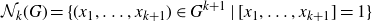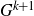1. Introduction and results
Let G be a (Hausdorff) compact group. Then G has a unique normalised Haar measure denoted by
![]() ${\mathbf m}_G$
. The following question is proposed by Martino, Tointon, Valiunas and Ventura in [Reference Martino, Tointon, Valiunas and Ventura4, question 1·20].
${\mathbf m}_G$
. The following question is proposed by Martino, Tointon, Valiunas and Ventura in [Reference Martino, Tointon, Valiunas and Ventura4, question 1·20].
Question 1·1 [Reference Martino, Tointon, Valiunas and Ventura4, question 1·20]. Let G be a compact group, and suppose that
![]() ${\mathcal N}_k(G) = \{(x_1,\dots, x_{k+1}) \in G^{k+1} \;|\; [x_1, \dots, x_{k+1}] = 1\}$
has positive Haar measure in
${\mathcal N}_k(G) = \{(x_1,\dots, x_{k+1}) \in G^{k+1} \;|\; [x_1, \dots, x_{k+1}] = 1\}$
has positive Haar measure in
![]() $G^{k+1}$
. Does G have an open k-step nilpotent subgroup?
$G^{k+1}$
. Does G have an open k-step nilpotent subgroup?
Here
![]() $[x,y]:=x^{-1}y^{-1}xy$
for elements x,y of a group and
$[x,y]:=x^{-1}y^{-1}xy$
for elements x,y of a group and
![]() $[x_1,\dots,x_k,x_{k+1}]$
is a left normed commutator defined inductively as
$[x_1,\dots,x_k,x_{k+1}]$
is a left normed commutator defined inductively as
![]() $[[x_1,\dots,x_k],x_{k+1}]$
for
$[[x_1,\dots,x_k],x_{k+1}]$
for
![]() $k\geq 2$
.
$k\geq 2$
.
A positive answer to Question 1.1 is known for
![]() $k=1$
(see [Reference Hofmann and Russo3, theorem 1·2]). It follows from [Reference Martino, Tointon, Valiunas and Ventura4, theorem 1·19] that Question 1·1 has positive answer for arbitrary k whenever we further assume that G is totally disconnected (i.e., profinite). Here we give a positive answer to Question 1·1 for
$k=1$
(see [Reference Hofmann and Russo3, theorem 1·2]). It follows from [Reference Martino, Tointon, Valiunas and Ventura4, theorem 1·19] that Question 1·1 has positive answer for arbitrary k whenever we further assume that G is totally disconnected (i.e., profinite). Here we give a positive answer to Question 1·1 for
![]() $k=2$
(see Theorem 1·2 below).
$k=2$
(see Theorem 1·2 below).
Theorem 1·2 Let G be a compact group, and suppose that
![]() ${\mathcal N}_2(G) = \{(x_1,x_2, x_3) \in G\times G \times G \;|\; [x_1, x_2, x_3] = 1\}$
has positive Haar measure in
${\mathcal N}_2(G) = \{(x_1,x_2, x_3) \in G\times G \times G \;|\; [x_1, x_2, x_3] = 1\}$
has positive Haar measure in
![]() $G\times G \times G$
. Then G has an open 2-step nilpotent subgroup.
$G\times G \times G$
. Then G has an open 2-step nilpotent subgroup.
2. A preliminary lemma
We need the following lemma in the proof of our main result.
Lemma 2·1 Suppose that
![]() $x_1,x_2,x_3,g_1,g_2,g_3$
are elements of a group such that
$x_1,x_2,x_3,g_1,g_2,g_3$
are elements of a group such that
![]() $[x_1u_1,x_2u_2,x_3u_3]=1$
for each triple of the following triples
$[x_1u_1,x_2u_2,x_3u_3]=1$
for each triple of the following triples
![]() $(u_1,u_2,u_3)$
:
$(u_1,u_2,u_3)$
:
 \begin{eqnarray*} &&(1,1,1),(g_1,g_2,g_3),(g_1,g_2,1),(g_1,1,g_2);\\[2pt] &&(g_1,1,1),(g_1,1,g_3),(1,1,g_1),(1,g_2,g_1);\\[2pt] && (1,g_2,1),(1,1,g_2),(1,g_2,g_3),(1,1,g_3).\end{eqnarray*}
\begin{eqnarray*} &&(1,1,1),(g_1,g_2,g_3),(g_1,g_2,1),(g_1,1,g_2);\\[2pt] &&(g_1,1,1),(g_1,1,g_3),(1,1,g_1),(1,g_2,g_1);\\[2pt] && (1,g_2,1),(1,1,g_2),(1,g_2,g_3),(1,1,g_3).\end{eqnarray*}
Then
![]() $[g_1,g_2,g_3]=1$
.
$[g_1,g_2,g_3]=1$
.
Proof. Note that [x,y] denotes
![]() $x^{-1}y^{-1}xy$
and
$x^{-1}y^{-1}xy$
and
![]() $[x,y,z]:=[[x,y],z]$
for arbitrary elements x,y,z of a group. We will throughout use famous commutator calculus identities:
$[x,y,z]:=[[x,y],z]$
for arbitrary elements x,y,z of a group. We will throughout use famous commutator calculus identities:
![]() $[xy,z]=[x,z]^y[y,z]$
(
$[xy,z]=[x,z]^y[y,z]$
(
![]() $\dagger$
) and
$\dagger$
) and
![]() $[x,yz]=[x,z][x,y]^z$
(
$[x,yz]=[x,z][x,y]^z$
(
![]() $\dagger \dagger$
) for all elements x,y,z of a group, where
$\dagger \dagger$
) for all elements x,y,z of a group, where
![]() $g^h$
denotes
$g^h$
denotes
![]() $h^{-1}gh$
. In the following (i) refers to the equality
$h^{-1}gh$
. In the following (i) refers to the equality
![]() $[x_1u_1,x_2u_2,x_3u_3]=1$
, where
$[x_1u_1,x_2u_2,x_3u_3]=1$
, where
![]() $(u_1,u_2,u_3)$
is the ith triple counting them from left to right starting at the top.
$(u_1,u_2,u_3)$
is the ith triple counting them from left to right starting at the top.
 \begin{eqnarray*} 1&=&[x_1g_1,x_2g_2,g_3]=[[x_1g_1,g_2][x_1g_1,x_2]^{g_2},g_3] \;\; {\textrm{by}} \; (\dagger \dagger), \; (2) \; {\textrm{and}} \; (3) \\[2pt] &=&[[x_1g_1,g_2][x_1g_1,x_2],g_3] \;\; {\textrm{by}} \; (4) \; {\textrm{and}} \; (5) \\[2pt] &=&[x_1g_1,g_2,g_3]=[[x_1,g_2]^{g_1}[g_1,g_2],g_3] \;\; {\textrm{by}} \; (\dagger), \; (5) \; {\textrm{and}} \; (6). \;\;\;\; {\textrm{(I)}} \end{eqnarray*}
\begin{eqnarray*} 1&=&[x_1g_1,x_2g_2,g_3]=[[x_1g_1,g_2][x_1g_1,x_2]^{g_2},g_3] \;\; {\textrm{by}} \; (\dagger \dagger), \; (2) \; {\textrm{and}} \; (3) \\[2pt] &=&[[x_1g_1,g_2][x_1g_1,x_2],g_3] \;\; {\textrm{by}} \; (4) \; {\textrm{and}} \; (5) \\[2pt] &=&[x_1g_1,g_2,g_3]=[[x_1,g_2]^{g_1}[g_1,g_2],g_3] \;\; {\textrm{by}} \; (\dagger), \; (5) \; {\textrm{and}} \; (6). \;\;\;\; {\textrm{(I)}} \end{eqnarray*}
On the other hand,
 \begin{eqnarray*} 1&=&[x_1,x_2g_2,g_1] \;\; {\textrm{by}} \; (8) \; {\textrm{and}} \; (9)\\[2pt] &=&[[x_1,g_2][x_1,x_2]^{g_2},g_1]=[[x_1,g_2][x_1,x_2],g_1] \;\; {\textrm{by}} \; (\dagger \dagger), \; (1) \; {\textrm{and}} \; (10)\\[2pt] &=&[x_1,g_2,g_1] \;\; {\textrm{by}} \; (1) \; {\textrm{and}} \; (7). \;\;\;\; {\textrm{(II)}} \end{eqnarray*}
\begin{eqnarray*} 1&=&[x_1,x_2g_2,g_1] \;\; {\textrm{by}} \; (8) \; {\textrm{and}} \; (9)\\[2pt] &=&[[x_1,g_2][x_1,x_2]^{g_2},g_1]=[[x_1,g_2][x_1,x_2],g_1] \;\; {\textrm{by}} \; (\dagger \dagger), \; (1) \; {\textrm{and}} \; (10)\\[2pt] &=&[x_1,g_2,g_1] \;\; {\textrm{by}} \; (1) \; {\textrm{and}} \; (7). \;\;\;\; {\textrm{(II)}} \end{eqnarray*}
Also,
 \begin{eqnarray*} 1&=&[x_1,x_2g_2,g_3] \;\; {\textrm{by}} \; (9) \; {\textrm{and}} \; (11)\\[2pt] &=&[[x_1,g_2][x_1,x_2]^{g_2},g_3]=[[x_1,g_2][x_1,x_2],g_3] \;\; {\textrm{by}} \; (\dagger \dagger), \; (1) \; {\textrm{and}} \; (10)\\[2pt] &=&[x_1,g_2,g_3] \;\; {\textrm{by}} \; (1) \; {\textrm{and}} \; (12). \;\;\;\; {\textrm{(III)}}\end{eqnarray*}
\begin{eqnarray*} 1&=&[x_1,x_2g_2,g_3] \;\; {\textrm{by}} \; (9) \; {\textrm{and}} \; (11)\\[2pt] &=&[[x_1,g_2][x_1,x_2]^{g_2},g_3]=[[x_1,g_2][x_1,x_2],g_3] \;\; {\textrm{by}} \; (\dagger \dagger), \; (1) \; {\textrm{and}} \; (10)\\[2pt] &=&[x_1,g_2,g_3] \;\; {\textrm{by}} \; (1) \; {\textrm{and}} \; (12). \;\;\;\; {\textrm{(III)}}\end{eqnarray*}
Now it follows from (I), (II) and (III) that
![]() $[g_1,g_2,g_3]=1$
.
$[g_1,g_2,g_3]=1$
.
Remark. The “left version” (
![]() $g_ix_j$
instead of
$g_ix_j$
instead of
![]() $x_jg_i$
) of Lemma 1·2 is not clear to hold. The validity of a similar result to Lemma 1·2 for commutators with length more than 3 is also under question.
$x_jg_i$
) of Lemma 1·2 is not clear to hold. The validity of a similar result to Lemma 1·2 for commutators with length more than 3 is also under question.
3. Compact groups with many elements satisfying the 2-step nilpotent law
We need the “right version” of [Reference Soleimani Malekan, Abdollahi and Ebrahimi5, theorem 2·3] as follows.
Theorem 3·1 If A is a measurable subset with positive Haar measure in a compact group G, then for any positive integer k there exists an open subset U of G containing 1 such that
![]() $\mathbf{m}_G(A \cap Au_1 \cap \cdots \cap Au_k) >0$
for all
$\mathbf{m}_G(A \cap Au_1 \cap \cdots \cap Au_k) >0$
for all
![]() $u_1,\dots,u_k \in U$
.
$u_1,\dots,u_k \in U$
.
Proof. Since
![]() $\mathbf{m}_G(A)=\mathbf{m}_G(A^{-1})$
, it follows from [Reference Soleimani Malekan, Abdollahi and Ebrahimi5, theorem 2·3] that there exists an open subset V of G containing 1 such that
$\mathbf{m}_G(A)=\mathbf{m}_G(A^{-1})$
, it follows from [Reference Soleimani Malekan, Abdollahi and Ebrahimi5, theorem 2·3] that there exists an open subset V of G containing 1 such that
for all
![]() $v_1,\dots,v_k \in V$
. Now take
$v_1,\dots,v_k \in V$
. Now take
![]() $U:=V^{-1}$
which is an open subset of G containing 1. Thus for all
$U:=V^{-1}$
which is an open subset of G containing 1. Thus for all
![]() $u_1,\dots,u_k \in U$
$u_1,\dots,u_k \in U$
 \begin{eqnarray*} \mathbf{m}_G(A \cap Au_1 \cap \cdots \cap Au_k) &=&\mathbf{m}_G((A \cap Au_1 \cap \cdots \cap Au_k)^{-1})\\[2pt] &=&\mathbf{m}_G(A^{-1} \cap u_1^{-1}A^{-1} \cap \cdots \cap u_k^{-1}A^{-1})>0 \end{eqnarray*}
\begin{eqnarray*} \mathbf{m}_G(A \cap Au_1 \cap \cdots \cap Au_k) &=&\mathbf{m}_G((A \cap Au_1 \cap \cdots \cap Au_k)^{-1})\\[2pt] &=&\mathbf{m}_G(A^{-1} \cap u_1^{-1}A^{-1} \cap \cdots \cap u_k^{-1}A^{-1})>0 \end{eqnarray*}
This completes the proof.
Now we can prove our main result.
Proof of Theorem 1·2. Let
![]() $X:={\mathcal N}_2(G)$
. It follows from Theorem 3·1 and [Reference Hewitt and Ross2, theorem 4·5] that there exists an open subset
$X:={\mathcal N}_2(G)$
. It follows from Theorem 3·1 and [Reference Hewitt and Ross2, theorem 4·5] that there exists an open subset
![]() $U=U^{-1}$
of G containing 1 such that
$U=U^{-1}$
of G containing 1 such that
for all
![]() $\bar{u}_1,\dots,\bar{u}_{11} \in U\times U \times U$
. Now take arbitrary elements
$\bar{u}_1,\dots,\bar{u}_{11} \in U\times U \times U$
. Now take arbitrary elements
![]() $g_1,g_2,g_3 \in U$
and consider
$g_1,g_2,g_3 \in U$
and consider
 \begin{eqnarray*} \bar{u}_1&=&(g_1^{-1},g_2^{-1},g_3^{-1}), \bar{u}_2=(g_1^{-1},g_2^{-1},1), \bar{u}_3=(g_1^{-1},1,g_2^{-1})\\[2pt] \bar{u}_4 &=&(g_1^{-1},1,1),\bar{u}_5=(g_1^{-1},1,g_3^{-1}), \bar{u}_6=(1,1,g_1^{-1}),\bar{u}_7=(1,g_2^{-1},g_1^{-1})\\[2pt] \bar{u}_8 &=&(1,g_2^{-1},1), \bar{u}_9=(1,1,g_2^{-1}), \bar{u}_{10}=(1,g_2^{-1},g_3^{-1}), \bar{u}_{11}=(1,1,g_3^{-1}). \end{eqnarray*}
\begin{eqnarray*} \bar{u}_1&=&(g_1^{-1},g_2^{-1},g_3^{-1}), \bar{u}_2=(g_1^{-1},g_2^{-1},1), \bar{u}_3=(g_1^{-1},1,g_2^{-1})\\[2pt] \bar{u}_4 &=&(g_1^{-1},1,1),\bar{u}_5=(g_1^{-1},1,g_3^{-1}), \bar{u}_6=(1,1,g_1^{-1}),\bar{u}_7=(1,g_2^{-1},g_1^{-1})\\[2pt] \bar{u}_8 &=&(1,g_2^{-1},1), \bar{u}_9=(1,1,g_2^{-1}), \bar{u}_{10}=(1,g_2^{-1},g_3^{-1}), \bar{u}_{11}=(1,1,g_3^{-1}). \end{eqnarray*}
By
![]() $(*)$
, there exists
$(*)$
, there exists
![]() $(x_1,x_2,x_3)\in X$
such that all the following 3-tuples are in X:
$(x_1,x_2,x_3)\in X$
such that all the following 3-tuples are in X:
 \begin{eqnarray*} &&(x_1g_1,x_2g_2,x_3g_3),(x_1g_1,x_2g_2,x_3),(x_1g_1,x_2,x_3g_2) \\[2pt] &&(x_1g_1,x_2,x_3),(x_1g_1,x_2,x_3g_3),(x_1,x_2,x_3g_1),(x_1,x_2g_2,x_3g_1)\\[2pt] &&(x_1,x_2g_2,x_3),(x_1,x_2,x_3g_2),(x_1,x_2g_2,x_3g_3),(x_1,x_2,x_3g_3). \end{eqnarray*}
\begin{eqnarray*} &&(x_1g_1,x_2g_2,x_3g_3),(x_1g_1,x_2g_2,x_3),(x_1g_1,x_2,x_3g_2) \\[2pt] &&(x_1g_1,x_2,x_3),(x_1g_1,x_2,x_3g_3),(x_1,x_2,x_3g_1),(x_1,x_2g_2,x_3g_1)\\[2pt] &&(x_1,x_2g_2,x_3),(x_1,x_2,x_3g_2),(x_1,x_2g_2,x_3g_3),(x_1,x_2,x_3g_3). \end{eqnarray*}
Now Lemma 2·1 implies that
![]() $[g_1,g_2,g_3]=1$
. Therefore the subgroup
$[g_1,g_2,g_3]=1$
. Therefore the subgroup
![]() $H:=\langle U \rangle$
generated by U is 2-step nilpotent. Since
$H:=\langle U \rangle$
generated by U is 2-step nilpotent. Since
![]() $H=\bigcup _{n\in {\mathbb N}} U^n$
, H is open in G. This completes the proof.
$H=\bigcup _{n\in {\mathbb N}} U^n$
, H is open in G. This completes the proof.
We finish with the following open question that would resolve Question 1·1 for arbitrary k:
Question 3·2 Are there finitely many words
![]() $w_{ij}$
(
$w_{ij}$
(
![]() $1 \leq i \leq n$
,
$1 \leq i \leq n$
,
![]() $1 \leq j \leq k+1$
) in the free group on
$1 \leq j \leq k+1$
) in the free group on
![]() $k+1$
generators such that if G is a compact group,
$k+1$
generators such that if G is a compact group,
![]() $(x_1, \dots, x_{k+1})$
,
$(x_1, \dots, x_{k+1})$
,
![]() $u=(u_1, \dots, u_{k+1}) \in G^{k+1}$
and
$u=(u_1, \dots, u_{k+1}) \in G^{k+1}$
and
![]() $[x_1 w_{i1}(u), \dots, x_{k+1} w_{i,k+1}(u)] = 1$
for all
$[x_1 w_{i1}(u), \dots, x_{k+1} w_{i,k+1}(u)] = 1$
for all
![]() $i \in \{1,\dots,n\}$
then
$i \in \{1,\dots,n\}$
then
![]() $[u_1, \dots, u_{k+1}] = 1$
?
$[u_1, \dots, u_{k+1}] = 1$
?
Acknowledgements
The authors are grateful to the referee for their valuable comments. The research of the second author was in part supported by a grant from Iran National Science Foundation (INSF) (No: 99010672).