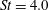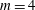1 Introduction
The prediction of and reduction of noise radiated by turbulent jets constitute two challenging technological problems. For commercial aircraft, noise regulations provide the driving factor, whereas for military applications, the primary concern is the hearing loss of personnel. Both issues motivate the search for noise-reduction solutions (Bowes et al. Reference Bowes, Bowler, Carnes, Fratarangelo, Rumpf, Heiser, Huff and Moin2009). The conception of effective noise-control strategies relies on a clear understanding of the underlying flow physics, and on the development of associated reduced-order models. In addition to the lower computational expense that such models present, in comparison with large-eddy or direct numerical simulation, they have the added advantage of providing physical insight into the mechanisms of sound generation (Sinha et al. Reference Sinha, Rodríguez, Brès and Colonius2014).
The coherent part of the velocity field of high-Reynolds-number turbulent jets comprises a wavepacket (Jordan & Colonius Reference Jordan and Colonius2013): a hydrodynamic wave with amplitude growth due to the Kelvin–Helmholtz instability of the shear layer, followed by stabilisation and decay. Such structures are characterised by a high degree of azimuthal, radial and streamwise organisation. While their contribution to the turbulent kinetic energy is small, they are important for sound radiation on account of the said organisation.
Wavepacket modelling is based on a linearisation of the Navier–Stokes system using the mean field as a base flow. The resulting linearised system neglects explicit nonlinear interactions between wavepackets and turbulence; such interactions can only occur via the mean flow, established by Reynolds stresses associated with the energy-containing turbulent eddies (Crighton & Gaster Reference Crighton and Gaster1976). More recent studies (McKeon & Sharma Reference McKeon and Sharma2010; Towne et al. Reference Towne, Colonius, Jordan, Cavalieri and Brès2015; Jeun, Nichols & Jovanović Reference Jeun, Nichols and Jovanović2016; Semeraro et al. Reference Semeraro, Jaunet, Jordan, Cavalieri and Lesshafft2016) model the aforementioned nonlinear interactions as a forcing term in the linearised system; wavepackets then arise as optimal flow responses, obtained by an analysis of the resolvent operator in the frequency domain. As a consequence of the convective non-normality of the jet, the optimal forcing is concentrated upstream, near or inside the nozzle, with nearly zero support in the downstream region. Disturbance growth then occurs downstream due to the Kelvin–Helmholtz instability of the shear layer (Garnaud et al. Reference Garnaud, Lesshafft, Schmid and Huerre2013; Semeraro et al. Reference Semeraro, Jaunet, Jordan, Cavalieri and Lesshafft2016). Because of this, the optimal wavepacket can often be computed using a homogeneous linear model, with an unsteady upstream boundary condition imposed, and which plays the role of the optimal forcing identified by the resolvent analysis. The validity of the model is then verified a posteriori, as in Petersen & Samet (Reference Petersen and Samet1988) or Gudmundsson & Colonius (Reference Gudmundsson and Colonius2011) for forced and unforced jets respectively. Because of the slow streamwise variation of the mean-flow characteristics of turbulent jets, the parabolised stability equations have been found to constitute a suitable dynamic ansatz, and it is this model that we consider in this work.
The agreement observed between experiment and wavepacket-based reduced-order models, particularly in regions upstream of the end of the jet potential core, has motivated many studies. In addition to the round subsonic jets studied in the works cited above, linear wavepacket models have been used to model coaxial (Gloor, Obrist & Kleiser Reference Gloor, Obrist and Kleiser2013) and supersonic jets (Malik & Chang Reference Malik and Chang2000; Ray & Lele Reference Ray and Lele2007; Nichols & Lele Reference Nichols and Lele2011; Sinha et al. Reference Sinha, Rodríguez, Brès and Colonius2014). For the latter, wavepackets can be readily extended to the acoustic field to obtain Mach-wave radiation. Recently, Sinha et al. (Reference Sinha, Rodríguez, Brès and Colonius2014) compared wavepacket model predictions with results from large-eddy simulations of cold and heated supersonic jets, and found encouraging agreement for the peak far-field radiation. Sound radiation by wavepackets in subsonic jets is more subtle, depending on details of the amplitude envelope (Crighton & Huerre Reference Crighton and Huerre1990) and the two-point coherence (Cavalieri & Agarwal Reference Cavalieri and Agarwal2014). These mechanisms are the subject of ongoing research, which considers either simplified kinematic sound-source models (Avital & Sandham Reference Avital and Sandham1997; Obrist Reference Obrist2009; Maia et al. Reference Maia, Jordan, Jaunet and Cavalieri2017) or the coupling of dynamic wavepacket models with an acoustic analogy (Sandham & Salgado Reference Sandham and Salgado2008).
The parabolised stability equations (PSE) have also proved useful in providing a physical interpretation of the mechanisms underpinning noise reductions obtained by forcing a turbulent jet (Koenig et al. Reference Koenig, Sasaki, Cavalieri, Jordan and Gervais2016). Parabolised-stability-equation-based transfer functions have been shown to enable real-time estimation of the downstream evolution of wavepackets in a high-Reynolds-number turbulent jet (Sasaki et al. Reference Sasaki, Piantanida, Cavalieri and Jordan2017) and closed-loop control of fluctuations in a low-Reynolds-number shear layer (Sasaki et al. Reference Sasaki, Tissot, Cavalieri, Jordan and Biau2016).
Nearly all of the cited studies focus on low-frequency disturbances, as wavepackets are most readily evaluated for these low frequencies. However, high-frequency fluctuations in turbulent jets are of considerable interest. For instance, it remains unclear whether high-frequency sound is driven by what is often referred to as ‘fine-scale turbulence’ or by high-frequency wavepacket motion. How nozzle conditions influence sound radiation (Harper-Bourne Reference Harper-Bourne2010; Fontaine et al. Reference Fontaine, Elliott, Austin and Freund2015) is another open question. The extension of wavepacket models to higher frequencies and azimuthal modes would open up new perspectives for addressing these issues, and it is this that motivates the work we present here.
One of the central difficulties we face in trying to educe high-frequency wavepackets from turbulent jets is posed by the small amplitudes of the high-frequency fluctuations. Figure 1 shows the experimentally measured power spectral densities (PSDs) of the axial velocity on the centreline of a jet studied previously by this group (Cavalieri et al. Reference Cavalieri, Rodríguez, Jordan, Colonius and Gervais2013). For Strouhal numbers above one, the spectra fall below the noise floor of the measurement and cannot be educed for comparison with models.
Figure 1. Experimental PSDs for the axial velocity (
$u_{x}$
) fluctuation on the jet centreline for several axial positions (
$x$
). The non-dimensionalisation considers the mean velocity of the jet (
$U$
).
Furthermore, decomposition of the velocity fluctuations into azimuthal wavenumbers higher than zero is not possible with single hotwire measurements, as the necessary spatial information would be unavailable. An azimuthal decomposition could be accomplished with stereoscopic time-resolved particle image velocimetry (STRPIV) (Cavalieri et al. Reference Cavalieri, Rodríguez, Jordan, Colonius and Gervais2013; Jaunet, Jordan & Cavalieri Reference Jaunet, Jordan and Cavalieri2017), which is limited to low Strouhal numbers, or a near-field microphone array, which must be located outside the turbulent region of the jet, where the low amplitudes of high-frequency wavepackets again preclude accurate measurement.
It is for these reasons that we here work with data provided by the experimentally validated high-fidelity large-eddy simulation (LES) of Brès et al. (Reference Brès, Jaunet, Le Rallic, Jordan, Colonius and Lele2015). This has been shown to closely match the experimentally measured hydrodynamic and acoustic field of a Mach 0.9 jet, thanks to careful computation of the turbulent boundary layer inside the nozzle.
Comparisons are made after the application of a spectral proper orthogonal decomposition (POD) filter to the LES pressure fluctuations. The POD separates the original data into orthogonal sets, ordered by their energy content. Each set presents a spatial correlation over significant distances and it is therefore known to educe the signature of linear wavepackets in turbulent jets (Gudmundsson & Colonius Reference Gudmundsson and Colonius2011). The first mode, which contains the highest energy content, has been used in several other studies in comparison with wavepacket formulations, such as the PSE (Cavalieri et al. Reference Cavalieri, Rodríguez, Jordan, Colonius and Gervais2013; Sinha et al. Reference Sinha, Rodríguez, Brès and Colonius2014; Beneddine et al. Reference Beneddine, Sipp, Arnault, Dandois and Lesshafft2016). Further details regarding the POD calculation may be found in Towne, Schmidt & Colonius (Reference Towne, Schmidt and Colonius2017b ).
This article is organised as follows. In § 2, a brief description of the LES database is provided, along with some details of the PSE method. Section 3 presents PSE–LES comparisons and a discussion of the results. Conclusions are given in § 4.
2 Mathematical model
The LES database corresponds to an isothermal Mach 0.9 turbulent jet, issued from a convergent-straight nozzle. The simulation was performed using the flow solver Charles (Brès et al.
Reference Brès, Ham, Nichols and Lele2017), developed at Cascade Technologies, and reproduces the conditions of a companion experiment conducted at the Pprime Institute; this same simulation has been used in other studies by this group (Schmidt et al.
Reference Schmidt, Towne, Colonius, Cavalieri, Jordan and Brès2017; Towne et al.
Reference Towne, Cavalieri, Jordan, Colonius, Schmidt, Jaunet and Brès2017a
). The Reynolds number, defined as
$Re=\unicode[STIX]{x1D70C}UD/\unicode[STIX]{x1D707}$
, where
$\unicode[STIX]{x1D70C}$
,
$U$
,
$D$
and
$\unicode[STIX]{x1D707}$
are respectively the mean density, velocity, diameter and viscosity of the jet, is approximately one million. Computation of the far-field noise is based on the frequency-domain permeable formulation of the Ffowcs Williams–Hawkings equation (Ffowcs Williams & Hawkings Reference Ffowcs Williams and Hawkings1969).
The LES data used throughout this work were computed on a 69-million-grid-point mesh with refined resolution in the jet. To replicate the effects of the boundary layer trip present in the companion experiment and to ensure an initially turbulent jet, near-wall adaptive mesh refinement, synthetic turbulence and wall modelling are applied inside the nozzle. This leads to fully turbulent nozzle-exit boundary layers, as shown in figure 2, presenting good agreement with the experimental measurements; the only noticeable difference is for the maximum of root mean square (RMS) values at
$r=0.5$
, with the peak probably missed by the experimental measurements due to limited spatial resolution.
To facilitate postprocessing and analysis, the data were interpolated from the original unstructured LES mesh onto structured cylindrical grids with equi-distanced points in the azimuthal direction, enabling azimuthal decomposition in Fourier space. The LES results show excellent agreement with experimental far-field noise measurements up to
$St=4.0$
, as shown in figure 3, which is important for the present study. Further details of the LES methodology, grid resolution study and validation with experiments are presented in Brès et al. (Reference Brès, Jordan, Colonius, Le Rallic, Jaunet and Lele2014, Reference Brès, Jaunet, Le Rallic, Jordan, Colonius and Lele2015, Reference Brès, Jaunet, Le Rallic, Jordan, Towne, Schmidt, Colonius, Cavalieri and Lele2016).
Figure 2. Nozzle-exit boundary layer profiles from experiment (circles) and LES cases (solid line): (a) time-averaged streamwise velocity; (b) RMS of the streamwise velocity.
Figure 3. Comparison between the LES predicted acoustic field (solid line) and experiment (circles) at two positions, at 50 diameters from the nozzle, in relation to the jet axis: (a)
$\unicode[STIX]{x1D719}=90$
and (b)
$\unicode[STIX]{x1D719}=150$
.
For comparison with the PSE solutions, the first spectral POD mode of the pressure fluctuations obtained from the LES is considered, as in Sinha et al. (Reference Sinha, Rodríguez, Brès and Colonius2014). The energy norm for the decomposition was introduced by Chu (Reference Chu1965).
Fluctuations are compared with solutions of the linear PSEs (Herbert Reference Herbert1997). Details of the PSE formalism, the numerical strategy used for its solution and a validation can be found in Sasaki et al. (Reference Sasaki, Piantanida, Cavalieri and Jordan2017) and will not be reproduced here, for the sake of brevity. The initial conditions for the PSE, shape functions and eigenvalues, are obtained from the solution of a generalised eigenvalue problem, derived from the locally parallel assumption, using the Euler equations for a compressible flow. The procedure is outlined in Sasaki et al. (Reference Sasaki, Piantanida, Cavalieri and Jordan2017).
The mean flow is fitted by an expression similar to that used by Fontaine et al. (Reference Fontaine, Elliott, Austin and Freund2015), which, considering the current non-dimensionalisation, becomes
$$\begin{eqnarray}\overline{u}(r)=\frac{M}{4}\left[1-\tanh \left(\frac{r_{0}}{4\unicode[STIX]{x1D703}_{1}}\left[\frac{r}{r_{0}}-\frac{r_{0}}{r}\right]\right)\right]\left[1-\tanh \left(\frac{r_{0}}{4\unicode[STIX]{x1D703}_{2}}\left[\frac{r-r_{s}}{r_{0}}-\frac{r_{0}}{r}\right]\right)\right],\end{eqnarray}$$
where the parameters
$r_{0}$
,
$r_{s}$
,
$\unicode[STIX]{x1D703}_{1}$
and
$\unicode[STIX]{x1D703}_{2}$
are determined via a least-squares fit. Equation (2.1) permits the sharp gradients and details of the mean flow in the near nozzle to be accurately reproduced. The radial discretisation follows Lesshafft & Huerre (Reference Lesshafft and Huerre2007), with 500 Chebyshev collocation points, half of which are between
$r=0$
and
$r=0.8D$
, where
$D$
is the diameter of the jet.
3 Comparison of linear PSE and LES
As mentioned in § 2, prior to initiation of the PSE calculations, a locally parallel computation is made to obtain the initial shape functions and eigenvalues. The method is started with the Kelvin–Helmholtz mode, and we are interested in cases where it is unstable and is expected to dominate the dynamics of the flow. Figure 4 shows the behaviour of the spatial growth rate, the imaginary part of the wavenumber
$\unicode[STIX]{x1D6FC}$
, as a function of the Strouhal number
$St$
, for seven axial positions and azimuthal wavenumbers of
$m=0$
and
$m=4$
. Very close to the nozzle, the flow is unstable at a Strouhal number of 8.0. Moving downstream, we observe that stabilisation occurs rapidly, and at
$X/D>0.2$
, only Strouhal numbers below 3 remain unstable.
It should be noted that very near the nozzle the behaviour of the growth rates for the different azimuthal wavenumbers is almost the same. This could be interpreted by noting that the shear-layer thickness is small in this region, when compared with the azimuthal wavelengths considered, rendering an equivalent trend for the two cases. Further downstream, where the shear layer is thicker, the differences become more apparent, as may be observed in figure 4.
The results in figure 4 imply that in order to observe such high-frequency behaviour in the simulation, one is limited to regions very close to the nozzle-exit plane. Details of the boundary layer in this region need therefore to be accurately captured.
Figure 4. Growth rates obtained from a locally parallel Euler calculation close to the nozzle for
$m=0$
(solid) and
$m=4$
(dashed), for seven different axial positions. The behaviour for
$x=0.5$
and
$x=1.0$
is zoomed.
Comparisons are made with the first POD mode for each frequency, as POD is known to educe the signature of linear wavepackets, as discussed in the introduction. Figure 5 shows the real part of the pressure fluctuations of the first POD mode, for
$m=0$
and
$St=4.1$
, where the wavepacket character of the flow is evident, particularly in the upstream region where spatial amplification occurs by the Kelvin–Helmholtz mechanism. The downstream region displays more complex dynamics, studied recently by Jordan et al. (Reference Jordan, Zhang, Lehnasch and Cavalieri2017) and Tissot et al. (Reference Tissot, Zhang, Lajús, Cavalieri and Jordan2017).
Figure 5. The first POD mode for the axisymmetric pressure fluctuations at
$St=4.1$
extracted from the LES. The white box highlights the region where the comparisons will be made with the linear PSE simulation.
Figure 6 presents a comparison between the PSE prediction and the first POD, using in both cases the real part of the pressure. The sample Strouhal numbers taken were 2 and 4, and comparisons were made for
$m=0$
. The free amplitude of the linear PSE solution was chosen to best match the amplitudes of the POD mode, and the comparison focuses on the upstream region of amplification of the Kelvin–Helmholtz wavepacket. In figure 7, the radial shape of the fluctuations is shown, for the same Strouhal numbers, also for the axisymmetric case. The axial positions
$x=0.3$
and
$x=0.5$
are considered; however, the same trends are seen up to
$x\approx 1.0$
for these frequencies.
Figure 6. The POD and PSE pressure data in (a,c) and (b,d) for
$St$
of 2.0 (a,b) and 4.0 (c,d), for the axisymmetric mode,
$m=0$
. Similar trends are observed for intermediate frequencies and higher azimuthal numbers, until
$m=4$
.
Figure 7. Comparison of the radial behaviour of the PSDs of the pressure fluctuations between the LES (solid) and PSE prediction (dashed), for the axisymmetric mode.
We observe that the PSE solutions closely match the first POD mode, with a typical wavepacket shape in
$x$
clearly visible in the POD mode and accurately modelled by the PSE. The growth and decay of the fluctuations in the neighbourhood of
$r=0.5$
are correctly described by the PSE method. The most significant differences appear when
$r$
is close to zero. For this Mach 0.9 jet, in particular, there are other relevant modes, corresponding to trapped acoustic waves in the potential core. Such modes, which decay to zero towards the jet shear layer, are not accounted for in the present computation and are responsible for the radially oscillatory behaviour seen in the pressure fluctuations. These modes have been thoroughly studied by (Schmidt et al.
Reference Schmidt, Towne, Colonius, Cavalieri, Jordan and Brès2017) and Towne et al. (Reference Towne, Cavalieri, Jordan, Colonius, Schmidt, Jaunet and Brès2017a
), and are outside the scope of this article.
As the Strouhal number is increased, disturbances become more concentrated on the shear layer, as expected from linear stability. Figures 6 and 7 show results for
$m=0$
, but similar behaviour was found for azimuthal wavenumbers up to
$m=4$
and the intermediate Strouhal numbers.
In order to present the agreement for several values of the Strouhal number and axial positions in a compact manner, following Cavalieri et al. (Reference Cavalieri, Rodríguez, Jordan, Colonius and Gervais2013), we define the metric
$$\begin{eqnarray}\unicode[STIX]{x1D6FD}(x,St,m)=\frac{\langle p_{PSE}(x,r,St,m),p_{POD}(x,r,St,m)\rangle }{\Vert p_{PSE}(x,r,St,m)\Vert \Vert p_{POD}(x,r,St,m)\Vert },\end{eqnarray}$$
where
$p$
is the pressure fluctuation and the inner product is defined as
$$\begin{eqnarray}\langle f(r),g(r)\rangle =\int _{0}^{\infty }f(r)g^{\ast }(r)r\,\text{d}r.\end{eqnarray}$$
Equation (3.1) provides a measurement of the similarity between the radial shapes at a given frequency/axial position:
$\unicode[STIX]{x1D6FD}=1$
implies perfect agreement whereas
$\unicode[STIX]{x1D6FD}=0$
implies that the two functions are completely uncorrelated. Figure 8 shows the behaviour of this metric for azimuthal numbers varying from 0 to 4. Similarly to our previous observations (Cavalieri et al.
Reference Cavalieri, Rodríguez, Jordan, Colonius and Gervais2013), values above 0.9 are observed for Strouhal numbers below 1.0. However, significant values of this parameter are also observed for Strouhal numbers as high as 4.0. The region of agreement shows a correlation with the region where
$\unicode[STIX]{x1D6FC}_{i}$
becomes negative, indicating a switch between growth and decay for the PSE prediction for the wavepackets. When this happens,
$\unicode[STIX]{x1D6FD}$
rapidly decreases to values close to zero. For all of the frequency/azimuthal wavenumber combinations considered, this switch in behaviour occurs further upstream as the frequency is increased.
Figure 8. Behaviour of the
$\unicode[STIX]{x1D6FD}$
metric for azimuthal wavenumbers from 0 to 4. The dashed line indicates the
$St$
–
$x$
combination where the PSE render a prediction of stable behaviour for the fluctuations.
As shown by Semeraro et al. (Reference Semeraro, Jaunet, Jordan, Cavalieri and Lesshafft2016) and Towne et al. (Reference Towne, Schmidt and Colonius2017b ), if the nonlinear terms in the Navier–Stokes system behave as stochastic white-noise forcing, there exists an equivalence between the first POD mode and the optimal flow response obtained from a resolvent analysis. Moreover, the convective non-normality typical of Kelvin–Helmholtz instability leads to optimal forcings concentrated upstream, often inside the nozzle, as presented in the works of Semeraro et al. (Reference Semeraro, Jaunet, Jordan, Cavalieri and Lesshafft2016) and Jordan et al. (Reference Jordan, Zhang, Lehnasch and Cavalieri2017). The linear PSE replace such forcings by an upstream boundary condition, which explains its success in matching the first POD mode from the LES. However, close agreement is only obtained for regions of significant spatial amplification; this is in accordance with the study by Beneddine et al. (Reference Beneddine, Sipp, Arnault, Dandois and Lesshafft2016), which states a strong convective instability as one of the necessary ingredients for the validity of the PSE in predicting the spatial structure of the fluctuations. Furthermore, it should be noted that the white-noise assumption is strong, and nonlinearities can be expected to comprise colour, with amplitudes varying in space and non-zero coherence lengths, for instance. This will result in differences between the POD and the PSE, but for regions of the parameter space with strong Kelvin–Helmholtz amplification, the flow response appears to be largely independent of the forcing details, and is thus accurately matched by the linear PSE.
4 Conclusions
A detailed comparison between the PSE and an experimentally validated high-fidelity LES was undertaken, where the LES data were considered in terms of their first POD mode. The objective was to evaluate the range of frequencies and azimuthal wavenumbers for which the linear PSE accurately model wavepackets in the turbulent jet. The comparisons reveal a close agreement between the data and the linear model up to
$St\approx 4.0$
and
$m=4$
, extending significantly the range of validity of wavepacket models.
The good agreement is primarily observed for the growth phase of the linear waves, and shows, for the range of
$St$
and
$m$
considered, that the growth of fluctuation energy in the near-nozzle region is largely linear, despite the fully turbulent character of the nozzle boundary layer. The agreement between the PSE and LES deteriorates downstream of the position where the Kelvin–Helmholtz mode has reached its maximum. This discrepancy, which had been observed previously in the works of Gudmundsson & Colonius (Reference Gudmundsson and Colonius2011) and Cavalieri et al. (Reference Cavalieri, Rodríguez, Jordan, Colonius and Gervais2013), for
$St\leqslant 1.0$
has been recently investigated in the works of Jordan et al. (Reference Jordan, Zhang, Lehnasch and Cavalieri2017) and Tissot et al. (Reference Tissot, Zhang, Lajús, Cavalieri and Jordan2017), where the non-modal growth is shown to play an important role in determining the behaviour of the fluctuations in this region.
Acknowledgements
K.S. acknowledges financial support from Capes and FAPESP, grant number 2016/25187-4. A.V.G.C. and P.J. acknowledge support from the Science Without Borders programme (project number A073/2013). A.V.G.C. was supported by a CNPq research scholarship, and by CNPq grant 444796/2014-2. T.C. gratefully acknowledges support from the Office of Naval Research under contract N0014-11- 1-0753. The LES studies are supported by the NAVAIR SBIR project, under the supervision of Dr J. T. Spyropoulos. The main calculations were carried out on CRAY XE6 machines at DoD supercomputer facilities at ERDC DSRC.
