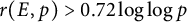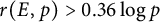1 Introduction
Let
$E/\mathbb {F}_p$
be an elliptic curve. Recall that there exist unique positive integers
$L,M$
such that
$$ \begin{align*} E(\mathbb{F}_p)\cong \mathbb{Z}/L\mathbb{Z}\times \mathbb{Z}/M\mathbb{Z} \end{align*} $$
and
$L\mid M$
. Here, M is the maximal order of a point of
$E(\mathbb {F}_p)$
. In order to find a point on
$E/\mathbb {F}_p$
of maximal order, a natural strategy is to compute the orders of points with x-coordinates
$0, 1, 2, \dots $
and continue until the desired point is found. In practice, this works fairly well. A natural question is how long this process takes in the worst case.
Along these lines, fix an elliptic curve
$E/\mathbb {Q}$
and let p be a prime of good reduction. Let
$r(E,p)$
denote the minimal x-coordinate of a point of maximal order in the reduction
$E/\mathbb {F}_p$
. The goal of this note is to prove the following two lower bounds on
$r(E,p)$
.
Theorem 1.1 Let
$E/\mathbb {Q}$
be an elliptic curve. There are infinitely many primes p such that
$$ \begin{align*}r(E,p)> 0.72\log\log p. \end{align*} $$
Theorem 1.2 Let
$E/\mathbb {Q}$
be an elliptic curve. Under GRH, there are infinitely many primes p such that
$$ \begin{align*}r(E,p)>0.36\log p. \end{align*} $$
These results can be viewed as elliptic curve analogues of lower bounds on the least primitive root
$r(p)$
of a prime p. Pillai [Reference Pillai14] proved that there is a positive constant C such that
$r(p)> C\log \log p$
for infinitely many p. Using Linnik’s theorem in Pillai’s proof, Fridlender [Reference Fridlender6] and Salié [Reference Salié15] improved the result to the following. We include a proof since it inspired the result of the present paper.
Theorem 1.3 [Reference Fridlender6, Reference Salié15]
There exists a positive constant C such that
$r(p)> C\log p$
for infinitely many p.
Proof Linnik’s theorem says that there exist constants c and L such that every arithmetic progression
$a+bn$
with
$\gcd (a,b)=1$
contains a prime
$p<c\cdot b^L$
. For
$x>0$
large, let
$k=\prod \ell $
, where the product is taken over all primes
$\ell \le x$
. By Linnik’s theorem, there exists a prime
$p=1$
mod
$4k$
with
$p<c\cdot (4k)^L$
. It follows from quadratic reciprocity that every positive prime divisor of k is a quadratic residue for such a prime p. This implies that all positive integers
$n\leq x$
are quadratic residues for p and therefore cannot be primitive roots mod p. By the prime number theorem,
$\log k \sim x$
. Therefore,
$$ \begin{align*} r(p)> x\sim \log k> C\log p \end{align*} $$
for some constant C that is independent of x.▪
The bound
$\log p$
above has been improved to
$\log p \log \log \log p$
by Graham–Ringrose [Reference Graham and Ringrose7] unconditionally and to
$\log p \log \log p$
by Montgomery [Reference Montgomery13] under the generalized Riemann hypothesis.
For an elliptic curve
$$ \begin{align*} E:\; y^2=f(x)= x^3+Ax+B \end{align*} $$
with
$A, B\in \mathbb Z$
, we follow a similar approach in the search for a prime p for which
$r(E,p)$
is large. First, we force
$E(\mathbb {F}_p)$
to have even order by requiring
$f(x)$
to factor into linear factors mod p. Next, let N be a large integer. We force all points
$(x,y)$
with
$0\le x\le N$
to be doubles of other points in
$E(\mathbb {F}_p)$
. Since
$E(F_p)$
has even order, these points cannot have maximal order. Finally, we use an explicit version of the Chebotarev Density Theorem to give an upper bound for p in terms of N, which can be transformed into the desired lower bound for N in terms of p.
It is reasonable to ask what can be said in terms of an upper bound. In the classical setting, bounding
$r(p)$
from above is a well-studied problem (see, for instance, [Reference Erdős4, Reference Erdős and Shapiro5, Reference Hua8, Reference Vinogradov19]; see [Reference Dubrois and Dumas3] for computational issues). The best known bound along these lines is the Burgess bound [Reference Burgess2], which states that
$r(p)\ll p^{\frac {1}{4}+\epsilon }$
. Under GRH, a result of Shoup [Reference Shoup16] yields the stronger statement
$r(p) \ll \log ^6 p$
.
Igor Shparlinski has pointed out to us that in the elliptic curve case, one can obtain
$r(E,p) = O( p^{\frac {1}{2}+\epsilon })$
via results from [Reference Kohel and Shparlinski10]. This is done by using the analogue of the last section of [Reference Burgess2] and the technique of Theorem 2 of [Reference Kohel and Shparlinski10], combined with the estimate of Theorem 1 of [Reference Kohel and Shparlinski10] for characters supported on
$\mathbb {Z}/M\mathbb {Z}$
. Computations suggest that the true order of
$r(E,p)$
is smaller and that Theorem 1.2 is almost sharp, perhaps missing by no more than a power of
$\log \log p$
. See Section 3.
2 The proofs
Proof of Theorems 1.1 and 1.2
. Fix
$N>0$
. Let
$E/\mathbb {Q}$
be an elliptic curve over
$\mathbb {Q}$
given by Weierstrass equation
$$ \begin{align*} y^2=f(x)=x^3+Ax+B, \end{align*} $$
where
$A,B\in \mathbb {Z}$
. We are going to construct a suitable polynomial by constructing several factors and multiplying them together.
Let
$\{p_1,\dots ,p_m\}$
consist of the distinct prime divisors of the discriminant of
$E/\mathbb {Q}$
and the primes up to and including
$7$
. Let
$g(z)= z^2-\prod _{i=1}^m p_i$
. This polynomial is constructed for the following technical reason: If a prime p is unramified in the splitting field of
$g(z)$
, then p is a prime of good reduction for E.
Recall that the x-coordinate of the doubling of a point
$(x,y)\ne \infty $
is given by
$$ \begin{align*} h(x)=\frac{r(x)}{s(x)}, \: \text{ where } r(x)=x^4-2Ax^2-8Bx+A^2, \:\: s(x)=4x^3+4Ax+4B. \end{align*} $$
For
$0\leq j\leq N$
, let
$\xi _j(z)=r(z)-js(z)$
.
Let
$$ \begin{align*}T(z)=f(z)g(z) \prod_{j=0}^N \xi_j(z), \end{align*} $$
and let F be the splitting field of
$T(z)$
. If p splits completely in
$F/\mathbb {Q}$
, then each of the factors of
$T(z)$
factors into linear factors over
$\mathbb {F}_p$
. Since p is unramified in
$F/\mathbb {Q}$
and
$g(z)$
is a factor of
$T(z)$
, it follows that
$p>7$
and is a prime of good reduction for E. Since
$f(z)$
factors, the two-torsion is contained in
$E(\mathbb {F}_p)$
, so
$E(\mathbb {F}_p)$
has even order.
Suppose
$P=(j,y)\in E(\mathbb {F}_p)$
for some
$0\le j\le N$
. Since
$\xi _j(z)$
factors into linear factors mod p, there exists
$x_1\in \mathbb {F}_p$
such that
$\xi _j(x_1)\equiv 0\ \pmod p$
. Let
$y_1\in \mathbb {F}_{p^2}$
satisfy
$y_1^2\equiv f(x_1)$
. Since the resultant of
$r(z)$
and
$s(z)$
is
$(4A^3+27B^2)^2$
, which is not divisible by p by assumption, we cannot have
$s(x_1)\equiv 0\ \pmod p$
. Therefore,
$ (j, y)= 2(x_1, y_1)$
for a suitable choice of sign of
$y_1$
. Suppose
$y_1\not \in \mathbb {F}_p$
. Since
$y_1^2\in \mathbb {F}_p$
, the Galois conjugate of
$y_1$
is
$-y_1$
. Taking conjugates yields
$ (j, y)= 2(x_1, -y_1)= -2(x_1, y_1)= -(j, y)$
. Therefore,
$(j, y)$
is a point of order 2. Since
$p>7$
, the Hasse bound implies that
$|E(\mathbb {F}_p)|> 4$
, so
$(j,y)$
cannot be a point of maximal order. On the other hand, if
$y_1\in \mathbb {F}_p$
, then
$(j, y)=2(x_1, y_1)$
implies that
$(j, y)$
cannot have maximal order. Therefore,
$r(E,p)>N$
.
To finish the proof, we need an upper bound on the smallest p. This estimate uses an explicit Chebotarev Density Theorem, which bounds p in terms of the discriminant of the splitting field F. The next few lemmas bound this discriminant.
Lemma 2.1 Let
$L/K$
be an extension of number fields with rings of integers
$\mathcal {O}_L$
and
$\mathcal {O}_K$
, respectively. The different
$\mathfrak {D}_{L/K}$
of
$L/K$
is the ideal generated by
$\{g'(\alpha )\}$
, where
$\alpha $
runs through elements of
$\mathcal {O}_L$
such that
$L=K(\alpha )$
and g runs through monic polynomials in
$\mathcal {O}_K[x]$
satisfying
$g(\alpha )=0$
.
Proof See for instance [Reference Lang12, Proposition III.3]. Note that the usual statement of this result requires g to be the minimal polynomial of
$\alpha $
. However, if
$m(x)$
is the minimal polynomial for
$\alpha $
, then
$g(x)=m(x)h(x)$
for some
$h(x)\in \mathcal {O}_K[x]$
and
$g'(\alpha )=m'(\alpha )h(\alpha )$
, which is in the ideal generated by
$m'(\alpha )$
. Therefore, including polynomials g that are potentially reducible does not affect the ideal
$\mathfrak {D}_{L/K}$
.▪
Henceforth, all mentions of discriminants are understood to refer to discriminants over
$\mathbb {Q}$
. The following result is probably well-known, but we could not find a good reference so we include a proof.
Lemma 2.2 Suppose
$K/\mathbb {Q}$
is a field extension given as
$K=K_1\cdots K_n$
. Then
$$ \begin{align*}|\operatorname{\textrm{disc}}(K)|\leq \prod_{i=1}^n |\operatorname{\textrm{disc}}(K_i)|^{[K:K_i]}.\end{align*} $$
Proof (cf. [Reference Toyama18]) Consider the tower of fields
$\mathbb {Q} \subseteq K_1 \subseteq K_1K_2 \subseteq \cdots \subseteq K=K_1K_2\cdots K_n$
. The different of
$(K_1K_2\cdots K_{i})/( K_1 K_2 \cdots K_{i-1})$
divides the different
$\mathfrak D_i$
of
$K_i/\mathbb {Q}$
, by Lemma 2.1. Since differents multiply in towers, the different of
$K/\mathbb {Q}$
divides
$\mathfrak D_1 \mathfrak D_2\cdots \mathfrak D_n$
. Taking the norm from K to
$\mathbb {Q}$
yields the result.▪
Lemma 2.3 Let
$f\in \mathbb {Z}[x]$
be a monic polynomial with no repeated roots and let F be the splitting field of f. Let
$d=[F:\mathbb {Q}]$
. Then
$\operatorname {\textrm {disc}}(F)^2\text { divides }\operatorname {\textrm {disc}}(f)^{d}$
.
Proof Let
$f(x)=\prod _{i=1}^n (x-\beta _i)$
. For
$i>0$
, let
$K_i=\mathbb {Q}(\beta _1,\beta _2,\dots , \beta _i)$
. Let
$f_i(x)=\prod _{j=i+1}^n (x-\beta _j)$
. Since
$K_{i+1}=K_{i}(\beta _{i+1})$
and
$f_i(\beta _{i+1})=0$
, the different
$\mathfrak {D}_{K_{i+1}/K_i}$
divides
$$ \begin{align*}f'(\beta_{i+1})=\prod_{j=i+2}^n (\beta_{i+1}-\beta_j)\end{align*} $$
by Lemma 2.1. Since differents multiply in towers, we have that
$\mathfrak {D}_{F/\mathbb {Q}}$
divides the ideal generated by
$$ \begin{align*}\prod_{i=0}^{n-2} \prod_{j=i+2}^n (\beta_{i+1}-\beta_j)=\prod_{i<j} (\beta_i-\beta_j)=\operatorname{\textrm{disc}}(f)^{1/2}.\end{align*} $$
Squaring and taking norms, we obtain the result.▪
By Lemma 2.3, the discriminant of splitting field
$K_f$
of
$f(z)$
divides
$(4A^3+27B^2)^3$
. The discriminant of the splitting field
$K_g$
of
$g(z)$
divides
$4\prod _{i=1}^m p_i$
. A computation shows that the discriminant of
$\xi _j(z)$
is
$$ \begin{align*}2^{12}(-4A^3-27B^2)f(j)^2. \end{align*} $$
Therefore, the discriminant of the splitting field
$K_j$
of
$\xi _j(z)$
divides
$2^{144}(-4A^3-27B^2)^{12}f(j)^{24}$
.
Lemma 2.4 Let
$y^2=x^3+Ax+B$
define an elliptic curve over a field L of characteristic not 2 and assume
$E(L)$
contains
$E[2]$
. Let
$j\in L$
and let
$\tilde {L}$
be the splitting field of
$$ \begin{align*}\xi_j(x) = x^4-2Ax^2-8Bx+A^2- j(4x^3+4Ax+4B).\end{align*} $$
Then
$[\tilde {L} : L]$
divides
$4$
.
Proof Let
$y'=\sqrt {j^3+Aj+B}$
and
$L'=L(y')$
. Then
$(j, y')\in E(L')$
. Let
$(a, b)\in E(\overline {L})$
satisfy
$2(a, b)= (j, y')$
and let
$L'(a, b)$
be the field generated by a and b. Since
$E[2]\subseteq E(L')$
, all four solutions of
$2(a, b)= (j, y')$
have coordinates in
$L'(a, b)$
, and
$\text {Gal}(L'(a, b)/L')$
is isomorphic to a subgroup of
$E[2]$
. Since
$L'(a, b)$
contains the splitting field of
$\xi _j(x)$
, we conclude that the splitting field has degree over L dividing 8.
Note that
$-A^3-27B^2$
is a square in L, and therefore the discriminant of
$\xi _j(z)$
is a square in L. It follows that the Galois group of
$\xi _j(x)$
is a subgroup of
$A_4$
, hence has degree dividing 12. Since the degree also divides 8, the degree divides 4.▪
The splitting field F of
$T(z)$
is
$K_fK_gK_0K_1\cdots K_N$
. Therefore,
$$ \begin{align*} [F : \mathbb{Q}] \le 6\cdot 2\cdot 4^{N+1}. \end{align*} $$
If
$K_j= \mathbb {Q}$
for some j, then we can omit that field from our calculations. Therefore, when we apply Lemma 2.2 to the present situation, we can bound the remaining exponents
$[F : K_i]$
by
$[F : \mathbb {Q}]/2$
and obtain
$$ \begin{align*} |\text{disc}(F)| &\le \left(C_E \prod_{0\le j\le N}C_E' |f(j)|^{24}\right)^{6\cdot 4^{N+1}}\\ &\le \left((C_E'' N)^{72(N+1)}\right)^{6\cdot 4^{N+1}}\\ & = (C_E'' N)^{432(N+1)4^{N+1}}, \end{align*} $$
where
$C_E$
,
$C_E'$
, and
$C_E''$
are constants depending only on the elliptic curve E and where we have bounded
$f(j)$
by a constant times
$N^3$
.
We now can estimate the smallest prime p that splits completely in
$F/\mathbb {Q}$
. A theorem of Ahn and Kwon [Reference Ahn and Kwon1] states that
$p< |\text {disc}(F)|^{12577}$
. Therefore,
$$ \begin{align*} \log\log p & < \log 12577 + \log\log |\text{disc}(F)|\\ &\le \log 12577+ \log\left(432(N+1)4^{N+1}\right) + \log\log C_E'' N\\ &= N\log 4 + o(N)\\ &< N/0.72 \end{align*} $$
when N is sufficiently large. But
$r(E,p)> N$
for this p, so the proof of Theorem 1.1 is complete.
Assuming the generalized Riemann hypothesis for the Dedekind zeta function of F, Lagarias and Odlyzko [Reference Lagarias and Odlyzko11] show that there exists
$p<C_0(\log (|\text {disc}(F)|))^2$
for some
$C_0>0$
. Therefore,
$$ \begin{align*} \log p & < \log C_0 + 2\log\log |\text{disc}(F)|\\ &\le 2\log(4) N + o(N)\\ &< N/0.36 \end{align*} $$
when N is sufficiently large. Therefore,
$r(E,p)> N > 0.36 \log p$
for this p. This completes the proof of Theorem 1.2.
Remark. As the proof indicates, the constants
$0.72$
and
$0.36$
can be replaced by any
$k_1 <1/\log 4$
and
$k_2<1/\log 16$
, respectively. The constant
$12577$
in the bound of Ahn and Kwon is also not crucial; the existence of such a constant is enough for our purposes. A recent preprint of Kadiri and Wong [Reference Kadiri and Wong9] improves the constant to
$310$
.
3 Numerical results
For each of the elliptic curves in this section, we computed
$r(E, p)$
as p ran through primes of good reduction less than
$3\times 10^6$
. If a value was larger than
$r(E, q)$
for all
$q<p$
, we recorded p and
$r(E, p)$
. The results are given in Tables 1–7. We omit the data for primes
$p<100$
since they are too small to consider in the asymptotic behavior. The calculations were done in Sage [Reference Stein17].
Table 1
$y^2=x^3+x$
.
Table 2
$y^2=x^3-x$
.
Table 3
$y^2=x^3+1$
.
Table 4
$y^2=x^3-385875x-113447250$
.
Table 5
$y^2=x^3+x+1$
.
Table 6
$y^2=x^3-13392x - 1080432$
.
Table 7
$y^2=x^3-7x +6$
.
The third and fourth columns of each table compare
$r(E, p)$
to
$\log p \log \log p$
and
$\log p (\log \log p)^2$
. It is well known that
$\log \log p$
grows so slowly that it is often not easy to recognize what power is appropriate. In the present case, the ratio of
$\log \log (2\times 10^6)$
to
$\log \log 200$
is
$1.6$
, and this is representative of the range of primes in our data. So the numbers in the third and fourth columns sometimes exhibit a definite increase or decrease when the power of
$\log \log p$
is modified. But other times, it is not readily apparent which power is appropriate. For each column, we computed the slope of the least-squares line through the data points and listed the result in the last line of the table. For example, for the fourth column of Table 1, we used the points
$(1, 1.49), (2, 0.94), (3, 1.10), \dots , (14, 1.38)$
. The least-squares line has slope
$0.018$
. In three of the tables, the absolute value of the slope is smaller in the third column and in the other four tables the absolute value of the slope is smaller in the second column. We do not have an explanation for the potential variation of exponents. It seems reasonable to guess that an upper bound of the form
$r(E, p) \le C \log p (\log \log p)^{\delta }$
is possible. In other words, the estimate of Theorem 2 is probably sharp, except for powers of
$\log \log p$
and smaller contributions. As mentioned in Section 1, Montgomery [Reference Montgomery13] showed under GRH that the smallest quadratic nonresidue is
$\Omega (\log p \log \log p)$
. The numerical results for elliptic curves indicate that a similar result is possible for elliptic curves. (Of course the estimate of Theorem 1 is probably not close to sharp, unless GRH is false.)
The first four curves have complex multiplication by
$\mathbb Z[i]$
,
$\mathbb Z[i]$
,
$\mathbb Z[(1+\sqrt {-3})/2]$
, and
$\mathbb Z[(1+\sqrt {-7})/2]$
, respectively. All of the p that occur are supersingular primes for their respective curves with the exception of
$p=13007$
in Table 4. For these supersingular primes, the group
$E(\mathbb {F}_p)$
has order
$p+1$
and is either cyclic or cyclic times a group of order 2. This can be seen as follows. The Frobenius map is given by
$\sqrt {-p}$
in the endomorphism ring. If the full n-torsion is contained in
$E(\mathbb {F}_p)$
, then the Frobenius endomorphism must be congruent to 1 mod n. But
$(\sqrt {-p}-1)/n$
is not integral when
$n>2$
. It follows that
$E(\mathbb {F}_p)$
is either
$\mathbb {Z}/(p+1)/Z$
, or
$\mathbb {Z}/\frac {p+1}{2}\mathbb {Z}\times \mathbb {Z}/2\mathbb {Z}$
. The latter is always the case for the curve
$y^2=x^3-x$
. However, for the other three curves, only one point of order 2 is in
$E(\mathbb {F}_p)$
, so the group is cyclic. A cyclic group sometimes has fewer elements of maximal order than a noncyclic abelian group of the same order. However, it is not clear why almost every example is a supersingular prime.
The curves in the last three tables do not have complex multiplication (the last curve is the Weierstrass form for
$X_0(11)$
). The values of
$r(E, p)$
are somewhat smaller than those for the curves with complex multiplication. Perhaps this reflects the fact that supersingular primes are less frequent, but a good explanation is yet to be found.
The curves in Tables 2 and 7 have noncyclic two-torsion over
$\mathbb Q$
, hence mod each of the primes p considered. This phenomenon seems to cause larger values of
$r(E,p)$
.
An interesting situation occurs in Tables 1 and 2, where the prime 537599 is in both tables. Note that in Table 1, the group
$E(\mathbb {F}_p)$
is cyclic of order
$537600 = 2^{10}\cdot 3\cdot 5^2\cdot 7$
, which is a very smooth number. This lowers the probability that a randomly chosen element is a generator. In fact,
$\phi (537600)/537600= 8/35$
. The group for the curve in Table 2 is the product of a cyclic group of order
$2^{9}\cdot 3\cdot 5^2\cdot 7$
times a group of order 2. The probability is again 8/35 that a randomly chosen element of the group has maximal order. These probabilities are low, but it still seems to be a lucky coincidence that this p occurs in both tables. The smoothness of the group order is probably not the deciding factor. There are several smooth numbers close to each of the primes in our table. For example, the Mersenne prime
$2^{19}-1= 524287$
yields
$r(E,p)=3$
for
$y^2=x^3+x$
and
$r(E,p)= 4$
for
$y^2=x^3-x$
, and both curves have
$2^{19}$
points. The more relevant property might be the existence of several small prime factors of
$n=p+1$
(in the supersingular case for the present curves) since this makes
$\phi (n)/n$
small. But this does not guarantee that
$r(E,p)$
is large. An example is
$p=570569$
, where
$p+1=2\cdot 3\cdot 5\cdot 7\cdot 11\cdot 13\cdot 19$
. But
$r(E,p)=6$
for both
$y^2=x^3+x$
and
$y^2=x^3-x$
. It would be interesting to find a good explanation, if one exists, for the double occurrence of 537599.
