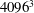1 Introduction
Many fundamental studies of turbulent flow are, for important reasons, devoted to the canonical geometries of isotropic turbulence with no mean velocity gradients, or to flows dominated by mean shear with or without wall boundaries. However, many turbulent flows also undergo changes in cross-section, e.g. flows through nozzles and diffusers, where the effects of deformation by irrotational mean strain are of great interest. Mean strain rates give rise to anisotropy, which weakens when the strain is removed. A considerable body of work is known for the return-to-isotropy problem in Reynolds stress closures (Lumley & Newman Reference Lumley and Newman1977; Speziale Reference Speziale1991). However, at a more detailed level, the nature of anisotropy development at different scale sizes, which is important for subgrid-scale modelling (Liu, Katz & Meneveau Reference Liu, Katz and Meneveau1999), is still not well understood (Sagaut & Cambon Reference Sagaut and Cambon2008).
Assuming incompressibility, three principal sub-classes of irrotational mean strain can be identified, namely: (i) axisymmetric contraction (one extensional direction and two equally compressive directions), (ii) axisymmetric expansion (two equally extensional directions and one compressive direction) and (iii) plane strain (one extensional direction and one compressive direction). A number of experimental (Gence & Mathieu Reference Gence and Mathieu1979; Liu et al. Reference Liu, Katz and Meneveau1999; Choi & Lumley Reference Choi and Lumley2001; Ayyalasomayajula & Warhaft Reference Ayyalasomayajula and Warhaft2006; Brown, Parsheh & Aidun Reference Brown, Parsheh and Aidun2006) and numerical (Lee & Reynolds Reference Lee and Reynolds1985; Zusi & Perot Reference Zusi and Perot2013, Reference Zusi and Perot2014) studies covering one or more of these sub-classes are known. All three sub-classes are distinct and important. However, axisymmetric contraction and expansion (as well as relaxation therefrom) are more closely related to flows through conduits of variable cross-section in engineering devices, and to converging and diverging sections in laboratory wind tunnel facilities. A number of early experimental (Uberoi Reference Uberoi1956; Mills & Corrsin Reference Mills and Corrsin1959; Reynolds & Tucker Reference Reynolds and Tucker1975; Warhaft Reference Warhaft1980) and theoretical (Batchelor & Proudman Reference Batchelor and Proudman1954) studies focused on the response of isotropic turbulence subjected to axisymmetric contraction. Velocity fluctuations are (as expected from the Reynolds stress transport equations) suppressed in the extensional direction but amplified in the compressive directions. The small scales also depart from isotropy when the strain rate is large (Uberoi Reference Uberoi1956). However, in these early studies, the Reynolds number was usually limited, and no attempt was made to investigate the Reynolds number dependence of the flow.
In this paper, we present a computational investigation of turbulence under axisymmetric contraction and subsequent relaxation, with a special interest in conditions corresponding to experiments. In particular, we refer closely to the experimental data of Ayyalasomayajula & Warhaft (Reference Ayyalasomayajula and Warhaft2006) (AW henceforth) in which grid-generated turbulence was passed through an axisymmetric contraction of area ratio 4 : 1. Using both passive and active grids, the experiments of AW covered a range of Reynolds numbers (40–470, based on the Taylor scale). A significant result was that a qualitative change in the form of the transverse one-dimensional (1-D) spectra occurred during relaxation (referred to as a ‘double peak’) only if the Reynolds number was sufficiently high. Increasing departures from rapid distortion theory (RDT) (Savill Reference Savill1987) were also observed as the Reynolds number was increased.
Although strained turbulence becomes less anisotropic upon removal of strain (Sarkar & Speziale Reference Sarkar and Speziale1990; Choi & Lumley Reference Choi and Lumley2001), a full return to isotropy is not guaranteed. For example, the simulations of Chasnov (Reference Chasnov1995) and Davidson, Okamoto & Kaneda (Reference Davidson, Okamoto and Kaneda2012) showed that for anisotropic Saffman turbulence (Saffman Reference Saffman1967; Krogstad & Davidson Reference Krogstad and Davidson2010), the large scales do not return to isotropy. Changes in the form of the spectra measured by AW also imply that different scales respond differently to both the application and removal of strain. To understand the mechanisms involved it is necessary to study spectral transfer resulting from nonlinear interactions and pressure-strain correlations between different scale sizes and velocity components (in the extensional versus compressive directions). Direct numerical simulations (DNS) using Fourier pseudo-spectral methods are well suited to provide the detailed information necessary for this purpose.
It is well known that, provided the strain rate is uniform in space, turbulence under irrotational mean strain is homogeneous and can be simulated on a solution domain that deforms with the mean flow (Rogallo Reference Rogallo1981). A number of such simulations, with strain rates held constant in time, have been helpful in examining the structure of Reynolds stress anisotropy (Lee & Reynolds Reference Lee and Reynolds1985), assessing turbulence models (Zusi & Perot Reference Zusi and Perot2013, Reference Zusi and Perot2014) and understanding inertial and fluid particle statistics (Lee et al. Reference Lee, Gylfason, Perlekar and Toschi2015). However as in the case of Gualtieri & Meneveau (Reference Gualtieri and Meneveau2010) (in conjunction with Chen, Meneveau & Katz (Reference Chen, Meneveau and Katz2006)), a time-dependent strain rate in the DNS is necessary to facilitate comparisons with experiment, where typically the turbulence evolves in space rather than in time.
In this work we have developed a smoothly varying time-dependent strain rate to closely mimic the laboratory conditions of AW. A series of numerical simulations in a deforming periodic domain have been performed to study the effect of the Reynolds number and possible numerical or sampling limitations of the results. To capture the natural behaviours of both large- and small-scale motions faithfully, simulation parameters are chosen to ensure that, at all times, the large scales are sufficiently well sampled along the shortest side of the solution domain, while the small scales are sufficiently well resolved along the direction of coarsest grid spacing. A pre-simulation is first carried out in order to produce a state of fully developed isotropic turbulent flow before strain is applied. The highest grid resolution is
![]() $4096^{3}$
. During the application of strain, the small scales become strongly anisotropic, but in contrast to the large scales, they return to isotropy quickly when strain is removed. For the case of highest pre-strain Reynolds number (95 based on the Taylor scale), we find clear evidence of the characteristic change in spectral shape that AW reported in their higher Reynolds number experiments during the relaxation phase. Detailed analyses of the evolution of axisymmetric spectra (Mininni, Rosenberg & Pouquet Reference Mininni, Rosenberg and Pouquet2012) in the simulations show that this feature is the result of a strong contrast in rates of return to isotropy between the large scales and the small scales, with this contrast being stronger at higher Reynolds number.
$4096^{3}$
. During the application of strain, the small scales become strongly anisotropic, but in contrast to the large scales, they return to isotropy quickly when strain is removed. For the case of highest pre-strain Reynolds number (95 based on the Taylor scale), we find clear evidence of the characteristic change in spectral shape that AW reported in their higher Reynolds number experiments during the relaxation phase. Detailed analyses of the evolution of axisymmetric spectra (Mininni, Rosenberg & Pouquet Reference Mininni, Rosenberg and Pouquet2012) in the simulations show that this feature is the result of a strong contrast in rates of return to isotropy between the large scales and the small scales, with this contrast being stronger at higher Reynolds number.
The remaining sections of this paper are organized as follows. In § 2, we present our numerical method including the governing equations on a domain deforming with the mean flow, the development of a time-dependent strain rate used to model the wind tunnel contraction of AW and the formulation of evolution equations for spectra. In § 3, we give details on the pre-simulation approach and a list of several simulations conducted for both physical (Reynolds number) and numerical (domain size and grid resolution) reasons. In § 4, we focus on the response of initially isotropic turbulence to the time-dependent axisymmetric contraction. In § 5, we present results for the relaxation phase that begins when the strain rate is turned off. A number of 1-D spectra are shown which display features similar to those reported by AW in their experiments. Finally, in § 6 we summarize the conclusions from this work and briefly discuss some possible paths for further investigation. In the Appendix we show that our numerical results are robust by comparing simulations on domains of different size and grid resolution.
2 Mathematical formulation and numerical approach
The use of a solution domain that deforms according to an axisymmetric time-dependent strain rate, which is in turn constructed to model a laboratory turbulent flow with a spatially evolving cross-section, requires some special care in both the conduct of the simulation and the subsequent data analysis, as we discuss below.
2.1 Solution algorithm in a deforming, anisotropic domain
Rogallo (Reference Rogallo1981) introduced the coordinate transformation
![]() $\unicode[STIX]{x1D709}_{i}=\unicode[STIX]{x1D609}_{ij}(t)x_{j}$
, in which the deforming coordinate system
$\unicode[STIX]{x1D709}_{i}=\unicode[STIX]{x1D609}_{ij}(t)x_{j}$
, in which the deforming coordinate system
![]() $\unicode[STIX]{x1D709}_{i}$
is related to the laboratory coordinates
$\unicode[STIX]{x1D709}_{i}$
is related to the laboratory coordinates
![]() $x_{i}$
through the metric tensor
$x_{i}$
through the metric tensor
![]() $\unicode[STIX]{x1D609}_{ij}(t)$
. Summation over repeated Latin indices is implied throughout the text. The deforming coordinates are required to move with the mean flow, according to
$\unicode[STIX]{x1D609}_{ij}(t)$
. Summation over repeated Latin indices is implied throughout the text. The deforming coordinates are required to move with the mean flow, according to
where
![]() $\langle U_{i}\rangle$
is the mean velocity. In this coordinate system the turbulence is homogeneous, and periodic boundary conditions are applicable provided the mean velocity gradients are uniform in space. The continuity and momentum equations become
$\langle U_{i}\rangle$
is the mean velocity. In this coordinate system the turbulence is homogeneous, and periodic boundary conditions are applicable provided the mean velocity gradients are uniform in space. The continuity and momentum equations become
For irrotational axisymmetric contraction, the mean deformation tensor is given by (Lee & Reynolds Reference Lee and Reynolds1985)
 $$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\langle U_{i}\rangle }{\unicode[STIX]{x2202}x_{j}}=\frac{2}{\sqrt{3}}S(t)\left[\begin{array}{@{}ccc@{}}1 & 0 & 0\\ 0 & \displaystyle -\frac{1}{2} & 0\\ 0 & 0 & \displaystyle -\frac{1}{2}\end{array}\right]\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\langle U_{i}\rangle }{\unicode[STIX]{x2202}x_{j}}=\frac{2}{\sqrt{3}}S(t)\left[\begin{array}{@{}ccc@{}}1 & 0 & 0\\ 0 & \displaystyle -\frac{1}{2} & 0\\ 0 & 0 & \displaystyle -\frac{1}{2}\end{array}\right]\end{eqnarray}$$
with
![]() $S(t)\geqslant 0$
. The solution domain is orthogonal at all times, such that only the diagonal elements of
$S(t)\geqslant 0$
. The solution domain is orthogonal at all times, such that only the diagonal elements of
![]() $\unicode[STIX]{x1D609}_{ij}(t)$
are non-zero. Solving (2.1) leads to (for
$\unicode[STIX]{x1D609}_{ij}(t)$
are non-zero. Solving (2.1) leads to (for
![]() $\unicode[STIX]{x1D6FC}=1,2,3$
, no summation)
$\unicode[STIX]{x1D6FC}=1,2,3$
, no summation)
where
![]() $\unicode[STIX]{x1D609}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}}^{0}\equiv \unicode[STIX]{x1D609}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}}(0)$
and
$\unicode[STIX]{x1D609}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}}^{0}\equiv \unicode[STIX]{x1D609}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}}(0)$
and
![]() $\exp [f_{\unicode[STIX]{x1D6FC}}(t)]$
is the total strain in each direction with
$\exp [f_{\unicode[STIX]{x1D6FC}}(t)]$
is the total strain in each direction with
Figure 1 shows a schematic of how the domain is deformed during the application of strain. At any time
![]() $t$
, the length of the domain on each side given by
$t$
, the length of the domain on each side given by
![]() $L_{\unicode[STIX]{x1D6FC}}=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D609}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}}(t)$
varies as
$L_{\unicode[STIX]{x1D6FC}}=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D609}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}}(t)$
varies as
![]() $L_{\unicode[STIX]{x1D6FC}}(t)=L_{\unicode[STIX]{x1D6FC}}^{0}\exp [f_{\unicode[STIX]{x1D6FC}}(t)]$
where
$L_{\unicode[STIX]{x1D6FC}}(t)=L_{\unicode[STIX]{x1D6FC}}^{0}\exp [f_{\unicode[STIX]{x1D6FC}}(t)]$
where
![]() $L_{\unicode[STIX]{x1D6FC}}^{0}$
is the initial length. While the number of grid points is fixed, the grid spacings and hence also resolution in each direction vary. Correspondingly, the wavenumbers represented in each direction of the domain are given by
$L_{\unicode[STIX]{x1D6FC}}^{0}$
is the initial length. While the number of grid points is fixed, the grid spacings and hence also resolution in each direction vary. Correspondingly, the wavenumbers represented in each direction of the domain are given by
![]() $k_{\unicode[STIX]{x1D6FC}}(n_{\unicode[STIX]{x1D6FC}},t)=n_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D609}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}}(t)$
, where
$k_{\unicode[STIX]{x1D6FC}}(n_{\unicode[STIX]{x1D6FC}},t)=n_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D609}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}}(t)$
, where
![]() $n_{\unicode[STIX]{x1D6FC}}=-N_{\unicode[STIX]{x1D6FC}}/2+1,\cdots \,,N_{\unicode[STIX]{x1D6FC}}/2$
, and
$n_{\unicode[STIX]{x1D6FC}}=-N_{\unicode[STIX]{x1D6FC}}/2+1,\cdots \,,N_{\unicode[STIX]{x1D6FC}}/2$
, and
![]() $N_{\unicode[STIX]{x1D6FC}}$
is the number of grid points in the
$N_{\unicode[STIX]{x1D6FC}}$
is the number of grid points in the
![]() $x_{\unicode[STIX]{x1D6FC}}$
direction. The maximum resolved wavenumber in each direction after truncation is
$x_{\unicode[STIX]{x1D6FC}}$
direction. The maximum resolved wavenumber in each direction after truncation is
![]() $k_{max,\unicode[STIX]{x1D6FC}}(t)=\sqrt{2}N_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D609}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}}(t)/3$
. As the simulation proceeds and the domain becomes deformed from its original shape, it is necessary to check that the large scales continue to be well contained within the domain in all directions, while the small scales likewise remain well resolved (Gualtieri & Meneveau Reference Gualtieri and Meneveau2010).
$k_{max,\unicode[STIX]{x1D6FC}}(t)=\sqrt{2}N_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D609}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}}(t)/3$
. As the simulation proceeds and the domain becomes deformed from its original shape, it is necessary to check that the large scales continue to be well contained within the domain in all directions, while the small scales likewise remain well resolved (Gualtieri & Meneveau Reference Gualtieri and Meneveau2010).

Figure 1. Grid deformation under axisymmetric contraction with a total elongation of 4 in the
![]() $x_{1}$
direction. The grid metrics in the
$x_{1}$
direction. The grid metrics in the
![]() $x_{2}$
and
$x_{2}$
and
![]() $x_{3}$
directions are equal.
$x_{3}$
directions are equal.
2.2 A time-dependent strain as a model for experiment
In most wind tunnel experiments the change in cross-section is gradual, which results in a smooth variation of the mean velocity with distance downstream along the wind tunnel centreline. The mean strain rate along the wind tunnel centreline is thus readily established as a function of the spatial coordinates. However, as a fluid element passes through the wind tunnel, the spatially varying mean strain rate is experienced in a time-dependent manner. To model the mean strain rates from experimental wind tunnels in our time-dependent DNS, we apply a spatially uniform, but time-dependent mean strain rate that corresponds to the local value of the mean strain rate that a fluid element experiences as it passes through the wind tunnel (Pearson Reference Pearson1959). This is accomplished by introducing a convective time
![]() $t$
as the time taken for a fluid element travelling with the mean flow to reach a position
$t$
as the time taken for a fluid element travelling with the mean flow to reach a position
![]() $x$
from a reference location
$x$
from a reference location
![]() $x_{a}$
. (Here
$x_{a}$
. (Here
![]() $x$
alone, or
$x$
alone, or
![]() $x_{a}$
etc. without tensor subscripts shall refer to distances measured along the wind tunnel centreline.) We write
$x_{a}$
etc. without tensor subscripts shall refer to distances measured along the wind tunnel centreline.) We write
According to (2.5)–(2.6), by this time
![]() $t$
the grid metric in the extensional direction will be
$t$
the grid metric in the extensional direction will be
The integral in (2.8) can be evaluated through a change of variables,
![]() $\text{d}\unicode[STIX]{x1D70F}=\text{d}x/\langle U_{1}(x)\rangle$
(suggested by (2.7)). After some simplifications, we obtain
$\text{d}\unicode[STIX]{x1D70F}=\text{d}x/\langle U_{1}(x)\rangle$
(suggested by (2.7)). After some simplifications, we obtain
Since the applied mean strain is volume preserving, the product of the three diagonal metric factors
![]() $\unicode[STIX]{x1D609}_{11}\unicode[STIX]{x1D609}_{22}\unicode[STIX]{x1D609}_{33}$
is fixed, while axisymmetry requires
$\unicode[STIX]{x1D609}_{11}\unicode[STIX]{x1D609}_{22}\unicode[STIX]{x1D609}_{33}$
is fixed, while axisymmetry requires
![]() $\unicode[STIX]{x1D609}_{22}=\unicode[STIX]{x1D609}_{33}$
. As a result, the change in the transverse grid metrics is given by
$\unicode[STIX]{x1D609}_{22}=\unicode[STIX]{x1D609}_{33}$
. As a result, the change in the transverse grid metrics is given by
Since in the simulation the turbulence is advanced in time instead of space, at each time step from
![]() $t_{n}$
to
$t_{n}$
to
![]() $t_{n}+\unicode[STIX]{x0394}t$
, it is necessary to solve (2.7) for a new spatial location
$t_{n}+\unicode[STIX]{x0394}t$
, it is necessary to solve (2.7) for a new spatial location
![]() $x$
, so that the new metric factors can be evaluated according to (2.9)–(2.10). In addition, at every time step the metric factors are used to form the viscous integrating factors (Rogallo Reference Rogallo1981). The solution to (2.7) and the calculation of the integrating factors are carried out using QUADPACK (Piessens et al.
Reference Piessens, de Doncker-Kapenga, Überhuber and Kahaner1983).
$x$
, so that the new metric factors can be evaluated according to (2.9)–(2.10). In addition, at every time step the metric factors are used to form the viscous integrating factors (Rogallo Reference Rogallo1981). The solution to (2.7) and the calculation of the integrating factors are carried out using QUADPACK (Piessens et al.
Reference Piessens, de Doncker-Kapenga, Überhuber and Kahaner1983).
In the experiments of AW, the mean streamwise velocity
![]() $\langle U_{1}(x)\rangle$
along the centreline of the wind tunnel is well described by an error function, which yields a Gaussian profile for the mean extensional strain (see figure 2 of AW). We consider the functional form
$\langle U_{1}(x)\rangle$
along the centreline of the wind tunnel is well described by an error function, which yields a Gaussian profile for the mean extensional strain (see figure 2 of AW). We consider the functional form
where the five parameters
![]() $a$
,
$a$
,
![]() $b$
,
$b$
,
![]() $c$
,
$c$
,
![]() $x_{a}$
and
$x_{a}$
and
![]() $x_{b}$
are chosen so the mean strain closely matches the experiments in a non-dimensional sense, and the origin of the
$x_{b}$
are chosen so the mean strain closely matches the experiments in a non-dimensional sense, and the origin of the
![]() $x$
-axis has been placed at the location of maximum mean velocity gradient. In the experiments, some appreciable strain also existed immediately upstream and downstream of the physical beginning and ending locations of the contraction. To incorporate this feature in our DNS, we specify two intermediate locations
$x$
-axis has been placed at the location of maximum mean velocity gradient. In the experiments, some appreciable strain also existed immediately upstream and downstream of the physical beginning and ending locations of the contraction. To incorporate this feature in our DNS, we specify two intermediate locations
![]() $x_{i}$
and
$x_{i}$
and
![]() $x_{f}$
satisfying
$x_{f}$
satisfying
![]() $x_{a}<x_{i}<x_{f}<x_{b}$
(
$x_{a}<x_{i}<x_{f}<x_{b}$
(
![]() $x_{i}$
and
$x_{i}$
and
![]() $x_{f}$
correspond to the vertical lines in figure 2 of AW). Since these two locations are approximately equally far from the location of maximum strain rate, we take
$x_{f}$
correspond to the vertical lines in figure 2 of AW). Since these two locations are approximately equally far from the location of maximum strain rate, we take
![]() $x_{i}=-x_{f}$
. The straining ‘period’ in the DNS is considered to be the entire phase of the simulation during which there is non-zero mean strain, corresponding to the physical distance between
$x_{i}=-x_{f}$
. The straining ‘period’ in the DNS is considered to be the entire phase of the simulation during which there is non-zero mean strain, corresponding to the physical distance between
![]() $x_{a}$
and
$x_{a}$
and
![]() $x_{b}$
. Figure 2(a) presents a sketch of an error function mean velocity profile with these locations marked for later reference. While
$x_{b}$
. Figure 2(a) presents a sketch of an error function mean velocity profile with these locations marked for later reference. While
![]() $x_{i}$
and
$x_{i}$
and
![]() $x_{f}$
are used to specify the mean velocity variation, we report pre- and post-contraction statistics at
$x_{f}$
are used to specify the mean velocity variation, we report pre- and post-contraction statistics at
![]() $x_{a}$
and
$x_{a}$
and
![]() $x_{b}$
, respectively.
$x_{b}$
, respectively.

Figure 2. (a) Schematic of mean velocity profile in experiments, and (b) examples of non-dimensional strain rate
![]() $S\unicode[STIX]{x1D70F}_{a}$
as function of convective time in experiments and DNS. In (b): ○ (black) is for the AW
$S\unicode[STIX]{x1D70F}_{a}$
as function of convective time in experiments and DNS. In (b): ○ (black) is for the AW
![]() $R_{\unicode[STIX]{x1D706}}=260$
experiment, ▫ (blue) for AW
$R_{\unicode[STIX]{x1D706}}=260$
experiment, ▫ (blue) for AW
![]() $R_{\unicode[STIX]{x1D706}}=40$
experiment, ▴ (magenta) for
$R_{\unicode[STIX]{x1D706}}=40$
experiment, ▴ (magenta) for
![]() $S_{0}^{\ast }=25$
numerical, ♦ (green) for
$S_{0}^{\ast }=25$
numerical, ♦ (green) for
![]() $S_{0}^{\ast }=20$
numerical and ▾ (red) for
$S_{0}^{\ast }=20$
numerical and ▾ (red) for
![]() $S_{0}^{\ast }=15$
numerical.
$S_{0}^{\ast }=15$
numerical.
For a systematic procedure for choosing the five curve-fit parameters noted above, we need five constraints to control both the spatial spread of the profile and its maximum velocity gradient (which is proportional to the product
![]() $ab$
). First, since the value of
$ab$
). First, since the value of
![]() $c$
does not affect the strain rate, it is arbitrary provided it is large enough to ensure that
$c$
does not affect the strain rate, it is arbitrary provided it is large enough to ensure that
![]() $\langle U_{1}(x)\rangle >0$
for all
$\langle U_{1}(x)\rangle >0$
for all
![]() $x$
. Second, we specify the velocity ratio
$x$
. Second, we specify the velocity ratio
![]() $\langle U_{1}(x_{f})\rangle /\langle U_{1}(x_{i})\rangle$
at a value close to the experiment. Third, we require that the strain rate
$\langle U_{1}(x_{f})\rangle /\langle U_{1}(x_{i})\rangle$
at a value close to the experiment. Third, we require that the strain rate
![]() $S$
at
$S$
at
![]() $x=0$
, denoted by
$x=0$
, denoted by
![]() $S_{0}$
, corresponds to a non-dimensional strain
$S_{0}$
, corresponds to a non-dimensional strain
![]() $S_{0}^{\ast }$
formed from
$S_{0}^{\ast }$
formed from
![]() $S_{0}$
and a large-eddy time scale of the turbulence before strain is applied. Specifically, we define
$S_{0}$
and a large-eddy time scale of the turbulence before strain is applied. Specifically, we define
![]() $S_{0}^{\ast }=S_{0}\unicode[STIX]{x1D70F}_{a}$
, where
$S_{0}^{\ast }=S_{0}\unicode[STIX]{x1D70F}_{a}$
, where
![]() $\unicode[STIX]{x1D70F}_{a}=(2K/\langle \unicode[STIX]{x1D716}\rangle )_{a}$
, with
$\unicode[STIX]{x1D70F}_{a}=(2K/\langle \unicode[STIX]{x1D716}\rangle )_{a}$
, with
![]() $K$
and
$K$
and
![]() $\unicode[STIX]{x1D716}$
being the turbulence kinetic energy and the dissipation rate. Fourth, the starting location
$\unicode[STIX]{x1D716}$
being the turbulence kinetic energy and the dissipation rate. Fourth, the starting location
![]() $x_{a}$
is chosen to give a desired non-dimensional strain rate at
$x_{a}$
is chosen to give a desired non-dimensional strain rate at
![]() $x_{a}$
based on the experiments. Finally, the ending location
$x_{a}$
based on the experiments. Finally, the ending location
![]() $x_{b}$
is chosen to achieve a desired velocity ratio
$x_{b}$
is chosen to achieve a desired velocity ratio
![]() $\langle U_{1}(x_{b})\rangle /\langle U_{1}(x_{a})\rangle$
, i.e. deformation, for the entire straining period.
$\langle U_{1}(x_{b})\rangle /\langle U_{1}(x_{a})\rangle$
, i.e. deformation, for the entire straining period.
Figure 2(b) shows a qualitative comparison of the non-dimensional strain rate profiles obtained numerically from three values of
![]() $S_{0}^{\ast }$
with experimental data derived from AW at two values of the pre-strain Reynolds number. Experimental data in this figure are obtained first by applying curve fits of a form similar to (2.11) and then differentiating. The non-dimensional strain rates are plotted at convective times
$S_{0}^{\ast }$
with experimental data derived from AW at two values of the pre-strain Reynolds number. Experimental data in this figure are obtained first by applying curve fits of a form similar to (2.11) and then differentiating. The non-dimensional strain rates are plotted at convective times
![]() $t$
in the laboratory facility obtained using (2.7) and normalized by large-eddy turnover times obtained from table 1 of AW. The numerical strain rates are obtained using the aforementioned procedure with
$t$
in the laboratory facility obtained using (2.7) and normalized by large-eddy turnover times obtained from table 1 of AW. The numerical strain rates are obtained using the aforementioned procedure with
![]() $c=10$
,
$c=10$
,
![]() $bx_{f}=0.9$
, a velocity ratio
$bx_{f}=0.9$
, a velocity ratio
![]() $\langle U_{1}(x_{f})\rangle /\langle U_{1}(x_{i})\rangle =2.85$
, a starting non-dimensional strain rate of
$\langle U_{1}(x_{f})\rangle /\langle U_{1}(x_{i})\rangle =2.85$
, a starting non-dimensional strain rate of
![]() $0.3$
at
$0.3$
at
![]() $x_{a}$
and an overall velocity ratio
$x_{a}$
and an overall velocity ratio
![]() $\langle U_{1}(x_{b})\rangle /\langle U_{1}(x_{a})\rangle =4$
. The resulting strain rate profiles are similar to those in the experiments, suggesting that the procedures described here model the mean velocity variation in the wind tunnel contraction well.
$\langle U_{1}(x_{b})\rangle /\langle U_{1}(x_{a})\rangle =4$
. The resulting strain rate profiles are similar to those in the experiments, suggesting that the procedures described here model the mean velocity variation in the wind tunnel contraction well.
2.3 Spectral evolution and rapid-distortion theory
To understand the dynamical processes underlying the change in shape of the energy spectrum under applied strain, we need to compute various terms in the spectral evolution equations. In isotropic turbulence, computation of the nonlinear transfer spectrum of the kinetic energy (e.g. Domaradzki & Rogallo Reference Domaradzki and Rogallo1990; Yeung, Brasseur & Wang Reference Yeung, Brasseur and Wang1995) in spherical wavenumber shells is sufficient. However, in this work we also have to consider pressure-strain correlations and systematic anisotropy, which requires individual components of spectra in one- and two-dimensional partitions of wavenumber space. In addition, the mean strain distorts the wavenumbers on a deforming domain, leading to transport of the spectrum in wavenumber space (Pope Reference Pope2000).
In Fourier space, the fluctuating velocity on a deforming periodic domain evolves by
where the metric factors in (2.3) are expressed through time dependence of the wave vector
![]() $\boldsymbol{k}$
,
$\boldsymbol{k}$
,
![]() $\hat{p}(\boldsymbol{k})$
is the Fourier coefficient of the fluctuating pressure,
$\hat{p}(\boldsymbol{k})$
is the Fourier coefficient of the fluctuating pressure,
![]() $G_{i}(\boldsymbol{k})=\text{i}k_{j}\widehat{u_{i}u_{j}}$
and
$G_{i}(\boldsymbol{k})=\text{i}k_{j}\widehat{u_{i}u_{j}}$
and
![]() $\text{i}=\sqrt{-1}$
. It is important to distinguish between rapid pressure and slow pressure, which respond to the mean flow and the velocity fluctuations respectively; we write
$\text{i}=\sqrt{-1}$
. It is important to distinguish between rapid pressure and slow pressure, which respond to the mean flow and the velocity fluctuations respectively; we write
![]() $\hat{p}=\hat{p}^{r}+\hat{p}^{s}$
. Both are obtained by solving well-known Poisson equations. The spectral covariance
$\hat{p}=\hat{p}^{r}+\hat{p}^{s}$
. Both are obtained by solving well-known Poisson equations. The spectral covariance
![]() $\unicode[STIX]{x1D60C}_{ij}(\boldsymbol{k})\equiv \langle \hat{u} _{i}^{\ast }(\boldsymbol{k})\hat{u} _{j}(\boldsymbol{k})\rangle$
(where superscript
$\unicode[STIX]{x1D60C}_{ij}(\boldsymbol{k})\equiv \langle \hat{u} _{i}^{\ast }(\boldsymbol{k})\hat{u} _{j}(\boldsymbol{k})\rangle$
(where superscript
![]() $\ast$
denotes complex conjugates) is in general complex valued, although because mean shear is absent we are only concerned with the diagonal components, which are real. We can write
$\ast$
denotes complex conjugates) is in general complex valued, although because mean shear is absent we are only concerned with the diagonal components, which are real. We can write
where terms on the right-hand side represent, respectively, production due to the mean velocity gradient, redistribution due to rapid pressure and slow pressure, spectral transfer due to nonlinear terms and dissipation due to viscosity. Specifically, these terms are:
The angled brackets in these equations represent averaging over multiple realizations, i.e. ensemble averaging, which we perform for the majority of our simulations detailed later. When axisymmetric contraction is applied the production term is negative for
![]() $\unicode[STIX]{x1D60C}_{11}(\boldsymbol{k})$
, but positive for
$\unicode[STIX]{x1D60C}_{11}(\boldsymbol{k})$
, but positive for
![]() $\unicode[STIX]{x1D60C}_{22}(\boldsymbol{k})$
and
$\unicode[STIX]{x1D60C}_{22}(\boldsymbol{k})$
and
![]() $\unicode[STIX]{x1D60C}_{33}(\boldsymbol{k})$
, thus causing anisotropy directly, especially at the large scales. The pressure-strain term exchanges energy among the diagonal components
$\unicode[STIX]{x1D60C}_{33}(\boldsymbol{k})$
, thus causing anisotropy directly, especially at the large scales. The pressure-strain term exchanges energy among the diagonal components
![]() $\unicode[STIX]{x1D60C}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}}(\boldsymbol{k})$
and is traceless due to incompressibility, for both rapid and slow pressures. The rapid pressure is present only while strain is applied, while slow pressure is also important during relaxation. Since nonlinear transfer redistributes energy in Fourier space, each component of
$\unicode[STIX]{x1D60C}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}}(\boldsymbol{k})$
and is traceless due to incompressibility, for both rapid and slow pressures. The rapid pressure is present only while strain is applied, while slow pressure is also important during relaxation. Since nonlinear transfer redistributes energy in Fourier space, each component of
![]() $T_{ij}(\boldsymbol{k})$
integrates to zero over wavenumber space. Integrating (2.13) over all wavenumbers gives the Reynolds stress transport equation for homogeneous turbulence, which is
$T_{ij}(\boldsymbol{k})$
integrates to zero over wavenumber space. Integrating (2.13) over all wavenumbers gives the Reynolds stress transport equation for homogeneous turbulence, which is
where
![]() $s_{ij}$
is the fluctuating strain rate.
$s_{ij}$
is the fluctuating strain rate.
In (2.13), only the production and rapid pressure-strain terms depend directly on the mean strain rate. As a result, if the strain rate is very strong, i.e. very rapid compared to the time scales of the turbulence, this equation can be simplified by retaining only
![]() $P_{ij}(\boldsymbol{k})$
and
$P_{ij}(\boldsymbol{k})$
and
![]() $\unicode[STIX]{x1D6F1}_{ij}^{r}(\boldsymbol{k})$
, while neglecting viscous dissipation and the nonlinear effects of slow pressure and spectral transfer. The behaviour of the energy spectrum tensor can then be described by inviscid RDT (Townsend Reference Townsend1976; Savill Reference Savill1987). Although in practice the strain rates in experiments and simulations are necessarily finite, comparisons with RDT theory are still useful for a better understanding.
$\unicode[STIX]{x1D6F1}_{ij}^{r}(\boldsymbol{k})$
, while neglecting viscous dissipation and the nonlinear effects of slow pressure and spectral transfer. The behaviour of the energy spectrum tensor can then be described by inviscid RDT (Townsend Reference Townsend1976; Savill Reference Savill1987). Although in practice the strain rates in experiments and simulations are necessarily finite, comparisons with RDT theory are still useful for a better understanding.
The use of a deforming domain, and hence a time-dependent set of wave vectors in our simulations, requires some care when interpreting spectra. It would be useful to relate the 1-D spectrum
![]() $\unicode[STIX]{x1D60C}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}}(k_{\unicode[STIX]{x1D6FD}})$
to its equivalent representation
$\unicode[STIX]{x1D60C}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}}(k_{\unicode[STIX]{x1D6FD}})$
to its equivalent representation
![]() $\unicode[STIX]{x1D60C}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}}^{0}(k_{\unicode[STIX]{x1D6FD}}^{0})$
as a function of the pre-strain wavenumbers
$\unicode[STIX]{x1D60C}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}}^{0}(k_{\unicode[STIX]{x1D6FD}}^{0})$
as a function of the pre-strain wavenumbers
![]() $k_{\unicode[STIX]{x1D6FD}}^{0}$
. This would clearly show how a set of modes (those perpendicular to an initial
$k_{\unicode[STIX]{x1D6FD}}^{0}$
. This would clearly show how a set of modes (those perpendicular to an initial
![]() $k_{1}$
) are affected by the strain. The integrals of these spectra over the corresponding wavenumbers
$k_{1}$
) are affected by the strain. The integrals of these spectra over the corresponding wavenumbers
![]() $k_{\unicode[STIX]{x1D6FD}}$
and
$k_{\unicode[STIX]{x1D6FD}}$
and
![]() $k_{\unicode[STIX]{x1D6FD}}^{0}$
are both equal to
$k_{\unicode[STIX]{x1D6FD}}^{0}$
are both equal to
![]() $\langle u_{\unicode[STIX]{x1D6FC}}^{2}\rangle$
. At any time
$\langle u_{\unicode[STIX]{x1D6FC}}^{2}\rangle$
. At any time
![]() $t$
during the straining period, the current and pre-strain wavenumbers are related by
$t$
during the straining period, the current and pre-strain wavenumbers are related by
where
![]() $\unicode[STIX]{x1D609}_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FD}}^{0}/\unicode[STIX]{x1D609}_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FD}}(t)$
is the total deformation in the
$\unicode[STIX]{x1D609}_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FD}}^{0}/\unicode[STIX]{x1D609}_{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FD}}(t)$
is the total deformation in the
![]() $x_{\unicode[STIX]{x1D6FD}}$
direction. A change of variables between the integrals in
$x_{\unicode[STIX]{x1D6FD}}$
direction. A change of variables between the integrals in
![]() $k_{\unicode[STIX]{x1D6FD}}$
and
$k_{\unicode[STIX]{x1D6FD}}$
and
![]() $k_{\unicode[STIX]{x1D6FD}}^{0}$
then gives the relation
$k_{\unicode[STIX]{x1D6FD}}^{0}$
then gives the relation
Following AW, we present most of our 1-D spectral results in terms of the pre-strain wavenumbers during the application of strain, and in terms of the post-strain wavenumbers (which are fixed) during the relaxation period.

Figure 3. Ring decomposition of wavenumber space for axisymmetric turbulence. The axis of axisymmetry
![]() $\unicode[STIX]{x1D740}$
is in the
$\unicode[STIX]{x1D740}$
is in the
![]() $\boldsymbol{k}_{1}$
direction, and the ring is perpendicular to
$\boldsymbol{k}_{1}$
direction, and the ring is perpendicular to
![]() $\unicode[STIX]{x1D740}$
. The longitude with respect to
$\unicode[STIX]{x1D740}$
. The longitude with respect to
![]() $\boldsymbol{k}_{2}$
is
$\boldsymbol{k}_{2}$
is
![]() $\unicode[STIX]{x1D703}$
and the colatitude with respect to
$\unicode[STIX]{x1D703}$
and the colatitude with respect to
![]() $\unicode[STIX]{x1D740}$
is
$\unicode[STIX]{x1D740}$
is
![]() $\unicode[STIX]{x1D719}$
.
$\unicode[STIX]{x1D719}$
.
Statistics in axisymmetric turbulence are rotationally symmetric about a preferred direction
![]() $\unicode[STIX]{x1D740}$
(Batchelor Reference Batchelor1946), which in this study is the extensional direction. Figure 3 shows a decomposition of Fourier space motivated by this rotational symmetry, such that spectral quantities are expressed as functions of
$\unicode[STIX]{x1D740}$
(Batchelor Reference Batchelor1946), which in this study is the extensional direction. Figure 3 shows a decomposition of Fourier space motivated by this rotational symmetry, such that spectral quantities are expressed as functions of
![]() $k_{1}$
and the wavenumber magnitude in the cross-sectional plane
$k_{1}$
and the wavenumber magnitude in the cross-sectional plane
![]() $k_{r}=\sqrt{k_{2}^{2}+k_{3}^{2}}$
. We can also write
$k_{r}=\sqrt{k_{2}^{2}+k_{3}^{2}}$
. We can also write
![]() $k_{r}=k\sin \unicode[STIX]{x1D719}$
, where
$k_{r}=k\sin \unicode[STIX]{x1D719}$
, where
![]() $k=\sqrt{\boldsymbol{k}\cdot \boldsymbol{k}}$
and
$k=\sqrt{\boldsymbol{k}\cdot \boldsymbol{k}}$
and
![]() $0\leqslant \unicode[STIX]{x1D719}\leqslant \unicode[STIX]{x03C0}$
is the colatitude with respect to
$0\leqslant \unicode[STIX]{x1D719}\leqslant \unicode[STIX]{x03C0}$
is the colatitude with respect to
![]() $\unicode[STIX]{x1D740}$
. The spectral covariance
$\unicode[STIX]{x1D740}$
. The spectral covariance
![]() $\unicode[STIX]{x1D60C}_{ij}(\boldsymbol{k})$
defined earlier is a discrete version of the velocity spectrum tensor
$\unicode[STIX]{x1D60C}_{ij}(\boldsymbol{k})$
defined earlier is a discrete version of the velocity spectrum tensor
![]() $\unicode[STIX]{x1D6F7}_{ij}(\boldsymbol{k})$
(whose integral in wavenumber space gives
$\unicode[STIX]{x1D6F7}_{ij}(\boldsymbol{k})$
(whose integral in wavenumber space gives
![]() $\langle u_{i}u_{j}\rangle$
). We define the axisymmetric spectrum tensor as
$\langle u_{i}u_{j}\rangle$
). We define the axisymmetric spectrum tensor as
from which the 1-D spectra can be recovered by
where the factor of 2 is used to collect contributions from both positive and negative values of
![]() $k_{1}$
. Axisymmetric representations of the spectra are useful in studies of rotating (Clark di Leoni et al.
Reference Clark di Leoni, Cobelli, Mininni and Dmitruk2014) and stably stratified turbulent flows (Godeferd & Staquet Reference Godeferd and Staquet2003). Evolution equations for the axisymmetric spectra and 1-D spectra are readily obtained by integration of (2.13) over rings and planes in wavenumber space, respectively. For isotropic turbulence, the contours of the axisymmetric energy spectrum
$k_{1}$
. Axisymmetric representations of the spectra are useful in studies of rotating (Clark di Leoni et al.
Reference Clark di Leoni, Cobelli, Mininni and Dmitruk2014) and stably stratified turbulent flows (Godeferd & Staquet Reference Godeferd and Staquet2003). Evolution equations for the axisymmetric spectra and 1-D spectra are readily obtained by integration of (2.13) over rings and planes in wavenumber space, respectively. For isotropic turbulence, the contours of the axisymmetric energy spectrum
![]() $E_{A}(k_{1},k_{r})\equiv {\textstyle \frac{1}{2}}A_{ii}(k_{1},k_{r})$
multiplied by
$E_{A}(k_{1},k_{r})\equiv {\textstyle \frac{1}{2}}A_{ii}(k_{1},k_{r})$
multiplied by
![]() $1/\sin \unicode[STIX]{x1D719}$
are circles in the
$1/\sin \unicode[STIX]{x1D719}$
are circles in the
![]() $(k_{1},k_{r})$
plane (Mininni et al.
Reference Mininni, Rosenberg and Pouquet2012). In practice, the axisymmetric spectra are formed by summing over Fourier modes residing in rings of finite thickness. Because the computational space is Cartesian, the distribution of modes in rings at small
$(k_{1},k_{r})$
plane (Mininni et al.
Reference Mininni, Rosenberg and Pouquet2012). In practice, the axisymmetric spectra are formed by summing over Fourier modes residing in rings of finite thickness. Because the computational space is Cartesian, the distribution of modes in rings at small
![]() $k_{r}$
is significantly uneven, which can lead to some noise in contours of the axisymmetric spectra. A node-density correction factor is applied in a manner similar to those used for 3-D spectra collected into discrete spherical shells in wavenumber space (Eswaran & Pope Reference Eswaran and Pope1988).
$k_{r}$
is significantly uneven, which can lead to some noise in contours of the axisymmetric spectra. A node-density correction factor is applied in a manner similar to those used for 3-D spectra collected into discrete spherical shells in wavenumber space (Eswaran & Pope Reference Eswaran and Pope1988).
3 Pre-simulation and the choice of numerical parameters
In our simulations we are interested in the effects of strain applied to a velocity field that is physically well developed, well sampled and well resolved. To produce such an initial state, we carry out a ‘pre-simulation’ of decaying isotropic turbulence evolving from a Gaussian velocity field with a specified energy spectrum. The mean strain rate is turned on when the turbulence shows clear evidence of a power-law decay in its kinetic energy, and of non-Gaussianity in the statistics of velocity gradient fluctuations. The initial energy spectrum chosen is of the form (Pope Reference Pope2000, pp. 232–234)
where
![]() $f_{L}(kL)$
controls the shape of the energy containing range,
$f_{L}(kL)$
controls the shape of the energy containing range,
![]() $f_{\unicode[STIX]{x1D702}}(k\unicode[STIX]{x1D702})$
gives exponential decay in the dissipation range,
$f_{\unicode[STIX]{x1D702}}(k\unicode[STIX]{x1D702})$
gives exponential decay in the dissipation range,
![]() $k$
is the wavenumber magnitude,
$k$
is the wavenumber magnitude,
![]() $C_{K}$
is the Kolmogorov constant (taken as 1.62 (Yeung & Zhou Reference Yeung and Zhou1997)),
$C_{K}$
is the Kolmogorov constant (taken as 1.62 (Yeung & Zhou Reference Yeung and Zhou1997)),
![]() $\langle \unicode[STIX]{x1D716}\rangle$
is the mean dissipation rate,
$\langle \unicode[STIX]{x1D716}\rangle$
is the mean dissipation rate,
![]() $L$
is a measure of the size of the large scales and
$L$
is a measure of the size of the large scales and
![]() $\unicode[STIX]{x1D702}=(\unicode[STIX]{x1D708}^{3}/\langle \unicode[STIX]{x1D716}\rangle )^{1/4}$
is the Kolmogorov length scale. Other constants appearing in the model spectrum functions include
$\unicode[STIX]{x1D702}=(\unicode[STIX]{x1D708}^{3}/\langle \unicode[STIX]{x1D716}\rangle )^{1/4}$
is the Kolmogorov length scale. Other constants appearing in the model spectrum functions include
![]() $p_{0}=2$
,
$p_{0}=2$
,
![]() $\unicode[STIX]{x1D6FD}=5.2$
,
$\unicode[STIX]{x1D6FD}=5.2$
,
![]() $c_{\unicode[STIX]{x1D702}}=0.4$
and
$c_{\unicode[STIX]{x1D702}}=0.4$
and
![]() $c_{L}=(1.262C_{K})^{3}\approx 8.55$
. With
$c_{L}=(1.262C_{K})^{3}\approx 8.55$
. With
![]() $p_{0}=2$
, the fitting function
$p_{0}=2$
, the fitting function
![]() $f_{L}(kL)$
gives
$f_{L}(kL)$
gives
![]() $E(k)\sim k^{2}$
for small
$E(k)\sim k^{2}$
for small
![]() $k$
.
$k$
.
The non-cubic and deforming nature of the solution domain implies that both large-scale sampling and small-scale resolution are dependent on time and direction. The shape of the pre-simulation domain is illustrated in the left of figure 1. We measure large-scale sampling by comparing the integral length scales with the shortest side of the domain, and small-scale resolution by comparing the Kolmogorov scales with the coarsest grid spacing. As the turbulence decays and the length scales grow, large-scale sampling worsens, but small-scale resolution improves. To ensure that the large scales are initially well sampled, we choose the spectrum parameter
![]() $L$
to be a small fraction of the shortest dimension
$L$
to be a small fraction of the shortest dimension
![]() $L_{1}^{0}$
. Resolution of the small scales in cubic domains is often expressed by the non-dimensional parameters
$L_{1}^{0}$
. Resolution of the small scales in cubic domains is often expressed by the non-dimensional parameters
![]() $\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}$
and
$\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}$
and
![]() $k_{max}\unicode[STIX]{x1D702}$
. Although good resolution requires
$k_{max}\unicode[STIX]{x1D702}$
. Although good resolution requires
![]() $\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}\lesssim 2$
(corresponding to
$\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}\lesssim 2$
(corresponding to
![]() $k_{max}\unicode[STIX]{x1D702}\gtrsim 1.5$
) (Donzis, Yeung & Sreenivasan Reference Donzis, Yeung and Sreenivasan2008), a larger initial value of
$k_{max}\unicode[STIX]{x1D702}\gtrsim 1.5$
) (Donzis, Yeung & Sreenivasan Reference Donzis, Yeung and Sreenivasan2008), a larger initial value of
![]() $\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}$
for a pre-simulation is acceptable since the resolution improves as the turbulence decays. In this work, we must consider directional resolution parameters
$\unicode[STIX]{x0394}x/\unicode[STIX]{x1D702}$
for a pre-simulation is acceptable since the resolution improves as the turbulence decays. In this work, we must consider directional resolution parameters
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FC}}/\unicode[STIX]{x1D702}$
(
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FC}}/\unicode[STIX]{x1D702}$
(
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FC}}\equiv \unicode[STIX]{x0394}x_{\unicode[STIX]{x1D6FC}}$
is the grid spacing in the
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FC}}\equiv \unicode[STIX]{x0394}x_{\unicode[STIX]{x1D6FC}}$
is the grid spacing in the
![]() $x_{\unicode[STIX]{x1D6FC}}$
direction), because the grid spacing in each direction varies. For the pre-simulation, the grid spacing is coarsest in the
$x_{\unicode[STIX]{x1D6FC}}$
direction), because the grid spacing in each direction varies. For the pre-simulation, the grid spacing is coarsest in the
![]() $x_{2}$
and
$x_{2}$
and
![]() $x_{3}$
directions, so we specify an initial value of
$x_{3}$
directions, so we specify an initial value of
![]() $\unicode[STIX]{x1D702}$
such that
$\unicode[STIX]{x1D702}$
such that
![]() $\unicode[STIX]{x1D6E5}_{2}/\unicode[STIX]{x1D702}$
(which equals
$\unicode[STIX]{x1D6E5}_{2}/\unicode[STIX]{x1D702}$
(which equals
![]() $\unicode[STIX]{x1D6E5}_{3}/\unicode[STIX]{x1D702}$
) takes an acceptable value.
$\unicode[STIX]{x1D6E5}_{3}/\unicode[STIX]{x1D702}$
) takes an acceptable value.
Table 1. Initial conditions for the pre-simulations. For each run, ‘count’ is the number of independent simulations. In the first block, number of grid points and initial grid metric factors are
![]() $N_{\unicode[STIX]{x1D6FC}}$
and
$N_{\unicode[STIX]{x1D6FC}}$
and
![]() $\unicode[STIX]{x1D609}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}}^{0}$
, respectively. The second block lists the Taylor-scale Reynolds number and indicators of large-scale sampling and small-scale resolution. Longitudinal integral length scales given by
$\unicode[STIX]{x1D609}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}}^{0}$
, respectively. The second block lists the Taylor-scale Reynolds number and indicators of large-scale sampling and small-scale resolution. Longitudinal integral length scales given by
![]() $\ell _{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}}$
and
$\ell _{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}}$
and
![]() $\unicode[STIX]{x1D702}$
is the Kolmogorov length scale. Domain length and grid spacing in the
$\unicode[STIX]{x1D702}$
is the Kolmogorov length scale. Domain length and grid spacing in the
![]() $x_{\unicode[STIX]{x1D6FC}}$
direction are given by
$x_{\unicode[STIX]{x1D6FC}}$
direction are given by
![]() $L_{\unicode[STIX]{x1D6FC}}$
and
$L_{\unicode[STIX]{x1D6FC}}$
and
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FC}}$
, respectively. Length scales
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D6FC}}$
, respectively. Length scales
![]() $L$
and
$L$
and
![]() $\unicode[STIX]{x1D702}_{0}$
are inputs to the model spectrum function. Kinematic viscosity for all simulations is
$\unicode[STIX]{x1D702}_{0}$
are inputs to the model spectrum function. Kinematic viscosity for all simulations is
![]() $\unicode[STIX]{x1D708}=2.8\times 10^{-3}$
(arbitrary units).
$\unicode[STIX]{x1D708}=2.8\times 10^{-3}$
(arbitrary units).

Table 1 summarizes the pre-simulation initial conditions in this work. Run 1 is a baseline, low Reynolds number simulation comparable to the lowest Reynolds number experiment reported by AW. The modest size of this run allows us to perform multiple independent realizations (Overholt & Pope Reference Overholt and Pope1996), which is useful for statistical reliability since time averaging is not applicable. Runs 2–5 are effectively at the same Reynolds number as Run 1, but designed to check the influence of the domain size and grid resolution. In Runs 2 and 3, the domain size is unchanged, but the grid spacing is refined by a factor of 2 first along the
![]() $x_{1}$
direction, and then the
$x_{1}$
direction, and then the
![]() $x_{2}$
and
$x_{2}$
and
![]() $x_{3}$
directions. Run 4 shows, relative to Run 1, the effects of improved small-scale resolution in the
$x_{3}$
directions. Run 4 shows, relative to Run 1, the effects of improved small-scale resolution in the
![]() $x_{1}$
direction accompanied by improved large-scale sampling in the
$x_{1}$
direction accompanied by improved large-scale sampling in the
![]() $x_{2}$
and
$x_{2}$
and
![]() $x_{3}$
directions. Run 5 presents a case in which the domain size is doubled in all directions compared to Run 1, while the grid spacings are unchanged.
$x_{3}$
directions. Run 5 presents a case in which the domain size is doubled in all directions compared to Run 1, while the grid spacings are unchanged.
In Runs 6 and 7, we increase the Reynolds number by using the same domain size (i.e. the same grid metrics) as Run 1, and refining the grid spacing to resolve a smaller initial Kolmogorov scale. We also conduct two simulations on
![]() $4096^{3}$
grids (Runs 8 and 9) to investigate the influence of the domain size and grid resolution on Run 7. Compared to Run 7, Run 8 gives improved small-scale resolution in the
$4096^{3}$
grids (Runs 8 and 9) to investigate the influence of the domain size and grid resolution on Run 7. Compared to Run 7, Run 8 gives improved small-scale resolution in the
![]() $x_{1}$
direction, and improved large-scale sampling in the
$x_{1}$
direction, and improved large-scale sampling in the
![]() $x_{2}$
and
$x_{2}$
and
![]() $x_{3}$
directions. Finally, Run 9 improves large-scale sampling compared to Run 7 by doubling the domain length in all directions.
$x_{3}$
directions. Finally, Run 9 improves large-scale sampling compared to Run 7 by doubling the domain length in all directions.
Table 2. Simulation parameters at the onset of straining, labelled with subscript or superscript
![]() $a$
. Parameters with subscript 0 taken from initial conditions for the pre-simulations (see table 1 for
$a$
. Parameters with subscript 0 taken from initial conditions for the pre-simulations (see table 1 for
![]() $R_{\unicode[STIX]{x1D706}}^{0}$
). In the second block
$R_{\unicode[STIX]{x1D706}}^{0}$
). In the second block
![]() $\ell _{11}$
and
$\ell _{11}$
and
![]() $\ell _{22}$
are longitudinal integral length scales, and
$\ell _{22}$
are longitudinal integral length scales, and
![]() $\ell _{21}$
is the transverse integral length scale in the
$\ell _{21}$
is the transverse integral length scale in the
![]() $x_{1}$
direction. The domain does not deform during the pre-simulation, so
$x_{1}$
direction. The domain does not deform during the pre-simulation, so
![]() $L_{1}^{a}=L_{1}^{0}$
and
$L_{1}^{a}=L_{1}^{0}$
and
![]() $L_{2}^{a}=L_{2}^{0}$
. With the shorthand
$L_{2}^{a}=L_{2}^{0}$
. With the shorthand
![]() $u_{i,j}=\unicode[STIX]{x2202}u_{i}/\unicode[STIX]{x2202}x_{j}$
the third block shows the skewness (
$u_{i,j}=\unicode[STIX]{x2202}u_{i}/\unicode[STIX]{x2202}x_{j}$
the third block shows the skewness (
![]() $S$
) and flatness (
$S$
) and flatness (
![]() $F$
) of longitudinal velocity gradients.
$F$
) of longitudinal velocity gradients.

Table 2 summarizes the state of each run at the end of the pre-simulation period, just before strain is applied. The turbulence kinetic energy, dissipation rate and Taylor-scale Reynolds number at this time (designated by subscript or superscript
![]() $a$
) are all (as a result of decay) lower than their initial values (designated by subscript or superscript 0). Large-scale sampling has worsened by this time, as indicated by the larger integral length scales, but small-scale resolution has improved. The integral length scales approximately satisfy
$a$
) are all (as a result of decay) lower than their initial values (designated by subscript or superscript 0). Large-scale sampling has worsened by this time, as indicated by the larger integral length scales, but small-scale resolution has improved. The integral length scales approximately satisfy
![]() $\ell _{11}=2\ell _{21}$
, which is indicative of isotropy. Non-Gaussianity is evident in the skewness factors of longitudinal velocity gradients reaching approximately
$\ell _{11}=2\ell _{21}$
, which is indicative of isotropy. Non-Gaussianity is evident in the skewness factors of longitudinal velocity gradients reaching approximately
![]() $-0.5$
, and the flatness factors reaching values that increase with Reynolds number. It appears that
$-0.5$
, and the flatness factors reaching values that increase with Reynolds number. It appears that
![]() $u_{1,1}\equiv \unicode[STIX]{x2202}u_{1}/\unicode[STIX]{x2202}x_{1}$
is slightly more non-Gaussian than
$u_{1,1}\equiv \unicode[STIX]{x2202}u_{1}/\unicode[STIX]{x2202}x_{1}$
is slightly more non-Gaussian than
![]() $u_{3,3}\equiv \unicode[STIX]{x2202}u_{3}/\unicode[STIX]{x2202}x_{3}$
, which may be the result of better small-scale resolution in the
$u_{3,3}\equiv \unicode[STIX]{x2202}u_{3}/\unicode[STIX]{x2202}x_{3}$
, which may be the result of better small-scale resolution in the
![]() $x_{1}$
direction compared to the
$x_{1}$
direction compared to the
![]() $x_{2}$
and
$x_{2}$
and
![]() $x_{3}$
directions. In all runs, the ratios of transverse to longitudinal velocity gradient variances are within 0.5 % of the isotropic value of 2. All components of the Reynolds stress anisotropy tensor are
$x_{3}$
directions. In all runs, the ratios of transverse to longitudinal velocity gradient variances are within 0.5 % of the isotropic value of 2. All components of the Reynolds stress anisotropy tensor are
![]() $3\times 10^{-3}$
or smaller, showing that a state of isotropic turbulence is obtained despite the non-cubic shape of the domain.
$3\times 10^{-3}$
or smaller, showing that a state of isotropic turbulence is obtained despite the non-cubic shape of the domain.
4 Application of strain
Following the pre-simulation we apply a time-dependent axisymmetric contraction until the domain elongates by a factor of 4 in the
![]() $x_{1}$
direction. Using the approach and parameters detailed in § 2.2, we apply mean strain rates characterized by a peak non-dimensional strain
$x_{1}$
direction. Using the approach and parameters detailed in § 2.2, we apply mean strain rates characterized by a peak non-dimensional strain
![]() $S_{0}^{\ast }=25$
. In § 4.1 we present single-point moments, and in § 4.2 we study the evolution of the spectra.
$S_{0}^{\ast }=25$
. In § 4.1 we present single-point moments, and in § 4.2 we study the evolution of the spectra.
Table 3. Post-contraction (subscript or superscript
![]() $b$
) parameters and post- to pre-contraction parameter ratios. See tables 1 and 2 for descriptions of symbols.
$b$
) parameters and post- to pre-contraction parameter ratios. See tables 1 and 2 for descriptions of symbols.

4.1 Single-point moments
We first provide data in table 3 that summarizes the post-contraction state of each run, to be followed by figures that show the evolution of important statistics over the complete straining period. The post-contraction shape of the domains is as shown in the right of figure 1, with a decrease in
![]() $\unicode[STIX]{x1D609}_{11}$
and increase in
$\unicode[STIX]{x1D609}_{11}$
and increase in
![]() $\unicode[STIX]{x1D609}_{22}$
and
$\unicode[STIX]{x1D609}_{22}$
and
![]() $\unicode[STIX]{x1D609}_{33}$
relative to their pre-contraction values in table 1. As the domain deforms and the physical length scales of the turbulence evolve, large-scale sampling and small-scale resolution (second block in table 3) change. The post-contraction domains are still large compared with the integral length scales, indicating that large-scale sampling is still adequate. It is worth noting that the ratio
$\unicode[STIX]{x1D609}_{33}$
relative to their pre-contraction values in table 1. As the domain deforms and the physical length scales of the turbulence evolve, large-scale sampling and small-scale resolution (second block in table 3) change. The post-contraction domains are still large compared with the integral length scales, indicating that large-scale sampling is still adequate. It is worth noting that the ratio
![]() $L_{1}/\ell _{21}$
has dropped compared to its pre-contraction value, despite a factor of 4 increase in
$L_{1}/\ell _{21}$
has dropped compared to its pre-contraction value, despite a factor of 4 increase in
![]() $L_{1}$
. This implies a substantial increase in the transverse integral length scale
$L_{1}$
. This implies a substantial increase in the transverse integral length scale
![]() $\ell _{21}$
, which is consistent with the formation of coherent longitudinal vortices in the extensional direction (Rogers & Moin Reference Rogers and Moin1987). As expected, small-scale resolution worsens in the direction where the domain is stretched (
$\ell _{21}$
, which is consistent with the formation of coherent longitudinal vortices in the extensional direction (Rogers & Moin Reference Rogers and Moin1987). As expected, small-scale resolution worsens in the direction where the domain is stretched (
![]() $x_{1}$
), but improves in the directions where the domain is compressed (
$x_{1}$
), but improves in the directions where the domain is compressed (
![]() $x_{2}$
and
$x_{2}$
and
![]() $x_{3}$
).
$x_{3}$
).
Continuing in table 3, the turbulence kinetic energy is amplified in all cases, with the amplification ratio nearly independent of the Reynolds number. The dissipation rate also increases, but less so at higher Reynolds number. It is clear that the turbulence becomes anisotropic, as velocity fluctuations in the extensional and compressive directions are suppressed and amplified, respectively. Anisotropy at the small scales is also seen in the statistics of velocity gradient fluctuations, such as the ratio of transverse to longitudinal velocity gradient variances, which differ from the isotropic value of 2. Apparently, in the higher Reynolds number runs, the ratio
![]() $\langle u_{2,1}^{2}\rangle /\langle u_{1,1}^{2}\rangle$
becomes less anisotropic but
$\langle u_{2,1}^{2}\rangle /\langle u_{1,1}^{2}\rangle$
becomes less anisotropic but
![]() $\langle u_{3,2}^{2}\rangle /\langle u_{2,2}^{2}\rangle$
is nearly fixed at close to 3, which (as we discuss further later in this subsection) is an indication of quasi two-dimensionality in the cross-sectional plane.
$\langle u_{3,2}^{2}\rangle /\langle u_{2,2}^{2}\rangle$
is nearly fixed at close to 3, which (as we discuss further later in this subsection) is an indication of quasi two-dimensionality in the cross-sectional plane.
Third and fourth moments of longitudinal velocity gradients are also included in table 3. In 3-D incompressible isotropic turbulence, the skewness of the longitudinal velocity gradient is negative, and related to the phenomenon of vortex stretching (Batchelor Reference Batchelor1953; Tavoularis, Bennett & Corrsin Reference Tavoularis, Bennett and Corrsin1978). However, as reported by AW and others (Mills & Corrsin Reference Mills and Corrsin1959; Sjögren & Johansson Reference Sjögren and Johansson1998), we find that axisymmetric contraction causes the skewness of
![]() $\unicode[STIX]{x2202}u_{1}/\unicode[STIX]{x2202}x_{1}$
to undergo a change in sign, with its magnitude increasing with the Reynolds number. In contrast, the skewness of
$\unicode[STIX]{x2202}u_{1}/\unicode[STIX]{x2202}x_{1}$
to undergo a change in sign, with its magnitude increasing with the Reynolds number. In contrast, the skewness of
![]() $\unicode[STIX]{x2202}u_{3}/\unicode[STIX]{x2202}x_{3}$
remains negative but its magnitude is reduced compared to that observed in isotropic turbulence. At the same time, we observe an increase in the flatness of
$\unicode[STIX]{x2202}u_{3}/\unicode[STIX]{x2202}x_{3}$
remains negative but its magnitude is reduced compared to that observed in isotropic turbulence. At the same time, we observe an increase in the flatness of
![]() $\unicode[STIX]{x2202}u_{1}/\unicode[STIX]{x2202}x_{1}$
and a decrease in the flatness of
$\unicode[STIX]{x2202}u_{1}/\unicode[STIX]{x2202}x_{1}$
and a decrease in the flatness of
![]() $\unicode[STIX]{x2202}u_{3}/\unicode[STIX]{x2202}x_{3}$
during the contraction. The flatness of
$\unicode[STIX]{x2202}u_{3}/\unicode[STIX]{x2202}x_{3}$
during the contraction. The flatness of
![]() $\unicode[STIX]{x2202}u_{1}/\unicode[STIX]{x2202}x_{1}$
also increases with Reynolds number, which is consistent with AW. A comparison of the post-contraction flatness of
$\unicode[STIX]{x2202}u_{1}/\unicode[STIX]{x2202}x_{1}$
also increases with Reynolds number, which is consistent with AW. A comparison of the post-contraction flatness of
![]() $\unicode[STIX]{x2202}u_{1}/\unicode[STIX]{x2202}x_{1}$
between runs with different resolution (Run 2 and 8 versus 1 and 7, respectively) suggests that higher-order derivative statistics in this work are affected by finite resolution in the extensional direction. However, we are mainly interested in lower-order quantities such as spectra, for which the lower-resolution simulations are adequate. We show in the Appendix that the major results from this paper are not affected.
$\unicode[STIX]{x2202}u_{1}/\unicode[STIX]{x2202}x_{1}$
between runs with different resolution (Run 2 and 8 versus 1 and 7, respectively) suggests that higher-order derivative statistics in this work are affected by finite resolution in the extensional direction. However, we are mainly interested in lower-order quantities such as spectra, for which the lower-resolution simulations are adequate. We show in the Appendix that the major results from this paper are not affected.
It is also useful to compare DNS, which uses a finite strain rate, to RDT. Following the pre-simulation, we evolve the Fourier coefficients of the velocity field according to well-known relations for inviscid RDT (Townsend Reference Townsend1976; Lee & Reynolds Reference Lee and Reynolds1985). Each velocity field is subjected to a 4 : 1 area ratio axisymmetric contraction. We then ensemble-average statistics over all realizations for each run, e.g. over the 16 simulations comprising Run 1. RDT predicts
![]() $K_{b}/K_{a}=2.1$
and
$K_{b}/K_{a}=2.1$
and
![]() $\langle \unicode[STIX]{x1D716}\rangle _{b}/\langle \unicode[STIX]{x1D716}\rangle _{a}=5.5$
for all runs, which are considerably different from the DNS results presented in table 3. The extent of large-scale anisotropy is predicted well by RDT; it gives
$\langle \unicode[STIX]{x1D716}\rangle _{b}/\langle \unicode[STIX]{x1D716}\rangle _{a}=5.5$
for all runs, which are considerably different from the DNS results presented in table 3. The extent of large-scale anisotropy is predicted well by RDT; it gives
![]() $\unicode[STIX]{x1D623}_{11}^{b}=-0.3$
and
$\unicode[STIX]{x1D623}_{11}^{b}=-0.3$
and
![]() $\unicode[STIX]{x1D623}_{22}^{b}=0.15$
for all runs. There is more discrepancy between the DNS and RDT when examining velocity derivative statistics. For example, RDT estimates
$\unicode[STIX]{x1D623}_{22}^{b}=0.15$
for all runs. There is more discrepancy between the DNS and RDT when examining velocity derivative statistics. For example, RDT estimates
![]() $\langle u_{2,1}^{2}\rangle _{b}/\langle u_{1,1}^{2}\rangle _{b}=8$
, which is markedly different from the DNS results. The velocity derivative statistic
$\langle u_{2,1}^{2}\rangle _{b}/\langle u_{1,1}^{2}\rangle _{b}=8$
, which is markedly different from the DNS results. The velocity derivative statistic
![]() $\langle u_{3,2}^{2}\rangle _{b}/\langle u_{2,2}^{2}\rangle _{b}$
, however, takes a post-contraction value of 3 with RDT, which is very similar to the DNS results. Table 4 shows the RDT predictions for higher-order velocity derivative statistics. While RDT fails to predict a positive value for the skewness of
$\langle u_{3,2}^{2}\rangle _{b}/\langle u_{2,2}^{2}\rangle _{b}$
, however, takes a post-contraction value of 3 with RDT, which is very similar to the DNS results. Table 4 shows the RDT predictions for higher-order velocity derivative statistics. While RDT fails to predict a positive value for the skewness of
![]() $\unicode[STIX]{x2202}u_{1}/\unicode[STIX]{x2202}x_{1}$
, a small negative value of the skewness of
$\unicode[STIX]{x2202}u_{1}/\unicode[STIX]{x2202}x_{1}$
, a small negative value of the skewness of
![]() $\unicode[STIX]{x2202}u_{3}/\unicode[STIX]{x2202}x_{3}$
is consistent with the DNS at lower Reynolds numbers. The large increase in the flatness of
$\unicode[STIX]{x2202}u_{3}/\unicode[STIX]{x2202}x_{3}$
is consistent with the DNS at lower Reynolds numbers. The large increase in the flatness of
![]() $\unicode[STIX]{x2202}u_{1}/\unicode[STIX]{x2202}x_{1}$
at high Reynolds numbers, and the decrease in the flatness of
$\unicode[STIX]{x2202}u_{1}/\unicode[STIX]{x2202}x_{1}$
at high Reynolds numbers, and the decrease in the flatness of
![]() $\unicode[STIX]{x2202}u_{3}/\unicode[STIX]{x2202}x_{3}$
observed in the DNS are not predicted by RDT.
$\unicode[STIX]{x2202}u_{3}/\unicode[STIX]{x2202}x_{3}$
observed in the DNS are not predicted by RDT.

Figure 4. Evolution of (a)
![]() $K$
and
$K$
and
![]() $\langle \unicode[STIX]{x1D716}\rangle$
normalized by initial values for Runs 4, 6 and 8, (b) budget for
$\langle \unicode[STIX]{x1D716}\rangle$
normalized by initial values for Runs 4, 6 and 8, (b) budget for
![]() $\text{d}K/\text{d}t$
normalized by
$\text{d}K/\text{d}t$
normalized by
![]() $\langle \unicode[STIX]{x1D716}\rangle _{a}$
for Runs 4 and 8, and (c) non-dimensional strain rates for Runs 4, 6 and 8. In (a), solid curves (red) for
$\langle \unicode[STIX]{x1D716}\rangle _{a}$
for Runs 4 and 8, and (c) non-dimensional strain rates for Runs 4, 6 and 8. In (a), solid curves (red) for
![]() $K(t)/K_{a}$
for the three runs are almost coincident, and dashed curves (blue) are for
$K(t)/K_{a}$
for the three runs are almost coincident, and dashed curves (blue) are for
![]() $\langle \unicode[STIX]{x1D716}(t)\rangle /\langle \unicode[STIX]{x1D716}\rangle _{a}$
, with
$\langle \unicode[STIX]{x1D716}(t)\rangle /\langle \unicode[STIX]{x1D716}\rangle _{a}$
, with
![]() $R_{\unicode[STIX]{x1D706}}$
increasing in the direction of the arrow. In (b), dashed curves with open symbols are for Run 4, and solid curves with filled symbols for Run 8: ▪ and ▫ (blue) for production, ● and ○ (red) for minus the dissipation, and ▴ and ▵ (black) for overall rate of change. In (c), mean strain rate normalized by large-eddy turnover time
$R_{\unicode[STIX]{x1D706}}$
increasing in the direction of the arrow. In (b), dashed curves with open symbols are for Run 4, and solid curves with filled symbols for Run 8: ▪ and ▫ (blue) for production, ● and ○ (red) for minus the dissipation, and ▴ and ▵ (black) for overall rate of change. In (c), mean strain rate normalized by large-eddy turnover time
![]() $\unicode[STIX]{x1D70F}$
(upper red curves) and Kolmogorov time scale
$\unicode[STIX]{x1D70F}$
(upper red curves) and Kolmogorov time scale
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
(lower blue curves), with
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
(lower blue curves), with
![]() $R_{\unicode[STIX]{x1D706}}$
increasing in the directions of the arrows.
$R_{\unicode[STIX]{x1D706}}$
increasing in the directions of the arrows.
Table 4. Post-contraction skewness and flatness of longitudinal velocity gradients predicted by rapid-distortion theory.

For information on the evolution of the turbulence during the period of axisymmetric contraction, and to facilitate comparison with previous studies, it is useful to show results against the total deformation at a given time, rather than time itself. Figure 4 shows, as a function of
![]() $L_{1}(t)/L_{1}^{0}$
(which ranges from 1 to 4 for a 4 : 1 contraction ratio), in (a) the evolution of turbulence kinetic energy and dissipation rate, in (b) various terms in the turbulence kinetic energy budget and in (c) the non-dimensional mean strain rates. To focus on the effects of the Reynolds number we have selected data from Runs 4, 6 and 8 (see table 1). For homogeneous turbulence the turbulence kinetic energy budget is governed by production and dissipation, as
$L_{1}(t)/L_{1}^{0}$
(which ranges from 1 to 4 for a 4 : 1 contraction ratio), in (a) the evolution of turbulence kinetic energy and dissipation rate, in (b) various terms in the turbulence kinetic energy budget and in (c) the non-dimensional mean strain rates. To focus on the effects of the Reynolds number we have selected data from Runs 4, 6 and 8 (see table 1). For homogeneous turbulence the turbulence kinetic energy budget is governed by production and dissipation, as
It can be seen that both
![]() $K$
and
$K$
and
![]() $\langle \unicode[STIX]{x1D716}\rangle$
initially decay since it takes finite time for production (initially zero) to grow to exceed the dissipation. Subsequently, as both variables grow, the evolution of
$\langle \unicode[STIX]{x1D716}\rangle$
initially decay since it takes finite time for production (initially zero) to grow to exceed the dissipation. Subsequently, as both variables grow, the evolution of
![]() $K$
is almost independent of the Reynolds number, while dissipation grows less rapidly at high Reynolds number. Because of the form of the strain rate profile (figure 2), both
$K$
is almost independent of the Reynolds number, while dissipation grows less rapidly at high Reynolds number. Because of the form of the strain rate profile (figure 2), both
![]() $K$
and
$K$
and
![]() $\langle \unicode[STIX]{x1D716}\rangle$
decrease towards the end of the straining period when the strain rate is weak. The production term in frame (b) is driven by the mean flow and is essentially the same for all Reynolds numbers simulated. It is also dominant over dissipation during the straining period, which explains why the kinetic energy evolution is nearly identical for all runs. The non-dimensional strain rates in frame (c) indicate that the strain rates are strong compared to the time scales of the large-scale motions, but actually weak from the perspective of the small scales.
$\langle \unicode[STIX]{x1D716}\rangle$
decrease towards the end of the straining period when the strain rate is weak. The production term in frame (b) is driven by the mean flow and is essentially the same for all Reynolds numbers simulated. It is also dominant over dissipation during the straining period, which explains why the kinetic energy evolution is nearly identical for all runs. The non-dimensional strain rates in frame (c) indicate that the strain rates are strong compared to the time scales of the large-scale motions, but actually weak from the perspective of the small scales.
The production of turbulence kinetic energy by mean strain requires anisotropy in the Reynolds stresses, which is expressed by the anisotropy tensor
![]() $\unicode[STIX]{x1D623}_{ij}=\langle u_{i}u_{j}\rangle /(2K)-\unicode[STIX]{x1D6FF}_{ij}/3$
, and its second and third coordinate-frame invariants. We use the definitions
$\unicode[STIX]{x1D623}_{ij}=\langle u_{i}u_{j}\rangle /(2K)-\unicode[STIX]{x1D6FF}_{ij}/3$
, and its second and third coordinate-frame invariants. We use the definitions
where here
![]() $\unicode[STIX]{x1D702}$
is not to be confused with the Kolmogorov scale. For isotropic turbulence subjected to axisymmetric contraction the invariants satisfy
$\unicode[STIX]{x1D702}$
is not to be confused with the Kolmogorov scale. For isotropic turbulence subjected to axisymmetric contraction the invariants satisfy
Figure 5 shows for Runs 4 and 8, (a) the evolution of the Reynolds stresses, (b) the evolution of the anisotropy tensor elements
![]() $\unicode[STIX]{x1D623}_{11}$
and
$\unicode[STIX]{x1D623}_{11}$
and
![]() $\unicode[STIX]{x1D623}_{22}$
and (c) the invariants
$\unicode[STIX]{x1D623}_{22}$
and (c) the invariants
![]() $\unicode[STIX]{x1D709}$
and
$\unicode[STIX]{x1D709}$
and
![]() $\unicode[STIX]{x1D702}$
. The results suggest that the large-scale anisotropy is completely determined by the total deformation at any time
$\unicode[STIX]{x1D702}$
. The results suggest that the large-scale anisotropy is completely determined by the total deformation at any time
![]() $t$
, but is independent of the Reynolds number. Since the large-scale anisotropy depends only on the total deformation, the anisotropy development is the same as observed in simulations with constant strain rates (Lee & Reynolds Reference Lee and Reynolds1985), and can be predicted almost exactly by RDT. Although (4.3) is in principle exact, in numerical results it is not guaranteed if the large scales contributing the most to the Reynolds stress tensor are not sampled well in a domain of finite size. Our present results show that the large scales are sufficiently well sampled.
$t$
, but is independent of the Reynolds number. Since the large-scale anisotropy depends only on the total deformation, the anisotropy development is the same as observed in simulations with constant strain rates (Lee & Reynolds Reference Lee and Reynolds1985), and can be predicted almost exactly by RDT. Although (4.3) is in principle exact, in numerical results it is not guaranteed if the large scales contributing the most to the Reynolds stress tensor are not sampled well in a domain of finite size. Our present results show that the large scales are sufficiently well sampled.

Figure 5. Evolution of (a) Reynolds stresses normalized by
![]() $q_{a}^{2}=2K_{a}$
, (b) components of the Reynolds stress anisotropy tensor and (c) anisotropy tensor invariants for Run 4 (dashed curves with open symbols) and Run 8 (solid curves with filled symbols). Symbols ▪ and ▫ (red) are for
$q_{a}^{2}=2K_{a}$
, (b) components of the Reynolds stress anisotropy tensor and (c) anisotropy tensor invariants for Run 4 (dashed curves with open symbols) and Run 8 (solid curves with filled symbols). Symbols ▪ and ▫ (red) are for
![]() $\langle u_{1}^{2}\rangle /q_{a}^{2}$
,
$\langle u_{1}^{2}\rangle /q_{a}^{2}$
,
![]() $\unicode[STIX]{x1D623}_{11}$
and
$\unicode[STIX]{x1D623}_{11}$
and
![]() $\unicode[STIX]{x1D709}$
in each respective figure. Symbols ● and ○ (blue) are for
$\unicode[STIX]{x1D709}$
in each respective figure. Symbols ● and ○ (blue) are for
![]() $\langle u_{2}^{2}\rangle /q_{a}^{2}$
,
$\langle u_{2}^{2}\rangle /q_{a}^{2}$
,
![]() $\unicode[STIX]{x1D623}_{22}$
and
$\unicode[STIX]{x1D623}_{22}$
and
![]() $\unicode[STIX]{x1D702}$
in each respective figure. Dashed lines in (c) are for the two-dimensional isotropic limit.
$\unicode[STIX]{x1D702}$
in each respective figure. Dashed lines in (c) are for the two-dimensional isotropic limit.

Figure 6. Reynolds stress budgets normalized by initial dissipation rate
![]() $\langle \unicode[STIX]{x1D716}\rangle _{a}$
during the application of strain for Run 4 (dashed curves with open symbols) and Run 8 (solid curves with filled symbols). Budget terms for
$\langle \unicode[STIX]{x1D716}\rangle _{a}$
during the application of strain for Run 4 (dashed curves with open symbols) and Run 8 (solid curves with filled symbols). Budget terms for
![]() $\text{d}\langle u_{1}^{2}\rangle /\text{d}t$
are shown in (a) and budget terms for
$\text{d}\langle u_{1}^{2}\rangle /\text{d}t$
are shown in (a) and budget terms for
![]() $\text{d}\langle u_{2}^{2}\rangle /\text{d}t$
in (b): ▾ and ▿ (red) are for production, ▴ and ▵ (magenta) for rapid pressure strain, ♦ and ♢ (green) for slow pressure strain, ● and ○ (blue) for dissipation, and the sum of all budget terms is marked by ▪ and ▫ (black).
$\text{d}\langle u_{2}^{2}\rangle /\text{d}t$
in (b): ▾ and ▿ (red) are for production, ▴ and ▵ (magenta) for rapid pressure strain, ♦ and ♢ (green) for slow pressure strain, ● and ○ (blue) for dissipation, and the sum of all budget terms is marked by ▪ and ▫ (black).
The development of anisotropy in the Reynolds stress tensor can be analysed further using the Reynolds stress transport equation (2.19). Figure 6 presents the terms in the balance equations for (a)
![]() $\langle u_{1}^{2}\rangle$
and (b)
$\langle u_{1}^{2}\rangle$
and (b)
![]() $\langle u_{2}^{2}\rangle$
, using data from Runs 4 and 8. For the production terms, in this flow
$\langle u_{2}^{2}\rangle$
, using data from Runs 4 and 8. For the production terms, in this flow
![]() $P_{11}<0$
whereas
$P_{11}<0$
whereas
![]() $P_{22}>0$
. The rapid pressure-strain term quickly counteracts the anisotropy generated by the production term. The slow pressure-strain term, on the other hand, becomes significant only at later times, and is more important at higher Reynolds number. In frame (b) the production effect is clearly the dominant term in the Reynolds stress budget for
$P_{22}>0$
. The rapid pressure-strain term quickly counteracts the anisotropy generated by the production term. The slow pressure-strain term, on the other hand, becomes significant only at later times, and is more important at higher Reynolds number. In frame (b) the production effect is clearly the dominant term in the Reynolds stress budget for
![]() $\langle u_{2}^{2}\rangle$
, being resisted only weakly by the rapid pressure strain at early times and viscous dissipation at later times. In both frames of this figure the production terms (of either sign) reach peak amplitude at intermediate times, which is a consequence of the time-dependent strain rate and is different from results from simulations of constant strain (Lee & Reynolds Reference Lee and Reynolds1985).
$\langle u_{2}^{2}\rangle$
, being resisted only weakly by the rapid pressure strain at early times and viscous dissipation at later times. In both frames of this figure the production terms (of either sign) reach peak amplitude at intermediate times, which is a consequence of the time-dependent strain rate and is different from results from simulations of constant strain (Lee & Reynolds Reference Lee and Reynolds1985).

Figure 7. Evolution of (a) mean-square vorticities normalized by dissipation rate and (b) velocity derivative statistics for Run 4 (dashed curves with open symbols) and Run 8 (solid curves with filled symbols). In (a), ▪ and ▫ (black) are for
![]() $\unicode[STIX]{x1D708}\langle \unicode[STIX]{x1D714}_{1}^{2}\rangle /\langle \unicode[STIX]{x1D716}\rangle _{a}$
, ● and ○ (red) for
$\unicode[STIX]{x1D708}\langle \unicode[STIX]{x1D714}_{1}^{2}\rangle /\langle \unicode[STIX]{x1D716}\rangle _{a}$
, ● and ○ (red) for
![]() $\unicode[STIX]{x1D708}\langle \unicode[STIX]{x1D714}_{2}^{2}\rangle /\langle \unicode[STIX]{x1D716}\rangle _{a}$
and ▴ and ▵ (blue) for
$\unicode[STIX]{x1D708}\langle \unicode[STIX]{x1D714}_{2}^{2}\rangle /\langle \unicode[STIX]{x1D716}\rangle _{a}$
and ▴ and ▵ (blue) for
![]() $\unicode[STIX]{x1D708}\langle \unicode[STIX]{x1D714}_{3}^{2}\rangle /\langle \unicode[STIX]{x1D716}\rangle _{a}$
. Let
$\unicode[STIX]{x1D708}\langle \unicode[STIX]{x1D714}_{3}^{2}\rangle /\langle \unicode[STIX]{x1D716}\rangle _{a}$
. Let
![]() $u_{i,j}=\unicode[STIX]{x2202}u_{i}/\unicode[STIX]{x2202}x_{j}$
. In (b), ▪ and ▫ (red) are for
$u_{i,j}=\unicode[STIX]{x2202}u_{i}/\unicode[STIX]{x2202}x_{j}$
. In (b), ▪ and ▫ (red) are for
![]() $\langle u_{2,1}^{2}\rangle /\langle u_{1,1}^{2}\rangle$
, ● and ○ (blue) for
$\langle u_{2,1}^{2}\rangle /\langle u_{1,1}^{2}\rangle$
, ● and ○ (blue) for
![]() $\langle u_{1,2}^{2}\rangle /\langle u_{2,2}^{2}\rangle$
, ♦ and ♢ (magenta) for
$\langle u_{1,2}^{2}\rangle /\langle u_{2,2}^{2}\rangle$
, ♦ and ♢ (magenta) for
![]() $-\langle u_{1,1}^{2}\rangle /\langle u_{2,3}u_{3,2}\rangle$
, ▴ and ▵ (green) for
$-\langle u_{1,1}^{2}\rangle /\langle u_{2,3}u_{3,2}\rangle$
, ▴ and ▵ (green) for
![]() $\langle u_{3,2}^{2}\rangle /\langle u_{2,2}^{2}\rangle$
, and ▾ and ▿ (black) for
$\langle u_{3,2}^{2}\rangle /\langle u_{2,2}^{2}\rangle$
, and ▾ and ▿ (black) for
![]() $-\langle u_{2,2}^{2}\rangle /\langle u_{2,3}u_{3,2}\rangle$
. Values for
$-\langle u_{2,2}^{2}\rangle /\langle u_{2,3}u_{3,2}\rangle$
. Values for
![]() $\langle u_{3,2}^{2}\rangle /\langle u_{2,2}^{2}\rangle$
and
$\langle u_{3,2}^{2}\rangle /\langle u_{2,2}^{2}\rangle$
and
![]() $-\langle u_{2,2}^{2}\rangle /\langle u_{2,3}u_{3,2}\rangle$
in two-dimensional isotropic turbulence marked by horizontal dashed lines at 3 and 1, respectively.
$-\langle u_{2,2}^{2}\rangle /\langle u_{2,3}u_{3,2}\rangle$
in two-dimensional isotropic turbulence marked by horizontal dashed lines at 3 and 1, respectively.
Although large-scale statistics show little dependence on the Reynolds number, small-scale statistics, such as the dissipation rate in figure 4(a), show a strong Reynolds number dependence. It was already observed in table 3 that the small scales become anisotropic during the straining period. The geometry of axisymmetric contraction also suggests that vorticity components in different directions (
![]() $\unicode[STIX]{x1D714}_{1}$
versus
$\unicode[STIX]{x1D714}_{1}$
versus
![]() $\unicode[STIX]{x1D714}_{2}$
and
$\unicode[STIX]{x1D714}_{2}$
and
![]() $\unicode[STIX]{x1D714}_{3}$
) will have different statistics. We therefore investigate the behaviour of both vorticity and velocity gradient fluctuations below, with data given in the two frames of figure 7, respectively.
$\unicode[STIX]{x1D714}_{3}$
) will have different statistics. We therefore investigate the behaviour of both vorticity and velocity gradient fluctuations below, with data given in the two frames of figure 7, respectively.
In homogeneous turbulence we can write
Figure 7(a) shows, for Runs 4 and 8, the three mean-squared vorticities, normalized by the viscosity and the pre-contraction dissipation rate. As expected from the geometry, axisymmetric contraction amplifies and aligns vorticity in the extensional direction while reducing vorticity in the compressive directions (Rogers & Moin Reference Rogers and Moin1987), but the effects are weaker at higher Reynolds number. This dependence on the Reynolds number can be understood by noting that (lower curves in figure 4
c) as the Reynolds number increases (in the order Runs 4, 6, 8) the value of the non-dimensional strain rate
![]() $S\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
becomes smaller. In other words, as the range of time scales in the flow widens with increasing Reynolds number, the strain rate becomes weaker with respect to the small scales. Hence, at higher Reynolds numbers, the fluctuating vorticity is less responsive to the applied strain, as reflected in the weaker amplification of
$S\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
becomes smaller. In other words, as the range of time scales in the flow widens with increasing Reynolds number, the strain rate becomes weaker with respect to the small scales. Hence, at higher Reynolds numbers, the fluctuating vorticity is less responsive to the applied strain, as reflected in the weaker amplification of
![]() $\langle \unicode[STIX]{x1D714}_{1}^{2}\rangle$
in figure 7(a).
$\langle \unicode[STIX]{x1D714}_{1}^{2}\rangle$
in figure 7(a).
To further assess departures from local isotropy using statistics of the velocity gradients, we can compare the simulation data with a number of relations that apply for 3-D incompressible isotropic turbulence, such as (with
![]() $\unicode[STIX]{x1D6FC}\neq \unicode[STIX]{x1D6FD}$
)
$\unicode[STIX]{x1D6FC}\neq \unicode[STIX]{x1D6FD}$
)
It is worth noting that figure 7(b) shows that during straining,
![]() $\langle u_{3,2}^{2}\rangle /\langle u_{2,2}^{2}\rangle$
and
$\langle u_{3,2}^{2}\rangle /\langle u_{2,2}^{2}\rangle$
and
![]() $-\langle u_{2,2}^{2}\rangle /\langle u_{2,3}u_{3,2}\rangle$
approach asymptotic limits 3 and 1, respectively. This can be explained by generalizing (4.5) and (4.6) to
$-\langle u_{2,2}^{2}\rangle /\langle u_{2,3}u_{3,2}\rangle$
approach asymptotic limits 3 and 1, respectively. This can be explained by generalizing (4.5) and (4.6) to
![]() $n$
-dimensional isotropic turbulence, where
$n$
-dimensional isotropic turbulence, where
![]() $n\geqslant 2$
. We have, for
$n\geqslant 2$
. We have, for
![]() $\unicode[STIX]{x1D6FC}\neq \unicode[STIX]{x1D6FD}$
(Pope Reference Pope2000; Gotoh et al.
Reference Gotoh, Watanabe, Shiga, Nakano and Suzuki2007)
$\unicode[STIX]{x1D6FC}\neq \unicode[STIX]{x1D6FD}$
(Pope Reference Pope2000; Gotoh et al.
Reference Gotoh, Watanabe, Shiga, Nakano and Suzuki2007)

Figure 8. Axisymmetric energy spectrum for (a–c) Run 4 and (d–f) Run 8 (a,d) before the application of strain, (b,e) half way through straining (
![]() $L_{1}/L_{1}^{0}=2$
) and (c,f) at the end of the straining period. Contour levels decrease by a factor of 10. Spectra plotted against the instantaneously distorting wavenumbers, and multiplied by 2 to recover
$L_{1}/L_{1}^{0}=2$
) and (c,f) at the end of the straining period. Contour levels decrease by a factor of 10. Spectra plotted against the instantaneously distorting wavenumbers, and multiplied by 2 to recover
![]() $K$
when integrating over
$K$
when integrating over
![]() $k_{r}$
and non-negative
$k_{r}$
and non-negative
![]() $k_{1}$
. Simulation cutoff wavenumbers marked by outermost black boundary. Spectra normalized by
$k_{1}$
. Simulation cutoff wavenumbers marked by outermost black boundary. Spectra normalized by
![]() $\sin \unicode[STIX]{x1D719}=k_{r}/k$
to obtain circular contours in isotropic turbulence; data for
$\sin \unicode[STIX]{x1D719}=k_{r}/k$
to obtain circular contours in isotropic turbulence; data for
![]() $k_{r}=0$
omitted from plot.
$k_{r}=0$
omitted from plot.
4.2 Spectral evolution
Results discussed above indicate that anisotropy in the mean flow and the large-scale motions ultimately lead to strong anisotropy in the small scales. This observation implies that isotropy in the flow is scale dependent, which is best explored through spectral quantities in wavenumber space. We consider an axisymmetric representation of the energy spectrum (§ 2.3), 1-D spectra like those measured in the experiments of AW, and various terms in the spectral energy budget (based on (2.13)).
Figure 8 shows contour plots of the axisymmetric energy spectrum
![]() $E_{A}(k_{1},k_{r})$
for Runs 4 and 8 before the straining period (a,d), half way through the straining period (b,e), and at the end of the straining period (c,f). If the turbulence is isotropic the energy spectrum would depend only on
$E_{A}(k_{1},k_{r})$
for Runs 4 and 8 before the straining period (a,d), half way through the straining period (b,e), and at the end of the straining period (c,f). If the turbulence is isotropic the energy spectrum would depend only on
![]() $k=\sqrt{k_{1}^{2}+k_{r}^{2}}$
, which means isocontours of
$k=\sqrt{k_{1}^{2}+k_{r}^{2}}$
, which means isocontours of
![]() $E_{A}(k_{1},k_{r})$
(after the normalization discussed in § 2.3) would be circles in the (
$E_{A}(k_{1},k_{r})$
(after the normalization discussed in § 2.3) would be circles in the (
![]() $k_{1},k_{r}$
) plane. This is indeed the case for the pre-contraction spectra in frames (a) and (d), except that the shape of the contours is distorted near the simulation cutoff wavenumbers, which are marked by the outermost black elliptical boundaries in the plots. As the strain is applied (from the left column to the right column), the spectra change significantly. The post-contraction energy spectra in frames (c) and (f) are highly anisotropic at all scales of motion (with non-circular contours), which is consistent with the large-scale and small-scale anisotropy observed for single-point moments in § 4.1. The contours in frame (c) for Run 4 show evidence of stronger anisotropy than those in frame (f) for Run 8. This is in agreement with the results for single-point moments, which showed that the small scales become more anisotropic during the application of strain at lower Reynolds number. During straining, the domain is lengthened in the
$k_{1},k_{r}$
) plane. This is indeed the case for the pre-contraction spectra in frames (a) and (d), except that the shape of the contours is distorted near the simulation cutoff wavenumbers, which are marked by the outermost black elliptical boundaries in the plots. As the strain is applied (from the left column to the right column), the spectra change significantly. The post-contraction energy spectra in frames (c) and (f) are highly anisotropic at all scales of motion (with non-circular contours), which is consistent with the large-scale and small-scale anisotropy observed for single-point moments in § 4.1. The contours in frame (c) for Run 4 show evidence of stronger anisotropy than those in frame (f) for Run 8. This is in agreement with the results for single-point moments, which showed that the small scales become more anisotropic during the application of strain at lower Reynolds number. During straining, the domain is lengthened in the
![]() $x_{1}$
direction but shortened in
$x_{1}$
direction but shortened in
![]() $x_{2}$
and
$x_{2}$
and
![]() $x_{3}$
. This results in wavenumber distortion, where the wavenumbers in
$x_{3}$
. This results in wavenumber distortion, where the wavenumbers in
![]() $k_{1}$
decrease while those in
$k_{1}$
decrease while those in
![]() $k_{2}$
and
$k_{2}$
and
![]() $k_{3}$
increase. Close observation of figure 8 reveals that the cutoff wavenumber boundary for each simulation is distorted as the strain is applied. Wavenumber distortion causes energy to accumulate in long-wavelength (low-wavenumber) modes in the extensional direction, which is consistent with the formation of long coherent vortical structures in the extensional direction (Rogers & Moin Reference Rogers and Moin1987).
$k_{3}$
increase. Close observation of figure 8 reveals that the cutoff wavenumber boundary for each simulation is distorted as the strain is applied. Wavenumber distortion causes energy to accumulate in long-wavelength (low-wavenumber) modes in the extensional direction, which is consistent with the formation of long coherent vortical structures in the extensional direction (Rogers & Moin Reference Rogers and Moin1987).

Figure 9. Comparison of pre- and post-contraction longitudinal (a,c,e) and transverse (b,d,f) 1-D spectra, for DNS Run 4 at low Reynolds number (a,b), DNS Run 8 at higher Reynolds number (c,d) and the high Reynolds number experiment of AW (e,f), all shown as functions of pre-contraction wavenumbers. Experimental data are reproduced from figure 11 of AW by permission of the authors. Solid lines (black) are for pre-contraction DNS or experiment, dashed (red) for post-contraction DNS or experiment and dashed-dotted (blue) for post-contraction RDT. Insets in each frame show the same spectra but multiplied by the wavenumber (e.g.
![]() $k_{1}^{0}\unicode[STIX]{x1D60C}_{22}^{0}(k_{1}^{0})$
), such that the areas under the curve on log–linear scales give the mean-squared velocities. For the DNS, the transverse spectra
$k_{1}^{0}\unicode[STIX]{x1D60C}_{22}^{0}(k_{1}^{0})$
), such that the areas under the curve on log–linear scales give the mean-squared velocities. For the DNS, the transverse spectra
![]() $\unicode[STIX]{x1D60C}_{22}^{0}(k_{1}^{0})$
and
$\unicode[STIX]{x1D60C}_{22}^{0}(k_{1}^{0})$
and
![]() $\unicode[STIX]{x1D60C}_{33}^{0}(k_{1}^{0})$
are averaged with each other when producing frames (b) and (d). Such averaging is motivated by the axisymmetry of the turbulence.
$\unicode[STIX]{x1D60C}_{33}^{0}(k_{1}^{0})$
are averaged with each other when producing frames (b) and (d). Such averaging is motivated by the axisymmetry of the turbulence.
To characterize the scale-dependent anisotropy between different velocity components, we show in figure 9 the 1-D spectra of the
![]() $u_{1}$
and
$u_{1}$
and
![]() $u_{2}$
velocity fluctuations for low and high Reynolds numbers in the DNS (top and middle rows, respectively), compared with the highest Reynolds number data in the AW experiments (bottom row, from AW figure 11, with permission). The spectra are, based on rationale discussed earlier in § 2.3, all shown as functions of the initial (pre-contraction) wavenumbers. The effect of strain on
$u_{2}$
velocity fluctuations for low and high Reynolds numbers in the DNS (top and middle rows, respectively), compared with the highest Reynolds number data in the AW experiments (bottom row, from AW figure 11, with permission). The spectra are, based on rationale discussed earlier in § 2.3, all shown as functions of the initial (pre-contraction) wavenumbers. The effect of strain on
![]() $\unicode[STIX]{x1D60C}_{11}^{0}(k_{1}^{0})$
is a decrease at low wavenumbers but an increase at high wavenumbers. As the Reynolds number increases, a pronounced rightward shift is seen to develop in the peak of
$\unicode[STIX]{x1D60C}_{11}^{0}(k_{1}^{0})$
is a decrease at low wavenumbers but an increase at high wavenumbers. As the Reynolds number increases, a pronounced rightward shift is seen to develop in the peak of
![]() $k_{1}^{0}\unicode[STIX]{x1D60C}_{11}^{0}(k_{1}^{0})$
in both the DNS and experiment (red dashed lines in the insets of frames (c) and (e)). The effect of the mean strain on
$k_{1}^{0}\unicode[STIX]{x1D60C}_{11}^{0}(k_{1}^{0})$
in both the DNS and experiment (red dashed lines in the insets of frames (c) and (e)). The effect of the mean strain on
![]() $\unicode[STIX]{x1D60C}_{22}^{0}(k_{1}^{0})$
is, in contrast, an increase in the spectrum at all values of
$\unicode[STIX]{x1D60C}_{22}^{0}(k_{1}^{0})$
is, in contrast, an increase in the spectrum at all values of
![]() $k_{1}^{0}$
, with a milder change in the spectrum shape and a weaker Reynolds number dependence. The suppression of
$k_{1}^{0}$
, with a milder change in the spectrum shape and a weaker Reynolds number dependence. The suppression of
![]() $\langle u_{1}^{2}\rangle$
and amplification of
$\langle u_{1}^{2}\rangle$
and amplification of
![]() $\langle u_{2}^{2}\rangle$
are also indicated by changes in the area under the curves in the inset to each figure.
$\langle u_{2}^{2}\rangle$
are also indicated by changes in the area under the curves in the inset to each figure.
In figure 9 we have included inviscid RDT results for comparison. While the theory appears to reasonably predict the shape of
![]() $\unicode[STIX]{x1D60C}_{11}^{0}(k_{1}^{0})$
at low wavenumbers, it can be seen that the theory fails to capture the rightward shift in
$\unicode[STIX]{x1D60C}_{11}^{0}(k_{1}^{0})$
at low wavenumbers, it can be seen that the theory fails to capture the rightward shift in
![]() $k_{1}^{0}\unicode[STIX]{x1D60C}_{11}^{0}(k_{1}^{0})$
at high Reynolds number as discussed above, while it over-predicts the amplification of
$k_{1}^{0}\unicode[STIX]{x1D60C}_{11}^{0}(k_{1}^{0})$
at high Reynolds number as discussed above, while it over-predicts the amplification of
![]() $\unicode[STIX]{x1D60C}_{22}^{0}(k_{1}^{0})$
at low wavenumbers. This indicates the physical mechanisms neglected in RDT, namely nonlinear energy transfer, slow pressure strain and viscous dissipation, play a significant role in the evolution of the spectral structure of the Reynolds stresses.
$\unicode[STIX]{x1D60C}_{22}^{0}(k_{1}^{0})$
at low wavenumbers. This indicates the physical mechanisms neglected in RDT, namely nonlinear energy transfer, slow pressure strain and viscous dissipation, play a significant role in the evolution of the spectral structure of the Reynolds stresses.
The roles and relative importance of physical processes governing the evolution of the spectra described above can be studied using the spectral budget equation (2.13), which was written for the case of a single Fourier mode. The balance equations for the 1-D spectra parameterized by the initial wavenumbers are obtained by integrating (2.13) over planes perpendicular to
![]() $k_{1}$
, and then dividing by the total deformation (like in (2.21)). We then multiply the terms by
$k_{1}$
, and then dividing by the total deformation (like in (2.21)). We then multiply the terms by
![]() $k_{1}^{0}$
to study the evolution of the compensated spectra (the insets in figure 9). We are interested in determining what causes the rightward shift in the peak of
$k_{1}^{0}$
to study the evolution of the compensated spectra (the insets in figure 9). We are interested in determining what causes the rightward shift in the peak of
![]() $k_{1}^{0}\unicode[STIX]{x1D60C}_{11}^{0}(k_{1}^{0})$
at high Reynolds numbers, and what causes the general disagreement between the RDT and DNS spectra at high wavenumbers in all simulations. In figure 10 the balance terms are shown at different times and different Reynolds numbers. As expected for axisymmetric contraction, the production term is negative for the spectrum of
$k_{1}^{0}\unicode[STIX]{x1D60C}_{11}^{0}(k_{1}^{0})$
at high Reynolds numbers, and what causes the general disagreement between the RDT and DNS spectra at high wavenumbers in all simulations. In figure 10 the balance terms are shown at different times and different Reynolds numbers. As expected for axisymmetric contraction, the production term is negative for the spectrum of
![]() $u_{1}$
, but positive for the spectrum of
$u_{1}$
, but positive for the spectrum of
![]() $u_{2}$
. The rapid pressure strain counteracts the generation of anisotropy by taking the opposite sign of the production term, but a net tendency for anisotropy still persists. The nonlinear term is negative for low
$u_{2}$
. The rapid pressure strain counteracts the generation of anisotropy by taking the opposite sign of the production term, but a net tendency for anisotropy still persists. The nonlinear term is negative for low
![]() $k_{1}^{0}$
and positive for high
$k_{1}^{0}$
and positive for high
![]() $k_{1}^{0}$
, indicating that there is a forward cascade of energy to high
$k_{1}^{0}$
, indicating that there is a forward cascade of energy to high
![]() $k_{1}^{0}$
. This forward cascade opposes the tendency for energy to pile up near the
$k_{1}^{0}$
. This forward cascade opposes the tendency for energy to pile up near the
![]() $k_{1}^{0}=0$
plane during straining (see figure 8). The overall magnitude of the nonlinear transfer term is greater for
$k_{1}^{0}=0$
plane during straining (see figure 8). The overall magnitude of the nonlinear transfer term is greater for
![]() $k_{1}^{0}\unicode[STIX]{x1D60C}_{22}^{0}(k_{1}^{0})$
compared to
$k_{1}^{0}\unicode[STIX]{x1D60C}_{22}^{0}(k_{1}^{0})$
compared to
![]() $k_{1}^{0}\unicode[STIX]{x1D60C}_{11}^{0}(k_{1}^{0})$
, which is likely due to the fact that
$k_{1}^{0}\unicode[STIX]{x1D60C}_{11}^{0}(k_{1}^{0})$
, which is likely due to the fact that
![]() $\langle u_{2}^{2}\rangle$
is amplified during the straining, while
$\langle u_{2}^{2}\rangle$
is amplified during the straining, while
![]() $\langle u_{1}^{2}\rangle$
is suppressed.
$\langle u_{1}^{2}\rangle$
is suppressed.
In our simulations, the magnitude of the strain reaches a maximum and then decreases. To see how this is reflected in the spectral budgets, we present data for Run 8 at two deformations in figure 10(c–f). The production and rapid pressure-strain terms (which depend on the mean strain rate) in the bottom row are smaller than those in the middle row. As the production terms weaken, the relative importance of the nonlinear terms (especially at intermediate and high wavenumbers) increases. This is also the case for the slow pressure-strain term, which peaks at intermediate wavenumbers close to the peak observed for
![]() $k_{1}^{0}\unicode[STIX]{x1D60C}_{11}^{0}(k_{1}^{0})$
. We may conclude, therefore, that the slow pressure strain, which is neglected in RDT theory, is the main contributor to rightward shift in
$k_{1}^{0}\unicode[STIX]{x1D60C}_{11}^{0}(k_{1}^{0})$
. We may conclude, therefore, that the slow pressure strain, which is neglected in RDT theory, is the main contributor to rightward shift in
![]() $k_{1}^{0}\unicode[STIX]{x1D60C}_{11}^{0}(k_{1}^{0})$
both in our DNS and the experiments of AW. The increasing importance of slow pressure strain at later times noted here is also consistent with a similar feature in figure 6 addressed in § 4.1. On the other hand, the slow pressure-strain term is not as important to the evolution of
$k_{1}^{0}\unicode[STIX]{x1D60C}_{11}^{0}(k_{1}^{0})$
both in our DNS and the experiments of AW. The increasing importance of slow pressure strain at later times noted here is also consistent with a similar feature in figure 6 addressed in § 4.1. On the other hand, the slow pressure-strain term is not as important to the evolution of
![]() $k_{1}^{0}\unicode[STIX]{x1D60C}_{22}^{0}(k_{1}^{0})$
, which (besides production) is heavily influenced by nonlinear transfer at intermediate and high wavenumbers.
$k_{1}^{0}\unicode[STIX]{x1D60C}_{22}^{0}(k_{1}^{0})$
, which (besides production) is heavily influenced by nonlinear transfer at intermediate and high wavenumbers.
5 Relaxation of axisymmetric turbulence
The results in § 4 show that application of strain causes anisotropy at both the large and small scales. In this section we examine the relaxation that occurs when the mean strain is removed and the turbulence decays. We focus on varying degrees of return to isotropy as seen in single-point moments and axisymmetric and 1-D spectra. We also investigate the effects of nonlinear transfer and slow pressure fluctuations.

Figure 10. Terms from (2.13) contributing to the evolution of the 1-D compensated spectra, normalized by the pre-contraction dissipation rate and shown as functions of pre-contraction wavenumbers. (a,b)
![]() $L_{1}(t)/L_{1}^{0}=2.5$
from Run 4; (c,d)
$L_{1}(t)/L_{1}^{0}=2.5$
from Run 4; (c,d)
![]() $L_{1}(t)/L_{1}^{0}=2.5$
from Run 8; (e,f)
$L_{1}(t)/L_{1}^{0}=2.5$
from Run 8; (e,f)
![]() $L_{1}(t)/L_{1}^{0}=3.5$
from Run 8. Left and right columns show data for
$L_{1}(t)/L_{1}^{0}=3.5$
from Run 8. Left and right columns show data for
![]() $k_{1}^{0}\unicode[STIX]{x1D60C}_{11}^{0}(k_{1}^{0})$
and
$k_{1}^{0}\unicode[STIX]{x1D60C}_{11}^{0}(k_{1}^{0})$
and
![]() $k_{1}^{0}\unicode[STIX]{x1D60C}_{22}^{0}(k_{1}^{0})$
, respectively. In all frames: ▵ (black solid line) is for production, ▿ (magenta) for rapid pressure strain, ○ (green) for slow pressure-strain, ▫ (blue) for nonlinear transfer, ♢ (red) for minus the dissipation, and
$k_{1}^{0}\unicode[STIX]{x1D60C}_{22}^{0}(k_{1}^{0})$
, respectively. In all frames: ▵ (black solid line) is for production, ▿ (magenta) for rapid pressure strain, ○ (green) for slow pressure-strain, ▫ (blue) for nonlinear transfer, ♢ (red) for minus the dissipation, and
![]() $+$
(black dashed line) for total rate of change. Data for
$+$
(black dashed line) for total rate of change. Data for
![]() $k_{1}^{0}\unicode[STIX]{x1D60C}_{22}^{0}(k_{1}^{0})$
averaged with data for
$k_{1}^{0}\unicode[STIX]{x1D60C}_{22}^{0}(k_{1}^{0})$
averaged with data for
![]() $k_{1}^{0}\unicode[STIX]{x1D60C}_{33}^{0}(k_{1}^{0})$
due to the axisymmetry of the turbulence.
$k_{1}^{0}\unicode[STIX]{x1D60C}_{33}^{0}(k_{1}^{0})$
due to the axisymmetry of the turbulence.

Figure 11. Relaxation of (a) Reynolds stresses normalized by
![]() $q_{b}^{2}=2K_{b}$
, (b) components of the anisotropy tensor, and (c) anisotropy tensor invariants for Runs 4 (▾ and ▿, in blue), 6 (● and ○, in red), and 8 (▪ and ▫, in black). Upper curves are for
$q_{b}^{2}=2K_{b}$
, (b) components of the anisotropy tensor, and (c) anisotropy tensor invariants for Runs 4 (▾ and ▿, in blue), 6 (● and ○, in red), and 8 (▪ and ▫, in black). Upper curves are for
![]() $\langle u_{2}^{2}\rangle /q_{b}^{2}$
,
$\langle u_{2}^{2}\rangle /q_{b}^{2}$
,
![]() $\unicode[STIX]{x1D623}_{22}$
and
$\unicode[STIX]{x1D623}_{22}$
and
![]() $\unicode[STIX]{x1D702}$
in each figure, respectively. Lower curves are for
$\unicode[STIX]{x1D702}$
in each figure, respectively. Lower curves are for
![]() $\langle u_{1}^{2}\rangle /q_{b}^{2}$
,
$\langle u_{1}^{2}\rangle /q_{b}^{2}$
,
![]() $\unicode[STIX]{x1D623}_{11}$
and
$\unicode[STIX]{x1D623}_{11}$
and
![]() $\unicode[STIX]{x1D709}$
in each figure, respectively. Dashed lines at 0 in (b) and (c) denote values for isotropic turbulence.
$\unicode[STIX]{x1D709}$
in each figure, respectively. Dashed lines at 0 in (b) and (c) denote values for isotropic turbulence.
Figure 11 shows the component energy ratios and Reynolds stress anisotropy tensor information as functions of time since the end of strain, normalized by the time scale
![]() $\unicode[STIX]{x1D70F}=2K/\langle \unicode[STIX]{x1D716}\rangle$
at post-strain conditions. It is clear that anisotropy decreases significantly in the earlier stages of relaxation, slightly more rapidly if the Reynolds number is higher (Runs 6 and 8). However, the data also strongly suggest that the large scales will either not return to isotropy fully or will take almost an indefinitely long time to do so. This is consistent with the DNS of Davidson et al. (Reference Davidson, Okamoto and Kaneda2012) and large-eddy simulations of Chasnov (Reference Chasnov1995), which both showed persistent anisotropy at the large scales for axisymmetric Saffman turbulence (
$\unicode[STIX]{x1D70F}=2K/\langle \unicode[STIX]{x1D716}\rangle$
at post-strain conditions. It is clear that anisotropy decreases significantly in the earlier stages of relaxation, slightly more rapidly if the Reynolds number is higher (Runs 6 and 8). However, the data also strongly suggest that the large scales will either not return to isotropy fully or will take almost an indefinitely long time to do so. This is consistent with the DNS of Davidson et al. (Reference Davidson, Okamoto and Kaneda2012) and large-eddy simulations of Chasnov (Reference Chasnov1995), which both showed persistent anisotropy at the large scales for axisymmetric Saffman turbulence (
![]() $E(k)\sim k^{2}$
as
$E(k)\sim k^{2}$
as
![]() $k\rightarrow 0$
). This consistency in trend is perhaps not surprising, since our pre-simulation initial conditions are also of the Saffman type (due to the choice
$k\rightarrow 0$
). This consistency in trend is perhaps not surprising, since our pre-simulation initial conditions are also of the Saffman type (due to the choice
![]() $p_{0}=2$
in (3.1)). We have also checked for long-time effects by extending Runs 1 and 5 to relaxation times several times longer than shown in the figure. As the integral length scales grow during the extended relaxation period, the axisymmetry property
$p_{0}=2$
in (3.1)). We have also checked for long-time effects by extending Runs 1 and 5 to relaxation times several times longer than shown in the figure. As the integral length scales grow during the extended relaxation period, the axisymmetry property
![]() $\unicode[STIX]{x1D709}=-\unicode[STIX]{x1D702}$
does not hold as well for the smaller domain (Run 1), but a finite level of anisotropy is likely to persist even at asymptotically large times.
$\unicode[STIX]{x1D709}=-\unicode[STIX]{x1D702}$
does not hold as well for the smaller domain (Run 1), but a finite level of anisotropy is likely to persist even at asymptotically large times.

Figure 12. Relaxation of (a) vorticity contributions to dissipation rate and (b) velocity gradient statistics for Run 4 (dashed curves with open symbols) and Run 8 (solid curves with filled symbols). In (a), ▪ and ▫ (black) are for
![]() $\unicode[STIX]{x1D708}\langle \unicode[STIX]{x1D714}_{1}^{2}\rangle /\langle \unicode[STIX]{x1D716}\rangle _{b}$
, ● and ○ (red) for
$\unicode[STIX]{x1D708}\langle \unicode[STIX]{x1D714}_{1}^{2}\rangle /\langle \unicode[STIX]{x1D716}\rangle _{b}$
, ● and ○ (red) for
![]() $\unicode[STIX]{x1D708}\langle \unicode[STIX]{x1D714}_{2}^{2}\rangle /\langle \unicode[STIX]{x1D716}\rangle _{b}$
, and ▴ and ▵ (blue) for
$\unicode[STIX]{x1D708}\langle \unicode[STIX]{x1D714}_{2}^{2}\rangle /\langle \unicode[STIX]{x1D716}\rangle _{b}$
, and ▴ and ▵ (blue) for
![]() $\unicode[STIX]{x1D708}\langle \unicode[STIX]{x1D714}_{3}^{2}\rangle /\langle \unicode[STIX]{x1D716}\rangle _{b}$
. Let
$\unicode[STIX]{x1D708}\langle \unicode[STIX]{x1D714}_{3}^{2}\rangle /\langle \unicode[STIX]{x1D716}\rangle _{b}$
. Let
![]() $u_{i,j}=\unicode[STIX]{x2202}u_{i}/\unicode[STIX]{x2202}x_{j}$
. In (b), ▪ and ▫ (red) are for
$u_{i,j}=\unicode[STIX]{x2202}u_{i}/\unicode[STIX]{x2202}x_{j}$
. In (b), ▪ and ▫ (red) are for
![]() $\langle u_{2,1}^{2}\rangle /\langle u_{1,1}^{2}\rangle$
, ▴ and ▵ (green) for
$\langle u_{2,1}^{2}\rangle /\langle u_{1,1}^{2}\rangle$
, ▴ and ▵ (green) for
![]() $\langle u_{3,2}^{2}\rangle /\langle u_{2,2}^{2}\rangle$
, ▾ and ▿ (black) for
$\langle u_{3,2}^{2}\rangle /\langle u_{2,2}^{2}\rangle$
, ▾ and ▿ (black) for
![]() $-\langle u_{2,2}^{2}\rangle /\langle u_{2,3}u_{3,2}\rangle$
, and horizontal line at 2 for three-dimensional isotropic turbulence.
$-\langle u_{2,2}^{2}\rangle /\langle u_{2,3}u_{3,2}\rangle$
, and horizontal line at 2 for three-dimensional isotropic turbulence.
The concept of local isotropy in turbulence suggests the small scales may become isotropic during relaxation. Figure 12 shows the mean-square vorticity components and several ratios of derivative covariances during relaxation for Runs 4 and 8. Since these are small-scale quantities we have normalized time by the (post-contraction) Kolmogorov time scale. In frame (a),
![]() $\langle \unicode[STIX]{x1D714}_{1}^{2}\rangle$
initially decreases rapidly, while
$\langle \unicode[STIX]{x1D714}_{1}^{2}\rangle$
initially decreases rapidly, while
![]() $\langle \unicode[STIX]{x1D714}_{2}^{2}\rangle$
and
$\langle \unicode[STIX]{x1D714}_{2}^{2}\rangle$
and
![]() $\langle \unicode[STIX]{x1D714}_{3}^{2}\rangle$
increase before decreasing. By approximately
$\langle \unicode[STIX]{x1D714}_{3}^{2}\rangle$
increase before decreasing. By approximately
![]() $20~\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
, which for Run 8 corresponds to
$20~\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$
, which for Run 8 corresponds to
![]() $t/\unicode[STIX]{x1D70F}_{b}\approx 0.22$
, the mean-square vorticities are almost equal (while the Reynolds stresses in figure 11 are still very anisotropic). In frame (b), velocity derivative variance and covariance ratios also return to their isotropic value of 2. Similar to AW (their figure 24), the ratio
$t/\unicode[STIX]{x1D70F}_{b}\approx 0.22$
, the mean-square vorticities are almost equal (while the Reynolds stresses in figure 11 are still very anisotropic). In frame (b), velocity derivative variance and covariance ratios also return to their isotropic value of 2. Similar to AW (their figure 24), the ratio
![]() $\langle u_{2,1}^{2}\rangle /\langle u_{1,1}^{2}\rangle$
initially undershoots, and then increases toward the isotropic value.
$\langle u_{2,1}^{2}\rangle /\langle u_{1,1}^{2}\rangle$
initially undershoots, and then increases toward the isotropic value.

Figure 13. Relaxation of (a) skewness and (b) flatness of longitudinal velocity gradients for Run 4 (dashed curves with open symbols) and Run 8 (solid curves with filled symbols): ▪ and ▫ (red) for statistics of
![]() $\unicode[STIX]{x2202}u_{1}/\unicode[STIX]{x2202}x_{1}$
and ● and ○ (blue) for statistics of
$\unicode[STIX]{x2202}u_{1}/\unicode[STIX]{x2202}x_{1}$
and ● and ○ (blue) for statistics of
![]() $\unicode[STIX]{x2202}u_{3}/\unicode[STIX]{x2202}x_{3}$
.
$\unicode[STIX]{x2202}u_{3}/\unicode[STIX]{x2202}x_{3}$
.
For higher-order moments, figure 13 shows the post-contraction evolution of skewness and flatness factors of the longitudinal velocity gradients. The general trend is towards a skewness in the neighbourhood of
![]() $-$
0.5, which is typical of isotropic turbulence, and a flatness factor higher than 3 showing a noticeable increase with the Reynolds number. For Run 4 the skewness and flatness factors show a transient overshoot, which then gives way to the trend noted above. It is also interesting that, as a measure of isotropy, the flatness factors of
$-$
0.5, which is typical of isotropic turbulence, and a flatness factor higher than 3 showing a noticeable increase with the Reynolds number. For Run 4 the skewness and flatness factors show a transient overshoot, which then gives way to the trend noted above. It is also interesting that, as a measure of isotropy, the flatness factors of
![]() $\unicode[STIX]{x2202}u_{1}/\unicode[STIX]{x2202}x_{1}$
and
$\unicode[STIX]{x2202}u_{1}/\unicode[STIX]{x2202}x_{1}$
and
![]() $\unicode[STIX]{x2202}u_{3}/\unicode[STIX]{x2202}x_{3}$
become nearly equal faster than the corresponding skewness factors. The relatively slow equilibration of the skewness factors could be due to their connection with the energy cascade, which also depends on the large scales.
$\unicode[STIX]{x2202}u_{3}/\unicode[STIX]{x2202}x_{3}$
become nearly equal faster than the corresponding skewness factors. The relatively slow equilibration of the skewness factors could be due to their connection with the energy cascade, which also depends on the large scales.

Figure 14. Relaxation of axisymmetric energy spectrum for (a–c) Run 4 and (d–f) Run 8 at (a,d)
![]() $t/\unicode[STIX]{x1D70F}_{b}=0.05$
, (b,e)
$t/\unicode[STIX]{x1D70F}_{b}=0.05$
, (b,e)
![]() $t/\unicode[STIX]{x1D70F}_{b}=0.1$
, and (c,f)
$t/\unicode[STIX]{x1D70F}_{b}=0.1$
, and (c,f)
![]() $t/\unicode[STIX]{x1D70F}_{b}=0.2$
. Contour levels decrease by a factor of 10. Spectra plotted against post-contraction wavenumbers and multiplied by two to recover
$t/\unicode[STIX]{x1D70F}_{b}=0.2$
. Contour levels decrease by a factor of 10. Spectra plotted against post-contraction wavenumbers and multiplied by two to recover
![]() $K$
when integrating over
$K$
when integrating over
![]() $k_{r}$
and non-negative
$k_{r}$
and non-negative
![]() $k_{1}$
. Simulation cutoff wavenumbers marked by outermost black boundary. Spectra normalized by
$k_{1}$
. Simulation cutoff wavenumbers marked by outermost black boundary. Spectra normalized by
![]() $\sin \unicode[STIX]{x1D719}=k_{r}/k$
to obtain circular contours in isotropic turbulence; data for
$\sin \unicode[STIX]{x1D719}=k_{r}/k$
to obtain circular contours in isotropic turbulence; data for
![]() $k_{r}=0$
not plotted.
$k_{r}=0$
not plotted.
The fact that the large scales and the small scales return to isotropy (at least partially) at different rates in time suggest that, at a given time in the relaxation phase, the spectra may display a series of non-trivial shapes. In figure 14 we present the post-contraction evolution of the axisymmetric energy spectrum for Runs 4 and 8 (a–c and d–f, respectively), at three relatively early time instants corresponding to
![]() $t/\unicode[STIX]{x1D70F}_{b}=0.05$
(a,d),
$t/\unicode[STIX]{x1D70F}_{b}=0.05$
(a,d),
![]() $t/\unicode[STIX]{x1D70F}_{b}=0.1$
(b,e) and
$t/\unicode[STIX]{x1D70F}_{b}=0.1$
(b,e) and
![]() $t/\unicode[STIX]{x1D70F}_{b}=0.2$
(c,f). While the axisymmetric spectra immediately following the contraction are highly anisotropic (figure 8
c,f), a trend towards a more isotropic appearance (circular contours in the
$t/\unicode[STIX]{x1D70F}_{b}=0.2$
(c,f). While the axisymmetric spectra immediately following the contraction are highly anisotropic (figure 8
c,f), a trend towards a more isotropic appearance (circular contours in the
![]() $(k_{1},k_{r})$
plane) is evident at high wavenumbers during relaxation. This relaxation occurs faster for Run 8 because it has a greater contrast in time scales between the large scales and the small scales. Because the energy spectrum evolves only according to dissipation and energy redistribution (through the nonlinear term), the increase in the axisymmetric energy spectrum at high
$(k_{1},k_{r})$
plane) is evident at high wavenumbers during relaxation. This relaxation occurs faster for Run 8 because it has a greater contrast in time scales between the large scales and the small scales. Because the energy spectrum evolves only according to dissipation and energy redistribution (through the nonlinear term), the increase in the axisymmetric energy spectrum at high
![]() $k_{1}$
implies that there is a strong energy transfer to higher
$k_{1}$
implies that there is a strong energy transfer to higher
![]() $k_{1}$
during the initial relaxation period. Consistent with large-scale statistics in figure 11, we observe that anisotropy persists at low
$k_{1}$
during the initial relaxation period. Consistent with large-scale statistics in figure 11, we observe that anisotropy persists at low
![]() $k_{1}$
and low
$k_{1}$
and low
![]() $k_{r}$
during relaxation.
$k_{r}$
during relaxation.

Figure 15. Relaxation of (a,c,e) longitudinal and (b,d,f) transverse 1-D spectra, for (a,b) DNS Run 4, (c,d) DNS Run 8 and (e,f) high Reynolds number AW experiment. Experimental data are reproduced from figure 19 of AW by permission of the authors. Insets multiply spectra by
![]() $k_{1}$
. Time (for the DNS) or downstream evolution (for the experiments) increasing in directions of arrows. For DNS, curves at
$k_{1}$
. Time (for the DNS) or downstream evolution (for the experiments) increasing in directions of arrows. For DNS, curves at
![]() $t/\unicode[STIX]{x1D70F}_{b}=0$
(black),
$t/\unicode[STIX]{x1D70F}_{b}=0$
(black),
![]() $t/\unicode[STIX]{x1D70F}_{b}=0.1$
(red, not included in (c) log-log plot for clarity),
$t/\unicode[STIX]{x1D70F}_{b}=0.1$
(red, not included in (c) log-log plot for clarity),
![]() $t/\unicode[STIX]{x1D70F}_{b}=0.2$
(blue),
$t/\unicode[STIX]{x1D70F}_{b}=0.2$
(blue),
![]() $t/\unicode[STIX]{x1D70F}_{b}=0.4$
(green),
$t/\unicode[STIX]{x1D70F}_{b}=0.4$
(green),
![]() $t/\unicode[STIX]{x1D70F}_{b}=0.6$
(light blue, not included in top row) and
$t/\unicode[STIX]{x1D70F}_{b}=0.6$
(light blue, not included in top row) and
![]() $t/\unicode[STIX]{x1D70F}_{b}=0.8$
(magenta, not included in (a)). For DNS,
$t/\unicode[STIX]{x1D70F}_{b}=0.8$
(magenta, not included in (a)). For DNS,
![]() $\unicode[STIX]{x1D60C}_{22}(k_{1})$
and
$\unicode[STIX]{x1D60C}_{22}(k_{1})$
and
![]() $\unicode[STIX]{x1D60C}_{33}(k_{1})$
averaged with each other for frames (b) and (d) due to axisymmetry.
$\unicode[STIX]{x1D60C}_{33}(k_{1})$
averaged with each other for frames (b) and (d) due to axisymmetry.
The strong energy transfer to higher wavenumbers in the extensional direction is expected to have a significant effect on both longitudinal and transverse 1-D spectra, which are shown in figure 15 for DNS Runs 4 and 8 (a,b and c,d, respectively) at different times (increasing in the directions of the arrows) during relaxation. To facilitate comparison with experiment we have also included (with permission), in e–f, experimental data from figure 19 of AW. The longitudinal spectrum
![]() $\unicode[STIX]{x1D60C}_{11}(k_{1})$
initially increases during relaxation (primarily at high wavenumbers), corresponding to an increase of both
$\unicode[STIX]{x1D60C}_{11}(k_{1})$
initially increases during relaxation (primarily at high wavenumbers), corresponding to an increase of both
![]() $\langle u_{1}^{2}\rangle$
(see figure 11
a) and
$\langle u_{1}^{2}\rangle$
(see figure 11
a) and
![]() $\langle (\unicode[STIX]{x2202}u_{1}/\unicode[STIX]{x2202}x_{1})^{2}\rangle$
during the early relaxation period. In contrast, the transverse spectrum
$\langle (\unicode[STIX]{x2202}u_{1}/\unicode[STIX]{x2202}x_{1})^{2}\rangle$
during the early relaxation period. In contrast, the transverse spectrum
![]() $\unicode[STIX]{x1D60C}_{22}(k_{1})$
shows a decrease at low wavenumbers accompanied by an increase at high wavenumbers, corresponding to a reduction of
$\unicode[STIX]{x1D60C}_{22}(k_{1})$
shows a decrease at low wavenumbers accompanied by an increase at high wavenumbers, corresponding to a reduction of
![]() $\langle u_{2}^{2}\rangle$
and
$\langle u_{2}^{2}\rangle$
and
![]() $\langle u_{3}^{2}\rangle$
even though mean-square transverse velocity gradients increase. At high Reynolds numbers the compensated spectrum
$\langle u_{3}^{2}\rangle$
even though mean-square transverse velocity gradients increase. At high Reynolds numbers the compensated spectrum
![]() $k_{1}\unicode[STIX]{x1D60C}_{22}(k_{1})$
in the inset of frame (d) develops a ‘double-peak’ structure, which was a major finding in the AW experiments (frame (f)). The evolution of this part of the spectrum is non-monotonic in time, with the feature being most prominent in at
$k_{1}\unicode[STIX]{x1D60C}_{22}(k_{1})$
in the inset of frame (d) develops a ‘double-peak’ structure, which was a major finding in the AW experiments (frame (f)). The evolution of this part of the spectrum is non-monotonic in time, with the feature being most prominent in at
![]() $t/\unicode[STIX]{x1D70F}_{b}=0.2$
(frame (d) dark blue). As noted by AW, this ‘double-peak’ structure during relaxation appears to be a distinctive result of high Reynolds number. The observations here confirm that the simulations are successfully reproducing key flow physics in the experiments. We can address the physical mechanisms contributing to this double peak by analysing the spectral energy budget, as below.
$t/\unicode[STIX]{x1D70F}_{b}=0.2$
(frame (d) dark blue). As noted by AW, this ‘double-peak’ structure during relaxation appears to be a distinctive result of high Reynolds number. The observations here confirm that the simulations are successfully reproducing key flow physics in the experiments. We can address the physical mechanisms contributing to this double peak by analysing the spectral energy budget, as below.

Figure 16. Terms from (2.13) contributing to the evolution of 1-D compensated spectra for (a,b) Run 4 and (c,d) Run 8 at
![]() $t/\unicode[STIX]{x1D70F}_{b}=0.05$
into relaxation, normalized by dissipation rate
$t/\unicode[STIX]{x1D70F}_{b}=0.05$
into relaxation, normalized by dissipation rate
![]() $\langle \unicode[STIX]{x1D716}\rangle _{b}$
. Terms for
$\langle \unicode[STIX]{x1D716}\rangle _{b}$
. Terms for
![]() $k_{1}\unicode[STIX]{x1D60C}_{11}(k_{1})$
in (a,c) and terms averaged for
$k_{1}\unicode[STIX]{x1D60C}_{11}(k_{1})$
in (a,c) and terms averaged for
![]() $k_{1}\unicode[STIX]{x1D60C}_{22}(k_{1})$
and
$k_{1}\unicode[STIX]{x1D60C}_{22}(k_{1})$
and
![]() $k_{1}\unicode[STIX]{x1D60C}_{33}(k_{1})$
in (b,d) ○ (green) for slow pressure strain, ▫ (blue) for nonlinear transfer, ♢ (red) for minus the dissipation and
$k_{1}\unicode[STIX]{x1D60C}_{33}(k_{1})$
in (b,d) ○ (green) for slow pressure strain, ▫ (blue) for nonlinear transfer, ♢ (red) for minus the dissipation and
![]() $+$
(black dashed line) for total rate of change.
$+$
(black dashed line) for total rate of change.
As done in figure 10 for turbulence during the application of strain, we present in figure 16 the balance of terms that govern the evolution of the 1-D compensated spectra early in the relaxation period (
![]() $t/\unicode[STIX]{x1D70F}_{b}=0.05$
) for Runs 4 and 8. For both runs, the evolution of
$t/\unicode[STIX]{x1D70F}_{b}=0.05$
) for Runs 4 and 8. For both runs, the evolution of
![]() $k_{1}\unicode[STIX]{x1D60C}_{11}(k_{1})$
(in frames (a) and (c)) is dominated by the slow pressure-strain term (circles in green), which is positive over a wide range of wavenumbers. The integral of the pressure-strain term gives the pressure-strain correlation, which promotes isotropy by increasing
$k_{1}\unicode[STIX]{x1D60C}_{11}(k_{1})$
(in frames (a) and (c)) is dominated by the slow pressure-strain term (circles in green), which is positive over a wide range of wavenumbers. The integral of the pressure-strain term gives the pressure-strain correlation, which promotes isotropy by increasing
![]() $\langle u_{1}^{2}\rangle$
while decreasing
$\langle u_{1}^{2}\rangle$
while decreasing
![]() $\langle u_{2}^{2}\rangle$
and
$\langle u_{2}^{2}\rangle$
and
![]() $\langle u_{3}^{2}\rangle$
. For both
$\langle u_{3}^{2}\rangle$
. For both
![]() $k_{1}\unicode[STIX]{x1D60C}_{11}(k_{1})$
and
$k_{1}\unicode[STIX]{x1D60C}_{11}(k_{1})$
and
![]() $k_{1}\unicode[STIX]{x1D60C}_{22}(k_{1})$
, the nonlinear term (squares in blue) shows the characteristics of a forward cascade in
$k_{1}\unicode[STIX]{x1D60C}_{22}(k_{1})$
, the nonlinear term (squares in blue) shows the characteristics of a forward cascade in
![]() $k_{1}$
, being negative at low
$k_{1}$
, being negative at low
![]() $k_{1}$
, but positive at high
$k_{1}$
, but positive at high
![]() $k_{1}$
. This forward cascade from low
$k_{1}$
. This forward cascade from low
![]() $k_{1}$
to high
$k_{1}$
to high
![]() $k_{1}$
during relaxation is likely a consequence of a prior accumulation of energy near the
$k_{1}$
during relaxation is likely a consequence of a prior accumulation of energy near the
![]() $k_{1}=0$
plane during the contraction (see figure 8 frames (c) and (f), and discussion for figure 14). A comparison between the left and right columns of this figure shows that the nonlinear term plays a more important role in the evolution of
$k_{1}=0$
plane during the contraction (see figure 8 frames (c) and (f), and discussion for figure 14). A comparison between the left and right columns of this figure shows that the nonlinear term plays a more important role in the evolution of
![]() $k_{1}\unicode[STIX]{x1D60C}_{22}(k_{1})$
than for
$k_{1}\unicode[STIX]{x1D60C}_{22}(k_{1})$
than for
![]() $k_{1}\unicode[STIX]{x1D60C}_{11}(k_{1})$
. At intermediate and high wavenumbers, the nonlinear transfer is strong enough to exceed dissipation and pressure strain combined, leading to an increase in
$k_{1}\unicode[STIX]{x1D60C}_{11}(k_{1})$
. At intermediate and high wavenumbers, the nonlinear transfer is strong enough to exceed dissipation and pressure strain combined, leading to an increase in
![]() $k_{1}\unicode[STIX]{x1D60C}_{22}(k_{1})$
during the early phase of relaxation. A comparison of frames (b) and (d) also indicates that as the Reynolds number increases, nonlinear spectral transfer becomes stronger, while the effects of viscous dissipation are shifted towards higher wavenumbers. Since (in frame (d)) nonlinear transfer is the term of largest overall magnitude, it is a principal contributor to the change in shape of the transverse spectrum observed in both the AW experiments and our numerical simulations.
$k_{1}\unicode[STIX]{x1D60C}_{22}(k_{1})$
during the early phase of relaxation. A comparison of frames (b) and (d) also indicates that as the Reynolds number increases, nonlinear spectral transfer becomes stronger, while the effects of viscous dissipation are shifted towards higher wavenumbers. Since (in frame (d)) nonlinear transfer is the term of largest overall magnitude, it is a principal contributor to the change in shape of the transverse spectrum observed in both the AW experiments and our numerical simulations.
While results on the balance terms for the compensated spectra in figure 16 explain the reduction in
![]() $k_{1}\unicode[STIX]{x1D60C}_{22}(k_{1})$
at low wavenumbers and the increase in
$k_{1}\unicode[STIX]{x1D60C}_{22}(k_{1})$
at low wavenumbers and the increase in
![]() $k_{1}\unicode[STIX]{x1D60C}_{22}(k_{1})$
at high wavenumbers, the occurrence of a double-peak structure in
$k_{1}\unicode[STIX]{x1D60C}_{22}(k_{1})$
at high wavenumbers, the occurrence of a double-peak structure in
![]() $k_{1}\unicode[STIX]{x1D60C}_{22}(k_{1})$
at higher Reynolds number is more subtle. It may be noted that a higher Reynolds number gives a wider range of scales, and that results in figure 14 show that at higher Reynolds number (frames d–f) the high
$k_{1}\unicode[STIX]{x1D60C}_{22}(k_{1})$
at higher Reynolds number is more subtle. It may be noted that a higher Reynolds number gives a wider range of scales, and that results in figure 14 show that at higher Reynolds number (frames d–f) the high
![]() $k_{1}$
region of the axisymmetric energy spectrum increased quickly. A similar feature is seen in the transverse 1-D spectrum (figure 15
d), which exhibited a rapid increase at high wavenumbers early in the relaxation period. This is in contrast with a slower increase of the spectrum at high wavenumbers for the lower Reynolds number case shown in figure 15(b). In other words, the double-peak structure can be interpreted as the result of a slower decrease of
$k_{1}$
region of the axisymmetric energy spectrum increased quickly. A similar feature is seen in the transverse 1-D spectrum (figure 15
d), which exhibited a rapid increase at high wavenumbers early in the relaxation period. This is in contrast with a slower increase of the spectrum at high wavenumbers for the lower Reynolds number case shown in figure 15(b). In other words, the double-peak structure can be interpreted as the result of a slower decrease of
![]() $\unicode[STIX]{x1D60C}_{22}(k_{1})$
at low
$\unicode[STIX]{x1D60C}_{22}(k_{1})$
at low
![]() $k_{1}$
combined with a faster increase at high
$k_{1}$
combined with a faster increase at high
![]() $k_{1}$
, provided the contrast in time scales between these two processes is sufficiently strong, thus requiring high Reynolds number.
$k_{1}$
, provided the contrast in time scales between these two processes is sufficiently strong, thus requiring high Reynolds number.
The formation of two peaks in
![]() $k_{1}\unicode[STIX]{x1D60C}_{22}(k_{1})$
also depends on what processes influence the wavenumbers between the two peaks. For Run 8 this wavenumber range is approximately
$k_{1}\unicode[STIX]{x1D60C}_{22}(k_{1})$
also depends on what processes influence the wavenumbers between the two peaks. For Run 8 this wavenumber range is approximately
![]() $2\lesssim k_{1}\lesssim 10$
. If a forward cascade of energy occurs in
$2\lesssim k_{1}\lesssim 10$
. If a forward cascade of energy occurs in
![]() $k_{1}$
, we expect the curve
$k_{1}$
, we expect the curve
![]() $T_{22}(k_{1})$
to undergo a change in sign, which is evident in figure 16(d) at
$T_{22}(k_{1})$
to undergo a change in sign, which is evident in figure 16(d) at
![]() $k_{1}\approx 5$
(although the figure plots
$k_{1}\approx 5$
(although the figure plots
![]() $k_{1}T_{22}(k_{1})$
). The wavenumber location of this change in sign is nearly fixed during the relaxation period, and is located between the two peaks that emerge in
$k_{1}T_{22}(k_{1})$
). The wavenumber location of this change in sign is nearly fixed during the relaxation period, and is located between the two peaks that emerge in
![]() $k_{1}\unicode[STIX]{x1D60C}_{22}(k_{1})$
. In this wavenumber range as the nonlinear term is close to zero, the pressure strain and dissipation terms become more important. Hence, while the strong decrease in the spectrum at low wavenumbers and the rapid increase in the spectrum at high wavenumbers are primarily results of strong nonlinear interactions, the formation of two clearly visible peaks in
$k_{1}\unicode[STIX]{x1D60C}_{22}(k_{1})$
. In this wavenumber range as the nonlinear term is close to zero, the pressure strain and dissipation terms become more important. Hence, while the strong decrease in the spectrum at low wavenumbers and the rapid increase in the spectrum at high wavenumbers are primarily results of strong nonlinear interactions, the formation of two clearly visible peaks in
![]() $k_{1}\unicode[STIX]{x1D60C}_{22}(k_{1})$
depends subtly on pressure strain and dissipation effects in the wavenumber region between the two peaks. This effect is likely to become more prominent at higher Reynolds numbers which will support an even wider range of scales.
$k_{1}\unicode[STIX]{x1D60C}_{22}(k_{1})$
depends subtly on pressure strain and dissipation effects in the wavenumber region between the two peaks. This effect is likely to become more prominent at higher Reynolds numbers which will support an even wider range of scales.
As suggested throughout this section, the small scales become isotropic during relaxation, while the large scales appear to retain a significant degree of anisotropy for a very long time. The scale-dependent degree of return to isotropy was first observed for the axisymmetric energy spectrum in figure 14, where contours of kinetic energy at high wavenumbers became nearly circular for the higher Reynolds number simulation. To assess the scale-dependent anisotropy quantitatively we can also compare with theoretical relations for spectra in isotropic turbulence, such as

Figure 17. Post-contraction spectral isotropy for Run 8. In (a), isotropy of 1-D component spectra measured with (5.1) at (time increasing in the directions of the arrows)
![]() $t/\unicode[STIX]{x1D70F}_{b}=0$
(red, steepest curve),
$t/\unicode[STIX]{x1D70F}_{b}=0$
(red, steepest curve),
![]() $t/\unicode[STIX]{x1D70F}_{b}=0.05$
(green, intermediate curve) and
$t/\unicode[STIX]{x1D70F}_{b}=0.05$
(green, intermediate curve) and
![]() $t/\unicode[STIX]{x1D70F}_{b}=0.2$
(blue, plateau at 1 present); dashed line at 1 is for isotropic turbulence. In (b), measured (dashed blue) 3-D energy spectrum compared with calculated spectrum using (5.2) (solid red) at
$t/\unicode[STIX]{x1D70F}_{b}=0.2$
(blue, plateau at 1 present); dashed line at 1 is for isotropic turbulence. In (b), measured (dashed blue) 3-D energy spectrum compared with calculated spectrum using (5.2) (solid red) at
![]() $t/\unicode[STIX]{x1D70F}_{b}=0.2$
.
$t/\unicode[STIX]{x1D70F}_{b}=0.2$
.
6 Conclusions
In this paper we presented a numerical investigation of isotropic turbulence subjected to irrotational axisymmetric contraction and subsequent relaxation. A series of direct numerical simulations with grid resolution up to
![]() $4096^{3}$
have been conducted. Special care was taken to mimic the flow physics in the wind tunnel experiments of Ayyalasomayajula & Warhaft (Reference Ayyalasomayajula and Warhaft2006), which used an axisymmetric contraction with a 4 : 1 area ratio. The development of anisotropy and the physical mechanisms behind scale-dependent anisotropy during the contraction and subsequent relaxation are of fundamental interest.
$4096^{3}$
have been conducted. Special care was taken to mimic the flow physics in the wind tunnel experiments of Ayyalasomayajula & Warhaft (Reference Ayyalasomayajula and Warhaft2006), which used an axisymmetric contraction with a 4 : 1 area ratio. The development of anisotropy and the physical mechanisms behind scale-dependent anisotropy during the contraction and subsequent relaxation are of fundamental interest.
Although homogeneous turbulence subjected to spatially uniform mean velocity gradients can be simulated in a solution domain moving with the mean flow, time-dependent mean strain rates are necessary to produce flow conditions corresponding to experiments in spatially evolving wind tunnels. Accordingly, we have developed a technique to specify a time-dependent strain rate based on the convective time for fluid travelling along the wind tunnel centreline. The resulting strain rates in the DNS are, in non-dimensional form, similar to the strain rate histories in the AW experiments. Before applying the strain, a pre-simulation is first carried out with a specified initial energy spectrum to obtain physically realistic conditions of unforced isotropic turbulence. The Reynolds numbers simulated in this work are limited by numerical constraints on large-scale sampling and small-scale resolution, which are compounded by the non-cubic aspect ratio of the solution domains. A domain sufficiently large along its shortest dimension compared to the integral length scales is required to ensure that the numerical solution remains statistically axisymmetric at all times.
As expected, axisymmetric contraction leads to anisotropy in the Reynolds stress tensor. Velocity fluctuations are suppressed in the extensional direction but amplified in the compressive directions. The degree of anisotropy is independent of Reynolds number but is a function of the total strain applied. The small scales also become anisotropic. Mean-square vorticity in the extensional direction is enhanced (figure 7), and changes are observed in the skewness of the longitudinal velocity gradients. Rapid distortion theory (RDT) predicts anisotropy at the large scales well but not at the small scales, which implies that nonlinear effects excluded in RDT play an important role. The axisymmetry about the
![]() $x_{1}$
direction motivates the use of spectra extracted as functions of
$x_{1}$
direction motivates the use of spectra extracted as functions of
![]() $k_{1}$
and the wavenumber magnitude in the transverse plane
$k_{1}$
and the wavenumber magnitude in the transverse plane
![]() $k_{r}=\sqrt{k_{2}^{2}+k_{3}^{2}}$
. The axisymmetric energy spectrum becomes anisotropic at all scales of motion during the application of strain, and shows that energy is accumulated in long-wavelength (low
$k_{r}=\sqrt{k_{2}^{2}+k_{3}^{2}}$
. The axisymmetric energy spectrum becomes anisotropic at all scales of motion during the application of strain, and shows that energy is accumulated in long-wavelength (low
![]() $k_{1}$
) modes in the
$k_{1}$
) modes in the
![]() $x_{1}$
direction (figure 8). The effect of strain on the longitudinal 1-D spectrum of
$x_{1}$
direction (figure 8). The effect of strain on the longitudinal 1-D spectrum of
![]() $u_{1}$
fluctuations is a decrease at low wavenumbers but an increase at high wavenumbers (figure 9). At high Reynolds number the compensated form of this spectrum shows a rightward shift to higher wavenumbers as a consequence of the nonlinear effects of slow pressure strain.
$u_{1}$
fluctuations is a decrease at low wavenumbers but an increase at high wavenumbers (figure 9). At high Reynolds number the compensated form of this spectrum shows a rightward shift to higher wavenumbers as a consequence of the nonlinear effects of slow pressure strain.
Following the removal of the mean strain, the small scales relax faster than the large scales. The contrast in relaxation time scales becomes more apparent as the range of time scales in the flow increases with increasing Reynolds number. Statistics of velocity gradients show a return to local isotropy, whereas a residual level of anisotropy in the Reynolds stresses appears to persist indefinitely. The axisymmetric energy spectrum at high Reynolds number quickly becomes isotropic at high wavenumbers (small scales), whereas at low Reynolds number the spectrum is slow in its return to isotropy (figure 14). In close correspondence with the AW experiments, the compensated transverse spectrum
![]() $k_{1}\unicode[STIX]{x1D60C}_{22}(k_{1})$
undergoes a qualitative change at higher Reynolds number, where a ‘double-peak’ structure emerges at intermediate times during relaxation (figure 15
d). Analyses of the spectral budget following the contraction (figure 16) indicate that the transverse 1-D spectrum is dominated by nonlinear energy transfer to high
$k_{1}\unicode[STIX]{x1D60C}_{22}(k_{1})$
undergoes a qualitative change at higher Reynolds number, where a ‘double-peak’ structure emerges at intermediate times during relaxation (figure 15
d). Analyses of the spectral budget following the contraction (figure 16) indicate that the transverse 1-D spectrum is dominated by nonlinear energy transfer to high
![]() $k_{1}$
wavenumbers, and that slow pressure strain and viscous dissipation also play a role in establishing the double-peak structure in
$k_{1}$
wavenumbers, and that slow pressure strain and viscous dissipation also play a role in establishing the double-peak structure in
![]() $k_{1}\unicode[STIX]{x1D60C}_{22}(k_{1})$
. The formation of the double-peak structure requires that the high wavenumbers (small scales) relax very quickly compared to the low wavenumbers (large scales), and thus requires a high Reynolds number and a wide range of scales.
$k_{1}\unicode[STIX]{x1D60C}_{22}(k_{1})$
. The formation of the double-peak structure requires that the high wavenumbers (small scales) relax very quickly compared to the low wavenumbers (large scales), and thus requires a high Reynolds number and a wide range of scales.
In summary, the motivation for this work was to see whether DNS could reproduce the experimental finding by AW that turbulence under axisymmetric contraction and subsequent relaxation undergoes a qualitative change as the Reynolds number is increased. We also wanted to use the detail available in DNS to help explain the underlying physical mechanisms controlling these flows. Through a series of computations using a time-dependent strain rate formulated to mimic the AW wind tunnel, the numerical simulations are successful in reproducing and helping to explain the experimental observations. The behaviour of turbulence under irrotational, axisymmetric straining is a canonical problem (Lumley & Newman Reference Lumley and Newman1977) for which there is a continuing need for data at high Reynolds number (Warhaft Reference Warhaft2009). The results of this study have implications for engineering devices such as nozzles and diffusers where high Reynolds number turbulent flows are typically subjected to axisymmetric contraction, relaxation or expansion. The mixing of passive scalars, especially small temperature fluctuations, in these flows (Gylfason & Warhaft Reference Gylfason and Warhaft2009) is also a subject of both theoretical significance and practical interest.

Figure 18. Comparison of relaxing 1-D (a,c) longitudinal and (b,d) transverse spectra for (a,b) Runs 7 and 8 and (c,d) Runs 7 and 9. Solid black curves are for Run 7, dashed coloured curves for Runs 8 and 9. Time increasing in the directions of the arrows. Curves correspond to the same physical times shown for figure 15(c,d).
![]() $\unicode[STIX]{x1D60C}_{22}(k_{1})$
and
$\unicode[STIX]{x1D60C}_{22}(k_{1})$
and
![]() $\unicode[STIX]{x1D60C}_{33}(k_{1})$
averaged with each other for frames (b) and (d) due to axisymmetry.
$\unicode[STIX]{x1D60C}_{33}(k_{1})$
averaged with each other for frames (b) and (d) due to axisymmetry.
Acknowledgements
The authors gratefully acknowledge support from the Fluid Dynamics Program of the National Science Foundation, under Grant CBET-1510749. The first author is also supported by the Science, Mathematics, and Research for Transformation scholarship program through the Air Force Research Laboratory. The computations and data analyses reported in this paper were performed primarily using advanced computational facilities provided by the Texas Advanced Computation Center (TACC) under the XSEDE program supported by NSF. We are indebted to Professor Z. Warhaft for his kind encouragement and many valuable discussions, and Professor S. Ayyalasomayajula for kindly providing the experimental data included in figures 9 and 15. Helpful comments from the referees are also much appreciated.
Appendix. Influence of domain size and grid resolution
We showed in figure 15 that DNS of isotropic turbulence subjected to axisymmetric contraction at high Reynolds number reproduce key features of the 1-D spectra measured by AW (most notably the double-peak structure in
![]() $k_{1}\unicode[STIX]{x1D60C}_{22}(k_{1})$
). It is important to check that these results are not contaminated by the size of the computational domain or the grid resolution. In this Appendix we compare the relaxing 1-D spectra for the highest Reynolds number case on the different grids provided by Runs 7, 8 and 9. Run 7 is the baseline configuration on a
$k_{1}\unicode[STIX]{x1D60C}_{22}(k_{1})$
). It is important to check that these results are not contaminated by the size of the computational domain or the grid resolution. In this Appendix we compare the relaxing 1-D spectra for the highest Reynolds number case on the different grids provided by Runs 7, 8 and 9. Run 7 is the baseline configuration on a
![]() $2048^{3}$
grid, while Runs 8 and 9 employ
$2048^{3}$
grid, while Runs 8 and 9 employ
![]() $4096^{3}$
grid points. Run 8 improves upon Run 7 by doubling the domain length in the
$4096^{3}$
grid points. Run 8 improves upon Run 7 by doubling the domain length in the
![]() $x_{2}$
and
$x_{2}$
and
![]() $x_{3}$
directions (improving large-scale sampling), and halving the grid spacing in the
$x_{3}$
directions (improving large-scale sampling), and halving the grid spacing in the
![]() $x_{1}$
direction (improving resolution in
$x_{1}$
direction (improving resolution in
![]() $x_{1}$
). On the other hand, Run 9 improves upon Run 7 by doubling the domain length in all directions, which improves large-scale sampling in all directions. In figure 18 we overlay the longitudinal and transverse spectra for Runs 7 and 8 (a,b) and Runs 7 and 9 (c,d) at the same instants of time during relaxation that were used in figure 15(c,d) for Run 8 alone. As expected, in frames (a) and (b) Run 8 shows results advancing further into the high-wavenumber dissipation range, while in frames (c) and (d) Run 9 shows results extending to a lower range of wavenumbers. Most importantly, results at intermediate wavenumbers show little difference between Runs 7 and 8 and likewise between Runs 7 and 9. This demonstrates the most important conclusions from this work, including the emergence of a double-peak structure in
$x_{1}$
). On the other hand, Run 9 improves upon Run 7 by doubling the domain length in all directions, which improves large-scale sampling in all directions. In figure 18 we overlay the longitudinal and transverse spectra for Runs 7 and 8 (a,b) and Runs 7 and 9 (c,d) at the same instants of time during relaxation that were used in figure 15(c,d) for Run 8 alone. As expected, in frames (a) and (b) Run 8 shows results advancing further into the high-wavenumber dissipation range, while in frames (c) and (d) Run 9 shows results extending to a lower range of wavenumbers. Most importantly, results at intermediate wavenumbers show little difference between Runs 7 and 8 and likewise between Runs 7 and 9. This demonstrates the most important conclusions from this work, including the emergence of a double-peak structure in
![]() $k_{1}\unicode[STIX]{x1D60C}_{22}(k_{1})$
during relaxation, are numerically robust and not compromised by either finite domain size or finite grid spacing.
$k_{1}\unicode[STIX]{x1D60C}_{22}(k_{1})$
during relaxation, are numerically robust and not compromised by either finite domain size or finite grid spacing.