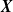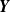1. Introduction
Let
${\bf X}=(X_1,\ldots,X_n)$
be a vector of non-negative dependent and identically distributed (d.i.d.) random variables with an absolutely continuous distribution F, survival function
$\overline{F}=1-F$
, and density function f. The joint distribution function of X is given by
\begin{equation*} {F}_{{\textbf{X}}}({\textbf{X}})=\mathbb{P}(X_1\leq x_1,\ldots,X_n\leq x_n)=\mathbb{C}({F}(x_1),\ldots,{F}(x_n)),\end{equation*}
where
${\bf x}=(x_1,\ldots,x_n)$
and
$\mathbb{C}$
is the multivariate distribution copula on
$[0,1]^n$
with uniformly distributed marginals on [0,Reference Amini-Seresht and Khaledi1]. The joint survival (or reliability) function of
${\textbf{X}}$
has the form
\begin{equation*}\overline{F}_{{\textbf{X}}}({\textbf{X}})=\mathbb{P}(X_1> x_1,\ldots,X_n> x_n)=\mathbb{\widehat{C}}(\overline{F}(x_1),\ldots,\overline{F}(x_n)),\end{equation*}
where
$\overline{F}$
is the survival function; it is also referred to as a reliability copula (see Nelsen [Reference Nelsen18]). Now let
$\overline{\mathbb{K}}_i(\overline{F}(x))=\mathbb{\widehat{C}}(\overline{F}(x)\boldsymbol{1}_i,\boldsymbol{1}_{n-i})$
denote the survival function of the series system
$X_{1:i}=\min(X_1,\ldots, X_i)$
, where the entries of both
$\boldsymbol{1}_i$
and
$\boldsymbol{1}_{n-i}$
are all ones, with
$\overline{\mathbb{K}}_1(\overline{F}(x))=\overline{F}(x)$
and
$\overline{\mathbb{K}}_n(\overline{F}(x))=\mathbb{\widehat{C}}(\overline{F}(x),\ldots,\overline{F}(x))$
.
We now define the survival function of a generalized finite mixture model (wherein the mixing proportions may be negative) from these i-dimensional marginals of
$\mathbb{\widehat{C}}$
as follows:
\begin{equation}\overline{H}_{{\textbf{X}},\textbf{a}}(\overline{F}(x))=\sum_{i=1}^na_i\overline{\mathbb{K}}_i(\overline{F}(x)),\end{equation}
where
$\textbf{a}=(a_1,\ldots,a_n)$
are some real numbers (weights) such that
$\sum_{i=1}^n a_i=1$
. Note that if all the weights are positive, then the mixture model in (1) becomes a pure mixture model. If some of the weights are negative, then the mixture in (1) becomes a generalized mixture model. Suppose
$u=\overline{F}(x)$
for all
$u\in[0,1]$
; then (1) can be rewritten as
\begin{equation*}\overline{H}_{\textbf{a}}(u)=\sum_{i=1}^na_i\overline{\mathbb{K}}_i(u),\end{equation*}
where
$\overline{H}_{\textbf{a}}(u)$
is a proper distribution function from [0,1] to [0,1] with
${H}_{\textbf{a}}(0)=0$
and
${H}_{\textbf{a}}(1)=1$
. Moreover, the distribution function corresponding to the generalized mixture model in (1) is given by
\begin{equation*}{H}_{{\textbf{X}},\textbf{a}}(\overline{F}(x))=\sum_{i=1}^na_i{\mathbb{K}}_i(\overline{F}(x)),\end{equation*}
where
${H}_{{\textbf{X}},\textbf{a}}(\overline{F}(x))=1-\overline{H}_{{\textbf{X}},\textbf{a}}(\overline{F}(x))$
and
$\mathbb{K}_i(\overline{F}(x))=1-\overline{\mathbb{K}}_i(\overline{F}(x))$
.
The aim of this paper is to compare two statistical models having distributions of the above form, according to the hazard rate and the reversed hazard rate orders. Many statistical models discussed in the literature are indeed special cases of the model in (1). Here are some examples.
-
• k-out-of-n systems. A k-out-of-n system with n components works if at least k components work or equivalently at most
$n-k$
components have failed. Thus its lifetime is simply the
$(n-k+1)$
th order statistic among the lifetimes of n components. Evidently series and parallel systems are n-out-of-n and 1-out-of-n systems, respectively. In Section 3 it will be shown that the lifetime distribution of a k-out-of-n system with dependent components is a special case of the generalized mixture model in (1) (e.g. (3)). -
• Coherent systems. A system is said to be coherent if it has no irrelevant components and the structure function of the system is monotone in each argument (i.e. an improvement of a component cannot lead to a deterioration in the system performance). In Section 3.2 it will be shown that the survival function of a coherent system with d.i.d. components can be written as in (1) with the vector of weights
$\textbf{a}=(a_1,\ldots,a_n)$
, so it is also a special case of the generalized mixture model.
Stochastic comparisons of two lifetimes of such systems from various aspects (such as two systems having i.i.d. components or d.i.d. components, two systems having the same vector of signature or different vectors of signature, two systems having the same components or different components, and so on) have been extensively studied and discussed in the literature. For more details, the reader is referred to the recent works of Navarro et al. [Reference Navarro, del Águila, Sordo and Suárez-Llorens15,Reference Navarro, del Águila, Sordo and Suárez-Llorens16] and the references therein. Motivated by these comparison results in the present work, we introduce a flexible model to compare lifetimes of systems under quite general conditions.
We specifically establish some general results for the comparison of two generalized mixture models in (1) in the sense of hazard rate and reversed hazard rate orders.
We first briefly review some notions of stochastic orderings and ageing properties that are used in the subsequent sections of this paper. Let
$\mathbb{R}=(-\infty,+\infty)$
and
$\mathbb{R}^+=[0,+\infty)$
. Throughout this paper we use increasing to mean non-decreasing and decreasing to mean non-increasing.
Definition 1. Let X and Y be two non-negative random variables with density functions f and g, distribution functions F and G, survival functions
$\overline{F}=1-F$
and
$\overline{G}=1-G$
, hazard rate functions
$r_X={{f}/{\overline{F}}}$
and
$r_Y={{g}/{\overline{G}}}$
, and reversed hazard rate functions
$\tilde{r}_X={{f}/{F}}$
and
$\tilde{r}_Y={{g}/{G}}$
, respectively. Then:
-
• X is said to be smaller than Y in the likelihood ratio order (denoted by
$X\leq_{lr} Y$
) if
${{g(x)}/{f(x)}}$
is increasing in x, -
• X is said to be smaller than Y in the hazard rate order (denoted by
$X\leq_{hr} Y$
) if
${{\overline{G}(x)}/{\overline{F}(x)}}$
is increasing in x or equivalently
$r_X(x)\geq r_Y(x)$
for all x, -
• X is said to be smaller than Y in the reversed hazard rate order (denoted by
$X\leq_{rh} Y$
) if
${{{G}(x)}/{{F}(x)}}$
is increasing in x or equivalently
$\tilde{r}_X(x)\leq \tilde{r}_Y(x)$
for all x, -
• X is said to be smaller than Y in the usual stochastic order (denoted by
$X\leq_{\rm st} Y$
) if
$\overline{F}(x)\leq \overline{G}(x)$
for all
$x\in\mathbb{R}^{+}$
or equivalently
$\textsf{E}[\phi(X)]\leq[\geq] \textsf{E}[\phi(Y)]$
for any increasing [decreasing] function
$\phi:\mathbb{R}\rightarrow\mathbb{R}$
for which the involved expectations exist.
It is well known that
\begin{equation*}X \leq_{lr} Y\Longrightarrow X \leq_{hr[rh]} Y \Longrightarrow X \leq_{st} Y,\end{equation*}
but neither reversed hazard rate order nor hazard rate order implies the other. For more detailed discussions of the above stochastic orderings, one may refer to the books by Shaked and Shanthikumar [Reference Shaked and Shanthikumar21] and MÜller and Stoyan [Reference MÜller and Stoyan13].
Let
${\textbf{X}}$
and
${\textbf{Y}}$
be two independent vectors of d.i.d. random variables in which the
$X_i$
and
$Y_i$
have distribution functions F and G, respectively, and let
$H_{{\textbf{X}},\textbf{a}}$
and
$H_{{\textbf{Y}},\textbf{a}}$
denote the generalized finite mixture models having the distribution functions as in (1) corresponding to vectors
${\textbf{X}}$
and
${\textbf{Y}}$
, respectively. Several authors have studied stochastic comparisons of mixture models; see Amini-Seresht and Khaledi [Reference Amini-Seresht and Khaledi1], Khaledi and Shaked [Reference Khaledi and Shaked8], Belzunce et al. [Reference Belzunce, Mercader, Ruiz and Spizzichino4], Gupta et al. [Reference Gupta, Dhariyal and Misra7], Gupta and Gupta [Reference Gupta and Gupta6], Li and Da [Reference Li and Da10], Li and Zhao [Reference Li and Zhao11], and Misra et al. [Reference Misra, Gupta and Gupta12]. Recently, Hernandez (2007) and Navarro et al. [Reference Navarro, Guillamón and Ruiz17] obtained some stochastic comparison results for generalized mixtures involving only two independent components. Navarro [Reference Navarro14] considered generalized mixture models with independent components and obtained some conditions for comparing the lifetime distributions of generalized mixtures in the sense of hazard rate, reversed hazard rate, and likelihood ratio orders. Some results for comparing two finite mixture models, which generalize the results of Navarro [Reference Navarro14], have been presented recently by Amini-Seresht and Zhang [Reference Amini-Seresht and Zhang2]. But comparison of two generalized mixture models with dependent components has not been discussed so far in the literature, to the best of our knowledge. Motivated by this, we will first consider two statistical models
$H_{{\textbf{X}},\textbf{a}}$
and
$H_{{\textbf{Y}},\textbf{a}}$
having different components and the same weights, and establish some ordering results between them in the sense of hazard rate and reversed hazard rate orders. Next we consider
$H_{{\textbf{X}},\textbf{a}}$
and
$H_{{\textbf{X}},\textbf{b}}$
having the same components with different weights, and establish results with respect to different stochastic orders. Finally we apply these results to compare the lifetimes of k-out-of-n systems and coherent systems.
2. Main results
In this section we obtain some general results for the comparison of general mixture models in (1) in the following two cases: two mixture models formed from two sets of random vectors,
${\textbf{X}}$
and
${\textbf{Y}}$
, with the same weights, and two mixture models formed from one random vector of components,
${\textbf{X}}$
, with different weights.
2.1. Stochastic comparisons of mixture models with two different random vectors
Theorem 1. Let
$H_{{\textbf{X}},\textbf{a}}$
and
$H_{{\textbf{Y}},\textbf{a}}$
be two generalized finite mixture models with d.i.d. components
${\textbf{X}}$
and
${\textbf{Y}}$
, respectively, and having the same copula function. If
-
(i)
$\dfrac{u\overline{H}'_{\textbf{a}}(u)}{\overline{H}_{\textbf{a}}(u)}$
is decreasing in u for all
$u\in(0,1)$
, and -
(ii)
$X_1\leq_{hr}Y_1$
,
then
${H}_{{\textbf{X}},\textbf{a}}\leq_{hr}{H}_{{\textbf{Y}},\textbf{a}}$
.
Proof. To obtain the desired result, it is enough to show that
\[\Psi_1(x)=\dfrac{\overline{H}_{{\textbf{Y}},\textbf{a}}(\overline{G}(x))}{\overline{H}_{{\textbf{X}},\textbf{a}}(\overline{F}(x))}\]
is increasing in
$x\in\mathbb{R}^+$
. With the derivative of
$\Psi_1$
, denoted by
$\Psi'_1$
, it can be found that
\begin{align*}\Psi'_1(x) &\overset{\operatorname{sgn}}= r_X(x)\dfrac{\overline{F}(x)\overline{H}'_{{\textbf{X}},\textbf{a}}(\overline{F}(x))}{\overline{H}_{{\textbf{X}},\textbf{a}}(\overline{F}(x))}-r_Y(x)\dfrac{\overline{G}(x)\overline{H}'_{{\textbf{Y}},\textbf{a}}(\overline{G}(x))}{\overline{H}_{{\textbf{Y}},\textbf{a}}(\overline{G}(x))}\\[3pt] &\geq r_Y(x)\Big[\dfrac{u\overline{H}'_{\textbf{a}}(u)}{\overline{H}_{\textbf{a}}(u)}-\dfrac{v\overline{H}'_{\textbf{a}}(v)}{\overline{H}_{\textbf{a}}(v)}\Big]\\*&\geq 0,\end{align*}
where
$u=\overline{F}(x)$
for all
$x\in\mathbb{R}^+$
and
$v=\overline{G}(x)$
for all
$x\in\mathbb{R}^+$
. The first inequality follows from the assumption that
$X_1\leq_{hr}Y_1$
, while the second inequality follows from assumption (i) and the fact that
$u\leq v$
. This completes the proof of the theorem.□
Theorem 2. Let
$H_{{\textbf{X}},\textbf{a}}$
and
$H_{{\textbf{Y}},\textbf{a}}$
be two generalized finite mixture models with d.i.d. components
${\textbf{X}}$
and
${\textbf{Y}}$
, respectively, and having the same copula function. If
-
(i)
$\dfrac{(1-u)\overline{H}'_{\textbf{a}}(u)}{1-\overline{H}_{\textbf{a}}(u)}$
is increasing in u for all
$u\in(0,1)$
, and -
(ii)
$X_1\leq_{rh}Y_1$
,
then
${H}_{{\textbf{X}},\textbf{a}}\leq_{rh}{H}_{{\textbf{Y}},\textbf{a}}$
.
Proof. Using the same arguments as in the proof of Theorem 1, it is enough to show that
\[\Psi_2(x)=\dfrac{1-\overline{H}_{{\textbf{Y}},\textbf{a}}(\overline{G}(x))}{1-\overline{H}_{{\textbf{X}},\textbf{a}}(\overline{F}(x))}\]
is increasing in
$x\in\mathbb{R}^+$
. With the derivative of
$\Psi_2$
, denoted by
$\Psi'_2$
, it can be found that
\begin{align*}\Psi'_2(x) &\overset{\operatorname{sgn}}= \tilde{r}_Y(x)\dfrac{(1-\overline{G}(x))\overline{H}'_{{\textbf{Y}},\textbf{a}}(\overline{G}(x))}{1-\overline{H}_{{\textbf{Y}},\textbf{a}}(\overline{G}(x))}-\tilde{r}_X(x)\dfrac{(1-\overline{F}(x))\overline{H}'_{{\textbf{X}},\textbf{a}}(\overline{F}(x))}{1-\overline{H}_{{\textbf{X}},\textbf{a}}(\overline{F}(x))}\\[3pt] &\geq \tilde{r}_X(x)\Big[\dfrac{(1-v)\overline{H}'_{\textbf{a}}(v)}{1-\overline{H}_{\textbf{a}}(v)}-\dfrac{(1-u)\overline{H}'_{\textbf{a}}(u)}{1-\overline{H}_{\textbf{a}}(u)}\Big] \\*&\geq 0,\end{align*}
where
$u=\overline{F}(x)$
for all
$x\in\mathbb{R}^+$
and
$v=\overline{G}(x)$
for all
$x\in\mathbb{R}^+$
. The first inequality follows from the assumption that
$X_1\leq_{rh}Y_1$
while the second inequality follows from assumption (i) and the fact that
$u\leq v$
. This completes the proof of the theorem.□
2.2. Stochastic comparisons of mixture models with the same random vector
We now consider two mixture models,
$H_{{\textbf{X}},\textbf{a}}$
and
$H_{{\textbf{X}},\textbf{b}}$
, having the same d.i.d. components but with different vectors of weights,
$\textbf{a}$
and
$\textbf{b}$
, respectively. We then establish some sufficient conditions for the comparison of the two mixture models with respect to hazard rate and reversed hazard rate orderings.
Theorem 3. Let
$H_{{\textbf{X}},\textbf{a}}$
and
$H_{{\textbf{X}},\textbf{b}}$
be two generalized finite mixture models with d.i.d. components
${\textbf{X}}$
and vectors of weights
$\textbf{a}$
and
$\textbf{b}$
, respectively. If
-
(i)
$\dfrac{u\overline{\mathbb{K}}'_j(u)}{\overline{\mathbb{K}}_j(u)}$
is increasing in j for all
$1\leq j\leq n$
, and -
(ii)
$a_ib_j\leq a_jb_i$
for all
$1\leq i\leq j\leq n$
.
then
${H}_{{\textbf{X}},\textbf{a}}\leq_{hr}{H}_{{\textbf{X}},\textbf{b}}$
,
Proof. To obtain the desired result, it is enough to show that
\[\Psi_3(x)=\dfrac{\sum_{j=1}^nb_j\overline{\mathbb{K}}_j(\overline{F}(x))}{\sum_{i=1}^na_i\overline{\mathbb{K}}_i(\overline{F}(x))}\]
is increasing in
$x\in \mathbb{R}^+$
. Taking the derivative of
$\Psi_3$
with respect to x, we obtain
\begin{align*}\Psi_3'(x) &\overset{\operatorname{sgn}}= \sum_{i=1}^n\sum_{j=1}^n\Big[ a_ib_jif(x)\overline{\mathbb{K}}'_i(\overline{F}(x))\overline{\mathbb{K}}_j(\overline{F}(x))-a_ib_jjf(x)\overline{\mathbb{K}}'_j(\overline{F}(x))\overline{\mathbb{K}}_i(\overline{F}(x))\Big]\\* &= r_X(x)\sum_{i=1}^n\sum_{j=1}^na_ib_j\biggl[i\dfrac{\overline{F}(x)\overline{\mathbb{K}}'_i(\overline{F}(x))}{\overline{\mathbb{K}}_i(\overline{F}(x))}-j\dfrac{\overline{F}(x)\overline{\mathbb{K}}'_j(\overline{F}(x))}{\overline{\mathbb{K}}_j(\overline{F}(x))}\biggr] {\overline{\mathbb{K}}_i(\overline{F}(x))}{\overline{\mathbb{K}}_j(\overline{F}(x))}\\ &= r_X(x)\sum_{i=1}^n\sum_{j=i}^na_ib_j\biggl[i\dfrac{\overline{F}(x)\overline{\mathbb{K}}'_i(\overline{F}(x))}{\overline{\mathbb{K}}_i(\overline{F}(x))}-j\dfrac{\overline{F}(x)\overline{\mathbb{K}}'_j(\overline{F}(x))}{\overline{\mathbb{K}}_j(\overline{F}(x))}\biggr] {\overline{\mathbb{K}}_i(\overline{F}(x))}{\overline{\mathbb{K}}_j(\overline{F}(x))}\\* & \quad\, +r_X(x)\sum_{i=1}^n\sum_{j=i}^na_jb_i\biggl[j\dfrac{\overline{F}(x)\overline{\mathbb{K}}'_j(\overline{F}(x))}{\overline{\mathbb{K}}_j(\overline{F}(x))}-i\dfrac{\overline{F}(x)\overline{\mathbb{K}}'_i(\overline{F}(x))}{\overline{\mathbb{K}}_i(\overline{F}(x))}\biggr] {\overline{\mathbb{K}}_j(\overline{F}(x))}{\overline{\mathbb{K}}_i(\overline{F}(x))}\\ &= r_X(x)\sum_{i=1}^n\sum_{j=i}^n[a_jb_i-a_ib_j].\biggl[j\dfrac{\overline{F}(x)\overline{\mathbb{K}}'_j(\overline{F}(x))}{\overline{\mathbb{K}}_j(\overline{F}(x))}-i\dfrac{\overline{F}(x)\overline{\mathbb{K}}'_i(\overline{F}(x))}{\overline{\mathbb{K}}_i(\overline{F}(x))}\biggr]\\* & \quad\, \times {\overline{\mathbb{K}}_j(\overline{F}(x))}{\overline{\mathbb{K}}_i(\overline{F}(x))}:=\Delta.\end{align*}
Thus it is now enough to show that
$\Delta$
is non-negative. Setting
$\overline{F}(x)=u$
,
$\Delta$
can be expressed as
\begin{align*}\Delta &= r_X(x)\sum_{i=1}^n\sum_{j=i}^n[a_jb_i-a_ib_j]\biggl[j\dfrac{u\overline{\mathbb{K}}'_j(u)}{\overline{\mathbb{K}}_j(u)}-i\dfrac{u\overline{\mathbb{K}}'_i(u)}{\overline{\mathbb{K}}_i(u)}\biggr]\times {\overline{\mathbb{K}}_j(u)}{\overline{\mathbb{K}}_i(u)}\\[3pt] &\geq r_X(x)\sum_{i=1}^n\sum_{j=i}^n[a_jb_i-a_ib_j]i\biggl[\dfrac{u\overline{\mathbb{K}}'_j(u)}{\overline{\mathbb{K}}_j(u)}-\dfrac{u\overline{\mathbb{K}}'_i(u)}{\overline{\mathbb{K}}_i(u)}\biggr]\times {\overline{\mathbb{K}}_j(u)}{\overline{\mathbb{K}}_i(u)}\\[3pt] &\geq 0 ,\end{align*}
where the first inequality follows from the fact that
$1\leq i\leq j\leq n$
, while the second inequality follows from assumptions (i) and (ii) and that
$1\leq i\leq j\leq n$
.□
Theorem 4. Let
$H_{{\textbf{X}},\textbf{a}}$
and
$H_{{\textbf{X}},\textbf{b}}$
be two generalized finite mixture models with d.i.d. components
${\textbf{X}}$
and vectors of weights
$\textbf{a}$
and
$\textbf{b}$
, respectively. If
-
(i)
$\dfrac{(1-u){\mathbb{K}}'_j(u)}{1-\overline{\mathbb{K}}_j(u)}$
is increasing in j for all
$1\leq j\leq n$
, and -
(ii)
$a_ib_j\leq a_jb_i$
for all
$1\leq i\leq j\leq n$
.
then
${H}_{{\textbf{X}},\textbf{a}}\leq_{rh}{H}_{{\textbf{X}},\textbf{b}}$
,
Proof. As in the proof of Theorem 3, it is enough to show that
\[\Psi_3(x)=\dfrac{\sum_{j=1}^nb_j{\mathbb{K}}_j(\overline{F}(x))}{\sum_{i=1}^na_i{\mathbb{K}}_i(\overline{F}(x))}\]
is increasing in
$x\in \mathbb{R}^+$
. Taking the derivative of
$\Psi_3$
with respect to x, we obtain
\begin{align*}\Psi_3'(x) &\overset{\operatorname{sgn}}= \sum_{i=1}^n\sum_{j=1}^n\biggl[ a_ib_jif(x)\overline{\mathbb{K}}'_i(\overline{F}(x))\overline{\mathbb{K}}_j(\overline{F}(x))-a_ib_jjf(x)\overline{\mathbb{K}}'_j(\overline{F}(x))\overline{\mathbb{K}}_i(\overline{F}(x))\biggr]\\[3pt] &= \tilde{r}_X(x)\sum_{i=1}^n\sum_{j=1}^na_ib_j\biggl[i\dfrac{{F}(x){\mathbb{K}}'_i(\overline{F}(x))}{{\mathbb{K}}_i(\overline{F}(x))}-j\dfrac{{F}(x){\mathbb{K}}'_j(\overline{F}(x))}{\overline{\mathbb{K}}_j(\overline{F}(x))}\biggr] {{\mathbb{K}}_i(\overline{F}(x))}{{\mathbb{K}}_j(\overline{F}(x))}\\[3pt] &= \tilde{r}_X(x)\sum_{i=1}^n\sum_{j=i}^na_ib_j\biggl[i\dfrac{{F}(x){\mathbb{K}}'_i(\overline{F}(x))}{{\mathbb{K}}_i(\overline{F}(x))}-j\dfrac{{F}(x){\mathbb{K}}'_j(\overline{F}(x))}{{\mathbb{K}}_j(\overline{F}(x))}\biggr] {{\mathbb{K}}_i(\overline{F}(x))}{{\mathbb{K}}_j(\overline{F}(x))}\\[3pt] &\quad\, +\tilde{r}_X(x)\sum_{i=1}^n\sum_{j=i}^na_jb_i\biggl[j\dfrac{{F}(x){\mathbb{K}}'_j(\overline{F}(x))}{{\mathbb{K}}_j(\overline{F}(x))}-i\dfrac{{F}(x){\mathbb{K}}'_i(\overline{F}(x))}{{\mathbb{K}}_i(\overline{F}(x))}\biggr] {{\mathbb{K}}_j(\overline{F}(x))}{{\mathbb{K}}_i(\overline{F}(x))}\\[3pt] &= \tilde{r}_X(x)\sum_{i=1}^n\sum_{j=i}^n[a_jb_i-a_ib_j]\biggl[j\dfrac{{F}(x){\mathbb{K}}'_j(\overline{F}(x))}{{\mathbb{K}}_j(\overline{F}(x))}-i\dfrac{{F}(x){\mathbb{K}}'_i({F}(x))}{{\mathbb{K}}_i(\overline{F}(x))}\biggr]\\[3pt] & \quad\, \times {{\mathbb{K}}_j({F}(x))}{{\mathbb{K}}_i(\overline{F}(x))}:=\Delta^{\star}.\end{align*}
Therefore it is now enough to show that
$\Delta^{\star}$
is non-negative. Setting
$u=\overline{F}(x)$
,
$\Delta^{\star}$
can be expressed as
\begin{align*}\Delta^{\star} &= \tilde{r}_X(x)\sum_{i=1}^n\sum_{j=i}^n[a_jb_i-a_ib_j]\biggl[j\dfrac{(1-u){\mathbb{K}}'_j(u)}{1-\overline{\mathbb{K}}_j(u)}-i\dfrac{(1-u){\mathbb{K}}'_i(u)}{1-\overline{\mathbb{K}}_i(u)}\biggr]\times {{\mathbb{K}}_j(u)}{{\mathbb{K}}_i(u)}\\[3pt] &\geq \tilde{r}_X(x)\sum_{i=1}^n\sum_{j=i}^n[a_jb_i-a_ib_j]i\biggl[\dfrac{(1-u){\mathbb{K}}'_j(u)}{1-\overline{\mathbb{K}}_j(u)}-\dfrac{(1-u){\mathbb{K}}'_i(u)}{1-\overline{\mathbb{K}}_i(u)}\biggr]\times {{\mathbb{K}}_j(u)}{{\mathbb{K}}_i(u)}\\[3pt] &\geq 0 ,\end{align*}
where the first inequality follows from the fact that
$1\leq i\leq j\leq n$
while the second inequality follows from assumptions (i) and (ii) and that
$1\leq i\leq j\leq n$
.□
3. Applications
In this section we use the results in the last section to compare the lifetimes of two k-out-of-n and two coherent systems.
3.1. Comparison of k-out-of-n systems
The k-out-of-n systems are well-known reliability structures that have been studied extensively in reliability theory. Kuo and Zuo [Reference Kuo and Zuo9] have provided a comprehensive discussion of k-out-of-n systems. In this subsection we show that the distribution function and survival function of a k-out-of-n system with d.i.d. components can be written as in (1) with the vector of weights
$\textbf{a}=(0,0,\ldots,a_k,\ldots,a_n)$
.
Let
$X_{1:n}\leq\cdots\leq X_{n:n}$
denote the order statistics of the random variables
$X_1,\ldots,X_n$
. Further, let
$T^{\textbf{X}}_{k|n}$
denote the lifetime of a k-out-of-n system. Its survival function can be written as (see Gupta [5, p.˜839])
\begin{equation}\overline{F}_{T^{\textbf{X}}_{k|n}}(x)=\mathbb{P}(X_{n-k+1:n}>x)=\sum_{i=k}^n(-1)^{i-k}\binom{i-1}{k-1}\binom{n}{i}\overline{F}_{1:i}(x),\end{equation}
where
$\overline{F}_{1:j}(x)$
is the survival function of order statistic
$X_{1:j}$
.
As the system has d.i.d. components, (2) can be rewritten as
\begin{align}\overline{F}_{T^{\textbf{X}}_{k|n}}(x) &= \sum_{i=k}^n(-1)^{i-k}\binom{i-1}{k-1}\binom{n}{i}\mathbb{\widehat{C}}(\overline{F}(x)\boldsymbol{1}_i,\boldsymbol{1}_{n-i})\notag\\[3pt] &= \sum_{i=1}^na_i\overline{\mathbb{K}}_i(\overline{F}(x))\notag\\[3pt] &:= \overline{H}_{k|n,\textbf{a}}(\overline{F}(x)),\end{align}
where
\[a_i=(-1)^{i-k}\binom{i-1}{k-1}\binom{n}{i}\quad\text{and}\quad\textbf{a}=(0,0,\ldots,a_k,\ldots,a_n).\]
In particular, if
$k=n$
, then
$T_{n|n}=X_{1:n}$
and
\[\overline{H}_{{n|n},\textbf{a}}(\overline{F}(x))=\mathbb{\widehat{C}}(\overline{F}(x),\ldots,\overline{F}(x)).\]
Note that the vector of weights for such a system is
$\textbf{a}=(0,0,\ldots,0,1,0,\ldots,0)$
. For example, in the case of
$k=4$
, for the parallel system
$T_{1:4}=X_{4:4}$
we have
\[\overline{H}_{{1|4},\textbf{a}_4}(\overline{F}(x))=\sum_{i=1}^4a_i\overline{\mathbb{K}}_i(\overline{F}(x)),\]
where the vector of weights is
$\textbf{a}=(4,-6,4,-1)$
.
We now present some results comparing the lifetimes of k-out-of-n systems with respect to hazard rate and reversed hazard rate orders.
Proposition 1. Let
$T^{\textbf{X}}_{k|n}$
and
$T^{\textbf{Y}}_{k|n}$
be the lifetimes of two k-out-of-n systems with d.i.d. components
${\textbf{X}}$
and
${\textbf{Y}}$
, respectively. If
-
(i)
$\dfrac{u\overline{H}'_{k|n,\textbf{a}}(u)}{\overline{H}_{k|n,\textbf{a}}(u)}$
is decreasing in u for all
$u\in(0,1)$
, and -
(ii)
$X_1\leq_{hr}Y_1$
,
then
$T^{\textbf{X}}_{k|n}\leq_{hr}T^{\textbf{Y}}_{k|n}$
.
Proposition 2. Let
$T^{\textbf{X}}_{k|n}$
and
$T^{\textbf{Y}}_{k|n}$
be two generalized finite mixture models with d.i.d. components
${\textbf{X}}$
and
${\textbf{Y}}$
, respectively. If
-
(i)
$\dfrac{(1-u){H}'_{k|n,\textbf{a}}(u)}{1-\overline{H}_{k|n,\textbf{a}}(u)}$
is increasing in u for all
$u\in(0,1)$
, and -
(ii)
$X_1\leq_{rh}Y_1$
,
then
$T^{\textbf{X}}_{k|n}\leq_{rh}T^{\textbf{Y}}_{k|n}$
.
Example 1. Let us consider the comparison in hazard rate order of two k-out-of-3 systems. Suppose that component lifetimes
${\textbf{X}}=(X_1,X_2,X_3)$
and
${\textbf{Y}}=(Y_1,Y_2,Y_3)$
in the two systems are d.i.d. with common distributions F and G, respectively, such that
$X_1\leq_{hr}Y_1$
. Further, let the random vectors
${\textbf{X}}$
and
${\textbf{Y}}$
have the same joint distribution with Farlie–Gumbel–Morgenstern (FGM) survival copula given by
\[\mathbb{C}(u_1,\ldots,u_n)=\Pi_{i=1}^nu_i [1+\theta\Pi_{i=1}^n(1-u_i)],\quad -1\leq\theta\leq 1,\]
Let us now compare the two k-out-of-3 systems under this dependence model when
$\theta=0.2$
. First, let us consider the 2-out-of-3 system with lifetime
$T_{2|3}^{\textbf{X}}=X_{2:3}$
. It is then easy to see that
\begin{align*}\overline{H}_{2|3,\textbf{a}}(\overline{F}(x)) &= \sum_{i=1}^3a_i\overline{\mathbb{K}}_i(\overline{F}(x))= 3\overline{F}^2(x)-2\overline{F}^3(x)(1+0.2(1-\overline{F}(x))^3),\end{align*}
where
$\textbf{a}=(0,3,-2)$
. Similarly, for
$k=3$
, it is easy to see that the vector of weights is
$(3,-3,1)$
, and thus we have
\begin{align*}\overline{H}_{3|3,\textbf{a}}(\overline{F}(x)) &= \sum_{i=1}^3a_i\overline{\mathbb{K}}_i(\overline{F}(x))= 3\overline{F}(x)-3\overline{F}^2(x)+\overline{F}^3(x)(1+0.2(1-\overline{F}(x))^3).\end{align*}
For all
$u\in(0,1)$
, let us define
\[\Delta_k(u)=\dfrac{u\overline{H}'_{k|3,\textbf{a}}(u)}{\overline{H}_{k|3,\textbf{a}}(u)},\quad k=2,3.\]
In Figure 1, we have plotted the ratios
$\Delta_k(u)$
,
$k=2,3$
, from which we see that both are strictly decreasing in
$u\in(0,1)$
. Hence
$T^{\textbf{X}}_{k|3}\leq_{hr}T^{\textbf{Y}}_{k|3}$
,
$k=2,3$
.
3.2. Comparisons of coherent systems with the different structure
Consider a system with n components. Suppose
${\bf X}=(X_1,\ldots,X_n)$
correspond to the lifetimes of the n d.i.d. component lifetimes, where the
$X_i$
have a common distribution function F. The stochastic comparisons of coherent systems with d.i.d. components have recently been discussed by some researchers; for example, see Amini-Seresht et al. [Reference Amini-Seresht, Zhang and Balakrishnan3], Navarro et al. [Reference Navarro, del Águila, Sordo and Suárez-Llorens15], and Samaniego and Navarro [Reference Samaniego and Navarro20].
Figure 1. Plot of
$\Delta_k(u)$
,
$k=2,3$
for all
$u\in(0,1)$
.
In this subsection we show that the survival function of a coherent system with d.i.d. components can be written as in (1) with the vector of weights
$\textbf{a}=(a_1,\ldots,a_n)$
. Let us denote the lifetime of a coherent system by
$T_{\Phi}({\textbf{a}})=\Phi(X_1,\ldots,X_n)$
, where
$\Phi$
is the structure function. Samaniego [Reference Samaniego19] proved that the survival functions of the system lifetime
$T_{\Phi}({\textbf{a}})$
have the form
\begin{equation*}\overline{F}_{T_{\Phi}({\textbf{a}})}(t)=\sum_{k=1}^{n}p_{n-k+1}\overline{F}_{n-k+1:n}(t),\end{equation*}
where
$p_{n-k+1}=\mathbb{P}(T_{\Phi}({\textbf{a}})=X_{n-k+1:n})$
.
From (3), the survival function of
$T_{\Phi}({\textbf{a}})$
can then be expressed as
\begin{align*}\overline{F}_{T_{\Phi}({\textbf{a}})}(x) &= \sum_{k=1}^{n}\sum_{i=k}^np_{n-k+1}(-1)^{i-k}\binom{i-1}{k-1}\binom{n}{i}\mathbb{\widehat{C}}(\overline{F}(x)\boldsymbol{1}_i,\boldsymbol{1}_{n-i})\\* &= \sum_{i=1}^n\sum_{k=1}^{i}p_{n-k+1}(-1)^{i-k}\binom{i-1}{k-1}\binom{n}{i}\mathbb{\widehat{C}}(\overline{F}(x)\boldsymbol{1}_i,\boldsymbol{1}_{n-i})\\ &= \sum_{i=1}^na_i\mathbb{\widehat{C}}(\overline{F}(x)\boldsymbol{1}_i,\boldsymbol{1}_{n-i})\notag\\* &= \overline{H}_{\textbf{a}}(\overline{F}(x)),\end{align*}
where
\[ a_i=\binom{n}{i}\sum_{k=1}^{i}p_{n-k+1}(-1)^{i-k}\binom{i-1}{k-1} \quad\text{for $i=1,\ldots,n$.} \]
Hence the survival function of a coherent system can be obtained by using this representation. For example, for a coherent system with lifetime
$T_{\Phi}=\min(X_1,\max(X_2,X_3))$
, where
$X_1,X_2,X_3$
are d.i.d. and have a joint distribution with survival copula
$\mathbb{\widehat{C}}$
, its survival function can be expressed as
\begin{align*}\overline{F}_{T_{\Phi}}(x) &= 2\mathbb{\widehat{C}}(\overline{F}(x),\overline{F}(x),1)-\mathbb{\widehat{C}}(\overline{F}(x),\overline{F}(x),\overline{F}(x))\\* &= \sum_{i=1}^3a_i\mathbb{\widehat{C}}(\overline{F}(x)\boldsymbol{1}_i,\boldsymbol{1}_{3-i}),\end{align*}
where
$\textbf{a}=(0,2,-1)$
.
Proposition 3. Let
$T_{\Phi_1}({\textbf{a}})$
and
$T_{\Phi_2}({\textbf{b}})$
be the lifetimes of two coherent systems with the same d.i.d. components, where
$\Phi_1$
and
$\Phi_2$
are the different structure functions and
$\textbf{a}$
and
$\textbf{b}$
are the corresponding vectors of weights, respectively. Under the assumptions of Theorem 3, we then have
$T_{\Phi_1}({\textbf{a}})\leq_{hr}T_{\Phi_2}({\textbf{b}})$
.
Proposition 4. Let
$T_{\Phi_1}({\textbf{a}})$
and
$T_{\Phi_2}({\textbf{b}})$
be the lifetimes of two coherent systems with the same d.i.d. components, where
$\Phi_1$
and
$\Phi_2$
are the different structure functions and
$\textbf{a}$
and
$\textbf{b}$
are the vectors of weights, respectively. Under the assumptions of Theorem 4, we then have
$T_{\Phi_1}({\textbf{a}})\leq_{rh}T_{\Phi_2}({\textbf{b}_n})$
.
Example 2. Let us consider the comparison in hazard rate order of two coherent systems with lifetimes
$T_{\Phi_1}(\textbf{a}_3)=\min(X_1,\max(X_2,X_3))$
and
$T_{\Phi_2}(\textbf{b}_3)=T^{{\textbf{X}}}_{2|3}$
, where
${\textbf{X}}=(X_1,X_2,X_3)$
have the joint distribution with survival copula given in Example 1 with
$\theta=0.2$
, and the vectors of weights are
$\textbf{a}_3=(0,2,-1)$
and
$\textbf{b}_3=(0,3,-2)$
, respectively. It is easy to check that
$a_ib_j\leq a_jb_i$
for all
$1\leq i\leq i\leq 3$
. Thus condition (ii) of Theorem 3 is satisfied. Hence it is enough to check condition (i) of Theorem 3. It can be seen that
\[\dfrac{u\overline{\mathbb{K}}'_1(u)}{\overline{\mathbb{K}}_1(u)}=1,\quad \dfrac{u\overline{\mathbb{K}}'_2(u)}{\overline{\mathbb{K}}_2(u)}=2\]
and
\[\dfrac{u\overline{\mathbb{K}}'_3(u)}{\overline{\mathbb{K}}_3(u)}=3-0.6\dfrac{u(1-u)^2}{1+0.2(1-u)^3}=3-\psi(u).\]
Note that
$\psi(0)=\psi(1)=0$
and
$\max_{u\in(0,1)}\psi(u)=\psi(0.353)=0.0841056$
, which implies
$0\leq\psi(u)\leq 0.0841056$
for all
$u\in[0,1]$
. So, from these observations, it follows that
${{u\overline{\mathbb{K}}'_j(u)}/{\overline{\mathbb{K}}_j(u)}}$
is increasing in j for all
$1\leq j\leq 3$
. Therefore, from Proposition 3, we have
$T_{\Phi_1}(\textbf{a}_3)\leq_{hr}T_{\Phi_2}(\textbf{b}_3)$
.
