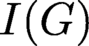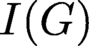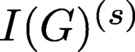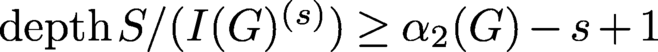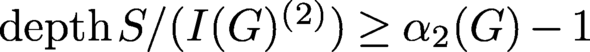1 Introduction
Let
![]() $\mathbb {K}$
be a field and
$\mathbb {K}$
be a field and
![]() $S = \mathbb {K}[x_1,\ldots ,x_n]$
be the polynomial ring in n variables over
$S = \mathbb {K}[x_1,\ldots ,x_n]$
be the polynomial ring in n variables over
![]() $\mathbb {K}$
. Computing and finding bounds for the depth (or equivalently, projective dimension) of homogenous ideals of S and their powers have been studied by several authors (see, e.g., [Reference Burch3], [Reference Caviglia, Hà, Herzog, Kummini, Terai and Trung4], [Reference Dao and Schweig5], [Reference Fouli and Morey8], [Reference Hà, Trung and Trung9], [Reference Herzog and Hibi11], [Reference Hoa, Kimura, Terai and Trung12], [Reference Nguyen and Trung13]).
$\mathbb {K}$
. Computing and finding bounds for the depth (or equivalently, projective dimension) of homogenous ideals of S and their powers have been studied by several authors (see, e.g., [Reference Burch3], [Reference Caviglia, Hà, Herzog, Kummini, Terai and Trung4], [Reference Dao and Schweig5], [Reference Fouli and Morey8], [Reference Hà, Trung and Trung9], [Reference Herzog and Hibi11], [Reference Hoa, Kimura, Terai and Trung12], [Reference Nguyen and Trung13]).
In [Reference Fouli, Hà and Morey7], Fouli et al. introduced the notion of initially regular sequence. Using this notion, they provided a method for estimating the depth of a homogenous ideal. To be more precise, let
![]() $I\subset S$
be a homogenous ideal and let
$I\subset S$
be a homogenous ideal and let
![]() $\{x_{i,j} \mid 1\leq i\leq q, 0\leq j\leq t_i\}$
be a subset of distinct variables of S. Suppose
$\{x_{i,j} \mid 1\leq i\leq q, 0\leq j\leq t_i\}$
be a subset of distinct variables of S. Suppose
![]() $\mathrm {in}_<(I)$
is the initial ideal of I with respect to a fixed monomial order
$\mathrm {in}_<(I)$
is the initial ideal of I with respect to a fixed monomial order
![]() $<$
and assume that
$<$
and assume that
![]() $\{u_1, \ldots , u_m\}$
is the set of minimal monomial generators of
$\{u_1, \ldots , u_m\}$
is the set of minimal monomial generators of
![]() $\mathrm {in}_<(I)$
. It is shown in [Reference Fouli, Hà and Morey7, Theorem 3.11] that
$\mathrm {in}_<(I)$
. It is shown in [Reference Fouli, Hà and Morey7, Theorem 3.11] that
![]() $ \operatorname {\mathrm {depth}} S/I\geq q$
, provided that the following conditions hold.
$ \operatorname {\mathrm {depth}} S/I\geq q$
, provided that the following conditions hold.
-
(i) The monomials
 $u_1, u_2, \ldots , u_m$
are not divisible by
$u_1, u_2, \ldots , u_m$
are not divisible by
 $x_{i,j}^2$
for
$x_{i,j}^2$
for
 $1\leq i\leq q$
and
$1\leq i\leq q$
and
 $1\leq j\leq t_i$
.
$1\leq j\leq t_i$
. -
(ii) For
 $i=1, 2, \ldots , q$
, if a monomial in
$i=1, 2, \ldots , q$
, if a monomial in
 $\{u_1, \ldots , u_m\}$
is divisible by
$\{u_1, \ldots , u_m\}$
is divisible by
 $x_{i,0}$
, then it is also divisible by
$x_{i,0}$
, then it is also divisible by
 $x_{i,j}$
, for some integer
$x_{i,j}$
, for some integer
 $1\leq j\leq t_i$
.
$1\leq j\leq t_i$
.
In Section 2, we provide an alternative proof for this result (see Proposition 2.1). Our proof is based on a short exact sequence argument, while in [Reference Fouli, Hà and Morey7], the authors construct an initially regular sequence to prove their result.
Fouli et al. [Reference Fouli, Hà and Morey6] observed that the above result provides a combinatorial lower bound for the depth of edge ideals of graphs. Indeed, for every graph G with edge ideal
![]() $I(G)$
, we have
$I(G)$
, we have
where
![]() $\alpha _2(G)$
denotes the so-called star packing number of G (see Section 2 for the definition of star packing number and see Corollary 2.2 for more details about the above inequality). It is proven in [Reference Fouli, Hà and Morey6, Theorem 3.7] that the above inequality can be extended to powers of
$\alpha _2(G)$
denotes the so-called star packing number of G (see Section 2 for the definition of star packing number and see Corollary 2.2 for more details about the above inequality). It is proven in [Reference Fouli, Hà and Morey6, Theorem 3.7] that the above inequality can be extended to powers of
![]() $I(G)$
when G is a forest. More precisely, for every forest G and for every integer
$I(G)$
when G is a forest. More precisely, for every forest G and for every integer
![]() $s\geq 1$
, the inequality
$s\geq 1$
, the inequality
holds. On the other hand, we know from [Reference Simis, Vasconcelos and Villarreal16, Theorem 5.9] that for every forest G, the sth ordinary and symbolic powers of
![]() $I(G)$
coincide. Hence, inequality (†) essentially says that for every forest G and any positive integer s,
$I(G)$
coincide. Hence, inequality (†) essentially says that for every forest G and any positive integer s,
 $$ \begin{align} \begin{array}{rl} \operatorname{\mathrm{depth}} S/I(G)^{(s)} \geq \alpha_2(G)-s+1. \end{array} \end{align} $$
$$ \begin{align} \begin{array}{rl} \operatorname{\mathrm{depth}} S/I(G)^{(s)} \geq \alpha_2(G)-s+1. \end{array} \end{align} $$
In Theorem 3.4, we generalize [Reference Fouli, Hà and Morey6, Theorem 3.7] by proving inequality (‡) for any chordal graph. Moreover, we show that inequality (‡) with
![]() $s=2$
is true for any graph G (see Theorem 4.2).
$s=2$
is true for any graph G (see Theorem 4.2).
2 Preliminaries and known results
In this section, we provide the definitions and the known results which will be used in the next sections.
Let G be a simple graph with vertex set
 $V(G)=\big \{x_1, \ldots , x_n\big \}$
and edge set
$V(G)=\big \{x_1, \ldots , x_n\big \}$
and edge set
![]() $E(G)$
. So, we identify the vertices of G with the variables of S. Also, by abusing the notation, every edge of G will be written by the product of the vertices. For a vertex
$E(G)$
. So, we identify the vertices of G with the variables of S. Also, by abusing the notation, every edge of G will be written by the product of the vertices. For a vertex
![]() $x_i$
, the neighbor set of
$x_i$
, the neighbor set of
![]() $x_i$
is
$x_i$
is
![]() $N_G(x_i)=\{x_j\mid x_ix_j\in E(G)\}$
. We set
$N_G(x_i)=\{x_j\mid x_ix_j\in E(G)\}$
. We set
![]() $N_G[x_i]=N_G(x_i)\cup \{x_i\}$
and call it the closed neighborhood of
$N_G[x_i]=N_G(x_i)\cup \{x_i\}$
and call it the closed neighborhood of
![]() $x_i$
. The cardinality of
$x_i$
. The cardinality of
![]() $N_G(x_i)$
is the degree of
$N_G(x_i)$
is the degree of
![]() $x_i$
and will be denoted by
$x_i$
and will be denoted by
![]() $\mathrm {deg}_G(x_i)$
. For every subset
$\mathrm {deg}_G(x_i)$
. For every subset
![]() $U\subset V(G)$
, the graph
$U\subset V(G)$
, the graph
![]() $G\setminus U$
has vertex set
$G\setminus U$
has vertex set
![]() $V(G\setminus U)=V(G)\setminus U$
and edge set
$V(G\setminus U)=V(G)\setminus U$
and edge set
![]() $E(G\setminus U)=\{e\in E(G)\mid e\cap U=\emptyset \}$
. A subgraph H of G is called induced provided that two vertices of H are adjacent if and only if they are adjacent in G. A graph G is called chordal if it has no induced cycle of length at least four. A subset W of
$E(G\setminus U)=\{e\in E(G)\mid e\cap U=\emptyset \}$
. A subgraph H of G is called induced provided that two vertices of H are adjacent if and only if they are adjacent in G. A graph G is called chordal if it has no induced cycle of length at least four. A subset W of
![]() $V(G)$
is a clique of G if every two distinct vertices of W are adjacent in G. A vertex x of G is a simplicial vertex if
$V(G)$
is a clique of G if every two distinct vertices of W are adjacent in G. A vertex x of G is a simplicial vertex if
![]() $N_G(x)$
is a clique. It is well-known that every chordal graph has a simplicial vertex. A subset C of
$N_G(x)$
is a clique. It is well-known that every chordal graph has a simplicial vertex. A subset C of
![]() $V(G)$
is a vertex cover of G if every edge of G is incident to at least one vertex of C. A vertex cover C is a minimal vertex cover if no proper subset of C is a vertex cover of G. The set of minimal vertex covers of G will be denoted by
$V(G)$
is a vertex cover of G if every edge of G is incident to at least one vertex of C. A vertex cover C is a minimal vertex cover if no proper subset of C is a vertex cover of G. The set of minimal vertex covers of G will be denoted by
![]() $\mathcal {C}(G)$
. A subset A of
$\mathcal {C}(G)$
. A subset A of
![]() $V(G)$
is called an independent subset of G if there are no edges among the vertices of A. Obviously, A is independent if and only if
$V(G)$
is called an independent subset of G if there are no edges among the vertices of A. Obviously, A is independent if and only if
![]() $V(G)\setminus A$
is a vertex cover of G.
$V(G)\setminus A$
is a vertex cover of G.
The edge ideal of a graph G is defined as
 $$\begin{align*}I(G)=\big(x_ix_j \, |\, x_ix_j\in E(G)\big)\subset S.\end{align*}$$
$$\begin{align*}I(G)=\big(x_ix_j \, |\, x_ix_j\in E(G)\big)\subset S.\end{align*}$$
For a subset C of
 $\big \{x_1, \ldots , x_n\big \}$
, we denote by
$\big \{x_1, \ldots , x_n\big \}$
, we denote by
![]() $\mathfrak {p}_C$
, the monomial prime ideal which is generated by the variables belonging to C. It is well-known that for every graph G,
$\mathfrak {p}_C$
, the monomial prime ideal which is generated by the variables belonging to C. It is well-known that for every graph G,
 $$\begin{align*}I(G)=\bigcap_{C\in \mathcal{C}(G)}\mathfrak{p}_C.\end{align*}$$
$$\begin{align*}I(G)=\bigcap_{C\in \mathcal{C}(G)}\mathfrak{p}_C.\end{align*}$$
Let I be an ideal of S and let
![]() $\mathrm {Min}(I)$
denote the set of minimal primes of I. For every integer
$\mathrm {Min}(I)$
denote the set of minimal primes of I. For every integer
![]() $s\geq 1$
, the sth symbolic power of I, denoted by
$s\geq 1$
, the sth symbolic power of I, denoted by
![]() $I^{(s)}$
, is defined to be
$I^{(s)}$
, is defined to be
 $$\begin{align*}I^{(s)}=\bigcap_{\frak{p}\in \mathrm{Min}(I)} \mathrm{Ker}(S\rightarrow (S/I^s)_{\frak{p}}).\end{align*}$$
$$\begin{align*}I^{(s)}=\bigcap_{\frak{p}\in \mathrm{Min}(I)} \mathrm{Ker}(S\rightarrow (S/I^s)_{\frak{p}}).\end{align*}$$
Let I be a squarefree monomial ideal in S and suppose that I has the irredundant primary decomposition
where every
![]() $\frak {p}_i$
is an ideal generated by a subset of the variables of S. It follows from [Reference Herzog and Hibi10, Proposition 1.4.4] that for every integer
$\frak {p}_i$
is an ideal generated by a subset of the variables of S. It follows from [Reference Herzog and Hibi10, Proposition 1.4.4] that for every integer
![]() $s\geq 1$
,
$s\geq 1$
,
 $$\begin{align*}I^{(s)}=\frak{p}_1^s\cap\cdots\cap \frak{p}_r^s.\end{align*}$$
$$\begin{align*}I^{(s)}=\frak{p}_1^s\cap\cdots\cap \frak{p}_r^s.\end{align*}$$
We set
![]() $I^{(s)}=S$
, for any integer
$I^{(s)}=S$
, for any integer
![]() $s\leq 0$
.
$s\leq 0$
.
It is clear that for any graph G and every integer
![]() $s\geq 1$
,
$s\geq 1$
,
 $$\begin{align*}I(G)^{(s)}=\bigcap_{C\in \mathcal{C}(G)}\mathfrak{p}_C^s.\end{align*}$$
$$\begin{align*}I(G)^{(s)}=\bigcap_{C\in \mathcal{C}(G)}\mathfrak{p}_C^s.\end{align*}$$
As it was mentioned in introduction, Fouli et al. [Reference Fouli, Hà and Morey7] detected a method to bound the depth of a homogenous ideal. We provide an alternative proof for their result. Recall that for every monomial u and for every variable
![]() $x_i$
, the degree of u with respect to
$x_i$
, the degree of u with respect to
![]() $x_i$
is denoted by
$x_i$
is denoted by
 $\mathrm {deg}_{x_i}(u)$
. Also, for every monomial ideal I, the set of its minimal monomial generators is denoted by
$\mathrm {deg}_{x_i}(u)$
. Also, for every monomial ideal I, the set of its minimal monomial generators is denoted by
![]() $G(I)$
.
$G(I)$
.
Proposition 2.1 ([Reference Fouli, Hà and Morey7], Theorem 3.11).
Let I be a proper homogenous ideal of S and let
![]() $<$
be a monomial order. Assume that
$<$
be a monomial order. Assume that
![]() $A=\{x_{i,j} \mid 1\leq i\leq q, 0\leq j\leq t_i\}$
is a subset of distinct variables of S, such that the following conditions are satisfied.
$A=\{x_{i,j} \mid 1\leq i\leq q, 0\leq j\leq t_i\}$
is a subset of distinct variables of S, such that the following conditions are satisfied.
-
(i) For every pair of integers
 $1\leq i\leq q$
,
$1\leq i\leq q$
,
 $1\leq j\leq t_i$
and for every
$1\leq j\leq t_i$
and for every
 $u\in G(\mathrm {in}_<(I))$
, we have
$u\in G(\mathrm {in}_<(I))$
, we have
 $\mathrm {deg}_{x_{i,j}}(u)\leq 1$
.
$\mathrm {deg}_{x_{i,j}}(u)\leq 1$
. -
(ii) For
 $i=1, 2, \ldots , q$
, if a monomial
$i=1, 2, \ldots , q$
, if a monomial
 $u\in G(\mathrm {in}_<(I))$
is divisible by
$u\in G(\mathrm {in}_<(I))$
is divisible by
 $x_{i,0}$
, then it is also divisible by
$x_{i,0}$
, then it is also divisible by
 $x_{i,j}$
, for some integer
$x_{i,j}$
, for some integer
 $1\leq j\leq t_i$
.
$1\leq j\leq t_i$
.
Then
![]() $ \operatorname {\mathrm {depth}} S/I\geq q$
.
$ \operatorname {\mathrm {depth}} S/I\geq q$
.
Proof. It is known that
![]() $ \operatorname {\mathrm {depth}} S/I\geq \operatorname {\mathrm {depth}} S/\mathrm {in}_<(I)$
(see, e.g., [Reference Herzog and Hibi10, Theorem 3.3.4]). Hence, replacing I by
$ \operatorname {\mathrm {depth}} S/I\geq \operatorname {\mathrm {depth}} S/\mathrm {in}_<(I)$
(see, e.g., [Reference Herzog and Hibi10, Theorem 3.3.4]). Hence, replacing I by
![]() $\mathrm {in}_<(I)$
, we may suppose that I is a monomial ideal. We use induction on
$\mathrm {in}_<(I)$
, we may suppose that I is a monomial ideal. We use induction on
![]() $|A|$
. There is nothing to prove for
$|A|$
. There is nothing to prove for
![]() $|A|=0$
, as in this case
$|A|=0$
, as in this case
![]() $q=0$
. Therefore, assume that
$q=0$
. Therefore, assume that
![]() $|A|\geq 1$
. If
$|A|\geq 1$
. If
![]() $t_i=0$
, for every
$t_i=0$
, for every
![]() $i=1, 2, \ldots , q$
, then it follows from condition (ii) that
$i=1, 2, \ldots , q$
, then it follows from condition (ii) that
![]() $x_{1,0}, \ldots , x_{q,0}$
do not divide the minimal monomial generators of I. In particular, they form a regular sequences on
$x_{1,0}, \ldots , x_{q,0}$
do not divide the minimal monomial generators of I. In particular, they form a regular sequences on
![]() $S/I$
and the assertion follows. Thus, suppose that
$S/I$
and the assertion follows. Thus, suppose that
![]() $t_i\geq 1$
, for some i with
$t_i\geq 1$
, for some i with
![]() $1\leq i\leq q$
. Without loss of generality, suppose
$1\leq i\leq q$
. Without loss of generality, suppose
![]() $i=1$
. Consider the following short exact sequence:
$i=1$
. Consider the following short exact sequence:
This yields that
 $$ \begin{align} \begin{array}{rl} \operatorname{\mathrm{depth}} S/I \geq \min \big\{\operatorname{\mathrm{depth}} S/(I:x_{1,t_1}), \operatorname{\mathrm{depth}} S/(I,x_{1,t_1})\big\}. \end{array} \end{align} $$
$$ \begin{align} \begin{array}{rl} \operatorname{\mathrm{depth}} S/I \geq \min \big\{\operatorname{\mathrm{depth}} S/(I:x_{1,t_1}), \operatorname{\mathrm{depth}} S/(I,x_{1,t_1})\big\}. \end{array} \end{align} $$
By condition (i), the variable
![]() $x_{1,t_1}$
does not appear in the minimal monomial generators of
$x_{1,t_1}$
does not appear in the minimal monomial generators of
![]() $(I:x_{1,t_1})$
. In particular,
$(I:x_{1,t_1})$
. In particular,
![]() $x_{1,t_1}$
is a regular element on
$x_{1,t_1}$
is a regular element on
![]() $S/(I:x_{1,t_1})$
. Let
$S/(I:x_{1,t_1})$
. Let
![]() $S^{\prime }$
be the polynomial ring obtained from S by deleting the variable
$S^{\prime }$
be the polynomial ring obtained from S by deleting the variable
![]() $x_{1,t_1}$
(in other words,
$x_{1,t_1}$
(in other words,
![]() $S^{\prime }\cong S/(x_{1,t_1})$
). Set
$S^{\prime }\cong S/(x_{1,t_1})$
). Set
![]() $I^{\prime }:=(I:x_{1,t_1})\cap S^{\prime }$
. It follows that
$I^{\prime }:=(I:x_{1,t_1})\cap S^{\prime }$
. It follows that
 $$\begin{align*}\operatorname{\mathrm{depth}} S/(I:x_{1,t_1})=\operatorname{\mathrm{depth}} S/((I:x_{1,t_1}), x_{1,t_1})+1=\operatorname{\mathrm{depth}} S^{\prime}/I^{\prime}+1.\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{depth}} S/(I:x_{1,t_1})=\operatorname{\mathrm{depth}} S/((I:x_{1,t_1}), x_{1,t_1})+1=\operatorname{\mathrm{depth}} S^{\prime}/I^{\prime}+1.\end{align*}$$
Clearly,
![]() $I^{\prime }$
satisfies the assumptions with respect to the set
$I^{\prime }$
satisfies the assumptions with respect to the set
![]() $\{x_{i,j} \mid 2\leq i\leq q, 0\leq j\leq t_i\}$
of variables. Thus, the induction hypothesis implies that
$\{x_{i,j} \mid 2\leq i\leq q, 0\leq j\leq t_i\}$
of variables. Thus, the induction hypothesis implies that
![]() $ \operatorname {\mathrm {depth}} S^{\prime }/I^{\prime }\geq q-1$
. Hence, we deduce from the above equalities that
$ \operatorname {\mathrm {depth}} S^{\prime }/I^{\prime }\geq q-1$
. Hence, we deduce from the above equalities that
Using inequality (1), it suffices to prove that
![]() $ \operatorname {\mathrm {depth}} S/(I,x_{1,t_1})\geq q$
. Set
$ \operatorname {\mathrm {depth}} S/(I,x_{1,t_1})\geq q$
. Set
![]() $I^{\prime \prime }:=I\cap S^{\prime }$
. Then
$I^{\prime \prime }:=I\cap S^{\prime }$
. Then
![]() $S/(I,x_{1,t_1})\cong S^{\prime }/I^{\prime \prime }$
. Put
$S/(I,x_{1,t_1})\cong S^{\prime }/I^{\prime \prime }$
. Put
![]() $t_1^{\prime }:=t_1-1$
and
$t_1^{\prime }:=t_1-1$
and
![]() $t_i^{\prime }:=t_i$
, for
$t_i^{\prime }:=t_i$
, for
![]() $i=2, \ldots , q$
. Obviously,
$i=2, \ldots , q$
. Obviously,
![]() $I^{\prime \prime }$
satisfies the assumptions with respect to the set
$I^{\prime \prime }$
satisfies the assumptions with respect to the set
![]() $\{x_{i,j} \mid 1\leq i\leq q, 0\leq j\leq t_i^{\prime }\}$
of variables. Therefore, we conclude from the induction hypothesis that
$\{x_{i,j} \mid 1\leq i\leq q, 0\leq j\leq t_i^{\prime }\}$
of variables. Therefore, we conclude from the induction hypothesis that
 $$\begin{align*}\operatorname{\mathrm{depth}} S/(I,x_{1,t_1})=\operatorname{\mathrm{depth}} S^{\prime}/I^{\prime\prime}\geq q.\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{depth}} S/(I,x_{1,t_1})=\operatorname{\mathrm{depth}} S^{\prime}/I^{\prime\prime}\geq q.\end{align*}$$
Let G be a graph and x be a vertex of G. The subgraph
![]() $\mathrm {St}(x)$
of G with vertex set
$\mathrm {St}(x)$
of G with vertex set
![]() $N_G[x]$
and edge set
$N_G[x]$
and edge set
![]() $\{xy\, |\, y\in N_G(x)\}$
is called a star with center x. A star packing of G is a family
$\{xy\, |\, y\in N_G(x)\}$
is called a star with center x. A star packing of G is a family
![]() $\mathcal {X}$
of stars in G which are pairwise disjoint, that is,
$\mathcal {X}$
of stars in G which are pairwise disjoint, that is,
![]() $V(\mathrm {St}(x))\cap V(\mathrm {St}(x^{\prime }))=\emptyset $
, for
$V(\mathrm {St}(x))\cap V(\mathrm {St}(x^{\prime }))=\emptyset $
, for
![]() $\mathrm {St}(x), \mathrm {St}(x^{\prime })\in \mathcal {X}$
with
$\mathrm {St}(x), \mathrm {St}(x^{\prime })\in \mathcal {X}$
with
![]() $x\neq x^{\prime }$
. The quantity
$x\neq x^{\prime }$
. The quantity
 $$\begin{align*}\max\big\{|\mathcal{X}|\, |\, \mathcal{X} \ \text{is a star packing of } G\big\}\end{align*}$$
$$\begin{align*}\max\big\{|\mathcal{X}|\, |\, \mathcal{X} \ \text{is a star packing of } G\big\}\end{align*}$$
is called the star packing number of G. Following [Reference Fouli, Hà and Morey6], we denote the star packing number of G by
![]() $\alpha _2(G)$
.
$\alpha _2(G)$
.
The following corollary is an immediate consequence of Proposition 2.1, and it was indeed observed in [Reference Fouli, Hà and Morey6].
Corollary 2.2 ([Reference Fouli, Hà and Morey6]).
For every graph G, we have
Proof. Let
![]() $x_{1,0}, \ldots , x_{q,0}$
be the centers of stars in a largest star packing of G. Moreover, for
$x_{1,0}, \ldots , x_{q,0}$
be the centers of stars in a largest star packing of G. Moreover, for
![]() $1\leq i\leq q$
, assume that
$1\leq i\leq q$
, assume that
![]() $N_G(x_{i,0})=\{x_{i,1}, \ldots , x_{i,t_i}\}$
. Then the assumptions of Proposition 2.1 are satisfied and it follows that
$N_G(x_{i,0})=\{x_{i,1}, \ldots , x_{i,t_i}\}$
. Then the assumptions of Proposition 2.1 are satisfied and it follows that
3 Symbolic powers of edge ideals of chordal graphs
In this section, we prove the first main result of this paper, Theorem 3.4 which states that inequality (‡) is true for every chordal graph G and for any integer
![]() $s\geq 1$
. In order to prove this result, we first need to estimate the star packing number of the graph obtained from G by deleting a certain subset of its vertices. This will be done in the following two lemmas.
$s\geq 1$
. In order to prove this result, we first need to estimate the star packing number of the graph obtained from G by deleting a certain subset of its vertices. This will be done in the following two lemmas.
Lemma 3.1. Let G be a graph and let W be a subset of
![]() $V(G)$
. Then for every
$V(G)$
. Then for every
 $A\subseteq \bigcup _{x\in W}N_G[x]$
, we have
$A\subseteq \bigcup _{x\in W}N_G[x]$
, we have
Proof. Let
![]() $\mathcal {S}$
be the set of the centers of stars in a largest star packing of G. In particular,
$\mathcal {S}$
be the set of the centers of stars in a largest star packing of G. In particular,
![]() $|\mathcal {S}|=\alpha _2(G)$
. Since every vertex in A belongs to the closed neighborhood of a vertex in W, it follows from the definition of star packing that
$|\mathcal {S}|=\alpha _2(G)$
. Since every vertex in A belongs to the closed neighborhood of a vertex in W, it follows from the definition of star packing that
![]() $|\mathcal {S}\cap A|\leq | W|$
. Then the stars in
$|\mathcal {S}\cap A|\leq | W|$
. Then the stars in
![]() $G\setminus A$
centered at the vertices in
$G\setminus A$
centered at the vertices in
![]() $\mathcal {S}\setminus A$
form a star packing in
$\mathcal {S}\setminus A$
form a star packing in
![]() $G\setminus A$
of size at least
$G\setminus A$
of size at least
![]() $\alpha _2(G)-| W|$
. Therefore,
$\alpha _2(G)-| W|$
. Therefore,
![]() $\alpha _2(G\setminus A)\geq \alpha _2(G)-|W|$
.
$\alpha _2(G\setminus A)\geq \alpha _2(G)-|W|$
.
Lemma 3.2. Assume that G is a graph and
![]() $W=\{x_1, \ldots , x_d\}$
is a clique of G. Let A be a subset of
$W=\{x_1, \ldots , x_d\}$
is a clique of G. Let A be a subset of
![]() $V(G)$
such that
$V(G)$
such that
-
(i)
 $A\subseteq \bigcup _{i=1}^dN_G(x_i)$
,
$A\subseteq \bigcup _{i=1}^dN_G(x_i)$
, -
(ii)
 $N_G(x_1)\setminus \{x_2, \ldots , x_d\} \subseteq A$
, and
$N_G(x_1)\setminus \{x_2, \ldots , x_d\} \subseteq A$
, and -
(iii)
 $x_1\notin A$
.
$x_1\notin A$
.
Then
![]() $\alpha _2(G\setminus A)\geq \alpha _2(G)-d+1$
.
$\alpha _2(G\setminus A)\geq \alpha _2(G)-d+1$
.
Proof. Let
![]() $\mathcal {S}$
be the set of the centers of stars in a largest star packing of G. Thanks to (i), similar to the proof of Lemma 3.1, we have
$\mathcal {S}$
be the set of the centers of stars in a largest star packing of G. Thanks to (i), similar to the proof of Lemma 3.1, we have
![]() $|\mathcal {S}\cap A|\leq d$
. If
$|\mathcal {S}\cap A|\leq d$
. If
![]() $|\mathcal {S}\cap A|\leq d-1$
, then the stars in
$|\mathcal {S}\cap A|\leq d-1$
, then the stars in
![]() $G\setminus A$
centered at the vertices in
$G\setminus A$
centered at the vertices in
![]() $\mathcal {S}\setminus A$
form a star packing in
$\mathcal {S}\setminus A$
form a star packing in
![]() $G\setminus A$
of size at least
$G\setminus A$
of size at least
![]() $\alpha _2(G)-d+1$
. Thus, the assertion follows in this case. Therefore, suppose
$\alpha _2(G)-d+1$
. Thus, the assertion follows in this case. Therefore, suppose
![]() $|\mathcal {S}\cap A|=d$
. In this case, we have
$|\mathcal {S}\cap A|=d$
. In this case, we have
 $$\begin{align*}x_1, \ldots, x_d\in \bigcup_{x\in \mathcal{S}\cap A}N_G(x).\end{align*}$$
$$\begin{align*}x_1, \ldots, x_d\in \bigcup_{x\in \mathcal{S}\cap A}N_G(x).\end{align*}$$
It again follows from the definition of star packing that
 $$\begin{align*}x_1, \ldots, x_d\notin \bigcup_{x\in \mathcal{S}\setminus A}N_{G\setminus A}(x).\end{align*}$$
$$\begin{align*}x_1, \ldots, x_d\notin \bigcup_{x\in \mathcal{S}\setminus A}N_{G\setminus A}(x).\end{align*}$$
Therefore, we conclude from condition (ii) that
 $$ \begin{align*} N_{G\setminus A}[x_1]\cap \big(\bigcup_{x\in \mathcal{S}\setminus A}N_{G\setminus A}(x)\big)\subseteq \{x_1, \ldots, x_d\}\cap \big(\bigcup_{x\in \mathcal{S}\setminus A}N_{G\setminus A}(x)\big)=\emptyset. \end{align*} $$
$$ \begin{align*} N_{G\setminus A}[x_1]\cap \big(\bigcup_{x\in \mathcal{S}\setminus A}N_{G\setminus A}(x)\big)\subseteq \{x_1, \ldots, x_d\}\cap \big(\bigcup_{x\in \mathcal{S}\setminus A}N_{G\setminus A}(x)\big)=\emptyset. \end{align*} $$
As a consequence, the stars in
![]() $G\setminus A$
centered at the vertices in
$G\setminus A$
centered at the vertices in
![]() $(\mathcal {S}\setminus A)\cup \{x_1\}$
form a star packing in
$(\mathcal {S}\setminus A)\cup \{x_1\}$
form a star packing in
![]() $G\setminus A$
of size
$G\setminus A$
of size
![]() $\alpha _2(G)-d+1$
. This completes the proof of the lemma.
$\alpha _2(G)-d+1$
. This completes the proof of the lemma.
We are now ready to prove that inequality (‡) holds for any chordal graph. Indeed, we are able to prove the following stronger result.
Proposition 3.3. Let G be a chordal graph. Suppose H and
![]() $H^{\prime }$
are subgraphs of G with
$H^{\prime }$
are subgraphs of G with
Assume further that H is a chordal graph. Then for every integer
![]() $s\geq 1$
,
$s\geq 1$
,
 $$\begin{align*}\operatorname{\mathrm{depth}} S/(I(H)^{(s)}S+I(H^{\prime})S)\geq \alpha_2(G)-s+1.\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{depth}} S/(I(H)^{(s)}S+I(H^{\prime})S)\geq \alpha_2(G)-s+1.\end{align*}$$
Proof. As the isolated vertices have no effect on edge ideals, we assume that
![]() $V(H)=V(H^{\prime })=V(G)$
(i.e., we extend the vertex sets of H and
$V(H)=V(H^{\prime })=V(G)$
(i.e., we extend the vertex sets of H and
![]() $H^{\prime }$
to
$H^{\prime }$
to
![]() $V(G)$
). We use induction on
$V(G)$
). We use induction on
![]() $s+|E(H)|$
. For
$s+|E(H)|$
. For
![]() $s=1$
, we have
$s=1$
, we have
 $I(H)^{(s)}+I(H^{\prime })=I(G)$
and the assertion follows from Corollary 2.2. Therefore, suppose
$I(H)^{(s)}+I(H^{\prime })=I(G)$
and the assertion follows from Corollary 2.2. Therefore, suppose
![]() $s\geq 2$
. If
$s\geq 2$
. If
![]() $E(H)=\emptyset $
, then
$E(H)=\emptyset $
, then
![]() $I(H^{\prime })=I(G)$
and again we have the required inequality by Corollary 2.2. Hence, we assume
$I(H^{\prime })=I(G)$
and again we have the required inequality by Corollary 2.2. Hence, we assume
![]() $|E(H)|\geq 1$
.
$|E(H)|\geq 1$
.
To simplify the notations, we set
 $I:=I(H)^{(s)}+I(H^{\prime })$
. Since H is a chordal graph, it has a simplicial vertex, say
$I:=I(H)^{(s)}+I(H^{\prime })$
. Since H is a chordal graph, it has a simplicial vertex, say
![]() $x_1$
, with nonzero degree. Without loss of generality, suppose
$x_1$
, with nonzero degree. Without loss of generality, suppose
 $N_H(x_1)=\big \{x_2, \ldots , x_d\big \}$
, for some integer
$N_H(x_1)=\big \{x_2, \ldots , x_d\big \}$
, for some integer
![]() $d\geq 2$
. Consider the following short exact sequence:
$d\geq 2$
. Consider the following short exact sequence:
 $$ \begin{align*} 0\longrightarrow \frac{S}{(I:x_1\cdots x_d)}\longrightarrow \frac{S}{I}\longrightarrow \frac{S}{(I,x_1\cdots x_d)}\longrightarrow 0. \end{align*} $$
$$ \begin{align*} 0\longrightarrow \frac{S}{(I:x_1\cdots x_d)}\longrightarrow \frac{S}{I}\longrightarrow \frac{S}{(I,x_1\cdots x_d)}\longrightarrow 0. \end{align*} $$
Using depth lemma [Reference Bruns and Herzog2, Proposition 1.2.9], we have
 $$ \begin{align} \begin{array}{rl} \operatorname{\mathrm{depth}} S/I \geq \min \big\{\operatorname{\mathrm{depth}} S/(I:x_1\cdots x_d), \operatorname{\mathrm{depth}} S/(I,x_1\cdots x_d)\big\}. \end{array} \end{align} $$
$$ \begin{align} \begin{array}{rl} \operatorname{\mathrm{depth}} S/I \geq \min \big\{\operatorname{\mathrm{depth}} S/(I:x_1\cdots x_d), \operatorname{\mathrm{depth}} S/(I,x_1\cdots x_d)\big\}. \end{array} \end{align} $$
By assumption, for every pair of integers
![]() $i\neq j$
, with
$i\neq j$
, with
![]() $1\leq i,j\leq d$
we have
$1\leq i,j\leq d$
we have
![]() $x_ix_j\in E(H)$
. Therefore,
$x_ix_j\in E(H)$
. Therefore,
![]() $x_ix_j$
is not an edge of
$x_ix_j$
is not an edge of
![]() $H^{\prime }$
. Set
$H^{\prime }$
. Set
 $$\begin{align*}U:=\bigcup_{i=1}^dN_{H^{\prime}}[x_i]\end{align*}$$
$$\begin{align*}U:=\bigcup_{i=1}^dN_{H^{\prime}}[x_i]\end{align*}$$
and
 $$\begin{align*}U^{\prime}:=\bigcup_{i=1}^dN_{H^{\prime}}(x_i).\end{align*}$$
$$\begin{align*}U^{\prime}:=\bigcup_{i=1}^dN_{H^{\prime}}(x_i).\end{align*}$$
Then using [Reference Seyed Fakhari14, Lemma 2], we have
 $$ \begin{align*} (I:x_1\cdots x_d)&=\big((I(H)^{(s)}+I(H^{\prime})):x_1\cdots x_d\big)\\ & =I(H)^{(s-d+1)}+I(H^{\prime}\setminus U) +\big(\text{the ideal generated by}\ U^{\prime}\big)\\ & =I(H\setminus U^{\prime})^{(s-d+1)}+I(H^{\prime}\setminus U)+\big(\text{the ideal generated by }\ U^{\prime}\big). \end{align*} $$
$$ \begin{align*} (I:x_1\cdots x_d)&=\big((I(H)^{(s)}+I(H^{\prime})):x_1\cdots x_d\big)\\ & =I(H)^{(s-d+1)}+I(H^{\prime}\setminus U) +\big(\text{the ideal generated by}\ U^{\prime}\big)\\ & =I(H\setminus U^{\prime})^{(s-d+1)}+I(H^{\prime}\setminus U)+\big(\text{the ideal generated by }\ U^{\prime}\big). \end{align*} $$
This yields that
 $$\begin{align*}\operatorname{\mathrm{depth}} S/(I:x_1\cdots x_d)=\operatorname{\mathrm{depth}} S^{\prime}/(I(H\setminus U^{\prime})^{(s-d+1)}+I(H^{\prime}\setminus U)),\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{depth}} S/(I:x_1\cdots x_d)=\operatorname{\mathrm{depth}} S^{\prime}/(I(H\setminus U^{\prime})^{(s-d+1)}+I(H^{\prime}\setminus U)),\end{align*}$$
where
![]() $S^{\prime }=\mathbb {K}[x_i: 1\leq i\leq n, i\notin U^{\prime }]$
. Let
$S^{\prime }=\mathbb {K}[x_i: 1\leq i\leq n, i\notin U^{\prime }]$
. Let
![]() $G^{\prime }$
be the union of
$G^{\prime }$
be the union of
![]() $H\setminus U^{\prime }$
and
$H\setminus U^{\prime }$
and
![]() $H^{\prime }\setminus U$
. In fact,
$H^{\prime }\setminus U$
. In fact,
![]() $G^{\prime }$
is the induced subgraph of G on
$G^{\prime }$
is the induced subgraph of G on
![]() $V(G)\setminus U^{\prime }$
. Clearly,
$V(G)\setminus U^{\prime }$
. Clearly,
![]() $N_G(x_1)\setminus \{x_2, \ldots , x_d\}$
is contained in
$N_G(x_1)\setminus \{x_2, \ldots , x_d\}$
is contained in
![]() $U^{\prime }$
. Then the above equality together with Lemma 3.2 and the induction hypothesis implies that
$U^{\prime }$
. Then the above equality together with Lemma 3.2 and the induction hypothesis implies that
Using inequalities (2) and (3), it is enough to prove that
For every integer k with
![]() $1\leq k\leq d-1$
, let
$1\leq k\leq d-1$
, let
![]() $J_k$
be the ideal generated by all the squarefree monomials of degree k on variables
$J_k$
be the ideal generated by all the squarefree monomials of degree k on variables
![]() $x_2, \ldots , x_d$
. We continue in the following steps.
$x_2, \ldots , x_d$
. We continue in the following steps.
Step 1. Let
![]() $1\leq k\leq d-2$
be a fixed integer and assume that
$1\leq k\leq d-2$
be a fixed integer and assume that
![]() $\{u_1, \ldots , u_t\}$
is the set of minimal monomial generators of
$\{u_1, \ldots , u_t\}$
is the set of minimal monomial generators of
![]() $x_1J_k$
. In particular, every
$x_1J_k$
. In particular, every
![]() $u_j$
is divisible by
$u_j$
is divisible by
![]() $x_1$
and
$x_1$
and
![]() $\mathrm {deg}(u_j)=k+1$
. For every integer j with
$\mathrm {deg}(u_j)=k+1$
. For every integer j with
![]() $1\leq j\leq t$
, we prove that
$1\leq j\leq t$
, we prove that
 $$ \begin{align*} & \operatorname{\mathrm{depth}} S/(I+x_1J_{k+1}+(u_1, \ldots, u_{j-1}))\\ & \geq\min\big\{\operatorname{\mathrm{depth}} S/(I+x_1J_{k+1}+(u_1, \ldots, u_j)), \alpha_2(G)-s+1\big\}. \end{align*} $$
$$ \begin{align*} & \operatorname{\mathrm{depth}} S/(I+x_1J_{k+1}+(u_1, \ldots, u_{j-1}))\\ & \geq\min\big\{\operatorname{\mathrm{depth}} S/(I+x_1J_{k+1}+(u_1, \ldots, u_j)), \alpha_2(G)-s+1\big\}. \end{align*} $$
(Note that for
![]() $j=1$
, we have
$j=1$
, we have
![]() $I+x_1J_{k+1}+(u_1, \ldots , u_{j-1})=I+x_1J_{k+1}$
.)
$I+x_1J_{k+1}+(u_1, \ldots , u_{j-1})=I+x_1J_{k+1}$
.)
Consider the following short exact sequence.
 $$ \begin{align*} 0 & \longrightarrow \frac{S}{(I+x_1J_{k+1}+(u_1, \ldots, u_{j-1})):u_j}\longrightarrow \frac{S}{I+x_1J_{k+1}+(u_1, \ldots, u_{j-1})}\\ & \longrightarrow \frac{S}{I+x_1J_{k+1}+(u_1, \ldots, u_j)}\longrightarrow 0. \end{align*} $$
$$ \begin{align*} 0 & \longrightarrow \frac{S}{(I+x_1J_{k+1}+(u_1, \ldots, u_{j-1})):u_j}\longrightarrow \frac{S}{I+x_1J_{k+1}+(u_1, \ldots, u_{j-1})}\\ & \longrightarrow \frac{S}{I+x_1J_{k+1}+(u_1, \ldots, u_j)}\longrightarrow 0. \end{align*} $$
As a consequence,
 $$ \begin{align*} & \operatorname{\mathrm{depth}} S/(I+x_1J_{k+1}+(u_1, \ldots, u_{j-1}))\geq\\& \min\big\{\operatorname{\mathrm{depth}} S/((I+x_1J_{k+1}+(u_1, \ldots, u_{j-1})):u_j), \operatorname{\mathrm{depth}} S/(I+x_1J_{k+1}+(u_1, \ldots, u_j))\big\}. \end{align*} $$
$$ \begin{align*} & \operatorname{\mathrm{depth}} S/(I+x_1J_{k+1}+(u_1, \ldots, u_{j-1}))\geq\\& \min\big\{\operatorname{\mathrm{depth}} S/((I+x_1J_{k+1}+(u_1, \ldots, u_{j-1})):u_j), \operatorname{\mathrm{depth}} S/(I+x_1J_{k+1}+(u_1, \ldots, u_j))\big\}. \end{align*} $$
Therefore, to complete this step, it is sufficient to show that
Set
For any
![]() $x_i\in U_j$
, the monomial
$x_i\in U_j$
, the monomial
![]() $x_iu_j$
is a squarefree monomial of degree
$x_iu_j$
is a squarefree monomial of degree
![]() $k+2$
. Hence,
$k+2$
. Hence,
![]() $x_iu_j$
belongs to
$x_iu_j$
belongs to
![]() $x_1J_{k+1}$
. This shows that
$x_1J_{k+1}$
. This shows that
 $$\begin{align*}(\text{the ideal generated by }\ U_j)\subseteq \big((x_1J_{k+1}+(u_1, \ldots, u_{j-1})):u_j\big).\end{align*}$$
$$\begin{align*}(\text{the ideal generated by }\ U_j)\subseteq \big((x_1J_{k+1}+(u_1, \ldots, u_{j-1})):u_j\big).\end{align*}$$
We show the reverse inclusion holds too.
Since
![]() $x_1J_{k+1}+(u_1, \ldots , u_{j-1})$
is a squarefree monomial ideal, it follows that
$x_1J_{k+1}+(u_1, \ldots , u_{j-1})$
is a squarefree monomial ideal, it follows that
 $$\begin{align*}\big((x_1J_{k+1}+(u_1, \ldots, u_{j-1})):u_j\big)\end{align*}$$
$$\begin{align*}\big((x_1J_{k+1}+(u_1, \ldots, u_{j-1})):u_j\big)\end{align*}$$
is also a squarefree monomial ideal. On the other hand, every monomial generator of
![]() $x_1J_{k+1}+(u_1, \ldots , u_{j-1})$
is a monomial over
$x_1J_{k+1}+(u_1, \ldots , u_{j-1})$
is a monomial over
![]() $x_1, \ldots , x_d$
. This implies that every monomial generator of
$x_1, \ldots , x_d$
. This implies that every monomial generator of
 $\big ((x_1J_{k+1}+(u_1, \ldots , u_{j-1})):u_j\big )$
is also a squarefree monomial over the variables
$\big ((x_1J_{k+1}+(u_1, \ldots , u_{j-1})):u_j\big )$
is also a squarefree monomial over the variables
![]() $x_1, \ldots , x_d$
. Assume that v is a minimal generator of
$x_1, \ldots , x_d$
. Assume that v is a minimal generator of
 $\big ((x_1J_{k+1}+(u_1, \ldots , u_{j-1})):u_j\big )$
. If v is not equal to any of the variables belonging to
$\big ((x_1J_{k+1}+(u_1, \ldots , u_{j-1})):u_j\big )$
. If v is not equal to any of the variables belonging to
![]() $U_j$
, then by definition of
$U_j$
, then by definition of
![]() $U_j$
, every variable dividing v, also divides
$U_j$
, every variable dividing v, also divides
![]() $u_j$
. As v is a squarefree monomial, we have
$u_j$
. As v is a squarefree monomial, we have
![]() $v\mid u_j$
. Since
$v\mid u_j$
. Since
we deduce that
 $$\begin{align*}u_j^2\in x_1J_{k+1}+(u_1, \ldots, u_{j-1}),\end{align*}$$
$$\begin{align*}u_j^2\in x_1J_{k+1}+(u_1, \ldots, u_{j-1}),\end{align*}$$
which implies that
because
![]() $x_1J_{k+1}+(u_1, \ldots , u_{j-1})$
is a squarefree monomial ideal. This is contradiction, as the degree of
$x_1J_{k+1}+(u_1, \ldots , u_{j-1})$
is a squarefree monomial ideal. This is contradiction, as the degree of
![]() $u_j$
is strictly less than the degree of any monomial in
$u_j$
is strictly less than the degree of any monomial in
![]() $x_1J_{k+1}$
and
$x_1J_{k+1}$
and
![]() $u_j\notin (u_1, \ldots , u_{j-1})$
. Hence,
$u_j\notin (u_1, \ldots , u_{j-1})$
. Hence,
 $$ \begin{align} \begin{array}{rl} \big((x_1J_{k+1}+(u_1, \ldots, u_{j-1})):u_j\big)=(\text{the ideal generated by} U_j). \end{array} \end{align} $$
$$ \begin{align} \begin{array}{rl} \big((x_1J_{k+1}+(u_1, \ldots, u_{j-1})):u_j\big)=(\text{the ideal generated by} U_j). \end{array} \end{align} $$
Let
![]() $W_j$
be the set of variables dividing
$W_j$
be the set of variables dividing
![]() $u_j$
. In other words,
$u_j$
. In other words,
![]() $W_j=\{x_1, \ldots , x_d\}\setminus U_j$
. We remind that for any pair of integers
$W_j=\{x_1, \ldots , x_d\}\setminus U_j$
. We remind that for any pair of integers
![]() $1\leq i, j\leq d$
, the vertices
$1\leq i, j\leq d$
, the vertices
![]() $x_i$
and
$x_i$
and
![]() $x_j$
are not adjacent in
$x_j$
are not adjacent in
![]() $H^{\prime }$
. Set
$H^{\prime }$
. Set
 $$\begin{align*}U_j^{\prime}:=\bigcup_{x_i\in W_j}N_{H^{\prime}}[x_i]\end{align*}$$
$$\begin{align*}U_j^{\prime}:=\bigcup_{x_i\in W_j}N_{H^{\prime}}[x_i]\end{align*}$$
and
 $$\begin{align*}U_j^{\prime\prime}:=\bigcup_{x_i\in W_j}N_{H^{\prime}}(x_i).\end{align*}$$
$$\begin{align*}U_j^{\prime\prime}:=\bigcup_{x_i\in W_j}N_{H^{\prime}}(x_i).\end{align*}$$
Using equality (4), we conclude that
 $$ \begin{align*} & \big((I+x_1J_{k+1}+(u_1, \ldots, u_{j-1})):u_j\big)\\ & =\big((I(H)^{(s)}+I(H^{\prime})+x_1J_{k+1}+(u_1, \ldots, u_{j-1})):u_j\big)\\ & =(I(H)^{(s)}:u_j)+I(H^{\prime}\setminus U_j^{\prime})+(\text{the ideal generated by }\ U_j\cup U_j^{\prime\prime})\\ & =\big(I\big(H\setminus (U_j\cup U_j^{\prime\prime})\big)^{(s)}:u_j\big)+I\big(H^{\prime}\setminus (U_j\cup U_j^{\prime})\big)\\ & +(\text{the ideal generated by } U_j\cup U_j^{\prime\prime}). \end{align*} $$
$$ \begin{align*} & \big((I+x_1J_{k+1}+(u_1, \ldots, u_{j-1})):u_j\big)\\ & =\big((I(H)^{(s)}+I(H^{\prime})+x_1J_{k+1}+(u_1, \ldots, u_{j-1})):u_j\big)\\ & =(I(H)^{(s)}:u_j)+I(H^{\prime}\setminus U_j^{\prime})+(\text{the ideal generated by }\ U_j\cup U_j^{\prime\prime})\\ & =\big(I\big(H\setminus (U_j\cup U_j^{\prime\prime})\big)^{(s)}:u_j\big)+I\big(H^{\prime}\setminus (U_j\cup U_j^{\prime})\big)\\ & +(\text{the ideal generated by } U_j\cup U_j^{\prime\prime}). \end{align*} $$
Set
 $H_j:=H\setminus (U_j\cup U_j^{\prime \prime })$
and
$H_j:=H\setminus (U_j\cup U_j^{\prime \prime })$
and
 $H_j^{\prime }:=H^{\prime }\setminus (U_j\cup U_j^{\prime })$
. Then
$H_j^{\prime }:=H^{\prime }\setminus (U_j\cup U_j^{\prime })$
. Then
![]() $H_j$
is a chordal graph, and
$H_j$
is a chordal graph, and
![]() $x_1$
is a simplicial vertex of
$x_1$
is a simplicial vertex of
![]() $H_j$
. It is also clear that
$H_j$
. It is also clear that
 $N_{H_j}[x_1]$
is the set of variables divining
$N_{H_j}[x_1]$
is the set of variables divining
![]() $u_j$
. It thus follows from [Reference Seyed Fakhari14, Lemma 2] and the above equalities that
$u_j$
. It thus follows from [Reference Seyed Fakhari14, Lemma 2] and the above equalities that
 $$ \begin{align*} & \big((I+x_1J_{k+1}+(u_1, \ldots, u_{j-1})):u_j\big)=I(H_j)^{(s-k)}+I(H_j^{\prime})\\ & +(\text{the ideal generated by }\ U_j\cup U_j^{\prime\prime}). \end{align*} $$
$$ \begin{align*} & \big((I+x_1J_{k+1}+(u_1, \ldots, u_{j-1})):u_j\big)=I(H_j)^{(s-k)}+I(H_j^{\prime})\\ & +(\text{the ideal generated by }\ U_j\cup U_j^{\prime\prime}). \end{align*} $$
This yields that
 $$\begin{align*}\operatorname{\mathrm{depth}} S/((I+x_1J_{k+1}+(u_1, \ldots, u_{j-1})):u_j)=\operatorname{\mathrm{depth}} S_j/(I(H_j)^{(s-k)}+I(H_j^{\prime})),\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{depth}} S/((I+x_1J_{k+1}+(u_1, \ldots, u_{j-1})):u_j)=\operatorname{\mathrm{depth}} S_j/(I(H_j)^{(s-k)}+I(H_j^{\prime})),\end{align*}$$
where
 $S_j=\mathbb {K}[x_i: 1\leq i\leq n, i\notin U_j\cup U_j^{\prime \prime }]$
. Let
$S_j=\mathbb {K}[x_i: 1\leq i\leq n, i\notin U_j\cup U_j^{\prime \prime }]$
. Let
![]() $G_j$
be the union of
$G_j$
be the union of
![]() $H_j$
and
$H_j$
and
 $H_j^{\prime }$
. Then
$H_j^{\prime }$
. Then
![]() $G_j$
is the induced subgraph of G on
$G_j$
is the induced subgraph of G on
 $V(G)\setminus (U_j\cup U_j^{\prime \prime })$
. We conclude from Lemma 3.2 (by considering the clique
$V(G)\setminus (U_j\cup U_j^{\prime \prime })$
. We conclude from Lemma 3.2 (by considering the clique
![]() $W_j$
) that
$W_j$
) that
where the last equality follows from the fact that
![]() $\mathrm {deg}(u_j)=k+1$
. Hence, the induction hypothesis implies that
$\mathrm {deg}(u_j)=k+1$
. Hence, the induction hypothesis implies that
 $$ \begin{align*} & \operatorname{\mathrm{depth}} S/((I+x_1J_{k+1}+(u_1, \ldots, u_{j-1})):u_j)=\operatorname{\mathrm{depth}} S_j/(I(H_j)^{(s-k)}+I(H_j^{\prime}))\\ & \geq \alpha_2(G_j)-(s-k)+1\geq \alpha_2(G)-s+1, \end{align*} $$
$$ \begin{align*} & \operatorname{\mathrm{depth}} S/((I+x_1J_{k+1}+(u_1, \ldots, u_{j-1})):u_j)=\operatorname{\mathrm{depth}} S_j/(I(H_j)^{(s-k)}+I(H_j^{\prime}))\\ & \geq \alpha_2(G_j)-(s-k)+1\geq \alpha_2(G)-s+1, \end{align*} $$
and this step is complete.
Step 2. Let
![]() $1\leq k\leq d-2$
be a fixed integer. By a repeated use of Step 1, we have
$1\leq k\leq d-2$
be a fixed integer. By a repeated use of Step 1, we have
 $$ \begin{align*} & \operatorname{\mathrm{depth}} S/(I+x_1J_{k+1}) \geq\min\big\{\operatorname{\mathrm{depth}} S/(I+x_1J_{k+1}+(u_1, \ldots, u_t)), \alpha_2(G)-s+1\big\}\\ & =\min\big\{\operatorname{\mathrm{depth}} S/(I+x_1J_k), \alpha_2(G)-s+1\big\}. \end{align*} $$
$$ \begin{align*} & \operatorname{\mathrm{depth}} S/(I+x_1J_{k+1}) \geq\min\big\{\operatorname{\mathrm{depth}} S/(I+x_1J_{k+1}+(u_1, \ldots, u_t)), \alpha_2(G)-s+1\big\}\\ & =\min\big\{\operatorname{\mathrm{depth}} S/(I+x_1J_k), \alpha_2(G)-s+1\big\}. \end{align*} $$
Step 3. It follows from Step 2 that
 $$ \begin{align*} & \operatorname{\mathrm{depth}} S/(I,x_1\cdots x_d)=\operatorname{\mathrm{depth}} S/(I+x_1J_{d-1})\\ & \geq\min\big\{\operatorname{\mathrm{depth}} S/(I+x_1J_{d-2}), \alpha_2(G)-s+1\big\}\\ & \geq\min\big\{\operatorname{\mathrm{depth}} S/(I+x_1J_{d-3}), \alpha_2(G)-s+1\big\}\\ & \geq \cdots \geq\min\big\{\operatorname{\mathrm{depth}} S/(I+x_1J_1), \alpha_2(G)-s+1\big\}. \end{align*} $$
$$ \begin{align*} & \operatorname{\mathrm{depth}} S/(I,x_1\cdots x_d)=\operatorname{\mathrm{depth}} S/(I+x_1J_{d-1})\\ & \geq\min\big\{\operatorname{\mathrm{depth}} S/(I+x_1J_{d-2}), \alpha_2(G)-s+1\big\}\\ & \geq\min\big\{\operatorname{\mathrm{depth}} S/(I+x_1J_{d-3}), \alpha_2(G)-s+1\big\}\\ & \geq \cdots \geq\min\big\{\operatorname{\mathrm{depth}} S/(I+x_1J_1), \alpha_2(G)-s+1\big\}. \end{align*} $$
In particular,
 $$ \begin{align} \begin{array}{rl} \operatorname{\mathrm{depth}} S/(I,x_1\cdots x_d)\geq\min\big\{\operatorname{\mathrm{depth}} S/\big(I+(x_1x_2, x_1x_3, \ldots, x_1x_d)\big), \alpha_2(G)-s+1\big\}. \end{array} \end{align} $$
$$ \begin{align} \begin{array}{rl} \operatorname{\mathrm{depth}} S/(I,x_1\cdots x_d)\geq\min\big\{\operatorname{\mathrm{depth}} S/\big(I+(x_1x_2, x_1x_3, \ldots, x_1x_d)\big), \alpha_2(G)-s+1\big\}. \end{array} \end{align} $$
Step 4. Let L be the graph obtained from H, by deleting the edges
![]() $x_1x_2, \ldots , x_1x_d$
. Then L is the disjoint union of
$x_1x_2, \ldots , x_1x_d$
. Then L is the disjoint union of
![]() $H\setminus x_1$
and the isolated vertex
$H\setminus x_1$
and the isolated vertex
![]() $x_1$
. In particular, L is a chordal graph. Also, let
$x_1$
. In particular, L is a chordal graph. Also, let
![]() $L^{\prime }$
be the graph obtained from
$L^{\prime }$
be the graph obtained from
![]() $H^{\prime }$
, by adding the edges
$H^{\prime }$
, by adding the edges
![]() $x_1x_2, \ldots , x_1x_d$
. Then
$x_1x_2, \ldots , x_1x_d$
. Then
It follows from [Reference Seyed Fakhari15, Lemma 3.2] and the induction hypothesis that
 $$ \begin{align*} & \operatorname{\mathrm{depth}} S/(I+(x_1x_2, x_1x_3, \ldots, x_1x_d))\\ & =\operatorname{\mathrm{depth}} S/(I(H)^{(s)}+I(H^{\prime})+(x_1x_2, x_1x_3, \ldots, x_1x_d)\big)\\ & =\operatorname{\mathrm{depth}} S/((I(L)^{(s)}+I(L^{\prime})))\geq \alpha_2(G)-s+1. \end{align*} $$
$$ \begin{align*} & \operatorname{\mathrm{depth}} S/(I+(x_1x_2, x_1x_3, \ldots, x_1x_d))\\ & =\operatorname{\mathrm{depth}} S/(I(H)^{(s)}+I(H^{\prime})+(x_1x_2, x_1x_3, \ldots, x_1x_d)\big)\\ & =\operatorname{\mathrm{depth}} S/((I(L)^{(s)}+I(L^{\prime})))\geq \alpha_2(G)-s+1. \end{align*} $$
Finally, inequality (5) implies that
Now, inequalities (2), (3), and (6) complete the proof of the proposition.
The following theorem is the main result of this section and follows easily from Proposition 3.3.
Theorem 3.4. Let G be a chordal graph. Then for every integer
![]() $s\geq 1$
, we have
$s\geq 1$
, we have
 $$\begin{align*}\operatorname{\mathrm{depth}} S/(I(G)^{(s)})\geq\alpha_2(G)-s+1.\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{depth}} S/(I(G)^{(s)})\geq\alpha_2(G)-s+1.\end{align*}$$
Proof. The assertion follows from Proposition 3.3 by substituting
![]() $H=G$
and
$H=G$
and
![]() $H^{\prime }=\emptyset $
.
$H^{\prime }=\emptyset $
.
4 Second symbolic power of edge ideals
The aim of this section is to show that inequality (‡) is true for
![]() $s=2$
(Theorem 4.2). To prove this result, we need to bound the depth of ideals of the form
$s=2$
(Theorem 4.2). To prove this result, we need to bound the depth of ideals of the form
 $\big (I(G)^{(k)}:xy\big )$
, where
$\big (I(G)^{(k)}:xy\big )$
, where
![]() $xy$
is an edge of G. To achieve this goal, we will use the following lemma in the case of
$xy$
is an edge of G. To achieve this goal, we will use the following lemma in the case of
![]() $k=2$
.
$k=2$
.
Lemma 4.1. Let G be a graph and
![]() $xy$
be an edge of G. Then for any integer
$xy$
be an edge of G. Then for any integer
![]() $k\geq 2$
, we have
$k\geq 2$
, we have
 $$\begin{align*}\big(I(G)^{(k)}:xy\big)=\big(I(G)^{(k-1)}:x\big)\cap \big(I(G)^{(k-1)}:y\big).\end{align*}$$
$$\begin{align*}\big(I(G)^{(k)}:xy\big)=\big(I(G)^{(k-1)}:x\big)\cap \big(I(G)^{(k-1)}:y\big).\end{align*}$$
Proof. Let u be a monomial in
 $\big (I(G)^{(k)}:xy\big )$
. Then
$\big (I(G)^{(k)}:xy\big )$
. Then
 $uxy\in I(G)^{(k)}$
. Clearly, this implies that
$uxy\in I(G)^{(k)}$
. Clearly, this implies that
 $ux\in I(G)^{(k-1)}$
. Therefore,
$ux\in I(G)^{(k-1)}$
. Therefore,
 $u\in \big (I(G)^{(k-1)}:x\big )$
. Similarly, u belongs to
$u\in \big (I(G)^{(k-1)}:x\big )$
. Similarly, u belongs to
 $\big (I(G)^{(k-1)}:y\big )$
. Hence,
$\big (I(G)^{(k-1)}:y\big )$
. Hence,
 $$\begin{align*}\big(I(G)^{(k)}:xy\big)\subseteq\big(I(G)^{(k-1)}:x\big)\cap \big(I(G)^{(k-1)}:y\big).\end{align*}$$
$$\begin{align*}\big(I(G)^{(k)}:xy\big)\subseteq\big(I(G)^{(k-1)}:x\big)\cap \big(I(G)^{(k-1)}:y\big).\end{align*}$$
To prove the reverse inclusion, let v be a monomial in
 $$\begin{align*}\big(I(G)^{(k-1)}:x\big)\cap \big(I(G)^{(k-1)}:y\big).\end{align*}$$
$$\begin{align*}\big(I(G)^{(k-1)}:x\big)\cap \big(I(G)^{(k-1)}:y\big).\end{align*}$$
We must show that
 $vxy\in I(G)^{(k)}$
. It is enough to prove that for any minimal vertex cover C of G, we have
$vxy\in I(G)^{(k)}$
. It is enough to prove that for any minimal vertex cover C of G, we have
 $vxy\in \mathfrak {p}_C^k$
. So, let C be a minimal vertex cover of G. It follows from
$vxy\in \mathfrak {p}_C^k$
. So, let C be a minimal vertex cover of G. It follows from
![]() $xy\in E(G)$
that C contains at least one of the vertices x and y. Without loss of generality, suppose
$xy\in E(G)$
that C contains at least one of the vertices x and y. Without loss of generality, suppose
![]() $x\in C$
. Since
$x\in C$
. Since
 $v\in \big (I(G)^{(k-1)}:y\big )$
, we have
$v\in \big (I(G)^{(k-1)}:y\big )$
, we have
 $vy\in I(G)^{(k-1)}\subseteq \mathfrak {p}_C^{k-1}$
. This together with
$vy\in I(G)^{(k-1)}\subseteq \mathfrak {p}_C^{k-1}$
. This together with
![]() $x\in \mathfrak {p}_C$
implies that
$x\in \mathfrak {p}_C$
implies that
 $vxy\in \mathfrak {p}_C^k$
.
$vxy\in \mathfrak {p}_C^k$
.
The following theorem is the second main result of this paper.
Theorem 4.2. For any graph G, we have
 $$\begin{align*}\operatorname{\mathrm{depth}} S/I(G)^{(2)}\geq \alpha_2(G)-1.\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{depth}} S/I(G)^{(2)}\geq \alpha_2(G)-1.\end{align*}$$
Proof. Set
![]() $I:=I(G)$
and let
$I:=I(G)$
and let
![]() $G(I)=\{u_1, \ldots , u_m\}$
be the set of minimal monomial generators of I. For every integer i with
$G(I)=\{u_1, \ldots , u_m\}$
be the set of minimal monomial generators of I. For every integer i with
![]() $1\leq i\leq m$
consider the short exact sequence
$1\leq i\leq m$
consider the short exact sequence
 $$ \begin{align*} 0 & \longrightarrow \frac{S}{(I^{(2)}+(u_1, \ldots, u_{i-1})):u_i}\longrightarrow \frac{S}{I^{(2)}+(u_1, \ldots, u_{i-1})}\\ & \longrightarrow \frac{S}{I^{(2)}+(u_1, \ldots, u_i)}\longrightarrow 0, \end{align*} $$
$$ \begin{align*} 0 & \longrightarrow \frac{S}{(I^{(2)}+(u_1, \ldots, u_{i-1})):u_i}\longrightarrow \frac{S}{I^{(2)}+(u_1, \ldots, u_{i-1})}\\ & \longrightarrow \frac{S}{I^{(2)}+(u_1, \ldots, u_i)}\longrightarrow 0, \end{align*} $$
where for
![]() $i=1$
, the ideal
$i=1$
, the ideal
![]() $(u_1, \ldots , u_{i-1})$
is the zero ideal. It follows from depth Lemma [Reference Bruns and Herzog2, Proposition 1.2.9] that
$(u_1, \ldots , u_{i-1})$
is the zero ideal. It follows from depth Lemma [Reference Bruns and Herzog2, Proposition 1.2.9] that
 $$ \begin{align*} & \operatorname{\mathrm{depth}} S/(I^{(2)}+(u_1, \ldots, u_{i-1}))\\ & \geq \min\big\{\operatorname{\mathrm{depth}} S/((I^{(2)}+(u_1, \ldots, u_{i-1})):u_i), \operatorname{\mathrm{depth}} S/(I^{(2)}+(u_1, \ldots, u_i))\big\}. \end{align*} $$
$$ \begin{align*} & \operatorname{\mathrm{depth}} S/(I^{(2)}+(u_1, \ldots, u_{i-1}))\\ & \geq \min\big\{\operatorname{\mathrm{depth}} S/((I^{(2)}+(u_1, \ldots, u_{i-1})):u_i), \operatorname{\mathrm{depth}} S/(I^{(2)}+(u_1, \ldots, u_i))\big\}. \end{align*} $$
Using the above inequalities inductively, we have
 $$ \begin{align*} & \operatorname{\mathrm{depth}} S/I^{(2)}\\ & \geq\min\bigg\{\operatorname{\mathrm{depth}} S/(I^{(2)}+I), \min\big\{\operatorname{\mathrm{depth}} S/((I^{(2)}+(u_1, \ldots, u_{i-1})):u_i)\mid 1\leq i\leq m\big\}\bigg\}\\ & =\min\big\{\operatorname{\mathrm{depth}} S/I, \operatorname{\mathrm{depth}} S/((I^{(2)}+(u_1, \ldots, u_{i-1})):u_i)\mid 1\leq i\leq m\big\}\\ & \geq\min\big\{\alpha_2(G), \operatorname{\mathrm{depth}} S/((I^{(2)}+(u_1, \ldots, u_{i-1})):u_i)\mid 1\leq i\leq m\big\}, \end{align*} $$
$$ \begin{align*} & \operatorname{\mathrm{depth}} S/I^{(2)}\\ & \geq\min\bigg\{\operatorname{\mathrm{depth}} S/(I^{(2)}+I), \min\big\{\operatorname{\mathrm{depth}} S/((I^{(2)}+(u_1, \ldots, u_{i-1})):u_i)\mid 1\leq i\leq m\big\}\bigg\}\\ & =\min\big\{\operatorname{\mathrm{depth}} S/I, \operatorname{\mathrm{depth}} S/((I^{(2)}+(u_1, \ldots, u_{i-1})):u_i)\mid 1\leq i\leq m\big\}\\ & \geq\min\big\{\alpha_2(G), \operatorname{\mathrm{depth}} S/((I^{(2)}+(u_1, \ldots, u_{i-1})):u_i)\mid 1\leq i\leq m\big\}, \end{align*} $$
where the last inequality follows from Corollary 2.2. Hence, it is enough to show that
 $$\begin{align*}\operatorname{\mathrm{depth}} S/((I^{(2)}+(u_1, \ldots, u_{i-1})):u_i)\geq \alpha_2(G)-1,\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{depth}} S/((I^{(2)}+(u_1, \ldots, u_{i-1})):u_i)\geq \alpha_2(G)-1,\end{align*}$$
for every integer i with
![]() $1\leq i\leq m$
.
$1\leq i\leq m$
.
Fix an integer i with
![]() $1\leq i\leq m$
and assume that
$1\leq i\leq m$
and assume that
![]() $u_i=xy$
. By [Reference Banerjee1, Theorem 4.12], for every pair of integers
$u_i=xy$
. By [Reference Banerjee1, Theorem 4.12], for every pair of integers
![]() $1\leq j< i\leq m$
, one of the following conditions holds.
$1\leq j< i\leq m$
, one of the following conditions holds.
-
(i)
 $(u_j:u_i) \subseteq (I^2:u_i)\subseteq (I^{(2)}:u_i)$
; or
$(u_j:u_i) \subseteq (I^2:u_i)\subseteq (I^{(2)}:u_i)$
; or -
(ii) there exists an integer
 $k\leq i-1$
such that
$k\leq i-1$
such that
 $(u_k:u_i)$
is generated by a variable, and
$(u_k:u_i)$
is generated by a variable, and
 $(u_j:u_i)\subseteq (u_k:u_i)$
.
$(u_j:u_i)\subseteq (u_k:u_i)$
.
We know from (i) and (ii) above that
 $$ \begin{align} \begin{array}{rl} \big((I^{(2)}+ (u_1, \ldots, u_{i-1})):u_i\big)=(I^{(2)}:u_i)+(\text{some variables}). \end{array} \end{align} $$
$$ \begin{align} \begin{array}{rl} \big((I^{(2)}+ (u_1, \ldots, u_{i-1})):u_i\big)=(I^{(2)}:u_i)+(\text{some variables}). \end{array} \end{align} $$
Let A be the set of variables belonging to
 $\big ((I^{(2)}+ (u_1, \ldots , u_{i-1})):u_i\big )$
. Assume that
$\big ((I^{(2)}+ (u_1, \ldots , u_{i-1})):u_i\big )$
. Assume that
![]() $x\in A$
. This means that
$x\in A$
. This means that
![]() $x^2y$
belongs to the ideal
$x^2y$
belongs to the ideal
 $I^{(2)}+(u_1, \ldots , u_{i-1})$
. Since
$I^{(2)}+(u_1, \ldots , u_{i-1})$
. Since
![]() $u_1, \ldots , u_{i-1}$
do not divide
$u_1, \ldots , u_{i-1}$
do not divide
![]() $x^2y$
, we deduce that
$x^2y$
, we deduce that
 $x^2y\in I(G)^{(2)}$
. But this is a contradiction, as
$x^2y\in I(G)^{(2)}$
. But this is a contradiction, as
![]() $C:=V(G)\setminus \{x\}$
is a vertex cover of G with
$C:=V(G)\setminus \{x\}$
is a vertex cover of G with
 $x^2y\notin \mathfrak {p}_C^2$
. Therefore,
$x^2y\notin \mathfrak {p}_C^2$
. Therefore,
![]() $x\notin A$
. Similarly,
$x\notin A$
. Similarly,
![]() $y\notin A$
. It follows from
$y\notin A$
. It follows from
![]() $x,y\notin A$
and equality (7) that
$x,y\notin A$
and equality (7) that
 $$ \begin{align*} & \big((I^{(2)}+ (u_1, \ldots, u_{i-1})):u_i\big)=\big(I^{(2)}:u_i\big)+(\text{the ideal generated by } A)\\ & =\big(I^{(2)}+ (\text{the ideal generated by } A)):u_i\big)\\ & =\big(I(G\setminus A)^{(2)}+(\text{the ideal generated by } A)):u_i\big)\\ & =\big(I(G\setminus A)^{(2)}:u_i\big)+(\text{the ideal generated by } A). \end{align*} $$
$$ \begin{align*} & \big((I^{(2)}+ (u_1, \ldots, u_{i-1})):u_i\big)=\big(I^{(2)}:u_i\big)+(\text{the ideal generated by } A)\\ & =\big(I^{(2)}+ (\text{the ideal generated by } A)):u_i\big)\\ & =\big(I(G\setminus A)^{(2)}+(\text{the ideal generated by } A)):u_i\big)\\ & =\big(I(G\setminus A)^{(2)}:u_i\big)+(\text{the ideal generated by } A). \end{align*} $$
Therefore,
 $$ \begin{align} \begin{array}{rl} \operatorname{\mathrm{depth}} S/((I^{(2)}+ (u_1, \ldots, u_{i-1})):u_i)=\operatorname{\mathrm{depth}} S_A/(I(G\setminus A)^{(2)}:u_i), \end{array} \end{align} $$
$$ \begin{align} \begin{array}{rl} \operatorname{\mathrm{depth}} S/((I^{(2)}+ (u_1, \ldots, u_{i-1})):u_i)=\operatorname{\mathrm{depth}} S_A/(I(G\setminus A)^{(2)}:u_i), \end{array} \end{align} $$
where
![]() $S_A=\mathbb {K}[x_i: 1\leq i\leq n, x_i\notin A]$
. It follows from Lemma 4.1 that
$S_A=\mathbb {K}[x_i: 1\leq i\leq n, x_i\notin A]$
. It follows from Lemma 4.1 that
 $$\begin{align*}(I(G\setminus A)^{(2)}:u_i)=(I(G\setminus A):x)\cap(I(G\setminus A):y).\end{align*}$$
$$\begin{align*}(I(G\setminus A)^{(2)}:u_i)=(I(G\setminus A):x)\cap(I(G\setminus A):y).\end{align*}$$
Consider the following short exact sequence.
 $$ \begin{align*} 0 & \longrightarrow \frac{S_A}{(I(G\setminus A)^{(2)}:u_i)}\longrightarrow \frac{S_A}{(I(G\setminus A):x)}\oplus\frac{S_A}{(I(G\setminus A):y)}\\ & \longrightarrow \frac{S_A}{(I(G\setminus A):x)+(I(G\setminus A):y)}\longrightarrow 0. \end{align*} $$
$$ \begin{align*} 0 & \longrightarrow \frac{S_A}{(I(G\setminus A)^{(2)}:u_i)}\longrightarrow \frac{S_A}{(I(G\setminus A):x)}\oplus\frac{S_A}{(I(G\setminus A):y)}\\ & \longrightarrow \frac{S_A}{(I(G\setminus A):x)+(I(G\setminus A):y)}\longrightarrow 0. \end{align*} $$
Applying depth lemma [Reference Bruns and Herzog2, Proposition 1.2.9] on the above exact sequence, it suffices to prove that
-
(a)
 $ \operatorname {\mathrm {depth}} S_A/(I(G\setminus A):x) \geq \alpha _2(G)-1$
,
$ \operatorname {\mathrm {depth}} S_A/(I(G\setminus A):x) \geq \alpha _2(G)-1$
, -
(b)
 $ \operatorname {\mathrm {depth}} S_A/(I(G\setminus A):y) \geq \alpha _2(G)-1$
, and
$ \operatorname {\mathrm {depth}} S_A/(I(G\setminus A):y) \geq \alpha _2(G)-1$
, and -
(c)
 $ \operatorname {\mathrm {depth}} S_A/((I(G\setminus A):x)+(I(G\setminus A):y))\geq \alpha _2(G)-2$
.
$ \operatorname {\mathrm {depth}} S_A/((I(G\setminus A):x)+(I(G\setminus A):y))\geq \alpha _2(G)-2$
.
To prove (a), note that
 $$ \begin{align*} (I(G\setminus A):x)&=I(G\setminus(A\cup N_{G\setminus A}[x]))+(\text{the ideal generated by }\ N_{G\setminus A}(x))\\ & =I(G\setminus(A\cup N_G[x]))+(\text{the ideal generated by }\ N_{G\setminus A}(x)). \end{align*} $$
$$ \begin{align*} (I(G\setminus A):x)&=I(G\setminus(A\cup N_{G\setminus A}[x]))+(\text{the ideal generated by }\ N_{G\setminus A}(x))\\ & =I(G\setminus(A\cup N_G[x]))+(\text{the ideal generated by }\ N_{G\setminus A}(x)). \end{align*} $$
Hence,
where
![]() $S^{\prime }=\mathbb {K}[x_i: 1\leq i\leq n, x_i\notin A\cup N_G(x)]$
. Obviously, x is a regular element of
$S^{\prime }=\mathbb {K}[x_i: 1\leq i\leq n, x_i\notin A\cup N_G(x)]$
. Obviously, x is a regular element of
![]() $S^{\prime }/I(G\setminus (A\cup N_G[x]))$
. Therefore, Corollary 2.2 implies that
$S^{\prime }/I(G\setminus (A\cup N_G[x]))$
. Therefore, Corollary 2.2 implies that
Assume that
![]() $A\subseteq N_G(x)\cup N_G(y)$
. It then follows from Lemma 3.1 that
$A\subseteq N_G(x)\cup N_G(y)$
. It then follows from Lemma 3.1 that
Hence, we conclude from equality (9) and inequality (10) that
Thus, to complete the proof of (a), we only need to show that
![]() $A\subseteq N_G(x)\cup N_G(y)$
.
$A\subseteq N_G(x)\cup N_G(y)$
.
Let z be an arbitrary variable in A and suppose
![]() $z\notin N_G(x)\cup N_G(y)$
. Then the only edge dividing
$z\notin N_G(x)\cup N_G(y)$
. Then the only edge dividing
![]() $zu_i=zxy$
is
$zu_i=zxy$
is
![]() $u_i$
. In particular,
$u_i$
. In particular,
 $$ \begin{align} \begin{array}{rl} z\notin \big((u_1, \ldots, u_{i-1}):u_i). \end{array} \end{align} $$
$$ \begin{align} \begin{array}{rl} z\notin \big((u_1, \ldots, u_{i-1}):u_i). \end{array} \end{align} $$
Moreover, since
![]() $\{z,x\}$
is an independent subset of G, we conclude that
$\{z,x\}$
is an independent subset of G, we conclude that
![]() $C^{\prime }=V(G)\setminus \{z,x\}$
is a vertex cover of G with
$C^{\prime }=V(G)\setminus \{z,x\}$
is a vertex cover of G with
 $zu_i=zxy\notin \mathfrak {p}_{C^{\prime }}^2$
. Thus,
$zu_i=zxy\notin \mathfrak {p}_{C^{\prime }}^2$
. Thus,
 $zu_i\notin I^{(2)}$
. This means that
$zu_i\notin I^{(2)}$
. This means that
 $z\notin (I^{(2)}:u_i)$
. This, together with (11) implies that
$z\notin (I^{(2)}:u_i)$
. This, together with (11) implies that
 $$\begin{align*}z\notin\big((I^{(2)}, u_1, \ldots, u_{i-1}):u_i\big),\end{align*}$$
$$\begin{align*}z\notin\big((I^{(2)}, u_1, \ldots, u_{i-1}):u_i\big),\end{align*}$$
which is a contradiction. Therefore,
![]() $z\in N_G(x)\cup N_G(y)$
. Hence,
$z\in N_G(x)\cup N_G(y)$
. Hence,
![]() $A\subseteq N_G(x)\cup N_G(y)$
and this completes the proof of (a). The proof of (b) is similar to the proof of (a). We now prove (c).
$A\subseteq N_G(x)\cup N_G(y)$
and this completes the proof of (a). The proof of (b) is similar to the proof of (a). We now prove (c).
Note that
 $$ \begin{align*} & (I(G\setminus A):x)+(I(G\setminus A):y)\\ & =I(G\setminus(A\cup N_{G\setminus A}[x]\cup N_{G\setminus A}[y]))+(\text{the ideal generated by } N_{G\setminus A}[x]\cup N_{G\setminus A}[y])\\ & =I(G\setminus(A\cup N_G[x]\cup N_G[y]))+(\text{the ideal generated by }\ N_{G\setminus A}[x]\cup N_{G\setminus A}[y])\\ & =I(G\setminus(N_G[x]\cup N_G[y]))+(\text{the ideal generated by }\ N_{G\setminus A}[x]\cup N_{G\setminus A}[y]), \end{align*} $$
$$ \begin{align*} & (I(G\setminus A):x)+(I(G\setminus A):y)\\ & =I(G\setminus(A\cup N_{G\setminus A}[x]\cup N_{G\setminus A}[y]))+(\text{the ideal generated by } N_{G\setminus A}[x]\cup N_{G\setminus A}[y])\\ & =I(G\setminus(A\cup N_G[x]\cup N_G[y]))+(\text{the ideal generated by }\ N_{G\setminus A}[x]\cup N_{G\setminus A}[y])\\ & =I(G\setminus(N_G[x]\cup N_G[y]))+(\text{the ideal generated by }\ N_{G\setminus A}[x]\cup N_{G\setminus A}[y]), \end{align*} $$
where the last equality follows from
![]() $A\subseteq N_G(x)\cup N_G(y)$
. We conclude that
$A\subseteq N_G(x)\cup N_G(y)$
. We conclude that
where
 $S^{\prime \prime }=\mathbb {K}\big [x_i: 1\leq i\leq n, x_i\notin N_G[x]\cup N_G[y]\big ]$
. Using Corollary 2.2 and Lemma 3.1, we deuce that
$S^{\prime \prime }=\mathbb {K}\big [x_i: 1\leq i\leq n, x_i\notin N_G[x]\cup N_G[y]\big ]$
. Using Corollary 2.2 and Lemma 3.1, we deuce that
Finally, the assertion of (c) follows from equality (12) and the above inequality. This completes the proof of the theorem.
Acknowledgment
The author would like to thank the referee for a careful reading of the paper and for valuable comments.