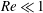1 Introduction
Collective behaviours are ubiquitous in biological and natural systems with large numbers of individuals acting with or being influenced by other individuals (Vicsek & Zafeiris Reference Vicsek and Zafeiris2012). Of particular interest are collections of actively moving bodies in a fluid where the flow-mediated interaction plays a crucial role. Biological examples include active collective locomotion with low Reynolds number (
![]() $Re\ll 1$
), e.g. swimming micro-organisms (Saintillan & Shelley Reference Saintillan and Shelley2008; Lauga & Powers Reference Lauga and Powers2009; Zhang et al.
Reference Zhang, Beer, Florin and Swinney2010) and animal collectives with
$Re\ll 1$
), e.g. swimming micro-organisms (Saintillan & Shelley Reference Saintillan and Shelley2008; Lauga & Powers Reference Lauga and Powers2009; Zhang et al.
Reference Zhang, Beer, Florin and Swinney2010) and animal collectives with
![]() $Re\sim 10^{2}{-}10^{6}$
, such as insect swarms (Kelley & Ouellette Reference Kelley and Ouellette2013), fish schools (Weihs Reference Weihs1973) and bird flocks (Portugal et al.
Reference Portugal, Hubel, Fritz, Heese, Trobe, Voelkl, Hailes, Wilson and Usherwood2014), in which the long-lasting inertial effects lead to more complex flows (Ramananarivo et al.
Reference Ramananarivo, Fang, Oza, Zhang and Ristroph2016).
$Re\sim 10^{2}{-}10^{6}$
, such as insect swarms (Kelley & Ouellette Reference Kelley and Ouellette2013), fish schools (Weihs Reference Weihs1973) and bird flocks (Portugal et al.
Reference Portugal, Hubel, Fritz, Heese, Trobe, Voelkl, Hailes, Wilson and Usherwood2014), in which the long-lasting inertial effects lead to more complex flows (Ramananarivo et al.
Reference Ramananarivo, Fang, Oza, Zhang and Ristroph2016).
For the animal collectives, considerable attention has been paid to the social traits of collective behaviours, such as foraging, reproduction, and defence from predators (Parrish & Edelstein-Keshet Reference Parrish and Edelstein-Keshet1999; Couzin et al. Reference Couzin, Krause, Franks and Levin2005). However, several issues about the role of hydrodynamics in collective locomotion are still open questions. One important and intriguing issue is the role of flows on the emergence of the collective pattern. The fluid dynamicist Lighthill (Reference Lighthill1975) once conjectured that the orderly patterns could arise spontaneously as a consequence of passive flow-mediated interactions, without the need for ‘elaborate control mechanisms’. This hypothesis, which is referred to as the ‘Lighthill conjecture’, has never been tested for groups on a larger scale (Zhu, He & Zhang Reference Zhu, He and Zhang2014; Ramananarivo et al. Reference Ramananarivo, Fang, Oza, Zhang and Ristroph2016). The other issue concerns the hydrodynamic advantage. It is plausible that the individuals in collective locomotion are energy efficient due to favourable flow interactions that occur in specific formations (Weihs Reference Weihs1973; Portugal et al. Reference Portugal, Hubel, Fritz, Heese, Trobe, Voelkl, Hailes, Wilson and Usherwood2014). However, quantitative information is limited because it is difficult to measure in experiments.
Because the two-body system is the simplest individual-level model, two passively flapping bodies (Ristroph & Zhang Reference Ristroph and Zhang2008; Alben Reference Alben2009) and actively flapping flags or hydrofoils (Boschitsch, Dewey & Smits Reference Boschitsch, Dewey and Smits2014; Uddin, Huang & Sung Reference Uddin, Huang and Sung2015) were studied to investigate their collective behaviour. However, in these studies the individuals were held fixed in the flow. A more realistic self-propelled model for an actively moving body was developed for further study (Alben & Shelley Reference Alben and Shelley2005; Hua, Zhu & Lu Reference Hua, Zhu and Lu2013). Recently the hydrodynamic behaviour of two self-propelled flapping filaments was studied numerically (Zhu et al. Reference Zhu, He and Zhang2014). The results show that multiple stable tandem configurations can be formed passively from vortex-body interactions (Zhu et al. Reference Zhu, He and Zhang2014). The ‘vortex locking’ mechanism was proposed, i.e., stable configurations can be spontaneously formed by locking the trajectories onto the vortex centres (Zhu et al. Reference Zhu, He and Zhang2014).
Moreover, the collective locomotion dynamics of two flapping wings swimming in a tandem array was also studied experimentally (Becker et al. Reference Becker, Masoud, Newbolt, Shelley and Ristroph2015; Ramananarivo et al. Reference Ramananarivo, Fang, Oza, Zhang and Ristroph2016). Becker et al. (Reference Becker, Masoud, Newbolt, Shelley and Ristroph2015) have shown that arrays of flapping and self-propelled wings select slow or fast modes due to constructive or destructive wing–wake interactions, respectively. In the study, they chose a periodic boundary condition horizontally, which implicitly means that there exist infinite plate interactions. In this way, each wing swims within the wakes of others. However, the horizontal spacing between the two plates was fixed so the configuration was imposed in the study of Becker et al. (Reference Becker, Masoud, Newbolt, Shelley and Ristroph2015). Hence, the set-up and physical mechanism are significantly different from that in Zhu et al. (Reference Zhu, He and Zhang2014). Ramananarivo et al. (Reference Ramananarivo, Fang, Oza, Zhang and Ristroph2016) have shown that for two flapping plates, collective locomotion at enhanced speed and in orderly formations can emerge from flow interactions alone. Direct measurements of hydrodynamic forces acting on the follower reveal springlike restoring forces that maintain group cohesion (Ramananarivo et al. Reference Ramananarivo, Fang, Oza, Zhang and Ristroph2016). The idea of a hydrodynamic potential is also introduced in the study of Ramananarivo et al. (Reference Ramananarivo, Fang, Oza, Zhang and Ristroph2016). It is a useful tool which we adopted here to analyse schooling stability. They noted a speed increase for pairs relative to a single body, indicating an influence on the leader by the follower. When the gap spacing is large, lack of flow feedback to the leading wing from the follower makes it effectively an isolated swimmer (Ramananarivo et al. Reference Ramananarivo, Fang, Oza, Zhang and Ristroph2016). To some extent, these studies support the perspective of the Lighthill conjecture for the two-body system. However, it is still unknown whether and to what extent the Lighthill conjecture is valid for a larger group.
To further verify the Lighthill conjecture, here we numerically investigate the hydrodynamic schooling of multi-body self-propelled systems consisting of flexible flapping plates. Self-propulsion is induced by the prescribed heave motion at the leading edge of each plate but whose longitudinal swimming is free. Two orderly schooling states are identified. The hydrodynamic interaction is analysed to reveal the mechanism. In addition, the schooling performances of the two states, including the cruising speed and swimming efficiency, are also discussed.
The remainder of this paper is organized as follows. The physical problem and mathematical formulation are presented in § 2. The numerical method and validation are described in § 3. Detailed results are discussed in § 4 and concluding remarks are addressed in § 5.
2 Physical problem and mathematical formulation
Here a self-propelled system consisting of
![]() $N$
flapping flexible plates in a tandem configuration (see figure 1
a) is investigated. Plates with identical length
$N$
flapping flexible plates in a tandem configuration (see figure 1
a) is investigated. Plates with identical length
![]() $L$
are immersed in an initially stationary viscous incompressible fluid. The leading edges of the plates are forced to heave sinusoidally and in phase with identical amplitude
$L$
are immersed in an initially stationary viscous incompressible fluid. The leading edges of the plates are forced to heave sinusoidally and in phase with identical amplitude
![]() $A$
and frequency
$A$
and frequency
![]() $f$
in the lateral direction. The forced vertical motions of the leading edges are prescribed by
$f$
in the lateral direction. The forced vertical motions of the leading edges are prescribed by
![]() $y(t)=A\cos (2\unicode[STIX]{x03C0}ft)$
with zero active pitching angle. The longitudinal distance between the leading edges of plates
$y(t)=A\cos (2\unicode[STIX]{x03C0}ft)$
with zero active pitching angle. The longitudinal distance between the leading edges of plates
![]() $i$
and
$i$
and
![]() $j$
is denoted by
$j$
is denoted by
![]() $D_{i,j}$
.
$D_{i,j}$
.
![]() $G_{i,i+1}$
denotes the longitudinal distance between the trailing edge of the plate and the leading edge of its following plate, i.e.,
$G_{i,i+1}$
denotes the longitudinal distance between the trailing edge of the plate and the leading edge of its following plate, i.e.,
![]() $G_{i,i+1}=D_{i,i+1}-1$
. In all simulations, if not specified, initially the plates are equally spaced with
$G_{i,i+1}=D_{i,i+1}-1$
. In all simulations, if not specified, initially the plates are equally spaced with
![]() $G_{i,i+1}=G_{0}$
, where
$G_{i,i+1}=G_{0}$
, where
![]() $i=1,2,\ldots N-1$
.
$i=1,2,\ldots N-1$
.
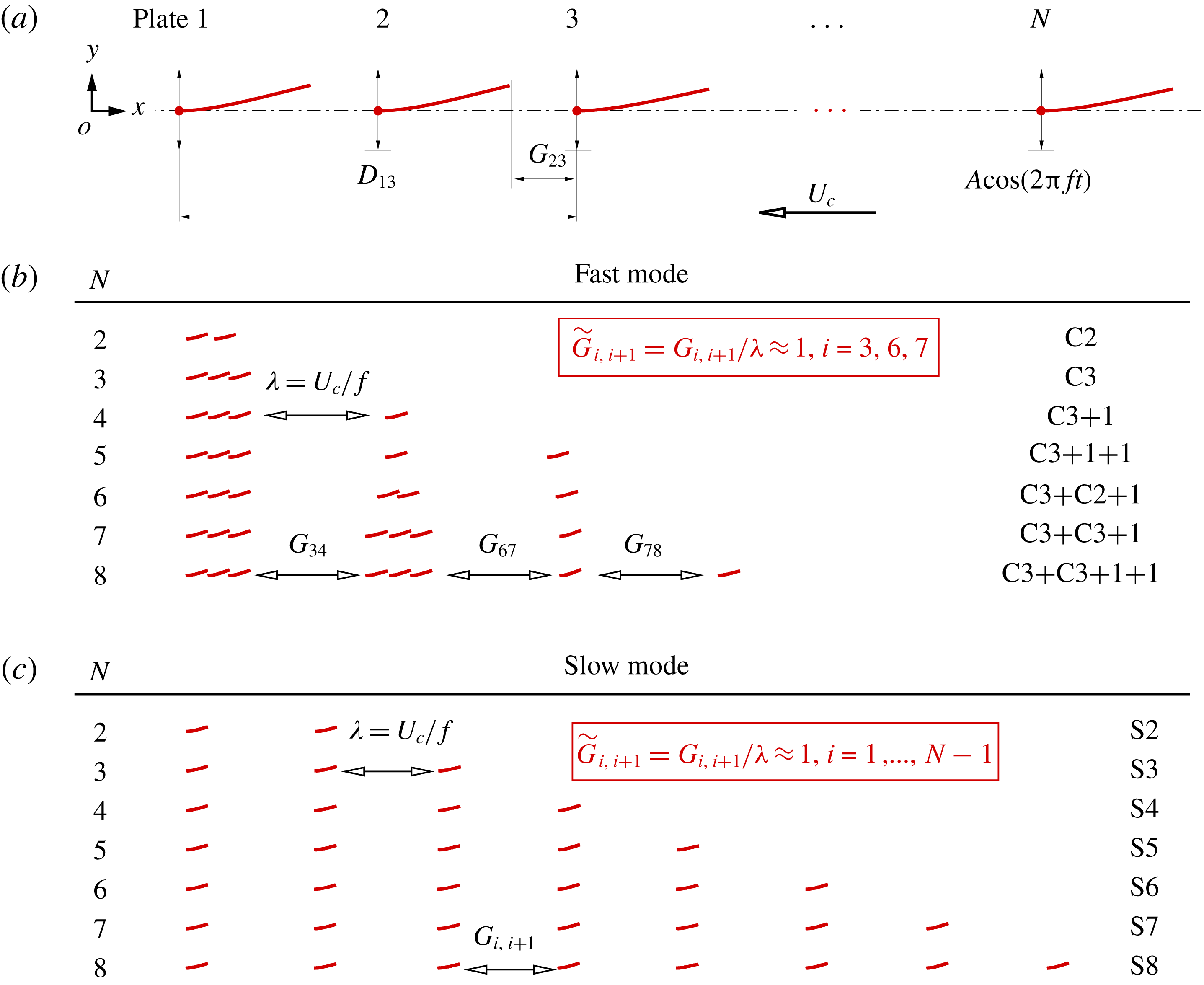
Figure 1. (a) Schematic diagram for the multi-body self-propelled system consisting of
![]() $N$
flapping flexible plates in a tandem configuration. The longitudinal distance
$N$
flapping flexible plates in a tandem configuration. The longitudinal distance
![]() $D$
, gap distance
$D$
, gap distance
![]() $G$
and flapping amplitude
$G$
and flapping amplitude
![]() $A$
have been normalized by the dimensional length of the plate
$A$
have been normalized by the dimensional length of the plate
![]() $L$
. Snapshots of the orderly configurations for (b) the fast mode and (c) the slow mode. The notations ‘C’ and ‘S’ represent compact and sparse configurations, respectively. The number just following the notation denotes the number of plates in the subgroup (if any) or the group. For example, ‘C3+C2+1’ represents 3, 2 and 1 plates in the first, second and third subgroups in the compact configuration, respectively.
$L$
. Snapshots of the orderly configurations for (b) the fast mode and (c) the slow mode. The notations ‘C’ and ‘S’ represent compact and sparse configurations, respectively. The number just following the notation denotes the number of plates in the subgroup (if any) or the group. For example, ‘C3+C2+1’ represents 3, 2 and 1 plates in the first, second and third subgroups in the compact configuration, respectively.
In this system, the fluid flow is governed by the incompressible Navier–Stokes equations
where
![]() $\boldsymbol{v}$
is the velocity,
$\boldsymbol{v}$
is the velocity,
![]() $p$
the pressure,
$p$
the pressure,
![]() $\unicode[STIX]{x1D70C}$
the density of the fluid,
$\unicode[STIX]{x1D70C}$
the density of the fluid,
![]() $\unicode[STIX]{x1D707}$
the dynamic viscosity, and
$\unicode[STIX]{x1D707}$
the dynamic viscosity, and
![]() $\boldsymbol{f}_{b}$
the body force term. The deformation and motion of plates are described by the structural equation (Hua et al.
Reference Hua, Zhu and Lu2013),
$\boldsymbol{f}_{b}$
the body force term. The deformation and motion of plates are described by the structural equation (Hua et al.
Reference Hua, Zhu and Lu2013),
where
![]() $s$
is the Lagrangian coordinate along the plates,
$s$
is the Lagrangian coordinate along the plates,
![]() $\boldsymbol{X}(s,t)=(X(s,t),Y(s,t))$
is the position vector of the plates,
$\boldsymbol{X}(s,t)=(X(s,t),Y(s,t))$
is the position vector of the plates,
![]() $\boldsymbol{F}_{s}$
is the Lagrangian force exerted on the plates by the surrounding fluid and
$\boldsymbol{F}_{s}$
is the Lagrangian force exerted on the plates by the surrounding fluid and
![]() $\unicode[STIX]{x1D70C}_{l}$
is the structural linear mass density.
$\unicode[STIX]{x1D70C}_{l}$
is the structural linear mass density.
![]() $Eh$
and
$Eh$
and
![]() $EI$
are the structural stretching and bending rigidity, respectively.
$EI$
are the structural stretching and bending rigidity, respectively.
For the structural equation, the boundary condition at the leading edges of the plates is
![]() $-Eh(1-|\unicode[STIX]{x2202}\boldsymbol{X}/\unicode[STIX]{x2202}s|^{-1})\unicode[STIX]{x2202}X/\unicode[STIX]{x2202}s+EI\unicode[STIX]{x2202}^{3}X/\unicode[STIX]{x2202}^{3}s=0$
,
$-Eh(1-|\unicode[STIX]{x2202}\boldsymbol{X}/\unicode[STIX]{x2202}s|^{-1})\unicode[STIX]{x2202}X/\unicode[STIX]{x2202}s+EI\unicode[STIX]{x2202}^{3}X/\unicode[STIX]{x2202}^{3}s=0$
,
![]() $Y(t)=y(t)$
,
$Y(t)=y(t)$
,
![]() $\unicode[STIX]{x2202}\boldsymbol{X}/\unicode[STIX]{x2202}s=(1,0)$
, and the boundary condition at the free ends of the plates is
$\unicode[STIX]{x2202}\boldsymbol{X}/\unicode[STIX]{x2202}s=(1,0)$
, and the boundary condition at the free ends of the plates is
![]() $-Eh(1-|\unicode[STIX]{x2202}\boldsymbol{X}/\unicode[STIX]{x2202}s|^{-1})\unicode[STIX]{x2202}\boldsymbol{X}/\unicode[STIX]{x2202}s+EI\unicode[STIX]{x2202}^{3}\boldsymbol{X}/\unicode[STIX]{x2202}^{3}s=0$
,
$-Eh(1-|\unicode[STIX]{x2202}\boldsymbol{X}/\unicode[STIX]{x2202}s|^{-1})\unicode[STIX]{x2202}\boldsymbol{X}/\unicode[STIX]{x2202}s+EI\unicode[STIX]{x2202}^{3}\boldsymbol{X}/\unicode[STIX]{x2202}^{3}s=0$
,
![]() $\unicode[STIX]{x2202}^{2}\boldsymbol{X}/\unicode[STIX]{x2202}s^{2}=0$
.
$\unicode[STIX]{x2202}^{2}\boldsymbol{X}/\unicode[STIX]{x2202}s^{2}=0$
.
Following the scheme in Zou & He (Reference Zou and He1997), a constant pressure with
![]() $\boldsymbol{v}=0$
is imposed at all boundaries except for the outlet.
$\boldsymbol{v}=0$
is imposed at all boundaries except for the outlet.
![]() $\unicode[STIX]{x2202}\boldsymbol{v}/\unicode[STIX]{x2202}x=0$
with the constant pressure imposed at the outlet (Zou & He Reference Zou and He1997). At the initial time, the fluid velocity field is zero in the entire computational domain.
$\unicode[STIX]{x2202}\boldsymbol{v}/\unicode[STIX]{x2202}x=0$
with the constant pressure imposed at the outlet (Zou & He Reference Zou and He1997). At the initial time, the fluid velocity field is zero in the entire computational domain.
The characteristic quantities
![]() $\unicode[STIX]{x1D70C}$
,
$\unicode[STIX]{x1D70C}$
,
![]() $L$
and
$L$
and
![]() $U_{ref}$
are chosen to normalize the above equations. Here,
$U_{ref}$
are chosen to normalize the above equations. Here,
![]() $U_{ref}$
is the maximum flapping velocity of the plunging motion, i.e.
$U_{ref}$
is the maximum flapping velocity of the plunging motion, i.e.
![]() $U_{ref}=2\unicode[STIX]{x03C0}ALf$
. The dimensionless governing parameters are described as follows: the Reynolds number
$U_{ref}=2\unicode[STIX]{x03C0}ALf$
. The dimensionless governing parameters are described as follows: the Reynolds number
![]() $Re=\unicode[STIX]{x1D70C}U_{ref}L/\unicode[STIX]{x1D707}$
, the stretching stiffness
$Re=\unicode[STIX]{x1D70C}U_{ref}L/\unicode[STIX]{x1D707}$
, the stretching stiffness
![]() $S=Eh/\unicode[STIX]{x1D70C}U_{ref}^{2}L$
, the bending stiffness
$S=Eh/\unicode[STIX]{x1D70C}U_{ref}^{2}L$
, the bending stiffness
![]() $K=EI/\unicode[STIX]{x1D70C}U_{ref}^{2}L^{3}$
, the mass ratio of the plates and the fluid
$K=EI/\unicode[STIX]{x1D70C}U_{ref}^{2}L^{3}$
, the mass ratio of the plates and the fluid
![]() $M=\unicode[STIX]{x1D70C}_{l}/\unicode[STIX]{x1D70C}L$
, the heaving amplitude
$M=\unicode[STIX]{x1D70C}_{l}/\unicode[STIX]{x1D70C}L$
, the heaving amplitude
![]() $A$
, the number of group member
$A$
, the number of group member
![]() $N$
, and the initial gap spacing
$N$
, and the initial gap spacing
![]() $G_{0}$
.
$G_{0}$
.
3 Numerical method and validation
The Navier–Stokes equations are solved numerically by the lattice Boltzmann method (LBM) (Chen & Doolen Reference Chen and Doolen1998). The deformation and motion of each plate are described by a structural equation, i.e., equation (2.3). Each structural equation is solved by a finite element method in the Lagrange coordinate independently (Doyle Reference Doyle2001). For each plate, boundary conditions for the leading and trailing ends are imposed. The movement of each plate (Lagrange points) is coupled with the LBM solver through immersed boundary methods (Peskin Reference Peskin2002; Mittal & Iaccarino Reference Mittal and Iaccarino2005). The body force term
![]() $\boldsymbol{f}_{b}$
in (2.1) represents an interaction force between the fluid and the immersed boundary to enforce the no-slip velocity boundary condition. A detailed description of the numerical method can be found elsewhere (Hua et al.
Reference Hua, Zhu and Lu2013; Hua, Zhu & Lu Reference Hua, Zhu and Lu2014).
$\boldsymbol{f}_{b}$
in (2.1) represents an interaction force between the fluid and the immersed boundary to enforce the no-slip velocity boundary condition. A detailed description of the numerical method can be found elsewhere (Hua et al.
Reference Hua, Zhu and Lu2013; Hua, Zhu & Lu Reference Hua, Zhu and Lu2014).
Based on our convergence studies with different computational domains, the computational domain for fluid flow is chosen as
![]() $(D_{1N}+50)L\times 40L$
in the
$(D_{1N}+50)L\times 40L$
in the
![]() $x$
and
$x$
and
![]() $y$
directions. The domain is large enough so that the blocking effects of the boundaries are not significant.
$y$
directions. The domain is large enough so that the blocking effects of the boundaries are not significant.
In the
![]() $x$
and
$x$
and
![]() $y$
directions, the mesh is uniform with spacing
$y$
directions, the mesh is uniform with spacing
![]() $\unicode[STIX]{x0394}x=\unicode[STIX]{x0394}y=0.01L$
. The time step is
$\unicode[STIX]{x0394}x=\unicode[STIX]{x0394}y=0.01L$
. The time step is
![]() $\unicode[STIX]{x0394}t=T/10\,000$
for the simulations of fluid flow and plate deformation, with
$\unicode[STIX]{x0394}t=T/10\,000$
for the simulations of fluid flow and plate deformation, with
![]() $T=1/f$
being the flapping period. Moreover, a finite moving computational domain (Hua et al.
Reference Hua, Zhu and Lu2013) is used in the
$T=1/f$
being the flapping period. Moreover, a finite moving computational domain (Hua et al.
Reference Hua, Zhu and Lu2013) is used in the
![]() $x$
direction to allow the plates to move for a sufficiently long time. As the plate travels one lattice spacing in the
$x$
direction to allow the plates to move for a sufficiently long time. As the plate travels one lattice spacing in the
![]() $x$
direction, the computational domain is shifted, i.e. one layer being added at the inlet and another layer being removed at the outlet (Hua et al.
Reference Hua, Zhu and Lu2013).
$x$
direction, the computational domain is shifted, i.e. one layer being added at the inlet and another layer being removed at the outlet (Hua et al.
Reference Hua, Zhu and Lu2013).
Figure 2. (a) Numerical validation. Lines and symbols represent the present results and those in Zhu et al. (Reference Zhu, He and Zhang2014), respectively. (b) Grid-independence study. A case of two self-propelled plates in a tandem configuration is simulated. In the case, the key parameters,
![]() $Re=200$
,
$Re=200$
,
![]() $A=0.5$
,
$A=0.5$
,
![]() $M=0.2$
,
$M=0.2$
,
![]() $K=0.8$
,
$K=0.8$
,
![]() $S=1000$
and
$S=1000$
and
![]() $G_{0}=8.0$
, are identical to those in Zhu et al. (Reference Zhu, He and Zhang2014).
$G_{0}=8.0$
, are identical to those in Zhu et al. (Reference Zhu, He and Zhang2014).
![]() $U_{c}$
is the cruising speed.
$U_{c}$
is the cruising speed.
To validate the present numerical method, the coupling locomotion of two self-propelled plates in a tandem configuration is simulated. Figure 2(a) shows the cruising speeds of the leading and following plates as a function of time. It is seen that the present results agree well with those of Zhu et al. (Reference Zhu, He and Zhang2014). Moreover, the cruising speeds of the leading plate obtained from different grid resolutions are shown in figure 2(b). It is seen that
![]() $\unicode[STIX]{x0394}x/L=0.01$
is sufficient to achieve accurate results. In addition, the numerical strategy used in this study has been validated and successfully applied to a wide range of flows, such as the dynamics of fluid flow over a circular flexible plate (Hua et al.
Reference Hua, Zhu and Lu2014) and the locomotion of a flapping flexible plate (Hua et al.
Reference Hua, Zhu and Lu2013).
$\unicode[STIX]{x0394}x/L=0.01$
is sufficient to achieve accurate results. In addition, the numerical strategy used in this study has been validated and successfully applied to a wide range of flows, such as the dynamics of fluid flow over a circular flexible plate (Hua et al.
Reference Hua, Zhu and Lu2014) and the locomotion of a flapping flexible plate (Hua et al.
Reference Hua, Zhu and Lu2013).
4 Results and discussion
In our simulations, the typical non-dimensional parameters are:
![]() $Re=200$
,
$Re=200$
,
![]() $A=0.5$
,
$A=0.5$
,
![]() $M=0.2$
,
$M=0.2$
,
![]() $S=1000$
and
$S=1000$
and
![]() $K=1$
. Here, the stretching stiffness of plate is chosen to be large enough (
$K=1$
. Here, the stretching stiffness of plate is chosen to be large enough (
![]() $S=1000$
) so that the stretching deformation is negligible. Usually the bending stiffness
$S=1000$
) so that the stretching deformation is negligible. Usually the bending stiffness
![]() $K$
of a fish is
$K$
of a fish is
![]() $O(1)$
; for example, the tail fin of a goldfish (Carassius auratus) has a bending stiffness of
$O(1)$
; for example, the tail fin of a goldfish (Carassius auratus) has a bending stiffness of
![]() $2.5\sim 23$
(Hua et al.
Reference Hua, Zhu and Lu2013). (It is noted that the characteristic velocities are
$2.5\sim 23$
(Hua et al.
Reference Hua, Zhu and Lu2013). (It is noted that the characteristic velocities are
![]() $U_{ref}=2\unicode[STIX]{x03C0}ALf$
and
$U_{ref}=2\unicode[STIX]{x03C0}ALf$
and
![]() $U_{ref}=Lf$
in the present study and Hua et al. (Reference Hua, Zhu and Lu2013), respectively.) In our study
$U_{ref}=Lf$
in the present study and Hua et al. (Reference Hua, Zhu and Lu2013), respectively.) In our study
![]() $K$
is fixed to be unity. At
$K$
is fixed to be unity. At
![]() $M=0.2$
, an isolated plate with
$M=0.2$
, an isolated plate with
![]() $K=1$
achieves the maximum cruising speed. These parameters are also consistent with those in Zhu et al. (Reference Zhu, He and Zhang2014). In our study,
$K=1$
achieves the maximum cruising speed. These parameters are also consistent with those in Zhu et al. (Reference Zhu, He and Zhang2014). In our study,
![]() $N\in [2,8]$
,
$N\in [2,8]$
,
![]() $G_{0}\in (0,6]$
; they are variable.
$G_{0}\in (0,6]$
; they are variable.
4.1 Schooling states
The cruising speed of the
![]() $i$
th plate is defined as the averaged forward speed at the equilibrium state, i.e.
$i$
th plate is defined as the averaged forward speed at the equilibrium state, i.e.
![]() $U_{c,i}=\int _{0}^{T}u_{i}(t)\,\text{d}t/T=\int _{0}^{T}|\unicode[STIX]{x2202}_{t}X_{i}(0,t)|\,\text{d}t/T$
, where
$U_{c,i}=\int _{0}^{T}u_{i}(t)\,\text{d}t/T=\int _{0}^{T}|\unicode[STIX]{x2202}_{t}X_{i}(0,t)|\,\text{d}t/T$
, where
![]() $u_{i}(t)$
is the instantaneous speed of the
$u_{i}(t)$
is the instantaneous speed of the
![]() $i$
th plate. At the equilibrium state, the cruising speed of the whole group is
$i$
th plate. At the equilibrium state, the cruising speed of the whole group is
![]() $U_{c}=U_{c,i}$
,
$U_{c}=U_{c,i}$
,
![]() $i=1,2,\ldots N$
.
$i=1,2,\ldots N$
.
Results of our simulations show that two distinct stable schooling states emerge spontaneously. According to
![]() $U_{c}$
, they are classified as the fast and slow modes. Figures 1(b) and 1(c) show snapshots of the configurations for the two modes, respectively. It is seen that the two modes can also be identified according to the spatial configuration of the plates. The emergence of distinct orderly formations depends on
$U_{c}$
, they are classified as the fast and slow modes. Figures 1(b) and 1(c) show snapshots of the configurations for the two modes, respectively. It is seen that the two modes can also be identified according to the spatial configuration of the plates. The emergence of distinct orderly formations depends on
![]() $G_{0}$
. In particular, the compact and sparse configurations appear when
$G_{0}$
. In particular, the compact and sparse configurations appear when
![]() $G_{0}\leqslant 2.3$
and
$G_{0}\leqslant 2.3$
and
![]() $2.5\leqslant G_{0}\leqslant 6$
, respectively. For the effect of the initial gap spacing
$2.5\leqslant G_{0}\leqslant 6$
, respectively. For the effect of the initial gap spacing
![]() $G_{0}$
, we can imagine that if
$G_{0}$
, we can imagine that if
![]() $G_{0}$
is large enough, the interactions between plates are negligible and the plates flap and move independently. Hence we do not intend to investigate cases with too large
$G_{0}$
is large enough, the interactions between plates are negligible and the plates flap and move independently. Hence we do not intend to investigate cases with too large
![]() $G_{0}$
, and limit the present study to the range
$G_{0}$
, and limit the present study to the range
![]() $G_{0}\leqslant 6$
.
$G_{0}\leqslant 6$
.
For the fast mode, as the group size increases, the group may spontaneously split into several subgroups or individuals. Each subgroup in the compact mode consists of up to three members (see figure 1
b). For the slow mode with a sparse configuration, when
![]() $G_{0}\geqslant 5$
, at the equilibrium state the gap spacings between any two neighbouring plates are identical and subgroups are not observed, as shown in figure 1(c). For corresponding flow fields, please refer to the supplementary movies available at https://doi.org/10.1017/jfm.2018.634. Typical cases of the fast mode ‘C3+1’ and ‘C3+C2+1’ are shown in Movies 1 and 2, respectively. Typical cases of the slow mode ‘S4’, ‘S6’, ‘S6+S2’, and ‘S8’ are shown in Movies 3–6, respectively. The notations ‘C’ and ‘S’ represent compact and sparse configurations, respectively. The number just following the notation denotes the number of plates in the subgroup (if any) or the group.
$G_{0}\geqslant 5$
, at the equilibrium state the gap spacings between any two neighbouring plates are identical and subgroups are not observed, as shown in figure 1(c). For corresponding flow fields, please refer to the supplementary movies available at https://doi.org/10.1017/jfm.2018.634. Typical cases of the fast mode ‘C3+1’ and ‘C3+C2+1’ are shown in Movies 1 and 2, respectively. Typical cases of the slow mode ‘S4’, ‘S6’, ‘S6+S2’, and ‘S8’ are shown in Movies 3–6, respectively. The notations ‘C’ and ‘S’ represent compact and sparse configurations, respectively. The number just following the notation denotes the number of plates in the subgroup (if any) or the group.

Figure 3. Dynamics of the orderly formations. (a,b) The distances between the following plates and the leading plate, i.e.,
![]() $D_{1,i}$
(
$D_{1,i}$
(
![]() $i=2,\ldots ,N$
) and (c,d) the schooling number as a function of time. (a,c) Case ‘C3+C3+1+1’. (b,d) Case ‘S8’. In both cases
$i=2,\ldots ,N$
) and (c,d) the schooling number as a function of time. (a,c) Case ‘C3+C3+1+1’. (b,d) Case ‘S8’. In both cases
![]() $N=8$
.
$N=8$
.
To quantitatively describe the evolution of the orderly formations, two typical cases with
![]() $N=8$
,
$N=8$
,
![]() $G_{0}=1$
and
$G_{0}=1$
and
![]() $N=8$
,
$N=8$
,
![]() $G_{0}=5$
are taken as examples. The locations of the following plates (i.e.
$G_{0}=5$
are taken as examples. The locations of the following plates (i.e.
![]() $i=2,\ldots ,N$
) described by
$i=2,\ldots ,N$
) described by
![]() $D_{1i}$
as a function of time for the two cases are shown in figures 3(a,b). It is seen that when
$D_{1i}$
as a function of time for the two cases are shown in figures 3(a,b). It is seen that when
![]() $t>15T$
, all distances
$t>15T$
, all distances
![]() $D_{1i}$
reach equilibrium states in both cases. The cases
$D_{1i}$
reach equilibrium states in both cases. The cases
![]() $G_{0}=1$
and
$G_{0}=1$
and
![]() $G_{0}=5$
evolve to two distinct equilibrium states: the compact (‘C3+C3+1+1’) and sparse (‘S8’) configurations, respectively.
$G_{0}=5$
evolve to two distinct equilibrium states: the compact (‘C3+C3+1+1’) and sparse (‘S8’) configurations, respectively.
The schooling number introduced by Becker et al. (Reference Becker, Masoud, Newbolt, Shelley and Ristroph2015) has been used to quantify collective patterns of the two-wing system (Becker et al.
Reference Becker, Masoud, Newbolt, Shelley and Ristroph2015; Ramananarivo et al.
Reference Ramananarivo, Fang, Oza, Zhang and Ristroph2016). Here it is defined as
![]() $\widetilde{G}_{i,i+1}=G_{i,i+1}/\unicode[STIX]{x1D706}$
, where
$\widetilde{G}_{i,i+1}=G_{i,i+1}/\unicode[STIX]{x1D706}$
, where
![]() $\unicode[STIX]{x1D706}=U_{c}/f$
is the wavelength. In the fast mode, the schooling numbers within the compact subgroups, such as
$\unicode[STIX]{x1D706}=U_{c}/f$
is the wavelength. In the fast mode, the schooling numbers within the compact subgroups, such as
![]() $\widetilde{G}_{12}$
and
$\widetilde{G}_{12}$
and
![]() $\widetilde{G}_{23}$
, approximately converge to zero, whereas the inter-subgroup schooling numbers, such as
$\widetilde{G}_{23}$
, approximately converge to zero, whereas the inter-subgroup schooling numbers, such as
![]() $\widetilde{G}_{34}$
and
$\widetilde{G}_{34}$
and
![]() $\widetilde{G}_{67}$
, approximately approach unity (see figure 1
b ‘C3+C3+1+1’). In the slow mode illustrated in figure 1(c), the inter-individual schooling numbers are also close to unity.
$\widetilde{G}_{67}$
, approximately approach unity (see figure 1
b ‘C3+C3+1+1’). In the slow mode illustrated in figure 1(c), the inter-individual schooling numbers are also close to unity.
Figures 3(c) and 3(d) show the schooling numbers of the fast and slow modes, respectively. In the fast mode, the inter-individual spacings within the compact subgroups, such as
![]() $\widetilde{G}_{12}$
and
$\widetilde{G}_{12}$
and
![]() $\widetilde{G}_{23}$
in figure 3(a), approximately converge to zero, whereas the inter-subgroup schooling numbers, such as
$\widetilde{G}_{23}$
in figure 3(a), approximately converge to zero, whereas the inter-subgroup schooling numbers, such as
![]() $\widetilde{G}_{34}$
and
$\widetilde{G}_{34}$
and
![]() $\widetilde{G}_{67}$
, approximately approach unity. In the slow mode, the inter-individual schooling numbers within the group are identical, i.e.
$\widetilde{G}_{67}$
, approximately approach unity. In the slow mode, the inter-individual schooling numbers within the group are identical, i.e.
![]() $\widetilde{G}_{i,i+1}=1$
,
$\widetilde{G}_{i,i+1}=1$
,
![]() $i=1,2,\ldots ,7$
.
$i=1,2,\ldots ,7$
.
For the fast mode, the maximum number of members in the compact subgroup,
![]() $n$
, does not always have to be three. It depends on the initial gap spacing. For the case
$n$
, does not always have to be three. It depends on the initial gap spacing. For the case
![]() $N=4$
with uniform gap spacing
$N=4$
with uniform gap spacing
![]() $G_{0}=1$
, ‘C3+1’ would appear (see figure 4
a). When the initial gap spacing is non-uniform (see the caption of figure 4), the fast mode with a leading subgroup consisting of four or five plates would also emerge. In figure 4(b,c), the instantaneous vorticity structures at equilibrium states for cases ‘C4+1’ and ‘C5+1’ are shown. The schooling number
$G_{0}=1$
, ‘C3+1’ would appear (see figure 4
a). When the initial gap spacing is non-uniform (see the caption of figure 4), the fast mode with a leading subgroup consisting of four or five plates would also emerge. In figure 4(b,c), the instantaneous vorticity structures at equilibrium states for cases ‘C4+1’ and ‘C5+1’ are shown. The schooling number
![]() $\widetilde{G}=G/\unicode[STIX]{x1D706}$
is found to be unity for all three cases in figure 4, where
$\widetilde{G}=G/\unicode[STIX]{x1D706}$
is found to be unity for all three cases in figure 4, where
![]() $G$
is the gap distance between the additional plate ‘1’ and its front neighbour. It indicates that there is similar hydrodynamic mechanism in the fast mode with compact configurations, which is not dependent on
$G$
is the gap distance between the additional plate ‘1’ and its front neighbour. It indicates that there is similar hydrodynamic mechanism in the fast mode with compact configurations, which is not dependent on
![]() $n$
. The cruising speed of the leading compact subgroups is listed in table 1. It is seen that the larger
$n$
. The cruising speed of the leading compact subgroups is listed in table 1. It is seen that the larger
![]() $n$
is, the faster the whole group travels. A possible reason is that the compact plates in a subgroup act as a longer plate, which has a larger
$n$
is, the faster the whole group travels. A possible reason is that the compact plates in a subgroup act as a longer plate, which has a larger
![]() $U_{c}$
(Rosellini & Zhang Reference Rosellini and Zhang2007).
$U_{c}$
(Rosellini & Zhang Reference Rosellini and Zhang2007).

Figure 4. Formation of ‘C4’ and ‘C5’ in the compact configurations. Typical instantaneous vorticity structures of the compact configurations at
![]() $t/T=1/4$
: (a) case ‘C3+1’ with the uniform initial separation
$t/T=1/4$
: (a) case ‘C3+1’ with the uniform initial separation
![]() $G_{0}=1$
, (b) case ‘C4+1’ with
$G_{0}=1$
, (b) case ‘C4+1’ with
![]() $G_{i,i+1}(t=0)=1$
(
$G_{i,i+1}(t=0)=1$
(
![]() $i=1,2,3$
) and
$i=1,2,3$
) and
![]() $G_{45}(t=0)=0.5$
, and (c) case ‘C5+1’ with
$G_{45}(t=0)=0.5$
, and (c) case ‘C5+1’ with
![]() $G_{i,i+1}(t=0)=1$
(
$G_{i,i+1}(t=0)=1$
(
![]() $i=1,2,3,4$
) and
$i=1,2,3,4$
) and
![]() $G_{56}(t=0)=0.5$
.
$G_{56}(t=0)=0.5$
.
Table 1. The cruising speed
![]() $U_{c}$
of groups with leading compact subgroups ‘
$U_{c}$
of groups with leading compact subgroups ‘
![]() $\text{C}n$
’,
$\text{C}n$
’,
![]() $n=2$
, 3, 4 and 5. The results of the slow mode and the isolated plate are also presented.
$n=2$
, 3, 4 and 5. The results of the slow mode and the isolated plate are also presented.

It is worth noting that for the slow mode, the group may also split, which depends on the initial configuration. For example, when the initial gap distance
![]() $G_{0}=3$
, the stable formation consisting of two subgroups is observed. It is referred to as ‘S6+S2’ (see Movie 5). The front and rear subgroups contain six and two plates, respectively. The gap spacings within the subgroups are uniform, e.g.
$G_{0}=3$
, the stable formation consisting of two subgroups is observed. It is referred to as ‘S6+S2’ (see Movie 5). The front and rear subgroups contain six and two plates, respectively. The gap spacings within the subgroups are uniform, e.g.
![]() $\widetilde{G}_{i,i+1}=1$
(
$\widetilde{G}_{i,i+1}=1$
(
![]() $i=1,2,\ldots ,5$
and 7), and the inter-subgroup spacing is
$i=1,2,\ldots ,5$
and 7), and the inter-subgroup spacing is
![]() $\widetilde{G}_{67}=2$
.
$\widetilde{G}_{67}=2$
.
4.2 Schooling stability
These stable and orderly formations with spontaneously selected integer values of schooling numbers are a result of long-range wake–plate interactions. The vorticity contours at
![]() $t/T=1/4$
for the cases ‘C3’ and ‘S6’ are shown in figures 5(a) and 5(b), respectively. It is seen that the wakes of the ‘C3’ and ‘S6’ evolve from a chaotic and perturbed state to an orderly vortex street along the distance downstream through vorticity merging and dissipation. Suppose the case of ‘C3’ reaches a stable state as shown in figure 5(a); if an additional plate is inserted into the wake of ‘C3’, it would be ‘locked’ into several discrete equilibrium positions. Which equilibrium position it adopts depends on the initial gap spacing
$t/T=1/4$
for the cases ‘C3’ and ‘S6’ are shown in figures 5(a) and 5(b), respectively. It is seen that the wakes of the ‘C3’ and ‘S6’ evolve from a chaotic and perturbed state to an orderly vortex street along the distance downstream through vorticity merging and dissipation. Suppose the case of ‘C3’ reaches a stable state as shown in figure 5(a); if an additional plate is inserted into the wake of ‘C3’, it would be ‘locked’ into several discrete equilibrium positions. Which equilibrium position it adopts depends on the initial gap spacing
![]() $G_{34}$
. The circumstance of the case ‘S6’ is similar. The locations labelled by the up arrows approximately have integer schooling numbers, i.e.
$G_{34}$
. The circumstance of the case ‘S6’ is similar. The locations labelled by the up arrows approximately have integer schooling numbers, i.e.
![]() $\widetilde{G}\approx 1,2,\ldots ,6$
. This observation is consistent with that of the two-body system (Zhu et al.
Reference Zhu, He and Zhang2014; Ramananarivo et al.
Reference Ramananarivo, Fang, Oza, Zhang and Ristroph2016), indicating that the additional plates are able to keep pace with oncoming wake of the leading subgroup even though the flow perturbation increases compared to the two-body system.
$\widetilde{G}\approx 1,2,\ldots ,6$
. This observation is consistent with that of the two-body system (Zhu et al.
Reference Zhu, He and Zhang2014; Ramananarivo et al.
Reference Ramananarivo, Fang, Oza, Zhang and Ristroph2016), indicating that the additional plates are able to keep pace with oncoming wake of the leading subgroup even though the flow perturbation increases compared to the two-body system.
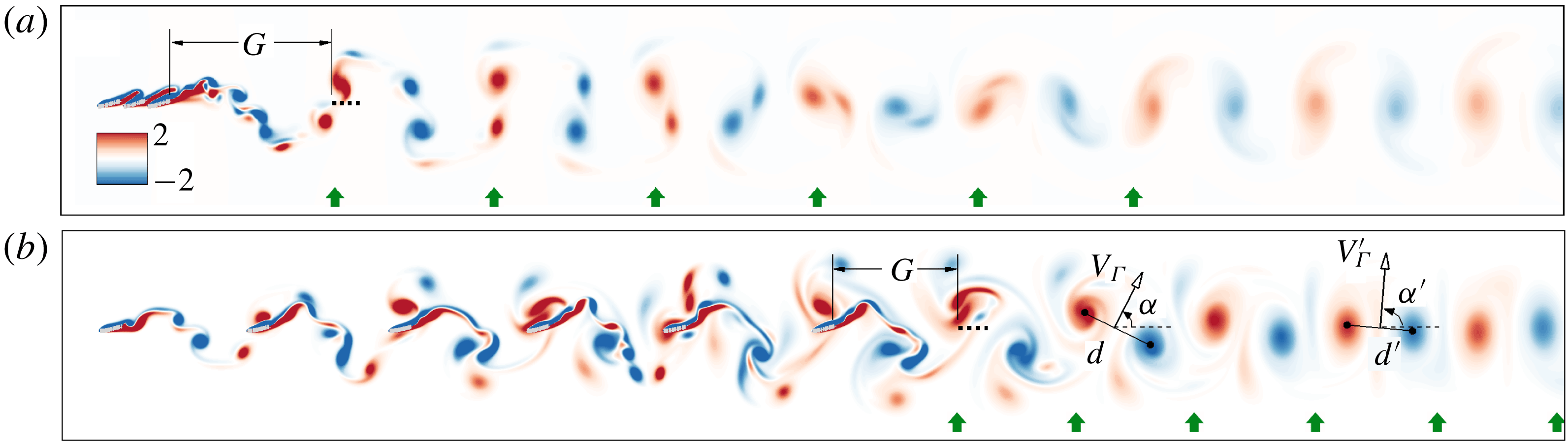
Figure 5. Instantaneous vorticity contours for the cases ‘C3’ (a) and ‘S6’ (b) at
![]() $t/T=1/4$
. If an additional plate (represented by the bold dashed line) is inserted into the wake, the six sequential equilibrium locations are marked with green up arrows near the
$t/T=1/4$
. If an additional plate (represented by the bold dashed line) is inserted into the wake, the six sequential equilibrium locations are marked with green up arrows near the
![]() $x$
-axis.
$x$
-axis.
![]() $G$
is the gap distance between the additional plate and its front neighbour.
$G$
is the gap distance between the additional plate and its front neighbour.
![]() $\unicode[STIX]{x1D6FC}$
,
$\unicode[STIX]{x1D6FC}$
,
![]() $\unicode[STIX]{x1D6FC}^{\prime }$
are the orientation angles between the dipole-induced velocities
$\unicode[STIX]{x1D6FC}^{\prime }$
are the orientation angles between the dipole-induced velocities
![]() $V_{\unicode[STIX]{x1D6E4}}$
,
$V_{\unicode[STIX]{x1D6E4}}$
,
![]() $V_{\unicode[STIX]{x1D6E4}}^{\prime }$
and the
$V_{\unicode[STIX]{x1D6E4}}^{\prime }$
and the
![]() $x$
-axis.
$x$
-axis.
![]() $d$
and
$d$
and
![]() $d^{\prime }$
are distances between two vortex centres.
$d^{\prime }$
are distances between two vortex centres.
To further explore the mechanism for the emergence of the equilibrium positions, the hydrodynamic forces on the additional or the trailing plate in the cases of ‘C3’ and ‘S6’ (see figure 5) are calculated. For convenience, the simulations were performed in an inertial coordinate system moving with velocity
![]() $U_{c}$
in the negative
$U_{c}$
in the negative
![]() $x$
-direction. It is noted that before the simulations, the equilibrium states for cases of ‘C3’ and ‘S6’ and their
$x$
-direction. It is noted that before the simulations, the equilibrium states for cases of ‘C3’ and ‘S6’ and their
![]() $U_{c}$
have been figured out. In the inertial frame, the oncoming flow has a uniform longitudinal velocity of
$U_{c}$
have been figured out. In the inertial frame, the oncoming flow has a uniform longitudinal velocity of
![]() $U_{c}$
and the longitudinal locations of the plates are fixed to be those at the equilibrium state. Figure 6(a) shows the net horizontal force
$U_{c}$
and the longitudinal locations of the plates are fixed to be those at the equilibrium state. Figure 6(a) shows the net horizontal force
![]() $F_{x}$
acting on the trailing plate as a function of
$F_{x}$
acting on the trailing plate as a function of
![]() $\widetilde{G}$
for the cases ‘C3
$\widetilde{G}$
for the cases ‘C3
![]() $+1$
’ and ‘S6
$+1$
’ and ‘S6
![]() $+1$
’. It is seen that for both the modes, there are several discrete points with
$+1$
’. It is seen that for both the modes, there are several discrete points with
![]() $F_{x}=0$
, such as
$F_{x}=0$
, such as
![]() $\widetilde{G}\approx 1,1.4,2,2.5,3,\ldots .$
However, only the points with negative
$\widetilde{G}\approx 1,1.4,2,2.5,3,\ldots .$
However, only the points with negative
![]() $\text{d}F_{x}/\text{d}\widetilde{G}$
are stable, at which
$\text{d}F_{x}/\text{d}\widetilde{G}$
are stable, at which
![]() $\widetilde{G}\approx 1,2,3\ldots .$
The hydrodynamic force near the stable equilibrium positions is a springlike restoring force with
$\widetilde{G}\approx 1,2,3\ldots .$
The hydrodynamic force near the stable equilibrium positions is a springlike restoring force with
![]() $F_{x}\approx -k(\widetilde{G}-\widetilde{G}^{eq})$
, where
$F_{x}\approx -k(\widetilde{G}-\widetilde{G}^{eq})$
, where
![]() $\widetilde{G}^{eq}$
is the
$\widetilde{G}^{eq}$
is the
![]() $i$
th stable equilibrium location and
$i$
th stable equilibrium location and
![]() $k=-\text{d}F_{x}/\text{d}\widetilde{G}$
is analogous to the spring constant. In addition, the emergence of equilibrium positions may be illustrated in terms of a hydrodynamic potential, which is defined as the integral of force with respect to distance, i.e.
$k=-\text{d}F_{x}/\text{d}\widetilde{G}$
is analogous to the spring constant. In addition, the emergence of equilibrium positions may be illustrated in terms of a hydrodynamic potential, which is defined as the integral of force with respect to distance, i.e.
![]() $\unicode[STIX]{x1D6F9}(\widetilde{G})=-\int F_{x}\,\text{d}\widetilde{G}$
. As shown in figure 6(b), there are stable wells in the potential energy landscape. The well bottoms correspond to the stable equilibrium states, at which
$\unicode[STIX]{x1D6F9}(\widetilde{G})=-\int F_{x}\,\text{d}\widetilde{G}$
. As shown in figure 6(b), there are stable wells in the potential energy landscape. The well bottoms correspond to the stable equilibrium states, at which
![]() $\widetilde{G}^{eq}\approx 1,2,3,4$
. The peak points are unstable equilibrium states which are not observed in the simulations.
$\widetilde{G}^{eq}\approx 1,2,3,4$
. The peak points are unstable equilibrium states which are not observed in the simulations.
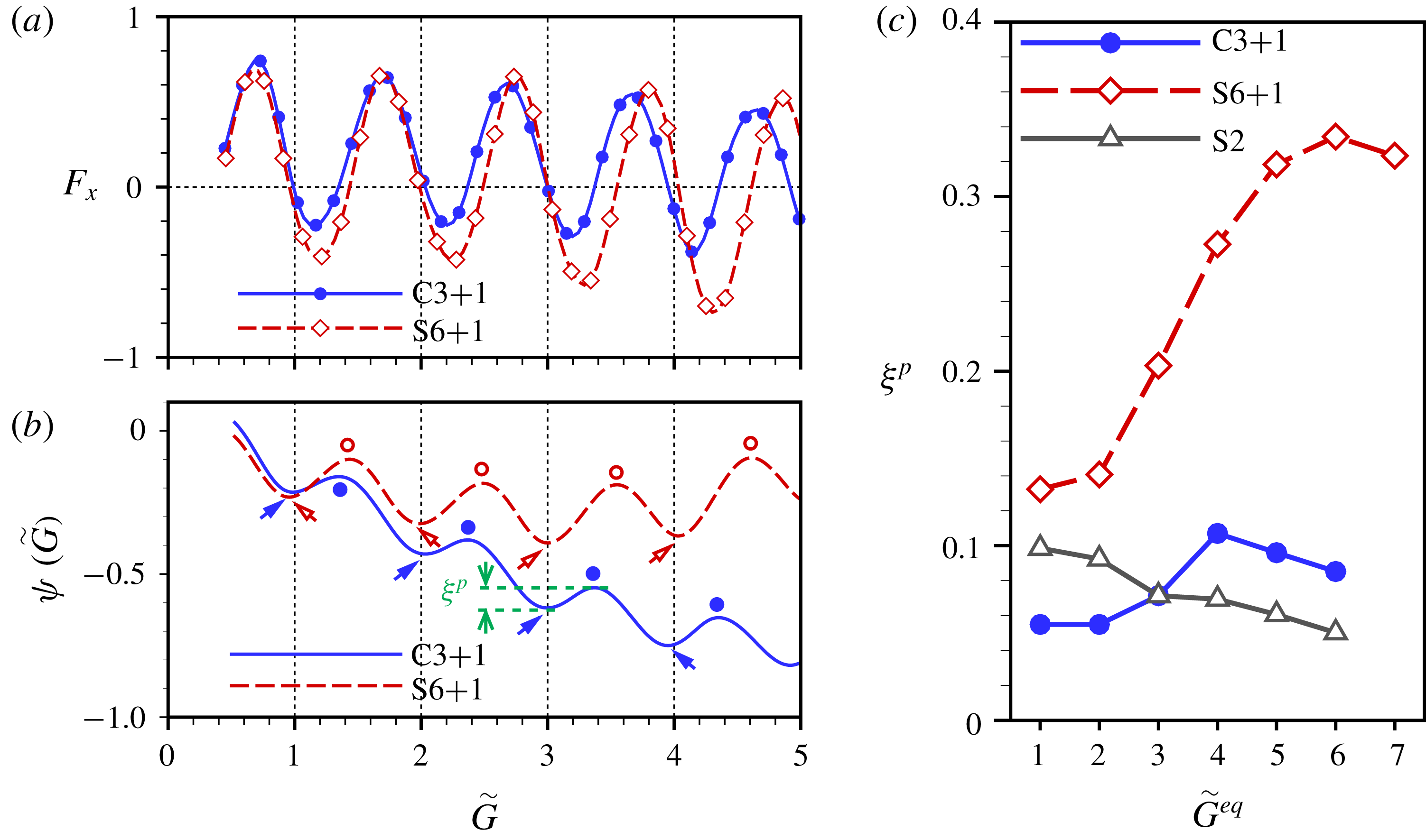
Figure 6. Hydrodynamic forces
![]() $F_{x}$
(a) and potentials
$F_{x}$
(a) and potentials
![]() $\unicode[STIX]{x1D6F9}(\widetilde{G})=-\int F_{x}\,\text{d}\widetilde{G}$
(b) as a function of
$\unicode[STIX]{x1D6F9}(\widetilde{G})=-\int F_{x}\,\text{d}\widetilde{G}$
(b) as a function of
![]() $\widetilde{G}$
,
$\widetilde{G}$
,
![]() $\widetilde{G}=G/\unicode[STIX]{x1D706}$
. The valleys (well bottoms) and peaks of
$\widetilde{G}=G/\unicode[STIX]{x1D706}$
. The valleys (well bottoms) and peaks of
![]() $\unicode[STIX]{x1D6F9}$
are marked with arrows and circles, showing the stable (
$\unicode[STIX]{x1D6F9}$
are marked with arrows and circles, showing the stable (
![]() $\widetilde{G}^{eq}$
) and unstable equilibrium locations, respectively. Well depth
$\widetilde{G}^{eq}$
) and unstable equilibrium locations, respectively. Well depth
![]() $\unicode[STIX]{x1D709}^{p}$
at
$\unicode[STIX]{x1D709}^{p}$
at
![]() $\widetilde{G}^{eq}=3$
for the case ‘C3+1’ is shown as an example. (c)
$\widetilde{G}^{eq}=3$
for the case ‘C3+1’ is shown as an example. (c)
![]() $\unicode[STIX]{x1D709}^{p}$
as a function of
$\unicode[STIX]{x1D709}^{p}$
as a function of
![]() $\widetilde{G}^{eq}$
.
$\widetilde{G}^{eq}$
.
To evaluate the tolerance for flow perturbation at the stable positions, the well depths in the curve of
![]() $\unicode[STIX]{x1D6F9}(\widetilde{G})$
, which are denoted by
$\unicode[STIX]{x1D6F9}(\widetilde{G})$
, which are denoted by
![]() $\unicode[STIX]{x1D709}^{p}$
, are measured. Figure 6(c) shows
$\unicode[STIX]{x1D709}^{p}$
, are measured. Figure 6(c) shows
![]() $\unicode[STIX]{x1D709}^{p}$
as a function of stable position
$\unicode[STIX]{x1D709}^{p}$
as a function of stable position
![]() $\widetilde{G}^{eq}$
for the cases ‘C3+1’ and ‘S6+1’, as well as the slow mode for the two-plate system (‘S2’). It is seen that for the case ‘S2’,
$\widetilde{G}^{eq}$
for the cases ‘C3+1’ and ‘S6+1’, as well as the slow mode for the two-plate system (‘S2’). It is seen that for the case ‘S2’,
![]() $\unicode[STIX]{x1D709}^{p}$
decreases with
$\unicode[STIX]{x1D709}^{p}$
decreases with
![]() $\widetilde{G}^{eq}$
, which is consistent with the experimental result in the two-body system (Ramananarivo et al.
Reference Ramananarivo, Fang, Oza, Zhang and Ristroph2016). In contrast, for the larger groups, such as ‘C3+1’ and ‘S6+1’,
$\widetilde{G}^{eq}$
, which is consistent with the experimental result in the two-body system (Ramananarivo et al.
Reference Ramananarivo, Fang, Oza, Zhang and Ristroph2016). In contrast, for the larger groups, such as ‘C3+1’ and ‘S6+1’,
![]() $\unicode[STIX]{x1D709}^{p}$
increases and then decreases with increasing
$\unicode[STIX]{x1D709}^{p}$
increases and then decreases with increasing
![]() $\widetilde{G}^{eq}$
. In other words, for all equilibrium cases of ‘C3+1’, the case with the trailing plate at
$\widetilde{G}^{eq}$
. In other words, for all equilibrium cases of ‘C3+1’, the case with the trailing plate at
![]() $\widetilde{G}^{eq}=4$
is more stable than the cases of
$\widetilde{G}^{eq}=4$
is more stable than the cases of
![]() $\widetilde{G}^{eq}=1,2,3$
and
$\widetilde{G}^{eq}=1,2,3$
and
![]() $\widetilde{G}^{eq}=5,6$
. For the trailing plate in the wake of the leading subgroup, the stability around its equilibrium state is relevant to the vertical flow induced by the vortices. From figure 5(b), it is seen that
$\widetilde{G}^{eq}=5,6$
. For the trailing plate in the wake of the leading subgroup, the stability around its equilibrium state is relevant to the vertical flow induced by the vortices. From figure 5(b), it is seen that
![]() $\unicode[STIX]{x1D6FC}^{\prime }$
is closer to
$\unicode[STIX]{x1D6FC}^{\prime }$
is closer to
![]() $90^{\circ }$
than
$90^{\circ }$
than
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $d^{\prime }$
is smaller than
$d^{\prime }$
is smaller than
![]() $d$
, where
$d$
, where
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FC}^{\prime }$
are the orientation angles between the dipole-induced velocities
$\unicode[STIX]{x1D6FC}^{\prime }$
are the orientation angles between the dipole-induced velocities
![]() $V_{\unicode[STIX]{x1D6E4}}$
,
$V_{\unicode[STIX]{x1D6E4}}$
,
![]() $V_{\unicode[STIX]{x1D6E4}}^{\prime }$
and the
$V_{\unicode[STIX]{x1D6E4}}^{\prime }$
and the
![]() $x$
-axis, and
$x$
-axis, and
![]() $d$
and
$d$
and
![]() $d^{\prime }$
are distances between two vortex centres. Although the vortex circulation
$d^{\prime }$
are distances between two vortex centres. Although the vortex circulation
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
at
$\unicode[STIX]{x1D6E4}^{\prime }$
at
![]() $\widetilde{G}^{eq}\approx 4$
is slightly smaller than
$\widetilde{G}^{eq}\approx 4$
is slightly smaller than
![]() $\unicode[STIX]{x1D6E4}$
at
$\unicode[STIX]{x1D6E4}$
at
![]() $\widetilde{G}^{eq}\approx 2$
, the vertical component of the dipole-induced velocity
$\widetilde{G}^{eq}\approx 2$
, the vertical component of the dipole-induced velocity
![]() $V_{\unicode[STIX]{x1D6E4}}^{\prime }\sin \unicode[STIX]{x1D6FC}^{\prime }$
at
$V_{\unicode[STIX]{x1D6E4}}^{\prime }\sin \unicode[STIX]{x1D6FC}^{\prime }$
at
![]() $\widetilde{G}^{eq}\approx 4$
is larger according to the vortex-dipole model
$\widetilde{G}^{eq}\approx 4$
is larger according to the vortex-dipole model
![]() $V_{\unicode[STIX]{x1D6E4}}^{\prime }\sin \unicode[STIX]{x1D6FC}^{\prime }=(\unicode[STIX]{x1D6E4}^{\prime }/2\unicode[STIX]{x03C0}d^{\prime })\sin \unicode[STIX]{x1D6FC}^{\prime }$
(Godoy-Diana et al.
Reference Godoy-Diana, Marais, Aider and Wesfreid2009). It would result in an enhanced hydrodynamic restoring force at
$V_{\unicode[STIX]{x1D6E4}}^{\prime }\sin \unicode[STIX]{x1D6FC}^{\prime }=(\unicode[STIX]{x1D6E4}^{\prime }/2\unicode[STIX]{x03C0}d^{\prime })\sin \unicode[STIX]{x1D6FC}^{\prime }$
(Godoy-Diana et al.
Reference Godoy-Diana, Marais, Aider and Wesfreid2009). It would result in an enhanced hydrodynamic restoring force at
![]() $\widetilde{G}^{eq}\approx 4$
(Wu & Chwang Reference Wu and Chwang1975; Ramananarivo et al.
Reference Ramananarivo, Fang, Oza, Zhang and Ristroph2016) and therefore the value of
$\widetilde{G}^{eq}\approx 4$
(Wu & Chwang Reference Wu and Chwang1975; Ramananarivo et al.
Reference Ramananarivo, Fang, Oza, Zhang and Ristroph2016) and therefore the value of
![]() $\unicode[STIX]{x1D709}^{p}$
at
$\unicode[STIX]{x1D709}^{p}$
at
![]() $\widetilde{G}^{eq}=4$
is enhanced compared to that at
$\widetilde{G}^{eq}=4$
is enhanced compared to that at
![]() $\widetilde{G}^{eq}=2$
. On the other hand, when
$\widetilde{G}^{eq}=2$
. On the other hand, when
![]() $\widetilde{G}^{eq}$
becomes larger, e.g.
$\widetilde{G}^{eq}$
becomes larger, e.g.
![]() $\widetilde{G}^{eq}\geqslant 7$
,
$\widetilde{G}^{eq}\geqslant 7$
,
![]() $\unicode[STIX]{x1D709}^{p}$
would decrease because the wake–plate interaction is diminished for the trailing plate due to vortex dissipation.
$\unicode[STIX]{x1D709}^{p}$
would decrease because the wake–plate interaction is diminished for the trailing plate due to vortex dissipation.
For the two-plate system, using the ‘vortex locking’ mechanism, Zhu et al. (Reference Zhu, He and Zhang2014) explained the energy benefit of the rear plate. Meanwhile, they also mentioned that if the rear plate slaloms between the vortex cores, it is not able to obtain the energy benefit. However, the mechanism is not true for the multiple plate system. From supplementary Movie 2, it is seen that in the ‘C3+C2+1’ configuration, the last plate (
![]() $i=6$
) moves forward by slaloming between the vortex cores, instead of swimming through the vortex cores. This slaloming behaviour is also beneficial to enhancing propulsive performance because the last plate moves approximately 1.3 times faster than an isolated plate. Moreover, because the wakes of a multi-body group may become disorganized as the group grows, the ‘vortex locking’ mechanism is also not valid. Supplementary Movies 5 and 6 show that even encountering a disordered oncoming vortical structure, the last plate in case ‘S8’ is still able to hold its position in the stable configuration.
$i=6$
) moves forward by slaloming between the vortex cores, instead of swimming through the vortex cores. This slaloming behaviour is also beneficial to enhancing propulsive performance because the last plate moves approximately 1.3 times faster than an isolated plate. Moreover, because the wakes of a multi-body group may become disorganized as the group grows, the ‘vortex locking’ mechanism is also not valid. Supplementary Movies 5 and 6 show that even encountering a disordered oncoming vortical structure, the last plate in case ‘S8’ is still able to hold its position in the stable configuration.
For the multiple plate system, the mechanism of ‘hydrodynamic force generation by effective flapping speed’ (Wu & Chwang Reference Wu and Chwang1975; Ramananarivo et al.
Reference Ramananarivo, Fang, Oza, Zhang and Ristroph2016) seems more general and appropriate than ‘vortex locking’. The mechanism states ‘hydrodynamic force on the follower is due to the vorticity induced by the leader’, specifically the thrust is mainly induced by ‘effective wing flapping speed’ (i.e., the relative vertical velocity of the wing and the fluid) (Ramananarivo et al.
Reference Ramananarivo, Fang, Oza, Zhang and Ristroph2016). In the above discussion the mechanism is adopted to explain why the hydrodynamic restoring force at
![]() $\widetilde{G}^{eq}=4$
is enhanced.
$\widetilde{G}^{eq}=4$
is enhanced.
4.3 Schooling performance
To quantify the schooling performance of each plate, the swimming efficiency
![]() $\unicode[STIX]{x1D702}_{i}$
is defined as the ratio of the kinetic energy of the
$\unicode[STIX]{x1D702}_{i}$
is defined as the ratio of the kinetic energy of the
![]() $i$
th plate and its input work, i.e.
$i$
th plate and its input work, i.e.
![]() $\unicode[STIX]{x1D702}_{i}=(1/2)MU_{c,i}^{2}/W_{i}$
, where the input work
$\unicode[STIX]{x1D702}_{i}=(1/2)MU_{c,i}^{2}/W_{i}$
, where the input work
![]() $W_{i}$
is computed as a time integral of the input power
$W_{i}$
is computed as a time integral of the input power
![]() $P_{i}$
required to produce the oscillation and the forward movement (Hua et al.
Reference Hua, Zhu and Lu2013; Zhu et al.
Reference Zhu, He and Zhang2014), i.e.
$P_{i}$
required to produce the oscillation and the forward movement (Hua et al.
Reference Hua, Zhu and Lu2013; Zhu et al.
Reference Zhu, He and Zhang2014), i.e.
![]() $W_{i}=\int _{0}^{T}P_{i}(t)\,\text{d}t=-\int _{0}^{T}\int _{0}^{1}\boldsymbol{F}_{s,i}(s,t)\boldsymbol{\cdot }\unicode[STIX]{x2202}_{t}\boldsymbol{X}_{i}(s,t)\,\text{d}s\,\text{d}t$
. The swimming efficiency of the whole group is
$W_{i}=\int _{0}^{T}P_{i}(t)\,\text{d}t=-\int _{0}^{T}\int _{0}^{1}\boldsymbol{F}_{s,i}(s,t)\boldsymbol{\cdot }\unicode[STIX]{x2202}_{t}\boldsymbol{X}_{i}(s,t)\,\text{d}s\,\text{d}t$
. The swimming efficiency of the whole group is
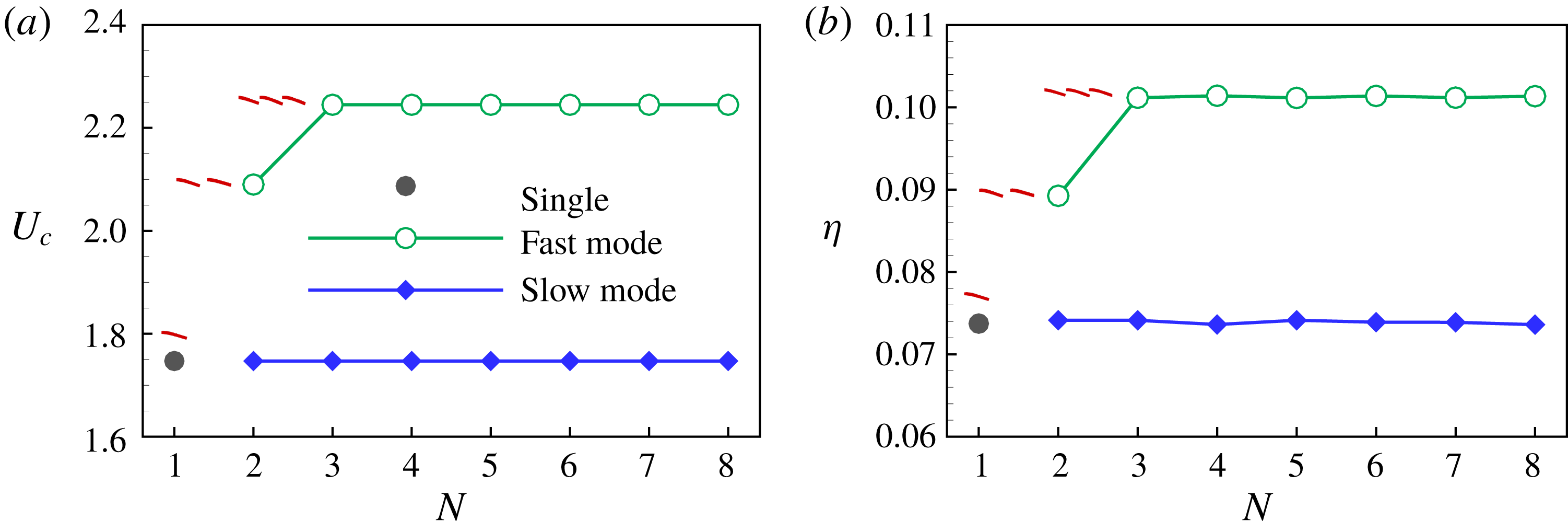
Figure 7. Schooling performance of the groups. (a) The cruising speed and (b) the swimming efficiency as a function of the group size
![]() $N$
. Small snapshots of the leading subgroup or individual are shown in red.
$N$
. Small snapshots of the leading subgroup or individual are shown in red.
Figure 7(a,b) show the cruising speed and the swimming efficiency of the group as a function of
![]() $N$
for the cases in figure 1(b,c). For the slow mode, the groups’ cruising speeds and their efficiencies are almost identical to those of the isolated swimmer. In contrast, for the fast mode, the groups have larger
$N$
for the cases in figure 1(b,c). For the slow mode, the groups’ cruising speeds and their efficiencies are almost identical to those of the isolated swimmer. In contrast, for the fast mode, the groups have larger
![]() $U_{c}$
with higher
$U_{c}$
with higher
![]() $\unicode[STIX]{x1D702}$
compared to the isolated case. For the groups with
$\unicode[STIX]{x1D702}$
compared to the isolated case. For the groups with
![]() $N>3$
,
$N>3$
,
![]() $U_{c}\approx 2.24$
and
$U_{c}\approx 2.24$
and
![]() $\unicode[STIX]{x1D702}\approx 0.10$
, they are approximately 1.3 times those of the isolated plate, as shown in figure 7.
$\unicode[STIX]{x1D702}\approx 0.10$
, they are approximately 1.3 times those of the isolated plate, as shown in figure 7.
Moreover, it is interesting to see that the leading subgroup plays the role of ‘leading goose’; namely, the following subgroups or individuals would keep pace with the leading ones to achieve a uniform cruising speed, although they may have different speeds in isolated swimming. Taking case ‘C3+C2+1’ (see figure 1) as an example, we can see that if the subgroups ‘C3’, ‘C2’, and the individual ‘1’ swim independently, the cruising speeds are 2.24, 2.09 and 1.75 (see table 1), respectively. However, when swimming together as a group, they achieve a uniform cruising speed
![]() $U_{c}=2.24$
, as shown in figure 7(a). Meanwhile, the swimming efficiency of the group members ‘C2’ and ‘1’ is improved (see figure 7
b). In the fast mode, following the leading packed subgroup, the rear subgroups or individuals take advantage of the oncoming wake. These conclusions indicate the hydrodynamic force not only acts as an restoring force to maintain schooling cohesion but also provides a drafting force to rear subgroups so as to improve their schooling performance.
$U_{c}=2.24$
, as shown in figure 7(a). Meanwhile, the swimming efficiency of the group members ‘C2’ and ‘1’ is improved (see figure 7
b). In the fast mode, following the leading packed subgroup, the rear subgroups or individuals take advantage of the oncoming wake. These conclusions indicate the hydrodynamic force not only acts as an restoring force to maintain schooling cohesion but also provides a drafting force to rear subgroups so as to improve their schooling performance.
5 Concluding remarks
In summary, the collective locomotion of multiple self-propelled plates in a tandem configuration is investigated numerically. Two schooling states, i.e., the fast mode with compact configuration and the slow mode with sparse configuration, emerge spontaneously solely due to the flow-mediated interactions among the individuals. The Lighthill conjecture (Lighthill Reference Lighthill1975) was supported by the results of multiple self-propelled plates, which is beyond the cases of the two-body system considered elsewhere (Zhu et al. Reference Zhu, He and Zhang2014; Ramananarivo et al. Reference Ramananarivo, Fang, Oza, Zhang and Ristroph2016).
Schooling stability analysis shows the mechanism for the emergence of the equilibrium positions. It is found that the hydrodynamic force near the stable equilibrium positions is a springlike restoring force. In addition, the emergence of equilibrium positions can be illustrated in terms of a hydrodynamic potential; there are stable wells in the potential energy landscape. The well bottoms correspond to the stable equilibrium states.
The well depths
![]() $\unicode[STIX]{x1D709}^{p}$
in the curve of
$\unicode[STIX]{x1D709}^{p}$
in the curve of
![]() $\unicode[STIX]{x1D6F9}(\widetilde{G})$
are examined to quantify the tolerance for flow perturbation at the stable positions. For the two-plate system, the well depth
$\unicode[STIX]{x1D6F9}(\widetilde{G})$
are examined to quantify the tolerance for flow perturbation at the stable positions. For the two-plate system, the well depth
![]() $\unicode[STIX]{x1D709}^{p}$
decreases with increasing
$\unicode[STIX]{x1D709}^{p}$
decreases with increasing
![]() $\widetilde{G}^{eq}$
, while for multiple plates, the well depth
$\widetilde{G}^{eq}$
, while for multiple plates, the well depth
![]() $\unicode[STIX]{x1D709}^{p}$
may increase first and then decrease with
$\unicode[STIX]{x1D709}^{p}$
may increase first and then decrease with
![]() $\widetilde{G}^{eq}$
.
$\widetilde{G}^{eq}$
.
For the multiple plate system, the last plate may move forward by slaloming between the vortex cores, instead of swimming through the vortex cores. The ‘vortex locking’ mechanism (Zhu et al. Reference Zhu, He and Zhang2014) is no longer valid. The mechanism of ‘hydrodynamic force generation by effective flapping speed’ (Wu & Chwang Reference Wu and Chwang1975; Ramananarivo et al. Reference Ramananarivo, Fang, Oza, Zhang and Ristroph2016) seems more general and appropriate.
For the slow mode, the groups’ cruising speeds and their efficiencies are almost identical to those of the isolated swimmer. In contrast, for the fast mode, the groups have larger
![]() $U_{c}$
with higher
$U_{c}$
with higher
![]() $\unicode[STIX]{x1D702}$
compared to the isolated case. In terms of the cruising speed and efficiency of the whole group, the leading subgroup or individual plays the role of ‘leading goose’. It seems that the hydrodynamic force also provides a drafting force to rear subgroups so as to improve their schooling performance.
$\unicode[STIX]{x1D702}$
compared to the isolated case. In terms of the cruising speed and efficiency of the whole group, the leading subgroup or individual plays the role of ‘leading goose’. It seems that the hydrodynamic force also provides a drafting force to rear subgroups so as to improve their schooling performance.
The present study is a generalization of the two-plate system (Zhu et al.
Reference Zhu, He and Zhang2014) to more wings/flappers (up to
![]() $O(10)$
) and the Lighthill conjecture is further validated on a larger scale. There are some limitations in our study. First, the present model is only two-dimensional, but extending it to the three-dimensional case would be helpful to examine the role of body shape. Second the actuation of the swimming is simple, i.e., only the leading edge of the plate is forced to oscillate sinusoidally. To mimic the actuation of a real fish, a better actuation model, e.g., the neuromechanical model for a lamprey (Tytell et al.
Reference Tytell, Hsu, Williams, Cohen and Fauci2010), should be applied rather than the simplified oscillation model here. If the three-dimensional body shape and a better actuation model are considered, the fish schooling behaviour revealed may be more reasonable.
$O(10)$
) and the Lighthill conjecture is further validated on a larger scale. There are some limitations in our study. First, the present model is only two-dimensional, but extending it to the three-dimensional case would be helpful to examine the role of body shape. Second the actuation of the swimming is simple, i.e., only the leading edge of the plate is forced to oscillate sinusoidally. To mimic the actuation of a real fish, a better actuation model, e.g., the neuromechanical model for a lamprey (Tytell et al.
Reference Tytell, Hsu, Williams, Cohen and Fauci2010), should be applied rather than the simplified oscillation model here. If the three-dimensional body shape and a better actuation model are considered, the fish schooling behaviour revealed may be more reasonable.
Acknowledgements
This work was supported by the Natural Science Foundation of China (NSFC) grant nos 11372304 and 11621202. H.B.H. is supported by NSFC grant no. 11772326.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2018.634.