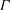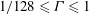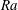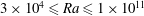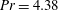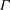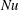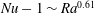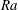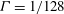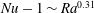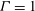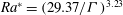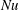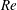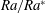1 Introduction
Rayleigh–Bénard (RB) convection occurs in a fluid layer heated from below and cooled from above when the temperature difference is sufficient to initiate instability. This classical paradigm has far-reaching implications for industrial processes, and for fundamental physics in astrophysical and geophysical convections, and its importance is testified to by the large number of studies over the past decade (Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009; Lohse & Xia Reference Lohse and Xia2010; Chillà & Schumacher Reference Chillà and Schumacher2012; Xia Reference Xia2013). Convective heat transfer, in terms of the Nusselt number
![]() $Nu$
, is a fundamental issue in thermal convection, and it has been widely accepted that the heat exchange in RB convection is dictated by the thermal plumes. Typically, plumes organize themselves into the so-called large-scale circulation (LSC) to efficiently transport heat across the convection cell (Kadanoff Reference Kadanoff2001; Shang et al.
Reference Shang, Qiu, Tong and Xia2003; Xi, Lam & Xia Reference Xi, Lam and Xia2004), and this mechanism is regarded as the standard mode of heat transfer in classical RB convection for a closed convection cell of aspect ratio around one.
$Nu$
, is a fundamental issue in thermal convection, and it has been widely accepted that the heat exchange in RB convection is dictated by the thermal plumes. Typically, plumes organize themselves into the so-called large-scale circulation (LSC) to efficiently transport heat across the convection cell (Kadanoff Reference Kadanoff2001; Shang et al.
Reference Shang, Qiu, Tong and Xia2003; Xi, Lam & Xia Reference Xi, Lam and Xia2004), and this mechanism is regarded as the standard mode of heat transfer in classical RB convection for a closed convection cell of aspect ratio around one.
The geometric properties, such as the cell geometry and the lateral extent (characterized by the aspect ratio
![]() $\unicode[STIX]{x1D6E4}$
), strongly influence the LSC and thus the motion of plumes. An example for the influence of cell geometry is that in a cylindrical cell of aspect ratio around one the LSC is manifested as a single-roll structure meandering azimuthally (Cioni, Ciliberto & Sommeria Reference Cioni, Ciliberto and Sommeria1997; Brown, Nikolaenko & Ahlers Reference Brown, Nikolaenko and Ahlers2005; Sun, Xi & Xia Reference Sun, Xi and Xia2005b
; Xi, Zhou & Xia Reference Xi, Zhou and Xia2006), but it becomes largely confined along the cell diagonal when cubic cells are used instead. Besides the shape of cell, varying
$\unicode[STIX]{x1D6E4}$
), strongly influence the LSC and thus the motion of plumes. An example for the influence of cell geometry is that in a cylindrical cell of aspect ratio around one the LSC is manifested as a single-roll structure meandering azimuthally (Cioni, Ciliberto & Sommeria Reference Cioni, Ciliberto and Sommeria1997; Brown, Nikolaenko & Ahlers Reference Brown, Nikolaenko and Ahlers2005; Sun, Xi & Xia Reference Sun, Xi and Xia2005b
; Xi, Zhou & Xia Reference Xi, Zhou and Xia2006), but it becomes largely confined along the cell diagonal when cubic cells are used instead. Besides the shape of cell, varying
![]() $\unicode[STIX]{x1D6E4}$
is the alternative method for changing the nature of LSC. As
$\unicode[STIX]{x1D6E4}$
is the alternative method for changing the nature of LSC. As
![]() $\unicode[STIX]{x1D6E4}$
is increased from one, the original single-roll structure becomes multi-roll (Funfschilling et al.
Reference Funfschilling, Brown, Nikolaenko and Ahlers2005; Sun et al.
Reference Sun, Ren, Song and Xia2005a
). As
$\unicode[STIX]{x1D6E4}$
is increased from one, the original single-roll structure becomes multi-roll (Funfschilling et al.
Reference Funfschilling, Brown, Nikolaenko and Ahlers2005; Sun et al.
Reference Sun, Ren, Song and Xia2005a
). As
![]() $\unicode[STIX]{x1D6E4}$
is decreased from one, LSC will be strongly suppressed by the closer no-slip walls, as reflected by more frequent flow reversals in quasi-2D convection (Ni, Huang & Xia Reference Ni, Huang and Xia2015; Huang & Xia Reference Huang and Xia2016). One question is whether the distinct flow patterns brought about by changing geometric parameters would also influence the convective heat transfer, through a possible modification of plume properties. This leads to the study of geometrical effect on heat transport in RB convection (Grossmann & Lohse Reference Grossmann and Lohse2003; Ching & Tam Reference Ching and Tam2006; Bailon-Cuba, Emran & Schumacher Reference Bailon-Cuba, Emran and Schumacher2010; van der Poel et al.
Reference van der Poel, Stevens, Sugiyama and Lohse2012; Zhou et al.
Reference Zhou, Liu, Li and Zhong2012; Huang et al.
Reference Huang, Kaczorowski, Ni and Xia2013; Wagner & Shishkina Reference Wagner and Shishkina2013; Chong et al.
Reference Chong, Huang, Kaczorowski and Xia2015). A number of experimental studies in fluids with
$\unicode[STIX]{x1D6E4}$
is decreased from one, LSC will be strongly suppressed by the closer no-slip walls, as reflected by more frequent flow reversals in quasi-2D convection (Ni, Huang & Xia Reference Ni, Huang and Xia2015; Huang & Xia Reference Huang and Xia2016). One question is whether the distinct flow patterns brought about by changing geometric parameters would also influence the convective heat transfer, through a possible modification of plume properties. This leads to the study of geometrical effect on heat transport in RB convection (Grossmann & Lohse Reference Grossmann and Lohse2003; Ching & Tam Reference Ching and Tam2006; Bailon-Cuba, Emran & Schumacher Reference Bailon-Cuba, Emran and Schumacher2010; van der Poel et al.
Reference van der Poel, Stevens, Sugiyama and Lohse2012; Zhou et al.
Reference Zhou, Liu, Li and Zhong2012; Huang et al.
Reference Huang, Kaczorowski, Ni and Xia2013; Wagner & Shishkina Reference Wagner and Shishkina2013; Chong et al.
Reference Chong, Huang, Kaczorowski and Xia2015). A number of experimental studies in fluids with
![]() $Pr>1$
(e.g. water) have found that heat transport in RB convection is actually insensitive to the nature of LSC (Wu & Libchaber Reference Wu and Libchaber1992; Xia & Lui Reference Xia and Lui1997; Funfschilling et al.
Reference Funfschilling, Brown, Nikolaenko and Ahlers2005; Nikolaenko et al.
Reference Nikolaenko, Brown, Funfschilling and Ahlers2005; Zhou et al.
Reference Zhou, Liu, Li and Zhong2012). These observations can be understood as follows. The thermal boundary layer is buffered by a thicker viscous boundary layer in the case of
$Pr>1$
(e.g. water) have found that heat transport in RB convection is actually insensitive to the nature of LSC (Wu & Libchaber Reference Wu and Libchaber1992; Xia & Lui Reference Xia and Lui1997; Funfschilling et al.
Reference Funfschilling, Brown, Nikolaenko and Ahlers2005; Nikolaenko et al.
Reference Nikolaenko, Brown, Funfschilling and Ahlers2005; Zhou et al.
Reference Zhou, Liu, Li and Zhong2012). These observations can be understood as follows. The thermal boundary layer is buffered by a thicker viscous boundary layer in the case of
![]() $Pr>1$
(van der Poel, Stevens & Lohse Reference van der Poel, Stevens and Lohse2011). However, by reducing
$Pr>1$
(van der Poel, Stevens & Lohse Reference van der Poel, Stevens and Lohse2011). However, by reducing
![]() $\unicode[STIX]{x1D6E4}$
to much less than one, Huang et al. (Reference Huang, Kaczorowski, Ni and Xia2013) and Chong et al. (Reference Chong, Huang, Kaczorowski and Xia2015) have discovered something highly non-trivial – heat flux increases significantly under geometrical confinement. Chong et al. (Reference Chong, Huang, Kaczorowski and Xia2015) have furthermore found three regimes based on the various heat transport behaviours: Regime I: classical boundary-layer-controlled regime in which heat flux is insensitive to the change in
$\unicode[STIX]{x1D6E4}$
to much less than one, Huang et al. (Reference Huang, Kaczorowski, Ni and Xia2013) and Chong et al. (Reference Chong, Huang, Kaczorowski and Xia2015) have discovered something highly non-trivial – heat flux increases significantly under geometrical confinement. Chong et al. (Reference Chong, Huang, Kaczorowski and Xia2015) have furthermore found three regimes based on the various heat transport behaviours: Regime I: classical boundary-layer-controlled regime in which heat flux is insensitive to the change in
![]() $\unicode[STIX]{x1D6E4}$
; Regime II: plume-controlled regime in which heat flux increases significantly with decreasing
$\unicode[STIX]{x1D6E4}$
; Regime II: plume-controlled regime in which heat flux increases significantly with decreasing
![]() $\unicode[STIX]{x1D6E4}$
owing to the increased plume coherency; and Regime III: severely confined regime in which heat flux drops dramatically with decreasing
$\unicode[STIX]{x1D6E4}$
owing to the increased plume coherency; and Regime III: severely confined regime in which heat flux drops dramatically with decreasing
![]() $\unicode[STIX]{x1D6E4}$
. The present study further shows that Regime III should be restricted to cases well above the onset of convection in which
$\unicode[STIX]{x1D6E4}$
. The present study further shows that Regime III should be restricted to cases well above the onset of convection in which
![]() $Nu$
–
$Nu$
–
![]() $Ra$
possesses steep scaling. We remark that the three regimes were previously recognized for
$Ra$
possesses steep scaling. We remark that the three regimes were previously recognized for
![]() $Pr=4.38$
, but the regime transition may depend on
$Pr=4.38$
, but the regime transition may depend on
![]() $Pr$
as well. For
$Pr$
as well. For
![]() $Pr=0.786$
, the 3D simulations with
$Pr=0.786$
, the 3D simulations with
![]() $10^{5}\leqslant Ra\leqslant 10^{9}$
by Wagner & Shishkina (Reference Wagner and Shishkina2013) have shown that decreasing
$10^{5}\leqslant Ra\leqslant 10^{9}$
by Wagner & Shishkina (Reference Wagner and Shishkina2013) have shown that decreasing
![]() $\unicode[STIX]{x1D6E4}$
can lead to a significant drop in
$\unicode[STIX]{x1D6E4}$
can lead to a significant drop in
![]() $Nu$
, but Regime II has not been realized for their explored parameter range.
$Nu$
, but Regime II has not been realized for their explored parameter range.
Previous studies of highly confined RB convection (
![]() $\unicode[STIX]{x1D6E4}\ll 1$
) have mainly considered how
$\unicode[STIX]{x1D6E4}\ll 1$
) have mainly considered how
![]() $Nu$
responds to a reducing
$Nu$
responds to a reducing
![]() $\unicode[STIX]{x1D6E4}$
, while ignoring the question of whether heat transport scaling of
$\unicode[STIX]{x1D6E4}$
, while ignoring the question of whether heat transport scaling of
![]() $Nu$
versus Rayleigh number
$Nu$
versus Rayleigh number
![]() $Ra$
would differ in the three regimes. One of the few experimental studies on highly confined RB convection (Huang & Xia Reference Huang and Xia2016) has provided a
$Ra$
would differ in the three regimes. One of the few experimental studies on highly confined RB convection (Huang & Xia Reference Huang and Xia2016) has provided a
![]() $Nu{-}Ra$
relationship in Regime II, in which the classical scaling with exponents between
$Nu{-}Ra$
relationship in Regime II, in which the classical scaling with exponents between
![]() $1/4$
and
$1/4$
and
![]() $1/3$
is found. Those authors analysed the bulk and boundary layer contributions to the scaling in terms of the model of Grossmann & Lohse (Reference Grossmann and Lohse2000, Reference Grossmann and Lohse2001) and found that the weight of the boundary layer contribution relative to the bulk contribution increases with decreasing
$1/3$
is found. Those authors analysed the bulk and boundary layer contributions to the scaling in terms of the model of Grossmann & Lohse (Reference Grossmann and Lohse2000, Reference Grossmann and Lohse2001) and found that the weight of the boundary layer contribution relative to the bulk contribution increases with decreasing
![]() $\unicode[STIX]{x1D6E4}$
. However, Regime III has been barely touched in previous studies (see figure 1), so the
$\unicode[STIX]{x1D6E4}$
. However, Regime III has been barely touched in previous studies (see figure 1), so the
![]() $Nu$
–
$Nu$
–
![]() $Ra$
relation in this regime remains unexplored.
$Ra$
relation in this regime remains unexplored.

Figure 1. Phase diagram of different regimes of heat transport under geometrical confinement. I represents the classical boundary-layer-controlled regime; II represents the plume-controlled regime; and III represents the severely confined regime. The dashed line separating I and II is
![]() $\unicode[STIX]{x1D6E4}=12.42Ra^{-0.21}$
, which is determined by the spacing between plumes, and that separating II and III is
$\unicode[STIX]{x1D6E4}=12.42Ra^{-0.21}$
, which is determined by the spacing between plumes, and that separating II and III is
![]() $\unicode[STIX]{x1D6E4}=29.37Ra^{-0.31}$
, which is identified by the optimal aspect ratio for achieving the maximum
$\unicode[STIX]{x1D6E4}=29.37Ra^{-0.31}$
, which is identified by the optimal aspect ratio for achieving the maximum
![]() $Nu$
(Chong et al.
Reference Chong, Huang, Kaczorowski and Xia2015). The solid line is
$Nu$
(Chong et al.
Reference Chong, Huang, Kaczorowski and Xia2015). The solid line is
![]() $Ra=Ra_{c}$
, with
$Ra=Ra_{c}$
, with
![]() $Ra_{c}=482.4\unicode[STIX]{x1D6E4}^{-2.0\pm 0.1}$
, which indicates the onset
$Ra_{c}=482.4\unicode[STIX]{x1D6E4}^{-2.0\pm 0.1}$
, which indicates the onset
![]() $Ra$
for different
$Ra$
for different
![]() $\unicode[STIX]{x1D6E4}$
; and the dotted line is
$\unicode[STIX]{x1D6E4}$
; and the dotted line is
![]() $Ra=5Ra_{c}$
. Note that
$Ra=5Ra_{c}$
. Note that
![]() $Ra_{c}\leqslant Ra\leqslant 5Ra_{c}$
is the transition region before reaching Regime III. Purple squares and green triangles denote the experimental and DNS data from Huang et al. (Reference Huang, Kaczorowski, Ni and Xia2013) and Chong et al. (Reference Chong, Huang, Kaczorowski and Xia2015), respectively. Orange stars denote the DNS data for cubic geometry from Kaczorowski & Xia (Reference Kaczorowski and Xia2013) as a baseline for comparing with the confined cases. Red circles represent the new simulations performed in the present study. All cases are for fluid with
$Ra_{c}\leqslant Ra\leqslant 5Ra_{c}$
is the transition region before reaching Regime III. Purple squares and green triangles denote the experimental and DNS data from Huang et al. (Reference Huang, Kaczorowski, Ni and Xia2013) and Chong et al. (Reference Chong, Huang, Kaczorowski and Xia2015), respectively. Orange stars denote the DNS data for cubic geometry from Kaczorowski & Xia (Reference Kaczorowski and Xia2013) as a baseline for comparing with the confined cases. Red circles represent the new simulations performed in the present study. All cases are for fluid with
![]() $Pr=4.38$
.
$Pr=4.38$
.
In the present study we have conducted highly resolved direct numerical simulations (DNS) of confined Rayleigh–Bénard convection over a large region of the parameter space, with the aspect ratio spanning over two decades and the Rayleigh number spanning seven decades. The width-to-height aspect ratio
![]() $\unicode[STIX]{x1D6E4}$
has been reduced to as low as
$\unicode[STIX]{x1D6E4}$
has been reduced to as low as
![]() $1/128$
to fully explore the severely confined regime (Regime III). With such small
$1/128$
to fully explore the severely confined regime (Regime III). With such small
![]() $\unicode[STIX]{x1D6E4}$
, Regime III could be explored for almost four decades of
$\unicode[STIX]{x1D6E4}$
, Regime III could be explored for almost four decades of
![]() $Ra$
, which enabled us to investigate the scalings of
$Ra$
, which enabled us to investigate the scalings of
![]() $Nu$
and the Reynolds number
$Nu$
and the Reynolds number
![]() $Re$
with
$Re$
with
![]() $Ra$
in Regime III and the corresponding flow topologies.
$Ra$
in Regime III and the corresponding flow topologies.
2 Numerical procedure and set-ups
The simulation determines the non-dimensional velocities
![]() $\boldsymbol{u}=(u_{x},u_{y},u_{z})$
with the temperature field
$\boldsymbol{u}=(u_{x},u_{y},u_{z})$
with the temperature field
![]() $T$
for the incompressible flow by numerically integrating the three-dimensional Navier–Stokes equations in Cartesian geometry within the Oberbeck–Boussinesq approximation,
$T$
for the incompressible flow by numerically integrating the three-dimensional Navier–Stokes equations in Cartesian geometry within the Oberbeck–Boussinesq approximation,
where
![]() $Ra=\unicode[STIX]{x1D6FC}g\unicode[STIX]{x0394}TH^{3}/\unicode[STIX]{x1D708}\unicode[STIX]{x1D705}$
and
$Ra=\unicode[STIX]{x1D6FC}g\unicode[STIX]{x0394}TH^{3}/\unicode[STIX]{x1D708}\unicode[STIX]{x1D705}$
and
![]() $Pr=\unicode[STIX]{x1D708}/\unicode[STIX]{x1D705}$
are the Rayleigh number and the Prandtl number with
$Pr=\unicode[STIX]{x1D708}/\unicode[STIX]{x1D705}$
are the Rayleigh number and the Prandtl number with
![]() $\unicode[STIX]{x1D6FC}$
,
$\unicode[STIX]{x1D6FC}$
,
![]() $\unicode[STIX]{x1D708}$
and
$\unicode[STIX]{x1D708}$
and
![]() $\unicode[STIX]{x1D705}$
denoting the thermal expansion coefficient, kinematic viscosity and thermal diffusivity of fluid;
$\unicode[STIX]{x1D705}$
denoting the thermal expansion coefficient, kinematic viscosity and thermal diffusivity of fluid;
![]() $g$
is the gravitational acceleration and
$g$
is the gravitational acceleration and
![]() $\unicode[STIX]{x0394}T$
the temperature difference across the system height
$\unicode[STIX]{x0394}T$
the temperature difference across the system height
![]() $H$
. The equations are solved in non-dimensional form by using the system height
$H$
. The equations are solved in non-dimensional form by using the system height
![]() $H$
, free-fall velocity
$H$
, free-fall velocity
![]() $\sqrt{\unicode[STIX]{x1D6FD}g\unicode[STIX]{x0394}TH}$
and global temperature difference
$\sqrt{\unicode[STIX]{x1D6FD}g\unicode[STIX]{x0394}TH}$
and global temperature difference
![]() $\unicode[STIX]{x0394}T$
as the respective normalization scales. In this dimensionless form, the range of temperature should be
$\unicode[STIX]{x0394}T$
as the respective normalization scales. In this dimensionless form, the range of temperature should be
![]() $-0.5\leqslant T\leqslant 0.5$
. The velocity boundary conditions of the simulations are that all walls are no-slip and impermeable. And the temperature boundary conditions are that the sidewall is adiabatic while the top and bottom surfaces are isothermal with top (bottom) surface fixed at
$-0.5\leqslant T\leqslant 0.5$
. The velocity boundary conditions of the simulations are that all walls are no-slip and impermeable. And the temperature boundary conditions are that the sidewall is adiabatic while the top and bottom surfaces are isothermal with top (bottom) surface fixed at
![]() $T=-0.5$
(
$T=-0.5$
(
![]() $T=0.5$
).
$T=0.5$
).
The code solves the equations through the finite-volume method on a staggered grid with fourth-order accuracy in space. The convective and diffusive terms in the equations are temporally advanced by the leapfrog and Euler forward methods respectively. A major concern for DNS in RB convection is to resolve the smallest relevant scale in turbulent flows, which is either the Kolmogorov length
![]() $\unicode[STIX]{x1D702}_{k}$
or the Batchelor length
$\unicode[STIX]{x1D702}_{k}$
or the Batchelor length
![]() $\unicode[STIX]{x1D702}_{b}$
depending on whether
$\unicode[STIX]{x1D702}_{b}$
depending on whether
![]() $Pr<1$
or
$Pr<1$
or
![]() $Pr>1$
. The global estimations of both length scales in dimensionless form are expressed as
$Pr>1$
. The global estimations of both length scales in dimensionless form are expressed as
![]() $\unicode[STIX]{x1D702}_{k}=\sqrt{Pr}/[Ra(Nu-1)]^{1/4}$
and
$\unicode[STIX]{x1D702}_{k}=\sqrt{Pr}/[Ra(Nu-1)]^{1/4}$
and
![]() $\unicode[STIX]{x1D702}_{b}=1/[Ra(Nu-1)]^{1/4}$
, and this implies that the number of grid points necessary along a dimension roughly doubles when
$\unicode[STIX]{x1D702}_{b}=1/[Ra(Nu-1)]^{1/4}$
, and this implies that the number of grid points necessary along a dimension roughly doubles when
![]() $Ra$
increases tenfold. Due to the non-uniform distribution of the length scales over space, a stricter resolution requirement is needed near the boundary layers (Shishkina et al.
Reference Shishkina, Stevens, Grossmann and Lohse2010). Those requirements were taken into consideration to perform reliable simulations, and therefore
$Ra$
increases tenfold. Due to the non-uniform distribution of the length scales over space, a stricter resolution requirement is needed near the boundary layers (Shishkina et al.
Reference Shishkina, Stevens, Grossmann and Lohse2010). Those requirements were taken into consideration to perform reliable simulations, and therefore
![]() $N_{z}=2304$
grid points have been adopted along the vertical direction for our largest explored
$N_{z}=2304$
grid points have been adopted along the vertical direction for our largest explored
![]() $Ra$
(
$Ra$
(
![]() $=1\times 10^{11}$
). The results were collected when the simulations had reached the statistical steady state as judged by the convergence of global
$=1\times 10^{11}$
). The results were collected when the simulations had reached the statistical steady state as judged by the convergence of global
![]() $Nu$
over time. For details of the code validation, details of the numerical scheme and an a priori check on the grid design, we refer to the previous publications (Kaczorowski et al.
Reference Kaczorowski, Shishkin, Shishkina and Wagner2008; Kaczorowski & Xia Reference Kaczorowski and Xia2013; Kaczorowski, Chong & Xia Reference Kaczorowski, Chong and Xia2014).
$Nu$
over time. For details of the code validation, details of the numerical scheme and an a priori check on the grid design, we refer to the previous publications (Kaczorowski et al.
Reference Kaczorowski, Shishkin, Shishkina and Wagner2008; Kaczorowski & Xia Reference Kaczorowski and Xia2013; Kaczorowski, Chong & Xia Reference Kaczorowski, Chong and Xia2014).

Figure 2. (a,b)
![]() $Nu$
versus
$Nu$
versus
![]() $Ra$
, (c)
$Ra$
, (c)
![]() $Nu-1$
versus
$Nu-1$
versus
![]() $Ra$
and (d)
$Ra$
and (d)
![]() $Re$
versus
$Re$
versus
![]() $Ra$
for
$Ra$
for
![]() $\unicode[STIX]{x1D6E4}=1$
,
$\unicode[STIX]{x1D6E4}=1$
,
![]() $1/8$
,
$1/8$
,
![]() $1/16$
,
$1/16$
,
![]() $1/32$
,
$1/32$
,
![]() $1/64$
and
$1/64$
and
![]() $1/128$
. The dashed lines are power-law fittings under the scheme: the data within
$1/128$
. The dashed lines are power-law fittings under the scheme: the data within
![]() $5Ra_{c}\leqslant Ra\leqslant Ra^{\ast }$
are fitted for
$5Ra_{c}\leqslant Ra\leqslant Ra^{\ast }$
are fitted for
![]() $\unicode[STIX]{x1D6E4}\leqslant 1/8$
(represented as solid symbols) where
$\unicode[STIX]{x1D6E4}\leqslant 1/8$
(represented as solid symbols) where
![]() $Ra_{c}$
is the onset
$Ra_{c}$
is the onset
![]() $Ra$
and
$Ra$
and
![]() $Ra^{\ast }$
is the
$Ra^{\ast }$
is the
![]() $Ra$
for transition between Regimes II and III, while the full range of
$Ra$
for transition between Regimes II and III, while the full range of
![]() $Ra$
is used for
$Ra$
is used for
![]() $\unicode[STIX]{x1D6E4}=1$
. Note that to focus on the scaling observed well above the onset, data with
$\unicode[STIX]{x1D6E4}=1$
. Note that to focus on the scaling observed well above the onset, data with
![]() $Ra<5Ra_{c}$
are not shown in (c,d).
$Ra<5Ra_{c}$
are not shown in (c,d).
We present the result from
![]() $100$
cases in total,
$100$
cases in total,
![]() $74$
cases from the new simulations combined with
$74$
cases from the new simulations combined with
![]() $26$
cases from our previous numerical data sets (Kaczorowski & Xia Reference Kaczorowski and Xia2013; Chong et al.
Reference Chong, Huang, Kaczorowski and Xia2015), with the width-to-height aspect ratio
$26$
cases from our previous numerical data sets (Kaczorowski & Xia Reference Kaczorowski and Xia2013; Chong et al.
Reference Chong, Huang, Kaczorowski and Xia2015), with the width-to-height aspect ratio
![]() $\unicode[STIX]{x1D6E4}$
spanning over two decades (
$\unicode[STIX]{x1D6E4}$
spanning over two decades (
![]() $1/128\leqslant \unicode[STIX]{x1D6E4}\leqslant 1$
) while the length-to-height aspect ratio is kept fixed at
$1/128\leqslant \unicode[STIX]{x1D6E4}\leqslant 1$
) while the length-to-height aspect ratio is kept fixed at
![]() $1$
,
$1$
,
![]() $Ra$
spans almost seven decades (
$Ra$
spans almost seven decades (
![]() $3\times 10^{4}\leqslant Ra\leqslant 1\times 10^{11}$
) and
$3\times 10^{4}\leqslant Ra\leqslant 1\times 10^{11}$
) and
![]() $Pr$
is fixed at
$Pr$
is fixed at
![]() $Pr=4.38$
. To focus on the severely confined regime, five small
$Pr=4.38$
. To focus on the severely confined regime, five small
![]() $\unicode[STIX]{x1D6E4}$
values are studied in detail here (
$\unicode[STIX]{x1D6E4}$
values are studied in detail here (
![]() $\unicode[STIX]{x1D6E4}=1/8$
,
$\unicode[STIX]{x1D6E4}=1/8$
,
![]() $1/16$
,
$1/16$
,
![]() $1/32$
,
$1/32$
,
![]() $1/64$
and
$1/64$
and
![]() $1/128$
), together with
$1/128$
), together with
![]() $\unicode[STIX]{x1D6E4}=1$
cases as the baseline. The
$\unicode[STIX]{x1D6E4}=1$
cases as the baseline. The
![]() $Ra{-}\unicode[STIX]{x1D6E4}$
combination of the new simulations and our previous data sets are summarized in the phase diagram shown in figure 1.
$Ra{-}\unicode[STIX]{x1D6E4}$
combination of the new simulations and our previous data sets are summarized in the phase diagram shown in figure 1.
3 Results and discussion
The first important quantity to be examined is the global convective heat flux, expressed as
![]() $Nu-1$
where
$Nu-1$
where
![]() $Nu-1=0$
represents the case of pure conduction. The heat flux across a horizontal plane can be calculated through
$Nu-1=0$
represents the case of pure conduction. The heat flux across a horizontal plane can be calculated through
![]() $Nu_{s}=\langle (RaPr)^{1/2}u_{z}T-\unicode[STIX]{x2202}T/\unicode[STIX]{x2202}z\rangle _{x,y,t}$
, where
$Nu_{s}=\langle (RaPr)^{1/2}u_{z}T-\unicode[STIX]{x2202}T/\unicode[STIX]{x2202}z\rangle _{x,y,t}$
, where
![]() $\langle .\rangle _{x,y,t}$
represents the averaging over the horizontal plane and a sufficiently long period of time.
$\langle .\rangle _{x,y,t}$
represents the averaging over the horizontal plane and a sufficiently long period of time.
![]() $Nu$
is estimated by averaging
$Nu$
is estimated by averaging
![]() $Nu_{s}$
over every horizontal plane. Besides the direct measurement of heat flux,
$Nu_{s}$
over every horizontal plane. Besides the direct measurement of heat flux,
![]() $Nu$
can also be estimated from the exact relations with the globally averaged viscous and thermal dissipation rates, which are
$Nu$
can also be estimated from the exact relations with the globally averaged viscous and thermal dissipation rates, which are
![]() $Nu=\langle \unicode[STIX]{x1D716}_{u}\rangle (RaPr)^{1/2}+1$
and
$Nu=\langle \unicode[STIX]{x1D716}_{u}\rangle (RaPr)^{1/2}+1$
and
![]() $Nu=\langle \unicode[STIX]{x1D716}_{T}\rangle (RaPr)^{1/2}$
, with
$Nu=\langle \unicode[STIX]{x1D716}_{T}\rangle (RaPr)^{1/2}$
, with
![]() $\langle .\rangle$
representing averaging over the entire domain and infinite time,
$\langle .\rangle$
representing averaging over the entire domain and infinite time,
![]() $\unicode[STIX]{x1D716}_{u}=(Ra/Pr)^{-1/2}\sum _{i}\sum _{j}(1/2)(\unicode[STIX]{x2202}u_{i}/\unicode[STIX]{x2202}x_{j}+\unicode[STIX]{x2202}u_{j}/\unicode[STIX]{x2202}x_{i})^{2}$
and
$\unicode[STIX]{x1D716}_{u}=(Ra/Pr)^{-1/2}\sum _{i}\sum _{j}(1/2)(\unicode[STIX]{x2202}u_{i}/\unicode[STIX]{x2202}x_{j}+\unicode[STIX]{x2202}u_{j}/\unicode[STIX]{x2202}x_{i})^{2}$
and
![]() $\unicode[STIX]{x1D716}_{T}=(RaPr)^{-1/2}\sum _{i}(\unicode[STIX]{x2202}T/\unicode[STIX]{x2202}x_{i})^{2}$
. Here the average of the three values is taken as the numerically measured
$\unicode[STIX]{x1D716}_{T}=(RaPr)^{-1/2}\sum _{i}(\unicode[STIX]{x2202}T/\unicode[STIX]{x2202}x_{i})^{2}$
. Here the average of the three values is taken as the numerically measured
![]() $Nu$
and their standard deviation represents the error. Another important global transport quantity is the Reynolds number
$Nu$
and their standard deviation represents the error. Another important global transport quantity is the Reynolds number
![]() $Re$
, which characterizes the flow intensity and is defined as
$Re$
, which characterizes the flow intensity and is defined as
![]() $\sqrt{\langle \boldsymbol{u}^{2}\rangle }(Ra/Pr)^{1/2}$
(note that the large-scale flow velocity is ill-defined for small
$\sqrt{\langle \boldsymbol{u}^{2}\rangle }(Ra/Pr)^{1/2}$
(note that the large-scale flow velocity is ill-defined for small
![]() $\unicode[STIX]{x1D6E4}$
because the LSC has been strongly suppressed for highly confined cases).
$\unicode[STIX]{x1D6E4}$
because the LSC has been strongly suppressed for highly confined cases).
In order to capture the onset Rayleigh number
![]() $Ra_{c}$
for convection, we first examine
$Ra_{c}$
for convection, we first examine
![]() $Nu$
versus
$Nu$
versus
![]() $Ra$
in figure 2(a,b) instead of
$Ra$
in figure 2(a,b) instead of
![]() $Nu-1$
versus
$Nu-1$
versus
![]() $Ra$
. The
$Ra$
. The
![]() $Ra_{c}$
for each case of small
$Ra_{c}$
for each case of small
![]() $\unicode[STIX]{x1D6E4}$
between
$\unicode[STIX]{x1D6E4}$
between
![]() $1/128$
and
$1/128$
and
![]() $1/8$
is identified based on the fact that
$1/8$
is identified based on the fact that
![]() $Nu$
settles at one when
$Nu$
settles at one when
![]() $Ra$
is below
$Ra$
is below
![]() $Ra_{c}$
, and the values are listed in table 1. We find that
$Ra_{c}$
, and the values are listed in table 1. We find that
![]() $Ra_{c}$
obeys a power-law relation with
$Ra_{c}$
obeys a power-law relation with
![]() $\unicode[STIX]{x1D6E4}$
, i.e.
$\unicode[STIX]{x1D6E4}$
, i.e.
![]() $Ra_{c}=482.4\unicode[STIX]{x1D6E4}^{-2.0\pm 0.1}$
(figure 3
a). This scaling exponent agrees excellently with
$Ra_{c}=482.4\unicode[STIX]{x1D6E4}^{-2.0\pm 0.1}$
(figure 3
a). This scaling exponent agrees excellently with
![]() $Ra_{c}\sim \unicode[STIX]{x1D6E4}^{-2}$
(for
$Ra_{c}\sim \unicode[STIX]{x1D6E4}^{-2}$
(for
![]() $\unicode[STIX]{x1D6E4}\ll 1$
), which was derived from linear stability analysis that was originally developed for Hele-Shaw convection (Bizon et al.
Reference Bizon, Werne, Predtechensky, Julien, McCormick, Swift and Swinney1997). Figure 2(a,b) also reveals that, after
$\unicode[STIX]{x1D6E4}\ll 1$
), which was derived from linear stability analysis that was originally developed for Hele-Shaw convection (Bizon et al.
Reference Bizon, Werne, Predtechensky, Julien, McCormick, Swift and Swinney1997). Figure 2(a,b) also reveals that, after
![]() $Ra$
exceeds
$Ra$
exceeds
![]() $Ra_{c}$
, there exists a transition region for
$Ra_{c}$
, there exists a transition region for
![]() $Nu$
before it clearly exhibits a power-law behaviour. In this work, we mainly focus on the scaling relation that occurs for
$Nu$
before it clearly exhibits a power-law behaviour. In this work, we mainly focus on the scaling relation that occurs for
![]() $Ra$
well above
$Ra$
well above
![]() $Ra_{c}$
. Thus, only the data points with
$Ra_{c}$
. Thus, only the data points with
![]() $Ra\geqslant 5Ra_{c}$
are included for scaling analysis.
$Ra\geqslant 5Ra_{c}$
are included for scaling analysis.

Figure 3. (a) Onset Rayleigh number
![]() $Ra_{c}$
versus
$Ra_{c}$
versus
![]() $\unicode[STIX]{x1D6E4}$
. Exponents for the power laws
$\unicode[STIX]{x1D6E4}$
. Exponents for the power laws
![]() $Nu-1\sim Ra^{\unicode[STIX]{x1D6FD}_{Nu-1}}$
and
$Nu-1\sim Ra^{\unicode[STIX]{x1D6FD}_{Nu-1}}$
and
![]() $Re\sim Ra^{\unicode[STIX]{x1D6FD}_{Re}}$
in the severely confined regime versus
$Re\sim Ra^{\unicode[STIX]{x1D6FD}_{Re}}$
in the severely confined regime versus
![]() $\unicode[STIX]{x1D6E4}$
: (b)
$\unicode[STIX]{x1D6E4}$
: (b)
![]() $\unicode[STIX]{x1D6FD}_{Nu-1}$
and (c)
$\unicode[STIX]{x1D6FD}_{Nu-1}$
and (c)
![]() $\unicode[STIX]{x1D6FD}_{Re}$
, with the lines drawn to guide the eye.
$\unicode[STIX]{x1D6FD}_{Re}$
, with the lines drawn to guide the eye.
Table 1. Onset Rayleigh number
![]() $Ra_{c}$
and scaling exponents from the relations
$Ra_{c}$
and scaling exponents from the relations
![]() $Nu-1\sim Ra^{\unicode[STIX]{x1D6FD}_{Nu-1}}$
and
$Nu-1\sim Ra^{\unicode[STIX]{x1D6FD}_{Nu-1}}$
and
![]() $Re\sim Ra^{\unicode[STIX]{x1D6FD}_{Re}}$
fitted to data lying in the severely confined regime.
$Re\sim Ra^{\unicode[STIX]{x1D6FD}_{Re}}$
fitted to data lying in the severely confined regime.

Figure 2(c) plots
![]() $Nu-1$
versus
$Nu-1$
versus
![]() $Ra$
for different
$Ra$
for different
![]() $\unicode[STIX]{x1D6E4}$
on a log–log scale, which readily shows the power-law relation. As a baseline we first examine the case for
$\unicode[STIX]{x1D6E4}$
on a log–log scale, which readily shows the power-law relation. As a baseline we first examine the case for
![]() $\unicode[STIX]{x1D6E4}=1$
(black squares). The power-law fitting represented by the black dashed line yields
$\unicode[STIX]{x1D6E4}=1$
(black squares). The power-law fitting represented by the black dashed line yields
![]() $Nu-1=0.106Ra^{0.308\pm 0.001}$
over the full range of explored
$Nu-1=0.106Ra^{0.308\pm 0.001}$
over the full range of explored
![]() $Ra$
,
$Ra$
,
![]() $1\times 10^{6}\leqslant Ra\leqslant 1\times 10^{10}$
, indicating that the scaling in this range for the case of
$1\times 10^{6}\leqslant Ra\leqslant 1\times 10^{10}$
, indicating that the scaling in this range for the case of
![]() $\unicode[STIX]{x1D6E4}=1$
can be described by a single power law. For the confined cases (
$\unicode[STIX]{x1D6E4}=1$
can be described by a single power law. For the confined cases (
![]() $\unicode[STIX]{x1D6E4}\leqslant 1/8$
) and over the range of
$\unicode[STIX]{x1D6E4}\leqslant 1/8$
) and over the range of
![]() $Ra$
explored, the convective state may straddle various regimes in the phase diagram shown in figure 1, implying the possibility of having multiple scalings. Indeed, as can be clearly seen from figure 2(c), data for the cases of small
$Ra$
explored, the convective state may straddle various regimes in the phase diagram shown in figure 1, implying the possibility of having multiple scalings. Indeed, as can be clearly seen from figure 2(c), data for the cases of small
![]() $\unicode[STIX]{x1D6E4}$
exhibit different scaling behaviours as
$\unicode[STIX]{x1D6E4}$
exhibit different scaling behaviours as
![]() $Ra$
increases. The sharp change of scaling takes place at the boundary separating Regime II and Regime III, i.e.
$Ra$
increases. The sharp change of scaling takes place at the boundary separating Regime II and Regime III, i.e.
![]() $\unicode[STIX]{x1D6E4}=29.37Ra^{-0.31}$
(Chong et al.
Reference Chong, Huang, Kaczorowski and Xia2015), which leads us to identify a Rayleigh number for this regime transition,
$\unicode[STIX]{x1D6E4}=29.37Ra^{-0.31}$
(Chong et al.
Reference Chong, Huang, Kaczorowski and Xia2015), which leads us to identify a Rayleigh number for this regime transition,
![]() $Ra^{\ast }=(29.37/\unicode[STIX]{x1D6E4})^{3.23}$
. We fit the data for individual
$Ra^{\ast }=(29.37/\unicode[STIX]{x1D6E4})^{3.23}$
. We fit the data for individual
![]() $\unicode[STIX]{x1D6E4}$
separately for data points with
$\unicode[STIX]{x1D6E4}$
separately for data points with
![]() $Ra<Ra^{\ast }$
(represented by the solid symbols), with the fitting indicated by the dashed lines in corresponding colours in figure 2(c,d). For instance, the case of
$Ra<Ra^{\ast }$
(represented by the solid symbols), with the fitting indicated by the dashed lines in corresponding colours in figure 2(c,d). For instance, the case of
![]() $\unicode[STIX]{x1D6E4}=1/128$
(red star) exhibits the scaling exponent of 0.61 over three decades of
$\unicode[STIX]{x1D6E4}=1/128$
(red star) exhibits the scaling exponent of 0.61 over three decades of
![]() $Ra$
(
$Ra$
(
![]() $5\times 10^{7}\leqslant Ra\leqslant 1\times 10^{11}$
), which is much larger than 0.31 for
$5\times 10^{7}\leqslant Ra\leqslant 1\times 10^{11}$
), which is much larger than 0.31 for
![]() $\unicode[STIX]{x1D6E4}=1$
. We also examine
$\unicode[STIX]{x1D6E4}=1$
. We also examine
![]() $Re$
similarly (figure 2
d), which yields the scaling
$Re$
similarly (figure 2
d), which yields the scaling
![]() $Re\sim Ra^{0.80\pm 0.01}$
for
$Re\sim Ra^{0.80\pm 0.01}$
for
![]() $\unicode[STIX]{x1D6E4}=1/128$
, contrasting sharply with the scaling
$\unicode[STIX]{x1D6E4}=1/128$
, contrasting sharply with the scaling
![]() $Re\sim Ra^{0.522\pm 0.003}$
for
$Re\sim Ra^{0.522\pm 0.003}$
for
![]() $\unicode[STIX]{x1D6E4}=1$
. Details of the fitting exponents in the severely confined regime (Regime III) for each
$\unicode[STIX]{x1D6E4}=1$
. Details of the fitting exponents in the severely confined regime (Regime III) for each
![]() $\unicode[STIX]{x1D6E4}$
are shown in table 1 and plotted in figure 3(b,c). It is seen that the scaling exponents for both
$\unicode[STIX]{x1D6E4}$
are shown in table 1 and plotted in figure 3(b,c). It is seen that the scaling exponents for both
![]() $Nu$
and
$Nu$
and
![]() $Re$
increase with decreasing
$Re$
increase with decreasing
![]() $\unicode[STIX]{x1D6E4}$
in Regime III. The exponents also seem to approach some asymptotic values, and for the sake of discussion we take the exponents for
$\unicode[STIX]{x1D6E4}$
in Regime III. The exponents also seem to approach some asymptotic values, and for the sake of discussion we take the exponents for
![]() $\unicode[STIX]{x1D6E4}=1/128$
(smallest value explored) as the proxy for those values. To verify this, it will be highly desirable to have 3D simulations for
$\unicode[STIX]{x1D6E4}=1/128$
(smallest value explored) as the proxy for those values. To verify this, it will be highly desirable to have 3D simulations for
![]() $\unicode[STIX]{x1D6E4}$
much smaller than
$\unicode[STIX]{x1D6E4}$
much smaller than
![]() $1/128$
in the future. However, it will be a difficult task for DNS because of the infinitesimally small time step needed for small grid spacing along the confinement direction for
$1/128$
in the future. However, it will be a difficult task for DNS because of the infinitesimally small time step needed for small grid spacing along the confinement direction for
![]() $\unicode[STIX]{x1D6E4}\ll 1$
.
$\unicode[STIX]{x1D6E4}\ll 1$
.
The above scaling behaviour can be shown more clearly by the compensated plots. Figure 4(a) displays
![]() $(Nu-1)Ra^{-0.61}$
versus
$(Nu-1)Ra^{-0.61}$
versus
![]() $Ra$
, which also demonstrates that the scaling in the severely confined regime is not strictly universal (before entering the asymptotic state). Figure 4(a) also clearly demonstrates that, on increasing
$Ra$
, which also demonstrates that the scaling in the severely confined regime is not strictly universal (before entering the asymptotic state). Figure 4(a) also clearly demonstrates that, on increasing
![]() $Ra$
, the steep scaling observed in Regime III returns to the classical scaling (black dashed line) upon entering the plume-controlled regime (Regime II), which is more evident for the cases
$Ra$
, the steep scaling observed in Regime III returns to the classical scaling (black dashed line) upon entering the plume-controlled regime (Regime II), which is more evident for the cases
![]() $\unicode[STIX]{x1D6E4}=1/8$
and
$\unicode[STIX]{x1D6E4}=1/8$
and
![]() $\unicode[STIX]{x1D6E4}=1/16$
. The return to the classical scaling in Regime II is actually in agreement with the previous experimental finding (Huang & Xia Reference Huang and Xia2016). Similarly, the compensated plot of
$\unicode[STIX]{x1D6E4}=1/16$
. The return to the classical scaling in Regime II is actually in agreement with the previous experimental finding (Huang & Xia Reference Huang and Xia2016). Similarly, the compensated plot of
![]() $Re\,Ra^{-0.80}$
versus
$Re\,Ra^{-0.80}$
versus
![]() $Ra$
(figure 4
b) also reveals how the scaling tends from 0.69 to 0.80 as
$Ra$
(figure 4
b) also reveals how the scaling tends from 0.69 to 0.80 as
![]() $\unicode[STIX]{x1D6E4}$
decreases from
$\unicode[STIX]{x1D6E4}$
decreases from
![]() $1/8$
to
$1/8$
to
![]() $1/128$
, and how the steep scaling in the severely confined regime transits to the classical scaling (black dashed line).
$1/128$
, and how the steep scaling in the severely confined regime transits to the classical scaling (black dashed line).

Figure 4. Compensated plots of (a)
![]() $(Nu-1)Ra^{-0.61}$
and (b)
$(Nu-1)Ra^{-0.61}$
and (b)
![]() $Re\,Ra^{-0.80}$
versus
$Re\,Ra^{-0.80}$
versus
![]() $Ra$
for six values of
$Ra$
for six values of
![]() $\unicode[STIX]{x1D6E4}$
between
$\unicode[STIX]{x1D6E4}$
between
![]() $1/128$
and 1. The power-law fitting is the same as in figure 2.
$1/128$
and 1. The power-law fitting is the same as in figure 2.

Figure 5. Colour-graded instantaneous field of the dimensionless temperature
![]() $T$
taken at vertical mid-plane (midway along the confinement direction) for three different
$T$
taken at vertical mid-plane (midway along the confinement direction) for three different
![]() $Ra$
,
$Ra$
,
![]() $1\times 10^{8}$
(a,d,g),
$1\times 10^{8}$
(a,d,g),
![]() $1\times 10^{9}$
(b,e,h) and
$1\times 10^{9}$
(b,e,h) and
![]() $1\times 10^{10}$
(c,f,i), and for three different
$1\times 10^{10}$
(c,f,i), and for three different
![]() $\unicode[STIX]{x1D6E4}$
,
$\unicode[STIX]{x1D6E4}$
,
![]() $\unicode[STIX]{x1D6E4}=1$
(a–c),
$\unicode[STIX]{x1D6E4}=1$
(a–c),
![]() $\unicode[STIX]{x1D6E4}=1/32$
(d–f) and
$\unicode[STIX]{x1D6E4}=1/32$
(d–f) and
![]() $\unicode[STIX]{x1D6E4}=1/128$
(g–i). Here the reddish colour indicates the hot fluid while the bluish colour indicates the cold fluid.
$\unicode[STIX]{x1D6E4}=1/128$
(g–i). Here the reddish colour indicates the hot fluid while the bluish colour indicates the cold fluid.
The scaling transition observed for the global quantities may be associated with changes in flow topology. Figure 5 shows slices of the instantaneous dimensionless temperature field taken at the vertical mid-plane, where the reddish and bluish colours represent hot and cold plumes respectively. Figure 5(a,b,c) shows the temperature fields for
![]() $\unicode[STIX]{x1D6E4}=1$
at
$\unicode[STIX]{x1D6E4}=1$
at
![]() $Ra=1\times 10^{8}$
,
$Ra=1\times 10^{8}$
,
![]() $1\times 10^{9}$
and
$1\times 10^{9}$
and
![]() $1\times 10^{10}$
respectively, which are examples of the flow topology in the classical ‘less confined’ situation. The figures clearly demonstrate that thermal plumes of mushroom-like morphology detach from the top and bottom thermal boundary layers. These plumes cluster mainly on either side of the wall as they are driven by the LSC (note that the main circulating plane of LSC is along the diagonal). With
$1\times 10^{10}$
respectively, which are examples of the flow topology in the classical ‘less confined’ situation. The figures clearly demonstrate that thermal plumes of mushroom-like morphology detach from the top and bottom thermal boundary layers. These plumes cluster mainly on either side of the wall as they are driven by the LSC (note that the main circulating plane of LSC is along the diagonal). With
![]() $Ra$
increasing from
$Ra$
increasing from
![]() $1\times 10^{8}$
to
$1\times 10^{8}$
to
![]() $1\times 10^{10}$
, figure 5(c) demonstrates that plumes become more fragmented (Zhou & Xia Reference Zhou and Xia2010), suggesting smaller scales being excited by stronger thermal forcing. For
$1\times 10^{10}$
, figure 5(c) demonstrates that plumes become more fragmented (Zhou & Xia Reference Zhou and Xia2010), suggesting smaller scales being excited by stronger thermal forcing. For
![]() $\unicode[STIX]{x1D6E4}=1/32$
, as shown in figure 5(d–f), plumes extending the entire cell height have been observed for
$\unicode[STIX]{x1D6E4}=1/32$
, as shown in figure 5(d–f), plumes extending the entire cell height have been observed for
![]() $Ra=1\times 10^{8}$
and
$Ra=1\times 10^{8}$
and
![]() $1\times 10^{9}$
, which are cases in the severely confined regime; whereas highly coherent plumes have been observed for
$1\times 10^{9}$
, which are cases in the severely confined regime; whereas highly coherent plumes have been observed for
![]() $Ra=1\times 10^{10}$
, in which convective flow has entered the plume-controlled Regime II. The flow topology in severely confined Regime III has also been demonstrated by the smallest explored
$Ra=1\times 10^{10}$
, in which convective flow has entered the plume-controlled Regime II. The flow topology in severely confined Regime III has also been demonstrated by the smallest explored
![]() $\unicode[STIX]{x1D6E4}$
(
$\unicode[STIX]{x1D6E4}$
(
![]() $=1/128$
) as shown in figure 5(g–i). It can be seen that the main feature of flow topology becomes the finger-like columns of hot and cold thermal plumes, in contrast to the typical picture of mushroom-like fragmented thermal plumes in the classical regime. Thus, the transition into Regime III leads to the formation of the long-lived columns of thermal plumes that extend the entire cell height. With increasing
$=1/128$
) as shown in figure 5(g–i). It can be seen that the main feature of flow topology becomes the finger-like columns of hot and cold thermal plumes, in contrast to the typical picture of mushroom-like fragmented thermal plumes in the classical regime. Thus, the transition into Regime III leads to the formation of the long-lived columns of thermal plumes that extend the entire cell height. With increasing
![]() $Ra$
, not only does the scale of the heat columns become smaller, the columns also become less straight, which is the signature of vanishing vertical coherency as the flow becomes more unstable under stronger thermal driving. Furthermore, figure 5(i) demonstrates a state where mushroom-like plumes grow into column-like plumes; this coalescence of plumes has also been found in a porous medium (Hewitt, Neufeld & Lister Reference Hewitt, Neufeld and Lister2012). At even larger
$Ra$
, not only does the scale of the heat columns become smaller, the columns also become less straight, which is the signature of vanishing vertical coherency as the flow becomes more unstable under stronger thermal driving. Furthermore, figure 5(i) demonstrates a state where mushroom-like plumes grow into column-like plumes; this coalescence of plumes has also been found in a porous medium (Hewitt, Neufeld & Lister Reference Hewitt, Neufeld and Lister2012). At even larger
![]() $Ra$
, the plume-controlled regime should be reached and the dominating feature becomes the highly coherent giant plumes (Huang et al.
Reference Huang, Kaczorowski, Ni and Xia2013; Chong et al.
Reference Chong, Huang, Kaczorowski and Xia2015), and eventually the fragmented plumes.
$Ra$
, the plume-controlled regime should be reached and the dominating feature becomes the highly coherent giant plumes (Huang et al.
Reference Huang, Kaczorowski, Ni and Xia2013; Chong et al.
Reference Chong, Huang, Kaczorowski and Xia2015), and eventually the fragmented plumes.
Our study has revealed a new state of thermal convection in which the scaling of the global quantities and the flow topology are strikingly different from their classical counterparts. With sufficiently small
![]() $\unicode[STIX]{x1D6E4}$
and a sufficiently wide range in
$\unicode[STIX]{x1D6E4}$
and a sufficiently wide range in
![]() $Ra$
, thus giving rise to a sufficiently wide Regime III, the transition from Regime III to Regime II and Regime I can be clearly observed from the scalings of the global heat and momentum transport. Also, Regime III possesses a new type of flow topology in the form of column-like plumes. The emergence of finger-like, long-lived heat columns observed here and the multiple transitions in highly confined RB convection observed by Chong et al. (Reference Chong, Huang, Kaczorowski and Xia2015) are a result of the interplay between stabilizing and destabilizing forces, i.e. the viscous drag from walls as a result of severe confinement and the thermal driving force. It is interesting to note that similarities exist between the present system and other types of convective flows under different forms of stabilizing and destabilizing forces, such as rotating RB convection (Stevens et al.
Reference Stevens, Zhong, Clercx, Ahlers and Lohse2009; King, Stellmach & Aurnou Reference King, Stellmach and Aurnou2012; Wei, Weiss & Ahlers Reference Wei, Weiss and Ahlers2015) and double diffusive convection (Yang, Verzicco & Lohse Reference Yang, Verzicco and Lohse2016), in which the forces that suppress the convective flow are the rotation and the stabilizing scalar gradient respectively. For rotating RB convection under vigorous rotation, there exists a regime with convective Taylor columns (Grooms et al.
Reference Grooms, Julien, Weiss and Knobloch2010), and such columnar flow topology is associated with a very steep
$Ra$
, thus giving rise to a sufficiently wide Regime III, the transition from Regime III to Regime II and Regime I can be clearly observed from the scalings of the global heat and momentum transport. Also, Regime III possesses a new type of flow topology in the form of column-like plumes. The emergence of finger-like, long-lived heat columns observed here and the multiple transitions in highly confined RB convection observed by Chong et al. (Reference Chong, Huang, Kaczorowski and Xia2015) are a result of the interplay between stabilizing and destabilizing forces, i.e. the viscous drag from walls as a result of severe confinement and the thermal driving force. It is interesting to note that similarities exist between the present system and other types of convective flows under different forms of stabilizing and destabilizing forces, such as rotating RB convection (Stevens et al.
Reference Stevens, Zhong, Clercx, Ahlers and Lohse2009; King, Stellmach & Aurnou Reference King, Stellmach and Aurnou2012; Wei, Weiss & Ahlers Reference Wei, Weiss and Ahlers2015) and double diffusive convection (Yang, Verzicco & Lohse Reference Yang, Verzicco and Lohse2016), in which the forces that suppress the convective flow are the rotation and the stabilizing scalar gradient respectively. For rotating RB convection under vigorous rotation, there exists a regime with convective Taylor columns (Grooms et al.
Reference Grooms, Julien, Weiss and Knobloch2010), and such columnar flow topology is associated with a very steep
![]() $Nu{-}Ra$
scaling, having an exponent as large as 3.6 when the Ekman number
$Nu{-}Ra$
scaling, having an exponent as large as 3.6 when the Ekman number
![]() $Ek$
reaches
$Ek$
reaches
![]() $10^{-7}$
(Cheng et al.
Reference Cheng, Stellmach, Ribeiro, Grannan, King and Aurnou2015). Such a scaling transition in rotating RB convection is related to the crossing of Ekman and thermal boundary layers, and a rescaled Rayleigh number
$10^{-7}$
(Cheng et al.
Reference Cheng, Stellmach, Ribeiro, Grannan, King and Aurnou2015). Such a scaling transition in rotating RB convection is related to the crossing of Ekman and thermal boundary layers, and a rescaled Rayleigh number
![]() $Ra\,Ek^{3/2}$
has been introduced (King et al.
Reference King, Stellmach and Aurnou2012) to understand the observed
$Ra\,Ek^{3/2}$
has been introduced (King et al.
Reference King, Stellmach and Aurnou2012) to understand the observed
![]() $Nu$
behaviour. Here, for severely confined RB convection, the new scaling is found in Regime III, which is entered when
$Nu$
behaviour. Here, for severely confined RB convection, the new scaling is found in Regime III, which is entered when
![]() $Ra$
is smaller than a
$Ra$
is smaller than a
![]() $\unicode[STIX]{x1D6E4}$
-dependent value
$\unicode[STIX]{x1D6E4}$
-dependent value
![]() $Ra^{\ast }=(29.37/\unicode[STIX]{x1D6E4})^{3.23}$
. Therefore, a rescaled Rayleigh number
$Ra^{\ast }=(29.37/\unicode[STIX]{x1D6E4})^{3.23}$
. Therefore, a rescaled Rayleigh number
![]() $Ra/Ra^{\ast }=1.84\times 10^{-5}Ra\unicode[STIX]{x1D6E4}^{3.23}$
may be suitable for revealing the regime transition.
$Ra/Ra^{\ast }=1.84\times 10^{-5}Ra\unicode[STIX]{x1D6E4}^{3.23}$
may be suitable for revealing the regime transition.

Figure 6. The shift factors
![]() $C_{1}$
,
$C_{1}$
,
![]() $C_{2}$
and
$C_{2}$
and
![]() $C_{3}$
versus
$C_{3}$
versus
![]() $\unicode[STIX]{x1D6E4}$
in (a), (b) and (c), respectively. Here
$\unicode[STIX]{x1D6E4}$
in (a), (b) and (c), respectively. Here
![]() $C_{1}$
,
$C_{1}$
,
![]() $C_{2}$
and
$C_{2}$
and
![]() $C_{3}$
are arbitrarily chosen factors such that
$C_{3}$
are arbitrarily chosen factors such that
![]() $C_{1}(\unicode[STIX]{x1D6E4})(Nu-1)Ra^{-0.61}$
,
$C_{1}(\unicode[STIX]{x1D6E4})(Nu-1)Ra^{-0.61}$
,
![]() $C_{2}(\unicode[STIX]{x1D6E4})Re\,Ra^{-0.52}$
and
$C_{2}(\unicode[STIX]{x1D6E4})Re\,Ra^{-0.52}$
and
![]() $C_{3}(\unicode[STIX]{x1D6E4})Re\,Ra^{-0.80}$
collapse onto more or less single curves. Compensated plots of (d)
$C_{3}(\unicode[STIX]{x1D6E4})Re\,Ra^{-0.80}$
collapse onto more or less single curves. Compensated plots of (d)
![]() $(Nu-1)Ra^{-0.31}$
, (e)
$(Nu-1)Ra^{-0.31}$
, (e)
![]() $(Nu-1)Ra^{-0.61}\unicode[STIX]{x1D6E4}^{-0.88}$
, (f)
$(Nu-1)Ra^{-0.61}\unicode[STIX]{x1D6E4}^{-0.88}$
, (f)
![]() $Re\,Ra^{-0.52}\unicode[STIX]{x1D6E4}^{-0.31}$
and (g)
$Re\,Ra^{-0.52}\unicode[STIX]{x1D6E4}^{-0.31}$
and (g)
![]() $Re\,Ra^{-0.80}\unicode[STIX]{x1D6E4}^{-1.23}$
versus the rescaled Rayleigh number
$Re\,Ra^{-0.80}\unicode[STIX]{x1D6E4}^{-1.23}$
versus the rescaled Rayleigh number
![]() $Ra/Ra^{\ast }=1.84\times 10^{-5}Ra\unicode[STIX]{x1D6E4}^{3.23}$
for six different values of
$Ra/Ra^{\ast }=1.84\times 10^{-5}Ra\unicode[STIX]{x1D6E4}^{3.23}$
for six different values of
![]() $\unicode[STIX]{x1D6E4}$
. Here the grey dotted line indicates the boundary separating Regimes III and II as found by Chong et al. (Reference Chong, Huang, Kaczorowski and Xia2015).
$\unicode[STIX]{x1D6E4}$
. Here the grey dotted line indicates the boundary separating Regimes III and II as found by Chong et al. (Reference Chong, Huang, Kaczorowski and Xia2015).
With the rescaled
![]() $Ra$
, the compensated plot
$Ra$
, the compensated plot
![]() $(Nu-1)Ra^{-0.31}$
collapsed onto more or less a single curve whereas the plot
$(Nu-1)Ra^{-0.31}$
collapsed onto more or less a single curve whereas the plot
![]() $(Nu-1)Ra^{-0.61}$
can also be collapsed by multiplying by a
$(Nu-1)Ra^{-0.61}$
can also be collapsed by multiplying by a
![]() $\unicode[STIX]{x1D6E4}$
-dependent shift factor
$\unicode[STIX]{x1D6E4}$
-dependent shift factor
![]() $C_{1}$
, where its
$C_{1}$
, where its
![]() $\unicode[STIX]{x1D6E4}$
-dependence is shown in figure 6(a). Similar to
$\unicode[STIX]{x1D6E4}$
-dependence is shown in figure 6(a). Similar to
![]() $Nu$
, the plots of
$Nu$
, the plots of
![]() $Re\,Ra^{-0.52}$
and
$Re\,Ra^{-0.52}$
and
![]() $Re\,Ra^{-0.80}$
use the shift factors
$Re\,Ra^{-0.80}$
use the shift factors
![]() $C_{2}$
and
$C_{2}$
and
![]() $C_{3}$
for collapsing the data, and the
$C_{3}$
for collapsing the data, and the
![]() $\unicode[STIX]{x1D6E4}$
-dependence of these factors is shown in figure 6(b,c). Interestingly,
$\unicode[STIX]{x1D6E4}$
-dependence of these factors is shown in figure 6(b,c). Interestingly,
![]() $C_{1}$
,
$C_{1}$
,
![]() $C_{2}$
and
$C_{2}$
and
![]() $C_{3}$
all have a power-law dependence on
$C_{3}$
all have a power-law dependence on
![]() $\unicode[STIX]{x1D6E4}$
, with the coefficients all close to one, i.e.
$\unicode[STIX]{x1D6E4}$
, with the coefficients all close to one, i.e.
![]() $C_{1}=1.06\unicode[STIX]{x1D6E4}^{-0.88\pm 0.02}$
,
$C_{1}=1.06\unicode[STIX]{x1D6E4}^{-0.88\pm 0.02}$
,
![]() $C_{2}=0.88\unicode[STIX]{x1D6E4}^{-0.31\pm 0.03}$
and
$C_{2}=0.88\unicode[STIX]{x1D6E4}^{-0.31\pm 0.03}$
and
![]() $C_{3}=0.86\unicode[STIX]{x1D6E4}^{-1.23\pm 0.04}$
. After determining the power-law dependence on
$C_{3}=0.86\unicode[STIX]{x1D6E4}^{-1.23\pm 0.04}$
. After determining the power-law dependence on
![]() $\unicode[STIX]{x1D6E4}$
, the compensated
$\unicode[STIX]{x1D6E4}$
, the compensated
![]() $(Nu-1)Ra^{-0.31}$
and
$(Nu-1)Ra^{-0.31}$
and
![]() $(Nu-1)Ra^{-0.61}\unicode[STIX]{x1D6E4}^{-0.88}$
, using exponents for the classical and severely confined regimes, are plotted versus the rescaled Rayleigh number
$(Nu-1)Ra^{-0.61}\unicode[STIX]{x1D6E4}^{-0.88}$
, using exponents for the classical and severely confined regimes, are plotted versus the rescaled Rayleigh number
![]() $Ra/Ra^{\ast }$
in figure 6(d,e). The results clearly demonstrate the crossover of the
$Ra/Ra^{\ast }$
in figure 6(d,e). The results clearly demonstrate the crossover of the
![]() $Nu$
scaling. For
$Nu$
scaling. For
![]() $Ra>Ra^{\ast }$
over the explored range of
$Ra>Ra^{\ast }$
over the explored range of
![]() $Ra$
, the curves follow the classical scaling. And for
$Ra$
, the curves follow the classical scaling. And for
![]() $Ra<Ra^{\ast }$
, the scaling becomes much steeper than the classical one. Figure 6(e) shows the compensated plot by using the exponent 0.61 corresponding to the smallest explored
$Ra<Ra^{\ast }$
, the scaling becomes much steeper than the classical one. Figure 6(e) shows the compensated plot by using the exponent 0.61 corresponding to the smallest explored
![]() $\unicode[STIX]{x1D6E4}$
(
$\unicode[STIX]{x1D6E4}$
(
![]() $\unicode[STIX]{x1D6E4}=1/128$
), and thus the curve for
$\unicode[STIX]{x1D6E4}=1/128$
), and thus the curve for
![]() $\unicode[STIX]{x1D6E4}=1/128$
is flat for
$\unicode[STIX]{x1D6E4}=1/128$
is flat for
![]() $Ra<Ra^{\ast }$
, whereas curves for
$Ra<Ra^{\ast }$
, whereas curves for
![]() $\unicode[STIX]{x1D6E4}>1/128$
are not totally flat for
$\unicode[STIX]{x1D6E4}>1/128$
are not totally flat for
![]() $Ra<Ra^{\ast }$
but sufficient to indicate the steep scaling in severely confined regimes in contrast to the classical scaling. Similar behaviours are observed for the global momentum transport
$Ra<Ra^{\ast }$
but sufficient to indicate the steep scaling in severely confined regimes in contrast to the classical scaling. Similar behaviours are observed for the global momentum transport
![]() $Re$
. Figure 6(f,g) shows the compensated
$Re$
. Figure 6(f,g) shows the compensated
![]() $Re\,Ra^{-0.52}\unicode[STIX]{x1D6E4}^{-0.31}$
and
$Re\,Ra^{-0.52}\unicode[STIX]{x1D6E4}^{-0.31}$
and
![]() $Re\,Ra^{-0.80}\unicode[STIX]{x1D6E4}^{-1.23}$
, again using exponents for the classical and severely confined regimes respectively, versus the rescaled
$Re\,Ra^{-0.80}\unicode[STIX]{x1D6E4}^{-1.23}$
, again using exponents for the classical and severely confined regimes respectively, versus the rescaled
![]() $Ra$
, which demonstrates the clear transition at
$Ra$
, which demonstrates the clear transition at
![]() $Ra=Ra^{\ast }$
. We note that the collapsing of the data for
$Ra=Ra^{\ast }$
. We note that the collapsing of the data for
![]() $Re$
is less good than that for
$Re$
is less good than that for
![]() $Nu$
; this may be related to the fact that the definition of the Reynolds number is scale-dependent and confinement may have changed the characteristic scale for the Reynolds number.
$Nu$
; this may be related to the fact that the definition of the Reynolds number is scale-dependent and confinement may have changed the characteristic scale for the Reynolds number.
4 Concluding remarks
In summary, we have made a preliminary exploration of severely confined turbulent Rayleigh–Bénard convection over a wide range of width-to-height aspect ratio
![]() $\unicode[STIX]{x1D6E4}$
, with
$\unicode[STIX]{x1D6E4}$
, with
![]() $1/128\leqslant \unicode[STIX]{x1D6E4}\leqslant 1$
and
$1/128\leqslant \unicode[STIX]{x1D6E4}\leqslant 1$
and
![]() $3\times 10^{4}\leqslant Ra\leqslant 1\times 10^{11}$
. We first determined the
$3\times 10^{4}\leqslant Ra\leqslant 1\times 10^{11}$
. We first determined the
![]() $\unicode[STIX]{x1D6E4}$
-dependence of the critical
$\unicode[STIX]{x1D6E4}$
-dependence of the critical
![]() $Ra$
for convection,
$Ra$
for convection,
![]() $Ra_{c}=482.4\unicode[STIX]{x1D6E4}^{-2.0\pm 0.1}$
, which is found to agree excellently with a previous theoretical result. The study then reveals how severe geometrical confinement induces transitions in global heat and momentum transport and in flow topology from the classical regime to a new regime characterized by steep scaling exponents and column-like plumes. For example, the scalings for
$Ra_{c}=482.4\unicode[STIX]{x1D6E4}^{-2.0\pm 0.1}$
, which is found to agree excellently with a previous theoretical result. The study then reveals how severe geometrical confinement induces transitions in global heat and momentum transport and in flow topology from the classical regime to a new regime characterized by steep scaling exponents and column-like plumes. For example, the scalings for
![]() $\unicode[STIX]{x1D6E4}=1/128$
lying in the severely confined regime (Regime III) are
$\unicode[STIX]{x1D6E4}=1/128$
lying in the severely confined regime (Regime III) are
![]() $Nu-1\sim Ra^{0.61}$
and
$Nu-1\sim Ra^{0.61}$
and
![]() $Re\sim Ra^{0.80}$
, which contrast sharply with
$Re\sim Ra^{0.80}$
, which contrast sharply with
![]() $Nu-1\sim Ra^{0.31}$
and
$Nu-1\sim Ra^{0.31}$
and
![]() $Re\sim Ra^{0.52}$
observed at
$Re\sim Ra^{0.52}$
observed at
![]() $\unicode[STIX]{x1D6E4}=1$
in Regime I. Based on the boundary separating the plume-controlled and severely confined regimes, a Rayleigh number for regime transition,
$\unicode[STIX]{x1D6E4}=1$
in Regime I. Based on the boundary separating the plume-controlled and severely confined regimes, a Rayleigh number for regime transition,
![]() $Ra^{\ast }=(29.37/\unicode[STIX]{x1D6E4})^{3.23}$
, has been identified. It is found that, for both
$Ra^{\ast }=(29.37/\unicode[STIX]{x1D6E4})^{3.23}$
, has been identified. It is found that, for both
![]() $Nu$
and
$Nu$
and
![]() $Re$
, a rather sharp crossover in their scaling behaviours occurs at
$Re$
, a rather sharp crossover in their scaling behaviours occurs at
![]() $Ra/Ra^{\ast }=1.84\times 10^{-5}Ra\unicode[STIX]{x1D6E4}^{3.23}=1$
. This relationship implies that the new scalings for
$Ra/Ra^{\ast }=1.84\times 10^{-5}Ra\unicode[STIX]{x1D6E4}^{3.23}=1$
. This relationship implies that the new scalings for
![]() $Nu$
and
$Nu$
and
![]() $Re$
can be observed over a wider range of
$Re$
can be observed over a wider range of
![]() $Ra$
for smaller values of
$Ra$
for smaller values of
![]() $\unicode[STIX]{x1D6E4}$
.
$\unicode[STIX]{x1D6E4}$
.
Finally, we remark that the transition in severely confined RB convection is somewhat similar to that in rotating RB convection with the emergence of steep heat transfer scaling and columnar flow topology under extremely stabilizing conditions (severe confinement and vigorous rotation respectively). Though the analogy between confined RB and rotating RB convection needs to be made more quantitatively, the more well-studied rotating RB convection may provide insight into the steep scaling identified here and the formation of column-like plumes. As heat transport in severely confined environments exists widely in the modern electronics industry, our study should be of some relevance to certain engineering applications.
Acknowledgements
We thank S.-D. Huang for helpful discussions and M. Kaczorowski for his help with numerical simulations. This work was supported by the Hong Kong RGC (grant no. CUHK404513) and through a Hong Kong PhD Fellowship, and by a CUHK Direct Grant (project no. 3132740). We also thank the support of computational resources by the Leibnitz-Rechenzentrum Munich (project no. pr47vi).