1 Introduction
To understand the propagation of energetic particles through a plasma is a very fundamental problem with a variety of applications in plasma physics, space science and astrophysics. The motion of such particles is described by transport equations and their solutions provide a particle distribution function. As explained in detail in Schlickeiser (Reference Schlickeiser2002) there are different levels at which the transport can be described. The most fundamental description is provided by the relativistic Vlasov equation from which a pitch-angle-dependent Fokker–Planck equation can be derived. The latter equation can contain different transport processes ranging from pitch-angle scattering to perpendicular diffusion, stochastic acceleration and adiabatic focusing. It is usually assumed that if the aforementioned Fokker–Planck equation is averaged over all pitch angles, and if a late time limit is considered, one obtains a diffusive transport equation. Pitch-angle-dependent and averaged cosmic ray transport equations are solved in order to describe the acceleration of particles at shock waves or their motion through the solar system, the interstellar medium or the extra galactic space (see, e.g. Li et al. Reference Li, Shalchi, Ao, Zank and Verkhoglyadova2012; Ferrand et al. Reference Ferrand, Danos, Shalchi, Safi-Harb, Edmon and Mendygral2014; Zank Reference Zank2014; Engelbrecht & Burger Reference Engelbrecht and Burger2015; Miyake, Muraishi & Yanagita Reference Miyake, Muraishi and Yanagita2015; Mulcahy et al. Reference Mulcahy, Fletcher, Beck, Mitra and Scaife2016; Porth et al. Reference Porth, Vorster, Lyutikov and Engelbrecht2016; Strauss, Dresing & Engelbrecht Reference Strauss, Dresing and Engelbrecht2017).
For some applications one could concentrate on the motion of charged particles along a mean magnetic field. Usually this type of transport is called parallel diffusion and it is assumed that parallel transport is the most important process. For example it controls the life time of cosmic rays in the Milky Way (see, e.g. Swordy et al. Reference Swordy, Mueller, Meyer, L’Heureux and Grunsfeld1990; Schlickeiser Reference Schlickeiser2002; Shalchi & Schlickeiser Reference Shalchi and Schlickeiser2005). Therefore, one can focus on the analytical and numerical study of the two-dimensional Fokker–Planck equation which provides the particle distribution as a function of time, parallel position and pitch angle.Footnote 1 This type of distribution function also enters nonlinear theories for perpendicular transport, as shown in Shalchi (Reference Shalchi2010, Reference Shalchi2017).
An exact analytical solution of the Fokker–Planck equation is difficult to find. Although some progress has been made recently (see Malkov Reference Malkov2017), such solutions are either based on approximations or involve numerical calculations. For some applications such as the formulation of nonlinear theories for perpendicular transport, exact and pure analytical solutions are desired.
It is the purpose of the current paper to derive exact analytical forms of the first 14 moments of the pitch-angle-dependent cosmic ray Fokker–Planck equation for an arbitrary initial pitch angle. Such explicit formulas for the moments can be important for different applications as also demonstrated in the present article. In all cases we recover the formulas derived previously for the initial pitch-angle-averaged case (see, e.g. Malkov Reference Malkov2017).
The remainder of this paper is organized as follows. After discussing transport equations and some general properties in § 2, the moments are derived step by step in § 3. In § 4 we consider the characteristic function in nonlinear diffusion theory as an example for the applicability of our findings. In § 4 we summarize and conclude.
2 Transport equations
The general Fokker–Planck equation of cosmic ray transport is complicated and contains several terms such as perpendicular diffusion or stochastic acceleration (see, e.g. Skilling Reference Skilling1975; Schlickeiser Reference Schlickeiser2002; Zank Reference Zank2014). For some applications one can neglect such terms and consider the limit that both the magnetic field and the plasma flow are weakly non-uniform. In this case one obtains a simpler, two-dimensional version of the Fokker–Planck equation which is valid in the plasma flow frame (see, e.g. Schlickeiser Reference Schlickeiser2002, for a detailed derivation and discussion)
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}t}+v\unicode[STIX]{x1D707}\frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}z}=\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}}\left[D_{\unicode[STIX]{x1D707}\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D707})\frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}}\right]\!, & \displaystyle\end{eqnarray}$$
where we have used the pitch-angle Fokker–Planck coefficient
$D_{\unicode[STIX]{x1D707}\unicode[STIX]{x1D707}}$
. The solution of this equation provides the particle distribution function
$f=f(\unicode[STIX]{x1D707},z,t)$
where we have used time
$t$
, the particle position along the mean magnetic field
$z$
and the pitch-angle cosine
$\unicode[STIX]{x1D707}$
. It has to be emphasized that the parameter
$D_{\unicode[STIX]{x1D707}\unicode[STIX]{x1D707}}$
still depends on the particle speed or momentum. The latter parameters, however, are just parameters which do not change the form of the solution
$f=f(\unicode[STIX]{x1D707},z,t)$
. If the latter function is averaged over all values of
$\unicode[STIX]{x1D707}$
, and if a late time limit is considered, one finds a usual diffusion equation of the form (see, e.g. Schlickeiser Reference Schlickeiser2002; Shalchi Reference Shalchi2009; Zank Reference Zank2014)
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}M}{\unicode[STIX]{x2202}t}=\unicode[STIX]{x1D705}_{\Vert }\frac{\unicode[STIX]{x2202}^{2}M}{\unicode[STIX]{x2202}z^{2}}, & \displaystyle\end{eqnarray}$$
where we have used the pitch-angle-averaged distribution function
$$\begin{eqnarray}\displaystyle & \displaystyle M(z,t)=\frac{1}{2}\int _{-1}^{+1}\text{d}\unicode[STIX]{x1D707}\,f(\unicode[STIX]{x1D707},z,t). & \displaystyle\end{eqnarray}$$
Equation (2.2) is also known as the heat transport equation. The parallel spatial diffusion coefficient
$\unicode[STIX]{x1D705}_{\Vert }$
therein is related to the pitch-angle Fokker–Planck coefficient
$D_{\unicode[STIX]{x1D707}\unicode[STIX]{x1D707}}$
via the famous relation (see, e.g. Earl (Reference Earl1974) for a systematic derivation)
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D705}_{\Vert }=\frac{v^{2}}{8}\int _{-1}^{+1}\text{d}\unicode[STIX]{x1D707}\,\frac{(1-\unicode[STIX]{x1D707}^{2})^{2}}{D_{\unicode[STIX]{x1D707}\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D707})}. & \displaystyle\end{eqnarray}$$
It has to be emphasized that generalizations can be found in the literature in which a telegrapher equation has been derived and discussed in the context of cosmic ray transport (see, e.g. Litvinenko & Schlickeiser Reference Litvinenko and Schlickeiser2013; Litvinenko et al. Reference Litvinenko, Effenberger and Schlickeiser2015; Tautz & Lerche Reference Tautz and Lerche2016; Malkov Reference Malkov2017).
For sharp initial conditions
$M(z,t=0)=\unicode[STIX]{x1D6FF}(z)$
, equation (2.2) has a Gaussian solution of the form
$$\begin{eqnarray}\displaystyle & \displaystyle M(z,t)=\frac{1}{\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D705}_{\Vert }t}}\text{e}^{-z^{2}/(4\unicode[STIX]{x1D705}_{\Vert }t)}. & \displaystyle\end{eqnarray}$$
The characteristic function of a transport equation is defined via
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \text{e}^{\text{i}kz}\rangle =\frac{1}{2}\int _{-1}^{+1}\text{d}\unicode[STIX]{x1D707}\int _{-\infty }^{+\infty }\text{d}z\,\text{e}^{\text{i}kz}f(\unicode[STIX]{x1D707},z,t)\equiv \int _{-\infty }^{+\infty }\text{d}z\,\text{e}^{\text{i}kz}M(z,t) & \displaystyle\end{eqnarray}$$
corresponding to the Fourier transform of the distribution function. The characteristic function of a usual diffusion equation (see (2.2) of the current paper) is given by
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \text{e}^{\text{i}kz}\rangle =\text{e}^{-\unicode[STIX]{x1D705}_{\Vert }k^{2}t}. & \displaystyle\end{eqnarray}$$
The latter function can easily be derived by combining (2.5) and (2.6). The characteristic function will be discussed in more detail in § 4 of this paper.
3 The moments of the Fokker–Planck equation
It is the purpose of the current article to derive analytical forms for the first 14 moments of (2.1). In order to do this we need to specify the scattering parameter
$D_{\unicode[STIX]{x1D707}\unicode[STIX]{x1D707}}$
. In the following we employ the isotropic model (see, e.g. Shalchi et al. (Reference Shalchi, Škoda, Tautz and Schlickeiser2009) for a justification of this form and more details)
$$\begin{eqnarray}\displaystyle & \displaystyle D_{\unicode[STIX]{x1D707}\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D707})=D\left(1-\unicode[STIX]{x1D707}^{2}\right), & \displaystyle\end{eqnarray}$$
and the Fokker–Planck equation (2.1) becomes
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}t}+v\unicode[STIX]{x1D707}\frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}z}=D\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}}\left[\left(1-\unicode[STIX]{x1D707}^{2}\right)\frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}}\right]. & \displaystyle\end{eqnarray}$$
The parameter
$D$
used here is just a constant in the sense that it does not depend on
$\unicode[STIX]{x1D707}$
. However,
$D$
can depend on particle properties such as momentum as well as magnetic field properties.
Some moments of the Fokker–Planck equation have been computed before (see, e.g. Shalchi Reference Shalchi2006). In order to derive a general relation for the moments we follow Malkov (Reference Malkov2017) and multiply (3.2) by
$z^{n}\unicode[STIX]{x1D707}^{m}$
, integrate over all positions and average over all pitch angles. We find
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\langle z^{n}\unicode[STIX]{x1D707}^{m}\rangle =nv\langle z^{n-1}\unicode[STIX]{x1D707}^{m+1}\rangle +m(m-1)D\langle z^{n}\unicode[STIX]{x1D707}^{m-2}\rangle -m(m+1)D\langle z^{n}\unicode[STIX]{x1D707}^{m}\rangle , & \displaystyle\end{eqnarray}$$
where we have used
$$\begin{eqnarray}\displaystyle & \displaystyle \langle z^{n}\unicode[STIX]{x1D707}^{m}\rangle =\frac{1}{2}\int _{-1}^{+1}\text{d}\unicode[STIX]{x1D707}\int _{-\infty }^{+\infty }\text{d}z\,z^{n}\unicode[STIX]{x1D707}^{m}\,f(\unicode[STIX]{x1D707},z,t) & \displaystyle\end{eqnarray}$$
and
$f(\unicode[STIX]{x1D707},z=\pm \infty ,t)=0$
. If the moments
$\langle z^{n-1}\unicode[STIX]{x1D707}^{m+1}\rangle$
and
$\langle z^{n}\unicode[STIX]{x1D707}^{m-2}\rangle$
are known, differential equation (3.3) can be solved analytically. In the following paragraphs we compute the first 14 moments by solving (3.3). Alternatively, the moments could be derived from equation (8) of Malkov (Reference Malkov2017). The latter equation provides an inductive algorithm to compute moments by integration of exponential and power functions.
3.1 The moment
$\langle \unicode[STIX]{x1D707}\rangle$
For
$n=0$
and
$m=1$
, equation (3.3) becomes
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\langle \unicode[STIX]{x1D707}\rangle =-2D\langle \unicode[STIX]{x1D707}\rangle . & \displaystyle\end{eqnarray}$$
We can easily solve the latter ordinary differential equation. By using the initial pitch-angle cosine
$\unicode[STIX]{x1D707}_{0}$
the solution is
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \unicode[STIX]{x1D707}\rangle =\unicode[STIX]{x1D707}_{0}\,\text{e}^{-2Dt}. & \displaystyle\end{eqnarray}$$
If we also average over all initial pitch-angle cosine values, this becomes
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \langle \unicode[STIX]{x1D707}\rangle \rangle =0, & \displaystyle\end{eqnarray}$$
for all times. Here we have used the notation
$\langle \langle \ldots \rangle \rangle$
which stands for average over
$\unicode[STIX]{x1D707}$
and
$\unicode[STIX]{x1D707}_{0}$
, i.e.
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \langle A\rangle \rangle =\frac{1}{2}\int _{-1}^{+1}\text{d}\unicode[STIX]{x1D707}_{0}\langle A\rangle =\frac{1}{4}\int _{-1}^{+1}\text{d}\unicode[STIX]{x1D707}_{0}\int _{-1}^{+1}\text{d}\unicode[STIX]{x1D707}\int _{-\infty }^{+\infty }\text{d}z\,A\left(\unicode[STIX]{x1D707}_{0},\unicode[STIX]{x1D707},z,t\right). & \displaystyle\end{eqnarray}$$
However, the correlation between the initial pitch-angle cosine
$\unicode[STIX]{x1D707}_{0}$
and
$\unicode[STIX]{x1D707}$
is given by
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \langle \unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D707}\rangle \rangle =\frac{1}{2}\int _{-1}^{+1}\text{d}\unicode[STIX]{x1D707}_{0}\,\unicode[STIX]{x1D707}_{0}^{2}\text{e}^{-2Dt}=\frac{1}{3}\text{e}^{-2Dt}. & \displaystyle\end{eqnarray}$$
Therefore, the velocity correlation function is
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \langle v_{z}(t)v_{z}(0)\rangle \rangle =\frac{v^{2}}{3}\text{e}^{-vt/\unicode[STIX]{x1D706}_{\Vert }}, & \displaystyle\end{eqnarray}$$
where we have used the parallel mean free path
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D706}_{\Vert }=v/(2D). & \displaystyle\end{eqnarray}$$
Velocity correlation functions of the form (3.10) are often used in theories for perpendicular diffusion (see, e.g. Owens Reference Owens1974; Matthaeus et al.
Reference Matthaeus, Qin, Bieber and Zank2003) but this exponential form is only correct for an isotropic
$D_{\unicode[STIX]{x1D707}\unicode[STIX]{x1D707}}$
(see Shalchi (Reference Shalchi2011a
) for a detailed discussion of this matter).
The so-called Taylor–Green–Kubo formula (see Taylor Reference Taylor1922; Green Reference Green1951; Kubo Reference Kubo1957) allows us to compute a running diffusion coefficient via
$$\begin{eqnarray}\displaystyle d_{\Vert }(\unicode[STIX]{x1D707}_{0},t) & = & \displaystyle \int _{0}^{t}\text{d}\unicode[STIX]{x1D70F}\langle v_{z}(\unicode[STIX]{x1D70F})v_{z}(0)\rangle \nonumber\\ \displaystyle & = & \displaystyle v^{2}\int _{0}^{t}\text{d}\unicode[STIX]{x1D70F}\,\unicode[STIX]{x1D707}_{0}^{2}\text{e}^{-2D\unicode[STIX]{x1D70F}}\nonumber\\ \displaystyle & = & \displaystyle \frac{v^{2}\unicode[STIX]{x1D707}_{0}^{2}}{2D}\left(1-\text{e}^{-2Dt}\right)\!,\end{eqnarray}$$
where we have employed (3.6) again. In the limit
$t\rightarrow \infty$
this becomes
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D705}_{\Vert }(\unicode[STIX]{x1D707}_{0})=\frac{v^{2}\unicode[STIX]{x1D707}_{0}^{2}}{2D} & \displaystyle\end{eqnarray}$$
and if we average over all initial pitch-angle cosine values we obtain
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D705}_{\Vert }=\frac{v^{2}}{6D}. & \displaystyle\end{eqnarray}$$
The latter form can alternatively be obtained by combining the isotropic form (3.1) with Earl’s relation (2.4). If we average (3.12) directly over
$\unicode[STIX]{x1D707}_{0}$
, we derive
$$\begin{eqnarray}\displaystyle & \displaystyle d_{\Vert }(t)=\unicode[STIX]{x1D705}_{\Vert }\left(1-\text{e}^{-vt/\unicode[STIX]{x1D706}_{\Vert }}\right). & \displaystyle\end{eqnarray}$$
For
$t\rightarrow 0$
we can expand the exponential in (3.12) to derive
$$\begin{eqnarray}\displaystyle & \displaystyle d_{\Vert }(\unicode[STIX]{x1D707}_{0},t)\rightarrow v^{2}\unicode[STIX]{x1D707}_{0}^{2}t, & \displaystyle\end{eqnarray}$$
corresponding to ballistic transport. In figure 1 we visualize (3.15) to show the turnover from the initial ballistic regime to the normal diffusive regime.
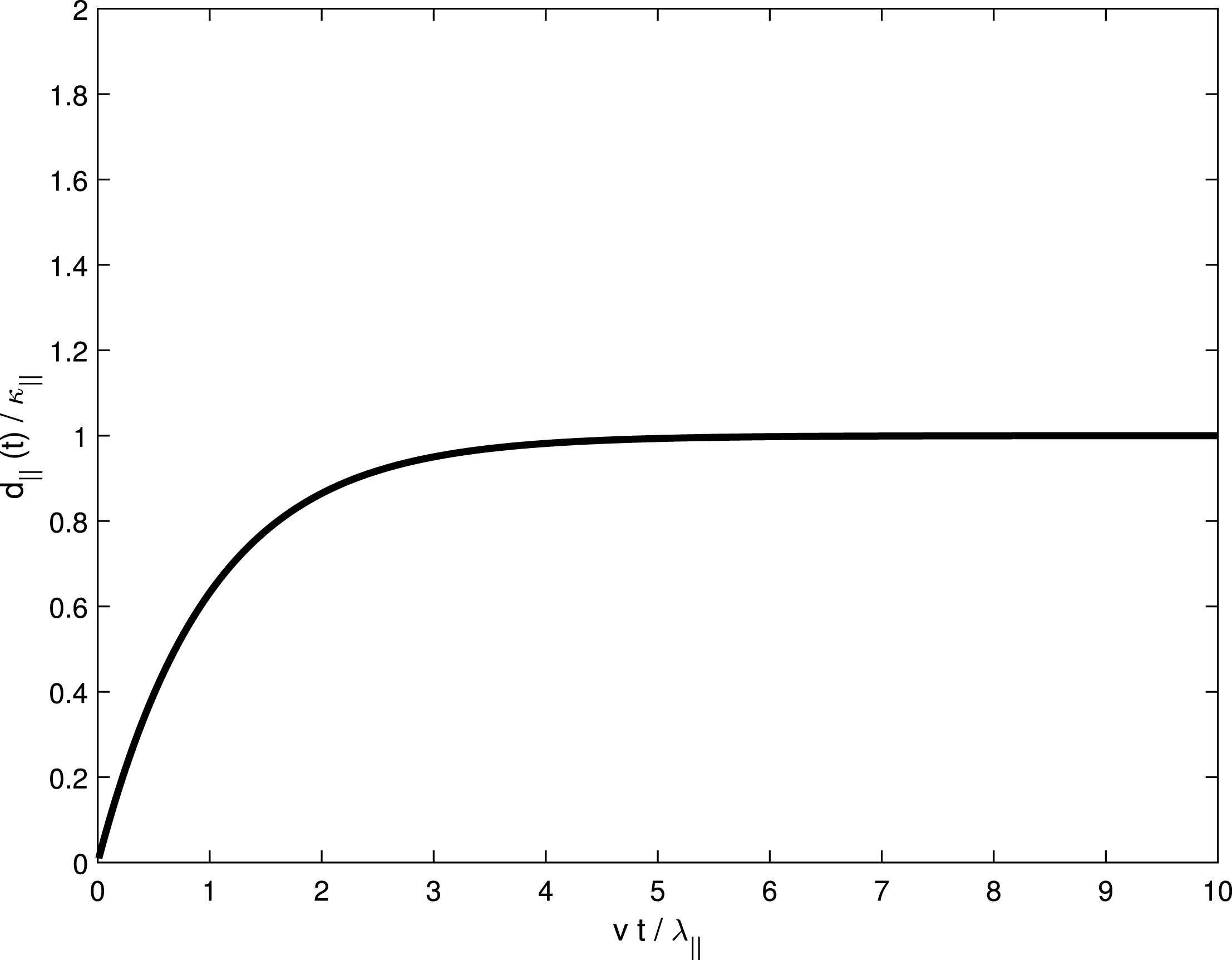
Figure 1. The running diffusion coefficient normalized with respect to the late time diffusion coefficient
$d_{\Vert }(t)/\unicode[STIX]{x1D705}_{\Vert }$
versus dimensionless time
$vt/\unicode[STIX]{x1D706}_{\Vert }$
.
3.2 The moment
$\langle \unicode[STIX]{x1D707}^{2}\rangle$
For
$n=0$
and
$m=2$
, equation (3.3) becomes
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\langle \unicode[STIX]{x1D707}^{2}\rangle =2D\left(1-3\langle \unicode[STIX]{x1D707}^{2}\rangle \right). & \displaystyle\end{eqnarray}$$
The latter equation has the homogeneous solution
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \unicode[STIX]{x1D707}^{2}\rangle _{h}=C\text{e}^{-6Dt}, & \displaystyle\end{eqnarray}$$
with the constant
$C$
which will be determined below. Furthermore, a particular solution is provided by the constant
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \unicode[STIX]{x1D707}^{2}\rangle _{p}={\textstyle \frac{1}{3}}. & \displaystyle\end{eqnarray}$$
By using again the initial pitch angle
$\unicode[STIX]{x1D707}_{0}$
, we can write the solution of (3.17) as a superposition of homogeneous and particular solutions
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \unicode[STIX]{x1D707}^{2}\rangle =\left(\unicode[STIX]{x1D707}_{0}^{2}-{\textstyle \frac{1}{3}}\right)\text{e}^{-6Dt}+{\textstyle \frac{1}{3}}. & \displaystyle\end{eqnarray}$$
For
$t\rightarrow \infty$
we obtain
$\langle \unicode[STIX]{x1D707}^{2}\rangle \rightarrow 1/3$
as expected. This asymptotic limit does not depend on the initial pitch-angle cosine
$\unicode[STIX]{x1D707}_{0}$
due to the pitch-angle isotropization process. If (3.20) is averaged over all
$\unicode[STIX]{x1D707}_{0}$
we derive
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \langle \unicode[STIX]{x1D707}^{2}\rangle \rangle ={\textstyle \frac{1}{3}} & \displaystyle\end{eqnarray}$$
in agreement with the formula derived in Malkov (Reference Malkov2017).
3.3 The moment
$\langle \unicode[STIX]{x1D707}^{3}\rangle$
For
$n=0$
and
$m=3$
, equation (3.3) becomes
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\langle \unicode[STIX]{x1D707}^{3}\rangle =6D\langle \unicode[STIX]{x1D707}\rangle -12D\langle \unicode[STIX]{x1D707}^{3}\rangle , & \displaystyle\end{eqnarray}$$
where the moment
$\langle \unicode[STIX]{x1D707}\rangle$
is given by (3.6). The homogeneous solution of (3.22) is
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \unicode[STIX]{x1D707}^{3}\rangle _{h}=C\text{e}^{-12Dt}. & \displaystyle\end{eqnarray}$$
In order to derive the particular solution, we combine (3.6) and (3.22)
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\langle \unicode[STIX]{x1D707}^{3}\rangle =6D\unicode[STIX]{x1D707}_{0}\text{e}^{-2Dt}-12D\langle \unicode[STIX]{x1D707}^{3}\rangle , & \displaystyle\end{eqnarray}$$
which has the particular solution
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \unicode[STIX]{x1D707}^{3}\rangle _{p}=A\text{e}^{-2Dt}. & \displaystyle\end{eqnarray}$$
If the latter ansatz is combined with (3.22), we derive
$$\begin{eqnarray}\displaystyle & \displaystyle A={\textstyle \frac{3}{5}}\unicode[STIX]{x1D707}_{0} & \displaystyle\end{eqnarray}$$
and, thus, the total solution is
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \unicode[STIX]{x1D707}^{3}\rangle =C\text{e}^{-12Dt}+{\textstyle \frac{3}{5}}\unicode[STIX]{x1D707}_{0}\text{e}^{-2Dt}. & \displaystyle\end{eqnarray}$$
The remaining parameter
$C$
can be replaced by the initial pitch-angle cosine
$\unicode[STIX]{x1D707}_{0}$
and we finally obtain
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \unicode[STIX]{x1D707}^{3}\rangle =\left(\unicode[STIX]{x1D707}_{0}^{3}-{\textstyle \frac{3}{5}}\unicode[STIX]{x1D707}_{0}\right)\text{e}^{-12Dt}+{\textstyle \frac{3}{5}}\unicode[STIX]{x1D707}_{0}\text{e}^{-2Dt}. & \displaystyle\end{eqnarray}$$
For
$t\rightarrow \infty$
we find
$\langle \unicode[STIX]{x1D707}^{3}\rangle \rightarrow 0$
due to the pitch-angle isotropization process. Furthermore, we derive
$\langle \langle \unicode[STIX]{x1D707}^{3}\rangle \rangle =0$
as expected due to symmetry.
3.4 The moment
$\langle \unicode[STIX]{x1D707}^{4}\rangle$
For
$n=0$
and
$m=4$
, equation (3.3) becomes
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\langle \unicode[STIX]{x1D707}^{4}\rangle =12D\langle \unicode[STIX]{x1D707}^{2}\rangle -20D\langle \unicode[STIX]{x1D707}^{4}\rangle , & \displaystyle\end{eqnarray}$$
where the moment
$\langle \unicode[STIX]{x1D707}^{2}\rangle$
is given by (3.20). The homogeneous solution of (3.29) is
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \unicode[STIX]{x1D707}^{4}\rangle _{h}=C\text{e}^{-20Dt}. & \displaystyle\end{eqnarray}$$
To compute the particular solution, we combine (3.29) and (3.20) to find
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\langle \unicode[STIX]{x1D707}^{4}\rangle =12D\left[\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{1}{3}\right)\text{e}^{-6Dt}+\frac{1}{3}\right]-20D\langle \unicode[STIX]{x1D707}^{4}\rangle . & \displaystyle\end{eqnarray}$$
In order to determine the particular solution, we employ the ansatz
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \unicode[STIX]{x1D707}^{4}\rangle _{p}=A+B\text{e}^{-6Dt}. & \displaystyle\end{eqnarray}$$
By using this in (3.31) we find after straightforward algebra
$$\begin{eqnarray}\displaystyle & \displaystyle A={\textstyle \frac{1}{5}} & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle & \displaystyle B={\textstyle \frac{6}{7}}\left(\unicode[STIX]{x1D707}_{0}^{2}-{\textstyle \frac{1}{3}}\right). & \displaystyle\end{eqnarray}$$
Therefore, the total solution of (3.29) is given by
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \unicode[STIX]{x1D707}^{4}\rangle =C\text{e}^{-20Dt}+{\textstyle \frac{1}{5}}+{\textstyle \frac{6}{7}}\left(\unicode[STIX]{x1D707}_{0}^{2}-{\textstyle \frac{1}{3}}\right)\text{e}^{-6Dt}. & \displaystyle\end{eqnarray}$$
The remaining constant
$C$
can be replaced by the initial pitch-angle cosine
$\unicode[STIX]{x1D707}_{0}$
. We obtain
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \unicode[STIX]{x1D707}^{4}\rangle =\left[\unicode[STIX]{x1D707}_{0}^{4}-{\textstyle \frac{6}{7}}\left(\unicode[STIX]{x1D707}_{0}^{2}-{\textstyle \frac{1}{3}}\right)-{\textstyle \frac{1}{5}}\right]\text{e}^{-20Dt}+{\textstyle \frac{1}{5}}+{\textstyle \frac{6}{7}}\left(\unicode[STIX]{x1D707}_{0}^{2}-{\textstyle \frac{1}{3}}\right)\text{e}^{-6Dt}. & \displaystyle\end{eqnarray}$$
In the late time limit
$t\rightarrow \infty$
we find
$\langle \unicode[STIX]{x1D707}^{4}\rangle \rightarrow 1/5$
as expected. Furthermore, we can average (3.36) over the initial pitch-angle cosine
$\unicode[STIX]{x1D707}_{0}$
to deduce
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \langle \unicode[STIX]{x1D707}^{4}\rangle \rangle ={\textstyle \frac{1}{5}}. & \displaystyle\end{eqnarray}$$
3.5 The moment
$\langle z\rangle$
For
$n=1$
and
$m=0$
, equation (3.3) becomes
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\langle z\rangle =v\langle \unicode[STIX]{x1D707}\rangle . & \displaystyle\end{eqnarray}$$
The quantity at the right-hand side can be replaced by (3.6) and we find
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\langle z\rangle =v\unicode[STIX]{x1D707}_{0}\text{e}^{-2Dt}. & \displaystyle\end{eqnarray}$$
We can easily integrate the latter formula to derive
$$\begin{eqnarray}\displaystyle & \displaystyle \langle z\rangle =\frac{v\unicode[STIX]{x1D707}_{0}}{2D}\left(1-\text{e}^{-2Dt}\right)\equiv \unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D706}_{\Vert }\left(1-\text{e}^{-vt/\unicode[STIX]{x1D706}_{\Vert }}\right). & \displaystyle\end{eqnarray}$$
For
$t\rightarrow \infty$
we find for the penetration depth
$$\begin{eqnarray}\displaystyle & \displaystyle \langle z\rangle _{t\rightarrow \infty }=\frac{v\unicode[STIX]{x1D707}_{0}}{2D}\equiv \unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D706}_{\Vert }. & \displaystyle\end{eqnarray}$$
Therefore, the maximal penetration depth is
$\pm \unicode[STIX]{x1D706}_{\Vert }$
. If we average (3.40) over all initial pitch angles we find
$\langle \langle z\rangle \rangle =0$
. For
$t\rightarrow 0$
, on the other hand, we derive from (3.40)
$$\begin{eqnarray}\displaystyle & \displaystyle \langle z\rangle \rightarrow v\unicode[STIX]{x1D707}_{0}t & \displaystyle\end{eqnarray}$$
corresponding to the unperturbed motion of the particle.
3.6 The moment
$\langle z\unicode[STIX]{x1D707}\rangle$
For
$n=m=1$
, equation (3.3) becomes
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\langle z\unicode[STIX]{x1D707}\rangle =v\langle \unicode[STIX]{x1D707}^{2}\rangle -2D\langle z\unicode[STIX]{x1D707}\rangle . & \displaystyle\end{eqnarray}$$
The homogeneous solution is provided by
$$\begin{eqnarray}\displaystyle & \displaystyle \langle z\unicode[STIX]{x1D707}\rangle _{h}=C\text{e}^{-2Dt}. & \displaystyle\end{eqnarray}$$
To obtain the particular solution, we first replace
$\langle \unicode[STIX]{x1D707}^{2}\rangle$
at the right-hand side of (3.43) by (3.20) to write
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\langle z\unicode[STIX]{x1D707}\rangle +2D\langle z\unicode[STIX]{x1D707}\rangle =v\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{1}{3}\right)\text{e}^{-6Dt}+\frac{v}{3}. & \displaystyle\end{eqnarray}$$
The latter equation has the particular solution
$$\begin{eqnarray}\displaystyle & \displaystyle \langle z\unicode[STIX]{x1D707}\rangle _{p}=\frac{v}{4D}\left(\frac{1}{3}-\unicode[STIX]{x1D707}_{0}^{2}\right)\text{e}^{-6Dt}+\frac{v}{6D}. & \displaystyle\end{eqnarray}$$
By superposing homogeneous and particular solutions, and by using
$\langle z\unicode[STIX]{x1D707}\rangle =0$
for
$t=0$
, we obtain
$$\begin{eqnarray}\displaystyle & \displaystyle \langle z\unicode[STIX]{x1D707}\rangle =\frac{v}{4D}\left(\unicode[STIX]{x1D707}_{0}^{2}-1\right)\text{e}^{-2Dt}+\frac{v}{4D}\left(\frac{1}{3}-\unicode[STIX]{x1D707}_{0}^{2}\right)\text{e}^{-6Dt}+\frac{v}{6D}. & \displaystyle\end{eqnarray}$$
Again we can consider the limit
$t\rightarrow \infty$
to find
$$\begin{eqnarray}\displaystyle & \displaystyle \langle v_{z}(t)\unicode[STIX]{x0394}z(t)\rangle \equiv v\langle z\unicode[STIX]{x1D707}\rangle =\frac{v^{2}}{6D}=\unicode[STIX]{x1D705}_{\Vert } & \displaystyle\end{eqnarray}$$
corresponding to the parallel diffusion coefficient. Furthermore, we can average (3.47) also over the initial pitch-angle cosine
$\unicode[STIX]{x1D707}_{0}$
to find
$$\begin{eqnarray}\displaystyle & \displaystyle v\langle \langle z\unicode[STIX]{x1D707}\rangle \rangle =\frac{v^{2}}{6D}\left(1-\text{e}^{-2Dt}\right)\equiv \unicode[STIX]{x1D705}_{\Vert }\left(1-\text{e}^{-vt/\unicode[STIX]{x1D706}_{\Vert }}\right) & \displaystyle\end{eqnarray}$$
in agreement with (3.15).
3.7 The moment
$\langle z\unicode[STIX]{x1D707}^{2}\rangle$
For
$n=1$
and
$m=2$
, equation (3.3) becomes
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\langle z\unicode[STIX]{x1D707}^{2}\rangle =v\langle \unicode[STIX]{x1D707}^{3}\rangle +2D\langle z\rangle -6D\langle z\unicode[STIX]{x1D707}^{2}\rangle , & \displaystyle\end{eqnarray}$$
where the moments
$\langle \unicode[STIX]{x1D707}^{3}\rangle$
and
$\langle z\rangle$
are given by (3.28) and (3.40), respectively. The homogeneous solution of (3.50) is
$$\begin{eqnarray}\displaystyle & \displaystyle \langle z\unicode[STIX]{x1D707}^{2}\rangle _{h}=C\text{e}^{-6Dt}. & \displaystyle\end{eqnarray}$$
In order to compute the particular solution, we combine (3.28) and (3.40) with (3.50) to find
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\langle z\unicode[STIX]{x1D707}^{2}\rangle =v\left(\unicode[STIX]{x1D707}_{0}^{3}-\frac{3}{5}\unicode[STIX]{x1D707}_{0}\right)\text{e}^{-12Dt}-\frac{2}{5}v\unicode[STIX]{x1D707}_{0}\text{e}^{-2Dt}+v\unicode[STIX]{x1D707}_{0}-6D\langle z\unicode[STIX]{x1D707}^{2}\rangle . & \displaystyle\end{eqnarray}$$
For the particular solution we can employ the ansatz
$$\begin{eqnarray}\displaystyle & \displaystyle \langle z\unicode[STIX]{x1D707}^{2}\rangle _{p}=A+B\text{e}^{-12Dt}+E\text{e}^{-2Dt}. & \displaystyle\end{eqnarray}$$
By combining the latter form with (3.50), we derive, after straightforward algebra,
$$\begin{eqnarray}\displaystyle & \displaystyle A=\frac{v\unicode[STIX]{x1D707}_{0}}{6D},\quad B=-\frac{v\unicode[STIX]{x1D707}_{0}}{6D}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{3}{5}\right), & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle & \displaystyle E=-\frac{v\unicode[STIX]{x1D707}_{0}}{10D}. & \displaystyle\end{eqnarray}$$
Therefore, the particular solution is known. In combination with the homogeneous solution (3.51) we, thus, derive
$$\begin{eqnarray}\displaystyle & \displaystyle \langle z\unicode[STIX]{x1D707}^{2}\rangle =C\text{e}^{-6Dt}+\frac{v\unicode[STIX]{x1D707}_{0}}{6D}-\frac{v\unicode[STIX]{x1D707}_{0}}{6D}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{3}{5}\right)\text{e}^{-12Dt}-\frac{v\unicode[STIX]{x1D707}_{0}}{10D}\text{e}^{-2Dt}. & \displaystyle\end{eqnarray}$$
For
$t=0$
we need to satisfy
$\langle z\unicode[STIX]{x1D707}^{2}\rangle =0$
. This condition allows us to determine the remaining constant
$C$
. One can show that
$$\begin{eqnarray}\displaystyle & \displaystyle C=\frac{v\unicode[STIX]{x1D707}_{0}}{6D}\left(\unicode[STIX]{x1D707}_{0}^{2}-1\right) & \displaystyle\end{eqnarray}$$
and, thus, we obtain for the solution of (3.50)
$$\begin{eqnarray}\displaystyle & \displaystyle \langle z\unicode[STIX]{x1D707}^{2}\rangle =\frac{v\unicode[STIX]{x1D707}_{0}}{6D}\left(\unicode[STIX]{x1D707}_{0}^{2}-1\right)\text{e}^{-6Dt}+\frac{v\unicode[STIX]{x1D707}_{0}}{6D}-\frac{v\unicode[STIX]{x1D707}_{0}}{6D}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{3}{5}\right)\text{e}^{-12Dt}-\frac{v\unicode[STIX]{x1D707}_{0}}{10D}\text{e}^{-2Dt}. & \displaystyle\end{eqnarray}$$
One can very easily show that
$\langle \langle z\unicode[STIX]{x1D707}^{2}\rangle \rangle =0$
.
3.8 The moment
$\langle z\unicode[STIX]{x1D707}^{3}\rangle$
For
$n=1$
and
$m=3$
, equation (3.3) becomes
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\langle z\unicode[STIX]{x1D707}^{3}\rangle =v\langle \unicode[STIX]{x1D707}^{4}\rangle +6D\langle z\unicode[STIX]{x1D707}\rangle -12D\langle z\unicode[STIX]{x1D707}^{3}\rangle , & \displaystyle\end{eqnarray}$$
where the moments
$\langle \unicode[STIX]{x1D707}^{4}\rangle$
and
$\langle z\unicode[STIX]{x1D707}\rangle$
are given by (3.36) and (3.47), respectively. The homogeneous solution of (3.59) is
$$\begin{eqnarray}\displaystyle & \displaystyle \langle z\unicode[STIX]{x1D707}^{3}\rangle _{h}=C\text{e}^{-12Dt}. & \displaystyle\end{eqnarray}$$
In order to compute the particular solution, we combine (3.36) and (3.47) with (3.59) to find
$$\begin{eqnarray}\displaystyle \frac{\text{d}}{\text{d}t}\langle z\unicode[STIX]{x1D707}^{3}\rangle & = & \displaystyle v\left[\unicode[STIX]{x1D707}_{0}^{4}-\frac{6}{7}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{1}{3}\right)-\frac{1}{5}\right]\text{e}^{-20Dt}-\frac{9v}{14}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{1}{3}\right)\text{e}^{-6Dt}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{3v}{2}\left(\unicode[STIX]{x1D707}_{0}^{2}-1\right)\text{e}^{-2Dt}+\frac{6v}{5}-12D\langle z\unicode[STIX]{x1D707}^{3}\rangle .\end{eqnarray}$$
For the particular solution we can employ the ansatz
$$\begin{eqnarray}\displaystyle & \displaystyle \langle z\unicode[STIX]{x1D707}^{3}\rangle _{p}=A+B\text{e}^{-20Dt}+E\text{e}^{-6Dt}+F\text{e}^{-2Dt}. & \displaystyle\end{eqnarray}$$
We find after lengthy straightforward algebra
$$\begin{eqnarray}\displaystyle & \displaystyle \left.\begin{array}{@{}c@{}}\displaystyle A=\frac{v}{10D},\\[15.0pt] \displaystyle B=-\frac{v}{8D}\left[\unicode[STIX]{x1D707}_{0}^{4}-\frac{6}{7}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{1}{3}\right)-\frac{1}{5}\right],\\[15.0pt] \displaystyle E=\frac{3v}{28D}\left(\frac{1}{3}-\unicode[STIX]{x1D707}_{0}^{2}\right),\end{array}\right\} & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle & \displaystyle F=\frac{3v}{20D}\left(\unicode[STIX]{x1D707}_{0}^{2}-1\right). & \displaystyle\end{eqnarray}$$
The total solution of (3.59) can be obtained by superposing the homogeneous solution and the particular solution. The remaining constant
$C$
in the homogeneous solution (3.60) can be obtained from the initial condition
$\langle z\unicode[STIX]{x1D707}^{3}\rangle =0$
for
$t=0$
. We find
$$\begin{eqnarray}\displaystyle & \displaystyle C=\frac{v}{40D}\left(5\unicode[STIX]{x1D707}_{0}^{4}-6\unicode[STIX]{x1D707}_{0}^{2}+1\right). & \displaystyle\end{eqnarray}$$
Finally we derive
$$\begin{eqnarray}\displaystyle \hspace{-24.0pt}\langle z\unicode[STIX]{x1D707}^{3}\rangle & = & \displaystyle \frac{v}{10D}+\frac{3v}{20D}\left(\unicode[STIX]{x1D707}_{0}^{2}-1\right)\text{e}^{-2Dt}+\frac{3v}{28D}\left(\frac{1}{3}-\unicode[STIX]{x1D707}_{0}^{2}\right)\text{e}^{-6Dt}\nonumber\\ \displaystyle & & \displaystyle \displaystyle +\,\frac{v}{40D}\left(5\unicode[STIX]{x1D707}_{0}^{4}-6\unicode[STIX]{x1D707}_{0}^{2}+1\right)\text{e}^{-12Dt}-\frac{v}{8D}\left[\unicode[STIX]{x1D707}_{0}^{4}-\frac{6}{7}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{1}{3}\right)-\frac{1}{5}\right]\text{e}^{-20Dt}.\end{eqnarray}$$
If we average over all
$\unicode[STIX]{x1D707}_{0}$
, we derive
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \langle z\unicode[STIX]{x1D707}^{3}\rangle \rangle =\frac{v}{10D}\left(1-\text{e}^{-2Dt}\right). & \displaystyle\end{eqnarray}$$
3.9 The moment
$\langle z^{2}\rangle$
For
$n=2$
and
$m=0$
, equation (3.3) becomes
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\langle z^{2}\rangle =2v\langle z\unicode[STIX]{x1D707}\rangle . & \displaystyle\end{eqnarray}$$
We can directly see that
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{2}\frac{\text{d}}{\text{d}t}\langle z^{2}\rangle =v\langle z\unicode[STIX]{x1D707}\rangle \equiv \langle v_{z}(t)\unicode[STIX]{x0394}z(t)\rangle . & \displaystyle\end{eqnarray}$$
This relation is well known in diffusion theory (see, e.g. Shalchi (Reference Shalchi2011b
) for more details). In order to replace
$\langle \unicode[STIX]{x1D707}z\rangle$
therein, we employ (3.47) to derive
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\langle z^{2}\rangle =\frac{v^{2}}{2D}\left(\unicode[STIX]{x1D707}_{0}^{2}-1\right)\text{e}^{-2Dt}+\frac{v^{2}}{2D}\left(\frac{1}{3}-\unicode[STIX]{x1D707}_{0}^{2}\right)\text{e}^{-6Dt}+\frac{v^{2}}{3D}. & \displaystyle\end{eqnarray}$$
The latter equation can easily be integrated. Together with the initial condition
$\langle z^{2}\rangle =0$
for
$t=0$
, we find
$$\begin{eqnarray}\displaystyle & \displaystyle \langle z^{2}\rangle =\frac{v^{2}}{4D^{2}}\left(\unicode[STIX]{x1D707}_{0}^{2}-1\right)\left(1-\text{e}^{-2Dt}\right)+\frac{v^{2}}{12D^{2}}\left(\frac{1}{3}-\unicode[STIX]{x1D707}_{0}^{2}\right)\left(1-\text{e}^{-6Dt}\right)+\frac{v^{2}t}{3D}. & \displaystyle\end{eqnarray}$$
For early times this becomes
$$\begin{eqnarray}\displaystyle & \displaystyle \langle z^{2}\rangle _{t\rightarrow 0}\rightarrow v^{2}\unicode[STIX]{x1D707}_{0}^{2}t^{2} & \displaystyle\end{eqnarray}$$
corresponding to the unperturbed motion. For late times we obtain
$$\begin{eqnarray}\displaystyle & \displaystyle \langle z^{2}\rangle _{t\rightarrow \infty }=\frac{v^{2}t}{3D}\equiv 2\unicode[STIX]{x1D705}_{\Vert }t, & \displaystyle\end{eqnarray}$$
which does not depend on the initial pitch-angle cosine
$\unicode[STIX]{x1D707}_{0}$
. Equation (3.73) corresponds to a normal diffusive motion. If we average (3.71) over all initial pitch angles, we find
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \langle z^{2}\rangle \rangle =\frac{v^{2}t}{3D}-\frac{v^{2}}{6D^{2}}\left(1-\text{e}^{-2Dt}\right) & \displaystyle\end{eqnarray}$$
in agreement with Malkov (Reference Malkov2017).
3.10 The moment
$\langle z^{2}\unicode[STIX]{x1D707}\rangle$
For
$n=2$
and
$m=1$
, equation (3.3) becomes
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\langle z^{2}\unicode[STIX]{x1D707}\rangle =2v\langle z\unicode[STIX]{x1D707}^{2}\rangle -2D\langle z^{2}\unicode[STIX]{x1D707}\rangle , & \displaystyle\end{eqnarray}$$
where the moment
$\langle z\unicode[STIX]{x1D707}^{2}\rangle$
is given by (3.58). The homogeneous solution of (3.75) is
$$\begin{eqnarray}\displaystyle & \displaystyle \langle z^{2}\unicode[STIX]{x1D707}\rangle _{h}=C\text{e}^{-2Dt}. & \displaystyle\end{eqnarray}$$
In order to compute the particular solution, we combine (3.58) with (3.75) to find
$$\begin{eqnarray}\displaystyle \frac{\text{d}}{\text{d}t}\langle z^{2}\unicode[STIX]{x1D707}\rangle & = & \displaystyle \frac{v^{2}\unicode[STIX]{x1D707}_{0}}{3D}\left(\unicode[STIX]{x1D707}_{0}^{2}-1\right)\text{e}^{-6Dt}+\frac{v^{2}\unicode[STIX]{x1D707}_{0}}{3D}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{v^{2}\unicode[STIX]{x1D707}_{0}}{3D}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{3}{5}\right)\text{e}^{-12Dt}-\frac{v^{2}\unicode[STIX]{x1D707}_{0}}{5D}\text{e}^{-2Dt}-2D\langle \unicode[STIX]{x1D707}z^{2}\rangle .\end{eqnarray}$$
For the particular solution we can employ the ansatz
$$\begin{eqnarray}\displaystyle & \displaystyle \langle z^{2}\unicode[STIX]{x1D707}\rangle _{p}=A+B\text{e}^{-12Dt}+E\text{e}^{-6Dt}+F(t)\text{e}^{-2Dt}. & \displaystyle\end{eqnarray}$$
It has to be pointed out that
$F(t)$
needs to be a function of time. A constant coefficient
$F$
would not work in this particular case. By combining the latter form with (3.77), we find after straightforward algebra
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle A=\frac{v^{2}\unicode[STIX]{x1D707}_{0}}{6D^{2}},\\[15.0pt] \displaystyle B=\frac{v^{2}\unicode[STIX]{x1D707}_{0}}{30D^{2}}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{3}{5}\right)\!,\\[15.0pt] \displaystyle E=\frac{v^{2}\unicode[STIX]{x1D707}_{0}}{12D^{2}}\left(1-\unicode[STIX]{x1D707}_{0}^{2}\right),\end{array}\right\} & & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle & \displaystyle F(t)=-\frac{v^{2}\unicode[STIX]{x1D707}_{0}t}{5D}. & \displaystyle\end{eqnarray}$$
The total solution is a superposition of homogeneous and particular solutions. The remaining constant
$C$
in (3.76) can be determined from the initial condition
$\langle z^{2}\unicode[STIX]{x1D707}\rangle =0$
for
$t=0$
. After more lengthy algebra we obtain
$$\begin{eqnarray}\displaystyle & \displaystyle C=\frac{v^{2}\unicode[STIX]{x1D707}_{0}}{20D^{2}}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{23}{5}\right). & \displaystyle\end{eqnarray}$$
Therewith the total solution of (3.75) becomes
$$\begin{eqnarray}\displaystyle \langle z^{2}\unicode[STIX]{x1D707}\rangle & = & \displaystyle \frac{v^{2}\unicode[STIX]{x1D707}_{0}}{20D^{2}}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{23}{5}\right)\text{e}^{-2Dt}+\frac{v^{2}\unicode[STIX]{x1D707}_{0}}{6D^{2}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{v^{2}\unicode[STIX]{x1D707}_{0}}{30D^{2}}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{3}{5}\right)\text{e}^{-12Dt}+\frac{v^{2}\unicode[STIX]{x1D707}_{0}}{12D^{2}}\left(1-\unicode[STIX]{x1D707}_{0}^{2}\right)\text{e}^{-6Dt}-\frac{v^{2}\unicode[STIX]{x1D707}_{0}t}{5D}\text{e}^{-2Dt}.\end{eqnarray}$$
We can very easily show that
$\langle \langle z^{2}\unicode[STIX]{x1D707}\rangle \rangle =0$
as expected.
3.11 The moment
$\langle z^{2}\unicode[STIX]{x1D707}^{2}\rangle$
For
$n=2$
and
$m=2$
, equation (3.3) becomes
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\langle z^{2}\unicode[STIX]{x1D707}^{2}\rangle =2v\langle z\unicode[STIX]{x1D707}^{3}\rangle +2D\langle z^{2}\rangle -6D\langle z^{2}\unicode[STIX]{x1D707}^{2}\rangle , & \displaystyle\end{eqnarray}$$
where the moments
$\langle z\unicode[STIX]{x1D707}^{3}\rangle$
and
$\langle z^{2}\rangle$
are given by (3.66) and (3.71), respectively. The homogeneous solution of (3.83) is
$$\begin{eqnarray}\displaystyle & \displaystyle \langle z^{2}\unicode[STIX]{x1D707}^{2}\rangle _{h}=C\text{e}^{-6Dt}. & \displaystyle\end{eqnarray}$$
In order to determine the particular solution we need to combine (3.83) with (3.66) and (3.71). We then obtain
$$\begin{eqnarray}\displaystyle \frac{\text{d}}{\text{d}t}\langle z^{2}\unicode[STIX]{x1D707}^{2}\rangle & = & \displaystyle \frac{v^{2}}{5D}+\frac{3v^{2}}{10D}\left(\unicode[STIX]{x1D707}_{0}^{2}-1\right)\text{e}^{-2Dt}+\frac{3v^{2}}{14D}\left(\frac{1}{3}-\unicode[STIX]{x1D707}_{0}^{2}\right)\text{e}^{-6Dt}\nonumber\\ \displaystyle & & \displaystyle +\frac{v^{2}}{20D}\left(5\unicode[STIX]{x1D707}_{0}^{4}-6\unicode[STIX]{x1D707}_{0}^{2}+1\right)\text{e}^{-12Dt}\nonumber\\ \displaystyle & & \displaystyle -\frac{v^{2}}{4D}\left[\unicode[STIX]{x1D707}_{0}^{4}-\frac{6}{7}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{1}{3}\right)-\frac{1}{5}\right]\text{e}^{-20Dt}\nonumber\\ \displaystyle & & \displaystyle +\frac{v^{2}}{2D}\left(\unicode[STIX]{x1D707}_{0}^{2}-1\right)\left(1-\text{e}^{-2Dt}\right)\nonumber\\ \displaystyle & & \displaystyle +\frac{v^{2}}{6D}\left(\frac{1}{3}-\unicode[STIX]{x1D707}_{0}^{2}\right)\left(1-\text{e}^{-6Dt}\right)+\frac{2v^{2}t}{3}-6D\langle z^{2}\unicode[STIX]{x1D707}^{2}\rangle .\end{eqnarray}$$
For the particular solution we can employ the ansatz
$$\begin{eqnarray}\displaystyle & \displaystyle \langle z^{2}\unicode[STIX]{x1D707}^{2}\rangle _{p}=A(t)+B\text{e}^{-20Dt}+E\text{e}^{-12Dt}+F(t)\text{e}^{-6Dt}+G\text{e}^{-2Dt}, & \displaystyle\end{eqnarray}$$
where the factors
$A(t)$
and
$F(t)$
need to be functions of time. After lengthy straightforward algebra we find for the coefficients and functions therein
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle A(t)=\frac{v^{2}t}{9D}+\frac{v^{2}\unicode[STIX]{x1D707}_{0}^{2}}{18D^{2}}-\frac{8v^{2}}{135D^{2}},\\[15.0pt] \displaystyle B=\frac{v^{2}}{56D^{2}}\left[\unicode[STIX]{x1D707}_{0}^{4}-\frac{6}{7}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{1}{3}\right)-\frac{1}{5}\right],\\[15.0pt] \displaystyle E=-\frac{v^{2}}{120D^{2}}(5\unicode[STIX]{x1D707}_{0}^{4}-6\unicode[STIX]{x1D707}_{0}^{2}+1),\\[15.0pt] \displaystyle F(t)=\frac{v^{2}t}{21D}\left(\frac{1}{3}-\unicode[STIX]{x1D707}_{0}^{2}\right),\end{array}\right\} & & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle & \displaystyle G=\frac{v^{2}}{20D^{2}}\left(1-\unicode[STIX]{x1D707}_{0}^{2}\right). & \displaystyle\end{eqnarray}$$
The total solution is a superposition of homogeneous and particular solutions. The remaining constant
$C$
in (3.84) can be determined from the initial condition
$\langle z^{2}\unicode[STIX]{x1D707}^{2}\rangle =0$
for
$t=0$
. After lengthy straightforward algebra we obtain
$$\begin{eqnarray}\displaystyle C & = & \displaystyle \frac{8v^{2}}{135D^{2}}-\frac{v^{2}\unicode[STIX]{x1D707}_{0}^{2}}{18D^{2}}-\frac{v^{2}}{56D^{2}}\left[\unicode[STIX]{x1D707}_{0}^{4}-\frac{6}{7}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{1}{3}\right)-\frac{1}{5}\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{v^{2}}{120D^{2}}\left(5\unicode[STIX]{x1D707}_{0}^{4}-6\unicode[STIX]{x1D707}_{0}^{2}+1\right)-\frac{v^{2}}{20D^{2}}\left(1-\unicode[STIX]{x1D707}_{0}^{2}\right).\end{eqnarray}$$
The solution of (3.83) is, therefore,
$$\begin{eqnarray}\displaystyle \langle z^{2}\unicode[STIX]{x1D707}^{2}\rangle & = & \displaystyle \left\{\hspace{-2.0pt}\frac{8v^{2}}{135D^{2}}-\frac{v^{2}\unicode[STIX]{x1D707}_{0}^{2}}{18D^{2}}-\frac{v^{2}}{56D^{2}}\left[\unicode[STIX]{x1D707}_{0}^{4}-\frac{6}{7}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{1}{3}\right)-\frac{1}{5}\right]\right.\nonumber\\ \displaystyle & & \displaystyle +\,\frac{v^{2}}{120D^{2}}\left(5\unicode[STIX]{x1D707}_{0}^{4}-6\unicode[STIX]{x1D707}_{0}^{2}+1\right)-\left.\frac{v^{2}}{20D^{2}}\left(1-\unicode[STIX]{x1D707}_{0}^{2}\right)\hspace{-2.0pt}\right\}\text{e}^{-6Dt}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{v^{2}t}{9D}+\frac{v^{2}\unicode[STIX]{x1D707}_{0}^{2}}{18D^{2}}-\frac{8v^{2}}{135D^{2}}+\frac{v^{2}}{56D^{2}}\left[\unicode[STIX]{x1D707}_{0}^{4}-\frac{6}{7}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{1}{3}\right)-\frac{1}{5}\right]\text{e}^{-20Dt}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{v^{2}}{120D^{2}}\left(5\unicode[STIX]{x1D707}_{0}^{4}-6\unicode[STIX]{x1D707}_{0}^{2}+1\right)\text{e}^{-12Dt}+\frac{v^{2}t}{21D}\left(\frac{1}{3}-\unicode[STIX]{x1D707}_{0}^{2}\right)\text{e}^{-6Dt}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{v^{2}}{20D^{2}}\left(1-\unicode[STIX]{x1D707}_{0}^{2}\right)\text{e}^{-2Dt}.\end{eqnarray}$$
In the late time limit, we can neglect all exponential functions and constants to find
$$\begin{eqnarray}\displaystyle & \displaystyle \langle z^{2}\unicode[STIX]{x1D707}^{2}\rangle _{t\rightarrow \infty }\rightarrow \frac{v^{2}t}{9D}. & \displaystyle\end{eqnarray}$$
If we average (3.90) over the initial pitch-angle cosine
$\unicode[STIX]{x1D707}_{0}$
, we find
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \langle z^{2}\unicode[STIX]{x1D707}^{2}\rangle \rangle =\frac{v^{2}}{135D^{2}}\text{e}^{-6Dt}+\frac{v^{2}}{30D^{2}}\text{e}^{-2Dt}+\frac{v^{2}t}{9D}-\frac{11v^{2}}{270D^{2}}. & \displaystyle\end{eqnarray}$$
3.12 The moment
$\langle z^{3}\rangle$
For
$n=3$
and
$m=0$
, equation (3.3) becomes
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\langle z^{3}\rangle =3v\langle z^{2}\unicode[STIX]{x1D707}\rangle , & \displaystyle\end{eqnarray}$$
where the moment
$\langle z^{2}\unicode[STIX]{x1D707}\rangle$
is given by (3.82). If we integrate (3.93) and by using
$\langle z^{3}\rangle =0$
for
$t=0$
, we derive
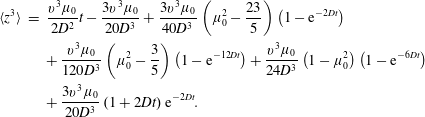$$\begin{eqnarray}\displaystyle \langle z^{3}\rangle & = & \displaystyle \frac{v^{3}\unicode[STIX]{x1D707}_{0}}{2D^{2}}t-\frac{3v^{3}\unicode[STIX]{x1D707}_{0}}{20D^{3}}+\frac{3v^{3}\unicode[STIX]{x1D707}_{0}}{40D^{3}}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{23}{5}\right)\left(1-\text{e}^{-2Dt}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{v^{3}\unicode[STIX]{x1D707}_{0}}{120D^{3}}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{3}{5}\right)\left(1-\text{e}^{-12Dt}\right)+\frac{v^{3}\unicode[STIX]{x1D707}_{0}}{24D^{3}}\left(1-\unicode[STIX]{x1D707}_{0}^{2}\right)\left(1-\text{e}^{-6Dt}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{3v^{3}\unicode[STIX]{x1D707}_{0}}{20D^{3}}\left(1+2Dt\right)\text{e}^{-2Dt}.\end{eqnarray}$$
We can easily see that if we average (3.94) over the initial pitch-angle cosine
$\unicode[STIX]{x1D707}_{0}$
, we find
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \langle z^{3}\rangle \rangle =0. & \displaystyle\end{eqnarray}$$
This result was also obtained by Malkov (Reference Malkov2017). Equation (3.94) provides a generalization of the latter result, because it is valid for an arbitrary initial pitch-angle cosine
$\unicode[STIX]{x1D707}_{0}$
.
If we consider the limit
$t\rightarrow \infty$
, equation (3.94) becomes
$$\begin{eqnarray}\displaystyle & \displaystyle \langle z^{3}\rangle _{t\rightarrow \infty }=\frac{v^{3}\unicode[STIX]{x1D707}_{0}}{2D^{2}}t & \displaystyle\end{eqnarray}$$
corresponding to a linear increase.
3.13 The moment
$\langle z^{3}\unicode[STIX]{x1D707}\rangle$
For
$n=3$
and
$m=1$
, equation (3.3) becomes
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\langle z^{3}\unicode[STIX]{x1D707}\rangle =3v\langle z^{2}\unicode[STIX]{x1D707}^{2}\rangle -2D\langle z^{3}\unicode[STIX]{x1D707}\rangle , & \displaystyle\end{eqnarray}$$
where the moment
$\langle z^{2}\unicode[STIX]{x1D707}^{2}\rangle$
is given by (3.90). The homogeneous solution of (3.97) is
$$\begin{eqnarray}\displaystyle & \displaystyle \langle z^{3}\unicode[STIX]{x1D707}\rangle _{h}=C\text{e}^{-2Dt}. & \displaystyle\end{eqnarray}$$
In order to compute the particular solution, we combine (3.90) with (3.97) to find
$$\begin{eqnarray}\displaystyle \frac{\text{d}}{\text{d}t}\langle z^{3}\unicode[STIX]{x1D707}\rangle & = & \displaystyle -\frac{3v^{3}}{56D^{2}}\left[\unicode[STIX]{x1D707}_{0}^{4}-\frac{6}{7}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{1}{3}\right)-\frac{1}{5}\right]\left(\text{e}^{-6Dt}-\text{e}^{-20Dt}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{v^{3}}{40D^{2}}\left(5\unicode[STIX]{x1D707}_{0}^{4}-6\unicode[STIX]{x1D707}_{0}^{2}+1\right)\left(\text{e}^{-6Dt}-\text{e}^{-12Dt}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{3v^{3}}{20D^{2}}\left(1-\unicode[STIX]{x1D707}_{0}^{2}\right)\left(\text{e}^{-6Dt}-\text{e}^{-2Dt}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{v^{3}t}{7D}\left(\frac{1}{3}-\unicode[STIX]{x1D707}_{0}^{2}\right)\text{e}^{-6Dt}+\frac{8v^{3}}{45D^{2}}\left(\text{e}^{-6Dt}-1\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{v^{3}\unicode[STIX]{x1D707}_{0}^{2}}{6D^{2}}\left(1-\text{e}^{-6Dt}\right)+\frac{v^{3}t}{3D}-2D\langle z^{3}\unicode[STIX]{x1D707}\rangle .\end{eqnarray}$$
For the particular solution we can employ the ansatz
$$\begin{eqnarray}\displaystyle & \displaystyle \langle z^{3}\unicode[STIX]{x1D707}\rangle _{p}=A(t)+B\text{e}^{-20Dt}+E\text{e}^{-12Dt}+F(t)\text{e}^{-6Dt}+G(t)\text{e}^{-2Dt}, & \displaystyle\end{eqnarray}$$
where
$A(t)$
,
$F(t)$
and
$G(t)$
need to be functions of time. If this is used in (3.99) we find after long algebra
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle A(t)=\frac{v^{3}t}{6D^{2}}+\frac{v^{3}}{12D^{3}}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{31}{15}\right)\\[15.0pt] \displaystyle B=-\frac{v^{3}}{336D^{3}}\left[\unicode[STIX]{x1D707}_{0}^{4}-\frac{6}{7}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{1}{3}\right)-\frac{1}{5}\right],\\[15.0pt] \displaystyle E=\frac{v^{3}}{400D^{3}}\left(5\unicode[STIX]{x1D707}_{0}^{4}-6\unicode[STIX]{x1D707}_{0}^{2}+1\right)\end{array}\right\} & & \displaystyle\end{eqnarray}$$
as well as
$$\begin{eqnarray}\displaystyle F(t) & = & \displaystyle -\frac{v^{3}}{28D^{3}}\left(\frac{1}{4}+Dt\right)\left(\frac{1}{3}-\unicode[STIX]{x1D707}_{0}^{2}\right)-\frac{2v^{3}}{45D^{3}}+\frac{v^{3}\unicode[STIX]{x1D707}_{0}^{2}}{24D^{3}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{3v^{3}}{224D^{3}}\left[\unicode[STIX]{x1D707}_{0}^{4}-\frac{6}{7}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{1}{3}\right)-\frac{1}{5}\right]\nonumber\\ \displaystyle & & \displaystyle -\,\frac{v^{3}}{160D^{3}}\left(5\unicode[STIX]{x1D707}_{0}^{4}-6\unicode[STIX]{x1D707}_{0}^{2}+1\right)+\frac{3v^{3}}{80D^{3}}\left(1-\unicode[STIX]{x1D707}_{0}^{2}\right)\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle & \displaystyle G(t)=\frac{3v^{3}t}{20D^{2}}\left(1-\unicode[STIX]{x1D707}_{0}^{2}\right). & \displaystyle\end{eqnarray}$$
The remaining constant
$C$
in (3.98) can be determined from the initial condition
$\langle z^{3}\unicode[STIX]{x1D707}\rangle =0$
for
$t=0$
. After lengthy straightforward algebra we obtain
$$\begin{eqnarray}\displaystyle C & = & \displaystyle -\frac{v^{3}}{12D^{3}}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{31}{15}\right)-\frac{v^{3}}{96D^{3}}\left[\unicode[STIX]{x1D707}_{0}^{4}-\frac{6}{7}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{1}{3}\right)-\frac{1}{5}\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{3v^{3}}{800D^{3}}\left(5\unicode[STIX]{x1D707}_{0}^{4}-6\unicode[STIX]{x1D707}_{0}^{2}+1\right)+\frac{v^{3}}{112D^{3}}\left(\frac{1}{3}-\unicode[STIX]{x1D707}_{0}^{2}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{2v^{3}}{45D^{3}}-\frac{v^{3}\unicode[STIX]{x1D707}_{0}^{2}}{24D^{3}}-\frac{3v^{3}}{80D^{3}}\left(1-\unicode[STIX]{x1D707}_{0}^{2}\right).\end{eqnarray}$$
Therefore, we find
$$\begin{eqnarray}\displaystyle \langle z^{3}\unicode[STIX]{x1D707}\rangle & = & \displaystyle \frac{v^{3}t}{6D^{2}}+\frac{v^{3}}{12D^{3}}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{31}{15}\right)-\frac{v^{3}}{336D^{3}}\left[\unicode[STIX]{x1D707}_{0}^{4}-\frac{6}{7}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{1}{3}\right)-\frac{1}{5}\right]\text{e}^{-20Dt}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{v^{3}}{400D^{3}}\left(5\unicode[STIX]{x1D707}_{0}^{4}-6\unicode[STIX]{x1D707}_{0}^{2}+1\right)\text{e}^{-12Dt}+\left\{\hspace{-2.0pt}-\frac{v^{3}}{28D^{3}}\left(\frac{1}{4}+Dt\right)\left(\frac{1}{3}-\unicode[STIX]{x1D707}_{0}^{2}\right)\right.\nonumber\\ \displaystyle & & \displaystyle -\,\frac{2v^{3}}{45D^{3}}+\frac{v^{3}\unicode[STIX]{x1D707}_{0}^{2}}{24D^{3}}+\frac{3v^{3}}{224D^{3}}\left[\unicode[STIX]{x1D707}_{0}^{4}-\frac{6}{7}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{1}{3}\right)-\frac{1}{5}\right]\nonumber\\ \displaystyle & & \displaystyle -\,\left.\frac{v^{3}}{160D^{3}}\left(5\unicode[STIX]{x1D707}_{0}^{4}-6\unicode[STIX]{x1D707}_{0}^{2}+1\right)+\frac{3v^{3}}{80D^{3}}\left(1-\unicode[STIX]{x1D707}_{0}^{2}\right)\hspace{-2.0pt}\right\}\text{e}^{-6Dt}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{3v^{3}t}{20D^{2}}\left(1-\unicode[STIX]{x1D707}_{0}^{2}\right)\text{e}^{-2Dt}+\left\{\hspace{-2.0pt}-\frac{v^{3}}{12D^{3}}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{31}{15}\right)\right.\nonumber\\ \displaystyle & & \displaystyle -\,\frac{v^{3}}{96D^{3}}\left[\unicode[STIX]{x1D707}_{0}^{4}-\frac{6}{7}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{1}{3}\right)-\frac{1}{5}\right]+\frac{3v^{3}}{800D^{3}}\left(5\unicode[STIX]{x1D707}_{0}^{4}-6\unicode[STIX]{x1D707}_{0}^{2}+1\right)\nonumber\\ \displaystyle & & \displaystyle \left.+\frac{v^{3}}{112D^{3}}\left(\frac{1}{3}-\unicode[STIX]{x1D707}_{0}^{2}\right)+\frac{2v^{3}}{45D^{3}}-\frac{v^{3}\unicode[STIX]{x1D707}_{0}^{2}}{24D^{3}}-\frac{3v^{3}}{80D^{3}}\left(1-\unicode[STIX]{x1D707}_{0}^{2}\right)\hspace{-2.0pt}\right\}\text{e}^{-2Dt}.\end{eqnarray}$$
In the limit
$t\rightarrow \infty$
, we omit the terms with exponentials as well as the constant terms and, thus, equation (3.105) becomes
$$\begin{eqnarray}\displaystyle & \displaystyle \langle z^{3}\unicode[STIX]{x1D707}\rangle \rightarrow \frac{v^{3}t}{6D^{2}}. & \displaystyle\end{eqnarray}$$
If we average (3.105) over the initial pitch-angle cosine
$\unicode[STIX]{x1D707}_{0}$
, we find
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \langle z^{3}\unicode[STIX]{x1D707}\rangle \rangle =\frac{v^{3}t}{6D^{2}}-\frac{13v^{3}}{90D^{3}}-\frac{v^{3}}{180D^{3}}\text{e}^{-6Dt}+\left(\frac{v^{3}t}{10D^{2}}+\frac{3v^{3}}{20D^{3}}\right)\text{e}^{-2Dt}. & \displaystyle\end{eqnarray}$$
3.14 The moment
$\langle z^{4}\rangle$
For
$n=4$
and
$m=0$
, equation (3.3) becomes
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\langle z^{4}\rangle =4v\langle z^{3}\unicode[STIX]{x1D707}\rangle , & \displaystyle\end{eqnarray}$$
where the moment
$\langle \unicode[STIX]{x1D707}z^{3}\rangle$
is given by (3.105). By using the parameters and functions
$A(t)$
,
$B$
,
$E$
,
$F(t)$
,
$G(t)$
and
$C$
given by (3.101)–(3.104), we can write differential equation (3.108) as
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\langle z^{4}\rangle =4vA(t)+4vB\text{e}^{-20Dt}+4vE\text{e}^{-12Dt}+4vF(t)\text{e}^{-6Dt}+4vG(t)\text{e}^{-2Dt}+4vC\text{e}^{-2Dt}. & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
With
$\langle z^{4}\rangle =0$
for
$t=0$
, we can integrate the latter equation so that
$$\begin{eqnarray}\displaystyle \langle z^{4}\rangle & = & \displaystyle 4v\int _{0}^{t}\text{d}t^{\prime }\,A(t^{\prime })+4vB\int _{0}^{t}\text{d}t^{\prime }\,\text{e}^{-20Dt^{\prime }}+4vE\int _{0}^{t}\text{d}t^{\prime }\,\text{e}^{-12Dt^{\prime }}\nonumber\\ \displaystyle & & \displaystyle +\,4v\int _{0}^{t}\text{d}t^{\prime }\,F(t^{\prime })\text{e}^{-6Dt^{\prime }}+4v\int _{0}^{t}\text{d}t^{\prime }\,G(t^{\prime })\text{e}^{-2Dt^{\prime }}+4vC\int _{0}^{t}\text{d}t^{\prime }\,\text{e}^{-2Dt^{\prime }}.\end{eqnarray}$$
The only integral which is not trivial has the form
$$\begin{eqnarray}\displaystyle \int _{0}^{t}\text{d}x\,x\text{e}^{-\unicode[STIX]{x1D6FC}x}=\frac{1}{\unicode[STIX]{x1D6FC}^{2}}\left[1-\left(1+\unicode[STIX]{x1D6FC}t\right)\text{e}^{-\unicode[STIX]{x1D6FC}t}\right]. & & \displaystyle\end{eqnarray}$$
With this integral we derive
$$\begin{eqnarray}\displaystyle \langle z^{4}\rangle & = & \displaystyle \frac{v^{4}t^{2}}{3D^{2}}+\frac{v^{4}t}{3D^{3}}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{31}{15}\right)+\frac{vB}{5D}\left(1-\text{e}^{-20Dt}\right)+\frac{vE}{3D}\left(1-\text{e}^{-12Dt}\right)\nonumber\\ \displaystyle & & \displaystyle +\,\frac{2vF_{0}}{3D}\left(1-\text{e}^{-6Dt}\right)+\frac{vF_{1}}{9D^{2}}\left[1-\left(1+6Dt\right)\text{e}^{-6Dt}\right]\nonumber\\ \displaystyle & & \displaystyle +\,\frac{3v^{4}}{20D^{4}}\left(1-\unicode[STIX]{x1D707}_{0}^{2}\right)\left[1-\left(1+2Dt\right)\text{e}^{-2Dt}\right]+\frac{2vC}{D}\left(1-\text{e}^{-2Dt}\right)\!,\end{eqnarray}$$
where we have used
$$\begin{eqnarray}\displaystyle & \displaystyle F_{1}=-\frac{v^{3}}{28D^{2}}\left(\frac{1}{3}-\unicode[STIX]{x1D707}_{0}^{2}\right) & \displaystyle\end{eqnarray}$$
and
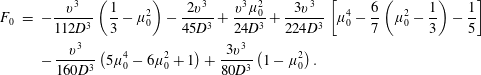$$\begin{eqnarray}\displaystyle F_{0} & = & \displaystyle -\frac{v^{3}}{112D^{3}}\left(\frac{1}{3}-\unicode[STIX]{x1D707}_{0}^{2}\right)-\frac{2v^{3}}{45D^{3}}+\frac{v^{3}\unicode[STIX]{x1D707}_{0}^{2}}{24D^{3}}+\frac{3v^{3}}{224D^{3}}\left[\unicode[STIX]{x1D707}_{0}^{4}-\frac{6}{7}\left(\unicode[STIX]{x1D707}_{0}^{2}-\frac{1}{3}\right)-\frac{1}{5}\right]\nonumber\\ \displaystyle & & \displaystyle -\,\frac{v^{3}}{160D^{3}}\left(5\unicode[STIX]{x1D707}_{0}^{4}-6\unicode[STIX]{x1D707}_{0}^{2}+1\right)+\frac{3v^{3}}{80D^{3}}\left(1-\unicode[STIX]{x1D707}_{0}^{2}\right).\end{eqnarray}$$
The parameters
$B$
,
$C$
and
$E$
are given by (3.101) and (3.104).
In the limit
$t\rightarrow \infty$
, equation (3.112) becomes
$$\begin{eqnarray}\displaystyle & \displaystyle \langle z^{4}\rangle \rightarrow \frac{v^{4}t^{2}}{3D^{2}}=12\unicode[STIX]{x1D705}_{\Vert }^{2}t^{2}. & \displaystyle\end{eqnarray}$$
Furthermore, we can average (3.112) over the initial pitch-angle cosine
$\unicode[STIX]{x1D707}_{0}$
to deduce
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \langle z^{4}\rangle \rangle =\frac{v^{4}t^{2}}{3D^{2}}-\frac{26v^{4}t}{45D^{3}}+\frac{107v^{4}}{270D^{4}}+\frac{v^{4}}{270D^{4}}\text{e}^{-6Dt}-\left(\frac{2v^{4}}{5D^{4}}+\frac{v^{4}t}{5D^{3}}\right)\text{e}^{-2Dt}. & \displaystyle\end{eqnarray}$$
The latter formula agrees perfectly with Malkov (Reference Malkov2017). We would like to emphasize that (3.112) provides a generalization of (3.116) because it is correct for an arbitrary initial pitch-angle cosine
$\unicode[STIX]{x1D707}_{0}$
.
4 The characteristic function
In the previous section we have computed moments of the pitch-angle-dependent Fokker–Planck equation. Compared to previous work our findings depend on the initial pitch-angle cosine
$\unicode[STIX]{x1D707}_{0}$
. In the following we consider an application of such analytical results by exploring the characteristic function and related quantities. Those are important for analytical formulations of nonlinear theories describing the motion of energetic particles across a mean magnetic field.
The characteristic function of a distribution function is defined via (2.6) corresponding to the Fourier transform of that function. After employing a Taylor expansion of the exponential function we derive
$$\begin{eqnarray}\displaystyle & \displaystyle \left\langle \text{e}^{\text{i}kz}\right\rangle =\mathop{\sum }_{n=0}^{\infty }\frac{1}{n!}(\text{i}k)^{n}\langle z^{n}\rangle . & \displaystyle\end{eqnarray}$$
By only taking into account the first four terms therein, we can approximate
$$\begin{eqnarray}\displaystyle & \displaystyle \left\langle \text{e}^{\text{i}kz}\right\rangle \approx 1+\text{i}k\langle z\rangle -{\textstyle \frac{1}{2}}k^{2}\langle z^{2}\rangle -{\textstyle \frac{1}{6}}\text{i}k^{3}\langle z^{3}\rangle +{\textstyle \frac{1}{24}}k^{4}\langle z^{4}\rangle . & \displaystyle\end{eqnarray}$$
The characteristic function of the diffusion equation is given by (2.7). A Taylor expansion of the latter function yields
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \text{e}^{\text{i}kz}\rangle _{D}=\mathop{\sum }_{n=0}^{\infty }\frac{1}{n!}\left(-\unicode[STIX]{x1D705}_{\Vert }k^{2}t\right)^{n}\approx 1-\unicode[STIX]{x1D705}_{\Vert }k^{2}t+\frac{1}{2}\unicode[STIX]{x1D705}_{\Vert }^{2}k^{4}t^{2}+\cdots & \displaystyle\end{eqnarray}$$
If we compare (4.2) and (4.3), we find
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \langle z\rangle _{D}=0,\\[5.0pt] \displaystyle \langle z^{2}\rangle _{D}=2\unicode[STIX]{x1D705}_{\Vert }t,\\[5.0pt] \displaystyle \langle z^{3}\rangle _{D}=0,\end{array}\right\} & & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle & \displaystyle \langle z^{4}\rangle _{D}=12\unicode[STIX]{x1D705}_{\Vert }^{2}t^{2}. & \displaystyle\end{eqnarray}$$
In nonlinear theories for perpendicular diffusion, one needs to know correlations of the form
$\langle \langle \unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D707}\text{e}^{\text{i}kz}\rangle \rangle$
(see, e.g. Matthaeus et al.
Reference Matthaeus, Qin, Bieber and Zank2003; Shalchi Reference Shalchi2010). If we expand again as above, we find
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \langle \unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D707}\text{e}^{\text{i}kz}\rangle \rangle \approx \langle \langle \unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D707}\rangle \rangle +\text{i}k\langle \langle \unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D707}z\rangle \rangle -{\textstyle \frac{1}{2}}k^{2}\langle \langle \unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D707}z^{2}\rangle \rangle . & \displaystyle\end{eqnarray}$$
For the moments we can employ (3.9), (3.47) and (3.82). If we multiply the latter moments by
$\unicode[STIX]{x1D707}_{0}$
and average over all
$\unicode[STIX]{x1D707}_{0}$
, we find
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \langle \langle \unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D707}\rangle \rangle ={\textstyle \frac{1}{3}}\text{e}^{-vt/\unicode[STIX]{x1D706}_{\Vert }}\\[10.0pt] \displaystyle \langle \langle \unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D707}z\rangle \rangle =0,\end{array}\right\} & & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \langle \unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D707}z^{2}\rangle \rangle =\frac{v^{2}}{18D^{2}}+\frac{v^{2}}{90D^{2}}\text{e}^{-6Dt}-\frac{v^{2}}{15D^{2}}\left(1+Dt\right)\text{e}^{-2Dt}. & \displaystyle\end{eqnarray}$$
Therewith, equation (4.6) becomes
$$\begin{eqnarray}\displaystyle & \displaystyle \langle \langle \unicode[STIX]{x1D707}_{0}\unicode[STIX]{x1D707}\text{e}^{\text{i}kz}\rangle \rangle \approx \frac{1}{3}\text{e}^{-vt/\unicode[STIX]{x1D706}_{\Vert }}-\frac{1}{2}k^{2}\left[\frac{v^{2}}{18D^{2}}+\frac{v^{2}}{90D^{2}}\text{e}^{-6Dt}-\frac{v^{2}}{15D^{2}}\left(1+Dt\right)\text{e}^{-2Dt}\right]. & \displaystyle\end{eqnarray}$$
The latter formula can be written as
$$\begin{eqnarray}\displaystyle & \displaystyle \langle v_{z}(t)v_{z}(0)\text{e}^{\text{i}kz}\rangle =\frac{v^{2}}{3}\text{e}^{-vt/\unicode[STIX]{x1D706}_{\Vert }}\left[1+\frac{v^{2}k^{2}}{10D^{2}}\left(1+Dt\right)\right]-\frac{v^{4}k^{2}}{36D^{2}}-\frac{v^{4}k^{2}}{180D^{2}}\text{e}^{-3vt/\unicode[STIX]{x1D706}_{\Vert }}. & \displaystyle\end{eqnarray}$$
In the limit
$t\rightarrow \infty$
, this becomes
$$\begin{eqnarray}\displaystyle & \displaystyle \langle v_{z}(t)v_{z}(0)\text{e}^{\text{i}kz}\rangle _{t\rightarrow \infty }=-\frac{v^{4}k^{2}}{36D^{2}}=-\unicode[STIX]{x1D705}_{\Vert }^{2}k^{2}. & \displaystyle\end{eqnarray}$$
In Matthaeus et al. (Reference Matthaeus, Qin, Bieber and Zank2003) the following model was used
$$\begin{eqnarray}\displaystyle & \displaystyle \langle v_{z}(t)v_{z}(0)\text{e}^{\text{i}kz}\rangle _{M}\approx v^{2}\langle \unicode[STIX]{x1D707}\unicode[STIX]{x1D707}_{0}\rangle \langle \text{e}^{\text{i}kz}\rangle =\frac{v^{2}}{3}\text{e}^{-vt/\unicode[STIX]{x1D706}_{\Vert }}\text{e}^{-\unicode[STIX]{x1D705}_{\Vert }k^{2}t}. & \displaystyle\end{eqnarray}$$
If we expand up to second order in
$k$
, this becomes
$$\begin{eqnarray}\displaystyle & \displaystyle \langle v_{z}(t)v_{z}(0)\text{e}^{\text{i}kz}\rangle _{M}\approx \frac{v^{2}}{3}\text{e}^{-vt/\unicode[STIX]{x1D706}_{\Vert }}\left(1-\unicode[STIX]{x1D705}_{\Vert }k^{2}t\right)\!, & \displaystyle\end{eqnarray}$$
which disagrees with (4.12). In Shalchi (Reference Shalchi2017), on the other hand, the following form was proposed
$$\begin{eqnarray}\displaystyle & \displaystyle \langle v_{z}(t)v_{z}(0)\text{e}^{\text{i}kz}\rangle _{S}=-\unicode[STIX]{x1D705}_{\Vert }^{2}k^{2}\text{e}^{-\unicode[STIX]{x1D705}_{\Vert }k^{2}t}. & \displaystyle\end{eqnarray}$$
In the lowest non-vanishing order in
$k$
, this becomes
$$\begin{eqnarray}\displaystyle & \displaystyle \langle v_{z}(t)v_{z}(0)\text{e}^{\text{i}kz}\rangle _{S}\approx -\unicode[STIX]{x1D705}_{\Vert }^{2}k^{2}. & \displaystyle\end{eqnarray}$$
Therefore, we conclude that the Shalchi (Reference Shalchi2017) model agrees with the exact calculations presented in the current paper up to second order in
$k$
.
As pointed out in Shalchi (Reference Shalchi2010) one needs to know correlations involving particle positions and velocities in order to formulate advanced nonlinear theories for perpendicular diffusion. In the following we consider the time derivative of the characteristic function
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\langle \text{e}^{\text{i}kz}\rangle =\mathop{\sum }_{n=0}^{\infty }\frac{1}{n!}(\text{i}k)^{n}\frac{\text{d}}{\text{d}t}\langle z^{n}\rangle , & \displaystyle\end{eqnarray}$$
where we have used again expansion (4.1). For the time derivative of the moment
$\langle z^{n}\rangle$
we can employ
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{d}}{\text{d}t}\langle z^{n}\rangle =nv\langle z^{n-1}\unicode[STIX]{x1D707}\rangle =\langle nz^{n-1}v_{z}\rangle =\left\langle \frac{\text{d}}{\text{d}t}z^{n}\right\rangle . & \displaystyle\end{eqnarray}$$
The latter formula is derived from (3.3) by setting
$m=0$
therein. Furthermore, we have used again
$v_{z}=v\unicode[STIX]{x1D707}$
. With relation (4.17), equation (4.16) becomes
$$\begin{eqnarray}\displaystyle \frac{\text{d}}{\text{d}t}\langle \text{e}^{\text{i}kz}\rangle & = & \displaystyle \mathop{\sum }_{n=0}^{\infty }\frac{1}{n!}(\text{i}k)^{n}\langle nz^{n-1}v_{z}\rangle \nonumber\\ \displaystyle & = & \displaystyle \text{i}k\mathop{\sum }_{n=1}^{\infty }\frac{1}{(n-1)!}(\text{i}k)^{n-1}\langle z^{n-1}v_{z}\rangle \nonumber\\ \displaystyle & = & \displaystyle \text{i}k\langle v_{z}\text{e}^{\text{i}kz}\rangle .\end{eqnarray}$$
This relation was used in Shalchi (Reference Shalchi2017) in order to derive a time-dependent theory for perpendicular diffusion. In the current paper we confirmed its validity.
5 Summary and conclusion
To solve the pitch-angle-dependent Fokker–Planck equation of energetic particle transport is a difficult task. However, for several applications a pitch-angle and position-dependent particle distribution function is desired. In some cases one is only interested in the late time limit for which a diffusion approximation can be used (see, e.g. Schlickeiser Reference Schlickeiser2002; Shalchi Reference Shalchi2009; Zank Reference Zank2014). In other cases, however, one needs a description of the transport which is valid for early (non-diffusive) times as well.
In the current paper we have derived exact analytical formulas for the first 14 moments of the form
$\langle z^{n}\unicode[STIX]{x1D707}^{m}\rangle$
. The presented results were obtained for an isotropic pitch-angle scattering coefficient but for an arbitrary initial pitch-angle cosine
$\unicode[STIX]{x1D707}_{0}$
. Previous formulas derived for the moments (see, e.g. Shalchi Reference Shalchi2006; Malkov Reference Malkov2017) can be obtained by considering the initial pitch-angle cosine average of the formulas derived in the present article.
To find moments which depend on the parameter
$\unicode[STIX]{x1D707}_{0}$
is important for applications such as the formulation of nonlinear theories for perpendicular transport (see, e.g. Shalchi Reference Shalchi2010, Reference Shalchi2017). In the current paper we, therefore, considered characteristic functions as an example and have tested different ad hoc assumptions used previously in nonlinear diffusion theories. Further applications of the moments calculated in the present article will be considered in the future.
Acknowledgements
A.S. acknowledges support by the Natural Sciences and Engineering Research Council (NSERC) of Canada.
