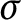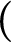1 Introduction
All spaces under consideration are separable and metrizable.
A subset A of a topological space X is called a C-set in X if A can be written as an intersection of clopen subsets of X. A
$\sigma $
C-set is a countable union of C-sets. A space X is said to be almost zero-dimensional provided every point
$x\in X$
has a neighborhood basis consisting of C-sets in X.
A space X is cohesive if every point
$x\in X$
has a neighborhood that contains no non-empty clopen subset of X. Clearly, every cohesive space is nowhere zero-dimensional. The converse is false, even for almost zero-dimensional spaces [Reference Dijkstra10]. Spaces that are both almost zero-dimensional and cohesive include:
$$ \begin{align*}\textit{Erd\H{o}s space }& &&\mathfrak E=\big\{x\in \ell^2:x_i\in\mathbb Q\text{ for each }i<\omega\big\}&\text{and}\\\begin{aligned}\textit{complete Erd\H{o}s space }\\ {\phantom{\big\{}}\end{aligned} & && \begin{aligned} \mathfrak E_{\mathrm c}=\big\{x\in \ell^2:x_i & \in \{0\}\cup \{1/n:n=1,2,3,\ldots\}\\ &\text{ for each }i<\omega\big\}, \end{aligned} \end{align*} $$
where
$\ell ^{2}$
stands for the Hilbert space of square summable sequences of real numbers. Other examples include the homeomorphism groups of the Sierpiński carpet and Menger universal curve [Reference Dijkstra8, Reference Oversteegen and Tymchatyn33], and various endpoint sets in complex dynamics [Reference Alhabib and Rempe-Gillen2, Reference Lipham31].
Almost zero-dimensionality of
$\mathfrak E$
and
$\mathfrak E_{\mathrm c}$
follows from the fact that each closed
$\varepsilon $
-ball in either space is closed in the zero-dimensional topology inherited from
$\mathbb Q^\omega $
, which is weaker than the
$\ell ^{2}$
-norm topology. The spaces are cohesive, because all non-empty clopen subsets of
$\mathfrak E$
and
$\mathfrak E_{\mathrm c}$
are unbounded in the
$\ell ^{2}$
-norm as proved by Erdős [Reference Erdős18]. Thus, if we add a point
$\infty $
to
$\ell ^{2}$
whose neighborhoods are the complements of bounded sets, then we have that
$\mathfrak E\cup \{\infty \}$
and
$\mathfrak E_{\mathrm c}\cup \{\infty \}$
are connected. The following result is Proposition 5.4 in Dijkstra and van Mill [Reference Dijkstra and van Mill12].
Proposition 1.1 Every almost zero-dimensional cohesive space has a one-point connectification. If a space has a one-point connectification, then it is cohesive.
Actually, open subsets of non-singleton connected spaces are cohesive, because cohesion is open hereditary [Reference Dijkstra and van Mill12, Remark 5.2]. More information on cohesion and one-point connectifications can be found in [Reference Abry, Dijkstra and van Mill1].
In Section 3, we will show that every cohesive almost zero-dimensional space E is homeomorphic to a dense subset
${E'}\subset \mathfrak E_{\mathrm c}$
such that
$E{'}\cup \{\infty \}$
is connected. The result is largely a consequence of earlier work by Dijkstra and van Mill [Reference Dijkstra and van Mill12, Chapters 4 and 5]. We apply the embedding to show that every cohesive almost zero-dimensional subspace of (Cantor set)
$\!\!\times \mathbb R$
is nowhere dense, and there is a continuous one-to-one image of complete Erdős space that is totally disconnected but not almost zero-dimensional.
In Section 4, we examine C-sets and the rim-type of almost zero-dimensional spaces. We say that X is rational at
$x\in X$
if x has a neighborhood basis of open sets with countable boundaries. In [Reference Nishiura and Tymchatyn32, §6, Example, p. 596], Nishiura and Tymchatyn implicitly proved that
$D^{\mathrm e}$
, the set of endpoints of Lelek’s fan [Reference Lelek27, §9], is not rational at any of its points. Results in [Reference Bula and Oversteegen5, Reference Charatonik6, Reference Kawamura, Oversteegen and Tymchatyn23] later established that
$D^{\mathrm e}\simeq \mathfrak E_{\mathrm c}$
, so
$\mathfrak E_{\mathrm c}$
is nowhere rational. Working in
$\ell ^{2}$
, Banakh [Reference Banakh3] recently demonstrated that each bounded open subset of
$\mathfrak E$
has an uncountable boundary. We generalize these results by proving that each cohesive almost zero-dimensional space is nowhere rational. Moreover, every rim-
$\sigma $
-compact almost zero-dimensional space is zero-dimensional. We also find that in almost zero-dimensional spaces cohesion is preserved if we delete
$\sigma $
-compacta. These results follow from Theorem 4.4, which states that closed
$\sigma $
C-sets in almost zero-dimensional spaces are C-sets.
In Section 5, we will construct a rim-discrete connected space
$\tau $
with an explosion point. The example is partially based on [Reference Lipham30, Example 1], which was constructed by the second author to answer a question from the Houston Problem Book [Reference Cook, Ingram and Lelek7]. The pulverized complement of the explosion point will be a rim-discrete totally disconnected set that is not zero-dimensional, in contrast with Section 4 results. Additionally, the rim-discrete property guarantees the entire connected set has a rational compactification [Reference Iliadis19, Reference Iliadis and Tymchatyn20, Reference Tymchatyn35]. We therefore solve [Reference Cook, Ingram and Lelek7, Problem 79] in the context of explosion point spaces. Results from Section 4 indicate that this new solution is optimal.
In general, ZD
$\!\!\!\implies $
AZD
$\!\!\!\implies $
TD
$\!\!\!\implies $
HD, where we used abbreviations for zero-dimensional, almost zero-dimensional, totally disconnected, and hereditarily disconnected. In certain contexts, these implications can be reversed. For example,
$$ \begin{align*} \mathrm{HD}\stackrel{(1)\;}{\implies}\mathrm{TD}\stackrel{(2)\;}{\implies}\mathrm{AZD}\stackrel{(3)\;}{\implies}\mathrm{ZD} \end{align*} $$
for subsets of hereditarily locally connected continua [Reference Kuratowski24, §50 IV Theorem 9]. As mentioned above, the implication (3) is valid in the larger class of subsets of rational continua. But [Reference Lipham30, Example 1] and the example
$\tau $
in Section 5 show that (1) and (2) are generally false in that context.
2 Preliminaries
A space X is hereditarily disconnected if every connected subset of X contains at most one point. A space X is totally disconnected if every singleton in X is a C-set. A point x in a connected space X is:
-
• a dispersion point if
$X\backslash \{x\}$
is hereditarily disconnected; -
• an explosion point if
$X\backslash \{x\}$
is totally disconnected.
If P is a topological property, then a space X is rim-P provided X has a basis of open sets whose boundaries have the property P: Rational
$\equiv $
rim-countable. Zero-dimensional
$\equiv $
rim-empty.
For A a subset of a space
$X,$
we let
$A^{\mathrm {o}}$
,
$\overline A$
, and
$\partial A$
denote the interior, the closure, and the boundary of A in X, respectively.
Throughout the paper,
$\mathfrak C$
will denote the middle-third Cantor set in
$[0,1]$
. The coordinate projections in
$\mathbb R ^{2}$
are denoted
$\pi _{0}$
and
$\pi _{1}$
;
$\pi _{0}(\langle x,y\rangle )=x$
and
$\pi _{1}(\langle x,y\rangle )=y$
. We define
$ \nabla :[0,1]^{2}\to [0,1]^{2}$
by
$\langle x,y\textstyle \rangle \mapsto \langle xy+\frac {1}{2}(1-y),y\rangle .$
The image of
$\nabla $
is the region enclosed by the triangle with vertices
$\langle 0,1\rangle $
,
$\langle \frac {1}{2},0\rangle $
, and
$\langle 1,1\rangle $
. Note that
$\nabla \restriction [0,1]\times (0,1]$
is a homeomorphism and
$\textstyle \nabla ^{-1}(\langle \frac {1}{2},0\rangle )=[0,1]\times \{0\}.$
For each
$X\subset \mathfrak C\times (0,1]$
we put
$$ \begin{align*} \underset{.}{\nabla}X= \nabla(X)\cup \bigg\{ \big\langle\frac{1}{2},0\big\rangle \bigg\}. \end{align*} $$
The Cantor fan is the set
$\nabla (\mathfrak C\times [0,1])= \underset{.}{\nabla}(\mathfrak C\times (0,1])$
, see Figure 1.
Given
$X\subset \mathfrak C$
, a function
$\varphi :X\to [0,1]$
is upper semi-continuous (abbreviated USC) if
$\varphi ^{-1}[0,t)$
is open in X for every
$t\in [0,1]$
. Define
$$ \begin{align*} G^\varphi_{0}&=\{\langle x,\varphi(x)\rangle:\varphi(x)>0\},\\ L^\varphi_{0}&=\{\langle x,t\rangle:0\leq t\leq \varphi(x)\}. \end{align*} $$
We say
$\varphi $
is a Lelek function if
$\varphi $
is USC and
$G^\varphi _{0}$
is dense in
$L^{\varphi }_{0}$
. Lelek functions with domain
$\mathfrak C$
exist, and if
$\varphi $
is a Lelek function with domain
$\mathfrak C,$
then
$\nabla L^\varphi _{0}$
is a Lelek fan; see Figure 2. For example, let
$\|\;\;\|$
be the
$\ell ^{2}$
-norm and identify
$\mathfrak C$
with the Cantor set
$(\{0\}\cup \{1/n:n=1,2,3,\ldots \})^\omega $
. Define
$\eta (x)=1/(1+\|x\|)$
, where
$1/\infty =0$
. Then
$\mathfrak E_{\mathrm c}$
is homeomorphic to
$G^\eta _{0}$
,
$\eta :\mathfrak C\to [0,1]$
is a Lelek function, and
$\nabla L^\eta _{0}$
is a Lelek fan; see [Reference Roberts34] and the proof of [Reference Dijkstra9, Theorem 3].
Figure 1 Cantor fan.
Figure 2 Lelek fan.
3 Embedding into Fans and Complete Erdős Space
Let E be any non-empty cohesive almost zero-dimensional space. Dijkstra and van Mill proved the following: There is a Lelek function
$\chi :X\to [0,1)$
such that E is homeomorphic to
$G^\chi _{0}$
, and hence E admits a dense embedding in
$\mathfrak E_{\mathrm c}$
[Reference Dijkstra and van Mill12, Proposition 5.10]. We observe the following theorem.
Theorem 3.1 For the Lelek function
$\chi $
constructed in [Reference Dijkstra and van Mill12],
$\underset{.}{\nabla} G^\chi _{0}$
is connected. Thus, there is a dense homeomorphic embedding
$\alpha :E\hookrightarrow \mathfrak E_{\mathrm c}$
such that
$\alpha (E)\cup \{\infty \}$
is connected.
Proof In [Reference Dijkstra and van Mill12],
$\chi $
is constructed via two USC functions,
$\varphi $
and
$\psi ,$
which have the same zero-dimensional domain X. First,
$\varphi $
is given by [Reference Dijkstra and van Mill12, Lemma 4.11] such that E is homeomorphic to
$G^\varphi _{0}$
. And then, in the proof of [Reference Dijkstra and van Mill12, Lemma 5.8],
$\psi $
is defined by
$\psi (x)=\lim _{\varepsilon \to 0^+}\inf J_\varepsilon (x)$
, where
$$ \begin{align*} U_\varepsilon(x)&=\{y\in X:d(x,y)<\varepsilon),\\ J_\varepsilon(x)&=\big\{t\in [0,1):U_\varepsilon(x)\times (t,1)\cap G^\varphi_{0}\\&\qquad\text{ contains no non-empty clopen subset of }G^\varphi_{0}\big\}. \end{align*} $$
Notice that
$J_\varepsilon (x)$
becomes larger as
$\varepsilon $
decreases, so its infimum decreases. Thus,
$\psi (x)$
is well defined. Finally,
$\chi $
is defined so that
$\langle x,\varphi (x)\rangle \mapsto \langle x,\chi (x)\rangle $
is a homeomorphism and
$\chi \leq \varphi -\psi $
[Reference Dijkstra and van Mill12, Lemma 4.9].
To prove that
$ \underset{.}{\nabla} G^\chi _{0}$
is connected, we let A be any non-empty clopen subset of
$G^\chi _{0}$
and show that
$0\in \overline {\pi _{1}(A)}$
. Define
$y=\inf \{\varphi (x): x\in \pi _{0}(A)\}$
and let
$\varepsilon>0$
. Pick an
$x\in \pi _{0}(A)$
with
$\varphi (x)<y+\varepsilon $
. Since
$\{\langle x,\varphi (x)\rangle :x\in \pi _{0}(A)\}$
is a clopen subset of
$G^\varphi _{0}$
and X is zero-dimensional,
$\psi (x)\geq y$
. We have
$\langle x,\chi (x)\rangle \in A$
and
$$ \begin{align*} \pi_{1}(\langle x,\chi(x)\rangle)=\chi(x)\leq \varphi(x)-\psi(x)<(y+\varepsilon)-y=\varepsilon. \end{align*} $$
Since
$\varepsilon $
was an arbitrary positive number, this shows that
$0\in \overline {\pi _{1}(A)}$
.
We will now construct
$\alpha $
. Since
$\chi $
is Lelek, X is perfect, so we can assume X is dense in
$\mathfrak C$
. Now
$\chi $
extends to a Lelek function
$ \overline {\chi }:\mathfrak C\to [0,1]$
such that
$G^\chi _{0}$
is dense in
$G^{\overline {\chi }}_{0}$
[Reference Dijkstra and van Mill12, Lemma 4.8]. In particular,
$\nabla L^{\overline {\chi }}_{0}$
is a Lelek fan. By [Reference Bula and Oversteegen5, Reference Charatonik6], the Lelek fan is unique, so there is a homeomorphism
$\Xi :\nabla L^{\overline {\chi }}_{0}\to \nabla L^\eta _{0}$
(recall
$\eta $
from Section 2). We observe that
$\Xi (\textstyle \underset{.}{\nabla}G^{\overline {\chi }}_{0})=\textstyle \underset{.}{\nabla}G^\eta _{0}\simeq \mathfrak E_{\mathrm c}\cup \{\infty \}$
. So there is a homeomorphism
$\gamma :\textstyle \underset{.}{\nabla}G^{\overline {\chi }}_{0}\to \mathfrak E_{\mathrm c}\cup \{\infty \}$
. We know there is also a homeomorphism
$\beta :E\to \textstyle \boldsymbol {\nabla }G^\chi _{0}$
. Let
$\alpha =\gamma \circ \beta $
, and notice that
$\alpha (E)\cup \{\infty \}=\gamma (\textstyle \underset{.}{\nabla}G^{{\chi }}_{0})$
is connected.▪
Corollary 3.2 If Y is a complete space containing E, then there is a complete cohesive almost zero-dimensional space
${E'}$
such that
$E\subset {E'}\subset Y$
.
Proof Let
$\alpha :E\hookrightarrow \mathfrak E_{\mathrm c}$
be given by Theorem 3.1. Since Y and
$\mathfrak E_{\mathrm c}$
are both complete, Lavrentiev’s Theorem [Reference Engelking17, Theorem 4.3.21] says
$\alpha $
extends to a homeomorphism between
$G_\delta $
-sets
${E'}$
and A such that
$E\subset {E'}\subset Y$
and
$\alpha (E)\subset A\subset \mathfrak E_{\mathrm c}$
. Since
$\alpha (E)$
is dense in
$\mathfrak E_{\mathrm c}$
and
$\alpha (E)\cup \{\infty \}$
is connected,
$A\cup \{\infty \}$
is connected. So
${E'}$
is cohesive.▪
Theorem 3.3 Every cohesive almost zero-dimensional subset of
$\mathfrak C\times \mathbb R$
is nowhere dense.
Proof Cohesion is open-hereditary [Reference Dijkstra and van Mill12, Remark 5.2]. By self-similarity of
$\mathfrak C\times \mathbb R$
, it therefore suffices to show there is no dense cohesive almost zero-dimensional subspace of
$\mathfrak C\times \mathbb R$
. Suppose on the contrary that E is such a space. By Corollary 3.2, there is a complete cohesive almost zero-dimensional
$X\subset \mathfrak C\times \mathbb R$
such that
$E\subset X$
. Then X is a dense
$G_\delta $
-subset of
$\mathfrak C\times \mathbb R$
, so by [Reference Brouwer4, Reference Kuratowski and Ulam25], there exists
$c\in \mathfrak C$
such that
$\overline {X\cap (\{c\}\times \mathbb R)}=\{c\}\times \mathbb R$
. Let
$x=\langle c,r\rangle \in X$
. We obtain a contradiction by showing that X is zero-dimensional at x. Let
$V\times (a,b)$
be any regular open subset of
$\mathfrak C\times \mathbb R$
that contains x. There exist an
$r_{1}\in (a,r)$
and an
$r_{2}\in (r,b)$
such that
$x_{1}=\langle c,r_{1}\rangle $
and
$x_{2}= \langle c,r_{2}\rangle $
are in
$ X$
. Since X is totally disconnected, there are X-clopen sets
$W_{1}$
and
$W_{2}$
such that
$x_{1}\in W_{1}$
,
$x_{2}\in W_{2}$
, and
$x\notin W_{1}\cup W_{2}$
. Let
$U_{1},U_{2}\subset V$
be
$\mathfrak C$
-clopen sets such that
$x_{i}\in (U_{i}\times \{r_{i}\})\cap X\subset W_{i}$
for each
$i\in \{1,2\}$
. Then
$[(U_{1}\cap U_{2})\times [r_{1},r_{2}]\backslash (W_{1}\cup W_{2})]\cap X$
is an X-clopen subset of
$V\times (a,b),$
which contains x. This shows that X is zero-dimensional at x. ▪
Theorem 3.3 shows that a certain continuous one-to-one image of
$\mathfrak E_{\mathrm c}$
is totally disconnected but not almost zero-dimensional. Define
$$ \begin{align*} f:\mathfrak E_{\mathrm c}\longrightarrow \big(\{0\}\cup \{1/n:n=1,2,3,\ldots\}\big)^\omega\times [0,1] \end{align*} $$
by
$\textstyle f(x)=\big \langle x,\frac {1+\sin \|x\|}{2}\big \rangle .$
Let
$Y=f(\mathfrak E_{\mathrm c})$
. Clearly, f is one-to-one and continuous, and Y is totally disconnected. The example Y is essentially the same as [Reference Lipham29, Example
${X}_2$
], and therefore, by [Reference Lipham29, Propositions 3 and 5], Y is dense in
$\mathfrak C\times [0,1]$
and
$\nabla Y$
is connected. Thus, Y is cohesive. By Theorem 3.3, Y is not almost zero-dimensional. Both this example and the space
$\tau $
constructed in Section 5 show that Theorem 3.3 does not extend to totally disconnected spaces.
4
$\sigma $
C-sets and Rim-type
Remark 4.1 If
$x\in A^{\mathrm {o}}\subset X$
with
$\partial A$
a C-set in
$X,$
then there is a clopen set C with
$x\in C$
and
$C\cap \partial A=\varnothing ,$
and hence
$C\cap A^{\mathrm {o}}=C\cap \overline A$
is also clopen. Consequently, rim-C is equivalent to zero-dimensional.
Lemma 4.2 For every two disjoint C-sets in a space, there is a clopen set containing one and missing the other.
Proof This is identical to the proof of [Reference Engelking16, Lemma 1.2.6]. ▪
Theorem 4.3 Let A be a subset of an almost zero-dimensional space X. If there is a
$\sigma $
C-set B with
$\partial A\subset B\subset \overline A$
, then
$\overline A$
is a C-set.
Proof Suppose
$B=\bigcup \{B_{i}:i<\omega \}$
where each
$B_{i}$
is a C-set, and
$\partial A\subset B\subset \overline A$
. To prove
$\overline A$
is a C-set, it suffices to show that for every
$x\in X\backslash \overline A,$
there is an X-clopen set C such that
$x\in C\subset X\backslash \overline A$
.
Let
$x\in X\backslash \overline A$
. By the Lindelöf property and almost zero-dimensionality, it is possible to write the open set
$X\backslash \overline A$
as the union of countably many C-sets in X whose interiors cover
$X\backslash \overline A$
. The property of being a C-set is closed under finite unions, so there is an increasing sequence of C-sets
$D_{0}\subset D_{1}\subset \ldots $
with
$x\in D_{0}$
and
$$ \begin{align*} \textstyle\bigcup \{D_{i}:i<\omega\}= \bigcup \{ D_{i} ^{\mathrm{o}}:i<\omega\}=X\backslash \overline A. \end{align*} $$
By Lemma 4.2, for each
$i<\omega $
there is an X-clopen set
$C_{i}$
such that
$D_{i}\subset C_{i}\subset X\backslash B_{i}.$
Let
$\textstyle C=\bigcap \{C_{i}:i<\omega \}\backslash A^{\mathrm {o}}$
. Clearly, C is closed,
$x\in C$
, and
$$ \begin{align*} C\subset X\backslash (A^{\mathrm{o}}\cup B) = X\backslash \overline A. \end{align*} $$
Further, if
$y\in C,$
then there exists
$j<\omega $
such that
$y\in D_{j}^{\mathrm {o}}$
. The open set
$D_{j}^{\mathrm {o}}\cap \bigcap \{C_{i}:i<j\}$
witnesses that
$y\in C^{\mathrm {o}}$
. This shows C is open and thus clopen.▪
Theorem 4.4 In an almost zero-dimensional space, every closed
$\sigma $
C-set is a C-set.
Proof Given a closed
$\sigma $
C-set A, apply Theorem 4.3 with
$B=A$
. ▪
With Remark 4.1 we get the following corollary.
Corollary 4.5 Every rim-
$\sigma $
C almost zero-dimensional space is zero-dimensional.
Since compacta are C-sets in totally disconnected spaces, we also have the following corollary.
Corollary 4.6 Every almost zero-dimensional space that is rim-
$\sigma $
-compact or rational is zero-dimensional.
A space is called nowhere rim-
$\sigma $
C (nowhere rim-
$\sigma $
-compact, resp., nowhere rational) if no point has a neighborhood basis consisting of sets that have boundaries that are
$\sigma $
C-sets (
$\sigma $
-compact, resp., countable). With Theorem 4.4 and Remark 4.1, we also find the following corollary.
Corollary 4.7 Cohesive almost zero-dimensional spaces are nowhere rim-
$\sigma $
C and hence nowhere rim-
$\sigma $
-compact and nowhere rational.
Thus, there are no rim-
$\sigma $
-compact or rational connected spaces Y with a point p such that
$Y\backslash \{p\}$
is almost zero-dimensional, using Proposition 1.1.
Theorem 4.8 If X almost zero-dimensional,
$Y=X\cup \{p\}$
is connected, and
$K\subset X$
is
$\sigma $
-compact, then
$Y\backslash K$
is connected.
Proof Suppose X is almost zero-dimensional, Y is connected, and
$K\subset X$
is
$\sigma $
-compact. Striving for a contradiction, suppose
$Y\backslash K$
is not connected. Then
$Y\backslash K$
is the union of two non-empty relatively closed subsets A and B such that
$A\cap B=\varnothing $
. We can assume that
$p\in B$
. The closures of A and B in the open set
$Y\backslash (\overline A\cap \overline B)$
are disjoint, so they are contained in disjoint Y-open sets U and V. Note that
$\partial U$
in Y is contained in K and is, therefore,
$\sigma $
-compact and hence a
$\sigma $
C-set in the totally disconnected space X. By Theorem 4.4,
$\partial A$
is a C-set in X. So by Remark 4.1, U contains a nonempty clopen subset C of X. Note that X is open in Y and U is contained in the Y-closed set
$Y\backslash B,$
so C is also clopen in Y. This violates the assumption that Y is connected.▪
Since
$\mathfrak E\cup \{\infty \}$
and
$\mathfrak E_{\mathrm c}\cup \{\infty \}$
are connected we have the following corollary.
Corollary 4.9 Bounded neighborhoods in
$\mathfrak E$
and
$\mathfrak E_{\mathrm c}$
do not have
$\sigma $
-compact boundaries.
Combining Theorem 4.8 with Proposition 1.1 we find the following theorem.
Theorem 4.10 If X is cohesive and almost zero-dimensional and
$K\subset X$
is
$\sigma $
-compact, then
$X\backslash K$
is cohesive.
For the spaces
$\mathfrak E$
,
$\mathfrak E_{\mathrm c}$
, and
$\mathfrak E_{\mathrm c} ^\omega $
there is a stronger result: in these spaces
$\sigma $
-compacta are negligible; see [Reference Dijkstra11, Reference Dijkstra and van Mill13, Reference Kawamura, Oversteegen and Tymchatyn23].
A connected space X is
$\sigma $
-connected if X cannot be written as the union of
$\omega $
-many pairwise disjoint non-empty closed subsets. Note that the Sierpiński Theorem [Reference Engelking17, Theorem 6.1.27] states that every continuum is
$\sigma $
-connected. Lelek [Reference Lelek26, P4] asked whether every connected space with a dispersion point is
$\sigma $
-connected. Duda [Reference Duda15, Example 5] answered this question in the negative.
Theorem 4.11 If a space X contains an open almost zero-dimensional subspace O with
$O\not =\varnothing $
and
$X\backslash O\not =\varnothing ,$
then X is not
$\sigma $
-connected.
Proof We can assume that X is connected. Since O is almost zero-dimensional and open, we can find for every
$x\in O,$
a C-set
$A_{x}$
in O that is closed in X and with
$x\in A_{x}^{\mathrm {o}}$
. Select a countable subcovering
$\{B_{i}:i<\omega \}$
of
$\{A_{x}:x\in O\}$
. Since the union of two C-sets is a C-set, we can arrange that
$B_{i}\subset B_{i+1}$
for each
$i<\omega $
. Also, we can assume that
$B_{0}=\varnothing $
. Since
$B_{i}$
is a C-set in
$O,$
we can find an O-clopen covering
$\mathcal{C}_{i}$
of
$O\backslash B_{i}$
. We can assume that
$\mathcal C_{i}=\{C_{ij}:j<\omega \}$
is countable. Moreover, by clopenness we can arrange that
$\mathcal C_{i}$
is a disjoint collection. Consider the countable closed disjoint covering
$$ \begin{align*} \mathcal F=\big(\{X\backslash O\}\cup \{C_{ij}\cap B_{i+1}:i,j<\omega\}\big)\backslash\{\varnothing\} \end{align*} $$
of X. If
$\mathcal F$
is finite, then O is closed and hence clopen, violating the connectedness of X. Thus, X is not
$\sigma $
-connected. ▪
Since every cohesive almost zero-dimensional space has a one-point connectification by Proposition 1.1 it produces an example in answer to Lelek’s question. These examples are explosion point spaces rather than just dispersion point spaces. In particular, we have that
$\mathfrak E\cup \{\infty \}$
and
$\mathfrak E_{\mathrm c}\cup \{\infty \}$
are counterexamples. Note that
$\mathfrak E_{\mathrm c}\cup \{\infty \}$
is complete, which is optimal, because
$\sigma $
-compact dispersion point spaces cannot exist.
5 A Rim-discrete Space with an Explosion Point
Let
$\mathfrak C$
,
$\nabla $
and
$ \underset{.}{\nabla}$
be as defined in Section 2. We will construct a function
$\tau :P \to (0,1)$
with domain
$P\subset \mathfrak C$
such that:
-
(1)
$\tau $
is a dense subset of
$\mathfrak C\times (0,1)$
; -
(2)
$ \underset{.}{\nabla}\tau $
is connected; -
(3)
$ \underset{.}{\nabla}\tau $
is rim-discrete.
Here, we identify a function like
$\tau $
with its graph in the product topology. Clearly,
$\tau $
will be totally disconnected. Note that
$\tau $
cannot be almost zero-dimensional by (2), (3), and Corollary 4.6 or (1), (2), and Theorem 3.3.
5.1 Construction of Z
We begin by constructing a rim-discrete connectible set
$Z\subset \mathfrak C\times \mathbb R$
similar to Y in [Reference Lipham30, Example 1].
Let E be the set of endpoints of connected components of
$\mathbb R \backslash \mathfrak C$
. For each
$\sigma \in 2^{<\omega }$
, let
$n=\operatorname {\mathrm {dom}}(\sigma )$
and define
$$ \begin{align*} B(\sigma)=\bigg[ \sum\limits_{k=0}^{n-1} \frac{2\sigma(k)}{3^{k+1}}, \sum\limits_{k=0}^{n-1} \frac{2\sigma(k)}{3^{k+1}}+\frac{1}{3^{n}}\bigg]\cap \mathfrak C. \end{align*} $$
Here,
$B(\varnothing )=[0,1]\cap \mathfrak C=\mathfrak C$
. The set of all
$B(\sigma )$
’s is the canonical clopen basis for
$\mathfrak C$
.
Suppose
$\sigma \in 2^{<\omega }$
, Q is a countable dense subset of
$ B(\sigma )\backslash E$
, and a and b are real numbers with
$a<b$
. Fix an enumeration
$\{q_{m}:m<\omega \}$
for Q, and define a function
$$ \begin{align*} f=f_{\langle Q,\sigma,a,b\rangle}:B(\sigma)\longrightarrow [a,b] \end{align*} $$
by the formula
$$ \begin{align*} \textstyle f(c)=a+(b-a)\cdot \sum\{2^{-m-1}:m<\omega\text{ and } q_{m}<c\}. \end{align*} $$
Note that:
-
■ f is well defined and non-decreasing;
-
■
$f\restriction B(\sigma )\backslash E$
is one-to-one; -
■ f has the same value at consecutive elements of E;
-
■ Q is the set of discontinuities of f; and
-
■ the discontinuity at
$q_{m}$
is caused by a jump of height
$(b-a)\cdot 2^{-m-1}$
.
Let
$$ \begin{align*} D=\textstyle D_{\langle Q,\sigma,a,b\rangle}=f\cup \bigcup \{\{q_{m}\}\times [f(q_{m}),f(q_{m})+(b-a)\cdot2^{-m-1}]:m<\omega\}. \end{align*} $$
Thus, D is equal to (the graph of) f together with vertical arcs corresponding to the jumps in f. Note that
$\pi _{1}(D)=[a,b]$
and D is compact.
Let
$\{Q^{n}_{i}:n,i<\omega \}$
be a collection of pairwise disjoint countable dense subsets of
$\mathfrak C\backslash E$
. As in [Reference Lipham30, Example 1], it is possible to recursively define a sequence
$\mathcal R_{0},\mathcal R_{1}, \ldots $
of finite partial tilings of
$\mathfrak C\times \mathbb R$
so that for each
$n<\omega $
:
-
(i)
$\mathcal R_{n}$
consists of rectangles
$R^{n}_{i}=B(\sigma ^{n}_{i})\times [a^{n}_{i},b^{n}_{i}]$
, where
$i<|\mathcal R_{n}|<\omega $
,
$\sigma ^{n}_{i}\in 2^{n}$
, and
$0<b^{n}_{i}-a^{n}_{i}\leq \frac {1}{n+1}$
for all
$i<|\mathcal R_{n}|$
; -
(ii) the sets
$$ \begin{align*} D^{n}_{i}=D_{\langle Q^{n}_{i}\cap B(\sigma^{n}_{i}),\sigma^{n}_{i},a^{n}_{i},b^{n}_{i}\rangle} \end{align*} $$
are such that
$D^{n}_{i}\cap D^{k}_{j}=\varnothing $
whenever
$k< n$
or
$i\neq j$
; -
(iii) for every arc
$I\subset \mathfrak C\times [-n,n+1]\backslash \bigcup \{D^{k}_{i}:k\leq n\text { and }i<|\mathcal R_{k}|\},$
there are integers
$i<|\mathcal R_{n}|$
,
$k\leq n$
, and
$j<|\mathcal R_{k}|$
such that
$I\subset R^{n}_{i}\cup R^{k}_{j}$
and
$d(I,D^{k}_{j})\leq \frac {1}{3^{n}}$
, where d is the standard metric on
$\mathbb R^{2}$
.
Let
$M^{n}_{i}$
be the (discrete) set of midpoints of the vertical arcs in
$D^{n}_{i}$
. The key difference between the sets
$M^{n}_{i}$
and the
$T^{n}_{i}(M)$
defined in [Reference Lipham30, Example 1] is that here we have guaranteed
$\pi _{0}(M^{n}_{i})\cap \pi _{0}(M^{k}_{j})\subset Q^{n}_{i}\cap Q^{k}_{j}=\varnothing $
whenever
$n\neq k$
or
$i\neq j$
, whereas a vertical line could intersect multiple
$T^{n}_{i}(M)$
’s.
Let
$\{D_{n}:n<\omega \}$
and
$\{M_{n}:n<\omega \}$
be the sets of all
$D^{n}_{i}$
’s and
$M^{n}_{i}$
’s, respectively. Properties (i) through (iii) guarantee the set
$Z=\mathfrak C\times \mathbb R \backslash \bigcup \{D_{n}\backslash M_{n}:n<\omega \}$
is rim-discrete; see [Reference Lipham30, Claims 1 and 3]. Essentially,
$\tau $
will be a subset of Z containing all
$M_{n}$
’s, but will be vertically compressed from
$\mathfrak C\times \mathbb R$
into
$\mathfrak C\times (0,1)$
.
5.2 Construction of
$\overline g$
We now construct a connected function
$\overline g$
(i.e., a function with a connected graph) on which
$\tau $
will be based.
Let
$\xi :\mathbb R \to (0,1)$
be a homeomorphism, e.g.
$\xi =\frac {1}{2}+ \frac {1}{\pi }\arctan $
. Let
$\phi :[0,1]\to [0,1]$
be the Cantor function [Reference Dovgoshey, Martio, Ryazanov and Vuorinen14], and put
$\textstyle \Phi =\phi \times \xi .$
Then each
$\Phi (D_{n})$
is an arc which resembles the graph of
$\phi $
reflected across the diagonal
$x=y$
. See Figure 3.
Figure 3 Graph of
$\phi $
(blue) and its “inverse” (red).
Note that
$\phi (E)$
is the set of dyadic rationals in
$[0,1]$
. Let
$$ \begin{align*} g=\textstyle(\phi(E)\times\{0\})\cup \bigcup\{\Phi(M_{n}):n<\omega\}. \end{align*} $$
Since
$\pi _{0}\restriction M_{n}$
is one-to-one and the
$\pi _{0}(M_{n})$
’s are pairwise disjoint, g is a function. Also,
$$ \begin{align*} \operatorname{\mathrm{dom}}(g)=\textstyle\phi(E)\cup \bigcup \{\pi_{0}(\Phi(M_{n})):n<\omega\} \end{align*} $$
is countable and
$\operatorname {\mathrm {ran}}(g)\subset [0,1)$
. Our goal is to extend g to a connected function
$\overline g:[0,1]\to (-1,1)$
. This will be accomplished with the help of two claims. By a continuum, we shall mean a compact connected metrizable space with more than one point.
Claim 5.1 Fix
$n<\omega $
and put
$D=D_{n}$
and
$M=M_{n}$
. Let
$A\subset [0,1]$
have a dense complement and let
$K\subset \Phi (D)\cup (A\times (-1,1))$
be a continuum. If
$|\pi _{0}(K)|>1,$
then
$K\cap \Phi (M)\neq \varnothing $
.
Proof Let a and b be two points in K such that
$\pi _{0}(a)<\pi _{0}(b)$
. Since
$\pi _{0}(K)$
is an interval contained in the union of the zero-dimensional set A and the interval
$\pi _{0}(D),$
we have
$\pi _{0}(K)\subset \pi _{0}(D)$
. Noting that
$\pi _{0}(M)$
is dense in
$\pi _{0}(D),$
we find a
$p\in \Phi (M)$
such that
$\pi _{0}(p)\in (\pi _{0}(a),\pi _{0}(b))$
. If
$p\notin K$
, then we can find
$c, d \in [0,1]\backslash A$
such that
$U=[c,d]\times \{\pi _{1}(p)\}$
is disjoint from K and
$\pi _{0}(a)<c<\pi _{0}(p)<d<\pi _{0}(b)$
. Then
$U\cup (\{c\}\times (\pi _{1}(p),1))\cup (\{d\}\times (-1,\pi _{1}(p))$
separates K with a and b on opposite sides. This contradicts our assumption that K is connected. Therefore,
$p\in K$
. ▪
Claim 5.2 Let
$A\subset [0,1]$
be any countable set, and let
$K\subset \bigcup \{\Phi (D_{n}):n<\omega \}\cup (A\times (-1,1))$
be a continuum. If
$|\pi _{0}(K)|>1,$
then
$K\cap \Phi (M_{n})\neq \varnothing $
for some
$n<\omega $
.
Proof For each
$x\in [0,1]$
, let
$K_{x}=K\cap (\{x\}\times (-1,1))$
. Let
$\mathcal K$
be the decomposition of K consisting of every connected component of every non-empty
$K_{x}$
. Applying [Reference Engelking17, Lemma 6.2.21] to the perfect map
$\pi _{0}\restriction K$
, we see that
$\mathcal K$
is upper semi-continuous. If
$q:K\to {K'}$
is the associated (closed) quotient mapping, then
${K'}$
is also a continuum. Consider the countable covering
$\mathcal V$
of
$ {K'}$
consisting of the compacta
$q(K_{x})$
for
$x\in A$
and
$q(\Phi (D_{n})\cap K)$
for all
$n<\omega $
. By the Baire Category Theorem, there is an element of
$\mathcal{V}$
that has nonempty interior in
$ {K'}$
and hence contains a (non-degenerate) continuum
$ {C'}$
by [Reference Engelking17, Theorem 6.1.25]. Each
$q(K_{x})$
is zero-dimensional by [Reference Engelking17, Theorem 6.2.24], so
$ {C'}\subset q(\Phi (D_{n})\cap K)$
for some
$n<\omega $
. Since q is a closed monotone map, the pre-image
$C=q^{-1}( {C'})$
is a continuum by [Reference Engelking17, Theorem 6.1.29]. Note that
$|\pi _{0}(C)|>1,$
because otherwise
${C'}$
would be a subset of some zero-dimensional
$q(K_{x})$
. If
$x\notin A,$
then each connected component of
$K_{x}$
is contained in a single
$\Phi (D_{i})$
by the Sierpiński Theorem [Reference Engelking17, Theorem 6.1.27], because the
$\Phi (D_{i})$
’s are disjoint. Thus,
$q(\Phi (D_{n})\cap K_{x})$
is disjoint from
$q(\Phi (D_{i})\cap K_{x})$
for each
$i\not =n$
. So
$C\subset (A\times (-1,1))\cup \Phi (D_{n})$
. By Claim 5.1, we have that
$C\cap \Phi (M_{n})\neq \varnothing $
. ▪
Now let
$\{x_\alpha :\alpha <\mathfrak c\}$
enumerate the set
$[0,1]\backslash \operatorname {\mathrm {dom}}(g)$
. Let
$\{K_\gamma :\gamma <\mathfrak c\}$
be the set of continua in
$[0,1]\times (-1,1)$
such that:
-
■
$K_\gamma $
is not contained in any vertical line; -
■
$K_\gamma \cap \Phi (M_{n})= \varnothing $
for all
$n<\omega $
.
For each
$\alpha <\mathfrak c,$
let
$l_{\alpha }=(\{x_\alpha \}\times (-1,1))\backslash \bigcup \{\Phi (D_{n}):n<\omega \}$
. By transfinite induction, we define for each
$\alpha <\mathfrak c$
an ordinal
$$ \begin{align*} \gamma(\alpha)=\min\{\gamma<\mathfrak c:l_\alpha\cap K_\gamma\neq\varnothing \text{ and } \gamma\neq \gamma(\beta)\text{ for any }\beta<\alpha\}. \end{align*} $$
We verify that the one-to one function
$\gamma :\mathfrak c\to \mathfrak c$
is well defined. Let
$\alpha <\mathfrak c,$
so
$x_\alpha \notin \operatorname {\mathrm {dom}}(g)$
and
$x_\alpha \notin \pi _{0}(\Phi (M_{n}))$
for each n. Since
$M_{n}$
contains the midpoints of all vertical intervals in
$D_{n},$
we have that
$\{x_\alpha \}\times (-1,1)$
contains at most one point of
$\Phi (D_{n})$
. Let A be the countable set
$$ \begin{align*} \bigcup\limits_{n<\omega}\pi_{1}(\{x_\alpha\}\times(-1,1))\cap\Phi(D_{n}))\cup\Phi(M_{n})). \end{align*} $$
If
$a\in (-1,1)\backslash A,$
then
$K=[0,1]\times \{a\}$
misses every
$\Phi (M_{n}),$
so
$K=K_\beta $
for some
$\beta <\mathfrak c$
. Also, we have
$l_\alpha \cap K_\beta \not =\varnothing $
. Since
$|(-1,1)\backslash A|=\mathfrak c,$
we have that
$\gamma $
is well defined.
For every
$\alpha <\mathfrak c,$
choose a
$y_\alpha \in \pi _{1}( l_\alpha \cap K_{\gamma (\alpha )})$
. Define
$$ \begin{align*} \overline g=g\cup \{\langle x_\alpha,y_\alpha\rangle:\alpha<\mathfrak c\} \end{align*} $$
and note that
$\overline g:[0,1]\to (-1,1)$
is a function. To prove that the graph of
$\overline g$
is connected, let K be a continuum in
$[0,1]\times (-1,1)$
such that
$|\pi _{0}(K)|>1$
. We show that
$K\cap \overline g\not =\varnothing $
. The set K intersects some
$\Phi (M_{n})$
, which is a subset of
$\overline g$
, or
$K=K_\alpha $
for some
$\alpha <\mathfrak c$
. By the contraposition of Claim 5.2, the projection
$A=\pi _{0}(K_\alpha \backslash \bigcup \{\Phi (D_{n}):n<\omega \})$
is uncountable. A is a continuous image of a Polish space, so, in fact, it has cardinality
$\mathfrak c$
by [Reference Jech21, Corollary 11.20]. Since
$[0,1]\backslash \{x_\beta :\beta <\mathfrak c\}= \operatorname {\mathrm {dom}}(g)$
is countable, this means
$B=\{\beta <\mathfrak c:l_\beta \cap K_\alpha \neq \varnothing \}$
has cardinality
$\mathfrak c$
. Assuming that
$K_\alpha \cap \overline g=\varnothing $
we find that
$\alpha $
cannot be in the range of
$\overline g$
. If
$\beta \in B,$
then
$l_\beta \cap K_\alpha \not =\varnothing ,$
so by the definition of
$\gamma ,$
we have
$\gamma (\beta )<\alpha $
. Thus,
$\gamma \restriction B$
is a one-to-one function from B into
$\{\delta :\delta <\alpha \},$
and we have the desired contradiction. So (the graph of)
$\overline g$
intersects each continuum in
$[0,1]\times (-1,1)$
not lying wholly in a vertical line. By [Reference Jones22, Theorem 2],
$\overline g$
is connected.
5.3 Definition and Properties of
$\tau $
Observe that
$\overline g\circ \phi \subset (\mathfrak C\times (-1,1))\cup ([0,1]\times \{0\})$
. Let
$$ \begin{align*} \textstyle\tau=(\overline g\circ \phi)\cap (0,1)^{2}. \end{align*} $$
The domain of
$\tau $
is the set
$P=\pi _{0}(\tau )\subset \mathfrak C$
.
Let
$X=\nabla (\overline g \cap ((0,1)\times [0,1)))$
. If A is any clopen subset of X with
$\langle \frac {1}{2},0\rangle \in A$
, then
$A=X$
. Otherwise,
$\nabla ^{-1}(X\backslash A)$
would be a non-empty proper clopen subset of
$\overline g$
, contrary to the fact that
$\overline g$
is connected. Therefore, X is connected. Note that
$\textstyle \underset{.}{\nabla}\tau \simeq X$
, so
$\textstyle \underset{.}{\nabla}\tau $
is also connected. Finally, let
$\textstyle \Xi = \operatorname {\mathrm {id}}_{\mathfrak C}\times \xi .$
By [Reference Lipham30, Claims 3 and 4] and the construction of Z,
$ \underset{.}{\nabla}\Xi (Z)$
is rim-discrete. We have
$ \underset{.}{\nabla}\tau \subset \underset{.}{\nabla}\Xi (Z)$
, so
$ \underset{.}{\nabla}\tau $
is rim-discrete.
5.4 Two Questions
A continuum is Suslinian if it contains no uncountable collection of pairwise disjoint (non-degenerate) subcontinua [Reference Lelek28]. The class of Suslinian continua is slightly larger than the class of rational continua.
Question 5.3 Can
$\mathfrak E_{\mathrm c}$
be embedded into a Suslinian continuum?
Question 5.4 Can
$\mathfrak E_{\mathrm c}$
be densely embedded into the plane
$\mathbb R ^{2}$
?
Added July 2020
E. D. Tymchatyn informed the authors that Question 5.3 has a positive answer. There is, in fact, a Suslinian dendroid that homeomorphically contains the set of endpoints of the Lelek fan. The example is due to Tymchatyn and P. Minc.
