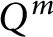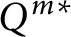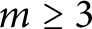1 Introduction
In this paper, we study real hypersurfaces of the complex quadric
![]() $Q^m$
and the complex hyperbolic quadric
$Q^m$
and the complex hyperbolic quadric
![]() $Q^{m*}$
for
$Q^{m*}$
for
![]() $m\ge 3$
. Due to their different background, we consider these two ambient spaces separately.
$m\ge 3$
. Due to their different background, we consider these two ambient spaces separately.
First, recall that the complex quadric of dimension m is defined by
![]() $Q^m:=\{[(z_0,z_1,\ldots ,z_{m+1})]\in \mathbb {C}P^{m+1}: z_0^2+z_1^2+\cdots +z_{m+1}^2=0\}$
, where
$Q^m:=\{[(z_0,z_1,\ldots ,z_{m+1})]\in \mathbb {C}P^{m+1}: z_0^2+z_1^2+\cdots +z_{m+1}^2=0\}$
, where
![]() $\mathbb {C}P^{m+1}$
is the
$\mathbb {C}P^{m+1}$
is the
![]() $(m+1)$
-dimensional complex projective space equipped with the Fubini–Study metric g of constant holomorphic sectional curvature
$(m+1)$
-dimensional complex projective space equipped with the Fubini–Study metric g of constant holomorphic sectional curvature
![]() $4$
, and
$4$
, and
![]() $z_0,\ldots ,z_{m+1}$
are the homogeneous coordinates on
$z_0,\ldots ,z_{m+1}$
are the homogeneous coordinates on
![]() $\mathbb {C}P^{m+1}$
. Being as a complex hypersurface of
$\mathbb {C}P^{m+1}$
. Being as a complex hypersurface of
![]() $\mathbb {C}P^{m+1}$
with the induced metric, denoted still by g,
$\mathbb {C}P^{m+1}$
with the induced metric, denoted still by g,
![]() $Q^m$
is a compact and Einstein Riemannian symmetric space (see Reckziegel [Reference Reckziegel22], Smyth [Reference Smyth23], and Berndt and Suh [Reference Berndt and Suh3]). Besides the Kähler structure J that is induced from that of
$Q^m$
is a compact and Einstein Riemannian symmetric space (see Reckziegel [Reference Reckziegel22], Smyth [Reference Smyth23], and Berndt and Suh [Reference Berndt and Suh3]). Besides the Kähler structure J that is induced from that of
![]() $\mathbb {C}P^{m+1}$
,
$\mathbb {C}P^{m+1}$
,
![]() $Q^m$
carries another important geometric structure A, being called the almost product structure in [Reference Li, Ma, Van der Veken, Vrancken and Wang16], and they are related by
$Q^m$
carries another important geometric structure A, being called the almost product structure in [Reference Li, Ma, Van der Veken, Vrancken and Wang16], and they are related by
![]() $AJ=-JA$
(see [Reference Berndt and Suh3, Reference Reckziegel22]). The complex quadric
$AJ=-JA$
(see [Reference Berndt and Suh3, Reference Reckziegel22]). The complex quadric
![]() $Q^m$
is an important Riemannian manifold, so the study of its submanifolds is significant, which has attracted many geometers. To see the results, among others, we refer to Smyth [Reference Smyth23], Reckziegel [Reference Reckziegel22], Berndt and Suh [Reference Berndt and Suh3], and the many literatures citing them, which could be looked up from MathSciNet.
$Q^m$
is an important Riemannian manifold, so the study of its submanifolds is significant, which has attracted many geometers. To see the results, among others, we refer to Smyth [Reference Smyth23], Reckziegel [Reference Reckziegel22], Berndt and Suh [Reference Berndt and Suh3], and the many literatures citing them, which could be looked up from MathSciNet.
Next, as the noncompact dual of
![]() $Q^m$
, the m-dimensional complex hyperbolic quadric
$Q^m$
, the m-dimensional complex hyperbolic quadric
![]() $Q^{m\ast }$
is a simply connected Riemannian symmetric space whose curvature tensor is the negative of that of
$Q^{m\ast }$
is a simply connected Riemannian symmetric space whose curvature tensor is the negative of that of
![]() $Q^m$
. It is known that
$Q^m$
. It is known that
![]() $Q^{m\ast }$
cannot be realized as a homogeneous complex hypersurface of the complex hyperbolic space
$Q^{m\ast }$
cannot be realized as a homogeneous complex hypersurface of the complex hyperbolic space
![]() $\mathbb {C}H^{m+1}$
(see [Reference Klein and Suh13, Reference Smyth23]), whereas Montiel and Romero [Reference Montiel and Romero19] proved that it can be isometrically immersed indeed into the indefinite complex hyperbolic space
$\mathbb {C}H^{m+1}$
(see [Reference Klein and Suh13, Reference Smyth23]), whereas Montiel and Romero [Reference Montiel and Romero19] proved that it can be isometrically immersed indeed into the indefinite complex hyperbolic space
![]() $\mathbb {C}H_1^{m+1}(-c)$
(
$\mathbb {C}H_1^{m+1}(-c)$
(
![]() $c>0$
) as a complex Einstein hypersurface. Accordingly, similar to the complex quadric
$c>0$
) as a complex Einstein hypersurface. Accordingly, similar to the complex quadric
![]() $Q^{m}$
, the complex hyperbolic quadric
$Q^{m}$
, the complex hyperbolic quadric
![]() $Q^{m\ast }$
also admits two important geometric structures, namely an almost product structure (also called real structure) and the Kähler structure, which are still denoted by A and J, and they also satisfy
$Q^{m\ast }$
also admits two important geometric structures, namely an almost product structure (also called real structure) and the Kähler structure, which are still denoted by A and J, and they also satisfy
![]() $AJ=-JA$
. These two structures satisfy the same properties of those two in
$AJ=-JA$
. These two structures satisfy the same properties of those two in
![]() $Q^m$
. For more details about the complex hyperbolic quadric
$Q^m$
. For more details about the complex hyperbolic quadric
![]() $Q^{m\ast }$
, we refer the readers to [Reference Klein and Suh13, Reference Montiel and Romero19, Reference Suh25, Reference Suh, Pérez and Woo27, Reference Van der Veken and Wijffels28].
$Q^{m\ast }$
, we refer the readers to [Reference Klein and Suh13, Reference Montiel and Romero19, Reference Suh25, Reference Suh, Pérez and Woo27, Reference Van der Veken and Wijffels28].
Now, we can state the main result of this paper as the following nonexistence theorem.
Theorem 1.1 There do not exist any locally conformally flat real hypersurfaces in both the complex quadric
![]() $Q^m$
and the complex hyperbolic quadric
$Q^m$
and the complex hyperbolic quadric
![]() $Q^{m*}$
with
$Q^{m*}$
with
![]() $m\ge 3$
.
$m\ge 3$
.
Recall that an n-dimensional Riemannian manifold
![]() $(M^n,g)$
is said to be locally conformally flat if it admits a coordinate covering
$(M^n,g)$
is said to be locally conformally flat if it admits a coordinate covering
![]() $\{(U_\alpha , x^i_\alpha );\,\alpha \in \Lambda \}$
such that
$\{(U_\alpha , x^i_\alpha );\,\alpha \in \Lambda \}$
such that
 $g(\frac {\partial \ }{\partial x^i_\alpha }, \frac {\partial \ }{\partial x^j_\alpha })= e^{f_\alpha }\delta _{ij}$
, for
$g(\frac {\partial \ }{\partial x^i_\alpha }, \frac {\partial \ }{\partial x^j_\alpha })= e^{f_\alpha }\delta _{ij}$
, for
![]() $1\le i,j\le n$
, and each
$1\le i,j\le n$
, and each
![]() $\alpha \in \Lambda $
, where
$\alpha \in \Lambda $
, where
![]() $f_\alpha $
is a smooth function defined on
$f_\alpha $
is a smooth function defined on
![]() $U_\alpha $
. For
$U_\alpha $
. For
![]() $n\ge 4$
, it is well known that
$n\ge 4$
, it is well known that
![]() $(M^n,g)$
is locally conformally flat if and only if the Weyl curvature tensor of
$(M^n,g)$
is locally conformally flat if and only if the Weyl curvature tensor of
![]() $(M^n,g)$
vanishes identically. The study of (locally) conformally flat manifolds is an important subject in Riemannian geometry, and particularly from the viewpoint of submanifold theory. Our motivation of proving Theorem 1.1 lies in the latter. Historically, there are many researches on the conformally flat hypersurfaces in Riemannian manifolds. When the ambient space is the space forms, such studies are given, e.g., in [Reference Cartan4, Reference do Carmo, Dajczer and Mercuri9, Reference Nishikawa and Maeda20, Reference Pinkall21] and many latter references citing them. When the ambient space is the complex space form
$(M^n,g)$
vanishes identically. The study of (locally) conformally flat manifolds is an important subject in Riemannian geometry, and particularly from the viewpoint of submanifold theory. Our motivation of proving Theorem 1.1 lies in the latter. Historically, there are many researches on the conformally flat hypersurfaces in Riemannian manifolds. When the ambient space is the space forms, such studies are given, e.g., in [Reference Cartan4, Reference do Carmo, Dajczer and Mercuri9, Reference Nishikawa and Maeda20, Reference Pinkall21] and many latter references citing them. When the ambient space is the complex space form
![]() $M^n(c)$
of constant holomorphic sectional curvature
$M^n(c)$
of constant holomorphic sectional curvature
![]() $c\not =0$
, based on a series studies of Kon [Reference Kon14], Cecil and Ryan [Reference Cecil and Ryan5], and Montiel [Reference Montiel18], Ki et al. [Reference Ki, Nakagawa and Suh11] proved that it admits no real hypersurfaces with harmonic Weyl tensor for
$c\not =0$
, based on a series studies of Kon [Reference Kon14], Cecil and Ryan [Reference Cecil and Ryan5], and Montiel [Reference Montiel18], Ki et al. [Reference Ki, Nakagawa and Suh11] proved that it admits no real hypersurfaces with harmonic Weyl tensor for
![]() $n\ge 3$
. It follows that there are no conformally flat real hypersurfaces in such a complex space form
$n\ge 3$
. It follows that there are no conformally flat real hypersurfaces in such a complex space form
![]() $M^n(c)$
.
$M^n(c)$
.
Related to Theorem 1.1, it is worth mentioning that there are many researches on the real hypersurfaces of the complex quadric
![]() $Q^m$
very recently. For instance, under additional conditions, Suh [Reference Suh24] studied real and Hopf hypersurfaces of
$Q^m$
very recently. For instance, under additional conditions, Suh [Reference Suh24] studied real and Hopf hypersurfaces of
![]() $Q^m$
with harmonic curvature, and also, under some special conditions, Suh [Reference Suh and Hwang26] investigated real and Hopf hypersurfaces of
$Q^m$
with harmonic curvature, and also, under some special conditions, Suh [Reference Suh and Hwang26] investigated real and Hopf hypersurfaces of
![]() $Q^m$
with commuting Ricci tensor. On the other hand, without the Hopf condition, Loo [Reference Loo17] studied the pseudo-Einstein hypersurfaces of
$Q^m$
with commuting Ricci tensor. On the other hand, without the Hopf condition, Loo [Reference Loo17] studied the pseudo-Einstein hypersurfaces of
![]() $Q^m$
and obtained meaningful results in some special cases.
$Q^m$
and obtained meaningful results in some special cases.
To prove Theorem 1.1, we note that for the complex quadric
![]() $Q^m$
and the complex hyperbolic quadric
$Q^m$
and the complex hyperbolic quadric
![]() $Q^{m*}$
, the curvature tensors are much more complicated than that of the complex space forms and the Gauss equations become very difficult to solve directly. This makes the problem of investigating conformally flat real hypersurfaces of
$Q^{m*}$
, the curvature tensors are much more complicated than that of the complex space forms and the Gauss equations become very difficult to solve directly. This makes the problem of investigating conformally flat real hypersurfaces of
![]() $Q^m$
and
$Q^m$
and
![]() $Q^{m*}$
quite different from that of the nonflat complex space forms. In order to get out of this difficulty, our proof of Theorem 1.1 makes use of a new approach, the so-called Tsinghua principle due to H. Li, L. Vrancken, and X. Wang (see a statement in Section 3 of [Reference Antić, Li, Vrancken and Wang1]). Roughly speaking, this remarkable principle helps us to use the Codazzi equation and the Ricci identity in a new way to obtain some nice linear equations involving the components of the second fundamental form. For readers’ better understanding, we will elaborate on the Tsinghua principle in Section 3.
$Q^{m*}$
quite different from that of the nonflat complex space forms. In order to get out of this difficulty, our proof of Theorem 1.1 makes use of a new approach, the so-called Tsinghua principle due to H. Li, L. Vrancken, and X. Wang (see a statement in Section 3 of [Reference Antić, Li, Vrancken and Wang1]). Roughly speaking, this remarkable principle helps us to use the Codazzi equation and the Ricci identity in a new way to obtain some nice linear equations involving the components of the second fundamental form. For readers’ better understanding, we will elaborate on the Tsinghua principle in Section 3.
Remark 1.1 The complex quadric
![]() $Q^2$
is isometric to the Riemannian product of two
$Q^2$
is isometric to the Riemannian product of two
![]() $2$
-spheres with constant curvature, whereas the complex hyperbolic quadric
$2$
-spheres with constant curvature, whereas the complex hyperbolic quadric
![]() $Q^{2*}$
is isometric to the Riemannian product of two hyperbolic plane
$Q^{2*}$
is isometric to the Riemannian product of two hyperbolic plane
![]() $H^2$
with constant negative curvature (cf. [Reference Berndt and Suh3, Reference Van der Veken and Wijffels28]). Therefore, contrary to cases
$H^2$
with constant negative curvature (cf. [Reference Berndt and Suh3, Reference Van der Veken and Wijffels28]). Therefore, contrary to cases
![]() $Q^m$
and
$Q^m$
and
![]() $Q^{m*}$
for
$Q^{m*}$
for
![]() $m\ge 3$
, in both
$m\ge 3$
, in both
![]() $Q^2$
and
$Q^2$
and
![]() $Q^{2*}$
, there do exist conformally flat hypersurfaces. Indeed, for any curve
$Q^{2*}$
, there do exist conformally flat hypersurfaces. Indeed, for any curve
![]() $\Gamma \hookrightarrow \mathbb {S}^2(1)$
(resp.
$\Gamma \hookrightarrow \mathbb {S}^2(1)$
(resp.
![]() $\tilde \Gamma \hookrightarrow H^2(-1)$
),
$\tilde \Gamma \hookrightarrow H^2(-1)$
),
![]() $\Gamma \times \mathbb {S}^2(1)$
(resp.
$\Gamma \times \mathbb {S}^2(1)$
(resp.
![]() $\tilde \Gamma \times H^2(-1)$
) is a conformally flat hypersurface of
$\tilde \Gamma \times H^2(-1)$
) is a conformally flat hypersurface of
![]() $\mathbb {S}^2(1)\times \mathbb {S}^2(1)$
(resp.
$\mathbb {S}^2(1)\times \mathbb {S}^2(1)$
(resp.
![]() $H^2(-1)\times H^2(-1)$
). On the other hand, to our knowledge, the problem of classifying conformally flat hypersurfaces in either
$H^2(-1)\times H^2(-1)$
). On the other hand, to our knowledge, the problem of classifying conformally flat hypersurfaces in either
![]() $Q^2$
or
$Q^2$
or
![]() $Q^{2*}$
is still open.
$Q^{2*}$
is still open.
This paper is organized as follows. In Section 2, we review some basic materials of the complex quadric
![]() $Q^m$
, and, particularly, we derive several fundamental equations for real hypersurfaces of
$Q^m$
, and, particularly, we derive several fundamental equations for real hypersurfaces of
![]() $Q^m$
. In Section 3, as crucial steps toward the proof of Theorem 1.1, we introduce the Tsinghua principle by proving two lemmas. In Section 4, we complete the proof of Theorem 1.1 for
$Q^m$
. In Section 3, as crucial steps toward the proof of Theorem 1.1, we introduce the Tsinghua principle by proving two lemmas. In Section 4, we complete the proof of Theorem 1.1 for
![]() $Q^m$
. Finally, in Section 5, thanks to the similarities between
$Q^m$
. Finally, in Section 5, thanks to the similarities between
![]() $Q^m$
and
$Q^m$
and
![]() $Q^{m*}$
, we give an outline proof of Theorem 1.1 for
$Q^{m*}$
, we give an outline proof of Theorem 1.1 for
![]() $Q^{m*}$
.
$Q^{m*}$
.
2 Preliminaries
In this section, we shall introduce the basic materials only about the complex quadric
![]() $Q^m$
and its real hypersurfaces. For those about the complex hyperbolic quadric
$Q^m$
and its real hypersurfaces. For those about the complex hyperbolic quadric
![]() $Q^{m*}$
that are completely similar, we refer to [Reference Klein and Suh13, Reference Suh25, Reference Suh, Pérez and Woo27, Reference Van der Veken and Wijffels28] for details.
$Q^{m*}$
that are completely similar, we refer to [Reference Klein and Suh13, Reference Suh25, Reference Suh, Pérez and Woo27, Reference Van der Veken and Wijffels28] for details.
2.1 The complex quadric
As described in the introduction section, the complex quadric
![]() $Q^m$
is equipped with a canonical Kähler structure, denoted by
$Q^m$
is equipped with a canonical Kähler structure, denoted by
![]() $\{J,g\}$
, induced from that of
$\{J,g\}$
, induced from that of
![]() $\mathbb {C}P^{m+1}$
. For the purpose of this paper, we shall assume
$\mathbb {C}P^{m+1}$
. For the purpose of this paper, we shall assume
![]() $m\ge 3$
in the sequel.
$m\ge 3$
in the sequel.
For a nonzero vector
![]() $z\in \mathbb {C}^{m+2}$
, we denote by
$z\in \mathbb {C}^{m+2}$
, we denote by
![]() $[z]$
the complex span of z, that is,
$[z]$
the complex span of z, that is,
![]() $[z]=\{\lambda z|\lambda \in \mathbb {C}^\ast \}$
. For
$[z]=\{\lambda z|\lambda \in \mathbb {C}^\ast \}$
. For
![]() $[z]\in Q^m$
, the tangent space
$[z]\in Q^m$
, the tangent space
![]() $T_{[z]}Q^m$
can be identified canonically with
$T_{[z]}Q^m$
can be identified canonically with
![]() $\mathbb {C}^{m+2}\ominus ([z]\oplus [\bar {z}])$
in
$\mathbb {C}^{m+2}\ominus ([z]\oplus [\bar {z}])$
in
![]() $\mathbb {C}^{m+2}$
. Note that
$\mathbb {C}^{m+2}$
. Note that
![]() $\zeta =-\bar {z}$
is a unit normal vector of
$\zeta =-\bar {z}$
is a unit normal vector of
![]() $Q^m$
in
$Q^m$
in
![]() $\mathbb {C}P^{m+1}$
at the point
$\mathbb {C}P^{m+1}$
at the point
![]() $[z]$
, and the shape operator
$[z]$
, and the shape operator
![]() $A_{\zeta }$
of
$A_{\zeta }$
of
![]() $Q^m$
in
$Q^m$
in
![]() $\mathbb {C}P^{m+1}$
with respect to
$\mathbb {C}P^{m+1}$
with respect to
![]() $\zeta $
is given by
$\zeta $
is given by
![]() $A_{\zeta }w=\bar {w}$
for all
$A_{\zeta }w=\bar {w}$
for all
![]() $w\in T_{[z]}Q^m$
. Thus, restricted to
$w\in T_{[z]}Q^m$
. Thus, restricted to
![]() $T_{[z]}Q^m$
,
$T_{[z]}Q^m$
,
![]() $A_{\zeta }$
is the complex conjugation. Moreover, acting on the complex vector space
$A_{\zeta }$
is the complex conjugation. Moreover, acting on the complex vector space
![]() $T_{[z]}Q^m$
, the shape operator
$T_{[z]}Q^m$
, the shape operator
![]() $A_{\zeta }$
is an anticommuting involution such that
$A_{\zeta }$
is an anticommuting involution such that
 $A_{\zeta }^2=Id$
and
$A_{\zeta }^2=Id$
and
![]() $AJ=-JA$
. Hence, we have
$AJ=-JA$
. Hence, we have
![]() $T_{[z]}Q^m=V(A_{\zeta })\oplus JV(A_{\zeta })$
, where
$T_{[z]}Q^m=V(A_{\zeta })\oplus JV(A_{\zeta })$
, where
 $V(A_{\zeta })=\mathbb {R}^{m+2}\cap T_{[z]}Q^m$
is the
$V(A_{\zeta })=\mathbb {R}^{m+2}\cap T_{[z]}Q^m$
is the
![]() $(+1)$
-eigenspace and
$(+1)$
-eigenspace and
 $JV(A_{\zeta })=\mathbf {i}\mathbb {R}^{m+2}\cap T_{[z]}Q^m$
is the
$JV(A_{\zeta })=\mathbf {i}\mathbb {R}^{m+2}\cap T_{[z]}Q^m$
is the
![]() $(-1)$
-eigenspace of
$(-1)$
-eigenspace of
![]() $A_{\zeta }$
, respectively. Because the normal space
$A_{\zeta }$
, respectively. Because the normal space
![]() $\nu _{[z]}Q^m$
of
$\nu _{[z]}Q^m$
of
![]() $Q^m$
in
$Q^m$
in
![]() $\mathbb {C}P^{m+1}$
at
$\mathbb {C}P^{m+1}$
at
![]() $[z]$
is a complex subspace of
$[z]$
is a complex subspace of
 $T_{[z]}\mathbb {C}P^{m+1}$
of complex dimension one, every unit normal vector in
$T_{[z]}\mathbb {C}P^{m+1}$
of complex dimension one, every unit normal vector in
![]() $\nu _{[z]}Q^m$
can be written as
$\nu _{[z]}Q^m$
can be written as
![]() $\lambda \bar {z}$
with some
$\lambda \bar {z}$
with some
![]() $\lambda \in S^1\subset \mathbb {C}$
, and it holds that
$\lambda \in S^1\subset \mathbb {C}$
, and it holds that
![]() $V(A_{\lambda \bar {z}})=\lambda V(A_{\bar {z}})$
. We denote by
$V(A_{\lambda \bar {z}})=\lambda V(A_{\bar {z}})$
. We denote by
![]() $\mathfrak {A}$
the set of all shape operators of
$\mathfrak {A}$
the set of all shape operators of
![]() $Q^m\hookrightarrow \mathbb {C}P^{m+1}$
associated with unit normal vector fields. Then,
$Q^m\hookrightarrow \mathbb {C}P^{m+1}$
associated with unit normal vector fields. Then,
![]() $\mathfrak {A}$
is an
$\mathfrak {A}$
is an
![]() $S^1$
-sub-bundle of the endomorphism bundle End(
$S^1$
-sub-bundle of the endomorphism bundle End(
![]() $TQ^m$
), consisting of complex conjugations on the tangent spaces of
$TQ^m$
), consisting of complex conjugations on the tangent spaces of
![]() $Q^m$
. In summary, we have
$Q^m$
. In summary, we have
Lemma 2.1 (cf. [Reference Reckziegel22, Reference Smyth23])
For each
![]() $A\in \mathfrak {A}$
, it holds that
$A\in \mathfrak {A}$
, it holds that
The sub-bundle
![]() $\mathfrak {A}$
is commonly called consisting of complex conjugations (cf. [Reference Reckziegel22]). On the other hand, Lemma 2.1 implies, in particular, that
$\mathfrak {A}$
is commonly called consisting of complex conjugations (cf. [Reference Reckziegel22]). On the other hand, Lemma 2.1 implies, in particular, that
![]() $\mathfrak {A}$
is a family of almost product structures on
$\mathfrak {A}$
is a family of almost product structures on
![]() $Q^m$
(cf. [Reference Li, Ma, Van der Veken, Vrancken and Wang16]), and we will use the latter term in this paper. Furthermore, because the second fundamental form of the embedding
$Q^m$
(cf. [Reference Li, Ma, Van der Veken, Vrancken and Wang16]), and we will use the latter term in this paper. Furthermore, because the second fundamental form of the embedding
![]() $Q^m\hookrightarrow \mathbb {C}P^{m+1}$
is parallel,
$Q^m\hookrightarrow \mathbb {C}P^{m+1}$
is parallel,
![]() $\mathfrak {A}$
is contained in a parallel sub-bundle of End(
$\mathfrak {A}$
is contained in a parallel sub-bundle of End(
![]() $TQ^m$
). It follows that, for each almost product structure
$TQ^m$
). It follows that, for each almost product structure
![]() $A\in \mathfrak {A}$
, there exists a one-form q on
$A\in \mathfrak {A}$
, there exists a one-form q on
![]() $Q^m$
such that it holds the relation (see [Reference Smyth23])
$Q^m$
such that it holds the relation (see [Reference Smyth23])
where
![]() $\bar {\nabla }$
denotes the Levi–Civita connection of
$\bar {\nabla }$
denotes the Levi–Civita connection of
![]() $Q^m$
.
$Q^m$
.
The Gauss equation for the complex hypersurface
![]() $Q^m\hookrightarrow \mathbb {C}P^{m+1}$
implies that the Riemannian curvature tensor
$Q^m\hookrightarrow \mathbb {C}P^{m+1}$
implies that the Riemannian curvature tensor
![]() $\bar {R}$
of
$\bar {R}$
of
![]() $Q^m$
can be expressed in terms of the Riemannian metric g, the complex structure J, and a generic
$Q^m$
can be expressed in terms of the Riemannian metric g, the complex structure J, and a generic
![]() $A\in \mathfrak {A}$
as follows (cf. [Reference Reckziegel22]):
$A\in \mathfrak {A}$
as follows (cf. [Reference Reckziegel22]):
 $$ \begin{align} \begin{aligned} \bar{R}(X,Y)Z=&g(Y,Z)X-g(X,Z)Y+g(JY,Z)JX-g(JX,Z)JY\\ &-2g(JX,Y)JZ+g(AY,Z)AX-g(AX,Z)AY\\ &+g(JAY,Z)JAX-g(JAX,Z)JAY, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \bar{R}(X,Y)Z=&g(Y,Z)X-g(X,Z)Y+g(JY,Z)JX-g(JX,Z)JY\\ &-2g(JX,Y)JZ+g(AY,Z)AX-g(AX,Z)AY\\ &+g(JAY,Z)JAX-g(JAX,Z)JAY, \end{aligned} \end{align} $$
where it should be noted that
![]() $\bar {R}$
is independent of the special choice of
$\bar {R}$
is independent of the special choice of
![]() $A\in \mathfrak {A}$
.
$A\in \mathfrak {A}$
.
According to Reckziegel [Reference Reckziegel22], a real
![]() $2$
-dimensional linear subspace
$2$
-dimensional linear subspace
![]() $\sigma $
of
$\sigma $
of
![]() $T_{[z]}Q^m$
is called a
$T_{[z]}Q^m$
is called a
![]() $2$
-flat if the curvature tensor
$2$
-flat if the curvature tensor
![]() $\bar {R}$
of
$\bar {R}$
of
![]() $Q^m$
vanishes identically on
$Q^m$
vanishes identically on
![]() $\sigma $
. A nonzero tangent vector
$\sigma $
. A nonzero tangent vector
![]() $W\in T_{[z]}Q^m$
is called
$W\in T_{[z]}Q^m$
is called
![]() $\mathfrak {A}$
-singular if it is contained in more than one
$\mathfrak {A}$
-singular if it is contained in more than one
![]() $2$
-flat. There are two types of
$2$
-flat. There are two types of
![]() $\mathfrak {A}$
-singular tangent vectors for
$\mathfrak {A}$
-singular tangent vectors for
![]() $Q^m$
, namely,
$Q^m$
, namely,
![]() $\mathfrak {A}$
-principal and
$\mathfrak {A}$
-principal and
![]() $\mathfrak {A}$
-isotropic tangent vectors, described as follows (cf. [Reference Berndt and Suh3, Reference Reckziegel22]):
$\mathfrak {A}$
-isotropic tangent vectors, described as follows (cf. [Reference Berndt and Suh3, Reference Reckziegel22]):
-
1. If there exists an almost product structure
 $A\in \mathfrak {A}_{[z]}$
such that
$A\in \mathfrak {A}_{[z]}$
such that
 $W\in V(A)$
, then W is
$W\in V(A)$
, then W is
 $\mathfrak {A}$
-singular. Such
$\mathfrak {A}$
-singular. Such
 $W\in T_{[z]}Q^m$
is called an
$W\in T_{[z]}Q^m$
is called an
 $\mathfrak {A}$
-principal tangent vector.
$\mathfrak {A}$
-principal tangent vector. -
2. If there exists an almost product structure
 $A\in \mathfrak {A}_{[z]}$
and two orthonormal vectors
$A\in \mathfrak {A}_{[z]}$
and two orthonormal vectors
 $X,Y\in V(A)$
such that
$X,Y\in V(A)$
such that
 $\frac {W}{\|W\|}=\frac {X+JY}{\sqrt {2}}$
, then W is
$\frac {W}{\|W\|}=\frac {X+JY}{\sqrt {2}}$
, then W is
 $\mathfrak {A}$
-singular. In this case, we have
$\mathfrak {A}$
-singular. In this case, we have
 $g(AW,W)=0$
and
$g(AW,W)=0$
and
 $W\in T_{[z]}Q^m$
is called an
$W\in T_{[z]}Q^m$
is called an
 $\mathfrak {A}$
-isotropic tangent vector.
$\mathfrak {A}$
-isotropic tangent vector.
Further results about the complex quadric are referred to [Reference Berndt and Suh3, Reference Klein12, Reference Reckziegel22].
2.2 Hypersurfaces of the complex quadric
We begin with introducing the basic formulas. Let M be a hypersurface of
![]() $Q^m$
and N its unit normal vector field. For a generic almost product structure
$Q^m$
and N its unit normal vector field. For a generic almost product structure
![]() $A\in \mathfrak {A}$
and an arbitrary tangent vector field X of M, we have the decomposition
$A\in \mathfrak {A}$
and an arbitrary tangent vector field X of M, we have the decomposition
where
![]() $\phi X$
(resp.
$\phi X$
(resp.
![]() $TX$
) and
$TX$
) and
![]() $\eta (X)N$
(resp.
$\eta (X)N$
(resp.
![]() $\mu (X)N$
) are the tangent and normal parts of
$\mu (X)N$
) are the tangent and normal parts of
![]() $JX$
(resp.
$JX$
(resp.
![]() $AX$
), respectively. Here,
$AX$
), respectively. Here,
![]() $\phi $
and T are tensor fields of type
$\phi $
and T are tensor fields of type
![]() $(1,1)$
, and
$(1,1)$
, and
![]() $\eta $
and
$\eta $
and
![]() $\mu $
are
$\mu $
are
![]() $1$
-forms over M. Then, by definition, we have the following relations:
$1$
-forms over M. Then, by definition, we have the following relations:
 $$ \begin{align} \left\{ \begin{aligned} &\eta(X)=g(X,\xi),\ \ \eta(\phi X)=0,\ \ \phi^2X=-X+\eta(X)\xi,\\ &g(\phi X,Y)=-g(X,\phi Y),\ \ g(\phi X,\phi Y)=g(X,Y)-\eta(X)\eta(Y),\\ &g(TX,Y)=g(X,TY),\ \ \mu(X)=g(AX,N), \end{aligned}\right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &\eta(X)=g(X,\xi),\ \ \eta(\phi X)=0,\ \ \phi^2X=-X+\eta(X)\xi,\\ &g(\phi X,Y)=-g(X,\phi Y),\ \ g(\phi X,\phi Y)=g(X,Y)-\eta(X)\eta(Y),\\ &g(TX,Y)=g(X,TY),\ \ \mu(X)=g(AX,N), \end{aligned}\right. \end{align} $$
where
![]() $\xi :=-JN$
is called the Reeb vector field of M. The equations in (2.5) show that
$\xi :=-JN$
is called the Reeb vector field of M. The equations in (2.5) show that
![]() $\{\phi ,\xi ,\eta \}$
determines an almost contact structure on M.
$\{\phi ,\xi ,\eta \}$
determines an almost contact structure on M.
Let
![]() $\nabla $
be the induced connection on M with R its Riemannian curvature tensor. The formulas of Gauss and Weingarten state that
$\nabla $
be the induced connection on M with R its Riemannian curvature tensor. The formulas of Gauss and Weingarten state that
where S is the shape operator of
![]() $M\hookrightarrow Q^m$
.
$M\hookrightarrow Q^m$
.
Next, we calculate the covariant derivatives of the tensors
![]() $\phi ,\eta ,T$
, and
$\phi ,\eta ,T$
, and
![]() $\mu $
. These basic equations are necessary for our proof of Theorem 1.1.
$\mu $
. These basic equations are necessary for our proof of Theorem 1.1.
Lemma 2.2 The covariant derivatives of the tensors
![]() $\phi ,T,\mu $
, and
$\phi ,T,\mu $
, and
![]() $\eta $
are given by
$\eta $
are given by
![]() $:$
$:$
Proof These equations are derived by direct calculations. Specifically, we have the following derivation by using the basic equations in (2.2), (2.5), and (2.6):
 $$ \begin{align*} \nabla_X \xi&=-\bar{\nabla}_X JN-g(SX,\xi)N=-J\bar{\nabla}_X N-g(SX,\xi)N\\ &=JSX-g(SX,\xi)N=\phi SX, \end{align*} $$
$$ \begin{align*} \nabla_X \xi&=-\bar{\nabla}_X JN-g(SX,\xi)N=-J\bar{\nabla}_X N-g(SX,\xi)N\\ &=JSX-g(SX,\xi)N=\phi SX, \end{align*} $$
 $$ \begin{align*} (\nabla_X \phi)Y&=\nabla_X {\phi Y}-\phi\nabla_X Y=\bar{\nabla}_X {\phi Y} -g(SX,\phi Y)N-\phi\nabla_X Y\\ &=[\bar{\nabla}_X (JY-\eta(Y)N)]^\top-\phi\nabla_X Y\\ &=[(\bar{\nabla}_X J)Y+J\bar{\nabla}_X Y]^\top-\eta(Y)\bar{\nabla}_X N-\phi\nabla_X Y\\ &=-g(SX,Y)\xi+\eta(Y)SX, \end{align*} $$
$$ \begin{align*} (\nabla_X \phi)Y&=\nabla_X {\phi Y}-\phi\nabla_X Y=\bar{\nabla}_X {\phi Y} -g(SX,\phi Y)N-\phi\nabla_X Y\\ &=[\bar{\nabla}_X (JY-\eta(Y)N)]^\top-\phi\nabla_X Y\\ &=[(\bar{\nabla}_X J)Y+J\bar{\nabla}_X Y]^\top-\eta(Y)\bar{\nabla}_X N-\phi\nabla_X Y\\ &=-g(SX,Y)\xi+\eta(Y)SX, \end{align*} $$
 $$ \begin{align*} (\nabla_X T)Y&=\nabla_X {TY}-T\nabla_X Y=\bar{\nabla}_X {TY}-g(SX,TY)N-T\nabla_X Y\\ &=[\bar{\nabla}_X (AY-\mu(Y)N)]^\top-T\nabla_X Y\\ &=[(\bar{\nabla}_X A)Y+A\bar{\nabla}_X Y]^\top-\mu(Y)\bar{\nabla}_X N-T\nabla_X Y\\ &=[q(X)JAY+g(SX,Y)AN]^\top+\mu(Y)SX\\ &=q(X)[\phi TY-\mu(Y)\xi]+g(SX,Y)[-\phi T\xi+\mu(\xi)\xi]+\mu(Y)SX, \end{align*} $$
$$ \begin{align*} (\nabla_X T)Y&=\nabla_X {TY}-T\nabla_X Y=\bar{\nabla}_X {TY}-g(SX,TY)N-T\nabla_X Y\\ &=[\bar{\nabla}_X (AY-\mu(Y)N)]^\top-T\nabla_X Y\\ &=[(\bar{\nabla}_X A)Y+A\bar{\nabla}_X Y]^\top-\mu(Y)\bar{\nabla}_X N-T\nabla_X Y\\ &=[q(X)JAY+g(SX,Y)AN]^\top+\mu(Y)SX\\ &=q(X)[\phi TY-\mu(Y)\xi]+g(SX,Y)[-\phi T\xi+\mu(\xi)\xi]+\mu(Y)SX, \end{align*} $$
 $$ \begin{align*} (\nabla_X \mu)Y&=X(\mu(Y))-\mu(\nabla_X Y)\\ &=g(\bar{\nabla}_X {AY},N) +g(AY,\bar{\nabla}_X N)-g(A\bar{\nabla}_X Y-g(SX,Y)AN,N)\\ &=g((\bar{\nabla}_X A)Y,N)-g(SX,TY)+g(SX,Y)g(AN,N)\\ &=g(q(X)JAY,N)-g(SX,TY)+g(SX,Y)g(AN,N)\\ &=q(X)g(TY,\xi)-g(SX,TY)-g(SX,Y)g(T\xi,\xi), \end{align*} $$
$$ \begin{align*} (\nabla_X \mu)Y&=X(\mu(Y))-\mu(\nabla_X Y)\\ &=g(\bar{\nabla}_X {AY},N) +g(AY,\bar{\nabla}_X N)-g(A\bar{\nabla}_X Y-g(SX,Y)AN,N)\\ &=g((\bar{\nabla}_X A)Y,N)-g(SX,TY)+g(SX,Y)g(AN,N)\\ &=g(q(X)JAY,N)-g(SX,TY)+g(SX,Y)g(AN,N)\\ &=q(X)g(TY,\xi)-g(SX,TY)-g(SX,Y)g(T\xi,\xi), \end{align*} $$
where
![]() $\cdot ^\top $
denotes the tangential part.▪
$\cdot ^\top $
denotes the tangential part.▪
Third, by using the decomposition of A and the expression of the curvature tensor of
![]() $Q^m$
, we have the following Gauss and Codazzi equations of M:
$Q^m$
, we have the following Gauss and Codazzi equations of M:
 $$ \begin{align} R(X,Y)Z=&g(Y,Z)X-g(X,Z)Y+g(\phi Y,Z)\phi X-g(\phi X,Z)\phi Y\nonumber\\ &-2g(\phi X,Y)\phi Z+g(AY,Z)(AX)^\top-g(AX,Z)(AY)^\top\nonumber\\ &+g(JAY,Z)(JAX)^\top-g(JAX,Z)(JAY)^\top\nonumber\\ &+g(SZ,Y)SX-g(SZ,X)SY, \end{align} $$
$$ \begin{align} R(X,Y)Z=&g(Y,Z)X-g(X,Z)Y+g(\phi Y,Z)\phi X-g(\phi X,Z)\phi Y\nonumber\\ &-2g(\phi X,Y)\phi Z+g(AY,Z)(AX)^\top-g(AX,Z)(AY)^\top\nonumber\\ &+g(JAY,Z)(JAX)^\top-g(JAX,Z)(JAY)^\top\nonumber\\ &+g(SZ,Y)SX-g(SZ,X)SY, \end{align} $$
 $$ \begin{align} g\big((\nabla_X S)Y&-(\nabla_Y S)X,Z\big)=\eta(X)g(\phi Y,Z)-\eta(Y)g(\phi X,Z)\nonumber\\ &-2g(\phi X,Y)\eta(Z)+\mu(X)g(TY,Z)-\mu(Y)g(TX,Z)\nonumber\\ &-g(TX,\xi)g(TY,\phi Z)-g(TX,\xi)\mu(Y)\eta(Z)\nonumber\\ &+g(TY,\xi)g(TX,\phi Z)+g(TY,\xi)\mu(X)\eta(Z). \end{align} $$
$$ \begin{align} g\big((\nabla_X S)Y&-(\nabla_Y S)X,Z\big)=\eta(X)g(\phi Y,Z)-\eta(Y)g(\phi X,Z)\nonumber\\ &-2g(\phi X,Y)\eta(Z)+\mu(X)g(TY,Z)-\mu(Y)g(TX,Z)\nonumber\\ &-g(TX,\xi)g(TY,\phi Z)-g(TX,\xi)\mu(Y)\eta(Z)\nonumber\\ &+g(TY,\xi)g(TX,\phi Z)+g(TY,\xi)\mu(X)\eta(Z). \end{align} $$
Contracting Y and Z in (2.12), we get the Ricci tensor of M (cf. (4.1) of [Reference Suh24]):
 $$ \begin{align} \text{Ric}\,(X,Y)&=(2m-1)g(X,Y)-3\eta(X)\eta(Y)-g(AN,N)g(AX,Y)\nonumber\\ &\quad +g(AX,N)g(AN,Y)-g(A\xi,N)g(JAX,Y)\nonumber\\ &\quad +g(A\xi,X)g(A\xi,Y)+Hg(SX,Y)-g(S^2X,Y)\nonumber\\ &=(2m-1)g(X,Y)-3\eta(X)\eta(Y)+g(T\xi,\xi)g(TX,Y)\nonumber\\ &\quad +\mu(X)\mu(Y)+\mu(\xi)g(TX,\phi Y)+\mu(\xi)\mu(X)\eta(Y)\nonumber\\ &\quad +g(TX,\xi)g(TY,\xi)+Hg(SX,Y)-g(S^2X,Y), \end{align} $$
$$ \begin{align} \text{Ric}\,(X,Y)&=(2m-1)g(X,Y)-3\eta(X)\eta(Y)-g(AN,N)g(AX,Y)\nonumber\\ &\quad +g(AX,N)g(AN,Y)-g(A\xi,N)g(JAX,Y)\nonumber\\ &\quad +g(A\xi,X)g(A\xi,Y)+Hg(SX,Y)-g(S^2X,Y)\nonumber\\ &=(2m-1)g(X,Y)-3\eta(X)\eta(Y)+g(T\xi,\xi)g(TX,Y)\nonumber\\ &\quad +\mu(X)\mu(Y)+\mu(\xi)g(TX,\phi Y)+\mu(\xi)\mu(X)\eta(Y)\nonumber\\ &\quad +g(TX,\xi)g(TY,\xi)+Hg(SX,Y)-g(S^2X,Y), \end{align} $$
where
![]() $H=\mathrm {tr}\,S$
denotes the mean curvature of the hypersurface M.
$H=\mathrm {tr}\,S$
denotes the mean curvature of the hypersurface M.
Let
![]() $\nabla ^2 S$
denote the second covariant derivative of S, defined by:
$\nabla ^2 S$
denote the second covariant derivative of S, defined by:
Then, we have the following Ricci identity:
 $$ \begin{align} g\big((\nabla^{2}S)(X,Y,Z),&W\big)-g\big((\nabla^{2}S)(Y,X,Z),W\big)\nonumber\\ &=-g\big(R(X,Y)Z,SW\big)-g\big(R(X,Y)W,SZ\big). \end{align} $$
$$ \begin{align} g\big((\nabla^{2}S)(X,Y,Z),&W\big)-g\big((\nabla^{2}S)(Y,X,Z),W\big)\nonumber\\ &=-g\big(R(X,Y)Z,SW\big)-g\big(R(X,Y)W,SZ\big). \end{align} $$
Notice that the tangent bundle
![]() $TM$
of M splits orthogonally into
$TM$
of M splits orthogonally into
![]() $TM=\mathcal {C}\oplus \mathcal {F}$
, where
$TM=\mathcal {C}\oplus \mathcal {F}$
, where
![]() $\mathcal {C}=\text {ker}(\eta )$
is the maximal complex sub-bundle of
$\mathcal {C}=\text {ker}(\eta )$
is the maximal complex sub-bundle of
![]() $TM$
and
$TM$
and
![]() $\mathcal {F}=\mathbb {R}\xi $
. When restricted to
$\mathcal {F}=\mathbb {R}\xi $
. When restricted to
![]() $\mathcal {C}$
, the structure tensor field
$\mathcal {C}$
, the structure tensor field
![]() $\phi $
coincides with the complex structure J. Moreover, at each point
$\phi $
coincides with the complex structure J. Moreover, at each point
![]() $[z]\in M$
, the set
$[z]\in M$
, the set
defines a maximal
![]() $\mathfrak {A}_{[z]}$
-invariant subspace of
$\mathfrak {A}_{[z]}$
-invariant subspace of
![]() $T_{[z]}M$
.
$T_{[z]}M$
.
According to Proposition 3 of [Reference Reckziegel22], at each point
![]() $[z]\in M$
, we can choose
$[z]\in M$
, we can choose
![]() $A\in \mathfrak {A}_{[z]}$
and two orthonormal vectors
$A\in \mathfrak {A}_{[z]}$
and two orthonormal vectors
![]() $Z_1,Z_2\in V(A)$
such that the unit normal vector field N takes the form
$Z_1,Z_2\in V(A)$
such that the unit normal vector field N takes the form
where the parameter function t satisfies
![]() $0\leq t\leq \frac {\pi }{4}$
. Using
$0\leq t\leq \frac {\pi }{4}$
. Using
![]() $\xi =-JN$
, we further get
$\xi =-JN$
, we further get
 $$ \begin{align*} AN=\cos t\,Z_1-\sin t\,JZ_2,\\ \xi=\sin t\,Z_2-\cos t\,JZ_1,\\ A\xi=\sin t\,Z_2+\cos t\,JZ_1. \end{align*} $$
$$ \begin{align*} AN=\cos t\,Z_1-\sin t\,JZ_2,\\ \xi=\sin t\,Z_2-\cos t\,JZ_1,\\ A\xi=\sin t\,Z_2+\cos t\,JZ_1. \end{align*} $$
This implies that
![]() $g(A\xi ,N)=0$
and
$g(A\xi ,N)=0$
and
![]() $A\xi \in T_{[z]}M$
.
$A\xi \in T_{[z]}M$
.
Remark 2.1 From the above facts, we can get the following conclusions:
-
(1) If
 $N_{[z]}$
is
$N_{[z]}$
is
 $\mathfrak {A}$
-principal, we have
$\mathfrak {A}$
-principal, we have
 $t=0$
at
$t=0$
at
 $[z]$
,
$[z]$
,
 $\mathcal {Q}_{[z]}=\mathcal {C}_{[z]}$
, and
$\mathcal {Q}_{[z]}=\mathcal {C}_{[z]}$
, and
 $\dim \mathcal {Q}_{[z]}=2m-2$
. For each
$\dim \mathcal {Q}_{[z]}=2m-2$
. For each
 $A\in \mathfrak {A}_{[z]}$
, (2.1) implies that
$A\in \mathfrak {A}_{[z]}$
, (2.1) implies that
 $A|_{\mathcal {Q}_{[z]}}$
has two eigenvalues
$A|_{\mathcal {Q}_{[z]}}$
has two eigenvalues
 $1$
and
$1$
and
 $-1$
. For
$-1$
. For
 $\varepsilon \in \{1,-1\}$
, if denoting by
$\varepsilon \in \{1,-1\}$
, if denoting by
 $\mathcal {Q}(\varepsilon )$
the eigenspace of
$\mathcal {Q}(\varepsilon )$
the eigenspace of
 $A|_{\mathcal {Q}}$
corresponding to
$A|_{\mathcal {Q}}$
corresponding to
 $\varepsilon $
, then it holds that
$\varepsilon $
, then it holds that
 $J\mathcal {Q}(1)=\mathcal {Q}(-1)$
and
$J\mathcal {Q}(1)=\mathcal {Q}(-1)$
and
 $\dim \mathcal {Q}(1)=\dim \mathcal {Q}(-1)=m-1$
.
$\dim \mathcal {Q}(1)=\dim \mathcal {Q}(-1)=m-1$
. -
(2) If
 $N_{[z]}$
is not
$N_{[z]}$
is not
 $\mathfrak {A}$
-principal, we get
$\mathfrak {A}$
-principal, we get
 $\mathcal {Q}_{[z]}=\{N_{[z]},\xi _{[z]},AN_{[z]},A\xi _{[z]}\}^\bot $
for any
$\mathcal {Q}_{[z]}=\{N_{[z]},\xi _{[z]},AN_{[z]},A\xi _{[z]}\}^\bot $
for any
 $A\in \mathfrak {A}_{[z]}$
, and
$A\in \mathfrak {A}_{[z]}$
, and
 $\dim \mathcal {Q}_{[z]}=2(m-2)$
. For each
$\dim \mathcal {Q}_{[z]}=2(m-2)$
. For each
 $A\in \mathfrak {A}_{[z]}$
, (2.1) implies that
$A\in \mathfrak {A}_{[z]}$
, (2.1) implies that
 $A|_{\mathcal {Q}_{[z]}}$
has two eigenvalues
$A|_{\mathcal {Q}_{[z]}}$
has two eigenvalues
 $1$
and
$1$
and
 $-1$
. Moreover, it holds that
$-1$
. Moreover, it holds that
 $J\mathcal {Q}(1)=\mathcal {Q}(-1)$
and
$J\mathcal {Q}(1)=\mathcal {Q}(-1)$
and
 $\dim \mathcal {Q}(1)=\dim \mathcal {Q}(-1)=m-2$
.
$\dim \mathcal {Q}(1)=\dim \mathcal {Q}(-1)=m-2$
.
Finally, we recall the following lemma due to Berndt and Suh [Reference Berndt and Suh3] (cf. also [Reference Loo17]). This lemma is very helpful for simplifying our latter calculations. Specifically, it allows us to choose locally, under appropriate conditions, the almost product structure
![]() $A\in \mathfrak {A}$
such that
$A\in \mathfrak {A}$
such that
![]() $A\xi \in TM$
and
$A\xi \in TM$
and
![]() $g(AN,\xi )=0$
.
$g(AN,\xi )=0$
.
Lemma 2.3 (cf. [Reference Berndt and Suh3] and [Reference Loo17])
Let M be a hypersurface of
![]() $Q^m$
with unit normal vector field N and
$Q^m$
with unit normal vector field N and
![]() $\xi =-JN$
. Then, we have
$\xi =-JN$
. Then, we have
![]() $:$
$:$
-
(a) If N is
 $\mathfrak {A}$
-principal on an open set
$\mathfrak {A}$
-principal on an open set
 $U\subset M$
, then there exists an almost product structure
$U\subset M$
, then there exists an almost product structure
 $A\in \mathfrak {A}$
on U such that
$A\in \mathfrak {A}$
on U such that
 $AN=N$
.
$AN=N$
. -
(b) If N is not
 $\mathfrak {A}$
-principal at
$\mathfrak {A}$
-principal at
 $[z]\in M$
, then there exist a neighborhood U of
$[z]\in M$
, then there exist a neighborhood U of
 $[z]$
and an almost product structure
$[z]$
and an almost product structure
 $A\in \mathfrak {A}$
on U such that
$A\in \mathfrak {A}$
on U such that
 $A\xi \in TM$
.
$A\xi \in TM$
.
3 Key lemmas related to the Tsinghua principle
We begin with establishing the following general lemma about real hypersurfaces of the complex quadric.
Lemma 3.1 Let M be a real hypersurface in the complex quadric
![]() $Q^m\ (m\geq 3)$
. Then, for a generic almost product structure
$Q^m\ (m\geq 3)$
. Then, for a generic almost product structure
![]() $A\in \mathfrak {A}$
and any tangent vector fields
$A\in \mathfrak {A}$
and any tangent vector fields
![]() $W,X,Y,Z\in TM$
, we have
$W,X,Y,Z\in TM$
, we have
 $$ \begin{align} -\mathop{\mathfrak{S}}\limits_{WXY} \big\{g(R(W,X)Y,SZ) +g(R(W,X)Z,SY)\big\}=\mathop{\mathfrak{S}}\limits_{WXY}\mathbf{I}(W,X,Y,Z), \end{align} $$
$$ \begin{align} -\mathop{\mathfrak{S}}\limits_{WXY} \big\{g(R(W,X)Y,SZ) +g(R(W,X)Z,SY)\big\}=\mathop{\mathfrak{S}}\limits_{WXY}\mathbf{I}(W,X,Y,Z), \end{align} $$
where
 $\mathop {\mathfrak {S}}\limits _{WXY}$
denotes the cyclic summation over
$\mathop {\mathfrak {S}}\limits _{WXY}$
denotes the cyclic summation over
![]() $W,X$
, and Y, and
$W,X$
, and Y, and
 $$ \begin{align*} \mathbf{I}&(W,X,Y,Z):=-g(SW,\phi X)g(\phi Y,Z)+g(SW,\phi Y)g(\phi X,Z)\\ &+2g(SW,\phi Z)g(\phi X,Y)-3g(SW,Y)\eta(X)\eta(Z)+3g(SW,X)\eta(Y)\eta(Z)\\ &-[g(TX,SW)+\eta(T\xi)g(SW,X)]g(TY,Z)+\mu(X)g(SW,Y)\mu(Z)\\ &+[g(TY,SW)+\eta(T\xi)g(SW,Y)]g(TX,Z)-\mu(Y)g(SW,X)\mu(Z)\\ &-[g(SW,X)\mu(\xi)+\mu(X)\eta(SW)]g(TY,\phi Z)-g(TX,\phi SW)g(TY,\phi Z)\\ &+\eta(TX)g(SW,Y)\eta(TZ)-g(SW,X)\mu(\xi)\mu(Y)\eta(Z)-g(TX,\phi SW)\mu(Y)\eta(Z)\\ &+[g(SW,Y)\mu(\xi)+\mu(Y)\eta(SW)]g(TX,\phi Z)+g(TY,\phi SW)g(TX,\phi Z)\\ &-\eta(TY)g(SW,X)\eta(TZ)+g(SW,Y)\mu(\xi)\mu(X)\eta(Z)+g(TY,\phi SW)\mu(X)\eta(Z). \end{align*} $$
$$ \begin{align*} \mathbf{I}&(W,X,Y,Z):=-g(SW,\phi X)g(\phi Y,Z)+g(SW,\phi Y)g(\phi X,Z)\\ &+2g(SW,\phi Z)g(\phi X,Y)-3g(SW,Y)\eta(X)\eta(Z)+3g(SW,X)\eta(Y)\eta(Z)\\ &-[g(TX,SW)+\eta(T\xi)g(SW,X)]g(TY,Z)+\mu(X)g(SW,Y)\mu(Z)\\ &+[g(TY,SW)+\eta(T\xi)g(SW,Y)]g(TX,Z)-\mu(Y)g(SW,X)\mu(Z)\\ &-[g(SW,X)\mu(\xi)+\mu(X)\eta(SW)]g(TY,\phi Z)-g(TX,\phi SW)g(TY,\phi Z)\\ &+\eta(TX)g(SW,Y)\eta(TZ)-g(SW,X)\mu(\xi)\mu(Y)\eta(Z)-g(TX,\phi SW)\mu(Y)\eta(Z)\\ &+[g(SW,Y)\mu(\xi)+\mu(Y)\eta(SW)]g(TX,\phi Z)+g(TY,\phi SW)g(TX,\phi Z)\\ &-\eta(TY)g(SW,X)\eta(TZ)+g(SW,Y)\mu(\xi)\mu(X)\eta(Z)+g(TY,\phi SW)\mu(X)\eta(Z). \end{align*} $$
Proof We shall calculate the expression of the cyclic summation
 $$ \begin{align} \mathfrak{B}:=\mathop{\mathfrak{S}}\limits_{WXY} \big\{g((\nabla^2 S)(W,X,Y),Z)- g((\nabla^2 S)(W,Y,X),Z)\big\} \end{align} $$
$$ \begin{align} \mathfrak{B}:=\mathop{\mathfrak{S}}\limits_{WXY} \big\{g((\nabla^2 S)(W,X,Y),Z)- g((\nabla^2 S)(W,Y,X),Z)\big\} \end{align} $$
in two different ways. On the one hand, taking the covariant derivative of the Codazzi equation (2.13), we can get
 $$ \begin{align*} &g((\nabla^2 S)(W,X,Y),Z)-g((\nabla^2 S)(W,Y,X),Z)\\ &=(\nabla_W\eta)(X)g(\phi Y,Z)+\eta(X)g((\nabla_W\phi)Y,Z)-(\nabla_W\eta)(Y)g(\phi X,Z)\\ &-\eta(Y)g((\nabla_W\phi)X,Z)-2g((\nabla_W\phi)X,Y)\eta(Z)-2g(\phi X,Y)(\nabla_W\eta)(Z)\\ &+(\nabla_W\mu)(X)g(TY,Z)+\mu(X)g((\nabla_WT)Y,Z)-(\nabla_W\mu)(Y)g(TX,Z)\\ &-\mu(Y)g((\nabla_WT)X,Z)-g((\nabla_WT)X,\xi)g(TY,\phi Z)-g(TX,\nabla_W\xi)g(TY,\phi Z)\\ &-g(TX,\xi)g((\nabla_WT)Y,\phi Z)-g(TX,\xi)g(TY,(\nabla_W\phi)Z)\\ &-g((\nabla_WT)X,\xi)\mu(Y)\eta(Z)-g(TX,\nabla_W\xi)\mu(Y)\eta(Z)-g(TX,\xi)(\nabla_W\mu)(Y)\eta(Z)\\ &-g(TX,\xi)\mu(Y)(\nabla_W\eta)(Z)+g((\nabla_WT)Y,\xi)g(TX,\phi Z)\\ &+g(TY,\nabla_W\xi)g(TX,\phi Z)+g(TY,\xi)g((\nabla_WT)X,\phi Z)\\ &+g(TY,\xi)g(TX,(\nabla_W\phi)Z)+g((\nabla_WT)Y,\xi)\mu(X)\eta(Z)\\&+g(TY,\nabla_W\xi)\mu(X)\eta(Z)+g(TY,\xi)(\nabla_W\mu)(X)\eta(Z)+g(TY,\xi)\mu(X)(\nabla_W\eta)(Z). \end{align*} $$
$$ \begin{align*} &g((\nabla^2 S)(W,X,Y),Z)-g((\nabla^2 S)(W,Y,X),Z)\\ &=(\nabla_W\eta)(X)g(\phi Y,Z)+\eta(X)g((\nabla_W\phi)Y,Z)-(\nabla_W\eta)(Y)g(\phi X,Z)\\ &-\eta(Y)g((\nabla_W\phi)X,Z)-2g((\nabla_W\phi)X,Y)\eta(Z)-2g(\phi X,Y)(\nabla_W\eta)(Z)\\ &+(\nabla_W\mu)(X)g(TY,Z)+\mu(X)g((\nabla_WT)Y,Z)-(\nabla_W\mu)(Y)g(TX,Z)\\ &-\mu(Y)g((\nabla_WT)X,Z)-g((\nabla_WT)X,\xi)g(TY,\phi Z)-g(TX,\nabla_W\xi)g(TY,\phi Z)\\ &-g(TX,\xi)g((\nabla_WT)Y,\phi Z)-g(TX,\xi)g(TY,(\nabla_W\phi)Z)\\ &-g((\nabla_WT)X,\xi)\mu(Y)\eta(Z)-g(TX,\nabla_W\xi)\mu(Y)\eta(Z)-g(TX,\xi)(\nabla_W\mu)(Y)\eta(Z)\\ &-g(TX,\xi)\mu(Y)(\nabla_W\eta)(Z)+g((\nabla_WT)Y,\xi)g(TX,\phi Z)\\ &+g(TY,\nabla_W\xi)g(TX,\phi Z)+g(TY,\xi)g((\nabla_WT)X,\phi Z)\\ &+g(TY,\xi)g(TX,(\nabla_W\phi)Z)+g((\nabla_WT)Y,\xi)\mu(X)\eta(Z)\\&+g(TY,\nabla_W\xi)\mu(X)\eta(Z)+g(TY,\xi)(\nabla_W\mu)(X)\eta(Z)+g(TY,\xi)\mu(X)(\nabla_W\eta)(Z). \end{align*} $$
Then, by straightforward calculations of the RHS, with the use of equations in (2.5) and Lemma 2.2, we can obtain
Here, we note that the terms involving
![]() $q(W)$
are cancelled out with each other. Interestingly, when taking the covariant derivative of the Codazzi equation for a Lagrangian submanifold of
$q(W)$
are cancelled out with each other. Interestingly, when taking the covariant derivative of the Codazzi equation for a Lagrangian submanifold of
![]() $Q^m$
, this phenomenon also occurred in [Reference Li, Ma, Van der Veken, Vrancken and Wang16].
$Q^m$
, this phenomenon also occurred in [Reference Li, Ma, Van der Veken, Vrancken and Wang16].
Now, from (3.3), we have
 $$ \begin{align} \mathfrak{B}=\mathop{\mathfrak{S}}\limits_{WXY}\mathbf{I}(W,X,Y,Z). \end{align} $$
$$ \begin{align} \mathfrak{B}=\mathop{\mathfrak{S}}\limits_{WXY}\mathbf{I}(W,X,Y,Z). \end{align} $$
On the other hand, the cyclic summation
![]() $\mathfrak {B}$
can be rewritten as
$\mathfrak {B}$
can be rewritten as
 $$ \begin{align} \mathfrak{B}=\mathop{\mathfrak{S}}\limits_{WXY}\big\{g((\nabla^{2}S)(W,X,Y),Z) -g((\nabla^{2}S)(X,W,Y),Z)\big\}. \end{align} $$
$$ \begin{align} \mathfrak{B}=\mathop{\mathfrak{S}}\limits_{WXY}\big\{g((\nabla^{2}S)(W,X,Y),Z) -g((\nabla^{2}S)(X,W,Y),Z)\big\}. \end{align} $$
Then, we can apply the Ricci identity (2.15), so that, from (3.5), we obtain
 $$ \begin{align} \mathfrak{B}=-\mathop{\mathfrak{S}}\limits_{WXY} \big\{g(R(W,X)Y,SZ) +g(R(W,X)Z,SY)\big\}. \end{align} $$
$$ \begin{align} \mathfrak{B}=-\mathop{\mathfrak{S}}\limits_{WXY} \big\{g(R(W,X)Y,SZ) +g(R(W,X)Z,SY)\big\}. \end{align} $$
Remark 3.1 The method used in the proof of Lemma 3.1 is elementary and is called the Tsinghua principle. This remarkable technique has been applied in many different situations since its first successful attempt in [Reference Dioos, Vrancken and Wang8], see [Reference Antić, Li, Vrancken and Wang1, Reference Cheng, Hu, Moruz and Vrancken6, Reference Cheng, Hu, Moruz and Vrancken7, Reference Li, Ma, Van der Veken, Vrancken and Wang16, Reference Hu, Moruz, Vrancken and Yao29] for details. Essentially, it establishes a bridge between the Codazzi equation and the Ricci identity by calculating the cyclic sum of the second covariant derivative of the second fundamental form. The significance of the Tsinghua principle lies in that, under appropriate conditions, it simplifies some higher-order equations of the second fundamental form into linear equations.
Next, for a conformally flat real hypersurface M of
![]() $Q^m$
, Lemma 3.1 reduces to the following lemma, which is crucial for the proof of Theorem 1.1.
$Q^m$
, Lemma 3.1 reduces to the following lemma, which is crucial for the proof of Theorem 1.1.
Lemma 3.2 Let M be a conformally flat real hypersurface in the complex quadric
![]() $Q^m\ (m\geq 3)$
. Then, for a generic almost product structure
$Q^m\ (m\geq 3)$
. Then, for a generic almost product structure
![]() $A\in \mathfrak {A}$
and any tangent vector fields
$A\in \mathfrak {A}$
and any tangent vector fields
![]() $W,X,Y,Z\in TM$
, we have
$W,X,Y,Z\in TM$
, we have
 $$ \begin{align} \mathop{\mathfrak{S}}\limits_{WXY}\mathbf{II}(W,X,Y,Z) =\mathop{\mathfrak{S}}\limits_{WXY}\mathbf{I}(W,X,Y,Z), \end{align} $$
$$ \begin{align} \mathop{\mathfrak{S}}\limits_{WXY}\mathbf{II}(W,X,Y,Z) =\mathop{\mathfrak{S}}\limits_{WXY}\mathbf{I}(W,X,Y,Z), \end{align} $$
where
![]() $\mathbf {I}(W,X,Y,Z)$
is defined as in Lemma 3.1
, and
$\mathbf {I}(W,X,Y,Z)$
is defined as in Lemma 3.1
, and
 $$ \begin{align*} \mathbf{II}&(W,X,Y,Z):=\frac{3}{2m-3}\big[\eta(Y)\eta(SX)-\eta(X)\eta(SY)\big]g(W,Z)\\ &+\frac{1}{2m-3}\Big\{\eta(T\xi)\big[g(TX,SY)-g(TY,SX)\big]+\mu(X)\mu(SY)-\mu(Y)\mu(SX)\\ &-\mu(\xi)\big[g(TY,\phi SX)-g(TX,\phi SY)+\mu(Y)\eta(SX)-\mu(X)\eta(SY)\big]\\ &+\eta(TX)\eta(TSY)-\eta(TY)\eta(TSX)\Big\}g(W,Z). \end{align*} $$
$$ \begin{align*} \mathbf{II}&(W,X,Y,Z):=\frac{3}{2m-3}\big[\eta(Y)\eta(SX)-\eta(X)\eta(SY)\big]g(W,Z)\\ &+\frac{1}{2m-3}\Big\{\eta(T\xi)\big[g(TX,SY)-g(TY,SX)\big]+\mu(X)\mu(SY)-\mu(Y)\mu(SX)\\ &-\mu(\xi)\big[g(TY,\phi SX)-g(TX,\phi SY)+\mu(Y)\eta(SX)-\mu(X)\eta(SY)\big]\\ &+\eta(TX)\eta(TSY)-\eta(TY)\eta(TSX)\Big\}g(W,Z). \end{align*} $$
Proof The conformally flatness of the real hypersurface M implies that it has vanishing Weyl curvature tensor or, equivalently, its Riemannian curvature tensor R takes the following form:
 $$ \begin{align} g(R(X,Y)Z,W)=&\frac{1}{2m-3}\big\{\text{Ric}(Y,Z)g(X,W)-\text{Ric}(X,Z)g(Y,W)\nonumber\\ &+\text{Ric}(X,W)g(Y,Z)-\text{Ric}(Y,W)g(X,Z)\big\}\nonumber\\ &+\frac{r}{(2m-2)(2m-3)}\big\{g(X,Z)g(Y,W)-g(Y,Z)g(X,W)\big\}, \end{align} $$
$$ \begin{align} g(R(X,Y)Z,W)=&\frac{1}{2m-3}\big\{\text{Ric}(Y,Z)g(X,W)-\text{Ric}(X,Z)g(Y,W)\nonumber\\ &+\text{Ric}(X,W)g(Y,Z)-\text{Ric}(Y,W)g(X,Z)\big\}\nonumber\\ &+\frac{r}{(2m-2)(2m-3)}\big\{g(X,Z)g(Y,W)-g(Y,Z)g(X,W)\big\}, \end{align} $$
where r denotes the scalar curvature of M. Substituting (3.8) into (3.6), we obtain
 $$ \begin{align} \mathfrak{B}=\frac{1}{2m-3}\mathop{\mathfrak{S}}\limits_{WXY} \big\{g(W,Z)[\text{Ric}(X,SY)-\text{Ric}(Y,SX)]\big\}. \end{align} $$
$$ \begin{align} \mathfrak{B}=\frac{1}{2m-3}\mathop{\mathfrak{S}}\limits_{WXY} \big\{g(W,Z)[\text{Ric}(X,SY)-\text{Ric}(Y,SX)]\big\}. \end{align} $$
By using (2.14), we finally have that
 $$ \begin{align} \mathfrak{B}=\mathop{\mathfrak{S}}\limits_{WXY}\mathbf{II}(W,X,Y,Z). \end{align} $$
$$ \begin{align} \mathfrak{B}=\mathop{\mathfrak{S}}\limits_{WXY}\mathbf{II}(W,X,Y,Z). \end{align} $$
4 Proof of Theorem 1.1 for
 $Q^m$
$Q^m$
In order to complete the proof of Theorem 1.1 for
![]() $Q^m\ (m\ge 3)$
, we suppose on the contrary that
$Q^m\ (m\ge 3)$
, we suppose on the contrary that
![]() $Q^m$
admits a conformally flat real hypersurface M. First of all, with the help of Lemma 3.2, we can prove the following lemma.
$Q^m$
admits a conformally flat real hypersurface M. First of all, with the help of Lemma 3.2, we can prove the following lemma.
Lemma 4.1 Let M be a conformally flat real hypersurface in the complex quadric
![]() $Q^m\ (m\geq 3)$
. Then, the unit normal vector field of M must be
$Q^m\ (m\geq 3)$
. Then, the unit normal vector field of M must be
![]() $\mathfrak {A}$
-principal everywhere.
$\mathfrak {A}$
-principal everywhere.
Proof We argue by contradiction. Assume that at some point
![]() $[z]\in M$
, the unit normal vector
$[z]\in M$
, the unit normal vector
![]() $N_{[z]}$
is not
$N_{[z]}$
is not
![]() $\mathfrak {A}$
-principal. By Lemma 2.3, there exist a neighborhood U around
$\mathfrak {A}$
-principal. By Lemma 2.3, there exist a neighborhood U around
![]() $[z]$
in M and an almost product structure
$[z]$
in M and an almost product structure
![]() $A\in \mathfrak {A}$
on U such that
$A\in \mathfrak {A}$
on U such that
![]() $A\xi \in TM$
and
$A\xi \in TM$
and
![]() $\mu (\xi )=g(A\xi ,N)=0$
. It follows that there exist a unit tangent vector field
$\mu (\xi )=g(A\xi ,N)=0$
. It follows that there exist a unit tangent vector field
![]() $e_1\in \mathcal {C}$
and functions
$e_1\in \mathcal {C}$
and functions
![]() $a,c$
with
$a,c$
with
![]() $c>0$
such that
$c>0$
such that
Then, we get
![]() $\eta (T\xi )=g(T\xi ,\xi )=-a$
.
$\eta (T\xi )=g(T\xi ,\xi )=-a$
.
Put
![]() $e_2=Je_1,e_{2m-1}=\xi $
. From (2.1) and that
$e_2=Je_1,e_{2m-1}=\xi $
. From (2.1) and that
![]() $\dim {\mathcal {Q}}=2m-4$
on U, we can choose orthogonal unit tangent vector fields
$\dim {\mathcal {Q}}=2m-4$
on U, we can choose orthogonal unit tangent vector fields
![]() $\{e_3,\ldots ,e_{2m-2}\}$
such that
$\{e_3,\ldots ,e_{2m-2}\}$
such that
Then,
![]() $\{e_i\}_{i=1}^{2m-1}$
forms a local orthonormal frame field of M with the following properties:
$\{e_i\}_{i=1}^{2m-1}$
forms a local orthonormal frame field of M with the following properties:
 $$ \begin{align} \left\{ \begin{aligned} &AN=aN+ce_1,\ \ Ae_1=cN-ae_1,\ \ Ae_2=ce_{2m-1}+ae_2,\\[-1mm] &Ae_{2p-3}=e_{2p-3},\ \ Ae_{2p-2}=-e_{2p-2},\ \ 3\le p\le m,\\[-1mm] &Ae_{2m-1}=ce_{2}-ae_{2m-1}. \end{aligned}\right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &AN=aN+ce_1,\ \ Ae_1=cN-ae_1,\ \ Ae_2=ce_{2m-1}+ae_2,\\[-1mm] &Ae_{2p-3}=e_{2p-3},\ \ Ae_{2p-2}=-e_{2p-2},\ \ 3\le p\le m,\\[-1mm] &Ae_{2m-1}=ce_{2}-ae_{2m-1}. \end{aligned}\right. \end{align} $$
Put
 $Se_i=\sum _{j=1}^{2m-1}a_{ij}e_j$
,
$Se_i=\sum _{j=1}^{2m-1}a_{ij}e_j$
,
![]() $1\leq i\leq 2m-1$
, where
$1\leq i\leq 2m-1$
, where
![]() $a_{ij}=a_{ji},\ 1\leq i,j\leq 2m-1$
.
$a_{ij}=a_{ji},\ 1\leq i,j\leq 2m-1$
.
Now, we apply for Lemma 3.2 with
![]() $A\in \mathfrak {A}$
being chosen as above.
$A\in \mathfrak {A}$
being chosen as above.
By choosing appropriate
![]() $W=e_i,\, X=e_j,\, Y=e_k,\, Z=e_l$
,
$W=e_i,\, X=e_j,\, Y=e_k,\, Z=e_l$
,
![]() $1\leq i,j,k,l\leq 2m-1$
, with the use of (2.4), (4.2),
$1\leq i,j,k,l\leq 2m-1$
, with the use of (2.4), (4.2),
![]() $\mu (\xi )=0$
, and
$\mu (\xi )=0$
, and
![]() $\eta (T\xi )=-a$
, we can calculate
$\eta (T\xi )=-a$
, we can calculate
![]() $\mathbf {I}(W,X,Y,Z)$
and
$\mathbf {I}(W,X,Y,Z)$
and
![]() $\mathbf {II}(W,X,Y,Z)$
directly. As the result, by (3.7), we shall obtain a system of linear equations of the components
$\mathbf {II}(W,X,Y,Z)$
directly. As the result, by (3.7), we shall obtain a system of linear equations of the components
![]() $\{a_{ij}\}$
. For instance, for
$\{a_{ij}\}$
. For instance, for
![]() $3\leq p\leq m$
, letting
$3\leq p\leq m$
, letting
![]() $(W,X,Y,Z)=(e_1,e_2,e_{2m-1},e_{2p-3}),\ (e_1,e_2,e_{2m-1},e_{2p-2})$
, respectively, by direct calculations, we have
$(W,X,Y,Z)=(e_1,e_2,e_{2m-1},e_{2p-3}),\ (e_1,e_2,e_{2m-1},e_{2p-2})$
, respectively, by direct calculations, we have
 $$ \begin{align*} \left\{ \begin{aligned} &\mathbf{I}(e_1,e_2,e_{2m-1},e_{2p-3})=\mathbf{I}(e_2,e_{2m-1},e_1,e_{2p-3})=0,\\ &\mathbf{I}(e_{2m-1},e_1,e_2,e_{2p-3})=2a_{{2p-2},{2m-1}};\\ &\mathbf{I}(e_1,e_2,e_{2m-1},e_{2p-2})=\mathbf{I}(e_2,e_{2m-1},e_1,e_{2p-2})=0,\\ &\mathbf{I}(e_{2m-1},e_1,e_2,e_{2p-2})=-2a_{{2p-3},{2m-1}};\\ &\mathbf{II}(e_1,e_2,e_{2m-1},e_{2p-3})=\mathbf{II}(e_2,e_{2m-1},e_1,e_{2p-3}) =\mathbf{II}(e_{2m-1},e_1,e_2,e_{2p-3})=0;\\ &\mathbf{II}(e_1,e_2,e_{2m-1},e_{2p-2})=\mathbf{II}(e_2,e_{2m-1},e_1,e_{2p-2}) =\mathbf{II}(e_{2m-1},e_1,e_2,e_{2p-2})=0. \end{aligned}\right. \end{align*} $$
$$ \begin{align*} \left\{ \begin{aligned} &\mathbf{I}(e_1,e_2,e_{2m-1},e_{2p-3})=\mathbf{I}(e_2,e_{2m-1},e_1,e_{2p-3})=0,\\ &\mathbf{I}(e_{2m-1},e_1,e_2,e_{2p-3})=2a_{{2p-2},{2m-1}};\\ &\mathbf{I}(e_1,e_2,e_{2m-1},e_{2p-2})=\mathbf{I}(e_2,e_{2m-1},e_1,e_{2p-2})=0,\\ &\mathbf{I}(e_{2m-1},e_1,e_2,e_{2p-2})=-2a_{{2p-3},{2m-1}};\\ &\mathbf{II}(e_1,e_2,e_{2m-1},e_{2p-3})=\mathbf{II}(e_2,e_{2m-1},e_1,e_{2p-3}) =\mathbf{II}(e_{2m-1},e_1,e_2,e_{2p-3})=0;\\ &\mathbf{II}(e_1,e_2,e_{2m-1},e_{2p-2})=\mathbf{II}(e_2,e_{2m-1},e_1,e_{2p-2}) =\mathbf{II}(e_{2m-1},e_1,e_2,e_{2p-2})=0. \end{aligned}\right. \end{align*} $$
It then follows from (3.7) that
In the following, we shall carry the above procedures repeatedly, but the detailed calculation process will be omitted. To start, for
![]() $3\leq p\leq m$
, taking in (3.7),
$3\leq p\leq m$
, taking in (3.7),
respectively, and using the fact
![]() $c>0$
, we obtain
$c>0$
, we obtain
For
![]() $3\leq p\leq m$
, taking in (3.7),
$3\leq p\leq m$
, taking in (3.7),
respectively, with the use of (4.4), we obtain
For
![]() $3\leq p\leq m$
, taking in (3.7),
$3\leq p\leq m$
, taking in (3.7),
respectively, with the use of (4.4), we obtain
For
![]() $3\leq p\leq m$
, taking in (3.7),
$3\leq p\leq m$
, taking in (3.7),
respectively, together with (4.6) and
![]() $c>0$
, we obtain
$c>0$
, we obtain
For
![]() $3\leq p\leq m$
, taking in (3.7),
$3\leq p\leq m$
, taking in (3.7),
respectively, together with (4.3) and
![]() $c>0$
, we obtain
$c>0$
, we obtain
 $$ \begin{align*}\frac{2m-3+2a}{2m-3}a_{2,{2p-3}}=0, \ \ \frac{2m-3-2a}{2m-3}a_{2,{2p-2}}=0,\ \ 3\leq p\leq m. \end{align*} $$
$$ \begin{align*}\frac{2m-3+2a}{2m-3}a_{2,{2p-3}}=0, \ \ \frac{2m-3-2a}{2m-3}a_{2,{2p-2}}=0,\ \ 3\leq p\leq m. \end{align*} $$
Then, as
![]() $m\geq 3$
and
$m\geq 3$
and
![]() $-1 < a < 1$
, we deduce that
$-1 < a < 1$
, we deduce that
For
![]() $3\leq p\leq m$
, taking in (3.7),
$3\leq p\leq m$
, taking in (3.7),
respectively, together with (4.3), (4.8), and
![]() $c>0$
, we obtain
$c>0$
, we obtain
If
![]() $m=3$
, then the above calculations show that
$m=3$
, then the above calculations show that
![]() $Se_i=a_{ii}e_i,\ 1\le i\le 5$
, and
$Se_i=a_{ii}e_i,\ 1\le i\le 5$
, and
![]() $a_{11}=\cdots =a_{55}$
. Hence, M is totally umbilical and
$a_{11}=\cdots =a_{55}$
. Hence, M is totally umbilical and
![]() $S\phi =\phi S$
holds. This is equivalent to that M has isometric Reeb flow. But, Corollary 1.3 of [Reference Berndt and Suh3] states that there are no real hypersurfaces with isometric Reeb flow in the odd-dimensional complex quadric
$S\phi =\phi S$
holds. This is equivalent to that M has isometric Reeb flow. But, Corollary 1.3 of [Reference Berndt and Suh3] states that there are no real hypersurfaces with isometric Reeb flow in the odd-dimensional complex quadric
![]() $Q^{2k+1}$
for each
$Q^{2k+1}$
for each
![]() $k\ge 1$
. As desired, we get a contradiction.
$k\ge 1$
. As desired, we get a contradiction.
Next, we continue with the discussions for
![]() $m\geq 4$
.
$m\geq 4$
.
For
![]() $3\leq p,s\leq m$
and
$3\leq p,s\leq m$
and
![]() $p\neq s$
, taking in (3.7),
$p\neq s$
, taking in (3.7),
 $$ \begin{align*} (W,X,Y,Z)=&(e_{2p-3},e_1,e_2,e_{2s-3}),\ (e_{2p-3},e_1,e_2,e_{2s-2}),\\ &(e_{2p-2},e_1,e_2,e_{2s-3}),\ (e_{2p-2},e_1,e_2,e_{2s-2}), \end{align*} $$
$$ \begin{align*} (W,X,Y,Z)=&(e_{2p-3},e_1,e_2,e_{2s-3}),\ (e_{2p-3},e_1,e_2,e_{2s-2}),\\ &(e_{2p-2},e_1,e_2,e_{2s-3}),\ (e_{2p-2},e_1,e_2,e_{2s-2}), \end{align*} $$
respectively, we obtain
From the above calculations, we see that
![]() $Se_i=a_{ii}e_i,\ 1\le i\le 2m-1$
, and
$Se_i=a_{ii}e_i,\ 1\le i\le 2m-1$
, and
![]() $a_{11}=\cdots =a_{2m-1,2m-1}$
. Hence, M is totally umbilical and
$a_{11}=\cdots =a_{2m-1,2m-1}$
. Hence, M is totally umbilical and
![]() $S\phi =\phi S$
holds, so M has isometric Reeb flow. But, according to Theorem 1.1 and Proposition 4.1 of Berndt and Suh [Reference Berndt and Suh3], there are no totally umbilical real hypersurfaces with isometric Reeb flow in the complex quadric
$S\phi =\phi S$
holds, so M has isometric Reeb flow. But, according to Theorem 1.1 and Proposition 4.1 of Berndt and Suh [Reference Berndt and Suh3], there are no totally umbilical real hypersurfaces with isometric Reeb flow in the complex quadric
![]() $Q^m\ (m\geq 4)$
. This gives again a contradiction.
$Q^m\ (m\geq 4)$
. This gives again a contradiction.
From the above contradictions, we have completed the proof of Lemma 4.1. ▪
Remark 4.1 Our proof of Lemma 4.1 strongly depends on the results of [Reference Berndt and Suh3]. In Theorem 1.1 of [Reference Berndt and Suh3], Berndt and Suh classified real hypersurfaces with isometric Reeb flow in the complex quadrics
![]() $Q^m\ (m\ge 3)$
. Moreover, in Proposition 4.1 of [Reference Berndt and Suh3], the authors calculated the geometric invariants of all real hypersurfaces with isometric Reeb flow in the complex quadrics
$Q^m\ (m\ge 3)$
. Moreover, in Proposition 4.1 of [Reference Berndt and Suh3], the authors calculated the geometric invariants of all real hypersurfaces with isometric Reeb flow in the complex quadrics
![]() $Q^{2k}\ (k\ge 2)$
, showing that each of such real hypersurfaces has at least three distinct principal curvatures. Very recently, Hu and Yin [Reference Hu and Yin10] obtained new characterizations of the real hypersurfaces with isometric Reeb flow in the complex quadric.
$Q^{2k}\ (k\ge 2)$
, showing that each of such real hypersurfaces has at least three distinct principal curvatures. Very recently, Hu and Yin [Reference Hu and Yin10] obtained new characterizations of the real hypersurfaces with isometric Reeb flow in the complex quadric.
Now, by Lemma 4.1, the unit normal vector field N of the conformally flat real hypersurface M is
![]() $\mathfrak {A}$
-principal everywhere. According to Lemma 2.3, there exists an almost product structure
$\mathfrak {A}$
-principal everywhere. According to Lemma 2.3, there exists an almost product structure
![]() $A\in \mathfrak {A}$
such that
$A\in \mathfrak {A}$
such that
![]() $AN=N$
and
$AN=N$
and
![]() $A\xi =-\xi $
. Thus, we have
$A\xi =-\xi $
. Thus, we have
![]() $T\xi =-\xi $
and
$T\xi =-\xi $
and
![]() $\mu (X)=g(AX,N)=0$
for any
$\mu (X)=g(AX,N)=0$
for any
![]() $X\in TM$
.
$X\in TM$
.
Put
![]() $e_{2m-1}=\xi $
. From (2.1) and that
$e_{2m-1}=\xi $
. From (2.1) and that
![]() $\dim {\mathcal {Q}}=2m-2$
, we can choose unit tangent vector fields
$\dim {\mathcal {Q}}=2m-2$
, we can choose unit tangent vector fields
so that
![]() $\{e_i\}_{i=1}^{2m-1}$
forms a local orthonormal frame field of M with the following properties:
$\{e_i\}_{i=1}^{2m-1}$
forms a local orthonormal frame field of M with the following properties:
Put again
 $Se_i=\sum _{j=1}^{2m-1}a_{ij}e_j$
, where
$Se_i=\sum _{j=1}^{2m-1}a_{ij}e_j$
, where
![]() $a_{ij}=a_{ji}$
,
$a_{ij}=a_{ji}$
,
![]() $1\leq i,j\leq 2m-1$
.
$1\leq i,j\leq 2m-1$
.
Now, we apply for Lemma 3.2 with
![]() $A\in \mathfrak {A}$
being chosen as above.
$A\in \mathfrak {A}$
being chosen as above.
By choosing appropriate
![]() $W=e_i,\, X=e_j,\, Y=e_k,\, Z=e_l$
,
$W=e_i,\, X=e_j,\, Y=e_k,\, Z=e_l$
,
![]() $1\leq i,j,k,l\leq 2m-1$
, with the use of (2.4), (4.11),
$1\leq i,j,k,l\leq 2m-1$
, with the use of (2.4), (4.11),
![]() $T\xi =-\xi $
, and that
$T\xi =-\xi $
, and that
![]() $\mu (X)=0$
, for any
$\mu (X)=0$
, for any
![]() $X\in TM$
, we can calculate
$X\in TM$
, we can calculate
![]() $\mathbf {I}(W,X,Y,Z)$
and
$\mathbf {I}(W,X,Y,Z)$
and
![]() $\mathbf {II}(W,X,Y,Z)$
directly. Then, by (3.7), we will obtain a system of linear equations of the components
$\mathbf {II}(W,X,Y,Z)$
directly. Then, by (3.7), we will obtain a system of linear equations of the components
![]() $\{a_{ij}\}$
. The procedure is essentially totally similar to that in the proof of Lemma 4.1. Thus, for simplicity, most of the detailed calculations below will be omitted.
$\{a_{ij}\}$
. The procedure is essentially totally similar to that in the proof of Lemma 4.1. Thus, for simplicity, most of the detailed calculations below will be omitted.
For
![]() $2\leq p,s\leq m$
and
$2\leq p,s\leq m$
and
![]() $p\neq s$
, taking in (3.7),
$p\neq s$
, taking in (3.7),
respectively, we can obtain
It follows that
![]() $S\xi =a_{{2m-1},{2m-1}} \xi $
, and therefore, M is a Hopf hypersurface such that its unit normal vector field is
$S\xi =a_{{2m-1},{2m-1}} \xi $
, and therefore, M is a Hopf hypersurface such that its unit normal vector field is
![]() $\mathfrak {A}$
-principal everywhere. Then, we can apply for Theorem 14 of [Reference Loo17] or Theorem 2 of [Reference Lee and Suh15] to obtain that M is an open part of a tube around a totally geodesic
$\mathfrak {A}$
-principal everywhere. Then, we can apply for Theorem 14 of [Reference Loo17] or Theorem 2 of [Reference Lee and Suh15] to obtain that M is an open part of a tube around a totally geodesic
![]() $Q^{m-1}\hookrightarrow Q^m$
. Thus, by Proposition 4.1 of [Reference Berndt and Suh2], we have
$Q^{m-1}\hookrightarrow Q^m$
. Thus, by Proposition 4.1 of [Reference Berndt and Suh2], we have
 $$ \begin{align*}Se_{2p-3}=-\frac{2}{\alpha}e_{2p-3},\ \ Se_{2p-2}=0, \ \ S\xi=\alpha \xi,\ \ \text{for all}\ 2\leq p\leq m. \end{align*} $$
$$ \begin{align*}Se_{2p-3}=-\frac{2}{\alpha}e_{2p-3},\ \ Se_{2p-2}=0, \ \ S\xi=\alpha \xi,\ \ \text{for all}\ 2\leq p\leq m. \end{align*} $$
Finally, letting
![]() $(W,X,Y,Z)=(e_3,e_2,e_4,e_1)$
, by direct calculations, we have
$(W,X,Y,Z)=(e_3,e_2,e_4,e_1)$
, by direct calculations, we have
 $$ \begin{align*} \left\{ \begin{aligned} &\mathbf{I}(e_3,e_2,e_4,e_1)=-\frac{4}{\alpha},\ \ \mathbf{I}(e_2,e_4,e_3,e_1)= \mathbf{I}(e_4,e_3,e_2,e_1)=0;\\ &\mathbf{II}(e_3,e_2,e_4,e_1)=\mathbf{II}(e_2,e_4,e_3,e_1)= \mathbf{II}(e_4,e_3,e_2,e_1)=0. \end{aligned}\right. \end{align*} $$
$$ \begin{align*} \left\{ \begin{aligned} &\mathbf{I}(e_3,e_2,e_4,e_1)=-\frac{4}{\alpha},\ \ \mathbf{I}(e_2,e_4,e_3,e_1)= \mathbf{I}(e_4,e_3,e_2,e_1)=0;\\ &\mathbf{II}(e_3,e_2,e_4,e_1)=\mathbf{II}(e_2,e_4,e_3,e_1)= \mathbf{II}(e_4,e_3,e_2,e_1)=0. \end{aligned}\right. \end{align*} $$
It then follows from (3.7) that
 $\frac {4}{\alpha }=0$
. This is a contradiction, by which we have completed the proof of Theorem 1.1 for the complex quadric
$\frac {4}{\alpha }=0$
. This is a contradiction, by which we have completed the proof of Theorem 1.1 for the complex quadric
![]() $Q^m\ (m\ge 3)$
.
$Q^m\ (m\ge 3)$
.
Corollary 4.1 The complex quadric
![]() $Q^m\ (m\geq 3)$
does not admit real hypersurface of constant sectional curvature.
$Q^m\ (m\geq 3)$
does not admit real hypersurface of constant sectional curvature.
Remark 4.2 Corollary 4.1 follows also from Theorem 21 of [Reference Loo17], where it was shown that the complex quadric
![]() $Q^m\ (m\geq 3)$
admits no Einstein real hypersurfaces.
$Q^m\ (m\geq 3)$
admits no Einstein real hypersurfaces.
5 Proof of Theorem 1.1 for
 $Q^{m*}$
$Q^{m*}$
To begin, we first note that, like the complex quadric
![]() $Q^{m}$
, the set
$Q^{m}$
, the set
![]() $\mathfrak {A}$
of all almost product structures of
$\mathfrak {A}$
of all almost product structures of
![]() $Q^{m\ast }$
is also an
$Q^{m\ast }$
is also an
![]() $S^1$
-sub-bundle of the endomorphism bundle End(
$S^1$
-sub-bundle of the endomorphism bundle End(
![]() $TQ^{m*}$
), and there are also two types of singular tangent vectors for the complex hyperbolic quadric
$TQ^{m*}$
), and there are also two types of singular tangent vectors for the complex hyperbolic quadric
![]() $Q^{m*}$
:
$Q^{m*}$
:
![]() $\mathfrak {A}$
-principal and
$\mathfrak {A}$
-principal and
![]() $\mathfrak {A}$
-isotropic.
$\mathfrak {A}$
-isotropic.
Now, suppose on the contrary that the complex hyperbolic quadric
![]() $Q^{m\ast }\ (m\geq 3)$
admits a conformally flat real hypersurface
$Q^{m\ast }\ (m\geq 3)$
admits a conformally flat real hypersurface
![]() $\bar {M}$
, with N and S a unit normal vector field and the shape operator, respectively, and g and
$\bar {M}$
, with N and S a unit normal vector field and the shape operator, respectively, and g and
![]() $\nabla $
be the induced metric and the corresponding Levi–Civita connection on
$\nabla $
be the induced metric and the corresponding Levi–Civita connection on
![]() $\bar {M}$
, respectively. Then, there is also naturally an almost contact structure
$\bar {M}$
, respectively. Then, there is also naturally an almost contact structure
![]() $\{\phi ,\xi ,\eta \}$
, a type
$\{\phi ,\xi ,\eta \}$
, a type
![]() $(1,1)$
tensor field T, and a
$(1,1)$
tensor field T, and a
![]() $1$
-form
$1$
-form
![]() $\mu $
induced from a generic almost product structure
$\mu $
induced from a generic almost product structure
![]() $A\in \mathfrak {A}$
on
$A\in \mathfrak {A}$
on
![]() $\bar {M}$
.
$\bar {M}$
.
In the following, we outline the proof in three steps, which are essentially the same as the proof of Theorem 1.1 for
![]() $Q^m\ (m\ge 3)$
.
$Q^m\ (m\ge 3)$
.
Step 1. The real hypersurface
![]() $\bar {M}$
in
$\bar {M}$
in
![]() $Q^{m\ast }\ (m\geq 3)$
satisfies equation (3.7).
$Q^{m\ast }\ (m\geq 3)$
satisfies equation (3.7).
As mentioned in the introduction, the almost product structure A and the Kähler structure J of
![]() $Q^{m\ast }$
also satisfy (2.1) and (2.2) (see [Reference Klein and Suh13, Reference Suh25, Reference Suh, Pérez and Woo27, Reference Van der Veken and Wijffels28]), and it makes the tensors
$Q^{m\ast }$
also satisfy (2.1) and (2.2) (see [Reference Klein and Suh13, Reference Suh25, Reference Suh, Pérez and Woo27, Reference Van der Veken and Wijffels28]), and it makes the tensors
![]() $\phi ,T,\mu $
, and
$\phi ,T,\mu $
, and
![]() $\eta $
on
$\eta $
on
![]() $\bar {M}$
also satisfy the equations (2.7)–(2.11) in Lemma 2.2. Because the Riemannian curvature tensor of
$\bar {M}$
also satisfy the equations (2.7)–(2.11) in Lemma 2.2. Because the Riemannian curvature tensor of
![]() $Q^{m\ast }$
is exactly opposite to the Riemannian curvature tensor of
$Q^{m\ast }$
is exactly opposite to the Riemannian curvature tensor of
![]() $Q^m$
, it makes both the Gauss–Codazzi equations and the Ricci tensor of
$Q^m$
, it makes both the Gauss–Codazzi equations and the Ricci tensor of
![]() $\bar {M}$
a slightly different from (2.12)–(2.14): some terms change at most by negative signs. However, when we apply for the Tsinghua principle with
$\bar {M}$
a slightly different from (2.12)–(2.14): some terms change at most by negative signs. However, when we apply for the Tsinghua principle with
![]() $\bar {M}$
, following the same discussions as in Section 3, we see that Lemma 3.2 still holds for conformally flat real hypersurfaces in
$\bar {M}$
, following the same discussions as in Section 3, we see that Lemma 3.2 still holds for conformally flat real hypersurfaces in
![]() $Q^{m\ast }\ (m\geq 3)$
.
$Q^{m\ast }\ (m\geq 3)$
.
Step 2. The unit normal vector field of
![]() $\bar {M}$
must be
$\bar {M}$
must be
![]() $\mathfrak {A}$
-principal everywhere.
$\mathfrak {A}$
-principal everywhere.
In fact, if otherwise, the unit normal vector field N is assumed locally not
![]() $\mathfrak {A}$
-principal. By Lemma 3.2 of [Reference Suh25], there exists an almost product structure
$\mathfrak {A}$
-principal. By Lemma 3.2 of [Reference Suh25], there exists an almost product structure
![]() $A\in \mathfrak {A}$
in local such that
$A\in \mathfrak {A}$
in local such that
![]() $A\xi \in T\bar {M}$
and
$A\xi \in T\bar {M}$
and
![]() $\mu (\xi )=g(A\xi ,N)=0$
. Similarly, we can also choose a local frame field
$\mu (\xi )=g(A\xi ,N)=0$
. Similarly, we can also choose a local frame field
![]() $\{e_i\}_{i=1}^{2m-1}$
of
$\{e_i\}_{i=1}^{2m-1}$
of
![]() $\bar {M}$
satisfying equations (4.1) and (4.2) as in the proof of Lemma 4.1. Then, following the same calculations as in the proof of Lemma 4.1, we can show that
$\bar {M}$
satisfying equations (4.1) and (4.2) as in the proof of Lemma 4.1. Then, following the same calculations as in the proof of Lemma 4.1, we can show that
![]() $\bar {M}$
is totally umbilical and
$\bar {M}$
is totally umbilical and
![]() $S\phi =\phi S$
holds. Thus,
$S\phi =\phi S$
holds. Thus,
![]() $\bar {M}$
has isometric Reeb flow. But, according to Theorem 1.1 and Proposition 4.1 of Suh [Reference Suh25], there are no totally umbilical real hypersurfaces with isometric Reeb flow in the complex hyperbolic quadric
$\bar {M}$
has isometric Reeb flow. But, according to Theorem 1.1 and Proposition 4.1 of Suh [Reference Suh25], there are no totally umbilical real hypersurfaces with isometric Reeb flow in the complex hyperbolic quadric
![]() $Q^{m\ast }\ (m\geq 3)$
. This gives a contradiction.
$Q^{m\ast }\ (m\geq 3)$
. This gives a contradiction.
Step 3. The unit normal vector field of
![]() $\bar {M}$
cannot be
$\bar {M}$
cannot be
![]() $\mathfrak {A}$
-principal everywhere.
$\mathfrak {A}$
-principal everywhere.
In fact, if the unit normal vector field N is
![]() $\mathfrak {A}$
-principal, there exists an almost product structure
$\mathfrak {A}$
-principal, there exists an almost product structure
![]() $A\in \mathfrak {A}$
such that
$A\in \mathfrak {A}$
such that
![]() $AN=N$
and
$AN=N$
and
![]() $A\xi =-\xi $
. We can find a local frame field
$A\xi =-\xi $
. We can find a local frame field
![]() $\{e_i\}_{i=1}^{2m-1}$
(
$\{e_i\}_{i=1}^{2m-1}$
(
![]() $e_{2m-1}=\xi $
) of
$e_{2m-1}=\xi $
) of
![]() $\bar {M}$
satisfying the same equations as (4.11). Then, by similar calculations as taking in (3.7),
$\bar {M}$
satisfying the same equations as (4.11). Then, by similar calculations as taking in (3.7),
for
![]() $2\leq p,s\leq m$
and
$2\leq p,s\leq m$
and
![]() $p\neq s$
, respectively, we can show that
$p\neq s$
, respectively, we can show that
![]() $S\xi =\alpha \xi $
. Therefore,
$S\xi =\alpha \xi $
. Therefore,
![]() $\bar {M}$
is a Hopf hypersurface such that the unit normal vector field is
$\bar {M}$
is a Hopf hypersurface such that the unit normal vector field is
![]() $\mathfrak {A}$
-principal everywhere. Then, according to Lemma 4.2 (ii) of [Reference Suh, Pérez and Woo27], by choosing the almost product structure
$\mathfrak {A}$
-principal everywhere. Then, according to Lemma 4.2 (ii) of [Reference Suh, Pérez and Woo27], by choosing the almost product structure
![]() $A\in \mathfrak {A}$
such that
$A\in \mathfrak {A}$
such that
![]() $AN=N$
, it holds
$AN=N$
, it holds
![]() $ASX=SX$
for any
$ASX=SX$
for any
![]() $X\in \mathcal {C}$
.
$X\in \mathcal {C}$
.
As
![]() $\bar {M}$
is a Hopf hypersurface with
$\bar {M}$
is a Hopf hypersurface with
![]() $\mathfrak {A}$
-principal unit normal vector field, the above fact implies that
$\mathfrak {A}$
-principal unit normal vector field, the above fact implies that
![]() $SAX=SX$
for all
$SAX=SX$
for all
![]() $X\in \mathcal {C}$
. It follows that
$X\in \mathcal {C}$
. It follows that
![]() $S\mathcal {Q}(-1)=0$
, where
$S\mathcal {Q}(-1)=0$
, where
![]() $\mathcal {Q}(-1)$
is the eigenspace of
$\mathcal {Q}(-1)$
is the eigenspace of
![]() $A|_{\mathcal {C}}$
corresponding to the eigenvalue
$A|_{\mathcal {C}}$
corresponding to the eigenvalue
![]() $-1$
. Then, for any
$-1$
. Then, for any
![]() $X\in \mathcal {Q}(-1)$
, Lemma 3.4 of [Reference Suh, Pérez and Woo27] shows that
$X\in \mathcal {Q}(-1)$
, Lemma 3.4 of [Reference Suh, Pérez and Woo27] shows that
![]() $\alpha S\phi X=2\phi X$
. It follows that
$\alpha S\phi X=2\phi X$
. It follows that
![]() $\alpha \not =0$
and
$\alpha \not =0$
and
 $SX=\frac {2}{\alpha }X$
for all
$SX=\frac {2}{\alpha }X$
for all
![]() $X\in \mathcal {Q}(1)=J\mathcal {Q}(-1)$
. Thus, we have
$X\in \mathcal {Q}(1)=J\mathcal {Q}(-1)$
. Thus, we have
 $$ \begin{align*}Se_{2p-3}=\frac{2}{\alpha}e_{2p-3},\ \ Se_{2p-2}=0, \ \ S\xi=\alpha \xi,\ \ \text{for all}\ 2\leq p\leq m. \end{align*} $$
$$ \begin{align*}Se_{2p-3}=\frac{2}{\alpha}e_{2p-3},\ \ Se_{2p-2}=0, \ \ S\xi=\alpha \xi,\ \ \text{for all}\ 2\leq p\leq m. \end{align*} $$
Finally, taking
![]() $(W,X,Y,Z)=(e_3,e_2,e_4,e_1)$
in (3.7), by direct calculations, we have
$(W,X,Y,Z)=(e_3,e_2,e_4,e_1)$
in (3.7), by direct calculations, we have
 $\frac {4}{\alpha }=0$
. This is a contradiction.
$\frac {4}{\alpha }=0$
. This is a contradiction.
In summary, we have completed the proof of Theorem 1.1 for
![]() $Q^{m*}\ (m\ge 3)$
.
$Q^{m*}\ (m\ge 3)$
.
Corollary 5.1 The complex hyperbolic quadric
![]() $Q^{m\ast }\ (m\geq 3)$
does not admit real hypersurface of constant sectional curvature.
$Q^{m\ast }\ (m\geq 3)$
does not admit real hypersurface of constant sectional curvature.
Acknowledgment
We would like to express our sincere gratitude for the referee for his/her valuable comments, which impel us to have modified the original version, so that Theorem 1.1 includes the statement that the complex hyperbolic quadric
![]() $Q^{m\ast }$
does not admit any locally conformally flat real hypersurfaces for
$Q^{m\ast }$
does not admit any locally conformally flat real hypersurfaces for
![]() $m\ge 3$
.
$m\ge 3$
.