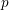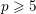1 Introduction
Building upon the work of Pappas and Zhu [Reference Pappas and ZhuPZ13], Levin defines in [Reference LevinLev16] candidates for parahoric local models of Shimura varieties for reductive groups of the form ![]() $\operatorname{Res}_{K/F}(G_{0})$ where
$\operatorname{Res}_{K/F}(G_{0})$ where ![]() $G_{0}$ splits over a tamely ramified extension of
$G_{0}$ splits over a tamely ramified extension of ![]() $K$, and
$K$, and ![]() $K/F$ is a finite (possibly wildly ramified) extension. The present paper is a follow-up of [Reference Haines and RicharzHR18], in which we prove the test function conjecture for these local models. The method follows closely [Reference Haines and RicharzHR18], and we only explain new arguments in detail, but repeat as much as necessary for the sake of readability. For a detailed introduction and further references we refer the reader to the introduction of [Reference Haines and RicharzHR18].
$K/F$ is a finite (possibly wildly ramified) extension. The present paper is a follow-up of [Reference Haines and RicharzHR18], in which we prove the test function conjecture for these local models. The method follows closely [Reference Haines and RicharzHR18], and we only explain new arguments in detail, but repeat as much as necessary for the sake of readability. For a detailed introduction and further references we refer the reader to the introduction of [Reference Haines and RicharzHR18].
Let us mention that the paper is supplemented in § 3 by a general study of relative affine Grassmannians and loop groups formed using a general Cartier divisor as in the work of Beilinson and Drinfeld [Reference Beilinson and DrinfeldBD99]. This unifies the frameworks of [Reference Pappas and ZhuPZ13, Reference LevinLev16] in mixed characteristic, of [Reference HeinlothHei10, Reference ZhuZhu14, Reference ZhuZhu15, Reference RicharzRic16b] in equal characteristic, and of [Reference Fedorov and PaninFP15, Reference FedorovFed16] on the Grothendieck–Serre conjecture; cf. Examples 3.1 below. As an application, we identify the torus fixed points and their attractor and repeller loci in the sense of Drinfeld [Reference DrinfeldDri13] (cf. also [Reference HesselinkHes81]) for these relative affine Grassmannians; cf. Theorem 3.17.
1.1 Formulation of the main result
Let ![]() $p$ be a prime number. Let
$p$ be a prime number. Let ![]() $F/\mathbb{Q}_{p}$ be a finite extension with residue field
$F/\mathbb{Q}_{p}$ be a finite extension with residue field ![]() $k_{F}$ of cardinality
$k_{F}$ of cardinality ![]() $q$. Let
$q$. Let ![]() $\bar{F}/F$ be a separable closure, and denote by
$\bar{F}/F$ be a separable closure, and denote by ![]() $\unicode[STIX]{x1D6E4}_{F}$ the Galois group with inertia subgroup
$\unicode[STIX]{x1D6E4}_{F}$ the Galois group with inertia subgroup ![]() $I_{F}$ and fixed geometric Frobenius lift
$I_{F}$ and fixed geometric Frobenius lift ![]() $\unicode[STIX]{x1D6F7}_{F}\in \unicode[STIX]{x1D6E4}_{F}$.
$\unicode[STIX]{x1D6F7}_{F}\in \unicode[STIX]{x1D6E4}_{F}$.
Let ![]() $K/F$ be a finite extension, and let
$K/F$ be a finite extension, and let ![]() $G_{0}$ be a (connected) reductive
$G_{0}$ be a (connected) reductive ![]() $K$-group which splits over a tamely ramified extension. We are interested in the group of Weil restrictions
$K$-group which splits over a tamely ramified extension. We are interested in the group of Weil restrictions ![]() $G=\operatorname{Res}_{K/F}(G_{0})$ which is a reductive
$G=\operatorname{Res}_{K/F}(G_{0})$ which is a reductive ![]() $F$-group but now possibly wildly ramified depending on
$F$-group but now possibly wildly ramified depending on ![]() $K/F$.
$K/F$.
Let ![]() ${\mathcal{G}}$ be a parahoric
${\mathcal{G}}$ be a parahoric ![]() ${\mathcal{O}}_{F}$-group scheme in the sense of Bruhat and Tits [Reference Bruhat and TitsBT84] with generic fiber
${\mathcal{O}}_{F}$-group scheme in the sense of Bruhat and Tits [Reference Bruhat and TitsBT84] with generic fiber ![]() $G$. Note that
$G$. Note that ![]() ${\mathcal{G}}=\operatorname{Res}_{{\mathcal{O}}_{K}/{\mathcal{O}}_{F}}({\mathcal{G}}_{0})$ for a unique parahoric
${\mathcal{G}}=\operatorname{Res}_{{\mathcal{O}}_{K}/{\mathcal{O}}_{F}}({\mathcal{G}}_{0})$ for a unique parahoric ![]() ${\mathcal{O}}_{K}$-group scheme
${\mathcal{O}}_{K}$-group scheme ![]() ${\mathcal{G}}_{0}$ with generic fiber
${\mathcal{G}}_{0}$ with generic fiber ![]() $G_{0}$; cf. Corollary 4.8. We fix
$G_{0}$; cf. Corollary 4.8. We fix ![]() $\{\unicode[STIX]{x1D707}\}$ a (not necessarily minuscule) conjugacy class of geometric cocharacters in
$\{\unicode[STIX]{x1D707}\}$ a (not necessarily minuscule) conjugacy class of geometric cocharacters in ![]() $G$ defined over a finite (separable) extension
$G$ defined over a finite (separable) extension ![]() $E/F$.
$E/F$.
Attached to the triple ![]() $(G,\{\unicode[STIX]{x1D707}\},{\mathcal{G}})$ is the (flat) local model
$(G,\{\unicode[STIX]{x1D707}\},{\mathcal{G}})$ is the (flat) local model
which is a flat projective ![]() ${\mathcal{O}}_{E}$-scheme; cf. [Reference Pappas and ZhuPZ13] if
${\mathcal{O}}_{E}$-scheme; cf. [Reference Pappas and ZhuPZ13] if ![]() $K=F$ and [Reference LevinLev16] for general
$K=F$ and [Reference LevinLev16] for general ![]() $K/F$ (cf. also Definition 4.18). The generic fiber
$K/F$ (cf. also Definition 4.18). The generic fiber ![]() $M_{\{\unicode[STIX]{x1D707}\},E}$ is naturally the Schubert variety in the affine Grassmannian of
$M_{\{\unicode[STIX]{x1D707}\},E}$ is naturally the Schubert variety in the affine Grassmannian of ![]() $G/E$ associated with the class
$G/E$ associated with the class ![]() $\{\unicode[STIX]{x1D707}\}$. The special fiber
$\{\unicode[STIX]{x1D707}\}$. The special fiber ![]() $M_{\{\unicode[STIX]{x1D707}\},k_{E}}$ is equidimensional, but neither irreducible nor a divisor with normal crossings in general.
$M_{\{\unicode[STIX]{x1D707}\},k_{E}}$ is equidimensional, but neither irreducible nor a divisor with normal crossings in general.
Fix a prime number ![]() $\ell \not =p$, and fix
$\ell \not =p$, and fix ![]() in order to define half Tate twists. Let
in order to define half Tate twists. Let ![]() $d_{\unicode[STIX]{x1D707}}$ be the dimension of the generic fiber
$d_{\unicode[STIX]{x1D707}}$ be the dimension of the generic fiber ![]() $M_{\{\unicode[STIX]{x1D707}\},E}$, and denote the normalized intersection complex by
$M_{\{\unicode[STIX]{x1D707}\},E}$, and denote the normalized intersection complex by
cf. § 5.2.1. Under the geometric Satake equivalence [Reference GinzburgGin95, Reference LusztigLus83, Reference Beilinson and DrinfeldBD99, Reference Mirković and VilonenMV07, Reference RicharzRic14, Reference Richarz and ZhuRZ15, Reference ZhuZhu17], the complex ![]() $\operatorname{IC}_{\{\unicode[STIX]{x1D707}\}}$ corresponds to the
$\operatorname{IC}_{\{\unicode[STIX]{x1D707}\}}$ corresponds to the ![]() $^{L}G_{E}=G^{\vee }\rtimes \unicode[STIX]{x1D6E4}_{E}$-representation
$^{L}G_{E}=G^{\vee }\rtimes \unicode[STIX]{x1D6E4}_{E}$-representation ![]() $V_{\{\unicode[STIX]{x1D707}\}}$ of highest weight
$V_{\{\unicode[STIX]{x1D707}\}}$ of highest weight ![]() $\{\unicode[STIX]{x1D707}\}$ defined in [Reference Haines, Diamond, Kassaei and KimHai14, 6.1]; cf. [Reference Haines and RicharzHR18, Corollary 3.12]. Note that we have
$\{\unicode[STIX]{x1D707}\}$ defined in [Reference Haines, Diamond, Kassaei and KimHai14, 6.1]; cf. [Reference Haines and RicharzHR18, Corollary 3.12]. Note that we have ![]() $G^{\vee }=\operatorname{Ind}_{\unicode[STIX]{x1D6E4}_{K}}^{\unicode[STIX]{x1D6E4}_{F}}(G_{0}^{\vee })$ as groups over
$G^{\vee }=\operatorname{Ind}_{\unicode[STIX]{x1D6E4}_{K}}^{\unicode[STIX]{x1D6E4}_{F}}(G_{0}^{\vee })$ as groups over ![]() $\bar{\mathbb{Q}}_{\ell }$ under which
$\bar{\mathbb{Q}}_{\ell }$ under which ![]() $V_{\{\unicode[STIX]{x1D707}\}}=\boxtimes _{\unicode[STIX]{x1D713}}V_{\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D713}}}$; cf. Lemma 5.6.
$V_{\{\unicode[STIX]{x1D707}\}}=\boxtimes _{\unicode[STIX]{x1D713}}V_{\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D713}}}$; cf. Lemma 5.6.
Let ![]() $E_{0}/F$ be the maximal unramified subextension of
$E_{0}/F$ be the maximal unramified subextension of ![]() $E/F$, and let
$E/F$, and let ![]() $\unicode[STIX]{x1D6F7}_{E}=\unicode[STIX]{x1D6F7}_{E_{0}}=\unicode[STIX]{x1D6F7}_{F}^{[E_{0}:F]}$ and
$\unicode[STIX]{x1D6F7}_{E}=\unicode[STIX]{x1D6F7}_{E_{0}}=\unicode[STIX]{x1D6F7}_{F}^{[E_{0}:F]}$ and ![]() $q_{E}=q_{E_{0}}=q^{[E_{0}:F]}$. The semisimple trace of Frobenius function on the sheaf of nearby cycles
$q_{E}=q_{E_{0}}=q^{[E_{0}:F]}$. The semisimple trace of Frobenius function on the sheaf of nearby cycles
is naturally a function in the center ![]() ${\mathcal{Z}}(G(E_{0}),{\mathcal{G}}({\mathcal{O}}_{E_{0}}))$ of the parahoric Hecke algebra; cf. [Reference Pappas and ZhuPZ13, Theorem 10.14], [Reference LevinLev16, Theorem 5.3.3] and § 6.3. We remark that
${\mathcal{Z}}(G(E_{0}),{\mathcal{G}}({\mathcal{O}}_{E_{0}}))$ of the parahoric Hecke algebra; cf. [Reference Pappas and ZhuPZ13, Theorem 10.14], [Reference LevinLev16, Theorem 5.3.3] and § 6.3. We remark that ![]() $\unicode[STIX]{x1D70F}_{\{\unicode[STIX]{x1D707}\}}^{\text{ss}}$ lives in the center of the
$\unicode[STIX]{x1D70F}_{\{\unicode[STIX]{x1D707}\}}^{\text{ss}}$ lives in the center of the ![]() $\bar{\mathbb{Q}}_{\ell }$-valued Hecke algebra attached to function field analogues of
$\bar{\mathbb{Q}}_{\ell }$-valued Hecke algebra attached to function field analogues of ![]() $(G_{E_{0}},{\mathcal{G}}_{{\mathcal{O}}_{E_{0}}},E_{0})$; we are implicitly identifying this with
$(G_{E_{0}},{\mathcal{G}}_{{\mathcal{O}}_{E_{0}}},E_{0})$; we are implicitly identifying this with ![]() ${\mathcal{Z}}(G(E_{0}),{\mathcal{G}}({\mathcal{O}}_{E_{0}}))$ via Lemma 4.12.
${\mathcal{Z}}(G(E_{0}),{\mathcal{G}}({\mathcal{O}}_{E_{0}}))$ via Lemma 4.12.
Our main result, the test function conjecture for local models for Weil-restricted groups, characterizes the function ![]() $\unicode[STIX]{x1D70F}_{\{\unicode[STIX]{x1D707}\}}^{\operatorname{ss}}$, extending the main result of [Reference Haines and RicharzHR18] to the Weil-restricted situation. It confirms that even for these local models, the local geometry of Shimura varieties at places of parahoric bad reduction can be related to automorphic-type data, as required by the Langlands–Kottwitz method.
$\unicode[STIX]{x1D70F}_{\{\unicode[STIX]{x1D707}\}}^{\operatorname{ss}}$, extending the main result of [Reference Haines and RicharzHR18] to the Weil-restricted situation. It confirms that even for these local models, the local geometry of Shimura varieties at places of parahoric bad reduction can be related to automorphic-type data, as required by the Langlands–Kottwitz method.
Main Theorem. Let ![]() $(G,\{\unicode[STIX]{x1D707}\},{\mathcal{G}})$ be a triple as above. Let
$(G,\{\unicode[STIX]{x1D707}\},{\mathcal{G}})$ be a triple as above. Let ![]() $E/F$ be a finite separable extension over which
$E/F$ be a finite separable extension over which ![]() $\{\unicode[STIX]{x1D707}\}$ is defined, and let
$\{\unicode[STIX]{x1D707}\}$ is defined, and let ![]() $E_{0}/F$ be the maximal unramified subextension. Then
$E_{0}/F$ be the maximal unramified subextension. Then
where ![]() $z_{\{\unicode[STIX]{x1D707}\}}^{\text{ss}}=z_{{\mathcal{G}},\{\unicode[STIX]{x1D707}\}}^{\text{ss}}\in {\mathcal{Z}}(G(E_{0}),{\mathcal{G}}({\mathcal{O}}_{E_{0}}))$ is the unique function which acts on any
$z_{\{\unicode[STIX]{x1D707}\}}^{\text{ss}}=z_{{\mathcal{G}},\{\unicode[STIX]{x1D707}\}}^{\text{ss}}\in {\mathcal{Z}}(G(E_{0}),{\mathcal{G}}({\mathcal{O}}_{E_{0}}))$ is the unique function which acts on any ![]() ${\mathcal{G}}({\mathcal{O}}_{E_{0}})$-spherical smooth irreducible
${\mathcal{G}}({\mathcal{O}}_{E_{0}})$-spherical smooth irreducible ![]() $\bar{\mathbb{Q}}_{\ell }$-representation
$\bar{\mathbb{Q}}_{\ell }$-representation ![]() $\unicode[STIX]{x1D70B}$ by the scalar
$\unicode[STIX]{x1D70B}$ by the scalar
where ![]() $s(\unicode[STIX]{x1D70B})\in [(G^{\vee })^{I_{E_{0}}}\rtimes \unicode[STIX]{x1D6F7}_{E_{0}}]_{\operatorname{ss}}/(G^{\vee })^{I_{E_{0}}}$ is the Satake parameter for
$s(\unicode[STIX]{x1D70B})\in [(G^{\vee })^{I_{E_{0}}}\rtimes \unicode[STIX]{x1D6F7}_{E_{0}}]_{\operatorname{ss}}/(G^{\vee })^{I_{E_{0}}}$ is the Satake parameter for ![]() $\unicode[STIX]{x1D70B}$ [Reference HainesHai15]. The function
$\unicode[STIX]{x1D70B}$ [Reference HainesHai15]. The function ![]() $q_{E_{0}}^{d_{\unicode[STIX]{x1D707}}/2}\unicode[STIX]{x1D70F}_{\{\unicode[STIX]{x1D707}\}}^{\operatorname{ss}}$ takes values in
$q_{E_{0}}^{d_{\unicode[STIX]{x1D707}}/2}\unicode[STIX]{x1D70F}_{\{\unicode[STIX]{x1D707}\}}^{\operatorname{ss}}$ takes values in ![]() $\mathbb{Z}$ and is independent of
$\mathbb{Z}$ and is independent of ![]() $\ell \neq p$ and
$\ell \neq p$ and ![]() $q^{1/2}\in \bar{\mathbb{Q}}_{\ell }$.
$q^{1/2}\in \bar{\mathbb{Q}}_{\ell }$.
The construction of ![]() $s(\unicode[STIX]{x1D70B})$ is also reviewed in [Reference Haines and RicharzHR18, § 7.2], and the values of
$s(\unicode[STIX]{x1D70B})$ is also reviewed in [Reference Haines and RicharzHR18, § 7.2], and the values of ![]() $z_{\{\unicode[STIX]{x1D707}\}}^{\text{ss}}$ are studied in [Reference Haines and RicharzHR18, § 7.7]; cf. § 6.5. The definition of the local models
$z_{\{\unicode[STIX]{x1D707}\}}^{\text{ss}}$ are studied in [Reference Haines and RicharzHR18, § 7.7]; cf. § 6.5. The definition of the local models ![]() $M_{\{\unicode[STIX]{x1D707}\}}$ depends on certain auxiliary choices (cf. Remark 4.19), but the function
$M_{\{\unicode[STIX]{x1D707}\}}$ depends on certain auxiliary choices (cf. Remark 4.19), but the function ![]() $\unicode[STIX]{x1D70F}_{\{\unicode[STIX]{x1D707}\}}^{\text{ss}}$ depends canonically only on the data
$\unicode[STIX]{x1D70F}_{\{\unicode[STIX]{x1D707}\}}^{\text{ss}}$ depends canonically only on the data ![]() $(G,\{\unicode[STIX]{x1D707}\},{\mathcal{G}})$.
$(G,\{\unicode[STIX]{x1D707}\},{\mathcal{G}})$.
As an application of our main theorem we prove in § 7 the test function conjecture for (modified) local models attached to all groups and prime numbers ![]() $p\geqslant 5$. This relies on the fact that when
$p\geqslant 5$. This relies on the fact that when ![]() $p\geqslant 5$ any adjoint reductive
$p\geqslant 5$ any adjoint reductive ![]() $F$-group is isomorphic to a product of Weil restrictions of scalars of tamely ramified groups; cf. (7.1) below. In Theorem 6.7 and § 6.3 we also show that the variant of the main theorem holds, where semisimple traces are replaced by traces with respect to any fixed lift
$F$-group is isomorphic to a product of Weil restrictions of scalars of tamely ramified groups; cf. (7.1) below. In Theorem 6.7 and § 6.3 we also show that the variant of the main theorem holds, where semisimple traces are replaced by traces with respect to any fixed lift ![]() $\unicode[STIX]{x1D6F7}_{E}$ of geometric Frobenius.
$\unicode[STIX]{x1D6F7}_{E}$ of geometric Frobenius.
1.2 Other results
Our methods can be used to obtain results on the fixed point (respectively, attractor and repeller) locus of ![]() $\mathbb{G}_{m}$-actions on fusion Grassmannians (cf. Theorem A below), and the special fiber of local models (cf. Theorem B below).
$\mathbb{G}_{m}$-actions on fusion Grassmannians (cf. Theorem A below), and the special fiber of local models (cf. Theorem B below).
1.2.1 Fusion Grassmannians
Let ![]() $F$ be any field, and let
$F$ be any field, and let ![]() $G$ be a reductive
$G$ be a reductive ![]() $F$-group. For each
$F$-group. For each ![]() $n\geqslant 0$, there is the fusion Grassmannian
$n\geqslant 0$, there is the fusion Grassmannian ![]() $\operatorname{Gr}_{G,n}\rightarrow \mathbb{A}_{F}^{n}$ defined in [Reference Beilinson and DrinfeldBD99] which parametrizes isomorphism classes of
$\operatorname{Gr}_{G,n}\rightarrow \mathbb{A}_{F}^{n}$ defined in [Reference Beilinson and DrinfeldBD99] which parametrizes isomorphism classes of ![]() $G$-bundles on the affine line together with a trivialization away from
$G$-bundles on the affine line together with a trivialization away from ![]() $n$ points. Given a cocharacter
$n$ points. Given a cocharacter ![]() $\unicode[STIX]{x1D712}:\mathbb{G}_{m,F}\rightarrow G$, we obtain a fiberwise
$\unicode[STIX]{x1D712}:\mathbb{G}_{m,F}\rightarrow G$, we obtain a fiberwise ![]() $\mathbb{G}_{m}$-action on the family
$\mathbb{G}_{m}$-action on the family ![]() $\operatorname{Gr}_{G,n}\rightarrow \mathbb{A}_{F}^{n}$, and we are interested in determining the diagram on the fixed point ind-scheme and attractor (respectively, repeller) ind-scheme
$\operatorname{Gr}_{G,n}\rightarrow \mathbb{A}_{F}^{n}$, and we are interested in determining the diagram on the fixed point ind-scheme and attractor (respectively, repeller) ind-scheme
cf. (2.1). Let ![]() $M\subset G$ be the centralizer of
$M\subset G$ be the centralizer of ![]() $\unicode[STIX]{x1D712}$, which is a Levi subgroup. The dynamic method promulgated in [Reference Conrad, Gabber and PrasadCGP10] defines a pair of parabolic subgroups
$\unicode[STIX]{x1D712}$, which is a Levi subgroup. The dynamic method promulgated in [Reference Conrad, Gabber and PrasadCGP10] defines a pair of parabolic subgroups ![]() $(P^{+},P^{-})$ in
$(P^{+},P^{-})$ in ![]() $G$ such that
$G$ such that ![]() $P^{+}\,\cap \,P^{-}=M$; see the formulation of Theorem 3.17. The natural maps
$P^{+}\,\cap \,P^{-}=M$; see the formulation of Theorem 3.17. The natural maps ![]() $M\leftarrow P^{\pm }\rightarrow G$ induce maps of fusion Grassmannians
$M\leftarrow P^{\pm }\rightarrow G$ induce maps of fusion Grassmannians
An extension of the method used in the proof of [Reference Haines and RicharzHR18, Proposition 3.4] allows us to prove the following result.
Theorem A. For each ![]() $n\in \mathbb{Z}_{{\geqslant}0}$, there is a commutative diagram of
$n\in \mathbb{Z}_{{\geqslant}0}$, there is a commutative diagram of ![]() $\mathbb{A}_{F}^{n}$-ind-schemes
$\mathbb{A}_{F}^{n}$-ind-schemes

where the vertical maps are isomorphisms.
Theorem A is a special case of Theorem 3.17 which applies to general reductive group schemes over ![]() $\mathbb{A}_{F}^{n}$ which are not necessarily defined over
$\mathbb{A}_{F}^{n}$ which are not necessarily defined over ![]() $F$. Let us point out that [Reference Haines and RicharzHR18, Proposition 3.4] implies that Theorem A holds fiberwise. However, we do not know how to prove sufficiently good flatness properties of
$F$. Let us point out that [Reference Haines and RicharzHR18, Proposition 3.4] implies that Theorem A holds fiberwise. However, we do not know how to prove sufficiently good flatness properties of ![]() $\operatorname{Gr}_{G,n}\rightarrow \mathbb{A}_{F}^{n}$ in order to deduce the more general result from the fiberwise result.
$\operatorname{Gr}_{G,n}\rightarrow \mathbb{A}_{F}^{n}$ in order to deduce the more general result from the fiberwise result.
The tensor structure on the constant term functors in geometric Langlands is constructed in [Reference Beilinson and DrinfeldBD99, Reference Mirković and VilonenMV07]. In [Reference GaitsgoryGai07, Reference ReichRei12], it is explained how to use the nearby cycles to define the fusion structure used in the geometric Satake isomorphism. Theorem A together with [Reference RicharzRic19, Theorem 3.3] gives another way of constructing the tensor structure on the constant term functors, even without passing to the underlying reduced ind-schemes; cf. the proof of [Reference Haines and RicharzHR18, Theorem 3.16].
1.2.2 Special fibers of local models
As in [Reference Haines and RicharzHR18, § 6.3.1], we use the commutation of nearby cycles with constant terms to determine the irreducible components of the geometric special fiber ![]() $M_{\{\unicode[STIX]{x1D707}\},\bar{k}}$ of the local models. Recall that, by construction (cf. Definition 4.18), there is a closed embedding
$M_{\{\unicode[STIX]{x1D707}\},\bar{k}}$ of the local models. Recall that, by construction (cf. Definition 4.18), there is a closed embedding
where ![]() ${\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}$ is the (partial) affine flag variety attached to the function field analogue
${\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}$ is the (partial) affine flag variety attached to the function field analogue ![]() ${\mathcal{G}}^{\flat }/k_{F}[\![u]\!]$ of
${\mathcal{G}}^{\flat }/k_{F}[\![u]\!]$ of ![]() ${\mathcal{G}}/{\mathcal{O}}_{F}$; cf. Theorem 4.13 and Proposition 4.15(ii). As envisioned by Kottwitz and Rapoport, the geometric special fiber
${\mathcal{G}}/{\mathcal{O}}_{F}$; cf. Theorem 4.13 and Proposition 4.15(ii). As envisioned by Kottwitz and Rapoport, the geometric special fiber ![]() $M_{\{\unicode[STIX]{x1D707}\},\bar{k}}$ should be the union of the Schubert varieties
$M_{\{\unicode[STIX]{x1D707}\},\bar{k}}$ should be the union of the Schubert varieties ![]() ${\mathcal{F}}l_{{\mathcal{G}}^{\flat },\bar{k}}^{{\leqslant}w}\subset {\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat },\bar{k}}$ where
${\mathcal{F}}l_{{\mathcal{G}}^{\flat },\bar{k}}^{{\leqslant}w}\subset {\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat },\bar{k}}$ where ![]() $w$ ranges over the
$w$ ranges over the ![]() $\{\unicode[STIX]{x1D707}\}$-admissible set
$\{\unicode[STIX]{x1D707}\}$-admissible set ![]() $\operatorname{Adm}_{\{\unicode[STIX]{x1D707}\}}^{\mathbf{f}}\subset W_{\mathbf{f}}\backslash W/W_{\mathbf{f}}$ where
$\operatorname{Adm}_{\{\unicode[STIX]{x1D707}\}}^{\mathbf{f}}\subset W_{\mathbf{f}}\backslash W/W_{\mathbf{f}}$ where ![]() ${\mathcal{G}}={\mathcal{G}}_{\mathbf{f}}$ and
${\mathcal{G}}={\mathcal{G}}_{\mathbf{f}}$ and ![]() $W=W(G,F)$ denotes the Iwahori–Weyl group. Here we are identifying the Iwahori–Weyl groups attached to
$W=W(G,F)$ denotes the Iwahori–Weyl group. Here we are identifying the Iwahori–Weyl groups attached to ![]() $G/F$ and
$G/F$ and ![]() $G^{\flat }/k_{F}((u))$ by Lemma 4.11. The following result verifies their prediction; cf. Theorem 5.14.
$G^{\flat }/k_{F}((u))$ by Lemma 4.11. The following result verifies their prediction; cf. Theorem 5.14.
Theorem B. The smooth locus ![]() $(M_{\{\unicode[STIX]{x1D707}\}})^{\operatorname{sm}}$ is fiberwise dense in
$(M_{\{\unicode[STIX]{x1D707}\}})^{\operatorname{sm}}$ is fiberwise dense in ![]() $M_{\{\unicode[STIX]{x1D707}\}}$, and on reduced subschemes a union of the Schubert varieties
$M_{\{\unicode[STIX]{x1D707}\}}$, and on reduced subschemes a union of the Schubert varieties
In particular, the geometric special fiber ![]() $M_{\{\unicode[STIX]{x1D707}\},\bar{k}}$ is generically reduced.
$M_{\{\unicode[STIX]{x1D707}\},\bar{k}}$ is generically reduced.
If ![]() $p\nmid |\unicode[STIX]{x1D70B}_{1}(G_{\operatorname{der}})|$, then Theorem B is [Reference Pappas and ZhuPZ13, Theorem 9.3] for
$p\nmid |\unicode[STIX]{x1D70B}_{1}(G_{\operatorname{der}})|$, then Theorem B is [Reference Pappas and ZhuPZ13, Theorem 9.3] for ![]() $K=F$, and [Reference LevinLev16, Theorem 2.3.5] when
$K=F$, and [Reference LevinLev16, Theorem 2.3.5] when ![]() $K\neq F$. We have removed this condition on
$K\neq F$. We have removed this condition on ![]() $p$ and thereby conclude that the Kottwitz–Rapoport strata in the special fiber are enumerated by the
$p$ and thereby conclude that the Kottwitz–Rapoport strata in the special fiber are enumerated by the ![]() $\{\unicode[STIX]{x1D707}\}$-admissible set for all local models constructed in [Reference Pappas and ZhuPZ13, Reference LevinLev16].
$\{\unicode[STIX]{x1D707}\}$-admissible set for all local models constructed in [Reference Pappas and ZhuPZ13, Reference LevinLev16].
1.3 Overview
In § 2 we recall a few facts about ![]() $\mathbb{G}_{m}$-actions for convenience. The following § 3 studies relative affine Grassmannians formed using a general Cartier divisor. In § 4 we recall the definition of Weil-restricted local models and results from [Reference LevinLev16] which are needed in the sequel. These results are applied in § 5 to study
$\mathbb{G}_{m}$-actions for convenience. The following § 3 studies relative affine Grassmannians formed using a general Cartier divisor. In § 4 we recall the definition of Weil-restricted local models and results from [Reference LevinLev16] which are needed in the sequel. These results are applied in § 5 to study ![]() $\mathbb{G}_{m}$-actions on Beilinson–Drinfeld affine Grassmannians for Weil-restricted groups. In § 6 we formulate and prove the test function conjecture for Weil-restricted local models.
$\mathbb{G}_{m}$-actions on Beilinson–Drinfeld affine Grassmannians for Weil-restricted groups. In § 6 we formulate and prove the test function conjecture for Weil-restricted local models.
1.4 Conventions on ind-algebraic spaces
Let ![]() ${\mathcal{O}}$ be a ring, and denote by
${\mathcal{O}}$ be a ring, and denote by ![]() ${\mathcal{O}}\operatorname{ - Alg}$ the category of
${\mathcal{O}}\operatorname{ - Alg}$ the category of ![]() ${\mathcal{O}}$-algebras equipped with the fpqc topology. An
${\mathcal{O}}$-algebras equipped with the fpqc topology. An ![]() ${\mathcal{O}}$-space
${\mathcal{O}}$-space ![]() $X$ is a sheaf on the site
$X$ is a sheaf on the site ![]() ${\mathcal{O}}\operatorname{ - Alg}$, and we denote the category of
${\mathcal{O}}\operatorname{ - Alg}$, and we denote the category of ![]() ${\mathcal{O}}$-spaces by
${\mathcal{O}}$-spaces by ![]() $\text{Sp}_{{\mathcal{O}}}$. As each object in the site
$\text{Sp}_{{\mathcal{O}}}$. As each object in the site ![]() ${\mathcal{O}}\operatorname{ - Alg}$ is quasi-compact, the pretopology on
${\mathcal{O}}\operatorname{ - Alg}$ is quasi-compact, the pretopology on ![]() ${\mathcal{O}}\operatorname{ - Alg}$ is generated by finite covering families, and hence filtered colimits exist in
${\mathcal{O}}\operatorname{ - Alg}$ is generated by finite covering families, and hence filtered colimits exist in ![]() $\text{Sp}_{{\mathcal{O}}}$ and can be computed in the category of presheaves.
$\text{Sp}_{{\mathcal{O}}}$ and can be computed in the category of presheaves.
The category ![]() $\operatorname{Sp}_{{\mathcal{O}}}$ contains the category of
$\operatorname{Sp}_{{\mathcal{O}}}$ contains the category of ![]() ${\mathcal{O}}$-schemes
${\mathcal{O}}$-schemes ![]() $\text{Sch}_{{\mathcal{O}}}$ as a full subcategory. An
$\text{Sch}_{{\mathcal{O}}}$ as a full subcategory. An ![]() ${\mathcal{O}}$-algebraic space is a
${\mathcal{O}}$-algebraic space is a ![]() ${\mathcal{O}}$-space
${\mathcal{O}}$-space ![]() $X$ such that
$X$ such that ![]() $X\rightarrow X\times _{{\mathcal{O}}}X$ is relatively representable, and such that there exists an étale surjective map from a scheme
$X\rightarrow X\times _{{\mathcal{O}}}X$ is relatively representable, and such that there exists an étale surjective map from a scheme ![]() $U\rightarrow X$. By a theorem of Gabber [StaPro, Tag 03W8] this agrees with the usual definition of algebraic spaces using étale or fppf sheaves.
$U\rightarrow X$. By a theorem of Gabber [StaPro, Tag 03W8] this agrees with the usual definition of algebraic spaces using étale or fppf sheaves.
The category of ![]() ${\mathcal{O}}$-algebraic spaces is denoted
${\mathcal{O}}$-algebraic spaces is denoted ![]() $\text{AlgSp}_{{\mathcal{O}}}$. There are full embeddings
$\text{AlgSp}_{{\mathcal{O}}}$. There are full embeddings ![]() $\text{Sch}_{{\mathcal{O}}}\subset \text{AlgSp}_{{\mathcal{O}}}\subset \text{Sp}_{{\mathcal{O}}}$. A map of
$\text{Sch}_{{\mathcal{O}}}\subset \text{AlgSp}_{{\mathcal{O}}}\subset \text{Sp}_{{\mathcal{O}}}$. A map of ![]() ${\mathcal{O}}$-spaces
${\mathcal{O}}$-spaces ![]() $X\rightarrow Y$ is called representable (respectively, schematic) if for every scheme
$X\rightarrow Y$ is called representable (respectively, schematic) if for every scheme ![]() $T\rightarrow Y$ the fiber product
$T\rightarrow Y$ the fiber product ![]() $X\times _{Y}T$ is representable by an algebraic space (respectively, scheme).
$X\times _{Y}T$ is representable by an algebraic space (respectively, scheme).
An ![]() ${\mathcal{O}}$-ind-algebraic space (respectively,
${\mathcal{O}}$-ind-algebraic space (respectively, ![]() ${\mathcal{O}}$-ind-scheme) is a contravariant functor
${\mathcal{O}}$-ind-scheme) is a contravariant functor
such that there exists a presentation as presheaves ![]() $X=\text{colim}_{i}X_{i}$ where
$X=\text{colim}_{i}X_{i}$ where ![]() $\{{X_{i}\}}_{i\in I}$ is a filtered system of
$\{{X_{i}\}}_{i\in I}$ is a filtered system of ![]() ${\mathcal{O}}$-algebraic spaces (respectively,
${\mathcal{O}}$-algebraic spaces (respectively, ![]() ${\mathcal{O}}$-schemes)
${\mathcal{O}}$-schemes) ![]() $X_{i}$ with transition maps being (schematic) closed immersions. Since filtered colimits in
$X_{i}$ with transition maps being (schematic) closed immersions. Since filtered colimits in ![]() $\operatorname{Sp}_{{\mathcal{O}}}$ can be computed in presheaves, every
$\operatorname{Sp}_{{\mathcal{O}}}$ can be computed in presheaves, every ![]() ${\mathcal{O}}$-ind-algebraic space (respectively,
${\mathcal{O}}$-ind-algebraic space (respectively, ![]() ${\mathcal{O}}$-ind-scheme) is an
${\mathcal{O}}$-ind-scheme) is an ![]() ${\mathcal{O}}$-space. The category of
${\mathcal{O}}$-space. The category of ![]() ${\mathcal{O}}$-ind-algebraic spaces (respectively,
${\mathcal{O}}$-ind-algebraic spaces (respectively, ![]() ${\mathcal{O}}$-ind-schemes)
${\mathcal{O}}$-ind-schemes) ![]() $\operatorname{IndAlgSp}_{{\mathcal{O}}}$ (respectively,
$\operatorname{IndAlgSp}_{{\mathcal{O}}}$ (respectively, ![]() $\operatorname{IndSch}_{{\mathcal{O}}}$) is the full subcategory of
$\operatorname{IndSch}_{{\mathcal{O}}}$) is the full subcategory of ![]() $\operatorname{Sp}_{{\mathcal{O}}}$ whose objects are
$\operatorname{Sp}_{{\mathcal{O}}}$ whose objects are ![]() ${\mathcal{O}}$-ind-algebraic spaces (respectively,
${\mathcal{O}}$-ind-algebraic spaces (respectively, ![]() ${\mathcal{O}}$-ind-schemes). If
${\mathcal{O}}$-ind-schemes). If ![]() $X=\operatorname{colim}_{i}X_{i}$ and
$X=\operatorname{colim}_{i}X_{i}$ and ![]() $Y=\text{colim}_{j}Y_{j}$ are presentations of ind-algebraic spaces (respectively, ind-schemes), and if each
$Y=\text{colim}_{j}Y_{j}$ are presentations of ind-algebraic spaces (respectively, ind-schemes), and if each ![]() $X_{i}$ is quasi-compact, then as sets
$X_{i}$ is quasi-compact, then as sets
because every map ![]() $X_{i}\rightarrow Y$ factors over some
$X_{i}\rightarrow Y$ factors over some ![]() $Y_{j}$ by quasi-compactness of
$Y_{j}$ by quasi-compactness of ![]() $X_{i}$. The category
$X_{i}$. The category ![]() $\text{IndAlgSp}_{{\mathcal{O}}}$ (respectively,
$\text{IndAlgSp}_{{\mathcal{O}}}$ (respectively, ![]() $\text{IndSch}_{{\mathcal{O}}}$) is closed under fiber products, that is,
$\text{IndSch}_{{\mathcal{O}}}$) is closed under fiber products, that is, ![]() $\operatorname{colim}_{(i,j)}(X_{i}\times _{{\mathcal{O}}}Y_{j})$ is a presentation of
$\operatorname{colim}_{(i,j)}(X_{i}\times _{{\mathcal{O}}}Y_{j})$ is a presentation of ![]() $X\times _{{\mathcal{O}}}Y$. If
$X\times _{{\mathcal{O}}}Y$. If ![]() ${\mathcal{P}}$ is a property of algebraic spaces (respectively, schemes), then an
${\mathcal{P}}$ is a property of algebraic spaces (respectively, schemes), then an ![]() ${\mathcal{O}}$-ind-algebraic space (respectively,
${\mathcal{O}}$-ind-algebraic space (respectively, ![]() ${\mathcal{O}}$-ind-scheme)
${\mathcal{O}}$-ind-scheme) ![]() $X$ is said to have
$X$ is said to have ![]() $\text{ind-}{\mathcal{P}}$ if there exists a presentation
$\text{ind-}{\mathcal{P}}$ if there exists a presentation ![]() $X=\text{colim}_{i}X_{i}$ where each
$X=\text{colim}_{i}X_{i}$ where each ![]() $X_{i}$ has property
$X_{i}$ has property ![]() ${\mathcal{P}}$. A map
${\mathcal{P}}$. A map ![]() $f:X\rightarrow Y$ of
$f:X\rightarrow Y$ of ![]() ${\mathcal{O}}$-ind-algebraic spaces (respectively,
${\mathcal{O}}$-ind-algebraic spaces (respectively, ![]() ${\mathcal{O}}$-ind-schemes) is said to have property
${\mathcal{O}}$-ind-schemes) is said to have property ![]() ${\mathcal{P}}$ if
${\mathcal{P}}$ if ![]() $f$ is representable and, for all schemes
$f$ is representable and, for all schemes ![]() $T\rightarrow Y$, the pullback
$T\rightarrow Y$, the pullback ![]() $f\times _{Y}T$ has property
$f\times _{Y}T$ has property ![]() ${\mathcal{P}}$. Note that every representable quasi-compact map of
${\mathcal{P}}$. Note that every representable quasi-compact map of ![]() ${\mathcal{O}}$-ind-schemes is schematic.
${\mathcal{O}}$-ind-schemes is schematic.
2 Actions of  $\mathbb{G}_{m}$ on ind-algebraic spaces
$\mathbb{G}_{m}$ on ind-algebraic spaces
We recall the setup and some notation from [Reference DrinfeldDri13, Reference RicharzRic19]. Let ![]() ${\mathcal{O}}$ be a ring, and let
${\mathcal{O}}$ be a ring, and let ![]() $X$ be an
$X$ be an ![]() ${\mathcal{O}}$-algebraic space (or
${\mathcal{O}}$-algebraic space (or ![]() ${\mathcal{O}}$-ind-algebraic space) equipped with an action of
${\mathcal{O}}$-ind-algebraic space) equipped with an action of ![]() $\mathbb{G}_{m}$ which is trivial on
$\mathbb{G}_{m}$ which is trivial on ![]() ${\mathcal{O}}$. There are the following three functors on the category of
${\mathcal{O}}$. There are the following three functors on the category of ![]() ${\mathcal{O}}$-algebras:
${\mathcal{O}}$-algebras:
 $$\begin{eqnarray}\begin{array}{@{}rcl@{}}X^{0}:\; & R\longmapsto \; & \operatorname{Hom}_{R}^{\mathbb{G}_{m}}(R,X),\\ X^{+}:\; & R\longmapsto \; & \operatorname{Hom}_{R}^{\mathbb{G}_{m}}((\mathbb{A}_{R}^{1})^{+},X),\\ X^{-}:\; & R\longmapsto \; & \operatorname{Hom}_{R}^{\mathbb{G}_{m}}((\mathbb{A}_{R}^{1})^{-},X),\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}rcl@{}}X^{0}:\; & R\longmapsto \; & \operatorname{Hom}_{R}^{\mathbb{G}_{m}}(R,X),\\ X^{+}:\; & R\longmapsto \; & \operatorname{Hom}_{R}^{\mathbb{G}_{m}}((\mathbb{A}_{R}^{1})^{+},X),\\ X^{-}:\; & R\longmapsto \; & \operatorname{Hom}_{R}^{\mathbb{G}_{m}}((\mathbb{A}_{R}^{1})^{-},X),\end{array}\end{eqnarray}$$ where ![]() $(\mathbb{A}_{R}^{1})^{+}$ (respectively,
$(\mathbb{A}_{R}^{1})^{+}$ (respectively, ![]() $(\mathbb{A}_{R}^{1})^{-}$) is
$(\mathbb{A}_{R}^{1})^{-}$) is ![]() $\mathbb{A}_{R}^{1}$ with the usual (respectively, opposite)
$\mathbb{A}_{R}^{1}$ with the usual (respectively, opposite) ![]() $\mathbb{G}_{m}$-action. The functor
$\mathbb{G}_{m}$-action. The functor ![]() $X^{0}$ is the functor of
$X^{0}$ is the functor of ![]() $\mathbb{G}_{m}$-fixed points in
$\mathbb{G}_{m}$-fixed points in ![]() $X$, and
$X$, and ![]() $X^{+}$ (respectively,
$X^{+}$ (respectively, ![]() $X^{-}$) is called the attractor (respectively, repeller). Informally speaking,
$X^{-}$) is called the attractor (respectively, repeller). Informally speaking, ![]() $X^{+}$ (respectively,
$X^{+}$ (respectively, ![]() $X^{-}$) is the space of points
$X^{-}$) is the space of points ![]() $x$ such that the limit
$x$ such that the limit ![]() $\lim _{\unicode[STIX]{x1D706}\rightarrow 0}\unicode[STIX]{x1D706}\cdot x$ (respectively,
$\lim _{\unicode[STIX]{x1D706}\rightarrow 0}\unicode[STIX]{x1D706}\cdot x$ (respectively, ![]() $\lim _{\unicode[STIX]{x1D706}\rightarrow \infty }\unicode[STIX]{x1D706}\cdot x$) exists. The functors (2.1) come equipped with natural maps
$\lim _{\unicode[STIX]{x1D706}\rightarrow \infty }\unicode[STIX]{x1D706}\cdot x$) exists. The functors (2.1) come equipped with natural maps
where ![]() $X^{\pm }\rightarrow X^{0}$ (respectively,
$X^{\pm }\rightarrow X^{0}$ (respectively, ![]() $X^{\pm }\rightarrow X$) is given by evaluating a morphism at the zero section (respectively, at the unit section). We say that the
$X^{\pm }\rightarrow X$) is given by evaluating a morphism at the zero section (respectively, at the unit section). We say that the ![]() $\mathbb{G}_{m}$-action on an algebraic space
$\mathbb{G}_{m}$-action on an algebraic space ![]() $X$ is étale (respectively, Zariski) locally linearizable if the
$X$ is étale (respectively, Zariski) locally linearizable if the ![]() $\mathbb{G}_{m}$-action lifts – necessarily uniquely – to an étale cover which is affine; cf. [Reference RicharzRic19, Definition 1.6]. We say that a
$\mathbb{G}_{m}$-action lifts – necessarily uniquely – to an étale cover which is affine; cf. [Reference RicharzRic19, Definition 1.6]. We say that a ![]() $\mathbb{G}_{m}$-action on an
$\mathbb{G}_{m}$-action on an ![]() $S$-ind-algebraic space
$S$-ind-algebraic space ![]() $X$ is étale (respectively, Zariski) locally linearizable if there is a
$X$ is étale (respectively, Zariski) locally linearizable if there is a ![]() $\mathbb{G}_{m}$-stable presentation with equivariant transition maps
$\mathbb{G}_{m}$-stable presentation with equivariant transition maps ![]() $X=\operatorname{colim}_{i}X_{i}$ where the
$X=\operatorname{colim}_{i}X_{i}$ where the ![]() $\mathbb{G}_{m}$-action on each
$\mathbb{G}_{m}$-action on each ![]() $X_{i}$ is étale (respectively, Zariski) locally linearizable. We use the following representability properties of the functors (2.1); cf. [Reference Haines and RicharzHR18, Theorem 2.1].
$X_{i}$ is étale (respectively, Zariski) locally linearizable. We use the following representability properties of the functors (2.1); cf. [Reference Haines and RicharzHR18, Theorem 2.1].
Theorem 2.1. Let ![]() $X=\operatorname{colim}_{i}X_{i}$ be an
$X=\operatorname{colim}_{i}X_{i}$ be an ![]() ${\mathcal{O}}$-ind-algebraic space equipped with an étale locally linearizable
${\mathcal{O}}$-ind-algebraic space equipped with an étale locally linearizable ![]() $\mathbb{G}_{m}$-action.
$\mathbb{G}_{m}$-action.
(i) The subfunctor
 $X^{0}=\operatorname{colim}_{i}X_{i}^{0}$ is representable by a closed sub-ind-algebraic space of
$X^{0}=\operatorname{colim}_{i}X_{i}^{0}$ is representable by a closed sub-ind-algebraic space of  $X$.
$X$.(ii) The functor
 $X^{\pm }=\operatorname{colim}_{i}X_{i}^{\pm }$ is representable, and the map
$X^{\pm }=\operatorname{colim}_{i}X_{i}^{\pm }$ is representable, and the map  $X^{\pm }\rightarrow X$ is representable and quasi-compact. The map
$X^{\pm }\rightarrow X$ is representable and quasi-compact. The map  $X^{\pm }\rightarrow X^{0}$ is ind-affine with geometrically connected fibers and induces a bijection on connected components
$X^{\pm }\rightarrow X^{0}$ is ind-affine with geometrically connected fibers and induces a bijection on connected components  $\unicode[STIX]{x1D70B}_{0}(X^{\pm })\simeq \unicode[STIX]{x1D70B}_{0}(X^{0})$ of the underlying topological spaces.
$\unicode[STIX]{x1D70B}_{0}(X^{\pm })\simeq \unicode[STIX]{x1D70B}_{0}(X^{0})$ of the underlying topological spaces.(iii) If
 $X=\operatorname{colim}_{i}X_{i}$ is of ind-finite presentation (respectively, an ind-scheme; respectively, separated), so are
$X=\operatorname{colim}_{i}X_{i}$ is of ind-finite presentation (respectively, an ind-scheme; respectively, separated), so are  $X^{0}$ and
$X^{0}$ and  $X^{\pm }$.
$X^{\pm }$.
The proof is like that of [Reference Haines and RicharzHR18, Theorem 2.1], using the representability results of [Reference RicharzRic19, Theorem 1.8]. We record the following lemma for later use.
Lemma 2.2. For ![]() $n\in \mathbb{Z}_{{>}0}$, let
$n\in \mathbb{Z}_{{>}0}$, let ![]() $X_{1},\ldots ,X_{n}$ be
$X_{1},\ldots ,X_{n}$ be ![]() ${\mathcal{O}}$-algebraic spaces (or
${\mathcal{O}}$-algebraic spaces (or ![]() ${\mathcal{O}}$-ind-algebraic spaces) equipped with an étale locally linearizable
${\mathcal{O}}$-ind-algebraic spaces) equipped with an étale locally linearizable ![]() $\mathbb{G}_{m}$-action. Then the diagonal
$\mathbb{G}_{m}$-action. Then the diagonal ![]() $\mathbb{G}_{m}$-action on the product
$\mathbb{G}_{m}$-action on the product ![]() $\prod _{i=1}^{n}X_{i}$ is étale locally linearizable, and the canonical maps
$\prod _{i=1}^{n}X_{i}$ is étale locally linearizable, and the canonical maps
are isomorphisms.
Proof. If, for each ![]() $i$, the map
$i$, the map ![]() $U_{i}\rightarrow X_{i}$ is an étale local linearization, then the product
$U_{i}\rightarrow X_{i}$ is an étale local linearization, then the product ![]() $\prod _{i=1}^{n}U_{i}\rightarrow \prod _{i=1}^{n}X_{i}$ is an étale local linearization. It is easy to check on the level of functors that the maps are isomorphisms.◻
$\prod _{i=1}^{n}U_{i}\rightarrow \prod _{i=1}^{n}X_{i}$ is an étale local linearization. It is easy to check on the level of functors that the maps are isomorphisms.◻
3 Affine Grassmannians for Cartier divisors
In this section we give a self-contained treatment of affine Grassmannians for non-constant group schemes over relative curves which are formed using a formal neighborhood of a general Cartier divisor. This extends the work of Beilinson and Drinfeld [Reference Beilinson and DrinfeldBD99], and is inspired by the work of Fedorov and Panin [Reference Fedorov and PaninFP15, Reference FedorovFed16] and Levin [Reference LevinLev16].
3.1 Definitions and examples
Let ![]() ${\mathcal{O}}$ be a Noetherian ring. Let
${\mathcal{O}}$ be a Noetherian ring. Let ![]() $X$ be a smooth
$X$ be a smooth ![]() ${\mathcal{O}}$-curve, that is, the structure map
${\mathcal{O}}$-curve, that is, the structure map ![]() $X\rightarrow \operatorname{Spec}({\mathcal{O}})$ is of finite presentation and smooth of pure dimension
$X\rightarrow \operatorname{Spec}({\mathcal{O}})$ is of finite presentation and smooth of pure dimension ![]() $1$. Let
$1$. Let ![]() $D\subset X$ be a relative effective Cartier divisor which is finite and flat over
$D\subset X$ be a relative effective Cartier divisor which is finite and flat over ![]() ${\mathcal{O}}$. Let
${\mathcal{O}}$. Let ![]() ${\mathcal{G}}$ be a smooth affine
${\mathcal{G}}$ be a smooth affine ![]() $X$-group scheme.
$X$-group scheme.
To the triple ![]() $(X,{\mathcal{G}},D)$, we associate the functor
$(X,{\mathcal{G}},D)$, we associate the functor ![]() $\operatorname{Gr}_{{\mathcal{G}}}=\operatorname{Gr}_{(X,{\mathcal{G}},D)}$ on the category of
$\operatorname{Gr}_{{\mathcal{G}}}=\operatorname{Gr}_{(X,{\mathcal{G}},D)}$ on the category of ![]() ${\mathcal{O}}$-algebras which assigns to every
${\mathcal{O}}$-algebras which assigns to every ![]() $R$ the set of isomorphism classes of tuples
$R$ the set of isomorphism classes of tuples ![]() $({\mathcal{F}},\unicode[STIX]{x1D6FC})$ with
$({\mathcal{F}},\unicode[STIX]{x1D6FC})$ with
where ![]() ${\mathcal{F}}_{0}$ denotes the trivial
${\mathcal{F}}_{0}$ denotes the trivial ![]() ${\mathcal{G}}$-torsor. Fpqc descent for schemes affine over
${\mathcal{G}}$-torsor. Fpqc descent for schemes affine over ![]() $X_{R}$ implies that
$X_{R}$ implies that ![]() $\operatorname{Gr}_{{\mathcal{G}}}$ is an
$\operatorname{Gr}_{{\mathcal{G}}}$ is an ![]() ${\mathcal{O}}$-space. As
${\mathcal{O}}$-space. As ![]() ${\mathcal{G}}$ is smooth affine and hence of finite presentation, the functor
${\mathcal{G}}$ is smooth affine and hence of finite presentation, the functor ![]() $\operatorname{Gr}_{{\mathcal{G}}}$ commutes with filtered colimits of
$\operatorname{Gr}_{{\mathcal{G}}}$ commutes with filtered colimits of ![]() ${\mathcal{O}}$-algebras. Further, if
${\mathcal{O}}$-algebras. Further, if ![]() $R$ is an
$R$ is an ![]() ${\mathcal{O}}$-algebra, then as functors on
${\mathcal{O}}$-algebra, then as functors on ![]() $R\text{-Alg}$,
$R\text{-Alg}$,
If we replace ![]() $D$ by a positive multiple
$D$ by a positive multiple ![]() $nD$ for some
$nD$ for some ![]() $n\geqslant 1$, then
$n\geqslant 1$, then ![]() $X\backslash D=X\backslash nD$, and hence, as
$X\backslash D=X\backslash nD$, and hence, as ![]() ${\mathcal{O}}$-functors,
${\mathcal{O}}$-functors,
The following examples are special cases of the general setup.
Example 3.1. (i) Affine Grassmannians/flag varieties. Let ![]() ${\mathcal{O}}=F$ be a field, and let
${\mathcal{O}}=F$ be a field, and let ![]() $D=\{x\}$ for some point
$D=\{x\}$ for some point ![]() $x\in X(F)$. Then on completed local rings
$x\in X(F)$. Then on completed local rings ![]() ${\mathcal{O}}_{x}\simeq F[\![t_{x}]\!]$ where
${\mathcal{O}}_{x}\simeq F[\![t_{x}]\!]$ where ![]() $t_{x}$ denotes a local parameter at
$t_{x}$ denotes a local parameter at ![]() $x\in X$. If
$x\in X$. If ![]() ${\mathcal{G}}=G\,\otimes _{F}\,X$ for some smooth affine
${\mathcal{G}}=G\,\otimes _{F}\,X$ for some smooth affine ![]() $F$-group
$F$-group ![]() $G$, then
$G$, then ![]() $\operatorname{Gr}_{G}:=\operatorname{Gr}_{{\mathcal{G}}}$ is (by the Beauville–Laszlo theorem [Reference Beauville and LaszloBL95]) the ‘affine Grassmannian’ formed using the local parameter
$\operatorname{Gr}_{G}:=\operatorname{Gr}_{{\mathcal{G}}}$ is (by the Beauville–Laszlo theorem [Reference Beauville and LaszloBL95]) the ‘affine Grassmannian’ formed using the local parameter ![]() $t_{x}$, that is, the ind-scheme given by the étale sheafification of the functor
$t_{x}$, that is, the ind-scheme given by the étale sheafification of the functor ![]() $R\mapsto G(R((t_{x})))/G(R[\![t_{x}]\!])$. In general, the functor
$R\mapsto G(R((t_{x})))/G(R[\![t_{x}]\!])$. In general, the functor ![]() $\operatorname{Gr}_{{\mathcal{G}}}$ is the ‘twisted affine flag variety’ for the group scheme
$\operatorname{Gr}_{{\mathcal{G}}}$ is the ‘twisted affine flag variety’ for the group scheme ![]() ${\mathcal{G}}\otimes _{X}F[\![t_{x}]\!]$ in the sense of [Reference Pappas and RapoportPR08].
${\mathcal{G}}\otimes _{X}F[\![t_{x}]\!]$ in the sense of [Reference Pappas and RapoportPR08].
(ii) Mixed characteristic. Let ![]() ${\mathcal{O}}={\mathcal{O}}_{F}$ be the valuation ring of a finite extension
${\mathcal{O}}={\mathcal{O}}_{F}$ be the valuation ring of a finite extension ![]() $F/\mathbb{Q}_{p}$. Let
$F/\mathbb{Q}_{p}$. Let ![]() $K/F$ be a finite totally ramified extension with uniformizer
$K/F$ be a finite totally ramified extension with uniformizer ![]() $\unicode[STIX]{x1D71B}\in K$. Let
$\unicode[STIX]{x1D71B}\in K$. Let ![]() $X=\mathbb{A}_{{\mathcal{O}}_{F}}^{1}$ with global coordinate denoted by
$X=\mathbb{A}_{{\mathcal{O}}_{F}}^{1}$ with global coordinate denoted by ![]() $z$, and let
$z$, and let ![]() $D=\{Q=0\}$, where
$D=\{Q=0\}$, where ![]() $Q\in {\mathcal{O}}_{F}[z]$ is the minimal polynomial of
$Q\in {\mathcal{O}}_{F}[z]$ is the minimal polynomial of ![]() $\unicode[STIX]{x1D71B}$ over
$\unicode[STIX]{x1D71B}$ over ![]() $F$ (an Eisenstein polynomial). Let
$F$ (an Eisenstein polynomial). Let ![]() ${\mathcal{G}}$ be the
${\mathcal{G}}$ be the ![]() $X$-group scheme constructed in [Reference Pappas and ZhuPZ13, Theorem 4.1] if
$X$-group scheme constructed in [Reference Pappas and ZhuPZ13, Theorem 4.1] if ![]() $K=F$, and in [Reference LevinLev16, Theorem 3.3.3] otherwise; here it is denoted by
$K=F$, and in [Reference LevinLev16, Theorem 3.3.3] otherwise; here it is denoted by ![]() $\text{}\underline{{\mathcal{G}}}$ (see Theorem 4.13). Then
$\text{}\underline{{\mathcal{G}}}$ (see Theorem 4.13). Then ![]() $\operatorname{Gr}_{{\mathcal{G}}}$ is the
$\operatorname{Gr}_{{\mathcal{G}}}$ is the ![]() ${\mathcal{O}}_{F}$-ind-scheme defined in [Reference Pappas and ZhuPZ13, Equation (6.11)] if
${\mathcal{O}}_{F}$-ind-scheme defined in [Reference Pappas and ZhuPZ13, Equation (6.11)] if ![]() $K=F$, and in [Reference LevinLev16, Definition 4.1.1] otherwise; here we denote it by
$K=F$, and in [Reference LevinLev16, Definition 4.1.1] otherwise; here we denote it by ![]() $\operatorname{Gr}_{\tilde{{\mathcal{G}}}}$ (see § 4.4.1).
$\operatorname{Gr}_{\tilde{{\mathcal{G}}}}$ (see § 4.4.1).
(iii) Equal characteristic. Let ![]() $F$ be a field, and let
$F$ be a field, and let ![]() $C$ be a smooth affine
$C$ be a smooth affine ![]() $F$-curve. Let
$F$-curve. Let ![]() ${\mathcal{O}}=\unicode[STIX]{x1D6E4}(C,{\mathcal{O}}_{C})$ be the global sections, and let
${\mathcal{O}}=\unicode[STIX]{x1D6E4}(C,{\mathcal{O}}_{C})$ be the global sections, and let ![]() $X=C\times _{F}C=C_{{\mathcal{O}}}$. Let
$X=C\times _{F}C=C_{{\mathcal{O}}}$. Let ![]() ${\mathcal{G}}_{0}$ be a smooth affine
${\mathcal{G}}_{0}$ be a smooth affine ![]() ${\mathcal{O}}$-group scheme, and let
${\mathcal{O}}$-group scheme, and let ![]() ${\mathcal{G}}={\mathcal{G}}_{0}\otimes _{{\mathcal{O}}}X$. Let
${\mathcal{G}}={\mathcal{G}}_{0}\otimes _{{\mathcal{O}}}X$. Let ![]() $D:=\unicode[STIX]{x1D6E5}(C)$ be the diagonal divisor in
$D:=\unicode[STIX]{x1D6E5}(C)$ be the diagonal divisor in ![]() $X$. If
$X$. If ![]() $C=\mathbb{A}_{F}^{1}$, then
$C=\mathbb{A}_{F}^{1}$, then ![]() $\operatorname{Gr}_{{\mathcal{G}}}$ is the ind-scheme defined in [Reference ZhuZhu14, Equation (3.1.1)]. If
$\operatorname{Gr}_{{\mathcal{G}}}$ is the ind-scheme defined in [Reference ZhuZhu14, Equation (3.1.1)]. If ![]() $x\in C(F)$ is a point, and
$x\in C(F)$ is a point, and ![]() ${\mathcal{O}}_{x}\rightarrow {\mathcal{O}}$ denotes the completed local ring, then
${\mathcal{O}}_{x}\rightarrow {\mathcal{O}}$ denotes the completed local ring, then ![]() $\operatorname{Gr}_{{\mathcal{G}}}\otimes _{{\mathcal{O}}}{\mathcal{O}}_{x}$ is the ind-scheme defined in [Reference RicharzRic16b, Definition 2.3]. Let us remark that this is a special case of the general setup in [Reference HeinlothHei10, § 2].
$\operatorname{Gr}_{{\mathcal{G}}}\otimes _{{\mathcal{O}}}{\mathcal{O}}_{x}$ is the ind-scheme defined in [Reference RicharzRic16b, Definition 2.3]. Let us remark that this is a special case of the general setup in [Reference HeinlothHei10, § 2].
(iv) Fusion Grassmannians. Let ![]() $F$ be a field, and let
$F$ be a field, and let ![]() $C$ be an affine curve over
$C$ be an affine curve over ![]() $F$. The
$F$. The ![]() $d$th symmetric product
$d$th symmetric product ![]() $C^{(d)}$ is by [Reference Deligne, Artin, Grothendieck and VerdierSGA4, Example XVII, Proposition 6.3.9] the moduli space of degree-
$C^{(d)}$ is by [Reference Deligne, Artin, Grothendieck and VerdierSGA4, Example XVII, Proposition 6.3.9] the moduli space of degree-![]() $d$ effective Cartier divisors on
$d$ effective Cartier divisors on ![]() $C$. Let
$C$. Let ![]() $\operatorname{Spec}({\mathcal{O}}):=C^{(d)}$, and let
$\operatorname{Spec}({\mathcal{O}}):=C^{(d)}$, and let ![]() $D:=C^{(d)}$ be the universal degree-
$D:=C^{(d)}$ be the universal degree-![]() $d$ divisor on
$d$ divisor on ![]() $X:=C\times _{F}C^{(d)}=C_{{\mathcal{O}}}$. For a smooth affine
$X:=C\times _{F}C^{(d)}=C_{{\mathcal{O}}}$. For a smooth affine ![]() $F$-group scheme
$F$-group scheme ![]() $G$, let
$G$, let ![]() ${\mathcal{G}}=G\otimes _{F}X$. Then the ind-scheme
${\mathcal{G}}=G\otimes _{F}X$. Then the ind-scheme ![]() $\operatorname{Gr}_{{\mathcal{G}}}\times _{\operatorname{Spec}({\mathcal{O}})}C^{d}$ is the fusion Grassmannian defined in [Reference Beilinson and DrinfeldBD99, 5.3.11].
$\operatorname{Gr}_{{\mathcal{G}}}\times _{\operatorname{Spec}({\mathcal{O}})}C^{d}$ is the fusion Grassmannian defined in [Reference Beilinson and DrinfeldBD99, 5.3.11].
(v) Generically trivial bundles. If ![]() $X=\mathbb{A}_{{\mathcal{O}}}^{1}$ and
$X=\mathbb{A}_{{\mathcal{O}}}^{1}$ and ![]() ${\mathcal{G}}$ is split reductive, then the functor
${\mathcal{G}}$ is split reductive, then the functor ![]() $\operatorname{Gr}_{{\mathcal{G}}}$ in (3.1) is the moduli space of objects used in [Reference FedorovFed16, Theorem 2].
$\operatorname{Gr}_{{\mathcal{G}}}$ in (3.1) is the moduli space of objects used in [Reference FedorovFed16, Theorem 2].
3.1.1 Loop groups
The functor ![]() $\operatorname{Gr}_{{\mathcal{G}}}$ is related to loop groups as follows. For an
$\operatorname{Gr}_{{\mathcal{G}}}$ is related to loop groups as follows. For an ![]() ${\mathcal{O}}$-algebra
${\mathcal{O}}$-algebra ![]() $R$, let
$R$, let ![]() $(X_{R}/D_{R})\,\,\widehat{\text{}}\,$ be the formal affineFootnote 1 scheme defined by
$(X_{R}/D_{R})\,\,\widehat{\text{}}\,$ be the formal affineFootnote 1 scheme defined by ![]() $D_{R}$ in
$D_{R}$ in ![]() $X_{R}$, and denote by
$X_{R}$, and denote by ![]() $R[\![D]\!]$ its ring of regular functions. Explicitly, if
$R[\![D]\!]$ its ring of regular functions. Explicitly, if ![]() ${\mathcal{I}}_{R}\subset {\mathcal{O}}_{X_{R}}$ is the ideal sheaf for
${\mathcal{I}}_{R}\subset {\mathcal{O}}_{X_{R}}$ is the ideal sheaf for ![]() $D_{R}$, then
$D_{R}$, then ![]() $(D_{R},{\mathcal{O}}_{X_{R}}/{\mathcal{I}}_{R}^{n})$ is an affine scheme
$(D_{R},{\mathcal{O}}_{X_{R}}/{\mathcal{I}}_{R}^{n})$ is an affine scheme ![]() $\text{Spec}(A_{n})$ for all
$\text{Spec}(A_{n})$ for all ![]() $n\geqslant 1$, and
$n\geqslant 1$, and ![]() $R[\![D]\!]\overset{\text{def}}{=}\varprojlim A_{n}=\varprojlim \unicode[STIX]{x1D6E4}(D_{R},{\mathcal{O}}_{X_{R}}/{\mathcal{I}}_{R}^{n})$. Let
$R[\![D]\!]\overset{\text{def}}{=}\varprojlim A_{n}=\varprojlim \unicode[STIX]{x1D6E4}(D_{R},{\mathcal{O}}_{X_{R}}/{\mathcal{I}}_{R}^{n})$. Let ![]() $\hat{D}_{R}=\operatorname{Spec}(R[\![D]\!])$ be the associated affine (true) scheme. The map
$\hat{D}_{R}=\operatorname{Spec}(R[\![D]\!])$ be the associated affine (true) scheme. The map ![]() $(X_{R}/D_{R})\,\,\widehat{\text{}}\rightarrow X_{R}$ uniquely extends to a map
$(X_{R}/D_{R})\,\,\widehat{\text{}}\rightarrow X_{R}$ uniquely extends to a map ![]() $p:\hat{D}_{R}\rightarrow X_{R}$ by [Reference BhattBha16, Theorem 1.1],Footnote 2 and
$p:\hat{D}_{R}\rightarrow X_{R}$ by [Reference BhattBha16, Theorem 1.1],Footnote 2 and ![]() $p^{-1}(D_{R})\simeq D_{R}$ defines a relative effective Cartier divisor on
$p^{-1}(D_{R})\simeq D_{R}$ defines a relative effective Cartier divisor on ![]() $\hat{D}_{R}$. Let
$\hat{D}_{R}$. Let ![]() $\hat{D}_{R}^{o}=\hat{D}_{R}\backslash D_{R}$. As
$\hat{D}_{R}^{o}=\hat{D}_{R}\backslash D_{R}$. As ![]() $D_{R}$ is a Cartier divisor in
$D_{R}$ is a Cartier divisor in ![]() $\hat{D}_{R}$, it is locally principal, and hence the complement
$\hat{D}_{R}$, it is locally principal, and hence the complement ![]() $\hat{D}_{R}^{o}:=\operatorname{Spec}(R((D)))$ is an affine scheme. The (twisted) loop group
$\hat{D}_{R}^{o}:=\operatorname{Spec}(R((D)))$ is an affine scheme. The (twisted) loop group ![]() $L{\mathcal{G}}=L_{D}{\mathcal{G}}$ is the functor on the category of
$L{\mathcal{G}}=L_{D}{\mathcal{G}}$ is the functor on the category of ![]() ${\mathcal{O}}$-algebras
${\mathcal{O}}$-algebras
The positive (twisted) loop group ![]() $L^{+}{\mathcal{G}}=L_{D}^{+}{\mathcal{G}}$ is the functor on the category of
$L^{+}{\mathcal{G}}=L_{D}^{+}{\mathcal{G}}$ is the functor on the category of ![]() ${\mathcal{O}}$-algebras
${\mathcal{O}}$-algebras
As every Cartier divisor is locally defined by a single non-zero divisor, we see that ![]() $L^{+}{\mathcal{G}}\subset L{\mathcal{G}}$ is a subgroup functor. Let us explain why these functors are representable in this generality.
$L^{+}{\mathcal{G}}\subset L{\mathcal{G}}$ is a subgroup functor. Let us explain why these functors are representable in this generality.
Lemma 3.2. (i) The functor ![]() $L^{+}{\mathcal{G}}$ (respectively,
$L^{+}{\mathcal{G}}$ (respectively, ![]() $L{\mathcal{G}}$) is representable by an affine scheme (respectively, ind-affine ind-scheme). In particular,
$L{\mathcal{G}}$) is representable by an affine scheme (respectively, ind-affine ind-scheme). In particular, ![]() $L^{+}{\mathcal{G}}$ and
$L^{+}{\mathcal{G}}$ and ![]() $L{\mathcal{G}}$ are
$L{\mathcal{G}}$ are ![]() ${\mathcal{O}}$-spaces.
${\mathcal{O}}$-spaces.
(ii) The scheme ![]() $L^{+}{\mathcal{G}}$ is a faithfully flat affine
$L^{+}{\mathcal{G}}$ is a faithfully flat affine ![]() ${\mathcal{O}}$-group scheme which is pro-smooth.
${\mathcal{O}}$-group scheme which is pro-smooth.
Proof. Part (i) is true for every affine scheme ![]() ${\mathcal{G}}$ of finite presentation over
${\mathcal{G}}$ of finite presentation over ![]() ${\mathcal{O}}$: Let
${\mathcal{O}}$: Let ![]() ${\mathcal{G}}=\mathbb{A}_{{\mathcal{O}}}^{1}$ first. Denote by
${\mathcal{G}}=\mathbb{A}_{{\mathcal{O}}}^{1}$ first. Denote by ![]() $I_{D}$ the invertible ideal defined by
$I_{D}$ the invertible ideal defined by ![]() $D$ in
$D$ in ![]() ${\mathcal{O}}[\![D]\!]$. By the preceding discussion, the ring
${\mathcal{O}}[\![D]\!]$. By the preceding discussion, the ring ![]() ${\mathcal{O}}[\![D]\!]/I_{D}$ is isomorphic to the global sections of
${\mathcal{O}}[\![D]\!]/I_{D}$ is isomorphic to the global sections of ![]() $D$ and both are finite locally free
$D$ and both are finite locally free ![]() ${\mathcal{O}}$-modules; cf. [StaPro, Tag 0B9C]. For any
${\mathcal{O}}$-modules; cf. [StaPro, Tag 0B9C]. For any ![]() $a\in \mathbb{Z}$, we form
$a\in \mathbb{Z}$, we form ![]() $I_{D}^{a}$ as an invertible
$I_{D}^{a}$ as an invertible ![]() ${\mathcal{O}}[\![D]\!]$-module. For
${\mathcal{O}}[\![D]\!]$-module. For ![]() $a\leqslant b$, denote by
$a\leqslant b$, denote by ![]() $E_{[a,b]}$ the
$E_{[a,b]}$ the ![]() ${\mathcal{O}}$-module
${\mathcal{O}}$-module ![]() $I_{D}^{a}/I_{D}^{b}$ which is also finite locally free (hence reflexive) by an induction argument. As
$I_{D}^{a}/I_{D}^{b}$ which is also finite locally free (hence reflexive) by an induction argument. As ![]() $b$ varies, the set of
$b$ varies, the set of ![]() ${\mathcal{O}}$-modules
${\mathcal{O}}$-modules ![]() $\{{E_{[a,b]}\}}_{b\geqslant a}$ forms an inverse system, and
$\{{E_{[a,b]}\}}_{b\geqslant a}$ forms an inverse system, and ![]() ${\mathcal{O}}[\![D]\!]=\text{lim}_{b\geqslant 0}E_{[0,b]}$ by definition. It follows that
${\mathcal{O}}[\![D]\!]=\text{lim}_{b\geqslant 0}E_{[0,b]}$ by definition. It follows that ![]() $I_{D}^{a}=\text{lim}_{b\geqslant a}E_{[a,b]}$ for any
$I_{D}^{a}=\text{lim}_{b\geqslant a}E_{[a,b]}$ for any ![]() $a\in \mathbb{Z}$. In particular, we get
$a\in \mathbb{Z}$. In particular, we get ![]() ${\mathcal{O}}((D))=\text{colim}_{a}\text{lim}_{b\geqslant a}E_{[a,b]}$. As
${\mathcal{O}}((D))=\text{colim}_{a}\text{lim}_{b\geqslant a}E_{[a,b]}$. As ![]() $E_{[a,b]}$ is a reflexive
$E_{[a,b]}$ is a reflexive ![]() ${\mathcal{O}}$-module, we get for every
${\mathcal{O}}$-module, we get for every ![]() ${\mathcal{O}}$-algebra
${\mathcal{O}}$-algebra ![]() $R$ that
$R$ that
where ![]() $\mathbb{V}_{[a,b]}=\operatorname{Spec}(\text{Sym}^{\otimes }(E_{[a,b]})^{\ast })$ for every pair
$\mathbb{V}_{[a,b]}=\operatorname{Spec}(\text{Sym}^{\otimes }(E_{[a,b]})^{\ast })$ for every pair ![]() $b\geqslant a$. Taking limits shows that
$b\geqslant a$. Taking limits shows that
is identified with the ![]() $R$-points of the affine
$R$-points of the affine ![]() ${\mathcal{O}}$-scheme
${\mathcal{O}}$-scheme ![]() $\text{lim}_{b\geqslant 0}\mathbb{V}_{[0,b]}$. The same argument shows that
$\text{lim}_{b\geqslant 0}\mathbb{V}_{[0,b]}$. The same argument shows that ![]() $R\mapsto \mathbb{A}_{{\mathcal{O}}}^{1}(R((D)))$ is representable by the ind-affine ind-scheme
$R\mapsto \mathbb{A}_{{\mathcal{O}}}^{1}(R((D)))$ is representable by the ind-affine ind-scheme ![]() $\text{colim}_{a}\text{lim}_{b\geqslant a}\mathbb{V}_{[a,b]}$. This gives part (i) in the case
$\text{colim}_{a}\text{lim}_{b\geqslant a}\mathbb{V}_{[a,b]}$. This gives part (i) in the case ![]() ${\mathcal{G}}=\mathbb{A}_{{\mathcal{O}}}^{1}$. For the general case, one verifies that the
${\mathcal{G}}=\mathbb{A}_{{\mathcal{O}}}^{1}$. For the general case, one verifies that the ![]() $L^{+}$-construction (respectively,
$L^{+}$-construction (respectively, ![]() $L$-construction) commutes with taking finite products and equalizers, and that finite products and equalizers are constructed termwise in the category of ind-schemes. Hence, the lemma follows for
$L$-construction) commutes with taking finite products and equalizers, and that finite products and equalizers are constructed termwise in the category of ind-schemes. Hence, the lemma follows for ![]() $L^{+}\mathbb{A}_{{\mathcal{O}}}^{n}$ (respectively,
$L^{+}\mathbb{A}_{{\mathcal{O}}}^{n}$ (respectively, ![]() $L\mathbb{A}_{{\mathcal{O}}}^{n}$). A finite presentation
$L\mathbb{A}_{{\mathcal{O}}}^{n}$). A finite presentation ![]() ${\mathcal{G}}=\operatorname{Spec}({\mathcal{O}}[t_{1},\ldots ,t_{n}]/(f_{1},\ldots ,f_{m}))$ realizes
${\mathcal{G}}=\operatorname{Spec}({\mathcal{O}}[t_{1},\ldots ,t_{n}]/(f_{1},\ldots ,f_{m}))$ realizes ![]() ${\mathcal{G}}$ as the equalizer of the two maps
${\mathcal{G}}$ as the equalizer of the two maps ![]() $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}:\mathbb{A}_{{\mathcal{O}}}^{n}\rightarrow \mathbb{A}_{{\mathcal{O}}}^{m}$ where
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}:\mathbb{A}_{{\mathcal{O}}}^{n}\rightarrow \mathbb{A}_{{\mathcal{O}}}^{m}$ where ![]() $\unicode[STIX]{x1D711}$ is given by the functions
$\unicode[STIX]{x1D711}$ is given by the functions ![]() $f_{1},\ldots ,f_{m}$ and
$f_{1},\ldots ,f_{m}$ and ![]() $\unicode[STIX]{x1D713}$ is the composition of the structure map with the zero section. Hence,
$\unicode[STIX]{x1D713}$ is the composition of the structure map with the zero section. Hence, ![]() $L^{+}{\mathcal{G}}$ (respectively,
$L^{+}{\mathcal{G}}$ (respectively, ![]() $L{\mathcal{G}}$) is the equalizer of
$L{\mathcal{G}}$) is the equalizer of ![]() $L^{+}\unicode[STIX]{x1D711}$ and
$L^{+}\unicode[STIX]{x1D711}$ and ![]() $L^{+}\unicode[STIX]{x1D713}$ (respectively,
$L^{+}\unicode[STIX]{x1D713}$ (respectively, ![]() $L\unicode[STIX]{x1D711}$ and
$L\unicode[STIX]{x1D711}$ and ![]() $L\unicode[STIX]{x1D713}$) in the category of schemes (respectively, ind-schemes). As equalizers define closed subschemes and
$L\unicode[STIX]{x1D713}$) in the category of schemes (respectively, ind-schemes). As equalizers define closed subschemes and ![]() $L^{+}\mathbb{A}_{{\mathcal{O}}}^{n}$ is affine (respectively,
$L^{+}\mathbb{A}_{{\mathcal{O}}}^{n}$ is affine (respectively, ![]() $L\mathbb{A}_{{\mathcal{O}}}^{n}$ ind-affine), (i) follows.
$L\mathbb{A}_{{\mathcal{O}}}^{n}$ ind-affine), (i) follows.
Part (ii) is true for every smooth affine ![]() ${\mathcal{O}}$-scheme
${\mathcal{O}}$-scheme ![]() ${\mathcal{G}}$, necessarily of finite presentation. For
${\mathcal{G}}$, necessarily of finite presentation. For ![]() $n\geqslant 0$, let
$n\geqslant 0$, let ![]() $D_{n}=\operatorname{Spec}({\mathcal{O}}[\![D]\!]/I_{D}^{n+1})$ be the
$D_{n}=\operatorname{Spec}({\mathcal{O}}[\![D]\!]/I_{D}^{n+1})$ be the ![]() $n$th infinitesimal neighborhood of
$n$th infinitesimal neighborhood of ![]() $D$ in
$D$ in ![]() $X$. The Weil restriction of scalars
$X$. The Weil restriction of scalars ![]() ${\mathcal{G}}_{n}:=\operatorname{Res}_{D_{n}/{\mathcal{O}}}({\mathcal{G}}\times _{X}D_{n})$ is a smooth affine
${\mathcal{G}}_{n}:=\operatorname{Res}_{D_{n}/{\mathcal{O}}}({\mathcal{G}}\times _{X}D_{n})$ is a smooth affine ![]() ${\mathcal{O}}$-group scheme; cf. [Reference Bosch, Lütkebohmert and RaynaudBLR90, § 7.6, Theorem 4, Proposition 5]. For varying
${\mathcal{O}}$-group scheme; cf. [Reference Bosch, Lütkebohmert and RaynaudBLR90, § 7.6, Theorem 4, Proposition 5]. For varying ![]() $n$, these groups fit into an inverse system
$n$, these groups fit into an inverse system ![]() ${\mathcal{G}}_{m}\rightarrow {\mathcal{G}}_{n}$ for
${\mathcal{G}}_{m}\rightarrow {\mathcal{G}}_{n}$ for ![]() $m\geqslant n$, and the natural map of functors
$m\geqslant n$, and the natural map of functors
is an isomorphism. This proves (ii), and the lemma follows. ◻
Remark 3.3. If ![]() $nD$ is a positive multiple of
$nD$ is a positive multiple of ![]() $D$, then there is a canonical isomorphism
$D$, then there is a canonical isomorphism ![]() ${\mathcal{O}}[\![D]\!]\overset{\simeq \;}{\rightarrow }{\mathcal{O}}[\![nD]\!]$ (respectively,
${\mathcal{O}}[\![D]\!]\overset{\simeq \;}{\rightarrow }{\mathcal{O}}[\![nD]\!]$ (respectively, ![]() ${\mathcal{O}}((D))\overset{\simeq \;}{\rightarrow }{\mathcal{O}}((nD))$). Indeed, as
${\mathcal{O}}((D))\overset{\simeq \;}{\rightarrow }{\mathcal{O}}((nD))$). Indeed, as ![]() $I_{nD}=I_{D}^{n}\subset I_{D}$, the ring
$I_{nD}=I_{D}^{n}\subset I_{D}$, the ring ![]() ${\mathcal{O}}[\![D]\!]$ is complete with respect to the
${\mathcal{O}}[\![D]\!]$ is complete with respect to the ![]() $I_{nD}$-adic topology, and hence
$I_{nD}$-adic topology, and hence ![]() ${\mathcal{O}}[\![D]\!]\simeq \operatorname{lim}_{k\geqslant 0}R[\![D]\!]/I_{nD}^{k}=R[\![nD]\!]$.
${\mathcal{O}}[\![D]\!]\simeq \operatorname{lim}_{k\geqslant 0}R[\![D]\!]/I_{nD}^{k}=R[\![nD]\!]$.
Lemma 3.4. (i) The loop group ![]() $L{\mathcal{G}}$ represents the functor on the category of
$L{\mathcal{G}}$ represents the functor on the category of ![]() ${\mathcal{O}}$-algebras which assigns to every
${\mathcal{O}}$-algebras which assigns to every ![]() $R$ the set of isomorphism classes of triples
$R$ the set of isomorphism classes of triples ![]() $({\mathcal{F}},\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$, where
$({\mathcal{F}},\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$, where ![]() ${\mathcal{F}}$ is a
${\mathcal{F}}$ is a ![]() ${\mathcal{G}}$-torsor on
${\mathcal{G}}$-torsor on ![]() $X_{R}$, and
$X_{R}$, and ![]() $\unicode[STIX]{x1D6FC}:{\mathcal{F}}|_{X_{R}\backslash D_{R}}\stackrel{\simeq }{\longrightarrow }{\mathcal{F}}_{0}$ (respectively,
$\unicode[STIX]{x1D6FC}:{\mathcal{F}}|_{X_{R}\backslash D_{R}}\stackrel{\simeq }{\longrightarrow }{\mathcal{F}}_{0}$ (respectively, ![]() $\unicode[STIX]{x1D6FD}:{\mathcal{F}}_{0}\stackrel{\simeq }{\longrightarrow }{\mathcal{F}}|_{\hat{D}_{R}}$) is a trivialization over
$\unicode[STIX]{x1D6FD}:{\mathcal{F}}_{0}\stackrel{\simeq }{\longrightarrow }{\mathcal{F}}|_{\hat{D}_{R}}$) is a trivialization over ![]() $X_{R}\backslash D_{R}$ (respectively,
$X_{R}\backslash D_{R}$ (respectively, ![]() $\hat{D}_{R}$).
$\hat{D}_{R}$).
(ii) The projection ![]() $L{\mathcal{G}}\rightarrow \operatorname{Gr}_{{\mathcal{G}}}$,
$L{\mathcal{G}}\rightarrow \operatorname{Gr}_{{\mathcal{G}}}$, ![]() $({\mathcal{F}},\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\rightarrow ({\mathcal{F}},\unicode[STIX]{x1D6FC})$ is a right
$({\mathcal{F}},\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\rightarrow ({\mathcal{F}},\unicode[STIX]{x1D6FC})$ is a right ![]() $L^{+}{\mathcal{G}}$-torsor in the étale topology, and induces an isomorphism of sheaves
$L^{+}{\mathcal{G}}$-torsor in the étale topology, and induces an isomorphism of sheaves ![]() $L{\mathcal{G}}/L^{+}{\mathcal{G}}\stackrel{\simeq }{\longrightarrow }\;\operatorname{Gr}_{{\mathcal{G}}}$.
$L{\mathcal{G}}/L^{+}{\mathcal{G}}\stackrel{\simeq }{\longrightarrow }\;\operatorname{Gr}_{{\mathcal{G}}}$.
Proof. Part (i) is deduced from the Beauville–Laszlo theorem [Reference Beauville and LaszloBL95]; cf. [Reference Beilinson and DrinfeldBD99, § 2.12] for a further discussion (cf. also [Reference Pappas and ZhuPZ13, Lemma 6.1]). For (ii), it is enough to prove that the projection ![]() $L{\mathcal{G}}\rightarrow \operatorname{Gr}_{{\mathcal{G}}}$ admits sections étale locally.
$L{\mathcal{G}}\rightarrow \operatorname{Gr}_{{\mathcal{G}}}$ admits sections étale locally.
Let ![]() $R$ be an
$R$ be an ![]() ${\mathcal{O}}$-algebra, and let
${\mathcal{O}}$-algebra, and let ![]() ${\mathcal{F}}\rightarrow \hat{D}_{R}$ be a
${\mathcal{F}}\rightarrow \hat{D}_{R}$ be a ![]() ${\mathcal{G}}$-torsor. We have to show that
${\mathcal{G}}$-torsor. We have to show that ![]() ${\mathcal{F}}$ is trivial étale locally on
${\mathcal{F}}$ is trivial étale locally on ![]() $R$, that is, admits a
$R$, that is, admits a ![]() $\hat{D}_{R}$-section étale locally on
$\hat{D}_{R}$-section étale locally on ![]() $R$. By applying the lifting criterion for smoothness and an algebraization result for sections (algebraization is easy because
$R$. By applying the lifting criterion for smoothness and an algebraization result for sections (algebraization is easy because ![]() ${\mathcal{F}}$ is affine), it is enough to show that the restriction
${\mathcal{F}}$ is affine), it is enough to show that the restriction ![]() ${\mathcal{F}}|_{D_{R}}\rightarrow D_{R}$ admits a section étale locally on
${\mathcal{F}}|_{D_{R}}\rightarrow D_{R}$ admits a section étale locally on ![]() $R$. Since the functor
$R$. Since the functor ![]() ${\mathcal{F}}|_{D_{R}}:R\text{-Alg}\rightarrow \text{Sets},B\mapsto {\mathcal{F}}(D_{B})$ commutes with filtered colimits (because
${\mathcal{F}}|_{D_{R}}:R\text{-Alg}\rightarrow \text{Sets},B\mapsto {\mathcal{F}}(D_{B})$ commutes with filtered colimits (because ![]() ${\mathcal{F}}$ is a scheme locally of finite presentation [StaPro, 01ZC]), we may assume without loss of generality that
${\mathcal{F}}$ is a scheme locally of finite presentation [StaPro, 01ZC]), we may assume without loss of generality that ![]() $R$ is a strictly Henselian local
$R$ is a strictly Henselian local ![]() ${\mathcal{O}}$-algebra. Now by assumption on
${\mathcal{O}}$-algebra. Now by assumption on ![]() $D$ the
$D$ the ![]() $R$-algebra
$R$-algebra ![]() $R^{\prime }:=\unicode[STIX]{x1D6E4}(D_{R},{\mathcal{O}}_{D_{R}})$ is finite, and hence a direct product of Henselian local rings
$R^{\prime }:=\unicode[STIX]{x1D6E4}(D_{R},{\mathcal{O}}_{D_{R}})$ is finite, and hence a direct product of Henselian local rings ![]() $R^{\prime }=R_{1}\times \cdots \times R_{n}$; cf. [StaPro, 04GH]. As
$R^{\prime }=R_{1}\times \cdots \times R_{n}$; cf. [StaPro, 04GH]. As ![]() $R$ is strictly Henselian, each
$R$ is strictly Henselian, each ![]() $R_{i}$ is strictly Henselian as well (because a finite extension of a separably closed field is separably closed). But each non-empty smooth scheme over a finite product of strictly Henselian local rings admits a section by Hensel’s lemma. This finishes the proof.◻
$R_{i}$ is strictly Henselian as well (because a finite extension of a separably closed field is separably closed). But each non-empty smooth scheme over a finite product of strictly Henselian local rings admits a section by Hensel’s lemma. This finishes the proof.◻
Lemma 3.4(ii) shows that there is a transitive action map
Let us look at the fibers of (3.8) over ![]() ${\mathcal{O}}$.
${\mathcal{O}}$.
Corollary 3.5. (i) Let ![]() $F$ be a field, and let
$F$ be a field, and let ![]() ${\mathcal{O}}\rightarrow F$ be a ring morphism. The underlying reduced subscheme
${\mathcal{O}}\rightarrow F$ be a ring morphism. The underlying reduced subscheme ![]() $D_{F,\operatorname{red}}\subset D_{F}$ is an effective Cartier divisor on
$D_{F,\operatorname{red}}\subset D_{F}$ is an effective Cartier divisor on ![]() $X_{F}$, and we write
$X_{F}$, and we write ![]() $D_{F,\operatorname{red}}=\sum _{i=1}^{n}D_{i}$ where
$D_{F,\operatorname{red}}=\sum _{i=1}^{n}D_{i}$ where ![]() $D_{i}$ are distinct irreducible, that is, the
$D_{i}$ are distinct irreducible, that is, the ![]() $D_{i}$ are closed points of
$D_{i}$ are closed points of ![]() $X_{F}$. There is a canonical isomorphism of
$X_{F}$. There is a canonical isomorphism of ![]() $F$-spaces
$F$-spaces
compatible with the action of ![]() $L{\mathcal{G}}_{(X,{\mathcal{G}},D)}\otimes _{{\mathcal{O}}}F\simeq \prod _{i=1}^{n}L{\mathcal{G}}_{(X_{F},{\mathcal{G}}_{F},D_{i})}$.
$L{\mathcal{G}}_{(X,{\mathcal{G}},D)}\otimes _{{\mathcal{O}}}F\simeq \prod _{i=1}^{n}L{\mathcal{G}}_{(X_{F},{\mathcal{G}}_{F},D_{i})}$.
(ii) Let ![]() ${\mathcal{O}}=F$ be a field, and let
${\mathcal{O}}=F$ be a field, and let ![]() $D=[x]$ be the divisor on
$D=[x]$ be the divisor on ![]() $X$ defined by a closed point
$X$ defined by a closed point ![]() $x\in X$. The residue field
$x\in X$. The residue field ![]() $K:=\unicode[STIX]{x1D705}(x)$ is a finite field extension, and we assume that
$K:=\unicode[STIX]{x1D705}(x)$ is a finite field extension, and we assume that ![]() $K/F$ is separable. There is a canonical isomorphism of
$K/F$ is separable. There is a canonical isomorphism of ![]() $F$-spaces
$F$-spaces
compatible with the action of ![]() $L{\mathcal{G}}_{(X,{\mathcal{G}},D)}\simeq \operatorname{Res}_{K/F}(L{\mathcal{G}}_{(X_{K},{\mathcal{G}}_{X_{K}},D)})$.
$L{\mathcal{G}}_{(X,{\mathcal{G}},D)}\simeq \operatorname{Res}_{K/F}(L{\mathcal{G}}_{(X_{K},{\mathcal{G}}_{X_{K}},D)})$.
Proof. For (i), we may by (3.2) assume ![]() ${\mathcal{O}}=F$. It is immediate from Remark 3.3 that for any
${\mathcal{O}}=F$. It is immediate from Remark 3.3 that for any ![]() ${\mathcal{O}}$-algebra
${\mathcal{O}}$-algebra ![]() $R$, we have
$R$, we have ![]() $R[\![D_{\operatorname{red}}]\!]\simeq R[\![D]\!]$ (respectively,
$R[\![D_{\operatorname{red}}]\!]\simeq R[\![D]\!]$ (respectively, ![]() $R((D_{\operatorname{red}}))\simeq R((D))$). Further, there is a canonical isomorphism
$R((D_{\operatorname{red}}))\simeq R((D))$). Further, there is a canonical isomorphism
because ![]() $X$ is of dimension
$X$ is of dimension ![]() $1$, and hence
$1$, and hence ![]() $D_{i}\cap D_{j}=\varnothing$ for
$D_{i}\cap D_{j}=\varnothing$ for ![]() $i\not =j$. Part (i) follows from Lemma 3.4(ii).
$i\not =j$. Part (i) follows from Lemma 3.4(ii).
For (ii), first note that if we consider ![]() $D$ as the divisor on
$D$ as the divisor on ![]() $X_{K}$ defined by the
$X_{K}$ defined by the ![]() $K$-point
$K$-point ![]() $x$, then
$x$, then ![]() $\operatorname{Gr}_{(X_{K},{\mathcal{G}}_{X_{K}},D)}$ is the twisted affine Grassmannian over
$\operatorname{Gr}_{(X_{K},{\mathcal{G}}_{X_{K}},D)}$ is the twisted affine Grassmannian over ![]() $K$; cf. Example 3.1(i). Let
$K$; cf. Example 3.1(i). Let ![]() $\tilde{K}/F$ be the splitting field of
$\tilde{K}/F$ be the splitting field of ![]() $K$ which is a finite Galois extension with Galois group
$K$ which is a finite Galois extension with Galois group ![]() $\tilde{\unicode[STIX]{x1D6E4}}$. There is a canonical isomorphism of
$\tilde{\unicode[STIX]{x1D6E4}}$. There is a canonical isomorphism of ![]() $\tilde{K}$-algebras
$\tilde{K}$-algebras
which is ![]() $\tilde{\unicode[STIX]{x1D6E4}}$-equivariant for the action
$\tilde{\unicode[STIX]{x1D6E4}}$-equivariant for the action ![]() $\unicode[STIX]{x1D6FE}\ast (c_{\unicode[STIX]{x1D713}})_{\unicode[STIX]{x1D713}}\mapsto (\unicode[STIX]{x1D6FE}(c_{\unicode[STIX]{x1D713}}))_{\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D713}}$ on the target. Applying this isomorphism to
$\unicode[STIX]{x1D6FE}\ast (c_{\unicode[STIX]{x1D713}})_{\unicode[STIX]{x1D713}}\mapsto (\unicode[STIX]{x1D6FE}(c_{\unicode[STIX]{x1D713}}))_{\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D713}}$ on the target. Applying this isomorphism to ![]() $D\otimes _{F}\tilde{K}$, we obtain by (i) a
$D\otimes _{F}\tilde{K}$, we obtain by (i) a ![]() $\tilde{\unicode[STIX]{x1D6E4}}$-equivariant isomorphism
$\tilde{\unicode[STIX]{x1D6E4}}$-equivariant isomorphism
compatible with the actions of the loop groups. The canonical descent datum on the source in (3.9) induces a descent datum on the target of (3.9) which implies (ii). ◻
Let us point out some useful compatibility with Weil restriction of scalars.
Corollary 3.6. Let ![]() $X^{\prime }\rightarrow X$ be a finite flat surjective map of smooth quasi-projective
$X^{\prime }\rightarrow X$ be a finite flat surjective map of smooth quasi-projective ![]() ${\mathcal{O}}$-curves, and assume
${\mathcal{O}}$-curves, and assume ![]() ${\mathcal{G}}=\operatorname{Res}_{X^{\prime }/X}({\mathcal{G}}^{\prime })$ for a smooth affine
${\mathcal{G}}=\operatorname{Res}_{X^{\prime }/X}({\mathcal{G}}^{\prime })$ for a smooth affine ![]() $X^{\prime }$-group scheme
$X^{\prime }$-group scheme ![]() ${\mathcal{G}}^{\prime }$. If
${\mathcal{G}}^{\prime }$. If ![]() $D^{\prime }:=D\times _{X}X^{\prime }$, then the natural map is an isomorphism of
$D^{\prime }:=D\times _{X}X^{\prime }$, then the natural map is an isomorphism of ![]() ${\mathcal{O}}$-spaces
${\mathcal{O}}$-spaces
Proof. Since ![]() $X^{\prime }\rightarrow X$ is finite flat surjective, the closed subscheme
$X^{\prime }\rightarrow X$ is finite flat surjective, the closed subscheme ![]() $D^{\prime }\subset X^{\prime }$ is a relative effective Cartier divisor which is finite flat over
$D^{\prime }\subset X^{\prime }$ is a relative effective Cartier divisor which is finite flat over ![]() ${\mathcal{O}}$. Hence, the functor
${\mathcal{O}}$. Hence, the functor ![]() $\operatorname{Gr}_{(X^{\prime },{\mathcal{G}}^{\prime },D^{\prime })}$ is well defined. Using Lemma 3.4(ii), the map (3.10) is induced for any
$\operatorname{Gr}_{(X^{\prime },{\mathcal{G}}^{\prime },D^{\prime })}$ is well defined. Using Lemma 3.4(ii), the map (3.10) is induced for any ![]() ${\mathcal{O}}$-algebra
${\mathcal{O}}$-algebra ![]() $R$ by the canonical map of
$R$ by the canonical map of ![]() $R$-algebras
$R$-algebras
If ![]() $R$ is Noetherian, then the first map (hence the second map) is an isomorphism by [StaPro, 00MA] because
$R$ is Noetherian, then the first map (hence the second map) is an isomorphism by [StaPro, 00MA] because ![]() $X^{\prime }\rightarrow X$ is finite. In particular, (3.10) is an isomorphism for any Noetherian
$X^{\prime }\rightarrow X$ is finite. In particular, (3.10) is an isomorphism for any Noetherian ![]() ${\mathcal{O}}$-algebra
${\mathcal{O}}$-algebra ![]() $R$. As both functors in (3.10) commute with filtered colimits of
$R$. As both functors in (3.10) commute with filtered colimits of ![]() ${\mathcal{O}}$-algebras, the corollary follows.◻
${\mathcal{O}}$-algebras, the corollary follows.◻
Lemma 3.7. Let ![]() ${\mathcal{O}}^{\prime }\rightarrow {\mathcal{O}}$ be a finite étale map of Noetherian rings. Then the composition
${\mathcal{O}}^{\prime }\rightarrow {\mathcal{O}}$ be a finite étale map of Noetherian rings. Then the composition ![]() $X\rightarrow \operatorname{Spec}({\mathcal{O}})\rightarrow \operatorname{Spec}({\mathcal{O}}^{\prime })$ is a smooth curve as well, and there is a canonical isomorphism of functors
$X\rightarrow \operatorname{Spec}({\mathcal{O}})\rightarrow \operatorname{Spec}({\mathcal{O}}^{\prime })$ is a smooth curve as well, and there is a canonical isomorphism of functors
Proof. If ![]() $T\rightarrow \operatorname{Spec}({\mathcal{O}}^{\prime })$ is a test scheme, then
$T\rightarrow \operatorname{Spec}({\mathcal{O}}^{\prime })$ is a test scheme, then ![]() $X\times _{\operatorname{Spec}({\mathcal{O}})}(\operatorname{Spec}({\mathcal{O}})\times _{\operatorname{Spec}({\mathcal{O}}^{\prime })}T)=X\times _{\operatorname{Spec}({\mathcal{O}}^{\prime })}T$. The lemma follows immediately from the definitions.◻
$X\times _{\operatorname{Spec}({\mathcal{O}})}(\operatorname{Spec}({\mathcal{O}})\times _{\operatorname{Spec}({\mathcal{O}}^{\prime })}T)=X\times _{\operatorname{Spec}({\mathcal{O}}^{\prime })}T$. The lemma follows immediately from the definitions.◻
3.1.2 Basic representability properties
The starting point is the following lemma, and we sketch its proof.
Lemma 3.8. If ![]() ${\mathcal{G}}=\operatorname{Gl}_{n,X}$, then the functor
${\mathcal{G}}=\operatorname{Gl}_{n,X}$, then the functor ![]() $\operatorname{Gr}_{{\mathcal{G}}}$ is representable by an ind-projective
$\operatorname{Gr}_{{\mathcal{G}}}$ is representable by an ind-projective ![]() ${\mathcal{O}}$-ind-scheme.
${\mathcal{O}}$-ind-scheme.
Proof. Let ![]() $R$ be an
$R$ be an ![]() ${\mathcal{O}}$-algebra. If
${\mathcal{O}}$-algebra. If ![]() ${\mathcal{G}}=\operatorname{Gl}_{n,X}$, then
${\mathcal{G}}=\operatorname{Gl}_{n,X}$, then ![]() $\operatorname{Gr}_{{\mathcal{G}}}(R)$ classifies rank-
$\operatorname{Gr}_{{\mathcal{G}}}(R)$ classifies rank-![]() $n$ vector bundles
$n$ vector bundles ![]() ${\mathcal{E}}$ on
${\mathcal{E}}$ on ![]() $X_{R}$ together with an isomorphism
$X_{R}$ together with an isomorphism ![]() ${\mathcal{E}}|_{U_{R}}\simeq {\mathcal{O}}_{U_{R}}^{n}$ where
${\mathcal{E}}|_{U_{R}}\simeq {\mathcal{O}}_{U_{R}}^{n}$ where ![]() $U_{R}:=(X\backslash D)_{R}$. Let
$U_{R}:=(X\backslash D)_{R}$. Let ![]() ${\mathcal{I}}_{D_{R}}\subset {\mathcal{O}}_{X_{R}}$ be the invertible ideal sheaf defined by
${\mathcal{I}}_{D_{R}}\subset {\mathcal{O}}_{X_{R}}$ be the invertible ideal sheaf defined by ![]() $D_{R}\subset X_{R}$. For
$D_{R}\subset X_{R}$. For ![]() $N\geqslant 1$, let
$N\geqslant 1$, let ![]() $\operatorname{Gr}_{{\mathcal{G}},N}$ be the
$\operatorname{Gr}_{{\mathcal{G}},N}$ be the ![]() ${\mathcal{O}}$-space whose
${\mathcal{O}}$-space whose ![]() $R$-valued points are rank-
$R$-valued points are rank-![]() $n$ vector bundles
$n$ vector bundles ![]() ${\mathcal{E}}$ on
${\mathcal{E}}$ on ![]() $X_{R}$ such that, as
$X_{R}$ such that, as ![]() ${\mathcal{O}}_{X_{R}}$-modules,
${\mathcal{O}}_{X_{R}}$-modules,
Every vector bundle is locally free and by bounding the poles (respectively, zeros) of basis elements, one gets, as ![]() ${\mathcal{O}}$-spaces,
${\mathcal{O}}$-spaces,
We claim that each ![]() $\operatorname{Gr}_{{\mathcal{G}},N}$ is representable by a
$\operatorname{Gr}_{{\mathcal{G}},N}$ is representable by a ![]() $\operatorname{Quot}$-scheme as follows. The
$\operatorname{Quot}$-scheme as follows. The ![]() ${\mathcal{O}}_{X_{R}}$-module
${\mathcal{O}}_{X_{R}}$-module ![]() ${\mathcal{E}}_{N,R}:=({\mathcal{I}}_{D}^{-N}/{\mathcal{I}}_{D}^{N})^{n}\otimes _{{\mathcal{O}}}R$ is coherent and locally free over
${\mathcal{E}}_{N,R}:=({\mathcal{I}}_{D}^{-N}/{\mathcal{I}}_{D}^{N})^{n}\otimes _{{\mathcal{O}}}R$ is coherent and locally free over ![]() $R$. Let
$R$. Let ![]() $\operatorname{Quot}_{N}$ be the
$\operatorname{Quot}_{N}$ be the ![]() ${\mathcal{O}}$-space whose
${\mathcal{O}}$-space whose ![]() $R$-points are coherent
$R$-points are coherent ![]() ${\mathcal{O}}_{X_{R}}$-module quotients
${\mathcal{O}}_{X_{R}}$-module quotients ![]() ${\mathcal{E}}_{N,R}{\twoheadrightarrow}{\mathcal{Q}}$ which are locally free
${\mathcal{E}}_{N,R}{\twoheadrightarrow}{\mathcal{Q}}$ which are locally free ![]() $R$-modules. The functor
$R$-modules. The functor ![]() $\operatorname{Quot}_{N}$ is representable by a projective
$\operatorname{Quot}_{N}$ is representable by a projective ![]() ${\mathcal{O}}$-scheme by the theory of
${\mathcal{O}}$-scheme by the theory of ![]() $\operatorname{Quot}$-schemes applied to the finite flat
$\operatorname{Quot}$-schemes applied to the finite flat ![]() ${\mathcal{O}}$-scheme
${\mathcal{O}}$-scheme ![]() $2ND$, and the coherent
$2ND$, and the coherent ![]() ${\mathcal{O}}_{2ND}={\mathcal{O}}_{X}/{\mathcal{I}}_{D}^{2N}$-module
${\mathcal{O}}_{2ND}={\mathcal{O}}_{X}/{\mathcal{I}}_{D}^{2N}$-module ![]() ${\mathcal{E}}_{N,{\mathcal{O}}}$. More precisely, in the notation of [Reference FantechiFan05, § 5.1.4], one has a finite disjoint union
${\mathcal{E}}_{N,{\mathcal{O}}}$. More precisely, in the notation of [Reference FantechiFan05, § 5.1.4], one has a finite disjoint union
and the representability result is then a theorem of Grothendieck [Reference FantechiFan05, § 5.5.2, Theorem 5.14]. Note that the structure sheaf ![]() ${\mathcal{O}}_{2ND}$ is relatively ample for
${\mathcal{O}}_{2ND}$ is relatively ample for ![]() $2ND\rightarrow \operatorname{Spec}({\mathcal{O}})$ because the map is finite (cf. [StaPro, Tag 01VG, 28.35.6]). Concretely,
$2ND\rightarrow \operatorname{Spec}({\mathcal{O}})$ because the map is finite (cf. [StaPro, Tag 01VG, 28.35.6]). Concretely, ![]() $\operatorname{Quot}_{N}$ is the closed subscheme of the Grassmannian
$\operatorname{Quot}_{N}$ is the closed subscheme of the Grassmannian
which is cut out by the condition that the quotients are stable under the finitely many nilpotent operators ![]() $u_{1},\ldots ,u_{n}$ on
$u_{1},\ldots ,u_{n}$ on ![]() ${\mathcal{E}}_{N,{\mathcal{O}}}$ induced by some presentation
${\mathcal{E}}_{N,{\mathcal{O}}}$ induced by some presentation ![]() $2ND=\operatorname{Spec}({\mathcal{O}}[u_{1},\ldots ,u_{n}]/J)$. Hence, to prove the lemma it is enough to show that, as functors,
$2ND=\operatorname{Spec}({\mathcal{O}}[u_{1},\ldots ,u_{n}]/J)$. Hence, to prove the lemma it is enough to show that, as functors,
We need to check that ![]() ${\mathcal{Q}}:=({\mathcal{I}}_{D_{R}}^{-N})^{n}/{\mathcal{E}}$ is a locally free
${\mathcal{Q}}:=({\mathcal{I}}_{D_{R}}^{-N})^{n}/{\mathcal{E}}$ is a locally free ![]() $R$-module. This follows from the isomorphism as
$R$-module. This follows from the isomorphism as ![]() $R$-modules
$R$-modules ![]() ${\mathcal{O}}_{U_{R}}^{n}/{\mathcal{E}}\simeq \bigoplus _{k\geqslant 0}{\mathcal{I}}_{D_{R}}^{-k-1}{\mathcal{E}}/{\mathcal{I}}_{D_{R}}^{-k}{\mathcal{E}}$, and the short exact sequence
${\mathcal{O}}_{U_{R}}^{n}/{\mathcal{E}}\simeq \bigoplus _{k\geqslant 0}{\mathcal{I}}_{D_{R}}^{-k-1}{\mathcal{E}}/{\mathcal{I}}_{D_{R}}^{-k}{\mathcal{E}}$, and the short exact sequence
cf. also the argument in [Reference ZhuZhu17, Lemma 1.1.5]. Conversely, let ![]() ${\mathcal{Q}}\in \operatorname{Quot}_{N}(R)$, and define the coherent
${\mathcal{Q}}\in \operatorname{Quot}_{N}(R)$, and define the coherent ![]() ${\mathcal{O}}_{X_{R}}$-module
${\mathcal{O}}_{X_{R}}$-module
We need to show that ![]() ${\mathcal{E}}$ is a rank-
${\mathcal{E}}$ is a rank-![]() $n$ vector bundle on
$n$ vector bundle on ![]() $X_{R}$. Covering
$X_{R}$. Covering ![]() $X_{R}$ with affine schemes, we may assume
$X_{R}$ with affine schemes, we may assume ![]() $X_{R}=\operatorname{Spec}(S)$ is affine. Let
$X_{R}=\operatorname{Spec}(S)$ is affine. Let ![]() $\mathfrak{p}\subset S$ be a prime ideal lying over a prime ideal
$\mathfrak{p}\subset S$ be a prime ideal lying over a prime ideal ![]() $\mathfrak{m}:=\mathfrak{p}\cap R\subset R$. By [StaPro, Tag 00M] applied to the map of local rings
$\mathfrak{m}:=\mathfrak{p}\cap R\subset R$. By [StaPro, Tag 00M] applied to the map of local rings ![]() $R_{\mathfrak{m}}\rightarrow S_{\mathfrak{p}}$ and the module
$R_{\mathfrak{m}}\rightarrow S_{\mathfrak{p}}$ and the module ![]() ${\mathcal{E}}_{\mathfrak{p}}$ (note that
${\mathcal{E}}_{\mathfrak{p}}$ (note that ![]() ${\mathcal{E}}_{\mathfrak{p}}$ is still
${\mathcal{E}}_{\mathfrak{p}}$ is still ![]() $R_{\mathfrak{m}}$-flat), to prove
$R_{\mathfrak{m}}$-flat), to prove ![]() ${\mathcal{E}}_{\mathfrak{p}}$ is free over
${\mathcal{E}}_{\mathfrak{p}}$ is free over ![]() $S_{\mathfrak{p}}$ we are reduced to the case where
$S_{\mathfrak{p}}$ we are reduced to the case where ![]() $R$ is a field. In the case where
$R$ is a field. In the case where ![]() $R$ is a field,
$R$ is a field, ![]() ${\mathcal{E}}\subset ({\mathcal{I}}_{D_{R}}^{-N})^{n}$ is a torsion-free rank-
${\mathcal{E}}\subset ({\mathcal{I}}_{D_{R}}^{-N})^{n}$ is a torsion-free rank-![]() $n$ submodule, and since
$n$ submodule, and since ![]() $X_{R}\rightarrow \operatorname{Spec}(R)$ is a smooth curve,
$X_{R}\rightarrow \operatorname{Spec}(R)$ is a smooth curve, ![]() ${\mathcal{E}}$ is a vector bundle.◻
${\mathcal{E}}$ is a vector bundle.◻
Remark 3.9. Using Lemma 3.4(ii), the set ![]() $\operatorname{Gr}_{\operatorname{Gl}_{n,X}}({\mathcal{O}})$ can be identified with the set of
$\operatorname{Gr}_{\operatorname{Gl}_{n,X}}({\mathcal{O}})$ can be identified with the set of ![]() ${\mathcal{O}}[\![D]\!]$-lattices in
${\mathcal{O}}[\![D]\!]$-lattices in ![]() ${\mathcal{O}}((D))$, that is, in the notation of Lemma 3.2, the set of
${\mathcal{O}}((D))$, that is, in the notation of Lemma 3.2, the set of ![]() ${\mathcal{O}}[\![D]\!]$-submodules
${\mathcal{O}}[\![D]\!]$-submodules ![]() $M\subset {\mathcal{O}}((D))$ such that for some
$M\subset {\mathcal{O}}((D))$ such that for some ![]() $N\gg 0$,
$N\gg 0$, ![]() $(I_{D}^{N})^{n}\subset M\subset (I_{D}^{-N})^{n}$ and
$(I_{D}^{N})^{n}\subset M\subset (I_{D}^{-N})^{n}$ and ![]() $(I_{D}^{-N})^{n}/M$ is a locally free
$(I_{D}^{-N})^{n}/M$ is a locally free ![]() ${\mathcal{O}}$-module.
${\mathcal{O}}$-module.
Proposition 3.10. If ![]() ${\mathcal{G}}{\hookrightarrow}G$ is a monomorphism of smooth
${\mathcal{G}}{\hookrightarrow}G$ is a monomorphism of smooth ![]() $X$-affine
$X$-affine ![]() $X$-group schemes such that the fppf quotient
$X$-group schemes such that the fppf quotient ![]() $G/{\mathcal{G}}$ is a
$G/{\mathcal{G}}$ is a ![]() $X$-quasi-affine scheme (respectively,
$X$-quasi-affine scheme (respectively, ![]() $X$-affine scheme), then the map
$X$-affine scheme), then the map ![]() $\operatorname{Gr}_{{\mathcal{G}}}\rightarrow \operatorname{Gr}_{G}$ is representable by a quasi-compact immersion (respectively, closed immersion).
$\operatorname{Gr}_{{\mathcal{G}}}\rightarrow \operatorname{Gr}_{G}$ is representable by a quasi-compact immersion (respectively, closed immersion).
Proof. Following the proof of [Reference ZhuZhu17, Proposition 1.2.6], it is enough to establish the analogue of [Reference ZhuZhu17, Lemma 1.2.7]. Let ![]() $R$ an
$R$ an ![]() ${\mathcal{O}}$-algebra, and let
${\mathcal{O}}$-algebra, and let ![]() $p:V\rightarrow \hat{D}_{R}$ be an affine scheme of finite presentation. Let
$p:V\rightarrow \hat{D}_{R}$ be an affine scheme of finite presentation. Let ![]() $s$ be a section of
$s$ be a section of ![]() $p$ over
$p$ over ![]() $\hat{D}_{R}^{o}$. We need to prove that the presheaf assigning, to any
$\hat{D}_{R}^{o}$. We need to prove that the presheaf assigning, to any ![]() $R$-algebra
$R$-algebra ![]() $R^{\prime }$, the set of sections
$R^{\prime }$, the set of sections ![]() $s^{\prime }$ of
$s^{\prime }$ of ![]() $p$ over
$p$ over ![]() $\hat{D}_{R^{\prime }}$ such that
$\hat{D}_{R^{\prime }}$ such that ![]() $s^{\prime }|_{\hat{D}_{R^{\prime }}^{o}}=s|_{\hat{D}_{R^{\prime }}^{o}}\!$, is representable by a closed subscheme of
$s^{\prime }|_{\hat{D}_{R^{\prime }}^{o}}=s|_{\hat{D}_{R^{\prime }}^{o}}\!$, is representable by a closed subscheme of ![]() $\operatorname{Spec}(R)$. Indeed, choosing a closed embedding
$\operatorname{Spec}(R)$. Indeed, choosing a closed embedding ![]() $V\subset \mathbb{A}_{\hat{D}_{R}}^{n}$ for some
$V\subset \mathbb{A}_{\hat{D}_{R}}^{n}$ for some ![]() $n\gg 0$ and using that
$n\gg 0$ and using that ![]() $R[\![D]\!]\subset R((D))$ is injective, we reduce to the case
$R[\![D]\!]\subset R((D))$ is injective, we reduce to the case ![]() $V=\mathbb{A}_{\hat{D}_{R}}^{n}$. The presheaf in question is representable by the locus on
$V=\mathbb{A}_{\hat{D}_{R}}^{n}$. The presheaf in question is representable by the locus on ![]() $\operatorname{Spec}(R)$ where the class
$\operatorname{Spec}(R)$ where the class ![]() $\bar{s}$ of the section
$\bar{s}$ of the section ![]() $s\in V(\hat{D}_{R}^{o})=R((D))^{n}$ in
$s\in V(\hat{D}_{R}^{o})=R((D))^{n}$ in ![]() $(R((D))/R[\![D]\!])^{n}$ vanishes. With the notation of Lemma 3.2, we have
$(R((D))/R[\![D]\!])^{n}$ vanishes. With the notation of Lemma 3.2, we have ![]() $\bar{s}\in E_{[-N,0]}\otimes _{{\mathcal{O}}}R$ for some
$\bar{s}\in E_{[-N,0]}\otimes _{{\mathcal{O}}}R$ for some ![]() $N\gg 0$. As
$N\gg 0$. As ![]() $E_{[-N,0]}$ is a reflexive
$E_{[-N,0]}$ is a reflexive ![]() ${\mathcal{O}}$-module, we see that giving an element of
${\mathcal{O}}$-module, we see that giving an element of ![]() $E_{[-N,0]}\otimes _{{\mathcal{O}}}R$ is equivalent to giving a map of
$E_{[-N,0]}\otimes _{{\mathcal{O}}}R$ is equivalent to giving a map of ![]() $R$-schemes
$R$-schemes ![]() $\operatorname{Spec}(R)\rightarrow \mathbb{V}(E_{[-N,0]}\otimes _{{\mathcal{O}}}R)$. Then the presheaf in question is representable by the equalizer of the two maps corresponding to the elements
$\operatorname{Spec}(R)\rightarrow \mathbb{V}(E_{[-N,0]}\otimes _{{\mathcal{O}}}R)$. Then the presheaf in question is representable by the equalizer of the two maps corresponding to the elements ![]() $\bar{s},0\in E_{[-N,0]}\otimes _{{\mathcal{O}}}R$ which is a closed subscheme of
$\bar{s},0\in E_{[-N,0]}\otimes _{{\mathcal{O}}}R$ which is a closed subscheme of ![]() $\operatorname{Spec}(R)$.◻
$\operatorname{Spec}(R)$.◻
Corollary 3.11. (i) If there exists a monomorphism ![]() ${\mathcal{G}}{\hookrightarrow}\operatorname{Gl}_{n,X}$ such that the fppf quotient is a
${\mathcal{G}}{\hookrightarrow}\operatorname{Gl}_{n,X}$ such that the fppf quotient is a ![]() $X$-quasi-affine scheme (respectively, an
$X$-quasi-affine scheme (respectively, an ![]() $X$-affine scheme), then
$X$-affine scheme), then ![]() $\operatorname{Gr}_{{\mathcal{G}}}=\operatorname{colim}_{i}\operatorname{Gr}_{{\mathcal{G}},i}$ is representable by a separated
$\operatorname{Gr}_{{\mathcal{G}}}=\operatorname{colim}_{i}\operatorname{Gr}_{{\mathcal{G}},i}$ is representable by a separated ![]() ${\mathcal{O}}$-ind-scheme of ind-finite type (respectively, separated ind-proper
${\mathcal{O}}$-ind-scheme of ind-finite type (respectively, separated ind-proper ![]() ${\mathcal{O}}$-ind-scheme). Each
${\mathcal{O}}$-ind-scheme). Each ![]() $\operatorname{Gr}_{{\mathcal{G}},i}$ can be chosen to be
$\operatorname{Gr}_{{\mathcal{G}},i}$ can be chosen to be ![]() $L^{+}{\mathcal{G}}$-stable.
$L^{+}{\mathcal{G}}$-stable.
(ii) If in (i) the representation ![]() ${\mathcal{G}}{\hookrightarrow}\operatorname{Gl}_{n,X}$ exists étale locally on
${\mathcal{G}}{\hookrightarrow}\operatorname{Gl}_{n,X}$ exists étale locally on ![]() ${\mathcal{O}}$, then
${\mathcal{O}}$, then ![]() $\operatorname{Gr}_{{\mathcal{G}}}=\operatorname{colim}_{i}\operatorname{Gr}_{{\mathcal{G}},i}$ is a separated
$\operatorname{Gr}_{{\mathcal{G}}}=\operatorname{colim}_{i}\operatorname{Gr}_{{\mathcal{G}},i}$ is a separated ![]() ${\mathcal{O}}$-ind-algebraic space of ind-finite presentation (respectively, separated ind-proper
${\mathcal{O}}$-ind-algebraic space of ind-finite presentation (respectively, separated ind-proper ![]() ${\mathcal{O}}$-ind-algebraic space). Each
${\mathcal{O}}$-ind-algebraic space). Each ![]() $\operatorname{Gr}_{{\mathcal{G}},i}$ can be chosen to be
$\operatorname{Gr}_{{\mathcal{G}},i}$ can be chosen to be ![]() $L^{+}{\mathcal{G}}$-stable.
$L^{+}{\mathcal{G}}$-stable.
(iii) If ![]() ${\mathcal{G}}=G\,\otimes _{{\mathcal{O}}}\,X$ is constant and
${\mathcal{G}}=G\,\otimes _{{\mathcal{O}}}\,X$ is constant and ![]() $G$ is a reductive
$G$ is a reductive ![]() ${\mathcal{O}}$-group scheme, then
${\mathcal{O}}$-group scheme, then ![]() $\operatorname{Gr}_{{\mathcal{G}}}$ is representable by an ind-proper
$\operatorname{Gr}_{{\mathcal{G}}}$ is representable by an ind-proper ![]() ${\mathcal{O}}$-ind-algebraic space.
${\mathcal{O}}$-ind-algebraic space.
Proof. Part (i) is immediate from Lemma 3.8 and Proposition 3.10.
For (ii), we use part (i) together with Lemma 3.12 below. Note that the diagonal of ![]() $\operatorname{Gr}_{{\mathcal{G}}}$ being representable by a closed immersion follows from the same property of
$\operatorname{Gr}_{{\mathcal{G}}}$ being representable by a closed immersion follows from the same property of ![]() $\operatorname{Gr}_{\operatorname{Gl}_{n,{\mathcal{O}}}}$ and the effectivity of descent for closed immersions. Further, if
$\operatorname{Gr}_{\operatorname{Gl}_{n,{\mathcal{O}}}}$ and the effectivity of descent for closed immersions. Further, if ![]() ${\mathcal{O}}\rightarrow {\mathcal{O}}^{\prime }$ is étale, then the method of Lemma 3.12 shows that an
${\mathcal{O}}\rightarrow {\mathcal{O}}^{\prime }$ is étale, then the method of Lemma 3.12 shows that an ![]() $L^{+}{\mathcal{G}}\otimes _{{\mathcal{O}}}{\mathcal{O}}^{\prime }$-stable presentation of
$L^{+}{\mathcal{G}}\otimes _{{\mathcal{O}}}{\mathcal{O}}^{\prime }$-stable presentation of ![]() $\operatorname{Gr}_{{\mathcal{G}}}\otimes _{{\mathcal{O}}}{\mathcal{O}}^{\prime }$ induces an
$\operatorname{Gr}_{{\mathcal{G}}}\otimes _{{\mathcal{O}}}{\mathcal{O}}^{\prime }$ induces an ![]() $L^{+}{\mathcal{G}}$-stable presentation of
$L^{+}{\mathcal{G}}$-stable presentation of ![]() $\operatorname{Gr}_{{\mathcal{G}}}$ (because
$\operatorname{Gr}_{{\mathcal{G}}}$ (because ![]() $L^{+}{\mathcal{G}}$ is affine and flat, and taking the scheme-theoretic image commutes with flat base change).
$L^{+}{\mathcal{G}}$ is affine and flat, and taking the scheme-theoretic image commutes with flat base change).
For (iii), note that after an étale cover ![]() ${\mathcal{O}}\rightarrow {\mathcal{O}}^{\prime }$, the group scheme
${\mathcal{O}}\rightarrow {\mathcal{O}}^{\prime }$, the group scheme ![]() $G_{{\mathcal{O}}^{\prime }}:=G\otimes _{{\mathcal{O}}}{\mathcal{O}}^{\prime }$ is split reductive and, in particular, linearly reductive. If we choose a closed immersion
$G_{{\mathcal{O}}^{\prime }}:=G\otimes _{{\mathcal{O}}}{\mathcal{O}}^{\prime }$ is split reductive and, in particular, linearly reductive. If we choose a closed immersion ![]() $G_{{\mathcal{O}}^{\prime }}{\hookrightarrow}\operatorname{Gl}_{n,{\mathcal{O}}^{\prime }}$, then the quotient
$G_{{\mathcal{O}}^{\prime }}{\hookrightarrow}\operatorname{Gl}_{n,{\mathcal{O}}^{\prime }}$, then the quotient ![]() $\operatorname{Gl}_{n,{\mathcal{O}}^{\prime }}/G_{{\mathcal{O}}^{\prime }}$ is representable by an affine scheme by [Reference AlperAlp14, Corollary 9.7.7], and (iii) follows from (ii).◻
$\operatorname{Gl}_{n,{\mathcal{O}}^{\prime }}/G_{{\mathcal{O}}^{\prime }}$ is representable by an affine scheme by [Reference AlperAlp14, Corollary 9.7.7], and (iii) follows from (ii).◻
Lemma 3.12. Let ![]() $X$ be an
$X$ be an ![]() ${\mathcal{O}}$-space with schematic diagonal, and such that there exists a étale surjective (as sheaves) map of
${\mathcal{O}}$-space with schematic diagonal, and such that there exists a étale surjective (as sheaves) map of ![]() ${\mathcal{O}}$-spaces
${\mathcal{O}}$-spaces ![]() $U\rightarrow X$ with
$U\rightarrow X$ with ![]() $U$ an
$U$ an ![]() ${\mathcal{O}}$-ind-scheme. If either
${\mathcal{O}}$-ind-scheme. If either ![]() $U\rightarrow X$ is quasi-compact or
$U\rightarrow X$ is quasi-compact or ![]() $U$ is quasi-separated, then
$U$ is quasi-separated, then ![]() $X$ is an
$X$ is an ![]() ${\mathcal{O}}$-ind-algebraic space.
${\mathcal{O}}$-ind-algebraic space.
Proof. Given a presentation ![]() $U=\operatorname{colim}_{i\in I}U_{i}$ with
$U=\operatorname{colim}_{i\in I}U_{i}$ with ![]() $U_{i}$ being schemes, we need to construct a presentation
$U_{i}$ being schemes, we need to construct a presentation ![]() $X=\operatorname{colim}_{i\in I}X_{i}$ with
$X=\operatorname{colim}_{i\in I}X_{i}$ with ![]() $X_{i}$ being algebraic spaces. For each
$X_{i}$ being algebraic spaces. For each ![]() $i$, consider
$i$, consider ![]() $U_{i}\subset U\rightarrow X$. We define
$U_{i}\subset U\rightarrow X$. We define ![]() $X_{i}^{\prime }$ to be the scheme-theoretic image of the map
$X_{i}^{\prime }$ to be the scheme-theoretic image of the map
This is well defined for the following reason. Since ![]() $U_{i}\times _{X}U$ is a quasi-compact scheme, the map (3.12) factors through
$U_{i}\times _{X}U$ is a quasi-compact scheme, the map (3.12) factors through ![]() $U_{j}\subset U$ for some
$U_{j}\subset U$ for some ![]() $j\gg i$. In either case,
$j\gg i$. In either case, ![]() $U\rightarrow X$ quasi-compact or
$U\rightarrow X$ quasi-compact or ![]() $U$ quasi-separated, the map (3.12) is quasi-compact. By [StaPro, 01R8], the scheme-theoretic image behaves well for quasi-compact maps, and
$U$ quasi-separated, the map (3.12) is quasi-compact. By [StaPro, 01R8], the scheme-theoretic image behaves well for quasi-compact maps, and ![]() $X_{i}^{\prime }\subset U_{j}$ is a quasi-compact closed subscheme. As scheme-theoretic images of quasi-compact maps commute with flat base change [StaPro, Tag 081I], the scheme
$X_{i}^{\prime }\subset U_{j}$ is a quasi-compact closed subscheme. As scheme-theoretic images of quasi-compact maps commute with flat base change [StaPro, Tag 081I], the scheme ![]() $X_{i}^{\prime }$ is equipped with a descent datum relative to
$X_{i}^{\prime }$ is equipped with a descent datum relative to ![]() $U\rightarrow X$, and defines a closed
$U\rightarrow X$, and defines a closed ![]() ${\mathcal{O}}$-subspace
${\mathcal{O}}$-subspace ![]() $X_{i}\subset X$ together with an étale surjective map
$X_{i}\subset X$ together with an étale surjective map ![]() $X_{i}^{\prime }\rightarrow X_{i}$. As
$X_{i}^{\prime }\rightarrow X_{i}$. As ![]() $X_{i}\subset X$ is closed, the diagonal of
$X_{i}\subset X$ is closed, the diagonal of ![]() $X_{i}$ is schematic, and
$X_{i}$ is schematic, and ![]() $X_{i}$ is a quasi-compact algebraic space. By construction the
$X_{i}$ is a quasi-compact algebraic space. By construction the ![]() $X_{i}$ form a filtered direct system indexed by the poset
$X_{i}$ form a filtered direct system indexed by the poset ![]() $I$, and the canonical map
$I$, and the canonical map ![]() $\operatorname{colim}_{i\in I}X_{i}\rightarrow X$ is an isomorphism (because
$\operatorname{colim}_{i\in I}X_{i}\rightarrow X$ is an isomorphism (because ![]() $U\rightarrow X$ is a sheaf surjection, and
$U\rightarrow X$ is a sheaf surjection, and ![]() $\operatorname{colim}_{i}X_{i}^{\prime }=U$ by construction).◻
$\operatorname{colim}_{i}X_{i}^{\prime }=U$ by construction).◻
Remark 3.13. It would be nice to give a proof of representability of ![]() $\operatorname{Gr}_{{\mathcal{G}}}$ which does not refer to the choice of an embedding
$\operatorname{Gr}_{{\mathcal{G}}}$ which does not refer to the choice of an embedding ![]() ${\mathcal{G}}{\hookrightarrow}\operatorname{Gl}_{n,X}$.
${\mathcal{G}}{\hookrightarrow}\operatorname{Gl}_{n,X}$.
3.2 The open cell
In this subsection and the next, we apply our methods to prove Theorem 3.17, a generalization of Theorem A from the introduction. The results are not used in the proof of our main theorem.
We specialize to the case where ![]() $X=\mathbb{A}_{{\mathcal{O}}}^{1}$, and where
$X=\mathbb{A}_{{\mathcal{O}}}^{1}$, and where ![]() ${\mathcal{G}}=G\otimes _{{\mathcal{O}}}X$ is constant, that is, the base change of a smooth affine
${\mathcal{G}}=G\otimes _{{\mathcal{O}}}X$ is constant, that is, the base change of a smooth affine ![]() ${\mathcal{O}}$-group scheme
${\mathcal{O}}$-group scheme ![]() $G$ of finite presentation. In this case, we denote
$G$ of finite presentation. In this case, we denote ![]() $L_{D}{\mathcal{G}}$ (respectively,
$L_{D}{\mathcal{G}}$ (respectively, ![]() $L_{D}^{+}{\mathcal{G}}$; respectively,
$L_{D}^{+}{\mathcal{G}}$; respectively, ![]() $\operatorname{Gr}_{(X,{\mathcal{G}},D)}$) by
$\operatorname{Gr}_{(X,{\mathcal{G}},D)}$) by ![]() $LG=L_{D}G$ (respectively,
$LG=L_{D}G$ (respectively, ![]() $L^{+}G=L_{D}^{+}G$; respectively,
$L^{+}G=L_{D}^{+}G$; respectively, ![]() $\operatorname{Gr}_{G}=\operatorname{Gr}_{(X,G,D)}$).
$\operatorname{Gr}_{G}=\operatorname{Gr}_{(X,G,D)}$).
Since ![]() $D\subset \mathbb{A}_{{\mathcal{O}}}^{1}$ is assumed to be finite over
$D\subset \mathbb{A}_{{\mathcal{O}}}^{1}$ is assumed to be finite over ![]() ${\mathcal{O}}$, the subscheme
${\mathcal{O}}$, the subscheme ![]() $D\subset \mathbb{P}_{{\mathcal{O}}}^{1}$ is closed and defines a relative effective Cartier divisor. In particular, Lemma 3.4(ii) (the Beauville–Laszlo lemma) implies that
$D\subset \mathbb{P}_{{\mathcal{O}}}^{1}$ is closed and defines a relative effective Cartier divisor. In particular, Lemma 3.4(ii) (the Beauville–Laszlo lemma) implies that ![]() $\operatorname{Gr}_{(\mathbb{A}_{{\mathcal{O}}}^{1},G,D)}=\operatorname{Gr}_{(\mathbb{P}_{{\mathcal{O}}}^{1},G,D)}$ by extending torsors trivially to
$\operatorname{Gr}_{(\mathbb{A}_{{\mathcal{O}}}^{1},G,D)}=\operatorname{Gr}_{(\mathbb{P}_{{\mathcal{O}}}^{1},G,D)}$ by extending torsors trivially to ![]() $\infty$.
$\infty$.
The negative loop group is the functor on the category of ![]() ${\mathcal{O}}$-algebras
${\mathcal{O}}$-algebras
Then ![]() $L^{-}G$ is an
$L^{-}G$ is an ![]() ${\mathcal{O}}$-space which is a subgroup functor
${\mathcal{O}}$-space which is a subgroup functor ![]() $L^{-}G\subset LG$.
$L^{-}G\subset LG$.
Lemma 3.14. The functor ![]() $L^{-}G$ is representable by an ind-affine ind-scheme locally of ind-finite presentation over
$L^{-}G$ is representable by an ind-affine ind-scheme locally of ind-finite presentation over ![]() ${\mathcal{O}}$.
${\mathcal{O}}$.
Proof. That the affine schemes are of finite presentation follows from the fact that ![]() $L^{-}G$ commutes with filtered colimits (because
$L^{-}G$ commutes with filtered colimits (because ![]() $G$ is of finite presentation). One verifies that
$G$ is of finite presentation). One verifies that ![]() $L^{-}$ commutes with finite products and equalizers, and hence the proof of representability is reduced to the case
$L^{-}$ commutes with finite products and equalizers, and hence the proof of representability is reduced to the case ![]() $G=\mathbb{A}_{{\mathcal{O}}}^{1}$; cf. the proof of Lemma 3.2. We have to show that the functor on the category of
$G=\mathbb{A}_{{\mathcal{O}}}^{1}$; cf. the proof of Lemma 3.2. We have to show that the functor on the category of ![]() ${\mathcal{O}}$-algebras
${\mathcal{O}}$-algebras ![]() $R$ given by the global sections
$R$ given by the global sections ![]() $R\mapsto \unicode[STIX]{x1D6E4}({\mathcal{O}}_{\mathbb{P}_{R}^{1}\backslash D_{R}})$ is representable by an ind-affine ind-scheme. But, as
$R\mapsto \unicode[STIX]{x1D6E4}({\mathcal{O}}_{\mathbb{P}_{R}^{1}\backslash D_{R}})$ is representable by an ind-affine ind-scheme. But, as ![]() $R$-modules,
$R$-modules, ![]() $\unicode[STIX]{x1D6E4}({\mathcal{O}}_{\mathbb{P}_{R}^{1}\backslash D_{R}})=\operatorname{colim}_{n}\unicode[STIX]{x1D6E4}({\mathcal{O}}_{\mathbb{P}_{R}^{1}}(nD_{R}))$, and we claim that
$\unicode[STIX]{x1D6E4}({\mathcal{O}}_{\mathbb{P}_{R}^{1}\backslash D_{R}})=\operatorname{colim}_{n}\unicode[STIX]{x1D6E4}({\mathcal{O}}_{\mathbb{P}_{R}^{1}}(nD_{R}))$, and we claim that ![]() $\unicode[STIX]{x1D6E4}({\mathcal{O}}_{\mathbb{P}_{R}^{1}}(nD_{R}))$ is finite locally free: indeed, this follows from the short exact sequence
$\unicode[STIX]{x1D6E4}({\mathcal{O}}_{\mathbb{P}_{R}^{1}}(nD_{R}))$ is finite locally free: indeed, this follows from the short exact sequence
and the vanishing of ![]() $H_{\text{Zar}}^{1}(\mathbb{P}_{R}^{1},{\mathcal{O}}_{\mathbb{P}_{R}^{1}})$. This proves the lemma.◻
$H_{\text{Zar}}^{1}(\mathbb{P}_{R}^{1},{\mathcal{O}}_{\mathbb{P}_{R}^{1}})$. This proves the lemma.◻
Now define ![]() $L^{--}G=\ker (L^{-}G\rightarrow G)$ for
$L^{--}G=\ker (L^{-}G\rightarrow G)$ for ![]() $g\mapsto g(\infty )$. Then the intersection
$g\mapsto g(\infty )$. Then the intersection ![]() $L^{--}G\cap L^{+}G$ is trivial inside
$L^{--}G\cap L^{+}G$ is trivial inside ![]() $LG$, and we consider the orbit map
$LG$, and we consider the orbit map
where ![]() $e_{0}\in \operatorname{Gr}_{G}$ denotes the base point.
$e_{0}\in \operatorname{Gr}_{G}$ denotes the base point.
Lemma 3.15. The map (3.14) is representable by an open immersion, and identifies ![]() $L^{--}G$ with those pairs
$L^{--}G$ with those pairs ![]() $({\mathcal{F}},\unicode[STIX]{x1D6FC})$ where
$({\mathcal{F}},\unicode[STIX]{x1D6FC})$ where ![]() ${\mathcal{F}}$ is the trivial torsor.
${\mathcal{F}}$ is the trivial torsor.
Proof. The argument is the same as the deformation argument given in [Reference Haines and RicharzHR18, Lemma 3.1], and we do not repeat it here. ◻
3.3 Geometry of  $\mathbb{G}_{m}$-actions on
$\mathbb{G}_{m}$-actions on  $\operatorname{Gr}_{G}$
$\operatorname{Gr}_{G}$
We assume ![]() $X=\mathbb{A}_{{\mathcal{O}}}^{1}$, and
$X=\mathbb{A}_{{\mathcal{O}}}^{1}$, and ![]() ${\mathcal{G}}=G\otimes _{{\mathcal{O}}}X$ with
${\mathcal{G}}=G\otimes _{{\mathcal{O}}}X$ with ![]() $G$ being a reductive
$G$ being a reductive ![]() ${\mathcal{O}}$-group scheme with connected (and hence geometrically connected) fibers. Let
${\mathcal{O}}$-group scheme with connected (and hence geometrically connected) fibers. Let ![]() $\unicode[STIX]{x1D712}:\mathbb{G}_{m,{\mathcal{O}}}\rightarrow G$ be an
$\unicode[STIX]{x1D712}:\mathbb{G}_{m,{\mathcal{O}}}\rightarrow G$ be an ![]() ${\mathcal{O}}$-rational cocharacter. The cocharacter
${\mathcal{O}}$-rational cocharacter. The cocharacter ![]() $\unicode[STIX]{x1D712}$ induces via the composition
$\unicode[STIX]{x1D712}$ induces via the composition
a left ![]() $\mathbb{G}_{m}$-action on the affine Grassmannian
$\mathbb{G}_{m}$-action on the affine Grassmannian ![]() $\operatorname{Gr}_{G}\rightarrow \operatorname{Spec}({\mathcal{O}})$. As in (2.2), we obtain maps of
$\operatorname{Gr}_{G}\rightarrow \operatorname{Spec}({\mathcal{O}})$. As in (2.2), we obtain maps of ![]() ${\mathcal{O}}$-spaces
${\mathcal{O}}$-spaces
Let us mention the following lemma which implies the ind-representability of the spaces (3.16), in light of Theorem 2.1 and Corollary 3.11.
Lemma 3.16. The ![]() $\mathbb{G}_{m}$-action on
$\mathbb{G}_{m}$-action on ![]() $\operatorname{Gr}_{G}$ is étale locally linearizable.
$\operatorname{Gr}_{G}$ is étale locally linearizable.
Proof. After an étale cover ![]() ${\mathcal{O}}\rightarrow {\mathcal{O}}^{\prime }$, there exists a closed immersion
${\mathcal{O}}\rightarrow {\mathcal{O}}^{\prime }$, there exists a closed immersion ![]() $\operatorname{Gr}_{G_{{\mathcal{O}}}^{\prime }}\rightarrow \operatorname{Gr}_{\operatorname{Gl}_{n,{\mathcal{O}}^{\prime }}}$ (cf. Proposition 3.11(iii)) which is
$\operatorname{Gr}_{G_{{\mathcal{O}}}^{\prime }}\rightarrow \operatorname{Gr}_{\operatorname{Gl}_{n,{\mathcal{O}}^{\prime }}}$ (cf. Proposition 3.11(iii)) which is ![]() $\mathbb{G}_{m}$-equivariant with respect to the action on
$\mathbb{G}_{m}$-equivariant with respect to the action on ![]() $\operatorname{Gr}_{\operatorname{Gl}_{n,{\mathcal{O}}^{\prime }}}$ given by the cocharacter
$\operatorname{Gr}_{\operatorname{Gl}_{n,{\mathcal{O}}^{\prime }}}$ given by the cocharacter ![]() $\mathbb{G}_{m,{\mathcal{O}}^{\prime }}\overset{\unicode[STIX]{x1D712}\,}{\rightarrow }G_{{\mathcal{O}}^{\prime }}\rightarrow \operatorname{Gl}_{n,{\mathcal{O}}^{\prime }}$. The proof of Lemma 3.12 shows that an
$\mathbb{G}_{m,{\mathcal{O}}^{\prime }}\overset{\unicode[STIX]{x1D712}\,}{\rightarrow }G_{{\mathcal{O}}^{\prime }}\rightarrow \operatorname{Gl}_{n,{\mathcal{O}}^{\prime }}$. The proof of Lemma 3.12 shows that an ![]() $L^{+}G_{{\mathcal{O}}^{\prime }}$-stable presentation of
$L^{+}G_{{\mathcal{O}}^{\prime }}$-stable presentation of ![]() $\operatorname{Gr}_{G_{{\mathcal{O}}^{\prime }}}$ by quasi-compact schemes induces an
$\operatorname{Gr}_{G_{{\mathcal{O}}^{\prime }}}$ by quasi-compact schemes induces an ![]() $L^{+}G$-stable presentation of
$L^{+}G$-stable presentation of ![]() $\operatorname{Gr}_{G}$ by quasi-compact algebraic spaces. To prove the lemma it is enough to show that the
$\operatorname{Gr}_{G}$ by quasi-compact algebraic spaces. To prove the lemma it is enough to show that the ![]() $\mathbb{G}_{m}$-action on
$\mathbb{G}_{m}$-action on ![]() $\operatorname{Gr}_{\operatorname{Gl}_{n,{\mathcal{O}}^{\prime }}}$ is Zariski locally linearizable, and we reduce to the case
$\operatorname{Gr}_{\operatorname{Gl}_{n,{\mathcal{O}}^{\prime }}}$ is Zariski locally linearizable, and we reduce to the case ![]() ${\mathcal{O}}={\mathcal{O}}^{\prime }$,
${\mathcal{O}}={\mathcal{O}}^{\prime }$, ![]() $G=\operatorname{Gl}_{n,{\mathcal{O}}}$. By [Reference ConradCon14, Propositions 6.2.11 and 3.1.9], Zariski locally on
$G=\operatorname{Gl}_{n,{\mathcal{O}}}$. By [Reference ConradCon14, Propositions 6.2.11 and 3.1.9], Zariski locally on ![]() ${\mathcal{O}}$ the cocharacter
${\mathcal{O}}$ the cocharacter ![]() $\unicode[STIX]{x1D712}$ lies in a split maximal torus in
$\unicode[STIX]{x1D712}$ lies in a split maximal torus in ![]() $\operatorname{Gl}_{n,{\mathcal{O}}}$ which is
$\operatorname{Gl}_{n,{\mathcal{O}}}$ which is ![]() ${\mathcal{O}}$-conjugate to the diagonal matrices in
${\mathcal{O}}$-conjugate to the diagonal matrices in ![]() $\operatorname{Gl}_{n,{\mathcal{O}}}$, and hence is after conjugation with a permutation matrix dominant. In this way, we reduce to the case where
$\operatorname{Gl}_{n,{\mathcal{O}}}$, and hence is after conjugation with a permutation matrix dominant. In this way, we reduce to the case where ![]() $\unicode[STIX]{x1D712}$ is a standard dominant cocharacter given by
$\unicode[STIX]{x1D712}$ is a standard dominant cocharacter given by ![]() $\unicode[STIX]{x1D706}\mapsto \operatorname{diag}(\unicode[STIX]{x1D706}^{a_{1}},\ldots ,\unicode[STIX]{x1D706}^{a_{n}})$ for some integers
$\unicode[STIX]{x1D706}\mapsto \operatorname{diag}(\unicode[STIX]{x1D706}^{a_{1}},\ldots ,\unicode[STIX]{x1D706}^{a_{n}})$ for some integers ![]() $a_{1}\geqslant \cdots \geqslant a_{n}$. With the notation of Lemma 3.8, it is now immediate that the
$a_{1}\geqslant \cdots \geqslant a_{n}$. With the notation of Lemma 3.8, it is now immediate that the ![]() $\mathbb{G}_{m}$-action on
$\mathbb{G}_{m}$-action on ![]() $\operatorname{Quot}_{N}\subset \operatorname{Grass}({\mathcal{E}}_{N,{\mathcal{O}}})$ is linear, and compatible with the transition maps for varying
$\operatorname{Quot}_{N}\subset \operatorname{Grass}({\mathcal{E}}_{N,{\mathcal{O}}})$ is linear, and compatible with the transition maps for varying ![]() $N$. The lemma follows.◻
$N$. The lemma follows.◻
Our aim is to express (3.16) in terms of group-theoretical data related to the cocharacter ![]() $\unicode[STIX]{x1D712}$; cf. Theorem 3.17 below.
$\unicode[STIX]{x1D712}$; cf. Theorem 3.17 below.
Let ![]() $\unicode[STIX]{x1D712}$ act on
$\unicode[STIX]{x1D712}$ act on ![]() $G$ via conjugation
$G$ via conjugation ![]() $(\unicode[STIX]{x1D706},g)\mapsto \unicode[STIX]{x1D712}(\unicode[STIX]{x1D706})\cdot g\cdot \unicode[STIX]{x1D712}(g)^{-1}$. The fixed points
$(\unicode[STIX]{x1D706},g)\mapsto \unicode[STIX]{x1D712}(\unicode[STIX]{x1D706})\cdot g\cdot \unicode[STIX]{x1D712}(g)^{-1}$. The fixed points ![]() $M=G^{0}$ (respectively, the attractor
$M=G^{0}$ (respectively, the attractor ![]() $P^{+}=G^{+}$; respectively, the repeller
$P^{+}=G^{+}$; respectively, the repeller ![]() $P^{-}=G^{-}$) define a closed subgroup of
$P^{-}=G^{-}$) define a closed subgroup of ![]() $G$ which is smooth of finite presentation over
$G$ which is smooth of finite presentation over ![]() ${\mathcal{O}}$; cf. [Reference MargauxMar15]. The group
${\mathcal{O}}$; cf. [Reference MargauxMar15]. The group ![]() $M$ is the centralizer of
$M$ is the centralizer of ![]() $\unicode[STIX]{x1D712}$, and is by the classical theory over a field a reductive
$\unicode[STIX]{x1D712}$, and is by the classical theory over a field a reductive ![]() ${\mathcal{O}}$-group scheme which is fiberwise connected (hence fiberwise geometrically connected). By (2.2) we have natural maps of
${\mathcal{O}}$-group scheme which is fiberwise connected (hence fiberwise geometrically connected). By (2.2) we have natural maps of ![]() ${\mathcal{O}}$-groups
${\mathcal{O}}$-groups
Theorem 3.17. The maps (3.17) induce a commutative diagram of ![]() ${\mathcal{O}}$-ind-algebraic spaces
${\mathcal{O}}$-ind-algebraic spaces

where the vertical maps ![]() $\unicode[STIX]{x1D704}^{0}$ and
$\unicode[STIX]{x1D704}^{0}$ and ![]() $\unicode[STIX]{x1D704}^{\pm }$ are isomorphisms.
$\unicode[STIX]{x1D704}^{\pm }$ are isomorphisms.
Remark 3.18. (i) An interesting example to which Theorem 3.17 applies is the case of fusion Grassmannians ![]() $\operatorname{Gr}_{G}\rightarrow \mathbb{A}_{F}^{n}$; cf. Example 3.1(iv) withFootnote 3
$\operatorname{Gr}_{G}\rightarrow \mathbb{A}_{F}^{n}$; cf. Example 3.1(iv) withFootnote 3 ![]() $C=\mathbb{A}_{F}^{1}$. Hence, Theorem 3.17 implies Theorem A from the introduction. Note that the group
$C=\mathbb{A}_{F}^{1}$. Hence, Theorem 3.17 implies Theorem A from the introduction. Note that the group ![]() $G$ need not be defined over
$G$ need not be defined over ![]() $F$, but can be a general reductive group scheme over the
$F$, but can be a general reductive group scheme over the ![]() $n$th symmetric power
$n$th symmetric power ![]() $(\mathbb{A}_{F}^{1})^{(n)}$. Changing the setup slightly, the group
$(\mathbb{A}_{F}^{1})^{(n)}$. Changing the setup slightly, the group ![]() $G$ could even be a general reductive group scheme over
$G$ could even be a general reductive group scheme over ![]() $\mathbb{A}_{F}^{n}$ (take
$\mathbb{A}_{F}^{n}$ (take ![]() $D=\operatorname{Spec}({\mathcal{O}})=\mathbb{A}_{F}^{n}$,
$D=\operatorname{Spec}({\mathcal{O}})=\mathbb{A}_{F}^{n}$, ![]() $X=\mathbb{A}_{F}^{n}\times _{F}\mathbb{A}_{F}^{1}$ and consider the divisor
$X=\mathbb{A}_{F}^{n}\times _{F}\mathbb{A}_{F}^{1}$ and consider the divisor ![]() $\mathbb{A}_{F}^{n}\rightarrow \mathbb{A}_{F}^{n}\times \mathbb{A}_{F}^{1}$,
$\mathbb{A}_{F}^{n}\rightarrow \mathbb{A}_{F}^{n}\times \mathbb{A}_{F}^{1}$, ![]() $(x_{i})_{i}\mapsto ((x_{i})_{i},\sum _{i}x_{i})$ for
$(x_{i})_{i}\mapsto ((x_{i})_{i},\sum _{i}x_{i})$ for ![]() $i=1,\ldots ,n$). (ii) Note that Theorem 3.17 also generalizes [Reference Haines and RicharzHR18, Proposition 3.4] and justifies [Reference Haines and RicharzHR18, sentence containing (3.33)].
$i=1,\ldots ,n$). (ii) Note that Theorem 3.17 also generalizes [Reference Haines and RicharzHR18, Proposition 3.4] and justifies [Reference Haines and RicharzHR18, sentence containing (3.33)].
3.3.1 Construction of  $\unicode[STIX]{x1D704}^{0}$ and
$\unicode[STIX]{x1D704}^{0}$ and  $\unicode[STIX]{x1D704}^{\pm }$
$\unicode[STIX]{x1D704}^{\pm }$
The strategy of construction is the same as in [Reference Haines and RicharzHR18], which we recall for the sake of readability.
As the ![]() $\mathbb{G}_{m}$-action on
$\mathbb{G}_{m}$-action on ![]() $\operatorname{Gr}_{M}$ is trivial, the natural map
$\operatorname{Gr}_{M}$ is trivial, the natural map ![]() $\operatorname{Gr}_{M}\rightarrow \operatorname{Gr}_{G}$ factors as
$\operatorname{Gr}_{M}\rightarrow \operatorname{Gr}_{G}$ factors as ![]() $\operatorname{Gr}_{M}\rightarrow (\operatorname{Gr}_{G})^{0}\rightarrow \operatorname{Gr}_{G}$, which defines
$\operatorname{Gr}_{M}\rightarrow (\operatorname{Gr}_{G})^{0}\rightarrow \operatorname{Gr}_{G}$, which defines ![]() $\unicode[STIX]{x1D704}^{0}$. For the map
$\unicode[STIX]{x1D704}^{0}$. For the map ![]() $\unicode[STIX]{x1D704}^{\pm }$, we use the Rees construction explained in Heinloth [Reference HeinlothHei18, 1.6.2]. The
$\unicode[STIX]{x1D704}^{\pm }$, we use the Rees construction explained in Heinloth [Reference HeinlothHei18, 1.6.2]. The ![]() $\mathbb{G}_{m}$-action
$\mathbb{G}_{m}$-action ![]() $P^{\pm }\times \mathbb{G}_{m,{\mathcal{O}}}\rightarrow P^{\pm },(p,\unicode[STIX]{x1D706})\mapsto \unicode[STIX]{x1D712}(\unicode[STIX]{x1D706}^{\pm })\cdot p\,\cdot \,\unicode[STIX]{x1D712}(\unicode[STIX]{x1D706}^{\pm })^{-1}$ via conjugation extends via the monoid action of
$P^{\pm }\times \mathbb{G}_{m,{\mathcal{O}}}\rightarrow P^{\pm },(p,\unicode[STIX]{x1D706})\mapsto \unicode[STIX]{x1D712}(\unicode[STIX]{x1D706}^{\pm })\cdot p\,\cdot \,\unicode[STIX]{x1D712}(\unicode[STIX]{x1D706}^{\pm })^{-1}$ via conjugation extends via the monoid action of ![]() $\mathbb{A}^{1}$ on
$\mathbb{A}^{1}$ on ![]() $(\mathbb{A}_{{\mathcal{O}}}^{1})^{\pm }$ in (2.1) to a monoid action
$(\mathbb{A}_{{\mathcal{O}}}^{1})^{\pm }$ in (2.1) to a monoid action
such that ![]() $m_{\unicode[STIX]{x1D712}}(p,0)\in M$. We let
$m_{\unicode[STIX]{x1D712}}(p,0)\in M$. We let ![]() $\operatorname{gr}_{\unicode[STIX]{x1D712}}:P^{\pm }\times \mathbb{A}_{{\mathcal{O}}}^{1}\rightarrow P^{\pm }\times \mathbb{A}_{{\mathcal{O}}}^{1}$,
$\operatorname{gr}_{\unicode[STIX]{x1D712}}:P^{\pm }\times \mathbb{A}_{{\mathcal{O}}}^{1}\rightarrow P^{\pm }\times \mathbb{A}_{{\mathcal{O}}}^{1}$, ![]() $(p,\unicode[STIX]{x1D706})\mapsto (m_{\unicode[STIX]{x1D712}}(p,\unicode[STIX]{x1D706}),\unicode[STIX]{x1D706})$, viewed as an
$(p,\unicode[STIX]{x1D706})\mapsto (m_{\unicode[STIX]{x1D712}}(p,\unicode[STIX]{x1D706}),\unicode[STIX]{x1D706})$, viewed as an ![]() $\mathbb{A}_{{\mathcal{O}}}^{1}$-group homomorphism. Then the restriction
$\mathbb{A}_{{\mathcal{O}}}^{1}$-group homomorphism. Then the restriction ![]() $\operatorname{gr}_{\unicode[STIX]{x1D712}}\!|_{\{1\}}$ is the identity, whereas
$\operatorname{gr}_{\unicode[STIX]{x1D712}}\!|_{\{1\}}$ is the identity, whereas ![]() $\operatorname{gr}_{\unicode[STIX]{x1D712}}\!|_{\{0\}}$ is the composition
$\operatorname{gr}_{\unicode[STIX]{x1D712}}\!|_{\{0\}}$ is the composition ![]() $P^{\pm }\rightarrow M\rightarrow P^{\pm }$. For a point
$P^{\pm }\rightarrow M\rightarrow P^{\pm }$. For a point ![]() $({\mathcal{F}}^{\pm },\unicode[STIX]{x1D6FC}^{\pm })\in \operatorname{Gr}_{P^{\pm }}(R)$, the Rees bundle is
$({\mathcal{F}}^{\pm },\unicode[STIX]{x1D6FC}^{\pm })\in \operatorname{Gr}_{P^{\pm }}(R)$, the Rees bundle is
where ![]() $\operatorname{gr}_{\unicode[STIX]{x1D712},\ast }$ denotes the pushforward under the
$\operatorname{gr}_{\unicode[STIX]{x1D712},\ast }$ denotes the pushforward under the ![]() $\mathbb{A}^{1}$-group homomorphism. Then the restriction
$\mathbb{A}^{1}$-group homomorphism. Then the restriction ![]() $\operatorname{Rees}_{\unicode[STIX]{x1D712}}({\mathcal{F}}^{\pm },\unicode[STIX]{x1D6FC}^{\pm })|_{\{1\}_{R}}$ is equal to
$\operatorname{Rees}_{\unicode[STIX]{x1D712}}({\mathcal{F}}^{\pm },\unicode[STIX]{x1D6FC}^{\pm })|_{\{1\}_{R}}$ is equal to ![]() $({\mathcal{F}}^{\pm },\unicode[STIX]{x1D6FC}^{\pm })$, whereas
$({\mathcal{F}}^{\pm },\unicode[STIX]{x1D6FC}^{\pm })$, whereas ![]() $\operatorname{Rees}_{\unicode[STIX]{x1D712}}({\mathcal{F}}^{\pm },\unicode[STIX]{x1D6FC}^{\pm })|_{\{0\}_{R}}$ is the image of
$\operatorname{Rees}_{\unicode[STIX]{x1D712}}({\mathcal{F}}^{\pm },\unicode[STIX]{x1D6FC}^{\pm })|_{\{0\}_{R}}$ is the image of ![]() $({\mathcal{F}}^{\pm },\unicode[STIX]{x1D6FC}^{\pm })$ under the composition
$({\mathcal{F}}^{\pm },\unicode[STIX]{x1D6FC}^{\pm })$ under the composition ![]() $\operatorname{Gr}_{P^{\pm }}\rightarrow \operatorname{Gr}_{M}\rightarrow \operatorname{Gr}_{P^{\pm }}$. One checks that
$\operatorname{Gr}_{P^{\pm }}\rightarrow \operatorname{Gr}_{M}\rightarrow \operatorname{Gr}_{P^{\pm }}$. One checks that ![]() $\operatorname{Rees}_{\unicode[STIX]{x1D712}}({\mathcal{F}}^{\pm },\unicode[STIX]{x1D6FC}^{\pm })$ is
$\operatorname{Rees}_{\unicode[STIX]{x1D712}}({\mathcal{F}}^{\pm },\unicode[STIX]{x1D6FC}^{\pm })$ is ![]() $\mathbb{G}_{m}$-equivariant, and hence defines an
$\mathbb{G}_{m}$-equivariant, and hence defines an ![]() $R$-point of
$R$-point of ![]() $(\operatorname{Gr}_{P^{\pm }})^{\pm }$. As the Rees construction is functorial, we obtain a map of
$(\operatorname{Gr}_{P^{\pm }})^{\pm }$. As the Rees construction is functorial, we obtain a map of ![]() ${\mathcal{O}}$-spaces
${\mathcal{O}}$-spaces
which is inverse to the map ![]() $(\operatorname{Gr}_{P^{\pm }})^{\pm }\rightarrow \operatorname{Gr}_{P^{\pm }}$ given by evaluating at the unit section. We define the map
$(\operatorname{Gr}_{P^{\pm }})^{\pm }\rightarrow \operatorname{Gr}_{P^{\pm }}$ given by evaluating at the unit section. We define the map ![]() $\operatorname{Gr}_{P^{\pm }}\rightarrow (\operatorname{Gr}_{G})^{\pm }$ to be the composition
$\operatorname{Gr}_{P^{\pm }}\rightarrow (\operatorname{Gr}_{G})^{\pm }$ to be the composition ![]() $\operatorname{Gr}_{P^{\pm }}\simeq (\operatorname{Gr}_{P^{\pm }})^{\pm }\rightarrow (\operatorname{Gr}_{G})^{\pm }$ where the latter map is deduced from the natural map
$\operatorname{Gr}_{P^{\pm }}\simeq (\operatorname{Gr}_{P^{\pm }})^{\pm }\rightarrow (\operatorname{Gr}_{G})^{\pm }$ where the latter map is deduced from the natural map ![]() $\operatorname{Gr}_{P^{\pm }}\rightarrow \operatorname{Gr}_{G}$. This constructs the commutative diagram (3.18).
$\operatorname{Gr}_{P^{\pm }}\rightarrow \operatorname{Gr}_{G}$. This constructs the commutative diagram (3.18).
We claim that the map ![]() $\unicode[STIX]{x1D704}^{0}$ (respectively,
$\unicode[STIX]{x1D704}^{0}$ (respectively, ![]() $\unicode[STIX]{x1D704}^{\pm }$) is representable by a quasi-compact immersion. By [Reference ConradCon14, Theorem 2.4.1], the fppf quotient
$\unicode[STIX]{x1D704}^{\pm }$) is representable by a quasi-compact immersion. By [Reference ConradCon14, Theorem 2.4.1], the fppf quotient ![]() $G/M$ is quasi-affine, and hence
$G/M$ is quasi-affine, and hence ![]() $\unicode[STIX]{x1D704}^{0}$ is representable by a quasi-compact immersion by Proposition 3.10. Note that since
$\unicode[STIX]{x1D704}^{0}$ is representable by a quasi-compact immersion by Proposition 3.10. Note that since ![]() $M$ is reductive, the space
$M$ is reductive, the space ![]() $\operatorname{Gr}_{M}$ is ind-proper and hence
$\operatorname{Gr}_{M}$ is ind-proper and hence ![]() $\unicode[STIX]{x1D704}^{0}$ is even a closed immersion. For
$\unicode[STIX]{x1D704}^{0}$ is even a closed immersion. For ![]() $\unicode[STIX]{x1D704}^{\pm }$, we use that quasi-compact immersions are of effective descent (cf. [StaPro, Tag 0247, 02JR]), and after passing to an étale ring extension of
$\unicode[STIX]{x1D704}^{\pm }$, we use that quasi-compact immersions are of effective descent (cf. [StaPro, Tag 0247, 02JR]), and after passing to an étale ring extension of ![]() ${\mathcal{O}}$, we reduce to the case where
${\mathcal{O}}$, we reduce to the case where ![]() $G$ is linearly reductive. As in the proof of Corollary 3.11, we choose
$G$ is linearly reductive. As in the proof of Corollary 3.11, we choose ![]() $G{\hookrightarrow}\operatorname{Gl}_{n,{\mathcal{O}}}$ such that
$G{\hookrightarrow}\operatorname{Gl}_{n,{\mathcal{O}}}$ such that ![]() $\operatorname{Gl}_{n,{\mathcal{O}}}/G$ is quasi-affine (or even affine). Let
$\operatorname{Gl}_{n,{\mathcal{O}}}/G$ is quasi-affine (or even affine). Let ![]() $Q^{+}\subset \operatorname{Gl}_{n,{\mathcal{O}}}$ (respectively,
$Q^{+}\subset \operatorname{Gl}_{n,{\mathcal{O}}}$ (respectively, ![]() $Q^{-}\subset \operatorname{Gl}_{n,{\mathcal{O}}}$) be the attractor (respectively, repeller) subgroup defined by the cocharacter
$Q^{-}\subset \operatorname{Gl}_{n,{\mathcal{O}}}$) be the attractor (respectively, repeller) subgroup defined by the cocharacter ![]() $\mathbb{G}_{m,{\mathcal{O}}}\overset{\unicode[STIX]{x1D712}}{\rightarrow }G\rightarrow \operatorname{Gl}_{n,{\mathcal{O}}}$. Then we have
$\mathbb{G}_{m,{\mathcal{O}}}\overset{\unicode[STIX]{x1D712}}{\rightarrow }G\rightarrow \operatorname{Gl}_{n,{\mathcal{O}}}$. Then we have ![]() $P^{\pm }=Q^{\pm }\times _{\operatorname{Gl}_{n,{\mathcal{O}}}}G$. The quotient
$P^{\pm }=Q^{\pm }\times _{\operatorname{Gl}_{n,{\mathcal{O}}}}G$. The quotient ![]() $Q^{\pm }/P^{\pm }$ is an algebraic space of finite presentation over
$Q^{\pm }/P^{\pm }$ is an algebraic space of finite presentation over ![]() ${\mathcal{O}}$, and the map
${\mathcal{O}}$, and the map ![]() $i:Q^{\pm }/P^{\pm }{\hookrightarrow}\operatorname{Gl}_{n,{\mathcal{O}}}/G$ is a monomorphism of finite type (hence separated and quasi-finite, by [StaPro, Tag 0463, 59.27.10]). Thus,
$i:Q^{\pm }/P^{\pm }{\hookrightarrow}\operatorname{Gl}_{n,{\mathcal{O}}}/G$ is a monomorphism of finite type (hence separated and quasi-finite, by [StaPro, Tag 0463, 59.27.10]). Thus, ![]() $Q^{\pm }/P^{\pm }$ is a scheme, and the map
$Q^{\pm }/P^{\pm }$ is a scheme, and the map ![]() $i$ is quasi-affine by Zariski’s main theorem. In particular,
$i$ is quasi-affine by Zariski’s main theorem. In particular, ![]() $Q^{\pm }/P^{\pm }$ is quasi-affine as well. Now there is a commutative diagram of
$Q^{\pm }/P^{\pm }$ is quasi-affine as well. Now there is a commutative diagram of ![]() ${\mathcal{O}}$-spaces
${\mathcal{O}}$-spaces
 $$\begin{eqnarray}\begin{array}{@{}c@{}}\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}c@{}}\end{array}\end{eqnarray}$$ constructed as follows. The map ![]() $\operatorname{Gr}_{G}\rightarrow \operatorname{Gr}_{\operatorname{Gl}_{n,{\mathcal{O}}}}$ is a quasi-compact immersion by Proposition 3.10, and as
$\operatorname{Gr}_{G}\rightarrow \operatorname{Gr}_{\operatorname{Gl}_{n,{\mathcal{O}}}}$ is a quasi-compact immersion by Proposition 3.10, and as ![]() $\operatorname{Gr}_{G}$ is ind-proper, it is a closed immersion. Hence, the square is Cartesian by general properties of attractor (respectively, repeller) ind-schemes. This also constructs the dotted arrow in (3.22) which is the map
$\operatorname{Gr}_{G}$ is ind-proper, it is a closed immersion. Hence, the square is Cartesian by general properties of attractor (respectively, repeller) ind-schemes. This also constructs the dotted arrow in (3.22) which is the map ![]() $\unicode[STIX]{x1D704}^{\pm }$. Further, the map
$\unicode[STIX]{x1D704}^{\pm }$. Further, the map ![]() $\operatorname{Gr}_{Q^{\pm }}\rightarrow (\operatorname{Gr}_{\operatorname{Gl}_{n,{\mathcal{O}}}})^{\pm }$ is an isomorphism by Lemma 3.19 below. The map
$\operatorname{Gr}_{Q^{\pm }}\rightarrow (\operatorname{Gr}_{\operatorname{Gl}_{n,{\mathcal{O}}}})^{\pm }$ is an isomorphism by Lemma 3.19 below. The map ![]() $\operatorname{Gr}_{P^{\pm }}\rightarrow \operatorname{Gr}_{Q^{\pm }}$ is a quasi-compact immersion because
$\operatorname{Gr}_{P^{\pm }}\rightarrow \operatorname{Gr}_{Q^{\pm }}$ is a quasi-compact immersion because ![]() $Q^{\pm }/P^{\pm }$ is quasi-affine. Since
$Q^{\pm }/P^{\pm }$ is quasi-affine. Since ![]() $(\operatorname{Gr}_{G})^{\pm }\rightarrow (\operatorname{Gr}_{\operatorname{Gl}_{n,{\mathcal{O}}}})^{\pm }$ is a closed immersion, the map
$(\operatorname{Gr}_{G})^{\pm }\rightarrow (\operatorname{Gr}_{\operatorname{Gl}_{n,{\mathcal{O}}}})^{\pm }$ is a closed immersion, the map ![]() $\unicode[STIX]{x1D704}^{\pm }$ is a quasi-compact immersion.
$\unicode[STIX]{x1D704}^{\pm }$ is a quasi-compact immersion.
Lemma 3.19. If ![]() $G=\operatorname{Gl}_{n,{\mathcal{O}}}$, then the maps
$G=\operatorname{Gl}_{n,{\mathcal{O}}}$, then the maps ![]() $\unicode[STIX]{x1D704}^{0}$ and
$\unicode[STIX]{x1D704}^{0}$ and ![]() $\unicode[STIX]{x1D704}^{\pm }$ are isomorphisms.
$\unicode[STIX]{x1D704}^{\pm }$ are isomorphisms.
Proof. As in the proof of Lemma 3.16, we reduce to the case where ![]() $\unicode[STIX]{x1D712}$ is a standard dominant cocharacter. Then
$\unicode[STIX]{x1D712}$ is a standard dominant cocharacter. Then ![]() $\unicode[STIX]{x1D712}$ corresponds to a
$\unicode[STIX]{x1D712}$ corresponds to a ![]() $\mathbb{Z}$-grading on
$\mathbb{Z}$-grading on ![]() $V:={\mathcal{O}}^{n}$, say
$V:={\mathcal{O}}^{n}$, say ![]() $V=\bigoplus _{i\in \mathbb{Z}}V_{i}$, compatible with the standard
$V=\bigoplus _{i\in \mathbb{Z}}V_{i}$, compatible with the standard ![]() ${\mathcal{O}}$-basis of
${\mathcal{O}}$-basis of ![]() $V$. The group
$V$. The group ![]() $M$ (respectively,
$M$ (respectively, ![]() $P^{+}$/
$P^{+}$/![]() $P^{-}$) is a standard Levi (respectively, standard parabolic) of automorphisms of
$P^{-}$) is a standard Levi (respectively, standard parabolic) of automorphisms of ![]() $V$ preserving the grading (respectively, the ascending/descending filtration induced from the grading). In the description of Lemma 3.8, the subfunctor
$V$ preserving the grading (respectively, the ascending/descending filtration induced from the grading). In the description of Lemma 3.8, the subfunctor ![]() $\operatorname{Gr}_{M}$ (respectively,
$\operatorname{Gr}_{M}$ (respectively, ![]() $\operatorname{Gr}_{P^{\pm }}$) consists of those vector bundles
$\operatorname{Gr}_{P^{\pm }}$) consists of those vector bundles ![]() ${\mathcal{E}}\in \operatorname{Gr}_{G}(R)$ compatible with the grading (respectively, filtration induced by the grading) on
${\mathcal{E}}\in \operatorname{Gr}_{G}(R)$ compatible with the grading (respectively, filtration induced by the grading) on ![]() $V\otimes _{{\mathcal{O}}}{\mathcal{O}}_{U_{R}}$. Likewise, the grading on
$V\otimes _{{\mathcal{O}}}{\mathcal{O}}_{U_{R}}$. Likewise, the grading on ![]() $V$ induces in the notation of Lemma 3.8 gradings on
$V$ induces in the notation of Lemma 3.8 gradings on ![]() ${\mathcal{E}}_{N,{\mathcal{O}}}=V\otimes _{{\mathcal{O}}}({\mathcal{I}}_{D}^{-N}/{\mathcal{I}}_{D}^{N})$ for each
${\mathcal{E}}_{N,{\mathcal{O}}}=V\otimes _{{\mathcal{O}}}({\mathcal{I}}_{D}^{-N}/{\mathcal{I}}_{D}^{N})$ for each ![]() $N\geqslant 1$. As in Lemma 3.16, we have a closed
$N\geqslant 1$. As in Lemma 3.16, we have a closed ![]() $\mathbb{G}_{m}$-equivariant immersion, and hence the diagram of
$\mathbb{G}_{m}$-equivariant immersion, and hence the diagram of ![]() ${\mathcal{O}}$-schemes
${\mathcal{O}}$-schemes

is cartesian, and likewise on attractor (respectively, repeller) schemes. The equality ![]() $\operatorname{Grass}({\mathcal{E}}_{N,{\mathcal{O}}})^{0}=\prod _{i\in \mathbb{Z}}\operatorname{Grass}(V_{i}\,\otimes _{{\mathcal{O}}}\,({\mathcal{I}}_{D}^{-N}/{\mathcal{I}}_{D}^{N}))$ is immediate, and one checks that
$\operatorname{Grass}({\mathcal{E}}_{N,{\mathcal{O}}})^{0}=\prod _{i\in \mathbb{Z}}\operatorname{Grass}(V_{i}\,\otimes _{{\mathcal{O}}}\,({\mathcal{I}}_{D}^{-N}/{\mathcal{I}}_{D}^{N}))$ is immediate, and one checks that ![]() $\operatorname{Grass}(V\otimes _{{\mathcal{O}}}({\mathcal{I}}_{D}^{-N}/{\mathcal{I}}_{D}^{N}))^{\pm }$ is the subfunctor of those subspaces in
$\operatorname{Grass}(V\otimes _{{\mathcal{O}}}({\mathcal{I}}_{D}^{-N}/{\mathcal{I}}_{D}^{N}))^{\pm }$ is the subfunctor of those subspaces in ![]() ${\mathcal{E}}_{N,{\mathcal{O}}}$ compatible with the filtration. The lemma follows.◻
${\mathcal{E}}_{N,{\mathcal{O}}}$ compatible with the filtration. The lemma follows.◻
3.3.2 Proof of Theorem 3.17
We need a lemma first. By functoriality of the loop group construction, the ![]() $\mathbb{G}_{m}$-action on
$\mathbb{G}_{m}$-action on ![]() $G$ via
$G$ via ![]() $\unicode[STIX]{x1D712}$-conjugation gives a
$\unicode[STIX]{x1D712}$-conjugation gives a ![]() $\mathbb{G}_{m}$-action on
$\mathbb{G}_{m}$-action on ![]() $LG$ (respectively,
$LG$ (respectively, ![]() $L^{+}G$; respectively,
$L^{+}G$; respectively, ![]() $L^{-}G$). There are natural monomorphisms on negative loop groups
$L^{-}G$). There are natural monomorphisms on negative loop groups
Proof. Replacing ![]() ${\mathcal{O}}$ by an étale cover, we may assume that there exists a closed embedding
${\mathcal{O}}$ by an étale cover, we may assume that there exists a closed embedding ![]() $G{\hookrightarrow}\operatorname{Gl}_{n,{\mathcal{O}}}$. By the proof of Lemma 3.14 (respectively, Lemma 3.2(i)), the induced map
$G{\hookrightarrow}\operatorname{Gl}_{n,{\mathcal{O}}}$. By the proof of Lemma 3.14 (respectively, Lemma 3.2(i)), the induced map ![]() $L^{-}G\rightarrow L^{-}\operatorname{Gl}_{n,{\mathcal{O}}}$ is a closed immersion.
$L^{-}G\rightarrow L^{-}\operatorname{Gl}_{n,{\mathcal{O}}}$ is a closed immersion.
Let ![]() $\unicode[STIX]{x1D712}^{\prime }:\mathbb{G}_{m,{\mathcal{O}}}\overset{\unicode[STIX]{x1D712}\,}{\rightarrow }G\rightarrow \operatorname{Gl}_{n,{\mathcal{O}}}$, and denote the fixed point group (respectively, attractor/repeller group) by
$\unicode[STIX]{x1D712}^{\prime }:\mathbb{G}_{m,{\mathcal{O}}}\overset{\unicode[STIX]{x1D712}\,}{\rightarrow }G\rightarrow \operatorname{Gl}_{n,{\mathcal{O}}}$, and denote the fixed point group (respectively, attractor/repeller group) by ![]() $L$ (respectively,
$L$ (respectively, ![]() $Q^{\pm }$). It is straightforward to check
$Q^{\pm }$). It is straightforward to check ![]() $L^{-}M=L^{-}G\cap L^{-}L$ (respectively,
$L^{-}M=L^{-}G\cap L^{-}L$ (respectively, ![]() $L^{-}P^{\pm }=L^{-}G\cap L^{-}Q^{\pm }$) and
$L^{-}P^{\pm }=L^{-}G\cap L^{-}Q^{\pm }$) and ![]() $(L^{-}G)^{0}=L^{-}G\cap (L^{-}\operatorname{Gl}_{n,{\mathcal{O}}})^{0}$ (respectively,
$(L^{-}G)^{0}=L^{-}G\cap (L^{-}\operatorname{Gl}_{n,{\mathcal{O}}})^{0}$ (respectively, ![]() $(L^{-}G)^{\pm }=L^{-}G\cap (L^{-}\operatorname{Gl}_{n,{\mathcal{O}}})^{\pm }$). Hence, we may assume
$(L^{-}G)^{\pm }=L^{-}G\cap (L^{-}\operatorname{Gl}_{n,{\mathcal{O}}})^{\pm }$). Hence, we may assume ![]() $G=\operatorname{Gl}_{n,{\mathcal{O}}}$.
$G=\operatorname{Gl}_{n,{\mathcal{O}}}$.
After passing to a Zariski cover of ![]() ${\mathcal{O}}$, we may assume that
${\mathcal{O}}$, we may assume that ![]() $\unicode[STIX]{x1D712}$ is a standard dominant cocharacter; cf. proof of Lemma 3.16. We have for every
$\unicode[STIX]{x1D712}$ is a standard dominant cocharacter; cf. proof of Lemma 3.16. We have for every ![]() ${\mathcal{O}}$-algebra
${\mathcal{O}}$-algebra ![]() $R$,
$R$,
Let ![]() $g\in (L^{-}\operatorname{Gl}_{n,{\mathcal{O}}})^{0}(R)$. To show
$g\in (L^{-}\operatorname{Gl}_{n,{\mathcal{O}}})^{0}(R)$. To show ![]() $g\in (L^{-}M)(R)$, we can take
$g\in (L^{-}M)(R)$, we can take ![]() $S=R[t,t^{-1}]$ to see that the desired entries in the matrix
$S=R[t,t^{-1}]$ to see that the desired entries in the matrix ![]() $g$ vanish. The case of
$g$ vanish. The case of ![]() $(L^{-}G)^{\pm }$ is similar, and the lemma follows.◻
$(L^{-}G)^{\pm }$ is similar, and the lemma follows.◻
First case. Let ![]() ${\mathcal{O}}=F$ be a field. By fpqc descent, we may assume that
${\mathcal{O}}=F$ be a field. By fpqc descent, we may assume that ![]() $F$ is algebraically closed. Then
$F$ is algebraically closed. Then ![]() $D_{\operatorname{red}}=\sum _{i=1}^{d}[x_{i}]$ for pairwise distinct points
$D_{\operatorname{red}}=\sum _{i=1}^{d}[x_{i}]$ for pairwise distinct points ![]() $x_{i}\in X(F)$. If
$x_{i}\in X(F)$. If ![]() $d=1$, the maps
$d=1$, the maps ![]() $\unicode[STIX]{x1D704}^{0}$ and
$\unicode[STIX]{x1D704}^{0}$ and ![]() $\unicode[STIX]{x1D704}^{\pm }$ are isomorphisms in light of Example 3.1(i) and [Reference Haines and RicharzHR18, Proposition 3.4]. In general, by Corollary 3.5 each ind-scheme in (3.18) is a direct product of
$\unicode[STIX]{x1D704}^{\pm }$ are isomorphisms in light of Example 3.1(i) and [Reference Haines and RicharzHR18, Proposition 3.4]. In general, by Corollary 3.5 each ind-scheme in (3.18) is a direct product of ![]() $d$ copies (compatible with the maps) of classical affine Grassmannians formed using local parameters at
$d$ copies (compatible with the maps) of classical affine Grassmannians formed using local parameters at ![]() $x_{i}$. The
$x_{i}$. The ![]() $\mathbb{G}_{m}$-action on the product via
$\mathbb{G}_{m}$-action on the product via
is the diagonal action, and we conclude using Lemma 2.2 and the case ![]() $d=1$.
$d=1$.
Second case. Let ![]() ${\mathcal{O}}$ be an Artinian local ring with maximal ideal
${\mathcal{O}}$ be an Artinian local ring with maximal ideal ![]() $\mathfrak{m}$, and residue field
$\mathfrak{m}$, and residue field ![]() $F$. Passing to the strict Henselization, we may assume that
$F$. Passing to the strict Henselization, we may assume that ![]() $F$ is separably closed. The restriction of
$F$ is separably closed. The restriction of ![]() $\unicode[STIX]{x1D704}^{0}$ (respectively,
$\unicode[STIX]{x1D704}^{0}$ (respectively, ![]() $\unicode[STIX]{x1D704}^{\pm }$) to the open cell
$\unicode[STIX]{x1D704}^{\pm }$) to the open cell ![]() $L^{--}M$ (respectively,
$L^{--}M$ (respectively, ![]() $L^{--}P^{\pm }$) is an isomorphism by Lemma 3.20. By Lemma 3.15, there is the open subset
$L^{--}P^{\pm }$) is an isomorphism by Lemma 3.20. By Lemma 3.15, there is the open subset
of ![]() $\operatorname{Gr}_{M}$ (respectively,
$\operatorname{Gr}_{M}$ (respectively, ![]() $\operatorname{Gr}_{P^{\pm }}$), where the union runs over all
$\operatorname{Gr}_{P^{\pm }}$), where the union runs over all ![]() $m\in LM({\mathcal{O}})$ (respectively,
$m\in LM({\mathcal{O}})$ (respectively, ![]() $p\in LP^{\pm }({\mathcal{O}})$). The
$p\in LP^{\pm }({\mathcal{O}})$). The ![]() $LM$-equivariance (respectively,
$LM$-equivariance (respectively, ![]() $LP^{\pm }$-equivariance) of
$LP^{\pm }$-equivariance) of ![]() $\unicode[STIX]{x1D704}^{0}$ (respectively,
$\unicode[STIX]{x1D704}^{0}$ (respectively, ![]() $\unicode[STIX]{x1D704}^{\pm }$) implies that
$\unicode[STIX]{x1D704}^{\pm }$) implies that ![]() $\unicode[STIX]{x1D704}^{0}|_{V_{M}}$ (respectively,
$\unicode[STIX]{x1D704}^{0}|_{V_{M}}$ (respectively, ![]() $\unicode[STIX]{x1D704}^{\pm }|_{V_{P^{\pm }}}$) is an isomorphism. As
$\unicode[STIX]{x1D704}^{\pm }|_{V_{P^{\pm }}}$) is an isomorphism. As ![]() $\operatorname{Gr}_{M}$ (respectively,
$\operatorname{Gr}_{M}$ (respectively, ![]() $\operatorname{Gr}_{P^{\pm }}$) is a nilpotent thickening of
$\operatorname{Gr}_{P^{\pm }}$) is a nilpotent thickening of ![]() $\operatorname{Gr}_{M}\otimes _{{\mathcal{O}}}F$ (respectively,
$\operatorname{Gr}_{M}\otimes _{{\mathcal{O}}}F$ (respectively, ![]() $\operatorname{Gr}_{P^{\pm }}\otimes _{{\mathcal{O}}}F$), it is enough to show that
$\operatorname{Gr}_{P^{\pm }}\otimes _{{\mathcal{O}}}F$), it is enough to show that ![]() $V_{M}$ (respectively,
$V_{M}$ (respectively, ![]() $V_{P^{\pm }}$) contains the special fiber. As
$V_{P^{\pm }}$) contains the special fiber. As ![]() $G$ splits over
$G$ splits over ![]() $F$ (because separably closed), the points
$F$ (because separably closed), the points ![]() $\operatorname{Gr}_{M}(F)\subset \operatorname{Gr}_{M}$ (respectively,
$\operatorname{Gr}_{M}(F)\subset \operatorname{Gr}_{M}$ (respectively, ![]() $\operatorname{Gr}_{P^{\pm }}(F)\subset \operatorname{Gr}_{P^{\pm }}$) are dense, which follows from the density of
$\operatorname{Gr}_{P^{\pm }}(F)\subset \operatorname{Gr}_{P^{\pm }}$) are dense, which follows from the density of ![]() $\mathbb{A}_{F}^{n}(F)\subset \mathbb{A}_{F}^{n}$ and the cellular structure of these spaces. Thus, it suffices to show that
$\mathbb{A}_{F}^{n}(F)\subset \mathbb{A}_{F}^{n}$ and the cellular structure of these spaces. Thus, it suffices to show that ![]() $\operatorname{Gr}_{M}(F)\subset V_{M}$ (respectively,
$\operatorname{Gr}_{M}(F)\subset V_{M}$ (respectively, ![]() $\operatorname{Gr}_{P^{\pm }}(F)\subset V_{P^{\pm }}$). In view of Lemma 3.4(ii), it suffices to show that the reduction map
$\operatorname{Gr}_{P^{\pm }}(F)\subset V_{P^{\pm }}$). In view of Lemma 3.4(ii), it suffices to show that the reduction map ![]() $LM({\mathcal{O}})\rightarrow LM(F)$ (respectively,
$LM({\mathcal{O}})\rightarrow LM(F)$ (respectively, ![]() $LP^{\pm }({\mathcal{O}})\rightarrow LP^{\pm }(F)$) is surjective. As
$LP^{\pm }({\mathcal{O}})\rightarrow LP^{\pm }(F)$) is surjective. As ![]() ${\mathcal{O}}$ is Artinian, the ring
${\mathcal{O}}$ is Artinian, the ring ![]() ${\mathcal{O}}((D))$ is (semi-local) Artinian, and the reduction map
${\mathcal{O}}((D))$ is (semi-local) Artinian, and the reduction map ![]() ${\mathcal{O}}((D))\rightarrow F((D))$ is surjective with nilpotent kernel
${\mathcal{O}}((D))\rightarrow F((D))$ is surjective with nilpotent kernel ![]() $\mathfrak{m}((D))$. Hence, the desired surjectivity follows from the formal lifting criterion using the smoothness of
$\mathfrak{m}((D))$. Hence, the desired surjectivity follows from the formal lifting criterion using the smoothness of ![]() $M$ (respectively,
$M$ (respectively, ![]() $P^{\pm }$). This handles the second case.
$P^{\pm }$). This handles the second case.
The general case. Passing to an étale extension of ![]() ${\mathcal{O}}$, we may assume that (3.18) is a diagram of ind-schemes; cf. Corollary 3.11. In view of (3.2), the closed immersion
${\mathcal{O}}$, we may assume that (3.18) is a diagram of ind-schemes; cf. Corollary 3.11. In view of (3.2), the closed immersion ![]() $\unicode[STIX]{x1D704}^{0}$ (respectively, quasi-compact immersion
$\unicode[STIX]{x1D704}^{0}$ (respectively, quasi-compact immersion ![]() $\unicode[STIX]{x1D704}^{\pm }$) is fiberwise bijective, and hence bijective. Now Theorem 3.17 follows from Lemma 3.21 below using the second case.
$\unicode[STIX]{x1D704}^{\pm }$) is fiberwise bijective, and hence bijective. Now Theorem 3.17 follows from Lemma 3.21 below using the second case.
Lemma 3.21. Let ![]() ${\mathcal{O}}$ be a Noetherian ring, and let
${\mathcal{O}}$ be a Noetherian ring, and let ![]() $\unicode[STIX]{x1D704}:Y\rightarrow Z$ be a quasi-compact immersion of finite type
$\unicode[STIX]{x1D704}:Y\rightarrow Z$ be a quasi-compact immersion of finite type ![]() ${\mathcal{O}}$-schemes. If
${\mathcal{O}}$-schemes. If ![]() $\unicode[STIX]{x1D704}$ is set-theoretically bijective, and if, for every maximal ideal
$\unicode[STIX]{x1D704}$ is set-theoretically bijective, and if, for every maximal ideal ![]() $\mathfrak{m}\subset {\mathcal{O}}$ and every
$\mathfrak{m}\subset {\mathcal{O}}$ and every ![]() $n\geqslant 1$, the reduction
$n\geqslant 1$, the reduction ![]() $\unicode[STIX]{x1D704}\otimes {\mathcal{O}}/\mathfrak{m}^{n}$ is an isomorphism, then
$\unicode[STIX]{x1D704}\otimes {\mathcal{O}}/\mathfrak{m}^{n}$ is an isomorphism, then ![]() $\unicode[STIX]{x1D704}$ is an isomorphism.
$\unicode[STIX]{x1D704}$ is an isomorphism.
Proof. By [StaPro, Tag 01QV], the map ![]() $\unicode[STIX]{x1D704}$ factors as an open immersion followed by a closed immersion:
$\unicode[STIX]{x1D704}$ factors as an open immersion followed by a closed immersion: ![]() $Y\rightarrow \bar{Y}\rightarrow Z$. As
$Y\rightarrow \bar{Y}\rightarrow Z$. As ![]() $\unicode[STIX]{x1D704}$ is bijective, we have
$\unicode[STIX]{x1D704}$ is bijective, we have ![]() $Y=\bar{Y}$ and
$Y=\bar{Y}$ and ![]() $\unicode[STIX]{x1D704}$ is a bijective closed immersion. Being an isomorphism is local on the target, and we may assume that
$\unicode[STIX]{x1D704}$ is a bijective closed immersion. Being an isomorphism is local on the target, and we may assume that ![]() $Z=\operatorname{Spec}(A)$ and hence
$Z=\operatorname{Spec}(A)$ and hence ![]() $Y=\operatorname{Spec}(B)$ are affine. The map of
$Y=\operatorname{Spec}(B)$ are affine. The map of ![]() ${\mathcal{O}}$-algebras
${\mathcal{O}}$-algebras ![]() $\unicode[STIX]{x1D704}^{\#}:A\rightarrow B$ is surjective (because closed immersion), and each element in
$\unicode[STIX]{x1D704}^{\#}:A\rightarrow B$ is surjective (because closed immersion), and each element in ![]() $I:=\ker (\unicode[STIX]{x1D704}^{\#})$ is nilpotent (because
$I:=\ker (\unicode[STIX]{x1D704}^{\#})$ is nilpotent (because ![]() $\unicode[STIX]{x1D704}^{\#}$ is bijective on spectra). It is enough to show that for the localization
$\unicode[STIX]{x1D704}^{\#}$ is bijective on spectra). It is enough to show that for the localization ![]() $I_{\mathfrak{m}}=0$ for all maximal ideals
$I_{\mathfrak{m}}=0$ for all maximal ideals ![]() $\mathfrak{m}\subset {\mathcal{O}}$. Without loss of generality, we may assume that
$\mathfrak{m}\subset {\mathcal{O}}$. Without loss of generality, we may assume that ![]() ${\mathcal{O}}$ is local with maximal ideal
${\mathcal{O}}$ is local with maximal ideal ![]() $\mathfrak{m}$. If
$\mathfrak{m}$. If ![]() $\mathfrak{m}A=A$, that is, the fiber of
$\mathfrak{m}A=A$, that is, the fiber of ![]() $Z$ over
$Z$ over ![]() $\mathfrak{m}$ is empty, there is nothing to prove, and we may assume that
$\mathfrak{m}$ is empty, there is nothing to prove, and we may assume that ![]() $\mathfrak{m}A\subset A$ is a proper ideal. As
$\mathfrak{m}A\subset A$ is a proper ideal. As ![]() $A/\mathfrak{m}^{n}A\rightarrow B/\mathfrak{m}^{n}B$ is an isomorphism for all
$A/\mathfrak{m}^{n}A\rightarrow B/\mathfrak{m}^{n}B$ is an isomorphism for all ![]() $n\geqslant 1$, we have
$n\geqslant 1$, we have ![]() $I\subset \bigcap _{n\geqslant 1}\mathfrak{m}^{n}A$. But since
$I\subset \bigcap _{n\geqslant 1}\mathfrak{m}^{n}A$. But since ![]() $\mathfrak{m}^{n}A=(\mathfrak{m}A)^{n}$ and
$\mathfrak{m}^{n}A=(\mathfrak{m}A)^{n}$ and ![]() $\mathfrak{m}A\subset A$ is a proper ideal in a Noetherian ring, we have
$\mathfrak{m}A\subset A$ is a proper ideal in a Noetherian ring, we have ![]() $\bigcap _{n\geqslant 1}\mathfrak{m}^{n}A=0$ by Krull’s intersection theorem. The lemma follows.◻
$\bigcap _{n\geqslant 1}\mathfrak{m}^{n}A=0$ by Krull’s intersection theorem. The lemma follows.◻
4 Local models for Weil-restricted groups
In this section we collect a few properties of the Weil-restricted affine Grassmannians as constructed in [Reference LevinLev16]. We provide proofs for several statements which appear to be well known but for which we could not find proofs in the literature.
4.1 Notation
Let ![]() $F/\mathbb{Q}_{p}$ be a finite extension with ring of integers
$F/\mathbb{Q}_{p}$ be a finite extension with ring of integers ![]() ${\mathcal{O}}_{F}$, and residue field
${\mathcal{O}}_{F}$, and residue field ![]() $k$ with
$k$ with ![]() $q$ elements. Let
$q$ elements. Let ![]() $K/F$ be a finite extension with ring of integers
$K/F$ be a finite extension with ring of integers ![]() ${\mathcal{O}}_{K}$ and residue field
${\mathcal{O}}_{K}$ and residue field ![]() $k_{0}/k$. Let
$k_{0}/k$. Let ![]() $K_{0}/F$ denote the maximal unramified subextension of
$K_{0}/F$ denote the maximal unramified subextension of ![]() $K/F$, with the same residue field
$K/F$, with the same residue field ![]() $k_{0}/k$. Fix a uniformizer
$k_{0}/k$. Fix a uniformizer ![]() $\unicode[STIX]{x1D71B}$ of
$\unicode[STIX]{x1D71B}$ of ![]() $K$, and denote by
$K$, and denote by ![]() $Q\in K_{0}[u]$ the minimal polynomial, that is,
$Q\in K_{0}[u]$ the minimal polynomial, that is, ![]() $Q$ is the unique irreducible normalized polynomial with
$Q$ is the unique irreducible normalized polynomial with ![]() $Q(\unicode[STIX]{x1D71B})=0$. Note that
$Q(\unicode[STIX]{x1D71B})=0$. Note that ![]() $Q\in {\mathcal{O}}_{K_{0}}[u]$, and that
$Q\in {\mathcal{O}}_{K_{0}}[u]$, and that ![]() $Q\equiv u^{[K:K_{0}]}\;\text{mod}\;\unicode[STIX]{x1D71B}$.
$Q\equiv u^{[K:K_{0}]}\;\text{mod}\;\unicode[STIX]{x1D71B}$.
Let ![]() $\breve{F}$ (respectively,
$\breve{F}$ (respectively, ![]() $\breve{K}$; respectively,
$\breve{K}$; respectively, ![]() $\breve{K}_{0}$) denote the completion of the maximal unramified extension of
$\breve{K}_{0}$) denote the completion of the maximal unramified extension of ![]() $F$ (respectively,
$F$ (respectively, ![]() $K$; respectively,
$K$; respectively, ![]() $K_{0}$) inside a fixed algebraic closure
$K_{0}$) inside a fixed algebraic closure ![]() $\bar{F}$, and let
$\bar{F}$, and let ![]() $\unicode[STIX]{x1D70E}\in \text{Aut}(\breve{F}/F)$ denote the Frobenius generator. We note that
$\unicode[STIX]{x1D70E}\in \text{Aut}(\breve{F}/F)$ denote the Frobenius generator. We note that ![]() $\breve{F}=\breve{K}_{0}$.
$\breve{F}=\breve{K}_{0}$.
In § 4.4 below, we specialize the general setup of § 3 to the case where ![]() ${\mathcal{O}}={\mathcal{O}}_{F}$,
${\mathcal{O}}={\mathcal{O}}_{F}$, ![]() $X=\mathbb{A}_{{\mathcal{O}}_{K_{0}}}^{1}$ is viewed as a smooth curve over
$X=\mathbb{A}_{{\mathcal{O}}_{K_{0}}}^{1}$ is viewed as a smooth curve over ![]() ${\mathcal{O}}$, and
${\mathcal{O}}$, and ![]() $D$ is defined by
$D$ is defined by ![]() $\{Q=0\}$. We first summarize some properties of parahoric groups for Weil-restricted groups (see § 4.2), and the group schemes
$\{Q=0\}$. We first summarize some properties of parahoric groups for Weil-restricted groups (see § 4.2), and the group schemes ![]() $\text{}\underline{{\mathcal{G}}}_{0}$ over
$\text{}\underline{{\mathcal{G}}}_{0}$ over ![]() $X=\mathbb{A}_{{\mathcal{O}}_{K_{0}}}^{1}$ constructed in [Reference Pappas and ZhuPZ13, Reference LevinLev16] (see § 4.3).
$X=\mathbb{A}_{{\mathcal{O}}_{K_{0}}}^{1}$ constructed in [Reference Pappas and ZhuPZ13, Reference LevinLev16] (see § 4.3).
4.2 Parahoric group schemes for Weil-restricted groups
Let ![]() $G_{0}$ be a reductive
$G_{0}$ be a reductive ![]() $K$-group. Fix a maximal
$K$-group. Fix a maximal ![]() $K$-split torus
$K$-split torus ![]() $A_{0}$, and a maximal
$A_{0}$, and a maximal ![]() $\breve{K}$-split torus
$\breve{K}$-split torus ![]() $S_{0}$ containing
$S_{0}$ containing ![]() $A_{0}$ and defined over
$A_{0}$ and defined over ![]() $K$. Let
$K$. Let ![]() $M_{0}=Z_{G_{0}}(A_{0})$ denote the centralizer of
$M_{0}=Z_{G_{0}}(A_{0})$ denote the centralizer of ![]() $A_{0}$ which is a minimal
$A_{0}$ which is a minimal ![]() $K$-Levi subgroup of
$K$-Levi subgroup of ![]() $G_{0}$, and let
$G_{0}$, and let ![]() $T_{0}=Z_{G_{0}}(S_{0})$ be the centralizer of
$T_{0}=Z_{G_{0}}(S_{0})$ be the centralizer of ![]() $S_{0}$. Then
$S_{0}$. Then ![]() $T_{0}$ is a maximal torus because
$T_{0}$ is a maximal torus because ![]() $G_{0,\breve{K}}$ is quasi-split by Steinberg’s theorem.
$G_{0,\breve{K}}$ is quasi-split by Steinberg’s theorem.
We are interested in parahoric subgroups of the Weil restriction of scalars ![]() $G:=\operatorname{Res}_{K/F}(G_{0})$. We will first need to classify the maximal
$G:=\operatorname{Res}_{K/F}(G_{0})$. We will first need to classify the maximal ![]() $F$-split tori in
$F$-split tori in ![]() $G$.
$G$.
Lemma 4.1. Suppose ![]() $T_{0}$ is any
$T_{0}$ is any ![]() $K$-torus, so that
$K$-torus, so that ![]() $T=\operatorname{Res}_{K/F}(T_{0})$ is an
$T=\operatorname{Res}_{K/F}(T_{0})$ is an ![]() $F$-torus. Then there is a canonical isomorphism of groups
$F$-torus. Then there is a canonical isomorphism of groups
In particular, the ![]() $F$-split rank of
$F$-split rank of ![]() $T$ is the
$T$ is the ![]() $K$-split rank of
$K$-split rank of ![]() $T_{0}$.
$T_{0}$.
Proof. Recall that ![]() $T$ represents the functor on
$T$ represents the functor on ![]() $F$-tori which sends the
$F$-tori which sends the ![]() $F$-torus
$F$-torus ![]() $T^{\prime }$ to
$T^{\prime }$ to
We deduce that ![]() $X_{\ast }(\operatorname{Res}_{K/F}(T_{0}))=\text{Ind}_{\unicode[STIX]{x1D6E4}_{K}}^{\unicode[STIX]{x1D6E4}_{F}}(X_{\ast }(T_{0}))\cong X_{\ast }(T_{0})\otimes _{\mathbb{Z}[\unicode[STIX]{x1D6E4}_{K}]}\mathbb{Z}[\unicode[STIX]{x1D6E4}_{F}]$ (since
$X_{\ast }(\operatorname{Res}_{K/F}(T_{0}))=\text{Ind}_{\unicode[STIX]{x1D6E4}_{K}}^{\unicode[STIX]{x1D6E4}_{F}}(X_{\ast }(T_{0}))\cong X_{\ast }(T_{0})\otimes _{\mathbb{Z}[\unicode[STIX]{x1D6E4}_{K}]}\mathbb{Z}[\unicode[STIX]{x1D6E4}_{F}]$ (since ![]() $[\unicode[STIX]{x1D6E4}_{F}:\unicode[STIX]{x1D6E4}_{K}]<\infty$). Then the
$[\unicode[STIX]{x1D6E4}_{F}:\unicode[STIX]{x1D6E4}_{K}]<\infty$). Then the ![]() $H_{0}$-version of Shapiro’s lemma gives
$H_{0}$-version of Shapiro’s lemma gives ![]() $(X_{\ast }(T_{0})\otimes _{\mathbb{Z}[\unicode[STIX]{x1D6E4}_{K}]}\mathbb{Z}[\unicode[STIX]{x1D6E4}_{F}])_{\unicode[STIX]{x1D6E4}_{F}}=X_{\ast }(T_{0})_{\unicode[STIX]{x1D6E4}_{K}}$, which implies the lemma.◻
$(X_{\ast }(T_{0})\otimes _{\mathbb{Z}[\unicode[STIX]{x1D6E4}_{K}]}\mathbb{Z}[\unicode[STIX]{x1D6E4}_{F}])_{\unicode[STIX]{x1D6E4}_{F}}=X_{\ast }(T_{0})_{\unicode[STIX]{x1D6E4}_{K}}$, which implies the lemma.◻
Under the bijection
![]() $T^{\prime }\rightarrow \operatorname{Res}_{K/F}(G_{0})$ is injective if and only if the corresponding morphism
$T^{\prime }\rightarrow \operatorname{Res}_{K/F}(G_{0})$ is injective if and only if the corresponding morphism ![]() $T_{K}^{\prime }\rightarrow G_{0}$ is injective. Since any
$T_{K}^{\prime }\rightarrow G_{0}$ is injective. Since any ![]() $K$-split torus is of the form
$K$-split torus is of the form ![]() $T_{K}^{\prime }$ for a unique
$T_{K}^{\prime }$ for a unique ![]() $F$-split torus
$F$-split torus ![]() $T^{\prime }$, this shows that the rank of a maximal
$T^{\prime }$, this shows that the rank of a maximal ![]() $F$-split torus in
$F$-split torus in ![]() $\operatorname{Res}_{K/F}(G_{0})$ is the same as the rank of a maximal
$\operatorname{Res}_{K/F}(G_{0})$ is the same as the rank of a maximal ![]() $K$-split torus in
$K$-split torus in ![]() $G_{0}$. For the maximal
$G_{0}$. For the maximal ![]() $K$-split torus
$K$-split torus ![]() $A_{0}\subset G_{0}$, we write
$A_{0}\subset G_{0}$, we write ![]() $A_{0}=A_{K}$ for a unique
$A_{0}=A_{K}$ for a unique ![]() $F$-split torus
$F$-split torus ![]() $A$. Using the canonical embedding
$A$. Using the canonical embedding ![]() $A{\hookrightarrow}\operatorname{Res}_{K/F}(A_{K})=\operatorname{Res}_{K/F}(A_{0})$, we see that
$A{\hookrightarrow}\operatorname{Res}_{K/F}(A_{K})=\operatorname{Res}_{K/F}(A_{0})$, we see that ![]() $A$ is the
$A$ is the ![]() $F$-split component of
$F$-split component of ![]() $\operatorname{Res}_{K/F}(A_{0})$ and also a maximal
$\operatorname{Res}_{K/F}(A_{0})$ and also a maximal ![]() $F$-split torus in
$F$-split torus in ![]() $G$.
$G$.
From now on, we will abuse notation and denote by ![]() $A$ the image of
$A$ the image of ![]() $A{\hookrightarrow}\operatorname{Res}_{K/F}(A_{0}){\hookrightarrow}\operatorname{Res}_{K/F}(G_{0})=G$ (even though
$A{\hookrightarrow}\operatorname{Res}_{K/F}(A_{0}){\hookrightarrow}\operatorname{Res}_{K/F}(G_{0})=G$ (even though ![]() $A$ is not a Weil restriction of a torus). The discussion following (4.2) shows that
$A$ is not a Weil restriction of a torus). The discussion following (4.2) shows that ![]() $A_{0}\mapsto A$ gives a bijection between maximal
$A_{0}\mapsto A$ gives a bijection between maximal ![]() $K$-split tori in
$K$-split tori in ![]() $G_{0}$ and maximal
$G_{0}$ and maximal ![]() $F$-split tori in
$F$-split tori in ![]() $G$.
$G$.
Let us note that since ![]() $S_{0}$ is
$S_{0}$ is ![]() $\breve{K}$-split (and using
$\breve{K}$-split (and using ![]() $\breve{K}_{0}\otimes _{K_{0}}K=\breve{K}$) there exists a unique subtorus
$\breve{K}_{0}\otimes _{K_{0}}K=\breve{K}$) there exists a unique subtorus ![]() $S_{0}^{\prime }{\hookrightarrow}\operatorname{Res}_{K/K_{0}}(S_{0})$ which is a maximal
$S_{0}^{\prime }{\hookrightarrow}\operatorname{Res}_{K/K_{0}}(S_{0})$ which is a maximal ![]() $\breve{K}_{0}$-split torus in
$\breve{K}_{0}$-split torus in ![]() $\operatorname{Res}_{K/K_{0}}(G_{0})$ defined over
$\operatorname{Res}_{K/K_{0}}(G_{0})$ defined over ![]() $K_{0}$ and of the same rank as
$K_{0}$ and of the same rank as ![]() $S_{0}$. We let
$S_{0}$. We let ![]() $S$ denote the image of
$S$ denote the image of ![]() $\operatorname{Res}_{K_{0}/F}(S_{0}^{\prime }){\hookrightarrow}\operatorname{Res}_{K_{0}/F}(\operatorname{Res}_{K/K_{0}}(S_{0}))=\operatorname{Res}_{K/F}S_{0}$ which is a maximal
$\operatorname{Res}_{K_{0}/F}(S_{0}^{\prime }){\hookrightarrow}\operatorname{Res}_{K_{0}/F}(\operatorname{Res}_{K/K_{0}}(S_{0}))=\operatorname{Res}_{K/F}S_{0}$ which is a maximal ![]() $\breve{F}$-split torus in
$\breve{F}$-split torus in ![]() $G$ defined over
$G$ defined over ![]() $F$.
$F$.
Lemma 4.2. Letting ![]() $M=\operatorname{Res}_{K/F}(M_{0})$ and
$M=\operatorname{Res}_{K/F}(M_{0})$ and ![]() $T=\operatorname{Res}_{K/F}(T_{0})$, we have
$T=\operatorname{Res}_{K/F}(T_{0})$, we have ![]() $M=Z_{G}(A)$ and
$M=Z_{G}(A)$ and ![]() $T=Z_{G}(S)$ as subgroups of
$T=Z_{G}(S)$ as subgroups of ![]() $G=\operatorname{Res}_{K/F}(G_{0})$.
$G=\operatorname{Res}_{K/F}(G_{0})$.
Proof. Both containments ‘![]() $\subseteq$’ are obvious. For ‘
$\subseteq$’ are obvious. For ‘![]() $\supseteq$’ we note that the torus
$\supseteq$’ we note that the torus ![]() $A_{\bar{F}}$ is the diagonal torus inside
$A_{\bar{F}}$ is the diagonal torus inside ![]() $\prod _{K{\hookrightarrow}\bar{F}}A_{0}\otimes _{K,\unicode[STIX]{x1D713}}\bar{F}$. Considering its centralizer inside
$\prod _{K{\hookrightarrow}\bar{F}}A_{0}\otimes _{K,\unicode[STIX]{x1D713}}\bar{F}$. Considering its centralizer inside ![]() $\prod _{K{\hookrightarrow}\bar{F}}G_{0}\otimes _{K,\unicode[STIX]{x1D713}}\bar{F}$ proves
$\prod _{K{\hookrightarrow}\bar{F}}G_{0}\otimes _{K,\unicode[STIX]{x1D713}}\bar{F}$ proves ![]() $M=Z_{G}(A)$. Since
$M=Z_{G}(A)$. Since ![]() $Z_{G}(S)$ is necessarily a maximal torus, the inclusion
$Z_{G}(S)$ is necessarily a maximal torus, the inclusion ![]() $T\subseteq Z_{G}(S)$ is also an equality.◻
$T\subseteq Z_{G}(S)$ is also an equality.◻
The correspondence ![]() $A\leftrightarrow A_{0}$ induces a correspondence between the apartments in the (extended) Bruhat–Tits buildings
$A\leftrightarrow A_{0}$ induces a correspondence between the apartments in the (extended) Bruhat–Tits buildings ![]() $\mathscr{B}(G,F)$ and
$\mathscr{B}(G,F)$ and ![]() $\mathscr{B}(G_{0},K)$. We will show that there is a canonical isomorphism
$\mathscr{B}(G_{0},K)$. We will show that there is a canonical isomorphism
equivariant for the action of ![]() $G(F)=G_{0}(K)$, and compatible with an identification of apartments
$G(F)=G_{0}(K)$, and compatible with an identification of apartments ![]() $\mathscr{A}(G,A,F)=\mathscr{A}(G_{0},A_{0},K)$.
$\mathscr{A}(G,A,F)=\mathscr{A}(G_{0},A_{0},K)$.
The Iwahori–Weyl group ![]() $W=W(G,A,F)$ is the group
$W=W(G,A,F)$ is the group
where ![]() $M(F)_{1}$ is the unique parahoric subgroup of the minimal Levi
$M(F)_{1}$ is the unique parahoric subgroup of the minimal Levi ![]() $M$; cf. [Reference Haines and RapoportHR08, Reference RicharzRic16a]. (By Lemma 4.2,
$M$; cf. [Reference Haines and RapoportHR08, Reference RicharzRic16a]. (By Lemma 4.2, ![]() $M$ is a minimal
$M$ is a minimal ![]() $F$-Levi subgroup of
$F$-Levi subgroup of ![]() $G$.) We define
$G$.) We define ![]() $\breve{W}=W(G,S,\breve{F})$ analogously. In the following we will use the identification
$\breve{W}=W(G,S,\breve{F})$ analogously. In the following we will use the identification ![]() $\breve{F}\otimes _{F}K=\prod _{[K_{0}:F]}\breve{K}$ which is
$\breve{F}\otimes _{F}K=\prod _{[K_{0}:F]}\breve{K}$ which is ![]() $\unicode[STIX]{x1D70E}$-equivariant for the action
$\unicode[STIX]{x1D70E}$-equivariant for the action ![]() $\unicode[STIX]{x1D70E}(a_{j})_{j}=(\unicode[STIX]{x1D70E}a_{j-1})_{j}$ on the product.
$\unicode[STIX]{x1D70E}(a_{j})_{j}=(\unicode[STIX]{x1D70E}a_{j-1})_{j}$ on the product.
Lemma 4.3. There is a canonical identification of Iwahori–Weyl groups
Proof. As in Lemma 4.2, one shows ![]() $\operatorname{Norm}_{G}(A)=\operatorname{Res}_{K/F}(\operatorname{Norm}_{G_{0}}(A_{0}))$, and hence
$\operatorname{Norm}_{G}(A)=\operatorname{Res}_{K/F}(\operatorname{Norm}_{G_{0}}(A_{0}))$, and hence ![]() $\operatorname{Norm}_{G}(A)(F)=\operatorname{Norm}_{G_{0}}(A_{0})(K)$. By Lemma 4.4 below,
$\operatorname{Norm}_{G}(A)(F)=\operatorname{Norm}_{G_{0}}(A_{0})(K)$. By Lemma 4.4 below, ![]() $M(F)_{1}=M_{0}(K)_{1}$. The first equality follows and the second is similar.◻
$M(F)_{1}=M_{0}(K)_{1}$. The first equality follows and the second is similar.◻
Lemma 4.4. Let ![]() $G(F)_{1}\subset G(F)$ denote the Kottwitz kernel, that is,
$G(F)_{1}\subset G(F)$ denote the Kottwitz kernel, that is, ![]() $G(F)_{1}=G(F)\cap G(\breve{F})_{1}$ with
$G(F)_{1}=G(F)\cap G(\breve{F})_{1}$ with
where ![]() $\unicode[STIX]{x1D705}_{G}$ is the Kottwitz homomorphism of [Reference KottwitzKot97, § 7]. Then
$\unicode[STIX]{x1D705}_{G}$ is the Kottwitz homomorphism of [Reference KottwitzKot97, § 7]. Then ![]() $G(\breve{F})_{1}=\prod _{[K_{0}:F]}G_{0}(\breve{K})_{1}$ and
$G(\breve{F})_{1}=\prod _{[K_{0}:F]}G_{0}(\breve{K})_{1}$ and ![]() $G(F)_{1}=G_{0}(K)_{1}$.
$G(F)_{1}=G_{0}(K)_{1}$.
Proof. The result is clear when ![]() $G_{0}$ is a torus:
$G_{0}$ is a torus: ![]() $G(\breve{F})_{1}$ and
$G(\breve{F})_{1}$ and ![]() $\prod _{[K_{0}:F]}G_{0}(\breve{K})_{1}$ coincide with the unique maximal bounded subgroup of
$\prod _{[K_{0}:F]}G_{0}(\breve{K})_{1}$ coincide with the unique maximal bounded subgroup of
Thus, by a variation of Lemma 4.1, ![]() $\unicode[STIX]{x1D705}_{G}:G(\breve{F})\rightarrow X_{\ast }(G)_{I_{F}}$ is the direct product over
$\unicode[STIX]{x1D705}_{G}:G(\breve{F})\rightarrow X_{\ast }(G)_{I_{F}}$ is the direct product over ![]() $[K_{0}:K]$-many copies of
$[K_{0}:K]$-many copies of ![]() $\unicode[STIX]{x1D705}_{G_{0}}:G_{0}(\breve{K})\rightarrow X_{\ast }(G_{0})_{I_{K}}$. Clearly the result holds for
$\unicode[STIX]{x1D705}_{G_{0}}:G_{0}(\breve{K})\rightarrow X_{\ast }(G_{0})_{I_{K}}$. Clearly the result holds for ![]() $G_{0}=G_{0,\text{sc}}$ and hence for
$G_{0}=G_{0,\text{sc}}$ and hence for ![]() $G_{0,\text{der}}=G_{0,\text{sc}}$ by reduction to the torus case. Finally, the general case follows by the method of
$G_{0,\text{der}}=G_{0,\text{sc}}$ by reduction to the torus case. Finally, the general case follows by the method of ![]() $z$-extensions as in the construction of
$z$-extensions as in the construction of ![]() $\unicode[STIX]{x1D705}_{G_{0}}$ [Reference KottwitzKot97, § 7.4].◻
$\unicode[STIX]{x1D705}_{G_{0}}$ [Reference KottwitzKot97, § 7.4].◻
Lemma 4.5. There is a canonical isomorphism of apartments ![]() $\mathscr{A}(G,S,\breve{F})=\mathscr{A}(G_{0},S_{0},\breve{F}\otimes _{F}K)$ compatible with the action of the Iwahori–Weyl groups
$\mathscr{A}(G,S,\breve{F})=\mathscr{A}(G_{0},S_{0},\breve{F}\otimes _{F}K)$ compatible with the action of the Iwahori–Weyl groups ![]() $W(G,S,\breve{F})=W(G_{0},S_{0},\breve{F}\otimes _{F}K)$ and the action of the Frobenius
$W(G,S,\breve{F})=W(G_{0},S_{0},\breve{F}\otimes _{F}K)$ and the action of the Frobenius ![]() $\unicode[STIX]{x1D70E}$.
$\unicode[STIX]{x1D70E}$.
Proof. Let ![]() $\breve{\unicode[STIX]{x1D6F4}}_{G}$ (respectively,
$\breve{\unicode[STIX]{x1D6F4}}_{G}$ (respectively, ![]() $\breve{\unicode[STIX]{x1D6F4}}_{G_{0}}$) denote the Bruhat–Tits échelonnage root system attached to
$\breve{\unicode[STIX]{x1D6F4}}_{G_{0}}$) denote the Bruhat–Tits échelonnage root system attached to ![]() $(G,S)$ (respectively,
$(G,S)$ (respectively, ![]() $(G_{0},S_{0})$). Taking
$(G_{0},S_{0})$). Taking ![]() $T_{0}=T_{0,\text{sc}}$ in Lemma 4.1 and using [Reference Haines and RapoportHR08, Lemma 15], we obtain an equality of coroot lattices
$T_{0}=T_{0,\text{sc}}$ in Lemma 4.1 and using [Reference Haines and RapoportHR08, Lemma 15], we obtain an equality of coroot lattices
By considering minimal positive generators of these lattices, we deduce that ![]() $\breve{\unicode[STIX]{x1D6F4}}_{G}=\prod _{[K_{0}:F]}\breve{\unicode[STIX]{x1D6F4}}_{G_{0}}$. As all identifications are canonical this isomorphism is compatible with the action of
$\breve{\unicode[STIX]{x1D6F4}}_{G}=\prod _{[K_{0}:F]}\breve{\unicode[STIX]{x1D6F4}}_{G_{0}}$. As all identifications are canonical this isomorphism is compatible with the action of ![]() $\unicode[STIX]{x1D70E}$ on both sides. This gives the identification of affine root hyperplanes needed to prove the isomorphism of apartments
$\unicode[STIX]{x1D70E}$ on both sides. This gives the identification of affine root hyperplanes needed to prove the isomorphism of apartments
The isomorphism is equivariant for ![]() $W(G,S,\breve{F})=W(G_{0},S_{0},\breve{F}\otimes _{F}K)$ and
$W(G,S,\breve{F})=W(G_{0},S_{0},\breve{F}\otimes _{F}K)$ and ![]() $\unicode[STIX]{x1D70E}$.◻
$\unicode[STIX]{x1D70E}$.◻
Proposition 4.6. There is a canonical isomorphism ![]() $\mathscr{B}(G,F)\,\simeq \,\mathscr{B}(G_{0},K)$, equivariant for the action of
$\mathscr{B}(G,F)\,\simeq \,\mathscr{B}(G_{0},K)$, equivariant for the action of ![]() $G(F)=G_{0}(K)$, and compatible with an identification of apartments
$G(F)=G_{0}(K)$, and compatible with an identification of apartments ![]() $\mathscr{A}(G,A,F)=\mathscr{A}(G_{0},A_{0},K)$.
$\mathscr{A}(G,A,F)=\mathscr{A}(G_{0},A_{0},K)$.
Proof. By construction ![]() $\mathscr{B}(G_{0},\breve{K})=(G_{0}(\breve{K})\times \mathscr{A}(G_{0},S_{0},\breve{K}))/\sim$, where
$\mathscr{B}(G_{0},\breve{K})=(G_{0}(\breve{K})\times \mathscr{A}(G_{0},S_{0},\breve{K}))/\sim$, where ![]() $(g,x)\sim (g^{\prime },x^{\prime })$ if there exists
$(g,x)\sim (g^{\prime },x^{\prime })$ if there exists ![]() $n\in \text{Norm}_{G_{0}}(S_{0})(\breve{K})$ such that
$n\in \text{Norm}_{G_{0}}(S_{0})(\breve{K})$ such that ![]() $n\cdot x=x^{\prime }$ and
$n\cdot x=x^{\prime }$ and ![]() $g^{-1}g^{\prime }n\in U_{x}$. Here
$g^{-1}g^{\prime }n\in U_{x}$. Here ![]() $U_{x}$ is the subgroup of
$U_{x}$ is the subgroup of ![]() $G_{0}(\breve{K})$ generated by the affine root groups
$G_{0}(\breve{K})$ generated by the affine root groups ![]() $U_{\unicode[STIX]{x1D6FC}+r}$ associated to
$U_{\unicode[STIX]{x1D6FC}+r}$ associated to ![]() $\unicode[STIX]{x1D6FC}+r$ with
$\unicode[STIX]{x1D6FC}+r$ with ![]() $\unicode[STIX]{x1D6FC}(x)+r\geqslant 0$, for
$\unicode[STIX]{x1D6FC}(x)+r\geqslant 0$, for ![]() $(\unicode[STIX]{x1D6FC},r)\in \breve{\unicode[STIX]{x1D6F4}}_{G_{0}}\times \mathbb{Z}$. Because
$(\unicode[STIX]{x1D6FC},r)\in \breve{\unicode[STIX]{x1D6F4}}_{G_{0}}\times \mathbb{Z}$. Because ![]() $\breve{\unicode[STIX]{x1D6F4}}_{G}=\prod _{[K_{0}:F]}\breve{\unicode[STIX]{x1D6F4}}_{G_{0}}$, the equivalence relation for
$\breve{\unicode[STIX]{x1D6F4}}_{G}=\prod _{[K_{0}:F]}\breve{\unicode[STIX]{x1D6F4}}_{G_{0}}$, the equivalence relation for ![]() $G$ is the
$G$ is the ![]() $[K_{0}:F]$-fold product of the equivalence relation for
$[K_{0}:F]$-fold product of the equivalence relation for ![]() $G_{0}$. Using Lemma 4.5, this proves
$G_{0}$. Using Lemma 4.5, this proves
equivariantly for ![]() $\unicode[STIX]{x1D70E}$, and the proposition follows by étale descent; cf. [Reference Bruhat and TitsBT84, § 5.1].◻
$\unicode[STIX]{x1D70E}$, and the proposition follows by étale descent; cf. [Reference Bruhat and TitsBT84, § 5.1].◻
Let ![]() $\mathbf{f}$ be a facet of
$\mathbf{f}$ be a facet of ![]() $\mathscr{A}(G,A,F)$, and denote by
$\mathscr{A}(G,A,F)$, and denote by ![]() $\mathbf{f}_{0}$ the corresponding facet in
$\mathbf{f}_{0}$ the corresponding facet in ![]() $\mathscr{A}(G_{0},A_{0},K)$. Let
$\mathscr{A}(G_{0},A_{0},K)$. Let ![]() ${\mathcal{G}}_{\mathbf{f}}$ (respectively,
${\mathcal{G}}_{\mathbf{f}}$ (respectively, ![]() ${\mathcal{G}}_{\mathbf{f}_{0}}$) be the associated parahoric group scheme over
${\mathcal{G}}_{\mathbf{f}_{0}}$) be the associated parahoric group scheme over ![]() ${\mathcal{O}}_{F}$ (respectively,
${\mathcal{O}}_{F}$ (respectively, ![]() ${\mathcal{O}}_{K}$).
${\mathcal{O}}_{K}$).
Proposition 4.7. There is a canonical isomorphism of ![]() ${\mathcal{O}}_{F}$-group schemes
${\mathcal{O}}_{F}$-group schemes ![]() ${\mathcal{G}}_{\mathbf{f}}\simeq \operatorname{Res}_{{\mathcal{O}}_{K}/{\mathcal{O}}_{F}}({\mathcal{G}}_{\mathbf{f}_{0}})$ inducing the identity on generic fibers.
${\mathcal{G}}_{\mathbf{f}}\simeq \operatorname{Res}_{{\mathcal{O}}_{K}/{\mathcal{O}}_{F}}({\mathcal{G}}_{\mathbf{f}_{0}})$ inducing the identity on generic fibers.
Proof. By the defining property of parahoric group schemes, it suffices to check that the group ![]() ${\mathcal{H}}:=\operatorname{Res}_{{\mathcal{O}}_{K}/{\mathcal{O}}_{F}}({\mathcal{G}}_{\mathbf{f}_{0}})$ is a smooth affine
${\mathcal{H}}:=\operatorname{Res}_{{\mathcal{O}}_{K}/{\mathcal{O}}_{F}}({\mathcal{G}}_{\mathbf{f}_{0}})$ is a smooth affine ![]() ${\mathcal{O}}_{F}$-group scheme of finite type with (geometrically) connected special fiber, with the property that
${\mathcal{O}}_{F}$-group scheme of finite type with (geometrically) connected special fiber, with the property that ![]() ${\mathcal{H}}({\mathcal{O}}_{\breve{F}})$ is the intersection of the Kottwitz kernel
${\mathcal{H}}({\mathcal{O}}_{\breve{F}})$ is the intersection of the Kottwitz kernel ![]() $G(\breve{F})_{1}$ with the pointwise fixer in
$G(\breve{F})_{1}$ with the pointwise fixer in ![]() $G(\breve{F})$ of
$G(\breve{F})$ of ![]() $\mathbf{f}$ which we view as a subset of the building over
$\mathbf{f}$ which we view as a subset of the building over ![]() $\breve{F}$; cf. [Reference Haines and RapoportHR08]. The
$\breve{F}$; cf. [Reference Haines and RapoportHR08]. The ![]() ${\mathcal{O}}_{F}$-group
${\mathcal{O}}_{F}$-group ![]() ${\mathcal{H}}$ is smooth affine and of finite type by general properties of Weil restriction of scalars; cf. [Reference Bosch, Lütkebohmert and RaynaudBLR90, § 7.6, Theorem 4, Proposition 5]. If
${\mathcal{H}}$ is smooth affine and of finite type by general properties of Weil restriction of scalars; cf. [Reference Bosch, Lütkebohmert and RaynaudBLR90, § 7.6, Theorem 4, Proposition 5]. If ![]() $R={\mathcal{O}}_{K}/\unicode[STIX]{x1D71B}^{[K:K_{0}]}$, then the special fiber is given by
$R={\mathcal{O}}_{K}/\unicode[STIX]{x1D71B}^{[K:K_{0}]}$, then the special fiber is given by
which is a successive extension of smooth (geometrically) connected groups, and hence (geometrically) connected. As ![]() $\prod _{[K_{0}:F]}\breve{K}=K\otimes _{F}\breve{F}$ we have
$\prod _{[K_{0}:F]}\breve{K}=K\otimes _{F}\breve{F}$ we have ![]() ${\mathcal{H}}({\mathcal{O}}_{\breve{F}})=\prod _{[K_{0}:F]}{\mathcal{G}}_{\mathbf{f}_{0}}({\mathcal{O}}_{\breve{K}})$ which is the intersection of
${\mathcal{H}}({\mathcal{O}}_{\breve{F}})=\prod _{[K_{0}:F]}{\mathcal{G}}_{\mathbf{f}_{0}}({\mathcal{O}}_{\breve{K}})$ which is the intersection of ![]() $\prod _{[K_{0}:F]}G_{0}(\breve{K})_{1}=G(\breve{F})_{1}$ (Lemma 4.4) with the pointwise fixer in
$\prod _{[K_{0}:F]}G_{0}(\breve{K})_{1}=G(\breve{F})_{1}$ (Lemma 4.4) with the pointwise fixer in ![]() $\prod _{[K_{0}:F]}G_{0}(\breve{K})$ of
$\prod _{[K_{0}:F]}G_{0}(\breve{K})$ of ![]() $\mathbf{f}$, by Lemma 4.5. The proposition follows.◻
$\mathbf{f}$, by Lemma 4.5. The proposition follows.◻
Corollary 4.8. Every parahoric ![]() ${\mathcal{O}}_{F}$-group scheme of
${\mathcal{O}}_{F}$-group scheme of ![]() $G$ is of the form
$G$ is of the form ![]() $\operatorname{Res}_{{\mathcal{O}}_{K}/{\mathcal{O}}_{F}}({\mathcal{G}}_{\mathbf{f}_{0}})$ for a unique facet
$\operatorname{Res}_{{\mathcal{O}}_{K}/{\mathcal{O}}_{F}}({\mathcal{G}}_{\mathbf{f}_{0}})$ for a unique facet ![]() $\mathbf{f}_{0}\subset \mathscr{B}(G,K)$.◻
$\mathbf{f}_{0}\subset \mathscr{B}(G,K)$.◻
The subgroup ![]() $W_{\mathbf{f}}=W_{\mathbf{f}}(G,A,F)$ of
$W_{\mathbf{f}}=W_{\mathbf{f}}(G,A,F)$ of ![]() $W$ associated with
$W$ associated with ![]() $\mathbf{f}$ is the group
$\mathbf{f}$ is the group
The isomorphism ![]() $W(G,A,F)=W(G_{0},A_{0},K)$ induces
$W(G,A,F)=W(G_{0},A_{0},K)$ induces ![]() $W_{\mathbf{f}}(G,A,F)=W_{\mathbf{f}_{0}}(G_{0},A_{0},K)$. Let us point out a consequence of Proposition 4.6 which is used later.
$W_{\mathbf{f}}(G,A,F)=W_{\mathbf{f}_{0}}(G_{0},A_{0},K)$. Let us point out a consequence of Proposition 4.6 which is used later.
Corollary 4.9. There is a canonical identification ![]() ${\mathcal{Z}}(G(F),{\mathcal{G}}_{\mathbf{f}}({\mathcal{O}}_{F}))={\mathcal{Z}}(G_{0}(K),{\mathcal{G}}_{\mathbf{f}_{0}}({\mathcal{O}}_{K}))$ of centers of parahoric Hecke algebras compatible with the Bernstein isomorphism of [Reference Haines, Diamond, Kassaei and KimHai14, Theorem 11.10.1], where the Haar measures are normalized to give
${\mathcal{Z}}(G(F),{\mathcal{G}}_{\mathbf{f}}({\mathcal{O}}_{F}))={\mathcal{Z}}(G_{0}(K),{\mathcal{G}}_{\mathbf{f}_{0}}({\mathcal{O}}_{K}))$ of centers of parahoric Hecke algebras compatible with the Bernstein isomorphism of [Reference Haines, Diamond, Kassaei and KimHai14, Theorem 11.10.1], where the Haar measures are normalized to give ![]() ${\mathcal{G}}_{\mathbf{f}}({\mathcal{O}}_{F})={\mathcal{G}}_{\mathbf{f}_{0}}({\mathcal{O}}_{K})$ volume
${\mathcal{G}}_{\mathbf{f}}({\mathcal{O}}_{F})={\mathcal{G}}_{\mathbf{f}_{0}}({\mathcal{O}}_{K})$ volume ![]() $1$.
$1$.
Proof. In view of ![]() ${\mathcal{G}}_{\mathbf{f}}({\mathcal{O}}_{F})={\mathcal{G}}_{\mathbf{f}_{0}}({\mathcal{O}}_{K})$, the equality of the centers is clear, and all that remains is to show the compatibility with the Bernstein isomorphism. This follows from the equality
${\mathcal{G}}_{\mathbf{f}}({\mathcal{O}}_{F})={\mathcal{G}}_{\mathbf{f}_{0}}({\mathcal{O}}_{K})$, the equality of the centers is clear, and all that remains is to show the compatibility with the Bernstein isomorphism. This follows from the equality
combined with the definition of Bernstein isomorphisms given by the integration formula (e.g. [Reference Haines, Diamond, Kassaei and KimHai14, 11.11]) and the isomorphism of finite relative Weyl groups ![]() $W_{0}(G,A,F)=W_{0}(G_{0},A_{0},K)$ consistent with Lemma 4.3.◻
$W_{0}(G,A,F)=W_{0}(G_{0},A_{0},K)$ consistent with Lemma 4.3.◻
4.3 Group schemes over  $\mathbb{A}_{{\mathcal{O}}_{K_{0}}}^{1}$
$\mathbb{A}_{{\mathcal{O}}_{K_{0}}}^{1}$
Let ![]() $G_{0}$ be a reductive
$G_{0}$ be a reductive ![]() $K$-group which splits over a tamely ramified extension, and let
$K$-group which splits over a tamely ramified extension, and let ![]() $G:=\operatorname{Res}_{K/F}(G_{0})$. Fix a chain of subgroups
$G:=\operatorname{Res}_{K/F}(G_{0})$. Fix a chain of subgroups ![]() $A_{0}\subset S_{0}\subset T_{0}\subset M_{0}$ in
$A_{0}\subset S_{0}\subset T_{0}\subset M_{0}$ in ![]() $G_{0}$ as in § 4.2 with corresponding chain of subgroups
$G_{0}$ as in § 4.2 with corresponding chain of subgroups ![]() $A\subset S\subset T\subset M$ in
$A\subset S\subset T\subset M$ in ![]() $G$. Further, fix a parabolic
$G$. Further, fix a parabolic ![]() $K$-subgroup
$K$-subgroup ![]() $P_{0}$ containing
$P_{0}$ containing ![]() $M_{0}$ in
$M_{0}$ in ![]() $G_{0}$, and let
$G_{0}$, and let ![]() $P:=\operatorname{Res}_{K/F}(P_{0})$ in
$P:=\operatorname{Res}_{K/F}(P_{0})$ in ![]() $G$.
$G$.
In [Reference Pappas and ZhuPZ13, § 3], a reductive ![]() ${\mathcal{O}}_{K}[u^{\pm }]$-group scheme
${\mathcal{O}}_{K}[u^{\pm }]$-group scheme ![]() $\text{}\underline{G}_{0}$ admitting a maximal torus, and with connected fibers, is constructed. As observed in [Reference LevinLev16, § 3.1; Proposition 3.3], the group scheme
$\text{}\underline{G}_{0}$ admitting a maximal torus, and with connected fibers, is constructed. As observed in [Reference LevinLev16, § 3.1; Proposition 3.3], the group scheme ![]() $\text{}\underline{G}_{0}$ is defined over
$\text{}\underline{G}_{0}$ is defined over ![]() ${\mathcal{O}}_{K_{0}}[u^{\pm }]$ in the following sense.
${\mathcal{O}}_{K_{0}}[u^{\pm }]$ in the following sense.
Proposition 4.10. (i) There exists a reductive ![]() ${\mathcal{O}}_{K_{0}}[u^{\pm }]$-group
${\mathcal{O}}_{K_{0}}[u^{\pm }]$-group ![]() $\text{}\underline{G}_{0}$ together with a tuple of smooth closed
$\text{}\underline{G}_{0}$ together with a tuple of smooth closed ![]() ${\mathcal{O}}_{K_{0}}[u^{\pm }]$-subgroups
${\mathcal{O}}_{K_{0}}[u^{\pm }]$-subgroups ![]() $(\text{}\underline{A}_{0},\text{}\underline{S}_{0},\text{}\underline{T}_{0},\text{}\underline{M}_{0},\text{}\underline{P}_{0})$ and an isomorphism of
$(\text{}\underline{A}_{0},\text{}\underline{S}_{0},\text{}\underline{T}_{0},\text{}\underline{M}_{0},\text{}\underline{P}_{0})$ and an isomorphism of ![]() $K$-groups
$K$-groups
where ![]() $\text{}\underline{A}_{0}$ is a maximal
$\text{}\underline{A}_{0}$ is a maximal ![]() ${\mathcal{O}}_{K_{0}}[u^{\pm }]$-split torus,
${\mathcal{O}}_{K_{0}}[u^{\pm }]$-split torus, ![]() $\text{}\underline{S}_{0}$ a maximal
$\text{}\underline{S}_{0}$ a maximal ![]() ${\mathcal{O}}_{\breve{K}_{0}}[u^{\pm }]$-split torus defined over
${\mathcal{O}}_{\breve{K}_{0}}[u^{\pm }]$-split torus defined over ![]() ${\mathcal{O}}_{K_{0}}[u^{\pm }]$,
${\mathcal{O}}_{K_{0}}[u^{\pm }]$, ![]() $\text{}\underline{T}_{0}$ its centralizer,
$\text{}\underline{T}_{0}$ its centralizer, ![]() $\text{}\underline{M}_{0}$ the centralizer of
$\text{}\underline{M}_{0}$ the centralizer of ![]() $\text{}\underline{A}_{0}$ (a minimal Levi), and
$\text{}\underline{A}_{0}$ (a minimal Levi), and ![]() $\text{}\underline{P}_{0}$ a parabolic
$\text{}\underline{P}_{0}$ a parabolic ![]() ${\mathcal{O}}_{K_{0}}[u^{\pm }]$-subgroup with Levi
${\mathcal{O}}_{K_{0}}[u^{\pm }]$-subgroup with Levi ![]() $\text{}\underline{M}_{0}$.
$\text{}\underline{M}_{0}$.
(ii) The base change ![]() $\text{}\underline{G}_{{\mathcal{O}}_{\breve{K}_{0}}[u^{\pm }]}$ is quasi-split. In particular,
$\text{}\underline{G}_{{\mathcal{O}}_{\breve{K}_{0}}[u^{\pm }]}$ is quasi-split. In particular, ![]() $\text{}\underline{T}_{0}$ is a maximal torus.
$\text{}\underline{T}_{0}$ is a maximal torus.
Proof. Let us recall some elements of the construction as needed later. Let ![]() $\tilde{K}/K$ be a tamely ramified Galois extension which splits
$\tilde{K}/K$ be a tamely ramified Galois extension which splits ![]() $G_{0}$. After possibly enlarging
$G_{0}$. After possibly enlarging ![]() $\tilde{K}$, we may assume:
$\tilde{K}$, we may assume:
(1) the group
 $G_{0}$ is quasi-split over the maximal unramified subextension
$G_{0}$ is quasi-split over the maximal unramified subextension  $\tilde{K}_{0}$ of
$\tilde{K}_{0}$ of  $\tilde{K}/F$;
$\tilde{K}/F$;(2) there exist a uniformizer
 $\tilde{\unicode[STIX]{x1D71B}}\in \tilde{K}$ and an integer
$\tilde{\unicode[STIX]{x1D71B}}\in \tilde{K}$ and an integer  $\tilde{e}\geqslant 1$ such that
$\tilde{e}\geqslant 1$ such that  $\unicode[STIX]{x1D71B}=\tilde{\unicode[STIX]{x1D71B}}^{\tilde{e}}$, and therefore
$\unicode[STIX]{x1D71B}=\tilde{\unicode[STIX]{x1D71B}}^{\tilde{e}}$, and therefore  $\tilde{K}\overset{{\sim}}{\leftarrow }\tilde{K}_{0}[v]/Q(v^{\tilde{e}})$ via
$\tilde{K}\overset{{\sim}}{\leftarrow }\tilde{K}_{0}[v]/Q(v^{\tilde{e}})$ via  $\tilde{\unicode[STIX]{x1D71B}}\leftarrow v$;
$\tilde{\unicode[STIX]{x1D71B}}\leftarrow v$;(3)
 $\tilde{K}_{0}$ contains a primitive
$\tilde{K}_{0}$ contains a primitive  $\tilde{e}$th root of unity (cf. [Reference Pappas and ZhuPZ13, § 3.1]).
$\tilde{e}$th root of unity (cf. [Reference Pappas and ZhuPZ13, § 3.1]).
There is a cocartesian diagramFootnote 4 of ![]() ${\mathcal{O}}_{K_{0}}$-algebras
${\mathcal{O}}_{K_{0}}$-algebras

One can prove that ![]() ${\mathcal{O}}_{\tilde{K}_{0}}[v]/{\mathcal{O}}_{K_{0}}[u]$ is a ramified Galois cover with group isomorphic to
${\mathcal{O}}_{\tilde{K}_{0}}[v]/{\mathcal{O}}_{K_{0}}[u]$ is a ramified Galois cover with group isomorphic to ![]() $\tilde{\unicode[STIX]{x1D6E4}}:=\operatorname{Gal}(\tilde{K}/K)$; for this we use that
$\tilde{\unicode[STIX]{x1D6E4}}:=\operatorname{Gal}(\tilde{K}/K)$; for this we use that ![]() $\tilde{K}_{0}$ contains a primitive
$\tilde{K}_{0}$ contains a primitive ![]() $\tilde{e}$th root of unity. As in [Reference Pappas and ZhuPZ13, § 3], the
$\tilde{e}$th root of unity. As in [Reference Pappas and ZhuPZ13, § 3], the ![]() ${\mathcal{O}}_{K_{0}}[u^{\pm }]$-group scheme
${\mathcal{O}}_{K_{0}}[u^{\pm }]$-group scheme ![]() $\text{}\underline{G}_{0}$ is constructed in [Reference LevinLev16, § 3.1] by descending a suitable choice of Chevalley model for
$\text{}\underline{G}_{0}$ is constructed in [Reference LevinLev16, § 3.1] by descending a suitable choice of Chevalley model for ![]() $G_{0,\tilde{K}}$ along the étale ring extension
$G_{0,\tilde{K}}$ along the étale ring extension ![]() ${\mathcal{O}}_{\tilde{K}_{0}}[v^{\pm }]/{\mathcal{O}}_{K_{0}}[u^{\pm }]$; see [Reference Pappas and ZhuPZ13, § 3] and [Reference LevinLev16, § 3.1] for details. See also Example 4.14.◻
${\mathcal{O}}_{\tilde{K}_{0}}[v^{\pm }]/{\mathcal{O}}_{K_{0}}[u^{\pm }]$; see [Reference Pappas and ZhuPZ13, § 3] and [Reference LevinLev16, § 3.1] for details. See also Example 4.14.◻
Let us denote
Then ![]() $G_{0}^{\flat }$ is a reductive group over
$G_{0}^{\flat }$ is a reductive group over ![]() $K_{0}^{\flat }:=k_{0}((u))$, and
$K_{0}^{\flat }:=k_{0}((u))$, and ![]() $(A_{0}^{\flat },S_{0}^{\flat },T_{0}^{\flat },M_{0}^{\flat },P_{0}^{\flat })$ are analogous to the corresponding groups above; cf. the discussion in [Reference Pappas and ZhuPZ13, 4.1.2–4.1.3] and [Reference LevinLev16, 3.3]. Further, we obtain a canonical identification of the apartments
$(A_{0}^{\flat },S_{0}^{\flat },T_{0}^{\flat },M_{0}^{\flat },P_{0}^{\flat })$ are analogous to the corresponding groups above; cf. the discussion in [Reference Pappas and ZhuPZ13, 4.1.2–4.1.3] and [Reference LevinLev16, 3.3]. Further, we obtain a canonical identification of the apartments
for both ![]() $\unicode[STIX]{x1D705}=K_{0},k_{0}$; cf. [Reference Pappas and ZhuPZ13, 4.1.3] and [Reference LevinLev16, Proposition 3.3.1 ff.]. In particular, we have
$\unicode[STIX]{x1D705}=K_{0},k_{0}$; cf. [Reference Pappas and ZhuPZ13, 4.1.3] and [Reference LevinLev16, Proposition 3.3.1 ff.]. In particular, we have ![]() $\mathscr{A}(G_{0},A_{0},K_{0})=\mathscr{A}(G_{0}^{\flat },A_{0}^{\flat },K_{0}^{\flat })$ for
$\mathscr{A}(G_{0},A_{0},K_{0})=\mathscr{A}(G_{0}^{\flat },A_{0}^{\flat },K_{0}^{\flat })$ for ![]() $\unicode[STIX]{x1D705}=k_{0}$. Thus, we may think of
$\unicode[STIX]{x1D705}=k_{0}$. Thus, we may think of ![]() $G_{0}^{\flat }$ as an equal characteristic analogue of
$G_{0}^{\flat }$ as an equal characteristic analogue of ![]() $G_{0}$ of the same Dynkin type.
$G_{0}$ of the same Dynkin type.
We now introduce the equal characteristic analogue ![]() $G^{\flat }$ of
$G^{\flat }$ of ![]() $G$ by restriction of scalars along the unramified extension
$G$ by restriction of scalars along the unramified extension ![]() $K_{0}/F$: we define the sextuple of
$K_{0}/F$: we define the sextuple of ![]() $k((u))$-groups
$k((u))$-groups
where ![]() $G^{\flat }=\operatorname{Res}_{K_{0}^{\flat }/F^{\flat }}(G_{0}^{\flat })$ is a reductive group over
$G^{\flat }=\operatorname{Res}_{K_{0}^{\flat }/F^{\flat }}(G_{0}^{\flat })$ is a reductive group over ![]() $F^{\flat }:=k((u))$, and likewise
$F^{\flat }:=k((u))$, and likewise ![]() $(S^{\flat },T^{\flat },M^{\flat },P^{\flat })$ are obtained from
$(S^{\flat },T^{\flat },M^{\flat },P^{\flat })$ are obtained from ![]() $(S_{0}^{\flat },T_{0}^{\flat },M_{0}^{\flat },P_{0}^{\flat })$ by restriction of scalars along the unramified extension
$(S_{0}^{\flat },T_{0}^{\flat },M_{0}^{\flat },P_{0}^{\flat })$ by restriction of scalars along the unramified extension ![]() $K_{0}^{\flat }/F^{\flat }$. Here
$K_{0}^{\flat }/F^{\flat }$. Here ![]() $A^{\flat }$ is the maximal
$A^{\flat }$ is the maximal ![]() $F^{\flat }$-split subtorus inside
$F^{\flat }$-split subtorus inside ![]() $\operatorname{Res}_{K_{0}^{\flat }/F^{\flat }}(A_{0}^{\flat })$.
$\operatorname{Res}_{K_{0}^{\flat }/F^{\flat }}(A_{0}^{\flat })$.
Combining (4.7) with Proposition 4.6, we obtain a canonical identification of the apartments
We shall use the following two results in § 6 below.
Lemma 4.11. There is an identification of Iwahori–Weyl groups ![]() $W(G,A,F)=W(G^{\flat },A^{\flat },F^{\flat })$ which is compatible with the action on the apartments under the identification (4.9).
$W(G,A,F)=W(G^{\flat },A^{\flat },F^{\flat })$ which is compatible with the action on the apartments under the identification (4.9).
Proof. Over ![]() $\breve{F}$ we obtain a
$\breve{F}$ we obtain a ![]() $\unicode[STIX]{x1D70E}$-equivariant isomorphism according to [Reference Pappas and ZhuPZ13, 4.1.2] and [Reference LevinLev16, 3.3.0.1], compatible with the action on the apartments. The general case follows by taking
$\unicode[STIX]{x1D70E}$-equivariant isomorphism according to [Reference Pappas and ZhuPZ13, 4.1.2] and [Reference LevinLev16, 3.3.0.1], compatible with the action on the apartments. The general case follows by taking ![]() $\unicode[STIX]{x1D70E}$-fixed points from [Reference RicharzRic16a, § 1.2] (cf. also [Reference Pappas and ZhuPZ13, 4.1.3] and [Reference LevinLev16, Proposition 3.3.1 ii)]).◻
$\unicode[STIX]{x1D70E}$-fixed points from [Reference RicharzRic16a, § 1.2] (cf. also [Reference Pappas and ZhuPZ13, 4.1.3] and [Reference LevinLev16, Proposition 3.3.1 ii)]).◻
Now let ![]() ${\mathcal{G}}={\mathcal{G}}_{\mathbf{f}}$ be a parahoric
${\mathcal{G}}={\mathcal{G}}_{\mathbf{f}}$ be a parahoric ![]() ${\mathcal{O}}_{F}$-group scheme of
${\mathcal{O}}_{F}$-group scheme of ![]() $G$ whose facet
$G$ whose facet ![]() $\mathbf{f}$ is contained in
$\mathbf{f}$ is contained in ![]() $\mathscr{A}(G,A,F)$. Then under (4.9) we obtain a unique facet
$\mathscr{A}(G,A,F)$. Then under (4.9) we obtain a unique facet ![]() $\mathbf{f}^{\flat }\subset \mathscr{A}(G^{\flat },A^{\flat },F^{\flat })$, and hence a parahoric
$\mathbf{f}^{\flat }\subset \mathscr{A}(G^{\flat },A^{\flat },F^{\flat })$, and hence a parahoric ![]() ${\mathcal{O}}_{F^{\flat }}$-group scheme
${\mathcal{O}}_{F^{\flat }}$-group scheme ![]() ${\mathcal{G}}^{\flat }:={\mathcal{G}}_{\mathbf{f}^{\flat }}$ of
${\mathcal{G}}^{\flat }:={\mathcal{G}}_{\mathbf{f}^{\flat }}$ of ![]() $G^{\flat }$.
$G^{\flat }$.
Lemma 4.12. There is a canonical identification ![]() ${\mathcal{Z}}(G(F),{\mathcal{G}}({\mathcal{O}}_{F}))={\mathcal{Z}}(G^{\flat }(F^{\flat }),{\mathcal{G}}^{\flat }({\mathcal{O}}_{F^{\flat }}))$ of centers of parahoric Hecke algebras, where the Haar measures are normalized to give
${\mathcal{Z}}(G(F),{\mathcal{G}}({\mathcal{O}}_{F}))={\mathcal{Z}}(G^{\flat }(F^{\flat }),{\mathcal{G}}^{\flat }({\mathcal{O}}_{F^{\flat }}))$ of centers of parahoric Hecke algebras, where the Haar measures are normalized to give ![]() ${\mathcal{G}}({\mathcal{O}}_{F})$ (respectively,
${\mathcal{G}}({\mathcal{O}}_{F})$ (respectively, ![]() ${\mathcal{G}}^{\flat }({\mathcal{O}}_{F^{\flat }})$) volume
${\mathcal{G}}^{\flat }({\mathcal{O}}_{F^{\flat }})$) volume ![]() $1$.
$1$.
Proof. Applying Lemma 4.11 for ![]() $M$, we obtain an identification of abelian groups
$M$, we obtain an identification of abelian groups
where ![]() $M(F)_{1}$ (respectively,
$M(F)_{1}$ (respectively, ![]() $M^{\flat }(F^{\flat })_{1}$) is the unique parahoric group scheme of
$M^{\flat }(F^{\flat })_{1}$) is the unique parahoric group scheme of ![]() $M(F)$ (respectively,
$M(F)$ (respectively, ![]() $M^{\flat }(F^{\flat })$). The result follows via the Bernstein isomorphisms [Reference Haines, Diamond, Kassaei and KimHai14, Theorem 11.10.1]
$M^{\flat }(F^{\flat })$). The result follows via the Bernstein isomorphisms [Reference Haines, Diamond, Kassaei and KimHai14, Theorem 11.10.1]
noting that the finite relative Weyl groups of ![]() $(G,A,F)$ and
$(G,A,F)$ and ![]() $(G^{\flat },A^{\flat },F^{\flat })$ are isomorphic compatible with the action on
$(G^{\flat },A^{\flat },F^{\flat })$ are isomorphic compatible with the action on ![]() $\unicode[STIX]{x1D6EC}_{M}=\unicode[STIX]{x1D6EC}_{M^{\flat }}$.◻
$\unicode[STIX]{x1D6EC}_{M}=\unicode[STIX]{x1D6EC}_{M^{\flat }}$.◻
Theorem 4.13. Fix ![]() $(\text{}\underline{G}_{0},\text{}\underline{A}_{0},\text{}\underline{S}_{0},\text{}\underline{T}_{0})$ and
$(\text{}\underline{G}_{0},\text{}\underline{A}_{0},\text{}\underline{S}_{0},\text{}\underline{T}_{0})$ and ![]() ${\mathcal{G}}_{\mathbf{f}}$ with
${\mathcal{G}}_{\mathbf{f}}$ with ![]() $\mathbf{f}\subset \mathscr{A}(G,A,F)$ as above. There exists a tuple of smooth affine
$\mathbf{f}\subset \mathscr{A}(G,A,F)$ as above. There exists a tuple of smooth affine ![]() ${\mathcal{O}}_{K_{0}}[u]$-group schemes
${\mathcal{O}}_{K_{0}}[u]$-group schemes ![]() $(\text{}\underline{{\mathcal{G}}}_{0},\text{}\underline{{\mathcal{A}}}_{0},\text{}\underline{{\mathcal{S}}}_{0},\text{}\underline{{\mathcal{T}}}_{0})$ with geometrically connected fibers satisfying the following properties.
$(\text{}\underline{{\mathcal{G}}}_{0},\text{}\underline{{\mathcal{A}}}_{0},\text{}\underline{{\mathcal{S}}}_{0},\text{}\underline{{\mathcal{T}}}_{0})$ with geometrically connected fibers satisfying the following properties.
(i) The restriction
 $(\text{}\underline{{\mathcal{G}}}_{0},\text{}\underline{{\mathcal{A}}}_{0},\text{}\underline{{\mathcal{S}}}_{0},\text{}\underline{{\mathcal{T}}}_{0})|_{{\mathcal{O}}_{K_{0}}[u^{\pm }]}$ is
$(\text{}\underline{{\mathcal{G}}}_{0},\text{}\underline{{\mathcal{A}}}_{0},\text{}\underline{{\mathcal{S}}}_{0},\text{}\underline{{\mathcal{T}}}_{0})|_{{\mathcal{O}}_{K_{0}}[u^{\pm }]}$ is  $(\text{}\underline{G}_{0},\text{}\underline{A}_{0},\text{}\underline{S}_{0},\text{}\underline{T}_{0})$ as
$(\text{}\underline{G}_{0},\text{}\underline{A}_{0},\text{}\underline{S}_{0},\text{}\underline{T}_{0})$ as  ${\mathcal{O}}_{K_{0}}[u^{\pm }]$-groups.
${\mathcal{O}}_{K_{0}}[u^{\pm }]$-groups.(ii) The base change of
 $\text{}\underline{{\mathcal{G}}}_{0}$ under
$\text{}\underline{{\mathcal{G}}}_{0}$ under  ${\mathcal{O}}_{K_{0}}[u]\rightarrow {\mathcal{O}}_{K}$,
${\mathcal{O}}_{K_{0}}[u]\rightarrow {\mathcal{O}}_{K}$,  $u\mapsto \unicode[STIX]{x1D71B}$ is the parahoric group
$u\mapsto \unicode[STIX]{x1D71B}$ is the parahoric group  ${\mathcal{G}}={\mathcal{G}}_{\mathbf{f}}$.
${\mathcal{G}}={\mathcal{G}}_{\mathbf{f}}$.(iii) The base change of
 $\text{}\underline{{\mathcal{G}}}_{0}$ under
$\text{}\underline{{\mathcal{G}}}_{0}$ under  ${\mathcal{O}}_{K_{0}}[u]\rightarrow \unicode[STIX]{x1D705}[\![u]\!]$,
${\mathcal{O}}_{K_{0}}[u]\rightarrow \unicode[STIX]{x1D705}[\![u]\!]$,  $u\mapsto u$ for both
$u\mapsto u$ for both  $\unicode[STIX]{x1D705}=K_{0},k_{0}$ is the parahoric group scheme for
$\unicode[STIX]{x1D705}=K_{0},k_{0}$ is the parahoric group scheme for  $\text{}\underline{G}_{0,\unicode[STIX]{x1D705}((u))}$ attached to
$\text{}\underline{G}_{0,\unicode[STIX]{x1D705}((u))}$ attached to  $\mathbf{f}$ under (4.7).
$\mathbf{f}$ under (4.7).(iv) The group
 $\text{}\underline{{\mathcal{A}}}_{0}$ is a split
$\text{}\underline{{\mathcal{A}}}_{0}$ is a split  ${\mathcal{O}}_{K_{0}}[u]$-torus,
${\mathcal{O}}_{K_{0}}[u]$-torus,  $\text{}\underline{{\mathcal{S}}}$ a
$\text{}\underline{{\mathcal{S}}}$ a  ${\mathcal{O}}_{K_{0}}[u]$-torus which splits over
${\mathcal{O}}_{K_{0}}[u]$-torus which splits over  ${\mathcal{O}}_{\breve{F}}[u]$ and
${\mathcal{O}}_{\breve{F}}[u]$ and  $\text{}\underline{{\mathcal{T}}}$ is a smooth affine
$\text{}\underline{{\mathcal{T}}}$ is a smooth affine  ${\mathcal{O}}_{K_{0}}[u]$-group scheme such that
${\mathcal{O}}_{K_{0}}[u]$-group scheme such that  $\text{}\underline{{\mathcal{T}}}_{0}\otimes \unicode[STIX]{x1D705}[\![u]\!]$ is the neutral component of the lft (locally finite type) Néron model of
$\text{}\underline{{\mathcal{T}}}_{0}\otimes \unicode[STIX]{x1D705}[\![u]\!]$ is the neutral component of the lft (locally finite type) Néron model of  $\text{}\underline{T}_{0,\unicode[STIX]{x1D705}((u))}$, for
$\text{}\underline{T}_{0,\unicode[STIX]{x1D705}((u))}$, for  $\unicode[STIX]{x1D705}=K_{0},k_{0}$.
$\unicode[STIX]{x1D705}=K_{0},k_{0}$.
The group ![]() $\text{}\underline{{\mathcal{G}}}_{0}$ is uniquely determined (up to unique isomorphism) by properties (i) and (iii) for
$\text{}\underline{{\mathcal{G}}}_{0}$ is uniquely determined (up to unique isomorphism) by properties (i) and (iii) for ![]() $\unicode[STIX]{x1D705}=K_{0}$, and so is the tuple
$\unicode[STIX]{x1D705}=K_{0}$, and so is the tuple ![]() $(\text{}\underline{{\mathcal{A}}}_{0},\text{}\underline{{\mathcal{S}}}_{0},\text{}\underline{{\mathcal{T}}}_{0})$ using (iv).
$(\text{}\underline{{\mathcal{A}}}_{0},\text{}\underline{{\mathcal{S}}}_{0},\text{}\underline{{\mathcal{T}}}_{0})$ using (iv).
Proof. This is [Reference LevinLev16, Theorem 3.3.3, Proposition 3.3.4]; cf. also [Reference Pappas and ZhuPZ13, Theorem 4.1, esp. 4.2.1] for the uniqueness assertion. ◻
Example 4.14. Suppose ![]() $G_{0}=T_{0}$ is a tamely ramified torus over
$G_{0}=T_{0}$ is a tamely ramified torus over ![]() $K$. Let
$K$. Let ![]() $T_{H}$ be the split torus over
$T_{H}$ be the split torus over ![]() ${\mathcal{O}}_{K_{0}}$ such that
${\mathcal{O}}_{K_{0}}$ such that ![]() $T_{0}$ is given by a 1-cocycle
$T_{0}$ is given by a 1-cocycle
Explicitly,
We let ![]() $T_{H}\otimes _{{\mathcal{O}}_{K_{0}}}\tilde{{\mathcal{O}}}_{0}[v]$ be the split torus over
$T_{H}\otimes _{{\mathcal{O}}_{K_{0}}}\tilde{{\mathcal{O}}}_{0}[v]$ be the split torus over ![]() $\tilde{{\mathcal{O}}}_{0}[v]:={\mathcal{O}}_{\tilde{K}_{0}}[v]$ (cf. (4.5)), which is endowed with Galois actions
$\tilde{{\mathcal{O}}}_{0}[v]:={\mathcal{O}}_{\tilde{K}_{0}}[v]$ (cf. (4.5)), which is endowed with Galois actions ![]() $\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FE})\otimes \unicode[STIX]{x1D6FE}$ for
$\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FE})\otimes \unicode[STIX]{x1D6FE}$ for ![]() $\unicode[STIX]{x1D6FE}\in \tilde{\unicode[STIX]{x1D6E4}}$ which we view as Galois descent data used to give a torus over
$\unicode[STIX]{x1D6FE}\in \tilde{\unicode[STIX]{x1D6E4}}$ which we view as Galois descent data used to give a torus over ![]() ${\mathcal{O}}_{K_{0}}[u]$. Explicitly, we define
${\mathcal{O}}_{K_{0}}[u]$. Explicitly, we define ![]() $\text{}\underline{T}_{0}/{\mathcal{O}}_{K_{0}}[u^{\pm }]$ and
$\text{}\underline{T}_{0}/{\mathcal{O}}_{K_{0}}[u^{\pm }]$ and ![]() $\text{}\underline{{\mathcal{T}}}_{0}/{\mathcal{O}}_{K_{0}}[u]$ by
$\text{}\underline{{\mathcal{T}}}_{0}/{\mathcal{O}}_{K_{0}}[u]$ by
and ![]() $\text{}\underline{{\mathcal{T}}}_{0}$ as the (fiberwise) neutral component of
$\text{}\underline{{\mathcal{T}}}_{0}$ as the (fiberwise) neutral component of
Write ![]() $\text{Gal}(\tilde{K}/K)=\langle \unicode[STIX]{x1D6FE}\rangle \rtimes \langle \unicode[STIX]{x1D70E}\rangle$ where
$\text{Gal}(\tilde{K}/K)=\langle \unicode[STIX]{x1D6FE}\rangle \rtimes \langle \unicode[STIX]{x1D70E}\rangle$ where ![]() $\unicode[STIX]{x1D6FE}$ generates the inertia subgroup and
$\unicode[STIX]{x1D6FE}$ generates the inertia subgroup and ![]() $\unicode[STIX]{x1D70E}$ is a lift of a generator of
$\unicode[STIX]{x1D70E}$ is a lift of a generator of ![]() $\text{Gal}(\tilde{K}^{\text{un}}/K)$ for
$\text{Gal}(\tilde{K}^{\text{un}}/K)$ for ![]() $\tilde{K}^{\text{un}}/K$ the maximal unramified subextension of
$\tilde{K}^{\text{un}}/K$ the maximal unramified subextension of ![]() $\tilde{K}/K$. Then
$\tilde{K}/K$. Then ![]() $\text{}\underline{T}_{0}$ is realized as an
$\text{}\underline{T}_{0}$ is realized as an ![]() $\text{Aut}(\breve{K}_{0}/K_{0})$-descent of
$\text{Aut}(\breve{K}_{0}/K_{0})$-descent of
This shows that the formation of ![]() $\text{}\underline{T}_{0}$ commutes with base change
$\text{}\underline{T}_{0}$ commutes with base change ![]() $\mathbb{A}_{E_{0}}^{1}\rightarrow \mathbb{A}_{K_{0}}^{1}$, where
$\mathbb{A}_{E_{0}}^{1}\rightarrow \mathbb{A}_{K_{0}}^{1}$, where ![]() $E_{0}/K_{0}$ is any unramified extension. Similar remarks apply to
$E_{0}/K_{0}$ is any unramified extension. Similar remarks apply to ![]() $\text{}\underline{{\mathcal{T}}}_{0}$.
$\text{}\underline{{\mathcal{T}}}_{0}$.
4.4 Affine Grassmannians and local models
We continue with the notation as in § 4.1. Recall that we fix a uniformizer ![]() $\unicode[STIX]{x1D71B}\in K$ with Eisenstein polynomial
$\unicode[STIX]{x1D71B}\in K$ with Eisenstein polynomial ![]() $Q\in {\mathcal{O}}_{K_{0}}[u]$. Let
$Q\in {\mathcal{O}}_{K_{0}}[u]$. Let ![]() $(G_{0},A_{0},S_{0},T_{0})$ be tamely ramified over
$(G_{0},A_{0},S_{0},T_{0})$ be tamely ramified over ![]() $K$, and fix a spreading
$K$, and fix a spreading ![]() $(\text{}\underline{G}_{0},\text{}\underline{A}_{0},\text{}\underline{S}_{0},\text{}\underline{T}_{0})$ defined over
$(\text{}\underline{G}_{0},\text{}\underline{A}_{0},\text{}\underline{S}_{0},\text{}\underline{T}_{0})$ defined over ![]() ${\mathcal{O}}_{K_{0}}[u^{\pm }]$ as in Proposition 4.10. Let
${\mathcal{O}}_{K_{0}}[u^{\pm }]$ as in Proposition 4.10. Let ![]() $(G,A,S,T)$ be constructed from
$(G,A,S,T)$ be constructed from ![]() $(G_{0},A_{0},S_{0},T_{0})$ by Weil restriction of scalars along
$(G_{0},A_{0},S_{0},T_{0})$ by Weil restriction of scalars along ![]() $K/F$ as in § 4.2. Choose a facet
$K/F$ as in § 4.2. Choose a facet ![]() $\mathbf{f}\in \mathscr{A}(G,A,F)$, and let
$\mathbf{f}\in \mathscr{A}(G,A,F)$, and let ![]() ${\mathcal{G}}:={\mathcal{G}}_{\mathbf{f}}$ be the corresponding parahoric
${\mathcal{G}}:={\mathcal{G}}_{\mathbf{f}}$ be the corresponding parahoric ![]() ${\mathcal{O}}_{F}$-group scheme for
${\mathcal{O}}_{F}$-group scheme for ![]() $G$. Associated with these data, we have the tuple
$G$. Associated with these data, we have the tuple ![]() $(\text{}\underline{{\mathcal{G}}}_{0},\text{}\underline{{\mathcal{A}}}_{0},\text{}\underline{{\mathcal{S}}}_{0},\text{}\underline{{\mathcal{T}}}_{0})$ of smooth affine group schemes over
$(\text{}\underline{{\mathcal{G}}}_{0},\text{}\underline{{\mathcal{A}}}_{0},\text{}\underline{{\mathcal{S}}}_{0},\text{}\underline{{\mathcal{T}}}_{0})$ of smooth affine group schemes over ![]() $X:=\operatorname{Spec}({\mathcal{O}}_{K_{0}}[u])$ constructed in Theorem 4.13. Since
$X:=\operatorname{Spec}({\mathcal{O}}_{K_{0}}[u])$ constructed in Theorem 4.13. Since ![]() ${\mathcal{O}}_{K_{0}}/{\mathcal{O}}_{F}$ is finite étale, we can view
${\mathcal{O}}_{K_{0}}/{\mathcal{O}}_{F}$ is finite étale, we can view ![]() $X$ as a smooth curve over
$X$ as a smooth curve over ![]() ${\mathcal{O}}_{F}$. Let
${\mathcal{O}}_{F}$. Let ![]() $D\subset X$ be the closed subscheme defined by
$D\subset X$ be the closed subscheme defined by ![]() $\{Q=0\}$ viewed as a relative effective Cartier divisor over
$\{Q=0\}$ viewed as a relative effective Cartier divisor over ![]() ${\mathcal{O}}_{F}$. We are interested in local models for the group
${\mathcal{O}}_{F}$. We are interested in local models for the group ![]() $G=\operatorname{Res}_{K/F}(G_{0})$ with level structure given by the parahoric
$G=\operatorname{Res}_{K/F}(G_{0})$ with level structure given by the parahoric ![]() ${\mathcal{O}}_{F}$-group
${\mathcal{O}}_{F}$-group ![]() ${\mathcal{G}}={\mathcal{G}}_{\mathbf{f}}=\operatorname{Res}_{{\mathcal{O}}_{K}/{\mathcal{O}}_{F}}({\mathcal{G}}_{\mathbf{f}_{0}})$; cf. Proposition 4.7.
${\mathcal{G}}={\mathcal{G}}_{\mathbf{f}}=\operatorname{Res}_{{\mathcal{O}}_{K}/{\mathcal{O}}_{F}}({\mathcal{G}}_{\mathbf{f}_{0}})$; cf. Proposition 4.7.
4.4.1 Affine Grassmannians for Weil-restricted groups
![]() $\!\!$The Beilinson–Drinfeld Grassmannian
$\!\!$The Beilinson–Drinfeld Grassmannian
from (3.1) specializes to [Reference LevinLev16, Definition 4.1.1] for ![]() $K_{0}=F$. By Lemma 3.7, we have
$K_{0}=F$. By Lemma 3.7, we have
Hence, our definition of ![]() $\operatorname{Gr}_{{\mathcal{G}}}$ agrees with [Reference LevinLev16, Proposition 4.1.8 ff.].
$\operatorname{Gr}_{{\mathcal{G}}}$ agrees with [Reference LevinLev16, Proposition 4.1.8 ff.].
We think of (4.11) as being the Beilinson–Drinfeld Grassmannian associated with the parahoric ![]() ${\mathcal{O}}_{F}$-group scheme
${\mathcal{O}}_{F}$-group scheme ![]() ${\mathcal{G}}$. Explicitly,
${\mathcal{G}}$. Explicitly, ![]() $\operatorname{Gr}_{{\mathcal{G}}}$ is the functor on the category of
$\operatorname{Gr}_{{\mathcal{G}}}$ is the functor on the category of ![]() ${\mathcal{O}}_{F}$-algebras
${\mathcal{O}}_{F}$-algebras ![]() $R$ given by the isomorphism classes of tuples
$R$ given by the isomorphism classes of tuples ![]() $({\mathcal{F}},\unicode[STIX]{x1D6FC})$ with
$({\mathcal{F}},\unicode[STIX]{x1D6FC})$ with
where ![]() ${\mathcal{F}}^{0}$ denotes the trivial torsor. If
${\mathcal{F}}^{0}$ denotes the trivial torsor. If ![]() $Q=u-\unicode[STIX]{x1D71B}$ (i.e.
$Q=u-\unicode[STIX]{x1D71B}$ (i.e. ![]() $K=F$) then
$K=F$) then ![]() $\operatorname{Gr}_{{\mathcal{G}}}$ is the Beilinson–Drinfeld Grassmannian defined in [Reference Pappas and ZhuPZ13, 6.2.3; (6.11)].
$\operatorname{Gr}_{{\mathcal{G}}}$ is the Beilinson–Drinfeld Grassmannian defined in [Reference Pappas and ZhuPZ13, 6.2.3; (6.11)].
For an ![]() ${\mathcal{O}}_{F}$-algebra
${\mathcal{O}}_{F}$-algebra ![]() $R$, we have the regular functions on the completion of
$R$, we have the regular functions on the completion of ![]() $X_{R}$ along
$X_{R}$ along ![]() $D_{R}$, namely the
$D_{R}$, namely the ![]() ${\mathcal{O}}_{K_{0}}[u]$-algebra
${\mathcal{O}}_{K_{0}}[u]$-algebra ![]() $R[\![D]\!]=\operatorname{lim}_{N}(R\,\otimes _{{\mathcal{O}}_{F}}\,{\mathcal{O}}_{K_{0}})[u]/(Q^{N})$, and likewise
$R[\![D]\!]=\operatorname{lim}_{N}(R\,\otimes _{{\mathcal{O}}_{F}}\,{\mathcal{O}}_{K_{0}})[u]/(Q^{N})$, and likewise ![]() .With the notation of § 3.1.1, we have the loop group
.With the notation of § 3.1.1, we have the loop group
and the positive loop group
By Lemma 3.4, there is a natural isomorphism ![]() $L{\mathcal{G}}/L^{+}{\mathcal{G}}\simeq \operatorname{Gr}_{{\mathcal{G}}}$, and thus a transitive action morphism
$L{\mathcal{G}}/L^{+}{\mathcal{G}}\simeq \operatorname{Gr}_{{\mathcal{G}}}$, and thus a transitive action morphism
The following proposition is [Reference LevinLev16, Propositions 4.1.6 and 4.1.8].
Proposition 4.15. (i) The generic fiber of (4.13) is isomorphic to
where ![]() $L_{z}G(R)=G(R((z)))=G((K\otimes _{F}R)((z)))$ is the loop group for
$L_{z}G(R)=G(R((z)))=G((K\otimes _{F}R)((z)))$ is the loop group for ![]() $G=\operatorname{Res}_{K/F}(G)$ formed using the parameter
$G=\operatorname{Res}_{K/F}(G)$ formed using the parameter ![]() $z:=u-\unicode[STIX]{x1D71B}\in K[u]$, and
$z:=u-\unicode[STIX]{x1D71B}\in K[u]$, and ![]() $\operatorname{Gr}_{G}$ is, as in Example 3.1 (i), the affine Grassmannian for the group
$\operatorname{Gr}_{G}$ is, as in Example 3.1 (i), the affine Grassmannian for the group ![]() $G\otimes _{F}F[\![z]\!]$, that is, the étale sheaf associated with the functor on
$G\otimes _{F}F[\![z]\!]$, that is, the étale sheaf associated with the functor on ![]() $F$-algebras
$F$-algebras ![]() $R\mapsto G(R((z)))/G(R[\![z]\!])$.
$R\mapsto G(R((z)))/G(R[\![z]\!])$.
(ii) The special fiber of (4.13) is canonically isomorphic to
where ![]() $L{\mathcal{G}}^{\flat }(R)={\mathcal{G}}^{\flat }(R((u)))$ is the twisted affine loop group for the parahoric
$L{\mathcal{G}}^{\flat }(R)={\mathcal{G}}^{\flat }(R((u)))$ is the twisted affine loop group for the parahoric ![]() $k_{F}[\![u]\!]$-group scheme
$k_{F}[\![u]\!]$-group scheme ![]() ${\mathcal{G}}^{\flat }={\mathcal{G}}_{\mathbf{f}^{\flat }}$ of
${\mathcal{G}}^{\flat }={\mathcal{G}}_{\mathbf{f}^{\flat }}$ of ![]() $G^{\flat }$ as in (4.9), and
$G^{\flat }$ as in (4.9), and ![]() ${\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}$ is the twisted affine flag variety for
${\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}$ is the twisted affine flag variety for ![]() ${\mathcal{G}}^{\flat }/k_{F}[\![u]\!]$ defined in [Reference Pappas and RapoportPR08], that is, the étale-sheaf associated with the functor on
${\mathcal{G}}^{\flat }/k_{F}[\![u]\!]$ defined in [Reference Pappas and RapoportPR08], that is, the étale-sheaf associated with the functor on ![]() $k_{F}$-algebras
$k_{F}$-algebras ![]() $R\mapsto {\mathcal{G}}^{\flat }(R((u)))/{\mathcal{G}}^{\flat }(R[\![u]\!])$.
$R\mapsto {\mathcal{G}}^{\flat }(R((u)))/{\mathcal{G}}^{\flat }(R[\![u]\!])$.
Proof. Let ![]() $L_{D/{\mathcal{O}}_{K_{0}}}^{+}\text{}\underline{{\mathcal{G}}}_{0}$ denote the positive loop group attached to
$L_{D/{\mathcal{O}}_{K_{0}}}^{+}\text{}\underline{{\mathcal{G}}}_{0}$ denote the positive loop group attached to ![]() $D$ and the curve
$D$ and the curve ![]() $\mathbb{A}_{{\mathcal{O}}_{K_{0}}}^{1}\!$, and let
$\mathbb{A}_{{\mathcal{O}}_{K_{0}}}^{1}\!$, and let ![]() $L_{D/{\mathcal{O}}_{K_{0}}}\text{}\underline{{\mathcal{G}}}_{0}$ be the corresponding loop group. We then have
$L_{D/{\mathcal{O}}_{K_{0}}}\text{}\underline{{\mathcal{G}}}_{0}$ be the corresponding loop group. We then have
and likewise for the positive loop group. We may use Theorem 4.13 to compute the generic and special fibers of the right-hand side. For example, if ![]() ${\mathcal{G}}_{0}^{\flat }:=\text{}\underline{{\mathcal{G}}}_{0}\otimes k_{0}[\![u]\!]$, then the special fiber of
${\mathcal{G}}_{0}^{\flat }:=\text{}\underline{{\mathcal{G}}}_{0}\otimes k_{0}[\![u]\!]$, then the special fiber of ![]() $L{\mathcal{G}}$ is
$L{\mathcal{G}}$ is
and likewise for the positive loop group. This together with Lemma 3.7 reduces us to the case where ![]() $K_{0}=F$. Then part (ii) is Corollary 3.5(i). For (i), note that the natural maps
$K_{0}=F$. Then part (ii) is Corollary 3.5(i). For (i), note that the natural maps ![]() $\operatorname{Res}_{K/F}(L_{z}G_{0})\rightarrow L_{z}\operatorname{Res}_{K/F}(G_{0})$ and
$\operatorname{Res}_{K/F}(L_{z}G_{0})\rightarrow L_{z}\operatorname{Res}_{K/F}(G_{0})$ and ![]() $\operatorname{Res}_{K/F}(\operatorname{Gr}_{G_{0}})\rightarrow \operatorname{Gr}_{\operatorname{Res}_{K/F}(G_{0})}$ are isomorphisms; cf. [Reference Pappas and RapoportPR08, (1.2)] and [Reference LevinLev13, § 2.6]. Note that
$\operatorname{Res}_{K/F}(\operatorname{Gr}_{G_{0}})\rightarrow \operatorname{Gr}_{\operatorname{Res}_{K/F}(G_{0})}$ are isomorphisms; cf. [Reference Pappas and RapoportPR08, (1.2)] and [Reference LevinLev13, § 2.6]. Note that ![]() $Q(z+\unicode[STIX]{x1D71B})\in zK[z]$. Hence, by induction on
$Q(z+\unicode[STIX]{x1D71B})\in zK[z]$. Hence, by induction on ![]() $n\geqslant 1$, the map
$n\geqslant 1$, the map ![]() $u\mapsto z+\unicode[STIX]{x1D71B}$ sets up an isomorphism
$u\mapsto z+\unicode[STIX]{x1D71B}$ sets up an isomorphism ![]() $F[u]/(Q^{n})\overset{{\sim}}{\rightarrow }K[z]/(z^{n})$, and hence
$F[u]/(Q^{n})\overset{{\sim}}{\rightarrow }K[z]/(z^{n})$, and hence ![]() $F[\![u]\!]\overset{{\sim}}{\rightarrow }K[\![z]\!]$. Similarly, we remark that, for any
$F[\![u]\!]\overset{{\sim}}{\rightarrow }K[\![z]\!]$. Similarly, we remark that, for any ![]() $F$-algebra
$F$-algebra ![]() $R$,
$R$, ![]() $u\mapsto z+\unicode[STIX]{x1D71B}$ gives an isomorphism
$u\mapsto z+\unicode[STIX]{x1D71B}$ gives an isomorphism ![]() $R[\![u]\!]\cong (R\otimes _{F}K)[\![z]\!]$. Let
$R[\![u]\!]\cong (R\otimes _{F}K)[\![z]\!]$. Let ![]() $\text{}\underline{{\mathcal{G}}}_{K[\![z]\!]}:=\text{}\underline{{\mathcal{G}}}_{0}\otimes _{{\mathcal{O}}_{F}[u]}K[\![z]\!]$, and denote by
$\text{}\underline{{\mathcal{G}}}_{K[\![z]\!]}:=\text{}\underline{{\mathcal{G}}}_{0}\otimes _{{\mathcal{O}}_{F}[u]}K[\![z]\!]$, and denote by ![]() $\operatorname{Gr}_{\text{}\underline{{\mathcal{G}}}_{K[\![z]\!]}}$ the twisted affine Grassmannian for
$\operatorname{Gr}_{\text{}\underline{{\mathcal{G}}}_{K[\![z]\!]}}$ the twisted affine Grassmannian for ![]() $\text{}\underline{{\mathcal{G}}}_{K[\![z]\!]}$; cf. Example 3.1(i). In view of Corollary 3.5, or the above remark, the generic fiber of (4.13) is canonically isomorphic to the action morphism
$\text{}\underline{{\mathcal{G}}}_{K[\![z]\!]}$; cf. Example 3.1(i). In view of Corollary 3.5, or the above remark, the generic fiber of (4.13) is canonically isomorphic to the action morphism
Hence, as in [Reference Pappas and ZhuPZ13, § 6.2.6] and [Reference LevinLev16, Proposition 4.1.6], it suffices to give an isomorphism of ![]() $K[\![z]\!]$-groups
$K[\![z]\!]$-groups ![]() $\text{}\underline{{\mathcal{G}}}_{K[\![z]\!]}\simeq G_{0}\otimes _{K}K[\![z]\!]$. But as
$\text{}\underline{{\mathcal{G}}}_{K[\![z]\!]}\simeq G_{0}\otimes _{K}K[\![z]\!]$. But as ![]() $u$ is invertible in
$u$ is invertible in ![]() $K[\![z]\!]$, we have
$K[\![z]\!]$, we have ![]() $\text{}\underline{{\mathcal{G}}}_{K[\![z]\!]}=\text{}\underline{G}_{0}\otimes _{{\mathcal{O}}_{F}[u^{\pm }]}K[\![z]\!]$. With the notation of (4.5), the group scheme
$\text{}\underline{{\mathcal{G}}}_{K[\![z]\!]}=\text{}\underline{G}_{0}\otimes _{{\mathcal{O}}_{F}[u^{\pm }]}K[\![z]\!]$. With the notation of (4.5), the group scheme ![]() $\text{}\underline{G}_{0}$ is constructed by descent from
$\text{}\underline{G}_{0}$ is constructed by descent from ![]() ${\mathcal{O}}_{\tilde{K}_{0}}[v^{\pm }]$ where it is a constant Chevalley group scheme. As in [Reference Pappas and ZhuPZ13, (6.9)], it is enough to give a commutative diagram of
${\mathcal{O}}_{\tilde{K}_{0}}[v^{\pm }]$ where it is a constant Chevalley group scheme. As in [Reference Pappas and ZhuPZ13, (6.9)], it is enough to give a commutative diagram of ![]() $\tilde{\unicode[STIX]{x1D6E4}}$-covers
$\tilde{\unicode[STIX]{x1D6E4}}$-covers

which matches the ![]() $\tilde{\unicode[STIX]{x1D6E4}}$-action on
$\tilde{\unicode[STIX]{x1D6E4}}$-action on ![]() ${\mathcal{O}}_{\tilde{K}_{0}}[v^{\pm }]/{\mathcal{O}}_{F}[u^{\pm }]$ via (4.5) with the
${\mathcal{O}}_{\tilde{K}_{0}}[v^{\pm }]/{\mathcal{O}}_{F}[u^{\pm }]$ via (4.5) with the ![]() $\tilde{\unicode[STIX]{x1D6E4}}$-action on the coefficients in
$\tilde{\unicode[STIX]{x1D6E4}}$-action on the coefficients in ![]() $\tilde{K}[\![z]\!]$ (see below for why this is enough). As in [Reference Pappas and ZhuPZ13, (6.9)], the isomorphism is given on rings by
$\tilde{K}[\![z]\!]$ (see below for why this is enough). As in [Reference Pappas and ZhuPZ13, (6.9)], the isomorphism is given on rings by ![]() $v\mapsto \tilde{\unicode[STIX]{x1D71B}}\cdot (1+z)$ and
$v\mapsto \tilde{\unicode[STIX]{x1D71B}}\cdot (1+z)$ and ![]() $z\mapsto b\cdot z$ with
$z\mapsto b\cdot z$ with
The map ![]() $\unicode[STIX]{x1D70F}$ is the
$\unicode[STIX]{x1D70F}$ is the ![]() $K$-algebra morphism given by
$K$-algebra morphism given by ![]() $z\mapsto b\cdot z$. (To see that the horizontal morphism is an isomorphism, observe that
$z\mapsto b\cdot z$. (To see that the horizontal morphism is an isomorphism, observe that ![]() $K[\![z]\!]=K[\![bz]\!]$, and let
$K[\![z]\!]=K[\![bz]\!]$, and let ![]() $f(z)\in K[\![z]\!]$ be such that
$f(z)\in K[\![z]\!]$ be such that ![]() $f(bz)=(1+z)^{-1}$; then
$f(bz)=(1+z)^{-1}$; then ![]() $v\otimes f(z)\mapsto \tilde{\unicode[STIX]{x1D71B}}$ and the morphism is surjective. One sees it is injective using an
$v\otimes f(z)\mapsto \tilde{\unicode[STIX]{x1D71B}}$ and the morphism is surjective. One sees it is injective using an ![]() ${\mathcal{O}}_{F}[u]$-basis for
${\mathcal{O}}_{F}[u]$-basis for ![]() ${\mathcal{O}}_{\tilde{K}_{0}}[v]$ of the form
${\mathcal{O}}_{\tilde{K}_{0}}[v]$ of the form ![]() $a_{i}v^{j}$ for
$a_{i}v^{j}$ for ![]() $a_{i}\in {\mathcal{O}}_{\tilde{F}_{0}}$ to write any element in the source uniquely in the form
$a_{i}\in {\mathcal{O}}_{\tilde{F}_{0}}$ to write any element in the source uniquely in the form ![]() $\sum _{i,j}a_{i}v^{j}\otimes f_{ij}$ for
$\sum _{i,j}a_{i}v^{j}\otimes f_{ij}$ for ![]() $f_{ij}\in K[\![z]\!]$. To see that diagram (
$f_{ij}\in K[\![z]\!]$. To see that diagram (
) suffices, note that the right oblique arrow is isomorphic via ![]() $\tilde{K}[\![z]\!]\overset{{\sim}}{\rightarrow }\tilde{K}[\![z]\!]$,
$\tilde{K}[\![z]\!]\overset{{\sim}}{\rightarrow }\tilde{K}[\![z]\!]$, ![]() $z\mapsto b\cdot z$ to the arrow
$z\mapsto b\cdot z$ to the arrow ![]() $\text{Spec}(\tilde{K}[\![z]\!])\rightarrow \text{Spec}(K[\![z]\!])$ induced by the inclusion
$\text{Spec}(\tilde{K}[\![z]\!])\rightarrow \text{Spec}(K[\![z]\!])$ induced by the inclusion ![]() $K[\![z]\!]{\hookrightarrow}\tilde{K}[\![z]\!]$.)◻
$K[\![z]\!]{\hookrightarrow}\tilde{K}[\![z]\!]$.)◻
Recall from [Reference Pappas and ZhuPZ13, Corollary 11.7] that there exists a closed immersion of ![]() $X$-groups
$X$-groups ![]() $\text{}\underline{{\mathcal{G}}}_{0}{\hookrightarrow}\operatorname{Gl}_{n,X}$ such that the quotient
$\text{}\underline{{\mathcal{G}}}_{0}{\hookrightarrow}\operatorname{Gl}_{n,X}$ such that the quotient ![]() $\operatorname{Gl}_{n,X}/\text{}\underline{{\mathcal{G}}}_{0}$ is quasi-affine. Thus, the
$\operatorname{Gl}_{n,X}/\text{}\underline{{\mathcal{G}}}_{0}$ is quasi-affine. Thus, the ![]() ${\mathcal{O}}_{F}$-space
${\mathcal{O}}_{F}$-space ![]() $\operatorname{Gr}_{{\mathcal{G}}}=\operatorname{Gr}_{(X,\text{}\underline{{\mathcal{G}}}_{0},D)}$ is representable by a separated
$\operatorname{Gr}_{{\mathcal{G}}}=\operatorname{Gr}_{(X,\text{}\underline{{\mathcal{G}}}_{0},D)}$ is representable by a separated ![]() ${\mathcal{O}}_{F}$-ind-scheme of ind-finite type; cf. Corollary 3.11. We need the following stronger statement.
${\mathcal{O}}_{F}$-ind-scheme of ind-finite type; cf. Corollary 3.11. We need the following stronger statement.
Theorem 4.16. The Beilinson–Drinfeld Grassmannian ![]() $\operatorname{Gr}_{{\mathcal{G}}}=\operatorname{colim}_{i}\operatorname{Gr}_{{\mathcal{G}},i}$ is representable by an ind-projective
$\operatorname{Gr}_{{\mathcal{G}}}=\operatorname{colim}_{i}\operatorname{Gr}_{{\mathcal{G}},i}$ is representable by an ind-projective ![]() ${\mathcal{O}}_{F}$-ind-scheme, and, for each
${\mathcal{O}}_{F}$-ind-scheme, and, for each ![]() $i$, the projective
$i$, the projective ![]() ${\mathcal{O}}_{F}$-scheme
${\mathcal{O}}_{F}$-scheme ![]() $\operatorname{Gr}_{{\mathcal{G}},i}$ can be chosen to be
$\operatorname{Gr}_{{\mathcal{G}},i}$ can be chosen to be ![]() $L^{+}{\mathcal{G}}$-stable compatible with the transition maps.
$L^{+}{\mathcal{G}}$-stable compatible with the transition maps.
Proof. By Lemma 3.7 we reduce to the case where ![]() $K_{0}=F$. Then the ind-projectivity is proven in [Reference LevinLev16, Theorem 4.2.11, Proposition 5.1.5]. If
$K_{0}=F$. Then the ind-projectivity is proven in [Reference LevinLev16, Theorem 4.2.11, Proposition 5.1.5]. If ![]() $G$ is unramified, the proof is considerably simpler; cf. [Reference LevinLev16, Proposition 2.2.8]. The proof relies on the existence and properties of specialization morphisms
$G$ is unramified, the proof is considerably simpler; cf. [Reference LevinLev16, Proposition 2.2.8]. The proof relies on the existence and properties of specialization morphisms
where ![]() $\operatorname{Gr}_{{\mathcal{T}}}\subset \operatorname{Gr}_{{\mathcal{G}}}$ is the part induced from the maximal torus; cf. Lemma 4.17 below. Levin constructs this map ‘by hand’ in [Reference LevinLev16, Proposition 4.2.8]. We will follow a more conceptual approach which avoids constructing
$\operatorname{Gr}_{{\mathcal{T}}}\subset \operatorname{Gr}_{{\mathcal{G}}}$ is the part induced from the maximal torus; cf. Lemma 4.17 below. Levin constructs this map ‘by hand’ in [Reference LevinLev16, Proposition 4.2.8]. We will follow a more conceptual approach which avoids constructing ![]() $\text{sp}$ ahead of time and the calculations that entails. Our outline is as follows.
$\text{sp}$ ahead of time and the calculations that entails. Our outline is as follows.
(a) Prove
 $\text{Gr}_{{\mathcal{T}}}\rightarrow \operatorname{Spec}({\mathcal{O}}_{F})$ is ind-finite, using the method of [Reference RicharzRic16b, Lemma 2.20] (§ 4.4.2).
$\text{Gr}_{{\mathcal{T}}}\rightarrow \operatorname{Spec}({\mathcal{O}}_{F})$ is ind-finite, using the method of [Reference RicharzRic16b, Lemma 2.20] (§ 4.4.2).(b) Deduce existence of the specialization maps for
 ${\mathcal{T}}$ via the valuative criterion of properness, and prove the required compatibility with Kottwitz homomorphisms (§ 4.4.3).
${\mathcal{T}}$ via the valuative criterion of properness, and prove the required compatibility with Kottwitz homomorphisms (§ 4.4.3).(c) Use (b) to show that each local model has non-empty special fiber and deduce by [Reference RicharzRic16b, Lemma 2.22] that each local model is proper (§ 4.4.5).
(d) Conclude that
 $\text{Gr}_{{\mathcal{G}}}\rightarrow \operatorname{Spec}({\mathcal{O}}_{F})$ is ind-proper (§ 4.4.6).
$\text{Gr}_{{\mathcal{G}}}\rightarrow \operatorname{Spec}({\mathcal{O}}_{F})$ is ind-proper (§ 4.4.6).
In view of Lemma 3.8 and Corollary 3.11, the ind-properness of ![]() $\operatorname{Gr}_{{\mathcal{G}}}$ implies the theorem. Steps (a)–(d) are explicated in the next several subsections, and with them the proof is concluded.◻
$\operatorname{Gr}_{{\mathcal{G}}}$ implies the theorem. Steps (a)–(d) are explicated in the next several subsections, and with them the proof is concluded.◻
4.4.2  $\text{Gr}_{{\mathcal{T}}}$ is ind-finite
$\text{Gr}_{{\mathcal{T}}}$ is ind-finite
Recall that we have already reduced to the case ![]() $K_{0}=F$ so that
$K_{0}=F$ so that ![]() $K/F$ is totally ramified. Without loss of generality, we further assume that
$K/F$ is totally ramified. Without loss of generality, we further assume that ![]() $F=\breve{F}$,
$F=\breve{F}$, ![]() ${\mathcal{O}}_{F}={\mathcal{O}}_{\breve{F}}$. Here we use that the formation of the affine Grassmannian (4.11) and the group scheme
${\mathcal{O}}_{F}={\mathcal{O}}_{\breve{F}}$. Here we use that the formation of the affine Grassmannian (4.11) and the group scheme ![]() $\text{}\underline{{\mathcal{T}}}_{0}$ from Theorem 4.13 is compatible with unramified base change; cf. also Example 4.14. We show that
$\text{}\underline{{\mathcal{T}}}_{0}$ from Theorem 4.13 is compatible with unramified base change; cf. also Example 4.14. We show that ![]() $\operatorname{Gr}_{{\mathcal{T}}}:=\operatorname{Gr}_{(X,\text{}\underline{{\mathcal{T}}}_{0},D)}$ is ind-proper over
$\operatorname{Gr}_{{\mathcal{T}}}:=\operatorname{Gr}_{(X,\text{}\underline{{\mathcal{T}}}_{0},D)}$ is ind-proper over ![]() ${\mathcal{O}}_{F}$, where
${\mathcal{O}}_{F}$, where ![]() $X=\mathbb{A}_{{\mathcal{O}}_{F}}^{1}$ and
$X=\mathbb{A}_{{\mathcal{O}}_{F}}^{1}$ and ![]() $D=\{Q=0\}$. It is then ind-finite, since this holds fiberwise by Proposition 4.15. We proceed in two steps as follows.
$D=\{Q=0\}$. It is then ind-finite, since this holds fiberwise by Proposition 4.15. We proceed in two steps as follows.
Step 1. First assume that ![]() $T=\operatorname{Res}_{K/F}(T_{0})$, where
$T=\operatorname{Res}_{K/F}(T_{0})$, where ![]() $T_{0}$ is an induced
$T_{0}$ is an induced ![]() $K$-torus which splits over a tamely ramified extension. Then
$K$-torus which splits over a tamely ramified extension. Then ![]() $T_{0}$ is isomorphic to a finite product of
$T_{0}$ is isomorphic to a finite product of ![]() $K$-tori of the form
$K$-tori of the form ![]() $T_{1}:=\operatorname{Res}_{K_{1}/K}(\mathbb{G}_{m})$, where
$T_{1}:=\operatorname{Res}_{K_{1}/K}(\mathbb{G}_{m})$, where ![]() $K_{1}/K$ is a tamely ramified finite field extension. Note that
$K_{1}/K$ is a tamely ramified finite field extension. Note that ![]() $K_{1}/K$ is totally ramified by our assumption
$K_{1}/K$ is totally ramified by our assumption ![]() $F=\breve{F}$. Accordingly, the
$F=\breve{F}$. Accordingly, the ![]() $\mathbb{A}_{{\mathcal{O}}_{F}}^{1}$-group scheme
$\mathbb{A}_{{\mathcal{O}}_{F}}^{1}$-group scheme ![]() $\text{}\underline{{\mathcal{T}}}_{0}$ is isomorphic to a finite product of
$\text{}\underline{{\mathcal{T}}}_{0}$ is isomorphic to a finite product of ![]() $\mathbb{A}_{{\mathcal{O}}_{F}}^{1}$-group schemes of the form
$\mathbb{A}_{{\mathcal{O}}_{F}}^{1}$-group schemes of the form
where ![]() $v^{[K_{1}:K]}=u$. After fixing a uniformizer
$v^{[K_{1}:K]}=u$. After fixing a uniformizer ![]() $\unicode[STIX]{x1D71B}_{1}\in K_{1}$ with
$\unicode[STIX]{x1D71B}_{1}\in K_{1}$ with ![]() $(\unicode[STIX]{x1D71B}_{1})^{[K_{1}:K]}=\unicode[STIX]{x1D71B}$ (possible because
$(\unicode[STIX]{x1D71B}_{1})^{[K_{1}:K]}=\unicode[STIX]{x1D71B}$ (possible because ![]() $F=\breve{F}$), this can be verified using Example 4.14 (use that, in this case,
$F=\breve{F}$), this can be verified using Example 4.14 (use that, in this case, ![]() $T_{H}\otimes \tilde{{\mathcal{O}}}_{0}[v]\cong (\mathbb{G}_{m,\tilde{{\mathcal{O}}}_{0}[v]})^{[K_{1}:K]}$ with
$T_{H}\otimes \tilde{{\mathcal{O}}}_{0}[v]\cong (\mathbb{G}_{m,\tilde{{\mathcal{O}}}_{0}[v]})^{[K_{1}:K]}$ with ![]() $\text{Gal}(K_{1}/K)$ acting via the permutation of the factors). Likewise, the affine Grassmannian
$\text{Gal}(K_{1}/K)$ acting via the permutation of the factors). Likewise, the affine Grassmannian ![]() $\operatorname{Gr}_{{\mathcal{T}}}$ is a finite
$\operatorname{Gr}_{{\mathcal{T}}}$ is a finite ![]() ${\mathcal{O}}_{F}$-product of the affine Grassmannians
${\mathcal{O}}_{F}$-product of the affine Grassmannians ![]() $\operatorname{Gr}_{(X,\text{}\underline{{\mathcal{T}}}_{1},D)}$, where
$\operatorname{Gr}_{(X,\text{}\underline{{\mathcal{T}}}_{1},D)}$, where ![]() $X=\mathbb{A}_{{\mathcal{O}}_{F}}^{1}$ and
$X=\mathbb{A}_{{\mathcal{O}}_{F}}^{1}$ and![]() $D=\{Q(u)=0\}$. Hence, we reduce to the case where
$D=\{Q(u)=0\}$. Hence, we reduce to the case where ![]() $\text{}\underline{{\mathcal{T}}}_{0}=\text{}\underline{{\mathcal{T}}}_{1}$, that is,
$\text{}\underline{{\mathcal{T}}}_{0}=\text{}\underline{{\mathcal{T}}}_{1}$, that is, ![]() $T=\operatorname{Res}_{K_{1}/K}(\mathbb{G}_{m})$. By Corollary 3.6, there is an equality of ind-schemes
$T=\operatorname{Res}_{K_{1}/K}(\mathbb{G}_{m})$. By Corollary 3.6, there is an equality of ind-schemes
where ![]() $X^{\prime }=\mathbb{A}_{{\mathcal{O}}_{F}}^{1}=\operatorname{Spec}({\mathcal{O}}_{F}[v])$ and
$X^{\prime }=\mathbb{A}_{{\mathcal{O}}_{F}}^{1}=\operatorname{Spec}({\mathcal{O}}_{F}[v])$ and ![]() $D^{\prime }=\{Q(v^{[K_{1}:K]})=0\}$. We reduce to the case
$D^{\prime }=\{Q(v^{[K_{1}:K]})=0\}$. We reduce to the case ![]() $X=X^{\prime }$,
$X=X^{\prime }$, ![]() $\text{}\underline{{\mathcal{T}}}_{0}=\mathbb{G}_{m}$ and
$\text{}\underline{{\mathcal{T}}}_{0}=\mathbb{G}_{m}$ and ![]() $D=D^{\prime }$. Then
$D=D^{\prime }$. Then ![]() $\operatorname{Gr}_{(X,\mathbb{G}_{m},D)}$ is ind-projective (hence ind-proper) by Lemma 3.8.
$\operatorname{Gr}_{(X,\mathbb{G}_{m},D)}$ is ind-projective (hence ind-proper) by Lemma 3.8.
Step 2. Now let ![]() $T=\operatorname{Res}_{K/F}(T_{0})$, where
$T=\operatorname{Res}_{K/F}(T_{0})$, where ![]() $T_{0}$ is a
$T_{0}$ is a ![]() $K$-torus which splits over a tamely ramified extension. As in [Reference KottwitzKot97, § 7], we choose a surjection of
$K$-torus which splits over a tamely ramified extension. As in [Reference KottwitzKot97, § 7], we choose a surjection of ![]() $K$-tori
$K$-tori ![]() $T_{1}\rightarrow T_{0}$ where
$T_{1}\rightarrow T_{0}$ where ![]() $T_{1}$ is induced, and where the kernel
$T_{1}$ is induced, and where the kernel ![]() $T_{2}:=\ker (T_{1}\rightarrow T)$ is a
$T_{2}:=\ker (T_{1}\rightarrow T)$ is a ![]() $K$-torus. Note that
$K$-torus. Note that ![]() $T_{1}$ can be chosen to split over a tamely ramified extension (and so does
$T_{1}$ can be chosen to split over a tamely ramified extension (and so does ![]() $T_{2}$ as well). The proof of [Reference Kisin and PappasKP18, Proposition 2.2.2] adapts to our setup, and the map
$T_{2}$ as well). The proof of [Reference Kisin and PappasKP18, Proposition 2.2.2] adapts to our setup, and the map ![]() $T_{1}\rightarrow T_{0}$ extends to a map of
$T_{1}\rightarrow T_{0}$ extends to a map of ![]() $X$-groups
$X$-groups ![]() $\text{}\underline{{\mathcal{T}}}_{1}\rightarrow \text{}\underline{{\mathcal{T}}}_{0}$ with kernel
$\text{}\underline{{\mathcal{T}}}_{1}\rightarrow \text{}\underline{{\mathcal{T}}}_{0}$ with kernel ![]() $\text{}\underline{{\mathcal{T}}}_{2}$ an
$\text{}\underline{{\mathcal{T}}}_{2}$ an ![]() $X$-group scheme extending
$X$-group scheme extending ![]() $T_{2}$. (Instead of using [Reference Kisin and PappasKP18], one can also deduce this by making use of the prescription given in Example 4.14.) We claim that the resulting map of
$T_{2}$. (Instead of using [Reference Kisin and PappasKP18], one can also deduce this by making use of the prescription given in Example 4.14.) We claim that the resulting map of ![]() ${\mathcal{O}}_{F}$-ind-schemes
${\mathcal{O}}_{F}$-ind-schemes
is surjective on the underlying topological spaces. Clearly, this can be tested on the fibers of (4.18) over ![]() ${\mathcal{O}}_{F}$ which are determined by Proposition 4.15. The geometric generic fiber of (4.18) is isomorphic (on the underlying topological spaces) to the map of discrete groups
${\mathcal{O}}_{F}$ which are determined by Proposition 4.15. The geometric generic fiber of (4.18) is isomorphic (on the underlying topological spaces) to the map of discrete groups ![]() $X_{\ast }(\operatorname{Res}_{K/F}(T_{1}))\rightarrow X_{\ast }(\operatorname{Res}_{K/F}(T_{0}))$ which is surjective because
$X_{\ast }(\operatorname{Res}_{K/F}(T_{1}))\rightarrow X_{\ast }(\operatorname{Res}_{K/F}(T_{0}))$ which is surjective because ![]() $T_{1}\rightarrow T_{0}$ is surjective and its kernel
$T_{1}\rightarrow T_{0}$ is surjective and its kernel ![]() $T_{2}$ is a torus (that is, connected). The geometric special fiber of (4.18) is under the Kottwitz map isomorphic to
$T_{2}$ is a torus (that is, connected). The geometric special fiber of (4.18) is under the Kottwitz map isomorphic to ![]() $X_{\ast }(T_{1}^{\flat })_{I_{k((u))}}\rightarrow X_{\ast }(T_{0}^{\flat })_{I_{k((u))}}$ which is induced by
$X_{\ast }(T_{1}^{\flat })_{I_{k((u))}}\rightarrow X_{\ast }(T_{0}^{\flat })_{I_{k((u))}}$ which is induced by ![]() $T_{1}^{\flat }:=\text{}\underline{{\mathcal{T}}}_{1}\otimes k((u))\rightarrow \text{}\underline{{\mathcal{T}}}_{0}\otimes k((u))=:T_{0}^{\flat }$. This map is isomorphic to
$T_{1}^{\flat }:=\text{}\underline{{\mathcal{T}}}_{1}\otimes k((u))\rightarrow \text{}\underline{{\mathcal{T}}}_{0}\otimes k((u))=:T_{0}^{\flat }$. This map is isomorphic to ![]() $X_{\ast }(T_{1})_{I_{K}}\rightarrow X_{\ast }(T_{0})_{I_{K}}$ which follows by applying the Kottwitz map to the identification (4.10). As in [Reference KottwitzKot97, § 7 (7.2.5)], the desired surjectivity now follows from
$X_{\ast }(T_{1})_{I_{K}}\rightarrow X_{\ast }(T_{0})_{I_{K}}$ which follows by applying the Kottwitz map to the identification (4.10). As in [Reference KottwitzKot97, § 7 (7.2.5)], the desired surjectivity now follows from ![]() $T_{2}$ being a
$T_{2}$ being a ![]() $K$-torus. By Step 1, the
$K$-torus. By Step 1, the ![]() ${\mathcal{O}}_{F}$-scheme
${\mathcal{O}}_{F}$-scheme ![]() $\operatorname{Gr}_{{\mathcal{T}}_{1}}$ is ind-proper and maps surjectively onto the separated ind-scheme
$\operatorname{Gr}_{{\mathcal{T}}_{1}}$ is ind-proper and maps surjectively onto the separated ind-scheme ![]() $\operatorname{Gr}_{{\mathcal{T}}}$ which is therefore ind-proper as well. This concludes § 4.4.2.
$\operatorname{Gr}_{{\mathcal{T}}}$ which is therefore ind-proper as well. This concludes § 4.4.2.
4.4.3 The specialization map
Once ![]() $\text{Gr}_{{\mathcal{G}}}$ is known to be ind-proper, by the valuative criterion for properness there exists a specialization map
$\text{Gr}_{{\mathcal{G}}}$ is known to be ind-proper, by the valuative criterion for properness there exists a specialization map
In the case where ![]() $G_{0}=T_{0}$ is a maximal torus, and hence
$G_{0}=T_{0}$ is a maximal torus, and hence ![]() $\text{}\underline{{\mathcal{G}}}_{0}=\text{}\underline{{\mathcal{T}}}_{0}$ is as in Theorem 4.13(iv), we therefore know the existence of the specialization map. It is made explicit in [Reference Pappas and ZhuPZ13, Lemma 9.8] and [Reference LevinLev16, Proposition 4.2.8]. Recall the following result for later use (which compared to [Reference LevinLev16] is proved in a more conceptual way here).
$\text{}\underline{{\mathcal{G}}}_{0}=\text{}\underline{{\mathcal{T}}}_{0}$ is as in Theorem 4.13(iv), we therefore know the existence of the specialization map. It is made explicit in [Reference Pappas and ZhuPZ13, Lemma 9.8] and [Reference LevinLev16, Proposition 4.2.8]. Recall the following result for later use (which compared to [Reference LevinLev16] is proved in a more conceptual way here).
Lemma 4.17. Let ![]() $\unicode[STIX]{x1D6E4}_{F}$ denote the Galois group of
$\unicode[STIX]{x1D6E4}_{F}$ denote the Galois group of ![]() $F$, and likewise
$F$, and likewise ![]() $\unicode[STIX]{x1D6E4}_{k}$ and
$\unicode[STIX]{x1D6E4}_{k}$ and ![]() $\unicode[STIX]{x1D6E4}_{k_{0}}$. There is a commutative diagram of abelian groups
$\unicode[STIX]{x1D6E4}_{k_{0}}$. There is a commutative diagram of abelian groups

which is Galois equivariant for the ![]() $\unicode[STIX]{x1D6E4}_{F}$-action on the top covering the
$\unicode[STIX]{x1D6E4}_{F}$-action on the top covering the ![]() $\unicode[STIX]{x1D6E4}_{k}$-action on the bottom.
$\unicode[STIX]{x1D6E4}_{k}$-action on the bottom.
Proof. The top arrow is the natural isomorphism, and the map ![]() $\operatorname{pr}$ is the canonical projection to the coinvariants. Let us construct the bottom arrow. Note that
$\operatorname{pr}$ is the canonical projection to the coinvariants. Let us construct the bottom arrow. Note that ![]() $X_{\ast }(\operatorname{Res}_{K/F}(T_{0}))=\text{Ind}_{\unicode[STIX]{x1D6E4}_{K}}^{\unicode[STIX]{x1D6E4}_{F}}(X_{\ast }(T_{0}))$ is an induced Galois module by the proof of Lemma 4.1. Shapiro’s lemma induces a
$X_{\ast }(\operatorname{Res}_{K/F}(T_{0}))=\text{Ind}_{\unicode[STIX]{x1D6E4}_{K}}^{\unicode[STIX]{x1D6E4}_{F}}(X_{\ast }(T_{0}))$ is an induced Galois module by the proof of Lemma 4.1. Shapiro’s lemma induces a ![]() $\unicode[STIX]{x1D6E4}_{k}$-equivariant isomorphism
$\unicode[STIX]{x1D6E4}_{k}$-equivariant isomorphism
(For any ![]() $\mathbb{Z}[\unicode[STIX]{x1D6E4}_{K}]$-module
$\mathbb{Z}[\unicode[STIX]{x1D6E4}_{K}]$-module ![]() $M$, we have
$M$, we have ![]() $(M\,\otimes _{\mathbb{Z}[\unicode[STIX]{x1D6E4}_{K}]}\,\mathbb{Z}[\unicode[STIX]{x1D6E4}_{F}])_{I_{F}}=M_{I_{K}}\,\otimes _{\mathbb{Z}[\unicode[STIX]{x1D6E4}_{k_{0}}]}\,\mathbb{Z}[\unicode[STIX]{x1D6E4}_{k}]$ canonically.) Further, the Kottwitz map (cf. [Reference KottwitzKot97, § 7]) applied to (4.10) in the case of
$(M\,\otimes _{\mathbb{Z}[\unicode[STIX]{x1D6E4}_{K}]}\,\mathbb{Z}[\unicode[STIX]{x1D6E4}_{F}])_{I_{F}}=M_{I_{K}}\,\otimes _{\mathbb{Z}[\unicode[STIX]{x1D6E4}_{k_{0}}]}\,\mathbb{Z}[\unicode[STIX]{x1D6E4}_{k}]$ canonically.) Further, the Kottwitz map (cf. [Reference KottwitzKot97, § 7]) applied to (4.10) in the case of ![]() $T_{0}(\breve{K})$ (respectively,
$T_{0}(\breve{K})$ (respectively, ![]() $T_{0}^{\flat }(\bar{k}((u)))$) induces a
$T_{0}^{\flat }(\bar{k}((u)))$) induces a ![]() $\unicode[STIX]{x1D6E4}_{k_{0}}$-equivariant isomorphism
$\unicode[STIX]{x1D6E4}_{k_{0}}$-equivariant isomorphism ![]() $X_{\ast }(T_{0}^{\flat })_{I_{K_{0}^{\flat }}}\simeq X_{\ast }(T_{0})_{I_{K}}$. Applying the induction functor, we deduce a
$X_{\ast }(T_{0}^{\flat })_{I_{K_{0}^{\flat }}}\simeq X_{\ast }(T_{0})_{I_{K}}$. Applying the induction functor, we deduce a ![]() $\unicode[STIX]{x1D6E4}_{k}$-equivariant isomorphism
$\unicode[STIX]{x1D6E4}_{k}$-equivariant isomorphism
Finally, we use ![]() ${\mathcal{F}}\!\ell _{{\mathcal{T}}^{\flat }}=\operatorname{Res}_{k_{0}/k}({\mathcal{F}}\!\ell _{{\mathcal{T}}_{0}^{\flat }})$ (cf. (4.16)) together with the isomorphism induced by the Kottwitz map
${\mathcal{F}}\!\ell _{{\mathcal{T}}^{\flat }}=\operatorname{Res}_{k_{0}/k}({\mathcal{F}}\!\ell _{{\mathcal{T}}_{0}^{\flat }})$ (cf. (4.16)) together with the isomorphism induced by the Kottwitz map
which is ![]() $\unicode[STIX]{x1D6E4}_{k_{0}}$-equivariant as well. This induces the
$\unicode[STIX]{x1D6E4}_{k_{0}}$-equivariant as well. This induces the ![]() $\unicode[STIX]{x1D6E4}_{k}$-equivariant isomorphism
$\unicode[STIX]{x1D6E4}_{k}$-equivariant isomorphism
The bottom arrow in (4.20) is defined to be the composition of (4.21), (4.22) and (4.23).
All that remains is to prove the commutativity, which is a reformulation of [Reference LevinLev16, Proposition 4.2.8]: the composition ![]() $\operatorname{pr}$ with the inverse of (4.21) is the map given by
$\operatorname{pr}$ with the inverse of (4.21) is the map given by ![]() $\unicode[STIX]{x1D707}^{\prime }\mapsto \bar{\unicode[STIX]{x1D706}}_{\unicode[STIX]{x1D707}^{\prime }}$ in the notation of [Reference LevinLev16]. We show the commutativity as follows. The diagram is compatible with unramified extensions, and we reduce to the case
$\unicode[STIX]{x1D707}^{\prime }\mapsto \bar{\unicode[STIX]{x1D706}}_{\unicode[STIX]{x1D707}^{\prime }}$ in the notation of [Reference LevinLev16]. We show the commutativity as follows. The diagram is compatible with unramified extensions, and we reduce to the case ![]() $K_{0}=F$. Changing notation, we may now assume that
$K_{0}=F$. Changing notation, we may now assume that ![]() $F=\breve{F}$,
$F=\breve{F}$, ![]() $k=\bar{k}$. The diagram (4.20) is functorial in the tamely ramified
$k=\bar{k}$. The diagram (4.20) is functorial in the tamely ramified ![]() $K$-torus
$K$-torus ![]() $T_{0}$. Arguing as in § 4.4.2 Step 2, we choose an induced tamely ramified
$T_{0}$. Arguing as in § 4.4.2 Step 2, we choose an induced tamely ramified ![]() $K$-torus
$K$-torus ![]() $T_{1}{\twoheadrightarrow}T_{0}$ with kernel being a torus. Each item in the diagram for
$T_{1}{\twoheadrightarrow}T_{0}$ with kernel being a torus. Each item in the diagram for ![]() $T_{1}$ maps surjectively onto each item in the diagram for
$T_{1}$ maps surjectively onto each item in the diagram for ![]() $T_{0}$, and we reduce to the case where
$T_{0}$, and we reduce to the case where ![]() $T_{0}=T_{1}$ is an induced tamely ramified
$T_{0}=T_{1}$ is an induced tamely ramified ![]() $K$-torus. Arguing as in § 4.4.2 Step 1, the torus
$K$-torus. Arguing as in § 4.4.2 Step 1, the torus ![]() $T_{0}$ is a product of
$T_{0}$ is a product of ![]() $K$-tori of the form
$K$-tori of the form ![]() $\operatorname{Res}_{K_{1}/K}(\mathbb{G}_{m})$ with
$\operatorname{Res}_{K_{1}/K}(\mathbb{G}_{m})$ with ![]() $K_{1}/K$ being totally (tamely) ramified. Accordingly, each item in the diagram (4.20) splits as a product compatible with the maps, and we reduce to the case where
$K_{1}/K$ being totally (tamely) ramified. Accordingly, each item in the diagram (4.20) splits as a product compatible with the maps, and we reduce to the case where ![]() $T_{0}=\operatorname{Res}_{K_{1}/K}(\mathbb{G}_{m})$. Replacing the pair
$T_{0}=\operatorname{Res}_{K_{1}/K}(\mathbb{G}_{m})$. Replacing the pair ![]() $(X,D)$ with the pair
$(X,D)$ with the pair ![]() $(X^{\prime },D^{\prime })$ as in § 4.4.2 Step 1, we reduce further to the case where
$(X^{\prime },D^{\prime })$ as in § 4.4.2 Step 1, we reduce further to the case where ![]() $T_{0}=\mathbb{G}_{m}$. In this case, we have for the (global) loop group
$T_{0}=\mathbb{G}_{m}$. In this case, we have for the (global) loop group
where ![]() $Q\in {\mathcal{O}}_{F}[u]$ is the minimal polynomial of
$Q\in {\mathcal{O}}_{F}[u]$ is the minimal polynomial of ![]() $\unicode[STIX]{x1D71B}\in K$ over
$\unicode[STIX]{x1D71B}\in K$ over ![]() $F$. Writing
$F$. Writing ![]() $Q=(u-a_{1})\cdot \ldots \cdot (u-a_{d})$ for
$Q=(u-a_{1})\cdot \ldots \cdot (u-a_{d})$ for ![]() $d=[K:F]$ and pairwise distinct elements
$d=[K:F]$ and pairwise distinct elements ![]() $a_{1},\ldots ,a_{d}\in {\mathcal{O}}_{\bar{F}}$, we compute for the generic fiber
$a_{1},\ldots ,a_{d}\in {\mathcal{O}}_{\bar{F}}$, we compute for the generic fiber
For ![]() $i=1,\ldots ,d$, let
$i=1,\ldots ,d$, let ![]() $v_{i}$ be the
$v_{i}$ be the ![]() $(u-a_{i})$-adic valuation of
$(u-a_{i})$-adic valuation of ![]() $\bar{F}((u-a_{i}))$. The specialization map (4.19) is explicitly given by the map
$\bar{F}((u-a_{i}))$. The specialization map (4.19) is explicitly given by the map
where we use that ![]() $Q\equiv u^{[K:F]}\;\text{mod}\;\unicode[STIX]{x1D71B}$. One checks that (4.20) commutes for
$Q\equiv u^{[K:F]}\;\text{mod}\;\unicode[STIX]{x1D71B}$. One checks that (4.20) commutes for ![]() $T_{0}=\mathbb{G}_{m}$. which finishes the proof of the lemma.◻
$T_{0}=\mathbb{G}_{m}$. which finishes the proof of the lemma.◻
4.4.4 Local models for Weil-restricted groups
We now recall the definition of local models for the pair ![]() $(G,{\mathcal{G}})=(\operatorname{Res}_{K/F}(G_{0}),\operatorname{Res}_{{\mathcal{O}}_{K}/{\mathcal{O}}_{F}}({\mathcal{G}}_{\mathbf{f}_{0}}))$. Let
$(G,{\mathcal{G}})=(\operatorname{Res}_{K/F}(G_{0}),\operatorname{Res}_{{\mathcal{O}}_{K}/{\mathcal{O}}_{F}}({\mathcal{G}}_{\mathbf{f}_{0}}))$. Let ![]() $\{\unicode[STIX]{x1D707}\}$ be a
$\{\unicode[STIX]{x1D707}\}$ be a ![]() $G(\bar{F})$-conjugacy class of geometric cocharacters with reflex field
$G(\bar{F})$-conjugacy class of geometric cocharacters with reflex field ![]() $E/F$. For a representative
$E/F$. For a representative ![]() $\unicode[STIX]{x1D707}\in \{\unicode[STIX]{x1D707}\}$, the associated Schubert variety is the reduced
$\unicode[STIX]{x1D707}\in \{\unicode[STIX]{x1D707}\}$, the associated Schubert variety is the reduced ![]() $L_{z}^{+}G_{\bar{F}}$-orbit closure
$L_{z}^{+}G_{\bar{F}}$-orbit closure
The ![]() $\bar{F}$-scheme
$\bar{F}$-scheme ![]() $\operatorname{Gr}_{G}^{{\leqslant}\{\unicode[STIX]{x1D707}\}}$ is defined over the reflex field
$\operatorname{Gr}_{G}^{{\leqslant}\{\unicode[STIX]{x1D707}\}}$ is defined over the reflex field ![]() $E=E(\{\unicode[STIX]{x1D707}\})$, that is, the field of definition of
$E=E(\{\unicode[STIX]{x1D707}\})$, that is, the field of definition of ![]() $\{\unicode[STIX]{x1D707}\}$ which is a finite extension of
$\{\unicode[STIX]{x1D707}\}$ which is a finite extension of ![]() $F$, and is a (geometrically irreducible) projective
$F$, and is a (geometrically irreducible) projective ![]() $E$-variety.
$E$-variety.
The following definition is [Reference Pappas and ZhuPZ13, Definition 7.1] if ![]() $K/F$ is tamely ramified, and [Reference LevinLev16, Definition 4.2.1] in general; cf. [Reference LevinLev16, Proposition 4.2.4].
$K/F$ is tamely ramified, and [Reference LevinLev16, Definition 4.2.1] in general; cf. [Reference LevinLev16, Proposition 4.2.4].
Definition 4.18. The local model ![]() $M_{\{\unicode[STIX]{x1D707}\}}=M(\text{}\underline{G}_{0},{\mathcal{G}}_{\mathbf{f}},\{\unicode[STIX]{x1D707}\},\unicode[STIX]{x1D71B})$ is the scheme-theoretic closure of the locally closed subscheme
$M_{\{\unicode[STIX]{x1D707}\}}=M(\text{}\underline{G}_{0},{\mathcal{G}}_{\mathbf{f}},\{\unicode[STIX]{x1D707}\},\unicode[STIX]{x1D71B})$ is the scheme-theoretic closure of the locally closed subscheme
where ![]() $\operatorname{Gr}_{G}^{{\leqslant}\{\unicode[STIX]{x1D707}\}}$ is as in (4.24).
$\operatorname{Gr}_{G}^{{\leqslant}\{\unicode[STIX]{x1D707}\}}$ is as in (4.24).
By definition, the local model ![]() $M_{\{\unicode[STIX]{x1D707}\}}$ is a closed flat
$M_{\{\unicode[STIX]{x1D707}\}}$ is a closed flat ![]() $L^{+}{\mathcal{G}}_{{\mathcal{O}}_{E}}$-invariant subscheme of
$L^{+}{\mathcal{G}}_{{\mathcal{O}}_{E}}$-invariant subscheme of ![]() $(\operatorname{Gr}_{{\mathcal{G}}}\otimes _{{\mathcal{O}}_{F}}{\mathcal{O}}_{E})_{\operatorname{red}}$ which is uniquely determined up to unique isomorphism by the data
$(\operatorname{Gr}_{{\mathcal{G}}}\otimes _{{\mathcal{O}}_{F}}{\mathcal{O}}_{E})_{\operatorname{red}}$ which is uniquely determined up to unique isomorphism by the data ![]() $(\text{}\underline{G}_{0},{\mathcal{G}}_{\mathbf{f}},\{\unicode[STIX]{x1D707}\},\unicode[STIX]{x1D71B})$. Its generic fiber
$(\text{}\underline{G}_{0},{\mathcal{G}}_{\mathbf{f}},\{\unicode[STIX]{x1D707}\},\unicode[STIX]{x1D71B})$. Its generic fiber ![]() $M_{\{\unicode[STIX]{x1D707}\}}\otimes E=\operatorname{Gr}_{G,E}^{{\leqslant}\{\unicode[STIX]{x1D707}\}}$ is a (geometrically irreducible) variety, and the special fiber
$M_{\{\unicode[STIX]{x1D707}\}}\otimes E=\operatorname{Gr}_{G,E}^{{\leqslant}\{\unicode[STIX]{x1D707}\}}$ is a (geometrically irreducible) variety, and the special fiber ![]() $M_{\{\unicode[STIX]{x1D707}\}}\otimes k_{E}$ is equidimensional; cf. [Reference Görtz and WedhornGW10, Theorem 14.114]. By Proposition 4.15, the map
$M_{\{\unicode[STIX]{x1D707}\}}\otimes k_{E}$ is equidimensional; cf. [Reference Görtz and WedhornGW10, Theorem 14.114]. By Proposition 4.15, the map ![]() $\operatorname{Gr}_{{\mathcal{G}}}\rightarrow \operatorname{Spec}({\mathcal{O}}_{F})$ is fiberwise ind-proper, and hence the map
$\operatorname{Gr}_{{\mathcal{G}}}\rightarrow \operatorname{Spec}({\mathcal{O}}_{F})$ is fiberwise ind-proper, and hence the map ![]() $M_{\{\unicode[STIX]{x1D707}\}}\rightarrow \operatorname{Spec}({\mathcal{O}}_{E})$ is fiberwise proper. Note that there is a closed embedding into the flag variety
$M_{\{\unicode[STIX]{x1D707}\}}\rightarrow \operatorname{Spec}({\mathcal{O}}_{E})$ is fiberwise proper. Note that there is a closed embedding into the flag variety
which identifies the reduced locus ![]() $(M_{\{\unicode[STIX]{x1D707}\}}\otimes k_{E})_{\operatorname{red}}$ with a union of Schubert varieties in
$(M_{\{\unicode[STIX]{x1D707}\}}\otimes k_{E})_{\operatorname{red}}$ with a union of Schubert varieties in ![]() ${\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat },k_{E}}$.
${\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat },k_{E}}$.
Remark 4.19. The local model ![]() $M_{\{\unicode[STIX]{x1D707}\}}$ should up to unique isomorphism only depend on the data
$M_{\{\unicode[STIX]{x1D707}\}}$ should up to unique isomorphism only depend on the data ![]() $(G,{\mathcal{G}},\{\unicode[STIX]{x1D707}\})$. The uniqueness of
$(G,{\mathcal{G}},\{\unicode[STIX]{x1D707}\})$. The uniqueness of ![]() $M_{\{\unicode[STIX]{x1D707}\}}$ is a separate question, and not of importance for the present paper. We refer the reader to [Reference Pappas and ZhuPZ13, Remark 3.2] for remarks on the uniqueness of
$M_{\{\unicode[STIX]{x1D707}\}}$ is a separate question, and not of importance for the present paper. We refer the reader to [Reference Pappas and ZhuPZ13, Remark 3.2] for remarks on the uniqueness of ![]() $\text{}\underline{G}_{0}$, and to [Reference LevinLev16, Remark 4.2.5] for remarks on the independence of
$\text{}\underline{G}_{0}$, and to [Reference LevinLev16, Remark 4.2.5] for remarks on the independence of ![]() $M_{\{\unicode[STIX]{x1D707}\}}$ on the choice of the uniformizer
$M_{\{\unicode[STIX]{x1D707}\}}$ on the choice of the uniformizer ![]() $\unicode[STIX]{x1D71B}\in K$. In the recent preprint [Reference He, Pappas and RapoportHPR18, Theorem 2.7], it is shown the ind-scheme
$\unicode[STIX]{x1D71B}\in K$. In the recent preprint [Reference He, Pappas and RapoportHPR18, Theorem 2.7], it is shown the ind-scheme ![]() $\operatorname{Gr}_{{\mathcal{G}}}$ for
$\operatorname{Gr}_{{\mathcal{G}}}$ for ![]() $K=F$ depends up to equivariant isomorphism only on the data
$K=F$ depends up to equivariant isomorphism only on the data ![]() $(G,{\mathcal{G}})$. So
$(G,{\mathcal{G}})$. So ![]() $M_{\{\unicode[STIX]{x1D707}\}}$ for
$M_{\{\unicode[STIX]{x1D707}\}}$ for ![]() $K=F$ depends up to equivariant isomorphism only on the data
$K=F$ depends up to equivariant isomorphism only on the data ![]() $(G,{\mathcal{G}},\{\unicode[STIX]{x1D707}\})$. Note that [Reference He, Pappas and RapoportHPR18, Conjecture 2.12] uniquely characterizes
$(G,{\mathcal{G}},\{\unicode[STIX]{x1D707}\})$. Note that [Reference He, Pappas and RapoportHPR18, Conjecture 2.12] uniquely characterizes ![]() $M_{\{\unicode[STIX]{x1D707}\}}$ for
$M_{\{\unicode[STIX]{x1D707}\}}$ for ![]() $K=F$ in the case where
$K=F$ in the case where ![]() $\{\unicode[STIX]{x1D707}\}$ is minuscule.
$\{\unicode[STIX]{x1D707}\}$ is minuscule.
4.4.5 Each local model is proper
For every conjugacy class ![]() $\{\unicode[STIX]{x1D707}\}$, we need to show that the local model
$\{\unicode[STIX]{x1D707}\}$, we need to show that the local model ![]() $M_{\{\unicode[STIX]{x1D707}\}}$ is proper over
$M_{\{\unicode[STIX]{x1D707}\}}$ is proper over ![]() ${\mathcal{O}}_{E}$, where
${\mathcal{O}}_{E}$, where ![]() $E=E(\{\unicode[STIX]{x1D707}\})$ is the reflex field. In view of [Reference RicharzRic16b, Lemma 2.20] and the discussion after Definition 4.18, all that remains is to show that the special fiber of
$E=E(\{\unicode[STIX]{x1D707}\})$ is the reflex field. In view of [Reference RicharzRic16b, Lemma 2.20] and the discussion after Definition 4.18, all that remains is to show that the special fiber of ![]() $M_{\{\unicode[STIX]{x1D707}\}}$ is non-empty. The inclusion
$M_{\{\unicode[STIX]{x1D707}\}}$ is non-empty. The inclusion ![]() $\text{}\underline{{\mathcal{T}}}_{0}\subset \text{}\underline{{\mathcal{G}}}_{0}$ induces a map of
$\text{}\underline{{\mathcal{T}}}_{0}\subset \text{}\underline{{\mathcal{G}}}_{0}$ induces a map of ![]() ${\mathcal{O}}_{F}$-ind-schemes
${\mathcal{O}}_{F}$-ind-schemes
In the notation of Proposition 4.15, the geometric generic fiber ![]() $M_{\{\unicode[STIX]{x1D707}\}}(\bar{F})$ contains the element
$M_{\{\unicode[STIX]{x1D707}\}}(\bar{F})$ contains the element
for any representative ![]() $\unicode[STIX]{x1D707}\in X_{\ast }(\tilde{T})$ of
$\unicode[STIX]{x1D707}\in X_{\ast }(\tilde{T})$ of ![]() $\{\unicode[STIX]{x1D707}\}$. As
$\{\unicode[STIX]{x1D707}\}$. As ![]() $\operatorname{Gr}_{{\mathcal{T}}}$ is ind-finite (hence ind-proper) by § 4.4.2, the element
$\operatorname{Gr}_{{\mathcal{T}}}$ is ind-finite (hence ind-proper) by § 4.4.2, the element ![]() $\unicode[STIX]{x1D707}\in \operatorname{Gr}_{{\mathcal{T}}}(\bar{F})$ uniquely extends to a point
$\unicode[STIX]{x1D707}\in \operatorname{Gr}_{{\mathcal{T}}}(\bar{F})$ uniquely extends to a point ![]() $\tilde{\unicode[STIX]{x1D707}}\in \operatorname{Gr}_{{\mathcal{T}}}({\mathcal{O}}_{\bar{F}})$ by the valuative criterion for properness. Composed with (4.26), this defines a point (still denoted)
$\tilde{\unicode[STIX]{x1D707}}\in \operatorname{Gr}_{{\mathcal{T}}}({\mathcal{O}}_{\bar{F}})$ by the valuative criterion for properness. Composed with (4.26), this defines a point (still denoted) ![]() $\tilde{\unicode[STIX]{x1D707}}\in \operatorname{Gr}_{{\mathcal{G}}}({\mathcal{O}}_{\bar{F}})$. Since
$\tilde{\unicode[STIX]{x1D707}}\in \operatorname{Gr}_{{\mathcal{G}}}({\mathcal{O}}_{\bar{F}})$. Since ![]() $M_{\{\unicode[STIX]{x1D707}\}}\subset \operatorname{Gr}_{{\mathcal{G}},{\mathcal{O}}_{E}}$ is a closed subscheme, we have
$M_{\{\unicode[STIX]{x1D707}\}}\subset \operatorname{Gr}_{{\mathcal{G}},{\mathcal{O}}_{E}}$ is a closed subscheme, we have
and its special fiber ![]() $\bar{\unicode[STIX]{x1D707}}:=\tilde{\unicode[STIX]{x1D707}}_{\bar{k}}\in M_{\{\unicode[STIX]{x1D707}\}}(\bar{k})$ is non-empty. This concludes § 4.4.5.
$\bar{\unicode[STIX]{x1D707}}:=\tilde{\unicode[STIX]{x1D707}}_{\bar{k}}\in M_{\{\unicode[STIX]{x1D707}\}}(\bar{k})$ is non-empty. This concludes § 4.4.5.
4.4.6 Conclusion of proof of Theorem 4.16
We need to show that ![]() $\operatorname{Gr}_{{\mathcal{G}}}\rightarrow \operatorname{Spec}({\mathcal{O}}_{F})$ is ind-proper. It suffices to prove that the map
$\operatorname{Gr}_{{\mathcal{G}}}\rightarrow \operatorname{Spec}({\mathcal{O}}_{F})$ is ind-proper. It suffices to prove that the map ![]() $(\operatorname{Gr}_{{\mathcal{G}}}\otimes {\mathcal{O}}_{\bar{F}})_{\operatorname{red}}\rightarrow \operatorname{Spec}({\mathcal{O}}_{\bar{F}})$ is ind-proper. In view of § 4.4.5, we have to show that the closed immersion
$(\operatorname{Gr}_{{\mathcal{G}}}\otimes {\mathcal{O}}_{\bar{F}})_{\operatorname{red}}\rightarrow \operatorname{Spec}({\mathcal{O}}_{\bar{F}})$ is ind-proper. In view of § 4.4.5, we have to show that the closed immersion
is an equality. Here ![]() $\{\unicode[STIX]{x1D707}\}$ ranges over all
$\{\unicode[STIX]{x1D707}\}$ ranges over all ![]() $G(\bar{F})$-conjugacy classes of geometric cocharacters. As both ind-schemes in (4.28) are reduced, one can check the equality on the underlying topological spaces. As in [Reference RicharzRic16b, § 2.5] (respectively, [Reference LevinLev16, Theorem 4.2.11]), this follows from Lemma 4.17 combined with (4.25) and (4.27). This concludes § 4.4.6, and hence the proof of Theorem 4.16.
$G(\bar{F})$-conjugacy classes of geometric cocharacters. As both ind-schemes in (4.28) are reduced, one can check the equality on the underlying topological spaces. As in [Reference RicharzRic16b, § 2.5] (respectively, [Reference LevinLev16, Theorem 4.2.11]), this follows from Lemma 4.17 combined with (4.25) and (4.27). This concludes § 4.4.6, and hence the proof of Theorem 4.16.
5 Actions of  $\mathbb{G}_{m}$ on Weil-restricted affine Grassmannians
$\mathbb{G}_{m}$ on Weil-restricted affine Grassmannians
5.1 Geometry of  $\mathbb{G}_{m}$-actions on affine Grassmannians
$\mathbb{G}_{m}$-actions on affine Grassmannians
Fix the data and notation as in § 4.4. In particular, we denote the group schemes over ![]() $X=\mathbb{A}_{{\mathcal{O}}_{K_{0}}}^{1}$ by
$X=\mathbb{A}_{{\mathcal{O}}_{K_{0}}}^{1}$ by ![]() $(\text{}\underline{{\mathcal{G}}}_{0},\text{}\underline{{\mathcal{A}}}_{0},\text{}\underline{{\mathcal{S}}}_{0},\text{}\underline{{\mathcal{T}}}_{0})$.
$(\text{}\underline{{\mathcal{G}}}_{0},\text{}\underline{{\mathcal{A}}}_{0},\text{}\underline{{\mathcal{S}}}_{0},\text{}\underline{{\mathcal{T}}}_{0})$.
5.1.1 Main geometric result
Let ![]() $\unicode[STIX]{x1D712}:\mathbb{G}_{m,K}\rightarrow A_{0}\subset G_{0}$ be a cocharacter which acts on
$\unicode[STIX]{x1D712}:\mathbb{G}_{m,K}\rightarrow A_{0}\subset G_{0}$ be a cocharacter which acts on ![]() $G_{0}$ by conjugation. As in (3.17), the centralizer is a Levi subgroup
$G_{0}$ by conjugation. As in (3.17), the centralizer is a Levi subgroup ![]() $M_{0}\subset G_{0}$, and the attractor (respectively, repeller) subgroup
$M_{0}\subset G_{0}$, and the attractor (respectively, repeller) subgroup ![]() $P_{0}^{+}$ (respectively,
$P_{0}^{+}$ (respectively, ![]() $P_{0}^{-}$) is a parabolic subgroup with
$P_{0}^{-}$) is a parabolic subgroup with ![]() $P_{0}^{+}\cap P_{0}^{-}=M_{0}$. Further, we have semidirect product decompositions
$P_{0}^{+}\cap P_{0}^{-}=M_{0}$. Further, we have semidirect product decompositions ![]() $P_{0}^{\pm }=M_{0}\rtimes N_{0}^{\pm }$ defined over
$P_{0}^{\pm }=M_{0}\rtimes N_{0}^{\pm }$ defined over ![]() $K$.
$K$.
Via the fixed isomorphism ![]() $\text{}\underline{{\mathcal{G}}}_{0,K}\simeq G$ compatible with
$\text{}\underline{{\mathcal{G}}}_{0,K}\simeq G$ compatible with ![]() $\text{}\underline{{\mathcal{A}}}_{0,K}\simeq A_{0}$, we may view
$\text{}\underline{{\mathcal{A}}}_{0,K}\simeq A_{0}$, we may view ![]() $\unicode[STIX]{x1D712}$ as a cocharacter of
$\unicode[STIX]{x1D712}$ as a cocharacter of ![]() $\text{}\underline{{\mathcal{A}}}_{0,K}$. As
$\text{}\underline{{\mathcal{A}}}_{0,K}$. As ![]() $X$ is connected and
$X$ is connected and ![]() $\text{}\underline{{\mathcal{A}}}$ a split torus,
$\text{}\underline{{\mathcal{A}}}$ a split torus, ![]() $\unicode[STIX]{x1D712}$ extends uniquely to a cocharacter also denoted by
$\unicode[STIX]{x1D712}$ extends uniquely to a cocharacter also denoted by
Hence, the cocharacter ![]() $\unicode[STIX]{x1D712}$ acts by conjugation on
$\unicode[STIX]{x1D712}$ acts by conjugation on ![]() $\text{}\underline{{\mathcal{G}}}_{0}$ via the rule
$\text{}\underline{{\mathcal{G}}}_{0}$ via the rule ![]() $\mathbb{G}_{m,X}\times _{X}\text{}\underline{{\mathcal{G}}}_{0}\rightarrow \text{}\underline{{\mathcal{G}}}_{0}$,
$\mathbb{G}_{m,X}\times _{X}\text{}\underline{{\mathcal{G}}}_{0}\rightarrow \text{}\underline{{\mathcal{G}}}_{0}$, ![]() $(\unicode[STIX]{x1D706},g)\mapsto \unicode[STIX]{x1D712}(\unicode[STIX]{x1D706})\cdot g\cdot \unicode[STIX]{x1D712}(\unicode[STIX]{x1D706})^{-1}$. Using the dynamic method promulgated in [Reference Conrad, Gabber and PrasadCGP10], the functors (2.1) define
$(\unicode[STIX]{x1D706},g)\mapsto \unicode[STIX]{x1D712}(\unicode[STIX]{x1D706})\cdot g\cdot \unicode[STIX]{x1D712}(\unicode[STIX]{x1D706})^{-1}$. Using the dynamic method promulgated in [Reference Conrad, Gabber and PrasadCGP10], the functors (2.1) define ![]() $X$-subgroup schemes of
$X$-subgroup schemes of ![]() $\text{}\underline{{\mathcal{G}}}_{0}$ given by the fixed points
$\text{}\underline{{\mathcal{G}}}_{0}$ given by the fixed points ![]() $\text{}\underline{{\mathcal{M}}}_{0}=\text{}\underline{{\mathcal{G}}}_{0}^{0,\unicode[STIX]{x1D712}}$, and the attractor
$\text{}\underline{{\mathcal{M}}}_{0}=\text{}\underline{{\mathcal{G}}}_{0}^{0,\unicode[STIX]{x1D712}}$, and the attractor ![]() $\text{}\underline{{\mathcal{P}}}_{0}^{+}=\text{}\underline{{\mathcal{G}}}_{0}^{+,\unicode[STIX]{x1D712}}$ (respectively, the repeller
$\text{}\underline{{\mathcal{P}}}_{0}^{+}=\text{}\underline{{\mathcal{G}}}_{0}^{+,\unicode[STIX]{x1D712}}$ (respectively, the repeller ![]() $\text{}\underline{{\mathcal{P}}}_{0}^{-}=\text{}\underline{{\mathcal{G}}}_{0}^{-,\unicode[STIX]{x1D712}}$). Note that
$\text{}\underline{{\mathcal{P}}}_{0}^{-}=\text{}\underline{{\mathcal{G}}}_{0}^{-,\unicode[STIX]{x1D712}}$). Note that ![]() $\text{}\underline{{\mathcal{M}}}_{0}$ is by definition the schematic centralizer of
$\text{}\underline{{\mathcal{M}}}_{0}$ is by definition the schematic centralizer of ![]() $\unicode[STIX]{x1D712}$ in
$\unicode[STIX]{x1D712}$ in ![]() $\text{}\underline{{\mathcal{G}}}_{0}$.
$\text{}\underline{{\mathcal{G}}}_{0}$.
Lemma 5.1. (i) The ![]() $X$-group schemes
$X$-group schemes ![]() $\text{}\underline{{\mathcal{M}}}_{0}$ and
$\text{}\underline{{\mathcal{M}}}_{0}$ and ![]() $\text{}\underline{{\mathcal{P}}}_{0}^{\pm }$ are smooth closed subgroup schemes of
$\text{}\underline{{\mathcal{P}}}_{0}^{\pm }$ are smooth closed subgroup schemes of ![]() $\text{}\underline{{\mathcal{G}}}_{0}$ with geometrically connected fibers.
$\text{}\underline{{\mathcal{G}}}_{0}$ with geometrically connected fibers.
(ii) The centralizer ![]() $\text{}\underline{{\mathcal{M}}}_{0}$ is a parahoric
$\text{}\underline{{\mathcal{M}}}_{0}$ is a parahoric ![]() $X$-group scheme for
$X$-group scheme for ![]() $M_{0}$ in the sense of Theorem 4.13.
$M_{0}$ in the sense of Theorem 4.13.
(iii) There is a semidirect product decomposition as ![]() $X$-group schemes
$X$-group schemes ![]() $\text{}\underline{{\mathcal{P}}}_{0}^{\pm }=\text{}\underline{{\mathcal{M}}}_{0}\ltimes \text{}\underline{{\mathcal{N}}}_{0}^{\pm }$ where
$\text{}\underline{{\mathcal{P}}}_{0}^{\pm }=\text{}\underline{{\mathcal{M}}}_{0}\ltimes \text{}\underline{{\mathcal{N}}}_{0}^{\pm }$ where ![]() $\text{}\underline{{\mathcal{N}}}_{0}^{\pm }$ is a smooth affine group scheme with geometrically connected fibers.
$\text{}\underline{{\mathcal{N}}}_{0}^{\pm }$ is a smooth affine group scheme with geometrically connected fibers.
(iv) The fixed isomorphism ![]() $\text{}\underline{G}_{0,K}\simeq G_{0}$ induces isomorphisms of
$\text{}\underline{G}_{0,K}\simeq G_{0}$ induces isomorphisms of ![]() $K[\![z]\!]$-groups
$K[\![z]\!]$-groups ![]() $\text{}\underline{{\mathcal{M}}}_{0,K[\![z]\!]}\simeq M_{0}\otimes _{K}K[\![z]\!]$, and
$\text{}\underline{{\mathcal{M}}}_{0,K[\![z]\!]}\simeq M_{0}\otimes _{K}K[\![z]\!]$, and ![]() $\text{}\underline{{\mathcal{P}}}_{0,K[\![z]\!]}^{\pm }\simeq P_{0}^{\pm }\otimes _{K}K[\![z]\!]$ compatible with the semidirect product decomposition in (iii).
$\text{}\underline{{\mathcal{P}}}_{0,K[\![z]\!]}^{\pm }\simeq P_{0}^{\pm }\otimes _{K}K[\![z]\!]$ compatible with the semidirect product decomposition in (iii).
Proof. The method of [Reference Haines and RicharzHR18, Lemma 5.16] extends to give (i), (ii) and (iii) of the lemma. Part (iv) is immediate from the construction of ![]() $\unicode[STIX]{x1D712}$ and the proof of Proposition 4.15(i).◻
$\unicode[STIX]{x1D712}$ and the proof of Proposition 4.15(i).◻
By (2.2), there are natural maps of ![]() $X$-group schemes
$X$-group schemes
The maps (5.2) induce, by functoriality of Beilinson–Drinfeld Grassmannians, maps of ![]() ${\mathcal{O}}_{F}$-spaces
${\mathcal{O}}_{F}$-spaces
where ![]() $\operatorname{Gr}_{{\mathcal{G}}}:=\operatorname{Gr}_{(X,\text{}\underline{{\mathcal{G}}}_{0},D)}$ (respectively,
$\operatorname{Gr}_{{\mathcal{G}}}:=\operatorname{Gr}_{(X,\text{}\underline{{\mathcal{G}}}_{0},D)}$ (respectively, ![]() $\operatorname{Gr}_{{\mathcal{M}}}:=\operatorname{Gr}_{(X,\text{}\underline{{\mathcal{M}}}_{0},D)}$; respectively,
$\operatorname{Gr}_{{\mathcal{M}}}:=\operatorname{Gr}_{(X,\text{}\underline{{\mathcal{M}}}_{0},D)}$; respectively, ![]() $\operatorname{Gr}_{{\mathcal{P}}^{\pm }}:=\operatorname{Gr}_{(X,\text{}\underline{{\mathcal{P}}}_{0}^{\pm },D)}$) by notational convention. In light of [Reference Pappas and ZhuPZ13, Corollary 11.7] and Corollary 3.11(i), the functors in (5.3) are representable by separated
$\operatorname{Gr}_{{\mathcal{P}}^{\pm }}:=\operatorname{Gr}_{(X,\text{}\underline{{\mathcal{P}}}_{0}^{\pm },D)}$) by notational convention. In light of [Reference Pappas and ZhuPZ13, Corollary 11.7] and Corollary 3.11(i), the functors in (5.3) are representable by separated ![]() ${\mathcal{O}}_{F}$-ind-schemes of ind-finite type. Note that, by Theorem 4.16(i) and Lemma 5.1(ii), the
${\mathcal{O}}_{F}$-ind-schemes of ind-finite type. Note that, by Theorem 4.16(i) and Lemma 5.1(ii), the ![]() ${\mathcal{O}}_{F}$-ind-schemes
${\mathcal{O}}_{F}$-ind-schemes ![]() $\operatorname{Gr}_{{\mathcal{G}}}$ and
$\operatorname{Gr}_{{\mathcal{G}}}$ and ![]() $\operatorname{Gr}_{{\mathcal{M}}}$ are even ind-projective. The
$\operatorname{Gr}_{{\mathcal{M}}}$ are even ind-projective. The ![]() ${\mathcal{O}}_{F}$-ind-scheme
${\mathcal{O}}_{F}$-ind-scheme ![]() $\operatorname{Gr}_{{\mathcal{P}}}$ is never ind-projective besides the trivial cases.
$\operatorname{Gr}_{{\mathcal{P}}}$ is never ind-projective besides the trivial cases.
By functoriality of the loop group, we obtain via the composition
a ![]() $\mathbb{G}_{m,{\mathcal{O}}_{F}}$-action on
$\mathbb{G}_{m,{\mathcal{O}}_{F}}$-action on ![]() $\operatorname{Gr}_{{\mathcal{G}}}\rightarrow \operatorname{Spec}({\mathcal{O}}_{F})$.
$\operatorname{Gr}_{{\mathcal{G}}}\rightarrow \operatorname{Spec}({\mathcal{O}}_{F})$.
Lemma 5.2. The ![]() $\mathbb{G}_{m}$-action on
$\mathbb{G}_{m}$-action on ![]() $\operatorname{Gr}_{{\mathcal{G}}}$ is Zariski locally linearizable.
$\operatorname{Gr}_{{\mathcal{G}}}$ is Zariski locally linearizable.
Proof. By [Reference Pappas and ZhuPZ13, Corollary 11.7] there exists an monomorphism of ![]() $X$-groups
$X$-groups ![]() $\text{}\underline{{\mathcal{G}}}_{0}{\hookrightarrow}\operatorname{Gl}_{n,X}$ such that the fppf quotient
$\text{}\underline{{\mathcal{G}}}_{0}{\hookrightarrow}\operatorname{Gl}_{n,X}$ such that the fppf quotient ![]() $\operatorname{Gl}_{n,X}/\text{}\underline{{\mathcal{G}}}_{0}$ is quasi-affine. Hence, the induced monomorphism
$\operatorname{Gl}_{n,X}/\text{}\underline{{\mathcal{G}}}_{0}$ is quasi-affine. Hence, the induced monomorphism ![]() $\unicode[STIX]{x1D704}:\operatorname{Gr}_{{\mathcal{G}}}{\hookrightarrow}\operatorname{Gr}_{\operatorname{Gl}_{n,X}}$ is representable by a quasi-compact immersion (cf. Proposition 3.10) which is even a closed immersion because
$\unicode[STIX]{x1D704}:\operatorname{Gr}_{{\mathcal{G}}}{\hookrightarrow}\operatorname{Gr}_{\operatorname{Gl}_{n,X}}$ is representable by a quasi-compact immersion (cf. Proposition 3.10) which is even a closed immersion because ![]() $\operatorname{Gr}_{{\mathcal{G}}}$ is ind-proper; cf. Theorem 4.16. The map
$\operatorname{Gr}_{{\mathcal{G}}}$ is ind-proper; cf. Theorem 4.16. The map ![]() $\unicode[STIX]{x1D704}$ is
$\unicode[STIX]{x1D704}$ is ![]() $\mathbb{G}_{m}$-equivariant for the cocharacter
$\mathbb{G}_{m}$-equivariant for the cocharacter ![]() $\mathbb{G}_{m,X}\overset{\unicode[STIX]{x1D712}}{\rightarrow }\text{}\underline{{\mathcal{G}}}_{0}\rightarrow \operatorname{Gl}_{n,X}$, and we reduce to the case
$\mathbb{G}_{m,X}\overset{\unicode[STIX]{x1D712}}{\rightarrow }\text{}\underline{{\mathcal{G}}}_{0}\rightarrow \operatorname{Gl}_{n,X}$, and we reduce to the case ![]() $\text{}\underline{{\mathcal{G}}}_{0}=\operatorname{Gl}_{n,X}$. By [Reference ConradCon14, Proposition 6.2.11] (use
$\text{}\underline{{\mathcal{G}}}_{0}=\operatorname{Gl}_{n,X}$. By [Reference ConradCon14, Proposition 6.2.11] (use ![]() $\operatorname{Pic}(X)=0$), the cocharacter
$\operatorname{Pic}(X)=0$), the cocharacter ![]() $\unicode[STIX]{x1D712}:\mathbb{G}_{m,X}\rightarrow \operatorname{Gl}_{n,X}$ is conjugate to a cocharacter with values in the standard diagonal torus, and hence defined over
$\unicode[STIX]{x1D712}:\mathbb{G}_{m,X}\rightarrow \operatorname{Gl}_{n,X}$ is conjugate to a cocharacter with values in the standard diagonal torus, and hence defined over ![]() ${\mathcal{O}}_{F}$. The lemma follows from the proof of Lemma 3.16.◻
${\mathcal{O}}_{F}$. The lemma follows from the proof of Lemma 3.16.◻
In light of Theorems 4.16 and 2.1, we obtain maps of separated ![]() ${\mathcal{O}}_{F}$-ind-schemes
${\mathcal{O}}_{F}$-ind-schemes
The following theorem compares (5.3) with (5.5).
Theorem 5.3. The maps induce a commutative diagram of ![]() ${\mathcal{O}}_{F}$-ind-schemes
${\mathcal{O}}_{F}$-ind-schemes

where the maps ![]() $\unicode[STIX]{x1D704}^{0}$ and
$\unicode[STIX]{x1D704}^{0}$ and ![]() $\unicode[STIX]{x1D704}^{\pm }$ satisfy the following properties.
$\unicode[STIX]{x1D704}^{\pm }$ satisfy the following properties.
(i) In the generic fiber, the diagram is isomorphic to (5.7) below, and the maps
 $\unicode[STIX]{x1D704}_{F}^{0}$ and
$\unicode[STIX]{x1D704}_{F}^{0}$ and  $\unicode[STIX]{x1D704}_{F}^{\pm }$ are isomorphisms.
$\unicode[STIX]{x1D704}_{F}^{\pm }$ are isomorphisms.(ii) In the special fiber, the diagram is isomorphic to (5.8) below, and the maps
 $\unicode[STIX]{x1D704}_{k}^{0}$ and
$\unicode[STIX]{x1D704}_{k}^{0}$ and  $\unicode[STIX]{x1D704}_{k}^{\pm }$ are closed immersions which are open immersions on the underlying reduced loci.
$\unicode[STIX]{x1D704}_{k}^{\pm }$ are closed immersions which are open immersions on the underlying reduced loci.(iii) The maps
 $\unicode[STIX]{x1D704}^{0}$ and
$\unicode[STIX]{x1D704}^{0}$ and  $\unicode[STIX]{x1D704}^{\pm }$ are closed immersions which are open immersions on the underlying reduced loci.
$\unicode[STIX]{x1D704}^{\pm }$ are closed immersions which are open immersions on the underlying reduced loci.
The diagram is constructed as follows. The fppf quotient ![]() $\text{}\underline{{\mathcal{G}}}_{0}/\text{}\underline{{\mathcal{M}}}_{0}$ is quasi-affine by [Reference ConradCon14, Theorem 2.4.1], which implies that the map
$\text{}\underline{{\mathcal{G}}}_{0}/\text{}\underline{{\mathcal{M}}}_{0}$ is quasi-affine by [Reference ConradCon14, Theorem 2.4.1], which implies that the map ![]() $\operatorname{Gr}_{{\mathcal{M}}}\rightarrow \operatorname{Gr}_{{\mathcal{G}}}$ as in the proof of Lemma 5.2 is representable by a closed immersion. Since the
$\operatorname{Gr}_{{\mathcal{M}}}\rightarrow \operatorname{Gr}_{{\mathcal{G}}}$ as in the proof of Lemma 5.2 is representable by a closed immersion. Since the ![]() $\mathbb{G}_{m}$-action on
$\mathbb{G}_{m}$-action on ![]() $\operatorname{Gr}_{{\mathcal{M}}}$ is trivial, the map factors as
$\operatorname{Gr}_{{\mathcal{M}}}$ is trivial, the map factors as ![]() $\operatorname{Gr}_{{\mathcal{M}}}\rightarrow (\operatorname{Gr}_{{\mathcal{G}}})^{0}\rightarrow \operatorname{Gr}_{{\mathcal{G}}}$, and we obtain the closed immersion
$\operatorname{Gr}_{{\mathcal{M}}}\rightarrow (\operatorname{Gr}_{{\mathcal{G}}})^{0}\rightarrow \operatorname{Gr}_{{\mathcal{G}}}$, and we obtain the closed immersion ![]() $\unicode[STIX]{x1D704}^{0}$.
$\unicode[STIX]{x1D704}^{0}$.
The map ![]() $\unicode[STIX]{x1D704}^{\pm }$ is given via a Rees construction in terms of the moduli description (4.12); cf. § 3.3.1. Alternatively, if we choose a monomorphism of
$\unicode[STIX]{x1D704}^{\pm }$ is given via a Rees construction in terms of the moduli description (4.12); cf. § 3.3.1. Alternatively, if we choose a monomorphism of ![]() $X$-groups
$X$-groups ![]() $\text{}\underline{{\mathcal{G}}}_{0}{\hookrightarrow}\operatorname{Gl}_{n,X}$ such that
$\text{}\underline{{\mathcal{G}}}_{0}{\hookrightarrow}\operatorname{Gl}_{n,X}$ such that ![]() $\operatorname{Gl}_{n,X}/\text{}\underline{{\mathcal{G}}}_{0}$ is quasi-affine (cf. [Reference Pappas and ZhuPZ13, Corollary 11.7]), then the same argument as in (3.22) applies, and we conclude that
$\operatorname{Gl}_{n,X}/\text{}\underline{{\mathcal{G}}}_{0}$ is quasi-affine (cf. [Reference Pappas and ZhuPZ13, Corollary 11.7]), then the same argument as in (3.22) applies, and we conclude that ![]() $\unicode[STIX]{x1D704}^{\pm }$ is representable by a quasi-compact immersion. We do not repeat the argument here, but instead refer the reader to § 3.3.1 for details. This constructs the commutative diagram (5.6).
$\unicode[STIX]{x1D704}^{\pm }$ is representable by a quasi-compact immersion. We do not repeat the argument here, but instead refer the reader to § 3.3.1 for details. This constructs the commutative diagram (5.6).
Proof of Theorem 5.3.
(i) In the generic fiber, by (4.14) and Lemma 5.1(iv), (5.6) is the commutative diagram of ![]() $F$-ind-schemes
$F$-ind-schemes

where ![]() $G=\operatorname{Res}_{K/F}(G_{0})$ (respectively,
$G=\operatorname{Res}_{K/F}(G_{0})$ (respectively, ![]() $M=\operatorname{Res}_{K/F}(M_{0})$; respectively,
$M=\operatorname{Res}_{K/F}(M_{0})$; respectively, ![]() $P^{\pm }=\operatorname{Res}_{K/F}(P_{0}^{\pm })$). The
$P^{\pm }=\operatorname{Res}_{K/F}(P_{0}^{\pm })$). The ![]() $\mathbb{G}_{m}$-action on the diagram is induced by the
$\mathbb{G}_{m}$-action on the diagram is induced by the ![]() $L_{z}^{+}$-construction applied to the cocharacter
$L_{z}^{+}$-construction applied to the cocharacter
combined with the inclusion ![]() $\mathbb{G}_{m,F}\subset L_{z}^{+}\mathbb{G}_{m,F}$. We claim that the conjugation action of
$\mathbb{G}_{m,F}\subset L_{z}^{+}\mathbb{G}_{m,F}$. We claim that the conjugation action of ![]() $\tilde{\unicode[STIX]{x1D712}}$ on
$\tilde{\unicode[STIX]{x1D712}}$ on ![]() $G$ gives the group of fixed points
$G$ gives the group of fixed points ![]() $M=G^{0,\tilde{\unicode[STIX]{x1D712}}}$ and the attractor (respectively, repeller) group
$M=G^{0,\tilde{\unicode[STIX]{x1D712}}}$ and the attractor (respectively, repeller) group ![]() $P^{+}=G^{+,\tilde{\unicode[STIX]{x1D712}}}$ (respectively,
$P^{+}=G^{+,\tilde{\unicode[STIX]{x1D712}}}$ (respectively, ![]() $P^{-}=G^{-,\tilde{\unicode[STIX]{x1D712}}}$). Indeed, the canonical maps of
$P^{-}=G^{-,\tilde{\unicode[STIX]{x1D712}}}$). Indeed, the canonical maps of ![]() $F$-subgroups of
$F$-subgroups of ![]() $G$,
$G$,
are isomorphisms. By descent, it is enough to prove this after passing to ![]() $\bar{F}$. But
$\bar{F}$. But ![]() $G\otimes _{F}\bar{F}\simeq \prod _{K{\hookrightarrow}\bar{F}}G_{0}\otimes _{K,\unicode[STIX]{x1D713}}\bar{F}$, where the
$G\otimes _{F}\bar{F}\simeq \prod _{K{\hookrightarrow}\bar{F}}G_{0}\otimes _{K,\unicode[STIX]{x1D713}}\bar{F}$, where the ![]() $\mathbb{G}_{m}$-action induced by
$\mathbb{G}_{m}$-action induced by ![]() $\tilde{\unicode[STIX]{x1D712}}$ is the diagonal action on the product. Lemma 2.2 implies the claim. Part (i) follows from [Reference Haines and RicharzHR18, Proposition 3.4] applied to the pair
$\tilde{\unicode[STIX]{x1D712}}$ is the diagonal action on the product. Lemma 2.2 implies the claim. Part (i) follows from [Reference Haines and RicharzHR18, Proposition 3.4] applied to the pair ![]() $(G,\tilde{\unicode[STIX]{x1D712}})$.
$(G,\tilde{\unicode[STIX]{x1D712}})$.
(ii) In the special fiber, (5.6) is the commutative diagram of ![]() $k$-ind-schemes
$k$-ind-schemes

The ![]() $\mathbb{G}_{m}$-action on the diagram is given as follows. Base-changing (5.1) along
$\mathbb{G}_{m}$-action on the diagram is given as follows. Base-changing (5.1) along ![]() ${\mathcal{O}}_{K_{0}}[u]\rightarrow k_{0}[\![u]\!]$ and taking restriction of scalars along
${\mathcal{O}}_{K_{0}}[u]\rightarrow k_{0}[\![u]\!]$ and taking restriction of scalars along ![]() $k_{0}[\![u]\!]/k[\![u]\!]$, we obtain the cocharacter
$k_{0}[\![u]\!]/k[\![u]\!]$, we obtain the cocharacter
which factors through ![]() ${\mathcal{A}}^{\flat }\subset {\mathcal{G}}^{\flat }$, the natural
${\mathcal{A}}^{\flat }\subset {\mathcal{G}}^{\flat }$, the natural ![]() $k[\![u]\!]$-extension of the maximal
$k[\![u]\!]$-extension of the maximal ![]() $k((u))$-split torus
$k((u))$-split torus ![]() $A^{\flat }\subset G^{\flat }$ in (4.8). Then
$A^{\flat }\subset G^{\flat }$ in (4.8). Then ![]() $\mathbb{G}_{m,k}$ acts on the diagram via
$\mathbb{G}_{m,k}$ acts on the diagram via ![]() $\unicode[STIX]{x1D712}^{\flat }$ after applying the
$\unicode[STIX]{x1D712}^{\flat }$ after applying the ![]() $L^{+}$-construction combined with the inclusion
$L^{+}$-construction combined with the inclusion ![]() $\mathbb{G}_{m,k}\subset L^{+}\mathbb{G}_{m,k[\![u]\!]}$. Since taking fixed points (respectively, attractors; respectively, repellers) commutes with base change [Reference RicharzRic19, (1.3)] and is compatible with restriction of scalars along étale extensions, we have
$\mathbb{G}_{m,k}\subset L^{+}\mathbb{G}_{m,k[\![u]\!]}$. Since taking fixed points (respectively, attractors; respectively, repellers) commutes with base change [Reference RicharzRic19, (1.3)] and is compatible with restriction of scalars along étale extensions, we have ![]() ${\mathcal{M}}^{\flat }=({\mathcal{G}}^{\flat })^{0,\unicode[STIX]{x1D712}^{\flat }}$ and
${\mathcal{M}}^{\flat }=({\mathcal{G}}^{\flat })^{0,\unicode[STIX]{x1D712}^{\flat }}$ and ![]() ${\mathcal{P}}^{\flat ,\pm }=({\mathcal{G}}^{\flat })^{\pm ,\unicode[STIX]{x1D712}^{\flat }}$. Part (ii) follows from [Reference Haines and RicharzHR18, Proposition 4.7] applied to the pair
${\mathcal{P}}^{\flat ,\pm }=({\mathcal{G}}^{\flat })^{\pm ,\unicode[STIX]{x1D712}^{\flat }}$. Part (ii) follows from [Reference Haines and RicharzHR18, Proposition 4.7] applied to the pair ![]() $({\mathcal{G}}^{\flat },\unicode[STIX]{x1D712}^{\flat })$.
$({\mathcal{G}}^{\flat },\unicode[STIX]{x1D712}^{\flat })$.
(iii) This follows as in [Reference Haines and RicharzHR18, Theorem 5.5, 5.17] using Proposition 5.5 below, and we sketch the argument for convenience. With the notation of Proposition 5.5, the map ![]() $\unicode[STIX]{x1D704}^{0}$ (respectively,
$\unicode[STIX]{x1D704}^{0}$ (respectively, ![]() $\unicode[STIX]{x1D704}^{\pm }$) factors as a set-theoretically bijective quasi-compact immersion
$\unicode[STIX]{x1D704}^{\pm }$) factors as a set-theoretically bijective quasi-compact immersion
where ![]() $(\operatorname{Gr}_{{\mathcal{G}}})^{0,c}$ (respectively,
$(\operatorname{Gr}_{{\mathcal{G}}})^{0,c}$ (respectively, ![]() $(\operatorname{Gr}_{{\mathcal{G}}})^{\pm ,c}$) is an open and closed
$(\operatorname{Gr}_{{\mathcal{G}}})^{\pm ,c}$) is an open and closed ![]() ${\mathcal{O}}_{F}$-sub-ind-scheme of
${\mathcal{O}}_{F}$-sub-ind-scheme of ![]() $(\operatorname{Gr}_{{\mathcal{G}}})^{0}$ (respectively,
$(\operatorname{Gr}_{{\mathcal{G}}})^{0}$ (respectively, ![]() $(\operatorname{Gr}_{{\mathcal{G}}})^{\pm }$). But any such map
$(\operatorname{Gr}_{{\mathcal{G}}})^{\pm }$). But any such map ![]() $\unicode[STIX]{x1D704}^{0,c}$ (respectively,
$\unicode[STIX]{x1D704}^{0,c}$ (respectively, ![]() $\unicode[STIX]{x1D704}^{\pm ,c}$) is a closed immersion which is an isomorphism on the underlying reduced loci; cf. [Reference Haines and RicharzHR18, Lemma 5.8].◻
$\unicode[STIX]{x1D704}^{\pm ,c}$) is a closed immersion which is an isomorphism on the underlying reduced loci; cf. [Reference Haines and RicharzHR18, Lemma 5.8].◻
We record the following properties.
Lemma 5.4. (i) The map ![]() $(\operatorname{Gr}_{{\mathcal{G}}})^{\pm }\rightarrow \operatorname{Gr}_{{\mathcal{G}}}$ is schematic.
$(\operatorname{Gr}_{{\mathcal{G}}})^{\pm }\rightarrow \operatorname{Gr}_{{\mathcal{G}}}$ is schematic.
(ii) The map ![]() $(\operatorname{Gr}_{{\mathcal{G}}})^{\pm }\rightarrow (\operatorname{Gr}_{{\mathcal{G}}})^{0}$ is ind-affine with geometrically connected fibers, and induces an isomorphism on the group of connected components
$(\operatorname{Gr}_{{\mathcal{G}}})^{\pm }\rightarrow (\operatorname{Gr}_{{\mathcal{G}}})^{0}$ is ind-affine with geometrically connected fibers, and induces an isomorphism on the group of connected components ![]() $\unicode[STIX]{x1D70B}_{0}((\operatorname{Gr}_{{\mathcal{G}}})^{\pm })\simeq \unicode[STIX]{x1D70B}_{0}((\operatorname{Gr}_{{\mathcal{G}}})^{0})$.
$\unicode[STIX]{x1D70B}_{0}((\operatorname{Gr}_{{\mathcal{G}}})^{\pm })\simeq \unicode[STIX]{x1D70B}_{0}((\operatorname{Gr}_{{\mathcal{G}}})^{0})$.
Proof. These are general properties of attractors in ind-schemes endowed with étale locally linearizable ![]() $\mathbb{G}_{m}$-actions; cf. Lemma 5.2, and Theorem 2.1(ii) or [Reference Haines and RicharzHR18, Theorem 2.1(ii)].◻
$\mathbb{G}_{m}$-actions; cf. Lemma 5.2, and Theorem 2.1(ii) or [Reference Haines and RicharzHR18, Theorem 2.1(ii)].◻
The following proposition decomposes the image of the maps ![]() $\unicode[STIX]{x1D704}^{0}$ and
$\unicode[STIX]{x1D704}^{0}$ and ![]() $\unicode[STIX]{x1D704}^{\pm }$ into connected components, and will be important in what follows.
$\unicode[STIX]{x1D704}^{\pm }$ into connected components, and will be important in what follows.
Proposition 5.5. Let either ![]() $N=N^{+}$ or
$N=N^{+}$ or ![]() $N=N^{-}$. There exists an open and closed
$N=N^{-}$. There exists an open and closed ![]() ${\mathcal{O}}_{F}$-ind-subscheme
${\mathcal{O}}_{F}$-ind-subscheme ![]() $(\operatorname{Gr}_{{\mathcal{G}}})^{0,c}$ (respectively,
$(\operatorname{Gr}_{{\mathcal{G}}})^{0,c}$ (respectively, ![]() $(\operatorname{Gr}_{{\mathcal{G}}})^{\pm ,c}$) of
$(\operatorname{Gr}_{{\mathcal{G}}})^{\pm ,c}$) of ![]() $(\operatorname{Gr}_{{\mathcal{G}}})^{0}$ (respectively,
$(\operatorname{Gr}_{{\mathcal{G}}})^{0}$ (respectively, ![]() $(\operatorname{Gr}_{{\mathcal{G}}})^{\pm }$) together with a disjoint decomposition, depending up to sign on the choice of
$(\operatorname{Gr}_{{\mathcal{G}}})^{\pm }$) together with a disjoint decomposition, depending up to sign on the choice of ![]() $N$, as
$N$, as ![]() ${\mathcal{O}}_{F}$-ind-schemes
${\mathcal{O}}_{F}$-ind-schemes
which has the following properties.
(i) The map
 $\unicode[STIX]{x1D704}^{0}:\operatorname{Gr}_{{\mathcal{M}}}\rightarrow (\operatorname{Gr}_{{\mathcal{G}}})^{0}$ (respectively,
$\unicode[STIX]{x1D704}^{0}:\operatorname{Gr}_{{\mathcal{M}}}\rightarrow (\operatorname{Gr}_{{\mathcal{G}}})^{0}$ (respectively,  $\unicode[STIX]{x1D704}^{\pm }:\operatorname{Gr}_{{\mathcal{P}}^{\pm }}\rightarrow (\operatorname{Gr}_{{\mathcal{G}}})^{\pm }$) factors through
$\unicode[STIX]{x1D704}^{\pm }:\operatorname{Gr}_{{\mathcal{P}}^{\pm }}\rightarrow (\operatorname{Gr}_{{\mathcal{G}}})^{\pm }$) factors through  $(\operatorname{Gr}_{{\mathcal{G}}})^{0,c}$ (respectively,
$(\operatorname{Gr}_{{\mathcal{G}}})^{0,c}$ (respectively,  $(\operatorname{Gr}_{{\mathcal{G}}})^{\pm ,c}$), inducing a closed immersion
$(\operatorname{Gr}_{{\mathcal{G}}})^{\pm ,c}$), inducing a closed immersion  $\unicode[STIX]{x1D704}^{0,c}:\operatorname{Gr}_{{\mathcal{M}}}\rightarrow (\operatorname{Gr}_{{\mathcal{G}}})^{0,c}$ (respectively,
$\unicode[STIX]{x1D704}^{0,c}:\operatorname{Gr}_{{\mathcal{M}}}\rightarrow (\operatorname{Gr}_{{\mathcal{G}}})^{0,c}$ (respectively,  $\unicode[STIX]{x1D704}^{\pm ,c}:\operatorname{Gr}_{{\mathcal{P}}^{\pm }}\rightarrow (\operatorname{Gr}_{{\mathcal{G}}})^{\pm ,c}$) which is an isomorphism on reduced loci.
$\unicode[STIX]{x1D704}^{\pm ,c}:\operatorname{Gr}_{{\mathcal{P}}^{\pm }}\rightarrow (\operatorname{Gr}_{{\mathcal{G}}})^{\pm ,c}$) which is an isomorphism on reduced loci.(ii) The complement
 $(\operatorname{Gr}_{{\mathcal{G}}})^{0}\backslash (\operatorname{Gr}_{{\mathcal{G}}})^{0,c}$ (respectively,
$(\operatorname{Gr}_{{\mathcal{G}}})^{0}\backslash (\operatorname{Gr}_{{\mathcal{G}}})^{0,c}$ (respectively,  $(\operatorname{Gr}_{{\mathcal{G}}})^{\pm }\backslash (\operatorname{Gr}_{{\mathcal{G}}})^{\pm ,c}$ ) has empty generic fiber, that is, is concentrated in the special fiber.
$(\operatorname{Gr}_{{\mathcal{G}}})^{\pm }\backslash (\operatorname{Gr}_{{\mathcal{G}}})^{\pm ,c}$ ) has empty generic fiber, that is, is concentrated in the special fiber.
Proof. The proof closely follows [Reference Haines and RicharzHR18, Propositions 5.7 and 5.21]. We recall some steps of the construction. Let us denote ![]() ${\mathcal{O}}:={\mathcal{O}}_{F}$ and
${\mathcal{O}}:={\mathcal{O}}_{F}$ and ![]() $\breve{{\mathcal{O}}}:={\mathcal{O}}_{\breve{F}}$. Let
$\breve{{\mathcal{O}}}:={\mathcal{O}}_{\breve{F}}$. Let ![]() $\unicode[STIX]{x1D70B}_{1}(M)=X_{\ast }(T)/X_{\ast }(T_{M_{\operatorname{sc}}})$ be the algebraic fundamental group of
$\unicode[STIX]{x1D70B}_{1}(M)=X_{\ast }(T)/X_{\ast }(T_{M_{\operatorname{sc}}})$ be the algebraic fundamental group of ![]() $M$ in the sense of [Reference BorovoiBor98], and denote by
$M$ in the sense of [Reference BorovoiBor98], and denote by ![]() $\unicode[STIX]{x1D70B}_{1}(M)_{I_{F}}$ the coinvariants. By [Reference Pappas and RapoportPR08, Theorem 5.1], the group of connected components is given by
$\unicode[STIX]{x1D70B}_{1}(M)_{I_{F}}$ the coinvariants. By [Reference Pappas and RapoportPR08, Theorem 5.1], the group of connected components is given by
where the last equality follows from the proof of Lemma 4.11. Note that ![]() $\unicode[STIX]{x1D70B}_{1}(M)_{I_{F}}=\text{Ind}_{\unicode[STIX]{x1D6E4}_{k_{0}}}^{\unicode[STIX]{x1D6E4}_{k}}\unicode[STIX]{x1D70B}_{1}(M_{0})_{I_{K}}$; cf. (4.21). Since
$\unicode[STIX]{x1D70B}_{1}(M)_{I_{F}}=\text{Ind}_{\unicode[STIX]{x1D6E4}_{k_{0}}}^{\unicode[STIX]{x1D6E4}_{k}}\unicode[STIX]{x1D70B}_{1}(M_{0})_{I_{K}}$; cf. (4.21). Since ![]() $\operatorname{Gr}_{{\mathcal{M}},\breve{{\mathcal{O}}}}\rightarrow \operatorname{Spec}(\breve{{\mathcal{O}}})$ is ind-proper and
$\operatorname{Gr}_{{\mathcal{M}},\breve{{\mathcal{O}}}}\rightarrow \operatorname{Spec}(\breve{{\mathcal{O}}})$ is ind-proper and ![]() $\breve{{\mathcal{O}}}$ is Henselian, the natural map
$\breve{{\mathcal{O}}}$ is Henselian, the natural map
is an isomorphism by [Reference DeligneSGA4½, Arcata; IV-2; Proposition 2.1]. This shows that there is a decomposition into connected components
such that ![]() $(\operatorname{Gr}_{{\mathcal{M}},\breve{{\mathcal{O}}}})_{\bar{\unicode[STIX]{x1D708}}}\otimes \bar{k}\simeq ({\mathcal{F}}\!\ell _{{\mathcal{M}}^{\flat },\bar{k}})_{\bar{\unicode[STIX]{x1D708}}}$. By Lemma 4.17, the generic fiber decomposes as
$(\operatorname{Gr}_{{\mathcal{M}},\breve{{\mathcal{O}}}})_{\bar{\unicode[STIX]{x1D708}}}\otimes \bar{k}\simeq ({\mathcal{F}}\!\ell _{{\mathcal{M}}^{\flat },\bar{k}})_{\bar{\unicode[STIX]{x1D708}}}$. By Lemma 4.17, the generic fiber decomposes as ![]() $(\operatorname{Gr}_{{\mathcal{M}},\breve{{\mathcal{O}}}})_{\bar{\unicode[STIX]{x1D708}}}\otimes \bar{F}\simeq \coprod _{\unicode[STIX]{x1D708}\mapsto \bar{\unicode[STIX]{x1D708}}}(\operatorname{Gr}_{M,\bar{F}})_{\unicode[STIX]{x1D708}}$, where
$(\operatorname{Gr}_{{\mathcal{M}},\breve{{\mathcal{O}}}})_{\bar{\unicode[STIX]{x1D708}}}\otimes \bar{F}\simeq \coprod _{\unicode[STIX]{x1D708}\mapsto \bar{\unicode[STIX]{x1D708}}}(\operatorname{Gr}_{M,\bar{F}})_{\unicode[STIX]{x1D708}}$, where ![]() $\unicode[STIX]{x1D708}\in \unicode[STIX]{x1D70B}_{1}(M)$ runs over the elements which map to
$\unicode[STIX]{x1D708}\in \unicode[STIX]{x1D70B}_{1}(M)$ runs over the elements which map to ![]() $\bar{\unicode[STIX]{x1D708}}$ under the reduction map
$\bar{\unicode[STIX]{x1D708}}$ under the reduction map ![]() $\unicode[STIX]{x1D70B}_{1}(M)\rightarrow \unicode[STIX]{x1D70B}_{1}(M)_{I_{F}}$.
$\unicode[STIX]{x1D70B}_{1}(M)\rightarrow \unicode[STIX]{x1D70B}_{1}(M)_{I_{F}}$.
By Theorem 5.3(i) and (ii), it is easy to see that the closed immersion ![]() $\unicode[STIX]{x1D704}^{0}:\operatorname{Gr}_{{\mathcal{M}},\breve{{\mathcal{O}}}}\rightarrow (\operatorname{Gr}_{{\mathcal{G}},\breve{{\mathcal{O}}}})^{0}$ is open on the underlying topological spaces (e.g. its image is closed under generization), that is, the image identifies each connected component of
$\unicode[STIX]{x1D704}^{0}:\operatorname{Gr}_{{\mathcal{M}},\breve{{\mathcal{O}}}}\rightarrow (\operatorname{Gr}_{{\mathcal{G}},\breve{{\mathcal{O}}}})^{0}$ is open on the underlying topological spaces (e.g. its image is closed under generization), that is, the image identifies each connected component of ![]() $\operatorname{Gr}_{{\mathcal{M}},\breve{{\mathcal{O}}}}$ with a connected component of
$\operatorname{Gr}_{{\mathcal{M}},\breve{{\mathcal{O}}}}$ with a connected component of ![]() $(\operatorname{Gr}_{{\mathcal{G}},\breve{{\mathcal{O}}}})^{0}$. Using Lemma 5.4(ii), we get an inclusion
$(\operatorname{Gr}_{{\mathcal{G}},\breve{{\mathcal{O}}}})^{0}$. Using Lemma 5.4(ii), we get an inclusion
For ![]() $\bar{\unicode[STIX]{x1D708}}\in \unicode[STIX]{x1D70B}_{1}(M)_{I_{F}}$, we denote the corresponding connected component of
$\bar{\unicode[STIX]{x1D708}}\in \unicode[STIX]{x1D70B}_{1}(M)_{I_{F}}$, we denote the corresponding connected component of ![]() $(\operatorname{Gr}_{{\mathcal{G}},\breve{{\mathcal{O}}}})^{0}$ (respectively,
$(\operatorname{Gr}_{{\mathcal{G}},\breve{{\mathcal{O}}}})^{0}$ (respectively, ![]() $(\operatorname{Gr}_{{\mathcal{G}},\breve{{\mathcal{O}}}})^{\pm }$) by
$(\operatorname{Gr}_{{\mathcal{G}},\breve{{\mathcal{O}}}})^{\pm }$) by ![]() $(\operatorname{Gr}_{{\mathcal{G}}})_{\bar{\unicode[STIX]{x1D708}}}^{0}$ (respectively,
$(\operatorname{Gr}_{{\mathcal{G}}})_{\bar{\unicode[STIX]{x1D708}}}^{0}$ (respectively, ![]() $(\operatorname{Gr}_{{\mathcal{G}}})_{\bar{\unicode[STIX]{x1D708}}}^{\pm }$).
$(\operatorname{Gr}_{{\mathcal{G}}})_{\bar{\unicode[STIX]{x1D708}}}^{\pm }$).
Let ![]() $\unicode[STIX]{x1D70C}$ denote the half-sum of the roots in
$\unicode[STIX]{x1D70C}$ denote the half-sum of the roots in ![]() $\operatorname{Res}_{K/F}(N)_{\bar{F}}$ with respect to
$\operatorname{Res}_{K/F}(N)_{\bar{F}}$ with respect to ![]() $\operatorname{Res}_{K/F}(T)_{\bar{F}}$. For
$\operatorname{Res}_{K/F}(T)_{\bar{F}}$. For ![]() $\unicode[STIX]{x1D70B}_{1}(M)\ni \unicode[STIX]{x1D708}\mapsto \bar{\unicode[STIX]{x1D708}}\in \unicode[STIX]{x1D70B}_{1}(M)_{I_{F}}$, and
$\unicode[STIX]{x1D70B}_{1}(M)\ni \unicode[STIX]{x1D708}\mapsto \bar{\unicode[STIX]{x1D708}}\in \unicode[STIX]{x1D70B}_{1}(M)_{I_{F}}$, and ![]() $\dot{\unicode[STIX]{x1D708}}\in X_{\ast }(\operatorname{Res}_{K/F}(T))$ a lift of
$\dot{\unicode[STIX]{x1D708}}\in X_{\ast }(\operatorname{Res}_{K/F}(T))$ a lift of ![]() $\unicode[STIX]{x1D708}$, we define the integer
$\unicode[STIX]{x1D708}$, we define the integer ![]() $n_{\unicode[STIX]{x1D708}}:=\langle 2\unicode[STIX]{x1D70C},\dot{\unicode[STIX]{x1D708}}\rangle$ (respectively,
$n_{\unicode[STIX]{x1D708}}:=\langle 2\unicode[STIX]{x1D70C},\dot{\unicode[STIX]{x1D708}}\rangle$ (respectively, ![]() $n_{\bar{\unicode[STIX]{x1D708}}}:=\langle 2\unicode[STIX]{x1D70C},\dot{\unicode[STIX]{x1D708}}\rangle$) which is well defined independent of the choice of
$n_{\bar{\unicode[STIX]{x1D708}}}:=\langle 2\unicode[STIX]{x1D70C},\dot{\unicode[STIX]{x1D708}}\rangle$) which is well defined independent of the choice of ![]() $\dot{\unicode[STIX]{x1D708}}$; cf. [Reference Haines and RicharzHR18, (3.19)]. Note that we have
$\dot{\unicode[STIX]{x1D708}}$; cf. [Reference Haines and RicharzHR18, (3.19)]. Note that we have ![]() $n_{\unicode[STIX]{x1D708}}=n_{\bar{\unicode[STIX]{x1D708}}}$ for all
$n_{\unicode[STIX]{x1D708}}=n_{\bar{\unicode[STIX]{x1D708}}}$ for all ![]() $\unicode[STIX]{x1D708}\mapsto \bar{\unicode[STIX]{x1D708}}$ by definition. For fixed
$\unicode[STIX]{x1D708}\mapsto \bar{\unicode[STIX]{x1D708}}$ by definition. For fixed ![]() $m\in \mathbb{Z}$, we consider the disjoint union
$m\in \mathbb{Z}$, we consider the disjoint union
where the disjoint sum is indexed by all ![]() $\bar{\unicode[STIX]{x1D708}}\in \unicode[STIX]{x1D70B}_{1}(M)_{I_{F}}$ such that
$\bar{\unicode[STIX]{x1D708}}\in \unicode[STIX]{x1D70B}_{1}(M)_{I_{F}}$ such that ![]() $n_{\bar{\unicode[STIX]{x1D708}}}=m$. The Galois action preserves the integers
$n_{\bar{\unicode[STIX]{x1D708}}}=m$. The Galois action preserves the integers ![]() $n_{\bar{\unicode[STIX]{x1D708}}}$, and hence the ind-scheme
$n_{\bar{\unicode[STIX]{x1D708}}}$, and hence the ind-scheme ![]() $(\operatorname{Gr}_{{\mathcal{G}}})_{m}^{0}$ (respectively,
$(\operatorname{Gr}_{{\mathcal{G}}})_{m}^{0}$ (respectively, ![]() $(\operatorname{Gr}_{{\mathcal{G}}})_{m}^{\pm }$) is defined over
$(\operatorname{Gr}_{{\mathcal{G}}})_{m}^{\pm }$) is defined over ![]() ${\mathcal{O}}$. Note that
${\mathcal{O}}$. Note that ![]() $(\operatorname{Gr}_{{\mathcal{G}}})_{m}^{\pm }$ is the preimage of
$(\operatorname{Gr}_{{\mathcal{G}}})_{m}^{\pm }$ is the preimage of ![]() $(\operatorname{Gr}_{{\mathcal{G}}})_{m}^{0}$ along
$(\operatorname{Gr}_{{\mathcal{G}}})_{m}^{0}$ along ![]() $(\operatorname{Gr}_{{\mathcal{G}}})^{\pm }\rightarrow (\operatorname{Gr}_{{\mathcal{G}}})^{0}$. We obtain a decomposition as
$(\operatorname{Gr}_{{\mathcal{G}}})^{\pm }\rightarrow (\operatorname{Gr}_{{\mathcal{G}}})^{0}$. We obtain a decomposition as ![]() ${\mathcal{O}}$-ind-schemes
${\mathcal{O}}$-ind-schemes
Properties (i) and (ii) are immediate from the construction. ◻
5.2 Cohomology of  $\mathbb{G}_{m}$-actions on affine Grassmannians
$\mathbb{G}_{m}$-actions on affine Grassmannians
The conventions are the same as in [Reference Haines and RicharzHR18, § 3.4]. We fix a prime ![]() $\ell \not =p$ and an algebraic closure
$\ell \not =p$ and an algebraic closure ![]() $\bar{\mathbb{Q}}_{\ell }$ of
$\bar{\mathbb{Q}}_{\ell }$ of ![]() $\mathbb{Q}_{\ell }$. We fix once and for all
$\mathbb{Q}_{\ell }$. We fix once and for all ![]() $q^{1/2}\in \bar{\mathbb{Q}}_{\ell }$ and the square root of the cyclotomic character
$q^{1/2}\in \bar{\mathbb{Q}}_{\ell }$ and the square root of the cyclotomic character ![]() $\operatorname{cycl}:\unicode[STIX]{x1D6E4}_{F}\rightarrow \bar{\mathbb{Z}}_{\ell }^{\times }$ which maps any lift of the geometric Frobenius
$\operatorname{cycl}:\unicode[STIX]{x1D6E4}_{F}\rightarrow \bar{\mathbb{Z}}_{\ell }^{\times }$ which maps any lift of the geometric Frobenius ![]() $\unicode[STIX]{x1D6F7}_{F}$ to
$\unicode[STIX]{x1D6F7}_{F}$ to ![]() $q^{-1/2}$. The Tate twists are normalized such that the geometric Frobenius
$q^{-1/2}$. The Tate twists are normalized such that the geometric Frobenius ![]() $\unicode[STIX]{x1D6F7}_{F}$ acts on
$\unicode[STIX]{x1D6F7}_{F}$ acts on ![]() $\bar{\mathbb{Q}}_{\ell }(-1/2)$ by
$\bar{\mathbb{Q}}_{\ell }(-1/2)$ by ![]() $q^{1/2}$.
$q^{1/2}$.
For a separated ind-scheme ![]() $X=\operatorname{colim}_{i}X_{i}$ of finite type over a field (e.g.
$X=\operatorname{colim}_{i}X_{i}$ of finite type over a field (e.g. ![]() $F$) or a discrete valuation ring (e.g.
$F$) or a discrete valuation ring (e.g. ![]() ${\mathcal{O}}_{F}$), we denote the bounded derived category
${\mathcal{O}}_{F}$), we denote the bounded derived category ![]() $D_{c}^{b}(X)=D_{c}^{b}(X,\bar{\mathbb{Q}}_{\ell })$ of
$D_{c}^{b}(X)=D_{c}^{b}(X,\bar{\mathbb{Q}}_{\ell })$ of ![]() $\bar{\mathbb{Q}}_{\ell }$-complexes with constructible cohomologies by
$\bar{\mathbb{Q}}_{\ell }$-complexes with constructible cohomologies by
There is the full abelian subcategory ![]() $\operatorname{Perv}(X)\subset D_{c}^{b}(X)$ of perverse sheaves; cf. [Reference ZhuZhu17, A.1] in the setting of ind-schemes, for example. For a complex
$\operatorname{Perv}(X)\subset D_{c}^{b}(X)$ of perverse sheaves; cf. [Reference ZhuZhu17, A.1] in the setting of ind-schemes, for example. For a complex ![]() ${\mathcal{A}}\in D_{c}^{b}(X)$, we denote for any
${\mathcal{A}}\in D_{c}^{b}(X)$, we denote for any ![]() $n\in \mathbb{Z}$ the shifted and twisted complex by
$n\in \mathbb{Z}$ the shifted and twisted complex by
Let us briefly recall the nearby cycles functor. Let ![]() $S=\operatorname{Spec}({\mathcal{O}}_{F})$ with open (respectively, closed) point
$S=\operatorname{Spec}({\mathcal{O}}_{F})$ with open (respectively, closed) point ![]() $\unicode[STIX]{x1D702}=\operatorname{Spec}(F)$ (respectively,
$\unicode[STIX]{x1D702}=\operatorname{Spec}(F)$ (respectively, ![]() $s=\operatorname{Spec}(k)$). Let
$s=\operatorname{Spec}(k)$). Let ![]() $\bar{\unicode[STIX]{x1D702}}:=\operatorname{Spec}(\bar{F})\rightarrow \unicode[STIX]{x1D702}$ (respectively,
$\bar{\unicode[STIX]{x1D702}}:=\operatorname{Spec}(\bar{F})\rightarrow \unicode[STIX]{x1D702}$ (respectively, ![]() $\bar{s}:=\operatorname{Spec}(\bar{k})\rightarrow s$) denote the geometric point with Galois group
$\bar{s}:=\operatorname{Spec}(\bar{k})\rightarrow s$) denote the geometric point with Galois group ![]() $\unicode[STIX]{x1D6E4}=\operatorname{Gal}(\bar{\unicode[STIX]{x1D702}}/\unicode[STIX]{x1D702})$. Let
$\unicode[STIX]{x1D6E4}=\operatorname{Gal}(\bar{\unicode[STIX]{x1D702}}/\unicode[STIX]{x1D702})$. Let ![]() $\bar{S}$ denote the integral closure of
$\bar{S}$ denote the integral closure of ![]() $S$ in
$S$ in ![]() $\bar{\unicode[STIX]{x1D702}}$. This gives rise to the
$\bar{\unicode[STIX]{x1D702}}$. This gives rise to the ![]() $7$-tuple
$7$-tuple ![]() $(S,\unicode[STIX]{x1D702},s,\bar{S},\bar{\unicode[STIX]{x1D702}},\bar{s},\unicode[STIX]{x1D6E4})$. Now if
$(S,\unicode[STIX]{x1D702},s,\bar{S},\bar{\unicode[STIX]{x1D702}},\bar{s},\unicode[STIX]{x1D6E4})$. Now if ![]() $X$ is an
$X$ is an ![]() ${\mathcal{O}}_{F}$-ind-scheme of ind-finite type, there is by [Reference Deligne and KatzSGA7, Example XIII] (cf. also [Reference IllusieIll94, App]) the functor of nearby cycles
${\mathcal{O}}_{F}$-ind-scheme of ind-finite type, there is by [Reference Deligne and KatzSGA7, Example XIII] (cf. also [Reference IllusieIll94, App]) the functor of nearby cycles
where ![]() $D_{c}^{b}(X_{s}\times _{S}\unicode[STIX]{x1D702})$ denotes the bounded derived category of
$D_{c}^{b}(X_{s}\times _{S}\unicode[STIX]{x1D702})$ denotes the bounded derived category of ![]() $\bar{\mathbb{Q}}_{\ell }$-sheaves on
$\bar{\mathbb{Q}}_{\ell }$-sheaves on ![]() $X_{\bar{s}}$ with constructible cohomologies, and with a continuous action of
$X_{\bar{s}}$ with constructible cohomologies, and with a continuous action of ![]() $\unicode[STIX]{x1D6E4}$ compatible with the action on
$\unicode[STIX]{x1D6E4}$ compatible with the action on ![]() $X_{\bar{s}}$. The nearby cycles preserve perversity and restrict to a functor
$X_{\bar{s}}$. The nearby cycles preserve perversity and restrict to a functor ![]() $\unicode[STIX]{x1D6F9}_{X}:\operatorname{Perv}(X_{\unicode[STIX]{x1D702}})\rightarrow \operatorname{Perv}(X_{s}\times _{S}\unicode[STIX]{x1D702})$. We refer the reader to [Reference Pappas and ZhuPZ13, § 10] for the extension to ind-schemes.
$\unicode[STIX]{x1D6F9}_{X}:\operatorname{Perv}(X_{\unicode[STIX]{x1D702}})\rightarrow \operatorname{Perv}(X_{s}\times _{S}\unicode[STIX]{x1D702})$. We refer the reader to [Reference Pappas and ZhuPZ13, § 10] for the extension to ind-schemes.
For a map of ![]() ${\mathcal{O}}_{F}$-ind-schemes
${\mathcal{O}}_{F}$-ind-schemes ![]() $f:X\rightarrow Y$, the nearby cycles are functorial in the obvious way; cf. [Reference Deligne and KatzSGA7, Example XIII, 1.2.7–1.2.9]. Further, if
$f:X\rightarrow Y$, the nearby cycles are functorial in the obvious way; cf. [Reference Deligne and KatzSGA7, Example XIII, 1.2.7–1.2.9]. Further, if ![]() $f$ is a nilpotent thickening, that is, a closed immersion defined by an nilpotent ideal sheaf, then
$f$ is a nilpotent thickening, that is, a closed immersion defined by an nilpotent ideal sheaf, then ![]() $f$ induces
$f$ induces ![]() $\unicode[STIX]{x1D6F9}_{X}\simeq \unicode[STIX]{x1D6F9}_{Y}$.
$\unicode[STIX]{x1D6F9}_{X}\simeq \unicode[STIX]{x1D6F9}_{Y}$.
5.2.1 Geometric Satake for Weil restrictions
Recall the geometric Satake equivalence from [Reference GinzburgGin95, Reference LusztigLus83, Reference Beilinson and DrinfeldBD99, Reference Mirković and VilonenMV07, Reference RicharzRic14, Reference Richarz and ZhuRZ15, Reference ZhuZhu17]. We work under the same conventions as in [Reference Haines and RicharzHR18, § 3.4], and we refer the reader to that work for more details.
Let ![]() $G_{0}$ be a reductive group over
$G_{0}$ be a reductive group over ![]() $K$. We are interested in the geometric Satake isomorphism for the group
$K$. We are interested in the geometric Satake isomorphism for the group ![]() $G=\operatorname{Res}_{K/F}(G_{0})$. For a conjugacy class
$G=\operatorname{Res}_{K/F}(G_{0})$. For a conjugacy class ![]() $\{\unicode[STIX]{x1D707}\}$ of geometric cocharacters in
$\{\unicode[STIX]{x1D707}\}$ of geometric cocharacters in ![]() $G$, denote the inclusion of the open
$G$, denote the inclusion of the open ![]() $L_{z}^{+}G_{\bar{F}}$-orbit by
$L_{z}^{+}G_{\bar{F}}$-orbit by
cf. (4.24). The map ![]() $j$ is defined over the reflex field
$j$ is defined over the reflex field ![]() $E=E(\{\unicode[STIX]{x1D707}\})$. We define the normalized intersection complex by
$E=E(\{\unicode[STIX]{x1D707}\})$. We define the normalized intersection complex by
where ![]() $d_{\unicode[STIX]{x1D707}}$ denotes the dimension of
$d_{\unicode[STIX]{x1D707}}$ denotes the dimension of ![]() $\operatorname{Gr}_{G}^{{\leqslant}\{\unicode[STIX]{x1D707}\}}$. The category
$\operatorname{Gr}_{G}^{{\leqslant}\{\unicode[STIX]{x1D707}\}}$. The category ![]() $P_{L_{z}^{+}G}(\operatorname{Gr}_{G})$ of
$P_{L_{z}^{+}G}(\operatorname{Gr}_{G})$ of ![]() $L_{z}^{+}G$-equivariant perverse sheaves (cf. [Reference ZhuZhu17, A.1] for equivariant perverse sheaves on ind-schemes) is generated by the intersection complexes (5.11) and local systems concentrated on the base point
$L_{z}^{+}G$-equivariant perverse sheaves (cf. [Reference ZhuZhu17, A.1] for equivariant perverse sheaves on ind-schemes) is generated by the intersection complexes (5.11) and local systems concentrated on the base point ![]() $e_{0}\in \operatorname{Gr}_{G}(F)$. More precisely, every indecomposable object in
$e_{0}\in \operatorname{Gr}_{G}(F)$. More precisely, every indecomposable object in ![]() $P_{L_{z}^{+}G}(\operatorname{Gr}_{G})$ is of the form
$P_{L_{z}^{+}G}(\operatorname{Gr}_{G})$ is of the form
where ![]() ${\mathcal{L}}$ is a
${\mathcal{L}}$ is a ![]() $\bar{\mathbb{Q}}_{\ell }$-local system on
$\bar{\mathbb{Q}}_{\ell }$-local system on ![]() $e_{0}=\operatorname{Spec}(F)$. The Satake category
$e_{0}=\operatorname{Spec}(F)$. The Satake category ![]() $\operatorname{Sat}_{G}$ is the full subcategory of
$\operatorname{Sat}_{G}$ is the full subcategory of ![]() $P_{L_{z}^{+}G}(\operatorname{Gr}_{G})$ generated by objects (5.12) where the local system
$P_{L_{z}^{+}G}(\operatorname{Gr}_{G})$ generated by objects (5.12) where the local system ![]() ${\mathcal{L}}$ is trivial over a finite field extension
${\mathcal{L}}$ is trivial over a finite field extension ![]() $\tilde{F}/F$.
$\tilde{F}/F$.
We view ![]() $\unicode[STIX]{x1D6E4}_{F}$ as a pro-algebraic group, and we let
$\unicode[STIX]{x1D6E4}_{F}$ as a pro-algebraic group, and we let ![]() $\operatorname{Rep}_{\bar{\mathbb{Q}}_{\ell }}^{\operatorname{alg}}(\unicode[STIX]{x1D6E4}_{F})$ be the category of algebraic
$\operatorname{Rep}_{\bar{\mathbb{Q}}_{\ell }}^{\operatorname{alg}}(\unicode[STIX]{x1D6E4}_{F})$ be the category of algebraic ![]() $\bar{\mathbb{Q}}_{\ell }$-representations of
$\bar{\mathbb{Q}}_{\ell }$-representations of ![]() $\unicode[STIX]{x1D6E4}_{F}$, that is, finite-dimensional representations which factor through a finite quotient of
$\unicode[STIX]{x1D6E4}_{F}$, that is, finite-dimensional representations which factor through a finite quotient of ![]() $\unicode[STIX]{x1D6E4}_{F}$. There is the Tate twisted global cohomology functor
$\unicode[STIX]{x1D6E4}_{F}$. There is the Tate twisted global cohomology functor

By the geometric Satake equivalence, the functor ![]() $\unicode[STIX]{x1D714}$ can be upgraded to an equivalence of abelian tensor categories
$\unicode[STIX]{x1D714}$ can be upgraded to an equivalence of abelian tensor categories
where ![]() $^{L}G=G^{\vee }\rtimes \unicode[STIX]{x1D6E4}_{F}$ denotes the
$^{L}G=G^{\vee }\rtimes \unicode[STIX]{x1D6E4}_{F}$ denotes the ![]() $L$-group viewed as a pro-algebraic group over
$L$-group viewed as a pro-algebraic group over ![]() $\bar{\mathbb{Q}}_{\ell }$. The tensor structure on
$\bar{\mathbb{Q}}_{\ell }$. The tensor structure on ![]() $\operatorname{Sat}_{G}$ is given by the convolution of perverse sheaves; cf. § 5.5 below. The normalized intersection complex
$\operatorname{Sat}_{G}$ is given by the convolution of perverse sheaves; cf. § 5.5 below. The normalized intersection complex ![]() $\operatorname{IC}_{\{\unicode[STIX]{x1D707}\}}$ is an object in the category
$\operatorname{IC}_{\{\unicode[STIX]{x1D707}\}}$ is an object in the category ![]() $\operatorname{Sat}_{G_{E}}$, and its cohomology
$\operatorname{Sat}_{G_{E}}$, and its cohomology ![]() $\unicode[STIX]{x1D714}(\operatorname{IC}_{\{\unicode[STIX]{x1D707}\}})$ is under the geometric Satake equivalence (
$\unicode[STIX]{x1D714}(\operatorname{IC}_{\{\unicode[STIX]{x1D707}\}})$ is under the geometric Satake equivalence (
) the ![]() $^{L}G_{E}:=G^{\vee }\rtimes \unicode[STIX]{x1D6E4}_{E}$-representation
$^{L}G_{E}:=G^{\vee }\rtimes \unicode[STIX]{x1D6E4}_{E}$-representation ![]() $V_{\{\unicode[STIX]{x1D707}\}}$ of highest weight
$V_{\{\unicode[STIX]{x1D707}\}}$ of highest weight ![]() $\{\unicode[STIX]{x1D707}\}$ defined in [Reference Haines, Diamond, Kassaei and KimHai14, § 6.1]; cf. [Reference Haines and RicharzHR18, Corollary 3.12].
$\{\unicode[STIX]{x1D707}\}$ defined in [Reference Haines, Diamond, Kassaei and KimHai14, § 6.1]; cf. [Reference Haines and RicharzHR18, Corollary 3.12].
Let us describe the dual group ![]() $G^{\vee }=\operatorname{Res}_{K/F}(G_{0})^{\vee }$ and the representation
$G^{\vee }=\operatorname{Res}_{K/F}(G_{0})^{\vee }$ and the representation ![]() $V_{\{\unicode[STIX]{x1D707}\}}$ explicitly in terms of
$V_{\{\unicode[STIX]{x1D707}\}}$ explicitly in terms of ![]() $G_{0}^{\vee }$. Of course,
$G_{0}^{\vee }$. Of course, ![]() $G^{\vee }$ is canonically isomorphic to the product
$G^{\vee }$ is canonically isomorphic to the product ![]() $\prod _{K{\hookrightarrow}\bar{F}}G_{0}^{\vee }$, but the Galois action does not respect the factors in general.
$\prod _{K{\hookrightarrow}\bar{F}}G_{0}^{\vee }$, but the Galois action does not respect the factors in general.
Let ![]() $\text{}\underline{\operatorname{Hom}}_{\bar{\mathbb{Q}}_{\ell }}(\unicode[STIX]{x1D6E4}_{F},G_{0}^{\vee })$ be the sheaf of
$\text{}\underline{\operatorname{Hom}}_{\bar{\mathbb{Q}}_{\ell }}(\unicode[STIX]{x1D6E4}_{F},G_{0}^{\vee })$ be the sheaf of ![]() $\bar{\mathbb{Q}}_{\ell }$-scheme morphisms where again
$\bar{\mathbb{Q}}_{\ell }$-scheme morphisms where again ![]() $\unicode[STIX]{x1D6E4}_{F}$ is viewed as a pro-algebraic group. Then
$\unicode[STIX]{x1D6E4}_{F}$ is viewed as a pro-algebraic group. Then ![]() $\text{}\underline{\operatorname{Hom}}_{\bar{\mathbb{Q}}_{\ell }}(\unicode[STIX]{x1D6E4}_{F},G_{0}^{\vee })$ is a group functor, and the pro-algebraic group
$\text{}\underline{\operatorname{Hom}}_{\bar{\mathbb{Q}}_{\ell }}(\unicode[STIX]{x1D6E4}_{F},G_{0}^{\vee })$ is a group functor, and the pro-algebraic group ![]() $\unicode[STIX]{x1D6E4}_{K}$ acts on
$\unicode[STIX]{x1D6E4}_{K}$ acts on ![]() $\text{}\underline{\operatorname{Hom}}_{\bar{\mathbb{Q}}_{\ell }}(\unicode[STIX]{x1D6E4}_{F},G_{0}^{\vee })$ via
$\text{}\underline{\operatorname{Hom}}_{\bar{\mathbb{Q}}_{\ell }}(\unicode[STIX]{x1D6E4}_{F},G_{0}^{\vee })$ via ![]() $\bar{\mathbb{Q}}_{\ell }$-group automorphisms by the rule
$\bar{\mathbb{Q}}_{\ell }$-group automorphisms by the rule ![]() $(\unicode[STIX]{x1D6FE}\ast f)(g)=\unicode[STIX]{x1D6FE}(f(\unicode[STIX]{x1D6FE}^{-1}g))$. Following [Reference BorelBor79, I.5], we define the induced group as the
$(\unicode[STIX]{x1D6FE}\ast f)(g)=\unicode[STIX]{x1D6FE}(f(\unicode[STIX]{x1D6FE}^{-1}g))$. Following [Reference BorelBor79, I.5], we define the induced group as the ![]() $\unicode[STIX]{x1D6E4}_{K}$-fixed point sheaf
$\unicode[STIX]{x1D6E4}_{K}$-fixed point sheaf
which is a group functor. Note that choosing any finite extension ![]() $\tilde{K}/K$ which is Galois over
$\tilde{K}/K$ which is Galois over ![]() $F$ and splits
$F$ and splits ![]() $G_{0}$, we get an isomorphism of
$G_{0}$, we get an isomorphism of ![]() $\bar{\mathbb{Q}}_{\ell }$-groups
$\bar{\mathbb{Q}}_{\ell }$-groups
where ![]() $\unicode[STIX]{x1D6E4}_{\tilde{K}/K}=\operatorname{Gal}(\tilde{K}/K)$ (respectively,
$\unicode[STIX]{x1D6E4}_{\tilde{K}/K}=\operatorname{Gal}(\tilde{K}/K)$ (respectively, ![]() $\unicode[STIX]{x1D6E4}_{\tilde{K}/F}=\operatorname{Gal}(\tilde{K}/F)$). In particular,
$\unicode[STIX]{x1D6E4}_{\tilde{K}/F}=\operatorname{Gal}(\tilde{K}/F)$). In particular, ![]() $I_{\unicode[STIX]{x1D6E4}_{K}}^{\unicode[STIX]{x1D6E4}_{F}}(G_{0}^{\vee })$ is an algebraic group, and is the colimit indexed by the filtered direct system (5.16) indexed by the splitting fields
$I_{\unicode[STIX]{x1D6E4}_{K}}^{\unicode[STIX]{x1D6E4}_{F}}(G_{0}^{\vee })$ is an algebraic group, and is the colimit indexed by the filtered direct system (5.16) indexed by the splitting fields ![]() $\tilde{K}$. In this way, we get, as in [Reference BorelBor79, I.5], an
$\tilde{K}$. In this way, we get, as in [Reference BorelBor79, I.5], an ![]() $\unicode[STIX]{x1D6E4}_{F}$-equivariant isomorphism of algebraic
$\unicode[STIX]{x1D6E4}_{F}$-equivariant isomorphism of algebraic ![]() $\bar{\mathbb{Q}}_{\ell }$-groups
$\bar{\mathbb{Q}}_{\ell }$-groups
Let us turn to the representation ![]() $V_{\{\unicode[STIX]{x1D707}\}}$. We write the conjugacy class as
$V_{\{\unicode[STIX]{x1D707}\}}$. We write the conjugacy class as ![]() $\{\unicode[STIX]{x1D707}\}=(\{\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D713}}\})_{\unicode[STIX]{x1D713}}$ according to
$\{\unicode[STIX]{x1D707}\}=(\{\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D713}}\})_{\unicode[STIX]{x1D713}}$ according to ![]() $G_{\bar{F}}\simeq \prod _{\unicode[STIX]{x1D713}:K{\hookrightarrow}\bar{F}}G_{0}\otimes _{\unicode[STIX]{x1D713},K}\bar{F}$. The reflex field
$G_{\bar{F}}\simeq \prod _{\unicode[STIX]{x1D713}:K{\hookrightarrow}\bar{F}}G_{0}\otimes _{\unicode[STIX]{x1D713},K}\bar{F}$. The reflex field ![]() $E$ of
$E$ of ![]() $\{\unicode[STIX]{x1D707}\}$ is the intersection (inside
$\{\unicode[STIX]{x1D707}\}$ is the intersection (inside ![]() $\bar{F}$) of the reflex fields
$\bar{F}$) of the reflex fields ![]() $E_{\unicode[STIX]{x1D713}}$ of
$E_{\unicode[STIX]{x1D713}}$ of ![]() $\{\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D713}}\}$. For each
$\{\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D713}}\}$. For each ![]() $\unicode[STIX]{x1D713}$, let
$\unicode[STIX]{x1D713}$, let ![]() $V_{\{\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D713}}\}}$ denote the representation of
$V_{\{\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D713}}\}}$ denote the representation of ![]() $G_{0}^{\vee }$ of highest weight
$G_{0}^{\vee }$ of highest weight ![]() $\{\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D713}}\}$, where we view
$\{\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D713}}\}$, where we view ![]() $\{\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D713}}\}$ as a Weyl orbit in the dual torus
$\{\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D713}}\}$ as a Weyl orbit in the dual torus ![]() $X^{\ast }(T^{\vee })$. The following lemma is immediate from the construction, and left to the reader.
$X^{\ast }(T^{\vee })$. The following lemma is immediate from the construction, and left to the reader.
Lemma 5.6. The ![]() $\prod _{\unicode[STIX]{x1D713}}G_{0}^{\vee }$-representation
$\prod _{\unicode[STIX]{x1D713}}G_{0}^{\vee }$-representation ![]() $\boxtimes _{\unicode[STIX]{x1D713}}V_{\{\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D713}}\}}$ uniquely extends to the
$\boxtimes _{\unicode[STIX]{x1D713}}V_{\{\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D713}}\}}$ uniquely extends to the ![]() $^{L}G_{E}=G^{\vee }\rtimes \unicode[STIX]{x1D6E4}_{E}$ representation
$^{L}G_{E}=G^{\vee }\rtimes \unicode[STIX]{x1D6E4}_{E}$ representation ![]() $V_{\{\unicode[STIX]{x1D707}\}}$ defined above. ◻
$V_{\{\unicode[STIX]{x1D707}\}}$ defined above. ◻
5.2.2 Constant terms commute with nearby cycles
We proceed with the notation as in § 5.1, and view the cocharacter ![]() $\unicode[STIX]{x1D712}$ as in (5.1). Combining Theorem 5.3 and Proposition 5.5 from the previous section, we have constructed a commutative diagram of
$\unicode[STIX]{x1D712}$ as in (5.1). Combining Theorem 5.3 and Proposition 5.5 from the previous section, we have constructed a commutative diagram of ![]() ${\mathcal{O}}_{F}$-ind-schemes
${\mathcal{O}}_{F}$-ind-schemes

The generic fiber of (
5.18) is (5.7), and the special fiber of (
5.18) is (5.8). The maps ![]() $\unicode[STIX]{x1D704}^{0,c}:\operatorname{Gr}_{{\mathcal{M}}}{\hookrightarrow}(\operatorname{Gr}_{{\mathcal{G}}})^{0,c}$ and
$\unicode[STIX]{x1D704}^{0,c}:\operatorname{Gr}_{{\mathcal{M}}}{\hookrightarrow}(\operatorname{Gr}_{{\mathcal{G}}})^{0,c}$ and ![]() $\unicode[STIX]{x1D704}^{\pm ,c}:\operatorname{Gr}_{{\mathcal{P}}^{\pm }}{\hookrightarrow}(\operatorname{Gr}_{{\mathcal{G}}})^{\pm ,c}$ are nilpotent thickenings by Proposition 5.5, and we may and do identify their derived categories of
$\unicode[STIX]{x1D704}^{\pm ,c}:\operatorname{Gr}_{{\mathcal{P}}^{\pm }}{\hookrightarrow}(\operatorname{Gr}_{{\mathcal{G}}})^{\pm ,c}$ are nilpotent thickenings by Proposition 5.5, and we may and do identify their derived categories of ![]() $\ell$-adic complexes. Then there is a natural isomorphism of functors
$\ell$-adic complexes. Then there is a natural isomorphism of functors ![]() $D_{c}^{b}(\operatorname{Gr}_{M})\rightarrow D_{c}^{b}({\mathcal{F}}\!\ell _{{\mathcal{M}}^{\flat }}\times _{S}\unicode[STIX]{x1D702})$,
$D_{c}^{b}(\operatorname{Gr}_{M})\rightarrow D_{c}^{b}({\mathcal{F}}\!\ell _{{\mathcal{M}}^{\flat }}\times _{S}\unicode[STIX]{x1D702})$,
We write ![]() $\unicode[STIX]{x1D6F9}_{{\mathcal{G}}}=\unicode[STIX]{x1D6F9}_{\operatorname{Gr}_{{\mathcal{G}}}}$ (respectively,
$\unicode[STIX]{x1D6F9}_{{\mathcal{G}}}=\unicode[STIX]{x1D6F9}_{\operatorname{Gr}_{{\mathcal{G}}}}$ (respectively, ![]() $\unicode[STIX]{x1D6F9}_{{\mathcal{M}}}=\unicode[STIX]{x1D6F9}_{\operatorname{Gr}_{{\mathcal{M}}}}$) in what follows. Since
$\unicode[STIX]{x1D6F9}_{{\mathcal{M}}}=\unicode[STIX]{x1D6F9}_{\operatorname{Gr}_{{\mathcal{M}}}}$) in what follows. Since ![]() $\unicode[STIX]{x1D704}^{0,c}$ and
$\unicode[STIX]{x1D704}^{0,c}$ and ![]() $\unicode[STIX]{x1D704}^{\pm ,c}$ are nilpotent thickenings, Proposition 5.5 gives us a decomposition
$\unicode[STIX]{x1D704}^{\pm ,c}$ are nilpotent thickenings, Proposition 5.5 gives us a decomposition
according to the choice of the parabolic ![]() $P^{\pm }$. We use the generic and the special fiber of diagram (
$P^{\pm }$. We use the generic and the special fiber of diagram (
) to define normalized geometric constant term functors as follows.
Definition 5.7. We define the functor ![]() $\operatorname{CT}_{M}:D_{c}^{b}(\operatorname{Gr}_{G})\rightarrow D_{c}^{b}(\operatorname{Gr}_{M})$ (respectively,
$\operatorname{CT}_{M}:D_{c}^{b}(\operatorname{Gr}_{G})\rightarrow D_{c}^{b}(\operatorname{Gr}_{M})$ (respectively, ![]() $\operatorname{CT}_{{\mathcal{M}}^{\flat }}:D_{c}^{b}({\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}\times _{S}\unicode[STIX]{x1D702})\rightarrow D_{c}^{b}({\mathcal{F}}\!\ell _{{\mathcal{M}}^{\flat }}\times _{S}\unicode[STIX]{x1D702})$) as the shifted pull-push functor
$\operatorname{CT}_{{\mathcal{M}}^{\flat }}:D_{c}^{b}({\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}\times _{S}\unicode[STIX]{x1D702})\rightarrow D_{c}^{b}({\mathcal{F}}\!\ell _{{\mathcal{M}}^{\flat }}\times _{S}\unicode[STIX]{x1D702})$) as the shifted pull-push functor
As in [Reference Haines and RicharzHR18, Theorem 6.1, (6.11)], the functorialities of nearby cycles give a transformation of functors ![]() $D_{c}^{b}(\operatorname{Gr}_{G})\rightarrow D_{c}^{b}({\mathcal{F}}\!\ell _{{\mathcal{M}}^{\flat }}\times _{S}\unicode[STIX]{x1D702})$ as
$D_{c}^{b}(\operatorname{Gr}_{G})\rightarrow D_{c}^{b}({\mathcal{F}}\!\ell _{{\mathcal{M}}^{\flat }}\times _{S}\unicode[STIX]{x1D702})$ as
Theorem 5.8. The transformation (5.20) is an isomorphism of functors ![]() $\operatorname{Sat}_{G}\rightarrow D_{c}^{b}({\mathcal{F}}\!\ell _{{\mathcal{M}}^{\flat }}\times _{S}\unicode[STIX]{x1D702})$. In particular, for every
$\operatorname{Sat}_{G}\rightarrow D_{c}^{b}({\mathcal{F}}\!\ell _{{\mathcal{M}}^{\flat }}\times _{S}\unicode[STIX]{x1D702})$. In particular, for every ![]() ${\mathcal{A}}\in \operatorname{Sat}_{G}$, the complex
${\mathcal{A}}\in \operatorname{Sat}_{G}$, the complex ![]() $\operatorname{CT}_{{\mathcal{M}}^{\flat }}\circ \unicode[STIX]{x1D6F9}_{{\mathcal{G}}}({\mathcal{A}})$ is naturally an object in the category
$\operatorname{CT}_{{\mathcal{M}}^{\flat }}\circ \unicode[STIX]{x1D6F9}_{{\mathcal{G}}}({\mathcal{A}})$ is naturally an object in the category ![]() $\operatorname{Perv}_{L^{+}{\mathcal{M}}^{\flat }}({\mathcal{F}}\!\ell _{{\mathcal{M}}^{\flat }}\times _{S}\unicode[STIX]{x1D702})$.
$\operatorname{Perv}_{L^{+}{\mathcal{M}}^{\flat }}({\mathcal{F}}\!\ell _{{\mathcal{M}}^{\flat }}\times _{S}\unicode[STIX]{x1D702})$.
Proof. Every object in ![]() $\operatorname{Sat}_{G}$ is
$\operatorname{Sat}_{G}$ is ![]() $\mathbb{G}_{m}$-equivariant. In view of Theorem 5.3 and (5.18), the extension of the method used in [Reference Haines and RicharzHR18, Theorem 6.5] to this more general situation is obvious. We do not repeat the arguments.◻
$\mathbb{G}_{m}$-equivariant. In view of Theorem 5.3 and (5.18), the extension of the method used in [Reference Haines and RicharzHR18, Theorem 6.5] to this more general situation is obvious. We do not repeat the arguments.◻
5.3 Constant terms for tori
We aim to make Theorem 5.8 more explicit in the special case where ![]() $M=T$ is a torus; cf. Theorem 5.12 and Corollary 5.13. We retain the notation of § 5.2.
$M=T$ is a torus; cf. Theorem 5.12 and Corollary 5.13. We retain the notation of § 5.2.
Let ![]() $\operatorname{Sat}_{{\mathcal{T}}^{\flat }}\subset \operatorname{Perv}_{L^{+}{\mathcal{T}}^{\flat }}({\mathcal{F}}\!\ell _{{\mathcal{T}}^{\flat }}\times _{S}\unicode[STIX]{x1D702})$ denote the semisimple full subcategory defined as in [Reference RicharzRic16a, Definition 5.10]. By [Reference RicharzRic16a, Theorem 5.11], the category
$\operatorname{Sat}_{{\mathcal{T}}^{\flat }}\subset \operatorname{Perv}_{L^{+}{\mathcal{T}}^{\flat }}({\mathcal{F}}\!\ell _{{\mathcal{T}}^{\flat }}\times _{S}\unicode[STIX]{x1D702})$ denote the semisimple full subcategory defined as in [Reference RicharzRic16a, Definition 5.10]. By [Reference RicharzRic16a, Theorem 5.11], the category ![]() $\operatorname{Sat}_{{\mathcal{T}}^{\flat }}$ has a Tannakian structure with tensor structure given by the convolution product, and with fiber functor given by the global sections functor
$\operatorname{Sat}_{{\mathcal{T}}^{\flat }}$ has a Tannakian structure with tensor structure given by the convolution product, and with fiber functor given by the global sections functor ![]() $\unicode[STIX]{x1D714}_{{\mathcal{T}}^{\flat }}:\operatorname{Sat}_{{\mathcal{T}}^{\flat }}\rightarrow \operatorname{Rep}_{\bar{\mathbb{Q}}_{\ell }}(\unicode[STIX]{x1D6E4}_{F})$,
$\unicode[STIX]{x1D714}_{{\mathcal{T}}^{\flat }}:\operatorname{Sat}_{{\mathcal{T}}^{\flat }}\rightarrow \operatorname{Rep}_{\bar{\mathbb{Q}}_{\ell }}(\unicode[STIX]{x1D6E4}_{F})$, ![]() ${\mathcal{A}}\mapsto \operatorname{H}^{0}({\mathcal{F}}\!\ell _{{\mathcal{T}}^{\flat },\bar{k}},{\mathcal{A}}_{\bar{k}})$. Note that
${\mathcal{A}}\mapsto \operatorname{H}^{0}({\mathcal{F}}\!\ell _{{\mathcal{T}}^{\flat },\bar{k}},{\mathcal{A}}_{\bar{k}})$. Note that ![]() ${\mathcal{F}}\!\ell _{{\mathcal{T}}^{\flat }}$ is ind-finite, and hence there is no higher cohomology and the convolution product is given by the usual tensor product. Further, for every
${\mathcal{F}}\!\ell _{{\mathcal{T}}^{\flat }}$ is ind-finite, and hence there is no higher cohomology and the convolution product is given by the usual tensor product. Further, for every ![]() ${\mathcal{A}}\in \operatorname{Sat}_{{\mathcal{T}}^{\flat }}$ the
${\mathcal{A}}\in \operatorname{Sat}_{{\mathcal{T}}^{\flat }}$ the ![]() $\unicode[STIX]{x1D6E4}_{F}$-action on
$\unicode[STIX]{x1D6E4}_{F}$-action on ![]() $\unicode[STIX]{x1D714}_{{\mathcal{T}}^{\flat }}({\mathcal{A}})$ factors by definition through a finite quotient.
$\unicode[STIX]{x1D714}_{{\mathcal{T}}^{\flat }}({\mathcal{A}})$ factors by definition through a finite quotient.
Lemma 5.9. The functor ![]() $\unicode[STIX]{x1D714}_{{\mathcal{T}}^{\flat }}$ can be upgraded to an equivalence of Tannakian categories
$\unicode[STIX]{x1D714}_{{\mathcal{T}}^{\flat }}$ can be upgraded to an equivalence of Tannakian categories
where ![]() $^{L}T_{r}=(T^{\vee })^{I_{F}}\rtimes \unicode[STIX]{x1D6E4}_{F}$ viewed as a pro-algebraic subgroup of
$^{L}T_{r}=(T^{\vee })^{I_{F}}\rtimes \unicode[STIX]{x1D6E4}_{F}$ viewed as a pro-algebraic subgroup of ![]() $^{L}T$. Here the subscript
$^{L}T$. Here the subscript ![]() $(\cdot )_{r}$ stands for ‘ramified’.
$(\cdot )_{r}$ stands for ‘ramified’.
Proof. By Lemma 4.17, there are ![]() $\operatorname{Gal}(\bar{k}/k)$-isomorphisms of abelian groups
$\operatorname{Gal}(\bar{k}/k)$-isomorphisms of abelian groups
where the equivariance of the last isomorphism holds by construction of the dual torus. This induces a ![]() $\operatorname{Gal}(\bar{k}/k)$-equivariant isomorphism of
$\operatorname{Gal}(\bar{k}/k)$-equivariant isomorphism of ![]() $\bar{k}$-schemes
$\bar{k}$-schemes
By definition, the objects in ![]() $\operatorname{Sat}_{{\mathcal{T}}^{\flat }}$ are finite-dimensional
$\operatorname{Sat}_{{\mathcal{T}}^{\flat }}$ are finite-dimensional ![]() $\bar{\mathbb{Q}}_{\ell }$-vector spaces on (5.21) (viewed as complexes concentrated in cohomological degree
$\bar{\mathbb{Q}}_{\ell }$-vector spaces on (5.21) (viewed as complexes concentrated in cohomological degree ![]() $0$) together with an action of
$0$) together with an action of ![]() $\unicode[STIX]{x1D6E4}_{F}$ which is equivariant over the base, and which factors through a finite quotient. The lemma follows from this description.◻
$\unicode[STIX]{x1D6E4}_{F}$ which is equivariant over the base, and which factors through a finite quotient. The lemma follows from this description.◻
The following proposition is the analogue of [Reference Pappas and ZhuPZ13, Theorems 10.18, 10.23] in the special case of a torus.
Proposition 5.10. There is a commutative diagram of Tannakian categories

where ![]() $\operatorname{res}$ denotes the restriction of representations along the inclusion
$\operatorname{res}$ denotes the restriction of representations along the inclusion ![]() $\text{}^{L}T_{r}\subset \text{}^{L}T$.
$\text{}^{L}T_{r}\subset \text{}^{L}T$.
Proof. This is a reformulation of Lemma 4.17 as follows. In view of (5.14) and Lemma 5.9 the diagram is well defined, and it suffices to prove the commutativity. Let ![]() $f:\operatorname{Gr}_{T}\rightarrow \operatorname{Spec}({\mathcal{O}}_{F})$ denote the structure map. Since
$f:\operatorname{Gr}_{T}\rightarrow \operatorname{Spec}({\mathcal{O}}_{F})$ denote the structure map. Since ![]() $f$ is ind-proper, there is a
$f$ is ind-proper, there is a ![]() $\unicode[STIX]{x1D6E4}_{F}$-equivariant isomorphism
$\unicode[STIX]{x1D6E4}_{F}$-equivariant isomorphism
and passing to the zeroth cohomology defines a ![]() $\unicode[STIX]{x1D6E4}_{F}$-equivariant isomorphism
$\unicode[STIX]{x1D6E4}_{F}$-equivariant isomorphism ![]() $\unicode[STIX]{x1D6FC}:\operatorname{res}\circ \,\unicode[STIX]{x1D714}_{T}\simeq \unicode[STIX]{x1D714}_{{\mathcal{T}}^{\flat }}\circ \unicode[STIX]{x1D6F9}_{{\mathcal{T}}}$. We have to show that
$\unicode[STIX]{x1D6FC}:\operatorname{res}\circ \,\unicode[STIX]{x1D714}_{T}\simeq \unicode[STIX]{x1D714}_{{\mathcal{T}}^{\flat }}\circ \unicode[STIX]{x1D6F9}_{{\mathcal{T}}}$. We have to show that ![]() $\unicode[STIX]{x1D6FC}$ is a map of
$\unicode[STIX]{x1D6FC}$ is a map of ![]() $\text{}^{L}T_{r}$-representations. As we already know the
$\text{}^{L}T_{r}$-representations. As we already know the ![]() $\unicode[STIX]{x1D6E4}_{F}$-equivariance, it is enough to check that
$\unicode[STIX]{x1D6E4}_{F}$-equivariance, it is enough to check that ![]() $\unicode[STIX]{x1D6FC}$ is a map of
$\unicode[STIX]{x1D6FC}$ is a map of ![]() $(T^{\vee })^{I_{F}}$-representations, that is, respects the grading by
$(T^{\vee })^{I_{F}}$-representations, that is, respects the grading by ![]() $X^{\ast }((T^{\vee })^{I_{F}})=X_{\ast }(T)_{I_{F}}$ on the underlying
$X^{\ast }((T^{\vee })^{I_{F}})=X_{\ast }(T)_{I_{F}}$ on the underlying ![]() $\bar{\mathbb{Q}}_{\ell }$-vector spaces. By (5.9), we have a decomposition into connected components
$\bar{\mathbb{Q}}_{\ell }$-vector spaces. By (5.9), we have a decomposition into connected components
where ![]() $(\operatorname{Gr}_{{\mathcal{T}},{\mathcal{O}}_{\breve{F}}})_{\bar{\unicode[STIX]{x1D708}}}\otimes \bar{k}=\{\bar{\unicode[STIX]{x1D708}}\}$ and
$(\operatorname{Gr}_{{\mathcal{T}},{\mathcal{O}}_{\breve{F}}})_{\bar{\unicode[STIX]{x1D708}}}\otimes \bar{k}=\{\bar{\unicode[STIX]{x1D708}}\}$ and ![]() $(\operatorname{Gr}_{{\mathcal{T}},{\mathcal{O}}_{\breve{F}}})_{\bar{\unicode[STIX]{x1D708}}}\otimes \bar{F}=\coprod _{\unicode[STIX]{x1D708}\mapsto \bar{\unicode[STIX]{x1D708}}}\{\unicode[STIX]{x1D708}\}$ on the underlying reduced subschemes; cf. also Lemma 4.17. The proposition follows from the fact that nearby cycles of a disjoint sum are computed as the sum of the single components.◻
$(\operatorname{Gr}_{{\mathcal{T}},{\mathcal{O}}_{\breve{F}}})_{\bar{\unicode[STIX]{x1D708}}}\otimes \bar{F}=\coprod _{\unicode[STIX]{x1D708}\mapsto \bar{\unicode[STIX]{x1D708}}}\{\unicode[STIX]{x1D708}\}$ on the underlying reduced subschemes; cf. also Lemma 4.17. The proposition follows from the fact that nearby cycles of a disjoint sum are computed as the sum of the single components.◻
Remark 5.11. It would be interesting to see whether the analogue of Proposition 5.10 for more general very special parahoric group schemes as in [Reference Pappas and ZhuPZ13, Theorems 10.18, 10.23] holds true.
Combining Proposition 5.10 with Theorem 5.8, we arrive as in [Reference Haines and RicharzHR18, § 6.2] at the following theorem which is the analogue of [Reference Arkhipov and BezrukavnikovAB09, Theorem 4] in our situation.
Theorem 5.12. (i) For every ![]() ${\mathcal{A}}\in \operatorname{Sat}_{G}$, one has
${\mathcal{A}}\in \operatorname{Sat}_{G}$, one has ![]() $\operatorname{CT}_{{\mathcal{T}}^{\flat }}\circ \unicode[STIX]{x1D6F9}_{{\mathcal{G}}}({\mathcal{A}})\in \operatorname{Sat}_{{\mathcal{T}}^{\flat }}$.
$\operatorname{CT}_{{\mathcal{T}}^{\flat }}\circ \unicode[STIX]{x1D6F9}_{{\mathcal{G}}}({\mathcal{A}})\in \operatorname{Sat}_{{\mathcal{T}}^{\flat }}$.
(ii) The functor ![]() $\operatorname{CT}_{{\mathcal{T}}^{\flat }}\,\circ \,\unicode[STIX]{x1D6F9}_{{\mathcal{G}}}:\operatorname{Sat}_{G}\rightarrow \operatorname{Sat}_{{\mathcal{T}}^{\flat }}$ admits a unique structure of a tensor functor together with an isomorphism
$\operatorname{CT}_{{\mathcal{T}}^{\flat }}\,\circ \,\unicode[STIX]{x1D6F9}_{{\mathcal{G}}}:\operatorname{Sat}_{G}\rightarrow \operatorname{Sat}_{{\mathcal{T}}^{\flat }}$ admits a unique structure of a tensor functor together with an isomorphism ![]() $\unicode[STIX]{x1D714}_{{\mathcal{T}}^{\flat }}\,\circ \,\operatorname{CT}_{{\mathcal{T}}^{\flat }}\,\circ \,\unicode[STIX]{x1D6F9}_{{\mathcal{G}}}\simeq \unicode[STIX]{x1D714}_{G}$. Under the geometric Satake equivalence, it corresponds to the restriction of representations
$\unicode[STIX]{x1D714}_{{\mathcal{T}}^{\flat }}\,\circ \,\operatorname{CT}_{{\mathcal{T}}^{\flat }}\,\circ \,\unicode[STIX]{x1D6F9}_{{\mathcal{G}}}\simeq \unicode[STIX]{x1D714}_{G}$. Under the geometric Satake equivalence, it corresponds to the restriction of representations ![]() $\operatorname{res}:\operatorname{Rep}_{\bar{\mathbb{Q}}_{\ell }}(\text{}^{L}G)\rightarrow \operatorname{Rep}_{\bar{\mathbb{Q}}_{\ell }}(\text{}^{L}T_{r})$ along the inclusion
$\operatorname{res}:\operatorname{Rep}_{\bar{\mathbb{Q}}_{\ell }}(\text{}^{L}G)\rightarrow \operatorname{Rep}_{\bar{\mathbb{Q}}_{\ell }}(\text{}^{L}T_{r})$ along the inclusion ![]() $\text{}^{L}T_{r}\subset \text{}^{L}G$.◻
$\text{}^{L}T_{r}\subset \text{}^{L}G$.◻
We now apply Theorem 5.12 in a special case. For more details, we refer to [Reference Haines and RicharzHR18, § 6.2.1] which is analogous. Assume ![]() $F=\breve{F}$, and hence that
$F=\breve{F}$, and hence that ![]() $K/F$ is totally ramified. Let
$K/F$ is totally ramified. Let ![]() $\unicode[STIX]{x1D712}:\mathbb{G}_{m,K}\rightarrow A_{0}\subset G_{0}$ be a regular cocharacter (i.e. its centralizer
$\unicode[STIX]{x1D712}:\mathbb{G}_{m,K}\rightarrow A_{0}\subset G_{0}$ be a regular cocharacter (i.e. its centralizer ![]() $M_{0}=T_{0}$ is a maximal torus), and let the parahoric
$M_{0}=T_{0}$ is a maximal torus), and let the parahoric ![]() ${\mathcal{O}}_{K}$-group scheme
${\mathcal{O}}_{K}$-group scheme ![]() ${\mathcal{G}}_{0}$ be an Iwahori. Hence,
${\mathcal{G}}_{0}$ be an Iwahori. Hence, ![]() ${\mathcal{G}}=\operatorname{Res}_{{\mathcal{O}}_{K}/{\mathcal{O}}_{F}}({\mathcal{G}}_{0})$ is an Iwahori
${\mathcal{G}}=\operatorname{Res}_{{\mathcal{O}}_{K}/{\mathcal{O}}_{F}}({\mathcal{G}}_{0})$ is an Iwahori ![]() ${\mathcal{O}}_{F}$-group scheme as well; cf. Proposition 4.7. There is a decomposition into connected components
${\mathcal{O}}_{F}$-group scheme as well; cf. Proposition 4.7. There is a decomposition into connected components
where ![]() $W=W(G,A,F)=W(G_{0},A_{0},K)$ is the Iwahori–Weyl group; cf. Lemma 4.3. Let
$W=W(G,A,F)=W(G_{0},A_{0},K)$ is the Iwahori–Weyl group; cf. Lemma 4.3. Let ![]() $\unicode[STIX]{x1D6EC}_{T}=T(F)/{\mathcal{T}}({\mathcal{O}}_{F})\subset W$ be the subset of ‘translation’ elements. Let
$\unicode[STIX]{x1D6EC}_{T}=T(F)/{\mathcal{T}}({\mathcal{O}}_{F})\subset W$ be the subset of ‘translation’ elements. Let ![]() $X_{\ast }(T)_{I_{F}}\simeq \unicode[STIX]{x1D6EC}_{T},\bar{\unicode[STIX]{x1D706}}\mapsto t^{\bar{\unicode[STIX]{x1D706}}}$ be the isomorphism given by the Kottwitz map. Let
$X_{\ast }(T)_{I_{F}}\simeq \unicode[STIX]{x1D6EC}_{T},\bar{\unicode[STIX]{x1D706}}\mapsto t^{\bar{\unicode[STIX]{x1D706}}}$ be the isomorphism given by the Kottwitz map. Let ![]() $2\unicode[STIX]{x1D70C}\in X^{\ast }(T)$ be the sum of the positive roots contained in the positive Borel
$2\unicode[STIX]{x1D70C}\in X^{\ast }(T)$ be the sum of the positive roots contained in the positive Borel ![]() $B^{+}$ of
$B^{+}$ of ![]() $G_{\bar{F}}$ determined by
$G_{\bar{F}}$ determined by ![]() $\unicode[STIX]{x1D712}$. Then the integer
$\unicode[STIX]{x1D712}$. Then the integer ![]() $\langle 2\unicode[STIX]{x1D70C},\bar{\unicode[STIX]{x1D706}}\rangle :=\langle 2\unicode[STIX]{x1D70C},\unicode[STIX]{x1D706}\rangle$ is well defined independent of the choice of
$\langle 2\unicode[STIX]{x1D70C},\bar{\unicode[STIX]{x1D706}}\rangle :=\langle 2\unicode[STIX]{x1D70C},\unicode[STIX]{x1D706}\rangle$ is well defined independent of the choice of ![]() $\unicode[STIX]{x1D706}\in X_{\ast }(T)$ with
$\unicode[STIX]{x1D706}\in X_{\ast }(T)$ with ![]() $\unicode[STIX]{x1D706}\mapsto \bar{\unicode[STIX]{x1D706}}$.
$\unicode[STIX]{x1D706}\mapsto \bar{\unicode[STIX]{x1D706}}$.
Corollary 5.13. Let ![]() $V\in \operatorname{Rep}_{\bar{\mathbb{Q}}_{\ell }}(G^{\vee })$, and denote by
$V\in \operatorname{Rep}_{\bar{\mathbb{Q}}_{\ell }}(G^{\vee })$, and denote by ![]() ${\mathcal{A}}_{V}\in \operatorname{Sat}_{G,\bar{F}}$ the object with
${\mathcal{A}}_{V}\in \operatorname{Sat}_{G,\bar{F}}$ the object with ![]() $\unicode[STIX]{x1D714}_{G,\bar{F}}({\mathcal{A}}_{V})=V$. As
$\unicode[STIX]{x1D714}_{G,\bar{F}}({\mathcal{A}}_{V})=V$. As ![]() $\bar{\mathbb{Q}}_{\ell }$-vector spaces, the compactly supported cohomology groups are given by the equality
$\bar{\mathbb{Q}}_{\ell }$-vector spaces, the compactly supported cohomology groups are given by the equality
where ![]() $V(\bar{\unicode[STIX]{x1D706}})$ is the
$V(\bar{\unicode[STIX]{x1D706}})$ is the ![]() $\bar{\unicode[STIX]{x1D706}}$-weight space in
$\bar{\unicode[STIX]{x1D706}}$-weight space in ![]() $V|_{(T^{\vee })^{I_{F}}}$.◻
$V|_{(T^{\vee })^{I_{F}}}$.◻
5.4 Special fibers of local models
Levin proved in [Reference LevinLev16, Theorem 2.3.5] the analogue of the following theorem in the special case where ![]() $p\nmid |\unicode[STIX]{x1D70B}_{1}(G_{\operatorname{der}})|$. As in [Reference Haines and RicharzHR18, §§ 6.2 and 6.3], Corollary 5.13 can be used to obtain this result on the special fibers of local models, with no hypothesis on
$p\nmid |\unicode[STIX]{x1D70B}_{1}(G_{\operatorname{der}})|$. As in [Reference Haines and RicharzHR18, §§ 6.2 and 6.3], Corollary 5.13 can be used to obtain this result on the special fibers of local models, with no hypothesis on ![]() $p$. We do not need this result for the proof of our main theorem, but include it for completeness: together with the corresponding result in [Reference Haines and RicharzHR18], we can conclude that the admissible sets
$p$. We do not need this result for the proof of our main theorem, but include it for completeness: together with the corresponding result in [Reference Haines and RicharzHR18], we can conclude that the admissible sets ![]() $\text{Adm}_{\{\unicode[STIX]{x1D707}\}}^{\mathbf{f}}$ parametrize the strata in the special fiber of
$\text{Adm}_{\{\unicode[STIX]{x1D707}\}}^{\mathbf{f}}$ parametrize the strata in the special fiber of ![]() $M_{\{\unicode[STIX]{x1D707}\}}$for all known local models
$M_{\{\unicode[STIX]{x1D707}\}}$for all known local models ![]() $M_{\{\unicode[STIX]{x1D707}\}}$.
$M_{\{\unicode[STIX]{x1D707}\}}$.
The following theorem is precisely the analogue of [Reference Haines and RicharzHR18, Theorem 6.12] in the current Weil restriction setting. We will assume for simplicity here that ![]() $K_{0}=F$; a similar result holds without this assumption. Since
$K_{0}=F$; a similar result holds without this assumption. Since ![]() $\breve{K}=K\breve{F}$, we may work over
$\breve{K}=K\breve{F}$, we may work over ![]() $F=\breve{F}$, so that
$F=\breve{F}$, so that ![]() $K=\breve{K}$ and
$K=\breve{K}$ and ![]() $k=\bar{k}$. The special fiber
$k=\bar{k}$. The special fiber ![]() $M_{\{\unicode[STIX]{x1D707}\},k}$ and the relevant Schubert varieties live in the affine flag variety attached to equal characteristic analogues
$M_{\{\unicode[STIX]{x1D707}\},k}$ and the relevant Schubert varieties live in the affine flag variety attached to equal characteristic analogues ![]() $G^{\flat }=G_{k(\!(u)\!)}^{\flat },A^{\flat }=S^{\flat }$ defined in (4.8), and by Lemmas 4.3 and 4.11 there is an identification of Iwahori–Weyl groups
$G^{\flat }=G_{k(\!(u)\!)}^{\flat },A^{\flat }=S^{\flat }$ defined in (4.8), and by Lemmas 4.3 and 4.11 there is an identification of Iwahori–Weyl groups
For ![]() $w\in W$, we define the Schubert variety
$w\in W$, we define the Schubert variety ![]() ${\mathcal{F}}l_{{\mathcal{G}}^{\flat }}^{{\leqslant}w}$ exactly as in [Reference Haines and RicharzHR18, § 3.2].
${\mathcal{F}}l_{{\mathcal{G}}^{\flat }}^{{\leqslant}w}$ exactly as in [Reference Haines and RicharzHR18, § 3.2].
Theorem 5.14. The smooth locus ![]() $(M_{\{\unicode[STIX]{x1D707}\}})^{\operatorname{sm}}$ is fiberwise dense in
$(M_{\{\unicode[STIX]{x1D707}\}})^{\operatorname{sm}}$ is fiberwise dense in ![]() $M_{\{\unicode[STIX]{x1D707}\}}$, and on reduced subschemes
$M_{\{\unicode[STIX]{x1D707}\}}$, and on reduced subschemes
In particular, the special fiber ![]() $M_{\{\unicode[STIX]{x1D707}\},k}$ is generically reduced.
$M_{\{\unicode[STIX]{x1D707}\},k}$ is generically reduced.
Proof. We may imitate the proof of [Reference Haines and RicharzHR18, Theorem 6.12]. First we follow the method of [Reference RicharzRic16b, Lemma 3.12] to prove ![]() $\text{Adm}_{\{\unicode[STIX]{x1D707}\}}^{\mathbf{f}}\subseteq \text{Supp}_{\{\unicode[STIX]{x1D707}\}}^{\mathbf{f}}:=\text{Supp}\,\unicode[STIX]{x1D6F9}_{{\mathcal{G}}_{\mathbf{f}}}(\text{IC}_{\{\unicode[STIX]{x1D707}\}})$, using our Lemma 4.17 in place of [Reference RicharzRic16b, Lemma 2.21].
$\text{Adm}_{\{\unicode[STIX]{x1D707}\}}^{\mathbf{f}}\subseteq \text{Supp}_{\{\unicode[STIX]{x1D707}\}}^{\mathbf{f}}:=\text{Supp}\,\unicode[STIX]{x1D6F9}_{{\mathcal{G}}_{\mathbf{f}}}(\text{IC}_{\{\unicode[STIX]{x1D707}\}})$, using our Lemma 4.17 in place of [Reference RicharzRic16b, Lemma 2.21].
Also as in [Reference Haines and RicharzHR18, Theorem 6.12], we reduce to the case where ![]() $\mathbf{f}=\mathbf{a}$. Then is it enough to show that if
$\mathbf{f}=\mathbf{a}$. Then is it enough to show that if ![]() $w\in \text{Supp}_{\{\unicode[STIX]{x1D707}\}}^{\mathbf{a}}$ is maximal, then
$w\in \text{Supp}_{\{\unicode[STIX]{x1D707}\}}^{\mathbf{a}}$ is maximal, then ![]() $w\in \text{Adm}_{\{\unicode[STIX]{x1D707}\}}^{\mathbf{a}}$. Now we choose a regular cocharacter
$w\in \text{Adm}_{\{\unicode[STIX]{x1D707}\}}^{\mathbf{a}}$. Now we choose a regular cocharacter ![]() $\unicode[STIX]{x1D712}:\mathbb{G}_{m,K}\rightarrow A_{0}\subset G_{0}$, and use Corollary 5.13 as follows. As
$\unicode[STIX]{x1D712}:\mathbb{G}_{m,K}\rightarrow A_{0}\subset G_{0}$, and use Corollary 5.13 as follows. As ![]() $\bar{\mathbb{Q}}_{\ell }$-vector spaces, we have
$\bar{\mathbb{Q}}_{\ell }$-vector spaces, we have
because ![]() ${\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}^{{\leqslant}w}\cap ({\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }})_{w}^{+}\subset {\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}^{w}$ is non-empty by [Reference Haines and RicharzHR18, Lemma 6.10], and because up to shift and twist
${\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}^{{\leqslant}w}\cap ({\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }})_{w}^{+}\subset {\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}^{w}$ is non-empty by [Reference Haines and RicharzHR18, Lemma 6.10], and because up to shift and twist ![]() $\unicode[STIX]{x1D6F9}_{{\mathcal{G}}}(\operatorname{IC}_{\{\unicode[STIX]{x1D707}\}})|_{{\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}^{w}}={\bar{\mathbb{Q}}_{\ell }}^{d}$ for some
$\unicode[STIX]{x1D6F9}_{{\mathcal{G}}}(\operatorname{IC}_{\{\unicode[STIX]{x1D707}\}})|_{{\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}^{w}}={\bar{\mathbb{Q}}_{\ell }}^{d}$ for some ![]() $d>0$ since
$d>0$ since ![]() $w\in \text{Supp}_{\{\unicode[STIX]{x1D707}\}}^{\mathbf{a}}$ is maximal. Thus, Corollary 5.13 applies to show
$w\in \text{Supp}_{\{\unicode[STIX]{x1D707}\}}^{\mathbf{a}}$ is maximal. Thus, Corollary 5.13 applies to show ![]() $w=t^{\bar{\unicode[STIX]{x1D706}}}$ for some
$w=t^{\bar{\unicode[STIX]{x1D706}}}$ for some ![]() $\bar{\unicode[STIX]{x1D706}}\in X_{\ast }(T)_{I_{F}}$ which is a weight in
$\bar{\unicode[STIX]{x1D706}}\in X_{\ast }(T)_{I_{F}}$ which is a weight in ![]() $V_{\{\unicode[STIX]{x1D707}\}}|_{(G^{\vee })^{I_{F}}}$. As in [Reference Haines and RicharzHR18, Theorem 6.12], we can conclude that
$V_{\{\unicode[STIX]{x1D707}\}}|_{(G^{\vee })^{I_{F}}}$. As in [Reference Haines and RicharzHR18, Theorem 6.12], we can conclude that ![]() $w=t^{\bar{\unicode[STIX]{x1D706}}}\in \text{Adm}_{\{\unicode[STIX]{x1D707}\}}^{\mathbf{a}}$ by citing [Reference HainesHai18, Theorem 4.2 and (7.11-12)].◻
$w=t^{\bar{\unicode[STIX]{x1D706}}}\in \text{Adm}_{\{\unicode[STIX]{x1D707}\}}^{\mathbf{a}}$ by citing [Reference HainesHai18, Theorem 4.2 and (7.11-12)].◻
5.5 Central sheaves
We recall some facts on central sheaves which will be used in what follows. We proceed with the notation as in § 4.4. Let ![]() $\operatorname{Perv}_{L^{+}{\mathcal{G}}^{\flat }}({\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}\times _{S}\unicode[STIX]{x1D702})$ be the category of
$\operatorname{Perv}_{L^{+}{\mathcal{G}}^{\flat }}({\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}\times _{S}\unicode[STIX]{x1D702})$ be the category of ![]() $L^{+}{\mathcal{G}}^{\flat }$-equivariant perverse sheaves compatible with a continuous Galois action; cf. [Reference Pappas and ZhuPZ13, Definition 10.3].
$L^{+}{\mathcal{G}}^{\flat }$-equivariant perverse sheaves compatible with a continuous Galois action; cf. [Reference Pappas and ZhuPZ13, Definition 10.3].
Recall that for objects in ![]() $\operatorname{Perv}_{L^{+}{\mathcal{G}}^{\flat }}({\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}\times _{S}\unicode[STIX]{x1D702})$ there is the convolution product defined by Lusztig [Reference LusztigLus83]. Consider the convolution diagram
$\operatorname{Perv}_{L^{+}{\mathcal{G}}^{\flat }}({\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}\times _{S}\unicode[STIX]{x1D702})$ there is the convolution product defined by Lusztig [Reference LusztigLus83]. Consider the convolution diagram
For ![]() ${\mathcal{A}},{\mathcal{B}}\in \operatorname{Perv}_{L^{+}{\mathcal{G}}^{\flat }}({\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}\times _{S}\unicode[STIX]{x1D702})$, let
${\mathcal{A}},{\mathcal{B}}\in \operatorname{Perv}_{L^{+}{\mathcal{G}}^{\flat }}({\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}\times _{S}\unicode[STIX]{x1D702})$, let ![]() ${\mathcal{A}}\,\tilde{\times }\,{\mathcal{B}}$ be the (unique up to canonical isomorphism) complex on
${\mathcal{A}}\,\tilde{\times }\,{\mathcal{B}}$ be the (unique up to canonical isomorphism) complex on ![]() ${\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}\,\tilde{\times }\,{\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}$ such that
${\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}\,\tilde{\times }\,{\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}$ such that ![]() $q^{\ast }({\mathcal{A}}\boxtimes {\mathcal{B}})\simeq p^{\ast }({\mathcal{A}}\,\tilde{\times }\,{\mathcal{B}})$. By definition
$q^{\ast }({\mathcal{A}}\boxtimes {\mathcal{B}})\simeq p^{\ast }({\mathcal{A}}\,\tilde{\times }\,{\mathcal{B}})$. By definition
In the following, we consider ![]() $P_{L^{+}{\mathcal{G}}^{\flat }}({\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }})$ as a full subcategory of
$P_{L^{+}{\mathcal{G}}^{\flat }}({\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }})$ as a full subcategory of ![]() $P_{L^{+}{\mathcal{G}}^{\flat }}({\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}\times _{S}\unicode[STIX]{x1D702})$.
$P_{L^{+}{\mathcal{G}}^{\flat }}({\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}\times _{S}\unicode[STIX]{x1D702})$.
Let ![]() $W=W(G,A,K)=W(G^{\flat },A^{\flat },F^{\flat })$ be the associated Iwahori–Weyl group; cf. Lemma 4.11. For each
$W=W(G,A,K)=W(G^{\flat },A^{\flat },F^{\flat })$ be the associated Iwahori–Weyl group; cf. Lemma 4.11. For each ![]() $w\in W$, the associated Schubert variety
$w\in W$, the associated Schubert variety ![]() ${\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}^{{\leqslant}w}\subset {\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}$ is defined over
${\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}^{{\leqslant}w}\subset {\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}$ is defined over ![]() $k_{F}$. Let
$k_{F}$. Let ![]() $j:{\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}^{w}{\hookrightarrow}{\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}^{{\leqslant}w}$, and denote by
$j:{\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}^{w}{\hookrightarrow}{\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}^{{\leqslant}w}$, and denote by ![]() $\operatorname{IC}_{w}=j_{!\ast }(\bar{\mathbb{Q}}_{\ell }[\dim ({\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}^{w})])$ the intersection complex. We have the functor of nearby cycles
$\operatorname{IC}_{w}=j_{!\ast }(\bar{\mathbb{Q}}_{\ell }[\dim ({\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}^{w})])$ the intersection complex. We have the functor of nearby cycles
The next theorem follows from [Reference Pappas and ZhuPZ13, Theorem 10.5] if ![]() $K/F$ is tamely ramified, and from [Reference LevinLev16, Theorem 5.2.10] in general.
$K/F$ is tamely ramified, and from [Reference LevinLev16, Theorem 5.2.10] in general.
Theorem 5.15 (Gaitsgory, Zhu, Pappas and Zhu, Levin).
For each ![]() ${\mathcal{A}}\in \operatorname{Perv}_{L_{z}^{+}G}(\operatorname{Gr}_{G})$, and
${\mathcal{A}}\in \operatorname{Perv}_{L_{z}^{+}G}(\operatorname{Gr}_{G})$, and ![]() $w\in W$, both convolutions
$w\in W$, both convolutions ![]() $\unicode[STIX]{x1D6F9}_{{\mathcal{G}}}({\mathcal{A}})\star \operatorname{IC}_{w}$,
$\unicode[STIX]{x1D6F9}_{{\mathcal{G}}}({\mathcal{A}})\star \operatorname{IC}_{w}$, ![]() $\operatorname{IC}_{w}\star \unicode[STIX]{x1D6F9}_{{\mathcal{G}}}({\mathcal{A}})$ are objects in
$\operatorname{IC}_{w}\star \unicode[STIX]{x1D6F9}_{{\mathcal{G}}}({\mathcal{A}})$ are objects in ![]() $P_{L^{+}{\mathcal{G}}^{\flat }}({\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}\times _{S}\unicode[STIX]{x1D702})$, and as such there is a canonical isomorphism
$P_{L^{+}{\mathcal{G}}^{\flat }}({\mathcal{F}}\!\ell _{{\mathcal{G}}^{\flat }}\times _{S}\unicode[STIX]{x1D702})$, and as such there is a canonical isomorphism
Proof. If ![]() ${\mathcal{A}}=\operatorname{IC}_{\{\unicode[STIX]{x1D707}\}}$ where
${\mathcal{A}}=\operatorname{IC}_{\{\unicode[STIX]{x1D707}\}}$ where ![]() $\{\unicode[STIX]{x1D707}\}$ is a class which is defined over
$\{\unicode[STIX]{x1D707}\}$ is a class which is defined over ![]() $F$, then the theorem is a special case of [Reference LevinLev16, Theorem 5.2.10] which follows the method of [Reference Pappas and ZhuPZ13, Theorem 10.5]. However, the proof given there works for general objects
$F$, then the theorem is a special case of [Reference LevinLev16, Theorem 5.2.10] which follows the method of [Reference Pappas and ZhuPZ13, Theorem 10.5]. However, the proof given there works for general objects ![]() ${\mathcal{A}}\in P_{L_{z}^{+}G}(\operatorname{Gr}_{G})$, and only uses that the support
${\mathcal{A}}\in P_{L_{z}^{+}G}(\operatorname{Gr}_{G})$, and only uses that the support ![]() $\operatorname{Supp}({\mathcal{A}})$ is finite-dimensional and defined over
$\operatorname{Supp}({\mathcal{A}})$ is finite-dimensional and defined over ![]() $F$. We do not repeat the arguments here.◻
$F$. We do not repeat the arguments here.◻
6 Test functions for Weil-restricted local models
6.1 Preliminaries
Recall that we let ![]() $G=\operatorname{Res}_{K/F}(G_{0})$ and
$G=\operatorname{Res}_{K/F}(G_{0})$ and ![]() $^{L}G=G^{\vee }\rtimes \unicode[STIX]{x1D6E4}_{F}$. Recall that
$^{L}G=G^{\vee }\rtimes \unicode[STIX]{x1D6E4}_{F}$. Recall that ![]() $\{\unicode[STIX]{x1D707}\}$ is defined over a field
$\{\unicode[STIX]{x1D707}\}$ is defined over a field ![]() $E$, a separable field extension of
$E$, a separable field extension of ![]() $F$ which is a possibly non-trivial extension of the reflex field, and that
$F$ which is a possibly non-trivial extension of the reflex field, and that ![]() $E_{0}/F$ is the maximal unramified subextension of
$E_{0}/F$ is the maximal unramified subextension of ![]() $E/F$. We have
$E/F$. We have ![]() $V_{\{\unicode[STIX]{x1D707}\}}\in \text{Rep}(\text{}^{L}G_{E})$ and
$V_{\{\unicode[STIX]{x1D707}\}}\in \text{Rep}(\text{}^{L}G_{E})$ and ![]() $I(V_{\{\unicode[STIX]{x1D707}\}})\in \text{Rep}(\text{}^{L}G_{E_{0}})$, where
$I(V_{\{\unicode[STIX]{x1D707}\}})\in \text{Rep}(\text{}^{L}G_{E_{0}})$, where ![]() $I(V):=\text{Ind}_{\text{}^{L}G_{E}}^{\text{}^{L}G_{E_{0}}}(V)$ for
$I(V):=\text{Ind}_{\text{}^{L}G_{E}}^{\text{}^{L}G_{E_{0}}}(V)$ for ![]() $V\in \text{Rep}(\text{}^{L}G_{E})$. Writing
$V\in \text{Rep}(\text{}^{L}G_{E})$. Writing ![]() ${\mathcal{G}}:={\mathcal{G}}_{\mathbf{f}}$ and
${\mathcal{G}}:={\mathcal{G}}_{\mathbf{f}}$ and ![]() ${\mathcal{G}}_{0}:={\mathcal{G}}_{\mathbf{f}_{\mathbf{0}}}$, the parahoric group scheme of
${\mathcal{G}}_{0}:={\mathcal{G}}_{\mathbf{f}_{\mathbf{0}}}$, the parahoric group scheme of ![]() $G=\operatorname{Res}_{K/F}(G_{0})$ is given by
$G=\operatorname{Res}_{K/F}(G_{0})$ is given by ![]() ${\mathcal{G}}=\operatorname{Res}_{{\mathcal{O}}_{K}/{\mathcal{O}}_{F}}({\mathcal{G}}_{0})$ by Corollary 4.8.
${\mathcal{G}}=\operatorname{Res}_{{\mathcal{O}}_{K}/{\mathcal{O}}_{F}}({\mathcal{G}}_{0})$ by Corollary 4.8.
Because the representation ![]() $I(V_{\{\unicode[STIX]{x1D707}\}})$ is ‘defined over
$I(V_{\{\unicode[STIX]{x1D707}\}})$ is ‘defined over ![]() $E_{0}$’ (not
$E_{0}$’ (not ![]() $F$), it is convenient to reformulate the test function conjecture after base-changing all geometric objects from
$F$), it is convenient to reformulate the test function conjecture after base-changing all geometric objects from ![]() ${\mathcal{O}}_{F}$ to
${\mathcal{O}}_{F}$ to ![]() ${\mathcal{O}}_{E_{0}}$. This ultimately allows us to reduce to the case where
${\mathcal{O}}_{E_{0}}$. This ultimately allows us to reduce to the case where ![]() $E_{0}=F$ (see the end of this subsection, and § 6.3 below). The next few lemmas are ingredients toward this reduction.
$E_{0}=F$ (see the end of this subsection, and § 6.3 below). The next few lemmas are ingredients toward this reduction.
Lemma 6.1. The following statements hold.
(i) We may write
 $K_{0}\otimes _{F}E=\prod _{j}E_{j}$ and
$K_{0}\otimes _{F}E=\prod _{j}E_{j}$ and  $K_{0}\otimes _{F}E_{0}=\prod _{j}E_{j,0}$, where
$K_{0}\otimes _{F}E_{0}=\prod _{j}E_{j,0}$, where  $E_{j}/K_{0}$ is a finite extension of fields with maximal unramified subextension
$E_{j}/K_{0}$ is a finite extension of fields with maximal unramified subextension  $E_{j,0}/K_{0}$, and where
$E_{j,0}/K_{0}$, and where  $j$ ranges over the finite index set of
$j$ ranges over the finite index set of  $\unicode[STIX]{x1D6E4}_{K_{0}}$-orbits of
$\unicode[STIX]{x1D6E4}_{K_{0}}$-orbits of  $F$-embeddings
$F$-embeddings  $E_{0}\rightarrow \bar{K}_{0}$, that is, over the set
$E_{0}\rightarrow \bar{K}_{0}$, that is, over the set  $\unicode[STIX]{x1D6E4}_{E_{0}}\backslash \unicode[STIX]{x1D6E4}_{F}/\unicode[STIX]{x1D6E4}_{K_{0}}$. Similarly, for rings of integers we have
$\unicode[STIX]{x1D6E4}_{E_{0}}\backslash \unicode[STIX]{x1D6E4}_{F}/\unicode[STIX]{x1D6E4}_{K_{0}}$. Similarly, for rings of integers we have  ${\mathcal{O}}_{K_{0}}\otimes _{{\mathcal{O}}_{F}}{\mathcal{O}}_{E_{0}}=\prod _{j}{\mathcal{O}}_{E_{j,0}}$. Furthermore, the inertia groups satisfy
${\mathcal{O}}_{K_{0}}\otimes _{{\mathcal{O}}_{F}}{\mathcal{O}}_{E_{0}}=\prod _{j}{\mathcal{O}}_{E_{j,0}}$. Furthermore, the inertia groups satisfy  $I_{E}=I_{E_{j}}\subset I_{E_{0}}=I_{E_{j,0}}$.
$I_{E}=I_{E_{j}}\subset I_{E_{0}}=I_{E_{j,0}}$.(ii)
 $K\otimes _{F}E_{0}=\prod _{j}KE_{j,0}$.
$K\otimes _{F}E_{0}=\prod _{j}KE_{j,0}$.(iii) The canonical map
 $\unicode[STIX]{x1D6E4}_{E_{0}}\backslash \unicode[STIX]{x1D6E4}_{F}/\unicode[STIX]{x1D6E4}_{K}\rightarrow \unicode[STIX]{x1D6E4}_{E_{0}}\backslash \unicode[STIX]{x1D6E4}_{F}/\unicode[STIX]{x1D6E4}_{K_{0}}$ is a bijection.
$\unicode[STIX]{x1D6E4}_{E_{0}}\backslash \unicode[STIX]{x1D6E4}_{F}/\unicode[STIX]{x1D6E4}_{K}\rightarrow \unicode[STIX]{x1D6E4}_{E_{0}}\backslash \unicode[STIX]{x1D6E4}_{F}/\unicode[STIX]{x1D6E4}_{K_{0}}$ is a bijection.
Proof. Write ![]() $K_{0}\otimes _{F}E_{0}=\prod _{j}E_{j,0}$ and
$K_{0}\otimes _{F}E_{0}=\prod _{j}E_{j,0}$ and ![]() $E=E_{0}[X]/(Q)$, where
$E=E_{0}[X]/(Q)$, where ![]() $Q$ is an Eisenstein polynomial over
$Q$ is an Eisenstein polynomial over ![]() ${\mathcal{O}}_{E_{0}}$. Each extension
${\mathcal{O}}_{E_{0}}$. Each extension ![]() $E_{j,0}/F$ is unramified, and so
$E_{j,0}/F$ is unramified, and so ![]() $Q$ remains an Eisenstein polynomial in the overfield
$Q$ remains an Eisenstein polynomial in the overfield ![]() $E_{j,0}$ of
$E_{j,0}$ of ![]() $E_{0}$. As
$E_{0}$. As ![]() $K_{0}\otimes _{F}E=\prod _{j}E_{j,0}[X]/(Q)=:\prod _{j}E_{j}$, it follows that
$K_{0}\otimes _{F}E=\prod _{j}E_{j,0}[X]/(Q)=:\prod _{j}E_{j}$, it follows that ![]() $E_{j}/E_{j,0}$ is totally ramified and that
$E_{j}/E_{j,0}$ is totally ramified and that ![]() $E_{j}=EE_{j,0}$, from which it follows that
$E_{j}=EE_{j,0}$, from which it follows that ![]() $E_{j}/E$ is unramified and hence
$E_{j}/E$ is unramified and hence ![]() $I_{E}=I_{E_{j}}$.
$I_{E}=I_{E_{j}}$.
Since ![]() $K/K_{0}$ is totally ramified,
$K/K_{0}$ is totally ramified, ![]() $K\otimes _{K_{0}}E_{j,0}=KE_{j,0}$, which implies (ii).
$K\otimes _{K_{0}}E_{j,0}=KE_{j,0}$, which implies (ii).
Abstractly ![]() $K_{0}\otimes _{F}E$ is a product of fields indexed by the set
$K_{0}\otimes _{F}E$ is a product of fields indexed by the set ![]() $\unicode[STIX]{x1D6E4}_{E}\backslash \unicode[STIX]{x1D6E4}_{F}/\unicode[STIX]{x1D6E4}_{K_{0}}$, and this set coincides with
$\unicode[STIX]{x1D6E4}_{E}\backslash \unicode[STIX]{x1D6E4}_{F}/\unicode[STIX]{x1D6E4}_{K_{0}}$, and this set coincides with ![]() $\unicode[STIX]{x1D6E4}_{E_{0}}\backslash \unicode[STIX]{x1D6E4}_{F}/\unicode[STIX]{x1D6E4}_{K_{0}}$ by the above argument. Interchanging the roles of
$\unicode[STIX]{x1D6E4}_{E_{0}}\backslash \unicode[STIX]{x1D6E4}_{F}/\unicode[STIX]{x1D6E4}_{K_{0}}$ by the above argument. Interchanging the roles of ![]() $E$ and
$E$ and ![]() $K$, we also get the bijection in (iii).◻
$K$, we also get the bijection in (iii).◻
Lemma 6.2. We have ![]() $G_{E_{0}}=\prod _{j}\operatorname{Res}_{KE_{j,0}/E_{0}}G_{0,KE_{j,0}}$ and
$G_{E_{0}}=\prod _{j}\operatorname{Res}_{KE_{j,0}/E_{0}}G_{0,KE_{j,0}}$ and ![]() ${\mathcal{G}}_{{\mathcal{O}}_{E_{0}}}=\prod _{j}\operatorname{Res}_{{\mathcal{O}}_{KE_{j,0}}/{\mathcal{O}}_{E_{0}}}{\mathcal{G}}_{0,{\mathcal{O}}_{KE_{j,0}}}$.
${\mathcal{G}}_{{\mathcal{O}}_{E_{0}}}=\prod _{j}\operatorname{Res}_{{\mathcal{O}}_{KE_{j,0}}/{\mathcal{O}}_{E_{0}}}{\mathcal{G}}_{0,{\mathcal{O}}_{KE_{j,0}}}$.
Proof. This is a consequence of the compatibility of Weil restriction of scalars with base change along the ring extension ![]() $F\rightarrow E_{0}$ (respectively,
$F\rightarrow E_{0}$ (respectively, ![]() ${\mathcal{O}}_{F}\rightarrow {\mathcal{O}}_{E_{0}}$) and Lemma 6.1(i) and (ii).◻
${\mathcal{O}}_{F}\rightarrow {\mathcal{O}}_{E_{0}}$) and Lemma 6.1(i) and (ii).◻
By [Reference BorelBor79, I.5] (cf. (5.17)) there are natural identifications
where we abbreviate ![]() $I_{K}^{F}:=I_{\unicode[STIX]{x1D6E4}_{K}}^{\unicode[STIX]{x1D6E4}_{F}}$ for the induction functor. Using Lemma 6.2, we obtain the following lemma.
$I_{K}^{F}:=I_{\unicode[STIX]{x1D6E4}_{K}}^{\unicode[STIX]{x1D6E4}_{F}}$ for the induction functor. Using Lemma 6.2, we obtain the following lemma.
Lemma 6.3. We have an identification
Let ![]() $X=\mathbb{A}_{{\mathcal{O}}_{K_{0}}}^{1}=\text{Spec}({\mathcal{O}}_{K_{0}}[u])$ and
$X=\mathbb{A}_{{\mathcal{O}}_{K_{0}}}^{1}=\text{Spec}({\mathcal{O}}_{K_{0}}[u])$ and ![]() $D=\{Q=0\}$, viewed as a relative effective Cartier divisor on
$D=\{Q=0\}$, viewed as a relative effective Cartier divisor on ![]() $X$ which is finite and flat over
$X$ which is finite and flat over ![]() $\text{Spec}({\mathcal{O}}_{F})$. The following lemma helps us to determine
$\text{Spec}({\mathcal{O}}_{F})$. The following lemma helps us to determine ![]() $\text{Gr}_{(X/{\mathcal{O}}_{F},\text{}\underline{{\mathcal{G}}}_{0},D)}\otimes _{{\mathcal{O}}_{F}}{\mathcal{O}}_{E_{0}}$; it handles the special case where
$\text{Gr}_{(X/{\mathcal{O}}_{F},\text{}\underline{{\mathcal{G}}}_{0},D)}\otimes _{{\mathcal{O}}_{F}}{\mathcal{O}}_{E_{0}}$; it handles the special case where ![]() $K/F$ is totally ramified.
$K/F$ is totally ramified.
Lemma 6.4. Assume ![]() $K_{0}=F$, let
$K_{0}=F$, let ![]() $K^{\prime }=E_{0}K$, which is the maximal unramified subextension of
$K^{\prime }=E_{0}K$, which is the maximal unramified subextension of ![]() $KE/K$, and let
$KE/K$, and let ![]() ${\mathcal{O}}_{K^{\prime }}={\mathcal{O}}_{K}\otimes _{{\mathcal{O}}_{F}}{\mathcal{O}}_{E_{0}}$ be its ring of integers. Since
${\mathcal{O}}_{K^{\prime }}={\mathcal{O}}_{K}\otimes _{{\mathcal{O}}_{F}}{\mathcal{O}}_{E_{0}}$ be its ring of integers. Since ![]() ${\mathcal{O}}_{K_{0}}={\mathcal{O}}_{F}$, note
${\mathcal{O}}_{K_{0}}={\mathcal{O}}_{F}$, note ![]() $\text{}\underline{{\mathcal{G}}}_{0}$ is defined over
$\text{}\underline{{\mathcal{G}}}_{0}$ is defined over ![]() ${\mathcal{O}}_{F}[u]$. Then we have identifications:
${\mathcal{O}}_{F}[u]$. Then we have identifications:
(i)
 $\text{}\underline{{\mathcal{G}}}_{0}\otimes _{{\mathcal{O}}_{F}[u]}{\mathcal{O}}_{E_{0}}[u]=\text{}\underline{{\mathcal{G}}_{{\mathcal{O}}_{K^{\prime }}}}_{0}=:\text{}\underline{{\mathcal{G}}}_{0,{\mathcal{O}}_{E_{0}}}$;
$\text{}\underline{{\mathcal{G}}}_{0}\otimes _{{\mathcal{O}}_{F}[u]}{\mathcal{O}}_{E_{0}}[u]=\text{}\underline{{\mathcal{G}}_{{\mathcal{O}}_{K^{\prime }}}}_{0}=:\text{}\underline{{\mathcal{G}}}_{0,{\mathcal{O}}_{E_{0}}}$;(ii)
 $(L_{D}\text{}\underline{{\mathcal{G}}}_{0})\otimes _{{\mathcal{O}}_{F}}{\mathcal{O}}_{E_{0}}=L_{D_{{\mathcal{O}}_{E_{0}}}}\text{}\underline{{\mathcal{G}}}_{0,{\mathcal{O}}_{E_{0}}}$ (and similarly for
$(L_{D}\text{}\underline{{\mathcal{G}}}_{0})\otimes _{{\mathcal{O}}_{F}}{\mathcal{O}}_{E_{0}}=L_{D_{{\mathcal{O}}_{E_{0}}}}\text{}\underline{{\mathcal{G}}}_{0,{\mathcal{O}}_{E_{0}}}$ (and similarly for  $L_{D}^{+}$);
$L_{D}^{+}$);(iii)
 $\text{Gr}_{(X,\text{}\underline{{\mathcal{G}}}_{0},D)}\otimes _{{\mathcal{O}}_{F}}{\mathcal{O}}_{E_{0}}=\text{Gr}_{(X_{{\mathcal{O}}_{E_{0}}},\,\text{}\underline{{\mathcal{G}}}_{0,{\mathcal{O}}_{E_{0}}},\,D_{{\mathcal{O}}_{E_{0}}})}$.
$\text{Gr}_{(X,\text{}\underline{{\mathcal{G}}}_{0},D)}\otimes _{{\mathcal{O}}_{F}}{\mathcal{O}}_{E_{0}}=\text{Gr}_{(X_{{\mathcal{O}}_{E_{0}}},\,\text{}\underline{{\mathcal{G}}}_{0,{\mathcal{O}}_{E_{0}}},\,D_{{\mathcal{O}}_{E_{0}}})}$.
Proof. Part (i) follows because the formation of ![]() $\text{}\underline{G}_{0}$ and
$\text{}\underline{G}_{0}$ and ![]() $\text{}\underline{{\mathcal{G}}}_{0}$ as in [Reference LevinLev13, Proposition 3.1.2 and Theorem 3.3.3] is compatible with change of base
$\text{}\underline{{\mathcal{G}}}_{0}$ as in [Reference LevinLev13, Proposition 3.1.2 and Theorem 3.3.3] is compatible with change of base ![]() ${\mathcal{O}}_{F}[u^{\pm }]\rightarrow {\mathcal{O}}_{E_{0}}[u^{\pm }]$ (respectively,
${\mathcal{O}}_{F}[u^{\pm }]\rightarrow {\mathcal{O}}_{E_{0}}[u^{\pm }]$ (respectively, ![]() ${\mathcal{O}}_{F}[u]\rightarrow {\mathcal{O}}_{E_{0}}[u]$); see also Example 4.14. Part (ii) follows formally from part (i) and the identities
${\mathcal{O}}_{F}[u]\rightarrow {\mathcal{O}}_{E_{0}}[u]$); see also Example 4.14. Part (ii) follows formally from part (i) and the identities ![]() $R[\![D_{{\mathcal{O}}_{E_{0}}}]\!]=\mathop{\varprojlim }\nolimits_{n}R[u]/Q^{n}=R[\![D]\!]$ (respectively,
$R[\![D_{{\mathcal{O}}_{E_{0}}}]\!]=\mathop{\varprojlim }\nolimits_{n}R[u]/Q^{n}=R[\![D]\!]$ (respectively, ![]() $R((D_{{\mathcal{O}}_{E_{0}}}))=(\mathop{\varprojlim }\nolimits_{n}R[u]/Q^{n})[1/Q]=R((D))$) for
$R((D_{{\mathcal{O}}_{E_{0}}}))=(\mathop{\varprojlim }\nolimits_{n}R[u]/Q^{n})[1/Q]=R((D))$) for ![]() ${\mathcal{O}}_{E_{0}}$-algebras
${\mathcal{O}}_{E_{0}}$-algebras ![]() $R$. Part (iii) follows from part (ii) and Lemma 3.4(ii).◻
$R$. Part (iii) follows from part (ii) and Lemma 3.4(ii).◻
Proposition 6.5. In the notation above, there are canonical isomorphisms
 $$\begin{eqnarray}\displaystyle \text{Gr}_{(X/{\mathcal{O}}_{F},\text{}\underline{{\mathcal{G}}}_{0},D)}\otimes _{{\mathcal{O}}_{F}}{\mathcal{O}}_{E_{0}} & = & \displaystyle \mathop{\prod }_{j}\operatorname{Res}_{{\mathcal{O}}_{E_{j,0}}/{\mathcal{O}}_{E_{0}}}(\text{Gr}_{(X/{\mathcal{O}}_{K_{0}},\text{}\underline{{\mathcal{G}}}_{0},D)}\otimes _{{\mathcal{O}}_{K_{0}}}{\mathcal{O}}_{E_{j,0}})\nonumber\\ \displaystyle & = & \displaystyle \mathop{\prod }_{j}\operatorname{Res}_{{\mathcal{O}}_{E_{j,0}}/{\mathcal{O}}_{E_{0}}}(\text{Gr}_{(X_{{\mathcal{O}}_{E_{j,0}}}/{\mathcal{O}}_{E_{j,0}},\,\,\text{}\underline{{\mathcal{G}}}_{0,{\mathcal{O}}_{E_{j,0}}}\!\!,\,D\otimes _{{\mathcal{O}}_{K_{0}}}{\mathcal{O}}_{E_{j,0}})}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Gr}_{(X/{\mathcal{O}}_{F},\text{}\underline{{\mathcal{G}}}_{0},D)}\otimes _{{\mathcal{O}}_{F}}{\mathcal{O}}_{E_{0}} & = & \displaystyle \mathop{\prod }_{j}\operatorname{Res}_{{\mathcal{O}}_{E_{j,0}}/{\mathcal{O}}_{E_{0}}}(\text{Gr}_{(X/{\mathcal{O}}_{K_{0}},\text{}\underline{{\mathcal{G}}}_{0},D)}\otimes _{{\mathcal{O}}_{K_{0}}}{\mathcal{O}}_{E_{j,0}})\nonumber\\ \displaystyle & = & \displaystyle \mathop{\prod }_{j}\operatorname{Res}_{{\mathcal{O}}_{E_{j,0}}/{\mathcal{O}}_{E_{0}}}(\text{Gr}_{(X_{{\mathcal{O}}_{E_{j,0}}}/{\mathcal{O}}_{E_{j,0}},\,\,\text{}\underline{{\mathcal{G}}}_{0,{\mathcal{O}}_{E_{j,0}}}\!\!,\,D\otimes _{{\mathcal{O}}_{K_{0}}}{\mathcal{O}}_{E_{j,0}})}).\nonumber\end{eqnarray}$$Proof. The first equality is proved using Lemma 3.7. The second equality follows by applying Lemma 6.4(iii) to each factor indexed by ![]() $j$, replacing the data
$j$, replacing the data ![]() $(F,K,E_{0})$ with
$(F,K,E_{0})$ with ![]() $(K_{0},K,E_{j,0})$.◻
$(K_{0},K,E_{j,0})$.◻
Recall that ![]() $\text{}\underline{{\mathcal{G}}}_{0}$ is defined using the following data: the totally ramified extension
$\text{}\underline{{\mathcal{G}}}_{0}$ is defined using the following data: the totally ramified extension ![]() $K/K_{0}$, the
$K/K_{0}$, the ![]() $K_{0}$-group
$K_{0}$-group ![]() $G_{0}$, the facet
$G_{0}$, the facet ![]() $\mathbf{f}_{0}$, and the choice of spreading
$\mathbf{f}_{0}$, and the choice of spreading ![]() $\text{}\underline{G}_{0}/{\mathcal{O}}_{K_{0}}[u^{\pm }]$; and the generic fiber of
$\text{}\underline{G}_{0}/{\mathcal{O}}_{K_{0}}[u^{\pm }]$; and the generic fiber of ![]() $\text{Gr}_{(X/{\mathcal{O}}_{F},\text{}\underline{{\mathcal{G}}},D)}$ is the affine Grassmannian for
$\text{Gr}_{(X/{\mathcal{O}}_{F},\text{}\underline{{\mathcal{G}}},D)}$ is the affine Grassmannian for ![]() $G=\operatorname{Res}_{K/F}G_{0}$, by Proposition 4.15. By contrast
$G=\operatorname{Res}_{K/F}G_{0}$, by Proposition 4.15. By contrast ![]() $\text{}\underline{{\mathcal{G}}}_{0,{\mathcal{O}}_{E_{j,0}}}$ is defined from the data: the totally ramified extension
$\text{}\underline{{\mathcal{G}}}_{0,{\mathcal{O}}_{E_{j,0}}}$ is defined from the data: the totally ramified extension ![]() $KE_{j,0}/E_{j,0}$, the
$KE_{j,0}/E_{j,0}$, the ![]() $E_{j,0}$-group
$E_{j,0}$-group ![]() $G_{0,E_{j,0}}$, the facet
$G_{0,E_{j,0}}$, the facet ![]() $\mathbf{f}_{0}$, and the spreading
$\mathbf{f}_{0}$, and the spreading ![]() $\text{}\underline{G}_{0,{\mathcal{O}}_{E_{j,0}}[u^{\pm }]}$; and the generic fiber of
$\text{}\underline{G}_{0,{\mathcal{O}}_{E_{j,0}}[u^{\pm }]}$; and the generic fiber of ![]() $\text{Gr}_{(X_{{\mathcal{O}}_{E_{j,0}}}/{\mathcal{O}}_{E_{j,0}},\,\,\text{}\underline{{\mathcal{G}}}_{0,{\mathcal{O}}_{E_{j,0}}}\!\!,\,D\otimes _{{\mathcal{O}}_{K_{0}}}{\mathcal{O}}_{E_{j,0}})}$ is the affine Grassmannian for
$\text{Gr}_{(X_{{\mathcal{O}}_{E_{j,0}}}/{\mathcal{O}}_{E_{j,0}},\,\,\text{}\underline{{\mathcal{G}}}_{0,{\mathcal{O}}_{E_{j,0}}}\!\!,\,D\otimes _{{\mathcal{O}}_{K_{0}}}{\mathcal{O}}_{E_{j,0}})}$ is the affine Grassmannian for ![]() $\operatorname{Res}_{KE_{j,0}/E_{j,0}}G_{0,KE_{j,0}}$. So when restricting attention to the part inside the Weil restriction in the
$\operatorname{Res}_{KE_{j,0}/E_{j,0}}G_{0,KE_{j,0}}$. So when restricting attention to the part inside the Weil restriction in the ![]() $j$th factor, we are in the situation ‘
$j$th factor, we are in the situation ‘![]() $F=E_{0}$’ and ‘
$F=E_{0}$’ and ‘![]() $K_{0}=F$’. Our next goal is to show how we may effectively reduce our problem to the study of each
$K_{0}=F$’. Our next goal is to show how we may effectively reduce our problem to the study of each ![]() $\text{Gr}_{(X_{{\mathcal{O}}_{E_{j,0}}}/{\mathcal{O}}_{E_{j,0}},\,\,\text{}\underline{{\mathcal{G}}}_{0,{\mathcal{O}}_{E_{j,0}}}\!\!,\,D\otimes _{{\mathcal{O}}_{K_{0}}}{\mathcal{O}}_{E_{j,0}})}$ separately.
$\text{Gr}_{(X_{{\mathcal{O}}_{E_{j,0}}}/{\mathcal{O}}_{E_{j,0}},\,\,\text{}\underline{{\mathcal{G}}}_{0,{\mathcal{O}}_{E_{j,0}}}\!\!,\,D\otimes _{{\mathcal{O}}_{K_{0}}}{\mathcal{O}}_{E_{j,0}})}$ separately.
6.2 Statement of theorem
Given an irreducible algebraic representation ![]() $V$ of
$V$ of ![]() $\text{}^{L}G$, we define the parity
$\text{}^{L}G$, we define the parity ![]() $d_{V}\in \mathbb{Z}/2\mathbb{Z}$ as in [Reference Haines and RicharzHR18, (7.11)]. Then we define the function
$d_{V}\in \mathbb{Z}/2\mathbb{Z}$ as in [Reference Haines and RicharzHR18, (7.11)]. Then we define the function ![]() $\unicode[STIX]{x1D70F}_{{\mathcal{G}},V}^{\text{ss}}$ on
$\unicode[STIX]{x1D70F}_{{\mathcal{G}},V}^{\text{ss}}$ on ![]() $\text{Gr}_{{\mathcal{G}}}(k_{F})$ by the identity
$\text{Gr}_{{\mathcal{G}}}(k_{F})$ by the identity
We extend this definition to general representations ![]() $V$ of
$V$ of ![]() $\text{}^{L}G$ (not necessarily irreducible) by linearity. By Theorem 5.15, Lemma 4.12, and Corollary 4.9, we may view
$\text{}^{L}G$ (not necessarily irreducible) by linearity. By Theorem 5.15, Lemma 4.12, and Corollary 4.9, we may view ![]() $\unicode[STIX]{x1D70F}_{{\mathcal{G}},V}^{\text{ss}}$ as an element in the Hecke algebra
$\unicode[STIX]{x1D70F}_{{\mathcal{G}},V}^{\text{ss}}$ as an element in the Hecke algebra ![]() ${\mathcal{Z}}(G(F),{\mathcal{G}}({\mathcal{O}}_{F}))$. Given any algebraic representation
${\mathcal{Z}}(G(F),{\mathcal{G}}({\mathcal{O}}_{F}))$. Given any algebraic representation ![]() $V$, we also define
$V$, we also define ![]() $z_{{\mathcal{G}},V}^{\text{ss}}\in {\mathcal{Z}}(G(F),{\mathcal{G}}({\mathcal{O}}_{F}))$ to be the unique function such that, if
$z_{{\mathcal{G}},V}^{\text{ss}}\in {\mathcal{Z}}(G(F),{\mathcal{G}}({\mathcal{O}}_{F}))$ to be the unique function such that, if ![]() $\unicode[STIX]{x1D70B}$ is an irreducible smooth representation of
$\unicode[STIX]{x1D70B}$ is an irreducible smooth representation of ![]() $G(F)$ on a
$G(F)$ on a ![]() $\bar{\mathbb{Q}}_{\ell }$-vector space such that
$\bar{\mathbb{Q}}_{\ell }$-vector space such that ![]() $\unicode[STIX]{x1D70B}^{{\mathcal{G}}({\mathcal{O}}_{F})}\neq 0$, then
$\unicode[STIX]{x1D70B}^{{\mathcal{G}}({\mathcal{O}}_{F})}\neq 0$, then ![]() $z_{{\mathcal{G}},V}^{\text{ss}}$ acts on
$z_{{\mathcal{G}},V}^{\text{ss}}$ acts on ![]() $\unicode[STIX]{x1D70B}^{{\mathcal{G}}({\mathcal{O}}_{F})}$ by the scalar
$\unicode[STIX]{x1D70B}^{{\mathcal{G}}({\mathcal{O}}_{F})}$ by the scalar ![]() $\text{tr}(s(\unicode[STIX]{x1D70B})\mid V^{1\rtimes I_{F}})$, where
$\text{tr}(s(\unicode[STIX]{x1D70B})\mid V^{1\rtimes I_{F}})$, where ![]() $s(\unicode[STIX]{x1D70B})$ is the Satake parameter of
$s(\unicode[STIX]{x1D70B})$ is the Satake parameter of ![]() $\unicode[STIX]{x1D70B}$ as defined in [Reference HainesHai15].
$\unicode[STIX]{x1D70B}$ as defined in [Reference HainesHai15].
Theorem 6.6. For ![]() $(G,{\mathcal{G}},V)$ as above, we have the equality
$(G,{\mathcal{G}},V)$ as above, we have the equality ![]() $\unicode[STIX]{x1D70F}_{{\mathcal{G}},V}^{\text{ss}}=z_{{\mathcal{G}},V}^{\text{ss}}$.
$\unicode[STIX]{x1D70F}_{{\mathcal{G}},V}^{\text{ss}}=z_{{\mathcal{G}},V}^{\text{ss}}$.
Recall that taking inertia invariants does not commute in general with forming tensor products of representations. Because of the products and unramified Weil restrictions appearing in Lemma 6.3 and Proposition 6.5, it is problematic to reduce our main theorem to Theorem 6.6. Instead we need a variant of Theorem 6.6without semisimplifying the trace, for a fixed lift ![]() $\unicode[STIX]{x1D6F7}$of geometric Frobenius. This is formulated as follows. For each fixed lift
$\unicode[STIX]{x1D6F7}$of geometric Frobenius. This is formulated as follows. For each fixed lift ![]() $\unicode[STIX]{x1D6F7}$, we define a function
$\unicode[STIX]{x1D6F7}$, we define a function ![]() $z_{{\mathcal{G}},V}^{\unicode[STIX]{x1D6F7}}\in {\mathcal{Z}}(G(F),{\mathcal{G}}({\mathcal{O}}_{F}))$; similarly, we define a function
$z_{{\mathcal{G}},V}^{\unicode[STIX]{x1D6F7}}\in {\mathcal{Z}}(G(F),{\mathcal{G}}({\mathcal{O}}_{F}))$; similarly, we define a function ![]() $\unicode[STIX]{x1D70F}_{{\mathcal{G}},V}^{\unicode[STIX]{x1D6F7}}$ on
$\unicode[STIX]{x1D70F}_{{\mathcal{G}},V}^{\unicode[STIX]{x1D6F7}}$ on ![]() $\text{Gr}_{{\mathcal{G}}}(k_{F})$ (see Appendix A). By the same arguments due to Gaitsgory, Pappas and Zhu, and Levin cited above, this function can be viewed as an element of
$\text{Gr}_{{\mathcal{G}}}(k_{F})$ (see Appendix A). By the same arguments due to Gaitsgory, Pappas and Zhu, and Levin cited above, this function can be viewed as an element of ![]() ${\mathcal{Z}}(G(F),{\mathcal{G}}({\mathcal{O}}_{F}))$.
${\mathcal{Z}}(G(F),{\mathcal{G}}({\mathcal{O}}_{F}))$.
Theorem 6.7. For ![]() $(G,{\mathcal{G}},V)$ as above and for every fixed choice of lift
$(G,{\mathcal{G}},V)$ as above and for every fixed choice of lift ![]() $\unicode[STIX]{x1D6F7}$ of geometric Frobenius, we have the equality
$\unicode[STIX]{x1D6F7}$ of geometric Frobenius, we have the equality ![]() $\unicode[STIX]{x1D70F}_{{\mathcal{G}},V}^{\unicode[STIX]{x1D6F7}}=z_{{\mathcal{G}},V}^{\unicode[STIX]{x1D6F7}}$.
$\unicode[STIX]{x1D70F}_{{\mathcal{G}},V}^{\unicode[STIX]{x1D6F7}}=z_{{\mathcal{G}},V}^{\unicode[STIX]{x1D6F7}}$.
In fact we will prove Theorem 6.7, and we deduce Theorem 6.6 immediately by Lemma A.1. However, we will not require Theorem 6.6, but only Theorem 6.7, to prove our main theorem.
6.3 Reducing the main theorem to Theorem 6.7
Following the method of [Reference Haines and RicharzHR18, 7.3], we show that the main theorem is a consequence of Theorem 6.7 as follows. Recall that ![]() $V_{\{\unicode[STIX]{x1D707}\}}$ is a representation of
$V_{\{\unicode[STIX]{x1D707}\}}$ is a representation of ![]() $\text{}^{L}G_{E}=G^{\vee }\rtimes \unicode[STIX]{x1D6E4}_{E}$, the
$\text{}^{L}G_{E}=G^{\vee }\rtimes \unicode[STIX]{x1D6E4}_{E}$, the ![]() $L$-group of
$L$-group of ![]() $\operatorname{Res}_{K/F}(G_{0})\,\otimes _{F}E$, and that
$\operatorname{Res}_{K/F}(G_{0})\,\otimes _{F}E$, and that ![]() $I(V_{\{\unicode[STIX]{x1D707}\}})$ is a representation of
$I(V_{\{\unicode[STIX]{x1D707}\}})$ is a representation of ![]() $\text{}^{L}G_{E_{0}}=G^{\vee }\rtimes \unicode[STIX]{x1D6E4}_{E_{0}}$, the
$\text{}^{L}G_{E_{0}}=G^{\vee }\rtimes \unicode[STIX]{x1D6E4}_{E_{0}}$, the ![]() $L$-group of
$L$-group of ![]() $\operatorname{Res}_{K/F}(G_{0})\,\otimes _{F}E_{0}$. Arguing as in [Reference Haines and RicharzHR18, § 7.3], up to the sign
$\operatorname{Res}_{K/F}(G_{0})\,\otimes _{F}E_{0}$. Arguing as in [Reference Haines and RicharzHR18, § 7.3], up to the sign ![]() $(-1)^{d_{\unicode[STIX]{x1D707}}}$ the function
$(-1)^{d_{\unicode[STIX]{x1D707}}}$ the function ![]() $\unicode[STIX]{x1D70F}_{\{\unicode[STIX]{x1D707}\}}^{\text{ss}}$ is identified with the function in
$\unicode[STIX]{x1D70F}_{\{\unicode[STIX]{x1D707}\}}^{\text{ss}}$ is identified with the function in ![]() ${\mathcal{Z}}(G(E_{0}),{\mathcal{G}}({\mathcal{O}}_{E_{0}}))$
${\mathcal{Z}}(G(E_{0}),{\mathcal{G}}({\mathcal{O}}_{E_{0}}))$
Also, ![]() $z_{\{\unicode[STIX]{x1D707}\}}^{\text{ss}}$ acts on
$z_{\{\unicode[STIX]{x1D707}\}}^{\text{ss}}$ acts on ![]() $\unicode[STIX]{x1D70B}^{{\mathcal{G}}({\mathcal{O}}_{E_{0}})}\neq 0$ by
$\unicode[STIX]{x1D70B}^{{\mathcal{G}}({\mathcal{O}}_{E_{0}})}\neq 0$ by
Therefore, to prove the main theorem, it suffices to prove ![]() $\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{{\mathcal{O}}_{E_{0}}},I(V_{\{\unicode[STIX]{x1D707}\}})}^{\text{ss}}=z_{{\mathcal{G}}_{{\mathcal{O}}_{E_{0}}},I(V_{\{\unicode[STIX]{x1D707}\}})}^{\text{ss}}$. All irreducible constituents of
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{{\mathcal{O}}_{E_{0}}},I(V_{\{\unicode[STIX]{x1D707}\}})}^{\text{ss}}=z_{{\mathcal{G}}_{{\mathcal{O}}_{E_{0}}},I(V_{\{\unicode[STIX]{x1D707}\}})}^{\text{ss}}$. All irreducible constituents of ![]() $I(V_{\{\unicode[STIX]{x1D707}\}})$ have the same parity, so we may replace
$I(V_{\{\unicode[STIX]{x1D707}\}})$ have the same parity, so we may replace ![]() $I(V_{\{\unicode[STIX]{x1D707}\}})$ with an arbitrary irreducible representation
$I(V_{\{\unicode[STIX]{x1D707}\}})$ with an arbitrary irreducible representation ![]() $V$ of
$V$ of ![]() $\text{}^{L}G_{E_{0}}$. By Lemma A.1, it suffices to prove
$\text{}^{L}G_{E_{0}}$. By Lemma A.1, it suffices to prove
for every fixed lift ![]() $\unicode[STIX]{x1D6F7}_{E_{0}}$ of geometric Frobenius.
$\unicode[STIX]{x1D6F7}_{E_{0}}$ of geometric Frobenius.
Now ![]() $\text{}^{L}G_{E_{0}}=(\prod _{j}I_{E_{j,0}}^{E_{0}}\,(\operatorname{Res}_{KE_{j,0}/E_{j,0}}G_{0,KE_{j,0}})^{\vee })\rtimes \unicode[STIX]{x1D6E4}_{E_{0}}$ by Lemma 6.3. Because
$\text{}^{L}G_{E_{0}}=(\prod _{j}I_{E_{j,0}}^{E_{0}}\,(\operatorname{Res}_{KE_{j,0}/E_{j,0}}G_{0,KE_{j,0}})^{\vee })\rtimes \unicode[STIX]{x1D6E4}_{E_{0}}$ by Lemma 6.3. Because ![]() $E_{j,0}/E_{0}$ is unramified (cf. Lemma 6.1(i)), any irreducible representation
$E_{j,0}/E_{0}$ is unramified (cf. Lemma 6.1(i)), any irreducible representation ![]() $V$ is built up, as explained in the Appendix A, from irreducible representations of
$V$ is built up, as explained in the Appendix A, from irreducible representations of ![]() $\text{}^{L}(\operatorname{Res}_{KE_{j,0}/E_{j,0}}G_{0,KE_{j,0}})$. There is a parallel description of the corresponding perverse sheaves on the generic fiber of
$\text{}^{L}(\operatorname{Res}_{KE_{j,0}/E_{j,0}}G_{0,KE_{j,0}})$. There is a parallel description of the corresponding perverse sheaves on the generic fiber of ![]() $\text{Gr}_{{\mathcal{G}},{\mathcal{O}}_{E_{0}}}$, thanks to Proposition 6.5. Using Lemmas A.2 and A.3, we easily see that (6.4) will be proved if we can prove Theorem 6.7 for any irreducible representation of
$\text{Gr}_{{\mathcal{G}},{\mathcal{O}}_{E_{0}}}$, thanks to Proposition 6.5. Using Lemmas A.2 and A.3, we easily see that (6.4) will be proved if we can prove Theorem 6.7 for any irreducible representation of ![]() $\text{}^{L}(\operatorname{Res}_{KE_{j,0}/E_{j,0}}G_{0,KE_{j,0}})$ and corresponding nearby cycles along
$\text{}^{L}(\operatorname{Res}_{KE_{j,0}/E_{j,0}}G_{0,KE_{j,0}})$ and corresponding nearby cycles along ![]() $\text{Gr}_{(X_{{\mathcal{O}}_{E_{j,0}}}/{\mathcal{O}}_{E_{j,0}},\,\,\text{}\underline{{\mathcal{G}}}_{0,{\mathcal{O}}_{E_{j,0}}}\!\!,\,D\otimes _{{\mathcal{O}}_{K_{0}}}{\mathcal{O}}_{E_{j,0}})}$.
$\text{Gr}_{(X_{{\mathcal{O}}_{E_{j,0}}}/{\mathcal{O}}_{E_{j,0}},\,\,\text{}\underline{{\mathcal{G}}}_{0,{\mathcal{O}}_{E_{j,0}}}\!\!,\,D\otimes _{{\mathcal{O}}_{K_{0}}}{\mathcal{O}}_{E_{j,0}})}$.
Therefore, we may assume ![]() $F=E_{0}$ henceforth, and we have seen that in order to prove the main theorem it is enough to prove Theorem 6.7, and in fact we may even assume
$F=E_{0}$ henceforth, and we have seen that in order to prove the main theorem it is enough to prove Theorem 6.7, and in fact we may even assume ![]() $K_{0}=F$ (i.e. that
$K_{0}=F$ (i.e. that ![]() $K/F$ is totally ramified), and that
$K/F$ is totally ramified), and that ![]() $V$ is an irreducible representation of
$V$ is an irreducible representation of ![]() $\text{}^{L}G$. By the argument of [Reference Haines and RicharzHR18, Lemma 7.7], we may also assume that
$\text{}^{L}G$. By the argument of [Reference Haines and RicharzHR18, Lemma 7.7], we may also assume that ![]() $V|_{G^{\vee }\rtimes I_{F}}$ is irreducible, whenever convenient.
$V|_{G^{\vee }\rtimes I_{F}}$ is irreducible, whenever convenient.
6.4 Proof of Theorem 6.7
As above, we will assume ![]() $V|_{G^{\vee }\rtimes I_{F}}$ is irreducible. Following the proof of [Reference Haines and RicharzHR18, Theorem 7.6], there are three main steps:
$V|_{G^{\vee }\rtimes I_{F}}$ is irreducible. Following the proof of [Reference Haines and RicharzHR18, Theorem 7.6], there are three main steps:
(1) reduction to minimal
 $F$-Levi subgroups of
$F$-Levi subgroups of  $G$;
$G$;(2) reduction from anisotropic mod center groups to quasi-split groups;
(3) proof for quasi-split groups.
The proofs work exactly the same way as in [Reference Haines and RicharzHR18], with only a few additional remarks. For Step 1, we use Lemma 4.2 to ensure that a minimal ![]() $F$-Levi subgroup of
$F$-Levi subgroup of ![]() $G$ is of the form
$G$ is of the form ![]() $M=\operatorname{Res}_{K/F}(M_{0})$, for
$M=\operatorname{Res}_{K/F}(M_{0})$, for ![]() $M_{0}$ a minimal
$M_{0}$ a minimal ![]() $K$-Levi subgroup of
$K$-Levi subgroup of ![]() $G$; in light of Theorem 5.15 and Theorem 5.8, the argument of [Reference Haines and RicharzHR18] goes through to reduce us to proving Theorem 6.7 for
$G$; in light of Theorem 5.15 and Theorem 5.8, the argument of [Reference Haines and RicharzHR18] goes through to reduce us to proving Theorem 6.7 for ![]() $M$, that is, for
$M$, that is, for ![]() $\text{Gr}_{(X,\text{}\underline{{\mathcal{M}}}_{0},D)}$.
$\text{Gr}_{(X,\text{}\underline{{\mathcal{M}}}_{0},D)}$.
For Step 2, we assume ![]() $G$ is
$G$ is ![]() $F$-anisotropic mod center and we observe that if
$F$-anisotropic mod center and we observe that if ![]() $G_{0}^{\ast }$ is a
$G_{0}^{\ast }$ is a ![]() $K$-quasi-split inner form of
$K$-quasi-split inner form of ![]() $G_{0}$, then
$G_{0}$, then ![]() $G^{\ast }=\operatorname{Res}_{K/F}(G_{0}^{\ast })$ is an
$G^{\ast }=\operatorname{Res}_{K/F}(G_{0}^{\ast })$ is an ![]() $F$-quasi-split inner form of
$F$-quasi-split inner form of ![]() $G$. More to the point,
$G$. More to the point, ![]() $\text{Gr}_{(X,\text{}\underline{{\mathcal{G}}}_{0},D)}$ and
$\text{Gr}_{(X,\text{}\underline{{\mathcal{G}}}_{0},D)}$ and ![]() $\text{Gr}_{(X,\text{}\underline{{\mathcal{G}}}_{0}^{\ast },D)}$ become isomorphic over
$\text{Gr}_{(X,\text{}\underline{{\mathcal{G}}}_{0}^{\ast },D)}$ become isomorphic over ![]() $\breve{{\mathcal{O}}}_{F}$ and hence we may think of them as the same geometrically, with differing Galois actions
$\breve{{\mathcal{O}}}_{F}$ and hence we may think of them as the same geometrically, with differing Galois actions ![]() $\unicode[STIX]{x1D6F7}$ and
$\unicode[STIX]{x1D6F7}$ and ![]() $\unicode[STIX]{x1D6F7}^{\ast }$ of the geometric Frobenius element; applying the argument of [Reference Haines and RicharzHR18], we reduce to proving Theorem 6.7 for
$\unicode[STIX]{x1D6F7}^{\ast }$ of the geometric Frobenius element; applying the argument of [Reference Haines and RicharzHR18], we reduce to proving Theorem 6.7 for ![]() $G^{\ast }$, that is, for
$G^{\ast }$, that is, for ![]() $\text{Gr}_{(X,\text{}\underline{{\mathcal{G}}}_{0}^{\ast },D)}$.
$\text{Gr}_{(X,\text{}\underline{{\mathcal{G}}}_{0}^{\ast },D)}$.
For Step 3, we apply Step 1 to ![]() $G^{\ast }$, and we are reduced to proving the theorem for a torus of the form
$G^{\ast }$, and we are reduced to proving the theorem for a torus of the form ![]() $T^{\ast }=\operatorname{Res}_{K/F}(T_{0}^{\ast })$, that is, for
$T^{\ast }=\operatorname{Res}_{K/F}(T_{0}^{\ast })$, that is, for ![]() $\text{Gr}_{(X,\text{}\underline{{\mathcal{T}}}_{0}^{\ast },D)}$. The theorem for any torus
$\text{Gr}_{(X,\text{}\underline{{\mathcal{T}}}_{0}^{\ast },D)}$. The theorem for any torus ![]() $T=\operatorname{Res}_{K/F}(T_{0})$ is easy. Let us explain, following the method of [Reference Haines and RicharzHR18, § 7.6]. Let
$T=\operatorname{Res}_{K/F}(T_{0})$ is easy. Let us explain, following the method of [Reference Haines and RicharzHR18, § 7.6]. Let ![]() $V$ be a representation of
$V$ be a representation of ![]() $T^{\vee }\rtimes \unicode[STIX]{x1D6E4}_{F}$ such that
$T^{\vee }\rtimes \unicode[STIX]{x1D6E4}_{F}$ such that ![]() $V|_{T^{\vee }\rtimes I_{F}}$ is irreducible. As in [Reference Haines and RicharzHR18, Definition 7.11], let
$V|_{T^{\vee }\rtimes I_{F}}$ is irreducible. As in [Reference Haines and RicharzHR18, Definition 7.11], let ![]() $\unicode[STIX]{x1D714}_{V}\in \unicode[STIX]{x1D70B}_{1}(T)_{I_{F}}^{\unicode[STIX]{x1D6F7}}$ be the common image of the
$\unicode[STIX]{x1D714}_{V}\in \unicode[STIX]{x1D70B}_{1}(T)_{I_{F}}^{\unicode[STIX]{x1D6F7}}$ be the common image of the ![]() $T^{\vee }$-weights in
$T^{\vee }$-weights in ![]() $V|_{T^{\vee }}$. Then
$V|_{T^{\vee }}$. Then ![]() $\unicode[STIX]{x1D714}_{V}$ can be viewed as the unique
$\unicode[STIX]{x1D714}_{V}$ can be viewed as the unique ![]() $k$-rational point in the support of
$k$-rational point in the support of ![]() $\unicode[STIX]{x1D6F9}(\text{Sat}(V|_{T^{\vee }\rtimes I_{F}}))$, and also as the element indexing the unique coset in the support of
$\unicode[STIX]{x1D6F9}(\text{Sat}(V|_{T^{\vee }\rtimes I_{F}}))$, and also as the element indexing the unique coset in the support of ![]() $z_{{\mathcal{T}},V}^{\unicode[STIX]{x1D6F7}}$. Further, by Proposition 5.10, we have an identification of
$z_{{\mathcal{T}},V}^{\unicode[STIX]{x1D6F7}}$. Further, by Proposition 5.10, we have an identification of ![]() $\text{}^{L}T_{r}=(T^{\vee })^{I_{F}}\rtimes \unicode[STIX]{x1D6E4}_{F}$-modules
$\text{}^{L}T_{r}=(T^{\vee })^{I_{F}}\rtimes \unicode[STIX]{x1D6E4}_{F}$-modules
By the Grothendieck–Lefschetz fixed point theorem, it suffices to prove
The second equality comes from the identifications ![]() $\mathbb{H}^{\ast }(\text{Gr}_{T,\bar{F}},\text{Sat}(V))=\mathbb{H}^{0}(\text{Gr}_{T,\bar{F}},\text{Sat}(V))=V$ as
$\mathbb{H}^{\ast }(\text{Gr}_{T,\bar{F}},\text{Sat}(V))=\mathbb{H}^{0}(\text{Gr}_{T,\bar{F}},\text{Sat}(V))=V$ as ![]() $\text{}^{L}T$-representations under the Satake correspondence. Therefore we need to prove the first equality. Note that all the weights in
$\text{}^{L}T$-representations under the Satake correspondence. Therefore we need to prove the first equality. Note that all the weights in ![]() $V$ are
$V$ are ![]() $I_{F}$-conjugate, and
$I_{F}$-conjugate, and ![]() $z_{{\mathcal{T}},V}^{\unicode[STIX]{x1D6F7}}$ acts on a weakly unramified character
$z_{{\mathcal{T}},V}^{\unicode[STIX]{x1D6F7}}$ acts on a weakly unramified character ![]() $\unicode[STIX]{x1D712}:T(F)/T(F)_{1}\rightarrow \bar{\mathbb{Q}}_{\ell }^{\times }$ by the scalar
$\unicode[STIX]{x1D712}:T(F)/T(F)_{1}\rightarrow \bar{\mathbb{Q}}_{\ell }^{\times }$ by the scalar
the second equality holding since ![]() $s^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D712})\in (T^{\vee })^{I_{F}}\rtimes \unicode[STIX]{x1D6F7}$. Thus
$s^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D712})\in (T^{\vee })^{I_{F}}\rtimes \unicode[STIX]{x1D6F7}$. Thus ![]() $z_{{\mathcal{T}},V}^{\unicode[STIX]{x1D6F7}}=\text{tr}(\unicode[STIX]{x1D6F7}\mid V)\,\unicode[STIX]{x1D7D9}_{\unicode[STIX]{x1D714}_{V}}$, as desired. This completes the proof of Step 3 and therefore of Theorem 6.7.◻
$z_{{\mathcal{T}},V}^{\unicode[STIX]{x1D6F7}}=\text{tr}(\unicode[STIX]{x1D6F7}\mid V)\,\unicode[STIX]{x1D7D9}_{\unicode[STIX]{x1D714}_{V}}$, as desired. This completes the proof of Step 3 and therefore of Theorem 6.7.◻
6.5 Values of test functions
As in the main theorem of [Reference Haines and RicharzHR18], the function ![]() $q_{E_{0}}^{d_{\unicode[STIX]{x1D707}}/2}z_{{\mathcal{G}},\{\unicode[STIX]{x1D707}\}}^{\text{ss}}$ takes values in
$q_{E_{0}}^{d_{\unicode[STIX]{x1D707}}/2}z_{{\mathcal{G}},\{\unicode[STIX]{x1D707}\}}^{\text{ss}}$ takes values in ![]() $\mathbb{Z}$ and is independent of
$\mathbb{Z}$ and is independent of ![]() $\ell \neq p$. The proof given in [Reference Haines and RicharzHR18, § 7.7] uses only general facts about the Bernstein functions and related combinatorics, and applies equally well to all groups, including those which are Weil-restricted groups such as
$\ell \neq p$. The proof given in [Reference Haines and RicharzHR18, § 7.7] uses only general facts about the Bernstein functions and related combinatorics, and applies equally well to all groups, including those which are Weil-restricted groups such as ![]() $G$.
$G$.
7 Test functions for modified local models
The aim of this final section is to formulate and prove the test function conjecture for all reductive groups and all primes ![]() $p\geqslant 5$ using the modified local models introduced in [Reference He, Pappas and RapoportHPR18, § 2.6]. This is a consequence of our main theorem and some geometric results in [Reference Haines and RicharzHR19]; cf. Corollary 7.4 below.
$p\geqslant 5$ using the modified local models introduced in [Reference He, Pappas and RapoportHPR18, § 2.6]. This is a consequence of our main theorem and some geometric results in [Reference Haines and RicharzHR19]; cf. Corollary 7.4 below.
7.1 Modified local models
We denote by ![]() $G$ a reductive group over a non-archimedean local field
$G$ a reductive group over a non-archimedean local field ![]() $F$ of mixed characteristic
$F$ of mixed characteristic ![]() $(0,p)$. We fix an isomorphism
$(0,p)$. We fix an isomorphism
where each ![]() $K_{j}/F$ is a finite field extension, and each
$K_{j}/F$ is a finite field extension, and each ![]() $G_{j}$ is an absolutely simple, reductive
$G_{j}$ is an absolutely simple, reductive ![]() $K_{j}$-group. We assume that each
$K_{j}$-group. We assume that each ![]() $G_{j}$ is tamely ramified. This is only a restriction for
$G_{j}$ is tamely ramified. This is only a restriction for ![]() $p=2,3$: whenever
$p=2,3$: whenever ![]() $p\geqslant 5$ this assumption is automatically satisfied by the classification (cf. [Reference TitsTit77, § 1.12; § 4]; see also [Reference Pappas and RapoportPR08, § 7.a]).
$p\geqslant 5$ this assumption is automatically satisfied by the classification (cf. [Reference TitsTit77, § 1.12; § 4]; see also [Reference Pappas and RapoportPR08, § 7.a]).
We further fix a facet ![]() $\mathbf{f}\subset \mathscr{B}(G,F)$ which corresponds to facets
$\mathbf{f}\subset \mathscr{B}(G,F)$ which corresponds to facets ![]() $\mathbf{f}_{j}\subset \mathscr{B}(G_{j},K_{j})$,
$\mathbf{f}_{j}\subset \mathscr{B}(G_{j},K_{j})$, ![]() $j\in J$, under the identifications
$j\in J$, under the identifications
deduced from Proposition 4.6 applied to each pair ![]() $(G_{j},K_{j}/F)$. We denote by
$(G_{j},K_{j}/F)$. We denote by ![]() ${\mathcal{G}}={\mathcal{G}}_{\mathbf{f}}$ over
${\mathcal{G}}={\mathcal{G}}_{\mathbf{f}}$ over ![]() ${\mathcal{O}}_{F}$ and by
${\mathcal{O}}_{F}$ and by ![]() ${\mathcal{G}}_{j}={\mathcal{G}}_{\mathbf{f}_{j}}$ over
${\mathcal{G}}_{j}={\mathcal{G}}_{\mathbf{f}_{j}}$ over ![]() ${\mathcal{O}}_{K_{j}}$ the associated parahoric group schemes.
${\mathcal{O}}_{K_{j}}$ the associated parahoric group schemes.
We fix a uniformizer ![]() $\unicode[STIX]{x1D71B}_{j}\in K_{j}$ and an
$\unicode[STIX]{x1D71B}_{j}\in K_{j}$ and an ![]() ${\mathcal{O}}_{K_{j,0}}[u^{\pm }]$-extension
${\mathcal{O}}_{K_{j,0}}[u^{\pm }]$-extension ![]() $\text{}\underline{G}_{j,0}$ of
$\text{}\underline{G}_{j,0}$ of ![]() $G_{j}$ where
$G_{j}$ where ![]() $K_{j,0}/F$ denotes the maximal unramified subextension in
$K_{j,0}/F$ denotes the maximal unramified subextension in ![]() $K_{j}/F$. Each geometric conjugacy class of cocharacters
$K_{j}/F$. Each geometric conjugacy class of cocharacters ![]() $\{\unicode[STIX]{x1D707}\}$ in
$\{\unicode[STIX]{x1D707}\}$ in ![]() $G$ induces a geometric conjugacy class
$G$ induces a geometric conjugacy class ![]() $\{\unicode[STIX]{x1D707}_{\operatorname{ad}}\}$ in
$\{\unicode[STIX]{x1D707}_{\operatorname{ad}}\}$ in ![]() $G_{\operatorname{ad}}$ and hence for each
$G_{\operatorname{ad}}$ and hence for each ![]() $j\in J$ a geometric conjugacy class
$j\in J$ a geometric conjugacy class ![]() $\{\unicode[STIX]{x1D707}_{j}\}$ in
$\{\unicode[STIX]{x1D707}_{j}\}$ in ![]() $\operatorname{Res}_{K_{j}/F}(G_{j})$. We note that the reflex field
$\operatorname{Res}_{K_{j}/F}(G_{j})$. We note that the reflex field ![]() $E$ of
$E$ of ![]() $\{\unicode[STIX]{x1D707}\}$ is naturally an overfield of the reflex field
$\{\unicode[STIX]{x1D707}\}$ is naturally an overfield of the reflex field ![]() $E_{j}$ of
$E_{j}$ of ![]() $\{\unicode[STIX]{x1D707}_{j}\}$.
$\{\unicode[STIX]{x1D707}_{j}\}$.
Definition 7.1. The modified local model ![]() $\mathbb{M}_{{\mathcal{G}}}(G,\{\unicode[STIX]{x1D707}\})=\mathbb{M}(K_{j}/F,\text{}\underline{G}_{j,0},\mathbf{f}_{j},\{\unicode[STIX]{x1D707}_{j}\},\unicode[STIX]{x1D71B}_{j}\,;\,j\in J)$ is the
$\mathbb{M}_{{\mathcal{G}}}(G,\{\unicode[STIX]{x1D707}\})=\mathbb{M}(K_{j}/F,\text{}\underline{G}_{j,0},\mathbf{f}_{j},\{\unicode[STIX]{x1D707}_{j}\},\unicode[STIX]{x1D71B}_{j}\,;\,j\in J)$ is the ![]() ${\mathcal{O}}_{E}$-product of the
${\mathcal{O}}_{E}$-product of the ![]() ${\mathcal{O}}_{E}$-schemes
${\mathcal{O}}_{E}$-schemes
where ![]() $M_{\{\unicode[STIX]{x1D707}_{j}\}}=M(K_{j}/F,\text{}\underline{G}_{j,0},\mathbf{f}_{j},\{\unicode[STIX]{x1D707}_{j}\},\unicode[STIX]{x1D71B}_{j})$ is the local model over
$M_{\{\unicode[STIX]{x1D707}_{j}\}}=M(K_{j}/F,\text{}\underline{G}_{j,0},\mathbf{f}_{j},\{\unicode[STIX]{x1D707}_{j}\},\unicode[STIX]{x1D71B}_{j})$ is the local model over ![]() ${\mathcal{O}}_{E_{j}}$ as in § 4.4.4, and
${\mathcal{O}}_{E_{j}}$ as in § 4.4.4, and ![]() $M_{\{\unicode[STIX]{x1D707}_{j}\}}^{\operatorname{norm}}\rightarrow M_{\{\unicode[STIX]{x1D707}_{j}\}}$ denotes its normalization.
$M_{\{\unicode[STIX]{x1D707}_{j}\}}^{\operatorname{norm}}\rightarrow M_{\{\unicode[STIX]{x1D707}_{j}\}}$ denotes its normalization.
For convenience we summarize the results on the modified local models obtained in [Reference Pappas and ZhuPZ13, Reference LevinLev16, Reference He, Pappas and RapoportHPR18, Reference Haines and RicharzHR19].
Theorem 7.2. (i) If ![]() $G$ splits over a tamely ramified extension of
$G$ splits over a tamely ramified extension of ![]() $F$, then
$F$, then ![]() $\mathbb{M}_{{\mathcal{G}}}(G,\{\unicode[STIX]{x1D707}\})$ is isomorphic to the modified local model defined in [Reference He, Pappas and RapoportHPR18, § 2.6].
$\mathbb{M}_{{\mathcal{G}}}(G,\{\unicode[STIX]{x1D707}\})$ is isomorphic to the modified local model defined in [Reference He, Pappas and RapoportHPR18, § 2.6].
(ii) A morphism of local model triples ![]() $(G^{\prime },\{\unicode[STIX]{x1D707}^{\prime }\},{\mathcal{G}}^{\prime })\rightarrow (G,\{\unicode[STIX]{x1D707}\},{\mathcal{G}})$ with
$(G^{\prime },\{\unicode[STIX]{x1D707}^{\prime }\},{\mathcal{G}}^{\prime })\rightarrow (G,\{\unicode[STIX]{x1D707}\},{\mathcal{G}})$ with ![]() $G_{\operatorname{ad}}^{\prime }\simeq G_{\operatorname{ad}}$ satisfying the tameness assumption in (7.1) induces an isomorphism of
$G_{\operatorname{ad}}^{\prime }\simeq G_{\operatorname{ad}}$ satisfying the tameness assumption in (7.1) induces an isomorphism of ![]() ${\mathcal{O}}_{E^{\prime }}$-schemes
${\mathcal{O}}_{E^{\prime }}$-schemes
(iii) The modified local model ![]() $\mathbb{M}_{{\mathcal{G}}}(G,\{\unicode[STIX]{x1D707}\})$ is normal with geometrically reduced special fiber, and if
$\mathbb{M}_{{\mathcal{G}}}(G,\{\unicode[STIX]{x1D707}\})$ is normal with geometrically reduced special fiber, and if ![]() $p>2$ it is Cohen–Macaulay as well.
$p>2$ it is Cohen–Macaulay as well.
Proof. As in [Reference He, Pappas and RapoportHPR18, § 2.6] we choose for each ![]() $j\in J$ a suitable
$j\in J$ a suitable ![]() $z$-extension
$z$-extension ![]() $\tilde{G}_{j}\rightarrow G_{j}$ whose derived group
$\tilde{G}_{j}\rightarrow G_{j}$ whose derived group ![]() $\tilde{G}_{j,\operatorname{der}}$ is simply connected. Then the geometric conjugacy class
$\tilde{G}_{j,\operatorname{der}}$ is simply connected. Then the geometric conjugacy class ![]() $\{\unicode[STIX]{x1D707}_{j}\}$ in
$\{\unicode[STIX]{x1D707}_{j}\}$ in ![]() $\operatorname{Res}_{K_{j}/F}(G_{j})$ can be lifted to
$\operatorname{Res}_{K_{j}/F}(G_{j})$ can be lifted to ![]() $\{\tilde{\unicode[STIX]{x1D707}}_{j}\}$ in
$\{\tilde{\unicode[STIX]{x1D707}}_{j}\}$ in ![]() $\operatorname{Res}_{K_{j}/F}(\tilde{G}_{j})$ with the same reflex field
$\operatorname{Res}_{K_{j}/F}(\tilde{G}_{j})$ with the same reflex field ![]() $\tilde{E}_{j}=E_{j}$; cf. [Reference He, Pappas and RapoportHPR18, § 2.6]. Denote by
$\tilde{E}_{j}=E_{j}$; cf. [Reference He, Pappas and RapoportHPR18, § 2.6]. Denote by ![]() $\tilde{\mathbf{f}}_{j}$ the facet of
$\tilde{\mathbf{f}}_{j}$ the facet of ![]() $\tilde{G}_{j}$ corresponding to
$\tilde{G}_{j}$ corresponding to ![]() $\mathbf{f}_{j}$. This induces a morphism of
$\mathbf{f}_{j}$. This induces a morphism of ![]() ${\mathcal{O}}_{E_{j}}$-schemes on Weil-restricted local models
${\mathcal{O}}_{E_{j}}$-schemes on Weil-restricted local models
where ![]() $\tilde{\text{}\underline{G}}_{j,0}\rightarrow \text{}\underline{G}_{j,0}$ is an
$\tilde{\text{}\underline{G}}_{j,0}\rightarrow \text{}\underline{G}_{j,0}$ is an ![]() ${\mathcal{O}}_{K_{j,0}}[u^{\pm }]$-extension of
${\mathcal{O}}_{K_{j,0}}[u^{\pm }]$-extension of ![]() $\tilde{G}_{j}\rightarrow G_{j}$. Now for tamely ramified extensions
$\tilde{G}_{j}\rightarrow G_{j}$. Now for tamely ramified extensions ![]() $K_{j}/F$ the Weil-restricted local models agree by [Reference LevinLev16, Proposition 4.2.4] with the local models of [Reference Pappas and ZhuPZ13]. Further, the morphism (7.2) is a finite, birational, universal homeomorphism by [Reference Haines and RicharzHR19, Corollary 2.3]. Since
$K_{j}/F$ the Weil-restricted local models agree by [Reference LevinLev16, Proposition 4.2.4] with the local models of [Reference Pappas and ZhuPZ13]. Further, the morphism (7.2) is a finite, birational, universal homeomorphism by [Reference Haines and RicharzHR19, Corollary 2.3]. Since ![]() $M_{\{\tilde{\unicode[STIX]{x1D707}}_{j}\}}$ is normal by [Reference Pappas and ZhuPZ13, Theorem 9.1] (see also [Reference LevinLev16, Theorem 4.2.7]), the map induces an isomorphism
$M_{\{\tilde{\unicode[STIX]{x1D707}}_{j}\}}$ is normal by [Reference Pappas and ZhuPZ13, Theorem 9.1] (see also [Reference LevinLev16, Theorem 4.2.7]), the map induces an isomorphism ![]() $M_{\{\tilde{\unicode[STIX]{x1D707}}_{j}\}}\simeq M_{\{\tilde{\unicode[STIX]{x1D707}}_{j}\}}^{\operatorname{norm}}$ on normalizations, and the former are the modified local models of [Reference He, Pappas and RapoportHPR18, § 2.6]. Extending scalars to
$M_{\{\tilde{\unicode[STIX]{x1D707}}_{j}\}}\simeq M_{\{\tilde{\unicode[STIX]{x1D707}}_{j}\}}^{\operatorname{norm}}$ on normalizations, and the former are the modified local models of [Reference He, Pappas and RapoportHPR18, § 2.6]. Extending scalars to ![]() ${\mathcal{O}}_{E}$ and taking the product over
${\mathcal{O}}_{E}$ and taking the product over ![]() $j\in J$ implies part (i). Part (iii) follows from [Reference Haines and RicharzHR19, Corollary 2.5]; see also the references cited there. For part (ii) we remark that the morphism is a finite, birational, universal homeomorphism by the same reasoning as in (i), and that the target is normal: its generic fiber is normal by definition and its special fiber is reduced by (iii). As the local model is flat and of finite type, the target is normal by Serre’s criterion; cf. [Reference Pappas and ZhuPZ13, Proposition 9.2]. ◻
$j\in J$ implies part (i). Part (iii) follows from [Reference Haines and RicharzHR19, Corollary 2.5]; see also the references cited there. For part (ii) we remark that the morphism is a finite, birational, universal homeomorphism by the same reasoning as in (i), and that the target is normal: its generic fiber is normal by definition and its special fiber is reduced by (iii). As the local model is flat and of finite type, the target is normal by Serre’s criterion; cf. [Reference Pappas and ZhuPZ13, Proposition 9.2]. ◻
Remark 7.3. As in Remark 4.19 one can show that ![]() $\mathbb{M}_{{\mathcal{G}}}(G,\{\unicode[STIX]{x1D707}\})$ depends up to equivariant isomorphism only on the data
$\mathbb{M}_{{\mathcal{G}}}(G,\{\unicode[STIX]{x1D707}\})$ depends up to equivariant isomorphism only on the data ![]() $(G,\{\unicode[STIX]{x1D707}\},{\mathcal{G}})$, which justifies the notation.
$(G,\{\unicode[STIX]{x1D707}\},{\mathcal{G}})$, which justifies the notation.
We also record the following property which is important for the proof of the test function conjecture.
Corollary 7.4. The product of the normalization morphisms
is finite, birational and a universal homeomorphism. In particular, this morphism induces an equivalence on the associated étale topoi of source and target [StaPro, 03SI].
Proof. This is immediate from the isomorphism ![]() $M_{\{\tilde{\unicode[STIX]{x1D707}}_{j}\}}\simeq M_{\{\tilde{\unicode[STIX]{x1D707}}_{j}\}}^{\operatorname{norm}}$,
$M_{\{\tilde{\unicode[STIX]{x1D707}}_{j}\}}\simeq M_{\{\tilde{\unicode[STIX]{x1D707}}_{j}\}}^{\operatorname{norm}}$, ![]() $j\in J$, in the proof of Theorem 7.2(i), together with [Reference Haines and RicharzHR19, Corollary 2.3].◻
$j\in J$, in the proof of Theorem 7.2(i), together with [Reference Haines and RicharzHR19, Corollary 2.3].◻
7.2 Test functions
Let ![]() $(G,\{\unicode[STIX]{x1D707}\},{\mathcal{G}})$ be a triple as above, where
$(G,\{\unicode[STIX]{x1D707}\},{\mathcal{G}})$ be a triple as above, where ![]() $G/F$ satisfies the tameness assumption in (7.1). Denote by
$G/F$ satisfies the tameness assumption in (7.1). Denote by ![]() $\mathbb{M}_{\{\unicode[STIX]{x1D707}\}}=\mathbb{M}_{{\mathcal{G}}}(G,\{\unicode[STIX]{x1D707}\})$ the modified local model as in Definition 7.1. For a finite extension
$\mathbb{M}_{\{\unicode[STIX]{x1D707}\}}=\mathbb{M}_{{\mathcal{G}}}(G,\{\unicode[STIX]{x1D707}\})$ the modified local model as in Definition 7.1. For a finite extension ![]() $E/F$ over which
$E/F$ over which ![]() $\{\unicode[STIX]{x1D707}\}$ is defined, we consider the associated semisimple trace of Frobenius function on the sheaf of nearby cycles
$\{\unicode[STIX]{x1D707}\}$ is defined, we consider the associated semisimple trace of Frobenius function on the sheaf of nearby cycles
where ![]() $\operatorname{IC}_{\{\unicode[STIX]{x1D707}\}}$ denotes the normalized intersection complex of the generic fiber of
$\operatorname{IC}_{\{\unicode[STIX]{x1D707}\}}$ denotes the normalized intersection complex of the generic fiber of ![]() $\mathbb{M}_{\{\unicode[STIX]{x1D707}\}}$. As an application of our main theorem we deduce the test function conjecture for modified local models.
$\mathbb{M}_{\{\unicode[STIX]{x1D707}\}}$. As an application of our main theorem we deduce the test function conjecture for modified local models.
Theorem 7.5. Let ![]() $(G,\{\unicode[STIX]{x1D707}\},{\mathcal{G}})$ be as above, and denote by
$(G,\{\unicode[STIX]{x1D707}\},{\mathcal{G}})$ be as above, and denote by ![]() $E/F$ an extension which contains the reflex field of
$E/F$ an extension which contains the reflex field of ![]() $\{\unicode[STIX]{x1D707}\}$. Let
$\{\unicode[STIX]{x1D707}\}$. Let ![]() $E_{0}/F$ be the maximal unramified subextension. Then
$E_{0}/F$ be the maximal unramified subextension. Then ![]() $\unicode[STIX]{x1D70F}_{\{\unicode[STIX]{x1D707}\}}^{\operatorname{ss}}$ naturally defines an element in
$\unicode[STIX]{x1D70F}_{\{\unicode[STIX]{x1D707}\}}^{\operatorname{ss}}$ naturally defines an element in ![]() ${\mathcal{Z}}(G(E_{0}),{\mathcal{G}}({\mathcal{O}}_{E_{0}}))$, and one has
${\mathcal{Z}}(G(E_{0}),{\mathcal{G}}({\mathcal{O}}_{E_{0}}))$, and one has
where ![]() $z_{\{\unicode[STIX]{x1D707}\}}^{\text{ss}}\in {\mathcal{Z}}(G(E_{0}),{\mathcal{G}}({\mathcal{O}}_{E_{0}}))$ is the unique function which acts on any
$z_{\{\unicode[STIX]{x1D707}\}}^{\text{ss}}\in {\mathcal{Z}}(G(E_{0}),{\mathcal{G}}({\mathcal{O}}_{E_{0}}))$ is the unique function which acts on any ![]() ${\mathcal{G}}({\mathcal{O}}_{E_{0}})$-spherical smooth irreducible
${\mathcal{G}}({\mathcal{O}}_{E_{0}})$-spherical smooth irreducible ![]() $\bar{\mathbb{Q}}_{\ell }$-representation
$\bar{\mathbb{Q}}_{\ell }$-representation ![]() $\unicode[STIX]{x1D70B}$ by the scalar
$\unicode[STIX]{x1D70B}$ by the scalar
where ![]() $s(\unicode[STIX]{x1D70B})\in [(G^{\vee })^{I_{E_{0}}}\rtimes \unicode[STIX]{x1D6F7}_{E_{0}}]_{\operatorname{ss}}/(G^{\vee })^{I_{E_{0}}}$ is the Satake parameter for
$s(\unicode[STIX]{x1D70B})\in [(G^{\vee })^{I_{E_{0}}}\rtimes \unicode[STIX]{x1D6F7}_{E_{0}}]_{\operatorname{ss}}/(G^{\vee })^{I_{E_{0}}}$ is the Satake parameter for ![]() $\unicode[STIX]{x1D70B}$ [Reference HainesHai15]. The function
$\unicode[STIX]{x1D70B}$ [Reference HainesHai15]. The function ![]() $q_{E_{0}}^{d_{\unicode[STIX]{x1D707}}/2}\unicode[STIX]{x1D70F}_{\{\unicode[STIX]{x1D707}\}}^{\operatorname{ss}}$ takes values in
$q_{E_{0}}^{d_{\unicode[STIX]{x1D707}}/2}\unicode[STIX]{x1D70F}_{\{\unicode[STIX]{x1D707}\}}^{\operatorname{ss}}$ takes values in ![]() $\mathbb{Z}$ and is independent of
$\mathbb{Z}$ and is independent of ![]() $\ell \neq p$ and
$\ell \neq p$ and ![]() $q^{1/2}\in \bar{\mathbb{Q}}_{\ell }$.
$q^{1/2}\in \bar{\mathbb{Q}}_{\ell }$.
Proof. First, we will show that ![]() $\unicode[STIX]{x1D70F}_{\{\unicode[STIX]{x1D707}\}}^{\text{ss}}$ naturally defines an element of
$\unicode[STIX]{x1D70F}_{\{\unicode[STIX]{x1D707}\}}^{\text{ss}}$ naturally defines an element of ![]() ${\mathcal{Z}}(G(E_{0}),{\mathcal{G}}({\mathcal{O}}_{E_{0}}))$ for which we need to prove the analogue of (6.2). As in (7.1) we denote by
${\mathcal{Z}}(G(E_{0}),{\mathcal{G}}({\mathcal{O}}_{E_{0}}))$ for which we need to prove the analogue of (6.2). As in (7.1) we denote by ![]() $(H_{j},\{\unicode[STIX]{x1D707}_{j}\},{\mathcal{H}}_{j})$,
$(H_{j},\{\unicode[STIX]{x1D707}_{j}\},{\mathcal{H}}_{j})$, ![]() $j\in J$, the local model triple where
$j\in J$, the local model triple where ![]() $H_{j}:=\operatorname{Res}_{K_{j}/F}(G_{j})$ and
$H_{j}:=\operatorname{Res}_{K_{j}/F}(G_{j})$ and ![]() ${\mathcal{H}}_{j}:=\operatorname{Res}_{{\mathcal{O}}_{K_{j}}/{\mathcal{O}}_{F}}({\mathcal{G}}_{j})$. Note that
${\mathcal{H}}_{j}:=\operatorname{Res}_{{\mathcal{O}}_{K_{j}}/{\mathcal{O}}_{F}}({\mathcal{G}}_{j})$. Note that ![]() $G_{\operatorname{ad}}=\prod _{j}H_{j}$ and
$G_{\operatorname{ad}}=\prod _{j}H_{j}$ and ![]() ${\mathcal{G}}_{\operatorname{ad}}=\prod _{j}{\mathcal{H}}_{j}$. For the next statement, observe that
${\mathcal{G}}_{\operatorname{ad}}=\prod _{j}{\mathcal{H}}_{j}$. For the next statement, observe that ![]() $\text{IC}_{\{\unicode[STIX]{x1D707}\}}=\text{Sat}(V_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}})$ under the equivalence of étale topoi of Corollary 7.4 for the generic fibers
$\text{IC}_{\{\unicode[STIX]{x1D707}\}}=\text{Sat}(V_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}})$ under the equivalence of étale topoi of Corollary 7.4 for the generic fibers ![]() $\mathbb{M}_{\{\unicode[STIX]{x1D707}\},E}$ and
$\mathbb{M}_{\{\unicode[STIX]{x1D707}\},E}$ and ![]() $\prod _{j}M_{\{\unicode[STIX]{x1D707}_{j}\}}\otimes _{{\mathcal{O}}_{E_{j}}}E\subset \operatorname{Gr}_{{\mathcal{G}}_{\operatorname{ad}},{\mathcal{O}}_{E_{0}}}\otimes _{{\mathcal{O}}_{E_{0}}}E=\text{Gr}_{G_{\text{ad},E}}$.
$\prod _{j}M_{\{\unicode[STIX]{x1D707}_{j}\}}\otimes _{{\mathcal{O}}_{E_{j}}}E\subset \operatorname{Gr}_{{\mathcal{G}}_{\operatorname{ad}},{\mathcal{O}}_{E_{0}}}\otimes _{{\mathcal{O}}_{E_{0}}}E=\text{Gr}_{G_{\text{ad},E}}$.
Lemma 7.6. We have
where ![]() $\unicode[STIX]{x1D6F9}_{\operatorname{ad}}$ denotes the nearby cycles functor for
$\unicode[STIX]{x1D6F9}_{\operatorname{ad}}$ denotes the nearby cycles functor for ![]() $\operatorname{Gr}_{{\mathcal{G}}_{\operatorname{ad}},{\mathcal{O}}_{E_{0}}}=\prod _{j}\text{Gr}_{{\mathcal{H}}_{j},{\mathcal{O}}_{E_{0}}}$.
$\operatorname{Gr}_{{\mathcal{G}}_{\operatorname{ad}},{\mathcal{O}}_{E_{0}}}=\prod _{j}\text{Gr}_{{\mathcal{H}}_{j},{\mathcal{O}}_{E_{0}}}$.
Proof. The argument follows the proof of (6.2) as in [Reference Haines and RicharzHR18, § 7.3]. Consider the finite morphism
Abbreviate the nearby cycles for ![]() $\operatorname{Gr}_{{\mathcal{G}}_{\operatorname{ad}},{\mathcal{O}}_{E_{0}}}\otimes _{{\mathcal{O}}_{E_{0}}}{\mathcal{O}}_{E}$ by
$\operatorname{Gr}_{{\mathcal{G}}_{\operatorname{ad}},{\mathcal{O}}_{E_{0}}}\otimes _{{\mathcal{O}}_{E_{0}}}{\mathcal{O}}_{E}$ by ![]() $\unicode[STIX]{x1D6F9}_{\operatorname{ad},E}$. We have
$\unicode[STIX]{x1D6F9}_{\operatorname{ad},E}$. We have
 $$\begin{eqnarray}\displaystyle \text{tr}^{\text{ss}}(\unicode[STIX]{x1D6F7}_{E}\mid \unicode[STIX]{x1D6F9}_{\operatorname{ad},E}(\text{Sat}(V_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}}))) & = & \displaystyle \text{tr}^{\text{ss}}(\unicode[STIX]{x1D6F7}_{E_{0}}\mid f_{\bar{s},\ast }\unicode[STIX]{x1D6F9}_{\operatorname{ad},E}(\text{Sat}(V_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}})))\nonumber\\ \displaystyle & = & \displaystyle \text{tr}^{\text{ss}}(\unicode[STIX]{x1D6F7}_{E_{0}}\mid \unicode[STIX]{x1D6F9}_{\operatorname{ad}}(f_{\unicode[STIX]{x1D702},\ast }\text{Sat}(V_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}})))\nonumber\\ \displaystyle & = & \displaystyle \text{tr}^{\text{ss}}(\unicode[STIX]{x1D6F7}_{E_{0}}\mid \unicode[STIX]{x1D6F9}_{\operatorname{ad}}(\text{Sat}(I(V_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}})))).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{tr}^{\text{ss}}(\unicode[STIX]{x1D6F7}_{E}\mid \unicode[STIX]{x1D6F9}_{\operatorname{ad},E}(\text{Sat}(V_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}}))) & = & \displaystyle \text{tr}^{\text{ss}}(\unicode[STIX]{x1D6F7}_{E_{0}}\mid f_{\bar{s},\ast }\unicode[STIX]{x1D6F9}_{\operatorname{ad},E}(\text{Sat}(V_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}})))\nonumber\\ \displaystyle & = & \displaystyle \text{tr}^{\text{ss}}(\unicode[STIX]{x1D6F7}_{E_{0}}\mid \unicode[STIX]{x1D6F9}_{\operatorname{ad}}(f_{\unicode[STIX]{x1D702},\ast }\text{Sat}(V_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}})))\nonumber\\ \displaystyle & = & \displaystyle \text{tr}^{\text{ss}}(\unicode[STIX]{x1D6F7}_{E_{0}}\mid \unicode[STIX]{x1D6F9}_{\operatorname{ad}}(\text{Sat}(I(V_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}})))).\nonumber\end{eqnarray}$$We used the analogue of [Reference HainesHai18, Lemma 8.1] for the first equality, proper base change for the second equality and [Reference Haines and RicharzHR18, Proposition 3.14] for the final equality. By the topological invariance of the étale site in Corollary 7.4 we have
which proves the lemma. ◻
By Lemma 7.6 (combined with Theorem 5.15), the test function
naturally defines an element of ![]() ${\mathcal{Z}}(G_{\operatorname{ad}}(E_{0}),{\mathcal{G}}_{\operatorname{ad}}({\mathcal{O}}_{E_{0}}))$. By § 7.3 below, the natural projection
${\mathcal{Z}}(G_{\operatorname{ad}}(E_{0}),{\mathcal{G}}_{\operatorname{ad}}({\mathcal{O}}_{E_{0}}))$. By § 7.3 below, the natural projection ![]() $p:G\rightarrow G_{\operatorname{ad}}$ induces a canonical morphism of algebras
$p:G\rightarrow G_{\operatorname{ad}}$ induces a canonical morphism of algebras
There is a disjoint union
where ![]() $G(E_{0})_{\unicode[STIX]{x1D714}}=\unicode[STIX]{x1D705}_{G,E_{0}}^{-1}(\unicode[STIX]{x1D714})$ is the fiber of the Kottwitz morphism
$G(E_{0})_{\unicode[STIX]{x1D714}}=\unicode[STIX]{x1D705}_{G,E_{0}}^{-1}(\unicode[STIX]{x1D714})$ is the fiber of the Kottwitz morphism ![]() $\unicode[STIX]{x1D705}_{G,E_{0}}:G(E_{0})\rightarrow \unicode[STIX]{x1D70B}_{1}(G)_{I}$ with
$\unicode[STIX]{x1D705}_{G,E_{0}}:G(E_{0})\rightarrow \unicode[STIX]{x1D70B}_{1}(G)_{I}$ with ![]() $I=I_{E_{0}}=I_{F}$ (use
$I=I_{E_{0}}=I_{F}$ (use ![]() $E_{0}/F$ unramified), and likewise for
$E_{0}/F$ unramified), and likewise for ![]() $G$ replaced by
$G$ replaced by ![]() $G_{\operatorname{ad}}$. The key observation is proved in Lemma 7.7 below: if
$G_{\operatorname{ad}}$. The key observation is proved in Lemma 7.7 below: if ![]() $\unicode[STIX]{x1D714}\mapsto \unicode[STIX]{x1D714}_{\operatorname{ad}}$ under the map
$\unicode[STIX]{x1D714}\mapsto \unicode[STIX]{x1D714}_{\operatorname{ad}}$ under the map ![]() $\unicode[STIX]{x1D70B}_{1}(G)_{I}\rightarrow \unicode[STIX]{x1D70B}_{1}(G_{\operatorname{ad}})_{I}$, then
$\unicode[STIX]{x1D70B}_{1}(G)_{I}\rightarrow \unicode[STIX]{x1D70B}_{1}(G_{\operatorname{ad}})_{I}$, then ![]() $p_{\ast }$ restricts to an isomorphism
$p_{\ast }$ restricts to an isomorphism
on the functions whose support is contained in ![]() $G(E_{0})_{\unicode[STIX]{x1D714}}$ (respectively, in
$G(E_{0})_{\unicode[STIX]{x1D714}}$ (respectively, in ![]() $G_{\operatorname{ad}}(E_{0})_{\unicode[STIX]{x1D714}_{\operatorname{ad}}}$). We apply this to
$G_{\operatorname{ad}}(E_{0})_{\unicode[STIX]{x1D714}_{\operatorname{ad}}}$). We apply this to ![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\{\unicode[STIX]{x1D707}\}}$, the image of
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\{\unicode[STIX]{x1D707}\}}$, the image of ![]() $\{\unicode[STIX]{x1D707}\}$ inside
$\{\unicode[STIX]{x1D707}\}$ inside ![]() $\unicode[STIX]{x1D70B}_{1}(G)_{I}$. To explain, note that the representation
$\unicode[STIX]{x1D70B}_{1}(G)_{I}$. To explain, note that the representation ![]() $I(V_{\{\unicode[STIX]{x1D707}\}})$ of
$I(V_{\{\unicode[STIX]{x1D707}\}})$ of ![]() $\text{}^{L}G_{E_{0}}$ need not be irreducible, but all its
$\text{}^{L}G_{E_{0}}$ need not be irreducible, but all its ![]() $B^{\vee }$-highest
$B^{\vee }$-highest ![]() $T^{\vee }$ are
$T^{\vee }$ are ![]() $I_{E_{0}}$-conjugate to
$I_{E_{0}}$-conjugate to ![]() $\unicode[STIX]{x1D707}$. Similar remarks apply to the restriction
$\unicode[STIX]{x1D707}$. Similar remarks apply to the restriction ![]() $I(V_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}})$ of
$I(V_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}})$ of ![]() $I(V_{\{\unicode[STIX]{x1D707}\}})$ to
$I(V_{\{\unicode[STIX]{x1D707}\}})$ to ![]() $\text{}^{L}(G_{\text{ad}})_{E_{0}}$; note as well that
$\text{}^{L}(G_{\text{ad}})_{E_{0}}$; note as well that ![]() $\unicode[STIX]{x1D714}_{\{\unicode[STIX]{x1D707}\}}\mapsto \unicode[STIX]{x1D714}_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}}$. Geometrically, this means that the support of (7.3) is contained in the connected component of
$\unicode[STIX]{x1D714}_{\{\unicode[STIX]{x1D707}\}}\mapsto \unicode[STIX]{x1D714}_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}}$. Geometrically, this means that the support of (7.3) is contained in the connected component of ![]() $\text{Gr}_{{\mathcal{G}}_{\text{ad}}}\otimes _{{\mathcal{O}}_{F}}k_{E_{0}}$ indexed by
$\text{Gr}_{{\mathcal{G}}_{\text{ad}}}\otimes _{{\mathcal{O}}_{F}}k_{E_{0}}$ indexed by ![]() $\unicode[STIX]{x1D714}_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}}$, and hence it belongs to
$\unicode[STIX]{x1D714}_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}}$, and hence it belongs to ![]() ${\mathcal{Z}}(G_{\text{ad}}(E_{0}),{\mathcal{G}}_{\text{ad}}({\mathcal{O}}_{E_{0}}))_{\unicode[STIX]{x1D714}_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}}}\!$. Finally, via (7.5) we see that
${\mathcal{Z}}(G_{\text{ad}}(E_{0}),{\mathcal{G}}_{\text{ad}}({\mathcal{O}}_{E_{0}}))_{\unicode[STIX]{x1D714}_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}}}\!$. Finally, via (7.5) we see that ![]() $\unicode[STIX]{x1D70F}_{\{\unicode[STIX]{x1D707}\}}^{\operatorname{ss}}$ identifies with an element of
$\unicode[STIX]{x1D70F}_{\{\unicode[STIX]{x1D707}\}}^{\operatorname{ss}}$ identifies with an element of ![]() ${\mathcal{Z}}(G(E_{0}),{\mathcal{G}}({\mathcal{O}}_{E_{0}}))_{\unicode[STIX]{x1D714}_{\{\unicode[STIX]{x1D707}\}}}\subset {\mathcal{Z}}(G(E_{0}),{\mathcal{G}}({\mathcal{O}}_{E_{0}}))$.
${\mathcal{Z}}(G(E_{0}),{\mathcal{G}}({\mathcal{O}}_{E_{0}}))_{\unicode[STIX]{x1D714}_{\{\unicode[STIX]{x1D707}\}}}\subset {\mathcal{Z}}(G(E_{0}),{\mathcal{G}}({\mathcal{O}}_{E_{0}}))$.
Next we prove the equality of ![]() $\unicode[STIX]{x1D70F}_{\{\unicode[STIX]{x1D707}\}}^{\operatorname{ss}}=z_{\{\unicode[STIX]{x1D707}\}}^{\operatorname{ss}}$ as elements of
$\unicode[STIX]{x1D70F}_{\{\unicode[STIX]{x1D707}\}}^{\operatorname{ss}}=z_{\{\unicode[STIX]{x1D707}\}}^{\operatorname{ss}}$ as elements of ![]() ${\mathcal{Z}}(G(E_{0}),{\mathcal{G}}({\mathcal{O}}_{E_{0}}))$. Their values then satisfy the required integrality properties independently of the choice of
${\mathcal{Z}}(G(E_{0}),{\mathcal{G}}({\mathcal{O}}_{E_{0}}))$. Their values then satisfy the required integrality properties independently of the choice of ![]() $\ell \neq p$ and
$\ell \neq p$ and ![]() $q^{1/2}\in \bar{\mathbb{Q}}_{\ell }$ by § 6.5. It is enough to show the equality
$q^{1/2}\in \bar{\mathbb{Q}}_{\ell }$ by § 6.5. It is enough to show the equality ![]() $\unicode[STIX]{x1D70F}_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}}^{\operatorname{ss}}=z_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}}^{\operatorname{ss}}$, that is, the equality of the two functions when they are viewed as elements of
$\unicode[STIX]{x1D70F}_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}}^{\operatorname{ss}}=z_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}}^{\operatorname{ss}}$, that is, the equality of the two functions when they are viewed as elements of ![]() ${\mathcal{Z}}(G_{\operatorname{ad}}(E_{0}),{\mathcal{G}}_{\operatorname{ad}}({\mathcal{O}}_{E_{0}}))$ via (7.5). Here
${\mathcal{Z}}(G_{\operatorname{ad}}(E_{0}),{\mathcal{G}}_{\operatorname{ad}}({\mathcal{O}}_{E_{0}}))$ via (7.5). Here ![]() $\unicode[STIX]{x1D70F}_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}}^{\text{ss}}$ is just a relabeling of (7.3) and we are using Lemma 7.7 below with
$\unicode[STIX]{x1D70F}_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}}^{\text{ss}}$ is just a relabeling of (7.3) and we are using Lemma 7.7 below with ![]() $V=I(V_{\{\unicode[STIX]{x1D707}\}})$ and
$V=I(V_{\{\unicode[STIX]{x1D707}\}})$ and ![]() $V_{\text{ad}}=I(V_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}})$ to justify that
$V_{\text{ad}}=I(V_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}})$ to justify that ![]() $z_{\{\unicode[STIX]{x1D707}\}}^{\text{ss}}\mapsto z_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}}^{\text{ss}}$ under (7.5).
$z_{\{\unicode[STIX]{x1D707}\}}^{\text{ss}}\mapsto z_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}}^{\text{ss}}$ under (7.5).
Fix a lift of geometric Frobenius ![]() $\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D6F7}_{E_{0}}$. We will show that
$\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D6F7}_{E_{0}}$. We will show that ![]() $\unicode[STIX]{x1D70F}_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}}^{\unicode[STIX]{x1D6F7}}=z_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}}^{\unicode[STIX]{x1D6F7}}$; cf. Appendix A. The result will then follow from Lemma A.1 by averaging over the different lifts
$\unicode[STIX]{x1D70F}_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}}^{\unicode[STIX]{x1D6F7}}=z_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}}^{\unicode[STIX]{x1D6F7}}$; cf. Appendix A. The result will then follow from Lemma A.1 by averaging over the different lifts ![]() $\unicode[STIX]{x1D6F7}$.
$\unicode[STIX]{x1D6F7}$.
For each ![]() $j\in J$ as in (7.1), we denote by
$j\in J$ as in (7.1), we denote by ![]() $\unicode[STIX]{x1D70F}_{\{\unicode[STIX]{x1D707}_{j}\}}^{\unicode[STIX]{x1D6F7}}$ (respectively,
$\unicode[STIX]{x1D70F}_{\{\unicode[STIX]{x1D707}_{j}\}}^{\unicode[STIX]{x1D6F7}}$ (respectively, ![]() $z_{\{\unicode[STIX]{x1D707}_{j}\}}^{\unicode[STIX]{x1D6F7}}$) the central functions associated with the local model triple
$z_{\{\unicode[STIX]{x1D707}_{j}\}}^{\unicode[STIX]{x1D6F7}}$) the central functions associated with the local model triple ![]() $(H_{j},\{\unicode[STIX]{x1D707}_{j}\},{\mathcal{H}}_{j})$ over the extension
$(H_{j},\{\unicode[STIX]{x1D707}_{j}\},{\mathcal{H}}_{j})$ over the extension ![]() $E/F$. Parallel to (7.3) we have
$E/F$. Parallel to (7.3) we have
where ![]() $\unicode[STIX]{x1D6F9}_{j}$ stands for the nearby cycles functor for
$\unicode[STIX]{x1D6F9}_{j}$ stands for the nearby cycles functor for ![]() $\operatorname{Gr}_{{\mathcal{H}}_{j}}\otimes _{{\mathcal{O}}_{F}}{\mathcal{O}}_{E}$. The tameness assumption in (7.1) guarantees that Theorem 6.7, and in particular (6.4), is applicable, and we deduce the equality
$\operatorname{Gr}_{{\mathcal{H}}_{j}}\otimes _{{\mathcal{O}}_{F}}{\mathcal{O}}_{E}$. The tameness assumption in (7.1) guarantees that Theorem 6.7, and in particular (6.4), is applicable, and we deduce the equality
as functions in ![]() ${\mathcal{Z}}(H_{j}(E_{0}),{\mathcal{H}}_{j}({\mathcal{O}}_{E_{0}}))$ for all
${\mathcal{Z}}(H_{j}(E_{0}),{\mathcal{H}}_{j}({\mathcal{O}}_{E_{0}}))$ for all ![]() $j\in J$. Recall that
$j\in J$. Recall that ![]() $\text{IC}_{\{\unicode[STIX]{x1D707}\}}=\text{Sat}(V_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}})$ can be expressed as the external tensor product
$\text{IC}_{\{\unicode[STIX]{x1D707}\}}=\text{Sat}(V_{\{\unicode[STIX]{x1D707}_{\text{ad}}\}})$ can be expressed as the external tensor product ![]() $\boxtimes _{j}\text{Sat}(V_{\{\unicode[STIX]{x1D707}_{j}\}})=\boxtimes _{j}\text{IC}_{\{\unicode[STIX]{x1D707}_{j}\}}$ on the generic fiber
$\boxtimes _{j}\text{Sat}(V_{\{\unicode[STIX]{x1D707}_{j}\}})=\boxtimes _{j}\text{IC}_{\{\unicode[STIX]{x1D707}_{j}\}}$ on the generic fiber ![]() $\operatorname{Gr}_{{\mathcal{G}}_{\operatorname{ad}},{\mathcal{O}}_{E_{0}}}\otimes _{{\mathcal{O}}_{E_{0}}}E=\prod _{j}\text{Gr}_{H_{j},E}$. Since the formation of the non-semisimplified functions commutes with direct products of groups by Lemma A.2, we get the equality
$\operatorname{Gr}_{{\mathcal{G}}_{\operatorname{ad}},{\mathcal{O}}_{E_{0}}}\otimes _{{\mathcal{O}}_{E_{0}}}E=\prod _{j}\text{Gr}_{H_{j},E}$. Since the formation of the non-semisimplified functions commutes with direct products of groups by Lemma A.2, we get the equality
inside ![]() ${\mathcal{Z}}(G_{\operatorname{ad}}(E_{0}),{\mathcal{G}}_{\operatorname{ad}}({\mathcal{O}}_{E_{0}}))=\prod _{j}{\mathcal{Z}}(H_{j}(E_{0}),{\mathcal{H}}_{j}({\mathcal{O}}_{E_{0}}))$. We have also used the equality
${\mathcal{Z}}(G_{\operatorname{ad}}(E_{0}),{\mathcal{G}}_{\operatorname{ad}}({\mathcal{O}}_{E_{0}}))=\prod _{j}{\mathcal{Z}}(H_{j}(E_{0}),{\mathcal{H}}_{j}({\mathcal{O}}_{E_{0}}))$. We have also used the equality ![]() $\sum _{j}d_{\unicode[STIX]{x1D707}_{j}}\equiv d_{\unicode[STIX]{x1D707}}\;\text{mod}\;2$. This completes the proof of the theorem.◻
$\sum _{j}d_{\unicode[STIX]{x1D707}_{j}}\equiv d_{\unicode[STIX]{x1D707}}\;\text{mod}\;2$. This completes the proof of the theorem.◻
7.3 Passing to adjoint groups
In this section we do not need any tameness assumptions – the arguments hold for general groups. We work over the unramified extension ![]() $E_{0}/F$. Let
$E_{0}/F$. Let ![]() $Z$ be the center of
$Z$ be the center of ![]() $G$. Let
$G$. Let ![]() $A,S,T,M$ be as usual for the
$A,S,T,M$ be as usual for the ![]() $E_{0}$-group
$E_{0}$-group ![]() $G$, and denote by
$G$, and denote by ![]() $A_{\text{ad}},S_{\text{ad}},T_{\text{ad}},M_{\text{ad}}$ their images under the canonical map
$A_{\text{ad}},S_{\text{ad}},T_{\text{ad}},M_{\text{ad}}$ their images under the canonical map ![]() $p:G\rightarrow G_{\text{ad}}=G/Z$. Recall that
$p:G\rightarrow G_{\text{ad}}=G/Z$. Recall that ![]() $M_{\operatorname{ad}}$ is not the adjoint group of
$M_{\operatorname{ad}}$ is not the adjoint group of ![]() $M$, but is a minimal
$M$, but is a minimal ![]() $E_{0}$-Levi subgroup of
$E_{0}$-Levi subgroup of ![]() $G_{\operatorname{ad}}$. Let
$G_{\operatorname{ad}}$. Let ![]() ${\mathcal{G}}$ (respectively,
${\mathcal{G}}$ (respectively, ![]() ${\mathcal{G}}_{\mathbf{a}}$) be the parahoric group
${\mathcal{G}}_{\mathbf{a}}$) be the parahoric group ![]() ${\mathcal{O}}_{E_{0}}$-scheme with generic fiber
${\mathcal{O}}_{E_{0}}$-scheme with generic fiber ![]() $G_{E_{0}}$ attached to a facet
$G_{E_{0}}$ attached to a facet ![]() $\mathbf{f}$ (respectively, an alcove
$\mathbf{f}$ (respectively, an alcove ![]() $\mathbf{a}$ with
$\mathbf{a}$ with ![]() $\mathbf{f}\subset \bar{\mathbf{a}}$). Let
$\mathbf{f}\subset \bar{\mathbf{a}}$). Let ![]() ${\mathcal{G}}_{\text{ad}}$ (respectively,
${\mathcal{G}}_{\text{ad}}$ (respectively, ![]() ${\mathcal{G}}_{\text{ad},\mathbf{a}}$) be their analogues for
${\mathcal{G}}_{\text{ad},\mathbf{a}}$) be their analogues for ![]() $G_{\text{ad}}$. The morphism
$G_{\text{ad}}$. The morphism ![]() $p:G(E_{0})\rightarrow G_{\text{ad}}(E_{0})$ sends
$p:G(E_{0})\rightarrow G_{\text{ad}}(E_{0})$ sends ![]() ${\mathcal{G}}({\mathcal{O}}_{E_{0}})$ into
${\mathcal{G}}({\mathcal{O}}_{E_{0}})$ into ![]() ${\mathcal{G}}_{\text{ad}}({\mathcal{O}}_{E_{0}})$, and so by the étoffé property of
${\mathcal{G}}_{\text{ad}}({\mathcal{O}}_{E_{0}})$, and so by the étoffé property of ![]() ${\mathcal{G}}$,
${\mathcal{G}}$, ![]() $p$ extends to an
$p$ extends to an ![]() ${\mathcal{O}}_{E_{0}}$-morphism
${\mathcal{O}}_{E_{0}}$-morphism ![]() $p:{\mathcal{G}}\rightarrow {\mathcal{G}}_{\text{ad}}$; cf. [Reference Bruhat and TitsBT84, 1.7]. Similarly, we have
$p:{\mathcal{G}}\rightarrow {\mathcal{G}}_{\text{ad}}$; cf. [Reference Bruhat and TitsBT84, 1.7]. Similarly, we have ![]() $p:{\mathcal{G}}_{\mathbf{a}}\rightarrow {\mathcal{G}}_{\text{ad},\mathbf{a}}$.
$p:{\mathcal{G}}_{\mathbf{a}}\rightarrow {\mathcal{G}}_{\text{ad},\mathbf{a}}$.
Let ![]() ${\mathcal{O}}$ stand for either
${\mathcal{O}}$ stand for either ![]() ${\mathcal{O}}_{E_{0}}$ or
${\mathcal{O}}_{E_{0}}$ or ![]() ${\mathcal{O}}_{\breve{E}_{0}}$, with
${\mathcal{O}}_{\breve{E}_{0}}$, with ![]() $K$ its fraction field. In general, the natural maps
$K$ its fraction field. In general, the natural maps ![]() $p:{\mathcal{G}}({\mathcal{O}})\rightarrow {\mathcal{G}}_{\text{ad}}({\mathcal{O}})$ and
$p:{\mathcal{G}}({\mathcal{O}})\rightarrow {\mathcal{G}}_{\text{ad}}({\mathcal{O}})$ and ![]() $G(K)/{\mathcal{G}}({\mathcal{O}})\rightarrow G_{\text{ad}}(K)/{\mathcal{G}}_{\text{ad}}({\mathcal{O}})\!)$ are not surjective. Nevertheless, using [Reference Bruhat and TitsBT84, 5.2.4], if
$G(K)/{\mathcal{G}}({\mathcal{O}})\rightarrow G_{\text{ad}}(K)/{\mathcal{G}}_{\text{ad}}({\mathcal{O}})\!)$ are not surjective. Nevertheless, using [Reference Bruhat and TitsBT84, 5.2.4], if ![]() ${\mathcal{M}}_{\text{ad}}$ (respectively,
${\mathcal{M}}_{\text{ad}}$ (respectively, ![]() ${\mathcal{T}}_{\text{ad}}$) denotes the unique parahoric group scheme for
${\mathcal{T}}_{\text{ad}}$) denotes the unique parahoric group scheme for ![]() $M_{\text{ad}}$ (respectively,
$M_{\text{ad}}$ (respectively, ![]() $T_{\text{ad}}$), one can check that
$T_{\text{ad}}$), one can check that ![]() $p({\mathcal{G}}({\mathcal{O}}_{E_{0}}))\cdot {\mathcal{M}}_{\text{ad}}({\mathcal{O}}_{E_{0}})={\mathcal{G}}_{\text{ad}}({\mathcal{O}}_{E_{0}})$ (respectively,
$p({\mathcal{G}}({\mathcal{O}}_{E_{0}}))\cdot {\mathcal{M}}_{\text{ad}}({\mathcal{O}}_{E_{0}})={\mathcal{G}}_{\text{ad}}({\mathcal{O}}_{E_{0}})$ (respectively, ![]() $p({\mathcal{G}}({\mathcal{O}}_{\breve{E}_{0}}))\cdot {\mathcal{T}}_{\text{ad}}({\mathcal{O}}_{\breve{E}_{0}})={\mathcal{G}}_{\text{ad}}({\mathcal{O}}_{\breve{E}_{0}})$). This implies that
$p({\mathcal{G}}({\mathcal{O}}_{\breve{E}_{0}}))\cdot {\mathcal{T}}_{\text{ad}}({\mathcal{O}}_{\breve{E}_{0}})={\mathcal{G}}_{\text{ad}}({\mathcal{O}}_{\breve{E}_{0}})$). This implies that ![]() $p$ takes any
$p$ takes any ![]() ${\mathcal{G}}({\mathcal{O}})$-orbit in
${\mathcal{G}}({\mathcal{O}})$-orbit in ![]() $G(K)/{\mathcal{G}}({\mathcal{O}})$ onto a
$G(K)/{\mathcal{G}}({\mathcal{O}})$ onto a ![]() ${\mathcal{G}}_{\text{ad}}({\mathcal{O}})$-orbit in
${\mathcal{G}}_{\text{ad}}({\mathcal{O}})$-orbit in ![]() $G_{\text{ad}}(K)/{\mathcal{G}}_{\text{ad}}({\mathcal{O}})$, since
$G_{\text{ad}}(K)/{\mathcal{G}}_{\text{ad}}({\mathcal{O}})$, since ![]() ${\mathcal{M}}_{\text{ad}}({\mathcal{O}}_{E_{0}})$ (respectively,
${\mathcal{M}}_{\text{ad}}({\mathcal{O}}_{E_{0}})$ (respectively, ![]() ${\mathcal{T}}_{\text{ad}}({\mathcal{O}}_{\breve{E}_{0}})$) is normalized by the group
${\mathcal{T}}_{\text{ad}}({\mathcal{O}}_{\breve{E}_{0}})$) is normalized by the group ![]() $N_{G_{\text{ad}}}(A_{\text{ad}})(E_{0})$ (respectively,
$N_{G_{\text{ad}}}(A_{\text{ad}})(E_{0})$ (respectively, ![]() $N_{G_{\text{ad}}}(S_{\text{ad}})(\breve{E}_{0})$) giving rise to representatives of those
$N_{G_{\text{ad}}}(S_{\text{ad}})(\breve{E}_{0})$) giving rise to representatives of those ![]() ${\mathcal{G}}_{\text{ad}}({\mathcal{O}})$-orbits.
${\mathcal{G}}_{\text{ad}}({\mathcal{O}})$-orbits.
Write ![]() ${\mathcal{O}}={\mathcal{O}}_{E_{0}}$ and
${\mathcal{O}}={\mathcal{O}}_{E_{0}}$ and ![]() $\breve{{\mathcal{O}}}={\mathcal{O}}_{\breve{E}_{0}}$. We make some abbreviations: Iwahori subgroups
$\breve{{\mathcal{O}}}={\mathcal{O}}_{\breve{E}_{0}}$. We make some abbreviations: Iwahori subgroups ![]() $\breve{I}={\mathcal{G}}_{\mathbf{a}}(\breve{{\mathcal{O}}})$ and
$\breve{I}={\mathcal{G}}_{\mathbf{a}}(\breve{{\mathcal{O}}})$ and ![]() $I={\mathcal{G}}_{\mathbf{a}}({\mathcal{O}})$; parahoric subgroups
$I={\mathcal{G}}_{\mathbf{a}}({\mathcal{O}})$; parahoric subgroups ![]() $\breve{J}={\mathcal{G}}(\breve{{\mathcal{O}}})$ and
$\breve{J}={\mathcal{G}}(\breve{{\mathcal{O}}})$ and ![]() $J={\mathcal{G}}({\mathcal{O}})$. Similarly define their analogues for
$J={\mathcal{G}}({\mathcal{O}})$. Similarly define their analogues for ![]() $G_{\text{ad}}$:
$G_{\text{ad}}$: ![]() $\breve{I}_{\text{ad}}$,
$\breve{I}_{\text{ad}}$, ![]() $I_{\text{ad}}$,
$I_{\text{ad}}$, ![]() $\breve{J}_{\text{ad}}$, and
$\breve{J}_{\text{ad}}$, and ![]() $J_{\text{ad}}$. Let
$J_{\text{ad}}$. Let ![]() $W_{0}$ denote the finite relative Weyl group for
$W_{0}$ denote the finite relative Weyl group for ![]() $G/E_{0}$. There are decompositions of the Iwahori–Weyl groups over
$G/E_{0}$. There are decompositions of the Iwahori–Weyl groups over ![]() $E_{0}$:
$E_{0}$:
and ![]() $p:W\rightarrow W_{\text{ad}}$ is compatible with these decompositions. In general,
$p:W\rightarrow W_{\text{ad}}$ is compatible with these decompositions. In general, ![]() $p$ maps
$p$ maps ![]() $\unicode[STIX]{x1D6FA}_{\mathbf{a}}$ to
$\unicode[STIX]{x1D6FA}_{\mathbf{a}}$ to ![]() $\unicode[STIX]{x1D6FA}_{\mathbf{a}_{\text{ad}}}$, but neither surjectively nor injectively. However, for each fixed
$\unicode[STIX]{x1D6FA}_{\mathbf{a}_{\text{ad}}}$, but neither surjectively nor injectively. However, for each fixed ![]() $\unicode[STIX]{x1D714}\in \unicode[STIX]{x1D6FA}_{\mathbf{a}}$ with image
$\unicode[STIX]{x1D714}\in \unicode[STIX]{x1D6FA}_{\mathbf{a}}$ with image ![]() $\unicode[STIX]{x1D714}_{\text{ad}}\in \unicode[STIX]{x1D6FA}_{\mathbf{a}_{\text{ad}}}$, we obtain an isomorphism
$\unicode[STIX]{x1D714}_{\text{ad}}\in \unicode[STIX]{x1D6FA}_{\mathbf{a}_{\text{ad}}}$, we obtain an isomorphism
Recall that ![]() ${\mathcal{H}}(G(E_{0}),I)$ is generated by
${\mathcal{H}}(G(E_{0}),I)$ is generated by ![]() $T_{w}^{G}=1_{I{\dot{w}}I}$, where
$T_{w}^{G}=1_{I{\dot{w}}I}$, where ![]() ${\dot{w}}\in N_{G}(T)(E_{0})$ is a lift of
${\dot{w}}\in N_{G}(T)(E_{0})$ is a lift of ![]() $w\in W(G)$ along the Kottwitz homomorphism
$w\in W(G)$ along the Kottwitz homomorphism ![]() $\unicode[STIX]{x1D705}_{G,E_{0}}$. The algebra
$\unicode[STIX]{x1D705}_{G,E_{0}}$. The algebra ![]() ${\mathcal{H}}(G(E_{0}),I)$ has an Iwahori–Matsumoto presentation, that is, it is isomorphic to an affine Hecke algebra over
${\mathcal{H}}(G(E_{0}),I)$ has an Iwahori–Matsumoto presentation, that is, it is isomorphic to an affine Hecke algebra over ![]() $\mathbb{Z}[v,v^{-1}]$ with possibly unequal parameters, after a specialization
$\mathbb{Z}[v,v^{-1}]$ with possibly unequal parameters, after a specialization ![]() $v\mapsto \sqrt{q_{E_{0}}}\in \bar{\mathbb{Q}}_{\ell }$; cf. [Reference Haines, Diamond, Kassaei and KimHai14, 11.3.2] or [Reference RostamiRos15] for a proof in this generality. The map
$v\mapsto \sqrt{q_{E_{0}}}\in \bar{\mathbb{Q}}_{\ell }$; cf. [Reference Haines, Diamond, Kassaei and KimHai14, 11.3.2] or [Reference RostamiRos15] for a proof in this generality. The map ![]() $T_{w}^{G}\mapsto T_{p(w)}^{G_{\text{ad}}}$ respects the braid and quadratic relations, hence gives an algebra homomorphism
$T_{w}^{G}\mapsto T_{p(w)}^{G_{\text{ad}}}$ respects the braid and quadratic relations, hence gives an algebra homomorphism
Let ![]() $e_{J}$ and
$e_{J}$ and ![]() $e_{J_{\text{ad}}}$ be the idempotents corresponding to
$e_{J_{\text{ad}}}$ be the idempotents corresponding to ![]() $J$ and
$J$ and ![]() $J_{\text{ad}}$; these both correspond to the same set of reflections in
$J_{\text{ad}}$; these both correspond to the same set of reflections in ![]() $W_{\text{sc}}$ (those which fix
$W_{\text{sc}}$ (those which fix ![]() $\mathbf{f}$). Therefore, using the usual relations in the Iwahori–Hecke algebra to understand the products of such idempotents by the standard generators
$\mathbf{f}$). Therefore, using the usual relations in the Iwahori–Hecke algebra to understand the products of such idempotents by the standard generators ![]() $T_{w}^{G}$, we see that the map
$T_{w}^{G}$, we see that the map
where ![]() $w_{\text{ad}}=p(w)$, determines a homomorphism of algebras
$w_{\text{ad}}=p(w)$, determines a homomorphism of algebras
The homomorphism above preserves centers; to see this one uses the Bernstein presentation of ![]() ${\mathcal{H}}(G(E_{0}),I)$ and
${\mathcal{H}}(G(E_{0}),I)$ and ![]() ${\mathcal{H}}(G_{\text{ad}}(E_{0}),I_{\text{ad}})$ (we refer to [Reference RostamiRos15] for a proof of the Bernstein presentation in this most general setting). Put
${\mathcal{H}}(G_{\text{ad}}(E_{0}),I_{\text{ad}})$ (we refer to [Reference RostamiRos15] for a proof of the Bernstein presentation in this most general setting). Put ![]() $\unicode[STIX]{x1D6EC}_{M}=X^{\ast }(Z(M^{\vee })^{I_{E_{0}}})^{\unicode[STIX]{x1D6F7}}$. The Bernstein presentations reflect the decomposition
$\unicode[STIX]{x1D6EC}_{M}=X^{\ast }(Z(M^{\vee })^{I_{E_{0}}})^{\unicode[STIX]{x1D6F7}}$. The Bernstein presentations reflect the decomposition ![]() $W=\unicode[STIX]{x1D6EC}_{M}\rtimes W_{0}$ of (7.6), and, for each
$W=\unicode[STIX]{x1D6EC}_{M}\rtimes W_{0}$ of (7.6), and, for each ![]() $W_{0}$-orbit
$W_{0}$-orbit ![]() $\bar{\unicode[STIX]{x1D706}}\subset \unicode[STIX]{x1D6EC}_{M}$, there is a basis element
$\bar{\unicode[STIX]{x1D706}}\subset \unicode[STIX]{x1D6EC}_{M}$, there is a basis element ![]() $z_{\bar{\unicode[STIX]{x1D706}}}\in {\mathcal{Z}}(G(E_{0}),I)$; cf. [Reference Haines, Diamond, Kassaei and KimHai14, 11.10.2]. The map sends
$z_{\bar{\unicode[STIX]{x1D706}}}\in {\mathcal{Z}}(G(E_{0}),I)$; cf. [Reference Haines, Diamond, Kassaei and KimHai14, 11.10.2]. The map sends ![]() $z_{\bar{\unicode[STIX]{x1D706}}}$ to
$z_{\bar{\unicode[STIX]{x1D706}}}$ to ![]() $z_{\bar{\unicode[STIX]{x1D706}}_{\operatorname{ad}}}$. To see this, we write out each of
$z_{\bar{\unicode[STIX]{x1D706}}_{\operatorname{ad}}}$. To see this, we write out each of ![]() $z_{\bar{\unicode[STIX]{x1D706}}}$ and
$z_{\bar{\unicode[STIX]{x1D706}}}$ and ![]() $z_{\bar{\unicode[STIX]{x1D706}}_{\operatorname{ad}}}$ in terms of the standard basis elements
$z_{\bar{\unicode[STIX]{x1D706}}_{\operatorname{ad}}}$ in terms of the standard basis elements ![]() $T_{w}^{G}$ and
$T_{w}^{G}$ and ![]() $T_{p(w)}^{G_{\text{ad}}}$. (Use that the alcove walk description of Bernstein functions depends only on the combinatorics of
$T_{p(w)}^{G_{\text{ad}}}$. (Use that the alcove walk description of Bernstein functions depends only on the combinatorics of ![]() $W_{\text{sc}}$; cf. [Reference Haines and RapoportHR12, § 14.2].) Hence the diagram
$W_{\text{sc}}$; cf. [Reference Haines and RapoportHR12, § 14.2].) Hence the diagram

commutes, where the vertical arrows are the Bernstein isomorphisms of [Reference Haines, Diamond, Kassaei and KimHai14, 11.10.1].
Now, the top arrow is neither injective nor surjective in general. To remedy this, we establish the analogue of (7.7) on the level of centers. Assume ![]() $V\in \text{Rep}(\text{}^{L}G_{E_{0}})$ has the following property:
$V\in \text{Rep}(\text{}^{L}G_{E_{0}})$ has the following property:
(e.g. ![]() $V|_{G^{\vee }\rtimes I_{E_{0}}}$ is irreducible). Then the restriction
$V|_{G^{\vee }\rtimes I_{E_{0}}}$ is irreducible). Then the restriction ![]() $V_{\text{ad}}:=V|_{\text{}^{L}(G_{\text{ad}})_{E_{0}}}$ has the same property. Let
$V_{\text{ad}}:=V|_{\text{}^{L}(G_{\text{ad}})_{E_{0}}}$ has the same property. Let ![]() $\unicode[STIX]{x1D714}_{V}\in \unicode[STIX]{x1D70B}_{1}(G)_{I_{E_{0}}}^{\unicode[STIX]{x1D6F7}_{E}}$ be the common image of the
$\unicode[STIX]{x1D714}_{V}\in \unicode[STIX]{x1D70B}_{1}(G)_{I_{E_{0}}}^{\unicode[STIX]{x1D6F7}_{E}}$ be the common image of the ![]() $\unicode[STIX]{x1D706}_{i}\in X_{\ast }(T)$ appearing as
$\unicode[STIX]{x1D706}_{i}\in X_{\ast }(T)$ appearing as ![]() $B^{\vee }$-highest
$B^{\vee }$-highest ![]() $T^{\vee }$-weights in
$T^{\vee }$-weights in ![]() $V|_{G^{\vee }}$, and define
$V|_{G^{\vee }}$, and define ![]() $\unicode[STIX]{x1D714}_{V_{\text{ad}}}$ similarly. Note that
$\unicode[STIX]{x1D714}_{V_{\text{ad}}}$ similarly. Note that ![]() $\unicode[STIX]{x1D714}_{V}\mapsto \unicode[STIX]{x1D714}_{V_{\text{ad}}}$ under
$\unicode[STIX]{x1D714}_{V}\mapsto \unicode[STIX]{x1D714}_{V_{\text{ad}}}$ under ![]() $\unicode[STIX]{x1D70B}_{1}(G)_{I_{E_{0}}}\rightarrow \unicode[STIX]{x1D70B}_{1}(G_{\text{ad}})_{I_{E_{0}}}$, that is,
$\unicode[STIX]{x1D70B}_{1}(G)_{I_{E_{0}}}\rightarrow \unicode[STIX]{x1D70B}_{1}(G_{\text{ad}})_{I_{E_{0}}}$, that is, ![]() $(\unicode[STIX]{x1D714}_{V})_{\text{ad}}=\unicode[STIX]{x1D714}_{V_{\text{ad}}}$.
$(\unicode[STIX]{x1D714}_{V})_{\text{ad}}=\unicode[STIX]{x1D714}_{V_{\text{ad}}}$.
Let ![]() ${\mathcal{H}}(G(E_{0}),J)_{\unicode[STIX]{x1D714}_{V}}$ be the subspace generated by the elements
${\mathcal{H}}(G(E_{0}),J)_{\unicode[STIX]{x1D714}_{V}}$ be the subspace generated by the elements ![]() $e_{J}T_{w}^{G}e_{J}$,
$e_{J}T_{w}^{G}e_{J}$, ![]() $w\in W_{\text{sc}}\rtimes \,\unicode[STIX]{x1D714}_{V}$. Define
$w\in W_{\text{sc}}\rtimes \,\unicode[STIX]{x1D714}_{V}$. Define ![]() ${\mathcal{Z}}(G(E_{0}),J)_{\unicode[STIX]{x1D714}_{V}}={\mathcal{H}}(G(E_{0}),J)_{\unicode[STIX]{x1D714}_{V}}\cap {\mathcal{Z}}(G(E_{0}),J)$. As in (7.4) these are the functions supported on
${\mathcal{Z}}(G(E_{0}),J)_{\unicode[STIX]{x1D714}_{V}}={\mathcal{H}}(G(E_{0}),J)_{\unicode[STIX]{x1D714}_{V}}\cap {\mathcal{Z}}(G(E_{0}),J)$. As in (7.4) these are the functions supported on ![]() $G(E_{0})_{\unicode[STIX]{x1D714}_{V}}\subset G(E_{0})$.
$G(E_{0})_{\unicode[STIX]{x1D714}_{V}}\subset G(E_{0})$.
Lemma 7.7. Assume ![]() $V$ satisfies property
$V$ satisfies property ![]() $(\ast )$; for example,
$(\ast )$; for example, ![]() $V=I(V_{\{\unicode[STIX]{x1D707}\}})$. Then the map
$V=I(V_{\{\unicode[STIX]{x1D707}\}})$. Then the map ![]() $p_{\ast }:{\mathcal{Z}}(G(E_{0}),J)\rightarrow {\mathcal{Z}}(G_{\text{ad}}(E_{0}),J_{\operatorname{ad}})$ induces a vector space isomorphism
$p_{\ast }:{\mathcal{Z}}(G(E_{0}),J)\rightarrow {\mathcal{Z}}(G_{\text{ad}}(E_{0}),J_{\operatorname{ad}})$ induces a vector space isomorphism
taking ![]() $z_{{\mathcal{G}},V}^{\unicode[STIX]{x1D6F7}}$ to
$z_{{\mathcal{G}},V}^{\unicode[STIX]{x1D6F7}}$ to ![]() $z_{{\mathcal{G}}_{\text{ad}},V_{\operatorname{ad}}}^{\unicode[STIX]{x1D6F7}}$.
$z_{{\mathcal{G}}_{\text{ad}},V_{\operatorname{ad}}}^{\unicode[STIX]{x1D6F7}}$.
Proof. Since ![]() $p(z_{\bar{\unicode[STIX]{x1D706}}})=z_{\bar{\unicode[STIX]{x1D706}}_{\operatorname{ad}}}$ for
$p(z_{\bar{\unicode[STIX]{x1D706}}})=z_{\bar{\unicode[STIX]{x1D706}}_{\operatorname{ad}}}$ for ![]() $\bar{\unicode[STIX]{x1D706}}$ (respectively,
$\bar{\unicode[STIX]{x1D706}}$ (respectively, ![]() $\bar{\unicode[STIX]{x1D706}}_{\operatorname{ad}}$) ranging over
$\bar{\unicode[STIX]{x1D706}}_{\operatorname{ad}}$) ranging over ![]() $W_{0}$-orbits in
$W_{0}$-orbits in ![]() $\unicode[STIX]{x1D6EC}_{M}\cap (W_{\text{sc}}\rtimes \unicode[STIX]{x1D714}_{V})$ (respectively, in
$\unicode[STIX]{x1D6EC}_{M}\cap (W_{\text{sc}}\rtimes \unicode[STIX]{x1D714}_{V})$ (respectively, in ![]() $\unicode[STIX]{x1D6EC}_{M_{\operatorname{ad}}}\cap (W_{\text{sc}}\rtimes \unicode[STIX]{x1D714}_{V_{\operatorname{ad}}})$), the first statement is clear. All that remains is to show that
$\unicode[STIX]{x1D6EC}_{M_{\operatorname{ad}}}\cap (W_{\text{sc}}\rtimes \unicode[STIX]{x1D714}_{V_{\operatorname{ad}}})$), the first statement is clear. All that remains is to show that ![]() $p_{\ast }(z_{{\mathcal{G}},V}^{\unicode[STIX]{x1D6F7}})=z_{{\mathcal{G}}_{\operatorname{ad}},V_{\operatorname{ad}}}^{\unicode[STIX]{x1D6F7}}$.
$p_{\ast }(z_{{\mathcal{G}},V}^{\unicode[STIX]{x1D6F7}})=z_{{\mathcal{G}}_{\operatorname{ad}},V_{\operatorname{ad}}}^{\unicode[STIX]{x1D6F7}}$.
Using the construction of Satake parameters ([Reference HainesHai15, § 9], [Reference HainesHai17]), the map ![]() $G\rightarrow G_{\operatorname{ad}}$ induces a commutative diagram (here for notational convenience we write
$G\rightarrow G_{\operatorname{ad}}$ induces a commutative diagram (here for notational convenience we write ![]() $\widehat{G}$ in place of
$\widehat{G}$ in place of ![]() $G^{\vee }$):
$G^{\vee }$):

Fix ![]() $V\in \text{Rep}(\text{}^{L}G_{E})$. Starting with the regular function
$V\in \text{Rep}(\text{}^{L}G_{E})$. Starting with the regular function ![]() $g^{\ast }\rtimes \unicode[STIX]{x1D6F7}^{\ast }\mapsto \text{tr}(g^{\ast }\rtimes \unicode[STIX]{x1D6F7}^{\ast }\mid V)$ on the variety in the upper right corner, we pull back along the diagram to get a regular function on the lower left-hand corner. Pulling back in one way yields
$g^{\ast }\rtimes \unicode[STIX]{x1D6F7}^{\ast }\mapsto \text{tr}(g^{\ast }\rtimes \unicode[STIX]{x1D6F7}^{\ast }\mid V)$ on the variety in the upper right corner, we pull back along the diagram to get a regular function on the lower left-hand corner. Pulling back in one way yields ![]() $z_{{\mathcal{G}}_{\operatorname{ad}},V_{\operatorname{ad}}}^{\unicode[STIX]{x1D6F7}}$, and pulling back in the other way, by (7.8), yields
$z_{{\mathcal{G}}_{\operatorname{ad}},V_{\operatorname{ad}}}^{\unicode[STIX]{x1D6F7}}$, and pulling back in the other way, by (7.8), yields ![]() $p_{\ast }(z_{{\mathcal{G}},V}^{\unicode[STIX]{x1D6F7}})$.◻
$p_{\ast }(z_{{\mathcal{G}},V}^{\unicode[STIX]{x1D6F7}})$.◻
Acknowledgements
The authors thank Michael Rapoport for funding, the University of Maryland for logistical support which made this research possible, and the anonymous referee for useful suggestions leading to the results in § 7. The second named author thanks the DFG (German Research Foundation) for financial support during the academic year 2018.
Appendix A Non-semisimplified trace
A.1 Basic definitions
Let ![]() $V\in \text{Rep}(\text{}^{L}G)$, and let
$V\in \text{Rep}(\text{}^{L}G)$, and let ![]() $\unicode[STIX]{x1D6F7}\in \text{Gal}(\bar{F}/F)$ denote a fixed lift of geometric Frobenius. Let
$\unicode[STIX]{x1D6F7}\in \text{Gal}(\bar{F}/F)$ denote a fixed lift of geometric Frobenius. Let ![]() ${\mathcal{G}}/{\mathcal{O}}_{F}$ denote a parahoric group scheme. Define
${\mathcal{G}}/{\mathcal{O}}_{F}$ denote a parahoric group scheme. Define ![]() $z_{{\mathcal{G}},V}^{\unicode[STIX]{x1D6F7}}\in {\mathcal{Z}}(G(F),{\mathcal{G}}({\mathcal{O}}_{F}))$ to be the unique function such that, if
$z_{{\mathcal{G}},V}^{\unicode[STIX]{x1D6F7}}\in {\mathcal{Z}}(G(F),{\mathcal{G}}({\mathcal{O}}_{F}))$ to be the unique function such that, if ![]() $\unicode[STIX]{x1D70B}$ is an irreducible smooth representation of
$\unicode[STIX]{x1D70B}$ is an irreducible smooth representation of ![]() $G(F)$ on a
$G(F)$ on a ![]() $\bar{\mathbb{Q}}_{\ell }$-vector space such that
$\bar{\mathbb{Q}}_{\ell }$-vector space such that ![]() $\unicode[STIX]{x1D70B}^{{\mathcal{G}}({\mathcal{O}}_{F})}\neq 0$, then
$\unicode[STIX]{x1D70B}^{{\mathcal{G}}({\mathcal{O}}_{F})}\neq 0$, then ![]() $z_{{\mathcal{G}},V}^{\unicode[STIX]{x1D6F7}}$ acts on
$z_{{\mathcal{G}},V}^{\unicode[STIX]{x1D6F7}}$ acts on ![]() $\unicode[STIX]{x1D70B}^{{\mathcal{G}}({\mathcal{O}}_{F})}$ by the scalar
$\unicode[STIX]{x1D70B}^{{\mathcal{G}}({\mathcal{O}}_{F})}$ by the scalar
where ![]() $s^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D70B})\in [(G^{\vee })^{I_{F}}\rtimes \unicode[STIX]{x1D6F7}]_{\text{ss}}/(G^{\vee })^{I_{F}}$ is the Satake parameter of
$s^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D70B})\in [(G^{\vee })^{I_{F}}\rtimes \unicode[STIX]{x1D6F7}]_{\text{ss}}/(G^{\vee })^{I_{F}}$ is the Satake parameter of ![]() $\unicode[STIX]{x1D70B}$ as defined in [Reference HainesHai15], relative to the fixed choice of
$\unicode[STIX]{x1D70B}$ as defined in [Reference HainesHai15], relative to the fixed choice of ![]() $\unicode[STIX]{x1D6F7}$.
$\unicode[STIX]{x1D6F7}$.
Similarly, if ![]() $V$ is irreducible with parity
$V$ is irreducible with parity ![]() $d_{V}\in \mathbb{Z}/2\mathbb{Z}$ as in [Reference Haines and RicharzHR18, (7.11)], we define the function
$d_{V}\in \mathbb{Z}/2\mathbb{Z}$ as in [Reference Haines and RicharzHR18, (7.11)], we define the function ![]() $\unicode[STIX]{x1D70F}_{{\mathcal{G}},V}^{\unicode[STIX]{x1D6F7}}$ on
$\unicode[STIX]{x1D70F}_{{\mathcal{G}},V}^{\unicode[STIX]{x1D6F7}}$ on ![]() $\text{Gr}_{{\mathcal{G}}}(k_{F})$ by the identity
$\text{Gr}_{{\mathcal{G}}}(k_{F})$ by the identity
We extend by linearity to define ![]() $\unicode[STIX]{x1D70F}_{{\mathcal{G}},V}^{\unicode[STIX]{x1D6F7}}$ for all
$\unicode[STIX]{x1D70F}_{{\mathcal{G}},V}^{\unicode[STIX]{x1D6F7}}$ for all ![]() $V$. By the same arguments which proved Theorem 5.15, Lemma 4.12 and Corollary 4.9, we may view
$V$. By the same arguments which proved Theorem 5.15, Lemma 4.12 and Corollary 4.9, we may view ![]() $\unicode[STIX]{x1D70F}_{{\mathcal{G}},V}^{\unicode[STIX]{x1D6F7}}$ as an element in the Hecke algebra
$\unicode[STIX]{x1D70F}_{{\mathcal{G}},V}^{\unicode[STIX]{x1D6F7}}$ as an element in the Hecke algebra ![]() ${\mathcal{Z}}(G(F),{\mathcal{G}}({\mathcal{O}}_{F}))$.
${\mathcal{Z}}(G(F),{\mathcal{G}}({\mathcal{O}}_{F}))$.
A.2 Averaging over inertia
Choose any normal finite-index subgroup ![]() $I_{1}\subseteq I_{F}$ having the property that
$I_{1}\subseteq I_{F}$ having the property that ![]() $1\rtimes I_{1}$ acts trivially on
$1\rtimes I_{1}$ acts trivially on ![]() $V$ and
$V$ and ![]() $I_{1}$ acts purely unipotently on all cohomology stalks of
$I_{1}$ acts purely unipotently on all cohomology stalks of ![]() $\unicode[STIX]{x1D6F9}_{\text{Gr}_{{\mathcal{G}}}}(\text{Sat}(V))$.
$\unicode[STIX]{x1D6F9}_{\text{Gr}_{{\mathcal{G}}}}(\text{Sat}(V))$.
Lemma A.1. Let ![]() $\dot{\unicode[STIX]{x1D6FE}}\in I_{F}$ range over a set of lifts of the elements
$\dot{\unicode[STIX]{x1D6FE}}\in I_{F}$ range over a set of lifts of the elements ![]() $\unicode[STIX]{x1D6FE}\in I_{F}/I_{1}$. Then
$\unicode[STIX]{x1D6FE}\in I_{F}/I_{1}$. Then
Consequently, ![]() $\unicode[STIX]{x1D70F}_{{\mathcal{G}},V}^{\text{ss}}=z_{{\mathcal{G}},V}^{\text{ss}}$, if
$\unicode[STIX]{x1D70F}_{{\mathcal{G}},V}^{\text{ss}}=z_{{\mathcal{G}},V}^{\text{ss}}$, if ![]() $\unicode[STIX]{x1D70F}_{{\mathcal{G}},V}^{\unicode[STIX]{x1D6F7}}=z_{{\mathcal{G}},V}^{\unicode[STIX]{x1D6F7}}$ for all lifts
$\unicode[STIX]{x1D70F}_{{\mathcal{G}},V}^{\unicode[STIX]{x1D6F7}}=z_{{\mathcal{G}},V}^{\unicode[STIX]{x1D6F7}}$ for all lifts ![]() $\unicode[STIX]{x1D6F7}$ of Frobenius.
$\unicode[STIX]{x1D6F7}$ of Frobenius.
Proof. Let ![]() $H$ be a finite group acting on a finite-dimensional
$H$ be a finite group acting on a finite-dimensional ![]() $\bar{\mathbb{Q}}_{\ell }$-vector space
$\bar{\mathbb{Q}}_{\ell }$-vector space ![]() ${\mathcal{V}}$. Let
${\mathcal{V}}$. Let ![]() $\unicode[STIX]{x1D6F7}$ denote an arbitrary linear operator on
$\unicode[STIX]{x1D6F7}$ denote an arbitrary linear operator on ![]() ${\mathcal{V}}$. Then we have the identity
${\mathcal{V}}$. Then we have the identity
Now in a cohomology stalk of ![]() $\unicode[STIX]{x1D6F9}_{\text{Gr}_{{\mathcal{G}}}}(\text{Sat}(V))$, choose a
$\unicode[STIX]{x1D6F9}_{\text{Gr}_{{\mathcal{G}}}}(\text{Sat}(V))$, choose a ![]() $\text{Gal}(\bar{F}/F)$-stable filtration on which
$\text{Gal}(\bar{F}/F)$-stable filtration on which ![]() $I_{F}$ acts through a finite quotient on the associated graded module, denoted
$I_{F}$ acts through a finite quotient on the associated graded module, denoted ![]() ${\mathcal{V}}$. Then (A.3) yields (A.1). Similarly, using that
${\mathcal{V}}$. Then (A.3) yields (A.1). Similarly, using that ![]() $1\rtimes I_{F}$ already acts through a finite quotient on
$1\rtimes I_{F}$ already acts through a finite quotient on ![]() $V$, we obtain (A.2).◻
$V$, we obtain (A.2).◻
A.3 Products and unramified Weil restrictions
A.3.1 Products
Let ![]() $G_{j}$,
$G_{j}$, ![]() $j=1,\ldots ,n$, be connected reductive groups with corresponding parahoric groups
$j=1,\ldots ,n$, be connected reductive groups with corresponding parahoric groups ![]() ${\mathcal{G}}_{j}$. Write
${\mathcal{G}}_{j}$. Write ![]() $G=\prod _{j}G_{j}$ and
$G=\prod _{j}G_{j}$ and ![]() ${\mathcal{G}}=\prod _{j}{\mathcal{G}}_{j}$.
${\mathcal{G}}=\prod _{j}{\mathcal{G}}_{j}$.
Suppose ![]() $V_{j}$ are representations of
$V_{j}$ are representations of ![]() $\text{}^{L}G_{j}$. We form the dual group
$\text{}^{L}G_{j}$. We form the dual group ![]() $\text{}^{L}(\prod _{j}G_{j})=(\prod _{j}G^{\vee })\rtimes \unicode[STIX]{x1D6E4}$, with
$\text{}^{L}(\prod _{j}G_{j})=(\prod _{j}G^{\vee })\rtimes \unicode[STIX]{x1D6E4}$, with ![]() $\unicode[STIX]{x1D6E4}=\text{Gal}(\bar{F}/F)$ acting diagonally on the factors.
$\unicode[STIX]{x1D6E4}=\text{Gal}(\bar{F}/F)$ acting diagonally on the factors.
Lemma A.2. Let ![]() $V=\boxtimes _{j}V_{j}$, the representation of
$V=\boxtimes _{j}V_{j}$, the representation of ![]() $\text{}^{L}(\prod _{j}G_{j})$ with
$\text{}^{L}(\prod _{j}G_{j})$ with ![]() $\unicode[STIX]{x1D6E4}$ acting diagonally in the obvious manner. Then we have equalities of functions in
$\unicode[STIX]{x1D6E4}$ acting diagonally in the obvious manner. Then we have equalities of functions in ![]() ${\mathcal{Z}}(G(F),{\mathcal{G}}({\mathcal{O}}_{F}))=\prod _{j}{\mathcal{Z}}(G_{j}(F),{\mathcal{G}}({\mathcal{O}}_{F}))$:
${\mathcal{Z}}(G(F),{\mathcal{G}}({\mathcal{O}}_{F}))=\prod _{j}{\mathcal{Z}}(G_{j}(F),{\mathcal{G}}({\mathcal{O}}_{F}))$:
A.3.2 Unramified Weil restrictions
Let ![]() $F_{n}/F$ be a finite unramified extension of degree
$F_{n}/F$ be a finite unramified extension of degree ![]() $n$, and let
$n$, and let ![]() $G_{0}$ be a connected reductive
$G_{0}$ be a connected reductive ![]() $F_{n}$-group; let
$F_{n}$-group; let ![]() $G=\operatorname{Res}_{F_{n}/F}G_{0}$. Then
$G=\operatorname{Res}_{F_{n}/F}G_{0}$. Then ![]() $\text{}^{L}G$ identifies with the induced group
$\text{}^{L}G$ identifies with the induced group ![]() $\text{}^{L}G=(I_{F_{n}}^{F}G_{0}^{\vee })\rtimes \unicode[STIX]{x1D6E4}_{F}$, where
$\text{}^{L}G=(I_{F_{n}}^{F}G_{0}^{\vee })\rtimes \unicode[STIX]{x1D6E4}_{F}$, where ![]() $\unicode[STIX]{x1D6E4}_{F}$ acts on the
$\unicode[STIX]{x1D6E4}_{F}$ acts on the ![]() $\bar{\mathbb{Q}}_{\ell }$-group
$\bar{\mathbb{Q}}_{\ell }$-group ![]() $I_{F_{n}}^{F}G_{0}^{\vee }\cong \,\prod _{j=0}^{n-1}G_{0}^{\vee }$ in the obvious way. Explicitly, as a
$I_{F_{n}}^{F}G_{0}^{\vee }\cong \,\prod _{j=0}^{n-1}G_{0}^{\vee }$ in the obvious way. Explicitly, as a ![]() $\unicode[STIX]{x1D6E4}_{n}$-group
$\unicode[STIX]{x1D6E4}_{n}$-group ![]() $I_{F_{n}}^{F}G_{0}^{\vee }=\,\prod _{j=0}^{n-1}\,\text{}^{\unicode[STIX]{x1D6F7}^{-j}}G_{0}^{\vee }$, where
$I_{F_{n}}^{F}G_{0}^{\vee }=\,\prod _{j=0}^{n-1}\,\text{}^{\unicode[STIX]{x1D6F7}^{-j}}G_{0}^{\vee }$, where ![]() $\text{}^{\unicode[STIX]{x1D6F7}^{0}}G_{0}^{\vee }$ is
$\text{}^{\unicode[STIX]{x1D6F7}^{0}}G_{0}^{\vee }$ is ![]() $G_{0}^{\vee }$ endowed with the given action of
$G_{0}^{\vee }$ endowed with the given action of ![]() $\unicode[STIX]{x1D6E4}_{n}$, and
$\unicode[STIX]{x1D6E4}_{n}$, and ![]() $\text{}^{\unicode[STIX]{x1D6F7}^{-j}}G_{0}^{\vee }$ is the same group but with
$\text{}^{\unicode[STIX]{x1D6F7}^{-j}}G_{0}^{\vee }$ is the same group but with ![]() $\unicode[STIX]{x1D6E4}_{n}$ acting through the given action precomposed with the automorphism
$\unicode[STIX]{x1D6E4}_{n}$ acting through the given action precomposed with the automorphism ![]() $\unicode[STIX]{x1D6FE}_{n}\mapsto \unicode[STIX]{x1D6F7}^{j}\unicode[STIX]{x1D6FE}_{n}\unicode[STIX]{x1D6F7}^{-j}$. The action of
$\unicode[STIX]{x1D6FE}_{n}\mapsto \unicode[STIX]{x1D6F7}^{j}\unicode[STIX]{x1D6FE}_{n}\unicode[STIX]{x1D6F7}^{-j}$. The action of ![]() $\unicode[STIX]{x1D6F7}$ on
$\unicode[STIX]{x1D6F7}$ on ![]() $I_{F_{n}}^{F}G_{0}^{\vee }$ is given by
$I_{F_{n}}^{F}G_{0}^{\vee }$ is given by ![]() $(g_{0},g_{1},\ldots ,g_{n-1})\mapsto (g_{1},g_{2},\ldots ,g_{n-1},\unicode[STIX]{x1D6F7}^{n}(g_{0}))$.
$(g_{0},g_{1},\ldots ,g_{n-1})\mapsto (g_{1},g_{2},\ldots ,g_{n-1},\unicode[STIX]{x1D6F7}^{n}(g_{0}))$.
An irreducible algebraic representation of ![]() $\text{}^{L}G$ is of the form
$\text{}^{L}G$ is of the form ![]() $V=\,\boxtimes _{j=0}^{n-1}\,\text{}^{\unicode[STIX]{x1D6F7}^{-j}}V_{0}$, where
$V=\,\boxtimes _{j=0}^{n-1}\,\text{}^{\unicode[STIX]{x1D6F7}^{-j}}V_{0}$, where ![]() $V_{0}$ is an irreducible representation of
$V_{0}$ is an irreducible representation of ![]() $\text{}^{L}G_{0}=G_{0}^{\vee }\rtimes \unicode[STIX]{x1D6E4}_{n}$, and
$\text{}^{L}G_{0}=G_{0}^{\vee }\rtimes \unicode[STIX]{x1D6E4}_{n}$, and ![]() $\unicode[STIX]{x1D6E4}_{n}$ acts on
$\unicode[STIX]{x1D6E4}_{n}$ acts on ![]() $\text{}^{\unicode[STIX]{x1D6F7}^{-j}}V_{0}$ by precomposing the given action on
$\text{}^{\unicode[STIX]{x1D6F7}^{-j}}V_{0}$ by precomposing the given action on ![]() $V_{0}$ with the automorphism
$V_{0}$ with the automorphism ![]() $\unicode[STIX]{x1D6FE}_{n}\mapsto \unicode[STIX]{x1D6F7}^{j}\unicode[STIX]{x1D6FE}_{n}\unicode[STIX]{x1D6F7}^{-j}$. Then, as before,
$\unicode[STIX]{x1D6FE}_{n}\mapsto \unicode[STIX]{x1D6F7}^{j}\unicode[STIX]{x1D6FE}_{n}\unicode[STIX]{x1D6F7}^{-j}$. Then, as before, ![]() $\unicode[STIX]{x1D6E4}_{F}=\langle \unicode[STIX]{x1D6F7}\rangle \unicode[STIX]{x1D6E4}_{F_{n}}$ operates as follows:
$\unicode[STIX]{x1D6E4}_{F}=\langle \unicode[STIX]{x1D6F7}\rangle \unicode[STIX]{x1D6E4}_{F_{n}}$ operates as follows: ![]() $\unicode[STIX]{x1D6E4}_{F_{n}}$ acts ‘diagonally’ on vectors of the form
$\unicode[STIX]{x1D6E4}_{F_{n}}$ acts ‘diagonally’ on vectors of the form ![]() $v_{0}\boxtimes v_{1}\boxtimes \cdots \boxtimes v_{n-1}$, and
$v_{0}\boxtimes v_{1}\boxtimes \cdots \boxtimes v_{n-1}$, and ![]() $\unicode[STIX]{x1D6F7}$ sends such a vector to the vector
$\unicode[STIX]{x1D6F7}$ sends such a vector to the vector ![]() $v_{1}\boxtimes v_{2}\boxtimes \cdots \boxtimes v_{n-1}\boxtimes \unicode[STIX]{x1D6F7}^{n}(v_{0})$.
$v_{1}\boxtimes v_{2}\boxtimes \cdots \boxtimes v_{n-1}\boxtimes \unicode[STIX]{x1D6F7}^{n}(v_{0})$.
Lemma A.3. We have the identity
and this implies the identities
in ![]() ${\mathcal{Z}}(G(F),{\mathcal{G}}({\mathcal{O}}_{F}))={\mathcal{Z}}(G_{0}(F_{n}),{\mathcal{G}}_{0}({\mathcal{O}}_{F_{n}}))$.
${\mathcal{Z}}(G(F),{\mathcal{G}}({\mathcal{O}}_{F}))={\mathcal{Z}}(G_{0}(F_{n}),{\mathcal{G}}_{0}({\mathcal{O}}_{F_{n}}))$.
Proof. The first identity is a special case of a result of Saito and Shintani; cf. [Reference FengFen20, Lemma 6.12]. The other assertions follow from this one. ◻