We advocate the use of cluster algebras and their $y$-variables in the study of hyperbolic 3-manifolds. We study hyperbolic structures on the mapping tori of pseudo-Anosov mapping classes of punctured surfaces, and show that cluster $y$-variables naturally give the solutions of the edge-gluing conditions of ideal tetrahedra. We also comment on the completeness of hyperbolic structures.

We introduce the notion of exact tilting objects, which are partial tilting objects $T$ inducing an equivalence between the abelian category generated by $T$ and the category of modules over the endomorphism algebra of $T$. Given a chain of sufficiently negative rational curves on a rational surface, we construct an exceptional sequence whose universal extension is an exact tilting object. For a chain of $(-2)$-curves, we obtain an equivalence with modules over a well-known algebra.

A recent result by the authors gives an explicit construction for a universal deformation of a formal group $\unicode[STIX]{x1D6F7}$ of finite height over a finite field $k$. This provides in particular a parametrization of the set of deformations of $\unicode[STIX]{x1D6F7}$ over the ring ${\mathcal{O}}$ of Witt vectors over $k$. Another parametrization of the same set can be obtained through the Dieudonné theory. We find an explicit relation between these parameterizations. As a consequence, we obtain an explicit expression for the action of $\text{Aut}_{k}(\unicode[STIX]{x1D6F7})$ on the set of ${\mathcal{O}}$-deformations of $\unicode[STIX]{x1D6F7}$ in the coordinate system defined by the universal deformation. This generalizes a formula of Gross and Hopkins and the authors’ result for one-dimensional formal groups.

Given an odd prime $p$, we investigate the position of simple modules in the stable Auslander–Reiten quiver of the principal block of a finite group with noncyclic abelian Sylow $p$-subgroups. In particular, we prove a reduction to finite simple groups. In the case that the characteristic is $3$, we prove that simple modules in the principal block all lie at the end of their components.

The Galois representation associated to a $p$-divisible group over a normal complete noetherian local ring with perfect residue field is described in terms of its Dieudonné display. As a consequence, the Kisin module associated to a commutative finite flat $p$-group scheme via Dieudonné displays is related to its Galois representation in the expected way.

In this paper, we prove that the set of equivalence classes of dormant opers of rank $p-1$ over a projective smooth curve of genus ${\geqslant}2$ over an algebraically closed field of characteristic $p>0$ is of cardinality one.

In this paper, we investigate the set of accumulation points of normalized roots of infinite Coxeter groups for certain class of their action. Concretely, we prove the conjecture proposed in [6, Section 3.2] in the case where the equipped Coxeter matrices are of type $(n-1,1)$, where $n$ is the rank. Moreover, we obtain that the set of such accumulation points coincides with the closure of the orbit of one point of normalized limit roots. In addition, in order to prove our main results, we also investigate some properties on fixed points of the action.

For a pair 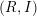$(R,I)$, where 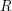$R$ is a standard graded domain of dimension $d$ over an algebraically closed field of characteristic 0, and 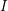$I$ is a graded ideal of finite colength, we prove that the existence of 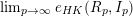$\lim _{p\rightarrow \infty }e_{HK}(R_{p},I_{p})$ is equivalent, for any fixed 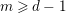$m\geqslant d-1$, to the existence of 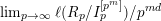$\lim _{p\rightarrow \infty }\ell (R_{p}/I_{p}^{[p^{m}]})/p^{md}$. This we get as a consequence of Theorem 1.1: as 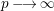$p\longrightarrow \infty$, the convergence of the Hilbert–Kunz (HK) density function $f(R_{p},I_{p})$ is equivalent to the convergence of the truncated HK density functions 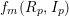$f_{m}(R_{p},I_{p})$ (in 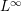$L^{\infty }$ norm) of the mod 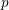$p$reductions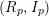$(R_{p},I_{p})$, for any fixed 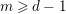$m\geqslant d-1$. In particular, to define the HK density function 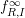$f_{R,I}^{\infty }$ in char 0, it is enough to prove the existence of 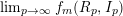$\lim _{p\rightarrow \infty }f_{m}(R_{p},I_{p})$, for any fixed 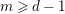$m\geqslant d-1$. This allows us to prove the existence of 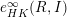$e_{HK}^{\infty }(R,I)$ in many new cases, for example, when Proj R is a Segre product of curves.

The main goal of this paper is to show that Castelnuovo–Enriques’ $P_{12}$- theorem (a precise version of the rough classification of algebraic surfaces) also holds for algebraic surfaces $S$ defined over an algebraically closed field $k$ of positive characteristic ($\text{char}(k)=p>0$). The result relies on a main theorem describing the growth of the plurigenera for properly elliptic or properly quasielliptic surfaces (surfaces with Kodaira dimension equal to 1). We also discuss the limit cases, i.e., the families of surfaces which show that the result of the main theorem is sharp.