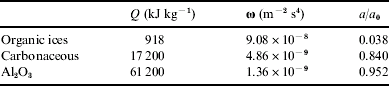Introduction
The Stardust probe (Brownlee et al. Reference Brownlee, Tsou, Anderson, Hanner, Newburn, Sekanina, Clark, Hörz, Zolensky, Kissel, McDonnell, Sandford and Tuzzolino2003) crossed the coma of Comet Wild 2 on 2 January, 2004 (Brownlee et al. Reference Brownlee, Horz, Newburn, Zolensky, Duxbury, Sandford, Sekanina, Tsou, Hanner, Clark, Green and Kissel2004). 3 cm depth panels of low-density (0.005 g cm−3 at the front face of each panel increasing linearly to 0.05 g cm−3 at the rear face), highly porous aerogel composed of silicon dioxide were deployed on the outside of the probe to capture cometary particles of ~10 μm. At capture, the relative speed between the aerogel and the coma was 6 km s−1, so the impact initial velocity of the particles onto the panels would have been distributed around a mean of 6 km s−1. Around 1200 particles larger than 1 μm in diameter are believed to have been collected by the aerogel (Burchell et al. Reference Burchell, Fairey, Wozniakiewicz, Brownlee, Hörz, Kearsley, See, Tsou, Westphal and Green2008). Two years later the samples were recovered to Earth and made available to an international consortium for analysis.
Stardust brought back to Earth the first samples of cometary particles collected from the coma shortly after emission and also collected contemporary interplanetary dust during its mission. Some two-thirds of the hypervelocity impacts of small particles onto the surface of aerogel produced roughly cylindrical cone shaped tracks ranging from 10−9 m to 10−4 m in length, with initial diameters approximately three orders of magnitude greater than the original particle diameter. The particles that produced these tracks are referred to as Type A particles (Trigo-Rodriguez et al. Reference Trigo-Rodriguez, Dominguez, Burchell, Hörz and Llorca2008); the reminder of the impacting particles disaggregated producing cavities within the aerogel are called Types B and C particles. In this present work we will focus on the carrot-shaped tracks produced by Type A particles; the turnip-shaped tracks created by the break up of Types B and C particles will be the subject of later work. On recovery of the aerogel tiles, residues of the particles have been recovered from the track walls and terminal grains (Brownlee et al. Reference Brownlee, Tsou, Aléon, Alexander, Araki, Bajt, Baratta, Bastien, Bland and Bleuet2006).
Aerogels are highly-porous, supercritically dried gels that have been manufactured since the 1930s and have numerous applications in scientific research (Tillotson & Hrubesh Reference Tillotson and Hrubesh1992). Their usefulness in capturing extraterrestrial particles was first raised at a series of workshops in the early 1990s and aerogel panels have been deployed on several space missions (see Burchell et al. (Reference Burchell, Creighton, Cole, Mann and Kearsley2001) for a short review). The use of aerogel to capture hypervelocity particles has been the subject of much experimental study (Tsou et al. Reference Tsou, Brownlee, Laurance, Hrubesh and Albee1988; Hörz et al. Reference Hörz, Cintala, See and Nakamura-Messenger2008); however, relatively little work has been carried out on the temperature profiles of micrometre-sized particles captured by aerogel (Anderson Reference Anderson1988; Noguchi et al. Reference Noguchi, Nakamura, Okudaira, Yano, Sugita and Burchell2007; Hörz et al. Reference Hörz, Cintala, See and Nakamura-Messenger2008; Trigo-Rodriguez et al. Reference Trigo-Rodriguez, Dominguez, Burchell, Hörz and Llorca2008). The study of samples from Comet Wild 2 at 1.86 AU has revealed a number of refractory Fe-Ni metals, Fe-Ni sulphides and ferromagnesian silicates ~1–10 μm in diameter (Zolensky et al. Reference Zolensky, Zega, Yano, Wirick, Westphal, Weisberg, Weber, Warren, Velbel and Tsuchiyama2006). No volatile material has been detected in the tracks of particles embedded within the aerogel.
A key question to consider when analysing the results of the Stardust mission is how complete was the capture of particles? The power released by a micrometre-sized hypervelocity particle decelerated within a microsecond is of the order of kilowatts. This release of energy can significantly alter the physical and chemical composition of the original particle. In general, cometary particles are highly heterogeneous and contain a mixture of volatile and refractory material; determining the thermal history of the particle during its capture is essential to be able to infer the composition of the original particle from the recovered sample. Here we construct a simple analytical model for the temperature profile of hypervelocity particles impacting within aerogel.
At solar distances of 1.86 AU the ambient temperature of aerogel is approximately the ambient black-body temperature (212 K) and its mean free path is of the order of its pore diameter ~10−8 m. The mean free path of the aerogel is several orders of magnitude lower than that of the radius of the cometary fragments captured by Stardust, which were typically between 10−5–10−4 m. Under these conditions the aerogel can be considered as a continuous fluid surrounding the particle, which will experience a drag force proportional to the square of its velocity within the aerogel (Coulson Reference Coulson2006).
The interaction between the aerogel and a high-speed particle is not well understood and presents a difficult problem in hydrodynamic modelling to determine the pressure and temperature history of the particle's trajectory (Dominguez et al. Reference Domínguez, Westphal, Jones and Phillips2004). In this current work, we consider two simplified models for the deceleration of hypervelocity particles captured in aerogel; both models assume a velocity squared drag force. The first model assumes that the mass of the particle remains constant during capture and the second that mass is lost due to ablation of the particle by interacting with the aerogel. In each case, the velocity and temperature profiles as a function of the track length through the aerogel are obtained.
Constant mass approximation
Consider a spherical particle of radius a, composed of a uniform density ρm, impacting parallel to the normal of a semi-infinite slab of aerogel with density ρg, at a relative velocity of v 0, typically ~6 km s−1. The density of the aerogel used on the Stardust panels varied linearly with depth, so that ρg is a function of the displacement of the particle within the aerogel. For simplicity and to allow a comparison with aerogel experiments on Earth (Hörz et al. Reference Hörz, Cintala, See and Nakamura-Messenger2008), we assume an effective average density independent of displacement. On entering the aerogel the particle experiences a drag force proportional to the square of its velocity and its equation of motion through the aerogel is given by
where x is the path length of the particle within the aerogel, such that x=0 corresponds to the boundary between the aerogel and free space; and Γ is the drag coefficient between the aerogel and the particle. If the radius of the particle is independent of both v and x, e.g. its mass remains constant as it decelerates through the aerogel, then Eq. (1) reduces to
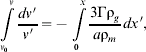
which yields
Figure 1 shows the velocity profile of 30 μm radius particles composed from materials of different densities (0.6 g cm−3, 2.6 g cm−3 and 4.0 g cm−3) impacting into 0.06 g cm−3 density aerogel with an initial velocity of 6.1 km s−1. Cometary fragments composed of organic materials typically have a densities ~0.6 g cm−3, while metallic and refractory particles have higher densities, e.g. aluminium oxide ~4 g cm−3 and carbon ~2.6 g cm−3.
Fig. 1. Velocity profiles (plotted on a log scale) for 30 μm radius particles impacting into 0.02 g cm−3 density aerogel with an initial velocity of 6 km s−1. The organic ice particles have a density of 0.6 g cm−3, the carbonaceous particles 2.4 g cm−3 and the aluminium oxide particles 4 g cm−3.
It is assumed that the particles come to rest when the pressure on the forward hemisphere of the particle is less than the crushing strength of the aerogel (1.24×104 Pa) (Trigo-Rodriguez et al. Reference Trigo-Rodriguez, Dominguez, Burchell, Hörz and Llorca2008). The pressure on the forward hemisphere of the particle is ~ρmv 2 for the materials considered in Fig. 1; this corresponds to a final particle velocity of ~1 m s−1.
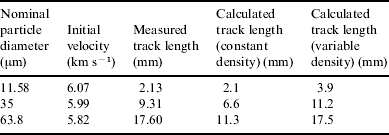
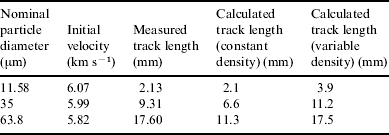
Assuming that the drag coefficient between the particle and the aerogel is Γ=1, and the track lengths for captured organics and carbonaceous particles are ~2.7 and 10.5 mm respectively, metallic aluminium oxide particles penetrate further into the aerogel with path lengths of ~20 mm. Analysis of Type A particle tracks recovered by the Stardust mission has recovered the remains of refractory particles from tracks ~1–100 mm in length (Burchell et al. Reference Burchell, Fairey, Wozniakiewicz, Brownlee, Hörz, Kearsley, See, Tsou, Westphal and Green2008).
Laboratory experiments that used a gas gun to impact glass beads into the linearly varying density aerogel used on Stardust have been performed by Burchell et al. (Reference Burchell, Fairey, Wozniakiewicz, Brownlee, Hörz, Kearsley, See, Tsou, Westphal and Green2008). The predictions of Eq. (3) compare reasonably well with the results of these experiments (see Table 1). If the density of the aerogel is assumed to be a function of displacement, to take account of the varying density of the Stardust aerogel, the velocity profile becomes
where λ is the ratio between the final and the initial densities of the aerogel and L is the depth of the aerogel panel (for Stardust aerogel, λ=10 and L=3 cm). Table 1 shows that the track lengths predicted by Eq. (4) agree better with the experimental results obtained by Burchell et al. (Reference Burchell, Fairey, Wozniakiewicz, Brownlee, Hörz, Kearsley, See, Tsou, Westphal and Green2008) than those predicted by Eq. (3) (using an averaged aerogel density) for track lengths approximately greater than 10 mm.
Table 1. The total track lengths for glass spheres impacted into aerogel with a density that increased linearly from 0.005 to 0.05 g cm−3 over a depth of 3 cm as measured by Burchell et al. (Reference Burchell, Fairey, Wozniakiewicz, Brownlee, Hörz, Kearsley, See, Tsou, Westphal and Green2008), compared with lengths calculated from Eqs. (3) and (4), with the density of glass spheres set to 2.6 g cm−3 and the drag coefficient to unity
As the particle is decelerated, it experiences frictional heating from the aerogel. The skin depth of the one-dimensional heat equation suggests that particles with radii <500 μm are too small to maintain temperature gradients during flash heating over ~1 μs (Coulson & Wickramasinghe Reference Coulson and Wickramasinghe2003); however, recent examination of Stardust particles estimates thermal gradients with about 2770 K μm−1 were estimated near the surface of the grains (<2 μm thick) (Noguchi et al. Reference Noguchi, Nakamura, Okudaira, Yano, Sugita and Burchell2007). As a simplification, we will assume that the 10–100 μm grains captured by Stardust can be treated as being at a single temperature T.
Ignoring energy losses through conduction, mass loss and ionization, the energy gained through frictional heating can be considered to be dissipated in the form of infrared radiation by the particle. The wavelength of the emitted radiation varies from 2 to 12 μm; particles with radii greater than 12 μm can be considered as black-body radiating according to Wein's law, where the energy of the emitted radiation is proportional to T 4 (Coulson & Wickramasinghe Reference Coulson and Wickramasinghe2007).
The majority of the kinetic energy lost from the particle goes into heating the aerogel and the particle. By energy balance, the energy emitted by the particle is equal to its loss of kinetic energy:
where α is the fraction of energy that goes into heating the particle (assumed to be 0.5); the mass of the particle is 
, σ is the Stefan-Boltzmann constant, T 0 is the ambient temperature and ε is the emistivity of the particle. Inserting the velocity profile given by Eq. (3) into the energy balance equation gives the temperature of the particle during its deceleration within the aerogel:
Figure 2 shows the temperature profiles for 30 μm radius particles of varying densities. Cometary ices attain maximum temperatures of approximately 1400 K; while carbonaceous and aluminium oxide particles experience maximum temperatures of 1611 K and 1811 K, respectively. For all three types of particle the maximum temperature exceeds, or is close to, the melting point of the particle, so the effects of mass loss during deceleration are an important feature to model. Above the melting point of the particle the temperatures given by Eq. (6) are no longer accurate; at these high temperatures, energy is removed by both mass loss and phase changes as the particle melts. The next section considers a simplified model for particle ablation.
Fig. 2. Particle temperature profiles for 30 μm radius particles impacting into 0.02 g cm−3 density aerogel with an initial velocity of 6 km s−1. The organic ice particles have a density of 0.6 g cm−3, the carbonaceous particles 2.4 g cm−3 and the aluminium oxide particles 4 g cm−3.
A model for ablating particles
Ablation of a particle reduces its surface area s and so reduces the effects of the drag force and the magnitude of heating experienced. In general, the ratio of the particle's surface area to the initial surface area is proportional to some power β of the ratio of its mass to its original mass (Brohnsten Reference Bronhsten1983):
This expression can be simplified by making the assumption that the particle remains spherical during its deceleration within the aerogel; the variation of the mass can be expressed with respect to the change in its radius a
Ablation refers to the removal of molecules from the particle during interactions with the bow wave in the aerogel. Ablation can be considered as analogous to evaporation, since it occurs at all temperatures as opposed to sublimation or boiling of the particle, which only occur once the particle's temperature exceeds its melting and boiling points respectively. The mass lost per unit time is proportional to the amount of aerogel encountered, which is proportional to the velocity u, multiplied by the kinetic energy deposited by the aerogel which is proportional to u 2. Hence the rate of change in mass due to ablation is equal to
where Λ is the coefficient of heat transfer between the aerogel and the particle, and Q is the heat of ablation of the particle.
The pressure on the leading face of the particle is proportional to the Stokes law drag force v 2, which, for hypervelocity impacts of a particle into aerogel, is less than the pressure of the ablated material v 3. So, a cloud of ablated molecules shields the particle from direct collisions with the aerogel; e.g. a bow shock is formed between the aerogel and the particle. This implies that the majority of heat exchanged between the particle and the aerogel is by radiative transfer. The value of Λ, the coefficient of heat transfer, is not equal to the heat capacity of the aerogel. The details of the interaction between the ablated material forming the bow shock and the particle are complicated and have been excluded from the model for simplicity.
Using the chain rule to combine Eqs. (8) and (9), the rate of change of the particle's radius is given by
Writing the equation of motion for the particle as a function of velocity and time and combining with Eq. (10) and integrating gives an expression for the radius of the particle as a function of velocity
Substituting Eq. (11) for a into Eq. (2), we find
Making the substitution U=v 2 and integrating over the path of the particle in the aerogel produces
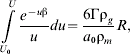
where 
and R is the path length through the aerogel.
The integral on the left-hand side of Eq. (13) can be expanded as a power series and integrated term by term to give
![\eqalign{\int\limits_{a}^{b} {{e^{ \minus \rmomega t} } \over t}dt \equals \tab \int\limits_{a}^{b} {dt\left\{ {{1 \over t} \minus \rmomega \plus {{\rmomega ^{\setnum{2}} t} \over {2\hskip1\exclam }} \plus \cdots \plus \lpar\hskip-1 { \minus 1} \rpar^{n} {{\rmomega ^{n} t^{n \minus \setnum{1}} } \over {n\hskip1\exclam }}} \right\}} \cr \equals \tab \left[ {\ln t \minus \rmomega t \plus {{\rmomega ^{\setnum{2}} t^{\setnum{2}} } \over {2 \cdot 2\hskip1\exclam }} \plus \cdots \plus \lpar\hskip-1 { \minus 1} \rpar ^{n} {{\rmomega ^{n} t^{n} } \over {n \cdot n\hskip1\exclam }}} \right]_{a}^{b}.}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151007145715609-0872:S147355040800431X_eqn14.gif?pub-status=live)
This series converges if |ωt|<1; from (13), 
, where U=v 2.
We make the simplification that the coefficient of heat transfer between the aerogel and the particle is the same for all densities of particle and set Λ equal to unity. In the case of a particle decelerating in aerogel, U is initially large and so |ωt|<1 implies that ω is small; e.g. the particle has a high heat of ablation. In these circumstances the series reduces to lnt and Eq. (13) reduces to the velocity profile obtained in Eq. (3) for a particle of constant mass.
In practice this expression is often greater than unity and so the integral diverges. The integral can be expanded as an asymptotic series (see the Appendix) to obtain
![\eqalign{\tab e^{ \minus \rmomega U} \left[ {{1 \over {\rmomega U}} \minus {1 \over {\rmomega ^{\setnum{2}} U^{\setnum{2}} }} \minus \cdots \minus {{n\hskip1\exclam } \over {\rmomega ^{n \plus \setnum{1}} U^{n \plus \setnum{1}} }}} \right] \minus e^{ \minus \rmomega U_{\setnum{0}} } \cr \tab \quad\times \left[ {{1 \over {\rmomega U_{\setnum{0}} }} \minus {1 \over {\rmomega ^{\setnum{2}} U_{\setnum{0}} ^{\setnum{2}} }} \minus \cdots \minus {{n\hskip1\exclam } \over {\rmomega ^{n \plus \setnum{1}} U_{\setnum{0}} ^{n \plus \setnum{1}} }}} \right] \equals {6 \over {a_{\setnum{0}} }}{{\rmrho_{g} } \over {\rmrho _{m} }}\rmGamma R.}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151007145715609-0872:S147355040800431X_eqn15.gif?pub-status=live)
From the Appendix, the error in the asymptotic series expansion is at a minimum when the series is truncated when n~ωU.
An estimate for the value of the asymptotic where the error is minimal may be obtained by considering
![{{e^{ \minus \rmomega t} } \over {\rmomega t}}\!\left[ {1 \minus {1 \over {\rmomega t}} \minus \cdots \minus {{n\hskip1\exclam } \over {\rmomega ^{n} t^{n} }}} \right] \!\lt\! {{e^{ \minus \rmomega t} } \over {\rmomega t}}\!\left[ {1 \minus {1 \over {\rmomega t}} \minus \cdots \minus {1 \over {\rmomega ^{n} t^{n} }}} \right].](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151007145715609-0872:S147355040800431X_eqn16.gif?pub-status=live){kind=small}
For small n, this can be calculated directly. As n becomes large, the sum of the first n terms of the series on the right-hand side is equal to
When ωU 0≫1, Eq. (15) may be approximated as
![U\lpar R \rpar \sim {{e^{ \minus {{\rmomega U} \over {\left( {m \minus \setnum{1}} \right)}}} } \over \rmomega }\left[ {{6 \over {a_{\setnum{0}} }}{{\rmrho _{g} } \over {\rmrho _{m} }}\rmGamma R \plus {{e^{ \minus \rmomega U_{\setnum{0}} } } \over {\rmomega ^{n \minus \setnum{1}} U_{\setnum{0}}^{n \minus \setnum{1}} }}} \right]^{ \minus {\setnum{1} \over {m \minus \setnum{1}}}} \comma](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151007145715609-0872:S147355040800431X_eqn17.gif?pub-status=live){kind=small}
where ωU~m and ωU 0~n. Eq. (17) is only strictly valid over the range U∊[U min, U 0], where U min~Q is the threshold energy for ablation. For U<U min~Q, the velocity profile is described by Eq. (3).
In the limit, U→Q, and the velocity can be approximated as
![U\lpar R \rpar \sim {1 \over \rmomega }\left[ {{6 \over {a_{\setnum{0}} }}{{\rmrho _{g} } \over {\rmrho_{m} }}\rmGamma R \plus {{e^{ \minus \rmomega U_{\setnum{0}} } } \over {\rmomega ^{n \minus \setnum{1}} U_{\setnum{0}}^{n \minus \setnum{1}} }}} \right]^{ \minus \setnum{1}}.](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151007145715609-0872:S147355040800431X_eqn18.gif?pub-status=live){kind=small}
The size of the error produced by this approximation can be estimated from the magnitude of the discontinuity at the boundary where R=0:
and
For most practical applications, the error equates to a temperature difference on the boundary of less than 1 K, since U(R→+0)→U 0 as U→U 0 and m→n.
The temperature profile of the particle ablating through the aerogel is given by the radiation balance equation used above, but with the radius as a function of velocity
From Eqs. (17) and (11) the temperature profile can be approximated as
![\lpar T \minus T_{\setnum{0}} \rpar ^{\setnum{4}} \equals {1 \over 6}{{\rmrho _{m} } \over {\rmsigma \rmepsi }}{{a_{\setnum{0}} } \over \rmomega }e^{ \minus \rmomega U_{\setnum{0}} } \left[ {{6 \over {a_{\setnum{0}} }}{{\rmrho _{g} } \over {\rmrho _{m} }}\rmGamma R \plus {{e^{ \minus \rmomega U_{\setnum{0}} } } \over {\rmomega ^{n \minus \setnum{1}} U_{\setnum{0}}^{n \minus \setnum{1}} }}} \right]^{ \minus \setnum{1}} \comma](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151007145715609-0872:S147355040800431X_eqn20.gif?pub-status=live){kind=small}
in the limit U→Q and where n is large.
In general it is difficult to derive a general expression for the velocity profile of the ablating particle as a function of its track length in aerogel; however, using Eq. (11) and the approximations of Eqs. (18) and (20), the radius, velocity, track length and temperature of the particle can be calculated at U=U min. The velocity of the particle then follows the constant mass profile of Eq. (3), with the calculated values of the particle's radius, velocity, track length and temperature used for the initial conditions.
Figure 3 shows the temperature profiles for a range of idealized particles with differing densities, but with the same heat of ablation. The temperature initially falls off rapidly until 
, where the temperature decreases as R −1.
Fig. 3. Velocity profiles according to Eq. (20) for 15 μm radius particles impacting into 0.02 g cm−3 density aerogel with an initial velocity of 6 km s−1. The particles are composed of hypothetical materials with densities of 0.6 g cm−3, 2 g cm−3 and 4 g cm−3 with ω=1.28×10−7.
Results
From the previous section, the critical parameter in determining the fate of a particle captured in aerogel is its specific heat of ablation, Q. The final radius of the particle is given by integrating Eq. (11) between U min and U 0 to give
where U 0 is the square of the initial particle velocity; e.g. U 0=(6.1 km s−1)2. In the limit U min→Q, the ratio of the final radius of the particle to its initial radius is 
; e.g. mass loss is greatest for low values of Q.
Values of Q are given in Table 2. Volatile materials composed of organic ices typically have low values of Q and so are quickly reduced to less than 4% of their original radius after traversing through ~1.1 mm of aerogel. Volatile cometary fragments lose more than 96% of their kinetic energy through ablation.
Table 2. Energies of ablation (Lide Reference Lide2008) for different particle compositions and corresponding values of ω and the ratio of the final radius to the initial a/a0
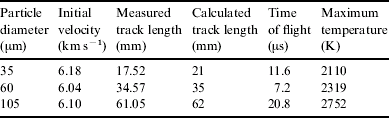
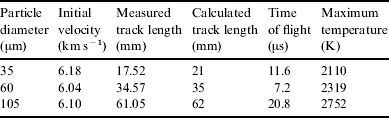
Particles composed of refractory substances such as Al2O3 have values of Q⩾U 0; such particles experience intense ablation, but only for a small fraction of their transit time through the aerogel, so that their deceleration can be adequately described by Eq. (3). Hörz et al. (Reference Hörz, Cintala, See and Nakamura-Messenger2008) have conducted experiments firing 35, 60 and 105 μm diameter aluminium oxide spheres into 0.02 g cm−3 aerogel at hypervelocities of 6.04–6.18 km s−1. From post firing analysis of the aerogel, the track length produced by each particle was obtained. Using Eq. (3), the velocity profiles for these three sizes of particle are plotted in Fig. 4. From this the total track length (when, as in the second section, v<1 m s−1) can be found; Table 3 shows the total track lengths obtained from Fig. 4 compared with the experimental results obtained by Hörz et al. (Reference Hörz, Cintala, See and Nakamura-Messenger2008). When the drag coefficient Γ is set to 0.5, it can be seen that the results obtained by Eq. (3) are very close to the track lengths obtained experimentally.
Fig. 4. The velocity profiles (plotted on a log scale) given by Eq. (3) for aluminium oxide particles of diameters of 35 μm, 60 μm and 105 μm; and a density of 4 g cm−3 impacting into aerogel of density 0.02 g cm−3.
Table 3. The total track lengths for Al2O3 spheres impacted into 0.02 g cm−3 aerogel as measured by Hörz et al. (Reference Hörz, Cintala, See and Nakamura-Messenger2008), compared with lengths calculated from Eq. (3), with the density of Al2O3 spheres set to 4 g cm−3 and the drag coefficient to 0.5
From substituting 
in the left-hand side of Eq. (3) and integrating, the time of flight of the particle inside the aerogel is
![t \equals {1 \over {v_{\setnum{0}} }}{a \over 3}{{\rmrho _{m} } \over {\rmrho _{g} }}{1 \over \rmGamma }\left[ {e^{{{\setnum{3}\rmGamma \rmrho _{g} } \over {a\rmrho _{m} }}L} \minus 1} \right]\comma](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151007145715609-0872:S147355040800431X_eqn22.gif?pub-status=live){kind=small}
where L is the track length of the particle. For typical Stardust track lengths of 1–10 mm, the time of flight is of the order of microseconds, in good agreement with the observations of Noguchi et al. (Reference Noguchi, Nakamura, Okudaira, Yano, Sugita and Burchell2007). Table 3 gives the times of flight for different Al2O3 spheres from the work of Hörz et al. (Reference Hörz, Cintala, See and Nakamura-Messenger2008), which shows typical timescales of tens of microseconds.
Figure 5 shows the temperature profiles for these particles and the maximum particle temperature is given in Table 3. The particles experienced maximum temperatures greater than 2100 K; this is consistent with the work of Hörz et al. (Reference Hörz, Cintala, See and Nakamura-Messenger2008), who found that these particles experienced temperatures that were close to, or exceeded, 2245 K, the melting point of Al2O3.
Fig. 5. The temperature profiles for the aluminium oxide particles shown in Fig. 4.
For particles composed of volatile materials such as cometary ices, the velocity profile follows Eq. (14) until U<U min~Q. Beyond this the mass can be treated as approximately constant and Eq. (3) can be used to describe its velocity. On impacting into the aerogel, the maximum temperature experienced by the particle is ~1400 K, which falls off roughly proportionally to R −1 in accordance with Eq. (18). Ablation ceases after the particle has travelled ~1.1 mm through the aerogel, when its deceleration now varies as ~e −R (see Fig. 6). The particle experiences an average temperature ~600 K during its deceleration, which takes ~1 μs: sufficient to considerably modify a 10–100 μm sized particle.
Fig. 6. The temperature profile for a 60 μm radius particle composed of organic ices with an average density of 0.6 g cm−3, impacting into 0.02 g cm−3 density aerogel with an initial velocity of 6 km s−1.
Conclusion
The simple, semi-analytical models developed in the second and third sections suggest that hypervelocity impacts ~6 km s−1 produce intense flash heating within micrometre-sized particles. Low-density, volatile particles, such as those formed from organics with low decomposition temperatures, experience peak temperatures of over 1000 K on capture by aerogel. High-density, refractory particles, such as metal oxides and silicates, experience even greater maximum temperatures of greater than 2000 K. For both types of particle, these maximum temperatures exceed their melting point and the duration of intense heating of ~1 μs is long enough to cause physical and chemical changes to the composition of the particles. Despite the simplifications introduced in both models to overcome the complexity of the particle, aerogel interaction results compare well to impact experiments and analysis of particle tracks captured by the Stardust mission.
Comet P81/Wild 2 is a short-period comet, thought to have originated from the Kuiper Belt. One of the main hopes for the Stardust mission was the chance to recover pristine particles that had remained unaltered since their formation during the early evolution of the Solar System. These particles are believed to be a highly inhomogeneous collection of metals and silicates as well as complex organics; knowledge of their detailed physical structure as well as chemical composition would provide valuable information about the formation of the Solar System from the surrounding interstellar medium. The combination of ablation and melting of the captured particles limits the useful information that can be extracted from the Stardust data. The intense heating associated with capture in aerogel limits the possibility of the recovery of intact volatile organic ices by missions similar to Stardust. From an astrobiological perspective recovery of micrometre-sized organic material from within a comet would be a significant step to validating existing theories of panspermia (Hoyle & Wickramasinghe Reference Hoyle and Wickramsinghe1978; Burchell Reference Burchell2004).
The models derived are able to predict the track lengths for different density materials to a reasonable degree of accuracy. Obtaining analytical expressions for the velocity and temperature of the particle as a function of displacement within the aerogel allows the duration of particle heating to be estimated, which compares well with the results of analysis of particles obtained by Stardust. Both of the models derived are highly sensitive to the parameters such as particle density, radius and drag coefficient. A valid criticism of these models is that a certain amount of ‘fine tuning’ of the parameters enables a wide number of initial particle sizes or densities to agree with the results of the experiment. The particles recovered are far from homogeneous or regular in shape and so attempts to reconstruct the original composition of a particle from its track length are difficult. Future work will attempt to construct the velocity profiles of particles using hydrodynamics to reduce the number of physical assumptions and simplifications used to obtain the analytic expression presented here.
Appendix A: Asymptotic expansions
Definition A1
Consider an expansion of a function f(z):U⊂픺→픺, z∊픺, in inverse powers of z,
If the series on the right-hand side diverges, then f(z) can be written as an asymptotic series,
providing
![\lim \limits_{z \to \infty } \left( {z^{n} \left[ {{{f\left( z \right)} \over {\rmphi \left( z \right)}} \minus \sum\limits_{j \equals \setnum{0}}^{n} {{{a_{j} } \over {z^{j} }}} } \right]} \right) \to 0.](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151007145715609-0872:S147355040800431X_eqnU12.gif?pub-status=live){kind=small}
Theorem A1
can be expressed as an asymptotic series of the form
![f\lpar U\comma U_{\setnum{0}} \rpar \equals \left[ {e^{ \minus \rmomega U} \left[ {{1 \over {\rmomega U}} \minus {1 \over {\rmomega ^{\setnum{2}} U^{\setnum{2}} }} \minus \cdots \minus {{n\hskip1\exclam } \over {\rmomega ^{n \plus \setnum{1}} U^{n \plus \setnum{1}} }}} \right]} \right]_{U_{\setnum{0}} }^{U}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151007145715609-0872:S147355040800431X_eqnU14.gif?pub-status=live){kind=small}
.
Proof
Repeated integration by parts gives
![\eqalign{\it{\int\limits_{U_{\setnum{0}} }^{U} {{{e^{ \minus \rmomega t} } \over t}dt}} \equals \tab {\it\left[ {e^{ \minus \rmomega t} \left[ {{{\rm 1} \over {\rmomega t}} \minus {{\rm 1} \over {\rmomega ^{\setnum{2}} t^{\setnum{2}} }} \minus \cdots \minus {{n\hskip1\exclam } \over {\rmomega ^{n \plus \setnum{1}} t^{n \plus \setnum{1}} }}} \right]} \right]_{U_{\setnum{0}} }^{U}} \cr \tab {\it \minus \lpar {n \plus {\rm 1}} \rpar \exclam \int\limits_{U_{\setnum{0}} }^{U} {{{e^{ \minus \rmomega t} } \over {\rmomega ^{n \plus \setnum{2}} t^{n \plus \setnum{2}} }}dt}. }](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151007145715609-0872:S147355040800431X_eqnU15.gif?pub-status=live)
Approximating f(z) as
![f\lpar z \rpar \simeq \sum\limits_{j \equals \setnum{0}}^{\infty } {{{a_{j} } \over {z^{j} }} \equals \left[ {{1 \over {\rmomega t}} \minus {1 \over {\rmomega ^{\setnum{2}} t^{\setnum{2}} }} \minus \cdots \minus {{n\hskip1\exclam } \over {\rmomega ^{n \plus \setnum{1}} t^{n \plus \setnum{1}} }}} \right]} _{U_{\setnum{0}} }^{U}.](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151007145715609-0872:S147355040800431X_eqnU16.gif?pub-status=live){kind=small}
By application of the ratio test,
e.g. the series diverges and the difference between successive terms is at a minimum when j~ωt.
Let ɸ(t)=e −ωt. Hence
![\eqalign{\hskip-4 \left[ {\lim\limits_{t \to \infty } \left\vert {t^{n} \left( {{{f\left( t \right)} \over {\rmphi \left( t \right)}} \!\minus\! \sum\limits_{j \equals \setnum{0}}^{\infty } {{{a_{j} } \over {t^{j} }}} } \right)} \right\vert} \right]_{U_{\setnum{0}} }^{U} \!\!\!\!\equals\!\tab\left[ {\left\vert {\left( {n \plus 1} \right)\exclam t^{n} e^{\rmomega t} \!\int\limits_{t}^{\infty }\!\! {{{e^{ \minus \rmomega t}}^{\prime} } \over {\rmomega ^{n \plus \setnum{2}} t\prime{^{n \plus \setnum{2}} }}}dt} \prime } \right\vert} \right]_{U_{\setnum{0}} }^{U} \cr\tab\!\!\!\!\!\!\lt\! \left[ {\left\vert {{{\left( {n \plus 1} \right)\exclam } \over {\rmomega ^{n \plus \setnum{2}} }}{{e^{ \minus \rmomega t} } \over t}\int\limits_{t}^{\infty } {e^{ \minus \rmomega t} }^{\prime} dt} \prime } \right\vert} \right]_{U_{\setnum{0}} }^{U} \cr}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151007145715609-0872:S147355040800431X_eqnU18.gif?pub-status=live)
and, by integrating by parts,
![\eqalign{\tab\hskip106pt\Rightarrow\! \left[ {\lim\limits_{t \to \infty } \left\vert {t^{n} \left( {{{f\left( t \right)} \over {\rmphi \left( t \right)}} \minus \sum\limits_{j \equals \setnum{0}}^{\infty } {{{a_{j} } \over {t^{j} }}} } \right)} \right\vert} \right]_{U_{\setnum{0}} }^{U}\!\! \to 0\cr\tab \hskip248pt\square}}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151007145715609-0872:S147355040800431X_eqnU19.gif?pub-status=live)
From the above, the error obtained by approximating f(U, U 0) by truncating this asymptotic series at the nth term is less than
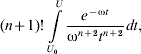
which is simply the next term in the series.
