1 Introduction
Very soon after Drinfeld’s suggestion [Reference Drinfeld9] to study set-theoretic solutions
![]() $S\colon X^2\rightarrow X^2$
to the Yang–Baxter equation
$S\colon X^2\rightarrow X^2$
to the Yang–Baxter equation
in
![]() $X^3$
, these solutions found increasing attention during the past 30 years (see, e.g., [Reference Angiono, Galindo and Vendramin1, Reference Catino and Rizzo4–Reference Dehornoy8, Reference Etingof, Schedler and Soloviev10–Reference Gateva-Ivanova12, Reference Gateva-Ivanova14, Reference Gateva-Ivanova and Van den Bergh15, Reference Lebed and Vendramin18, Reference Lu, Yan and Zhu19, Reference Rump21, Reference Rump23, Reference Rump25–Reference Weinstein and Xu30]. Due to their close connection with braidings, they arise in various topics, including noncommutative regular rings [Reference Gateva-Ivanova13, Reference Gateva-Ivanova14], regular affine groups [Reference Catino, Colazzo and Stefanelli2–Reference Catino and Rizzo4], Hopf–Galois theory [Reference Angiono, Galindo and Vendramin1, Reference Childs6, Reference Featherstonhaugh, Caranti and Childs11, Reference Guarnieri and Vendramin16], and Garside groups [Reference Chouraqui and Godelle7, Reference Dehornoy8, Reference Rump23].
$X^3$
, these solutions found increasing attention during the past 30 years (see, e.g., [Reference Angiono, Galindo and Vendramin1, Reference Catino and Rizzo4–Reference Dehornoy8, Reference Etingof, Schedler and Soloviev10–Reference Gateva-Ivanova12, Reference Gateva-Ivanova14, Reference Gateva-Ivanova and Van den Bergh15, Reference Lebed and Vendramin18, Reference Lu, Yan and Zhu19, Reference Rump21, Reference Rump23, Reference Rump25–Reference Weinstein and Xu30]. Due to their close connection with braidings, they arise in various topics, including noncommutative regular rings [Reference Gateva-Ivanova13, Reference Gateva-Ivanova14], regular affine groups [Reference Catino, Colazzo and Stefanelli2–Reference Catino and Rizzo4], Hopf–Galois theory [Reference Angiono, Galindo and Vendramin1, Reference Childs6, Reference Featherstonhaugh, Caranti and Childs11, Reference Guarnieri and Vendramin16], and Garside groups [Reference Chouraqui and Godelle7, Reference Dehornoy8, Reference Rump23].
A first systematic study of involutive solutions was undertaken by Etingof et al. [Reference Etingof, Schedler and Soloviev10] who introduced the structure group
![]() $(G_X;\circ )$
of a solution
$(G_X;\circ )$
of a solution
![]() $S(x,y)=({{}}^xy,x^y)$
, generated by X, with relations
$S(x,y)=({{}}^xy,x^y)$
, generated by X, with relations
![]() $x\circ y ={{}}^xy\circ x^y$
. A solution S is said to be nondegenerate if the component maps
$x\circ y ={{}}^xy\circ x^y$
. A solution S is said to be nondegenerate if the component maps
![]() $y\mapsto {{}}^xy$
and
$y\mapsto {{}}^xy$
and
![]() $y\mapsto y^x$
are invertible for all
$y\mapsto y^x$
are invertible for all
![]() $x\in X$
. In [Reference Rump21], it was shown that left nondegenerate involutive solutions S are equivalent to cycle sets, that is, sets X with a single binary operation
$x\in X$
. In [Reference Rump21], it was shown that left nondegenerate involutive solutions S are equivalent to cycle sets, that is, sets X with a single binary operation
![]() $\cdot $
such that the self-maps
$\cdot $
such that the self-maps
![]() $\sigma (x)\colon X\rightarrow X$
with
$\sigma (x)\colon X\rightarrow X$
with
![]() $\sigma (x)(y):=x\cdot y$
are bijective, and X satisfies the equation
$\sigma (x)(y):=x\cdot y$
are bijective, and X satisfies the equation
Furthermore, it was shown that finite cycle sets are (two-sided) nondegenerate.
The structure group
![]() $G_X$
of a nondegenerate cycle set X is obtained by a process of discrete integration where equation (1.1) plays the role of an integrability condition. More precisely, X embeds into
$G_X$
of a nondegenerate cycle set X is obtained by a process of discrete integration where equation (1.1) plays the role of an integrability condition. More precisely, X embeds into
![]() $G_X$
, and the operation on X extends to
$G_X$
, and the operation on X extends to
![]() $G_X$
and makes
$G_X$
and makes
![]() $G_X$
into a cycle set. The action
$G_X$
into a cycle set. The action
![]() $G_X\times X\rightarrow X$
given by
$G_X\times X\rightarrow X$
given by
![]() $(a,x)\mapsto a\cdot x$
leads to a factor group
$(a,x)\mapsto a\cdot x$
leads to a factor group
![]() $G(X)$
of
$G(X)$
of
![]() $G_X$
, acting faithfully on X, such that
$G_X$
, acting faithfully on X, such that
![]() $G(X)$
is generated by the permutations
$G(X)$
is generated by the permutations
![]() $\sigma (x)$
with
$\sigma (x)$
with
![]() $x\in X$
. Therefore,
$x\in X$
. Therefore,
![]() $G(X)$
is called the permutation group of X. If X is nondegenerate,
$G(X)$
is called the permutation group of X. If X is nondegenerate,
![]() $G(X)$
is also a cycle set, induced by the cycle set structure of
$G(X)$
is also a cycle set, induced by the cycle set structure of
![]() $G_X$
.
$G_X$
.
Until now, several types of cycle sets with an underlying group structure have been found. The cycle sets
![]() $G_X$
and
$G_X$
and
![]() $G(X)$
are two examples. Both are braces [Reference Rump22], that is, additive abelian groups with a ring-like multiplication where
$G(X)$
are two examples. Both are braces [Reference Rump22], that is, additive abelian groups with a ring-like multiplication where
![]() $(G_X;\circ )$
plays the role of an adjoint group, similar to that of a radical ring:
$(G_X;\circ )$
plays the role of an adjoint group, similar to that of a radical ring:
![]() $a\circ b=ab+a+b$
. Any brace satisfies
$a\circ b=ab+a+b$
. Any brace satisfies
so that equation (1.1) follows by the commutativity of addition. Etingof et al. [Reference Etingof, Schedler and Soloviev10] already considered affine solutions to the Yang–Baxter equation. These also can be described as cycle sets with an underlying abelian group. In [Reference Rump24], we studied two other types of cycle set structures on an abelian group. Given the close connection between group structures and symmetries, the cumulative occurrence of groups in relation with cycle sets indicates a high level of inner balance of this structure. Surprisingly, there is another connection with groups arising in the context of coverings.
In this paper, we introduce a class of self-maps of a group G, leading to a cycle set structure on G, such that the universal covering of any cycle set is of that type. In [Reference Rump26], we developed a general covering theory which applies to noninvolutive and even degenerate solutions to the Yang–Baxter equation. Here, we focus upon the involutive case. To highlight the analogy with topological coverings of connected spaces, special attention is payed to irreducible cycle sets, consisting of a single orbit under the permutation group.
By [Reference Rump26, Theorem 6], every cycle set X has a universal covering
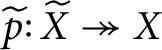 $\widetilde {p}\colon \widetilde {X}\twoheadrightarrow X$
, a cycle set morphism which does not change the permutation group
$\widetilde {p}\colon \widetilde {X}\twoheadrightarrow X$
, a cycle set morphism which does not change the permutation group
![]() $G(X)$
, and does not increase the set of
$G(X)$
, and does not increase the set of
![]() $G(X)$
-orbits. Like in topology, it is universal, hence essentially unique, so that it factors through each covering of X. The relationship between X and
$G(X)$
-orbits. Like in topology, it is universal, hence essentially unique, so that it factors through each covering of X. The relationship between X and
![]() $\widetilde {X}$
is determined by the fundamental groupoid
$\widetilde {X}$
is determined by the fundamental groupoid
![]() $\pi _1(X)$
, which can be replaced by a group if X is irreducible. Thus, in order to classify all irreducible cycle sets, the main step consists in the knowledge of cycle sets arising as universal coverings, i.e., those with a trivial fundamental group. In [Reference Rump27], these uniconnected cycle sets, analogous to simply connected spaces, are classified in the nondegenerate case. Here, we remove the restriction by characterizing arbitrary uniconnected cycle sets as groups with a specific self-map (Theorem 3.2).
$\pi _1(X)$
, which can be replaced by a group if X is irreducible. Thus, in order to classify all irreducible cycle sets, the main step consists in the knowledge of cycle sets arising as universal coverings, i.e., those with a trivial fundamental group. In [Reference Rump27], these uniconnected cycle sets, analogous to simply connected spaces, are classified in the nondegenerate case. Here, we remove the restriction by characterizing arbitrary uniconnected cycle sets as groups with a specific self-map (Theorem 3.2).
Using a result of [Reference Rump28], we show that nondegenerate uniconnected cycle sets are equivalent to braces with a distinguished generator (Theorem 3.3). Here, the uniconnected cycle set structure differs from the cycle set structure as a brace! As a corollary, it follows that a uniconnected cycle set is nondegenerate if and only if its underlying group is the adjoint group of a brace. It turns out that a great many of universal coverings are degenerate: For example, each group with a right-invariant lattice structure (e.g., Artin’s braid group) gives rise to a degenerate uniconnected cycle set (Example 1). A class of nondegenerate uniconnected cycle sets is obtained from differential groups (Example 2).
2 Preliminaries
In this section, we briefly recall some facts on cycle sets needed in what follows. A set X with a binary operation
![]() $\cdot $
is said to be a cycle set [Reference Rump21] if the left multiplication
$\cdot $
is said to be a cycle set [Reference Rump21] if the left multiplication
![]() $\sigma (x)$
:
$\sigma (x)$
:
![]() $y\mapsto x\cdot y$
is invertible, and the equation (1.1) holds for all
$y\mapsto x\cdot y$
is invertible, and the equation (1.1) holds for all
![]() $x,y,z\in X$
. So
$x,y,z\in X$
. So
![]() $\sigma $
defines a map
$\sigma $
defines a map
into the permutation group
![]() $\mathfrak {S}(X)$
. The subgroup
$\mathfrak {S}(X)$
. The subgroup
![]() $G(X)$
of
$G(X)$
of
![]() $\mathfrak {S}(X)$
generated by the image of
$\mathfrak {S}(X)$
generated by the image of
![]() $\sigma $
is said to be the permutation group of X. The image
$\sigma $
is said to be the permutation group of X. The image
![]() $\sigma (X)$
admits a well-defined operation
$\sigma (X)$
admits a well-defined operation
so that equation (1.1) is retained for
![]() $\sigma (X)$
, the retraction [Reference Etingof, Schedler and Soloviev10, Reference Rump21] of X. In general,
$\sigma (X)$
, the retraction [Reference Etingof, Schedler and Soloviev10, Reference Rump21] of X. In general,
![]() $\sigma (X)$
is not a cycle set, unless X is nondegenerate, that is, the square map
$\sigma (X)$
is not a cycle set, unless X is nondegenerate, that is, the square map
![]() $x\mapsto x\cdot x$
is bijective. The retraction
$x\mapsto x\cdot x$
is bijective. The retraction
![]() $\sigma (X)$
is then again nondegenerate, so that the retraction process can be iterated. Finite cycle sets are always nondegenerate [Reference Rump21, Theorem 2].
$\sigma (X)$
is then again nondegenerate, so that the retraction process can be iterated. Finite cycle sets are always nondegenerate [Reference Rump21, Theorem 2].
A brace A is a cycle set with an abelian group structure satisfying
for all
![]() $a,b,c\in A$
. Note that equation (1.1) follows by equation (2.3) and the commutativity of
$a,b,c\in A$
. Note that equation (1.1) follows by equation (2.3) and the commutativity of
![]() $(A;+)$
. Equation (2.2) says that
$(A;+)$
. Equation (2.2) says that
![]() $\sigma (a)$
is a group automorphism for all
$\sigma (a)$
is a group automorphism for all
![]() $a\in A$
. As a cycle set, any brace A is nondegenerate. Moreover, it is a group with respect to the operation
$a\in A$
. As a cycle set, any brace A is nondegenerate. Moreover, it is a group with respect to the operation
where
![]() $a^b:=\sigma (b)^{-1}(a)$
. The group
$a^b:=\sigma (b)^{-1}(a)$
. The group
![]() $A^\circ :=(A;\circ )$
is called the adjoint group of A. Typical examples of braces are radical rings R (=Jacobson radicals of rings, viewed as pseudorings) with the operation
$A^\circ :=(A;\circ )$
is called the adjoint group of A. Typical examples of braces are radical rings R (=Jacobson radicals of rings, viewed as pseudorings) with the operation
![]() $a\cdot b:=b(1+a)^{-1}$
. Then, the adjoint group is given by Jacobson’s circle operation [Reference Jacobson17]
$a\cdot b:=b(1+a)^{-1}$
. Then, the adjoint group is given by Jacobson’s circle operation [Reference Jacobson17]
In accordance with Jacobson’s notation [Reference Jacobson17], we write
![]() $a'$
for the inverse in the adjoint group of a brace. Note that the unit element of
$a'$
for the inverse in the adjoint group of a brace. Note that the unit element of
![]() $A^\circ $
is 0.
$A^\circ $
is 0.
For any nondegenerate cycle set X, the permutation group
![]() $G(X)$
is the adjoint group of a unique brace
$G(X)$
is the adjoint group of a unique brace
![]() $A(X)$
such that
$A(X)$
such that
![]() $\sigma \colon X\rightarrow A(X)$
is a cycle set morphism. A subset of a brace A is said to be a cycle base [Reference Rump22, Definition 4] if it is invariant under the adjoint group
$\sigma \colon X\rightarrow A(X)$
is a cycle set morphism. A subset of a brace A is said to be a cycle base [Reference Rump22, Definition 4] if it is invariant under the adjoint group
![]() $A^\circ $
and generates the additive group of A. By [Reference Rump28, Proposition 10], a brace A is generated by an element
$A^\circ $
and generates the additive group of A. By [Reference Rump28, Proposition 10], a brace A is generated by an element
![]() $e\in A$
if and only if
$e\in A$
if and only if
![]() $X:=\{e^a\:|\:a\in A\}$
is a cycle base of A. Thus, each transitive cycle base (i.e., such that
$X:=\{e^a\:|\:a\in A\}$
is a cycle base of A. Thus, each transitive cycle base (i.e., such that
![]() $A^\circ $
acts transitively on it) is given by a generator
$A^\circ $
acts transitively on it) is given by a generator
![]() $e\in A$
.
$e\in A$
.
A right ideal [Reference Rump22] of a brace A is an additive subgroup which is invariant under the action of
![]() $A^\circ $
. By equation (2.4), any right ideal is a subbrace. For radical rings, this concept coincides with the usual one. We say that a brace A is a torsion brace if each
$A^\circ $
. By equation (2.4), any right ideal is a subbrace. For radical rings, this concept coincides with the usual one. We say that a brace A is a torsion brace if each
![]() $a\in A$
is of finite order in
$a\in A$
is of finite order in
![]() $(A;+)$
. For a torsion brace A, equation (2.2) implies that the primary decomposition of the additive group is a decomposition into right ideals.
$(A;+)$
. For a torsion brace A, equation (2.2) implies that the primary decomposition of the additive group is a decomposition into right ideals.
The fundamental groupoid [Reference Rump26]
![]() $\pi _1(X)$
of a cycle set X has X as set of objects, and pairs
$\pi _1(X)$
of a cycle set X has X as set of objects, and pairs
![]() $(a,x)\in G(X)\times X$
as morphisms from x to
$(a,x)\in G(X)\times X$
as morphisms from x to
![]() $a(x)$
. Composition is the obvious one:
$a(x)$
. Composition is the obvious one:
given by
![]() $(a,b(x))(b,x):=(ab,x)$
. Inverses are
$(a,b(x))(b,x):=(ab,x)$
. Inverses are
![]() $(a,x)^{-1}:=(a^{-1},a(x))$
. The isomorphism classes of objects in
$(a,x)^{-1}:=(a^{-1},a(x))$
. The isomorphism classes of objects in
![]() $\pi _1(X)$
form a set
$\pi _1(X)$
form a set
![]() $C(X)$
, consisting of the
$C(X)$
, consisting of the
![]() $G(X)$
-orbits of X. Any morphism
$G(X)$
-orbits of X. Any morphism
![]() $f\colon X\rightarrow Y$
of cycle sets induces a map
$f\colon X\rightarrow Y$
of cycle sets induces a map
![]() $C(f)\colon C(X)\rightarrow C(Y)$
. If f is surjective, it gives rise to a commutative diagram
$C(f)\colon C(X)\rightarrow C(Y)$
. If f is surjective, it gives rise to a commutative diagram

with a surjective group homomorphism
![]() $G(f)$
. We call
$G(f)$
. We call
![]() $f\colon X\twoheadrightarrow Y$
a covering [Reference Rump26] if
$f\colon X\twoheadrightarrow Y$
a covering [Reference Rump26] if
![]() $C(f)$
and
$C(f)$
and
![]() $G(f)$
are bijective. By [Reference Rump26, Theorem 6], any cycle set X admits a covering
$G(f)$
are bijective. By [Reference Rump26, Theorem 6], any cycle set X admits a covering
![]() $\widetilde {X}\twoheadrightarrow X$
which is universal in the sense that it factors uniquely though each covering
$\widetilde {X}\twoheadrightarrow X$
which is universal in the sense that it factors uniquely though each covering
![]() $Y\twoheadrightarrow X$
, so that
$Y\twoheadrightarrow X$
, so that
![]() $\widetilde {X}\rightarrow Y$
is again a covering. Cycle sets X with no proper coverings
$\widetilde {X}\rightarrow Y$
is again a covering. Cycle sets X with no proper coverings
![]() $Y\twoheadrightarrow X$
are characterized by their fundamental groupoid which is skeletal.
$Y\twoheadrightarrow X$
are characterized by their fundamental groupoid which is skeletal.
A cycle set X is said to be indecomposable if
![]() $G(X)$
acts transitively on X, that is,
$G(X)$
acts transitively on X, that is,
![]() $|C(X)|=1$
. Then,
$|C(X)|=1$
. Then,
![]() $\widetilde {X}$
is indecomposable, too. Thus,
$\widetilde {X}$
is indecomposable, too. Thus,
![]() $G(X)=G(\widetilde {X})$
acts freely and transitively on
$G(X)=G(\widetilde {X})$
acts freely and transitively on
![]() $\widetilde {X}$
. Being quite analogous to simply connected topological spaces, such cycle sets are called uniconnected [Reference Rump27].
$\widetilde {X}$
. Being quite analogous to simply connected topological spaces, such cycle sets are called uniconnected [Reference Rump27].
3 Bracial self-maps of groups
Let
![]() $\varepsilon \colon G\rightarrow G$
be a self-map of a group G. We define the kernel of
$\varepsilon \colon G\rightarrow G$
be a self-map of a group G. We define the kernel of
![]() $\varepsilon $
to be the subgroup
$\varepsilon $
to be the subgroup
For a group homomorphism
![]() $\varepsilon $
, this concept coincides with the usual one. Note, however, that
$\varepsilon $
, this concept coincides with the usual one. Note, however, that
![]() $\mbox {Ker}\,\varepsilon $
need not be normal for an arbitrary self-map
$\mbox {Ker}\,\varepsilon $
need not be normal for an arbitrary self-map
![]() $\varepsilon $
.
$\varepsilon $
.
Definition 3.1 We call a cycle set structure
![]() $(B;\odot )$
on a group B bracial if it satisfies
$(B;\odot )$
on a group B bracial if it satisfies
![]() $a\odot b=b(a\odot 1)$
for all
$a\odot b=b(a\odot 1)$
for all
![]() $a,b\in B$
.
$a,b\in B$
.
Thus, B is uniquely determined by its group structure and the self-map
We call
![]() $\varepsilon $
the structure map and
$\varepsilon $
the structure map and
![]() $\varepsilon (B)$
the image of B. The kernel
$\varepsilon (B)$
the image of B. The kernel
![]() $\mbox {Ker}\,B:=\mbox {Ker}\,\varepsilon $
of
$\mbox {Ker}\,B:=\mbox {Ker}\,\varepsilon $
of
![]() $\varepsilon $
will be called the kernel of B. In terms of
$\varepsilon $
will be called the kernel of B. In terms of
![]() $\varepsilon $
, we have
$\varepsilon $
, we have
Proposition 1 A self-map
![]() $\varepsilon \colon B\rightarrow B$
of a group B defines a bracial cycle set if and only if it satisfies the equation
$\varepsilon \colon B\rightarrow B$
of a group B defines a bracial cycle set if and only if it satisfies the equation
 $$ \begin{align} \varepsilon\bigl(a\varepsilon(b)^{-1}\bigr)\varepsilon(b)= \varepsilon\bigl(b\varepsilon(a)^{-1}\bigr)\varepsilon(a). \end{align} $$
$$ \begin{align} \varepsilon\bigl(a\varepsilon(b)^{-1}\bigr)\varepsilon(b)= \varepsilon\bigl(b\varepsilon(a)^{-1}\bigr)\varepsilon(a). \end{align} $$
Proof. For
![]() $a,b,c\in B$
, we have
$a,b,c\in B$
, we have
 $$\begin{align*} (a\odot b)\odot(a\odot c)&=b\varepsilon(a)^{-1}\odot c\varepsilon(a)^{-1}=c\varepsilon(a)^{-1}\varepsilon(b\varepsilon(a)^{-1})^{-1}\\&= c(\varepsilon\bigl(b\varepsilon(a)^{-1}\bigr)\varepsilon(a))^{-1}.\end{align*}$$
$$\begin{align*} (a\odot b)\odot(a\odot c)&=b\varepsilon(a)^{-1}\odot c\varepsilon(a)^{-1}=c\varepsilon(a)^{-1}\varepsilon(b\varepsilon(a)^{-1})^{-1}\\&= c(\varepsilon\bigl(b\varepsilon(a)^{-1}\bigr)\varepsilon(a))^{-1}.\end{align*}$$
Equation (3.1) says that this expression is symmetric in a and b.▪
Consider the subgroup
![]() $\langle \varepsilon (B)\rangle $
of B generated by the image of B. For
$\langle \varepsilon (B)\rangle $
of B generated by the image of B. For
![]() $a,b\in B$
, we have
$a,b\in B$
, we have
![]() $a\odot b=b(a\odot 1)=b\varepsilon (a)^{-1}$
. Therefore, the right regular representation of B induces a group isomorphism
$a\odot b=b(a\odot 1)=b\varepsilon (a)^{-1}$
. Therefore, the right regular representation of B induces a group isomorphism
onto the permutation group of B, which maps
![]() $a\in \langle \varepsilon (B)\rangle $
to the right multiplication
$a\in \langle \varepsilon (B)\rangle $
to the right multiplication
![]() $b\mapsto ba^{-1}$
. On the other hand, we have a map
$b\mapsto ba^{-1}$
. On the other hand, we have a map
with
![]() $\sigma (a)(b):=a\odot b$
. So the isomorphism (3.2) yields a factorization
$\sigma (a)(b):=a\odot b$
. So the isomorphism (3.2) yields a factorization

Theorem 3.1 Let B be a bracial cycle set. Then,
![]() $G(B)$
acts freely on B. The subset
$G(B)$
acts freely on B. The subset
![]() $\langle \varepsilon (B)\rangle $
of B is a uniconnected subcycle set. The left cosets of
$\langle \varepsilon (B)\rangle $
of B is a uniconnected subcycle set. The left cosets of
![]() $\langle \varepsilon (B)\rangle $
are the
$\langle \varepsilon (B)\rangle $
are the
![]() $G(B)$
-orbits of B.
$G(B)$
-orbits of B.
Proof. Assume that
![]() $\alpha (b)=b$
for some
$\alpha (b)=b$
for some
![]() $\alpha \in G(B)$
and
$\alpha \in G(B)$
and
![]() $b\in B$
. Then,
$b\in B$
. Then,
![]() $b=b\pi ^{-1}(\alpha )^{-1}$
, which yields
$b=b\pi ^{-1}(\alpha )^{-1}$
, which yields
![]() $\pi ^{-1}(\alpha )=1$
, that is,
$\pi ^{-1}(\alpha )=1$
, that is,
![]() $\alpha = 1_B$
. For
$\alpha = 1_B$
. For
![]() $a\in \langle \varepsilon (B)\rangle $
and
$a\in \langle \varepsilon (B)\rangle $
and
![]() $b\in B$
, we have
$b\in B$
, we have
![]() $b\odot a =a\varepsilon (b)^{-1} \in \langle \varepsilon (B)\rangle $
. Thus,
$b\odot a =a\varepsilon (b)^{-1} \in \langle \varepsilon (B)\rangle $
. Thus,
![]() $\langle \varepsilon (B)\rangle $
is a subcycle set. By induction, the equation
$\langle \varepsilon (B)\rangle $
is a subcycle set. By induction, the equation
![]() $b\odot a=a\varepsilon (b)^{-1}$
shows that the cycle set
$b\odot a=a\varepsilon (b)^{-1}$
shows that the cycle set
![]() $\langle \varepsilon (B)\rangle $
is indecomposable, hence uniconnected. Moreover, the equation implies that the left cosets of
$\langle \varepsilon (B)\rangle $
is indecomposable, hence uniconnected. Moreover, the equation implies that the left cosets of
![]() $\langle \varepsilon (B)\rangle $
are the
$\langle \varepsilon (B)\rangle $
are the
![]() $G(B)$
-orbits of B. ▪
$G(B)$
-orbits of B. ▪
As a consequence, we get a classification of uniconnected cycle sets.
Theorem 3.2 A bracial cycle set B is uniconnected if and only if
![]() $\langle \varepsilon (B) \rangle =B$
. Conversely, every uniconnected cycle set B is bracial and satisfies
$\langle \varepsilon (B) \rangle =B$
. Conversely, every uniconnected cycle set B is bracial and satisfies
![]() $\langle \varepsilon (B)\rangle =B$
.
$\langle \varepsilon (B)\rangle =B$
.
Proof. The first statement follows by Theorem 3.1. Conversely, let
![]() $(B;\odot )$
be any uniconnected cycle set. Choose an element
$(B;\odot )$
be any uniconnected cycle set. Choose an element
![]() $1\in B$
. Then, there is a bijection
$1\in B$
. Then, there is a bijection
![]() $\gamma \colon G(B)\mathop{\longrightarrow}\limits^{\sim}\, B$
with
$\gamma \colon G(B)\mathop{\longrightarrow}\limits^{\sim}\, B$
with
![]() $\gamma (\alpha ):=\alpha (1)$
. So the map
$\gamma (\alpha ):=\alpha (1)$
. So the map
![]() $\sigma \colon B\rightarrow G(B)$
with
$\sigma \colon B\rightarrow G(B)$
with
![]() $\sigma (a)(b)=a\odot b$
satisfies
$\sigma (a)(b)=a\odot b$
satisfies
![]() $\sigma (a)=\gamma ^{-1}(a\odot 1)$
. Define a multiplication in B as follows:
$\sigma (a)=\gamma ^{-1}(a\odot 1)$
. Define a multiplication in B as follows:
For given
![]() $a,b\in B$
, consider the automorphisms
$a,b\in B$
, consider the automorphisms
![]() $\alpha :=\gamma ^{-1}(a)$
and
$\alpha :=\gamma ^{-1}(a)$
and
![]() $\beta :=\gamma ^{-1}(b)$
in
$\beta :=\gamma ^{-1}(b)$
in
![]() $G(B)$
. Because
$G(B)$
. Because
![]() $\gamma (\alpha \beta )=\alpha \gamma (\beta )$
, we have
$\gamma (\alpha \beta )=\alpha \gamma (\beta )$
, we have
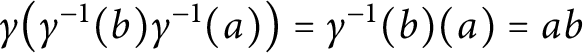 $\gamma \bigl (\gamma ^{-1}(b)\gamma ^{-1}(a)\bigr )= \gamma ^{-1}(b)(a)=ab$
, which yields
$\gamma \bigl (\gamma ^{-1}(b)\gamma ^{-1}(a)\bigr )= \gamma ^{-1}(b)(a)=ab$
, which yields
![]() $\gamma ^{-1}(ab)=\gamma ^{-1}(b) \gamma ^{-1}(a)$
. Thus, equation (3.4) defines a group structure on B with an isomorphism
$\gamma ^{-1}(ab)=\gamma ^{-1}(b) \gamma ^{-1}(a)$
. Thus, equation (3.4) defines a group structure on B with an isomorphism
In particular, we obtain
![]() $\langle \varepsilon (B)\rangle =B$
. For
$\langle \varepsilon (B)\rangle =B$
. For
![]() $a,b\in B$
, equation (3.4) gives
$a,b\in B$
, equation (3.4) gives
![]() $a\odot b=\sigma (a)(b)=\gamma ^{-1}(a\odot 1) (b)=b(a\odot 1)$
. Whence B is a bracial cycle set. ▪
$a\odot b=\sigma (a)(b)=\gamma ^{-1}(a\odot 1) (b)=b(a\odot 1)$
. Whence B is a bracial cycle set. ▪
In [Reference Rump27, Theorem 2], nondegenerate uniconnected cycle sets are classified in terms of braces with a transitive cycle base. The following example shows that uniconnected cycle sets need not be nondegenerate.
Example 1 Let G be a right
![]() $\ell $
-group [Reference Rump23], that is, a group with a lattice order, satisfying
$\ell $
-group [Reference Rump23], that is, a group with a lattice order, satisfying
for all
![]() $a,b,c\in G$
. Consider the self-map
$a,b,c\in G$
. Consider the self-map
![]() $\varepsilon \colon G\rightarrow G$
given by
$\varepsilon \colon G\rightarrow G$
given by
![]() $\varepsilon (a):=a\vee 1$
. Then,
$\varepsilon (a):=a\vee 1$
. Then,
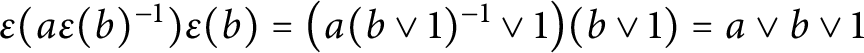 $\varepsilon (a\varepsilon (b)^{-1})\varepsilon (b)=\bigl (a(b\vee 1)^{-1}\vee 1\bigr )(b\vee 1)=a\vee b\vee 1$
, which is symmetric in a and b. Hence,
$\varepsilon (a\varepsilon (b)^{-1})\varepsilon (b)=\bigl (a(b\vee 1)^{-1}\vee 1\bigr )(b\vee 1)=a\vee b\vee 1$
, which is symmetric in a and b. Hence,
![]() $\varepsilon $
makes G into a bracial cycle set. The kernel of
$\varepsilon $
makes G into a bracial cycle set. The kernel of
![]() $\varepsilon $
is
$\varepsilon $
is
![]() $\{1\}$
, while the image
$\{1\}$
, while the image
![]() $\varepsilon (G)$
is the positive cone of G. Therefore, the corresponding cycle set
$\varepsilon (G)$
is the positive cone of G. Therefore, the corresponding cycle set
![]() $(G;\odot )$
with
$(G;\odot )$
with
![]() $a\odot b:=b (a\vee 1)^{-1}$
is uniconnected. However,
$a\odot b:=b (a\vee 1)^{-1}$
is uniconnected. However,
![]() $(G;\odot )$
is degenerate: For
$(G;\odot )$
is degenerate: For
![]() $a\geqslant 1$
, we have
$a\geqslant 1$
, we have
![]() $a\odot a=a(a\vee 1)^{-1}=1$
. So the square map
$a\odot a=a(a\vee 1)^{-1}=1$
. So the square map
![]() $a\mapsto a\odot a$
is not injective if
$a\mapsto a\odot a$
is not injective if
![]() $|G|\ne 1$
.
$|G|\ne 1$
.
The diagram (3.3) shows that the structure map
![]() $\varepsilon $
of a bracial cycle set B gives the retraction
$\varepsilon $
of a bracial cycle set B gives the retraction
![]() $\varepsilon (B)$
of B. By [Reference Rump21, Section 6], this implies that the cycle set structure of B induces a well-defined binary operation on
$\varepsilon (B)$
of B. By [Reference Rump21, Section 6], this implies that the cycle set structure of B induces a well-defined binary operation on
![]() $\varepsilon (B)$
:
$\varepsilon (B)$
:
Indeed,
![]() $\varepsilon (b)=\varepsilon (c)$
implies that
$\varepsilon (b)=\varepsilon (c)$
implies that
![]() $\varepsilon (b\varepsilon (a)^{-1}) \varepsilon (a)=\varepsilon (a\varepsilon (b)^{-1})\varepsilon (b)=\varepsilon (a\varepsilon (c)^{-1}) \varepsilon (c)=\varepsilon (c\varepsilon (a)^{-1})\varepsilon (a)$
, which yields
$\varepsilon (b\varepsilon (a)^{-1}) \varepsilon (a)=\varepsilon (a\varepsilon (b)^{-1})\varepsilon (b)=\varepsilon (a\varepsilon (c)^{-1}) \varepsilon (c)=\varepsilon (c\varepsilon (a)^{-1})\varepsilon (a)$
, which yields
![]() $\varepsilon (b\varepsilon (a)^{-1})=\varepsilon (c\varepsilon (a)^{-1})$
. Thus,
$\varepsilon (b\varepsilon (a)^{-1})=\varepsilon (c\varepsilon (a)^{-1})$
. Thus,
![]() $\varepsilon (a) \cdot \varepsilon (b)$
does not depend on the choice of b. So the operation (3.5) satisfies equation (1.1), which makes
$\varepsilon (a) \cdot \varepsilon (b)$
does not depend on the choice of b. So the operation (3.5) satisfies equation (1.1), which makes
![]() $\varepsilon (B)$
into a cycle set if B is nondegenerate. In general, however,
$\varepsilon (B)$
into a cycle set if B is nondegenerate. In general, however,
![]() $(\varepsilon (B);\cdot )$
is not a subcycle set of
$(\varepsilon (B);\cdot )$
is not a subcycle set of
![]() $(B;\odot )$
.
$(B;\odot )$
.
Example 2 Let C be a differential group [Reference Mac Lane20], that is, an abelian group with an endomorphism
![]() $d\colon C\rightarrow C$
satisfying
$d\colon C\rightarrow C$
satisfying
![]() $d^2=0$
. For an element
$d^2=0$
. For an element
![]() $b\in C$
with
$b\in C$
with
![]() $db\ne 0$
, we define
$db\ne 0$
, we define
![]() $\varepsilon (x):=dx+b$
. Then,
$\varepsilon (x):=dx+b$
. Then,
![]() $\varepsilon (x-\varepsilon (y))+\varepsilon (y)=d(x+y)-db+2b$
. By symmetry, this gives a bracial cycle set C with
$\varepsilon (x-\varepsilon (y))+\varepsilon (y)=d(x+y)-db+2b$
. By symmetry, this gives a bracial cycle set C with
![]() $x\odot y=y-\varepsilon (x)=y-dx-b$
. Because
$x\odot y=y-\varepsilon (x)=y-dx-b$
. Because
![]() $1-d$
is invertible, the cycle set is nondegenerate. However,
$1-d$
is invertible, the cycle set is nondegenerate. However,
![]() $\varepsilon (C)$
is not a subcycle set. Indeed,
$\varepsilon (C)$
is not a subcycle set. Indeed,
![]() $\varepsilon (x)\odot \varepsilon (y)=d(y-b)\notin \varepsilon (C)$
, because
$\varepsilon (x)\odot \varepsilon (y)=d(y-b)\notin \varepsilon (C)$
, because
![]() $db\ne 0$
. The subcycle set
$db\ne 0$
. The subcycle set
![]() $\langle \varepsilon (C)\rangle = dC+\mathbb {Z} b$
is uniconnected.
$\langle \varepsilon (C)\rangle = dC+\mathbb {Z} b$
is uniconnected.
Now, we turn our attention to the nondegenerate case. Note that a bracial cycle set B is nondegenerate if and only if the map
![]() $a\mapsto a \varepsilon (a)^{-1}$
is bijective.
$a\mapsto a \varepsilon (a)^{-1}$
is bijective.
Definition 3.2 We call a self-map
![]() $\varepsilon \colon G\rightarrow G$
of a group G right invariant if the implication
$\varepsilon \colon G\rightarrow G$
of a group G right invariant if the implication
holds for
![]() $a,b,c\in G$
.
$a,b,c\in G$
.
Let
![]() $\varepsilon \colon G\rightarrow G$
be a self-map with kernel H. Because
$\varepsilon \colon G\rightarrow G$
be a self-map with kernel H. Because
![]() $ac=(ab^{-1}) bc$
, condition (3.6) says that
$ac=(ab^{-1}) bc$
, condition (3.6) says that
![]() $\varepsilon (a)=\varepsilon (b)$
if and only if
$\varepsilon (a)=\varepsilon (b)$
if and only if
![]() $ab^{-1}\in H$
. So the fibers of
$ab^{-1}\in H$
. So the fibers of
![]() $\varepsilon $
are the right cosets of H. Therefore,
$\varepsilon $
are the right cosets of H. Therefore,
![]() $\varepsilon $
induces a bijection
$\varepsilon $
induces a bijection
![]() $\overline {\varepsilon }\colon G\backslash H\mathop{\longrightarrow}\limits^{\sim}\, \varepsilon (G)$
from the set
$\overline {\varepsilon }\colon G\backslash H\mathop{\longrightarrow}\limits^{\sim}\, \varepsilon (G)$
from the set
![]() $G\backslash H$
of right cosets onto the image of
$G\backslash H$
of right cosets onto the image of
![]() $\varepsilon $
. In Example 2, but not in Example 1, the map
$\varepsilon $
. In Example 2, but not in Example 1, the map
![]() $\varepsilon $
is right invariant.
$\varepsilon $
is right invariant.
Proposition 2 Let G be a group with a right invariant self-map
![]() $\varepsilon \colon G\rightarrow G$
. Then,
$\varepsilon \colon G\rightarrow G$
. Then,
(with
![]() $g,a\in G$
) defines a transitive action of G on the image of
$g,a\in G$
) defines a transitive action of G on the image of
![]() $\varepsilon $
.
$\varepsilon $
.
Proof. Because
![]() $\varepsilon $
is right invariant, equation (3.7) gives a well-defined map
$\varepsilon $
is right invariant, equation (3.7) gives a well-defined map
![]() $G\times \varepsilon (G)\rightarrow \varepsilon (G)$
. Furthermore,
$G\times \varepsilon (G)\rightarrow \varepsilon (G)$
. Furthermore,
![]() $gh\cdot \varepsilon (a)=\varepsilon (ah^{-1}g^{-1})=g\cdot \varepsilon (ah^{-1})=g\cdot (h\cdot \varepsilon (a))$
and
$gh\cdot \varepsilon (a)=\varepsilon (ah^{-1}g^{-1})=g\cdot \varepsilon (ah^{-1})=g\cdot (h\cdot \varepsilon (a))$
and
![]() $1\cdot \varepsilon (a)=\varepsilon (a)$
. Thus, equation (3.7) defines an action on
$1\cdot \varepsilon (a)=\varepsilon (a)$
. Thus, equation (3.7) defines an action on
![]() $\varepsilon (G)$
. Because
$\varepsilon (G)$
. Because
![]() $aG=G$
, this action is transitive. ▪
$aG=G$
, this action is transitive. ▪
Proposition 3 The structure map
![]() $\varepsilon \colon B\rightarrow B$
of a nondegenerate uniconnected cycle set B is right invariant.
$\varepsilon \colon B\rightarrow B$
of a nondegenerate uniconnected cycle set B is right invariant.
Proof. The diagram (3.3) shows that
![]() $\varepsilon (a)=\varepsilon (b)$
is equivalent to
$\varepsilon (a)=\varepsilon (b)$
is equivalent to
![]() $\sigma (a)=\sigma (b)$
. Assuming this, we have to show that
$\sigma (a)=\sigma (b)$
. Assuming this, we have to show that
![]() $\sigma (ac)= \sigma (bc)$
holds for all
$\sigma (ac)= \sigma (bc)$
holds for all
![]() $c\in B$
. Because B is uniconnected, it is enough to verify the equivalence
$c\in B$
. Because B is uniconnected, it is enough to verify the equivalence
Indeed,
![]() $\sigma (a)=\sigma (b)$
implies
$\sigma (a)=\sigma (b)$
implies
![]() $(c\odot a) \odot (c\odot d)=(a\odot c)\odot (a\odot d)= (b\odot c)\odot (b\odot d)=(c\odot b)\odot (c\odot d)$
for all
$(c\odot a) \odot (c\odot d)=(a\odot c)\odot (a\odot d)= (b\odot c)\odot (b\odot d)=(c\odot b)\odot (c\odot d)$
for all
![]() $d\in B$
. Thus,
$d\in B$
. Thus,
![]() $\sigma (c\odot a)=\sigma (c\odot b)$
. Conversely, assume that
$\sigma (c\odot a)=\sigma (c\odot b)$
. Conversely, assume that
![]() $\sigma (c\odot a)=\sigma (c\odot b)$
. Then,
$\sigma (c\odot a)=\sigma (c\odot b)$
. Then,
![]() $(a\odot c)\odot (a\odot c)= (c\odot a)\odot (c\odot c)=(c\odot b)\odot (c\odot c)=(b\odot c)\odot (b\odot c)$
. Because B is nondegenerate, we obtain
$(a\odot c)\odot (a\odot c)= (c\odot a)\odot (c\odot c)=(c\odot b)\odot (c\odot c)=(b\odot c)\odot (b\odot c)$
. Because B is nondegenerate, we obtain
![]() $a\odot c=b\odot c$
. As B is uniconnected, this implies that
$a\odot c=b\odot c$
. As B is uniconnected, this implies that
![]() $\sigma (a)=\sigma (b)$
.▪
$\sigma (a)=\sigma (b)$
.▪
For a nondegenerate bracial cycle set B, the group
![]() $G(B)$
is the adjoint group of a brace. So the group isomorphism (3.2) also makes
$G(B)$
is the adjoint group of a brace. So the group isomorphism (3.2) also makes
![]() $\langle \varepsilon (B)\rangle $
into a brace
$\langle \varepsilon (B)\rangle $
into a brace
![]() $A(B)$
. Taking
$A(B)$
. Taking
![]() $\pi $
as an identification, we get a factorization
$\pi $
as an identification, we get a factorization

which identifies
![]() $\varepsilon (B)$
with the image of
$\varepsilon (B)$
with the image of
![]() $\sigma $
.
$\sigma $
.
Theorem 3.3 Let B be a brace, generated by
![]() $e\in B$
. Then, there is a unique self-map
$e\in B$
. Then, there is a unique self-map
![]() $\varepsilon \colon B\rightarrow B$
with
$\varepsilon \colon B\rightarrow B$
with
![]() $\varepsilon (0)=e$
such that
$\varepsilon (0)=e$
such that
![]() $\varepsilon $
is the structure map of a nondegenerate uniconnected cycle set with group
$\varepsilon $
is the structure map of a nondegenerate uniconnected cycle set with group
![]() $B^\circ $
. Conversely, every nondegenerate uniconnected cycle set arises in this way.
$B^\circ $
. Conversely, every nondegenerate uniconnected cycle set arises in this way.
Proof. By [Reference Rump28, Proposition 10],
![]() $X:=\{e^a\:|\:a\in B\}$
is a transitive cycle base of B. So [Reference Rump27, Theorem 2] shows that the operation
$X:=\{e^a\:|\:a\in B\}$
is a transitive cycle base of B. So [Reference Rump27, Theorem 2] shows that the operation
makes B into a nondegenerate uniconnected cycle set. In particular,
![]() $(B;\odot )$
is a bracial cycle set with
$(B;\odot )$
is a bracial cycle set with
![]() $\varepsilon (a)=(a\odot 0)'=e^a$
. Thus,
$\varepsilon (a)=(a\odot 0)'=e^a$
. Thus,
![]() $\varepsilon (B)=X$
and
$\varepsilon (B)=X$
and
![]() $\varepsilon (0)=e$
. By Propositions 2 and 3, the structure map
$\varepsilon (0)=e$
. By Propositions 2 and 3, the structure map
![]() $\varepsilon $
is unique:
$\varepsilon $
is unique:
![]() $\varepsilon (a)=\varepsilon (0\circ a)= \varepsilon (0)^a=e^a$
.
$\varepsilon (a)=\varepsilon (0\circ a)= \varepsilon (0)^a=e^a$
.
Conversely, let B be a nondegenerate uniconnected cycle set. Because
![]() $\varepsilon (B)$
is the retraction of B, the map
$\varepsilon (B)$
is the retraction of B, the map
![]() $\varepsilon \colon B\twoheadrightarrow \varepsilon (B)$
is a cycle set morphism. So the cycle set morphism (3.8) shows that
$\varepsilon \colon B\twoheadrightarrow \varepsilon (B)$
is a cycle set morphism. So the cycle set morphism (3.8) shows that
![]() $\iota $
is a morphism of cycle sets. Thus,
$\iota $
is a morphism of cycle sets. Thus,
![]() $\varepsilon (B)$
is a cycle base of
$\varepsilon (B)$
is a cycle base of
![]() $A(X)$
. Equation (3.5) shows that it is transitive.
$A(X)$
. Equation (3.5) shows that it is transitive.
By equation (3.5), the action (3.7) coincides with the adjoint action in
![]() $A(B)$
. Hence,
$A(B)$
. Hence,
![]() $\varepsilon (a)=a^{-1}\cdot \varepsilon (1)=\varepsilon (1)^a$
for all
$\varepsilon (a)=a^{-1}\cdot \varepsilon (1)=\varepsilon (1)^a$
for all
![]() $a \in A(B)$
. Thus,
$a \in A(B)$
. Thus,
![]() $a\odot b=b\varepsilon (a)^{-1}=b(\varepsilon (1)^a)^{-1}$
. By [Reference Rump27, Theorem 2], the proof is complete. ▪
$a\odot b=b\varepsilon (a)^{-1}=b(\varepsilon (1)^a)^{-1}$
. By [Reference Rump27, Theorem 2], the proof is complete. ▪
Corollary A uniconnected cycle set B is nondegenerate if and only if B is the adjoint group of a brace.
Proof. By [Reference Rump27, Proposition 2], a cycle set is nondegenerate if and only if it is a cycle base of a brace. ▪



