Published online by Cambridge University Press: 01 March 2004
The Rayleigh–Taylor instability (RTI) of a laser-accelerated ablative surface of a thin plasma layer in an inertial fusion energy (IFE) target with incompressible electrically conducting plasma in the presence of a transverse magnetic field is investigated using linear stability analysis. A simple theory based on Stokes-lubrication approximation is proposed. It is shown that the effect of a transverse magnetic field is to reduce the growth rate of RTI considerably over the value it would have in the absence of a magnetic field. This is useful in the extraction of IFE efficiently.
In this article we report the Rayleigh–Taylor instability (RTI) of a laser-accelerated ablative surface of a thin plasma layer in an inertial fusion energy (IFE) target shell with an incompressible viscous, electrically conducting plasma in the presence of a transverse magnetic field. The RTI occurs at an ablative surface between the dense and less dense plasma if the dense plasma is accelerated by the less dense plasma. It is one of the physical mechanisms and limits the performance of laser fusion IFE targets. Hence, the additional mitigation of the RTI growth rate is needed to achieve high gain of IFE.
At present, mechanisms like a gradual variation of density instead of an abrupt change in a heterogeneous inviscid fluid and compressible inviscid fluid without a foam layer have been used to reduce the growth rate of RTI. The results of numerous experiments and numerical simulations of the RTI growth rate of compressible inviscid fluid at the ablation surface fit the following generalized dispersion formula (see Kanuer et al., 2000):

where n is the growth rate, [ell ] is the wave number of the perturbation, g is the acceleration due to gravity at the interface, A is the Atwood number, ε is a constant multiplying the density gradient correction term, L is the density scale length at the ablative surface, β is a constant multiplying the ablation stabilization term, and va is the velocity across the ablation surface. The first term on the right-hand side of Eq. (1) is the classical growth rate of a classical RTI for an inviscid incompressible fluid and the second term is the effect of compressibility. We note that with a suitable choice of ε, L, A, and β, we can get the compressible fluid results of Takabe et al. (1985), Kilkenny et al. (1994), Betti et al. (1995), Lindl (1995), and Bychkov et al. (1994). During the past approximately 10 years, porous IFE-relevant ablation layers with foam have been considered by IFE researchers (Sethian et al., 1999; Batani et al., 2000; and references therein) to reduce the RTI growth rate. To our knowledge, there is no definite analytical formula to predict the effect of foam to reduce the growth rate. Recently, Rudraiah (2003) has shown that the nondeformable porous lining made up of foametal porous material or aloxite porous material on one side and the IFE target shell filled with viscous incompressible fluid on the other side bounded by rigid surface reduces the RTI growth rate, np, considerably and derived the formula
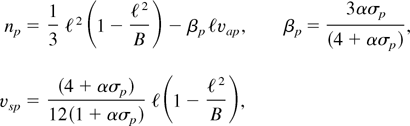
where the subscript p denotes the quantities in the presence of porous lining, B is the Bond number, which is a measure of gravitational effect to surface tension effect, σp is the permeability of the porous lining, α is the slip parameter (see Rudraiah, 1985) vap is the velocity across the ablative surface lined with porous lining and other quantities are as defined in Eq. (1). From Eq. (2), Rudraiah (2003) had obtained the maximum wave number
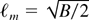
and the corresponding maximum growth rate nmp is
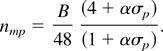
From this he had obtained
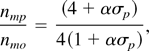
where
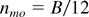
is the maximum growth rate in the absence of porous lining. From Eq. (1) with β = 3, A = 0.9 Takabe et al. (1985) have obtained
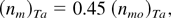
where the subscript Ta refers to the results of Takabe et al. (1985). From Eq. (7) Takabe et al. (1985) have concluded that the growth rate of a RTI is reduced to 45% of the classical value (nmo)Ta. For foam material used in the experiments of Beavers and Joseph (1967), the slip parameter α ranges from 0.1 to 4.0 and porous parameter σp ranges from 4 to 20. For α = 0.1 and σp = 4.0, Eq. (5) reduces to nmp = 0.7857nmo. From this result Rudraiah (2003) had concluded that the maximum growth rate, nmp, is reduced to 78.57% of nmo. In particular he (Rudraiah 2003) has shown that the reduction of the growth rate is possible even up to 80% for a proper choice of the porous parameters α and σp. Physically, this reduction in growth rate in the presence of porous lining is due to the contraction and expansion of flow in the pores, which absorbs some of the energy that would go otherwise into the target.
We know that in continuum plasma the effect of a transverse magnetic field is to suppress the perturbations by converting the kinetic energy in to magnetic energy. In classical plasma, that is, incompressible, inviscid, perfectly conducting fluid in the presence of a transverse magnetic field, called the classical problem of Magneto Rayleigh Taylor Instability (MRTI) has been extensively investigated in the literature (see Chandrasekhar, 1961). However, the MRTI of a laser-accelerated ablative surface of a thin target shell with viscous, electrically conducting incompressible plasma in the presence of a transverse magnetic field and surface tension has not been given much attention. The study of it is the main object of the present article with the motivation to know whether a suitable strength of a transverse magnetic field can reduce the RTI growth rate in the presence of viscous shear and surface tension without considering the mechanism of porous lining. It is also the objective to derive a simple analytical formula analogous to Rudraiah's formula (2).
To achieve these objectives, the plan of this article is as follows. In Section 2, the basic equations, the relevant boundary and surface conditions and approximations are given. The dispersion relation is obtained in Section 3 using linear stability analysis. The formula for the growth rate in the presence of a magnetic field and the absence of a porous lining, analogous to Eq. (2) is also derived in this section. Some important conclusions are drawn in the Section 4.
We consider a thin target shell in the form of a film of unperturbed thickness h filled with light incompressible viscous electrically conducting plasma of constant density ρ1 bounded on one side by a rigid surface and on the other side by an incompressible heavy viscous electrically conducting plasma of density ρ2 of an infinite extent with an interface between the two plasma layers subject to a transverse magnetic field and surface tension (see Fig. 1). This assumption on density is needed for the RTI as defined in Section 1. The fluid within the shell is set in motion by the laser-accelerated ablative surface. At time t, the fluctuations of the interface are amplified and the local thickness becomes a function of the position and time t and we have y = h + η(x,t) where η(x,t) is the surface displacement. We consider a rectangular coordinate system (x,y) as shown in the Figure 1, with the x-axis parallel to the shell and the y-axis normal to it with η(x,t) as the perturbed interface.

Physical configuration.
The basic equations for conducting, incompressible, viscous and electrically conducting plasma in the film are the conservation of momentum,
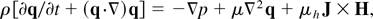
and the conservation of mass for an incompressible plasma,
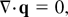
where q = (u,v) is the velocity, J = σ[E + σhq × H] is the current density, ∇ × E = −μh∂H/∂t, ∇·E = 0, ∇·H = 0, E is the electric field, H is the magnetic field, μ is the viscosity, μh is the magnetic permeability, and σ is the electrical conductivity of fluid. These equations must be supplemented with suitable boundary and surface conditions. These equations are sufficient for our purpose because we deal with electrically conducting fluid of small conductivity σ, so that the induced magnetic field can be neglected in comparison with the applied magnetic field.
In this article, we deal only with a linear two-dimensional RTI in continuum plasma considering infinitesimally small disturbances superposed on the basic state. The basic state is quiescent and the interface is flat. Further, the following stokes and lubrication approximations (see Babchin et al., 1983, Rudraiah et al., 1997) will greatly simplify the analysis: (1) η << h. This assumption helps to ignore the variation of horizontal velocity u with respect to x. (2) The Bond number B = δh2/γ << 1, which implies the gravitational effect is small compared to the surface tension effect where γ is the surface tension and δ = g(ϱamp;2 − ϱamp;1) is the normal stress. (3) The Reynolds number R = Uh2/Lν << 1, where ν is the kinematic viscosity, which enables us to neglect inertial force because of very viscous fluid. (4) The magnetic Reynolds number Rm = μhσUh << 1 because of small electrical conductivity. This enables us to ignore the induced magnetic field compared to the applied magnetic and electric fields. (5) The Strouhal number
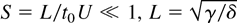
, where t0 and U are the characteristic time and velocity, which enables us to ignore local acceleration in the momentum equation. These approximations, which are valid when the wavelength of the instability of the ablative surface is large compared to the thickness of the layer, are useful to ignore many terms, particularly nonlinear terms in the basic Eq. (8). We also assume that heavy fluid bounding the lighter fluid is almost static because of creeping flow approximation, which is needed to study RT instability (see Babchin et al., 1983). Under these approximations, the basic Eq. (8) reduces to, after making the resulting equations dimensionless using the scales h for length, δh for pressure, δh2/μ for velocity, and μ/δh for time, the form
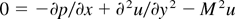
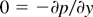
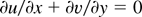
where
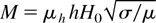
is the Hartmann number and H0 is the applied transverse magnetic field. These equations have to be solved using the following boundary and surface conditions. The no-slip condition at the rigid surface is
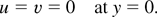
No shear at the free surface is
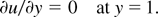
The dynamic condition is
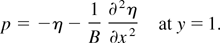
For linear analysis, the kinematic condition is
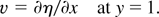
Solving Eq. (10) and, using the conditions (13) to (16), we get
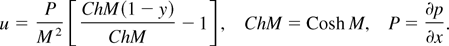
Integrating Eq. (12) with respect to y from 0 to 1 and simplifying, we get
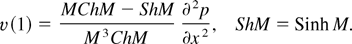
From Eq. (16), using normal mode solution of the form η = η0ei[ell ]x+nt and using Eqs. (15) and (18), we get the dispersion relation of the form
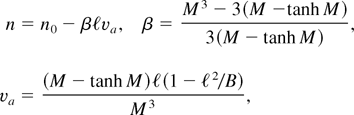
where n is the growth rate, [ell ] is the wave number, B is the Bond number, and
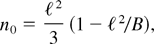
obtained from Eq. (19) in the limit of M → 0, and for convenience we call it a classical value.
This Eq. (19) clearly shows that the effect of the magnetic field is to reduce the growth rate of a RTI considerably compared to the one in the absence of a magnetic field. The physical reason for this reduction is that the transverse magnetic field suppresses the flow by converting the kinetic energy into magnetic energy.
In the present article, a self-consistent analytical approach is used to study linear RTI of ablatively laser-accelerated targets filled with an incompressible electrically conducting viscous plasma in the presence of a transverse magnetic field. The RTI growth rate formula given by Eq. (19) is analogous to the one given by Eq. (1) for a compressible fluid, and Eq. (2) for a porous lining.
Setting n = 0 in Eq. (19), we obtain the cutoff wave number [ell ]ct, above which the RTI mode is stabilized and is found to be
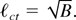
The maximum wave number [ell ]m obtained from Eq. (19) by setting ∂n/∂[ell ] = 0 is
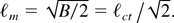
Eqs. (21) and (22) are true even for the case in the absence of a magnetic field (i.e., M = 0) given by Eq. (20) and for convenience we call them a classical result. The maximum growth rate, nm, for the corresponding [ell ]m given by Eq. (22) is
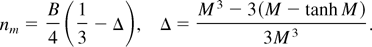
Similarly n0m, from Eq. (20) using Eq. (22), is
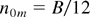
From these, we get the ratio of maximum growth rate nm to n0m, given by
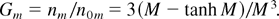
Relation (19) is plotted in Figure 2 for the growth rate n versus the wave number [ell ] for M = 1 and for different values of B. We see that the perturbations of the interface having a wave number smaller than [ell ]ct are amplified when δ > 0 (i.e., ρ1 < ρ2) and the growth rate decreases with a decrease in B, implying an increase in surface tension. That is, an increase in surface tension makes the interface more stable. Similar behavior is observed even for M = 10 and we found that an increase in M decreases the growth rate considerably. To know the amount of reduction in the growth rate caused by a magnetic field compared to that in the absence of magnetic field, Eq. (25) is numerically computed for different values of M ranging from 10−2 to 102 and the results are tabulated in Table 1 and are also plotted in Figure 3 with Gm versus M. We see that the decrease in the growth rate compared to the classical one is very steep for M in the range of 10−1 to 101, and the ratio Gm becomes independent of M for values M > 10 tending to the value 0.0003. For M = 1, we find that Gm = 0.71522, that is, the maximum growth rate is reduced to 71.52% of the classical value n0m. However, at M = 10 we find that the maximum growth rate is reduced by 97.3% of the classical value n0m. Similarly for M = 100 and above, we find that the maximum growth rate is reduced to 2.7% of the classical value n0m. From this we conclude that an increase in the value of the magnetic field, that is M, reduces considerably the growth rate compared to the classical value. This information is useful in the extraction of IFE efficiently by maintaining the symmetry of the target.
Ratio Gm for maximum growth rate for different M


The growth rate n versus wave number [ell ] for M = 1 and for different Bond numbers B.
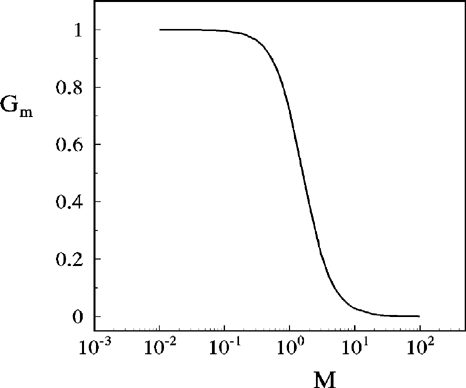
Ratio of maximum growth rate Gm versus M.
The work reported here is supported by the Department of Science and Technology (DST), New Delhi under the project No. SP/12/PC-03/2000. The authors gratefully acknowledge the financial support of DST, New Delhi.

Physical configuration.

Ratio Gm for maximum growth rate for different M

The growth rate n versus wave number [ell ] for M = 1 and for different Bond numbers B.
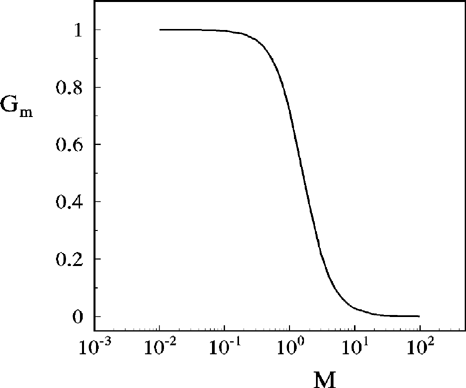
Ratio of maximum growth rate Gm versus M.