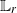1. Introduction
Sequential Monte Carlo (SMC) algorithms are used to approximate expectations with respect to a sequence of probability measures as well as the normalising constants of those measures. These techniques have found numerous applications in statistics, signal processing, physics, and related fields (see, e.g., [Reference Künsch21] for a recent review). These algorithms proceed in a sequential manner by generating a collection of N conditionally independent particles at each time step. An alternative to these schemes in which the particles at each time step are sampled instead according to a single Markov chain Monte Carlo (MCMC) chain was proposed early on by [Reference Berzuini, Best, Gilks and Larizza6]. Over recent years, there has been a renewed interest in such ideas as there is empirical evidence that these methods can outperform standard SMC algorithms in interesting scenarios (see, e.g., [Reference Carmi, Septier and Godsill8], [Reference Golightly and Wilkinson15], [Reference Pal and Coates28] ,[Reference Septier, Pang, Carmi and Godsill31], and [Reference Septier and Peters32] for novel applications and extensions). These methods have been termed sequential MCMC methods in the literature. However, in this work, we will also refer to these as MCMC particle filters (MCMC-PFs), to convey the idea that they rely on the same importance-sampling construction as particle methods.
Although there is a wealth of theoretical results available for SMC algorithms—see, for example, [Reference Del Moral10]—to the best of our knowledge, no convergence guarantees have yet been provided for MCMC-PFs. The present work fills this gap by providing an ![]() $\mathbb{L}_r$
-inequality (which implies a strong law of large numbers) and a central limit theorem for the Monte Carlo estimators of expectations and normalising constants obtained through MCMC-PFs. Our results show that compared to conventional particle filters (PFs), the asymptotic variance of estimators obtained by MCMC-PFs includes additional terms which can be identified as the excess variance arising from the autocorrelation of the MCMC chains used to generate the particles. This implies that a standard PF always provides estimators with a lower asymptotic variance than the corresponding MCMC-PF if both algorithms target the same distributions and if the latter relies on MCMC kernels which are positive, i.e. which induce positive autocorrelations of all orders.
$\mathbb{L}_r$
-inequality (which implies a strong law of large numbers) and a central limit theorem for the Monte Carlo estimators of expectations and normalising constants obtained through MCMC-PFs. Our results show that compared to conventional particle filters (PFs), the asymptotic variance of estimators obtained by MCMC-PFs includes additional terms which can be identified as the excess variance arising from the autocorrelation of the MCMC chains used to generate the particles. This implies that a standard PF always provides estimators with a lower asymptotic variance than the corresponding MCMC-PF if both algorithms target the same distributions and if the latter relies on MCMC kernels which are positive, i.e. which induce positive autocorrelations of all orders.
However, MCMC-PFs exhibit a significant advantage over regular PFs. The popular fully-adapted auxiliary particle filter (FA-APF) introduced by [Reference Pitt and Shephard29] typically significantly outperforms the bootstrap particle filter (BPF) of [Reference Gordon, Salmond and Smith16], for example when approximating the optimal filter for state-space models in the presence of informative measurements. Unfortunately, the FA-APF is implementable for only a very restricted class of models, whereas the MCMC-PF version of the FA-APF is much more widely applicable. In scenarios in which the FA-APF is not implementable, but its MCMC-PF version is, and in which the MCMC kernels used by the latter are sufficiently rapidly mixing, the MCMC-PF can substantially outperform implementable but rather inefficient standard PFs such as the BPF.
2. MCMC-PFs
2.1. Notation
Let ![]() $(\Omega, \mathcal{A}, \mathbb{P})$
be some probability space and denote expectation with respect to
$(\Omega, \mathcal{A}, \mathbb{P})$
be some probability space and denote expectation with respect to ![]() $\mathbb{P}$
by
$\mathbb{P}$
by ![]() $\mathbb{E}$
. For some set measurable space
$\mathbb{E}$
. For some set measurable space ![]() $(H, \mathcal{H})$
, we let
$(H, \mathcal{H})$
, we let ![]() $\mathcal{B}(H)$
denote the Banach space of all bounded, real-valued,
$\mathcal{B}(H)$
denote the Banach space of all bounded, real-valued, ![]() $\mathcal{H}$
-measurable functions on H, equipped with the uniform norm
$\mathcal{H}$
-measurable functions on H, equipped with the uniform norm ![]() $\lVert f \rVert \coloneqq \sup_{x \in H} \lvert f(x)\rvert$
. We also endow this space with the Borel
$\lVert f \rVert \coloneqq \sup_{x \in H} \lvert f(x)\rvert$
. We also endow this space with the Borel ![]() $\sigma$
-algebra (with respect to
$\sigma$
-algebra (with respect to ![]() $\lVert \,\cdot\, \rVert$
), and the product spaces
$\lVert \,\cdot\, \rVert$
), and the product spaces ![]() $\mathcal{B}(H) \times \mathcal{B}(H)$
and
$\mathcal{B}(H) \times \mathcal{B}(H)$
and ![]() $\mathcal{B}(H)^d$
for
$\mathcal{B}(H)^d$
for ![]() $d \in \mathbb{N}$
with the associated product
$d \in \mathbb{N}$
with the associated product ![]() $\sigma$
-algebras. We also define the subsets
$\sigma$
-algebras. We also define the subsets ![]() $\mathcal{B}_1(H) \coloneqq \{\,f \in \mathcal{B}(H) \mid \lVert f \rVert \leq 1\}$
. Finally, we let
$\mathcal{B}_1(H) \coloneqq \{\,f \in \mathcal{B}(H) \mid \lVert f \rVert \leq 1\}$
. Finally, we let ![]() $\textbf{1} \in \mathcal{B}(H)$
denote the unit function on H, i.e.
$\textbf{1} \in \mathcal{B}(H)$
denote the unit function on H, i.e. ![]() $\textbf{1} \equiv 1$
.
$\textbf{1} \equiv 1$
.
Let ![]() $\mathcal{M}(H)$
denote the Banach space of all finite and signed measures on
$\mathcal{M}(H)$
denote the Banach space of all finite and signed measures on ![]() $(H, \mathcal{H})$
equipped with the total variation norm
$(H, \mathcal{H})$
equipped with the total variation norm ![]() $\smash{\lVert \mu \rVert \coloneqq \frac{1}{2} \sup_{f \in \mathcal{B}_1(H)} \lvert \mu(\,f) \rvert}$
, where we use the shorthand
$\smash{\lVert \mu \rVert \coloneqq \frac{1}{2} \sup_{f \in \mathcal{B}_1(H)} \lvert \mu(\,f) \rvert}$
, where we use the shorthand ![]() $\smash{\mu(\,f) \coloneqq \int_{H} f(x) \mu(\textrm{d} x)}$
, for any
$\smash{\mu(\,f) \coloneqq \int_{H} f(x) \mu(\textrm{d} x)}$
, for any ![]() $\mu \in \mathcal{M}(H)$
and any
$\mu \in \mathcal{M}(H)$
and any ![]() $f \in \mathcal{B}(H)$
. We define
$f \in \mathcal{B}(H)$
. We define ![]() $\smash{\mathcal{P}(H) \subset \mathcal{M}(H)}$
to be the set of all probability measures on
$\smash{\mathcal{P}(H) \subset \mathcal{M}(H)}$
to be the set of all probability measures on ![]() $(H, \mathcal{H})$
. For any
$(H, \mathcal{H})$
. For any ![]() $\nu \in \mathcal{P}(H)$
, and any
$\nu \in \mathcal{P}(H)$
, and any ![]() $\smash{f, g \in \mathcal{B}(H)}$
, we further define
$\smash{f, g \in \mathcal{B}(H)}$
, we further define ![]() $\smash{{\textrm{cov}}_{\nu}[\,f, g] \coloneqq \nu([\,f - \nu(\,f)][g - \nu(g)])}$
and
$\smash{{\textrm{cov}}_{\nu}[\,f, g] \coloneqq \nu([\,f - \nu(\,f)][g - \nu(g)])}$
and ![]() $\smash{{\textrm{var}}_{\nu}[\,f] \coloneqq {\textrm{cov}}_{\nu}[\,f, f]}$
.
$\smash{{\textrm{var}}_{\nu}[\,f] \coloneqq {\textrm{cov}}_{\nu}[\,f, f]}$
.
Let ![]() $({H^\prime}, {\mathcal{H}^\prime})$
be another measurable space. For any bounded integral operator
$({H^\prime}, {\mathcal{H}^\prime})$
be another measurable space. For any bounded integral operator ![]() $\smash{M\colon \mathcal{B}({H^\prime}) \to \mathcal{B}(H)}$
, defined by
$\smash{M\colon \mathcal{B}({H^\prime}) \to \mathcal{B}(H)}$
, defined by ![]() $\smash{f \mapsto M(\,f)(x) \coloneqq \int_{H^\prime} f(z) M(x, \textrm{d} z)}$
for any
$\smash{f \mapsto M(\,f)(x) \coloneqq \int_{H^\prime} f(z) M(x, \textrm{d} z)}$
for any ![]() $x \in H$
, we define
$x \in H$
, we define ![]() $\smash{[\mu \otimes M](\,f) =\allowbreak \int_{H \times {H^\prime}} \mu(\textrm{d} x) M(x,\textrm{d} y) f(x,y)}$
for any
$\smash{[\mu \otimes M](\,f) =\allowbreak \int_{H \times {H^\prime}} \mu(\textrm{d} x) M(x,\textrm{d} y) f(x,y)}$
for any ![]() $\mu$
in
$\mu$
in ![]() $\mathcal{P}(H)$
and
$\mathcal{P}(H)$
and ![]() $f \in \mathcal{B}(H \times {H^\prime})$
. We also define the operator norm
$f \in \mathcal{B}(H \times {H^\prime})$
. We also define the operator norm ![]() $\smash{\lVert M \rVert \coloneqq\sup_{f \in \mathcal{B}_1({H^\prime})} \lVert M(\,f)\rVert}$
as well as the Dobrushin coefficient:
$\smash{\lVert M \rVert \coloneqq\sup_{f \in \mathcal{B}_1({H^\prime})} \lVert M(\,f)\rVert}$
as well as the Dobrushin coefficient: ![]() $\smash{\beta(M) \coloneqq \sup_{(x,y) \in {H^\prime} \times {H^\prime}} \lVert M(x,\,\cdot\,) - M(y, \,\cdot\,)\rVert}$
.
$\smash{\beta(M) \coloneqq \sup_{(x,y) \in {H^\prime} \times {H^\prime}} \lVert M(x,\,\cdot\,) - M(y, \,\cdot\,)\rVert}$
.
Finally, ‘![]() ${\mathrel{\mathop{\rightarrow}\nolimits_{\text{\upshape{a.s.}}}}}$
’ denotes almost sure convergence with respect to
${\mathrel{\mathop{\rightarrow}\nolimits_{\text{\upshape{a.s.}}}}}$
’ denotes almost sure convergence with respect to ![]() $\mathbb{P}$
and ‘
$\mathbb{P}$
and ‘![]() ${\mathrel{\mathop{\rightarrow}\nolimits_{\text{\upshape{d}}}}}$
’ denotes convergence in distribution.
${\mathrel{\mathop{\rightarrow}\nolimits_{\text{\upshape{d}}}}}$
’ denotes convergence in distribution.
2.2. Path-space Feynman–Kac model
We want to approximate expectations under some distributions which are related to a distribution flow ![]() $(\eta_n)_{n \geq 1}$
on spaces
$(\eta_n)_{n \geq 1}$
on spaces ![]() $(\textbf{E}_n, {\boldsymbol{\mathcal{E}}_{\!{n}}})$
—with
$(\textbf{E}_n, {\boldsymbol{\mathcal{E}}_{\!{n}}})$
—with ![]() $(\textbf{E}_1, {\boldsymbol{\mathcal{E}}_{\!{1}}}) \coloneqq (E, \mathcal{E})$
and
$(\textbf{E}_1, {\boldsymbol{\mathcal{E}}_{\!{1}}}) \coloneqq (E, \mathcal{E})$
and ![]() $(\textbf{E}_n, {\boldsymbol{\mathcal{E}}_{\!{n}}}) \coloneqq (\textbf{E}_{n-1} \times E, {\boldsymbol{\mathcal{E}}_{\!{n-1}}} \otimes \mathcal{E})$
, for
$(\textbf{E}_n, {\boldsymbol{\mathcal{E}}_{\!{n}}}) \coloneqq (\textbf{E}_{n-1} \times E, {\boldsymbol{\mathcal{E}}_{\!{n-1}}} \otimes \mathcal{E})$
, for ![]() $n > 1$
—of increasing dimension, where
$n > 1$
—of increasing dimension, where
for some positive finite measure ![]() $\gamma_n$
on
$\gamma_n$
on ![]() $(\textbf{E}_n, {\boldsymbol{\mathcal{E}}_{\!{n}}})$
and typically unknown normalising constant
$(\textbf{E}_n, {\boldsymbol{\mathcal{E}}_{\!{n}}})$
and typically unknown normalising constant ![]() $\mathcal{Z}_n \coloneqq \gamma_n(\textbf{1})$
. Throughout this work, we write
$\mathcal{Z}_n \coloneqq \gamma_n(\textbf{1})$
. Throughout this work, we write ![]() $\textbf{x}_p \coloneqq x_{1:p} = (\textbf{x}_{p-1}, x_p)$
and
$\textbf{x}_p \coloneqq x_{1:p} = (\textbf{x}_{p-1}, x_p)$
and ![]() $\textbf{z}_p \coloneqq z_{1:p} = (\textbf{z}_{p-1}, z_p)$
.
$\textbf{z}_p \coloneqq z_{1:p} = (\textbf{z}_{p-1}, z_p)$
.
We assume that the target distributions are induced by a Feynman–Kac model on the path space [Reference Del Moral10]. That is, there exist an initial distribution ![]() $M_1 \coloneqq \eta_1 \in \mathcal{P}(\textbf{E}_1)$
, a sequence of Markov transition kernels
$M_1 \coloneqq \eta_1 \in \mathcal{P}(\textbf{E}_1)$
, a sequence of Markov transition kernels ![]() $M_n\colon \textbf{E}_{n-1} \times \mathcal{E} \to [0, 1]$
for
$M_n\colon \textbf{E}_{n-1} \times \mathcal{E} \to [0, 1]$
for ![]() $n>1$
, and a sequence of bounded (without loss of generality we take the bound to be 1) measurable potential functions
$n>1$
, and a sequence of bounded (without loss of generality we take the bound to be 1) measurable potential functions ![]() $G_n\colon \textbf{E}_n \to (0,1]$
for
$G_n\colon \textbf{E}_n \to (0,1]$
for ![]() $n\geq1$
, such that for any
$n\geq1$
, such that for any ![]() $f_n \in \mathcal{B}(\textbf{E}_n)$
,
$f_n \in \mathcal{B}(\textbf{E}_n)$
,
where we have defined the two-parameter semigroup
 \begin{align*} Q_{p,q}(\,f_q)(\textbf{x}_p) \coloneqq \begin{cases} [Q_{p+1} \cdots Q_q](\,f_q)(\textbf{x}_p) & \text{if $p
< q$,}\\[3pt] f_p(\textbf{x}_p) & \text{if $p = q$,} \end{cases}\end{align*}
\begin{align*} Q_{p,q}(\,f_q)(\textbf{x}_p) \coloneqq \begin{cases} [Q_{p+1} \cdots Q_q](\,f_q)(\textbf{x}_p) & \text{if $p
< q$,}\\[3pt] f_p(\textbf{x}_p) & \text{if $p = q$,} \end{cases}\end{align*}
for any ![]() $1 \leq p \leq q \leq n$
, with
$1 \leq p \leq q \leq n$
, with
This implies that ![]() $\gamma_{1} = \eta_1$
and, for
$\gamma_{1} = \eta_1$
and, for ![]() $n > 1$
,
$n > 1$
,
where we have defined the following family of probability measures, indexed by ![]() $\mu \in \mathcal{P}(\textbf{E}_{n-1})$
:
$\mu \in \mathcal{P}(\textbf{E}_{n-1})$
:
 \begin{align*} {\Phi_{n}^{\mu}}(\textrm{d} \textbf{x}_n) & \coloneqq \begin{dcases} M_1(\textrm{d} \textbf{x}_1) = \eta_1(\textrm{d} \textbf{x}_1), & \text{if $n = 1$,}\\[3pt] \frac{G_{n-1}(\textbf{x}_{n-1})}{\mu(G_{n-1})}[\mu \otimes M_n](\textrm{d} \textbf{x}_n) , & \text{if $n > 1$.} \end{dcases}\end{align*}
\begin{align*} {\Phi_{n}^{\mu}}(\textrm{d} \textbf{x}_n) & \coloneqq \begin{dcases} M_1(\textrm{d} \textbf{x}_1) = \eta_1(\textrm{d} \textbf{x}_1), & \text{if $n = 1$,}\\[3pt] \frac{G_{n-1}(\textbf{x}_{n-1})}{\mu(G_{n-1})}[\mu \otimes M_n](\textrm{d} \textbf{x}_n) , & \text{if $n > 1$.} \end{dcases}\end{align*}
We note that ![]() $\smash{{\Phi_{1}^{\mu}}}$
does not actually depend on
$\smash{{\Phi_{1}^{\mu}}}$
does not actually depend on ![]() $\mu$
, but we keep
$\mu$
, but we keep ![]() $\mu$
in the superscript in order to avoid the need to treat the case
$\mu$
in the superscript in order to avoid the need to treat the case ![]() $n=1$
separately.
$n=1$
separately.
For later use, we also define the family of normalised operators
Note that this implies that ![]() $\eta_n(\,f_n) = \eta_p \widebar{Q}_{p,n}(\,f_n)$
for any
$\eta_n(\,f_n) = \eta_p \widebar{Q}_{p,n}(\,f_n)$
for any ![]() $1 \leq p \leq n$
and any
$1 \leq p \leq n$
and any ![]() $f_n \in \mathcal{B}(\textbf{E}_n)$
.
$f_n \in \mathcal{B}(\textbf{E}_n)$
.
2.3. Generic MCMC-PF algorithm
In Algorithm 1, we summarise a generic MCMC-PF scheme for constructing sampling approximations ![]() $\eta_n^N$
of
$\eta_n^N$
of ![]() $\eta_n$
. It admits all the MCMC-PF discussed in this work as special cases. This algorithm is essentially a PF in which the particles are not sampled conditionally independently from
$\eta_n$
. It admits all the MCMC-PF discussed in this work as special cases. This algorithm is essentially a PF in which the particles are not sampled conditionally independently from ![]() ${\Phi_{n}^{\mu}}$
at step n, for some
${\Phi_{n}^{\mu}}$
at step n, for some ![]() $\mu \in \mathcal{P}(\textbf{E}_{n-1})$
, but are instead sampled according to a Markov chain with initial distribution
$\mu \in \mathcal{P}(\textbf{E}_{n-1})$
, but are instead sampled according to a Markov chain with initial distribution ![]() ${\kappa_{n}^{\mu}}\in \mathcal{P}(\textbf{E}_{n})$
and Markov transition kernels
${\kappa_{n}^{\mu}}\in \mathcal{P}(\textbf{E}_{n})$
and Markov transition kernels ![]() ${K_{n}^{\mu}}\colon \textbf{E}_{n} \times {\boldsymbol{\mathcal{E}}_{\!{n}}} \to [0, 1]$
which are invariant with respect to
${K_{n}^{\mu}}\colon \textbf{E}_{n} \times {\boldsymbol{\mathcal{E}}_{\!{n}}} \to [0, 1]$
which are invariant with respect to ![]() ${\Phi_{n}^{\mu}}$
, i.e.
${\Phi_{n}^{\mu}}$
, i.e. ![]() $\smash{{\Phi_{n}^{\mu}} {K_{n}^{\mu}} = {\Phi_{n}^{\mu}}}$
. Recall that
$\smash{{\Phi_{n}^{\mu}} {K_{n}^{\mu}} = {\Phi_{n}^{\mu}}}$
. Recall that ![]() $\smash{{\Phi_{1}^{\mu}}}$
does not actually depend on
$\smash{{\Phi_{1}^{\mu}}}$
does not actually depend on ![]() $\mu$
(and we also assume that the same is true for
$\mu$
(and we also assume that the same is true for ![]() ${\kappa_{1}^{\mu}}$
and
${\kappa_{1}^{\mu}}$
and ![]() ${K_{1}^{\mu}}$
), so that we need not define
${K_{1}^{\mu}}$
), so that we need not define ![]() $\eta_0^N$
.
$\eta_0^N$
.
Algorithm 1. (Generic MCMC-PF.) At time ![]() $n \geq 1$
,
$n \geq 1$
,
(1) sample
 ${\boldsymbol{\xi}_{{n}}^{1}} \sim \smash{{\kappa_{n}^{\eta^{N}_{n-1}}}}$
and
${\boldsymbol{\xi}_{{n}}^{1}} \sim \smash{{\kappa_{n}^{\eta^{N}_{n-1}}}}$
and  ${\boldsymbol{\xi}_{{n}}^{i}} \sim \smash{{K_{n}^{\eta^{N}_{n-1}}}}({\boldsymbol{\xi}_{{n}}^{i-1}}, \,\cdot\,)$
, for
${\boldsymbol{\xi}_{{n}}^{i}} \sim \smash{{K_{n}^{\eta^{N}_{n-1}}}}({\boldsymbol{\xi}_{{n}}^{i-1}}, \,\cdot\,)$
, for  $2 \leq i \leq N$
;
$2 \leq i \leq N$
;(2) set
 $\eta_n^N \coloneqq \frac{1}{N} \sum_{i=1}^N \delta_{{\boldsymbol{\xi}_{{n}}^{i}}}$
.
$\eta_n^N \coloneqq \frac{1}{N} \sum_{i=1}^N \delta_{{\boldsymbol{\xi}_{{n}}^{i}}}$
.
For any time ![]() $n \geq 1$
and for any
$n \geq 1$
and for any ![]() $f_n \in \mathcal{B}(\textbf{E}_n)$
,
$f_n \in \mathcal{B}(\textbf{E}_n)$
, ![]() $\smash{\gamma_n^N(\,f_n) \coloneqq \eta_n^N(\,f_n) \prod_{p=1}^{n-1} \eta_p^N(G_p)}$
is an estimate of
$\smash{\gamma_n^N(\,f_n) \coloneqq \eta_n^N(\,f_n) \prod_{p=1}^{n-1} \eta_p^N(G_p)}$
is an estimate of ![]() $\gamma_n(\,f_n)$
. In particular, an estimate of the normalising constant
$\gamma_n(\,f_n)$
. In particular, an estimate of the normalising constant ![]() $\mathcal{Z}_n$
is
$\mathcal{Z}_n$
is
 \begin{align} \mathcal{Z}_n^N \coloneqq \gamma_n^N(\textbf{1}) = \prod_{p=1}^{n-1} \eta_p^N(G_p) = \prod_{p=1}^{n-1} \frac{1}{N} \sum_{i=1}^N G_p({\boldsymbol{\xi}_{{p}}^{i}}). \end{align}
\begin{align} \mathcal{Z}_n^N \coloneqq \gamma_n^N(\textbf{1}) = \prod_{p=1}^{n-1} \eta_p^N(G_p) = \prod_{p=1}^{n-1} \frac{1}{N} \sum_{i=1}^N G_p({\boldsymbol{\xi}_{{p}}^{i}}). \end{align}
We hereafter write ![]() ${\Phi_{n}^{N}} \coloneqq {\Phi_{n}^{\eta^{N}_{n-1}}}$
,
${\Phi_{n}^{N}} \coloneqq {\Phi_{n}^{\eta^{N}_{n-1}}}$
, ![]() ${\kappa_{n}^{N}} \coloneqq {\kappa_{n}^{\eta^{N}_{n-1}}}$
, and
${\kappa_{n}^{N}} \coloneqq {\kappa_{n}^{\eta^{N}_{n-1}}}$
, and ![]() ${K_{n}^{N}} \coloneqq {K_{n}^{\eta^{N}_{n-1}}}$
to simplify the notation. Note that standard PFs are a special case of Algorithm 1 corresponding to
${K_{n}^{N}} \coloneqq {K_{n}^{\eta^{N}_{n-1}}}$
to simplify the notation. Note that standard PFs are a special case of Algorithm 1 corresponding to ![]() ${K_{n}^{N}}(\textbf{x}_{n}, \,\cdot\,) \equiv {\Phi_{n}^{N}}(\!\cdot\!) = {\kappa_{n}^{N}}(\!\cdot\!)$
. Unfortunately, implementing standard PFs can become prohibitively costly whenever there is no cheap way of generating N independent and identically distributed (IID) samples from
${K_{n}^{N}}(\textbf{x}_{n}, \,\cdot\,) \equiv {\Phi_{n}^{N}}(\!\cdot\!) = {\kappa_{n}^{N}}(\!\cdot\!)$
. Unfortunately, implementing standard PFs can become prohibitively costly whenever there is no cheap way of generating N independent and identically distributed (IID) samples from ![]() ${\Phi_{n}^{N}}$
—which can be the case when
${\Phi_{n}^{N}}$
—which can be the case when ![]() ${\Phi_{n}^{N}}$
is chosen for reasons of statistical efficiency rather than computational convenience, as in the case of the FA-APF of [Reference Pitt and Shephard29]. In contrast, Algorithm 1 only requires the construction of MCMC kernels which leave this distribution invariant.
${\Phi_{n}^{N}}$
is chosen for reasons of statistical efficiency rather than computational convenience, as in the case of the FA-APF of [Reference Pitt and Shephard29]. In contrast, Algorithm 1 only requires the construction of MCMC kernels which leave this distribution invariant.
Practitioners typically initialise the Markov chains close to stationarity by selecting ![]() ${\kappa_{n}^{N}}=[\eta_{n-1}^N \otimes M^{\prime}_n] ({K_{n}^{N}})^{N_{\textrm{burnin}} }$
for some approximation
${\kappa_{n}^{N}}=[\eta_{n-1}^N \otimes M^{\prime}_n] ({K_{n}^{N}})^{N_{\textrm{burnin}} }$
for some approximation ![]() $M^{\prime}_n(\textbf{x}_{n-1}, \textrm{d} x_n)$
of
$M^{\prime}_n(\textbf{x}_{n-1}, \textrm{d} x_n)$
of ![]() $M_n(\textbf{x}_{n-1}, \textrm{d} x_n)$
(see, e.g., [Reference Carmi, Septier and Godsill8], [Reference Golightly and Wilkinson15] ,[Reference Septier, Pang, Carmi and Godsill31], [Reference Septier and Peters32]). Here,
$M_n(\textbf{x}_{n-1}, \textrm{d} x_n)$
(see, e.g., [Reference Carmi, Septier and Godsill8], [Reference Golightly and Wilkinson15] ,[Reference Septier, Pang, Carmi and Godsill31], [Reference Septier and Peters32]). Here, ![]() $N_{\textrm{burnin}} \geq 1$
denotes a suitably large number of iterations whose samples are discarded as ‘burn-in’. Corollary 1, below, will demonstrate that, under regularity conditions, such algorithms can provide strongly consistent estimates of quantities of interest in spite of this out-of-equilibrium initialisation.
$N_{\textrm{burnin}} \geq 1$
denotes a suitably large number of iterations whose samples are discarded as ‘burn-in’. Corollary 1, below, will demonstrate that, under regularity conditions, such algorithms can provide strongly consistent estimates of quantities of interest in spite of this out-of-equilibrium initialisation.
In situations in which it is possible to initialise the Markov chains at stationarity, i.e. in which we can initialise ![]() $\smash{{\boldsymbol{\xi}_{{n}}^{1}} \sim {\kappa_{n}^{N}}={\Phi_{n}^{N}}}$
, [Reference Finke, Doucet and Johansen14] showed that the estimator
$\smash{{\boldsymbol{\xi}_{{n}}^{1}} \sim {\kappa_{n}^{N}}={\Phi_{n}^{N}}}$
, [Reference Finke, Doucet and Johansen14] showed that the estimator ![]() $\mathcal{Z}_n^N$
given in (2) is unbiased as for standard PFs [Reference Del Moral10]. This unbiasedness property permits—in principle—the use of MCMC-PFs within pseudo-marginal algorithms [Reference Andrieu and Roberts3], and thus makes it possible to perform Bayesian parameter inference for state-space models. As such an initialisation only requires one draw from
$\mathcal{Z}_n^N$
given in (2) is unbiased as for standard PFs [Reference Del Moral10]. This unbiasedness property permits—in principle—the use of MCMC-PFs within pseudo-marginal algorithms [Reference Andrieu and Roberts3], and thus makes it possible to perform Bayesian parameter inference for state-space models. As such an initialisation only requires one draw from ![]() $\smash{{\Phi_{n}^{N}}}$
, the use of relatively expensive methods, such as rejection sampling, may be justifiable. This is in contrast to standard PFs, which require N such draws, the cost of which may be prohibitive. However, as we discuss below in Subsections 2.5 and 4.2, the main advantage of MCMC-PFs over standard PFs is that the former can sometimes be implemented in scenarios in which the potential functions
$\smash{{\Phi_{n}^{N}}}$
, the use of relatively expensive methods, such as rejection sampling, may be justifiable. This is in contrast to standard PFs, which require N such draws, the cost of which may be prohibitive. However, as we discuss below in Subsections 2.5 and 4.2, the main advantage of MCMC-PFs over standard PFs is that the former can sometimes be implemented in scenarios in which the potential functions ![]() $G_n$
cannot be evaluated and then the estimate
$G_n$
cannot be evaluated and then the estimate ![]() $\smash{\mathcal{Z}_n^N}$
from (2) cannot be evaluated either.
$\smash{\mathcal{Z}_n^N}$
from (2) cannot be evaluated either.
Furthermore, the conditional SMC scheme proposed in [Reference Andrieu, Doucet and Holenstein1] can also be extended to MCMC-PFs as demonstrated in [Reference Shestopaloff and Neal33]. As discussed in [Reference Finke, Doucet and Johansen14], the resulting ‘conditional’ MCMC-PF can be used within the particle Gibbs sampler from [Reference Andrieu and Roberts3]. Importantly, it requires neither the construction of a suitable initial distribution ![]() $\smash{{\kappa_{n}^{N}}}$
nor the ability to evaluate the potential functions
$\smash{{\kappa_{n}^{N}}}$
nor the ability to evaluate the potential functions ![]() $G_n$
.
$G_n$
.
The literature on MCMC algorithms provides numerous ways in which to construct the Markov kernels ![]() ${K_{n}^{\mu}}$
. For instance, we could use Metropolis–Hastings (MH) [Reference Berzuini, Best, Gilks and Larizza6], the Metropolis-adjusted Langevin algorithm, Hamiltonian Monte Carlo and hybrid kernels [Reference Septier, Pang, Carmi and Godsill31], [Reference Septier and Peters32], or kernels based on invertible particle flow ideas [Reference Li and Coates22] or on the bouncy particle sampler [Reference Pal and Coates28]. As an illustration, Example 1 describes a simple independent MH kernel with a proposal distribution tailored to our setting.
${K_{n}^{\mu}}$
. For instance, we could use Metropolis–Hastings (MH) [Reference Berzuini, Best, Gilks and Larizza6], the Metropolis-adjusted Langevin algorithm, Hamiltonian Monte Carlo and hybrid kernels [Reference Septier, Pang, Carmi and Godsill31], [Reference Septier and Peters32], or kernels based on invertible particle flow ideas [Reference Li and Coates22] or on the bouncy particle sampler [Reference Pal and Coates28]. As an illustration, Example 1 describes a simple independent MH kernel with a proposal distribution tailored to our setting.
Example 1. (Independent MH.) For any ![]() $n \geq 1$
and any
$n \geq 1$
and any ![]() $\mu \in \mathcal{P}(\textbf{E}_{n-1})$
, define the proposal distribution
$\mu \in \mathcal{P}(\textbf{E}_{n-1})$
, define the proposal distribution
 \begin{align*} {\Pi_{n}^{\mu}}(\textrm{d} \textbf{x}_n) & \coloneqq \begin{dcases} R_1(\textrm{d} \textbf{x}_1) & \text{if $n = 1$,}\\[3pt] \frac{F_{n-1}(\textbf{x}_{n-1})}{\mu(F_{n-1})}[\mu \otimes R_n](\textrm{d} \textbf{x}_n) & \text{if $n > 1$,} \end{dcases}\end{align*}
\begin{align*} {\Pi_{n}^{\mu}}(\textrm{d} \textbf{x}_n) & \coloneqq \begin{dcases} R_1(\textrm{d} \textbf{x}_1) & \text{if $n = 1$,}\\[3pt] \frac{F_{n-1}(\textbf{x}_{n-1})}{\mu(F_{n-1})}[\mu \otimes R_n](\textrm{d} \textbf{x}_n) & \text{if $n > 1$,} \end{dcases}\end{align*}
for some sequence of nonnegative bounded measurable functions ![]() $F_n\colon \textbf{E}_n \to [0,\infty)$
, some distribution
$F_n\colon \textbf{E}_n \to [0,\infty)$
, some distribution ![]() $R_1 \in \mathcal{P}(\textbf{E}_1)$
with
$R_1 \in \mathcal{P}(\textbf{E}_1)$
with ![]() $M_1 \ll R_1$
, and some sequence of Markov transition kernels
$M_1 \ll R_1$
, and some sequence of Markov transition kernels ![]() $R_n\colon \textbf{E}_{n-1} \times \mathcal{E} \to [0, 1]$
with
$R_n\colon \textbf{E}_{n-1} \times \mathcal{E} \to [0, 1]$
with ![]() $M_n(\textbf{x}_{n-1}, \,\cdot\,) \ll R_n(\textbf{x}_{n-1}, \,\cdot\,)$
, for any
$M_n(\textbf{x}_{n-1}, \,\cdot\,) \ll R_n(\textbf{x}_{n-1}, \,\cdot\,)$
, for any ![]() $\textbf{x}_{n-1} \in \textbf{E}_{n-1}$
; for any
$\textbf{x}_{n-1} \in \textbf{E}_{n-1}$
; for any ![]() $n \geq 1$
, both
$n \geq 1$
, both ![]() $F_{n-1}$
and
$F_{n-1}$
and ![]() $R_n$
are assumed to satisfy
$R_n$
are assumed to satisfy
The independent MH kernel ![]() ${K_{n}^{\mu}}$
with proposal distribution
${K_{n}^{\mu}}$
with proposal distribution ![]() ${\Pi_{n}^{\mu}}$
and target/invariant distribution
${\Pi_{n}^{\mu}}$
and target/invariant distribution ![]() ${\Phi_{n}^{\mu}}$
is given by
${\Phi_{n}^{\mu}}$
is given by
 \begin{align*} {K_{n}^{\mu}}(\textbf{x}_n, \textrm{d} \textbf{z}_n) & \coloneqq \alpha_n(\textbf{x}_n, \textbf{z}_n) {\Pi_{n}^{\mu}}(\textrm{d} \textbf{z}_n)\\[3pt] & \quad + \biggl(1 - \int_{\textbf{E}_n}\alpha_n(\textbf{x}_n, \textrm{d} \textbf{x}^{\prime}_n) {\Pi_{n}^{\mu}}(\textrm{d} \textbf{x}^{\prime}_n)\biggr) \delta_{\textbf{x}_n}(\textrm{d} \textbf{z}_n), \end{align*}
\begin{align*} {K_{n}^{\mu}}(\textbf{x}_n, \textrm{d} \textbf{z}_n) & \coloneqq \alpha_n(\textbf{x}_n, \textbf{z}_n) {\Pi_{n}^{\mu}}(\textrm{d} \textbf{z}_n)\\[3pt] & \quad + \biggl(1 - \int_{\textbf{E}_n}\alpha_n(\textbf{x}_n, \textrm{d} \textbf{x}^{\prime}_n) {\Pi_{n}^{\mu}}(\textrm{d} \textbf{x}^{\prime}_n)\biggr) \delta_{\textbf{x}_n}(\textrm{d} \textbf{z}_n), \end{align*}
with acceptance probability
 \begin{align} \alpha_n(\textbf{x}_n, \textbf{z}_n) & \coloneqq 1 \wedge \dfrac{\textrm{d} {\Phi_{n}^{\mu}}}{\textrm{d} {\Pi_{n}^{\mu}}}(\textbf{z}_n) \bigg/ \dfrac{\textrm{d} {\Phi_{n}^{\mu}}}{\textrm{d} {\Pi_{n}^{\mu}}}(\textbf{x}_n)\nonumber\\[4pt]
& = 1 \wedge \dfrac{\dfrac{G_{n-1}}{F_{n-1}}(\textbf{z}_{n-1})}{\dfrac{G_{n-1}}{F_{n-1}}(\textbf{x}_{n-1})} \dfrac{\dfrac{\textrm{d} M_n(\textbf{z}_{n-1}, \,\cdot\,)}{\textrm{d} R_n(\textbf{z}_{n-1}, \,\cdot\,)}(z_n)}{\dfrac{\textrm{d} M_n(\textbf{x}_{n-1}, \,\cdot\,)}{\textrm{d} R_n(\textbf{x}_{n-1}, \,\cdot\,)}(x_n)}. \end{align}
\begin{align} \alpha_n(\textbf{x}_n, \textbf{z}_n) & \coloneqq 1 \wedge \dfrac{\textrm{d} {\Phi_{n}^{\mu}}}{\textrm{d} {\Pi_{n}^{\mu}}}(\textbf{z}_n) \bigg/ \dfrac{\textrm{d} {\Phi_{n}^{\mu}}}{\textrm{d} {\Pi_{n}^{\mu}}}(\textbf{x}_n)\nonumber\\[4pt]
& = 1 \wedge \dfrac{\dfrac{G_{n-1}}{F_{n-1}}(\textbf{z}_{n-1})}{\dfrac{G_{n-1}}{F_{n-1}}(\textbf{x}_{n-1})} \dfrac{\dfrac{\textrm{d} M_n(\textbf{z}_{n-1}, \,\cdot\,)}{\textrm{d} R_n(\textbf{z}_{n-1}, \,\cdot\,)}(z_n)}{\dfrac{\textrm{d} M_n(\textbf{x}_{n-1}, \,\cdot\,)}{\textrm{d} R_n(\textbf{x}_{n-1}, \,\cdot\,)}(x_n)}. \end{align}
This acceptance probability notably does not depend on ![]() $\mu$
.
$\mu$
.
2.4. Computational cost
If we are interested only in approximating the normalising constant ![]() $\mathcal{Z}_n$
, and if
$\mathcal{Z}_n$
, and if ![]() $G_{n-1}(\textbf{x}_{n-1})$
and
$G_{n-1}(\textbf{x}_{n-1})$
and ![]() $M_n(\textbf{x}_{n-1}, \,\cdot\,)$
depend upon only a fixed number of the most recent component(s) of
$M_n(\textbf{x}_{n-1}, \,\cdot\,)$
depend upon only a fixed number of the most recent component(s) of ![]() $\textbf{x}_{n-1}$
(as is the case in the state-space models discussed below), Algorithm 1 can be implemented at a per-time-step complexity (in both space and time) that is linear in the number of particles N and constant in the time horizon n.
$\textbf{x}_{n-1}$
(as is the case in the state-space models discussed below), Algorithm 1 can be implemented at a per-time-step complexity (in both space and time) that is linear in the number of particles N and constant in the time horizon n.
2.5. Application to state-space models
Let ![]() $(F, \mathcal{F})$
be another measurable space. The MCMC-PF may be used for (but is not limited to) performing inference in a state-space model given by the bivariate Markov chain
$(F, \mathcal{F})$
be another measurable space. The MCMC-PF may be used for (but is not limited to) performing inference in a state-space model given by the bivariate Markov chain ![]() $(X_n, Y_n)_{n \geq 1}$
on
$(X_n, Y_n)_{n \geq 1}$
on ![]() $(E \times F, \mathcal{E} \vee \mathcal{F})$
with initial distribution
$(E \times F, \mathcal{E} \vee \mathcal{F})$
with initial distribution ![]() $L_1(\textrm{d} x_1) g_1(x_1, y_1)\psi(\textrm{d} y_1)$
and with Markov transition kernels (for any
$L_1(\textrm{d} x_1) g_1(x_1, y_1)\psi(\textrm{d} y_1)$
and with Markov transition kernels (for any ![]() $n > 1$
)
$n > 1$
)
Here, ![]() $L_1 \in \mathcal{P}(E)$
is some initial distribution for
$L_1 \in \mathcal{P}(E)$
is some initial distribution for ![]() $X_1$
, and
$X_1$
, and ![]() $L_{n} \,:\, E \times \mathcal{E} \to [0, 1]$
, for
$L_{n} \,:\, E \times \mathcal{E} \to [0, 1]$
, for ![]() $n > 1$
, is a Markov transition kernel. Furthermore,
$n > 1$
, is a Markov transition kernel. Furthermore, ![]() $\psi$
is some suitable
$\psi$
is some suitable ![]() $\sigma$
-finite dominating measure on
$\sigma$
-finite dominating measure on ![]() $(F, \mathcal{F})$
and some positive bounded function
$(F, \mathcal{F})$
and some positive bounded function ![]() $g_n(\,\cdot\,, y_n)$
so that
$g_n(\,\cdot\,, y_n)$
so that ![]() $g_n(x_n, y_n) \psi(\textrm{d} y_n)$
represents the transition kernels for the observation at time n. Usually, we can only observe realisations of
$g_n(x_n, y_n) \psi(\textrm{d} y_n)$
represents the transition kernels for the observation at time n. Usually, we can only observe realisations of ![]() $(Y_n)_{n \geq 1}$
, whereas the process
$(Y_n)_{n \geq 1}$
, whereas the process ![]() $(X_n)_{n \geq 1}$
is latent.
$(X_n)_{n \geq 1}$
is latent.
Assume that we have observed realisations ![]() $\textbf{y}_n = (y_1, \dotsc, y_n)$
of
$\textbf{y}_n = (y_1, \dotsc, y_n)$
of ![]() $\textbf{Y}_n \coloneqq (Y_1, \dotsc, Y_n)$
; then we often wish to compute (expectations under) the
$\textbf{Y}_n \coloneqq (Y_1, \dotsc, Y_n)$
; then we often wish to compute (expectations under) the
• filter:
 $\pi_n(\,f_n) \coloneqq \mathbb{E}[\,f_n(\textbf{X}_n)|\textbf{Y}_n = \textbf{y}_n]$
, for
$\pi_n(\,f_n) \coloneqq \mathbb{E}[\,f_n(\textbf{X}_n)|\textbf{Y}_n = \textbf{y}_n]$
, for  $f_n \in \mathcal{B}(\textbf{E}_n)$
;
$f_n \in \mathcal{B}(\textbf{E}_n)$
;• predictor:
 $\tilde{\pi}_n(\,f_n) \coloneqq \mathbb{E}[\,f_n(\textbf{X}_n)|\textbf{Y}_{n-1} = \textbf{y}_{n-1}]$
, for
$\tilde{\pi}_n(\,f_n) \coloneqq \mathbb{E}[\,f_n(\textbf{X}_n)|\textbf{Y}_{n-1} = \textbf{y}_{n-1}]$
, for  $f_n \in \mathcal{B}(\textbf{E}_n)$
;
$f_n \in \mathcal{B}(\textbf{E}_n)$
;• marginal likelihood:
 $\mathcal{L}_n \coloneqq \mathbb{E}[\prod_{p=1}^{n} g_p(X_p, y_p)]$
.
$\mathcal{L}_n \coloneqq \mathbb{E}[\prod_{p=1}^{n} g_p(X_p, y_p)]$
.
Note that the definitions of ‘filter’ and ‘predictor’ here refer to the historical process, as we are taking a path-space approach. These terms are sometimes reserved for the final-component marginals of ![]() $\pi_n$
and
$\pi_n$
and ![]() $\tilde{\pi}_n$
; we will use the terms marginal filter and marginal predictor for those objects.
$\tilde{\pi}_n$
; we will use the terms marginal filter and marginal predictor for those objects.
Example 2. (BPF-type flow.) If, for any ![]() $n \geq 1$
,
$n \geq 1$
,
then ![]() $\eta_n = \tilde{\pi}_n$
is the time-n predictor,
$\eta_n = \tilde{\pi}_n$
is the time-n predictor, ![]() $\eta_n(G_nf_n)/\eta_n(G_n) = \pi_n(\,f_n)$
recovers the time-n filter, and
$\eta_n(G_nf_n)/\eta_n(G_n) = \pi_n(\,f_n)$
recovers the time-n filter, and ![]() $\mathcal{Z}_{n+1} = \mathcal{L}_{n}$
is the marginal likelihood associated with the observations
$\mathcal{Z}_{n+1} = \mathcal{L}_{n}$
is the marginal likelihood associated with the observations ![]() $\textbf{y}_{n}$
(with
$\textbf{y}_{n}$
(with ![]() $\mathcal{Z}_1 = 1$
).
$\mathcal{Z}_1 = 1$
).
In this case, Algorithm 1 can be implemented (e.g. using the independent MH kernel from Example 1) as long as ![]() $g_n$
,
$g_n$
, ![]() $F_{n}$
, and
$F_{n}$
, and ![]() $\textrm{d} L_{n}(x_{n-1}, \,\cdot\,) / \textrm{d} R_n(\textbf{x}_{n-1},\,\cdot\,)$
can be evaluated pointwise.
$\textrm{d} L_{n}(x_{n-1}, \,\cdot\,) / \textrm{d} R_n(\textbf{x}_{n-1},\,\cdot\,)$
can be evaluated pointwise.
Example 3. (FA-APF-type flow.) If, for any ![]() $n \geq 1$
,
$n \geq 1$
,
then ![]() $\eta_n = \pi_n$
is the time-n filter,
$\eta_n = \pi_n$
is the time-n filter, ![]() $\eta_{n-1}\otimes L_n = \tilde{\pi}_n$
recovers the time-n predictor, and
$\eta_{n-1}\otimes L_n = \tilde{\pi}_n$
recovers the time-n predictor, and ![]() $\mathcal{Z}_n = \mathcal{L}_{n}$
is the marginal likelihood associated with the observations
$\mathcal{Z}_n = \mathcal{L}_{n}$
is the marginal likelihood associated with the observations ![]() $\textbf{y}_{n}$
.
$\textbf{y}_{n}$
.
For this flow, it follows from (1) that sampling ![]() ${\boldsymbol{\xi}_{{n}}^{i}}$
from
${\boldsymbol{\xi}_{{n}}^{i}}$
from ![]() ${\Phi_{n}^{N}}$
requires first sampling an index
${\Phi_{n}^{N}}$
requires first sampling an index ![]() $J = j \in \{1,...,N\}$
with probability proportional to
$J = j \in \{1,...,N\}$
with probability proportional to ![]() $G_{n-1}({\boldsymbol{\xi}_{{n-1}}^{j}})$
, setting the first
$G_{n-1}({\boldsymbol{\xi}_{{n-1}}^{j}})$
, setting the first ![]() $n-1$
components of
$n-1$
components of ![]() $\smash{{\boldsymbol{\xi}_{{n}}^{i}}}$
equal to
$\smash{{\boldsymbol{\xi}_{{n}}^{i}}}$
equal to ![]() $\smash{{\boldsymbol{\xi}_{{n-1}}^{j}}}$
, and then sampling the final component according to
$\smash{{\boldsymbol{\xi}_{{n-1}}^{j}}}$
, and then sampling the final component according to ![]() $\smash{M_{n}({\boldsymbol{\xi}_{{n-1}}^{j}}, \,\cdot\,)}$
. There are many scenarios in which this is not feasible as both (6) and (7) involve an intractable integral. However, designing an MCMC kernel of invariant distribution
$\smash{M_{n}({\boldsymbol{\xi}_{{n-1}}^{j}}, \,\cdot\,)}$
. There are many scenarios in which this is not feasible as both (6) and (7) involve an intractable integral. However, designing an MCMC kernel of invariant distribution ![]() ${\Phi_{n}^{N}}$
is a much easier task, as the product
${\Phi_{n}^{N}}$
is a much easier task, as the product ![]() $G_{n-1}(\textbf{x}_{n-1})M_{n}(\textbf{x}_{n-1}, \textrm{d} x_{n})$
does not involve any intractable integral. For example, if we use the independent MH kernel from Example 1 then the acceptance probability in (4) reduces to the following (for simplicity, we take
$G_{n-1}(\textbf{x}_{n-1})M_{n}(\textbf{x}_{n-1}, \textrm{d} x_{n})$
does not involve any intractable integral. For example, if we use the independent MH kernel from Example 1 then the acceptance probability in (4) reduces to the following (for simplicity, we take ![]() $F_{n-1} \equiv 1$
):
$F_{n-1} \equiv 1$
):
 \begin{align*} \alpha_n(\textbf{x}_n, \textbf{z}_n) & = 1 \wedge \dfrac{g_{n}(z_n, y_n)}{g_{n}(x_{n}, y_n)} \dfrac{\dfrac{\textrm{d} L_n(z_{n-1}, \,\cdot\,)}{\textrm{d} R_n(\textbf{z}_{n-1}, \,\cdot\,)}(z_n)}{\dfrac{\textrm{d} L_n(x_{n-1}, \,\cdot\,)}{\textrm{d} R_n(\textbf{x}_{n-1}, \,\cdot\,)}(x_n)}. \end{align*}
\begin{align*} \alpha_n(\textbf{x}_n, \textbf{z}_n) & = 1 \wedge \dfrac{g_{n}(z_n, y_n)}{g_{n}(x_{n}, y_n)} \dfrac{\dfrac{\textrm{d} L_n(z_{n-1}, \,\cdot\,)}{\textrm{d} R_n(\textbf{z}_{n-1}, \,\cdot\,)}(z_n)}{\dfrac{\textrm{d} L_n(x_{n-1}, \,\cdot\,)}{\textrm{d} R_n(\textbf{x}_{n-1}, \,\cdot\,)}(x_n)}. \end{align*}
Example 4. (General auxiliary particle filter (APF)-type flow.) Let ![]() $\eta_1$
be some approximation of
$\eta_1$
be some approximation of ![]() $\pi_1$
. For
$\pi_1$
. For ![]() $n \geq 1$
, let
$n \geq 1$
, let ![]() $M_{n+1}(\textbf{x}_{n}, \textrm{d} x_{n+1})$
be some approximation of (7), and let
$M_{n+1}(\textbf{x}_{n}, \textrm{d} x_{n+1})$
be some approximation of (7), and let
 \begin{align*} G_n(\textbf{x}_n) &\coloneqq \begin{dcases} \frac{\textrm{d} L_1}{\textrm{d} \eta_1}(x_1) g_1(x_1, y_1) \tilde{g}_1(x_1, y_2) & \text{if $n = 1$,}\\[3pt] \frac{\textrm{d} L_n(x_{n-1}, \,\cdot\,)}{\textrm{d} M_n(\textbf{x}_{n-1}, \,\cdot\,)}(x_n) \frac{g_n(x_n, y_n) \tilde{g}_n(x_n, y_{n+1})}{\tilde{g}_{n-1}(x_{n-1}, y_n)} & \text{if $n > 1$.} \end{dcases} \end{align*}
\begin{align*} G_n(\textbf{x}_n) &\coloneqq \begin{dcases} \frac{\textrm{d} L_1}{\textrm{d} \eta_1}(x_1) g_1(x_1, y_1) \tilde{g}_1(x_1, y_2) & \text{if $n = 1$,}\\[3pt] \frac{\textrm{d} L_n(x_{n-1}, \,\cdot\,)}{\textrm{d} M_n(\textbf{x}_{n-1}, \,\cdot\,)}(x_n) \frac{g_n(x_n, y_n) \tilde{g}_n(x_n, y_{n+1})}{\tilde{g}_{n-1}(x_{n-1}, y_n)} & \text{if $n > 1$.} \end{dcases} \end{align*}
Here, ![]() $\tilde{g}_n(x_n, y_{n+1})$
denotes some tractable approximation of (6) which can be evaluated pointwise. More generally, we could incorporate information from observations at times
$\tilde{g}_n(x_n, y_{n+1})$
denotes some tractable approximation of (6) which can be evaluated pointwise. More generally, we could incorporate information from observations at times ![]() $n+1,\dotsc,n+l$
for some
$n+1,\dotsc,n+l$
for some ![]() $l \geq 1$
into
$l \geq 1$
into ![]() $M_{n+1}(\textbf{x}_{n}, \textrm{d} x_{n+1})$
and replace
$M_{n+1}(\textbf{x}_{n}, \textrm{d} x_{n+1})$
and replace ![]() $\tilde{g}_n(x_n, y_{n+1})$
by some approximation of
$\tilde{g}_n(x_n, y_{n+1})$
by some approximation of ![]() $\smash{\int_{E^l} \prod_{p=n+1}^{n+l} L_{p}(\textbf{x}_{p-1}, \textrm{d} x_p) g_p(x_p, y_p)}$
, as in the case of lookahead methods (see [Reference Lin, Chen and Liu23], for example).
$\smash{\int_{E^l} \prod_{p=n+1}^{n+l} L_{p}(\textbf{x}_{p-1}, \textrm{d} x_p) g_p(x_p, y_p)}$
, as in the case of lookahead methods (see [Reference Lin, Chen and Liu23], for example).
Note that the (general) APF flow admits the two other flows as special cases. That is, taking ![]() $M_n$
as in (5) and
$M_n$
as in (5) and ![]() $\tilde{g}_n \equiv 1$
yields the BPF-type flow; taking
$\tilde{g}_n \equiv 1$
yields the BPF-type flow; taking ![]() $M_n$
as in (7) and
$M_n$
as in (7) and ![]() $\tilde{g}_n(x_n, y_{n+1}) = L_{n+1}(g_{n+1}(\,\cdot\,, y_{n+1}))(x_n)$
yields the FA-APF-type flow.
$\tilde{g}_n(x_n, y_{n+1}) = L_{n+1}(g_{n+1}(\,\cdot\,, y_{n+1}))(x_n)$
yields the FA-APF-type flow.
In the remainder of this work, we will refer to Algorithm 1 as the MCMC bootstrap particle filter (MCMC-BPF) whenever the distribution flow ![]() $(\eta_n)_{n \geq 1}$
is defined as in Example 2, as the MCMC fully-adapted auxiliary particle filter (MCMC-FA-APF) whenever the flow is defined as in Example 3, and as MCMC auxiliary particle filters (MCMC-APF) whenever the flow is defined as in Example 4. Furthermore, we drop the prefix ‘MCMC’ when referring to the conventional PF-analogues of these algorithms, i.e. in the case that
$(\eta_n)_{n \geq 1}$
is defined as in Example 2, as the MCMC fully-adapted auxiliary particle filter (MCMC-FA-APF) whenever the flow is defined as in Example 3, and as MCMC auxiliary particle filters (MCMC-APF) whenever the flow is defined as in Example 4. Furthermore, we drop the prefix ‘MCMC’ when referring to the conventional PF-analogues of these algorithms, i.e. in the case that ![]() $\smash{{K_{n}^{\mu}}(\textbf{x}_n,\,\cdot\,) \equiv {\Phi_{n}^{\mu}} = {\kappa_{n}^{\mu}}}$
.
$\smash{{K_{n}^{\mu}}(\textbf{x}_n,\,\cdot\,) \equiv {\Phi_{n}^{\mu}} = {\kappa_{n}^{\mu}}}$
.
3. Main results
In this section, we state an ![]() $\mathbb{L}_r$
-inequality (Proposition 1)—which also implies a strong law of large numbers (SLLN) (Corollary 1)—and a central limit theorem (CLT) (Proposition 2) for the approximations of the normalised and unnormalised flows
$\mathbb{L}_r$
-inequality (Proposition 1)—which also implies a strong law of large numbers (SLLN) (Corollary 1)—and a central limit theorem (CLT) (Proposition 2) for the approximations of the normalised and unnormalised flows ![]() $(\eta_n)_{n \geq 1}$
and
$(\eta_n)_{n \geq 1}$
and ![]() $(\gamma_n)_{n \geq 1}$
generated by an MCMC-PF.
$(\gamma_n)_{n \geq 1}$
generated by an MCMC-PF.
3.1. Assumptions
We make the following assumptions about the MCMC kernels used to sample the particles at each time step.
(A1) For any
 $n \geq 1$
, there exists
$n \geq 1$
, there exists  $i_n \in \mathbb{N}$
and
$i_n \in \mathbb{N}$
and  $\varepsilon_n(K) \in (0,1]$
such that for all
$\varepsilon_n(K) \in (0,1]$
such that for all  $\mu \in \mathcal{P}(\textbf{E}_{n-1})$
and all
$\mu \in \mathcal{P}(\textbf{E}_{n-1})$
and all  $\textbf{x}_n, \textbf{z}_n \in \textbf{E}_n$
,
$\textbf{x}_n, \textbf{z}_n \in \textbf{E}_n$
,
 \begin{align*} ({K_{n}^{\mu}})^{i_n}(\textbf{x}_n, \,\cdot\,) \geq \varepsilon_n(K) ({K_{n}^{\mu}})^{i_n}(\textbf{z}_n, \,\cdot\,). \end{align*}
\begin{align*} ({K_{n}^{\mu}})^{i_n}(\textbf{x}_n, \,\cdot\,) \geq \varepsilon_n(K) ({K_{n}^{\mu}})^{i_n}(\textbf{z}_n, \,\cdot\,). \end{align*}
(A2) For any
 $n\geq 1$
, there exists a constant
$n\geq 1$
, there exists a constant  ${\widebar{\varGamma}_{n}} < \infty$
and a family of bounded integral operators
${\widebar{\varGamma}_{n}} < \infty$
and a family of bounded integral operators  $({\varGamma_{n}^{\mu}})_{\mu \in \mathcal{P}(\textbf{E}_{n-1})}$
from
$({\varGamma_{n}^{\mu}})_{\mu \in \mathcal{P}(\textbf{E}_{n-1})}$
from  $\mathcal{B}(\textbf{E}_n)$
to
$\mathcal{B}(\textbf{E}_n)$
to  $\mathcal{B}(\textbf{E}_{n-1})$
such that for any
$\mathcal{B}(\textbf{E}_{n-1})$
such that for any  $(\nu, \mu) \in \mathcal{P}(\textbf{E}_{n-1})^2$
and any
$(\nu, \mu) \in \mathcal{P}(\textbf{E}_{n-1})^2$
and any  $f_n \in \mathcal{B}(\textbf{E}_n)$
,
and
$f_n \in \mathcal{B}(\textbf{E}_n)$
,
and \begin{align*} \lVert [{K_{n}^{\nu}} - {K_{n}^{\mu}}](\,f_n) \rVert &\leq \int_{\mathcal{B}(\textbf{E}_{n-1})} \lvert [\nu - \mu](g) \rvert {\varGamma_{n}^{\mu}}(\,f_n, \textrm{d} g) \end{align*}
\begin{align*} \lVert [{K_{n}^{\nu}} - {K_{n}^{\mu}}](\,f_n) \rVert &\leq \int_{\mathcal{B}(\textbf{E}_{n-1})} \lvert [\nu - \mu](g) \rvert {\varGamma_{n}^{\mu}}(\,f_n, \textrm{d} g) \end{align*}
 \begin{align*} \int_{\mathcal{B}(\textbf{E}_{n-1})} \lVert g \rVert {\varGamma_{n}^{\mu}}(\,f_n, \textrm{d} g) \leq \lVert f_n \rVert {\widebar{\varGamma}_{n}}. \end{align*}
\begin{align*} \int_{\mathcal{B}(\textbf{E}_{n-1})} \lVert g \rVert {\varGamma_{n}^{\mu}}(\,f_n, \textrm{d} g) \leq \lVert f_n \rVert {\widebar{\varGamma}_{n}}. \end{align*}
The first assumption on the MCMC kernels ensures that they are suitably ergodic (it corresponds to assuming that the kernels used are uniformly ergodic, uniformly in their invariant distribution) and is the only assumption required to obtain the ![]() $\mathbb{L}_r$
-inequality and the SLLN. More precisely, recall that for any bounded integral operator
$\mathbb{L}_r$
-inequality and the SLLN. More precisely, recall that for any bounded integral operator ![]() $M\colon \mathcal{B}(H) \to \mathcal{B}(H)$
, the associated Dobrushin coefficient is given by
$M\colon \mathcal{B}(H) \to \mathcal{B}(H)$
, the associated Dobrushin coefficient is given by ![]() $\beta(M) \coloneqq \sup_{(x,y) \in H \times H} \lVert M(x,\,\cdot\,) - M(y, \,\cdot\,)\rVert$
. Note that Assumption A1 implies that
$\beta(M) \coloneqq \sup_{(x,y) \in H \times H} \lVert M(x,\,\cdot\,) - M(y, \,\cdot\,)\rVert$
. Note that Assumption A1 implies that
In particular, if ![]() $({\boldsymbol{\xi}_{{p}}^{i}})_{i \geq 1}$
and
$({\boldsymbol{\xi}_{{p}}^{i}})_{i \geq 1}$
and ![]() $({\tilde{\boldsymbol{\xi}}}{}^{i}_{p})_{i \geq 1}$
are Markov chains with transition kernels
$({\tilde{\boldsymbol{\xi}}}{}^{i}_{p})_{i \geq 1}$
are Markov chains with transition kernels ![]() ${K_{n}^{\mu}}$
, with
${K_{n}^{\mu}}$
, with ![]() $\smash{({\tilde{\boldsymbol{\xi}}}{}^{i}_{p})_{i \geq 1}}$
initialised from stationarity, then a standard coupling argument shows that also implies that for any
$\smash{({\tilde{\boldsymbol{\xi}}}{}^{i}_{p})_{i \geq 1}}$
initialised from stationarity, then a standard coupling argument shows that also implies that for any ![]() $N, r \geq 1$
and any
$N, r \geq 1$
and any ![]() $f_n \in \mathcal{B}(\textbf{E}_n)$
with
$f_n \in \mathcal{B}(\textbf{E}_n)$
with ![]() $\lVert f_n\rVert \leq 1$
,
$\lVert f_n\rVert \leq 1$
,
 \begin{align} \mathbb{E}\biggl[\biggl\lvert \sum_{i=1}^N f_n({\boldsymbol{\xi}_{{n}}^{i}}) - f_n({\tilde{\boldsymbol{\xi}}}{}^{i}_{n}) \biggr\rvert^r\biggr]^{\mathrlap{\frac{1}{r}}} & \leq \sum_{\smash{i=1}}^{\smash{N}} \mathbb{E}\bigl[\bigl\lvert f_n({\boldsymbol{\xi}_{{n}}^{i}}) - f_n({\tilde{\boldsymbol{\xi}}}{}^{i}_{n}) \bigr\rvert^r\bigr]^{\frac{1}{r}}\nonumber\\ & \leq 2 \lVert f_n \rVert \sum_{\smash{i=1}}^{\smash{N}} (1 - \varepsilon_n(K))^{\lfloor i/i_n \rfloor}\nonumber\\ & \leq 2 i_n / \varepsilon_n(K) \eqqcolon {\widebar{T}_{n}}. \end{align}
\begin{align} \mathbb{E}\biggl[\biggl\lvert \sum_{i=1}^N f_n({\boldsymbol{\xi}_{{n}}^{i}}) - f_n({\tilde{\boldsymbol{\xi}}}{}^{i}_{n}) \biggr\rvert^r\biggr]^{\mathrlap{\frac{1}{r}}} & \leq \sum_{\smash{i=1}}^{\smash{N}} \mathbb{E}\bigl[\bigl\lvert f_n({\boldsymbol{\xi}_{{n}}^{i}}) - f_n({\tilde{\boldsymbol{\xi}}}{}^{i}_{n}) \bigr\rvert^r\bigr]^{\frac{1}{r}}\nonumber\\ & \leq 2 \lVert f_n \rVert \sum_{\smash{i=1}}^{\smash{N}} (1 - \varepsilon_n(K))^{\lfloor i/i_n \rfloor}\nonumber\\ & \leq 2 i_n / \varepsilon_n(K) \eqqcolon {\widebar{T}_{n}}. \end{align}
The second assumption on the MCMC kernels is a local Lipschitz condition. As shown in Lemma 3, this assumption ensures that for any ![]() $r \geq 1$
,
$r \geq 1$
, ![]() $\sqrt{N}$
-convergence of
$\sqrt{N}$
-convergence of ![]() $\smash{[\eta_{n-1}^N - \eta_{n-1}](\,f_{n-1})}$
to zero in
$\smash{[\eta_{n-1}^N - \eta_{n-1}](\,f_{n-1})}$
to zero in ![]() $\mathbb{L}_r$
(for all
$\mathbb{L}_r$
(for all ![]() $f_{n-1} \in \mathcal{B}(\textbf{E}_{n-1})$
) implies
$f_{n-1} \in \mathcal{B}(\textbf{E}_{n-1})$
) implies ![]() $\sqrt{N}$
-convergence of
$\sqrt{N}$
-convergence of ![]() ${\lVert [ K_n^{\eta_{\smash{n-1}}^{N}} - {K_{n}^{\eta_{n-1}}}](\,f_{n})\rVert}$
to zero in
${\lVert [ K_n^{\eta_{\smash{n-1}}^{N}} - {K_{n}^{\eta_{n-1}}}](\,f_{n})\rVert}$
to zero in ![]() $\mathbb{L}_r$
. By extension, in the proof of the CLT, specifically in Lemma 4, this property enables us to conclude that the (suitably scaled) variance of the particle approximation converges to a well-defined limiting asymptotic variance as
$\mathbb{L}_r$
. By extension, in the proof of the CLT, specifically in Lemma 4, this property enables us to conclude that the (suitably scaled) variance of the particle approximation converges to a well-defined limiting asymptotic variance as ![]() $N \to \infty$
.
$N \to \infty$
.
Assumptions and are similar to those imposed in [Reference Bercu, Del Moral and Doucet5]. They are strong and rarely hold for non-compact spaces. It might be possible to adopt weaker conditions such as those in [Reference Andrieu, Jasra, Doucet and Del Moral2 ], but this would involve substantially more technical and complicated proofs. As an illustration, we show that Assumptions and hold if we employ the independent MH kernels from Example 1, at least if E is finite.
Example 5. (Independent MH, continued.
) Assumption is satisfied thanks to [Reference Mengersen and Tweedie26, Theorem 2.1]. To see this, note that by (3), for any ![]() $n \geq 1$
and any
$n \geq 1$
and any ![]() $\mu \in \mathcal{P}(\textbf{E}_{n-1})$
, since
$\mu \in \mathcal{P}(\textbf{E}_{n-1})$
, since ![]() $F_{n-1}$
is bounded and
$F_{n-1}$
is bounded and ![]() $G_{n-1} > 0$
,
$G_{n-1} > 0$
,
Assumption was proved for finite spaces E (and in the case ![]() $F_{n} \equiv 1$
,
$F_{n} \equiv 1$
, ![]() $R_n = M_n$
) in [Reference Bercu, Del Moral and Doucet5, Section 2].
$R_n = M_n$
) in [Reference Bercu, Del Moral and Doucet5, Section 2].
When proving time-uniform convergence results, we also make the following assumptions on the mutation kernels and potential functions of the Feynman–Kac model. The first of these ensures that Assumption holds uniformly in time. The second and third of these constitute strong mixing conditions that have been extensively used in the analysis of SMC algorithms; although they can often be relaxed in similar settings, this comes at the cost of greatly complicating the analysis (see, e.g., [Reference Whiteley36], [Reference Douc, Moulines and Olsson12]).
(B1)
 $\bar{\imath} \coloneqq \sup_{n \geq 1} i_n < \infty$
and
$\bar{\imath} \coloneqq \sup_{n \geq 1} i_n < \infty$
and  $\varepsilon(K) \coloneqq \inf_{n \geq 1} \varepsilon_n(K) > 0$
.
$\varepsilon(K) \coloneqq \inf_{n \geq 1} \varepsilon_n(K) > 0$
.(B2) There exist
 ${m} \in \mathbb{N}$
and
${m} \in \mathbb{N}$
and  $\varepsilon(M) \in (0,1]$
such that for any
$\varepsilon(M) \in (0,1]$
such that for any  $n \geq 1$
, any
$n \geq 1$
, any  $\textbf{x}_n, \textbf{z}_n \in \textbf{E}_n$
and any
$\textbf{x}_n, \textbf{z}_n \in \textbf{E}_n$
and any  $\varphi \in \mathcal{B}(E)$
,
$\varphi \in \mathcal{B}(E)$
,
 \begin{align*} \MoveEqLeft \int_{E^m} \biggl[\prod_{\smash{p=1}}^{m} M_{n+p}(\textbf{x}_{n+p-1}, \textrm{d} x_{n+p})\biggr]\varphi(x_{n+{m}})\\ & \geq \varepsilon(M) \int_{E^{m}} \biggl[\prod_{p=1}^{\smash{{m}}} M_{n+p}(\textbf{z}_{n+p-1}, \textrm{d} z_{n+p})\biggr]\varphi(z_{n+{m}}). \end{align*}
\begin{align*} \MoveEqLeft \int_{E^m} \biggl[\prod_{\smash{p=1}}^{m} M_{n+p}(\textbf{x}_{n+p-1}, \textrm{d} x_{n+p})\biggr]\varphi(x_{n+{m}})\\ & \geq \varepsilon(M) \int_{E^{m}} \biggl[\prod_{p=1}^{\smash{{m}}} M_{n+p}(\textbf{z}_{n+p-1}, \textrm{d} z_{n+p})\biggr]\varphi(z_{n+{m}}). \end{align*}
(B3) There exist
 $l \in \mathbb{N}$
and
$l \in \mathbb{N}$
and  $\varepsilon(G) \in (0,1]$
such that for any
$\varepsilon(G) \in (0,1]$
such that for any  $n \geq 1$
and any
$n \geq 1$
and any  $\textbf{x}_n, \textbf{z}_n \in \textbf{E}_n$
,
$\textbf{x}_n, \textbf{z}_n \in \textbf{E}_n$
,
 \begin{align*} G_n(\textbf{x}_n) = G_n((\textbf{z}_{n-l-1}, x_{((n-l) {\vee} 1):n})) \quad \text{and} \quad G_n(\textbf{x}_n) \geq \varepsilon(G) G_n(\textbf{z}_n). \end{align*}
\begin{align*} G_n(\textbf{x}_n) = G_n((\textbf{z}_{n-l-1}, x_{((n-l) {\vee} 1):n})) \quad \text{and} \quad G_n(\textbf{x}_n) \geq \varepsilon(G) G_n(\textbf{z}_n). \end{align*}
Under these conditions, time-uniform bounds will be obtained when the test function under study has supremum norm of at most 1 and depends upon only its final coordinate marginal; i.e. we will restrict our attention to test functions ![]() $f_n \in \smash{\mathcal{B}_1^\star}(\textbf{E}_n)^d$
, where
$f_n \in \smash{\mathcal{B}_1^\star}(\textbf{E}_n)^d$
, where ![]() $\smash{\mathcal{B}_1^\star(\textbf{E}_n) \coloneqq \{ f^{\prime}_n \in \mathcal{B}^\star(\textbf{E}_n) \,|\,\lVert f^{\prime}_n\rVert \leq 1\}}$
with
$\smash{\mathcal{B}_1^\star(\textbf{E}_n) \coloneqq \{ f^{\prime}_n \in \mathcal{B}^\star(\textbf{E}_n) \,|\,\lVert f^{\prime}_n\rVert \leq 1\}}$
with
Here, for any ![]() $n \geq 1$
,
$n \geq 1$
, ![]() $\zeta_{n}\,:\, \textbf{E}_n \to E$
denotes the canonical final-coordinate projection operator defined through
$\zeta_{n}\,:\, \textbf{E}_n \to E$
denotes the canonical final-coordinate projection operator defined through ![]() $\textbf{x}_n \mapsto \zeta_{n}(\textbf{x}_n) \coloneqq x_n$
. In the state-space model context this corresponds, essentially, to considering the approximation of the marginal filter and predictor rather than their path-space analogues.
$\textbf{x}_n \mapsto \zeta_{n}(\textbf{x}_n) \coloneqq x_n$
. In the state-space model context this corresponds, essentially, to considering the approximation of the marginal filter and predictor rather than their path-space analogues.
3.2. Strong law of large numbers
The first main result in this work is the ![]() $\mathbb{L}_r$
-inequality given in Proposition 1, the proof of which will be given in Appendix C. As an immediate consequence, we obtain the SLLN stated in Corollary 1.
$\mathbb{L}_r$
-inequality given in Proposition 1, the proof of which will be given in Appendix C. As an immediate consequence, we obtain the SLLN stated in Corollary 1.
Proposition 1. (![]() $\mathbb{L}_r$
-inequality.) Under Assumption , for each
$\mathbb{L}_r$
-inequality.) Under Assumption , for each ![]() $r,n \geq 1$
there exist
$r,n \geq 1$
there exist ![]() ${a_{n}}, {b_{r}} < \infty$
such that for any
${a_{n}}, {b_{r}} < \infty$
such that for any ![]() $f_n \in \mathcal{B}(\textbf{E}_n)$
and any
$f_n \in \mathcal{B}(\textbf{E}_n)$
and any ![]() $N \geq 1$
,
$N \geq 1$
,
Under the additional Assumptions and if ![]() $f_n \in \smash{\mathcal{B}_1^\star}(\textbf{E}_n)$
, the right-hand side of (9) is bounded uniformly in time; i.e. there exists
$f_n \in \smash{\mathcal{B}_1^\star}(\textbf{E}_n)$
, the right-hand side of (9) is bounded uniformly in time; i.e. there exists ![]() $a < \infty $
such that
$a < \infty $
such that ![]() $\sup_{n \geq 1 }a_n \leq a$
.
$\sup_{n \geq 1 }a_n \leq a$
.
Corollary 1. (Strong law of large numbers.) Under Assumption , for any ![]() $n,d \geq 1$
and
$n,d \geq 1$
and ![]() $f_n \in \mathcal{B}(\textbf{E}_n)^d$
, as
$f_n \in \mathcal{B}(\textbf{E}_n)^d$
, as ![]() $N\to \infty$
,
$N\to \infty$
,
(1)
 $\eta_n^N(\,f_n) {\mathrel{\mathop{\rightarrow}\nolimits_{\text{\upshape{a.s.}}}}} \eta_n(\,f_n)$
;
$\eta_n^N(\,f_n) {\mathrel{\mathop{\rightarrow}\nolimits_{\text{\upshape{a.s.}}}}} \eta_n(\,f_n)$
;(2)
 $\gamma_n^N(\,f_n) {\mathrel{\mathop{\rightarrow}\nolimits_{\text{\upshape{a.s.}}}}} \gamma_n(\,f_n)$
.
$\gamma_n^N(\,f_n) {\mathrel{\mathop{\rightarrow}\nolimits_{\text{\upshape{a.s.}}}}} \gamma_n(\,f_n)$
.
Proof. Without loss of generality, we prove the result for scalar-valued test functions ![]() $f_n \in \mathcal{B}(\textbf{E}_n)$
. Part 1 is a direct consequence of Proposition 1, for some
$f_n \in \mathcal{B}(\textbf{E}_n)$
. Part 1 is a direct consequence of Proposition 1, for some ![]() $r > 2$
, using the Borel–Cantelli lemma together with Markov’s inequality. Part 2 follows from Part 1 and boundedness of the potential functions
$r > 2$
, using the Borel–Cantelli lemma together with Markov’s inequality. Part 2 follows from Part 1 and boundedness of the potential functions ![]() $G_p$
, i.e.
$G_p$
, i.e.
 \begin{align*} \gamma_n^N(\,f_n) = \eta_n^N(\,f_n) \prod_{p=1}^{n-1} \eta_p^N(G_p) {\mathrel{\mathop{\rightarrow}\nolimits_{\text{\upshape{a.s.}}}}} \eta_n(\,f_n) \prod_{p=1}^{n-1} \eta_p(G_p) = \gamma_n(\,f_n), \end{align*}
\begin{align*} \gamma_n^N(\,f_n) = \eta_n^N(\,f_n) \prod_{p=1}^{n-1} \eta_p^N(G_p) {\mathrel{\mathop{\rightarrow}\nolimits_{\text{\upshape{a.s.}}}}} \eta_n(\,f_n) \prod_{p=1}^{n-1} \eta_p(G_p) = \gamma_n(\,f_n), \end{align*}
as ![]() $N \to \infty$
. This completes the proof.
$N \to \infty$
. This completes the proof.
3.3. Central limit theorem
The second main result is Proposition 2, which adapts the usual CLT for SMC algorithms from [Reference Del Moral10, Propositions 9.4.1 & 9.4.2] to our setting. Its proof is given in Appendix C. As in [Reference Del Moral and Doucet11], [Reference Bercu, Del Moral and Doucet5], we will make extensive use of the resolvent operators ![]() ${T_{n}^{\mu}}$
, defined, for any
${T_{n}^{\mu}}$
, defined, for any ![]() $\mu \in \mathcal{P}(\textbf{E}_{n-1})$
and any
$\mu \in \mathcal{P}(\textbf{E}_{n-1})$
and any ![]() $f_n \in \mathcal{B}(\textbf{E}_n)$
, by
$f_n \in \mathcal{B}(\textbf{E}_n)$
, by
 \begin{equation*} {T_{n}^{\mu}}(\,f_n) \coloneqq \sum_{j = 0}^\infty [({K_{n}^{\mu}})^j - {\Phi_{n}^{\mu}}](\,f_n).\end{equation*}
\begin{equation*} {T_{n}^{\mu}}(\,f_n) \coloneqq \sum_{j = 0}^\infty [({K_{n}^{\mu}})^j - {\Phi_{n}^{\mu}}](\,f_n).\end{equation*}
These operators satisfy the Poisson equation
Under Assumption , [Reference Bercu, Del Moral and Doucet5, Proposition 3.1] shows that, for ![]() ${\widebar{T}_{n}}$
as defined in (8),
${\widebar{T}_{n}}$
as defined in (8),
In the following, for ![]() $n\geq 1$
, we consider a vector-valued test function
$n\geq 1$
, we consider a vector-valued test function ![]() $f_n = (\,f_n^u)_{1 \leq u \leq d} \in \mathcal{B}(\textbf{E}_n)^d$
. Using the resolvent operators, for any
$f_n = (\,f_n^u)_{1 \leq u \leq d} \in \mathcal{B}(\textbf{E}_n)^d$
. Using the resolvent operators, for any ![]() $1 \leq u, v \leq d$
, we define the covariance function
$1 \leq u, v \leq d$
, we define the covariance function ![]() ${C_{n}^{\mu}}(\,f_n^u,f_n^v)\colon \textbf{E}_n \to \mathbb{R}$
by
${C_{n}^{\mu}}(\,f_n^u,f_n^v)\colon \textbf{E}_n \to \mathbb{R}$
by
 \begin{align} \MoveEqLeft{C_{n}^{\mu}}(\,f_n^u,f_n^v)(\textbf{x}_n)\nonumber\\[4pt] & \coloneqq {K_{n}^{\mu}}[({T_{n}^{\mu}}(\,f_n^u)-{K_{n}^{\mu}}{T_{n}^{\mu}}(\,f_n^u)(\textbf{x}_n))({T_{n}^{\mu}}(\,f_n^v)-{K_{n}^{\mu}}{T_{n}^{\mu}}(\,f_n^v)(\textbf{x}_n))](\textbf{x}_n) \\[4pt] & = {\textrm{cov}}_{{K_{n}^{\mu}}(\textbf{x}_n,\,\cdot\,)}[{T_{n}^{\mu}}(\,f_n^u), {T_{n}^{\mu}}(\,f_n^v)]\nonumber\end{align}
\begin{align} \MoveEqLeft{C_{n}^{\mu}}(\,f_n^u,f_n^v)(\textbf{x}_n)\nonumber\\[4pt] & \coloneqq {K_{n}^{\mu}}[({T_{n}^{\mu}}(\,f_n^u)-{K_{n}^{\mu}}{T_{n}^{\mu}}(\,f_n^u)(\textbf{x}_n))({T_{n}^{\mu}}(\,f_n^v)-{K_{n}^{\mu}}{T_{n}^{\mu}}(\,f_n^v)(\textbf{x}_n))](\textbf{x}_n) \\[4pt] & = {\textrm{cov}}_{{K_{n}^{\mu}}(\textbf{x}_n,\,\cdot\,)}[{T_{n}^{\mu}}(\,f_n^u), {T_{n}^{\mu}}(\,f_n^v)]\nonumber\end{align}
for any ![]() $\textbf{x}_n \in \textbf{E}_n$
. Under Assumption , we have
$\textbf{x}_n \in \textbf{E}_n$
. Under Assumption , we have ![]() ${C_{n}^{\mu}}(\,f_n^u,f_n^v) \in \mathcal{B}(\textbf{E}_n)$
for any
${C_{n}^{\mu}}(\,f_n^u,f_n^v) \in \mathcal{B}(\textbf{E}_n)$
for any ![]() $1 \leq u, v \leq d$
and any
$1 \leq u, v \leq d$
and any ![]() $\mu \in \mathcal{P}(\textbf{E}_{n-1})$
. Indeed, using (12), it is straightforward to check that
$\mu \in \mathcal{P}(\textbf{E}_{n-1})$
. Indeed, using (12), it is straightforward to check that
Throughout the remainder of this work, let ![]() $V = (V_n)_{n \geq 1}$
be a sequence of independent and centred Gaussian fields with
$V = (V_n)_{n \geq 1}$
be a sequence of independent and centred Gaussian fields with
and define the (d,d)-matrix ![]() $\varSigma_n(\,f_n) \coloneqq (\varSigma_n(\,f_n^u, f_n^v))_{1\leq u,v\leq d}$
by
$\varSigma_n(\,f_n) \coloneqq (\varSigma_n(\,f_n^u, f_n^v))_{1\leq u,v\leq d}$
by
 \begin{equation} \varSigma_n(\,f_n^u, f_n^v) \coloneqq \sum_{p=1}^n \mathbb{E}[V_n(\widebar{Q}_{p,n}(\,f_n^u))V_n(\widebar{Q}_{p,n}(\,f_n^v))], \end{equation}
\begin{equation} \varSigma_n(\,f_n^u, f_n^v) \coloneqq \sum_{p=1}^n \mathbb{E}[V_n(\widebar{Q}_{p,n}(\,f_n^u))V_n(\widebar{Q}_{p,n}(\,f_n^v))], \end{equation}
for any ![]() $n \geq 1$
, any
$n \geq 1$
, any ![]() $f_n = (\,f_n^u)_{1 \leq u \leq d} \in \mathcal{B}(\textbf{E}_n)^d$
, and any
$f_n = (\,f_n^u)_{1 \leq u \leq d} \in \mathcal{B}(\textbf{E}_n)^d$
, and any ![]() $1 \leq u,v \leq d$
. Additionally, let
$1 \leq u,v \leq d$
. Additionally, let ![]() $N(0, \varSigma)$
denote a (multivariate) centred Gaussian distribution with some covariance matrix
$N(0, \varSigma)$
denote a (multivariate) centred Gaussian distribution with some covariance matrix ![]() $\varSigma$
.
$\varSigma$
.
Proposition 2. (Central limit theorem.) Under Assumptions and , for any ![]() $n,d \geq 1$
and any
$n,d \geq 1$
and any ![]() $f_n \in \mathcal{B}(\textbf{E}_n)^d$
, as
$f_n \in \mathcal{B}(\textbf{E}_n)^d$
, as ![]() $N \to \infty$
,
$N \to \infty$
,
 \begin{align*} \frac{\sqrt{N}}{\gamma_n(\textbf{1})} [\gamma_n^N - \gamma_n](\,f_n) & {\mathrel{\mathop{\rightarrow}\nolimits_{\text{\upshape{d}}}}} \sum_{p=1}^n V_p(\widebar{Q}_{p,n}(\,f_n)) \sim N(0, \varSigma_n(\,f_n)),\end{align*}
\begin{align*} \frac{\sqrt{N}}{\gamma_n(\textbf{1})} [\gamma_n^N - \gamma_n](\,f_n) & {\mathrel{\mathop{\rightarrow}\nolimits_{\text{\upshape{d}}}}} \sum_{p=1}^n V_p(\widebar{Q}_{p,n}(\,f_n)) \sim N(0, \varSigma_n(\,f_n)),\end{align*}
and likewise, writing ![]() $\bar{f}_n \coloneqq f_n - \eta_n(\,f_n)$
,
$\bar{f}_n \coloneqq f_n - \eta_n(\,f_n)$
,
 \begin{align} \sqrt{N}[\eta_n^N - \eta_n](\,f_n) & {\mathrel{\mathop{\rightarrow}\nolimits_{\text{\upshape{d}}}}} \sum_{p=1}^n V_p(\widebar{Q}_{p,n}(\bar{f}_n)) \sim N(0, \varSigma_n(\bar{f}_n)).\end{align}
\begin{align} \sqrt{N}[\eta_n^N - \eta_n](\,f_n) & {\mathrel{\mathop{\rightarrow}\nolimits_{\text{\upshape{d}}}}} \sum_{p=1}^n V_p(\widebar{Q}_{p,n}(\bar{f}_n)) \sim N(0, \varSigma_n(\bar{f}_n)).\end{align}
Under the additional Assumptions and if ![]() $f_n \in \smash{\mathcal{B}_1^\star}(\textbf{E}_n)^d$
, the asymptotic variance in (17) is bounded uniformly in time, i.e. there exists
$f_n \in \smash{\mathcal{B}_1^\star}(\textbf{E}_n)^d$
, the asymptotic variance in (17) is bounded uniformly in time, i.e. there exists ![]() $c < \infty$
such that
$c < \infty$
such that
where the supremum is over all ![]() $n \geq 1$
,
$n \geq 1$
, ![]() $f_n \in \smash{\mathcal{B}_1^\star}(\textbf{E}_n)^d$
, and
$f_n \in \smash{\mathcal{B}_1^\star}(\textbf{E}_n)^d$
, and ![]() $1 \leq u,v \leq d$
.
$1 \leq u,v \leq d$
.
4. Comparison with standard PFs
4.1. Variance decomposition
In this section, we first examine the asymptotic variance from Proposition 2. We then illustrate the trade-off between MCMC-PFs and standard PFs.
To ease the exposition, we consider only scalar-valued test functions ![]() $f_n \in \mathcal{B}(\textbf{E}_n)$
throughout this section. As noted in [Reference Bercu, Del Moral and Doucet5, Proposition 3.6], the terms
$f_n \in \mathcal{B}(\textbf{E}_n)$
throughout this section. As noted in [Reference Bercu, Del Moral and Doucet5, Proposition 3.6], the terms ![]() ${\Phi_{n}^{\mu}} {C_{n}^{\mu}}(\,f_n, f_n)$
from (15), which, via (16), appear in the expressions for the asymptotic variance in Proposition 2, can be written in the following form, which is more commonly used in the MCMC literature:
${\Phi_{n}^{\mu}} {C_{n}^{\mu}}(\,f_n, f_n)$
from (15), which, via (16), appear in the expressions for the asymptotic variance in Proposition 2, can be written in the following form, which is more commonly used in the MCMC literature:
 \begin{align} {\Phi_{n}^{\mu}} {C_{n}^{\mu}}(\,f_n, f_n) & = \textstyle \int_{\textbf{E}_n^2} {\Phi_{n}^{\mu}}(\textrm{d} \textbf{x}_n){K_{n}^{\mu}}(\textbf{x}_n, \textrm{d} \textbf{z}_n)\bigl[{T_{n}^{\mu}}(\,f_n)(\textbf{z}_n) - {K_{n}^{\mu}} {T_{n}^{\mu}}(\,f_n)(\textbf{x}_n)\bigr]^2\nonumber\\[4pt] & = {\Phi_{n}^{\mu}}\bigl({T_{n}^{\mu}}(\,f_n)^2 - {K_{n}^{\mu}}{T_{n}^{\mu}}(\,f_n)^2\bigr)\nonumber\\[4pt] & = {\Phi_{n}^{\mu}}\bigl({T_{n}^{\mu}}(\,f_n)^2 - [{\Phi_{n}^{\mu}}(\,f_n) - f_n + {T_{n}^{\mu}}(\,f_n)]^2\bigr) \quad \text{[by (10)]}\nonumber\\[4pt] & = {\Phi_{n}^{\mu}}\bigl(- [\,f_n - {\Phi_{n}^{\mu}}(\,f_n)]^2 - 2[{\Phi_{n}^{\mu}}(\,f_n) - f_n]{T_{n}^{\mu}}(\,f_n)\bigr)\nonumber\\[4pt] & = {\Phi_{n}^{\mu}}\bigl(- [\,f_n - {\Phi_{n}^{\mu}}(\,f_n)]^2 + 2 f_n{T_{n}^{\mu}}(\,f_n)\bigr) \quad \text{[by (11)]}\nonumber\\[4pt] &= {\textrm{var}}_{{\Phi_{n}^{\mu}}}[\,f_n] \times \textrm{iact}_{{K_{n}^{\mu}}}[\,f_n]. \end{align}
\begin{align} {\Phi_{n}^{\mu}} {C_{n}^{\mu}}(\,f_n, f_n) & = \textstyle \int_{\textbf{E}_n^2} {\Phi_{n}^{\mu}}(\textrm{d} \textbf{x}_n){K_{n}^{\mu}}(\textbf{x}_n, \textrm{d} \textbf{z}_n)\bigl[{T_{n}^{\mu}}(\,f_n)(\textbf{z}_n) - {K_{n}^{\mu}} {T_{n}^{\mu}}(\,f_n)(\textbf{x}_n)\bigr]^2\nonumber\\[4pt] & = {\Phi_{n}^{\mu}}\bigl({T_{n}^{\mu}}(\,f_n)^2 - {K_{n}^{\mu}}{T_{n}^{\mu}}(\,f_n)^2\bigr)\nonumber\\[4pt] & = {\Phi_{n}^{\mu}}\bigl({T_{n}^{\mu}}(\,f_n)^2 - [{\Phi_{n}^{\mu}}(\,f_n) - f_n + {T_{n}^{\mu}}(\,f_n)]^2\bigr) \quad \text{[by (10)]}\nonumber\\[4pt] & = {\Phi_{n}^{\mu}}\bigl(- [\,f_n - {\Phi_{n}^{\mu}}(\,f_n)]^2 - 2[{\Phi_{n}^{\mu}}(\,f_n) - f_n]{T_{n}^{\mu}}(\,f_n)\bigr)\nonumber\\[4pt] & = {\Phi_{n}^{\mu}}\bigl(- [\,f_n - {\Phi_{n}^{\mu}}(\,f_n)]^2 + 2 f_n{T_{n}^{\mu}}(\,f_n)\bigr) \quad \text{[by (11)]}\nonumber\\[4pt] &= {\textrm{var}}_{{\Phi_{n}^{\mu}}}[\,f_n] \times \textrm{iact}_{{K_{n}^{\mu}}}[\,f_n]. \end{align}
Here, for any probability measure ![]() $\nu \in \mathcal{P}(\textbf{E}_n)$
and any
$\nu \in \mathcal{P}(\textbf{E}_n)$
and any ![]() $\nu$
-invariant Markov kernel K, we have defined the integrated autocorrelation time (IACT):
$\nu$
-invariant Markov kernel K, we have defined the integrated autocorrelation time (IACT):
 \begin{align*} \textrm{iact}_{K}[\,f_n] & \coloneqq 1 + 2 \sum_{j=1}^\infty \frac{{\textrm{cov}}_{\nu}[\,f_n, K^j(\,f_n)]}{{\textrm{var}}_{\nu}[\,f_n]}. \end{align*}
\begin{align*} \textrm{iact}_{K}[\,f_n] & \coloneqq 1 + 2 \sum_{j=1}^\infty \frac{{\textrm{cov}}_{\nu}[\,f_n, K^j(\,f_n)]}{{\textrm{var}}_{\nu}[\,f_n]}. \end{align*}
If the MCMC kernels ![]() ${K_{n}^{\mu}}$
are perfectly mixing, that is if
${K_{n}^{\mu}}$
are perfectly mixing, that is if ![]() ${K_{n}^{\mu}}(\textbf{x}_n, \,\cdot\,) = {\Phi_{n}^{\mu}}(\!\cdot\!)$
for all
${K_{n}^{\mu}}(\textbf{x}_n, \,\cdot\,) = {\Phi_{n}^{\mu}}(\!\cdot\!)$
for all ![]() $\textbf{x}_n \in \textbf{E}_n$
, then
$\textbf{x}_n \in \textbf{E}_n$
, then ![]() $\textrm{iact}_{{K_{n}^{\mu}}}[\,f_n] = 1$
, i.e.
$\textrm{iact}_{{K_{n}^{\mu}}}[\,f_n] = 1$
, i.e. ![]() ${\Phi_{n}^{\mu}} {C_{n}^{\mu}}(\,f_n, f_n) = {\textrm{var}}_{{\Phi_{n}^{\mu}}}[\,f_n]$
, and the expressions for the asymptotic variances in Proposition 2 (as specified through (15) and (16)) simplify to those obtained in [Reference Chopin9], [Reference Del Moral10] ,[Reference Künsch20] for conventional SMC algorithms. Thus, by the decomposition from (19), the terms appearing in the asymptotic variance of the MCMC-PF are equal to those appearing in the asymptotic variance of standard PFs multiplied by the IACT associated with the MCMC kernels used to generate the particles.
${\Phi_{n}^{\mu}} {C_{n}^{\mu}}(\,f_n, f_n) = {\textrm{var}}_{{\Phi_{n}^{\mu}}}[\,f_n]$
, and the expressions for the asymptotic variances in Proposition 2 (as specified through (15) and (16)) simplify to those obtained in [Reference Chopin9], [Reference Del Moral10] ,[Reference Künsch20] for conventional SMC algorithms. Thus, by the decomposition from (19), the terms appearing in the asymptotic variance of the MCMC-PF are equal to those appearing in the asymptotic variance of standard PFs multiplied by the IACT associated with the MCMC kernels used to generate the particles.
To derive a variance ordering between standard PFs and MCMC-PFs, we assume in the remainder of this section that the MCMC operators are self-adjoint and positive, in the sense that ![]() $[{\Phi_{n}^{\mu}} \otimes {K_{n}^{\mu}}](\,f_n \otimes f_n) \geq 0$
for any
$[{\Phi_{n}^{\mu}} \otimes {K_{n}^{\mu}}](\,f_n \otimes f_n) \geq 0$
for any ![]() ${\Phi_{n}^{\mu}}$
-square integrable real-valued functions
${\Phi_{n}^{\mu}}$
-square integrable real-valued functions ![]() $f_n$
. For positive (and self-adjoint) MCMC operators, the IACT terms are greater than 1 for any
$f_n$
. For positive (and self-adjoint) MCMC operators, the IACT terms are greater than 1 for any ![]() $f_n \in \mathcal{B}(\textbf{E}_n)$
([Reference Liu24, p. 20] as cited in [Reference Mira27, Theorem 3.7.1]). They thus represent the variance ‘penalty’ incurred due to the additional between-particle positive correlations in MCMC-PFs relative to standard PFs. We note that this assumption is mild since the MCMC kernels which could be deployed in practical settings are almost always positive. Examples of positive operators include the independent MH kernel [Reference Liu25] discussed in Example 1, the MH kernel with Gaussian or Student-t random walk proposals [Reference Baxendale4] or autoregressive positively correlated proposals with normal or Student-t innovations [Reference Doucet, Pitt, Deligiannidis and Kohn13], and some versions of the hit-and-run and slice sampling algorithms [Reference Rudolf and Ullrich30].
$f_n \in \mathcal{B}(\textbf{E}_n)$
([Reference Liu24, p. 20] as cited in [Reference Mira27, Theorem 3.7.1]). They thus represent the variance ‘penalty’ incurred due to the additional between-particle positive correlations in MCMC-PFs relative to standard PFs. We note that this assumption is mild since the MCMC kernels which could be deployed in practical settings are almost always positive. Examples of positive operators include the independent MH kernel [Reference Liu25] discussed in Example 1, the MH kernel with Gaussian or Student-t random walk proposals [Reference Baxendale4] or autoregressive positively correlated proposals with normal or Student-t innovations [Reference Doucet, Pitt, Deligiannidis and Kohn13], and some versions of the hit-and-run and slice sampling algorithms [Reference Rudolf and Ullrich30].
4.2. Variance–variance trade-off
There is an efficiency trade-off involved in deciding whether to employ a standard PF or an MCMC-PF for a particular application. For the same distribution flow ![]() $(\eta_n)_{n \geq 1}$
, the former always has a lower asymptotic variance than the latter if the MCMC draws are positively correlated. However, as we seek to illustrate in the remainder of this section, an MCMC-PF may still be preferable (in terms of asymptotic variance) to a standard PF in certain situations, even if a positive MCMC kernel is used, because it can sometimes be used to target a more efficient distribution flow, i.e. a flow for which the variance terms
$(\eta_n)_{n \geq 1}$
, the former always has a lower asymptotic variance than the latter if the MCMC draws are positively correlated. However, as we seek to illustrate in the remainder of this section, an MCMC-PF may still be preferable (in terms of asymptotic variance) to a standard PF in certain situations, even if a positive MCMC kernel is used, because it can sometimes be used to target a more efficient distribution flow, i.e. a flow for which the variance terms ![]() ${\textrm{var}}_{{\Phi_{n}^{\mu}}}[\,f_n]$
are reduced far enough to compensate for the IACT-based ‘penalty’ terms
${\textrm{var}}_{{\Phi_{n}^{\mu}}}[\,f_n]$
are reduced far enough to compensate for the IACT-based ‘penalty’ terms ![]() $\textrm{iact}_{{K_{n}^{\mu}}}[\,f_n]$
in (19). Additionally, the computational cost of generating one particle in an MCMC-PF can be smaller than the corresponding cost in a standard PF.
$\textrm{iact}_{{K_{n}^{\mu}}}[\,f_n]$
in (19). Additionally, the computational cost of generating one particle in an MCMC-PF can be smaller than the corresponding cost in a standard PF.
As an illustration, we compare the asymptotic variances of approximations ![]() $\pi_n^N$
of the filter
$\pi_n^N$
of the filter ![]() $\pi_n$
computed using either the standard PFs or MCMC-PFs targeting the BPF and FA-APF flows in the state-space model from Subsection 2.5. In the remainder of this section, we let
$\pi_n$
computed using either the standard PFs or MCMC-PFs targeting the BPF and FA-APF flows in the state-space model from Subsection 2.5. In the remainder of this section, we let ![]() $S_{p,n}\colon \mathcal{B}(\textbf{E}_p) \to \mathcal{B}(\textbf{E}_n)$
be a kernel that satisfies
$S_{p,n}\colon \mathcal{B}(\textbf{E}_p) \to \mathcal{B}(\textbf{E}_n)$
be a kernel that satisfies ![]() $\pi_p S_{p,n} = \pi_n$
and is given by
$\pi_p S_{p,n} = \pi_n$
and is given by
 \begin{align*} S_{p,n}(\,f_n)(\textbf{x}_p) & \coloneqq \frac{\mathcal{L}_p}{\mathcal{L}_n} \int_{\textbf{E}_n} f_n(\textbf{z}_n) \delta_{\textbf{x}_p}(\textrm{d} \textbf{z}_p) \smashoperator{\prod_{q=p+1}^n} g_{q}(z_q, y_q) L_{q}(z_{q-1}, \textrm{d} z_q).\end{align*}
\begin{align*} S_{p,n}(\,f_n)(\textbf{x}_p) & \coloneqq \frac{\mathcal{L}_p}{\mathcal{L}_n} \int_{\textbf{E}_n} f_n(\textbf{z}_n) \delta_{\textbf{x}_p}(\textrm{d} \textbf{z}_p) \smashoperator{\prod_{q=p+1}^n} g_{q}(z_q, y_q) L_{q}(z_{q-1}, \textrm{d} z_q).\end{align*}
We begin by deriving expressions for the asymptotic variances in each case.
• BPF flow. For the BPF flow from Example 2, expectations under the filter
 $\pi_n(\,f_n) = \eta_n(G_nf_n)/\eta_n(G_n)$
are approximated by
$\pi_n(\,f_n) = \eta_n(G_nf_n)/\eta_n(G_n)$
are approximated by  $\pi_n^N(\,f_n) = \eta_n^N(G_nf_n)/\eta_n^N(G_n)$
. Accounting for this transformation, e.g. as in [Reference Johansen and Doucet17], yields
As Corollary 1 ensures that
$\pi_n^N(\,f_n) = \eta_n^N(G_nf_n)/\eta_n^N(G_n)$
. Accounting for this transformation, e.g. as in [Reference Johansen and Doucet17], yields
As Corollary 1 ensures that \begin{align*} [\pi_n^N - \pi_n](\,f_n) & = \frac{\eta_n(G_n)}{\eta_n^N(G_n)} \frac{\eta_n^N(G_n[\,f_n - \pi_n(\,f_n)])}{\eta_n(G_n)}\\[3pt] & = \frac{\eta_n(G_n)}{\eta_n^N(G_n)} [\eta_n^N - \eta_n](G_n[\,f_n - \pi_n(\,f_n)]/\eta_n(G_n)). \end{align*}
\begin{align*} [\pi_n^N - \pi_n](\,f_n) & = \frac{\eta_n(G_n)}{\eta_n^N(G_n)} \frac{\eta_n^N(G_n[\,f_n - \pi_n(\,f_n)])}{\eta_n(G_n)}\\[3pt] & = \frac{\eta_n(G_n)}{\eta_n^N(G_n)} [\eta_n^N - \eta_n](G_n[\,f_n - \pi_n(\,f_n)]/\eta_n(G_n)). \end{align*}
 $\eta_n(G_n)/\eta_n^N(G_n) {\mathrel{\mathop{\rightarrow}\nolimits_{\text{\upshape{a.s.}}}}} 1$
, Slutsky’s lemma and Proposition 2 are sufficient to show that for the BPF and MCMC-BPF, respectively,
$\eta_n(G_n)/\eta_n^N(G_n) {\mathrel{\mathop{\rightarrow}\nolimits_{\text{\upshape{a.s.}}}}} 1$
, Slutsky’s lemma and Proposition 2 are sufficient to show that for the BPF and MCMC-BPF, respectively,  $\sqrt{N}[\pi_n^N - \pi_n](\,f_n)$
converges in distribution to a Gaussian distribution with zero mean and variance
(20)
$\sqrt{N}[\pi_n^N - \pi_n](\,f_n)$
converges in distribution to a Gaussian distribution with zero mean and variance
(20) \begin{align} {\varSigma_{n}^{\text{BPF}}}(\,f_n) &\, = \sum_{p=1}^n {\textrm{var}}_{\tilde{\pi}_p}[\tilde{f}_{p,n}],\,\qquad\qquad\end{align}
(21)where, using that
\begin{align} {\varSigma_{n}^{\text{BPF}}}(\,f_n) &\, = \sum_{p=1}^n {\textrm{var}}_{\tilde{\pi}_p}[\tilde{f}_{p,n}],\,\qquad\qquad\end{align}
(21)where, using that \begin{align} {\varSigma_{n}^{\text{MCMC-BPF}}}(\,f_n) & \,= \sum_{p=1}^n {\textrm{var}}_{\tilde{\pi}_p}[\tilde{f}_{p,n}] \times \textrm{iact}_{{K_{p}^{{\tilde{\pi}}_{p-1}}}}[\tilde{f}_{p,n}], \end{align}
\begin{align} {\varSigma_{n}^{\text{MCMC-BPF}}}(\,f_n) & \,= \sum_{p=1}^n {\textrm{var}}_{\tilde{\pi}_p}[\tilde{f}_{p,n}] \times \textrm{iact}_{{K_{p}^{{\tilde{\pi}}_{p-1}}}}[\tilde{f}_{p,n}], \end{align}
 $\eta_n(G_n [\,f_n - \pi_n(\,f_n)]/\eta_n(G_n)) = 0$
,
$\eta_n(G_n [\,f_n - \pi_n(\,f_n)]/\eta_n(G_n)) = 0$
,
 \begin{align*} \tilde{f}_{p,n}(\textbf{x}_p) & \coloneqq \widebar{Q}_{p,n}(G_n[\,f_n - \pi_n(\,f_n)]/\eta_n(G_n))(\textbf{x}_p)\\ & = g_p(x_p, y_{p}) \frac{\mathcal{L}_{p-1}}{\mathcal{L}_p} S_{p,n}(\,f_n - \pi_n(\,f_n))(\textbf{x}_p). \end{align*}
\begin{align*} \tilde{f}_{p,n}(\textbf{x}_p) & \coloneqq \widebar{Q}_{p,n}(G_n[\,f_n - \pi_n(\,f_n)]/\eta_n(G_n))(\textbf{x}_p)\\ & = g_p(x_p, y_{p}) \frac{\mathcal{L}_{p-1}}{\mathcal{L}_p} S_{p,n}(\,f_n - \pi_n(\,f_n))(\textbf{x}_p). \end{align*}
• FA-APF flow. For the FA-APF flow from Example 3,
 $\pi_n = \eta_n$
, so that we may approximate the filter by
$\pi_n = \eta_n$
, so that we may approximate the filter by  $\pi_n^N \coloneqq \eta_n^N$
. Hence, Proposition 2 shows that for the FA-APF and MCMC-FA-APF, respectively,
$\pi_n^N \coloneqq \eta_n^N$
. Hence, Proposition 2 shows that for the FA-APF and MCMC-FA-APF, respectively,  $\sqrt{N}[\pi_n^N - \pi_n](\,f_n)$
converges in distribution to a Gaussian distribution with zero mean and variance
(22)
$\sqrt{N}[\pi_n^N - \pi_n](\,f_n)$
converges in distribution to a Gaussian distribution with zero mean and variance
(22) \begin{align} {\varSigma_{n}^{\text{FA-APF}}}(\,f_n) & \,= \sum_{p=1}^n {\textrm{var}}_{\pi_p}[\,f_{p,n}],\qquad\qquad\, \end{align}
(23)where
\begin{align} {\varSigma_{n}^{\text{FA-APF}}}(\,f_n) & \,= \sum_{p=1}^n {\textrm{var}}_{\pi_p}[\,f_{p,n}],\qquad\qquad\, \end{align}
(23)where \begin{align} {\varSigma_{n}^{\text{MCMC-FA-APF}}}(\,f_n) & \,= \sum_{p=1}^n {\textrm{var}}_{\pi_p}[\,f_{p,n}] \times \textrm{iact}_{{K_{p}^{{\pi_{p-1}}}}}[\,f_{p,n}], \end{align}
\begin{align} {\varSigma_{n}^{\text{MCMC-FA-APF}}}(\,f_n) & \,= \sum_{p=1}^n {\textrm{var}}_{\pi_p}[\,f_{p,n}] \times \textrm{iact}_{{K_{p}^{{\pi_{p-1}}}}}[\,f_{p,n}], \end{align}
 \begin{align*} f_{p,n}(\textbf{x}_p) \coloneqq \widebar{Q}_{p,n}(\,f_n - \pi_n(\,f_n))(\textbf{x}_p) = S_{p,n}(\,f_n - \pi_n(\,f_n))(\textbf{x}_p). \end{align*}
\begin{align*} f_{p,n}(\textbf{x}_p) \coloneqq \widebar{Q}_{p,n}(\,f_n - \pi_n(\,f_n))(\textbf{x}_p) = S_{p,n}(\,f_n - \pi_n(\,f_n))(\textbf{x}_p). \end{align*}
For the remainder of this section, assume that the asymptotic variance of the standard FA-APF is lower than that of the standard BPF for the given state-space model. More precisely, we assume that for each ![]() $p \leq n$
,
$p \leq n$
,
and hence that
This is thought to hold in many applications and has been empirically verified e.g. in [Reference Snyder, Bengtsson and Morzfeld35], although it is possible to construct counterexamples [Reference Johansen and Doucet18]. Assuming that the MCMC kernels ![]() ${K_{p}^{\mu}}$
are positive operators, the IACTs take values in
${K_{p}^{\mu}}$
are positive operators, the IACTs take values in ![]() $[1,\infty)$
, and hence
$[1,\infty)$
, and hence
However, as noted in Example 3, there are many scenarios where FA-APF cannot be implemented as we cannot generate N (conditionally) IID samples from ![]() ${\Phi_{n}^{N}}$
. In this case, practitioners typically have to resort to using the standard BPF instead. In contrast, the MCMC-FA-APF can usually be implemented. In such circumstances, use of MCMC-PFs (specifically in the form of the MCMC-FA-APF) can be preferable, e.g. if the variance reductions attained by targeting the FA-APF flow are large enough to outweigh the additional variance due to the increased particle correlation, i.e. if for each
${\Phi_{n}^{N}}$
. In this case, practitioners typically have to resort to using the standard BPF instead. In contrast, the MCMC-FA-APF can usually be implemented. In such circumstances, use of MCMC-PFs (specifically in the form of the MCMC-FA-APF) can be preferable, e.g. if the variance reductions attained by targeting the FA-APF flow are large enough to outweigh the additional variance due to the increased particle correlation, i.e. if for each ![]() $1 \leq p \leq n$
,
$1 \leq p \leq n$
,
because then
4.3. Numerical illustration
We end this section by illustrating the ‘variance–variance trade-off’ mentioned above on two instances of the state-space model from Subsection 2.5.
The first model is a state-space model on a binary space ![]() $E = F \coloneqq \{0,1\}$
and with
$E = F \coloneqq \{0,1\}$
and with ![]() $n=2$
observations:
$n=2$
observations: ![]() $y_1 = y_2 = 0$
. Furthermore, for some
$y_1 = y_2 = 0$
. Furthermore, for some ![]() $\alpha, \varepsilon \in [0, 1]$
and for any
$\alpha, \varepsilon \in [0, 1]$
and for any ![]() $x_1, x_2 \in E$
,
$x_1, x_2 \in E$
, ![]() $\mu \in \mathcal{P}(\textbf{E}_{n-1})$
and any
$\mu \in \mathcal{P}(\textbf{E}_{n-1})$
and any ![]() $n \in \{1,2\}$
,
$n \in \{1,2\}$
,
 \begin{align*} L_1(\{x_1\}) &\coloneqq 1/2, \quad L_2(x_1, \{x_2\}) \coloneqq \alpha {\textbf{1}}\{x_2 = x_1\} + (1-\alpha) {\textbf{1}}\{x_2 \neq x_1\},\\[3pt] g_n(x_n, y_n) &\coloneqq 0.99 {\textbf{1}}\{y_n = x_n\} + 0.01 {\textbf{1}}\{y_n \neq x_n\},\\[3pt] {K_{n}^{\mu}}(\textbf{x}_{n}, \,\cdot\,) &\coloneqq \varepsilon \delta_{\textbf{x}_{n}} + (1-\varepsilon) {\Phi_{n}^{\mu}}.\end{align*}
\begin{align*} L_1(\{x_1\}) &\coloneqq 1/2, \quad L_2(x_1, \{x_2\}) \coloneqq \alpha {\textbf{1}}\{x_2 = x_1\} + (1-\alpha) {\textbf{1}}\{x_2 \neq x_1\},\\[3pt] g_n(x_n, y_n) &\coloneqq 0.99 {\textbf{1}}\{y_n = x_n\} + 0.01 {\textbf{1}}\{y_n \neq x_n\},\\[3pt] {K_{n}^{\mu}}(\textbf{x}_{n}, \,\cdot\,) &\coloneqq \varepsilon \delta_{\textbf{x}_{n}} + (1-\varepsilon) {\Phi_{n}^{\mu}}.\end{align*}
While this is clearly only a toy model, we consider it for two reasons. Firstly, it allows us to analytically evaluate the asymptotic variances for standard PFs and MCMC-PFs given in (20), (21), (22) and (23). Secondly, as discussed in [Reference Johansen and Doucet18], the model allows us to select the parameter ![]() $\alpha$
in such a way that the FA-APF has either a lower or a higher asymptotic variance than the BPF.
$\alpha$
in such a way that the FA-APF has either a lower or a higher asymptotic variance than the BPF.
Figure 1 displays the asymptotic variances relative to the asymptotic variance of the standard BPF for the test function ![]() $f_2(\textbf{x}_{2}) = x_2$
for two different values of the parameter
$f_2(\textbf{x}_{2}) = x_2$
for two different values of the parameter ![]() $\alpha$
. As displayed in the first panel, a relatively large value of
$\alpha$
. As displayed in the first panel, a relatively large value of ![]() $\alpha$
leads to the somewhat contrived case that the BPF is more efficient than the FA-APF. However, as displayed in the second panel, a small value of
$\alpha$
leads to the somewhat contrived case that the BPF is more efficient than the FA-APF. However, as displayed in the second panel, a small value of ![]() $\alpha$
makes the FA-APF more efficient than the BPF. This is because if the system is in state 0 at time 1, the time-2 proposal used by the FA-APF incorporates the observation
$\alpha$
makes the FA-APF more efficient than the BPF. This is because if the system is in state 0 at time 1, the time-2 proposal used by the FA-APF incorporates the observation ![]() $y_2 = 0$
, whereas the time-2 proposal used by the BPF almost always proposes moves to state 1. In this case, the MCMC-FA-APF then outperforms the BPF as long as the autocorrelation of the MCMC kernels used by the former,
$y_2 = 0$
, whereas the time-2 proposal used by the BPF almost always proposes moves to state 1. In this case, the MCMC-FA-APF then outperforms the BPF as long as the autocorrelation of the MCMC kernels used by the former, ![]() $\varepsilon$
, is not too large.
$\varepsilon$
, is not too large.

Figure 1: Asymptotic variances (relative to the asymptotic variance of the BPF) of the algorithms discussed in Subsection 4.2 in the case that the BPF flow is more efficient than the FA-APF flow (first panel) and in the case that the BPF flow is less efficient than the FA-APF flow (second panel).
We stress that in practical situations, one might expect a much more pronounced difference between the performance of the FA-APF and the BPF than is observed in this toy model; hence Markov kernels with rather modest mixing properties can sometimes still give rise to an MCMC-FA-APF that outperforms the BPF. Indeed, such algorithms showed dramatic improvements in the practical applications in [Reference Septier and Peters32], and the MCMC-FA-APF also outperforms the BPF in our second model, discussed below.
The second model is a d-dimensional linear Gaussian state-space model. Let ![]() $E = F \coloneqq \mathbb{R}^d$
and write realisations of the d-dimensional state and observation vectors at time n as
$E = F \coloneqq \mathbb{R}^d$
and write realisations of the d-dimensional state and observation vectors at time n as ![]() $x_n = (x_{n,i})_{1 \leq i \leq d}$
and
$x_n = (x_{n,i})_{1 \leq i \leq d}$
and ![]() $y_n = (y_{n,i})_{1 \leq i \leq d}$
, respectively; then
$y_n = (y_{n,i})_{1 \leq i \leq d}$
, respectively; then
 \begin{align*} \frac{\textrm{d} L_1}{\textrm{d} \lambda^{\otimes d}}(x_1) &= \prod_{i=1}^d \phi(x_{1,i}), \quad \frac{\textrm{d} L_n(x_{n-1}, \,\cdot\,)}{\textrm{d} \lambda^{\otimes d}}(x_n) = \prod_{i=1}^{\smash{d}} \phi(x_{n,i} - x_{n-1,i}/2),\\[3pt] g_n(x_n, y_n) &= \prod_{i=1}^d \phi(x_{n,i} - y_{n,i}),\end{align*}
\begin{align*} \frac{\textrm{d} L_1}{\textrm{d} \lambda^{\otimes d}}(x_1) &= \prod_{i=1}^d \phi(x_{1,i}), \quad \frac{\textrm{d} L_n(x_{n-1}, \,\cdot\,)}{\textrm{d} \lambda^{\otimes d}}(x_n) = \prod_{i=1}^{\smash{d}} \phi(x_{n,i} - x_{n-1,i}/2),\\[3pt] g_n(x_n, y_n) &= \prod_{i=1}^d \phi(x_{n,i} - y_{n,i}),\end{align*}
where ![]() $\lambda$
denotes the Lebesgue measure on
$\lambda$
denotes the Lebesgue measure on ![]() $\mathbb{R}$
and
$\mathbb{R}$
and ![]() $\phi$
denotes a Lebesgue-density of a univariate standard normal distribution. We take
$\phi$
denotes a Lebesgue-density of a univariate standard normal distribution. We take ![]() ${K_{n}^{\mu}}(\textbf{x}_{n}, \,\cdot\,)$
to be an MH kernel with proposal
${K_{n}^{\mu}}(\textbf{x}_{n}, \,\cdot\,)$
to be an MH kernel with proposal
 \begin{align*} {\Pi_{n}^{\mu}}(\textbf{x}_n, \textrm{d} \textbf{z}_n) & = \begin{dcases} R(x_1, \textrm{d} z_1) & \text{if $n = 1$,}\\[3pt] \frac{F_{n-1}(\textbf{z}_{n-1})}{\mu(F_{n-1})} \mu(\textrm{d} \textbf{z}_{n-1}) R(x_n, \textrm{d} z_n) & \text{if $n > 1$,} \end{dcases}\end{align*}
\begin{align*} {\Pi_{n}^{\mu}}(\textbf{x}_n, \textrm{d} \textbf{z}_n) & = \begin{dcases} R(x_1, \textrm{d} z_1) & \text{if $n = 1$,}\\[3pt] \frac{F_{n-1}(\textbf{z}_{n-1})}{\mu(F_{n-1})} \mu(\textrm{d} \textbf{z}_{n-1}) R(x_n, \textrm{d} z_n) & \text{if $n > 1$,} \end{dcases}\end{align*}
where R is a Gaussian random-walk kernel on E with transition density
 \begin{align*} \frac{\textrm{d} R(x_{n}, \,\cdot\,)}{\textrm{d} \lambda^{\otimes d}}(z_n) = \prod_{i=1}^d \sqrt{d} \phi(\sqrt{d}[z_{n,i} - x_{n,i}]),\end{align*}
\begin{align*} \frac{\textrm{d} R(x_{n}, \,\cdot\,)}{\textrm{d} \lambda^{\otimes d}}(z_n) = \prod_{i=1}^d \sqrt{d} \phi(\sqrt{d}[z_{n,i} - x_{n,i}]),\end{align*}
and where ![]() $F_n(\textbf{x}_n) = g_n(x_n, y_n)$
for the MCMC-BPF and
$F_n(\textbf{x}_n) = g_n(x_n, y_n)$
for the MCMC-BPF and ![]() $F_n \equiv 1$
for the MCMC-FA-APF.
$F_n \equiv 1$
for the MCMC-FA-APF.
For the MCMC-BPF, the MCMC chains at each time step are initialised from stationarity, i.e.
as this is almost always possible in practice. For the MCMC-FA-APF, the MCMC chains are initialised by discarding the first ![]() $N_{\textrm{burnin}} = 100$
samples as burn-in, i.e.
$N_{\textrm{burnin}} = 100$
samples as burn-in, i.e. ![]() $\kappa_n^\mu = [\mu \mathbin{\otimes} L_n]({K_{n}^{\mu}})^{N_{\textrm{burnin}}}$
.
$\kappa_n^\mu = [\mu \mathbin{\otimes} L_n]({K_{n}^{\mu}})^{N_{\textrm{burnin}}}$
.
Figure 2 displays estimates of the marginal likelihood relative to the true marginal likelihood obtained from the (MCMC-)BPF and (MCMC-)FA-APF. In this case, the MCMC-FA-APF outperforms the BPF in both dimension ![]() $d=1$
and
$d=1$
and ![]() $d=5$
.
$d=5$
.

Figure 2: Relative estimates of the marginal likelihood ![]() $\mathcal{L}_n$
in the linear Gaussian state-space model, generated by the algorithms discussed in Subsection 4.2 using
$\mathcal{L}_n$
in the linear Gaussian state-space model, generated by the algorithms discussed in Subsection 4.2 using ![]() $N=10,000$
particles (with the MCMC-FA-APF using
$N=10,000$
particles (with the MCMC-FA-APF using ![]() $N=10,000 - N_{\textrm{burnin}}$
particles to compensate for the additional cost of generating the samples discarded as burn-in). Based on 1,000 independent runs of each algorithm, each run using a different observation sequence of length
$N=10,000 - N_{\textrm{burnin}}$
particles to compensate for the additional cost of generating the samples discarded as burn-in). Based on 1,000 independent runs of each algorithm, each run using a different observation sequence of length ![]() $n=10$
sampled from the model. For the BPF flow,
$n=10$
sampled from the model. For the BPF flow, ![]() $\mathcal{L}_n = \mathcal{Z}_{n+1} = \gamma_n(G_n)$
is estimated by
$\mathcal{L}_n = \mathcal{Z}_{n+1} = \gamma_n(G_n)$
is estimated by ![]() $\mathcal{L}_n^N \coloneqq \gamma_n^N(G_n)$
; for the FA-APF flow,
$\mathcal{L}_n^N \coloneqq \gamma_n^N(G_n)$
; for the FA-APF flow, ![]() $\mathcal{L}_n = \mathcal{Z}_n = \gamma_n(\textbf{1})$
is estimated by
$\mathcal{L}_n = \mathcal{Z}_n = \gamma_n(\textbf{1})$
is estimated by ![]() $\mathcal{L}_n^N \coloneqq \mathcal{Z}_n^N = \gamma_n^N(\textbf{1})$
.
$\mathcal{L}_n^N \coloneqq \mathcal{Z}_n^N = \gamma_n^N(\textbf{1})$
.
Note that Assumptions A1–A2 and B1–B3 are violated in this example. The results therefore appear to lend some support to the conjecture that these assumptions are stronger than necessary for the results of Propositions 1–2 to hold.
5. Conclusion
In this work, we have established an ![]() $\mathbb{L}_r$
-inequality (which implies an SLLN) and a central limit theorem for a class of algorithms known as sequential MCMC methods or or MCMC particle filters (MCMC-PFs) and provided conditions under which the associated errors can be controlled uniformly in time. When the MCMC-PFs are based around MCMC operators that are positive (in the sense of inducing positive autocorrelations of all orders), the asymptotic variances of particle filter (PF) estimators are always lower than those of the corresponding MCMC-PF estimators. However, even if the MCMC kernels provide positively correlated draws, MCMC-PFs can remain of practical interest compared to PFs. Indeed, there are many scenarios in which a sophisticated PF such as the fully-adapted auxiliary particle filter (FA-APF) would significantly outperform a bootstrap particle filter (BPF) but cannot be implemented, whereas the corresponding MCMC-FA-APF is essentially always applicable. If the MCMC operators used within the MCMC-FA-APF are thus displaying ‘reasonable’ integrated autocorrelation time, the asymptotic variance of the resulting estimators can be smaller than that of an implementable PF such as the BPF.
$\mathbb{L}_r$
-inequality (which implies an SLLN) and a central limit theorem for a class of algorithms known as sequential MCMC methods or or MCMC particle filters (MCMC-PFs) and provided conditions under which the associated errors can be controlled uniformly in time. When the MCMC-PFs are based around MCMC operators that are positive (in the sense of inducing positive autocorrelations of all orders), the asymptotic variances of particle filter (PF) estimators are always lower than those of the corresponding MCMC-PF estimators. However, even if the MCMC kernels provide positively correlated draws, MCMC-PFs can remain of practical interest compared to PFs. Indeed, there are many scenarios in which a sophisticated PF such as the fully-adapted auxiliary particle filter (FA-APF) would significantly outperform a bootstrap particle filter (BPF) but cannot be implemented, whereas the corresponding MCMC-FA-APF is essentially always applicable. If the MCMC operators used within the MCMC-FA-APF are thus displaying ‘reasonable’ integrated autocorrelation time, the asymptotic variance of the resulting estimators can be smaller than that of an implementable PF such as the BPF.
Appendix A. Sampling error decomposition
A.1. Proof strategy
Recall that given an approximation ![]() $\smash{\eta^{N}_{p-1}}$
of
$\smash{\eta^{N}_{p-1}}$
of ![]() $\eta_{p-1}$
, Algorithm 1 replaces
$\eta_{p-1}$
, Algorithm 1 replaces ![]() $\smash{{\Phi_{p}^{\eta^{N}_{p-1}}}}$
by a sampling-approximation
$\smash{{\Phi_{p}^{\eta^{N}_{p-1}}}}$
by a sampling-approximation ![]() $\smash{\eta_{p}^N}$
which is generated via an MCMC algorithm. This strategy is necessary because
$\smash{\eta_{p}^N}$
which is generated via an MCMC algorithm. This strategy is necessary because ![]() $\smash{{\Phi_{p}^{\mu}}}$
is typically intractable for any probability measure
$\smash{{\Phi_{p}^{\mu}}}$
is typically intractable for any probability measure ![]() $\mu$
. However, it introduces an additional local error at each time step.
$\mu$
. However, it introduces an additional local error at each time step.
In this section, we relate the ‘global’ approximation error at time n, ![]() $\smash{\eta_n^N(\,f_n) -\eta_n(\,f_n)}$
, to the local errors introduced at times
$\smash{\eta_n^N(\,f_n) -\eta_n(\,f_n)}$
, to the local errors introduced at times ![]() $1 \leq p \leq n$
via a well-known telescoping-sum decomposition. Key to the proofs of our main results is then a martingale approximation of the local errors given in Section B. The proofs of Propositions 1 and 2 and are then given in Section C. Specifically, in Subsection C.2, we give a proof of the
$1 \leq p \leq n$
via a well-known telescoping-sum decomposition. Key to the proofs of our main results is then a martingale approximation of the local errors given in Section B. The proofs of Propositions 1 and 2 and are then given in Section C. Specifically, in Subsection C.2, we give a proof of the ![]() $\mathbb{L}_r$
-inequality (Proposition 1) which relies on induction (in the time index p). In this context, the martingale approximation allows us to appeal to the Burkholder–Davis–Gundy inequality for martingales to control the local error at time p in
$\mathbb{L}_r$
-inequality (Proposition 1) which relies on induction (in the time index p). In this context, the martingale approximation allows us to appeal to the Burkholder–Davis–Gundy inequality for martingales to control the local error at time p in ![]() $\mathbb{L}_r$
. Similarly, in Subsection C.3, we give a proof of the CLT (Proposition 2). In this context, the martingale approximation allows us to appeal to the CLT for triangular arrays of martingale difference sequences in order to show that the local errors converge in distribution to independent centred Gaussian random variables.
$\mathbb{L}_r$
. Similarly, in Subsection C.3, we give a proof of the CLT (Proposition 2). In this context, the martingale approximation allows us to appeal to the CLT for triangular arrays of martingale difference sequences in order to show that the local errors converge in distribution to independent centred Gaussian random variables.
To simplify the notation, for any ![]() $n \geq 1$
, we will hereafter often write
$n \geq 1$
, we will hereafter often write
 \begin{align*} {\Phi_{n}^{N}} & \coloneqq {\Phi_{n}^{\eta^{N}_{n-1}}}, \quad {K_{n}^{N}} \coloneqq {K_{n}^{\eta^{N}_{n-1}}}, \quad {T_{n}^{N}} \coloneqq {T_{n}^{\eta^{N}_{n-1}}}, \quad {C_{n}^{N}} \coloneqq {C_{n}^{\eta^{N}_{n-1}}},\\ {\Phi_{n}^{}} &\coloneqq {\Phi_{n}^{\eta_{n-1}}} (= \eta_n), \quad {K_{n}^{}} \coloneqq {K_{n}^{\eta_{n-1}}}, \quad {T_{n}^{}} \coloneqq {T_{n}^{\eta_{n-1}}}, \quad {C_{n}^{}} \coloneqq {C_{n}^{\eta_{n-1}}}.\end{align*}
\begin{align*} {\Phi_{n}^{N}} & \coloneqq {\Phi_{n}^{\eta^{N}_{n-1}}}, \quad {K_{n}^{N}} \coloneqq {K_{n}^{\eta^{N}_{n-1}}}, \quad {T_{n}^{N}} \coloneqq {T_{n}^{\eta^{N}_{n-1}}}, \quad {C_{n}^{N}} \coloneqq {C_{n}^{\eta^{N}_{n-1}}},\\ {\Phi_{n}^{}} &\coloneqq {\Phi_{n}^{\eta_{n-1}}} (= \eta_n), \quad {K_{n}^{}} \coloneqq {K_{n}^{\eta_{n-1}}}, \quad {T_{n}^{}} \coloneqq {T_{n}^{\eta_{n-1}}}, \quad {C_{n}^{}} \coloneqq {C_{n}^{\eta_{n-1}}}.\end{align*}
In addition, for any ![]() $1 \leq p \leq n$
and any
$1 \leq p \leq n$
and any ![]() $f_n \in \mathcal{B}(\textbf{E}_n)$
, we define the family of probability measures
$f_n \in \mathcal{B}(\textbf{E}_n)$
, we define the family of probability measures ![]() $\smash{{\Phi_{p,n}^{\mu}}}$
associated with the Feynman–Kac model by
$\smash{{\Phi_{p,n}^{\mu}}}$
associated with the Feynman–Kac model by ![]() $\smash{{\Phi_{p,n}^{\mu}}(\,f_n) \coloneqq \mu Q_{p,n}(\,f_n) /\mu Q_{p,n}(\textbf{1})}$
. Furthermore, we allow
$\smash{{\Phi_{p,n}^{\mu}}(\,f_n) \coloneqq \mu Q_{p,n}(\,f_n) /\mu Q_{p,n}(\textbf{1})}$
. Furthermore, we allow ![]() $\smash{f \coloneqq (\,f_n)_{n \geq 1}}$
to denote a sequence of test functions where for any
$\smash{f \coloneqq (\,f_n)_{n \geq 1}}$
to denote a sequence of test functions where for any ![]() $n \geq 1$
,
$n \geq 1$
, ![]() $\smash{f_n = (\,f_n^u)_{1 \leq u \leq d} \in \mathcal{B}(\textbf{E}_n)^d}$
. For any
$\smash{f_n = (\,f_n^u)_{1 \leq u \leq d} \in \mathcal{B}(\textbf{E}_n)^d}$
. For any ![]() $\smash{1 \leq u \leq d}$
, we also sometimes write
$\smash{1 \leq u \leq d}$
, we also sometimes write ![]() $\smash{f^u \coloneqq (\,f_n^u)_{n \geq 1}}$
.
$\smash{f^u \coloneqq (\,f_n^u)_{n \geq 1}}$
.
A.2. Global-error decomposition
To control the overall approximation error at time n, we make use of a telescoping-sum decomposition commonly used in the analysis of Feynman-Kac models (see, e.g., [Reference Del Moral10, Chapter 7]):
 \begin{align} \sqrt{N}[\eta_n^N- \eta_n](\,f_n) & = \sqrt{N} \sum_{p=1}^n {\Phi_{p,n}^{\eta_p^N}}(\,f_n) - {\Phi_{p,n}^{{\Phi_{p}}^{N}}}(\,f_n). \end{align}
\begin{align} \sqrt{N}[\eta_n^N- \eta_n](\,f_n) & = \sqrt{N} \sum_{p=1}^n {\Phi_{p,n}^{\eta_p^N}}(\,f_n) - {\Phi_{p,n}^{{\Phi_{p}}^{N}}}(\,f_n). \end{align}
Here, we recall that ![]() $\smash{{\Phi_{1}^{\mu}}}$
does not depend on
$\smash{{\Phi_{1}^{\mu}}}$
does not depend on ![]() $\mu$
, so that
$\mu$
, so that ![]() $\smash{{\Phi_{1}^{\eta^{N}_{0}}} = {\Phi_{1}^{N}} = \eta_1}$
without the need for actually defining
$\smash{{\Phi_{1}^{\eta^{N}_{0}}} = {\Phi_{1}^{N}} = \eta_1}$
without the need for actually defining ![]() $\smash{\eta_{0}^N}$
. Note that the pth term in the sum on the right-hand side can be viewed as the part of the overall approximation error at time n that can be attributed to the local error introduced at time p. Specifically, the local error at time p is a consequence of propagating the particle system from time
$\smash{\eta_{0}^N}$
. Note that the pth term in the sum on the right-hand side can be viewed as the part of the overall approximation error at time n that can be attributed to the local error introduced at time p. Specifically, the local error at time p is a consequence of propagating the particle system from time ![]() $p-1$
to time p not by the nonlinear semigroup of the limiting model, which would yield
$p-1$
to time p not by the nonlinear semigroup of the limiting model, which would yield ![]() $\smash{{\Phi_{p}^{N}}}$
, but by forming an approximation
$\smash{{\Phi_{p}^{N}}}$
, but by forming an approximation ![]() $\smash{\eta_p^N}$
of
$\smash{\eta_p^N}$
of ![]() $\smash{{\Phi_{p}^{N}}}$
via MCMC sampling. That is, the local error at time p—which is propagated to time n via the probability measures
$\smash{{\Phi_{p}^{N}}}$
via MCMC sampling. That is, the local error at time p—which is propagated to time n via the probability measures ![]() $\smash{{\Phi_{p,n}^{\mu}}}$
in (24)—is given by
$\smash{{\Phi_{p,n}^{\mu}}}$
in (24)—is given by
It is well known (see Subsection C.1
for details) that the ‘strong mixing’ Assumption is sufficient to guarantee stability of the probability measures ![]() $\smash{{\Phi_{p,n}^{\mu}}}$
, so that the influence of earlier local errors diminishes over time. This stability property therefore plays a key rôle in establishing the time-uniform bounds on the
$\smash{{\Phi_{p,n}^{\mu}}}$
, so that the influence of earlier local errors diminishes over time. This stability property therefore plays a key rôle in establishing the time-uniform bounds on the ![]() $\mathbb{L}_r$
-errors and on the asymptotic variance in Propositions 1 and 2.
$\mathbb{L}_r$
-errors and on the asymptotic variance in Propositions 1 and 2.
A.3. Local-error decomposition
For the purpose of isolating the part of the error that is due to to a potential non-stationary initialisation of the MCMC chains, let ![]() $\smash{({\tilde{\boldsymbol{\xi}}_{{p}}^{i}})_{i \geq 1}}$
be a Markov chain which evolves according to the same transition kernels as
$\smash{({\tilde{\boldsymbol{\xi}}_{{p}}^{i}})_{i \geq 1}}$
be a Markov chain which evolves according to the same transition kernels as ![]() $\smash{({\boldsymbol{\xi}_{{p}}^{i}})_{i \geq 1}}$
but which is initialised from stationarity, i.e.
$\smash{({\boldsymbol{\xi}_{{p}}^{i}})_{i \geq 1}}$
but which is initialised from stationarity, i.e. ![]() $\smash{{\tilde{\boldsymbol{\xi}}_{{p}}^{1}} \sim {\Phi_{p}^{N}}}$
and
$\smash{{\tilde{\boldsymbol{\xi}}_{{p}}^{1}} \sim {\Phi_{p}^{N}}}$
and ![]() $\smash{{\tilde{\boldsymbol{\xi}}_{{p}}^{i}} \sim {K_{n}^{N}}({\tilde{\boldsymbol{\xi}}_{{p}}^{i-1}}, \,\cdot\,)}$
, for
$\smash{{\tilde{\boldsymbol{\xi}}_{{p}}^{i}} \sim {K_{n}^{N}}({\tilde{\boldsymbol{\xi}}_{{p}}^{i-1}}, \,\cdot\,)}$
, for ![]() $2 \leq i \leq N$
. Furthermore, let
$2 \leq i \leq N$
. Furthermore, let ![]() $\smash{\tilde{\eta}_p^N \coloneqq \frac{1}{N}\sum_{i=1}^N \delta_{{\tilde{\boldsymbol{\xi}}_{{p}}^{i}}}}$
denote the associated occupation measure. The local error defined in (25) can then be decomposed as
$\smash{\tilde{\eta}_p^N \coloneqq \frac{1}{N}\sum_{i=1}^N \delta_{{\tilde{\boldsymbol{\xi}}_{{p}}^{i}}}}$
denote the associated occupation measure. The local error defined in (25) can then be decomposed as
where
 \begin{align} \widetilde{V}_p^N(\,f_p) & \coloneqq \sqrt{N}[\tilde{\eta}_p^N - {\Phi_{p}^{N}}](\,f_p),\nonumber\\ R_p^N(\,f_p) & \coloneqq \sqrt{N}[\eta_p^N - \tilde{\eta}_p^N](\,f_p),\end{align}
\begin{align} \widetilde{V}_p^N(\,f_p) & \coloneqq \sqrt{N}[\tilde{\eta}_p^N - {\Phi_{p}^{N}}](\,f_p),\nonumber\\ R_p^N(\,f_p) & \coloneqq \sqrt{N}[\eta_p^N - \tilde{\eta}_p^N](\,f_p),\end{align}
represent, respectively, the local error introduced at time p if the MCMC chain used to generate the sampling-approximation of ![]() $\smash{{\Phi_{p}^{N}}}$
is initialised from stationarity and the additional error due to non-stationary initialisation. Tighter control of the latter could be obtained by explicitly coupling
$\smash{{\Phi_{p}^{N}}}$
is initialised from stationarity and the additional error due to non-stationary initialisation. Tighter control of the latter could be obtained by explicitly coupling ![]() $\smash{({\tilde{\boldsymbol{\xi}}}{}^{i}_{p})_{i \geq 1}}$
and
$\smash{({\tilde{\boldsymbol{\xi}}}{}^{i}_{p})_{i \geq 1}}$
and ![]() $\smash{({\boldsymbol{\xi}_{{p}}^{i}})_{i \geq 1}}$
, but it is sufficient for our purposes to treat the two systems as being entirely independent.
$\smash{({\boldsymbol{\xi}_{{p}}^{i}})_{i \geq 1}}$
, but it is sufficient for our purposes to treat the two systems as being entirely independent.
Using the tower property of conditional expectation, it can be easily checked that ![]() $\smash{\mathbb{E}[\widetilde{V}_p^N(\,f_p)] = 0}$
as in standard PFs. However, contrary to standard PFs, the particles
$\smash{\mathbb{E}[\widetilde{V}_p^N(\,f_p)] = 0}$
as in standard PFs. However, contrary to standard PFs, the particles ![]() $\smash{{\tilde{\boldsymbol{\xi}}}{}^{i}_{p}}$
and
$\smash{{\tilde{\boldsymbol{\xi}}}{}^{i}_{p}}$
and ![]() $\smash{{\tilde{\boldsymbol{\xi}}}{}^{j}_{p}}$
, for
$\smash{{\tilde{\boldsymbol{\xi}}}{}^{j}_{p}}$
, for ![]() $i \neq j$
, are not necessarily conditionally independent given
$i \neq j$
, are not necessarily conditionally independent given ![]() $\smash{\mathcal{F}_{p-1}^{N,N}}$
, where
$\smash{\mathcal{F}_{p-1}^{N,N}}$
, where ![]() $\smash{\mathcal{F}_{0}^{N,N} \coloneqq \{\emptyset, \Omega\}}$
and, for any
$\smash{\mathcal{F}_{0}^{N,N} \coloneqq \{\emptyset, \Omega\}}$
and, for any ![]() $p \geq 1$
and
$p \geq 1$
and ![]() $1 \leq k \leq N$
,
$1 \leq k \leq N$
,
Because of the lack of conditional independence, we obtain, for any ![]() $1 \leq u \leq d$
,
$1 \leq u \leq d$
,
 \begin{align} \!\!\!\!\!\!\!\mathbb{E}[\widetilde{V}_p^N(\,f_p^u)^2] & = \mathbb{E}\Bigl[\mathbb{E}\bigl(\widetilde{V}_p^N(\,f_p^u)^2\big|\mathcal{F}_{p-1}^{N,N}\bigr)\Bigr] \nonumber\\[4pt] & = \mathbb{E}\Bigl[{\Phi_{p}^{N}}\bigl[(\,f_p^u- {\Phi_{p}^{N}}(\,f_p^u))^2\bigr]\Bigr]\nonumber\\[4pt] & \quad + 2 \sum_{j=1}^{N-1}\biggl(1-\frac{j}{N}\biggr) \mathbb{E}\Bigl[{\Phi_{p}^{N}}\bigl[(\,f_p^u- {\Phi_{p}^{N}}(\,f_p^u))({K_{p}^{N}})^j(\,f_p^u- {\Phi_{p}^{N}}(\,f_p^u))\bigr]\Bigr].\!\!\!\!\!\!\!\! \end{align}
\begin{align} \!\!\!\!\!\!\!\mathbb{E}[\widetilde{V}_p^N(\,f_p^u)^2] & = \mathbb{E}\Bigl[\mathbb{E}\bigl(\widetilde{V}_p^N(\,f_p^u)^2\big|\mathcal{F}_{p-1}^{N,N}\bigr)\Bigr] \nonumber\\[4pt] & = \mathbb{E}\Bigl[{\Phi_{p}^{N}}\bigl[(\,f_p^u- {\Phi_{p}^{N}}(\,f_p^u))^2\bigr]\Bigr]\nonumber\\[4pt] & \quad + 2 \sum_{j=1}^{N-1}\biggl(1-\frac{j}{N}\biggr) \mathbb{E}\Bigl[{\Phi_{p}^{N}}\bigl[(\,f_p^u- {\Phi_{p}^{N}}(\,f_p^u))({K_{p}^{N}})^j(\,f_p^u- {\Phi_{p}^{N}}(\,f_p^u))\bigr]\Bigr].\!\!\!\!\!\!\!\! \end{align}
To see this, note that (conditional on ![]() $\smash{\mathcal{F}_{p-1}^{N,N}}$
) the inner expectation in (28) is simply the variance of
$\smash{\mathcal{F}_{p-1}^{N,N}}$
) the inner expectation in (28) is simply the variance of ![]() $\smash{ N^{-1/2} \sum_{i=1}^N h(\textbf{Y}^i)}$
, where
$\smash{ N^{-1/2} \sum_{i=1}^N h(\textbf{Y}^i)}$
, where ![]() $\smash{h(\textbf{y}) \coloneqq f_p^u(\textbf{y}) - {\Phi_{p}^{N}}(\,f_p^u)}$
and where
$\smash{h(\textbf{y}) \coloneqq f_p^u(\textbf{y}) - {\Phi_{p}^{N}}(\,f_p^u)}$
and where ![]() $(\textbf{Y}^i)_{i \geq 1}$
is a stationary Markov chain with invariant distribution
$(\textbf{Y}^i)_{i \geq 1}$
is a stationary Markov chain with invariant distribution ![]() ${\Phi_{p}^{N}}$
and transition kernels
${\Phi_{p}^{N}}$
and transition kernels ![]() $\smash{{K_{p}^{N}}}$
. The last line then follows by exploiting stationarity of that Markov chain and grouping equivalent terms. This is a generalisation, when
$\smash{{K_{p}^{N}}}$
. The last line then follows by exploiting stationarity of that Markov chain and grouping equivalent terms. This is a generalisation, when ![]() ${K_{p}^{\mu}}$
is not perfectly mixing, of the result for a standard PF in which
${K_{p}^{\mu}}$
is not perfectly mixing, of the result for a standard PF in which ![]() $\smash{{K_{p}^{\mu}}(\textbf{x}_p, \,\cdot\,) = {\Phi_{p}^{\mu}} = {\kappa_{p}^{\mu}}}$
for all
$\smash{{K_{p}^{\mu}}(\textbf{x}_p, \,\cdot\,) = {\Phi_{p}^{\mu}} = {\kappa_{p}^{\mu}}}$
for all ![]() $\textbf{x}_p \in \textbf{E}_p$
, in which case
$\textbf{x}_p \in \textbf{E}_p$
, in which case
Following [Reference Del Moral and Doucet11], [Reference Bercu, Del Moral and Doucet5], we further decompose (26) as
 \begin{align*} \widetilde{V}_p^N(\,f_p) & = \frac{1}{\sqrt{N}} \sum_{i=1}^N \bigl[\,f_p({\tilde{\boldsymbol{\xi}}}{}^{i}_{p}) - {\Phi_{p}^{N}}(\,f_p)\bigr]\\ & = \frac{1}{\sqrt{N}}\sum_{i=1}^{\smash{N}} \bigl[{T_{p}^{N}}(\,f_p)({\tilde{\boldsymbol{\xi}}}{}^{i}_{p}) - {K_{p}^{N}}{T_{p}^{N}}(\,f_p)({\tilde{\boldsymbol{\xi}}}{}^{i}_{p})\bigr] \quad \text{[by (\linkref{10}{10})]}\\ & = U_p^N(\,f_p) + L_p^{N}(\,f_p), \end{align*}
\begin{align*} \widetilde{V}_p^N(\,f_p) & = \frac{1}{\sqrt{N}} \sum_{i=1}^N \bigl[\,f_p({\tilde{\boldsymbol{\xi}}}{}^{i}_{p}) - {\Phi_{p}^{N}}(\,f_p)\bigr]\\ & = \frac{1}{\sqrt{N}}\sum_{i=1}^{\smash{N}} \bigl[{T_{p}^{N}}(\,f_p)({\tilde{\boldsymbol{\xi}}}{}^{i}_{p}) - {K_{p}^{N}}{T_{p}^{N}}(\,f_p)({\tilde{\boldsymbol{\xi}}}{}^{i}_{p})\bigr] \quad \text{[by (\linkref{10}{10})]}\\ & = U_p^N(\,f_p) + L_p^{N}(\,f_p), \end{align*}
where, letting ![]() $\smash{{\tilde{\boldsymbol{\xi}}}{}^{N+1}_{p}}$
be a random variable distributed, independently conditional upon
$\smash{{\tilde{\boldsymbol{\xi}}}{}^{N+1}_{p}}$
be a random variable distributed, independently conditional upon ![]() $\smash{\mathcal{F}_p^{N,N}}$
, according to
$\smash{\mathcal{F}_p^{N,N}}$
, according to ![]() ${{K_{p}^{N}}({\tilde{\boldsymbol{\xi}}}{}^{N}_{p}, \,\cdot\,)}$
, we have (weakly) defined
${{K_{p}^{N}}({\tilde{\boldsymbol{\xi}}}{}^{N}_{p}, \,\cdot\,)}$
, we have (weakly) defined
 \begin{align*} U_p^N(\,f_p) & \coloneqq \frac{1}{\sqrt{N}}\sum_{i=1}^N \bigl[{T_{p}^{N}}(\,f_p)({\tilde{\boldsymbol{\xi}}}{}^{i+1}_{p}) - {K_{p}^{N}}{T_{p}^{N}}(\,f_p)({\tilde{\boldsymbol{\xi}}}{}^{i}_{p})\bigr],\\ L_p^{N}(\,f_p) & \coloneqq \frac{1}{\sqrt{N}} \bigl[{T_{p}^{N}}(\,f_p)({\tilde{\boldsymbol{\xi}}}{}^{1}_{p}) - {T_{p}^{N}}(\,f_p)({\tilde{\boldsymbol{\xi}}}{}^{N+1}_{p})\bigr].\end{align*}
\begin{align*} U_p^N(\,f_p) & \coloneqq \frac{1}{\sqrt{N}}\sum_{i=1}^N \bigl[{T_{p}^{N}}(\,f_p)({\tilde{\boldsymbol{\xi}}}{}^{i+1}_{p}) - {K_{p}^{N}}{T_{p}^{N}}(\,f_p)({\tilde{\boldsymbol{\xi}}}{}^{i}_{p})\bigr],\\ L_p^{N}(\,f_p) & \coloneqq \frac{1}{\sqrt{N}} \bigl[{T_{p}^{N}}(\,f_p)({\tilde{\boldsymbol{\xi}}}{}^{1}_{p}) - {T_{p}^{N}}(\,f_p)({\tilde{\boldsymbol{\xi}}}{}^{N+1}_{p})\bigr].\end{align*}
This allows us to write the local error at time p as
In the next section, we show that the terms ![]() $\smash{L_p^{N}}$
and
$\smash{L_p^{N}}$
and ![]() $\smash{R_p^N}$
vanish as
$\smash{R_p^N}$
vanish as ![]() $N \to \infty$
, so that the local sampling error at time p,
$N \to \infty$
, so that the local sampling error at time p, ![]() $\smash{V_p^N}$
, can be approximated by
$\smash{V_p^N}$
, can be approximated by ![]() $\smash{U_p^N}$
. The latter has a martingale property which is at the centre of our proofs of the
$\smash{U_p^N}$
. The latter has a martingale property which is at the centre of our proofs of the ![]() $\mathbb{L}_r$
-inequality from Proposition 1 and the CLT from Proposition 2.
$\mathbb{L}_r$
-inequality from Proposition 1 and the CLT from Proposition 2.
Appendix B. Martingale construction
B.1. Martingale approximation at time p
For a given p, ![]() $1 \leq p \leq n$
, and every
$1 \leq p \leq n$
, and every ![]() $N \in \mathbb{N}$
, define the filtration
$N \in \mathbb{N}$
, define the filtration ![]() $\smash{\mathcal{F}_p^N \coloneqq (\mathcal{F}_p^{N,i})_{0 \leq i \leq N}}$
, where
$\smash{\mathcal{F}_p^N \coloneqq (\mathcal{F}_p^{N,i})_{0 \leq i \leq N}}$
, where ![]() $\smash{\mathcal{F}_p^{N,i}}$
is given by (27) with the convention that
$\smash{\mathcal{F}_p^{N,i}}$
is given by (27) with the convention that ![]() $\smash{\mathcal{F}_p^{N,0} = \mathcal{F}_{p-1}^{N,N}}$
. We now construct a martingale approximation of the local error at time p as the number of particles grows. That is, we show that for
$\smash{\mathcal{F}_p^{N,0} = \mathcal{F}_{p-1}^{N,N}}$
. We now construct a martingale approximation of the local error at time p as the number of particles grows. That is, we show that for ![]() $1 \leq p \leq n$
and each
$1 \leq p \leq n$
and each ![]() $N \in \mathbb{N}$
,
$N \in \mathbb{N}$
, ![]() $\smash{U_p^N(\,f_p)}$
is the terminal value of an
$\smash{U_p^N(\,f_p)}$
is the terminal value of an ![]() $\smash{\mathcal{F}_p^N}$
-martingale (and for fixed p these martingales, indexed by N, form a triangular array), while
$\smash{\mathcal{F}_p^N}$
-martingale (and for fixed p these martingales, indexed by N, form a triangular array), while ![]() $\smash{L_p^{N}(\,f_p)}$
and
$\smash{L_p^{N}(\,f_p)}$
and ![]() $\smash{R_p^N(\,f_p)}$
are remainder terms which vanish almost surely as
$\smash{R_p^N(\,f_p)}$
are remainder terms which vanish almost surely as ![]() $N \to \infty$
.
$N \to \infty$
.
• Martingale. For each
 $N\geq 1$
,
$N\geq 1$
,  $\smash{U_p^N(\,f_p) = \sum_{i=1}^N\varDelta U_p^{N,i+1}(\,f_p)}$
is the terminal value of a martingale defined through the
$\smash{U_p^N(\,f_p) = \sum_{i=1}^N\varDelta U_p^{N,i+1}(\,f_p)}$
is the terminal value of a martingale defined through the  $\smash{\mathcal{F}_p^N}$
-martingale difference sequence
$\smash{\mathcal{F}_p^N}$
-martingale difference sequence  $\smash{(\varDelta U_p^{N,i+1}(\,f_p))_{1 \leq i \leq N}}$
, whereIndeed, for any
$\smash{(\varDelta U_p^{N,i+1}(\,f_p))_{1 \leq i \leq N}}$
, whereIndeed, for any \begin{align*} \varDelta U_p^{N,i+1}(\,f_p) \coloneqq \frac{1}{\sqrt{N}}\bigl[{T_{p}^{N}}(\,f_p)({\tilde{\boldsymbol{\xi}}}{}^{i+1}_{p}) - {K_{p}^{N}}{T_{p}^{N}}(\,f_p)({\tilde{\boldsymbol{\xi}}}{}^{i}_{p})\bigr]. \end{align*}
\begin{align*} \varDelta U_p^{N,i+1}(\,f_p) \coloneqq \frac{1}{\sqrt{N}}\bigl[{T_{p}^{N}}(\,f_p)({\tilde{\boldsymbol{\xi}}}{}^{i+1}_{p}) - {K_{p}^{N}}{T_{p}^{N}}(\,f_p)({\tilde{\boldsymbol{\xi}}}{}^{i}_{p})\bigr]. \end{align*}
 $1 \leq i \leq N$
and any
$1 \leq i \leq N$
and any  $1 \leq u,v \leq d$
,
(30)
$1 \leq u,v \leq d$
,
(30) \begin{align} \mathbb{E}\bigl[\varDelta U_p^{N,i+1}(\,f_p^u)\big|\mathcal{F}_p^{N,i}\bigr] & = 0, \end{align}
(31)where the second line follows directly from the definition in (13).
\begin{align} \mathbb{E}\bigl[\varDelta U_p^{N,i+1}(\,f_p^u)\big|\mathcal{F}_p^{N,i}\bigr] & = 0, \end{align}
(31)where the second line follows directly from the definition in (13). \begin{align} \mathbb{E}\bigl[\varDelta U_p^{N,i+1}(\,f_p^u)\varDelta U_p^{N,i+1}(\,f_p^v)\big|\mathcal{F}_p^{N,i}\bigr] & = \frac{1}{N}{C_{p}^{N}}(\,f_p^u, f_p^v)({\tilde{\boldsymbol{\xi}}}{}^{i}_{p}), \end{align}
\begin{align} \mathbb{E}\bigl[\varDelta U_p^{N,i+1}(\,f_p^u)\varDelta U_p^{N,i+1}(\,f_p^v)\big|\mathcal{F}_p^{N,i}\bigr] & = \frac{1}{N}{C_{p}^{N}}(\,f_p^u, f_p^v)({\tilde{\boldsymbol{\xi}}}{}^{i}_{p}), \end{align}
• Remainder. By (12), for any
 $1 \leq u \leq d$
, the remainder signed measure
$1 \leq u \leq d$
, the remainder signed measure  $L_p^{N}$
is bounded as
(32)By (8 ), under Assumption , for any
$L_p^{N}$
is bounded as
(32)By (8 ), under Assumption , for any \begin{align} \lvert L_p^{N}(\,f_p^u) \rvert \leq \frac{2}{\sqrt{N}} \lvert {T_{p}^{N}}(\,f_p^u) \rvert \leq \frac{2 {\widebar{T}_{p}} \lVert f_p^u \rVert}{\sqrt{N}}. \end{align}
\begin{align} \lvert L_p^{N}(\,f_p^u) \rvert \leq \frac{2}{\sqrt{N}} \lvert {T_{p}^{N}}(\,f_p^u) \rvert \leq \frac{2 {\widebar{T}_{p}} \lVert f_p^u \rVert}{\sqrt{N}}. \end{align}
 $N, r \in \mathbb{N}$
and any
$N, r \in \mathbb{N}$
and any  $1 \leq u \leq d$
, we have
(33)Note that by Markov’s inequality and the Borel–Cantelli lemma, (33) implies that
$1 \leq u \leq d$
, we have
(33)Note that by Markov’s inequality and the Borel–Cantelli lemma, (33) implies that \begin{align} \mathbb{E}\bigl[ \lvert R_p^N(\,f_p^u)\rvert^r \bigr]^{\frac{1}{r}} \leq \frac{{\widebar{T}_{p}}\lVert f_p^u \rVert}{\sqrt{N}}. \end{align}
\begin{align} \mathbb{E}\bigl[ \lvert R_p^N(\,f_p^u)\rvert^r \bigr]^{\frac{1}{r}} \leq \frac{{\widebar{T}_{p}}\lVert f_p^u \rVert}{\sqrt{N}}. \end{align}
 $R_p^N(\,f_p^u) {\mathrel{\mathop{\rightarrow}\nolimits_{\text{\upshape{a.s.}}}}} 0$
as
$R_p^N(\,f_p^u) {\mathrel{\mathop{\rightarrow}\nolimits_{\text{\upshape{a.s.}}}}} 0$
as  $N \to \infty$
.
$N \to \infty$
.
B.2. Martingale approximation up to time n
For any ![]() $N \geq 1$
, the sum of all local errors up time n—of which we again construct a martingale approximation—is given by
$N \geq 1$
, the sum of all local errors up time n—of which we again construct a martingale approximation—is given by
 \begin{align*} \mathcal{V}_n^N(\,f) & \coloneqq \sum_{p=1}^n V_p^N(\,f_p) = \mathcal{U}_n^N(\,f) + \mathcal{L}_n^N(\,f) + \mathcal{R}_n^N(\,f).\end{align*}
\begin{align*} \mathcal{V}_n^N(\,f) & \coloneqq \sum_{p=1}^n V_p^N(\,f_p) = \mathcal{U}_n^N(\,f) + \mathcal{L}_n^N(\,f) + \mathcal{R}_n^N(\,f).\end{align*}
The three quantities appearing on the right-hand side are defined as follows.
• Martingale. Let
 $\smash{\mathcal{F}^N \coloneqq (\mathcal{F}_n^N)_{n \geq 1}}$
with
$\smash{\mathcal{F}^N \coloneqq (\mathcal{F}_n^N)_{n \geq 1}}$
with  $\smash{\mathcal{F}_p^N \coloneqq \mathcal{F}_p^{N,N}}$
; then the terms
define an
$\smash{\mathcal{F}_p^N \coloneqq \mathcal{F}_p^{N,N}}$
; then the terms
define an \begin{align*} \mathcal{U}_n^N(\,f) \coloneqq \sum_{p=1}^n U_p^N(\,f_p) \end{align*}
\begin{align*} \mathcal{U}_n^N(\,f) \coloneqq \sum_{p=1}^n U_p^N(\,f_p) \end{align*}
 $\smash{\mathcal{F}^N}$
-martingale
$\smash{\mathcal{F}^N}$
-martingale  $\smash{(\mathcal{U}_n^N(\,f))_{n \geq 1}}$
. As detailed in Section C.3, these martingales can be constructed by combining martingale increments from the local error decompositions in an appropriate lexicographic order. Again, we will treat this collection, indexed by N, as a triangular array.
$\smash{(\mathcal{U}_n^N(\,f))_{n \geq 1}}$
. As detailed in Section C.3, these martingales can be constructed by combining martingale increments from the local error decompositions in an appropriate lexicographic order. Again, we will treat this collection, indexed by N, as a triangular array.• Remainder. Again,
constitute remainder terms. Note that for any \begin{equation*} \mathcal{L}_n^N(\,f) \coloneqq \sum_{p=1}^n L_p^N(\,f_p) \quad \text{and} \quad \mathcal{R}_n^N(\,f) \coloneqq \sum_{p=1}^n R_p^N(\,f_p) \end{equation*}
\begin{equation*} \mathcal{L}_n^N(\,f) \coloneqq \sum_{p=1}^n L_p^N(\,f_p) \quad \text{and} \quad \mathcal{R}_n^N(\,f) \coloneqq \sum_{p=1}^n R_p^N(\,f_p) \end{equation*}
 $n \geq 1$
and any
$n \geq 1$
and any  $1 \leq u \leq d$
, by (32) and (33),
$1 \leq u \leq d$
, by (32) and (33),
 \begin{equation*} \lim_{N \to \infty} \lvert \mathcal{L}^{N}_{n}(f^u) \rvert = 0 \quad \text{and} \quad \lvert \mathcal{R}_n^N(\,f^u)\rvert {\mathrel{\mathop{\rightarrow}\nolimits_{\text{\upshape{a.s.}}}}} 0. \end{equation*}
\begin{equation*} \lim_{N \to \infty} \lvert \mathcal{L}^{N}_{n}(f^u) \rvert = 0 \quad \text{and} \quad \lvert \mathcal{R}_n^N(\,f^u)\rvert {\mathrel{\mathop{\rightarrow}\nolimits_{\text{\upshape{a.s.}}}}} 0. \end{equation*}
Appendix C. Convergence proofs
C.1. Auxiliary results needed for time-uniform bounds
For any ![]() $1 \leq p \leq n$
and any
$1 \leq p \leq n$
and any ![]() $f_n \in \mathcal{B}(\textbf{E}_n)$
, we define
$f_n \in \mathcal{B}(\textbf{E}_n)$
, we define
In the remainder of this work, whenever we restrict our analysis to test functions ![]() $f_n \in \smash{\mathcal{B}^\star(\textbf{E}_n)^d}$
, we can replace
$f_n \in \smash{\mathcal{B}^\star(\textbf{E}_n)^d}$
, we can replace ![]() $\beta(P_{p,n})$
by
$\beta(P_{p,n})$
by
where the supremum is over all ![]() $\textbf{x}_p, \textbf{z}_p \in \textbf{E}_p$
and all
$\textbf{x}_p, \textbf{z}_p \in \textbf{E}_p$
and all ![]() $f^{\prime}_n \in \smash{\mathcal{B}^\star(\textbf{E}_n)}$
such that
$f^{\prime}_n \in \smash{\mathcal{B}^\star(\textbf{E}_n)}$
such that ![]() $\lVert f^{\prime}_n\rVert \leq 1$
.
$\lVert f^{\prime}_n\rVert \leq 1$
.
Lemma 1. Under Assumptions and , for any ![]() $1 \leq p \leq n$
,
$1 \leq p \leq n$
,
 \begin{align*} {\widebar{T}_{p}} & \leq \widebar{T}, \quad \text{where} \quad \widebar{T} \coloneqq 2 \bar{\imath} / \varepsilon(K) < \infty;\\ r_{p,n} & \leq \bar{r}, \quad \text{where} \quad \bar{r} \coloneqq \varepsilon(G)^{-(m+l)} \varepsilon(M)^{-1} < \infty;\\ \beta^\star(P_{p,n}) & \leq \bar{\beta}^{\lfloor (n-p)/m \rfloor}, \quad \text{where} \quad \bar{\beta} \coloneqq (1 - \varepsilon(G)^{m+l} \varepsilon(M)^2) <1.\end{align*}
\begin{align*} {\widebar{T}_{p}} & \leq \widebar{T}, \quad \text{where} \quad \widebar{T} \coloneqq 2 \bar{\imath} / \varepsilon(K) < \infty;\\ r_{p,n} & \leq \bar{r}, \quad \text{where} \quad \bar{r} \coloneqq \varepsilon(G)^{-(m+l)} \varepsilon(M)^{-1} < \infty;\\ \beta^\star(P_{p,n}) & \leq \bar{\beta}^{\lfloor (n-p)/m \rfloor}, \quad \text{where} \quad \bar{\beta} \coloneqq (1 - \varepsilon(G)^{m+l} \varepsilon(M)^2) <1.\end{align*}
Proof. This follows by arguments similar to those used in the proof of [Reference Del Moral10, Proposition 4.3.3].
C.2. Auxiliary results needed for the  $\mathbb{L}_r$
-inequality
$\mathbb{L}_r$
-inequality
Lemma 2. Under Assumption , for any ![]() $r \geq 1$
, there exists
$r \geq 1$
, there exists ![]() ${b_{r}} < \infty$
such that for any
${b_{r}} < \infty$
such that for any ![]() $n \geq 1$
, any
$n \geq 1$
, any ![]() $f_n \in \mathcal{B}(\textbf{E}_n)$
, and any
$f_n \in \mathcal{B}(\textbf{E}_n)$
, and any ![]() $N \in \mathbb{N}$
,
$N \in \mathbb{N}$
,
Proof. Without loss of generality, assume that ![]() $\lVert f_n \rVert \leq 1$
. The quadratic variation associated with the martingale
$\lVert f_n \rVert \leq 1$
. The quadratic variation associated with the martingale ![]() $U_n^N(\,f_n)$
satisfies
$U_n^N(\,f_n)$
satisfies
 \begin{align*} \sum_{\smash{i=1}}^N \mathbb{E}\bigl(\varDelta U_n^{N,i+1}(\,f_n)^2\big|\mathcal{F}_n^{N,i}\bigr) & = \tilde{\eta}_n^N {C_{n}^{N}}(\,f_n,f_n) \quad \text{[by (\linkref{31}{31})]}\\ & \leq 4 \smash{{\widebar{T}_{n}}^{\,2}} \quad \text{[by (\linkref{14}{14})].} \end{align*}
\begin{align*} \sum_{\smash{i=1}}^N \mathbb{E}\bigl(\varDelta U_n^{N,i+1}(\,f_n)^2\big|\mathcal{F}_n^{N,i}\bigr) & = \tilde{\eta}_n^N {C_{n}^{N}}(\,f_n,f_n) \quad \text{[by (\linkref{31}{31})]}\\ & \leq 4 \smash{{\widebar{T}_{n}}^{\,2}} \quad \text{[by (\linkref{14}{14})].} \end{align*}
Hence, by the Burkholder–Davis–Gundy inequality (see, e.g., [Reference Kallenberg19, Theorem 17.7]) there exists ![]() ${b_{r}} < \infty$
such that
${b_{r}} < \infty$
such that
This completes the proof.
We are now ready to prove the ![]() $\mathbb{L}_r$
-inequality in Proposition 1.
$\mathbb{L}_r$
-inequality in Proposition 1.
Proof. Without loss of generality, assume that ![]() $\lVert f_n\rVert \leq 1$
for all
$\lVert f_n\rVert \leq 1$
for all ![]() $n \geq 1$
and that the constants
$n \geq 1$
and that the constants ![]() ${b_{r}}$
in Lemma 2 satisfy
${b_{r}}$
in Lemma 2 satisfy ![]() $\inf_{r \geq 1} b_r \geq 1$
.
$\inf_{r \geq 1} b_r \geq 1$
.
We begin by proving the first part of the proposition, i.e. the ![]() $\mathbb{L}_r$
-error bound without the additional Assumptions . The proof proceeds by induction on n by similar arguments as in [Reference Brockwell, Del Moral and Doucet7]. At time
$\mathbb{L}_r$
-error bound without the additional Assumptions . The proof proceeds by induction on n by similar arguments as in [Reference Brockwell, Del Moral and Doucet7]. At time ![]() $n=1$
, by Minkowski’s inequality combined with Lemma 2 as well as (32) and (33), we have
$n=1$
, by Minkowski’s inequality combined with Lemma 2 as well as (32) and (33), we have
 \begin{align*} \sqrt{N} \mathbb{E}\bigl[\lvert [\eta_1^N - \eta_1](\,f_1) \rvert^r \bigr]^{\frac{1}{r}} & = \sqrt{N} \mathbb{E}\bigl[\lvert [\eta_1^N - {\Phi_{1}^{N}}](\,f_1) \rvert^r \bigr]^{\frac{1}{r}}\\ & \leq \mathbb{E}\bigl[\lvert U_1^N(\,f_1) \rvert^r \bigr]^{\frac{1}{r}} + \mathbb{E}\bigl[\lvert L_1^N (\,f_1) \rvert^r \bigr]^{\frac{1}{r}} + \mathbb{E}\bigl[\lvert R_1^N (\,f_1) \rvert^r \bigr]^{\frac{1}{r}}\\ & \leq 2 {b_{r}} {\widebar{T}_{1}} + \frac{3 {\widebar{T}_{1}}}{\sqrt{N}} \leq a_1 {b_{r}}, \end{align*}
\begin{align*} \sqrt{N} \mathbb{E}\bigl[\lvert [\eta_1^N - \eta_1](\,f_1) \rvert^r \bigr]^{\frac{1}{r}} & = \sqrt{N} \mathbb{E}\bigl[\lvert [\eta_1^N - {\Phi_{1}^{N}}](\,f_1) \rvert^r \bigr]^{\frac{1}{r}}\\ & \leq \mathbb{E}\bigl[\lvert U_1^N(\,f_1) \rvert^r \bigr]^{\frac{1}{r}} + \mathbb{E}\bigl[\lvert L_1^N (\,f_1) \rvert^r \bigr]^{\frac{1}{r}} + \mathbb{E}\bigl[\lvert R_1^N (\,f_1) \rvert^r \bigr]^{\frac{1}{r}}\\ & \leq 2 {b_{r}} {\widebar{T}_{1}} + \frac{3 {\widebar{T}_{1}}}{\sqrt{N}} \leq a_1 {b_{r}}, \end{align*}
e.g. with ![]() $a_1 \coloneqq 5 {\widebar{T}_{1}} < \infty$
.
$a_1 \coloneqq 5 {\widebar{T}_{1}} < \infty$
.
Assume now that the first part of the proposition holds at time ![]() $n-1$
, for some
$n-1$
, for some ![]() $n > 1$
. By Minkowski’s inequality,
$n > 1$
. By Minkowski’s inequality,
 \begin{align} \MoveEqLeft \sqrt{N} \mathbb{E}\bigl[\lvert [\eta_n^N - \eta_n](\,f_n) \rvert^r \bigr]^{\frac{1}{r}}\nonumber\\ & \leq \sqrt{N} \mathbb{E}\bigl[\lvert [\eta_n^N - {\Phi_{n}^{N}}](\,f_n) \rvert^r \bigr]^{\frac{1}{r}} + \sqrt{N} \mathbb{E}\bigl[\lvert [{\Phi_{n}^{N}} - \eta_n](\,f_n) \rvert^r \bigr]^{\frac{1}{r}} \end{align}
\begin{align} \MoveEqLeft \sqrt{N} \mathbb{E}\bigl[\lvert [\eta_n^N - \eta_n](\,f_n) \rvert^r \bigr]^{\frac{1}{r}}\nonumber\\ & \leq \sqrt{N} \mathbb{E}\bigl[\lvert [\eta_n^N - {\Phi_{n}^{N}}](\,f_n) \rvert^r \bigr]^{\frac{1}{r}} + \sqrt{N} \mathbb{E}\bigl[\lvert [{\Phi_{n}^{N}} - \eta_n](\,f_n) \rvert^r \bigr]^{\frac{1}{r}} \end{align}
e.g. with ![]() $\smash{a_n \coloneqq 5 {\widebar{T}_{n}} + 2 a_{n-1} /\eta_{n-1}(G_{n-1}) < \infty}$
. Here, the bound on the first term in (34) follows by the same arguments as at time 1. The bound on the second term in (34) follows from the following decomposition (note that
$\smash{a_n \coloneqq 5 {\widebar{T}_{n}} + 2 a_{n-1} /\eta_{n-1}(G_{n-1}) < \infty}$
. Here, the bound on the first term in (34) follows by the same arguments as at time 1. The bound on the second term in (34) follows from the following decomposition (note that ![]() $\eta_{n-1}(Q_n(\textbf{1})) = \eta_{n-1}(G_{n-1})$
):
$\eta_{n-1}(Q_n(\textbf{1})) = \eta_{n-1}(G_{n-1})$
):
 \begin{align*} \MoveEqLeft \eta_{n-1}(G_{n-1}) \lvert [{\Phi_{n}^{N}} - \eta_n](\,f_n) \rvert\\[3pt] & = \bigl\lvert \eta_{n-1}(G_{n-1}) {\Phi_{n}^{N}}(\,f_n) - \eta_{n-1}^N(Q_n(\,f_n)) + \eta_{n-1}^N(Q_n(\,f_n)) - \eta_{n-1}(Q_n(\,f_n)) \bigr\rvert\\[3pt] & = \bigl\lvert {\Phi_{n}^{N}}(\,f_n) [\eta_{n-1} - \eta_{n-1}^N](Q_n(\textbf{1})) + [\eta_{n-1}^N - \eta_{n-1}](Q_n(\,f_n)) \bigr\rvert\\[3pt] & \leq \lVert {\Phi_{n}^{N}}(\,f_n) \rVert \lvert [\eta_{n-1} - \eta_{n-1}^N](Q_n(\textbf{1}))\rvert + \lvert [\eta_{n-1}^N - \eta_{n-1}](Q_n(\,f_n)) \rvert. \end{align*}
\begin{align*} \MoveEqLeft \eta_{n-1}(G_{n-1}) \lvert [{\Phi_{n}^{N}} - \eta_n](\,f_n) \rvert\\[3pt] & = \bigl\lvert \eta_{n-1}(G_{n-1}) {\Phi_{n}^{N}}(\,f_n) - \eta_{n-1}^N(Q_n(\,f_n)) + \eta_{n-1}^N(Q_n(\,f_n)) - \eta_{n-1}(Q_n(\,f_n)) \bigr\rvert\\[3pt] & = \bigl\lvert {\Phi_{n}^{N}}(\,f_n) [\eta_{n-1} - \eta_{n-1}^N](Q_n(\textbf{1})) + [\eta_{n-1}^N - \eta_{n-1}](Q_n(\,f_n)) \bigr\rvert\\[3pt] & \leq \lVert {\Phi_{n}^{N}}(\,f_n) \rVert \lvert [\eta_{n-1} - \eta_{n-1}^N](Q_n(\textbf{1}))\rvert + \lvert [\eta_{n-1}^N - \eta_{n-1}](Q_n(\,f_n)) \rvert. \end{align*}
Minkowski’s inequality along with ![]() $\lVert Q_n(\textbf{1})\rVert \leq 1$
and
$\lVert Q_n(\textbf{1})\rVert \leq 1$
and ![]() $\lVert Q_n(\,f_n) \rVert \leq 1$
as well as the bound
$\lVert Q_n(\,f_n) \rVert \leq 1$
as well as the bound ![]() $\smash{\lVert {\Phi_{n}^{N}}(\,f_n) \rVert \leq \lVert f_n\rVert \leq 1}$
combined with the induction assumption then readily yields the bound given in (35), i.e.
$\smash{\lVert {\Phi_{n}^{N}}(\,f_n) \rVert \leq \lVert f_n\rVert \leq 1}$
combined with the induction assumption then readily yields the bound given in (35), i.e.
This completes the first part of the proposition.
As the bounds obtained through the previous induction proof cannot easily be made time-uniform, we prove the second part of the proposition via the more conventional telescoping-sum decomposition given in (24). Using the arguments in [Reference Del Moral10, pp. 244–246], we obtain the following bound for the pth term in the telescoping sum:
 \begin{align*} \sqrt{N}\lvert [{\Phi_{p,n}^{\eta_p^N}} - {\Phi_{p,n}^{{\Phi_{p}}^{N}}}](\,f_n) \rvert & \leq 2 \sqrt{N} \lvert [\eta_p^N - {\Phi_{p}^{N}}](\widebar{Q}_{p,n}^N(\,f_n)) \rvert r_{p,n} \beta(P_{p,n})\\ & = 2 \lvert [ U_p^N + L_p^N + R_p^N ] (\widebar{Q}_{p,n}^N(\,f_n)) \rvert r_{p,n} \beta(P_{p,n}), \end{align*}
\begin{align*} \sqrt{N}\lvert [{\Phi_{p,n}^{\eta_p^N}} - {\Phi_{p,n}^{{\Phi_{p}}^{N}}}](\,f_n) \rvert & \leq 2 \sqrt{N} \lvert [\eta_p^N - {\Phi_{p}^{N}}](\widebar{Q}_{p,n}^N(\,f_n)) \rvert r_{p,n} \beta(P_{p,n})\\ & = 2 \lvert [ U_p^N + L_p^N + R_p^N ] (\widebar{Q}_{p,n}^N(\,f_n)) \rvert r_{p,n} \beta(P_{p,n}), \end{align*}
where the second line is due to (29) and where
 \begin{align*} \widebar{Q}_{p,n}^N(\,f_n) & \coloneqq \frac{Q_{p,n}^N(\,f_n)}{\lVert Q_{p,n}^N(\,f_n) \rVert},\\ Q_{p,n}^N(\,f_n) &\coloneqq \frac{Q_{p,n}(\textbf{1})}{{\Phi_{p}^{N}}(Q_{p,n}(\textbf{1}))} P_{p,n}\biggl(\,f_n - \frac{{\Phi_{p}^{N}}(Q_{p,n}(\,f_n))}{{\Phi_{p}^{N}}(Q_{p,n}(\textbf{1}))}\biggr).\end{align*}
\begin{align*} \widebar{Q}_{p,n}^N(\,f_n) & \coloneqq \frac{Q_{p,n}^N(\,f_n)}{\lVert Q_{p,n}^N(\,f_n) \rVert},\\ Q_{p,n}^N(\,f_n) &\coloneqq \frac{Q_{p,n}(\textbf{1})}{{\Phi_{p}^{N}}(Q_{p,n}(\textbf{1}))} P_{p,n}\biggl(\,f_n - \frac{{\Phi_{p}^{N}}(Q_{p,n}(\,f_n))}{{\Phi_{p}^{N}}(Q_{p,n}(\textbf{1}))}\biggr).\end{align*}
Hence, by (24),
 \begin{align*} & \sqrt{N} \mathbb{E}\bigl[\lvert [\eta_n^N - \eta_n](\,f_n) \rvert^r\bigr]^{\frac{1}{r}}\\
& \quad\leq 2 \sum_{p=1}^n \mathbb{E}\bigl[\lvert [ U_p^N + L_p^N + R_p^N ] (\widebar{Q}_{p,n}^N(\,f_n)) \rvert^r\bigr]^{\frac{1}{r}} r_{p,n} \beta(P_{p,n})\\
& \quad\leq 2 \sum_{p=1}^n \Bigl(2 {b_{r}} {\widebar{T}_{p}} + \frac{3 {\widebar{T}_{p}}}{\sqrt{N}}\Bigr) r_{p,n} \beta(P_{p,n}) \leq a_n b_r \end{align*}
\begin{align*} & \sqrt{N} \mathbb{E}\bigl[\lvert [\eta_n^N - \eta_n](\,f_n) \rvert^r\bigr]^{\frac{1}{r}}\\
& \quad\leq 2 \sum_{p=1}^n \mathbb{E}\bigl[\lvert [ U_p^N + L_p^N + R_p^N ] (\widebar{Q}_{p,n}^N(\,f_n)) \rvert^r\bigr]^{\frac{1}{r}} r_{p,n} \beta(P_{p,n})\\
& \quad\leq 2 \sum_{p=1}^n \Bigl(2 {b_{r}} {\widebar{T}_{p}} + \frac{3 {\widebar{T}_{p}}}{\sqrt{N}}\Bigr) r_{p,n} \beta(P_{p,n}) \leq a_n b_r \end{align*}
with ![]() $\smash{a_n \coloneqq 10 \sum_{p=1}^n {\widebar{T}_{p}} r_{p,n} \beta(P_{p,n})}$
, where the last line follows from Minkowski’s inequality combined with Lemma 2, (32), and (33). Since
$\smash{a_n \coloneqq 10 \sum_{p=1}^n {\widebar{T}_{p}} r_{p,n} \beta(P_{p,n})}$
, where the last line follows from Minkowski’s inequality combined with Lemma 2, (32), and (33). Since ![]() $f_n \in \smash{\mathcal{B}^\star(\textbf{E}_n)}$
, we can replace
$f_n \in \smash{\mathcal{B}^\star(\textbf{E}_n)}$
, we can replace ![]() $\smash{\beta(P_{p,n})}$
by
$\smash{\beta(P_{p,n})}$
by ![]() $\smash{\beta^\star(P_{p,n})}$
in the derivation above. Lemma 1 then yields the time-uniform bound
$\smash{\beta^\star(P_{p,n})}$
in the derivation above. Lemma 1 then yields the time-uniform bound
 \begin{align*} a_n \leq 10 \widebar{T} \bar{r} \sum_{p=1}^n \bar{\beta}^{\lfloor (n -p)/m\rfloor} \leq 10 \widebar{T} \bar{r} m \sum_{n=0}^\infty \bar{\beta}^n \leq \frac{20 \bar{\imath} m }{\varepsilon(K) \varepsilon(M)^3 \varepsilon(G)^{2(m+l)}} \eqqcolon a.\end{align*}
\begin{align*} a_n \leq 10 \widebar{T} \bar{r} \sum_{p=1}^n \bar{\beta}^{\lfloor (n -p)/m\rfloor} \leq 10 \widebar{T} \bar{r} m \sum_{n=0}^\infty \bar{\beta}^n \leq \frac{20 \bar{\imath} m }{\varepsilon(K) \varepsilon(M)^3 \varepsilon(G)^{2(m+l)}} \eqqcolon a.\end{align*}
This completes the proof.
C.3. Auxiliary results needed for the CLT
In this subsection, we prove the CLT stated in Proposition 2. The proof relies on Lemma 4, which establishes convergence of the covariance function, and whose proof in turn relies on Lemma 3. The latter illustrates how local Lipschitz conditions of the type given in Assumption A2 are used within this work.
Lemma 3. For measurable spaces ![]() $(H, \mathcal{H})$
and
$(H, \mathcal{H})$
and ![]() $({H^\prime}, {\mathcal{H}^\prime})$
, let
$({H^\prime}, {\mathcal{H}^\prime})$
, let ![]() $M^{\nu} \colon \mathcal{B}({H^\prime}) \to \mathcal{B}(H)$
be bounded integral operators indexed by
$M^{\nu} \colon \mathcal{B}({H^\prime}) \to \mathcal{B}(H)$
be bounded integral operators indexed by ![]() $\nu \in \mathcal{P}(H)$
. Let
$\nu \in \mathcal{P}(H)$
. Let ![]() $\smash{(\mu^N)_{N \geq 1}}$
be a sequence of random probability measures on
$\smash{(\mu^N)_{N \geq 1}}$
be a sequence of random probability measures on ![]() $(H, \mathcal{H})$
and
$(H, \mathcal{H})$
and ![]() $\mu \in \mathcal{P}(H)$
. Assume that
$\mu \in \mathcal{P}(H)$
. Assume that
(1) for any
 $r \geq 1$
, there exists
$r \geq 1$
, there exists  $b_r < \infty$
such that for any
$b_r < \infty$
such that for any  $g \in \mathcal{B}(H)$
and any
$g \in \mathcal{B}(H)$
and any  $N \geq 1$
,
(36)
$N \geq 1$
,
(36) \begin{align} \mathbb{E}\bigl[\lvert [\mu^N - \mu](g)\rvert^r\bigr]^{\frac{1}{r}} \leq \frac{b_r}{\sqrt{N}} \lVert g \rVert; \end{align}
\begin{align} \mathbb{E}\bigl[\lvert [\mu^N - \mu](g)\rvert^r\bigr]^{\frac{1}{r}} \leq \frac{b_r}{\sqrt{N}} \lVert g \rVert; \end{align}
(2) there exist a constant
 $\smash{{\widebar{\varGamma}_{}} < \infty}$
and a family of bounded integral operators
$\smash{{\widebar{\varGamma}_{}} < \infty}$
and a family of bounded integral operators  $({\varGamma_{}^{\nu}})_{\nu \in \mathcal{P}(H)}$
from
$({\varGamma_{}^{\nu}})_{\nu \in \mathcal{P}(H)}$
from  $\smash{\mathcal{B}({H^\prime})}$
into
$\smash{\mathcal{B}({H^\prime})}$
into  $\mathcal{B}(H)$
such that for any
$\mathcal{B}(H)$
such that for any  $f \in \mathcal{B}({H^\prime})$
and any
$f \in \mathcal{B}({H^\prime})$
and any  $\nu_0,\nu_1 \in \mathcal{P}(H)$
,
(37)with
$\nu_0,\nu_1 \in \mathcal{P}(H)$
,
(37)with \begin{align} \lVert [M^{\nu_1} - M^{\nu_0}](\,f) \rVert & \leq \int_{\mathcal{B}(H)} \lvert [\nu_1 - \nu_0](g)\rvert {\varGamma_{}^{\nu_0}}(\,f, \textrm{d} g), \end{align}
(38)
\begin{align} \lVert [M^{\nu_1} - M^{\nu_0}](\,f) \rVert & \leq \int_{\mathcal{B}(H)} \lvert [\nu_1 - \nu_0](g)\rvert {\varGamma_{}^{\nu_0}}(\,f, \textrm{d} g), \end{align}
(38) \begin{align} \int_{\mathcal{B}(H)} \lVert g\rVert {\varGamma_{}^{\nu_0}}(\,f, \textrm{d} g) \leq \lVert f \rVert {\widebar{\varGamma}_{}}. \end{align}
\begin{align} \int_{\mathcal{B}(H)} \lVert g\rVert {\varGamma_{}^{\nu_0}}(\,f, \textrm{d} g) \leq \lVert f \rVert {\widebar{\varGamma}_{}}. \end{align}
Then for any ![]() $r\geq1$
,
$r\geq1$
, ![]() $f \in \mathcal{B}({H^\prime})$
, and
$f \in \mathcal{B}({H^\prime})$
, and ![]() $N \geq 1$
,
$N \geq 1$
,
Proof. For any ![]() $r \geq 1$
,
$r \geq 1$
,
 \begin{align*} \mathbb{E}[\lVert [M^{\mu^{\raisebox{-1pt}{$\scriptscriptstyle{N}$}}} - M^{\mu}](\,f)\rVert^r]^{\frac{1}{r}} & \leq \mathbb{E}\biggl[\biggl\lvert \int_{\mathcal{B}(H)} \lvert [\mu^N - \mu](g)\rvert {\varGamma_{}^{\mu}}(\,f, \textrm{d} g) \biggr\rvert^r\biggr]^{\frac{1}{r}}\\& \leq \int_{\mathcal{B}(H)} \mathbb{E}[\lvert [\mu^N - \mu](g)\rvert^r ]^{\frac{1}{r}} {\varGamma_{}^{\mu}}(\,f, \textrm{d} g)\\ & \leq \frac{b_r}{\sqrt{N}} \int_{\mathcal{B}(H)} \lVert g\rVert {\varGamma_{}^{\mu}}(\,f, \textrm{d} g)\\ & \leq \frac{b_r {\widebar{\varGamma}_{}}}{\sqrt{N}} \lVert f \rVert.\end{align*}
\begin{align*} \mathbb{E}[\lVert [M^{\mu^{\raisebox{-1pt}{$\scriptscriptstyle{N}$}}} - M^{\mu}](\,f)\rVert^r]^{\frac{1}{r}} & \leq \mathbb{E}\biggl[\biggl\lvert \int_{\mathcal{B}(H)} \lvert [\mu^N - \mu](g)\rvert {\varGamma_{}^{\mu}}(\,f, \textrm{d} g) \biggr\rvert^r\biggr]^{\frac{1}{r}}\\& \leq \int_{\mathcal{B}(H)} \mathbb{E}[\lvert [\mu^N - \mu](g)\rvert^r ]^{\frac{1}{r}} {\varGamma_{}^{\mu}}(\,f, \textrm{d} g)\\ & \leq \frac{b_r}{\sqrt{N}} \int_{\mathcal{B}(H)} \lVert g\rVert {\varGamma_{}^{\mu}}(\,f, \textrm{d} g)\\ & \leq \frac{b_r {\widebar{\varGamma}_{}}}{\sqrt{N}} \lVert f \rVert.\end{align*}
Here, the first line follows from (37); the second line is due to the convexity of the ![]() $\mathbb{L}_r$
-norm; the last two lines follow from (36) and (38), respectively.
$\mathbb{L}_r$
-norm; the last two lines follow from (36) and (38), respectively.
Lemma 4. Under Assumptions
–
, for any ![]() $n \geq 1$
, there exists
$n \geq 1$
, there exists ![]() ${\widebar{\varUpsilon}_{n}} < \infty$
such that for any
${\widebar{\varUpsilon}_{n}} < \infty$
such that for any ![]() $N,r \geq 1$
and any
$N,r \geq 1$
and any ![]() $(\,f_n, g_n) \in \mathcal{B}(\textbf{E}_n)^2$
,
$(\,f_n, g_n) \in \mathcal{B}(\textbf{E}_n)^2$
,
where ![]() $a_{n-1}, b_r < \infty$
are from Proposition 1.
$a_{n-1}, b_r < \infty$
are from Proposition 1.
Proof. We use a similar argument to that used in the first part of the proof of [Reference Bercu, Del Moral and Doucet5
, Theorem 3.5]. That is, under Assumptions and , and using [Reference Bercu, Del Moral and Doucet5, Proposition 3.1], a telescoping-sum decomposition allows us to find a constant ![]() $\smash{{\widebar{\varUpsilon}_{n}} < \infty}$
and a family of bounded integral operators
$\smash{{\widebar{\varUpsilon}_{n}} < \infty}$
and a family of bounded integral operators ![]() $({\varUpsilon_{n}^{\nu}})_{\nu \in \mathcal{P}(\textbf{E}_{n-1})}$
from
$({\varUpsilon_{n}^{\nu}})_{\nu \in \mathcal{P}(\textbf{E}_{n-1})}$
from ![]() $\smash{\mathcal{B}(\textbf{E}_{n})^2}$
into
$\smash{\mathcal{B}(\textbf{E}_{n})^2}$
into ![]() $\mathcal{B}(\textbf{E}_{n-1})$
such that for any
$\mathcal{B}(\textbf{E}_{n-1})$
such that for any ![]() $(\nu,\mu) \in \mathcal{P}(\textbf{E}_{n-1})^2$
,
$(\nu,\mu) \in \mathcal{P}(\textbf{E}_{n-1})^2$
,
with
The proof is then completed by appealing to Lemma 3.
We now prove the following proposition, which adapts [Reference Finke, Doucet and Johansen5, Proposition 4.3] (see also [Reference Del Moral10, Theorem 9.3.1]) to our setting.
Proposition 3. Let ![]() $f \coloneqq (\,f_n)_{n \geq 1}$
, where
$f \coloneqq (\,f_n)_{n \geq 1}$
, where ![]() $\smash{f_n = (\,f_n^u)_{1 \leq u \leq d} \in \mathcal{B}(\textbf{E}_n)^d}$
. The sequence of martingales
$\smash{f_n = (\,f_n^u)_{1 \leq u \leq d} \in \mathcal{B}(\textbf{E}_n)^d}$
. The sequence of martingales ![]() $\smash{\mathcal{U}^N(\,f) = (\mathcal{U}_n^N(\,f))_{n \geq 1}}$
converges in law as
$\smash{\mathcal{U}^N(\,f) = (\mathcal{U}_n^N(\,f))_{n \geq 1}}$
converges in law as ![]() $N \to \infty$
to a Gaussian martingale
$N \to \infty$
to a Gaussian martingale ![]() $\mathcal{U}(\,f) = (\mathcal{U}_n(\,f))_{n \geq 1}$
such that for any
$\mathcal{U}(\,f) = (\mathcal{U}_n(\,f))_{n \geq 1}$
such that for any ![]() $n \geq 1$
and any
$n \geq 1$
and any ![]() $1 \leq u,v\leq d$
,
$1 \leq u,v\leq d$
,
 \begin{align*} \langle \mathcal{U}(\,f^u), \mathcal{U}(\,f^v)\rangle_n & = \sum_{p=1}^n \eta_p {C_{p}^{}}(\,f_p^u, f_p^v). \end{align*}
\begin{align*} \langle \mathcal{U}(\,f^u), \mathcal{U}(\,f^v)\rangle_n & = \sum_{p=1}^n \eta_p {C_{p}^{}}(\,f_p^u, f_p^v). \end{align*}
Proof. We begin by re-indexing the processes defined above. For any ![]() $(p,i) \in \mathbb{N} \times \{1,\dotsc,N\}$
, define the bijection
$(p,i) \in \mathbb{N} \times \{1,\dotsc,N\}$
, define the bijection ![]() $\smash{\theta^N}$
by
$\smash{\theta^N}$
by
Define the filtration ![]() $\smash{\mathcal{G}^N \coloneqq (\mathcal{G}_k^N)_{k \geq 1}}$
, where
$\smash{\mathcal{G}^N \coloneqq (\mathcal{G}_k^N)_{k \geq 1}}$
, where ![]() $\smash{\mathcal{G}_k^N \coloneqq \vee_{(p,i)\colon \theta^N(p,i) \leq k} \mathcal{F}_{p}^{N,i}}$
. We then have
$\smash{\mathcal{G}_k^N \coloneqq \vee_{(p,i)\colon \theta^N(p,i) \leq k} \mathcal{F}_{p}^{N,i}}$
. We then have ![]() $\smash{\mathcal{U}_n^N(\,f) = \widetilde{\mathcal{U}}_k^N(\,f)}$
whenever
$\smash{\mathcal{U}_n^N(\,f) = \widetilde{\mathcal{U}}_k^N(\,f)}$
whenever ![]() $\smash{k = \theta^N(n,N)}$
, where
$\smash{k = \theta^N(n,N)}$
, where
 \begin{align*} \widetilde{\mathcal{U}}_k^N(\,f) \coloneqq \sum_{j=1}^k \varDelta \widetilde{\mathcal{U}}_j^N(\,f)\end{align*}
\begin{align*} \widetilde{\mathcal{U}}_k^N(\,f) \coloneqq \sum_{j=1}^k \varDelta \widetilde{\mathcal{U}}_j^N(\,f)\end{align*}
defines a ![]() $\smash{\mathcal{G}^N}$
-martingale
$\smash{\mathcal{G}^N}$
-martingale ![]() $\smash{(\widetilde{\mathcal{U}}_k^N(\,f))_{k \geq 1}}$
with increments
$\smash{(\widetilde{\mathcal{U}}_k^N(\,f))_{k \geq 1}}$
with increments
Indeed, by (30) and (31), for any ![]() $1 \leq u,v\leq d$
,
$1 \leq u,v\leq d$
,
 \begin{align*} \mathbb{E}\bigl[\varDelta \widetilde{\mathcal{U}}_j^N(\,f^u)\big|\mathcal{G}_{j-1}^N\bigr] & = 0, \\ \mathbb{E}\bigl[\varDelta \widetilde{\mathcal{U}}_j^N(\,f^u)\varDelta \widetilde{\mathcal{U}}_j^N(\,f^v)\big|\mathcal{G}_{j-1}^N\bigr] & = \frac{1}{N}{C_{p}^{N}}(\,f_p^u, f_p^v)({\tilde{\boldsymbol{\xi}}}{}^{i}_{p}), \end{align*}
\begin{align*} \mathbb{E}\bigl[\varDelta \widetilde{\mathcal{U}}_j^N(\,f^u)\big|\mathcal{G}_{j-1}^N\bigr] & = 0, \\ \mathbb{E}\bigl[\varDelta \widetilde{\mathcal{U}}_j^N(\,f^u)\varDelta \widetilde{\mathcal{U}}_j^N(\,f^v)\big|\mathcal{G}_{j-1}^N\bigr] & = \frac{1}{N}{C_{p}^{N}}(\,f_p^u, f_p^v)({\tilde{\boldsymbol{\xi}}}{}^{i}_{p}), \end{align*}
where ![]() $p \geq 1$
and
$p \geq 1$
and ![]() $1 \leq i \leq N$
satisfy
$1 \leq i \leq N$
satisfy ![]() $\smash{\theta^N(p,i) = j}$
.
$\smash{\theta^N(p,i) = j}$
.
We now apply the CLT for triangular arrays of martingale difference sequences (see, e.g., [Reference Shiryaev34, Section VII.8, Theorem 4; p. 543]). The Lindeberg condition is satisfied because the test functions ![]() $f_n$
are bounded. Finally, for any
$f_n$
are bounded. Finally, for any ![]() $p \geq 1$
,
$p \geq 1$
,
 \begin{align*} \smashoperator{\sum_{\smash{k=(pN)+1}}^{(p+1)N}} \;\mathbb{E}[\varDelta \widetilde{\mathcal{U}}_k^N(\,f^u)\varDelta \widetilde{\mathcal{U}}_k^N(\,f^v)|\mathcal{G}_{k-1}^N] & = \frac{1}{N} \smashoperator{\sum_{i=1}^{\smash{N}}} {C_{p}^{N}}(\,f_p^u, f_p^v)({\tilde{\boldsymbol{\xi}}}{}^{i}_{p})\\ & = \tilde{\eta}_p^N {C_{p}^{N}}(\,f_p^u, f_p^v)\\ & {\mathrel{\mathop{\rightarrow}\nolimits_{\text{\upshape{a.s.}}}}} \eta_p {C_{p}^{}}(\,f_p^u, f_p^v).\end{align*}
\begin{align*} \smashoperator{\sum_{\smash{k=(pN)+1}}^{(p+1)N}} \;\mathbb{E}[\varDelta \widetilde{\mathcal{U}}_k^N(\,f^u)\varDelta \widetilde{\mathcal{U}}_k^N(\,f^v)|\mathcal{G}_{k-1}^N] & = \frac{1}{N} \smashoperator{\sum_{i=1}^{\smash{N}}} {C_{p}^{N}}(\,f_p^u, f_p^v)({\tilde{\boldsymbol{\xi}}}{}^{i}_{p})\\ & = \tilde{\eta}_p^N {C_{p}^{N}}(\,f_p^u, f_p^v)\\ & {\mathrel{\mathop{\rightarrow}\nolimits_{\text{\upshape{a.s.}}}}} \eta_p {C_{p}^{}}(\,f_p^u, f_p^v).\end{align*}
The last line follows by Markov’s inequality combined with the Borel–Cantelli lemma after noting that for any ![]() $r,p \geq 1$
, Minkowski’s inequality combined with (33), Lemma 4, and Proposition 1 guarantees the existence of
$r,p \geq 1$
, Minkowski’s inequality combined with (33), Lemma 4, and Proposition 1 guarantees the existence of ![]() $a^{\prime}_p, b^{\prime}_r < \infty$
such that for any
$a^{\prime}_p, b^{\prime}_r < \infty$
such that for any ![]() $N \geq 1$
,
$N \geq 1$
,
 \begin{align*} \mathbb{E}\bigl[ \lVert \tilde{\eta}_p^N {C_{p}^{N}}(\,f_p^u, f_p^v) - \eta_p {C_{p}^{}}(\,f_p^u, f_p^v) \rVert^r\bigr]^{\frac{1}{r}} & \leq \mathbb{E}\bigl[ \lVert [\tilde{\eta}_p^N - \eta_p^N] ({C_{p}^{N}}(\,f_p^u, f_p^v)) \rVert^r\bigr]^{\frac{1}{r}}\\ & \quad + \mathbb{E}\bigl[ \lVert {C_{p}^{N}}(\,f_p^u, f_p^v) - {C_{p}^{}}(\,f_p^u, f_p^v) \rVert^r\bigr]^{\frac{1}{r}} \\ & \quad + \mathbb{E}\bigl[ \lVert [\eta_p^N - \eta_p ] ({C_{p}^{}}(\,f_p^u, f_p^v)) \rVert^r\bigr]^{\frac{1}{r}}\\ & \leq \frac{a^{\prime}_p b^{\prime}_r}{\sqrt{N}} \lVert f_n^u\rVert \lVert f_n^v \rVert.\end{align*}
\begin{align*} \mathbb{E}\bigl[ \lVert \tilde{\eta}_p^N {C_{p}^{N}}(\,f_p^u, f_p^v) - \eta_p {C_{p}^{}}(\,f_p^u, f_p^v) \rVert^r\bigr]^{\frac{1}{r}} & \leq \mathbb{E}\bigl[ \lVert [\tilde{\eta}_p^N - \eta_p^N] ({C_{p}^{N}}(\,f_p^u, f_p^v)) \rVert^r\bigr]^{\frac{1}{r}}\\ & \quad + \mathbb{E}\bigl[ \lVert {C_{p}^{N}}(\,f_p^u, f_p^v) - {C_{p}^{}}(\,f_p^u, f_p^v) \rVert^r\bigr]^{\frac{1}{r}} \\ & \quad + \mathbb{E}\bigl[ \lVert [\eta_p^N - \eta_p ] ({C_{p}^{}}(\,f_p^u, f_p^v)) \rVert^r\bigr]^{\frac{1}{r}}\\ & \leq \frac{a^{\prime}_p b^{\prime}_r}{\sqrt{N}} \lVert f_n^u\rVert \lVert f_n^v \rVert.\end{align*}
As a result, for any ![]() $n \geq 1$
, as
$n \geq 1$
, as ![]() $N \to \infty$
,
$N \to \infty$
,
 \begin{equation*} \smashoperator{\sum_{k=1}^{(n+1)N}} \mathbb{E}[\varDelta \widetilde{\mathcal{U}}_k^N(\,f^u)\varDelta \widetilde{\mathcal{U}}_k^N(\,f^v)|\mathcal{G}_{k-1}^N] {\mathrel{\mathop{\rightarrow}\nolimits_{\text{\upshape{a.s.}}}}} \sum_{p=1}^n \eta_p {C_{p}^{}}(\,f_p^u, f_p^v).\end{equation*}
\begin{equation*} \smashoperator{\sum_{k=1}^{(n+1)N}} \mathbb{E}[\varDelta \widetilde{\mathcal{U}}_k^N(\,f^u)\varDelta \widetilde{\mathcal{U}}_k^N(\,f^v)|\mathcal{G}_{k-1}^N] {\mathrel{\mathop{\rightarrow}\nolimits_{\text{\upshape{a.s.}}}}} \sum_{p=1}^n \eta_p {C_{p}^{}}(\,f_p^u, f_p^v).\end{equation*}
This completes the proof.
As an immediate consequence of Proposition 3, we obtain the following corollary. Its proof is a straightforward modification of the proof of [Reference Del Moral10, Corollary 9.3.1].
Corollary 2. As ![]() $N \to \infty$
, the sequence of random fields
$N \to \infty$
, the sequence of random fields ![]() $\smash{V^N = (V_n^N)_{n\geq 1}}$
converges in law (and in the sense of convergence of finite-dimensional marginals) to the sequence of independent and centred Gaussian random fields
$\smash{V^N = (V_n^N)_{n\geq 1}}$
converges in law (and in the sense of convergence of finite-dimensional marginals) to the sequence of independent and centred Gaussian random fields ![]() $V = (V_n)_{n \geq 1}$
with covariance function as defined in (15).
$V = (V_n)_{n \geq 1}$
with covariance function as defined in (15).
We are now ready to give the proof of the CLT in Proposition 2.
Proof. The proof of the CLT now follows by replacing [Reference Del Moral10, Theorem 9.3.1 & Corollary 9.3.1] in the proofs of [Reference Del Moral10, Propositions 9.4.1 & 9.4.2] with Proposition 3 and Corollary 2, respectively.
For the time-uniform bound on the asymptotic variance in (17), we note that for any ![]() $1 \leq u \leq d$
,
$1 \leq u \leq d$
,
 \begin{align*} \lVert \widebar{Q}_{p,n}(\,f_n^u - \eta_n(\,f_n^u)) \rVert & = \biggl\lVert \frac{Q_{p,n}(\textbf{1})}{\eta_p Q_{p,n}(\textbf{1})} \bigl[P_{p,n}(\,f_n^u) - \Psi_{p,n}^{\eta_p}P_{p,n}(\,f_n^u)\bigr]\biggr\rVert\\ & \leq r_{p,n} \lVert [{\textrm{Id}}- \Psi_{p,n}^{\eta_p}] P_{p,n}(\,f_n^u)\rVert\\ & \leq 2 \lVert f_n^u \rVert r_{p,n} \beta^\star(P_{p,n}), \end{align*}
\begin{align*} \lVert \widebar{Q}_{p,n}(\,f_n^u - \eta_n(\,f_n^u)) \rVert & = \biggl\lVert \frac{Q_{p,n}(\textbf{1})}{\eta_p Q_{p,n}(\textbf{1})} \bigl[P_{p,n}(\,f_n^u) - \Psi_{p,n}^{\eta_p}P_{p,n}(\,f_n^u)\bigr]\biggr\rVert\\ & \leq r_{p,n} \lVert [{\textrm{Id}}- \Psi_{p,n}^{\eta_p}] P_{p,n}(\,f_n^u)\rVert\\ & \leq 2 \lVert f_n^u \rVert r_{p,n} \beta^\star(P_{p,n}), \end{align*}
where we have used that ![]() $\eta_n = \Psi_{p,n}^{\eta_p}P_{p,n}$
, where
$\eta_n = \Psi_{p,n}^{\eta_p}P_{p,n}$
, where
Hence, by (14) and Lemma 1, the time-uniform bound on the asymptotic variance in (18) holds, e.g. with
 \begin{align*} c \coloneqq 8 \widebar{T}^2 \bar{r}^2 \sum_{p=1}^n \bar{\beta}^{2 \lfloor (n -p)/m\rfloor} \leq 8 \widebar{T}^2 \bar{r}^2 m \sum_{n=0}^\infty \bar{\beta}^n \leq \frac{32 \bar{\imath}^2 m }{\varepsilon(K)^2 \varepsilon(M)^4 \varepsilon(G)^{3(m+l)}}.\end{align*}
\begin{align*} c \coloneqq 8 \widebar{T}^2 \bar{r}^2 \sum_{p=1}^n \bar{\beta}^{2 \lfloor (n -p)/m\rfloor} \leq 8 \widebar{T}^2 \bar{r}^2 m \sum_{n=0}^\infty \bar{\beta}^n \leq \frac{32 \bar{\imath}^2 m }{\varepsilon(K)^2 \varepsilon(M)^4 \varepsilon(G)^{3(m+l)}}.\end{align*}
This completes the proof.
Acknowledgement
This work was partially supported by funding from the Lloyd’s Register Foundation–Alan Turing Institute Programme on Data-Centric Engineering.