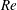1 Introduction
Solid bodies forced to oscillate in a fluid may, as a result, undergo a net motion, provided their shape breaks an appropriate symmetry. Yet, in the absence of inertia (i.e. when the Reynolds number
$Re$
is strictly zero), no net motion can arise from time-reciprocal actuation due to the linearity of Stokes’ equations (Purcell Reference Purcell1977). Above a critical
$Re_{c}=O(1)$
, a symmetric rigid body can achieve unidirectional locomotion as a result of symmetry-breaking instability resulting from the nonlinear inertial contribution to the Navier–Stokes equations (Alben & Shelley Reference Alben and Shelley2005). The purpose of the present work is to analyse the emergence of self-propulsion at small but finite
$Re$
(i.e. the effect of inertia is weak but non-negligible) for oscillating asymmetric particles. Indeed one could expect that asymmetric flows, resulting from asymmetric boundary conditions, will push the particle, thereby inducing non-zero average motion (Nadal & Lauga Reference Nadal and Lauga2014).
Artificial microswimmers have received much recent attention, thanks to their potential application to drug delivery or water treatment (Sundararajan et al. Reference Sundararajan, Lammert, Zudans, Crespi and Sen2008; Tiwari, Behari & Sen Reference Tiwari, Behari and Sen2008; Martinez-Pedrero & Tierno Reference Martinez-Pedrero and Tierno2015), or their fundamental interest in the study of active matter (see, for example Buttinoni et al. Reference Buttinoni, Bialké, Kümmel, Löwen, Bechinger and Speck2013; Palacci et al. Reference Palacci, Sacanna, Steinberg, Pine and Chaikin2013; Bechinger et al. Reference Bechinger, Di Leonardo, Löwen, Reichhardt, Volpe and Volpe2016). Among the many possible routes to self-propulsion, swimming in self-generated physico-chemical gradients, i.e. autophoresis (Moran & Posner Reference Moran and Posner2017), as well as bubble-generating (Wang & Wu Reference Wang and Wu2014; Li, Rozen & Wang Reference Li, Rozen and Wang2016) or magnetically actuated microswimmers (Dreyfus et al. Reference Dreyfus, Baudry, Roper, Fermigier, Stone and Bibette2005) have received particular attention. In these examples, a front–back asymmetry in the design of the system is necessary. Yet, symmetry-breaking and self-propulsion can also be achieved by exploiting an instability (Bricard et al. Reference Bricard, Caussin, Desreumaux, Dauchot and Bartolo2013; Michelin, Lauga & Bartolo Reference Michelin, Lauga and Bartolo2013; Izri et al. Reference Izri, Van Der Linden, Michelin and Dauchot2014) or flexibility (Wiggins & Goldstein Reference Wiggins and Goldstein1998).
Recently, passive rigid particles levitating in the nodal planes of an acoustic stationary wave have been observed to self-propel in a plane orthogonal to their direction of excitation (Wang et al.
Reference Wang, Castro, Hoyos and Mallouk2012). To explain such findings, Nadal & Lauga (Reference Nadal and Lauga2014) proposed an acoustic streaming mechanism, suggesting that near-spherical particles with asphericity parameter
$\unicode[STIX]{x1D716}$
can achieve a net
$O(\unicode[STIX]{x1D716}Re)$
propulsion, in the low-frequency limit. Several studies have since stood upon the results of Nadal & Lauga to account for their observations (see, for example Ahmed et al.
Reference Ahmed, Wang, Bai, Gentekos, Hoyos and Mallouk2016; Soto et al.
Reference Soto, Wagner, Garcia-Gradilla, Gillespie, Lakshmipathy, Karshalev, Angell, Chen and Wang2016; Sabrina et al.
Reference Sabrina, Tasinkevych, Ahmed, Brooks, Olivera de la Cruz, Mallouk and Bishop2018).
In contrast, we here demonstrate analytically that no net motion can arise at
$O(\unicode[STIX]{x1D716}Re)$
from a time-reciprocal oscillation and that self-propulsion, if any, must arise at higher order. In § 2, the governing equations for an oscillating particle are presented. In § 3, we introduce the particle geometry and the Taylor expansions of the velocity fields in
$Re$
and
$\unicode[STIX]{x1D716}$
. In §§ 4 and 5, we compute the net motion of the particle at the first two orders in
$Re$
. In § 6, we discuss our results and conclude.
2 Governing equations
We consider here a rigid and homogeneous particle of typical size
$R$
oscillating with frequency
$\unicode[STIX]{x1D714}$
and amplitude
$a$
in an incompressible and Newtonian fluid of kinematic viscosity
$\unicode[STIX]{x1D708}$
. Using
$R$
,
$a\unicode[STIX]{x1D714}$
and
$1/\unicode[STIX]{x1D714}$
, respectively, as reference length, velocity and time scales, the dimensionless Navier–Stokes and continuity equations read (Zhang & Stone Reference Zhang and Stone1998)
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D706}^{2}\unicode[STIX]{x2202}_{t}\boldsymbol{u}+Re\unicode[STIX]{x1D735}\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{u}=\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D748},\quad \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}=0, & & \displaystyle\end{eqnarray}$$
with
$\unicode[STIX]{x1D748}=-p\unicode[STIX]{x1D644}+(\unicode[STIX]{x1D735}\boldsymbol{u}+\unicode[STIX]{x1D735}^{\top }\boldsymbol{u})$
, the dimensionless stress tensor. The Reynolds number and reduced frequency are respectively defined as
$Re=a\unicode[STIX]{x1D714}R/\unicode[STIX]{x1D708}$
and
$\unicode[STIX]{x1D706}^{2}=(R/\unicode[STIX]{x1D6FF})^{2}$
, with
$\unicode[STIX]{x1D6FF}=\sqrt{\unicode[STIX]{x1D708}/\unicode[STIX]{x1D714}}$
the viscous penetration depth. More precisely, a translational oscillation is imposed to the particle along the
$\boldsymbol{e}_{x}$
direction,
$\tilde{\boldsymbol{U}}=\text{e}^{\text{i}t}\boldsymbol{e}_{x}$
, and the particle is free to move along the other directions, and is thus force-free along the
$yz$
plane and torque-free about any axis. The longitudinal and angular velocities of the particle resulting from its imposed oscillation are
$\boldsymbol{U}=U_{y}\boldsymbol{e}_{y}+U_{z}\boldsymbol{e}_{z}$
and
$\unicode[STIX]{x1D734}=\unicode[STIX]{x1D6FA}_{x}\boldsymbol{e}_{x}+\unicode[STIX]{x1D6FA}_{y}\boldsymbol{e}_{y}+\unicode[STIX]{x1D6FA}_{z}\boldsymbol{e}_{z}$
. In the frame of reference of the laboratory, the boundary conditions read
$$\begin{eqnarray}\displaystyle \boldsymbol{u}|_{S}=\tilde{\boldsymbol{U}}+\boldsymbol{U}+\unicode[STIX]{x1D734}\times \boldsymbol{r},\quad \boldsymbol{u}|_{\boldsymbol{r}\rightarrow \infty }=\mathbf{0}. & & \displaystyle\end{eqnarray}$$
In order to determine
$\boldsymbol{U}$
and
$\unicode[STIX]{x1D734}$
following an approach analogous to that of Lorentz’ reciprocal theorem (Happel & Brenner Reference Happel and Brenner1965), the auxiliary problem of a particle of the same instantaneous geometry in a steady Stokes flow is considered:
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\widehat{\unicode[STIX]{x1D748}}=\mathbf{0},\quad \unicode[STIX]{x1D735}\boldsymbol{\cdot }\widehat{\boldsymbol{u}}=0, & & \displaystyle\end{eqnarray}$$
with boundary conditions
$$\begin{eqnarray}\displaystyle \widehat{\boldsymbol{u}}|_{S}=\widehat{\boldsymbol{U}}+\widehat{\unicode[STIX]{x1D734}}\times \boldsymbol{r},\quad \widehat{\boldsymbol{u}}|_{\boldsymbol{r}\rightarrow \infty }=\mathbf{0}. & & \displaystyle\end{eqnarray}$$
Let us stress that the particle is rigid so that by instantaneous geometry one should understand that the surface boundary of the auxiliary problem matches that of its real counterpart at each time. Using (2.1) and (2.3), one obtains
$$\begin{eqnarray}\displaystyle \int _{V}[\widehat{\boldsymbol{u}}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D748})-\boldsymbol{u}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\widehat{\unicode[STIX]{x1D748}})]\,\text{d}V=Re\int _{V}\widehat{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{u}\,\text{d}V+\unicode[STIX]{x1D706}^{2}\int _{V}\widehat{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x2202}_{t}\boldsymbol{u}\,\text{d}V. & & \displaystyle\end{eqnarray}$$
Using the divergence theorem together with the continuity equations, equation (2.5) reduces to
$$\begin{eqnarray}\displaystyle \int _{S_{\infty }-S}(\widehat{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x1D748}-\boldsymbol{u}\boldsymbol{\cdot }\widehat{\unicode[STIX]{x1D748}})\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}S=Re\int _{V}\widehat{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{u}\,\text{d}V+\unicode[STIX]{x1D706}^{2}\int _{V}\widehat{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x2202}_{t}\boldsymbol{u}\,\text{d}V. & & \displaystyle\end{eqnarray}$$
Because
$\boldsymbol{u},\widehat{\boldsymbol{u}}\sim 1/r$
and
$\unicode[STIX]{x1D748},\widehat{\unicode[STIX]{x1D748}}\sim 1/r^{2}$
when
$r\rightarrow \infty$
(see e.g. Happel & Brenner Reference Happel and Brenner1965), the surface integral at infinity in (2.6) vanishes. The boundary conditions (2.2) and (2.4) then yield
$$\begin{eqnarray}\displaystyle (\tilde{\boldsymbol{U}}+\boldsymbol{U})\boldsymbol{\cdot }\widehat{\boldsymbol{F}}+\unicode[STIX]{x1D734}\boldsymbol{\cdot }\widehat{\boldsymbol{L}}-\widehat{\boldsymbol{U}}\boldsymbol{\cdot }\boldsymbol{F}-\widehat{\unicode[STIX]{x1D734}}\boldsymbol{\cdot }\boldsymbol{L}=Re\int _{V}\widehat{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{u}\,\text{d}V+\unicode[STIX]{x1D706}^{2}\int _{V}\widehat{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x2202}_{t}\boldsymbol{u}\,\text{d}V, & & \displaystyle\end{eqnarray}$$
with
$\boldsymbol{F}=\int _{S}\unicode[STIX]{x1D748}\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}S$
and
$\boldsymbol{L}=\int _{S}(\boldsymbol{r}\times \unicode[STIX]{x1D748})\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}S$
(respectively
$\hat{\boldsymbol{F}}$
and
$\hat{\boldsymbol{L}}$
), the force and torque in the real (respectively auxiliary) problem. For the real problem,
$\boldsymbol{F}$
and
$\boldsymbol{L}$
derive from Newton’s laws:
$$\begin{eqnarray}\displaystyle \boldsymbol{F}=\overline{\unicode[STIX]{x1D70C}}\unicode[STIX]{x2202}_{t}\boldsymbol{U},\quad \boldsymbol{L}=\unicode[STIX]{x2202}_{t}(\unicode[STIX]{x1D645}\boldsymbol{\cdot }\unicode[STIX]{x1D734}), & & \displaystyle\end{eqnarray}$$
with
$\bar{\unicode[STIX]{x1D70C}}$
the particle-to-fluid density ratio and
$\unicode[STIX]{x1D645}$
the particle’s inertia tensor. For the auxiliary problem,
$\hat{\boldsymbol{F}}$
and
$\hat{\boldsymbol{L}}$
are linearly related to
$\hat{\boldsymbol{U}}$
and
$\hat{\unicode[STIX]{x1D734}}$
through the possibly non-diagonal resistance matrix (Kim & Karrila Reference Kim and Karrila1991). In order to compute the particle motion
$(\boldsymbol{U},\unicode[STIX]{x1D734})$
, we shall consider in (2.7) either (i) an auxiliary steady propulsion
$(\hat{\boldsymbol{U}},\mathbf{0})$
with
$\hat{\boldsymbol{U}}\Vert \boldsymbol{U}$
to determine
$\boldsymbol{U}$
, or (ii) an auxiliary steady rotation
$(\mathbf{0},\hat{\unicode[STIX]{x1D734}})$
with
$\hat{\unicode[STIX]{x1D734}}\Vert \unicode[STIX]{x1D734}$
to determine
$\unicode[STIX]{x1D734}$
. Note that finding the contribution at
$O(Re^{n})$
of the first term on the right-hand side of (2.7) relies on the knowledge of the velocity field
$\boldsymbol{u}$
at
$O(Re^{n-1})$
only, hence the possibility of a recursive calculation order by order in
$Re$
. Conversely, computing the second term will rely on peculiar symmetry and time-average considerations to be made explicit below. Note that for a homogeneous particle, the above formulation also applies to the motion of a particle exposed to a uniform oscillating flow
$-\tilde{\boldsymbol{U}}$
, once inertial forces are accounted for as a modified pressure.
3 Nearly spherical particles in low-
$Re$
flows
We consider a nearly spherical particle of volume
${\mathcal{V}}$
and centre of mass
$O$
. By choosing
$R=(3{\mathcal{V}}/4\unicode[STIX]{x03C0})^{1/3}$
and taking
$O$
as the origin of the system of axes, one can define the particle’s geometry through
$r=1+\unicode[STIX]{x1D716}f(\boldsymbol{n})$
with
$\unicode[STIX]{x1D716}\ll 1$
. By construction
$f$
satisfies
$$\begin{eqnarray}\displaystyle \int _{S}f(\boldsymbol{n})\,\text{d}S=0,\quad \int _{S}f(\boldsymbol{n})\boldsymbol{n}\,\text{d}S=\mathbf{0}. & & \displaystyle\end{eqnarray}$$
The governing equations are first linearised with respect to
$Re\ll 1$
, e.g. defining
$\boldsymbol{u}=\boldsymbol{u}_{0}+Re\boldsymbol{u}_{1}+O(Re^{2})$
, and each order is further expanded as a regular perturbation problem in
$\unicode[STIX]{x1D716}\ll 1$
, e.g.
$\boldsymbol{u}_{k}=\boldsymbol{u}_{k}^{0}+\unicode[STIX]{x1D716}\boldsymbol{u}_{k}^{\unicode[STIX]{x1D716}}+O(\unicode[STIX]{x1D716}^{2})$
with
$k=0,1$
. Note that
$\unicode[STIX]{x1D716}$
must remain small compared to all other dimensionless length scales, i.e.
$\unicode[STIX]{x1D716}\ll 1$
(particle radius) and
$\unicode[STIX]{x1D716}\ll 1/\unicode[STIX]{x1D706}$
(viscous boundary layer thickness). In the following sections, we shall consider the problems at
$O(Re^{k}\unicode[STIX]{x1D716}^{\ell })$
, and successively look into the two leading orders in
$Re$
.
4 Zeroth order in
$Re$
At leading order
$O(Re^{0})$
, equations (2.1) and (2.2) become
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D706}^{2}\unicode[STIX]{x2202}_{t}\boldsymbol{u}_{0}=-\unicode[STIX]{x1D735}p_{0}+\unicode[STIX]{x1D735}^{2}\boldsymbol{u}_{0},\quad \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}_{0}=0, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}_{0}|_{S}=\tilde{\boldsymbol{U}}+\boldsymbol{U}_{0}+\unicode[STIX]{x1D734}_{0}\times \boldsymbol{r},\quad \boldsymbol{u}_{0}|_{\boldsymbol{r}\rightarrow \infty }=\mathbf{0}, & & \displaystyle\end{eqnarray}$$
and (2.7) reduces to
$$\begin{eqnarray}\displaystyle (\tilde{\boldsymbol{U}}+\boldsymbol{U}_{0})\boldsymbol{\cdot }\widehat{\boldsymbol{F}}+\unicode[STIX]{x1D734}_{0}\boldsymbol{\cdot }\widehat{\boldsymbol{L}}-\widehat{\boldsymbol{U}}\boldsymbol{\cdot }\boldsymbol{F}_{0}-\widehat{\unicode[STIX]{x1D734}}\boldsymbol{\cdot }\boldsymbol{L}_{0}=\unicode[STIX]{x1D706}^{2}\int _{V}\widehat{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x2202}_{t}\boldsymbol{u}_{0}\,\text{d}V, & & \displaystyle\end{eqnarray}$$
and this result is expanded as a linear perturbation in
$\unicode[STIX]{x1D716}$
below.
4.1 Perfect sphere –
$O(Re^{0}\unicode[STIX]{x1D716}^{0})$
While it is quite clear that no net motion can arise at
$O(\unicode[STIX]{x1D716}^{0}Re^{0})$
(i.e. unsteady Stokes flow around a spherical particle), we briefly rederive this result to provide the reader with the general methodology. At leading order
$O(\unicode[STIX]{x1D716}^{0})$
, equation (4.3) becomes
$$\begin{eqnarray}\displaystyle (\tilde{\boldsymbol{U}}+\boldsymbol{U}_{0}^{0})\boldsymbol{\cdot }\widehat{\boldsymbol{F}}^{0}+\unicode[STIX]{x1D734}_{0}^{0}\boldsymbol{\cdot }\widehat{\boldsymbol{L}}^{0}-\widehat{\boldsymbol{U}}\boldsymbol{\cdot }\boldsymbol{F}_{0}^{0}-\widehat{\unicode[STIX]{x1D734}}\boldsymbol{\cdot }\boldsymbol{L}_{0}^{0}=\unicode[STIX]{x1D706}^{2}\int _{V_{0}}\widehat{\boldsymbol{u}}^{0}\boldsymbol{\cdot }\unicode[STIX]{x2202}_{t}\boldsymbol{u}_{0}^{0}\,\text{d}V, & & \displaystyle\end{eqnarray}$$
where
$V_{0}$
denotes the volume of fluid outside the reference unit sphere. First, recalling
$\widehat{\boldsymbol{U}}\Vert \boldsymbol{U}_{0}^{0}$
provides
$\widehat{\boldsymbol{U}}\boldsymbol{\cdot }\tilde{\boldsymbol{U}}=0$
. Second, the velocity field
$\widehat{\boldsymbol{u}}^{0}$
(respectively
$\boldsymbol{u}_{0}^{0}$
) is linear with respect to
$\widehat{\boldsymbol{U}}$
(respectively
$\tilde{\boldsymbol{U}}$
), and axisymmetric about the axis holding the vector
$\widehat{\boldsymbol{U}}$
(respectively
$\tilde{\boldsymbol{U}}$
) and passing through the centre of mass of the particle. As a result, using the expression of
$\widehat{\boldsymbol{u}}^{0}$
and
$\boldsymbol{u}_{0}^{0}$
(appendix A) shows that the RHS of (4.4) does not include any contribution from the forcing
$\tilde{\boldsymbol{U}}$
. There is therefore no net motion at this order, i.e.
$\boldsymbol{U}_{0}^{0}=\mathbf{0}$
. A similar reasoning shows that
$\unicode[STIX]{x1D734}_{0}^{0}=\mathbf{0}$
as well. This last result imposes the rotation velocity of the particle to be at least first order (either in
$\unicode[STIX]{x1D716}$
or
$Re$
). The forcing and induced rotation act therefore on two separate time scales. As a consequence, at leading order, the geometry of the particle,
$f$
, can be considered constant over the
$O(1)$
period of the forcing (fast time scale).
4.2 Near-sphere correction –
$O(Re^{0}\unicode[STIX]{x1D716}^{1})$
At
$O(\unicode[STIX]{x1D716}^{1})$
, equation (4.3) becomes
$$\begin{eqnarray}\displaystyle & & \displaystyle \boldsymbol{U}_{0}^{\unicode[STIX]{x1D716}}\boldsymbol{\cdot }\widehat{\boldsymbol{F}}^{0}+\unicode[STIX]{x1D734}_{0}^{\unicode[STIX]{x1D716}}\boldsymbol{\cdot }\widehat{\boldsymbol{L}}^{0}+\tilde{\boldsymbol{U}}\boldsymbol{\cdot }\widehat{\boldsymbol{F}}^{\unicode[STIX]{x1D716}}-\widehat{\boldsymbol{U}}\boldsymbol{\cdot }\boldsymbol{F}_{0}^{\unicode[STIX]{x1D716}}-\widehat{\unicode[STIX]{x1D734}}\boldsymbol{\cdot }\boldsymbol{L}_{0}^{\unicode[STIX]{x1D716}}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D706}^{2}\int _{V_{0}}(\widehat{\boldsymbol{u}}^{\unicode[STIX]{x1D716}}\boldsymbol{\cdot }\unicode[STIX]{x2202}_{t}\boldsymbol{u}_{0}^{0}+\widehat{\boldsymbol{u}}^{0}\boldsymbol{\cdot }\unicode[STIX]{x2202}_{t}\boldsymbol{u}_{0}^{\unicode[STIX]{x1D716}})\,\text{d}V-\unicode[STIX]{x1D706}^{2}\int _{S_{0}}f\widehat{\boldsymbol{u}}^{0}\boldsymbol{\cdot }\unicode[STIX]{x2202}_{t}\boldsymbol{u}_{0}^{0}\,\text{d}S,\end{eqnarray}$$
where the surface integral is the
$O(\unicode[STIX]{x1D716})$
contribution from the difference of the volume integrals on
$V$
and
$V_{0}$
(e.g. Zhang & Stone Reference Zhang and Stone1998). The analysis of Zhang & Stone (Reference Zhang and Stone1998) shows that the rotation of a torque-free homogeneous near-sphere resulting from an
$O(1)$
imposed translation is
$O(\unicode[STIX]{x1D716}^{2})$
and thus
$\unicode[STIX]{x1D734}_{0}^{\unicode[STIX]{x1D716}}=\mathbf{0}$
. Consequently the torque
$\boldsymbol{L}_{0}^{\unicode[STIX]{x1D716}}$
linked to
$\unicode[STIX]{x1D734}_{0}^{\unicode[STIX]{x1D716}}$
through Newton’s law (2.8) vanishes as well. Using (2.4) and (3.1), the last term in (4.5) vanishes exactly:
$$\begin{eqnarray}\displaystyle \int _{S_{0}}f\widehat{\boldsymbol{u}}^{0}\boldsymbol{\cdot }\unicode[STIX]{x2202}_{t}\boldsymbol{u}_{0}^{0}\,\text{d}S=(\dot{\tilde{\boldsymbol{U}}}\times \widehat{\unicode[STIX]{x1D734}})\boldsymbol{\cdot }\int _{S_{0}}f\boldsymbol{n}\,\text{d}S=0. & & \displaystyle\end{eqnarray}$$
Since we are interested in the net motion of the particle, we take the time-average over the fast time scale (forcing period) of (4.5). The
$\langle \text{RHS}\rangle _{t}$
can be shown to vanish because
$\boldsymbol{u}_{0}^{\unicode[STIX]{x1D716}}$
and
$\boldsymbol{u}_{0}^{0}$
are periodic in time, and the integration domains are time-independent. Therefore
$$\begin{eqnarray}\displaystyle \langle \boldsymbol{U}_{0}^{\unicode[STIX]{x1D716}}\rangle _{t}\boldsymbol{\cdot }\widehat{\boldsymbol{F}}^{0}-\widehat{\boldsymbol{U}}\boldsymbol{\cdot }\langle \boldsymbol{F}_{0}^{\unicode[STIX]{x1D716}}\rangle _{t}=0. & & \displaystyle\end{eqnarray}$$
Equation (4.7) is linear with no net contribution of the forcing
$\tilde{\boldsymbol{U}}$
: no net motion can occur at
$O(Re^{0}\unicode[STIX]{x1D716}^{1})$
,
$\langle \boldsymbol{U}_{0}^{\unicode[STIX]{x1D716}}\rangle _{t}=\mathbf{0}$
.
5 First order in
$Re$
At
$O(Re^{1})$
, equations (2.1) and (2.2) become
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D706}^{2}\unicode[STIX]{x2202}_{t}\boldsymbol{u}_{1}+\unicode[STIX]{x1D735}\boldsymbol{u}_{0}\boldsymbol{\cdot }\boldsymbol{u}_{0}=-\unicode[STIX]{x1D735}p_{1}+\unicode[STIX]{x1D735}^{2}\boldsymbol{u}_{1},\quad \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}_{1}=0, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}_{1}|_{S}=\boldsymbol{U}_{1}+\unicode[STIX]{x1D734}_{1}\times \boldsymbol{r},\quad \boldsymbol{u}_{1}|_{\boldsymbol{r}\rightarrow \infty }=\mathbf{0}, & & \displaystyle\end{eqnarray}$$
and (2.7) reduces to
$$\begin{eqnarray}\displaystyle \boldsymbol{U}_{1}\boldsymbol{\cdot }\widehat{\boldsymbol{F}}+\unicode[STIX]{x1D734}_{1}\boldsymbol{\cdot }\widehat{\boldsymbol{L}}-\widehat{\boldsymbol{U}}\boldsymbol{\cdot }\boldsymbol{F}_{1}-\widehat{\unicode[STIX]{x1D734}}\boldsymbol{\cdot }\boldsymbol{L}_{1}=\int _{V}\widehat{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}_{0}\boldsymbol{\cdot }\boldsymbol{u}_{0}\,\text{d}V+\unicode[STIX]{x1D706}^{2}\int _{V}\widehat{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x2202}_{t}\boldsymbol{u}_{1}\,\text{d}V. & & \displaystyle\end{eqnarray}$$
Note that here, in addition to the unsteady forcing, the nonlinear convective term acts as a source term in (5.3). Because it is quadratic in velocity, one might expect that its average in time is non-zero, which could in turn yield net particle motion.
5.1 Perfect sphere –
$O(Re^{1}\unicode[STIX]{x1D716}^{0})$
At leading order
$O(\unicode[STIX]{x1D716}^{0})$
(5.3) becomes
$$\begin{eqnarray}\displaystyle \boldsymbol{U}_{1}^{0}\boldsymbol{\cdot }\widehat{\boldsymbol{F}}^{0}+\unicode[STIX]{x1D734}_{1}^{0}\boldsymbol{\cdot }\widehat{\boldsymbol{L}}^{0}-\widehat{\boldsymbol{U}}\boldsymbol{\cdot }\boldsymbol{F}_{1}^{0}-\widehat{\unicode[STIX]{x1D734}}\boldsymbol{\cdot }\boldsymbol{L}_{1}^{0}=\int _{V_{0}}\widehat{\boldsymbol{u}}^{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}_{0}^{0}\boldsymbol{\cdot }\boldsymbol{u}_{0}^{0}\,\text{d}V+\unicode[STIX]{x1D706}^{2}\int _{V_{0}}\widehat{\boldsymbol{u}}^{0}\boldsymbol{\cdot }\unicode[STIX]{x2202}_{t}\boldsymbol{u}_{1}^{0}\,\text{d}V.\quad & & \displaystyle\end{eqnarray}$$
The symmetry properties of
$\widehat{\boldsymbol{u}}^{0}$
and
$\boldsymbol{u}_{0}^{0}$
(appendix A) impose that the first term on the RHS of (5.4) vanishes. The second term on the RHS vanishes as well because it is the integral of the scalar product between two axisymmetric fields about orthogonal principal directions. Therefore (5.4) becomes
$$\begin{eqnarray}\displaystyle \boldsymbol{U}_{1}^{0}\boldsymbol{\cdot }\widehat{\boldsymbol{F}}^{0}+\unicode[STIX]{x1D734}_{1}^{0}\boldsymbol{\cdot }\widehat{\boldsymbol{L}}^{0}-\widehat{\boldsymbol{U}}\boldsymbol{\cdot }\boldsymbol{F}_{1}^{0}-\widehat{\unicode[STIX]{x1D734}}\boldsymbol{\cdot }\boldsymbol{L}_{1}^{0}=\mathbf{0}, & & \displaystyle\end{eqnarray}$$
implying that, very much like for
$O(Re^{0}\unicode[STIX]{x1D716}^{0})$
,
$\boldsymbol{U}_{1}^{0}=\mathbf{0}$
and
$\unicode[STIX]{x1D734}_{1}^{0}=\mathbf{0}$
.
5.2 Near-sphere correction –
$O(Re^{1}\unicode[STIX]{x1D716}^{1})$
At
$O(\unicode[STIX]{x1D716}^{1})$
, and using (2.8) together with (5.5), (5.3) becomes
$$\begin{eqnarray}\displaystyle & & \displaystyle \boldsymbol{U}_{1}^{\unicode[STIX]{x1D716}}\boldsymbol{\cdot }\widehat{\boldsymbol{F}}^{0}+\unicode[STIX]{x1D734}_{1}^{\unicode[STIX]{x1D716}}\boldsymbol{\cdot }\widehat{\boldsymbol{L}}^{0}-\widehat{\boldsymbol{U}}\boldsymbol{\cdot }\boldsymbol{F}_{1}^{\unicode[STIX]{x1D716}}-\widehat{\unicode[STIX]{x1D734}}\boldsymbol{\cdot }\boldsymbol{L}_{1}^{\unicode[STIX]{x1D716}}=-\int _{S_{0}}f\,\widehat{\boldsymbol{u}}^{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}_{0}^{0}\boldsymbol{\cdot }\boldsymbol{u}_{0}^{0}\,\text{d}S\nonumber\\ \displaystyle & & \displaystyle \quad +\,\int _{V_{0}}(\widehat{\boldsymbol{u}}^{\unicode[STIX]{x1D716}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}_{0}^{0}\boldsymbol{\cdot }\boldsymbol{u}_{0}^{0}+\widehat{\boldsymbol{u}}^{0}\boldsymbol{\cdot }[\unicode[STIX]{x1D735}\boldsymbol{u}_{0}^{0}\boldsymbol{\cdot }\boldsymbol{u}_{0}^{\unicode[STIX]{x1D716}}+\unicode[STIX]{x1D735}\boldsymbol{u}_{0}^{\unicode[STIX]{x1D716}}\boldsymbol{\cdot }\boldsymbol{u}_{0}^{0}])\,\text{d}V\nonumber\\ \displaystyle & & \displaystyle \quad +\,\unicode[STIX]{x1D706}^{2}\int _{V_{0}}(\widehat{\boldsymbol{u}}^{0}\boldsymbol{\cdot }\unicode[STIX]{x2202}_{t}\boldsymbol{u}_{1}^{\unicode[STIX]{x1D716}}+\widehat{\boldsymbol{u}}^{\unicode[STIX]{x1D716}}\boldsymbol{\cdot }\unicode[STIX]{x2202}_{t}\boldsymbol{u}_{1}^{0})\,\text{d}V-\unicode[STIX]{x1D706}^{2}\int _{S_{0}}f\widehat{\boldsymbol{u}}^{0}\boldsymbol{\cdot }\unicode[STIX]{x2202}_{t}\boldsymbol{u}_{1}^{0}\,\text{d}S.\end{eqnarray}$$
Taking the average in time of (5.6) over the forcing period, and using that
$\boldsymbol{u}_{1}^{\unicode[STIX]{x1D716}}$
and
$\boldsymbol{u}_{1}^{0}$
are periodic and that
$\boldsymbol{F}_{1}^{\unicode[STIX]{x1D716}}$
and
$\boldsymbol{L}_{1}^{\unicode[STIX]{x1D716}}$
are temporal derivatives of periodic functions (2.8), one finally obtains
$$\begin{eqnarray}\displaystyle & \displaystyle 6\unicode[STIX]{x03C0}\langle \boldsymbol{U}_{1}^{\unicode[STIX]{x1D716}}\rangle _{t}\boldsymbol{\cdot }\widehat{\boldsymbol{U}}+8\unicode[STIX]{x03C0}\langle \unicode[STIX]{x1D734}_{1}^{\unicode[STIX]{x1D716}}\rangle _{t}\boldsymbol{\cdot }\widehat{\unicode[STIX]{x1D734}}=-v_{1}^{\unicode[STIX]{x1D716}},\quad \text{with} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle v_{1}^{\unicode[STIX]{x1D716}}=\left\langle \int _{V_{0}}(\widehat{\boldsymbol{u}}^{\unicode[STIX]{x1D716}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}_{0}^{0}\boldsymbol{\cdot }\boldsymbol{u}_{0}^{0}+\widehat{\boldsymbol{u}}^{0}\boldsymbol{\cdot }[\unicode[STIX]{x1D735}\boldsymbol{u}_{0}^{0}\boldsymbol{\cdot }\boldsymbol{u}_{0}^{\unicode[STIX]{x1D716}}+\unicode[STIX]{x1D735}\boldsymbol{u}_{0}^{\unicode[STIX]{x1D716}}\boldsymbol{\cdot }\boldsymbol{u}_{0}^{0}])\,\text{d}V-\int _{S_{0}}f\widehat{\boldsymbol{u}}^{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}_{0}^{0}\boldsymbol{\cdot }\boldsymbol{u}_{0}^{0}\,\text{d}S\right\rangle _{t}\qquad & \displaystyle\end{eqnarray}$$
where we have used
$\widehat{\boldsymbol{F}}^{0}=-6\unicode[STIX]{x03C0}\widehat{\boldsymbol{U}}$
and
$\widehat{\boldsymbol{L}}^{0}=-8\unicode[STIX]{x03C0}\widehat{\unicode[STIX]{x1D734}}$
. Integrating by parts, and using the expressions of
$\widehat{\boldsymbol{u}}^{0}$
and
$\boldsymbol{u}_{0}^{0}$
(appendix A), one obtains
$$\begin{eqnarray}\displaystyle v_{1}^{\unicode[STIX]{x1D716}}=\int _{V_{0}}(\widehat{\boldsymbol{u}}^{\unicode[STIX]{x1D716}}\boldsymbol{\cdot }\boldsymbol{G}_{1}(\boldsymbol{r})-\langle \boldsymbol{u}_{0}^{\unicode[STIX]{x1D716}}\boldsymbol{\cdot }\boldsymbol{G}_{2}(\boldsymbol{r})\rangle _{t})\,\text{d}V, & & \displaystyle\end{eqnarray}$$
with the vector fields
$\boldsymbol{G}_{1}$
and
$\boldsymbol{G}_{2}$
defined as
$\boldsymbol{G}_{1}=\langle \unicode[STIX]{x1D735}\boldsymbol{u}_{0}^{0}\boldsymbol{\cdot }\boldsymbol{u}_{0}^{0}\rangle _{t}$
and
$\boldsymbol{G}_{2}=[\unicode[STIX]{x1D735}\widehat{\boldsymbol{u}}^{0}+(\unicode[STIX]{x1D735}\widehat{\boldsymbol{u}}^{0})^{T}]\boldsymbol{\cdot }\boldsymbol{u}_{0}^{0}$
, whose expressions are provided in appendix A.
Using domain perturbation, the velocity field
$\boldsymbol{u}_{0}^{\unicode[STIX]{x1D716}}$
(respectively
$\widehat{\boldsymbol{u}}^{\unicode[STIX]{x1D716}}$
) is solution of (4.1) (respectively (2.3)) with the following boundary conditions on the unit sphere (see appendix B):
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{u}_{0}^{\unicode[STIX]{x1D716}}|_{r=1}=-f(\boldsymbol{n})\unicode[STIX]{x2202}_{r}\boldsymbol{u}_{0}^{0}|_{r=1}+\boldsymbol{U}_{0}^{\unicode[STIX]{x1D716}}+\unicode[STIX]{x1D734}_{0}^{\unicode[STIX]{x1D716}}\times \boldsymbol{r}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \widehat{\boldsymbol{u}}^{\unicode[STIX]{x1D716}}|_{r=1}=-f(\boldsymbol{n})\unicode[STIX]{x2202}_{r}\widehat{\boldsymbol{u}}^{0}|_{r=1}. & \displaystyle\end{eqnarray}$$
$\unicode[STIX]{x1D734}_{0}^{\unicode[STIX]{x1D716}}=\mathbf{0}$
. A second one arises from the fact that the Stokes problem with the uniform boundary condition
$\boldsymbol{U}_{0}^{\unicode[STIX]{x1D716}}$
on the unit sphere does not contribute to particle motion, as demonstrated in § 5.1. As a consequence, only the first contribution to
$\boldsymbol{u}_{0}^{\unicode[STIX]{x1D716}}|_{r=1}$
in (5.10a
) provides a net contribution to
$v_{1}^{\unicode[STIX]{x1D716}}$
.For clarity, we now distinguish the cases of pure translation and pure rotation.
5.2.1 Translation
Setting
$\widehat{\unicode[STIX]{x1D734}}=\mathbf{0}$
, equation (5.9) simplifies after some algebraic calculations using the definitions of
$\boldsymbol{G}_{1}$
,
$\boldsymbol{G}_{2}$
,
$\widehat{\boldsymbol{u}}^{\unicode[STIX]{x1D700}}$
and
$\boldsymbol{u}_{0}^{\unicode[STIX]{x1D700}}$
(appendices A and B):
$$\begin{eqnarray}\displaystyle v_{1}^{\unicode[STIX]{x1D716}}={\mathcal{K}}(\unicode[STIX]{x1D706})[f\boldsymbol{n}\boldsymbol{n}\boldsymbol{n}]_{\boldsymbol{n}}\boldsymbol{\vdots }\,\boldsymbol{e}_{\boldsymbol{x}}\boldsymbol{e}_{\boldsymbol{x}}\widehat{\boldsymbol{U}}, & & \displaystyle\end{eqnarray}$$
where
$[\bullet ]_{\boldsymbol{n}}$
denotes the average over the unit sphere:
$[\bullet ]_{\boldsymbol{n}}=\int _{S_{0}}\bullet (\boldsymbol{n})\,\text{d}S$
, and
$\boldsymbol{\vdots }$
denotes the three-fold tensorial contraction. Quite remarkably, equation (5.11) provides the expression of the net translational velocity as a product of a function of
$\unicode[STIX]{x1D706}$
and a functional of
$f$
. The tensorial contraction, together with the angular symmetry properties of the inertial forcing, ensure that only a limited set of the spherical harmonic components of the shape function
$f$
can contribute to a net motion. Further algebraic calculations show that
${\mathcal{K}}(\unicode[STIX]{x1D706})$
conveniently reduces to
${\mathcal{K}}(\unicode[STIX]{x1D706})=\int _{r=1}^{\infty }(\text{d}{\mathcal{J}}_{\unicode[STIX]{x1D706}}(r)/\text{d}r)\,\text{d}r$
with
$$\begin{eqnarray}\displaystyle {\mathcal{J}}_{\unicode[STIX]{x1D706}}(r) & = & \displaystyle -\frac{1}{4}\text{Re}\left[\frac{27(1-r^{2})}{16\unicode[STIX]{x1D706}_{0}^{4}r^{8}} (\!-3|\unicode[STIX]{x1D6EC}_{0}|^{2}+2\overline{\unicode[STIX]{x1D6EC}_{0}}(3+3\unicode[STIX]{x1D706}_{0}r-\unicode[STIX]{x1D706}_{0}^{2}r^{2})\text{e}^{\unicode[STIX]{x1D706}_{0}(1-r)}\right.\nonumber\\ \displaystyle & & \displaystyle -\left.(3+3\unicode[STIX]{x1D706}_{0}r+(\unicode[STIX]{x1D706}_{0}r)^{2})(\overline{1+\unicode[STIX]{x1D706}_{0}r-\unicode[STIX]{x1D706}_{0}^{2}r^{2}})\text{e}^{2\text{Re}[\unicode[STIX]{x1D706}_{0}](1-r)}\! )\right],\end{eqnarray}$$
where an overbar denotes the complex conjugate,
$\text{Re}[z]$
is the real part operator of
$z$
and
$\unicode[STIX]{x1D6EC}_{0}=1+\unicode[STIX]{x1D706}_{0}+\unicode[STIX]{x1D706}_{0}^{2}/3$
with
$\unicode[STIX]{x1D706}_{0}=\unicode[STIX]{x1D706}\text{e}^{-i\unicode[STIX]{x03C0}/4}$
. Therefore, using
${\mathcal{J}}_{\unicode[STIX]{x1D706}}(\infty )={\mathcal{J}}_{\unicode[STIX]{x1D706}}(1)=0$
, one finds the central result of the present communication:
$$\begin{eqnarray}\displaystyle \langle \boldsymbol{U}_{1}^{\unicode[STIX]{x1D716}}\rangle _{t}=\mathbf{0}. & & \displaystyle\end{eqnarray}$$
No translational net motion can arise at first order (both in
$Re$
and non-sphericity
$\unicode[STIX]{x1D716}$
) from geometric asymmetry. This result stems from the fact that the near-field (
$r=O(1)$
) and far-field (
$r\gg 1$
) contributions to the inertial forcing compensate exactly.
5.2.2 Rotation
Considering now
$\widehat{\boldsymbol{U}}=\mathbf{0}$
, the same method provides
$$\begin{eqnarray}\displaystyle v_{1}^{\unicode[STIX]{x1D716}}={\mathcal{L}}(\unicode[STIX]{x1D706})[f\boldsymbol{n}\boldsymbol{n}]_{\boldsymbol{n}}\boldsymbol{ : }\boldsymbol{e}_{\boldsymbol{x}}(\boldsymbol{e}_{\boldsymbol{x}}\times \widehat{\unicode[STIX]{x1D734}}), & & \displaystyle\end{eqnarray}$$
with
$$\begin{eqnarray}\displaystyle {\mathcal{L}}(\unicode[STIX]{x1D706}) & = & \displaystyle \frac{1}{256}\text{Im}\left\{\frac{1}{\unicode[STIX]{x1D6EC}_{0}} [\!-48(\unicode[STIX]{x1D706}_{0}(\unicode[STIX]{x1D706}_{0}(\unicode[STIX]{x1D706}_{0}(\unicode[STIX]{x1D706}_{0}+6)+18)+30)+24)|\unicode[STIX]{x1D706}_{0}|^{2}F(2\text{Re}(\unicode[STIX]{x1D706}_{0}))\right.\nonumber\\ \displaystyle & & \displaystyle +\,3\text{i}(\unicode[STIX]{x1D706}_{0}(\unicode[STIX]{x1D706}_{0}(\unicode[STIX]{x1D706}_{0}(\unicode[STIX]{x1D706}_{0}+9)+27)+42)+30)\unicode[STIX]{x1D706}_{0}^{2}\bar{\unicode[STIX]{x1D6EC}_{0}}F(\unicode[STIX]{x1D706}_{0})\nonumber\\ \displaystyle & & \displaystyle +\,3\text{i}(\unicode[STIX]{x1D706}_{0}(\unicode[STIX]{x1D706}_{0}(\unicode[STIX]{x1D706}_{0}(\unicode[STIX]{x1D706}_{0}+3)+33)+78)+66)\unicode[STIX]{x1D706}_{0}^{2}\unicode[STIX]{x1D6EC}_{0}F(\text{i}\unicode[STIX]{x1D706}_{0})\nonumber\\ \displaystyle & & \displaystyle +\,(1-\text{i})\unicode[STIX]{x1D706}_{0}^{7}+(3-7\text{i})\unicode[STIX]{x1D706}_{0}^{6}-(5+35\text{i})\unicode[STIX]{x1D706}_{0}^{5}-(6+108\text{i})\unicode[STIX]{x1D706}_{0}^{4}-(60+210\text{i})\unicode[STIX]{x1D706}_{0}^{3}\nonumber\\ \displaystyle & & \displaystyle -\left.(264+306\text{i})\unicode[STIX]{x1D706}_{0}^{2}-(348+360\text{i})\unicode[STIX]{x1D706}_{0}-132\text{i}\!]\right\},\end{eqnarray}$$
with
$F(z)=[\text{Chi}(z)-\text{Shi}(z)]\text{e}^{z}$
where
$\text{Chi}/\text{Shi}$
are the hyperbolic cosine/sine integral functions respectively (Abramowitz & Stegun Reference Abramowitz and Stegun1965). We note from (5.8) and (5.14) that (i) no rotation is obtained along the direction of oscillation (i.e.
$\langle \unicode[STIX]{x1D734}_{1}^{\unicode[STIX]{x1D716}}\rangle _{t}\boldsymbol{\cdot }\tilde{\boldsymbol{U}}=0$
) and that (ii) the particle dynamics is an overdamped rotation towards an equilibrium position. The oscillation direction
$\tilde{\boldsymbol{U}}$
is aligned with a principal direction of the symmetric and traceless second-order tensor
$[f\boldsymbol{n}\boldsymbol{n}]_{\boldsymbol{n}}$
with positive or negative eigenvalue depending on the sign of
${\mathcal{L}}$
. Further, the function
$\langle {\mathcal{L}}\rangle _{t}$
changes sign for
$\unicode[STIX]{x1D706}_{c}\approx 3.6$
, resulting in a shift in the equilibrium orientation between
$\unicode[STIX]{x1D706}<\unicode[STIX]{x1D706}_{c}$
and
$\unicode[STIX]{x1D706}>\unicode[STIX]{x1D706}_{c}$
. This transition confirms fundamental differences in the streaming flow and associated forcing between small and large frequencies, as already observed by Collis, Chakraborty & Sader (Reference Collis, Chakraborty and Sader2017) when studying numerically the propulsion of an oscillating asymmetric dumbbell.
6 Conclusion
In this work, we analysed the translation and rotation resulting from the oscillation of a homogeneous near-sphere up to
$O(\unicode[STIX]{x1D716}Re)$
, showing analytically that no net translation occurs regardless of the oscillation frequency and despite the geometric asymmetry of the particle. This result, which contradicts the conclusions of Nadal & Lauga (Reference Nadal and Lauga2014), stems from the exact cancellation of the streaming flow forcing in the immediate vicinity of the particle and far away from it, making it difficult to capture numerically, as any discretisation introduces necessarily a truncation error. We also show that a transient rotation can stir back the particle towards one of its equilibrium positions.
Notwithstanding, our results do not contradict the numerical observations of Collis et al. (Reference Collis, Chakraborty and Sader2017) for which a weak front–back asymmetry of a dumbbell was sufficient to produce a net motion at that order: in that case, the elongated shape of the particle combined with the small asymmetry of the two spheres leads to an
$O(1)$
periodic rotation of the system, which is at the heart of the self-propulsion, when coupled to the oscillating translation – in contrast, such rotation is absent at
$O(\unicode[STIX]{x1D716}Re)$
in the case of a near-sphere. All together, developing net motion around an asymmetric particle appears to require an
$O(\unicode[STIX]{x1D716})$
rotation/translation coupling, as obtained for instance using density inhomogeneities.
Acknowledgements
We are grateful to F. Nadal and E. Lauga for insightful discussions on this problem. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme under Grant Agreement 714027 (SM).
Appendix A. Unsteady Stokes flow past a spherical particle
A.1 Oscillating flow
The complex velocity field around a sphere oscillating at velocity
$\tilde{\boldsymbol{U}}$
reads (Kim & Karrila Reference Kim and Karrila1991)
$\boldsymbol{u}_{0}^{0}=A\tilde{\boldsymbol{U}}+B(\tilde{\boldsymbol{U}}\boldsymbol{\cdot }\boldsymbol{n})\boldsymbol{n}$
where
$$\begin{eqnarray}\displaystyle & \displaystyle A(r,\unicode[STIX]{x1D706})=\frac{3}{2\unicode[STIX]{x1D706}_{0}^{2}r^{3}}[-\unicode[STIX]{x1D6EC}_{0}+(1+\unicode[STIX]{x1D706}_{0}r+\unicode[STIX]{x1D706}_{0}^{2}r^{2})\text{e}^{\unicode[STIX]{x1D706}_{0}(1-r)}], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle B(r,\unicode[STIX]{x1D706})=\frac{3}{2\unicode[STIX]{x1D706}_{0}^{2}r^{3}}[3\unicode[STIX]{x1D6EC}_{0}-(3+3\unicode[STIX]{x1D706}_{0}r+\unicode[STIX]{x1D706}_{0}^{2}r^{2})\text{e}^{\unicode[STIX]{x1D706}_{0}(1-r)}], & \displaystyle\end{eqnarray}$$
and where
$\unicode[STIX]{x1D706}_{0}=\unicode[STIX]{x1D706}\text{e}^{-\text{i}\unicode[STIX]{x03C0}/4}$
and
$\unicode[STIX]{x1D6EC}_{0}=1+\unicode[STIX]{x1D706}_{0}+\unicode[STIX]{x1D706}_{0}^{2}/3$
. Recalling that
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D735}\boldsymbol{u}_{0}^{0}=A^{\prime }\tilde{\boldsymbol{U}}\boldsymbol{n}+B^{\prime }(\tilde{\boldsymbol{U}}\boldsymbol{\cdot }\boldsymbol{n})\boldsymbol{n}\boldsymbol{n}+\frac{B}{r}(\unicode[STIX]{x1D644}-\boldsymbol{n}\boldsymbol{n})(\tilde{\boldsymbol{U}}\boldsymbol{\cdot }\boldsymbol{n})+\frac{B}{r}\boldsymbol{n}(\unicode[STIX]{x1D644}-\boldsymbol{n}\boldsymbol{n})\boldsymbol{\cdot }\tilde{\boldsymbol{U}}, & & \displaystyle\end{eqnarray}$$
one may compute
$\boldsymbol{G}_{1}=\langle \unicode[STIX]{x1D735}\boldsymbol{u}_{0}^{0}\boldsymbol{\cdot }\boldsymbol{u}_{0}^{0}\rangle _{t}$
, that is,
$$\begin{eqnarray}\displaystyle \boldsymbol{G}_{1}=\frac{1}{2}\text{Re}[(A+B)\overline{[A^{\prime }\unicode[STIX]{x1D644}\boldsymbol{n}+B^{\prime }\boldsymbol{n}\boldsymbol{n}\boldsymbol{n}]}+\frac{A\overline{B}}{r}[\boldsymbol{n}(\unicode[STIX]{x1D644}-\boldsymbol{n}\boldsymbol{n})+(\unicode[STIX]{x1D644}-\boldsymbol{n}\boldsymbol{n})\boldsymbol{n}]]\,\boldsymbol{ : }\,\boldsymbol{e}_{\boldsymbol{x}}\boldsymbol{e}_{\boldsymbol{x}}. & & \displaystyle\end{eqnarray}$$
A.2 Steady translation
The particular case of a steady translating sphere (
$\unicode[STIX]{x1D706}=0$
) at velocity
$\widehat{\boldsymbol{U}}$
is given by
$\widehat{\boldsymbol{u}}^{0}=\widehat{A}\widehat{\boldsymbol{U}}+\widehat{B}(\widehat{\boldsymbol{U}}\boldsymbol{\cdot }\boldsymbol{n})\boldsymbol{n}$
, where
$$\begin{eqnarray}\displaystyle \widehat{A}(r)=\frac{3}{4r}+\frac{1}{4r^{3}},\quad \widehat{B}(r)=\frac{3}{4}\left(\frac{1}{r}-\frac{1}{r^{3}}\right). & & \displaystyle\end{eqnarray}$$
One may compute
$\boldsymbol{G}_{2}=\unicode[STIX]{x1D735}\widehat{\boldsymbol{u}}_{0}^{0}\boldsymbol{\cdot }\boldsymbol{u}_{0}^{0}+\boldsymbol{u}_{0}^{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\widehat{\boldsymbol{u}}_{0}^{0}$
, that is,
$$\begin{eqnarray}\displaystyle \boldsymbol{G}_{2} & = & \displaystyle \widehat{A}^{\prime }A\boldsymbol{n}\unicode[STIX]{x1D644}\,\boldsymbol{ : }\,\widehat{\boldsymbol{U}}\tilde{\boldsymbol{U}}+\widehat{A}^{\prime }(A+B)\unicode[STIX]{x1D644}\boldsymbol{n}\,\boldsymbol{ : }\,\tilde{\boldsymbol{U}}\widehat{\boldsymbol{U}}+(\widehat{A}^{\prime }B+2\widehat{B}^{\prime }(A+B))\boldsymbol{n}\boldsymbol{n}\boldsymbol{n}\,\boldsymbol{ : }\,\tilde{\boldsymbol{U}}\widehat{\boldsymbol{U}}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\widehat{B}A}{r}[\boldsymbol{n}(\unicode[STIX]{x1D644}-\boldsymbol{n}\boldsymbol{n})\,\boldsymbol{ : }\,\tilde{\boldsymbol{U}}\widehat{\boldsymbol{U}}+2(\unicode[STIX]{x1D644}-\boldsymbol{n}\boldsymbol{n})\boldsymbol{n}\,\boldsymbol{ : }\,\widehat{\boldsymbol{U}}\tilde{\boldsymbol{U}}]+\frac{\widehat{B}(A+B)}{r}(\unicode[STIX]{x1D644}-\boldsymbol{n}\boldsymbol{n})\boldsymbol{n}\,\boldsymbol{ : }\,\tilde{\boldsymbol{U}}\widehat{\boldsymbol{U}}.\qquad\end{eqnarray}$$
A.3 Steady rotation
The velocity field around a steady rotating sphere reads
$\widehat{\boldsymbol{u}}^{0}=\widehat{\unicode[STIX]{x1D734}}\times \boldsymbol{n}/r^{2}$
. Computing
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\widehat{\boldsymbol{u}}^{0}\boldsymbol{\cdot }\boldsymbol{u}_{0}^{0}=\frac{1}{r^{3}}[\widehat{\unicode[STIX]{x1D734}}\times \boldsymbol{u}_{0}^{0}-3(\boldsymbol{u}_{0}^{0}\boldsymbol{\cdot }\boldsymbol{n})(\widehat{\unicode[STIX]{x1D734}}\times \boldsymbol{n})], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{u}_{0}^{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\widehat{\boldsymbol{u}}^{0}=\frac{1}{r^{3}}[\boldsymbol{u}_{0}^{0}\times \widehat{\unicode[STIX]{x1D734}}-3\boldsymbol{u}_{0}^{0}\boldsymbol{\cdot }(\widehat{\unicode[STIX]{x1D734}}\times \boldsymbol{n})\boldsymbol{n}], & \displaystyle\end{eqnarray}$$
one obtains the expression of
$\boldsymbol{G}_{2}=\unicode[STIX]{x1D735}\widehat{\boldsymbol{u}}_{0}^{0}\boldsymbol{\cdot }\boldsymbol{u}_{0}^{0}+\boldsymbol{u}_{0}^{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\widehat{\boldsymbol{u}}_{0}^{0}$
as
$$\begin{eqnarray}\displaystyle \boldsymbol{G}_{2}=-\frac{3A}{r^{3}}(\tilde{\boldsymbol{U}}\times \widehat{\unicode[STIX]{x1D734}})\boldsymbol{\cdot }\boldsymbol{n}\boldsymbol{n}-\frac{3(A+B)}{r^{3}}(\tilde{\boldsymbol{U}}\boldsymbol{\cdot }\boldsymbol{n})(\widehat{\unicode[STIX]{x1D734}}\times \boldsymbol{n}). & & \displaystyle\end{eqnarray}$$
Appendix B. Unsteady Stokes flow past a nearly spherical particle
Here we compute the velocity field solution of the unsteady Stokes problem around a nearly spherical particle:
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D706}^{2}\unicode[STIX]{x2202}_{t}\boldsymbol{u}_{0}^{\unicode[STIX]{x1D716}}=-\unicode[STIX]{x1D735}p_{0}^{\unicode[STIX]{x1D716}}+\unicode[STIX]{x1D735}^{2}\boldsymbol{u}_{0}^{\unicode[STIX]{x1D716}},\quad \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u}_{0}^{\unicode[STIX]{x1D716}}=0, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{u}_{0}^{\unicode[STIX]{x1D716}}|_{r=1}=-f(\boldsymbol{n})\unicode[STIX]{x2202}_{r}\boldsymbol{u}_{0}^{0}|_{r=1},\quad \boldsymbol{u}_{0}|_{\boldsymbol{r}\rightarrow \infty }=\mathbf{0}. & & \displaystyle\end{eqnarray}$$
In Fourier space the boundary condition on the surface of the particle (B 2) takes the form (Zhang & Stone Reference Zhang and Stone1998)
$$\begin{eqnarray}\displaystyle \boldsymbol{u}_{0}^{\unicode[STIX]{x1D716}}|_{r=1}=\frac{3f(\boldsymbol{n})}{2}(1+\unicode[STIX]{x1D706}_{0})(\unicode[STIX]{x1D644}-\boldsymbol{n}\boldsymbol{n})\boldsymbol{\cdot }\tilde{\boldsymbol{U}}. & & \displaystyle\end{eqnarray}$$
Following Sani (Reference Sani1963), we perform a reconstruction of the velocity field from its radial component and associated vorticity:
$$\begin{eqnarray}\displaystyle \boldsymbol{u}_{0}^{\unicode[STIX]{x1D716}}=u_{0,r}^{\unicode[STIX]{x1D716}}\boldsymbol{n}+r^{2}\mathop{\sum }_{n=1}^{\infty }\frac{1}{n(n+1)}[\unicode[STIX]{x1D735}_{s}(\unicode[STIX]{x1D6FB}^{2}u_{r,n})-\boldsymbol{n}\times \unicode[STIX]{x1D735}_{s}\unicode[STIX]{x1D712}_{r,n}], & & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D735}_{s}=\unicode[STIX]{x1D735}-\boldsymbol{n}\unicode[STIX]{x2202}_{r}$
and where
$u_{r,n}$
denotes the
$n$
th mode in the spherical harmonics basis of the radial component of
$\boldsymbol{u}_{0}^{\unicode[STIX]{x1D716}}$
. The latter satisfies in time-Fourier space the equation
$\unicode[STIX]{x1D735}^{2}(\text{i}\unicode[STIX]{x1D706}^{2}+\unicode[STIX]{x1D735}^{2})(ru_{0,r}^{\unicode[STIX]{x1D716}})=0$
. The function
$\unicode[STIX]{x1D712}_{r,n}$
is the
$n$
th mode of the radial component of
$\unicode[STIX]{x1D735}\times \boldsymbol{u}_{0}^{\unicode[STIX]{x1D716}}$
, satisfying
$(\unicode[STIX]{x1D735}^{2}+\text{i}\unicode[STIX]{x1D706}^{2})(r\unicode[STIX]{x1D712}_{r}^{\unicode[STIX]{x1D716}})=0$
. Defining
$p$
and
$q$
through
$$\begin{eqnarray}\displaystyle p=-\frac{2\unicode[STIX]{x1D735}_{s}\boldsymbol{\cdot }\boldsymbol{u}_{0}^{\unicode[STIX]{x1D716}}|_{r=1}}{3(1+\unicode[STIX]{x1D706}_{0})},\quad q=\frac{2\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{s}\times \boldsymbol{u}_{0}^{\unicode[STIX]{x1D716}}|_{r=1}}{3(1+\unicode[STIX]{x1D706}_{0})}, & & \displaystyle\end{eqnarray}$$
one finally obtains
$$\begin{eqnarray}\displaystyle \boldsymbol{u}_{0}^{\unicode[STIX]{x1D716}}=\frac{1}{r}\mathop{\sum }_{n=1}^{\infty }\mathop{\sum }_{m=-n}^{n}U_{n}p_{n}^{m}Y_{n}^{m}\boldsymbol{n}+\mathop{\sum }_{n=1}^{\infty }\mathop{\sum }_{m=-n}^{n}\frac{r^{2}V_{n}p_{n}^{m}}{n(n+1)}\unicode[STIX]{x1D735}Y_{n}^{m}-\mathop{\sum }_{n=1}^{\infty }\mathop{\sum }_{m=-n}^{n}\frac{rX_{n}q_{n}^{m}}{n(n+1)}\boldsymbol{n}\times \unicode[STIX]{x1D735}Y_{n}^{m}, & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where
$p_{n}^{m}$
and
$q_{n}^{m}$
denote respectively the modes of
$p$
and
$q$
in the spherical harmonics basis
$(Y_{n}^{m})$
, and
$U_{n}$
,
$V_{n}$
and
$X_{n}$
follow:
$$\begin{eqnarray}\displaystyle & \displaystyle U_{n}(r,\unicode[STIX]{x1D706})=\frac{3}{2}(1+\unicode[STIX]{x1D706}_{0})\frac{h_{n}^{(1)}(\overline{\unicode[STIX]{x1D706}_{0}}r)-\displaystyle \frac{h_{n}^{(1)}(\overline{\unicode[STIX]{x1D706}_{0}})}{r^{n+1}}}{(2n+1)h_{n}^{(1)}(\overline{\unicode[STIX]{x1D706}_{0}})-\overline{\unicode[STIX]{x1D706}_{0}}h_{n+1}^{(1)}(\overline{\unicode[STIX]{x1D706}_{0}})}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle V_{n}(r,\unicode[STIX]{x1D706})=\frac{U_{n}(r,\unicode[STIX]{x1D706})}{r^{2}}+\frac{\unicode[STIX]{x2202}_{r}U_{n}(r,\unicode[STIX]{x1D706})}{r}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle X_{n}(r,\unicode[STIX]{x1D706})=\frac{3}{2}(1+\unicode[STIX]{x1D706}_{0})\frac{h_{n}^{(1)}(\overline{\unicode[STIX]{x1D706}_{0}}r)}{h_{n}^{(1)}(\overline{\unicode[STIX]{x1D706}_{0}})}, & \displaystyle\end{eqnarray}$$
with
$h_{n}$
the spherical Hankel function of the first kind and order
$n$
(Abramowitz & Stegun Reference Abramowitz and Stegun1965). In (B 5), the functions
$p$
and
$q$
defined on the surface of the unit sphere are directly related to the shape function
$f$
through (B 2). Using (3.1), they further satisfy
$$\begin{eqnarray}\displaystyle [p]_{\boldsymbol{n}}=[q]_{\boldsymbol{n}}=0,\quad [q\boldsymbol{n}]_{\boldsymbol{n}}=0, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle [\unicode[STIX]{x1D735}p\boldsymbol{n}]_{\boldsymbol{n}}=[\boldsymbol{n}\unicode[STIX]{x1D735}p]_{\boldsymbol{n}}=[p\boldsymbol{n}\boldsymbol{n}]_{\boldsymbol{n}}=-2[f\boldsymbol{n}\boldsymbol{n}\boldsymbol{n}]_{\boldsymbol{n}}\boldsymbol{\cdot }\tilde{\boldsymbol{U}}. & & \displaystyle\end{eqnarray}$$
Note that these results can be transposed to obtain
$\widehat{\boldsymbol{u}}^{\unicode[STIX]{x1D716}}$
taking
$\unicode[STIX]{x1D706}=0$
for the translation problem. And a similar approach can be used in the rotating case.
