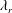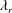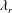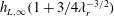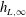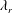1 Introduction
Impact of a drop onto a solid surface is not only commonly seen in nature, but is related to a variety of applications in industry; examples are inkjet printing (Derby Reference Derby2010), surface coating (Rukosuyev, Barannyk & Oshkai Reference Rukosuyev, Barannyk and Oshkai2016) and spray cooling (Zhou, Chen & Wang Reference Zhou, Chen and Wang2017). Spreading and retraction of the drop on the solid surfaces are the key processes in the impact dynamics, and may be accompanied by fascinating flow phenomena such as splashing (Riboux & Gordillo Reference Riboux and Gordillo2014; Stevens Reference Stevens2014) and bouncing (Liu et al. Reference Liu, Moevius, Xu, Qian, Yeomans and Wang2014); recent reviews can be found in Yarin (Reference Yarin2006) and Josserand & Thoroddsen (Reference Josserand and Thoroddsen2016). The parameter spaces of the flow phenomena are usually described by the dimensionless groups
$$\begin{eqnarray}Re=\frac{\unicode[STIX]{x1D70C}U_{0}D}{\unicode[STIX]{x1D707}},\quad We=\frac{\unicode[STIX]{x1D70C}U_{0}^{2}D}{\unicode[STIX]{x1D6FE}}\end{eqnarray}$$
and the wettability of the solid surface (represented by the contact angle
$\unicode[STIX]{x1D703}$
). Here,
$U_{0}$
is the impact velocity,
$D$
is the diameter, and
$\unicode[STIX]{x1D70C}$
,
$\unicode[STIX]{x1D707}$
and
$\unicode[STIX]{x1D6FE}$
denote the density, viscosity and surface tension of the drop respectively.
The dynamics of drop spreading and retraction has been extensively investigated for drop impact onto a flat plate (Biance, Clanet & Quere Reference Biance, Clanet and Quere2004; Clanet, BéGuin & Richard Reference Clanet, BÉGuin and Richard2004; Bartolo, Josserand & Bonn Reference Bartolo, Josserand and Bonn2005). For liquids of low viscosity, it has been experimentally observed that the early spreading is insensitive to the wettability of the solid surface. At low
$U_{0}$
, the radius of the wetted area varies with an inertia–capillary time scale as
$r(t)\sim (\unicode[STIX]{x1D6FE}D/\unicode[STIX]{x1D70C})^{1/4}t^{1/2}$
(Biance et al.
Reference Biance, Clanet and Quere2004); at relatively high
$U_{0}$
, it varies with an inertial time scale as
$r(t)\sim (U_{0}D)^{1/2}t^{1/2}$
(Kim, Feng & Chun Reference Kim, Feng and Chun2000), and the radius of the maximal wetted area
$r_{max}$
follows
$r_{max}/D\sim We^{1/4}$
(Clanet et al.
Reference Clanet, BÉGuin and Richard2004). For drops with relatively high impact velocity, Bartolo et al. (Reference Bartolo, Josserand and Bonn2005) experimentally observed that the drop retraction is independent of the impact velocity. In particular, the retraction velocity,
${\dot{r}}(t)$
, follows
${\dot{r}}(t)/r_{max}\sim (\unicode[STIX]{x1D70C}D^{3}/\unicode[STIX]{x1D6FE})^{-1/2}$
when the inertial and capillary forces are dominant, and
${\dot{r}}(t)/r_{max}\sim (\unicode[STIX]{x1D707}D/\unicode[STIX]{x1D6FE})^{-1}$
when the capillary and viscous forces are dominant.
Drop impact onto more complex substrates has attracted more and more attention recently (Liu et al.
Reference Liu, Andrew, Li, Yeomans and Wang2015; Dressaire, Sauret & Boulogne Reference Dressaire, Sauret and Boulogne2016). It has been shown that the geometry of the substrate can significantly affect the impact dynamics and results in flow phenomena different from those on a flat plate. A typical example is drop impact onto a sphere of radius
$R$
, in which the aspect ratio of the sphere to the drop,
$\unicode[STIX]{x1D706}_{r}=2R/D$
, is expected to play an important role. At
$We\sim 500$
,
$Re\sim O(10^{4})$
and
$\unicode[STIX]{x1D706}_{r}\sim 1$
, Rozhkov, Prunet-Foch & Vignes-Adler (Reference Rozhkov, Prunet-Foch and Vignes-Adler2002) experimentally observed the detachment of the liquid film from the target, forming a thin and conical lamella. At similar
$Re$
and
$We$
, Bakshi, Roisman & Tropea (Reference Bakshi, Roisman and Tropea2007) investigated the spreading of the liquid film on the sphere surface for various values of
$\unicode[STIX]{x1D706}_{r}$
, and suggested that the spreading dynamics could be divided into three stages: drop deformation, inertia-dominated spreading and viscosity-dominated spreading. Mitra, Sathe & Doroodchi (Reference Mitra, Sathe and Doroodchi2013) observed drop rebound off of the sphere after impact at relatively small
$Re$
and
$We$
; later, they theoretically analysed the maximum wetted area based on energy conservation (Mitra et al.
Reference Mitra, Nguyen, Doroodchi, Pareek, Joshi and Evans2016). Irrespective of these successes in experiments, it remains unclear how the aspect ratio influences the dynamics of spreading and retraction after impact, either qualitatively or quantitatively.
In this paper, we numerically investigate the drop deposition on a sphere after impact at moderate Reynolds and Weber numbers (
$We$
ranges from 25 to 400 and
$Re\sim O(10^{3})$
). The aim of our study is to provide a full understanding of the dynamics of the spreading and retraction on the sphere through numerical simulation and theoretical analysis. An axisymmetric diffuse-interface immersed-boundary method (Liu & Ding Reference Liu and Ding2015) is used for this purpose after being validated against experiments. Based on the numerical results, we investigate flow details that are not accessible in experiments, identify the key regimes in the spreading and retraction, analyse the results by scaling laws, and quantitatively evaluate the effect of
$\unicode[STIX]{x1D706}_{r}$
on the impact dynamics.
2 Methodology
We consider here a liquid drop impacting on a sphere, and investigate its dynamics using an axisymmetric diffuse-interface immersed-boundary method (Liu & Ding Reference Liu and Ding2015). This method allows for simulation of incompressible multiphase flows involving rigid objects of irregular shape and moving contact lines. The liquid–gas interface is represented by the volume fraction of the liquid,
$C_{L}$
, the evolution of which is governed by
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}C_{L}}{\unicode[STIX]{x2202}t}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }(\boldsymbol{u}C_{L})=\frac{1}{Pe}\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D713},\end{eqnarray}$$
where the chemical potential
$\unicode[STIX]{x1D713}$
is defined as
$$\begin{eqnarray}\unicode[STIX]{x1D713}=C_{L}^{3}-1.5C_{L}^{2}+0.5C_{L}-C_{L}C_{S}(1-C_{L}-C_{S})-Cn^{2}\unicode[STIX]{x1D6FB}^{2}C_{L}\end{eqnarray}$$
and the Cahn number
$Cn$
is a dimensionless measure of the thickness of the diffuse interface. The Péclet number is set to
$Pe=1/Cn$
(Liu & Ding Reference Liu and Ding2015). To simulate the motion of contact lines on the curved substrate, a characteristic moving contact line model (Lee & Kim Reference Lee and Kim2011; Liu & Ding Reference Liu and Ding2015) is used to update
$C_{L}$
at the embedded solid objects. The distribution of the volume fraction of the solid,
$C_{S}$
, is prescribed according to the position of the sphere. More details of the numerical implementation can be found in Liu & Ding (Reference Liu and Ding2015).
The method is verified by comparing with our experiments on drop impact onto a sphere, despite the fact that the same codes have been used to simulate water entry problems and the obtained results compared favourably with experiments (Ding et al.
Reference Ding, Chen, Liu, Zhang, Gao and Lu2015). The experimental set-up includes polished steel spheres of 3 mm in diameter, which are fixed on a steel needle, and droplets of size between 2 mm and 2.5 mm. The impact velocity ranges from
$0.5~\text{m}~\text{s}^{-1}$
to
$1.5~\text{m}~\text{s}^{-1}$
by adjusting the height of drop release. The impact dynamics is recorded by a high-speed camera at 1500 f.p.s. with a resolution of
$1024\times 1400$
pixels. The advancing contact angle is measured on a flat steel surface. The comparison between the experimental and numerical results with a mesh spacing of
$\unicode[STIX]{x0394}x=0.003$
is presented in figure 1. Unless otherwise stated, the interface in the simulation is represented by the
$C=0.5$
contour, and
$t=0$
corresponds to the moment when the drop comes into contact with the sphere. Clearly, a good agreement has been achieved. Figure 2 shows the grid independence study with
$\unicode[STIX]{x0394}x=0.002$
, 0.003 and 0.005. We found that the results with
$\unicode[STIX]{x0394}x=0.002$
and 0.003 are virtually overlapped with respect to the drop shape at
$t=0.9$
. Therefore, in the following, we use a Cartesian mesh with
$\unicode[STIX]{x0394}x=0.003$
in the simulations.
Figure 1. Snapshots of drop impact onto a solid sphere, in which a water drop of
$D=2.22$
mm hits a steel sphere of 3 mm in diameter at an impact velocity of
$U_{0}=0.74~\text{m}~\text{s}^{-1}$
. The advancing contact angle
$\unicode[STIX]{x1D703}_{A}=95^{\circ }$
in experiments. Numerical results at
$We=16.8$
,
$Re=1638$
,
$\unicode[STIX]{x1D703}=95^{\circ }$
and
$\unicode[STIX]{x1D706}_{r}=1.35$
(solid curves) are superimposed on the experimental results at dimensionless times
$tU_{0}/D=0.2$
, 0.45, 0.9 and 1.35 (from left to right).
Figure 2. Convergence study for a drop impacting onto a sphere at
$tU_{0}/D=0.9$
. The flow parameters are the same as in figure 1. The numerical results are obtained on meshes of different resolution:
$\unicode[STIX]{x0394}x=0.002$
(solid), 0.003 (dash-dotted) and 0.005 (dotted).
Figure 3. Snapshots of drop impact onto a sphere at
$Re=1068$
,
$We=144$
,
$\unicode[STIX]{x1D706}_{r}=2.6$
and
$\unicode[STIX]{x1D703}=60^{\circ }$
; the dimensionless times
$tU_{0}/D$
from (a) to (f) correspond to 0.25, 0.5, 2, 4.25, 10 and 15 respectively. In each panel, the pressure contour (left) and velocity vectors (right) are shown, and the arrow in the sphere indicates the reference vector.
Figure 4. Time evolution of the angular position of the contact line in drop impact at
$Re=1068$
and
$\unicode[STIX]{x1D703}=60^{\circ }$
, for (a)
$We=144$
and various
$\unicode[STIX]{x1D706}_{r}$
, and (b)
$\unicode[STIX]{x1D706}_{r}=2.6$
and various
$We$
.
3 Results and discussion
3.1 Flow features
Typical features of interface dynamics after drop impact at moderate Reynolds and Weber numbers can be observed in figure 3, where sequences of drop shapes are shown at
$Re=1068$
,
$We=144$
,
$\unicode[STIX]{x1D703}=60^{\circ }$
and
$\unicode[STIX]{x1D706}_{r}=2.6$
. At short times, the drop impact leads to high pressure at the north pole of the sphere and the occurrence of a thin layer of liquid film, which spreads out to wet the sphere. At later times (
$2\leqslant tU_{0}/D\leqslant 4.25$
), a rim occurs near the front of liquid film. After reaching the maximum wetted area (at
$tU_{0}/D=4.25$
), the film front retracts. In the subsequent dewetting process, the rim grows slowly by gathering the liquid in the film.
To quantitatively assess the effect of the aspect ratio on the impact dynamics, we performed two sets of numerical experiments, one with
$Re=1068$
,
$We=144$
,
$\unicode[STIX]{x1D703}=60^{\circ }$
and various
$\unicode[STIX]{x1D706}_{r}$
, and the other with
$Re=1068$
,
$\unicode[STIX]{x1D703}=60^{\circ }$
,
$\unicode[STIX]{x1D706}_{r}=2.6$
and various
$We$
. The temporal evolution of the contact line position is shown in figure 4, in terms of the azimuthal angle
$\unicode[STIX]{x1D709}$
(see figure 3
c). Several observations can be made from these results. First, at short times (
$tU_{0}/D\leqslant 2$
), the spreading rate of the drop on the sphere,
$\text{d}\unicode[STIX]{x1D709}/\text{d}t$
, appears to be independent of
$We$
but dependent on
$\unicode[STIX]{x1D706}_{r}$
(figure 4
b). Second, the contact line retracts at a roughly constant speed in all cases, although the value of the speed may vary. Third, the drop is seen to oscillate on the sphere before reaching its equilibrium state, and the oscillation frequency is found to be independent of the impact velocity and
$\unicode[STIX]{x1D706}_{r}$
. This can be interpreted by taking the drop as a spring with the coefficient of surface tension as the stiffness, which has an oscillatory period of
$4\sqrt{\unicode[STIX]{x1D70C}D^{3}/(6\unicode[STIX]{x1D6FE})}$
(Fedorchenko & Wang Reference Fedorchenko and Wang2004).
Figure 5. Snapshots of the drop shape at
$Re=1068$
,
$We=144$
and
$\unicode[STIX]{x1D703}=60^{\circ }$
for different values of
$\unicode[STIX]{x1D706}_{r}$
. The dimensionless times
$tU_{0}/D$
from (a) to (d) correspond to 0.5, 1, 2 and 3 respectively.
3.2 Thickness of the liquid film
Figure 5 shows snapshots of the drop shape at
$Re=1068$
,
$We=144$
and
$\unicode[STIX]{x1D703}=60^{\circ }$
for various values of
$\unicode[STIX]{x1D706}_{r}$
. For the convenience of comparison, the drop shapes are projected onto the plane with respect to
$\unicode[STIX]{x1D706}_{r}\unicode[STIX]{x1D6FD}$
and
$r$
(see the definitions of
$\unicode[STIX]{x1D6FD}$
and
$r$
in figure 3
f), along with the results of drop impact onto a flat substrate. The results show that there are two stages of wetting, characterized by film spreading and rim development respectively. For a fixed
$\unicode[STIX]{x1D706}_{r}$
, the thickness of the liquid film has more or less the same value in the first stage of wetting, and it is also observed that the film thickness decreases with increase of
$\unicode[STIX]{x1D706}_{r}$
. In order to quantitatively measure it, we define the thickness of the liquid film
$h_{L}$
as the mean thickness at
$tU_{0}/D=0.5$
. In the second stage, the inertia remaining in the liquid film drives the liquid to spread, and the liquid film becomes thinner and thinner at the centre due to the lack of liquid supply; on the other hand, the spreading rate of the film is significantly hindered by the capillary force, leading to the occurrence of the rim.
Figure 6 shows the variation of
$h_{L}$
as a function of
$We$
in a log–log scale. We can see that the relation
$h_{L}/D\sim We^{-1/2}$
holds for various values of
$\unicode[STIX]{x1D706}_{r}$
. This observation is consistent with experiments on drop impact onto a flat substrate (Clanet et al.
Reference Clanet, BÉGuin and Richard2004), in which the film thickness was found to be related to the balance between the surface tension and the vertical deceleration of the impacting drop,
$a_{D}$
(
${\sim}U_{0}^{2}/D$
). Similarly to the capillary length (defined as
$\sqrt{\unicode[STIX]{x1D6FE}/(\unicode[STIX]{x1D70C}g)}$
), the deformation of the drop in the impact process will have a length scale characterized by
$\sqrt{\unicode[STIX]{x1D6FE}/(\unicode[STIX]{x1D70C}a_{D})}=D/\sqrt{We}$
. It is reasonable to expect that this length scale will correspond to the film thickness
$h_{L}$
. In this sense, the relation
$h_{L}/D\sim We^{-1/2}$
indicates the balance between the deceleration and the surface tension. However,
$h_{L}$
deviates from this relation at relatively large
$We$
, primarily because the drop impact is affected by the viscosity of the impinging liquid. To quantitatively measure the significance of the liquid viscosity, Clanet et al. (Reference Clanet, BÉGuin and Richard2004) defined an impact factor
$P=We\,Re^{-4/5}$
, and they experimentally found that the viscous effect played an important role when
$P>0.3$
. For the cases considered here, i.e.
$Re=1068$
, this suggests that the transition will occur at
$We>79$
. This is consistent with our numerical simulations, and, moreover, it is interesting to see that
$h_{L}/D\sim We^{-1/4}$
after the transition (see the inset of figure 6).
It is clear from figure 6 that
$h_{L}$
is dependent on
$\unicode[STIX]{x1D706}_{r}$
. This can be understood by the fact that the smaller the sphere is, the less acceleration the drop experiences during impact, and consequently the larger
$h_{L}$
is. We found that the dependence can be well fitted by
$$\begin{eqnarray}h_{L}\sim h_{L,\infty }(1+3/4\unicode[STIX]{x1D706}_{r}^{-3/2}),\end{eqnarray}$$
where
$h_{L,\infty }$
represents the value of
$h_{L}$
when
$\unicode[STIX]{x1D706}_{r}\rightarrow \infty$
. The rescaled results for the film thickness for different values of
$\unicode[STIX]{x1D706}_{r}$
are nearly overlapped, as shown in the inset of figure 6. Moreover, the fitting of the film thickness in (3.1) suggests that
$h_{L,\infty }=0.052D$
at
$Re=1068$
,
$We=144$
and
$\unicode[STIX]{x1D703}=60^{\circ }$
; by contrast, the simulation of drop impact onto a flat substrate yields a rather close value, i.e.
$h_{L,\infty }=0.045D$
.
Figure 6. Film thickness
$h_{L}$
as a function of
$We$
at
$Re=1068$
,
$\unicode[STIX]{x1D703}=60^{\circ }$
and various values of
$\unicode[STIX]{x1D706}_{r}$
. The dashed line denotes a slope of
$1/2$
. In the inset,
$D^{\ast }$
represents
$(1+3/4\unicode[STIX]{x1D706}_{r}^{-3/2})D$
, and the dashed and solid lines denote slopes of
$1/2$
and
$1/4$
respectively.
3.3 Wetting dynamics
A scaling law is presented here to analyse the wetting dynamics dominated by the inertia of the drop. Provided that the liquid film spreads on the sphere at a rate of
$R\,\text{d}\unicode[STIX]{x1D709}/\text{d}t$
, it would require a mass flux of
${\sim}2\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}R^{2}h_{L}\sin \unicode[STIX]{x1D709}\,\text{d}\unicode[STIX]{x1D709}/\text{d}t$
to maintain its spreading. The mass flux should be supplied by the remaining drop above the liquid film, driven by the kinetic energy of the drop. Therefore, it has order
${\sim}\unicode[STIX]{x03C0}D^{2}\unicode[STIX]{x1D70C}U_{0}/4$
. If we assume that the mass supply does not change significantly in the early stage of wetting, mass conservation of the liquid phase suggests
$$\begin{eqnarray}2\unicode[STIX]{x1D706}_{r}^{2}h_{L}\sin \unicode[STIX]{x1D709}\frac{\text{d}\unicode[STIX]{x1D709}}{\text{d}t}\sim U_{0}.\end{eqnarray}$$
Since
$h_{L}$
has a roughly uniform thickness during the impact and
$h_{L}/D\sim 1+3/4\unicode[STIX]{x1D706}_{r}^{-3/2}$
, the integration of (3.2) from
$t=0$
yields
$$\begin{eqnarray}\unicode[STIX]{x1D706}_{r}^{2}(1-\cos \unicode[STIX]{x1D709})\sim \frac{t\,U_{0}}{(1+3/4\unicode[STIX]{x1D706}_{r}^{-3/2})D}.\end{eqnarray}$$
When
$h_{L}\ll R$
, the left-hand side of (3.3) is equivalent to the dimensionless wetted area. Therefore, (3.3) states that the wetted area should increase linearly with the dimensionless time
$\unicode[STIX]{x1D70F}=(t\,U_{0})/((1+3/4\unicode[STIX]{x1D706}_{r}^{-3/2})D)$
at the early impact. Figure 7(a) shows the numerical results for the wetted area as a function of
$\unicode[STIX]{x1D70F}$
at
$Re=1068$
,
$We=144$
and
$\unicode[STIX]{x1D703}=60^{\circ }$
for various values of
$\unicode[STIX]{x1D706}_{r}$
. It is clear that (3.3) provides a good prediction of the wetting dynamics for
$\unicode[STIX]{x1D70F}\leqslant 1.5$
, during which the results for different values of
$\unicode[STIX]{x1D706}_{r}$
collapse into a straight line. At
$\unicode[STIX]{x1D70F}=1.5$
, the drop evolves into a ‘pancake’ with a thickness of approximately
$h_{L}$
(see, e.g., figure 3
c). The numerical results deviate from the theoretical prediction afterwards because of the invalid assumption of uniform film thickness. Figure 7(a) also shows that the maximal wetted area on spheres of different sizes decreases monotonically with
$\unicode[STIX]{x1D706}_{r}$
. Figure 7(b) shows the maximal wetted area (in terms of its arclength
$\unicode[STIX]{x1D706}_{r}\unicode[STIX]{x1D709}_{max}$
) as a function of
$We$
at
$Re=1068$
,
$\unicode[STIX]{x1D706}_{r}=2.6$
and
$\unicode[STIX]{x1D703}=60^{\circ }$
. We can observe that
$\unicode[STIX]{x1D706}_{r}\unicode[STIX]{x1D709}_{max}\sim We^{1/4}$
for
$We<75$
, and
$\unicode[STIX]{x1D706}_{r}\unicode[STIX]{x1D709}_{max}\sim We^{1/8}$
for
$We>75$
. This can be naturally derived from mass conservation, which suggests that the maximal wetted area should be inversely proportional to the film thickness.
Figure 7. Results at
$Re=1068$
and
$\unicode[STIX]{x1D703}=60^{\circ }$
. (a) Time evolution of the wetted area in terms of
$\unicode[STIX]{x1D706}_{r}^{2}(1-\cos \unicode[STIX]{x1D709})$
at
$We=144$
;
$\unicode[STIX]{x1D70F}$
denotes
$t\,U_{0}/((1+3/4\unicode[STIX]{x1D706}_{r}^{-3/2})D)$
. The solid straight line represents a linear fitting and the dash-dotted line indicates the moment at which the drop evolves into a layer of liquid film of uniform thickness; see, e.g., figure 3(c). (b) The maximal wetted area (in terms of
$\unicode[STIX]{x1D706}_{r}\unicode[STIX]{x1D709}_{max}$
) as a function of
$We$
at
$\unicode[STIX]{x1D706}_{r}=2.6$
. The dash-dotted and dashed lines denote slopes of
$1/4$
and
$1/8$
respectively.
For small values of
$\unicode[STIX]{x1D709}$
, (3.3) can be further simplified, i.e.
$\unicode[STIX]{x1D706}_{r}\unicode[STIX]{x1D709}\sim (tU_{0}/D)^{1/2}$
. Under extreme conditions such as
$\unicode[STIX]{x1D706}_{r}\rightarrow \infty$
(i.e. a flat substrate), this implies that the radius of the wetted area,
$L$
, should satisfy
$L/D\sim (tU_{0}/D)^{1/2}$
. This is in good agreement with previous numerical studies (Kim et al.
Reference Kim, Feng and Chun2000).
3.4 Rate of rim retraction
In the retraction stage, the capillary force acts as the driving force to pull the rim back, while the inertia and viscosity are the resisting forces. Due to the relative significance of the two resisting forces, which can be represented by the Ohnesorge number
$Oh(=\sqrt{We}/Re)$
, the retraction speed may exhibit different dependence on the Weber number (Bartolo et al.
Reference Bartolo, Josserand and Bonn2005). For a drop with low viscosity, the motion of the rim can be modelled by
$$\begin{eqnarray}\displaystyle \frac{\text{d}}{\text{d}t}\left(mR\frac{\text{d}\unicode[STIX]{x1D709}}{\text{d}t}\right)=F_{c}, & & \displaystyle\end{eqnarray}$$
where
$m$
is the mass of the rim and
$F_{c}=2\unicode[STIX]{x03C0}R\sin \unicode[STIX]{x1D709}(1-\cos \unicode[STIX]{x1D703})\unicode[STIX]{x1D6FE}$
is the capillary force acting on the rim. Based on the observation of a constant angular velocity of retraction
$\text{d}\unicode[STIX]{x1D709}/\text{d}t$
(see figure 4), (3.4) can be simplified as
$$\begin{eqnarray}\displaystyle R\frac{\text{d}\unicode[STIX]{x1D709}}{\text{d}t}\frac{\text{d}m}{\text{d}t}=F_{c}. & & \displaystyle\end{eqnarray}$$
With the assumption of a stationary liquid film (see, e.g., figure 3
d,e for the velocity distribution in the film), the mass flux of the rim,
$\text{d}m/\text{d}t$
, can be approximated by
$2\unicode[STIX]{x03C0}R^{2}\,h_{min}\,\unicode[STIX]{x1D70C}\sin \unicode[STIX]{x1D709}\,\text{d}\unicode[STIX]{x1D709}/\text{d}t$
, where
$h_{min}$
is the film thickness when the film has the maximal wetted area (or
$\unicode[STIX]{x1D709}$
reaches its maximum value,
$\unicode[STIX]{x1D709}_{max}$
). Volume conservation suggests that
$h_{min}\sim D/(\unicode[STIX]{x1D706}_{r}^{2}(1-\cos \unicode[STIX]{x1D709}_{max}))$
. Therefore, the retraction speed follows
$$\begin{eqnarray}\displaystyle \frac{\text{d}\unicode[STIX]{x1D709}}{\text{d}t}\sim \frac{\sqrt{(1-\cos \unicode[STIX]{x1D703})(1-\cos \unicode[STIX]{x1D709}_{max})}}{\unicode[STIX]{x1D70F}_{i}}, & & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D70F}_{i}=\sqrt{\unicode[STIX]{x1D70C}D^{3}/\unicode[STIX]{x1D6FE}}$
is the inertial–capillary time scale. Figure 8(a) shows
$\unicode[STIX]{x1D709}/(1-\cos \unicode[STIX]{x1D709}_{max})^{1/2}$
as a function of
$t/\unicode[STIX]{x1D70F}_{i}$
for
$Oh<0.008$
. All of the numerical results appear to collapse into a single line in the retraction stage, and thus are in good agreement with the theoretical analysis in (3.6). On the other hand,
$1-\cos \unicode[STIX]{x1D709}_{max}$
approaches
$\unicode[STIX]{x1D709}_{max}^{2}$
when
$\unicode[STIX]{x1D706}_{r}\rightarrow \infty$
, and thus (3.6) can be rewritten as
${\dot{r}}/r_{max}\sim \unicode[STIX]{x1D70F}_{i}^{-1}$
. This is consistent with the results for a flat substrate by Bartolo et al. (Reference Bartolo, Josserand and Bonn2005).
For a drop with high viscosity, the viscous effect
$F_{v}$
near the contact line can be modelled by a linear force–velocity relation (de Gennes Reference de Gennes1985), such that
$F_{v}\sim \unicode[STIX]{x1D707}R^{2}\unicode[STIX]{x1D709}(\text{d}\unicode[STIX]{x1D709}/\text{d}t)$
. Therefore, the balance between
$F_{v}$
and
$F_{c}$
yields
$$\begin{eqnarray}\displaystyle \frac{\text{d}\unicode[STIX]{x1D709}}{\text{d}t}\sim \frac{(1-\cos \unicode[STIX]{x1D703})\sin \unicode[STIX]{x1D709}}{\unicode[STIX]{x1D706}_{r}\unicode[STIX]{x1D709}}\,\unicode[STIX]{x1D70F}_{v}^{-1}, & & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D70F}_{v}=\unicode[STIX]{x1D707}D/\unicode[STIX]{x1D6FE}$
is the viscous–capillary time scale. Figure 8(b) shows the numerical results for drop retraction with
$Oh>0.013$
, in terms of
$\unicode[STIX]{x1D709}\,\unicode[STIX]{x1D709}_{max}/\sin \unicode[STIX]{x1D709}_{max}$
versus the time
$t/\unicode[STIX]{x1D70F}_{v}$
. We can observe that the results are roughly parallel to each other in the retraction stage, suggesting that (3.7) gives a good prediction of the rim retraction in the viscous–capillary regime.
Figure 8. (a) Inertial–capillary retraction at
$Oh<0.008$
, in terms of
$\unicode[STIX]{x1D709}$
rescaled by
$(1-\cos \unicode[STIX]{x1D709}_{max})^{1/2}$
versus
$t/\unicode[STIX]{x1D70F}_{i}$
, and (b) viscous–capillary retraction at
$Oh>0.013$
, in terms of
$\unicode[STIX]{x1D709}$
rescaled by
$\sin \unicode[STIX]{x1D709}_{max}/\unicode[STIX]{x1D709}_{max}$
versus
$t/\unicode[STIX]{x1D70F}_{v}$
.
4 Conclusion
Drop impact onto a sphere was numerically investigated at moderate Reynolds and Weber numbers using a diffuse-interface immersed-boundary method, with the aim of providing a quantitative evaluation of the effect of
$\unicode[STIX]{x1D706}_{r}$
on the dynamics of drop spreading and retraction. Based on the numerical results, it was found that the thickness of the liquid film,
$h_{L}$
, can be well approximated by
$h_{L}\sim h_{L,\infty }(1+3/4\unicode[STIX]{x1D706}_{r}^{-3/2})$
. The variation of
$h_{L}$
with the Weber number appears to have two scaling laws,
$h_{L}/D\sim We^{-1/2}$
for
$Oh<0.008$
and
$h_{L}/D\sim We^{-1/4}$
for
$Oh>0.008$
, primarily due to the viscous effect becoming significant at relatively large
$Oh$
. It is very interesting to see that coincidentally at roughly the same parameters (
$Oh\approx 0.008$
or
$We\approx 75$
and
$Re=1068$
), the regime transition also occurs in the drop retraction and the maximal wetting area when varying the Weber number. At the early stage of spreading, the temporal variation of the wetted area was shown to be independent of
$\unicode[STIX]{x1D706}_{r}$
when the time was rescaled by the thickness of the liquid film, due to the fact that the impact inertia is dominant during that period. The retraction rates were theoretically analysed by taking
$\unicode[STIX]{x1D706}_{r}$
into account, and the theoretical prediction was consistent with the numerical results.
Acknowledgements
The authors are grateful for the support of the National Natural Science Foundation of China (grant nos. 11425210, 11621202, 11672288), the Chinese Academy of Sciences (grant no. XDB22040103) and the Fundamental Research Funds for the Central Universities.
