I. INTRODUCTION
Grazing incidence X-ray scattering is a powerful tool for investigating rough surface and interface structures (Parratt, Reference Parratt1954; Nevot and Croce, Reference Nevot and Croce1980; Sinha et al., Reference Sinha, Sirota, Garoff and Stanley1988; Holy et al., Reference Holy, Kubena, Ohlidal, Lischka and Plotz1993; Daillant and Gibaud, Reference Daillant and Gibaud1999; Sakurai, Reference Sakurai2009; Fujii et al., Reference Fujii, Nakayama and Yoshida2004, Reference Fujii, Komai and Ikeda2005; Fujii, Reference Fujii2010, Reference Fujii2011). In many previous studies of X-ray reflectometry, X-ray reflectivity was based on Parratt formalism (Parratt, Reference Parratt1954), coupled with the use of the theory of Nevot and Croce to include roughness (Nevot and Croce, Reference Nevot and Croce1980). However, the calculated results of X-ray reflectivity often showed strange results where the amplitude of the oscillation because of the interference effects would increase for a rougher surface. These strange results disagree with reality and suggest that there is a problem in how the effect of roughness is incorporated into Parratt formalism, and hence the effect of roughness is not accurately represented in the theoretical formula of X-ray reflectivity. In our previous study, we proposed that these strange results originated because of neglect of the effect of a decrease in the intensity of refracted X rays because of diffuse scattering at a rough surface and interface (Fujii, Reference Fujii2010, Reference Fujii2011).
In the present study, we propose more clearly that the strange results originated from a currently used equation because of a serious error in which the Fresnel transmission coefficient in the reflectivity equation is increased at a rough interface. We investigate the calculated result of X-ray reflectivity based on Parratt formalism (Parratt, Reference Parratt1954) with the effect of the roughness incorporated by the theory of Nevot–Croce (Nevot and Croce, Reference Nevot and Croce1980), and present a new accurate formalism to correct the error.
II. X-RAY REFLECTIVITY CACULATIONS
The reflectance of an N-layer multilayer system can be calculated using the recursive formalism given by Parratt (Reference Parratt1954). In the following, we show in detail the process of obtaining Parratt's expression and, further, show that this expression requires conservation of energy at the interface. We go on to show that the dispersion of energy by interface roughness cannot be correctly accounted for Parratt's expression.
A. X-ray reflectivity from a flat surface of a multilayer with flat interfaces
First, we consider the reflection from a flat surface of a multilayer with flat interfaces. We take the vertical direction to the surface as the z-axis, with the positive direction pointing towards the bulk. The scattering plane is made the x–z plane. Following that approach, let n j be the refractive index of the jth layer. The wave vector kj of the jth layer is related to the refractive index n j of the jth layer by
$${\bi k}_j \cdot {\bi k}_j=n_j ^2 {\bi k}_0 \cdot {\bi k}_0\comma \; \quad {\bi k}_0 \cdot {\bi k}_0=k^2$$as this necessitates that the x,y-direction components of the wave vector are constant, then the z-direction component of the wave vector of the jth layer is
$$k_{\,j{\rm\comma }z}=\sqrt {n_j ^2\, k^2 - k_{{\rm 0\comma }x} ^2 } .$$The electric fields Ej, E′j below the interface between the j − 1th layer and jth layer are expressed as
$$\eqalign{{\bi E}_j \lpar z_{\,j - 1\comma j} \rpar &={\bi A}_j \exp \!\lsqb {\rm i}\lpar k_{\,j\comma x} x+k_{\,j\comma y} y - \omega t\rpar \rsqb \comma \; \cr {\bi E}^{\prime}_j \lpar z_{\,j - 1\comma j} \rpar &={\bi A}^{\prime}_j \exp \!\lsqb {\rm i}\lpar k_{\,j\comma x} x+k_{\,j\comma y} y - \omega t\rpar \rsqb .}$$The amplitudes A j and A′ j at the jth layer are derived from the equations for the interface between the j − 1 and j layers and the electric field variation within the jth layer with depth h j as expressed by the following matrix:
$$\eqalign {\left(\matrix{{\bi A}^{\prime}_{\,j - 1} \exp \lpar - {\rm i}k_{\,j - 1\comma z} h_{\,j - 1} \rpar \hfill \cr {\bi A}_j \hfill} \right)& =\left(\matrix{{\bi \Psi }_{\,j - 1\comma j} \quad {\bi \Phi }_{\,j\comma j - 1} \hfill \cr {\bi \Phi }_{\,j - 1\comma j} \quad {\bi \Psi }_{\,j\comma j - 1} \hfill} \right)\cr & \quad \times \left(\matrix{{\bi A}_{\,j - 1} \exp \lpar {\rm i}k_{\,j - 1\comma z} h_{\,j - 1} \rpar \hfill \cr {\bi A}{\bf ^{\prime}}_j \hfill} \right)\comma \; }$$where Ψ j−1,j and Φ j−1,j are the Fresnel coefficient tensors for reflection and refraction at the interface between the j − 1 and j layers. For s-polarization, the Fresnel coefficients are
$$\eqalign {{\bi \Phi} _{j - 1\comma j\comma yy} & =\displaystyle{{ 2k_{j - 1\comma z}} \over {k_{j - 1\comma z} + k_{j \comma z}}}\comma \cr \Phi _{j\comma j - 1\comma yy} & = \displaystyle{{2k_{j\comma z}} \over {k_{j - 1\comma z} + k_{j\comma z}}}\, \Psi _{j - 1\comma j\comma yy} = \displaystyle{{k_{j - 1\comma z} - k_{j\comma z}} \over {k_{j - 1\comma z} + k_{j\comma z}}}\comma \cr \Psi _{j\comma j - 1\comma yy} & = \displaystyle{{k_{j\comma z} - k_{j - 1\comma z}} \over {k_{j - 1\comma z} + k_{j\comma z}}}.}$$The reflection coefficient is defined as the ratio Ro,1 of the reflected electric field to the incident electric field at the surface of the material and is given by
$${\bi A}{\bf ^{\prime}}_0={\bi R}_{0\comma 1} {\bi A}_0 .$$The reflection coefficient Rj−1,j of the electric field E′j−1 to the electric field Ej−1 at the interface of j − 1th layer and jth layer is
$${\bi A}^{\prime}_{\,j- 1}={\bi R}_{\,j - 1\comma j} {\bi A}_{\,j - 1}$$and the ratio Rj−1,j is related to the ratio Rj,j+1 as follows:
$$\eqalign {{\bi R}_{\,j - 1\comma j}&=\displaystyle{{{\bi \Psi }_{\,j - 1\comma j}+\lpar {\bi \Phi }_{\,j - 1\comma j} {\bi \Phi }_{\,j\comma j - 1} - {\bi \Psi }_{\,j - 1\comma j} {\bi \Psi }_{\,j\comma j - 1} \rpar {\bi R}_{\,j\comma j+1} } \over {1 - {\bi \Psi }_{\,j\comma j - 1} {\bi R}_{\,j\comma j+1} }}\cr & \quad \times \exp \lpar 2{\rm i}k_{\,j - 1\comma z} h_{\,j - 1}\rpar.}$$Here, from the relation between the Fresnel coefficient for reflection and the Fresnel coefficient for refraction,
$${\bi \Phi }_{\,j - 1\comma j} {\bi \Phi }_{\,j\comma j - 1} - {\bi \Psi }_{\,j - 1\comma j} {\bi \Psi }_{\,j\comma j - 1}=1\comma \;$$
$${\bi \Psi }_{j - 1\comma j}=- {\bi \Psi }_{j\comma j - 1}\comma \;$$we can formulate the following relationship:
$${\bi R}_{\,j - 1\comma j}=\displaystyle{{{\bi \Psi }_{\,j - 1\comma j}+{\bi R}_{\,j\comma j+1} } \over {1+{\bi \Psi }_{\,j - 1\comma j} {\bi R}_{\,j\comma j+1} }}\exp \lpar 2{\rm i}k_{\,j - 1\comma z} h_{\,j - 1} \rpar .$$It is reasonable to assume that no wave will be reflected back from the substrate, so that,
$${\bi R}_{N\comma N+1}=0.$$Then, the X-ray reflectivity is simply,
$$R=\left\vert {R_{0\comma 1} } \right\vert ^2 .$$Thus, we obtain Parratt's expression.
B. Previous calculations of X-ray reflectivity when roughness exists at the surface and interface
When the surface and interface have roughness, the Fresnel coefficient for reflection is reduced (Vidal and Vincent, Reference Vidal and Vincent1984; Sinha et al., Reference Sinha, Sirota, Garoff and Stanley1988; Holy et al., Reference Holy, Kubena, Ohlidal, Lischka and Plotz1993, Reference Holy, Pietsch and Baumbach1999; Boer, Reference Boer1995; Daillant and Gibaud, Reference Daillant and Gibaud1999; Fujii et al., Reference Fujii, Nakayama and Yoshida2004, Reference Fujii, Komai and Ikeda2005; Sakurai, Reference Sakurai2009; Fujii, Reference Fujii2010, Reference Fujii2011). The effect of roughness was previously put into calculation based on the theory of Nevot and Croce (Reference Nevot and Croce1980). The effect of such roughness was taken into account only through the effect of changes in density of the medium in a vertical direction to the surface and interface. With the use of relevant roughness parameters such as the root-mean-square (rms) roughness σ j−1,j of the jth layer, the reduced Fresnel reflection coefficient Ψ′ for s-polarization is transformed as shown below:
$${\it \Psi} ^{\prime}_{\,j\comma j - 1}={\it \Psi} _{\,j\comma j - 1} \!\exp \!\lpar\! - 2k_{\,j\comma z} k_{\,j - 1\comma z} \sigma _{\,j\comma j - 1}^2 \rpar$$and the X-ray reflectivity is calculated using the following equation:
$$R_{\,j - 1\comma j}=\displaystyle{{R_{\,j\comma j+1}+{\it \Psi} ^{\prime}_{\,j - 1\comma j} } \over {1+R_{\,j\comma j+1} {\it \Psi} ^{\prime}_{\,j - 1\comma j} }}\exp \!\lpar 2{\rm i}k_{\,j - 1{\rm\comma }z} h_{\,j - 1} \rpar .$$Figure 1 shows the reflectivity from a tungsten-covered silicon wafer calculated by the theory in use prior to this work.
Figure 1. X-ray reflectivity from a silicon wafer covered with a thin (10 nm) tungsten film calculated by the theory in use prior to this work. Solid line shows the case of a flat surface. Dashed line shows the case of a surface with an rms surface roughness of 0.3 nm.
The ratio of the oscillation amplitude to the value of the reflectivity from a surface with an rms surface roughness of 0.3 nm (dashed line) does not decrease but increases near the angle of incidence of 1.8°. We now consider the above strange result of X-ray reflectivity, which was based on Parratt formalism (Parratt, Reference Parratt1954) with the use of the Nevot and Croce approach to account for roughness (Nevot and Croce, Reference Nevot and Croce1980). In that calculation, the X-ray reflectivity is derived using the relation of reflection coefficient R j−1,j and R j,j+1 as Eq. (15). However, the relationship between the reflection coefficients R j−1,j and R j,j+1 was originally derived as the following equation:
$$\eqalign {{\bi R}_{j - 1\comma j}&=\displaystyle{{{\bi \Psi }^{\prime}_{j - 1\comma j}+\lpar {\bi \Phi }^{\prime}_{j - 1\comma j} {\bi \Phi }^{\prime}_{j\comma j - 1} - {\bi \Psi }^{\prime}_{j - 1\comma j} {\bi \Psi }^{\prime}_{j\comma j - 1} \rpar {\bi R}_{j\comma j+1} } \over {1 - {\bi \Psi }^{\prime}_{j\comma j - 1} {\bi R}_{j\comma j+1} }} \cr & \quad \times \exp \lpar 2{\rm i}k_{j - 1\comma z} h_{j - 1} \rpar.} $$Here, the following conditional relations between the Fresnel coefficient for reflection and refraction are relevant to the above equation,
$$\eqalign{&{\bi \Phi }^{\prime}_{\,j - 1\comma j} {\bi \Phi }^{\prime}_{\,j\comma j - 1} - {\bi \Psi }^{\prime}_{\,j - 1\comma j} {\bi \Psi }^{\prime}_{\,j\comma j - 1}=1\comma \; \cr & \quad {\bi \Psi }^{\prime}_{\,j - 1\comma j}=- {\bi \Psi }^{\prime}_{j\comma j - 1}\comma \;}$$then,
$${\bi \Phi }^{\prime}_{\,j - 1\comma j} {\bi \Phi }^{\prime}_{\,j\comma j - 1}=1 - {\bi \Psi }^{\prime 2} _{\,j\comma j - 1} .$$The Fresnel coefficients for refraction at the rough interface are derived using the Fresnel reflection coefficient Ψ as follows:
$$\eqalign {& {\bi \Phi }^{\prime}_{\,j - 1\comma j} {\bi \Phi }^{\prime}_{\,j\comma j - 1} - {\bi \Phi }_{\,j - 1\comma j} {\bi \Phi }_{\,j\comma j - 1}={\bi \Psi }^2 _{\,j\comma j - 1} \cr & \quad \times \left({1 - \exp\! \lpar \!\!-\! 2k_{\,j\comma z} k_{\,j - 1\comma z} \sigma _{\,j\comma j - 1}^2 \rpar } \right)\gt 0}$$
$$\eqalign {{\bi \Phi }^{\prime}_{j - 1\comma j} {\bi \Phi }^{\prime}_{j\comma j - 1}& ={\bi \Phi }_{j - 1\comma j} {\bi \Phi }_{j\comma j - 1}+\left({1 - {\bi \Phi }_{j - 1\comma j} {\bi \Phi }_{j\comma j - 1} } \right)\cr & \quad\times \left({1 - \!\exp\! \lpar \!- 2k_{j\comma z} k_{j - 1\comma z} \sigma _{j\comma j - 1}^2 \rpar } \right).}$$Therefore, the Fresnel coefficients for refraction at the rough interface are necessarily larger than the Fresnel coefficient for refraction at the flat interface. The resulting increase in transmission coefficient completely overpowers any decrease in the value of reflection coefficient. These coefficients for refraction obviously contain an error as the penetration of X-rays should decrease at a rough interface because of diffuse scattering. We propose that the unnatural results in the previous calculation of X-ray reflectivity originate from the fact that diffuse scattering was not considered. In fact, Eq. (15) contains the X-ray energy conservation rule at the interface as the following identity equation for the Fresnel coefficient:
$${\it \Phi} _{j - 1\comma j} {\it \Phi} _{j\comma j - 1} - {\it \Psi} _{j - 1\comma j} {\it \Psi} _{j\comma j - 1}={\it \Phi} _{j - 1\comma j} {\it \Phi} _{j\comma j - 1}+{\it \Psi}_{\,j - 1\comma j} ^2=1.$$When the Fresnel coefficients at the rough interface obey the following equations:
$${\bi \Phi }^{\prime}_{j - 1\comma j} {\bi \Phi }^{\prime}_{j\comma j - 1} - {\bi \Psi }^{\prime}_{j - 1\comma j} {\bi \Psi }^{\prime}_{j\comma j - 1}=1\comma \; \quad {\bi \Psi }^{\prime}_{j - 1\comma j}=- {\bi \Psi }^{\prime}_{j\comma j - 1}\comma \;$$these coefficients fulfill X-ray energy flow conservation at the interface, and so diffuse scattering was not considered at the rough interface.
This conservation expression should not apply any longer when the Fresnel reflection coefficient is replaced by the reduced coefficient Ψ′ when there is roughening at the interface. Therefore, calculating the reflectivity using this reduced Fresnel reflection coefficient Ψ′ in Eq. (15) will incorrectly increase the Fresnel transmission coefficient Φ′, i.e., Φ < Φ′.
The penetration of X-rays should decrease at the rough interface because of diffuse scattering. Therefore, the identity equations for the Fresnel coefficients become,
$$\eqalign {{\it \Phi}^{\prime}_{\,j - 1\comma j} {\it \Phi} ^{\prime}_{\,j\comma j - 1} - {\it \Psi} ^{\prime}_{\,j - 1\comma j} {\it \Psi} ^{\prime}_{\,j\comma j - 1}& ={\it \Phi} ^{\prime}_{\,j - 1\comma j} {\it \Phi}^{\prime}_{\,j\comma j - 1}\cr & \quad +{\it \Psi} _{\,j - 1\comma j} ^{\prime 2}=1 - D^2\lt 1\comma \; }$$where D 2 is a decrease because of diffuse scattering. Then, in the calculation of X-ray reflectivity when there is roughening at the surface or the interface, the Fresnel transmission coefficient Φ′ should be used for the reduced coefficient. Several theories exist to describe the influence of roughness on X-ray scattering (Sinha et al., Reference Sinha, Sirota, Garoff and Stanley1988; Holy et al., Reference Holy, Kubena, Ohlidal, Lischka and Plotz1993, Reference Holy, Pietsch and Baumbach1999; Daillant and Gibaud, Reference Daillant and Gibaud1999). When the surface and interface are both rough, the Fresnel coefficient for refraction has been derived in several theories (Vidal and Vincent, Reference Vidal and Vincent1984; Sinha et al., Reference Sinha, Sirota, Garoff and Stanley1988; Holy et al., Reference Holy, Kubena, Ohlidal, Lischka and Plotz1993, Reference Holy, Pietsch and Baumbach1999; Boer, Reference Boer1995).
C. A new formula for reflectivity of rough multilayer surface
When the z position of the interface of 0th layer and 1st layer z o,1 fluctuates vertically as a function of the lateral position because of interface roughness, the relations between the amplitudes A 0, A′ 0, A 1, and A′ 1 are derived by use of the Fresnel coefficient tensor Φ for refraction and the Fresnel coefficient tensor Ψ for reflection as follows:
$$\eqalign{&\left(\matrix{A^{\prime}_0 \hfill \cr A_1 \hfill} \right)=\cr&\left(\matrix{{\bi \Psi }_{0\comma 1} \displaystyle{{\exp \!\lpar {\rm i}\lpar k_{1\comma z}+k_{0\comma z} \rpar z_{0\comma 1} \rpar } \over {\exp \lpar {\rm i} \lpar - k_{0\comma z}+k_{1\comma z} \rpar z_{0\comma 1} \rpar }}\comma \; \qquad{\bi \Phi }_{1\comma 0} \exp \lpar {\rm i} \lpar k_{0\comma z} - k_{1\comma z} \rpar z_{0\comma 1} \rpar \hfill \cr {\bi \Phi }_{0\comma 1} \exp \lpar {\rm i}\lpar - k_{1\comma z}+k_{0\comma z} \rpar z_{0\comma 1} \rpar \comma \; \qquad{\bi \Psi }_{1\comma 0} \displaystyle{{\exp \lpar {\rm i}\lpar - k_{0\comma z} - k_{1\comma z} \rpar z_{0\comma 1} \rpar } \over {\exp \lpar {\rm i}\lpar - k_{0\comma z}+k_{1\comma z} \rpar z_{0\comma 1} \rpar }} \hfill} \right)\cr&\quad\times\left(\matrix{A_0 \hfill \cr A^{\prime}_1 \hfill} \right).}$$We therefore consider the derivation of the average value of the following matrix.
We take the average value of this matrix. For Gaussian statistics of standard deviation value σ, the Fresnel reflection coefficient Ψ′ is as follows:
$$\eqalign {{\bi \Psi }^{\prime}_{0\comma 1}&={\bi \Psi }_{0\comma 1} \displaystyle{{\left\langle {\exp \lpar {\rm i}\lpar k_{1\comma z}+k_{0\comma z} \rpar z_{0\comma 1} \rpar } \right\rangle } \over {\left\langle {\exp \lpar {\rm i}\lpar - k_{0\comma z}+k_{1\comma z} \rpar z_{0\comma 1} \rpar } \right\rangle }}\cr \quad &={\bi \Psi }_{0\comma 1} \displaystyle{{\exp \lpar - {\textstyle{1 \over 2}}\lpar k_{0\comma z}+k_{1\comma z} \rpar ^2 \sigma _{0\comma 1} ^2 \rpar } \over {\exp \lpar - {\textstyle{1 \over 2}}\lpar k_{0\comma z} - k_{1\comma z} \rpar ^2 \sigma _{0\comma 1} ^2 \rpar }}\cr \quad &={\bi \Psi }_{0\comma 1} \exp \lpar - 2k_{0\comma z} k_{1\comma z} \sigma _{0\comma 1} ^2 \rpar .}$$These reduced reflection coefficients accord with the result in prior works (Vidal and Vincent, Reference Vidal and Vincent1984; Sinha et al., Reference Sinha, Sirota, Garoff and Stanley1988; Holy et al., 1993, 1999; Boer, Reference Boer1995; Daillant and Gibaud, Reference Daillant and Gibaud1999; Sakurai, Reference Sakurai2009). SinceX-rays penetrating an interface reflect from the interface below, and penetrate former interface again without fail, it is necessary to treat the refraction coefficients Φ′ 0,1 and Φ′ 1,0 collectively.
$$\eqalign{&{\bi \Phi }^{\prime}_{0\comma 1} {\bi \Phi }^{\prime}_{1\comma 0} \cr & \quad=\left\langle {{\bi \Phi }_{0\comma 1} \exp \lpar {\rm i}\lpar - k_{1\comma z}+k_{0\comma z} \rpar z_{0\comma 1} \rpar {\bi \Phi }_{1\comma 0} \exp \lpar i\lpar k_{0\comma z} - k_{1\comma z} \rpar z_{0\comma 1} \rpar } \right\rangle \cr & \quad ={\bi \Phi }_{0\comma 1} {\bi \Phi }_{1\comma 0} \left\langle {\exp \lpar {\rm i}\lpar - k_{1\comma z}+k_{0\comma z} \rpar z_{0\comma 1} \rpar \exp \lpar i\lpar k_{0\comma z} - k_{1\comma z} \rpar z_{0\comma 1} \rpar } \right\rangle \cr &\quad={\bi \Phi }_{0\comma 1} {\bi \Phi }_{1\comma 0} \left\langle {\exp \lpar {\rm i}\lpar 2k_{0\comma z} - 2k_{1\comma z} \rpar z_{0\comma 1} \rpar } \right\rangle \cr &\quad={\bi \Phi }_{0\comma 1} {\bi \Phi }_{1\comma 0} \exp \lpar - 2\lpar k_{0\comma z} - k_{1\comma z} \rpar ^2 \sigma _{0\comma 1} ^2 \rpar.}$$Then the Fresnel coefficients Ψ′ and Φ′ are reduced as follows:
$$\eqalign{\left(\matrix{A^{\prime}_0 \hfill \cr A_1 \hfill} \right)\cr &\hskip-25pt=\left(\matrix{{\bi \Psi }_{0\comma 1} \exp \lpar - 2k_{0\comma z} k_{1\comma z} \sigma _{0\comma 1} ^2 \rpar \comma \; \quad {\bi \Phi }_{1\comma 0} \exp \lpar - \lpar k_{0\comma z} - k_{1\comma z} \rpar ^2 \sigma _{0\comma 1} ^2 \rpar \hfill \cr {\bi \Phi }_{0\comma 1} \exp \lpar - \lpar k_{0\comma z} - k_{1\comma z} \rpar ^2 \sigma _{0\comma 1} ^2 \rpar \comma \; \quad {\bi \Psi }_{1\comma 0} \exp \lpar - 2k_{0\comma z} k_{1\comma z} \sigma _{0\comma 1} ^2 \rpar \hfill} \right) \cr & \hskip-25pt\times\left(\matrix{A_0 \hfill \cr A^{\prime}_1 \hfill} \right).}$$The Fresnel refraction coefficients Φ′ derived by this method are reduced, and can be used to calculate the reflectivity from rough surface and interface. Therefore, we calculate the reflectivity using these newly derived Fresnel coefficients in an accurate reflectivity equation of R j−1,j and R j,j+1 as follows:
$$\eqalign {{\bi R}_{\,j - 1\comma j}& =\displaystyle{{{\bi \Psi }^{\prime}_{\,j - 1\comma j}+\lpar {\bi \Phi }^{\prime}_{\,j - 1\comma j} {\bi \Phi }^{\prime}_{\,j\comma j - 1} - {\bi \Psi }^{\prime}_{\,j - 1\comma j} {\bi \Psi }^{\prime}_{\,j\comma j - 1} \rpar {\bi R}_{\,j\comma j+1} } \over {1 - {\bi \Psi }^{\prime}_{\,j\comma j - 1} {\bi R}_{\,j\comma j+1} }}\cr & \quad\times \exp \lpar 2{\rm i}k_{\,j - 1\comma z} h_{\,j - 1} \rpar .}$$Based on the above considerations, we again calculated the X-ray reflectivity of the W/Si system, but now considered the effect of attenuation in the refracted X-rays by diffuse scattering resulting from surface roughness. However, the reduced refraction coefficient in prior work varies (Vidal and Vincent, Reference Vidal and Vincent1984; Sinha et al., Reference Sinha, Sirota, Garoff and Stanley1988; Holy et al., Reference Holy, Kubena, Ohlidal, Lischka and Plotz1993, Reference Holy, Pietsch and Baumbach1999; Boer, Reference Boer1995; Daillant and Gibaud, Reference Daillant and Gibaud1999; Fujii et al., Reference Fujii, Nakayama and Yoshida2004, Reference Fujii, Komai and Ikeda2005; Sakurai, Reference Sakurai2009; Fujii, Reference Fujii2010, Reference Fujii2011). Then, about the reduced refraction coefficient, reduction is the same as the reflection coefficient applied.
In the reflectivity curve from a surface with an rms surface roughness of 0.3 nm (dashed line), the amplitude of oscillation in Figure 1 has reduced in Figure 2. These results are now physically reasonable. The strange results seen in Figure 1 have disappeared in Figure 2. It seems natural that the effect of interference does decrease at a rough surface and interface, because the amount of coherent X-rays should reduce because of diffuse scattering.
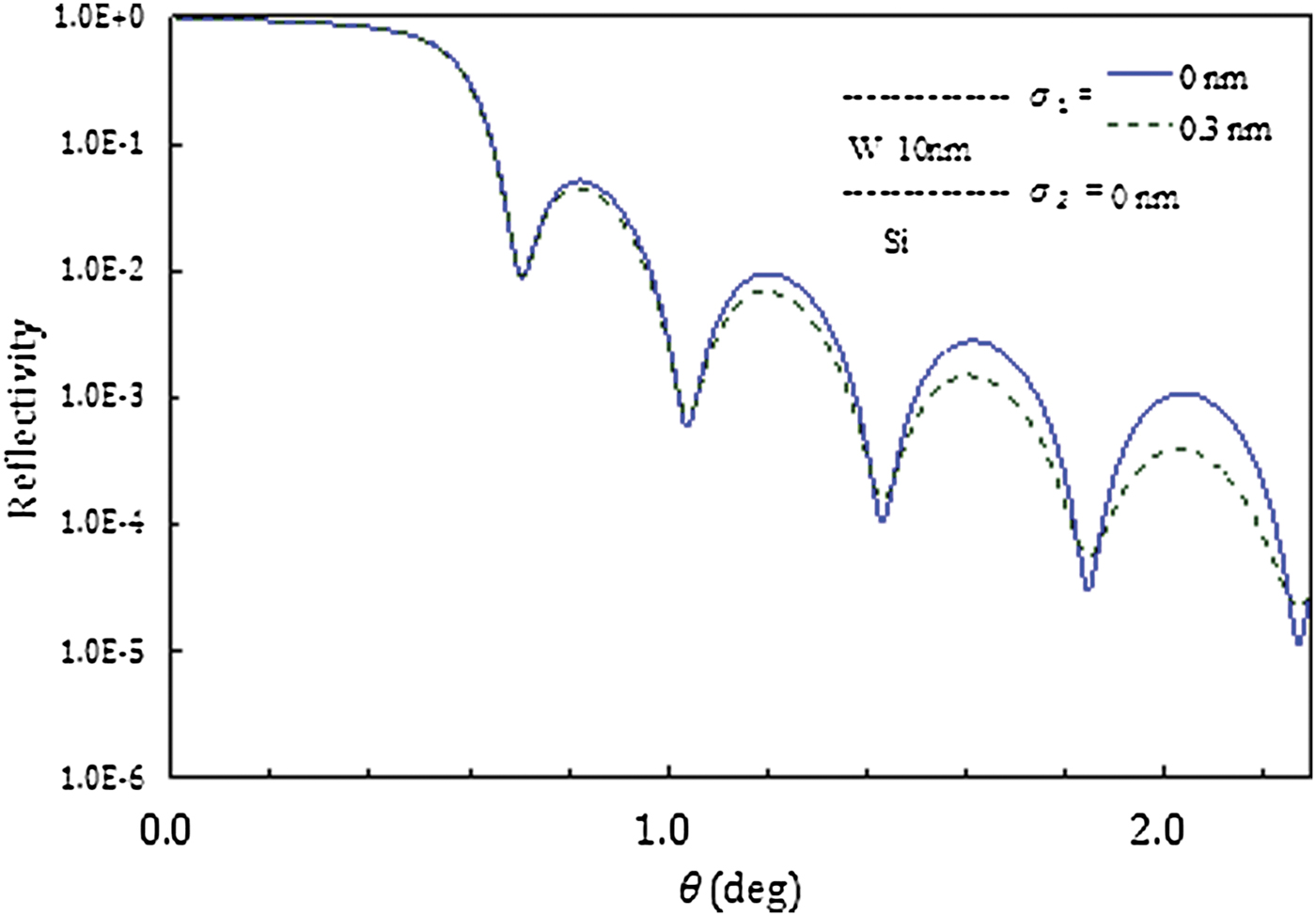
Figure 2. X-ray reflectivity from a silicon wafer covered with a thin (10 nm) tungsten film calculated by the new calculation that considered diffuse scattering. Solid line shows the case of a flat surface. Dashed line shows the case of a surface with an rms surface roughness of 0.3 nm.
III. CONCLUSION
We have investigated the fact that the calculated results of X-ray reflectivity based on Parratt formalism with the effect of the roughness incorporated by the theory of Nevot–Croce show a strange phenomenon in which the amplitude of the oscillation because of the interference effects increase in the case of the rougher surface. We found that the strange results originate in the currently used equation where the Fresnel refraction coefficient in the reflectivity equation is increased at a rough interface. The increase in the transmission coefficient completely overpowers any decrease in the value of the reflection coefficient because of the lack of consideration of diffuse scattering. Then, we have developed a new formalism that corrects this error, producing more accurate estimates of the X-ray reflectivity for systems having surface and interfacial roughness, taking into account the effect of roughness-induced diffuse scattering. The new, accurate formalism is completely described in detail. The X-ray reflectivity R is derived by use of accurate reflectivity equations for R j−1,j and R j,j+1 as the following:
$$\eqalign {&R=\left\vert {R_{0\comma 1} } \right\vert ^2\comma \; \quad R_{N\comma N+1}=0\comma \; \cr & \quad R_{\,j - 1\comma j}=\displaystyle{{{\it \Psi} ^{\prime}_{\,j - 1\comma j}+\lpar {\it \Phi}^{\prime}_{\,j - 1\comma j} {\it \Phi} ^{\prime}_{\,j\comma j - 1} - {\it \Psi} ^{\prime}_{\,j - 1\comma j} {\it \Psi} ^{\prime}_{\,j\comma j - 1} \rpar R_{\,j\comma j+1} } \over {1 - {\it \Psi}^{\prime}_{\,j\comma j - 1} R_{\,j\comma j+1} }}\cr & \quad \quad \qquad \times\exp \lpar 2{\rm i}k_{\,j - 1\comma z} h_{\,j - 1} \rpar \comma \; }$$where the Fresnel coefficients Ψ′ for reflection and Φ′ for refraction are reduced. The reflectivity calculated with this new, accurate formalism, gives a physically reasonable result. Here, the reduced Fresnel coefficients Ψ′ and Φ′ in the reflectivity equation need further research and we will continue to refine this theory. The use of this equation resolves the strange numerical results that occurred in the previous calculations that neglected diffuse scattering and is expected that the buried interface structure can now be analyzed more accurately.
