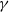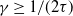1. Introduction
The study of percolation properties of infinite random graphs traces back many decades, and many of the classical results are already available in textbook form; see for example the monographs [Reference Bollobás and Riordan3, Reference Grimmett15, Reference Meester and Roy25]. The first results for percolation in the continuum
![]() $\mathbb{R}^d$
were presented in the landmark paper by Gilbert [Reference Gilbert11], where nontrivial regimes of existence and absence of percolation (i.e., existence of an unbounded connected component) were established for the Poisson–Gilbert graph, i.e., where the set of nodes is given by a homogeneous Poisson point process (PPP), and edges are drawn between two nodes whenever their distance is below a certain fixed positive connectivity threshold. The context of telecommunication systems was already mentioned there.
$\mathbb{R}^d$
were presented in the landmark paper by Gilbert [Reference Gilbert11], where nontrivial regimes of existence and absence of percolation (i.e., existence of an unbounded connected component) were established for the Poisson–Gilbert graph, i.e., where the set of nodes is given by a homogeneous Poisson point process (PPP), and edges are drawn between two nodes whenever their distance is below a certain fixed positive connectivity threshold. The context of telecommunication systems was already mentioned there.
In order to make the model more flexible, instead of using a fixed connectivity threshold, the nodes in the PPP can also be marked with independent random radii, drawn from a common distribution, with two nodes connected by an edge whenever their distance is below the sum of the associated radii. In view of our topic in this paper, we call the resulting model a Poisson–Gilbert graph with random radii, whose percolation properties can equivalently be expressed in terms of the corresponding Poisson Boolean model with random radii. We note that a wide range of results for percolation for this model are available; see for example [Reference Ahlberg, Tassion and Teixeira1, Reference Gouéré12–Reference Gouéré and Théret14, Reference Meester and Roy25] and references therein. Starting from the seminal book [Reference Matheron24], many results about the original Poisson Boolean model with spherical grains have been extended to more general grains, but in the present paper we focus on the classical case when the Boolean model is a union of balls (with random radii).
In view of applications in wireless telecommunication systems, the extension of Poisson–Gilbert graphs to Gilbert graphs based on Cox point processes (CPPs), i.e., PPPs with random intensity measure, allows one to study long-range communication properties in device-to-device networks where devices are placed according to a PPP in a random environment that is represented by the intensity measure of the CPP. Recently, continuum percolation and further properties of such Cox–Gilbert graphs have been studied under certain conditions of stabilization and connectedness; see [Reference Cali5, Reference Hirsch, Jahnel and Cali16] and below. However, in these works, the edge-drawing rule remained, as in the classical case of the Poisson–Gilbert graph, based on a fixed connectivity threshold.
In the very recent manuscript [Reference Jahnel, Tóbiás, Ca and li18], continuum percolation results are first presented for Cox–Gilbert graphs where, as in the Poisson–Gilbert graph with random radii, each node is equipped with a random radius, and edges are placed between any two nodes whenever their distance is below the sum of the radii. In this case, again under certain stabilization and connectedness assumptions, most of the percolation properties of the Poisson–Gilbert graph with random radii can be reproduced also for this Cox–Gilbert graph with random radii. We note that here, similarly to [Reference Meester and Roy25], percolation properties of the Gilbert graphs are again expressed in terms of the underlying Cox Boolean models with random radii.
Moving beyond a setting where edges are placed between pairs of points based on their mutual distance and their associated radii, another line of research aims towards a different kind of extension of Gilbert graphs with respect to the edges. Starting with the papers [Reference Dousse, Baccelli and Thiran8, Reference Dousse9], still based on a homogeneous PPP in
![]() $\mathbb{R}^2$
, the edge-drawing mechanism is replaced by a highly non-local rule using the signal-to-interference-plus-noise ratio (SINR), which we describe precisely and more generally in (2.1). In words, very roughly, a pair of Poisson points is connected by an edge only if the weighted distance between the points is sufficiently small compared to the accumulated weighted distances of all the other points, the so-called interference. This definition is very much inspired by applications in wireless telecommunication networks, where the success of a transmission between network components is highly dependent on the relative signal strength between the components compared to the other (unwanted) signals present in the medium. In the simplest case, only the relative distances between points enter the SINR, giving rise to the SINR graph on PPPs, or the Poisson SINR graph. Let us note that this definition introduces long-range, or even infinite-range, dependencies for the construction of edges into the system. This is the setting considered in [Reference Dousse, Baccelli and Thiran8, Reference Dousse9], where, using comparison techniques with the Poisson–Gilbert graph, again nontrivial percolation properties are established. Let us mention that the SINR graph has very different monotonicity properties compared to the Poisson–Gilbert graph, which makes it more interesting but also harder to analyze. To see this, note that due to the definition of the SINR, an increase in the number of points also leads to an increase in the unwanted interference and thus to the potential loss of edges. On the other hand, for the Poisson–Gilbert graph, the connectivity increases if points are added into the system.
$\mathbb{R}^2$
, the edge-drawing mechanism is replaced by a highly non-local rule using the signal-to-interference-plus-noise ratio (SINR), which we describe precisely and more generally in (2.1). In words, very roughly, a pair of Poisson points is connected by an edge only if the weighted distance between the points is sufficiently small compared to the accumulated weighted distances of all the other points, the so-called interference. This definition is very much inspired by applications in wireless telecommunication networks, where the success of a transmission between network components is highly dependent on the relative signal strength between the components compared to the other (unwanted) signals present in the medium. In the simplest case, only the relative distances between points enter the SINR, giving rise to the SINR graph on PPPs, or the Poisson SINR graph. Let us note that this definition introduces long-range, or even infinite-range, dependencies for the construction of edges into the system. This is the setting considered in [Reference Dousse, Baccelli and Thiran8, Reference Dousse9], where, using comparison techniques with the Poisson–Gilbert graph, again nontrivial percolation properties are established. Let us mention that the SINR graph has very different monotonicity properties compared to the Poisson–Gilbert graph, which makes it more interesting but also harder to analyze. To see this, note that due to the definition of the SINR, an increase in the number of points also leads to an increase in the unwanted interference and thus to the potential loss of edges. On the other hand, for the Poisson–Gilbert graph, the connectivity increases if points are added into the system.
Now, similarly to the generalization of a Poisson–Gilbert graph to a Poisson–Gilbert graph with random radii, SINR graphs can also be generalized in the sense that each point is equipped with an independent power random variable. These powers enter the definition of the SINR as presented in (2.1) and represent the individual signal strengths of the network components. For the case of the SINR graph with random powers based on PPPs, or the Poisson SINR graph with random powers, the paper [Reference Kong and Yeh21] presents first results similar to the assertions presented in [Reference Dousse, Baccelli and Thiran8, Reference Dousse9] under very strong boundedness assumptions on the powers. Let us note that the definition of an SINR graph with random powers already appears in [Reference Dousse, Baccelli and Thiran8], but the only proven result of this paper for this setting is about degree bounds (cf. Section 4.2). The first steps towards understanding the case of unbounded powers in the Poisson SINR graph with random powers were made recently in [Reference Löffler22]. In this master’s thesis, supervised by the authors, results in the spirit of one of our main theorems, Theorem 2.1, are presented under much stronger assumptions and only for the case of an underlying homogeneous PPP. The thesis [Reference Löffler22] also provides sufficient conditions for the absence of percolation for small intensities of the PPP. Before [Reference Löffler22], no positive assertions about percolation in an SINR graph with unbounded random powers had been known in the literature; regarding the case of bounded random powers, see also Section 4.
On the other hand, in [Reference Tóbiás28], the two extensions described above were for the first time considered jointly, giving rise to the SINR graph based on CPPs, the Cox SINR graph, but without random powers. In [Reference Tóbiás28] it was established that for sufficiently large intensities and sufficiently connected environments, the Cox SINR graph percolates almost surely at least for nonvanishing interference. In [Reference Tóbiás27, Section 4.2.3.4] it was anticipated that the case of random but bounded powers might easily be handled via the same methods; see Section 4.1 for further details.
The present paper now completes this line of research by analyzing the Cox SINR graph with random powers, which are also not necessarily bounded. More precisely, in our first main result, Theorem 2.1, we present sufficient conditions for the existence of a supercritical percolation phase, i.e., a nontrivial regime for the intensity of the underlying CPP and nonvanishing interference, such that the Cox SINR graph with random powers percolates. This substantially extends the results of [Reference Dousse, Baccelli and Thiran8–Reference Franceschetti and Meester10] from the case of a homogeneous PPP in
![]() $\mathbb{R}^2$
with constant powers to that of a CPP in
$\mathbb{R}^2$
with constant powers to that of a CPP in
![]() $\mathbb{R}^d$
,
$\mathbb{R}^d$
,
![]() $d \geq 2$
, with random and possibly unbounded powers, combining the methods of [Reference Tóbiás28] for the case of a CPP with constant powers and those of [Reference Löffler22] for the case of a PPP with random powers (both in dimension 2 or higher). We will discuss the relationship of Theorem 2.1 to these results in detail in Section 4.
$d \geq 2$
, with random and possibly unbounded powers, combining the methods of [Reference Tóbiás28] for the case of a CPP with constant powers and those of [Reference Löffler22] for the case of a PPP with random powers (both in dimension 2 or higher). We will discuss the relationship of Theorem 2.1 to these results in detail in Section 4.
Our second main result, Theorem 2.2, establishes a uniform bound on the strength of the interference, above which no percolation is possible. In essence, this theorem claims that there is no percolation in the SINR graph whenever the degree of its vertices is bounded by 2. The fact that SINR graphs with nonvanishing interference have bounded degrees originates from [Reference Dousse, Baccelli and Thiran8, Theorem 1]; however, in that paper, only the simple assertion that SINR graphs with degrees bounded by 1 do not percolate was proven, and this has not been improved until the present paper.
Finally, in our third main result, Theorem 2.3, we state that in the case of the Poisson SINR graph with constant powers, indeed, the critical intensity for percolation in the presence of interference can be represented via the critical intensity of an associated Poisson–Gilbert graph. This result extends the two-dimensional statement [Reference Dousse9, Theorem 1] to higher dimensions, although its proof is rather different from the proof in [Reference Dousse9].
The organization of the manuscript is as follows. In Section 2, we present the setting and main results but postpone the introduction of our main technical conditions for the CPP, namely stabilization and asymptotic essential connectedness. These conditions are presented in Section 3 together with examples of CPPs for which our main results are applicable. In Section 4 we present the proof strategies for our main results and give further background on how they relate to previous results in the literature. Finally, in Section 5, we give the detailed proofs.
2. Setting and main results
For
![]() $\lambda>0$
, let
$\lambda>0$
, let
![]() ${\textbf{X}}^\lambda=\{(x_i,P_i)\}_{i \in \mathbb{N}}$
be an independent and identically distributed (i.i.d.) marked CPP in
${\textbf{X}}^\lambda=\{(x_i,P_i)\}_{i \in \mathbb{N}}$
be an independent and identically distributed (i.i.d.) marked CPP in
![]() $\mathbb{R}^d\times[0,\infty)$
for
$\mathbb{R}^d\times[0,\infty)$
for
![]() $d \geq 1$
, with directing measure
$d \geq 1$
, with directing measure
![]() $\lambda\Lambda\otimes\mu$
where
$\lambda\Lambda\otimes\mu$
where
![]() $\Lambda$
is stationary with
$\Lambda$
is stationary with
![]() $\mathbb{E}[\Lambda(Q_1)]=1$
and
$\mathbb{E}[\Lambda(Q_1)]=1$
and
![]() $Q_n=[\!-n/2,n/2]^d$
for
$Q_n=[\!-n/2,n/2]^d$
for
![]() $n >0$
. Here,
$n >0$
. Here,
![]() $\Lambda$
is a random element in the space
$\Lambda$
is a random element in the space
![]() $\mathbb M$
of Borel measures on
$\mathbb M$
of Borel measures on
![]() $\mathbb{R}^d$
equipped with the usual evaluation
$\mathbb{R}^d$
equipped with the usual evaluation
![]() $\sigma$
-algebra, and
$\sigma$
-algebra, and
![]() $\mu$
is a Borel probability measure on
$\mu$
is a Borel probability measure on
![]() $[0,\infty)$
, the common distribution of the marks
$[0,\infty)$
, the common distribution of the marks
![]() $P=\{P_i\}_{i\in \mathbb{N}}$
. We consider the SINR graph with vertex set given by the first component of
$P=\{P_i\}_{i\in \mathbb{N}}$
. We consider the SINR graph with vertex set given by the first component of
![]() ${\textbf{X}}^\lambda$
, which we denote by
${\textbf{X}}^\lambda$
, which we denote by
![]() $X^\lambda=\{x_i\}_{i\in \mathbb{N}}$
. Here, the pair of vertices
$X^\lambda=\{x_i\}_{i\in \mathbb{N}}$
. Here, the pair of vertices
![]() $x_i, x_j\in X^\lambda$
, with
$x_i, x_j\in X^\lambda$
, with
![]() $x_i\neq x_j$
, is connected by an edge if and only if
$x_i\neq x_j$
, is connected by an edge if and only if
 \begin{equation} \begin{split} P_i\ell(|x_i-x_j|)&>\tau\bigg({N_o} + \gamma \sum_{k \in \mathbb{N} \setminus \{ i,j\}} P_k \ell(|x_k-x_j|)\bigg) \quad\text{and }\\[3pt] P_j\ell(|x_i-x_j|)&>\tau\bigg({N_o} + \gamma \sum_{k \in \mathbb{N} \setminus \{ i,j\}} P_k \ell(|x_k-x_i|)\bigg). \end{split} \end{equation}
\begin{equation} \begin{split} P_i\ell(|x_i-x_j|)&>\tau\bigg({N_o} + \gamma \sum_{k \in \mathbb{N} \setminus \{ i,j\}} P_k \ell(|x_k-x_j|)\bigg) \quad\text{and }\\[3pt] P_j\ell(|x_i-x_j|)&>\tau\bigg({N_o} + \gamma \sum_{k \in \mathbb{N} \setminus \{ i,j\}} P_k \ell(|x_k-x_i|)\bigg). \end{split} \end{equation}
In (2.1),
![]() $\tau>0$
is fixed and called the SINR threshold, the constant
$\tau>0$
is fixed and called the SINR threshold, the constant
![]() ${N_o}\ge 0$
represents noise,
${N_o}\ge 0$
represents noise,
![]() $r\mapsto\ell(r)\in [0,\infty)$
is referred to as the path-loss function, and
$r\mapsto\ell(r)\in [0,\infty)$
is referred to as the path-loss function, and
![]() $\gamma\ge0$
is called the interference-cancellation factor. The random variables
$\gamma\ge0$
is called the interference-cancellation factor. The random variables
![]() $P_i$
,
$P_i$
,
![]() $i\in \mathbb{N}$
, are often called random powers, and the term
$i\in \mathbb{N}$
, are often called random powers, and the term
is referred to as interference. We will use the notation
![]() ${G_{\gamma}({\textbf{X}}^\lambda)}$
to indicate the SINR graph, suppressing the dependencies on
${G_{\gamma}({\textbf{X}}^\lambda)}$
to indicate the SINR graph, suppressing the dependencies on
![]() $\tau$
,
$\tau$
,
![]() ${N_o}$
, and
${N_o}$
, and
![]() $\ell$
, but highlighting the dependence on
$\ell$
, but highlighting the dependence on
![]() $\gamma$
; see Figure 1 for an illustration. We refer to [Reference Dousse, Baccelli and Thiran8, Section 1] for further interpretation of the modeling parameters.
$\gamma$
; see Figure 1 for an illustration. We refer to [Reference Dousse, Baccelli and Thiran8, Section 1] for further interpretation of the modeling parameters.

Figure 1. A typical realization of a Cox SINR graph (with blue vertices and black edges) with directing measure given by the edge-length measure of a two-dimensional Poisson–Voronoi tessellation (in red) in a box, with
![]() ${N_o}=1$
,
${N_o}=1$
,
![]() $\gamma=0.3$
,
$\gamma=0.3$
,
![]() $\tau=0.2$
, constant powers equal to 1, and a suitable path-loss function
$\tau=0.2$
, constant powers equal to 1, and a suitable path-loss function
![]() $\ell$
. The interference-cancellation factor is set to
$\ell$
. The interference-cancellation factor is set to
![]() $\gamma=1/(2\tau)$
. We see only a few vertices having degree two, the largest connected component is of size three, and there are no cycles in the graph.
$\gamma=1/(2\tau)$
. We see only a few vertices having degree two, the largest connected component is of size three, and there are no cycles in the graph.
The SINR graph has a nice interpretation in the study of device-to-device telecommunication systems where the devices of
![]() $X^\lambda$
can communicate directly with each other if their mutual distance, represented by the path-loss function, and their individual powers are sufficiently strong to overcome thermal noise plus all the interference coming from the other devices. If this is the case, then the ability to communicate is represented by an undirected edge.
$X^\lambda$
can communicate directly with each other if their mutual distance, represented by the path-loss function, and their individual powers are sufficiently strong to overcome thermal noise plus all the interference coming from the other devices. If this is the case, then the ability to communicate is represented by an undirected edge.
Our main interest lies in percolation properties of the SINR graph, as first studied in [Reference Dousse, Baccelli and Thiran8–Reference Franceschetti and Meester10]. A cluster in
![]() ${G_{\gamma}({\textbf{X}}^\lambda)}$
is a maximal connected component. We say that
${G_{\gamma}({\textbf{X}}^\lambda)}$
is a maximal connected component. We say that
![]() ${G_{\gamma}({\textbf{X}}^\lambda)}$
percolates if
${G_{\gamma}({\textbf{X}}^\lambda)}$
percolates if
![]() ${G_{\gamma}({\textbf{X}}^\lambda)}$
contains an unbounded connected component. Clusters and percolation are defined analogously in the case of any graph having a vertex set that is included in
${G_{\gamma}({\textbf{X}}^\lambda)}$
contains an unbounded connected component. Clusters and percolation are defined analogously in the case of any graph having a vertex set that is included in
![]() $\mathbb{R}^d$
,
$\mathbb{R}^d$
,
![]() $d \geq 1$
, and is locally finite. Here we focus on the following key quantities. First, the critical interference-cancellation factor is defined as
$d \geq 1$
, and is locally finite. Here we focus on the following key quantities. First, the critical interference-cancellation factor is defined as
In words, it represents the maximal amount of interference that can be added to the system and still maintain percolation. Second, the critical intensity is defined as
which describes the smallest intensity such that for all larger intensities, the addition of a small amount of interference does not destroy percolation.
For the statement of our first main result, we assume certain decorrelation and connectivity properties for the directing measure
![]() $\Lambda$
of the underlying CPP. The precise definitions for
$\Lambda$
of the underlying CPP. The precise definitions for
![]() $\Lambda$
to be stabilizing, b-dependent, or asymptotically essentially connected are technical and will be presented in Definitions 3.1 and 3.2 in Section 3, where we will also mention a number of relevant examples of random measures satisfying these definitions. We denote by
$\Lambda$
to be stabilizing, b-dependent, or asymptotically essentially connected are technical and will be presented in Definitions 3.1 and 3.2 in Section 3, where we will also mention a number of relevant examples of random measures satisfying these definitions. We denote by
![]() $P_o$
a generic power random variable distributed according to
$P_o$
a generic power random variable distributed according to
![]() $\mu$
and put
$\mu$
and put
![]() $P_{\sup}=\textrm{ess\,sup} \mu$
. We call the path-loss function
$P_{\sup}=\textrm{ess\,sup} \mu$
. We call the path-loss function
![]() $\ell$
well-behaved if
$\ell$
well-behaved if
![]() $\ell$
is continuous, constant on
$\ell$
is continuous, constant on
![]() $[0,d_o]$
for some
$[0,d_o]$
for some
![]() $d_o \geq 0$
, and strictly decreasing on
$d_o \geq 0$
, and strictly decreasing on
![]() $[d_o,\infty) \cap \mathrm{supp}(\ell)$
, and satisfies
$[d_o,\infty) \cap \mathrm{supp}(\ell)$
, and satisfies
![]() $\int_0^\infty r^{d-1} \ell(r) \textrm{d} r <\infty$
. Our first result establishes percolation for the SINR graph based on CPPs with random powers.
$\int_0^\infty r^{d-1} \ell(r) \textrm{d} r <\infty$
. Our first result establishes percolation for the SINR graph based on CPPs with random powers.
Theorem 2.1. Let
![]() $d \geq 2$
,
$d \geq 2$
,
![]() ${N_o},\tau>0$
,
${N_o},\tau>0$
,
![]() $P_{\sup}=\infty$
; let
$P_{\sup}=\infty$
; let
![]() $\Lambda$
be stabilizing and
$\Lambda$
be stabilizing and
![]() $\ell$
well-behaved. Then
$\ell$
well-behaved. Then
![]() $\lambda^*_\textrm{c}<\infty$
holds if at least one of the following conditions is satisfied:
$\lambda^*_\textrm{c}<\infty$
holds if at least one of the following conditions is satisfied:
-
1. The path-loss function
 $\ell$
has unbounded support,
$\ell$
has unbounded support,
 $\Lambda$
is b-dependent for some
$\Lambda$
is b-dependent for some
 $b>0$
, and both
$b>0$
, and both
 $\mathbb{E}[\exp(\alpha \Lambda(Q_1))]<\infty$
and
$\mathbb{E}[\exp(\alpha \Lambda(Q_1))]<\infty$
and
 $\mathbb{E}[\exp(\alpha P_o)]<\infty$
hold for some
$\mathbb{E}[\exp(\alpha P_o)]<\infty$
hold for some
 $\alpha>0$
.
$\alpha>0$
. -
2. The path-loss function
 $\ell$
has bounded support,
$\ell$
has bounded support,
 $\mathbb{E}[P_o]<\infty$
, and
$\mathbb{E}[P_o]<\infty$
, and
 $\Lambda$
is asymptotically essentially connected.
$\Lambda$
is asymptotically essentially connected. -
3. The path-loss function
 $\ell$
has bounded support,
$\ell$
has bounded support,
 $\mathbb{E}[P_o]<\infty$
, and
$\mathbb{E}[P_o]<\infty$
, and
 $\sup \mathrm{supp}(\ell)$
is larger than c, where c is a finite constant depending on
$\sup \mathrm{supp}(\ell)$
is larger than c, where c is a finite constant depending on
 $\Lambda$
,
$\Lambda$
,
 $\tau$
, and
$\tau$
, and
 ${N_o}$
.
${N_o}$
.
As discussed in the introduction, Theorem 2.1 extends similar results known for the case of a homogeneous PPP in
![]() $\mathbb{R}^2$
with constant powers to the case of a CPP in
$\mathbb{R}^2$
with constant powers to the case of a CPP in
![]() $\mathbb{R}^d$
,
$\mathbb{R}^d$
,
![]() $d \geq 2$
, with random and possibly unbounded powers. Let us note that the complementary assertion that
$d \geq 2$
, with random and possibly unbounded powers. Let us note that the complementary assertion that
![]() $\lambda^*_\textrm{c}>0$
can be deduced in certain cases based on recent results on Cox–Gilbert graphs with random radii; see [Reference Jahnel, Tóbiás, Ca and li18] and Section 4.1 for more details.
$\lambda^*_\textrm{c}>0$
can be deduced in certain cases based on recent results on Cox–Gilbert graphs with random radii; see [Reference Jahnel, Tóbiás, Ca and li18] and Section 4.1 for more details.
Our second main result establishes a uniform upper bound on the critical interference-cancellation factor. For this assertion we assume the basic nondegeneracy property that
![]() $X^\lambda$
is nonequidistant, which is satisfied for a very large class of CPPs, including many examples relevant to wireless telecommunication systems; see Section 3. This means that for all
$X^\lambda$
is nonequidistant, which is satisfied for a very large class of CPPs, including many examples relevant to wireless telecommunication systems; see Section 3. This means that for all
![]() $i,j,k,l\in \mathbb{N}$
,
$i,j,k,l\in \mathbb{N}$
,
![]() $| x_i-x_j|=| x_k-x_l|>0$
implies
$| x_i-x_j|=| x_k-x_l|>0$
implies
![]() $\{ i,j\} = \{ k,l \}$
and
$\{ i,j\} = \{ k,l \}$
and
![]() $| x_i|=| x_j|$
implies
$| x_i|=| x_j|$
implies
![]() $i\neq j$
, almost surely. Clearly, this property implies that the point process
$i\neq j$
, almost surely. Clearly, this property implies that the point process
![]() $X^\lambda$
is simple; furthermore, if
$X^\lambda$
is simple; furthermore, if
![]() $X^\lambda$
is nonequidistant for some
$X^\lambda$
is nonequidistant for some
![]() $\lambda>0$
, then it is nonequidistant for every
$\lambda>0$
, then it is nonequidistant for every
![]() $\lambda>0$
. As for a (pathological) counterexample, note that if
$\lambda>0$
. As for a (pathological) counterexample, note that if
![]() $\Lambda$
is the sum of Dirac measures at the points of the randomly shifted lattice
$\Lambda$
is the sum of Dirac measures at the points of the randomly shifted lattice
![]() $\mathbb{Z}^d+U$
, where U is a uniform random variable in
$\mathbb{Z}^d+U$
, where U is a uniform random variable in
![]() $[0,1]^d$
, the associated CPP is simple, stationary, but not nonequidistant.
$[0,1]^d$
, the associated CPP is simple, stationary, but not nonequidistant.
Theorem 2.2. Let
![]() $d \geq 1$
,
$d \geq 1$
,
![]() ${N_o}\geq 0$
, and
${N_o}\geq 0$
, and
![]() $\tau,\lambda>0$
, and assume that
$\tau,\lambda>0$
, and assume that
![]() $X^\lambda$
is nonequidistant for all
$X^\lambda$
is nonequidistant for all
![]() $\lambda>0$
. Then
$\lambda>0$
. Then
![]() $\gamma(\lambda) \leq 1/(2\tau)$
.
$\gamma(\lambda) \leq 1/(2\tau)$
.
Note that we do not require any stabilization or connectedness, and also we impose no direct restrictions on
![]() $\mu$
and
$\mu$
and
![]() $\ell$
. The proof of Theorem 2.2 rests on showing absence of percolation in the SINR graph with a maximal degree given by 2. The fact that SINR graphs with
$\ell$
. The proof of Theorem 2.2 rests on showing absence of percolation in the SINR graph with a maximal degree given by 2. The fact that SINR graphs with
![]() $\gamma>0$
have degrees less than
$\gamma>0$
have degrees less than
![]() $1+1/(\tau\gamma)$
is already stated in [Reference Dousse, Baccelli and Thiran8, Theorem 1]; an immediate consequence of this assertion is that there is no percolation in the case
$1+1/(\tau\gamma)$
is already stated in [Reference Dousse, Baccelli and Thiran8, Theorem 1]; an immediate consequence of this assertion is that there is no percolation in the case
![]() $\gamma \geq 1/\tau$
when degrees are at most 1. These claims can easily be seen to hold for any simple point process in any dimension, although in [Reference Dousse, Baccelli and Thiran8] only the case of a two-dimensional homogeneous PPP is considered. Theorem 2.2 is the first improvement of this bound since then, applicable to stationary CPPs and thus in particular also covering the case of homogeneous PPPs in all dimensions.
$\gamma \geq 1/\tau$
when degrees are at most 1. These claims can easily be seen to hold for any simple point process in any dimension, although in [Reference Dousse, Baccelli and Thiran8] only the case of a two-dimensional homogeneous PPP is considered. Theorem 2.2 is the first improvement of this bound since then, applicable to stationary CPPs and thus in particular also covering the case of homogeneous PPPs in all dimensions.
Finally, our third main result states that the critical intensity parameter for the SINR graph can be represented as the critical threshold for percolation of an associated Gilbert graph in any dimension. For this we assume a simpler setting in which
![]() $\Lambda$
equals the Lebesgue measure, i.e., the CPP is in fact a PPP, and the powers are non-random and given by
$\Lambda$
equals the Lebesgue measure, i.e., the CPP is in fact a PPP, and the powers are non-random and given by
![]() $p>0$
. Note that for
$p>0$
. Note that for
![]() $\gamma=0$
, the SINR graph is in fact a Poisson–Gilbert graph (cf. [Reference Gilbert11]) with connection radius given by
$\gamma=0$
, the SINR graph is in fact a Poisson–Gilbert graph (cf. [Reference Gilbert11]) with connection radius given by
which is a well-defined quantity if
![]() $\ell(0)>\tau N_o/p$
and the conditions of Theorem 2.1 on
$\ell(0)>\tau N_o/p$
and the conditions of Theorem 2.1 on
![]() $\ell$
hold.
$\ell$
hold.
Recall that the Gilbert graph based on a simple point process Y with connection radius
![]() $r>0$
has vertex set Y and an edge between two different points of Y whenever the distance between the two points is less than r, and the name ‘Poisson–Gilbert graph’ corresponds to the case when Y is a homogeneous PPP. It is a standard result in continuum percolation that for the Poisson–Gilbert graph with connection radius
$r>0$
has vertex set Y and an edge between two different points of Y whenever the distance between the two points is less than r, and the name ‘Poisson–Gilbert graph’ corresponds to the case when Y is a homogeneous PPP. It is a standard result in continuum percolation that for the Poisson–Gilbert graph with connection radius
![]() $r\in (0,\infty)$
in
$r\in (0,\infty)$
in
![]() $d \geq 2$
dimensions, there exists a unique critical intensity
$d \geq 2$
dimensions, there exists a unique critical intensity
![]() $\lambda_\textrm{c}(r) \in (0,\infty)$
that separates a supercritical regime, where
$\lambda_\textrm{c}(r) \in (0,\infty)$
that separates a supercritical regime, where
![]() $\lambda>\lambda_\textrm{c}(r)$
, in which the Gilbert graph percolates with probability one, from a subcritical regime, where
$\lambda>\lambda_\textrm{c}(r)$
, in which the Gilbert graph percolates with probability one, from a subcritical regime, where
![]() $\lambda<\lambda_\textrm{c}(r)$
, in which the Gilbert graph does not percolate almost surely; see for example [Reference Meester and Roy25, Section 3].
$\lambda<\lambda_\textrm{c}(r)$
, in which the Gilbert graph does not percolate almost surely; see for example [Reference Meester and Roy25, Section 3].
Theorem 2.3. Let
![]() $d \geq 2$
,
$d \geq 2$
,
![]() ${N_o},\tau,p>0$
, and
${N_o},\tau,p>0$
, and
![]() $\Lambda(\textrm{d} x)=\textrm{d} x$
; let
$\Lambda(\textrm{d} x)=\textrm{d} x$
; let
![]() $\ell$
be well-behaved with
$\ell$
be well-behaved with
![]() $\ell(0) > \tau {N_o}/p$
. Then
$\ell(0) > \tau {N_o}/p$
. Then
![]() $\lambda^*_\textrm{c}=\lambda_\textrm{c}(r_\textrm{B})$
.
$\lambda^*_\textrm{c}=\lambda_\textrm{c}(r_\textrm{B})$
.
Theorem 2.3 extends the result [Reference Dousse9, Theorem 1] to dimensions
![]() $d\ge3$
using new techniques; see Section 4 for details.
$d\ge3$
using new techniques; see Section 4 for details.
In the following section we present our main technical conditions together with examples for which our main theorems are applicable.
3. Stabilization, asymptotic essential connectedness, and examples
The following definitions were recently introduced in [Reference Hirsch, Jahnel and Cali16] in order to prove existence of a unique nontrivial critical intensity threshold for Cox–Gilbert graphs with fixed connectivity threshold. Let us recall that
![]() $Q_n=[\!-n/2,n/2]^d$
for
$Q_n=[\!-n/2,n/2]^d$
for
![]() $n>0$
and
$n>0$
and
![]() $d \in \mathbb{N}$
; let
$d \in \mathbb{N}$
; let
![]() $Q_n(x)=Q_n+x$
denote the box with side length n, centered at
$Q_n(x)=Q_n+x$
denote the box with side length n, centered at
![]() $x\in\mathbb{R}^d$
, and let
$x\in\mathbb{R}^d$
, and let
![]() ${\operatorname {dist}}(x,A):=\inf\{|x-y|\colon y\in A\}$
for
${\operatorname {dist}}(x,A):=\inf\{|x-y|\colon y\in A\}$
for
![]() $x \in \mathbb{R}^d$
and
$x \in \mathbb{R}^d$
and
![]() $A \subset \mathbb{R}^d$
. We start with the definition of stabilization, which can be understood as a quantitative spatial mixing property of the directing measure of a CPP.
$A \subset \mathbb{R}^d$
. We start with the definition of stabilization, which can be understood as a quantitative spatial mixing property of the directing measure of a CPP.
Definition 3.1.
(Stabilization.) The random measure
![]() $\Lambda$
is called stabilizing if there exists a random field of stabilization radii
$\Lambda$
is called stabilizing if there exists a random field of stabilization radii
![]() $R=\{ R_x \}_{x\in \mathbb{R}^d}$
defined on the same probability space as
$R=\{ R_x \}_{x\in \mathbb{R}^d}$
defined on the same probability space as
![]() $\Lambda$
such that, writing
$\Lambda$
such that, writing
the following hold:
-
1.
 $(\Lambda,R)$
is jointly stationary.
$(\Lambda,R)$
is jointly stationary. -
2. We have
 $\lim_{n \uparrow \infty} \mathbb P(R(Q_n)<n)=1$
.
$\lim_{n \uparrow \infty} \mathbb P(R(Q_n)<n)=1$
. -
3. For all
 $n \geq 1$
, non-negative bounded measurable functions
$n \geq 1$
, non-negative bounded measurable functions
 $f \colon \mathbb M \to [0,\infty)$
, and finite
$f \colon \mathbb M \to [0,\infty)$
, and finite
 $\varphi \subset \mathbb{R}^d$
with
$\varphi \subset \mathbb{R}^d$
with
 ${\operatorname {dist}}(x,\varphi\setminus \{ x \})>3n$
for all
${\operatorname {dist}}(x,\varphi\setminus \{ x \})>3n$
for all
 $x \in \varphi$
, the following random variables are independent:
where for a measurable set
$x \in \varphi$
, the following random variables are independent:
where for a measurable set \begin{equation*} f(\Lambda_{Q_n(x)}) \unicode{x1D7D9} \{ R(Q_n(x)) <n \}, \qquad x \in \varphi, \end{equation*}
\begin{equation*} f(\Lambda_{Q_n(x)}) \unicode{x1D7D9} \{ R(Q_n(x)) <n \}, \qquad x \in \varphi, \end{equation*}
 $A \subseteq \mathbb{R}^d$
,
$A \subseteq \mathbb{R}^d$
,
 $\Lambda_A$
denotes the restriction of
$\Lambda_A$
denotes the restriction of
 $\Lambda$
to A.
$\Lambda$
to A.
A stronger form of stabilization is when
![]() $\Lambda$
is b-dependent. That is, the restrictions
$\Lambda$
is b-dependent. That is, the restrictions
![]() $\Lambda_A$
and
$\Lambda_A$
and
![]() $\Lambda_B$
of
$\Lambda_B$
of
![]() $\Lambda$
to the measurable sets
$\Lambda$
to the measurable sets
![]() $A,B\subset\mathbb{R}^d$
are independent whenever
$A,B\subset\mathbb{R}^d$
are independent whenever
![]() ${\operatorname {dist}}(A,B)>b$
for some
${\operatorname {dist}}(A,B)>b$
for some
![]() $b>0$
. For b-dependence of subsets of
$b>0$
. For b-dependence of subsets of
![]() $\mathbb{Z}^d$
we will use the analogous definition but with
$\mathbb{Z}^d$
we will use the analogous definition but with
![]() ${\operatorname {dist}}$
replaced by the
${\operatorname {dist}}$
replaced by the
![]() $\ell^{\infty}$
-distance.
$\ell^{\infty}$
-distance.
Next we give a definition of asymptotic essential connectedness, a suitable way of capturing connectedness of the support of the directing measure of a CPP with high probability.
Definition 3.2.
(Asymptotic essential connectedness.) The stabilizing random measure
![]() $\Lambda$
with stabilization radius field R is asymptotically essentially connected if for all
$\Lambda$
with stabilization radius field R is asymptotically essentially connected if for all
![]() $n \geq 1$
, whenever
$n \geq 1$
, whenever
![]() $R(Q_{2n})<n/2$
, we have that
$R(Q_{2n})<n/2$
, we have that
-
i.
 $\mathrm{supp}(\Lambda_{Q_n})$
contains a connected component of diameter at least
$\mathrm{supp}(\Lambda_{Q_n})$
contains a connected component of diameter at least
 $n/3$
, and
$n/3$
, and -
ii. any two connected components of
 $\mathrm{supp}(\Lambda_{Q_n})$
of diameter at least
$\mathrm{supp}(\Lambda_{Q_n})$
of diameter at least
 $n/9$
are contained in the same connected component of
$n/9$
are contained in the same connected component of
 $\mathrm{supp}(\Lambda_{Q_{2n}})$
.
$\mathrm{supp}(\Lambda_{Q_{2n}})$
.
The class of stabilizing random measures includes a number of interesting and relevant examples, for instance directing measures given via random tessellations based on PPPs. As already proven in [Reference Hirsch, Jahnel and Cali16, Section 3.1], for example, the edge-length measures of Poisson–Voronoi tessellations are asymptotically essentially connected (and hence also stabilizing), and it was also pointed out there that the same property for Poisson–Delaunay tessellations can be proven very similarly. It is nevertheless easy to see that these intensity measures are not b-dependent for any
![]() $b>0$
. However, let us note that the edge-length measures of Poisson line tessellations in
$b>0$
. However, let us note that the edge-length measures of Poisson line tessellations in
![]() $\mathbb{R}^2$
are not even stabilizing.
$\mathbb{R}^2$
are not even stabilizing.
Stabilizing random measures that are absolutely continuous with respect to the Lebesgue measure include the directing measure of some modulated PPPs or shot-noise fields with compactly supported kernel. For the purpose of the present paper, a modulated PPP is defined with directing measure
![]() $\Lambda(\textrm{d} x)=\lambda\unicode{x1D7D9}\{x\in \Xi\}\textrm{d} x+ \lambda'\unicode{x1D7D9}\{x\notin \Xi\}\textrm{d} x$
, for some Poisson Boolean model
$\Lambda(\textrm{d} x)=\lambda\unicode{x1D7D9}\{x\in \Xi\}\textrm{d} x+ \lambda'\unicode{x1D7D9}\{x\notin \Xi\}\textrm{d} x$
, for some Poisson Boolean model
![]() $\Xi$
with constant connection radii, where the definition of a Poisson Boolean model (with constant connection radii) will be presented at the beginning of Section 5.3, and
$\Xi$
with constant connection radii, where the definition of a Poisson Boolean model (with constant connection radii) will be presented at the beginning of Section 5.3, and
![]() $\lambda,\lambda'\ge0$
. As noted in [Reference Hirsch, Jahnel and Cali16, Section 2.1], the intensity measure that this definition yields is easily seen to be b-dependent for some
$\lambda,\lambda'\ge0$
. As noted in [Reference Hirsch, Jahnel and Cali16, Section 2.1], the intensity measure that this definition yields is easily seen to be b-dependent for some
![]() $b>0$
, and if
$b>0$
, and if
![]() $\lambda$
and
$\lambda$
and
![]() $\lambda'$
are positive, then
$\lambda'$
are positive, then
![]() $\Lambda$
is asymptotically essentially connected. There exist examples, both for
$\Lambda$
is asymptotically essentially connected. There exist examples, both for
![]() $\lambda>0$
and
$\lambda>0$
and
![]() $\lambda'=0$
and for
$\lambda'=0$
and for
![]() $\lambda=0$
and
$\lambda=0$
and
![]() $\lambda'>0$
, such that asymptotic essential connectedness fails; see [Reference Tóbiás28, Section 2.5.1] for details. However, if
$\lambda'>0$
, such that asymptotic essential connectedness fails; see [Reference Tóbiás28, Section 2.5.1] for details. However, if
![]() $\Xi$
is in the supercritical regime for percolation and
$\Xi$
is in the supercritical regime for percolation and
![]() $\lambda>0$
, then
$\lambda>0$
, then
![]() $\Lambda$
is asymptotically essentially connected, which follows from [Reference Penrose and Pisztora26, Theorems 2 and 5], as was observed in [Reference Hirsch, Jahnel and Cali16, Section 2.1]. The general definition of a modulated PPP can be found in [Reference Chiu, Stoyan, Kendall and Mecke6, Section 5.2.2]; there, the construction is similar to the case presented in our paper, but
$\Lambda$
is asymptotically essentially connected, which follows from [Reference Penrose and Pisztora26, Theorems 2 and 5], as was observed in [Reference Hirsch, Jahnel and Cali16, Section 2.1]. The general definition of a modulated PPP can be found in [Reference Chiu, Stoyan, Kendall and Mecke6, Section 5.2.2]; there, the construction is similar to the case presented in our paper, but
![]() $\Xi$
can be a general random closed subset of
$\Xi$
can be a general random closed subset of
![]() $\mathbb{R}^d$
, and hence the arising directing measure need not even be stabilizing, as explained in [Reference Tóbiás28, Section 2.5.1]. Finally, without going into details, let us mention that in the case when
$\mathbb{R}^d$
, and hence the arising directing measure need not even be stabilizing, as explained in [Reference Tóbiás28, Section 2.5.1]. Finally, without going into details, let us mention that in the case when
![]() $\Xi$
is a Poisson Boolean model with random radii, it is possible that the corresponding directing measure is stabilizing but not b-dependent for any
$\Xi$
is a Poisson Boolean model with random radii, it is possible that the corresponding directing measure is stabilizing but not b-dependent for any
![]() $b>0$
; see [Reference Jahnel, Tóbiás, Ca and li18, Example 3.4].
$b>0$
; see [Reference Jahnel, Tóbiás, Ca and li18, Example 3.4].
Shot-noise fields have directing measures of the form
![]() $\Lambda(\textrm{d} x)=\sum_{i\in \mathbb N}\kappa(y_i-x)\textrm{d} x $
, with
$\Lambda(\textrm{d} x)=\sum_{i\in \mathbb N}\kappa(y_i-x)\textrm{d} x $
, with
![]() $(y_i)_{i\in \mathbb N}$
a homogeneous PPP and
$(y_i)_{i\in \mathbb N}$
a homogeneous PPP and
![]() $\kappa\colon \mathbb{R}^d\to[0,\infty)$
compactly supported; cf. [Reference Hirsch, Jahnel and Cali16, Example 2.2]. They are always b-dependent for some
$\kappa\colon \mathbb{R}^d\to[0,\infty)$
compactly supported; cf. [Reference Hirsch, Jahnel and Cali16, Example 2.2]. They are always b-dependent for some
![]() $b>0$
, but not asymptotically essentially connected in general (see [Reference Hirsch, Jahnel and Cali16, Section 2.1]); however, in some relevant cases they are (see [Reference Tóbiás28, Section 2.5.1]).
$b>0$
, but not asymptotically essentially connected in general (see [Reference Hirsch, Jahnel and Cali16, Section 2.1]); however, in some relevant cases they are (see [Reference Tóbiás28, Section 2.5.1]).
In the following section, we lay out the strategies for the proofs of our main results, and comment on limitations and further extensions of the statements presented.
4. Methods and discussion
4.1. Strategy of proof and discussion for Theorem 2.1
As mentioned in the introduction, the statement of Theorem 2.1 is an extension of the results of [Reference Löffler22] to the case of stabilizing CPPs. For the proof, we combine the approach used in [Reference Löffler22, Theorem 4.5] for handling random radii and the approach used in [Reference Tóbiás28, Theorem 2.4] for dealing with the spatial correlations of the directing measure
![]() $\Lambda$
of the CPP. To begin with, an easy coupling argument (see [Reference Tóbiás27, Section 4.2.3.4]) implies that as long as the powers are bounded, all positive results of [Reference Tóbiás28] about percolation in the Cox SINR graph for asymptotically essentially connected
$\Lambda$
of the CPP. To begin with, an easy coupling argument (see [Reference Tóbiás27, Section 4.2.3.4]) implies that as long as the powers are bounded, all positive results of [Reference Tóbiás28] about percolation in the Cox SINR graph for asymptotically essentially connected
![]() $\Lambda$
are applicable. More precisely, we have the following proposition for the Cox SINR graph with random bounded powers.
$\Lambda$
are applicable. More precisely, we have the following proposition for the Cox SINR graph with random bounded powers.
Proposition 4.1. ([Reference Tóbiás28, Theorem 2.4 and Proposition 2.7].) Let
![]() $d\ge 2$
,
$d\ge 2$
,
![]() ${N_o},\tau>0$
, and
${N_o},\tau>0$
, and
![]() $\mathbb{P}(P_o>0)>0$
; let
$\mathbb{P}(P_o>0)>0$
; let
![]() $\Lambda$
be stabilizing and
$\Lambda$
be stabilizing and
![]() $\ell$
well-behaved. If
$\ell$
well-behaved. If
![]() $P_{\sup}<\infty$
and
$P_{\sup}<\infty$
and
![]() $\ell(0)>\tau{N_o}/P_{\sup}$
, then
$\ell(0)>\tau{N_o}/P_{\sup}$
, then
![]() $\lambda^*_\textrm{c}<\infty$
holds if at least one of the following conditions is satisfied:
$\lambda^*_\textrm{c}<\infty$
holds if at least one of the following conditions is satisfied:
-
1. The path-loss function
 $\ell$
has unbounded support,
$\ell$
has unbounded support,
 $\Lambda$
is b-dependent for some
$\Lambda$
is b-dependent for some
 $b>0$
,
$b>0$
,
 $\mathbb{E}[\exp(\alpha\Lambda(Q_1))]<\infty$
holds for some
$\mathbb{E}[\exp(\alpha\Lambda(Q_1))]<\infty$
holds for some
 $\alpha>0$
, and at least one of the following conditions holds:
$\alpha>0$
, and at least one of the following conditions holds:
 $\Lambda$
is asymptotically essentially connected, or
$\Lambda$
is asymptotically essentially connected, or
 $P_{\sup}$
is sufficiently large.
$P_{\sup}$
is sufficiently large. -
2. The path-loss function
 $\ell$
has bounded support, and
$\ell$
has bounded support, and
 $\Lambda$
is asymptotically essentially connected.
$\Lambda$
is asymptotically essentially connected. -
3. The path-loss function
 $\ell$
has bounded support, and
$\ell$
has bounded support, and
 $\sup \mathrm{supp}(\ell)$
and
$\sup \mathrm{supp}(\ell)$
and
 $P_{\sup}$
are both sufficiently large.
$P_{\sup}$
are both sufficiently large.
Note that we have formulated Condition 1 in Proposition 4.1 more generally than the statement in [Reference Tóbiás28], and Condition 3 does not appear in [Reference Tóbiás28]. However, the proof from [Reference Tóbiás28] can also be adapted to these more general cases. Indeed, let us first explain how the case of a constant power
![]() $\mu=\delta_p$
,
$\mu=\delta_p$
,
![]() $p>0$
, can be handled using the methods of [Reference Tóbiás28]. The cases where
$p>0$
, can be handled using the methods of [Reference Tóbiás28]. The cases where
![]() $\Lambda$
is asymptotically essentially connected in Proposition 4.1 for constant powers are covered by [Reference Tóbiás28, Theorem 2.4, Part (2)]. Furthermore, the methods of the proof of [Reference Tóbiás28, Proposition 2.7] apply to the case when
$\Lambda$
is asymptotically essentially connected in Proposition 4.1 for constant powers are covered by [Reference Tóbiás28, Theorem 2.4, Part (2)]. Furthermore, the methods of the proof of [Reference Tóbiás28, Proposition 2.7] apply to the case when
![]() $\Lambda$
is stabilizing but not necessary asymptotically essentially connected. To see this, note that the arguments of that proof require the connection radii
$\Lambda$
is stabilizing but not necessary asymptotically essentially connected. To see this, note that the arguments of that proof require the connection radii
![]() $r_\textrm{B}$
(see (2.4)) to be large enough. Now, if
$r_\textrm{B}$
(see (2.4)) to be large enough. Now, if
![]() $\mathrm{supp}(\ell)$
is unbounded, then one can always make
$\mathrm{supp}(\ell)$
is unbounded, then one can always make
![]() $r_\textrm{B}$
arbitrarily large by choosing the power value p sufficiently large, which corresponds to the case of large
$r_\textrm{B}$
arbitrarily large by choosing the power value p sufficiently large, which corresponds to the case of large
![]() $P_{\sup}=p$
in Condition 1. Otherwise, this is not always possible, because
$P_{\sup}=p$
in Condition 1. Otherwise, this is not always possible, because
![]() $\sup_{p>0} \ell^{-1}(\tau N_0/p)$
equals the finite number
$\sup_{p>0} \ell^{-1}(\tau N_0/p)$
equals the finite number
![]() $\sup \mathrm{supp}(\ell)$
. However, once
$\sup \mathrm{supp}(\ell)$
. However, once
![]() $\sup \mathrm{supp}(\ell)$
is sufficiently large, one can make
$\sup \mathrm{supp}(\ell)$
is sufficiently large, one can make
![]() $r_\textrm{B}$
sufficiently large so that the proof of [Reference Tóbiás28, Proposition 2.7] becomes applicable. Hence, we see that Proposition 4.1 indeed follows from [Reference Tóbiás28] for fixed
$r_\textrm{B}$
sufficiently large so that the proof of [Reference Tóbiás28, Proposition 2.7] becomes applicable. Hence, we see that Proposition 4.1 indeed follows from [Reference Tóbiás28] for fixed
![]() $p>0$
. Now, if
$p>0$
. Now, if
![]() $\mu$
is not concentrated at one point, then one can always choose
$\mu$
is not concentrated at one point, then one can always choose
![]() $p_2 \geq p_1>0$
such that
$p_2 \geq p_1>0$
such that
![]() $\mu([p_1,\infty))>0$
and
$\mu([p_1,\infty))>0$
and
![]() $\mu((p_2,\infty))=0$
. Then, if
$\mu((p_2,\infty))=0$
. Then, if
![]() $p_1$
is sufficiently large, the above arguments imply that there exists an infinite connected component in the subgraph of the SINR graph spanned by all vertices
$p_1$
is sufficiently large, the above arguments imply that there exists an infinite connected component in the subgraph of the SINR graph spanned by all vertices
![]() $x_i$
where
$x_i$
where
![]() $i \in \mathbb{N}$
is such that
$i \in \mathbb{N}$
is such that
![]() $P_i>p_1$
, for all sufficiently large
$P_i>p_1$
, for all sufficiently large
![]() $\lambda>0$
and all sufficiently small
$\lambda>0$
and all sufficiently small
![]() $\gamma>0$
. Here, we bound all power values corresponding to the interferences by
$\gamma>0$
. Here, we bound all power values corresponding to the interferences by
![]() $p_2$
from above. See Section 5.1, Step 1, for further details of a very similar argument. We conclude that
$p_2$
from above. See Section 5.1, Step 1, for further details of a very similar argument. We conclude that
![]() $\lambda^*_\textrm{c}<\infty$
holds under the assumptions of Proposition 4.1. Given Proposition 4.1, in the present paper it suffices to prove the case when
$\lambda^*_\textrm{c}<\infty$
holds under the assumptions of Proposition 4.1. Given Proposition 4.1, in the present paper it suffices to prove the case when
![]() $P_{\sup}=\infty$
. We prove Theorem 2.1 in Section 5.1.
$P_{\sup}=\infty$
. We prove Theorem 2.1 in Section 5.1.
Let us comment on some further aspects of Theorem 2.1. First, as for Condition 2 in Theorem 2.1, an extension to the general stabilizing case is not possible in general. Indeed, even if
![]() $P_o$
has very heavy tails, as soon as
$P_o$
has very heavy tails, as soon as
![]() $\mathrm{supp}(\ell)$
is bounded, the radii of the associated Cox–Gilbert graph with random radii are bounded. Then it is not hard to exhibit examples of stabilizing directing measures
$\mathrm{supp}(\ell)$
is bounded, the radii of the associated Cox–Gilbert graph with random radii are bounded. Then it is not hard to exhibit examples of stabilizing directing measures
![]() $\Lambda$
such that
$\Lambda$
such that
![]() $\lambda^*_\textrm{c}=\infty$
; see the examples in [Reference Tóbiás28, Section 2.5.1].
$\lambda^*_\textrm{c}=\infty$
; see the examples in [Reference Tóbiás28, Section 2.5.1].
Second, if
![]() $\Lambda$
is such that
$\Lambda$
is such that
![]() $\Lambda(Q_1)$
is almost surely bounded, then the exponential-moment condition
$\Lambda(Q_1)$
is almost surely bounded, then the exponential-moment condition
of Condition 1 in Theorem 2.1 clearly holds for all
![]() $\alpha >0$
. For example, this is the case for the modulated PPP with
$\alpha >0$
. For example, this is the case for the modulated PPP with
![]() $\lambda,\lambda' \geq 0$
. Furthermore, (4.1) holds for shot-noise fields for all
$\lambda,\lambda' \geq 0$
. Furthermore, (4.1) holds for shot-noise fields for all
![]() $\alpha>0$
; see e.g. [Reference Tóbiás28, Section 2.5.1]. For Poisson–Voronoi and Poisson–Delaunay tessellations, the b-dependence assumption in Condition 1 fails for all
$\alpha>0$
; see e.g. [Reference Tóbiás28, Section 2.5.1]. For Poisson–Voronoi and Poisson–Delaunay tessellations, the b-dependence assumption in Condition 1 fails for all
![]() $b>0$
, and hence percolation in the SINR graph can only be concluded for compactly supported
$b>0$
, and hence percolation in the SINR graph can only be concluded for compactly supported
![]() $\ell$
. On the other hand, it was verified in [Reference Jahnel and Tóbiás17] that for these two kinds of tessellations in two dimensions,
$\ell$
. On the other hand, it was verified in [Reference Jahnel and Tóbiás17] that for these two kinds of tessellations in two dimensions,
![]() $\mathbb{E}[\exp(\alpha\Lambda(Q_1))]<\infty$
holds for all
$\mathbb{E}[\exp(\alpha\Lambda(Q_1))]<\infty$
holds for all
![]() $\alpha>0$
; it is not known whether the same holds in higher dimension.
$\alpha>0$
; it is not known whether the same holds in higher dimension.
Third, the moment conditions on
![]() $P_o$
may look surprising at first. Indeed, why do we need to upper-bound moments of
$P_o$
may look surprising at first. Indeed, why do we need to upper-bound moments of
![]() $P_o$
in order to guarantee percolation in an SINR graph? This is indeed counterintuitive in view of the Gilbert graph since there larger radii would lead to better connectivity. However, in the SINR graph, as mentioned above, larger powers also increase interference and thus also might decrease connectivity. The classical approach used in [Reference Blaszczyszyn and Yogeshwaran2, Reference Dousse9, Reference Tóbiás28] to establish percolation in SINR graphs is to show that the underlying Gilbert graph satisfies some strong connectivity properties, and that at the same time the interferences can be uniformly bounded on large connected areas. We follow this approach as well; however, the random powers dictate several workarounds.
$P_o$
in order to guarantee percolation in an SINR graph? This is indeed counterintuitive in view of the Gilbert graph since there larger radii would lead to better connectivity. However, in the SINR graph, as mentioned above, larger powers also increase interference and thus also might decrease connectivity. The classical approach used in [Reference Blaszczyszyn and Yogeshwaran2, Reference Dousse9, Reference Tóbiás28] to establish percolation in SINR graphs is to show that the underlying Gilbert graph satisfies some strong connectivity properties, and that at the same time the interferences can be uniformly bounded on large connected areas. We follow this approach as well; however, the random powers dictate several workarounds.
Fourth, Condition 1 in Theorem 2.1 is not necessarily optimal. However, we believe that if percolation with unbounded
![]() $\mathrm{supp}(\ell)$
and without exponential moments of
$\mathrm{supp}(\ell)$
and without exponential moments of
![]() $P_o$
is possible, then the proof for this statement must be rather different from ours. An interference-control argument may not be possible at all; instead one should be able to show that the SINR values are sufficiently large for many transitions, yielding satisfactory connectivity of the network for percolation. Let us mention a similar problem. It was conjectured in [Reference Dousse, Baccelli and Thiran8] that in the case with constant powers, in order to have percolation in the SINR graph for large
$P_o$
is possible, then the proof for this statement must be rather different from ours. An interference-control argument may not be possible at all; instead one should be able to show that the SINR values are sufficiently large for many transitions, yielding satisfactory connectivity of the network for percolation. Let us mention a similar problem. It was conjectured in [Reference Dousse, Baccelli and Thiran8] that in the case with constant powers, in order to have percolation in the SINR graph for large
![]() $\lambda$
,
$\lambda$
,
![]() $\ell$
has only to have integrable tails but may explode at zero. However, the setting where
$\ell$
has only to have integrable tails but may explode at zero. However, the setting where
![]() $\lim_{r \downarrow 0} \ell(r)=\infty$
is such that the classical interference-control argument, as exhibited in [Reference Dousse9], certainly cannot work. Indeed, the interferences are almost surely finite, but they have infinite expectation (see [Reference Daley7]); hence there is no hope of applying a version of the exponential Markov inequality. Let us also note that the results of [Reference Daley7] imply that, if the tails of
$\lim_{r \downarrow 0} \ell(r)=\infty$
is such that the classical interference-control argument, as exhibited in [Reference Dousse9], certainly cannot work. Indeed, the interferences are almost surely finite, but they have infinite expectation (see [Reference Daley7]); hence there is no hope of applying a version of the exponential Markov inequality. Let us also note that the results of [Reference Daley7] imply that, if the tails of
![]() $\ell$
are not integrable, then SINR graphs with
$\ell$
are not integrable, then SINR graphs with
![]() $\gamma>0$
have no edges.
$\gamma>0$
have no edges.
Finally, under the assumptions of Theorem 2.1 on
![]() $\ell$
, for
$\ell$
, for
![]() $\gamma=0$
, the SINR graph
$\gamma=0$
, the SINR graph
![]() $G_{0}(\textbf{X}^\lambda)$
is a Gilbert graph with i.i.d. random radii
$G_{0}(\textbf{X}^\lambda)$
is a Gilbert graph with i.i.d. random radii
![]() $R_i=\ell^{-1}(\tau N_o/P_i)$
. Let
$R_i=\ell^{-1}(\tau N_o/P_i)$
. Let
![]() $R_o$
denote a generic random variable having the same distribution as
$R_o$
denote a generic random variable having the same distribution as
![]() $R_i$
. Now, if all other parameters are kept fixed, it is easy to see that
$R_i$
. Now, if all other parameters are kept fixed, it is easy to see that
![]() $\gamma \mapsto \mathbb{P}({G_{\gamma}({\textbf{X}}^\lambda)} \text{ percolates})$
is decreasing. Hence, if almost surely there is no percolation in the SINR graph for
$\gamma \mapsto \mathbb{P}({G_{\gamma}({\textbf{X}}^\lambda)} \text{ percolates})$
is decreasing. Hence, if almost surely there is no percolation in the SINR graph for
![]() $\gamma=0$
, then the same holds for all
$\gamma=0$
, then the same holds for all
![]() $\gamma>0$
. Furthermore, as already mentioned, percolation properties of Gilbert graphs can equivalently be expressed in terms of the corresponding Boolean models. Thus, the recent result [Reference Jahnel, Tóbiás, Ca and li18, Theorem 2.6, Part (2)] about existence of a subcritical phase in Cox Boolean models immediately implies the following assertion. If
$\gamma>0$
. Furthermore, as already mentioned, percolation properties of Gilbert graphs can equivalently be expressed in terms of the corresponding Boolean models. Thus, the recent result [Reference Jahnel, Tóbiás, Ca and li18, Theorem 2.6, Part (2)] about existence of a subcritical phase in Cox Boolean models immediately implies the following assertion. If
![]() $\Lambda$
is
$\Lambda$
is
![]() $\phi$
-stabilizing and
$\phi$
-stabilizing and
![]() $R_o$
is unbounded with
$R_o$
is unbounded with
![]() $\mathbb{E}[R_o^d]<\infty$
, then
$\mathbb{E}[R_o^d]<\infty$
, then
![]() $\lambda^*_\textrm{c}>0$
. Here, the notion of
$\lambda^*_\textrm{c}>0$
. Here, the notion of
![]() $\phi$
-stabilization (cf. [Reference Jahnel, Tóbiás, Ca and li18, Definition 2.5]) is very similar to our definition of stabilization, and many relevant stabilizing examples are also
$\phi$
-stabilization (cf. [Reference Jahnel, Tóbiás, Ca and li18, Definition 2.5]) is very similar to our definition of stabilization, and many relevant stabilizing examples are also
![]() $\phi$
-stabilizing. This observation complements the result
$\phi$
-stabilizing. This observation complements the result
![]() $\lambda^*_\textrm{c}<\infty$
in Theorem 2.1. Moreover, it improves the assertion of [Reference Tóbiás27, Section 4.2.3.4] that
$\lambda^*_\textrm{c}<\infty$
in Theorem 2.1. Moreover, it improves the assertion of [Reference Tóbiás27, Section 4.2.3.4] that
![]() $\lambda^*_\textrm{c}<\infty$
holds for bounded
$\lambda^*_\textrm{c}<\infty$
holds for bounded
![]() $P_o$
(equivalently, bounded
$P_o$
(equivalently, bounded
![]() $R_o$
) if
$R_o$
) if
![]() $\Lambda$
is stabilizing and
$\Lambda$
is stabilizing and
![]() $\ell$
satisfies the assumptions of Theorem 2.1 with
$\ell$
satisfies the assumptions of Theorem 2.1 with
![]() $\ell(0) > \tau {N_o}/{\operatorname {essinf}} \mu$
or
$\ell(0) > \tau {N_o}/{\operatorname {essinf}} \mu$
or
![]() $\ell(0) \leq \tau {N_o}/P_{\sup}$
.
$\ell(0) \leq \tau {N_o}/P_{\sup}$
.
4.2. Strategy of proof and discussion for Theorem 2.2
Recall that we call a maximal connected component in a graph a cluster. As already pointed out in [Reference Dousse, Baccelli and Thiran8, Theorem 1], for
![]() $\gamma>0$
, all degrees in
$\gamma>0$
, all degrees in
![]() ${G_{\gamma}({\textbf{X}}^\lambda)}$
, where
${G_{\gamma}({\textbf{X}}^\lambda)}$
, where
![]() $X^\lambda$
is a PPP, are less than
$X^\lambda$
is a PPP, are less than
![]() $1+1/(\tau\gamma)$
for any choice of
$1+1/(\tau\gamma)$
for any choice of
![]() $\lambda,\tau>0$
and
$\lambda,\tau>0$
and
![]() ${N_o} \geq 0$
. In other words, each vertex in
${N_o} \geq 0$
. In other words, each vertex in
![]() ${G_{\gamma}({\textbf{X}}^\lambda)}$
has at most
${G_{\gamma}({\textbf{X}}^\lambda)}$
has at most
![]() $1+1/(\tau\gamma)$
neighbors. It is not hard to see that this property remains true if the PPP is replaced by a CPP, or even any simple point process; see [Reference Tóbiás27, Section A.3]. Thanks to the degree bounds, any such Cox SINR graph with random powers for which
$1+1/(\tau\gamma)$
neighbors. It is not hard to see that this property remains true if the PPP is replaced by a CPP, or even any simple point process; see [Reference Tóbiás27, Section A.3]. Thanks to the degree bounds, any such Cox SINR graph with random powers for which
![]() $\gamma \geq 1/\tau$
has no infinite cluster since it has degrees bounded by 1. For
$\gamma \geq 1/\tau$
has no infinite cluster since it has degrees bounded by 1. For
![]() $\gamma \in [1/(2\tau),1/\tau)$
, we have an a priori degree bound of 2, which implies that all maximal connected components of SINR graphs are finite cycles or paths that are infinite in zero, one, or two directions. This is reminiscent of a one-dimensional percolation model, and thus the conjecture is that it contains no infinite clusters under general assumptions on the directing measure of the CPP; see Figure 2 for an illustration. The following proposition shows that this is indeed true for the Cox SINR graph with random powers.
$\gamma \in [1/(2\tau),1/\tau)$
, we have an a priori degree bound of 2, which implies that all maximal connected components of SINR graphs are finite cycles or paths that are infinite in zero, one, or two directions. This is reminiscent of a one-dimensional percolation model, and thus the conjecture is that it contains no infinite clusters under general assumptions on the directing measure of the CPP; see Figure 2 for an illustration. The following proposition shows that this is indeed true for the Cox SINR graph with random powers.

Figure 2. A typical realization of a Cox SINR graph (with blue vertices and black edges) with directing measure given by the edge-length measure of a two-dimensional Poisson–Voronoi tessellation (in red) in a box, with
![]() ${N_o}=P_o=\tau=1$
and a suitable path-loss function
${N_o}=P_o=\tau=1$
and a suitable path-loss function
![]() $\ell$
. The interference-cancellation factor is set to
$\ell$
. The interference-cancellation factor is set to
![]() $\gamma=1/(2\tau)$
. We see only a few vertices having degree two, the largest connected component is of size three, and there are no cycles in the graph. As indicated by Proposition 4.2 the graph is highly disconnected.
$\gamma=1/(2\tau)$
. We see only a few vertices having degree two, the largest connected component is of size three, and there are no cycles in the graph. As indicated by Proposition 4.2 the graph is highly disconnected.
Proposition 4.2. Let
![]() $d\ge 1$
,
$d\ge 1$
,
![]() ${N_o}\geq 0$
,
${N_o}\geq 0$
,
![]() $\tau>0$
, and
$\tau>0$
, and
![]() $\gamma \geq 1/(2\tau)$
; then for
$\gamma \geq 1/(2\tau)$
; then for
![]() $\Lambda$
nonequidistant,
$\Lambda$
nonequidistant,
The statement of Theorem 2.2 is an immediate consequence of Proposition 4.2, the proof of which can be found in Section 5.2. The proof employs a delicate configuration-wise analysis of the SINR graph, which seems to be new in the literature. Moreover, we expect the proof to hold for SINR graphs based on a large class of simple nonequidistant stationary point processes.
Let us comment on a further aspect of Theorem 2.2. It can be observed that the proof of Proposition 4.2 does not use the precise numerical relation
![]() $\gamma \geq 1/(2\tau)$
, but rather just the fact that the SINR graph has degrees at most 2. Hence, once
$\gamma \geq 1/(2\tau)$
, but rather just the fact that the SINR graph has degrees at most 2. Hence, once
![]() $\Lambda$
is nonequidistant, the result holds as soon as the SINR graph has degrees bounded by 2. Note for example that if
$\Lambda$
is nonequidistant, the result holds as soon as the SINR graph has degrees bounded by 2. Note for example that if
![]() $N_o>0$
,
$N_o>0$
,
![]() $P_o$
is bounded, and
$P_o$
is bounded, and
![]() $\ell$
is continuous on
$\ell$
is continuous on
![]() $[0,\infty)$
, then one can derive a stricter upper bound on the degrees (depending on several parameters) along the lines of the proof of [Reference Dousse, Baccelli and Thiran8, Theorem 1].
$[0,\infty)$
, then one can derive a stricter upper bound on the degrees (depending on several parameters) along the lines of the proof of [Reference Dousse, Baccelli and Thiran8, Theorem 1].
4.3. Strategy of proof for Theorem 2.3
As mentioned previously, we have
![]() $G_{0}(X^\lambda)=g_{r_\textrm{B}}(X^\lambda)$
for all
$G_{0}(X^\lambda)=g_{r_\textrm{B}}(X^\lambda)$
for all
![]() $\lambda>0$
in the Poisson SINR graph with fixed powers p, where
$\lambda>0$
in the Poisson SINR graph with fixed powers p, where
![]() $r_\textrm{B}$
is defined in (2.4). We use
$r_\textrm{B}$
is defined in (2.4). We use
![]() $X^\lambda$
instead of
$X^\lambda$
instead of
![]() ${\textbf{X}}^\lambda$
since the marks are non-random. Moreover, note that the increase of the interference-cancellation factor
${\textbf{X}}^\lambda$
since the marks are non-random. Moreover, note that the increase of the interference-cancellation factor
![]() $\gamma$
can only lead to edges being removed from the graph, and hence there is a monotonicity of
$\gamma$
can only lead to edges being removed from the graph, and hence there is a monotonicity of
![]() $G_{\gamma}(X^\lambda)$
with respect to
$G_{\gamma}(X^\lambda)$
with respect to
![]() $\gamma$
. Additionally, there is a monotonicity of
$\gamma$
. Additionally, there is a monotonicity of
![]() $g_{r_\textrm{B}}(X^\lambda)$
with respect to
$g_{r_\textrm{B}}(X^\lambda)$
with respect to
![]() $\lambda$
, which together implies that
$\lambda$
, which together implies that
![]() $\lambda^*_\textrm{c}\geq \lambda_\textrm{c}(r_\textrm{B})$
.
$\lambda^*_\textrm{c}\geq \lambda_\textrm{c}(r_\textrm{B})$
.
Theorem 2.3 states that for PPPs and with constant powers, one actually has
![]() $\lambda^*_\textrm{c}= \lambda_\textrm{c}(r_\textrm{B})$
. This result is already known in two dimensions: see [Reference Dousse9, Theorem 1]. In words, this result states that for any
$\lambda^*_\textrm{c}= \lambda_\textrm{c}(r_\textrm{B})$
. This result is already known in two dimensions: see [Reference Dousse9, Theorem 1]. In words, this result states that for any
![]() $\lambda>0$
such that the Poisson–Gilbert graph
$\lambda>0$
such that the Poisson–Gilbert graph
![]() $g_{r_\textrm{B}}(X^\lambda)$
is supercritical, there exists
$g_{r_\textrm{B}}(X^\lambda)$
is supercritical, there exists
![]() $\gamma>0$
such that the Poisson SINR graph
$\gamma>0$
such that the Poisson SINR graph
![]() $G_{\gamma}(X^\lambda)$
also percolates. See [Reference Blaszczyszyn and Yogeshwaran2, Section 3.4] for extensions of this result in the two-dimensional case in the context of sub-Poisson point processes.
$G_{\gamma}(X^\lambda)$
also percolates. See [Reference Blaszczyszyn and Yogeshwaran2, Section 3.4] for extensions of this result in the two-dimensional case in the context of sub-Poisson point processes.
The proof of [Reference Dousse9, Theorem 1] employs Russo–Seymour–Welsh-type arguments for the Poisson–Gilbert graph in two dimensions; see [Reference Meester and Roy25, Section 4] and [Reference Dousse9, Section 3]. These arguments have no known analogue in the Poisson case for
![]() $d \geq 3$
, or in the general Cox case even for
$d \geq 3$
, or in the general Cox case even for
![]() $d=2$
. Note that the results of [Reference Tóbiás28] imply only that
$d=2$
. Note that the results of [Reference Tóbiás28] imply only that
![]() $\lambda^*_\textrm{c}<\infty$
for
$\lambda^*_\textrm{c}<\infty$
for
![]() $d \geq 3$
and
$d \geq 3$
and
![]() $\Lambda(\textrm{d} x)=\textrm{d} x$
. However, [Reference Hirsch, Jahnel and Cali16, Section 2.1] includes some further observations about Gilbert graphs in
$\Lambda(\textrm{d} x)=\textrm{d} x$
. However, [Reference Hirsch, Jahnel and Cali16, Section 2.1] includes some further observations about Gilbert graphs in
![]() $d \geq 3$
dimensions, originating from results of [Reference Penrose and Pisztora26], that allow us to conclude Theorem 2.3 in higher dimensions. We will carry out the proof of Theorem 2.3 in Section 5.3, recalling also the corresponding results of [Reference Penrose and Pisztora26].
$d \geq 3$
dimensions, originating from results of [Reference Penrose and Pisztora26], that allow us to conclude Theorem 2.3 in higher dimensions. We will carry out the proof of Theorem 2.3 in Section 5.3, recalling also the corresponding results of [Reference Penrose and Pisztora26].
5. Proofs
For the proofs it will be convenient to define the SINR of
![]() $x_i,x_j \in X^\lambda$
,
$x_i,x_j \in X^\lambda$
,
![]() $x_i \neq x_j$
, via
$x_i \neq x_j$
, via
5.1. Proof of Theorem 1
In this section, we carry out the proof under Condition 1 of the theorem. The proofs under Conditions 2 and 3 are rather easy extensions of this proof that use some additional arguments [Reference Hirsch, Jahnel and Cali16, Reference Tóbiás28], which are omitted from our paper but included in the extended online version [Reference Jahnel and Tóbiás19].
Assume for the rest of this section that Condition 1 holds. For fixed
![]() $\lambda$
and
$\lambda$
and
![]() $\gamma$
, in order to show that
$\gamma$
, in order to show that
![]() ${G_{\gamma}({\textbf{X}}^\lambda)}$
percolates, it suffices to verify that a subgraph of it contains an infinite cluster. Our proof consists of four steps. First, for
${G_{\gamma}({\textbf{X}}^\lambda)}$
percolates, it suffices to verify that a subgraph of it contains an infinite cluster. Our proof consists of four steps. First, for
![]() $\gamma,\lambda>0$
, we define a subgraph that is included in a Cox–Gilbert graph (with constant connection radii). Second, we map this subgraph to a lattice percolation model and show that this discrete model percolates for large
$\gamma,\lambda>0$
, we define a subgraph that is included in a Cox–Gilbert graph (with constant connection radii). Second, we map this subgraph to a lattice percolation model and show that this discrete model percolates for large
![]() $\lambda$
for a suitable choice of auxiliary parameters. In particular, since
$\lambda$
for a suitable choice of auxiliary parameters. In particular, since
![]() $\Lambda$
is assumed only to be stabilizing, the connection radius of the Gilbert graph must be large enough so that the graph percolates for large
$\Lambda$
is assumed only to be stabilizing, the connection radius of the Gilbert graph must be large enough so that the graph percolates for large
![]() $\lambda$
. In this step, we are able to employ multiple arguments of [Reference Dousse9, Reference Hirsch, Jahnel and Cali16, Reference Tóbiás28]. Our interference-control assertion, Proposition 5.1, is presented here. Third, using the subgraph, we make a choice of
$\lambda$
. In this step, we are able to employ multiple arguments of [Reference Dousse9, Reference Hirsch, Jahnel and Cali16, Reference Tóbiás28]. Our interference-control assertion, Proposition 5.1, is presented here. Third, using the subgraph, we make a choice of
![]() $\gamma>0$
such that percolation in the discrete model implies percolation in the SINR graph
$\gamma>0$
such that percolation in the discrete model implies percolation in the SINR graph
![]() ${G_{\gamma}({\textbf{X}}^\lambda)}$
, which is done analogously to [Reference Dousse9]. Fourth, we carry out the proof of Proposition 5.1, combining arguments of [Reference Dousse9, Reference Tóbiás28] for SINR graphs with constant powers and arguments used in [Reference Löffler22] for Poisson SINR graphs with random powers.
${G_{\gamma}({\textbf{X}}^\lambda)}$
, which is done analogously to [Reference Dousse9]. Fourth, we carry out the proof of Proposition 5.1, combining arguments of [Reference Dousse9, Reference Tóbiás28] for SINR graphs with constant powers and arguments used in [Reference Löffler22] for Poisson SINR graphs with random powers.
STEP 1. A subgraph of the SINR graph.
We first present a general construction of a subgraph of
![]() ${G_{\gamma}({\textbf{X}}^\lambda)}$
for
${G_{\gamma}({\textbf{X}}^\lambda)}$
for
![]() $\gamma,\lambda>0$
. Let
$\gamma,\lambda>0$
. Let
![]() $r_o>d_o$
. Since both
$r_o>d_o$
. Since both
![]() $P_o$
and
$P_o$
and
![]() $\mathrm{supp}(\ell)$
are unbounded, we have
$\mathrm{supp}(\ell)$
are unbounded, we have
Let us define the independent thinning
of
![]() $X^\lambda$
with survival probability
$X^\lambda$
with survival probability
![]() $p(r_o)$
. According to [Reference Kingman20, Colouring Theorem],
$p(r_o)$
. According to [Reference Kingman20, Colouring Theorem],
![]() $X^{\lambda,-}$
is a CPP with directing measure
$X^{\lambda,-}$
is a CPP with directing measure
![]() $\lambda p(r_o)\Lambda$
. Now, let us define a subgraph
$\lambda p(r_o)\Lambda$
. Now, let us define a subgraph
![]() $G^-_{\gamma}({\textbf{X}}^\lambda)$
of
$G^-_{\gamma}({\textbf{X}}^\lambda)$
of
![]() ${G_{\gamma}({\textbf{X}}^\lambda)}$
as follows. The vertex set is
${G_{\gamma}({\textbf{X}}^\lambda)}$
as follows. The vertex set is
![]() $X^{\lambda,-}$
, and two vertices
$X^{\lambda,-}$
, and two vertices
![]() $x_i,x_j \in X^{\lambda,-}$
,
$x_i,x_j \in X^{\lambda,-}$
,
![]() $x_i \neq x_j$
, are connected by an edge if and only if
$x_i \neq x_j$
, are connected by an edge if and only if
and the analogously defined
![]() $\mathrm{SINR}^-(x_j,x_i,{\textbf{X}}^\lambda)$
also exceeds
$\mathrm{SINR}^-(x_j,x_i,{\textbf{X}}^\lambda)$
also exceeds
![]() $\tau$
. Note that for
$\tau$
. Note that for
![]() $x_i,x_j \in X^{\lambda,-}$
, in the numerator of
$x_i,x_j \in X^{\lambda,-}$
, in the numerator of
![]() $\mathrm{SINR}(x_i,x_j,{\textbf{X}}^\lambda)$
, for the power of
$\mathrm{SINR}(x_i,x_j,{\textbf{X}}^\lambda)$
, for the power of
![]() $x_i$
we have
$x_i$
we have
![]() $P_i \geq \tau {N_o}/\ell(r_o)$
, whereas the denominators of (5.1) and (5.2) are equal, and the same holds with the roles of i and j interchanged. Hence,
$P_i \geq \tau {N_o}/\ell(r_o)$
, whereas the denominators of (5.1) and (5.2) are equal, and the same holds with the roles of i and j interchanged. Hence,
![]() $G^-_{\gamma}({\textbf{X}}^\lambda)$
is indeed a subgraph of
$G^-_{\gamma}({\textbf{X}}^\lambda)$
is indeed a subgraph of
![]() ${G_{\gamma}({\textbf{X}}^\lambda)}$
for any
${G_{\gamma}({\textbf{X}}^\lambda)}$
for any
![]() $\gamma \geq 0$
. As for
$\gamma \geq 0$
. As for
![]() $\gamma=0$
,
$\gamma=0$
,
![]() $G^-_{0}({\textbf{X}}^\lambda)$
equals the Cox–Gilbert graph
$G^-_{0}({\textbf{X}}^\lambda)$
equals the Cox–Gilbert graph
![]() $g_{r_o}(X^{\lambda,-})$
with connection radius
$g_{r_o}(X^{\lambda,-})$
with connection radius
![]() $r_o$
and vertex set
$r_o$
and vertex set
![]() $X^{\lambda,-}$
. In words, in order to obtain
$X^{\lambda,-}$
. In words, in order to obtain
![]() $G^-_{\gamma}({\textbf{X}}^\lambda)$
from
$G^-_{\gamma}({\textbf{X}}^\lambda)$
from
![]() ${G_{\gamma}({\textbf{X}}^\lambda)}$
, one first thins out vertices with small powers, so as to get rid of vertices with small values of the connection radius
${G_{\gamma}({\textbf{X}}^\lambda)}$
, one first thins out vertices with small powers, so as to get rid of vertices with small values of the connection radius
![]() $r_\textrm{B}^i$
, where
$r_\textrm{B}^i$
, where
Then one bounds the powers of the remaining vertices by
![]() $\tau {N_o}/\ell(r_o)$
from below.
$\tau {N_o}/\ell(r_o)$
from below.
STEP 2. Mapping the subgraph to a lattice-percolation problem and percolation on the lattice.
Now we are in a position to adapt to the setting of [Reference Tóbiás28, Section 3.2.2] and use strong connectivity of
![]() $g_{r_o}(X^{\lambda,-})$
in case
$g_{r_o}(X^{\lambda,-})$
in case
![]() $r_o$
is sufficiently large and
$r_o$
is sufficiently large and
![]() $\lambda$
is chosen according to
$\lambda$
is chosen according to
![]() $r_o$
. Together with an interference-control argument presented below, this will allow us to verify Condition 1 of Theorem 2.1.
$r_o$
. Together with an interference-control argument presented below, this will allow us to verify Condition 1 of Theorem 2.1.
First, let us recall the definition of rescalings of a Gilbert graph, which were also used in [Reference Tóbiás28]. For
![]() $c>0$
and a Gilbert graph G with connection radius
$c>0$
and a Gilbert graph G with connection radius
![]() $r>0$
, deterministic vertex set
$r>0$
, deterministic vertex set
![]() $V \subset \mathbb{R}^d$
,
$V \subset \mathbb{R}^d$
,
![]() $d \geq 1$
, and edge set
$d \geq 1$
, and edge set
![]() $E=\{ (x,y) \in V\times V \colon x \neq y, |x-y|<r \}$
, the graph cG is defined with vertex set
$E=\{ (x,y) \in V\times V \colon x \neq y, |x-y|<r \}$
, the graph cG is defined with vertex set
![]() $cV=\{cx\colon x\in V\}$
and edge set
$cV=\{cx\colon x\in V\}$
and edge set
![]() $cE=\{ (cx,cy) \colon (x,y) \in E \}$
. It is easy to see that cG is a Gilbert graph with vertex set cV and connection radius cr. For Gilbert graphs with random vertex sets (e.g., if the vertex set is given by a random simple point process), rescalings of the graph are defined realization-wise. From the proof of Theorem 2.9 (Convergence in Bounded Domains) in [Reference Hirsch, Jahnel and Cali16, Section 7.1], we know that in the coupled limit
$cE=\{ (cx,cy) \colon (x,y) \in E \}$
. It is easy to see that cG is a Gilbert graph with vertex set cV and connection radius cr. For Gilbert graphs with random vertex sets (e.g., if the vertex set is given by a random simple point process), rescalings of the graph are defined realization-wise. From the proof of Theorem 2.9 (Convergence in Bounded Domains) in [Reference Hirsch, Jahnel and Cali16, Section 7.1], we know that in the coupled limit
![]() $\widetilde r \uparrow \infty, \, \widetilde \lambda \downarrow 0$
and
$\widetilde r \uparrow \infty, \, \widetilde \lambda \downarrow 0$
and
![]() $\widetilde \lambda \widetilde r^d = \widetilde \varrho>0$
, we have that
$\widetilde \lambda \widetilde r^d = \widetilde \varrho>0$
, we have that
![]() $\widetilde r^{-1} g_{\widetilde r}(X^{\widetilde \lambda})$
converges weakly to the graph
$\widetilde r^{-1} g_{\widetilde r}(X^{\widetilde \lambda})$
converges weakly to the graph
![]() $g_{1}(Y^{\widetilde \varrho})$
, where
$g_{1}(Y^{\widetilde \varrho})$
, where
![]() $Y^{\varrho}$
is a homogeneous PPP with intensity
$Y^{\varrho}$
is a homogeneous PPP with intensity
![]() $\varrho$
. Let us note that in [Reference Hirsch, Jahnel and Cali16, Section 7.1] this convergence is formulated equivalently for the Boolean model, and the crucial point is that the convergence is guaranteed only in compact domains.
$\varrho$
. Let us note that in [Reference Hirsch, Jahnel and Cali16, Section 7.1] this convergence is formulated equivalently for the Boolean model, and the crucial point is that the convergence is guaranteed only in compact domains.
Let
![]() $\varrho_\textrm{c}(1)$
be such that the Poisson–Gilbert graph
$\varrho_\textrm{c}(1)$
be such that the Poisson–Gilbert graph
![]() $g_{1}(Y^{\varrho_\textrm{c}(1)})$
is critical. Then, due to the scale invariance of Poisson–Gilbert graphs [Reference Meester and Roy25, Section 2.2], for
$g_{1}(Y^{\varrho_\textrm{c}(1)})$
is critical. Then, due to the scale invariance of Poisson–Gilbert graphs [Reference Meester and Roy25, Section 2.2], for
![]() $\varrho>\varrho_\textrm{c}(1)$
, we can choose a smaller intensity
$\varrho>\varrho_\textrm{c}(1)$
, we can choose a smaller intensity
![]() $\varrho'<\varrho$
such that
$\varrho'<\varrho$
such that
![]() $g_{1}(Y^{\varrho'})$
is still supercritical. Now, for
$g_{1}(Y^{\varrho'})$
is still supercritical. Now, for
![]() $r>d_o$
, we define
$r>d_o$
, we define
![]() $r_o(r)=r(\varrho/\varrho')^{1/d}$
,
$r_o(r)=r(\varrho/\varrho')^{1/d}$
,
![]() $\lambda(r)=\varrho' r^{-d} (p(r_o(r)))^{-1}$
, and
$\lambda(r)=\varrho' r^{-d} (p(r_o(r)))^{-1}$
, and
![]() $p(r)=\tau {N_o}/\ell(r_o(r))$
. Noting that
$p(r)=\tau {N_o}/\ell(r_o(r))$
. Noting that
![]() $g_r(X^{\lambda(r),-})$
is a Cox–Gilbert graph with connection radius r and stabilizing intensity
$g_r(X^{\lambda(r),-})$
is a Cox–Gilbert graph with connection radius r and stabilizing intensity
![]() $p(r_o(r)) \lambda(r)=\varrho' r^{-d}$
, we have that
$p(r_o(r)) \lambda(r)=\varrho' r^{-d}$
, we have that
![]() $r^{-1}g_r(X^{\lambda(r),-})$
converges to the supercritical graph
$r^{-1}g_r(X^{\lambda(r),-})$
converges to the supercritical graph
![]() $g_1(Y^{\varrho'})$
on compact sets, as r tends to infinity.
$g_1(Y^{\varrho'})$
on compact sets, as r tends to infinity.
Furthermore, recalling that R denotes the stabilization radii of
![]() $\Lambda$
, we put
$\Lambda$
, we put
![]() $R(Q)=\sup_{x \in Q \cap \mathbb{Q}^d} R_x$
for any measurable set
$R(Q)=\sup_{x \in Q \cap \mathbb{Q}^d} R_x$
for any measurable set
![]() $Q \subseteq \mathbb{R}^d$
.
$Q \subseteq \mathbb{R}^d$
.
Using these notions, we construct a renormalized percolation process on
![]() $\mathbb{Z}^d$
as follows. For
$\mathbb{Z}^d$
as follows. For
![]() $n \geq 1$
and
$n \geq 1$
and
![]() $r>d_o$
, the site
$r>d_o$
, the site
![]() $z \in \mathbb{Z}^d$
is (r, n)-good if the following conditions hold:
$z \in \mathbb{Z}^d$
is (r, n)-good if the following conditions hold:
-
1.
 $R(Q_{6rn}(rnz))<rn/2$
.
$R(Q_{6rn}(rnz))<rn/2$
. -
2.
 $X^{\lambda(r),-} \cap Q_{rn}(rnz) \neq \varnothing$
.
$X^{\lambda(r),-} \cap Q_{rn}(rnz) \neq \varnothing$
. -
3. Every pair
 $x_i,x_j \in X^{\lambda(r),-} \cap Q_{3rn}(rnz)$
is connected by a path in
$x_i,x_j \in X^{\lambda(r),-} \cap Q_{3rn}(rnz)$
is connected by a path in
 $g_r(X^{\lambda(r),-}) \cap Q_{6rn}(rnz)$
.
$g_r(X^{\lambda(r),-}) \cap Q_{6rn}(rnz)$
.
The site
![]() $z \in \mathbb{Z}^d$
is (r, n)-bad if it is not (r, n)-good. Note that the process of (r, n)-good sites is 7-dependent thanks to the definition of stabilization. The following lemma is verified in [Reference Tóbiás28, Section 3.2.2]. However, since in [Reference Tóbiás28] it is not formulated as a lemma, and two different proofs are presented for
$z \in \mathbb{Z}^d$
is (r, n)-bad if it is not (r, n)-good. Note that the process of (r, n)-good sites is 7-dependent thanks to the definition of stabilization. The following lemma is verified in [Reference Tóbiás28, Section 3.2.2]. However, since in [Reference Tóbiás28] it is not formulated as a lemma, and two different proofs are presented for
![]() $d=2$
and
$d=2$
and
![]() $d \geq 3$
, we provide a self-contained proof here for the reader’s convenience.
$d \geq 3$
, we provide a self-contained proof here for the reader’s convenience.
Lemma 5.1. ([Reference Tóbiás28].) Assume that the general conditions of Theorem 2.1 plus Condition 1 hold. Then, for all sufficiently large
![]() $\lambda>0$
and for all
$\lambda>0$
and for all
![]() $n \geq 1$
and
$n \geq 1$
and
![]() $r >d_o$
with rn sufficiently large, there exists
$r >d_o$
with rn sufficiently large, there exists
![]() $q_A=q_A(\lambda,rn) <1$
such that for any
$q_A=q_A(\lambda,rn) <1$
such that for any
![]() $N \in \mathbb{N}$
and pairwise distinct
$N \in \mathbb{N}$
and pairwise distinct
![]() $z_1,\ldots,z_N \in\mathbb{Z}^d$
,
$z_1,\ldots,z_N \in\mathbb{Z}^d$
,
Furthermore, for any
![]() $\varepsilon>0$
, one can choose
$\varepsilon>0$
, one can choose
![]() $\lambda$
and rn sufficiently large so that
$\lambda$
and rn sufficiently large so that
![]() $q_A <\varepsilon$
.
$q_A <\varepsilon$
.
Proof. For
![]() $z \in \mathbb{Z}^d$
, we write
$z \in \mathbb{Z}^d$
, we write
![]() $J_{n,r}(z)$
for the event that z satisfies Parts 2 and 3 of the definition of (r, n)-goodness. Then, for any n, r under consideration, the process of (r, n)-good sites is 7-dependent by the definition of stabilization. Furthermore, we write
$J_{n,r}(z)$
for the event that z satisfies Parts 2 and 3 of the definition of (r, n)-goodness. Then, for any n, r under consideration, the process of (r, n)-good sites is 7-dependent by the definition of stabilization. Furthermore, we write
![]() $F_n(z)$
for the event that in the definition of (1, n)-goodness, the PPP
$F_n(z)$
for the event that in the definition of (1, n)-goodness, the PPP
![]() $Y^{\varrho'}$
with intensity
$Y^{\varrho'}$
with intensity
![]() $\varrho'=\lambda(r)r^d$
satisfies Part 2 with
$\varrho'=\lambda(r)r^d$
satisfies Part 2 with
![]() $X^{\lambda(r),-}$
replaced by
$X^{\lambda(r),-}$
replaced by
![]() $Y^{\varrho'}$
and Part 3 with
$Y^{\varrho'}$
and Part 3 with
![]() $g_r(X^{\lambda(r),-})$
replaced by
$g_r(X^{\lambda(r),-})$
replaced by
![]() $g_1(Y^{\varrho'})$
everywhere. The probability of
$g_1(Y^{\varrho'})$
everywhere. The probability of
![]() $F_n(z)$
is independent of the choice of z and tends to 1 as
$F_n(z)$
is independent of the choice of z and tends to 1 as
![]() $n \to\infty$
thanks to the arguments of [Reference Hirsch, Jahnel and Cali16, Section 5.2], since the constant directing measure of the PPP
$n \to\infty$
thanks to the arguments of [Reference Hirsch, Jahnel and Cali16, Section 5.2], since the constant directing measure of the PPP
![]() $Y^{\varrho'}$
is certainly asymptotically essentially connected. Using a union bound and the well-known scale invariance of Poisson–Gilbert graphs, namely that for
$Y^{\varrho'}$
is certainly asymptotically essentially connected. Using a union bound and the well-known scale invariance of Poisson–Gilbert graphs, namely that for
![]() $\widetilde\lambda,\widetilde r>0$
,
$\widetilde\lambda,\widetilde r>0$
,
![]() $\widetilde r^{-1} g_{\widetilde r} (X^{\widetilde\lambda})$
equals
$\widetilde r^{-1} g_{\widetilde r} (X^{\widetilde\lambda})$
equals
![]() $g_1(X^{\widetilde \lambda \widetilde r^d})$
in distribution, we conclude that for
$g_1(X^{\widetilde \lambda \widetilde r^d})$
in distribution, we conclude that for
![]() $z \in \mathbb{Z}^d$
,
$z \in \mathbb{Z}^d$
,
This can be made arbitrarily close to zero by choosing first n large and then r large according to n, due to the weak convergence of
![]() $r^{-1} g_r(X^\lambda)$
to
$r^{-1} g_r(X^\lambda)$
to
![]() $g_1(Y^{\varrho'})$
on
$g_1(Y^{\varrho'})$
on
![]() $Q_{6n}(nz)$
as
$Q_{6n}(nz)$
as
![]() $r \to \infty$
,
$r \to \infty$
,
![]() $\lambda(r) \to 0$
,
$\lambda(r) \to 0$
,
![]() $r^d \lambda(r) = {\varrho'}$
.
$r^d \lambda(r) = {\varrho'}$
.
Hence, applying [Reference Liggett, Schonmann and Stacey23, Theorem 0.0], for all sufficiently large n and large enough r chosen according to n, the 7-dependent process of (r, n)-good sites is stochastically dominated from below by a supercritical independent site percolation process. Moreover, the probability that a site of the independent site percolation process is closed can be made arbitrarily close to 0 via further increasing nr. This implies the lemma.
We proceed similarly to [Reference Dousse9, Reference Tóbiás28] by defining ‘shifted’ versions of the path-loss function
![]() $\ell$
. For
$\ell$
. For
![]() $a\ge 0$
, define
$a\ge 0$
, define
Note that
![]() $\ell_0=\ell$
. Now, we define the shot-noise processes
$\ell_0=\ell$
. Now, we define the shot-noise processes
and note that
![]() $I_{0}(x)=I(x)$
. By the triangle inequality, for
$I_{0}(x)=I(x)$
. By the triangle inequality, for
![]() $a \geq 0$
,
$a \geq 0$
,
![]() $I(x) \leq I_{a}(z)$
holds for any
$I(x) \leq I_{a}(z)$
holds for any
![]() $z \in \mathbb{R}^d$
and
$z \in \mathbb{R}^d$
and
![]() $x \in Q_a(z)$
. Now, the interference-control argument consists in verifying the following proposition. For
$x \in Q_a(z)$
. Now, the interference-control argument consists in verifying the following proposition. For
![]() $z \in \mathbb{Z}^d$
, let us write
$z \in \mathbb{Z}^d$
, let us write
![]() $B_{r, n, M}(z)=\{ I_{6rn}(rnz) \leq M \}$
.
$B_{r, n, M}(z)=\{ I_{6rn}(rnz) \leq M \}$
.
Proposition 5.1. Assume that the general conditions of Theorem 2.1 plus Condition 1 hold. Then, for all
![]() $\lambda>0$
, for all
$\lambda>0$
, for all
![]() $n \geq 1$
and
$n \geq 1$
and
![]() $r>d_o$
with rn sufficiently large, and for all
$r>d_o$
with rn sufficiently large, and for all
![]() $M>0$
sufficiently large, there exists
$M>0$
sufficiently large, there exists
![]() $q_B=q_B(\lambda,rn,N) <1$
such that for all
$q_B=q_B(\lambda,rn,N) <1$
such that for all
![]() $N \in \mathbb{N}$
and for all pairwise distinct
$N \in \mathbb{N}$
and for all pairwise distinct
![]() $z_1,\ldots,z_N \in \mathbb{Z}^d$
we have
$z_1,\ldots,z_N \in \mathbb{Z}^d$
we have
Furthermore, for any
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $\lambda>0$
, one can choose rn and M sufficiently large so that
$\lambda>0$
, one can choose rn and M sufficiently large so that
![]() $q_B < \varepsilon$
.
$q_B < \varepsilon$
.
The proof of this proposition is postponed until Step 4. Once we have proved Proposition 5.1, we can derive the following corollary using a standard argument (see e.g. the proof of [Reference Dousse9, Proposition 3] or that of [Reference Tóbiás28, Proposition 3.1]). For
![]() $z \in \mathbb{Z}^d$
let us define
$z \in \mathbb{Z}^d$
let us define
![]() $C_{r, n, M}(z)=\{ z\text{ is }(r, n)\text{-good} \}\cap \{ I_{6rn}(rnz) \leq M \}$
.
$C_{r, n, M}(z)=\{ z\text{ is }(r, n)\text{-good} \}\cap \{ I_{6rn}(rnz) \leq M \}$
.
Corollary 5.1. Assume that the general conditions of Theorem 2.1 plus Condition 1 hold. Then, for all sufficiently large
![]() $\lambda>0$
, for all
$\lambda>0$
, for all
![]() $r>d_o$
and
$r>d_o$
and
![]() $n \geq 1$
with rn sufficiently large, and for all
$n \geq 1$
with rn sufficiently large, and for all
![]() $M>0$
sufficiently large, there exists
$M>0$
sufficiently large, there exists
![]() $q_C =q_C(\lambda,rn,M)<1$
such that for all
$q_C =q_C(\lambda,rn,M)<1$
such that for all
![]() $N \in \mathbb{N}$
and for all pairwise distinct
$N \in \mathbb{N}$
and for all pairwise distinct
![]() $z_1,\ldots,z_N \in \mathbb{Z}^d$
we have
$z_1,\ldots,z_N \in \mathbb{Z}^d$
we have
Furthermore, for any
![]() $\varepsilon>0$
, one can choose
$\varepsilon>0$
, one can choose
![]() $\lambda,rn,M$
sufficiently large so that
$\lambda,rn,M$
sufficiently large so that
![]() $q_C < \varepsilon$
.
$q_C < \varepsilon$
.
STEP 3. Percolation in the subgraph of the SINR graph.
Having Corollary 5.1 and employing a Peierls argument (cf. [Reference Grimmett15, Section 1.4]), we conclude that for
![]() $\lambda, rn,M$
sufficiently large, the process of (r, n)-good sites
$\lambda, rn,M$
sufficiently large, the process of (r, n)-good sites
![]() $z \in \mathbb{Z}^d$
such that
$z \in \mathbb{Z}^d$
such that
![]() $I_{6rn}(rnz) \leq M$
percolates. Thanks to exactly the same arguments as in the proof of Theorem 2.6 in [Reference Hirsch, Jahnel and Cali16, Section 5.2], this implies percolation of the Cox–Gilbert graph
$I_{6rn}(rnz) \leq M$
percolates. Thanks to exactly the same arguments as in the proof of Theorem 2.6 in [Reference Hirsch, Jahnel and Cali16, Section 5.2], this implies percolation of the Cox–Gilbert graph
![]() $G^-_{0}({\textbf{X}}^{\lambda(r)})=g_{r_o(r)}(X^{\lambda(r),-})$
. From this point of the proof it is classical to derive that
$G^-_{0}({\textbf{X}}^{\lambda(r)})=g_{r_o(r)}(X^{\lambda(r),-})$
. From this point of the proof it is classical to derive that
![]() $G^-_{\gamma}({\textbf{X}}^{\lambda(r)})$
percolates for small
$G^-_{\gamma}({\textbf{X}}^{\lambda(r)})$
percolates for small
![]() $\gamma>0$
; see [Reference Dousse9, Section 3.3]. For the convenience of the reader, let us give the details here. We define
$\gamma>0$
; see [Reference Dousse9, Section 3.3]. For the convenience of the reader, let us give the details here. We define
where the strict inequality holds because
![]() $r_o(r)>r>d_o$
and
$r_o(r)>r>d_o$
and
![]() $\ell$
has unbounded support. Then we have
$\ell$
has unbounded support. Then we have
Now, let
![]() $x_i,x_j \in X^{\lambda(r),-}$
be situated in
$x_i,x_j \in X^{\lambda(r),-}$
be situated in
![]() $Q_{rn}(rnz)$
and
$Q_{rn}(rnz)$
and
![]() $Q_{rn}(rnz')$
, respectively, for some sites
$Q_{rn}(rnz')$
, respectively, for some sites
![]() $z,z' \in\mathbb{Z}^d$
included in the same infinite cluster of the process of (r, n)-good sites
$z,z' \in\mathbb{Z}^d$
included in the same infinite cluster of the process of (r, n)-good sites
![]() $z \in \mathbb{Z}^d$
satisfying
$z \in \mathbb{Z}^d$
satisfying
![]() $I_{6rn}(rnz) \leq M$
, with
$I_{6rn}(rnz) \leq M$
, with
![]() $|x_i-x_j| < r$
. Then, for
$|x_i-x_j| < r$
. Then, for
![]() $\gamma<\gamma'$
, we have
$\gamma<\gamma'$
, we have
Thus,
![]() $x_i$
and
$x_i$
and
![]() $x_j$
are connected by an edge in
$x_j$
are connected by an edge in
![]() $G^-_{\gamma}({\textbf{X}}^\lambda)$
. Hence,
$G^-_{\gamma}({\textbf{X}}^\lambda)$
. Hence,
![]() ${G_{\gamma}({\textbf{X}}^\lambda)}$
also percolates. Thus, we can conclude Theorem 2.1 as soon as we have verified Proposition 5.1.
${G_{\gamma}({\textbf{X}}^\lambda)}$
also percolates. Thus, we can conclude Theorem 2.1 as soon as we have verified Proposition 5.1.
STEP 4. Proof of Proposition 5.1: the interference-control argument.
Similarly to [Reference Tóbiás28, Section 3.1.1], we split the interference into two parts. For
![]() $x \in \mathbb{R}^d$
,
$x \in \mathbb{R}^d$
,
![]() $n \geq 1$
, and
$n \geq 1$
, and
![]() $r>0$
, we put
$r>0$
, we put
 \begin{align*}& I_{6rn}^{\mathrm{in}} (x) = \sum_{x_i \in X^\lambda \cap Q_{12rn\sqrt d}(x)} \ell_{6rn}(|x_i-x|),\\[3pt] & I_{6rn}^{\mathrm{out}} (x) = \sum_{x_i \in X^\lambda \setminus Q_{12rn\sqrt d}(x)} \ell_{6rn}(|x_i-x|).\end{align*}
\begin{align*}& I_{6rn}^{\mathrm{in}} (x) = \sum_{x_i \in X^\lambda \cap Q_{12rn\sqrt d}(x)} \ell_{6rn}(|x_i-x|),\\[3pt] & I_{6rn}^{\mathrm{out}} (x) = \sum_{x_i \in X^\lambda \setminus Q_{12rn\sqrt d}(x)} \ell_{6rn}(|x_i-x|).\end{align*}
Then, for
![]() $M>0$
, if
$M>0$
, if
![]() $I_{6rn}(x)>M$
, then
$I_{6rn}(x)>M$
, then
![]() $I_{6rn}^{\mathrm{in}} (x)>M/2$
or
$I_{6rn}^{\mathrm{in}} (x)>M/2$
or
![]() $I_{6rn}^{\mathrm{out}} (x)>M/2$
. Using a union bound and the fact that M can be chosen arbitrarily large in Proposition 5.1, it suffices to conclude the proposition both with
$I_{6rn}^{\mathrm{out}} (x)>M/2$
. Using a union bound and the fact that M can be chosen arbitrarily large in Proposition 5.1, it suffices to conclude the proposition both with
![]() $B_{r, n, M}(z_i)$
replaced by
$B_{r, n, M}(z_i)$
replaced by
![]() $B_{r, n, M}^{\mathrm{in}}(z_i)$
and with
$B_{r, n, M}^{\mathrm{in}}(z_i)$
and with
![]() $B_{r, n, M}(z_i)$
replaced by
$B_{r, n, M}(z_i)$
replaced by
![]() $B_{r, n, M}^{\mathrm{out}}(z_i)$
everywhere in (5.6) for all
$B_{r, n, M}^{\mathrm{out}}(z_i)$
everywhere in (5.6) for all
![]() $i \in \{1,\ldots,N\}$
, where for
$i \in \{1,\ldots,N\}$
, where for
![]() $z \in \mathbb{Z}^d$
we write
$z \in \mathbb{Z}^d$
we write
![]() $B_{r, n, M}^{\mathrm{in}}(z)= \big\{ I_{6rn}^{\mathrm{in}}(rnz) \le M \big\}$
and
$B_{r, n, M}^{\mathrm{in}}(z)= \big\{ I_{6rn}^{\mathrm{in}}(rnz) \le M \big\}$
and
![]() $B_{r, n, M}^{\mathrm{out}}(z)= \big\{ I_{6rn}^{\mathrm{out}}(rnz) \le M \big\}$
. Indeed, having these assertions, we can combine them similarly to Corollary 5.1.
$B_{r, n, M}^{\mathrm{out}}(z)= \big\{ I_{6rn}^{\mathrm{out}}(rnz) \le M \big\}$
. Indeed, having these assertions, we can combine them similarly to Corollary 5.1.
We now verify Proposition 5.1 with
![]() $B_{r,n,M}(\cdot)$
replaced by
$B_{r,n,M}(\cdot)$
replaced by
![]() $B_{r,n,M}^{\mathrm{in}}(\cdot)$
everywhere. For this assertion, instead of the assumption that
$B_{r,n,M}^{\mathrm{in}}(\cdot)$
everywhere. For this assertion, instead of the assumption that
![]() $P_o$
and
$P_o$
and
![]() $\Lambda(Q_1)$
have some exponential moments, it suffices to assume they have a first moment (for
$\Lambda(Q_1)$
have some exponential moments, it suffices to assume they have a first moment (for
![]() $\Lambda(Q_1)$
this is automatic since
$\Lambda(Q_1)$
this is automatic since
![]() $\mathbb{E}[\Lambda(Q_1)]=1$
by assumption). To be more precise, we prove the following lemma.
$\mathbb{E}[\Lambda(Q_1)]=1$
by assumption). To be more precise, we prove the following lemma.
Lemma 5.2. Assume that the general conditions of Theorem 2.1 plus Condition 1 hold. Furthermore, let
![]() $\Lambda$
be stabilizing and let
$\Lambda$
be stabilizing and let
![]() $\mathbb{E}[P_o]<\infty$
. Then, for all
$\mathbb{E}[P_o]<\infty$
. Then, for all
![]() $\lambda>0$
, for all
$\lambda>0$
, for all
![]() $n \geq 1$
and
$n \geq 1$
and
![]() $r>d_o$
with rn sufficiently large, and for all
$r>d_o$
with rn sufficiently large, and for all
![]() $M>0$
sufficiently large, there exists
$M>0$
sufficiently large, there exists
![]() $q_B=q_B(\lambda,rn,N) <1$
such that for all
$q_B=q_B(\lambda,rn,N) <1$
such that for all
![]() $N \in \mathbb{N}$
and for all pairwise distinct
$N \in \mathbb{N}$
and for all pairwise distinct
![]() $z_1,\ldots,z_N \in \mathbb{Z}^d$
we have
$z_1,\ldots,z_N \in \mathbb{Z}^d$
we have
Furthermore, for any
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $\lambda>0$
, one can choose rn and M sufficiently large so that
$\lambda>0$
, one can choose rn and M sufficiently large so that
![]() $q_B < \varepsilon$
.
$q_B < \varepsilon$
.
Proof. We use the following auxiliary discrete percolation process. A site
![]() $z \in \mathbb{Z}^d$
is (r,n)-tame if the following hold:
$z \in \mathbb{Z}^d$
is (r,n)-tame if the following hold:
-
1.
 $R\big(Q_{12rn\sqrt d}(rnz)\big)<rn/2$
.
$R\big(Q_{12rn\sqrt d}(rnz)\big)<rn/2$
. -
2.
 $I_{6rn}^{\mathrm{in}}(rnz)\leq M $
.
$I_{6rn}^{\mathrm{in}}(rnz)\leq M $
.
A site
![]() $z \in \mathbb{Z}^d$
is (r, n)-wild if it is not (r, n)-tame. The process of (r, n)-tame sites is
$z \in \mathbb{Z}^d$
is (r, n)-wild if it is not (r, n)-tame. The process of (r, n)-tame sites is
![]() $\lceil 12 \sqrt d + 1\rceil$
-dependent according to the definition of stabilization. Thus, it follows from dependent-percolation theory [Reference Liggett, Schonmann and Stacey23, Theorem 0.0] that, in order to verify Lemma 5.2, it suffices to show that for all
$\lceil 12 \sqrt d + 1\rceil$
-dependent according to the definition of stabilization. Thus, it follows from dependent-percolation theory [Reference Liggett, Schonmann and Stacey23, Theorem 0.0] that, in order to verify Lemma 5.2, it suffices to show that for all
![]() $\lambda>0$
,
$\lambda>0$
,
![]() $\mathbb P(o\textrm{\ is}\ $
$\mathbb P(o\textrm{\ is}\ $
![]() $(r,n)\hbox{-}\textrm{wild})$
can be made arbitrarily close to zero by choosing first rn sufficiently large and then M large enough accordingly. We have
$(r,n)\hbox{-}\textrm{wild})$
can be made arbitrarily close to zero by choosing first rn sufficiently large and then M large enough accordingly. We have
The first term can be made arbitrarily small by choosing rn large enough, thanks to the definition of stabilization. Moreover, by the definition of
![]() $\ell_a$
(see (5.5)),
$\ell_a$
(see (5.5)),
In particular, using that the point process
![]() $\textbf{X}^\lambda$
is independently marked with
$\textbf{X}^\lambda$
is independently marked with
![]() $P_i$
having marginal distribution
$P_i$
having marginal distribution
![]() $\mu$
, and that
$\mu$
, and that
![]() $\Lambda$
is stationary with
$\Lambda$
is stationary with
![]() $\mathbb{E}[\Lambda(Q_1)]=1$
, it follows that
$\mathbb{E}[\Lambda(Q_1)]=1$
, it follows that
Thus, for any
![]() $n \geq 1$
and
$n \geq 1$
and
![]() $r>0$
,
$r>0$
,
![]() $\mathbb P\big(I_{6rn}^{\mathrm{in}}(o)>M\big)$
can be made arbitrarily small by choosing M large enough, given that
$\mathbb P\big(I_{6rn}^{\mathrm{in}}(o)>M\big)$
can be made arbitrarily small by choosing M large enough, given that
![]() $\mathbb{E}[P_o]<\infty$
. Thus, the statement of the lemma follows.
$\mathbb{E}[P_o]<\infty$
. Thus, the statement of the lemma follows.
It remains to verify Proposition 5.1 with
![]() $B_{r,n,M}(\cdot)$
replaced by
$B_{r,n,M}(\cdot)$
replaced by
![]() $B_{r,n,M}^{\mathrm{out}}(\cdot)$
everywhere. More precisely, thanks to the exponential-moment and b-dependence assumption on
$B_{r,n,M}^{\mathrm{out}}(\cdot)$
everywhere. More precisely, thanks to the exponential-moment and b-dependence assumption on
![]() $\Lambda$
, the proof can be completed analogously to the proof of [Reference Tóbiás28, Proposition 3.3] starting from [Reference Tóbiás28, Equation (3.15)], as soon as we have verified the following lemma. (In [Reference Tóbiás28] it is also assumed that
$\Lambda$
, the proof can be completed analogously to the proof of [Reference Tóbiás28, Proposition 3.3] starting from [Reference Tóbiás28, Equation (3.15)], as soon as we have verified the following lemma. (In [Reference Tóbiás28] it is also assumed that
![]() $\ell(0) \leq 1$
, but since M can be made arbitrarily large in Proposition 5.1,
$\ell(0) \leq 1$
, but since M can be made arbitrarily large in Proposition 5.1,
![]() $\ell(0) \leq 1$
can be assumed without loss of generality since for
$\ell(0) \leq 1$
can be assumed without loss of generality since for
![]() $\ell$
continuous, the function
$\ell$
continuous, the function
![]() $\widetilde \ell=\ell/\ell(0)$
satisfies
$\widetilde \ell=\ell/\ell(0)$
satisfies
![]() $\widetilde \ell(0)=1$
, and for
$\widetilde \ell(0)=1$
, and for
![]() $a \geq 0$
, we have
$a \geq 0$
, we have
![]() $ \ell_{a}=\ell(0)\widetilde \ell_a$
and hence
$ \ell_{a}=\ell(0)\widetilde \ell_a$
and hence
![]() $I_a(x)=\ell(0)\sum_{i \in \mathbb{N}} P_i \widetilde \ell_a(|x-x_i|)$
.)
$I_a(x)=\ell(0)\sum_{i \in \mathbb{N}} P_i \widetilde \ell_a(|x-x_i|)$
.)
Lemma 5.3. Under the general assumptions of Theorem 2.1 plus Condition 1, there exists a constant
![]() $c_o=c_o(\mu,\ell)>0$
such that for all sufficiently small
$c_o=c_o(\mu,\ell)>0$
such that for all sufficiently small
![]() $s>0$
, for all
$s>0$
, for all
![]() $\lambda>0$
, for all
$\lambda>0$
, for all
![]() $n \geq 1$
and
$n \geq 1$
and
![]() $r>d_o$
with
$r>d_o$
with
![]() $rn>0$
sufficiently large, and for all large enough
$rn>0$
sufficiently large, and for all large enough
![]() $M>0$
, for all
$M>0$
, for all
![]() $N\in\mathbb{N}$
and pairwise distinct
$N\in\mathbb{N}$
and pairwise distinct
![]() $z_1,\ldots,z_N \in \mathbb{Z}^d$
we have
$z_1,\ldots,z_N \in \mathbb{Z}^d$
we have
 \begin{equation}\begin{split}\mathbb{P}\big(B^{\mathrm{out}}_{r,n,M}(z_1)^\textrm{c}& \cap \ldots \cap B^{\mathrm{out}}_{r,n,M}(z_N)^\textrm{c}\big)\\[3pt]
\leq &\, \mathbb{E}\left[ \exp\left( c_o \lambda s \sum_{i=1}^N \int_{\mathbb{R}^d\setminus Q_{12rn\sqrt d}(rnz_i)} \ell_{6rn}(|rnz_i-x|) \Lambda(\textrm{d} x) \right) \right].\end{split}\end{equation}
\begin{equation}\begin{split}\mathbb{P}\big(B^{\mathrm{out}}_{r,n,M}(z_1)^\textrm{c}& \cap \ldots \cap B^{\mathrm{out}}_{r,n,M}(z_N)^\textrm{c}\big)\\[3pt]
\leq &\, \mathbb{E}\left[ \exp\left( c_o \lambda s \sum_{i=1}^N \int_{\mathbb{R}^d\setminus Q_{12rn\sqrt d}(rnz_i)} \ell_{6rn}(|rnz_i-x|) \Lambda(\textrm{d} x) \right) \right].\end{split}\end{equation}
Indeed, the right-hand side of (5.8) is the same as that of [Reference Tóbiás28, Equation (3.15)], and the assumptions on
![]() $\Lambda$
in the two proofs are also the same.
$\Lambda$
in the two proofs are also the same.
Proof of Lemma 5.2. We start with an estimate originating from [Reference Dousse9, Section 3.2]. By Markov’s inequality, for any
![]() $s>0$
,
$s>0$
,
 \begin{align}& \mathbb P\big( B^{\mathrm{out}}_{r,n,M}(z_1)^\textrm{c} \cap \ldots \cap B^{\mathrm{out}}_{r,n,M}(z_N)^\textrm{c}\big) = \mathbb P\big( I_{6rn}^{\mathrm{out}}(rnz_1)>M,\ldots,I_{6rn}^{\mathrm{out}}(rnz_N)>M \big)\nonumber\\[3pt]
& \leq \mathbb P \left( \sum_{i=1}^N I_{6rn}^{\mathrm{out}}(rnz_i) > N M \right)\nonumber\\[3pt]
& \leq \varepsilon^{-sNM} \mathbb{E} \left[ \exp\left( s \sum_{i=1}^N \sum_{x_k \in X^\lambda\setminus Q_{12rn\sqrt d}(nz_i)} P_k \ell_{6rn}(|rnz_i-x_k|) \right) \right]. \end{align}
\begin{align}& \mathbb P\big( B^{\mathrm{out}}_{r,n,M}(z_1)^\textrm{c} \cap \ldots \cap B^{\mathrm{out}}_{r,n,M}(z_N)^\textrm{c}\big) = \mathbb P\big( I_{6rn}^{\mathrm{out}}(rnz_1)>M,\ldots,I_{6rn}^{\mathrm{out}}(rnz_N)>M \big)\nonumber\\[3pt]
& \leq \mathbb P \left( \sum_{i=1}^N I_{6rn}^{\mathrm{out}}(rnz_i) > N M \right)\nonumber\\[3pt]
& \leq \varepsilon^{-sNM} \mathbb{E} \left[ \exp\left( s \sum_{i=1}^N \sum_{x_k \in X^\lambda\setminus Q_{12rn\sqrt d}(nz_i)} P_k \ell_{6rn}(|rnz_i-x_k|) \right) \right]. \end{align}
The randomness of the power values
![]() $P_k$
prevents us from continuing the proof analogously to [Reference Dousse9, Reference Tóbiás28]. On the other hand, similarly to [Reference Löffler22, Section 4.3] in the Poisson case, we can argue as follows. According to the Marking Theorem [Reference Kingman20, Section 5.2], the independently marked CPP
$P_k$
prevents us from continuing the proof analogously to [Reference Dousse9, Reference Tóbiás28]. On the other hand, similarly to [Reference Löffler22, Section 4.3] in the Poisson case, we can argue as follows. According to the Marking Theorem [Reference Kingman20, Section 5.2], the independently marked CPP
![]() $\textbf{X}^\lambda=\{ (x_i,P_i)\}_{i \in \mathbb{N}}$
is a CPP in
$\textbf{X}^\lambda=\{ (x_i,P_i)\}_{i \in \mathbb{N}}$
is a CPP in
![]() $\mathbb{R}^d \times [0,\infty)$
with directing measure
$\mathbb{R}^d \times [0,\infty)$
with directing measure
![]() $\Lambda \otimes \mu$
, where we recall that
$\Lambda \otimes \mu$
, where we recall that
![]() $\mu=\mathbb{P} \circ P_o^{-1}$
is the distribution of
$\mu=\mathbb{P} \circ P_o^{-1}$
is the distribution of
![]() $P_o$
. Hence, applying the Laplace functional of a CPP (cf. [Reference Kingman20, Sections 3.2 and 6]) to the function
$P_o$
. Hence, applying the Laplace functional of a CPP (cf. [Reference Kingman20, Sections 3.2 and 6]) to the function
![]() $f \colon \mathbb{R}^d \times [0,\infty) \to [0,\infty)$
,
$f \colon \mathbb{R}^d \times [0,\infty) \to [0,\infty)$
,
 \begin{equation*} f(x,p)=s\sum_{i=1}^N p \ell_{6rn}(|x-rnz_i|) \unicode{x1D7D9} \big\{ x \in \mathbb{R}^d \setminus Q_{12rn\sqrt d}(rnz_i) \big\}, \end{equation*}
\begin{equation*} f(x,p)=s\sum_{i=1}^N p \ell_{6rn}(|x-rnz_i|) \unicode{x1D7D9} \big\{ x \in \mathbb{R}^d \setminus Q_{12rn\sqrt d}(rnz_i) \big\}, \end{equation*}
we obtain
 \begin{align}&\mathbb{E} \left[ \exp\left( s \sum_{i=1}^N \sum_{x_k \in X^\lambda\setminus Q_{12rn\sqrt d}(rnz_i)} P_k \ell_{6rn}(|rnz_i-x_k|) \right) \right]\nonumber\\[3pt]
&= \mathbb{E} \left[ \exp \left( \lambda \int_{\mathbb{R}^d\setminus Q_{12rn\sqrt d}(rn z_i) } \int_{0}^{\infty} \left( \exp \left( sp \sum_{i=1}^N \ell_{6rn}(|rnz_i-x|)\right) -1 \right)
\mu(\textrm{d} p)\Lambda(\textrm{d} x) \right) \right]. \end{align}
\begin{align}&\mathbb{E} \left[ \exp\left( s \sum_{i=1}^N \sum_{x_k \in X^\lambda\setminus Q_{12rn\sqrt d}(rnz_i)} P_k \ell_{6rn}(|rnz_i-x_k|) \right) \right]\nonumber\\[3pt]
&= \mathbb{E} \left[ \exp \left( \lambda \int_{\mathbb{R}^d\setminus Q_{12rn\sqrt d}(rn z_i) } \int_{0}^{\infty} \left( \exp \left( sp \sum_{i=1}^N \ell_{6rn}(|rnz_i-x|)\right) -1 \right)
\mu(\textrm{d} p)\Lambda(\textrm{d} x) \right) \right]. \end{align}
Thanks to the exponential-moment assumption on
![]() $P_o$
from Condition 1, the moment-generating function
$P_o$
from Condition 1, the moment-generating function
is infinitely differentiable at
![]() $\alpha=0$
, with first derivative
$\alpha=0$
, with first derivative
![]() $\int_0^{\infty} p \mu(\textrm{d} p)=\mathbb{E}[P_o]<\infty$
. Note that
$\int_0^{\infty} p \mu(\textrm{d} p)=\mathbb{E}[P_o]<\infty$
. Note that
![]() $\sum_{i=1}^N \ell_{6rn}(|rnz_i-x|) $
is uniformly bounded in
$\sum_{i=1}^N \ell_{6rn}(|rnz_i-x|) $
is uniformly bounded in
![]() $x\in \mathbb{R}^d$
, rn, N, and pairwise distinct
$x\in \mathbb{R}^d$
, rn, N, and pairwise distinct
![]() $z_1,\dots, z_N$
; see [Reference Tóbiás28, Lemma 3.6]. Consequently, for any
$z_1,\dots, z_N$
; see [Reference Tóbiás28, Lemma 3.6]. Consequently, for any
![]() $C>1$
, the following holds for all sufficiently small
$C>1$
, the following holds for all sufficiently small
![]() $s>0$
(depending on C):
$s>0$
(depending on C):
 \begin{equation} \int_{0}^{\infty} \left( \exp \left( sp \sum_{i=1}^N\ell_{6rn}(|rnz_i-x|) \right)-1 \right) \mu(\textrm{d} p) \leq Cs \mathbb{E}[P_o] \sum_{i=1}^N \ell_{6rn}(|rnz_i-x|). \end{equation}
\begin{equation} \int_{0}^{\infty} \left( \exp \left( sp \sum_{i=1}^N\ell_{6rn}(|rnz_i-x|) \right)-1 \right) \mu(\textrm{d} p) \leq Cs \mathbb{E}[P_o] \sum_{i=1}^N \ell_{6rn}(|rnz_i-x|). \end{equation}
For such s, plugging (5.11) back into (5.10), starting from (5.9) we obtain
 \begin{multline} \mathbb{P}\big(B^{\mathrm{out}}_{r,n,M}(z_1)^\textrm{c} \cap \ldots \cap B^{\mathrm{out}}_{r,n,M}(z_N)^\textrm{c}\big)\\
\leq \mathbb{E}\left[ \exp\left( C \mathbb{E}[P_o] \lambda s \sum_{i=1}^N \int_{\mathbb{R}^d\setminus Q_{12rn\sqrt d}(rnz_i)} \ell_{6rn}(|rnz_i-x|)\Lambda(\textrm{d} x) \right) \right], \end{multline}
\begin{multline} \mathbb{P}\big(B^{\mathrm{out}}_{r,n,M}(z_1)^\textrm{c} \cap \ldots \cap B^{\mathrm{out}}_{r,n,M}(z_N)^\textrm{c}\big)\\
\leq \mathbb{E}\left[ \exp\left( C \mathbb{E}[P_o] \lambda s \sum_{i=1}^N \int_{\mathbb{R}^d\setminus Q_{12rn\sqrt d}(rnz_i)} \ell_{6rn}(|rnz_i-x|)\Lambda(\textrm{d} x) \right) \right], \end{multline}
which is (5.8) with
![]() $c_o=C \mathbb{E}[P_o]$
. With this we conclude the proof of the lemma.
$c_o=C \mathbb{E}[P_o]$
. With this we conclude the proof of the lemma.
5.2. Proof of Proposition 4.2
The strategy of the proof of Proposition 4.2 is the following. We first show that up to
![]() $\mathbb{P}$
-null sets, clusters are either finite or infinite in both directions, i.e., they contain no vertex of degree 1 in the case where they are infinite; see Lemma 5.4 below. Next, we assume for a contradiction that there exists an infinite cluster with positive probability. We then introduce a procedure that removes points from the infinite cluster that is closest to the origin in a certain sense. Thanks to elementary properties of the SINR graph, in the resulting configuration, the infinite cluster still remains infinite, but it contains a vertex of degree 1. Hence, the probability that the process takes values in the set of the resulting configurations is zero. What remains to show afterwards is that the probability that the process takes place in the set of original configurations is also zero, which leads to the desired contradiction. At this point it will be useful to compare the resulting configuration with an independent thinning of the original configuration in a certain ball, and this is where we make use of the fact that the underlying point process is a stationary CPP.
$\mathbb{P}$
-null sets, clusters are either finite or infinite in both directions, i.e., they contain no vertex of degree 1 in the case where they are infinite; see Lemma 5.4 below. Next, we assume for a contradiction that there exists an infinite cluster with positive probability. We then introduce a procedure that removes points from the infinite cluster that is closest to the origin in a certain sense. Thanks to elementary properties of the SINR graph, in the resulting configuration, the infinite cluster still remains infinite, but it contains a vertex of degree 1. Hence, the probability that the process takes values in the set of the resulting configurations is zero. What remains to show afterwards is that the probability that the process takes place in the set of original configurations is also zero, which leads to the desired contradiction. At this point it will be useful to compare the resulting configuration with an independent thinning of the original configuration in a certain ball, and this is where we make use of the fact that the underlying point process is a stationary CPP.
We assume throughout the proof that
![]() $\gamma \geq 1/(2\tau)$
, so that degrees in
$\gamma \geq 1/(2\tau)$
, so that degrees in
![]() ${G_{\gamma}({\textbf{X}}^\lambda)}$
are bounded by 2, and that
${G_{\gamma}({\textbf{X}}^\lambda)}$
are bounded by 2, and that
![]() $X^\lambda$
is nonequidistant (for all
$X^\lambda$
is nonequidistant (for all
![]() $\lambda>0$
). We can also assume that
$\lambda>0$
). We can also assume that
![]() $\mathbb{P}(P_o>0)>0$
in what follows, since otherwise the statement is trivially true. We start the proof with the following lemma, which excludes infinite paths that have an endpoint in the case where the degrees are bounded by 2, in a substantially more general setting.
$\mathbb{P}(P_o>0)>0$
in what follows, since otherwise the statement is trivially true. We start the proof with the following lemma, which excludes infinite paths that have an endpoint in the case where the degrees are bounded by 2, in a substantially more general setting.
Lemma 5.4. Let
![]() $g({\textbf{X}})$
be a random graph based on a stationary marked point process
$g({\textbf{X}})$
be a random graph based on a stationary marked point process
![]() ${\textbf{X}}=\{(x_i,P_i)\}_{i\in \mathbb{N}}$
with values in
${\textbf{X}}=\{(x_i,P_i)\}_{i\in \mathbb{N}}$
with values in
![]() $\mathbb{R}^d \times Z$
, where the mark space
$\mathbb{R}^d \times Z$
, where the mark space
![]() $(Z,\mathcal{Z})$
is an arbitrary measurable space,
$(Z,\mathcal{Z})$
is an arbitrary measurable space,
![]() $X=\{x_i\}_{i\in \mathbb{N}}$
is the vertex set, and the degree of all
$X=\{x_i\}_{i\in \mathbb{N}}$
is the vertex set, and the degree of all
![]() $x_i\in X$
,
$x_i\in X$
,
![]() $\deg(x_i)$
, is bounded by 2, almost surely. Let X have a finite intensity and consider the point process of degree-one points in infinite clusters,
$\deg(x_i)$
, is bounded by 2, almost surely. Let X have a finite intensity and consider the point process of degree-one points in infinite clusters,
Then
![]() $\mathbb{P}(\mathcal{X}_0(\mathbb{R}^d)=0)=1$
.
$\mathbb{P}(\mathcal{X}_0(\mathbb{R}^d)=0)=1$
.
We will apply this lemma to the SINR graph
![]() $g({\textbf{X}})={G_{\gamma}({\textbf{X}}^\lambda)}$
with
$g({\textbf{X}})={G_{\gamma}({\textbf{X}}^\lambda)}$
with
![]() $\lambda$
arbitrary,
$\lambda$
arbitrary,
![]() $\gamma \geq 1/(2\tau)$
, and
$\gamma \geq 1/(2\tau)$
, and
![]() $Z=[0,\infty)$
. The proof is based on a variant of the mass-transport principle (cf. [Reference Coupier, Dereudre and Le Stum4, Section 4.2] for instance).
$Z=[0,\infty)$
. The proof is based on a variant of the mass-transport principle (cf. [Reference Coupier, Dereudre and Le Stum4, Section 4.2] for instance).
Proof of Lemma 5.4. First, using the union bound and stationarity, it is enough to show that
![]() $\mathbb{E}[\mathcal{X}_0(Q_1)]=0$
. Let us define the point process of points in infinite clusters that are at distance equal to
$\mathbb{E}[\mathcal{X}_0(Q_1)]=0$
. Let us define the point process of points in infinite clusters that are at distance equal to
![]() $k\in\mathbb{N}_o$
from a point in
$k\in\mathbb{N}_o$
from a point in
![]() $\mathcal{X}_0$
,
$\mathcal{X}_0$
,
Thanks to the degree bound, every infinite cluster has at most one point in
![]() $\mathcal{X}_0$
, and
$\mathcal{X}_0$
, and
![]() $\mathbb{E}[\mathcal{X}_k(Q_1)]=\mathbb{E}[\mathcal{X}_0(Q_1)]$
for all
$\mathbb{E}[\mathcal{X}_k(Q_1)]=\mathbb{E}[\mathcal{X}_0(Q_1)]$
for all
![]() $k\in\mathbb{N}_o$
, by stationarity. However,
$k\in\mathbb{N}_o$
, by stationarity. However,
![]() $\sum_{k\ge 0}\mathbb{E}[\mathcal{X}_k(Q_1)]\le \mathbb{E}[X(Q_1)]<\infty$
, and thus
$\sum_{k\ge 0}\mathbb{E}[\mathcal{X}_k(Q_1)]\le \mathbb{E}[X(Q_1)]<\infty$
, and thus
![]() $\mathbb{E}[\mathcal{X}_0(Q_1)]=0$
.
$\mathbb{E}[\mathcal{X}_0(Q_1)]=0$
.
Let us denote by
![]() $(\mathcal{C}_i)_{0\le i< L}$
the L-many infinite clusters in
$(\mathcal{C}_i)_{0\le i< L}$
the L-many infinite clusters in
![]() ${G_{\gamma}({\textbf{X}}^\lambda)}$
, where
${G_{\gamma}({\textbf{X}}^\lambda)}$
, where
![]() $L\in \mathbb{N}\cup\{ \infty\}$
. For the proof of Proposition 4.2, it then suffices to show that
$L\in \mathbb{N}\cup\{ \infty\}$
. For the proof of Proposition 4.2, it then suffices to show that
We view
![]() ${\textbf{X}}^\lambda$
as the canonical process
${\textbf{X}}^\lambda$
as the canonical process
![]() ${\textbf{X}}^\lambda(\boldsymbol\omega)=\boldsymbol\omega$
on the set
${\textbf{X}}^\lambda(\boldsymbol\omega)=\boldsymbol\omega$
on the set
![]() $\textbf{N}$
of marked point configurations
$\textbf{N}$
of marked point configurations
![]() $\boldsymbol \omega$
in
$\boldsymbol \omega$
in
![]() $\mathbb{R}^d \times [0,\infty)$
such that
$\mathbb{R}^d \times [0,\infty)$
such that
![]() $\omega=\{ x_i \colon (x_i,p_i) \in \boldsymbol \omega \}$
is an infinite, locally-finite, nonequidistant point configuration on
$\omega=\{ x_i \colon (x_i,p_i) \in \boldsymbol \omega \}$
is an infinite, locally-finite, nonequidistant point configuration on
![]() $\mathbb{R}^d$
. The set of such point configurations
$\mathbb{R}^d$
. The set of such point configurations
![]() $\omega$
will be denoted by
$\omega$
will be denoted by
![]() $\textrm{N}$
. Note that
$\textrm{N}$
. Note that
![]() $\textbf{N}$
and N are equipped with the corresponding evaluation
$\textbf{N}$
and N are equipped with the corresponding evaluation
![]() $\sigma$
-fields.
$\sigma$
-fields.
Now we introduce an ordering in
![]() $\mathbb{R}^d\times [0,\infty)$
, which orders the points of the set according to the received signal power at a given point
$\mathbb{R}^d\times [0,\infty)$
, which orders the points of the set according to the received signal power at a given point
![]() $y \in \mathbb{R}^d$
(or equivalently, according to the received SINR values
$y \in \mathbb{R}^d$
(or equivalently, according to the received SINR values
![]() $\mathrm{SINR}(\cdot,y,\boldsymbol \omega)$
at y).
$\mathrm{SINR}(\cdot,y,\boldsymbol \omega)$
at y).
Definition 5.1. Let
![]() $(x,p),(z,r)\in\mathbb{R}^d \times [0,\infty)$
and
$(x,p),(z,r)\in\mathbb{R}^d \times [0,\infty)$
and
![]() $y \in \mathbb{R}^d$
. We say that (x, p) transmits a stronger signal to y than (z, r) does if one of the following conditions is satisfied:
$y \in \mathbb{R}^d$
. We say that (x, p) transmits a stronger signal to y than (z, r) does if one of the following conditions is satisfied:
-
i.
 $p \ell(| x-y |) > r \ell(| z-y |)$
, or
$p \ell(| x-y |) > r \ell(| z-y |)$
, or -
ii.
 $p \ell(| x-y |) = r \ell(| z-y |)$
and
$p \ell(| x-y |) = r \ell(| z-y |)$
and
 $| x-y |<| z-y|$
.
$| x-y |<| z-y|$
.
When talking about the marked CPP
![]() ${\textbf{X}}^\lambda$
, we will always assume that transmitters are associated with their own transmitted signal powers, and hence we will say ‘
${\textbf{X}}^\lambda$
, we will always assume that transmitters are associated with their own transmitted signal powers, and hence we will say ‘
![]() $x_i$
transmits a stronger signal to
$x_i$
transmits a stronger signal to
![]() $x_j$
than
$x_j$
than
![]() $x_l$
does’ instead of ‘
$x_l$
does’ instead of ‘
![]() $(x_i,P_i)$
transmits a stronger signal to
$(x_i,P_i)$
transmits a stronger signal to
![]() $x_j$
than
$x_j$
than
![]() $(x_l,P_l)$
does’, for any
$(x_l,P_l)$
does’, for any
![]() $i,j,l \in \mathbb{N}$
such that
$i,j,l \in \mathbb{N}$
such that
![]() $i \neq j$
and
$i \neq j$
and
![]() $l \neq j$
. It is easy to see that for
$l \neq j$
. It is easy to see that for
![]() ${\textbf{X}}^\lambda$
such that
${\textbf{X}}^\lambda$
such that
![]() $X^\lambda$
is nonequidistant, almost surely the following holds. For all
$X^\lambda$
is nonequidistant, almost surely the following holds. For all
![]() $i \in \mathbb{N}$
, the relation ‘
$i \in \mathbb{N}$
, the relation ‘
![]() $x_i$
transmits a stronger signal to
$x_i$
transmits a stronger signal to
![]() $x_j$
than
$x_j$
than
![]() $x_l$
does’ is a total ordering (i.e., irreflexive, antisymmetric, and transitive, with any two elements being comparable) on the set
$x_l$
does’ is a total ordering (i.e., irreflexive, antisymmetric, and transitive, with any two elements being comparable) on the set
![]() $\{ (i,l) \in \mathbb{N}^2 \colon i \neq j \text{ and } l \neq j \}$
, which we call the ordering of signal-weighted distance from receiver
$\{ (i,l) \in \mathbb{N}^2 \colon i \neq j \text{ and } l \neq j \}$
, which we call the ordering of signal-weighted distance from receiver
![]() $x_i$
. This fact indeed relies on the tiebreaking mechanism (ii): e.g., if
$x_i$
. This fact indeed relies on the tiebreaking mechanism (ii): e.g., if
![]() $\ell$
is constant on some interval (which is possible under the assumption of Proposition 4.2 and even under the stronger assumption of Theorem 2.1), then (i) does not define a total ordering on its own.
$\ell$
is constant on some interval (which is possible under the assumption of Proposition 4.2 and even under the stronger assumption of Theorem 2.1), then (i) does not define a total ordering on its own.
For
![]() $\boldsymbol\omega \in \textbf{N}$
and
$\boldsymbol\omega \in \textbf{N}$
and
![]() $x_o \in \omega$
, we can consider the vector
$x_o \in \omega$
, we can consider the vector
![]() $\textbf{V}(x_o,\boldsymbol \omega)=(\textbf{V}_n(x_o,\boldsymbol \omega))_{n \in \mathbb{N}_0}$
of the marked points of
$\textbf{V}(x_o,\boldsymbol \omega)=(\textbf{V}_n(x_o,\boldsymbol \omega))_{n \in \mathbb{N}_0}$
of the marked points of
![]() $\boldsymbol \omega$
ordered increasingly according to signal-weighted distance from receiver
$\boldsymbol \omega$
ordered increasingly according to signal-weighted distance from receiver
![]() $x_o$
. Then, we define
$x_o$
. Then, we define
![]() $\mathrm{V}_i(x_o,\boldsymbol \omega)$
as the first component of
$\mathrm{V}_i(x_o,\boldsymbol \omega)$
as the first component of
![]() $\textbf{V}_i(x_o,\boldsymbol \omega)$
, which we call the ith nearest neighbor of
$\textbf{V}_i(x_o,\boldsymbol \omega)$
, which we call the ith nearest neighbor of
![]() $x_o$
in signal-weighted order. In particular,
$x_o$
in signal-weighted order. In particular,
![]() $\mathrm{V}_0(x_o,\boldsymbol \omega)=x_o$
. Note that if the distribution
$\mathrm{V}_0(x_o,\boldsymbol \omega)=x_o$
. Note that if the distribution
![]() $\mu$
is concentrated in one point
$\mu$
is concentrated in one point
![]() $p>0$
, i.e.,
$p>0$
, i.e.,
![]() $\mu=\delta_p$
, then the ith nearest neighbor of
$\mu=\delta_p$
, then the ith nearest neighbor of
![]() $x_o$
in signal-weighted order is just the ith nearest neighbor of
$x_o$
in signal-weighted order is just the ith nearest neighbor of
![]() $x_o$
with respect to Euclidean distance.
$x_o$
with respect to Euclidean distance.
Now, if
![]() $x_o$
has degree two in
$x_o$
has degree two in
![]() $G_\gamma({\textbf{X}}^\lambda(\boldsymbol\omega))$
, then
$G_\gamma({\textbf{X}}^\lambda(\boldsymbol\omega))$
, then
![]() $x_o$
must be connected by an edge to both
$x_o$
must be connected by an edge to both
![]() $\mathrm{V}_1(x_o,\boldsymbol\omega)$
and
$\mathrm{V}_1(x_o,\boldsymbol\omega)$
and
![]() $\mathrm{V}_2(x_o,\boldsymbol\omega)$
, since the degree bound applies already for the edges towards
$\mathrm{V}_2(x_o,\boldsymbol\omega)$
, since the degree bound applies already for the edges towards
![]() $x_o$
. Moreover, both
$x_o$
. Moreover, both
![]() $\mathrm{V}_1(x_o,\boldsymbol\omega)$
and
$\mathrm{V}_1(x_o,\boldsymbol\omega)$
and
![]() $\mathrm{V}_2(x_o,\boldsymbol\omega)$
must also have
$\mathrm{V}_2(x_o,\boldsymbol\omega)$
must also have
![]() $x_o$
as one of their first two nearest neighbors in signal-weighted order; that is,
$x_o$
as one of their first two nearest neighbors in signal-weighted order; that is,
for all
![]() $i\in\{1,2\}$
. These signal-weighted nearest neighbor relations hold almost surely, in particular for every nonequidistant configuration
$i\in\{1,2\}$
. These signal-weighted nearest neighbor relations hold almost surely, in particular for every nonequidistant configuration
![]() $\boldsymbol\omega$
. The goal of using the configuration space
$\boldsymbol\omega$
. The goal of using the configuration space
![]() $\textbf{N}$
is to entirely exclude configurations that violate the degree bound or the signal-weighted nearest neighbor relations or that are not nonequidistant.
$\textbf{N}$
is to entirely exclude configurations that violate the degree bound or the signal-weighted nearest neighbor relations or that are not nonequidistant.
In the event
![]() $\{L\ge 1\}$
, let
$\{L\ge 1\}$
, let
![]() $\textbf{Z}=(Z,R)$
denote the closest point to the origin that has degree two and is contained in an infinite cluster. Without loss of generality, we will assume that this cluster is always equal to
$\textbf{Z}=(Z,R)$
denote the closest point to the origin that has degree two and is contained in an infinite cluster. Without loss of generality, we will assume that this cluster is always equal to
![]() $\mathcal{C}_0$
. Now, Proposition 4.2 immediately follows once we have verified the following proposition.
$\mathcal{C}_0$
. Now, Proposition 4.2 immediately follows once we have verified the following proposition.
Proposition 5.2. Consider the event
![]() $\{L\ge 1\}$
and define the random variable
$\{L\ge 1\}$
and define the random variable
Then, under the assumptions of Proposition 4.2, for any
![]() $i \geq 3$
, we have
$i \geq 3$
, we have
Proof of Proposition 4.2. Using a union bound and noting that
![]() $\{ L\ge 1 \}\subset \{I<\infty\}$
, Proposition 5.2 implies
$\{ L\ge 1 \}\subset \{I<\infty\}$
, Proposition 5.2 implies
![]() $\mathbb{P}(L\ge 1)=0$
, which is (5.17), and thus the proof of Proposition 4.2 is finished.
$\mathbb{P}(L\ge 1)=0$
, which is (5.17), and thus the proof of Proposition 4.2 is finished.
Proof of Proposition 5.2. For
![]() $\boldsymbol\omega\in \{L\ge 1\}$
, by definition, we have that
$\boldsymbol\omega\in \{L\ge 1\}$
, by definition, we have that
![]() $Z(\boldsymbol\omega)$
is connected by an edge to both
$Z(\boldsymbol\omega)$
is connected by an edge to both
![]() $\mathrm{V}_1(Z(\boldsymbol\omega), \boldsymbol\omega)$
and
$\mathrm{V}_1(Z(\boldsymbol\omega), \boldsymbol\omega)$
and
![]() $\mathrm{V}_2(Z(\boldsymbol\omega), \boldsymbol\omega)$
in
$\mathrm{V}_2(Z(\boldsymbol\omega), \boldsymbol\omega)$
in
![]() $G_\gamma({\textbf{X}}^\lambda(\boldsymbol\omega))$
. Furthermore, thanks to the degree bound of two, in the event
$G_\gamma({\textbf{X}}^\lambda(\boldsymbol\omega))$
. Furthermore, thanks to the degree bound of two, in the event
![]() $\{L\ge 1\}$
,
$\{L\ge 1\}$
,
![]() $\mathrm{V}_1(Z(\boldsymbol\omega), \boldsymbol\omega)$
and
$\mathrm{V}_1(Z(\boldsymbol\omega), \boldsymbol\omega)$
and
![]() $\mathrm{V}_2(Z(\boldsymbol\omega), \boldsymbol\omega)$
have no further joint neighbor in
$\mathrm{V}_2(Z(\boldsymbol\omega), \boldsymbol\omega)$
have no further joint neighbor in
![]() $G_\gamma({\textbf{X}}^\lambda(\boldsymbol\omega))$
, since otherwise
$G_\gamma({\textbf{X}}^\lambda(\boldsymbol\omega))$
, since otherwise
![]() $\mathcal{C}_0(\boldsymbol\omega)$
has a loop and cannot be infinite by the degree bound. Thus, for any
$\mathcal{C}_0(\boldsymbol\omega)$
has a loop and cannot be infinite by the degree bound. Thus, for any
![]() $i \geq 3$
, there exists
$i \geq 3$
, there exists
![]() $l \in \{1,2\}$
such that
$l \in \{1,2\}$
such that
![]() $\mathrm{V}_i(Z(\boldsymbol\omega), \boldsymbol\omega)$
and
$\mathrm{V}_i(Z(\boldsymbol\omega), \boldsymbol\omega)$
and
![]() $\mathrm{V}_l(Z(\boldsymbol\omega), \boldsymbol\omega)$
are not connected by an edge in
$\mathrm{V}_l(Z(\boldsymbol\omega), \boldsymbol\omega)$
are not connected by an edge in
![]() $G_\gamma({\textbf{X}}^\lambda(\boldsymbol\omega))$
. Let us denote the corresponding
$G_\gamma({\textbf{X}}^\lambda(\boldsymbol\omega))$
. Let us denote the corresponding
![]() $\mathrm{V}_l(Z(\boldsymbol\omega), \boldsymbol\omega)$
by
$\mathrm{V}_l(Z(\boldsymbol\omega), \boldsymbol\omega)$
by
![]() $M_i(\boldsymbol\omega)$
, and define
$M_i(\boldsymbol\omega)$
, and define
![]() $M_i(\boldsymbol\omega)=\mathrm{V}_1(Z(\boldsymbol\omega), \boldsymbol\omega)$
if neither
$M_i(\boldsymbol\omega)=\mathrm{V}_1(Z(\boldsymbol\omega), \boldsymbol\omega)$
if neither
![]() $\mathrm{V}_1(Z(\boldsymbol\omega), \boldsymbol\omega)$
nor
$\mathrm{V}_1(Z(\boldsymbol\omega), \boldsymbol\omega)$
nor
![]() $\mathrm{V}_2(Z(\boldsymbol\omega), \boldsymbol\omega)$
is connected to
$\mathrm{V}_2(Z(\boldsymbol\omega), \boldsymbol\omega)$
is connected to
![]() $\mathrm{V}_i(Z(\boldsymbol\omega), \boldsymbol\omega)$
by an edge. The element of
$\mathrm{V}_i(Z(\boldsymbol\omega), \boldsymbol\omega)$
by an edge. The element of
![]() $\{ \mathrm{V}_1(Z(\boldsymbol\omega), \boldsymbol\omega),\mathrm{V}_2( Z(\boldsymbol\omega), \boldsymbol\omega) \}$
not equal to
$\{ \mathrm{V}_1(Z(\boldsymbol\omega), \boldsymbol\omega),\mathrm{V}_2( Z(\boldsymbol\omega), \boldsymbol\omega) \}$
not equal to
![]() $M_i(\boldsymbol\omega)$
is denoted by
$M_i(\boldsymbol\omega)$
is denoted by
![]() $N_i(\boldsymbol\omega)$
. We will write Q for the signal power transmitted by
$N_i(\boldsymbol\omega)$
. We will write Q for the signal power transmitted by
![]() $M_i(\boldsymbol\omega)$
.
$M_i(\boldsymbol\omega)$
.
Let us fix
![]() $i \geq 3$
. Let
$i \geq 3$
. Let
![]() $\boldsymbol \omega \in \{L\ge 1\}$
be such that
$\boldsymbol \omega \in \{L\ge 1\}$
be such that
![]() $I(\boldsymbol \omega)=i$
. Let us define a thinned configuration
$I(\boldsymbol \omega)=i$
. Let us define a thinned configuration
We claim for
![]() $\mathbb{P}$
-almost all
$\mathbb{P}$
-almost all
![]() $\boldsymbol \omega \in \{L\ge 1\}\cap \{I=i\}$
that also
$\boldsymbol \omega \in \{L\ge 1\}\cap \{I=i\}$
that also
![]() $\boldsymbol \omega^i \in \{L\ge 1\}$
. For this, first note that the removal of finitely many points and their associated edges from an infinite cluster does not change the property that the cluster is infinite. However, the removal of points can still change the edge structure of the remaining points. In order to exclude this, we use the following fundamental property of the SINR graph. Assume that
$\boldsymbol \omega^i \in \{L\ge 1\}$
. For this, first note that the removal of finitely many points and their associated edges from an infinite cluster does not change the property that the cluster is infinite. However, the removal of points can still change the edge structure of the remaining points. In order to exclude this, we use the following fundamental property of the SINR graph. Assume that
![]() $\boldsymbol \omega,\boldsymbol \omega'$
are elements of
$\boldsymbol \omega,\boldsymbol \omega'$
are elements of
![]() $\textbf{N}$
such that
$\textbf{N}$
such that
![]() $\boldsymbol \omega \subseteq \boldsymbol \omega'$
. Then, for all
$\boldsymbol \omega \subseteq \boldsymbol \omega'$
. Then, for all
![]() $x,y \in \omega$
, if
$x,y \in \omega$
, if
![]() $\mathrm{SINR}(x,y,\boldsymbol \omega') >\tau$
, then
$\mathrm{SINR}(x,y,\boldsymbol \omega') >\tau$
, then
![]() $\mathrm{SINR}(x,y,\boldsymbol \omega) >\tau$
, which is clear from (5.1). In words, if we remove some vertices from an SINR graph, then edges of the SINR graphs between the remaining points stay preserved.
$\mathrm{SINR}(x,y,\boldsymbol \omega) >\tau$
, which is clear from (5.1). In words, if we remove some vertices from an SINR graph, then edges of the SINR graphs between the remaining points stay preserved.
Our next claim is that for
![]() $\boldsymbol\omega\in \{L\ge 1\}\cap \{I=i\}$
,
$\boldsymbol\omega\in \{L\ge 1\}\cap \{I=i\}$
,
![]() $\boldsymbol\omega^i$
is contained in
$\boldsymbol\omega^i$
is contained in
The proof of this claim in the simplest case
![]() $i=3$
is illustrated in Figure 3. For general
$i=3$
is illustrated in Figure 3. For general
![]() $i\ge 3$
, recall that Z cannot have degree higher than two in
$i\ge 3$
, recall that Z cannot have degree higher than two in
![]() $G_\gamma({\textbf{X}}^\lambda(\boldsymbol\omega^i))$
, whereas it has degree at least one and its cluster
$G_\gamma({\textbf{X}}^\lambda(\boldsymbol\omega^i))$
, whereas it has degree at least one and its cluster
![]() $\mathcal{C}_0(\boldsymbol\omega^i)$
is infinite in
$\mathcal{C}_0(\boldsymbol\omega^i)$
is infinite in
![]() $G_\gamma({\textbf{X}}^\lambda(\boldsymbol\omega^i))$
. Note also that the edge between
$G_\gamma({\textbf{X}}^\lambda(\boldsymbol\omega^i))$
. Note also that the edge between
![]() $Z(\boldsymbol\omega)$
and
$Z(\boldsymbol\omega)$
and
![]() $N_i(\boldsymbol\omega)$
still exists in
$N_i(\boldsymbol\omega)$
still exists in
![]() $G_\gamma({\textbf{X}}^\lambda(\boldsymbol\omega^i))$
. Furthermore, if
$G_\gamma({\textbf{X}}^\lambda(\boldsymbol\omega^i))$
. Furthermore, if
![]() $Z(\boldsymbol\omega)$
has degree two in
$Z(\boldsymbol\omega)$
has degree two in
![]() $G_\gamma({\textbf{X}}^\lambda(\boldsymbol\omega^i))$
, then it is connected to the second-nearest neighbor of
$G_\gamma({\textbf{X}}^\lambda(\boldsymbol\omega^i))$
, then it is connected to the second-nearest neighbor of
![]() $Z(\boldsymbol\omega)$
in signal-weighted order in
$Z(\boldsymbol\omega)$
in signal-weighted order in
![]() $\boldsymbol\omega^i$
, which is
$\boldsymbol\omega^i$
, which is
![]() $\mathrm{V}_2(Z(\boldsymbol\omega),\boldsymbol\omega^i)=\mathrm{V}_i(Z(\boldsymbol\omega),\boldsymbol\omega)$
, whereas
$\mathrm{V}_2(Z(\boldsymbol\omega),\boldsymbol\omega^i)=\mathrm{V}_i(Z(\boldsymbol\omega),\boldsymbol\omega)$
, whereas
![]() $\mathrm{V}_1(Z(\boldsymbol\omega),\boldsymbol\omega^i)=N_i(\boldsymbol\omega)$
. Now, since
$\mathrm{V}_1(Z(\boldsymbol\omega),\boldsymbol\omega^i)=N_i(\boldsymbol\omega)$
. Now, since
![]() $\boldsymbol\omega \notin B$
,
$\boldsymbol\omega \notin B$
,
![]() $\boldsymbol\omega \in \{L\ge 1\}$
, and
$\boldsymbol\omega \in \{L\ge 1\}$
, and
![]() $\mathrm{V}_i(Z(\boldsymbol\omega),\boldsymbol\omega) \in \mathcal{C}_0(\boldsymbol\omega)$
, it follows that
$\mathrm{V}_i(Z(\boldsymbol\omega),\boldsymbol\omega) \in \mathcal{C}_0(\boldsymbol\omega)$
, it follows that
![]() $\mathrm{V}_i(Z(\boldsymbol\omega),\boldsymbol\omega)$
has degree equal to two in
$\mathrm{V}_i(Z(\boldsymbol\omega),\boldsymbol\omega)$
has degree equal to two in
![]() $G_\gamma({\textbf{X}}^\lambda(\boldsymbol\omega))$
. Furthermore, it is neither connected to
$G_\gamma({\textbf{X}}^\lambda(\boldsymbol\omega))$
. Furthermore, it is neither connected to
![]() $M_i(\boldsymbol\omega)$
by an edge nor to
$M_i(\boldsymbol\omega)$
by an edge nor to
![]() $Z(\boldsymbol\omega)$
in this graph. Hence, both edges adjacent to
$Z(\boldsymbol\omega)$
in this graph. Hence, both edges adjacent to
![]() $\mathrm{V}_i(Z(\boldsymbol\omega),\boldsymbol\omega)$
also exist in
$\mathrm{V}_i(Z(\boldsymbol\omega),\boldsymbol\omega)$
also exist in
![]() $G_\gamma({\textbf{X}}^\lambda(\boldsymbol\omega^i))$
. But since
$G_\gamma({\textbf{X}}^\lambda(\boldsymbol\omega^i))$
. But since
![]() $\mathrm{V}_i(Z(\boldsymbol\omega),\boldsymbol\omega)$
has degree at most two in
$\mathrm{V}_i(Z(\boldsymbol\omega),\boldsymbol\omega)$
has degree at most two in
![]() $G_\gamma({\textbf{X}}^\lambda(\boldsymbol\omega^i))$
, it follows that
$G_\gamma({\textbf{X}}^\lambda(\boldsymbol\omega^i))$
, it follows that
![]() $Z(\boldsymbol\omega)$
and
$Z(\boldsymbol\omega)$
and
![]() $\mathrm{V}_i(Z(\boldsymbol\omega),\boldsymbol\omega)$
are not connected by an edge in this graph. Hence,
$\mathrm{V}_i(Z(\boldsymbol\omega),\boldsymbol\omega)$
are not connected by an edge in this graph. Hence,
![]() $\boldsymbol\omega^i \in B$
, which implies the claim.
$\boldsymbol\omega^i \in B$
, which implies the claim.

Figure 3. A visualization of the case
![]() $I(\boldsymbol\omega)=3$
for some realization
$I(\boldsymbol\omega)=3$
for some realization
![]() $\boldsymbol\omega\in \{L \geq 1\}$
.
$\boldsymbol\omega\in \{L \geq 1\}$
.
![]() $\mathrm{V}_3=\mathrm{V}_3(Z(\boldsymbol \omega),\boldsymbol\omega)$
is contained in the infinite cluster
$\mathrm{V}_3=\mathrm{V}_3(Z(\boldsymbol \omega),\boldsymbol\omega)$
is contained in the infinite cluster
![]() $\mathcal{C}_0=\mathcal{C}_0(\boldsymbol\omega)$
of the SINR graph
$\mathcal{C}_0=\mathcal{C}_0(\boldsymbol\omega)$
of the SINR graph
![]() $G_{\gamma}(\boldsymbol \omega)$
including
$G_{\gamma}(\boldsymbol \omega)$
including
![]() $Z=Z(\boldsymbol \omega)$
, and it is not a neighbor of
$Z=Z(\boldsymbol \omega)$
, and it is not a neighbor of
![]() $M_3=M_3(\boldsymbol\omega)$
, which in this example equals
$M_3=M_3(\boldsymbol\omega)$
, which in this example equals
![]() $\mathrm{V}_1=\mathrm{V}_1(Z(\boldsymbol\omega),\boldsymbol\omega)$
, while
$\mathrm{V}_1=\mathrm{V}_1(Z(\boldsymbol\omega),\boldsymbol\omega)$
, while
![]() $\mathrm{V}_2=\mathrm{V}_2(Z(\boldsymbol \omega),\boldsymbol\omega)=N_3=N_3(\boldsymbol\omega)$
. Hence, if
$\mathrm{V}_2=\mathrm{V}_2(Z(\boldsymbol \omega),\boldsymbol\omega)=N_3=N_3(\boldsymbol\omega)$
. Hence, if
![]() $\mathrm{V}_3$
has degree two in
$\mathrm{V}_3$
has degree two in
![]() $\mathcal{C}_0$
, then there are various possibilities respecting the degree bound of two to connect
$\mathcal{C}_0$
, then there are various possibilities respecting the degree bound of two to connect
![]() $\mathrm{V}_3$
to
$\mathrm{V}_3$
to
![]() $\mathcal{C}_0$
so that it is not connected to
$\mathcal{C}_0$
so that it is not connected to
![]() $M_3$
by an edge.
$M_3$
by an edge.
![]() $\mathrm{V}_3$
can be either a direct neighbor of
$\mathrm{V}_3$
can be either a direct neighbor of
![]() $\mathrm{V}_2$
(dashed line), or a later point of the path from Z to infinity starting with the edge from Z to
$\mathrm{V}_2$
(dashed line), or a later point of the path from Z to infinity starting with the edge from Z to
![]() $\mathrm{V}_2$
(dash-dotted lines), or a non-direct neighbor of
$\mathrm{V}_2$
(dash-dotted lines), or a non-direct neighbor of
![]() $\mathrm{V}_1$
on the path from Z to infinity starting with the edge from Z to
$\mathrm{V}_1$
on the path from Z to infinity starting with the edge from Z to
![]() $\mathrm{V}_1$
(dotted lines). Now, if
$\mathrm{V}_1$
(dotted lines). Now, if
![]() $M_3$
is removed from the realization, both edges adjacent to
$M_3$
is removed from the realization, both edges adjacent to
![]() $\mathrm{V}_3$
are preserved. Also, all edges from Z to infinity starting with the edge from Z to
$\mathrm{V}_3$
are preserved. Also, all edges from Z to infinity starting with the edge from Z to
![]() $\mathrm{V}_2$
are preserved, so that Z is still contained in an infinite cluster, but the edge from Z to
$\mathrm{V}_2$
are preserved, so that Z is still contained in an infinite cluster, but the edge from Z to
![]() $\mathrm{V}_1$
is removed. In the resulting configuration, the second-nearest neighbor of Z in signal-weighted order is
$\mathrm{V}_1$
is removed. In the resulting configuration, the second-nearest neighbor of Z in signal-weighted order is
![]() $\mathrm{V}_3$
, and hence this is the only point of the configuration that could be connected to Z by an edge. But
$\mathrm{V}_3$
, and hence this is the only point of the configuration that could be connected to Z by an edge. But
![]() $\mathrm{V}_3$
still cannot have degree 3 or more, so it cannot be connected to Z, which implies that in the new configuration Z is in an infinite cluster containing a point of degree one.
$\mathrm{V}_3$
still cannot have degree 3 or more, so it cannot be connected to Z, which implies that in the new configuration Z is in an infinite cluster containing a point of degree one.
Note that by Lemma 5.4, the set B is a
![]() $\mathbb{P}$
-null set, i.e.,
$\mathbb{P}$
-null set, i.e.,
This implies (5.14) and concludes the proof of Proposition 5.2 as soon as the following lemma is verified.
Lemma 5.5. Under the assumptions of Proposition 4.2, for any
![]() $i \geq 3$
,
$i \geq 3$
,
![]() $\mathbb{P}(\{L\ge1\}\cap \{ I=i \})>0$
implies
$\mathbb{P}(\{L\ge1\}\cap \{ I=i \})>0$
implies
![]() $\mathbb{P}\big( \big\{ \boldsymbol \omega^i \colon \boldsymbol \omega \in \{L\ge1\}\cap \{ I=i \} \big\}\big) >0$
.
$\mathbb{P}\big( \big\{ \boldsymbol \omega^i \colon \boldsymbol \omega \in \{L\ge1\}\cap \{ I=i \} \big\}\big) >0$
.
By Lemma 5.5—where we show that if the collection of thinned configurations is contained in a
![]() $\mathbb{P}$
-null set, then the non-thinned configurations also form a
$\mathbb{P}$
-null set, then the non-thinned configurations also form a
![]() $\mathbb{P}$
-null set—we see that (5.15) implies (5.14), which concludes the proof of Proposition 5.2.
$\mathbb{P}$
-null set—we see that (5.15) implies (5.14), which concludes the proof of Proposition 5.2.
Proof of Lemma 5.5. Let us fix
![]() $i \geq 3$
and assume that
$i \geq 3$
and assume that
![]() $\mathbb{P}(\{L\ge1\}\cap \{ I=i \})>0$
. Then, by continuity of measures, there exists
$\mathbb{P}(\{L\ge1\}\cap \{ I=i \})>0$
. Then, by continuity of measures, there exists
![]() $K>0$
such that
$K>0$
such that
where
![]() $B_K(o)$
denotes the open Euclidean ball of radius K in
$B_K(o)$
denotes the open Euclidean ball of radius K in
![]() $\mathbb{R}^d$
. Hence, there exists
$\mathbb{R}^d$
. Hence, there exists
![]() $n \geq i$
such that
$n \geq i$
such that
![]() $\mathbb{P}(C_{i,K,n})>0$
, where
$\mathbb{P}(C_{i,K,n})>0$
, where
 \begin{equation*}\begin{aligned} C_{i,K,n} =\big\{ \boldsymbol \omega \in \{L\ge1\}\cap \{I=i\} \colon &\#\big( \omega \cap B_K(o) \big)=n+1 \\[3pt] &\text{and }\mathrm{V}_j(Z(\boldsymbol\omega),\boldsymbol \omega) \in B_K(o), \forall j \in \{ 1,\ldots,i\}\big\}. \end{aligned} \end{equation*}
\begin{equation*}\begin{aligned} C_{i,K,n} =\big\{ \boldsymbol \omega \in \{L\ge1\}\cap \{I=i\} \colon &\#\big( \omega \cap B_K(o) \big)=n+1 \\[3pt] &\text{and }\mathrm{V}_j(Z(\boldsymbol\omega),\boldsymbol \omega) \in B_K(o), \forall j \in \{ 1,\ldots,i\}\big\}. \end{aligned} \end{equation*}
Conditional on the event
![]() $C_{i,K,n}$
, the marked point process
$C_{i,K,n}$
, the marked point process
![]() $(\textbf{X}^\lambda \setminus \{\textbf{Z} \})\cap B_K(o)$
has precisely n points.
$(\textbf{X}^\lambda \setminus \{\textbf{Z} \})\cap B_K(o)$
has precisely n points.
Now, for some fixed
![]() $q \in (0,1)$
, we can represent
$q \in (0,1)$
, we can represent
![]() $\textbf{X}^\lambda$
as
$\textbf{X}^\lambda$
as
![]() ${\textbf{X}}^{\lambda,1} \cup {\textbf{X}}^{\lambda,2}$
as follows. For
${\textbf{X}}^{\lambda,1} \cup {\textbf{X}}^{\lambda,2}$
as follows. For
![]() $K>0$
, let
$K>0$
, let
![]() $B_K(o)$
denote the open
$B_K(o)$
denote the open
![]() $\ell^2$
-ball of radius K around o. Let
$\ell^2$
-ball of radius K around o. Let
![]() ${\textbf{X}}^{\lambda,1}$
be given as the union of
${\textbf{X}}^{\lambda,1}$
be given as the union of
![]() $\textbf{X}^\lambda \setminus (B_K(o)\times [0,\infty))$
and the independent thinning of
$\textbf{X}^\lambda \setminus (B_K(o)\times [0,\infty))$
and the independent thinning of
![]() $\textbf{X}^\lambda \cap (B_K(o)\times [0,\infty))$
with survival probability q, and let
$\textbf{X}^\lambda \cap (B_K(o)\times [0,\infty))$
with survival probability q, and let
![]() ${\textbf{X}}^{\lambda,2}$
be the complementary thinning. That is, conditional on
${\textbf{X}}^{\lambda,2}$
be the complementary thinning. That is, conditional on
![]() $\textbf{X}^\lambda$
,
$\textbf{X}^\lambda$
,
![]() ${\textbf{X}}^{\lambda,1} \cap (B_K(o)\times [0,\infty))$
contains each point of
${\textbf{X}}^{\lambda,1} \cap (B_K(o)\times [0,\infty))$
contains each point of
![]() $\textbf{X}^\lambda \cap (B_K(o)\times [0,\infty))$
with probability q independent of the other points of this point process, and it contains no other points. Note further that
$\textbf{X}^\lambda \cap (B_K(o)\times [0,\infty))$
with probability q independent of the other points of this point process, and it contains no other points. Note further that
![]() ${\textbf{X}}^{\lambda,2}$
and
${\textbf{X}}^{\lambda,2}$
and
![]() ${\textbf{X}}^{\lambda,1} \cap (B_K(o)\times [0,\infty))$
are independent thinnings of
${\textbf{X}}^{\lambda,1} \cap (B_K(o)\times [0,\infty))$
are independent thinnings of
![]() $\textbf{X}^\lambda \cap (B_K(o)\times [0,\infty))$
with survival probabilities
$\textbf{X}^\lambda \cap (B_K(o)\times [0,\infty))$
with survival probabilities
![]() $1-q$
and q, respectively; moreover,
$1-q$
and q, respectively; moreover,
![]() ${\textbf{X}}^{\lambda,1}=\textbf{X}^\lambda \setminus {\textbf{X}}^{\lambda,2}$
,
${\textbf{X}}^{\lambda,1}=\textbf{X}^\lambda \setminus {\textbf{X}}^{\lambda,2}$
,
![]() ${\textbf{X}}^{\lambda,2} \setminus (B_K(o)\times [0,\infty))=\varnothing$
, and
${\textbf{X}}^{\lambda,2} \setminus (B_K(o)\times [0,\infty))=\varnothing$
, and
![]() ${\textbf{X}}^{\lambda,1} \setminus (B_K(o)\times [0,\infty))=\textbf{X}^\lambda \setminus (B_K(o)\times [0,\infty))$
. In order to provide a precise construction of the thinned processes, we choose a sequence
${\textbf{X}}^{\lambda,1} \setminus (B_K(o)\times [0,\infty))=\textbf{X}^\lambda \setminus (B_K(o)\times [0,\infty))$
. In order to provide a precise construction of the thinned processes, we choose a sequence
![]() $(J_m)_{m \in\mathbb{N}}$
of i.i.d. Bernoulli random variables with parameter q that is independent of
$(J_m)_{m \in\mathbb{N}}$
of i.i.d. Bernoulli random variables with parameter q that is independent of
![]() $\textbf{X}^\lambda$
, and given the realization
$\textbf{X}^\lambda$
, and given the realization
![]() $\boldsymbol \omega=\textbf{X}^\lambda(\boldsymbol \omega) = (\textbf{V}_i(Z(\boldsymbol\omega),\boldsymbol \omega))_{i \in \mathbb{N}_0}$
, the realizations of
$\boldsymbol \omega=\textbf{X}^\lambda(\boldsymbol \omega) = (\textbf{V}_i(Z(\boldsymbol\omega),\boldsymbol \omega))_{i \in \mathbb{N}_0}$
, the realizations of
![]() ${\textbf{X}}^{\lambda,1}(\boldsymbol \omega)$
and
${\textbf{X}}^{\lambda,1}(\boldsymbol \omega)$
and
![]() ${\textbf{X}}^{\lambda,2}(\boldsymbol \omega)$
are defined as follows, depending also on
${\textbf{X}}^{\lambda,2}(\boldsymbol \omega)$
are defined as follows, depending also on
![]() $(J_m)_{m \in\mathbb{N}}$
:
$(J_m)_{m \in\mathbb{N}}$
:
 \begin{equation*}\begin{aligned}{\textbf{X}}^{\lambda,1}(\boldsymbol \omega) & ={\textbf{X}}^{\lambda,1}(\boldsymbol \omega,(J_m)_{m \in \mathbb{N}}) = \{ \textbf{V}_m(Z(\boldsymbol\omega),\boldsymbol \omega) \colon J_m = 1, \textbf{V}_m(Z(\boldsymbol\omega),\boldsymbol \omega) \in B_K(o) \}\\[3pt] & \quad \cup \{ \textbf{Z}(\boldsymbol\omega) \} \cup \{\textbf{V}_m(Z(\boldsymbol\omega),\boldsymbol \omega) \colon \textbf{V}_m(Z(\boldsymbol\omega), \boldsymbol \omega) \in \mathbb{R}^d \setminus B_K(o) \} \end{aligned} \end{equation*}
\begin{equation*}\begin{aligned}{\textbf{X}}^{\lambda,1}(\boldsymbol \omega) & ={\textbf{X}}^{\lambda,1}(\boldsymbol \omega,(J_m)_{m \in \mathbb{N}}) = \{ \textbf{V}_m(Z(\boldsymbol\omega),\boldsymbol \omega) \colon J_m = 1, \textbf{V}_m(Z(\boldsymbol\omega),\boldsymbol \omega) \in B_K(o) \}\\[3pt] & \quad \cup \{ \textbf{Z}(\boldsymbol\omega) \} \cup \{\textbf{V}_m(Z(\boldsymbol\omega),\boldsymbol \omega) \colon \textbf{V}_m(Z(\boldsymbol\omega), \boldsymbol \omega) \in \mathbb{R}^d \setminus B_K(o) \} \end{aligned} \end{equation*}
and
It is clear that the respective projections
![]() $X^{\lambda,1}$
and
$X^{\lambda,1}$
and
![]() $X^{\lambda,2}$
of
$X^{\lambda,2}$
of
![]() ${\textbf{X}}^{\lambda,1}$
and
${\textbf{X}}^{\lambda,1}$
and
![]() ${\textbf{X}}^{\lambda,2}$
to the
${\textbf{X}}^{\lambda,2}$
to the
![]() $\mathbb{R}^d$
-coordinate are nonequidistant; furthermore,
$\mathbb{R}^d$
-coordinate are nonequidistant; furthermore,
![]() ${\textbf{X}}^{\lambda,1}$
can be represented as a random variable with values in
${\textbf{X}}^{\lambda,1}$
can be represented as a random variable with values in
![]() $\textbf{N}$
, defined on an enlarged probability space
$\textbf{N}$
, defined on an enlarged probability space
![]() $(\Omega',\mathcal{F}',\mathbb P')$
governing both the point process
$(\Omega',\mathcal{F}',\mathbb P')$
governing both the point process
![]() ${\textbf{X}}^\lambda$
and the sequence
${\textbf{X}}^\lambda$
and the sequence
![]() $(J_m)_{m \in \mathbb{N}}$
. In particular,
$(J_m)_{m \in \mathbb{N}}$
. In particular,
![]() $\mathbb{P}'({\textbf{X}}^\lambda \in \cdot) = \mathbb{P}({\textbf{X}}^\lambda \in \cdot)$
.
$\mathbb{P}'({\textbf{X}}^\lambda \in \cdot) = \mathbb{P}({\textbf{X}}^\lambda \in \cdot)$
.
The next property of stationary and nonequidistant CPPs is crucial for completing the proof of Lemma 5.5.
Lemma 5.6. Let
![]() $\Lambda$
be stationary and nonequidistant. Then, for any
$\Lambda$
be stationary and nonequidistant. Then, for any
![]() $K>0$
, the law of
$K>0$
, the law of
![]() ${\textbf{X}}^{\lambda,1}$
is absolutely continuous with respect to that of
${\textbf{X}}^{\lambda,1}$
is absolutely continuous with respect to that of
![]() ${\textbf{X}}^\lambda$
.
${\textbf{X}}^\lambda$
.
To be more precise, the absolute continuity is meant in this lemma in the following way, with respect to the probability space
![]() $(\Omega',\mathcal{F}',\mathbb P')$
on which
$(\Omega',\mathcal{F}',\mathbb P')$
on which
![]() ${\textbf{X}}^{\lambda,1}$
and
${\textbf{X}}^{\lambda,1}$
and
![]() ${\textbf{X}}^\lambda$
are jointly defined with
${\textbf{X}}^\lambda$
are jointly defined with
![]() $\mathbb P'({\textbf{X}}^\lambda \in \cdot)=\mathbb P({\textbf{X}}^\lambda \in \cdot)$
. Let
$\mathbb P'({\textbf{X}}^\lambda \in \cdot)=\mathbb P({\textbf{X}}^\lambda \in \cdot)$
. Let
![]() $G \in \mathcal{F}'$
be any event such that
$G \in \mathcal{F}'$
be any event such that
![]() $\mathbb{P}'({\textbf{X}}^{\lambda,1} \in G)>0$
; then we have
$\mathbb{P}'({\textbf{X}}^{\lambda,1} \in G)>0$
; then we have
![]() $\mathbb{P}'({\textbf{X}}^\lambda \in G)>0$
.
$\mathbb{P}'({\textbf{X}}^\lambda \in G)>0$
.
Proof of Lemma 5.6. Let F be an element of the evaluation
![]() $\sigma$
-algebra of
$\sigma$
-algebra of
![]() $\textbf{N}$
such that
$\textbf{N}$
such that
![]() $\mathbb{P}'({\textbf{X}}^{\lambda,1} \in F)>0$
. We have to show that
$\mathbb{P}'({\textbf{X}}^{\lambda,1} \in F)>0$
. We have to show that
![]() $\mathbb{P}(\textbf{X}^\lambda \in F)>0$
as well. Under the assumption that
$\mathbb{P}(\textbf{X}^\lambda \in F)>0$
as well. Under the assumption that
![]() $\mathbb{P}'({\textbf{X}}^{\lambda,1} \in F)>0$
, by continuity of measures, we can find
$\mathbb{P}'({\textbf{X}}^{\lambda,1} \in F)>0$
, by continuity of measures, we can find
![]() $K,l \in \mathbb{N}$
such that
$K,l \in \mathbb{N}$
such that
In other words, we have
![]() $0<\varepsilon = \mathbb{P}'\big({\textbf{X}}^{\lambda,1} \in G\big)$
, where
$0<\varepsilon = \mathbb{P}'\big({\textbf{X}}^{\lambda,1} \in G\big)$
, where
![]() $G = \{ \boldsymbol \omega \in F \colon \# (\boldsymbol \omega \cap ( B_K(o) \times$
$G = \{ \boldsymbol \omega \in F \colon \# (\boldsymbol \omega \cap ( B_K(o) \times$
![]() $[0,\infty)))=l \}$
. Thus,
$[0,\infty)))=l \}$
. Thus,
 \begin{equation*}\begin{aligned} \mathbb{P}\big(\textbf{X}^\lambda \in F\big) &\geq \mathbb{P}'\big(\textbf{X}^\lambda \in G, {\textbf{X}}^{\lambda,1} = \textbf{X}\big) \geq \mathbb{P}'\big({\textbf{X}}^{\lambda,1} \in G\big)\mathbb{P}'\big({\textbf{X}}^{\lambda,1} = \textbf{X}^\lambda | {\textbf{X}}^{\lambda,1} \in G\big) \\[3pt]
&= \varepsilon \mathbb{P}'\big({\textbf{X}}^{\lambda,1} = \textbf{X}^\lambda | {\textbf{X}}^{\lambda,1} \in G\big),\end{aligned}\end{equation*}
\begin{equation*}\begin{aligned} \mathbb{P}\big(\textbf{X}^\lambda \in F\big) &\geq \mathbb{P}'\big(\textbf{X}^\lambda \in G, {\textbf{X}}^{\lambda,1} = \textbf{X}\big) \geq \mathbb{P}'\big({\textbf{X}}^{\lambda,1} \in G\big)\mathbb{P}'\big({\textbf{X}}^{\lambda,1} = \textbf{X}^\lambda | {\textbf{X}}^{\lambda,1} \in G\big) \\[3pt]
&= \varepsilon \mathbb{P}'\big({\textbf{X}}^{\lambda,1} = \textbf{X}^\lambda | {\textbf{X}}^{\lambda,1} \in G\big),\end{aligned}\end{equation*}
and further,
According to (5.16), we have
where
![]() $a_n=\mathbb{E}'\big[ \mathbb{P}'\big({\textbf{X}}^{\lambda,1} \in G | \Lambda\big) \unicode{x1D7D9} \{ \Lambda(B_K(o)) \in [n,n+1) \} \big]$
, and thus there exists
$a_n=\mathbb{E}'\big[ \mathbb{P}'\big({\textbf{X}}^{\lambda,1} \in G | \Lambda\big) \unicode{x1D7D9} \{ \Lambda(B_K(o)) \in [n,n+1) \} \big]$
, and thus there exists
![]() $m\in\mathbb{N}_0$
with
$m\in\mathbb{N}_0$
with
![]() $a_m>0$
. Now, conditional on
$a_m>0$
. Now, conditional on
![]() $\Lambda$
,
$\Lambda$
,
![]() ${\textbf{X}}^{\lambda,1}$
is an i.i.d. marked PPP, and hence a PPP on
${\textbf{X}}^{\lambda,1}$
is an i.i.d. marked PPP, and hence a PPP on
![]() $\mathbb{R}^d \times [0,\infty)$
, which also implies that the complementary thinnings
$\mathbb{R}^d \times [0,\infty)$
, which also implies that the complementary thinnings
![]() ${\textbf{X}}^{\lambda,1}$
and
${\textbf{X}}^{\lambda,1}$
and
![]() ${\textbf{X}}^{\lambda,2}$
are independent given
${\textbf{X}}^{\lambda,2}$
are independent given
![]() $\Lambda$
; see the Colouring Theorem and the Marking Theorem in [Reference Kingman20]. Hence, we obtain
$\Lambda$
; see the Colouring Theorem and the Marking Theorem in [Reference Kingman20]. Hence, we obtain
 \begin{equation*}\begin{aligned}\mathbb{P}'\big({\textbf{X}}^{\lambda,2} = \varnothing, &{\textbf{X}}^{\lambda,1} \in G\big) = \mathbb{E}'\big[\mathbb{P}'\big({\textbf{X}}^{\lambda,2} = \varnothing|\Lambda\big) \mathbb{P}'\big({\textbf{X}}^{\lambda,1} \in G|\Lambda\big) \big] \\[3pt]
& = \sum_{n=0}^{\infty} \mathbb{E}'\big[ \varepsilon^{-(1-q)\Lambda(B_K(o))}\mathbb{P}'\big({\textbf{X}}^{\lambda,1} \in G |\Lambda\big) \unicode{x1D7D9}\{ \Lambda(B_K(o)) \in [n,n+1) \} \big]\\[3pt] & \geq \sum_{n=0}^{\infty} \varepsilon^{-(1-q)(n+1)} a_n\ge \varepsilon^{-(1-q)(m+1)} a_m>0,\end{aligned}\end{equation*}
\begin{equation*}\begin{aligned}\mathbb{P}'\big({\textbf{X}}^{\lambda,2} = \varnothing, &{\textbf{X}}^{\lambda,1} \in G\big) = \mathbb{E}'\big[\mathbb{P}'\big({\textbf{X}}^{\lambda,2} = \varnothing|\Lambda\big) \mathbb{P}'\big({\textbf{X}}^{\lambda,1} \in G|\Lambda\big) \big] \\[3pt]
& = \sum_{n=0}^{\infty} \mathbb{E}'\big[ \varepsilon^{-(1-q)\Lambda(B_K(o))}\mathbb{P}'\big({\textbf{X}}^{\lambda,1} \in G |\Lambda\big) \unicode{x1D7D9}\{ \Lambda(B_K(o)) \in [n,n+1) \} \big]\\[3pt] & \geq \sum_{n=0}^{\infty} \varepsilon^{-(1-q)(n+1)} a_n\ge \varepsilon^{-(1-q)(m+1)} a_m>0,\end{aligned}\end{equation*}
which verifies the lemma that the distribution of
![]() ${\textbf{X}}^{\lambda,1}$
is absolutely continuous with respect to that of
${\textbf{X}}^{\lambda,1}$
is absolutely continuous with respect to that of
![]() ${\textbf{X}}^\lambda$
.
${\textbf{X}}^\lambda$
.
Given Lemma 5.6, we now finish the proof of Lemma 5.5. Thanks to the assumption that
![]() $\mathbb{P}(C_{i,K,n})>0$
and using the definition of
$\mathbb{P}(C_{i,K,n})>0$
and using the definition of
![]() ${\textbf{X}}^{\lambda,1}$
,
${\textbf{X}}^{\lambda,1}$
,
 \begin{equation}\begin{aligned} \mathbb P' \big( {\textbf{X}}^{\lambda,1} \in& \{ \boldsymbol \omega^i \colon \boldsymbol \omega \in \{L\ge 1\} \cap \{ I=i \} \}\big) \geq \mathbb P' \big( {\textbf{X}}^{\lambda,1} \in \{ \boldsymbol \omega^i \colon \boldsymbol \omega \in C_{i,K,n} \} \big) \\[3pt] & \geq \mathbb P' \big( {\textbf{X}}^{\lambda,1} \in \{ \boldsymbol \omega^i \colon\boldsymbol \omega \in C_{i,K,n}\}, {\textbf{X}}^\lambda \in C_{i,K,n} \big) \\[3pt] & = \mathbb{P}(C_{i,K,n}) \mathbb P'\big({\textbf{X}}^{\lambda,1} \in \{\boldsymbol \omega^i \colon \boldsymbol \omega \in C_{i,K,n} \}| {\textbf{X}}^\lambda \in C_{i,K,n} \big) \\[3pt] & = \mathbb{P}(C_{i,K,n}) q^{n-i+2} (1-q)^{i-2}>0.\end{aligned} \end{equation}
\begin{equation}\begin{aligned} \mathbb P' \big( {\textbf{X}}^{\lambda,1} \in& \{ \boldsymbol \omega^i \colon \boldsymbol \omega \in \{L\ge 1\} \cap \{ I=i \} \}\big) \geq \mathbb P' \big( {\textbf{X}}^{\lambda,1} \in \{ \boldsymbol \omega^i \colon \boldsymbol \omega \in C_{i,K,n} \} \big) \\[3pt] & \geq \mathbb P' \big( {\textbf{X}}^{\lambda,1} \in \{ \boldsymbol \omega^i \colon\boldsymbol \omega \in C_{i,K,n}\}, {\textbf{X}}^\lambda \in C_{i,K,n} \big) \\[3pt] & = \mathbb{P}(C_{i,K,n}) \mathbb P'\big({\textbf{X}}^{\lambda,1} \in \{\boldsymbol \omega^i \colon \boldsymbol \omega \in C_{i,K,n} \}| {\textbf{X}}^\lambda \in C_{i,K,n} \big) \\[3pt] & = \mathbb{P}(C_{i,K,n}) q^{n-i+2} (1-q)^{i-2}>0.\end{aligned} \end{equation}
Finally, by Lemma 5.6, under
![]() $\mathbb P'$
the distribution of
$\mathbb P'$
the distribution of
![]() ${\textbf{X}}^{\lambda,1}$
is absolutely continuous with respect to that of
${\textbf{X}}^{\lambda,1}$
is absolutely continuous with respect to that of
![]() ${\textbf{X}}^\lambda$
. Hence, it follows from (5.18) that
${\textbf{X}}^\lambda$
. Hence, it follows from (5.18) that
which implies the lemma.
5.3. Proof of Theorem 2.3
This proof is similar to that of Theorem 2.1, Condition 1, but simpler. The new proof ingredient that we use here is the strong connectivity of any supercritical Poisson Boolean model [Reference Tóbiás28, Theorems 2 and 5] in the case of
![]() $d\geq 2$
, which allows us to improve the result that
$d\geq 2$
, which allows us to improve the result that
![]() $\lambda^*_\textrm{c}<\infty$
to
$\lambda^*_\textrm{c}<\infty$
to
![]() $\lambda^*_\textrm{c}=\lambda_\textrm{c}(r_\textrm{B})$
. First we introduce an adequate discrete percolation model and then we control the interferences.
$\lambda^*_\textrm{c}=\lambda_\textrm{c}(r_\textrm{B})$
. First we introduce an adequate discrete percolation model and then we control the interferences.
Throughout the proof,
![]() $X^\lambda=\{ x_i \}_{i \in \mathbb{N}}$
denotes a homogeneous PPP with intensity
$X^\lambda=\{ x_i \}_{i \in \mathbb{N}}$
denotes a homogeneous PPP with intensity
![]() $\lambda$
in
$\lambda$
in
![]() $\mathbb{R}^d$
, and we write
$\mathbb{R}^d$
, and we write
![]() $X^\lambda$
instead of
$X^\lambda$
instead of
![]() ${\textbf{X}}^\lambda$
since marks are non-random. Let us introduce the notion and elementary properties of Boolean models with (constant) radius
${\textbf{X}}^\lambda$
since marks are non-random. Let us introduce the notion and elementary properties of Boolean models with (constant) radius
![]() $r>0$
. The Poisson Boolean model
$r>0$
. The Poisson Boolean model
![]() $B(X^\lambda,r)$
(with constant connection radii r) is defined as
$B(X^\lambda,r)$
(with constant connection radii r) is defined as
Connecting any two different points
![]() $x_i,x_j \in X^\lambda$
by an edge whenever
$x_i,x_j \in X^\lambda$
by an edge whenever
we obtain the Poisson–Gilbert graph
![]() $g_{2r}(X^\lambda)$
with connection radius 2r. Percolation in this Gilbert graph is equivalent to the existence of an unbounded connected component in
$g_{2r}(X^\lambda)$
with connection radius 2r. Percolation in this Gilbert graph is equivalent to the existence of an unbounded connected component in
![]() $B(X^\lambda,r)$
, which we also refer to as percolation. Thus, one can speak about subcritical, critical, and supercritical Poisson Boolean models.
$B(X^\lambda,r)$
, which we also refer to as percolation. Thus, one can speak about subcritical, critical, and supercritical Poisson Boolean models.
Recall the definition of the radius
![]() $r_\textrm{B}$
from (2.4), and let us fix
$r_\textrm{B}$
from (2.4), and let us fix
![]() $\lambda>\lambda_\textrm{c}(r_\textrm{B})$
for the remainder of this section. Thanks to scale invariance of Poisson Boolean models [Reference Meester and Roy25, Section 2.2] and the well-behavedness of
$\lambda>\lambda_\textrm{c}(r_\textrm{B})$
for the remainder of this section. Thanks to scale invariance of Poisson Boolean models [Reference Meester and Roy25, Section 2.2] and the well-behavedness of
![]() $\ell$
, we can fix
$\ell$
, we can fix
![]() $r\in (d_o,r_\textrm{B})$
such that the Poisson Boolean model
$r\in (d_o,r_\textrm{B})$
such that the Poisson Boolean model
![]() $B(X^\lambda,r/2)$
associated to
$B(X^\lambda,r/2)$
associated to
![]() $g_{r}(X^\lambda)$
is still supercritical. The next lemma is an immediate consequence of the results in [Reference Penrose and Pisztora26, Section 1].
$g_{r}(X^\lambda)$
is still supercritical. The next lemma is an immediate consequence of the results in [Reference Penrose and Pisztora26, Section 1].
Lemma 5.7. ([Reference Penrose and Pisztora26].) Let
![]() $B(X^\lambda,r/2)$
be a supercritical Poisson Boolean model and let
$B(X^\lambda,r/2)$
be a supercritical Poisson Boolean model and let
![]() $x \in \mathbb{R}^d$
. With probability tending to one as
$x \in \mathbb{R}^d$
. With probability tending to one as
![]() $n \uparrow \infty$
, the following two statements hold:
$n \uparrow \infty$
, the following two statements hold:
-
1.
 $B(X^\lambda,r/2) \cap Q_n(x)$
contains a connected component of diameter at least
$B(X^\lambda,r/2) \cap Q_n(x)$
contains a connected component of diameter at least
 $n/3$
.
$n/3$
. -
2. Any two connected components of
 $B(X^\lambda,r/2) \cap Q_n(x)$
of diameter at least
$B(X^\lambda,r/2) \cap Q_n(x)$
of diameter at least
 $n/9$
each are contained in the same connected component of
$n/9$
each are contained in the same connected component of
 $B(X^\lambda,r/2) \cap Q_{2n}(x)$
.
$B(X^\lambda,r/2) \cap Q_{2n}(x)$
.
Using Lemma 5.7, we construct a renormalized percolation process on
![]() $\mathbb{Z}^d$
. For
$\mathbb{Z}^d$
. For
![]() $z \in \mathbb{Z}^d$
, let
$z \in \mathbb{Z}^d$
, let
![]() $\Xi_n(z)$
denote the union of all connected components of
$\Xi_n(z)$
denote the union of all connected components of
![]() $B(X^\lambda,r/2) \cap Q_n(z)$
that are of diameter at least
$B(X^\lambda,r/2) \cap Q_n(z)$
that are of diameter at least
![]() $n/3$
. For
$n/3$
. For
![]() $n \geq 1$
, we say that the site
$n \geq 1$
, we say that the site
![]() $z \in \mathbb{Z}^d$
is n-good if
$z \in \mathbb{Z}^d$
is n-good if
-
i.
 $\Xi_n(nz) \neq \varnothing$
, and
$\Xi_n(nz) \neq \varnothing$
, and -
ii. for any
 $z' \in \mathbb{Z}^d$
with
$z' \in \mathbb{Z}^d$
with
 $|z-z'|_\infty \leq 1$
, it holds that all pairs of connected components C of
$|z-z'|_\infty \leq 1$
, it holds that all pairs of connected components C of
 $\Xi_n(nz)$
and C
$\Xi_n(nz)$
and C
 $^{\prime}$
of
$^{\prime}$
of
 $\Xi_n(nz')$
are contained in the same connected component of
$\Xi_n(nz')$
are contained in the same connected component of
 $B(X^\lambda,r/2) \cap Q_{6n}(nz)$
.
$B(X^\lambda,r/2) \cap Q_{6n}(nz)$
.
The site
![]() $z \in \mathbb{Z}^d$
is n-bad if z is not n-good. We have the following lemma.
$z \in \mathbb{Z}^d$
is n-bad if z is not n-good. We have the following lemma.
Lemma 5.8. Under the assumptions of Theorem 2.3, for all
![]() $n \geq 1$
sufficiently large, there exists
$n \geq 1$
sufficiently large, there exists
![]() $q_{A}=q_A(\lambda,n) \in (0,1)$
such that for any
$q_{A}=q_A(\lambda,n) \in (0,1)$
such that for any
![]() $N \in \mathbb{N}$
and pairwise distinct
$N \in \mathbb{N}$
and pairwise distinct
![]() $z_1,\ldots,z_N \in \mathbb{Z}^d$
we have
$z_1,\ldots,z_N \in \mathbb{Z}^d$
we have
Furthermore, for any
![]() $\varepsilon>0$
, for all large enough n one can choose
$\varepsilon>0$
, for all large enough n one can choose
![]() $q_A$
such that
$q_A$
such that
![]() $q_A<\varepsilon$
.
$q_A<\varepsilon$
.
Proof. For
![]() $z \in \mathbb{Z}^d$
,
$z \in \mathbb{Z}^d$
,
![]() $\unicode{x1D7D9} \{ z\text{ is \textit{n}-good} \}$
is measurable with respect to
$\unicode{x1D7D9} \{ z\text{ is \textit{n}-good} \}$
is measurable with respect to
![]() $X^{\lambda} \cap(Q_{6n}(nz) \oplus B_{r/2}(o))$
, which is contained in
$X^{\lambda} \cap(Q_{6n}(nz) \oplus B_{r/2}(o))$
, which is contained in
![]() $X^\lambda \cap Q_{7n}(nz)$
for all n large enough; hence for all sufficiently large n the process of n-good sites is 7-dependent thanks to the independence property of the PPP
$X^\lambda \cap Q_{7n}(nz)$
for all n large enough; hence for all sufficiently large n the process of n-good sites is 7-dependent thanks to the independence property of the PPP
![]() $X^\lambda$
. Hence, by a standard argument (using dependent percolation theory [Reference Liggett, Schonmann and Stacey23], as in the proof of Lemma 5.2), it suffices to verify that
$X^\lambda$
. Hence, by a standard argument (using dependent percolation theory [Reference Liggett, Schonmann and Stacey23], as in the proof of Lemma 5.2), it suffices to verify that
The limit (5.20) can be verified along the lines of the proof of [Reference Hirsch, Jahnel and Cali16, Theorem 2.6] using an adequate interpretation of the Poisson Boolean model. More precisely, in view of Definition 3.2, the assertion of Lemma 5.7 is equivalent to the statement in [Reference Hirsch, Jahnel and Cali16, Section 2.1] that the (for all sufficiently large
![]() $b>0$
) b-dependent directing random measure
$b>0$
) b-dependent directing random measure
![]() $\Lambda$
given as
$\Lambda$
given as
![]() $\Lambda(\textrm{d} x)= \lambda_1 \unicode{x1D7D9} \{ x \in B(X^\lambda,r/2) \} \textrm{d} x$
is asymptotically essentially connected, where
$\Lambda(\textrm{d} x)= \lambda_1 \unicode{x1D7D9} \{ x \in B(X^\lambda,r/2) \} \textrm{d} x$
is asymptotically essentially connected, where
![]() $\lambda_1>0$
is such that
$\lambda_1>0$
is such that
![]() $\mathbb{E}[\Lambda(Q_1)]=1$
.
$\mathbb{E}[\Lambda(Q_1)]=1$
.
The other essential proof ingredient is the interference control. We recall the ‘shifted’ path-loss functions
![]() $\ell_a$
(5.5) and the shot-noise processes
$\ell_a$
(5.5) and the shot-noise processes
![]() $I_a(x),I(x)$
from Section 5.1, and also that by the triangle inequality, for
$I_a(x),I(x)$
from Section 5.1, and also that by the triangle inequality, for
![]() $a \geq 0$
,
$a \geq 0$
,
![]() $I(x) \leq I_{a}(z)$
holds for any
$I(x) \leq I_{a}(z)$
holds for any
![]() $z \in \mathbb{R}^d$
and
$z \in \mathbb{R}^d$
and
![]() $x \in Q_a(z)$
.
$x \in Q_a(z)$
.
For
![]() $n \geq 1$
and
$n \geq 1$
and
![]() $M>0$
, we say that
$M>0$
, we say that
![]() $z \in \mathbb{Z}^d$
is (n,M)-tame if
$z \in \mathbb{Z}^d$
is (n,M)-tame if
![]() $I_{7n}(nz) \leq M$
and (n,M)-wild otherwise. Then we have the following assertion, which holds for all
$I_{7n}(nz) \leq M$
and (n,M)-wild otherwise. Then we have the following assertion, which holds for all
![]() $\lambda$
such that
$\lambda$
such that
![]() $B(X^\lambda,r/2)$
is supercritical.
$B(X^\lambda,r/2)$
is supercritical.
Lemma 5.9. ([Reference Tóbiás28].) Under the assumptions of Theorem 2.3, for fixed
![]() $n \geq 1$
, for all sufficiently large
$n \geq 1$
, for all sufficiently large
![]() $M>0$
, there exists
$M>0$
, there exists
![]() $q_B=q_B(\lambda,n,M)\in (0,1)$
such that for any
$q_B=q_B(\lambda,n,M)\in (0,1)$
such that for any
![]() $N \in \mathbb{N}$
and pairwise distinct
$N \in \mathbb{N}$
and pairwise distinct
![]() $z_1,\ldots,z_N \in \mathbb{Z}^d$
we have
$z_1,\ldots,z_N \in \mathbb{Z}^d$
we have
Furthermore, for
![]() $\varepsilon>0$
, for any
$\varepsilon>0$
, for any
![]() $n \geq 1$
, for all sufficiently large M one can choose
$n \geq 1$
, for all sufficiently large M one can choose
![]() $q_B$
such that
$q_B$
such that
![]() $q_B < \varepsilon$
.
$q_B < \varepsilon$
.
Proof. Clearly, the Lebesgue measure
![]() $\Lambda$
is asymptotically essentially connected and b-dependent for any
$\Lambda$
is asymptotically essentially connected and b-dependent for any
![]() $b>0$
, and
$b>0$
, and
![]() $\Lambda(Q_1)$
has all exponential moments. Hence the lemma can be proven very similarly to [Reference Tóbiás28, Proposition 3.3] under the condition (2b) in [Reference Tóbiás28, Theorem 2.4]. The only difference is that in [Reference Tóbiás28],
$\Lambda(Q_1)$
has all exponential moments. Hence the lemma can be proven very similarly to [Reference Tóbiás28, Proposition 3.3] under the condition (2b) in [Reference Tóbiás28, Theorem 2.4]. The only difference is that in [Reference Tóbiás28],
![]() $I_{6n}(nz)$
was considered instead of
$I_{6n}(nz)$
was considered instead of
![]() $I_{7n}(nz)$
, but this makes no qualitative difference for the proof. Furthermore, the additional condition in [Reference Tóbiás28, Theorem 2.4] that
$I_{7n}(nz)$
, but this makes no qualitative difference for the proof. Furthermore, the additional condition in [Reference Tóbiás28, Theorem 2.4] that
![]() $\ell(0) \leq 1$
can be assumed to hold without loss of generality, for the same reason as in the proof of Proposition 5.1 (see the beginning of Step 4 in the proof of Theorem 2.1).
$\ell(0) \leq 1$
can be assumed to hold without loss of generality, for the same reason as in the proof of Proposition 5.1 (see the beginning of Step 4 in the proof of Theorem 2.1).
Equipped with these results, we can now prove our main theorem.
Proof of Theorem 2.3. For
![]() $n \geq 1$
and
$n \geq 1$
and
![]() $M>0$
, we say that the site
$M>0$
, we say that the site
![]() $z \in \mathbb{Z}^d$
is (n, M)-nice if it is both n-good and (n, M)-tame. We claim that for all sufficiently large n and accordingly chosen large enough M, the process of (n, M)-nice sites percolates. Indeed, this follows from combining the estimates of Lemmas 5.7 and 5.9, similarly to Corollary 5.1, and carrying out a Peierls argument.
$z \in \mathbb{Z}^d$
is (n, M)-nice if it is both n-good and (n, M)-tame. We claim that for all sufficiently large n and accordingly chosen large enough M, the process of (n, M)-nice sites percolates. Indeed, this follows from combining the estimates of Lemmas 5.7 and 5.9, similarly to Corollary 5.1, and carrying out a Peierls argument.
We claim that this assertion implies percolation in
![]() $G_{\gamma}(X^\lambda)$
for small
$G_{\gamma}(X^\lambda)$
for small
![]() $\gamma>0$
. Indeed, let n, M be so large that the process of (n, M)-nice sites percolates, and such that
$\gamma>0$
. Indeed, let n, M be so large that the process of (n, M)-nice sites percolates, and such that
![]() $Q_{6n}(o) \oplus B_{r/2}(o) \subseteq Q_{7n}(o)$
. Using a standard argument (cf. [Reference Dousse9] or Step 3 in the proof of Theorem 2.1, Condition 1), one can choose
$Q_{6n}(o) \oplus B_{r/2}(o) \subseteq Q_{7n}(o)$
. Using a standard argument (cf. [Reference Dousse9] or Step 3 in the proof of Theorem 2.1, Condition 1), one can choose
![]() $\gamma>0$
sufficiently small so that for any (n, M)-tame site z, all connections in
$\gamma>0$
sufficiently small so that for any (n, M)-tame site z, all connections in
![]() $g_r(X^\lambda) \cap Q_{7n}(nz)$
also exist in
$g_r(X^\lambda) \cap Q_{7n}(nz)$
also exist in
![]() $G_{\gamma}(X^\lambda) \cap Q_{7n}(nz)$
.
$G_{\gamma}(X^\lambda) \cap Q_{7n}(nz)$
.
Now, analogously to [Reference Hirsch, Jahnel and Cali16, Section 5.2], we can argue as follows. Let
![]() $\mathcal{C}$
be an infinite connected component of the process of sites that are (n, M)-nice. Let
$\mathcal{C}$
be an infinite connected component of the process of sites that are (n, M)-nice. Let
![]() $z,z' \in \mathcal{C} $
and let
$z,z' \in \mathcal{C} $
and let
![]() $\{ z_0=z,z_1,\ldots,z_{k-1},z_k=z' \}$
be a path in
$\{ z_0=z,z_1,\ldots,z_{k-1},z_k=z' \}$
be a path in
![]() $\mathcal{C}$
connecting z and z
$\mathcal{C}$
connecting z and z
![]() $^{\prime}$
. Then, thanks to n-goodness, for any
$^{\prime}$
. Then, thanks to n-goodness, for any
![]() $j=0,\ldots,k$
and for any
$j=0,\ldots,k$
and for any
![]() $x_j \in X^\lambda$
such that
$x_j \in X^\lambda$
such that
![]() $B_{r/2}(x_j) \cap Q_n(nz_j) \subseteq \Xi_n(nz_j)$
we have that
$B_{r/2}(x_j) \cap Q_n(nz_j) \subseteq \Xi_n(nz_j)$
we have that
![]() $x_j$
and
$x_j$
and
![]() $x_{j+1}$
are in the same connected component of
$x_{j+1}$
are in the same connected component of
![]() $B(X^\lambda,r/2)\cap Q_{6n}(nz_j)$
. In other words,
$B(X^\lambda,r/2)\cap Q_{6n}(nz_j)$
. In other words,
![]() $x_j$
and
$x_j$
and
![]() $x_{j+1}$
are connected in the Poisson–Gilbert graph
$x_{j+1}$
are connected in the Poisson–Gilbert graph
![]() $g_r(X^\lambda)$
via a path in
$g_r(X^\lambda)$
via a path in
![]() $Q_{7n}(nz_j)$
, where the additional unit of n comes from the fact that the centers of balls in the Boolean model might lie in a neighboring box. Hence, using (n, M)-tameness, we conclude that all edges of this path in
$Q_{7n}(nz_j)$
, where the additional unit of n comes from the fact that the centers of balls in the Boolean model might lie in a neighboring box. Hence, using (n, M)-tameness, we conclude that all edges of this path in
![]() $g_r(X^\lambda)$
also exist in
$g_r(X^\lambda)$
also exist in
![]() $G_{\gamma}(X^\lambda)$
. Thus,
$G_{\gamma}(X^\lambda)$
. Thus,
![]() $G_{\gamma}(X^\lambda)$
also percolates. Since
$G_{\gamma}(X^\lambda)$
also percolates. Since
![]() $\lambda>\lambda_\textrm{c}(r_\textrm{B})$
was arbitrary, the theorem follows.
$\lambda>\lambda_\textrm{c}(r_\textrm{B})$
was arbitrary, the theorem follows.
Acknowledgements
The authors thank E. Cali, A. Hinsen, C. Hirsch, W. König, and R. Löffler for interesting discussions and comments, with special thanks to R. Löffler for making her thesis available on arXiv and to A. Hinsen for helping create Figure 2.
Funding Information
This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy MATH+: The Berlin Mathematics Research Center, EXC-2046/1 project ID 390685689.
Competing Interests
There were no competing interests to declare which arose during the preparation or publication process for this article.