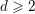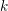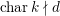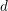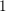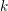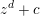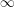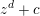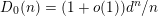1 Introduction
1.1 Dynatomic curves
Fix an integer 
$d\geqslant 2$. Let 
$k$ be a field such that 
$\operatorname{char}k\nmid d$. View 
$f=f_{c}:=z^{d}+c$ as a polynomial in 
$z$ with coefficients in 
$k[c]$. Let 
$f^{n}(z)$ be the 
$n$th iterate of 
$f$; in particular, 
$f^{0}(z):=z$. If 
$n$ and 
$m$ are nonnegative integers with 
$n>m$, then any irreducible factor of 
$f^{n}(z)-f^{m}(z)\in k[z,c]$ defines an affine curve over 
$k$. By a dynatomic curve over 
$k$, we mean any such curve, or its smooth projective model. Any 
$k$-point on such a curve yields 
$c_{0}\in k$ equipped with a preperiodic point in 
$k$, that is, an element 
$z_{0}\in k$ that under iteration 
$z^{d}+c_{0}$ eventually enters a cycle; the length of the cycle is called the eventual period. We consider two dynatomic curves to be different if the corresponding closed subschemes of 
$\mathbb{A}_{k}^{2}$ are distinct. Section 2 describes all dynatomic curves in characteristic 
$0$ explicitly.
1.2 Gonality
Let 
$\overline{k}$ be an algebraic closure of 
$k$. Let 
$\unicode[STIX]{x1D707}_{d}=\{x\in \overline{k}:x^{d}=1\}$.
For a curve 
$X$ over 
$k$, let 
$X_{\overline{k}}=X\times _{k}\overline{k}$. If 
$X$ is irreducible, define the gonality
$\unicode[STIX]{x1D6FE}(X)$ of 
$X$ as the least possible degree of a dominant rational map 
$X{\dashrightarrow}\mathbb{P}_{k}^{1}$. If 
$X$ is geometrically irreducible, define its 
$\overline{k}$-gonality as 
$\unicode[STIX]{x1D6FE}(X_{\overline{k}})$.
The following theorem, and its consequence, Theorem 1.7, are our main results.
Theorem 1.1. Fix 
$d\geqslant 2$ and 
$k$ such that 
$\operatorname{char}k\nmid d$. Suppose that 
$\unicode[STIX]{x1D707}_{d}\subset k$.
(a) Every dynatomic curve over
$k$ is geometrically irreducible.(b) If the dynatomic curves over
$k$ are listed in any order, their gonalities tend to $\infty$.
Remark 1.2. Part (a) of Theorem 1.1 can fail if 
$\unicode[STIX]{x1D707}_{d}\not \subset k$. See Remark 2.2.
Remark 1.3. In proving Theorem 1.1 in positive characteristic, we face the challenge that we do not know explicitly what the dynatomic curves are, since we are not sure whether the known factors of the polynomials 
$f^{n}(z)-f^{m}(z)$ are irreducible. Some results regarding the irreducibility of dynatomic curves in positive characteristic may be found in [Reference Doyle, Krieger, Obus, Pries, Rubinstein-Salzedo and WestDKO+19], but they are not sufficient for proving the full result. Instead, to overcome the difficulties, we use a novel argument that is specific to finite fields to prove that the degrees of dynatomic curves over the 
$c$-line must tend to infinity even though we do not know precisely what these curves are; see § 4.
Let us now introduce notation for our next result. Let 
$\unicode[STIX]{x1D707}(n)$ denote the Möbius 
$\unicode[STIX]{x1D707}$-function. Then 
$f^{n}(z)-z=\prod _{e|n}\unicode[STIX]{x1D6F7}_{e}(z,c)$, where
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{n}(z,c):=\mathop{\prod }_{e|n}(f^{e}(z)-z)^{\unicode[STIX]{x1D707}(n/e)}\in k[z,c].\end{eqnarray}$$ Let 
$Y_{1}^{\operatorname{dyn}}(n)$ be the curve defined by 
$\unicode[STIX]{x1D6F7}_{n}(z,c)=0$ in 
$\mathbb{A}_{k}^{2}$, and let 
$X_{1}^{\operatorname{dyn}}(n)$ be the normalization of its projective closure. To simplify notation, we omit the superscript dyn from now on. General points of 
$X_{1}(n)$ parameterize polynomials of the form 
$z^{d}+c$ equipped with a point of exact order 
$n$.
The morphism 
$(z,c)\mapsto (f(z),c)$ restricts to an order-
$n$ automorphism of 
$Y_{1}(n)$, so it induces an order-
$n$ automorphism 
$\unicode[STIX]{x1D70E}$ of 
$X_{1}(n)$. The quotient of 
$X_{1}(n)$ by the cyclic group generated by 
$\unicode[STIX]{x1D70E}$ is called 
$X_{0}(n)$. If 
$\operatorname{char}k=0$, it is known that 
$X_{1}(n)$ is geometrically irreducible (see [Reference BouschBou92, Reference Lau and SchleicherLS94, Reference MortonMor96]), so 
$X_{0}(n)$ is too.
Theorem 1.4. Fix 
$d\geqslant 2$ and a field 
$k$ of characteristic 
$0$. Then
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}(X_{0}(n))>\biggl(\frac{1}{2}-\frac{1}{2d}-o(1)\biggr)n\end{eqnarray}$$ as 
$n\rightarrow \infty$. In particular, 
$\unicode[STIX]{x1D6FE}(X_{0}(n))\rightarrow \infty$.
Remark 1.5. Our definition of dynatomic curve does not include quotient curves such as 
$X_{0}(n)$, so the conclusion 
$\unicode[STIX]{x1D6FE}(X_{0}(n))\rightarrow \infty$ of Theorem 1.4 does not follow from Theorem 1.1(b). In fact, our logic runs in the opposite direction: we use Theorem 1.4 in the proof of the characteristic-
$0$ case of Theorem 1.1(b).
Remark 1.6. Although the lower bound in Theorem 1.4 is linear in 
$n$, the best upper bound we know, 
$\unicode[STIX]{x1D6FE}(X_{0}(n))\leqslant (1+o(1))d^{n}/n$ (see Proposition 3.1(b)), is exponential in 
$n$.
To prove Theorem 1.4, we use that 
$X_{0}(n)$ already has a morphism to 
$\mathbb{P}^{1}$ of degree lower than expected for its genus, namely 
$X_{0}(n)\stackrel{c}{\rightarrow }\mathbb{P}^{1}$. If it also had a morphism to 
$\mathbb{P}^{1}$ of bounded degree, then the Castelnuovo–Severi inequality would make the genus of 
$X_{0}(n)$ smaller than it actually is, a contradiction. See § 3 for details.
To prove Theorem 1.1(b), we use different arguments in characteristic 
$0$ and characteristic 
${>}0$.
In characteristic 
$0$, we use that each dynatomic curve dominates 
$X_{1}(n)$ and hence also 
$X_{0}(n)$ for some 
$n$, so by Theorem 1.4 its gonality is large when 
$n$ is large; this lets us reduce to proving a gonality lower bound for the dynatomic curves above 
$X_{1}(n)$ for each fixed 
$n$. The latter curves for fixed 
$n$ come in towers, and we use the Castelnuovo–Severi inequality to work our way up each tower. See § 3.
In characteristic 
$p$, we prove that the irreducible components of 
$f^{n}(z)-f^{m}(z)$ have large degree over the 
$c$-line, and we use that to prove that over the finite field 
$\mathbb{F}_{q}:=\mathbb{F}_{p}(\unicode[STIX]{x1D707}_{d})$ their smooth projective models have so many 
$\mathbb{F}_{q}$-points over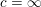 
$c=\infty$ that their 
$\mathbb{F}_{q}$-gonalities must be large. Finally, we use a result controlling how gonality of a curve changes when the base field is enlarged. See § 4.
1.3 Uniform boundedness of preperiodic points
The growth of gonalities of classical modular curves implies the strong uniform boundedness theorem for torsion points on elliptic curves over function fields (the function field analogue of Merel’s theorem [Reference MerelMer96]); see [Reference Nguyen and SaitoNS96, Theorem 0.3]. Similarly, from Theorem 1.1 we will deduce the following function field analogue of a case of the Morton–Silverman conjecture [Reference Morton and SilvermanMS94, p. 100].
Theorem 1.7 (Strong uniform boundedness theorem for preperiodic points over function fields).
Fix 
$d\geqslant 2$ and a field 
$k$ such that 
$\operatorname{char}k\nmid d$. Let 
$K$ be the function field of an integral curve over 
$k$. Fix a positive integer 
$D$. Then there exists 
$B=B(d,K,D)>0$ such that, for every field extension 
$L\supseteq K$ of degree 
${\leqslant}D$ and every 
$c\in L$ not algebraic over 
$k$, the number of preperiodic points of 
$z^{d}+c$ in 
$L$ is at most 
$B$. If 
$k$ is finite, the same holds with the words ‘not algebraic over 
$k$’ deleted.
Remark 1.8. As far as we know, Theorem 1.7 is the first theorem proving strong uniform boundedness of preperiodic points for all members of a nontrivial algebraic family of maps over a global field. See [Reference Doyle, Krieger, Obus, Pries, Rubinstein-Salzedo and WestDKO+19] for some related results and arguments; in particular, that article also explains the connection between uniform boundedness and gonality and geometric irreducibility, and proves geometric irreducibility of curves such as 
$\unicode[STIX]{x1D6F7}_{n}(z,c)=0$ modulo 
$p$ for many primes 
$p$. Our innovation, as mentioned above, is to show how to use finite fields to get the gonality and uniform boundedness results even without knowing that 
$\unicode[STIX]{x1D6F7}_{n}(z,c)=0$ modulo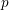 
$p$ is geometrically irreducible.
Remark 1.9. Theorem 1.7 is best possible in the sense that the words ‘not algebraic over 
$k$’ cannot be removed in general. For example, if 
$k$ is algebraically closed and 
$c\in k$, then all preperiodic points of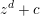 
$z^{d}+c$ lie in 
$k$ and hence also in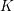 
$K$ and 
$L$; the number of them is generally not even finite, let alone uniformly bounded!
Another application of Theorem 1.1 is the following result, which over number fields provides a uniform bound on preperiodic points having a bounded eventual period.
Theorem 1.10. Fix integers 
$d\geqslant 2$, 
$D\geqslant 1$, and 
$N\geqslant 1$. Then there exists 
$B=B(d,D,N)>0$ such that, for every number field 
$K$ satisfying 
$[K:\mathbb{Q}]\leqslant D$ and every 
$c\in K$, the number of preperiodic points of 
$z^{d}+c$ in 
$K$ with eventual period at most 
$N$ is at most 
$B$.
Theorems 1.7 and 1.10 are proved in § 5. Theorem 1.10 implies that the strong uniform boundedness conjecture for periodic points over number fields implies the strong uniform boundedness conjecture for preperiodic points over number fields, as we now explain.
Corollary 1.11. Fix integers 
$d\geqslant 2$ and 
$D\geqslant 1$. Suppose that there exists a bound 
$N=N(d,D)$ such that, for every number field 
$K$ satisfying 
$[K:\mathbb{Q}]\leqslant D$ and every 
$c\in K$, every periodic point of 
$z^{d}+c$ in 
$K$ has period at most 
$N$. Then there exists a bound 
$B^{\prime }=B^{\prime }(d,D)$ such that, for every number field 
$K$ satisfying 
$[K:\mathbb{Q}]\leqslant D$ and every 
$c\in K$, the number of preperiodic points of 
$z^{d}+c$ in 
$K$ is at most 
$B^{\prime }$.
Proof. By assumption, if 
$[K:\mathbb{Q}]\leqslant D$ and 
$c\in K$, then the preperiodic points of 
$z^{d}+c$ in 
$K$ having eventual period at most 
$N$ are all the preperiodic points in 
$K$. Therefore the bound 
$B(d,D,N)$ of Theorem 1.10 is actually a bound on the total number of preperiodic points in 
$K$. Take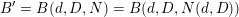 
$B^{\prime }=B(d,D,N)=B(d,D,N(d,D))$.◻
Remark 1.12. Eliminating the hypothesis that 
$N(d,D)$ exists in Corollary 1.11 seems extremely difficult. Proving that 
$N(2,1)$ exists is a problem that has been studied for over two decades, and even this smallest case seems far out of reach of existing methods. It amounts to ruling out all sufficiently large periods 
$n$ for quadratic polynomials over 
$\mathbb{Q}$, and entire articles have been devoted to ruling out just periods 
$4$ and 
$5$ [Reference MortonMor98b, Reference Flynn, Poonen and SchaeferFPS97]. Going further has so far relied on major conjectures: the Birch and Swinnerton-Dyer conjecture rules out period 
$6$ [Reference StollSto08], and the 
$abc$ conjecture and its generalizations contained in one of Vojta’s conjectures imply uniform boundedness for preperiodic points of 
$z^{d}+c$ over any fixed number field [Reference LooperLoo19].
2 Classification of dynatomic curves
For 
$m,n\geqslant 1$, let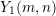 
$Y_{1}(m,n)$ be the curve over 
$k$ whose general points parameterize polynomials 
$z^{d}+c$ equipped with a preperiodic point that after exactly 
$m$ steps enters an 
$n$-cycle. This curve is the zero locus in 
$\mathbb{A}_{k}^{2}$ of the polynomial
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{m,n}(z,c):=\frac{\unicode[STIX]{x1D6F7}_{n}(f^{m}(z),c)}{\unicode[STIX]{x1D6F7}_{n}(f^{m-1}(z),c)}.\end{eqnarray}$$ For a general point 
$(z,c)\in Y_{1}(1,n)$, the elements 
$z$ and 
$f^{n}(z)$ are distinct preimages of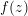 
$f(z)$, so 
$z=\unicode[STIX]{x1D701}f^{n}(z)$ for some 
$\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{d}-\{1\}$. Suppose that 
$\unicode[STIX]{x1D707}_{d}\subseteq k$. For each 
$\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{d}-\{1\}$, let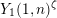 
$Y_{1}(1,n)^{\unicode[STIX]{x1D701}}$ be the subscheme of 
$Y_{1}(1,n)$ defined by the condition 
$z=\unicode[STIX]{x1D701}f^{n}(z)$, so
$$\begin{eqnarray}Y_{1}(1,n)=\mathop{\bigcup }_{\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{d}-\{1\}}Y_{1}(1,n)^{\unicode[STIX]{x1D701}}.\end{eqnarray}$$ Both 
$(z,c)\mapsto (f(z),c)$ and 
$(z,c)\mapsto (\unicode[STIX]{x1D701}^{-1}z,c)$ define isomorphisms 
$Y_{1}(1,n)^{\unicode[STIX]{x1D701}}\rightarrow Y_{1}(n)$. In particular, 
$Y_{1}(1,n)^{\unicode[STIX]{x1D701}}$ equals the curve 
$\unicode[STIX]{x1D6F7}_{n}(\unicode[STIX]{x1D701}^{-1}z,c)=0$ in 
$\mathbb{A}_{k}^{2}$. For 
$m\geqslant 2$, let 
$Y_{1}(m,n)^{\unicode[STIX]{x1D701}}$ be the inverse image of 
$Y_{1}(1,n)^{\unicode[STIX]{x1D701}}$ under
$$\begin{eqnarray}\displaystyle Y_{1}(m,n) & \longrightarrow & \displaystyle Y_{1}(1,n)\nonumber\\ \displaystyle (z,c) & \longmapsto & \displaystyle (f^{m-1}(z),c).\nonumber\end{eqnarray}$$ Then, for any 
$m,n\geqslant 1$,
$$\begin{eqnarray}Y_{1}(m,n)=\mathop{\bigcup }_{\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{d}-\{1\}}Y_{1}(m,n)^{\unicode[STIX]{x1D701}},\end{eqnarray}$$ and 
$Y_{1}(m,n)^{\unicode[STIX]{x1D701}}$ equals the curve 
$\unicode[STIX]{x1D6F7}_{n}(\unicode[STIX]{x1D701}^{-1}f^{m-1}(z),c)=0$ in 
$\mathbb{A}_{k}^{2}$. The decomposition (2) corresponds to a factorization
The following theorem is a collection of results from [Reference BouschBou92, Reference Lau and SchleicherLS94, Reference MortonMor96, Reference GaoGao16].
Theorem 2.1. Let 
$k$ be a field of characteristic 
$0$ such that 
$\unicode[STIX]{x1D707}_{d}\subset k$. Then the curves 
$Y_{1}(n)$ for 
$n\geqslant 1$ and the curves 
$Y_{1}(m,n)^{\unicode[STIX]{x1D701}}$ for 
$m,n\geqslant 1$ and 
$\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{d}-\{1\}$ are irreducible, so they are all the dynatomic curves over 
$k$.
Computer experiments (at least for 
$d=2$) suggest that Theorem 2.1 holds for any field 
$k$ such that 
$\operatorname{char}k\nmid d$ and 
$\unicode[STIX]{x1D707}_{d}\subset k$, but in positive characteristic this remains unproved. See [Reference Doyle, Krieger, Obus, Pries, Rubinstein-Salzedo and WestDKO+19], especially Theorems B and D, for progress in this direction.
Remark 2.2. If in Theorem 2.1 we drop the hypothesis that 
$\unicode[STIX]{x1D707}_{d}\subset k$, then the irreducible components of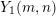 
$Y_{1}(m,n)$ over 
$k$ are in bijection with the 
$\operatorname{Gal}(k(\unicode[STIX]{x1D707}_{d})/k)$-orbits in 
$\unicode[STIX]{x1D707}_{d}-\{1\}$. An irreducible component corresponding to an orbit of size greater than 
$1$ is not geometrically irreducible.
3 Gonality in characteristic 0
Given a geometrically irreducible curve 
$X$ over 
$k$, let 
$g(X)$ denote the genus of its smooth projective model. Let 
$D_{0}(n)$ be the degree of the morphism 
$X_{0}(n)\stackrel{c}{\longrightarrow }\mathbb{P}^{1}$. Similarly, let 
$D_{1}(n)=\deg (X_{1}(n)\stackrel{c}{\longrightarrow }\mathbb{P}^{1})$.
Proposition 3.1. Fix 
$d\geqslant 2$, and fix a field 
$k$ of characteristic 
$0$.
(a) We have
$D_{1}(n)=(1+o(1))d^{n}$ as $n\rightarrow \infty$.(b) We have
$D_{0}(n)=(1+o(1))d^{n}/n$ as $n\rightarrow \infty$.(c) We have
$g(X_{0}(n))>(1/2-1/2d-o(1))d^{n}$ as $n\rightarrow \infty$.(d) The Galois group of (the Galois closure of) the covering
$X_{0}(n)\stackrel{c}{\longrightarrow }\mathbb{P}^{1}$ is the full symmetric group $S_{D_{0}(n)}$.
Proof. We may assume 
$k=\mathbb{C}$.
(a) See the proof of [Reference MortonMor96, Theorem 13(d)]. The estimate is deduced from 
$D_{1}(n)=\deg _{z}\unicode[STIX]{x1D6F7}_{n}=\sum _{e|n}\unicode[STIX]{x1D707}(n/e)d^{e}$, which follows from (1).
(b) The first morphism in the tower 
$X_{1}(n)\rightarrow X_{0}(n)\stackrel{c}{\longrightarrow }\mathbb{P}^{1}$ has degree 
$n$, so 
$D_{0}(n)=D_{1}(n)/n$. Substitute (a) into this.
(c) More precisely, 
$g(X_{0}(n))>(1/2-1/2d-1/n)d^{n}+O(nd^{n/2})$ as 
$n\rightarrow \infty$, by [Reference MortonMor96, Theorem 13(d)].
(d) This is a consequence of work by Bousch [Reference BouschBou92] for 
$d=2$, and Lau and Schleicher [Reference Lau and SchleicherLS94] for 
$d>2$. See also [Reference MortonMor98a, Theorem B] and [Reference SchleicherSch17].◻
A well-known strategy for obtaining lower bounds on gonality (cf. [Reference Nguyen and SaitoNS96] and [Reference PoonenPoo07, §2]) involves the following result, which will tell us roughly that if a high-genus curve has a relatively low-degree map to a low-genus curve, it cannot have a second such map that is independent of the first.
Proposition 3.2 (Castelnuovo–Severi inequality).
Let 
$F$, 
$F_{1}$, 
$F_{2}$ be function fields of curves over 
$k$, of genera 
$g$, 
$g_{1}$, 
$g_{2}$, respectively. Suppose that 
$F_{i}\subseteq F$ for 
$i=1,2$ and the compositum of 
$F_{1}$ and 
$F_{2}$ in 
$F$ equals 
$F$. Let 
$d_{i}=[F:F_{i}]$ for 
$i=1,2$. Then
$$\begin{eqnarray}g\leqslant d_{1}g_{1}+d_{2}g_{2}+(d_{1}-1)(d_{2}-1).\end{eqnarray}$$Proof. See [Reference StichtenothSti09, Theorem 3.11.3]. ◻
Proof of Theorem 1.4.
Let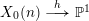 
$X_{0}(n)\stackrel{h}{\longrightarrow }\mathbb{P}^{1}$ be a dominant rational map of minimal degree.
Case I: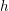 
$h$factors through 
$X_{0}(n)\stackrel{c}{\longrightarrow }\mathbb{P}^{1}$. Then
$$\begin{eqnarray}\deg h\geqslant D_{0}(n)=(1+o(1))\frac{d^{n}}{n}\end{eqnarray}$$ by Proposition 3.1(b), so 
$\deg h$ is much larger than 
$n$ when 
$n$ is large.
Case II: 
$h$does not factor through 
$X_{0}(n)\stackrel{c}{\longrightarrow }\mathbb{P}^{1}$. Then the compositum of 
$k(c)$ and 
$k(h)$ in the function field 
$k(X_{0}(n))$ is strictly larger than 
$k(c)$. Because of the Galois group (Proposition 3.1(d)), the only nontrivial extension of 
$k(c)$ in 
$k(X_{0}(n))$ is the whole field 
$k(X_{0}(n))$. Thus 
$k(c)$ and 
$k(h)$ generate 
$k(X_{0}(n))$. By Proposition 3.2,
$$\begin{eqnarray}g(X_{0}(n))\leqslant (D_{0}(n)-1)(\deg h-1).\end{eqnarray}$$Thus
$$\begin{eqnarray}\deg h\geqslant 1+\frac{g(X_{0}(n))}{D_{0}(n)-1}=\biggl(\frac{1}{2}-\frac{1}{2d}-o(1)\biggr)n\end{eqnarray}$$
The following lemma, which says in particular that 
$Y_{1}(m,n)^{\unicode[STIX]{x1D701}}\stackrel{z}{\rightarrow }\mathbb{A}^{1}$ is étale above 
$0$, will yield genus inequalities to combine with the Castelnuovo–Severi inequality in the proof of Theorem 1.1.
Lemma 3.3. Let 
$k$ be a field of characteristic 
$0$ such that 
$\unicode[STIX]{x1D707}_{d}\subseteq k$. Let 
$m$ and 
$n$ be positive integers, and let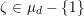 
$\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{d}-\{1\}$. Then the polynomial 
$\unicode[STIX]{x1D6F7}_{n}(\unicode[STIX]{x1D701}^{-1}f^{m-1}(0),c)\in k[c]$ has only simple roots, and their number is 
$d^{m-2}D_{1}(n)$ if 
$m\geqslant 2$.
Proof. First suppose that 
$n$ does not divide 
$m-1$. In this case, the roots of 
$\unicode[STIX]{x1D6F7}_{m,n}(0,c)$ are distinct by [Reference Hutz and TowsleyHT15, Theorem 1.1], and therefore the roots of 
$\unicode[STIX]{x1D6F7}_{n}(\unicode[STIX]{x1D701}^{-1}f^{m-1}(0),c)$ are distinct by (3).
Now suppose that 
$n$ divides 
$m-1$. By [Reference EpsteinEps12, Proposition A.1], the roots of 
$\unicode[STIX]{x1D6F7}_{n}(0,c)$ are simple. If 
$c$ is such a root, then the polynomial 
$f=f_{c}$ satisfies 
$f^{n}(0)=0$, so 
$f^{m-1}(0)=0$ and 
$\unicode[STIX]{x1D6F7}_{n}(\unicode[STIX]{x1D701}^{-1}f^{m-1}(0),c)=0$. Thus 
$\unicode[STIX]{x1D6F7}_{n}(0,c)$ divides 
$\unicode[STIX]{x1D6F7}_{n}(\unicode[STIX]{x1D701}^{-1}f^{m-1}(0),c)$. The factorization (3) yields
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D6F7}_{m,n}(0,c)}{\unicode[STIX]{x1D6F7}_{n}(0,c)^{d-1}}=\mathop{\prod }_{\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{d}-\{1\}}\frac{\unicode[STIX]{x1D6F7}_{n}(\unicode[STIX]{x1D701}^{-1}f^{m-1}(0),c)}{\unicode[STIX]{x1D6F7}_{n}(0,c)}.\end{eqnarray}$$ By [Reference Hutz and TowsleyHT15, Theorem 1.1], 
$\unicode[STIX]{x1D6F7}_{m,n}(0,c)/\unicode[STIX]{x1D6F7}_{n}(0,c)^{d-1}$ has only simple roots, none of which are also roots of 
$\unicode[STIX]{x1D6F7}_{n}(0,c)$. Combining this with (4) shows that 
$\unicode[STIX]{x1D6F7}_{n}(\unicode[STIX]{x1D701}^{-1}f^{m-1}(0),c)$ has only simple roots.
It remains to prove 
$\deg \unicode[STIX]{x1D6F7}_{n}(\unicode[STIX]{x1D701}^{-1}f^{m-1}(0),c)=d^{m-2}D_{1}(n)$. In fact, this is [Reference GaoGao16, Lemma 4.8]. In our notation, the argument is as follows. By induction on 
$m$, the degree of the polynomial 
$f^{m-1}(0)\in k[c]$ is 
$d^{m-2}$ if 
$m\geqslant 2$. Hence, by induction on 
$e$, we have 
$\deg f^{e}(\unicode[STIX]{x1D701}^{-1}f^{m-1}(0))=d^{e}d^{m-2}$ for each 
$e\geqslant 0$. Thus the 
$c$-degree of 
$f^{e}(\unicode[STIX]{x1D701}^{-1}f^{m-1}(0))-\unicode[STIX]{x1D701}^{-1}f^{m-1}(0)$ is 
$d^{m-2}$ times the 
$z$-degree of 
$f^{e}(z)-z$ for each 
$e\geqslant 1$. Substituting 
$\unicode[STIX]{x1D701}^{-1}f^{m-1}(0)$ for 
$z$ in (1) shows that
$$\begin{eqnarray}\deg _{c}\unicode[STIX]{x1D6F7}_{n}(\unicode[STIX]{x1D701}^{-1}f^{m-1}(0),c)=d^{m-2}\deg _{z}\unicode[STIX]{x1D6F7}_{n}(z,c)=d^{m-2}D_{1}(n).\end{eqnarray}$$◻
Proof of Theorem 1.1 in characteristic $0$.
(a) By Theorem 2.1, the dynatomic curves over 
$k$ are the curves 
$Y_{1}(n)$ and 
$Y_{1}(m,n)^{\unicode[STIX]{x1D701}}$, and they are geometrically irreducible.
(b) The curves 
$Y_{1}(n)$ and 
$Y_{1}(m,n)^{\unicode[STIX]{x1D701}}$ dominate 
$X_{0}(n)$, so their gonalities are at least the gonality of 
$X_{0}(n)$, by [Reference PoonenPoo07, Proposition A.1(vii)]. In light of Theorem 1.4, it remains to prove that in each tower
$$\begin{eqnarray}\cdots \longrightarrow Y_{1}(m,n)^{\unicode[STIX]{x1D701}}\longrightarrow Y_{1}(m-1,n)^{\unicode[STIX]{x1D701}}\longrightarrow \cdots \longrightarrow Y_{1}(1,n)^{\unicode[STIX]{x1D701}}\end{eqnarray}$$ for fixed 
$n$ and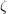 
$\unicode[STIX]{x1D701}$, the gonality tends to 
$\infty$ as 
$m\rightarrow \infty$.
Let 
$g_{m}=g(Y_{1}(m,n)^{\unicode[STIX]{x1D701}})$ and 
$\unicode[STIX]{x1D6FE}_{m}=\unicode[STIX]{x1D6FE}(Y_{1}(m,n)^{\unicode[STIX]{x1D701}})$. Let 
$Y_{1}(m,n)^{\unicode[STIX]{x1D701}}\stackrel{h}{\longrightarrow }\mathbb{P}^{1}$ be a dominant rational map of the minimal degree 
$\unicode[STIX]{x1D6FE}_{m}$.
Case I: 
$h$factors through a curve 
$Z$with 
$k(Y_{1}(m-1,n)^{\unicode[STIX]{x1D701}})\subseteq k(Z)\subsetneq k(Y_{1}(m,n)^{\unicode[STIX]{x1D701}})$. These inclusions imply 
$\unicode[STIX]{x1D6FE}_{m-1}\leqslant \unicode[STIX]{x1D6FE}(Z)$ (by [Reference PoonenPoo07, Proposition A.1(vii)]) and 
$2\unicode[STIX]{x1D6FE}(Z)\leqslant \deg h=\unicode[STIX]{x1D6FE}_{m}$, respectively. Combining these yields 
$\unicode[STIX]{x1D6FE}_{m}\geqslant 2\unicode[STIX]{x1D6FE}_{m-1}$. Thus 
$\unicode[STIX]{x1D6FE}_{m}$ grows, by induction on 
$m$.
Case II: 
$h$does not factor through any such curve 
$Z$. Denote by 
$\unicode[STIX]{x1D70B}_{m}$ the degree-
$d$ map
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{m}:Y_{1}(m,n)^{\unicode[STIX]{x1D701}} & \longrightarrow & \displaystyle Y_{1}(m-1,n)^{\unicode[STIX]{x1D701}}\nonumber\\ \displaystyle (z,c) & \longmapsto & \displaystyle (f(z),c),\nonumber\end{eqnarray}$$ and let 
$\widetilde{\unicode[STIX]{x1D70B}}_{m}:X_{1}(m,n)^{\unicode[STIX]{x1D701}}\rightarrow X_{1}(m-1,n)^{\unicode[STIX]{x1D701}}$ be its extension to the smooth projective models. Let 
$R_{m}$ be the ramification divisor of 
$\widetilde{\unicode[STIX]{x1D70B}}_{m}$.
Applying Proposition 3.2 to 
$\unicode[STIX]{x1D70B}_{m}$ and 
$h$ yields
$$\begin{eqnarray}g_{m}\leqslant dg_{m-1}+(d-1)(\unicode[STIX]{x1D6FE}_{m}-1),\end{eqnarray}$$ so it suffices to show that 
$g_{m}-dg_{m-1}\rightarrow \infty$ as 
$m\rightarrow \infty$. By Riemann–Hurwitz, this is equivalent to showing that 
$\deg R_{m}\rightarrow \infty$ as 
$m\rightarrow \infty$. In the fiber product diagram
both vertical morphisms are étale above 
$0$ by Lemma 3.3, while 
$f$ has ramification index 
$d$ at 
$0$, so 
$\widetilde{\unicode[STIX]{x1D70B}}^{m}$ has ramification index 
$d$ at each point of 
$Y_{1}(m,n)^{\unicode[STIX]{x1D701}}$ where 
$z=0$. For 
$m\geqslant 2$, the number of such points is 
$d^{m-2}D_{1}(n)$ by Lemma 3.3. Thus 
$\deg R_{m}\geqslant (d-1)d^{m-2}D_{1}(n)$, which tends to 
$\infty$ as 
$m\rightarrow \infty$.◻
4 Gonality in characteristic $p$
4.1 Reduction to the case of a finite field
Let 
$\mathbb{F}_{q}=\mathbb{F}_{p}(\unicode[STIX]{x1D707}_{d})$.
Lemma 4.1. Theorem 1.1 for 
$\mathbb{F}_{q}$ implies Theorem 1.1 for any characteristic 
$p$ field 
$k$ containing 
$\unicode[STIX]{x1D707}_{d}$.
Proof. Theorem 1.1(a) for 
$\mathbb{F}_{q}$ implies that the dynatomic curves over 
$k$ are just the base extensions of the dynatomic curves 
$X$ over 
$\mathbb{F}_{q}$, and that they are geometrically irreducible too. We will prove in § 4.4 that the smooth projective model of each 
$X$ has an 
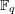$\mathbb{F}_{q}$-point. Then [Reference PoonenPoo07, Theorem 2.5(iii) and Proposition A.1(ii)] imply 
$\unicode[STIX]{x1D6FE}(X_{k})\geqslant \sqrt{\unicode[STIX]{x1D6FE}(X)}$, which implies Theorem 1.1(b) for 
$k$.◻
4.2 Symbolic dynamics
In order to prove the finiteness of the set of dynatomic curves of bounded degree over the 
$c$-line, and to prove that the dynatomic curves of higher degree have many 
$\mathbb{F}_{q}$-points above 
$c=\infty$, we need to analyze the splitting above 
$c=\infty$ in dynatomic curves. This splitting is given in Lemma 4.2 below. The symbolic dynamics approach yielding Lemma 4.2 is standard (cf. [Reference MortonMor96, Lemma 1]), but the ways that Lemma 4.2 will be applied in subsequent sections are not standard.
View 
$f(z)$ as a polynomial in 
$z$ over the local field 
$\mathbb{F}_{q}((c^{-1}))$. Normalize the valuation 
$v$ on 
$\mathbb{F}_{q}((c^{-1}))$ so that 
$v(c^{-1})=1$, and extend 
$v$ to an algebraic closure. Let 
$t=c^{-1/d}$, so 
$\mathbb{F}_{q}((t))$ is a totally tamely ramified extension of 
$\mathbb{F}_{q}((c^{-1}))$ of degree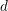 
$d$.
(a) For any nonnegative integers
$n>m$, the polynomial $f^{n}(z)-f^{m}(z)$ over $\mathbb{F}_{q}(c)$ is separable and splits completely over $\mathbb{F}_{q}((t))$.(b) Each zero of
$f^{n}(z)-f^{m}(z)$ has valuation $-1/d$ and generates $\mathbb{F}_{q}((t))$ over $\mathbb{F}_{q}((c^{-1}))$.
Proof. The ideas in the following argument are well known; cf. [Reference MortonMor96, Lemma 1].
(a) For each 
$d$th root of 
$-c$, interpreting 
$(-c+z)^{1/d}$ as 
$(-c)^{1/d}(1-c^{-1}z)^{1/d}$ and expanding 
$(1-c^{-1}z)^{1/d}$ in a binomial series defines a branch of the inverse of 
$z^{d}+c$ on the open disk 
$D:=\{z\in \mathbb{F}_{q}((t)):v(z)>v(c)\}$. Taking the derivative of 
$(-c+z)^{1/d}$ shows that each branch is a contracting map 
$D\rightarrow D$. These branches have disjoint images, each a smaller open disk around a different 
$d$th root of 
$-c$. Let 
$S$ be the set of these 
$d$ functions. Each finite sequence of elements of 
$S$ defines a composition of functions, and for each 
$m$, the images of the different 
$m$-fold compositions are disjoint open disks. For each infinite sequence 
$s_{1},s_{2},\ldots$ of elements of 
$S$, the images of 
$s_{1}\cdots s_{m}$ for 
$m\geqslant 1$ are nested open disks whose radii tend to 
$0$, so they have a unique point in their intersection; denote it 
$[s_{1}s_{2}\cdots \,]$. Any two distinct infinite sequences yield two points in disjoint disks, so these points are distinct. Since 
$f\circ s_{1}$ is the identity, 
$f$ maps 
$[s_{1}s_{2}\cdots \,]$ to 
$[s_{2}s_{3}\cdots \,]$. For fixed nonnegative integers 
$n>m$, any 
$n$-long sequence 
$s_{1},\ldots ,s_{n}$ in 
$S$ extends uniquely to an infinite sequence 
$(s_{i})$ satisfying 
$s_{i+n}=s_{i+m}$ for all 
$i\geqslant 1$, and then 
$[s_{1}s_{2}\cdots \,]$ is a zero of 
$f^{n}(z)-f^{m}(z)$. There are 
$d^{n}$ of these, so they are all the zeros. In particular, these zeros are distinct elements of 
$\mathbb{F}_{q}((t))$. This implies that 
$f^{n}(z)-f^{m}(z)$ is separable.
(b) The image of each 
$s\in S$ consists of elements of valuation exactly 
$-1/d$. Thus each element 
$[s_{1}s_{2}\cdots \,]$ has valuation 
$-1/d$. In particular, each zero of 
$f^{n}(z)-f^{m}(z)$ generates an extension field of 
$\mathbb{F}_{q}((c^{-1}))$ of ramification index divisible by 
$d$; this extension field can only be the whole field 
$\mathbb{F}_{q}((t))$.◻
4.3 Dynatomic curves of low degree
It is here that we use the trick requiring the ground field to be finite.
Lemma 4.3. For each 
$e\geqslant 1$, the set of dynatomic curves 
$X$ over 
$\mathbb{F}_{q}$ such that 
$\deg (X\stackrel{c}{\rightarrow }\mathbb{P}^{1})=e$ is finite.
Proof. Suppose that 
$Q(z)=\sum _{r=0}^{e}q_{r}z^{e-r}$ is a monic degree-
$e$ factor of 
$f^{n}(z)-f^{m}(z)$ over 
$\mathbb{F}_{q}(c)$ for some 
$n$ and 
$m$. For each 
$r$, the coefficient 
$q_{r}$ is the 
$r$th elementary symmetric polynomial evaluated at the negatives of the zeros of 
$Q$; those zeros have valuation 
$-1/d$ by Lemma 4.2(b), so 
$v(q_{r})\geqslant -r/d$. On the other hand, by Gauss’s lemma, 
$q_{r}\in \mathbb{F}_{q}[c]$, so 
$\deg q_{r}\leqslant r/d$. Thus there are only finitely many possibilities for each 
$q_{r}$, and hence finitely many possibilities for 
$Q$, each of which yields one dynatomic curve.◻
4.4 Gonality of dynatomic curves
Proof of Theorem 1.1.
By Lemma 4.1, we may assume that 
$k=\mathbb{F}_{q}$.
(a) Let 
$X$ be the smooth projective model of a dynatomic curve, corresponding to a factor of 
$f^{n}(z)-f^{m}(z)$ for some 
$n$ and 
$m$. By Lemma 4.2(b), 
$f^{n}(z)-f^{m}(z)$ splits completely over 
$\mathbb{F}_{q}((t))$, and the preimage of 
$\infty$ under 
$X\stackrel{c}{\rightarrow }\mathbb{P}^{1}$ consists of 
$\mathbb{F}_{q}$-points, each of ramification index 
$d$. Every irreducible component 
$Z$ of 
$X_{\overline{\mathbb{F}}_{q}}$ dominates 
$\mathbb{P}^{1}$ via 
$c$ and hence must contain one of those 
$\mathbb{F}_{q}$-points, say 
$x$. Then each 
$\operatorname{Gal}(\overline{\mathbb{F}}_{q}/\mathbb{F}_{q})$-conjugate of 
$Z$ contains 
$x$. On the other hand, since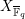 
$X_{\overline{\mathbb{F}}_{q}}$ is smooth, its irreducible components are disjoint. Thus 
$Z$ equals each of its conjugates, so 
$Z$ descends to an irreducible component of 
$X$, which must be 
$X$ itself. (This proves also that 
$X$ has an 
$\mathbb{F}_{q}$-point, as promised in the proof of Lemma 4.1.)
(b) To bound gonality from below, we use Ogg’s method of counting points over a finite field; cf. [Reference OggOgg74], [Reference PoonenPoo07, § 3], and [Reference Doyle, Krieger, Obus, Pries, Rubinstein-Salzedo and WestDKO+19, § 4]. Let 
$X$ be the smooth projective model of a dynatomic curve. Let 
$e=\deg (X\stackrel{c}{\rightarrow }\mathbb{P}^{1})$. Each preimage of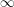 
$\infty$ in 
$X$ is an 
$\mathbb{F}_{q}$-point of ramification index 
$d$, so there are 
$e/d$ such points. On the other hand, 
$\mathbb{P}^{1}$ has only 
$q+1$ points over 
$\mathbb{F}_{q}$, so any nonconstant morphism 
$X\rightarrow \mathbb{P}^{1}$ has degree at least 
$e/(d(q+1))$. As 
$X$ varies, 
$e\rightarrow \infty$ by Lemma 4.3.◻
5 Strong uniform boundedness of preperiodic points
Proof of Theorem 1.7.
Without loss of generality, 
$K=k(u)$ for some indeterminate 
$u$. Given 
$L$, let 
$Y$ be the smooth projective integral curve over 
$k$ with function field 
$L$. The condition 
$[L:K]\leqslant D$ implies that 
$Y$ has gonality at most 
$D$, so each irreducible component of 
$Y_{\overline{k}}$ has gonality at most 
$D$. For 
$c\in L$ not algebraic over 
$k$, if 
$z\in L$ and 
$n>m$ satisfy 
$f^{n}(z)-f^{m}(z)=0$, then 
$(z,c)$ is a nonconstant and hence smooth 
$L$-point of the curve 
$f^{n}(z)-f^{m}(z)=0$ in 
$\mathbb{A}^{2}$, so it yields an 
$L$-point on a dynatomic curve 
$X$ corresponding to a factor of 
$f^{n}(z)-f^{m}(z)$. This 
$L$-point defines a nonconstant 
$k$-morphism 
$Y\rightarrow X$, so 
$\unicode[STIX]{x1D6FE}(X)\leqslant \unicode[STIX]{x1D6FE}(Y)\leqslant D$. By Theorem 1.1(b), this places a uniform bound on 
$n$. For each 
$n$, the number of preperiodic points of 
$z^{d}+c$ corresponding to that value of 
$n$ is uniformly bounded by 
$\sum _{m=0}^{n-1}\deg (f^{n}(z)-f^{m}(z))=nd^{n}$, so bounding 
$n$ bounds the number of preperiodic points too.
If 
$k$ is finite and 
$c$ lies in the maximal algebraic extension 
$\ell$ of 
$k$ in 
$L$, then all the preperiodic points of 
$z^{d}+c$ in 
$L$ are in 
$\ell$, but 
$[\ell :k]\leqslant D$, so the number of preperiodic points is uniformly bounded by 
$(\#k)^{D}$.◻
To prove Theorem 1.10, we need the following result of Frey [Reference FreyFre94, Proposition 2], which in turn relies on Faltings’s theorems on rational points on subvarieties of abelian varieties.
Lemma 5.1. Let 
$C$ be a curve defined over a number field 
$K$. Let 
$D\geqslant 1$. If there are infinitely many points 
$P\in C(\overline{K})$ of degree 
${\leqslant}D$ over 
$K$, then 
$\unicode[STIX]{x1D6FE}(C)\leqslant 2D$.
Proof of Theorem 1.10.
For each 
$(m,n)$, let 
$S_{m,n}$ be the set of 
$(z_{0},c)\in \overline{\mathbb{Q}}\times \overline{\mathbb{Q}}$ such that 
$z_{0}$ and 
$c$ belong to some number field 
$K$ of degree 
${\leqslant}D$, and iteration of 
$z^{d}+c$ maps 
$z_{0}$ into a cycle of length exactly 
$n$ after exactly 
$m$ steps; thus 
$S_{m,n}\subseteq Y_{1}(m,n)(\overline{\mathbb{Q}})$. Suppose that the conclusion fails; then, for some 
$n\leqslant N$, there exist infinitely many 
$m\geqslant 1$ for which 
$S_{m,n}$ is nonempty. Fix such an 
$n$.
Let 
$m_{0}\geqslant 1$. By choice of 
$n$, the disjoint union 
$\coprod _{m\geqslant m_{0}}S_{m,n}$ is infinite. For each 
$m\geqslant m_{0}$, the 
$c$-coordinate map 
$Y_{1}(m,n)\rightarrow \mathbb{A}^{1}$ factors through 
$Y_{1}(m_{0},n)$, so we obtain maps of sets
$$\begin{eqnarray}\coprod _{m\geqslant m_{0}}S_{m,n}\longrightarrow S_{m_{0},n}\longrightarrow \overline{\mathbb{Q}}.\end{eqnarray}$$ On the other hand, by Northcott’s theorem [Reference NorthcottNor50, Theorem 3], for any given 
$c\in \overline{\mathbb{Q}}$, the set of preperiodic points of 
$z^{d}+c$ of degree 
${\leqslant}D$ over 
$\mathbb{Q}$ is finite; thus each 
$c\in \overline{\mathbb{Q}}$ has finite preimage under the composition (5). Hence the image of (5) is infinite, so 
$S_{m_{0},n}$ is infinite. Thus some 
$\mathbb{Q}(\unicode[STIX]{x1D707}_{d})$-irreducible component 
$Y_{1}(m_{0},n)^{\unicode[STIX]{x1D701}}$ of 
$Y_{1}(m_{0},n)$ contains infinitely many points of degree 
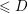${\leqslant}D$ over 
$\mathbb{Q}(\unicode[STIX]{x1D707}_{d})$. By Lemma 5.1, 
$\unicode[STIX]{x1D6FE}(Y_{1}(m_{0},n)^{\unicode[STIX]{x1D701}})\leqslant 2D$.
The previous paragraph applies for every integer 
$m_{0}\geqslant 1$, contradicting Theorem 1.1(b).◻
Acknowledgements
We thank Joseph Gunther, Holly Krieger, Andrew Obus, Padmavathi Srinivasan, Isabel Vogt, Robin Zhang, and anonymous referees for comments and discussions. Some of the initial ideas for an approach arose while the second author was participating in the American Institute of Mathematics workshop ‘The Uniform Boundedness Conjecture in Arithmetic Dynamics’ organized by Robert Benedetto, Liang-Chung Hsia, and Joseph H. Silverman, January 14–18, 2008, but the key ideas, especially those for getting around our ignorance regarding the irreducibility of dynatomic curves in characteristic 
$p$, were worked out in 2017, in response to some questions from Holly Krieger.
