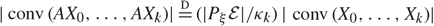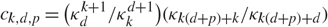1. Main results
1.1. Basic notation
First we introduce some basic notion of integral geometry following [Reference Schneider and Weil17]. The Euclidean space ℝd is equipped with the Euclidean scalar product ‹·, ·›. The volume is denoted by | · |. Some of the sets we consider have dimension less than d. In fact, we consider three classes: the convex hulls of k + 1 points, orthogonal projections to k-dimensinal linear subspaces, and intersections with k-dimensional affine subspaces, where k ∈ {0, …, d}. In this case, | · | stands for the k-dimensional volume.
The unit ball in ℝk is denoted by 
$\mathbb B^k$
. For p > 0, we write
\begin{align}\kappa_p\,:\!=\frac{\pi^{p/2}}{\Gamma (\kern1.5pt p/2+1)},\end{align}
where, for an integer k, we have 
$\kappa_k=|\mathbb B^k|$
.
For k ∈ {0, …, d}, the linear (respectively affine) Grassmannian of k-dimensional linear (respectively affine) subspaces of ℝd is denoted by Gd,k (respectively Ad,k) and is equipped with a unique rotation invariant (respectively rigid motion invariant) Haar measure νd,k (respectively μd,k), normalized by
\begin{align*}\nu_{d,k}(G_{d,k})=1\end{align*}
and
\begin{align*}\mu_{d,k}\left(\left\{E\in A_{d,k}\colon E\cap \mathbb B^d\ne\emptyset\right\}\right)=\kappa_{d-k},\end{align*}
respectively.
A compact convex subset K of ℝd with nonempty interior is called a convex body. We define the intrinsic volumes of K by Kubota’s formula,
\begin{align}V_k(K)={d \choose k}\,\frac{\kappa_d}{\kappa_k\kappa_{d-k}}\int_{G_{d,k}}|P_LK|\nu_{d,k}(\ dL),\end{align}
where PLK denotes the image of K under the orthogonal projection to L.
For L ∈ Gd,k (respectively E ∈ Ad,k), we denote by λL (respectively λE) the k-dimensional Lebesgue measures on L (respectively E).
1.2. Affine transformation of spherically symmetric distribution
For a fixed k ∈ {1, …, d}, consider random vectors X 0, …, Xk ∈ ℝd (not necessarily independent and identically distributed (i.i.d.)) with an arbitrary spherically symmetric joint distribution. By this we mean that the (k + 1)-tuple (UX 0, …, UXk) has the same distribution for any orthogonal d × d matrix U. The convex hull
\begin{align*}{\rm{conv(}}X_0,\dots,X_{k})\end{align*}
is a k-dimensional simplex (maybe degenerate) with well-defined k-dimensional volume
\begin{align}|{\rm{conv(}}X_0,\dots,X_{k})|.\end{align}
How does the volume in (1.3) change under affine transformations? For k = d, the answer is obvious: it is multiplied by the determinant of the transformation. The k < d case presents a more delicate problem.
Theorem 1.1. Let A be any nonsingular d × d matrix, and let ɛ be the ellipsoid defined by
\[\varepsilon : = \left\{ {x \in {\mathbb R^d}:{x^{\rm{T}}}{{({A^{\rm{T}}}A)}^{ - 1}}x \le 1} \right\}.\]
Then we have
\[|{\rm{conv(}}A{X_0}{\rm{,}} \ldots {\rm{,}}A{X_k}{\rm{)|}}\mathop {\rm{ = }}\limits^{\rm{D}} \frac{{|{P_\xi }\varepsilon }}{{{\kappa _k}}}|{\rm{conv(}}{X_{\rm{0}}}{\rm{,}} \ldots {\rm{,}}{X_k}{\rm{),}}\]
where Pξ denotes the orthogonal projection to a uniformly chosen random k-dimensional linear subspace ξ independent of X 0, …, Xk.
Due to Kubota’s formula (see (1.2)), 
$\mathbb E[|{P_\xi} \varepsilon|]$
is proportional to Vk(ɛ). Thus, taking the expectation in (1.5) and using the formula
\begin{align*}V_k\big(\mathbb B^d\big)={d \choose k}\frac{\kappa_d}{\kappa_{d-k}}\end{align*}
readily implies the following corollary.
Corollary 1.1. Under the assumptions of Theorem 1.1, we have
\begin{align}\mathbb E|{\rm{conv(}}AX_0,\dots,AX_{k})|={\frac{V_k(\varepsilon)}{V_k\big(\mathbb B^d\big)}}\mathbb E|{\rm{conv(}}X_0,\dots,X_{k})|.\end{align}
For a formula of Vk(ɛ), see [Reference Kabluchko and Zaporozhets11]. Relation (1.6) can be generalized to higher moments using the notion of generalized intrinsic volumes introduced in [Reference Dafnis and Paouris4], but we shall skip to describing details here.
The main ingredient of the proof of Theorem 1.1 is the following deterministic version of (1.5).
Proposition 1.1. Let A and ɛ be as in Theorem 1.1. Consider x1, …, xk ∈ ℝd and denote by L their span (linear hull). Then
\begin{align}|{\rm{conv (0, }}A{x_{\rm{1}}}{\rm{,}} \ldots {\rm{,}}A{x_k}{\rm{)| = }}\frac{{|{P_L}\varepsilon |}}{{{\kappa _k}}}|{\rm{conv(0, }}{x_{\rm{1}}}{\rm{,}} \ldots {\rm{, }}{x_{\rm{k}}}{\rm{)|}}{\rm{.}}\end{align}
Let us stress that here the origin is added to the convex hull.
Applying (1.7) to standard Gaussian vectors (details are in Section 2.3) leads to the following representation.
Corollary 1.2. Under the assumptions of Theorem 1.1, we have
\[\frac{{|{P_\xi }\varepsilon |}}{{{\kappa _k}}}\mathop = \limits^{\rm{D}} {\left( {\frac{{\det ({G^{\rm{T}}}{A^{\rm{T}}}AG)}}{{\det ({G^{\rm{T}}}G)}}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right.} 2}}}\mathop = \limits^{\rm{D}} {\left( {\frac{{\det (G_{^\lambda }^T{G_\lambda })}}{{\det ({G^{\rm{T}}}G)}}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right.} 2}}},\]
where G is a random d × k matrix with i.i.d. standard Gaussian entries Nij and Gλ is a random d × k matrix with the entries λiNij, where λ 1, …, λd denote the singular values of A.
Thus, we obtain the following version of (1.5).
Corollary 1.3. Under the assumptions of Theorem 1.1 and Corollary 1.2, we have
\[\begin{array}{*{20}{c}} {|{\rm{conv(}}A{X_0}{\rm{,}} \ldots {\rm{,}}A{X_k}{\rm{)|}}} \hfill & {\mathop = \limits^{\rm{D}} } \hfill & {{{\left( {\frac{{\det ({G^{\rm{T}}}{A^{\rm{T}}}AG)}}{{\det ({G^{\rm{T}}}G)}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right.} 2}}}|{\rm{conv(}}{X_0}{\rm{,}} \ldots {\rm{,}}{X_k}{\rm{)|}}} \hfill \\ {} \hfill & {\mathop = \limits^{\rm{D}} } \hfill & {{{\left( {\frac{{\det (G_{^\lambda }^T{G_\lambda })}}{{\det ({G^{\rm{T}}}G)}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right.} 2}}}|{\rm{conv(}}{X_0}{\rm{,}} \ldots {\rm{,}}{X_k}{\rm{)|}}} \hfill \\\end{array}\]
The important special case k = 1 corresponds to the distance between two random points.
Corollary 1.4. Under the assumptions of Theorem 1.1, we have
\[|A{X_0} - A{X_1}|\mathop = \limits^{\rm{D}} \sqrt {\frac{{\lambda _1^2N_1^2 + \cdots + \lambda _d^2N_d^2}}{{N_1^2 + \cdots + N_d^2}}} |{X_0} - {X_1}|,\]
where N 1, …, Nd are i.i.d. standard Gaussian variables and λ 1, …, λd denote the singular values of A.
1.3 Random points in ellipsoids
Now suppose that X 0, …, X k are independent and uniformly distributed in some convex body K ⊂ ℝd. A classical problem of stochastic geometry is to find the distribution of (1.3) starting with its moments
$$\mathbb E|{\rm{conv(}}{X_{\rm{0}}}{\rm{,}} \ldots {\rm{,}}{X_{\rm{k}}}{\rm{)}}{{\rm{|}}^p} = \frac{1}{{|K{|^{k + 1}}}}|{\rm{conv(}}{x_{\rm{0}}}{\rm{,}} \ldots {x_k}{\rm{)}}{{\rm{|}}^p}{\rm{d}}{x_{\rm{0}}}{\rm{,}} \ldots {\rm{d}}{x_k}.$$
The most studied case is d = 2, k = p = 1, when the problem reduces to calculating the mean distance between two uniformly chosen random points in a planar convex set (see [Reference Bäsel1], [Reference Borel2], [Reference Ghosh6], [Reference Mathai13, Chapter 2], and [Reference Santaló16, Chapter 4]).
For an arbitrary d and k = 1, there is an electromagnetic interpretation of (1.9) (see [Reference Hansen and Reitzner8]): a transmitter X 0 and a receiver X 1 are placed uniformly at random in K. It is empirically known that the power received decreases with an inverse distance law of the form 1/|X 0 - X 1|α, where α is the so-called path-loss exponent, which depends on the environment in which both are located (see [Reference Rappaport, Annamalai, Buehrer and Tranter15]). Thus, with k = 1 and p = -nα, (1.9) expresses the nth moment of the power received (n < d/α).
The case of arbitrary k and d was studied only for K being a ball. In [Reference Miles14] it was shown (see also [Reference Schneider and Weil17, Theorem 8.2.3]) that, for X 0, …, Xk uniformly distributed in the unit ball 
$\mathbb B^d\subset\mathbb R^d$
and for an integer p ≥ 0,
\begin{align}\mathbb E|{\rm{conv(}}X_0,\dots,X_{k})|^{\kern.5pt p}={\frac{1}{(k\hbox{{!}})^{p}}\frac{\kappa_{d+p}^{k+1}}{\kappa_{d}^{k+1}}\frac{\kappa_{k(d+p)+d}}{\kappa_{(k+1)(d+p)}} \frac{b_{d,k}}{b_{d+p,k}}},\end{align}
where κk is defined in (1.1) and for any real number q > k – 1 we write (see [Reference Schneider and Weil17, Equation (7.8)])
\begin{align}b_{q,k}\,:\!=\frac{\omega_{q-k+1}\cdots\omega_{q}}{\omega_1\cdots\omega_k},\end{align}
with ωp := pκp being equal to the area of the unit (p – 1)-dimensional sphere when p is integer.
In [Reference Kabluchko, Temesvari and Thäle10, Proposition 2.8] this relation was extended to all real p > – 1. It should be noted that Proposition 2.8 of [Reference Kabluchko, Temesvari and Thäle10] is formulated for real p ≥ 0 only, but in the proof (see p. 23) it is argued that by analytic continuation, the formula holds for all real p > -1 as well. Theorem 1.1 implies (for details see Section 2.4) the following generalization of (1.10) for ellipsoids. Recall that Pξ denotes the orthogonal projection to a uniformly chosen random k-dimensional linear subspace ξ independent of X 0, …, Xk.
Theorem 1.2. For X 0, …, Xk uniformly distributed in some nondegenerate ellipsoid ɛ ⊂ ℝd and any real number p > −1, we have
$$ \mathbb E|{\rm{conv (}}{X_0}{\rm{,}} \ldots {X_k}{\rm{)}}{{\rm{|}}^p} = \frac{1}{{(k!)p}}\frac{{\kappa _{d + p}^{k + 1}}}{{\kappa _d^{k + 1}}}\frac{{{\kappa _{k(d + p) + d}}}}{{{\kappa _{(k + 1) + (d + p)}}}}\frac{{{b_{d,k}}}}{{{b_{d + p,k}}}}\frac{{\mathbb E|{P_\xi }\varepsilon {|^p}}}{{\kappa _k^p}}.$$
Note that (1.12) is indeed a generalization of (1.10) since 
$P_\xi\mathbb B^d=\mathbb B^k$
a.s. and 
$|\mathbb B^k|^{\kern.5pt p}=\kappa_{k}^{\kern.5pt p}$
. For k = 1, (1.12) was recently obtained in [Reference Heinrich9].
For p = 1, the right-hand side of (1.12) is proportional to the kth intrinsic volume of ɛ (see (1.2)), which implies the following result (for details, see Section 2.5).
Corollary 1.5. For X 0, …, Xk uniformly distributed in some nondegenerate ellipsoid ɛ ⊂ ℝd, we have
\begin{align*}\mathbb E|{\rm{conv(}}X_0,\dots,X_{k})|=\frac{1}{2^k}\,\frac{((d+1)\hbox{{!}})^{k+1}}{((d+1)(k+1))\hbox{{!}}}\,\left(\frac{\kappa_{d+1}^{k+1}}{\kappa_{(d+1)(k+1)}}\right)^2\,V_k(\varepsilon).\end{align*}
Very recently, for X 0, …, Xk uniformly distributed in the unit ball 
$\mathbb B^d$
, the formula for the distribution of | conv (X 0, …, Xk)| has been derived in [Reference Grote, Kabluchko and Thäle7]. For a random variable η and α 1, α 2 > 0, we write η ~ B(α 1, α 2) to denote that η has a beta distribution with parameters α 1, α 2 and the density
\begin{align*}\frac{\Gamma(\alpha_1+\alpha_2)}{\Gamma(\alpha_1)\Gamma(\alpha_2)}t^{\alpha_1-1}\,(1-t)^{\alpha_2-1}, \qquad t\in(0,1).\end{align*}
It was shown in [Reference Grote, Kabluchko and Thäle7] that, for X 0, …, Xk uniformly distributed in $\mathbb B^d$
,
\begin{align}(k\hbox{{!}})^2\,\eta(1-\eta)^k\,|{\rm{conv(}}X_0,\dots,X_k)|^2 \mathop = \limits^{\rm{D}} (1-\eta')^k\,\eta_1\cdots\eta_k,\end{align}
where η, η′, η 1, …, ηk are independent random variables independent of X 0, …, Xk such that
\begin{align*}\eta,\eta'\sim B\bigg(\frac d2+1,\frac{kd}{2}\bigg), \qquad \eta_i\simB\bigg(\frac{d-k+i}{2},\frac{k-i}{2}+1\bigg).\end{align*}
Multiplying both sides of (1.13) by 
$|P_\xi\varepsilon|^2/\kappa_k^2$
and applying Theorem 1.1 and Corollary 1.2 (for details, see Section 2.4) leads to the following generalization of (1.13).
Theorem 1.3. For X 0, …, Xk uniformly distributed in some nondegenerate ellipsoid ɛ ⊂ ℝd, we have
\begin{align*}(k\hbox{{!}})^2 \eta (1-\eta)^k |{\rm{conv(}}X_0,\dots,X_k)|^2& \mathop = \limits^{\rm{D}} \kappa_k^{-2}(1-\eta')^k \eta_1\cdots\eta_k |P_\xi\varepsilon|^2\\& \mathop = \limits^{\rm{D}} (1-\eta')^k \eta_1\cdots\eta_k \left( {\frac{{\det (G_\lambda ^{\rm{T}}{G_\lambda })}}{{\det ({G^T}G)}}} \right),\end{align*}
where the matrices G and Gλ are defined in Corollary 1.2 and λ 1, …, λd denote the length of semi-axes of ɛ.
Taking k = 1 yields the distribution of the distance between two random points in ɛ.
Corollary 1.6. Under the assumptions of Theorem 1.3, we have
\begin{align*}\eta(1-\eta) \, |X_0-X_1|^2 \mathop = \limits^{\rm{D}} (1-\eta') \eta_1\left(\frac{\lambda_1^2N_1^2+\dots+\lambda_d^2N_d^2}{N_1^2+\dots+N_d^2}\right)\!,\end{align*}
where N 1, …, Nd are i.i.d. standard Gaussian variables.
1.4. Integral geometry formulae
Recall that Gd ,k and Ad ,k denote the linear and affine Grassmannians defined in Section 1.1.
For an arbitrary convex compact body K, p > −d, and k = 1, it is possible to express (1.9) in terms of the lengths of the one-dimensional sections of K (see [Reference Chakerian3] and [Reference Kingman12]):
\begin{align*} {\int {_{{K^2}}|{x_0} - {x_1}|} ^p}d{x_0} - d{x_1} = \frac{{2d{\kappa _d}}}{{(d + p)(d + p + 1)}}{\int {_{{A_{d,1}}}|K \cap E|} ^{p + d + 1}}{\mu _{d,1}}(dE).\end{align*}
This formula does not extend to k > 1. The next theorem shows that for ellipsoids this is possible.
Theorem 1.4. For any nondegenerate ellipsoid ɛ ⊂ ℝd, k ∈ {0, 1, …, d}, and any real number p > −d + k − 1, we have
\begin{align}{\int {_{{\varepsilon ^{k + 1}}}} |{\rm conv}({x_0}, \ldots ,{x_k}){|^p}d{x_0}, \ldots ,d{x_k} \\ = \frac{1}{{{{(k!)}^p}}}\frac{{\kappa _{d + p}^{k + 1}}}{{\kappa _k^{p + d + 1}}}\frac{{{\kappa _{k(d + p) + k}}}}{{{\kappa _{(k + 1) + (d + p)}}}}\frac{{{b_{d,k}}}}{{{b_{d + p,k}}}}\int {{A_{d,k}}} |\varepsilon \cap E{|^{p + d + 1}}{\mu _{d,k}}(dE).}\end{align}
The proof is given in Section 3.2.
Comparing this theorem with Theorem 1.2 readily gives the following connection between the volumes of k-dimensional cross-sections and projections of ellipsoids.
Theorem 1.5. Under the assumptions of Theorem 1.4, we have
\begin{align*}\frac{\kappa_{d}^{k+1}}{\kappa_k^{d+1}}\frac{\kappa_{k(d+p)+k}}{\kappa_{k(d+p)+d}} \int_{A_{d,k}}|\varepsilon\capE|^{p+d+1} \mu_{d,k}(dE)=|\varepsilon|^{k+1} \int_{G_{d,k}}|P_L\varepsilon|^{\kern.5pt p}\nu_{d,k}(dL).\end{align*}
For p = 0, we obtain the following integral formula.
Corollary 1.7. Under the assumptions of Theorem 1.4, we have
\begin{align}\int_{A_{d,k}}|\varepsilon\cap E|^{d+1}\mu_{d,k}(dE)=\frac{\kappa_k^{d+1}}{\kappa_{d}^{k+1}}\frac{\kappa_{d(k+1)}}{\kappa_{k(d+1)}}|\varepsilon|^{k+1}.\end{align}
This result may be regarded as an affine version of the following integral formula of Furstenberg and Tzkoni (see [Reference Furstenberg and Tzkoni5]):
\begin{align*}\int_{G_{d,k}}|\varepsilon\cap L|^d\nu_{d,k}(dL)=\frac{\kappa_k^d}{\kappa_d^k}|\varepsilon|^k.\end{align*}
Our next theorem generalizes this formula in the same way as (1.14) generalizes (1.15).
Theorem 1.6. For any nondegenerate ellipsoid ɛ ⊂ ℝd, k ∈ {0, 1, …, d}, and any real number p > −d + k, we have
\[\int {_{{\varepsilon ^k}}} |{\rm conv}(0,{x_1}, \ldots ,{x_k}){|^p}d{x_1}, \ldots ,d{x_k} = \frac{1}{{{{(k!)}^p}}}\frac{{\kappa _{d + p}^k}}{{\kappa _k^{p + d}}}\frac{{{b_{d,k}}}}{{{b_{d + p,k}}}}{\int {_{{G_{d,k}}}|\varepsilon \cap L|} ^{p + d}}{\nu _{d,k}}(dL).\]
In probabilistic language it may be formulated as
\begin{align*}|\mathbb E\!|^{k} {\rm conv}(0,{X_1},\dots,{X_k})|^{\kern.5pt p} =\frac{1}{(k\hbox{{!}})^{\kern.5pt p}}\frac{\kappa_{d+p}^{k}}{\kappa_k^{p+d}} \frac{b_{d,k}}{b_{d+p,k}}\mathbb E|\varepsilon\cap\xi|^{p+d},\end{align*}
where X 1, …, Xk are independent uniformly distributed random vectors in ɛ and ξ is a uniformly chosen random k-dimensional linear subspace in ℝd.
2. Proofs: part I
2.1. Proof of Theorem 1.1 assuming Proposition 1.1
First note that, with probability 1, the equation
\begin{align*}\frac{|P_\xi\varepsilon|}{\kappa_k}\cdot|{\rm{conv(}}X_0,\dots,X_{k})|=0\end{align*}
holds if and only if
\begin{align*}|{\rm{conv(}}AX_0,\dots,AX_{k})|=0,\end{align*}
which in turn is equivalent to
\begin{align*}\dim {\rm conv} (X_0,\dots, X_k)<k.\end{align*}
Therefore, to prove (1.5), it is enough to show that the conditional distributions of
\begin{align*}|{\rm{conv(}}AX_0,\dots,AX_{k})| \quad\text{and}\quad\frac{|P_\xi\varepsilon|}{\kappa_k}\, |{\rm{conv(}}X_0,\dots,X_{k})|\end{align*}
given dim conv (X 0, …, Xk) = k are equal. Thus, without loss of generality, we can assume that the simplex conv (X 0, …, Xk) is not degenerate with probability 1:
\begin{align}\dim {\rm conv}(X_0,\dots, X_k)=k \quad\text{a.s.}\end{align}
Our original proof was based on the Blaschke–Petkantschin formula and the characteristic function uniqueness theorem. (The original proof can be found in the first version of this paper available at https://arxiv.org/abs/1711.06578v1.) Later, Youri Davydov found a much simpler and nicer proof which also allows us to get rid of the assumption about the existence of the joint density of X 0, …, Xk. Let us present this proof.
Since the joint distribution of X 0, …, Xk is spherically symmetric, we have for any orthogonal matrix U
\begin{align}|{\rm{conv(}}AX_0,\dots,AX_{k})|&=|{\rm{conv(}}0, A(X_1-X_0),\dots,A(X_{k}-X_0)|\\&\mathop = \limits^{\rm{D}} |{\rm{conv(}}0, A(UX_1-UX_0),\dots,A(UX_{k}-UX_0)|.\end{align}
Now let 
$\Upsilon$
be a random orthogonal matrix chosen uniformly from SO(n) with respect to the probabilistic Haar measure and independently of X 0, …, Xk. By (2.1), with probability one the span of X 1 − X 0, …, Xk − X 0 is a k-dimensional linear subspace of ℝd. Thus, the span
\[\xi {\kern 1pt} : = \mathop {{\rm{span}}}\nolimits_ (\Upsilon {X_1} - \Upsilon {X_0}, \ldots ,\Upsilon {X_k} - \Upsilon {X_0})\]
is a random uniformly chosen k-dimensional linear subspace in ℝd independent of X 0, …, Xk. Applying Proposition 1.1 to the vectors 
$\Upsilon X_1-\Upsilon X_0,\dots,\Upsilon X_{k}-\Upsilon X_0$, we obtain
\[\begin{array}{l}|\mathop {{\rm{conv}}}(0,A(\Upsilon {X_1} - \Upsilon {X_0}), \ldots ,A(\Upsilon {X_k} - \Upsilon {X_0})|\\\quad \quad = \frac{{|{P_\xi\varepsilon}|}}{{{\kappa _k}}}{\kern 1pt} |\mathop {{\rm{conv}}}(0,\Upsilon {X_1} - \Upsilon {X_0}, \ldots ,\Upsilon {X_k} - \Upsilon {X_0})|\\\quad \quad = \frac{{|{P_\xi\varepsilon}|}}{{{\kappa _k}}}{\kern 1pt} |\mathop {{\rm{conv}}}\nolimits_ (\Upsilon {X_0},\Upsilon {X_1}, \ldots ,\Upsilon {X_k})|\\\mathop = \limits^{\rm{D}} \quad \quad \frac{{|{P_\xi\varepsilon}|}}{{{\kappa _k}}}{\kern 1pt} |\mathop {{\rm{conv}}}\nolimits_ ({X_0},{X_1}, \ldots ,{X_k})|.\end{array}\]
Combining this with (2.2) for 
$U=\Upsilon$
completes the proof.
2.2. Proof of Proposition 1.1
To avoid trivialities, we assume that dim L = k, i.e. x1, …, xk are in general position. Let e1, …, ek ∈ ℝd be some orthonormal basis in L. Let OL and X denote d × k matrices whose columns are e1, …, ek and x1, …, xk, respectively. It is easy to check that 
$O_LO_L^{\top}$
is a d × d matrix corresponding to the orthogonal projection operator PL. Thus,
\begin{align}O_LO_L^{\top}X=X.\end{align}
Recall that ɛ is defined by (1.4). It is known (see, e.g. [Reference Schweppe18, Appendix H]) that the orthogonal projection PLɛ is an ellipsoid in L and
\begin{align}| P_L\varepsilon|=\kappa_k \left[\det \left(O_L^{\top}HO_L\right)\right]^{1/2},\end{align}
where
\begin{align*}H: = {A^{\rm{T}}}A.\end{align*}
A well-known formula for the volume of a k-dimensional parallelepiped implies that, for any x1, …, xk ∈ ℝd,
\begin{align}|\mathop {{\rm{conv}}}(0,{x_1}, \ldots ,{x_k})| = \frac{1}{{k{\kern 1pt} \;!{\kern 1pt} }}{[\det ({X^{\rm{T}}}X)]^{1/2}}.\end{align}
Therefore,
\begin{align*}k{\kern 1pt} \;!{\kern 1pt} {\kern 1pt} |\mathop {{\rm{conv}}}(0,A{x_1}, \ldots ,A{x_k})| = {\left[ {\det ((AX{)^{\rm{T}}}AX)} \right]^{1/2}} = {\left[ {\det ({X^{\rm{T}}}HX)} \right]^{1/2}}.\end{align*}
Applying (2.3) produces
\begin{align}\det (X^{\rm{T}}HX) = \det (X^{\rm{T}}{O_L}{O_L^{\rm{T}}}H{O_L}{O_L^{\rm{T}}}X)\\ = \det ({O_L^{\rm{T}}}H{O_L})\det (X^{\rm{T}}{O_L})\det ({O_L^{\rm{T}}}X)\\ = \det ({O_L^{\rm{T}}}H{O_L})\det (X^{\rm{T}}{O_L}{O_L^{\rm{T}}}X)\\ = \det ({O_L^{\rm{T}}}H{O_L})\det (X^{\rm{T}}X),\end{align}
2.3. Proof of Corollary 1.2
Denote by G 1, …, Gk ∈ ℝd the columns of the matrix G. Hence, AG 1, …, AGk ∈ ℝd are the columns of the matrix AG. Using Proposition 1.1 with xi = Gi and applying (2.5) to G and AG gives
\begin{align*}{\left[ {\det ({G^{\rm{T}}}{A^{\rm{T}}}AG)} \right]^{1/2}} = \frac{{|{P_\eta }\varepsilon |}}{{{\kappa _k}}}{\left[ {\det ({G^{\rm{T}}}G)} \right]^{1/2}},\end{align*}
or
\begin{align*}{\left( {\frac{{\det ({G^{\rm{T}}}{A^{\rm{T}}}AG)}}{{\det ({G^{\rm{T}}}G)}}} \right)^{1/2}} = \frac{{|{P_\eta }\varepsilon |}}{{{\kappa _k}}},\end{align*}
where η is the span of G 1, …, Gk. Since G 1, …, Gk are i.i.d. standard Gaussian vectors, η is uniformly distributed in Gd ,k with respect to νd ,k (given dim η = k which holds a.s.), therefore, 
$\eta \mathop = \limits^{\rm{D}} \xi$
and the corollary follows.
2.4. Proofs of Theorem 1.2 and Theorem 1.3
For any nondegenerate ellipsoid ɛ, there exists a unique symmetric positive-definite d × d matrix A such that
\begin{align*}\varepsilon = A{\mathbb B^d} = \left\{ {x \in {\mathbb R^d}:\left\| {{A^{ - 1}}x} \right\| \le 1} \right\} = \left\{ {x \in {\mathbb R^d}:{x^{\rm{T}}}{A^{ - 2}}x \le 1} \right\}.\end{align*}
Since X 0, …, Xk are i.i.d. random vectors uniformly distributed in ɛ, then A −1X 0, …, A −1Xk are i.i.d. random vectors uniformly distributed in $\mathbb B^d$
. It follows from Theorem 1.1 that
\begin{align}|{{\rm conv(}}X_0,\dots,X_{k})| & = \left|{\rm conv}\left(AA^{-1}X_0,\dots,AA^{-1}X_{k}\right)\right|\notag\\& \mathop = \limits^{\rm{D}} \left|{\rm conv}\left(A^{-1}X_0,\dots,A^{-1}X_{k}\right)\right|\,\frac{|P_\xi\varepsilon|}{{\kappa_{k}}}.\end{align}
Taking the pth moment and applying (1.10) implies Theorem 1.2.
Now apply (1.13) to A −1X 0, …, A −1Xk:
\begin{align*}(k\hbox{{!}})^2\,\eta(1-\eta)^k\,\left|{\rm conv}\big(A^{-1}X_0,\dots,A^{-1}X_k\big)\right|^2 \mathop = \limits^{\rm{D}}(1-\eta')^k\,\eta_1\cdots\eta_k.\end{align*}
Multiplying by 
${|P_\xi\varepsilon|}/{\kappa_{k}^{\kern.5pt p}}$
and applying (2.6) implies the first equation in Theorem 1.3. The second equation follows from (1.8).
2.5. Proof of Corollary 1.5
From Kubota’s formula (see (1.2)) and Theorem 1.2, we have
\begin{align*}\mathbb E|{{\rm conv(}}X_0,\dots,X_{k})|=\alpha_{d,k} V_k(\varepsilon),\end{align*}
where
\begin{align*}\alpha_{d,k}\,:\!={\frac{1}{k\hbox{{!}}} \frac{\kappa_{d+1}^{k+1}}{\kappa_d^{k+1}}\frac{\kappa_{k(d+1)+d}}{\kappa_{(k+1)(d+1)}} \frac{b_{d,k}}{b_{d+1,k}}\frac{\kappa_{d-k}}{{d \choose k} \kappa_{d}}}.\end{align*}
From the definitions of bd ,k (see (1.11)) and κp (see (1.1)), we obtain
\begin{array}{l}{\alpha _{d,k}} = \frac{{\kappa _{d + 1}^{k + 1}}}{{\kappa _d^{k + 1}}}\frac{{{\kappa _{k(d + 1) + d}}}}{{{\kappa _{(k + 1)(d + 1)}}}}\frac{{(d + 1 - k){\kern 1pt} \;!{\kern 1pt} {\kern 1pt} {\kappa _{d - k + 1}}}}{{(d + 1){\kern 1pt} \;!{\kern 1pt} {\kern 1pt} {\kappa _{d + 1}}}}\frac{{{\kappa _{d - k}}}}{{{\kappa _d}}}\\ = \frac{{(d + 1 - k){\kern 1pt} \;!{\kern 1pt} }}{{{\pi ^{k/2}}(d + 1){\kern 1pt} \;!{\kern 1pt} }}{\left( {\frac{{\Gamma \left( {d/2 + 1} \right)}}{{\Gamma \left( {(d + 1)/2 + 1} \right)}}} \right)^{k + 1}}\\\quad {\kern 1pt} \times \frac{{\Gamma \left( {(k + 1)(d + 1)/2 + 1} \right)}}{{\Gamma \left( {((k + 1)d + k)/2 + 1} \right)}}\frac{{\Gamma \left( {(d + 1)/2 + 1} \right)}}{{\Gamma \left( {(d - k + 1)/2 + 1} \right)}}\frac{{\Gamma \left( {d/2 + 1} \right)}}{{\Gamma \left( {(d - k)/2 + 1} \right)}}.\end{array}
Using Legendre’s duplication formula for the gamma function,
\begin{align*}\Gamma(z)\,\Gamma\left(z+\tfrac12\right)=2^{1-2z} \pi^{1/2} \Gamma(2z),\end{align*}
the recursion (Г(1 + z) = zГ(z), and the fact that k, d ∈ ℤ, we obtain
\begin{array}{l}{\alpha _{d,k}} = \frac{{(d - k){\kern 1pt} \;!{\kern 1pt} }}{{{\pi ^{k/2}}d{\kern 1pt} \;!{\kern 1pt} }}\frac{{\Gamma \left( {(k + 1)(d + 1)/2 + 1} \right)}}{{\Gamma \left( {((k + 1)d + k)/2 + 1} \right)}}\frac{{\Gamma \left( {d/2 + 1/2} \right)\Gamma \left( {d/2 + 1} \right)}}{{\Gamma \left( {(d - k)/2 + 1/2} \right)\Gamma \left( {(d - k)/2 + 1} \right)}}\\\quad {\kern 1pt} \times {\left( {\frac{{\Gamma \left( {d/2 + 1} \right)}}{{\Gamma \left( {(d + 1)/2 + 1} \right)}}} \right)^{k + 1}}\\ = \frac{1}{{{{(2\sqrt \pi )}^k}}}\frac{{\Gamma \left( {(k + 1)(d + 1)/2 + 1} \right)}}{{\Gamma \left( {((k + 1)d + k)/2 + 1} \right)}}{\left( {\frac{{\Gamma \left( {d/2 + 1} \right)}}{{\Gamma \left( {(d + 1)/2 + 1} \right)}}} \right)^{k + 1}}\\ = \frac{1}{{{{(2\sqrt \pi )}^k}}}\frac{{{{\left( {\Gamma \left( {d/2 + 1} \right)\Gamma \left( {d/2 + 1 + 1/2} \right)} \right)}^{k + 1}}}}{{\Gamma \left( {(kd + d + k)/2 + 1} \right)\Gamma \left( {(kd + k + d)/2 + 1 + 1/2} \right)}}{\left( {\frac{{\kappa _{d + 1}^{k + 1}}}{{{\kappa _{(d + 1)(k + 1)}}}}} \right)^2}\\ = \frac{1}{{{2^k}}}\frac{{{{((d + 1){\kern 1pt} \;!{\kern 1pt} )}^{k + 1}}}}{{((d + 1)(k + 1)){\kern 1pt} \;!{\kern 1pt} }}{\left( {\frac{{\kappa _{d + 1}^{k + 1}}}{{{\kappa _{(d + 1)(k + 1)}}}}} \right)^2}.\end{array}
3. Proofs: part II
3.1. Blaschke–Petkantschin formula
In our further calculations we will need to integrate some nonnegative measurable function h of k-tuples of points in ℝd. To this end, we integrate first over the k-tuples of points in a fixed k-dimensional linear subspace L with respect to the product measure 
$\lambda_L^k$
and then integrate over Gd,k with respect to νd,k. The corresponding transformation formula is known as the linear Blaschke–Petkantschin formula (see [Reference Schneider and Weil17, Theorem 7.2.1]):
\[\begin{array}{l}\int_{{{({\mathbb R^d})}^k}} h({x_1}, \ldots ,{x_k}){\rm{d}}{x_1} \ldots {\rm{d}}{x_k}\\\quad = (k{\kern 1pt} \;!{\kern 1pt} {)^{d - k}}{b_{d,k}}\int_{{G_{d,k}}} \int_{{L^k}} h({x_1}, \ldots ,{x_k})|\mathop {{\rm{conv}}}(0,{x_1}, \ldots ,{x_k}{)|^{d - k}}\\\quad \quad \times {\lambda _L}({\rm{d}}{x_1}) \cdots {\lambda _L}({\rm{d}}{x_k}){\nu _{d,k}}({\rm{d}}L),\end{array}\]
where bd,k is defined in (1.11).
A similar affine version (see [Reference Schneider and Weil17, Theorem 7.2.7]) may be stated as follows:
\begin{array}{l}\int_{{{({\mathbb R^d})}^{k + 1}}} h({x_0}, \ldots ,{x_k}){\rm{d}}{x_0} \ldots {\rm{d}}{x_k}\\\quad = (k{\kern 1pt} \;!{\kern 1pt} {)^{d - k}}{b_{d,k}}\int_{{A_{d,k}}} \int_{{E^{k + 1}}} h({x_0}, \ldots ,{x_k})|\mathop {{\rm{conv}}}\nolimits_ ({x_0}, \ldots ,{x_k}{)|^{d - k}}\\\quad \quad \times {\lambda _E}({\rm{d}}{x_0}) \cdots {\lambda _E}({\rm{d}}{x_k}){\mu _{d,k}}({\rm{d}}E).\end{array}
3.2. Proof of Theorem 1.4
Let
\begin{align}{J := \int_{{\varepsilon^{k + 1}}} |{{\rm{conv}}}({x_0}, \ldots ,{x_k})|^p{\rm{d}}{x_0} \cdots {\rm{d}}{x_k} \\ = \int_{{{({\mathbb{R}^d})}^{k + 1}}} |{{\rm{conv}}}({{x}_0}, \ldots ,{x_k})|^p\prod\limits_{i = 0}^k 1_\varepsilon ({x_i}){\rm{d}}{x_0} \cdots {\rm{d}}{x_k}.}\end{align}
Using the affine Blaschke–Petkantschin formula (see (3.2)) with
\begin{align*}h({x_0}, \ldots ,{x_k}){\kern 1pt} : = |\mathop {{\rm{conv}}}\nolimits_ ({x_0}, \ldots ,{x_k}{)|^p}\prod\limits_{i = 0}^k {1_\varepsilon }({x_i})\end{align*}
yields
\begin{array}{l}J = (k{\kern 1pt} \;!{\kern 1pt} {)^{d - k}}{b_{d,k}}\int_{{A_{d,k}}} \int_{{E^{k + 1}}} |\mathop {{\rm{conv}}}\nolimits_ ({x_0}, \ldots ,{x_k}{)|^{p + d - k}}\\\quad \times \prod\limits_{i = 0}^k {1_\varepsilon }({x_i}){\lambda _E}({\rm{d}}{x_0}) \ldots {\lambda _E}({\rm{d}}{x_k}){\mu _{d,k}}({\rm{d}}E)\\ = (k{\kern 1pt} \;!{\kern 1pt} {)^{d - k}}{b_{d,k}}\int_{{A_{d,k}}} \int_{{{(E \cap \varepsilon )}^{k + 1}}} |\mathop {{\rm{conv}}}\nolimits_ ({x_0}, \ldots ,{x_k}{)|^{p + d - k}}{\kern 1pt} {\lambda _E}({\rm{d}}{x_0}) \cdots {\lambda _E}({\rm{d}}{x_k}){\mu _{d,k}}({\rm{d}}E).\end{array}
Now fix E ∈ Ad ,k. Applying Theorem 1.2 to the ellipsoid ɛ ∩ E gives
\begin{array}{l}\frac{1}{{|\varepsilon \cap E{|^{k + 1}}}}{\kern 1pt} \int_{{{(E \cap \varepsilon )}^{k + 1}}} |\mathop {{{\rm conv}}}\nolimits_ ({x_0}, \ldots ,{x_k}{)|^{p + d - k}}{\lambda _E}({\rm{d}}{x_0}) \cdots {\lambda _E}({\rm{d}}{x_k})\\\quad \quad = \frac{1}{{{{(k{\kern 1pt} \;!{\kern 1pt} )}^{p + d - k}}}}\frac{{\kappa _{d + p}^{k + 1}}}{{\kappa _k^{k + 1}}}\frac{{{\kappa _{k(d + p) + k}}}}{{{\kappa _{(k + 1)(d + p)}}}}\frac{{{b_{k,k}}}}{{{b_{d + p,k}}}}\frac{{|\varepsilon \cap E{|^{p + d - k}}}}{{\kappa _k^{p + d - k}}},\end{array}
which leads to
\begin{align*}J={\frac{1}{(k\hbox{{!}})^{\kern.5pt p}}}\frac{\kappa_{d+p}^{k+1}}{\kappa_k^{p+d+1}}\frac{\kappa_{k(d+p)+k}}{\kappa_{(k+1)(d+p)}} \frac{b_{d,k}}{b_{d+p,k}} \int_{A_{d,k}}|\varepsilon\cap E|^{p+d+1} \mu_{d,k}(d E).\end{align*}
3.3. Proof of Theorem 1.6
The proof is similar to the previous proof. Let
\begin{array}{l}J{\kern 1pt} : = \int_{{\varepsilon ^k}} |\mathop {{{\rm conv}}}(0,{x_1}, \ldots ,{x_k}{)|^p}{\rm{d}}{x_1} \cdots {\rm{d}}{x_k}\\ = \int_{{{({\mathbb R^d})}^k}} |\mathop {{ {\rm conv}}}(0,{x_1}, \ldots ,{x_k}{)|^p}\prod\limits_{i = 1}^k {1_\varepsilon }({x_i}){\rm{d}}{x_1} \cdots {\rm{d}}{x_k}.\end{array}
Using the linear Blaschke–Petkantschin formula (see (3.1)) with
\[h({x_1}, \ldots ,{x_k}){\kern 1pt} : = |\mathop {{\rm{conv}}}(0,{x_1}, \ldots ,{x_k}){|^p}\prod\limits_{i = 1}^k {1_{\cal E}}({x_i})\]
gives
\begin{array}{l}J = (k{\kern 1pt} \;!{\kern 1pt} {)^{d - k}}{b_{d,k}}{\kern 1pt} \int_{{G_{d,k}}} \int_{{L^k}} |\mathop {{\rm{conv}}}(0,{x_1}, \ldots ,{x_k}{)|^{p + d - k}}\\\quad \times \prod\limits_{i = 1}^k {1_{\cal E}}({x_i}){\lambda _L}({\rm{d}}{x_1}) \cdots {\lambda _L}({\rm{d}}{x_k}){\kern 1pt} {\nu _{d,k}}({\rm{d}}L)\\ = (k{\kern 1pt} \;!{\kern 1pt} {)^{d - k}}{b_{d,k}}\int_{{G_{d,k}}} \int_{{{(L \cap {\cal E})}^k}} |\mathop {{\rm{conv}}}(0,{x_1}, \ldots ,{x_k}{)|^{p + d - k}}{\kern 1pt} {\lambda _L}({\rm{d}}{x_1}) \cdots {\lambda _L}({\rm{d}}{x_k}){\nu _{d,k}}({\rm{d}}L).\end{array}
Fix L ∈ Gd ,k. Since ɛ ∩ L is an ellipsoid, there exists a linear transform AL : L→ℝk such that 
$A_L(\varepsilon\cap L)=\mathbb B^k$
. Applying the coordinate transform xi = AL yi, i = 1, 2, …, k, we get
\begin{array}{l}\int_{{{(L \cap {\cal E})}^k}} |\mathop {{\rm{conv}}}(0,{x_1}, \ldots ,{x_k}{)|^{p + d - k}}{\lambda _L}({\rm{d}}{x_1}) \cdots {\lambda _L}({\rm{d}}{x_k})\\\quad \quad = \frac{{|{\cal E} \cap L{|^{p + d}}}}{{\kappa _k^{p + d}}}\int_{{{({\mathbb B^k})}^k}} |\mathop {{\rm{conv}}}(0,{y_1}, \ldots ,{y_k}{)|^{p + d - k}}{\rm{d}}{y_1} \cdots {\rm{d}}{y_k}.\end{array}
It is known (see, e.g. [Reference Schneider and Weil17, Theorem 8.2.2]) that
\[\int_{{{({\mathbb B^k})}^k}} |\mathop {{{\rm conv}}}(0,{y_1}, \ldots ,{y_k}{)|^{p + d - k}}{\rm{d}}{y_1} \cdots {\rm{d}}{y_k} = (k{\kern 1pt} \;!{\kern 1pt} {)^{ - p - d + k}}\kappa _{d + p}^k\frac{{{b_{k,k}}}}{{{b_{d + p,k}}}}.\]]
Substituting (3.5) and (3.4) into (3.3) completes the proof.
Acknowledgements
The authors are grateful to Daniel Hug and Günter Last for helpful discussions and suggestions which improved this paper. The authors also gratefully acknowledge Youri Davydov who considerably simplified the proof of Theorem 1.1.
The work was done with the financial support of the Bielefeld University (Germany). The work of F. G. and D. Z. was supported by grant SFB 1283. The work of A. G. was supported by grant IRTG 2235. The work of D. Z. was supported by grant RFBR 16-01-00367 and by the Program of Fundamental Researches of the Russian Academy of Sciences, ‘Modern Problems of Fundamental Mathematics’.
