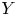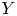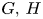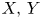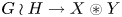1. Introduction
Recall that, given two groups $G$
and $H$
, the wreath product $G \wr H$
is defined as the semidirect product $( \bigoplus _H G ) \rtimes H$
where $H$
acts on the direct sum by permuting the coordinates. These groups are also called lamplighter groups, a terminology coined by Jim Cannon (see [Reference Parry18]). The family of lamplighter groups is well known in group theory and has been studied from various perspectives over the years. On the one hand, lamplighter groups have an easy and explicit definition, allowing an easy access to various properties and calculations. On the other hand, these groups are sufficiently exotic, i.e. sufficiently far away from most of the well-understood classes of groups exhibited in the literature, in order to exhibit interesting behaviours. The combination of these two observations probably explains the success of lamplighter groups, and why they are often used to produce counterexamples.
In this article, we are interested in the $L^{1}$
-geometry of wreath products. How taking the wreath product of two finitely generated groups can affect the compatibility between the geometry of the group and the geometry of an $L^{1}$
-space? In fact, because $L^{1}$
-spaces are median spaces and that, conversely, median spaces isometrically embed into $L^{1}$
-spaces [Reference Chatterji, Druţu and Haglund8], we can alternatively ask the previous question for median spaces. Recall that:
Definition 1.1 Let $X$
be a metric space. Given two points $x,\,y \in X$
, the interval between $x$
and $y$
is
Given any three points $x,\,y,\,z \in X$
, a point in the intersection $I(x,\,y) \cap I(y,\,z) \cap I(x,\,z)$
is a median point of $x$
, $y$
and $z$
. The space $X$
is median if any triple of points admits a unique median.
In this article, we use the point of view offered by median spaces. Our main goal is to transfer the wreath product between groups to an operation between median spaces that create another median space.
Definition 1.2 Let $X,\,Y$
be two median spaces and $1 \in X$
a basepoint. The diadem product $(X,\,1)\circledast Y$
(or simply $X \circledast Y$
) is the set of wreaths $(C,\,\varphi )$
, where
• $C$
is a convex subspace of $Y$ that is finitely generated (i.e. the convex hull of finitely many points);• $\varphi : Y \to X$
satisfies $\varphi (y)=1$ for all but finitely many $y \in Y$ (written $\varphi \in X^{(Y)}$),
endowed with the metric $\delta$
defined as
where $\varphi _1 \Delta \varphi _2$
denotes the set of points where $\varphi _1,\,\varphi _2$
differ and where $\mu (\cdot )$
denotes the measure of the collection of hyperplanes crossing the subspace under consideration (see § 3.1).
The idea to keep in mind is that a point in the diadem product is the data of a ‘finitely supported’ colouring of $Y$
by points of $X$
together with a finitely generated subspace representing the area where a lamplighter is allowed to modify the colouring. Thus, in order to go from a point $(C_1,\,\varphi _1)$
to a point $(C_2,\,\varphi _2)$
, one has to ‘move’ $C_1$
to $C_2$
in $Y$
in such a way that each point where $\varphi _1$
and $\varphi _2$
disagree belongs to one of the subspaces in our path from $C_1$
to $C_2$
, so that the lamplighter be able to modify $\varphi _1$
into $\varphi _2$
. The distance between $(C_1,\,\varphi _1)$
and $(C_2,\,\varphi _2)$
is then the sum of the cost to move from $C_1$
to $C_2$
with the cost to modify the colouring $\varphi _1$
to $\varphi _2$
. In order to formalize the former cost, we show that the set of finitely generated subspaces of a median graph can be endowed with a median metric, a result which is of independent interest:
Theorem 1.3 Let $X$
be a median space. The set $\mathcal {F}(X)$
of the non-empty finitely generated convex subspaces of $X$
is median when endowed with the metric
where $\mu (\cdot )$
refers to the measure of the collections of hyperplanes crossing the subspace under consideration.
We refer to § 2 for an illustration of diadem products in a simple case. Our definition of diadem products is inspired by [Reference Genevois12, § 9], where, given two groups $G,\,H$
with $H$
acting on a median graph, we constructed an action of $G \wr H$
on a quasi-median graph and deduced estimations on the $L^{2}$
-compression.
The central idea is that, given two finitely generated groups $G,\,H$
and two maps $\Phi,\,\Psi$
from our groups to median spaces $X,\,Y$
, we can construct a new median space, namely the diadem product $X \circledast Y$
, and a new map $\Phi \wr \Psi : G \wr H \to X \circledast Y$
in such a way that the amount of geometry preserved by $\Phi \wr \Psi$
is directly related to the amount of geometry preserved by $\Phi$
and $\Psi$
. We motivate this idea from two points of view.
Our first point of view is purely geometric: the wreath product of two finitely generated groups that embed nicely in median spaces also embeds nicely in some median space. In fact, instead of finitely generated groups, we can express our results for arbitrary graphs thanks to the following definition:
Definition 1.4 Let $G,\,H$
be two graphs and $1 \in G$
a basepoint. The wreath product $(G,\,1) \wr H$
(or simply $G \wr H$
) is the graph whose vertices are the pairs $(\varphi,\,h)$
where $h \in H$
and where $\varphi : H \to G$
satisfies $\varphi (k)=1$
for all but finitely many $k \in H$
(written $\varphi \in G^{(H)}$
), and whose edges link two vertices $(\varphi _1,\,y_1),\, (\varphi _2,\,y_2)$
if either $\varphi _1=\varphi _2$
and $y_1,\,y_2$
are adjacent in $H$
or $y_1=y_2$
and $\varphi _1,\,\varphi _2$
only differ at $y_1=y_2$
with $\varphi _1(y_1),\,\varphi _2(y_2)$
adjacent in $G$
.
Observe that, given two groups $G,\,H$
and two generating sets $R \subset G,\, S \subset H$
, we have
justifying our terminology.
Our first application of diadem products is that the wreath product of two (uniformly locally finite) graphs that coarsely embed in $L^{1}$
-spaces also embeds in some $L^{1}$
-space, or equivalently:
Theorem 1.5 Let $G,\,H$
be two graphs with $H$
uniformly locally finite. Then, $G \wr H$
coarsely embeds in a Hilbert space if and only if so do $G,\,H$
.
After the completion of this work, R. Tessera informed us that Theorem 1.5 can also be found in [Reference Cave and Dreesen7].
The property of being coarsely embeddable in some Hilbert space has been popularized by Yu in [Reference Yu23], where it is proved that a finitely generated group that coarsely embeds in some Hilbert space satisfies the famous Novikov conjecture.
Regarding Theorem 1.5, it is natural to ask whether a control on the metric distortion is possible. Recall that, given a Lipschitz map $f : R \to S$
between two metric spaces, one says that $f$
has compression $\geq \alpha$
if there exists some constant $C >0$
such that
The $L^{p}$
-compression of $R$
, denoted by $\alpha _p(R)$
, is the supremum of the $\alpha$
such that there exists a Lipschitz map of compression $\geq \alpha$
from $R$
to an $L^{p}$
-space. Roughly speaking, the $L^{p}$
-compression of a metric space is a real number between zero and one that quantifies the compatibility between the geometry of the space and the geometry of an $L^{p}$
-space. The first examples of finitely generated groups with $L^{2}$
-compression in $(0,\,1)$
, namely Thompson's group $F$
and the lamplighter group $\mathbb {Z} \wr \mathbb {Z}$
, are exhibited in [Reference Arzhantseva, Guba and Sapir1]. Since then, $L^{p}$
-compressions of wreath products have received a lot of attention (see for instance [Reference Austin, Naor and Peres2, Reference Brieussel and Zheng6, Reference Cornulier, Stalder and Valette11, Reference Li13, Reference Naor and Peres16, Reference Naor and Peres17, Reference Stalder and Valette20, Reference Tessera21]).
A quantitative version of Theorem 1.5 leads to the following statement:
Theorem 1.6 Let $G,\,H$
be two graphs with $H$
uniformly locally finite. Then,
However, this lower bound is not optimal in general. When $G$
and $H$
are Cayley graphs, [Reference Li13, Theorem 1.1] provides a better estimate.
We emphasize that having $L^{p}$
-compression one does not imply that the metric space under consideration admits a biLipschitz embedding in some $L^{p}$
-space. For instance, a finitely generated free group has $L^{2}$
-compression one but it does not admit a biLipschitz embedding in some Hilbert space [Reference Bourgain5]. Several wreath products are known to admit biLipschitz embedding in $L^{1}$
-spaces, such that $\mathbb {Z}_2 \wr \mathbb {Z}$
[Reference Naor and Peres16] and $\mathbb {Z}_2 \wr \mathbb {F}$
[Reference Cornulier, Stalder and Valette11] (see also [Reference Baudier, Motakis, Schlumprecht and Zsák3]), but the problem is difficult in general. For instance, in [Reference Naor and Peres17], the authors show that $\mathbb {Z}_2 \wr \mathbb {Z}^{2}$
has $L^{1}$
-compression one but leave the existence of a biLipschitz embedding as an open question. As an application of our diadem products, we prove that:
Theorem 1.7 Let $G,\,H$
be two graphs. Assume that $H$
is a uniformly locally finite median hyperbolic graph. If $G$
biLipschitz embeds into an $L^{1}$
-space, then so does $G \wr H$
.
For instance, the theorem applies to the groups $\mathbb {Z}_n \wr \mathbb {Z}$
, $\mathbb {Z}^{n} \wr \mathbb {Z}$
, $\mathbb {F}_n \wr \mathbb {Z}$
, $\mathbb {Z}_n \wr \mathbb {F}_r$
, $\mathbb {Z}^{n} \wr \mathbb {F}_r$
and $\mathbb {F}_n \wr \mathbb {F}_r$
. In fact, in all these cases, the median spaces are discrete, so our construction provides a biLipschitz embedding in an infinite Hamming cube $\{0,\,1\}^{(\mathbb {N})}$
.
Our second point of view dynamical: the wreath product of two groups that act nicely on $L^{1}$
-spaces also acts nicely on some $L^{1}$
-space. Such results are obtained by noticing that, if two groups act on two median spaces, then their wreath product acts on the diadem product of the corresponding spaces. In view of the characterization of Kazhdan's property (T) and a-T-menability provided by [Reference Chatterji, Druţu and Haglund8], we recover the two following known statements:
Theorem 1.8 Let $G,\,H$
be two non-trivial groups.
• [Reference Cherix, Martin and Valette10] $G\wr H$
has property (T) if and only if $H$ is finite and $G$ has property (T).• [Reference Cornulier, Stalder and Valette11] $G\wr H$
is a-T-menable if and only if so are $G$ and $H$.
Because a discrete group has property (T) if and only if it cannot act on a median space with unbounded orbits, a natural discrete analogue is the property (FW), asking that no action of the group on a median graph can have unbounded orbits. Similarly, being a-T-menable amounts to admitting a metrically proper action on a median space, and the corresponding discrete version of it, namely the property (PW), requires the existence of a metrically proper action on a median graph. By noticing that the diadem product of two median graphs produces a median graphs, we deduce a discrete analogue of Theorem 1.8:
Theorem 1.9 Let $G,\,H$
be two non-trivial groups.
• [Reference Leemann and Schneeberger14] $G\wr H$
has property (FW) if and only if $H$ is finite and $G$ have property (FW).• [Reference Cornulier, Stalder and Valette11] $G\wr H$
has property (PW) if and only if so do $G$ and $H$.
See also [Reference Genevois12] for another proof of the second point.
2. Warmup
In this section, we sketch the construction of a median graph associated with the wreath product $\mathbb {Z} \wr \mathbb {Z}^{2}$
. Our purpose is to motivate the definitions introduced in the next section and to illustrate them visually in a specific case.
An element of the wreath product $\mathbb {Z} \wr \mathbb {Z}^{2}$
, thought of as a lamplighter group, can be described by an infinite grid whose vertices are labelled by integers, such that all but finitely many vertices are labelled by $0$
, together with an arrow pointing to some vertex (see Figure 1). Formally, the labelled grid encodes the coordinate along $\bigoplus _{p \in \mathbb {Z}^{2}} \mathbb {Z}$
and the arrow the coordinate along $\mathbb {Z}^{2}$
. Moreover, $\mathbb {Z} \wr \mathbb {Z}^{2}$
has a natural generating set such that right-multiplying an element of $\mathbb {Z} \wr \mathbb {Z}^{2}$
by one of these generators corresponds to modifying the integer of the vertex where the arrow is (by adding $\pm 1$
) or to moving the arrow to an adjacent vertex.
Figure 1. Replacing the arrow with a rectangle.
Essentially, our construction lies on the following idea: replace the arrow of the previous description with a rectangle (whose corners have their coordinates in $\frac {1}{2} \mathbb {Z}$
) containing a single vertex of the grid (see Figure 1), and, instead of moving the arrow from one vertex to an adjacent vertex, move the sides of the rectangle independently (by $\pm 1$
). For instance, in order to move the rectangle from one vertex to an adjacent vertex, three moves are necessary; see Figure 2. More formally, we define a wreath as the data $(R,\, \varphi )$
of a rectangle $R$
and a map $\varphi : \mathbb {Z}^{2} \to \mathbb {Z}$
with finite support. Now, our elementary moves on a given wreath $(R,\, \varphi )$
are the followings: modify the integer of a vertex which belongs to (the interior of) $R$
by adding $\pm 1$
, or translate one (and only one) side of $R$
by a unit vector. Among the wreaths, we recover the group $\mathbb {Z} \wr \mathbb {Z}^{2}$
as the wreaths whose rectangles contain a single vertex of the grid. Moreover, we have a natural action of $\mathbb {Z} \wr \mathbb {Z}^{2}$
on the set of wreaths extending the left-multiplication:
Now, define the graph of wreaths $\mathfrak {W}$
(which will correspond to the diadem product of the two median graphs given by $\mathbb {Z}$
and $\mathbb {Z}^{2}$
) as the graph whose vertices are the wreaths and whose edges link two wreaths if one can be obtained from the other by an elementary move. We claim that $\mathfrak {W}$
is a median graph and that $\mathbb {Z} \wr \mathbb {Z}^{2}$
acts on it metrically properly.
Figure 2. Passing from a vertex to an adjacent vertex by elementary moves.
In order to link two wreaths $(R_1,\, \varphi _1)$
and $(R_2,\, \varphi _2)$
by a path in $\mathfrak {W}$
, we need to modify the integers at the points on which $\varphi _1,\,\varphi _2$
differ and to find a sequence of rectangles from $R_1$
to $R_2$
such that a rectangle is obtained from the previous one by an elementary move. Notice that, if we want to modify the integer at some point $p \in \mathbb {Z}^{2}$
, then one of our rectangles must contain $p$
in its interior, and $|\varphi _1(p)- \varphi _2(p)|$
elementary moves will be needed to transform $\varphi _1(p)$
to $\varphi _2(p)$
. Therefore, the distance between $(R_1,\, \varphi _1)$
and $(R_2,\, \varphi _2)$
in $\mathfrak {W}$
is equal to
where $\varphi _1 \Delta \varphi _2$
denotes the set of points on which the colourings $\varphi _1,\, \varphi _2$
differ and where $TC(R_1,\,F,\,R_2)$
denotes the minimal number of rectangles needed to connect $R_1$
to $R_2$
in such a way that any point of $F \subset \mathbb {Z}^{2}$
belongs to one of these rectangles.
However, it is not clear how to extend this formula to arbitrary median spaces. We need an alternative description of the metric. The key observation is that applying an elementary move to some rectangle $R$
amounts to adding/removing a hyperplane (here, a vertical or horizontal line of the form $\{n/2\} \times \mathbb {R}$
or $\mathbb {R} \times \{n / 2\}$
where $n \in \mathbb {Z}$
; see § 3.1 for the general case) to/from $R$
. With this idea in mind, it can be proved that
where $\mathcal {H}(S)$
denotes the set of hyperplanes separating at least two vertices of $S$
. The idea is essentially the following: if $J$
is a hyperplane separating two vertices of $R_1 \cup R_2 \cup F$
, then in our sequence of rectangles from $R_1$
to $R_2$
, we will need to add $J$
to one of these rectangles and next to remove it from another one, except if $J$
already crosses $R_1$
(so that we do not need to add it) or if it crosses $R_2$
(so that we do not need to remove it). See [Reference Genevois12, §9] for more information. Thus, the distance between $(R_1,\, \varphi _1)$
and $(R_2,\, \varphi _2)$
in the graph of wreaths $\mathfrak {W}$
is equal to
In the next sections, we will generalize these ideas to arbitrary median spaces.
3. Diadem products of median spaces
3.1. Preliminaries on median spaces
In this section, we give the preliminary material on median spaces which will be needed in the sequel. We refer to [Reference Chatterji, Druţu and Haglund8] and references therein for more information.
Definition 3.1 Let $X$
be a metric space. Given two points $x,\,y \in X$
, the interval between $x$
and $y$
is
Given any three points $x,\,y,\,z \in X$
, a point in the intersection $I(x,\,y) \cap I(y,\,z) \cap I(x,\,z)$
is a median point of $x$
, $y$
and $z$
. The space $X$
is median if any triple of points admits a unique median.
Important examples of median spaces are median graphs, since it was proved independently in [Reference Chepoi9, Reference Roller19] that they are precisely the one-skeletons of CAT(0) cube complexes. In fact, median spaces can be thought of as a ‘non-discrete’ generalization of these complexes. In particular, the technology of hyperplanes can be extended.
Definition 3.2 Let $X$
be a median space. A subspace $Y \subset X$
is convex if $I(x,\,y) \subset Y$
for every $x,\,y \in Y$
. A halfspace of $X$
is a convex subspace whose complement is convex as well. Finally, a hyperplane of $X$
is a pair $\{D,\,D^{c}\}$
where $D$
is a halfspace.
In a median graph, the distance between any two vertices coincides with the number of hyperplanes separating them. In order to generalize this idea to median spaces, we need to introduce measured wallspaces.
Definition 3.3 Let $X$
be a set. A wall $W$
is a partition $\{D,\,D^{c}\}$
of $X$
into two non-empty subsets; $D$
and $D^{c}$
are referred to as the halfspaces delimited by $W$
. Two points $x,\,y \in X$
are separated by a given wall $\{Y,\,Y^{c} \}$
if either $x \in Y$
and $y \in Y^{c}$
, or $x \in Y^{c}$
and $y \in Y$
.
The typical examples of walls we have in mind are hyperplanes in median spaces.
Definition 3.4 A measured wallspace $(X,\, \mathcal {W},\, \mathcal {B},\, \mu )$
is the data of a set $X$
, a collection of walls $\mathcal {W}$
, a $\sigma$
-algebra $\mathcal {B}$
on $\mathcal {W}$
and $\mu$
a measure on $\mathcal {B}$
, such that, for all points $x,\,y \in X$
the collection of walls $\mathcal {W}(x \mid y)$
separating $x$
and $y$
belongs to $\mathcal {B}$
and has finite $\mu$
-measure.
It is proved in [Reference Chatterji, Druţu and Haglund8] that a median space, together with its collection of hyperplanes, can be naturally endowed with a structure of measured wallspace which is compatible with the initial metric. More precisely,
Theorem 3.5 Let $(X,\,d)$
be a median space. There exist a $\sigma$
-algebra $\mathcal {B}$
and a measure $\mu$
defined on the set of hyperplanes of $X$
such that, for all points $x,\,y \in X,$
$\mathcal {W}(x \mid y)$
belongs to $\mathcal {B}$
and $\mu ( \mathcal {W}(x \mid y) )=d(x,\,y)$
.
Another useful tool in the study of median spaces is that it is possible to define projections on some subspaces.
Definition 3.6 Let $X$
be a metric space and $Y \subset X$
a subspace. Given two points $x \in X$
and $p \in Y$
, $p$
is a gate for $x$
in $Y$
if $p \in I(x,\,y)$
for every $y \in Y$
. If every point of $X$
admits a gate in $Y$
, we say that $Y$
is gated.
Clearly, if it exists, a gate of a point $x$
is the unique point of the subspace which minimizes the distance to $x$
. In particular, for any gated subspace $Y$
, it allows to define the projection of any point $x \in X$
onto $Y$
as the unique gate of $x$
in $Y$
.
Lemma 3.7 Let $X$
be a median space, $C \subset X$
a gated subspace and $x \in X$
a point. Any hyperplane separating $x$
from its projection onto $C$
separates $x$
from $C$
.
Proof. Let $x' \in C$
denote the projection of $x$
onto $C$
, and let $\{D,\,D^{c}\}$
be a hyperplane separating $x$
and $x'$
, say $x' \in D$
and $x \in D^{c}$
. For any point $z \in D^{c}$
, necessarily $I(x,\,z) \subset D^{c}$
by convexity. On the other hand, if $z \in C$
, then $I(x,\,z) \cap D \neq \emptyset$
since $x' \in I(x,\,z)$
. Therefore, $z \in D$
. This proves that $C \subset D$
, so that $\{D,\,D^{c} \}$
separates $x$
from $C$
.
For instance, it is proved in [Reference Chatterji, Druţu and Haglund8] that closed convex subspaces in complete median spaces are gated. In this paper, we are interested in the class of finitely generated convex subspaces.
Definition 3.8 In a median space $X$
, a convex subspace is finitely generated if it is the convex hull of finitely many points. We denote by $\mathcal {F}(X)$
the collection of all the non-empty finitely generated convex subspaces of $X$
.
Our main lemma about finitely generated convex subspaces is the following:
Lemma 3.9 Let $X$
be a median space and $C_1,\,C_2 \in \mathcal {F}(X)$
two subspaces. There exist two points $x_1 \in C_1$
and $x_2 \in C_2$
such that
Moreover, $x_1$
is a gate of $x_2$
in $C_1$
and similarly $x_2$
is a gate of $x_1$
in $C_2$
.
Proof. For any subset $F \subset X$
, define $M(F)= \{ m(x,\,y,\,z) \mid x,\,y,\,z \in F \}$
, and by induction
By construction, $\bigcup \limits _{n \geq 0} M^{n}(F)$
coincides with the median hull of $F$
, i.e. the smallest subset of $X$
containing $F$
which is stable under the median operation. Moreover, because the median hull of a finite set turns out to be finite according to [Reference Van de Vel22, Lemma 6.20], there exists some $N \geq 0$
such that $M^{n}(F)= \bigcup \limits _{n \geq 0} M^{n}(F)$
for every $n \geq N$
.
Let $F_1,\,F_2 \subset X$
be two finite subsets such that $C_1$
and $C_2$
are the convex hulls of $F_1$
and $F_2$
, respectively. Let $F$
denote the median hull of $F_1 \cup F_2$
; according to our previous observation, $F$
is finite. We claim that $F \subset C_1 \cup C_2$
. It is clear that $M^{0}(F_1 \cup F_2) \subset C_1 \cup C_2$
; and if $M^{n}(F_1 \cup F_2) \subset C_1 \cup C_2$
for some $n \geq 0$
, then any point $p \in M^{n+1}(F_1 \cup F_2)$
can be written as $p=m(x,\,y,\,z)$
for some $x,\,y,\,z \in C_1 \cup C_2$
, say with $x,\,y \in C_1$
, so that $p \in I(x,\,y) \subset C_1$
. Thus, it follows by induction that $M^{n}(F_1 \cup F_1) \subset C_1 \cup C_2$
for every $n \geq 0$
, hence $F \subset C_1 \cup C_2$
. We have proved more generally that
Fact 3.10 If $C_1$
and $C_2$
are the convex hulls of two subsets $F_1$
and $F_2$
respectively, then the median hull of $F_1 \cup F_2$
is included in $C_1 \cup C_2$
.
Now, fix two points $x_1 \in F \cap C_1$
and $x_2 \in F \cap C_2$
satisfying
Let $z \in F \cap C_1$
be a point. Because the median point $m$
of $x_1$
, $z$
and $x_2$
necessarily belongs to $F \cap C_1$
and that $d(x_1,\,x_2)=d(x_1,\,m)+d(m,\,x_2)$
, we deduce that $m=x_1$
, so that $x_1 \in I(z,\,x_2)$
. As a consequence, any hyperplane separating $x_1$
and $x_2$
must separate $z$
and $x_2$
. Indeed, if $\{ D,\,D^{c} \}$
is such a hyperplane, say with $x_2 \in D$
and $x_1 \in D^{c}$
, and if $z$
belongs to $D$
, then it follows that $x_1 \in I(z,\,x_2) \subset D$
by convexity of $D$
, which is absurd. Thus, we have proved that any hyperplane separating $x_1$
and $x_2$
separates $F \cap C_1$
and $x_2$
. By symmetry, our argument also implies that any hyperplane separating $x_1$
and $x_2$
separates $x_1$
and $F \cap C_2$
. Therefore, $\mathcal {W}(x_1 \mid x_2) \subset \mathcal {W}(F_1 \mid F_2)$
. The reverse inclusion being clear, it follows that $\mathcal {W}(x_1 \mid x_2) = \mathcal {W}(F_1 \mid F_2)$
. From the inequalities
we conclude that $d(x_1,\,x_2)=d(C_1,\,C_2)$
.
Now, we want to prove that $x_2$
is a gate of $x_1$
in $C_2$
. So, fix a point $w \in C_2$
. If $J$
is a hyperplane separating $x_2$
and $w$
, then $J$
does not separate $x_1$
and $x_2$
, because we know that the hyperplanes separating $x_1$
and $x_2$
are precisely the hyperplanes separating $C_1$
and $C_2$
, which do not intersect $C_2$
in particular. Equivalently, $\mathcal {W}(x_2 \mid w) \cap \mathcal {W}(x_1,\,x_2)= \emptyset$
. As a consequence, $\mathcal {W}(x_2 \mid w) \subset \mathcal {W}(x_1 \mid w)$
. Because any hyperplane separating $x_1$
and $x_2$
must separate $C_1$
and $C_2$
, and a fortiori $x_1$
and $w$
, it follows that
hence $d(x_1,\,w)=d(x_1,\,x_2)+d(x_2,\,w)$
. Thus, we have proved that $x_2$
is a gate of $x_1$
in $C_2$
. A symmetric argument proves that $x_1$
is a gate of $x_2$
in $C_1$
.
As a consequence of Lemma 3.9, it follows that finitely generated convex subspaces are gated, so that it will be possible to project points on such subspaces.
Corollary 3.11 In a median space, any finitely generated convex subspace is gated.
Proof. Let $X$
be a median space, $C \in \mathcal {F}(X)$
some subspace and $x \in X$
some point. Applying Lemma 3.9 to $\{x\}$
and $C$
provides the conclusion.
It is known that, in median spaces, any two disjoint convex subspaces are separated by at least one hyperplane. Another consequence of Lemma 3.9 is that, if these two subspaces are moreover finitely generated, then the collection of the hyperplanes separating them is measurable and has positive measure.
Corollary 3.12 Let $X$
be a median graph and $C_1,\, C_2 \in \mathcal {F}(X)$
two subspaces. If $C_1$
and $C_2$
are disjoint, then $\mu ( \mathcal {W}(C_1 \mid C_2) )>0$
.
Proof. Let $x_1 \in C_1$
and $x_2 \in C_2$
be the two points given by Lemma 3.9. Notice that, because $C_1$
and $C_2$
are disjoint, necessarily $x_1 \neq x_2$
. We have
which proves our corollary.
Finally, we conclude this section by noticing that being finitely generated is stable under intersection.
Lemma 3.13 Let $X$
be a median space and $C_1,\,C_2 \in \mathcal {F}(X)$
two subspaces. The intersection $C_1 \cap C_2$
is finitely generated.
Proof. Let $F_1,\,F_2 \subset X$
be two finite subsets such that $C_1$
and $C_2$
are the convex hulls of $F_1$
and $F_2$
, respectively. According to Fact 3.10, the median hull $F$
of $F_1 \cup F_2$
is included in $C_1 \cup C_2$
. Let $Q$
denote the convex hull of $F \cap C_1 \cap C_2$
. Notice that, because the convex hull of $F$
contains $C_1 \cup C_2$
, necessarily $C_1 \cap C_2 \subset Q$
. The reverse inclusion being clear, it follows that $Q= C_1 \cap C_2$
. Thus, $C_1 \cap C_2$
is the convex hull of $F$
, which is finite according to [Reference Van de Vel22, Lemma 6.20]. A fortiori, $C_1 \cap C_2$
is finitely generated.
3.2. The space of finitely generated convex subspaces
Recall that, given a median space, a convex subspace is finitely generated if it is the convex hull of finitely many points of $X$
. Notice that, if $C$
is such a subspace, then the set $\mathcal {H}(C)$
of the hyperplanes intersecting $C$
is measurable and has finite measure. Indeed, if $C$
is the convex hull of some finite set $\{ x_1,\, \ldots,\, x_n\}$
, then $\mathcal {H}(C)= \cup _{1 \leq i < j \leq n} \mathcal {W}(x_i \mid x_j)$
and $\mu (\mathcal {H}(C)) \leq \sum \nolimits _{1 \leq i < j \leq n} d(x_i,\,x_j)$
. The goal of this section is to exploit this observation in order to define a median metric on the set of finitely generated convex subspaces of a given median space.
In the sequel, we will use the following notation. Fix a median space $X$
. For any subset $F \subset X$
, we denote by $\mathcal {H}(F)$
the set of the hyperplanes separating two points of $F$
; alternatively, this is also the set of the hyperplanes intersecting the convex hull of $F$
. If $A_1,\, \ldots,\, A_n \subset X$
are subsets such that the convex hull of $A_1 \cup \cdots \cup A_n$
is finitely generated, we denote by $\mu (A_1 \cup \cdots \cup A _n)$
the measure of $\mathcal {H}(A_1 \cup \cdots \cup A_n)$
.
Definition 3.14 Given a median space $X$
, we denote by $\mathcal {F}(X)$
the set of non-empty finitely generated convex subspaces of $X$
, which we equip with the map $d : \mathcal {F}(X) \times \mathcal {F}(X) \to \mathbb {R}_+$
defined by
The idea to keep in mind is that one moves slightly a point $C \in \mathcal {F}(X)$
by adding/removing a small amount of hyperplanes to/from $C$
. When $X$
is a median graph, then $(\mathcal {F}(X),\,d)$
is again a (median) graph; see [Reference Genevois12, § 9.1] for more details. This allows us to give some examples more easily.
Example 3.15 Let $I$
be a set and let $X$
be the graph whose vertices are the finitely supported sequences $I \to \{0,\,1\}$
and whose edges connect two sequences whenever they differ at a single place. In other words, $X$
is the one-skeleton of a (possibly infinite-dimensional) cube. The convex subgraphs of $X$
are exactly the subgraphs of the form
Given two finite subsets $J,\,K \subset I$
, $X_J$
and $X_K$
are adjacent in $\mathcal {F}(X)$
if and only if the symmetric difference between $J$
and $K$
has size one. In other words, $\mathcal {F}(X)$
is isomorphic to the graph whose vertices are the finite subsets of $I$
and whose edges connect two subsets whenever their symmetric difference has size one. Thus, $\mathcal {F}(X)$
is again the one-skeleton of a (possibly infinite-dimensional) cube.
Example 3.16 Let $X$
denote the graph whose vertex-set is $\mathbb {Z}$
and whose edges connect two integers at distance one (i.e. $X$
is a bi-infinite line). The finite convex subgraphs of $X$
correspond to the intervals in $\mathbb {Z}$
, and two such intervals are connected by an edge in $\mathcal {F}(X)$
if and only if one is obtained from the other by shifting one side by one. In other words, $\mathcal {F}(X)$
is isomorphic to the subgraph $D:= \{ (a,\,b) \mid a \leq b\}$
of $X^{2}$
; see Figure 3. It is worth noticing that, given any two median graphs $A$
and $B$
, the graph $\mathcal {F}(A \times B)$
is isomorphic to $\mathcal {F}(A) \times \mathcal {F}(B)$
. Consequently, $\mathcal {F}(X^{n})$
is isomorphic to $D^{n}$
for every $n \geq 1$
.
Figure 3. The space $\mathcal {F}(X)$
when $X$
is a bi-infinite line or a tripod.
Example 3.17 Let $X$
be an infinite tripod, i.e. the graph obtained by gluing three infinite rays $R_1,\,R_2,\,R_3$
along their starting points $o$
. A convex subgraph in $X$
is either an interval in $R_1$
, $R_2$
or $R_3$
; or a subtripod (possibly degenerate, i.e. with a leg of length zero) with $o$
as its centre. Two finite intervals in $R_i$
(for a fixed $i \in \{1,\,2,\,3\}$
) are adjacent in $\mathcal {F}(X)$
if and only one can be obtained from the other by shifting one side by one. Consequently, one gets a copy of the positive part $D^{+}:= D \cap \mathbb {N}^{2}$
of the halfplane $D$
from Example 3.16 for each $i \{1,\,2,\,3\}$
. Observe that the vertices corresponding to subgraphs of $X$
containing $o$
are given by $\{0\} \times \mathbb {N} \subset D^{+}$
. Next, two finite subtripods are adjacent in $\mathcal {F}(X)$
if and only if one can be obtained from the other by shifting one leg by one. Because shifting the three legs are pairwise independent operations, one gets a product $C$
of three infinite rays in $\mathcal {F}(X)$
. Thus, $\mathcal {F}(X)$
can be obtained by gluing three copies of $D^{+}$
to $C$
(see Figure 3). For more ‘branching’ trees, the graph of finite subtrees is more difficult to draw because one quickly gets (one-skeleta of) high-dimensional cubes. For instance, in a $2$
-regular tree, if $S$
is a finite subtree with $n$
leaves, then adding edges to these leaves will provide (the one-skeleton of) an $n$
-cube.
The rest of the section is dedicated to the proof of the following statement.
Proposition 3.18 $(\mathcal {F}(X),\,d)$
is a median space.
The proposition extends [Reference Genevois12, Proposition 9.6], which shows that the space of finite convex subgraphs in a median graph is again a median graph.
The first thing to verify is that $d$
defines indeed a distance on $\mathcal {F}(X)$
.
Lemma 3.19 $(\mathcal {F}(X),\,d)$
is a metric space.
Proof. The map $d$
is clearly symmetric. Now, let $C_1,\,C_2 \in \mathcal {F}(X)$
be two distinct convex subspaces. Say that there exists some $x \in C_1 \backslash C_2$
. Notice that
On the other hand, if $x'$
denotes the projection of $x$
onto $C_2$
, then any hyperplane separating $x$
and $x'$
must separate $x$
and $C_2$
according to Lemma 3.7, so that
Therefore, we deduce that
which is positive because $x$
does not belong to $C_2$
. Thus, we have proved that $d$
is positive.
Next, we want to prove the triangle inequality. So let $C_1,\,C_2,\,C_3 \in \mathcal {F}(X)$
be three convex subspaces. First of all, notice that
Claim 3.20 The following inequality holds:
Indeed, for every hyperplane $J$
of $X$
, if we denote, respectively, by $L$
and $R$
the left-hand-side and the right-hand-side of the previous inequality, then
• if $J$
intersects either both $C_1$ and $C_2$, or both $C_2$ and $C_3$, then $L(J)=1=R(J)$;• if $J$
intersects either $C_1$ but not $C_2$, or $C_3$ but not $C_2$, then $L(J)=1$ and $R(J) \geq 1$;• if $J$
intersects $C_2$ but not $C_1$ nor $C_3$, then $L(J) \leq 1$ and $R(J)=1$;• if $J$
delimits a halfspace containing $C_1,\,C_2,\,C_3$, then $L(J)=0=R(J)$;• if $J$
separates $C_2$ and $C_1 \cup C_3$, then $L(J)=0$ and $R(J)=2$;• if $J$
separates either $C_1$ and $C_2 \cup C_3$, or $C_3$ and $C_1 \cup C_2$, then $L(J)=1=R(J)$.
This proves our claim. By integrating this inequality, we deduce that
As a consequence,
which proves the triangle inequality.
The next step towards the proof of Proposition 3.18 is to understand the intervals in our metric space.
Lemma 3.21 Let $X$
be a median space and $C,\,C_1,\,C_2 \in \mathcal {F}(X)$
three convex subspaces. The point $C$
belongs to the interval between $C_1$
and $C_2$
in $\mathcal {F}(X)$
if and only if the following three conditions are satisfied:
(i) $C$
is included in the convex hull of $C_1 \cup C_2;$(ii) any hyperplane intersecting both $C_1$
and $C_2$ must intersect $C;$(iii) no hyperplane intersecting $C_1$
separates $C$ and $C_2,$ and similarly, no hyperplane intersecting $C_2$ separates $C$ and $C_1$.
Proof. Because
and
it follows that $C$
belongs to $I(C_1,\,C_2)$
if and only if the equality
holds. Suppose that the three conditions of our statement hold. We want to prove that
so that the previous equality will follow by integration. For every hyperplane $J$
of $X$
, if we denote respectively by $L$
and $R$
the left-hand-side and the right-hand-side of our equality above, then
• if $J$
intersects either both $C_1$ and $C$, or both $C_2$ and $C$, then $L(J)=1=R(J)$;• if $J$
intersects $C_1$ but not $C$, then $J$ cannot intersect $C_2$ by condition $(ii)$ and it cannot separate $C_2$ and $C$ by condition $(iii)$, hence $L(J)=1 =R(J)$; if $J$ intersects $C_2$ but not $C$, the situation is symmetric;• if $J$
intersects $C$ but not $C_1$ nor $C_2$, then $J$ must separate $C_1$ and $C_2$ by condition $(i)$, so that $L(J) = 1 = R(J)$;• if $J$
delimits a halfspace containing $C_1,\,C_2,\,C$, then $L(J)=0=R(J)$;• $J$
cannot separate $C$ from $C_1 \cup C_2$ by condition $(i)$;• if $J$
separates either $C_1$ and $C \cup C_2$, or $C_2$ and $C_1 \cup C$, then $L(J)=1=R(J)$.
Thus, we have proved that, if $C$
satisfies the conditions $(i)$
, $(ii)$
and $(iii)$
, then it belongs to $I(C_1,\,C_2)$
.
Conversely, if we denote respectively by $L$
and $R$
the left-hand-side and the right-hand-side of the equality (3.2), we claim that, if $C$
does not satisfy one of the conditions $(i)$
, $(ii)$
or $(iii)$
, then the inequality $L < R$
holds on a set of positive measure. Because we already know from Claim 3.20 that the inequality $L \leq R$
holds everywhere, it follows by integrating this inequality that the equality (3.1) cannot hold, so that $C$
cannot belong to the interval $I(C_1,\,C_2)$
.
• If $C$
does not satisfy the condition $(i)$, there exists a point $x \in C$ which does not belong to the convex hull of $C_1 \cup C_2$. Let $x'$ denote the projection of $x$ onto this convex hull. According to Lemma 3.7, any hyperplane separating $x$ from $x'$ must separate $x$ from the convex hull of $C_1 \cup C_2$, so that $L(J)=0 < 1 \leq R(J)$ for every $J \in \mathcal {W}(x \mid x')$. On the other hand, $\mu ( \mathcal {W}( x \mid x' ) ) = d(x,\,x')$ is positive.• If $C$
does not satisfy either the condition $(ii)$ or the condition $(iii)$, there exists a halfspace $D$ intersecting both $C_1$ and $C_2$ but which is disjoint from $C$. Let $F_1,\,F_2 \subset X$ be two finite subsets such that $C_1$ and $C_2$ are the convex hulls of $F_1$ and $F_2$ respectively. Denote by $A$ the convex hull of $(F_1 \cap D) \cup (F_2 \cap D)$, and by $B$ the convex hull of $(F_1 \cap D^{c}) \cup (F_2 \cap D^{c}) \cup C$. Notice that $A$ and $B$ are non-empty two finitely generated convex subspaces separated by the hyperplane $\{D,\,D^{c}\}$. Moreover, $L(J) \leq 1 < 2= R(J)$ for every $J \in \mathcal {W}(A \mid B)$. On the other hand, because $A$ and $B$ are disjoint, we deduce from Corollary 3.12 that $\mathcal {W}(A \mid B)$ has positive measure.
This concludes the proof of our lemma.
Proof of Proposition 3.18. Let $C_1,\,C_2,\,C_3 \in \mathcal {F}(X)$
be three convex subspaces. Let $M$
denote the intersection of the convex hulls of $C_1 \cup C_2$
, $C_2 \cup C_3$
and $C_1 \cup C_3$
. Notice that $M$
is finitely generated according to Lemma 3.13, and is non-empty because $m(x_1,\,x_2,\,x_3) \in M$
for every $x_1 \in C_1$
, $x_2 \in C_2$
and $x_3 \in C_3$
. According to Lemma 3.21,
Let $C \in \mathcal {F}(X)$
be a convex subspace satisfying $C \subsetneq M$
. Fix a point $x \in M \backslash C$
, let $x'$
denote its projection onto $C$
and let $J$
be a hyperplane separating $x$
and $x'$
. Notice that, according to Lemma 3.7, $J$
separates $x$
and $x'$
. Moreover, two subcomplexes among $C_1,\,C_2,\,C_3$
cannot be both included into some halfspace $D$
delimited by $J$
since otherwise the convex hull of the union of these two subcomplexes, and a fortiori $M$
, would be included into $D$
, which is impossible because $J$
separates two points of $M$
, namely $x$
and $x'$
. Therefore, $J$
intersects at least one subcomplex among $C_1,\,C_2,\,C_3$
, say $C_1$
, and either separates $C_2$
and $C_3$
or intersects at least one of $C_2$
and $C_3$
. In the former case, if $C$
belongs to the same halfspace delimited by $J$
as $C_2$
, say, then we deduce from Lemma 3.21 that $C$
does not belong to $I(C_1,\,C_3)$
; in the latter case, if $J$
intersects both $C_1$
and $C_2$
, say, then we also deduce from Lemma 3.21 that $C$
does not belong to $I(C_1,\,C_2)$
.
Thus, we have proved that $M$
is the only candidate for a median point of $C_1,\,C_2,\,C_3$
. We claim that $M$
is such a median point.
Let $J$
be a hyperplane intersecting both $C_1$
and $C_2$
. So there exist points $x_1,\,y_1 \in C_2$
and $x_2,\,y_2 \in C_2$
such that $J$
separates $x_1$
and $y_1$
, and $x_2$
and $y_2$
; say that $x_1$
and $x_2$
belong to the same halfspace delimited by $J$
. Fix an arbitrary point $z \in C_3$
. Since halfspaces are convex, it follows that $m(x_1,\,x_2,\,z)$
belongs to the halfspace delimited by $J$
containing $x_1$
and $x_2$
, and that $m(y_1,\,y_2,\,z)$
belongs to the halfspace delimited by $J$
containing $y_1$
and $y_2$
, so $J$
separates the two points $m(x_1,\,x_2,\,z)$
and $m(y_1,\,y_2,\,z)$
of $M$
. A fortiori, $J$
intersects $M$
. Now, suppose by contradiction that there exists a hyperplane $J$
intersecting $C_1$
which separates $M$
and $C_2$
. As a consequence of our previous observation, $J$
cannot intersect $C_3$
. Moreover, $C_3$
cannot be included into the halfspace delimited by $J$
which contains $C_2$
, because otherwise the convex hull of $C_2 \cup C_3$
and $M$
would be separated by $J$
, which is impossible by the definition of $M$
. Therefore, $J$
separates $C_2$
and $C_3$
. Fix two arbitrary points $x_2 \in C_2$
and $x_3 \in C_3$
, and fix a point $x_1 \in C_1$
which belongs to the same halfspace delimited by $J$
as $x_2$
. Since halfspaces are convex, it follows that the point $m(x_1,\,x_2,\,x_3)$
of $M$
belongs to the same halfspace delimited by $J$
as $C_2$
, which contradicts the assumption that $J$
separates $C_2$
and $C$
. Therefore, no hyperplane intersecting $C_1$
separates $C$
and $C_2$
; and similarly, no hyperplane intersecting $C_2$
separates $C$
and $C_3$
.
Thanks to Lemma 3.21, we conclude that $M$
belongs to the interval $I(C_1,\,C_2)$
. By symmetry, we deduce that $M$
also belongs to the intervals $I(C_1,\,C_3)$
and $I(C_2,\,C_3)$
, so that $M \in I(C_1,\,C_2) \cap I(C_2,\,C_3) \cap I(C_1,\,C_3)$
, i.e. $M$
is a median point of $C_1,\,C_2,\,C_3$
.
3.3. The space of wreaths
We are now ready to define diadem products of median spaces and to study their geometry.
Definition 3.22 Let $X,\,Y$
be two median spaces and $1 \in X$
a basepoint. The diadem product $(X,\,1)\circledast Y$
is the set of wreaths $(C,\,\varphi )$
, where $C \in \mathcal {F}(Y)$
and where $\varphi : Y \to X$
satisfies $\varphi (y)=1$
for all but finitely many $y \in Y$
(written $\varphi \in X^{(Y)}$
in the sequel), endowed with the metric $\delta$
defined as
The fact that $\delta$
is indeed a metric will be justified later; see Corollary 3.26. The main result of this section is the following:
Theorem 3.23 A diadem product of two median spaces is a median space.
From now on, we fix two median spaces $X,\,Y$
and a basepoint $1 \in X$
, and for short we denote by $\mathfrak {W}$
the diadem product $(X,\,1) \circledast Y$
. Before proving the theorem, we need to introduce some preliminary material.
Definition 3.24 A leaf of $\mathfrak {W}$
is a subspace $\mathfrak {W}(\varphi ):= \{ (C,\, \varphi ) \mid C \in \mathcal {F}(Y) \},$
the map $\varphi \in X^{(Y)}$
being fixed.
Clearly, the map $C \mapsto (C,\,\varphi )$
defines an isometry $\mathcal {F}(Y) \to \mathfrak {W}(\varphi )$
, so that we already understand the geometry of the leaves of $\mathfrak {W}$
thanks to the previous section. Fixing a leaf $\mathfrak {W}(\varphi )$
, we define a projection
where $\overline {\cdot }$
denotes the convex hull. As a consequence of our first preliminary lemma below, this map is a ‘true’ projection, in the sense that $p_{\varphi }(x)$
is the unique point of the leaf $\mathfrak {W}(\varphi )$
minimizing the distance to a given point $x$
.
Lemma 3.25 For every $\varphi \in X^{(Y)},$
every $x \in \mathfrak {W}$
and every $y \in \mathfrak {W}(\varphi ),$
the following equality holds
Proof. If $x=(C,\,\psi )$
and $y= (Q,\, \varphi )$
, then the sum $\delta (x,\,p_{\varphi }(x))+ \delta (p_{\varphi }(x),\,y)$
simplifies as
which is precisely $\delta (x,\,y)$
.
Although this lemma is completely elementary, it has important consequences, and it will turn out to be fundamental in the proof of Theorem 3.23. For instance, we are able to show that $\delta$
defines a distance on $\mathfrak {W}$
.
Corollary 3.26 $(\mathfrak {W},\, \delta )$
is a metric space.
Proof. First of all, notice that the map $\delta$
is clearly symmetric.
Next, if two wreaths $(C_1,\, \varphi _1),\,(C_2,\, \varphi _2) \in \mathfrak {W}$
satisfy $\delta ((C_1,\,\varphi _1),\,(C_2,\, \varphi _2))=0$
, then necessarily $\sum \nolimits \limits _{y \in Y} d(\varphi _1(y),\, \varphi _2(y))=0$
for every $y \in Y$
. This implies that $\varphi _1=\varphi _2$
, i.e. our two wreaths belong to a common leaf $\mathfrak {W}(\varphi )$
. On the other hand, the restriction of $\delta$
to this leaf, namely $((Q_1,\,\varphi ),\,(Q_2,\, \varphi )) \mapsto d(Q_1,\,Q_2)$
, is a distance according to Lemma 3.19. Consequently, $C_1$
must be equal to $C_2$
, so that $(C_1,\, \varphi _1)= (C_2,\, \varphi _2)$
. We have proved that $\delta$
is positive-definite.
Finally, for any three wreaths $x=(C_1,\, \varphi _1)$
, $y=(C_2,\, \varphi _2)$
and $z=(C,\, \varphi )$
, we deduce from Lemma 3.25 that
On the other hand, since we know from Lemma 3.19 that the restriction of $\delta$
to the leaf $\mathfrak {W}(\varphi )$
, is a distance, it follows that $\delta (p_{\varphi }(x),\,z)+ \delta (z,\, p_{\varphi }(y)) \geq \delta (p_{\varphi }(x),\,p_{\varphi }(y))$
, hence
Notice that the sum in the right-hand-side of this inequality simplifies as
But if $y \in Y$
is a point on which $\varphi _1$
and $\varphi _2$
differ, necessarily either $\varphi (y)$
and $\varphi _1(y)$
or $\varphi (y)$
and $\varphi _2(y)$
will differ as well, i.e. $\varphi _1 \Delta \varphi _2 \subset \varphi _1 \Delta \varphi \cup \varphi \Delta \varphi _2$
. Therefore,
Thus, $\delta$
satisfies the triangle inequality.
Another consequence of Lemma 3.25 is that leaves are convex.
Corollary 3.27 A leaf in $\mathfrak {W}$
is convex.
Proof. Let $\varphi \in X^{(Y)}$
be a map, $x,\,y \in \mathfrak {W}(\varphi )$
two points, and $z \in I(x,\,y)$
a third point. As a consequence of Lemma 3.25,
On the other hand, we deduce from the triangle inequality that
Therefore, $\delta (z,\,p_{\varphi }(z))=0$
, which means that $z$
belongs to the leaf $\mathfrak {W}(\varphi )$
.
Our second (and last) preliminary lemma studies when intervals and leaves intersect.
Lemma 3.28 Let $\varphi \in X^{(Y)}$
be a map, and $(C_1,\, \varphi _1),\,(C_2,\, \varphi _2) \in \mathfrak {W}$
two wreaths. The leaf $\mathfrak {W}(\varphi )$
intersects the interval between $(C_1,\, \varphi _1)$
and $(C_2,\, \varphi _2)$
if and only if $\varphi (y)$
belongs to $I(\varphi _1(y),\,\varphi _2(y))$
for every $y \in Y$
.
Proof. For convenience, set $x=(C_1,\,\varphi _1)$
and $y= (C_2,\, \varphi _2)$
. The interval $I(x,\,y)$
intersects the leaf $\mathfrak {W}(\varphi )$
if and only if there exists some $z \in \mathfrak {W}(\varphi )$
satisfying $\delta (x,\,y)=\delta (x,\,z)+ \delta (z,\,y)$
. This equality is equivalent to
On the other hand, we know from the triangle inequality that
hence $\delta (p_{\varphi }(x),\,z)+ \delta (z,\,p_{\varphi }(y))=\delta (p_{\varphi }(x),\,p_{\varphi }(y))$
. It follows that
Fact 3.29 The interval $I(x,\,y)$
intersects the leaf $\mathfrak {W}(\varphi )$
if and only if
This equality simplifies as
Suppose that $I(x,\,y)$
intersects $\mathfrak {W}(\varphi )$
, so that the previous equality holds. From the triangle inequality, it follows that
On the other hand, $\varphi _1 \Delta \varphi _2 \subset \varphi _1 \Delta \varphi \cup \varphi \Delta \varphi _2$
. Indeed, if $y \in Y$
is a point at which $\varphi _1$
and $\varphi _2$
differ, necessarily $\varphi$
must differ at $y$
from either $\varphi _1$
or $\varphi _2$
. Therefore,
It follows that
so that Equation 3.3 provides
Thus, for every $y \in Y$
, the equality $d( \varphi _1(y),\, \varphi (y)) + d(\varphi (y),\,\varphi _2(y))= d(\varphi _1(y),\, \varphi _2(y))$
hods, which means that $\varphi (y) \in I(\varphi _1(y),\, \varphi _2(y))$
.
Conversely, suppose that $\varphi (y) \in I( \varphi _1(y),\, \varphi _2(y))$
for every $y \in Y$
. In particular, it implies that
Indeed, if $\varphi _1$
and $\varphi _2$
agree at some $y \in Y$
, then $\varphi (y) \in I(\varphi _1(y),\,\varphi _2(y))= \{ \varphi _1(y)=\varphi _2(y) \}$
, so that $\varphi$
necessarily agrees with $\varphi _1$
and $\varphi _2$
at $y$
. On the other hand, we already know that the converse inclusion holds (without any assumption), so we deduce that
Because our assumption also implies that
we conclude that Equation 3.3 holds, and finally that the interval $I(x,\,y)$
intersects the leaf $\mathfrak {W}(\varphi )$
.
We are finally ready to prove Theorem 3.23, namely that the diadem product of two median spaces is again a median space. Our proof below exploits the structure of leaves previously studied. It is worth noticing that, even though this observation will not be used in the sequel, a precise description of the median operator can be deduced from our argument. See Remark 3.30.
Proof of Theorem 3.23. Let $x=(C_1,\,\varphi _1)$
, $y=(C_2,\, \varphi _2)$
and $z=(C_3,\,\varphi _3)$
be three wreaths. Suppose that these three points of $\mathfrak {W}$
admit a median point $m=(C,\, \varphi ) \in \mathfrak {W}$
. It follows from Lemma 3.28 that, for every $y \in Y$
, $\varphi (y)$
belongs to $I(\varphi _1(y),\, \varphi _2(y)) \cap I(\varphi _2(y),\, \varphi _3(y)) \cap I(\varphi _1(y),\, \varphi _3(y))$
, which means that $\varphi (y)$
is the median point of $\varphi _1(y)$
, $\varphi _2(y)$
and $\varphi _3(y)$
in $X$
. So $\varphi$
is uniquely determined. Next, because the interval $I(x,\,y)$
intersects the leaf $\mathfrak {W}(\varphi )$
, we deduce from Fact 3.29 that
On the other hand,
Combining these two equalities yields
We show similarly that
and
Therefore, $m$
is also a median point of $p_{\varphi }(x)$
, $p_{\varphi }(y)$
and $p_{\varphi }(z)$
. Because the leaf $\mathfrak {W}(\varphi )$
is convex in $\mathfrak {W}$
, according to Corollary 3.27, and is a median space on its own right according to Proposition 3.18, it follows that $p_{\varphi }(x)$
, $p_{\varphi }(y)$
and $p_{\varphi }(z)$
admit a unique median point. Thus, we have proved that $x$
, $y$
and $z$
admit at most one median point.
Now, set $\varphi : y \mapsto m(\varphi _1(y),\, \varphi _2(y),\,\varphi _3(y))$
and let $m \in \mathfrak {W}(\varphi )$
denote the (unique) median point of $p_{\varphi }(x)$
, $p_{\varphi }(y)$
and $p_{\varphi }(z)$
. We want to prove that $m$
is a median point of $x$
, $y$
and $z$
. According to Lemma 3.28, the interval $I(x,\,y)$
intersects the leaf $\mathfrak {W}(\varphi )$
, so that we deduce from Fact 3.29 that
Similarly, we show that
Thus, $m$
belongs to $I(x,\,y) \cap I(y,\,z) \cap I(x,\,z)$
, i.e. $m$
is a median point of $x$
, $y$
and $z$
.
Remark 3.30 From the previous proof, we get a precise description of the median point $(M,\, \varphi )$
of three wreaths $(C_1,\, \varphi _1)$
, $(C_2,\, \varphi _2)$
and $(C_3,\, \varphi _3)$
. Indeed,
and $M$
is the convex hull of
3.4. Constructing median graphs
Let $X,\,Y$
be two median graphs and let $1 \in X$
be a basepoint. The distances between vertices of $X$
and $Y$
define two discrete median metrics, so that the distance $\delta$
on the diadem product $(X,\,1) \circledast Y$
turns out to be discrete as well, and median according to Theorem 3.23. Thus, $(X,\,1) \circledast Y$
can be thought of as a graph by linking any two points of $(X,\,1) \circledast Y$
at distance one apart by an edge, but does the resulting length metric coincide with $\delta$
? The next lemma shows that this is the case, making $(X,\,1) \circledast Y$
a median graph.
Lemma 3.31 If $X$
and $Y$
are two median graphs, then $(X,\,1) \circledast Y$
is a median graph.
Proof. For short, we set $\mathfrak {W} = (X,\,1) \circledast Y$
. Let $(C_1,\, \varphi _1),\,(C_2,\,\varphi _2) \in \mathfrak {W}$
be two wreaths. Define a sequence $R_1,\, \ldots,\, R_p \in \mathcal {F}(Y)$
of convex subcomplexes in the following way:
• $R_1=C_1$
;• if $n \geq 2$
and $C_1 \cup C_2 \cup \varphi _1 \Delta \varphi _2 \subsetneq R_n$, $R_{n+1}$ is the convex hull of $R_n \cup \{x \}$, where $x$ is a vertex of the convex hull of $C_1 \cup C_2 \cup \varphi _1 \Delta \varphi _2$ which does not belong $R_n$ but which is adjacent to one of its vertices.
Notice that $(R_i,\,\varphi _1)$
and $(R_{i+1},\,\varphi _1)$
are at distance one apart in $\mathfrak {W}$
for every $1 \leq i \leq p-1$
, and that $p= \# \mathcal {H}(C_1 \cup C_2 \cup \varphi _1 \Delta \varphi _2) \backslash \mathcal {H}(C_1)$
. Similarly, define a sequence $S_1,\, \ldots,\, S_q \in \mathcal {F}(Y)$
from the convex hull of $C_1 \cup C_2 \cup \varphi _1 \Delta \varphi _2$
to $C_2$
such that $(S_i,\,\varphi _2)$
and $(S_{i+1},\,\varphi _2)$
are at distance one apart in $\mathfrak {W}$
for every $1 \leq i \leq q-1$
and such that $q= \# \mathcal {H}(C_1 \cup C_2 \cup \varphi _1 \Delta \varphi _2) \backslash \mathcal {H}(C_2)$
. Finally, let $\psi _1,\, \ldots,\, \psi _r \in X^{(Y)}$
be a sequence of maps such that $\psi _1= \varphi _1$
, $\psi _r=\varphi _2$
, $s= \sum \nolimits \limits _{y \in Y} d(\varphi _1(y),\,\varphi _2(y))$
, and such that, for every $1 \leq i \leq r-1$
, $\psi _i$
and $\psi _{i+1}$
differ at a single vertex $y$
and $\psi _i(y)$
and $\psi _{i+1}(y)$
are adjacent. Notice that $(R_p,\,\psi _i)$
and $(R_p,\,\psi _{i+1})$
are at distance one apart in the $\mathfrak {W}$
for every $1 \leq i \leq r-1$
. Thus,
is a path in $\mathfrak {W}$
, thought of as a graph, from $(C_1,\, \varphi _1)$
to $(C_2,\, \varphi _2)$
and of length
which is precisely the distance between $(C_1,\, \varphi _1)$
and $(C_2,\, \varphi _2)$
. Consequently, the length distance on $\mathfrak {W}$
thought of as a graph coincides with $\delta$
. Because we know from Theorem 3.23 that $\delta$
is a median distance, it follows that $\mathfrak {W}$
is a median graph.
4. Coarse embeddings into $L^{1}$-spaces
In this section, our goal is to show that, if two finitely generated groups coarsely embed into median spaces, then we can combine these embeddings in order to coarsely embed the wreath product of our two groups into the diadem product of two corresponding median spaces. In fact, we will be able to work with graphs instead of groups thanks to the following definition:
Definition 4.1 Let $G,\,H$
be two graphs and $1 \in G$
a basepoint. The wreath product $(G,\,1) \wr H$
is the graph whose vertices are the pairs $(\varphi,\,h)$
where $h \in H$
and where $\varphi : H \to G$
satisfies $\varphi (h)=1$
for all but finitely many $h \in H$
(written $\varphi \in G^{(H)}$
in the sequel), and whose edges link two vertices $(\varphi _1,\,h_1),\, (\varphi _2,\,h_2)$
if either $\varphi _1=\varphi _2$
and $h_1,\,h_2$
are adjacent in $H$
or $h_1=h_2$
and $\varphi _1,\,\varphi _2$
only differ at $h_1=h_2$
with $\varphi _1(h_1),\,\varphi _2(h_2)$
adjacent in $X$
.
Observe that, for all $(\varphi _1,\,h_1),\,(\varphi _2,\,h_2) \in (G,\,1) \wr H$
, one has
where $\varphi _1 \Delta \varphi _2$
denotes the set of all points in $H$
where $\varphi _1,\,\varphi _2$
differ and where $\mathrm {TS}(a,\,S,\,b)$
denotes the shortest length of a path that starts from a point $a$
, that visits all the points in a set $S$
, and that ends at a point $b$
. Also, observe that, given two groups $A,\,B$
and two generating sets $R \subset A,\, S \subset B$
, we have
justifying our terminology.
Definition 4.2 Let $G,\,H$
be two graphs, $X,\,Y$
two median spaces, $1 \in G$
a basepoint, and $\Phi : G \to X,\, \Psi : H \hookrightarrow Y$
two maps with $\Psi$
injective. The wreath product $\Phi \wr \Psi : (G,\,1) \wr H \to (X,\,\Phi (1)) \circledast Y$
is
In the next subsections, we are going to show that, if $\Phi$
and $\Psi$
preserve the metrics of $G,\,H$
, then so does $\Phi \wr \Psi$
.
4.1. Wreath products of coarse embeddings
Until the proof of Theorem 1.5, we fix two graphs $G,\,H$
, a basepoint $1 \in G$
, two median spaces $X,\,Y$
, and two injective maps $\Phi : G \hookrightarrow X$
, $\Psi : H \hookrightarrow Y$
. Our goal is to prove the following statement:
Proposition 4.3 Assume that $H$
is uniformly locally finite. If $\Phi$
and $\Psi$
are coarse embeddings, then so is $\Phi \wr \Psi$
.
We begin by proving two preliminary lemmas.
Lemma 4.4 For all $(c_1,\,h_1),\,(c_2,\,h_2) \in (G,\,1) \wr H,$
Proof. For all $(c_1,\,h_1),\,(c_2,\,h_2) \in (G,\,1) \wr H$
, we have
and
where we have denoted $\Phi c_i \Psi ^{-1} : y \mapsto \left \{\begin {smallmatrix}\Phi (1) & \textrm {if } y \notin \mathrm {Im}(\Psi ) \\ \Phi (c_i(\Psi ^{-1}(y))) & \textrm {otherwise} \end {smallmatrix}\right.$
for $i=1,\,2$
by abuse of notation. These two observations, applied to the definition of $\delta$
, lead to the desired equality.
Lemma 4.5 $\Phi \wr \Psi$
is Lipschitz.
Proof. Let $(c_1,\,h_1),\,(c_2,\,h_2) \in (G,\,1) \wr H$
be two adjacent vertices. Either $c_1=c_2$
and $h_1,\,h_2$
are adjacent in $H$
, which implies according to Lemma 4.4 that
for some uniform constant $C_1$
; or $c_1,\,c_2$
differ only at $h_1=h_2$
and taking adjacent values, which implies according to Lemma 4.4 that
for some uniform constant $C_2$
. Therefore, we have
for all $(c_1,\,h_1),\,(c_2,\,h_2) \in (G,\,1) \wr H$
, concluding the proof of our lemma.
Proof of Proposition 4.3. Assume that $\delta ( \Phi \wr \Psi (c_1,\,h_1),\, \Phi \wr \Psi (c_2,\,h_2) ) \leq R$
for some $R$
. As a consequence of Lemma 4.4, for all $(c_1,\,h_1),\,(c_2,\,h_2) \in (G,\,1)\wr H$
, we have
hence $d(c_1(h),\,c_2(h)) \leq C$
for some uniform constant $C$
; we also have
Consequently,
is bounded above by a constant that depends only on $C$
, $R$
and the maximal degree of a vertex in $H$
. Together with Lemma 4.5, this concludes the proof that $\Phi \wr \Psi$
is a coarse embedding.
Proof of Theorem 1.5. Let $G,\,H$
be two graphs and $1 \in G$
a basepoint. If $G \wr H$
coarsely embeds in a Hilbert space, then so do $G,\,H$
since they isometrically embed in $G \wr H$
. Conversely, assume that $G,\,H$
coarsely embed in Hilbert spaces. It follows from [Reference Nowak15] that there exist two coarse embeddings $\Phi _0 : G \to X_0$
and $\Psi _0 : H \to Y_0$
in $L^{1}$
-spaces, and so in median spaces. We can make $\Phi _0$
injective in the following way. Let $X$
denote the metric space obtained from $X_0$
by gluing, for every $x \in X_0$
, the origins of $|\Phi _0^{-1}(x)|$
unit segments $[0,\,1]$
at $x$
. Next, define $\Phi : G \to X$
in such a way that, for every $x \in X_0$
, $\Phi$
sends the points in $\Phi _0^{-1}(x)$
to pairwise distinct endpoints of the new segments. Then, $X$
is a median space containing $X_0$
as a convex subspace and $\Phi : G \hookrightarrow X$
is an injective coarse embedding. Similarly, we construct an injective coarse embedding to a median space $\Psi : H \hookrightarrow Y$
from $Y_0$
and $\Psi _0 : H \to Y$
. We deduce from Proposition 4.3 that $\Phi \wr \Psi$
defines a coarse embedding from $(G,\,1) \wr H$
to the median space $(X,\, \Phi (1)) \circledast Y$
. As a median space always isometrically embeds in an $L^{1}$
-space [Reference Chatterji, Druţu and Haglund8], which itself coarse embeds in an $L^{2}$
-space, we conclude that $(G,\,1) \wr H$
coarsely embeds in a Hilbert space.
4.2. A word about $L^{1}$-compressions
Until the proof of Theorem 1.6, we fix two graphs $G,\,H$
, a basepoint $1 \in G$
, two median spaces $X,\,Y$
, and two injective coarse embeddings $\Phi : G \hookrightarrow X$
, $\Psi : H \hookrightarrow Y$
. Our goal is to prove the following statement:
Proposition 4.6 Assume that there exists $\gamma,\,C>0$
such that
If $\Phi,\, \Psi$
have respectively compressions $\geq \alpha,\, \geq \beta$
, then $\Phi \wr \Psi$
has compression $\geq \gamma \min (\alpha,\, \beta )$
.
Proof. We already know from Lemma 4.5 that $\Phi \wr \Psi$
is Lipschitz. Let $\epsilon >0$
be smaller than the smallest distance between two distinct points in $\mathrm {Im}(\Psi )$
. For convenience, we assume that $\epsilon \leq \min (2,\,2^{\beta }/C)$
. Notice that, for all $a,\,b \in \mathrm {Im}(\Psi )$
and $S \subset \mathrm {Im}(\Psi )$
finite, we have
where the second inequality is justified by $\mathrm {TS}(a,\,S,\,b) \geq (|S|+1) \epsilon \geq 2 \epsilon |S|$
. According to Lemma 4.4 and the previous observation, for all $(c_1,\,h_1),\,(c_2,\,h_2) \in (G,\,1) \wr H$
we have
for some uniform constants $C_1,\,C_2>0$
, proving that $\Phi \wr \Psi$
has compression $\geq \gamma \min (\alpha,\, \beta )$
as desired.
We denote by $\mathrm {TS}(Y)$
the supremum of the powers $\gamma$
such that $Y$
satisfies the condition mentioned in Proposition 4.6. In [Reference Genevois12], we investigated the possible values taken by $\mathrm {TS}(Y)$
when $Y$
a median graph. For instance, we proved that the following statements hold:
• [Reference Genevois12, Lemma 9.44, Corollary 9.52] If $Y$
is an unbounded median graph, then $\mathrm {TS}(Y)$ always belongs to $[1/2,\,2/3] \cup \{1\}$.• [Reference Genevois12, Proposition 9.45] If $Y$
is a uniformly locally finite median graph, then $\mathrm {TS}(Y)=1$ if and only if $Y$ is hyperbolic.• [Reference Genevois12, Corollary 9.53] If $Y$
is a median graph containing a cube of arbitrary large dimension, then $\mathrm {TS}(Y)=1/2$.• [Reference Genevois12, Lemma 9.50] $\mathrm {TS}(\mathbb {Z}^{d}) = d/(2d-1)$
for every $d \geq 1$.
The uniform lower bound $\mathrm {TS}(Y)$
extends easily to the general case:
Lemma 4.7 For all $a,\,b \in Y$
and $S \subset Y$
finite, we have
Proof. Fix an enumeration $S= \{s_1,\, \ldots,\, s_r\}$
. Then,
Proof of Theorem 1.6. If $\alpha _1(G)=0$
or $\alpha _1(H)=0$
, there is nothing to prove, so from now on, we assume that $\alpha _1(G),\, \alpha _1(H) \neq 0$
. Fix an $\epsilon >0$
and a Lipschitz embedding $\Phi : G \to X$
(respectively $\Psi : H : Y$
) to an $L^{1}$
-space having compression $\geq \alpha _1(G)- \epsilon$
(respectively $\geq \alpha _1(H)-\epsilon$
). Following the beginning of the proof of Theorem 1.5, we can assume without loss of generality that $\Phi,\,\Psi$
are injective. We know from Proposition 4.6 and Lemma 4.5 that $\Phi \wr \Psi$
is Lipschitz and has compression $\geq \mathrm {TS}(Y) \cdot (\min (\alpha _1(G),\,\alpha _1(H)) - \epsilon )$
, and we know from Lemma 4.7 that $\mathrm {TS}(Y) \geq 1/2$
. Because every median space isometrically embeds in an $L^{1}$
-space, it follows that there exists a Lipschitz embedding from $G \wr H$
to an $L^{1}$
-space that has compression $\geq ( \min (\alpha _1(G),\, \alpha _1(H))- \epsilon )/2$
. We conclude the proof by letting $\epsilon \to 0$
.
Proof of Theorem 1.7. Fix a biLipschitz embedding $\Phi : G \hookrightarrow X$
to an $L^{1}$
-space and set $\Psi = \mathrm {id}_H$
. According to [Reference Genevois12, Proposition 9.45], $\mathrm {TS}(Y)=1$
. Therefore, Proposition 4.6 and Lemma 4.5 imply that $\Phi \wr \Psi$
is a biLipschitz embedding to a median space. The desired conclusion follows from the fact that every median space isometrically embeds in an $L^{1}$
-space.
5. Actions on $L^{1}$-spaces
Fix two discrete groups $G,\,H$
respectively acting on two median spaces $X,\,Y$
, with two points $x_0 \in X,\, y_0 \in Y$
having trivial stabilizers. Observe that the wreath product $G \wr H$
naturally acts on the diadem product $\mathfrak {W}:= (X,\,x_0) \circledast Y$
by isometries via
where $\overline {\psi } : Y \to G$
is defined by $\overline {\psi }(g \cdot y_0)=\psi (g)$
for every $g \in H$
and $\overline {\psi }(y)=1$
for every $y \notin H \cdot y_0$
; if we view $H$
as a subset of $Y$
by taking its image under the orbit map associated to the basepoint $y_0$
(the orbit map being an embedding since $y_0$
has trivial stabilizer), then the map $\overline {\psi }$
is naturally an extension of $\psi$
. It is straightforward to verify that this defines an isometric action of $G \wr H$
on $(\mathfrak {W},\,\delta )$
.
In the next two sections, we show that $G \wr H \curvearrowright \mathfrak {W}$
inherits some properties from the actions $G \curvearrowright X$
and $H \curvearrowright Y$
.
5.1. Actions with unbounded orbits
First, we characterize when the action of the wreath product on the diadem product, as described above, has unbounded orbits.
Proposition 5.1 Let $G,\,H$
be two non-trivial groups acting on two median spaces $X,\,Y$
with two points $x_0 \in X,\, y_0 \in Y$
having trivial stabilizers. If $G \cdot x_0$
is unbounded or if $\mu (H \cdot y_0)$
is infinite, then $G \wr H$
acts on $(X,\,x_0) \circledast Y$
with unbounded orbits.
Proof. First, we observe that, if $G$
acts on $X$
with unbounded orbits, then $G$
(as the subgroup of $G \wr H$
indexed by $1 \in H$
) also acts on $X \circledast Y$
with unbounded orbits. Indeed, if $\varphi : Y \to X$
denotes the map always taking the value $x_0$
, then
hence $\delta ( g \cdot (\{y_0\},\,\varphi ),\, (\{y_0\},\,\varphi ) ) \geq d(x_0,\,g\cdot x_0)$
. The desired conclusion follows.
Next, we observe that, if $\mu (H \cdot y_0)$
is infinite, then $\bigoplus _H G$
acts on $X \circledast Y$
with unbounded orbits. Indeed, fix a finite subset $R \subset H$
and set $S:= \{h \cdot y_0 \mid h \in R\}$
. Fix a non-trivial element $g \in G$
and let $\psi : H \to G$
denote the map that is identically equal to $g$
on $R$
and identically trivial elsewhere. Notice that
where $\varphi : Y \to X$
is identically to $x_0$
, hence $\delta ( (1,\,\psi ) \cdot (\{y_0\},\, \varphi ),\, (\{y_0\},\, \varphi ) ) \geq 2 \mu (S)$
. Because $\mu (H \cdot y_0)$
is infinite, we can choose $R$
so that $\mu (S)$
is arbitrarily large, so the desired conclusion follows.
Theorem 1.8 essentially follows from the combination of [Reference Chatterji, Druţu and Haglund8] and Proposition 5.1. The only point to be careful with is that our construction starts with actions on median spaces having basepoints with trivial stabilizers. However, it essentially follows from [Reference Genevois12, Lemma 4.34] that the assumption is not restrictive. For completeness, we reproduce the argument below.
Lemma 5.2 Let $G$
be a group acting on a median space $X_0$
. Then, $G$
acts on a median space $X$
containing $X_0$
so that the action $G \curvearrowright X_0$
extends to an action $G \curvearrowright X$
and $X$
contains a vertex whose stabilizer is trivial. Moreover, the action $G \curvearrowright X$
is properly discontinuous (respectively metrically proper, cocompact, with unbounded orbits) if and only if the action $G \curvearrowright X_0$
is properly discontinuous (respectively metrically proper, cocompact, with unbounded orbits) as well.
Proof. Let $x_0 \in X_0$
be a base vertex and let $\Omega$
denote its $G$
-orbit. Let $X$
be the space constructed from $X_0$
by adding one point $(x,\,g)$
for every $x \in \Omega$
and $g \in \mathrm {stab}(x)$
, and one segment of length one between $x$
and $(x,\,g)$
for every $x \in \Omega$
and $g \in \mathrm {stab}(x)$
. It is straightforward to verify that $X$
is a median space.
Now, we extend the action $G \curvearrowright X_0$
to an action $G \curvearrowright X$
. For every $x \in \Omega$
, fix some $h_x \in G$
such that $h_x \cdot x_0=x$
. For every $g,\,k \in G$
and $x \in \Omega$
, define
notice that
so that $gkh_xh_{gx}^{-1} \in \mathrm {stab}(gx)$
. Moreover,
so we have defined a group action $G \curvearrowright X$
, which extends $G \curvearrowright X_0$
by construction.
Fixing some $x \in \Omega$
, we claim that the vertex $(x,\,1) \in X$
has trivial stabilizer. Indeed, if $g \in G$
fixes $(x,\,1)$
, then $(x,\,1)= g \cdot (x,\,1)= (gx,\, gh_xh_{gx}^{-1})$
. As a consequence, $gx=x$
, i.e. $g \in \mathrm {stab}(x)$
, so that $h_{gx}=h_x$
. Therefore, our relation becomes $(x,\,1)=(x,\,g)$
, hence $g=1$
.
This proves the first assertion of our lemma. Next, it is clear that the action $G \curvearrowright X$
is properly discontinuous (respectively metrically proper, cocompact, with unbounded orbits) if and only if the action $G \curvearrowright X_0$
is properly discontinuous (respectively metrically proper, cocompact, with unbounded orbits) as well.
Proofs of the first parts of Theorems 1.8 and 1.9. Let $H$
act on the tree $T_H$
whose vertex-set is $H \cup \{H\}$
and whose edges connect every $h \in H$
to $H$
. The vertex $1 \in T$
has trivial stabilizer and $\mu (H \cdot 1) = |H|$
. Similarly, let $G$
act on the tree $T_G$
constructed in the same way. If $H$
is infinite, it follows from Proposition 5.1 that $G \wr H$
acts on the median space $(T_G,\,1) \circledast T_H$
with unbounded orbits. Therefore, $G \wr H$
does not have property (T). If $G$
does not have property (T), then according to [Reference Chatterji, Druţu and Haglund8], it admits an action on a median space $X$
with unbounded orbits. According to Lemma 5.2, we can suppose without loss of generality that $X$
contains a point $x_0$
with trivial stabilizer. We conclude from Proposition 5.1 that $G \wr H$
acts on $(X,\,x_0) \circledast T_H$
with unbounded orbits, and consequently that $G \wr H$
does have property (T). Conversely, if $H$
is finite, then $G \wr H$
contains a finite-index subgroup isomorphic to a product of finitely many copies of $G$
, so it follows from basic properties satisfied by (T) that $G \wr H$
has property (T) if so does $G$
(see for instance [Reference Bekka, de la Harpe and Valette4]).
Thus, we have proved the first part of Theorem 1.8. As a consequence of Lemma 3.31, reproducing the same argument word for word proves the first part of Theorem 1.9.
5.2. Proper actions
Finally, we characterize when the action of the wreath product on the diadem product, as described at the beginning of § 5, is metrically proper.
Proposition 5.3 Let $G,\,H$
be two discrete groups acting on two median spaces $X,\,Y$
with two points $x_0 \in X,\, y_0 \in Y$
having trivial stabilizers. If the actions $G \curvearrowright X$
and $H \curvearrowright Y$
are metrically proper, then so is the action of $G \wr H$
on $\mathfrak {W}:= (X,\,x_0) \circledast Y$
.
Proof. It is sufficient to prove that, fixing some $R \geq 0$
, the set
is finite, where $\xi$
denotes the map $Y \to X$
constant to $x_0$
. So, by definition of $F$
, an element $(h,\,\psi )\in G \wr H$
belongs to $F$
if and only if
If $(h,\,\psi )$
is such an element, in particular
and since the action $H \curvearrowright Y$
is metrically proper, it follows that $h$
can take only finitely many values. Moreover, if we denote by $\mathrm {supp}(\psi )$
the set $\{ g \in H \mid \psi (h) \neq 1 \}$
, notice that $\overline {\psi } \xi \Delta \xi$
coincides with $\mathrm {supp}(\psi ) \cdot y_0$
. Consequently,
for every $s \in \mathrm {supp}(\psi )$
, so that, once again because the action $H \curvearrowright Y$
is metrically proper, there are only finitely many choices for $\mathrm {supp}(\psi )$
. Finally, notice that, for every $k \in \mathrm {supp}(\psi )$
,
so that, because the action $G \curvearrowright X$
is metrically proper, $\psi (k)$
can take only finitely many values. Thus, we have proved that there are only finitely many choices on $h$
and $\psi$
in order to have $(h,\,\psi ) \in F$
. A fortiori, $F$
must be finite.
Proofs of the second parts of Theorems 1.8 and 1.9. If $G \wr H$
is a-T-menable, then clearly $G$
and $H$
are also a-T-menable. Conversely, assume that $G$
and $H$
are a-T-menable. According to [Reference Chatterji, Druţu and Haglund8], $G$
(respectively $H$
) acts metrically properly on a median space $X$
(respectively $Y$
); as a consequence of Lemma 5.2, we can assume that $X$
(respectively $Y$
) contains a point $x_0$
(respectively $y_0$
) with trivial stabilizer. It follows from Proposition 5.3 that $G \wr H$
admits a metrically proper action on a median space, and we conclude from [Reference Chatterji, Druţu and Haglund8] that the wreath product is a-T-menable.
Thus, we have proved the second part of Theorem 1.8. As a consequence of Lemma 3.31, reproducing the same argument word for word proves the second part of Theorem 1.9.
We conclude this article by noticing that, in the context of median graphs, we are also able to construct properly discontinuous actions.
Theorem 5.4 If $G$
and $H$
are two groups acting properly discontinuously on some median graphs, then their wreath product $G \wr H$
acts properly discontinuously on a median graph as well.
Proof. Let $G$
and $H$
act properly discontinuously on median graphs $X$
and $Y$
respectively. By following Lemma 5.2 (or according to [Reference Genevois12, Lemma 4.34]), we can suppose without loss of generality that there exist vertices $x_0 \in X$
and $y_0 \in Y$
with trivial stabilizers. We deduce from Lemma 3.31 that the wreath product $G\wr H$
acts on the median graph $\mathfrak {W}:= (X,\,x_0) \circledast Y$
. We claim that this action is properly discontinuous, which amounts to saying that vertex-stabilizers of $\mathfrak {W}$
are finite.
So let $(C,\, \varphi ) \in \mathfrak {W}$
be a wreath. An element $(h,\,\psi ) \in G \wr H$
belongs to its stabilizer if and only if
i.e. $hC=C$
and $\overline {\psi }(\cdot )\varphi (h^{-1} \cdot )= \varphi (\cdot )$
. In a median graph, the convex hull of a finite set must be finite, so that, because the action $H \curvearrowright Y$
is properly discontinuous, there may exist only finitely many $h \in H$
satisfying $hC=C$
. From now on, suppose that $h \in H$
is fixed, and satisfies $hC=C$
. Notice that the condition $\overline {\psi }(\cdot )\varphi (h^{-1} \cdot )= \varphi (\cdot )$
implies that $\psi (g) \cdot \varphi (h^{-1}g \cdot y_0) = \varphi (g \cdot y_0)$
for every $g \in G$
. As a consequence, if we set $F= \{ g \in G \mid \varphi (g \cdot y_0) \neq x_0 \}$
, then, for every $g \notin F \cup h F$
, one has $\psi (g) \cdot x_0=x_0$
, so that $\psi (g)=1$
since the stabilizer of $x_0$
is trivial. On the other hand, $F$
is finite because
and because the action $G \curvearrowright X$
is properly discontinuous, so we have only finitely many choices for $\mathrm {supp}(\psi ) = \{ g \in G \mid \psi (g) \neq 1 \}$
. If $g \in F \cup hF$
, then there exist some $y_1,\,y_2 \in \Phi := \varphi (F \cup hF)$
such that $\psi (g) \cdot y_1=y_2$
; since $\Phi$
is finite and that the action $G \curvearrowright X$
is properly discontinuous, we deduce that we have only finitely many choices for $\psi (g)$
. Thus, we have proved that there exist only finitely many $h \in H$
and $\psi \in G^{H}$
such that $(h,\,\psi )$
belongs to the stabilizer of $(C,\, \varphi )$
, which precisely means that this stabilizer must be finite. This concludes the proof.
Acknowledgements
I am grateful to Elia Fioravanti for interesting discussions about median spaces; to Victor Chepoï, for having indicated to me the reference [Reference Van de Vel22]; and to Bruno Duchesne and Jérémie Brieussel for their comments on a previous version of my manuscript.
