Published online by Cambridge University Press: 10 June 2004
Seasonality has been a major research area in economics for several decades. The paper assesses the recent development in the literature on the treatment of seasonality in economics, and divides it into three interrelated groups. The first group, pure noise models, consists of methods based on the view that seasonality is noise contaminating the data or, more correctly, contaminating the information of interest for the economists. The second group, time-series models, treats seasonality as a more integrated part of the modeling strategy, with the choice of model being data driven. The third group, economic models of seasonality, introduces economic theory, that is, optimizing behavior, into the modeling of seasonality.
Seasonality has been a major research area in economics for several decades. Starting with Sims (1974) and Wallis (1974), continuing with two conferences organized by Arnold Zellner in 1976 and 1981 [see Zellner (1978, 1983)], the foundation was created for an upsurge in the interest of economists and econometricians in the proper treatment of seasonality within economics. The literature on the treatment of seasonality in economics can be divided into three interrelated groups. The first group, pure noise models, consists of methods based on the view that seasonality is noise contaminating the data or, more correctly, contaminating the information of interest for the economists—a view dating back at least to Jevons (1862, 1884) [see Hylleberg (1986)]. The second group, time-series models, treats seasonality as a more integrated part of the modeling strategy, but in a time-series fashion, that is, with the choice of model being data driven. The third group, economic models of seasonality, introduces economic theory, that is, optimizing behavior, into the modeling of seasonality. Obviously, the three groups are interrelated, and several of the subgroups could be placed differently.
The most prominent methods in the first group, and methods that are not treated here, are the methods applied to create official seasonally adjusted data published by the statistical offices. The applications in economics of seasonally adjusted time series published by the official data-gathering statistical offices are widespread. For many years the most commonly applied official seasonal adjustment procedure has been the X-11 method developed at the U.S. Bureau of the Census; see Shiskin et al. (1967). The X-11 procedure is described in Hylleberg (1986, 1992). The procedure has now been replaced in some places by X-12, which no doubt is a major improvement over X-11. X-121
X-12 is downloadable from http://www.census.gov/srd/www/x12a/.
See also http://www.modeleasy.com/tramosea.htm.
The text book by Ghysels and Osborn treats several of the topics discussed below in detail, and the book is recommended for those who want a thorough introduction into these areas.
A much simpler filter often applied to clean up the data in empirical econometric work is seasonal dummy variables, which are added to the regression equations [see Lovell (1963)] or the seasonal difference filter applied by Box and Jenkins (1970). The filtering may also take place in the frequency domain, that is, after a Fourier transformation of the data, as in the band spectrum regression method suggested by Engle (1974, 1980), and discussed by Hylleberg (1977, 1986), and Bunzel and Hylleberg (1982). Obviously, the general idea of band spectrum regression is almost identical to the now fashionable idea of the application of band pass filters, see Baxter and King (1999).
The second group consists of five interrelated modeling approaches. The first approach was basically suggested by Box and Jenkins (1970) and the basic model is a multiplicative extension of the ARIMA model. The second approach, the unobserved components models, specifies ARIMA models for the additive trend cycle component and seasonal ARIMA models for the additive seasonal component, and may be considered a restricted version of the general seasonal ARIMA model. A third approach is based on the time-varying parameter model presented and discussed by Hylleberg (1986), and the periodic autoregressive model or PAR model, introduced into econometrics by Osborn (1988) and Franses (1991). The fourth and closely related approach is based on the evolving seasonals models, originally suggested by Hannan et al. (1970), but reintroduced into econometrics by Hylleberg and Pagan (1997) as a flexible model nesting several of the seasonal time-series models such as the periodic model and the seasonal unit root model. The fifth approach is based on the idea that seasonality should be treated in a multivariate context, and the concepts of seasonal cointegration, periodic cointegration, and seasonal common features become central concepts [see Birchenhal et al. (1989), Hylleberg et al. (1990), Franses (1993), and Engle and Hylleberg (1996)].
Finally, the third group contains the integration of the concept and treatment of seasonality in economics, but, before we turn our attention to the three groups, let us shortly state the definition of seasonality that we apply here. Seasonality in economic time series is defined as
the systematic, although not necessarily regular, intra-year movement caused by the changes of the weather, the calendar, and timing of decisions, directly or indirectly through the production and consumption decisions made by agents of the economy. These decisions are influenced by endowments, the expectations and preferences of the agents, and the production techniques available in the economy.
Hylleberg (1992, p. 4)
The definition stresses both the characteristic features of the seasonal components, their causes, and the economic contents.
The use of seasonal dummy variables to filter quarterly and monthly time-series data is very popular in econometric applications. The dummy variable method was promoted by Lovell (1963), and it is designed to take care of a constant stable seasonal component. The popularity of the seasonal dummy variable method is partly due to its simplicity and the flexible way it can be used. By use of the famous Frisch and Waugh (1933) result, extended by Lovell (1963), it can be shown that the OLS coefficient estimator is the same irrespective of whether the seasonal dummies have been introduced into the regression as in the quarterly model
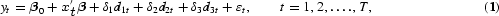
where xt is a vector of explanatory variables observed in period t, and djt, j=1, 2, 3, is a seasonal dummy variable with a value of 1 for t=j, j+4, j+8, …, and otherwise zero, or whether yt and xt or just xt have been seasonally adjusted by regressing them on the seasonal dummies and the constant term before running a regression using the seasonally adjusted data and no seasonal dummies.
The application of seasonal dummies may be justified in some cases. However, many economic time series exhibit a changing seasonal pattern, implying that the seasonal dynamics at best show up in the general dynamic specification of the model, but often are buried in the errors [see Hylleberg et al. (1993)].
A simple filter often applied in empirical econometric work is the seasonal difference filter (1−Ls), where s is the number of observations per year; typically s=2, 4, 12 or 52 [see Box and Jenkins (1970)]. The seasonal differencing of Box and Jenkins assumes that there are unit roots at all the seasonal frequencies in the autoregressive representation, and they recommend that the seasonal difference filter be applied until the transformed series is stationary. The seasonal difference filter can be written as (1−Ls)=(1−L)(1+L+L2+[sdot ][sdot ][sdot ][sdot ][sdot ][sdot ]+Ls−1), where the long-run- or zero-frequency unit root is in the first factor and the seasonal unit roots are in the seasonal summation filter S(L)=(1+L+L2+[sdot ][sdot ][sdot ][sdot ][sdot ][sdot ]+Ls−1). The seasonal summation filter has the real root −1 if s=2 (and indeed for any even s), the real −1, and the two complex conjugate roots ±i if s=4, and one real and five pairs of complex conjugate roots if s=12, etc.
Many empirical studies have applied the so-called HEGY test developed by Hylleberg et al. (1990) and Engle et al. (1993) for quarterly data and extended to monthly data by Franses (1991) and Beaulieu and Miron (1993). These tests are extensions of the well-known Dickey and Fuller (1979) test for a unit root at the long-run frequency (see also Dickey et al., 1984). Another test where the null is that of no unit root at the zero frequency is suggested by Kwiatkowski et al. (1992) (KPSS test) and extended to the seasonal frequencies by Canova and Hansen (1995).
The existence of seasonal unit roots in the data-generating process (DGP) implies a varying seasonal pattern where “summer may become winter.” In most cases, such a situation is not feasible and the finding of seasonal unit roots should be interpreted with care and taken as an indication of a varying seasonal pattern, where the unit root model is a parsimonious approximation and not the true DGP. Furthermore, a proper choice of the initial condition may render “summer may become winter” arbitrarily unlikely in finite samples, thus alleviating this main criticism on the existence of seasonal unit roots.
Recently, Arteche (2000) and Arteche and Robinson (2000), among others, have extended the analysis to seasonal long-memory or fractionally integrated models, for which a seasonal fractional difference filter would be appropriate in the Box-Jenkins spirit. Their estimation methods rely heavily on previous results from the analysis of standard (nonseasonal) long-memory or fractionally integrated models [see Granger and Joveux (1980), Hosking (1981), Geweke and Peter-Hudak (1983), Robinson (1995a,b)].
One source of such fractionally integrated models is the aggregation of stationary dynamic models. Granger (1981) showed that aggregating many AR(1) models with random coefficients leads to a time series with long memory. Long-memory models may also be the result of aggregation over time. Recently, these ideas have been extended to the seasonal case by Lildholdt (2001), who considers aggregation of stationary seasonal AR models and also has an extensive simulation study. Common examples of such aggregated models are production, price indices, and many other macroeconomic and financial time series.
Seasonal unit roots. In the standard unit root literature, a time series is said to be integrated of order d if its dth difference has a stationary and invertible ARMA representation. Hylleberg et al. (1990) generalized this to seasonal integration and defined a real-valued stochastic process {yt, t=0, ±1, …} to be integrated of order d at frequency ω if its spectral density satisfies

where g is a positive constant, the symbol “∼” means that the ratio of the left- and right-hand sides tends to 1, ω is a seasonal frequency, and d is a nonnegative integer. In case of quarterly data, ω={0, π, π/2, 3π/2}, where the frequency is measured in radians. When convenient, the seasonal frequency may also be represented as a fraction of a total circle, that is, as a fraction of
; hence ω=2πθ. A series whose spectral density satisfies (2) with ω=2πθ is denoted yt∼Iθ(d). An example is the process (1−L4) yt=εt, εt∼i.i.d.(0, σ2), which is integrated of order 1 at frequencies
.
In general, consider the autoregressive representation

where ϕ(L) is a finite lag polynomial. Suppose ϕ(L) has all its roots outside the unit circle except for possible unit roots at the long-run frequency ω=0 corresponding to L=1, semiannual frequency ω=π corresponding to L=−1, and annual frequencies ω={π/2, 3π/2} corresponding to L=±i. The standard unit root literature considers the estimation and testing of hypotheses regarding the long-run unit root L=1, and much of this work has now been generalized to include the seasonal cases L=−1 and/or L=±i.
Dickey et al. (1984) suggested a simple test [Dickey–Hasza–Fuller (DHF) test] for seasonal unit roots in the spirit of the Dickey and Fuller (1979) test for long-run unit roots. In the quarterly case, they suggest estimating the auxiliary regression
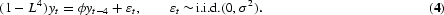
The DHF test statistic is the t-value corresponding to ϕ, which is nonstandard distributed and thus tabulated in Dickey et al. (1984). This test, however, is a joint test for unit roots at the long-run and all the seasonal frequencies; for instance, the polynomial (1−L4) can be written as (1−L)(1+L)(1−iL)(1+iL) and have the roots L={±1, ±i}.
To overcome the lack of flexibility in the DHF test, Hylleberg et al. (1990) refined this idea. By use of the result that any lag polynomial of order p, ϕ(L), with possible unit roots at each of the frequencies ω=0, π, [π/2, 3π/2], can be written as
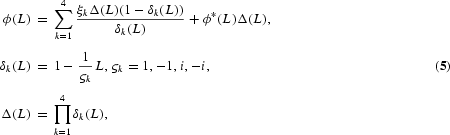
where ξk is a constant and ϕ*(z)=0 has all its roots outside the unit circle, it can be shown that, in the case of a quarterly time series, (3) can be written in the equivalent form
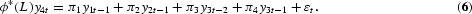
This is a generalized version of (4), where
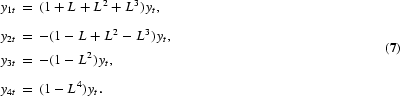
Notice that, in this representation, ϕ*(L) is a stationary and finite polynomial if ϕ(L) from (3) only has roots outside the unit circle except for possible unit roots at the long-run, semiannual, and annual frequencies.
The HEGY tests of the null hypothesis of a unit root are now conducted by simple t-value tests on π1 for the long-run unit root, π2 for the semiannual unit root, and F-value tests on π3, π4 for the annual unit roots. As in the Dickey-Fuller and DHF models, the statistics are not t- or F-distributed but have nonstandard distributions. Critical values for the t-tests are tabulated by Fuller (1976), while critical values for the F-test are tabulated by Hylleberg et al. (1990). The test for the complex unit roots may also be conducted by two tests based on the t-value on π3 and the t-value on π4. The t-value on π3 has a distribution as the DHF test with lag 2, provided π4=0. Hence, the test for complex unit roots using the t-values on π3 and π4 starts by testing π4=0 by the t-value on π4, which, under the null and ϕ*(L)=1, has a distribution tabulated by Hylleberg et al. (1990), and continues by testing π3=0 as in the DHF case. The F-value can be shown to be the sum of the squared t-values on π3 and π4. The t-tests are almost never used, possibly due to the fact that the t-tests cannot be saved by augmenting with lagged values of y4t in case of autocorrelation, as shown by Burridge and Taylor (2001). Tests for combinations of unit roots at the seasonal frequencies are suggested by Ghysels et al. (1994). See also Ghysels and Osborn (2001), who correctly argue that if the null hypothesis is four unit roots, that is, the proper transformation is (1−L4), the test applied should be an F-test of πi, i=1, 2, 3, 4, all equal to zero.
As in the Dickey-Fuller case the correct lag-augmentation in the auxiliary regression (6) is crucial. The errors need to be rendered white noise in order for the size to be close to the stipulated significance level, but the use of too many lag coefficients reduces the power of the tests.
Obviously, if the DGP contains a moving-average component, the augmentation of the autoregressive part may require long lags [see Hylleberg (1995)]. As is the case for the Dickey-Fuller test, the HEGY test may be seriously affected by moving-average terms with roots close to the unit circle [see, e.g., the Monte Carlo analyses of Rodrigues and Osborn (1999) and Ghysels et al. (1994)], but also one-time jumps in the series, often denoted structural breaks in the seasonal pattern, and noisy data with outliers may cause problems, as shown by a number of authors such as Ghysels et al. (1994, 1996), Harvey and Scott (1994), Canova and Hansen (1995), Breitung and Franses (1998), Franses and Vogelsang (1998), Haldrup et al. (2000), Taylor and Smith (2001), Kunst and Rutter (2002), Hassler and Rodrigues (2003), and others.
The sensitivity of the HEGY test to structural breaks has led to extensions, such as the one suggested by Hassler and Rodrigues (2003). They first examine the behavior of several seasonal unit root tests in the context of structural breaks, and show that the HEGY test and an LM\ variant of the HEGY test [see Breitung and Franses (1998) or Rodrigues (2002)] are asymptotically unaffected by a finite seasonal mean shift. However, in finite samples, both tests suffer from severe size and power distortions. To correct for this, Hassler and Rodrigues (2003) propose a new break-corrected LM-type test, which has asymptotic distributions already tabulated in the literature, but is robust to seasonal mean shifts. Furthermore, it is shown by a Monte Carlo experiment that although the test assumes that the break point is known a priori, it is robust to misspecification of the break time even in finite samples.
An alternative procedure was suggested by Canova and Hansen (1995) (CH procedure), who extended the KPSS test to the seasonal case. The KPSS test for a unit root at the zero frequency is based on a state-space representation of the process, often called the structural or unobserved components model, such as

where et is white noise with variance σ2e, and the errors et and εs are independent for all t and s. The null hypothesis of no unit root is parameterized as H0:σ2e=0. Canova and Hansen (1995) extend the test to the seasonal case by constructing similar models as (8) for the zero-frequency unit roots to each of the seasonal unit roots [see Section 2.2.3].
The CH test is an LM-type test based on the residuals from the auxiliary regression

where the regressand, yω, ω=0, π, or π/2, is a transformation of the observed variable, leaving only the corresponding potential unit root in the series. The regressors are deterministic seasonal terms (G) and other nonstochastic terms (X) present under the null hypothesis. Canova and Hansen (1995) use the first difference of the series as the regressand in order to remove a unit root at the zero frequency. However, for the T×1 error term to be of the form e=u+τCωξ, where u and ξ are independent white-noise errors, and where the known T×T matrix Cω projects ξ into a process with a unit root at frequency ω, the regressand must be free of unit roots at all frequencies except ω [see Hylleberg (1995) and Hylleberg and Pagan (1997)].
Then Canova and Hansen (1995) test the hypothesis H0:τ=0, i.e., the null is no unit root at the frequency ω against the alternative of a unit root, and the test statistic suggested by Canova and Hansen (1995) is

for frequencies ω=0, π, or (π/2, 3π/2). Here,
are the OLS residuals from the regression (9) and
is a consistent estimate of the long-run variance of et. The distribution of the Lω-test is nonstandard but depends only on the number of unit roots being tested, and is tabulated by Canova and Hansen (1995).
Besides the problems caused by the test being conditional on assumptions about the integratedness at other frequencies, the introduction of lagged dependent variables into the auxiliary regression may cause problems for testing for seasonal unit roots, unless sufficient care is exercised when choosing specific lags in the augmentation that do not conflict with the seasonal unit roots [see Canova and Hansen (1995) and Hylleberg (1995)]. Specifically, the use of lag 1 when testing for a semiannual unit root may ruin the test.
Recently, some authors have begun developing an optimality theory for seasonal unit root testing. Though no uniformly most-powerful test has been proposed (and most likely none exists), several attempts have been made applying other optimality criteria. The CH test is extended by Cancer (1998) who uses a parametric correction for autocorrelation instead of the nonparametric correction employed by CH. Thus, he is able to prove that his test is locally best invariant unbiased (LBIU). In a Monte Carlo study, Caner's test shows considerable power gains over the CH test. A related approach is considered by Tam and Reinsel (1997) who develop an LBIU test and a point optimal invariant (POI) test for a seasonal unit root in the MA representation, corresponding to seasonal overdifferencing. Thus, their null hypothesis is that of seasonal trend stationarity. By simulations it is shown that the LBIU test is approximately uniformly most powerful since its power curve is very close to the power envelope.
A recent promising addition to the battery of tests is the variance ratio test suggested by Taylor (2002). The test is an extension of a test for a unit root at the zero frequency suggested by Breitung (2002). For quarterly data, the null hypotheses considered are a unit root at the zero frequency, a unit root at the frequency π, and the complex unit root at the frequency π/2 (and the corresponding complex conjugate root at 3π/2), against their stationary alternatives. The test statistic of Breitung is

where
, and
is the residual from a regression of the observed variable xt on deterministic terms such as an intercept, a trend, and seasonal dummies. The null of a unit root is rejected for small values of VR. The necessary assumptions for the test are somewhat weaker than the assumptions for the HEGY test. Especially, one avoids the problems of finding the right lag augmentation, but prefiltering the observed series for possible unit roots at other frequencies is required and may cause problems in small samples.
Hylleberg (1995) argues that the CH test and the HEGY test complement each other. Kunst and Reutter (2002) consider the problem of choosing between the Caner test, the CH test, and the HEGY test, using a Bayesian decision setup, and Monte Carlo experiments show that the gains of such combinations over just applying the HEGY test are small in most cases.
Although unit root testing in the case of semiannual and quarterly data is relatively easy to perform in practice, and feasible in case of monthly observations, it is not possible in practice to handle cases where the auxiliary regressions contain more than 20 regressors as would be the case for weekly or daily data (even with several years of weekly or daily data).4
Note that sometimes the techniques are used to detect weekly effects in daily data, but here at most seven “seasons” are considered, not 52 or 365.
The results of a number of studies testing for seasonal unit roots in economic data series suggest the presence of one or more seasonal unit roots, but often not all required for the application of the seasonal difference filter, (1−Ls), advocated by Box and Jenkins (1970), or the application of the seasonal summation filter, S(L). Thus, these filters should be modified by applying a filter that removes the unit roots at the frequencies where they were found, and not at the frequencies where no unit roots can be detected. Another and maybe more satisfactory possibility would be to continue the analysis applying the theory of seasonal cointegration, which is the subject of Section 2.2.5.
Seasonal fractional integration. Recently, Arteche (2000) and Arteche and Robinson (2000) extended the analysis to include noninteger values of d in the definition (2) of an Iω(d) process. In particular, let {yt, t=0, ±1, …} be a real-valued stochastic process with spectral density satisfying (2) for any real number
. This defines a seasonal fractionally integrated process, which is said to have strong dependence or long memory at frequency ω since the autocorrelations die out at a hyperbolic rate in contrast to the much faster exponential rate in the weak dependence case. The parameter d determines the memory of the process, and its parameter space
is chosen to ensure that the process is stationary and invertible, that is, has a one-sided linear representation. If d=0, the spectral density is bounded at ω and the process has only weak dependence. For proofs of these properties and many more, see, for example, Granger and Joyeux (1980) or Hosking (1981).
When ω=0, the process has standard long memory and when ω is a seasonal frequency the process is said to have seasonal long memory. Many estimators of the memory parameter d and the scale parameter g have been developed in the standard long memory context. Beran (1994), Robinson (1994b), and Baillie (1996) provide overviews of both theoretical and empirical results in the area of (standard) long-memory processes in econometrics and time-series analyses up to about 1995. Basically, there are two dominant estimation methods. The semiparametric method [developed by Geweke and Porter-Hudak (1983), Künsch (1987), and Robinson (1995a,b)] assumes only the model (2) for the spectral density and uses a degenerating part of the periodogram around ω to estimate the model. It therefore has the advantage of being invariant to any dynamics at other frequencies; for example, when estimating standard long-memory models the estimator is invariant to short-run dynamics. Some estimators based on fully specified parametric models have also been developed [e.g., Fox and Taqqu (1986), Dahlhaus (1989), Robinson (1994a), and Nielsen (2004)], which are much more efficient using the entire sample, but will be inconsistent if the parametric model is specified incorrectly.
One of the two commonly used semiparametric estimators is the log-periodogram estimator originally introduced by Geweke and Porter-Hudak (1983), extended to seasonal long memory by Porter-Hudak (1990), and analyzed in detail by Robinson (1995b) and Arteche and Robinson (2000). Taking logs in (2) and inserting sample quantities, we get the approximate regression relationship
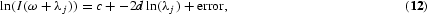
where λj=2πj/n are the Fourier frequencies and
is the periodogram of the observed process {yt, t=1, …, n}. The estimator
is defined as the OLS estimator in the regression (12) using j=±1, …, ±m, where m=m(n) is a bandwidth number that tends to infinity as n→∞. Under suitable regularity conditions, including {yt} being Gaussian and a restriction on the bandwidth, Arteche and Robinson (2000) showed consistency and asymptotic normality of the estimator.
The Gaussian semiparametric estimator (or local Whittle estimator) is attractive because of its nice asymptotic properties and very mild assumptions. The estimator is defined as the pair
that minimizes the (local Whittle likelihood) function
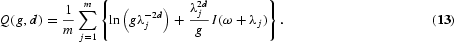
One drawback compared to log-periodogram estimation is that numerical optimization is needed. However, this estimator does not require the Gaussianity condition, and Arteche (2000) and Arteche and Robinson (2000) showed that
. An extremely simple asymptotic distribution facilitating easy asymptotic inference.
The problem with the semiparametric approach is that only
-consistency is achieved in comparison to
-consistency in the parametric case. Thus, the semiparametric approach is much less efficient than the parametric one since it requires at least m/n→0.
A more practical difficulty with the application of seasonal long-memory models or seasonal fractional models is caused by estimating several d parameters. Even in the standard long-memory model with only one d parameter, difficulties may arise, but in case of quarterly data where there are three possible d parameters, the testing procedure becomes very elaborate, with a sequence of clustered tests as in Gil-Alana and Robinson (1997); see also Robinson (1994a) and Nielsen (2004).
A natural way to analyze time series with a strong periodic component seems to be in the frequency domain, where the time series is represented as a weighted sum of cosine and sine waves. Hence, the time series are Fourier transformed and time-domain tools as autocovariance functions and cross-covariance functions are replaced by frequency-domain counterparts such as spectra and cross-spectra. The spectrum is the Fourier transformation of the autocovariance functions, and the autocovariance is the inverse Fourier transformation for the spectrum.5
In practice, estimation of the spectra often takes place as a histogram approximation or smoothing of the periodogram across adjacent frequencies. The periodogram is obtained as the norm of the Fourier-transformed time series.
In the so-called real-business-cycle literature, it has become common practice to filter out components such as the trend and also components with short periods such as the seasonal component, and concentrate on the so-called business-cycle component. This is done by applying band-pass filters, which ideally should leave only the business-cycle component in the series. For a recent discussion of band-pass filters, see Baxter and King (1999). However, application of such filters dates back a long time [see Hannan (1960)]. The application of band spectrum regression was further developed and analyzed by Engle (1974, 1980) and extended to the seasonal case by Hylleberg (1977, 1986) and Bunzel and Hylleberg (1982).
Band spectrum regression. Band spectrum regression is based on a frequency-domain representation of the time series. Let us assume that we have data series with T observations in a T×1 vector y and a T×k matrix X related by y=Xβ+ε, where ε is the disturbance term and β is a k×1 coefficient vector. The finite Fourier transformations of the data\ series are obtained by premultiplying the data matrices by a T×T matrix Ψ, with the k+1 row equal to
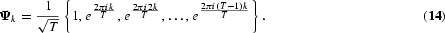
The Ψ matrix is complex and a Hermitian unitary matrix; that is, Ψ=Ψ[dagger] and Ψ[dagger]Ψ=I, where Ψ[dagger] is the transposed complex conjugate matrix of Ψ. Hence, the OLS estimate in the regression of the transformed series

is the same as the original OLS estimate. Let us premultiply the transformed model by a diagonal T×T matrix A with zeros and ones on the diagonal to obtain

The effect of having zeros along the diagonal of A is to take out the corresponding frequency components in the Fourier-transformed data series.
6Note that A must be symmetric around the southwest-northeast diagonal in order for the coefficient estimates to be real.
In case only the exact seasonal frequencies, i.e, π and π/2 in the quarterly case, are removed, OLS on (16) will produce coefficient estimates that are identical to those obtained by adding quarterly seasonal dummies to the regression equation.
The fact that some regression programs are unable to handle complex variables as in (16) implies that the filtered data should be transformed back to the time domain before applying the least-squares algorithm. The inverse Fourier transformation of the transformed filtered variables in the model is obtained by premultiplying (16) with Ψ.
One of the advantages of the band spectrum regression is that it is possible to test directly for the appropriate filtering, as argued by Engle (1974).
Band-pass filters. Most of the literature on the use of band-pass filters is connected to the real-business-cycle literature, following Hodrick and Prescott (1980), Prescott (1986), and Kydland and Prescott (1990). The focus of that literature is the business-cycle component, and the ideal band-pass filter is a filter that leaves out all the components not connected to the business cycle.
Obviously, similar procedures could be applied to leave out only the seasonal components. The ideal seasonal band-pass filter is a filter that leaves out the nonseasonal components of the economic time series.
Following Baxter and King (1999), for instance, it can be shown that an ideal seasonal band-pass filter that passes through only the frequencies
has frequency response function β(ω)=1 for
and β(ω)=0 elsewhere, has the form
, where
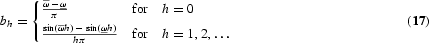
However, the filter
is an infinite moving average, and in practice, we are forced to apply an approximate finite moving-average filter, such as
.
If the optimization criteria are based on minimizing
, it can be shown that the optimal approximate band-pass filter is
for a given truncation K. Hence, the optimal approximating band-pass filter aK(L) is constructed from the ideal band-pass filter b(L) by letting the weights be equal within the truncation lag, that is, ak=bk for k=0, ±1, [sdot ][sdot ]±K.
The effect of the truncation with lag length K is to lose K observations at each end of the sample. However, a large K implies a better approximation. In fact, a small K may result in admitting substantial components just above
and below
, an effect called leakage, whereas the frequency response may be both below the unit frequency response (compression) and above it (exacerbation). Hence, there exists a trade-off between large and small K's for a given sample size T.
Whether one applies filtering in the frequency domain as in band spectrum regression or in the time domain as in band-pass filtering, the actual success of the filtering depends on the choice of bandwidth K, and the spectral characteristics of the series at hand. Even a small leakage in the filter may give rise to severe disturbances if the spectrum of the filtered series has mass at particular frequencies.
In the traditional analysis of Box and Jenkins (1970), the time series were made stationary by application of the filters (1−L) and/or (1−Ls)=(1−L)(1+L+L2+L3+[sdot ][sdot ][sdot ][sdot ][sdot ][sdot ]Ls−1), as many times as was deemed necessary from the form of the resulting autocorrelation function. After having obtained stationarity, the filtered series were modeled as an autoregressive moving-average, or ARMA, model. Both the AR and the MA part could be modeled as consisting of a nonseasonal and seasonal lag polynomial. Hence, the so-called Seasonal ARIMA model has the form
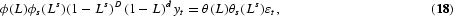
where ϕ(L) and θ(L) are invertible lag polynomials in L, while ϕs(Ls) and θs(Ls) are invertible lag polynomials in Ls.
In light of the results mentioned in the section on seasonal unit roots, the modeling strategy of Box and Jenkins may easily be refined to allow for situations where the nonstationarity exists only at some of the seasonal frequencies.
The model in (18) lends itself to a straightforward extension to the multivariate case but, unless constraints are invoked, the model will not be identified in the traditional econometric sense of the word. In Zellner and Palm (1974), the Box-Jenkins model and the traditional econometric modeling techniques are combined, and Plosser (1978) extends the approach to the seasonal case. The simultaneous modeling of both the seasonal and the nonseasonal components applying time series as well as econometric techniques is further developed by Hylleberg (1986), which also contains a long list of references.
When modeling processes with seasonal characteristics, complicated and high-order polynomials must be applied in the ARIMA representation [see Hylleberg (1992)]. As an alternative to this, the unobserved-components (UC) model was proposed. In its most general form, the model can be specified as

where μt is the trend-cycle component, γt is the seasonal component, and εt is an irregular component. It is assumed that μt and γt can be modeled as two distinct ARMA processes,

where the processes vt, wt, and εt are assumed to be independent, serially uncorrelated processes with zero means and variances σ2v, σ2w, and σε2. This class of models is also called unobserved-components autoregressive integrated moving-average models (UCARIMA) by Engle (1978).
Substituting (20) into (19), it is seen that the UC model can be equivalently specified as
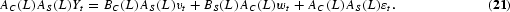
From this and the results of Granger and Morris (1976), it is seen that the UCARIMA model is a general ARIMA model with restrictions on the parameters. The restrictions may be derived from the estimated parameters of the unconstrained ARIMA model. Alternatively, the UC model may be specified as a so-called structural model following Harvey (1993).
The structural approach is based on a very simple and quite restrictive modeling of the components of interest such as trends, seasonals, and cycles. The model is often specified as (19). The trend is normally assumed to be stationary only in first or second differences, whereas γt is stationary when multiplied by the seasonal summation operator. In the basic structural model (BSM), the trend is specified as

where each of the error terms is independent, normally distributed. If σξ2=0, (22) collapses to a random walk plus drift. If ση2=0 as well, (19) corresponds to a model with a linear trend. The seasonal component is specified as

where s is the number of periods per year and wt∼N(0, σw2).
9Specifying the seasonal component this way makes it slowly changing by a mechanism that ensures that the sum of the seasonal components over any s consecutive time periods has an expected value of zero and a variance that remains constant over time.

where ξt=ηt−ηt−1+ζt−1 is equivalent to an MA(1) process. Expressing the model in form (24) makes the connection to the UCARIMA model in (21) clear.
Estimation of the general UC model is treated by Hylleberg (1986) and follows the same lines as the Box-Jenkins modeling procedure. Thus, the modeling procedure may be criticized on grounds similar to those for the general ARIMA models.
The statistical treatment in the structural approach is based on the state-space formulation, and the problems of specifying the ARMA models for the components are avoided by a priori restrictions. Harvey and Scott (1994) argue that the type of model above, which has a seasonal component evolving relatively slowly over time, can fit most economic time series. Nonetheless, the model presupposes a trend component with a unit root and a seasonal component with all possible seasonal unit roots present.10
The consumption function advocated by Harvey and Scott (1994) and found using the structural approach, is identical to a consumption function obtained by the seasonal cointegration approach, provided a common cointegration vector applies at the zero frequency and at all the seasonal frequencies.
The periodic model extends the nonperiodic time-series models by allowing the parameters to vary with the seasons. The periodic autoregressive (PAR) model assumes that the observations in each of the seasons can be described using different autoregressive models, and the same goes for the periodic extensions to the MA and ARMA models. Most of the research undertaken so far has focused on PAR models [see Franses (1996)].
Consider a quarterly times series yt that is observed for N years. The PAR(h) model can be written as
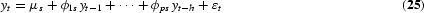
for s=1, 2, 3, 4 and t=1, 2, …, T=4N, or as
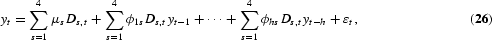
where Ds,t are seasonal dummies equal to 1 when t is falling in s and zero otherwise. The model may be estimated by maximum likelihood or OLS, which yields equal parameter estimates under normality of the error process and with fixed starting values. Testing for periodicity in (26) amounts to testing the hypothesis H0:ϕis=ϕi for s=1, 2, 3, 4 and i=1, 2, …, p. This hypothesis can be tested by a likelihood ratio test that is asymptotically χ3p2 under the null, irrespective of any unit roots in yt [see Boswijk and Franses (1995)]. The order of the PAR(h) model can be found using an information criterion or using a general-to-specific approach on (26).
11One problem arises because the testing strategies are prone to detect spurious periodic autoregressions [see Proietti (1998)].
Osborn (1991) shows that any PAR model can be described by a nonperiodic ARMA model. In general, however, the orders will be higher than in the PAR model. For example, a PAR(1) corresponds to a nonperiodic ARMA(4,3) model. Furthermore, it has been shown that estimating a nonperiodic model when the true DGP is a PAR can result in a lack of ability to reject the false nonperiodic model [see Franses (1996)]. Fitting a PAR model does not prevent the finding of a nonperiodic AR process, if the latter is in fact the DGP. In practice, it is thus recommended to start by selecting a PAR(h) model, and then tests whether the autoregressive parameters are periodically varying using the method described above.
A major weakness of the periodic model is that the available sample for estimation, given by N=n/s where s is the number of seasons, can be small. Furthermore, the identification of a periodic time-series model is not as easy as it is for nonperiodic models, since the periodic models have similarities with vector AR(MA) models. However, the models are easily estimated under the assumptions above, and standard type tests can be used to test the specification.
The periodic models can be considered special cases of what is referred to as the time-varying parameter models [see Hylleberg (1986)].
12Hylleberg and Pagan (1997) also note that the PAR models impose certain restrictions on the evolving seasonals model.
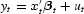
with seasonally varying coefficients, which in the most general form are specified as

where B(L) is a diagonal matrix with lag polynomials on the diagonal, A a matrix of coefficients, and γt is a vector of seasonal variables, while ξt is an error term. This model can be written in state-space form and estimated using the Kalman filter. A special case of (27) is the systematic nonrandom time-varying parameter model where
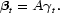
This model, in principle, constitutes no estimation problems if γt is known and the number of observations for each season is large.
13The same comment is valid for the PAR model, for which γt is equal to seasonal dummies and where Xt consists of lagged values of the dependent variable.
However, γt is rarely known and the number of observations for each season may be small. The latter problem can be addressed by restricting the parameters, and a sensible assumption is that the parameters vary smoothly over the seasons. This assumption was used by Gersovitz and MacKinnon (1978) applying Bayesian techniques. An alternative way to smooth the variation in the coefficients consists of restricting them to take on values along low-ordered polynomials. Estimation of this model can be done using a method like the one suggested by Almon (1965) for distributed lag models.
The evolving seasonals model was promulgated by Hannan in several articles in the 1960s [see Hannan et al. (1970)]. The model was revitalized by Hylleberg and Pagan (1997) and used to nest many of the most commonly applied seasonal models. Recently, the model has been used by Koop and Dijk (2000) to analyze seasonal models from a Bayesian perspective.
The evolving seasonals model for a quarterly time series is based on a representation such as
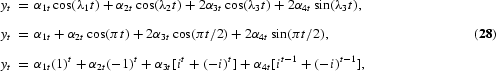
where λ1=0, λ2=π, λ3=π/2, cos(πt)=(−1)t, 2 cos(πt/2)=[it+(−i)t], 2 sin (πt/2)=[it−1+(−i)t−1], i2= −1, while αjt, j=1, 2, 3, 4, is a linear function of its own past and a stochastic term ejt, j=1, 2, 3, 4. For instance,

In such a model, α1t(1)t=α1t represents the trend component with the unit root at the zero frequency, α2t(−1)t represents the semiannual component with the root −1, while α3t[it+(−i)t]+α4t[it−1+(−i)t−1] represents the annual component with the complex conjugate roots ±i. Hylleberg and Pagan (1997) showed that the HEGY auxiliary regression in (6), rewritten as
, has an evolving seasonals model representation with
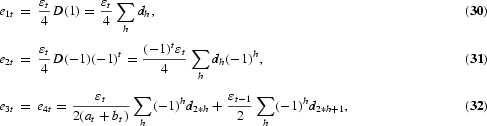
where at=it+(−i)t and bt=it−1+(−i)t−1.
From (28) to (32), it is seen that the HEGY auxiliary regression is an evolving seasonals model with α3t=α4t and the errors in the models for αjt, j=1, 2, 3, are perfectly correlated. A unit root at a given frequency implies that the corresponding ρj, j=1, 2, 3, is one. However, because αjt, j=1, 2, 3, are not observed, they must be estimated. Hylleberg and Pagan (1997) showed that
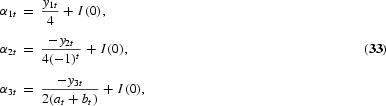
where yjt, j=1, 2, 3, is defined in Section 2.1.3 and I(0) means a stationary error. Inserting these expressions in (29) produces
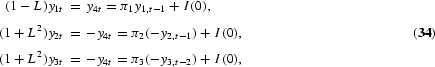
where πj=ρj−1, j=1, 2, 3.
Because the terms in the HEGY auxiliary regression are uncorrelated, one can perform the HEGY test by three regressions y4t=π1y1,t−1+I(0), y4t=π2y2,t−1+I(0), and y4t=π3y3,t−2+I(0), and testing null of πj=ρj−1=0, j=1, 2, 3, against the alternative that the πj′s are less than zero. For j=3 the test assumes that π4=0; that is, y3,t−1 is not in the HEGY regression.14
The HEGY F-test is based on a regression of the form

where the null is that (1+L2)y3t is stationary and the alternative is that the model for y3t has the form (1±γ1L+γ2L2)y3t=error.
The Canova-Hansen test may also be presented in the framework of the evolving seasonals model as shown by Hylleberg and Pagan (1997). Rewriting (33) and adding (29) with ρj=1, j=1, 2, 3, produce three state-space models
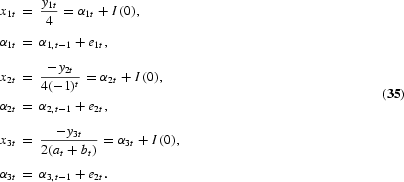
Applying a KPSS procedure as in Section 2.1.3 to each of the three state-space models implies seasonal unit root tests that coincide with the Canova-Hansen tests under their assumption that no other root exists in the data than possibly at the frequency under consideration. However, applying the KPSS procedure directly to (35) has the advantage that potential unit roots at the other frequencies do not matter, as shown by Hylleberg and Pagan (1997).
The PAR(p) may also be developed within the evolving seasonals model. Consider a simple version of (26) such as

Because Ds,t is a seasonal dummy variable taking the value 1 in the sth quarter and zero elsewhere, we can write the seasonal dummies as
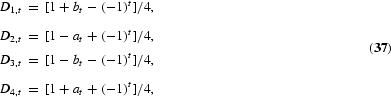
and it can be shown [see Hylleberg and Pagan (1997)] that (36) implies evolving seasonals models such as (28) with α3t=α4t and
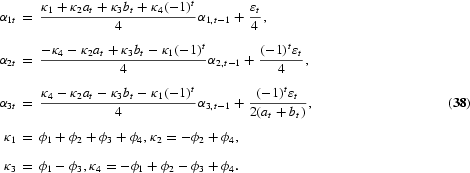
Hence, it is shown that several of the most popular seasonal models may be represented in the context of an evolving seasonals model.15
From the evolving seasonals model representation of the PAR model it is seen that the PAR model assumes that the seasonals as well as the stochastic trend evolve as a periodic model.
Koop and Dijk (2000) apply the evolving seasonals model (28) to nest the HEGY and CH auxiliary regressions as
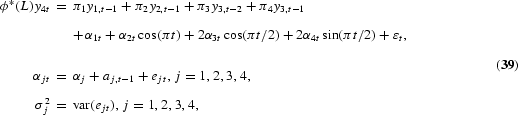
where a drift term has been added to the state equations.
16In their empirical work the only drift term allowed is in the state equation containing α1t.
The idea that the seasonal components of a set of economic time series are driven by a smaller set of common seasonal features seems a natural extension of the idea that the trend components of a set of economic time series are driven by common trends. In fact, the whole business of seasonal adjustment may be interpreted as an indirect approval of such a view.
If the seasonal components are integrated, the idea immediately leads to the concept of seasonal cointegration, introduced in the papers by Engle et al. (1989, 1993), and Hylleberg et al. (1990). In case the seasonal components are stationary, the idea leads to the concept of seasonal common features [see Engle and Hylleberg (1996)] whereas so-called periodic cointegration considers cointegration season by season [see Birchenhal et al. (1989), Franses (1993, 1996), Boswijk and Franses (1995), Franses and Kloek (1995), and Osborn (2000)].
Seasonal cointegration. Seasonal cointegration exists at a particular seasonal frequency if at least one linear combination of series, which are seasonally integrated at the particular frequency, is integrated of a lower order. For ease of exposition we concentrate on quarterly time series integrated of order 1, but the theory is easily extended to daily, weekly, or monthly data and to higher orders of integration. Quarterly time series may have unit roots at the annual frequency π/2 with period four quarters, at the semiannual frequency π with period two quarters, and/or at the long-run frequency 0. The cointegration theory at the semiannual frequency, where the root on the unit circle is real, is a straightforward extension of the cointegration theory at the long-run frequency. However, the complex unit roots at the annual frequency lead to the concept of polynomial cointegration, where cointegration exists if one can find at least one linear combination, including a lag of the seasonally integrated series, which is stationary.
In Hylleberg et al. (1990) and Engle et al. (1993), seasonal cointegration was analyzed along the path set up by Engle and Granger (1987). Consider the quarterly VAR model
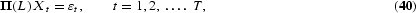
where Π(L) is a p×p matrix of lag polynomials of finite dimension, Xt is a p×1 vector of observations on the demeaned variables, while the p×1 disturbance vector is
. Under the assumptions that the p variables are integrated at the frequencies 0, π/2, 3π/2, and π, and that cointegration exists at these frequencies as well, the VAR model can be rewritten as a seasonal error correction model

where the transformed p×1 vectors Xj,t, j=1, 2, 3, 4, are defined as in (7), and where Z1t=β1′X1t and Z2t=β2′X2t contain the cointegrating relations at the long-run and semiannual frequencies, respectively, whereas Z3t=(β3′+β4′L)X3t contains the polynomial cointegrating vectors at the annual frequency. Engle et al. (1993) analyzed seasonal and nonseasonal cointegrating relations between the Japanese consumption and income, estimating the relations for Zjt, j=1, 2, 3, in the first step following the Granger-Engle two-step procedure.
The well-known drawbacks of this method, especially when the number of variables included exceeds two, are partly overcome by Lee (1992) who extended the maximum-likelihood-based methods of Johansen (1995) for cointegration at the long-run frequency, to cointegration at the semiannual frequency π.
To adopt the ML-based cointegration analysis at the annual frequency π/2 with the complex pair of unit roots ±i is somewhat more complicated, however.
To facilitate the analysis, a slightly different formulation of the seasonal error correction model is given by Johansen and Schaumburg (1999). In our notation, the formulation is
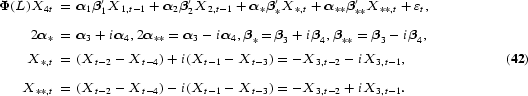
The formulation in (42), which is just a reformulation of (41),
17Equation (41) is obtained from (42) by inserting the definitions of α∗, β∗, X∗,t, and their complex conjugates α∗∗, β∗∗, X∗∗,t, and ordering the terms.
Note that (41) and (42) show the isomorphic between polynomial lags and complex variables. The general results may be found in Johansen and Schaumburg (1999) and Cubadda (2001). The relation between the cointegration vector
and the polynomial cointegration vector
is
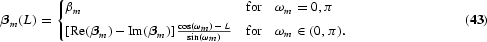
Brillinger (1981) extends the canonical correlation analysis to the case of complex variables and illustrates its similarities to the real-valued case. Based on these results, Cubadda (2001) then applies the usual Johansen (1995) approach based on canonical correlations to obtain tests for cointegration at all the frequencies of interest, that is, at the frequencies 0 and π with the real unit roots ±1 and at the frequency π/2 with the complex roots ±i.
Hence, for each of the frequencies of interest, the likelihood function is concentrated by a regression of X4t and X1,t−1, X2,t−1 or the complex pair (X∗,t, X∗∗,t) on the other regressors, resulting in the complex residual matrices U∗,t and V∗,t with complex conjugates U∗∗,t and V∗∗,t, respectively. After having purged X4t and X1,t−1, X2,t−1 or the complex pair (X∗,t, X∗∗,t) for the effects of the other regressors, the cointegration analysis is based on a canonical correlation analysis of the relations between U∗,t and V∗,t. The product matrices are
,
, and
, and the trace test of r or more cointegrating vectors is found as
, where
are the ordered eigenvalues of the problem

The corresponding (possibly complex) eigenvectors properly normalized are νj, j=1, 2 …., p, where the first r vectors form the cointegrating matrix β.
Critical values of the trace tests for the complex roots are supplied by Johansen and Schaumburg (1999) and Cubadda (2001), while the critical values for cointegration at the real root cases are found in Lee (1992) and Osterwald-Lenum (1992).
Furthermore, tests of linear hypotheses on the polynomial cointegration vectors may be executed as a χ2 test, similar to the test applied in the long-run cointegration case.
Periodic cointegration. To present some of the important concepts applied in the literature [e.g., Franses (1996), Osborn (2000), and Ghysels and Osborn (2001), let us define the observations of the sth quarter in year τ s=1, 2, 3, 4, τ=1, 2, …, N, as ysτ while the 4×1 vector
contains the observations from year τ. Consider the VAR model
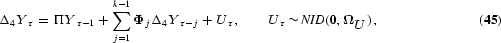
where Π and Φj are 4×4 coefficient matrices, ΩU a 4×4 covariance matrix, and Δ4=(1−L4), where L operates on the seasonal index s and not on τ. Hence,

and
.
The VAR model in (45) is written in error correction form and the number of cointegrating relations between the four series, one for each quarter, is determined by the rank of Π. Following Osborn (2000), we then have the following three definitions:
From Engle and Granger (1987) we have that two integrated series yt∼I(1) and xt∼I(1) are cointegrated if there exists a linear combination yt−βxt that is stationary. The vector 1, −β) is called the cointegration vector. In the notation above the series yt∼I(1) and xt∼I(1) are (nonperiodically) Cointegrated if each pair of annual series ysτ, xsτ is cointegrated with the same cointegration vector (1, −β) for all s=1, 2, 3, 4.
In the subsection on seasonal cointegration, we defined zero-frequency cointegration between two variables integrated at the zero frequency, yt∼I0(1) and xt∼I0(1), as existing if the transformed variables y1t and x1t [see (7)] cointegrate. Similarly, semiannual cointegration between two variables integrated at the semiannual frequency,
and
, exists if the transformed variables y1t and x1t [see (7)] cointegrate, whereas annual cointegration between two variables integrated at the annual frequency, yt∼I1/4(1) and xt∼I1/4(1), exists if the transformed variables y3t, x3t, and x3,t−1 [see (7)] polynomially cointegrate. Annual cointegration may also be expressed in terms of the complex transformations; in fact, annual cointegration exists if the complex pairs (y∗,t, x∗,t) and (y∗∗,t, x∗∗,t) cointegrate.
Full periodic cointegration exists if each pair of annual processes ysτ, xsτ cointegrates with cointegration vector (1, −βsP), but not all βsP=βP, for s=1, 2, 3, 4. Partial periodic cointegration exists if some but not all annual processes ysτ, xsτ cointegrate for s=1, 2, 3, 4. See Osborn (2000) for more details.
On the basis of these definitions, Osborn (2000) obtains a series of results that are summarized in Table 1. Osborn (2000) also suggests a series of tests for choosing between the different cointegration possibilities.

Common seasonal features. Although economic time series often exhibit nonstationary behavior, stationary economic variables exist as well, especially when conditioned on some deterministic pattern such as linear trends, seasonal dummies, and breaks. However, a set of stationary economic times series may also exhibit common behavior and, for instance, share a common seasonal pattern. The technique for finding such patterns, known as common seasonal features, is based on earlier contributions by Engle and Kozicki (1993) and Vahid and Engle (1993), defining common features. The common seasonal features were introduced by Engle and Hylleberg (1996), and further developed by Cubadda (1999).
Consider a multivariate autoregression written in error correction form as
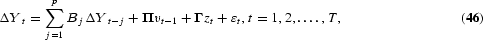
where Yt is k×1 vector of observations on the series of interest in period t and the error correction term is Πvt−1. The vector vt contains the cointegrating relations in case of cointegration at the zero frequency, and the number of cointegrating relations is equal to the rank of Π. If no cointegration exists, Π has full rank equal to k and the series are stationary. In the quarterly case, the vector zt is a vector of trigonometric seasonal dummies, such as {cos(2πht/4+2πj/T), h=1, 2; j∈(−δT≤j≤δT), sin(2πh4+2πj/T), h=1, 2; j∈(−δT≤j≤δT), j≠0, when h=2}. The use of trigonometric dummy variables facilitates the “modeling” of a varying seasonal pattern, since a proper choice of δ takes care of the neighboring frequencies to the exact seasonal frequencies, see Hylleberg (1986). Note that if δ=0, the trigonometric dummies defined above are equivalent to the usual seasonal dummies as described in Section 2.1.2.
The implication of a full rank of the k×m matrix Γ, equal to min [k, m], is that different linear combinations of the seasonal dummies in zt are needed to explain the seasonal behavior of the variables in Yt. However, if there are common seasonal features in these variables, we do not need all the different linear combinations, and the rank of Π is not full. Thus, a test of the number of common seasonal features can be based on the rank of Π [see Engle and Hylleberg (1996)].
The test is based on a reduced rank regression similar to the test for cointegration described earlier. Hence, the hypotheses are tested using a canonical correlation analysis between of zt and ΔYt, where both sets of variables are purged of the effect from the other variables in (46).
This kind of analysis has proved useful in some situations, but it is difficult to apply in case the number of variables is large, and the results are sensitive to the lag augmentation as in the case of cointegration. In addition, the somewhat arbitrary nature of the choice of zt poses difficulties.
Many economic time series have a strong seasonal component, and it is obvious that economic agents must react to that. Producers know that the demand for their products varies over the year, and the consumers know that certain products are only available at some periods or at least are cheaper in some periods than in others. Hence, the seasonal variation in economic time series must be an integrated part of the optimizing behavior of economic agents, and the seasonal variation in economic time series must be a result of the optimizing behavior of economic agents, reacting to exogenous factors such as the weather and the timing of holidays.
The fact that economic agents react and adjust to seasonal movements on the one hand, and influence them on the other, implies that the application of seasonal data in economic analysis may widen the possibilities for testing theories about economic behavior. The relative ease at which the agents may forecast at least some of the causes of the seasonality may be quite helpful in setting up testable models for production smoothing, for instance.
Apart from what is caused by the ease of forecasting exogenous factors, the type of optimizing behavior, and the agents' reactions to a seasonal phenomenon may be expected not to differ fundamentally from what is happening in a nonseasonal context. However, the recurrent characteristic of seasonality may be exploited. Such a recurrent characteristic may have important effects on adjustment cost, etc., seen in relation to adjustments to other cyclical, but less regular, phenomena. The recurrent characteristic may also have effect on the short- and long-run reaction to seasonal phenomena. In the short run, the farmers may adapt to the weather conditions in a passive way, but in the long run, investments in more effective species of grain, irrigation, etc., may change or smooth the effect of the weather.
In the following, we discuss how agents react and interact when faced with seasonal fluctuations.
There is no real dominating approach found in the literature, although there are two main branches. The first is the real-business-cycle approach [e.g., Chatterjee and Ravikumar (1992) or Braun and Evans (1995)]. These all work with a utility-optimizing consumer faced with some feasibility constraint. However, in most of this RBC branch, seasonality arises from deterministic shifts in tastes and technology, contradicting the empirical evidence that seasonality evolves in a stochastic fashion [e.g., Hylleberg et al. (1993)]. A few other papers incorporate seasonality through stochastic productivity shocks; see, for example, Wells (1997) and Cubbada et al. (2002). Christiano and Todd (2002) also discuss whether this conventional RBC model is sensible to the approximations usually made in the model.
A different approach is taken by Ghysels (1988), Miron and Zeldes (1988), and Miron (1996), who examine whether firms actually smooth production, and Beaulieu and Miron (1992a,b), Cecchetti and Kashyap (1996), and Cecchetti et al. (1997), who investigate whether there are significant connections between the business cycles and the seasonal cycles, and in general that seems to be the case.
Often the situation can be seen as though states change in accordance with the seasons, past actions, etc., whereafter the agents must decide on what to do. The problem can be made concrete by assuming that we can write the problem as an expected profit maximization
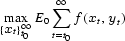
subject to some constraints
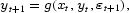
where xt is a vector containing, e.g., sales or production controlled by the firm; yt is a vector of states such as interest rates, storage capacity, inventory as well as the direct seasonality (e.g., average temperature); and εt+1 is a stochastic term.
If this problem obeys certain conditions of regularity [see, e.g., Stokey et al. (1989), it can be rewritten as a recursive problem. For concreteness, let the discount factor be constant and let the objective function be additively separable. In addition, let the seasonal shock have a Markov property. We can then rewrite the problem as a Bellman problem:
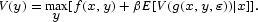
This functional equation almost always has a solution, and we can derive a rule of how the firm should choose xt, given the state yt. Unfortunately, the problem is generally too complicated to be given an analytical solution, and it is often necessary to find the solution by an iterative algorithm [see Rust (1996) and Judd (1998)].
Todd (1990) provides a framework to obtain analytic solutions using the linear quadratic approach. The main idea is to have the objective function being quadratic and the transition equations being linear, and to model seasonality by a periodic representation. Thus, the linear quadratic approach is quite restrictive.
Nonetheless, this approach is widely used for two main reasons. First, after all, the procedure is general enough to capture a very broad set of problems. Second, when the decision is derived from the model, the Euler equations—that is, the first-order conditions—provide estimable econometric equations. If data are available for some of the states and the final decisions, it is possible to test whether the model is compatible with actually observed behavior [Rust (1996)].
In an intertemporal dynamic model, a common result is that the presence of seasonality in an exogenous variable may induce power in the spectrum of the endogenous variables, both at the seasonal and nonseasonal frequencies. The reason for this is that agents generally will react to changes in their environment as well as in their information set, when they know that actions today will affect the future. An example that describes the intuition behind this result is the adjustment cost in production; e.g., if there is large cost associated with training workers, which implies that it may not be a good idea to fire workers in a period with low sales, or if the sales are expected to rise in the future.
There are several papers illustrating this fact. Ghysels (1988) sets up an intertemporal production model with the above-mentioned adjustment costs and an exogenous seasonal pattern introduced into the demand. It is then shown that seasonality is affecting the endogenous part of the model, not only at the seasonal frequencies but at all frequencies. This also illustrates the danger of applying prefiltered seasonal adjusted data. In some cases, it is shown that the distortions may be small, however [see Christiano and Todd (2002)].
Osborn (1988) extends Hall (1978) by including seasonal varying components in the utility function. The model is then tested with data from the United Kingdom, and even though the model is rejected, it still does better than the standard model.
A production-smoothing model is analyzed by Ghysels (1988), Miron and Zeldes (1988), and Miron (1996), but the empirical evidence is negative as the hypothesis of production smoothing is rejected, a finding that could be caused by the use of too-aggregated data. However, both empirical findings may also be due to misspecified models. The functional forms may be too restrictive or perhaps the agents may not have all the information that model builders normally assume.
A rather new approach, called robust control and advocated by Hansen and Sargent (2000), attacks this problem. The idea is to allow for the fact that the agent thinks the model could be misspecified and hence uses the information set available to him, and allows for the uncertainty. Thus, the agent is assumed to think of the model as a possibly misspecified model of the real model. It could be interesting to see this applied to models with seasonal characteristics.
Seasonality has been a major research area in economics for several decades. The paper assesses the recent development in the literature on the treatment of seasonality in economics, and divides it into three interrelated groups. The first group, pure noise model, consists of methods based on the view that seasonality is noise contaminating the data or, more correctly, contaminating the information of interest for the economists. The second group, time-series models, treats seasonality as a more integrated part of the modeling strategy, with the choice of model being data driven. The third group, economic models of seasonality, introduces economic theory, that is, optimizing behavior into the modeling of seasonality.
The recent development has been quite promising, where increasingly, the treatment of seasonal economic time series in economics is an integral part of the modeling process, and where there is an increased awareness that use of seasonally adjusted data very easily leads to errors and in addition throws away valuable information. The next step in the development should be a more elaborate integration of economic theory into the modeling process, a development that is as needed in the area of modeling seasonal economic time series as it is in most other areas of econometrics, if not all.
Paper presented as an invited paper at the METU conference in Ankara, September 2001. Earlier versions have been given at ESEM in Lausanne, August 2001; as the opening address at the Gdansk conference on East European Transition and EU Enlargement, A Quantitative Approach, June 2001; and as an invited paper to the conference on Seasonality in Economic and Financial Variables, held at the University of Algarve, Portugal, October 2000. It has also been presented at seminars at Universidade Technica de Lisboa, Copenhagen Business School, and at the University of Aarhus. Helpful comments from the participants and from referees are gratefully acknowledged.

Cointegration possibilitiesa