Cognition as an information source

Cognitive pattern recognition-and-selected response, following the model of Atlan and Cohen (Reference Atlan and Cohen1998), proceeds by convoluting an incoming external ‘sensory’ signal with an internal ‘ongoing activity’ – which includes, but is not limited to, a learned or inherited picture of the world – and, at some point, triggering an appropriate choice of an action from a larger set of those available based on a decision that the pattern of sensory activity requires a response. It is not necessary to specify how the pattern recognition system is trained, and hence possible to adopt a weak model, regardless of learning paradigm, that can be more formally described by the Rate Distortion Theorem that dictates the minimum channel capacity necessary to keep the average distortion in a transmitted signal below some fixed limit (Wallace, Reference Wallace2012). Fulfilling Atlan and Cohen's criterion of meaning-from-response, it is possible to define a language's contextual meaning entirely in terms of system output.

Most directly, cognition involves choice, choice reduces uncertainty, and the reduction of uncertainty directly implies the existence of an information source ‘dual’ to that cognition. This argument is breathtakingly sufficient, and places cognition and consciousness within the statistical regularities imposed by the asymptotic limit theorems of both information and control theories, and certain constraints imposed by physical theory through the recognition of information as a form of free energy (e.g. Feynman, Reference Feynman2000). However, a more formal model, a conceptual simplification of the standard neural network, can be made as follows.

A pattern of ‘sensory’ input – incorporating feedback from the external world – is expressed as an ordered sequence y ₀, y ₁, …. This is mixed in a systematic (but unspecified) algorithmic manner with internal ‘ongoing’ activity, a sequence w ₀, w ₁, …, to create a path of composite signals x = a ₀, a ₁, …, a _n, …, where a _j = f(y _j, w _j) for some function f. This path is then fed into a similarly unspecified decision function generating an output h(x) that is an element of one of two sets B ₀ and B ₁. We take B ₀ ≡ {b ₀, …, b _k}, B ₁ ≡ {b _k+1, …, b _m}.

The model permits a graded response, supposing that if h(x) ∈ B ₀ the pattern is not recognized, and if h(x) ∈ B ₁ the pattern is recognized and some action b _j, k + 1 ≤ j ≤ m takes place.

The principal focus is on those composite paths x triggering pattern recognition-and-response. Given a fixed initial state a ₀, such that h(a ₀) ∈ B ₀, we examine all possible subsequent paths x beginning with a ₀ and leading to the event h(x) ∈ B ₁. Thus h(a ₀, …, a _j) ∈ B ₀ for all 0 ≤ j < m, but h(a ₀, …, a _m) ∈ B ₁. The y _j, the ‘sensory’ input convoluted with the internal w _j, contains feedback from the external world, i.e. how well h matches intent with observation. Wallace (Reference Wallace2012) uses this comparison to define a Rate Distortion Function and an associated average distortion characterizing the ‘goodness-of-fit’ between what a cognitive entity perceives and what exists.

For each positive integer n let N(n) be the number of grammatical and syntactic high probability paths of length n that begin with some particular a ₀ having h(a ₀) ∈ B ₀ and lead to the condition h(x) ∈ B ₁. Call such paths ‘meaningful’ and assume N(n) to be considerably less than the number of all possible paths of length n – pattern recognition-and-response is comparatively rare. The essential assumption is that the longitudinal finite limit

(1)$$ H = \mathop {\lim }\limits_{n \to \infty } {\displaystyle{\log[N(n)]} \over {n}} $$

both exists and is independent of the path x. Call such a cognitive process ergodic. The essential idea surrounding an ergodic system is that time averages converge on ensemble averages.

Disjoint partition of state space is done according to sets of states which can be connected by meaningful paths from a particular base point, leading to a natural coset algebra of the system defining a groupoid (Wallace, Reference Wallace2012). A groupoid is an algebraic structure having a product that is not necessarily defined between all elements. The most simple example is a disjoint union of groups (e.g. Brown, Reference Brown1987).

It is thus possible to define an ergodic information source X associated with stochastic variates X _j having joint and conditional probabilities P(a ₀, …, a _n) and P(a _n|a ₀, …, a _n−1) such that appropriate joint and conditional Shannon uncertainties may be defined which satisfy the standard relations (Cover and Thomas, Reference Cover and Thomas2006).

(2)$$\eqalign{H[{\bf X}] & = \mathop {\lim }\limits_{n \to \infty } \,\displaystyle{{\log [N(n)]} \over n} \cr & = \mathop {\lim }\limits_{n \to \infty } H(X_n \vert X_0, \ldots ,X_{n - 1}) \cr & = \mathop {\lim }\limits_{n \to \infty } \displaystyle{{H(X_0, \ldots ,X_n)} \over n}} $$

where the Shannon uncertainties H are defined in terms of cross-sectional sums of the form $H = -\sum P_{k}\log [P_{k}]$. Again, the P _k constitute probability distributions, summing to 1 (Khinchin, Reference Khinchin1957; Ash, Reference Ash1990; Cover and Thomas, Reference Cover and Thomas2006).

This information source is taken as dual to the ergodic cognitive process.

Different quasi-languages will be defined by different divisions of the total universe of possible responses into various pairs of sets B ₀ and B ₁. Like the use of different distortion measures in the Rate Distortion Theorem, however, the underlying dynamics will all be qualitatively similar. Again, the Rate Distortion Theorem mandates R(D) as the minimum channel capacity needed to ensure that average distortion in a transmitted signal is below the fixed real positive value D, and will vary according to the nature of the channel studied.

Meaningful paths – creating an inherent grammar and syntax – have been defined entirely in terms of system response, as Atlan and Cohen (Reference Atlan and Cohen1998) propose.

In sum, if there are N(n) possible behavioral – and hence temporal – output paths of that information source having length n, then there will be a path-independent limit H such that equation (1) holds.

This is the Shannon uncertainty of the (stationary, ergodic) information source dual to the cognitive process.

Extension to path-dependent ‘nonergodic’ systems, for which the time average is not the same as the ensemble average, can be made using the fact that, for individual sequences x ⁿ = {a ₀, a ₁, …, a _n}, a path-wise uncertainty $\mathop {\lim }\nolimits_{n \to \infty } {\cal H}(x^{n})= {\cal H}(x)$ can always be defined, although it will not be given by a simple Shannon ‘entropy’ (Khinchin, Reference Khinchin1957 p. 72). See Wallace (Reference Wallace2018a) for details.

Cognitive phase transitions: constructing global workspaces

We envision the evolution of a broad set of unconscious cognitive modules within a reproducing organism that serves a number of independent purposes, ranging from the search for food and habitat, and the avoidance of predation, to modalities of reproduction. Thus even a simple organism will have a large network of unconscious cognitive modules that, necessarily, interact, if only by crosstalk information leakage.

Evolution can then take this interaction and run with it, across multiple physiological systems at different temporal scales, processes including wound healing, immune response, tumour control, gene expression, sociocultural cognition and so on (Wallace, Reference Wallace2012). The argument is direct.

Given a network of interacting (unconscious) cognitive modules of any sort, we can construct an interacting network of dual information sources, linked by crosstalk – a kind of inevitable information leakage between them.

That is, the information sources dual to an organism's set of cognitive modules are not independent, but are correlated, so that a joint information source can be defined as having the properties

(3)$$ H(X_{1},\ldots, X_{n}) \leq \sum_{\,j=1}^{n} H(X_{\,j}) $$

This is the information chain rule (Cover and Thomas, Reference Cover and Thomas2006) and has implications for metabolic energy consumption and regulation ina biological process. Recall Feynman's description of how information and free energy have an inherent duality. Feynman, in fact, defines information precisely as the free energy needed to erase a message. The argument is again direct, and for very simple systems it is easy to design an (idealized) machine that turns the information within a message directly into usable work – free energy. Information is a form of free energy (Feynman, Reference Feynman2000) and the construction and transmission of information within living things – the physical instantiation of information – consume considerable free energy, with inevitable massive losses via the second law of thermodynamics.

Suppose an intensity of available metabolic free energy is associated with each defined joint and individual information source H(X, Y), H(X), H(Y), e.g. rates M _X,Y, M _X, M _Y.

Again, although information is a form of free energy, there is a great entropic loss in its actual expression, so that the probability distribution of a source uncertainty H might be written in the standard Gibbs form (e.g. Landau and Lifshitz, Reference Landau and Lifshitz2007; Pettini, Reference Pettini2007) as

(4)$$ P[H] = {\displaystyle{\exp[-H/\kappa M]} \over {\int \exp[-H/\kappa M]{\rm d}H}} $$

assuming κ, the ‘translation rate’ of metabolic free energy into information, is very small.

To first order, then,

(5)$$ \hat{H}=\int H P[H] {\rm d}H \approx \kappa M $$

and, using equation (3),

(6)$$ \eqalign{{\hat H}(X,Y) & \leq \hat{H}(X) + {\hat H}(Y) \cr M_{X,Y} & \leq M_{X}+M_{Y}} $$

Thus, as a consequence of the information chain rule, allowing crosstalk consumes a lower rate of metabolic (or other) free energy than isolating information sources. That is, in general, it takes more free energy – higher total cost – to isolate a set of cognitive phenomena than it does allow them to engage in crosstalk, a signal interaction that, under typical circumstances, grows as the inverse square of the separation between circuits. This is a well-known problem in electrical engineering that can consume considerable attention and other resources for proper address.

For a given underlying network topology of n interacting information sources representing cognitive submodules of an organism – necessarily without isolated subcomponents – the average crosstalk between them, say ε(n), will be a monotonic increasing function of n. For that given network topology, there will be some critical value ε _C at which a giant component emerges. That is, at ε _C, a very large number of cognitive processes become suddenly linked into a joint ‘giant component’ information source. For random networks, this phenomenon has been fully studied, and the conditions under which a giant component occurs are well understood (e.g. Spenser, Reference Spenser2010). While other topologies impose different detailed conditions, the sudden emergence of a giant component is virtually universal, covering a very large class of networks. Thus, for any ε _C, there will be a critical number of dual information sources n _C such that ε(n) > ε _C if n > n _C.

This phase transition – from isolated individual components to a single ‘giant component’ – represents the onset of large-scale, dynamic, global broadcasts acting on a variety of scales of time as the organism becomes large enough to entertain a sufficient number of lower level cognitive modules.

The essential point is that this kind of phase transition to a ‘global broadcast’, necessarily involving changes in groupoid symmetry, is very general and will occur from the intra-organismal to societal level of organization in cognitive systems.

One suspects that evolutionary selection has, in fact, acted on cognitive network topology to favour forms that permit broadcasts – i.e., the establishment of a ‘giant component’ – at relatively low values of ε, albeit on varying timescales.

It was noted, after equation (1), that disjoint partition of state space is possible according to sets of states that can be connected by high probability paths to the same base point, leading to a groupoid structure characterizing the underlying network topology. Groupoids generalize ideas of both symmetry and equivalence class (e.g. Brown, Reference Brown1987), and ε can be taken as a temperature analog in a spontaneous symmetry breaking (or making) argument in Landau's sense (Landau and Lifshitz, Reference Landau and Lifshitz2007). That is, increasing ε, a measure of crosstalk – information leakage – between cognitive submodules, leads to a punctuated transition to a higher groupoid symmetry representing a global broadcast.

Nothing in this realization of the Baars model seems restricted to terrestrial biological entities. Indeed, even on Earth, we know of widely different brain structures that instantiate conscious behaviours, ranging from familiar mammalian and avian forms to reptiles, cephalopods, and perhaps insect colonies (Cartmill, Reference Cartmill2000; Griffin et al., Reference Griffin and Speck2004; Edelman et al., Reference Edelman, Baars and Seth2005).

The essential point, from an astrobiological perspective, is that any organism evolving a sufficiently large set of unconscious cognitive submodules is likely to undergo an evolutionary exaptation of the crosstalk (information leakage) between them into something having a shifting, tunable, global workspace/broadcast mechanism. Those broadcasts operating in the realm of a few hundred milliseconds would be analogous to consciousness-as-we-know-it.

The rate of cognition

We know that physiological global broadcasts, where underlying cognitive modules come together to address patterns of threat or opportunity, operate across very different timescales. Wound healing can take 18 months, while high-order animal consciousness operates in the realm of a few hundred milliseconds. How can consciousness be so fast? Here, we adapt the arguments of (Wallace, Reference Wallace2016a,Reference Wallaceb).

Recall the argument above, that in the cognitive process, an internal picture of the world is compared with incoming sensory data. Such comparison, involving transmission of information along with a ‘sensory/cognitive’ channel, permits definition of an average distortion between what is happening and what is perceived, and, via the Rate Distortion Theorem (Cover and Thomas, Reference Cover and Thomas2006), permits estimation of the minimum channel capacity needed to keep that average distortion below some limit. That is, to survive ‘real time’ challenge, the organism must maintain a good ongoing estimate of the external real world so that cognitive choices can be made, also in real time.

What are we to do with such a biological Rate Distortion Function? The approach is via Arrhenius' law (Laidler, Reference Laidler1987), which predicts an exponential rise in reaction rate withthe rise in temperature. Here, however, the ‘temperature’ is the rate of supply of metabolic free energy to the cognitive system of interest.

The energetics of terrestrial biological reactions are remarkable. At 300 K, molecular energies represent something like 2.5 KJ /mol⁻¹ of available free energy. The basic terrestrial biological energy reaction – the hydrolysis of adenosine triphosphate (ATP) to adenosine diphosphate – at 300 K, produces some 50 KJ /mol⁻¹, implying a ‘reaction temperature’ of 6000 K. A high rate of ATP delivery thus provides enough energy for very rapid biocogniton, given that neural tissues in higher animals consume an order of magnitude more metabolic free energy per unit time than other tissues.

A calculation

Given a simple chemical reaction of the form aA + bB → pP + qQ, the rate of change in the concentration of chemical species P – written [P] – is typically determined by an expression

(7)$$ {\rm d}[P]/{\rm d}t = k(T)[A]^{n}[B]^{m} $$

where n and m are constants depending on system structure. The reaction rate k is expressed by the Arrhenius relation as

(8)$$ k=\alpha \exp[-E_{a}/\kappa T] $$

where α is another characteristic constant, E _a is the reaction activation energy, T is the Kelvin temperature and κ a universal constant.

Note that exp[−E _a/κT] is, using the Boltzmann distribution, the fraction of molecular interactions having energy greater than E _a.

The basic idea can be adapted to cognitive physiological processes. Above, we have associated cognition with a dual information source (Wallace, Reference Wallace2012). High level cognition is usually an all-or-nothing phenomenon (Sergeant and Dehaene, Reference Sergeant and Dehaene2004) so that an incoming signal must exceed a threshold before becoming entrained into a characteristic general broadcast of large-scale developmental selection, very much akin to a slow form of consciousness (Wallace, Reference Wallace2012). Interest focuses on the Rate Distortion Function associated with the channel connecting the cognitive organism with an embedding and embodying ‘real time’ environment. Again, R(D) defines the minimum rate of information transmission needed to ensure that the average distortion between what is sent and what is received is less than or equal to D ≥ 0, according to an appropriate distortion measure. Assuming a threshold R ₀ for the perception of an incoming environmental signal, following Feynman (Reference Feynman2000) identification of information as a form of free energy, it is possible to write a Boltzmann-like probability as

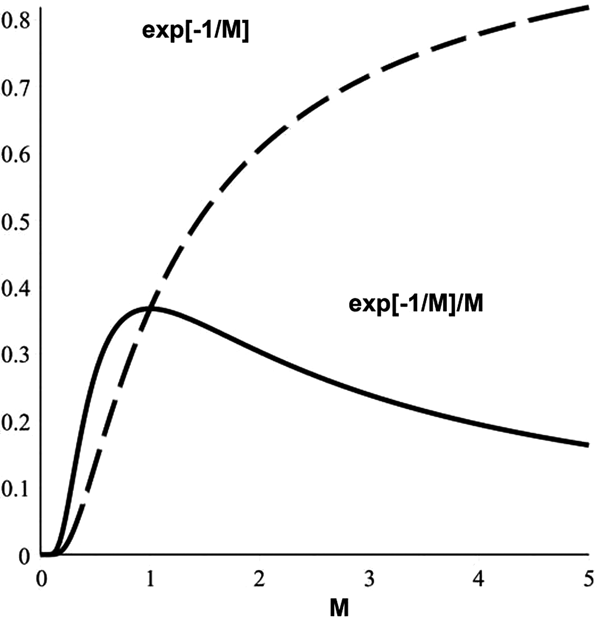
(9)$$ P[R \geq R_{0}] = {{\int_{R_{0}}^{\infty}\exp[-R/\omega M]{\rm d}R} \over {\int_{0}^{\infty}\exp[-R/\omega M]{\rm d}R}} =\exp[-R_{0}/\omega M] $$

where M is the rate at which metabolic free energy is provided to the cognitive process. Figure 1, showing exp (−1/M), follows. Also shown is the energetic efficiency measure exp (−1/M)/M. Peak efficiency – likely to be strongly selected for by evolutionary process – takes place at R ₀/ωM = 1.

Fig. 1. ‘Arrhenius’ relation for the rate of a cognitive physiological process as a function of the rate of metabolic free energy consumption. The rate of cognition – dotted line – at first increases exponentially witha supply of metabolic free energy but then tops out. The highest efficiency – solid line – occurs at the intermediate value M = R ₀/ω.

In sum, cognition rate first increases exponentially sharply with the rate of free energy supply M, but rapidly tops out, so that highest efficiency is at an intermediate value of M.

For terrestrial higher animals, nervous system tissues, operating with time constants of about 100 ms, do so by requiring an order of magnitude greater metabolic energy support than other tissues. High-level cognition in other astrobiologies may, in fact, operate with time constants shorter than 100 ms if they can evolve to supply metabolic free energy at sufficiently high rates.

A very general statistical model of the punctuated accession-to-consciousness involving the sudden formation of the global workspace that takes place when an incoming ‘sensory’ signal reaches threshold is given in the Mathematical Appendix.

Are ‘sleep cycles’ inevitable in rapid biocognition?

We have now developed enough formal machinery to address the question raised in the title, adapting, somewhat, the arguments of Wallace (Reference Wallace2016a).

As Maturana and Varela (Reference Maturana and Varela1980) argue, the cognition is ubiquitous at all scales and levels of organization of the living state. Gene expression mechanisms at the cellular level must choose when and how to activate, and are closely regulated as to time, place, and manner. Failure of regulation results in developmental disorders of varying severity. Blood pressure must not only change to meet metabolic and other demands, but it must be closely regulated to prevent explosive organic damage. Similarly, in higher animals, the ‘stream of consciousness’ must be closely regulated by ‘riverbanks’ that constrain it to realms useful to the animal and its social groupings (Baars Reference Baars1988; Wallace, Reference Wallace2005, Reference Wallace2012). We must, then, envision consciousness and its regulatory system as a paired dyad under a constraint on the maximum rate at which metabolic free energy is available.

Letting the subscript C represent consciousness and R its regulatory system, we thus seek to maximize an efficiency scalarization

(10)$$ \displaystyle{{\exp [ - K_{\rm C}/M_{\rm C}]} \over {M_{\rm C}}} + \displaystyle{{\exp [ - K_{\rm R}/M_{\rm R}]} \over {M_{\rm R}}} $$

subject to the constraint

(11)$$ M = M_{\rm C} + M_{\rm R} $$

This leads, most simply, to a standard Lagrangian optimization on

(12)$$L \equiv \displaystyle{{\exp [ - K_{\rm C}/M_{\rm C}]} \over {M_{\rm C}}} + \displaystyle{{\exp [ - K_{\rm R}/M_{\rm R}]} \over {M_R}} - \lambda (M - M_C - M_R)$$

where λ represents a ‘cost’ variable dual to M. Under sufficiently pathological conditions, the ‘cost’ cannot be met (Jin et al., Reference Jin, Hu and Zhou2008).

The Lagrange optimization condition is

(13)$$ \nabla_{M_{\rm C}, M_{\rm R}, \lambda}L = 0 $$

The resulting equation for solution pairs M _C, M _R implies the existence of several different possible optimization points for the system, strongly parameterized by the overall energy rate M. This expression represents an index theorem relating solutions of an analytic equation to underlying topological modes: increasing the number of systems to be optimized – adding terms of the form exp[−K _J/M _J]/M _J – increases the number of possible non-equilibrium quasi-stable states.

Making the first approximation to a sleep cycle, there will be only a small number of stages to the normal pattern. On Earth, these are NREM (non-rapid eye movement) sleep, which involves low rates of blood flow to the brain – low M – and REM sleep which can rival or exceed conscious state blood flows. Sleep states must, like all other neural processes, be highly regulated.

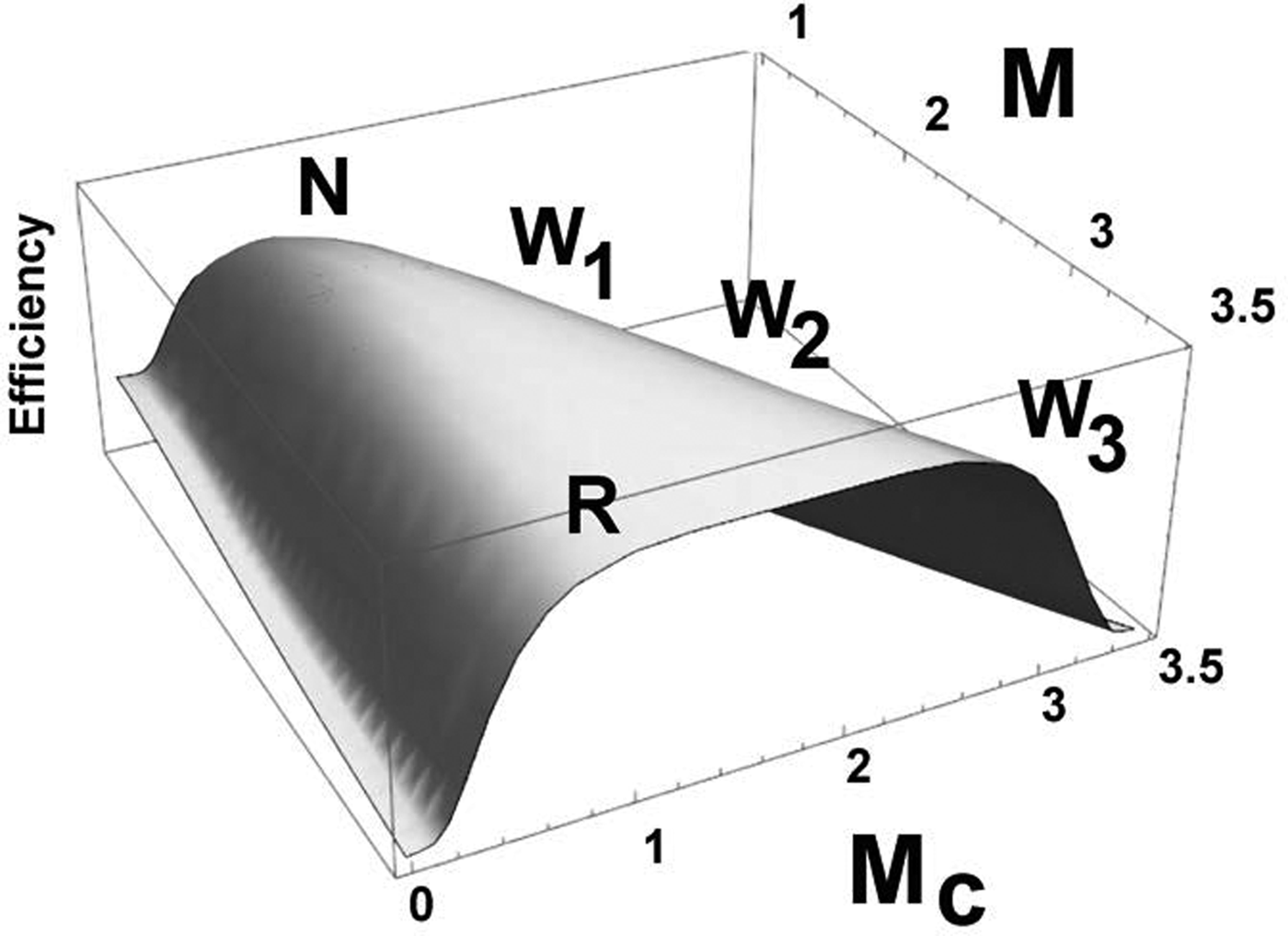
Taking the rate constants K _C ≈ K _R = K in equation (10), calculation shows a symmetric efficiency curve with one or two peaks, depending on the magnitude of M = M _C + M _R, as in Fig. 2. Taking K = 1, M _C + M _R = M = 1 → 3.6, we obtain a maximum efficiency index, (about 0.74) at M _C = M _R ≈ 1 for M ≈ 2, or along symmetric ridge points for larger M. The maximum value of 3.6 for M is chosen from Madsen and Vorstrup (Reference Madsen and Vorstrup1991), who found a 44% decline in cerebral metabolic rate during deep, slow-wave, NREM sleep.

Fig. 2. Following Wallace (Reference Wallace2016a), consciousness-and-regulator efficiency as a function of the metabolic free energy consumed by consciousness, M _C, for K _X = 1, M = M _C + M _R = 1 → 3.6. A single maximum dominates the low energy mode, suggesting NREM sleep, denoted N, representing a 44% decline from the maximum M. The maxima at higher energies are ridges, suggesting REM sleep/awake modes, denoted R, W. Normal transitions are from W to N, followed by N-R oscillation. During sleep modes, ‘regulator’ systems for consciousness may perform routine maintenance, as does the immune system when not coping with infection, wound healing, or malignancy. NREM sleep then becomes a transition path between the two more active states. Changing the values of the K _X markedly shifts the relative heights and widths of the peaks, suggesting an added control mode. Some work produces the sorts of models described in Booth and Diniz Behn (Reference Booth and Diniz Behn2014). The progression W ₁ → W ₂ → W ₃ would indicate increasing degrees of wakeful attention, requiring sequentially greater supplies of metabolic free energy. More convoluted evolutionary (or cultural) histories might impose other intermediate points for cycles on such energy/efficiency surfaces.

The highest efficiency peak is at the quiescent NREM-analog mode. At higher M there are two symmetric greatest efficiency points that suggest waking/active sleep modes in which REM ‘sleep’ seems to represent a parsimonious assumption of essential maintenance duties by systems otherwise dedicated to the regulation of awake consciousness. This appears to be similar to the immune system that, when not coping with infection, wound healing and malignancy, is committed to processes of routine cellular maintenance (Cohen, Reference Cohen2000).

Sleep deprivation may be very serious indeed.

As Harris et al. (Reference Harris, Jolivet and Attwell2012) put it,

It is known that the normal route from waking, the W point in Fig. 2, to REM sleep, the point R, is from W to N, and then down the other ridge from N to R. Direct transition from R to W does occur, and cycling between N and R is normal. In addition, occasional, culturally-dependent ‘trance states’ are known to exist that seem intermediate (e.g. Hubbard, Reference Hubbard2003).

The progression W ₁ → W ₂ → W ₃ in Fig. 2 could be taken as representing different degrees of attention within the waking state, each requiring a higher overall rate of metabolic free energy supply.

Note that higher values of K _C = K _R generate much broader symmetric curves with far less well-defined peaks, while lower values generate surfaces that are much more sharply peaked. Unequal values raise or lower one or the other ridge. Thus ‘tuning’ these parameters individually would provide significant added system control, causinga transition from ‘waking’ to various forms of ‘sleep’ states.

This model is consistent with Hobson's (Hobson (Reference Hobson2009), figure 4) picture of the Western sleep cycle, where the normal progression is from waking to low-energy NREM sleep, followed by oscillation between NREM mode and the high-energy REM state. Note that, in other cultures, other patterns have been observed (e.g. Wallace, Reference Wallace2017 Section 5.10 and references therein).

Figure 2 is also consistent with the observations of Hudson et al. (Reference Hudson, Calderon, Pfaff and Proekt2014) on the punctuated recovery to consciousness from anesthesia. See their figure 4C which identifies three hubs between which there is directed transition during recovery.

REM sleep is now understood as another state of consciousness that, compared to alert waking, is deficient in neuromuscular function, analytic ability, and transient episodic memory, while particularly rich in emotional cognition. Both waking and falling asleep involve complicated physiological processes to effect a transition between states. For some considerable time, researchers recognized the importance of the reticular activating mechanism in the change from sleep to waking (Evans, Reference Evans2003). Recently, an arousal inhibitory mechanism – a thalamo-cortical process – has been recognized which transfers the body from waking to sleep (Evans, Reference Evans2003). Other work (Saper et al., Reference Saper, Cano and Scammell2005; Lu et al., Reference Lu, Sherman and Saper2006) has identified a neural flip-flop switch structure which controls REM sleep.

The standard phenomenological model for sleep-as-we-know-it is the ‘two-process’ approach of Borbely (Reference Borbely1982) and Daan et al. (Reference Daan, Beersma and Borbely1984). As Skeldon et al. (Reference Skeldon, Dijk and Derks2014) put it, the homeostatic process takes the form of a relaxation oscillator that results in a monotonically increasing ‘sleep pressure’ during the wake that is dissipated during sleep. Switching from wake to sleep, and vice versa occurs at upper and lower threshold values of the sleep pressure respectively, where the thresholds are modulated by an approximately sinusoidal circadian oscillator. Skeldon et al. (Reference Skeldon, Dijk and Derks2014) go on to show that the two-process model is essentially the same as the slow-time dynamic of the neurologically-based Phillips and Robinson (Reference Phillips and Robinson2007) model.

We argue, then, that under Darwinian selection pressure for high rates of waking-state consciousness, patterns of transition analogous to Fig. 2 must be seen. These might perhaps involve adding one or more efficiency terms to Eq. (10), or more intermediate transition points on the plateau, generalizing the N − R − W and/or W ₁ → W ₂ → W ₃ progressions.

Intelligent aliens likely dream, although perhaps not in the ways we do, or of what we would call sheep.

Indeed, as Worthman and Melby (Reference Worthman, Melby and Carskadon2002) put the matter for humans,

In many respects, cultural differences already make us ‘aliens’ among ourselves. The intransigent difficulties of human inter-cultural communication should stand as a singular warning for scenarios involving ‘alien’ contacts. Recall that genetic differences between human populations are far less than those between chimpanzee populations.

We briefly explore this question further.

Consciousness and culture intertwined

The evolutionary anthropologist Robert Boyd has asserted that ‘Culture is as much a part of human biology as the enamel in our teeth,’ (Richerson and Boyd, Reference Richerson and Boyd2004) and, while many other animals on Earth display some measure of culture as learned and transmitted behaviour (Avital and Jablonka, Reference Avital and Jablonka2000), nothing defines humans quite like the interpenetration of mind and self with the embedding cultural milieu. Technology and its artefacts are, of course, one part of that milieu.

It is not difficult to extend the Baars model to include interaction with an embedding culture and with a hierarchical set of institutions within that culture seen as a generalized transmissible language associated with a nested set of information sources (Wallace, Reference Wallace2013, Reference Wallace2015). This includes both a form of niche construction (Wallace, Reference Wallace2010) and distributed cognitive institutions acting on various scales (Wallace and Fullilove Reference Wallace and Fullilove2008). This is most easily done by invoking the set of interacting information sources dual to cognitive process via network information theory (El Gamal and Kim, Reference El Gamal and Kim2010, p. 2–26): Given a basic set of such dual information sources, say (X ₁, …, X _k), that can be partitioned into two ordered sets, say $X({\cal J})$ and $X({\cal J}^{\prime })$, then the splitting criterion of the larger system becomes $H(X({\cal J})\vert X({\cal J}^{\prime }))$. Generalization to three or more such ordered sets seems direct and leads to a Baars-like theory of collective consciousness in which different global workspaces act at different scales of size and time (Wallace and Fullilove, Reference Wallace and Fullilove2008; Wallace, Reference Wallace2015).

As the anthropologists will attest, an astounding variety of culturally-driven institutions, associated forms of mind and self, and dynamics of interaction, graces the world. Typically, humans, whose overall genetic structure is more uniform than that of chimpanzee populations, do not communicate well across the many different cultural modes. Wallace (Reference Wallace2015) and Wallace and Fullilove (Reference Wallace and Fullilove2008) suggest that stabilizing complex systems of interacting cognitive institutions is exceedingly difficult, given that canonical inability to communicate, and the planet seems to be facing a serious crisis of sustainability.

More relevant, perhaps, are recent studies of the role of culture in ‘basic biological’ aspects of human perception, matters that ‘should’ be independent of culture.

They are not. We loosely follow the arguments of Wallace (Reference Wallace2018b).

Most particularly, Nisbett et al. (Reference Nisbett, Peng, Incheol and Norenzayan2001), continuing a long line of research (Markus and Kitayama, Reference Markus and Kitayama1991; Heine, Reference Heine2001), review an extensive literature on empirical studies of basic cognitive differences between individuals raised in East Asian and Western cultural heritages, which they characterize, respectively, as ‘holistic’ and ‘analytic’, finding that tools of thought embody a culture's intellectual history, that tools have theories built into them, and that users accept these theories, albeit unknowingly, when they use these tools.

Matsuda and Nisbett (Reference Matsuda and Nisbett2006) observed that, whereas East Asians view the world holistically, attending to the entire field and relations among objects, Westerners view the world analytically, focusing on the attributes of salient objects. Compared to Americans, East Asians were more sensitive to contextual changes than to focal object changes, These results strongly imply significant cultural variation in what may seem to be basic perceptual processes.

Similarly, Nisbett and Miyamoto (Reference Nisbett and Miyamoto2005) argue that fundamental perceptual processes are influenced by culture, establishing a dynamic relationship between the cultural context and perceptual processes. The central implication is that for humans, who have relatively little genetic variability across populations, basic perception can no longer be regarded as consisting of processes that are universal across all people at all times.

Wallace (Reference Wallace2007) explores analogous dynamics involving inattentional blindness and culture.

The inference, then, is that ‘alien’ species will have cognitive modalities also synergistic and intertwined with learned or inherited culture and that understanding and relating to such mutualistic constructs will be difficult indeed.

Quantum systems

The theory above is purely classical and produces Baars' results directly. Wallace (Wallace, Reference Wallace2005, Chapter 5, Section 6), however, does examine how quantum versions of the asymptotic limit theorems of information theory (e.g. Bjelakovic et al., Reference Bjelakovic, Kruger, Siegmund-Schultz and Szkola2003, Reference Bjelakovic, Kruger, Siegmund-Schultze and Szkola2004) might be used to generalize the model. Unfortunately, the quantum results are not well characterized, and an exact treatment is lacking, Nonetheless, it becomes quite clear that consciousness in quantum systems – at least those supporting relatively large coherence lengths – would be to consciousness-as-we-know-it much as a flask of superfluid helium is to a glass of water.

Tegmark (Reference Tegmark2000), in contrast to his later work, has convincingly argued the impossibility of macroscopic quantum treatments of consciousness at normal biological temperatures. Quantum effects at such temperatures are, of course, fully and strongly manifest at the molecular and neural levels as ‘chemistry’.

Since information is a form of free energy, even quantum systems having large coherence lengths will suffer second law heating through information transmission and transformation that will inherently limit the possible size of quantum-conscious structures. Typically 10⁹–10¹¹ interacting components are needed for high level mental function, involving large-scale information transfer. This scale of activity is likely to generate much heat and unlikely to be attained in quantum domains by an evolutionary process in the natural world, even if far smaller numbers of qubits are envisioned as sufficient for rapid lower level cognition.

The inference is, then, that the designs for ‘conscious quantum systems’ are likely to remain in the realm of perpetual motion machines of the second kind for some time. Indeed, proposals of this nature rapidly enter the notorious physics realm of ‘not even wrong’ (e.g. Penrose, Reference Penrose1994; Tegmark, Reference Tegmark2015).

Mathematical appendix

Activation of the rate-of-cognition expression from Fig. 1, F = exp [−K/M], first requires recognition that an incoming ‘sensory’ signal – in a large sense – deserves response. For working coalitions of low-level cognitive modules, we have argued that there is a topologically-defined threshold for such detection, depending on the wiring of the crosstalk. Most generally, we can write a stochastic differential equation of the form

(14)$$\eqalign{{\rm d}F_t & = ({\rm d}F/{\rm d}M \times {\rm d}M/{\rm d}t){\rm d}t + F_t{\rm d}B_t \cr & = F_t \left[\left(\displaystyle{K \over {M_t^2 }}\mathop {M_t}\limits^.\right){\rm d}t + {\rm d}B_t \right] \cr & = F_t{\rm d}Y_t} $$

where B _t is a ‘noise’ that may not be simple Brownian, and Y _t is a very general stochastic process.

Equation (14) is in precisely the form required by the Doleans-Dade exponential (Protter, Reference Protter2005), having an expectation in F that converges in probability as

(15)$$ {\cal E}(F) \rightarrow \propto \exp \left[Y_{t}-{\displaystyle{1} \over {2}}[Y_{t}, Y_{t}]\right] $$

where [Y _t, Y _t] ≥ 0 is the quadratic variation of the stochastic process Y _t (Protter, Reference Protter2005). Heuristically, by the Mean Value Theorem, if (1/2)d[Y _t, Y _t]/dt > dY _t/dt, then ${\cal E}(F) \rightarrow 0$ in probability, and the ‘switch’ is not activated.

Thus [Y _t, Y _t] can be taken as the noise-to-signal ratio of the incoming ‘sensory’ information, tuned according to the shifting topological configuration of the underlying network of ‘low level’ cognitive modules. For Brownian noise, d[Y _t, Y _t]/dt ≡ σ ², and the noise-to-signal ratio has clear meaning. For ‘colored’ noises more characteristic of real neural processes, matters are more complicated but still, fall within the treatment.

The basic result can be extended to more general cognition rate expressions than F = exp[−K/M] as follows.

We have, from eqations (9) and (10), leading to the expressions of equations (14) and (15), imposed a particular functional form for the effectiveness, efficiency, and the stochastic dynamics, of a tunable, cognitive ‘global broadcast’ network system responding to sensory challenge. More comprehensive results are available (Appleby et al., Reference Appleby, Mao and Rodkina2008).

We suppose that, instead of the specific form leading to equations (14) and (15), we can express the stochastic dynamics of a generalized measure ${\cal F}(M)$ as

(16)$$ {\rm d}{\cal F}_{t}=g({\cal F}_{t}){\rm d}t + h({\cal F}_{t}){\rm d}W_{t} $$

where dW _t is taken as Brownian noise, subject to the Lipschitz condition that, for a positive constant C, and for all ${\cal F}(M_{2})$ sufficiently near to some fixed point ${\cal F}(M_{1})$,

(17)$$ \vert g({\cal F}(M_{1}))-g({\cal F}(M_{2}))\vert \leq C\vert {\cal F}(M_{1})-{\cal F}(M_{2})\vert $$

We further assume that ${\cal F}(0)=0$, ‘no excitation of the global broadcast’ as above, is an ‘unstable equilibrium state’.

Then, Appleby et al. (Reference Appleby, Mao and Rodkina2008) show that, in one dimension, a function h can always be found that stabilizes an unstable equilibrium, i.e., keeps ${\cal F}(M,\,t)$ at zero. This generalizes the Doleans-Dade exponential of Eq. (15) to a much broader class of functions. On the one hand, sufficient ‘noise-to-signal’ ratio, measured by the function h, can keep a global broadcast from occurring, on the other, the function h itself is a tunable means of ensuring that, when incoming sensory signal is sufficiently large under the conditions defined by h, such a global broadcast can indeed take place.