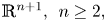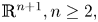1. Introduction
An algebraic hypersurface in the ![]() $(n+1)$-dimensional Euclidean space
$(n+1)$-dimensional Euclidean space ![]() $\mathbb {R}^{n+1},\,\;n\geq 2,$ is the zero set
$\mathbb {R}^{n+1},\,\;n\geq 2,$ is the zero set ![]() $M=P^{-1}(0)$ of a polynomial function
$M=P^{-1}(0)$ of a polynomial function ![]() $P:\mathbb {R}^{n+1}\to \mathbb {R}$. We say that
$P:\mathbb {R}^{n+1}\to \mathbb {R}$. We say that ![]() $M$ is regular if the gradient vector field
$M$ is regular if the gradient vector field ![]() $\nabla P$ of
$\nabla P$ of ![]() $P$ has no zeros on
$P$ has no zeros on ![]() $M$. The condition of regularity implies that
$M$. The condition of regularity implies that ![]() $M$ is a complete properly embedded hypersurface of
$M$ is a complete properly embedded hypersurface of ![]() $\mathbb {R}^{n+1}$.
$\mathbb {R}^{n+1}$.
There are many examples of algebraic hypersurfaces in ![]() $\mathbb {R}^{n+1}$ which have constant mean curvature. The basic examples of such hypersurfaces are hyperplanes, hyperspheres and round cylinders. In addition to them, we have, for example, the classical Enneper and Henneberg minimal surfaces in
$\mathbb {R}^{n+1}$ which have constant mean curvature. The basic examples of such hypersurfaces are hyperplanes, hyperspheres and round cylinders. In addition to them, we have, for example, the classical Enneper and Henneberg minimal surfaces in ![]() $\mathbb {R}^{3}$ [Reference Nitsche5], and the families of algebraic minimal cones in
$\mathbb {R}^{3}$ [Reference Nitsche5], and the families of algebraic minimal cones in ![]() $\mathbb {R}^{n+1}$ constructed in [Reference Tkachev12]. For other examples, see [Reference López4, Reference Odehnal6, Reference Perdomo and Tkachev8, Reference Small10, Reference Small11] and the references therein.
$\mathbb {R}^{n+1}$ constructed in [Reference Tkachev12]. For other examples, see [Reference López4, Reference Odehnal6, Reference Perdomo and Tkachev8, Reference Small10, Reference Small11] and the references therein.
Barbosa and do Carmo [Reference Barbosa and do Carmo3] proved that the only connected regular algebraic surfaces in ![]() $\mathbb {R}^{3}$ with non-zero constant mean curvature are the spheres and the right circular cylinders, a result that was already known for polynomials of degree less than or equal to three [Reference Perdomo7]. For generalizations of this result for globally subanalytic CMC surfaces in
$\mathbb {R}^{3}$ with non-zero constant mean curvature are the spheres and the right circular cylinders, a result that was already known for polynomials of degree less than or equal to three [Reference Perdomo7]. For generalizations of this result for globally subanalytic CMC surfaces in ![]() $\mathbb {R}^{3}$ see [Reference Barbosa, Birbrair, do Carmo and Fernandes2, Reference Sampaio9].
$\mathbb {R}^{3}$ see [Reference Barbosa, Birbrair, do Carmo and Fernandes2, Reference Sampaio9].
Motivated by the theorem mentioned in the previous paragraph and by the fact that the hyperspheres and the round cylinders are the only examples of regular algebraic hypersurfaces in ![]() $\mathbb {R}^{n+1}$ with non-zero constant mean curvature known so far, Barbosa and do Carmo [Reference Barbosa and do Carmo3, p. 177] proposed the following extension of their own result:
$\mathbb {R}^{n+1}$ with non-zero constant mean curvature known so far, Barbosa and do Carmo [Reference Barbosa and do Carmo3, p. 177] proposed the following extension of their own result:
The hyperspheres and the round cylinders are the only connected regular algebraic hypersurfaces in ![]() $\mathbb {R}^{n+1},\,\;n\geq 2$, with non-zero constant mean curvature.
$\mathbb {R}^{n+1},\,\;n\geq 2$, with non-zero constant mean curvature.
From Perdomo and Tkachev [Reference Perdomo and Tkachev8] we know that there are no regular algebraic hypersurfaces with non-zero constant mean curvature in ![]() $\mathbb {R}^{n+1},\,\;n\geq 2,$ defined by polynomials of degree
$\mathbb {R}^{n+1},\,\;n\geq 2,$ defined by polynomials of degree ![]() $3$. Here, we prove that there can be no examples defined by polynomials of any odd degree:
$3$. Here, we prove that there can be no examples defined by polynomials of any odd degree:
Theorem 1.1 Let ![]() $M^{n}$ be a regular algebraic hypersurface in
$M^{n}$ be a regular algebraic hypersurface in ![]() $\mathbb {R}^{n+1},\,n\geq 2,$ defined by a polynomial
$\mathbb {R}^{n+1},\,n\geq 2,$ defined by a polynomial ![]() $P$ of degree
$P$ of degree ![]() $m$. If
$m$. If ![]() $M^{n}$ has non-zero constant mean curvature, then
$M^{n}$ has non-zero constant mean curvature, then ![]() $m$ is even.
$m$ is even.
The theorem below shows that the question formulated by Barbosa and do Carmo has an affirmative answer for polynomials of degree less than or equal to three.
Theorem 1.2 Let ![]() $M^{n}$ be a regular algebraic hypersurface in
$M^{n}$ be a regular algebraic hypersurface in ![]() $\mathbb {R}^{n+1},\,\;n\geq 2,$ defined by a polynomial
$\mathbb {R}^{n+1},\,\;n\geq 2,$ defined by a polynomial ![]() $P$ of degree less than or equal to three. If
$P$ of degree less than or equal to three. If ![]() $M^{n}$ has non-zero constant mean curvature, then
$M^{n}$ has non-zero constant mean curvature, then ![]() $M^{n}$ is a hypersphere or a round cylinder.
$M^{n}$ is a hypersphere or a round cylinder.
Using theorem 1.1 one concludes that if ![]() $M^{n}\subset \mathbb {R}^{n+1},\,\;n\geq 2,$ is a regular algebraic hypersurface that has non-zero constant mean curvature and is defined by a polynomial
$M^{n}\subset \mathbb {R}^{n+1},\,\;n\geq 2,$ is a regular algebraic hypersurface that has non-zero constant mean curvature and is defined by a polynomial ![]() $P$ of degree
$P$ of degree ![]() $m\leq 3$, then
$m\leq 3$, then ![]() $m=2$, i.e.,
$m=2$, i.e., ![]() $M^{n}$ is a quadric hypersurface in
$M^{n}$ is a quadric hypersurface in ![]() $\mathbb {R}^{n+1}$. Thus, in the case
$\mathbb {R}^{n+1}$. Thus, in the case ![]() $n=2$, theorem 1.2 follows immediately from theorem 1.1 and the well-known classification of quadric surfaces in
$n=2$, theorem 1.2 follows immediately from theorem 1.1 and the well-known classification of quadric surfaces in ![]() $\mathbb {R}^{3}$. However, the situation is quite different for
$\mathbb {R}^{3}$. However, the situation is quite different for ![]() $n\geq 3$, since, to the best of our knowledge, there is not a classification of quadric hypersurfaces in
$n\geq 3$, since, to the best of our knowledge, there is not a classification of quadric hypersurfaces in ![]() $\mathbb {R}^{n+1}$ for
$\mathbb {R}^{n+1}$ for ![]() $n\geq 3$.
$n\geq 3$.
2. Our arguments
A polynomial ![]() $P:\mathbb {R}^{n+1}\to \mathbb {R}$ of degree
$P:\mathbb {R}^{n+1}\to \mathbb {R}$ of degree ![]() $m$ can be expressed in a unique way as the sum
$m$ can be expressed in a unique way as the sum
 \begin{equation} P=\sum_{i=0}^{m}P_i, \end{equation}
\begin{equation} P=\sum_{i=0}^{m}P_i, \end{equation}
where ![]() $P_m\neq 0$ and each
$P_m\neq 0$ and each ![]() $P_i$ is a homogeneous polynomial of degree
$P_i$ is a homogeneous polynomial of degree ![]() $i$. We call
$i$. We call ![]() $P_i,\,i=0,\,\ldots ,\,m,$ the homogeneous factors of
$P_i,\,i=0,\,\ldots ,\,m,$ the homogeneous factors of ![]() $P$, and
$P$, and ![]() $P_m$ the highest order homogeneous factor of
$P_m$ the highest order homogeneous factor of ![]() $P$. Since
$P$. Since ![]() $P_m$ clearly changes sign when
$P_m$ clearly changes sign when ![]() $m$ is odd, theorem 1.1 is a consequence of the stronger theorem below. From now on we consider that a regular algebraic hypersurface
$m$ is odd, theorem 1.1 is a consequence of the stronger theorem below. From now on we consider that a regular algebraic hypersurface ![]() $M=P^{-1}(0)$ is oriented by the global unit normal vector field
$M=P^{-1}(0)$ is oriented by the global unit normal vector field ![]() $N=\nabla P/|\nabla P|$.
$N=\nabla P/|\nabla P|$.
Theorem 2.1 Let ![]() $M^{n}$ be a regular algebraic hypersurface in
$M^{n}$ be a regular algebraic hypersurface in ![]() $\mathbb {R}^{n+1},\,\;n\geq 2$, given by a polynomial
$\mathbb {R}^{n+1},\,\;n\geq 2$, given by a polynomial ![]() $P$ of degree
$P$ of degree ![]() $m$. If
$m$. If ![]() $M^{n}$ has non-zero constant mean curvature, then the highest order homogeneous factor
$M^{n}$ has non-zero constant mean curvature, then the highest order homogeneous factor ![]() $P_m$ of
$P_m$ of ![]() $P$ is semi-definite, i.e., either
$P$ is semi-definite, i.e., either ![]() $P_m(x)\geq 0$ for all
$P_m(x)\geq 0$ for all ![]() $x\in \mathbb {R}^{n+1}$ or
$x\in \mathbb {R}^{n+1}$ or ![]() $P_m(x)\leq 0$ for all
$P_m(x)\leq 0$ for all ![]() $x\in \mathbb {R}^{n+1}$.
$x\in \mathbb {R}^{n+1}$.
Proof. Let (2.1) be the expression of ![]() $P$ as the sum of homogeneous polynomials. Writing a point in
$P$ as the sum of homogeneous polynomials. Writing a point in ![]() $\mathbb {R}^{n+1}$ as
$\mathbb {R}^{n+1}$ as ![]() $x=(x_1,\,\ldots ,\,x_{n+1})$, let
$x=(x_1,\,\ldots ,\,x_{n+1})$, let ![]() $U^{+}=\{x\in \mathbb {R}^{n+1}:P(x)>0\}$ and
$U^{+}=\{x\in \mathbb {R}^{n+1}:P(x)>0\}$ and ![]() $U^{-}=\{x\in \mathbb {R}^{n+1}:P(x)<0\}$. Since the mean curvature
$U^{-}=\{x\in \mathbb {R}^{n+1}:P(x)<0\}$. Since the mean curvature ![]() $H$ of
$H$ of ![]() $M$ is a non-zero constant by hypothesis, changing
$M$ is a non-zero constant by hypothesis, changing ![]() $P$ by
$P$ by ![]() $-P$ if necessary, we can assume that
$-P$ if necessary, we can assume that ![]() $H=c>0$. This means that the mean curvature vector
$H=c>0$. This means that the mean curvature vector ![]() $\overrightarrow {H}$ of
$\overrightarrow {H}$ of ![]() $M^{n}$ points in the direction of
$M^{n}$ points in the direction of ![]() $U^{+}$.
$U^{+}$.
By (2.1), for any ![]() $t\in \mathbb {R}$ and any vector
$t\in \mathbb {R}$ and any vector ![]() $v$ in the unit sphere
$v$ in the unit sphere ![]() $S^{n}_1$ we have
$S^{n}_1$ we have
and so
 \begin{equation} \frac{P(tv)}{t^{m}}-P_m(v)=\sum_{i=0}^{m-1}\frac{P_i(v)}{t^{m-i}},\quad v\in S^{n}_1,\ t\neq 0. \end{equation}
\begin{equation} \frac{P(tv)}{t^{m}}-P_m(v)=\sum_{i=0}^{m-1}\frac{P_i(v)}{t^{m-i}},\quad v\in S^{n}_1,\ t\neq 0. \end{equation}
Using (2.3) and the compactness of ![]() $S^{n}_1$, one easily sees that
$S^{n}_1$, one easily sees that ![]() $t^{-m}P(tv)\to P_m(v)$ uniformly on
$t^{-m}P(tv)\to P_m(v)$ uniformly on ![]() $S^{n}_1$ when
$S^{n}_1$ when ![]() $t\to \infty$.
$t\to \infty$.
Suppose, by contradiction, that ![]() $P_m$ changes sign. Then, since
$P_m$ changes sign. Then, since ![]() $P_m$ is homogeneous, there exists a vector
$P_m$ is homogeneous, there exists a vector ![]() $w$ in the unit sphere
$w$ in the unit sphere ![]() $S^{n}_1\subset \mathbb {R}^{n+1}$ such that
$S^{n}_1\subset \mathbb {R}^{n+1}$ such that ![]() $P_m(w)>0$. Hence, by continuity, there is a closed disk
$P_m(w)>0$. Hence, by continuity, there is a closed disk ![]() $W$ around
$W$ around ![]() $w$ in
$w$ in ![]() $S^{n}_1$ such that
$S^{n}_1$ such that ![]() $P_m(v)>P_m(w)/2$ for all
$P_m(v)>P_m(w)/2$ for all ![]() $v\in W$. Since
$v\in W$. Since ![]() $t^{-m}P(tv)\to P_m(v)$ uniformly on
$t^{-m}P(tv)\to P_m(v)$ uniformly on ![]() $S^{n}_1$, there exists
$S^{n}_1$, there exists ![]() $t_0>0$ such that
$t_0>0$ such that ![]() $|t^{-m}P(tv)-P_m(v)|< P_m(w)/4$ for all
$|t^{-m}P(tv)-P_m(v)|< P_m(w)/4$ for all ![]() $t>t_0$ and
$t>t_0$ and ![]() $v\in S^{n}_1$. Combining these informations, one obtains
$v\in S^{n}_1$. Combining these informations, one obtains
 \begin{align} t^{{-}m}P(tv)&\geq{-}|t^{{-}m}P(tv)-P_m(v)|+P_m(v)\nonumber\\ &>{-}\frac{1}{4}P_m(w)+\frac{1}{2}P_m(w)=\frac{1}{4}P_m(w)>0,\quad t>t_0,\ v\in W, \end{align}
\begin{align} t^{{-}m}P(tv)&\geq{-}|t^{{-}m}P(tv)-P_m(v)|+P_m(v)\nonumber\\ &>{-}\frac{1}{4}P_m(w)+\frac{1}{2}P_m(w)=\frac{1}{4}P_m(w)>0,\quad t>t_0,\ v\in W, \end{align}and so
Let ![]() $R$ be an arbitrary positive number. By (2.5), there exists a ball
$R$ be an arbitrary positive number. By (2.5), there exists a ball ![]() $B$ of radius
$B$ of radius ![]() $R$ in
$R$ in ![]() $\mathbb {R}^{n+1}$ such that
$\mathbb {R}^{n+1}$ such that ![]() $B\subset U^{+}$. Let
$B\subset U^{+}$. Let ![]() $x_0$ be the centre of
$x_0$ be the centre of ![]() $B$ and
$B$ and ![]() $f:M\to \mathbb {R}$ the function defined by
$f:M\to \mathbb {R}$ the function defined by ![]() $f(x)=||x-x_0||^{2}$. Since
$f(x)=||x-x_0||^{2}$. Since ![]() $M$ is a closed subset of
$M$ is a closed subset of ![]() $\mathbb {R}^{n+1}$, there is a point
$\mathbb {R}^{n+1}$, there is a point ![]() $p\in M$ such that
$p\in M$ such that ![]() $f(p)=\inf _M f$. Let
$f(p)=\inf _M f$. Let ![]() $v$ be an arbitrary unit vector of
$v$ be an arbitrary unit vector of ![]() $T_pM$ and
$T_pM$ and ![]() $\gamma :I\to M$ a smooth curve such that
$\gamma :I\to M$ a smooth curve such that ![]() $\gamma (0)=p$ and
$\gamma (0)=p$ and ![]() $\gamma '(0)=v$. Since the function
$\gamma '(0)=v$. Since the function ![]() $f(\gamma (t))$ attains a minimum at
$f(\gamma (t))$ attains a minimum at ![]() $t=0$, one has
$t=0$, one has
and
From (2.6) one obtains that ![]() $p-x_0$ is orthogonal to
$p-x_0$ is orthogonal to ![]() $T_pM$. Since
$T_pM$. Since ![]() $N$ points inward
$N$ points inward ![]() $U^{+}$ and
$U^{+}$ and ![]() $x_0\in U^{+}$, it follows that
$x_0\in U^{+}$, it follows that ![]() $N(p)=(x_0-p)/||x_0-p||$. Using this information in (2.7), one obtains
$N(p)=(x_0-p)/||x_0-p||$. Using this information in (2.7), one obtains
for any unit vector ![]() $v\in T_pM$, where
$v\in T_pM$, where ![]() $A$ is the shape operator of
$A$ is the shape operator of ![]() $M$ with respect to
$M$ with respect to ![]() $N$. Taking the trace in the above inequality and using the fact that
$N$. Taking the trace in the above inequality and using the fact that ![]() $p\not \in B$, one concludes that
$p\not \in B$, one concludes that
for every ![]() $R>0$, contradicting
$R>0$, contradicting ![]() $H=c>0$. This contradiction shows that
$H=c>0$. This contradiction shows that ![]() $P_m$ does not change sign, and the theorem is proved.
$P_m$ does not change sign, and the theorem is proved.
Remark 2.2 The arguments used in the proof of theorem 2.1 show that the complement of the zero set of any non-zero polynomial, in any number of variables, contains balls of arbitrarily large radius.
In the proof of theorem 1.2, as well as in the proof of corollary 2.5, we will use the following result, which is of interest in its own right. We believe this result is known, but since we were unable to find a reference in the literature, we will provide a proof for it here.
Lemma 2.3 Let ![]() $P:\mathbb {R}^{n+1}\to \mathbb {R}$ be a polynomial of degree
$P:\mathbb {R}^{n+1}\to \mathbb {R}$ be a polynomial of degree ![]() $m,\,\;m\geq 2$. If for some
$m,\,\;m\geq 2$. If for some ![]() $k,\,\;1\leq k\leq n,$
$k,\,\;1\leq k\leq n,$ ![]() $P(x)$ vanishes on
$P(x)$ vanishes on ![]() $S_r^{k}(a)\times \mathbb {R}^{n-k},$ where
$S_r^{k}(a)\times \mathbb {R}^{n-k},$ where ![]() $S_r^{k}(a)$ is the hypersphere of
$S_r^{k}(a)$ is the hypersphere of ![]() $\mathbb {R}^{k+1}$ of radius
$\mathbb {R}^{k+1}$ of radius ![]() $r$ and centre
$r$ and centre ![]() $a,$ then
$a,$ then ![]() $P(x)$ is divisible by the polynomial
$P(x)$ is divisible by the polynomial
 \[ Q(x)=\sum_{i=1}^{k+1}(x_i-a_i)^{2}-r^{2}. \]
\[ Q(x)=\sum_{i=1}^{k+1}(x_i-a_i)^{2}-r^{2}. \]Proof. We will prove the lemma in the case where ![]() $m=2d,\,\;d\geq 1$. The proof in the case that the degree of
$m=2d,\,\;d\geq 1$. The proof in the case that the degree of ![]() $P(x)$ is odd is entirely analogous and will be omitted.
$P(x)$ is odd is entirely analogous and will be omitted.
Assume first ![]() $a=0$ and
$a=0$ and ![]() $r=1$. Write
$r=1$. Write ![]() $P$ as
$P$ as
 \begin{equation} P=\sum_{i=0}^{d}P_{2i}+\sum_{i=0}^{d-1}P_{2i+1}, \end{equation}
\begin{equation} P=\sum_{i=0}^{d}P_{2i}+\sum_{i=0}^{d-1}P_{2i+1}, \end{equation}
where ![]() $P_j,\, j=0,\,\ldots ,\,2d,$ is a homogeneous polynomial of degree
$P_j,\, j=0,\,\ldots ,\,2d,$ is a homogeneous polynomial of degree ![]() $j$. By hypothesis, for every
$j$. By hypothesis, for every ![]() $v\in S^{k}_1(0)\times \mathbb {R}^{n-k}$ one has
$v\in S^{k}_1(0)\times \mathbb {R}^{n-k}$ one has
 \begin{align*} 0&=P(v) =\sum_{i=0}^{d}P_{2i}(v)+\sum_{i=0}^{d-1}P_{2i+1}(v),\\ 0&=P({-}v)=\sum_{i=0}^{d}P_{2i}(v)-\sum_{i=0}^{d-1}P_{2i+1}(v). \end{align*}
\begin{align*} 0&=P(v) =\sum_{i=0}^{d}P_{2i}(v)+\sum_{i=0}^{d-1}P_{2i+1}(v),\\ 0&=P({-}v)=\sum_{i=0}^{d}P_{2i}(v)-\sum_{i=0}^{d-1}P_{2i+1}(v). \end{align*}
From the two equalities above one obtains ![]() $\sum_{i=0}^{d}P_{2i}(v)=0=\sum_{i=0}^{d-1}P_{2i+1}(v)$, which implies
$\sum_{i=0}^{d}P_{2i}(v)=0=\sum_{i=0}^{d-1}P_{2i+1}(v)$, which implies
 \begin{equation} P_{2d}(v)={-}\sum_{i=0}^{d-1}P_{2i}(v),\quad P_{2d-1}(v)={-}\sum_{i=0}^{d-2}P_{2i+1}(v),\ \forall v\in S^{k}_1(0)\times\mathbb{R}^{n-k}. \end{equation}
\begin{equation} P_{2d}(v)={-}\sum_{i=0}^{d-1}P_{2i}(v),\quad P_{2d-1}(v)={-}\sum_{i=0}^{d-2}P_{2i+1}(v),\ \forall v\in S^{k}_1(0)\times\mathbb{R}^{n-k}. \end{equation}
Let ![]() $\{e_1,\,\ldots ,\,e_{n+1}\}$ be the canonical basis of
$\{e_1,\,\ldots ,\,e_{n+1}\}$ be the canonical basis of ![]() $\mathbb {R}^{n+1}$. For any
$\mathbb {R}^{n+1}$. For any ![]() $x=(x_1,\,\ldots ,\,x_{n+1})\in \mathbb {R}^{n+1}$ such that
$x=(x_1,\,\ldots ,\,x_{n+1})\in \mathbb {R}^{n+1}$ such that ![]() $y:=\sum_{i=1}^{k+1}x_ie_i\neq 0$ it holds that
$y:=\sum_{i=1}^{k+1}x_ie_i\neq 0$ it holds that ![]() $x/|y|\in S^{k}_1(0)\times \mathbb {R}^{n-k}$. By (2.8) and (2.9), for all such
$x/|y|\in S^{k}_1(0)\times \mathbb {R}^{n-k}$. By (2.8) and (2.9), for all such ![]() $x$ one has
$x$ one has
 \begin{align*} P(x)&=\sum_{i=0}^{d-1}P_{2i}(x)+P_{2d}(x)+\sum_{i=0}^{d-2}P_{2i+1}(x)+P_{2d-1}(x)\nonumber\\ &=\sum_{i=0}^{d-1}P_{2i}(x)+|y|^{2d}P_{2d}(x/|y|)+\sum_{i=0}^{d-2}P_{2i+1}(x)+|y|^{2d-1}P_{2d-1}(x/|y|)\nonumber\\ &=\sum_{i=0}^{d-1}P_{2i}(x)-|y|^{2d}\sum_{i=0}^{d-1}P_{2i}(x/|y|)+\sum_{i=0}^{d-2}P_{2i+1}(x)-|y|^{2d-1}\sum_{i=0}^{d-2}P_{2i+1}(x/|y|)\nonumber\\ &=\sum_{i=0}^{d-1}(1-|y|^{2(d-i)})P_{2i}(x)+\sum_{i=0}^{d-2}(1-|y|^{2(d-i-1)})P_{2i+1}(x).\nonumber \end{align*}
\begin{align*} P(x)&=\sum_{i=0}^{d-1}P_{2i}(x)+P_{2d}(x)+\sum_{i=0}^{d-2}P_{2i+1}(x)+P_{2d-1}(x)\nonumber\\ &=\sum_{i=0}^{d-1}P_{2i}(x)+|y|^{2d}P_{2d}(x/|y|)+\sum_{i=0}^{d-2}P_{2i+1}(x)+|y|^{2d-1}P_{2d-1}(x/|y|)\nonumber\\ &=\sum_{i=0}^{d-1}P_{2i}(x)-|y|^{2d}\sum_{i=0}^{d-1}P_{2i}(x/|y|)+\sum_{i=0}^{d-2}P_{2i+1}(x)-|y|^{2d-1}\sum_{i=0}^{d-2}P_{2i+1}(x/|y|)\nonumber\\ &=\sum_{i=0}^{d-1}(1-|y|^{2(d-i)})P_{2i}(x)+\sum_{i=0}^{d-2}(1-|y|^{2(d-i-1)})P_{2i+1}(x).\nonumber \end{align*}
Notice that the second term on the right-hand side of the above equality vanishes when ![]() $d=1$. Since
$d=1$. Since ![]() $(1-|y|^{2k})$ is divisible by
$(1-|y|^{2k})$ is divisible by ![]() $1-|y|^{2}$ for any integer
$1-|y|^{2}$ for any integer ![]() $k\geq 1$, it follows from the above equality that
$k\geq 1$, it follows from the above equality that
for some polynomial ![]() $R(x)$ of degree
$R(x)$ of degree ![]() $2(d-1)$. This proves the lemma in the case
$2(d-1)$. This proves the lemma in the case ![]() $a=0$ and
$a=0$ and ![]() $r=1$, since
$r=1$, since ![]() $|y|^{2}=\sum_{i=1}^{k+1}x_i^{2}$. To obtain the lemma in the general case, it suffices to apply (2.10) for the polynomial
$|y|^{2}=\sum_{i=1}^{k+1}x_i^{2}$. To obtain the lemma in the general case, it suffices to apply (2.10) for the polynomial ![]() $\overline {P}(x):=P(rx+a)$.
$\overline {P}(x):=P(rx+a)$.
Theorem 2.1 states that if a regular algebraic hypersurface in ![]() $\mathbb {R}^{n+1}$ has non-zero constant mean curvature, then the highest order homogeneous factor
$\mathbb {R}^{n+1}$ has non-zero constant mean curvature, then the highest order homogeneous factor ![]() $P_m$ of its defining polynomial
$P_m$ of its defining polynomial ![]() $P$ is semi-definite (in particular, the degree
$P$ is semi-definite (in particular, the degree ![]() $m$ of
$m$ of ![]() $P$ is even). Before proving theorem 1.2, for completeness let us say what happens in the case where
$P$ is even). Before proving theorem 1.2, for completeness let us say what happens in the case where ![]() $P_m$ is definite, i.e.
$P_m$ is definite, i.e. ![]() $P_m(x)\neq 0$ for all
$P_m(x)\neq 0$ for all ![]() $x\in \mathbb {R}^{n+1}-\{0\}$:
$x\in \mathbb {R}^{n+1}-\{0\}$:
Theorem 2.4 Let ![]() $M^{n}$ be a regular algebraic hypersurface in
$M^{n}$ be a regular algebraic hypersurface in ![]() $\mathbb {R}^{n+1},\,\;n\geq 2,$ defined by a polynomial
$\mathbb {R}^{n+1},\,\;n\geq 2,$ defined by a polynomial ![]() $P$ of degree
$P$ of degree ![]() $m$. If the highest order homogeneous factor
$m$. If the highest order homogeneous factor ![]() $P_m$ of
$P_m$ of ![]() $P$ is definite, then
$P$ is definite, then ![]() $M^{n}$ is compact. In particular, if
$M^{n}$ is compact. In particular, if ![]() $M^{n}$ has constant mean curvature, then
$M^{n}$ has constant mean curvature, then ![]() $M^{n}$ is a finite union of hyperspheres of
$M^{n}$ is a finite union of hyperspheres of ![]() $\mathbb {R}^{n+1}$.
$\mathbb {R}^{n+1}$.
Proof. Let (2.1) be the expression of ![]() $P$ as the sum of its homogeneous factors. Since
$P$ as the sum of its homogeneous factors. Since ![]() $P_m$ is definite by hypothesis, changing
$P_m$ is definite by hypothesis, changing ![]() $P$ by
$P$ by ![]() $-P$ if necessary we can assume that
$-P$ if necessary we can assume that ![]() $P_m(v)>0$ for all
$P_m(v)>0$ for all ![]() $v\in S^{n}_1$. Let
$v\in S^{n}_1$. Let ![]() $\alpha =\inf \{P_m(v):v\in S^{n}_1\}>0$. By the proof of theorem 2.1,
$\alpha =\inf \{P_m(v):v\in S^{n}_1\}>0$. By the proof of theorem 2.1,
Then there exists ![]() $t_0>0$ such that
$t_0>0$ such that ![]() $|t^{-m}P(tv)-P_m(v)|<\alpha /2$, for all
$|t^{-m}P(tv)-P_m(v)|<\alpha /2$, for all ![]() $t>t_0$ and
$t>t_0$ and ![]() $v\in S^{n}_1$, and so
$v\in S^{n}_1$, and so
for all ![]() $t>t_0$ and
$t>t_0$ and ![]() $v\in S^{n}_1$. Hence,
$v\in S^{n}_1$. Hence, ![]() $P(tv)>0$ for all
$P(tv)>0$ for all ![]() $t>t_0$ and
$t>t_0$ and ![]() $v\in S^{n}_1$, which implies that the set
$v\in S^{n}_1$, which implies that the set ![]() $U^{-}=\{x\in \mathbb {R}^{n+1}:P(x)<0\}$ is bounded. Since
$U^{-}=\{x\in \mathbb {R}^{n+1}:P(x)<0\}$ is bounded. Since ![]() $M=\partial (U^{-})$, one concludes that
$M=\partial (U^{-})$, one concludes that ![]() $M$ is compact.
$M$ is compact.
Assume now that ![]() $M^{n}$ has constant mean curvature. Since
$M^{n}$ has constant mean curvature. Since ![]() $M^{n}$ is embedded, by a well known theorem of Alexandrov [Reference Aleksandrov1] each connected component of
$M^{n}$ is embedded, by a well known theorem of Alexandrov [Reference Aleksandrov1] each connected component of ![]() $M^{n}$ is a hypersphere of
$M^{n}$ is a hypersphere of ![]() $\mathbb {R}^{n+1}$.
$\mathbb {R}^{n+1}$.
The following result is an immediate consequence of lemma 2.3 and theorem 2.4.
Corollary 2.5 Let ![]() $M^{n}$ be a regular algebraic hypersurface in
$M^{n}$ be a regular algebraic hypersurface in ![]() $\mathbb {R}^{n+1},\,\;n\geq 2,$ defined by an irreducible polynomial
$\mathbb {R}^{n+1},\,\;n\geq 2,$ defined by an irreducible polynomial ![]() $P$ of degree
$P$ of degree ![]() $m$. If the highest order homogeneous factor
$m$. If the highest order homogeneous factor ![]() $P_m$ of
$P_m$ of ![]() $P$ is definite and
$P$ is definite and ![]() $M^{n}$ has constant mean curvature, then
$M^{n}$ has constant mean curvature, then ![]() $M^{n}$ is a hypersphere of
$M^{n}$ is a hypersphere of ![]() $\mathbb {R}^{n+1}$.
$\mathbb {R}^{n+1}$.
Example 2.6 Let ![]() $P:\mathbb {R}^{3}\to \mathbb {R}$ be the polynomial defined by
$P:\mathbb {R}^{3}\to \mathbb {R}$ be the polynomial defined by
It is easy to see that the gradient ![]() $\nabla P$ of
$\nabla P$ of ![]() $P$ vanishes nowhere in
$P$ vanishes nowhere in ![]() $M^{2}:=P^{-1}(0)$. Then
$M^{2}:=P^{-1}(0)$. Then ![]() $M^{2}$ is a regular algebraic surface in
$M^{2}$ is a regular algebraic surface in ![]() $\mathbb {R}^{3}$. The highest order homogeneous factor of
$\mathbb {R}^{3}$. The highest order homogeneous factor of ![]() $P$ is
$P$ is ![]() $P_4=x^{4}+y^{4}+z^{4}+2x^{2}y^{2}+2x^{2}z^{2}+2y^{2}z^{2}$, which is clearly definite. Being the union of two disjoint unit spheres of
$P_4=x^{4}+y^{4}+z^{4}+2x^{2}y^{2}+2x^{2}z^{2}+2y^{2}z^{2}$, which is clearly definite. Being the union of two disjoint unit spheres of ![]() $\mathbb {R}^{3}$,
$\mathbb {R}^{3}$, ![]() $M^{2}$ has constant mean curvature. This shows that the hypothesis in corollary 2.5 that
$M^{2}$ has constant mean curvature. This shows that the hypothesis in corollary 2.5 that ![]() $P$ is irreducible cannot be dropped.
$P$ is irreducible cannot be dropped.
Proof of theorem 1.2. Since, by hypothesis, the degree ![]() $m$ of
$m$ of ![]() $P$ is less than or equal to
$P$ is less than or equal to ![]() $3$ and
$3$ and ![]() $M^{n}$ has non-zero constant mean curvature, it follows from theorem 1.1 that
$M^{n}$ has non-zero constant mean curvature, it follows from theorem 1.1 that ![]() $m=2$. Hence, we can express
$m=2$. Hence, we can express ![]() $P$ as
$P$ as
where ![]() $P_i,\,\;i=0,\,1,\,2$, is a homogeneous polynomial of degree
$P_i,\,\;i=0,\,1,\,2$, is a homogeneous polynomial of degree ![]() $i$ in the variables
$i$ in the variables ![]() $x_1,\,\ldots ,\,x_{n+1}$. Changing
$x_1,\,\ldots ,\,x_{n+1}$. Changing ![]() $P$ by
$P$ by ![]() $-P$ if necessary, we can assume that
$-P$ if necessary, we can assume that ![]() $H=c>0$. We will establish the theorem by proving that
$H=c>0$. We will establish the theorem by proving that
(![]() ${\dagger}$) Up to a rigid motion of
${\dagger}$) Up to a rigid motion of ![]() $\mathbb {R}^{n+1}$,
$\mathbb {R}^{n+1}$, ![]() $M^{n}=S^{k}\times \mathbb {R}^{n-k}$ for some
$M^{n}=S^{k}\times \mathbb {R}^{n-k}$ for some ![]() $k,\,\;1\leq k\leq n$, where
$k,\,\;1\leq k\leq n$, where ![]() $S^{k}$ is a hypersphere of
$S^{k}$ is a hypersphere of ![]() $\mathbb {R}^{k+1}$.
$\mathbb {R}^{k+1}$.
We will prove (![]() ${\dagger}$) by induction on
${\dagger}$) by induction on ![]() $n$. If
$n$. If ![]() $n=2$, it follows from the well known classification of quadric surfaces in
$n=2$, it follows from the well known classification of quadric surfaces in ![]() $\mathbb {R}^{3}$ and from the hypothesis that
$\mathbb {R}^{3}$ and from the hypothesis that ![]() $M$ has non-zero constant mean curvature that
$M$ has non-zero constant mean curvature that ![]() $M$ is a sphere or a right circular cylinder. This shows that (
$M$ is a sphere or a right circular cylinder. This shows that (![]() ${\dagger}$) holds for
${\dagger}$) holds for ![]() $n=2$.
$n=2$.
Assume now ![]() $n\geq 3$ and that (
$n\geq 3$ and that (![]() ${\dagger}$) holds for
${\dagger}$) holds for ![]() $n-1$. If
$n-1$. If ![]() $P_2$ is definite, then
$P_2$ is definite, then ![]() $M^{n}$ is a finite union of hyperspheres of
$M^{n}$ is a finite union of hyperspheres of ![]() $\mathbb {R}^{n+1}$ by theorem 2.4. Since the degree of
$\mathbb {R}^{n+1}$ by theorem 2.4. Since the degree of ![]() $P$ is two, it follows from lemma 2.3 that
$P$ is two, it follows from lemma 2.3 that ![]() $M^{n}$ is a single hypersphere of
$M^{n}$ is a single hypersphere of ![]() $\mathbb {R}^{n+1}$. Thus (
$\mathbb {R}^{n+1}$. Thus (![]() ${\dagger}$) holds for
${\dagger}$) holds for ![]() $n$ in the case that
$n$ in the case that ![]() $P_2$ is definite.
$P_2$ is definite.
If ![]() $P_2$ is indefinite, then there exists
$P_2$ is indefinite, then there exists ![]() $w\in S^{n}_1$ such that
$w\in S^{n}_1$ such that ![]() $P_2(w)=0$. Then, after a change of coordinates given by an orthogonal transformation that sends
$P_2(w)=0$. Then, after a change of coordinates given by an orthogonal transformation that sends ![]() $e_{n+1}$ to
$e_{n+1}$ to ![]() $w$, the polynomial P can be written as
$w$, the polynomial P can be written as
where ![]() $A_1(x_1,\,\ldots ,\,x_n)$ is a polynomial of degree
$A_1(x_1,\,\ldots ,\,x_n)$ is a polynomial of degree ![]() $\leq 1$ and
$\leq 1$ and ![]() $A_0(x_1,\,\ldots ,\,x_n)$ a polynomial of degree
$A_0(x_1,\,\ldots ,\,x_n)$ a polynomial of degree ![]() $\leq 2$.
$\leq 2$.
Claim. ![]() $A_1=0$.
$A_1=0$.
Assume that the claim is not true. Since the degree of ![]() $A_1$ is at most
$A_1$ is at most ![]() $1$, given
$1$, given ![]() $R>0$ there exists a closed ball
$R>0$ there exists a closed ball ![]() $B\subset \mathbb {R}^{n}$ of radius
$B\subset \mathbb {R}^{n}$ of radius ![]() $R$ on which
$R$ on which ![]() $A_1(x_1,\,\ldots , x_n)\neq 0$. If
$A_1(x_1,\,\ldots , x_n)\neq 0$. If ![]() $A_1>0$ on
$A_1>0$ on ![]() $B$, using (2.12) one easily verifies that
$B$, using (2.12) one easily verifies that ![]() $P(x_1,\,\ldots ,\,x_n,\,x_{n+1})>0$ for all
$P(x_1,\,\ldots ,\,x_n,\,x_{n+1})>0$ for all ![]() $(x_1,\,\ldots ,\,x_n)\in B$ and all
$(x_1,\,\ldots ,\,x_n)\in B$ and all ![]() $x_{n+1}>\max _B |A_0|/\min _B A_1$. Similarly, if
$x_{n+1}>\max _B |A_0|/\min _B A_1$. Similarly, if ![]() $A_1<0$ on
$A_1<0$ on ![]() $B$ one has
$B$ one has ![]() $P(x_1,\,\ldots ,\,x_n,\,x_{n+1})>0$ for all
$P(x_1,\,\ldots ,\,x_n,\,x_{n+1})>0$ for all ![]() $(x_1,\,\ldots ,\,x_n)\in B$ and all
$(x_1,\,\ldots ,\,x_n)\in B$ and all ![]() $x_{n+1}<\max _B |A_0|/\max _B A_1$. In either case, one sees that there is a ball of radius R in
$x_{n+1}<\max _B |A_0|/\max _B A_1$. In either case, one sees that there is a ball of radius R in ![]() $\mathbb {R}^{n+1}$ entirely contained in the set
$\mathbb {R}^{n+1}$ entirely contained in the set ![]() $U^{+}=\{x\in \mathbb {R}^{n+1}:P(x)>0\}$. Then, by an argument used in the proof of theorem 2.1,
$U^{+}=\{x\in \mathbb {R}^{n+1}:P(x)>0\}$. Then, by an argument used in the proof of theorem 2.1, ![]() $H\leq 1/R$ for every
$H\leq 1/R$ for every ![]() $R>0$, contradicting
$R>0$, contradicting ![]() $H=c>0$. This proves the claim.
$H=c>0$. This proves the claim.
By (2.12) and the claim above, ![]() $P(x_1,\,\ldots ,\,x_n,\,x_{n+1})=A_0(x_1,\,\ldots ,\,x_n)$, where
$P(x_1,\,\ldots ,\,x_n,\,x_{n+1})=A_0(x_1,\,\ldots ,\,x_n)$, where ![]() $A_0:\mathbb {R}^{n}\to \mathbb {R}$ is a polynomial of degree two in the variables
$A_0:\mathbb {R}^{n}\to \mathbb {R}$ is a polynomial of degree two in the variables ![]() $x_1,\,\ldots ,\,x_n$. Since 0 is a regular value for
$x_1,\,\ldots ,\,x_n$. Since 0 is a regular value for ![]() $P$, so is for
$P$, so is for ![]() $A_0$. Hence
$A_0$. Hence ![]() $M^{n}=M_0^{n-1}\times \mathbb {R}$, where
$M^{n}=M_0^{n-1}\times \mathbb {R}$, where ![]() $M_0^{n-1}=A_0^{-1}(0)$ is a regular algebraic hypersurface of
$M_0^{n-1}=A_0^{-1}(0)$ is a regular algebraic hypersurface of ![]() $\mathbb {R}^{n}$. Since
$\mathbb {R}^{n}$. Since ![]() $M^{n}$ has non-zero constant mean curvature, the same is true of
$M^{n}$ has non-zero constant mean curvature, the same is true of ![]() $M_0^{n-1}$. Then, by the induction hypothesis, up to a rigid motion of
$M_0^{n-1}$. Then, by the induction hypothesis, up to a rigid motion of ![]() $\mathbb {R}^{n}$ one has
$\mathbb {R}^{n}$ one has ![]() $M_0^{n-1}=S^{k}\times \mathbb {R}^{n-1-k}$, for some
$M_0^{n-1}=S^{k}\times \mathbb {R}^{n-1-k}$, for some ![]() $k,\,\;1\leq k\leq n-1$, where
$k,\,\;1\leq k\leq n-1$, where ![]() $S^{k}$ is a hypersphere of
$S^{k}$ is a hypersphere of ![]() $\mathbb {R}^{k+1}$. Hence
$\mathbb {R}^{k+1}$. Hence ![]() $M^{n}=S^{k}\times \mathbb {R}^{n-k}$, for some
$M^{n}=S^{k}\times \mathbb {R}^{n-k}$, for some ![]() $k,\,\;1\leq k\leq n-1$. This shows that (
$k,\,\;1\leq k\leq n-1$. This shows that (![]() ${\dagger}$) holds for
${\dagger}$) holds for ![]() $n$ also in the case that
$n$ also in the case that ![]() $P_2$ is indefinite. Then, by the induction principle, (
$P_2$ is indefinite. Then, by the induction principle, (![]() ${\dagger}$) holds for every
${\dagger}$) holds for every ![]() $n\geq 2$, and the theorem is proved.
$n\geq 2$, and the theorem is proved.
Acknowledgments
Work partially supported by FAPESP:2018/03721-4 (Brazil), FAPESP:2019/20854-0 (Brazil), FAPESP:2018/23202-1 (Brazil)