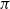1. Introduction
Markov chain Monte Carlo (MCMC) algorithms [Reference Brooks, Gelman, Jones and Meng6] are very widely used to explore and sample from a complicated high-dimensional target probability distribution
![]() $\pi$
. The most basic version of MCMC is the Metropolis algorithm [Reference Metropolis, Rosenbluth, Rosenbluth, Teller and Teller17, Reference Hastings10]. From a given state x, it proceeds by first proposing to move to a new state y, and then either accepting that proposal (i.e. moving to y), or rejecting that proposal (i.e. staying at x). The acceptance probability is given by
$\pi$
. The most basic version of MCMC is the Metropolis algorithm [Reference Metropolis, Rosenbluth, Rosenbluth, Teller and Teller17, Reference Hastings10]. From a given state x, it proceeds by first proposing to move to a new state y, and then either accepting that proposal (i.e. moving to y), or rejecting that proposal (i.e. staying at x). The acceptance probability is given by
![]() $\min[1, \, \pi(y) / \pi(x)]$
. If the proposal densities are symmetric (i.e. have the same probability of proposing y from x as of proposing x from y), this procedure ensures that the resulting Markov chain will be reversible with respect to
$\min[1, \, \pi(y) / \pi(x)]$
. If the proposal densities are symmetric (i.e. have the same probability of proposing y from x as of proposing x from y), this procedure ensures that the resulting Markov chain will be reversible with respect to
![]() $\pi$
, and thus have
$\pi$
, and thus have
![]() $\pi$
as its stationary density.
$\pi$
as its stationary density.
MCMC algorithms have a tendency to get stuck in local modes, which limits their effectiveness. Annealing and tempering methods [Reference Aarts and Korst1, Reference Geyer9, Reference Kirkpatrick, Gelatt and Vecchi12, Reference Marinari and Parisi16, Reference Pincus18] attempt to overcome this problem by considering different powers
![]() $\pi^\beta$
of the target density, where
$\pi^\beta$
of the target density, where
![]() $\beta \le 1$
is an inverse temperature. Here,
$\beta \le 1$
is an inverse temperature. Here,
![]() $\beta=1$
corresponds to the desired distribution, so those are the only samples which are ‘counted’. However, small positive values
$\beta=1$
corresponds to the desired distribution, so those are the only samples which are ‘counted’. However, small positive values
![]() $\beta \ll 1$
make the density flatter and thus much easier to traverse.
$\beta \ll 1$
make the density flatter and thus much easier to traverse.
Despite the tremendous success of tempering, these methods suffer from deficiencies, especially in high dimensions. In particular, tempering of distributions does not usually preserve the relative mass contained in each of the modes. To deal with this, [Reference Tawn, Roberts and Rosenthal31] introduced a weight-preserving transformation which overcomes the weight instability problem as long as all modes look reasonably Gaussian. Unfortunately, in applications that is often not the case, since modes often exhibit significant skewness.
An alternative approach, the Annealed Leap-Point Sampler (ALPS), is introduced in [Reference Tawn, Moores and Roberts29]. This algorithm instead considers very large values
![]() $\beta \gg 1$
, corresponding to very peaked target densities at very cold temperatures. (Large
$\beta \gg 1$
, corresponding to very peaked target densities at very cold temperatures. (Large
![]() $\beta$
are often used in optimisation algorithms such as simulated annealing [Reference Aarts and Korst1, Reference Kirkpatrick, Gelatt and Vecchi12, Reference Pincus18], but are not normally used by sampling algorithms.) Assuming smoothness, the resulting sharply peaked modes then become approximately Gaussian, thus facilitating simpler ways of moving between them. Furthermore, a weight-preserving transformation is performed to approximately preserve the probabilistic weight of each peak upon tempering.
$\beta$
are often used in optimisation algorithms such as simulated annealing [Reference Aarts and Korst1, Reference Kirkpatrick, Gelatt and Vecchi12, Reference Pincus18], but are not normally used by sampling algorithms.) Assuming smoothness, the resulting sharply peaked modes then become approximately Gaussian, thus facilitating simpler ways of moving between them. Furthermore, a weight-preserving transformation is performed to approximately preserve the probabilistic weight of each peak upon tempering.
For any MCMC algorithm, an important question is how quickly it converges to its stationary distribution
![]() $\pi$
. While there have been many attempts to bound MCMC convergence times directly (see, e.g., [Reference Rosenthal26] and the references therein), much of the effort has been focused on questions of computational complexity, i.e. how the algorithm’s running time grows as a function of other parameters (dimension, size of data, etc.).
$\pi$
. While there have been many attempts to bound MCMC convergence times directly (see, e.g., [Reference Rosenthal26] and the references therein), much of the effort has been focused on questions of computational complexity, i.e. how the algorithm’s running time grows as a function of other parameters (dimension, size of data, etc.).
One promising, though technically challenging, approach to determining the computational complexity of Metropolis algorithms is through the use of diffusion limits as the dimension
![]() $d\to\infty$
. Similar to how a symmetric random walk converges to Brownian motion under appropriate rescaling, certain transformations of some Metropolis algorithm components will converge to Langevin diffusions. This was originally exploited in [Reference Roberts, Gelman and Gilks21, Reference Roberts and Rosenthal22] to derive complexity and optimality results for ordinary random-walk-based Metropolis algorithms, and was later generalised to many other contexts [Reference Bédard and Rosenthal4, Reference Roberts and Rosenthal23, Reference Roberts and Rosenthal25]. Furthermore, the
$d\to\infty$
. Similar to how a symmetric random walk converges to Brownian motion under appropriate rescaling, certain transformations of some Metropolis algorithm components will converge to Langevin diffusions. This was originally exploited in [Reference Roberts, Gelman and Gilks21, Reference Roberts and Rosenthal22] to derive complexity and optimality results for ordinary random-walk-based Metropolis algorithms, and was later generalised to many other contexts [Reference Bédard and Rosenthal4, Reference Roberts and Rosenthal23, Reference Roberts and Rosenthal25]. Furthermore, the
![]() $d\to\infty$
limit of MCMC algorithms also provides good approximate information about processes of modest finite dimension; see, e.g., [Reference Roberts and Rosenthal23, Figure 4].
$d\to\infty$
limit of MCMC algorithms also provides good approximate information about processes of modest finite dimension; see, e.g., [Reference Roberts and Rosenthal23, Figure 4].
In this paper we apply the diffusion limits methodology to a ‘vanilla’ version of the ALPS algorithm, to study its convergence complexity. We prove (Theorem 3) that, under appropriate assumptions, a suitably scaled version of this ALPS algorithm converges to skew Brownian motion (cf. [Reference Lejay14]). This limit allows us to draw conclusions about the computational complexity of our algorithm, and to show (Corollaries 2 and 3) that, under appropriate assumptions, as the dimension
![]() $d\to\infty$
the vanilla ALPS algorithm mixes in time
$d\to\infty$
the vanilla ALPS algorithm mixes in time
![]() $O(d [\log d]^2)$
or O(d) depending on which version is used.
$O(d [\log d]^2)$
or O(d) depending on which version is used.
These results show that ALPS converges fairly quickly even in high dimension. This complexity order is similar to those previously derived for ordinary random-walk Metropolis [Reference Roberts, Gelman and Gilks21] and for simulated tempering [Reference Roberts and Rosenthal25], which were each shown to converge to dimension-free diffusions when sped up by a factor of d, thus showing that their complexity is O(d). The difference is that those previous results assumed an independent and identically distributed (i.i.d.) target of the form (1) and (3) with
![]() $J=1$
, and assumed immediate mixing between all modes at each
$J=1$
, and assumed immediate mixing between all modes at each
![]() $\beta$
, so it omitted the issue of moving between modes which often makes those algorithms exponentially slow [Reference Woodard, Schmidler and Huber32]. By contrast, the ALPS algorithm stores mode location information that is used in a special mode-jumping move to converge efficiently even when there are
$\beta$
, so it omitted the issue of moving between modes which often makes those algorithms exponentially slow [Reference Woodard, Schmidler and Huber32]. By contrast, the ALPS algorithm stores mode location information that is used in a special mode-jumping move to converge efficiently even when there are
![]() $J>1$
widely separated modes, as we now describe.
$J>1$
widely separated modes, as we now describe.
2. The ALPS algorithm
Tempering methods for MCMC usually consider powers
![]() $\pi^\beta$
for small values
$\pi^\beta$
for small values
![]() $\beta \in (0,1]$
, to make the target distribution flatter and thus allow for easier mixing between modes. By contrast, [Reference Tawn, Moores and Roberts29] introduces the ALPS algorithm, which instead uses large values
$\beta \in (0,1]$
, to make the target distribution flatter and thus allow for easier mixing between modes. By contrast, [Reference Tawn, Moores and Roberts29] introduces the ALPS algorithm, which instead uses large values
![]() $\beta \gg 1$
, combined with locally weight-preserving tempering distributions as in [Reference Tawn, Roberts and Rosenthal31] so the modes retain their relative masses. These choices make the modes of
$\beta \gg 1$
, combined with locally weight-preserving tempering distributions as in [Reference Tawn, Roberts and Rosenthal31] so the modes retain their relative masses. These choices make the modes of
![]() $\pi$
even more separated. However, under certain smoothness and integrability assumptions, they also make each mode appear approximately Gaussian and hence similarly shaped. This allows for auxiliary ‘mode-jumping’ Markov chain steps which move effectively between the different modes when
$\pi$
even more separated. However, under certain smoothness and integrability assumptions, they also make each mode appear approximately Gaussian and hence similarly shaped. This allows for auxiliary ‘mode-jumping’ Markov chain steps which move effectively between the different modes when
![]() $\beta$
is large. Then, as usual, only samples in the original temperature
$\beta$
is large. Then, as usual, only samples in the original temperature
![]() $\beta=1$
are ‘counted’ as actual samples from
$\beta=1$
are ‘counted’ as actual samples from
![]() $\pi$
.
$\pi$
.
To illustrate the idea of this algorithm, consider the following simple example in dimension
![]() $d=5$
. Suppose the target density
$d=5$
. Suppose the target density
![]() $\pi$
on
$\pi$
on
![]() ${\mathbb R}^5$
is a mixture of two skew-normal modes centered at
${\mathbb R}^5$
is a mixture of two skew-normal modes centered at
![]() $(\!-20,-20,-20,-20,-20)$
and (20, 20, 20, 20, 20) respectively, with scalings 1 and 2 respectively, and with shape parameter
$(\!-20,-20,-20,-20,-20)$
and (20, 20, 20, 20, 20) respectively, with scalings 1 and 2 respectively, and with shape parameter
![]() $\alpha=10$
; so, for all
$\alpha=10$
; so, for all
![]() $\theta\in{\mathbb R}^5$
,
$\theta\in{\mathbb R}^5$
,
 \begin{equation*}\pi(\theta) =(0.7) \prod_{i=1}^5 2 \, \phi\big( \theta_i+20 \big) \, \Phi\big( 10(\theta_i+20) \big) +(0.3) \prod_{i=1}^5 \phi\big( \tfrac{1}{2}(\theta_i-20) \big) \, \Phi\big( 5(\theta_i-20) \big) ,\end{equation*}
\begin{equation*}\pi(\theta) =(0.7) \prod_{i=1}^5 2 \, \phi\big( \theta_i+20 \big) \, \Phi\big( 10(\theta_i+20) \big) +(0.3) \prod_{i=1}^5 \phi\big( \tfrac{1}{2}(\theta_i-20) \big) \, \Phi\big( 5(\theta_i-20) \big) ,\end{equation*}
where as usual
![]() $\phi(x) = \frac{1}{\sqrt{2\pi}\,} \textrm{e}^{-x^2/2}$
and
$\phi(x) = \frac{1}{\sqrt{2\pi}\,} \textrm{e}^{-x^2/2}$
and
![]() $\Phi(x) = \int_{-\infty}^x \phi(u) \, \textrm{d} u$
; see Figure 1.
$\Phi(x) = \int_{-\infty}^x \phi(u) \, \textrm{d} u$
; see Figure 1.

Figure 1. The
![]() $\theta_1$
marginal of the target density in the illustrative example.
$\theta_1$
marginal of the target density in the illustrative example.
In such an example, it is very easy for a Markov chain to mix separately within either of the two modes. The challenge is to move between the modes (which is virtually impossible for a typical fixed-temperature Metropolis algorithm even in this simple five-dimensional example). The ALPS algorithm introduces a powerful independence-sampler-based move so that at very large inverse-temperature values
![]() $\beta \gg 1$
, the chain can exploit the near-Gaussianity of each of the modes to directly jump between them. Figure 2 shows a trace plot of the inverse temperature values
$\beta \gg 1$
, the chain can exploit the near-Gaussianity of each of the modes to directly jump between them. Figure 2 shows a trace plot of the inverse temperature values
![]() $\beta$
during one run of the algorithm, and also indicates by colour which of the two modes the chain is in (i.e. closest to). As can be seen from the plot, the chain stays in the same mode for long periods of time, and only switches modes when the values of
$\beta$
during one run of the algorithm, and also indicates by colour which of the two modes the chain is in (i.e. closest to). As can be seen from the plot, the chain stays in the same mode for long periods of time, and only switches modes when the values of
![]() $\beta$
are very large, at which point it jumps to either mode with its correct probability. (Note that this description is for the ‘vanilla’ version of ALPS; see Remark 1.)
$\beta$
are very large, at which point it jumps to either mode with its correct probability. (Note that this description is for the ‘vanilla’ version of ALPS; see Remark 1.)

Figure 2. Trace plot of the
![]() $\beta$
values in the illustrative example, coloured to indicate whether the chain is in mode 1 (light-grey) or mode 2 (black).
$\beta$
values in the illustrative example, coloured to indicate whether the chain is in mode 1 (light-grey) or mode 2 (black).
Figure 2 illustrates that the key to the ALPS algorithm’s success is moving rapidly between the large
![]() $\beta= \beta_\textrm{max} = 256$
values (which allow for mixing between the modes) and the small
$\beta= \beta_\textrm{max} = 256$
values (which allow for mixing between the modes) and the small
![]() $\beta=1$
value (which can be ‘counted’ as a sample from
$\beta=1$
value (which can be ‘counted’ as a sample from
![]() $\pi$
). However, it is not clear how quickly such mixing takes place, and in particular how it changes depending on the target
$\pi$
). However, it is not clear how quickly such mixing takes place, and in particular how it changes depending on the target
![]() $\pi$
and dimension d. To study this, we would like to prove a diffusion limit of a suitably scaled version of the
$\pi$
and dimension d. To study this, we would like to prove a diffusion limit of a suitably scaled version of the
![]() $\beta$
process, but it is not clear from Figure 2 what sort of limiting diffusive behaviour is available.
$\beta$
process, but it is not clear from Figure 2 what sort of limiting diffusive behaviour is available.
To better understand this algorithm’s convergence, we consider a suitable transformation of
![]() $\beta$
. Namely, we instead consider the values of
$\beta$
. Namely, we instead consider the values of
![]() $s \log(\beta_\textrm{max}/\beta)$
, where
$s \log(\beta_\textrm{max}/\beta)$
, where
![]() $s=1$
if the chain is in mode 1 or
$s=1$
if the chain is in mode 1 or
![]() $s=-1$
if the chain is in mode 2. The resulting process is shown in Figure 3, which suggests that this modified functional does indeed start to resemble a diffusive process. Indeed, away from the special value 0 (corresponding to
$s=-1$
if the chain is in mode 2. The resulting process is shown in Figure 3, which suggests that this modified functional does indeed start to resemble a diffusive process. Indeed, away from the special value 0 (corresponding to
![]() $\beta_\textrm{max}$
and the mode-jumping moves), the process looks roughly like Brownian motion. In fact, we prove in Theorem 3 that under appropriate assumptions and scalings, this modified process converges to a skew Brownian motion.
$\beta_\textrm{max}$
and the mode-jumping moves), the process looks roughly like Brownian motion. In fact, we prove in Theorem 3 that under appropriate assumptions and scalings, this modified process converges to a skew Brownian motion.

Figure 3. A trace plot of the transformed values
![]() $s \log(\beta_\textrm{max}/\beta)$
in the illustrative example, where
$s \log(\beta_\textrm{max}/\beta)$
in the illustrative example, where
![]() $s=+1$
or
$s=+1$
or
![]() $s=-1$
when the chain is in mode 1 or 2.
$s=-1$
when the chain is in mode 1 or 2.
More precisely, we shall prove diffusion limits for suitably rescaled versions of the ALPS algorithm, as the dimension
![]() $d\to\infty$
. We shall assume that the ALPS algorithm can easily jump between modes when it reaches the sufficiently large inverse temperature
$d\to\infty$
. We shall assume that the ALPS algorithm can easily jump between modes when it reaches the sufficiently large inverse temperature
![]() $\beta_\textrm{max}^{(d)}$
, but that it is stuck within one mode whenever
$\beta_\textrm{max}^{(d)}$
, but that it is stuck within one mode whenever
![]() $\beta < \beta_\textrm{max}^{(d)}$
. We therefore focus on how the inverse temperatures
$\beta < \beta_\textrm{max}^{(d)}$
. We therefore focus on how the inverse temperatures
![]() $\beta$
themselves are updated by the algorithm. In particular, we prove in Theorem 3 that a particular rescaling of the
$\beta$
themselves are updated by the algorithm. In particular, we prove in Theorem 3 that a particular rescaling of the
![]() $\beta$
process converges to skew Brownian motion [Reference Lejay14]. This in turn allows us to derive computational complexity results (Section 5).
$\beta$
process converges to skew Brownian motion [Reference Lejay14]. This in turn allows us to derive computational complexity results (Section 5).
Remark 1. The ‘vanilla’ ALPS algorithm studied herein differs in certain ways from the full ALPS algorithm for actual applications in [Reference Tawn, Moores and Roberts29]. For example, we assume the process mixes perfectly between modes when
![]() $\beta=\beta_\textrm{max}^{(d)}$
(due to near-Gaussianity and the algorithm’s auxiliary mode-jumping steps), and not at all when
$\beta=\beta_\textrm{max}^{(d)}$
(due to near-Gaussianity and the algorithm’s auxiliary mode-jumping steps), and not at all when
![]() $\beta<\beta_\textrm{max}^{(d)}$
, while the full algorithm mixes better and better at higher
$\beta<\beta_\textrm{max}^{(d)}$
, while the full algorithm mixes better and better at higher
![]() $\beta$
values but never perfectly. Also, the full algorithm actually uses parallel tempering, in which a separate chain is run at each temperature and their values are swapped; the single
$\beta$
values but never perfectly. Also, the full algorithm actually uses parallel tempering, in which a separate chain is run at each temperature and their values are swapped; the single
![]() $\beta$
process studied herein can then be thought of as following which of the chains is currently carrying state information between larger and smaller inverse temperatures and thus facilitating mixing (cf. [Reference Atchadé, Roberts and Rosenthal2, Section 4]). Finally, the full ALPS algorithm in [Reference Tawn, Moores and Roberts29] also makes use of the QuanTA transformation [Reference Tawn and Roberts30], an additional affine transformation to increase the efficiency of the temperature-swap moves, which we omit here; we discuss the effect of this extra QuanTA transformation in Corollary 3.
$\beta$
process studied herein can then be thought of as following which of the chains is currently carrying state information between larger and smaller inverse temperatures and thus facilitating mixing (cf. [Reference Atchadé, Roberts and Rosenthal2, Section 4]). Finally, the full ALPS algorithm in [Reference Tawn, Moores and Roberts29] also makes use of the QuanTA transformation [Reference Tawn and Roberts30], an additional affine transformation to increase the efficiency of the temperature-swap moves, which we omit here; we discuss the effect of this extra QuanTA transformation in Corollary 3.
3. Assumptions
We consider a version of the ALPS algorithm of [Reference Tawn, Moores and Roberts29]. We assume the chain always mixes immediately within each mode, but the chain can only jump between modes when at the sufficiently cold inverse temperature
![]() $\beta = \beta_\textrm{max}^{(d)}$
, at which point it immediately jumps to any of its modes with the correct probability weight.
$\beta = \beta_\textrm{max}^{(d)}$
, at which point it immediately jumps to any of its modes with the correct probability weight.
To facilitate theoretical analysis, we assume that the target density
![]() $\pi$
is a mixture of J normalised densities
$\pi$
is a mixture of J normalised densities
![]() $g_1,\ldots,g_J$
on
$g_1,\ldots,g_J$
on
![]() ${\mathbb R}^d$
with weights
${\mathbb R}^d$
with weights
![]() $w_1,\ldots,w_J$
, i.e.
$w_1,\ldots,w_J$
, i.e.
 \begin{equation}\pi(x) = \sum_{j=1}^J w_j g_j(x) , \qquad x\in{\mathbb R}^d . \end{equation}
\begin{equation}\pi(x) = \sum_{j=1}^J w_j g_j(x) , \qquad x\in{\mathbb R}^d . \end{equation}
We do not require the
![]() $g_j$
to be unimodal, but we shall nevertheless refer to them informally as the ‘modal components’ or ‘modes’ of
$g_j$
to be unimodal, but we shall nevertheless refer to them informally as the ‘modal components’ or ‘modes’ of
![]() $\pi$
, with the intuition that it is easy for MCMC to mix efficiently within each individual
$\pi$
, with the intuition that it is easy for MCMC to mix efficiently within each individual
![]() $g_j$
but difficult for it to jump between the different
$g_j$
but difficult for it to jump between the different
![]() $g_j$
.
$g_j$
.
We also assume that each state x is ‘allocated’ to (i.e. is ‘in’) one of the modes (e.g. whichever one’s centre it is closest to), such that the accept/reject probabilities when updating
![]() $\beta$
can be computed using only the mode
$\beta$
can be computed using only the mode
![]() $g_j$
of the current state, rather than the full density
$g_j$
of the current state, rather than the full density
![]() $\pi$
.
$\pi$
.
(This corresponds to considering the x values as elements of
![]() $\big({\mathbb R}^d\big)^J$
, with a different version of the state space
$\big({\mathbb R}^d\big)^J$
, with a different version of the state space
![]() ${\mathbb R}^d$
for each of the J modes; if the modes are well separated then, especially for large
${\mathbb R}^d$
for each of the J modes; if the modes are well separated then, especially for large
![]() $\beta$
, this will be a good approximation to the actual algorithm.)
$\beta$
, this will be a good approximation to the actual algorithm.)
Then, for each inverse temperature
![]() $\beta \ge 1$
we use the tempered distribution
$\beta \ge 1$
we use the tempered distribution
 \begin{equation}\pi_\beta(x) \propto\sum_{j=1}^J w_j \frac{[g_j(x)]^\beta}{\int [g_j(x)]^\beta \, \textrm{d} x} \,{=\!:}\,\sum_{j=1}^J w_j \, g_j^\beta(x) ,\end{equation}
\begin{equation}\pi_\beta(x) \propto\sum_{j=1}^J w_j \frac{[g_j(x)]^\beta}{\int [g_j(x)]^\beta \, \textrm{d} x} \,{=\!:}\,\sum_{j=1}^J w_j \, g_j^\beta(x) ,\end{equation}
where
![]() $g_j^\beta$
are the normalised powers of the
$g_j^\beta$
are the normalised powers of the
![]() $g_j$
. We assume the same weights
$g_j$
. We assume the same weights
![]() $w_j$
can be used for each
$w_j$
can be used for each
![]() $\beta$
due to a weight-preserving transformation as in [Reference Tawn, Roberts and Rosenthal31].
$\beta$
due to a weight-preserving transformation as in [Reference Tawn, Roberts and Rosenthal31].
In terms of these assumptions, the vanilla ALPS algorithm as we shall study it is defined by Algorithm 1.
Algorithm 1: The vanilla ALPS algorithm.

In our theoretical proofs below, we assume for simplicity (though see Remark 3) that we have just
![]() $J=2$
modes, of weights
$J=2$
modes, of weights
![]() $w_1$
and
$w_1$
and
![]() $w_2=1-w_1$
. To achieve limiting diffusions, we further assume, as in the original MCMC diffusion limit results [Reference Roberts, Gelman and Gilks21], that each of the individual components
$w_2=1-w_1$
. To achieve limiting diffusions, we further assume, as in the original MCMC diffusion limit results [Reference Roberts, Gelman and Gilks21], that each of the individual components
![]() $g_j$
consists of i.i.d. univariate coordinates, i.e. that, for each j, we have
$g_j$
consists of i.i.d. univariate coordinates, i.e. that, for each j, we have
 \begin{equation}g_j(x) = \prod_{i=1}^d \overline{g}_j(x_i)\end{equation}
\begin{equation}g_j(x) = \prod_{i=1}^d \overline{g}_j(x_i)\end{equation}
for some fixed one-dimensional density function
![]() $\overline{g}_j$
, where
$\overline{g}_j$
, where
![]() $x=(x_1,x_2,\ldots,x_d)$
. This allows us to apply the diffusion limit results of [Reference Roberts and Rosenthal25] within each individual target mode. (Although (3) is a very restrictive assumption, it is known [Reference Roberts and Rosenthal23] that conclusions drawn from this special case are often approximately applicable in much broader contexts.)
$x=(x_1,x_2,\ldots,x_d)$
. This allows us to apply the diffusion limit results of [Reference Roberts and Rosenthal25] within each individual target mode. (Although (3) is a very restrictive assumption, it is known [Reference Roberts and Rosenthal23] that conclusions drawn from this special case are often approximately applicable in much broader contexts.)
We also require assumptions on the
![]() $\beta$
values. Write the inverse temperatures as
$\beta$
values. Write the inverse temperatures as
for the process in dimension d. Similar to [Reference Atchadé, Roberts and Rosenthal2, Reference Roberts and Rosenthal25], following [Reference Predescu, Predescu and Ciobanu19, Reference Kone and Kofke13], we assume that the inverse temperatures are related by
for some fixed
![]() $C^1$
function
$C^1$
function
![]() $\ell$
. It is shown in [Reference Atchadé, Roberts and Rosenthal2, Reference Roberts and Rosenthal25] that in the single-mode i.i.d. case, the fastest limiting diffusion is obtained by using the choice
$\ell$
. It is shown in [Reference Atchadé, Roberts and Rosenthal2, Reference Roberts and Rosenthal25] that in the single-mode i.i.d. case, the fastest limiting diffusion is obtained by using the choice
for a fixed constant
![]() $\ell_0 \doteq 2.38$
, where
$\ell_0 \doteq 2.38$
, where
![]() $I(\beta) = {\rm Var}_{x \sim \overline{g}^\beta}(\log \overline{g}(x))$
. Inspired by this, in our later results we assume the proportionality condition that the quantities
$I(\beta) = {\rm Var}_{x \sim \overline{g}^\beta}(\log \overline{g}(x))$
. Inspired by this, in our later results we assume the proportionality condition that the quantities
![]() $I_j(\beta) \,{:\!=}\, {\rm Var}_{x \sim \overline{g}_j^\beta}(\log \overline{g}_j(x))$
for the different modes are proportional, i.e. there are positive constants
$I_j(\beta) \,{:\!=}\, {\rm Var}_{x \sim \overline{g}_j^\beta}(\log \overline{g}_j(x))$
for the different modes are proportional, i.e. there are positive constants
![]() $r_j$
and a
$r_j$
and a
![]() $C^1$
function
$C^1$
function
![]() $I_0 \,{:}\, \mathbb{R}_{+}\to\mathbb{R}_{+}$
such that
$I_0 \,{:}\, \mathbb{R}_{+}\to\mathbb{R}_{+}$
such that
and shall then correspondingly assume that
for some fixed constant
![]() $\ell_0>0$
.
$\ell_0>0$
.
One example is the exponential power family case, in which each of the mixture component factors
![]() $g_j$
is of the form
$g_j$
is of the form
![]() $g_j(x) \propto \textrm{e}^{-\lambda_j|x|^{r_j}}$
for some
$g_j(x) \propto \textrm{e}^{-\lambda_j|x|^{r_j}}$
for some
![]() $\lambda_j,r_j>0$
. It then follows from [Reference Atchadé, Roberts and Rosenthal2, Section 2.4] that
$\lambda_j,r_j>0$
. It then follows from [Reference Atchadé, Roberts and Rosenthal2, Section 2.4] that
![]() $I_j(\beta) = \beta^{-2}/r_j$
for
$I_j(\beta) = \beta^{-2}/r_j$
for
![]() $\beta>0$
, so the proportionality condition (7) holds with
$\beta>0$
, so the proportionality condition (7) holds with
![]() $I_0(\beta)=\beta^{-2}$
. The corresponding choice of
$I_0(\beta)=\beta^{-2}$
. The corresponding choice of
![]() $\ell$
from (6) is then
$\ell$
from (6) is then
![]() $\ell(\beta) = \beta/\sqrt{r_j}$
in mode j. This includes the Gaussian case, where each
$\ell(\beta) = \beta/\sqrt{r_j}$
in mode j. This includes the Gaussian case, where each
![]() $r_j=2$
and
$r_j=2$
and
![]() $\lambda_j = 1/\sigma_j^2$
.
$\lambda_j = 1/\sigma_j^2$
.
Remark 2. Our assumptions of immediate mixing within modes, and immediate mixing between modes when
![]() $\beta=\beta_\textrm{max}$
, is analogous to the corresponding assumptions in [Reference Tawn, Roberts and Rosenthal31, Section 5.1] for ordinary simulated tempering of immediate mixing within modes, and immediate mixing between modes when
$\beta=\beta_\textrm{max}$
, is analogous to the corresponding assumptions in [Reference Tawn, Roberts and Rosenthal31, Section 5.1] for ordinary simulated tempering of immediate mixing within modes, and immediate mixing between modes when
![]() $\beta=\beta_\textrm{min}$
(the hottest temperature). In practice, even within simple modes the mixing is not immediate, but rather takes, e.g., O(d) iterations for random-walk Metropolis (RWM) [Reference Roberts, Gelman and Gilks21], or
$\beta=\beta_\textrm{min}$
(the hottest temperature). In practice, even within simple modes the mixing is not immediate, but rather takes, e.g., O(d) iterations for random-walk Metropolis (RWM) [Reference Roberts, Gelman and Gilks21], or
![]() $O(d^{1/3})$
for Langevin algorithms [Reference Roberts and Rosenthal22], or
$O(d^{1/3})$
for Langevin algorithms [Reference Roberts and Rosenthal22], or
![]() $O(d^{1/4})$
for Hamiltonian (hybrid) Monte Carlo [Reference Beskos, Pillai, Roberts, Sanz-Serna and Stuart5]. Since we show that the
$O(d^{1/4})$
for Hamiltonian (hybrid) Monte Carlo [Reference Beskos, Pillai, Roberts, Sanz-Serna and Stuart5]. Since we show that the
![]() $\beta$
-mixing for ALPS takes at least O(d), it follows that if Langevin or Hamiltonian dynamics are used for the state-changing phase, then the states will mix at a faster order than the temperatures, thus effectively immediately, in which case our assumption of immediate mixing within modes is reasonable. By contrast, if RWM dynamics are used for the state-changing phase, then the interplay between the temperature convergence and state convergence would be more complicated, though it still works effectively in practice [Reference Tawn, Moores and Roberts29].
$\beta$
-mixing for ALPS takes at least O(d), it follows that if Langevin or Hamiltonian dynamics are used for the state-changing phase, then the states will mix at a faster order than the temperatures, thus effectively immediately, in which case our assumption of immediate mixing within modes is reasonable. By contrast, if RWM dynamics are used for the state-changing phase, then the interplay between the temperature convergence and state convergence would be more complicated, though it still works effectively in practice [Reference Tawn, Moores and Roberts29].
4. Main results
We now state various weak convergence results for various transformations of our process. (All proofs are deferred to Section 6.) Let
![]() $\beta^{(d)}(t)$
be the inverse temperature at time t for the process described by Algorithm 1 in dimension d. Let
$\beta^{(d)}(t)$
be the inverse temperature at time t for the process described by Algorithm 1 in dimension d. Let
![]() $\beta^{(d)}(N(dt))$
be a continuous-time version of the
$\beta^{(d)}(N(dt))$
be a continuous-time version of the
![]() $\beta^{(d)}(t)$
process, sped up by a factor of d, where
$\beta^{(d)}(t)$
process, sped up by a factor of d, where
![]() $\{N(t)\}$
is an independent standard rate-1 Poisson process. To combine the two modes into one single process, we further augment this process by multiplying it by
$\{N(t)\}$
is an independent standard rate-1 Poisson process. To combine the two modes into one single process, we further augment this process by multiplying it by
![]() $-1$
when the algorithm’s state is allocated to the second mode, while leaving it positive (unchanged) when state is allocated to the first mode, i.e.
$-1$
when the algorithm’s state is allocated to the second mode, while leaving it positive (unchanged) when state is allocated to the first mode, i.e.
 \begin{equation} X_t^{(d)} = \begin{cases} \beta^{(d)}({N(dt)}) & \textrm{in mode 1} , \\[3pt] - \beta^{(d)}({N(dt)}) \quad & \textrm{in mode 2} . \\ \end{cases}\end{equation}
\begin{equation} X_t^{(d)} = \begin{cases} \beta^{(d)}({N(dt)}) & \textrm{in mode 1} , \\[3pt] - \beta^{(d)}({N(dt)}) \quad & \textrm{in mode 2} . \\ \end{cases}\end{equation}
Our first diffusion limit result, following [Reference Roberts and Rosenthal25], states that within each mode, the inverse temperature process behaves identically to the case where there is only one mode (i.e.
![]() $J=1$
). To state it, we extend the definition of I to
$J=1$
). To state it, we extend the definition of I to
 \begin{equation} I(\beta) = \begin{cases} {\rm Var}_{x\sim f_1^\beta}(\log f_1(x)) , & \beta>0 , \\[3pt] {\rm Var}_{x\sim f_2^{|\beta|}}(\log f_2(x)) , \quad & \beta<0 . \\ \end{cases}\end{equation}
\begin{equation} I(\beta) = \begin{cases} {\rm Var}_{x\sim f_1^\beta}(\log f_1(x)) , & \beta>0 , \\[3pt] {\rm Var}_{x\sim f_2^{|\beta|}}(\log f_2(x)) , \quad & \beta<0 . \\ \end{cases}\end{equation}
Theorem 1. Assume the target distribution
![]() $\pi$
is of the form (1), with
$\pi$
is of the form (1), with
![]() $J=2$
modes of weights
$J=2$
modes of weights
![]() $w_1$
and
$w_1$
and
![]() $w_2=1-w_1$
, each having i.i.d. coordinates as in (3), with tempered distributions as in (2) for an inverse-temperatures list (4) related by (5). Then, away from its boundary points 1 and
$w_2=1-w_1$
, each having i.i.d. coordinates as in (3), with tempered distributions as in (2) for an inverse-temperatures list (4) related by (5). Then, away from its boundary points 1 and
![]() $\beta_\textrm{max}^{(d)}$
, the process
$\beta_\textrm{max}^{(d)}$
, the process
![]() $\big\{X_t^{(d)}\big\}$
from (9) converges weakly as
$\big\{X_t^{(d)}\big\}$
from (9) converges weakly as
![]() $d\to\infty$
to a fixed diffusion process X, which for
$d\to\infty$
to a fixed diffusion process X, which for
![]() $X^{(d)}>0$
satisfies
$X^{(d)}>0$
satisfies
 \begin{align} \textrm{d} X_t &= \bigg[2 \ell^2(X_t) \, \Phi\bigg( \frac{- \ell(X_t) I^{1/2}(X_t)}{2} \bigg) \bigg]^{1/2} \textrm{d} B_t \nonumber\\[3pt] &\qquad\qquad\quad\qquad + \bigg[\ell(X_t) \, \ell'(X_t) \ \Phi \bigg(\frac{-I^{1/2}(X_t) \ell(X_t)}{2}\bigg)\nonumber\\[3pt] &\qquad\qquad\quad\qquad\qquad - \ell^2(X_t) \bigg(\frac{\ell(X_t) I^{1/2}(X_t)}{ 2} \bigg)' \phi \bigg( \frac{-I^{1/2}(X_t) \ell(X_t)}{2} \bigg) \bigg] \textrm{d} t . \end{align}
\begin{align} \textrm{d} X_t &= \bigg[2 \ell^2(X_t) \, \Phi\bigg( \frac{- \ell(X_t) I^{1/2}(X_t)}{2} \bigg) \bigg]^{1/2} \textrm{d} B_t \nonumber\\[3pt] &\qquad\qquad\quad\qquad + \bigg[\ell(X_t) \, \ell'(X_t) \ \Phi \bigg(\frac{-I^{1/2}(X_t) \ell(X_t)}{2}\bigg)\nonumber\\[3pt] &\qquad\qquad\quad\qquad\qquad - \ell^2(X_t) \bigg(\frac{\ell(X_t) I^{1/2}(X_t)}{ 2} \bigg)' \phi \bigg( \frac{-I^{1/2}(X_t) \ell(X_t)}{2} \bigg) \bigg] \textrm{d} t . \end{align}
The same equation holds for
![]() $X_t<0$
, except with the sign of the drift reversed.
$X_t<0$
, except with the sign of the drift reversed.
As a check, (11) satisfies the general relation
![]() $\mu(x)= \tfrac{1}{2} \sigma^2(x)\frac{\textrm{d}}{{\textrm{d} x}} \log \pi(x) + \sigma(x) \sigma'(x)$
, which implies that
$\mu(x)= \tfrac{1}{2} \sigma^2(x)\frac{\textrm{d}}{{\textrm{d} x}} \log \pi(x) + \sigma(x) \sigma'(x)$
, which implies that
![]() $\pi$
is locally invariant for
$\pi$
is locally invariant for
![]() $X^{(d)}$
, i.e. that its generator G has
$X^{(d)}$
, i.e. that its generator G has
![]() $\pi (G f)(x) = 0$
for appropriate smooth f and for x in the interior of the domain. That is,
$\pi (G f)(x) = 0$
for appropriate smooth f and for x in the interior of the domain. That is,
![]() $\pi$
is stationary for
$\pi$
is stationary for
![]() $X^{(d)}$
locally within each mode, as expected.
$X^{(d)}$
locally within each mode, as expected.
However, Theorem 1 describes only what happens on each mode separately; it says nothing about the mode-jumping process itself. Moreover, its state space
![]() $(\!-\infty,-1]\cup [1,\infty)$
is not connected. In fact, we will see that as
$(\!-\infty,-1]\cup [1,\infty)$
is not connected. In fact, we will see that as
![]() $d\to\infty$
, the value
$d\to\infty$
, the value
![]() $\beta_\textrm{max}^{(d)}$
will go to infinity and hence never be reached in finite time. To resolve these issues, we make several transformations on the
$\beta_\textrm{max}^{(d)}$
will go to infinity and hence never be reached in finite time. To resolve these issues, we make several transformations on the
![]() $X^{(d)}_t$
process. First, for
$X^{(d)}_t$
process. First, for
![]() $|x| \ge 1$
, we define
$|x| \ge 1$
, we define
![]() $h(x) = \int_1^{|x|} \frac{1}{\ell (u)} \, \textrm{d} u$
. (For example, in the exponential power family case,
$h(x) = \int_1^{|x|} \frac{1}{\ell (u)} \, \textrm{d} u$
. (For example, in the exponential power family case,
![]() $I(\beta) \propto 1/\beta^2$
, so (8) gives
$I(\beta) \propto 1/\beta^2$
, so (8) gives
![]() $\ell(\beta) = I_0^{-1/2}(\beta) \, \ell_0 \propto \beta$
, whence
$\ell(\beta) = I_0^{-1/2}(\beta) \, \ell_0 \propto \beta$
, whence
![]() $h(x) = \int_1^{|x|} \frac{1}{\ell(u)} \, \textrm{d} u\propto \int_1^{|x|} \frac{1}{u} \, \textrm{d} u= \log|x|$
.) We then set
$h(x) = \int_1^{|x|} \frac{1}{\ell(u)} \, \textrm{d} u\propto \int_1^{|x|} \frac{1}{u} \, \textrm{d} u= \log|x|$
.) We then set
 \begin{equation}H_{t (h(\beta_\textrm{max}^{(d)}))^2}^{(d)} ={\rm sign}\left(X_{t h(\beta_\textrm{max}^{(d)})^2}^{(d)}\right) \left[ 1 + \frac{h\left( X^{(d)}_{t h(\beta_\textrm{max}^{(d)})^2} \right)}{h(\beta_\textrm{max}^{(d)})} \right] .\end{equation}
\begin{equation}H_{t (h(\beta_\textrm{max}^{(d)}))^2}^{(d)} ={\rm sign}\left(X_{t h(\beta_\textrm{max}^{(d)})^2}^{(d)}\right) \left[ 1 + \frac{h\left( X^{(d)}_{t h(\beta_\textrm{max}^{(d)})^2} \right)}{h(\beta_\textrm{max}^{(d)})} \right] .\end{equation}
Hence,
![]() $1 \le H_t^{(d)} \le 2$
in the first mode, and
$1 \le H_t^{(d)} \le 2$
in the first mode, and
![]() $-1 \ge H_t^{(d)} \ge -2$
in the second mode. Also,
$-1 \ge H_t^{(d)} \ge -2$
in the second mode. Also,
![]() $H_t^{(d)}$
speeds up
$H_t^{(d)}$
speeds up
![]() $X_t^{(d)}$
by a factor of
$X_t^{(d)}$
by a factor of
![]() $h\big(\beta_\textrm{max}^{(d)}\big)^2$
, and hence moves at Poisson rate
$h\big(\beta_\textrm{max}^{(d)}\big)^2$
, and hence moves at Poisson rate
![]() $d h\big(\beta_\textrm{max}^{(d)}\big)^2$
. This new process
$d h\big(\beta_\textrm{max}^{(d)}\big)^2$
. This new process
![]() $H_t^{(d)}$
satisfies the following.
$H_t^{(d)}$
satisfies the following.
Theorem 2. Under the set-up and assumptions of Theorem 1, on
![]() $(\!-2,-1) \cup (1,2)$
(i.e. away from its boundary points), the process
$(\!-2,-1) \cup (1,2)$
(i.e. away from its boundary points), the process
![]() $\big\{H_t^{(d)}\big\}$
from (12) converges weakly in the Skorokhod topology as
$\big\{H_t^{(d)}\big\}$
from (12) converges weakly in the Skorokhod topology as
![]() $d\to\infty$
to a limiting diffusion H which satisfies
$d\to\infty$
to a limiting diffusion H which satisfies
Furthermore, H leaves constant (uniform) densities locally invariant.
To make further progress, we now use the proportionality condition (7), with corresponding inverse-temperature spacing (8). It then follows from the extended definition (10) that
![]() $\ell(X_t) \, I^{1/2}(X_t) = \ell_0 r_1^{1/2}$
for
$\ell(X_t) \, I^{1/2}(X_t) = \ell_0 r_1^{1/2}$
for
![]() $X_t < 0$
, and
$X_t < 0$
, and
![]() $\ell(X_t) \, I^{1/2}(X_t) = \ell_0 r_2^{1/2}$
for
$\ell(X_t) \, I^{1/2}(X_t) = \ell_0 r_2^{1/2}$
for
![]() $X_t > 0$
, with
$X_t > 0$
, with
![]() $\big[ \ell(X_t) \, I^{1/2}(X_t) \big]' = 0$
for all
$\big[ \ell(X_t) \, I^{1/2}(X_t) \big]' = 0$
for all
![]() $X_t \not= 0$
. Hence, Theorem 2 immediately gives the following corollary.
$X_t \not= 0$
. Hence, Theorem 2 immediately gives the following corollary.
Corollary 1. Assume the set-up and assumptions of Theorem 1, and also the proportionality condition (7) with inverse-temperature spacing (8). Then, as
![]() $d\to\infty$
, the process
$d\to\infty$
, the process
![]() $\big\{H_t^{(d)}\big\}$
converges weakly in the Skorokhod topology to a limit process H on
$\big\{H_t^{(d)}\big\}$
converges weakly in the Skorokhod topology to a limit process H on
![]() $(\!-2,-1)$
and on (1,2), i.e. away from its boundary points. Furthermore, H is a diffusion, with drift 0, and with diffusion coefficient which is constant on each of the two intervals
$(\!-2,-1)$
and on (1,2), i.e. away from its boundary points. Furthermore, H is a diffusion, with drift 0, and with diffusion coefficient which is constant on each of the two intervals
![]() $(\!-2,-1)$
and (1,2). Specifically,
$(\!-2,-1)$
and (1,2). Specifically,
![]() $\textrm{d} H_t = s(H_t) \, \textrm{d} B_t$
, where
$\textrm{d} H_t = s(H_t) \, \textrm{d} B_t$
, where
![]() $s(H_t) = s_1$
for
$s(H_t) = s_1$
for
![]() $H_t \in (1,2)$
, and
$H_t \in (1,2)$
, and
![]() $s(H_t) = s_2$
for
$s(H_t) = s_2$
for
![]() $H_t \in (\!-2,-1)$
, with
$H_t \in (\!-2,-1)$
, with
Next, we need to join up the two parts of the domain
![]() $[-2,-1] \cup[1,2]$
of the process
$[-2,-1] \cup[1,2]$
of the process
![]() $H_t^{(d)}$
. Now, the original process can jump between modes when at the coldest temperture
$H_t^{(d)}$
. Now, the original process can jump between modes when at the coldest temperture
![]() $\beta_\textrm{max}^{(d)}$
, corresponding to the values
$\beta_\textrm{max}^{(d)}$
, corresponding to the values
![]() $\pm 2$
for the transformed process
$\pm 2$
for the transformed process
![]() $H_t^{(d)}$
. Hence, we let
$H_t^{(d)}$
. Hence, we let
 \begin{equation} Z_t^{(d)} = 2 {\rm sign}\big(H_t^{(d)}\big) - H_t^{(d)} = \begin{cases} 2 - H_t^{(d)} , & H_t^{(d)} \ge 1, \ \textrm{i.e. in mode 1} , \\[3pt] -2 - H_t^{(d)} , \quad & H_t^{(d)} \le -1, \ \textrm{i.e. in mode 2} , \\[3pt] \end{cases}\end{equation}
\begin{equation} Z_t^{(d)} = 2 {\rm sign}\big(H_t^{(d)}\big) - H_t^{(d)} = \begin{cases} 2 - H_t^{(d)} , & H_t^{(d)} \ge 1, \ \textrm{i.e. in mode 1} , \\[3pt] -2 - H_t^{(d)} , \quad & H_t^{(d)} \le -1, \ \textrm{i.e. in mode 2} , \\[3pt] \end{cases}\end{equation}
so that
![]() $Z_t^{(d)}$
has domain
$Z_t^{(d)}$
has domain
![]() $[-1,1]$
with mode-jumping at 0.
$[-1,1]$
with mode-jumping at 0.
However, by Corollary 1, the limit of the process
![]() $Z_t^{(d)}$
will still have diffusion coefficient
$Z_t^{(d)}$
will still have diffusion coefficient
![]() $s_1$
or
$s_1$
or
![]() $s_2$
on its positive and negative parts. We thus rescale the process by setting
$s_2$
on its positive and negative parts. We thus rescale the process by setting
(So, to recap,
![]() $W_t^{(d)}$
is defined in (16) in terms of
$W_t^{(d)}$
is defined in (16) in terms of
![]() $Z_t^{(d)}$
, which is defined in (15) in terms of
$Z_t^{(d)}$
, which is defined in (15) in terms of
![]() $H_t^{(d)}$
, which is defined in (12) in terms of
$H_t^{(d)}$
, which is defined in (12) in terms of
![]() $X_t^{(d)}$
, which is in turn defined in (9) in terms of the original inverse-temperature process
$X_t^{(d)}$
, which is in turn defined in (9) in terms of the original inverse-temperature process
![]() $\beta^{(d)}(t)$
, which itself arises from running Algorithm 1.) Then,
$\beta^{(d)}(t)$
, which itself arises from running Algorithm 1.) Then,
![]() $W^{(d)}_t$
has domain
$W^{(d)}_t$
has domain
![]() $\Big[{-}\frac{1}{s_2},\frac{1}{s_1}\Big]$
, and a limit which is actual Brownian motion on each of
$\Big[{-}\frac{1}{s_2},\frac{1}{s_1}\Big]$
, and a limit which is actual Brownian motion on each of
![]() $\Big({-}\frac{1}{s_2},0\Big)$
and
$\Big({-}\frac{1}{s_2},0\Big)$
and
![]() $\Big(0,\frac{1}{s_1}\Big)$
. The precise limit of this process requires the notion of skew Brownian motion, a generalisation of usual Brownian motion that, intuitively, behaves just like a Brownian motion except that the sign of each excursion from 0 is chosen using an independent Bernoulli random variable; for further details, constructions, and discussion see, e.g., [Reference Lejay14]. In terms of skew Brownian motion, we have the following theorem.
$\Big(0,\frac{1}{s_1}\Big)$
. The precise limit of this process requires the notion of skew Brownian motion, a generalisation of usual Brownian motion that, intuitively, behaves just like a Brownian motion except that the sign of each excursion from 0 is chosen using an independent Bernoulli random variable; for further details, constructions, and discussion see, e.g., [Reference Lejay14]. In terms of skew Brownian motion, we have the following theorem.
Theorem 3. Under the assumptions of Corollary 1, with
![]() $s_i$
as in (14), the process
$s_i$
as in (14), the process
![]() $\big\{W_t^{(d)}\big\}$
from (16) converges weakly in the Skorokhod topology as
$\big\{W_t^{(d)}\big\}$
from (16) converges weakly in the Skorokhod topology as
![]() $d\to\infty$
to a limit process W which is skew Brownian motion on
$d\to\infty$
to a limit process W which is skew Brownian motion on
![]() $\big[{-}\frac{1}{s_2},\frac{1}{s_1}\big]$
, with reflecting boundaries, and with excursion probabilities at 0 proportional to
$\big[{-}\frac{1}{s_2},\frac{1}{s_1}\big]$
, with reflecting boundaries, and with excursion probabilities at 0 proportional to
![]() $w_1 s_1$
(to go positive) and
$w_1 s_1$
(to go positive) and
![]() $w_2 s_2$
(to go negative).
$w_2 s_2$
(to go negative).
The above theorems are all proved in Section 6. First, we use them to investigate the computational complexity of the ALPS algorithm.
5. Computational complexity
Theorem 3 has implications for the computational complexity of the ALPS algorithm. Indeed, it shows that the limiting process W does not depend at all on the dimension d, and hence has convergence time O(1) as
![]() $d\to\infty$
. However, W was derived from the processes
$d\to\infty$
. However, W was derived from the processes
![]() $H_t^{(d)}$
and
$H_t^{(d)}$
and
![]() $Z_t^{(d)}$
, which sped up time by a factor of
$Z_t^{(d)}$
, which sped up time by a factor of
![]() $\Big(h\big(\beta_\textrm{max}^{(d)}\big)\Big)^2$
from the process
$\Big(h\big(\beta_\textrm{max}^{(d)}\big)\Big)^2$
from the process
![]() $X_t^{(d)}$
, which itself sped up time by a factor d. That is, W was sped up by a total factor of
$X_t^{(d)}$
, which itself sped up time by a factor d. That is, W was sped up by a total factor of
![]() $d \Big[h\big(\beta_\textrm{max}^{(d)}\big)\Big]^2$
. So, in the original scaling, the convergence time is
$d \Big[h\big(\beta_\textrm{max}^{(d)}\big)\Big]^2$
. So, in the original scaling, the convergence time is
![]() $O\Big(d \Big[h(\beta_\textrm{max}^{(d)})\Big]^2\Big)$
.
$O\Big(d \Big[h(\beta_\textrm{max}^{(d)})\Big]^2\Big)$
.
More formally, it is shown in [Reference Roberts and Rosenthal24, Theorem 1] that such diffusion limit convergence implies that for any
![]() $\epsilon>0$
, the convergence time
$\epsilon>0$
, the convergence time
![]() $T_\epsilon$
for each component of the original process to get within
$T_\epsilon$
for each component of the original process to get within
![]() $\epsilon$
of stationary in Kantorovich–Rubinstein distance, averaged over starting state chosen from stationarity, will be of the same order as the speedup factor. So, combining Theorem 3 and [Reference Roberts and Rosenthal24, Theorem 1] shows that, for the
$\epsilon$
of stationary in Kantorovich–Rubinstein distance, averaged over starting state chosen from stationarity, will be of the same order as the speedup factor. So, combining Theorem 3 and [Reference Roberts and Rosenthal24, Theorem 1] shows that, for the
![]() $\beta$
process of the vanilla ALPS algorithm, the convergence time
$\beta$
process of the vanilla ALPS algorithm, the convergence time
![]() $T_\epsilon$
is
$T_\epsilon$
is
![]() $O\big(d \big[h(\beta_\textrm{max}^{(d)})\big]^2\big)$
. Furthermore, this convergence time is indeed an appropriate measure of the algorithm’s efficiency, since it is proportional to the rate at which the
$O\big(d \big[h(\beta_\textrm{max}^{(d)})\big]^2\big)$
. Furthermore, this convergence time is indeed an appropriate measure of the algorithm’s efficiency, since it is proportional to the rate at which the
![]() $\beta$
values can complete a ‘round trip’ from one sample at
$\beta$
values can complete a ‘round trip’ from one sample at
![]() $\beta=1$
, to a mode jump at
$\beta=1$
, to a mode jump at
![]() $\beta=\beta_\textrm{max}$
, to another sample at
$\beta=\beta_\textrm{max}$
, to another sample at
![]() $\beta=1$
, and hence mix well between modes; similar approaches appear in [Reference Atchadé, Roberts and Rosenthal2, Reference Jacka and Hernández-Hernández11, Reference Syed, Bouchard-Côté, Deligiannidis and Doucet28].
$\beta=1$
, and hence mix well between modes; similar approaches appear in [Reference Atchadé, Roberts and Rosenthal2, Reference Jacka and Hernández-Hernández11, Reference Syed, Bouchard-Côté, Deligiannidis and Doucet28].
This raises the question of how
![]() $h\big(\beta_\textrm{max}^{(d)}\big)$
grows as a function of d. It is proved in [Reference Tawn, Moores and Roberts29] that for the ALPS process to mix modes efficiently, we need the maximum inverse temperature value
$h\big(\beta_\textrm{max}^{(d)}\big)$
grows as a function of d. It is proved in [Reference Tawn, Moores and Roberts29] that for the ALPS process to mix modes efficiently, we need the maximum inverse temperature value
![]() $\beta_\textrm{max}^{(d)}$
to grow linearly with dimension, i.e. we need to choose
$\beta_\textrm{max}^{(d)}$
to grow linearly with dimension, i.e. we need to choose
![]() $\beta_\textrm{max}^{(d)} \propto d$
. And, in the exponential power family case, as mentioned above,
$\beta_\textrm{max}^{(d)} \propto d$
. And, in the exponential power family case, as mentioned above,
![]() $I(\beta) \propto 1/\beta^2$
, which implies by (8) that
$I(\beta) \propto 1/\beta^2$
, which implies by (8) that
![]() $h(x) \propto \log|x|$
, so
$h(x) \propto \log|x|$
, so
![]() $h\big(\beta_\textrm{max}^{(d)}\big) \propto \log(d)$
. Hence, the complexity order
$h\big(\beta_\textrm{max}^{(d)}\big) \propto \log(d)$
. Hence, the complexity order
![]() $O\big(d \big[h(\beta_\textrm{max}^{(d)})\big]^2\big)$
equals
$O\big(d \big[h(\beta_\textrm{max}^{(d)})\big]^2\big)$
equals
![]() $O\big(d [\log d]^2\big)$
. That is, for the inverse temperature process to hit
$O\big(d [\log d]^2\big)$
. That is, for the inverse temperature process to hit
![]() $\beta_\textrm{max}^{(d)}$
and hence mix modes takes
$\beta_\textrm{max}^{(d)}$
and hence mix modes takes
![]() $O\big(d [\log d]^2\big)$
iterations.
$O\big(d [\log d]^2\big)$
iterations.
If we are not in the exponential power family case, then it may no longer be true that
![]() $I(\beta) \propto 1/\beta^2$
. However, as
$I(\beta) \propto 1/\beta^2$
. However, as
![]() $d,\beta\to\infty$
, under appropriate smoothness assumptions the densities in the different modes will become approximately Gaussian, which corresponds to the exponential power family case with
$d,\beta\to\infty$
, under appropriate smoothness assumptions the densities in the different modes will become approximately Gaussian, which corresponds to the exponential power family case with
![]() $r=2$
. And, it is proved in [Reference Tawn and Roberts30, Equation (66)] that if the first four moments converge to those of a Gaussian, then
$r=2$
. And, it is proved in [Reference Tawn and Roberts30, Equation (66)] that if the first four moments converge to those of a Gaussian, then
![]() $2\beta^2 I(\beta) \to 1$
, i.e. approximately
$2\beta^2 I(\beta) \to 1$
, i.e. approximately
![]() $I(\beta) \propto 1/\beta^2$
. Hence, from (8), approximately
$I(\beta) \propto 1/\beta^2$
. Hence, from (8), approximately
![]() $\ell(\beta) \propto \beta$
, so again
$\ell(\beta) \propto \beta$
, so again
![]() $h\big(\beta_\textrm{max}^{(d)}\big) \propto \log(d)$
, and the complexity order is still
$h\big(\beta_\textrm{max}^{(d)}\big) \propto \log(d)$
, and the complexity order is still
![]() $O\big(d [\log d]^2\big)$
as before. We summarise this conclusion as follows.
$O\big(d [\log d]^2\big)$
as before. We summarise this conclusion as follows.
Corollary 2. Under the assumptions of Corollary 1, if either (a) the densities of the two modes of
![]() $\pi$
are in the exponential power family, or (b) the two modes’ first four moments each converge to those of a Gaussian as
$\pi$
are in the exponential power family, or (b) the two modes’ first four moments each converge to those of a Gaussian as
![]() $d,\beta\to\infty$
, then the convergence times
$d,\beta\to\infty$
, then the convergence times
![]() $T_\epsilon$
for
$T_\epsilon$
for
![]() $\beta$
are
$\beta$
are
![]() $O\big(d [\log d]^2\big)$
as
$O\big(d [\log d]^2\big)$
as
![]() $d\to\infty$
.
$d\to\infty$
.
In a different direction, [Reference Tawn and Roberts30] introduces the QuanTA algorithm, which modifies parallel tempering’s usual temperature-swap moves by adjusting the x space in order to permit larger moves in the inverse temperature space. As a result of this, [Reference Tawn and Roberts30, Theorem 2] shows that the resulting
![]() $\ell(\beta)$
function is then proportional to
$\ell(\beta)$
function is then proportional to
![]() $\beta^{k/2}$
for some
$\beta^{k/2}$
for some
![]() $k>2$
(instead of proportional to
$k>2$
(instead of proportional to
![]() $\beta$
). In that case,
$\beta$
). In that case,
so that
![]() $h\big(\beta_\textrm{max}^{(d)}\big)$
is O(1) rather than
$h\big(\beta_\textrm{max}^{(d)}\big)$
is O(1) rather than
![]() $O(\log d)$
. This means that the convergence complexity
$O(\log d)$
. This means that the convergence complexity
![]() $O\Big(d \Big[h\big(\beta_\textrm{max}^{(d)}\big)\Big]^2\Big)$
becomes simply O(d), i.e. the
$O\Big(d \Big[h\big(\beta_\textrm{max}^{(d)}\big)\Big]^2\Big)$
becomes simply O(d), i.e. the
![]() $[\log d]^2$
factor vanishes. We summarise this observation as follows.
$[\log d]^2$
factor vanishes. We summarise this observation as follows.
Corollary 3. Under the assumptions of Corollary 1, if we instead run the version of the ALPS algorithm which uses the QuanTA modification of [Reference Tawn and Roberts30], then the convergence times
![]() $T_\epsilon$
for
$T_\epsilon$
for
![]() $\beta$
are
$\beta$
are
![]() $O\big(d [\log d]^2\big)$
as
$O\big(d [\log d]^2\big)$
as
![]() $d\to\infty$
.
$d\to\infty$
.
Comparing Corollaries 2 and 3, we see that the QuanTA modification improves the complexity bound by a factor of
![]() $[\log d]^2$
. This is not surprising, since QuanTA was specifically designed to make the algorithm move faster, especially under near-Gaussianity at large
$[\log d]^2$
. This is not surprising, since QuanTA was specifically designed to make the algorithm move faster, especially under near-Gaussianity at large
![]() $\beta$
, thus improving the mixing time. This improvement is also borne out through simulation experiments; see [Reference Tawn and Roberts30].
$\beta$
, thus improving the mixing time. This improvement is also borne out through simulation experiments; see [Reference Tawn and Roberts30].
Remark 3. (More than two modes). For simplicity, all of the above proofs assumed a mixture of just
![]() $J=2$
modes. However, similar analysis works more generally. Indeed, suppose
$J=2$
modes. However, similar analysis works more generally. Indeed, suppose
![]() $\pi$
is a mixture of
$\pi$
is a mixture of
![]() $J>2$
modes, of weights
$J>2$
modes, of weights
![]() $w_1,w_2,\ldots,w_J \ge 0$
where
$w_1,w_2,\ldots,w_J \ge 0$
where
![]() $\sum_{i=1}^J w_i = 1$
. Then, when
$\sum_{i=1}^J w_i = 1$
. Then, when
![]() $\beta(t)$
reaches
$\beta(t)$
reaches
![]() $\beta_\textrm{max}^{(d)}$
, the process chooses one of the J modes with probability
$\beta_\textrm{max}^{(d)}$
, the process chooses one of the J modes with probability
![]() $w_i$
(due to the auxiliary mode-jumping step). In this case, a theorem similar to Theorem 3 could be proved by similar methods. The processes
$w_i$
(due to the auxiliary mode-jumping step). In this case, a theorem similar to Theorem 3 could be proved by similar methods. The processes
![]() $\big\{W_t^{(d)}\big\}$
will converge not to skew Brownian motion but to Walsh’s Brownian motion, a process not on
$\big\{W_t^{(d)}\big\}$
will converge not to skew Brownian motion but to Walsh’s Brownian motion, a process not on
![]() $\Big[{-}\frac{1}{s_2},\frac{1}{s_1}\Big]$
but rather on a ‘star’ shape with J different line segments all meeting at the origin (corresponding to
$\Big[{-}\frac{1}{s_2},\frac{1}{s_1}\Big]$
but rather on a ‘star’ shape with J different line segments all meeting at the origin (corresponding to
![]() $\beta_\textrm{max}^{(d)}$
). Intuitively, this process behaves as Brownian motion within each segment, but chooses each excursion from the origin using an independent random variable with probabilities
$\beta_\textrm{max}^{(d)}$
). Intuitively, this process behaves as Brownian motion within each segment, but chooses each excursion from the origin using an independent random variable with probabilities
![]() $w_i$
; for further details, constructions, and discussion see, e.g., [Reference Barlow, Pitman and Yor3]. (The case
$w_i$
; for further details, constructions, and discussion see, e.g., [Reference Barlow, Pitman and Yor3]. (The case
![]() $J=2$
but
$J=2$
but
![]() $w_1\not=\frac{1}{2}$
corresponds to skew Brownian motion as in Theorem 3.) This in turn leads to the same complexity bound of
$w_1\not=\frac{1}{2}$
corresponds to skew Brownian motion as in Theorem 3.) This in turn leads to the same complexity bound of
![]() $O\big(d [\log d]^2\big)$
iterations (or O(d) iterations if using QuanTA) when
$O\big(d [\log d]^2\big)$
iterations (or O(d) iterations if using QuanTA) when
![]() $J>2$
as well.
$J>2$
as well.
6. Theorem proofs
In this section we prove the theorems stated in Section 4. Note that Theorem 1 essentially follows directly from the previous theoretical analysis of simulated tempering in [Reference Atchadé, Roberts and Rosenthal2, Reference Roberts and Rosenthal25], and Theorem 2 then follows from some additional computations using Itô’s formula. By contrast, Theorem 3 requires a different approach, to show that the modified
![]() $W^{(d)}$
process converges to reflecting skew Brownian motion, including delicate arguments to show the convergence of the corresponding infinitesimal generators, especially at the two endpoints and at the excursion point 0.
$W^{(d)}$
process converges to reflecting skew Brownian motion, including delicate arguments to show the convergence of the corresponding infinitesimal generators, especially at the two endpoints and at the excursion point 0.
6.1. Proof of Theorem 1
Since mixing between modes is only possible at
![]() $\beta_\textrm{max}^{(d)}$
, the dynamics for other
$\beta_\textrm{max}^{(d)}$
, the dynamics for other
![]() $\beta$
will be identical to the single-mode case (
$\beta$
will be identical to the single-mode case (
![]() $J=1$
) as covered in [Reference Atchadé, Roberts and Rosenthal2, Reference Roberts and Rosenthal25]. It therefore follows directly from [Reference Roberts and Rosenthal25, Theorem 6] that as
$J=1$
) as covered in [Reference Atchadé, Roberts and Rosenthal2, Reference Roberts and Rosenthal25]. It therefore follows directly from [Reference Roberts and Rosenthal25, Theorem 6] that as
![]() $d\to\infty$
, the process
$d\to\infty$
, the process
![]() $\{X_t\}$
converges weakly, at least on
$\{X_t\}$
converges weakly, at least on
![]() $X_t>0$
, to a diffusion limit
$X_t>0$
, to a diffusion limit
![]() $\{X_t\}_{t \ge 0}$
satisfying (11). The result for
$\{X_t\}_{t \ge 0}$
satisfying (11). The result for
![]() $X_t<0$
follows similarly.
$X_t<0$
follows similarly.
6.2. Proof of Theorem 2
We assume
![]() $x\in(1,2)$
; the proof for
$x\in(1,2)$
; the proof for
![]() $x\in(\!-2,-1)$
is virtually identical. Here
$x\in(\!-2,-1)$
is virtually identical. Here
![]() $H_t = h(X_t)$
, where
$H_t = h(X_t)$
, where
![]() $h'(x) = \ell(x)^{-1}$
, and
$h'(x) = \ell(x)^{-1}$
, and
![]() $h''(x) = -\ell'(x) \ell(x)^{-2}$
. Hence, by Itô’s formula,
$h''(x) = -\ell'(x) \ell(x)^{-2}$
. Hence, by Itô’s formula,
 \begin{align*}\textrm{d} H_t& = h'(X_t) dX_t + \frac{1}{2} h''(X_t) d\langle X \rangle_t \\[3pt]& = \ell(X_t)^{-1} \textrm{d} X_t - \frac{1}{2} \ell'(X_t) \ell(X_t)^{-2}\textrm{d} \langle X \rangle_t \\[3pt]& = \ell(X_t)^{-1}\left[2 \ell^2(X_t) \Phi\left( \frac{- \ell(X_t) I^{1/2}(X_t)}{ 2} \right) \right]^{1/2} \textrm{d} B_t \\[3pt] & \quad + \ell(X_t)^{-1} \ell(X_t) \ell'(X_t) \Phi \left(\frac{-I^{1/2}(X_t) \ell(X_t)}{ 2}\right) \textrm{d} t \\[3pt] & \quad - \ell^2(X_t) \left(\frac{\ell(X_t) I^{1/2}(X_t)}{ 2} \right)' \phi \left( \frac{-I^{1/2}(X_t) \ell(X_t)}{ 2} \right) \textrm{d} t \\[3pt] & \quad - \frac{1}{2} \ell'(X_t) \ell(X_t)^{-2} 2 \ell^2(X_t) \Phi\left( \frac{- \ell(X_t) I^{1/2}(X_t)}{ 2} \right) \textrm{d} t .\end{align*}
\begin{align*}\textrm{d} H_t& = h'(X_t) dX_t + \frac{1}{2} h''(X_t) d\langle X \rangle_t \\[3pt]& = \ell(X_t)^{-1} \textrm{d} X_t - \frac{1}{2} \ell'(X_t) \ell(X_t)^{-2}\textrm{d} \langle X \rangle_t \\[3pt]& = \ell(X_t)^{-1}\left[2 \ell^2(X_t) \Phi\left( \frac{- \ell(X_t) I^{1/2}(X_t)}{ 2} \right) \right]^{1/2} \textrm{d} B_t \\[3pt] & \quad + \ell(X_t)^{-1} \ell(X_t) \ell'(X_t) \Phi \left(\frac{-I^{1/2}(X_t) \ell(X_t)}{ 2}\right) \textrm{d} t \\[3pt] & \quad - \ell^2(X_t) \left(\frac{\ell(X_t) I^{1/2}(X_t)}{ 2} \right)' \phi \left( \frac{-I^{1/2}(X_t) \ell(X_t)}{ 2} \right) \textrm{d} t \\[3pt] & \quad - \frac{1}{2} \ell'(X_t) \ell(X_t)^{-2} 2 \ell^2(X_t) \Phi\left( \frac{- \ell(X_t) I^{1/2}(X_t)}{ 2} \right) \textrm{d} t .\end{align*}
In this last equation, the second and fourth terms cancel. Also, since
![]() $\Phi' = \phi$
, it follows from the chain rule that the third term can be written as
$\Phi' = \phi$
, it follows from the chain rule that the third term can be written as
This gives (13). Then, writing everything in terms of
![]() $H_t = h(X_t)$
, this becomes
$H_t = h(X_t)$
, this becomes
 \begin{align*} \textrm{d} H_t & = \left[ 2 \, \Phi\left( \frac{- \ell(h^{-1}(H_t)) I^{1/2}(h^{-1}(H_t))}{2} \right) \right]^{1/2} \textrm{d} B_t \\[3pt] & \quad + \ell(h^{-1}(H_t)) \bigg[ \Phi \left( \frac{-I^{1/2}(h^{-1}(H_t)) \ell(h^{-1}(H_t))}{2} \right) \bigg]' \textrm{d} t .\end{align*}
\begin{align*} \textrm{d} H_t & = \left[ 2 \, \Phi\left( \frac{- \ell(h^{-1}(H_t)) I^{1/2}(h^{-1}(H_t))}{2} \right) \right]^{1/2} \textrm{d} B_t \\[3pt] & \quad + \ell(h^{-1}(H_t)) \bigg[ \Phi \left( \frac{-I^{1/2}(h^{-1}(H_t)) \ell(h^{-1}(H_t))}{2} \right) \bigg]' \textrm{d} t .\end{align*}
Now, a diffusion of the form
![]() $\textrm{d} H_t = \sigma(H_t) \textrm{d} B_t +\mu(H_t) \textrm{d} t$
has locally invariant distribution
$\textrm{d} H_t = \sigma(H_t) \textrm{d} B_t +\mu(H_t) \textrm{d} t$
has locally invariant distribution
![]() $\pi$
provided that
$\pi$
provided that
![]() $\frac{1}{2} (\log\pi)' \sigma^2 + \sigma \sigma' = \mu$
. That holds for constant
$\frac{1}{2} (\log\pi)' \sigma^2 + \sigma \sigma' = \mu$
. That holds for constant
![]() $\pi$
if
$\pi$
if
![]() $\sigma \sigma' = \mu$
. In this case, we compute that
$\sigma \sigma' = \mu$
. In this case, we compute that
 \begin{align*} \sigma \sigma' = \frac12 (\sigma^2)' & = \frac{1}{2} \frac{\textrm{d}}{\textrm{d} H} \left[ 2 \, \Phi\left( \frac{- \ell(h^{-1}(H)) I^{1/2}(h^{-1}(H))}{2} \right) \right] \\[3pt] & = \frac12 \left( \frac{\textrm{d} H}{\textrm{d} X} \right)^{-1} \frac{\textrm{d}}{\textrm{d} X} \left[ 2 \, \Phi\left( \frac{- \ell(X) I^{1/2}(X)}{2} \right) \right] \\[3pt] & = \frac12 \left( \ell(X)^{-1} \right)^{-1} \left[ 2 \, \Phi\left( \frac{- \ell(X) I^{1/2}(X)}{2} \right) \right]^{\prime} \\[3pt] & = \ell(X) \left[ \Phi\left( \frac{- \ell(X) I^{1/2}(X)}{2} \right) \right]^{\prime} = \mu ,\end{align*}
\begin{align*} \sigma \sigma' = \frac12 (\sigma^2)' & = \frac{1}{2} \frac{\textrm{d}}{\textrm{d} H} \left[ 2 \, \Phi\left( \frac{- \ell(h^{-1}(H)) I^{1/2}(h^{-1}(H))}{2} \right) \right] \\[3pt] & = \frac12 \left( \frac{\textrm{d} H}{\textrm{d} X} \right)^{-1} \frac{\textrm{d}}{\textrm{d} X} \left[ 2 \, \Phi\left( \frac{- \ell(X) I^{1/2}(X)}{2} \right) \right] \\[3pt] & = \frac12 \left( \ell(X)^{-1} \right)^{-1} \left[ 2 \, \Phi\left( \frac{- \ell(X) I^{1/2}(X)}{2} \right) \right]^{\prime} \\[3pt] & = \ell(X) \left[ \Phi\left( \frac{- \ell(X) I^{1/2}(X)}{2} \right) \right]^{\prime} = \mu ,\end{align*}
thus showing that H leaves constant densities locally invariant.
6.3. Proof of Theorem 3
Let
![]() $w_\textrm{min}^{(d)} = - {1} / {s_2}$
and
$w_\textrm{min}^{(d)} = - {1} / {s_2}$
and
![]() $w_\textrm{max}^{(d)} = {1} / {s_1}$
be the endpoints of the domain of W. By Corollary 1,
$w_\textrm{max}^{(d)} = {1} / {s_1}$
be the endpoints of the domain of W. By Corollary 1,
![]() $\textrm{d} H_t =s(H_t) \, \textrm{d} B_t$
in the interior of its domain. Since
$\textrm{d} H_t =s(H_t) \, \textrm{d} B_t$
in the interior of its domain. Since
![]() $W_t = s(H_t)^{-1}\, H_t$
, it follows that
$W_t = s(H_t)^{-1}\, H_t$
, it follows that
![]() $W_t$
behaves like Brownian motion on
$W_t$
behaves like Brownian motion on
![]() $\big(\!-w_\textrm{min}^{(d)},0\big)$
and on
$\big(\!-w_\textrm{min}^{(d)},0\big)$
and on
![]() $\big(0,w_\textrm{max}^{(d)}\big)$
. It remains to show that the process converges weakly to skew Brownian motion, including at the boundary points
$\big(0,w_\textrm{max}^{(d)}\big)$
. It remains to show that the process converges weakly to skew Brownian motion, including at the boundary points
![]() $W_t=0,w_\textrm{min}^{(d)},w_\textrm{max}^{(d)}$
. We prove this result using infinitesimal generators, as we now explain.
$W_t=0,w_\textrm{min}^{(d)},w_\textrm{max}^{(d)}$
. We prove this result using infinitesimal generators, as we now explain.
6.3.1. Method of proof: Generators
To prove the weak convergence, it suffices by [Reference Ethier and Kurtz7, Corollary 8.7, Chapter 4] to show (similar to previous proofs of diffusion limits of MCMC algorithms in [Reference Bédard and Rosenthal4, Reference Roberts, Gelman and Gilks21, Reference Roberts and Rosenthal22]) that the infinitesimal generator
![]() $G^{(d)}$
of the process
$G^{(d)}$
of the process
![]() $W^{(d)}$
converges uniformly in x as
$W^{(d)}$
converges uniformly in x as
![]() $d\to\infty$
to the generator
$d\to\infty$
to the generator
![]() $G^*$
of skew Brownian motion, when applied to a core
$G^*$
of skew Brownian motion, when applied to a core
![]() $\mathcal{D}$
of functionals, i.e. that
$\mathcal{D}$
of functionals, i.e. that
 \begin{equation*}\lim_{d\to\infty}\, \sup_{x \in \left[w_\textrm{min}^{(d)},w_\textrm{max}^{(d)}\right]}\, \Big| G^{(d)}f(x) - G^*f(x) \Big| = 0 ,\qquad f \in \mathcal{D} ,\end{equation*}
\begin{equation*}\lim_{d\to\infty}\, \sup_{x \in \left[w_\textrm{min}^{(d)},w_\textrm{max}^{(d)}\right]}\, \Big| G^{(d)}f(x) - G^*f(x) \Big| = 0 ,\qquad f \in \mathcal{D} ,\end{equation*}
where
To this end, let
![]() $\mathcal{D}$
be the set of all functions
$\mathcal{D}$
be the set of all functions
![]() $f \,{:}\, \big[-w_\textrm{min}^{(d)},w_\textrm{max}^{(d)}\big]\to \mathbb{R}$
which are continuous and twice continuously differentiable on
$f \,{:}\, \big[-w_\textrm{min}^{(d)},w_\textrm{max}^{(d)}\big]\to \mathbb{R}$
which are continuous and twice continuously differentiable on
![]() $\big[w_\textrm{min}^{(d)},0\big]$
and also on
$\big[w_\textrm{min}^{(d)},0\big]$
and also on
![]() $\big[0,w_\textrm{max}^{(d)}\big]$
, with matching one-sided second derivatives
$\big[0,w_\textrm{max}^{(d)}\big]$
, with matching one-sided second derivatives
![]() $f''^+(0)=f''^-(0)$
, and skewed one-sided first derivatives satisfying
$f''^+(0)=f''^-(0)$
, and skewed one-sided first derivatives satisfying
![]() $w_1 s_1 f'^+(0)= w_2 s_2 f'^-(0)$
and
$w_1 s_1 f'^+(0)= w_2 s_2 f'^-(0)$
and
![]() $f'\big(w_\textrm{max}^{(d)}\big)=f'\big(w_\textrm{min}^{(d)}\big)=0$
. Then, it follows from, e.g., [Reference Liggett15] and [Reference Revuz and Yor20, Exercise 1.23, Chapter VII] that the generator of skew Brownian motion (with excursion weights proportional to
$f'\big(w_\textrm{max}^{(d)}\big)=f'\big(w_\textrm{min}^{(d)}\big)=0$
. Then, it follows from, e.g., [Reference Liggett15] and [Reference Revuz and Yor20, Exercise 1.23, Chapter VII] that the generator of skew Brownian motion (with excursion weights proportional to
![]() $w_1 s_1$
and
$w_1 s_1$
and
![]() $w_2 s_2$
respectively, and with reflections at
$w_2 s_2$
respectively, and with reflections at
![]() $w_\textrm{min}^{(d)}$
and
$w_\textrm{min}^{(d)}$
and
![]() $w_\textrm{max}^{(d)}$
) satisfies that
$w_\textrm{max}^{(d)}$
) satisfies that
![]() $G^*f(x) = \frac{1}{2} f''(x)$
for all
$G^*f(x) = \frac{1}{2} f''(x)$
for all
![]() $f\in \mathcal{D}$
, where f”(0) represents the common value
$f\in \mathcal{D}$
, where f”(0) represents the common value
![]() $f''^+(0) = f''^-(0)$
. Furthermore,
$f''^+(0) = f''^-(0)$
. Furthermore,
![]() $\mathcal{D}$
is clearly dense (in the sup norm) in the set of all
$\mathcal{D}$
is clearly dense (in the sup norm) in the set of all
![]() $C^2\big[w_\textrm{min}^{(d)},w_\textrm{max}^{(d)}\big]$
functions, so in the language of [Reference Ethier and Kurtz7],
$C^2\big[w_\textrm{min}^{(d)},w_\textrm{max}^{(d)}\big]$
functions, so in the language of [Reference Ethier and Kurtz7],
![]() $\mathcal{D}$
serves as a core of functions for which it suffices to prove that the generators converge.
$\mathcal{D}$
serves as a core of functions for which it suffices to prove that the generators converge.
It follows from Corollary 1, as discussed above, that, for any fixed
![]() $f\in \mathcal{D}$
,
$f\in \mathcal{D}$
,
That is, the generators do converge uniformly to
![]() $G^*$
, as required, at least for
$G^*$
, as required, at least for
![]() $w \not= 0, w_\textrm{min}^{(d)}, w_\textrm{max}^{(d)}$
, i.e. avoiding the mode-jumping value 0 and the reflecting boundaries
$w \not= 0, w_\textrm{min}^{(d)}, w_\textrm{max}^{(d)}$
, i.e. avoiding the mode-jumping value 0 and the reflecting boundaries
![]() $w_\textrm{min}^{(d)}$
and
$w_\textrm{min}^{(d)}$
and
![]() $w_\textrm{max}^{(d)}$
. To complete the proof, it suffices to prove that (17) also holds at
$w_\textrm{max}^{(d)}$
. To complete the proof, it suffices to prove that (17) also holds at
![]() $w=0,w_\textrm{min}^{(d)},w_\textrm{max}^{(d)}$
, i.e. to prove
$w=0,w_\textrm{min}^{(d)},w_\textrm{max}^{(d)}$
, i.e. to prove
6.3.2. Verification of (19) and (20)
The proofs of (19) and (20) are virtually identical, so here we prove (20).
If the original inverse-temperature process
![]() $\beta^{(d)}(t)$
proposes to move in time 1 from inverse temperature
$\beta^{(d)}(t)$
proposes to move in time 1 from inverse temperature
![]() $1+0=1$
to
$1+0=1$
to
![]() $1 + \ell(1) d^{-1/2}$
, then by (12), the
$1 + \ell(1) d^{-1/2}$
, then by (12), the
![]() $H^{(d)}_t$
process proposes to move at Poisson rate
$H^{(d)}_t$
process proposes to move at Poisson rate
![]() $\Big[d \, h\big(\beta_\textrm{max}^{(d)}\big)^2\Big]$
from
$\Big[d \, h\big(\beta_\textrm{max}^{(d)}\big)^2\Big]$
from
![]() $1 + \Big({0} / {h\big(\beta_\textrm{max}^{(d)}\big)}\Big) = 1$
to
$1 + \Big({0} / {h\big(\beta_\textrm{max}^{(d)}\big)}\Big) = 1$
to
 \begin{equation*}1 + \frac{h\big(1+\ell(1) d^{-1/2}\big)}{h\big(\beta_\textrm{max}^{(d)}\big)} =1 + \frac{1}{h\big(\beta_\textrm{max}^{(d)}\big)}\int_1^{1+\ell(1) d^{-1/2}} \frac{1}{\ell(u)} \, \textrm{d} u ,\end{equation*}
\begin{equation*}1 + \frac{h\big(1+\ell(1) d^{-1/2}\big)}{h\big(\beta_\textrm{max}^{(d)}\big)} =1 + \frac{1}{h\big(\beta_\textrm{max}^{(d)}\big)}\int_1^{1+\ell(1) d^{-1/2}} \frac{1}{\ell(u)} \, \textrm{d} u ,\end{equation*}
which, to first order as
![]() $d\to\infty$
, is equal to
$d\to\infty$
, is equal to
Simultaneously, the
![]() $Z^{(d)}_t$
process proposes to move from
$Z^{(d)}_t$
process proposes to move from
![]() $2-1=1$
to
$2-1=1$
to
![]() $2 - \big[1 + d^{-1/2} / h\big(\beta_\textrm{max}^{(d)}\big)\big] = 1 - d^{-1/2} / h\big(\beta_\textrm{max}^{(d)}\big)$
, and the
$2 - \big[1 + d^{-1/2} / h\big(\beta_\textrm{max}^{(d)}\big)\big] = 1 - d^{-1/2} / h\big(\beta_\textrm{max}^{(d)}\big)$
, and the
![]() $W^{(d)}_t$
process proposes to move from
$W^{(d)}_t$
process proposes to move from
![]() $w_\textrm{max}^{(d)}$
to
$w_\textrm{max}^{(d)}$
to
![]() $\big(w_\textrm{max}^{(d)}\big) - d^{-1/2} / s_1 h\big(\beta_\textrm{max}^{(d)}\big)$
. Let A be the probability that the original
$\big(w_\textrm{max}^{(d)}\big) - d^{-1/2} / s_1 h\big(\beta_\textrm{max}^{(d)}\big)$
. Let A be the probability that the original
![]() $\beta^{(d)}(t)$
process accepts a move from 1 to
$\beta^{(d)}(t)$
process accepts a move from 1 to
![]() $1 + \ell(1) d^{-1/2}$
. Then, since
$1 + \ell(1) d^{-1/2}$
. Then, since
![]() $\beta^{(d)}(t)$
proposes to move from 1 to
$\beta^{(d)}(t)$
proposes to move from 1 to
![]() $1 + \ell(1) d^{-1/2}$
with probability
$1 + \ell(1) d^{-1/2}$
with probability
![]() $1/2$
, it actually moves from 1 to
$1/2$
, it actually moves from 1 to
![]() $1 + \ell(1) d^{-1/2}$
with probability
$1 + \ell(1) d^{-1/2}$
with probability
![]() $A/2$
, otherwise it stays at 1. So, correspondingly,
$A/2$
, otherwise it stays at 1. So, correspondingly,
![]() $W_t^{(d)}$
moves from
$W_t^{(d)}$
moves from
![]() $w_\textrm{max}^{(d)}$
to
$w_\textrm{max}^{(d)}$
to
![]() $\big(w_\textrm{max}^{(d)}\big) - d^{-1/2} / s_1 h\big(\beta_\textrm{max}^{(d)}\big)$
. Furthermore, recall that
$\big(w_\textrm{max}^{(d)}\big) - d^{-1/2} / s_1 h\big(\beta_\textrm{max}^{(d)}\big)$
. Furthermore, recall that
![]() $W_t^{(d)}$
moves at Poisson rate
$W_t^{(d)}$
moves at Poisson rate
![]() $\Big[d \, h\big(\beta_\textrm{max}^{(d)}\big)^2\Big]$
, so it moves from
$\Big[d \, h\big(\beta_\textrm{max}^{(d)}\big)^2\Big]$
, so it moves from
![]() $w_\textrm{max}^{(d)}$
to
$w_\textrm{max}^{(d)}$
to
![]() $\big(w_\textrm{max}^{(d)}\big) - d^{-1/2} / s_1 h\big(\beta_\textrm{max}^{(d)}\big)$
at rate
$\big(w_\textrm{max}^{(d)}\big) - d^{-1/2} / s_1 h\big(\beta_\textrm{max}^{(d)}\big)$
at rate
![]() $\Big[d \, h\big(\beta_\textrm{max}^{(d)}\big)^2\Big] (A/2)$
. However, we instead consider a minor modification of the process
$\Big[d \, h\big(\beta_\textrm{max}^{(d)}\big)^2\Big] (A/2)$
. However, we instead consider a minor modification of the process
![]() $W_t^{(d)}$
which speeds up time by a factor of 2 whenever it is at
$W_t^{(d)}$
which speeds up time by a factor of 2 whenever it is at
![]() $w_\textrm{max}^{(d)}$
, i.e. it moves from there at Poisson rate
$w_\textrm{max}^{(d)}$
, i.e. it moves from there at Poisson rate
![]() $\Big[d \, h\big(\beta_\textrm{max}^{(d)}\big)^2\Big] (A)$
. This is equivalent to the original
$\Big[d \, h\big(\beta_\textrm{max}^{(d)}\big)^2\Big] (A)$
. This is equivalent to the original
![]() $\beta^{(d)}(t)$
process ‘reflecting’ by always proposing a positive move from 1, instead of proposing either a positive or a negative (always-rejected) move with probability
$\beta^{(d)}(t)$
process ‘reflecting’ by always proposing a positive move from 1, instead of proposing either a positive or a negative (always-rejected) move with probability
![]() $1/2$
each. We show in Section 7 that this minor modification will not change the limiting distribution of the
$1/2$
each. We show in Section 7 that this minor modification will not change the limiting distribution of the
![]() $W_t^{(d)}$
, and thus does not affect the proof.
$W_t^{(d)}$
, and thus does not affect the proof.
Thus, to first order as
![]() $\delta \searrow 0$
(i.e. up to o(1) errors), our modified process
$\delta \searrow 0$
(i.e. up to o(1) errors), our modified process
![]() $W_t^{(d)}$
will move from
$W_t^{(d)}$
will move from
![]() $w_\textrm{max}^{(d)}$
to
$w_\textrm{max}^{(d)}$
to
![]() $\big(w_\textrm{max}^{(d)}\big) - d^{-1/2} / s_1 h\big(\beta_\textrm{max}^{(d)}\big)$
at Poisson rate
$\big(w_\textrm{max}^{(d)}\big) - d^{-1/2} / s_1 h\big(\beta_\textrm{max}^{(d)}\big)$
at Poisson rate
![]() $\Big[d \, h\big(\beta_\textrm{max}^{(d)}\big)^2\Big] (A)$
. Hence, setting
$\Big[d \, h\big(\beta_\textrm{max}^{(d)}\big)^2\Big] (A)$
. Hence, setting
![]() $x=w_\textrm{max}^{(d)} = 1/s_1$
, we have
$x=w_\textrm{max}^{(d)} = 1/s_1$
, we have
 \begin{multline*} \frac{{\mathbb E}\big[f\big(W^{(d)}_{\delta}\big) \mid W^{(d)}_0=x\big] - f(x)}{{\delta}} \\ = \Big[d \, h\big(\beta_\textrm{max}^{(d)}\big)^2\Big] (A) \big[ f\big( \big(w_\textrm{max}^{(d)}\big) - d^{-1/2} / s_1 h\big(\beta_\textrm{max}^{(d)}\big) \big) - f(x) \big] + o(1) .\end{multline*}
\begin{multline*} \frac{{\mathbb E}\big[f\big(W^{(d)}_{\delta}\big) \mid W^{(d)}_0=x\big] - f(x)}{{\delta}} \\ = \Big[d \, h\big(\beta_\textrm{max}^{(d)}\big)^2\Big] (A) \big[ f\big( \big(w_\textrm{max}^{(d)}\big) - d^{-1/2} / s_1 h\big(\beta_\textrm{max}^{(d)}\big) \big) - f(x) \big] + o(1) .\end{multline*}
Then, taking a Taylor series expansion around
![]() $x=w_\textrm{max}^{(d)} = 1/s_1$
,
$x=w_\textrm{max}^{(d)} = 1/s_1$
,
 \begin{align*} & \frac{{\mathbb E}\Big[f\big(W^{(d)}_{\delta}\big) \mid W^{(d)}_0=x\Big] - f(x)}{{\delta}} \\[2pt] & \qquad = - \Big[d \, h\big(\beta_\textrm{max}^{(d)}\big)^2\Big] (A) \Big[ d^{-1/2} / s_1 h\big(\beta_\textrm{max}^{(d)}\big) \Big] f'\Big(w_\textrm{max}^{(d)}\Big) \\[2pt] & \qquad \quad + \tfrac{1}{2} \Big[d \, h\big(\beta_\textrm{max}^{(d)}\big)^2\Big] (A) \Big[ d^{-1/2} / s_1 h\big(\beta_\textrm{max}^{(d)}\big) \Big]^2 f''\big(w_\textrm{max}^{(d)}\big) + O(d^{-1/2}) + o(1) \\[2pt] & \qquad = - \Big[A d^{1/2} h\big(\beta_\textrm{max}^{(d)}\big) / s_1\Big] \, f'\big(w_\textrm{max}^{(d)}\big) + \tfrac{1}{2} \big[A / s_1^2\big] \, f''\big(w_\textrm{max}^{(d)}\big) + O(d^{-1/2}) + o(1) .\end{align*}
\begin{align*} & \frac{{\mathbb E}\Big[f\big(W^{(d)}_{\delta}\big) \mid W^{(d)}_0=x\Big] - f(x)}{{\delta}} \\[2pt] & \qquad = - \Big[d \, h\big(\beta_\textrm{max}^{(d)}\big)^2\Big] (A) \Big[ d^{-1/2} / s_1 h\big(\beta_\textrm{max}^{(d)}\big) \Big] f'\Big(w_\textrm{max}^{(d)}\Big) \\[2pt] & \qquad \quad + \tfrac{1}{2} \Big[d \, h\big(\beta_\textrm{max}^{(d)}\big)^2\Big] (A) \Big[ d^{-1/2} / s_1 h\big(\beta_\textrm{max}^{(d)}\big) \Big]^2 f''\big(w_\textrm{max}^{(d)}\big) + O(d^{-1/2}) + o(1) \\[2pt] & \qquad = - \Big[A d^{1/2} h\big(\beta_\textrm{max}^{(d)}\big) / s_1\Big] \, f'\big(w_\textrm{max}^{(d)}\big) + \tfrac{1}{2} \big[A / s_1^2\big] \, f''\big(w_\textrm{max}^{(d)}\big) + O(d^{-1/2}) + o(1) .\end{align*}
Since
![]() $f\in\mathcal{D}$
, we have
$f\in\mathcal{D}$
, we have
![]() $f'\big(w_\textrm{max}^{(d)}\big)=0$
, so the first term vanishes. Furthermore, it is shown in [Reference Tawn, Roberts and Rosenthal31] that, as
$f'\big(w_\textrm{max}^{(d)}\big)=0$
, so the first term vanishes. Furthermore, it is shown in [Reference Tawn, Roberts and Rosenthal31] that, as
![]() $d\to\infty$
,
$d\to\infty$
,
![]() $A \to 2 \, \Phi\left( {- \ell_0} / {2 \sqrt{r_1}} \right) = s_1^2$
. Hence,
$A \to 2 \, \Phi\left( {- \ell_0} / {2 \sqrt{r_1}} \right) = s_1^2$
. Hence,
so that
 \begin{align*} \lim_{d\to\infty} G^{(d)}f\big(w_\textrm{max}^{(d)}\big) & = \lim_{d\to\infty} \, \lim_{\delta \searrow 0} \frac{{\mathbb E}\big[f\big(W^{(d)}_\delta\big) \mid W^{(d)}_0=x\big] - f(x)}{\delta} \\[3pt] & = \tfrac{1}{2} f''\big(w_\textrm{max}^{(d)}\big) = G^*\big(w_\textrm{max}^{(d)}\big) ,\end{align*}
\begin{align*} \lim_{d\to\infty} G^{(d)}f\big(w_\textrm{max}^{(d)}\big) & = \lim_{d\to\infty} \, \lim_{\delta \searrow 0} \frac{{\mathbb E}\big[f\big(W^{(d)}_\delta\big) \mid W^{(d)}_0=x\big] - f(x)}{\delta} \\[3pt] & = \tfrac{1}{2} f''\big(w_\textrm{max}^{(d)}\big) = G^*\big(w_\textrm{max}^{(d)}\big) ,\end{align*}
as required.
6.3.3. Verification of (18)
To prove (18), note that if the original inverse-temperature process
![]() $\beta^{(d)}(t)$
proposes to move in time 1 from
$\beta^{(d)}(t)$
proposes to move in time 1 from
![]() $\beta_\textrm{max}^{(d)}$
to
$\beta_\textrm{max}^{(d)}$
to
![]() $\beta_\textrm{max}^{(d)} - \ell\big(\beta_\textrm{max}^{(d)}\big) d^{-1/2}$
in one of the two modes (with probabilities
$\beta_\textrm{max}^{(d)} - \ell\big(\beta_\textrm{max}^{(d)}\big) d^{-1/2}$
in one of the two modes (with probabilities
![]() $w_1$
and
$w_1$
and
![]() $w_2$
respectively), then by (12) the
$w_2$
respectively), then by (12) the
![]() $H^{(d)}_t$
process proposes to move at rate
$H^{(d)}_t$
process proposes to move at rate
![]() $\Big[d \, h\big(\beta_\textrm{max}^{(d)}\big)^2\Big]$
from
$\Big[d \, h\big(\beta_\textrm{max}^{(d)}\big)^2\Big]$
from
![]() $1+\big[{h\big(\beta_\textrm{max}^{(d)}\big)} / {h\big(\beta_\textrm{max}^{(d)}\big)}\big] = 2$
to
$1+\big[{h\big(\beta_\textrm{max}^{(d)}\big)} / {h\big(\beta_\textrm{max}^{(d)}\big)}\big] = 2$
to
 \begin{align*} \pm \left[ 1 + \frac{h\big( \beta_\textrm{max}^{(d)} - \ell\big(\beta_\textrm{max}^{(d)}\big) d^{-1/2} \big) }{h\big(\beta_\textrm{max}^{(d)}\big)} \right] & = \pm \left[ 2 - \frac{\int_{\beta_\textrm{max}^{(d)}-\ell\left(\beta_\textrm{max}^{(d)}\right) d^{-1/2}}^{\beta_\textrm{max}^{(d)}} \frac{1}{\ell(u)} \, \textrm{d} u }{h\big(\beta_\textrm{max}^{(d)}\big)} \right] \\[3pt] & \approx \pm \left[ 2 - \left( \ell\big(\beta_\textrm{max}^{(d)}\big) d^{-1/2} \right) \frac{1}{\ell\big(\beta_\textrm{max}^{(d)}\big)} \right] = \pm (2-d^{-1/2}) .\end{align*}
\begin{align*} \pm \left[ 1 + \frac{h\big( \beta_\textrm{max}^{(d)} - \ell\big(\beta_\textrm{max}^{(d)}\big) d^{-1/2} \big) }{h\big(\beta_\textrm{max}^{(d)}\big)} \right] & = \pm \left[ 2 - \frac{\int_{\beta_\textrm{max}^{(d)}-\ell\left(\beta_\textrm{max}^{(d)}\right) d^{-1/2}}^{\beta_\textrm{max}^{(d)}} \frac{1}{\ell(u)} \, \textrm{d} u }{h\big(\beta_\textrm{max}^{(d)}\big)} \right] \\[3pt] & \approx \pm \left[ 2 - \left( \ell\big(\beta_\textrm{max}^{(d)}\big) d^{-1/2} \right) \frac{1}{\ell\big(\beta_\textrm{max}^{(d)}\big)} \right] = \pm (2-d^{-1/2}) .\end{align*}
Simultaneously, the
![]() $Z^{(d)}_t$
process proposes to move from
$Z^{(d)}_t$
process proposes to move from
![]() $2-2=0$
to
$2-2=0$
to
![]() $\pm 2 - [\pm (2 - d^{-1/2})] = \pm d^{-1/2}$
, and the
$\pm 2 - [\pm (2 - d^{-1/2})] = \pm d^{-1/2}$
, and the
![]() $W^{(d)}_t$
process proposes to move from 0 to either
$W^{(d)}_t$
process proposes to move from 0 to either
![]() $d^{-1/2}/s_1$
or
$d^{-1/2}/s_1$
or
![]() $-d^{-1/2}/s_2$
. Hence, similar to the above (but without the minor modification), with
$-d^{-1/2}/s_2$
. Hence, similar to the above (but without the minor modification), with
![]() $x=0$
we have, to first order as
$x=0$
we have, to first order as
![]() $\delta\searrow 0$
,
$\delta\searrow 0$
,
 \begin{align} &\frac{{\mathbb E}[f(W_{\delta}) \mid W_0=x] - f(x)}{{\delta}} = \nonumber\\[3pt] & [d \, h\big(\beta_\textrm{max}^{(d)}\big)^2] \big( w_1 \alpha_1 [f ( d^{-1/2} / s_1 ) - f(0) ] + w_2 \alpha_2 [f (\!- d^{-1/2} / s_2 ) - f(0) ] \big) + o(1) ,\end{align}
\begin{align} &\frac{{\mathbb E}[f(W_{\delta}) \mid W_0=x] - f(x)}{{\delta}} = \nonumber\\[3pt] & [d \, h\big(\beta_\textrm{max}^{(d)}\big)^2] \big( w_1 \alpha_1 [f ( d^{-1/2} / s_1 ) - f(0) ] + w_2 \alpha_2 [f (\!- d^{-1/2} / s_2 ) - f(0) ] \big) + o(1) ,\end{align}
where
![]() $\alpha_i$
is the acceptance probability for the original process to accept a proposal to increase the inverse temperature from
$\alpha_i$
is the acceptance probability for the original process to accept a proposal to increase the inverse temperature from
![]() $\beta_\textrm{max}^{(d)}$
to
$\beta_\textrm{max}^{(d)}$
to
![]() $\beta_\textrm{max}^{(d)} - \ell\big(\beta_\textrm{max}^{(d)}\big) d^{-1/2}$
in mode i. Now, the argument in [Reference Tawn, Roberts and Rosenthal31] shows that, as
$\beta_\textrm{max}^{(d)} - \ell\big(\beta_\textrm{max}^{(d)}\big) d^{-1/2}$
in mode i. Now, the argument in [Reference Tawn, Roberts and Rosenthal31] shows that, as
![]() $d\to\infty$
,
$d\to\infty$
,
Hence, taking a Taylor series expansion around
![]() $x=0$
, we obtain from (21) that
$x=0$
, we obtain from (21) that
 \begin{align*} & \frac{{\mathbb E}[f(W_{\delta}) \mid W_0=x] - f(x)}{{\delta}} \\[3pt] & \qquad = d \, w_1 s_1^2 (d^{-1/2} / s_1 ) f'^+(0) + \tfrac{1}{2} d \, w_1 s_1^2 (d^{-1/2} / s_1 )^2 f''^+(0) + O(d \, d^{-3/2}) + o(1) \\[3pt] & \qquad \quad - d \, w_2 s_2^2 (d^{-1/2} / s_2 ) f'^-(0) + \tfrac{1}{2} d \, w_2 s_2^2 (d^{-1/2} / s_2 )^2 f''^-(0) + O(d \, d^{-3/2}) + o(1) \\[3pt] & \qquad = d^{1/2} [ w_1 s_1 f'^+(0) - w_2 s_2 f'^-(0) ] + \tfrac{1}{2} [ w_1 f''^+(0) + w_2 f''^-(0) ] + O(d^{-1/2}) + o(1) .\end{align*}
\begin{align*} & \frac{{\mathbb E}[f(W_{\delta}) \mid W_0=x] - f(x)}{{\delta}} \\[3pt] & \qquad = d \, w_1 s_1^2 (d^{-1/2} / s_1 ) f'^+(0) + \tfrac{1}{2} d \, w_1 s_1^2 (d^{-1/2} / s_1 )^2 f''^+(0) + O(d \, d^{-3/2}) + o(1) \\[3pt] & \qquad \quad - d \, w_2 s_2^2 (d^{-1/2} / s_2 ) f'^-(0) + \tfrac{1}{2} d \, w_2 s_2^2 (d^{-1/2} / s_2 )^2 f''^-(0) + O(d \, d^{-3/2}) + o(1) \\[3pt] & \qquad = d^{1/2} [ w_1 s_1 f'^+(0) - w_2 s_2 f'^-(0) ] + \tfrac{1}{2} [ w_1 f''^+(0) + w_2 f''^-(0) ] + O(d^{-1/2}) + o(1) .\end{align*}
Now, by the definition of
![]() $f\in \mathcal{D}$
,
$f\in \mathcal{D}$
,
![]() $w_1 s_1 f'^+(0) - w_2 s_2 f'^-(0) = 0$
, and
$w_1 s_1 f'^+(0) - w_2 s_2 f'^-(0) = 0$
, and
![]() $w_1 f''^+(0) + w_2 f''^-(0) = (w_1+w_2) f''(0) = f''(0)$
. Hence, we obtain finally that
$w_1 f''^+(0) + w_2 f''^-(0) = (w_1+w_2) f''(0) = f''(0)$
. Hence, we obtain finally that
so that
This establishes (18), and hence completes the proof of Theorem 3.
Remark 4. Because of our transformations converting
![]() $\beta^{(d)}(t)$
to
$\beta^{(d)}(t)$
to
![]() $W^{(d)}_t$
, the limiting process W in Theorem 4 was skew Brownian motion on a continuous interval. It is also possible to consider diffusions directly associated with a discrete graph; see, e.g., [Reference Freidlin and Weber8].
$W^{(d)}_t$
, the limiting process W in Theorem 4 was skew Brownian motion on a continuous interval. It is also possible to consider diffusions directly associated with a discrete graph; see, e.g., [Reference Freidlin and Weber8].
7. Appendix: Modified processes’ occupation times
Recall that the proof of (20) in Section 6.3.2 was actually for a minor modification of the process
![]() $W_t^{(d)}$
that speeds up time by a factor of 2 whenever it is in the state
$W_t^{(d)}$
that speeds up time by a factor of 2 whenever it is in the state
![]() $w_\textrm{max}^{(d)}$
. We now argue that this minor modification does not affect the limiting distribution. Indeed, since the modification corresponds to adjusting the rate of time, we can write the modified process as
$w_\textrm{max}^{(d)}$
. We now argue that this minor modification does not affect the limiting distribution. Indeed, since the modification corresponds to adjusting the rate of time, we can write the modified process as
![]() $\widehat{W}_t^{(d)}\equiv W_{\tau_d(t)}^{(d)}$
, where
$\widehat{W}_t^{(d)}\equiv W_{\tau_d(t)}^{(d)}$
, where
![]() $\tau_d(t)$
is the time scale including the occasional speedups. Clearly,
$\tau_d(t)$
is the time scale including the occasional speedups. Clearly,
![]() $\lim_{t \searrow 0} \tau_d(t) = 0$
. Also, it follows from Proposition 2 below that the fraction of time that the original process spends at
$\lim_{t \searrow 0} \tau_d(t) = 0$
. Also, it follows from Proposition 2 below that the fraction of time that the original process spends at
![]() $w_\textrm{max}^{(d)}$
converges to 0 as
$w_\textrm{max}^{(d)}$
converges to 0 as
![]() $d\to\infty$
. This implies that
$d\to\infty$
. This implies that
![]() $\lim_{d\to\infty} (\tau_d(t) / t) = 1$
. Since our process
$\lim_{d\to\infty} (\tau_d(t) / t) = 1$
. Since our process
![]() $W_t^{(d)}$
is continuous, this means that
$W_t^{(d)}$
is continuous, this means that
![]() $\lim_{d\to\infty} \Big|f\bigl(W_{\tau_d(t)}^{(d)}\bigr) - f\bigl(W_t^{(d)}\bigr)\Big| = 0$
. That is, the two processes have the same limiting behaviour as
$\lim_{d\to\infty} \Big|f\bigl(W_{\tau_d(t)}^{(d)}\bigr) - f\bigl(W_t^{(d)}\bigr)\Big| = 0$
. That is, the two processes have the same limiting behaviour as
![]() $d\to\infty$
. So, the diffusion limit is not affected by making our minor modification as above.
$d\to\infty$
. So, the diffusion limit is not affected by making our minor modification as above.
It remains to state and prove Proposition 2. We begin with a result about limiting probabilities for reflecting a simple symmetric random walk.
Proposition 1. Let
![]() $\{Y_n\}$
be a reflecting simple symmetric random walk on the state space
$\{Y_n\}$
be a reflecting simple symmetric random walk on the state space
![]() $\{0,1,2,\ldots,m\}$
, i.e. a discrete-time birth–death Markov chain with transition probabilities
$\{0,1,2,\ldots,m\}$
, i.e. a discrete-time birth–death Markov chain with transition probabilities
![]() $p_{i,i+1}=p_{i,i-1}=1/2$
for
$p_{i,i+1}=p_{i,i-1}=1/2$
for
![]() $1 \le i \le m-1$
, and
$1 \le i \le m-1$
, and
![]() $p_{0,1}=p_{m,m-1}=1$
. Then, for all
$p_{0,1}=p_{m,m-1}=1$
. Then, for all
![]() $m\in{\mathbb N}$
and all sufficiently large
$m\in{\mathbb N}$
and all sufficiently large
![]() $n\in{\mathbb N}$
,
$n\in{\mathbb N}$
,
![]() ${\mathbb P}(Y_n = 0) \le (2/\sqrt{n}) + (1/m)$
. Hence,
${\mathbb P}(Y_n = 0) \le (2/\sqrt{n}) + (1/m)$
. Hence,
![]() $\lim\limits_{n,m\to\infty} {\mathbb P}(Y_n = 0) = 0$
.
$\lim\limits_{n,m\to\infty} {\mathbb P}(Y_n = 0) = 0$
.

Figure 4. The lifting transformation function ‘g’ (when
![]() $m=10$
).
$m=10$
).
Proof. We condition on
![]() $Y_0=y$
; the general case then follows by taking expectation with respect to
$Y_0=y$
; the general case then follows by taking expectation with respect to
![]() $Y_0$
. We ‘lift’
$Y_0$
. We ‘lift’
![]() $\{Y_n\}$
to
$\{Y_n\}$
to
![]() ${\mathbb Z}$
by writing
${\mathbb Z}$
by writing
![]() $Y_n = g(Z_n)$
, where
$Y_n = g(Z_n)$
, where
![]() $\{Z_n\}$
is a simple symmetric random walk on all the integers
$\{Z_n\}$
is a simple symmetric random walk on all the integers
![]() ${\mathbb Z}$
, and
${\mathbb Z}$
, and
![]() $g(z) = \min_j |z-2jm|$
(see Figure 4). Then
$g(z) = \min_j |z-2jm|$
(see Figure 4). Then
 \begin{multline*} {\mathbb P}_y[Y_n=0] = {\mathbb P}_y[g(Z_n)=0] = \sum_{j\in{\mathbb Z}} {\mathbb P}_y[Z_n=2jm] \\ = \sum_{j\in{\mathbb Z}} {\mathbb P}_y\Big[{\rm Binomial}(n,1/2) = \frac{n}{2} + \frac{y}{2} + jm\Big] = \sum_{j\in{\mathbb Z}} h\left(\frac{n}{2}+\frac{y}{2}+jm\right) ,\end{multline*}
\begin{multline*} {\mathbb P}_y[Y_n=0] = {\mathbb P}_y[g(Z_n)=0] = \sum_{j\in{\mathbb Z}} {\mathbb P}_y[Z_n=2jm] \\ = \sum_{j\in{\mathbb Z}} {\mathbb P}_y\Big[{\rm Binomial}(n,1/2) = \frac{n}{2} + \frac{y}{2} + jm\Big] = \sum_{j\in{\mathbb Z}} h\left(\frac{n}{2}+\frac{y}{2}+jm\right) ,\end{multline*}
where
![]() $h(k) = {\mathbb P}[{\rm Binomial}(n,1/2) = k]$
. Now, h is maximised when
$h(k) = {\mathbb P}[{\rm Binomial}(n,1/2) = k]$
. Now, h is maximised when
![]() $k=n/2$
(or
$k=n/2$
(or
![]() $(n\pm 1)/2$
if n is odd), and decreases monotonically on either side of that. Hence, find
$(n\pm 1)/2$
if n is odd), and decreases monotonically on either side of that. Hence, find
![]() $j_*\in{\mathbb N}$
with
$j_*\in{\mathbb N}$
with
![]() $\frac{y}{2}+(j_*-1)m < 0 \le \frac{y}{2}+j_*m$
. It follows from Stirling’s approximation (see, e.g., [Reference Rosenthal27]) that to first order as
$\frac{y}{2}+(j_*-1)m < 0 \le \frac{y}{2}+j_*m$
. It follows from Stirling’s approximation (see, e.g., [Reference Rosenthal27]) that to first order as
![]() $n,k,n-k\to\infty$
,
$n,k,n-k\to\infty$
,
so in particular
![]() $h\left(\frac{n}{2}+\frac{y}{2}+j_*m\right) \le \sqrt{2/\pi n} + o_n(1) \le 1/\sqrt{n}$
for all sufficiently large n, and similarly for
$h\left(\frac{n}{2}+\frac{y}{2}+j_*m\right) \le \sqrt{2/\pi n} + o_n(1) \le 1/\sqrt{n}$
for all sufficiently large n, and similarly for
![]() $h\left(\frac{n}{2}+\frac{y}{2}+(j_*-1)m\right)$
. Then, by monotonicity, we have, for
$h\left(\frac{n}{2}+\frac{y}{2}+(j_*-1)m\right)$
. Then, by monotonicity, we have, for
![]() $j>j_*$
,
$j>j_*$
,
 \begin{multline*} h\bigg(\frac{n}{2}+\frac{y}{2}+jm\bigg) \le \frac{1}{m} \bigg[ h\bigg(\frac{n}{2}+\frac{y}{2}+(j-1)m+1\bigg)+h\bigg(\frac{n}{2}+\frac{y}{2}+(j-1)m+2\bigg) \\ + \cdots + h\bigg(\frac{n}{2}+\frac{y}{2}+jm\bigg) \bigg] .\end{multline*}
\begin{multline*} h\bigg(\frac{n}{2}+\frac{y}{2}+jm\bigg) \le \frac{1}{m} \bigg[ h\bigg(\frac{n}{2}+\frac{y}{2}+(j-1)m+1\bigg)+h\bigg(\frac{n}{2}+\frac{y}{2}+(j-1)m+2\bigg) \\ + \cdots + h\bigg(\frac{n}{2}+\frac{y}{2}+jm\bigg) \bigg] .\end{multline*}
Hence,
But
![]() $\sum_k h(k) = 1$
, so by symmetry
$\sum_k h(k) = 1$
, so by symmetry
![]() $\sum_{k>n/2} h(k) \le 1/2$
, and so
$\sum_{k>n/2} h(k) \le 1/2$
, and so
Thus,
Similarly,
Therefore, for all sufficiently large n,
as claimed.
Remark 5. Similar arguments show that
![]() $\lim\limits_{n,m\to\infty} {\mathbb P}(Y_n = z) = 0$
for any fixed number
$\lim\limits_{n,m\to\infty} {\mathbb P}(Y_n = z) = 0$
for any fixed number
![]() $z\in{\mathbb N}$
, by replacing ‘
$z\in{\mathbb N}$
, by replacing ‘
![]() $Z_n=2jm$
’ by ‘
$Z_n=2jm$
’ by ‘
![]() $Z_n=2jm+z$
’ and ‘
$Z_n=2jm+z$
’ and ‘
![]() $\frac{n}{2}+\frac{y}{2}$
’ by ‘
$\frac{n}{2}+\frac{y}{2}$
’ by ‘
![]() $\frac{n}{2}+\frac{y}{2}-\frac{z}{2}$
’ throughout the proof, though we do not use that fact here.
$\frac{n}{2}+\frac{y}{2}-\frac{z}{2}$
’ throughout the proof, though we do not use that fact here.
Corollary 4. Let
![]() $\{Y_n\}$
be as in Proposition 1. Let
$\{Y_n\}$
be as in Proposition 1. Let
![]() $N_0=\#\{i \,{:}\, 0 \le i \le n-1, \, Y_i=0\}$
be the occupation time of state 0 before time n. Then, as
$N_0=\#\{i \,{:}\, 0 \le i \le n-1, \, Y_i=0\}$
be the occupation time of state 0 before time n. Then, as
![]() $n,m\to\infty$
, the average occupation time
$n,m\to\infty$
, the average occupation time
![]() $N_0/n$
converges to 0 in probability.
$N_0/n$
converges to 0 in probability.
Proof. Let
![]() $I_i = \textbf{1}_{Y_i=0}$
be the indicator function of the event
$I_i = \textbf{1}_{Y_i=0}$
be the indicator function of the event
![]() $Y_i=0$
. Then, by Proposition 1,
$Y_i=0$
. Then, by Proposition 1,
![]() $\lim_{n,m\to\infty} {\mathbb E}[I_n] = \lim_{n,m\to\infty} {\mathbb P}[Y_n=0] = 0$
. Hence, using the theory of Cesàro sums,
$\lim_{n,m\to\infty} {\mathbb E}[I_n] = \lim_{n,m\to\infty} {\mathbb P}[Y_n=0] = 0$
. Hence, using the theory of Cesàro sums,
 \begin{equation*}\lim_{n,m\to\infty} {\mathbb E}[N_0/n]= \lim_{n,m\to\infty} {\mathbb E}\Bigg[ \sum_{i=0}^{n-1} I_i \Bigg] / n= \lim_{n,m\to\infty} \frac{1}{n} \, \sum_{i=0}^{n-1} {\mathbb E}[I_i]= \lim_{n,m\to\infty} {\mathbb E}[I_{n}]= 0 .\end{equation*}
\begin{equation*}\lim_{n,m\to\infty} {\mathbb E}[N_0/n]= \lim_{n,m\to\infty} {\mathbb E}\Bigg[ \sum_{i=0}^{n-1} I_i \Bigg] / n= \lim_{n,m\to\infty} \frac{1}{n} \, \sum_{i=0}^{n-1} {\mathbb E}[I_i]= \lim_{n,m\to\infty} {\mathbb E}[I_{n}]= 0 .\end{equation*}
Hence, by Markov’s inequality, since
![]() $N_0/n \ge 0$
, for any
$N_0/n \ge 0$
, for any
![]() $\epsilon>0$
we have
$\epsilon>0$
we have
so that
![]() $N_0/n \to 0$
in probability, as claimed.
$N_0/n \to 0$
in probability, as claimed.
Proposition 2. Let
![]() $\{X_n\}$
be a discrete-time birth–death Markov chain on the state space
$\{X_n\}$
be a discrete-time birth–death Markov chain on the state space
![]() $\{0,1,2,\ldots,m\}$
, with transition probabilities satisfying
$\{0,1,2,\ldots,m\}$
, with transition probabilities satisfying
![]() $p_{i,j}=0$
whenever
$p_{i,j}=0$
whenever
![]() $|j-i| \ge 2$
,
$|j-i| \ge 2$
,
![]() $p_{i,i+1}=p_{i,i-1}$
for all
$p_{i,i+1}=p_{i,i-1}$
for all
![]() $1 \le i \le m-1$
, and
$1 \le i \le m-1$
, and
![]() $p_{i,i} \le 1-a$
for some fixed constant
$p_{i,i} \le 1-a$
for some fixed constant
![]() $a>0$
. Let
$a>0$
. Let
![]() $N_0=\#\{i \,{:}\, 0 \le i \le n-1, \ X_i=0\}$
. Then, as
$N_0=\#\{i \,{:}\, 0 \le i \le n-1, \ X_i=0\}$
. Then, as
![]() $n,m\to\infty$
,
$n,m\to\infty$
,
![]() $N_0/n$
converges to 0 in probability.
$N_0/n$
converges to 0 in probability.
Proof. Let
![]() $\{J_k\}$
be the jump chain of
$\{J_k\}$
be the jump chain of
![]() $\{X_n\}$
, i.e. the Markov chain which copies
$\{X_n\}$
, i.e. the Markov chain which copies
![]() $\{X_n\}$
except omitting immediate repetitions of the same state, and let
$\{X_n\}$
except omitting immediate repetitions of the same state, and let
![]() $\{M_k\}$
count the number of repetitions. [For example, if the original chain
$\{M_k\}$
count the number of repetitions. [For example, if the original chain
![]() $\{X_n\}$
began
$\{X_n\}$
began
then the jump chain
![]() $\{J_k\}$
would begin
$\{J_k\}$
would begin
![]() $\{J_k\} = ( a, b, a, c, d, a, \ldots )$
and the corresponding multiplicity list
$\{J_k\} = ( a, b, a, c, d, a, \ldots )$
and the corresponding multiplicity list
![]() $\{M_k\}$
would begin
$\{M_k\}$
would begin
![]() $\{M_k\} = ( 1, 3, 2, 4, 2, \ldots )$
.] Then the assumptions imply that
$\{M_k\} = ( 1, 3, 2, 4, 2, \ldots )$
.] Then the assumptions imply that
![]() $\{J_k\}$
has the transition probabilities of a reflecting simple symmetric random walk, as in Proposition 1 and Corollary 4.
$\{J_k\}$
has the transition probabilities of a reflecting simple symmetric random walk, as in Proposition 1 and Corollary 4.
Now, let K(n) be the smallest integer with
![]() $M_1+\cdots+M_{K(n)} \ge n$
. Given
$M_1+\cdots+M_{K(n)} \ge n$
. Given
![]() $J_k$
, the random variable
$J_k$
, the random variable
![]() $M_k$
has the Geometric
$M_k$
has the Geometric
![]() $(1-p_{J_k J_k})$
distribution, so it is stochastically bounded above by the Geometric(a) distribution, from which it follows that
$(1-p_{J_k J_k})$
distribution, so it is stochastically bounded above by the Geometric(a) distribution, from which it follows that
![]() $\lim_{n\to\infty} K(n)= \infty$
with probability 1. Let
$\lim_{n\to\infty} K(n)= \infty$
with probability 1. Let
![]() $C_s=\#\{i \,{:}\, 0 \le i \le K(n), \ J_i=s\}$
. Then Corollary 4 implies that
$C_s=\#\{i \,{:}\, 0 \le i \le K(n), \ J_i=s\}$
. Then Corollary 4 implies that
![]() $\lim_{n,m\to\infty} (C_0/K(n)) = 0$
. On the other hand,
$\lim_{n,m\to\infty} (C_0/K(n)) = 0$
. On the other hand,
![]() $N_0$
is less than or equal to a sum of
$N_0$
is less than or equal to a sum of
![]() $C_0$
independent Geometric
$C_0$
independent Geometric
![]() $(1-p_{00})$
random variables, so
$(1-p_{00})$
random variables, so
![]() ${\mathbb E}[N_0 \mid C_0] = C_0/(1-p_{00}) \le C_0/a$
, and
${\mathbb E}[N_0 \mid C_0] = C_0/(1-p_{00}) \le C_0/a$
, and
![]() ${\mathbb P}[N_0 > 2C_0/a \mid C_0] \to 0$
as
${\mathbb P}[N_0 > 2C_0/a \mid C_0] \to 0$
as
![]() $n\to\infty$
. Also,
$n\to\infty$
. Also,
![]() $M_1+\cdots+M_{K(n)-1} \le n$
, and each
$M_1+\cdots+M_{K(n)-1} \le n$
, and each
![]() $M_i \ge 1$
, so
$M_i \ge 1$
, so
![]() $n \ge K(n)-1$
. We therefore conclude that
$n \ge K(n)-1$
. We therefore conclude that
as claimed.
Remark 6. It might be possible to instead obtain the conclusion of Proposition 2 via the ergodic theorem or the Markov chain law of large numbers, which states that for fixed m the average occupation time
![]() $N_0/n$
will converge to the stationary measure of the process at state 0. However, this would require conditions and bounds on the sequence of stationary measures as
$N_0/n$
will converge to the stationary measure of the process at state 0. However, this would require conditions and bounds on the sequence of stationary measures as
![]() $m\to\infty$
, so it would not be trivial (nor provide the explicit bound of Proposition 1), and we instead use the more direct and quantitative method described herein.
$m\to\infty$
, so it would not be trivial (nor provide the explicit bound of Proposition 1), and we instead use the more direct and quantitative method described herein.
Acknowledgements
We thank Alex Mijatovic and Neal Madras for very helpful comments related to Section 7, and thank the editor and referees for very insightful suggestions which greatly improved the manuscript.
Funding information
This research was partially supported by EPSRC grants EP/R018561/1 and EP/R034710/1 to GOR, and NSERC grant RGPIN-2019-04142 to JSR.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.