INTRODUCTION
The propagation dynamics of laser beams through nonlinear media has been extensively investigated; among many of the non-linear phenomena, the one which has attracted most attention is the self-focusing of the laser beams (Chioa et al., Reference Chioa, Garmire and Townes1964; Kelley, Reference Kelley1965; Sodha et al., Reference Sodha, Tripathi and Ghatak1976; Rasmussen & Rypdal, Reference Rasmussen and Rypdal1986; Silberbarg, Reference Silberbarg1990; Kothari & Abbi, Reference Kothari and Abbi1990; Snyder et al., Reference Snyder, Chen, Poladian and Mitchell1990; Hora, Reference Hora1991; Sprangle & Esarey, Reference Sprangle and Esarey1991; Desaix et al., Reference Desaix, Anderson and Lisak1991; Karlsson & Anderson, Reference Karlsson and Anderson1992; Milchberg et al., Reference Milchberg, Durfee and Mcllrath1995; Berge, Reference Berge1998; Upadhyaya et al., Reference Upadhyaya, Tripathi, Sharma and Pant2002, Saini & Gill, Reference Saini and Gill2006; Gill & Saini, Reference Gill and Saini2007; Yu et al., Reference Yu, Yu, Xu, Tian, Chen and Wong2007), because the nonlinear effects are highly sensitive to the irradiance distribution along the wavefront of the beam, which gets significantly affected by self focusing. The interest in self focusing can also be appreciated in the context of promising applications in laser-plasma interaction, specifically optical harmonic generation (Sprangle & Esarey, Reference Sprangle and Esarey1991; Milchberg et al., Reference Milchberg, Durfee and Mcllrath1995; Zhou et al., Reference Zhou, Peatross, Murnane, Kapteyn and Christov1996), X-ray generation (Eder et al., Reference Eder, Amendt, DaSilva, London, MacGowan, Matthaws, Penetrante, Rosen, Wilks, Donnelly, Falcone and Strobel1994), inertial confinement fusion (Tabak et al., Reference Tabak, Hammer, Glinisky, Kruer, Wilks, WoodWorth, Campbell, Perry and Mason1994; Deutsch et al., Reference Deutsch, Furukaw, Mima, Murakami and Nishihara1996), and laser driven accelerators and particle beams (Sprangle et al., Reference Sprangle, Esarey, Ting and Joyee1988; Umstadter et al., Reference Umstadter, Chen, Maksimchuk, Mourou and Wagner1996; Mora & Antonsen, Reference Mora and Antonsen1996; Andreev et al., Reference Andreev, Gorbunov, Kirsanov, Nakajima and Ogata1997, Reference Andreev, Gorbunov and Frolov1998; Amiranoff et al., Reference Amiranoff, Baton, Bernard, Cros, Descamps, Derchies, Jaquet, Malka, Marques, Matthieussent, Mine, Modena, Mora, Manillo and Nazmudin1998; Sari et al., Reference Sari, Osman, Doolan, Ghoranneviss, Hora, Hopfl, Benstetter and Hantehzadehi2005; Neff et al., Reference Neff, Knobloch, Hoffmann, Tauschwitz and Yu2006; Zhou et al., Reference Zhou, Yu and He2007; Chen et al., Reference Chen, Unick, Vafaei-Najafabadi, Tsui, Fedosejevs, Naseri, Masson-Laborde and Rozmus2008; Niu et al., Reference Niu, He, Qiao and Zhou2008).
So far the main thrust of the theoretical and experimental investigations on self focusing of a laser beam in a plasma has been directed toward the study of the propagation characteristics of a Gaussian beam (Akhmanov et al., Reference Akhmanov, Sukhorukov and Khokhlov1968; Hora, Reference Hora1969; Sodha et al., Reference Sodha, Ghatak and Tripathi1974a, Reference Sodha, Tripathi and Ghatak1976; Hora, Reference Hora1975; Jones et al., Reference Jones, Kane, Lalousis, Wiles and Hora1982; Hauser et al., Reference Hauser, Scheid and Hora1992; Esarey et al., Reference Esarey, Sprangle, Krall and Ting1997; Osman et al., Reference Osman, Castillo and Hora1999; Umstadter, Reference Umstadter2001; Sharma et al., Reference Sharma, Prakash, Verma and Sodha2003, Reference Sharma, Verma and Sodha2004). Nevertheless, a few papers have been published on the self focusing of super Gaussian beams (Nayyar, Reference Nayyar1986; Grow et al., Reference Grow, Ishaaya, Vuong, Gaeta, Gavish and Fibich2006; Fibich, Reference Fibich, Boyd, Lukishova and Shen2007), self trapping of degenerate modes of laser beams (Karlsson, Reference Karlsson1992), and self trapping of Bessel beams (Johannisson et al., Reference Johannisson, Anderson, Lisak and Marklund2003). Apart from these, great interest has recently been evinced in optical beams with central shadow, usually known as dark hollow beams (DHB) on account of their wide and attractive applications in the field of modern optics, atomic optics, and plasmas (Soding et al., Reference Soding, Grimm and Ovchinnikov1995; Kuga et al., Reference Kuga, Torii, Shiokawa, Hirano, Shimizu and Sasada1997; Ovchinnikov et al., Reference Ovchinnikov, Manek and Grimm1997; Yin et al., Reference Yin, Zhu, Wang, Wang and Jhe1998; Song et al., Reference Song, Milam and Hill1999; Xu et al., Reference Xu, Wang and Jhe2002; Cai et al., Reference Cai, Lu and Lin2003; Yin et al., Reference Yin, Gao and Zhu2003; York et al., Reference York, Milchberg, Palastro and Antonsen2008). To describe the DHBs (the beam with zero central intensity), several theoretical models like TEM01 mode doughnut beam, some higher order Bessel beams, superposition of off-axis Gaussian beams, and dark-hollow Gaussian beams etc. have been introduced (Arlt & Dholakiyia, Reference Arlt and Dholakia2000; Zhu et al., Reference Zhu, Tang, Sun, Wang and Liu2002; Ganic et al., Reference Ganic, Gan and Gu2003; Cai & Lin, Reference Cai and Lin2004; Deng et al., Reference Deng, Fu, Wei, Shao and Fan2005; Mei & Zhao, Reference Mei and Zhao2005); a number of experimental methods have been developed for the production of hollow laser beams (Herman & Wiggins, Reference Herman and Wiggins1991; Wang & Littman, Reference Wang and Littman1993; Lee et al., Reference Lee, Atewart, Choi and Fenichel1994).
In the relatively recent studies the propagation of various DHBs in paraxial optical systems and turbulent atmosphere, has been investigated in detail (Cai & He, Reference Cai and He2006; Cai & Zhang, Reference Cai and Zhang2006a, Reference Cai and Zhang2006b; Gao & Lu, Reference Gao and Lu2006; Mei & Zhao, Reference Mei and Zhao2006). A review of the literature highlights the fact that the propagation characteristics of DHBs in a plasma or other nonlinear media have not been studied to a significant extent; as an exception, the beam propagation in the TEM10 mode has been studied to some extent, in a plasma for regions around the axis and the maximum of irradiance, in the geometrical optics approximation (Sodha et al., Reference Sodha, Nayyar and Tripathi1974b; Sharma et al., Reference Sharma, Verma, Sodha and Tripathi2005). Prakash et al. (Reference Prakash, Sharma, Verma and Sodha2006) modified the theory by taking the saturating nature of nonlinearity and diffraction into account and considering a doughnut (TEM01) beam.
In this communication, the authors have investigated the self focusing of dark cylindrical hollow Gaussian beams (HGBs), in which the irradiance along the axis is zero, and the maximum is away from the axis. It should however be realized that some interesting effects (Feit & Fleck, Reference Feit and Fleck1988; Vidal & Johnston, Reference Vidal and Johnston1996; Johnston et al., Reference Johnston, Vidal and Fre'chette1997) predicted by detailed numerical simulation like breaking up into a number of beams can not be recovered in the cylindrical geometry; hence the theory has some limitations, particularly for beams with powers above the critical value. However, since cylindrical beams are commonly used, a theory for cylindrical beams (even approximate) is in order. A paraxial like approach, similar to the one given by Akhmanov et al. (Reference Akhmanov, Sukhorukov and Khokhlov1968) and developed by Sodha et al. (Reference Sodha, Ghatak and Tripathi1974a, Reference Sodha, Tripathi and Ghatak1976) has been used in the present analysis; the nonlinear dielectric function has been expanded in terms of radial distance from the maximum of irradiance, rather than that from the axis, as is the case with Gaussian beams.
Before proceeding further, it is instructive to consider the nonlinearities, responsible for focusing in plasma. In collisional plasmas, the electrons get heated to different temperatures in the transverse plane on account of the radial distribution of the field of the beams; in the steady-state the electron temperature distribution is determined by the balance of the Ohmic heating and the power loss by collisions with heavier particles (ions, molecules etc.), and thermal conduction. The radial redistribution of electron density (and thereby the dielectric function) is determined by balancing the gradient of the partial pressure of electrons and ions by the space charge field and making use of the charge neutrality condition. The collisional nonlinearity sets up in periods on the order of 1/δcνe, where δc is the fraction of excess energy lost by an electron in a collision, and νe is the electron collision frequency. The role of conduction is significant when (δcr 02/l 2) ≤ 1, where l is the mean free path of electrons; thermal conduction has not been considered in this paper. In this paper, the ions have been considered to be at constant temperature, which is justified when νim > δc,eiνei and the neutral atoms are abundant enough to provide a constant temperature sink; here νim refers to the frequency of ion-neutral atom collisions and the subscripts ei refer to electron ion collisions. The process of Ohmic heating of electrons by the wave and subsequent loss of energy to ions/atoms is also some times referred to as inverse bremsstrahlung.
For collisionless plasma, the ponderomotive force on electrons, proportional to the gradient of irradiance at a point causes a redistribution of electron density, and thereby the dielectric function; this nonlinearity sets in a period on the order of r 0/c s, where r 0 is the width of the beam, and c s is the ion sound speed.
For very high powers of the beams, the quiver velocity of the electrons is comparable to the speed of light in vacuum, and it causes a change in the electron mass, and thereby in the plasma frequency and the dielectric function. Thus the radial distribution of the irradiance of the beam causes a corresponding redistribution of the electron mass and hence of the dielectric function. This nonlinearity sets in periods on the order of ωpe−1, where ωpe is the plasma frequency. Situations, when ions play a significant role have not been considered.
In the present paper, to illustrate the nature of focusing/defocusing, the critical curves and the divider curves have been given as a plot of dimensionless radius of the beam Π0 and the power of the beam Π0 (Figs 1, 2a, and 2b). The regions, (1) above the critical curve, (2) between the critical and divider curves and (3) below the divider curve, characterize (1) focusing, (2) oscillatory divergence, and (3) steady divergence of the beam, respectively. The dependence of the focusing parameter on the distance of propagation has also been illustrated for typical points in the three regions of the beam power-radius space.
FOCUSING OF HOLLOW GAUSSIAN BEAM (HGB)
Propagation
Consider the propagation of a linearly polarized hollow Gaussian beam with its electric vector polarized along the y-axis, propagating in a homogeneous plasma along the z-axis. In the steady-state, the electric field vector E for such a beam may be expressed in a cylindrical coordinate system with azimuthal symmetry as
where
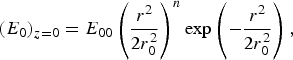
E 0 refers to the complex amplitude of the hollow Gaussian beam of initial beam width r 0, E 00 is a real constant characterizing the amplitude of the HGB, n is the order of the HGB and a positive integer, characterizing the shape of the HGB and position of its maximum, ω is the wave frequency, 
is the unit vector along the y-axis, and |E 0| describes the electric field maximum at 
. For n = 0, Eq. (2) represents a fundamental Gaussian beam of width r 0; however the interest of the present investigation is in higher order HGBs (i.e., n > 0).
The electric field vector E satisfies the wave equation (stationary frame),
where ɛ is the effective dielectric function of the plasma, and c is the speed of light in free space.
For transverse beams, the second term on Eq. (3) is zero. One can thus write the wave equation for the electromagnetic beam, as
Following Akhmanov et al. (1968) and Sodha et al. (Reference Sodha, Ghatak and Tripathi1974a, Reference Sodha, Tripathi and Ghatak1976), the solution of Eq. (4) can be chosen as
where A(r, z) is the complex amplitude of the electric field E0, 
, ɛ0(z) is the dielectric function, corresponding to the maximum electric field on the wavefront of the HGB (see Eq. (11)).
Substituting E0(r, z) from Eq. (5) in Eq. (4) and neglecting the term ∂2A/∂z 2 (assuming A(r, z) to be a slowly varying function of z), one obtains
The complex amplitude A(r, z) may be expressed as,
where S(r, z) is termed the eikonal associated with the hollow Gaussian beam. Substitution for A(r, z) from Eq. (7) in Eq. (6) and the separation of the real and imaginary parts, yields
and
To proceed further, one can adopt an approach, analogous to the paraxial approximation. Thus one may start by expressing Eqs (8) and (9) in terms of variables η and z, where
![{\rm \eta} = \left[\lpar r/r_0 f\rpar - \sqrt{2n}\right]\comma](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022040155221-0038:S0263034609000081_eqn10.gif?pub-status=live){kind=small}
r 0f(z) is the width of the beam, and 
is the position of the maximum irradiance for the propagating beam; it is shown later that in the paraxial like approximation, i.e., when 
, Eqs (8) and (9) lead to the maintenance of the HGB character during propagation. Since the irradiance of the beam is a function of r and z only, expansions of expressions for relevant parameters made along r, near the irradiance maximum via 
, are certainly justified in the paraxial like approximation; for n = 0 (Gaussian beam), the expansion is made (likewise) around r = 0 (as usual). Like the paraxial theory, the present analysis is strictly applicable when 
.
Thus from Eqs (8), (9), and (10) one obtains,
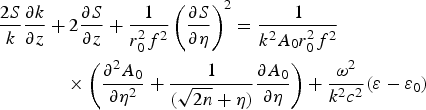
and
In the paraxial like approximation the relevant parameters (i.e., the dielectric function ɛ(r, z), eikonal and irradiance) may be expanded around the maximum of the HGB, i.e., around η = 0. Thus, one can express the dielectric function ɛ(η, z) around the maximum (η = 0) of the HGB as
where ɛ0(z) and ɛ2(z) are the coefficients associated with η0 and η2 in the expansion of ɛ(η, z) around η = 0. The expressions for these coefficients have been derived later.
Substitution for ɛ(η, z) from Eq. (13) in Eqs (11) and (12) leads to
and
One can express the solution of Eq. (15) following the paraxial like approximation 
as
with
where
φ(z) is an arbitrary function of z, and f(z) is the beam width parameter for the HGB.
Most of the power of the beam is concentrated in the region around η = 0. There is certainly some power of the beam beyond this limitation, which is accounted for in an approximate manner by Eq. (16), which in common with the variational and moment approaches, assures that the nature of r dependence of irradiance does not change with propagation. Eq. (16) also ensures conservation of power as the beam propagates.
Substituting from Eqs (16) and (17) for A 02 and S into Eq. (14) and equating the coefficients of η0 and η2 on both sides of the resulting equation, one obtains
and
where
and
The dependence of the beam width parameter f on the dimensionless distance of propagation ξ can be obtained by the numerical integration of Eq. (18) after putting suitable expressions for ɛ0 and ɛ2, and using the initial boundary conditions f = 1, df/dξ = 0 at ξ = 0; Φ is obtained by simultaneous solution of Eqs 18 and 19, taking the additional boundary condition Φ = 0, at ξ = 0 into account.
The Dielectric Function
Following Sodha et al. (1974a), the effective dielectric function of the plasma can be expressed as
where Ω = (ωpe/ω), ωpe = (4πN 0e 2/m)1/2 is the electron plasma frequency, N 0 is the undisturbed electron density of the plasma, N 0e is the electron density of the plasma in the presence of the electromagnetic field, m is the mass of the electron, and e is the electron charge.
Following the paraxial like approximation (i.e. 
) one can expand the dielectric function ɛ(η, z) in axial and radial parts around the maximum of E (η = 0). Thus one obtains from Eq. (13) and Eq. (20),
and
To obtain the above coefficients, one should expand E · E* in powers of η2; thus
where
and
With the help of Eqs (24) and (25) one can easily obtain ɛ0 and ɛ2 for a specific nature of the nonlinearity.
Ponderomotive Nonlinearity
For a collisionless plasma, the ponderomotive force on the electrons is proportional to the gradient of the irradiance, which causes a redistribution of the electron density, and thereby the dielectric function; this nonlinearity sets in a period on the order (r 0/c s), where r 0 is the width of the beam, and c s is the ion sound speed.
Hence, for a collisionless plasma at moderate fields (when the quiver speed of the electron is much smaller than the speed of light in vacuum), the modified electron density function N 0e is given (Akhmanov et al., Reference Akhmanov, Sukhorukov and Khokhlov1968; Sodha et al., Reference Sodha, Tripathi and Ghatak1976),
where,
k B is the Boltzmann constant, and T 0 is the temperature of the atoms/ions.
Substituting for N 0e from Eq. (26) in Eq. (20) and using Eqs (21), (22), (24), and (25), one can easily obtain ɛ0(z) and ɛ2(z) as
and
with p = βE 02/f 2 being proportional to the irradiance of the HGB at η = 0.
Collisional Nonlinearity
In collisional plasmas, the distribution of electron and ion temperatures takes place in the transverse plane on account of the nonuniform distribution of the electron temperature, caused by the radial dependence of the irradiance of the beam; this nonuniformity in temperature creates the pressure gradients of the electron and ion gases. In the steady state with plasma neutrality these pressure gradients are balanced by the space charge field, and lead to a redistribution of the electron density and hence the modified dielectric function. The collisional nonlinearity sets in a period 1/δcνe, where δc is the fractional loss of excess energy by an electron in a collision with heavier species (ions and neutral particles), and νe is the electron collision frequency. For collisional plasmas, the modified electron density N 0e may thus be expressed as (Akhmanov et al., Reference Akhmanov, Sukhorukov and Khokhlov1968; Sodha et al., Reference Sodha, Tripathi and Ghatak1976)
where
and the collision frequency νe is proportional to the s th power of the random electron speed. For electron-ion collision dominated plasma, one has s = −3 and for electron-neutral collision dominated plasma, it is s = 1. Eq. (21) is based on the fact that thermal conduction does not play a significant part in the energy balance of electrons, which is justified when (δcr 02/l 2) ≫1 (see Sodha et al., Reference Sodha, Tripathi and Ghatak1976). It is also assumed that the heavier particles are abundant enough to provide a heat sink at almost constant temperature for energy loss by the electrons.
Substituting for N 0e from Eq. (29) in Eq. (20) and by using Eq. (21), (22), (24), and (25), one can obtain expressions for ɛ0(z) and ɛ2(z) as,
and
where p = αE 02/f 2.
Relativistic Nonlinearity
For very high powers of the beams, the quiver speed of the electrons is comparable to the speed of light in vacuum, causing a change in the mass of the electron, and hence a change in the plasma frequency leads the modified dielectric function. Thus, the relativistic variation of the electron mass may also cause nonlinearity (Hora, Reference Hora1975; Kane & Hora, Reference Kane, Hora, Schwarz and Hora1977). This nonlinearity sets in a period on the order ωpe−1. The dielectric function for a circularly polarized beam can be expressed as
where γ=(e 2/m 02ω2c 2), m 0 is the rest mass of the electron and E is the amplitude of the beam.
From Eqs (21), (22), (24) (25), and (32) one can easily express ɛ0(z) and ɛ2(z) as
and
where p = γE 02/f 2.
Nature of Self Focusing: Critical and Divider Curves
Ponderomotive Nonlinearity
Using the expression for ɛ2(z) from Eq. (28), Eq. (18) ensures vanishing of d 2f/dξ2 for a value of p (say p c), corresponding to a beam width Π0f, when
which at ξ = 0 reduces to
where p 0 = βE 002.
Eq (36) represents the critical power curve plotted as Π0versus p 0 and separates the self focusing region from the rest. For the points lying above the critical power curve, the beam undergoes oscillatory convergence (self focusing), while for the points below this curve, the beam executes oscillatory divergence or steady divergence. The points on the curve lead to self trapped mode propagation of the HGB.
One should notice that Eqs (35) and (36) have the same algebraic form; this suggests that if during its propagation, the beam power and the beam width (p, Π0f) satisfy Eq. (35), the corresponding point in the f − ξ curve will be a point of inflection (d 2f/dξ2 = 0), a necessary condition for oscillatory convergence/divergence. However, all the points below the critical curve do not lead to a point of inflection, and hence lead to a steady divergence of the beam. The condition for any point (p, Π0f) to be a point of inflection is that it must satisfy Eq. (35). One can write Eq. (27) as
Therefore Eq. (35) reduces to
or
For p > 0, from Eq. (36) one has
or
These relations lead to
Therefore from Eq. (38) one obtains
Thus, for the point (p, Π0f) to arrive at a point of inflection (d 2f/dξ2 = 0), one must have the beam having initial point (p 0, Π0) lying above the curve
Eq. (40) represents a curve (Π0versus p 0) that further divides the region below the critical power curve in two regions, and has hence been termed the divider curve by Sharma et al. (2003). The area between the divider curve and the critical power curve represents the region of oscillatory divergence, while the area below the divider curve describes the region of steady divergence.
Collisional Nonlinearity
Using Eqs (30) and (31) for ɛ0(z) and ɛ2(z) with Eq. (18) and following a similar treatment (as in the preceding case) one can obtain the critical power curve and the divider curve as,
Critical power curve
Divider curve
with p 0 = αE 002.
Relativistic Nonlinearity (Circularly Polarized Beam)
Using the expression for ɛ0(z) and ɛ2(z) from Eqs (33) and (34) with Eq. (18), and following similar algebraic treatment as above, the expressions for the critical power curve and the divider curve can be written as,
Critical power curve
Divider curve
with p 0 = γE 002.
Power of the Hollow Gaussian Beam
The power of the hollow Gaussian beam with the irradiance distribution
can be expressed as
where ɛ(r, z) is the dielectric function of the plasma. For the circularly polarized beams, the right-hand-side gets multiplied by two. One can obtain the power of the HGB by using an appropriate dielectric function for all three kinds of nonlinearities.
Ponderomotive Nonlinearity
Using the dielectric function ɛ(r, z) from Eq. (20) and Eq. (26), Eq. (45) reduces to
![\eqalign{P &= {cr_0^2 \over 8{\rm \beta}} {\,p \over 2^{2{n}}} \vint\limits_0^{\infty} {\rm \lambda}^{2{n}} \exp \lpar\! -\!\lambda\rpar \cr &\quad \times \left[1 - \Omega^2 \exp \left(-\lpar p/2^{2{n}}\rpar \lambda^{2{n}} \exp \lpar\!\! -\!\lambda\rpar \right)\right]^{1/2} d\lambda\comma}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022040155221-0038:S0263034609000081_eqnU12.gif?pub-status=live)
where λ = (r 2/r 02f 2). The dimensionless power of the beam may be expressed as
![\eqalign{\Pi &= {8{\rm \beta} \over cr_0^2} P = {\,p \over 2^{2{n}}} \vint\limits_0^\infty \lambda^{2{n}} \exp \lpar\! -\!\lambda\rpar \cr &\quad \times \left[1 - \Omega^2 \exp \left(-\lpar p/2^{2{n}}\rpar \lambda^{2{n}} \exp \lpar\!\! -\!\lambda\rpar \right)\right]^{1/2} d\lambda\comma}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022040155221-0038:S0263034609000081_eqn46.gif?pub-status=live)
with p = βE 02/f 2. Further at z = 0, f = 1 the initial power is given as
![\eqalign{\Pi_0 &= {\,p_0 \over 2^{2{n}}} \vint\limits_0^{\infty} \lambda^{2{n}} \exp \lpar\!\! -\!\lambda\rpar \cr &\quad \times \left[1 - \Omega^2 \exp \left(-\lpar p_0 /2^{2{n}}\rpar \lambda^{2{n}} \exp \lpar \!\!-\!\!\lambda \rpar \right)\right]^{1/2} d{\rm \lambda}\comma}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022040155221-0038:S0263034609000081_eqn47.gif?pub-status=live)
with p 0 = βE 002.
Similarly the initial power of the HBG for collisional and relativistic nonlinearities may be expressed as
For Collisional Nonlinearity
![\eqalign{\Pi_0 &= {\,p_0 \over 2^{2{n}}} \vint\limits_0^\infty \lambda^{2{n}} \exp \lpar\!\! -\!\lambda\rpar \cr &\quad \times \left[1 - \Omega^2 \left(1 + \lpar p_0 /2^{2{n}}\rpar \lambda^{2{n}} \exp \lpar\!\! -\!\lambda\rpar \right)^{\lpar {\rm s} - 2\rpar /2}\right]^{1/2} d{\rm \lambda}}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022040155221-0038:S0263034609000081_eqn48.gif?pub-status=live)
with p 0 = αE 002.
For Relativistic Nonlinearity
![\eqalign{\Pi_0 &= {\,p_0 \over 2^{2{n}}} \vint\limits_0^\infty \lambda^{2{n}} \exp \lpar\!\! -\!\lambda\rpar \cr &\quad \times \left[1 - \Omega^2 \left(1 + \lpar p_0 /2^{2{n}}\rpar \lambda^{2{n}} \exp \lpar\!\! -\!\lambda\rpar \right)^{-1/2}\right]^{1/2} d {\rm \lambda}}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022040155221-0038:S0263034609000081_eqn49.gif?pub-status=live)
with p 0 = γE 002.
SCHEME OF COMPUTATION
To have a numerical appreciation of the results, the critical power curve, the divider curve, and the dependence of the beam width parameter f of the HGB on ξ have been computed for a chosen set of parameters and different kinds of nonlinearities.
To obtain the critical curve between initial power Π0 and initial beam width Π0, one first computes the critical curve with Π0 and p 0, as parameters using the appropriate equations (Eqs (36), (40), (41), (42), (43), and (44)) obtained herein and also computes the power Π0, corresponding to a set of values (p 0, Π0) on the critical curve, using Eq. (45). Thus one can obtain the critical curve with Π0 and Π0, as the parameters. The critical power curve and the divider curve Π0versus Π0 have been plotted for different kinds of nonlinearities for chosen sets of parameters Ω, s and n. The computations have also been made to investigate the dependence of the beam width parameter f, associated with the propagation of the hollow Gaussian beam on the dimensionless distance of propagation ξ in homogeneous plasmas. Starting with a combination of the parameters Π0, Π0, n, and Ω one can obtain the solution for the beam width parameter f by simultaneous numerical integration of Eqs (18) and (19) using suitable expressions for ɛ0 and ɛ2 under appropriate boundary conditions viz f = 1, df/dξ = 0 and Φ = 0 at ξ = 0.
NUMERICAL RESULTS AND DISCUSSION
In the present study, the propagation characteristics of a hollow Gaussian beam in plasma have been investigated; these are determined by the modified dielectric function around the maximum of the irradiance on the wavefront of the HGB. One can see from the irradiance distribution profile for HGB (Eq. (2)) that the radius of the bright ring increases when the order of the HGB n increases, which means that the area of the dark region across the HGB increases as n increases. It is instructive to remember that (1) the collisional nonlinearity sets in a period 1/δν, (2) the ponderomotive nonlinearity sets in a period r 0/c s where c s is the ionic sound speed, and (3) the relativistic nonlinearity sets in a period ωpe−1. The present steady state theory is valid when the duration of the laser radiation is longer than these characteristic times.
To have a better understanding of the phenomena and numerical appreciation of the results, the critical curves and the beam width parameter f as a function of dimensionless distance of propagation ξ have been computed for a set of parameters Π0, Π0, n, and for all the three kinds of nonlinearities. Further, these results for higher order HGB have been compared with corresponding results for a fundamental Gaussian beam (n = 0).
Figure 1 illustrates the dependence of the dimensionless initial power Π0 on the dimensionless initial beam width Π0 for self trapping, corresponding to the ponderomotive nonlinearity for various orders of the HGB. The figures show the critical as well as divider curves; thus the Π0 − Π0 space can be divided into three regions namely those corresponding to oscillatory focusing, oscillatory divergence, and steady divergence. If any initial point (Π0, Π0) lies on the critical power curve then d 2f/dξ2 vanishes at ξ = 0; since df/dξ is initially zero (for a plane wavefront) it continues to be zero and f remains equal to one as the HGB propagates through the plasma. Such propagation is termed as uniform waveguide propagation. For the initial point (Π0, Π0) lying above the critical power curve, d 2f/dξ2 < 0 and hence when the beam propagates through the plasma the power Π increases and the beam width Π0f decreases. Therefore, when the beam propagates the point (Π, Π) will move in the Π0 − Π0 space in the right downward direction and at some value of f it will reach the critical power curve (i.e., the point of inflection); beyond this df/dξ starts decreasing until df/dξ vanishes, i.e., f reaches a minimum. Thus, during the propagation of the beam, the beam width parameter f corresponding to such a point (lying above the critical power curve) oscillates between the initial value unity and a minimum. Similarly, for the initial point (Π0, Π0) lying between the critical power curve and the divider curve, the beam width parameter f oscillates as the beam propagates in the plasma between a maximum and the initial value unity. The points lying below the divider curve will never be able to attain a point of inflection and hence the beam having an initial point (Π0, Π0) in this region steadily diverges. The curves in Figure 1 indicate that the region for oscillatory divergence becomes narrower while self focusing and steady divergence occupy larger areas in the Π0 − Π0 space as the order of the HGB increases. The trend of the critical power curve gets reversed beyond some value of the critical power. This can be understood in terms of ɛ2(z), which at first rises rapidly to a maximum value (i.e., minimum self trapping width) and then falls sharply with increasing power of the beam for lower order HGBs. The divider curve shows that the beam width associated with the region of steady divergence increases with increasing order of the HGB. Further, a comparative study has been made for fundamental Gaussian beam, which follows a similar variation. The figure also suggests that the minimum self trapping width is lowest for n = 0 and increases with increasing order of the HGB.
Fig. 1. Variation of the initial beam width Π0 (=r 0ω/c) with the initial power Π0, for the propagation of various order HGBs in a collisionless plasma with dominant ponderomotive nonlinearity, for the parameter Ω2 = 0.8; the curves c and d refer to the critical power curve and divider curve respectively while the numerical subscripts 0, 1, 2, and 3 correspond to the order of the HGB n.
Figure 2a describes the curves corresponding to critical conditions for focusing and defocusing of the beam in an electron-ion collision dominant plasma (s = −3) for various orders of the HGBs; the curves display a trend like Figure 1. Further, the self focusing region occupies a larger area and a higher value of absolute minimum of the beam width for self trapping to occur for an electron-neutral collision dominant plasma (s = 1), in comparison with that for an electron-ion collision dominated (s = −3) plasma, in the Π0 − Π0 space; this comparison has been demonstrated in Figure 2b. The figure also suggests that for the same initial beam width Π0, self focusing is stronger for s = −3 for low power HGBs, it gets more pronounced for s = 1 with increasing power of the beam.
Fig. 2. (a) Variation of the initial beam width Π0 (=r 0ω/c) with the initial power Π0, for the propagation of various order HGBs in an electron-ion collision dominant plasma s = −3 for Ω2 = 0.8. The curves c and d refer to the critical power curve and divider curve respectively while the numerical subscripts 0, 1, 2, and 3 correspond to the order of the HGB n. (b) Critical power curves: The variation of the initial beam width 1/Π02 with the initial power Π0 for the propagation of HGBs of various orders in a collisional plasma for Ω2 = 0.8. The curves a, b and c refer to the order of the HGB n = 1, 2 and 3 respectively while the subscripts ei and en correspond to s = −3 and s = 1, respectively.
Figure 3a expresses the dependence of the beam width parameter f on the dimensionless distance of propagation ξ for a collisionless plasma with dominant ponderomotive nonlinearity. The figure describes the characteristic propagation of the HGB in the three regions namely self focusing, oscillatory divergence, and steady divergence for chosen points (Π0, Π0) from Figure 1 for n = 1; the focusing is more pronounced for the beam having high initial power and larger initial beam width. The effect of higher order of HGBs on the propagation has been depicted in Figure 3b, starting with fixed (Π0, Π0) for all the beams. It is seen that for low power beams that the self focusing character of the HGB decreases and leads to oscillatory divergence as n increases, but as the power of the beam increases the trend is seen to get reversed i.e., self focusing is more pronounced for higher order HGBs; this has been shown in Figure 3c.
Fig. 3. (a) Dependence of the dimensionless beam width parameter f on the dimensionless distance of propagation ξ, in a collisionless plasma with dominant ponderomotive nonlinearity, for the parameters Ω2 = 0.8 and first order HGB (n = 1); the curves refer to an arbitrarily chosen set of initial power and initial beam width (Π0, Π0) as indicated over the curves. (b) Variation of the dimensionless beam width parameter f on the dimensionless distance of propagation ξ, in a collisionless plasma with dominant ponderomotive nonlinearity for various order HGBs for Ω2 = 0.8, Π0 = 2 and Π0 = 4; the curves a, b, c and d refer to the order of the HGB n = 0, 1, 2 and 3 respectively. (c) Dependence of the dimensionless beam width parameter f on the dimensionless distance of propagation ξ, in a collisionless plasma with dominant ponderomotive nonlinearity for various order HGBs, for the parameters Ω2 = 0.8 and Π0 = 3; the curves a and b refer to the initial power of the beam Π0 = 2 and 10 respectively, while subscripts 1 and 3 correspond to the order of the HGB n.
The propagation of the various order HGBs in a collisional plasma has been illustrated in Figure 4 for s = 1, −3 starting with the same (Π0, Π0) for all the beams. The figure suggests stronger self focusing for s = −3 than for s = 1 (due to stronger nonlinearity for s = −3). Further, self focusing is more pronounced for s = −3 with increasing order of the HGB, while the opposite trend is observed for s = 1. All the f − ξ curves are in conformance with the above discussed critical curves.
Fig. 4. Variation of the dimensionless beam width parameter f on the dimensionless distance of propagation ξ, in a collisional plasma for various order HGBs, for the parameters Ω2 = 0.8, Π0 = 3 and Π0 = 4; the curves a, b and c refer to the order of the HGB n = 1, 2 and 3 respectively, while the subscripts ei and en correspond to s = −3 and s = 1 respectively.
One should notice that an expression for the dielectric function for relativistic nonlinearity (Eqs (33) and (34)), is exactly obtained by substituting s = 1 in the expression for the dielectric function for collisional nonlinearity (Eqs (30), (31)) with modified definition of p(=γE 02/f 2); therefore the results (in terms of p and Π) for relativistic nonlinearity are the same as those for s = 1 in collisional nonlinearity.
CONCLUSION
It is interesting to compare the propagation characteristics of the HGBs to those of the fundamental Gaussian beam. It is seen that the HGBs also exhibit three regions in the Π0 − Π0 space which follow a nature similar to that in the case of the Gaussian beam. The regions for self focusing and steady divergence occupy larger areas while the oscillatory divergence becomes narrower with respect to the Gaussian beam in Π0 − Π0 space for higher order HGBs. The nature of the critical curve involves that self focusing is more pronounced for lower orders for low power HGBs, while the trend just reverses for high power of the beam.
ACKNOWLEDGEMENT
The authors are grateful to the Department of Science and Technology, Government of India for financial support and to Prof. M. P. Verma for critical review of the manuscript.
