1. INTRODUCTION
Consider the discrete-time local level, or random walk plus noise,
unobserved components model of Harvey (1989, p.
19), extended to allow for a deterministic kernel,
at, for the univariate time series process
{yt}:
t = 1,…,T. We assume the initial condition
μ0 = 0, which implies no loss of generality, provided
at includes a constant and, for the present,
that the irregular and level disturbance processes
{εt} and {ηt} are
uncorrelated, both temporally and contemporaneously.
In the context of (1.1)-(1.2) considerable theoretical and empirical
interest have focused on the so-called stationarity testing problem. That
is, defining the signal-to-noise ratio in (1.1)-(1.2) as q =
ση2/σε2,
testing the null hypothesis of stationarity, H0 :
q = 0, against the unit root alternative, H1
: q > 0. Setting at = a,
a constant, Nyblom and Mäkeläinen (1983) demonstrate that the locally best invariant
(LBI) test of H0 against H1
rejects for large values of the statistic
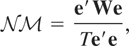
where e =
(e1,…,eT)′
is the T-vector of ordinary least squares (OLS) residuals
obtained from regressing yt on an intercept,
t = 1,…,T, and W is the so-called random
walk generating matrix with (i,j)th element equal to the
minimum of i and j, i,j =
1,…,T. King and Hillier (1985)
show that this is also a one-sided Lagrange multiplier test of
H0 against H1. Nyblom (1986) has extended the analysis of Nyblom and
Mäkeläinen (1983) to the case where
at = a + bt, a linear time
trend, in which case the LBI test is as given in (1.3) except that
e is now the vector of OLS residuals from regressing
yt on an intercept and trend. Further
generalizations are provided by Nabeya and Tanaka (1988), Kwiatkowski, Phillips, Schmidt, and Shin (1992), and Busetti and Harvey (2001).
Tanaka (1996, p. 368), inter alia,
demonstrates that under the local alternative,
Hc : q =
c2/T2, c ≥ 0, as
T → ∞
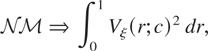
with
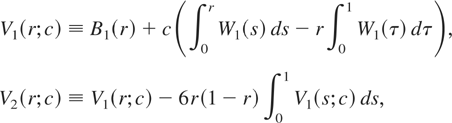
where ⇒ denotes weak convergence of the associated probability
measures and the nomenclature ξ = 1,2, is used exclusively throughout
this paper to indicate whether the deterministic kernel is a constant, in
which case ξ = 1, or a linear time trend, in which case ξ = 2. In
(1.4), B1(r) ≡
W0(r) − rW0(1),
r ∈ [0,1], is a standard Brownian bridge process,
defined via the standard Brownian motion
W0(r), whereas
W1(r) is a standard Brownian motion process
independent of W0(r).1
The result in (1.4) and those that follow also hold under
considerably weaker, martingale difference, conditions on the irregular
and level disturbance processes; see Stock (1994, pp. 2745, 2794–2799) for
details.
Where c = 0, Hc reduces to
H0, and hence (1.4) will give the limiting null
distribution of the LBI statistic,
of (1.3). For ξ = 1 and ξ = 2 these are, respectively, first- and
second-level Cramér–von Mises distributions with one degree
of freedom; see Harvey (2001) for further
discussion on the Cramér–von Mises family of distributions.
In what follows we will denote these Cramér–von Mises
distributions by VMξ(1), ξ = 1,2, upper tail
critical values from which are provided in, for example, Kwiatkowski et
al. (1992, p. 166) and Harvey (2001, pp. 4, 8). Moreover, from (1.4) the limiting
(local) power function of
under Hc for an α-level test will be
given by
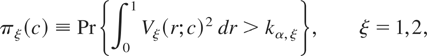
where kα,ξ is such that
.
For both ξ = 1 and ξ = 2, (1.6) is monotonically increasing in
c. These limiting power functions are graphed in Tanaka (1996, Figure 10.4, p. 389). Under the fixed
alternative H1 : q > 0,
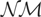
is of Op(T) and positive; see,
inter alia, Kwiatkowski et al. (1992, pp.
165–169). Consequently, the LBI test is consistent against fixed
alternatives.
Although the foregoing results were derived under the assumption of
uncorrelated disturbances, Bailey and Taylor (2002) have recently demonstrated that the form of the
LBI test, for a given deterministic kernel, is unaltered by allowing for
contemporaneous correlation between εt and
ηt: the so-called nonorthogonal model. Moreover,
they demonstrate that the limiting distribution theory in (1.4) for
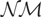
of (1.3) also remains appropriate under the nonorthogonal model.
The stationarity testing literature to date has started from the basic
presumption that the data are generated by the regularly spaced
discrete-time local level model, (1.1)-(1.2). However, as argued in Harvey
(1989, p. 479), “A continuous time model
is, in some ways, more fundamental than a discrete time model … a
good deal of the theory in economics and other subjects is based on
continuous time models.” Notably, continuous-time models provide a
framework that allows us to handle irregularly spaced data and highlights
the important distinctions that exist, in particular when the data are
irregularly spaced, between stock and flow variables. Stocks are variables
such as prices, unemployment, temperature, and the capital stock that can,
in principle, be observed at any given point in time, whereas flows are
variables such as rainfall, income, and consumption expenditures that are
defined with respect to an interval of time. It is perhaps surprising,
therefore, that stationarity tests have been widely applied to both
macroeconomic and financial data without any formal investigation into
what effects the stock-flow distinction has on the underlying testing
problem. Using continuous-time formulations of the local level model for
stock and flow variables, we undertake a detailed exploration of these
issues in this article.
In Section 2 we set out the continuous-time formulation of the local
level model for both stock and flow variables and derive the corresponding
discrete-time analogue models. In neither case do these analogue models
reduce to the discrete-time model (1.1)-(1.2), except where the
observations are regularly spaced. Even then, in the case of flow
variables one obtains the nonorthogonal discrete-time local level model.
This then allows us, in Section 3, to derive the LBI tests for the null
hypothesis that the signal-to-noise ratio in the continuous-time model is
zero against the alternative that it is positive in cases where the sample
observations are irregularly spaced through time. We demonstrate that the
form of the resulting LBI test, for a given pattern of intraobservation
intervals, is different for stock vis-à-vis flow variables. The
limiting null distributions of the LBI statistics are, in general,
nonpivotal. An exception occurs where the data are regularly sampled. Here
the LBI tests for stock and flow data both have pivotal
Cramér–von Mises distributions.
In Section 4 we analyze the case where the data are regularly sampled
and show that for stock variables the local limiting power of the LBI test
increases with the sampling frequency; that is, ceteris paribus, power is
higher for N years of monthly data than for N years of
annual data. Moreover, for stock variables we also show that the LBI test
is consistent against fixed alternatives for cases where the
continuous-time model is generated for a fixed time span but with the
sampling interval tending to zero. In contrast, we show that for flow
variables the local limiting power of the LBI test does not increase with
the sampling frequency, and that the LBI test is not consistent
when the time span is fixed and the sampling interval tends to zero.
Interestingly, these findings contrast with what has been found for the
Dickey–Fuller test by Phillips (1987),
Perron (1991), Ng (1995), and Chambers (2004).
However, this is perhaps not surprising given that our model effectively
reverses the role of the null and the alternative hypotheses, relative to
the Dickey–Fuller setup. Loosely speaking, in both models a stock
variable that admits a unit root appears “more nonstationary”
when it is observed with higher frequency, whereas a parallel, but
reversed, argument holds in the case of flow variables.
An interesting case of irregularly spaced data is provided by mixed
frequency data. An example of this is where some subsample of the complete
data set is observed annually and the remaining subsample comprises
quarterly observations. In Section 5 we derive explicit expressions for
the LBI stationarity tests for mixed frequency data, as special cases of
the tests derived in Section 3. We provide representations for the
limiting null distributions of the LBI statistics, demonstrating that
these depend on the fraction of the data observed in each subsample and on
the relative observation frequencies in the two subsamples. These
representations differ considerably between stock and flow variables. A
selection of critical values from these asymptotic distributions is
provided. We also consider tests that are based on statistics modified,
either by considering the two subsamples separately or by data
aggregation, so as to have limiting null distributions belonging to the
Cramér–von Mises family. The finite-sample power properties
of these tests are compared, via Monte Carlo simulation, with the LBI
tests. Our results suggest that the use of the aggregate data involves
only negligible losses in efficiency for the case of flow variables but
not for stock variables; in the latter case our simulations are decisively
in favor of the exact LBI tests developed in this paper.
2. CONTINUOUS-TIME LOCAL LEVEL MODELS FOR
STOCK AND FLOW DATA AND THEIR DISCRETE-TIME ANALOGUES
The continuous-time analogue of the discrete-time random walk
transition equation (1.2) is given by
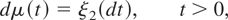
where ξ2(dt) is a random measure, defined
formally later. Formulating the continuous-time analogue of the
observation equation (1.1) is more involved. Because of the static nature
of (1.1), different continuous-time formulations of the observation
equation will necessarily be required for the separate cases of stock and
flow data because the former are measured at single points in time whereas
the latter are measured as integrals over the sampling interval. Consider
first the case of stock data. Here the appropriate observation equation is
given by
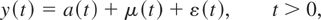
where a(t) is a deterministic kernel and
ε(t) is heuristically a serially uncorrelated mean-zero
process with variance σε2, as in Wymer
(1993). For the case of flow variables, the
corresponding observation equation is given by
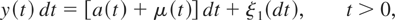
where ξ = (ξ1,ξ2)′ is a
two-dimensional random measure, defined on all subsets of the half-line 0
< t < ∞ with finite Lebesgue measure, satisfying
Assumption 2.1 of Bergstrom (1986), with
E [ξ(dt)] = 0 and E
[ξ(dt)ξ′(dt)] =
(dt)Σ, Σ = diag(σε2,
ση2). Heuristically speaking,
ξ(dt) can be thought of as a continuous-time white noise
process (for further discussion, see Bergstrom, 1984, p. 1157), and, moreover, (2.3) may be viewed as
(2.2) multiplied through by dt and with ε(t)
dt replaced by ξ1(dt).
Our continuous-time local level models for stock and flow data are
therefore given by (2.2)-(2.1) and (2.3)-(2.1), respectively. As with
(1.1)-(1.2), for both (2.2)-(2.1) and (2.3)-(2.1) we may assume the
initial condition μ(0) = 0 with no loss of generality, provided
a(t) contains an intercept term. Harvey and Stock (1993, pp. 58–59) and Chambers and McGarry (2002) specify the discrete-time observation equations
for stock and flow data directly. However, a comparison of (2.6)-(2.7) and
(2.9)-(2.10), which follow, with equations (9), (10), (12), and (25) of
Harvey and Stock (1993, pp. 58–64) shows
that the discrete-time analogues of (2.2)-(2.1) and (2.3)-(2.1) coincide
with the discrete-time models specified for stock and flow variables in
Harvey and Stock (1993). This point is also
recognized by Chambers and McGarry (2002), who
argue in the context of the discrete-time analogues that “the random
disturbance … can be interpreted either as the discrete time
realization of a genuine irregular component in continuous time …
or as a measurement error that is associated with the discrete time
sampling of the continuous time process” (p. 393).
Our formulations of the local level model for stock and flow variables
provide a general framework from which to examine the corresponding exact
discrete-time models, where the observations are sampled at possibly
irregular intervals. As with the stationarity tests outlined for the case
of the discrete-time local level model, (1.1)-(1.2) in Section 1, our
interest focuses on testing the null hypothesis of stationarity against
the unit root alternative in the continuous-time local level models. That
is, we wish to test the following hypothesis regarding the structural,
signal-to-noise ratio, parameter2
Notice that
the signal-to-noise ratios that are subsequently obtained for the
discrete-time analogues for stock and flow variables are derived, rather
than structural, parameters.
=
σ
η2/σ
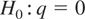
ε2 versus
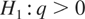
in (2.2)-(2.1)for stock variables and in (2.3)-(2.1) for flow
variables, using observations on the process that are available at
possibly irregular spaced discrete time points. In particular, we suppose
that the data are observed over the interval 0 < t ≤
N, where N denotes the span of the data, at
T irregular observation times {tτ}, τ
= 1,…,T, where tτ =
tτ−1 + δτ,
t0 = 0, with the intraobservation intervals,
δτ, expressed in calendar time units, such that
.
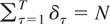
In a series of influential papers Bergstrom (1983, 1984, 1985), inter alia, sets out the theoretical treatment
of continuous-time autoregressive models and their estimation by Choleski
factorization of the Gaussian likelihood. Building upon this work, Harvey
(1989, Ch. 9) and Harvey and Stock (1993) consider a general class of state space models
in continuous time where the Gaussian likelihood estimation is carried out
via the Kalman filter. The continuous-time models in (2.2)-(2.1) and
(2.3)-(2.1) may be regarded as simple examples from this class of state
space models.3
More sophisticated models,
including those with common trends and cointegration in continuous time,
have been considered by Harvey and Stock (1988,
1989), Phillips (1991), and Comte (1999),
inter alia.
They are nevertheless important from the point of
view of constructing stationarity tests for the case of irregularly spaced
observations on stock and flow data, respectively. We now derive the
discrete-time analogues of (2.2)-(2.1) and (2.3)-(2.1).
2.1. Stock Variables
Consider first the case of a stock variable. Let
yτ = y(tτ),
μτ = μ(tτ),
aτ = a(tτ), and
ετ = ε(tτ). Evaluating
(2.2)-(2.1) at t = tτ, yields the
discrete-time analogue
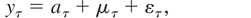
where ετ and ητ are
mean-zero, serially uncorrelated, and mutually orthogonal disturbances
with variances σε2 and
δτση2, respectively. It
is important to notice that, unlike the discrete-time model in
(1.1)-(1.2), the disturbances driving the level equation, (2.7), are
heteroskedastic when the observations are irregularly sampled, that is,
where δτ is not constant through the observed sample.
In the case where a(t) = a, then so
aτ = a, so that a constant in the
continuous-time local level model, (2.2)-(2.1), implies a constant in the
discrete-time analogue, (2.6)-(2.7). However, if a(t) =
a + bt, a linear trend, then aτ
= a + btτ, which will not, in general, be
of the form of a linear trend in τ. An obvious exception occurs where
δτ is fixed through the sample (the observations occur
at regular time points). In this case the discrete-time analogue
(2.6)-(2.7) clearly reduces to a discrete-time local level of the form
(1.1)-(1.2).
2.2. Flow Variables
An observed flow variable, which we denote by
Yτ, is obtained by integrating the (unobserved)
continuous-time analogue y(t) over the interval
(tτ−1,tτ],
namely,
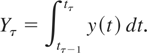
As demonstrated in Appendix A, one therefore obtains that the
discrete-time analogue of (2.3)-(2.1) is given by
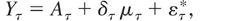
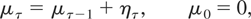
where
,
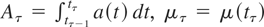
and ετ* and ητ are mean-zero,
serially uncorrelated disturbances. However, and in contrast to the case
of a stock variable, the disturbance in the measurement equation
ετ* is contemporaneously (but not temporally)
correlated with that of the transition equation ητ,
namely,
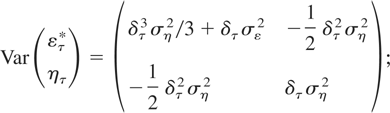
see also Harvey and Stock (1993).4
Notice that Harvey and Stock (1993) write (2.9) with μτ−1
in place of μτ and redefine ετ*
accordingly. Save for the minus sign in the expression for
Cov(ετ*,ητ), the two
representations coincide. Moreover, Chambers and McGarry (2002, p. 395) choose a different formulation where the
disturbance terms in the discrete-time observation and transition
equations are uncorrelated (both temporally and contemporaneously) but the
latter follows an MA(1) process. The nonorthogonal representation,
(2.9)-(2.10), is clearly the more useful in the context of this
paper.
As regards the deterministic kernel, if a(t) =
a, then Aτ =
aδτ, so that a constant in the continuous-time
local level model (2.3)-(2.1) does not imply a constant in the
discrete-time analogue model, unless δτ is fixed
through the sample. Moreover, if a(t) = a +
bt, a linear trend, then Aτ = (a
+ btτ −
(b/2)δτ)δτ: as with the
case of a stock variable, this reduces to a standard linear trend where
δτ is constant across the sample.
It is crucial to notice that, and again in contrast to the case of
stock variables, even where δτ is constant across the
sample, (2.9)-(2.10) does not reduce to the class of discrete-time local
level models as in (1.1)-(1.2), because of the contemporaneous correlation
between ετ* and ητ. However,
because our interest in this paper lies solely in developing optimal tests
of H0 of (2.4) against H1 of
(2.5), we know from the results of Bailey and Taylor (2002) that, in this regard, the orthogonal and
nonorthogonal local level models may be treated as if they were the same.
This point is pursued further in Section 3.3.
3. THE LBI TEST AGAINST THE PRESENCE OF A
RANDOM WALK COMPONENT
In this section we derive the LBI test of H0 of
(2.4) against H1 of (2.5) for the cases of both stock
and flow variables observed at (possibly irregularly spaced) discrete
points. These results show that there are significant and important
differences between the two cases. The LBI tests are obtained using the
framework of King and Hillier (1985).
The structure of the resulting LBI test statistics is shown to depend
on the intraobservation intervals, δτ, τ =
1,…,T, which may be regular or irregular. The former case
is pursued further in Sections 3.3 and 4, where it is shown that the
statistics simplify considerably. Two interesting examples of the latter
are the mixed frequency data and missing data cases. The first example is
pursued in detail in Section 5. Stationarity tests in the presence of
missing data obtain as special cases of the LBI tests outlined for stock
and flow variables in Sections 3.1 and 3.2, respectively, and we shall not
pursue such tests in any further detail here. However, for a setup that is
analogous to our stock variable case and under certain restrictions on the
intraobservation intervals, Nishino (2002)
provides an exploration of stationarity testing with missing data.
3.1. Stock Variables
Let yS =
(y1,…,yT)′
denote the T × 1 vector of observations when the observed
variable is a stock. From (2.6)-(2.7) and assuming Gaussianity, we
immediately obtain that
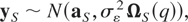
where aS is a T × 1 vector
with τth element aτ and
ΩS(q) =
IT + qVδ,
with Vδ a (T × T) matrix
with (i,j)th element equal to the minimum of
ti and tj,
i,j = 1,…,T.
A straightforward application of equation (6) of King and Hillier
(1985, p. 99) then yields that the LBI test of
H0 of (2.4) against H1 of (2.5) in
the case of a stock variable rejects for large values of the statistic
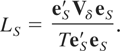
In (3.2), eS =
(e1,S,…,eT,S)′
is the vector of OLS residuals obtained from the projection onto the
deterministic component aS. For the linear
trend case, a(t) = a + bt and
eS is obtained from regressing
yτ on zS,τ =
(1,tτ)′, whereas in the case of a constant
level, a(t) = a, the elements of
eS are simply the deviations from the sample
mean.
The numerator of the statistic LS of
(3.2) may be written equivalently as the weighted sum of squared (reverse)
partial sums of the OLS residuals,
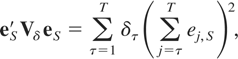
the weights being the sequence of intraobservation intervals
{δ1,…,δT}. Because of this
dependence on the δ1,…,δT
the null distribution of LS cannot be easily
obtained. An obvious exception, considered in Section 3.3, occurs when the
observations are sampled at regularly spaced intervals, that is, where
δτ is constant across the sample. However, because
LS is formed as the ratio of two quadratic
forms in Gaussian variables, the exact distribution of
LS under both H0 of (2.4)
and H1 of (2.5), for a given sequence,
{δ1,…,δT}, can be obtained
using the well-known Imhof (1961) routine.
3.2. Flow Variables
Consider now the case of a flow variable. Let
yF =
(Y1,…,YT)′
denote the T × 1 vector of observations on the flow
variable and let D =
diag(δ1,…,δT). In Appendix B
it is demonstrated that, from (2.9)-(2.10) and assuming Gaussianity,
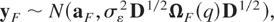
where aF is a T × 1 vector
with τth element Aτ and
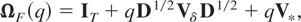
with Vδ defined as before, and where
V* is a symmetric matrix with
(i,j)th element, i ≤ j =
1,…,T,
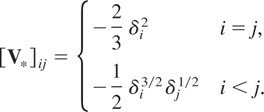
Again using equation (6) of King and Hillier (1985, p. 99), it then follows that the LBI test of
H0 of (2.4) against H1 of (2.5)
for the case of a flow variable rejects for large values of the
statistic
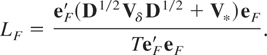
In the context of (3.6), eF =
(e1,F,…,eT,F)′
is the vector of OLS residuals from regressing
D−1/2yF on the
deterministic component
D−1/2aF. For
example, in the case of a constant level a(t) =
a, so that Aτ =
aδτ, one obtains that
eτ,F =
δτ−1/2(Yτ
− δτ [sum ]Yτ
/N), τ = 1,…,T.
Noting that the variance of
eF′V*eF
is of smaller order (in T) than that of
eF′D1/2VδD1/2eF
under both H0 of (2.4) and H1 of
(2.5), it follows that LF is asymptotically
equivalent to the simplified statistic
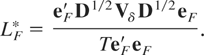
In what follows we will therefore concentrate our attention on
LF*. As with LS
of (3.2), the numerator of LF* of (3.7)
depends on the sequence of intraobservation intervals
{δ1,…,δT}. For a given
sequence, {δ1,…,δT}, the
exact distribution of LF*, and indeed
LF, can again be obtained using the Imhof
(1961) routine, whereas matters again simplify
greatly when δτ is constant across the sample.
3.3. LBI Tests when
δτ Is Constant
Suppose now that the intraobservation interval δτ
is constant, taking the fixed value δ, known as the sampling
interval, throughout the sample. As a consequence we obtain that
Vδ = δW, where W is the
random walk–generating matrix introduced in Section 1.
Consider first the case of a stock variable. Here we immediately
obtain from (3.2) that
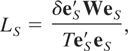
where eS are as defined following (3.2)
but with δτ ≡ δ. This implies that the
elements of eS are simply the demeaned or
detrended observations on yt for the case of
a constant or linear trend, respectively. Similarly, in the case of flow
variables, we obtain from (3.7) that
where eF are similarly the demeaned or
detrended observations on the flow variable Yτ for
a constant or linear trend, respectively.
Given the distributional properties established for the stock data,
yt, in (3.1) and the flow data,
Yτ, in (3.4), it follows immediately from (1.4)
and applications of the continuous mapping theorem (CMT) that, under
H0 of (2.4), LS and
LF* weakly converge, as T →
∞, to δ times a VMξ(1) distribution and
δ2 times a VMξ(1) distribution,
respectively.5
Recall from Section 1 that the
nomenclature VMξ(1), ξ = 1,2, denotes,
respectively, first- and second-level Cramér–von Mises
distributions with one degree of freedom.
Moreover, notice from
the discussion immediately following (3.6) that this result will also hold
for
LF. Indeed, we can say rather more than
that in this case: it is straightforward to show that when
δ
τ is constant throughout the sample, for a given value
of
T,
(
eF′
V*eF)/(
TeF′
eF)
collapses to a constant with respect to
eF.
Consequently,
LF and
LF* will have identical critical regions.
There is, therefore, no loss in efficiency from considering the test based
on the
LF* statistic in this case, which is
exact LBI.
In practice, when constructing the statistics
LS and LF* we
may set the calendar time unit δτ = 1 without altering
the critical regions of the associated tests. We may therefore define the
resulting LBI statistics as LS(δ)
≡ LS /δ and
LF*(δ) ≡
LF*/δ2, respectively,
which clearly coincide with the standard discrete-time stationarity test
statistic,
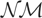
of (1.3), applied to the observed stock and flow data, respectively.
Moreover, both LS(δ) and
LF*(δ) will clearly have pivotal
VMξ(1) limiting null distributions so that the
critical values tabulated in Kwiatkowski et al. (1992) and Harvey (2001) may
be applied directly. For the remainder of this paper, where
δτ is fixed throughout the sample, any reference to LBI
tests will be taken to mean those based on the statistics
LS(δ) and
LF*(δ).
Empirical applications of the standard stationarity tests of Section 1
have concentrated in the main on regularly spaced macroeconomic
aggregates, such as income, output, and consumption, which are, by
definition, flow variables and, hence, will generate nonorthogonal
discrete-time local level models; see the discussion at the end of Section
2. Although Bailey and Taylor (2002) motivated
their research from purely statistical grounds, our results demonstrate
that their findings are also of central importance to the problem of
stationarity testing in economic data. They tell us that the standard
stationarity test will be exact LBI and with the same limiting null
distribution, irrespective of whether the data are generated as a stock or
flow variable, provided the data are observed at regularly spaced
intervals. However, as we shall see in the next section, the power
properties of the LBI tests do differ across the stock and flow cases.
Specifically, we show that the local limiting power function of the LBI
test for stock (flow) data depends (does not depend) on the sampling
frequency, δ−1, and that for a fixed data span
the LBI test for stock (flow) data is consistent (not consistent) against
fixed alternatives as the sampling frequency tends to infinity.
4. TEST POWER AND THE SAMPLING
FREQUENCY
In this section we suppose that the underlying process is generated by
the continuous-time local level model (2.2)-(2.1) for stock variables or
(2.3)-(2.1) for flow variables and that observations on
y(t) are made at intervals of length δ > 0 over
the interval 0 < t ≤ N, where N denotes
the span of the data. The number of observations is therefore given by
T = N/δ, and this quantity will clearly increase
if either N increases or δ decreases, or both. Our aim in
this section is to study the large-sample power properties of the LBI
tests appropriate for stock and flow variables. We first analyze in
Section 4.1 the behavior of the test statistics under a sequence of local
alternatives on the signal-to-noise ratio in the underlying continuous
time models, which are useful for computing the local limiting power
function of the tests as the time span increases to infinity.
Subsequently, in Section 4.2 we look at the large-sample behavior of the
statistics under fixed alternatives to establish the consistency (or
otherwise) of the tests. We show that fundamentally different results
emerge for stock and flow variables. Monte Carlo simulation results and
three empirical illustrations are provided in Sections 4.3 and 4.4,
respectively.
4.1. Behavior under Local Alternatives
The structural parameter of interest in both (2.2)-(2.1) and
(2.3)-(2.1) is the signal-to-noise ratio, q =
ση2/σε2.
For this parameter, a sequence of alternatives local to
H0 of (2.4) in the span of the data, N, is
therefore given by
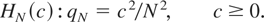
The subscript N has been placed on the signal-to-noise ratio
to highlight that this corresponds to a local alternative hypothesis and
also to distinguish it from the nomenclature used in Section 1. Notice
that ση2 =
c2σε2N−2,
under (4.1). Moreover, for c = 0,
HN(c) again reduces to
H0.
We now analyze the power properties of the LBI tests for both stock
and flow variables under HN(c) of
(4.1) as N → ∞. We show that for stock variables
asymptotic local power is an increasing function of the sampling frequency
δ−1, whereas for flow variables power is unaffected
by δ−1. As is subsequently demonstrated numerically
by Monte Carlo methods in Section 4.3, the asymptotic local distribution
theory provides a good approximation to the finite-sample impact of the
sampling frequency on power in both cases.
Consider first the case of a stock variable. It was demonstrated in
Section 2 that the exact discrete-time analogue of the continuous-time
model (2.2)-(2.1) is a random walk plus noise model with variances
σε2 and
δση2, respectively, observed for
T = N/δ periods. Using (2.6)-(2.7), the derived
signal-to-noise ratio, say qT,S
(where we use S to denote stock), in the discrete-time analogue
under HN(c) of (4.1) is therefore
given by
where
,
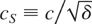
which is clearly an increasing function of the sampling frequency,
δ−1.
Therefore, it immediately follows from the results in Section 3.3 and
a comparison with (1.4) that, for given values of
will be an increasing function of the sampling frequency. The implication
of this is that the asymptotic local power of the LBI test in the case of
a stock variable will be higher the larger is the sampling frequency,
ceteris paribus, being a function of
.
Consider now the model for a flow variable. Noting again from Bailey
and Taylor (2002) that the contemporaneous
correlation between the signal and noise processes has no effect on the
local limiting distribution of the LBI statistic, exactly the same line of
argument can be used to analyze the power properties of the LBI test for
flow variables.
Using (2.9)-(2.10), noting that in this case the signal is
δμτ, it follows that the derived signal-to-noise
ratio for a discretely sampled flow variable, say
qT,F (where F denotes
flow), under the local alternative
HN(c) is given by
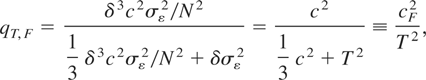
where
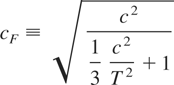
and is clearly such that limT→∞
cF = c. As N → ∞
with δ fixed, we see from (4.3) that the local limiting power of the
LBI test in the case of flow data depends only on ξ and the
noncentrality parameter, c, of (4.1). Crucially, it does not
depend on the sampling frequency δ−1. Consequently,
and in contrast to the case of stock variables, the local limiting power
of the LBI test for a given noncentrality parameter, c, will not
increase with the sampling frequency.
4.2. Behavior under Fixed Alternatives
We now consider the continuous-time model for stock and flow variables
(2.2)-(2.1) and (2.3)-(2.1) under the hypothesis that the signal-to-noise
ratio q =
ση2/σε2
is fixed and strictly greater than zero; that is, we are interested in the
behavior of the tests under a fixed alternative rather than under the
local alternative (4.1) of Section 4.1. In particular we will show that,
for a fixed time span N, as the sampling frequency tends to
infinity (δ → 0) the LBI test is consistent for the case of stock
variables but it is not consistent for flows. Where N →
∞ the test is consistent for both stock and flow data. The proof for
this case is not provided here because it follows immediately from
Kwiatkowski et al. (1992) and Bailey and Taylor
(2002).
Consider first the case of a stock variable. From (2.6)-(2.7), the
discrete time analogue, observed at a fixed time interval δ, can be
written as
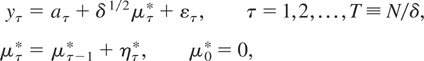
where ετ, ητ* are serially
uncorrelated and mutually orthogonal Gaussian disturbances with variances
σε2 and
ση2, respectively, and
aτ = Xτ′ β is a
deterministic component represented in terms of a k-dimensional
nonstochastic regressor Xτ with associated
coefficient vector β. We assume that Xτ
satisfies standard regularity conditions as in Phillips and Xiao (1998); that is, there exist a scaling matrix
ΛT and a bounded piecewise continuous function
X(r) such that (a) ΛT
X[lfloor ]Tr[rfloor ] → X(r) as
T → ∞ uniformly in r ∈ [0,1];
and (b)
,
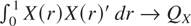
a positive definite matrix, as T → ∞. These
conditions are clearly met if the deterministic component is a constant
level or a linear trend, but they also allow for more general functions
such as piecewise polynomial trends.
From Section 3.3, the LBI statistic takes the form
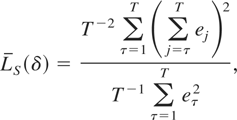
where eτ is the τth element of the vector
of OLS residuals eS, obtained from regressing
the observation vector yS =
(y1,…,yT)′
on the deterministic variables XS =
(X1′,…,XT)′.
As discussed in Section 3.3, (4.4) is the usual form of the LBI test of
stationarity for data sampled at constant intervals.
For a T-dimensional vector z denote by
its orthogonal projection onto the space spanned by
XS, that is, =
XS(XS′XS)−1XS′z,
with zτ being the τth element of
; clearly, if Xτ is a constant
regressor then zτ is just the average of the
elements of z. Then we can write the OLS residuals as
eτ = yτ −
yτ =
δ1/2(μτ* −
μτ*) + (ετ −
ετ). Now, as δ → 0 with
N fixed, and recalling that T = N/δ,
standard applications of the invariance principle and the CMT then yield,
for r ∈ [0,1], the following limiting results:
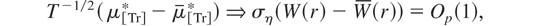
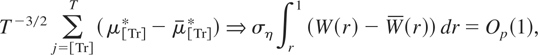
where W(r) is a standard Brownian motion process,
,
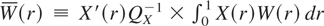
and [·] denotes the integer part of its argument. Notice
that if Xτ is a constant regressor, then
.
Therefore we immediately obtain from (4.5) and (4.6) that
,
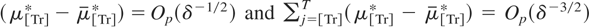
while using similar arguments
.
The numerator of the LBI statistic (4.4) is then seen to be of
Op(δ−1) whereas, because
e[Tr] = Op(1),
the denominator is of Op(1). Consequently, as
δ → 0 with fixed time span N, the LBI statistic (4.4) is
of Op(δ−1), and the
consistency property of the test follows. The qualitative prediction of
this large-sample result also appears evident in the finite-sample
simulation results reported in Table 1 in
Section 4.3.
Consider now the case of a flow variable. From (2.9)-(2.10) the
discrete-time analogue, observed at a fixed time interval δ, can be
written as
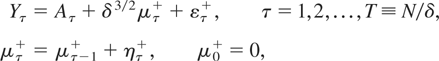
where
(ετ+,ητ+)′
are serially uncorrelated Gaussian disturbances with
and Aτ =
Xτ+ β+ is a
deterministic component. From Section 3.3, the LBI statistic is
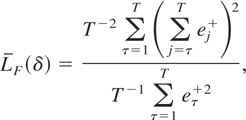
where eτ+ is the τth element of
the vector of OLS residuals eF, obtained from
regressing the observation vector yF =
(Y1,…,YT)′
on the deterministic variables XF =
(X1+′,…,XT+′)′.
Again, (4.7) is the usual form of the LBI test of stationarity for data
sampled at constant intervals.
Noticing that the random walk component in the observation equation is
scaled by δ3/2, rather than δ1/2 as
in the stock variable case, and adapting the previous arguments used for
the stock case, it is easily demonstrated that as δ → 0 with
N fixed, LF(δ) is of
Op(1) and consequently the LBI test is not
consistent in the case of flow data; cf. Table 1
in Section 4.3.
4.3. Monte Carlo Simulations
In this section we use Monte Carlo simulation methods to investigate
the finite-sample power properties of the LBI tests of Section 3.3. All
experiments reported in this paper were programmed using the random number
generator of the matrix programming language Ox 2.20 of Doornik (1998), over 10,000 Monte Carlo replications. All tests
were run at the nominal 5% asymptotic level, although other choices of the
nominal level did not alter the results qualitatively.
Specifically, we simulate data according to the discrete-time
analogues (2.6)-(2.7) for stock data and (2.9)-(2.10) for flow data over a
time span of N = 100 and setting δτ = δ
constant. Without loss of generality we set
σε2 = 1 and compute the tests across a
range of values of ση2 =
c2/N2, for c =
0,2.5,5,10,25, and of the sampling interval
.
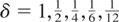
In each case the number of observations is therefore 100/δ.
Notice, therefore, that the implied signal-to-noise ratios in the
discrete-time analogue models for the cases of stock and flow variables
will be δc2/1002 and
,
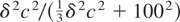
respectively; cf. (4.2)-(4.3).
We may think of this as data from an underlying continuous-time
process observed over a 100-year span at regular discrete intervals in
time corresponding to an annual, biannual, quarterly, bimonthly, and
monthly sampling frequency when
,
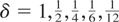
respectively. Without loss of generality, we have set the deterministic
kernel a(t) = 0 in what follows, because our tests are
constructed from exact invariant statistics.
Parts a and b of Table 1 report the
empirical rejection frequencies, as functions of c and δ, for
the tests that reject for large values of the LBI statistics
LS(δ) and
LF*(δ), for stock and flow variables,
respectively. The stock and flow statistics were constructed from the
residual vectors eS and
eF whose elements are the demeaned (ξ = 1
in part a) or detrended (ξ = 2 in part b) observations on the observed
stock and flow variables, respectively. Consequently all of the statistics
possess a VMξ(1) limiting distribution under
H0 of (2.4); cf. Section 3.3. The 5% asymptotic
critical value for the tests is therefore 0.461 for ξ = 1 and 0.149
for ξ = 2; see, for example, Harvey (2001).
Simulated rejection probabilities (× 100)
A number of important observations can be drawn from the results
presented in Table 1. First, in the case where
δ = 1 the power of the tests for stock and flow variables is almost
identical throughout. This is, of course, to be expected given that the
signal-to-noise ratio for stock variables is given by
c2/(T2δ) whereas for flow
variables it tends to c2/T2,
as T, the number of sample observations, increases; see Sections
4.1 and 4.2. Moreover, the observed powers reported in Table 1 for δ = 1 closely correspond with the
limiting power functions of Model A and Model B of Tanaka (1996, p. 390), respectively, despite being obtained
for the moderately small sample size of T = 100.
Second, for the case of flow variables we see from the results in
Table 1 that, ceteris paribus, power does not
increase as the sampling interval δ decreases, as predicted by the
limiting distribution theory in Section 4.2. Indeed, for a given value of
c, there are virtually no differences in power across the various
values of δ considered.
Third, in the case of stock variables we see that power increases as
δ decreases, other things equal. For example, in Table 1, part a, with c = 5 the power for
δ = 1, where we have annual observations on the underlying
continuous-time process, is 30.3%, but for data that have been observed
monthly throughout the sample the power of the test is dramatically
increased to 82.1%. Moreover, as predicted by the limiting distribution
theory in Section 4.1, the finite-sample local power of the test appears
closely related to the quantity
.
For example, c = 2.5,δ = ¼ and c = 5,δ =
1 both give cS = 5, whereas c = 5,
δ = ¼ and c = 10,δ = 1 both equate to
cS = 10. We see from the results in Table 1 that the power of the stock test for
c = 2.5,δ = ¼ and c = 5,δ = 1 is very
similar and is also very similar for c = 5,δ = ¼ and
c = 10,δ = 1.
Finally, notice that, as expected, the simulated powers reported in
part a of Table 1 are higher than the
corresponding entries in part b. This is due to the usual efficiency loss
resulting from the estimation of an extra parameter in the model with a
linear trend.
4.4. Empirical Illustrations
Figure 1 graphs the quarterly seasonally
unadjusted series of the Italian unemployment rate over the period
1980Q1–2003Q4; the data source is Istat, the Italian statistical
office. A random walk plus noise model, where a time-varying seasonal
component is also included as in Harvey (1989,
p. 42), satisfactorily tracks the data, with a standard error of 0.41 and
with no evidence of serial correlation in the Kalman filter residuals. The
maximum likelihood estimates of ση2 and
σε2 are 0.1279 and 0.0109, with
signal-to-noise ratio q = 11.73, whereas the variance of the
seasonal component is only 0.0003. The LBI test, applied to the seasonally
adjusted data,6
The data were seasonally
adjusted in the context of the basic structural model of Harvey (1989, p. 47), using the inbuilt seasonal adjustment
procedure in the STAMP 6.0 package of Koopman et al. (2000).
provides a sound rejection of the null
hypothesis of stationarity: the statistic (4.4) is equal to 1.827 compared
with the 10%, 5%, and 1% asymptotic critical values, which from Harvey
(
2001, p. 4) are 0.347, 0.461, and 0.743,
respectively. Even with a (superfluous) nonparametric long-run variance
correction of the form considered in Kwiatkowski et al. (
1992, pp. 164–165) employed, the null is still
rejected at at least the 5% significance level when a lag truncation of
three or less is used in the long-run variance estimator. As the
unemployment rate is a stock variable, on the basis of the foregoing
theoretical development one would expect, other things equal, less
evidence for rejection under the alternative if the stationarity test were
to be applied to annual data. Indeed, the LBI statistic applied to the
annual data (with no long-run variance correction) takes the greatly
reduced value 0.374, which is now only a borderline rejection at the 10%
significance level. It is also interesting to notice that fitting a random
walk plus noise model to the annual data yields
σ
η2 = 0.6418 (with
σ
ε2 approximately zero); this is not
inconsistent with what one would compute by multiplying by four the
variance in the quarterly model; cf. (2.6)-(2.7).
Italian unemployment rate, 1980Q1–2003Q4.
Consider now Figure 2, which graphs annual
and biennial data (the latter divided by two in the graph) on the flow of
the Nile over the period 1871–1970. The unit of measurement is cubic
meters times 108; see Koopman, Harvey, Doornik, and Shephard
(2000). It is known that the Aswan dam was
constructed in 1899, and consequently one has to account for a structural
break in the level of the series. The stationarity tests therefore have to
be run with a level change in the deterministic component. Critical values
for this case are provided in Busetti and Harvey (2001); for a breakpoint fraction equal to 0.3 the 10%
asymptotic critical value is 0.189. The LBI statistic for the biennial
data takes the value 0.086, signaling no evidence that a random walk
component is present in the data. Consonant with the large-sample theory,
doubling the number of observations by running the test on the annual data
does not alter our inference; the LBI statistic takes the value 0.089,
which is virtually unchanged from that obtained from the biennial
data.
Flow of the Nile, 1871–1970.
Figure 3 depicts the monthly inflation rate
in Japan, computed as first difference of the logarithm of the Consumer
Price Index; the source is the Bank of International Settlements.
Inflation can be regarded as a flow variable because it is the first
difference of a stock and it is clearly measured with respect to an
interval of time. Quarterly inflation can be calculated equivalently as a
three-period average of the monthly data or as the three-month differences
of the logarithm of the price index. To allow for serial dependence in the
series, we calculated the KPSS statistic (Kwiatkowski et al., 1992, equation (13), p. 165) (notice that this is just
the LBI statistic of (4.7) with the OLS variance estimator in the
denominator replaced by a corresponding long-run variance estimator), on
both monthly and quarterly inflation. We computed KPSS statistics over the
full-sample data (1985–2002, with a time span, N, equal to
72 quarters) and over the two subsamples 1985–1993 and
1994–2002, each of which has N = 36. The statistics were
calculated for two values, x = 4 and x = 8, of the lag
truncation parameter suggested in Kwiatkowski et al. (1992), [ell ] =
int[x(T/100)1/4], where
T is the number of sample observations. To account for
deterministic seasonal fluctuations in the series, the residuals used in
computing the statistics were obtained in each case from regressing the
observed data on a set of conventional seasonal dummies. Doing so does not
alter the large-sample behavior of the resulting statistics
vis-à-vis the case where only a constant is included; cf. Phillips
and Jin (2002).
Inflation rate in Japan, 1985M1–2002M12.
For the full-sample data there is rather strong evidence against the
null hypothesis of stationarity: for the monthly data with x = 4
and x = 8 the KPSS statistic takes the values 0.863 and 0.662,
respectively, which are significant at the 1% and 5% significance levels,
respectively; for the quarterly data the corresponding outcomes are 0.573
and 0.420, which are significant at the 5% and 10% levels, respectively.
In contrast, for the first subsample, 1985–1993, the outcomes for
the monthly (quarterly) data with x = 4 and x = 8 are
0.367 and 0.330 (0.311 and 0.229), whereas for the second subsample,
1994–2002, the corresponding outcomes are 0.282 and 0.283 (0.283 and
0.235), all but the first of which are insignificant at the 10% level.
These outcomes are consistent with the theoretical prediction that the
power of the test can only be increased by enlarging the span of the data.
Qualitatively similar results were also found for other subsamples of
length N = 36, so that the observed results are not merely
attributable to the particular sample split reported.
5. STATIONARITY TESTS WITH MIXED FREQUENCY
DATA
As Harvey (1989, p. 325) comments, “A
series may sometimes consist of observations at two different timing
intervals. For example, observations may, at first, only be available on
an annual basis, whereas later on they are collected every quarter.”
In this section we explore the impact of such mixed frequency data on
tests of H0 of (2.4) against H1 of
(2.5) for both stock and flow variables. Because both subsamples include
information about the trend, how we handle the mixed frequency data is
potentially important for the power properties of the resulting test.
In this section we derive the exact LBI tests for both stock and flow
variables in cases where we have a sample of mixed frequency data. We show
that the LBI statistics have nonpivotal limiting distributions. We compare
the exact LBI tests with simple modifications of these statistics,
constructed to have pivotal limiting distributions, and also tests that
are constructed from the aggregated data. The former are obtained by
applying the statistic
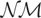
of (1.3) to each of the two subsamples and adding the resulting
statistics together, whereas the latter are tests that aggregate the more
frequently observed data so as to have the same sampling frequency as the
data from the first interval; see Harvey (1989,
p. 310).
In what follows, we suppose that for some λ ∈ [0,1]
the first [λT] observations have been made with a
sampling frequency of one, possibly annually as in Harvey's example
given previously, whereas the remaining T −
[λT] observations are made with a sampling
frequency of δ−1 ≥ 1;7
One might also consider the case where
δ−1 ≤ 1, that is, where observations become
available at less frequent intervals after time
[λT]. The theory that follows is also appropriate
to this case, but we choose to focus on δ−1 ≥ 1
because this seems more likely in practice. Moreover, although we have set
the sampling frequency in the first subsample to be one this also involves
no loss of generality.
for example, the case where the first half
of the available sample data consists of annual observations and the
second half of quarterly observations corresponds to λ = 0.5 and δ
= ¼. The corresponding sequence of intraobservation intervals will
therefore be given by
Consequently, the LBI tests for H0 of (2.4)
against H1 of (2.5) for the case of stock and flow
variables reject for large values of the statistics given in (3.2) and
(3.6), respectively, on setting the δτ as before in the
formulation thereof. Moreover, notice that
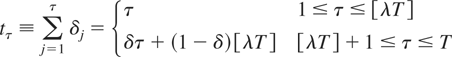
and thus N ≡ tT =
[λT] + δ(T −
[λT]).
The limiting distribution of the LBI statistic for the case of a stock
variable, LS, under H0 of
(2.4) follows using (3.3), (C.4) in Appendix C, and the CMT.
Specifically,
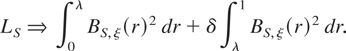
The form of the limiting process
BS,ξ(r) depends on the
deterministic component a(t). For ξ = 1, the
constant case, it was demonstrated in Section 2.1 that
aτ = a in (2.6)-(2.7), regardless of
δτ, and hence eS are
simply the demeaned observations on yτ.
Consequently, BS,1(r) will be a
standard Brownian bridge process. For ξ = 2, the linear trend case,
the form of the limiting process
BS,2(r) is more complicated and is
given in part C1 of Appendix C.
Turning to the flow variable case, the limiting distribution8
Recall from Section 3.2 that
LF* and LF are
asymptotically equivalent.
of
LF*
under
H0 of (2.4) can similarly be established as
Again the form of the limiting process
BF,ξ(r) depends on
a(t). For ξ = 1, it follows from the results in
Section 2.2 that Aτ = a for 1 ≤ τ
≤ [λT] and Aτ =
aδ for [λT] + 1 ≤ τ ≤
T, in (2.6)-(2.7). It then follows that the residual vector
eF has τth element
from which it follows, as demonstrated in part C2 of Appendix C,
that
where J ≡ (λ + δ(1 −
λ))−1(W(λ) +
δ1/2(W(1) − W(λ))) and
W(r) is a standard Brownian motion. The form of the
limiting process BF,2(r) is more
complicated and is given in part C3 of Appendix C.
As is clear from (5.2) and (5.3) the limiting null distributions of
the LS and LF*
statistics depend in a complicated manner on two nuisance parameters,
δ and λ. Consequently, asymptotic critical values for the two
tests will need to be tabulated across these two parameters. In parts a
and b of Table 2 we present the upper-tail 1%,
5%, and 10% fractiles from the right members of (5.2) and (5.3),
respectively, for
,
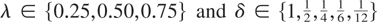
for both ξ = 1 (constant) and ξ = 2 (linear trend). In each case
these were calculated via direct simulation (i.e., approximating the limit
functionals using partial sums of normal random variables) for T
= 5,000, using 50,000 Monte Carlo replications.
Upper tail fractiles from the asymptotic null distributions of the
LS and LF*
statistics
There is, however, a simple way of obtaining statistics in both stock
and flow cases that have pivotal limiting null distributions in the
presence of mixed frequency observations. In what follows the subscript
index i is used to denote either the case of a stock variable,
i = S, or of a flow variable, i = F.
Define the vectors of OLS residuals
,
as follows. For the case of stock variables these are obtained from
regressing yτ on either
(1,hτ(λ))′, for the constant case, or,
for the linear trend case,
(1,τ,hτ(λ),τhτ(λ))′,
τ = 1,…T, where hτ(λ)
≡ 1(τ ≤ [λT]), 1(·) the usual
indicator function. For the case of flow variables the same regressions
are computed on replacing yτ by
Yτ.
Using these residuals we then construct the modified statistics
It is important to notice that for both stock and flow variables, the
left member of (5.4) is constructed by applying the statistic
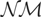
of (1.3) separately to each of the two subsamples,
{1,…,[λT]} and {[λT]
+ 1,…,T}, of stock or flow data and then taking the sum of
the two resulting subsample statistics. In doing so we are clearly
ignoring the information on the sequence of intraobservation intervals
δτ, τ = 1,…,T.
Because, in all cases considered,
,
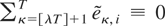
the two terms that appear in the right member of (5.4) are asymptotically
independent. Consequently, it trivially follows from the results in
Section 3 and the CMT that, under H0 of (2.4),
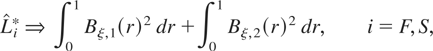
where Bξ,1(r) and
Bξ,2(r) are independent
VMξ(1) distributions, ξ = 1,2. By the additive
properties of the Cramér–von Mises family of distributions
(see Busetti and Harvey, 2001, p. 136), we
obtain that the right member of (5.5) is a pivotal ξth-level
Cramér–von Mises distribution with two degrees of freedom,
denoted VMξ(2), ξ = 1,2. Critical values from
the VM1(2) and VM2(2)
distributions are tabulated in Nyblom and Harvey (2000) and Harvey (2001).
One might also consider aggregating the second subsample of data such
that the aggregated observations in the second subsample have the same
sampling frequency as the data from the first interval. The aggregated
stock and flow data are given by
,
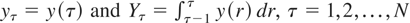
which we collect into the N-dimensional vectors
yS* =
(y1,y2,…,yN)′and
yF* =
(Y1,Y2,…,YN)′,
respectively. We then simply apply the standard stationarity test,
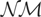
of (1.3), to yS* and
yF*, respectively. In what follows we will
denote the resulting statistics as LS,0 and
LF,0*, respectively. It is trivial to show
that both LS,0 and
LF,0* weakly converge under
H0 of (2.4), as T → ∞, to
VMξ(1) distributions, ξ = 1,2. For ξ = 1
the residuals used in constructing the LS,0
and LF,0* statistics are the demeaned
yS* and yF*,
respectively, whereas for ξ = 2 they are formed as the detrended
yS* and yF*,
respectively.
Both the modified statistics of (5.4) and the statistics based on the
aggregated data ignore the infraperiod aspect of the data. One might
expect that in the case of flow variables these tests will have very
similar power properties to the test based on
LF* (which is approximately LBI) because, as
shown in Section 4, power does not increase with the sampling frequency in
the case of flow variables. In contrast, the results in Section 4.3 would
lead us to expect significant power losses from ignoring the infraperiod
information in the case of stock variables. We now use numerical methods
to explore these issues further.
5.1. Monte Carlo Simulations
In this section we simulate mixed frequency data for
.
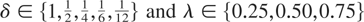
Using the observed data, yτ (stock) and
Yτ (flow), we compute the statistics
.
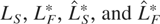
The first two statistics are then compared with the asymptotic 5%
critical values from Table 2, parts a and b, and
the latter two with the upper 5% point from the
VMξ(2) distribution, that is, 0.748 for a constant
level ξ = 1 and 0.247 for the linear trend case ξ = 2; see, for
example, Harvey (2001). In addition we also
consider the standard
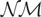
statistics, denoted LS,0 and
LF,0*, applied to the aggregated stock and
flow data, yS* and
yF*, as described previously.
Specifically, we simulate the local level process (1.1)-(1.2) for
t = 1,2,…,96/δ, across
.
Taking δ = 1 to represent yearly data, we consider the cases of
annual observations that become biannual, quarterly, bimonthly, monthly
when δ assume the values
,
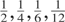
respectively. The signal-to-noise ratio is set to
ση2/σε2
= c2/(96/δ)2, for c =
0,2.5,5,10, so that we may simulate the power functions of the tests in
terms of the magnitude of the local alternative hypothesis in a process
generated with constant sampling frequency δ−1.
From this underlying data generating process (DGP) we obtain mixed
frequency observations for stock and flow variables, where the first
[λT] observations are sampled with unit frequency
(annual) and the remaining T − [λT]
observations are sampled with frequency δ−1 ≥ 1.
In particular, for each δ, data have been generated with frequency
δ−1 and then aggregated only in the first subsample
to obtain observations with unit frequency.9
Notice that the Monte Carlo experiments reported in this
section involve (partial) temporal aggregation over fixed time intervals
and thus are slightly different from those of Section 4.3, where data were
generated from the exact discrete-time analogues of the underlying
continuous-time process.
Notice that
T = 96 in all
cases, whereas λ varies among {0.25,0.50,0.75}.
Parts a–c of Table 3 report the
empirical rejection frequencies, as functions of c, δ, and
λ, for the tests that reject for large values of the LBI statistics
LS, LF*, the
simplified statistics
,
and the standard
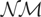
statistics LS,0,
LF,0* applied to the aggregated stock and
flow data, as explained in the previous section. Notice that the latter
two are computed for a number of observations equal to (λ + δ(1
− λ))T ≤ T.
Simulated rejection probabilities (× 100) for the mixed
frequency DGP
First notice that for δ = 1 the results in Table 3, parts a–c, are much the same because
here the observation frequency is constant throughout the sample.
Moreover, here the results for the LBI tests closely resemble the
simulated local limiting powers reported in Table
1, parts a and b, for δ = 1. Notice also that in Table 3, parts a–c, but not in Table 1, parts a and b, the time span N
increases as δ reduces: N = (λ/δ + 1 −
λ)T. It is therefore no surprise that the simulated power of
the tests for both stock and flow turns out to be, in general, an
increasing function of the sample frequency δ−1.
Consider now in particular part b of Table
3, where λ = 0.5, that is, the case where half of the data are
observed on an annual basis and the remaining half at higher frequency.
The empirical size, contained in the first six rows of the table where
c = 0, is reasonably close to the nominal asymptotic 5% level for
all reported tests. For stock variables the highest power is achieved by
using the LBI test LS. Here the power loss
from ignoring the more finely available observations and running the
standard Nyblom and Mäkeläinen (1983)
test on the aggregated data, namely, using the statistic
LS,0, is not negligible; for example, in the
case of constant level with
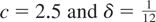
the use of the LBI test yields power of 42.1%, as against 26.8% when
using the corresponding aggregated data. Despite using all available data,
the modified test
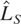
that combines the evidence in the two subsamples is less powerful than
,
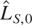
with power of 21.3% in the foregoing example. This is attributable to the
efficiency loss incurred by having to estimate additional parameters. For
flow variables, on the other hand, the power losses from using aggregate
data appear negligible. In the example used previously, where
,
the rejection frequencies are 77.8% for the LBI test
LF* and 74.5% for the Nyblom and
Mäkeläinen test LF,0* for the case
of constant level. Again, and for the same reason, lower power, 65.9%, is
obtained by running the modified test
.
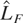
The results for the linear trend case are qualitatively similar to
those reported for a constant level, although for each configuration of
δ, λ, and c power is smaller. This is analogous to what
happens in the standard Nyblom and Mäkeläinen (1983) tests; cf. Kwiatkowski et al. (1992).
The results reported in parts a and c of Table
3, where λ is 0.25 and 0.75, respectively, are also broadly
similar to the corresponding results for λ = 0.50. The main difference
is the lower (respectively higher) power than in part b. This can be
easily explained by looking at the span of the data N =
(λ/δ + 1 − λ)T, which, for δ < 1, is
increasing in λ.
In summary, the Monte Carlo results strongly suggest using the LBI
test if the variables are stock; the critical values for λ ∈
{0.25,0.50,0.75} are provided in parts a and b of Table
2; for other values of λ they can be obtained from the authors
on request. For flow variables, on the other hand, it appears that
near-efficient tests can be obtained even when one ignores the more finely
available observations, because, as we have already seen, the limiting
power properties of the tests for flow variables depend on the span of the
data and not the number of sample observations.
6. CONCLUSIONS
Using a continuous-time framework in this paper we have derived
locally best invariant (LBI) stationarity tests for both stock and flow
data available at potentially irregularly spaced points in time. The
resulting tests were shown to differ between stock and flow variables. The
special case of mixed frequency data was analyzed in detail with
asymptotic critical values and a power study provided. Our results
suggested that tests based on statistics that ignore the infraperiod
aspect of the data, such as those constructed from aggregated data,
involve rather small losses in efficiency, relative to the LBI test, for
the case of flow variables but can incur significant efficiency losses
when dealing with stock variables. We have also demonstrated that where
the data are observed at regular intervals throughout the sample the LBI
tests for stock and flow data reduce to the form of the standard
stationarity test of, inter alia, Nyblom and Mäkeläinen (1983) applied to the observed stock and flow data,
respectively. These statistics were shown to have Cramér–von
Mises limiting null distributions. For regularly sampled data we also
demonstrated that the asymptotic local power of the LBI test increases
with the sampling frequency in the case of stock variables but not for
flow variables. Moreover, for a fixed time span the LBI test for stock
variables was shown to be consistent against a fixed alternative as the
sampling frequency increased to infinity. This was shown not to be true in
the case of flow variables.
Although we have focused on issues concerned with testing against a
unit root at frequency zero, the analysis of this paper can be extended to
the seasonal stationarity tests developed in, inter alia, Canova and
Hansen (1995). As an example, if one had mixed
frequency data observed first annually and then subsequently quarterly it
is clear that only the second subsample contains information useful in
constructing tests against seasonal frequency unit roots. However, if our
data were available first quarterly and then monthly, information on the
seasonal spectral frequencies π and π/2 (3π/2) would
be contained in both subsamples. Consequently, seasonal unit root tests
for mixed frequency data, akin to those developed in Section 5, can be
constructed to be more powerful (in the case of stock variables) than
those based on data where the monthly data are aggregated to quarterly
data. Moreover, by adopting a continuous-time framework one can also show
that, in the case of stock variables, tests against, for example, a pair
of complex conjugate unit roots at frequency π/2 (3π/2)
will be consistent against fixed alternatives for the case where a fixed
data span is available but where the sampling frequency tends to infinity
as a multiple of four.
APPENDIX A
From (2.2)-(2.1) we have that
where integrals are defined in the wide sense, with the exception of
those taken with respect to the random measure; see Bergstrom (1984). Defining
,
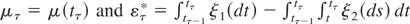
write (A.1) as
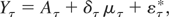
where the transition equation is given by
with
.
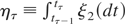
Using, for example, the results of Bergstrom (1984, 1986), we first have
that
.
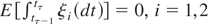
Moreover,
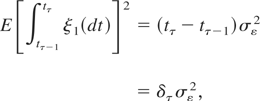
and, similarly, E
[ητ]2 =
δτση2, which establishes
the result for Var(ητ). Notice also that
{ητ} is serially independent.
The result for Var(ετ*) follows from (A.2) and
noting that
Again notice that {ετ*} is serially independent.
Finally,
whereas all noncontemporaneous covariances are zero.
APPENDIX B
From (2.9)-(2.10) the DGP for Yτ* ≡
Yτ − Aτ is given by
.
Consequently,
and, hence,
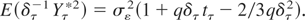
Similarly, for τ < s,
and, consequently,
APPENDIX C: Limiting Distributions of LBI
Statistics for Mixed Frequency Data
C1: Stock Variables with Linear Trend.
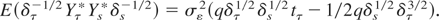
Under H0 of (2.4) the discrete-time model may be
written as
where
Let
denote the OLS estimators from (C.1). Using the following limiting
results (see also Busetti and Harvey, 2001, p.
146):
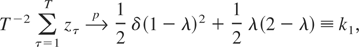
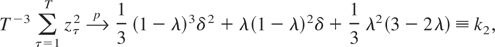
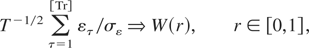
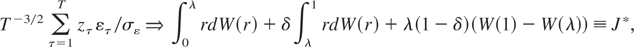
where W(r), r ∈ [0,1], is a
standard Brownian motion process, it is straightforward to establish
that
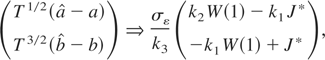
where k3 ≡ k2 −
k12.
Now, let
,
denote the corresponding OLS residuals from (C.1). Using the foregoing
limiting results and applications of the CMT we obtain that
where
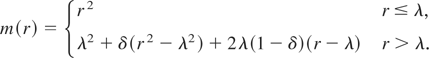
Notice that because there is a constant term in the regression,
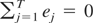
and thus
.
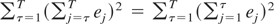
Because
,
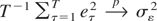
the stated limiting distribution, (5.2), then follows immediately using
applications of the CMT. Notice that for λ = 0,1 and/or δ = 1,
BS,2(r) reduces to a standard
second-level Brownian bridge process.
C2: Flow Variables with Constant Level.
Under H0 of (2.4) the discrete-time model may be
written as
where
The OLS estimator
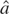
from (C.6) therefore satisfies
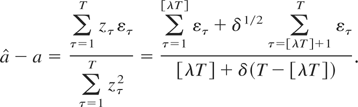
Proceeding as in part C1 of this Appendix, it is straightforward to
show that
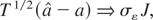
where J = (λ + δ(1 −
λ))−1(W(λ) +
δ1/2(W(1) − W(λ))) and
W(r), r ∈ [0,1], is a standard
Brownian motion process. Routine algebra establishes that
where
,
are the OLS residuals from (C.6). Using (C.8) and applications of the CMT
it is straightforward but tedious to demonstrate that
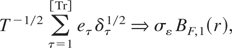
where BF,1(r) is as defined in
the main text. Notice that for λ = 0,1 and/or δ = 1,
BF,1(r) reduces to a standard
Brownian bridge process. The stated result then follows directly from
(C.9), (C.10), applications of the CMT, and the fact that
.
C3: Flow Variables with Linear Trend.
Under H0 of (2.4) the discrete-time model may be
written as
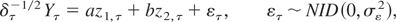
where
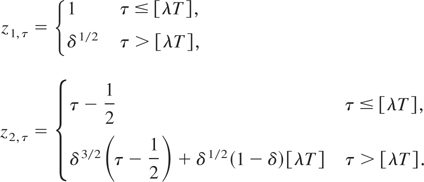
Using the following limiting results (see also Busetti and Harvey,
2001, p. 146):
where W(r), r ∈ [0,1], is a
standard Brownian motion process, it is straightforward to demonstrate
that
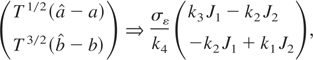
where k4 = k1
k3 − k22.
Now let
,
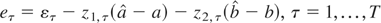
denote the OLS residuals from (C.11). Consequently, from the foregoing
limiting results and applications of the CMT, we obtain that
where
and where fa(r) = δ(1
− r), fb(r) =
½δ2(1 − r2) + λδ(1
− δ)(1 − r), Ja =
k4−1(k3
J1 − k2
J2), Jb =
−k4−1(k2
J1 − k1
J2). The stated result then follows directly from
(C.9), where eτ, τ = 1,…,T, in
(C.9) are now the OLS residuals from (C.11), applications of the CMT, and
the fact that
.
Again, notice that for λ = 0,1 and/or δ = 1,
BF,2(r) reduces to a standard
second-level Brownian bridge process.
