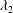1 Introduction
As a fundamental process in both classical and quantum turbulence, vortex reconnection has been intensively studied over recent decades (see, for example, Kida & Takaoka Reference Kida and Takaoka1994). Inspired by the recent experiment of Kleckner & Irvine (Reference Kleckner and Irvine2013) on the dynamics of a trefoil-knot vortex, we have considered a linearised model in which two skewed Burgers-type vortices are driven together by an axisymmetric straining velocity field (Kimura & Moffatt Reference Kimura and Moffatt2014). Within the limitations of that model, we demonstrated that the time scale of reconnection is independent of kinematic viscosity
$\unicode[STIX]{x1D708}$
in the limit
$\unicode[STIX]{x1D708}\rightarrow 0$
and that the initial helicity associated with the skewed configuration decays to zero during the reconnection process.
To elucidate the nonlinear effect of vortex–vortex interaction on the reconnection process, we then investigated the evolution of a vortex filament in the form of a figure of eight (an 8 nearly flattened on a plane), using a Biot–Savart model (Kimura & Moffatt Reference Kimura and Moffatt2017, hereafter KM17). In this, the closed loop of the filament was discretised into piecewise linear segments, and the velocity of each segment was calculated by evaluating the Biot–Savart integral as a sum of the interactions from all other segments (the cutoff method). While the ring sections of the figure-of-eight vortex move in opposite directions, the central sections first deform to a nearly antiparallel configuration and ultimately collide, producing a pair of cusps in the process. By systematically varying the number of segments, we controlled the numerical resolution and showed that the minimum separation of the colliding cusps scales as
$(t_{c}-t)^{1/2}$
, where
$t_{c}$
is the estimated collision time. We verified also that the scalings of the maximum velocity and the axial stretching rate at the cusps are very close to
$(t_{c}-t)^{-1/2}$
and
$(t_{c}-t)^{-1}$
, respectively. These are the scalings first obtained by Leray (Reference Leray1934) for possible self-similar solutions of the Navier–Stokes equations.
Scrutiny of the vortex configuration just before the instant of reconnection
$t_{c}$
suggests that there may exist a universal geometric configuration leading up to, and even during, the vortex reconnection process. We suggested this in KM17, in conformity with de Waele & Aarts (Reference de Waele and Aarts1994), who argued that a symmetric pyramid (or tent) structure, with a range of apex angle depending on initial conditions, is invariably formed before reconnection. (We note, however, that Tebbs, Youd & Barenghi (Reference Tebbs, Youd and Barenghi2011) have argued, on the basis of the Gross–Pitaevskii equation, that there may be other routes to reconnection.) In § 2 of the present paper, we investigate the approach further, starting with two initially tilted hyperbolic vortex filaments; this provides a simple representation of vortex reconnection, revealing some of the geometric properties involved. Two movies showing the approach to the reconnection singularity may be found in the supplementary movies available at https://doi.org/10.1017/jfm.2017.769.
There is much current interest in vortex reconnection in superfluid helium, usually studied through the Gross–Pitaevskii equation. Reconnection events have been experimentally detected, notably by Bewley et al. (Reference Bewley, Paoletti, Sreenivasan and Lathrop2008) and Fonda et al. (Reference Fonda, Meichie, Ouellette, Hormoz and Lathrop2014). A variety of reconnection events have also been very recently detected in a Bose–Einstein condensate (Serafini et al. Reference Serafini, Galantucci, Iseni, Bienaimé, Bisset, Barenghi, Dalfovo, Lamporesi and Ferrari2017). Experimental techniques in these contexts are developing rapidly, and provide added motivation for the present study.
In the classical fluid context, the Biot–Savart model can survive only for so long as the vortex cores (finite in reality) are not significantly deformed by the local straining process. For this reason the rate-of-strain tensor in the neighbourhood of the vortex tips plays a crucial role; we investigate its structure in § 3.
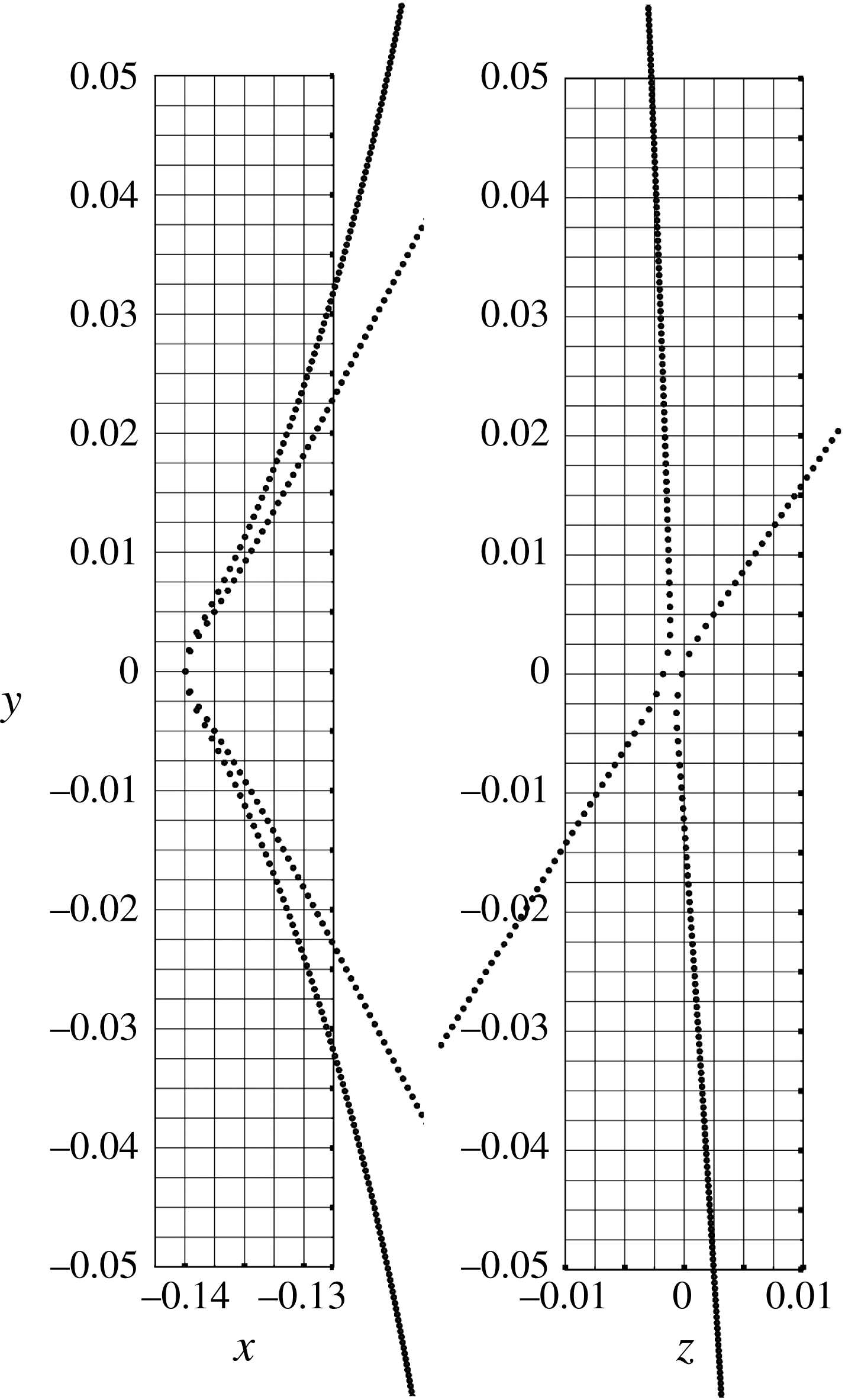
Figure 1. Blowup projections of the vortex configuration at the estimated reconnection time
$t=0.330772$
for the figure-of-eight vortex (Kimura & Moffatt Reference Kimura and Moffatt2017).
2 Tent model
Figure 1 shows two blowup projections of the centre part of the figure-of-eight vortex at the estimated reconnection time
$t=0.330772$
, with the number
$n$
of discretised segments (and so of nodes) equal to
$2^{15}=32\,768$
. The projection on the
$yz$
-plane (right) suggests rather strongly that the central sections are hyperbolic in shape. If however we look at the projection on the
$xy$
-plane (left), we see that the two branches of the hyperbola are not on a single plane but on planes symmetrically tilted at an angle
$\unicode[STIX]{x1D703}$
, say, to the horizontal.
Based on these observations, we propose the following parametrised curves for the branches of a ‘tilted hyperbola’, with circulations
$\unicode[STIX]{x1D6E4}_{1}$
and
$\unicode[STIX]{x1D6E4}_{2}\,(=-\unicode[STIX]{x1D6E4}_{1})$
, as the initial condition for a new ‘tent model’ of vortex-filament reconnection:
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{1}:\left\{\begin{array}{@{}l@{}}x(p,t)=c\cosh p\cos \unicode[STIX]{x1D703}\\ y(p,t)=(c/m)\sinh p\\ z(p,t)=-c\cosh p\sin \unicode[STIX]{x1D703}\end{array}\right.\quad \unicode[STIX]{x1D6E4}_{2}:\left\{\begin{array}{@{}l@{}}x(p,t)=-c\cosh p\cos \unicode[STIX]{x1D703}\\ y(p,t)=(c/m)\sinh p\\ z(p,t)=-c\cosh p\sin \unicode[STIX]{x1D703}\end{array}\right.\quad (-\infty <p<\infty ).\end{eqnarray}$$
These expressions are obtained by first parametrising a hyperbola
$x^{2}-m^{2}y^{2}=c^{2}$
and then imposing tilts symmetrically from the horizontal plane through angles
$\pm \unicode[STIX]{x1D703}$
; we may describe the resulting curve as a ‘tilted hyperbola’ of two branches. We shall allow for time dependence of the length scale of the interaction region
$c$
. Note that the arclength
$s(p)$
on either branch measured from
$p=0$
is given by
$|\text{d}\boldsymbol{x}/\text{d}s|=1=|\text{d}\boldsymbol{x}/\text{d}p|\,|\text{d}p/\text{d}s|$
, so that
$$\begin{eqnarray}s(p)=\frac{c}{m}\int _{0}^{p}(\cosh ^{2}q+m^{2}\sinh ^{2}q)^{1/2}\,\text{d}q.\end{eqnarray}$$
The radius of curvature at the tip of the hyperbola (
$p=0$
) is
$R_{0}=c/m^{2}$
. Taking
$kR_{0}$
as a characteristic length scale for suitable choice of
$k$
, we may non-dimensionalise with respect to this scale. We have adopted values
$c=0.1,m=0.35$
in the computations described below. This corresponds to the choice
$k=(0.35)^{2}/0.1\approx 1.225$
, and to an angle
$2\cot ^{-1}\unicode[STIX]{x1D6FC}\approx 141^{\circ }$
between the asymptotes of the hyperbola. If
$m$
and
$c$
are varied, then details (e.g. the singularity time
$t_{c}$
) change, but the results are qualitatively stable. As regards
$\unicode[STIX]{x1D703}$
, we adopt the value
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/4$
; there are good reasons for this choice, as will emerge in § 3 below.
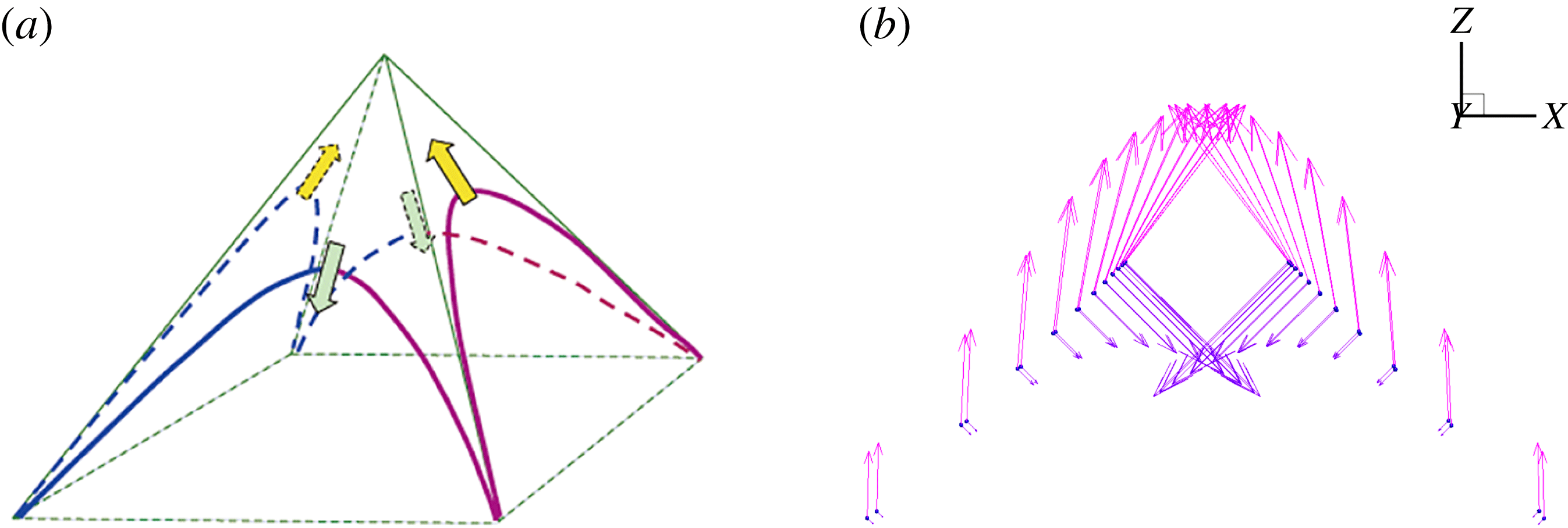
Figure 2. (a) Schematic view of the tent model. (b) Initial velocity vectors at points on
$\unicode[STIX]{x1D6E4}_{1}$
and
$\unicode[STIX]{x1D6E4}_{2}$
for
$m=0.35$
,
$c=0.1$
and
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/4$
in the
$xz$
-plane; pink vectors are total velocity
$\boldsymbol{v}_{1}+\boldsymbol{v}_{2}$
, and purple the self-velocity
$\boldsymbol{v}_{1}$
.
The Biot–Savart model is based on the Euler equations and, without viscosity or any other regularisation mechanisms, the solution diverges at
$t=t_{c}$
when the tips of the vortices collide and the curvature and velocity become infinite at the apex of the tent. If viscosity or any other regularisation mechanism is present, then the formation of a singularity may be averted and smooth reconnection can then presumably occur.
The tent model, as sketched in figure 2, can be continued to the post-reconnection situation on the assumption that the vortices simply exchange pairs on the edges of the tent at the moment of reconnection. Then two new vortices are located on the complementary surfaces of the tent. These new vortices are so oriented that they move apart, and the simplest assumption is that they ultimately recede on these complementary surfaces. Actually, the post-reconnection situation is in practice complicated by the fact that Kelvin waves are generated at the moment of reconnection and then propagate down the two vortices (Fonda et al.
Reference Fonda, Meichie, Ouellette, Hormoz and Lathrop2014). Ignoring this complication, with
$\unicode[STIX]{x1D70F}=t-t_{c}$
, and writing the vorticity field (2.1) before the singularity (
$\unicode[STIX]{x1D70F}<0$
) as
$\unicode[STIX]{x1D74E}(x,y,z,\unicode[STIX]{x1D70F})$
, then this simplest assumption would imply that the vorticity field after the singularity (
$\unicode[STIX]{x1D70F}>0$
) is obtained by reversing the sign of
$\unicode[STIX]{x1D74E}$
and rotating the configuration through
$\unicode[STIX]{x03C0}/2$
about the
$z$
-axis, i.e. for
$\unicode[STIX]{x1D70F}>0$
,
$$\begin{eqnarray}\unicode[STIX]{x1D74E}(x,y,z,\unicode[STIX]{x1D70F})=-\unicode[STIX]{x1D74E}(y,-x,z,-\unicode[STIX]{x1D70F}).\end{eqnarray}$$
The post-singularity tilted hyperbola may be said to be ‘conjugate’ to the pre-singularity tilted hyperbola. In the post-singularity situation, the change of sign of vorticity at the tips is what makes the vortices recede down the sloping faces of the tent. We note that the Euler equations admit the symmetry
$\boldsymbol{u}(\boldsymbol{x},\unicode[STIX]{x1D70F})=-\boldsymbol{u}(\boldsymbol{x},-\unicode[STIX]{x1D70F})$
,
$\unicode[STIX]{x1D74E}(\boldsymbol{x},\unicode[STIX]{x1D70F})=-\unicode[STIX]{x1D74E}(\boldsymbol{x},-\unicode[STIX]{x1D70F})$
; here, this symmetry is observed, but with the additional instantaneous rotation of the configuration through
$\unicode[STIX]{x03C0}/2$
about the
$z$
-axis at the singularity time
$\unicode[STIX]{x1D70F}=0$
. Under time reversal, the whole process is simply reversed.
This proposed model is consistent with the conclusion of de Waele & Aarts (Reference de Waele and Aarts1994) that a tent structure is formed by vortices as a universal route to reconnection; the asymptotes of our tilted hyperbola correspond to the edges of the tent and the vortices tend to the asymptotes, while the tips of the vortices approach the summit if
$c\rightarrow 0$
as
$t\rightarrow t_{c}$
. A similar model, but with different parametrisation, has been discussed by Boué et al. (Reference Boué, Khomenko, L’vov and Procaccia2013).
Substituting (2.1) into the Biot–Savart integral (as applied to vortex filaments, here with
$\text{d}\boldsymbol{x}=\boldsymbol{x}^{\prime }(s)\,\text{d}s=\boldsymbol{x}^{\prime }(p)\,\text{d}p$
),
$$\begin{eqnarray}\boldsymbol{u}(q)=-\frac{\unicode[STIX]{x1D6E4}}{4\unicode[STIX]{x03C0}}\int _{-\infty }^{\infty }\frac{(\boldsymbol{x}(q)-\boldsymbol{x}(p))\wedge \boldsymbol{x}^{\prime }(p)\,\text{d}p}{|\boldsymbol{x}(q)-\boldsymbol{x}(p)|^{3}},\end{eqnarray}$$
we obtain the velocity at
$q$
on
$\unicode[STIX]{x1D6E4}_{1}$
induced by
$\unicode[STIX]{x1D6E4}_{1}$
(its ‘self-velocity’) as
$$\begin{eqnarray}\boldsymbol{v}_{\mathbf{1}}(q)=\frac{\unicode[STIX]{x1D6E4}_{1}}{16\unicode[STIX]{x03C0}mc}\int _{-\infty }^{\infty }\frac{(\sin \unicode[STIX]{x1D703},0,\cos \unicode[STIX]{x1D703})\,\text{d}p}{\sinh \frac{1}{2}(p-q)[\sinh ^{2}\frac{1}{2}(p+q)+m^{-2}\cosh ^{2}\frac{1}{2}(p+q)]^{3/2}},\end{eqnarray}$$
and the velocity induced on
$\unicode[STIX]{x1D6E4}_{1}$
by
$\unicode[STIX]{x1D6E4}_{2}$
(the ‘induced velocity’) as
$$\begin{eqnarray}\displaystyle & & \displaystyle \boldsymbol{v}_{\mathbf{2}}(q)=\frac{\unicode[STIX]{x1D6E4}_{2}}{16\unicode[STIX]{x03C0}mc}\nonumber\\ \displaystyle & & \displaystyle \quad \times \int _{-\infty }^{\infty }\frac{(\sin \unicode[STIX]{x1D703}\sinh ^{2}\frac{1}{2}(p-q),m\sin \unicode[STIX]{x1D703}\cos \unicode[STIX]{x1D703}\sinh p\cosh q,\cos \unicode[STIX]{x1D703}\cosh ^{2}\frac{1}{2}(p+q))\,\text{d}p}{[\sinh ^{2}\frac{1}{2}(p-q)((\cos ^{2}\unicode[STIX]{x1D703}+m^{-2})\cosh ^{2}\frac{1}{2}(p+q)+\sin ^{2}\unicode[STIX]{x1D703}\sinh ^{2}\frac{1}{2}(p+q))+\cos ^{2}\unicode[STIX]{x1D703}\cosh ^{2}\frac{1}{2}(p+q)]^{3/2}}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
The singularity in
$\boldsymbol{v}_{1}(q)$
at
$p=q$
is regularised through the cutoff method used below. We may verify that this self-induced contribution is in the binormal direction on
$\unicode[STIX]{x1D6E4}_{1}$
and perpendicular to the plane containing
$\unicode[STIX]{x1D6E4}_{1}$
(figure 2).
For the evolution of
$\unicode[STIX]{x1D6E4}_{1}$
and
$\unicode[STIX]{x1D6E4}_{2}$
, we employ a method similar to that used by KM17. At
$t=0$
, the initial positions (2.1) of
$\unicode[STIX]{x1D6E4}_{1}$
and
$\unicode[STIX]{x1D6E4}_{2}$
are discretised and stretched by the double exponential formula,
$$\begin{eqnarray}p_{i}=\sinh \left(\frac{\unicode[STIX]{x03C0}}{2}\sinh (ih)\right)\quad (i=-N,\ldots ,-1,0,1,\ldots ,N).\end{eqnarray}$$
The velocity is evaluated at each point on
$\unicode[STIX]{x1D6E4}_{1}$
and
$\unicode[STIX]{x1D6E4}_{2}$
with a five-point finite-difference scheme with uneven grid points for the first derivatives. Figure 3 shows the positions of
$\unicode[STIX]{x1D6E4}_{1}$
and
$\unicode[STIX]{x1D6E4}_{2}$
with the velocity vectors at points near the centre part at (a)
$t=0.449646$
and (b)
$t=0.449716$
. (The total number of nodes here is
$n=19\,202$
.) At
$t=0.449646$
, the velocity vectors change continuously along
$\unicode[STIX]{x1D6E4}_{1}$
and
$\unicode[STIX]{x1D6E4}_{2}$
. At
$t=0.449716$
, however, these vectors are discontinuous at the centre point while new continuous sets of vectors form on parts of the reconnecting vortices. Two movies showing the velocity distribution on each vortex as the singularity is approached may be found in the supplementary material. (Similar behaviour was observed in the evolution of the figure-of-eight vortex (KM17).)
With the tent model, we find almost the same scaling properties as with the figure-of-eight vortex. Figure 4 summarises the scaling of the minimum distance
$D_{min}$
, the maximum velocity
$V_{max}$
and the maximum axial strain rate
$\unicode[STIX]{x1D70E}_{max}\equiv \boldsymbol{t}\boldsymbol{\cdot }\text{d}\boldsymbol{u}/\text{d}s$
(where
$\boldsymbol{t}$
is the unit tangent vector) as functions of
$t_{c}-t$
in log–log scale.
$D_{min}$
shows
$(t_{c}-t)^{1/2}$
scaling, and
$V_{max}$
and
$\unicode[STIX]{x1D70E}_{max}$
show scaling close to
$(t_{c}-t)^{-1/2}$
and
$(t_{c}-t)^{-1}$
, respectively, i.e. close to Leray scaling. But if we look closely at the scaling of
$V_{max}$
and
$\unicode[STIX]{x1D70E}_{max}$
, the magnitudes of the exponents are seen to be slightly above
$1/2$
and
$1$
, respectively, showing slight deviation from self-similar behaviour. We note that a
$|t_{c}-t|^{-1/2}$
scaling for
$D_{min}$
has been found both before and after the reconnection event by Zuccher et al. (Reference Zuccher, Caliari, Baggaley and Barenghi2012) (different scalings have, however, been reported by Hussain & Duraisamy (Reference Hussain and Duraisamy2011) and by Rorai et al. (Reference Rorai, Skipper, Kerr and Sreenivasan2016)).
Figure 3. Tent-model configuration and velocity vectors at points on the vortices
$\unicode[STIX]{x1D6E4}_{1}$
and
$\unicode[STIX]{x1D6E4}_{2}$
(
$m=0.35,c=0.1,\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/4,n=19\,202$
); (a)
$t=0.449646$
; (b)
$t=0.449716$
.
Figure 4. Scaling of (a) the minimum distance
$D_{min}$
, (b) the maximum velocity
$V_{max}$
, (c) the maximum axial strain rate
$\unicode[STIX]{x1D70E}_{max}\equiv \boldsymbol{t}(s)\boldsymbol{\cdot }\text{d}\boldsymbol{u}(s)/\text{d}s$
as a function of
$t_{c}-t$
in log–log scale; results of three resolutions,
$n=4802,9602,19\,202$
are compared (
$m=0.35$
,
$c=0.1$
,
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/4$
).
Figure 5. Projections of the tip part near
$t_{c}$
for
$n=19\,202$
; (a)
$xz$
-projections; (b)
$yz$
-projections.
Figure 6. (a) Curvature
$\unicode[STIX]{x1D705}(s,t)$
and (b) torsion
$\unicode[STIX]{x1D70F}(s,t)$
of
$\unicode[STIX]{x1D6E4}_{1}$
as functions of arclength
$s$
, at times
$t$
near to the singularity time
$t_{c}$
(
$m=0.35$
,
$c=0.1$
,
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/4$
,
$n=4802$
).
This deviation is evident in the appearance of inflection points on the filaments and a consequent tendency to form cusps (KM17) as the singularity is approached. Figure 5 shows (a) the
$xz$
-projections and (b) the
$yz$
-projections of the tip part of the vortices at times close to the singularity (with
$n=19\,202$
). The scaling exponent of the axial stretching is larger than the Leray exponent, implying a faster velocity in the
$z$
-direction at the tips, causing the appearance of inflection points and leading towards the cusped structure. The
$xz$
-projection also shows that the tips gradually leave the planes defined by the remote parts of the vortices. This means that the vortex filaments develop non-zero torsion near the tips,
$$\begin{eqnarray}\unicode[STIX]{x1D70F}=\frac{\boldsymbol{x}^{\prime \prime \prime }\boldsymbol{\cdot }(\boldsymbol{x}^{\prime }\wedge \boldsymbol{x}^{\prime \prime })}{(\boldsymbol{x}^{\prime }\wedge \boldsymbol{x}^{\prime \prime })\boldsymbol{\cdot }(\boldsymbol{x}^{\prime }\wedge \boldsymbol{x}^{\prime \prime })},\end{eqnarray}$$
where the prime signifies
$\text{d}/\text{d}p$
.
Figure 6 shows the curvature
$\unicode[STIX]{x1D705}(s,t)$
and torsion
$\unicode[STIX]{x1D70F}(s,t)$
of either vortex filament as functions of arclength
$s$
, at times
$t$
near to the singularity time
$t_{c}$
. The curvature is symmetric about
$s=0$
, with no zero, therefore no three-dimensional (3D) inflection point. We have verified that the maximum curvature (at the tip) scales as
$(t_{c}-t)^{-\unicode[STIX]{x1D707}}$
, where
$\unicode[STIX]{x1D707}=0.6027$
. This is somewhat greater than the value
$1/2$
that might be expected; we have no explanation for this at present, but again, it is an indication of the departure from Leray self-similarity. The inflection point observed in figure 5 is merely one on the two-dimensional (2D) projection of the curve on the
$xz$
-plane. This does show up, however, in figure 6(a) as a very distinct minimum of curvature which collapses towards the singularity point as
$t\rightarrow t_{c}$
. Figure 6(b) shows the torsion
$\unicode[STIX]{x1D70F}(s,t)$
, which is antisymmetric about
$s=0$
and has very pronounced peaks at the location of the curvature minima. These results are consistent with results obtained by Villois, Proment & Krstulovic (Reference Villois, Proment and Krstulovic2017) on the basis of the Gross–Pitaevskii model.
Two important properties of a deformed filament are its writhe
$Wr(t)$
and twist
$Tw(t)$
(Moffatt & Ricca Reference Moffatt and Ricca1992), and we know that in this case, for each tilted hyperbola,
$Wr+Tw=\text{const.}=0$
, since
$Wr=Tw=0$
initially. The twist
$Tw(t)$
is proportional to the integral of the torsion
$\unicode[STIX]{x1D70F}(s,t)$
along the complete length of the filament, and this remains zero for all
$t>0$
by virtue of the antisymmetry in
$s$
. This implies that
$Wr(t)=0$
also for all
$t>0$
, consistent with the interpretation of writhe as the average over all projections of the (signed) number of self-crossings of the curve: the tilted hyperbola is increasingly bent upwards from its original plane, but is not twisted about the
$z$
-direction, and therefore exhibits no self-crossings from any angle of projection.
Figure 7. Isosurfaces of
$\unicode[STIX]{x1D706}_{2}\,(m=0.35,c=0.1,\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/4,n=4802)$
; (a)
$t=0.473200$
with
$\unicode[STIX]{x1D706}_{2}=150$
(orange) and
$\unicode[STIX]{x1D706}_{2}=-150$
(blue); (b)
$t=0.489820$
with
$\unicode[STIX]{x1D706}_{2}=120$
(orange) and
$\unicode[STIX]{x1D706}_{2}=-120$
(blue).
Figure 8. Contours of
$\unicode[STIX]{x1D706}_{2}$
on the plane
$y=0$
; (a)
$t=0.473200$
; (b)
$t=0.489820$
(
$m=0.35,c=0.1,\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/4,n=4802$
).
3 Strain around the vortices
During the reconnection process, the vortices are subject to the local velocity gradient
$\unicode[STIX]{x1D735}\boldsymbol{v}$
, and the vortex cores, finite in reality, are inevitably deformed by the straining action. The nature of the deformation is determined by the eigenvalues
$\unicode[STIX]{x1D706}_{1}\geqslant \unicode[STIX]{x1D706}_{2}\geqslant \unicode[STIX]{x1D706}_{3}$
(
$\unicode[STIX]{x1D706}_{1}+\unicode[STIX]{x1D706}_{2}+\unicode[STIX]{x1D706}_{3}=0$
) of the rate-of-strain tensor
$\unicode[STIX]{x1D65A}=(\unicode[STIX]{x1D735}\boldsymbol{v}+(\unicode[STIX]{x1D735}\boldsymbol{v})^{\text{T}})/2$
. From the Biot–Savart integral (2.4), the deformation tensor at
$\boldsymbol{x}$
is
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}u_{j}(\boldsymbol{x})}{\unicode[STIX]{x2202}x_{i}}=\frac{\unicode[STIX]{x1D6E4}}{4\unicode[STIX]{x03C0}}\hspace{-1.0pt}\int \hspace{-1.0pt}\left[\frac{3(x_{i}-x_{i}(p))[(\boldsymbol{x}-\boldsymbol{x}(p))\wedge \text{d}\boldsymbol{x}(p)]_{j}}{|\boldsymbol{x}-\boldsymbol{x}(p)|^{5}}+\unicode[STIX]{x1D716}_{ijk}\frac{\text{d}x_{k}(p)}{|\boldsymbol{x}-\boldsymbol{x}(p)|^{3}}\right]\hspace{-3.0pt},\hspace{4.0pt}(i,j,k=1,2,3),\end{eqnarray}$$
where
$\unicode[STIX]{x1D716}_{ijk}$
is the Levi–Civita symbol.
Figure 7 shows the 3D isosurfaces of
$\unicode[STIX]{x1D706}_{2}$
near the vortices. Two times are selected: (a)
$t=0.473200$
and (b)
$t=0.489820$
. The isosurfaces are plotted by evaluating the nine components of (3.1) and, after symmetrising, by solving the cubic eigenvalue equation at
$200^{3}$
grid points around
$\unicode[STIX]{x1D6E4}_{1}$
and
$\unicode[STIX]{x1D6E4}_{2}$
. At the earlier time,
$\unicode[STIX]{x1D706}_{2}$
shows a dipole structure around the vortices (figure 7
a). As time advances, the positive parts of the dipole overlap near the tips of the vortices to produce another dipole structure on the symmetry plane
$x=0$
(figure 7
b). Figure 8 shows the contours of
$\unicode[STIX]{x1D706}_{2}$
on the plane
$y=0$
corresponding to figure 7; this shows details of the change around the tip. At
$t=0.473200$
, two tilted dipoles are observed which move along the zero level of
$\unicode[STIX]{x1D706}_{2}$
(figure 8
a). At
$t=0.489820$
, the positive parts of the dipoles overlap at the centre of the region. The combined dipoles squeeze the zero level of
$\unicode[STIX]{x1D706}_{2}$
towards a cusp at the tip while the ‘tails’ are straightened. By comparing figure 8(b) with figure 5, we may conjecture that it is the complicated local strain structure that leads to the appearance of inflection points and the development of cusps.
Table 1. Eigenvalues and eigenvectors of the rate-of-strain tensor at the tipping point on
$\unicode[STIX]{x1D6E4}_{1}$
at times
$t=0.47320$
and
$t=0.489820$
corresponding to figures 7 and 8.
A crucial issue concerns the structure of the principal rates of strain
$\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2}$
and
$\unicode[STIX]{x1D706}_{3}$
near the vortex tips. Table 1 shows the values of these eigenvalues and corresponding eigenvectors
$\boldsymbol{e}_{1},\boldsymbol{e}_{2}$
and
$\boldsymbol{e}_{3}$
at the tip of
$\unicode[STIX]{x1D6E4}_{1}$
at the two times corresponding to figures 7 and 8. The strain is evaluated by the total velocity produced by
$\unicode[STIX]{x1D6E4}_{1}$
and
$\unicode[STIX]{x1D6E4}_{2}$
(first three columns) and by the induced velocity produced by
$\unicode[STIX]{x1D6E4}_{2}$
alone (last three columns). The results may be summarised as follows:
-
(i)
$\unicode[STIX]{x1D706}_{1}+\unicode[STIX]{x1D706}_{2}+\unicode[STIX]{x1D706}_{3}=0$
, as expected by virtue of incompressibility. -
(ii)
$\unicode[STIX]{x1D706}_{2}>0$
, and
$\boldsymbol{e}_{2}$
is in the axial direction (parallel to the
$y$
-axis); each vortex is therefore persistently stretched at the tip. -
(iii) The eigenvectors
$\boldsymbol{e}_{1}$
and
$\boldsymbol{e}_{3}$
are in the
$xz$
-plane and are mutually orthogonal (as expected for a real symmetric matrix). -
(iv) The rate of strain produced by
$\unicode[STIX]{x1D6E4}_{2}$
alone is dominant at the tip of
$\unicode[STIX]{x1D6E4}_{1}$
, and the magnitudes of the
$x$
and
$z$
components of
$\boldsymbol{e}_{1}$
and
$\boldsymbol{e}_{3}$
are nearly equal; these vectors are therefore close to the directions
$z=\pm x$
.
The same results were obtained for a sequence of times up to
$t_{c}$
, and under modest variation of the parameters
$m$
and
$c$
, thus providing evidence for the accuracy of the computation. We note here that the straining in the
$xz$
-plane in the neighbourhood of the tip of
$\unicode[STIX]{x1D6E4}_{1}$
must tend to rotate the angle
$\unicode[STIX]{x1D703}$
of its plane towards the value
$\unicode[STIX]{x03C0}/4$
if it is not
$\unicode[STIX]{x03C0}/4$
initially. This is why we have chosen the value
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/4$
in the initial condition (2.1).
Direct numerical simulations (DNS) of the Euler equations by Brenner, Hormoz & Pumir (Reference Brenner, Hormoz and Pumir2016) and others have provided evidence of the flattening of vortex cores as the singularity time is approached. This must be a consequence of the positive rate-of-strain eigenvalue (here
$\unicode[STIX]{x1D706}_{1}$
) in the plane of cross-section of the vortex core. The Reynolds number dependence of this flattening when weak viscosity is taken into account remains a key issue, and will require much better numerical resolution than has so far been achieved.
In this context, it has been shown (Moffatt, Kida & Ohkitani Reference Moffatt, Kida and Ohkitani1994) that at very high Reynolds number, the cross-section of a stretched Burgers-type vortex remains nearly circular even when the straining flow is non-axisymmetric. There is therefore the possibility here that, at sufficiently high Reynolds number beyond the reach of present DNS, the vortex cross-sections, if assumed finite, may remain compact at leading order. We are currently investigating this possibility.
Acknowledgements
This work is supported by JSPS KAKENHI grant numbers JP24247014, JP16H01175. The authors thank Professor H. Fujiwara for helpful suggestions concerning the numerical methods.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2017.769.
