Introduction
In general, space plasmas, can be broadly modeled with Maxwellian velocity distribution. But with the advancement of satellite-based technologies and data therein it has been found in recent years, that most of these plasmas, especially those near to earth plasmas have high-energy tails and heat-flux shoulders, which may be due to the fact that these plasmas are quite inhomogeneous and semi-collisionless (Marsch et al. Reference Marsch, Mühlhäuser, Schwenn, Rosenbauer, Pilipp and Neubauer1982; Summers et al., Reference Summers, Xue and Thorne1994; Ma and Summers, Reference Ma and Summers1998). As a result, it has been established that these plasmas (especially the electron distributions) if modeled by a generalized Lorentzian or kappa distribution gives proper result rather than by a pure Maxwellian (Summers and Thorne, Reference Summers and Thorne1991; Reference Summers and Thorne1992). Dispersion relation in various multicomponent plasma has been investigated (Bala & Kaur, Reference Bala and Kaur2013). Lorentzian distribution has a spectral index κ which accounts for its high-energy tail. In the limit of κ→∞, it leads to a Maxwellian distribution function. Astrophysical plasma shows features and phenomena that prove that they contain non-thermal distributed electrons. For instance, the solar wind plasmas are usually found to be non-thermal distributed. In close proximity to earth, the solar wind plasmas usually have a density of ~30–100 cm−3 with velocity ~500 km/s and temperature reaching up to ~ 50 eV (Baumjohann and Treumann, Reference Baumjohann and Treumann1997). With the pioneering work of Zabusky and Kruskal (Reference Zabusky and Kruskal1965) on the one-dimensional (1D) solitary structure of the celebrated Korteweg–de Vries (KdV) equation in plasma physics, it has also played a major role in analyzing the non-linear phenomena in physical and biological sciences. Solitons are defined as spatially localized pulsed shape stable non-linear construct which retains their shape, identity, and energy in the mutual collision and is, therefore, the exact solution of a large number of the non-linear partial differential equation. They are formed due to the balance between the non-linear effects (that causes the steeping) and dispersive effects (that causes the broadening).
The KdV equation and the non-linear Schrödinger equation (NLSE) along with their different variants having used in the study of a large number of non-linear phenomena in astrophysical and laboratory produced plasma. Nakamura and Sarma (Reference Nakamura and Sarma2001) and Nakamura et al. (Reference Nakamura, Bailung and Shukla1999) have used this concept in their study of laboratory-produced plasma. The reductive perturbation technique which is used to derive the KdV equation describes the evolution of a non-modulated wave (a bare pulse without fast oscillation). The NLSE that governs the dynamics of a modulated wave packet deals with the fact that the non-linearity arising within the packet is balanced by the group dispersion resulting in the formation of a stationary envelope structured solution.
The electron–positron plasma exists in the magnetosphere of pulsars (Michel Reference Michel1982, Reference Michel1991) the early universe (Gibbons et al. Reference Gibbons, Hawking and Siklos1983), the bi-polar outflow in active galactic nuclei (Miller & Witta, Reference Miller and Witta1987). Though the astrophysical plasma dominantly contain electron and positron create a finite proportion of ion may be present forming effective electron–positron–ion (e–p–i) plasma. Similarly a small fraction of positron may be present in plasmas containing electrons and ions viz. tokamak plasma: in such cases the positron may be generated by the mechanism of pair production which may have possibly occurred due to collision between ran away electron (few MeV) and thermal particles (Helander & Ward, Reference Helander and Ward2003). It has been also reported when ultra-intense laser pulses interact with matter as in case of internal confinement fusion, the plasma produced there may also contain positron (Liang et al., Reference Liang, Wilks and Tabak1998; Gahn et al., Reference Gahn, Tsakiris, Pretzler, Witte, Delfin, Wahlstrom and Habs2000). The presence of ions may lead to the formation of the number of low-frequency mode which otherwise does not propagate in an electron–positron plasma. Therefore an e–p–i plasma is important in case of a laboratory plasma apart from the cosmological plasmas. The non-linear behavior in e–p–i plasma is more interesting from theoretical as well as experimental point of view.
Over the past few years the study of non-linear phenomena in electron–positron plasma has gained considerable interest. Ion-acoustic solitary structures and its dependence on various plasma parameters have been reported by Pillay and Bharuthram (Reference Pillay and Bharuthram1992), Ghosh and Bharuthram (Reference Ghosh and Bharuthram2008), Mahmood and Akhtar (Reference Mahmood and Akhtar2008), Gill et al. (Reference Gill, Kaur and Saini2003, Reference Gill, Bala, Kaur, Saini, Bansal and Kaur2004, Reference Gill, Singh, Kaur, Saini and Bala2007), Nejoh (Reference Nejoh1996a, Reference Nejohb), Mushtaq and Shah (Reference Mushtaq and Shah2005), and Popel et al. (Reference Popel, Vladimirov and Shukla2005). In recent times, modulation instabilities of different wave modes have been studied due to its importance in stable wave propagation. Watanabe (Reference Watanabe1977) reported about the modulation instability of monochromatic ion-acoustic wave in his experiment. Amplitude modulation in e–p–i plasma has been reported recently by Esfandyari-Kalejahi et al. (Reference Esfandyari-Kalejahi, Kourakis, Mehndipoor and Shukla2006), Jehan et al. (Reference Jehan, Salahuddin and Mirza2009), Kourakis et al. (Reference Kourakis, Esfandyari-Kalejahi, Mehdipoor and Shukla2006), and Salahuddin et al. (Reference Salahuddin, Saleem and Saddiq2002). Esfandyari studied the non-linear propagation of electrostatic wave packets in e–p–i plasma with varying positron concentration and other plasma parameters. The findings of Kourakis are rather interesting. According to him the presence of background ion species modify the characteristic features of excitation and alter the stability profile of modulated wave packet. Jehan reported that with an increase in positron condition there is a decrease in the maximum growth rate of instability.
Energetic electrons are in general non-thermally distributed and are abundant in space and laboratory plasmas; it has a significant effect on non-linear collective phenomena. Such distribution is also found in the magnetosphere. In 1994, Berezhiani et al. (Reference Berezhiani, El-Ashry and Mofiz1994) gave a theory of strong-electromagnetic-wave propagation in an e–p–i plasma. Cairns et al. (Reference Cairns, Mammun, Bingham, Bostrom, Dendy, Nairn and Shukla1995) proposed a non-thermal distribution of electron during their study of ion-acoustic solitary structure observed by FREJA satellite developed by Swedish space corporation on behalf of the national Swedish space board and reported the formation of compressive and rarefactive solitons. In the later years, Singh and Lakhina (Reference Singh and Lakhina2004) reported the modification of electron-acoustic solitary structures in the presence of non-thermal electrons. In the year 2008, Verheest and Pillay studied the dust acoustic solitary structures with positively charged dust particles and non-thermal electrons. They delimited a range of parameter where both positive and negative solitary structures may coexist. Using the same non-thermal distribution given by Cairns et al. Modulation instability in envelop solitary structures in un-magnetized plasma was reported by Kourakis and Shukla (Reference Kourakis and Shukla2005) and Tang and Xue (Reference Tang and Xue2004). Pakzad in 2009 studied ion-acoustic solitary waves and determined the parametric region for their existence. Saberian et al. (Reference Saberian, Esfandyari-Kalejahi and Akbari-Moghanjoughi2011) studied the ion-acoustic solitary waves in a relativistic e–p–i plasma using Sagdeev's pseudo-potential method. The relativistic dynamical equation was initially modeled by Lee and Choi (Reference Lee and Choi2007); Baluku and Hellberg (Reference Baluku and Hellberg2011) used the similar pseudo-potential method to study ion-acoustic solitary wave in e–p–i plasma with non-thermal electron and Boltzmann's positron.
In this paper, we studied the non-linear behavior of ion-acoustic solitary structures in an e–p–i plasma consisting non-thermal electrons and Boltzmann positrons. The findings are interesting from the theoretical and experimental point of view (astronomical and laboratory plasma). The novel finding in this paper is that we studied the small amplitude solitary structures and investigated the criteria of formation of envelope soliton. The transformation of the KdV equation into an NLSE to study amplitude modulation. The paper is organized in the following manner; section “Basic equations” provides the basic equations for the particles’ dynamics. Section “Linear dispersion characteristics” carries out the linear analysis and the linear dispersion relation is derived. Here we studied the dependence of linear dispersion on different plasma parameters. Section “KdV Equation and the solitary wave structures” derives the non-linear KdV equation and analyzes the formation and properties of ion-acoustic solitary wave structures. In the section “NLSE and the envelope soliton”, we investigate the properties of envelop soliton by transforming our KdV equation into an NLSE. In this section, we studied the stability criteria and also the growth rate of modulational instability. Finally, we discuss the results and conclude with some comments.
Basic equations
We consider an e–p–i plasma with non-thermal electrons and Boltzmann positrons. The dynamical equations for unidirectional propagation in such plasma are given by
The first equation is the fluid equation of continuity for the ions, the second one is the equation of motion for the ions. Equation (3) is the Poisson's equation.
Again, the ion pressure is given by
where k is the Boltzmann's constant.
Now, using normalization conditions, ![]() $\bar t \to {\rm \omega} _{\rm ci} t$,
$\bar t \to {\rm \omega} _{\rm ci} t$, ![]() ${\bar x} \to ((x{\rm \omega} _{\rm ci} )/(V_{T_{\rm e}} ))$,
${\bar x} \to ((x{\rm \omega} _{\rm ci} )/(V_{T_{\rm e}} ))$, ![]() $\overline {v_{\rm i}} \to (v_{\rm i} /V_{T_{\rm e}} )$, and
$\overline {v_{\rm i}} \to (v_{\rm i} /V_{T_{\rm e}} )$, and ![]() ${\bar {\rm \varphi}} \to ((e{\rm \varphi} )/(kT_{T{\rm e}} ))$,
${\bar {\rm \varphi}} \to ((e{\rm \varphi} )/(kT_{T{\rm e}} ))$, ![]() $\overline {n_{\rm \alpha}} \to (n_{\rm \alpha} /n_{\rm \alpha} 0 )$.
$\overline {n_{\rm \alpha}} \to (n_{\rm \alpha} /n_{\rm \alpha} 0 )$.
(where ![]() ${\rm \omega} _{\rm ci} = \sqrt {((4{\rm \pi} n_0 e^2 )/c^2 )} = \hbox{the electron plasma oscillation frequency}$.
${\rm \omega} _{\rm ci} = \sqrt {((4{\rm \pi} n_0 e^2 )/c^2 )} = \hbox{the electron plasma oscillation frequency}$. ![]() $V_{T_{\rm e}} = \hbox{Fermi thermal speed of electrons}$), we get the set of normalized equations are given by
$V_{T_{\rm e}} = \hbox{Fermi thermal speed of electrons}$), we get the set of normalized equations are given by
Here δ = (n i0/n e0) and p = (n p0/n e0) represent the equilibrium density ratios of ion-to-electron and positron-to-electron.
The non-thermal electron density is given by
 $$\eqalign{n_{\rm e} & = n_{{\rm e}0}\left\{ {\left[ {1 - {\rm \beta }\displaystyle{{e{\rm \varphi }} \over {kT_{\rm e}}}} \right] + {\rm \beta }{\left( {\displaystyle{{e{\rm \varphi }} \over {kT_{\rm e}}}} \right)}^2} \right\}\exp \left( {\displaystyle{{e{\rm \varphi }} \over {kT_{\rm e}}}} \right) \cr & = n_{{\rm e}0}\left\{ {\left[ {1 - \beta {{\rm \chi} {\rm \varphi} }} \right] + {\rm \beta }{\rm \chi }^2{\rm \varphi }^2} \right\}{\rm exp}({{\rm \chi} {\rm \varphi} }).}$$
$$\eqalign{n_{\rm e} & = n_{{\rm e}0}\left\{ {\left[ {1 - {\rm \beta }\displaystyle{{e{\rm \varphi }} \over {kT_{\rm e}}}} \right] + {\rm \beta }{\left( {\displaystyle{{e{\rm \varphi }} \over {kT_{\rm e}}}} \right)}^2} \right\}\exp \left( {\displaystyle{{e{\rm \varphi }} \over {kT_{\rm e}}}} \right) \cr & = n_{{\rm e}0}\left\{ {\left[ {1 - \beta {{\rm \chi} {\rm \varphi} }} \right] + {\rm \beta }{\rm \chi }^2{\rm \varphi }^2} \right\}{\rm exp}({{\rm \chi} {\rm \varphi} }).}$$Here β is the non-thermal parameter.
The Boltzmann distributed positron density is given by
where χ = (e/(kT)) is the reciprocal of electron temperature and σ = (T e/T p) is the reciprocal of positron temperature.
For charge neutrality, we have therefore
Using the same normalization it can be written as
Linear dispersion characteristics
In order to investigate the linear and non-linear behavior of ion-acoustic wave in the e–p–i plasma, we make the following perturbation expansions for the field quantities n i,n e,n p,v i, and φ about their values
 $$\left( {\matrix{ {n_{\rm i}} \cr {v_{\rm i}} \cr {\rm \varphi } \cr } } \right) = \left( {\matrix{ 1 \cr {v_0} \cr {{\rm \varphi }_0} \cr } } \right) + {\rm \varepsilon }\left( {\matrix{ {n_{\rm i}^{(1)} } \cr {v_{\rm i}^{(1)} } \cr {{\rm \varphi }^{(1)}} \cr } } \right) + {\rm \varepsilon }^2\left( {\matrix{ {n_{\rm i}^{(2)} } \cr {v_{\rm i}^{(2)} } \cr {{\rm \varphi }^{(2)}} \cr } } \right) + \cdots . $$
$$\left( {\matrix{ {n_{\rm i}} \cr {v_{\rm i}} \cr {\rm \varphi } \cr } } \right) = \left( {\matrix{ 1 \cr {v_0} \cr {{\rm \varphi }_0} \cr } } \right) + {\rm \varepsilon }\left( {\matrix{ {n_{\rm i}^{(1)} } \cr {v_{\rm i}^{(1)} } \cr {{\rm \varphi }^{(1)}} \cr } } \right) + {\rm \varepsilon }^2\left( {\matrix{ {n_{\rm i}^{(2)} } \cr {v_{\rm i}^{(2)} } \cr {{\rm \varphi }^{(2)}} \cr } } \right) + \cdots . $$Now, assuming that all the field variables are varying as exp[i(kx−ωt)], we get for normalized wave frequency ω and wavenumber k, we get the following dispersion relation:
 $$\eqalign{k^2 & = \left[\displaystyle{{k^2 - {({\rm \omega } - kv_0)}^2} \over {{\rm \delta } - k^2 - {({\rm \omega } - kv_0)}^2}}\right] \cr & \times \left({\rm \chi } + p{\rm \sigma} {\rm \chi } - {{\rm \beta} {\rm \chi }} + {\rm \beta }{\rm \chi }^2{\rm \varphi }_0 + 2{\rm \beta }{\rm \chi }^3{\rm \varphi }_0^2 \right).}$$
$$\eqalign{k^2 & = \left[\displaystyle{{k^2 - {({\rm \omega } - kv_0)}^2} \over {{\rm \delta } - k^2 - {({\rm \omega } - kv_0)}^2}}\right] \cr & \times \left({\rm \chi } + p{\rm \sigma} {\rm \chi } - {{\rm \beta} {\rm \chi }} + {\rm \beta }{\rm \chi }^2{\rm \varphi }_0 + 2{\rm \beta }{\rm \chi }^3{\rm \varphi }_0^2 \right).}$$
The dispersion relation exists for a particular range of wavenumber for given values of parameters where k is given by ![]() $k \gt \sqrt {({\rm \delta} /(1 - {\rm \beta} + p{ \rm \sigma} ))} $ (for v 0 = 0.2, β = 0.2, δ = 0.3, χ = 0.5, p = 0.7 σ = 0.3; k > 0.545).
$k \gt \sqrt {({\rm \delta} /(1 - {\rm \beta} + p{ \rm \sigma} ))} $ (for v 0 = 0.2, β = 0.2, δ = 0.3, χ = 0.5, p = 0.7 σ = 0.3; k > 0.545).
If we consider there is no streaming velocity of ion, that is, v 0 = 0 and considering quasi-linearity condition that is, φ0 = 0, then by replacing ![]() ${\rm \chi} = (1/{\rm \lambda} _{\rm D}^2 )$ we get
${\rm \chi} = (1/{\rm \lambda} _{\rm D}^2 )$ we get
 $$\displaystyle{{{\rm \omega }^2} \over {k^2}} = \displaystyle{1 \over {{\rm \lambda }_{\rm D}^2 }} - \displaystyle{{\rm \delta } \over {k^2{\rm \lambda }_{\rm D}^2 (1 - {\rm \beta } + p{\rm \sigma })}}.$$
$$\displaystyle{{{\rm \omega }^2} \over {k^2}} = \displaystyle{1 \over {{\rm \lambda }_{\rm D}^2 }} - \displaystyle{{\rm \delta } \over {k^2{\rm \lambda }_{\rm D}^2 (1 - {\rm \beta } + p{\rm \sigma })}}.$$This is the linear dispersion relation which has an extra term on the right-hand side when compared with Baluku and Hellberg (Reference Baluku and Hellberg2011). The extra term is the result of the inclusion of ion pressure in the momentum equation. Apart from this when we compare our dispersion relation with that obtained by Baliku et al. everything is same. Also when we consider β = 0 this gives in per perfect correspondence with the findings of Popel et al. (Reference Popel, Vladimirov and Shukla1995). While comparing the DR with that obtained by Pakzad (Reference Pakzad2009) the interpretation may be due to the fact that the distribution is a deviation from the Maxwellian one and the deviation is measured by a term β, and similarly, there exists a minimum value of M which is discussed in detail by Baluku.
It is found that the linear dispersion characteristics become steeper with an increase in the value of χ. It implies that as the electron temperature decreases the frequency increases with increase in wavenumber (Fig. 1). However, it has been found that there is no significant change in the dispersion characteristics with change in non-thermal parameter β (Fig. 2) or positron temperature because electrons provide the neutralizing effect.

Fig. 1. Dispersion relation for different value of χ.

Fig. 2. Dispersion curve for different value of non-thermal parameter β.
KdV Equation and the solitary wave structures
To investigate the behavior of small amplitude ion-acoustic wave, in the e–p–i plasma we need to study the KdV equation. The KdV equation describing the non-linear behavior of e–p–i plasma waves is derived by using the standard reductive perturbation technique. We introduce the usual stretching of space and time variables
where ε is a small dimensionless expansion parameter as a measure of the weakness of non-linearity, and M is a constant representing the phase velocity of the waves.
Now Eqs (5)–(7) are written in terms of the stretched coordinates ξ and τ, and the perturbation expansion given in Equation (12) is substituted. Solving for the equations lowest order in ε with the boundary condition that all the variables, that is, ![]() $n_i^{(1)} $,
$n_i^{(1)} $, ![]() $v_i^{(1)}, $ and φ(1) tends to zero as |ξ| → ∞
$v_i^{(1)}, $ and φ(1) tends to zero as |ξ| → ∞
 $$v_i^{(1)} = \displaystyle{{(M - v_0)} \over {\{ 1 - {\left( {M - v_0} \right)}^2\} }}{\rm \varphi }^{(1)}\,{\rm and}\,n_i^{(1)} = \displaystyle{{{\rm \varphi }^{(1)}} \over {\{ 1 - {\left( {M - v_0} \right)}^2\} }}$$
$$v_i^{(1)} = \displaystyle{{(M - v_0)} \over {\{ 1 - {\left( {M - v_0} \right)}^2\} }}{\rm \varphi }^{(1)}\,{\rm and}\,n_i^{(1)} = \displaystyle{{{\rm \varphi }^{(1)}} \over {\{ 1 - {\left( {M - v_0} \right)}^2\} }}$$Going to the next higher order terms in ε and after a few algebraic operations we get the KdV equation as
where
and
Here C is given by C = n e0 [(1 − β)χ + 3βχ3φ0 − p 2σχ].
The second and third terms of Eq. (17) are respectively the non-linear and dispersive terms. The coefficients A and B corresponding to non-linear and dispersive effect both depend onv 0. The solitary structure is the result of a balance between the non-linear and dispersive effects. While the non-linear effect steepens the solitary wave profile, the dispersive effect tries to broaden the solitary wave.
The solitary profiles depend heavily on the streaming velocity. With the increase in streaming velocity the width and amplitude of the solitary structures increase (Fig. 3). Similarly, with an increase in the positron density p (equivalent to a decrease in ion density) the solitary profiles become steeper (Fig. 4). This may be accounted for the fact that the positrons being lighter move faster than ions and they lead the solitary profiles of ion-acoustic waves. In either case, the ion density and positron density are complementary to each other and considering the mass of positrons or positive ions is immaterial as suggested by Verheest and Pillay (Reference Verheest and Pillay2008) and Baluku and Hellberg (Reference Baluku and Hellberg2011).

Fig. 3. Solitary profiles for different values of streaming velocity v 0.

Fig. 4. Solitary profiles for different values of ion (δ) and positron (p) density.
It is clear from Figure 5 that with a slight change in Mach number M both the amplitude and width of the solitary profile increases manifold. The reason behind this is simple. Because of the wave velocity the bulk of the plasma moves in unison thereby reflecting the high potential profiles. The width is also more due to the fact that when more particles form the wave structure there is more possibility that the particles disperse from it. Figure 6 shows that as the electron temperature decreases (which is equivalent to increase in χ) the solitary profiles become steeper. However, there is no significant change in the width. This is the result of the fact that as the temperature of the electrons is less, the randomness is also low which positively affects the ion concentration in the solitary profile thereby increasing its amplitude.

Fig. 5. Solitary profiles for different values of Mach number M.

Fig. 6. Solitary profiles for different values of electron temperature reciprocal factor (χ).
But in contrast to other parameters, it is found in Figure 7 that with the increase in non-thermal parameter the amplitude of the solitary wave decreases but its width does not change. As the non-thermal parameter directly relates to the deviation from equilibrium it is evident that as we move from equilibrium conditions the particle density falls and the dispersive forces act more effectively compared with the non-linear effects. Figure 8 further shows that the positron temperature enhances the peak of the solitary waves. This is due to the fact that as the temperature of the positron increases, its randomness is enhanced. Positrons being lighter than positive ions offshoot the bulk and push the ions to maintain charge neutrality. The comparatively inertial ions thus stick to their positions thereby creating a rather stable ion-acoustic solitary wave profile.

Fig. 7. Solitary profiles for different values of non-thermal parameter (β).

Fig. 8. Solitary profiles for different values of positron temperature reciprocal factor (σ).
NLSE and the envelope soliton
In order to study the modulational instability and the conditions of formation and properties of envelope soliton we transform our KdV equation into an NLSE by expanding Eq. (16) into a Fourier series and thereafter following regular technique:
Fourier expansion of a field quantity F is
 $$F = {\rm \varepsilon}^{2}{F_0} + \sum\limits_{s = 1}^\infty {\rm \varepsilon _s\{ F_s\exp (is {\rm \psi })} + F_s^{\ast} \exp ( - is{\rm \psi }).$$
$$F = {\rm \varepsilon}^{2}{F_0} + \sum\limits_{s = 1}^\infty {\rm \varepsilon _s\{ F_s\exp (is {\rm \psi })} + F_s^{\ast} \exp ( - is{\rm \psi }).$$F 0 and F s are assumed to vary very slowly with space and time.
Expanding φ as a Fourier series we get
Using perturbation expansion and using the stretched variables as
Therefore,
and
Equating the coefficient of the higher order of first harmonics we get
This is the NLSE. If we consider P = −3Bk and Q = (A 2/(6Bk)) where P represents the group dispersion coefficient and Q represents the non-linear coefficient in a regular NLSE, we obtain PQ = −(A 2/2); which is always negative so that the wave is always stable thus creating dark solitons.
The growth rate of non-linear effects depends on a lot of parameters. It has been found that with the increase in streaming velocity (v 0), the non-thermal parameter (β), reciprocal of electron temperature (χ) and positron density (p) the non-linearity increases whereas it decreases with increase in the value of Mach number (M) and ion density (δ). The width of the envelop soliton is studied by the dependence of P/Q on different plasma parameters (Figs 9–12).

Fig. 9. P/Q plots for different value of reciprocal electron temperature (χ).

Fig. 10. P/Q plots for different value of ion density (δ).
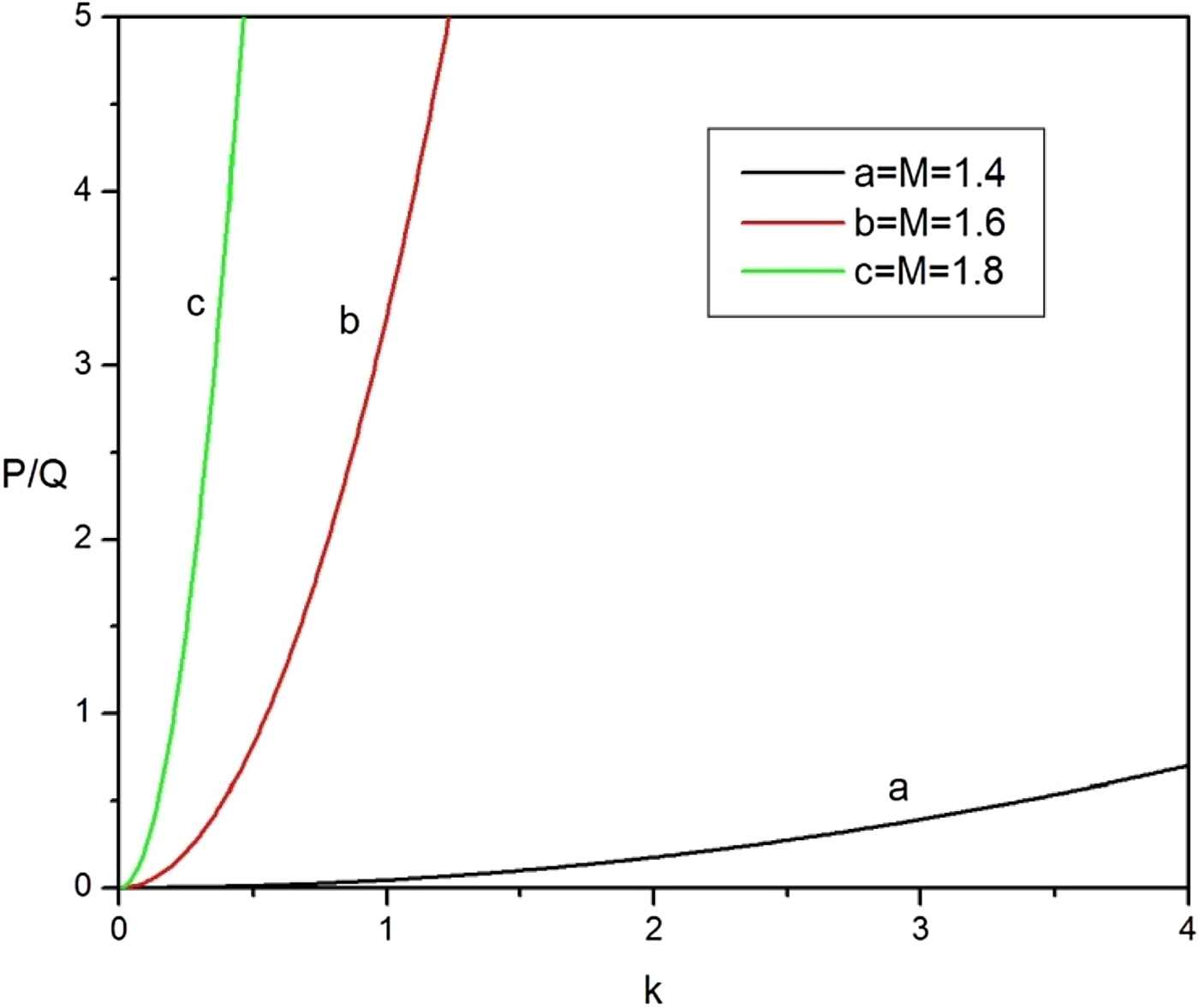
Fig. 11. P/Q plots for different value of Mach number (M).

Fig. 12. P/Q plots for different value of streaming velocity (v 0).
Figure 9 shows that width of the soliton decreases with increase in the value of χ. Or in short, as the electron temperature decreases the width of the envelop soliton shrinks and vice versa. This may be due to the fact that the effect due to electron temperature is reduced due to streaming of ions which prevents localization of thermally graded electrons. Similarly, as the ion density increases the envelop soliton shrinks. It widens with the increase in positron concentration (Fig. 10).
In contrary to these, Figure 11 shows that the width of the soliton increases with increase in Mach number. This is true because of the fact that if the solitary wave is moving with a high velocity it can only propagate if the dispersive effects are less (manifested by small width).
Figure 12 is rather interesting in nature. It shows that for streaming velocity v 0 = 0.5, the graph suddenly becomes less sleep. It implies that the width of the soliton suddenly decreases. This may be due to the fact that there exist some kind of resonance action between the velocity of the oscillating particles and the streaming velocity. This may result in energy dissipation and the slackening of the solitary structures.
Results and conclusion
In this paper, we have studied the linear and non-linear characteristics of a three-component plasma consisting non-thermal electrons and Boltzmann positrons. The linear dispersion characteristics have been found to depend on electron temperature mainly and almost independent of other plasma parameters. The KdV equation that describes the small amplitude solitary waves have been derived and its dependence on plasma parameters such as streaming velocity (v 0), non-thermal parameter (β), reciprocal of electron temperature (χ), positron density (p), Mach number (M), and ion density (δ) have been studied in details. Whereas it increases in amplitude (and/or) width for some it decreases with the others. Further, we have studied the conditions of formation and characteristic features of envelop soliton by deriving the NLSE and found out that only stable but compressive envelop solitons are formed. The dependence of the width of these solitons on various plasma parameters was also analyzed. The linear dispersion relation was found to agree with those obtained previously [Baluku]. Similarly, the properties of envelop solitons were also in consonance with previous findings. This work may further be extended with variable charges on the ions and incorporating dust particles.
APPENDIX
The normalized basic equations are
The perturbation expansion of the field variables are given by
 $$\left( {\matrix{ {n_{\rm i}} \cr {v_{\rm i}} \cr {\rm \varphi } \cr } } \right) = \left( {\matrix{ 1 \cr {v_0} \cr {{\rm \varphi }_0} \cr } } \right) + {\rm \varepsilon }\left( {\matrix{ {n_{\rm i}^{(1)} } \cr {v_{\rm i}^{(1)} } \cr {{\rm \varphi }^{(1)}} \cr } } \right) + {\rm \varepsilon }^2\left( {\matrix{ {n_{\rm i}^{(2)} } \cr {v_{\rm i}^{(2)} } \cr {{\rm \varphi }^{(2)}} \cr } } \right) + \cdots.$$
$$\left( {\matrix{ {n_{\rm i}} \cr {v_{\rm i}} \cr {\rm \varphi } \cr } } \right) = \left( {\matrix{ 1 \cr {v_0} \cr {{\rm \varphi }_0} \cr } } \right) + {\rm \varepsilon }\left( {\matrix{ {n_{\rm i}^{(1)} } \cr {v_{\rm i}^{(1)} } \cr {{\rm \varphi }^{(1)}} \cr } } \right) + {\rm \varepsilon }^2\left( {\matrix{ {n_{\rm i}^{(2)} } \cr {v_{\rm i}^{(2)} } \cr {{\rm \varphi }^{(2)}} \cr } } \right) + \cdots.$$The electrons have the non-thermal distributions is given by
 $$\eqalign{& n_{\rm e} = n_{{\rm e}0}\left\{ \left(1 - {\rm \beta }\displaystyle{{e{\rm \varphi }} \over {kT_{\rm e}}}\right) + {\rm \beta } \left(\displaystyle{{e{\rm \varphi }} \over {kT_{\rm e}}} \right)^2 \right\} \exp \left(\displaystyle{{e{\rm \varphi }} \over {kT_{\rm e}}}\right) \cr & \quad = n_{{\rm e}0} \left\{ \left(1 - {\rm \beta} {\rm \chi} {\rm \varphi }\right) + {\rm \beta }\left({\rm \chi} {\rm \varphi }\right)^2 \right\} \exp \left({\rm \chi} {\rm \varphi}\right) \cr & \qquad \left\{ 1 - \left(\displaystyle{{{\rm \omega } - kv_0} \over k}\right)^2 \right\} n_{\rm i} = {\rm \varphi }^{(1)}.}$$
$$\eqalign{& n_{\rm e} = n_{{\rm e}0}\left\{ \left(1 - {\rm \beta }\displaystyle{{e{\rm \varphi }} \over {kT_{\rm e}}}\right) + {\rm \beta } \left(\displaystyle{{e{\rm \varphi }} \over {kT_{\rm e}}} \right)^2 \right\} \exp \left(\displaystyle{{e{\rm \varphi }} \over {kT_{\rm e}}}\right) \cr & \quad = n_{{\rm e}0} \left\{ \left(1 - {\rm \beta} {\rm \chi} {\rm \varphi }\right) + {\rm \beta }\left({\rm \chi} {\rm \varphi }\right)^2 \right\} \exp \left({\rm \chi} {\rm \varphi}\right) \cr & \qquad \left\{ 1 - \left(\displaystyle{{{\rm \omega } - kv_0} \over k}\right)^2 \right\} n_{\rm i} = {\rm \varphi }^{(1)}.}$$The positron has the Boltzmann distribution and which is given by
Assuming space–time dependence of the field variables as e i(kx−ωt) we get,
From Continuity equations, we get by linearizing ε
Or,
From momentum equation of positron by linearizing ε we get
From these two equations, we get
 $$\left\{ 1 - \left(\displaystyle{{{\rm \omega} - kv_0} \over k}\right)^2 \right\} n_{\rm i}^{(1)} = {\rm \varphi} ^{(1)}. $$
$$\left\{ 1 - \left(\displaystyle{{{\rm \omega} - kv_0} \over k}\right)^2 \right\} n_{\rm i}^{(1)} = {\rm \varphi} ^{(1)}. $$From Poisson's equation
Replacing the value of ![]() $n_{\rm i}^{(1)} $ we get,
$n_{\rm i}^{(1)} $ we get,














