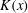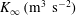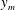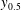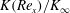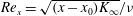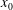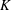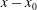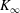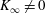1. Introduction
The flow under consideration is the plane turbulent wall jet without externally imposed stream (figure 1). The flow is steady and incompressible. Numerous papers have dealt with the subject of turbulent wall jets. The review articles by Narasimha, Narayan & Parthasarathy (Reference Narasimha, Narayan and Parthasarathy1973), Launder & Rodi (Reference Launder and Rodi1981, Reference Launder and Rodi1983) and Schneider & Goldstein (Reference Schneider and Goldstein1994) are worth mentioning. Unfortunately, not much can be found in the literature about the asymptotic downstream flow of turbulent wall jets. It appears that most authors hold the view that in this respect the turbulent wall jet behaves like a laminar wall jet. The latter tends to a flow with self-similar velocity distribution and vanishing jet momentum flux far downstream (cf. Schlichting & Gersten Reference Schlichting and Gersten2003, p. 180). However, it is overlooked that the asymptotic behaviour of the turbulent wall jet might be different from that of the laminar case.

Figure 1. Geometry and notations of the plane wall jet.
Myers, Schauer & Eustis (Reference Myers, Schauer and Eustis1963) were presumably the first who treated the asymptotic behaviour of turbulent wall jets. They described the wall-jet flow by an integral method. They concluded that, far downstream, the time-averaged velocity is
![]() $u\sim (x-x_{0})^{-1/2}$
and the half-maximum velocity distance is
$u\sim (x-x_{0})^{-1/2}$
and the half-maximum velocity distance is
![]() $y_{0.5}\sim (x-x_{0})$
. In other words, the wall jet tends to a turbulent half-free jet as limiting flow. As a consequence of this finding, the turbulent wall jet has a non-zero momentum flux far downstream. Furthermore, they found that the ratio
$y_{0.5}\sim (x-x_{0})$
. In other words, the wall jet tends to a turbulent half-free jet as limiting flow. As a consequence of this finding, the turbulent wall jet has a non-zero momentum flux far downstream. Furthermore, they found that the ratio
![]() $y_{m}/y_{0.5}$
(see figure 1) is not constant but rather a function of the streamwise coordinate
$y_{m}/y_{0.5}$
(see figure 1) is not constant but rather a function of the streamwise coordinate
![]() $x$
, tending to zero far downstream. The same result has been found by Hammond (Reference Hammond1982) in his analysis. When the velocity distribution shown in figure 1 is depicted in non-dimensional form, i.e.
$x$
, tending to zero far downstream. The same result has been found by Hammond (Reference Hammond1982) in his analysis. When the velocity distribution shown in figure 1 is depicted in non-dimensional form, i.e.
![]() $u/u_{m}=F(y/y_{0.5})$
, the wall distance of the point of maximum velocity decreases in the downstream direction. Finally, the point of maximum velocity reaches the wall. Consequently, the velocity distribution is like that of a bisected free jet. Therefore the flow of the wall jet further upstream can be considered as a perturbation of the turbulent half-free jet flow.
$u/u_{m}=F(y/y_{0.5})$
, the wall distance of the point of maximum velocity decreases in the downstream direction. Finally, the point of maximum velocity reaches the wall. Consequently, the velocity distribution is like that of a bisected free jet. Therefore the flow of the wall jet further upstream can be considered as a perturbation of the turbulent half-free jet flow.
Gersten & Herwig (Reference Gersten and Herwig1992, p. 753) treated the turbulent wall jet by a singular perturbation method. The problem is singular since the limiting solution (half-free jet) does not satisfy the no-slip condition at the wall. The perturbation analysis by Gersten & Herwig (Reference Gersten and Herwig1992) was limited to the first-order expansion and the theory was not compared with experimental results. In addition, and unfortunately, in the most important equation, the Greek letters
![]() ${\it\kappa}$
and
${\it\kappa}$
and
![]() ${\it\alpha}$
got lost in the printing process. This motivated the present corrected and considerably extended paper.
${\it\alpha}$
got lost in the printing process. This motivated the present corrected and considerably extended paper.
As mentioned above, many authors hold the view that the momentum flux
![]() $K(x)$
tends to zero for
$K(x)$
tends to zero for
![]() $x\rightarrow \infty$
. Examples of these authors are Narasimha et al. (Reference Narasimha, Narayan and Parthasarathy1973), Wygnanski, Katz & Horev (Reference Wygnanski, Katz and Horev1992), Schneider & Goldstein (Reference Schneider and Goldstein1994) and George et al. (Reference George, Abrahamsson, Eriksson, Karlsson, Löfdahl and Wosnik2000). Karlsson, Eriksson & Persson (Reference Karlsson, Eriksson, Persson, Adrian, Durâo, Durst, Heitor, Maeda and Whitelaw1993), Abrahamsson, Johansson & Löfdahl (Reference Abrahamsson, Johansson and Löfdahl1994), George et al. (Reference George, Abrahamsson, Eriksson, Karlsson, Löfdahl and Wosnik2000, cf. appendix B) and Barenblatt, Chorin & Prostokishin (Reference Barenblatt, Chorin and Prostokishin2005) investigated wall jets emerging from a wall perpendicular to the velocity vector of the inflow. For this kind of wall jet the theory of the present paper is not valid. As Schneider (Reference Schneider1985) has shown, the momentum flux of turbulent free jets emerging from orifices of plane walls decreases to zero far downstream. The same is, of course, true for a turbulent half-free jet. Therefore, wall jets emerging from a wall perpendicular to the inflow velocity vector have explicitly been excluded already in this investigation.
$x\rightarrow \infty$
. Examples of these authors are Narasimha et al. (Reference Narasimha, Narayan and Parthasarathy1973), Wygnanski, Katz & Horev (Reference Wygnanski, Katz and Horev1992), Schneider & Goldstein (Reference Schneider and Goldstein1994) and George et al. (Reference George, Abrahamsson, Eriksson, Karlsson, Löfdahl and Wosnik2000). Karlsson, Eriksson & Persson (Reference Karlsson, Eriksson, Persson, Adrian, Durâo, Durst, Heitor, Maeda and Whitelaw1993), Abrahamsson, Johansson & Löfdahl (Reference Abrahamsson, Johansson and Löfdahl1994), George et al. (Reference George, Abrahamsson, Eriksson, Karlsson, Löfdahl and Wosnik2000, cf. appendix B) and Barenblatt, Chorin & Prostokishin (Reference Barenblatt, Chorin and Prostokishin2005) investigated wall jets emerging from a wall perpendicular to the velocity vector of the inflow. For this kind of wall jet the theory of the present paper is not valid. As Schneider (Reference Schneider1985) has shown, the momentum flux of turbulent free jets emerging from orifices of plane walls decreases to zero far downstream. The same is, of course, true for a turbulent half-free jet. Therefore, wall jets emerging from a wall perpendicular to the inflow velocity vector have explicitly been excluded already in this investigation.
The basis of the following analysis is the hypothesis that the asymptotic momentum flux
![]() $K_{\infty }$
is not equal to zero. In § 2 it is shown by dimensional analysis that one single curve in the representation
$K_{\infty }$
is not equal to zero. In § 2 it is shown by dimensional analysis that one single curve in the representation
![]() $K/K_{\infty }=f(\mathit{Re}_{x})$
is valid for all turbulent wall jets far downstream. The analysis is based on a four-layer structure described in § 3. For known global functions
$K/K_{\infty }=f(\mathit{Re}_{x})$
is valid for all turbulent wall jets far downstream. The analysis is based on a four-layer structure described in § 3. For known global functions
![]() $y_{m}(x),y_{0.5}(x),u_{m}(x)$
and
$y_{m}(x),y_{0.5}(x),u_{m}(x)$
and
![]() $u_{{\it\tau}}(x)$
, which quite frequently can be found as results of experimental investigations, the details of the flow field are given in § 4. Here, self-similar velocity distributions are assumed for each of the four layers separately. In § 5 it is shown how the universal asymptotic formula for
$u_{{\it\tau}}(x)$
, which quite frequently can be found as results of experimental investigations, the details of the flow field are given in § 4. Here, self-similar velocity distributions are assumed for each of the four layers separately. In § 5 it is shown how the universal asymptotic formula for
![]() $K/K_{\infty }$
can be derived from the momentum-integral equation. In §§ 6–8 the four functions mentioned above are determined by a singular perturbation method. Finally, the theory is compared with experimental data in § 9.
$K/K_{\infty }$
can be derived from the momentum-integral equation. In §§ 6–8 the four functions mentioned above are determined by a singular perturbation method. Finally, the theory is compared with experimental data in § 9.
2. Dimensional analysis (for
 $K_{\infty }\neq 0$
)
$K_{\infty }\neq 0$
)
The maximum velocity
![]() $u_{m}$
of the turbulent wall jet with the asymptotic kinematic momentum flux
$u_{m}$
of the turbulent wall jet with the asymptotic kinematic momentum flux
![]() $K_{\infty }~(\text{m}^{3}~\text{s}^{-2})$
has the form
$K_{\infty }~(\text{m}^{3}~\text{s}^{-2})$
has the form
where
![]() $x_{0}$
is the coordinate of the virtual origin and
$x_{0}$
is the coordinate of the virtual origin and
![]() ${\it\nu}$
the kinematic viscosity. The asymptotic formula (2.1) is by definition independent of the slot width
${\it\nu}$
the kinematic viscosity. The asymptotic formula (2.1) is by definition independent of the slot width
![]() $b$
and the inlet momentum flux
$b$
and the inlet momentum flux
![]() $K_{j}$
.
$K_{j}$
.
Dimensional analysis leads to
where the Reynolds number is defined as
The one and only curve in the representation of (2.2) is universal and valid for all possible plane turbulent wall jets.
Also the following dimensionless combinations can depend only on the Reynolds number:
where
![]() $K$
is the (kinematic) momentum flux (see definition in (4.14)),
$K$
is the (kinematic) momentum flux (see definition in (4.14)),
![]() ${\it\rho}$
the density,
${\it\rho}$
the density,
![]() ${\it\tau}_{w}$
the wall shear stress,
${\it\tau}_{w}$
the wall shear stress,
![]() $y_{m}$
the wall distance of the maximum velocity and
$y_{m}$
the wall distance of the maximum velocity and
![]() $y_{0.5}$
the wall distance of the point with velocity
$y_{0.5}$
the wall distance of the point with velocity
![]() $u_{m}/2$
. All dimensionless combinations in (2.4) are also universal functions of
$u_{m}/2$
. All dimensionless combinations in (2.4) are also universal functions of
![]() $\mathit{Re}_{m}$
(examples in figure 2).
$\mathit{Re}_{m}$
(examples in figure 2).

Figure 2. Skin friction law
![]() $c_{f}(\mathit{Re}_{m})$
and thickness ratio
$c_{f}(\mathit{Re}_{m})$
and thickness ratio
![]() $y_{m}/y_{0.5}$
for turbulent plane wall jets. —— after (4.28), - - - - after Hammond (Reference Hammond1982), – – – after Launder & Rodi (Reference Launder and Rodi1981), -
$y_{m}/y_{0.5}$
for turbulent plane wall jets. —— after (4.28), - - - - after Hammond (Reference Hammond1982), – – – after Launder & Rodi (Reference Launder and Rodi1981), -
![]() $\cdot$
-
$\cdot$
-
![]() $\cdot$
- asymptote,
$\cdot$
- asymptote,
![]() $G=1$
in (4.28),
$G=1$
in (4.28),
![]() $\cdots \cdots$
after (6.1). Bars refer to experiments mentioned in table 1 presented in § 9; triangles are selected points for agreement with theory.
$\cdots \cdots$
after (6.1). Bars refer to experiments mentioned in table 1 presented in § 9; triangles are selected points for agreement with theory.
3. Flow model
The flow field consists of two parts: (i) the lower part
![]() $(y<y_{m})$
behaves like a turbulent boundary layer; (ii) the upper part
$(y<y_{m})$
behaves like a turbulent boundary layer; (ii) the upper part
![]() $(y>y_{m})$
behaves like a half-free jet. Similar to turbulent boundary layers the lower part of the wall jet can be divided into three layers: the viscous wall layer, the overlap layer and the so-called defect layer. Hence, the model of the wall-jet flow field under consideration has a four-layer structure. Furthermore it is assumed that the velocity distribution is self-similar, but separately in each of the four layers.
$(y>y_{m})$
behaves like a half-free jet. Similar to turbulent boundary layers the lower part of the wall jet can be divided into three layers: the viscous wall layer, the overlap layer and the so-called defect layer. Hence, the model of the wall-jet flow field under consideration has a four-layer structure. Furthermore it is assumed that the velocity distribution is self-similar, but separately in each of the four layers.
In many experimental investigations of turbulent wall jets the results focus on the global functions
![]() $y_{m}(x),y_{0.5}(x),u_{m}(x)$
and
$y_{m}(x),y_{0.5}(x),u_{m}(x)$
and
![]() $u_{{\it\tau}}(x)$
. In § 4 the flow field will be described in detail for the case that these four functions are given.
$u_{{\it\tau}}(x)$
. In § 4 the flow field will be described in detail for the case that these four functions are given.
4. Flow field
4.1. Asymptotic solution far downstream
As already mentioned in the introduction, the turbulent wall-jet flow will be considered as a perturbation of the turbulent half-free jet flow. Turbulent free shear flows are slender, i.e. the mean local lateral velocity component is small compared to the dominant mean flow velocity. The flow spreads gradually, thus axial gradients are small in comparison to lateral gradients. These features allow the application of boundary-layer equations in place of the full Navier–Stokes equations (see Pope Reference Pope2000, p. 111). Since the turbulent half-free jet flow is surrounded by quiescent fluid, the continuity equation and the momentum equation for the
![]() $x$
-direction are
$x$
-direction are
In (4.3) the similarity variable is
The dot in (4.3) refers to differentiation with respect to
![]() $\tilde{{\it\eta}}$
. The constant
$\tilde{{\it\eta}}$
. The constant
![]() $k$
is defined by
$k$
is defined by
From the continuity equation (4.1) it follows that
The momentum equation (4.2) leads to the shear stress:
Dimensional analysis requires that
![]() $y_{0.5}$
is proportional to
$y_{0.5}$
is proportional to
![]() $x-x_{0}$
, where
$x-x_{0}$
, where
![]() $x_{0}$
is the coordinate of the virtual origin of the half-free jet:
$x_{0}$
is the coordinate of the virtual origin of the half-free jet:
The rate of spreading of the half-free jet is
![]() $4{\it\alpha}k$
, and
$4{\it\alpha}k$
, and
![]() ${\it\alpha}$
is a slenderness parameter.
${\it\alpha}$
is a slenderness parameter.
As will be mentioned later, several turbulence models applied to turbulent free jets can be found in the literature. In the turbulence model used here it is assumed that the eddy viscosity
![]() ${\it\nu}_{t}$
is independent of
${\it\nu}_{t}$
is independent of
![]() $\tilde{{\it\eta}}$
(see Pope Reference Pope2000, p. 137).
$\tilde{{\it\eta}}$
(see Pope Reference Pope2000, p. 137).
Dimensional analysis then yields the ansatz
Therefore it follows for the shear stress that
Combination of (4.7) and (4.10) leads to a differential equation for the function
![]() $F(\tilde{{\it\eta}})$
. With
$F(\tilde{{\it\eta}})$
. With
![]() $U_{N}(x)\sim (x-x_{0})^{-1/2}$
the following ordinary differential equation results:
$U_{N}(x)\sim (x-x_{0})^{-1/2}$
the following ordinary differential equation results:
because the factor in front of
![]() $F^{3}$
in (4.7) vanishes.
$F^{3}$
in (4.7) vanishes.
The boundary conditions for
![]() $F(\tilde{{\it\eta}})$
are
$F(\tilde{{\it\eta}})$
are
The solution of (4.11) is
A comparison of this solution with experimental results will be discussed later in § 4.5.
The momentum flux
can now be determined for the turbulent half-free jet:
which is independent of
![]() $x$
. This leads to the formula
$x$
. This leads to the formula
The turbulence model expressed by (4.9) has been chosen here because of the simple solution for the velocity distribution
![]() ${\dot{F}}(\tilde{{\it\eta}})$
. Solutions for turbulent free jet flows with alternative turbulence modelling can also be found in the literature, for example Tollmien (Reference Tollmien1926), Saffman (Reference Saffman1970), Schneider & Mörwald (Reference Schneider and Mörwald1987) and Schneider (Reference Schneider1991). These solutions lead to different differential equations for
${\dot{F}}(\tilde{{\it\eta}})$
. Solutions for turbulent free jet flows with alternative turbulence modelling can also be found in the literature, for example Tollmien (Reference Tollmien1926), Saffman (Reference Saffman1970), Schneider & Mörwald (Reference Schneider and Mörwald1987) and Schneider (Reference Schneider1991). These solutions lead to different differential equations for
![]() $F(\tilde{{\it\eta}})$
and, hence, to different constants in (4.16). However, the hypothesis
$F(\tilde{{\it\eta}})$
and, hence, to different constants in (4.16). However, the hypothesis
![]() $K_{\infty }\neq 0$
proposed here would not be affected by the choice of the turbulence model for the half-free jet flow.
$K_{\infty }\neq 0$
proposed here would not be affected by the choice of the turbulence model for the half-free jet flow.
4.2. Viscous wall layer
In this case results for the viscous wall layer of turbulent boundary layers can be adopted, see Schlichting & Gersten (Reference Schlichting and Gersten2003, pp. 572, 523). The
![]() $x$
-component of the velocity is given by the universal distribution
$x$
-component of the velocity is given by the universal distribution
where
and
The limiting form of the function
![]() $F(y^{+})$
is
$F(y^{+})$
is
where
![]() ${\it\kappa}$
is called the Kármán constant and
${\it\kappa}$
is called the Kármán constant and
![]() $C^{+}$
is a further universal constant, determined from numerous experiments to be
$C^{+}$
is a further universal constant, determined from numerous experiments to be
![]() $C^{+}=5.0$
for smooth walls. In the literature, (4.20) is denoted as the ‘logarithmic law of the wall’. For high Reynolds numbers the
$C^{+}=5.0$
for smooth walls. In the literature, (4.20) is denoted as the ‘logarithmic law of the wall’. For high Reynolds numbers the
![]() $y$
-component of the velocity vanishes in the viscous wall layer, and the shear stress
$y$
-component of the velocity vanishes in the viscous wall layer, and the shear stress
![]() ${\it\tau}(x)$
is independent of
${\it\tau}(x)$
is independent of
![]() $y^{+}$
and, hence, equal to the wall shear stress
$y^{+}$
and, hence, equal to the wall shear stress
![]() ${\it\tau}_{w}(x)$
, see Schlichting & Gersten (Reference Schlichting and Gersten2003, p. 573). An analytic description of the universal function
${\it\tau}_{w}(x)$
, see Schlichting & Gersten (Reference Schlichting and Gersten2003, p. 573). An analytic description of the universal function
![]() $F(y^{+})$
is given in Schlichting & Gersten (Reference Schlichting and Gersten2003, p. 524).
$F(y^{+})$
is given in Schlichting & Gersten (Reference Schlichting and Gersten2003, p. 524).
4.3. Overlap layer
The wall layer
![]() $(y\leqslant y_{m})$
of turbulent wall jets has the same three-layer structure as turbulent boundary layers. These layers are the viscous wall layer, the so-called defect layer
$(y\leqslant y_{m})$
of turbulent wall jets has the same three-layer structure as turbulent boundary layers. These layers are the viscous wall layer, the so-called defect layer
![]() $(0\leqslant y\leqslant y_{m})$
and the overlap layer in between. The latter is part of the viscous wall layer and hence independent of
$(0\leqslant y\leqslant y_{m})$
and the overlap layer in between. The latter is part of the viscous wall layer and hence independent of
![]() $y_{m}$
, as well as part of the defect layer and hence independent of the kinematic viscosity
$y_{m}$
, as well as part of the defect layer and hence independent of the kinematic viscosity
![]() ${\it\nu}$
. Therefore the gradient of the velocity
${\it\nu}$
. Therefore the gradient of the velocity
![]() $u^{+}$
in the overlap layer is independent of
$u^{+}$
in the overlap layer is independent of
![]() ${\it\nu}$
and
${\it\nu}$
and
![]() $y_{m}$
.
$y_{m}$
.
Hence, the matching condition for the velocity gradient reads as follows:
where
is the dimensionless distance from the wall. Integrating the wall-layer part in (4.21) leads to (4.20). Integrating the defect-layer part in (4.21) leads to
where the integration constant is defined as
The matching condition for the velocity
![]() $u^{+}$
in the overlap layer reads as follows:
$u^{+}$
in the overlap layer reads as follows:
or
with
This implicit friction law
![]() $c_{f}=f(\mathit{Re}_{m})$
can be written in explicit form as
$c_{f}=f(\mathit{Re}_{m})$
can be written in explicit form as
where
The function
![]() $G({\it\Lambda};D,E)$
has been defined and tabulated by Gersten & Herwig (Reference Gersten and Herwig1992). More details are given in appendix A. The friction law according to (4.28) is shown in figure 2. The agreement with experimental data by Launder & Rodi (Reference Launder and Rodi1981) and Hammond (Reference Hammond1982) is very good. As will become apparent later, the limits
$G({\it\Lambda};D,E)$
has been defined and tabulated by Gersten & Herwig (Reference Gersten and Herwig1992). More details are given in appendix A. The friction law according to (4.28) is shown in figure 2. The agreement with experimental data by Launder & Rodi (Reference Launder and Rodi1981) and Hammond (Reference Hammond1982) is very good. As will become apparent later, the limits
![]() $\mathit{Re}_{m}\rightarrow \infty$
and
$\mathit{Re}_{m}\rightarrow \infty$
and
![]() ${\it\gamma}\rightarrow 0$
are equivalent to the limits
${\it\gamma}\rightarrow 0$
are equivalent to the limits
![]() $x\rightarrow \infty$
and
$x\rightarrow \infty$
and
![]() $\mathit{Re}_{x}\rightarrow \infty$
, respectively.
$\mathit{Re}_{x}\rightarrow \infty$
, respectively.
4.4. Defect layer
 $(0<y\leqslant y_{m})$
$(0<y\leqslant y_{m})$
4.4.1. Flow field
In the limiting case of infinite Reynolds number (which is equivalent to
![]() $y_{m}/y_{0.5}\rightarrow 0$
), the velocity
$y_{m}/y_{0.5}\rightarrow 0$
), the velocity
![]() $u(x,y)$
in the defect layer attains the value
$u(x,y)$
in the defect layer attains the value
![]() $u_{m}(x)$
. Therefore it seems natural to write the velocity in the form of a defect law
$u_{m}(x)$
. Therefore it seems natural to write the velocity in the form of a defect law
with
The continuity equation (4.1) leads to
When the velocity components are known, the shear stress can be determined by using the momentum equation (4.2). Transforming (4.2) into the
![]() $x,{\it\eta}$
coordinate system and using (4.32) leads to
$x,{\it\eta}$
coordinate system and using (4.32) leads to
where
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle A(x)=\frac{1}{u_{{\it\tau}}}\;\frac{\text{d}\left(y_{m}\;u_{m}\right)}{\text{d}x},\quad B(x)=-\frac{y_{m}}{u_{{\it\tau}}^{2}}\;\frac{\text{d}(u_{{\it\tau}}\;u_{m})\;}{\text{d}x},\\ \displaystyle C(x)=\frac{y_{m}}{u_{{\it\tau}}}\;\frac{\text{d}u_{{\it\tau}}}{\text{d}x},\quad D(x)=-\frac{1}{u_{{\it\tau}}}\;\frac{\text{d}(u_{{\it\tau}}\;y_{m})}{\text{d}x},\end{array}\right\},\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle A(x)=\frac{1}{u_{{\it\tau}}}\;\frac{\text{d}\left(y_{m}\;u_{m}\right)}{\text{d}x},\quad B(x)=-\frac{y_{m}}{u_{{\it\tau}}^{2}}\;\frac{\text{d}(u_{{\it\tau}}\;u_{m})\;}{\text{d}x},\\ \displaystyle C(x)=\frac{y_{m}}{u_{{\it\tau}}}\;\frac{\text{d}u_{{\it\tau}}}{\text{d}x},\quad D(x)=-\frac{1}{u_{{\it\tau}}}\;\frac{\text{d}(u_{{\it\tau}}\;y_{m})}{\text{d}x},\end{array}\right\},\end{eqnarray}$$
see Schlichting & Gersten (Reference Schlichting and Gersten2003, p. 574).
Splitting the shear stress into two parts
reduces the momentum equation (4.35) to
The term
![]() $s^{\prime }$
refers to differentiating
$s^{\prime }$
refers to differentiating
![]() $s(x,{\it\eta})$
with respect to
$s(x,{\it\eta})$
with respect to
![]() ${\it\eta}$
.
${\it\eta}$
.
Using the condition
![]() $s(x,0)=1$
, integration of (4.38) leads to
$s(x,0)=1$
, integration of (4.38) leads to
4.4.2. Determination of the function
 $f({\it\eta})$
$f({\it\eta})$
The function
![]() $f({\it\eta})$
represents the self-similarity of the velocity distribution in the defect layer according to (4.32). This function must satisfy the differential equation (4.38), which in this case must be independent of
$f({\it\eta})$
represents the self-similarity of the velocity distribution in the defect layer according to (4.32). This function must satisfy the differential equation (4.38), which in this case must be independent of
![]() $x$
. This means that
$x$
. This means that
![]() $A$
and
$A$
and
![]() $B$
in (4.38) must be constants, whereas
$B$
in (4.38) must be constants, whereas
![]() $C$
and
$C$
and
![]() $D$
will become negligibly small and
$D$
will become negligibly small and
![]() $s({\it\eta})$
depends only on
$s({\it\eta})$
depends only on
![]() ${\it\eta}$
.
${\it\eta}$
.
Now one should keep in mind that the defect layer of turbulent wall jets behaves like the defect layer of turbulent equilibrium boundary layers. The latter are defined by the self-similarity of the velocity distribution, see Schlichting & Gersten (Reference Schlichting and Gersten2003, p. 580). For turbulent equilibrium boundary layers the functions
![]() $A(x)$
and
$A(x)$
and
![]() $B(x)$
are constant for high Reynolds numbers. It is therefore appropriate to assume the analogous behaviour for the wall jet in the limit
$B(x)$
are constant for high Reynolds numbers. It is therefore appropriate to assume the analogous behaviour for the wall jet in the limit
![]() $\mathit{Re}_{x}\rightarrow \infty$
:
$\mathit{Re}_{x}\rightarrow \infty$
:
which will be verified in (4.47) after the following lines of formulae.
Introducing the characteristic length
leads to
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle A(x)=\frac{\text{d}\tilde{{\rm\Delta}}}{\text{d}x}+\frac{\tilde{{\rm\Delta}}}{u_{{\it\tau}}}\;\frac{\text{d}u_{{\it\tau}}}{\text{d}x},\quad B(x)=-\left(\frac{\tilde{{\rm\Delta}}}{u_{m}}\;\frac{\text{d}u_{m}}{\text{d}x}+\frac{\tilde{{\rm\Delta}}}{u_{{\it\tau}}}\;\frac{\text{d}u_{{\it\tau}}}{\text{d}x}\right)\\ \displaystyle C(x)={\it\gamma}\;\frac{\tilde{{\rm\Delta}}}{u_{{\it\tau}}}\;\frac{\text{d}u_{{\it\tau}}}{\text{d}x},\quad D(x)=-{\it\gamma}\;\left(A(x)+\frac{\tilde{{\rm\Delta}}}{{\it\gamma}}\;\frac{\text{d}{\it\gamma}}{\text{d}x}\right).\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle A(x)=\frac{\text{d}\tilde{{\rm\Delta}}}{\text{d}x}+\frac{\tilde{{\rm\Delta}}}{u_{{\it\tau}}}\;\frac{\text{d}u_{{\it\tau}}}{\text{d}x},\quad B(x)=-\left(\frac{\tilde{{\rm\Delta}}}{u_{m}}\;\frac{\text{d}u_{m}}{\text{d}x}+\frac{\tilde{{\rm\Delta}}}{u_{{\it\tau}}}\;\frac{\text{d}u_{{\it\tau}}}{\text{d}x}\right)\\ \displaystyle C(x)={\it\gamma}\;\frac{\tilde{{\rm\Delta}}}{u_{{\it\tau}}}\;\frac{\text{d}u_{{\it\tau}}}{\text{d}x},\quad D(x)=-{\it\gamma}\;\left(A(x)+\frac{\tilde{{\rm\Delta}}}{{\it\gamma}}\;\frac{\text{d}{\it\gamma}}{\text{d}x}\right).\end{array}\right\}\end{eqnarray}$$
From the definition of
![]() ${\it\gamma}$
in (4.27a
) it follows that
${\it\gamma}$
in (4.27a
) it follows that
Differentiation of (4.26) with respect to
![]() $x$
leads to
$x$
leads to
For the limit
![]() ${\it\gamma}\rightarrow 0$
the terms proportional to
${\it\gamma}\rightarrow 0$
the terms proportional to
![]() $\text{d}{\it\gamma}/\text{d}x$
in (4.42a−d
) and (4.43) are small compared to the other terms and can be neglected. In the flow far downstream
$\text{d}{\it\gamma}/\text{d}x$
in (4.42a−d
) and (4.43) are small compared to the other terms and can be neglected. In the flow far downstream
![]() $u_{m}(x)$
changes into
$u_{m}(x)$
changes into
![]() $U_{N}(x)$
according to (4.16). From (4.42b
) and (4.43) it follows that
$U_{N}(x)$
according to (4.16). From (4.42b
) and (4.43) it follows that
Therefore
![]() $\tilde{{\rm\Delta}}(x)$
is proportional to
$\tilde{{\rm\Delta}}(x)$
is proportional to
![]() $x-x_{0}$
or to
$x-x_{0}$
or to
![]() $y_{0.5}(x)$
according to (4.8):
$y_{0.5}(x)$
according to (4.8):
The limiting constant
![]() $A_{\infty }=A(x\rightarrow \infty )$
reads as follows:
$A_{\infty }=A(x\rightarrow \infty )$
reads as follows:
and, hence, equation (4.44) reduces to
which after integration leads to
where
![]() $\mathit{Re}_{x}$
is defined in (2.3). This formula shows clearly that the limit
$\mathit{Re}_{x}$
is defined in (2.3). This formula shows clearly that the limit
![]() $\mathit{Re}_{x}\rightarrow \infty$
is equivalent to the limit
$\mathit{Re}_{x}\rightarrow \infty$
is equivalent to the limit
![]() ${\it\gamma}\rightarrow 0$
. Combining (4.41) and (4.46) leads to
${\it\gamma}\rightarrow 0$
. Combining (4.41) and (4.46) leads to
The ratio
![]() $y_{m}/y_{0.5}$
tends to zero far downstream, as has been anticipated in the present hypothesis for
$y_{m}/y_{0.5}$
tends to zero far downstream, as has been anticipated in the present hypothesis for
![]() $K_{\infty }\neq 0$
.
$K_{\infty }\neq 0$
.
In § 6 equation (4.50) will be extended to an asymptotic series expansion (6.1). By using this extension it can be shown that the functions
![]() $A(x)$
and
$A(x)$
and
![]() $B(x)$
have for
$B(x)$
have for
![]() ${\it\gamma}\rightarrow 0$
the following asymptotic form:
${\it\gamma}\rightarrow 0$
the following asymptotic form:
The function
![]() $f({\it\eta})$
has to satisfy the following ordinary differential equation, which results from (4.39) for the limit
$f({\it\eta})$
has to satisfy the following ordinary differential equation, which results from (4.39) for the limit
![]() $x\rightarrow \infty$
:
$x\rightarrow \infty$
:
In order to enable the solution of the ordinary differential equation (4.52), a turbulence model is needed that provides a relation between
![]() $f({\it\eta})$
and
$f({\it\eta})$
and
![]() $s({\it\eta})$
. Instead of that, an indirect turbulence model will be applied here. A plausible function
$s({\it\eta})$
. Instead of that, an indirect turbulence model will be applied here. A plausible function
![]() $f({\it\eta})$
will be chosen and the corresponding function
$f({\it\eta})$
will be chosen and the corresponding function
![]() $s({\it\eta})$
can then be determined from (4.52).
$s({\it\eta})$
can then be determined from (4.52).
The function
![]() $f({\it\eta})$
must satisfy the following boundary conditions:
$f({\it\eta})$
must satisfy the following boundary conditions:
In particular the physical significance of the integration constant
![]() $\bar{C}$
is apparent in (4.24). The condition
$\bar{C}$
is apparent in (4.24). The condition
![]() $f^{\prime \prime \prime }({\it\eta}=1)=0$
results from ‘patching’ the term
$f^{\prime \prime \prime }({\it\eta}=1)=0$
results from ‘patching’ the term
![]() $\partial ^{2}u/\partial y^{2}$
of the defect layer and the outer layer at
$\partial ^{2}u/\partial y^{2}$
of the defect layer and the outer layer at
![]() $y=y_{m}$
(see (4.63)).
$y=y_{m}$
(see (4.63)).
For
![]() ${\it\eta}=1$
the value
${\it\eta}=1$
the value
![]() $f_{m}$
is a measure of
$f_{m}$
is a measure of
![]() $v(x,{\it\eta}=1)$
, and the conditions
$v(x,{\it\eta}=1)$
, and the conditions
![]() $f^{\prime }=0$
and
$f^{\prime }=0$
and
![]() $f^{\prime \prime }=0$
result from
$f^{\prime \prime }=0$
result from
![]() $u=u_{m}$
.
$u=u_{m}$
.
The following function consisting of a logarithmic term and a power series satisfies all boundary conditions appearing in (4.53) and (4.54):
with
In figure 3 the defect velocity
is compared with experimental data of Wygnanski et al. (Reference Wygnanski, Katz and Horev1992). The difference between theory and experiment may be attributed to the fact that the experiments refer to fairly low Reynolds numbers. The maximum of the absolute difference for
![]() $f^{\prime }({\it\eta})=5$
is about
$f^{\prime }({\it\eta})=5$
is about
![]() ${\rm\Delta}y=0.2~\text{mm}$
, which is surprisingly small. The theoretical curve
${\rm\Delta}y=0.2~\text{mm}$
, which is surprisingly small. The theoretical curve
![]() $f^{\prime }({\it\eta})$
does not depend on any empirical constant. It is proportional to
$f^{\prime }({\it\eta})$
does not depend on any empirical constant. It is proportional to
![]() $1/{\it\kappa}$
according to (4.55), where
$1/{\it\kappa}$
according to (4.55), where
![]() ${\it\kappa}$
is the well-defined ((4.21),
${\it\kappa}$
is the well-defined ((4.21),
![]() $\mathit{Re}\rightarrow \infty$
, zero pressure gradient) universal Kármán constant
$\mathit{Re}\rightarrow \infty$
, zero pressure gradient) universal Kármán constant
![]() ${\it\kappa}=0.41$
.
${\it\kappa}=0.41$
.

Figure 3. Self-similar distribution of the defect velocity in the defect layer.
4.5. Outer layer
 $(y\geqslant y_{m})$
$(y\geqslant y_{m})$
It is assumed that the distribution of the velocity is again self-similar:
where the similarity variable is
with
The dot designates differentiation with respect to
![]() $\bar{{\it\eta}}$
. The variable
$\bar{{\it\eta}}$
. The variable
![]() $\bar{{\it\eta}}$
is a generalization of the variable
$\bar{{\it\eta}}$
is a generalization of the variable
![]() $\tilde{{\it\eta}}$
in (4.4) for
$\tilde{{\it\eta}}$
in (4.4) for
![]() $y_{m}\neq 0$
.
$y_{m}\neq 0$
.
From the continuity equation it follows that
The momentum equation leads to the shear stress:
 $$\begin{eqnarray}\displaystyle \frac{{\it\tau}_{t}}{{\it\rho}} & = & \displaystyle u_{m}{\rm\Delta}\;\frac{\text{d}u_{m}}{\text{d}x}\;F\;{\dot{F}}+\frac{2}{3}\;u_{m}\;\left(2{\rm\Delta}\;\frac{\text{d}u_{m}}{\text{d}x}+u_{m}\;\frac{\text{d}{\rm\Delta}}{\text{d}x}\right)\;F^{3}\nonumber\\ \displaystyle & & \displaystyle +\,\left[\frac{\text{d}(y_{m}\;u_{{\it\tau}})}{\text{d}x}\;f_{m}-\frac{\text{d}(y_{m}\;u_{m})}{\text{d}x}\right]\;u_{m}\;{\dot{F}}+u_{{\it\tau}}^{2}+\frac{\text{d}(y_{m}\;u_{m}^{2}\;)}{\text{d}x}\nonumber\\ \displaystyle & & \displaystyle -\,\left[\;u_{{\it\tau}}\;\frac{\text{d}(y_{m}\;u_{m})}{\text{d}x}+y_{m}\;\frac{\text{d}(u_{{\it\tau}}\;u_{m})}{\text{d}x}+u_{m}\;\frac{\text{d}(y_{m}\;u_{{\it\tau}})}{\text{d}x}\right]\;f_{m}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{{\it\tau}_{t}}{{\it\rho}} & = & \displaystyle u_{m}{\rm\Delta}\;\frac{\text{d}u_{m}}{\text{d}x}\;F\;{\dot{F}}+\frac{2}{3}\;u_{m}\;\left(2{\rm\Delta}\;\frac{\text{d}u_{m}}{\text{d}x}+u_{m}\;\frac{\text{d}{\rm\Delta}}{\text{d}x}\right)\;F^{3}\nonumber\\ \displaystyle & & \displaystyle +\,\left[\frac{\text{d}(y_{m}\;u_{{\it\tau}})}{\text{d}x}\;f_{m}-\frac{\text{d}(y_{m}\;u_{m})}{\text{d}x}\right]\;u_{m}\;{\dot{F}}+u_{{\it\tau}}^{2}+\frac{\text{d}(y_{m}\;u_{m}^{2}\;)}{\text{d}x}\nonumber\\ \displaystyle & & \displaystyle -\,\left[\;u_{{\it\tau}}\;\frac{\text{d}(y_{m}\;u_{m})}{\text{d}x}+y_{m}\;\frac{\text{d}(u_{{\it\tau}}\;u_{m})}{\text{d}x}+u_{m}\;\frac{\text{d}(y_{m}\;u_{{\it\tau}})}{\text{d}x}\right]\;f_{m}.\end{eqnarray}$$
Equations (4.61) and (4.62) reduce to (4.6) and (4.7) for the limit
![]() $x\rightarrow \infty$
, when
$x\rightarrow \infty$
, when
![]() $y_{m}\rightarrow 0$
,
$y_{m}\rightarrow 0$
,
![]() $u_{m}\rightarrow U_{N}(x)$
and
$u_{m}\rightarrow U_{N}(x)$
and
![]() ${\rm\Delta}\rightarrow y_{0.5}/k$
are taken into account.
${\rm\Delta}\rightarrow y_{0.5}/k$
are taken into account.
At
![]() $y=y_{m}$
the values for
$y=y_{m}$
the values for
![]() $u$
,
$u$
,
![]() $\partial u/\partial y$
,
$\partial u/\partial y$
,
![]() $v$
and
$v$
and
![]() ${\it\tau}_{t}/{\it\rho}$
for the defect layer
${\it\tau}_{t}/{\it\rho}$
for the defect layer
![]() $({\it\eta}=1)$
and the outer layer
$({\it\eta}=1)$
and the outer layer
![]() $(\bar{{\it\eta}}=0)$
are equal (‘patching’). For
$(\bar{{\it\eta}}=0)$
are equal (‘patching’). For
![]() $\partial ^{2}u/\partial y^{2}$
the patching condition is as follows:
$\partial ^{2}u/\partial y^{2}$
the patching condition is as follows:
In the limit
![]() ${\it\gamma}\rightarrow 0$
it follows that
${\it\gamma}\rightarrow 0$
it follows that
![]() $f^{\prime \prime \prime }(1)=0$
in (4.53).
$f^{\prime \prime \prime }(1)=0$
in (4.53).
The function
![]() $F(\bar{{\it\eta}})$
is identical with
$F(\bar{{\it\eta}})$
is identical with
![]() $F(\tilde{{\it\eta}})$
. All results for
$F(\tilde{{\it\eta}})$
. All results for
![]() $F(\tilde{{\it\eta}})$
in § 4.1 can be used in this generalization. Figure 4 shows the comparison of the solution for the outer layer with experimental results of Tailland & Mathieu (Reference Tailland and Mathieu1967).
$F(\tilde{{\it\eta}})$
in § 4.1 can be used in this generalization. Figure 4 shows the comparison of the solution for the outer layer with experimental results of Tailland & Mathieu (Reference Tailland and Mathieu1967).

Figure 4. Self-similar velocity distribution in the outer layer.
4.6. Determination of the momentum flux
 $K(x)$
$K(x)$
The momentum flux
can now be determined if (4.32) and (4.58) are used for the integration. The result is
The constants are
The formula (4.65) can be used to determine the momentum flux
![]() $K$
when the global values in the formula are known.
$K$
when the global values in the formula are known.
5. Momentum-integral equation
The momentum flux
![]() $K(x)$
must satisfy the momentum-integral equation:
$K(x)$
must satisfy the momentum-integral equation:
A dimensionless friction velocity
is introduced, where
![]() $U_{N}(x)$
is given in (4.16). Then (5.1) can be written as
$U_{N}(x)$
is given in (4.16). Then (5.1) can be written as
where
The integration leads to the final formula (see appendix A):
(This equation without the term
![]() $O({\it\gamma}_{G}^{2})$
appears also in Gersten & Herwig (Reference Gersten and Herwig1992) and in Schlichting & Gersten (Reference Schlichting and Gersten2003). Unfortunately, there the Greek letters
$O({\it\gamma}_{G}^{2})$
appears also in Gersten & Herwig (Reference Gersten and Herwig1992) and in Schlichting & Gersten (Reference Schlichting and Gersten2003). Unfortunately, there the Greek letters
![]() ${\it\kappa}$
and
${\it\kappa}$
and
![]() ${\it\alpha}$
got lost in the printing process.)
${\it\alpha}$
got lost in the printing process.)
6. Wall-jet flow described by perturbation method
So far the flow field of the wall jet has been described for given functions
![]() $y_{m}(x),y_{0.5}(x),u_{m}(x)$
and
$y_{m}(x),y_{0.5}(x),u_{m}(x)$
and
![]() $u_{{\it\tau}}(x)$
. These functions are known in the limiting case
$u_{{\it\tau}}(x)$
. These functions are known in the limiting case
![]() $x\rightarrow \infty$
, see § 4.1. Now, for the general case, these functions will be described by a perturbation method. From (5.5) it is obvious to use
$x\rightarrow \infty$
, see § 4.1. Now, for the general case, these functions will be described by a perturbation method. From (5.5) it is obvious to use
![]() ${\it\gamma}_{G}$
as the perturbation parameter. The following power series expansions will be applied (with respect to
${\it\gamma}_{G}$
as the perturbation parameter. The following power series expansions will be applied (with respect to
![]() $A_{1}$
see (4.50)):
$A_{1}$
see (4.50)):
It is assumed that the asymptotic formula (see (4.8))
is generally valid, which is in accordance with experiments. Introducing (6.1) and (6.2) into (4.27) yields
where
The skin friction law (4.26) is now transformed into
with
In appendix A it is shown that the explicit solution of (6.6) is
where
7. Determination of the universal constants
It is desirable to determine the universal constants
![]() ${\it\alpha}$
,
${\it\alpha}$
,
![]() $A_{1}$
,
$A_{1}$
,
![]() $A_{2}$
,
$A_{2}$
,
![]() $B_{1}$
and
$B_{1}$
and
![]() $B_{2}$
defined in (4.8), (6.1) and (6.2) in such a way that the analysis is optimally concordant with existing experiments. Unfortunately, all existing experimental data on plane turbulent wall jets belong to rather low Reynolds numbers and, hence, are far away from the asymptotic state. Despite this deficiency, matching of the analysis with experimental data will be attempted.
$B_{2}$
defined in (4.8), (6.1) and (6.2) in such a way that the analysis is optimally concordant with existing experiments. Unfortunately, all existing experimental data on plane turbulent wall jets belong to rather low Reynolds numbers and, hence, are far away from the asymptotic state. Despite this deficiency, matching of the analysis with experimental data will be attempted.
Experimental results on six available turbulent wall-jet flows have been analysed. The main global values are listed in table 1 below. The constant
![]() ${\it\alpha}~(=\,\text{d}y_{0.5}/\text{d}x/(4k))$
introduced in (4.8) can be taken from Launder & Rodi (Reference Launder and Rodi1981), who analysed about 20 experimental investigations. They found
${\it\alpha}~(=\,\text{d}y_{0.5}/\text{d}x/(4k))$
introduced in (4.8) can be taken from Launder & Rodi (Reference Launder and Rodi1981), who analysed about 20 experimental investigations. They found
![]() ${\it\alpha}=0.021$
. This is in accordance with the mean value resulting from the experiments in the table (
${\it\alpha}=0.021$
. This is in accordance with the mean value resulting from the experiments in the table (
![]() $k$
from (4.66d
)):
$k$
from (4.66d
)):
Taking into account (4.16), (6.1) and (6.2) and comparing (5.5) and (4.65) provide the following two conditions that the constants
![]() $A_{1}$
,
$A_{1}$
,
![]() $A_{2}$
,
$A_{2}$
,
![]() $B_{1}$
and
$B_{1}$
and
![]() $B_{2}$
must satisfy:
$B_{2}$
must satisfy:
Table 1. Experimental data.

Two still missing relations between the constants follow from the condition that the experimental values of two particular wall-jet velocity profiles should coincide with the corresponding theoretical values. The following two points have been selected for the agreement with the theory:
Point I (from Tailland & Mathieu 3,
![]() $x-x_{0}=1.06~\text{m}$
)
$x-x_{0}=1.06~\text{m}$
)
Point II (from Tailland & Mathieu 1,
![]() $x-x_{0}=1.05~\text{m}$
)
$x-x_{0}=1.05~\text{m}$
)
In addition to (7.2) and (7.3), the (6.1) and (6.2) specified for each of these points lead finally to six nonlinear algebraic equations for
![]() $A_{1}$
,
$A_{1}$
,
![]() $A_{2}$
,
$A_{2}$
,
![]() $B_{1}$
,
$B_{1}$
,
![]() $B_{2}$
,
$B_{2}$
,
![]() ${\it\gamma}_{GI}$
and
${\it\gamma}_{GI}$
and
![]() ${\it\gamma}_{GII}$
. The results are the universal constants:
${\it\gamma}_{GII}$
. The results are the universal constants:
The positions of the points are given by:
The two selected points I and II are marked in figures 2 and 5 by triangles.

Figure 5. Universal functions.
![]() $K/K_{\infty }$
according to (5.5) and (6.6),
$K/K_{\infty }$
according to (5.5) and (6.6),
![]() $u_{m}\;y_{0.5}/{\it\nu}=\mathit{Re}_{m}\;y_{0.5}/y_{m}$
,
$u_{m}\;y_{0.5}/{\it\nu}=\mathit{Re}_{m}\;y_{0.5}/y_{m}$
,
![]() $\mathit{Re}_{m}$
and
$\mathit{Re}_{m}$
and
![]() ${\it\gamma}$
according to (6.4),
${\it\gamma}$
according to (6.4),
![]() ${\it\gamma}_{G}$
according to (6.6). Experiments: see table 1 for symbols.
${\it\gamma}_{G}$
according to (6.6). Experiments: see table 1 for symbols.
![]() ${\rm\Delta}$
denotes selected points for agreement with theory.
${\rm\Delta}$
denotes selected points for agreement with theory.
The numerical values of the universal constants should be considered preliminary until experimental data for higher Reynolds numbers become available.
8. Determination of the asymptotic momentum flux
 $K_{\infty }$
$K_{\infty }$
When the values
![]() $u_{m}$
,
$u_{m}$
,
![]() $y_{0.5}$
and
$y_{0.5}$
and
![]() ${\it\nu}$
at the position
${\it\nu}$
at the position
![]() $x-x_{0}$
are known, the asymptotic momentum flux
$x-x_{0}$
are known, the asymptotic momentum flux
![]() $K_{\infty }$
can be determined by using the universal function shown in figure 5. The combination
$K_{\infty }$
can be determined by using the universal function shown in figure 5. The combination
![]() $u_{m}\;y_{0.5}/{\it\nu}$
leads to the corresponding value
$u_{m}\;y_{0.5}/{\it\nu}$
leads to the corresponding value
![]() $\mathit{Re}_{x}$
and, via (2.3), to
$\mathit{Re}_{x}$
and, via (2.3), to
![]() $K_{\infty }$
. All positions
$K_{\infty }$
. All positions
![]() $x$
in a particular wall jet should lead to the same value
$x$
in a particular wall jet should lead to the same value
![]() $K_{\infty }$
. This would be true to a greater extent the further downstream the positions are. The mean value
$K_{\infty }$
. This would be true to a greater extent the further downstream the positions are. The mean value
![]() $\bar{K}_{\infty }$
of all analysed profiles of a particular wall jet is considered as the asymptotic momentum flux of this wall jet.
$\bar{K}_{\infty }$
of all analysed profiles of a particular wall jet is considered as the asymptotic momentum flux of this wall jet.
When the values
![]() $K$
and
$K$
and
![]() ${\it\nu}$
at the position
${\it\nu}$
at the position
![]() $x-x_{0}$
are known
$x-x_{0}$
are known
![]() $K_{\infty }$
can be determined by using the universal function for
$K_{\infty }$
can be determined by using the universal function for
![]() $K(\mathit{Re}_{x})/K_{\infty }$
, also shown in figure 5. Here an iteration process would lead to the solution
$K(\mathit{Re}_{x})/K_{\infty }$
, also shown in figure 5. Here an iteration process would lead to the solution
![]() $K_{\infty }$
.
$K_{\infty }$
.
9. Comparisons with experiments
Six turbulent wall jets documented in the literature have been analysed. The
![]() $\bar{K}_{\infty }$
-values and other characteristic parameters are listed in table 1. The values
$\bar{K}_{\infty }$
-values and other characteristic parameters are listed in table 1. The values
![]() $u_{m}\;y_{0.5}/{\it\nu}$
of the analysed wall jets are in good agreement with the theoretical universal curve in figure 5. The experimental results by Bradshaw & Gee (Reference Bradshaw and Gee1960) are not shown in figure 5 because they are practically identical with the results by Tailland & Mathieu 3 (Reference Tailland and Mathieu1967). The universal relation between
$u_{m}\;y_{0.5}/{\it\nu}$
of the analysed wall jets are in good agreement with the theoretical universal curve in figure 5. The experimental results by Bradshaw & Gee (Reference Bradshaw and Gee1960) are not shown in figure 5 because they are practically identical with the results by Tailland & Mathieu 3 (Reference Tailland and Mathieu1967). The universal relation between
![]() $K/\bar{K}_{\infty }$
and
$K/\bar{K}_{\infty }$
and
![]() $\mathit{Re}_{x}$
is also shown in figure 5.
$\mathit{Re}_{x}$
is also shown in figure 5.
The experimental data for the thickness ratio
![]() $y_{m}/y_{0.5}$
are given in table 1 for four wall jets. They are compared with the present theory in figure 2. The short bars refer to the values of
$y_{m}/y_{0.5}$
are given in table 1 for four wall jets. They are compared with the present theory in figure 2. The short bars refer to the values of
![]() $y_{m}/y_{0.5}$
according to the table averaged over the covered range of Reynolds numbers
$y_{m}/y_{0.5}$
according to the table averaged over the covered range of Reynolds numbers
![]() $\mathit{Re}_{m}$
. The authors obviously assumed that the thickness ratio is a constant for the entire wall jet. The analysis of this paper, however, shows that
$\mathit{Re}_{m}$
. The authors obviously assumed that the thickness ratio is a constant for the entire wall jet. The analysis of this paper, however, shows that
![]() $y_{m}/y_{0.5}$
decreases monotonically with increasing
$y_{m}/y_{0.5}$
decreases monotonically with increasing
![]() $\mathit{Re}_{m}$
. The dotted line in figure 2 corresponds to (6.1). It is a necessary condition for the hypothesis
$\mathit{Re}_{m}$
. The dotted line in figure 2 corresponds to (6.1). It is a necessary condition for the hypothesis
![]() $K_{\infty }\neq 0$
that
$K_{\infty }\neq 0$
that
![]() $y_{m}/y_{0.5}$
tends to zero for
$y_{m}/y_{0.5}$
tends to zero for
![]() $\mathit{Re}_{m}\rightarrow \infty$
(see
$\mathit{Re}_{m}\rightarrow \infty$
(see
![]() $u/u_{m}$
in figure 6).
$u/u_{m}$
in figure 6).

Figure 6. Distributions of velocity and shear stress at point II. ——
![]() ${\it\gamma}_{G}=0.0794$
,
${\it\gamma}_{G}=0.0794$
,
![]() $\mathit{Re}_{x}=2.1\times 10^{5}$
, after (9.1)–(9.4), ○ experiment, after Tailland & Mathieu (Reference Tailland and Mathieu1967).
$\mathit{Re}_{x}=2.1\times 10^{5}$
, after (9.1)–(9.4), ○ experiment, after Tailland & Mathieu (Reference Tailland and Mathieu1967).
The ratio of
![]() $K_{\infty }/K_{j}$
is not a universal constant, but it varies in the table between 0.19 and 0.45. It depends mainly on the velocity distribution at the inflow. Narasimha et al. (Reference Narasimha, Narayan and Parthasarathy1973) have non-dimensionalized
$K_{\infty }/K_{j}$
is not a universal constant, but it varies in the table between 0.19 and 0.45. It depends mainly on the velocity distribution at the inflow. Narasimha et al. (Reference Narasimha, Narayan and Parthasarathy1973) have non-dimensionalized
![]() $x-x_{0}$
by
$x-x_{0}$
by
![]() $K_{j}$
rather than by
$K_{j}$
rather than by
![]() $K_{\infty }$
as has been done in the present investigation. Asymptotic formulae should not depend on
$K_{\infty }$
as has been done in the present investigation. Asymptotic formulae should not depend on
![]() $K_{j}$
.
$K_{j}$
.
In figure 6 the theoretical distributions of the axial velocity and the shear stress are compared with experimental data of Tailland & Mathieu (Reference Tailland and Mathieu1967). The corresponding formulae (valid for all turbulent wall jets) are
 $$\begin{eqnarray}\displaystyle \frac{{\it\tau}_{t}}{{\it\rho}\;U_{N}^{2}} & = & \displaystyle 0.021\;\ddot{F}+[0.534\;\ddot{F}-0.0548\;{\dot{F}}]\;{\it\gamma}_{G}\nonumber\\ \displaystyle & & \displaystyle +\,[0.757\;\ddot{F}-0.866\;(F^{3}-1)-0.673\;{\dot{F}}]\;{\it\gamma}_{G}^{2}\quad \bar{{\it\eta}}\geqslant 0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{{\it\tau}_{t}}{{\it\rho}\;U_{N}^{2}} & = & \displaystyle 0.021\;\ddot{F}+[0.534\;\ddot{F}-0.0548\;{\dot{F}}]\;{\it\gamma}_{G}\nonumber\\ \displaystyle & & \displaystyle +\,[0.757\;\ddot{F}-0.866\;(F^{3}-1)-0.673\;{\dot{F}}]\;{\it\gamma}_{G}^{2}\quad \bar{{\it\eta}}\geqslant 0.\end{eqnarray}$$
It should be emphasized that the limiting solution does not satisfy the no-slip condition at the wall and has zero wall shear stress. The solution including the first-order disturbances satisfies the no-slip condition, but still has zero wall shear stress. Only if the second-order disturbances are taken into account does the shear stress have a finite value at the wall.
In figure 6 the special case
![]() ${\it\gamma}_{G}=0.0794$
is plotted and compared with the limiting curve
${\it\gamma}_{G}=0.0794$
is plotted and compared with the limiting curve
![]() ${\it\gamma}_{G}=0$
. Obviously, the comparisons between the analytical results and the experimental data in figures 2–6 make the hypothesis
${\it\gamma}_{G}=0$
. Obviously, the comparisons between the analytical results and the experimental data in figures 2–6 make the hypothesis
![]() $K_{\infty }\neq 0$
plausible. A definitely convincing verification, however, will be possible in the future, preferably by direct numerical solutions of turbulent wall jets.
$K_{\infty }\neq 0$
plausible. A definitely convincing verification, however, will be possible in the future, preferably by direct numerical solutions of turbulent wall jets.
Acknowledgements
I would like to thank Mrs G. Odemar and Professor Dr-Ing. H.-D. Papenfuß for their valuable assistance in the struggle to feed the computer with formulae and figures.
Appendix A. Function
 $G({\it\Lambda};D,E)$
$G({\it\Lambda};D,E)$
The following implicit equation for the function
![]() ${\it\gamma}(\mathit{Re})$
is considered:
${\it\gamma}(\mathit{Re})$
is considered:
In addition to the Kármán constant
![]() ${\it\kappa}$
the equation contains three further constants:
${\it\kappa}$
the equation contains three further constants:
![]() $n$
,
$n$
,
![]() $\hat{D}$
and
$\hat{D}$
and
![]() $\hat{E}$
. One can find this equation quite often in the context of the theory of turbulent shear flows near walls at high Reynolds numbers. The explicit solution of (A 1) is
$\hat{E}$
. One can find this equation quite often in the context of the theory of turbulent shear flows near walls at high Reynolds numbers. The explicit solution of (A 1) is
where
The function
![]() $G({\it\Lambda};D,E)$
has been defined and tabulated by Gersten & Herwig (Reference Gersten and Herwig1992). It satisfies the implicit algebraic equation
$G({\it\Lambda};D,E)$
has been defined and tabulated by Gersten & Herwig (Reference Gersten and Herwig1992). It satisfies the implicit algebraic equation
which is independent of
![]() ${\it\kappa}$
and
${\it\kappa}$
and
![]() $n$
. The asymptote for
$n$
. The asymptote for
![]() ${\it\Lambda}\rightarrow \infty$
is
${\it\Lambda}\rightarrow \infty$
is
 $$\begin{eqnarray}\displaystyle G({\it\Lambda}\rightarrow \infty ;D,\;E\;) & = & \displaystyle 1+\frac{1}{{\it\Lambda}}\;[2\ln {\it\Lambda}-D]+\frac{1}{{\it\Lambda}^{2}}\; [4\;\ln ^{2}{\it\Lambda}-4(1+D)\ln {\it\Lambda}\nonumber\\ \displaystyle & & \displaystyle +\,D^{2}+2\;D-E]+O({\it\Lambda}^{-3}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle G({\it\Lambda}\rightarrow \infty ;D,\;E\;) & = & \displaystyle 1+\frac{1}{{\it\Lambda}}\;[2\ln {\it\Lambda}-D]+\frac{1}{{\it\Lambda}^{2}}\; [4\;\ln ^{2}{\it\Lambda}-4(1+D)\ln {\it\Lambda}\nonumber\\ \displaystyle & & \displaystyle +\,D^{2}+2\;D-E]+O({\it\Lambda}^{-3}).\end{eqnarray}$$
Again for
![]() ${\it\Lambda}\rightarrow \infty$
the following integral has a rather simple solution:
${\it\Lambda}\rightarrow \infty$
the following integral has a rather simple solution:
Appendix B. Comment on the investigation by George et al. (Reference George, Abrahamsson, Eriksson, Karlsson, Löfdahl and Wosnik2000)
In the introduction of my paper it has been stated that the analysis by George et al. refers to plane turbulent wall jets emerging from a wall perpendicular to the jet. This statement has been based on the following facts: firstly, figure 1 in George et al. shows a wall jet of this kind. Secondly, practically all experiments quoted in that investigation refer to wall jets emerging from a perpendicular wall. Thirdly, it is assumed in that investigation that
![]() $y_{m}/y_{0.5}=0.17$
(table 1 in George et al. (Reference George, Abrahamsson, Eriksson, Karlsson, Löfdahl and Wosnik2000)). This is an arbitrary unproven assumption which forces
$y_{m}/y_{0.5}=0.17$
(table 1 in George et al. (Reference George, Abrahamsson, Eriksson, Karlsson, Löfdahl and Wosnik2000)). This is an arbitrary unproven assumption which forces
![]() $K_{\infty }$
to become zero.
$K_{\infty }$
to become zero.
Since the present analysis explicitly does not apply to wall jets emerging from a perpendicular wall, the investigation by George et al. has not been given further consideration in the present work.
If, however, one were to assume that the analysis of George et al. comprises also wall jets in the absence of a perpendicular wall, then two different asymptotic analyses are the consequence. Each asymptotic analysis is based on a different though unproven assumption (hypothesis). In George et al. it is assumed that
![]() $y_{m}/y_{0.5}=0.17$
, which leads to
$y_{m}/y_{0.5}=0.17$
, which leads to
![]() $K_{\infty }=0$
. In contrast, in the present analysis it is assumed that
$K_{\infty }=0$
. In contrast, in the present analysis it is assumed that
![]() $K_{\infty }\neq 0$
with the consequence that
$K_{\infty }\neq 0$
with the consequence that
![]() $y_{m}/y_{0.5}$
tends to zero when the Reynolds number tends to infinity. Another fundamental difference between the two analyses exists concerning the effect of the inflow momentum flux
$y_{m}/y_{0.5}$
tends to zero when the Reynolds number tends to infinity. Another fundamental difference between the two analyses exists concerning the effect of the inflow momentum flux
![]() $K_{j}~(=M_{0})$
. In George et al. the Reynolds number is built with
$K_{j}~(=M_{0})$
. In George et al. the Reynolds number is built with
![]() $M_{0}$
and hence all asymptotic formulae depend on
$M_{0}$
and hence all asymptotic formulae depend on
![]() $M_{0}$
. In contrast to this, in the present work the asymptotic formulae are by definition independent of the inflow values
$M_{0}$
. In contrast to this, in the present work the asymptotic formulae are by definition independent of the inflow values
![]() $M_{0}$
,
$M_{0}$
,
![]() $U_{0}$
and
$U_{0}$
and
![]() $b~(=\,\text{slot width})$
.
$b~(=\,\text{slot width})$
.
As has been mentioned above, it is hoped that direct numerical simulations will lead to a clarification at some future date.