1. INTRODUCTION
Blackwell (cf. [2,3]) used game-theoretic methods to obtain the following inequalities. Let

be a supermartingale such that |Xn| ≤ 1 and

for all n (0 < γ < 1). Then, for any a > 0,

In [3], he considered a martingale
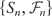
where |Xn| ≤ 1 and proved that for any positive constants a and b,
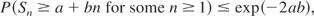
and for any positive b (0 < b < 1) and suitable r,
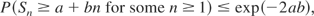
Ross [5] used a supermartingale argument to extend (2) and (3) for martingales

when −α ≤ Xn ≤ β(α,β > 0). These exponential inequalities result from the inherent subnormal character of the differences Xn. Therefore, it seems natural to widen the scope by assuming a suitable condition on the conditional moment generating function (mgf)
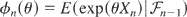
for wider applications. Consequently, the boundedness condition of Xn's is disposed and replaced by a subnormal condition on φn(θ), leading to an exponential supermartingale, and the subsequent inequalities are easily derived. Thus, the purpose of this article is to generalize Blackwell–Ross inequalities for martingales (supermartingales) under a subnormal structure on φn(θ) for wider scope and shorter and simpler proofs of earlier inequalities. Another variation of these inequalities is also given under a weaker condition leading to a sub-Poisson structure of φn(θ). Thus, our exponential supermartingale approach unifies and generalizes the known inequalities for broader applications without the condition of bounded martingale (supermartingale) differences.
2. THE MAIN RESULTS
Let
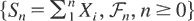
be a martingale (supermartingale) with conditional mgf
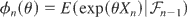
such that
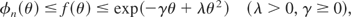
where f (θ) is a continuous positive function with f (0) = 1.
Using a suitable exponential supermartingale, we derive the basic inequality

for a suitable A ≤ 1. This inequality seems to be new under a subnormal structure that allows it to be true for martingales as well as supermartingales without the differences Xn's being bounded. The generalized version of (3) given later also appears to be new. The given generalizations unify and simplify the earlier known inequalities. All of the inequalities are derived from the following well-known supermartingale inequality.
Lemma: Let

be a positive supermartingale. Then, for m ≥ 1,
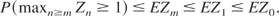
Proof: Let t = inf{n ≥ m : Zn ≥ 1} and t(k) = min(t,k), k ≥ m ≥ 1. Then
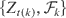
is a supermartingale by the optional stopping theorem and (4) follows from

by letting k → ∞. Most of the subsequent inequalities are based on the following proposition, which is the basic generalized inequality described earlier. It generalizes known inequalities under less restrictive conditions by shorter and simpler proofs.
Theorem: Let

be a martingale (supermartingale) such that the conditional moment generating function φn(θ) satisfies

where f (θ) is a continuous positive function such that f (0) = 1. Then for positive a and b,
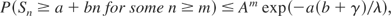
where A = e−bθ0f (θ0) ≤ 1 and θ0 = (b + γ)/λ. Moreover,
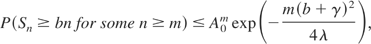
where A0 = exp(−(b − γ)θ0 /2) f (θ0) and θ0 = (b + γ)/2λ.
Proof: Let Zn(θ) = exp(θSn − aθ − bnθ), θ > 0. Clearly,

if θ = θ0 = (b + γ)/λ. Thus, Zn(θ0) is a positive supermartingale and, hence, (4) gives

It is clear that EZm(θ0) ≤ f (θ0)e−bθ0EZm−1(θ0) = AEZm−1(θ0) and, thus,

and (5) follows. To see (6), let g(s,n) = m(b − s) + sn, n ≥ m, s ≤ b, and note that bn ≥ g(s,n) for every n ≥ m, and a minimization consideration leads to the choice of s = s0 = (b − γ)/2. Thus,

and (5) gives

where A0 = exp(−½(b − γ)θ0) f (θ0) and θ0 = (b + γ)/2λ.
Remark 1: If b = 0, it is possible to improve (5) by assuming that f (θ) is convex and f′(0) < 0. Using the convexity and negative slope at θ = 0, it is easy to see that f (θ) = 1 has a unique solution θ1 ≥ θ0 = γ/2λ (γ > 0) defined earlier. Therefore, Zn(θ1) becomes a supermartingale and the bound in (5) becomes exp(−aθ1). This remark will be used later in connection with the special case leading to (1).
Special Cases: Let

be a supermartingale where −α ≤ Xn ≤ β and

for all n. For θ > 0, let m = (eβθ − e−αθ)/(α + β) and
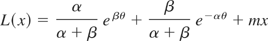
be the line through (−α,e−αθ) and (β,eβθ). Due to convexity, eθx ≤ L(x) and, hence,

Letting p = (α − γ)/(α + β) and q = (β + γ)/(α + β), we obtain
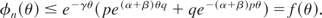
By Lemma A.6 of Alon and Spencer [1, p.235], we have

Consequently, (5) gives
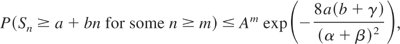
where A = f (θ0)e−bθ0, θ0 = 8(b + γ)/(α + β)2, and f (θ) is defined in (7). Similarly, (6) gives
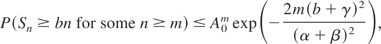
where A0 = exp(−½(b − γ)θ0) f (θ0) and θ0 = 4(b + γ)/(α + β)2.
If γ = 0, then the preceding inequalities become the ones obtained by Ross [5]. Moreover, Blackwell's inequality (1) is also included in (8) with a different bound. Since A ≤ 1 and setting b = 0 and α = β = 1, (8) becomes
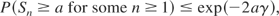
as opposed to the bound ((1 − γ)/(1 + γ))a. However, as mentioned in Remark 1, we can improve the bound (5) as follows. Clearly, in this special case, f (θ) defined in (7) becomes
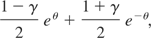
and the unique nonzero solution of f (θ) = 1 is

and the bound exp(−aθ1) in Remark 1 produces (1). Also, it should be noted that (1) gives a sharper bound than exp(−2aγ). In fact, ((1 − γ)/(1 + γ))a < exp(−2aγ), and the bound in (1) is attained. For example, let X1,X2,… be iid random variables such that P(X1 = −1) = q = (1 + γ)/2 and P(X1 = 1) = p = [(1 − γ)/2] (0 < γ < 1) so that EX1 = −γ. Set

and let f(a) = P(Sn ≥ a for some n ≥ 1) = P(Sn = a for some n ≥ 1), where a is a positive integer. A simple conditioning argument shows that f (a) = pf (a − 1) + q f (a + 1). Since f (a) < 1, the only nontrivial solution is f (a) = (p/q)a = ((1 − γ)/(1 + γ))a. It is also possible to find an analogue of the first part of (3) as follows. Consider Zn(θ) = exp(θSn − bnθ), θ > 0, and note that

. From (7), we have

where ψ(θ) = p exp((β − b)θ) + q exp(−(α + b)θ), α > γ ≥ 0, and b ≤ β. It is easy to see that ψ(θ) is convex and ψ(0) = 1 and ψ′(0) = −γ − b < 0. Hence, there exists θ* > 0 such that ψ(θ*) = 1, and there is θ1 (0 < θ1 < θ*) that minimizes ψ(θ); it occurs at

Also, note that ρ = ψ(θ1) < ψ(θ0) ≤ 1, where θ0 = 8(b + γ)/(α + β)2. Thus, EZn(θ1) ≤ ρEZn−1(θ1), and it follows that EZm(θ1) ≤ ρm. Hence, we obtain
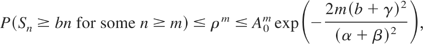
where the second bound is the same as obtained earlier by the use of Alon and Spencer's inequality for ψ(θ). This is the generalized version of (3) for nonsymmetrically bounded martingales (supermartingales), and the first bound ρm is certainly new. Also, it should be remarked that the left-hand probability is zero if b > β. In the special case α = β = 1 and γ = 0, our minimizing θ1 becomes
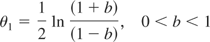
and
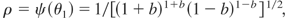
which produces Blackwell's inequality (3).
3. ANOTHER EXTENSION
We now consider a supermartingale
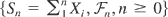
such that Xn ≤ β (β > 0) for all n (i.e., the differences Xn are bounded above only). With no loss of generality, we assume that β = 1. For θ > 0 and x ≤ 1, we will use the inequality
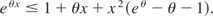
Inequality (9) is obvious from
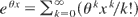
when 0 ≤ x ≤ 1. That (9) is true for x ≤ 0 follows from the elementary inequality eu ≤ 1 + u + ½u2, which follows from et ≥ 1 + t when integrated from u to zero. Replacing u by θx (x ≤ 0,θ > 0) and using the fact that eθ − θ − 1 ≥ ½θ2, (9) follows. Now let

and note from (9) that
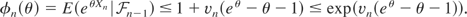
Now define
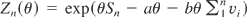
, θ > 0. Then
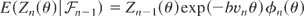
, and it follows from (10) that
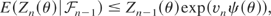
where ψ(θ) = eθ − (1 + b) θ − 1. We set ψ(θ) = 0, which has a unique solution θ0 = δ(b) > 0, so that Zn(θ0) is a supermartingale. Hence, we obtain from (4) that
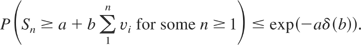
If we suppose that the vi's are constants, then
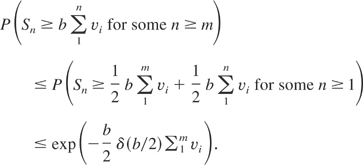
Properties of δ(b) have been noted in Lemma 1 of [4] (e.g., ln(1 + b) < δ(b) < 2b). These inequalities become useful for certain convergence problems. Clearly, if Sn is a martingale, then (12) continues to hold for |Sn| when the bound is multiplied by a factor of 2, and obviously
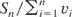
converges to zero a.s. provided
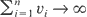
as n → ∞. As an example, let
,
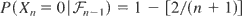
, and
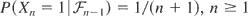
. Then vn = 2/(n + 1), and

converges to zero with probability 1, and the denominator is ∼ln(n) (as opposed to n in the usual strong law of large numbers).
Remark 2: If Xn ≤ β (β > 0), then replacing a by aβ and b by bβ in (11) and (12), the inequalities continue to hold. In addition, if

, then (11) continues to hold when a is replaced by (a + γ).
Remark 3: A final remark is that when 0 < θ < 1, then
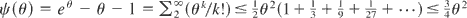
. Now set
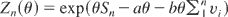
, where vi has been defined earlier. Clearly,
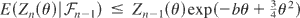
. Hence, letting θ0 = 4b/3, it follows that if b ≤ ¾, then (4) implies
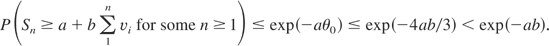
Moreover, if

is a martingale, then this inequality still hods with vi as the conditional variance of the martingale difference Xi.


