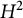1 Introduction
If T is a bounded linear operator on a Banach space E, then T is said to be embeddable into a strongly continuous semigroup if there exists
$(T_t)_{t \ge 0}$
a family of bounded linear operators on E, which is a strongly continous semigroup such that
$T = T_1$
.
This notion has been studied by T. Eisner, especially in the monograph [Reference Eisner10], and it turned out to be a very interesting and challenging problem. There is no known necessary and sufficient condition for any operator T on a Banach space, but T. Eisner showed that if T is embeddable, then
$\dim (\ker (T))$
and
$\text {codim}(\overline {\text {Im}}(T))$
are either
$0$
or
$\infty $
. This condition shows us that the forward shift operator S on
$H^2$
and all its powers are not embeddable into a strongly continous semigroup on
$H^2$
.
One of the first easy examples is the embedding of the Volterra operator
$V : f \in L^p([0,1]) \longmapsto Vf(x) = \int _0^x f(s) ~ds$
into the Riemann–Liouville semigroup on
$L^p([0,1])$
, for
$1 \le p < \infty $
[Reference Al Alam, Chalendar, El Chami, Fricain and Lefèvre1, Reference Arendt, Batty, Hieber and Neubrander2].
However, there exist some necessary and sufficient conditions for special classes of operators, and we highlight here the following result on isometric operators obtained by Eisner [Reference Eisner9] and [Reference Eisner10, Theorem V.1.19].
Theorem 1.1 Let
$V : H \rightarrow H$
be an isometry on a Hilbert space H. Then V is embeddable into a
$C_0$
-semigroup on H if and only if V is unitary or
$\text {codim}(VH) = \infty $
.
This theorem is very useful in the case of composition operators or analytic Toeplitz operators, where it is easy to characterize the isometric ones. The main goal of this paper is then to describe the embedding of such isometric operators and to make the associated semigroup explicit.
The paper is organized as follows. In Section 2, we recall some useful properties on (analytic) semigroup theory of operators and the main tools required on Hardy spaces. We also give a key lemma on Blaschke products for the main result on composition operators. Section 3 is concerned with the embedding of isometric composition operators and also the embedding of analytic Toeplitz operators. Finally, in Section 4, we show that the embedding of an isometry into a semigroup of contractions
$(T_t)_{t\geq 0}$
implies that each
$T_t$
is isometric. Moreover, the embedding of an isometry into a semigroup
$(T_t)_{t\geq 0}$
(not necessarily contractive) implies that, for each
$t>0$
,
$T_t$
is never compact.
2 Background and preliminaries
2.1 Strongly continuous semigroups of operators
Let E be a Banach space and
$(T_t)_{t \ge 0} \subset \mathcal {L}(E)$
, the space of all linear and bounded operators on E endowed with its usual norm. We say that
$(T_t)_{t \ge 0}$
is a strongly continuous semigroup or just a
$C_0$
-semigroup if
$$ \begin{align*}T_0 = Id, \quad T_{t+s} = T_t \circ T_s ,\quad t,s> 0,\end{align*} $$
and for all
$x \in E$
,
$$ \begin{align*}t \in \mathbb{R}_+ \longmapsto T_t x \text{ is continuous i.e.} \left\Vert T_t x - x\right\Vert{}_E \underset{t \rightarrow 0^+}{\longrightarrow} 0.\end{align*} $$
See, for example, [Reference Engel and Nagel11] for an introduction to semigroup theory of operators.
We recall here that an operator
$T \in \mathcal {L}(E)$
is embeddable into a
$C_0$
-semigroup on E if there exists
$(T_t)_{t \ge 0}$
a
$C_0$
-semigroup on E such that
$T = T_1$
. In this case, we write
$$ \begin{align*}T \hookrightarrow (T_t)_{t \ge 0}.\end{align*} $$
2.2 Analytic semiflows on
$\mathbb {D}$
Let
$\mathbb {D} = \{z \in \mathbb {C} : \left \lvert z \right \rvert < 1 \}$
be the open unit disc of the complex plane
$\mathbb {C}$
and
$(\varphi _t)_{t \ge 0}$
be a family of analytic self-maps of
$\mathbb {D}$
. We say that
$(\varphi _t)_{t \ge 0}$
is a semiflow of analytic self-maps of
$\mathbb {D}$
if
$$ \begin{align*}\varphi_0 = Id, \quad \varphi_{t + s} = \varphi_t \circ \varphi_s ,\quad t,s \geq 0,\end{align*} $$
and for all
$z\in \mathbb {D}$
,
$$ \begin{align*}t \in \mathbb{R}_+ \longmapsto \varphi_t (z)\text{~is continuous}.\end{align*} $$
Note that the pointwise continuity assumption is equivalent to the uniform continuity on all compact subsets of
$\mathbb {D}$
via Montel’s theorem.
It is a well known fact that when
$(\varphi _t)_{t \ge 0}$
is a semiflow of analytic self-maps of
$\mathbb {D}$
, each function
$\varphi _t$
is one-to-one. See [Reference Bracci, Contreras and Díaz-Madrigal6] for a proof using Cauchy–Lipschitz’s theory or [Reference Celariès and Chalendar7] for an alternative elementary proof. We recommend [Reference Bracci, Contreras and Díaz-Madrigal6] for a very complete state of the art of analytic semiflow theory.
In the same way, we say that
$\varphi \in \text {Hol}(\mathbb {D})$
is embeddable into a semiflow of analytic self-maps of
$\mathbb {D}$
if there exists
$(\varphi _t)_{t \ge 0}$
a semiflow of analytic self-maps of
$\mathbb {D}$
such that
$\varphi = \varphi _1$
. In this case, we write
$$ \begin{align*}\varphi \hookrightarrow (\varphi_t)_{t \ge 0}.\end{align*} $$
As an example, let
$\varphi $
be an elliptic automorphism of
$\mathbb {D}$
, i.e.,
$\varphi $
is an holomorphic and bijective function on
$\mathbb {D}$
with a fixed point
$\alpha \in \mathbb {D}$
. Equivalently, there exist
$\theta \in \mathbb {R}$
and
$\alpha \in \mathbb {D}$
such that
$$ \begin{align} \varphi = \tau_\alpha \circ R_\theta \circ \tau_\alpha,\text{ where } R_\theta : z \longmapsto e^{i\theta}z\text{ and } \tau_\alpha : z \longmapsto \frac{\alpha - z}{1 - \overline{\alpha}z}. \end{align} $$
Note that
$\tau _\alpha $
is an automorphism of
$\mathbb {D}$
, which coincides with its inverse. Thus,
$\varphi $
is embeddable into the following semiflow of analytic self-maps of
$\mathbb {D}$
:
$$ \begin{align*}\varphi_t = \tau_\alpha \circ R_{\theta t} \circ \tau_\alpha, \text{ with } R_{\theta t} : z \longmapsto e^{it\theta}z,\quad t\geq 0.\end{align*} $$
2.3 Hardy spaces and Blaschke products
Let
$\mathbb {T} = \{z \in \mathbb {C} : \left \lvert z \right \rvert = 1 \}$
be the unit circle endowed with the Lebesgue measure m. For
$0<p<\infty $
, we consider the Hardy space
$H^p=H^p(\mathbb {D})$
, which consists of functions f holomorphic on
$\mathbb {D}$
satisfying
$$\begin{align*}\left\Vert f\right\Vert{}_p= \sup_{0 \le r < 1}\left(\int_{\mathbb{T}} \left\lvert f(r\zeta) \right\rvert^p\,dm(\zeta)\right)^{1/p}<\infty. \end{align*}$$
Recall that for
$p=2$
,
$H^2$
is a reproducing kernel Hilbert space whose kernel is given by
$$\begin{align*}k_\lambda(z) = \frac{1}{1 - \overline{\lambda}z}, \quad \lambda, z \in \mathbb{D,} \end{align*}$$
meaning that
$$\begin{align*}f(\lambda) = \langle f, k_\lambda\rangle_2, \quad f \in H^2, \quad \lambda \in \mathbb{D}.\end{align*}$$
Moreover, we have
$\text {Span}_{H^2}(k_\lambda : \lambda \in \mathbb {D}) = H^2$
, where
$\text {Span}_{\mathcal H}(A)$
denotes the closure in
$\mathcal H$
of the subspace consisting of finite linear combinations of elements of A, where A is a family of vectors in a Hilbert space
$\mathcal H$
. Define by
$H_0^2$
the space of functions
$f \in H^2$
such that
$f(0) = 0$
.
We also define
$H^\infty = H^\infty (\mathbb {D})$
to be the class of bounded analytic functions on
$\mathbb {D}$
, endowed with the sup norm defined by
$\left \Vert f\right \Vert {}_\infty = \underset {z \in \mathbb {D}}{\sup } \left \lvert f(z) \right \rvert $
.
We also recall that a Blaschke product is a function of the form
$$ \begin{align} B(z) = e^{i\beta}z^k\prod_{n \ge 1} \frac{\left\lvert \alpha_n \right\rvert}{\alpha_n}\frac{\alpha_n - z}{1 - \overline{\alpha_n}z}, \quad z \in \mathbb{D,} \end{align} $$
where
$\beta \in \mathbb {R}$
,
$k \in \mathbb {N}\cup \{0\}$
and
$(\alpha _n)_{n \ge 1}$
is a finite or infinite sequence of
$\mathbb {D} \backslash \{0\}$
satisfying
$\sum _{n \ge 1} (1-\left \lvert \alpha _n \right \rvert ) < \infty $
. Then, B is an inner function on
$\mathbb {D}$
. When
$(\alpha _n)_{n \ge 1}$
is a finite sequence of
$\mathbb {D}$
, we say that B is a finite Blaschke product and one can easily check that such B are continuous on the closed unit disc. We refer the reader to [Reference Garcia, Mashreghi and Ross13] for more details about finite Blaschke products.
In the sequel, we consider the finite Blaschke product associated with a finite sequence
$(\alpha _n)_{1 \le n \le N}\subset \mathbb {D}$
defined by
$$ \begin{align} B(z) = \prod_{i=1}^N \frac{\alpha_i - z}{1 - \overline{\alpha_i}z}, \quad z \in \mathbb{D}. \end{align} $$
We know that the equation
$B(z) = \beta $
for
$\beta \in \mathbb {D}$
has exactly N solutions in
$\mathbb {D}$
, taking into account the multiplicity (see [Reference Garcia, Mashreghi and Ross13]). The following lemma is the key to differentiate them.
Lemma 2.1 Let
$\beta \in \mathbb {D} \backslash B( \text {Zero}(B'))$
. Then the equation
$B(z) = \beta $
has exactly N distinct solutions in
$\mathbb {D}$
.
Proof Let
$\beta \in \mathbb {D}$
. Then
$B(z) = \beta $
is equivalent to a polynomial equation of the form
$$\begin{align*}P(z)-\beta Q(z)=0\text{ with }P(z)= \prod_{i=1}^N (\alpha_i - z) \text{ and }Q(z)=\prod_{i=1}^N (1 - \overline{\alpha_i}z).\end{align*}$$
Since
$(-1)^{N}\left (1 - \beta \prod _{i=1}^N \overline {\alpha _i}\right ) \neq 0$
and since B maps
$\mathbb {D}$
to
$\mathbb {D}$
,
$\mathbb {T}$
to
$\mathbb {T}$
, and
$\{z\in \mathbb {C}:|z|>1\}$
to itself, there are N solutions in
$\mathbb {D}$
. It remains to prove that for suitable
$\beta $
the solutions are distinct.
Note that
$$ \begin{align*}B'(z) = \frac{P'(z)Q(z) - P(z)Q'(z)}{Q(z)^2},\end{align*} $$
and thus
$$ \begin{align*}P(z) - \beta Q(z) = 0 \text{~and~} P'(z) - \beta Q'(z) = 0\Longrightarrow B'(z)=0.\end{align*} $$
It follows that for
$\beta \in \mathbb {D} \backslash B( \text {Zero}(B'))$
, the equation
$B(z) = \beta $
has exactly N distinct solutions in
$\mathbb {D}$
.
We also recall the well known and very useful Frostman’s theorem [Reference Garcia, Mashreghi and Ross12] whose assertion is the following. Let
$\theta $
be an arbitrary inner function. Then there exists a set of measure zero with respect to the area measure (even a set of capacity zero)
$\Omega \subset \mathbb {D}$
such that for every
$\lambda \in \mathbb {D} \backslash \Omega $
, the so-called Frostman’s transform
$$ \begin{align*}\theta_\lambda := \tau_\lambda \circ \theta = \frac{\lambda - \theta}{1 - \overline{\lambda}\theta}\end{align*} $$
is a Blaschke product with simple zeros. Here recall that
$\tau _\lambda $
is the usual automorphism of
$\mathbb {D}$
defined by
$\tau _\lambda (z) = \frac {\lambda - z}{1 - \overline {\lambda }z}$
for
$z \in \mathbb {D}$
.
3 Embedding results
3.1 Composition operators on
$H^2$
First of all, recall that the main goal of this paper is to describe classes of operators, which can be embedded into a semigroup of operators. The isometric operators are of particular interest due to the necessary and sufficient condition in Theorem 1.1 on Hilbert spaces. The choice of composition operators on
$H^2$
is relevant since the isometric ones as well as the ones that are similar to isometries are fully characterized and, moreover, this class is quite rich. We define the composition operator
$C_\varphi $
with symbol
$\varphi $
on
$H^2$
by
$$ \begin{align*}C_\varphi : f \longmapsto f \circ \varphi, \quad f \in H^2.\end{align*} $$
This operator is well defined and bounded on
$H^2$
. See [Reference Shapiro17] for further information about those operators on
$H^2$
.
Moreover,
$C_\varphi $
is an isometry on
$H^2$
if and only if
$\varphi $
is inner and
$\varphi (0) = 0$
. In [Reference Bayart4], F. Bayart showed that
$C_\varphi $
is similar to an isometry on
$H^2$
if and only if
$\varphi $
is inner, and there exists
$\alpha \in \mathbb {D}$
such that
$\varphi (\alpha ) = \alpha $
. In other words,
$C_\varphi $
is similar to an isometry on
$H^2$
if and only if its symbol
$\varphi $
is an elliptic inner function.
In Arendt et al. [Reference Arendt, Chalendar, Kumar and Srivastava3] showed the following results.
-
• On the Bergman space
$\mathcal {A}^2$
(and even on its weighted versions
$\mathcal {A}^2_\beta $
for
$\beta> -1)$
,
$C_\varphi $
is similar to an isometry if and only if
$\varphi $
is an elliptic automorphism of
$\mathbb {D}$
. Thus, we will find a natural embedding according to (2.1) for
$C_\varphi $
, described later by Remark 3.1. -
• On the classical Dirichlet space
$\mathcal {D}$
,
$C_\varphi $
is similar to an isometry if and only if
$\varphi $
is a univalent full map with a fixed point in
$\mathbb {D}$
and the counting function
$n_\varphi $
associated to
$\varphi $
is essentially radial (see [Reference Arendt, Chalendar, Kumar and Srivastava3, Section 6]). Note that the existing criteria for the boundedness of
$C_\varphi $
is not that explicit and so the similarity to an isometry is much less easy to handle.
From now on, the space on which we study our operators are defined on the Hardy space
$H^2$
. Let
$\varphi : \mathbb {D} \to \mathbb {D}$
be analytic.
Remark 3.1 Observe that if
$\varphi \hookrightarrow (\varphi _t)_{t \ge 0}$
where
$(\varphi _t)_{t \ge 0}$
is a semiflow of analytic self-maps of
$\mathbb {D}$
, then
$C_\varphi \hookrightarrow (C_{\varphi _t})_{t \ge 0}$
where
$ (C_{\varphi _t})_{t \ge 0}$
is a
$C_0$
-semigroup on
$H^2$
.
Conversely if
$C_\varphi \hookrightarrow (T_t)_{t \ge 0}$
where
$(T_t)_{t \ge 0}$
is a
$C_0$
-semigroup of composition operators on
$H^2$
, then applying
$T_t$
to
$e_1(z) := z$
and using the fact that the convergence in
$H^2$
implies the pointwise convergence, we get the existence of
$(\varphi _t)_{t \ge 0}$
a semiflow of analytic self-maps of
$\mathbb {D}$
such that
$T_t = C_{\varphi _t}$
.
With the reproducing kernel Hilbert space property of
$H^2$
, we can give the following first sufficient condition of embedding for isometric composition operators. This is a key to understand the strategy of the proof of the main result.
Lemma 3.2 Let
$\varphi : \mathbb {D} \rightarrow \mathbb {D}$
be an inner function such that
$\varphi (0) = 0$
. Assume that there exists a sequence
$(z_k)_{k\geq 0}$
of distinct points in
$\mathbb {D} $
such that each
$z_k$
has at least two preimages by
$\varphi $
. Then
$C_\varphi $
is embeddable into a
$C_0$
-semigroup on
$H^2$
.
Proof Since
$\varphi $
is an inner function such that
$\varphi (0) = 0$
, it comes that
$C_\varphi $
is an isometry on
$H^2$
. Moreover, by hypothesis, for
$K \in \mathbb {N}$
, there exist
$(w_1, ..., w_K)$
and
$(w_1', ..., w_K') \in \mathbb {D}^K$
such that
$$ \begin{align*}\forall 1 \le i \le K, \quad w_i \neq w_i' \text{~and~} \varphi(w_i) = \varphi(w_i') = z_i.\end{align*} $$
For each
$1 \le i \le K$
, define the function
$f_i \in H^2$
by
$f_i = k_{w_i} - k_{w_i'}$
. Then, for all
$f \in H^2$
and for every
$1 \le i \le K$
,
$$ \begin{align*}\langle C_\varphi f, f_i\rangle_2 = \langle f \circ \varphi,k_{w_i}\rangle_2 - \langle f \circ \varphi,k_{w_i'}\rangle _2 = f \circ \varphi(w_i) - f \circ \varphi(w_i') = 0.\end{align*} $$
Therefore, we obtain that
$(f_i)_{1 \le i \le K} \subset \text {Im}(C_\varphi )^\perp $
. Since
$(f_i)_{1 \le i \le K}$
is a set of K linearly independent functions, where K is arbitrary large, we get that
$$ \begin{align*} \text{codim}(\text{Im}(C_\varphi)) = \dim(\text{Im}(C_\varphi)^\perp) = \infty. \end{align*} $$
Finally, we conclude with Theorem 1.1 and then
$C_\varphi $
is embeddable into a
$C_0$
-semigroup on
$H^2$
.
Recall that if
$\varphi $
is an elliptic automorphism, as in Section 2.2, then
$C_\varphi $
is embeddable into a semigroup of composition operators on
$H^2$
(see (2.1) and Remark 3.1). We refer the reader to [Reference Bracci, Contreras and Díaz-Madrigal6] for the remaining automorphism cases, for which there exist natural embeddings thanks to Remark 3.1.
Theorem 3.3 Every composition operator
$C_\varphi $
which is similar to an isometry on
$H^2$
is embeddable into a
$C_0$
-semigroup
$(T_t)_{t\geq 0}$
on
$H^2$
, which is not a semigroup of composition operators, unless
$\varphi $
is an automorphism.
Proof Let
$\varphi : \mathbb {D} \to \mathbb {D}$
be an analytic function. Then
$C_\varphi $
is similar to an isometry on
$H^2$
if and only if
$\varphi $
is inner and there exists
$\alpha \in \mathbb {D}$
such that
$\varphi (\alpha ) = \alpha $
. The case when
$\varphi $
is an elliptic automorphism is already done thanks to Remark 3.1. From now on, assume that
$\varphi $
is a nonautomorphic inner function with a fixed point
$\alpha \in \mathbb {D} $
.
Let us first remark that
$\varphi $
is not injective. Indeed,
-
• if
$\varphi $
is a Blaschke product as (2.2), then
$\varphi $
is not injective since
$0$
has at least two preimages; -
• if
$\varphi $
is not a Blaschke product, then according to Frostman’s theorem, the map
$\tau _a \circ \varphi = \frac {a - \varphi }{1 - \overline {a}\varphi }$
is a Blaschke product B with simple zeros for almost all
$a \in \mathbb {D}$
. Therefore,
$\varphi = \tau _a^{-1}(B)$
is not injective.
In that case, there is no semiflow of analytic self-maps of
$\mathbb {D}$
in which
$\varphi $
is embeddable. Therefore, from Remark 3.1,
$C_\varphi $
is not embeddable into a
$C_0$
-semigroup of composition operators on
$H^2$
. For
$\varphi (\alpha ) = \alpha $
, let us consider the application defined as follows
$$\begin{align*}\psi := \tau_\alpha \circ \varphi \circ \tau_\alpha.\end{align*}$$
Then
$\psi $
is an inner function such that
$\psi (0) = 0$
. Thus,
$C_\psi $
is an isometry of
$H^2$
and we get
$C_\varphi = C_{\tau _\alpha } \circ C_\psi \circ C_{\tau _\alpha }$
. Since
$C_{\tau _\alpha }$
is an isomorphism of
$H^2$
, it remains to show that
$C_\psi $
is embeddable into a
$C_0$
-semigroup on
$H^2$
.
-
• If
$\psi $
is a finite Blaschke product B, the conclusion follows from Lemmas 2.1 and 3.2, taking
$(z_k)_{k\geq 0}$
in
$\mathbb {D}\backslash B(\text {Zero}(B'))$
. -
• If
$\psi $
is inner but not a finite Blaschke product, according to Frostman’s theorem, the map
$\tau _\gamma \circ \psi =: B$
is a Blaschke product with simple zeros for almost all
$\gamma \in \mathbb {D}$
. In that case, we have (3.1)Denote by
$$ \begin{align} C_\psi H^2 & = \{ f \circ \psi : f \in H^2 \} \\ \nonumber & = \{ (f \circ \tau_\gamma) \circ (\tau_\gamma \circ \psi) : f \in H^2 \} \\ \nonumber & = \{ g \circ B : g \in H^2 \} = C_B H^2. \end{align} $$
$(w_k)_{k \ge 1}$
the sequence of simple zeros of B. Considering the sequence
$(k_{w_i} - k_{w_j})_{i,j \ge 1, i \neq j}$
of linearly independent functions of
$H^2$
, we deduce from (3.1) that The embedding of
$$ \begin{align*}\text{codim}(\text{Im}(C_\psi)) = \dim(\text{Im}(C_B)^\perp) = \infty.\end{align*} $$
$C_\psi $
follows from Theorem 1.1.
Finally, we conclude that
$C_\varphi $
is embeddable into the
$C_0$
-semigroup
$(C_{\tau _\alpha }T_tC_{\tau _\alpha })_{t \ge 0}$
on
$H^2$
, where
$C_\psi $
is embedded into a
$C_0$
-semigroup denoted by
$(T_t)_{t \ge 0}$
on
$H^2$
.
In order to describe the semigroup in which
$C_\varphi $
is embeddable, we need the following lemma that appears in [Reference Nordgren15, Lemma 5]. For the sake of completeness, we include a slightly different proof.
Lemma 3.4 Let
$\psi $
be an inner function such that
$\psi (0)=0$
and such that
$\psi $
is not an automorphism. Then
$\bigcap _{n\geq 0}C_\psi ^n H^2_0=\{0\}$
and thus 
, where 
stands for the constant function equal to
$1$
.
Proof Let
$g \in \bigcap _{n\geq 0}C_\psi ^n H_0^2$
. Then for each
$n \ge 1$
, there exists
$f_n \in H_0^2$
such that
$g(z) = f_n(\psi ^{[n]}(z))$
for every
$z \in \mathbb {D}$
with
$\psi ^{[n]} = \psi \circ \cdots \circ \psi $
(n times). Moreover,
$\left \Vert g\right \Vert {}_2 = \left \Vert f_n\right \Vert {}_2$
since
$C_\psi $
is isometric. Note that if
$g \neq 0$
, then there exists
$z_0 \in \mathbb {D}$
,
$z_0 \neq 0$
such that
$\left \lvert g(z_0) \right \rvert> 0$
. Since
$f_n \in H_0^2$
,
$f_n(0) = 0$
, there exists
$g_n \in H^2$
such that
$f_n(z) = zg_n(z)$
for every
$z \in \mathbb {D}$
, with
$\left \Vert g_n\right \Vert {}_2 = \left \Vert g\right \Vert {}_2$
. Finally, we get that
$$ \begin{align*} \left\lvert f_n(\psi^{[n]}(z_0)) \right\rvert & = \left\lvert \psi^{[n]}(z_0) \right\rvert\left\lvert g_n(\psi^{[n]}(z_0)) \right\rvert \\ & = \left\lvert \psi^{[n]}(z_0) \right\rvert\left\lvert \langle g_n,k_{\psi^{[n]}(z_0)}\rangle_2 \right\rvert \\ & \le \left\lvert \psi^{[n]}(z_0) \right\rvert\left\Vert g\right\Vert{}_2 \frac{1}{\sqrt{1 - \left\lvert \psi^{[n]}(z_0) \right\rvert^2}}. \end{align*} $$
Since
$0$
is the Denjoy–Wolff point of
$\psi $
, we get
$\psi ^{[n]}(z_0) \underset {n \rightarrow \infty }{\longrightarrow } 0$
. Then
$\left \lvert f_n(\psi ^{[n]}(z_0)) \right \rvert \underset {n \rightarrow \infty }{\longrightarrow } 0$
, and we get
$g(z_0) = 0$
, a contradiction. Consequently,
$\bigcap _{n\geq 0}C_\psi ^n H^2_0=\{0\}$
.
The second assertion of the lemma follows from the fact that if
$f \in \bigcap _{n \ge 0} C_\psi ^n H^2$
then 
. Indeed, in that case, for each
$n \ge 1$
, there exists
$h_n \in H^2$
such that
$f = C_\psi ^n h_n$
. Thus, 
. Since
$f(0) = h_n(\psi ^{[n]}(0)) = h_n(0)$
, we have 
with 
. Therefore, 
.
Corollary 3.5 Let
$\varphi $
be an inner function with a fixed point
$\alpha \in \mathbb {D}$
and such that
$\varphi $
is not an automorphism. Then
$C_\varphi $
on
$H^2$
is embeddable into the
$C_0$
-semigroup
$$\begin{align*}\left( M_{e^{it\theta}} \oplus C_{\tau_\alpha}U^*S_tU C_{\tau_\alpha}\right)_{t \ge 0},\end{align*}$$
with respect to the decomposition 
where
$U : H_0^2 \rightarrow L^2(\mathbb {R}_+, \text {Im}(C_\psi )^\perp )$
is unitary,
$\theta \in \mathbb {R}$
and
$(S_t)_{t \ge 0}$
is the right semigroup on
$L^2(\mathbb {R}_+, \text {Im}(C_\psi )^\perp )$
defined by
$$\begin{align*}(S_t f)(s)=\begin{cases} f(s-t) & s-t\geq 0\\ 0 & s-t<0 \end{cases}. \end{align*}$$
Proof First note that
$$ \begin{align} C_\varphi = C_{\tau_\alpha}C_\psi C_{\tau_\alpha}, \end{align} $$
where
$\psi $
is an inner function such that
$\psi (0)=0$
and
$\psi $
is not an automorphism. Therefore,
$C_\psi $
is isometric. Using Wold’s decomposition and Lemma 3.4, we obtain that
$H^2 = F \oplus ^\perp G$
with 
and, by the properties of the orthogonal direct sum,
$G := \bigoplus _{n \ge 0} C_\psi ^n(H^2 \ominus C_\psi H^2) = H_0^2$
. In that case,
$(C_\psi )_{|F}$
is unitary on a vector space of dimension
$1$
. Therefore,
$(C_\psi )_{|F} = M_{e^{i\theta }}$
for some
$\theta \in \mathbb {R}$
. On the other side,
$(C_\psi )_{|G}$
is unitarily equivalent to the right shift S on
$\ell ^2(\mathbb {N}, \text {Im}(C_\psi )^\perp )$
. According to the embedding of S by [Reference Eisner10, Proposition V.1.18], we obtain the embedding of
$C_\psi $
into the
$C_0$
-semigroup
$\left (M_{e^{it\theta }} \oplus U^*S_tU \right )_{t \ge 0}$
where
$U : H_0^2 \rightarrow L^2(\mathbb {R}_+, \text {Im}(C_\psi )^\perp )$
is unitary,
$\theta \in \mathbb {R}$
and
$(S_t)_{t \ge 0}$
is the right semigroup on
$L^2(\mathbb {R}_+, \text {Im}(C_\psi )^\perp )$
. We conclude the proof using (3.2).
Remark 3.6 Another special case is when the symbol
$\varphi $
is a linear fractional map of the unit disc. Indeed, we have a complete characterization of the embedding of
$\varphi $
according to its fixed points by [Reference Bracci, Contreras and Díaz-Madrigal5, Proposition 3.4]. Then, we have the natural embedding of
$C_\varphi $
by Remark 3.1. However, there are some examples where the embedding of
$C_\varphi $
into a
$C_0$
-semigroup of composition operators on
$H^2$
is not possible. To that aim, it suffices to consider
$\varphi $
the attractive elliptic function on
$\mathbb {D}$
defined by
$\varphi (z) = \frac {z}{z-2}$
. Indeed,
$\varphi $
does not satisfy the following required condition:
$$ \begin{align} \left\lvert \overline{\alpha} - \frac{1}{\beta} \right\rvert l \le \left\lvert \varphi'(\alpha) \right\rvert \left\lvert 1 - \frac{\alpha}{\beta} \right\rvert, \end{align} $$
where
$\alpha \in \mathbb {D}$
is its Denjoy–Wolff point,
$\beta \in (\mathbb {C} \cup \{\infty \}) \backslash \mathbb {D}$
its repulsive fixed point, and
$l = l(\varphi '(\alpha ))$
the length of the canonical spiral associated with
$\varphi '(\alpha ) \in \mathbb {D} \backslash \{0\}$
. Consequently,
$\varphi $
is not embeddable into a semiflow of analytic self-maps of
$\mathbb {D}$
. We refer the reader to [Reference Bracci, Contreras and Díaz-Madrigal6] for more information about Denjoy–Wolff theory.
Let us now introduce weighted composition operators. Let
$w \in H^2$
and
$\varphi : \mathbb {D} \to \mathbb {D}$
be analytic. We define the weighted composition operator
$C_{w, \varphi }$
with symbol
$\varphi $
and weight w by
$$ \begin{align*}C_{w, \varphi} : f \longmapsto w(f \circ \varphi), \quad f \in H^2.\end{align*} $$
Kumar and Partington [Reference Kumar and Partington14] proved that
$C_{w, \varphi }$
is an isometry on
$H^2$
if and only if
$\varphi $
is inner,
$\left \Vert w\right \Vert {}_2 = 1$
and
$\langle w,w \varphi ^n\rangle _2 = 0$
for every
$n \ge 1$
.
Chalendar and Partington [Reference Chalendar and Partington8] obtained the following result: if
$\varphi $
is inner, then there exists a weight
$w \in H^2$
such that
$C_{w, \varphi }$
is an isometry on
$H^2$
.
The combination of these two results gives the following sufficient condition about the embedding of weighted composition operators. The main interest of this assertion is that, provided that we make an appropriate choice of the weight, it is not required that the symbol of the composition operator has a fixed point in
$\mathbb {D}$
.
Theorem 3.7 Let
$\varphi $
be an inner function. Then there exists a weight
$w \in H^2$
such that
$C_{w, \varphi }$
is embeddable into a
$C_0$
-semigroup on
$H^2$
.
Proof Since
$\varphi $
is inner, there exists a weight
$w \in H^2$
such that
$C_{w, \varphi }$
is an isometry on
$H^2$
. Moreover, w satisfied
$\left \Vert w\right \Vert {}_2 = 1$
and
$\langle w,w \varphi ^n\rangle _2 = 0$
for every
$n \ge 1$
. It remains to show that
$\text {codim} (\text {Im}(C_{w, \varphi })) = \infty $
. Note that, for every
$\lambda \in \mathbb {D}$
and
$f \in H^2$
, we have
$$ \begin{align*}\langle C_{w, \varphi}f,k_\lambda\rangle_2 = w(\lambda)C_\varphi f(\lambda) = w(\lambda) (f \circ \varphi(\lambda)).\end{align*} $$
Then, we deduce that
$\langle C_{w, \varphi }f,k_\lambda \rangle _2 = 0$
if and only if
$w(\lambda ) = 0$
or
$f \circ \varphi (\lambda ) = 0$
. Take
$w = Bm$
where B is an infinite Blaschke product associated with a sequence
$(\lambda _n)_{n \ge 1} \subset \mathbb {D}$
satisfying
$\sum _{n \ge 1} (1 - \left \lvert \lambda _n \right \rvert ) < \infty $
and where
$m \in H^2$
satisfies
$\left \Vert m\right \Vert {}_2 = 1$
and
$\langle m,m \varphi ^n\rangle _2 = 0$
for every
$n \ge 1$
. Notice that since B is inner, we get
$\left \Vert w\right \Vert {}_2 = 1$
and
$\langle w,w \varphi ^n\rangle _2 = 0$
for every
$n \ge 1$
. Thus,
$C_{w, \varphi }$
is an isometry on
$H^2$
such that
$$ \begin{align*}\langle C_{w, \varphi}f,k_\lambda\rangle_2 = B(\lambda) m(\lambda) C_\varphi f(\lambda) = 0, \quad \lambda \in \{\lambda_n :n \ge 1\} \subset \mathbb{D}.\end{align*} $$
In other words, we deduce that
$\text {Span}_{H^2}(k_\lambda : \lambda \in \text {Zero}(B)) \subset \text {Im}(C_{w, \varphi })^\perp $
and
$$\begin{align*}\text{codim} (\text{Im}(C_{w, \varphi})) = \dim (\text{Im}(C_{w, \varphi})^\perp) = \infty.\end{align*}$$
Finally, for such a
$w \in H^2$
,
$C_{w, \varphi }$
is embeddable into a
$C_0$
-semigroup on
$H^2$
by Theorem 1.1.
Remark 3.8 The form of the
$C_0$
-semigroup in which
$C_{w, \varphi }$
is embeddable is less explicit than the one given in Corollary 3.5. Indeed, for
$\varphi $
an inner function and
$w \in H^2$
the weight such that
$C_{w, \varphi }$
is an isometry on
$H^2$
, by the Wold’s decomposition,
$H^2 = F \oplus ^\perp G$
where
$(C_{w, \varphi })_{|F}$
is unitary and
$(C_{w, \varphi })_{|G}$
is unitarily equivalent to the right shift on
$\ell ^2(\mathbb {N}, \text {Im}(C_{w, \varphi })^\perp )$
. Then, by [Reference Eisner10, Theorem V.1.14],
$C_{w, \varphi }$
is embeddable into the
$C_0$
-semigroup
$$ \begin{align*}\left (Z^* \left (e^{t \log (m)} \right)Z \oplus U^*S_tU \right )_{t \ge 0},\end{align*} $$
where
$\mu $
is a Borel measure,
$m \in L^\infty (\sigma ((C_{w, \varphi })_{|F}), \mu )$
is measurable and
$$\begin{align*}Z : F \rightarrow L^2(\sigma((C_{w, \varphi})_{|F}), \mu),\,\,\, U : G \rightarrow L^2(\mathbb{R}_+, \text{Im}(C_{w, \varphi})^\perp),\end{align*}$$
are unitary operators.
3.2 Analytic Toeplitz operators on
$H^2$
Let
$\varphi \in L^\infty (\mathbb {T})$
. We define the Toeplitz operator
$T_\varphi $
with symbol
$\varphi $
by
$$ \begin{align*}T_\varphi : f \longmapsto P_+(\varphi f), \quad f \in H^2,\end{align*} $$
where
$P_+$
denotes here the Riesz projection, i.e., the orthogonal projection of
$L^2(\mathbb {T})$
onto
$H^2$
. It is a bounded operator on
$H^2$
whose norm is equal to
$\|\varphi \|_\infty $
. See [Reference Garcia, Mashreghi and Ross12, Section 4] for the main properties about Toeplitz operators with symbols in
$L^\infty (\mathbb {T})$
. From now on, assume that
$\varphi \in H^\infty $
and note that
$T_\varphi $
is then the multiplication operator by
$\varphi $
. We have
$\ker (T_\varphi ) = \{0\}$
and
$\ker (T_\varphi ^*) = \mathcal {K}_\theta $
, thus
$$ \begin{align*}\text{codim}(\text{Im}(T_\varphi)) = \dim(\ker (T_\varphi^*)) = \dim (\mathcal{K}_\theta),\end{align*} $$
where
$\mathcal {K}_\theta := (\theta H^2)^\perp $
is the model space associated with
$\theta $
the inner part of
$\varphi $
. We refer the reader to [Reference Garcia, Mashreghi and Ross12] for a very nice introduction to model space theory. We also recall that
$T_\varphi $
is an isometry on
$H^2$
if and only if
$\varphi $
is inner.
Theorem 3.9 Let
$\varphi $
be a non constant inner function. Then
$T_\varphi $
is embeddable into a
$C_0$
-semigroup on
$H^2$
if and only if
$\varphi $
is not a finite Blaschke product. Moreover, the operators of the semigroup are analytic Toeplitz operators if and only if
$\varphi $
does not have any zero in
$\mathbb {D}$
.
Proof Let
$\varphi $
be a non constant inner function. Then
$T_\varphi $
is an isometry on
$H^2$
. By Theorem 1.1,
$T_\varphi $
is embeddable if and only if
$\text {codim}(\text {Im} (T_\varphi )) = \dim (\mathcal {K}_\varphi ) = \infty $
. We deduce then easily that
$T_\varphi $
is embeddable into a
$C_0$
-semigroup on
$H^2$
if and only if
$\varphi $
is not a finite Blaschke product (see [Reference Garcia, Mashreghi and Ross12, Proposition 5.5.19]). Denote by
$(R_t)_{t \ge 0}$
this semigroup. Let us recall that the commutant
$\{S\}'$
of S on
$H^2$
is given by
$$ \begin{align*}\{S\}' = \left \{ T_\psi : \psi \in H^\infty \right \}.\end{align*} $$
In that case,
$(R_t)_{t \ge 0}$
is a semigroup of analytic Toeplitz operators if and only there exists
$C \in \text {Hol}(\mathbb {D})$
satisfying
$\sup \{ \text {Re} (C(z)) : z \in \mathbb {D} \} < \infty $
and such that
$R_t = T_{e^{tC}}$
for every
$t \ge 0$
[Reference Seubert16]. In particular, we get
$R_1 = T_\varphi = T_{e^C}$
and
$\varphi = e^C$
, which does not vanish on
$\mathbb {D}$
. Reciprocally, if
$\varphi $
does not vanish on
$\mathbb {D}$
, then
$\varphi $
is an inner singular function of the form
$$ \begin{align*}\varphi(z) = \exp \left \{- \int_{\mathbb{T}} \frac{\zeta + z}{\zeta - z} ~d\mu(\zeta) \right \}, \quad z \in \mathbb{D,}\end{align*} $$
for
$\mu $
a finite positive measure of Borel on
$\mathbb {T}$
such that
$\mu $
is singular with respect to the Lebesgue measure m. It is easy to see, by considering, for every
$t \ge 0$
, the bounded analytic functions
$$ \begin{align*}\varphi_t(z) = \exp \left \{- t\int_{\mathbb{T}} \frac{\zeta + z}{\zeta - z} ~d\mu(\zeta) \right \}, \quad z \in \mathbb{D},\end{align*} $$
that
$T_\varphi $
is embeddable into the
$C_0$
-semigroup
$(M_{\varphi _t} = T_{\varphi _t})_{t \ge 0}$
of analytic Toeplitz operators on
$H^2$
.
The case of the isometric Toeplitz operators is now complete. The aim of the rest of this section is to investigate other analytic Toeplitz operators.
Lemma 3.10 Let
$\varphi $
be an outer function. Then
$T_\varphi $
is embeddable into a
$C_0$
-semigroup of analytic Toeplitz operators on
$H^2$
.
Proof It is an immediate consequence of the canonical representation of an outer function.
Proposition 3.11 Let
$\varphi = (BS_\mu ) \varphi _e \in H^\infty $
where B is a Blaschke product,
$S_\mu $
is an inner singular function and
$\varphi _e$
is an outer function. Assume that
$\varphi $
is not an outer nor an inner function. Then the following assertions hold:
-
(i) if
$B \equiv 1$
,
$T_\varphi $
is embeddable into a
$C_0$
-semigroup of analytic Toeplitz operators on
$H^2$
. -
(ii) if
$S_\mu \equiv 1$
and if B is a non constant finite Blaschke product,
$T_\varphi $
is not embeddable into a
$C_0$
-semigroup on
$H^2$
.
Proof We have:
-
(i) If
$B \equiv 1$
, then
$\varphi = S_\mu \varphi _e$
which does not vanish on
$\mathbb {D}$
. Let us remark that
$T_\varphi = T_{S_\mu \varphi _e} = M_{S_\mu }M_{\varphi _e}$
. Each term is embeddable into a
$C_0$
-semigroup on
$H^2$
which commutes, then
$T_\varphi $
is embeddable into the product of these two semigroups. -
(ii) If
$S_\mu \equiv 1$
and B is a non constant finite Blaschke product, then we get
$$ \begin{align*}\text{codim}(\text{Im}(T_\varphi)) = \dim (\mathcal{K}_B) \notin \{0, \infty \}.\end{align*} $$
We conclude with [Reference Eisner10, Theorem V.1.7].
Let us remark that according to Proposition 3.11, the remaining open question is the following.
Question 3.12 Do we have the embedding of
$T_\varphi $
when
$\varphi = B\phi $
, with B a non constant Blaschke product and
$\phi $
a nonvanishing analytic function on
$\mathbb {D}$
?
For that purpose, let us just note that on one side
$T_B$
is embeddable if and only if B is an infinite Blaschke product by Theorem 3.9. On the other side,
$T_{\phi }$
is embeddable from Proposition 3.11
$(i)$
. The following examples show the difficulty and the interest of this open question.
-
• Let
$B_1$
be a finite Blaschke product and
$B_2$
be an infinite Blaschke product. Then
$T_{B_1B_2}$
is embeddable by Theorem 3.9, whereas
$T_{B_1}$
is not embeddable. -
• Let B be an infinite Blaschke product and
$S_\mu $
be a singular inner function. Then
$T_{B}$
and
$T_{S_\mu }$
are embeddable into a
$C_0$
-semigroup denoted, respectively, by
$(A_t)_{t \ge 0}$
and
$(B_t)_{t \ge 0}$
by Theorem 3.9. Moreover,
$T_{BS_\mu }$
is also embeddable into a
$C_0$
-semigroup, which is not the product of
$(A_t)_{t \ge 0}$
and
$(B_t)_{t \ge 0}$
, even though
$T_B$
and
$T_{S_\mu }$
commute.
We end this section with a result on the embedding of Toeplitz operators whose symbol are polynomials.
Corollary 3.13 Let
$n \ge 1$
and
$P \in \mathcal {P}_n$
, where
$\mathcal {P}_n$
is the space of polynomials of degree at most n. Then
$T_P$
is embeddable into a
$C_0$
-semigroup on
$H^2$
if and only if P does not have any zero in
$\mathbb {D}$
.
Proof Let
$n \ge 1$
and
$P \in \mathcal {P}_n$
of the form
$$ \begin{align*}P(z) = a\prod_{k = 1}^n (z - \alpha_k)\prod_{j = 1}^m (z - \beta_j),\end{align*} $$
where
$a \in \mathbb {C} \backslash \{0\}$
,
$\left \lvert \alpha _k \right \rvert < 1$
for every
$1 \le k \le n$
and
$\left \lvert \beta _j \right \rvert \ge 1$
for every
$1 \le j \le m$
. It follows that
$P(z) = B(z)F(z)$
where B is the finite Blaschke product associated with the sequence
$(\alpha _k)_{1 \le k \le n}$
, and F is the outer function defined by
$F(z) = a \prod _{k = 1}^n (1 - \overline {\alpha _k}z) \prod _{j = 1}^m (z - \beta _j)$
. Then:
-
• if P does not have any zero in
$\mathbb {D}$
, i.e.,
$\alpha _k \notin \mathbb {D}$
for every
$1 \le k \le n$
, then
$B \equiv 1$
and P is outer. Therefore,
$T_P$
is embeddable into a
$C_0$
-semigroup on
$H^2$
according to Lemma 3.10. -
• if P has at least one zero in
$\mathbb {D}$
, then
$B \not \equiv 1$
. By Proposition 3.11
$(ii)$
,
$T_P$
is not embeddable into a
$C_0$
-semigroup on
$H^2$
.
4 Isometric operators and properties of semigroups
In this last section, we state two quite obvious results concerning the properties of the semigroup in terms of isometry or compactness where the operator embedded is isometric.
Proposition 4.1 Let
$V \in \mathcal {L}(H)$
be isometric. If V is embeddable into a
$C_0$
-semigroup of contractions
$(V_t)_{t \ge 0}$
on H, then
$V_t$
is isometric for every
$t \ge 0$
.
Proof Let us remark that since V is an isometry,
$V^n = V_n$
is also an isometry for every
$n \in \mathbb {N}$
. Assume that there exists
$t_0> 0$
such that
$V_{t_0}$
is not isometric. In that case, since
$V_{t_0}$
is a contraction, there exists
$x_0 \in H$
,
$\left \Vert x_0\right \Vert = 1$
such that
$\left \Vert V_{t_0}x_0\right \Vert < 1$
. But, for every
$N> t_0$
, we have on one hand
$$ \begin{align*}\left\Vert V_{N - t_0}V_{t_0}x_0\right\Vert = \left\Vert V_N x_0\right\Vert = 1,\end{align*} $$
and on the other hand
$$ \begin{align*}\left\Vert V_{N - t_0}V_{t_0}x_0\right\Vert \le \left\Vert V_{t_0}x_0\right\Vert < 1.\end{align*} $$
We obtain a contradiction, and so
$V_t$
is isometric for every
$t> 0$
.
Proposition 4.2 Let
$V \in \mathcal {L}(H)$
be isometric. If V is embeddable into a
$C_0$
-semigroup
$(V_t)_{t \ge 0}$
on H, then
$V_t$
is not compact for every
$t \ge 0$
.
Proof Assume that there exists
$t_0> 0$
such that
$V_{t_0}$
is compact. Since
$\mathcal {K}(H)$
is a bilateral ideal, it comes that
$V_t$
is compact for every
$t \ge t_0$
from the algebraic property of the semigroup. It comes also that, for every orthonormal sequence
$(e_n)_{n \ge 0}$
of H,
$\left \Vert V_t e_n\right \Vert \underset {n \rightarrow \infty }{\longrightarrow } 0$
for every
$t \ge t_0$
. But, since V is isometric,
$V_N = V^N$
is also isometric for every
$N \in \mathbb {N}$
, and we get
$$ \begin{align*}\left\Vert V_N e_n\right\Vert = \left\Vert e_n\right\Vert = 1.\end{align*} $$
For
$N \ge t_0$
, we obtain a contradiction and so
$V_t$
is not compact for every
$t> 0$
.
Acknowledgments
The authors are grateful to E. Fricain for his comments and useful remarks.
