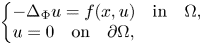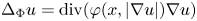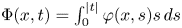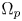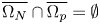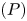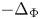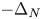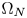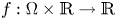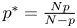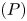1. Introduction
In this paper, we establish the existence of multiple solutions for the following class of quasilinear problems
where $\Omega \subset \mathbb {R}^{N}$![]() , with $N \geq 2$
, with $N \geq 2$![]() , is a smooth bounded domain, $\Delta _{\Phi }u={\rm div}\,(\varphi (x,|\nabla u|)\nabla u)$
, is a smooth bounded domain, $\Delta _{\Phi }u={\rm div}\,(\varphi (x,|\nabla u|)\nabla u)$![]() is the $\Phi$
is the $\Phi$![]() Laplace operator, where $\Phi (x,t)=\int _{0}^{|t|}\varphi (x,s)s\,ds, \varphi : \Omega \times [0,+\infty ) \to [0,+\infty )$
Laplace operator, where $\Phi (x,t)=\int _{0}^{|t|}\varphi (x,s)s\,ds, \varphi : \Omega \times [0,+\infty ) \to [0,+\infty )$![]() and $f: \Omega \times \mathbb {R} \to \mathbb {R}$
and $f: \Omega \times \mathbb {R} \to \mathbb {R}$![]() are continuous functions that satisfy some hypothesis that will be mentioned later on.
are continuous functions that satisfy some hypothesis that will be mentioned later on.
Before proceeding further, let us go through some known results associated with the $\Phi$![]() Laplace equations. In the recent past, the study of such equations concerning the existence theory has been a research topic of considerable attention. Such operator extends the $p$
Laplace equations. In the recent past, the study of such equations concerning the existence theory has been a research topic of considerable attention. Such operator extends the $p$![]() -Laplace operator, the variable exponent $p$
-Laplace operator, the variable exponent $p$![]() -Laplace operator, weighted $p$
-Laplace operator, weighted $p$![]() -Laplace operator, $p,q$
-Laplace operator, $p,q$![]() -Laplace operator and indeed occurs in many physical phenomena.
-Laplace operator and indeed occurs in many physical phenomena.
When $\Phi$![]() is independent of $x$
is independent of $x$![]() , solutions of $(P)$
, solutions of $(P)$![]() are investigated in the Orlicz-Sobolev space [Reference Pick, Kufner, John and Fučík44] and we refer the reader to Alves, Figueiredo and Santos [Reference Alves, Figueiredo and Santos7], Fukagai, Ito and Narukawa [Reference Fukagai, Ito and Narukawa29], Carvalho, Silva, Gonçalves and Goulart [Reference Carvalho, Silva, Gonçalves and Goulart15], Fukagai and Narukawa [Reference Fukagai and Narukawa28], Harjulehto and Hästö [Reference Harjulehto and Hästö32], and their references for the study of such PDEs. When $\Phi$
are investigated in the Orlicz-Sobolev space [Reference Pick, Kufner, John and Fučík44] and we refer the reader to Alves, Figueiredo and Santos [Reference Alves, Figueiredo and Santos7], Fukagai, Ito and Narukawa [Reference Fukagai, Ito and Narukawa29], Carvalho, Silva, Gonçalves and Goulart [Reference Carvalho, Silva, Gonçalves and Goulart15], Fukagai and Narukawa [Reference Fukagai and Narukawa28], Harjulehto and Hästö [Reference Harjulehto and Hästö32], and their references for the study of such PDEs. When $\Phi$![]() also depends on $x$
also depends on $x$![]() , we are led to study the problems in variable exponent Sobolev [Reference Diening, Hästo, Harjulehto and Ruzicka23, Reference Kováčik and Rákosník37] or Musielak–Sobolev spaces [Reference Chlebicka20, Reference Hudzik34, Reference Musielak43, Reference Pick, Kufner, John and Fučík44]. Differential equations in variable exponent Sobolev spaces have been studied extensively in the last years, most part of them involves the $p(x)$
, we are led to study the problems in variable exponent Sobolev [Reference Diening, Hästo, Harjulehto and Ruzicka23, Reference Kováčik and Rákosník37] or Musielak–Sobolev spaces [Reference Chlebicka20, Reference Hudzik34, Reference Musielak43, Reference Pick, Kufner, John and Fučík44]. Differential equations in variable exponent Sobolev spaces have been studied extensively in the last years, most part of them involves the $p(x)$![]() -Laplacian operator, see for example, Alves and Barreiro [Reference Alves and Barreiro2], Alves and Ferreira [Reference Alves and Ferreira3], Alves and Souto [Reference Alves and Souto6], Alves and Rădulescu [Reference Alves and Rădulescu5], Chabrowski and Fu [Reference Chabrowski and Fu18], Fan and Zhang [Reference Fan and Zhang27], Fan [Reference Fan25], Rădulescu and Repovš [Reference Rădulescu and Repovš46] and their references. However, Differential equations in general Musielak–Sobolev spaces have been studied very little, see for instance, Azroul, Benkirane, Shimi and Srati [Reference Azroul, Benkirane, Shimi and Srati10], Benkirane and Sidi El Vally [Reference Benkirane and Sidi El Vally11], Fan [Reference Fan26], Liu and Zhao [Reference Liu and Zhao40], Wang and Liu [Reference Wang and Liu51] and the references therein.
-Laplacian operator, see for example, Alves and Barreiro [Reference Alves and Barreiro2], Alves and Ferreira [Reference Alves and Ferreira3], Alves and Souto [Reference Alves and Souto6], Alves and Rădulescu [Reference Alves and Rădulescu5], Chabrowski and Fu [Reference Chabrowski and Fu18], Fan and Zhang [Reference Fan and Zhang27], Fan [Reference Fan25], Rădulescu and Repovš [Reference Rădulescu and Repovš46] and their references. However, Differential equations in general Musielak–Sobolev spaces have been studied very little, see for instance, Azroul, Benkirane, Shimi and Srati [Reference Azroul, Benkirane, Shimi and Srati10], Benkirane and Sidi El Vally [Reference Benkirane and Sidi El Vally11], Fan [Reference Fan26], Liu and Zhao [Reference Liu and Zhao40], Wang and Liu [Reference Wang and Liu51] and the references therein.
In the present paper, we will apply some recent results involving the Musielak–Sobolev spaces to study the existence of non-trivial solution for the problem $(P)$![]() . Next, we will state our main hypothesis on the functions $\Phi$
. Next, we will state our main hypothesis on the functions $\Phi$![]() and $\varphi$
and $\varphi$![]() :
:
(φ1) For each $x \in \Omega$
 , $\varphi (x,.)$
, $\varphi (x,.)$ is a $C^{1}$
is a $C^{1}$ function in the interval $(0,+\infty )$
function in the interval $(0,+\infty )$ .
.(φ2) $\varphi (x,t)$
 , $\partial _{t}(\varphi (x,t)t)>0$
, $\partial _{t}(\varphi (x,t)t)>0$ , for $x \in \Omega$
, for $x \in \Omega$ and $t>0$
and $t>0$ .
.(φ3) There exists $1< p< N< q< p^{*}$
 such that
\[ p-2\leq \frac{\varphi'(x,t)t}{\varphi(x,|t|)}\leq q-2, \text{ for } x \in \Omega \quad \mbox{and} \quad t > 0. \]
such that
\[ p-2\leq \frac{\varphi'(x,t)t}{\varphi(x,|t|)}\leq q-2, \text{ for } x \in \Omega \quad \mbox{and} \quad t > 0. \]
Arguing as in Fukagai, Ito and Narukawa [Reference Fukagai, Ito and Narukawa29], it is possible to prove with few modifications that if $\varphi$![]() satisfies the conditions $(\varphi _1)-(\varphi _3)$
satisfies the conditions $(\varphi _1)-(\varphi _3)$![]() , then the function $\Phi$
, then the function $\Phi$![]() is a generalized N-function.
is a generalized N-function.
The complementary function $\widetilde {\Phi }$![]() associated with $\Phi$
associated with $\Phi$![]() is given by the Legendre's transformation, that is,
is given by the Legendre's transformation, that is,
The functions $\Phi$![]() and $\widetilde {\Phi }$
and $\widetilde {\Phi }$![]() are complement of each other and $\widetilde {\Phi }$
are complement of each other and $\widetilde {\Phi }$![]() is also a generalized N-function. Hereafter, we also assume that for some constant $d_1$
is also a generalized N-function. Hereafter, we also assume that for some constant $d_1$![]() ,
,
(φ4) $\displaystyle \inf _{x \in \Omega }\Phi (x,1), \displaystyle \inf _{x \in \Omega }\widetilde {\Phi }(x,1) >0$
 .
.
The conditions $(\varphi _1)$![]() –$(\varphi _4)$
–$(\varphi _4)$![]() are very important in our approach, because they permit us to conclude that the Musielak–Orlicz space $L^{\Phi }(\Omega )$
are very important in our approach, because they permit us to conclude that the Musielak–Orlicz space $L^{\Phi }(\Omega )$![]() and Musielak–Sobolev space $W^{1,\Phi }(\Omega )$
and Musielak–Sobolev space $W^{1,\Phi }(\Omega )$![]() are reflexive and separable Banach spaces, for more details, see § 2.
are reflexive and separable Banach spaces, for more details, see § 2.
In a recent paper, Alves, Garain and Rădulescu [Reference Alves, Garain and Rădulescu8] proved the existence of at least one non-trivial solution for the following prototype problem
provided $\Omega$![]() is a smooth bounded domain in $\mathbb {R}^{N}$
is a smooth bounded domain in $\mathbb {R}^{N}$![]() with $N\geq 2$
with $N\geq 2$![]() , $f$
, $f$![]() is a continuous function, $\varphi :\Omega \times [0,+\infty )\to [0,+\infty )$
is a continuous function, $\varphi :\Omega \times [0,+\infty )\to [0,+\infty )$![]() satisfies the hypothesis $(\varphi _1)-(\varphi _4)$
satisfies the hypothesis $(\varphi _1)-(\varphi _4)$![]() above (see [Reference Alves, Garain and Rădulescu8] for precise assumptions).
above (see [Reference Alves, Garain and Rădulescu8] for precise assumptions).
In the present paper, as in [Reference Alves, Garain and Rădulescu8], $\Omega$![]() satisfies the following conditions: There are three smooth domains $\Omega _N, \Omega _q, \Omega _p \subset \Omega$
satisfies the following conditions: There are three smooth domains $\Omega _N, \Omega _q, \Omega _p \subset \Omega$![]() with non-empty interior such that
with non-empty interior such that
and there is $\delta >0$![]() such that
such that
Hereafter, if $A \subset \Omega$![]() , we denote by $A_\delta$
, we denote by $A_\delta$![]() to be the $\delta$
to be the $\delta$![]() -neighbourhood of $A$
-neighbourhood of $A$![]() restricted to $\Omega$
restricted to $\Omega$![]() , that is,
, that is,
Associated with the sets $\Omega _N, \Omega _q$![]() and $\Omega _p$
and $\Omega _p$![]() , there are three continuous functions $\eta _N,\eta _q,\eta _p:\overline {\Omega } \to [0,1]$
, there are three continuous functions $\eta _N,\eta _q,\eta _p:\overline {\Omega } \to [0,1]$![]() satisfying:
satisfying:
and

and for some positive constant $c_4$![]() ,
,
where $l>q$![]() and $\text {dist}(x, \partial (\Omega _q)_{\delta } \cap \Omega _p)=\inf \{|x-y|\,:\,y \in \partial (\Omega _q)_{\delta } \cap \Omega _p\}$
and $\text {dist}(x, \partial (\Omega _q)_{\delta } \cap \Omega _p)=\inf \{|x-y|\,:\,y \in \partial (\Omega _q)_{\delta } \cap \Omega _p\}$![]() .
.
Related to the function $f:\overline {\Omega } \times \mathbb {R} \to \mathbb {R}$![]() , we assume that it is a continuous function of one of the following forms:
, we assume that it is a continuous function of one of the following forms:

or
where $\lambda,\mu,\tau$![]() are positive parameters, $\alpha >0$
are positive parameters, $\alpha >0$![]() , $p^{*}>\zeta >q>N>p>\frac {N}{2}$
, $p^{*}>\zeta >q>N>p>\frac {N}{2}$![]() , $\beta >q$
, $\beta >q$![]() , where $p^{*}=\frac {Np}{N-p}$
, where $p^{*}=\frac {Np}{N-p}$![]() , $g:\overline {\Omega } \times \mathbb {R} \to \mathbb {R}$
, $g:\overline {\Omega } \times \mathbb {R} \to \mathbb {R}$![]() and $\tilde {\eta }_q: \overline {\Omega }\to [0,1]$
and $\tilde {\eta }_q: \overline {\Omega }\to [0,1]$![]() are continuous functions such that
are continuous functions such that
and
Related to the function $g$![]() , we assume the following conditions:
, we assume the following conditions:
for some $q_1>q$![]() and there is $\theta >q$
and there is $\theta >q$![]() such that
such that
where $G(x,t)=\int _{0}^{t}g(x,s)\,ds$![]() , for $t \in \mathbb {R}$
, for $t \in \mathbb {R}$![]() .
.
There exists a constant $c>0$![]() , such that
, such that
for some $q_2>q_1,$![]()
With these notation, we are ready to mention the last conditions on $\varphi$![]() . If $f$
. If $f$![]() is the form $(f_1)$
is the form $(f_1)$![]() , we assume for each $t>0$
, we assume for each $t>0$![]() the following:
the following:
(φ5) $\varphi (x,t) \geq t^{N-2}, \quad \mbox {for} \quad x \in \Omega _N \quad \mbox {and} \quad c_1 t^{N-2} \geq \varphi (x,t), \quad x \in \Omega _N \setminus \overline {(\Omega _q)_{\delta }}.$

(φ6) $\varphi (x,t) \geq \tau _1(x)t^{q-2}, \quad \mbox {for} \quad x \in (\Omega _q)_{\delta }$
 where $\tau _1:\overline {\Omega } \to \mathbb {R}$
where $\tau _1:\overline {\Omega } \to \mathbb {R}$ is a continuous function satisfying:
\[ \tau_1(x)>0, \quad \forall x \in (\Omega_q)_{\delta} \quad \mbox{and} \quad \tau_1(x)=0, \quad \forall x \in ((\Omega_q)_{\delta})^{c}. \]
is a continuous function satisfying:
\[ \tau_1(x)>0, \quad \forall x \in (\Omega_q)_{\delta} \quad \mbox{and} \quad \tau_1(x)=0, \quad \forall x \in ((\Omega_q)_{\delta})^{c}. \]
(φ7) $\tau _2(x)t^{q-2}+c_2t^{p-2} \geq \varphi (x,t) \geq t^{p-2}, \quad x \in \Omega _p$
 where $\tau _2:\overline {\Omega _p} \to \mathbb {R}$
where $\tau _2:\overline {\Omega _p} \to \mathbb {R}$ is a non-negative continuous function satisfying:
\[ \tau_2(x)\leq c_3 {\rm dist}(x, \partial(\Omega_q)_{\delta} \cap \Omega_p)^{s}, \quad \forall x \in \overline{\Omega_p} \cap (\Omega_q)_{\delta} \]for some $s>q$
is a non-negative continuous function satisfying:
\[ \tau_2(x)\leq c_3 {\rm dist}(x, \partial(\Omega_q)_{\delta} \cap \Omega_p)^{s}, \quad \forall x \in \overline{\Omega_p} \cap (\Omega_q)_{\delta} \]for some $s>q$
 and
\[ \tau_2(x)=0, \quad \forall x \in \overline{\Omega_p} \setminus \overline{(\Omega_q)_{\delta}}, \]for some constants $c_i>0$
and
\[ \tau_2(x)=0, \quad \forall x \in \overline{\Omega_p} \setminus \overline{(\Omega_q)_{\delta}}, \]for some constants $c_i>0$
 with $i=1,2,3.$
with $i=1,2,3.$
Now, if $f$![]() is the form $(f_2)$
is the form $(f_2)$![]() , the condition $(\varphi _5)$
, the condition $(\varphi _5)$![]() is assumed of the following way:
is assumed of the following way:
(φ5) $\varphi (x,t) \geq t^{N-2}, \quad \mbox {for} \quad x \in \Omega _N.$

As a model of a function that satisfies the conditions $(\varphi _1)-(\varphi _7)$![]() is the function $\varphi :{\Omega } \times [0,+\infty ) \to [0,+\infty )$
is the function $\varphi :{\Omega } \times [0,+\infty ) \to [0,+\infty )$![]() defined by
defined by
and so,
Motivated by the study made in [Reference Alves, Garain and Rădulescu8], we intend to prove the existence of multiple solutions for the problem $(Q)$![]() working with the same operator under the nonlinearities $(f_1)$
working with the same operator under the nonlinearities $(f_1)$![]() and $(f_2)$
and $(f_2)$![]() . Here we have two main results involving multiple solutions and their motivation are mentioned below.
. Here we have two main results involving multiple solutions and their motivation are mentioned below.
Our first main result is motivated by the study made by Wei and Wu [Reference Wei and Wu53], where the authors showed the existence of multiple solutions for the following class of problems involving the $p$![]() -Laplacian operator
-Laplacian operator
where $\Omega$![]() is a bounded domain, $\lambda$
is a bounded domain, $\lambda$![]() is a positive parameter and $f$
is a positive parameter and $f$![]() is a continuous function with subcritical growth and $p^{*}=\frac {Np}{N-p}$
is a continuous function with subcritical growth and $p^{*}=\frac {Np}{N-p}$![]() for $N > p$
for $N > p$![]() . Using a version of an abstract theorem due to Ambrosetti and Rabinowitz [Reference Ambrosetti and Rabinowitz9] that involves the genus theory for $C^{1}$
. Using a version of an abstract theorem due to Ambrosetti and Rabinowitz [Reference Ambrosetti and Rabinowitz9] that involves the genus theory for $C^{1}$![]() even functional, it was proved that given $n \in \mathbb {N}$
even functional, it was proved that given $n \in \mathbb {N}$![]() , there is $\lambda _*=\lambda _*(n)>0$
, there is $\lambda _*=\lambda _*(n)>0$![]() such that problem (1.4) has at least $n$
such that problem (1.4) has at least $n$![]() non-trivial solutions for $\lambda \in (0, \lambda _*)$
non-trivial solutions for $\lambda \in (0, \lambda _*)$![]() . In [Reference Silva and Xavier47], Silva and Xavier improved the main results proved in [Reference Wei and Wu53].
. In [Reference Silva and Xavier47], Silva and Xavier improved the main results proved in [Reference Wei and Wu53].
Here, we proved a version of the above-mentioned result for the problem $(P)$![]() and the statement of our result is the following.
and the statement of our result is the following.
Theorem 1.1 Assume $(g_0)-(g_3), (f_1)$![]() and $(\varphi _1)-(\varphi _7)$
and $(\varphi _1)-(\varphi _7)$![]() . Then, for each $k\in \mathbb {N},$
. Then, for each $k\in \mathbb {N},$![]() there exists positive real numbers $\lambda _k,\mu _k$
there exists positive real numbers $\lambda _k,\mu _k$![]() and $\tau _k$
and $\tau _k$![]() such that for $\lambda \geq \lambda _k,\mu \geq \mu _k$
such that for $\lambda \geq \lambda _k,\mu \geq \mu _k$![]() and $\tau \geq \tau _k,$
and $\tau \geq \tau _k,$![]() the problem $(P)$
the problem $(P)$![]() has at least $k$
has at least $k$![]() pairs of non-trivial solutions.
pairs of non-trivial solutions.
Our second result involves the existence of many rotationally non-equivalent and non-radial solutions. We would like to point out that the existence of many rotationally non-equivalent and non-radial solutions was considered in some problems involving the Laplacian operator. Brézis and Niremberg [Reference Brezis and Nirenberg13] proved the existence of non-radial positive solution for the following problem
where
for some $d>0$![]() . This type of phenomenon is known as symmetry breaking. In [Reference Coffman22], Coffman proved that the number of non-radial and rotationally non-equivalent positive solutions of (1.5) in $D$
. This type of phenomenon is known as symmetry breaking. In [Reference Coffman22], Coffman proved that the number of non-radial and rotationally non-equivalent positive solutions of (1.5) in $D$![]() tends to $+\infty$
tends to $+\infty$![]() as $r$
as $r$![]() tends to $+\infty$
tends to $+\infty$![]() , if $p > 1$
, if $p > 1$![]() and $N = 2$
and $N = 2$![]() or $1 < p < N/(N-2)$
or $1 < p < N/(N-2)$![]() and $N \geq 3$
and $N \geq 3$![]() .
.
Motivated by the above papers, some authors have studied this class of problems. For the subcritical case, we cite the papers of Li [Reference Li38], Lin [Reference Lin39], Suzuki [Reference Suzuki50] and references therein.
Related to the critical case, Wang and Willem [Reference Wang and Willem52] have shown the existence of multiple solutions for the following problem
where
The authors proved that for $0 < \lambda < \pi ^{2}$![]() and $n \in \mathbb {N}$
and $n \in \mathbb {N}$![]() , there exists $R(\lambda, n)$
, there exists $R(\lambda, n)$![]() such that for $r > R(\lambda, n)$
such that for $r > R(\lambda, n)$![]() , the equation (1.6) has at least $n$
, the equation (1.6) has at least $n$![]() non-radial and rotationally non-equivalent solutions. Motivated by [Reference Wang and Willem52], de Figueiredo and Miyagaki [Reference de Figueiredo and Miyagaki24] have considered the following problem
non-radial and rotationally non-equivalent solutions. Motivated by [Reference Wang and Willem52], de Figueiredo and Miyagaki [Reference de Figueiredo and Miyagaki24] have considered the following problem
where $f$![]() is a $C^{1}$
is a $C^{1}$![]() function with subcritical growth.
function with subcritical growth.
In [Reference Alves and de Freitas4], Alves and de Freitas showed the existence of many rotationally non-equivalent and non-radial solutions for a large class of quasilinear problems that have, in particular case, the problem below

Still related to this class of problem, we would like to cite the papers of Byeon [Reference Byeon14], Castro and Finan [Reference Castro and Finan16], Catrina and Wang [Reference Catrina and Wang17], Mizoguchi and Suzuki [Reference Mizoguchi and Suzuki42], Hirano and Mizoguchi [Reference Hirano and Mizoguchi33] and references therein.
Motivated by the bibliography cited above and more precisely, by results found in [Reference Alves and de Freitas4], [Reference de Figueiredo and Miyagaki24] and [Reference Wang and Willem52], we are ready to state our second main result; however, we need to fix some more conditions:
(φ8) $\Phi$
 is radial in relation with $x$
is radial in relation with $x$ that is $\Phi (|x|,t)=\Phi (x,t)$
that is $\Phi (|x|,t)=\Phi (x,t)$ for all $t>0$
for all $t>0$ .
.(φ9) There exists $\kappa \in (0, \frac {1}{2^{N+1}})$
 such that
\[ |\partial_s \Phi(s,t)| \leq \kappa \Phi(s,t), \, \forall (s,t) \in \mathbb{R}^{2}. \]
such that
\[ |\partial_s \Phi(s,t)| \leq \kappa \Phi(s,t), \, \forall (s,t) \in \mathbb{R}^{2}. \]
(η) The functions $\eta _N,\tilde {\eta }_q,\eta _p$
 and $g$
and $g$ are radial in $x$
are radial in $x$ , that is
\[ \eta_N(x)=\eta_N(|x|),\,\tilde{\eta}_q(x)=\tilde{\eta}(|x|),\,\eta_p(x)=\eta_p(|x|) \]and
, that is
\[ \eta_N(x)=\eta_N(|x|),\,\tilde{\eta}_q(x)=\tilde{\eta}(|x|),\,\eta_p(x)=\eta_p(|x|) \]and \[ g(x,t)=g(|x|,t), \]for all $x\in \Omega$
\[ g(x,t)=g(|x|,t), \]for all $x\in \Omega$
 and $t>0$
and $t>0$ .
.(ΩN) There is $\delta _1>0$
 such that
\[ \mathcal{A}=\left\{x \in \mathbb{R}^{N}\,:\, \frac{2r+1}{2}-\delta_1 \leq |x| \leq \frac{2r+1}{2}+\delta_1\right\} \subset \Omega_N\setminus\overline{(\Omega_q)_\delta}. \]
such that
\[ \mathcal{A}=\left\{x \in \mathbb{R}^{N}\,:\, \frac{2r+1}{2}-\delta_1 \leq |x| \leq \frac{2r+1}{2}+\delta_1\right\} \subset \Omega_N\setminus\overline{(\Omega_q)_\delta}. \]
(g4) $g(|x|,.)$
 is a $C^{1}$
is a $C^{1}$ function in the interval $(0,+\infty )$
function in the interval $(0,+\infty )$ and $\dfrac {g(|x|,t)}{|t|^{q-1}}$
and $\dfrac {g(|x|,t)}{|t|^{q-1}}$ is increasing for $t\neq 0$
is increasing for $t\neq 0$ uniformly in $x\in (\overline {\Omega _q})_{\frac {\delta }{2}}$
uniformly in $x\in (\overline {\Omega _q})_{\frac {\delta }{2}}$ .
.The reader is invited to see that $\Phi$
 given in (1.3) also satisfies $(\varphi _8)-(\varphi _{9})$
given in (1.3) also satisfies $(\varphi _8)-(\varphi _{9})$ , provided $(\eta )$
, provided $(\eta )$ holds.
holds.Our second main theorem has the following statement.
Theorem 1.2 Assume $\Omega =\Omega _r$![]() with $N\geq 2$
with $N\geq 2$![]() and $N\neq 3$
and $N\neq 3$![]() . Let $(f_2), (g_1),(g_2),(g_4),$
. Let $(f_2), (g_1),(g_2),(g_4),$![]() $(\eta ),$
$(\eta ),$![]() $(\Omega _N)$
$(\Omega _N)$![]() and $(\varphi _1)-(\varphi _{9})$
and $(\varphi _1)-(\varphi _{9})$![]() holds. Then, for each $n\in \mathbb {N},$
holds. Then, for each $n\in \mathbb {N},$![]() there exists $r_0=r_0(n)>0$
there exists $r_0=r_0(n)>0$![]() and $\lambda _0=\lambda _0(n)>0$
and $\lambda _0=\lambda _0(n)>0$![]() such that for $\lambda \geq \lambda _0$
such that for $\lambda \geq \lambda _0$![]() and $r\geq r_0,$
and $r\geq r_0,$![]() the problem $(P)$
the problem $(P)$![]() has at least $n$
has at least $n$![]() non-radial, rotationally non-equivalent and non-trivial solutions.
non-radial, rotationally non-equivalent and non-trivial solutions.
1.1. Our approach
To prove our main results (Theorem 1.1–1.2), we use variational methods. More precisely, for the proof of Theorem 1.1, we follow the approach from Wei and Wu [Reference Wei and Wu53] and Silva and Xavier [Reference Silva and Xavier47]. To this end, we use a result from Ambrosetti and Rabinowitz (see Lemma 4.1). To obtain Theorem 1.2, we adapt for our problem some ideas found in de Figueiredo and Miyagaki [Reference de Figueiredo and Miyagaki24] and Alves and de Freitas [Reference Alves and de Freitas4]. Here, we establish a Poincaré type inequality (Lemma 2.3) and a Strauss type result (Lemma 5.4) in the setting of Musielak–Sobolev spaces.
It is worth mentioning that, due to the double critical behaviour, the energy functionals associated with the problem $(P)$![]() do not satisfy the $(PS)$
do not satisfy the $(PS)$![]() -condition at some levels, which brings some difficulties to apply variational methods. To overcome such difficulties, we closely follow the approach introduced in [Reference Alves, Garain and Rădulescu8], where one needs to simultaneously employ the concentration compactness Lemma due to Lions in $W^{1,p}(\Omega _p)$
-condition at some levels, which brings some difficulties to apply variational methods. To overcome such difficulties, we closely follow the approach introduced in [Reference Alves, Garain and Rădulescu8], where one needs to simultaneously employ the concentration compactness Lemma due to Lions in $W^{1,p}(\Omega _p)$![]() found in Medeiros [Reference de Medeiros41], see Lemma 3.1, to obtain a useful estimate related to the critical exponent problem and a version of the Trundiger–Moser inequality in $W^{1,N}(\Omega _N)$
found in Medeiros [Reference de Medeiros41], see Lemma 3.1, to obtain a useful estimate related to the critical exponent problem and a version of the Trundiger–Moser inequality in $W^{1,N}(\Omega _N)$![]() by Cianchi [Reference Cianchi21], see Lemma 3.3, to deal with the exponential growth. Another difficulty appears since the trace of the functions on $\partial \Omega _p$
by Cianchi [Reference Cianchi21], see Lemma 3.3, to deal with the exponential growth. Another difficulty appears since the trace of the functions on $\partial \Omega _p$![]() and $\partial \Omega _N$
and $\partial \Omega _N$![]() may not vanish. We tackle this difficulty by applying the type of results that are used in the study of Neumann boundary value problems (Lemmas 3.4–3.5).
may not vanish. We tackle this difficulty by applying the type of results that are used in the study of Neumann boundary value problems (Lemmas 3.4–3.5).
1.2. Organization of the article
This article is organized as follows: In § 2, we discuss some preliminary results for the Musielak–Sobolev spaces, while in § 3, we show some technical results that will be used in our approach. In § 4 and § 5, we discuss some preliminaries required to prove our main results and finally, in § 6, we prove our main results (Theorems 1.1 and 1.2).
1.3. Notation
Throughout the paper, for $t>1$![]() , we denote by $t'=\frac {t}{t-1}$
, we denote by $t'=\frac {t}{t-1}$![]() . By $C$
. By $C$![]() , we mean a constant which may vary from line to line or even over the same line. If $C$
, we mean a constant which may vary from line to line or even over the same line. If $C$![]() depends on the parameters $r_1,r_2,\cdots,r_k$
depends on the parameters $r_1,r_2,\cdots,r_k$![]() , we write $C=C(r_1,r_2,\cdots,r_k)$
, we write $C=C(r_1,r_2,\cdots,r_k)$![]() .
.
2. A brief review about the Musielak–Sobolev spaces
In this section, we recall some results on Musielak–Orlicz and Musielak–Sobolev spaces. For more details, we refer to [Reference Chlebicka20, Reference Fan26, Reference Harjulehto and Hästö32, Reference Musielak43] and their references.
Let $\Omega \subset \mathbb {R}^{N}$![]() be a smooth bounded domain and $\Phi (x,t)=\int _{0}^{|t|}\varphi (x,s)s\,ds$
be a smooth bounded domain and $\Phi (x,t)=\int _{0}^{|t|}\varphi (x,s)s\,ds$![]() be a generalized N-function, that is, for each $t \in \mathbb {R}$
be a generalized N-function, that is, for each $t \in \mathbb {R}$![]() , the function $\Phi (., t)$
, the function $\Phi (., t)$![]() is measurable and for a.e. $x \in \Omega$
is measurable and for a.e. $x \in \Omega$![]() , the function $\Phi (x, .)$
, the function $\Phi (x, .)$![]() is an N-function. For the reader's convenience, we recall that a continuous function $A : \mathbb {R} \rightarrow [0,+\infty )$
is an N-function. For the reader's convenience, we recall that a continuous function $A : \mathbb {R} \rightarrow [0,+\infty )$![]() is an N-function if
is an N-function if
(i) $A$
 is convex.
is convex.(ii) $A = 0 \Leftrightarrow t = 0$
 .
.(iii) $\displaystyle \lim _{t\rightarrow 0}\frac {A(t)}{t}=0$
 and $\displaystyle \lim _{t\rightarrow +\infty }\frac {A(t)}{t}= +\infty$
and $\displaystyle \lim _{t\rightarrow +\infty }\frac {A(t)}{t}= +\infty$ .
.(iv) $A$
 is even.
is even.
The Musielak–Orlicz space $L^{\Phi }(\Omega )$![]() is defined by
is defined by

endowed with the Luxemburg norm
We say that an N-function $\Phi$![]() satisfies the $\Delta _{2}$
satisfies the $\Delta _{2}$![]() -condition, denote by $\Phi \in \Delta _{2}$
-condition, denote by $\Phi \in \Delta _{2}$![]() , if there exists a constant $K>0$
, if there exists a constant $K>0$![]() such that
such that
Arguing as in [Reference Pick, Kufner, John and Fučík44, Theorem 4.4.4], it follows that $\Phi$![]() satisfies the $\Delta _{2}$
satisfies the $\Delta _{2}$![]() -condition if and only if,
-condition if and only if,
Moreover, an important inequality involving $\Phi$![]() and its complementary function $\tilde {\Phi }$
and its complementary function $\tilde {\Phi }$![]() (see (1.1)) is a Young's type inequality given by
(see (1.1)) is a Young's type inequality given by
Using the above inequality, it is possible to prove a Hölder type inequality, that is,
Arguing as in [Reference Fukagai, Ito and Narukawa29], if $(\varphi _3)$![]() holds, we derive that
holds, we derive that
and
where
and
Hence, if ($\varphi _3$![]() ) holds, we have $\tilde {\Phi }$
) holds, we have $\tilde {\Phi }$![]() also satisfies the $\Delta _{2}$
also satisfies the $\Delta _{2}$![]() -condition.
-condition.
Arguing as in [Reference Fukagai, Ito and Narukawa29, Lemma A2], it is possible to prove that $\Phi$![]() and $\tilde {\Phi }$
and $\tilde {\Phi }$![]() satisfy the following inequality
satisfy the following inequality
The inequality $(\varphi _3)'$![]() is very important, because following the ideas of [Reference Fukagai, Ito and Narukawa29, Lemmas 2.1 and 2.5], it is possible to prove the following: Setting the functions
is very important, because following the ideas of [Reference Fukagai, Ito and Narukawa29, Lemmas 2.1 and 2.5], it is possible to prove the following: Setting the functions

we have
and
The Musielak–Sobolev space $W^{1,\Phi }(\Omega )$![]() can be defined by
can be defined by
with the norm
The conditions $(\varphi _1)-(\varphi _4)$![]() ensure that the spaces $L^{\Phi }(\Omega )$
ensure that the spaces $L^{\Phi }(\Omega )$![]() and $W^{1,\Phi }(\Omega )$
and $W^{1,\Phi }(\Omega )$![]() are reflexive and separable Banach spaces, for more details see [Reference Fan26, Propositions 1.6 and 1.8]. In what follows, $W_0^{1,\Phi }(\Omega )$
are reflexive and separable Banach spaces, for more details see [Reference Fan26, Propositions 1.6 and 1.8]. In what follows, $W_0^{1,\Phi }(\Omega )$![]() is defined as the closure of $C_0^{\infty }(\Omega )$
is defined as the closure of $C_0^{\infty }(\Omega )$![]() in $W_0^{1,\Phi }(\Omega )$
in $W_0^{1,\Phi }(\Omega )$![]() with respect to the above norm. Moreover, $\|u\|=|\nabla u|_{\Phi }$
with respect to the above norm. Moreover, $\|u\|=|\nabla u|_{\Phi }$![]() is a norm in $W_0^{1,\Phi }(\Omega )$
is a norm in $W_0^{1,\Phi }(\Omega )$![]() and if $(\varphi _1)-(\varphi _4)$
and if $(\varphi _1)-(\varphi _4)$![]() holds, by [Reference Gossez31, Lemma 5.7], $\|\,\,\|$
holds, by [Reference Gossez31, Lemma 5.7], $\|\,\,\|$![]() is equivalent to the norm $\|u\|_{1,\Phi }$
is equivalent to the norm $\|u\|_{1,\Phi }$![]() in $W_0^{1,\Phi }(\Omega )$
in $W_0^{1,\Phi }(\Omega )$![]() .
.
As a consequence of (2.5), we have the lemma below that will be used later on.
Proposition 2.1 The functional $\rho :W_0^{1,\Phi }(\Omega ) \to \mathbb {R}$![]() defined by
defined by
has the following properties:
(i) If $\left \Vert u\right \Vert \geq 1,$
 then $\left \Vert u\right \Vert ^{p}\leq \rho (u)\leq \left \Vert u\right \Vert ^{q}$
then $\left \Vert u\right \Vert ^{p}\leq \rho (u)\leq \left \Vert u\right \Vert ^{q}$ .
.(ii) If $\| u\| \leq 1,$
 then $\left \Vert u\right \Vert ^{q}\leq \rho (u)\leq \left \Vert u\right \Vert ^{p}$
then $\left \Vert u\right \Vert ^{q}\leq \rho (u)\leq \left \Vert u\right \Vert ^{p}$ .
.
In particular, $\rho (u)=1$![]() if and only if $\left \Vert u \right \Vert =1$
if and only if $\left \Vert u \right \Vert =1$![]() and if $(u_n) \subset W_0^{ 1,\Phi }( \Omega ),$
and if $(u_n) \subset W_0^{ 1,\Phi }( \Omega ),$![]() then $\left \Vert u_{n}\right \Vert \rightarrow 0$
then $\left \Vert u_{n}\right \Vert \rightarrow 0$![]() if and only if $\rho ( u_{n}) \rightarrow 0$
if and only if $\rho ( u_{n}) \rightarrow 0$![]() .
.
Remark 1 For the functional $\xi :L^{\Phi }(\Omega )\rightarrow \mathbb {R}$![]() given by
given by
the conclusion of Proposition 2.1 also holds, for example, if $(u_n) \subset L^{\Phi }( \Omega )$![]() , then $\left \vert u_{n}\right \vert _{\Phi }\rightarrow 0$
, then $\left \vert u_{n}\right \vert _{\Phi }\rightarrow 0$![]() if and only if $\xi (u_{n})\rightarrow 0$
if and only if $\xi (u_{n})\rightarrow 0$![]() .
.
From the definition of $W^{1,\Phi }(\Omega )$![]() and properties of $\Phi$
and properties of $\Phi$![]() , we have the continuous embedding
, we have the continuous embedding
for all $\omega \in (0,\delta )$![]() and the compact embedding
and the compact embedding
because $q>N$![]() , from where it follows that
, from where it follows that
is compact, which is crucial in our approach.
Next, we would like to state our last result found in [Reference Fan26, Theorem 2.2], which says the operator $-\Delta _{\Phi }: W_0^{1,\Phi }(\Omega ) \to (W_0^{1,\Phi }(\Omega ))^{*}$![]() belongs to the Class $(S_+)$
belongs to the Class $(S_+)$![]() .
.
Lemma 2.2 Assume the conditions $(\varphi _1)-(\varphi _7)$![]() . If $u_n \rightharpoonup u$
. If $u_n \rightharpoonup u$![]() in $W_0^{1,\Phi }(\Omega )$
in $W_0^{1,\Phi }(\Omega )$![]() and
and
then $u_n \to u$![]() in $W_0^{1,\Phi }(\Omega )$
in $W_0^{1,\Phi }(\Omega )$![]() .
.
Before concluding this section, we will show a version of Poincaré's inequality, which is a key point in the proof of Theorem 1.2.
Lemma 2.3 Assume $(\varphi _1)-(\varphi _4)$![]() and $(\varphi _{9})$
and $(\varphi _{9})$![]() . Then, there is $\Upsilon >0$
. Then, there is $\Upsilon >0$![]() independent of $r\geq 1$
independent of $r\geq 1$![]() such that
such that
Proof. Fix $p>1$![]() and $v \in C_{0}^{\infty }(\Omega _r)$
and $v \in C_{0}^{\infty }(\Omega _r)$![]() . Arguing as in [Reference Alves and de Freitas4, Lemma 3.1], we get
. Arguing as in [Reference Alves and de Freitas4, Lemma 3.1], we get

Now, taking the limit when $p \to 1$![]() and using the fact that $r \geq 1$
and using the fact that $r \geq 1$![]() , we derive that
, we derive that
Since $C_0^{\infty }(\mathbb {R}^{N})$![]() is dense in $W_0^{1,1}(\Omega _r)$
is dense in $W_0^{1,1}(\Omega _r)$![]() , it follows that
, it follows that
Now, for each $u \in W_0^{1,\Phi }(\Omega _r)$![]() , we know that $w=\Phi (x,u) \in W_0^{1,1}(\Omega _r)$
, we know that $w=\Phi (x,u) \in W_0^{1,1}(\Omega _r)$![]() and so,
and so,
Since $|\nabla \Phi (x,u)|\leq |\partial _s \Phi (x,|u|)|+\varphi (|u|)|u||\nabla u|$![]() , we obtain
, we obtain
Given $\epsilon >0$![]() , by $\Delta _2$
, by $\Delta _2$![]() condition, $(\varphi _{9})$
condition, $(\varphi _{9})$![]() , (2.2) and (2.3), there is $C_\epsilon >0$
, (2.2) and (2.3), there is $C_\epsilon >0$![]() such that
such that
for all $u \in W_0^{1,\Phi }(\Omega _r)$![]() . Thus, for $\epsilon =\frac {1}{2^{N+1}}$
. Thus, for $\epsilon =\frac {1}{2^{N+1}}$![]() and recalling that $\kappa < \frac {1}{2^{N+1}}$
and recalling that $\kappa < \frac {1}{2^{N+1}}$![]() , there is $\Upsilon >0$
, there is $\Upsilon >0$![]() independent of $r\geq 1$
independent of $r\geq 1$![]() such that
such that
3. Some technical results
The main goal of this section is to recall and prove some technical results that are crucial in the proof of our main result. Since we are going to work with double criticality, which involves the exponential critical growth and the critical growth $p^{*}$![]() , the next two results are crucial in our approach. The first one is a Concentration Compactness Lemma due to Lions for $W^{1,p}(\Theta )$
, the next two results are crucial in our approach. The first one is a Concentration Compactness Lemma due to Lions for $W^{1,p}(\Theta )$![]() explored in Medeiros [Reference de Medeiros41], where $\Theta \subset \mathbb {R}^{N}$
explored in Medeiros [Reference de Medeiros41], where $\Theta \subset \mathbb {R}^{N}$![]() is a smooth bounded domain.
is a smooth bounded domain.
Lemma 3.1 Let $(u_n)$![]() be a sequence in $W^{1,p}(\Theta )$
be a sequence in $W^{1,p}(\Theta )$![]() with $1< p< N$
with $1< p< N$![]() and $u_n \rightharpoonup u$
and $u_n \rightharpoonup u$![]() in $W^{1,p}(\Theta )$
in $W^{1,p}(\Theta )$![]() . If
. If
(i) $|\nabla u_n|^{p} \to \mu$
 weakly-$^{*}$
weakly-$^{*}$ in the sense of measure,
in the sense of measure,and
(ii) $|u_n|^{p^{*}} \to \nu$
 weakly-$^{*}$
weakly-$^{*}$ in the sense of measure,
in the sense of measure,then for at most a countable index set $J$
 , we have
\[ \left\{ \begin{array}{@{}l} (a)\quad \nu=|u|^{p^{*}}+\sum_{j \in J}\nu_j \delta_{x_j},\,\nu_j \geq 0.\\ (b)\quad \mu \geq |\nabla u|^{p}+\sum_{j \in J}\mu_j \delta_{x_j},\,\mu_j \geq 0.\\ (c)\,\, \mbox{If} \,\, x_j \in \Theta, \,\, \mbox{then} \quad S_p\nu_j^{\frac{p}{p^{*}}} \leq \mu_j.\\ (d)\,\, \mbox{If} \,\, x_j \in \partial \Theta, \,\, \mbox{then} \quad \dfrac{S_p}{2^{p/N}}\nu_j^{\frac{p}{p^{*}}} \leq \mu_j, \end{array} \right. \]where $p^{*}=\frac {Np}{N-p}$
, we have
\[ \left\{ \begin{array}{@{}l} (a)\quad \nu=|u|^{p^{*}}+\sum_{j \in J}\nu_j \delta_{x_j},\,\nu_j \geq 0.\\ (b)\quad \mu \geq |\nabla u|^{p}+\sum_{j \in J}\mu_j \delta_{x_j},\,\mu_j \geq 0.\\ (c)\,\, \mbox{If} \,\, x_j \in \Theta, \,\, \mbox{then} \quad S_p\nu_j^{\frac{p}{p^{*}}} \leq \mu_j.\\ (d)\,\, \mbox{If} \,\, x_j \in \partial \Theta, \,\, \mbox{then} \quad \dfrac{S_p}{2^{p/N}}\nu_j^{\frac{p}{p^{*}}} \leq \mu_j, \end{array} \right. \]where $p^{*}=\frac {Np}{N-p}$
 and $S_p$
and $S_p$ denotes the best constant of the embedding $D^{1,p}(\mathbb {R}^{N}) \hookrightarrow L^{p^{*}}(\mathbb {R}^{N})$
denotes the best constant of the embedding $D^{1,p}(\mathbb {R}^{N}) \hookrightarrow L^{p^{*}}(\mathbb {R}^{N})$ given by
(3.1)\begin{equation} S_p= \inf_{ {{ \begin{array}{l} u \in D^{1,p}(\mathbb{R}^{N}) \\ u \not=0 \end{array}}}} \displaystyle\frac{ \displaystyle\int_{\mathbb{R}^{N}}|\nabla u|^{p}\,{\rm d}x}{(\int_{\mathbb{R}^{N}}|u|^{p^{*}}\,{\rm d}x)^{\frac{p}{p^{*}}}}. \end{equation}
given by
(3.1)\begin{equation} S_p= \inf_{ {{ \begin{array}{l} u \in D^{1,p}(\mathbb{R}^{N}) \\ u \not=0 \end{array}}}} \displaystyle\frac{ \displaystyle\int_{\mathbb{R}^{N}}|\nabla u|^{p}\,{\rm d}x}{(\int_{\mathbb{R}^{N}}|u|^{p^{*}}\,{\rm d}x)^{\frac{p}{p^{*}}}}. \end{equation}
The proof of the above lemma follows by combining the arguments explored in Struwe [Reference Struwe49, Chapter I, Section 4] and the following Cherrier's inequality [Reference Cherrier19] below.
Lemma 3.2 Let $\Theta \subset \mathbb {R}^{N}$![]() be a smooth bounded domain and $p \in (1,N)$
be a smooth bounded domain and $p \in (1,N)$![]() . Then for each $\tau >0,$
. Then for each $\tau >0,$![]() there is $M_{\tau }>0$
there is $M_{\tau }>0$![]() such that
such that
The second result that we would like to point out is a version of Trundiger–Moser inequality in $W^{1,N}(\Theta )$![]() due to Cianchi [Reference Cianchi21, Theorem 1.1].
due to Cianchi [Reference Cianchi21, Theorem 1.1].
Lemma 3.3 Let $\Theta \subset \mathbb {R}^{N}$![]() be a smooth bounded domain for $N \geq 2$
be a smooth bounded domain for $N \geq 2$![]() and $u \in W^{1,N}(\Theta )$
and $u \in W^{1,N}(\Theta )$![]() . Then, there is a constant $C(\Theta )>0$
. Then, there is a constant $C(\Theta )>0$![]() such that
such that
where $u_{\Theta }=\frac {1}{|\Theta |}\int _{\Theta }u\,{\rm d}x$![]() is the mean value of $u$
is the mean value of $u$![]() in $\Theta,$
in $\Theta,$![]() $\alpha _N=N(\frac {w_N}{2})^{\frac {1}{N}}$
$\alpha _N=N(\frac {w_N}{2})^{\frac {1}{N}}$![]() and $w_N$
and $w_N$![]() is the volume of sphere $S^{N-1}$
is the volume of sphere $S^{N-1}$![]() . The integral on the left-hand of (3.2) is finite for each $u \in W^{1,N}(\Theta )$
. The integral on the left-hand of (3.2) is finite for each $u \in W^{1,N}(\Theta )$![]() even if $\alpha _N$
even if $\alpha _N$![]() is replaced by any other small positive number, but no inequality of type (3.2) can hold with a large constant in the place of $\alpha _N$
is replaced by any other small positive number, but no inequality of type (3.2) can hold with a large constant in the place of $\alpha _N$![]() .
.
From Lemma 3.3, for each $u \in W^{1,N}(\Theta )$![]() , we have
, we have
For the reader interested in Trudinger–Moser inequality for functions in $W^{1,N}(\Theta )$![]() , we would like to cite the papers due to Adimurthi and Yadava [Reference Adimurthi and Yadava1], Kaur and Sreenadh [Reference Kaur and Sreenadh36] and their references.
, we would like to cite the papers due to Adimurthi and Yadava [Reference Adimurthi and Yadava1], Kaur and Sreenadh [Reference Kaur and Sreenadh36] and their references.
As a consequence of Lemma 3.3, we have the following two results whose proof can be found in [Reference Alves, Garain and Rădulescu8].
Lemma 3.4 Given $t >1$![]() and $\alpha >0,$
and $\alpha >0,$![]() there is $r \in (0,1)$
there is $r \in (0,1)$![]() and $C=C(t,r,N)>0$
and $C=C(t,r,N)>0$![]() such that
such that
Lemma 3.5 Let $\alpha >0$![]() and $(u_n) \subset W^{1,N}(\Theta )$
and $(u_n) \subset W^{1,N}(\Theta )$![]() be a sequence satisfying $\|\nabla u_n\|^{N'}_{L^{N}(\Theta )}\leq \frac {\tau }{2^{N'}}\frac {\alpha _N}{\alpha }$
be a sequence satisfying $\|\nabla u_n\|^{N'}_{L^{N}(\Theta )}\leq \frac {\tau }{2^{N'}}\frac {\alpha _N}{\alpha }$![]() and $\|u_n\|_{L^{1}(\Theta )} \leq M$
and $\|u_n\|_{L^{1}(\Theta )} \leq M$![]() for some $\tau \in (0,1)$
for some $\tau \in (0,1)$![]() and $M>0$
and $M>0$![]() . Then, there is $t >1$
. Then, there is $t >1$![]() with $t \approx 1$
with $t \approx 1$![]() such that
such that
Hence, the sequence $f_n(x)=e^{\alpha |u_n(x)|^{N'}}$![]() is bounded in $L^{t}(\Theta )$
is bounded in $L^{t}(\Theta )$![]() .
.
As a consequence of Lemma 3.5, we have the corollary below.
Corollary 3.6 Let $(u_n) \subset W^{1,N}(\Theta )$![]() be a sequence as in Lemma 3.5. If $u_n(x) \to u(x)$
be a sequence as in Lemma 3.5. If $u_n(x) \to u(x)$![]() a.e. in $\Theta,$
a.e. in $\Theta,$![]() then $f_n \rightharpoonup f$
then $f_n \rightharpoonup f$![]() in $L^{t}(\Theta )$
in $L^{t}(\Theta )$![]() where $f(x)=e^{\alpha |u(x)|^{N'}},$
where $f(x)=e^{\alpha |u(x)|^{N'}},$![]() that is,
that is,
where $\frac {1}{t}+\frac {1}{t'}=1$![]() .
.
Our next result will help us to conclude that the energy functional associated with the problem $(P)$![]() is $C^{1}(W_0^{1,\Phi }(\Omega ),\mathbb {R})$
is $C^{1}(W_0^{1,\Phi }(\Omega ),\mathbb {R})$![]() . Since it follows as in Bezerra do Ó, Medeiros and Severo [Reference Bezerra do Ó, Medeiros and Severo12, Proposition 1], we will omit its proof.
. Since it follows as in Bezerra do Ó, Medeiros and Severo [Reference Bezerra do Ó, Medeiros and Severo12, Proposition 1], we will omit its proof.
Lemma 3.7 Let $(u_n) \subset W^{1,N}(\Theta )$![]() be a sequence such that $u_n \to u$
be a sequence such that $u_n \to u$![]() in $W^{1,N}(\Theta )$
in $W^{1,N}(\Theta )$![]() for some $u \in W^{1,N}(\Theta )$
for some $u \in W^{1,N}(\Theta )$![]() . Then, for some subsequence, still denoted by itself, there is $v \in W^{1,N}(\Theta )$
. Then, for some subsequence, still denoted by itself, there is $v \in W^{1,N}(\Theta )$![]() such that:
such that:
(i) $u_n(x) \to u(x)$
 a.e. in $\Theta$
a.e. in $\Theta$ .
.(ii) $|u_n(x)| \leq v(x)\,\,$
 a.e. in $\Theta$
a.e. in $\Theta$ for all $n \in \mathbb {N}$
for all $n \in \mathbb {N}$ .
.
4. Preliminaries for the proof of Theorem 1.1
To prove Theorem 1.1, we use the following result, whose proof follows similar arguments as in Ambrosetti and Rabinowitz [Reference Rabinowitz45]. Let $X$![]() be a Banach space, $K\subset X$
be a Banach space, $K\subset X$![]() be compact and $\gamma (Y)$
be compact and $\gamma (Y)$![]() be the genus of $Y\subset \Sigma,$
be the genus of $Y\subset \Sigma,$![]() where
where
Theorem 4.1 Suppose $I\in C^{1}(X,\mathbb {R})$![]() satisfies:
satisfies:
(a) $I(0)=0$
 , $I(u)=I(-u)$
, $I(u)=I(-u)$ for all $u\in X.$
for all $u\in X.$
(b) there exists $\alpha,\rho >0$
 such that
\[ I(u)\geq\alpha\,\,\forall\,\,||u||=\rho. \]
such that
\[ I(u)\geq\alpha\,\,\forall\,\,||u||=\rho. \]
(c) for every $\hat {X}\subset X$
 such that $\text {dim}\,\hat {X}<\infty,$
such that $\text {dim}\,\hat {X}<\infty,$ there exists $R=R(\hat {X})>0,$
there exists $R=R(\hat {X})>0,$ such that
\[ I(u)\leq 0,\text{ for every }u\in\hat{X}\setminus B_{R}(0); \]
such that
\[ I(u)\leq 0,\text{ for every }u\in\hat{X}\setminus B_{R}(0); \]
(d) there exists $M>0,$
 such that $I$
such that $I$ satisfies $(PS)_c$
satisfies $(PS)_c$ condition, for any $0< c< M.$
condition, for any $0< c< M.$
For each $m\in \mathbb {N},$![]() fix a finite-dimensional subspace $X_m$
fix a finite-dimensional subspace $X_m$![]() of $X$
of $X$![]() and consider $R_m=R(X_m)>0$
and consider $R_m=R(X_m)>0$![]() given by condition $(c).$
given by condition $(c).$![]() Now, define
Now, define
and
Then $0<\alpha \leq c_m\leq c_{m+1},$![]() and if $c_m< M,$
and if $c_m< M,$![]() the levels $c_j$
the levels $c_j$![]() for $j \in \{1,2,\ldots,m\}$
for $j \in \{1,2,\ldots,m\}$![]() are critical values of $I$
are critical values of $I$![]() . Moreover, if $c_1=c_2=\cdots =c_r=c< M,$
. Moreover, if $c_1=c_2=\cdots =c_r=c< M,$![]() then $\gamma (K_0)>r.$
then $\gamma (K_0)>r.$![]()
4.1. Functional setting
In what follows, we consider the associated energy functional $I:W_0^{1,\Phi }(\Omega ) \to \mathbb {R}$![]() given by
given by
where $F(x,t)=\int _{0}^{t}f(x,s)\, ds, \, t \in \mathbb {R}$![]() and $f$
and $f$![]() is either of the form $(f_1)$
is either of the form $(f_1)$![]() or $(f_2)$
or $(f_2)$![]() . Here, we would like to mention that, for the rest of the article, whenever we deal with $(f_1)$
. Here, we would like to mention that, for the rest of the article, whenever we deal with $(f_1)$![]() , we assume $\Omega$
, we assume $\Omega$![]() to be a smooth bounded domain in $\mathbb {R}^{N}$
to be a smooth bounded domain in $\mathbb {R}^{N}$![]() , $N\geq 2$
, $N\geq 2$![]() along with the hypothesis $(g_0)-(g_3)$
along with the hypothesis $(g_0)-(g_3)$![]() and $(\varphi _1)-(\varphi _7)$
and $(\varphi _1)-(\varphi _7)$![]() as in Theorem 1.1. For $(f_2)$
as in Theorem 1.1. For $(f_2)$![]() , we consider $\Omega =\Omega _r$
, we consider $\Omega =\Omega _r$![]() , $N\geq 2,$
, $N\geq 2,$![]() $N\neq 3$
$N\neq 3$![]() along with the hypothesis $(g_1),(g_2),(g_4), (\eta )$
along with the hypothesis $(g_1),(g_2),(g_4), (\eta )$![]() and $(\Omega _N)$
and $(\Omega _N)$![]() and $(\varphi _1)-(\varphi _{9})$
and $(\varphi _1)-(\varphi _{9})$![]() as in Theorem 1.2.
as in Theorem 1.2.
Lemma 4.2 Assume that $f$![]() is of form $(f_1)$
is of form $(f_1)$![]() or $(f_2)$
or $(f_2)$![]() . Then, the functional $I$
. Then, the functional $I$![]() belongs to $C^{1}(W_0^{1,\Phi }(\Omega ),\mathbb {R})$
belongs to $C^{1}(W_0^{1,\Phi }(\Omega ),\mathbb {R})$![]() and
and
Proof. See proof in [Reference Alves, Garain and Rădulescu8, Lemma 3.8]
Next, our goal is to prove that $I$![]() satisfies the geometric conditions of Theorem 4.1 and the well-known $(PS)$
satisfies the geometric conditions of Theorem 4.1 and the well-known $(PS)$![]() condition.
condition.
Lemma 4.3 Assume that $f$![]() is of the form $(f_1)$
is of the form $(f_1)$![]() . Then,
. Then,
(i) There are $r, \rho >0$
 such that
\[ I(u) \geq \rho, \quad \mbox{for} \quad \|u\|=r. \]
such that
\[ I(u) \geq \rho, \quad \mbox{for} \quad \|u\|=r. \]
(ii) For every $\hat {X}\subset W_{0}^{1,\Phi }(\Omega )$
 with $\dim \,\hat {X}<\infty,$
with $\dim \,\hat {X}<\infty,$ there exists $R=R(\hat {X})>0,$
there exists $R=R(\hat {X})>0,$ such that
\[ I(u)\leq 0,\text{ for all }u\in\hat{X}\setminus B_R(0). \]
such that
\[ I(u)\leq 0,\text{ for all }u\in\hat{X}\setminus B_R(0). \]
Proof. The proof of $(i)$![]() can be done as in [Reference Alves, Garain and Rădulescu8, Lemma 3.9].
can be done as in [Reference Alves, Garain and Rădulescu8, Lemma 3.9].
$(ii)$![]() Suppose for each $n\in \mathbb {N},$
Suppose for each $n\in \mathbb {N},$![]() there exists $u_n\in \hat {X}\setminus B_n(0)$
there exists $u_n\in \hat {X}\setminus B_n(0)$![]() such that
such that
From $(g_2)$![]() , it follows that
, it follows that
where $\chi =\min \{\theta,\beta,\zeta \}>q.$![]() Therefore, $f$
Therefore, $f$![]() satisfies the Ambrosetti–Rabinowitz condition. This gives the existence of positive constants $C,D$
satisfies the Ambrosetti–Rabinowitz condition. This gives the existence of positive constants $C,D$![]() such that
such that
Using Proposition 2.1-(ii) along with (4.5), we obtain
Since $\dim \,\hat {X}<\infty$![]() and $\chi >q$
and $\chi >q$![]() letting $n\to \infty$
letting $n\to \infty$![]() in (4.6), we arrive at a contradiction to our assumption (4.3). Hence $(ii)$
in (4.6), we arrive at a contradiction to our assumption (4.3). Hence $(ii)$![]() follows.
follows.
Lemma 4.4 Assume that $f$![]() is of the type $(f_1)$
is of the type $(f_1)$![]() or $(f_2)$
or $(f_2)$![]() . Then, every $(PS)$
. Then, every $(PS)$![]() sequence $(u_n)$
sequence $(u_n)$![]() of the functional $I$
of the functional $I$![]() is bounded in $W_0^{1,\Phi }(\Omega )$
is bounded in $W_0^{1,\Phi }(\Omega )$![]() .
.
Proof. Let $d>0$![]() and $(u_n)$
and $(u_n)$![]() be a $(PS)_d$
be a $(PS)_d$![]() sequence for $I$
sequence for $I$![]() . Then, there are constants $C_1,C_2>0$
. Then, there are constants $C_1,C_2>0$![]() such that
such that
If $f$![]() is of the type $(f_1)$
is of the type $(f_1)$![]() or $(f_2)$
or $(f_2)$![]() it is easy to check that (4.4) holds. Hence, by $(\varphi _3)'$
it is easy to check that (4.4) holds. Hence, by $(\varphi _3)'$![]() and the definition of $I$
and the definition of $I$![]() ,
,

Therefore,
If there is $(u_{n_j}) \subset (u_n)$![]() such that $\|u_{n_j}\| \geq 1$
such that $\|u_{n_j}\| \geq 1$![]() , then Proposition 2.1-(i) leads to
, then Proposition 2.1-(i) leads to
from where it follows the boundedness of $(u_{n_j})$![]() . This implies the boundedness of $(u_n)$
. This implies the boundedness of $(u_n)$![]() .
.
Corollary 4.5 Assume that $f$![]() is of the type $(f_1)$
is of the type $(f_1)$![]() or $(f_2)$
or $(f_2)$![]() and let $(u_n)$
and let $(u_n)$![]() be a $(PS)_d$
be a $(PS)_d$![]() sequence of $I$
sequence of $I$![]() with $d \in (0,M),$
with $d \in (0,M),$![]()
where $\chi =\min \{\theta,\beta,\zeta \}.$![]() Then,
Then,
Hence, without loss of generality, we can assume that there is $\tau \in (0,1)$![]() such that
such that
Proof. First of all, we must recall that
Therefore, by $(\varphi _5)$![]() ,
,

Hence,
leading to
which proves the lemma.
Lemma 4.6 Assume that $f$![]() is of the type $(f_1)$
is of the type $(f_1)$![]() or $(f_2)$
or $(f_2)$![]() . Then, the functional $I$
. Then, the functional $I$![]() verifies the $(PS)_d$
verifies the $(PS)_d$![]() condition for $d \in (0,M),$
condition for $d \in (0,M),$![]() where $M$
where $M$![]() was given in Corollary 4.5.
was given in Corollary 4.5.
Proof. The proof of this lemma follows as in [Reference Alves, Garain and Rădulescu8, Lemma 3.13]; however, for the reader's convenience, we will write the proof for $(f_1)$![]() , since for $(f_2)$
, since for $(f_2)$![]() , it follows with similar arguments. Let $(u_n)$
, it follows with similar arguments. Let $(u_n)$![]() be a $(PS)_d$
be a $(PS)_d$![]() sequence for $I$
sequence for $I$![]() . Then, by Lemma 4.4, $(u_n)$
. Then, by Lemma 4.4, $(u_n)$![]() is bounded in $W_0^{1,\Phi }(\Omega )$
is bounded in $W_0^{1,\Phi }(\Omega )$![]() . Since $W_0^{1,\Phi }(\Omega )$
. Since $W_0^{1,\Phi }(\Omega )$![]() is reflexive, we assume that for some subsequence, still denoted by itself, there is $u \in W_0^{1,\Phi }(\Omega )$
is reflexive, we assume that for some subsequence, still denoted by itself, there is $u \in W_0^{1,\Phi }(\Omega )$![]() such that
such that
and
Let us set
that is,
Consequently
From the definition of $f$![]() together with embedding (2.9),
together with embedding (2.9),

and
Consequently

By Corollary 4.5, the sequence $(u_n)$![]() satisfies
satisfies
for some $\tau \in (0,1)$![]() . Employing Corollary 3.6, there is $t>1$
. Employing Corollary 3.6, there is $t>1$![]() and $t \approx 1$
and $t \approx 1$![]() such that the sequence $h_n(x)=e^{\alpha |u_n(x)|^{N'}}$
such that the sequence $h_n(x)=e^{\alpha |u_n(x)|^{N'}}$![]() is weakly convergent to $h(x)=e^{\alpha |u(x)|^{N'}}$
is weakly convergent to $h(x)=e^{\alpha |u(x)|^{N'}}$![]() in $L^{t}(\Omega _N)$
in $L^{t}(\Omega _N)$![]() , that is,
, that is,
As
it follows that
that is,
Now, using the fact that
we also derive that
The above analysis ensures that

and then,
By [Reference Kavian35, Lemma 4.8],
then
Now, we are going to use the Concentration Compactness Lemma 3.1 to the sequence $(u_n) \subset W^{1,p}(\Omega _p)$![]() . From $(\varphi _6)$
. From $(\varphi _6)$![]() , for each open ball $B \subset (\Omega _q)_{\delta }$
, for each open ball $B \subset (\Omega _q)_{\delta }$![]() we have that the embedding $W^{1,\Phi }(\Omega ) \hookrightarrow C(\overline {B})$
we have that the embedding $W^{1,\Phi }(\Omega ) \hookrightarrow C(\overline {B})$![]() is compact, then as $(u_n)$
is compact, then as $(u_n)$![]() is a bounded $(PS)$
is a bounded $(PS)$![]() for $I$
for $I$![]() , it is possible to prove that for some subsequence, there holds
, it is possible to prove that for some subsequence, there holds
Since from $(\varphi _5)-(\varphi _7)$![]() , the embedding $W^{1,\Phi }(B) \hookrightarrow L^{\Phi }(B)$
, the embedding $W^{1,\Phi }(B) \hookrightarrow L^{\Phi }(B)$![]() is compact, the last limit together with the $\Delta _2$
is compact, the last limit together with the $\Delta _2$![]() -condition (2.1) implies that
-condition (2.1) implies that
Now, recalling that the embedding $W^{1,\Phi }(B) \hookrightarrow W^{1,p}(B)$![]() is continuous, we derive that
is continuous, we derive that
from where it follows that $x_i \in \overline {\Omega _p} \setminus (\Omega _q)_{\delta }$![]() for all $i \in J$
for all $i \in J$![]() . Now, our goal is proving that $J$
. Now, our goal is proving that $J$![]() must be a finite set. Have this in mind, we will consider $J=J_1 \cup J_2$
must be a finite set. Have this in mind, we will consider $J=J_1 \cup J_2$![]() where
where
and
If $i \in J_1$![]() , the condition $(\varphi _7)$
, the condition $(\varphi _7)$![]() says that $c_3t^{p-2} \geq \varphi (x,t) \geq t^{p-2}$
says that $c_3t^{p-2} \geq \varphi (x,t) \geq t^{p-2}$![]() for $x \in \overline {\Omega _p} \setminus \overline {(\Omega _q)_{\delta }}$
for $x \in \overline {\Omega _p} \setminus \overline {(\Omega _q)_{\delta }}$![]() . This fact permits us to repeat the same arguments explored in [Reference Garcia Azorero and Peral Alonso30, Lemma 2.3] to conclude that $J_1$
. This fact permits us to repeat the same arguments explored in [Reference Garcia Azorero and Peral Alonso30, Lemma 2.3] to conclude that $J_1$![]() is finite. Now, if $i \in J_2$
is finite. Now, if $i \in J_2$![]() , the situation is more subtle and we must be careful. In what follows let us consider $\tilde {\psi } \in C_{0}^{\infty }(\mathbb {R}^{N})$
, the situation is more subtle and we must be careful. In what follows let us consider $\tilde {\psi } \in C_{0}^{\infty }(\mathbb {R}^{N})$![]() such that
such that
For each $\epsilon >0$![]() , we set
, we set
Since $(u_n)$![]() is a bounded sequence in $W^{1,\Phi }(\Omega )$
is a bounded sequence in $W^{1,\Phi }(\Omega )$![]() , the sequence $(\psi u_n)$
, the sequence $(\psi u_n)$![]() is also bounded in $W^{1,\Phi }(\Omega )$
is also bounded in $W^{1,\Phi }(\Omega )$![]() and so, $I'(u_n)\psi u_n=o_n(1)$
and so, $I'(u_n)\psi u_n=o_n(1)$![]() . Hence,
. Hence,
Now, given $\xi >0$![]() , the Young's inequality (2.2) combined with (2.3) and $\Delta _2$
, the Young's inequality (2.2) combined with (2.3) and $\Delta _2$![]() -condition (2.1) gives
-condition (2.1) gives
for some $C_\xi >0$![]() . Note that by $(\varphi _7)$
. Note that by $(\varphi _7)$![]() ,
,

By Hölder's inequality

from where it follows that

Arguing as above, we also have

By change of variable,

Since $x_i \in \partial (\Omega _q)_{\delta } \cap \Omega _p$![]() , it follows that
, it follows that
and

As $s>q$![]() , it follows that
, it follows that
Now, the boundedness of $(u_n)$![]() in $W^{1,\Phi }(\Omega )$
in $W^{1,\Phi }(\Omega )$![]() together with Proposition (2.1), (4.9) and (4.10) ensures that
together with Proposition (2.1), (4.9) and (4.10) ensures that
for some $C>0$![]() . Since $\xi >0$
. Since $\xi >0$![]() is arbitrary, we can deduce that
is arbitrary, we can deduce that
The last limit together with the fact that $\varphi (x,t) \geq t^{p-2}$![]() for $x \in \Omega _p$
for $x \in \Omega _p$![]() permit us to conclude as in [Reference Garcia Azorero and Peral Alonso30, Lemma 2.3], that $J_2$
permit us to conclude as in [Reference Garcia Azorero and Peral Alonso30, Lemma 2.3], that $J_2$![]() is also finite. Consequently, $J$
is also finite. Consequently, $J$![]() is a finite set. However, in order to conclude the proof of the lemma, we need to show that $J$
is a finite set. However, in order to conclude the proof of the lemma, we need to show that $J$![]() is in fact an empty set. Seeking by a contradiction, assume that there is $i \in J$
is in fact an empty set. Seeking by a contradiction, assume that there is $i \in J$![]() . In this case, the argument explored in [Reference Garcia Azorero and Peral Alonso30] also says for us that
. In this case, the argument explored in [Reference Garcia Azorero and Peral Alonso30] also says for us that
Hence, by Lemma 3.1-(d),
As $|\nabla u_n|^{p} \to \mu$![]() weakly-$^{*}$
weakly-$^{*}$![]() in the sense of measure, we have
in the sense of measure, we have
and so,
Now, using once more the equality
we get
Taking the limit of $n \to +\infty$![]() , we find the inequality below
, we find the inequality below
which is a contradiction, showing that $J=\emptyset$![]() . Thereby, by Lemma 3.1-$(a)$
. Thereby, by Lemma 3.1-$(a)$![]() , $\nu =|u|^{p^{*}}$
, $\nu =|u|^{p^{*}}$![]() and
and
implying that $P_n=o_n(1)$![]() , that is,
, that is,
Now, it is enough to apply Lemma 2.2 to finish the proof.
Our last lemma in this section is as follows:
Lemma 4.7 Assume that $(f_1)$![]() holds. Then, for each $m\in \mathbb {N},$
holds. Then, for each $m\in \mathbb {N},$![]() there exists positive constants $\lambda _m, \mu _m$
there exists positive constants $\lambda _m, \mu _m$![]() and $\tau _m$
and $\tau _m$![]() such that
such that
for all $\lambda \geq \lambda _m, \mu \ge \mu _m$![]() and $\tau \geq \tau _m,$
and $\tau \geq \tau _m,$![]() where $M$
where $M$![]() is given by Corollary 4.5.
is given by Corollary 4.5.
Proof. First, we claim that for some positive constant $C>0,$![]() we have
we have

where $K\subset X_m$![]() is compact such that $\dim \,X_m<\infty.$
is compact such that $\dim \,X_m<\infty.$![]()
Indeed, if (4.11) does not hold, then there exists a sequence $\{u_n\}\subset K$![]() with $||u_n||=1$
with $||u_n||=1$![]() such that
such that

Since $\dim \,X_m<\infty,$![]() there exists a subsequence of $\{u_n\}$
there exists a subsequence of $\{u_n\}$![]() still denoted by $\{u_n\}$
still denoted by $\{u_n\}$![]() and $u\in K$
and $u\in K$![]() with $||u||=1$
with $||u||=1$![]() such that $u_{n_j}\to u$
such that $u_{n_j}\to u$![]() in $X_m.$
in $X_m.$![]() Then, letting $n\to \infty$
Then, letting $n\to \infty$![]() in (4.12), we obtain
in (4.12), we obtain
Hence, we have $u=0$![]() a.e. in each of the sets $\Omega _N,\Omega _q$
a.e. in each of the sets $\Omega _N,\Omega _q$![]() and $\Omega _p.$
and $\Omega _p.$![]() Now, since $\Omega =\Omega _N\cup \Omega _q\cup \Omega _p,$
Now, since $\Omega =\Omega _N\cup \Omega _q\cup \Omega _p,$![]() we have $u=0$
we have $u=0$![]() a.e. in $\Omega.$
a.e. in $\Omega.$![]() This contradicts the fact that $||u||=1.$
This contradicts the fact that $||u||=1.$![]() Hence the Claim (4.11) follows.
Hence the Claim (4.11) follows.
Now we choose $K=\overline {D}_m$![]() where $D_m$
where $D_m$![]() is given by (4.1). Since $h=I_d \in G_m$
is given by (4.1). Since $h=I_d \in G_m$![]() , the definition of $\Phi$
, the definition of $\Phi$![]() combined with (2.4) and $(f_1)$
combined with (2.4) and $(f_1)$![]() gives
gives

or equivalently

Now, when $||u||>1,$![]() we observe that
we observe that

where $l_1=\min \{\beta,q_2,\zeta \}$![]() , $\chi _1=\min \{\lambda,\mu,\tau \}$
, $\chi _1=\min \{\lambda,\mu,\tau \}$![]() and the constant $C$
and the constant $C$![]() is given by (4.11).
is given by (4.11).
Moreover, when $\|u\|\leq 1,$![]() we get
we get

where $l_2=\max \{\beta,q_2,\zeta \}$![]() , $\chi _1=\min \{\lambda,\mu,\tau \}$
, $\chi _1=\min \{\lambda,\mu,\tau \}$![]() and the constant $C$
and the constant $C$![]() is given by (4.11). Hence,
is given by (4.11). Hence,
where $l=l_1$![]() or $l_2.$
or $l_2.$![]()
Let, $w(t)=t^{p}+t^{q}-C\chi t^{l}$![]() . Then using the fact that $l>q>p,$
. Then using the fact that $l>q>p,$![]() it can be easily seen that $w$
it can be easily seen that $w$![]() achieves its maximum at $\hat {t}=\hat {t}(\lambda,\beta,\tau )>0$
achieves its maximum at $\hat {t}=\hat {t}(\lambda,\beta,\tau )>0$![]() which goes to $0$
which goes to $0$![]() as the parameters $\lambda,\mu,\tau$
as the parameters $\lambda,\mu,\tau$![]() goes to infinity. Hence there exists $\lambda _m,\mu _m,\tau _m$
goes to infinity. Hence there exists $\lambda _m,\mu _m,\tau _m$![]() such that for all $\lambda \geq \lambda _m,\mu \geq \mu _m$
such that for all $\lambda \geq \lambda _m,\mu \geq \mu _m$![]() and $\tau \geq \tau _m,$
and $\tau \geq \tau _m,$![]() we have
we have
where $M$![]() is given by Corollary 4.5. Hence, the Lemma follows.
is given by Corollary 4.5. Hence, the Lemma follows.
5. Preliminaries for the proof of Theorem 1.2
5.1. Functional setting
In what follows $f$![]() is of the type $(f_2)$
is of the type $(f_2)$![]() , $\Omega =\Omega _r$
, $\Omega =\Omega _r$![]() , see (1.7), $N\geq 2$
, see (1.7), $N\geq 2$![]() , $N\neq 3$
, $N\neq 3$![]() and the hypothesis $(g_1), (g_2), (g_4), (\varphi _1)-(\varphi _{9})$
and the hypothesis $(g_1), (g_2), (g_4), (\varphi _1)-(\varphi _{9})$![]() will be assumed, unless otherwise mentioned. Let us denote by $O(N)$
will be assumed, unless otherwise mentioned. Let us denote by $O(N)$![]() the group of $N\times N$
the group of $N\times N$![]() orthogonal matrices. For any integer $1\leq k<\infty$
orthogonal matrices. For any integer $1\leq k<\infty$![]() , let us consider the finite rotational subgroup $O_k$
, let us consider the finite rotational subgroup $O_k$![]() of $O(2)$
of $O(2)$![]() given by
given by
where $x=(x_1,x_2)\in \mathbb {R}^{2}$![]() and $l\in \{0,\ldots,k-1\}$
and $l\in \{0,\ldots,k-1\}$![]() . We define the subgroups of $O(N)$
. We define the subgroups of $O(N)$![]()
Associated with the above subgroups, we set the subspaces
endowed with the usual norm of $W^{1,\Phi }_0(\Omega _r)$![]() , that is,
, that is,
Hereafter, we denote by $I:W^{1,\Phi }_{0,H_k}(\Omega _r)\to \mathbb {R}$![]() the functional given by
the functional given by
Throughout this section, $J_{k,r}$![]() denotes the following real number
denotes the following real number
where
5.2. Properties of the levels $J_{k,r}$
Our first result concerns the positivity of $J_{k,r}$![]() .
.
Lemma 5.1 For any $1\leq k\leq \infty$![]() and $r>0,$
and $r>0,$![]() we have $J_{k,r}>0$
we have $J_{k,r}>0$![]() .
.
Proof. We prove the result in two steps.
Step 1. We claim that for every fixed $1\leq k\leq \infty$![]() and $r>0$
and $r>0$![]() , there exists a constant $\eta >0$
, there exists a constant $\eta >0$![]() such that
such that
Indeed, if (5.1) does not hold, there exists a sequence $(u_n)\in \mathcal {M}_{k,r}$![]() such that $||u_n||\to 0$
such that $||u_n||\to 0$![]() as $n\to \infty$
as $n\to \infty$![]() . From $u_n\in \mathcal {M}_{k,r}$
. From $u_n\in \mathcal {M}_{k,r}$![]() we have $I'(u_n)u_n=0$
we have $I'(u_n)u_n=0$![]() . Hence
. Hence
Due to the fact $||u_n||\to 0$![]() as $n\to \infty$
as $n\to \infty$![]() , without loss of generality we may assume that $||u_n||<1$
, without loss of generality we may assume that $||u_n||<1$![]() for all $n \in \mathbb {N}$
for all $n \in \mathbb {N}$![]() . Hence from $(\varphi _3)'$
. Hence from $(\varphi _3)'$![]() and Proposition 2.1, we can estimate the left-hand side of (5.2) as follows:
and Proposition 2.1, we can estimate the left-hand side of (5.2) as follows:
Now, we estimate the right-hand side of (5.2). Indeed,

Estimate of $I_1$![]() : As $||u_n|| \to 0$
: As $||u_n|| \to 0$![]() , by Hölder's inequality and Lemma 3.5 for some constant $C_1>0$
, by Hölder's inequality and Lemma 3.5 for some constant $C_1>0$![]() (independent of $n$
(independent of $n$![]() ), we have
), we have

Estimate of $I_2$![]() : From the condition $(g_1)$
: From the condition $(g_1)$![]() and the embedding (2.9) for some constant $C_2>0$
and the embedding (2.9) for some constant $C_2>0$![]() (independent of $n$
(independent of $n$![]() ) we deduce that
) we deduce that
Estimate of $I_3$![]() : It is clear that
: It is clear that
for some constant $C_3>0$![]() (independent of $n$
(independent of $n$![]() ).
).
Estimate of $I_4$![]() : By the embedding (2.9), the definition of $f_2$
: By the embedding (2.9), the definition of $f_2$![]() and the condition $(g_1)$
and the condition $(g_1)$![]() we have that
we have that
for some constant $C_4>0$![]() (independent of $n$
(independent of $n$![]() ).
).
Therefore, using the estimates (5.5), (5.6), (5.7) and (5.8) in (5.4), we obtain
for some constant $C>0$![]() (independent of $n$
(independent of $n$![]() ). Using (5.9) in (5.3), we have
). Using (5.9) in (5.3), we have
Since all the parameters $\beta,q_1$![]() and $p^{*}$
and $p^{*}$![]() are larger than $q$
are larger than $q$![]() , from (5.10) for some constant $\widehat {C}>0$
, from (5.10) for some constant $\widehat {C}>0$![]() (independent of $n$
(independent of $n$![]() ), we have
), we have
which is a contradiction to the fact $||u_n||\to 0$![]() . Hence (5.1) holds.
. Hence (5.1) holds.
Step 2. From the definition of $I$![]() , $(\varphi _3)'$
, $(\varphi _3)'$![]() and Proposition 2.1 for any $u\in \mathcal {M}_{k,r}$
and Proposition 2.1 for any $u\in \mathcal {M}_{k,r}$![]() , we have
, we have

where in the last line, we have used the estimate (5.1) from Step 1 and $\chi =\min \{\theta,\beta,p^{*}\}$![]() . This means that,
. This means that,
for every $1\leq k\leq \infty$![]() and all $r>0$
and all $r>0$![]() . Hence the result follows.
. Hence the result follows.
Lemma 5.2 For any integer $1\leq k<\infty,$![]() there exists $\lambda _0=\lambda _0(k)>0,$
there exists $\lambda _0=\lambda _0(k)>0,$![]() such that
such that
Proof. Fix $1\leq k<\infty$![]() . Due to $(\eta )$
. Due to $(\eta )$![]() , there exists $\gamma =\gamma (k) < \min \left \{\frac {1}{2},\delta _1\right \}$
, there exists $\gamma =\gamma (k) < \min \left \{\frac {1}{2},\delta _1\right \}$![]() such that the ball $B_{\gamma,r}:=B_{\gamma }((\frac {2r+1}{2},0,\ldots,0))\subset \Omega _N\setminus {\overline {(\Omega _q)_\delta }}$
such that the ball $B_{\gamma,r}:=B_{\gamma }((\frac {2r+1}{2},0,\ldots,0))\subset \Omega _N\setminus {\overline {(\Omega _q)_\delta }}$![]() satisfies
satisfies
Consider $v_r\in W^{1,\Phi }_0(B_{\delta,r})\setminus \{0\}$![]() and define
and define
By definition of $I$![]() , we observe that
, we observe that
Using
Therefore, using $(\varphi _3)'$![]() and (2.4), for every $t\geq 0$
and (2.4), for every $t\geq 0$![]() ,
,
As $\beta >q> p$![]() , we get that $I'(tv)tv\to -\infty$
, we get that $I'(tv)tv\to -\infty$![]() as $t\to +\infty$
as $t\to +\infty$![]() and $I'(tv)tv>0$
and $I'(tv)tv>0$![]() for $t \approx 0$
for $t \approx 0$![]() .
.
So, there exists $t_v>0$![]() such that $t_v v\in W^{1,\Phi }_{0,H_k}({\Omega _N\setminus {\overline {(\Omega _q)_\delta }}})\setminus \{0\}$
such that $t_v v\in W^{1,\Phi }_{0,H_k}({\Omega _N\setminus {\overline {(\Omega _q)_\delta }}})\setminus \{0\}$![]() with $I^{\prime }(t_v v)t_v v=0$
with $I^{\prime }(t_v v)t_v v=0$![]() . If we denote by $w=t_v v$
. If we denote by $w=t_v v$![]() , then
, then
Following similar arguments as in the proof of [Reference Alves, Garain and Rădulescu8, Lemma 3.11], we have

Now, we fix $\lambda _0=\lambda _0(k)>0$![]() such that for all $\lambda \geq \lambda _0$
such that for all $\lambda \geq \lambda _0$![]() , we have
, we have

Lemma 5.3 If $1\leq k<\infty$![]() and $\lambda \geq \lambda _0,$
and $\lambda \geq \lambda _0,$![]() then $J_{k,r}$
then $J_{k,r}$![]() is achieved.
is achieved.
Proof. Let $(v_n)\subset \mathcal {M}_{k,r}$![]() a minimizing sequence for $J_{k,r}$
a minimizing sequence for $J_{k,r}$![]() , i.e., $(v_n)\subset W^{1,\phi }_{0,H_k}(\Omega _r)\setminus \{0\}$
, i.e., $(v_n)\subset W^{1,\phi }_{0,H_k}(\Omega _r)\setminus \{0\}$![]() such that
such that
We claim that $(v_n)$![]() is bounded. Assume there is some $n$
is bounded. Assume there is some $n$![]() such that $||v_n||\geq 1$
such that $||v_n||\geq 1$![]() , since otherwise $(v_n)$
, since otherwise $(v_n)$![]() is bounded. Due to the fact $I(v_n)\to J_{k,r}$
is bounded. Due to the fact $I(v_n)\to J_{k,r}$![]() and $J_{k,r} \leq M$
and $J_{k,r} \leq M$![]() , where $M$
, where $M$![]() was given in Lemma 5.2, it follows that
was given in Lemma 5.2, it follows that

Therefore, $||v_n||\leq c$![]() if $\|v_n\| >1$
if $\|v_n\| >1$![]() , for some constant $c>0$
, for some constant $c>0$![]() independent of $n$
independent of $n$![]() . This shows that $(v_n)$
. This shows that $(v_n)$![]() is bounded.
is bounded.
Claim:
Indeed, using the Ekeland variational Principle (see Willem [Reference Willem54]), there exists a sequence $(w_n)\subset \mathcal {M}_{k,r}$![]() such that
such that
and
where $(\ell _n)\subset \mathbb {R}$![]() and $E(w)=I'(w)w$
and $E(w)=I'(w)w$![]() for $w\in W^{1,\Phi }_{0,H_k}(\Omega _r)$
for $w\in W^{1,\Phi }_{0,H_k}(\Omega _r)$![]() . Since $(v_n)$
. Since $(v_n)$![]() is bounded, we also have that $(w_n)$
is bounded, we also have that $(w_n)$![]() is bounded. Now, we prove that there exists $C >0$
is bounded. Now, we prove that there exists $C >0$![]() such that
such that
Indeed, we observe that

where in the second step, we have used that the function $\dfrac {\varphi (x,t)}{|t|^{q-3}t}$![]() is non-increasing for $t\neq 0$
is non-increasing for $t\neq 0$![]() , which is a consequence of $(\varphi _{3})$
, which is a consequence of $(\varphi _{3})$![]() , while that in the third step we have use the fact that $I^{\prime }(w_n)w_n=0$
, while that in the third step we have use the fact that $I^{\prime }(w_n)w_n=0$![]() , i.e.
, i.e.
respectively. Since $(w_n)$![]() is bounded in $W_{0}^{1,\Phi }(\Omega _r)$
is bounded in $W_{0}^{1,\Phi }(\Omega _r)$![]() and $J_{k,r}>0$
and $J_{k,r}>0$![]() , there exists $w\in W^{1,\Phi }(\Omega _r)\setminus \{0\}$
, there exists $w\in W^{1,\Phi }(\Omega _r)\setminus \{0\}$![]() such that $w_n\to w$
such that $w_n\to w$![]() strongly in $L^{\Phi }(\Omega _r)$
strongly in $L^{\Phi }(\Omega _r)$![]() and $w_n(x) \to w(x)$
and $w_n(x) \to w(x)$![]() a.e. in $\Omega _r$
a.e. in $\Omega _r$![]() for some subsequence. Then, by Fatou's lemma,
for some subsequence. Then, by Fatou's lemma,

From the hypothesis $(g_4)$![]() and the definition of $f_2$
and the definition of $f_2$![]() , we obtain
, we obtain
By contradiction, suppose
Then letting $n\to \infty$![]() in (5.15) and using (5.16) along with (5.17), we obtain
in (5.15) and using (5.16) along with (5.17), we obtain
which is absurd. Therefore, (5.14) holds.
From, (5.13)
and so, $\ell _n=o_n(1)$![]() . Since $(w_n)$
. Since $(w_n)$![]() is bounded we get $(E'(w_n))$
is bounded we get $(E'(w_n))$![]() is bounded. Hence from (5.13)
is bounded. Hence from (5.13)
Thus, without loss generality, we may assume
Since $(v_n)$![]() is bounded, there exists $v\in W^{1,\Phi }_{0.H_k}(\Omega _r)$
is bounded, there exists $v\in W^{1,\Phi }_{0.H_k}(\Omega _r)$![]() such that, for a subsequence, we have
such that, for a subsequence, we have

Now following exactly the proof of Lemma 4.6, we get $I(v_n)\to I(v)=J_{k,r}$![]() . Hence, $J_{k,r}$
. Hence, $J_{k,r}$![]() is achieved.
is achieved.
Now we establish the following Strauss-type result in Musielak–Sobolev space, which would be very useful to find a lower bound of $J_{\infty,r}$![]() .
.
Lemma 5.4 (A Strauss-type result in Musielak–Sobolev space) Assume that $(\varphi _1),$![]() $(\varphi _2),$
$(\varphi _2),$![]() $(\varphi _3),$
$(\varphi _3),$![]() $(\varphi _{8})-(\varphi _{9})$
$(\varphi _{8})-(\varphi _{9})$![]() holds and let $v\in W^{1,\Phi }(\mathbb {R}^{N})$
holds and let $v\in W^{1,\Phi }(\mathbb {R}^{N})$![]() be a radial function. Then
be a radial function. Then
where $\Phi ^{-1}(x,\cdot )$![]() denotes the inverse function of $\Phi (x,\cdot )$
denotes the inverse function of $\Phi (x,\cdot )$![]() restricted to $[0,+\infty )$
restricted to $[0,+\infty )$![]() and $C$
and $C$![]() is a positive constant independent of $v$
is a positive constant independent of $v$![]() .
.
Proof. We will establish the result for radial functions in $C_{0}^{\infty }(\mathbb {R}^{N})$![]() .
.
Let $v\in C_0^{\infty }(\mathbb {R}^{N})$![]() be radial and let $|x|=r$
be radial and let $|x|=r$![]() , $w(r)=v(x)$
, $w(r)=v(x)$![]() . Then, from $(\varphi _{8})$
. Then, from $(\varphi _{8})$![]()
Since $w\in C_0^{\infty }([0,\infty ))$![]() , for $b$
, for $b$![]() large enough,
large enough,

From (2.1), (2.2) and the $\Delta _2$![]() condition (2.1), for all $s\geq 0$
condition (2.1), for all $s\geq 0$![]() ,
,

From $(\varphi _{9})$![]() , for all $s\geq 0$
, for all $s\geq 0$![]() ,
,
Now using (5.19) and (5.20) in (5.18), we obtain
Hence, we can conclude that
From this, there is $C>0$![]() such that
such that
Since $\Phi$![]() is an even function, $\Phi (x,v(x))=\Phi (x,|v(x)|)$
is an even function, $\Phi (x,v(x))=\Phi (x,|v(x)|)$![]() for all $x\in \mathbb {R}^{N}$
for all $x\in \mathbb {R}^{N}$![]() and so,
and so,
From this,
where $\Phi ^{-1}(x, \cdot )$![]() denotes the inverse function of $\Phi (x, \cdot )$
denotes the inverse function of $\Phi (x, \cdot )$![]() restricted to $[0,+\infty )$
restricted to $[0,+\infty )$![]() . Now the result follows from the density of $C_0^{\infty }(\mathbb {R}^{N})$
. Now the result follows from the density of $C_0^{\infty }(\mathbb {R}^{N})$![]() in $W^{1,\Phi }(\mathbb {R}^{N})$
in $W^{1,\Phi }(\mathbb {R}^{N})$![]() , because $\Phi$
, because $\Phi$![]() satisfies the $\Delta _2$
satisfies the $\Delta _2$![]() condition.
condition.
Lemma 5.5 There exists $r_0=r_0(\lambda )>0$![]() such that for $\chi =\min \{\theta,\beta,p^{*}\}$
such that for $\chi =\min \{\theta,\beta,p^{*}\}$![]() ,
,
Proof. By contradiction, suppose there exists a sequence $(r_n)$![]() such that $r_n\to \infty$
such that $r_n\to \infty$![]() , satisfying
, satisfying
First, we claim that $J_{\infty,r_n}$![]() is attained, for all $n\in \mathbb {N}$
is attained, for all $n\in \mathbb {N}$![]() . In fact, for a fixed $n$
. In fact, for a fixed $n$![]() , let $(v_k)\subset \mathcal {M}_{\infty,r_n}$
, let $(v_k)\subset \mathcal {M}_{\infty,r_n}$![]() be a minimizing sequence for $J_{\infty,r_n}$
be a minimizing sequence for $J_{\infty,r_n}$![]() , i.e., $(v_k)\subset W^{1,\Phi }_{0,H_{\infty }}(\Omega _{r_n})\setminus \{0\}$
, i.e., $(v_k)\subset W^{1,\Phi }_{0,H_{\infty }}(\Omega _{r_n})\setminus \{0\}$![]() and satisfies
and satisfies
Note that

Now, we can repeat the same arguments employed in the proof of Lemma 5.3 to conclude that
where $v\in W^{1,\Phi }_{0,H_{\infty }}(\Omega _{r_n})$![]() is the limit of $(v_k)$
is the limit of $(v_k)$![]() in $W^{1,\Phi }_{0,H_{\infty }}(\Omega _{r_n})$
in $W^{1,\Phi }_{0,H_{\infty }}(\Omega _{r_n})$![]() . Then,
. Then,
Hence $I(v)=J_{\infty,r_n}$![]() . Note that $v\neq 0$
. Note that $v\neq 0$![]() , since by Lemma 5.1 $J_{\infty,r_n}>0$
, since by Lemma 5.1 $J_{\infty,r_n}>0$![]() . Therefore, $v\in \mathcal {M}_{\infty,r_n}$
. Therefore, $v\in \mathcal {M}_{\infty,r_n}$![]() and $J_{\infty,r_n}$
and $J_{\infty,r_n}$![]() is attained at $v$
is attained at $v$![]() .
.
Therefore, for each $n\in \mathbb {N}$![]() , we can choose a sequence $\{u_n\}\subset W^{1,\Phi }_{0,H_\infty }(\Omega _{r_n})\setminus \{0\}$
, we can choose a sequence $\{u_n\}\subset W^{1,\Phi }_{0,H_\infty }(\Omega _{r_n})\setminus \{0\}$![]() satisfying
satisfying
Proceeding as in (5.22)
which implies
Let $\{\tilde {u}_n\}$![]() be a sequence given by
be a sequence given by

Observe that the following properties hold:
(1) $\{\tilde {u}_n\}\subset W^{1,\Phi }_{H_{\infty }}(\mathbb {R}^{N})$
 ;
;(2) $||\tilde {u}_n||_{W^{1,\Phi }_{H_{\infty }}(\mathbb {R}^{N})}=||u_n||_{W^{1,N}_{0,H_{\infty }}(\Omega _{r_n})}$
 ;
;(3) $\tilde {u}_n \rightharpoonup 0\,\text {in}\, W^{1,\Phi }_{H_{\infty }}(\mathbb {R}^{N})\text { because }\tilde {u}_n(x)\to 0 \text { a.e. in }\mathbb {R}^{N}$
 .
.
Therefore, we have
From Lemma 5.4, we deduce that the sequence $\{\tilde {u}_n\}$![]() satisfies
satisfies
Using the fact that
and $(\varphi _3)'$![]() , it follows that given $\epsilon < \frac {p}{q \Upsilon }$
, it follows that given $\epsilon < \frac {p}{q \Upsilon }$![]() , where $\Upsilon$
, where $\Upsilon$![]() was given in Lemma 2.3, there exists $n_0 \in \mathbb {N}$
was given in Lemma 2.3, there exists $n_0 \in \mathbb {N}$![]() such that
such that

Since $r_n \to +\infty$![]() , without loss of generality we can assume that $r_n \geq 1$
, without loss of generality we can assume that $r_n \geq 1$![]() for all $n \in \mathbb {N}$
for all $n \in \mathbb {N}$![]() . Therefore, by the Poincaré inequality from Lemma 2.3,
. Therefore, by the Poincaré inequality from Lemma 2.3,
From (5.24), (5.25) and $(\varphi _3)$![]()

As $\tilde {u}_n \not =0$![]() for all $n \in \mathbb {N}$
for all $n \in \mathbb {N}$![]() , we get $p \leq \epsilon q \Upsilon$
, we get $p \leq \epsilon q \Upsilon$![]() , which is absurd. Hence, the result follows.
, which is absurd. Hence, the result follows.
Lemma 5.6 Suppose that $J_{km,r}$![]() is attained for some $1\leq k<\infty$
is attained for some $1\leq k<\infty$![]() and some $2\leq m<\infty$
and some $2\leq m<\infty$![]() . Suppose also that $J_{km,r}< J_{\infty,r}$
. Suppose also that $J_{km,r}< J_{\infty,r}$![]() . Then, $J_{k,r}< J_{km,r}$
. Then, $J_{k,r}< J_{km,r}$![]() .
.
Proof. Consider $u\in \mathcal {M}_{km,r}$![]() such that $I(u)=J_{km,r}$
such that $I(u)=J_{km,r}$![]() . Let $x=(\theta,\rho )$
. Let $x=(\theta,\rho )$![]() be the polar coordinates of $x\in \mathbb {R}^{2}$
be the polar coordinates of $x\in \mathbb {R}^{2}$![]() . Then, $u=u(\theta,\rho,|y|),\,y\in \mathbb {R}^{N-2}$
. Then, $u=u(\theta,\rho,|y|),\,y\in \mathbb {R}^{N-2}$![]() . Note that
. Note that

Define
We observe that,
(i) $v\in W^{1,\Phi }_{0,H_k}(\Omega _r)$
 ;
;(ii) $\Phi (\sqrt {\rho ^{2}+|y|^{2}},|\nabla v|)=\Phi (\sqrt {\rho ^{2}+|y|^{2}},(\frac {1}{\rho ^{2}m^{2}}u_\theta ^{2}+u_\rho ^{2}+|\nabla _y u|^{2})^{1/2})$
 ;
;(iii) $\int _{\Omega _r}F(|z|,v)\,{\rm d}x\,{\rm d}y=\int _{\Omega _r}F(|z|,u)\,{\rm d}x\,{\rm d}y$
 , where $z=(x,y) \in \Omega _r$
, where $z=(x,y) \in \Omega _r$ .
.
Proceeding similarly as in the proof of Lemma 5.2, there exists $t_0>0$![]() such that $t_0v\in \mathcal {M}_{k,r}$
such that $t_0v\in \mathcal {M}_{k,r}$![]() . For simplicity, let $v:=t_0 v$
. For simplicity, let $v:=t_0 v$![]() . Now, since $v\in \mathcal {M}_{k,r}$
. Now, since $v\in \mathcal {M}_{k,r}$![]() ,
,
Using $(ii)-(iii)$![]() ,
,

If $I(u)=J_{km,r}< J_{\infty,r}$![]() , then $u\notin W^{1,\Phi }_{0,H_{\infty }}(\Omega _r)$
, then $u\notin W^{1,\Phi }_{0,H_{\infty }}(\Omega _r)$![]() , then $u^{2}_{\theta }$
, then $u^{2}_{\theta }$![]() is not identically zero. Therefore, using that $m>1$
is not identically zero. Therefore, using that $m>1$![]() ,
,

which together with (5.26) implies $J_{k,r}< I(u)=J_{km,r}$![]() and the proof is complete.
and the proof is complete.
6. Proof of the main results
6.1. Proof of Theorem 1.1
By our assumption on $f_1$![]() , it is easy to verify that $I$
, it is easy to verify that $I$![]() is even and $I(0)=0$
is even and $I(0)=0$![]() . Moreover, from Lemma 4.2, Lemma 4.3 and Lemma 4.6, $I$
. Moreover, from Lemma 4.2, Lemma 4.3 and Lemma 4.6, $I$![]() satisfies all the properties in Lemma 4.1. Now from Lemma 4.7, there exists positive real numbers $\lambda _m,\mu _m,\tau _m$
satisfies all the properties in Lemma 4.1. Now from Lemma 4.7, there exists positive real numbers $\lambda _m,\mu _m,\tau _m$![]() such that for all $\lambda \geq \lambda _m,\mu \geq \mu _m$
such that for all $\lambda \geq \lambda _m,\mu \geq \mu _m$![]() and $\tau \geq \tau _m,$
and $\tau \geq \tau _m,$![]() we have
we have
Hence by Lemma 4.1, for every $\lambda \geq \lambda _m,\mu \geq \mu _m$![]() and $\tau \geq \tau _m,$
and $\tau \geq \tau _m,$![]() the problem $(P)$
the problem $(P)$![]() has at least $m$
has at least $m$![]() pairs of non-trivial solutions.
pairs of non-trivial solutions.
6.2. Proof of Theorem 1.2
By Lemma 5.2, for each $n\in \mathbb {N}$![]() , there exists $\lambda _0=\lambda _0(n)>0$
, there exists $\lambda _0=\lambda _0(n)>0$![]() satisfying
satisfying
On the other hand, by Lemma 5.5, there exists $r_0=r_0(\lambda _0,n)>0$![]() such that
such that
Thus,
for all $\lambda >\lambda _0$![]() and for all $r>r_0$
and for all $r>r_0$![]() . By Lemma 5.3, we have $J_{2^{n},r}$
. By Lemma 5.3, we have $J_{2^{n},r}$![]() is attained. So, we can apply Lemma 5.6 to get
is attained. So, we can apply Lemma 5.6 to get
Now $J_{2^{n-2}2,r}$![]() is also attained and satisfies
is also attained and satisfies
Again, by Lemma 5.6, we get $J_{2^{n-2},r}< J_{2^{n-1},r}$![]() . Inductively,
. Inductively,
for all $\lambda >\lambda _0$![]() and all $r>r_0$
and all $r>r_0$![]() .
.
Noting Lemma 4.2, from Lemma 5.3, minimizers of $J_{k,m}$![]() are critical points of $I$
are critical points of $I$![]() in $W^{1,\Phi }_{0,H_k}(\Omega _r)$
in $W^{1,\Phi }_{0,H_k}(\Omega _r)$![]() . Now, applying the Principle of symmetric criticality from [Reference Squassina48], it follows that they are critical points of $I$
. Now, applying the Principle of symmetric criticality from [Reference Squassina48], it follows that they are critical points of $I$![]() in $W^{1,\Phi }_0(\Omega _r)$
in $W^{1,\Phi }_0(\Omega _r)$![]() and therefore are solutions of $(P)$
and therefore are solutions of $(P)$![]() . Note that, due to Lemma 5.1, such solutions are non-trivial. Therefore, all minimizers of $J_{2^{m},r},\, m=1,\ldots,n$
. Note that, due to Lemma 5.1, such solutions are non-trivial. Therefore, all minimizers of $J_{2^{m},r},\, m=1,\ldots,n$![]() are non-radial, rotationally non-equivalent and non-trivial solutions of $(P)$
are non-radial, rotationally non-equivalent and non-trivial solutions of $(P)$![]() .
.
Acknowledgements
The authors want to thank the anonymous referee for his/her deep observations, careful reading and suggestions, which enabled us to improve this version of the manuscript. The third author thanks Ben Gurion University of the Negev, Israel for the nice hospitality.
C. O. Alves was partially supported by CNPq/Brazil 307045/2021-8, Projeto Universal FAPESQ 3031/2021.
On behalf of all authors, the corresponding author states that there is no competing interests.