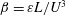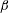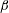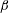1 Introduction
The Richardson–Kolmogorov cascade picture of fully developed turbulence relies on the assumption that the dissipation rate of turbulent kinetic energy remains finite in the limit of vanishing viscosity, i.e. on the dissipative anomaly (Frisch Reference Frisch1995; Eyink Reference Eyink2003). The behaviour of the mean dissipation rate
![]() $\unicode[STIX]{x1D700}$
as a function of viscosity is mostly studied in non-dimensional terms through the Reynolds-number dependence of the dimensionless dissipation factor
$\unicode[STIX]{x1D700}$
as a function of viscosity is mostly studied in non-dimensional terms through the Reynolds-number dependence of the dimensionless dissipation factor
![]() $\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D700}L/U^{3}$
(Batchelor Reference Batchelor1953), where
$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D700}L/U^{3}$
(Batchelor Reference Batchelor1953), where
![]() $U$
denotes the root-mean-square velocity and
$U$
denotes the root-mean-square velocity and
![]() $L$
the size of the largest eddies in the flow. The dimensionless dissipation rate is not only of interest in turbulence theory, as it enters adjustable coefficients in turbulence models such as the eddy viscosity in the
$L$
the size of the largest eddies in the flow. The dimensionless dissipation rate is not only of interest in turbulence theory, as it enters adjustable coefficients in turbulence models such as the eddy viscosity in the
![]() $k$
–
$k$
–
![]() $\unicode[STIX]{x1D700}$
model (Tannehill, Anderson & Pletcher Reference Tannehill, Anderson and Pletcher1997; Goto & Vassilicos Reference Goto and Vassilicos2009). The Smagorinsky constant in large-eddy simulations (LES) also depends on
$\unicode[STIX]{x1D700}$
model (Tannehill, Anderson & Pletcher Reference Tannehill, Anderson and Pletcher1997; Goto & Vassilicos Reference Goto and Vassilicos2009). The Smagorinsky constant in large-eddy simulations (LES) also depends on
![]() $\unicode[STIX]{x1D6FD}$
. Since its introduction, the question remains as to whether the infinite-Reynolds-number asymptote of
$\unicode[STIX]{x1D6FD}$
. Since its introduction, the question remains as to whether the infinite-Reynolds-number asymptote of
![]() $\unicode[STIX]{x1D6FD}$
is a universal quantity, i.e. whether it depends on the forces generating the turbulence and on the boundary conditions (Bos, Shao & Bertoglio Reference Bos, Shao and Bertoglio2007; Goto & Vassilicos Reference Goto and Vassilicos2009). Since
$\unicode[STIX]{x1D6FD}$
is a universal quantity, i.e. whether it depends on the forces generating the turbulence and on the boundary conditions (Bos, Shao & Bertoglio Reference Bos, Shao and Bertoglio2007; Goto & Vassilicos Reference Goto and Vassilicos2009). Since
![]() $\unicode[STIX]{x1D6FD}$
is related to the Kolmogorov constant
$\unicode[STIX]{x1D6FD}$
is related to the Kolmogorov constant
![]() $C_{K}$
(Lumley Reference Lumley1992), the question of universality concerning
$C_{K}$
(Lumley Reference Lumley1992), the question of universality concerning
![]() $\unicode[STIX]{x1D6FD}$
extends to the Kolmogorov constant. The latter has been an open question since the inference by Landau against universality of constants like
$\unicode[STIX]{x1D6FD}$
extends to the Kolmogorov constant. The latter has been an open question since the inference by Landau against universality of constants like
![]() $C_{K}$
(Landau & Lifshitz Reference Landau and Lifshitz1959; Frisch Reference Frisch1995). In particular, it is very difficult to disprove universality for forces acting at one single characteristic scale, as is the case for turbulence generated by a uniform grid in e.g. a wind tunnel (Frisch Reference Frisch1995). The present paper examines the universality of
$C_{K}$
(Landau & Lifshitz Reference Landau and Lifshitz1959; Frisch Reference Frisch1995). In particular, it is very difficult to disprove universality for forces acting at one single characteristic scale, as is the case for turbulence generated by a uniform grid in e.g. a wind tunnel (Frisch Reference Frisch1995). The present paper examines the universality of
![]() $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
![]() $C_{K}$
with respect to external forces which differ in their topological properties, namely their respective helicities, while acting at the same single characteristic length scale.
$C_{K}$
with respect to external forces which differ in their topological properties, namely their respective helicities, while acting at the same single characteristic length scale.
The value of
![]() $\unicode[STIX]{x1D6FD}$
has been measured in experiments (Sreenivasan Reference Sreenivasan1984, Reference Sreenivasan1998; Burattini, Lavoie & Antonia Reference Burattini, Lavoie and Antonia2005) as well as in direct numerical simulations (DNSs) (Wang et al.
Reference Wang, Chen, Brasseur and Wyngaard1996; Gotoh, Fukayama & Nakano Reference Gotoh, Fukayama and Nakano2002; Kaneda et al.
Reference Kaneda, Ishihara, Yokokawa, Itakura and Uno2003; Donzis, Sreenivasan & Yeung Reference Donzis, Sreenivasan and Yeung2005; Bos et al.
Reference Bos, Shao and Bertoglio2007; Goto & Vassilicos Reference Goto and Vassilicos2009; Yeung, Donzis & Sreenivasan Reference Yeung, Donzis and Sreenivasan2012; McComb et al.
Reference McComb, Berera, Yoffe and Linkmann2015; Yeung, Zhai & Sreenivasan Reference Yeung, Zhai and Sreenivasan2015; Ishihara et al.
Reference Ishihara, Morishita, Yokokawa, Uno and Kaneda2016). Although the experiments differed in the flow configuration and the DNSs in the properties of the external forcing and the run time, the results are generally consistent in terms of
$\unicode[STIX]{x1D6FD}$
has been measured in experiments (Sreenivasan Reference Sreenivasan1984, Reference Sreenivasan1998; Burattini, Lavoie & Antonia Reference Burattini, Lavoie and Antonia2005) as well as in direct numerical simulations (DNSs) (Wang et al.
Reference Wang, Chen, Brasseur and Wyngaard1996; Gotoh, Fukayama & Nakano Reference Gotoh, Fukayama and Nakano2002; Kaneda et al.
Reference Kaneda, Ishihara, Yokokawa, Itakura and Uno2003; Donzis, Sreenivasan & Yeung Reference Donzis, Sreenivasan and Yeung2005; Bos et al.
Reference Bos, Shao and Bertoglio2007; Goto & Vassilicos Reference Goto and Vassilicos2009; Yeung, Donzis & Sreenivasan Reference Yeung, Donzis and Sreenivasan2012; McComb et al.
Reference McComb, Berera, Yoffe and Linkmann2015; Yeung, Zhai & Sreenivasan Reference Yeung, Zhai and Sreenivasan2015; Ishihara et al.
Reference Ishihara, Morishita, Yokokawa, Uno and Kaneda2016). Although the experiments differed in the flow configuration and the DNSs in the properties of the external forcing and the run time, the results are generally consistent in terms of
![]() $\unicode[STIX]{x1D6FD}\leqslant 1$
. However, there is significant spread between the data points for experimental and numerical results alike. Similarly, experimentally measured values for the Kolmogorov constant
$\unicode[STIX]{x1D6FD}\leqslant 1$
. However, there is significant spread between the data points for experimental and numerical results alike. Similarly, experimentally measured values for the Kolmogorov constant
![]() $C_{K}$
resulted in consistent values
$C_{K}$
resulted in consistent values
![]() $C_{K}\simeq 1.6$
for different flow configurations albeit with considerable scatter in the data (Sreenivasan Reference Sreenivasan1995). Furthermore, the highest-resolution DNS of homogeneous isotropic turbulence carried out so far revealed a difference between the numerically and experimentally measured values of
$C_{K}\simeq 1.6$
for different flow configurations albeit with considerable scatter in the data (Sreenivasan Reference Sreenivasan1995). Furthermore, the highest-resolution DNS of homogeneous isotropic turbulence carried out so far revealed a difference between the numerically and experimentally measured values of
![]() $C_{K}$
, with
$C_{K}$
, with
![]() $C_{K}=1.8\pm 0.1$
obtained numerically (Ishihara et al.
Reference Ishihara, Morishita, Yokokawa, Uno and Kaneda2016). In summary, for both
$C_{K}=1.8\pm 0.1$
obtained numerically (Ishihara et al.
Reference Ishihara, Morishita, Yokokawa, Uno and Kaneda2016). In summary, for both
![]() $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
![]() $C_{K}$
the difference between the measured values is not large enough to support non-universality, nor is the statistical error small enough to disprove it.
$C_{K}$
the difference between the measured values is not large enough to support non-universality, nor is the statistical error small enough to disprove it.
Any question of universality, however, must be taken in the appropriate context, which is here that of ‘equilibrium turbulence’ (Batchelor Reference Batchelor1953; Vassilicos Reference Vassilicos2015), where the maximal inertial flux
![]() $\unicode[STIX]{x1D6F1}$
equals
$\unicode[STIX]{x1D6F1}$
equals
![]() $\unicode[STIX]{x1D700}$
. There are many flow configurations where the relation
$\unicode[STIX]{x1D700}$
. There are many flow configurations where the relation
![]() $\unicode[STIX]{x1D6F1}=\unicode[STIX]{x1D700}$
is violated, such as in decaying turbulence and for unsteady flows (Bos et al.
Reference Bos, Shao and Bertoglio2007; Valente & Vassilicos Reference Valente and Vassilicos2012; Valente, Onishi & da Silva Reference Valente, Onishi and da Silva2014; Vassilicos Reference Vassilicos2015; Bos & Rubinstein Reference Bos and Rubinstein2017), where the variation in the Taylor surrogate
$\unicode[STIX]{x1D6F1}=\unicode[STIX]{x1D700}$
is violated, such as in decaying turbulence and for unsteady flows (Bos et al.
Reference Bos, Shao and Bertoglio2007; Valente & Vassilicos Reference Valente and Vassilicos2012; Valente, Onishi & da Silva Reference Valente, Onishi and da Silva2014; Vassilicos Reference Vassilicos2015; Bos & Rubinstein Reference Bos and Rubinstein2017), where the variation in the Taylor surrogate
![]() $L/U^{3}$
describes variations of
$L/U^{3}$
describes variations of
![]() $\unicode[STIX]{x1D6F1}$
and not of
$\unicode[STIX]{x1D6F1}$
and not of
![]() $\unicode[STIX]{x1D700}$
(McComb et al.
Reference McComb, Berera, Salewski and Yoffe2010; Valente et al.
Reference Valente, Onishi and da Silva2014). In such cases, the value of
$\unicode[STIX]{x1D700}$
(McComb et al.
Reference McComb, Berera, Salewski and Yoffe2010; Valente et al.
Reference Valente, Onishi and da Silva2014). In such cases, the value of
![]() $\unicode[STIX]{x1D6FD}$
may differ from that for equilibrium turbulence for reasons connected with the unsteadiness of the flow. Therefore the present paper is only concerned with homogeneous turbulence maintained in a statistically stationary state by large-scale external forcing.
$\unicode[STIX]{x1D6FD}$
may differ from that for equilibrium turbulence for reasons connected with the unsteadiness of the flow. Therefore the present paper is only concerned with homogeneous turbulence maintained in a statistically stationary state by large-scale external forcing.
Recent numerical results suggest that
![]() $\unicode[STIX]{x1D6FD}$
depends on the number density of stagnation points in the large-scale flow field, i.e. on topological details of the large-scale flow (Goto & Vassilicos Reference Goto and Vassilicos2009). The dependence of the inertial flux (and thus
$\unicode[STIX]{x1D6FD}$
depends on the number density of stagnation points in the large-scale flow field, i.e. on topological details of the large-scale flow (Goto & Vassilicos Reference Goto and Vassilicos2009). The dependence of the inertial flux (and thus
![]() $\unicode[STIX]{x1D700}$
) on the topology of the flow field had already been inferred by Moffatt (Reference Moffatt1985, Reference Moffatt2014) through the effect of kinetic helicity on the nonlinear structure of the Navier–Stokes equations. The kinetic helicity is the
$\unicode[STIX]{x1D700}$
) on the topology of the flow field had already been inferred by Moffatt (Reference Moffatt1985, Reference Moffatt2014) through the effect of kinetic helicity on the nonlinear structure of the Navier–Stokes equations. The kinetic helicity is the
![]() $L^{2}$
-inner product
$L^{2}$
-inner product
![]() $(\boldsymbol{u},\unicode[STIX]{x1D74E})$
of the velocity field
$(\boldsymbol{u},\unicode[STIX]{x1D74E})$
of the velocity field
![]() $\boldsymbol{u}$
and the vorticity field
$\boldsymbol{u}$
and the vorticity field
![]() $\unicode[STIX]{x1D74E}=\unicode[STIX]{x1D735}\times \boldsymbol{u}$
. It is not only a measure of the alignment between velocity and vorticity and a conserved quantity under Euler evolution, but also a topological invariant of the Euler equations related to the linking number of infinitesimal vortex lines (Moffatt Reference Moffatt1969, Reference Moffatt1985). Since an alignment between
$\unicode[STIX]{x1D74E}=\unicode[STIX]{x1D735}\times \boldsymbol{u}$
. It is not only a measure of the alignment between velocity and vorticity and a conserved quantity under Euler evolution, but also a topological invariant of the Euler equations related to the linking number of infinitesimal vortex lines (Moffatt Reference Moffatt1969, Reference Moffatt1985). Since an alignment between
![]() $\boldsymbol{u}$
and
$\boldsymbol{u}$
and
![]() $\unicode[STIX]{x1D74E}$
results in a depletion of nonlinearity, regions of high helicity have been conjectured to be related to low levels of dissipation (Moffatt Reference Moffatt2014). Similar conclusions concerning a depletion of energy transfer in the presence of strong helicity had already been obtained by Kraichnan (Reference Kraichnan1973) based on interactions of helical Fourier modes. Although helicity is an inviscid invariant, it does not have a coercive effect on the dynamics compared to e.g. the enstrophy in two-dimensional turbulence, because it is in general not sign definite. However, once the helicity is made sign definite through a projection operation, the energy cascade direction is reversed (Biferale, Musacchio & Toschi Reference Biferale, Musacchio and Toschi2012, Reference Biferale, Musacchio and Toschi2013) and the corresponding helically projected Navier–Stokes equations admit globally regular solutions (Biferale & Titi Reference Biferale and Titi2013).
$\unicode[STIX]{x1D74E}$
results in a depletion of nonlinearity, regions of high helicity have been conjectured to be related to low levels of dissipation (Moffatt Reference Moffatt2014). Similar conclusions concerning a depletion of energy transfer in the presence of strong helicity had already been obtained by Kraichnan (Reference Kraichnan1973) based on interactions of helical Fourier modes. Although helicity is an inviscid invariant, it does not have a coercive effect on the dynamics compared to e.g. the enstrophy in two-dimensional turbulence, because it is in general not sign definite. However, once the helicity is made sign definite through a projection operation, the energy cascade direction is reversed (Biferale, Musacchio & Toschi Reference Biferale, Musacchio and Toschi2012, Reference Biferale, Musacchio and Toschi2013) and the corresponding helically projected Navier–Stokes equations admit globally regular solutions (Biferale & Titi Reference Biferale and Titi2013).
Owing to its aforementioned connection to nonlinear Navier–Stokes dynamics and its relevance to atmospheric physics (Lilly Reference Lilly1986), the effect of helicity has been studied in a variety of turbulent flows, including homogeneous isotropic turbulence (Chen, Chen & Eyink Reference Chen, Chen and Eyink2003a
; Chen et al.
Reference Chen, Chen, Eyink and Holm2003b
; Gledzer & Chkhetiani Reference Gledzer and Chkhetiani2015; Kessar et al.
Reference Kessar, Plunian, Stepanov and Balarac2015; Sahoo & Biferale Reference Sahoo and Biferale2015; Stepanov et al.
Reference Stepanov, Golbraikh, Frick and Shestakov2015; Alexakis Reference Alexakis2017), rotating turbulence (Mininni & Pouquet Reference Mininni and Pouquet2010a
,Reference Mininni and Pouquet
b
) and the atmospheric boundary layer (Deusebio & Lindborg Reference Deusebio and Lindborg2014). However, the dependence of
![]() $\unicode[STIX]{x1D6FD}$
on the helicity of the external force has never been investigated analytically or numerically. The present work aims to close this gap by providing both analytical estimates and numerical measurements of
$\unicode[STIX]{x1D6FD}$
on the helicity of the external force has never been investigated analytically or numerically. The present work aims to close this gap by providing both analytical estimates and numerical measurements of
![]() $\unicode[STIX]{x1D6FD}$
as a function of the helicity of the forcing. In view of universality, helicity is also a convenient tool to distinguish between forcing functions while keeping parameters such as characteristic length and time scales the same.
$\unicode[STIX]{x1D6FD}$
as a function of the helicity of the forcing. In view of universality, helicity is also a convenient tool to distinguish between forcing functions while keeping parameters such as characteristic length and time scales the same.
Mathematically rigorous bounds for the dissipation rate have been derived from the existence of weak solutions of the Navier–Stokes equations for a variety of wall-bounded flows (Howard Reference Howard1972; Busse Reference Busse1978; Doering & Constantin Reference Doering and Constantin1994; Kerswell Reference Kerswell1998; Nicodemus, Grossmann & Holthaus Reference Nicodemus, Grossmann and Holthaus1998) as well as for the case of periodic boundary conditions and sufficiently smooth forcing functions (Childress, Kerswell & Gilbert Reference Childress, Kerswell and Gilbert2001; Foias et al.
Reference Foias, Manley, Rosa and Temam2001; Doering & Foias Reference Doering and Foias2002). Concerning the dimensionless dissipation coefficient
![]() $\unicode[STIX]{x1D6FD}$
, Doering & Foias (Reference Doering and Foias2002) derived the following bound:
$\unicode[STIX]{x1D6FD}$
, Doering & Foias (Reference Doering and Foias2002) derived the following bound:
where
![]() $\unicode[STIX]{x1D6FD}_{\infty }$
and
$\unicode[STIX]{x1D6FD}_{\infty }$
and
![]() $\unicode[STIX]{x1D6FE}$
are constants depending on the forcing function (Doering & Foias Reference Doering and Foias2002), and
$\unicode[STIX]{x1D6FE}$
are constants depending on the forcing function (Doering & Foias Reference Doering and Foias2002), and
![]() $Re_{f}$
a Reynolds number defined with respect to the characteristic length scale of the external force. The value of the upper bound has been calculated and compared to experimental and numerical data for different flow configurations (Doering, Eckhardt & Schumacher Reference Doering, Eckhardt and Schumacher2003; Doering & Petrov Reference Doering, Petrov, Oberlack, Peinke, Kittel and Barth2005; Rollin, Dubief & Doering Reference Rollin, Dubief and Doering2011). In all cases the upper bound is approximately an order of magnitude larger than the measured value. However, for generalisations of Kolmogorov flow where the effect of different forcing scales has been studied, the predicted variation of
$Re_{f}$
a Reynolds number defined with respect to the characteristic length scale of the external force. The value of the upper bound has been calculated and compared to experimental and numerical data for different flow configurations (Doering, Eckhardt & Schumacher Reference Doering, Eckhardt and Schumacher2003; Doering & Petrov Reference Doering, Petrov, Oberlack, Peinke, Kittel and Barth2005; Rollin, Dubief & Doering Reference Rollin, Dubief and Doering2011). In all cases the upper bound is approximately an order of magnitude larger than the measured value. However, for generalisations of Kolmogorov flow where the effect of different forcing scales has been studied, the predicted variation of
![]() $\unicode[STIX]{x1D6FD}_{\infty }$
is in qualitative agreement with numerically obtained values for
$\unicode[STIX]{x1D6FD}_{\infty }$
is in qualitative agreement with numerically obtained values for
![]() $\unicode[STIX]{x1D6FD}$
(Rollin et al.
Reference Rollin, Dubief and Doering2011). In view of universality, following the arguments by Frisch (Reference Frisch1995), the dependence of
$\unicode[STIX]{x1D6FD}$
(Rollin et al.
Reference Rollin, Dubief and Doering2011). In view of universality, following the arguments by Frisch (Reference Frisch1995), the dependence of
![]() $\unicode[STIX]{x1D6FD}$
on the forcing band can indeed be expected.
$\unicode[STIX]{x1D6FD}$
on the forcing band can indeed be expected.
The aim of this paper is to demonstrate that the upper bound theory also captures the quantitative dependence of
![]() $\unicode[STIX]{x1D6FD}_{\infty }$
as a function of the helicity of the force independently of its time dependence, in the sense that it is able to predict non-universal relative values of
$\unicode[STIX]{x1D6FD}_{\infty }$
as a function of the helicity of the force independently of its time dependence, in the sense that it is able to predict non-universal relative values of
![]() $\unicode[STIX]{x1D6FD}_{\infty }$
in agreement with numerical results. For this purpose bounds for forces which differ in their level of helicity and dimensionality are calculated explicitly, and the upper bound theory is extended to include time-dependent forces. The main results of this analysis are as follows. (i) Helical forces lead to lower bounds for
$\unicode[STIX]{x1D6FD}_{\infty }$
in agreement with numerical results. For this purpose bounds for forces which differ in their level of helicity and dimensionality are calculated explicitly, and the upper bound theory is extended to include time-dependent forces. The main results of this analysis are as follows. (i) Helical forces lead to lower bounds for
![]() $\unicode[STIX]{x1D6FD}_{\infty }$
compared to non-helical forces. This supports the rationale of Moffatt (Reference Moffatt1985, Reference Moffatt2014) that a high level of helicity should inhibit the energy cascade. (ii) Dynamic forces lead to larger bounds than static forces, where the value of the bound depends now also on the characteristic time scale of the force. A comparison to DNS data then shows that the relative dependence of
$\unicode[STIX]{x1D6FD}_{\infty }$
compared to non-helical forces. This supports the rationale of Moffatt (Reference Moffatt1985, Reference Moffatt2014) that a high level of helicity should inhibit the energy cascade. (ii) Dynamic forces lead to larger bounds than static forces, where the value of the bound depends now also on the characteristic time scale of the force. A comparison to DNS data then shows that the relative dependence of
![]() $\unicode[STIX]{x1D6FD}_{\infty }$
on helicity as predicted by the upper bound theory is in good qualitative and quantitative agreement with numerically measured values of
$\unicode[STIX]{x1D6FD}_{\infty }$
on helicity as predicted by the upper bound theory is in good qualitative and quantitative agreement with numerically measured values of
![]() $\unicode[STIX]{x1D6FD}$
, and the results are independent of the dynamical details of the force. The relative values of
$\unicode[STIX]{x1D6FD}$
, and the results are independent of the dynamical details of the force. The relative values of
![]() $\unicode[STIX]{x1D6FD}_{\infty }$
are related to the relative values of the Kolmogorov constant
$\unicode[STIX]{x1D6FD}_{\infty }$
are related to the relative values of the Kolmogorov constant
![]() $C_{K}$
in order to predict a qualitative and quantitative dependence of
$C_{K}$
in order to predict a qualitative and quantitative dependence of
![]() $C_{K}$
on the helicity of the forcing. Finally, the effect helical forces on the Smagorinsky constant in LES is discussed.
$C_{K}$
on the helicity of the forcing. Finally, the effect helical forces on the Smagorinsky constant in LES is discussed.
This paper is organised as follows. The necessary mathematical concepts are introduced in § 2 alongside the statement of the main problem and a summary of the derivation of the general upper bound by Doering & Foias (Reference Doering and Foias2002). This method is applied to time-dependent forces in § 3, while the helicity dependence of static forces is studied in § 4, including implications for the Kolmogorov constant and the Smagorinsky constant in LES in §§ 4.2 and 4.3, respectively. A comparison to DNS data is carried out in § 5. The main results are summarised and discussed in § 6.
2 Background
The Navier–Stokes equations are considered on a three-dimensional domain
![]() $\unicode[STIX]{x1D6FA}=[0,L]^{3}$
with periodic boundary conditions
$\unicode[STIX]{x1D6FA}=[0,L]^{3}$
with periodic boundary conditions
where
![]() $\boldsymbol{u}(\cdot ,t)\in L^{2}(\unicode[STIX]{x1D6FA})$
is the velocity field,
$\boldsymbol{u}(\cdot ,t)\in L^{2}(\unicode[STIX]{x1D6FA})$
is the velocity field,
![]() $\unicode[STIX]{x1D708}$
the kinematic viscosity,
$\unicode[STIX]{x1D708}$
the kinematic viscosity,
![]() $P$
the pressure,
$P$
the pressure,
![]() $\boldsymbol{f}(\cdot ,t)\in L^{2}(\unicode[STIX]{x1D6FA})$
an external mechanical force and
$\boldsymbol{f}(\cdot ,t)\in L^{2}(\unicode[STIX]{x1D6FA})$
an external mechanical force and
![]() $\unicode[STIX]{x1D70C}$
the density which is set to unity for convenience. The initial conditions are assumed to be sufficiently well-behaved to allow weak solutions, i.e. solutions of the corresponding integral equation where all derivatives act on test functions, which are by definition infinitely many times differentiable. In the following such weak solutions are considered and any occurrence of a derivative acting on
$\unicode[STIX]{x1D70C}$
the density which is set to unity for convenience. The initial conditions are assumed to be sufficiently well-behaved to allow weak solutions, i.e. solutions of the corresponding integral equation where all derivatives act on test functions, which are by definition infinitely many times differentiable. In the following such weak solutions are considered and any occurrence of a derivative acting on
![]() $\boldsymbol{u}$
is understood as shorthand notation for
$\boldsymbol{u}$
is understood as shorthand notation for
![]() $\boldsymbol{u}$
integrated against the derivative of a smooth test function.
$\boldsymbol{u}$
integrated against the derivative of a smooth test function.
Leray (Reference Leray1934) established the existence of weak solutions of the Navier–Stokes equation in three spatial dimensions for square-integrable sufficiently regular initial conditions and external forces (Ladyshenskaya Reference Ladyshenskaya1969; Constantin & Foias Reference Constantin and Foias1988; Doering & Gibbon Reference Doering and Gibbon1995; Foias et al.
Reference Foias, Manley, Rosa and Temam2001). These weak solutions are square integrable and the existence result is valid for the three-dimensional torus as well as for the whole space
![]() $\mathbb{R}^{3}$
with the appropriate boundary conditions. Regarding the external force, sufficiently regular usually means that the Fourier coefficients of the force are square summable (or square integrable, in the case of
$\mathbb{R}^{3}$
with the appropriate boundary conditions. Regarding the external force, sufficiently regular usually means that the Fourier coefficients of the force are square summable (or square integrable, in the case of
![]() $\mathbb{R}^{3}$
) at all times and
$\mathbb{R}^{3}$
) at all times and
Furthermore, the forces must be solenoidal at all times.
For static forces Doering & Foias (Reference Doering and Foias2002) derived an upper bound on
![]() $\unicode[STIX]{x1D700}$
from weak solutions by decomposing the force
$\unicode[STIX]{x1D700}$
from weak solutions by decomposing the force
![]() $\boldsymbol{f}$
into an amplitude
$\boldsymbol{f}$
into an amplitude
![]() $f_{0}\in \mathbb{R}$
and a shape function
$f_{0}\in \mathbb{R}$
and a shape function
![]() $\unicode[STIX]{x1D753}\in L^{2}([0,1]^{3})$
, such that
$\unicode[STIX]{x1D753}\in L^{2}([0,1]^{3})$
, such that
where
![]() $L_{f}$
is the characteristic scale at which the force is acting. The shape function is further restricted by the requirements
$L_{f}$
is the characteristic scale at which the force is acting. The shape function is further restricted by the requirements
![]() $\Vert \unicode[STIX]{x1D753}\Vert _{2}=1$
and
$\Vert \unicode[STIX]{x1D753}\Vert _{2}=1$
and
![]() $\Vert \unicode[STIX]{x1D735}(-\unicode[STIX]{x1D6E5})^{-M}\unicode[STIX]{x1D753}\Vert _{\infty }<\infty$
for some
$\Vert \unicode[STIX]{x1D735}(-\unicode[STIX]{x1D6E5})^{-M}\unicode[STIX]{x1D753}\Vert _{\infty }<\infty$
for some
![]() $M\in \mathbb{N}$
. Such
$M\in \mathbb{N}$
. Such
![]() $M$
can always be found, with the minimum requirement for
$M$
can always be found, with the minimum requirement for
![]() $\unicode[STIX]{x1D753}\in L^{2}([0,1]^{3})$
being
$\unicode[STIX]{x1D753}\in L^{2}([0,1]^{3})$
being
![]() $M>1$
. A bound for
$M>1$
. A bound for
![]() $\unicode[STIX]{x1D700}$
was then derived from the energy inequality
$\unicode[STIX]{x1D700}$
was then derived from the energy inequality
by taking the inner product of the Navier–Stokes equations with
![]() $(-\unicode[STIX]{x1D6E5})^{-M}\boldsymbol{f}$
and integrating over the volume where several integrations by parts need to be carried out such that all derivatives act on the force instead of on the velocity field and the resulting inner products are bounded from above using the Cauchy–Schwarz and Hölder inequalities. Finally the long-time average
$(-\unicode[STIX]{x1D6E5})^{-M}\boldsymbol{f}$
and integrating over the volume where several integrations by parts need to be carried out such that all derivatives act on the force instead of on the velocity field and the resulting inner products are bounded from above using the Cauchy–Schwarz and Hölder inequalities. Finally the long-time average
![]() $\langle \cdot \rangle _{t}$
is taken (the time average can be placed on rigorous mathematical grounds by considering statistical solutions to the Navier–Stokes equations (Foias et al.
Reference Foias, Manley, Rosa and Temam2001)), resulting in
$\langle \cdot \rangle _{t}$
is taken (the time average can be placed on rigorous mathematical grounds by considering statistical solutions to the Navier–Stokes equations (Foias et al.
Reference Foias, Manley, Rosa and Temam2001)), resulting in
Substitution of the upper bound for
![]() $f_{0}$
into (2.5) and subsequent rearrangement then yields the following upper bound for
$f_{0}$
into (2.5) and subsequent rearrangement then yields the following upper bound for
![]() $\unicode[STIX]{x1D6FD}$
:
$\unicode[STIX]{x1D6FD}$
:
where
![]() $U=\langle \Vert \boldsymbol{u}\Vert _{2}^{2}\rangle _{t}^{1/2}$
and
$U=\langle \Vert \boldsymbol{u}\Vert _{2}^{2}\rangle _{t}^{1/2}$
and
hence both
![]() $\unicode[STIX]{x1D6FD}_{\infty }$
and
$\unicode[STIX]{x1D6FD}_{\infty }$
and
![]() $\unicode[STIX]{x1D6FE}$
are functionals of the shape function
$\unicode[STIX]{x1D6FE}$
are functionals of the shape function
![]() $\unicode[STIX]{x1D753}$
. Here, it is important to observe that unlike
$\unicode[STIX]{x1D753}$
. Here, it is important to observe that unlike
![]() $\unicode[STIX]{x1D6FD}_{\infty }$
,
$\unicode[STIX]{x1D6FD}_{\infty }$
,
![]() $\unicode[STIX]{x1D6FE}$
depends only on space-averaged quantities and is therefore fully described by the (spatial) regularity of the shape function, while
$\unicode[STIX]{x1D6FE}$
depends only on space-averaged quantities and is therefore fully described by the (spatial) regularity of the shape function, while
![]() $\unicode[STIX]{x1D6FD}_{\infty }$
is dominated by its local structure. The latter is brought about through
$\unicode[STIX]{x1D6FD}_{\infty }$
is dominated by its local structure. The latter is brought about through
![]() $\unicode[STIX]{x1D6FD}_{\infty }$
depending on the
$\unicode[STIX]{x1D6FD}_{\infty }$
depending on the
![]() $L^{\infty }$
-norm of the shape function, which involves single-point values.
$L^{\infty }$
-norm of the shape function, which involves single-point values.
3 Time-dependent forces
The first task is to extend the results of Doering & Foias (Reference Doering and Foias2002) to time-dependent forces. If, as above, the inner product of all terms in the Navier–Stokes equation with
![]() $(-\unicode[STIX]{x1D6E5})^{-M}\boldsymbol{f}$
is taken, an extra term arises on the left-hand side which does not necessarily vanish in the long-time average:
$(-\unicode[STIX]{x1D6E5})^{-M}\boldsymbol{f}$
is taken, an extra term arises on the left-hand side which does not necessarily vanish in the long-time average:
The main obstacle for an estimation of
![]() $\unicode[STIX]{x1D6FD}$
for time-dependent forces thus lies in that the new term on the left-hand side of (3.1) may not be bounded. This would occur if
$\unicode[STIX]{x1D6FD}$
for time-dependent forces thus lies in that the new term on the left-hand side of (3.1) may not be bounded. This would occur if
![]() $\boldsymbol{f}$
were rough in time. In order to proceed,
$\boldsymbol{f}$
were rough in time. In order to proceed,
![]() $\boldsymbol{f}$
could either be assumed to be temporally sufficiently well behaved, i.e.
$\boldsymbol{f}$
could either be assumed to be temporally sufficiently well behaved, i.e.
![]() $\boldsymbol{f}(\boldsymbol{x},\cdot )\in H^{1}([0,\infty ))$
, or convoluted with a filter kernel
$\boldsymbol{f}(\boldsymbol{x},\cdot )\in H^{1}([0,\infty ))$
, or convoluted with a filter kernel
![]() $G^{\unicode[STIX]{x1D70F}}\in H^{\infty }([0,\infty ))$
such that
$G^{\unicode[STIX]{x1D70F}}\in H^{\infty }([0,\infty ))$
such that
![]() $(G^{\unicode[STIX]{x1D70F}}\ast \boldsymbol{f})(\boldsymbol{x},\cdot )\in H^{1}([0,\infty ))$
. The latter approach introduces a time scale
$(G^{\unicode[STIX]{x1D70F}}\ast \boldsymbol{f})(\boldsymbol{x},\cdot )\in H^{1}([0,\infty ))$
. The latter approach introduces a time scale
![]() $\unicode[STIX]{x1D70F}$
, which will turn out to be useful in the assessment of the resulting upper bound of
$\unicode[STIX]{x1D70F}$
, which will turn out to be useful in the assessment of the resulting upper bound of
![]() $\unicode[STIX]{x1D6FD}$
. Therefore, instead of using (3.1), before taking the inner products the force is smoothed by convolution with
$\unicode[STIX]{x1D6FD}$
. Therefore, instead of using (3.1), before taking the inner products the force is smoothed by convolution with
![]() $G^{\unicode[STIX]{x1D70F}}$
, resulting in
$G^{\unicode[STIX]{x1D70F}}$
, resulting in
After some intermediate steps involving estimates of
![]() $G^{\unicode[STIX]{x1D70F}}$
and its time derivative which can be found in appendix A, one obtains
$G^{\unicode[STIX]{x1D70F}}$
and its time derivative which can be found in appendix A, one obtains
with
![]() $\unicode[STIX]{x1D714}=U/L_{f}=1/T$
denoting the frequency corresponding to the forcing-scale eddy turnover time and
$\unicode[STIX]{x1D714}=U/L_{f}=1/T$
denoting the frequency corresponding to the forcing-scale eddy turnover time and
![]() $\unicode[STIX]{x1D714}_{f}\leqslant 1/\unicode[STIX]{x1D70F}$
the characteristic frequency of the smoothed forcing, with
$\unicode[STIX]{x1D714}_{f}\leqslant 1/\unicode[STIX]{x1D70F}$
the characteristic frequency of the smoothed forcing, with
![]() $\unicode[STIX]{x1D70F}$
being set by the filter width. For static forcing
$\unicode[STIX]{x1D70F}$
being set by the filter width. For static forcing
![]() $\unicode[STIX]{x1D714}_{f}=0$
, the time averages in the definitions of the coefficients
$\unicode[STIX]{x1D714}_{f}=0$
, the time averages in the definitions of the coefficients
![]() $\unicode[STIX]{x1D6FD}_{\infty }$
and
$\unicode[STIX]{x1D6FD}_{\infty }$
and
![]() $\unicode[STIX]{x1D6FE}$
can be omitted, and the forms of
$\unicode[STIX]{x1D6FE}$
can be omitted, and the forms of
![]() $\unicode[STIX]{x1D6FD}_{\infty }$
and
$\unicode[STIX]{x1D6FD}_{\infty }$
and
![]() $\unicode[STIX]{x1D6FE}$
as in (2.8) are recovered. Dynamic forces can thus be expected to yield larger bounds due to the extra term in (2.8) which occurs only for time-dependent forces. This may imply that the bound becomes less tight for dynamic forces but it could also indicate that the value of
$\unicode[STIX]{x1D6FE}$
as in (2.8) are recovered. Dynamic forces can thus be expected to yield larger bounds due to the extra term in (2.8) which occurs only for time-dependent forces. This may imply that the bound becomes less tight for dynamic forces but it could also indicate that the value of
![]() $\unicode[STIX]{x1D6FD}$
for dynamic forces may be larger than for static forces. This point will be further assessed in § 5 using results from numerical simulations.
$\unicode[STIX]{x1D6FD}$
for dynamic forces may be larger than for static forces. This point will be further assessed in § 5 using results from numerical simulations.
4 Dependence of
 $\unicode[STIX]{x1D6FD}$
on the helicity of the force
$\unicode[STIX]{x1D6FD}$
on the helicity of the force
In order to highlight the influence of the helicity of the force on the upper bound of
![]() $\unicode[STIX]{x1D6FD}$
, the coefficients
$\unicode[STIX]{x1D6FD}$
, the coefficients
![]() $\unicode[STIX]{x1D6FD}_{\infty }$
and
$\unicode[STIX]{x1D6FD}_{\infty }$
and
![]() $\unicode[STIX]{x1D6FE}$
given in (2.8) are calculated explicitly for static forcing functions which differ in the helicity of their corresponding shape functions. For this purpose we consider two shape functions which are eigenfunctions of the curl operator
$\unicode[STIX]{x1D6FE}$
given in (2.8) are calculated explicitly for static forcing functions which differ in the helicity of their corresponding shape functions. For this purpose we consider two shape functions which are eigenfunctions of the curl operator
 $$\begin{eqnarray}\unicode[STIX]{x1D753}^{(1)}=\frac{1}{\sqrt{A^{2}+B^{2}+C^{2}}}\left(\begin{array}{@{}c@{}}A\sin 2\unicode[STIX]{x03C0}z+C\cos 2\unicode[STIX]{x03C0}y\\ B\sin 2\unicode[STIX]{x03C0}x+A\cos 2\unicode[STIX]{x03C0}z\\ C\sin 2\unicode[STIX]{x03C0}y+B\cos 2\unicode[STIX]{x03C0}x\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D753}^{(1)}=\frac{1}{\sqrt{A^{2}+B^{2}+C^{2}}}\left(\begin{array}{@{}c@{}}A\sin 2\unicode[STIX]{x03C0}z+C\cos 2\unicode[STIX]{x03C0}y\\ B\sin 2\unicode[STIX]{x03C0}x+A\cos 2\unicode[STIX]{x03C0}z\\ C\sin 2\unicode[STIX]{x03C0}y+B\cos 2\unicode[STIX]{x03C0}x\end{array}\right),\end{eqnarray}$$
and
 $$\begin{eqnarray}\unicode[STIX]{x1D753}^{(-1)}=\frac{1}{\sqrt{A^{2}+B^{2}+C^{2}}}\left(\begin{array}{@{}c@{}}A\cos 2\unicode[STIX]{x03C0}z+C\sin 2\unicode[STIX]{x03C0}y\\ B\cos 2\unicode[STIX]{x03C0}x+A\sin 2\unicode[STIX]{x03C0}z\\ C\cos 2\unicode[STIX]{x03C0}y+B\sin 2\unicode[STIX]{x03C0}x\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D753}^{(-1)}=\frac{1}{\sqrt{A^{2}+B^{2}+C^{2}}}\left(\begin{array}{@{}c@{}}A\cos 2\unicode[STIX]{x03C0}z+C\sin 2\unicode[STIX]{x03C0}y\\ B\cos 2\unicode[STIX]{x03C0}x+A\sin 2\unicode[STIX]{x03C0}z\\ C\cos 2\unicode[STIX]{x03C0}y+B\sin 2\unicode[STIX]{x03C0}x\end{array}\right),\end{eqnarray}$$
where
![]() $A,B,C\in \mathbb{R}$
and
$A,B,C\in \mathbb{R}$
and
![]() $\Vert \unicode[STIX]{x1D753}^{(\pm 1)}\Vert _{2}=1$
; see appendix B for further details. These shape functions are by construction fully helical, as their relative helicity is given by
$\Vert \unicode[STIX]{x1D753}^{(\pm 1)}\Vert _{2}=1$
; see appendix B for further details. These shape functions are by construction fully helical, as their relative helicity is given by
as
![]() $\unicode[STIX]{x1D753}^{(\pm 1)}$
are eigenfunctions of the curl operator with eigenvalues one and minus one, respectively. The latter also implies that
$\unicode[STIX]{x1D753}^{(\pm 1)}$
are eigenfunctions of the curl operator with eigenvalues one and minus one, respectively. The latter also implies that
![]() $\unicode[STIX]{x1D753}^{(1)}$
and
$\unicode[STIX]{x1D753}^{(1)}$
and
![]() $\unicode[STIX]{x1D753}^{(-1)}$
are orthogonal with respect to the
$\unicode[STIX]{x1D753}^{(-1)}$
are orthogonal with respect to the
![]() $L^{2}$
-inner product. A shape function
$L^{2}$
-inner product. A shape function
![]() $\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D753}})}$
of arbitrary relative helicity
$\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D753}})}$
of arbitrary relative helicity
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D753}}$
is then constructed by suitable linear combination of
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D753}}$
is then constructed by suitable linear combination of
![]() $\unicode[STIX]{x1D753}^{(1)}$
and
$\unicode[STIX]{x1D753}^{(1)}$
and
![]() $\unicode[STIX]{x1D753}^{(-1)}$
:
$\unicode[STIX]{x1D753}^{(-1)}$
:
Force functions
![]() $\boldsymbol{f}^{(\unicode[STIX]{x1D70C}_{f})}$
of a given relative helicity
$\boldsymbol{f}^{(\unicode[STIX]{x1D70C}_{f})}$
of a given relative helicity
![]() $\unicode[STIX]{x1D70C}_{f}\equiv \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D753}}$
are then constructed according to equation (2.4). A further assessment of the effect of dimensionality can be carried out by setting one or two of the coefficients
$\unicode[STIX]{x1D70C}_{f}\equiv \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D753}}$
are then constructed according to equation (2.4). A further assessment of the effect of dimensionality can be carried out by setting one or two of the coefficients
![]() $A,B$
or
$A,B$
or
![]() $C$
to zero.
$C$
to zero.
Before calculating the values of
![]() $\unicode[STIX]{x1D6FD}_{\infty }^{(\unicode[STIX]{x1D70C}_{f})}$
corresponding to
$\unicode[STIX]{x1D6FD}_{\infty }^{(\unicode[STIX]{x1D70C}_{f})}$
corresponding to
![]() $\boldsymbol{f}^{(\unicode[STIX]{x1D70C}_{f})}$
, certain topological and geometrical properties of the two functions corresponding to the cases
$\boldsymbol{f}^{(\unicode[STIX]{x1D70C}_{f})}$
, certain topological and geometrical properties of the two functions corresponding to the cases
![]() $\unicode[STIX]{x1D70C}_{f}=1$
and
$\unicode[STIX]{x1D70C}_{f}=1$
and
![]() $\unicode[STIX]{x1D70C}_{f}=0$
are discussed. The Navier–Stokes equations subject to a fully helical force
$\unicode[STIX]{x1D70C}_{f}=0$
are discussed. The Navier–Stokes equations subject to a fully helical force
![]() $\boldsymbol{f}^{(1)}$
with
$\boldsymbol{f}^{(1)}$
with
![]() $f_{0}^{(1)}=\unicode[STIX]{x1D708}k_{f}^{2}$
have an exact ‘laminar’ solution. (Here, laminar refers to vanishing nonlinearity, and does not necessarily imply a layered structure.) This solution is
$f_{0}^{(1)}=\unicode[STIX]{x1D708}k_{f}^{2}$
have an exact ‘laminar’ solution. (Here, laminar refers to vanishing nonlinearity, and does not necessarily imply a layered structure.) This solution is
![]() $\boldsymbol{f}^{(1)}$
itself; it is known as Arnol’d–Beltrami–Childress (ABC) flow (Childress Reference Childress1970; Dombre et al.
Reference Dombre, Frisch, Greene, Hénon, Mehr and Soward1986) and has been studied extensively in connection with dynamo action in magnetohydrodynamics (MHD). Depending on the values of
$\boldsymbol{f}^{(1)}$
itself; it is known as Arnol’d–Beltrami–Childress (ABC) flow (Childress Reference Childress1970; Dombre et al.
Reference Dombre, Frisch, Greene, Hénon, Mehr and Soward1986) and has been studied extensively in connection with dynamo action in magnetohydrodynamics (MHD). Depending on the values of
![]() $A,B$
and
$A,B$
and
![]() $C$
:
$C$
:
![]() $\boldsymbol{f}^{(1)}$
has up to eight stagnation points (Dombre et al.
Reference Dombre, Frisch, Greene, Hénon, Mehr and Soward1986). In contrast, a ‘laminar’ flow given by
$\boldsymbol{f}^{(1)}$
has up to eight stagnation points (Dombre et al.
Reference Dombre, Frisch, Greene, Hénon, Mehr and Soward1986). In contrast, a ‘laminar’ flow given by
![]() $\boldsymbol{f}^{(0)}$
has only the trivial stagnation points
$\boldsymbol{f}^{(0)}$
has only the trivial stagnation points
![]() $x=y=z=0$
and
$x=y=z=0$
and
![]() $x=y=z=\unicode[STIX]{x03C0}$
independently of the values of
$x=y=z=\unicode[STIX]{x03C0}$
independently of the values of
![]() $A,B$
and
$A,B$
and
![]() $C$
: see appendix D. The two functions also differ in terms of their symmetry groups: while the symmetry group of
$C$
: see appendix D. The two functions also differ in terms of their symmetry groups: while the symmetry group of
![]() $\boldsymbol{f}^{(1)}$
is isomorphic to
$\boldsymbol{f}^{(1)}$
is isomorphic to
![]() $\mathbb{Z}_{2}\times \mathbb{Z}_{2}\times \mathbb{Z}_{2}$
(Dombre et al.
Reference Dombre, Frisch, Greene, Hénon, Mehr and Soward1986), that of
$\mathbb{Z}_{2}\times \mathbb{Z}_{2}\times \mathbb{Z}_{2}$
(Dombre et al.
Reference Dombre, Frisch, Greene, Hénon, Mehr and Soward1986), that of
![]() $\boldsymbol{f}^{(0)}$
is isomorphic to
$\boldsymbol{f}^{(0)}$
is isomorphic to
![]() $\mathbb{Z}_{2}\times \mathbb{Z}_{2}$
(see appendix D).
$\mathbb{Z}_{2}\times \mathbb{Z}_{2}$
(see appendix D).
The dependence of the coefficients
![]() $\unicode[STIX]{x1D6FD}_{\infty }^{(\unicode[STIX]{x1D70C}_{f})}$
and
$\unicode[STIX]{x1D6FD}_{\infty }^{(\unicode[STIX]{x1D70C}_{f})}$
and
![]() $\unicode[STIX]{x1D6FE}^{(\unicode[STIX]{x1D70C}_{f})}$
on
$\unicode[STIX]{x1D6FE}^{(\unicode[STIX]{x1D70C}_{f})}$
on
![]() $\unicode[STIX]{x1D70C}_{f}$
is now obtained by straightforward analytical evaluation of the norms on the right-hand side of (2.8). Since
$\unicode[STIX]{x1D70C}_{f}$
is now obtained by straightforward analytical evaluation of the norms on the right-hand side of (2.8). Since
![]() $\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}$
consist of trigonometric functions they satisfy
$\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}$
consist of trigonometric functions they satisfy
![]() $(-\unicode[STIX]{x1D6E5})^{-M}\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}=\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}/(2\unicode[STIX]{x03C0})^{2M}$
, and the
$(-\unicode[STIX]{x1D6E5})^{-M}\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}=\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}/(2\unicode[STIX]{x03C0})^{2M}$
, and the
![]() $L^{2}$
-norm of their gradients is calculated directly:
$L^{2}$
-norm of their gradients is calculated directly:
 $$\begin{eqnarray}\displaystyle \Vert (-\unicode[STIX]{x1D6E5})^{-M/2}\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}\Vert _{2}^{2} & = & \displaystyle ((-\unicode[STIX]{x1D6E5})^{-M/2}\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})},(-\unicode[STIX]{x1D6E5})^{-M/2}\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})})\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})},(-\unicode[STIX]{x1D6E5})^{-M}\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})})=\frac{(\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})},\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})})}{(2\unicode[STIX]{x03C0})^{2M}}=\frac{1}{(2\unicode[STIX]{x03C0})^{2M}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Vert (-\unicode[STIX]{x1D6E5})^{-M/2}\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}\Vert _{2}^{2} & = & \displaystyle ((-\unicode[STIX]{x1D6E5})^{-M/2}\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})},(-\unicode[STIX]{x1D6E5})^{-M/2}\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})})\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})},(-\unicode[STIX]{x1D6E5})^{-M}\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})})=\frac{(\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})},\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})})}{(2\unicode[STIX]{x03C0})^{2M}}=\frac{1}{(2\unicode[STIX]{x03C0})^{2M}}.\end{eqnarray}$$
The evaluation of
![]() $\Vert \unicode[STIX]{x1D735}(-\unicode[STIX]{x1D6E5})^{-M}\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}\Vert _{\infty }=\Vert \unicode[STIX]{x1D735}\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}\Vert _{\infty }/(2\unicode[STIX]{x03C0})^{2M}$
proceeds explicitly by using the definition of the
$\Vert \unicode[STIX]{x1D735}(-\unicode[STIX]{x1D6E5})^{-M}\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}\Vert _{\infty }=\Vert \unicode[STIX]{x1D735}\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}\Vert _{\infty }/(2\unicode[STIX]{x03C0})^{2M}$
proceeds explicitly by using the definition of the
![]() $L^{\infty }$
-norm,
$L^{\infty }$
-norm,
where a sum over repeated indices is implied. Evaluating the last term in (4.6) for
![]() $\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}$
results in
$\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}$
results in
See appendix B for further details. The values for the norms are now combined according to (2.8), leading to
From (4.8) one obtains the following expression for the helicity dependence of the asymptote normalised by the zero-helicity value
![]() $\unicode[STIX]{x1D6FD}_{\infty }^{(0)}$
:
$\unicode[STIX]{x1D6FD}_{\infty }^{(0)}$
:
which implies
![]() $\unicode[STIX]{x1D6FD}_{\infty }^{(\unicode[STIX]{x1D70C}_{f})}/\unicode[STIX]{x1D6FD}_{\infty }^{(0)}\in [1/\sqrt{2},1]$
. That is, a helical large-scale force results in a lower estimate for the non-dimensional total asymptotic energy dissipation rate compared to a non-helical force, provided the forces are acting on the same single length scale. In contrast, the approach to the asymptote is independent of
$\unicode[STIX]{x1D6FD}_{\infty }^{(\unicode[STIX]{x1D70C}_{f})}/\unicode[STIX]{x1D6FD}_{\infty }^{(0)}\in [1/\sqrt{2},1]$
. That is, a helical large-scale force results in a lower estimate for the non-dimensional total asymptotic energy dissipation rate compared to a non-helical force, provided the forces are acting on the same single length scale. In contrast, the approach to the asymptote is independent of
![]() $\unicode[STIX]{x1D70C}_{f}$
following (4.9). Equation (4.10) is the first main result of this paper.
$\unicode[STIX]{x1D70C}_{f}$
following (4.9). Equation (4.10) is the first main result of this paper.
Since
![]() $\unicode[STIX]{x1D6FD}_{\infty }$
is also a measure of the inertial flux of the turbulent cascade for statistically steady turbulence in the infinite-Reynolds-number limit, it implies that a high level of helicity has a detrimental effect on the energy cascade. Thus the results obtained by the upper bound theory are qualitatively in accord with the predictions by Moffatt concerning the effect of helicity on turbulence dynamics. The latter prediction, however, was concerned with the helicity of the flow and not the forcing, which is assessed here. It is known that large-scale helicity injection does not lead to highly helical flows, as mirror symmetry is quickly recovered at successively smaller scales (Chen et al.
Reference Chen, Chen and Eyink2003a
; Deusebio & Lindborg Reference Deusebio and Lindborg2014; Kessar et al.
Reference Kessar, Plunian, Stepanov and Balarac2015). Hence (4.10) could perhaps best be viewed in terms of a large-scale control problem: through an adjustment in the helicity of the forcing it may be possible to regulate the value of the inertial flux across scales without having to invoke a depletion of nonlinearity in regions of high helicity at intermediate or small scales.
$\unicode[STIX]{x1D6FD}_{\infty }$
is also a measure of the inertial flux of the turbulent cascade for statistically steady turbulence in the infinite-Reynolds-number limit, it implies that a high level of helicity has a detrimental effect on the energy cascade. Thus the results obtained by the upper bound theory are qualitatively in accord with the predictions by Moffatt concerning the effect of helicity on turbulence dynamics. The latter prediction, however, was concerned with the helicity of the flow and not the forcing, which is assessed here. It is known that large-scale helicity injection does not lead to highly helical flows, as mirror symmetry is quickly recovered at successively smaller scales (Chen et al.
Reference Chen, Chen and Eyink2003a
; Deusebio & Lindborg Reference Deusebio and Lindborg2014; Kessar et al.
Reference Kessar, Plunian, Stepanov and Balarac2015). Hence (4.10) could perhaps best be viewed in terms of a large-scale control problem: through an adjustment in the helicity of the forcing it may be possible to regulate the value of the inertial flux across scales without having to invoke a depletion of nonlinearity in regions of high helicity at intermediate or small scales.
4.1 Variational approach for bidirectional static forces
The values for the bounds given in (4.8) and (4.9) do not depend on the dimensionality of the force because setting either one or two of the coefficients
![]() $A,B$
or
$A,B$
or
![]() $C$
in (4.1) and (4.2) to zero does not alter the results. However, for forces depending on only one spatial coordinate the upper bounds can be improved through a generalisation of the variational method developed by Doering et al. (Reference Doering, Eckhardt and Schumacher2003) for shear flows with unidirectional force, where the streamwise component of the Navier–Stokes equations is projected on a suitable multiplier function. The resulting upper bound on
$C$
in (4.1) and (4.2) to zero does not alter the results. However, for forces depending on only one spatial coordinate the upper bounds can be improved through a generalisation of the variational method developed by Doering et al. (Reference Doering, Eckhardt and Schumacher2003) for shear flows with unidirectional force, where the streamwise component of the Navier–Stokes equations is projected on a suitable multiplier function. The resulting upper bound on
![]() $\unicode[STIX]{x1D6FD}$
is then evaluated by minimisation over the set of multiplier functions (Doering et al.
Reference Doering, Eckhardt and Schumacher2003; Rollin et al.
Reference Rollin, Dubief and Doering2011).
$\unicode[STIX]{x1D6FD}$
is then evaluated by minimisation over the set of multiplier functions (Doering et al.
Reference Doering, Eckhardt and Schumacher2003; Rollin et al.
Reference Rollin, Dubief and Doering2011).
This method is not applicable for three-dimensional (3-D) forces, as an average over the direction of the force is taken. In order to apply it to the present case, set
![]() $A=B=0$
such that
$A=B=0$
such that
![]() $\unicode[STIX]{x1D753}=(\unicode[STIX]{x1D719}_{x}(y),0,\unicode[STIX]{x1D719}_{z}(y))$
for
$\unicode[STIX]{x1D753}=(\unicode[STIX]{x1D719}_{x}(y),0,\unicode[STIX]{x1D719}_{z}(y))$
for
![]() $y\in [0,1]$
, where
$y\in [0,1]$
, where
![]() $\unicode[STIX]{x1D719}_{x}$
and
$\unicode[STIX]{x1D719}_{x}$
and
![]() $\unicode[STIX]{x1D719}_{y}$
are periodic functions on
$\unicode[STIX]{x1D719}_{y}$
are periodic functions on
![]() $[0,1]$
. Let
$[0,1]$
. Let
![]() $\unicode[STIX]{x1D74D}=(\unicode[STIX]{x1D713}_{x}(y),0,\unicode[STIX]{x1D713}_{z}(y))$
be a function whose second derivative
$\unicode[STIX]{x1D74D}=(\unicode[STIX]{x1D713}_{x}(y),0,\unicode[STIX]{x1D713}_{z}(y))$
be a function whose second derivative
![]() $\unicode[STIX]{x1D733}=(\unicode[STIX]{x2202}_{y}\unicode[STIX]{x1D713}_{x},0,\unicode[STIX]{x2202}_{y}\unicode[STIX]{x1D713}_{z})$
is square integrable (i.e.
$\unicode[STIX]{x1D733}=(\unicode[STIX]{x2202}_{y}\unicode[STIX]{x1D713}_{x},0,\unicode[STIX]{x2202}_{y}\unicode[STIX]{x1D713}_{z})$
is square integrable (i.e.
![]() $\unicode[STIX]{x1D74D}\in H^{2}([0,1])$
) and which satisfies
$\unicode[STIX]{x1D74D}\in H^{2}([0,1])$
) and which satisfies
![]() $(\unicode[STIX]{x1D74D},\unicode[STIX]{x1D753})\neq 0$
. As in Doering et al. (Reference Doering, Eckhardt and Schumacher2003), consider
$(\unicode[STIX]{x1D74D},\unicode[STIX]{x1D753})\neq 0$
. As in Doering et al. (Reference Doering, Eckhardt and Schumacher2003), consider
![]() $\unicode[STIX]{x1D731}\equiv (-\unicode[STIX]{x2202}_{y}^{-1}\unicode[STIX]{x1D719}_{x},0,-\unicode[STIX]{x2202}_{y}^{-1}\unicode[STIX]{x1D719}_{z})$
, such that
$\unicode[STIX]{x1D731}\equiv (-\unicode[STIX]{x2202}_{y}^{-1}\unicode[STIX]{x1D719}_{x},0,-\unicode[STIX]{x2202}_{y}^{-1}\unicode[STIX]{x1D719}_{z})$
, such that
![]() $(\unicode[STIX]{x1D733},\unicode[STIX]{x1D731})=(\unicode[STIX]{x2202}_{y}\unicode[STIX]{x1D74D},-\unicode[STIX]{x2202}_{y}\unicode[STIX]{x1D753})=(\unicode[STIX]{x1D74D},\unicode[STIX]{x1D753})$
. Following the procedure outlined in § 2, i.e. taking the inner product of the Navier–Stokes equation with
$(\unicode[STIX]{x1D733},\unicode[STIX]{x1D731})=(\unicode[STIX]{x2202}_{y}\unicode[STIX]{x1D74D},-\unicode[STIX]{x2202}_{y}\unicode[STIX]{x1D753})=(\unicode[STIX]{x1D74D},\unicode[STIX]{x1D753})$
. Following the procedure outlined in § 2, i.e. taking the inner product of the Navier–Stokes equation with
![]() $\unicode[STIX]{x1D74D}$
and integrating by parts, one obtains
$\unicode[STIX]{x1D74D}$
and integrating by parts, one obtains
where
![]() $\tilde{\boldsymbol{u}}=(u_{x},u_{y},u_{z})=\boldsymbol{u}/U$
. The next step consists of a maximisation over all divergence-free normalised vector fields
$\tilde{\boldsymbol{u}}=(u_{x},u_{y},u_{z})=\boldsymbol{u}/U$
. The next step consists of a maximisation over all divergence-free normalised vector fields
![]() $\tilde{\boldsymbol{u}}$
. The inner products in the numerators on the right-hand side of (4.11) are considered separately, beginning with the inertial term
$\tilde{\boldsymbol{u}}$
. The inner products in the numerators on the right-hand side of (4.11) are considered separately, beginning with the inertial term
 $$\begin{eqnarray}\displaystyle (\tilde{\boldsymbol{u}},(\tilde{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\unicode[STIX]{x1D74D}) & = & \displaystyle \int _{\unicode[STIX]{x1D6FA}}\text{d}\boldsymbol{x}\,u_{x}u_{y}\unicode[STIX]{x2202}_{y}\unicode[STIX]{x1D713}_{x}(y)+u_{z}u_{y}\unicode[STIX]{x2202}_{y}\unicode[STIX]{x1D713}_{z}(y)=\int _{\unicode[STIX]{x1D6FA}}\text{d}\boldsymbol{x}\,u_{x}u_{y}\unicode[STIX]{x1D6F9}_{x}(y)+u_{z}u_{y}\unicode[STIX]{x1D6F9}_{z}(y)\nonumber\\ \displaystyle & = & \displaystyle \int _{\unicode[STIX]{x1D6FA}}\text{d}\boldsymbol{x}\,\tilde{\boldsymbol{u}}\boldsymbol{\cdot }u_{y}\unicode[STIX]{x1D733}(y)\leqslant \Vert \unicode[STIX]{x1D733}\Vert _{\infty }\Vert u_{y}\tilde{\boldsymbol{u}}^{\prime }\Vert _{1}=\Vert \unicode[STIX]{x1D733}\Vert _{\infty }\int _{\unicode[STIX]{x1D6FA}}\text{d}\boldsymbol{x}\,|u_{y}|\,|\sqrt{u_{x}^{2}+u_{z}^{2}}|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \Vert \unicode[STIX]{x1D733}\Vert _{\infty }\int _{\unicode[STIX]{x1D6FA}}\text{d}\boldsymbol{x}\,|u_{y}|(|u_{x}|+|u_{z}|)\leqslant \frac{\Vert \unicode[STIX]{x1D733}\Vert _{\infty }}{2}\int _{\unicode[STIX]{x1D6FA}}\text{d}\boldsymbol{x}\,u_{x}^{2}+u_{z}^{2}+2u_{y}^{2}\nonumber\\ \displaystyle & = & \displaystyle \frac{\Vert \unicode[STIX]{x1D733}\Vert _{\infty }}{2}\left(1+\int _{\unicode[STIX]{x1D6FA}}\text{d}\boldsymbol{x}\,u_{y}^{2}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\tilde{\boldsymbol{u}},(\tilde{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\unicode[STIX]{x1D74D}) & = & \displaystyle \int _{\unicode[STIX]{x1D6FA}}\text{d}\boldsymbol{x}\,u_{x}u_{y}\unicode[STIX]{x2202}_{y}\unicode[STIX]{x1D713}_{x}(y)+u_{z}u_{y}\unicode[STIX]{x2202}_{y}\unicode[STIX]{x1D713}_{z}(y)=\int _{\unicode[STIX]{x1D6FA}}\text{d}\boldsymbol{x}\,u_{x}u_{y}\unicode[STIX]{x1D6F9}_{x}(y)+u_{z}u_{y}\unicode[STIX]{x1D6F9}_{z}(y)\nonumber\\ \displaystyle & = & \displaystyle \int _{\unicode[STIX]{x1D6FA}}\text{d}\boldsymbol{x}\,\tilde{\boldsymbol{u}}\boldsymbol{\cdot }u_{y}\unicode[STIX]{x1D733}(y)\leqslant \Vert \unicode[STIX]{x1D733}\Vert _{\infty }\Vert u_{y}\tilde{\boldsymbol{u}}^{\prime }\Vert _{1}=\Vert \unicode[STIX]{x1D733}\Vert _{\infty }\int _{\unicode[STIX]{x1D6FA}}\text{d}\boldsymbol{x}\,|u_{y}|\,|\sqrt{u_{x}^{2}+u_{z}^{2}}|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \Vert \unicode[STIX]{x1D733}\Vert _{\infty }\int _{\unicode[STIX]{x1D6FA}}\text{d}\boldsymbol{x}\,|u_{y}|(|u_{x}|+|u_{z}|)\leqslant \frac{\Vert \unicode[STIX]{x1D733}\Vert _{\infty }}{2}\int _{\unicode[STIX]{x1D6FA}}\text{d}\boldsymbol{x}\,u_{x}^{2}+u_{z}^{2}+2u_{y}^{2}\nonumber\\ \displaystyle & = & \displaystyle \frac{\Vert \unicode[STIX]{x1D733}\Vert _{\infty }}{2}\left(1+\int _{\unicode[STIX]{x1D6FA}}\text{d}\boldsymbol{x}\,u_{y}^{2}\right),\end{eqnarray}$$
where
![]() $\tilde{\boldsymbol{u}}^{\prime }=(u_{x},0,u_{z})$
, while the monotonicity of the square-root was used in
$\tilde{\boldsymbol{u}}^{\prime }=(u_{x},0,u_{z})$
, while the monotonicity of the square-root was used in
![]() $\sqrt{u_{x}^{2}+u_{z}^{2}}\leqslant \sqrt{(|u_{x}|+|u_{z}|)^{2}}$
and the triangle inequality in
$\sqrt{u_{x}^{2}+u_{z}^{2}}\leqslant \sqrt{(|u_{x}|+|u_{z}|)^{2}}$
and the triangle inequality in
![]() $|u_{x}u_{y}|\leqslant (u_{x}^{2}+u_{y}^{2})/2$
. For the viscous term, one obtains
$|u_{x}u_{y}|\leqslant (u_{x}^{2}+u_{y}^{2})/2$
. For the viscous term, one obtains
since
![]() $\unicode[STIX]{x1D6F9}_{y}=0$
. The last term to evaluate is
$\unicode[STIX]{x1D6F9}_{y}=0$
. The last term to evaluate is
 $$\begin{eqnarray}\displaystyle |(\tilde{\boldsymbol{u}},\unicode[STIX]{x1D6E5}^{1/2}\unicode[STIX]{x1D731})| & = & \displaystyle |(\tilde{\boldsymbol{u}},\unicode[STIX]{x1D753})|=\left|\int _{\unicode[STIX]{x1D6FA}}\text{d}\boldsymbol{x}\,\unicode[STIX]{x1D719}_{x}u_{x}+\unicode[STIX]{x1D719}_{z}u_{z}\right|\leqslant \left|\int _{\unicode[STIX]{x1D6FA}}\text{d}\boldsymbol{x}\,\unicode[STIX]{x1D719}_{x}u_{x}\right|+\left|\int _{\unicode[STIX]{x1D6FA}}\text{d}\boldsymbol{x}\,\unicode[STIX]{x1D719}_{z}u_{z}\right|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \Vert \unicode[STIX]{x1D719}_{x}\Vert _{2}\Vert u_{x}\Vert _{2}+\Vert \unicode[STIX]{x1D719}_{z}\Vert _{2}\Vert u_{z}\Vert _{2}\leqslant \Vert u_{x}\Vert _{2}+\Vert u_{z}\Vert _{2},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |(\tilde{\boldsymbol{u}},\unicode[STIX]{x1D6E5}^{1/2}\unicode[STIX]{x1D731})| & = & \displaystyle |(\tilde{\boldsymbol{u}},\unicode[STIX]{x1D753})|=\left|\int _{\unicode[STIX]{x1D6FA}}\text{d}\boldsymbol{x}\,\unicode[STIX]{x1D719}_{x}u_{x}+\unicode[STIX]{x1D719}_{z}u_{z}\right|\leqslant \left|\int _{\unicode[STIX]{x1D6FA}}\text{d}\boldsymbol{x}\,\unicode[STIX]{x1D719}_{x}u_{x}\right|+\left|\int _{\unicode[STIX]{x1D6FA}}\text{d}\boldsymbol{x}\,\unicode[STIX]{x1D719}_{z}u_{z}\right|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \Vert \unicode[STIX]{x1D719}_{x}\Vert _{2}\Vert u_{x}\Vert _{2}+\Vert \unicode[STIX]{x1D719}_{z}\Vert _{2}\Vert u_{z}\Vert _{2}\leqslant \Vert u_{x}\Vert _{2}+\Vert u_{z}\Vert _{2},\end{eqnarray}$$
since the normalisation
![]() $\Vert \unicode[STIX]{x1D753}\Vert _{2}=1$
implies
$\Vert \unicode[STIX]{x1D753}\Vert _{2}=1$
implies
![]() $\Vert \unicode[STIX]{x1D719}_{x}\Vert _{2}\leqslant 1$
and
$\Vert \unicode[STIX]{x1D719}_{x}\Vert _{2}\leqslant 1$
and
![]() $\Vert \unicode[STIX]{x1D719}_{z}\Vert _{2}\leqslant 1$
. Following the procedure of Doering et al. (Reference Doering, Eckhardt and Schumacher2003), set
$\Vert \unicode[STIX]{x1D719}_{z}\Vert _{2}\leqslant 1$
. Following the procedure of Doering et al. (Reference Doering, Eckhardt and Schumacher2003), set
such that
where the inequality
![]() $2|xy|\leqslant x^{2}+y^{2}$
was used again. Now (4.11) can be written as
$2|xy|\leqslant x^{2}+y^{2}$
was used again. Now (4.11) can be written as
For
![]() $Re_{f}\rightarrow \infty$
the maximisation over
$Re_{f}\rightarrow \infty$
the maximisation over
![]() $\unicode[STIX]{x1D709}$
results in
$\unicode[STIX]{x1D709}$
results in
![]() $\unicode[STIX]{x1D709}=\sqrt{2/3}$
and
$\unicode[STIX]{x1D709}=\sqrt{2/3}$
and
![]() $\max _{\unicode[STIX]{x1D709}\in [0,1]}\unicode[STIX]{x1D709}(2-\unicode[STIX]{x1D709}^{2})/\sqrt{2}=4/\sqrt{27}$
, such that
$\max _{\unicode[STIX]{x1D709}\in [0,1]}\unicode[STIX]{x1D709}(2-\unicode[STIX]{x1D709}^{2})/\sqrt{2}=4/\sqrt{27}$
, such that
The remaining minimisation over the multiplier
![]() $\unicode[STIX]{x1D733}$
proceeds by minor modifications of the method devised by Doering et al. (Reference Doering, Eckhardt and Schumacher2003) and Rollin et al. (Reference Rollin, Dubief and Doering2011). For this purpose, consider
$\unicode[STIX]{x1D733}$
proceeds by minor modifications of the method devised by Doering et al. (Reference Doering, Eckhardt and Schumacher2003) and Rollin et al. (Reference Rollin, Dubief and Doering2011). For this purpose, consider
for any constant vector
![]() $\boldsymbol{C}=(C_{x},C_{y},C_{z})$
, as
$\boldsymbol{C}=(C_{x},C_{y},C_{z})$
, as
![]() $\unicode[STIX]{x1D713}_{x}$
and
$\unicode[STIX]{x1D713}_{x}$
and
![]() $\unicode[STIX]{x1D713}_{z}$
are periodic functions with zero mean. The inequality is saturated if
$\unicode[STIX]{x1D713}_{z}$
are periodic functions with zero mean. The inequality is saturated if
![]() $\unicode[STIX]{x1D731}-\boldsymbol{C}$
and
$\unicode[STIX]{x1D731}-\boldsymbol{C}$
and
![]() $\unicode[STIX]{x1D733}$
are fully aligned, that is if
$\unicode[STIX]{x1D733}$
are fully aligned, that is if
![]() $\unicode[STIX]{x1D733}$
is a unit vector pointing in the direction of
$\unicode[STIX]{x1D733}$
is a unit vector pointing in the direction of
![]() $\unicode[STIX]{x1D731}-\boldsymbol{C}$
. The minimum over
$\unicode[STIX]{x1D731}-\boldsymbol{C}$
. The minimum over
![]() $\unicode[STIX]{x1D733}$
in (4.19) is therefore realised for
$\unicode[STIX]{x1D733}$
in (4.19) is therefore realised for
from which the conditions for
![]() $\boldsymbol{C}$
realising the minimum become
$\boldsymbol{C}$
realising the minimum become
 $$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}C_{x}}\int _{0}^{1}\text{d}y\,\left.\sqrt{(\unicode[STIX]{x1D6F7}_{x}-C_{x})^{2}+(\unicode[STIX]{x1D6F7}_{z}-C_{z})^{2}}\right|_{C_{x,z}=C_{x,z}^{min}}\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{1}\frac{\unicode[STIX]{x1D6F7}_{x}-C_{x}^{min}}{\sqrt{(\unicode[STIX]{x1D6F7}_{x}-C_{x}^{min})^{2}+(\unicode[STIX]{x1D6F7}_{z}-C_{z}^{min})^{2}}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}C_{x}}\int _{0}^{1}\text{d}y\,\left.\sqrt{(\unicode[STIX]{x1D6F7}_{x}-C_{x})^{2}+(\unicode[STIX]{x1D6F7}_{z}-C_{z})^{2}}\right|_{C_{x,z}=C_{x,z}^{min}}\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{1}\frac{\unicode[STIX]{x1D6F7}_{x}-C_{x}^{min}}{\sqrt{(\unicode[STIX]{x1D6F7}_{x}-C_{x}^{min})^{2}+(\unicode[STIX]{x1D6F7}_{z}-C_{z}^{min})^{2}}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}C_{z}}\int _{0}^{1}\text{d}y\,\left.\sqrt{(\unicode[STIX]{x1D6F7}_{x}-C_{x})^{2}+(\unicode[STIX]{x1D6F7}_{z}-C_{z})^{2}}\right|_{C_{x,z}=C_{x,z}^{min}}\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{1}\frac{\unicode[STIX]{x1D6F7}_{z}-C_{z}^{min}}{\sqrt{(\unicode[STIX]{x1D6F7}_{x}-C_{x}^{min})^{2}+(\unicode[STIX]{x1D6F7}_{z}-C_{z}^{min})^{2}}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}C_{z}}\int _{0}^{1}\text{d}y\,\left.\sqrt{(\unicode[STIX]{x1D6F7}_{x}-C_{x})^{2}+(\unicode[STIX]{x1D6F7}_{z}-C_{z})^{2}}\right|_{C_{x,z}=C_{x,z}^{min}}\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{1}\frac{\unicode[STIX]{x1D6F7}_{z}-C_{z}^{min}}{\sqrt{(\unicode[STIX]{x1D6F7}_{x}-C_{x}^{min})^{2}+(\unicode[STIX]{x1D6F7}_{z}-C_{z}^{min})^{2}}}.\end{eqnarray}$$
For the periodic functions
![]() $\unicode[STIX]{x1D753}^{X}$
considered here
$\unicode[STIX]{x1D753}^{X}$
considered here
![]() $C_{x}^{min}=C_{z}^{min}=0$
satisfies these conditions. Hence the final result for the minimax problem in the limit
$C_{x}^{min}=C_{z}^{min}=0$
satisfies these conditions. Hence the final result for the minimax problem in the limit
![]() $Re_{f}\rightarrow \infty$
is
$Re_{f}\rightarrow \infty$
is
 $$\begin{eqnarray}\unicode[STIX]{x1D6FD}_{\infty }\leqslant \min _{\unicode[STIX]{x1D74D}}\max _{\tilde{\boldsymbol{u}}}\frac{(\tilde{\boldsymbol{u}},(\tilde{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\unicode[STIX]{x1D74D})(\tilde{\boldsymbol{u}},\unicode[STIX]{x1D6E5}^{1/2}\unicode[STIX]{x1D731})}{(\unicode[STIX]{x1D733},\unicode[STIX]{x1D731})}\leqslant \frac{4}{\sqrt{27}}\frac{1}{\displaystyle \int _{0}^{1}\,\text{d}y|\unicode[STIX]{x2202}_{y}^{-1}\unicode[STIX]{x1D753}|}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FD}_{\infty }\leqslant \min _{\unicode[STIX]{x1D74D}}\max _{\tilde{\boldsymbol{u}}}\frac{(\tilde{\boldsymbol{u}},(\tilde{\boldsymbol{u}}\boldsymbol{\cdot }\unicode[STIX]{x1D735})\unicode[STIX]{x1D74D})(\tilde{\boldsymbol{u}},\unicode[STIX]{x1D6E5}^{1/2}\unicode[STIX]{x1D731})}{(\unicode[STIX]{x1D733},\unicode[STIX]{x1D731})}\leqslant \frac{4}{\sqrt{27}}\frac{1}{\displaystyle \int _{0}^{1}\,\text{d}y|\unicode[STIX]{x2202}_{y}^{-1}\unicode[STIX]{x1D753}|}.\end{eqnarray}$$
The final step consists of an evaluation of the integral on the right-hand side of (4.24) for the static shape functions
![]() $\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}$
considered here for
$\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}$
considered here for
![]() $A=B=0$
, resulting in
$A=B=0$
, resulting in
See appendix C for the calculation. The ratio between the dissipation factors is now larger compared to the previous estimate in (4.10) because the minimisation procedure replaces the
![]() $L^{\infty }$
-norm of
$L^{\infty }$
-norm of
![]() $\unicode[STIX]{x1D6FB}^{-1}\unicode[STIX]{x1D753}$
with essentially the
$\unicode[STIX]{x1D6FB}^{-1}\unicode[STIX]{x1D753}$
with essentially the
![]() $L^{1}$
-norm. For the helical shape functions
$L^{1}$
-norm. For the helical shape functions
![]() $\unicode[STIX]{x1D753}^{(\pm 1)}$
one thus expects no effect from the minimisation owing to the fact that unlike for
$\unicode[STIX]{x1D753}^{(\pm 1)}$
one thus expects no effect from the minimisation owing to the fact that unlike for
![]() $\unicode[STIX]{x1D735}\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}$
with
$\unicode[STIX]{x1D735}\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}$
with
![]() $|\unicode[STIX]{x1D70C}_{f}|<1$
, the
$|\unicode[STIX]{x1D70C}_{f}|<1$
, the
![]() $L^{\infty }$
-norm of
$L^{\infty }$
-norm of
![]() $\unicode[STIX]{x1D735}\unicode[STIX]{x1D753}^{(\pm 1)}$
equals the
$\unicode[STIX]{x1D735}\unicode[STIX]{x1D753}^{(\pm 1)}$
equals the
![]() $L^{1}$
-norm.
$L^{1}$
-norm.
4.2 Implications for the value of the Kolmogorov constant
The dimensionless dissipation coefficient has a direct relation to the Kolmogorov constant
![]() $C_{K}$
, since the relation
$C_{K}$
, since the relation
![]() $\unicode[STIX]{x1D700}=\unicode[STIX]{x1D6FD}U^{3}/L_{f}$
can be viewed as a special case of Kolmogorov scaling formally extended to the turbulence production range (Lumley Reference Lumley1992). More precisely, if
$\unicode[STIX]{x1D700}=\unicode[STIX]{x1D6FD}U^{3}/L_{f}$
can be viewed as a special case of Kolmogorov scaling formally extended to the turbulence production range (Lumley Reference Lumley1992). More precisely, if
![]() $u_{\ell }$
is the magnitude of the velocity-field fluctuations at scale
$u_{\ell }$
is the magnitude of the velocity-field fluctuations at scale
![]() $\ell$
in the inertial range, then Kolmogorov scaling of the energy spectrum implies
$\ell$
in the inertial range, then Kolmogorov scaling of the energy spectrum implies
![]() $\unicode[STIX]{x1D700}\ell /u_{\ell }^{3}\sim C_{K}^{-2/3}=\text{const}$
. Formally extending this scaling to the production range, where
$\unicode[STIX]{x1D700}\ell /u_{\ell }^{3}\sim C_{K}^{-2/3}=\text{const}$
. Formally extending this scaling to the production range, where
![]() $\ell =L_{f}$
and
$\ell =L_{f}$
and
![]() $u_{\ell }\simeq U$
would yield the desired result, which by consequence implies
$u_{\ell }\simeq U$
would yield the desired result, which by consequence implies
![]() $C_{K}\sim \unicode[STIX]{x1D6FD}^{-2/3}$
. However, this is only justified if
$C_{K}\sim \unicode[STIX]{x1D6FD}^{-2/3}$
. However, this is only justified if
![]() $L_{f}$
lies in the inertial range, which is not the case at finite Reynolds number. That is, the argument can only be applied in the formal limit of infinite Reynolds number, where the inertial range extends through all
$L_{f}$
lies in the inertial range, which is not the case at finite Reynolds number. That is, the argument can only be applied in the formal limit of infinite Reynolds number, where the inertial range extends through all
![]() $k\neq 0$
. This limit corresponds to replacing
$k\neq 0$
. This limit corresponds to replacing
![]() $\unicode[STIX]{x1D6FD}$
with
$\unicode[STIX]{x1D6FD}$
with
![]() $\unicode[STIX]{x1D6FD}_{\infty }$
, which yields
$\unicode[STIX]{x1D6FD}_{\infty }$
, which yields
It is important to point out that this argument does not take into account that
![]() $\unicode[STIX]{x1D700}$
can vary locally, a point already made by Lumley (Reference Lumley1992). Therefore, the scaling given in (4.26) can only be viewed as an approximation. Equation (4.26) can now be used to obtain the ratio of Kolmogorov constants for helical and non-helical forces from the ratio
$\unicode[STIX]{x1D700}$
can vary locally, a point already made by Lumley (Reference Lumley1992). Therefore, the scaling given in (4.26) can only be viewed as an approximation. Equation (4.26) can now be used to obtain the ratio of Kolmogorov constants for helical and non-helical forces from the ratio
![]() $\unicode[STIX]{x1D6FD}_{\infty }^{(\unicode[STIX]{x1D70C}_{f})}/\unicode[STIX]{x1D6FD}_{\infty }^{(0)}$
:
$\unicode[STIX]{x1D6FD}_{\infty }^{(\unicode[STIX]{x1D70C}_{f})}/\unicode[STIX]{x1D6FD}_{\infty }^{(0)}$
:
For 3-D static forces, where the minimisation procedure cannot be applied, one obtains the following explicit dependence of the relative value of the Kolmogorov constant on the helicity of the external forcing from (4.10) and (4.27):
For shear flows where the minimisation procedure does apply, one obtains
The estimates hence result in the following range of values for the two extreme cases:
4.3 Implications for the Smagorinsky constant in LES
As mentioned in the Introduction, the value of
![]() $\unicode[STIX]{x1D6FD}$
is not only of theoretical interest because of its relation to the parametrisation of the subgrid scales in LES, such as for the Smagorinsky model (Smagorinsky Reference Smagorinsky1963). The aim of LES is to simulate only the motion at large and intermediate scales, while the effect of the small scales is modelled. More precisely, let
$\unicode[STIX]{x1D6FD}$
is not only of theoretical interest because of its relation to the parametrisation of the subgrid scales in LES, such as for the Smagorinsky model (Smagorinsky Reference Smagorinsky1963). The aim of LES is to simulate only the motion at large and intermediate scales, while the effect of the small scales is modelled. More precisely, let
![]() $\overline{\boldsymbol{u}}$
be the velocity field
$\overline{\boldsymbol{u}}$
be the velocity field
![]() $\boldsymbol{u}$
convoluted with a filter kernel
$\boldsymbol{u}$
convoluted with a filter kernel
![]() $G^{\unicode[STIX]{x1D6E5}}$
, where
$G^{\unicode[STIX]{x1D6E5}}$
, where
![]() $\unicode[STIX]{x1D6E5}$
is the characteristic filter width:
$\unicode[STIX]{x1D6E5}$
is the characteristic filter width:
![]() $\overline{\boldsymbol{u}}=G^{\unicode[STIX]{x1D6E5}}\ast \boldsymbol{u}$
. The evolution of the filtered field is then governed by the following equations:
$\overline{\boldsymbol{u}}=G^{\unicode[STIX]{x1D6E5}}\ast \boldsymbol{u}$
. The evolution of the filtered field is then governed by the following equations:
where
![]() $\unicode[STIX]{x1D70F}_{ij}^{\unicode[STIX]{x1D6E5}}=\overline{u_{i}u_{j}}-\overline{u}_{i}\overline{u}_{j}$
is the subgrid-scale stress tensor and we assume
$\unicode[STIX]{x1D70F}_{ij}^{\unicode[STIX]{x1D6E5}}=\overline{u_{i}u_{j}}-\overline{u}_{i}\overline{u}_{j}$
is the subgrid-scale stress tensor and we assume
![]() $\unicode[STIX]{x1D6E5}<L_{f}$
such that
$\unicode[STIX]{x1D6E5}<L_{f}$
such that
![]() $\overline{\boldsymbol{f}}=\boldsymbol{f}$
. Since
$\overline{\boldsymbol{f}}=\boldsymbol{f}$
. Since
![]() $\unicode[STIX]{x1D70F}_{ij}^{\unicode[STIX]{x1D6E5}}$
is not closed in term of
$\unicode[STIX]{x1D70F}_{ij}^{\unicode[STIX]{x1D6E5}}$
is not closed in term of
![]() $\overline{\boldsymbol{u}}$
, it must be modelled. The Smagorinsky model for
$\overline{\boldsymbol{u}}$
, it must be modelled. The Smagorinsky model for
![]() $\unicode[STIX]{x1D70F}_{ij}^{\unicode[STIX]{x1D6E5}}$
is based on the observation that the mean energy flux in 3-D turbulence proceeds from the large scales to the small scales, it models the deviatoric part of
$\unicode[STIX]{x1D70F}_{ij}^{\unicode[STIX]{x1D6E5}}$
is based on the observation that the mean energy flux in 3-D turbulence proceeds from the large scales to the small scales, it models the deviatoric part of
![]() $\unicode[STIX]{x1D70F}_{ij}^{\unicode[STIX]{x1D6E5}}$
as
$\unicode[STIX]{x1D70F}_{ij}^{\unicode[STIX]{x1D6E5}}$
as
where
![]() $\overline{\unicode[STIX]{x1D634}}_{ij}=(\unicode[STIX]{x2202}_{i}\overline{u}_{j}+\unicode[STIX]{x2202}_{j}\overline{u}_{i})$
is the resolved-scale strain tensor and
$\overline{\unicode[STIX]{x1D634}}_{ij}=(\unicode[STIX]{x2202}_{i}\overline{u}_{j}+\unicode[STIX]{x2202}_{j}\overline{u}_{i})$
is the resolved-scale strain tensor and
![]() $c_{S}$
the Smagorinsky constant, which is an adjustable parameter. Since the subgrid-scale energy transfer at scale
$c_{S}$
the Smagorinsky constant, which is an adjustable parameter. Since the subgrid-scale energy transfer at scale
![]() $\unicode[STIX]{x1D6E5}$
is given by
$\unicode[STIX]{x1D6E5}$
is given by
the Smagorinsky model leads to a pointwise non-negative subgrid-scale energy flux,
The Smagorinsky constant can be related to
![]() $\unicode[STIX]{x1D6FD}_{\infty }$
using the estimate by Lilly (Reference Lilly and Goldstine1967) for the value of the Smagorinsky constant for statistically steady homogeneous isotropic turbulence,
$\unicode[STIX]{x1D6FD}_{\infty }$
using the estimate by Lilly (Reference Lilly and Goldstine1967) for the value of the Smagorinsky constant for statistically steady homogeneous isotropic turbulence,
![]() $c_{S}=(3C_{K}/2)^{-4/3}/\unicode[STIX]{x03C0}$
, in combination with (4.26):
$c_{S}=(3C_{K}/2)^{-4/3}/\unicode[STIX]{x03C0}$
, in combination with (4.26):
 $$\begin{eqnarray}c_{S}=\frac{\left({\displaystyle \frac{2}{3C_{K}}}\right)^{4/3}}{\unicode[STIX]{x03C0}}\sim \unicode[STIX]{x1D6FD}_{\infty }^{1/2}.\end{eqnarray}$$
$$\begin{eqnarray}c_{S}=\frac{\left({\displaystyle \frac{2}{3C_{K}}}\right)^{4/3}}{\unicode[STIX]{x03C0}}\sim \unicode[STIX]{x1D6FD}_{\infty }^{1/2}.\end{eqnarray}$$
In terms of the dependence of
![]() $c_{S}$
on
$c_{S}$
on
![]() $\unicode[STIX]{x1D70C}_{f}$
, the above scaling results in a relative relation between
$\unicode[STIX]{x1D70C}_{f}$
, the above scaling results in a relative relation between
![]() $c_{S}$
and
$c_{S}$
and
![]() $\unicode[STIX]{x1D6FD}_{\infty }$
,
$\unicode[STIX]{x1D6FD}_{\infty }$
,
which implies the following dependence of
![]() $c_{S}$
on the relative helicity of the forcing,
$c_{S}$
on the relative helicity of the forcing,
for isotropic forcing, and
for shear flows. In summary, the values of
![]() $c_{S}$
decrease for increasing
$c_{S}$
decrease for increasing
![]() $\unicode[STIX]{x1D70C}_{f}$
, and in the case of a strongly helical force the usual value of
$\unicode[STIX]{x1D70C}_{f}$
, and in the case of a strongly helical force the usual value of
![]() $c_{S}\simeq 0.17$
(Lilly Reference Lilly and Goldstine1967) of the Smagorinsky constant should be decreased according to the corresponding values of
$c_{S}\simeq 0.17$
(Lilly Reference Lilly and Goldstine1967) of the Smagorinsky constant should be decreased according to the corresponding values of
![]() $\unicode[STIX]{x1D6FD}_{\infty }$
. Since the eddy viscosity
$\unicode[STIX]{x1D6FD}_{\infty }$
. Since the eddy viscosity
![]() $\unicode[STIX]{x1D708}_{E}=2(c_{S}\unicode[STIX]{x1D6E5})^{2}\sqrt{\overline{\unicode[STIX]{x1D634}}_{ij}\overline{\unicode[STIX]{x1D634}}_{ij}}$
depends quadratically on
$\unicode[STIX]{x1D708}_{E}=2(c_{S}\unicode[STIX]{x1D6E5})^{2}\sqrt{\overline{\unicode[STIX]{x1D634}}_{ij}\overline{\unicode[STIX]{x1D634}}_{ij}}$
depends quadratically on
![]() $c_{S}$
, it depends linearly on
$c_{S}$
, it depends linearly on
![]() $\unicode[STIX]{x1D6FD}_{\infty }$
, which results in a decrease of at least 10 % in the case of strongly helical forcing.
$\unicode[STIX]{x1D6FD}_{\infty }$
, which results in a decrease of at least 10 % in the case of strongly helical forcing.
In the context of subgrid-scale modelling, the effect of helicity is usually included through an extra model term (Yokoi & Yoshizawa Reference Yokoi and Yoshizawa1993; Li et al.
Reference Li, Meneveau, Chen and Eyink2006; Baerenzung et al.
Reference Baerenzung, Politano, Ponty and Pouquet2008; Inagaki, Yokoi & Hamba Reference Inagaki, Yokoi and Hamba2017), leading to an additional diffusion mechanism in the model. Here, the modelling of the unresolved inertial dynamics as a dissipative loss is the same and only the amount of dissipation is changed depending on the helicity of the external force. Li et al. (Reference Li, Meneveau, Chen and Eyink2006) investigated different subgrid-scale models in a priori and a posteriori analyses of isotropic helical turbulence. The effect of the newly introduced terms in helical subgrid-scale models was found to be quite small. Interestingly, the dynamic Smagorinsky model, where the model coefficient is adjusted in response to the flow, performed best in comparison with DNS data. An a posteriori analysis of the static Smagorinsky model with
![]() $c_{S}$
adjusted as discussed here could be of interest in this context.
$c_{S}$
adjusted as discussed here could be of interest in this context.
5 Numerical simulations
Equations (2.1)–(2.2) are solved numerically in a three-dimensional periodic domain of length
![]() $L_{box}=2\unicode[STIX]{x03C0}$
using a fully de-aliased pseudospectral code. In order to assess the influence of helicity, dimensionality and time dependence of the forcing on the value of the dimensionless dissipation coefficient, DNSs were carried out using different forcing functions, including the static forces constructed using the shape functions given in (4.2) and (4.1) according to (4.4). Simulation series carried out using these static shape functions are identified by the label S, followed by the dimensionality of the force and the relative helicity level. Here, the label 1D2C refers to one-dimensional two-component shape functions where e.g.
$L_{box}=2\unicode[STIX]{x03C0}$
using a fully de-aliased pseudospectral code. In order to assess the influence of helicity, dimensionality and time dependence of the forcing on the value of the dimensionless dissipation coefficient, DNSs were carried out using different forcing functions, including the static forces constructed using the shape functions given in (4.2) and (4.1) according to (4.4). Simulation series carried out using these static shape functions are identified by the label S, followed by the dimensionality of the force and the relative helicity level. Here, the label 1D2C refers to one-dimensional two-component shape functions where e.g.
![]() $A=B=0$
while 3D refers to three-dimensional forces with
$A=B=0$
while 3D refers to three-dimensional forces with
![]() $A=B=C$
. Since the different implementations of time-dependent forcing have little effect on the measured value for
$A=B=C$
. Since the different implementations of time-dependent forcing have little effect on the measured value for
![]() $\unicode[STIX]{x1D6FD}$
(Bos et al.
Reference Bos, Shao and Bertoglio2007), it is sufficient to consider only one type of time-dependent forcing for comparison to the static forces. The time-dependent forcing was given by a Gaussian distributed
$\unicode[STIX]{x1D6FD}$
(Bos et al.
Reference Bos, Shao and Bertoglio2007), it is sufficient to consider only one type of time-dependent forcing for comparison to the static forces. The time-dependent forcing was given by a Gaussian distributed
![]() $\unicode[STIX]{x1D6FF}(t)$
-correlated stochastic process, which is particularly suited to the present investigation because it gives optimal control over both kinetic energy and helicity injection rates. The helicity of the random force is set by expanding the Fourier modes
$\unicode[STIX]{x1D6FF}(t)$
-correlated stochastic process, which is particularly suited to the present investigation because it gives optimal control over both kinetic energy and helicity injection rates. The helicity of the random force is set by expanding the Fourier modes
![]() $\hat{\boldsymbol{f}}$
of the force field in a basis consisting of eigenfunctions of the curl operator (Constantin & Majda Reference Constantin and Majda1988; Waleffe Reference Waleffe1992), i.e. into positively and negatively helical modes, such that the helicity of the force can be adjusted exactly at each wavevector (Brandenburg Reference Brandenburg2001). Simulation series carried out using dynamic forcing are identified by the labels D1 and D2, followed by the helicity level of the force. All simulations of series S and D2 are carried out using
$\hat{\boldsymbol{f}}$
of the force field in a basis consisting of eigenfunctions of the curl operator (Constantin & Majda Reference Constantin and Majda1988; Waleffe Reference Waleffe1992), i.e. into positively and negatively helical modes, such that the helicity of the force can be adjusted exactly at each wavevector (Brandenburg Reference Brandenburg2001). Simulation series carried out using dynamic forcing are identified by the labels D1 and D2, followed by the helicity level of the force. All simulations of series S and D2 are carried out using
![]() $256^{3}$
collocation points, while simulations of series D1 were carried out using
$256^{3}$
collocation points, while simulations of series D1 were carried out using
![]() $512^{3}$
collocation points. The force always acts on the large scales
$512^{3}$
collocation points. The force always acts on the large scales
![]() $L_{f}=\unicode[STIX]{x03C0}/k_{f}$
, i.e. at wavenumbers
$L_{f}=\unicode[STIX]{x03C0}/k_{f}$
, i.e. at wavenumbers
![]() $k_{f}\leqslant 2.5$
for runs of series D1 and at
$k_{f}\leqslant 2.5$
for runs of series D1 and at
![]() $k_{f}=1$
for all other simulations. For case D2, the random force is equivalent to a phase-shifted ABC-flow with randomly chosen phases and values of
$k_{f}=1$
for all other simulations. For case D2, the random force is equivalent to a phase-shifted ABC-flow with randomly chosen phases and values of
![]() $A$
,
$A$
,
![]() $B$
and
$B$
and
![]() $C$
.
$C$
.
All runs are carried out with a fixed time step
![]() $\text{d}t$
chosen by the Courant–Friedrichs–Lewy criterion, where in the case of white-in-time forcing
$\text{d}t$
chosen by the Courant–Friedrichs–Lewy criterion, where in the case of white-in-time forcing
![]() $\text{d}t$
determines the characteristic frequency of the force by
$\text{d}t$
determines the characteristic frequency of the force by
![]() $\unicode[STIX]{x1D714}_{f}=2\unicode[STIX]{x03C0}/\text{d}t$
. According to (3.3), white-in-time forcing should therefore lead to a maximal weighting of the extra contribution to
$\unicode[STIX]{x1D714}_{f}=2\unicode[STIX]{x03C0}/\text{d}t$
. According to (3.3), white-in-time forcing should therefore lead to a maximal weighting of the extra contribution to
![]() $\unicode[STIX]{x1D6FD}_{\infty }$
originating from the time dependence of the forcing compared to forces with larger correlation times. Measurements are taken after the simulations have reached a statistically stationary state; all simulations are evolved for more than
$\unicode[STIX]{x1D6FD}_{\infty }$
originating from the time dependence of the forcing compared to forces with larger correlation times. Measurements are taken after the simulations have reached a statistically stationary state; all simulations are evolved for more than
![]() $25$
large-eddy turnover times in stationary state. It has been pointed out by Bos et al. (Reference Bos, Shao and Bertoglio2007) that averaging intervals of more than 10 large-eddy turnover times are necessary in order to obtain accurate values of
$25$
large-eddy turnover times in stationary state. It has been pointed out by Bos et al. (Reference Bos, Shao and Bertoglio2007) that averaging intervals of more than 10 large-eddy turnover times are necessary in order to obtain accurate values of
![]() $\unicode[STIX]{x1D6FD}$
. The long run time of the simulations is particularly important for the present study in order to distinguish the helicity dependence of the measured values of
$\unicode[STIX]{x1D6FD}$
. The long run time of the simulations is particularly important for the present study in order to distinguish the helicity dependence of the measured values of
![]() $\unicode[STIX]{x1D6FD}$
from the statistical error, resulting in a need to compromise between achievable run time and resolution. A summary of the numerical details including information on the small-scale resolution and measured values of
$\unicode[STIX]{x1D6FD}$
from the statistical error, resulting in a need to compromise between achievable run time and resolution. A summary of the numerical details including information on the small-scale resolution and measured values of
![]() $\unicode[STIX]{x1D700}$
,
$\unicode[STIX]{x1D700}$
,
![]() $U$
,
$U$
,
![]() $L$
and
$L$
and
![]() $\unicode[STIX]{x1D6FD}$
is given in table 1. For comparison purposes with results given in the literature for isotropic turbulence, where
$\unicode[STIX]{x1D6FD}$
is given in table 1. For comparison purposes with results given in the literature for isotropic turbulence, where
![]() $\unicode[STIX]{x1D6FD}_{L}=\unicode[STIX]{x1D700}L/U^{3}$
, with
$\unicode[STIX]{x1D6FD}_{L}=\unicode[STIX]{x1D700}L/U^{3}$
, with
![]() $L$
being the integral scale, is measured instead of
$L$
being the integral scale, is measured instead of
![]() $\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D700}L_{f}/U^{3}$
; values of
$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D700}L_{f}/U^{3}$
; values of
![]() $\unicode[STIX]{x1D6FD}_{L}$
are also provided in the table. For the same reason,
$\unicode[STIX]{x1D6FD}_{L}$
are also provided in the table. For the same reason,
![]() $U$
is calculated as
$U$
is calculated as
![]() $U=\sqrt{2E/3}$
, where
$U=\sqrt{2E/3}$
, where
![]() $E$
is the time-averaged kinetic energy per unit volume.
$E$
is the time-averaged kinetic energy per unit volume.
Table 1. Specifications of the numerical simulations.
![]() $N$
denotes the number of grid points in each Cartesian coordinate,
$N$
denotes the number of grid points in each Cartesian coordinate,
![]() $Re$
the Reynolds number with respect to the root-mean-square velocity
$Re$
the Reynolds number with respect to the root-mean-square velocity
![]() $U$
, the integral scale
$U$
, the integral scale
![]() $L$
and the kinematic viscosity
$L$
and the kinematic viscosity
![]() $\unicode[STIX]{x1D708}$
,
$\unicode[STIX]{x1D708}$
,
![]() $Re_{\unicode[STIX]{x1D706}}$
the Taylor-scale Reynolds number,
$Re_{\unicode[STIX]{x1D706}}$
the Taylor-scale Reynolds number,
![]() $\unicode[STIX]{x1D700}$
the dissipation rate,
$\unicode[STIX]{x1D700}$
the dissipation rate,
![]() $\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D700}L_{f}/U^{3}$
the dimensionless dissipation rate,
$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D700}L_{f}/U^{3}$
the dimensionless dissipation rate,
![]() $\unicode[STIX]{x1D6FD}_{L}=\unicode[STIX]{x1D700}L/U^{3}$
the dimensionless dissipation rate with respect to
$\unicode[STIX]{x1D6FD}_{L}=\unicode[STIX]{x1D700}L/U^{3}$
the dimensionless dissipation rate with respect to
![]() $L$
,
$L$
,
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FD}}$
and
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FD}}$
and
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FD}_{L}}$
the respective standard errors,
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D6FD}_{L}}$
the respective standard errors,
![]() $\unicode[STIX]{x1D70C}$
the relative kinetic helicity,
$\unicode[STIX]{x1D70C}$
the relative kinetic helicity,
![]() $\unicode[STIX]{x1D70C}_{f}$
the relative helicity of the forcing,
$\unicode[STIX]{x1D70C}_{f}$
the relative helicity of the forcing,
![]() $\unicode[STIX]{x1D702}$
the Kolmogorov microscale,
$\unicode[STIX]{x1D702}$
the Kolmogorov microscale,
![]() $k_{max}$
the highest resolved wavenumber,
$k_{max}$
the highest resolved wavenumber,
![]() $T=L/U$
the large-eddy turnover time and
$T=L/U$
the large-eddy turnover time and
![]() $t/T$
the steady-state run time in units of
$t/T$
the steady-state run time in units of
![]() $T$
. The values given for
$T$
. The values given for
![]() $\unicode[STIX]{x1D700}$
,
$\unicode[STIX]{x1D700}$
,
![]() $U$
,
$U$
,
![]() $L$
and
$L$
and
![]() $\unicode[STIX]{x1D70C}$
are ensemble averages, with the ensemble consisting of snapshots taken at intervals of
$\unicode[STIX]{x1D70C}$
are ensemble averages, with the ensemble consisting of snapshots taken at intervals of
![]() $T$
in order to obtain statistically independent samples. The identifiers D and S refer to dynamic and static forces, respectively. The two sets of simulations using static forces differ in the dimensionality of the force as indicated by the labels 3D and 1D2C.
$T$
in order to obtain statistically independent samples. The identifiers D and S refer to dynamic and static forces, respectively. The two sets of simulations using static forces differ in the dimensionality of the force as indicated by the labels 3D and 1D2C.

5.1 Comparison between numerical and analytical results
A comparison between the values of the rigorous bounds given in (4.8) and (4.25) and the measured values given in table 1 shows that the measured values are considerably smaller than the corresponding estimates. The range of values for the non-helical 3-D forces
![]() $0.43\leqslant {\unicode[STIX]{x1D6FD}_{L}}^{(0)}\leqslant 0.49$
obtained from the present DNSs are consistent with existing data from the literature for 3-D isotropic turbulence (Wang et al.
Reference Wang, Chen, Brasseur and Wyngaard1996; Gotoh et al.
Reference Gotoh, Fukayama and Nakano2002; Kaneda et al.
Reference Kaneda, Ishihara, Yokokawa, Itakura and Uno2003; Donzis et al.
Reference Donzis, Sreenivasan and Yeung2005; Yeung et al.
Reference Yeung, Donzis and Sreenivasan2012; McComb et al.
Reference McComb, Berera, Yoffe and Linkmann2015; Yeung et al.
Reference Yeung, Zhai and Sreenivasan2015; Ishihara et al.
Reference Ishihara, Morishita, Yokokawa, Uno and Kaneda2016), and the analytically obtained estimates differ by an order of magnitude from the measured values. Such a discrepancy between the measured value and the rigorous estimate has also been obtained for a particular type of dynamic forcing (Doering & Petrov Reference Doering, Petrov, Oberlack, Peinke, Kittel and Barth2005), given by
$0.43\leqslant {\unicode[STIX]{x1D6FD}_{L}}^{(0)}\leqslant 0.49$
obtained from the present DNSs are consistent with existing data from the literature for 3-D isotropic turbulence (Wang et al.
Reference Wang, Chen, Brasseur and Wyngaard1996; Gotoh et al.
Reference Gotoh, Fukayama and Nakano2002; Kaneda et al.
Reference Kaneda, Ishihara, Yokokawa, Itakura and Uno2003; Donzis et al.
Reference Donzis, Sreenivasan and Yeung2005; Yeung et al.
Reference Yeung, Donzis and Sreenivasan2012; McComb et al.
Reference McComb, Berera, Yoffe and Linkmann2015; Yeung et al.
Reference Yeung, Zhai and Sreenivasan2015; Ishihara et al.
Reference Ishihara, Morishita, Yokokawa, Uno and Kaneda2016), and the analytically obtained estimates differ by an order of magnitude from the measured values. Such a discrepancy between the measured value and the rigorous estimate has also been obtained for a particular type of dynamic forcing (Doering & Petrov Reference Doering, Petrov, Oberlack, Peinke, Kittel and Barth2005), given by
where
![]() $\hat{\boldsymbol{f}}(\boldsymbol{k},t)$
is the Fourier transform of the force and
$\hat{\boldsymbol{f}}(\boldsymbol{k},t)$
is the Fourier transform of the force and
![]() $E_{f}$
the total energy contained in the forcing band. The rigorous bound derived by Doering & Petrov (Reference Doering, Petrov, Oberlack, Peinke, Kittel and Barth2005) resulted in
$E_{f}$
the total energy contained in the forcing band. The rigorous bound derived by Doering & Petrov (Reference Doering, Petrov, Oberlack, Peinke, Kittel and Barth2005) resulted in
![]() $\unicode[STIX]{x1D6FD}_{\infty }=4\unicode[STIX]{x03C0}\sqrt{3/5}\simeq 9.73$
, which could be tightened to
$\unicode[STIX]{x1D6FD}_{\infty }=4\unicode[STIX]{x03C0}\sqrt{3/5}\simeq 9.73$
, which could be tightened to
![]() $\unicode[STIX]{x1D6FD}_{\infty }=2\sqrt{2}\unicode[STIX]{x03C0}$
assuming Kolmogorov scaling for the energy spectrum, i.e. interestingly to the same value as
$\unicode[STIX]{x1D6FD}_{\infty }=2\sqrt{2}\unicode[STIX]{x03C0}$
assuming Kolmogorov scaling for the energy spectrum, i.e. interestingly to the same value as
![]() $\unicode[STIX]{x1D6FD}_{\infty }^{(0)}$
obtained here for the static 3-D force.
$\unicode[STIX]{x1D6FD}_{\infty }^{(0)}$
obtained here for the static 3-D force.

Figure 1. Value of
![]() $\unicode[STIX]{x1D6FD}$
as a function of
$\unicode[STIX]{x1D6FD}$
as a function of
![]() $\unicode[STIX]{x1D70C}_{f}$
normalised by its value at
$\unicode[STIX]{x1D70C}_{f}$
normalised by its value at
![]() $\unicode[STIX]{x1D70C}_{f}=0$
from datasets D2, S3D and S1D2C compared to the analytical predictions in (4.10) and (4.25). (a)
$\unicode[STIX]{x1D70C}_{f}=0$
from datasets D2, S3D and S1D2C compared to the analytical predictions in (4.10) and (4.25). (a)
![]() $\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D700}L_{f}/U^{3}$
, (b)
$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D700}L_{f}/U^{3}$
, (b)
![]() $\unicode[STIX]{x1D6FD}_{L}=\unicode[STIX]{x1D700}L/U^{3}$
, where
$\unicode[STIX]{x1D6FD}_{L}=\unicode[STIX]{x1D700}L/U^{3}$
, where
![]() $L$
is the integral scale.
$L$
is the integral scale.
Figure 1 presents a comparison of values for
![]() $\unicode[STIX]{x1D6FD}^{(\unicode[STIX]{x1D70C}_{f})}/\unicode[STIX]{x1D6FD}^{(0)}$
(figure 1
a) and
$\unicode[STIX]{x1D6FD}^{(\unicode[STIX]{x1D70C}_{f})}/\unicode[STIX]{x1D6FD}^{(0)}$
(figure 1
a) and
![]() $\unicode[STIX]{x1D6FD}_{L}^{(\unicode[STIX]{x1D70C}_{f})}/\unicode[STIX]{x1D6FD}_{L}^{(0)}$
(figure 1
b) obtained from datasets D2, S3D and S1D2C and the analytical predictions of (4.10) and (4.25). As can be seen from the figure, the measured values are in broad agreement between the different datasets despite the lack of isotropy in case 1D2C and the dynamical nature of the forcing in case D2. Symmetries specific to the choice
$\unicode[STIX]{x1D6FD}_{L}^{(\unicode[STIX]{x1D70C}_{f})}/\unicode[STIX]{x1D6FD}_{L}^{(0)}$
(figure 1
b) obtained from datasets D2, S3D and S1D2C and the analytical predictions of (4.10) and (4.25). As can be seen from the figure, the measured values are in broad agreement between the different datasets despite the lack of isotropy in case 1D2C and the dynamical nature of the forcing in case D2. Symmetries specific to the choice
![]() $A=B=C$
in case S3D have therefore little or no influence on the value of
$A=B=C$
in case S3D have therefore little or no influence on the value of
![]() $\unicode[STIX]{x1D6FD}$
. Furthermore, the functional dependence of the ratios
$\unicode[STIX]{x1D6FD}$
. Furthermore, the functional dependence of the ratios
![]() $\unicode[STIX]{x1D6FD}^{(\unicode[STIX]{x1D70C}_{f})}/\unicode[STIX]{x1D6FD}^{(0)}$
and
$\unicode[STIX]{x1D6FD}^{(\unicode[STIX]{x1D70C}_{f})}/\unicode[STIX]{x1D6FD}^{(0)}$
and
![]() $\unicode[STIX]{x1D6FD}_{L}^{(\unicode[STIX]{x1D70C}_{f})}/\unicode[STIX]{x1D6FD}_{L}^{(0)}$
on
$\unicode[STIX]{x1D6FD}_{L}^{(\unicode[STIX]{x1D70C}_{f})}/\unicode[STIX]{x1D6FD}_{L}^{(0)}$
on
![]() $\unicode[STIX]{x1D70C}_{f}$
is consistent with the analytical predictions. This implies that although the upper bounds are by an order of magnitude higher than the measured values, there is good agreement between the analytical and the numerical results concerning the ratio
$\unicode[STIX]{x1D70C}_{f}$
is consistent with the analytical predictions. This implies that although the upper bounds are by an order of magnitude higher than the measured values, there is good agreement between the analytical and the numerical results concerning the ratio
![]() $\unicode[STIX]{x1D6FD}^{(\unicode[STIX]{x1D70C}_{f})}/\unicode[STIX]{x1D6FD}^{(0)}$
, which in the limit
$\unicode[STIX]{x1D6FD}^{(\unicode[STIX]{x1D70C}_{f})}/\unicode[STIX]{x1D6FD}^{(0)}$
, which in the limit
![]() $Re\rightarrow \infty$
is predicted to follow (4.10) for 3-D forces and (4.25) for shear flows. Differences between the
$Re\rightarrow \infty$
is predicted to follow (4.10) for 3-D forces and (4.25) for shear flows. Differences between the
![]() $\unicode[STIX]{x1D70C}_{f}$
-dependence of
$\unicode[STIX]{x1D70C}_{f}$
-dependence of
![]() $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
![]() $\unicode[STIX]{x1D6FD}_{L}$
originate from a
$\unicode[STIX]{x1D6FD}_{L}$
originate from a
![]() $\unicode[STIX]{x1D70C}_{f}$
-dependence of the integral scale, which is discussed briefly in § 5.3.
$\unicode[STIX]{x1D70C}_{f}$
-dependence of the integral scale, which is discussed briefly in § 5.3.
The effect of finite Reynolds number on the measurements can be quantified through the conventionally band-forced runs D1-0 and D1-1. For this purpose, it is useful to consider the empirical formula obtained by a least-squares fit to a dataset of
![]() $\unicode[STIX]{x1D6FD}_{L}$
resulting from DNSs of stationary homogeneous isotropic turbulence maintained with the dynamic forcing specified in (5.1) for
$\unicode[STIX]{x1D6FD}_{L}$
resulting from DNSs of stationary homogeneous isotropic turbulence maintained with the dynamic forcing specified in (5.1) for
![]() $k_{f}\leqslant 2.5$
(McComb et al.
Reference McComb, Berera, Yoffe and Linkmann2015),
$k_{f}\leqslant 2.5$
(McComb et al.
Reference McComb, Berera, Yoffe and Linkmann2015),
which yields
![]() $\unicode[STIX]{x1D6FD}_{L}(Re=834)=0.49$
, in good agreement with the measured value for run D1-0 shown in table 1. For run D1-1 the same equation is considered after adjusting the value of the asymptote according to the aforementioned estimates
$\unicode[STIX]{x1D6FD}_{L}(Re=834)=0.49$
, in good agreement with the measured value for run D1-0 shown in table 1. For run D1-1 the same equation is considered after adjusting the value of the asymptote according to the aforementioned estimates
which results in
![]() $\unicode[STIX]{x1D6FD}_{L}(Re=846)=0.45$
, again in good agreement with the measured value for run D1-1 shown in table 1. Hence the ratio 0.9 of the asymptotes and a helicity-independent approach to the asymptotes is consistent with the data.
$\unicode[STIX]{x1D6FD}_{L}(Re=846)=0.45$
, again in good agreement with the measured value for run D1-1 shown in table 1. Hence the ratio 0.9 of the asymptotes and a helicity-independent approach to the asymptotes is consistent with the data.
Concerning a possible influence of the time dependence of the forcing on the value of
![]() $\unicode[STIX]{x1D6FD}_{\infty }$
, the comparison of values for
$\unicode[STIX]{x1D6FD}_{\infty }$
, the comparison of values for
![]() $\unicode[STIX]{x1D6FD}$
obtained from runs D2 and S3D shown in table 1 demonstrates that the value of
$\unicode[STIX]{x1D6FD}$
obtained from runs D2 and S3D shown in table 1 demonstrates that the value of
![]() $\unicode[STIX]{x1D6FD}$
is comparable between the dynamically and the statically forced simulations, provided the forces act at the same length scales. Furthermore, the ratio
$\unicode[STIX]{x1D6FD}$
is comparable between the dynamically and the statically forced simulations, provided the forces act at the same length scales. Furthermore, the ratio
![]() $\unicode[STIX]{x1D6FD}^{(\unicode[STIX]{x1D70C}_{f})}/\unicode[STIX]{x1D6FD}^{(0)}$
appears to be largely unaffected by the time dependence of the forcing as can be seen in figure 1. That is, the dynamical details of the forcing have little influence on the value of
$\unicode[STIX]{x1D6FD}^{(\unicode[STIX]{x1D70C}_{f})}/\unicode[STIX]{x1D6FD}^{(0)}$
appears to be largely unaffected by the time dependence of the forcing as can be seen in figure 1. That is, the dynamical details of the forcing have little influence on the value of
![]() $\unicode[STIX]{x1D6FD}$
and possibly also on that of the asymptote
$\unicode[STIX]{x1D6FD}$
and possibly also on that of the asymptote
![]() $\unicode[STIX]{x1D6FD}_{\infty }$
. Note that the measured values of
$\unicode[STIX]{x1D6FD}_{\infty }$
. Note that the measured values of
![]() $\unicode[STIX]{x1D6FD}$
for the dynamically forced simulations D1-0 and D1-1 are higher than those obtained from D2-0 and D2-1, despite the larger Reynolds number which most probably results from differences in the range of wavenumbers the force is applied in. The dependence of
$\unicode[STIX]{x1D6FD}$
for the dynamically forced simulations D1-0 and D1-1 are higher than those obtained from D2-0 and D2-1, despite the larger Reynolds number which most probably results from differences in the range of wavenumbers the force is applied in. The dependence of
![]() $\unicode[STIX]{x1D6FD}$
on the width of the forcing band was studied analytically and numerically for Kolmogorov flow by Rollin et al. (Reference Rollin, Dubief and Doering2011). The analytical estimates suggested an increase of
$\unicode[STIX]{x1D6FD}$
on the width of the forcing band was studied analytically and numerically for Kolmogorov flow by Rollin et al. (Reference Rollin, Dubief and Doering2011). The analytical estimates suggested an increase of
![]() $\unicode[STIX]{x1D6FD}_{\infty }$
with the width of the forcing band, which was confirmed by DNS results. The behaviour observed here is consistent with these results, as runs of series D2 were forced at
$\unicode[STIX]{x1D6FD}_{\infty }$
with the width of the forcing band, which was confirmed by DNS results. The behaviour observed here is consistent with these results, as runs of series D2 were forced at
![]() $k_{f}=1$
in order to enable a like-for-like comparison to the statically forced series S3D runs, while runs of series D1 were forced more conventionally in the wavenumber band
$k_{f}=1$
in order to enable a like-for-like comparison to the statically forced series S3D runs, while runs of series D1 were forced more conventionally in the wavenumber band
![]() $1\leqslant k_{f}\leqslant 2.5$
in order to compare with results in the literature.
$1\leqslant k_{f}\leqslant 2.5$
in order to compare with results in the literature.
In summary, not only the qualitative but more importantly the relative quantitative helicity dependence of the measured values of
![]() $\unicode[STIX]{x1D6FD}$
is in good agreement with the helicity dependence of the upper bounds. Moreover, this dependence of
$\unicode[STIX]{x1D6FD}$
is in good agreement with the helicity dependence of the upper bounds. Moreover, this dependence of
![]() $\unicode[STIX]{x1D6FD}$
on the helicity of the forcing appears to be independent of its dynamical features.
$\unicode[STIX]{x1D6FD}$
on the helicity of the forcing appears to be independent of its dynamical features.
5.2 Kolmogorov constant
Concerning the Kolmogorov constant
![]() $C_{K}$
, recent numerical measurements (Ishihara et al.
Reference Ishihara, Morishita, Yokokawa, Uno and Kaneda2016) showed that accurate numerical measurements of
$C_{K}$
, recent numerical measurements (Ishihara et al.
Reference Ishihara, Morishita, Yokokawa, Uno and Kaneda2016) showed that accurate numerical measurements of
![]() $C_{K}$
require Taylor-scale Reynolds numbers
$C_{K}$
require Taylor-scale Reynolds numbers
![]() $Re_{\unicode[STIX]{x1D706}}\geqslant 700$
and hence very high resolution DNSs. Furthermore, numerical results at
$Re_{\unicode[STIX]{x1D706}}\geqslant 700$
and hence very high resolution DNSs. Furthermore, numerical results at
![]() $Re_{\unicode[STIX]{x1D706}}=2297$
requiring
$Re_{\unicode[STIX]{x1D706}}=2297$
requiring
![]() $12\,288^{3}$
collocation points revealed a difference between the numerically and experimentally measured values of
$12\,288^{3}$
collocation points revealed a difference between the numerically and experimentally measured values of
![]() $C_{K}$
, with
$C_{K}$
, with
![]() $C_{K}=1.8\pm 0.1$
obtained numerically (Ishihara et al.
Reference Ishihara, Morishita, Yokokawa, Uno and Kaneda2016) and
$C_{K}=1.8\pm 0.1$
obtained numerically (Ishihara et al.
Reference Ishihara, Morishita, Yokokawa, Uno and Kaneda2016) and
![]() $C_{K}\simeq 1.6$
obtained from experimental data for several flow configurations (Sreenivasan Reference Sreenivasan1995). The value of the Kolmogorov constant thus appears still to be an open question, and DNSs at much higher Reynolds numbers than those carried out in the present paper are necessary to test any predicted variations for the Kolmogorov constant such as those presented here.
$C_{K}\simeq 1.6$
obtained from experimental data for several flow configurations (Sreenivasan Reference Sreenivasan1995). The value of the Kolmogorov constant thus appears still to be an open question, and DNSs at much higher Reynolds numbers than those carried out in the present paper are necessary to test any predicted variations for the Kolmogorov constant such as those presented here.
5.3 Further observations
As can be seen from table 1, the integral scale is slightly larger for helical forces with
![]() $L^{(0)}/L^{(1)}\simeq 0.9$
consistently in all test cases. Although a proper interpretation of integral scale is perhaps ambiguous as the largest scales are dominated by the forcing in the present simulations, the measurements suggest that helically forced flows consist of larger eddies. This is expected given the depletion of nonlinearity in regions of high helicity (Moffatt Reference Moffatt1985, Reference Moffatt2014). Although mirror symmetry is generally recovered quickly at the small scales, (Kraichnan Reference Kraichnan1973; Chen et al.
Reference Chen, Chen and Eyink2003a
; Deusebio & Lindborg Reference Deusebio and Lindborg2014; Kessar et al.
Reference Kessar, Plunian, Stepanov and Balarac2015), the high level of helicity at the large scales diminishes the forward flux of kinetic energy and hence the efficiency of the kinetic energy cascade leading to less generation of small-scale turbulent fluctuations (Moffatt Reference Moffatt2014). In the decaying case, the same effect results in a delay in the onset of the decay for non-zero helicity (Polifke & Shtilman Reference Polifke and Shtilman1989). A similar conclusion can be achieved by noting that despite comparable large-scale and Taylor-scale Reynolds numbers, the helically forced turbulent flows are all better resolved, implying that the Kolmogorov microscale is larger for the helically forced simulations compared to the non-helically forced runs.
$L^{(0)}/L^{(1)}\simeq 0.9$
consistently in all test cases. Although a proper interpretation of integral scale is perhaps ambiguous as the largest scales are dominated by the forcing in the present simulations, the measurements suggest that helically forced flows consist of larger eddies. This is expected given the depletion of nonlinearity in regions of high helicity (Moffatt Reference Moffatt1985, Reference Moffatt2014). Although mirror symmetry is generally recovered quickly at the small scales, (Kraichnan Reference Kraichnan1973; Chen et al.
Reference Chen, Chen and Eyink2003a
; Deusebio & Lindborg Reference Deusebio and Lindborg2014; Kessar et al.
Reference Kessar, Plunian, Stepanov and Balarac2015), the high level of helicity at the large scales diminishes the forward flux of kinetic energy and hence the efficiency of the kinetic energy cascade leading to less generation of small-scale turbulent fluctuations (Moffatt Reference Moffatt2014). In the decaying case, the same effect results in a delay in the onset of the decay for non-zero helicity (Polifke & Shtilman Reference Polifke and Shtilman1989). A similar conclusion can be achieved by noting that despite comparable large-scale and Taylor-scale Reynolds numbers, the helically forced turbulent flows are all better resolved, implying that the Kolmogorov microscale is larger for the helically forced simulations compared to the non-helically forced runs.
A reduction in the formation of small-scale structures with increasing
![]() $\unicode[STIX]{x1D70C}_{f}$
is reminiscent of drag-reducing processes in wall-bounded flows. More precisely, at a given value of
$\unicode[STIX]{x1D70C}_{f}$
is reminiscent of drag-reducing processes in wall-bounded flows. More precisely, at a given value of
![]() $U$
a decrease in
$U$
a decrease in
![]() $\unicode[STIX]{x1D700}$
in homogeneous turbulence corresponds to a decrease in the wall shear stress in wall-bounded flows. Such an effect is indeed obtained with increasing
$\unicode[STIX]{x1D700}$
in homogeneous turbulence corresponds to a decrease in the wall shear stress in wall-bounded flows. Such an effect is indeed obtained with increasing
![]() $\unicode[STIX]{x1D70C}_{f}$
as shown in figure 2, where
$\unicode[STIX]{x1D70C}_{f}$
as shown in figure 2, where
![]() $\unicode[STIX]{x1D700}$
is presented as a function of
$\unicode[STIX]{x1D700}$
is presented as a function of
![]() $U$
. It can be quantified through the measure
$U$
. It can be quantified through the measure
which equals the ratio of the corresponding dissipation rates at fixed
![]() $U$
. From the analytical and numerical results, one obtains
$U$
. From the analytical and numerical results, one obtains
![]() $R(\unicode[STIX]{x1D70C}_{f}=1)\simeq 30\,\%$
.
$R(\unicode[STIX]{x1D70C}_{f}=1)\simeq 30\,\%$
.

Figure 2. Value of
![]() $\unicode[STIX]{x1D700}$
as a function of
$\unicode[STIX]{x1D700}$
as a function of
![]() $U$
on a logarithmic scale for datasets S1D2C, D2 and S3D. The solid line shows the scaling
$U$
on a logarithmic scale for datasets S1D2C, D2 and S3D. The solid line shows the scaling
![]() $\unicode[STIX]{x1D700}\sim U^{3}$
, which corresponds to a fixed value of
$\unicode[STIX]{x1D700}\sim U^{3}$
, which corresponds to a fixed value of
![]() $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
![]() $L_{f}$
. The grey shading indicates different values of
$L_{f}$
. The grey shading indicates different values of
![]() $\unicode[STIX]{x1D70C}_{f}$
. A trend can be observed: for a fixed value of
$\unicode[STIX]{x1D70C}_{f}$
. A trend can be observed: for a fixed value of
![]() $U$
, the dissipation rate decreases with increasing forcing helicity.
$U$
, the dissipation rate decreases with increasing forcing helicity.
6 Conclusions
Upper bounds for the dimensionless dissipation coefficient
![]() $\unicode[STIX]{x1D6FD}$
have been evaluated analytically depending on the relative helicity
$\unicode[STIX]{x1D6FD}$
have been evaluated analytically depending on the relative helicity
![]() $\unicode[STIX]{x1D70C}_{f}$
of the external forcing. The main results were: (i) helical forces lead to a lower estimate of the flux compared to a non-helical force, (ii) a time-dependent force results in a larger estimate of the flux compared to a static force, owing to an extra term appearing in the upper bound. The calculated values of
$\unicode[STIX]{x1D70C}_{f}$
of the external forcing. The main results were: (i) helical forces lead to a lower estimate of the flux compared to a non-helical force, (ii) a time-dependent force results in a larger estimate of the flux compared to a static force, owing to an extra term appearing in the upper bound. The calculated values of
![]() $\unicode[STIX]{x1D6FD}^{(\unicode[STIX]{x1D70C}_{f})}$
were subsequently compared with values obtained from DNSs which differed in the helicity level, the time dependence and the dimensionality of the forcing. The agreement between the theoretically and numerically obtained values is good concerning the ratio
$\unicode[STIX]{x1D6FD}^{(\unicode[STIX]{x1D70C}_{f})}$
were subsequently compared with values obtained from DNSs which differed in the helicity level, the time dependence and the dimensionality of the forcing. The agreement between the theoretically and numerically obtained values is good concerning the ratio
![]() $\unicode[STIX]{x1D6FD}^{(\unicode[STIX]{x1D70C}_{f})}/\unicode[STIX]{x1D6FD}^{(0)}$
despite a difference of an order of magnitude between theory and simulation results concerning the single quantities
$\unicode[STIX]{x1D6FD}^{(\unicode[STIX]{x1D70C}_{f})}/\unicode[STIX]{x1D6FD}^{(0)}$
despite a difference of an order of magnitude between theory and simulation results concerning the single quantities
![]() $\unicode[STIX]{x1D6FD}^{(\unicode[STIX]{x1D70C}_{f})}$
. Time-dependent forces do not lead to larger values of
$\unicode[STIX]{x1D6FD}^{(\unicode[STIX]{x1D70C}_{f})}$
. Time-dependent forces do not lead to larger values of
![]() $\unicode[STIX]{x1D6FD}^{(\unicode[STIX]{x1D70C}_{f})}$
compared to static forces, and the value of the ratio
$\unicode[STIX]{x1D6FD}^{(\unicode[STIX]{x1D70C}_{f})}$
compared to static forces, and the value of the ratio
![]() $\unicode[STIX]{x1D6FD}^{(\unicode[STIX]{x1D70C}_{f})}/\unicode[STIX]{x1D6FD}^{(0)}$
is comparable between static and dynamic forces. This indicates that the extra term that appears in the upper bounds for dynamic forces arises from an analytical difficulty in deriving tight estimates for dynamic forces and does not carry any relevant information concerning the value of the energy flux.
$\unicode[STIX]{x1D6FD}^{(\unicode[STIX]{x1D70C}_{f})}/\unicode[STIX]{x1D6FD}^{(0)}$
is comparable between static and dynamic forces. This indicates that the extra term that appears in the upper bounds for dynamic forces arises from an analytical difficulty in deriving tight estimates for dynamic forces and does not carry any relevant information concerning the value of the energy flux.
In summary, even though the actual estimates are not very tight, the upper bound theory captures well the dependence of helicity, i.e. of a topological property, of the force on the forward flux of kinetic energy not only qualitatively but also quantitatively. This result is robust under differences in the dynamical properties of the forcing. The forward flux of energy across the scales can thus be described by the spatial regularity and the helicity of the force, which in principle can be adjusted by the experimenter. Hence it may be possible to devise a particular type of force which controls this forward flux of energy, thus leading to a suppression or enhancement of turbulence and thus of e.g. nonlinear mixing or drag. The present results also suggest that detailed knowledge of the topological properties of a naturally occurring external force field may enable some predictions about the level of turbulence in a flow. Since
![]() $\unicode[STIX]{x1D6FD}$
is related to the model coefficient relating the turbulent kinetic energy to its dissipation rate in the
$\unicode[STIX]{x1D6FD}$
is related to the model coefficient relating the turbulent kinetic energy to its dissipation rate in the
![]() $k$
–
$k$
–
![]() $\unicode[STIX]{x1D700}$
model and to the eddy viscosity in LES, the present results may also be useful in practical applications concerned with flows subject to helical forces such as in atmospheric physics.
$\unicode[STIX]{x1D700}$
model and to the eddy viscosity in LES, the present results may also be useful in practical applications concerned with flows subject to helical forces such as in atmospheric physics.
Acknowledgements
Helpful discussions and suggestions by B. Eckhardt, C. Doering, L. Biferale and M. Buzzicotti are gratefully acknowledged. Part of the numerical work was carried out during a postdoctoral position at the University of Rome ‘Tor Vergata’ funded through the European Union’s Seventh Framework Programme (FP7/2007-2013) under grant agreement no. 339032.
Appendix A. Time-dependent forcing
Let
![]() $\boldsymbol{f}=f_{0}g(t)\unicode[STIX]{x1D753}(\boldsymbol{x}/L_{f})$
and consider a Gaussian filter function
$\boldsymbol{f}=f_{0}g(t)\unicode[STIX]{x1D753}(\boldsymbol{x}/L_{f})$
and consider a Gaussian filter function
![]() $G^{\unicode[STIX]{x1D70F}}$
, with characteristic time scale
$G^{\unicode[STIX]{x1D70F}}$
, with characteristic time scale
![]() $\unicode[STIX]{x1D70F}$
. From the energy inequality one obtains an upper bound for
$\unicode[STIX]{x1D70F}$
. From the energy inequality one obtains an upper bound for
![]() $\unicode[STIX]{x1D700}$
by the same boundedness argument as in the case of static forcing:
$\unicode[STIX]{x1D700}$
by the same boundedness argument as in the case of static forcing:
The next step proceeds similarly to the static case by taking the inner product of all terms in the Navier–Stokes equations with
![]() $G^{\unicode[STIX]{x1D70F}}\ast (-\unicode[STIX]{x1D6E5})^{-M}\boldsymbol{f}$
, and the arguments concerning the spatial dependence of the force are exactly the same. Each term in equation (3.2) is now considered separately, beginning with the new term on the left-hand side,
$G^{\unicode[STIX]{x1D70F}}\ast (-\unicode[STIX]{x1D6E5})^{-M}\boldsymbol{f}$
, and the arguments concerning the spatial dependence of the force are exactly the same. Each term in equation (3.2) is now considered separately, beginning with the new term on the left-hand side,
 $$\begin{eqnarray}\displaystyle -\langle ((-\unicode[STIX]{x1D6E5})^{-M}\unicode[STIX]{x2202}_{t}(G^{\unicode[STIX]{x1D70F}}\ast f_{i}),u_{i})\rangle _{t} & = & \displaystyle -\langle ((-\unicode[STIX]{x1D6E5})^{-M}\unicode[STIX]{x2202}_{t}G^{\unicode[STIX]{x1D70F}}\ast f_{i},u_{i})\rangle _{t}\nonumber\\ \displaystyle & = & \displaystyle \left\langle \frac{\unicode[STIX]{x1D70F}^{2}}{t^{3}}((-\unicode[STIX]{x1D6E5})^{-M}G^{\unicode[STIX]{x1D70F}}\ast f_{i},u_{i})\right\rangle _{t},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -\langle ((-\unicode[STIX]{x1D6E5})^{-M}\unicode[STIX]{x2202}_{t}(G^{\unicode[STIX]{x1D70F}}\ast f_{i}),u_{i})\rangle _{t} & = & \displaystyle -\langle ((-\unicode[STIX]{x1D6E5})^{-M}\unicode[STIX]{x2202}_{t}G^{\unicode[STIX]{x1D70F}}\ast f_{i},u_{i})\rangle _{t}\nonumber\\ \displaystyle & = & \displaystyle \left\langle \frac{\unicode[STIX]{x1D70F}^{2}}{t^{3}}((-\unicode[STIX]{x1D6E5})^{-M}G^{\unicode[STIX]{x1D70F}}\ast f_{i},u_{i})\right\rangle _{t},\end{eqnarray}$$
which results in
For the terms on the right-hand side one obtains
where in the last line
![]() $\langle (G^{\unicode[STIX]{x1D70F}}\ast g)g\rangle _{t}>0$
. Hence one obtains the upper bound
$\langle (G^{\unicode[STIX]{x1D70F}}\ast g)g\rangle _{t}>0$
. Hence one obtains the upper bound
which substituted into (A 1) yields after some rearrangement a bound on
![]() $\unicode[STIX]{x1D6FD}$
:
$\unicode[STIX]{x1D6FD}$
:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FD} & {\leqslant} & \displaystyle \frac{|\langle G^{\unicode[STIX]{x1D70F}}\ast g\rangle _{t}|\langle g\rangle _{t}}{\langle (G^{\unicode[STIX]{x1D70F}}\ast g)g\rangle _{t}}\left(\frac{|\langle (\unicode[STIX]{x1D70F}^{2}/t^{3})G^{\unicode[STIX]{x1D70F}}\ast g\rangle _{t}|}{|\langle G^{\unicode[STIX]{x1D70F}}\ast g\rangle _{t}|}\frac{L_{f}}{U}\frac{\Vert (-\unicode[STIX]{x1D6E5})^{-M}\unicode[STIX]{x1D753}\Vert _{2}\Vert \unicode[STIX]{x1D753}\Vert _{2}}{\Vert (-\unicode[STIX]{x1D6E5})^{-M/2}\unicode[STIX]{x1D753}\Vert _{2}^{2}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{\Vert \unicode[STIX]{x1D735}(-\unicode[STIX]{x1D6E5})^{-M}\unicode[STIX]{x1D753}\Vert _{\infty }\Vert \unicode[STIX]{x1D753}\Vert _{2}}{\Vert (-\unicode[STIX]{x1D6E5})^{-M/2}\unicode[STIX]{x1D753}\Vert _{2}^{2}}+\frac{1}{Re}\frac{\Vert (-\unicode[STIX]{x1D6E5})^{-M+1}\unicode[STIX]{x1D753}\Vert _{2}\Vert \unicode[STIX]{x1D753}\Vert _{2}}{\Vert (-\unicode[STIX]{x1D6E5})^{-M/2}\unicode[STIX]{x1D753}\Vert _{2}^{2}}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FD} & {\leqslant} & \displaystyle \frac{|\langle G^{\unicode[STIX]{x1D70F}}\ast g\rangle _{t}|\langle g\rangle _{t}}{\langle (G^{\unicode[STIX]{x1D70F}}\ast g)g\rangle _{t}}\left(\frac{|\langle (\unicode[STIX]{x1D70F}^{2}/t^{3})G^{\unicode[STIX]{x1D70F}}\ast g\rangle _{t}|}{|\langle G^{\unicode[STIX]{x1D70F}}\ast g\rangle _{t}|}\frac{L_{f}}{U}\frac{\Vert (-\unicode[STIX]{x1D6E5})^{-M}\unicode[STIX]{x1D753}\Vert _{2}\Vert \unicode[STIX]{x1D753}\Vert _{2}}{\Vert (-\unicode[STIX]{x1D6E5})^{-M/2}\unicode[STIX]{x1D753}\Vert _{2}^{2}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,\frac{\Vert \unicode[STIX]{x1D735}(-\unicode[STIX]{x1D6E5})^{-M}\unicode[STIX]{x1D753}\Vert _{\infty }\Vert \unicode[STIX]{x1D753}\Vert _{2}}{\Vert (-\unicode[STIX]{x1D6E5})^{-M/2}\unicode[STIX]{x1D753}\Vert _{2}^{2}}+\frac{1}{Re}\frac{\Vert (-\unicode[STIX]{x1D6E5})^{-M+1}\unicode[STIX]{x1D753}\Vert _{2}\Vert \unicode[STIX]{x1D753}\Vert _{2}}{\Vert (-\unicode[STIX]{x1D6E5})^{-M/2}\unicode[STIX]{x1D753}\Vert _{2}^{2}}\right).\end{eqnarray}$$
The summand on the right-hand side of the above inequality can be further approximated by considering
since both
![]() $G^{\unicode[STIX]{x1D70F}}$
and
$G^{\unicode[STIX]{x1D70F}}$
and
![]() $g$
are bounded, and
$g$
are bounded, and
since
![]() $G^{\unicode[STIX]{x1D70F}}=\exp (-\unicode[STIX]{x1D70F}^{2}/t^{2})$
goes to zero faster than any power for
$G^{\unicode[STIX]{x1D70F}}=\exp (-\unicode[STIX]{x1D70F}^{2}/t^{2})$
goes to zero faster than any power for
![]() $t\rightarrow 0$
. The average value is thus dominated by the integrand at
$t\rightarrow 0$
. The average value is thus dominated by the integrand at
![]() $t=\unicode[STIX]{x1D70F}$
and can be approximated as
$t=\unicode[STIX]{x1D70F}$
and can be approximated as
such that with the definitions
![]() $\unicode[STIX]{x1D714}_{f}=1/\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D714}_{f}=1/\unicode[STIX]{x1D70F}$
and
![]() $\unicode[STIX]{x1D714}=U/L_{f}$
one obtains (3.3).
$\unicode[STIX]{x1D714}=U/L_{f}$
one obtains (3.3).
Appendix B. Evaluation of norms for shape functions
 $\unicode[STIX]{x1D753}^{\unicode[STIX]{x1D70C}_{f}}$
.
$\unicode[STIX]{x1D753}^{\unicode[STIX]{x1D70C}_{f}}$
.
The terms to evaluate explicitly are
![]() $\Vert \unicode[STIX]{x1D735}(-\unicode[STIX]{x1D6E5})^{-M}\unicode[STIX]{x1D753}^{\unicode[STIX]{x1D70C}_{f}}\Vert _{\infty }$
and
$\Vert \unicode[STIX]{x1D735}(-\unicode[STIX]{x1D6E5})^{-M}\unicode[STIX]{x1D753}^{\unicode[STIX]{x1D70C}_{f}}\Vert _{\infty }$
and
![]() $\Vert \unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}\Vert ^{2}$
. We first establish that the fully helical shape functions are normalised to unity:
$\Vert \unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}\Vert ^{2}$
. We first establish that the fully helical shape functions are normalised to unity:
 $$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D753}^{(\pm 1)}\Vert _{2}^{2} & = & \displaystyle \frac{1}{|[0,1]^{3}|}\frac{1}{A^{2}+B^{2}+C^{2}}\int _{[0,1]^{3}}\text{d}x\,\text{d}y\,\text{d}z\,(\!B^{2}(\sin (2\unicode[STIX]{x03C0}x)^{2}+\cos (2\unicode[STIX]{x03C0}x)^{2})\nonumber\\ \displaystyle & & \displaystyle +\,C^{2}(\sin (2\unicode[STIX]{x03C0}y)^{2}+\cos (2\unicode[STIX]{x03C0}y)^{2})+A^{2}(\sin (2\unicode[STIX]{x03C0}z)^{2}+\cos (2\unicode[STIX]{x03C0}z)^{2})\!)=1.\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D753}^{(\pm 1)}\Vert _{2}^{2} & = & \displaystyle \frac{1}{|[0,1]^{3}|}\frac{1}{A^{2}+B^{2}+C^{2}}\int _{[0,1]^{3}}\text{d}x\,\text{d}y\,\text{d}z\,(\!B^{2}(\sin (2\unicode[STIX]{x03C0}x)^{2}+\cos (2\unicode[STIX]{x03C0}x)^{2})\nonumber\\ \displaystyle & & \displaystyle +\,C^{2}(\sin (2\unicode[STIX]{x03C0}y)^{2}+\cos (2\unicode[STIX]{x03C0}y)^{2})+A^{2}(\sin (2\unicode[STIX]{x03C0}z)^{2}+\cos (2\unicode[STIX]{x03C0}z)^{2})\!)=1.\qquad\end{eqnarray}$$
Since
![]() $\unicode[STIX]{x1D753}^{(\pm 1)}$
are eigenfunctions of the curl operator, they are also orthogonal with respect to the
$\unicode[STIX]{x1D753}^{(\pm 1)}$
are eigenfunctions of the curl operator, they are also orthogonal with respect to the
![]() $L^{2}$
-inner product, i.e.
$L^{2}$
-inner product, i.e.
![]() $(\unicode[STIX]{x1D753}^{(1)},\unicode[STIX]{x1D753}^{(-1)})=0$
. For a shape function with fractional relative helicity we therefore obtain
$(\unicode[STIX]{x1D753}^{(1)},\unicode[STIX]{x1D753}^{(-1)})=0$
. For a shape function with fractional relative helicity we therefore obtain
 $$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D719}^{(\unicode[STIX]{x1D70C}_{f})}\Vert _{2}^{2} & = & \displaystyle \left(\sqrt{\frac{1+\unicode[STIX]{x1D70C}_{f}}{2}}\unicode[STIX]{x1D753}^{(1)}+\sqrt{\frac{1-\unicode[STIX]{x1D70C}_{f}}{2}}\unicode[STIX]{x1D753}^{(-1)},\sqrt{\frac{1+\unicode[STIX]{x1D70C}_{f}}{2}}\unicode[STIX]{x1D753}^{(1)}+\sqrt{\frac{1-\unicode[STIX]{x1D70C}_{f}}{2}}\unicode[STIX]{x1D753}^{(-1)}\right)\nonumber\\ \displaystyle & = & \displaystyle \frac{1+\unicode[STIX]{x1D70C}_{f}}{2}\Vert \unicode[STIX]{x1D753}^{(1)}\Vert _{2}^{2}+\frac{1-\unicode[STIX]{x1D70C}_{f}}{2}\Vert \unicode[STIX]{x1D753}^{(-1)}\Vert _{2}^{2}=1.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D719}^{(\unicode[STIX]{x1D70C}_{f})}\Vert _{2}^{2} & = & \displaystyle \left(\sqrt{\frac{1+\unicode[STIX]{x1D70C}_{f}}{2}}\unicode[STIX]{x1D753}^{(1)}+\sqrt{\frac{1-\unicode[STIX]{x1D70C}_{f}}{2}}\unicode[STIX]{x1D753}^{(-1)},\sqrt{\frac{1+\unicode[STIX]{x1D70C}_{f}}{2}}\unicode[STIX]{x1D753}^{(1)}+\sqrt{\frac{1-\unicode[STIX]{x1D70C}_{f}}{2}}\unicode[STIX]{x1D753}^{(-1)}\right)\nonumber\\ \displaystyle & = & \displaystyle \frac{1+\unicode[STIX]{x1D70C}_{f}}{2}\Vert \unicode[STIX]{x1D753}^{(1)}\Vert _{2}^{2}+\frac{1-\unicode[STIX]{x1D70C}_{f}}{2}\Vert \unicode[STIX]{x1D753}^{(-1)}\Vert _{2}^{2}=1.\end{eqnarray}$$
The term
![]() $\Vert \unicode[STIX]{x1D735}(-\unicode[STIX]{x1D6E5})^{-M}\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}\Vert _{\infty }=\Vert \unicode[STIX]{x1D735}\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}\Vert _{\infty }/(2\unicode[STIX]{x03C0})^{2M}$
is calculated by first considering the gradients of the shape functions:
$\Vert \unicode[STIX]{x1D735}(-\unicode[STIX]{x1D6E5})^{-M}\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}\Vert _{\infty }=\Vert \unicode[STIX]{x1D735}\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}\Vert _{\infty }/(2\unicode[STIX]{x03C0})^{2M}$
is calculated by first considering the gradients of the shape functions:
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\unicode[STIX]{x1D753}^{(1)}=\frac{2\unicode[STIX]{x03C0}}{\sqrt{A^{2}+B^{2}+C^{2}}}\left(\begin{array}{@{}ccc@{}}0 & B\cos 2\unicode[STIX]{x03C0}x & -B\sin 2\unicode[STIX]{x03C0}x\\ -C\sin 2\unicode[STIX]{x03C0}y & 0 & C\cos 2\unicode[STIX]{x03C0}y\\ A\cos 2\unicode[STIX]{x03C0}z & -A\sin 2\unicode[STIX]{x03C0}z & 0\end{array}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\unicode[STIX]{x1D753}^{(1)}=\frac{2\unicode[STIX]{x03C0}}{\sqrt{A^{2}+B^{2}+C^{2}}}\left(\begin{array}{@{}ccc@{}}0 & B\cos 2\unicode[STIX]{x03C0}x & -B\sin 2\unicode[STIX]{x03C0}x\\ -C\sin 2\unicode[STIX]{x03C0}y & 0 & C\cos 2\unicode[STIX]{x03C0}y\\ A\cos 2\unicode[STIX]{x03C0}z & -A\sin 2\unicode[STIX]{x03C0}z & 0\end{array}\right), & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\unicode[STIX]{x1D753}^{(-1)}=\frac{2\unicode[STIX]{x03C0}}{\sqrt{A^{2}+B^{2}+C^{2}}}\left(\begin{array}{@{}ccc@{}}0 & -B\sin 2\unicode[STIX]{x03C0}x & B\cos 2\unicode[STIX]{x03C0}x\\ C\cos 2\unicode[STIX]{x03C0}y & 0 & -C\sin 2\unicode[STIX]{x03C0}y\\ -A\sin 2\unicode[STIX]{x03C0}z & A\cos 2\unicode[STIX]{x03C0}z & 0\end{array}\right). & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\unicode[STIX]{x1D753}^{(-1)}=\frac{2\unicode[STIX]{x03C0}}{\sqrt{A^{2}+B^{2}+C^{2}}}\left(\begin{array}{@{}ccc@{}}0 & -B\sin 2\unicode[STIX]{x03C0}x & B\cos 2\unicode[STIX]{x03C0}x\\ C\cos 2\unicode[STIX]{x03C0}y & 0 & -C\sin 2\unicode[STIX]{x03C0}y\\ -A\sin 2\unicode[STIX]{x03C0}z & A\cos 2\unicode[STIX]{x03C0}z & 0\end{array}\right). & \displaystyle\end{eqnarray}$$
Now the
![]() $L^{\infty }$
-norm of
$L^{\infty }$
-norm of
![]() $\unicode[STIX]{x1D735}\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}$
can be calculated. For this purpose, set
$\unicode[STIX]{x1D735}\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}$
can be calculated. For this purpose, set
![]() $\unicode[STIX]{x1D6FC}\equiv \sqrt{(1+\unicode[STIX]{x1D70C}_{f})/2}$
and
$\unicode[STIX]{x1D6FC}\equiv \sqrt{(1+\unicode[STIX]{x1D70C}_{f})/2}$
and
![]() $\unicode[STIX]{x1D6FE}\equiv \sqrt{(1-\unicode[STIX]{x1D70C}_{f})/2}$
, such that
$\unicode[STIX]{x1D6FE}\equiv \sqrt{(1-\unicode[STIX]{x1D70C}_{f})/2}$
, such that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \Vert \unicode[STIX]{x1D735}\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}\Vert _{\infty }=\sup _{\boldsymbol{x}\in [0,1]^{3}}\left(\mathop{\sum }_{i,j=1}^{3}\unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D719}_{j}^{(\unicode[STIX]{x1D70C}_{f})}\unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D719}_{j}^{(\unicode[STIX]{x1D70C}_{f})}\right)^{1/2}=\sup _{\boldsymbol{ x}\in [0,1]^{3}}\left(\mathop{\sum }_{i,j=1}^{3}\left[\unicode[STIX]{x2202}_{i}\left(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D719}_{j}^{(1)}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D719}_{j}^{(-1)}\right)\right]^{2}\right)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{2\unicode[STIX]{x03C0}}{\sqrt{A^{2}+B^{2}+C^{2}}}\sup _{\boldsymbol{x}\in [0,1]^{3}} (\!B^{2}[(\unicode[STIX]{x1D6FC}\cos 2\unicode[STIX]{x03C0}x-\unicode[STIX]{x1D6FE}\sin 2\unicode[STIX]{x03C0}x)^{2}+(\unicode[STIX]{x1D6FE}\cos 2\unicode[STIX]{x03C0}x-\unicode[STIX]{x1D6FC}\sin 2\unicode[STIX]{x03C0}x)^{2}]\nonumber\\ \displaystyle & & \displaystyle \qquad \quad +\,C^{2}[(\unicode[STIX]{x1D6FC}\cos 2\unicode[STIX]{x03C0}y-\unicode[STIX]{x1D6FE}\sin 2\unicode[STIX]{x03C0}y)^{2}+(\unicode[STIX]{x1D6FE}\cos 2\unicode[STIX]{x03C0}y-\unicode[STIX]{x1D6FC}\sin 2\unicode[STIX]{x03C0}y)^{2}]\nonumber\\ \displaystyle & & \displaystyle \qquad \quad +\,A^{2}[(\unicode[STIX]{x1D6FC}\cos 2\unicode[STIX]{x03C0}z-\unicode[STIX]{x1D6FE}\sin 2\unicode[STIX]{x03C0}z)^{2}+(\unicode[STIX]{x1D6FE}\cos 2\unicode[STIX]{x03C0}z-\unicode[STIX]{x1D6FC}\sin 2\unicode[STIX]{x03C0}z)^{2}]\!\!)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{2\unicode[STIX]{x03C0}}{\sqrt{A^{2}+B^{2}+C^{2}}}\sup _{\boldsymbol{x}\in [0,1]^{3}} (\!B^{2}[\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FE}^{2}-4\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}\cos 2\unicode[STIX]{x03C0}x\sin 2\unicode[STIX]{x03C0}x]\nonumber\\ \displaystyle & & \displaystyle \qquad \quad +\,C^{2}[\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FE}^{2}-4\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}\cos 2\unicode[STIX]{x03C0}y\sin 2\unicode[STIX]{x03C0}y]+A^{2}[\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FE}^{2}-4\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}\cos 2\unicode[STIX]{x03C0}z\sin 2\unicode[STIX]{x03C0}z]\!\!)^{1/2}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \Vert \unicode[STIX]{x1D735}\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}\Vert _{\infty }=\sup _{\boldsymbol{x}\in [0,1]^{3}}\left(\mathop{\sum }_{i,j=1}^{3}\unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D719}_{j}^{(\unicode[STIX]{x1D70C}_{f})}\unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D719}_{j}^{(\unicode[STIX]{x1D70C}_{f})}\right)^{1/2}=\sup _{\boldsymbol{ x}\in [0,1]^{3}}\left(\mathop{\sum }_{i,j=1}^{3}\left[\unicode[STIX]{x2202}_{i}\left(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D719}_{j}^{(1)}+\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D719}_{j}^{(-1)}\right)\right]^{2}\right)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{2\unicode[STIX]{x03C0}}{\sqrt{A^{2}+B^{2}+C^{2}}}\sup _{\boldsymbol{x}\in [0,1]^{3}} (\!B^{2}[(\unicode[STIX]{x1D6FC}\cos 2\unicode[STIX]{x03C0}x-\unicode[STIX]{x1D6FE}\sin 2\unicode[STIX]{x03C0}x)^{2}+(\unicode[STIX]{x1D6FE}\cos 2\unicode[STIX]{x03C0}x-\unicode[STIX]{x1D6FC}\sin 2\unicode[STIX]{x03C0}x)^{2}]\nonumber\\ \displaystyle & & \displaystyle \qquad \quad +\,C^{2}[(\unicode[STIX]{x1D6FC}\cos 2\unicode[STIX]{x03C0}y-\unicode[STIX]{x1D6FE}\sin 2\unicode[STIX]{x03C0}y)^{2}+(\unicode[STIX]{x1D6FE}\cos 2\unicode[STIX]{x03C0}y-\unicode[STIX]{x1D6FC}\sin 2\unicode[STIX]{x03C0}y)^{2}]\nonumber\\ \displaystyle & & \displaystyle \qquad \quad +\,A^{2}[(\unicode[STIX]{x1D6FC}\cos 2\unicode[STIX]{x03C0}z-\unicode[STIX]{x1D6FE}\sin 2\unicode[STIX]{x03C0}z)^{2}+(\unicode[STIX]{x1D6FE}\cos 2\unicode[STIX]{x03C0}z-\unicode[STIX]{x1D6FC}\sin 2\unicode[STIX]{x03C0}z)^{2}]\!\!)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{2\unicode[STIX]{x03C0}}{\sqrt{A^{2}+B^{2}+C^{2}}}\sup _{\boldsymbol{x}\in [0,1]^{3}} (\!B^{2}[\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FE}^{2}-4\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}\cos 2\unicode[STIX]{x03C0}x\sin 2\unicode[STIX]{x03C0}x]\nonumber\\ \displaystyle & & \displaystyle \qquad \quad +\,C^{2}[\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FE}^{2}-4\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}\cos 2\unicode[STIX]{x03C0}y\sin 2\unicode[STIX]{x03C0}y]+A^{2}[\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FE}^{2}-4\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}\cos 2\unicode[STIX]{x03C0}z\sin 2\unicode[STIX]{x03C0}z]\!\!)^{1/2}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Since
![]() $\sqrt{a}$
is a monotonic function for
$\sqrt{a}$
is a monotonic function for
![]() $a\in \mathbb{R}$
, the supremum is realised at a point
$a\in \mathbb{R}$
, the supremum is realised at a point
![]() $\boldsymbol{x}=(x,y,z)\in [0,1]^{3}$
where each summand is maximal. This is the case for
$\boldsymbol{x}=(x,y,z)\in [0,1]^{3}$
where each summand is maximal. This is the case for
![]() $x=y=z=1/8$
since
$x=y=z=1/8$
since
![]() $\cos \unicode[STIX]{x03C0}/4=1/\sqrt{2}$
and
$\cos \unicode[STIX]{x03C0}/4=1/\sqrt{2}$
and
![]() $\sin \unicode[STIX]{x03C0}/4=-1/\sqrt{2}$
, such that
$\sin \unicode[STIX]{x03C0}/4=-1/\sqrt{2}$
, such that
 $$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D735}\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}\Vert _{\infty } & = & \displaystyle \frac{2\unicode[STIX]{x03C0}}{\sqrt{A^{2}+B^{2}+C^{2}}}((A^{2}+B^{2}+C^{2})[\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FE}^{2}+2\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}])^{1/2}=2\unicode[STIX]{x03C0}|\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FE}|\nonumber\\ \displaystyle & = & \displaystyle \sqrt{2}\unicode[STIX]{x03C0}\left(\sqrt{1-\unicode[STIX]{x1D70C}_{f}}+\sqrt{1+\unicode[STIX]{x1D70C}_{f}}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D735}\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}\Vert _{\infty } & = & \displaystyle \frac{2\unicode[STIX]{x03C0}}{\sqrt{A^{2}+B^{2}+C^{2}}}((A^{2}+B^{2}+C^{2})[\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FE}^{2}+2\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}])^{1/2}=2\unicode[STIX]{x03C0}|\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FE}|\nonumber\\ \displaystyle & = & \displaystyle \sqrt{2}\unicode[STIX]{x03C0}\left(\sqrt{1-\unicode[STIX]{x1D70C}_{f}}+\sqrt{1+\unicode[STIX]{x1D70C}_{f}}\right).\end{eqnarray}$$
Finally, one obtains
Appendix C. Evaluation of the integrals in (4.24) for bidirectional static forces
Consider the two static forces
![]() $\unicode[STIX]{x1D753}^{(\pm 1)}$
for
$\unicode[STIX]{x1D753}^{(\pm 1)}$
for
![]() $A=B=0$
. For simplicity we set
$A=B=0$
. For simplicity we set
![]() $C=1$
, such that
$C=1$
, such that
 $$\begin{eqnarray}-\unicode[STIX]{x2202}_{y}^{-1}\unicode[STIX]{x1D753}^{(1)}=\frac{1}{2\unicode[STIX]{x03C0}}\left(\begin{array}{@{}c@{}}-\text{sin}2\unicode[STIX]{x03C0}y\\ 0\\ \cos 2\unicode[STIX]{x03C0}y\end{array}\right)\quad \text{and}\quad -\unicode[STIX]{x2202}_{y}^{-1}\unicode[STIX]{x1D753}^{(-1)}=\frac{1}{2\unicode[STIX]{x03C0}}\left(\begin{array}{@{}c@{}}\cos 2\unicode[STIX]{x03C0}y\\ 0\\ -\text{sin}2\unicode[STIX]{x03C0}y\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}-\unicode[STIX]{x2202}_{y}^{-1}\unicode[STIX]{x1D753}^{(1)}=\frac{1}{2\unicode[STIX]{x03C0}}\left(\begin{array}{@{}c@{}}-\text{sin}2\unicode[STIX]{x03C0}y\\ 0\\ \cos 2\unicode[STIX]{x03C0}y\end{array}\right)\quad \text{and}\quad -\unicode[STIX]{x2202}_{y}^{-1}\unicode[STIX]{x1D753}^{(-1)}=\frac{1}{2\unicode[STIX]{x03C0}}\left(\begin{array}{@{}c@{}}\cos 2\unicode[STIX]{x03C0}y\\ 0\\ -\text{sin}2\unicode[STIX]{x03C0}y\end{array}\right),\end{eqnarray}$$
such that
 $$\begin{eqnarray}-\unicode[STIX]{x2202}_{y}^{-1}\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}=\sqrt{\frac{1+\unicode[STIX]{x1D70C}_{f}}{2}}\left(\begin{array}{@{}c@{}}-\text{sin}2\unicode[STIX]{x03C0}y\\ 0\\ \cos 2\unicode[STIX]{x03C0}y\end{array}\right)+\sqrt{\frac{1-\unicode[STIX]{x1D70C}_{f}}{2}}\left(\begin{array}{@{}c@{}}\cos 2\unicode[STIX]{x03C0}y\\ 0\\ -\text{sin}2\unicode[STIX]{x03C0}y\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}-\unicode[STIX]{x2202}_{y}^{-1}\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}=\sqrt{\frac{1+\unicode[STIX]{x1D70C}_{f}}{2}}\left(\begin{array}{@{}c@{}}-\text{sin}2\unicode[STIX]{x03C0}y\\ 0\\ \cos 2\unicode[STIX]{x03C0}y\end{array}\right)+\sqrt{\frac{1-\unicode[STIX]{x1D70C}_{f}}{2}}\left(\begin{array}{@{}c@{}}\cos 2\unicode[STIX]{x03C0}y\\ 0\\ -\text{sin}2\unicode[STIX]{x03C0}y\end{array}\right).\end{eqnarray}$$
The evaluation of the integral on the right-hand side of (4.24) proceeds by explicit calculation. For convenience, set
![]() $\unicode[STIX]{x1D6FC}\equiv \sqrt{(1+\unicode[STIX]{x1D70C}_{f})/2}$
and
$\unicode[STIX]{x1D6FC}\equiv \sqrt{(1+\unicode[STIX]{x1D70C}_{f})/2}$
and
![]() $\unicode[STIX]{x1D6FE}\equiv \sqrt{(1-\unicode[STIX]{x1D70C}_{f})/2}$
, such that
$\unicode[STIX]{x1D6FE}\equiv \sqrt{(1-\unicode[STIX]{x1D70C}_{f})/2}$
, such that
 $$\begin{eqnarray}\displaystyle \int _{0}^{1}\text{d}y\,|\unicode[STIX]{x2202}_{y}^{-1}\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}| & = & \displaystyle \frac{1}{2\unicode[STIX]{x03C0}}\int _{0}^{1}\text{d}y\,\sqrt{(\unicode[STIX]{x1D6FC}\cos 2\unicode[STIX]{x03C0}y-\unicode[STIX]{x1D6FE}\sin 2\unicode[STIX]{x03C0}y)^{2}+(\unicode[STIX]{x1D6FE}\cos 2\unicode[STIX]{x03C0}y-\unicode[STIX]{x1D6FC}\sin 2\unicode[STIX]{x03C0}y)^{2}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2\unicode[STIX]{x03C0}}\int _{0}^{1}\text{d}y\,\sqrt{\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FE}^{2}-2\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}\sin 4\unicode[STIX]{x03C0}y}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2\unicode[STIX]{x03C0}}\int _{0}^{1}\text{d}y\,\sqrt{1-\sqrt{1-\unicode[STIX]{x1D70C}_{f}^{2}}\sin 4\unicode[STIX]{x03C0}y},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{0}^{1}\text{d}y\,|\unicode[STIX]{x2202}_{y}^{-1}\unicode[STIX]{x1D753}^{(\unicode[STIX]{x1D70C}_{f})}| & = & \displaystyle \frac{1}{2\unicode[STIX]{x03C0}}\int _{0}^{1}\text{d}y\,\sqrt{(\unicode[STIX]{x1D6FC}\cos 2\unicode[STIX]{x03C0}y-\unicode[STIX]{x1D6FE}\sin 2\unicode[STIX]{x03C0}y)^{2}+(\unicode[STIX]{x1D6FE}\cos 2\unicode[STIX]{x03C0}y-\unicode[STIX]{x1D6FC}\sin 2\unicode[STIX]{x03C0}y)^{2}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2\unicode[STIX]{x03C0}}\int _{0}^{1}\text{d}y\,\sqrt{\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FE}^{2}-2\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}\sin 4\unicode[STIX]{x03C0}y}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2\unicode[STIX]{x03C0}}\int _{0}^{1}\text{d}y\,\sqrt{1-\sqrt{1-\unicode[STIX]{x1D70C}_{f}^{2}}\sin 4\unicode[STIX]{x03C0}y},\end{eqnarray}$$
where the integrand has no closed-form antiderivative. For the extreme cases
![]() $\unicode[STIX]{x1D70C}_{f}=\pm 1$
and
$\unicode[STIX]{x1D70C}_{f}=\pm 1$
and
![]() $\unicode[STIX]{x1D70C}_{f}=0$
, one obtains
$\unicode[STIX]{x1D70C}_{f}=0$
, one obtains
 $$\begin{eqnarray}\displaystyle \int _{0}^{1}\text{d}y\,|\unicode[STIX]{x2202}_{y}^{-1}\unicode[STIX]{x1D753}^{(0)}| & = & \displaystyle \frac{1}{2\unicode[STIX]{x03C0}}\int _{0}^{1}\text{d}y\,\sqrt{1-\sin 4\unicode[STIX]{x03C0}y}=\frac{1}{2\unicode[STIX]{x03C0}}\int _{0}^{1}\text{d}y\,\sqrt{(\cos 2\unicode[STIX]{x03C0}y-\sin 2\unicode[STIX]{x03C0}y)^{2}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2\unicode[STIX]{x03C0}}\int _{0}^{1}\text{d}y\,\sqrt{2}|\sin (2\unicode[STIX]{x03C0}y+\unicode[STIX]{x03C0}/4)|=\frac{1}{2\unicode[STIX]{x03C0}}\int _{0}^{1}\text{d}y\,\sqrt{2}|\sin 2\unicode[STIX]{x03C0}y|=\frac{\sqrt{2}}{\unicode[STIX]{x03C0}^{2}}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{0}^{1}\text{d}y\,|\unicode[STIX]{x2202}_{y}^{-1}\unicode[STIX]{x1D753}^{(0)}| & = & \displaystyle \frac{1}{2\unicode[STIX]{x03C0}}\int _{0}^{1}\text{d}y\,\sqrt{1-\sin 4\unicode[STIX]{x03C0}y}=\frac{1}{2\unicode[STIX]{x03C0}}\int _{0}^{1}\text{d}y\,\sqrt{(\cos 2\unicode[STIX]{x03C0}y-\sin 2\unicode[STIX]{x03C0}y)^{2}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2\unicode[STIX]{x03C0}}\int _{0}^{1}\text{d}y\,\sqrt{2}|\sin (2\unicode[STIX]{x03C0}y+\unicode[STIX]{x03C0}/4)|=\frac{1}{2\unicode[STIX]{x03C0}}\int _{0}^{1}\text{d}y\,\sqrt{2}|\sin 2\unicode[STIX]{x03C0}y|=\frac{\sqrt{2}}{\unicode[STIX]{x03C0}^{2}}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Appendix D. Stagnation points and symmetries
In this appendix we consider the stagnation points and symmetries of a flow corresponding to
![]() $\unicode[STIX]{x1D753}^{(0)}$
, i.e. given by
$\unicode[STIX]{x1D753}^{(0)}$
, i.e. given by
 $$\begin{eqnarray}\boldsymbol{v}^{(0)}\equiv \left(\begin{array}{@{}c@{}}{\dot{x}}(t)\\ {\dot{y}}(t)\\ {\dot{z}}(t)\end{array}\right)=\left(\begin{array}{@{}c@{}}A\sin 2\unicode[STIX]{x03C0}z(t)+C\sin 2\unicode[STIX]{x03C0}y(t)\\ B\sin 2\unicode[STIX]{x03C0}x(t)+A\sin 2\unicode[STIX]{x03C0}z(t)\\ C\sin 2\unicode[STIX]{x03C0}y(t)+B\sin 2\unicode[STIX]{x03C0}x(t)\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}^{(0)}\equiv \left(\begin{array}{@{}c@{}}{\dot{x}}(t)\\ {\dot{y}}(t)\\ {\dot{z}}(t)\end{array}\right)=\left(\begin{array}{@{}c@{}}A\sin 2\unicode[STIX]{x03C0}z(t)+C\sin 2\unicode[STIX]{x03C0}y(t)\\ B\sin 2\unicode[STIX]{x03C0}x(t)+A\sin 2\unicode[STIX]{x03C0}z(t)\\ C\sin 2\unicode[STIX]{x03C0}y(t)+B\sin 2\unicode[STIX]{x03C0}x(t)\end{array}\right),\end{eqnarray}$$
on the periodic domain
![]() $[0,1)^{3}$
. The stagnation points of
$[0,1)^{3}$
. The stagnation points of
![]() $\boldsymbol{v}^{(0)}$
require
$\boldsymbol{v}^{(0)}$
require
![]() $\boldsymbol{v}^{(0)}=0$
, but
$\boldsymbol{v}^{(0)}=0$
, but
result in
![]() ${\dot{y}}(t)=-2C\sin 2\unicode[STIX]{x03C0}y(t)$
. Hence
${\dot{y}}(t)=-2C\sin 2\unicode[STIX]{x03C0}y(t)$
. Hence
![]() $\boldsymbol{v}^{(0)}=0$
if and only if
$\boldsymbol{v}^{(0)}=0$
if and only if
![]() $x=y=z=0$
or
$x=y=z=0$
or
![]() $x=y=z=\unicode[STIX]{x03C0}$
. The symmetry group of
$x=y=z=\unicode[STIX]{x03C0}$
. The symmetry group of
![]() $\boldsymbol{v}^{(0)}$
consists of the four elements
$\boldsymbol{v}^{(0)}$
consists of the four elements
![]() $\{\text{id},\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2},\unicode[STIX]{x1D70E}_{3}\}$
, where
$\{\text{id},\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2},\unicode[STIX]{x1D70E}_{3}\}$
, where
![]() $\text{id}$
denotes the identity transformation and
$\text{id}$
denotes the identity transformation and
Since
![]() $\unicode[STIX]{x1D70E}_{3}=\unicode[STIX]{x1D70E}_{1}\circ \unicode[STIX]{x1D70E}_{2}$
, the set
$\unicode[STIX]{x1D70E}_{3}=\unicode[STIX]{x1D70E}_{1}\circ \unicode[STIX]{x1D70E}_{2}$
, the set
![]() $\{\text{id},\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2},\unicode[STIX]{x1D70E}_{3}\}$
indeed forms a group. It is isomorphic to the direct product of the cyclic group of two elements
$\{\text{id},\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2},\unicode[STIX]{x1D70E}_{3}\}$
indeed forms a group. It is isomorphic to the direct product of the cyclic group of two elements
![]() $\mathbb{Z}_{2}$
with itself because
$\mathbb{Z}_{2}$
with itself because
![]() $\unicode[STIX]{x1D70E}_{i}^{2}=\text{id}$
for
$\unicode[STIX]{x1D70E}_{i}^{2}=\text{id}$
for
![]() $i\in \{1,2,3\}$
.
$i\in \{1,2,3\}$
.