Introduction
Nowadays indoor localization systems are getting a lot of attention, since there is a growing demand for indoor location-based services. As indoor environment is quite tough for radio waves propagation, especially when they are intended to be used for localization purposes, a need for new, precise, and accurate localization techniques arises.
There are many ways leading to estimation of indoor positions of tags, however systems based on propagation of radio waves are most popular. They do not share the limitation of vision- or ultrasound-based systems, which is the inability to propagate through walls [Reference Fontana and Gunderson1]. Of course, through-wall propagation deteriorates radio waves as well, it leads to their attenuation and introduces delays, but it does not preclude them from use in positioning systems. Majority of localization systems use measurements of received signal level, its time or angle of arrival to determine positions. Received Signal Strength (RSS) method is commonly used in WiFi or Bluetooth Low Energy (BLE)-based systems [2, 3]. However, it is prone to changes in radio propagation environment.
Measurements of time are most commonly used in ultrawideband (UWB) systems; the position is calculated based on Time of Arrival (TOA) or Time Difference of Arrival (TDOA) values. Systems utilizing those techniques offer good accuracy; the positioning errors are reaching dozens, or even single centimeters in favorable conditions.
Generally, localization systems consist of localized tags, infrastructure comprised of fixed-positioned anchor nodes and a system controller. The most popular system architecture is shown in Fig. 1(a). Implementation of TDOA technique in such a system has many advantages. Tags design can be simplified because their functionality is limited to transmission of signals. Anchors measure time of signals arrivals and send results to the system controller, which calculates TDOAs and determines tags positions. Communication links between anchor nodes can be provided with cable or wireless network.
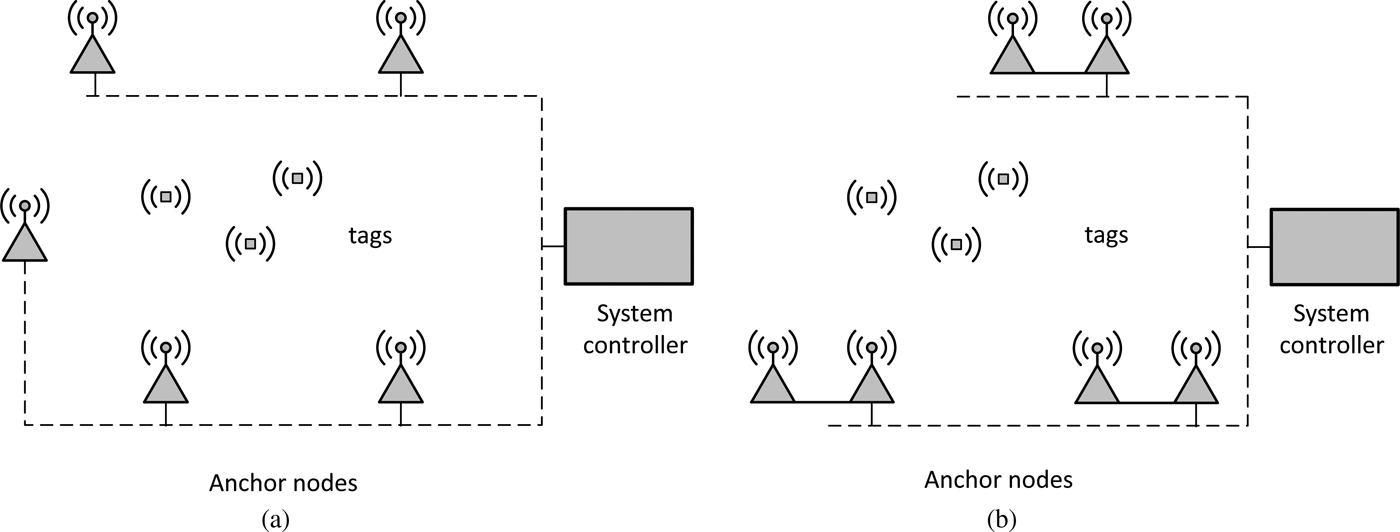
Fig. 1. A typical (a) and proposed (b) localization system architecture.
Determination of TDOAs for tags’ signals requires synchronization of anchors. Typically, it is achieved by transmission of synchronization signals over cable or wireless network. The need for providing synchronization signals to all anchors using cables may be tedious in indoor environment with lots of walls and obstacles. Moreover, distribution of such signals in case of system covering large areas is a demanding task.
The proposed system architecture (presented in Fig. 1(b)) illustrates the idea introduced in the paper. The system infrastructure consists of anchor nodes pairs, which measure TDOA independently and transmit the results to the system controller. The solution allows to release a requirement for global anchors synchronization. Only two nodes constituting a pair should be synchronized. The proposed solution is far more scalable. Synchronization of two nodes located close together is simpler and can be more accurate.
The article presents novel methods for synchronization of pair of anchor nodes, contains results of simulations and measurements. It also discusses influence of the synchronization process on the TDOA measurement rate. The presented solutions implement both cable and wireless connections between pairs of nodes and wireless connection to the system controller. The WiFi links are assumed to be used for this purpose.
Related works
Synchronization of anchor nodes is usually related to the synchronization of their clocks and may be treated in many ways. Most commonly it is referred to the synchronization of frequency or phase of the clock signal. However, in localization systems utilizing measurements of TOA or TDOA, for example, UWB localization systems, two main areas may be recognized:
• Clock synchronization, which is mainly tied to the frequency offset compensation. Each device is equipped with a clock signal source, which may be significantly affected by the temperature and humidity variations. Change of ambient conditions may cause the clocks to drift, which will have negative impact on the performed time measurements.
• Device synchronization, which can be understood, as maintaining the same time-base for all anchors. All devices have their own internal system counters, which may be used for timestamping of received packets (estimation of their TOA). A method for aligning those counters is necessary for the system to work properly.
Many of the commonly used solutions are inspired by the clock synchronization algorithms used within the internet or intranets, such as Cristian's algorithm, Precision Time Protocol (PTP), or Reference Broadcast Time (RBT) Synchronization used in wireless sensor networks.
There is a variety of methods described in the literature concerning synchronization in localization systems. Of course, the easiest solution is to provide cable connections between all devices [Reference Fontana and Gunderson1]. Despite its obvious drawbacks, such as complicated system installation and significant impact on the area where system is deployed, this approach is most commonly used in commercially available systems, such as Zebra's Dart [2] or Ubisense's Dimension4 [3]. Different approach was presented in [Reference Badawika and Kolakowski4, Reference Djaja-Jośko, Kołakowski and Modelski5]. It is less intrusive than straightforward connecting of all of the devices, as it relies on synchronizing only pairs of devices. That way, installation of the system is simplified, however at some cost of the versatility.
Another approach to synchronization is based on the wireless transmission of synchronization signals. In most cases, it consists in the placement of additional transmitting node which serves as a synchronization signal source or in the implementation of transmission scheme which allows for clock's drift compensation.
In [Reference McElroy, Neirynck and McLaughlin6–Reference Matsumoto, Kusano, Morokuma and Sakamura8], master tag, which periodically sends packets, is placed at a known position. It preferably has a high stability clock and therefore provides reference for the anchor nodes and measurements of the times of reception of the packets from other tags.
In [Reference Lee, Lin, Chin and Law9], a similar approach is presented. Master anchor node sends packets received by the tags and other anchors. Those anchors, after the reception, sequentially send their own packets after some predefined delays. All packets are received by the tags, which calculate their positions.
Significantly different approach was presented in [Reference Irahhauten, Nikookar and Klepper10], as it utilizes only one anchor node equipped with antenna array, hence there is no need for synchronization. It combines TOA technique with Direction of Arrival (DOA) and allows for 2D tag localization.
Methods presented in [Reference Zheng and Wu11, Reference Zhu and Ding12] rely on strictly structured message exchange between devices and modeling of imperfections in devices’ clocks, combined with more advanced data processing. Idea of modeling the clock and estimating its imperfections for further correction and synchronization is also analyzed in [Reference Xiao, Wang, Li and Zhang13, Reference Xie, Janssen and van der Veen14].
Anchor pairs
Architectures
The proposed system is based on pairs of anchor nodes. There are many variants of interfaces between anchors constituting the pair. Two exemplary solutions discussed in the article are shown in Fig. 2. Each pair consists of two anchors (A and B) which measure time of signal arrival. In order to calculate TDOA, measurement results should be expressed in the same time scale or the offset between anchors’ local times should be known and used for result correction. Keeping the offset steady requires synchronization of anchors clocks or correction of clock frequency deviations.
Fig. 2. Anchor pair architecture versions. WiFi, radio local area network transceiver; UWB, ultrawideband transceiver; PS, power supply unit.
Both configurations allow for use of different quality clock signal generators. It was assumed that more stable and of better tolerance clock source is provided in node A. Solutions differ with interfaces between nodes: wired is presented in Fig. 2(a), wireless is exploited in the design shown in Fig. 2(b).
According to the assumption that wireless connection is setup between anchor pairs and the system controller, WiFi modules are used for this purpose. In all architectures, UWB modules are responsible for UWB packets TOA measurements. Additionally, in the design shown in Fig. 2(b), they are used for exchange of measurement results and synchronization packets.
Cable interfaces give opportunity for power supply sharing. In case of wireless setup, each node should be powered separately.
TDOA determination with wired pair of nodes
TOA measurement performed in paired anchor nodes is illustrated in Fig. 3. Both nodes measure TOA with internal counters clocked with the signal derived from the same reference clock. At the moment of tag's packet transmission, the counter values in both nodes differ by Δt offset.
Fig. 3. Wire synchronization timing scheme.
After propagation times t p1 and t p2 the packet reaches both anchor nodes. Measured times of arrivals correspond to counter values T AT and T BT.
TDOA value can be expressed by:
$$TDOA = t_{\,p2}-t_{\,p1} = T_{BT}-T_{AT} + \tau _{AT}-\tau _{BT}-{\rm \Delta} t_{offset}, $$where: T AT, T BT – times of arrivals measured by nodes, τ A, τ B – internal delays in nodes, Δt offset – difference between counters in both nodes.
Difference of delays and Δt offset can be determined by placing the tag at a known position (TDOA is known) and performing a series of TOA measurement. By comparing calculated and known TDOA values, internal delay biases and counter offset can be calculated.
Uncertainties associated with measurements of times T AT and T BT have an impact on the uncertainty of TDOA determination. Total TDOA uncertainty is equal to:
$$\delta _{TDOA} = \sqrt {\delta _{RA}^2 + {\rm \;} \delta _{RB}^2 + \delta _{\tau off}^2}, $$where: δ RA, δ RB are uncertainties of measurements performed in both nodes (both values include internal delay uncertainty), δ τoff is the uncertainty of τ AT − τ BT − Δt offset component determination.
According to (2) TDOA determination uncertainty depends on uncertainties of TOA measurements δ RA, δ RB and the component related to calibration measurement. If the number of results collected during calibration process and averaged later in order to obtain τ AT − τ BT − Δt offset is large, the uncertainty δ τoff is much lower than δ RA, δ RB uncertainties and can be omitted.
Assuming the same design of the receiver in all anchor nodes and thus close uncertainty values, the TDOA uncertainty can be estimated as:
$$\delta _{TDOA}\approx \sqrt 2 {\rm \;} \delta _{RA}\approx \sqrt 2 {\rm \;} \delta _{RB}.$$TDOA determination with wirelessly synchronized nodes
Anchor nodes in configuration presented in Fig. 2(b) communicate only over UWB wireless link. The exchange of packets in this link is presented in Fig. 4.
Fig. 4. Exchange of packets between nodes in the pair, accumulation of time interval measurement error in node B.
Packet transmitted by the tag reaches both nodes and its times of arrival are recorded. Node B sends to the node A the packet containing measurement result and the time it was transmitted. Node A measures TOA and retrieves data from the packet. By comparing times of transmission of consecutive packets from node B with times of their arrival, node A is able to reduce errors caused by clock offset present in node B.
Node B clock offset is determined after each reception of data packet from node B. It can be expressed as:
$$\Delta t_{offset} = T_{RB1}-T_{TB1}-t_{\,pAB}-\tau _A{\rm.} $$If we assume that the both nodes clock frequencies difference is almost steady between packet “D” transmissions, the time measurement error cumulated within the period from T TB1 and T RTB2 can be estimated as:
$$\Delta T_{BT2} = (T_{RTB2}-T_{TB1})-\displaystyle{{(T_{RTB2}-T_{TB1})(T_{RB2}-T_{RB1})} \over {(T_{TB2}-T_{TB1})}}.$$TDOA value is equal to:
$$\eqalign{TDOA = &\,T_{RTB2} + {\rm \;} \Delta t_{offset}-\tau _B-T_{RTA2} + \tau _A + \Delta T_{BT2} \cr = &\,T_{RTB2}-T_{RTA2} + T_{RB1}-T_{TB1}-t_{\,pAB}-\Delta T_{BT2}-\tau_B.} $$Determination of TDOA besides measurement results requires determination of propagation time between nodes and internal delay in node B. As in the wired anchor pair architecture, both values can be evaluated from the results of measurement of the tag placed in a known location.
$$TDOA{\rm \;} = T_{RB1}-T_{RTA2}{\rm \;} -t_{\,pAB} + \displaystyle{{(T_{RTB2}-T_{TB1})(T_{RB2}-T_{RB1})} \over {(T_{TB2}-T_{TB1})}}-\tau _B.$$Uncertainty of TDOA calculated from (5) can be expressed as:
$$\delta _{TDOA} = \sqrt {\matrix{ {\displaystyle{{{(T_{TB2}-T_{RTB2})}^2 + {(T_{RTB2}-T_{TB1})}^2 + {(T_{RB2}-T_{RB1})}^2} \over {{(T_{TB2}-T_{TB1})}^2}}\delta _{RB}^2} \cr { + {(\delta _{RA})}^2} \cr { + {\left( {\displaystyle{{(T_{RTB2}-T_{{\rm TB}2})(T_{RB2}-T_{RB1})} \over {{(T_{TB2}-T_{TB1})}^2}}\delta_{TB}} \right)}^2 + {\left( {\displaystyle{{(T_{RTB2}-T_{TB1})(T_{RB2}-T_{RB1})} \over {{(T_{TB2}-T_{TB1})}^2}}\delta_{TB}} \right)}^2} \cr { + \delta _{tp}^2} \cr { + \delta _{\tau B}^2} \cr}}, $$where: δ RA, δ RB are uncertainties of measurements performed in both nodes (both values include internal delay uncertainty), δ TB is uncertainty of time of transmission determination, δ tp is the uncertainty of propagation time between anchor nodes determination, δ τB is the uncertainty of τ B determination. The derivation of the formula is included in Appendix.
The uncertainty can be estimated taking into account relations between measured times. Time interval between packets sent by anchor B is in the order of ms so it is significantly larger than propagation time between nodes or delays observed in nodes during packets reception.
The factors scaling δ TB and δ RB depend on the time interval between time of tag's packet arrival (T RTB2) and times of reference packets transmission from node B. If the T RTB2 is close to T TB2, the uncertainty can be estimated as:
$$\delta _{TDOA}\approx \sqrt {2\delta _{RB}^2 + {\lpar {\delta_{RA}} \rpar }^2 + {\lpar {\delta_{TB}} \rpar }^2 + \delta _{tp}^2 + \delta _{\tau B}^2}. $$For T RTB2 close to T TB1:
$$\delta _{TDOA}\approx \sqrt {3\delta _{RB}^2 + {\lpar {\delta_{RA}} \rpar }^2 + {\lpar {\delta_{TB}} \rpar }^2 + \delta _{tp}^2 + \delta _{\tau B}^2}. $$Typically, the process of packet transmission is controlled by internal digital circuits, and uncertainty of time of transmission determination δ TB is much lower than uncertainties related to TOA measurements. Uncertainty of propagation time and reception delay in node B measurements can be also significantly lower. Therefore, assuming that uncertainties of TOA measurements are the same in both nodes, the upper uncertainty value is bigger than in wired anchors configuration (3) and can be estimated as:
$$\delta _{TDOA}\approx 2\delta _{RB{\rm \;}} \approx 2\delta _{RA}{\rm \;} {\rm.} $$Impact of proposed architectures on positioning system performance
Typical positioning system should be able to localize many tags. The number of determined localizations per time period may be one of the measures of the system performance.
All the tags used in the system share the same radio resources. Random access to radio channel results in collisions deteriorating system performance. The problem can be solved by scheduling tags’ transmissions, but it requires two-way communication channel between the system and tags. Simpler solution depends on decreasing probability of collisions by randomizing tags’ transmission period. The second solution was investigated for the two proposed anchor pair architectures.
Performance of both architectures was investigated in Matlab environment. It was assumed that the packet structure conforms to IEEE 802.15.4a standard [15]. For the purpose of simulations, for the packets sent by the tags, preamble length was set to 2048 symbols and data rate to 110 kbps with data field consisting of one byte. It results in packet duration equal to 2.4 ms. For the wireless synchronization for the anchor's packet, 64 symbols long preamble was chosen along with same data rate as for the tags and data field consisting of 10 bytes. In such configuration, anchor's packet length was equal to 1 ms. Packet processing time in the receiver was assumed to be equal to 2.5 ms.
Total number of different tags transmitting packets was changed from 1 to 13 and transmission periods were changed from 50 ms to 3 s. Randomization of the transmission time was achieved by adding random component with uniform distribution, ranging from 0 to the half of the transmission period. For each combination of those parameters, 200 simulations were performed and obtained packet reception ratio results were averaged. For the simulation purposes, packet reception ratio was defined as the ratio of the number of received packets (successful reception was assumed in the situation when there was no overlapping between the packets and their processing time) to the total number of transmitted packets. Simulation results for architecture with wired connection between nodes are presented in Fig. 5 and the results for architecture with wirelessly connected nodes are shown in Fig. 6.
Fig. 5. Simulation results for wire synchronization architecture.
Fig. 6. Simulation results for wireless synchronization architecture.
As expected, probability of packet reception is higher for architecture with wire synchronization. There is no transmission of packets from the anchor node, and therefore radio link is occupied for shorter time and probability of packet collision is smaller.
However, for transmission periods higher than 1 s, for both architectures, probability of packet reception is above 90%.
In localization systems for three-dimensional localization of a tag, at least four anchor nodes are needed. In the proposed method, as TDOAs can be measured only between the nodes constituting the pair, a minimum of three pairs (six nodes) are needed. In case of wireless synchronization, every pair needs to exchange synchronization data, which could potentially lead to bottlenecking of the radio link. Fortunately, IEEE 802.15.4a standard allows for transmissions with different preamble codes, which eliminate possible interference between the nodes.
Experimental verification
Test arrangements
Both anchor pair architectures were tested with UWB modules based on DW1000 modules. DW1000 module integrates both analogue frontend and digital backend [16]. Its radio interface complies with IEEE standard 802.15.4a [15] (later consolidated into and superseded by IEEE Standard 802.15.4-2011 [17]).
The module allows for received signal TOA measurement with the 15.65 ps resolution, which is of crucial role when it comes to TDOA measurement.
In order for the module to work properly, external clock signal needs to be supplied and its choice may have significant impact on the performance of the measurements. This feature allows for distributing the same clock signal to two DW1000 equipped devices and was utilized in the proposed wired synchronization architecture.
Precision of DW1000's measurements was evaluated by measuring times of reception of continuously sent packets. Two receivers with different clock sources were used – one with standard crystal oscillator (XTAL) and one with Temperature Compensated Crystal Oscillator (TCXO). Results are shown in Fig. 7.
Fig. 7. Period measurement results comparison.
Significant drift is present in results gathered by XTAL-driven receiver, whereas in TCXO-based design, results are quite concentrated. For the latter, standard deviation of measured periods is equal to roughly 130 ps.
In DW1000 modules, packet reception timestamp is read from 40-bit register, where LSB stands for 15.65 ps [16]. Obtained value comes from DW1000's internal circuitry combining coarse timestamp with additional adjustments and is strictly tied to the system clock, generated using the earlier mentioned XTAL generator or TCXO and internal Phase Locked Loops (PLLs). As PLLs and other internal circuits are enabled on power-on, initial register values may differ between the two DW1000s.
DW1000 module is rather immune to multipath propagation influence on the reception of the data and TOA measurement. It is achieved by utilizing UWB technology and internal reception and timestamping algorithms based on channel impulse response estimation and first path detection.
Wired nodes
Test setup
The proposed TDOA determination method with a pair of wired synchronized nodes was experimentally investigated. The test setup is presented in Fig. 8. Tests were carried out in a classroom of size 6 by 6 m equipped with tables and chairs.
Fig. 8. Test setup for wire synchronized nodes.
Two anchor nodes were placed next to each other at the distance L at the same height, equal to 1.65 m. Both nodes were connected with the cable used for reference TCXO clock sharing. Measurement results were transferred to the PC over USB interfaces. Two sets of measurements were carried out, for two different distances (L) between the nodes.
The tag was placed in nine different positions at the height of 1.3 m. At each location, around 1200 TDOA measurements were performed. First measurement was done in such a position that the propagation times to both receivers were the same and therefore TDOA value was equal to 0 s. This measurement, referred as reference measurement (P0), was used to calculate Δt offset.
Test results
Empirical Cumulative Distribution Functions (CDFs) of measured TDOAs errors are presented in Figs 9 and 10 for the distances between anchors equal to 0.93 and 2.18 m, respectively. As a measurement error, absolute value of the difference between TDOAs measured and calculated from the distances to both node values was used.
Fig. 9. CDF for TDOA measurements errors for wire synchronization (distance between nodes equal to 0.93 m).
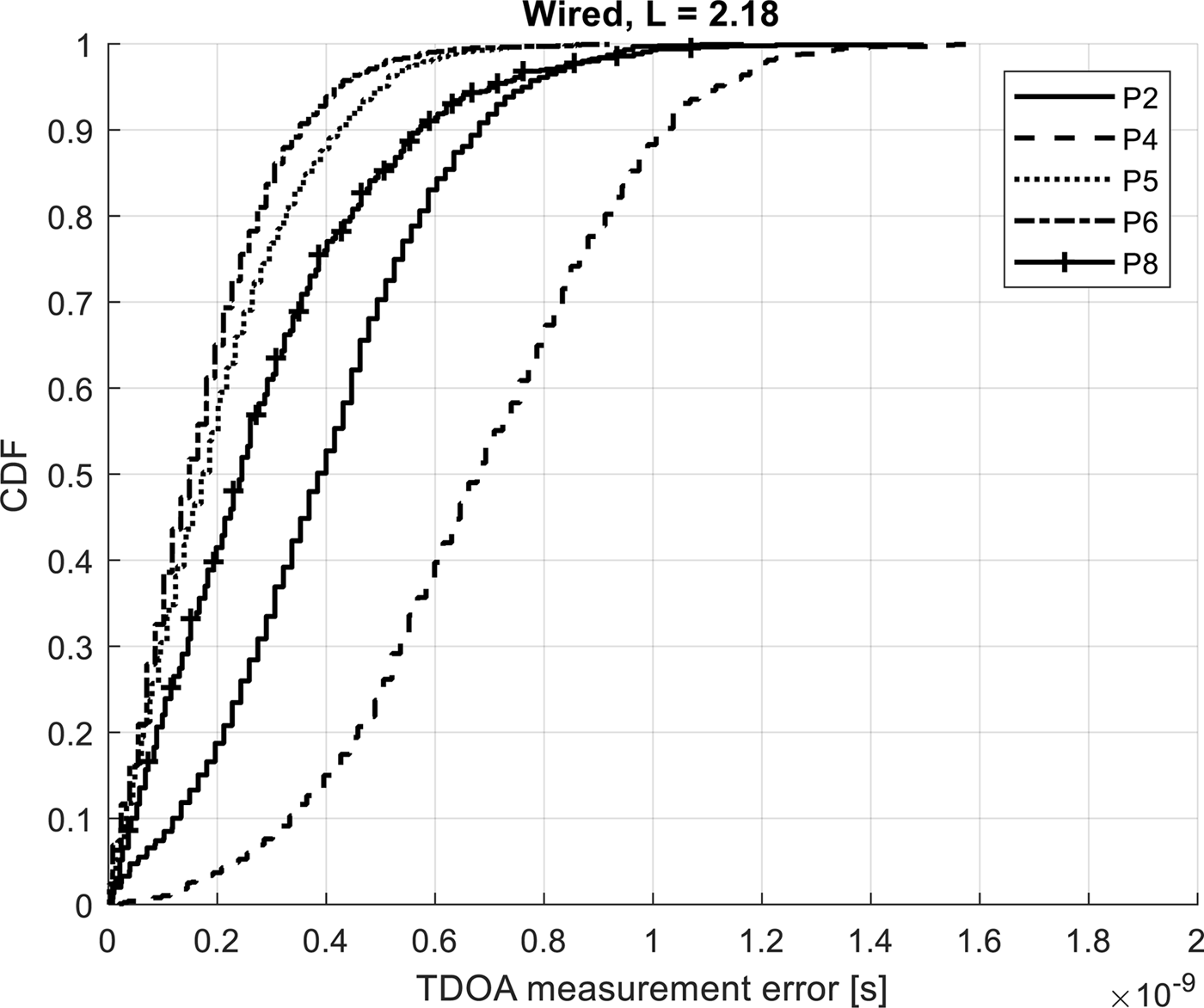
Fig. 10. CDF for TDOA measurements errors for wire synchronization (distance between nodes equal to 2.18 m).
The observable “step changes” visible on the presented figures are caused by the DW1000 counter's resolution of 15.65 ps.
Comparing the figures, it can be seen that in overall, TDOA values are more accurate for the separation between receivers equal to 0.93 m. It is mainly caused by the DW1000's dependence of TOA measurement on the signal level. There are two factors that have an impact on signal levels measured by nodes in one pair: difference of distances between the tag and the nodes and radiation pattern of nodes’ antennas (radiation patterns of antennas used in experiments are not purely omnidirectional and have a few dB pattern variations). By increasing the distance between antennas, we also increase the distance difference between the tag and the nodes for some tag locations. This effect is especially visible for the test points P2 and P4.
Wirelessly synchronized nodes
Test setup
The proposed TDOA determination method with wirelessly synchronized nodes was experimentally investigated. Tests were carried out in a laboratory room of size 6 by 6 m. Apart from the different room, test setup was the same as for the wire synchronized nodes shown in Fig. 8.
Node A, equipped with TCXO, was connected to the PC over USB interface, which was used to transfer measurement results.
The tag was placed in eight different positions at the height of 1.3 m. At each location, around 400 TDOA measurements were performed. Measurement marked with P0 was done in such position that the propagation times to both receivers were the same and therefore TDOA value was equal to 0 s. This measurement (reference measurement) was used to determine propagation time between nodes (t pAB) and internal delay in node B (τ B).
Test results
Empirical CDFs of measured TDOAs errors are presented in Figs 11 and 12 for distances between nodes equal to 0.93 and 2.18 m, respectively.
Fig. 11. CDF for TDOA measurements errors for wireless synchronization (distance between nodes equal to 0.93 m).
Fig. 12. CDF for TDOA measurements errors for wireless synchronization (distance between nodes equal to 2.18 m).
Similarly, to the results obtained using the wired synchronization between the nodes, results for the separation between the nodes equal to 0.93 were generally better than for 2.18 m, with the exception of the P5 point. Slightly different results for that point may be explained by the same phenomena observed for the test points P2 and P4 for the wired synchronization. This proves that the position of the tag and thus level of the received signal has an influence on the TDOA measurements.
Lack of “step changes” in the CDFs presented for the wireless synchronization can be explained by the way the TDOA values are calculated, which includes addition of the correction factors as shown in (5).
Comparison of results
In Table 1, standard deviations of obtained results are presented.
Table 1. Standard deviations of TDOA measurements
By comparing the results obtained for both synchronization methods, it can be seen that the wired synchronization slightly outperforms the wireless synchronization, which was expected and is in line with the estimations of the TDOA uncertainties presented in section “Anchor pairs”.
Conclusion
In the paper, two novel methods for TDOA estimation based on the connected pairs of anchor nodes equipped with DW1000 chips are evaluated. A brief explanation of methods is presented. One utilizes cable connections for nodes synchronization, second uses wireless links for that purpose.
Both methods were thoroughly analyzed, taking into account uncertainties of the measurements performed by the nodes in order to estimate uncertainties of estimated TDOA values. Additionally, simulations were conducted to evaluate the performance of the proposed methods in terms of probability of packet reception for assumed number of tags and transmission period.
Results of performed simulations and experiments show that the proposed methods are promising. As expected, simulations proved that architecture with cable synchronization allows for slightly higher probability of packet reception for assumed conditions.
Experiment results show that for both architectures, TDOAs are measured with errors smaller than 1 ns for 90% of cases. However, it is worth mentioning that the tests were performed in line of sight conditions between the tag and the anchor nodes. Significant errors in TDOA measurements may arise in case of non line of sight conditions, when measurements are carried out on reflected (or significantly delayed) signals, not direct ones.
Also, based on the results, it could be assumed that better TDOA measurement results may be achieved by placing the anchors close to each other. Unfortunately, apart from the distance between the nodes, there are other factors, such as size and layout of the area, placement of the pairs of nodes within the area and localization of tags, that have an influence on the accuracy of the TDOA measurements. Hence, there is no easy way to estimate the optimal allocation of the pairs of nodes and every deployment needs to be treated individually.
The proposed solutions would allow for higher scalability, easier deployment, and expansion of localization systems which would utilize them, while keeping TDOA measurement within reasonable accuracies (in the range of hundreds of picoseconds to single nanosecond).
Author ORCIDs
Vitomir Djaja-Josko, 0000-0002-2089-4641
Acknowledgements
The research leading to these results was partially funded by the National Centre for Research and Development under Grant Agreement AAL/Call2016/3/2017 (IONIS project).
Vitomir Djaja-Josko received the B.Sc. (2013) and M.Sc (2015) degrees in telecommunications from the Faculty of Electronics and Multimedia Technology, Warsaw University of Technology, Poland. He is pursuing the Ph.D. degree in the Institute of Radioelectronics and Multimedia Technology. He is currently a member of the research team working in the field of UWB technologies. His research interests include UWB signals, indoor localization, and synchronization methods in positioning systems.
Jerzy Kołakowski received the M.Sc. (1988) and Ph.D. (2000) degrees in telecommunications from the Warsaw University of Technology. Since 1988 he has been with the Institute of Radioelectronics and Multimedia Technology where he holds a position of Assistant Professor. He is a Member of the Management Board of the Foundation for the Development of Radiocommunications and Multimedia Technology. His current research interests include positioning systems, ultrawideband technology, and cellular systems.
Jozef Modelski is a Professor at the Warsaw University of Technology, Head of the Radiocommunications Division, IEEE Fellow, Member of the Polish Academy of Sciences, President of the URSI National Committee, 2009–10 IEEE Region 8 Director, Microwave and Radar Week Chair (from 2004). His research interests focus on microwave techniques, radiocommunications, and television. He has published over 300 technical papers, four monographs, obtained nine patents, and was a supervisor of 25 Ph.D. dissertations. He acts as a consultant to governmental agencies, industry, and telecommunication operators. Prof. Modelski is an active IEEE and European Microwave Association (EuMA) volunteer.
APPENDIX
Measurements of particular components in (5) are independent. Therefore, the total uncertainty of the measured TDOA can be estimated as:
$$\delta _{TDOA} = \sqrt {\matrix{ {{\left( {\left \vert {\displaystyle{{\partial TDOA} \over {\partial T_{RB1}}}} \right \vert \delta_{RB}} \right)}^2 + {\left( {\left \vert {\displaystyle{{\partial TDOA} \over {\partial T_{RB2}}}} \right \vert \delta_{RB}} \right)}^2 + \; {\left( {\left \vert {\displaystyle{{\partial TDOA} \over {\partial T_{RTA2}}}} \right \vert \delta_{RA}} \right)}^2} \cr { + {\left( {\left \vert {\displaystyle{{\partial TDOA} \over {\partial T_{RTB2}}}} \right \vert \delta_{RB}} \right)}^2 + {\left( {\left \vert {\displaystyle{{\partial TDOA} \over {\partial T_{TB1}}}} \right \vert \delta_{TB}} \right)}^2} \cr { + {\left( {\left \vert {\displaystyle{{\partial TDOA} \over {\partial T_{TB2}}}} \right \vert \delta_{TB}} \right)}^2 + {\left( {\left \vert {\displaystyle{{\partial TDOA} \over {\partial (t_{\,pAB})}}} \right \vert \delta_{tp}} \right)}^2 + {\left( {\left \vert {\displaystyle{{\partial TDOA} \over {\partial \tau_B)}}} \right \vert \; \delta_{\tau B}\; \;} \right)}^2} \cr}} $$
$$\delta _{TDOA} = \sqrt {\matrix{ {{\left( {\left( {1-\displaystyle{{\lpar {T_{RTB2}-T_{TB1}} \rpar } \over {\lpar {T_{TB2}-T_{TB1}} \rpar }}} \right)\delta_{RB}} \right)}^2 + {\left( {\displaystyle{{\lpar {T_{RTB2}-T_{TB1}} \rpar } \over {\lpar {T_{TB2}-T_{TB1}} \rpar }}\delta_{RB}} \right)}^2} { + \; {\lpar {\delta_{RA}} \rpar }^2 + {\left( {\displaystyle{{\lpar {T_{RB2}-T_{RB1}} \rpar } \over {\lpar {T_{TB2}-T_{TB1}} \rpar }}\delta_{RB}} \right)}^2} \cr { + {\left( {\displaystyle{{\lpar {T_{RTB2}-T_{TB2}} \rpar \lpar {T_{RB2}-T_{RB1}} \rpar } \over {{\lpar {T_{TB2}-T_{TB1}} \rpar }^2}}\delta_{TB}} \right)}^2 + {\left( {\displaystyle{{\lpar {T_{RTB2}-T_{TB1}} \rpar \lpar {T_{RB2}-T_{RB1}} \rpar } \over {{\lpar {T_{TB2}-T_{TB1}} \rpar }^2}}\delta_{TB}} \right)}^2} { + {\lpar {\delta_{tp}} \rpar }^2} { + \delta _{\tau B}^2} \cr}}. $$Finally:
$$\delta _{TDOA} = \sqrt {\matrix{ {\displaystyle{{{\lpar {T_{TB2}-T_{RTB2}} \rpar }^2 + {\lpar {T_{RTB2}-T_{TB1}} \rpar }^2 + {\lpar {T_{RB2}-T_{RB1}} \rpar }^2} \over {{\lpar {T_{TB2}-T_{TB1}} \rpar }^2}}\delta _{RB}^2} { + {\lpar {\delta_{RA}} \rpar }^2} \cr { + {\left( {\displaystyle{{\lpar {T_{RTB2}-T_{TB2}} \rpar \lpar {T_{RB2}-T_{RB1}} \rpar } \over {{\lpar {T_{TB2}-T_{TB1}} \rpar }^2}}\delta_{TB}} \right)}^2 + {\left( {\displaystyle{{\lpar {T_{RTB2}-T_{TB1}} \rpar \lpar {T_{RB2}-T_{RB1}} \rpar } \over {{\lpar {T_{TB2}-T_{TB1}} \rpar }^2}}\delta_{TB}} \right)}^2} { + \delta _{tp}^2} { + \delta _{\tau B}^2} \cr}}. $$
