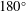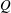1. Introduction
Flows in curved pipes are ubiquitous in industrial piping systems, microfluidic devices, and even biological systems. Furthermore, the widespread use of curved pipes in heat exchangers, chemical reactors and many other experimental flow systems demands an intimate knowledge of the flow details in these geometries. Centrifugal effects are significant in these flows and have been an area of active research. For example, flows in curved pipes are known to contain counter-rotating vortical features that can enhance heat and mass transfer (Dean Reference Dean1927; Austin & Seader Reference Austin and Seader1973). In applications where these effects are unwanted, a thorough understanding of the flow features and how to mitigate them is needed. For example, several studies of turbulent flow downstream of a bend have emphasized the long distances that these vortical structures can propagate in a straight pipe (Smits, Young & Bradshaw Reference Smits, Young and Bradshaw1979; Anwer, So & Lai Reference Anwer, So and Lai1989; So & Anwer Reference So and Anwer1993). However, the distances over which the flow evolves have not been quantified, even for laminar flows.
In this paper, we analyse the transition from fully developed laminar curved pipe flow to fully developed straight pipe flow. We solve for the flow field numerically using three-dimensional Navier–Stokes simulations. A sample simulation domain is shown in figure 1. Results detailing the grid validation and numerical convergence are presented in the Appendix. We focus our attention primarily on the straight pipe section downstream of the
$180^{\circ }$
curved pipe section. Decay lengths are calculated in the straight pipe using various physical parameters of the flow and are found to vary linearly with the Reynolds number. Scaling arguments are used to confirm this result. Similar results are presented for the decay of vortices in the outlets of a T-junction flow, where the flow enters through the base of the T and splits between the two outlet arms.
Figure 1. Flow in a curved pipe of diameter
$d$
with centreline curvature
$R$
. The simulation domain visualized from (a) top-down and (b) axial cross-sectional views. Arrows indicate the direction of flow. Mesh resolutions have been purposefully coarsened by a factor of eight for visualization purposes.
Dean theoretically derived a velocity profile for fully developed flow in slowly curving pipes with circular cross-sections, which qualitatively agreed with experiments (Dean Reference Dean1927, Reference Dean1928). Dean developed a first approximation to the secondary streamline flow in a curved pipe, in which two counter-rotating vortices form, with the flow moving from the inner to the outer edge of the pipe on the central plane. Thus, the streamlines travel in helical paths in fully developed laminar flow in curved pipes. This flow is governed by two dimensionless parameters, the Reynolds number and the pipe-to-curvature radius ratio. Using
${\it\rho}$
as the density of the fluid,
$u_{avg}$
as the average axial pipe velocity,
$d$
as the diameter of the pipe,
${\it\mu}$
as the dynamic viscosity of the fluid and
$R$
as the radius of curvature of the centreline of the pipe, the Reynolds number is defined as
$$\begin{eqnarray}\mathit{Re}=\frac{{\it\rho}u_{avg}d}{{\it\mu}},\end{eqnarray}$$
and the pipe-to-curvature radius ratio is given by
$$\begin{eqnarray}{\it\alpha}=\frac{d}{2R}.\end{eqnarray}$$
For slowly curving pipes,
${\it\alpha}\ll 1$
, Dean extended this analysis, showing that the behaviour of the flow could be reduced to a dependence on a single variable, now called the Dean number, which is commonly defined as
$$\begin{eqnarray}D=\mathit{Re}\,{\it\alpha}^{1/2}.\end{eqnarray}$$
For small Dean numbers, the solution for the velocity field can be expanded in powers of
$D$
(Dean Reference Dean1928). However,
$D$
is not necessarily small in many applications, so new solution methods were needed.
Since Dean’s original research, the flow in curved pipes has been a topic of substantial interest. Table 1 gives a short review of several of the studies related to curved pipe flow, including studies on developing curved pipe flow, laminar and turbulent fully developed curved pipe flow, and laminar and turbulent flow downstream of curved pipes. For example, Austin & Seader (Reference Austin and Seader1973) numerically solved the stream-function/vorticity formulation of the Navier–Stokes equation for fully developed curved pipe flow, confirming Dean’s conclusion that the Dean number was the main parameter governing the flow under certain conditions. In addition, Dennis & Riley (Reference Dennis and Riley1991) extended the results of Dean to large values of
$D$
, giving evidence for the existence of an asymptotic structure of the flow. Also, the development of flows in the entrance regions of curved pipes with varying inlet conditions has been studied. This flow has been solved using the method of matched asymptotic expansions for a uniform inlet velocity profile (Singh Reference Singh1974). In addition, a theoretical relationship for the entrance length in the curved pipe has been presented (Yao & Berger Reference Yao and Berger1975), although the authors only claim qualitative validity based on the assumptions of their model.
Table 1. A review of some studies related to flow in curved pipes, including developing flows and exit flows (laminar and turbulent).
Hot-wire anemometry has been used to study the entry region of curved pipes for laminar flow (Olson & Snyder Reference Olson and Snyder1985). Single-phase and two-phase particle/liquid flows in planar and helical pipes have been analysed theoretically and numerically (Liu & Masliyah Reference Liu and Masliyah1996; Tiwari, Antal & Podowski Reference Tiwari, Antal and Podowski2006). Turbulent flows in
$90^{\circ }$
and
$180^{\circ }$
bends with and without initial swirl have also been studied numerically (Pruvost, Legrand & Legentilhomme Reference Pruvost, Legrand and Legentilhomme2004). The swirling motions were strong enough to entirely suppress the Dean motions in some cases. Berger & Talbot (Reference Berger and Talbot1983) presented a comprehensive review of the laminar, incompressible flow in curved pipes. They reference research that touches on many aspects of curved pipe flow: varying cross-sections, developing flows, entry conditions, entry lengths, pressure drops, variable pipe curvatures, flexible walls, porous tubes, non-Newtonian fluids, multiphase flows, mass transfer flows, thermal effects and pulsatile flows.
Despite the abundance of research on flow in curved pipes and developing flow in curved pipes, almost no research exists concerning the decay that accompanies the transition from fully developed curved pipe flow back to fully developed straight pipe flow. To the best of our knowledge, almost all of the research that does exist concerning the flow downstream of a pipe bend deals exclusively with turbulent flow. For example, Tunstall & Harvey (Reference Tunstall and Harvey1968) studied the turbulent flow through a sharp
$90^{\circ }$
bend and documented a secondary flow that was dominated by a single clockwise or counterclockwise circulation about the pipe axis that switched the sense of rotation at a certain frequency. The switching could only occur if the bend angle was sufficiently acute. This flow showed little resemblance to the counter-rotating vortices observed in laminar flow (Dean Reference Dean1927, Reference Dean1928). In addition, Smits et al. (Reference Smits, Young and Bradshaw1979) measured the mean products of velocity fluctuations in turbulent boundary layers downstream of
$20^{\circ }$
and
$30^{\circ }$
angle bends and investigated the responses of the boundary layers to these ‘impulses’ of curvature and the decay of those responses downstream; the extremely slow recovery of the flow downstream of the bend was emphasized.
Hot-wire techniques have been used to measure mean velocity and Reynolds stress components downstream of
$90^{\circ }$
and
$180^{\circ }$
pipe bends (Anwer et al.
Reference Anwer, So and Lai1989; Sudo et al.
Reference Sudo, Sumida and Hibara2000). Steady and pulsatile turbulent flows in curved pipes have also been computed using the Reynolds-averaged Navier–Stokes technique and large eddy simulations (Hellström & Fuchs Reference Hellström and Fuchs2007). In addition, stereoscopic particle image velocimetry has been used to study the unsteady undulations of Dean vortices and bimodal ‘swirl switching’ downstream of a
$90^{\circ }$
pipe bend (Sakakibara & Machida Reference Sakakibara and Machida2012; Hellström et al.
Reference Hellström, Zlatinov, Cao and Smits2013) and to study the flow in a pipe bend with conditions similar to those in an internal combustion engine, using high Dean and Womersley numbers. The turbulent flow through a pipe bend and in a downstream outlet has also been studied for the case of added swirl in the inlet (Anwer & So Reference Anwer and So1993; So & Anwer Reference So and Anwer1993). None of the flow conditions in these studies bear a strong resemblance to the steady, laminar flow downstream of a curved pipe that we study here.
We have found few papers in the literature that study the laminar flow downstream of curved pipes. Two of these studies were experimental in nature and used laser-Doppler velocimetry to measure fluid velocities. In particular, experiments were performed for flow through a
$90^{\circ }$
bend with Reynolds numbers of 500 and 1093 (Enayet et al.
Reference Enayet, Gibson, Taylor and Yianneskis1982), although downstream measurements were only recorded at a single cross-sectional plane, one pipe diameter downstream in the outlet. Experiments were also performed for flow through a
$180^{\circ }$
bend with pipe-to-curvature radius ratios of 0.08 and 0.30, both at a Reynolds number of 400 (Fairbank & So Reference Fairbank and So1987). The influence of the pipe bend was found to propagate 14 pipe diameters downstream for the case of
${\it\alpha}=0.30$
and 11 pipe diameters for the case of
${\it\alpha}=0.08$
. However, the authors remarked that, using air as a working fluid, temperature variations in the experimental set-up were not sufficiently reduced, and buoyancy-driven secondary flows of the same order as the Dean flow polluted the experiments.
In the following sections, the methods, results, theoretical considerations, and conclusions of this study will be presented. Section 2 describes the numerical methods, flow geometries and simulation domains used, while § 3 presents theoretical considerations, including a linearization of the Navier–Stokes equations about the Poiseuille flow and the application of several useful scaling arguments for characterizing the flow. Section 4 presents numerical results for decay lengths in the outlet domain, and documents flow features of the decay process. Section 5 gives a comparison of the numerical results to the linearized theory. Section 6 applies these results to the flow in a T-junction. Section 7 presents conclusions and practical implications of this study. The Appendix presents the convergence studies we used to verify the accuracy of our simulations.
2. Methods
2.1. Numerical approach
We performed direct numerical simulations to solve for the laminar, steady, incompressible flow downstream of a
$180^{\circ }$
section of curved pipe of constant centreline curvature for a range of Reynolds numbers,
$\mathit{Re}$
, and pipe-to-curvature radius ratios,
${\it\alpha}$
. After scaling lengths by the pipe diameter
$d$
, velocities by the average axial pipe velocity
$u_{avg}$
, and pressures by the viscous scale
${\it\mu}u_{avg}/d$
, the basic equations governing the flow are the incompressible form of the steady Navier–Stokes and continuity equations:
$$\begin{eqnarray}\mathit{Re}\;\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}=-\boldsymbol{{\rm\nabla}}p+{\rm\nabla}^{2}\boldsymbol{u}\quad \text{and}\quad \boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u}=0,\end{eqnarray}$$
where
$p$
is the pressure and
$\boldsymbol{u}$
is the velocity vector. These equations are solved using the open-source computational fluid dynamics package OpenFOAM (Weller et al.
Reference Weller, Tabor, Jasak and Fureby1998), using the icoFoam solver, which implements the ‘pressure-implicit with splitting of operators’ (PISO) method described by Issa (Reference Issa1985, Reference Issa1986). This scheme solves a pressure–velocity formulation of the implicitly discretized time-dependent incompressible form of the Navier–Stokes equation. A predictor–corrector scheme is used to handle the coupling between the pressure and velocity non-iteratively, such that operations on the pressure are decoupled from operations on the velocity at each time step. The temporal evolution scheme is a second-order implicit Euler method, and the spatial derivatives are second-order accurate. The variables are defined at the cell centres, although velocities are interpolated to the surface centres for computing the velocity fluxes. The cumulative continuity errors, given by
$\sum (\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{u})$
, where the summation is over every finite volume cell in the simulation domain, are typically of the order of
$10^{-11}$
.
Since the PISO method is time-dependent, and our flows are expected to be steady for the range of
$\mathit{Re}$
and
${\it\alpha}$
that we study, the flow is given an initial condition and allowed to evolve towards the steady-state solution. The norm of the time derivative of the velocity field is used to monitor convergence in time. We define this norm as
$$\begin{eqnarray}\left\Vert \frac{\partial \boldsymbol{u}}{\partial t}\right\Vert ^{2}=\frac{1}{V}\int _{{\it\Omega}}\left(\frac{\partial \boldsymbol{u}}{\partial t}\right)^{2}\,\text{d}V,\end{eqnarray}$$
where
$V$
is the total volume of fluid, and the integration is over the entire simulation domain
${\it\Omega}$
.
As the solver approaches the steady-state solution, we expect the value of this norm to approach zero. However, an issue we have identified with the icoFoam solver is that this norm does not identically approach zero as the solver approaches the steady state. Instead, over the course of a simulation, the value of this norm decreases by approximately eight orders of magnitude, at which point the velocity/pressure fields begin to oscillate about a small orbit. This feature of the numerical convergence is documented in the Appendix, and is a numerical oscillation, not an analytical one; it is purely a numerical feature of the solver. On this numerical orbit,
$\Vert \partial \boldsymbol{u}/\partial t\Vert /\Vert \boldsymbol{u}\Vert \approx 10^{-4}$
or smaller. For the purposes of measuring transition lengths, velocity profiles and flow development to characterize the flow, this numerical oscillation does not appear to have any noticeable negative effects. Measuring transition lengths at various points on this numerical orbit results in identical transition lengths. For the purposes of this paper, we consider steady state to have been achieved once
$\Vert \partial \boldsymbol{u}/\partial t\Vert /\Vert \boldsymbol{u}\Vert \lesssim 10^{-4}$
and the solver has converged to the numerical orbit. For more details about the temporal convergence see the Appendix.
After steady state is achieved, built-in OpenFOAM utilities are used to calculate the wall shear stress, vorticity and velocity gradients. The open-source data visualization application ParaView is used to visualize the results and extract useful data, and MATLAB algorithms are used to analyse the results.
2.2. Vortex identification
In order to identify, quantify and visualize the vortices in the flow throughout the decay process as the flow evolves downstream of a pipe bend, we utilize the
$Q$
-criterion. This is a vortex identification technique (Hunt, Wray & Moin Reference Hunt, Wray and Moin1988), which is calculated using the rate-of-strain tensor
$(\unicode[STIX]{x1D640})$
and the vorticity tensor
$({\it\bf\Omega})$
, which are defined by
$$\begin{eqnarray}\unicode[STIX]{x1D640}={\textstyle \frac{1}{2}}(\boldsymbol{{\rm\nabla}}\boldsymbol{u}+(\boldsymbol{{\rm\nabla}}\boldsymbol{u})^{\text{T}})\quad \text{and}\quad {\it\bf\Omega}={\textstyle \frac{1}{2}}(\boldsymbol{{\rm\nabla}}\boldsymbol{u}-(\boldsymbol{{\rm\nabla}}\boldsymbol{u})^{\text{T}}).\end{eqnarray}$$
The
$Q$
-criterion is defined as
$$\begin{eqnarray}Q={\textstyle \frac{1}{2}}(\Vert {\it\bf\Omega}\Vert _{F}^{2}-\Vert \unicode[STIX]{x1D640}\Vert _{F}^{2}),\end{eqnarray}$$
where
$\Vert \cdot \Vert _{F}$
is the Frobenius norm, which is given by
$$\begin{eqnarray}\Vert \unicode[STIX]{x1D60C}\Vert _{F}^{2}=\mathop{\sum }_{i,j}|\unicode[STIX]{x1D60C}_{ij}|^{2}\quad \text{and}\quad \Vert {\it\bf\Omega}\Vert _{F}^{2}=\mathop{\sum }_{i,j}|{\it\Omega}_{ij}|^{2},\end{eqnarray}$$
where the
$\unicode[STIX]{x1D60C}_{ij}$
and
${\it\Omega}_{ij}$
are the elements of the rate-of-strain and vorticity tensors, respectively. Using this criterion, a vortex is defined as the spatial region where
$Q>0$
.
Generally speaking, the larger the
$Q$
-criterion, the stronger and more pronounced the vortical structure at that location, resulting in a numerical technique that can be used to visualize vortices. For example, figure 2 shows the
$Q$
-criterion along a slice taken through the centre of the vortices in our simulations, where
${\it\alpha}=0.07$
and
$\mathit{Re}=40$
, 50 and 60. As expected from the work of Dean (Reference Dean1927, Reference Dean1928), the vortical structures become stronger and more pronounced for a given
${\it\alpha}$
as the Reynolds number is increased. Thus, by plotting the
$Q$
-criterion we can visualize the vortical regions. Not only do we see that the vortices become relatively stronger and more pronounced as the Reynolds number increases, but below we will also show that the vortices propagate further into the outlet pipe as the Reynolds number increases.
Figure 2.
$Q$
-criterion on a slice through the vortex cores for
${\it\alpha}=0.07$
and (a)
$\mathit{Re}=40$
, (b)
$\mathit{Re}=50$
and (c)
$\mathit{Re}=60$
. The strength of the vortices increases with the Reynolds number. The vortices also propagate further into the outlet for larger
$\mathit{Re}$
. Arrows indicate the direction of flow. Vortices develop in the initial portion of the curved pipe section and propagate into the outlet as they decay. The calculated decay lengths,
$\ell _{d}$
, are also shown. The decay lengths increase as
$\mathit{Re}$
is increased, implying a further propagation of the vortices into the outlets.
2.3. Determining decay lengths
To characterize the flow downstream of a
$180^{\circ }$
curved pipe, we visualize streamlines, level-set contours of the
$Q$
-criterion, and velocity, pressure and vorticity fields on various cross-sections in the outlet pipe. In addition to characterizing the flow through visualization, we seek a quantitative relationship for the transition length of the decay process as a function of the Reynolds number and pipe-to-curvature-radius ratio. We evaluate transition lengths using four different approaches: (i) the wall-averaged shear stress about a cross-section, (ii) the integral of the magnitude of the vorticity on a cross-section, (iii) the maximum value of the
$Q$
-criterion on a cross-section and (iv) the norm of the perturbation velocity field
$\boldsymbol{u}^{\prime }$
(velocity
$\boldsymbol{u}$
minus fully developed Poiseuille flow
$\boldsymbol{u}_{p}$
) on a cross-section. This norm is defined as in (2.2) and is given by
$$\begin{eqnarray}\Vert \boldsymbol{u}^{\prime }\Vert ^{2}=\Vert \boldsymbol{u}-\boldsymbol{u}_{p}\Vert ^{2}=\frac{1}{V}\int _{{\it\Omega}}(\boldsymbol{u}-\boldsymbol{u}_{p})^{2}\,\text{d}V,\end{eqnarray}$$
where again
${\it\Omega}$
is the entire simulation domain and
$V$
is the total volume of
${\it\Omega}$
.
For each of the four approaches mentioned above, the ‘decay length’
$\ell _{d}$
is defined as the axial coordinate position
$z$
in the straight outlet pipe at which the given parameter of interest varies by less than 1 % from its fully developed value for all
$z\geqslant \ell _{d}$
. For each simulation, we take a slice through the cross-section at a given axial location. We then calculate the four aforementioned properties. Using these calculated values, we vary the axial position of the slice to determine the dependence of each parameter on the axial coordinate. Finally, we determine the transition lengths using the 1 % criterion, which is particularly useful since our experience is that not all parameters vary monotonically. For the case of parameters that vary monotonically, this criterion is equivalent to measuring the familiar 99 % transition length.
2.4. Geometry
An example simulation domain was shown previously in figure 1, featuring a straight inlet pipe section, a
$180^{\circ }$
curved pipe section and a straight outlet pipe section. Simulations were performed for pipe-to-curvature radius ratios
${\it\alpha}=d/2R=0.005$
, 0.01, 0.03, 0.07, 0.1, 0.15 and 0.25. In order to limit our study to the decay of fully developed curved pipe flow, the Reynolds numbers were chosen such that the inlet flow would have sufficient pipe length to become fully developed in the curved pipe section according to the four criteria previously mentioned. A safety margin was included in this selection process to ensure the flow was fully developed. Given a certain
${\it\alpha}$
, a maximum Reynolds number was selected such that the flow would be fully developed in the curved pipe section for a distance of at least 20 % of the total curved pipe length before entering the straight outlet. The maximum Reynolds number allowed for small values of
${\it\alpha}$
was higher than that for larger values of
${\it\alpha}$
. In particular, while the largest Reynolds number simulated for
${\it\alpha}=0.005$
was 800, the largest Reynolds number simulated for
${\it\alpha}=0.25$
was only 10. For higher Reynolds numbers, a fully developed curved pipe flow simply does not exist for large values of
${\it\alpha}$
since there is not a sufficient pipe length in the
$180^{\circ }$
curved section for the flow to become fully developed.
Using the curved pipe entrance length calculations reported by Yao & Berger (Reference Yao and Berger1975), initial estimates for the maximum Reynolds numbers were determined for each value of
${\it\alpha}$
. Using those Reynolds numbers, inlet/outlet lengths were estimated such that the flow would have sufficient length to become fully developed in the straight sections up- and downstream as well. These estimates were achieved using calculations of the entrance length for a straight pipe (see for example Mohanty & Asthana (Reference Mohanty and Asthana1978) as well as textbook estimates for laminar flow development, e.g. Fox, Pritchard & McDonald (Reference Fox, Pritchard and McDonald2009)). However, these inlet/outlet lengths were not sufficiently long because the decay lengths in the outlet downstream of a bend, which are the subject of this work, were roughly twice as long as the entrance lengths in a straight pipe for a given Reynolds number. Therefore, the inlet/outlet lengths were adjusted to ensure that the flow in those regions was fully developed with a safety margin for all Reynolds numbers. The inlet/outlet lengths and maximum Reynolds numbers for each value of
${\it\alpha}$
are summarized in table 2.
Table 2. Parameters for the numerical simulations: inlet/outlet lengths, maximum Reynolds numbers, and maximum Dean numbers corresponding to each value of pipe-to-curvature radius ratio.
2.5. Boundary and initial conditions
Numerical solutions of the fluid motions require both boundary and initial conditions for the pressure and velocity fields. The initial condition for the pressure field is a uniform value of zero. The outlet boundary condition on the domain is also given a uniform value of zero pressure for all time (only relative pressure differences matter for incompressible flow, so zero and even negative pressures are allowed by the solver). The gradient of pressure normal to the walls is zero for all time. The gradient of pressure normal to the inlet is also zero for all time, and although this inlet boundary condition is not correct, the pressure gradient converges rapidly downstream to the analytical value over a distance of just a few grid cells. Furthermore, the inlet is not the region of interest for this work, so this choice of boundary condition has a negligible influence on our results.
The initial condition for the velocity field is zero velocity throughout the domain. The outlet boundary condition for the velocity is a zero normal gradient in velocity, which assumes that the outlet flow is fully developed. This boundary condition would not be accurate for large Reynolds number simulations in which the vortical structures propagate beyond the outlet. However, we limit the maximum Reynolds numbers specifically to eliminate those cases, and we observe the development of the flow variables to confirm this boundary condition. The wall boundary condition is no-slip. The inlet boundary condition for the velocity is a fixed uniform value. Using these initial and boundary conditions, the simulations consist of a time evolution that proceeds towards steady state, as previously described.
3. Theoretical considerations: flow in the straight outlet
We now focus our attention on the flow in the straight outlet pipe. Our goal in this analysis is to rescale the linearized governing equations so as to eliminate
$\mathit{Re}$
and
${\it\alpha}$
from the governing equations and boundary conditions, and in this way identify the asymptotic structure for this laminar flow downstream of the bend. Before presenting our numerical results, we seek to provide an analytical scaling between the transition/decay length in the outlet pipe and the governing dimensionless parameters,
$\mathit{Re}$
and
${\it\alpha}$
. By linearizing and rescaling the Navier–Stokes and continuity equations, as well as our boundary conditions, we can eliminate the
${\it\alpha}$
-dependence and demonstrate a linear relationship between the Reynolds number and the characteristic length scale of the outlet decay. These conclusions will be justified by our numerical simulations in § 4.
To proceed, we assume that the velocity profile in the curved pipe section is a small perturbation away from the Poiseuille flow of a laminar fully developed straight pipe flow, i.e. if
$\boldsymbol{e}_{z}$
is the unit vector in the axial direction, then the Poiseuille velocity profile is given by
$\boldsymbol{u}=(1-4r^{2})\boldsymbol{e}_{z}$
, where the radial coordinate
$r$
has been non-dimensionalized by the pipe diameter
$d$
. We then linearize the basic equations about this Poiseuille flow. We will comment on the validity of this linearization in the following section by making direct use of our numerical results. We use cylindrical coordinates where we consider the region downstream of the bend, and define the velocity perturbation as
$\boldsymbol{u}^{\prime }=(u_{r}^{\prime },u_{{\it\theta}}^{\prime },u_{z}^{\prime })$
, where
$z$
is the axial direction of the straight outlet pipe. Here
${\it\theta}=0$
corresponds to the direction from the centreline of the pipe towards the outer edge of the curved pipe section, and the positive
${\it\theta}$
direction is chosen to be counterclockwise when looking upstream in the outlet section. The non-dimensional steady-state linearized equations are
$$\begin{eqnarray}\displaystyle & \displaystyle \mathit{Re}(1-4r^{2})\frac{\partial u_{r}^{\prime }}{\partial z}=-\frac{\partial p^{\prime }}{\partial r}+\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial u_{r}^{\prime }}{\partial r}\right)+\frac{1}{r^{2}}\frac{\partial ^{2}u_{r}^{\prime }}{\partial {\it\theta}^{2}}+\frac{\partial ^{2}u_{r}^{\prime }}{\partial z^{2}}-\frac{u_{r}^{\prime }}{r^{2}}-\frac{2}{r^{2}}\frac{\partial u_{{\it\theta}}^{\prime }}{\partial {\it\theta}},\qquad & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \mathit{Re}(1-4r^{2})\frac{\partial u_{{\it\theta}}^{\prime }}{\partial z}=-\frac{1}{r}\frac{\partial p^{\prime }}{\partial {\it\theta}}+\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial u_{{\it\theta}}^{\prime }}{\partial r}\right)+\frac{1}{r^{2}}\frac{\partial ^{2}u_{{\it\theta}}^{\prime }}{\partial {\it\theta}^{2}}+\frac{\partial ^{2}u_{{\it\theta}}^{\prime }}{\partial z^{2}}-\frac{u_{{\it\theta}}^{\prime }}{r^{2}}+\frac{2}{r^{2}}\frac{\partial u_{r}^{\prime }}{\partial {\it\theta}},\qquad & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \mathit{Re}(1-4r^{2})\frac{\partial u_{z}^{\prime }}{\partial z}-8\,\mathit{Re}\,r\,u_{r}^{\prime }=-\frac{\partial p^{\prime }}{\partial z}+\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial u_{z}^{\prime }}{\partial r}\right)+\frac{1}{r^{2}}\frac{\partial ^{2}u_{z}^{\prime }}{\partial {\it\theta}^{2}}+\frac{\partial ^{2}u_{z}^{\prime }}{\partial z^{2}},\qquad & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\frac{1}{r}\frac{\partial }{\partial r}(ru_{r}^{\prime })+\frac{1}{r}\frac{\partial u_{{\it\theta}}^{\prime }}{\partial {\it\theta}}+\frac{\partial u_{z}^{\prime }}{\partial z}=0.\end{eqnarray}$$
Next, we rescale the axial coordinate
$z$
by the Reynolds number, i.e.
$\tilde{z}=z/\mathit{Re}$
. To satisfy continuity we also scale the axial component of the perturbation velocity with the Reynolds number, i.e.
$\tilde{u} _{z}^{\prime }=u_{z}^{\prime }/\mathit{Re}$
. Rewriting the basic equations using these scalings and considering the case of large Reynolds numbers,
$\mathit{Re}\gg 1$
(but still a laminar flow), which eliminates
$z$
-derivatives on the right-hand side of (3.1), gives a set of four coupled, linear equations, independent of the Reynolds number:
$$\begin{eqnarray}\displaystyle & \displaystyle (1-4r^{2})\frac{\partial u_{r}^{\prime }}{\partial \tilde{z}}=-\frac{\partial p^{\prime }}{\partial r}+\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial u_{r}^{\prime }}{\partial r}\right)+\frac{1}{r^{2}}\frac{\partial ^{2}u_{r}^{\prime }}{\partial {\it\theta}^{2}}-\frac{u_{r}^{\prime }}{r^{2}}-\frac{2}{r^{2}}\frac{\partial u_{{\it\theta}}^{\prime }}{\partial {\it\theta}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle (1-4r^{2})\frac{\partial u_{{\it\theta}}^{\prime }}{\partial \tilde{z}}=-\frac{1}{r}\frac{\partial p^{\prime }}{\partial {\it\theta}}+\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial u_{{\it\theta}}^{\prime }}{\partial r}\right)+\frac{1}{r^{2}}\frac{\partial ^{2}u_{{\it\theta}}^{\prime }}{\partial {\it\theta}^{2}}-\frac{u_{{\it\theta}}^{\prime }}{r^{2}}+\frac{2}{r^{2}}\frac{\partial u_{r}^{\prime }}{\partial {\it\theta}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle (1-4r^{2})\frac{\partial \tilde{u} _{z}^{\prime }}{\partial \tilde{z}}-8\,r\,u_{r}^{\prime }=\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial \tilde{u} _{z}^{\prime }}{\partial r}\right)+\frac{1}{r^{2}}\frac{\partial ^{2}\tilde{u} _{z}^{\prime }}{\partial {\it\theta}^{2}}, & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\frac{1}{r}\frac{\partial }{\partial r}(ru_{r}^{\prime })+\frac{1}{r}\frac{\partial u_{{\it\theta}}^{\prime }}{\partial {\it\theta}}+\frac{\partial \tilde{u} _{z}^{\prime }}{\partial \tilde{z}}=0.\end{eqnarray}$$
These equations govern the evolution of the velocity perturbation in the straight outlet pipe section downstream of the curved pipe.
We must also consider the inlet boundary conditions to the straight outlet pipe. Specifically, this inlet condition is approximately the fully developed curved pipe flow. Although the effects of the straight outlet propagate upstream into the curved pipe a small distance, experience shows this effect can be neglected. For example, for the case
${\it\alpha}=0.005$
and
$\mathit{Re}=200~(D=14.1)$
, the difference between the straight outlet pipe inlet condition and Dean’s analytical curved pipe velocity profile
$\boldsymbol{u}_{D}$
is approximately
$$\begin{eqnarray}\Vert \boldsymbol{u}-\boldsymbol{u}_{D}\Vert /\Vert \boldsymbol{u}\Vert \approx 3.5\times 10^{-6},\end{eqnarray}$$
where the norm is given by
$$\begin{eqnarray}\Vert \cdot \Vert ^{2}=\frac{1}{S}\int _{{\it\Gamma}}(\cdot )^{2}\,\text{d}S.\end{eqnarray}$$
Here,
${\it\Gamma}$
is the cross-section at the inlet to the straight outlet section (
$z=0$
), and
$S$
is the area of that cross-section. Thus, the velocity profile entering the straight outlet is approximately the fully developed Dean profile (at least for
${\it\alpha}=0.005$
and
$\mathit{Re}=200$
).
Using Dean’s analytical velocity profile for the flow in a curved pipe, the perturbation velocity profile inlet condition (
$z=0$
) to the straight outlet pipe can be written as
$$\begin{eqnarray}\displaystyle & \displaystyle u_{r}^{\prime }(r,{\it\theta},0)=\frac{\mathit{Re}\,{\it\alpha}\cos {\it\theta}}{36}(1-4r^{2})^{2}(1-r^{2}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle u_{{\it\theta}}^{\prime }(r,{\it\theta},0)=-\frac{\mathit{Re}\,{\it\alpha}\sin {\it\theta}}{144}(1-4r^{2})(4-92r^{2}+112r^{4}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle u_{z}^{\prime }(r,{\it\theta},0)={\it\alpha}\,r\cos {\it\theta}(1-4r^{2})\left[-3+\frac{\mathit{Re}^{2}}{2880}(19-84r^{2}+144r^{4}-64r^{6})\right], & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}p^{\prime }(r,{\it\theta},0)=\frac{\mathit{Re}\,{\it\alpha}\,r\cos {\it\theta}}{3}(18-48r^{2}+64r^{4}).\end{eqnarray}$$
For large Reynolds numbers, in terms of linearized rescaled variables,
$\tilde{u} _{z}^{\prime }=u_{z}^{\prime }/\mathit{Re}$
can be approximated as
$$\begin{eqnarray}\tilde{u} _{z}^{\prime }(r,{\it\theta},0)=\frac{\mathit{Re}\,{\it\alpha}\,r\cos {\it\theta}}{2880}(1-4r^{2})(19-84r^{2}+144r^{4}-64r^{6}).\end{eqnarray}$$
Strictly speaking, Dean’s results were derived in the limit
$$\begin{eqnarray}\frac{D^{2}}{1440}\ll 1.\end{eqnarray}$$
However, as indicated in (3.3), the agreement is still reasonable when
$D^{2}/1440=\mathit{O}(0.1)$
. Below we will show that differences from the Dean solution occur when
$D^{2}/1440=\mathit{O}(1)$
.
These equations for
$u_{r}^{\prime }$
,
$u_{{\it\theta}}^{\prime }$
,
$\tilde{u} _{z}^{\prime }$
, and
$p^{\prime }$
set the inlet boundary condition for the straight outlet pipe. As can be seen, each is a linear function of both Reynolds number and the pipe-to-curvature radius ratio. Since the governing equations (3.2) for the perturbation are linear, we can rescale by the product
$\mathit{Re}\,{\it\alpha}$
, giving
$$\begin{eqnarray}U_{r}^{\prime }=\frac{u_{r}^{\prime }}{\mathit{Re}\,{\it\alpha}},\quad U_{{\it\theta}}^{\prime }=\frac{u_{{\it\theta}}^{\prime }}{\mathit{Re}\,{\it\alpha}},\quad U_{z}^{\prime }=\frac{\tilde{u} _{z}^{\prime }}{\mathit{Re}\,{\it\alpha}}\quad \text{and}\quad P^{\prime }=\frac{p^{\prime }}{\mathit{Re}\,{\it\alpha}},\end{eqnarray}$$
at the inlet (
$\tilde{z}=0$
). Thus, the linearized boundary-value problem downstream of the bend is
$$\begin{eqnarray}\displaystyle & \displaystyle (1-4r^{2})\frac{\partial U_{r}^{\prime }}{\partial \tilde{z}}=-\frac{\partial P^{\prime }}{\partial r}+\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial U_{r}^{\prime }}{\partial r}\right)+\frac{1}{r^{2}}\frac{\partial ^{2}U_{r}^{\prime }}{\partial {\it\theta}^{2}}-\frac{U_{r}^{\prime }}{r^{2}}-\frac{2}{r^{2}}\frac{\partial U_{{\it\theta}}^{\prime }}{\partial {\it\theta}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle (1-4r^{2})\frac{\partial U_{{\it\theta}}^{\prime }}{\partial \tilde{z}}=-\frac{1}{r}\frac{\partial P^{\prime }}{\partial {\it\theta}}+\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial U_{{\it\theta}}^{\prime }}{\partial r}\right)+\frac{1}{r^{2}}\frac{\partial ^{2}U_{{\it\theta}}^{\prime }}{\partial {\it\theta}^{2}}-\frac{U_{{\it\theta}}^{\prime }}{r^{2}}+\frac{2}{r^{2}}\frac{\partial U_{r}^{\prime }}{\partial {\it\theta}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle (1-4r^{2})\frac{\partial U_{z}^{\prime }}{\partial \tilde{z}}-8\,rU_{r}^{\prime }=\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial U_{z}^{\prime }}{\partial r}\right)+\frac{1}{r^{2}}\frac{\partial ^{2}U_{z}^{\prime }}{\partial {\it\theta}^{2}}, & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}\frac{1}{r}\frac{\partial }{\partial r}(rU_{r}^{\prime })+\frac{1}{r}\frac{\partial U_{{\it\theta}}^{\prime }}{\partial {\it\theta}}+\frac{\partial U_{z}^{\prime }}{\partial \tilde{z}}=0,\end{eqnarray}$$
subject to the inlet boundary conditions (
$\tilde{z}=0$
)
$$\begin{eqnarray}\displaystyle & \displaystyle U_{r}^{\prime }(r,{\it\theta},0)=\frac{\cos {\it\theta}}{36}(1-4r^{2})^{2}(-r^{2}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle U_{{\it\theta}}^{\prime }(r,{\it\theta},0)=-\frac{\sin {\it\theta}}{144}(1-4r^{2})(4-92r^{2}+112r^{4}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle U_{z}^{\prime }(r,{\it\theta},0)=\frac{r\cos {\it\theta}}{2880}(1-4r^{2})(19-84r^{2}+144r^{4}-64r^{6}), & \displaystyle\end{eqnarray}$$
and
$$\begin{eqnarray}P^{\prime }(r,{\it\theta},0)=\frac{r\cos {\it\theta}}{3}(18-48^{2}+64r^{4}).\end{eqnarray}$$
As stated in (3.6), the boundary conditions (3.9) are limited to flows with sufficiently small Dean numbers (
$D^{2}/1440\ll 1$
) (Dean Reference Dean1927). In practice, this limits the maximum Reynolds number for each value of
${\it\alpha}$
for which we might expect these boundary conditions to hold. Below we will compare the results of our numerical simulations with the conclusions from these scaling arguments.
We note that the flow downstream of a curved pipe could be solved numerically by solving (3.8) as long as the flow remains laminar, the inlet boundary condition remains a small perturbation to the Poiseuille flow, the Reynolds number is large enough, and the Dean number remains small enough for (3.9) to apply. In particular, the solution can be achieved by noting that, according to the proposed rescaling, the perturbation decays a fixed percentage over a length scale that varies linearly with the Reynolds number. Thus, a form of the velocity/pressure perturbation can be sought that includes a sum of modes that decay exponentially with the rescaled axial coordinate
$\tilde{z}$
if a finite pipe length domain is selected. Then, the governing equations, corresponding to (3.8), can be rewritten as a set of four coupled, linear, Sturm–Liouville-type ordinary differential equations. However, in practice these equations would still need to be solved numerically and thus would not provide any additional information about the flow beyond the direct numerical solutions that we have achieved below. Nevertheless, the theoretical scaling with Reynolds number of the relaxation of the linearized flow has been identified, and will be tested in § 5 by direct comparison with the full simulations.
4. Results and discussion
In this section, we develop a quantitative relationship relating the decay length
$\ell _{d}$
,
$\mathit{Re}$
and
${\it\alpha}$
. Also, we present several visualizations of the flow decay process in the downstream outlet. In § 5, we compare details of the flow with the linearized theory in § 3.
4.1. Decay lengths
As explained in § 2.3, we determine transition lengths based upon the wall shear stress, the vorticity, the
$Q$
-criterion and the norm of the axial gradient of the velocity field. Transition lengths for a given property are extracted by determining the axial
$z$
-coordinate corresponding to a 1 % deviation in that property from its fully developed value. Typical numerical results are shown in figure 3 for the case
${\it\alpha}=0.005$
and
$\mathit{Re}=800$
. Since the norm of the axial gradient of the velocity field (figure 3
d) consistently yields the largest transition length, we select that criterion to determine the overall decay lengths for the flows.
Figure 3. Numerical results for the outlet pipe flow for
${\it\alpha}=0.005$
and
$\mathit{Re}=800$
. Results shown are (a) the maximum value of the
$Q$
-criterion, (b) the wall-averaged shear stress, (c) the integral of the magnitude of the vorticity and (d) the norm of the axial gradient of the velocity field. All results are calculated on a cross-section taken at the respective
$z$
-values. Vorticity has been non-dimensionalized by
$u_{avg}/d$
, wall shear stress has been non-dimensionalized by
${\it\mu}u_{avg}/d$
, and
$z$
has been non-dimensionalized by
$d$
. Transition lengths are determined by finding the axial
$z$
-position corresponding to a 1 % deviation from the fully developed value, denoted by the vertical black lines.
Using the criterion based on the norm of the perturbation velocity field, the numerically determined relationship between the Reynolds number and the decay length downstream of the curved pipe section is shown in figure 4, which shows a linear relationship between decay length and
$\mathit{Re}$
, at least for
$\mathit{Re}>30$
; we anticipated the linear dependence using scaling arguments in § 3, based on a linearized flow analysis. Furthermore, figure 4 shows that the decay length does not depend on
${\it\alpha}$
; also as predicted from our scaling arguments. Below
$\mathit{Re}\approx 30$
, the viscous effects are comparable to or dominate the inertial effects, and the transition length approaches approximately one pipe diameter for small Reynolds numbers. This Reynolds number behaviour is consistent with other pipe flows of this type. For example, the entrance length in a developing straight pipe flow is known to be related linearly to the Reynolds number when
$\mathit{Re}$
is large, and the flow is known to develop on a length scale of the order of one pipe diameter when
$\mathit{Re}$
is small (Atkinson et al.
Reference Atkinson, Brocklebank, Card and Smith1969).
Although the flow is expected to be a function of both
${\it\alpha}$
and
$\mathit{Re}$
, our scaling arguments (§ 3) have shown that the pipe-to-curvature radius ratio should not have an effect on the decay length, based on assumptions of
$\mathit{Re}\gg 1$
and
$D^{2}/1440\ll 1$
. We now seek to verify this prediction with additional numerical results. Several decay lengths are shown in figure 5 for a range of
${\it\alpha}$
at two specific Reynolds numbers. The dependence on
${\it\alpha}$
appears to be negligible, at least relative to the dependence on
$\mathit{Re}$
. Relatively close, modest values of
$\mathit{Re}$
were chosen so that we could include results for the full range of
${\it\alpha}$
. Furthermore, this approach allows us to see that, while a 35-fold increase in
${\it\alpha}$
appears to have a negligible effect on the decay length, a 14 % increase in
$\mathit{Re}$
results in a distinctive increase in the decay length. The error bars displayed are plus and minus twice the length of the grid spacing in the axial flow direction. We note that, for the smaller values of
${\it\alpha}$
, we designed the geometries with larger values of
$\mathit{Re}$
in mind, because the total arc length of the curved section is greater for small
${\it\alpha}$
. Also, for larger values of
$\mathit{Re}$
, the axial velocity gradients are smaller. This feature allows us to use larger grid spacings in the axial directions for small values of
${\it\alpha}$
and explains the increase in the error bars for small values of
${\it\alpha}$
in figure 5. Considering figures 4 and 5 together, our numerical results demonstrate that the pipe-to-curvature radius ratio does not influence the perturbation velocity’s decay length, as anticipated by the scaling arguments in § 3.
Figure 5. Numerical results for the decay length as a function of the pipe-to-curvature radius ratio
$({\it\alpha})$
for
$\mathit{Re}=35$
and 40. The results show a negligible effect of
${\it\alpha}$
on the decay length.
Figure 6. Decay lengths calculated using the wall-averaged shear stress, the integral of the magnitude of the vorticity, the maximum value of the
$Q$
-criterion, and the norm of the perturbation velocity field
$\boldsymbol{u}^{\prime }$
.
We now investigate how the transition lengths associated with all of our physical properties vary with the Reynolds number. The decay lengths, as a function of
$\mathit{Re}$
, calculated using the wall shear stress, vorticity,
$Q$
-criterion and velocity perturbation, as previously described, are compared in figure 6. The decay lengths all display linear trends with the Reynolds number, at least for approximately
$\mathit{Re}>30$
. The decay lengths calculated using the wall shear stress and the vorticity show some irregularities when
$\mathit{Re}<30$
. This feature is due to the fact that these properties vary increasingly non-monotonically with the axial coordinate in the pipe outlet as the Reynolds number is increased. Thus, as a new oscillation in the wall shear stress and/or the vorticity emerges as the Reynolds number is increased, the corresponding 99 % transition length experiences unexpected jumps. However, we still see the key features: the decay lengths approach a constant value of the order of the pipe diameter at low Reynolds numbers, and they increase linearly with the Reynolds number for
$\mathit{Re}>30$
. The longest calculated lengths are found using the norm of the velocity perturbation. Using these results, a relationship, calculated using the criterion based on the norm of the perturbation velocity field
$\Vert \boldsymbol{u}^{\prime }\Vert$
, for the decay length
$\ell _{d}$
of fully developed curved pipe flow in a straight, tangent outlet pipe can be given by
$$\begin{eqnarray}\frac{\ell _{d}}{d}=0.1020\,\mathit{Re}-0.2070\quad \mathit{Re}>\mathit{O}(10).\end{eqnarray}$$
This formula is plotted in figure 4.
4.2. Decay process
Now we seek to understand the decay process further by visualizing the flow properties in the straight outlet pipe at various axial cross-sections downstream. Typical results are shown in figure 7 for the case
${\it\alpha}=0.005$
and
$\mathit{Re}=800$
, where we report the magnitude of the velocity perturbation, the pressure and the axial component of vorticity on cross-sectional slices taken at
$z=0$
,
$z=5$
,
$z=10$
and
$z=15$
. The results at
$z=0$
correspond approximately to the fully developed curved pipe flow (although the effects of the straight outlet pipe have propagated upstream a small distance into the curved pipe, as previously discussed). The leftmost column shows the magnitude of the velocity perturbation, overlaid with the streamlines of the secondary flow. The maximum magnitude of the velocity perturbation for this case is approximately
$0.67u_{avg}$
, which corresponds to the highest Dean number from our simulations (
$D=56.6$
), and so we might expect the velocity profile to no longer be a small perturbation about the Poiseuille flow
$\boldsymbol{u}_{p}$
. Indeed, we see that
$\Vert \boldsymbol{u}^{\prime }\Vert /\Vert \boldsymbol{u}_{p}\Vert \approx 0.28$
. Thus, the small perturbation assumption considered in § 3 may not be a good approximation, although the linear relationship between decay length and Reynolds number nonetheless holds, as shown in the previous section. For comparison,
$\Vert \boldsymbol{u}^{\prime }\Vert /\Vert \boldsymbol{u}_{p}\Vert \approx 0.073$
for
${\it\alpha}=0.005$
and
$\mathit{Re}=200$
, and is approximately 0.021 for
${\it\alpha}=0.005$
and
$\mathit{Re}=100$
.
Figure 7. Secondary streamlines and non-dimensional physical properties visualized at (a)
$z=0$
, (b)
$z=5$
, (c)
$z=10$
and (d)
$z=15$
from figure 1, for
${\it\alpha}=0.005$
and
$\mathit{Re}=800$
. The leftmost, centre and rightmost columns show the magnitude of the velocity perturbation, the pressure and the axial component of vorticity, respectively. The pressure is scaled by
${\it\mu}u_{avg}/d$
and vorticity has been scaled by
$u_{avg}/d$
. Coming out of the pipe bend, the left side of each cross-section corresponds to the inner surface of the curved pipe, and the right side of each cross-section corresponds to the outer surface of the curved pipe.
The middle column of figure 7 shows the pressure field on the same cross-sections. At
$z=0$
, the secondary pressure gradient is such that the pressure is highest on the side of the outer edge of the curved pipe (the right side of the figure), and the pressure is lowest on the inner edge, as expected from the predictions of Dean flow. However, immediately downstream of the curved pipe section, this pressure difference begins to equilibrate. The maximum pressure difference on a cross-section is approximately 0.24 % at
$z=0$
, 0.063 % at
$z=5$
, 0.013 % at
$z=10$
, and 0.0036 % at
$z=15$
. As the pressure difference decreases, we also observe that the lowest pressure on each cross-section shifts to correspond to the region of the vortex cores.
The rightmost column in figure 7 shows the axial component of vorticity non-dimensionalized by
$u_{avg}/d$
on each cross-section. The vortex cores correspond to the regions of largest magnitude of axial vorticity. We also observe that, as the vortices decay, their cores drift closer together and towards the outside edge of the pipe (to the right-hand side of the page). The drift to the right at least may be explained by a well-known behaviour of travelling vortex pairs, in which they drift under the action of their own induced velocity fields.
Since we expect the product
$\mathit{Re}\,{\it\alpha}$
to simply scale the parameters of the flow in the exit tube (having scaled it out of the linearized equations and boundary conditions in § 3), we seek to check this response with our numerical results. The effect of
${\it\alpha}$
on the decay process is visualized in figure 8 for
$\mathit{Re}=35$
and
${\it\alpha}=0.005$
, 0.03 and 0.07. The decay process is visually identical for the three cases, independent of
${\it\alpha}$
, as expected from our scaling arguments. However, we clearly see that the flow strength depends on
${\it\alpha}$
, since the magnitude of the vorticity is approximately 14 times greater for the case of
${\it\alpha}=0.07$
than the
${\it\alpha}=0.005$
case. Nonetheless, the value of
${\it\alpha}$
does not affect the decay process itself, having been effectively scaled out of both the governing equations and boundary conditions. We see this immediately by scaling the maximum magnitude of vorticity by
$\mathit{Re}\,{\it\alpha}$
for each case: for
${\it\alpha}=0.005$
,
$|{\it\omega}_{z}^{max}|/(\mathit{Re}\,{\it\alpha})\approx 0.26$
, for
${\it\alpha}=0.03$
,
$|{\it\omega}_{z}^{max}|/(\mathit{Re}\,{\it\alpha})\approx 0.26$
, and for
${\it\alpha}=0.07$
,
$|{\it\omega}_{z}^{max}|/(\mathit{Re}\,{\it\alpha})\approx 0.26$
.
Figure 8. Comparison of vorticity decay for
${\it\alpha}=0.005$
, 0.03 and 0.07 with
$\mathit{Re}=35$
. Results are shown with secondary streamlines at (a)
$z=0$
, (b)
$z=0.2$
, (c)
$z=0.4$
and (d)
$z=0.6$
from figure 1. Results demonstrate that vorticities scale with
$\mathit{Re}\,{\it\alpha}$
, as expected from our scaling arguments (
$|{\it\omega}_{z}^{max}|/(\mathit{Re}\,{\it\alpha})\approx \text{constant}$
).
5. Comparison with linearized theory
We can also understand details of the flow evolution in terms of the linearized theory and scaling arguments. Using the rescalings from § 3, we have successfully eliminated all dependence on the Reynolds number and pipe-to-curvature radius ratio from both the governing equations and the boundary conditions. This independence from
$\mathit{Re}$
and
${\it\alpha}$
is shown in figure 9, where we plot the magnitude of the maximum value of the numerically calculated rescaled axial velocity
$U_{z}^{\prime }$
on a cross-section versus the rescaled axial coordinate
$\tilde{z}$
for a range of
$\mathit{Re}$
and
${\it\alpha}$
. Similarly, in figure 10 we plot the magnitude of the maximum value of the rescaled secondary velocity component
$U_{sec}^{\prime }$
(the maximum velocity in the cross-section) versus the rescaled axial coordinate
$\tilde{z}$
. The figure insets show the data in the unscaled variables. We see that the data collapse when we apply the rescalings indicated in § 3.
Figure 9. Maximum magnitude of the numerically computed rescaled axial velocity component
$U_{z}^{\prime }$
versus the rescaled axial coordinate
$\tilde{z}$
. Data points are shown for a range of
$\mathit{Re}$
and
${\it\alpha}$
. The figure inset shows the unscaled
$u_{z}^{\prime }$
versus the unscaled axial coordinate
$z$
. The data collapse when we apply the scalings described in the text:
$\tilde{u} _{z}^{\prime }=u_{z}^{\prime }/Re$
, equation (3.7), and
$\tilde{z}=z/Re$
.
Figure 10. Maximum magnitude of the rescaled secondary velocity component
$U_{sec}^{\prime }$
(the maximum velocity in the cross-section) versus the rescaled axial coordinate
$\tilde{z}$
. Data points are shown for a range of
$\mathit{Re}$
and
${\it\alpha}$
. The figure inset shows the unscaled data. The data collapse when we apply the scalings of (3.7) and
$\tilde{z}=z/Re$
.
The data shown in figures 9 and 10 were selected such that
$D^{2}/1440\lesssim 0.3$
. Dean derived his velocity profile (3.5) for
$D^{2}\ll 1440$
, although the data still collapse when
$D^{2}/1440=\mathit{O}(0.1)$
. However, when
$D^{2}/1440$
approaches
$\mathit{O}(1)$
the results begin to diverge, and the scaling fails, as shown in figure 11, where we plot the maximum value of the
$Q$
-criterion rescaled by
$(\mathit{Re}\,{\it\alpha})^{2}$
. The
$Q$
-criterion is proportional to
$u_{r}^{\prime 2}$
and
$u_{{\it\theta}}^{\prime 2}$
. Thus, according to our scaling analysis in § 3,
$Q_{max}/(\mathit{Re}\,{\it\alpha})^{2}$
should be independent of
$\mathit{Re}$
and
${\it\alpha}$
when plotted against
$\tilde{z}$
. This result is exactly what we see in figure 11 for the cases with
$D^{2}/1440\lesssim 0.3$
. However, the scaling fails for the cases with
$D^{2}/1440=\mathit{O}(1)$
. The failure to collapse is due to the fact that the Dean velocity profile (3.5) no longer matches the fully developed curved pipe velocity profile when
$D^{2}/1440\geqslant \mathit{O}(1)$
.
Figure 11. Maximum value of the rescaled
$Q$
-criterion,
$Q_{max}/(\mathit{Re}\,{\it\alpha})^{2}$
, versus the rescaled axial coordinate
$\tilde{z}$
. Data points are shown for a range of
$\mathit{Re}$
and
${\it\alpha}$
. The data show that when
$D^{2}/1440\lesssim 0.3$
, the data collapse. However, when
$D^{2}/1440\approx \mathit{O}(1)$
, the data do not collapse. At these values of
$D^{2}/1440$
, Dean’s analytical velocity profile no longer holds.
So, after applying the scaling arguments presented in the linearized theory in § 3, the results of our numerical simulations collapse, at least for the ranges
$\mathit{Re}\gtrsim \mathit{O}(100)$
and
$D^{2}/1440\lesssim \mathit{O}(0.1)$
. Thus, by reporting a single numerical simulation with
$\mathit{Re}$
and
$D$
within these ranges, we can directly obtain the flow solution for every set of
$\mathit{Re}$
and
$D$
within these ranges by simply rescaling the results of our numerical solution, as described in § 3.
6. Application to the flow in a T-junction
The counter-rotating vortices that we study are not a unique feature to fully developed curved pipe flow. In fact, counter-rotating vortical structures are a common feature of the secondary motion of many flows in networks with bends and corners. We now demonstrate an analogy between the flow downstream of a curved pipe studied here and the flow in an impacting T-junction flow, where the flow enters through the base of the T and splits between the two outlet arms of the T. Most importantly, we consider whether or not any comparisons can be made between the decaying straight pipe outlet flow and the outlet flow in the arms of the T-junction. Steady-state simulations of the flow in T-junctions, along with descriptions of the numerical methods, initial conditions and boundary conditions used can be found in Vigolo, Radl & Stone (Reference Vigolo, Radl and Stone2014) and Chen, Rowley & Stone (Reference Chen, Rowley and Stone2015).
First, we seek to perform a visual comparison between the two flows, which we accomplish by plotting contours of the
$Q$
-criterion for a range of Reynolds numbers. For the T-junction case, we visualize the counter-rotating vortices in figure 12. Velocity streamlines are shown, along with a level set of the
$Q$
-contour. The vortices grow and propagate further downstream as the Reynolds number increases. For comparison, in figure 13 we show a single level set of the
$Q$
-contour for the flow downstream of a curved pipe which has a pipe-to-curvature radius ratio of
${\it\alpha}=0.005$
. Results are shown for
$\mathit{Re}=200$
, 400, 600 and 800. The leftmost edge of each figure represents the cross-sectional plane where
$z=0$
from figure 1. Streamlines are not added to this plot, because the magnitude of the secondary velocities is small, and the streamlines would appear nearly straight.
Figure 12. The steady-state solution of flow in a T-junction, shown as velocity streamlines (blue: low speed; white: high speed) and a single level set of the
$Q$
-contour (yellow); (a)
$\mathit{Re}=10$
, (b)
$\mathit{Re}=50$
, (c)
$\mathit{Re}=100$
, (d)
$\mathit{Re}=200$
, (e)
$\mathit{Re}=400$
, (f)
$\mathit{Re}=600$
. Arrows indicate the direction of flow. Results extracted from the numerical simulations of Chen et al. (Reference Chen, Rowley and Stone2015).
Figure 13. Level set of the
$Q$
-contour (red) in the straight outlet pipe for
${\it\alpha}=0.01$
; (a)
$\mathit{Re}=200$
, (b)
$\mathit{Re}=400$
, (c)
$\mathit{Re}=600$
, (d)
$\mathit{Re}=800$
.
Although the T-junction flow is visually more complicated than the flow in a straight pipe outlet from a curved section, we see that for both cases the vortices grow and propagate further downstream as the Reynolds number increases. We have shown that, for the straight pipe outlet flow, the characteristic length scale of the vortices scales linearly with the Reynolds number. We now ask whether this result also holds for the T-junction outlet flow, such that the characteristic length scale of the decay process in the arms of the T varies systematically with the Reynolds number.
In order to investigate this question, we calculate decay lengths for the vortical structures found in the outlets of the T-junction flow. Figure 14 shows the decay length (in channel widths) versus the Reynolds number that we calculated for the numerical results of Chen et al. (Reference Chen, Rowley and Stone2015). These results were found using the maximum value of the
$Q$
-criterion on a cross-section, as for the straight pipe outlet flow, as described in § 2. The data show a good linear fit. Thus we see that the decay lengths in the outlet arms of T-junction flow vary linearly with the Reynolds number, as for the case of decaying fully developed Dean flow.
Figure 14. Decay length (in channel widths) for the counter-rotating vortices found in the outlets of the flow in T-junctions based on the
$Q$
-criterion condition. Results extracted from the numerical simulations of Chen et al. (Reference Chen, Rowley and Stone2015).
For the case of the T-junction flow, the velocity profile entering each outlet arm is a large perturbation away from the fully developed square pipe velocity profile, unlike in the flow downstream of a curved pipe at modest Dean numbers. Furthermore, in the outlet arms, the secondary velocities can have magnitudes of the same order as the axial velocity. Thus, the linearization about the fully developed flow would most likely be a bad approximation for the flow in the outlet arms of a T-junction, at least at the Reynolds numbers studied here and by Chen et al. (Reference Chen, Rowley and Stone2015). Nevertheless, we find a linear relationship between the decay length and the Reynolds number. The results for the T-junction in figure 14 can be compared to the results for the outlet flow downstream of a curved pipe in figure 6. Both show a good linear relationship, differing only by a scale factor. The magnitude of the scale factor is expected to be a function of the differing inlet conditions and the pipe geometry (circular versus square). The key result, however, is that in both cases the characteristic axial length scale of the decay perturbation, non-dimensionalized by the channel width, varies proportional to
$\mathit{Re}$
.
Figure 15. Temporal convergence with
${\it\alpha}=0.01$
and
$\mathit{Re}=100$
.
7. Conclusion
Direct numerical simulations have been performed to investigate the downstream decay of fully developed curved pipe flow in a straight, tangential outlet downstream of a
$180^{\circ }$
pipe bend for a range of Reynolds numbers and pipe-to-curvature radius ratios. We quantified this decay process by calculating the transition lengths associated with the wall shear stress, vorticity,
$Q$
-criterion and velocity gradients in the outlet section. These decay lengths were found to have a linear dependence on the Reynolds number, with no dependence on the pipe-to-curvature radius ratio of the upstream curved pipe section. These dependencies were confirmed by applying judicious scaling arguments to the linearized governing equations and to the approximate boundary conditions. Velocity, pressure and vorticity fields were calculated and plotted in order to visualize the decay process. Finally, an analogy was found with the flow in the outlet arms of T-junction flow, where again a linear relationship was found between the decay length in the outlets and the Reynolds number.
The connection between this work and the flow in the outlets of a T-junction may suggest that some of the assumptions made in our scaling arguments could be relaxed and still result in linear relationships between decay lengths and the Reynolds number. Specifically, for the T-junction flow, the initial velocity perturbation in the outlet flow is large relative to the axial velocity, although our scaling arguments required a small velocity perturbation in order to perform the linearization. Nevertheless, we found a linear relationship also for the T-junction outlet case.
Figure 16. Grid convergence test results based on the magnitude of vorticity (
${\it\alpha}=0.03$
and
$\mathit{Re}=400$
).
This work provides a quantitative prediction for the transition length downstream of a curved pipe. These transition lengths may be relevant for systems that seek to minimize heat/mass transfer in certain regions of the flow or for systems that require precise Poiseuille flow conditions downstream of various other piping elements. Furthermore, prior to this work, the best estimates of such transition lengths would probably be the entrance length predictions in a straight pipe. However, such estimates could be off by 100 % or more, since (4.1) suggests that these decay lengths are nearly double the entrance length in a straight pipe (Atkinson et al. Reference Atkinson, Brocklebank, Card and Smith1969).
Future work could seek an analytical solution to (3.8) subject to the boundary conditions (3.9). As mentioned, a form of the velocity/pressure perturbation may be sought that includes a sum of modes that decay exponentially with the rescaled coordinate
$\tilde{z}$
. Furthermore, the analysis of Smith (Reference Smith1976) may be applied to the neighbourhood of the transition from the curved to the straight section in order to solve for the local structure of the boundary layer and to take into account the upstream influence on the local flow structure. Finally, this work may be extended to larger values of
$D$
, and additional appropriate scalings may be sought.
Acknowledgement
We thank the NSF for support via grant CBET-1234500.
Appendix. Numerical convergence
In order to verify numerical accuracy, both temporal and spatial convergence are monitored. As stated, temporal convergence is confirmed by monitoring the norm of the time derivative of the velocity vector field. Results representing the temporal convergence for the case with
${\it\alpha}=0.01$
and
$\mathit{Re}=100$
are shown in figure 15. As can be seen, the time derivative of the velocity decreases by almost eight orders of magnitude, at which time the solver oscillates about a small numerical orbit. On this numerical orbit,
$\Vert \partial \boldsymbol{u}/\partial t\Vert /\Vert \boldsymbol{u}\Vert \approx 10^{-4}$
or less. As mentioned, for the purposes of measuring transition lengths, velocity profiles and flow development, this numerical oscillation is not seen to have any noticeable effect. Measuring velocity profiles at various points on this oscillation never resulted in any change in measured transition lengths. This feature is likely due to the error introduced by this numerical oscillation on the transition length having a smaller order of magnitude than the error introduced by the spatial discretization itself. We also verify spatial convergence by performing a mesh refinement study at the largest Reynolds number chosen for each value of
${\it\alpha}$
. For these tests, the integral of the vorticity over the cross-sectional area of the pipe is plotted against the angle along the curved pipe. This is repeated for each value of
${\it\alpha}$
with simulation domains having
$2.0\times 10^{5}$
,
$4.0\times 10^{5}$
,
$8.0\times 10^{5}$
,
$1.6\times 10^{6}$
,
$3.2\times 10^{6}$
,
$6.4\times 10^{6}$
and
$1.28\times 10^{7}$
cells. Representative results are shown in figure 16. The results show monotonic convergence as the number of grid cells is doubled. Having performed such a convergence test for each value of
${\it\alpha}$
, we choose to perform all simulations using
$6.4\times 10^{6}$
cells.
