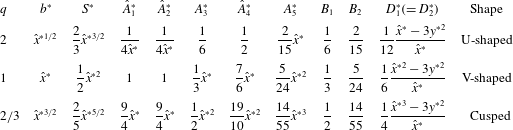1 Introduction
Long waves can be funnelled in converging basins whose cross-sections decrease in the direction of wave propagation. The funnelling effect is known to be responsible for extreme wave events of different scales, such as high tsunami run-up in narrow bays and local amplification of storm surges or tides over V-shaped gulfs. The earliest theory relevant to the phenomena is Green’s law, which is derived from the energy flux conservation of a progressive harmonic wave. It states that the wave amplitude in a converging channel increases with negative powers of the channel depth and width. While it is valid for waves sufficiently shorter than the transitional scale of the cross-section, Green’s law cannot be directly applied to wave amplification in strongly converging channels due to significant reflection (Rayleigh Reference Rayleigh1879; Lamb Reference Lamb1932). In case of embayment, which is closed at the end, incoming waves are fully reflected from the bay, regardless of the wavelength, to form standing waves with nodes and anti-nodes. Moreover, when the wavelength is smaller than the bay width, wave refraction occurs over laterally varying topography, affecting the energy transfer process inside the bay. In actual nonlinear problems, wave amplification is limited by the occurrence of wave breaking to further complicate the process.
Recent tsunami events have highlighted the complexity of the phenomena (e.g. Shimozono et al. Reference Shimozono, Sato, Okayasu, Tajima, Fritz, Liu and Takagawa2012; Didenkulova Reference Didenkulova2013). In particular, in the 2011 Tohoku tsunami, a large tsunami attacked a ria coast of Japan (the Sanriku Coast) that consists of numerous bays of several kilometres, marking extreme run-up heights in their inner coasts. The well-organized survey after the event provided us with a densely measured distribution of tsunami run-up heights throughout the coast (Mori & Takahashi Reference Mori and Takahashi2012). The dataset exhibits strong variations in run-up heights around the bays, and in some cases, contrary to Green’s law, large tsunami heights are found near the bay entrance rather than at the bay head (Liu et al. Reference Liu, Shimozono, Takagawa, Okayasu, Fritz, Sato and Tajima2013). The incident tsunami waveforms, which were captured by several wavemeter buoys off the coast, are characterized as a superposition of a long wave train and a short impulsive wave localized in its leading part. The distribution of run-up heights is largely attributed to complex behaviours of the shorter component since the longer component, whose wavelength is much larger than the bay scale, cannot produce the strong variation. Although the distribution of run-up heights could be reproduced to some extent by numerical models based on the two-dimensional nonlinear shallow water equations, the underlying physics is not well understood. It is desirable to clarify the mathematical structure of the problem to provide insights into the phenomena.
Various analytical solutions have been obtained for one-dimensional run-up problems. Pioneer work was done by Carrier & Greenspan (Reference Carrier and Greenspan1958), who presented a periodic long wave solution over an infinitely long slope. The nonlinear shallow water equations were transformed into a linear equation by the hodograph transform for the exact solution. Keller & Keller (Reference Keller and Keller1964) obtained a periodic wave solution on a finite slope connected to a flat bottom. The same solution was derived by Shuto (Reference Shuto1972) from the nonlinear shallow water equation in the Lagrangian description. The approaches for the periodic wave solutions were later extended by integral transforms for localized waves such as a solitary wave, N-wave and Lorentz wave (Synolakis Reference Synolakis1987; Pelinovsky & Mazova Reference Pelinovsky and Mazova1992; Tadepalli & Synolakis Reference Tadepalli and Synolakis1994). Simple formulas for the maximum run-up height resulted from these solutions, providing an understanding of how incoming waves of different wavelengths are amplified over sloping beds. The applicable range of the formula is limited by wave breaking, and the breaking criterion can be given as the condition at which the hodograph transform breaks down. Didenkulova, Pelinovsky & Soomere (Reference Didenkulova, Pelinovsky and Soomere2008) and Madsen & Schaeffer (Reference Madsen and Schaeffer2010) provided comprehensive overviews of the analytical solutions and breaking criteria for different types of incident waves. The analytical solutions for uniformly sloping beaches can also be viewed as those for rectangular bays of uniform width that linearly decrease water depth towards the bay head. For converging bays of decreasing cross-section, wave funnelling and refraction should modify these solutions, especially for relatively short incident waves.
Theoretical studies have also been conducted for long wave evolution in two-dimensional basins with decreasing cross-section. A common approach is to reduce the two-dimensional problems into quasi-one-dimensional problems using the section-integrated shallow water equations under the assumption that the basin width is sufficiently smaller than the wavelength (Stoker Reference Stoker1957). Several analytical solutions have been obtained, especially for tide propagation through converging channels. Inviscid solutions for channels with linearly decreasing depth and/or width are presented in Lamb (Reference Lamb1932). Many researchers later derived solutions for converging channels with friction, based on different assumptions, to discuss the balance of the frictional damping and topographic amplification (Jay Reference Jay1991; Friedrichs & Aubrey Reference Friedrichs and Aubrey1994; Prandle Reference Prandle2003; Savenije et al. Reference Savenije, Toffolon, Haas and Veling2008). On the other hand, only a few analytical studies have been conducted on the propagation and run-up of long waves in converging bays for which significant reflection is involved. Didenkulova & Pelinovsky (Reference Didenkulova and Pelinovsky2011) investigated periodic wave amplification in narrow bays whose depths linearly decreased in the longitudinal direction, whereas the cross-section was represented by an arbitrary power function. For the same types of bay topography, Zahibo et al. (Reference Zahibo, Pelinovsky, Golinko and Osipenko2006) applied the Carrier–Greenspan approach to the section-integrated shallow water equations to obtain a run-up solution as well as a breaking criterion for monochromatic waves. More recently, Rybkin, Pelinovsky & Didenkulova (Reference Rybkin, Pelinovsky and Didenkulova2014) has further generalized the approach for an arbitrary bay shape and incident waveform. Didenkulova, Didenkulov & Pelinovsky (Reference Didenkulova, Didenkulov and Pelinovsky2015) also discussed the influences of incoming wave shapes on run-up characteristics in converging bays. However, all of these solutions are independent of the bay width as they are based on the narrow bay assumption. Therefore, the two-dimensional effect through wave refraction is disregarded, which may become significant, especially where relatively short wave evolution is concerned.
In this study, analytical solutions for long periodic wave evolution in converging bays are derived from the section-integrated shallow water equations. Different types of converging bays are studied, in which water depth varies in both longitudinal and transverse directions at different rates. Unlike previous studies, we assume here that the transverse flow acceleration, which produces two-dimensionality in wave properties, is small but non-negligible. The two-dimensional shallow water equations can then be approximated by one-dimensional dispersive wave equations. Based on the analytical solutions of the higher-order equations, we investigate wave propagation and run-up characteristics considering the two-dimensional effect. Furthermore, we clarify the applicable range of the derived solutions through perturbation analysis and discuss wave behaviours beyond the limit, providing a comprehensive understanding of the problem.
2 Boundary value problem
2.1 Governing equations
We start the analytical investigation with the nonlinear shallow water equations neglecting the dispersion effect due to the vertical acceleration of bay water. This assumption is valid for a long wave propagating in a relatively shallow bay. For simplicity, we also disregard the bed friction effect since the ratio of the friction term to the acceleration term is small for relatively short waves that tend to be funnelled in bays of a typical scale. Hence, the two-dimensional continuity and momentum equations can be written in conservative form as
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial H}{\partial t}+\frac{\partial (Hu)}{\partial x}+\frac{\partial (Hv)}{\partial y}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial (Hu)}{\partial t}+\frac{\partial (Hu^{2})}{\partial x}+\frac{\partial (Huv)}{\partial y}+gH\frac{\partial {\it\eta}}{\partial x}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial (Hv)}{\partial t}+\frac{\partial (Huv)}{\partial x}+\frac{\partial (Hv^{2})}{\partial y}+gH\frac{\partial {\it\eta}}{\partial y}=0, & \displaystyle\end{eqnarray}$$
$t$
is time,
$x$
and
$y$
are spatial coordinates,
$H(x,y,t)$
is the total water depth,
${\it\eta}(x,y,t)$
is the water surface elevation above the undisturbed water surface,
$u(x,y,t)$
and
$v(x,y,t)$
are the depth-averaged velocities in the
$x$
and
$y$
directions, respectively and
$g$
is the gravity acceleration. The total water depth is expressed as
$H=h+{\it\eta}$
with the undisturbed water depth
$h(x,y)$
. The
$x$
coordinate is taken along the bay axis towards the bay head, whereas the
$y$
coordinate is set in the transverse direction, with the origin of the coordinates at the centre of the bay entrance. The bay geometry is assumed to be symmetric about the bay axis (
$x$
axis) with monotonically decreasing width and depth towards the bay head. The geometric symmetry allows us to consider only a half-domain (
$y\geqslant 0$
) and assume
$v=0$
along the bay axis (
$y=0$
) for normally incident waves. The bay scale is represented by three parameters: bay length
$l_{x}$
, bay entrance width
$l_{y}$
and bay entrance depth
$h_{0}$
(see figure 1).
The wave motion scale in the
$x$
direction is represented by the incident wavelength
$L_{0}$
, whereas that in the
$y$
direction is restricted by the bay width
$l_{y}$
. The two-dimensional problem can be reduced to a quasi-one-dimensional problem when
$l_{y}/L_{0}$
is small. In the following, we integrate (2.1) and (2.2) over the transverse extent of bay water to derive the section-integrated shallow water equations. In doing so, the kinematic lateral boundary condition is required:
$$\begin{eqnarray}\displaystyle v(x,B,t)=\frac{\partial B}{\partial t}+u(x,B,t)\frac{\partial B}{\partial x}, & & \displaystyle\end{eqnarray}$$
where
$B(x,t)$
is the transverse extent of water surface defined such that
$H(x,B(x,t),t)=0$
. The transverse extent is changing with time due to water surface evolution, and is separated into two components as
$B=b+{\it\xi}$
, where
$b(x)$
is the transverse extent of the undisturbed water surface that satisfies
$h(x,b(x))=0$
and
${\it\xi}(x,t)$
is the time-varying component.
First, we divide water surface elevation
${\it\eta}$
into its mean and varying components in the transverse direction. Rewriting (2.3) in the non-conservative form using (2.1) and integrating it from the bay centre (
$y=0$
) to an arbitrary
$y$
yields
$$\begin{eqnarray}\displaystyle {\it\eta}(x,y,t)={\it\eta}(x,0,t)-\frac{1}{g}\int _{0}^{y}\frac{\text{D}v}{\text{D}t}\,\text{d}y, & & \displaystyle\end{eqnarray}$$
where
$\text{D}/\text{D}t$
represents the substantial derivative. The second term on the right-hand side of (2.5) represents the transverse variation in water surface elevation. The mean water surface elevation
$\overline{{\it\eta}}$
can be obtained by averaging (2.5) over the transverse extent as
$$\begin{eqnarray}\displaystyle \bar{{\it\eta}}(x,t)={\it\eta}(x,0,t)-\frac{1}{gB}\int _{0}^{B}\int _{0}^{y}\frac{\text{D}v}{\text{D}t}\,\text{d}y\,\text{d}y. & & \displaystyle\end{eqnarray}$$
From (2.5) and (2.6),
${\it\eta}$
may be expressed as the sum of the mean and varying components:
${\it\eta}=\bar{{\it\eta}}+{\it\eta}^{\prime }$
with
$$\begin{eqnarray}\displaystyle {\it\eta}^{\prime }(x,y,t)=\frac{1}{gB}\int _{0}^{B}\int _{0}^{y}\frac{\text{D}v}{\text{D}t}\,\text{d}y\,\text{d}y-\frac{1}{g}\int _{0}^{y}\frac{\text{D}v}{\text{D}t}\,\text{d}y. & & \displaystyle\end{eqnarray}$$
Integrating (2.1) and (2.2) over the transverse extent using
$v(x,0,t)=0$
and the boundary condition (2.4), we obtain the section-integrated shallow water equations
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial }{\partial t}\int _{0}^{B}H\,\text{d}y+\frac{\partial }{\partial x}\int _{0}^{B}Hu\,\text{d}y=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial }{\partial t}\int _{0}^{B}Hu\,\text{d}y+\frac{\partial }{\partial x}\int _{0}^{B}Hu^{2}\,\text{d}y+g\left(\int _{0}^{B}H\,\text{d}y\right)\frac{\partial \bar{{\it\eta}}}{\partial x}+g\int _{0}^{B}H\frac{\partial {\it\eta}^{\prime }}{\partial x}\,\text{d}y=0. & \displaystyle\end{eqnarray}$$
Figure 1. Schematic illustration of the symmetric converging bay.
To simplify the expressions of (2.8) and (2.9), we also divide the longitudinal velocity
$u$
into the section-averaged component
$\bar{u}(x,t)$
and varying component
$u^{\prime }(x,y,t)$
as follows:
$$\begin{eqnarray}\displaystyle \bar{u}=\frac{1}{S}\int _{0}^{B}Hu\,\text{d}y,\quad u^{\prime }=u-\bar{u}\quad \text{with }S=\int _{0}^{B}H\,\text{d}y, & & \displaystyle\end{eqnarray}$$
where
$S(x,t)$
is the cross-sectional area of bay water varying with time. Substituting (2.10) into (2.8) and (2.9) yields
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial S}{\partial t}+\frac{\partial }{\partial x}(S\bar{u})=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial }{\partial t}(\bar{S}u)+\frac{\partial }{\partial x}(S\bar{u}^{2})+\frac{\partial }{\partial x}(S{u^{\prime }}^{2})+gS\frac{\partial \bar{{\it\eta}}}{\partial x}+g\int _{0}^{B}H\frac{\partial {\it\eta}^{\prime }}{\partial x}\,\text{d}y=0. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\!\!\!\!\begin{array}{@{}c@{}}\displaystyle x=L_{0}x^{\ast },\quad y=l_{y}y^{\ast },\quad t=\frac{L_{0}}{c_{0}}t^{\ast },\quad u={\it\varepsilon}c_{0}u^{\ast },\quad \bar{u}={\it\varepsilon}c_{0}\bar{u}^{\ast }\!,\quad v={\it\varepsilon}{\it\sigma}c_{0}v^{\ast }\!,\quad S=l_{y}h_{0}S^{\ast }\!,\!\\ \displaystyle H=h_{0}H^{\ast },\quad h=h_{0}h^{\ast },\quad {\it\eta}=a_{0}{\it\eta}^{\ast },\quad \bar{{\it\eta}}=a_{0}\bar{{\it\eta}}^{\ast },\quad B=l_{y}B^{\ast },\quad b=l_{y}b^{\ast },\quad {\it\xi}={\it\varepsilon}l_{y}{\it\xi}^{\ast },\!\end{array}\right\} & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where the superscript * denotes the dimensionless variables,
$a_{0}$
is the incident wave amplitude,
$c_{0}=\sqrt{gh_{0}}$
is the wave celerity at the bay entrance,
${\it\varepsilon}=a_{0}/h_{0}$
is the nonlinearity parameter and
${\it\sigma}=l_{y}/L_{0}$
is the relative bay width. The irrotationality of horizontal flows requires the scale of the varying component of the longitudinal velocity to be
$u^{\prime }={\it\varepsilon}{\it\sigma}^{2}c_{0}u^{\prime \ast }$
. Also, (2.7) suggests that the varying component of water surface elevation is scaled as
${\it\eta}^{\prime }=a_{0}{\it\sigma}^{2}{\it\eta}^{\prime \ast }$
. Inserting all the dimensionless variables into the equations above, we obtain
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial S^{\ast }}{\partial t^{\ast }}+{\it\varepsilon}\frac{\partial }{\partial x^{\ast }}(S^{\ast }\bar{u}^{\ast })=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial (S^{\ast }\bar{u}^{\ast })}{\partial t^{\ast }}+{\it\varepsilon}\frac{\partial (S^{\ast }\bar{u}^{\ast 2})}{\partial x^{\ast }}+{\it\varepsilon}{\it\sigma}^{4}\frac{\partial (S^{\ast }u^{\prime \ast 2})}{\partial x^{\ast }}+S^{\ast }\frac{\partial \bar{{\it\eta}}^{\ast }}{\partial x^{\ast }}+{\it\sigma}^{2}\int _{0}^{B^{\ast }}H^{\ast }\frac{\partial {{\it\eta}^{\prime }}^{\ast }}{\partial x^{\ast }}\,\text{d}y^{\ast }=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {{\it\eta}^{\prime }}^{\ast }=\frac{1}{B^{\ast }}\int _{0}^{B^{\ast }}\int _{0}^{y^{\ast }}\frac{\text{D}v^{\ast }}{\text{D}t^{\ast }}\,\text{d}y^{\ast }\,\text{d}y^{\ast }-\int _{0}^{y^{\ast }}\frac{\text{D}v^{\ast }}{\text{D}t^{\ast }}\,\text{d}y^{\ast }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{D}v^{\ast }}{\text{D}t^{\ast }}=\frac{\partial v^{\ast }}{\partial t^{\ast }}+{\it\varepsilon}u^{\ast }\frac{\partial v^{\ast }}{\partial x^{\ast }}+{\it\varepsilon}v^{\ast }\frac{\partial v^{\ast }}{\partial y^{\ast }}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle S^{\ast }=\int _{0}^{B^{\ast }}h^{\ast }\,\text{d}y^{\ast }+{\it\varepsilon}\int _{0}^{B^{\ast }}{\it\eta}^{\ast }\,\text{d}y^{\ast }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle H^{\ast }=h^{\ast }+{\it\varepsilon}{\it\eta}^{\ast }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle B^{\ast }=b^{\ast }+{\it\varepsilon}{\it\xi}^{\ast }. & \displaystyle\end{eqnarray}$$
${\it\sigma}$
. The former represents the advection by the varying component of longitudinal flows, while the latter represents the transverse flow effect. For narrow bays with small
${\it\sigma}$
, (2.15) can be simplified by neglecting these terms: 
$$\begin{eqnarray}\displaystyle \frac{\partial \bar{u}^{\ast }}{\partial t^{\ast }}+{\it\varepsilon}\bar{u}^{\ast }\frac{\partial \bar{u}^{\ast }}{\partial x^{\ast }}+\frac{\partial \bar{{\it\eta}}^{\ast }}{\partial x^{\ast }}=0. & & \displaystyle\end{eqnarray}$$
The set of (2.14) and (2.21) has been employed in previous studies to explore wave propagation and run-up characteristics in narrow bays (Zahibo et al.
Reference Zahibo, Pelinovsky, Golinko and Osipenko2006; Didenkulova et al.
Reference Didenkulova, Pelinovsky and Soomere2008; Didenkulova & Pelinovsky Reference Didenkulova and Pelinovsky2011; Rybkin et al.
Reference Rybkin, Pelinovsky and Didenkulova2014; Didenkulova et al.
Reference Didenkulova, Didenkulov and Pelinovsky2015). For specific types of bay geometries, Zahibo et al. (Reference Zahibo, Pelinovsky, Golinko and Osipenko2006) derived an analytical solution for monochromatic wave evolution through applying the hodograph transform to the equations. They described the nonlinear wave solution in terms of the linear solution that was obtained by neglecting the terms of
$O({\it\varepsilon})$
. This is possible because the linear dynamics determines the main structure of the solution, and the nonlinearity only plays a role in transforming the time and spatial coordinates. Therefore, the run-up height from their solution is identical to the one from the linear solution. This is valid only when the incident wave amplitude is small relative to the water depth at the bay entrance (
${\it\varepsilon}$
is small), because they linearized the holograph transform for assignment of the boundary value. However, this limitation is not severe because the nonlinearity at the bay entrance is often small in actual cases. Through comparisons with laboratory data, Synolakis (Reference Synolakis1991) confirmed that the linear theory predicts the run-up height over uniform slopes satisfactorily, although it does not correctly describe the details of wave profiles. Antuono & Brocchini (Reference Antuono and Brocchini2007) derived an analytical solution without linearizing the data assignment. Their results suggest that the error arising from the linearized assignment is a few per cent when
${\it\varepsilon}=0.05$
.
Unlike in the previous studies, we neglect the nonlinear terms of
$O({\it\varepsilon})$
, but keep the terms of
$O({\it\sigma}^{2})$
in (2.14)–(2.20). Therefore, we explore the effects of transverse flows in linear dynamics. As described above, the linearization does not severely restrict the applicability to actual problems for the energy transfer process in the bays. After some manipulation, we obtain the linearized continuity and momentum equations as
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial \bar{{\it\eta}}^{\ast }}{\partial t^{\ast }}+\frac{1}{b^{\ast }}\frac{\partial }{\partial x^{\ast }}(S^{\ast }\bar{u}^{\ast })=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial \bar{u}^{\ast }}{\partial t^{\ast }}+\frac{\partial \bar{{\it\eta}}^{\ast }}{\partial x^{\ast }}+\frac{{\it\sigma}^{2}}{S^{\ast }}\int _{0}^{b^{\ast }}h^{\ast }\frac{\partial {{\it\eta}^{\prime }}^{\ast }}{\partial x^{\ast }}\,\text{d}y^{\ast }=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {{\it\eta}^{\prime }}^{\ast }=\frac{1}{b^{\ast }}\int _{0}^{b^{\ast }}\int _{0}^{y^{\ast }}\frac{\partial v^{\ast }}{\partial t^{\ast }}\,\text{d}y^{\ast }\,\text{d}y^{\ast }-\int _{0}^{y^{\ast }}\frac{\partial v^{\ast }}{\partial t^{\ast }}\,\text{d}y^{\ast }. & \displaystyle\end{eqnarray}$$
$\bar{u}^{\ast }$
and
$\bar{{\it\eta}}^{\ast }$
, and the cross-sectional area
$S^{\ast }$
are now given by 
$$\begin{eqnarray}\displaystyle \bar{u}^{\ast }=\frac{1}{S^{\ast }}\int _{0}^{b^{\ast }}h^{\ast }u^{\ast }\,\text{d}y^{\ast },\quad \bar{{\it\eta}}^{\ast }=\frac{1}{b^{\ast }}\int _{0}^{b^{\ast }}{\it\eta}^{\ast }\,\text{d}y^{\ast },\quad S^{\ast }=\int _{0}^{b^{\ast }}h^{\ast }\,\text{d}y^{\ast }. & & \displaystyle\end{eqnarray}$$
For the sake of linearization, the transverse extent and cross-sectional area are no longer functions of time. In order to solve the equations, we need to express the transverse flow acceleration in (2.24) by
$\bar{u}^{\ast }$
and
$\bar{{\it\eta}}^{\ast }$
. Linearizing the continuity equation (2.1) and differentiating it with respect to time, we have the following relation in the dimensionless form:
$$\begin{eqnarray}\displaystyle \frac{\partial ^{2}{\it\eta}^{\ast }}{\partial t^{\ast 2}}+\frac{\partial ^{2}(h^{\ast }u^{\ast })}{\partial x^{\ast }\partial t^{\ast }}+\frac{\partial ^{2}(h^{\ast }v^{\ast })}{\partial y^{\ast }\partial t^{\ast }}=0. & & \displaystyle\end{eqnarray}$$
The transverse flow acceleration is given by integrating (2.26) from the bay centre (
$y^{\ast }=0$
) to an arbitrary
$y^{\ast }$
as
$$\begin{eqnarray}\displaystyle \frac{\partial v^{\ast }}{\partial t^{\ast }}=-\frac{1}{h^{\ast }}\int _{0}^{y^{\ast }}\frac{\partial ^{2}{\it\eta}^{\ast }}{\partial t^{\ast 2}}\,\text{d}y^{\ast }-\frac{1}{h^{\ast }}\frac{\partial }{\partial x^{\ast }}\int _{0}^{y^{\ast }}h^{\ast }\frac{\partial u^{\ast }}{\partial t^{\ast }}\,\text{d}y^{\ast }. & & \displaystyle\end{eqnarray}$$
Recalling that the laterally varying components of
$u^{\ast }$
and
${\it\eta}^{\ast }$
are of
$O({\it\sigma}^{2})$
, we rewrite (2.27) in terms of the mean variables as
$$\begin{eqnarray}\displaystyle \frac{\partial v^{\ast }}{\partial t^{\ast }}=-\frac{y^{\ast }}{h^{\ast }}\frac{\partial ^{2}\bar{{\it\eta}}^{\ast }}{\partial t^{\ast 2}}-\frac{1}{h^{\ast }}\int _{0}^{y^{\ast }}h^{\ast }\,\text{d}y^{\ast }\frac{\partial ^{2}\bar{u}^{\ast }}{\partial x^{\ast }\partial t^{\ast }}-\frac{1}{h^{\ast }}\frac{\partial }{\partial x^{\ast }}\left(\int _{0}^{y^{\ast }}h^{\ast }\,\text{d}y^{\ast }\right)\frac{\partial \bar{u}^{\ast }}{\partial t^{\ast }}+O({\it\sigma}^{2}).\quad & & \displaystyle\end{eqnarray}$$
Subsequently, equation (2.24) can be rewritten using (2.28) as
$$\begin{eqnarray}\displaystyle {{\it\eta}^{\prime }}^{\ast }=-I_{1}^{\ast }\frac{\partial ^{2}\bar{{\it\eta}}^{\ast }}{\partial t^{\ast 2}}-I_{2}^{\ast }\frac{\partial ^{2}\bar{u}^{\ast }}{\partial x^{\ast }\partial t^{\ast }}-I_{3}^{\ast }\frac{\partial \bar{u}^{\ast }}{\partial t^{\ast }}+O({\it\sigma}^{2}), & & \displaystyle\end{eqnarray}$$
where
$I_{1}^{\ast }$
,
$I_{2}^{\ast }$
and
$I_{3}^{\ast }$
are functions of
$x^{\ast }$
and
$y^{\ast }$
, which depend on the bay geometry:
$$\begin{eqnarray}\displaystyle & \displaystyle I_{1}^{\ast }=\frac{1}{b^{\ast }}\int _{0}^{b^{\ast }}{\it\gamma}_{1}^{\ast }\,\text{d}y^{\ast }-{\it\gamma}_{1}^{\ast } & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle I_{2}^{\ast }=\frac{1}{b^{\ast }}\int _{0}^{b^{\ast }}\int _{0}^{y^{\ast }}\frac{{\it\gamma}_{2}^{\ast }}{h^{\ast }}\,\text{d}y^{\ast }\,\text{d}y^{\ast }-\int _{0}^{y^{\ast }}\frac{{\it\gamma}_{2}^{\ast }}{h^{\ast }}\,\text{d}y^{\ast }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle I_{3}^{\ast }=\frac{1}{b^{\ast }}\int _{0}^{b^{\ast }}\int _{0}^{y^{\ast }}\frac{1}{h^{\ast }}\frac{\partial {\it\gamma}_{2}^{\ast }}{\partial x^{\ast }}\,\text{d}y^{\ast }\,\text{d}y^{\ast }-\int _{0}^{y^{\ast }}\frac{1}{h^{\ast }}\frac{\partial {\it\gamma}_{2}^{\ast }}{\partial x^{\ast }}\,\text{d}y^{\ast }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\gamma}_{1}^{\ast }=\int _{0}^{y^{\ast }}\frac{y^{\ast }}{h^{\ast }}\,\text{d}y^{\ast },\quad {\it\gamma}_{2}^{\ast }=\int _{0}^{y^{\ast }}h^{\ast }\,\text{d}y^{\ast }. & & \displaystyle\end{eqnarray}$$
We substitute (2.29) into (2.23) to obtain the momentum equation which is valid up to
$O({\it\sigma}^{2})$
:
$$\begin{eqnarray}\displaystyle (1-{\it\sigma}^{2}A_{1}^{\ast })\frac{\partial \bar{u}^{\ast }}{\partial t^{\ast }}+\frac{\partial \bar{{\it\eta}}^{\ast }}{\partial x^{\ast }}-{\it\sigma}^{2}\left[A_{2}^{\ast }\frac{\partial ^{2}\bar{{\it\eta}}^{\ast }}{\partial t^{\ast 2}}+A_{3}^{\ast }\frac{\partial ^{3}\bar{{\it\eta}}^{\ast }}{\partial x^{\ast }\partial t^{\ast 2}}+A_{4}^{\ast }\frac{\partial ^{2}\bar{u}^{\ast }}{\partial x^{\ast }\partial t^{\ast }}+A_{5}^{\ast }\frac{\partial ^{3}\bar{u}^{\ast }}{\partial x^{\ast 2}\partial t^{\ast }}\right]=O({\it\sigma}^{4}), & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where the coefficients
$A_{1}^{\ast }$
–
$A_{5}^{\ast }$
are functions of only
$x^{\ast }$
and are given by
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle A_{1}^{\ast }=\frac{1}{S^{\ast }}\int _{0}^{b^{\ast }}h^{\ast }\frac{\partial I_{3}^{\ast }}{\partial x^{\ast }}\,\text{d}y^{\ast },\quad A_{2}^{\ast }=\frac{1}{S^{\ast }}\int _{0}^{b}h^{\ast }\frac{\partial I_{1}^{\ast }}{\partial x^{\ast }}\,\text{d}y^{\ast },\quad A_{3}^{\ast }=\frac{1}{S^{\ast }}\int _{0}^{b^{\ast }}h^{\ast }I_{1}^{\ast }\,\text{d}y^{\ast },\\ \displaystyle A_{4}^{\ast }=\frac{1}{S^{\ast }}\int _{0}^{b^{\ast }}h^{\ast }\left(\frac{\partial I_{2}^{\ast }}{\partial x^{\ast }}+I_{3}^{\ast }\right)\,\text{d}y^{\ast }\quad \text{and}\quad A_{5}^{\ast }=\frac{1}{S^{\ast }}\int _{0}^{b^{\ast }}h^{\ast }I_{2}^{\ast }\,\text{d}y^{\ast }.\end{array}\right\}\quad & & \displaystyle\end{eqnarray}$$
The momentum equation (2.34) has a form similar to those of Boussinesq-type equations for dispersive waves, which generally involve third-order derivatives of the flow velocity and water surface elevation. The third-order derivative terms of the Boussineq-type equations arise from vertical flows, while those of (2.34) are attributed to transverse flows generated by the bay geometry. The dispersion effect by vertical flows has been studied for waves travelling over variable channels in the framework of the Korteweg–de Vries equations (Peregrine Reference Peregrine1968, Reference Peregrine1969; Teng & Wu Reference Teng and Wu1992, Reference Teng and Wu1994). The magnitude of this type of dispersion is represented by the relative depth
$h_{0}/L_{0}$
. Therefore, the relative importance of the present type of dispersion can be measured by
$l_{y}/h_{0}$
. This suggests that the present dispersion effect is dominant when the bay width is greater than the bay water depth. This condition is fulfilled by many bays that are widely open to the ocean. In some special cases of bay geometry, the coefficients of the higher-order terms in (2.34) can be expressed as power functions of
$x^{\ast }$
, which will be described in § 2.2. Given the bay geometry and incident wave condition, we can derive analytical solutions for
$\bar{{\it\eta}}$
and
$\bar{u}$
from the set of (2.22) and (2.34). Once the mean variables are determined, (2.29) enables us to obtain the two-dimensional wave profile inside the bay.
For later convenience, we introduce a new coordinate defined by
$$\begin{eqnarray}\displaystyle \hat{x}^{\ast }=1-\frac{x}{l_{x}}. & & \displaystyle\end{eqnarray}$$
The
$\hat{x}^{\ast }$
coordinate is directed towards the bay entrance with the origin at the bay head. Subsequently, equations (2.22) and (2.34) are rewritten in terms of the new coordinate as
$$\begin{eqnarray}\displaystyle {\it\nu}\frac{\partial \bar{{\it\eta}}^{\ast }}{\partial t^{\ast }}-\frac{\bar{u}^{\ast }}{b^{\ast }}\frac{\partial S^{\ast }}{\partial \hat{x}^{\ast }}-\frac{S^{\ast }}{b^{\ast }}\frac{\partial \bar{u}^{\ast }}{\partial \hat{x}^{\ast }}=0, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left({\it\nu}-\frac{{\it\sigma}^{2}}{{\it\nu}}\hat{A}_{1}^{\ast }\right)\frac{\partial \bar{u}^{\ast }}{\partial t^{\ast }}-\frac{\partial \bar{{\it\eta}}^{\ast }}{\partial \hat{x}^{\ast }}+{\it\sigma}^{2}\hat{A}_{2}^{\ast }\frac{\partial ^{2}\bar{{\it\eta}}^{\ast }}{\partial t^{\ast 2}}+{\it\sigma}^{2}A_{3}^{\ast }\frac{\partial ^{3}\bar{{\it\eta}}^{\ast }}{\partial \hat{x}^{\ast }\partial t^{\ast 2}}\nonumber\\ \displaystyle & & \displaystyle \qquad \qquad -\,\frac{{\it\sigma}^{2}}{{\it\nu}}\hat{A}_{4}^{\ast }\frac{\partial ^{2}\bar{u}^{\ast }}{\partial \hat{x}^{\ast }\partial t^{\ast }}-\frac{{\it\sigma}^{2}}{{\it\nu}}A_{5}^{\ast }\frac{\partial ^{3}\bar{u}^{\ast }}{\partial \hat{x}^{\ast 2}\partial t^{\ast }}=0,\end{eqnarray}$$
where
${\it\nu}=l_{x}/L_{0}$
represents the relative bay length to the representative wavelength. The higher-order terms of
$O({\it\sigma}^{4})$
are truncated in (2.38). The newly introduced coefficients
$\hat{A}_{1}^{\ast }$
,
$\hat{A}_{2}^{\ast }$
and
$\hat{A}_{4}^{\ast }$
are defined as follows:
$$\begin{eqnarray}\displaystyle \hat{A}_{1}^{\ast }=\frac{1}{S^{\ast }}\int _{0}^{b^{\ast }}h^{\ast }\frac{\partial \hat{I} _{3}^{\ast }}{\partial \hat{x}^{\ast }}\,\text{d}y^{\ast },\quad \hat{A}_{2}^{\ast }=\frac{1}{S^{\ast }}\int _{0}^{b}h^{\ast }\frac{\partial I_{1}^{\ast }}{\partial \hat{x}^{\ast }}\,\text{d}y^{\ast },\quad \hat{A}_{4}^{\ast }=\frac{1}{S^{\ast }}\int _{0}^{b^{\ast }}h^{\ast }\left(\frac{\partial I_{2}^{\ast }}{\partial \hat{x}^{\ast }}+\hat{I} _{3}^{\ast }\right)\,\text{d}y^{\ast }, & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
with
$$\begin{eqnarray}\displaystyle \hat{I} _{3}^{\ast }=\frac{1}{b^{\ast }}\int _{0}^{b^{\ast }}\int _{0}^{y^{\ast }}\frac{1}{h^{\ast }}\frac{\partial {\it\gamma}_{2}^{\ast }}{\partial \hat{x}^{\ast }}\,\text{d}y^{\ast }\,\text{d}y^{\ast }-\int _{0}^{y^{\ast }}\frac{1}{h^{\ast }}\frac{\partial {\it\gamma}_{2}^{\ast }}{\partial \hat{x}^{\ast }}\,\text{d}y^{\ast }. & & \displaystyle\end{eqnarray}$$
The set of (2.37) and (2.38) is employed as the governing equations in the present study. Using (2.37), the supplementary equation (2.29) for the varying component of water surface elevation can be rewritten in terms of the new coordinate as
$$\begin{eqnarray}\displaystyle {{\it\eta}^{\prime }}^{\ast }=D_{1}^{\ast }\frac{\partial ^{2}\bar{{\it\eta}}^{\ast }}{\partial t^{\ast 2}}-\frac{D_{2}^{\ast }}{{\it\nu}}\frac{\partial \bar{u}^{\ast }}{\partial t^{\ast }}, & & \displaystyle\end{eqnarray}$$
with
$$\begin{eqnarray}\displaystyle D_{1}^{\ast }=I_{2}^{\ast }\frac{b^{\ast }}{S^{\ast }}-I_{1}^{\ast },\quad D_{2}^{\ast }=\frac{I_{2}^{\ast }}{S^{\ast }}\frac{\partial S^{\ast }}{\partial \hat{x}^{\ast }}-\hat{I} _{3}^{\ast }, & & \displaystyle\end{eqnarray}$$
where
$D_{1}^{\ast }$
and
$D_{2}^{\ast }$
are functions of
$\hat{x}^{\ast }$
and
$y^{\ast }$
.
2.2 Topographic condition
To determine the coefficients of the governing equations, we need to specify the bay water depth
$h^{\ast }$
. The coefficients, which include triple or quadruple integrals of the
$h^{\ast }$
functions, can be analytically evaluated only for simple cases. Following the bay geometry used in Zahibo et al. (Reference Zahibo, Pelinovsky, Golinko and Osipenko2006), we limit our discussion to cases in which the bay water depth is represented by the sum of a linear function of
$\hat{x}^{\ast }$
and a power function of
$y^{\ast }$
:
$$\begin{eqnarray}\displaystyle h^{\ast }=\hat{x}^{\ast }-y^{\ast q}, & & \displaystyle\end{eqnarray}$$
where
$q$
is a real positive number. The water depth decreases linearly along the bay axis, and as a power law with an exponent
$q({>}0)$
in the transverse direction. The longitudinal variation of the bay water depth in some bays may be better represented by the power function of
$\hat{x}^{\ast }$
. However, in the general case, analytical solutions are not available for (2.37) and (2.38) unless the terms of
$O({\it\sigma}^{2})$
are neglected. The bay width and the cross-sectional area are therefore given by
$$\begin{eqnarray}\displaystyle b^{\ast }=\hat{x}^{\ast 1/q},\quad S^{\ast }=\frac{q}{q+1}\hat{x}^{\ast (1/q)+1}. & & \displaystyle\end{eqnarray}$$
At a smaller
$q$
value, the bay cross-section more strongly converges towards the bay head. Both horizontal and vertical sections are V-shaped when
$q=1$
and U-shaped when
$q=2$
. As
$q\rightarrow \infty$
, the bay shape approaches a rectangle, and wave characteristics become identical to those over a uniform slope. In this case, the coefficients of the higher-order terms in (2.38) are equal to zero. For
$q<1$
, the bay section strongly converges to form a cusp at the bay head. Figure 2 shows horizontal and vertical bay sections for three representative cases with
$q=$
2, 1 and
$2/3$
. We focus on the three bay types that cover a typical range of converging bay shapes. Table 1 summarizes
$b^{\ast }$
,
$S^{\ast }$
and the variable coefficients of (2.38) and (2.41) for the three cases. The five coefficients of (2.38) are commonly expressed as power functions of
$\hat{x}^{\ast }$
with integer exponents.
$D_{1}^{\ast }$
and
$D_{2}^{\ast }$
in (2.41) are identical to each other for the present geometric setting.
Figure 2. Planar shapes and vertical cross-sections of the converging bays with
$q=2,1$
and
$2/3$
. (a) Planar shapes, (b) vertical cross-sections at
$\hat{x}^{\ast }=0.5$
and
$\hat{x}^{\ast }=1$
.
2.3 Incident wave condition
The incident wave condition should be specified to close the boundary value problem. For simplicity, we consider the situation in which monochromatic waves are normally incident on the bays. Since incoming waves are reflected by the bay topography, the reflective waves must also be included in the boundary condition at the bay entrance (
$\hat{x}^{\ast }=1$
). Analogous to the classical run-up solution over plane beaches by Keller & Keller (Reference Keller and Keller1964), we assume a longitudinally uniform region with a constant cross-section that extends out of the bay entrance where incident and reflective monochromatic waves superpose one another. In actual situations, the cross-section at the bay entrance rapidly transits towards the outer sea with parallel depth contours. The present model does not account for lateral wave spreading over the transitional bathymetry out of the bay entrance. Therefore, the incident wave should be interpreted as the one coming into the bay after propagating over the transitional region. Consequently, the governing equations in the uniform region are obtained from (2.37) and (2.38) by neglecting
$\hat{x}^{\ast }$
derivatives of the geometric variables as
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\nu}\frac{\partial \bar{{\it\eta}}^{\ast }}{\partial t^{\ast }}-\frac{q}{q+1}\frac{\partial \bar{u}^{\ast }}{\partial \hat{x}^{\ast }}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\nu}\frac{\partial \bar{u}^{\ast }}{\partial t^{\ast }}-\frac{\partial \bar{{\it\eta}}^{\ast }}{\partial \hat{x}^{\ast }}+{\it\sigma}^{2}B_{1}\frac{\partial ^{3}\bar{{\it\eta}}^{\ast }}{\partial \hat{x}^{\ast }\partial t^{\ast 2}}-\frac{{\it\sigma}^{2}}{{\it\nu}}B_{2}\frac{\partial ^{3}\bar{u}^{\ast }}{\partial \hat{x}^{\ast 2}\partial t^{\ast }}=0, & \displaystyle\end{eqnarray}$$
$B_{1}$
and
$B_{2}$
are constants given in table 1. The two equations can be combined into a single equation in terms of
$\bar{u}^{\ast }$
: 
$$\begin{eqnarray}\displaystyle {\it\nu}^{2}\frac{\partial ^{2}\bar{u}^{\ast }}{\partial t^{\ast 2}}-\frac{q}{q+1}\frac{\partial ^{2}\bar{u}^{\ast }}{\partial \hat{x}^{\ast 2}}+{\it\sigma}^{2}\left(\frac{q}{q+1}B_{1}-B_{2}\right)\frac{\partial ^{3}\bar{u}^{\ast }}{\partial \hat{x}^{\ast 2}\partial t^{\ast 2}}=0. & & \displaystyle\end{eqnarray}$$
We assume that the monochromatic wave solution is expressed by
$$\begin{eqnarray}\displaystyle \bar{u}^{\ast }={\it\phi}(\hat{x}^{\ast })\text{e}^{-2\text{i}{\rm\pi}t^{\ast }}. & & \displaystyle\end{eqnarray}$$
Here, the representative wavelength is defined as
$L_{0}=2{\rm\pi}\sqrt{gh_{0}}/{\it\omega}$
with angular frequency
${\it\omega}$
of the incident wave. Substituting (2.48) into (2.47) yields a second-order linear differential equation
$$\begin{eqnarray}\displaystyle {\it\phi}^{\prime \prime }+{\it\kappa}^{2}{\it\phi}=0, & & \displaystyle\end{eqnarray}$$
with
$$\begin{eqnarray}\displaystyle {\it\kappa}^{2}=\frac{(1+q){\it\lambda}^{2}}{q\left[1+{\it\mu}^{2}\left\{B_{1}-\left(1+\displaystyle \frac{1}{q}\right)B_{2}\right\}\right]}, & & \displaystyle\end{eqnarray}$$
where
${\it\lambda}=2{\rm\pi}{\it\nu}={\it\omega}l_{x}/\sqrt{gh_{0}}$
and
${\it\mu}=2{\rm\pi}{\it\sigma}={\it\omega}l_{y}/\sqrt{gh_{0}}$
;
${\it\lambda}$
and
${\it\mu}$
are key parameters to characterize the wave solution. Since the parameter
${\it\kappa}$
is interpreted as a product of the wavenumber
$k$
and the bay length
$l_{x}$
, equation (2.50) represents the dispersion relation that relates the wavenumber
$k$
of the section-averaged wave to its frequency
${\it\omega}$
. It can be rewritten for the wave celerity as
$$\begin{eqnarray}\displaystyle c^{\ast }=\sqrt{\frac{q}{1+q}\left[1+{\it\mu}^{2}\left\{B_{1}-\left(1+\frac{1}{q}\right)B_{2}\right\}\right]}, & & \displaystyle\end{eqnarray}$$
where
$c^{\ast }={\it\omega}/k\sqrt{gh_{0}}$
is the dimensionless wave celerity. In the case of a narrow bay (
${\it\mu}\rightarrow 0$
), there is no frequency dispersion, and the wave celerity depends only on the bay geometry. Since
$B_{1}-(1+1/q)B_{2}<0$
holds for the three bay types, the wave celerity decreases with increasing
${\it\mu}$
. The frequency dispersion is interpreted as a consequence of wave refraction over the laterally varying topography. Wave refraction significantly elongates the effective path length of a relatively short wave. At a certain
${\it\mu}$
value, the wave celerity becomes zero, and a progressive wave solution does not exist in (2.49). This suggests the occurrence of total reflection due to strong wave refraction. The limiting values are calculated as
${\it\mu}\approx 5.5$
, 3.5 and 2.7 (
${\it\sigma}\approx$
0.87, 0.55 and 0.43) for
$q=2$
, 1 and
$2/3$
, respectively. However, the present solution is not valid for such high
${\it\sigma}$
values as the terms of
$O({\it\sigma}^{4})$
are truncated. Hence, the values do not represent the actual ones for the occurrence of the peculiar phenomenon. We will further discuss this issue using the perturbation method in § 4.1.
Substituting the solution of (2.49) into (2.48) and (2.45), we obtain the general solutions for
$\bar{u}^{\ast }$
and
$\bar{{\it\eta}}^{\ast }$
as
$$\begin{eqnarray}\displaystyle & \displaystyle \bar{u}^{\ast }(\hat{x}^{\ast },t^{\ast })=(C_{1}\text{e}^{-\text{i}{\it\kappa}\hat{x}^{\ast }}+C_{2}\text{e}^{\text{i}{\it\kappa}\hat{x}^{\ast }})\text{e}^{-2\text{i}{\rm\pi}t^{\ast }}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \bar{{\it\eta}}(\hat{x}^{\ast },t^{\ast })=\frac{q}{q+1}\frac{{\it\kappa}}{{\it\lambda}}(C_{1}\text{e}^{-\text{i}{\it\kappa}\hat{x}^{\ast }}-C_{2}\text{e}^{\text{i}{\it\kappa}\hat{x}^{\ast }})\text{e}^{-2\text{i}{\rm\pi}t^{\ast }}, & \displaystyle\end{eqnarray}$$
$C_{1}$
and
$C_{2}$
are constants. Letting
$K_{r}$
be the ratio of the reflected to the incident wave amplitude,
$\bar{{\it\eta}}^{\ast }$
and
$\bar{u}^{\ast }$
at the bay entrance
$(\hat{x}^{\ast }=1)$
are determined as 
$$\begin{eqnarray}\displaystyle & \displaystyle \bar{{\it\eta}}^{\ast }(1,t^{\ast })=(\text{e}^{-\text{i}{\it\kappa}}+K_{r}\text{e}^{\text{i}{\it\kappa}})\text{e}^{-2\text{i}{\rm\pi}t^{\ast }}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \bar{u}^{\ast }(1,t^{\ast })=\left(1+\frac{1}{q}\right)c^{\ast }(\text{e}^{-\text{i}{\it\kappa}}-K_{r}\text{e}^{\text{i}{\it\kappa}})\text{e}^{-2\text{i}{\rm\pi}t^{\ast }}. & \displaystyle\end{eqnarray}$$
$\bar{{\it\eta}}^{\ast }$
and
$\bar{u}^{\ast }$
at the bay entrance can be used as the boundary condition for deriving the wave solutions inside the bay.
3 Analytical solutions
We now derive the analytical solutions for monochromatic wave evolution in the converging bays of
$q=2$
, 1 and
$2/3$
. The governing equations (2.37) and (2.38) are combined to a single-variable differential equation in terms of
$\bar{u}^{\ast }$
, from which the monochromatic wave solution is derived under the boundary conditions given by (2.54) and (2.55). The resulting equation becomes the Bessel equation if the terms of
$O({\it\sigma}^{2})$
are neglected from the governing equations. In this case, unified analytical expressions for
$\bar{{\it\eta}}^{\ast }$
and
$\bar{u}^{\ast }$
are available for an arbitrary
$q$
value. In contrast, the higher-order equations have solutions in different forms for the three
$q$
values. Here, we first derive the leading-order solution neglecting the terms of
$O({\it\sigma}^{2})$
in § 3.1 and then separately deal with the three bay types for the higher-order solutions in §§ 3.2–3.4.
3.1 Leading-order solution
We first derive analytical solutions from the leading parts of the governing equations. Neglecting the terms of
$O({\it\sigma}^{2})$
, we obtain the leading-order momentum equation from (2.38) as
$$\begin{eqnarray}\displaystyle {\it\nu}\frac{\partial \bar{u}^{\ast }}{\partial t^{\ast }}-\frac{\partial \bar{{\it\eta}}^{\ast }}{\partial \hat{x}^{\ast }}=0. & & \displaystyle\end{eqnarray}$$
We substitute (2.44) into (2.37) to obtain the continuity equation
$$\begin{eqnarray}\displaystyle {\it\nu}\frac{\partial \bar{{\it\eta}}^{\ast }}{\partial t^{\ast }}-\bar{u}^{\ast }-\frac{q}{q+1}\hat{x}^{\ast }\frac{\partial \bar{u}^{\ast }}{\partial \hat{x}^{\ast }}=0. & & \displaystyle\end{eqnarray}$$
Combining (3.1) and (3.2), we have a single-variable equation with respect to
$\bar{u}^{\ast }$
$$\begin{eqnarray}\displaystyle {\it\nu}^{2}\frac{\partial ^{2}\bar{u}^{\ast }}{\partial t^{\ast 2}}-\frac{2q+1}{q+1}\frac{\partial \bar{u}^{\ast }}{\partial \hat{x}^{\ast }}-\frac{q}{q+1}\hat{x}^{\ast }\frac{\partial ^{2}\bar{u}^{\ast }}{\partial \hat{x}^{\ast 2}}=0. & & \displaystyle\end{eqnarray}$$
Assuming the form of the solution given by (2.48), (3.3) is transformed into an ordinary differential equation in terms of
${\it\phi}$
$$\begin{eqnarray}\displaystyle {\it\phi}^{\prime \prime }(\hat{x}^{\ast })+\frac{2q+1}{q}\frac{1}{\hat{x}^{\ast }}{\it\phi}^{\prime }(\hat{x}^{\ast })+\frac{q+1}{q}{\it\lambda}^{2}{\it\phi}(\hat{x}^{\ast })=0, & & \displaystyle\end{eqnarray}$$
which is the Bessel equation. The bounded solution of (3.4) is written
$$\begin{eqnarray}\displaystyle {\it\phi}(\hat{x}^{\ast })=C_{3}\hat{x}^{\ast -p^{2}/2}\text{J}_{1/q+1}(2p{\it\lambda}\hat{x}^{\ast 1/2}), & & \displaystyle\end{eqnarray}$$
where
$p=\sqrt{1+1/q}$
,
$C_{3}$
is an integration constant and the function
$\text{J}_{1/q+1}$
represents the Bessel function of the first kind of order
$1/q+1$
. Equation (3.5) is the same as the one obtained in Zahibo et al. (Reference Zahibo, Pelinovsky, Golinko and Osipenko2006) through the transformation of the nonlinear coordinates into linear ones. From (2.48) and (3.2), we have
$$\begin{eqnarray}\displaystyle & \displaystyle \bar{u}^{\ast }=C_{3}\hat{x}^{\ast -p^{2}/2}\text{J}_{1/q+1}(2p{\it\lambda}\hat{x}^{\ast 1/2})\text{e}^{-2\text{i}{\rm\pi}t^{\ast }}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \bar{{\it\eta}}^{\ast }=\frac{\text{i}C_{3}}{p}\hat{x}^{\ast -1/2q}\text{J}_{1/q}(2p{\it\lambda}\hat{x}^{\ast 1/2})\text{e}^{-2\text{i}{\rm\pi}t^{\ast }}. & \displaystyle\end{eqnarray}$$
$C_{3}$
, we use the boundary conditions for
$\bar{{\it\eta}}$
and
$\bar{u}$
at the bay entrance. Letting
$B_{1}=B_{2}=0$
in (2.50), the dispersion relation reads 
$$\begin{eqnarray}\displaystyle {\it\kappa}=\sqrt{\frac{1+q}{q}}{\it\lambda}. & & \displaystyle\end{eqnarray}$$
Subsequently, the wave celerity of the leading-order wave is given from (2.51) as
$$\begin{eqnarray}\displaystyle c^{\ast }=\sqrt{\frac{q}{1+q}}. & & \displaystyle\end{eqnarray}$$
Hence, the wave celerity does not depend on the wave frequency. Using the boundary conditions (2.54) and (2.55) with (3.9), we obtain the analytical solutions for
$\bar{{\it\eta}}^{\ast }$
and
$\bar{u}^{\ast }$
$$\begin{eqnarray}\displaystyle & \displaystyle \bar{{\it\eta}}^{\ast }=\frac{2\text{J}_{1/q}(2p{\it\lambda}\hat{x}^{\ast 1/2})}{\hat{x}^{\ast 1/2q}\{\text{J}_{1/q}(2p{\it\lambda})-\text{i}\text{J}_{1/q+1}(2p{\it\lambda})\}}\text{e}^{-\text{i}({\it\kappa}+2{\rm\pi}t^{\ast })}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \bar{u}^{\ast }=-\frac{2\text{i}p\text{J}_{1/q+1}(2p{\it\lambda}\hat{x}^{\ast 1/2})}{\hat{x}^{\ast p^{2}/2}\{\text{J}_{1/q}(2p{\it\lambda})-\text{i}\text{J}_{1/q+1}(2p{\it\lambda})\}}\text{e}^{-\text{i}({\it\kappa}+2{\rm\pi}t^{\ast })}. & \displaystyle\end{eqnarray}$$
$q\rightarrow \infty$
. The funnelling effect is mainly represented by a negative power function of
$\hat{x}^{\ast }$
with a different exponent by the bay type. Since the transverse variation in the water surface is ignored in the leading order, (3.10) represents the two-dimensional distribution of the water surface elevation, namely
${\it\eta}^{\ast }=\bar{{\it\eta}}^{\ast }$
. Therefore, the incoming wave propagates as a plane wave in the bays.
3.2 Higher-order solution for U-shaped bays (
$q=2$
)
When
$q=2$
, the higher-order governing equations (2.37) and (2.38) are written as
$$\begin{eqnarray}\displaystyle {\it\nu}\frac{\partial \bar{{\it\eta}}^{\ast }}{\partial t^{\ast }}-\bar{u}^{\ast }-\frac{2}{3}\hat{x}^{\ast }\frac{\partial \bar{u}^{\ast }}{\partial \hat{x}^{\ast }}=0, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left({\it\nu}-\frac{{\it\sigma}^{2}}{4{\it\nu}\hat{x}^{\ast }}\right)\frac{\partial \bar{u}^{\ast }}{\partial t^{\ast }}-\frac{\partial \bar{{\it\eta}}^{\ast }}{\partial \hat{x}^{\ast }}+\frac{{\it\sigma}^{2}}{4\hat{x}^{\ast }}\frac{\partial ^{2}\bar{{\it\eta}}^{\ast }}{\partial t^{\ast 2}}+\frac{{\it\sigma}^{2}}{6}\frac{\partial ^{3}\bar{{\it\eta}}^{\ast }}{\partial \hat{x}^{\ast }\partial t^{\ast 2}}\nonumber\\ \displaystyle & & \displaystyle \qquad \qquad -\,\frac{{\it\sigma}^{2}}{2{\it\nu}}\frac{\partial ^{2}\bar{u}^{\ast }}{\partial \hat{x}^{\ast }\partial t^{\ast }}-\frac{2{\it\sigma}^{2}}{15{\it\nu}}\hat{x}^{\ast }\frac{\partial ^{3}\bar{u}^{\ast }}{\partial \hat{x}^{\ast 2}\partial t^{\ast }}=0.\end{eqnarray}$$
The two equations can be combined into a single-variable equation in terms of
$\bar{u}^{\ast }$
$$\begin{eqnarray}\displaystyle {\it\nu}^{2}\frac{\partial ^{2}\bar{u}^{\ast }}{\partial t^{\ast 2}}-\frac{5}{3}\frac{\partial \bar{u}^{\ast }}{\partial \hat{x}^{\ast }}-\frac{2}{3}\hat{x}^{\ast }\frac{\partial ^{2}\bar{u}^{\ast }}{\partial \hat{x}^{\ast 2}}-\frac{{\it\sigma}^{2}}{18}\frac{\partial ^{3}\bar{u}^{\ast }}{\partial t^{\ast 2}\partial \hat{x}^{\ast }}-\frac{{\it\sigma}^{2}}{45}\hat{x}^{\ast }\frac{\partial ^{4}\bar{u}^{\ast }}{\partial \hat{x}^{\ast 2}\partial t^{\ast 2}}=0. & & \displaystyle\end{eqnarray}$$
Substituting (2.48) into (3.14) yields an ordinary differential equation in terms of
${\it\phi}$
$$\begin{eqnarray}\displaystyle {\it\phi}^{\prime \prime }(\hat{x}^{\ast })+\frac{5}{2\hat{x}^{\ast }}{\it\phi}^{\prime }(\hat{x}^{\ast })+\frac{3{\it\zeta}^{2}{\it\lambda}^{2}}{2\hat{x}^{\ast }}{\it\phi}(\hat{x}^{\ast })=0, & & \displaystyle\end{eqnarray}$$
where
${\it\zeta}=1/\sqrt{1-{\it\mu}^{2}/30}$
. The higher-order effect slightly modifies the last term of the leading-order equation (3.5). Since (3.15) is also the Bessel equation, the solution bounded at the bay head (
$\hat{x}^{\ast }=0$
) has the following form:
$$\begin{eqnarray}\displaystyle {\it\phi}=C_{4}\hat{x}^{\ast -3/4}\text{J}_{3/2}(\sqrt{6}{\it\zeta}{\it\lambda}\hat{x}^{\ast 1/2}), & & \displaystyle\end{eqnarray}$$
where
$C_{4}$
is an integration constant. Using (2.48) and (3.12), we obtain
$$\begin{eqnarray}\displaystyle & \displaystyle \bar{u}^{\ast }=C_{4}\hat{x}^{\ast -3/4}\text{J}_{3/2}(\sqrt{6}{\it\zeta}{\it\lambda}\hat{x}^{\ast 1/2})\text{e}^{-2\text{i}{\rm\pi}t^{\ast }}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \bar{{\it\eta}}^{\ast }=\frac{\sqrt{6}\text{i}C_{4}{\it\zeta}}{3}\hat{x}^{\ast -1/4}\text{J}_{1/2}(\sqrt{6}{\it\zeta}{\it\lambda}\hat{x}^{\ast 1/2})\text{e}^{-2\text{i}{\rm\pi}t^{\ast }}. & \displaystyle\end{eqnarray}$$
$C_{4}$
, we use the boundary conditions (2.54) and (2.55). For
$q=2$
, the dispersion relation (2.50) becomes 
$$\begin{eqnarray}\displaystyle {\it\kappa}=\sqrt{{\textstyle \frac{3}{2}}}{\it\zeta}{\it\lambda}. & & \displaystyle\end{eqnarray}$$
Therefore, the wave celerity of the mean wave is expressed as
$$\begin{eqnarray}\displaystyle c^{\ast }=\sqrt{\frac{2}{3}}{\it\zeta}^{-1}\approx \sqrt{\frac{2}{3}}\left(1-\frac{{\it\mu}^{2}}{60}\right). & & \displaystyle\end{eqnarray}$$
Equation (3.20) suggests that the higher-order effect contributes by slightly reducing the wave celerity. Using (2.54) and (2.55) together with (3.20), we determine
$C_{4}$
to obtain the mean wave solutions for
$\bar{{\it\eta}}^{\ast }$
and
$\bar{u}^{\ast }$
$$\begin{eqnarray}\displaystyle & \displaystyle \bar{{\it\eta}}^{\ast }=\frac{2\text{J}_{1/2}(\sqrt{6}{\it\zeta}{\it\lambda}\hat{x}^{\ast 1/2})}{\hat{x}^{\ast 1/4}\{\text{J}_{1/2}(\sqrt{6}{\it\zeta}{\it\lambda})-\text{i}\text{J}_{3/2}(\sqrt{6}{\it\zeta}{\it\lambda})\}}\text{e}^{-\text{i}({\it\kappa}+2{\rm\pi}t^{\ast })}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \bar{u}^{\ast }=-\frac{\sqrt{6}\text{i}\text{J}_{3/2}(\sqrt{6}{\it\zeta}{\it\lambda}\hat{x}^{\ast 1/2})}{{\it\zeta}\hat{x}^{\ast 3/4}\{\text{J}_{1/2}(\sqrt{6}{\it\zeta}{\it\lambda})-\text{i}\text{J}_{3/2}(\sqrt{6}{\it\zeta}{\it\lambda})\}}\text{e}^{-\text{i}({\it\kappa}+2{\rm\pi}t^{\ast })}. & \displaystyle\end{eqnarray}$$
${\it\zeta}=1$
). Substituting (3.21) and (3.22) into (2.41) provides the two-dimensional profile of water surface elevation to the same order of
${\it\sigma}$
as 
$$\begin{eqnarray}\displaystyle {\it\eta}^{\ast }=\bar{{\it\eta}}^{\ast }+\frac{{\it\mu}^{2}}{6}\frac{(\hat{x}^{\ast }-3y^{\ast 2})\text{J}_{5/2}(\sqrt{6}{\it\zeta}{\it\lambda}\hat{x}^{\ast 1/2})}{\hat{x}^{\ast 5/4}\{\text{J}_{1/2}(\sqrt{6}{\it\zeta}{\it\lambda})-\text{i}\text{J}_{3/2}(\sqrt{6}{\it\zeta}{\it\lambda})\}}\text{e}^{-\text{i}({\it\kappa}+2{\rm\pi}t^{\ast })}. & & \displaystyle\end{eqnarray}$$
The second term on the right-hand side is responsible for the transverse variation. The water surface elevation quadratically varies in the transverse direction.
Figure 3. Wave amplification inside the U-shaped bay (
$q=2$
) for different parameter sets of
${\it\mu}$
and
${\it\lambda}$
. (a) Wave amplification factor
$a/a_{0}$
, (b) higher-order contribution
$(a-a_{L})/a_{0}$
.
Figure 3 shows the distributions of wave amplitude inside U-shaped bays for different parameter sets of
${\it\mu}$
and
${\it\lambda}$
. The upper panels display the ratio of the wave amplitude to the incident wave amplitude
$a/a_{0}$
, whereas the lower panels represent the higher-order contributions given by
$(a-a_{L})/a_{0}$
with the leading-order wave amplitude
$a_{L}$
from (3.10). In cases of small
${\it\mu}$
, contour lines are parallel to the
$y^{\ast }$
-axis, suggesting that the transverse variation in the water surface is small. The effect of wave refraction intensifies as
${\it\mu}$
increases, and the contour lines become parabolic towards the bay head near the bay entrance. The wave amplitude around the bay head increases with
${\it\lambda}$
, as wave energy is transferred to the bay head with less reflection for shorter waves. Especially when
${\it\lambda}>1$
, drastic wave amplification occurs due to the strong funnelling effect. The wave refraction does not make a significant change in the energy transfer process within the present range of
${\it\mu}<1$
.
3.3 Higher-order solution for V-shaped bays (
$q=1$
)
For
$q=1$
, the governing equations (2.37) and (2.38) are expressed as
$$\begin{eqnarray}\displaystyle {\it\nu}\frac{\partial \bar{{\it\eta}}^{\ast }}{\partial t^{\ast }}-\bar{u}^{\ast }-\frac{1}{2}\hat{x}^{\ast }\frac{\partial \bar{u}^{\ast }}{\partial \hat{x}^{\ast }}=0, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left({\it\nu}-\frac{{\it\sigma}^{2}}{{\it\nu}}\right)\frac{\partial \bar{u}^{\ast }}{\partial t^{\ast }}-\frac{\partial \bar{{\it\eta}}^{\ast }}{\partial \hat{x}^{\ast }}+{\it\sigma}^{2}\frac{\partial ^{2}\bar{{\it\eta}}^{\ast }}{\partial t^{\ast 2}}+\frac{{\it\sigma}^{2}}{3}\hat{x}^{\ast }\frac{\partial ^{3}\bar{{\it\eta}}^{\ast }}{\partial \hat{x}^{\ast }\partial t^{\ast 2}}\nonumber\\ \displaystyle & & \displaystyle \qquad \qquad -\,\frac{7{\it\sigma}^{2}}{6{\it\nu}}\hat{x}^{\ast }\frac{\partial ^{2}\bar{u}^{\ast }}{\partial \hat{x}^{\ast }\partial t^{\ast }}-\frac{5{\it\sigma}^{2}}{24{\it\nu}}\hat{x}^{\ast 2}\frac{\partial ^{3}\bar{u}^{\ast }}{\partial \hat{x}^{\ast 2}\partial t^{\ast }}=0.\end{eqnarray}$$
The two equations are combined into a single-variable equation in terms of
$\bar{u}^{\ast }$
$$\begin{eqnarray}\displaystyle {\it\nu}^{2}\frac{\partial ^{2}\bar{u}^{\ast }}{\partial t^{\ast 2}}-\frac{3}{2}\frac{\partial \bar{u}^{\ast }}{\partial \hat{x}^{\ast }}-\frac{1}{2}\hat{x}^{\ast }\frac{\partial ^{2}\bar{u}^{\ast }}{\partial \hat{x}^{\ast 2}}-\frac{{\it\sigma}^{2}}{6}\hat{x}^{\ast }\frac{\partial ^{3}\bar{u}^{\ast }}{\partial \hat{x}^{\ast }\partial t^{\ast 2}}-\frac{{\it\sigma}^{2}}{24}\hat{x}^{\ast 2}\frac{\partial ^{4}\bar{u}^{\ast }}{\partial \hat{x}^{\ast 2}\partial t^{\ast 2}}=0. & & \displaystyle\end{eqnarray}$$
Substituting (2.48) into (3.26) yields
$$\begin{eqnarray}\displaystyle \hat{x}^{\ast }\left(1-\frac{{\it\mu}^{2}}{12}\hat{x}^{\ast }\right){\it\phi}^{\prime \prime }(\hat{x}^{\ast })+\left(3-\frac{{\it\mu}^{2}}{3}\hat{x}^{\ast }\right){\it\phi}^{\prime }(\hat{x}^{\ast })+2{\it\lambda}^{2}{\it\phi}(\hat{x}^{\ast })=0. & & \displaystyle\end{eqnarray}$$
Unlike the case of
$q=2$
,
${\it\phi}$
obeys the hypergeometric differential equation. The solution of (3.27) bounded at
$\hat{x}^{\ast }=0$
is given by
$$\begin{eqnarray}\displaystyle {\it\phi}(\hat{x}^{\ast })=C_{5}F\left({\it\alpha},{\it\beta},3;\frac{{\it\mu}^{2}\hat{x}^{\ast }}{12}\right), & & \displaystyle\end{eqnarray}$$
with
$$\begin{eqnarray}\displaystyle {\it\alpha}=\frac{3}{2}\left(1+\sqrt{1+\frac{32}{3r^{2}}}\right),\quad {\it\beta}=\frac{3}{2}\left(1-\sqrt{1+\frac{32}{3r^{2}}}\right), & & \displaystyle\end{eqnarray}$$
where
$C_{5}$
is an integration constant,
$r$
is the aspect ratio of the bay (
$=l_{y}/l_{x}$
) and
$F$
is the Gaussian hypergeometric function. From (3.28), (2.48) and (3.24), we obtain
$$\begin{eqnarray}\displaystyle & \displaystyle \bar{u}^{\ast }=C_{5}F\left({\it\alpha},{\it\beta},3;\frac{{\it\mu}^{2}\hat{x}^{\ast }}{12}\right)\text{e}^{-2\text{i}{\rm\pi}t^{\ast }}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \bar{{\it\eta}}^{\ast }=\frac{\text{i}C_{5}}{{\it\lambda}}F\left({\it\alpha},{\it\beta},2;\frac{{\it\mu}^{2}\hat{x}^{\ast }}{12}\right)\text{e}^{-2\text{i}{\rm\pi}t^{\ast }}. & \displaystyle\end{eqnarray}$$
$q=1$
becomes 
$$\begin{eqnarray}\displaystyle {\it\kappa}=\frac{{\it\lambda}}{\sqrt{\displaystyle \frac{1}{2}\left(1-\frac{{\it\mu}^{2}}{12}\right)}}. & & \displaystyle\end{eqnarray}$$
Therefore, the celerity of the mean wave is given by
$$\begin{eqnarray}\displaystyle c^{\ast }=\sqrt{\frac{1}{2}\left(1-\frac{{\it\mu}^{2}}{12}\right)}\approx \sqrt{\frac{1}{2}}\left(1-\frac{{\it\mu}^{2}}{24}\right). & & \displaystyle\end{eqnarray}$$
The higher-order effect on the wave celerity is larger than in the case of
$q=2$
. Using (2.54) and (2.55) with (3.33), we determine
$C_{5}$
to obtain the mean wave solution inside of the V-shaped bay
$$\begin{eqnarray}\displaystyle & \displaystyle \bar{{\it\eta}}^{\ast }=\frac{2F\left({\it\alpha},{\it\beta},2;\displaystyle \frac{{\it\mu}^{2}\hat{x}^{\ast }}{12}\right)}{F\left({\it\alpha},{\it\beta},2;\displaystyle \frac{{\it\mu}^{2}}{12}\right)-\text{i}\displaystyle \frac{{\it\kappa}}{2}F\left({\it\alpha},{\it\beta},3;\displaystyle \frac{{\it\mu}^{2}}{12}\right)}\text{e}^{-\text{i}({\it\kappa}+2{\rm\pi}t^{\ast })}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \bar{u}^{\ast }=-\frac{2\text{i}{\it\lambda}F\left({\it\alpha},{\it\beta},3;\displaystyle \frac{{\it\mu}^{2}\hat{x}^{\ast }}{12}\right)}{F\left({\it\alpha},{\it\beta},2;\displaystyle \frac{{\it\mu}^{2}}{12}\right)-\text{i}\displaystyle \frac{{\it\kappa}}{2}F\left({\it\alpha},{\it\beta},3;\displaystyle \frac{{\it\mu}^{2}}{12}\right)}\text{e}^{-\text{i}({\it\kappa}+2{\rm\pi}t^{\ast })}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\eta}^{\ast }=\bar{{\it\eta}}^{\ast }+\frac{{\it\mu}^{2}{\it\lambda}^{2}}{9}\frac{(\hat{x}^{\ast 2}-3y^{\ast 2})F\left({\it\alpha}+1,{\it\beta}+1,4;\displaystyle \frac{{\it\mu}^{2}\hat{x}^{\ast }}{12}\right)}{F\left({\it\alpha},{\it\beta},2;\displaystyle \frac{{\it\mu}^{2}}{12}\right)-\text{i}\displaystyle \frac{{\it\kappa}}{2}F\left({\it\alpha},{\it\beta},3;\displaystyle \frac{{\it\mu}^{2}}{12}\right)}\text{e}^{-\text{i}({\it\kappa}+2{\rm\pi}t^{\ast })}. & & \displaystyle\end{eqnarray}$$
The second term on the right-hand side of (3.36) describes the transverse variation in the water surface elevation, which is quadratic as in the case of
$q=2$
.
Figure 4. Wave amplification inside the V-shaped bay (
$q=1$
) for different parameter sets of
${\it\mu}$
and
${\it\lambda}$
. (a) Wave amplification factor
$a/a_{0}$
, (b) higher-order contribution
$(a-a_{L})/a_{0}$
.
Figure 4 shows the distributions of wave amplitude inside the V-shaped bays for different parameter sets of
${\it\mu}$
and
${\it\lambda}$
corresponding to those in figure 3. The wave amplitude distributions exhibit a similar tendency to that in figure 3 for U-shaped bays, but the transverse variation is stronger near the bay entrance where the bay cross-sectional area decreases more rapidly. In addition, the V-shaped bay more strongly funnels the incoming wave for large
${\it\lambda}$
, resulting in extreme wave amplification near the bay head. When
${\it\mu}$
is large, the higher-order effect contributes by increasing the wave amplitude around the bay entrance, while reducing it near the bay head. This is because stronger refraction forms standing waves in the transverse direction around the bay entrance, and prevents wave energy transfer into the bay.
3.4 Higher-order solution for cusped bays (
$q=2/3$
)
For the case of
$q=2/3$
, the governing equations (2.37) and (2.38) are rewritten as
$$\begin{eqnarray}\displaystyle \frac{\partial \bar{{\it\eta}}^{\ast }}{\partial t^{\ast }}-\bar{u}^{\ast }-\frac{2}{5}\hat{x}^{\ast }\frac{\partial \bar{u}^{\ast }}{\partial \hat{x}^{\ast }}=0, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left({\it\nu}-\frac{9{\it\sigma}^{2}}{4{\it\nu}}\hat{x}^{\ast }\right)\frac{\partial \bar{u}^{\ast }}{\partial t^{\ast }}-\frac{\partial \bar{{\it\eta}}^{\ast }}{\partial \hat{x}^{\ast }}+\frac{9{\it\sigma}^{2}}{4}\hat{x}^{\ast }\frac{\partial ^{2}\bar{{\it\eta}}^{\ast }}{\partial t^{\ast 2}}+\frac{{\it\sigma}^{2}}{2}\hat{x}^{\ast 2}\frac{\partial ^{3}\bar{{\it\eta}}^{\ast }}{\partial \hat{x}^{\ast }\partial t^{\ast 2}}\nonumber\\ \displaystyle & & \displaystyle \qquad \qquad -\,\frac{19{\it\sigma}^{2}}{10{\it\nu}}\hat{x}^{2\ast }\frac{\partial ^{2}\bar{u}^{\ast }}{\partial \hat{x}^{\ast }\partial t^{\ast }}-\frac{14{\it\sigma}^{2}}{55{\it\nu}}\hat{x}^{\ast 3}\frac{\partial ^{3}\bar{u}^{\ast }}{\partial \hat{x}^{\ast 2}\partial t^{\ast }}=0.\end{eqnarray}$$
The two equations are combined into a single-variable equation in terms of
$\bar{u}^{\ast }$
$$\begin{eqnarray}\displaystyle {\it\nu}^{2}\frac{\partial ^{2}\bar{u}^{\ast }}{\partial t^{\ast 2}}-\frac{7}{5}\frac{\partial \bar{u}^{\ast }}{\partial \hat{x}^{\ast }}-\frac{2}{5}\hat{x}^{\ast }\frac{\partial ^{2}\bar{u}^{\ast }}{\partial \hat{x}^{\ast 2}}-\frac{3{\it\sigma}^{2}}{10}\hat{x}^{\ast 2}\frac{\partial ^{3}\bar{u}^{\ast }}{\partial \hat{x}^{\ast }\partial t^{\ast 2}}-\frac{3{\it\sigma}^{2}}{55}\hat{x}^{\ast 3}\frac{\partial ^{4}\bar{u}^{\ast }}{\partial \hat{x}^{\ast 2}\partial t^{\ast 2}}=0. & & \displaystyle\end{eqnarray}$$
We then substitute (2.48) into (3.39) to have
$$\begin{eqnarray}\displaystyle \frac{2\hat{x}^{\ast }}{5}\left(1-\frac{3{\it\mu}^{2}\hat{x}^{\ast 2}}{22}\right){\it\phi}^{\prime \prime }(\hat{x}^{\ast })+\frac{7}{5}\left(1-\frac{3{\it\mu}^{2}\hat{x}^{\ast 2}}{14}\right){\it\phi}^{\prime }(\hat{x}^{\ast })+{\it\lambda}^{2}{\it\phi}(\hat{x}^{\ast })=0. & & \displaystyle\end{eqnarray}$$
The resulting equation is neither the Bessel equation nor the hypergeometric equation, as in the case of
$q=1$
or
$2$
. To change the form of the equation, we introduce a new variable defined by
$$\begin{eqnarray}\displaystyle {\it\chi}^{\ast }=\sqrt{\frac{3}{22}}{\it\mu}\hat{x}^{\ast }. & & \displaystyle\end{eqnarray}$$
The new variable leads (3.40) to
$$\begin{eqnarray}\displaystyle {\it\chi}^{\ast }(1-{\it\chi}^{\ast })(1+{\it\chi}^{\ast }){\it\phi}^{\prime \prime }({\it\chi}^{\ast })-\left(\frac{11}{2}{\it\chi}^{\ast 2}-\frac{7}{2}\right){\it\phi}^{\prime }({\it\chi}^{\ast })+\frac{5\sqrt{66}{\it\lambda}}{6r}{\it\phi}({\it\chi}^{\ast })=0, & & \displaystyle\end{eqnarray}$$
which is Heun’s equation. The bounded solution for (3.42) is
$$\begin{eqnarray}\displaystyle {\it\phi}=C_{6}E({\it\lambda};r;{\it\chi}^{\ast }), & & \displaystyle\end{eqnarray}$$
where
$C_{6}$
is an integration constant and the function
$E$
is introduced as an abbreviation of the local Heun function:
$$\begin{eqnarray}\displaystyle E({\it\lambda};r;{\it\chi}^{\ast })\equiv H\ell \left(-1,\frac{5\sqrt{66}{\it\lambda}}{6r};\frac{9}{2},0,\frac{7}{2},1;{\it\chi}^{\ast }\right). & & \displaystyle\end{eqnarray}$$
From (2.48), (3.37) and (3.43), we express the general solutions for
$\bar{u}$
and
$\bar{{\it\eta}}$
as
$$\begin{eqnarray}\displaystyle & \displaystyle \bar{u}^{\ast }=C_{6}E({\it\lambda};r;{\it\chi}^{\ast })\text{e}^{-2\text{i}{\rm\pi}t^{\ast }}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \bar{{\it\eta}}^{\ast }=\frac{\text{i}C_{6}}{{\it\lambda}}G({\it\lambda};r;{\it\chi}^{\ast })\text{e}^{-2\text{i}{\rm\pi}t^{\ast }}, & \displaystyle\end{eqnarray}$$
$G$
is defined by 
$$\begin{eqnarray}\displaystyle G({\it\lambda};r;{\it\chi}^{\ast })\equiv E({\it\lambda};r;{\it\chi}^{\ast })+{\textstyle \frac{2}{5}}{\it\chi}^{\ast }E^{\prime }({\it\lambda};r;{\it\chi}^{\ast }). & & \displaystyle\end{eqnarray}$$
Here,
$E^{\prime }({\it\lambda};r;{\it\chi}^{\ast })$
represents the differential of
$E({\it\lambda};r;{\it\chi}^{\ast })$
. Since the Heun function is represented by an infinite power series, the functional value of the differential can also be evaluated by a series through term-wise differentiation.
For
$q=2/3$
, the dispersion relation (2.50) becomes
$$\begin{eqnarray}\displaystyle {\it\kappa}=\frac{{\it\lambda}}{\sqrt{\displaystyle \frac{2}{5}\left(1-\displaystyle \frac{3{\it\mu}^{2}}{22}\right)}}. & & \displaystyle\end{eqnarray}$$
Therefore, the wave celerity is given by
$$\begin{eqnarray}\displaystyle c^{\ast }=\sqrt{\frac{2}{5}\left(1-\frac{3{\it\mu}^{2}}{22}\right)}\approx \sqrt{\frac{2}{5}}\left(1-\frac{3{\it\mu}^{2}}{44}\right). & & \displaystyle\end{eqnarray}$$
The higher-order reduction of the wave celerity is larger than the other bay types, since wave refraction more significantly elongates the effective wave path over the cusped cross-section. Using (2.54) and (2.55) together with (3.49) as the boundary conditions at
$\hat{x}^{\ast }=1$
, we obtain analytical solutions for
$\bar{{\it\eta}}^{\ast }$
and
$\bar{u}^{\ast }$
as
$$\begin{eqnarray}\displaystyle & \displaystyle \bar{{\it\eta}}^{\ast }=\frac{2G\left({\it\lambda};r;\sqrt{\frac{3}{22}}{\it\mu}\hat{x}^{\ast }\right)}{G\left({\it\lambda};r;\sqrt{\frac{3}{22}}{\it\mu}\right)-\frac{2}{5}\text{i}{\it\kappa}E\left({\it\lambda};r;\sqrt{\frac{3}{22}}{\it\mu}\right)}\text{e}^{-\text{i}({\it\kappa}+2{\rm\pi}t^{\ast })}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \bar{u}^{\ast }=-\frac{2\text{i}{\it\lambda}E\left({\it\lambda};r;\sqrt{\frac{3}{22}}{\it\mu}\hat{x}^{\ast }\right)}{G\left({\it\lambda};r;\sqrt{\frac{3}{22}}{\it\mu}\right)-\frac{2}{5}\text{i}{\it\kappa}E\left({\it\lambda};r;\sqrt{\frac{3}{22}}{\it\mu}\right)}\text{e}^{-\text{i}({\it\kappa}+2{\rm\pi}t^{\ast })}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\it\eta}^{\ast }=\bar{{\it\eta}}^{\ast }+\frac{{\it\mu}^{2}}{2}\frac{(\hat{x}^{\ast 3}-3y^{\ast 2})\left\{E\left({\it\lambda};r;\sqrt{\frac{3}{22}}{\it\mu}\hat{x}^{\ast }\right)-G\left({\it\lambda};r;\sqrt{\frac{3}{22}}{\it\mu}\hat{x}^{\ast }\right)\right\}}{\hat{x}^{\ast }\left\{G\left({\it\lambda};r;\sqrt{\frac{3}{22}}{\it\mu}\right)-\frac{2}{5}\text{i}{\it\kappa}E\left({\it\lambda};r;\sqrt{\frac{3}{22}}{\it\mu}\right)\right\}}\text{e}^{-\text{i}({\it\kappa}+2{\rm\pi}t^{\ast })}. & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
The transverse variation in wave amplitude remains quadratic as in the cases of the U-shaped and V-shaped bays.
Figure 5. Wave amplification inside the cusped-shaped bay (
$q=2/3$
) for different parameter sets of
${\it\mu}$
and
${\it\lambda}$
. (a) Wave amplification factor
$a/a_{0}$
, (b) higher-order contribution
$(a-a_{L})/a_{0}$
.
Figure 5 shows distributions of wave amplitude inside the cusped bays for different parameter sets of
${\it\mu}$
and
${\it\lambda}$
corresponding to those in figures 3 and 4. The general tendency of wave amplitude distribution is unchanged from those of the other bay types. The stronger wave refraction increases the curvature of the parabolic contour lines and more significantly reduces the wave amplitude in the bay head region for large
${\it\mu}$
. The funnelling effect is largest among the three bay types as the bay topography permits wave energy transfer with smaller reflection. However, the drastic wave amplification may be limited by the occurrence of wave breaking in actual nonlinear cases, which will be discussed later in § 4.2.
4 Discussion
The analytical solutions in the previous section were derived on the assumption of small
${\it\sigma}$
, namely that the bay width is sufficiently smaller than the representative wavelength. Therefore, they cannot correctly describe the actual phenomena beyond a certain value of
${\it\mu}$
. When the incident wavelength is small, wave funnelling is remarkable, but wave refraction also significantly affects the wave evolution process. In this section, we first clarify the applicable limit of the present approach and discuss wave propagation characteristics for large
${\it\mu}$
. Finally, we present the maximum run-up height in converging bays and how it is affected by the different processes such as wave funnelling, refraction and breaking.
4.1 Applicable range of the solutions
The present solutions suggest that a monochromatic wave propagating in the converging bays can be seen as a mean plane wave with weak two-dimensionality due to wave refraction. However, when
${\it\mu}$
exceeds a certain limit, we cannot assume the presence of the mean progressive wave since wave refraction produces a highly two-dimensional wave field. To estimate the limiting value of
${\it\mu}$
, one possible approach is to derive further higher-order solutions. However, it is difficult to analytically obtain them for the longitudinally varying topography given the complexity of the problem. Instead, we analyse asymptotic wave behaviours over the uniform cross-sections of the three types through the perturbation method.
The section-averaged momentum and continuity equations over the uniform region are obtained from (2.22) and (2.23) by introducing the geometrical set-up
$h^{\ast }=1-y^{\ast q}$
and
$S^{\ast }=q/(q+1)$
as
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial \bar{{\it\eta}}^{\ast }}{\partial t^{\ast }}+\frac{q}{q+1}\frac{\partial \bar{u}^{\ast }}{\partial x^{\ast }}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial \bar{u}^{\ast }}{\partial t^{\ast }}+\frac{q+1}{q}\int _{0}^{1}(1-y^{\ast q})\frac{\partial {\it\eta}^{\ast }}{\partial x^{\ast }}\,\text{d}y^{\ast }=0. & \displaystyle\end{eqnarray}$$
${\it\eta}^{\ast }$
in (4.2) by the mean variables,
$\bar{u}^{\ast }$
and
$\bar{{\it\eta}}^{\ast }$
. Two supplementary equations to determine
${\it\eta}^{\ast }$
are given, respectively, from (2.24) and (2.27) as 
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\eta}^{\ast }=\bar{{\it\eta}}^{\ast }+{\it\sigma}^{2}\left[\int _{0}^{1}\int _{0}^{y^{\ast }}\frac{\partial v^{\ast }}{\partial t^{\ast }}\,\text{d}y^{\ast }\,\text{d}y^{\ast }-\int _{0}^{y^{\ast }}\frac{\partial v^{\ast }}{\partial t^{\ast }}\,\text{d}y^{\ast }\right], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial v^{\ast }}{\partial t^{\ast }}=-\frac{1}{1-y^{\ast q}}\left[\int _{0}^{y^{\ast }}\frac{\partial ^{2}{\it\eta}^{\ast }}{\partial t^{\ast 2}}\,\text{d}y+\int _{0}^{y^{\ast }}(1-y^{\ast q})\frac{\partial ^{2}u^{\ast }}{\partial x^{\ast }\partial t^{\ast }}\,\text{d}y^{\ast }\right]. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\partial ^{2}u^{\ast }}{\partial y^{\ast }\partial t^{\ast }}={\it\sigma}^{2}\frac{\partial ^{2}v^{\ast }}{\partial x^{\ast }\partial t^{\ast }}, & & \displaystyle\end{eqnarray}$$
which means that the horizontal vorticity does not change over time. Laterally integrating (4.5) in the similar manner as we obtained (2.7), we have
$$\begin{eqnarray}\displaystyle \frac{\partial u^{\ast }}{\partial t^{\ast }}=\frac{\partial \bar{u}^{\ast }}{\partial t^{\ast }}-{\it\sigma}^{2}\left[\frac{q+1}{q}\int _{0}^{1}(1-y^{\ast q})\int _{0}^{y^{\ast }}\frac{\partial ^{2}v^{\ast }}{\partial t^{\ast }\partial x^{\ast }}\,\text{d}y^{\ast }\,\text{d}y^{\ast }-\int _{0}^{y^{\ast }}\frac{\partial ^{2}v^{\ast }}{\partial t^{\ast }\partial x^{\ast }}\,\text{d}y^{\ast }\right]. & & \displaystyle\end{eqnarray}$$
In order to apply the perturbation method, we approximate
${\it\eta}^{\ast }$
,
$u^{\ast }$
and
$v^{\ast }$
in series of
${\it\sigma}$
as
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}{\it\eta}^{\ast }=\bar{{\it\eta}}^{\ast }+{\it\sigma}^{2}{\it\eta}_{1}^{\ast }+{\it\sigma}^{4}{\it\eta}_{2}^{\ast }+\cdots \,,\\ u^{\ast }=\bar{u}^{\ast }+{\it\sigma}^{2}u_{1}^{\ast }+{\it\sigma}^{4}u_{2}^{\ast }+\cdots \,,\\ v^{\ast }=v_{1}^{\ast }+{\it\sigma}^{2}v_{2}^{\ast }+\cdots \,.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
Substituting (4.7) into (4.3), (4.4) and (4.6) yields the following recurrence equations for the
$n$
th-order components (
$n\geqslant 1$
):
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\eta}_{n}^{\ast }=\int _{0}^{1}\int _{0}^{y^{\ast }}\frac{\partial v_{n}^{\ast }}{\partial t^{\ast }}\,\text{d}y^{\ast }\,\text{d}y^{\ast }-\int _{0}^{y^{\ast }}\frac{\partial v_{n}^{\ast }}{\partial t^{\ast }}\,\text{d}y^{\ast }, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial v_{n}^{\ast }}{\partial t^{\ast }}=-\frac{1}{1-y^{\ast q}}\left[\int _{0}^{y^{\ast }}\frac{\partial ^{2}{\it\eta}_{n-1}^{\ast }}{\partial t^{\ast 2}}\,\text{d}y+\int _{0}^{y^{\ast }}(1-y^{\ast q})\frac{\partial ^{2}u_{n-1}^{\ast }}{\partial x^{\ast }\partial t^{\ast }}\,\text{d}y^{\ast }\right], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial u_{n}^{\ast }}{\partial t^{\ast }}=-\frac{q+1}{q}\int _{0}^{1}(1-y^{\ast q})\int _{0}^{y^{\ast }}\frac{\partial ^{2}v_{n}^{\ast }}{\partial t^{\ast }\partial x^{\ast }}\,\text{d}y^{\ast }\,\text{d}y^{\ast }+\int _{0}^{y^{\ast }}\frac{\partial ^{2}v_{n}^{\ast }}{\partial t^{\ast }\partial x^{\ast }}\,\text{d}y^{\ast }, & \displaystyle\end{eqnarray}$$
${\it\eta}_{0}^{\ast }=\bar{{\it\eta}}^{\ast }$
and
$u_{0}^{\ast }=\bar{u}^{\ast }$
. Therefore,
${\it\eta}_{n}^{\ast }$
can be successively obtained by the recurrence equations, and substituting it into (4.7) and (4.2) gives the
$n$
th-order momentum equation. Subsequently, the momentum and continuity equations are combined to produce a single-variable wave equation with respect to
$\bar{u}^{\ast }$
. The
$n$
th-order wave equation becomes the
$2n$
th-order partial differential equation. For derivation of the higher-order dispersion relation, we assume the solution to be of a travelling wave with a constant wavenumber and angular frequency. Substituting the assumed form into the wave equation yields the expression for the
$n$
th-order wave celerity
$c_{n}^{\ast }$
as 
$$\begin{eqnarray}\displaystyle c_{n}^{\ast }=\sqrt{\frac{q}{q+1}}(1+{\it\mu}^{2}s_{1}+{\it\mu}^{4}s_{2}+\cdots +{\it\mu}^{2n}s_{n}), & & \displaystyle\end{eqnarray}$$
where
$s_{n}$
is a coefficient for the
$n$
th-order correction to the wave celerity. The coefficient of the first-order term
$s_{1}$
was previously obtained using the Taylor expansion in (3.20), (3.33) or (3.49) for each bay type. Note that the wave celerity from the present analytical solution is slightly different from the first-order wave celerity in the asymptotic series. Table 2 summarizes the coefficients to the sixth order for the three bay types.
Figure 6. Dimensionless wave celerity of different order in terms of
${\it\mu}$
.
Table 2. Values of
$s_{n}$
to the sixth order.
The wave celerity is plotted against
${\it\mu}$
for different-order solutions (
$n=$
0, 1, 3, 6 and 9) in figure 6. The corresponding relationship from the present solution is also plotted in each figure (labelled
$c_{anal}^{\ast }$
), which agrees with that of the first-order wave celerity in the lower range of
${\it\mu}$
. The leading-order (0th-order) wave celerity is constant with
${\it\mu}$
, whereas the higher-order wave celerity deviates downward from it as
${\it\mu}$
increases. Hence, the wave refraction effect, which reduces the wave celerity, is underestimated by the lower-order solution for large
${\it\mu}$
. The
${\it\mu}$
value for
$c^{\ast }=0$
, which indicates the occurrence of total reflection, decreases as the higher-order terms are included up to a certain order. However, the very-high-order solutions (the sixth- and ninth-order solutions) conversely deviate upward from the lower-order solutions beyond a certain limit of
${\it\mu}$
that differs with the bay type. This oscillatory behaviour implies
${\it\mu}$
is out of the convergence radius of the asymptotic series. Although a rigorous proof is lacking, this convergence limit
${\it\mu}_{c}$
can be estimated from the asymptotic behaviours of the three cases as
$$\begin{eqnarray}\displaystyle {\it\mu}_{c}\approx \sqrt{2q}. & & \displaystyle\end{eqnarray}$$
The convergence limit provides the applicable limit of the perturbation approach. The
${\it\mu}_{c}$
values are approximately 2.0, 1.4 and 1.2, respectively, for
$q=2,1$
and
$2/3$
(the corresponding
${\it\sigma}$
values are 0.32, 0.23 and 0.18). When
${\it\mu}>{\it\mu}_{c}$
, the higher-order term is no longer a minor correction, and thus, the quasi-one-dimensional assumption breaks down. Beyond the limit, the two-dimensional wave field cannot be represented by the section-averaged travelling wave, and total reflection possibly occurs forming an evanescent wave towards the bay head. The results also suggest that the present solution provides a good approximation close to the limit with less than five percent error in the wave celerity. Since the applicable limit
${\it\mu}_{c}$
was not determined in a rigorous manner, we validate it by comparing the present solutions with numerical solutions of the two-dimensional shallow water equations, (2.1), (2.2) and (2.3). The supporting material provides the comparisons of the wave amplitude distribution at
${\it\mu}/{\it\mu}_{c}=0.5$
, 1.0 and 1.5 for the three bay types. The analytical solutions agree with the numerical results up to
${\it\mu}/{\it\mu}_{c}=1$
, whereas the two results rapidly deviate from each other as
${\it\mu}$
goes beyond
${\it\mu}_{c}$
. The results support the validity of the estimation.
4.2 Maximum run-up height
We finally discuss run-up characteristics of monochromatic waves in the different bay types on the basis of the analytical solutions. Analogous to the classical run-up solutions, the maximum run-up height
$R_{max}$
can be represented by the wave amplitude at the bay head (
$\hat{x}^{\ast }=0$
). For the leading-order solution, the maximum run-up height for arbitrary
$q$
can be expressed as
$$\begin{eqnarray}\displaystyle R_{max}^{\ast }=\frac{2(p{\it\lambda})^{1/q}}{{\rm\Gamma}(p^{2})\sqrt{\text{J}_{1/q}^{2}(2p{\it\lambda})+\text{J}_{1/q+1}^{2}(2p{\it\lambda})}}, & & \displaystyle\end{eqnarray}$$
where
$R_{max}^{\ast }=R_{max}/a_{0}$
is the dimensionless run-up height. This leads to the classical run-up solution over uniform slopes of Keller & Keller (Reference Keller and Keller1964) by letting
$q\rightarrow \infty$
$(p\rightarrow 1)$
:
$$\begin{eqnarray}\displaystyle R_{max}^{\ast }=\frac{2}{\sqrt{\text{J}_{0}^{2}(2{\it\lambda})+\text{J}_{1}^{2}(2{\it\lambda})}}. & & \displaystyle\end{eqnarray}$$
Also, for large
${\it\lambda}$
, (4.13) can be simplified using the asymptotic forms of the Bessel functions as
$$\begin{eqnarray}\displaystyle R_{max}^{\ast }=\frac{2\sqrt{{\rm\pi}}(p{\it\lambda})^{1/q+1/2}}{{\rm\Gamma}(p^{2})}. & & \displaystyle\end{eqnarray}$$
The run-up height is, therefore, expressed as the algebraic function of
${\it\lambda}$
. Equation (4.15) is identical to the one presented in Zahibo et al. (Reference Zahibo, Pelinovsky, Golinko and Osipenko2006).
For the higher-order solutions, a unified expression is not available for different bay types, and thus, it is given on a case-by-case basis as follows:
-
(i) U-shaped bay (
$q=2$
) (4.16)
$$\begin{eqnarray}\displaystyle R_{max}^{\ast }=\frac{4{\it\kappa}^{1/2}}{\sqrt{{\rm\pi}}\sqrt{\text{J}_{1/2}^{2}(\sqrt{6}{\it\zeta}{\it\lambda})+\text{J}_{3/2}^{2}(\sqrt{6}{\it\zeta}{\it\lambda})}}; & & \displaystyle\end{eqnarray}$$
-
(ii) V-shaped bay (
$q=1$
) (4.17)
$$\begin{eqnarray}\displaystyle R_{max}^{\ast }=\frac{2}{\sqrt{F\left({\it\alpha},{\it\beta},2;\displaystyle \frac{{\it\mu}^{2}}{12}\right)^{2}+\displaystyle \frac{{\it\kappa}^{2}}{4}F\left({\it\alpha},{\it\beta},3;\displaystyle \frac{{\it\mu}^{2}}{12}\right)^{2}}}; & & \displaystyle\end{eqnarray}$$
-
(iii) cusped bay (
$q=2/3$
) (4.18)
$$\begin{eqnarray}\displaystyle R_{max}^{\ast }=\frac{2}{\sqrt{G\left({\it\lambda};r;\sqrt{\frac{3}{22}}{\it\mu}\right)^{2}+\frac{4}{25}{\it\kappa}^{2}E\left({\it\lambda};r;\sqrt{\frac{3}{22}}{\it\mu}\right)^{2}}}. & & \displaystyle\end{eqnarray}$$
Note that the definition of
${\it\kappa}$
differs by the bay type and is given, respectively, in (3.19), (3.32) or (3.48). It was numerically confirmed that the higher-order solutions reduce to (4.13) in the limit of
${\it\mu}\rightarrow 0$
.
Figure 7 shows the relationships between
$R_{max}^{\ast }$
and
${\it\lambda}$
for the three bay types with different aspect ratios (
$r=$
0.25, 0.5 and 1) and plane beaches (
$q=\infty$
). The leading-order solutions for the three bay types are plotted with dashed lines (labelled
$R_{max0}^{\ast }$
), whereas the higher-order solutions are plotted with solid lines up to their applicable limits given by
${\it\mu}_{c}=\sqrt{2q}$
. When
${\it\lambda}<0.5$
, the dimensionless run-up height changes with neither
$q$
nor
$r$
, taking a nearly constant value of two. Incoming waves are not funnelled in the range due to reflection by the relatively strong convergence of the bay cross-section. As
${\it\lambda}$
increases, the funnelling effect intensifies to produce differences over the three bay types, causing larger amplification in bays with smaller
$q$
. Comparison of the leading- and higher-order solutions suggests that the wave refraction effect on the maximum run-up height also increases with increasing
${\it\lambda}$
. For large
${\it\mu}$
, the maximum run-up height is reduced from the leading-order solution for the cases of
$q=1$
and
$2/3$
, whereas it is slightly enhanced for the case of
$q=2$
, although the first-order solution contains a truncation error very close to the applicable limit. This is because the refracted waves are reflected out of the bay due to the strongly converging topography near the bay entrance for the former cases. Beyond the limit, the maximum run-up height should more significantly decrease compared to the leading-order solution due to the wave trapping at the bay entrance.
Figure 7. Relationships between
$R_{max}^{\ast }$
and
${\it\lambda}$
for different sets of the bay parameters
$q$
and
$r$
, and curves of wave breaking criteria for different
${\it\varepsilon}$
values.
As previously discussed in § 2.1, the linear solutions predict actual run-up heights well as long as
${\it\varepsilon}$
is small. This means that the energy transfer process in the bay is not significantly affected by the nonlinearity under the condition. However, the nonlinear advection causes wave breaking in the bay at a certain limit of
${\it\lambda}$
and suppresses the run-up height significantly. The breaking criterion can be specified as the breakdown point of the hodograph transform whose Jacobian goes to zero (Madsen & Schaeffer Reference Madsen and Schaeffer2010). Zahibo et al. (Reference Zahibo, Pelinovsky, Golinko and Osipenko2006) expressed the same criterion for monochromatic waves propagating in the converging bays with respect to the linear solution. It may be written in terms of the run-up height as
$$\begin{eqnarray}\displaystyle R_{max}^{\ast }=\frac{1}{{\it\varepsilon}{\it\lambda}^{2}}. & & \displaystyle\end{eqnarray}$$
It was determined as a condition for the appearance of discontinuity in the shoreline velocity that occurs at the ebb peak regardless of the
${\it\lambda}$
and
${\it\varepsilon}$
values. The breaking criteria for different
${\it\varepsilon}$
values are indicated by dash-dot-line curves in figure 7. Although they are based on the leading-order solution neglecting the terms of
$O({\it\sigma}^{2})$
, the criteria provide breaking limits within the applicable range of the present solution well, because the higher-order effect is not large. Therefore, given a value of
${\it\varepsilon}$
, the run-up amplification beyond the intersection of the run-up curve and the corresponding breaking curve will not be realized due to energy dissipation through wave breaking.
It may be worth discussing the case of the 2011 Tohoku tsunami based on figure 7. Numerous bays along the severely affected coast (the Sanriku Coast) typically have dimensions of
$h_{0}=80{-}100~\text{m}$
,
$l_{x}=4{-}6~\text{km}$
and
$l_{y}=1{-}2$
km with different shapes (Shimozono et al.
Reference Shimozono, Sato, Okayasu, Tajima, Fritz, Liu and Takagawa2012). The tsunami approaching the coast contained a predominant wave component with a period of approximately 40–50 min and a short impulsive wave of smaller than 10 min period localized in the leading predominant wave (Kawai et al.
Reference Kawai, Satoh, Kawaguchi and Seki2013). The
${\it\lambda}$
value for the predominant component was in the range of
${\it\lambda}<0.5$
for many bays, in which significant amplification could not occur. The observed variation in the run-up height was produced by the short wavelength component, which was in the range of strong funnelling (
${\it\lambda}>1.5$
). However, it was also in the critical range of the occurrence of wave breaking since its amplitude was up to several metres out of the bays, namely
${\it\varepsilon}=O(10^{-2})$
. Wave breaking dissipation limited the energy transfer to the bay head region in many bays. In strongly converging bays, wave refraction might further prevent the short wave intrusion, generating high run-up around its entrance through wave trapping. These probably explain why the tendency of wave funnelling was not clearly observed in the run-up height distribution along the coast. Indeed, large run-up heights were observed in converging bays of a relatively small scale where the short wave energy was brought to the bay head without being limited by both wave breaking and refraction. The highest run-up trace throughout the event, which was nearly 40 m above the mean sea level, was found at a small V-shaped bay of approximately 1 km length (Shimozono et al.
Reference Shimozono, Cui, Pietrzak, Fritz, Okayasu and Hooper2014).
5 Conclusions
This paper investigated propagation and run-up characteristics of long periodic waves in converging bays. We considered three types of symmetric bays that monotonically decrease their cross-sectional areas: U-shaped, V-shaped and cusped bays. The two-dimensional linear long wave equations reduce to one-dimensional dispersive wave equations under the assumption that the transverse flow acceleration is small. The analytical solutions are characterized by two parameters,
${\it\lambda}$
and
${\it\mu}$
. The longitudinal variation in wave amplitude inside the bay is represented with the different functions of
${\it\lambda}$
for the respective bay type. When
${\it\lambda}<0.5$
, incoming waves are not funnelled in the bays, and the run-up amplification factor remains nearly constant at two due to significant reflection through relatively rapid transition of the bay cross-section. The funnelling effect intensifies with increasing
${\it\lambda}$
and causes drastic wave amplification in the strongly converging bays. The higher-order effect with respect to
${\it\mu}$
is responsible for wave refraction over the laterally uneven topography. The refraction effect differently contributes to the wave amplitude in the bay head region depending on the bay type.
To clarify the applicable range of the derived solutions, we carried out the perturbation analysis to investigate asymptotic behaviours of the wave celerity over uniform cross-sections of the three types. The results suggest that the higher-order effect is no longer a minor correction to the leading-order plane-wave solution when
${\it\mu}$
exceeds
$\sqrt{2q}$
. Therefore, the incoming waves evolve into highly two-dimensional waves through strong wave refraction and total reflection probably occurs beyond the limit. Clarification of wave characteristics beyond the limit requires two-dimensional analysis since the quasi-one-dimensional assumption breaks down. Within the applicable range
${\it\mu}<\sqrt{2q}$
, the wave refraction effect on the maximum run-up height is small, and thus, run-up amplification is well predicted even if the higher-order effect is disregarded. However, the leading-order solution significantly underestimates the wave height around the bay entrance for large
${\it\mu}$
.
Acknowledgements
This study was supported by the Special Project ‘Integrated Research Project on Seismic and Tsunami Hazards around the Sea of Japan’ from the Ministry of Education, Culture, Sports, Science, and Technology of Japan, and Grant-in-Aid for Scientific Research no. 26820199 from Japan Society for the Promotion of Science.
