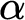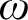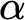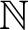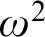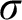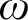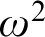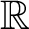1 Introduction
Let us call a subset A of
$\mathbb {R}$
clopen if
$A\setminus \mathbb {Q}$
is clopen in
$\mathbb {R}\setminus \mathbb {Q}$
. We study games of transfinite length whose payoff set is clopen when viewed as a subset of
$\mathbb {R}\setminus \mathbb {Q}$
(henceforth identified with
$\mathbb {N}^{\mathbb {N}}$
—the space of infinite sequences of natural numbers, viewed as a product of discrete spaces). More specifically, let
$\alpha $
be a countable wellorder and fix a bijection
$$ \begin{align*} \rho:\mathbb{N}\to\alpha. \end{align*} $$
For simplicity, we will assume that
$\rho $
is recursive, although this assumption can be dropped by relativizing to a real parameter. Fix
$A\subset \mathbb {R}$
(the payoff set) and consider a game of length
$\alpha $
in which two players, I and II, alternate turns playing natural numbers
$$ \begin{align*} \begin{array}{c|cccccccc} I & n(0) & & n(2) & &\ldots & n(\omega) & &\ldots\\ II & & n(1) & & n(3) & \ldots & & n(\omega+1) &\ldots \end{array} \end{align*} $$
After
$\alpha $
-many rounds have been played, the game ends. Player I wins if, and only if,
$$ \begin{align*} \big(n(\rho(0)), n(\rho(1)), n(\rho(2)), \ldots \big) \in A; \end{align*} $$
otherwise, Player II wins. We say that the game is determined if one of the players has a winning strategy. It is a classical theorem of Gale and Stewart [Reference Gale and Stewart5] that if A is clopen and
$\alpha = \omega $
(the order-type of
$\mathbb {N}$
), then the game is determined (in which case we say that A itself is determined). One may also view these games as having payoff set a clopen subset of
$\mathbb {N}^{\alpha }$
, with the product topology.
Gale and Stewart’s proof in fact shows that clopen games of length
$\omega +1$
are determined. A celebrated result of Martin [Reference Martin7] implies that clopen games of length
$\omega +\omega $
are also determined. Moreover, this is the extent of clopen determinacy provable in
${\mathsf {ZFC}}$
, Zermelo–Fraenkel set theory with the Axiom of Choice; i.e.,
${\mathsf {ZFC}}$
does not prove that clopen games of length
$\omega +\omega +1$
are determined. This is a theorem of Harrington (see [Reference Harrington6]). Determinacy for longer clopen games is, however, provable in natural extensions of
${\mathsf {ZFC}}$
by large cardinal axioms, and it is natural to ask the extent of clopen determinacy provable in theories stronger than
${\mathsf {ZFC}}$
. For example, clopen determinacy for games of length
$\omega ^2 + \omega $
is provable in the theory
${\mathsf {ZFC}} +$
“there are infinitely many Woodin cardinals,” but clopen determinacy for games of length
$\omega ^2 + \omega + 1$
is not.
Our work in this article takes a different direction, however. Namely, by using completely elementary methods, we prove that every long clopen game is reducible to a more complicated, but shorter, game. Some results in this direction are folklore. For example, it is not hard to show that clopen games of length
$\omega +\omega $
are determined if, and only if, Borel games of length
$\omega $
are determined. The argument generalizes to show that clopen games of length
$\alpha +\omega $
are determined if, and only if, Borel games of length
$\alpha $
are determined. Similarly, clopen games of even (resp. odd) length
$\alpha +1$
are determined if, and only if, open (resp. closed) games of length
$\alpha $
are determined. By combining these two observations, one can shorten clopen games of length
$\alpha + \omega + 1$
to analytic games of length
$\alpha $
. For similar reasons, the problem of shortening clopen games quickly reduces to the particular case in which the length is additively indecomposable (see Section 5 below). We include the proofs of these folklore results below.
Our first reduction of clopen games is, thus, from length
$\omega ^2$
to length
$\omega $
. Below, a set
$A\subset \mathbb {R}$
is
$\sigma $
-projective if it belongs to the smallest collection of subsets of
$\mathbb {R}$
containing all open sets and closed under continuous images, complements, and countable unions.
Theorem 1.1. The following are equivalent
$:$
-
1. Determinacy for clopen games of length
$\omega ^2$
. -
2. Determinacy for
$\sigma $
-projective games of length
$\omega $
.
As a consequence of Theorem 1.1 and the main result of [Reference Aguilera1], one obtains a characterization of clopen determinacy for games of length
$\omega ^2$
in terms of large-cardinal assumptions. A seemingly stronger form of the implication from (1) to (2) was proved in [Reference Aguilera, Müller and Schlicht3] (as well as a weak form of the implication from (2) to (1)), so we shall only prove the converse. In light of Theorem 1.1, one might conjecture that clopen games of any countable length can be shortened to length
$\omega $
. However, this is not the case. This is because clopen determinacy for games of length
$\omega ^2+\omega +1$
implies that
$\mathbb {R}^{\sharp }$
exists (this follows from a theorem of Trang [Reference Trang11], together with the observation on analytic games above). Since it is consistent that every set of reals in
$L(\mathbb {R})$
is determined, no determinacy assumption for games of length
$\omega $
can imply clopen determinacy of length
$\omega ^2+\omega +1$
(incidentally,
$\omega ^2+\omega +1$
is the least such ordinal).
However, as we will see, long clopen games can still be shortened. We will speak of some quantifiers on
$\mathbb {R}$
. Projections are usually denoted by the quantifier
$\exists $
, i.e., one writes
$\exists x\, A(x,y)$
for “
$\{x : A(x,y)\}$
is nonempty.” Another example is the game quantifier given by
$$ \begin{align*} \Game x\, A(x,y) \text{ if, and only if, Player I has a winning strategy for } \{x: A(x,y)\}. \end{align*} $$
Game quantifiers for longer games
$\Game _{\alpha }$
, as well as for games on
$\mathbb {R}$
,
$\Game ^{\mathbb {R}}$
, are defined similarly.
Definition 1.2. Let Q be a quantifier. We denote by
$\sigma (Q)$
the smallest
$\sigma $
-algebra on
$\mathbb {R}$
containing the open sets and closed under Q.
Similarly, if
$\{Q_{\iota }\}_{\iota }$
is a collection of quantifiers, we denote by
$\sigma (\{Q_{\iota }\}_{\iota })$
the smallest
$\sigma $
-algebra on
$\mathbb {R}$
containing the open sets and closed under each
$Q_{\iota }$
.
We remark that
$\sigma (\exists ) = \sigma (\Game )$
is the pointclass of all
$\sigma $
-projective sets. To see this, first observe that
$\sigma (\exists ) = \sigma (\Game )$
, because game quantifiers can be simulated by an existential quantifier followed by a universal quantifier. Every set in
$\sigma (\exists )$
is
$\sigma $
-projective because projection maps are continuous. Conversely, arbitary continuous functions are determined by their values on any countable dense subset of the reals and are thus each coded by single real, so A being a continuous image of B can be reduced to the existence of a real coding a continuous function which maps A to B. The shortening theorem for games of length
$\omega ^3$
is as follows:
Theorem 1.3. The following are equivalent
$:$
-
1. Determinacy for clopen games of length
$\omega ^{3}$
. -
2. Determinacy for games of length
$\omega ^2$
with payoff in
$\sigma (\Game ^{\mathbb {R}})$
.
Theorems 1.1 and 1.3 are both instances of a general theorem which is stated and proved in Section 4.
For expository reasons, we have chosen to include the proof of Theorem 1.1 in Section 3; it is similar to the general case, but easier.
2 Basic shortenings
In this section, we mention some folklore results whose proofs the reader might find helpful. Below, given
$A\subset \mathbb {R}\times \mathbb {R}$
, we write
$A_x$
for the set of all y such that
$(x,y) \in A$
.
Proposition 2.1. The following are equivalent for an even ordinal
$\alpha $
:
-
1. Determinacy for clopen games of length
$\alpha +1$
. -
2. Determinacy for open games of length
$\alpha $
.
Proof The assumption on
$\alpha $
being even is necessary because it guarantees that it is Player I who plays the last move in games of length
$\alpha +1$
. Given a clopen game A of length
$\alpha +1$
, consider a game B in which players I and II play
$\alpha $
-many natural numbers, producing a sequence x, after which Player I wins if and only if there is a move
$n\in \mathbb {N}$
such that
$x^{\frown } n$
is a winning move in A. Then B is an open game of length
$\alpha $
and each player has a winning strategy in A if and only if she has one in B.
Conversely, given an open game A of length
$\alpha $
, write
$A = \bigcup _{i\in \mathbb {N}}A_i$
as a union of basic open sets. Recall that basic open subsets of the Baire space are clopen. Consider a clopen game B where players I and II have to play
$\alpha $
many moves, producing a sequence x, after which Player I plays
$i\in \mathbb {N}$
. Player I wins if and only if
$x \in A_i$
. Since each
$A_i$
is a clopen game, B is a clopen game as well and, as before, each player has a winning strategy in A if and only if she has one in B. ⊣
Proposition 2.2. The following are equivalent
$:$
-
1. Determinacy for clopen games of length
$\alpha +\omega +1$
. -
2. Determinacy for
$\boldsymbol \Pi ^1_1$
games of length
$\alpha $
.
Proof Recall that a subset of
$\mathbb {R}$
is
$\boldsymbol \Pi ^1_1$
if and only if it is
$\Game \boldsymbol \Sigma ^0_1$
(see Moschovakis [Reference Moschovakis9]). Given a
$\Game \boldsymbol \Sigma ^0_1$
game A, there is an open set
$C \subset \mathbb {R}\times \mathbb {R}$
such that A has a payoff condition “ Player I wins the run x of the game if and only if Player I has a winning strategy for the game
$C_x$
.”
Given such a game A of length
$\alpha $
, consider the game B where two players produce a sequence x of length
$\alpha $
, after which they play the game
$C_x$
, with Player I taking the role of Player I in
$C_x$
, and Player II taking the role of Player II in
$C_x$
, thus producing a sequence y of length
$\omega $
. Player I wins B if y is a winning run for her in
$C_x$
. Each player has a winning strategy in A if and only if she has one in B. Thus reduces
$\boldsymbol \Pi ^1_1$
-determinacy for games of length
$\alpha $
to open determinacy for games of length
$\alpha +\omega $
; however, arguing as in the previous proposition (
$\omega $
is even), one can further reduce it to clopen determinacy for games of length
$\alpha +\omega +1$
.
Conversely, using the previous proposition, we see that clopen determinacy for games of length
$\alpha +\omega +1$
is equivalent to open determinacy for games of length
$\alpha +\omega $
. Thus, fix a
$\boldsymbol \Sigma ^0_1$
game A of length
$\alpha + \omega $
, say A. We consider a game B where players I and II alternate
$\alpha $
-many turns to produce a sequence x after which the game ends. Player I wins if and only if she has a winning strategy to win the rest of the game after x has been played. If Player I does not have such a strategy, then Player II must have one, because there are only
$\omega $
many moves remaining after x has been played, the payoff of A is open. It follows that each player has a winning strategy in A if and only if she has one in B. Since B is a game of length
$\alpha +\omega $
with payoff in
$\Game \boldsymbol \Sigma ^0_1$
, the result follows. ⊣
Proposition 2.3. The following are equivalent
$:$
-
1. Determinacy for clopen games of length
$\alpha +\omega $
. -
2. Determinacy for Borel games of length
$\alpha $
.
Proof This is proved like before, using the fact that
$\Delta ^1_1 = \Game \Delta ^0_1$
(see Moschovakis [Reference Moschovakis10] or Martin [Reference Martin8, Lemma 1.4.1]). ⊣
3 Shortening games of length
$\omega ^2$
Let
$A\subset \mathbb {R}\times \mathbb {R}$
be clopen. Hence,
$$ \begin{align*} \Game^{\mathbb{R}}A = \{x: \text{ Player I has a winning strategy in the game on } \mathbb{R} \text{ with payoff } A_x\}. \end{align*} $$
We define
$$ \begin{align*} \Game^{\mathbb{R}}\boldsymbol\Delta^0_1 = \{\Game^{\mathbb{R}}A: A \text{ is clopen}\}. \end{align*} $$
Recall that
$L_{\alpha }(\mathbb {R})$
is the
$\alpha $
th level of the constructible hierarchy relative to the set of all real numbers. It is given by transfinite recursion, setting
$L_0(\mathbb {R})$
equal to
$V_{\omega +1}$
,
$L_{\alpha +1}(\mathbb {R})$
equal to the collection of all subsets of
$L_{\alpha }(\mathbb {R})$
definable from finitely many elements of
$L_{\alpha }(\mathbb {R})$
, and
$L_{\lambda }(\mathbb {R}) = \bigcup _{\alpha <\lambda }L_{\alpha }(\mathbb {R})$
at limit stages. In particular, a subset of
$\mathbb {R}$
is
$\sigma $
-projective if, and only if, it belongs to
$L_{\omega _1}(\mathbb {R})$
(this is a simple, folklore fact, but a proof can be found in [Reference Aguilera, Müller and Schlicht3]).
Lemma 3.1.
$\Game ^{\mathbb {R}}\boldsymbol \Delta ^0_1\subset L_{\omega _1}(\mathbb {R})$
.
The converse of the lemma (for sets of reals) follows from the argument of [Reference Aguilera, Müller and Schlicht3].
Proof of the Lemma Suppose that a recursive procedure for coding finite and countably infinite sequences of real numbers by real numbers has been fixed, as well as a recursive relation
$\sqsubset $
so that
$x\sqsubset y$
if, and only if, x and y code sequences and x is a proper initial segment of y.
Let
$A\subset \mathbb {R}\times \mathbb {R}$
be clopen. For each
$x\in \mathbb {R}$
, there is a game of length
$\omega $
with moves in
$\mathbb {R}$
given by
$A_x$
. Let us identify this game with
$A_x$
. We shall show that
$\Game ^{\mathbb {R}} A \in L_{\omega _1}(\mathbb {R})$
. For every
$x\in \mathbb {R}$
, we define
$$ \begin{align*} T_x = \big\{t \in \mathbb{R}^{<\mathbb{N}}: \exists y\in\mathbb{R}^{\mathbb{N}}\,\exists z\in\mathbb{R}^{\mathbb{N}}\, \big(t\sqsubset y \wedge t\sqsubset z \wedge (x,y)\in A \wedge (x,z) \not \in A\big)\big\}. \end{align*} $$
Thus,
$T_x$
is the set of “ contested” positions in
$A_x$
. We define a binary relation on
$\mathbb {R}^2$
by
$$ \begin{align*} (x,y) \prec (w,z) \text{ if, and only if, } y \in \mathbb{R}^{<\mathbb{N}} \wedge x = w \wedge z \in T_w \wedge z \sqsubset y. \end{align*} $$
Since A is clopen, for every
$x\in \mathbb {R}$
and every
$y\in \mathbb {R}^{\mathbb {N}}$
, there is some
$n\in \mathbb {N}$
such that for every
$z\in \mathbb {R}^{\mathbb {N}}$
,
$$ \begin{align*} y\upharpoonright n = z\upharpoonright n \text{ implies } (y\in A_x\leftrightarrow z\in A_x). \end{align*} $$
It follows that
$\prec $
is wellfounded, so it has a rank function,
$\rho $
. The rank function is defined by
$$ \begin{align*} \rho(w,z) = \sup\big\{\rho(x,y) + 1: (x,y)\prec (w,z)\big\}. \end{align*} $$
Now,
$\prec $
is analytic, so, by e.g., the Kunen–Martin theorem (see, e.g., [Reference Moschovakis10, Theorem 2G.2]),
$\rho $
is bounded below
$\omega _1$
, say, by
$\eta $
. Let us write
$$ \begin{align*} y\prec_x z \text{ if, and only if, } (x,y) \prec (x,z), \end{align*} $$
and denote by
$\rho _x$
the associated rank function. For every
$x\in \mathbb {R}$
,
$\rho _x$
is bounded by
$\eta $
. If z is a partial play of
$A_x$
and
$\rho _x(z) = 0$
, i.e., if z is
$\prec _x$
-minimal, then it does not belong to
$T_x$
, so every extension of z to a full play in the game with payoff
$A_x$
is won by the same player. As in the effective proof of (short) clopen determinacy, define:
$$ \begin{align*} W_0(x) &= \big\{a\in\mathbb{R}^{<\mathbb{N}}: \exists y\in\mathbb{R}\,\forall z\in\mathbb{R}\, \big(a^{\frown} y^{\frown} z\not\in T_x\, \wedge \\ & \qquad\quad \exists w\in\mathbb{R}^{\mathbb{N}}\, \big(a^{\frown} y^{\frown} z \sqsubset w \wedge (x,w) \in A\big)\big) \big\};\\ W_{\alpha}(x) &= \Bigg\{a\in\mathbb{R}^{<\mathbb{N}}: \exists y\in\mathbb{R}\,\forall z\in\mathbb{R}\, \big(a^{\frown} y^{\frown} z\in \bigcup_{\xi<\alpha}W_{\xi}(x)\big) \Bigg\};\\ W_{\infty}(x) &= \bigcup_{\alpha\in{\mathsf{Ord}}}W_{\alpha}(x).\\ \end{align*} $$
It is not hard to see (in V, where the Axiom of Choice holds) that from a partial play a of even length, Player I has a winning strategy in
$A_x$
if
$a\in W_{\infty }(x)$
. Conversely, if
$a\not \in W_{\infty }(x)$
, then Player II has a strategy that prevents Player I from ever reaching a position in
$W_{\infty }(x)$
and ultimately wins. It follows that
$$ \begin{align*} \Game^{\mathbb{R}}A = \big\{x\in\mathbb{R}:\langle\ \rangle \in W_{\infty}(x)\big\}. \end{align*} $$
Let us refer to the least
$\xi $
such that
$y\in W_{\xi }(x)$
, if any, as the weight of y and denote it by
$w_x(y)$
. The point is that if a has weight
$\xi $
, then any extension of a of smaller weight has smaller rank in
$\prec _x$
. It follows that for every
$a\in W_{\infty }(x)$
,
$w_x(a)\leq \rho _x(a)$
. This is shown by an easy induction on the weight:
Put
$\xi = w_x(a)$
. Let us assume that
$0 < \xi $
, so there is
$y\in \mathbb {R}$
such that for all
$z\in \mathbb {R}$
,
$a^{\frown } y^{\frown } z$
has weight
$<\xi $
. By minimality of
$\xi $
, z can be chosen so that the weight of
$a^{\frown } y^{\frown } z$
is arbitrarily large below
$\xi $
(
$\xi $
could be a successor ordinal, in which case this means “ equal to the predecessor”). By induction hypothesis,
$$ \begin{align*} \xi = \sup\big\{w_x(a^{\frown} y^{\frown} z) + 1: z\in\mathbb{R}\big\} \leq \sup\big\{\rho_x(a^{\frown} y^{\frown} z) + 1: z\in\mathbb{R}\big\}. \end{align*} $$
It cannot be that
$a \not \in T_x$
, for this contradicts the assumption that
$w_x(a) \neq 0$
; thus,
$a \in T_x$
and, similarly,
$a^{\frown } y \in T_x$
, in which case we must have
$$ \begin{align*} \xi &\leq \sup\big\{\rho_x(a^{\frown} y^{\frown} z) + 1: z\in\mathbb{R} \big\} \\ &= \sup\big\{\rho_x(a^{\frown} y^{\frown} z) + 1: a^{\frown} y^{\frown} z \prec_x a^{\frown} y \big\} \\ &= \rho_x(a^{\frown} y). \end{align*} $$
It follows that
$\rho _x(a)$
is at least
$\xi +1$
. This proves the claim. It follows that
$$ \begin{align*} W_{\infty}(x) = W_{\eta}(x), \end{align*} $$
for every
$x\in \mathbb {R}$
.
Finally, the construction of
$W_{\eta }(x)$
can be carried out within
$L_{\omega _1}(\mathbb {R})$
, uniformly in x, so
$\Game ^{\mathbb {R}}A \in L_{\omega _1}(\mathbb {R})$
, as desired. ⊣
To prove Theorem 1.1, suppose that
$\sigma $
-projective games of length
$\omega $
are determined. Let A be a clopen set and consider the game of length
$\omega ^2$
on
$\mathbb {N}$
with payoff A. The argument to follow is a clopen version of one of Blass [Reference Blass4]. Unlike the situation in [Reference Blass4], we do not have too much determinacy to work with; however, we do not need much when dealing with clopen games, and we do not need uniformization.
Consider the following game:
$$ \begin{align} \begin{array}{c|ccccc} I & \sigma_0 & & \sigma_1 & &\ldots\\ II & & \tau_0 & & \tau_1 & \ldots \end{array} \end{align} $$
Here, players I and II take turns playing reals coding strategies for Gale–Stewart games. Player I wins if
$$ \begin{align*} (\sigma_0*\tau_0, \sigma_1*\tau_1, \ldots) \in A, \end{align*} $$
where
$\sigma *\tau $
denotes the result of facing off the strategies
$\sigma $
and
$\tau $
; otherwise, Player II wins. Instead of playing the game, the players simply reveal their strategies and use them compute a run of the game. This is a clopen game on reals, so it is determined by the Gale–Stewart Theorem [Reference Gale and Stewart5]. Clearly, if Player I has a winning strategy in this game, then she has one in the long game with payoff A. Suppose instead that Player II has a winning strategy; we claim she has one in the long game.
We will construct a strategy
$\tau $
for Player II in the long game with the property that every partial play by
$\tau $
is not a losing play for Player II. Since the game is clopen, there can be no full play in which the winner of the game has not been decided, so
$\tau $
will be a winning strategy. The strategy is constructed by blocks; first, we define it for plays of finite length. Given
$x\in \mathbb {R}$
, one may consider the following variant
$G_x$
of (1):
$$ \begin{align*} \begin{array}{c|ccccc} I & \sigma_1 & & \sigma_2 & &\ldots\\ II & & \tau_1 & & \tau_2 & \ldots \end{array} \end{align*} $$
Here, Player I wins if, and only if,
$$ \begin{align*} (x, \sigma_1*\tau_1, \ldots) \in A; \end{align*} $$
otherwise, Player II wins. This is also a clopen game, so the set
$$ \begin{align*} W = \{x\in\mathbb{R}: \text{ Player I has a winning strategy in } G_x\} \end{align*} $$
belongs to
$\Game ^{\mathbb {R}}\boldsymbol \Delta ^0_1$
, and thus to
$L_{\omega _1}(\mathbb {R})$
, by the lemma. By hypothesis,
$$ \begin{align*} L_{\omega_1}(\mathbb{R})\models{\mathsf{AD}}, \end{align*} $$
and so W is determined. Player I cannot have a winning strategy, for otherwise it could have been used as a first move to obtain a winning strategy in (1). Thus, Player II has a winning strategy in W. This will provide the restriction of
$\tau $
to the first
$\omega $
-many moves. Given the first
$\omega $
-many moves, say a, one repeats the argument above to obtain the restriction of
$\tau $
to moves of length
$\omega \cdot 2$
extending a. We describe how to do this. First observe that Player I does not have a winning strategy in
$G_a$
by the definition of W. We consider the set
$$ \begin{align*} W_a = \{x\in\mathbb{R}: \text{Player I has a winning strategy in } G_{a^{\frown} x}\}. \end{align*} $$
As before, this is a set in
$\Game ^{\mathbb {R}}\boldsymbol \Delta ^0_1$
which is determined by hypothesis and by the lemma. Player I cannot have winning strategy for
$W_a$
, for this would induce a winning strategy in
$G_a$
. Hence, Player II has a winning strategy for
$W_a$
. Following this strategy tells Player II what to do in turns
$\omega $
through
$\omega \cdot 2$
of A. By continuing this way, eventually one defines the response of
$\tau $
to every
$b \in \mathbb {N}^{<\omega ^2}$
, as desired. This completes the proof of Theorem 1.1.
4 Shortening games of length
$\omega ^{\alpha }$
In this section we study games of length
$\omega ^{\alpha }$
. We first assume
$\alpha $
is a successor ordinal and show:
Theorem 4.1. Let
$2\leq \alpha <\omega _1$
. The following are equivalent
$:$
-
1. Determinacy for clopen games of length
$\omega ^{\alpha +1}$
. -
2. Determinacy for games of length
$\omega ^{\alpha }$
with payoff in
$\sigma (\Game ^{\mathbb {R}}_{\omega ^{-1 + \alpha }})$
.
We shall only prove that (2) implies (1). As will be pointed out (see the proof of Lemma 4.2), the converse again follows from the argument of [Reference Aguilera, Müller and Schlicht3].
Let
$S = \{(B,i):$
Player I has a winning strategy in the game of length
$\omega ^{-1+\alpha }$
on
$\mathbb {R}$
with payoff B and
$i = 1$
, or else Player I does not have a winning strategy in the game of length
$\omega ^{-1+\alpha }$
on
$\mathbb {R}$
with payoff B and
$i = 0\}$
. Thus,
$L(\mathbb {R})[S]$
is the smallest inner model of
${\mathsf {ZF}}$
that “knows” whether each of its games of length
$\omega ^{-1+\alpha }$
on
$\mathbb {R}$
is won by Player I.
Lemma 4.2. Let
$2\leq \alpha <\omega _1$
. The following pointclasses all coincide
$:$
-
1.
$\sigma (\Game ^{\mathbb {R}}_{\omega ^{-1+\alpha }})$
, -
2.
$\sigma (\Game _{\omega ^{\alpha }})$
, -
3.
$\mathcal {P}(\mathbb {R})\cap L_{\omega _1}(\mathbb {R})[S]$
, -
4.
$\Game ^{\mathbb {R}}_{\omega ^{-1 + \alpha + 1}}\boldsymbol \Delta ^0_1$
.
Proof First, notice that for any adequateFootnote
1
pointclass
$\Gamma $
, the fact that
$$ \begin{align*} \Game^{\mathbb{R}}_{\omega^{-1+\alpha}}\Gamma = \Game_{\omega^{\alpha}}\Gamma \end{align*} $$
can be shown easily by considering games like the one in the previous section.Footnote
2
The equality between (1) and (2) now follows by a simple transfinite induction on the construction of the
$\sigma $
-algebras.
Let us prove the equality between (1) and (3). Clearly,
$L_{\omega _1}(\mathbb {R})[S]$
contains all reals and contains surjections
$$ \begin{align*} \pi_{\xi}: \mathbb{R} \twoheadrightarrow L_{\xi}(\mathbb{R})[S], \end{align*} $$
for each
$\xi <\omega _1$
. It follows that it is closed under countable sequences and in particular
$\mathcal {P}(\mathbb {R})\cap L_{\omega _1}(\mathbb {R})[S]$
is closed under countable unions. It is clearly closed under complements and
$\Game _{\omega ^{\alpha }}$
.
For the converse, we need to verify that every set of reals in
$L_{\omega _1}(\mathbb {R})[S]$
belongs to
$\sigma (\Game _{\omega ^{\alpha }})$
. For this, it suffices to show that for each
$\xi <\omega _1$
, there is a prewellordering
$\preceq _{\xi }$
of a subset of
$\mathbb {R}$
, with
$\preceq _{\xi }$
in
$\sigma (\Game _{\omega ^{\alpha }})$
, such that if
$\equiv _{\xi }$
denotes the induced equivalence relation and
$$ \begin{align*} x\prec_{\xi} y \leftrightarrow x\preceq_{\xi} y\wedge y \not\preceq_{\xi} x \end{align*} $$
denotes the strict part of
$\preceq _{\xi }$
, then
$$ \begin{align*} (\text{field}(\preceq_{\xi}),\prec_{\xi}, \equiv_{\xi})/{\equiv_{\xi}}\ \cong\ (L_{\xi}(\mathbb{R})[S], \in, =). \end{align*} $$
This is easily done by induction: for the successor case, suppose
$\preceq _{\xi }$
has been defined and let
$i_{\xi }:\text {field}(\preceq _{\xi })\to L_{\xi }(\mathbb {R})[S]$
be the isomorphism. Suppose moreover that
$i_{\xi }^{-1}[S\cap L_{\xi }(\mathbb {R})[S]]$
is in
$\sigma (\Game _{\omega ^{\alpha }})$
. We first define the prewellordering
$\preceq _{\xi +1}^*$
as an extension of
$$ \begin{align*} \big\{\big((\xi, x), (\xi, y)\big) : (x,y) \in\ \preceq_{\xi}\!\!\big\} \end{align*} $$
by setting
$(\xi ,x) \preceq _{\xi +1}^* (\xi +1,y)$
if, and only if, the following hold:Footnote
3
-
1. y is a tuple of the form
$(\phi , \vec b)$
, where
$\vec b = b_1,\ldots , b_n$
is a finite collection of reals in field
$(\preceq _{\xi })$
and
$\phi $
is a formula of arity n in the language of set theory extended with a predicate symbol
$\dot S$
; -
2. The structure
$(\text {field}(\preceq _{\xi }), \prec _{\xi })$
satisfies the formula
$\phi (x, b_1,\ldots , b_n)$
if equality is interpreted as
$\preceq _{\xi }$
-equivalence and
$\dot S$
is interpreted as
$i^{-1}_{\xi }[S \cap L_{\xi }(\mathbb {R})[S]]$
.
Then,
$\preceq _{\xi +1}$
is defined to be the extensional closure of
$\preceq _{\xi +1}^*$
, i.e., writing
$x \sim y$
if x and y have exactly the same
$\prec _{\xi +1}^*$
-predecessors, one also sets
$x\preceq _{\xi +1} y$
if
$x \sim y$
or there are
$u,v$
such that
$u\sim x$
,
$v\sim y$
, and
$u \preceq _{\xi +1}^* v$
. It is not hard to verify that this prewellordering is as required. Moreover, if one writes
$$ \begin{align*} i_{\xi+1}:\text{field}(\preceq_{\xi+1})\to L_{\xi+1}(\mathbb{R})[S] \end{align*} $$
for the isomorphism, the set
$i_{\xi +1}^{-1}[S\cap L_{\xi +1}(\mathbb {R})[S]]$
is definable from
$\preceq _{\xi +1}$
using the quantifier
$\Game _{\omega ^{\alpha }}$
and thus belongs to
$\sigma (\Game _{\omega ^{\alpha }})$
.
It remains to verify the equality between (3) and (4). We shall only prove that
$$ \begin{align*} \Game^{\mathbb{R}}_{\omega^{-1 + \alpha +1}}\boldsymbol\Delta^0_1 \subset \mathcal{P}(\mathbb{R}) \cap L_{\omega_1}(\mathbb{R})[S]. \end{align*} $$
The converse can be proved by an argument very similar to the one in [Reference Aguilera, Müller and Schlicht3, Section 3], using the equivalence of (2) and (3).
The proof is much like that of Lemma 3.1. We repeat it with the necessary changes. For notational simplicity, let us assume that
$\alpha $
is infinite, so that
$-1 + \alpha = \alpha $
. Let
$A\subset \mathbb {R}\times \mathbb {R}$
be clopen. For each
$x\in \mathbb {R}$
, there is a game of length
$\omega ^{ \alpha + 1}$
with moves in
$\mathbb {R}$
given by
$A_x$
. We need to show that
$\Game _{\omega ^{\alpha + 1}}^{\mathbb {R}} A \in L_{\omega _1}(\mathbb {R})[S]$
. Again, assuming some suitable coding of sequences of reals by reals, we define for every
$x\in \mathbb {R}$
:
$$ \begin{align*} T_x \kern1pt{=}\kern1pt \bigcup_{n \kern1pt{\in}\kern1pt \mathbb{N}} \big\{t \kern1pt{\in}\kern1pt \mathbb{R}^{\omega^{\alpha}\cdot n}: \exists y\in\mathbb{R}^{\omega^{\alpha+1}}\exists z\kern1pt{\in}\kern1pt\mathbb{R}^{\omega^{\alpha+1}}\! \big(t\kern1pt{\sqsubset}\kern1pt y\kern1pt{\wedge}\kern1pt t\kern1pt{\sqsubset}\kern1pt z \wedge (x,y)\in A \kern1pt{\wedge}\kern1pt (x,z) \kern1pt{\not \in}\kern1pt A\big)\!\big\}. \end{align*} $$
Define a binary relation on
$\mathbb {R}^2$
by
$$ \begin{align*} (x,y) \prec (w,z) \text{ if, and only if, } y \in \bigcup_{n\in\mathbb{N} }\mathbb{R}^{\omega^{\alpha}\cdot n} \wedge x = w \wedge z \in T_w \wedge z \sqsubset y. \end{align*} $$
As before, the fact that A is clopen implies that
$\prec $
is wellfounded, so it has a rank function,
$\rho $
, which is bounded by some
$\eta <\omega _1$
, by the analyticity of
$\prec $
. Define the relation
$\prec _x$
and its rank function
$\rho _x$
as before and set
$$ \begin{align*} W_0(x) &= \bigcup_{n\in\mathbb{N} } \big\{a\in\mathbb{R}^{\omega^{\alpha}\cdot n}: \Game^{\mathbb{R}}_{\omega^{\alpha}}\vec y\, \big(a^{\frown} \vec y \not\in T_x\, \wedge \\ & \qquad\qquad \exists w\in\mathbb{R}^{\omega^{\alpha+1}}\, \big(a^{\frown} \vec y \sqsubset w \wedge (x,w) \in A\big)\big) \big\};\\ W_{\alpha}(x) &= \bigcup_{n\in\mathbb{N} } \Bigg\{a\in\mathbb{R}^{\omega^{\alpha}\cdot n}: \Game^{\mathbb{R}}_{\omega^{\alpha}}\vec y\, \big(a^{\frown} \vec y \in \bigcup_{\xi<\alpha}W_{\xi}(x)\big) \Bigg\};\\ W_{\infty}(x) &= \bigcup_{\alpha\in{\mathsf{Ord}}}W_{\alpha}(x).\end{align*} $$
An inductive argument like the one in Lemma 3.1 shows that for each
$x\in \mathbb {R}$
and each partial play a, the least
$\xi $
such that
$y\in W_{\xi }(x)$
, if it exists, is at most
$\rho _x(a)$
: as before, denote the least such
$\xi $
by
$w_x(a)$
and call it the weight of a. Inductively, suppose that
$w_x(a)$
is defined and for all b weight smaller than a we have
$w_x(b) \leq \rho _x(b)$
. Since
$w_x(a) = \xi $
is defined, we have
$$ \begin{align} \Game^{\mathbb{R}}_{\omega^{\alpha}}\vec y\, \Bigg(a^{\frown} \vec y \in \bigcup_{\xi<\alpha}W_{\xi}(x)\Bigg)\end{align} $$
as witnessed by a winning strategy
$\Sigma $
for a game of length
$\omega ^{\alpha }$
on
$\mathbb {R}$
. Moreover, by the minimality of
$w_x(a)$
,
$\Sigma $
is necessarily such that as one considers all
$\vec y$
consistent with
$\Sigma $
as in (2), the weight of
$a^{\frown } \vec y$
is arbitrarily large below
$w_x(a)$
, i.e.,
$$ \begin{align*} w_x(a) = \sup\big\{w_x(a^{\frown} \vec y) + 1 : \vec y \in \mathbb{R}^{\omega^{\alpha}} \text{ and } \vec y = \Sigma(\vec b) \text{ for some } \vec b\big\}. \end{align*} $$
Without loss of generality we may assume
$\xi \neq 0$
, so that
$a \in T_x$
. Then, we have
$$ \begin{align*} w_x(a) &= \sup\big\{w_x(a^{\frown} \vec y) + 1 : \vec y \in \mathbb{R}^{\omega^{\alpha}} \text{ and } \vec y = \Sigma(\vec b) \text{ for some } \vec b \big\}\\ &\leq \sup\big\{\rho_x(a^{\frown} \vec y) + 1 : \vec y \in \mathbb{R}^{\omega^{\alpha}} \text{ and } \vec y = \Sigma(\vec b) \text{ for some } \vec b\big\}\\ &\leq\sup\big\{\rho_x(a^{\frown} \vec y) + 1 : a^{\frown} \vec y \prec_x a\big\}\\ &= \rho_x(a), \end{align*} $$
where the inequality going from the second line to the third follows from the fact that
$a \not \in T_x$
. This implies that
$$ \begin{align*} W_{\infty}(x) = W_{\eta}(x), \end{align*} $$
for every
$x\in \mathbb {R}$
.
It is easy to see that for every partial play a with length
$\omega ^{\alpha }\cdot n$
, for some
$n\in \mathbb {N}$
, Player I has a winning strategy from a in
$A_x$
if
$a\in W_{\infty }(x)$
. Conversely, if
$a\not \in W_{\infty }(x)$
, then Player I cannot have a winning strategy from a, for such a strategy would guarantee that every sufficiently long partial play consistent with it belongs to some
$W_{\alpha }(x)$
and thus that
$a \in W_{\infty }(x)$
(here, we do not conclude that Player II has a winning strategy, but we do not need to). Now, the set
$S_{\eta } = S\cap L_{\eta }(\mathbb {R})[S]$
belongs to
$L_{\omega _1}(\mathbb {R})[S]$
. Using
$S_{\eta }$
as a parameter, the construction of
$W_{\eta }(x)$
can be carried out within
$L_{\omega _1}(\mathbb {R})[S]$
, uniformly in x, whereby
$\Game _{\omega ^{\alpha +1}}^{\mathbb {R}}A$
belongs to
$L_{\omega _1}(\mathbb {R})[S]$
, as desired. ⊣
In the proof of Lemma 4.3 and below throughout, we use diagrams of the form
$$ \begin{align*} \begin{array}{c|ccccc} I & x_0 & & x_1 & &\ldots (<\omega^{\alpha})\\ II & & y_0 & & y_1 & \ldots(<\omega^{\alpha}) \end{array} \end{align*} $$
to describe games as before. The notation “
$(<\omega ^{\alpha })$
” indicates that the game is to last
$\omega ^{\alpha }$
-many turns.
Lemma 4.3. Let
$2\leq \alpha <\omega _1$
. Suppose that all games of length
$\omega ^{-1+\alpha }$
on
$\mathbb {R}$
with payoff in
$\sigma (\Game ^{\mathbb {R}}_{\omega ^{-1+\alpha }})$
are determined. Then, clopen games of length
$\omega ^{-1 +\alpha + 1}$
on
$\mathbb {R}$
are determined.
Proof Let A be a clopen game of length
$\omega ^{-1 +\alpha +1}$
on
$\mathbb {R}$
(so A is clopen when viewed as a set of reals). For every partial play p of A, let
$A_p$
denote the game A after p has been played. This is also a clopen game of length
$\omega ^{-1 +\alpha +1}$
on
$\mathbb {R}$
.
We consider the following game, which we denote by G:
$$ \begin{align*} \begin{array}{c|ccccc} I & x_0 & & x_1 & &\ldots (<\omega^{-1+\alpha})\\ II & & y_0 & & y_1 & \ldots(<\omega^{-1+\alpha}) \end{array} \end{align*} $$
At the end of the game, a sequence
$$ \begin{align*} p = (x_0, y_0, x_1, \ldots) \in \mathbb{R}^{\omega^{-1+\alpha}} \end{align*} $$
has been produced. Player I wins if she has a winning strategy in
$A_p$
. If Player I has a winning strategy in G, then she clearly has one in A.
Suppose Player I does not have a winning strategy in G. We describe a winning strategy for Player II in A. Note that G is a game of length
$\omega ^{-1 + \alpha }$
on
$\mathbb {R}$
with payoff in
$\Game ^{\mathbb {R}}_{\omega ^{-1 + \alpha + 1}}\boldsymbol \Delta ^0_1 = \sigma (\Game ^{\mathbb {R}}_{\omega ^{-1 + \alpha }})$
, so G is determined. Thus, Player II has a winning strategy in G, say
$\Sigma $
. Any play consistent with
$\Sigma $
produces an infinite sequence
$p_0$
such that Player I does not have a winning strategy in
$A_{p_0}$
.
Let
$p_0$
be any sequence produced this way. Consider the following game,
$G(p_0)$
:
$$ \begin{align} \begin{array}{c|ccccc} I & x_0 & & x_1 & &\ldots(<\omega^{-1+\alpha})\\ II & & y_0 & & y_1 & \ldots(<\omega^{-1+\alpha}) \end{array} \end{align} $$
At the end of the game, a sequence
$$ \begin{align*} p = (x_0, y_0, x_1, \ldots) \in \mathbb{R}^{\omega^{-1+\alpha}} \end{align*} $$
has been produced. Player I wins if she has a winning strategy in
$A_{p_0^{\frown } p}$
. Player I cannot have a winning strategy in this game, for it would yield a winning strategy in
$A_{p_0}$
. As before, this game belongs to
$\sigma (\Game ^{\mathbb {R}}_{\omega ^{-1 + \alpha }})$
and is thus determined. It follows that there is a winning strategy
$\Sigma (p_0)$
such that any play
$p_1$
consistent with it has the property that Player I does not have a winning strategy in
$A_{p_0^{\frown } p_1}$
.
The game A is clopen, so any full play won by Player I is won at a bounded stage. It follows that by repeating the above procedure one obtains a winning strategy for Player II in A.⊣
If
$\alpha $
is an infinite ordinal, then determinacy for games of length
$\omega ^{\alpha }$
on
$\mathbb {N}$
with payoff in
$\sigma (\Game ^{\mathbb {R}}_{\omega ^{\alpha }})$
implies determinacy for games of length
$\omega ^{\alpha }$
on
$\mathbb {R}$
with payoff in
$\sigma (\Game ^{\mathbb {R}}_{\omega ^{\alpha }})$
(this is simply because
$\omega ^{\alpha } = \omega \cdot \omega ^{\alpha }$
for infinite
$\alpha $
), and so the theorem follows from the preceding lemma. Oddly, if
$\alpha $
is finite, the proof requires an additional argument:
Lemma 4.4. Let
$2 \leq n < \omega $
. Suppose that games of length
$\omega ^{n}$
on
$\mathbb {N}$
with payoff in
$\sigma (\Game ^{\mathbb {R}}_{\omega ^{n - 1}})$
are determined. Then, clopen games of length
$\omega ^{n+1}$
are determined.
Proof Let us assume
$n = 2$
for simplicity, so we assume that games of length
$\omega ^2$
on
$\mathbb {N}$
with payoff in
$\sigma (\Game ^{\mathbb {R}})$
are determined and show that clopen games of length
$\omega ^3$
are determined. In this proof, unlike before, it will be convenient to maintain the distinction between games and their payoff sets.
Let A be a clopen set and let
$G(A)$
be the clopen game of length
$\omega ^3$
on A. We want to show that
$G(A)$
is determined. Let G be the following game on
$\mathbb {R}$
:
$$ \begin{align*} \begin{array}{c|ccccc} I & \sigma_0 & & \sigma_1 & &\ldots (<\omega^2)\\ II & & \tau_0 & & \tau_1 & \ldots (<\omega^2) \end{array} \end{align*} $$
Player I wins if, and only if,
$$ \begin{align*} (\sigma_0*\tau_0, \sigma_1*\tau_1,\ldots) \in A. \end{align*} $$
This is a clopen game on
$\mathbb {R}$
of length
$\omega ^2$
. Clearly, if I wins G, then I wins
$G(A)$
. By hypothesis, games of length
$\omega $
on
$\mathbb {R}$
with payoff in
$\sigma (\Game ^{\mathbb {R}})$
are determined, so Lemma 4.3 applies, i.e., clopen games of length
$\omega ^2$
on
$\mathbb {R}$
are determined. Hence, if Player I does not win G, then Player II does. If so, we need to construct a strategy for Player II in
$G(A)$
. As usual, it will be given by blocks, this time of length
$\omega ^2$
each. Given
$p \in \mathbb {R}^{\mathbb {N}}$
or
$p \in \mathbb {N}^{\omega ^2}$
, we define the game
$G(p)$
of length
$\omega ^2$
with moves in
$\mathbb {R}$
by
$$ \begin{align*} \begin{array}{c|ccccc} I & \sigma_0 & & \sigma_1 & &\ldots (<\omega^2)\\ II & & \tau_0 & & \tau_1 & \ldots (<\omega^2) \end{array} \end{align*} $$
Player I wins if, and only if,
$$ \begin{align*} (p,\sigma_0*\tau_0, \sigma_1*\tau_1,\ldots) \in A. \end{align*} $$
Let
$W = \{p:$
Player I has a winning strategy in
$G(p)\}$
. Since
$G(p)$
is a clopen game on
$\mathbb {R}$
of length
$\omega ^2$
for each p (uniformly), W is a set in
$\Game ^{\mathbb {R}}_{\omega ^2}\boldsymbol \Delta ^0_1$
. Let H be the game on
$\mathbb {R}$
of length
$\omega $
given by:
$$ \begin{align*} \begin{array}{c|ccccc} I & \sigma_0 & & \sigma_1 & &\ldots (<\omega)\\ II & & \tau_0 & & \tau_1 & \ldots (<\omega) \end{array} \end{align*} $$
Player I wins if, and only if,
$$ \begin{align*} (\sigma_0*\tau_0, \sigma_1*\tau_1,\ldots) \in W. \end{align*} $$
Note that Player I cannot have a winning strategy in H, since it would easily yield a winning strategy for G. Let
$H'$
be the game of length
$\omega ^2$
with moves in
$\mathbb {N}$
and payoff W. Player I cannot have a winning strategy in
$H'$
, for it would induce a winning strategy in H. Since
$H'$
is a game of length
$\omega ^2$
with moves in
$\mathbb {N}$
and payoff in
$\Game ^{\mathbb {R}}_{\omega ^2}\boldsymbol \Delta ^0_1$
, it is determined, so Player II has a winning strategy in
$H'$
. This strategy may act as a non-losing strategy for Player II to use throughout the first
$\omega ^2$
-many moves of
$G(A)$
. An argument as before completes the proof. ⊣
This completes the proof of Theorem 4.1. The analogue for limit ordinals is:
Theorem 4.5. Let
$\lambda $
be a countable limit ordinal. The following are equivalent
$:$
-
1. Determinacy for clopen games of length
$\omega ^{\lambda }$
. -
2. Determinacy for games of length
$\omega ^{\beta }$
with payoff in
$\sigma (\{\Game ^{\mathbb {R}}_{\omega ^{\iota }}\}_{\iota <\lambda })$
for all
$\beta <\lambda $
.
Theorem 4.5 is proved much like Theorem 4.1. The key observation is that, if
$\{\lambda _i:i\in \mathbb {N}\}$
is a sequence cofinal in
$\lambda $
, then games of length
$\omega ^{\lambda }$
can be decomposed into
$\omega $
-many blocks the ith of which has length
$\omega ^{\lambda _i}$
. We note that, in the process of proving Theorem 4.5, one shows the following analogue of Lemma 4.2, where
$S_{\lambda } = \{(\alpha , B,i): \alpha <\lambda $
and either Player I has a winning strategy in the game of length
$\omega ^{\alpha }$
on
$\mathbb {R}$
with payoff B and
$i = 1$
, or else Player I does not have a winning strategy in the game of length
$\omega ^{\alpha }$
on
$\mathbb {R}$
with payoff B and
$i = 0\}$
.
Lemma 4.6. Let
$\lambda $
be a countable limit ordinal. The following pointclasses all coincide
$:$
-
1.
$\sigma (\{\Game ^{\mathbb {R}}_{\omega ^{\iota }}\}_{\iota <\lambda })$
, -
2.
$\sigma (\{\Game _{\omega ^{\iota }}\}_{\iota <\lambda })$
, -
3.
$\mathcal {P}(\mathbb {R})\cap L_{\omega _1}(\mathbb {R})[S_{\lambda }]$
, -
4.
$\Game ^{\mathbb {R}}_{\omega ^{\lambda }}\boldsymbol \Delta ^0_1$
.
5 Shortening games of decomposable length
The proof from the last section (as well as the argument from [Reference Aguilera, Müller and Schlicht3]) adapts to shorten games of any countable length. For games of length
$\theta +1$
and
$\theta +\omega $
, this was mentioned already. Meanwhile, for games of other forms, we obtain the following analogues of Theorems 1.1, 4.1, and 4.1:
Theorem 5.1. Let
$\omega \leq \theta <\omega _1$
. The following are equivalent
$:$
-
1. Determinacy for clopen games of length
$\theta + \omega ^{2}$
. -
2. Determinacy for
$\sigma $
-projective games of length
$\theta $
.
Theorem 5.2. Let
$2\leq \alpha <\omega _1$
and
$\theta <\omega _1$
. The following are equivalent
$:$
-
1. Determinacy for clopen games of length
$\theta + \omega ^{\alpha +1}$
. -
2. Determinacy for games of length
$\max \{\theta ,\omega ^{\alpha }\}$
with payoff in
$\sigma (\Game ^{\mathbb {R}}_{\omega ^{-1 + \alpha }})$
.
Theorem 5.3. Let
$\lambda $
be a countable limit ordinal and
$\theta <\omega _1$
. The following are equivalent
$:$
-
1. Determinacy for clopen games of length
$\theta + \omega ^{\lambda }$
. -
2. Determinacy for games of length
$\gamma $
with payoff in
$\sigma (\{\Game ^{\mathbb {R}}_{\omega ^{\iota }}\}_{\iota <\lambda })$
for every
$\gamma \in \lambda \cup \{\theta \}$
.
The proofs of these theorems are very similar to the ones presented so far. They use (the statements of) Lemmata 3.1, 4.2, and 4.6, as well as the proofs of Theorem 1.1 and Lemmata 4.3 and 4.4. The key observation is that games of length
$\theta + \omega ^{\alpha }$
can be divided into
$\omega $
-many rounds, the first of which has length
$\theta $
and the rest of which have lengths that add up to
$\omega ^{\alpha }$
.
6 Open questions
Let us finish by mentioning some open problems that relate to the topic of this article. The main motivating question for this work is the following:
Question 6.1. Let
$\alpha $
be a countable ordinal. What is the consistency strength of determinacy for clopen games of length
$\alpha $
?
The answer is known in many cases, but not nearly all. An upper bound for ordinals of the form
$\omega ^2\cdot \beta $
(which is likely optimal) can be found in [Reference Aguilera2]. The proof relies on the results of this article. A particularly interesting case is the following:
Question 6.2. What is the consistency strength of clopen determinacy for games of length
$\omega \cdot 2+2$
?
Recall that clopen determinacy for games of length
$\omega \cdot 2+1$
is simply
$\boldsymbol \Pi ^1_1$
-determinacy (Proposition 2.2). It follows from work of Welch [Reference Welch12] that clopen determinacy for games of length
$\omega \cdot 2+2$
implies the existence of inner models with strong cardinals.
Acknowledgements
The problem giving rise to this article was motivated by earlier joint work with S. Müller and P. Schlicht. I would like to thank them for very fruitful conversations. This work was partially supported by a FWF grant I-4513 and FWO grant 3E017319.
