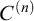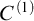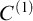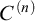1 Introduction
Reflection principles are one of the most important and ubiquitous phenomena in mathematics. Broadly speaking, one can formulate reflection principles by means of the slogan “If a structure enjoys some property, there is a small substructure satisfying the same property”. In practice small substructure is modulated by some given regular cardinal.
The dual version of reflection principles are the so called Compactness Principles. The way of defining a compactness principle is by means of the slogan “If every small substructure of a given structure enjoys some property then the structure satisfies the property, as well”. One can easily reformulate a reflection principle as a compactness and viceversa. Thus, the choice in the formulation of a given problem will depend on which of them is more illustrative. Mathematical Logic, and specially Set Theory, is one of the fields where many central questions are formulated in terms of reflection principles and consequently, its study becomes of special interest. Among many other examples, we can highlight the investigations on stationary reflection or the study of the tree property at regular cardinals.
From a platonistic conception, Set Theory is the field devoted to reveal the truths of the universe of sets. Long time ago Lévy and Montague proved the Reflection theorem (see e.g. [Reference Kunen13]) discovering that reflection is an intrinsic feature of the model-theoretic architecture of the universe of sets, V. More precisely, for each
$n\in \omega $
, they proved that the class of ordinals
$\alpha \in C^{(n)}$
such that
$V_{\alpha }\prec _n V$
is a proper club class. Short time after, Lévy noticed that the Reflection theorem is equivalent to Infinity plus Replacement, modulo the remaining
$\mathrm {ZF}$
axioms. This accentuates, even more, the belief that reflection is one of the cornerstones of Set Theory.
The model-theoretic machinery of elementary embeddings has been the responsible of reflection principles to become more and more sophisticated. Many of the well-known large cardinals notions are formulated as critical points of elementary embeddings
$j:V\rightarrow M$
between the universe and some transitive substructure
$M\subseteq V$
. The degree of agreement between these two structures depends on the specific properties of j.
The purpose of the present paper is to contribute to the investigation of the identity crises phenomenon in the section of the large cardinal hierarchy ranging between the first supercompact cardinal and Vopenka’s Principle (
$\mathrm {VP}$
on the sequel). These cardinals are known as
$C^{(n)}$
-cardinals and were introduced by Bagaria in [Reference Bagaria3] aiming for a sharp study of the strongest forms of reflection. Morally these families of large cardinal principles provide natural milestones on the road towards the ultimate reflection principle. For convenience hereafter we shall denote by
$\mathfrak{M},\ \mathfrak{K},\ \mathfrak{S}$
,
$\mathfrak{S}_{\omega_1}$
Footnote
1
and
$\mathfrak {E}$
the classes of measurable, strongly compact,
$\omega _1$
-strongly compact, supercompact and extendible cardinals, respectively. Similarly,
$\mathfrak {S}^{(n)}$
and
$\mathfrak {E}^{(n)}$
will stand for the families of
$C^{(n)}$
-supercompact and
$C^{(n)}$
-extendible cardinals, respectively. Any undefined notion may be consulted in Tsaprounis excellent Ph.D. dissertation [Reference Tsaprounis17].
Several studies on the topic of
$C^{(n)}$
-cardinals have been carried out succesfully by Bagaria and Tsaprounis whose investigations cover a broad spectrum embracing from the interplay of
$C^{(n)}$
-cardinals with forcing to applications to Category theory and Resurrection Axioms (see [Reference Bagaria3], [Reference Bagaria, Casacuberta, Mathias and Rosickỳ4], [Reference Tsaprounis19], [Reference Tsaprounis21], [Reference Tsaprounis18], [Reference Tsaprounis20]). Nonetheless, there is a natural notion in the setting of
$C^{(n)}$
-cardinals which remains elusive and mysterious:
$C^{(n)}$
-supercompactness.
Definition 1.1 (
$C^{(n)}$
-supercompactness [Reference Bagaria3])
A cardinal
$\kappa $
is
$\lambda $
-
$C^{(n)}$
-supercompact for some
$\lambda>\kappa $
, if there is an elementary embedding
$j: V\rightarrow M$
such that
$\mathrm {crit}(j)=\kappa $
,
$j(\kappa )>\lambda $
,
$M^{\lambda }\subseteq M$
and
$j(\kappa )\in C^{(n)}$
. A cardinal
$\kappa $
is
$C^{(n)}$
-supercompact if it is
$\lambda $
-
$C^{(n)}$
-supercompact, for each
$\lambda>\kappa $
.
Our purpose along the paper will answer the next three questions posed by Bagaria and Tsaprounis.
Question 1. Are the notions of supercompactness and
$C^{(1)}$
-supercompactness equivalent? More generally, given
$n\geq 1$
, is it true that the first supercompact is the same as the first
$C^{(n)}$
-supercompact?
Question 2. Do the classes of
$C^{(n)}$
-supercompact cardinals form a strictly increasing hierarchy?
Question 3. Let
$n\geq 1$
. Is it the first
$C^{(n)}$
-supercompact cardinal the first
$C^{(n)}$
-extendible?
Our contribution to settle the aforementioned questions can be summarized by the following two results:
Theorem 1.2. (Main Theorem 1)
Assume
$\mathrm {GCH}$
holds and let
$\kappa $
be a supercompact cardinal. Then there is a generic extension
$V^{\mathbb {P}}$
where
$\kappa $
is still supercompact but not
$C^{(1)}$
-supercompact. In fact there is no elementary embedding in
$V^{\mathbb {P}}$
,
$j:V^{\mathbb {P}}\rightarrow M$
, such that
$\mathrm {crit}(j)=\kappa $
,
$M^{\omega }\subseteq M$
and
$j(\kappa )$
being a limit cardinal.
Theorem 1.3. (Main Theorem 2)
Let
$n\geq 1$
,
$\kappa $
be a
$C^{(n)}$
-supercompact cardinal and
$\ell :\kappa \rightarrow \kappa $
be a
$\mathfrak {S}^{(n)}$
-fast function on
$\kappa $
. Then in the generic extension
$V^{\mathbb {M}}$
given by a Magidor product of Prikry forcings
$\kappa $
remains
$C^{(n)}$
-supercompact and in fact it is the first (
$\omega _1$
-) strongly compact. In particular, the following holds in
$V^{\mathbb {M}}$
:
$$ \begin{align*}\min\mathfrak{M}<\min\mathfrak{K}_{\omega_1}=\min \mathfrak{K}=\min \mathfrak{S}=\min \mathfrak{S}^{(n)}<\min\mathfrak{E}.\end{align*} $$
Both Theorem 1.2 and Theorem 1.3 settle in a negative way the former questions. Furthermore building on these ideas we shall show how to prove the following strengthenings:
Theorem 1.4. Assume
$\mathrm {GCH}\,$
holds and that there are two supercompact cardinals with a
$C^{(1)}$
-supercompact cardinal above them. Then there is a generic extension of the universe where the following holds:
$$ \begin{align*}\min\mathfrak{M}<\min\mathfrak{K}<\min\mathfrak{S}<\min\mathfrak{S}^{(1)}.\end{align*} $$
Theorem 1.5. (The ultimate identity crises)
Let
$\langle V,\in ,\kappa \rangle $
be a model of (large enough fragment of)
$\mathrm {ZFC}^{\star }$
plus
$C^{(<\omega )}-\mathrm {EXT}$
. Then in the generic extension
$V^{\mathbb {M}}$
it is true that
$$ \begin{align*}\min\mathfrak{M}<\min\mathfrak{K}_{\omega_1}=\min\mathfrak{K}=\min\mathfrak{S}=\min \mathfrak{S}^{(<\omega)}<\min\mathfrak{E}.\end{align*} $$
The notions
$C^{(<\omega )}-\mathrm {EXT}$
and
$\mathfrak {S}^{(<\omega )}$
will be introduced at the end of §3.
The structure of the paper is as follows. §2 will be devoted to the proofs of Theorems 1.2 and 1.4 while §3 will be focused on the proofs of Theorems 1.3 and 1.4. We shall end the paper with §4 and §5 where we respectively describe what is known up to the moment about
$C^{(n)}$
-supercompact cardinals and what are the possibles futures for the research of this topic. All the notions and notations are quite standard and can be easily found either in general manuals or in the bibliography quoted below.
2 The first
$C^{(1)}$
-supercompact can be greater than the first supercompact
The present section is devoted to the proof of Theorems 1.2 and 1.4. In particular, both results answer negatively Question 1. Before beginning with the details let us give a taste of the ideas involved in the proof of these results.
A classical theorem of Solovay asserts that if a cardinal
$\kappa $
is strongly compact then
$\square _{\lambda }$
fails, all
$\lambda \geq \kappa $
[Reference Solovay16]. More generally if
$\kappa $
is a supercompact cardinal then
$\square _{\lambda ,\mathrm {cf}(\lambda )}$
fails, for
$\mathrm {cf}(\lambda )<\kappa <\lambda $
(see Proposition 2.12). Therefore it is then natural to ask how much square can hold below a supercompact cardinal. Working in this direction Apter proved in [Reference Apter1] the consistency of a supercompact cardinal with the existence of
$\square _{\lambda }$
-sequences for each cardinal
$\lambda $
in a certain stationary subset of
$\kappa $
. On this respect it is worth to emphasize that this result is close to be optimal since there is no club
$C\subseteq \kappa $
where
$\square _{\lambda }$
holds, for each
$\lambda \in C$
. Indeed, let us assume aiming for a contradiction that
$\kappa $
is supercompact and
$C\subseteq \kappa $
is a club with the above property. Let U be the standard normal measure derived by some elementary embedding with critical point
$\kappa $
and M be the corresponding ultrapower. By normality of the measure
$C\in U$
, hence
$\square _{\kappa }$
holds in M, and furthermore it is not hard to show that
$(\kappa ^+)^M=\kappa ^+$
. Altogether one has that
$\square _{\kappa }$
holds, yielding a contradiction with the supercompactness of
$\kappa $
.
Broadly speaking, the main point to kill the
$C^{(1)}$
-supercompactness of a supercompact cardinal
$\kappa $
is to construct a generic extension where any elementary embedding witnessing the
$C^{(1)}$
-supercompactness of
$\kappa $
would yield to the existence of a
$\square _{\lambda }$
-sequence above
$\kappa $
. To implement this idea one needs to force many square sequences below
$\kappa $
and afterwards argue that this is upwards reflected by any
$C^{(1)}$
-supercompact embedding with critical point
$\kappa $
. This is interesting since it points out that despite the existence of many squares sequences is not an inconvenience for supercompactness it is for
$C^{(1)}$
-supercompactness.
Our forcing construction will be an Easton support iteration guided by some Laver function on
$\kappa $
of the canonical forcings for adding square sequences. Once one proves that this forcing is harmless with respect to the supercompactness of
$\kappa $
it is not hard to prove that there are no witnesses for
$C^{(1)}$
-supercompactness in the generic extension. In particular Theorem 1.2 yields to the next result of consistency:
Corollary 2.1.
$\mathrm {Con}(\mathrm {ZFC}\,+\mathrm {GCH}\,+\exists \kappa ,\lambda \,(\kappa ,\lambda \in \mathfrak {S}^{(1)}))$
implies
$\mathrm {Con}(\mathrm {ZFC}\,+\mathrm {GCH}\,+\min \mathfrak {S}<\min \mathfrak {S}^{(1)})$
.
Working on the ideas needed for the proof of Theorem 1.2 we will show in §2.2 how to use them to prove Theorem 1.4. As before, this result will automatically yield the following consistency result:
Corollary 2.2.
$\mathrm {Con}(\mathrm {ZFC}\,+\mathrm {GCH}\,+\exists \kappa ,\lambda \in \mathfrak {S}\,\exists \mu \in \mathfrak {S}^{(1)}(\lambda <\kappa <\mu ))$
implies
$\mathrm {Con}(\mathrm {ZFC}\, + \min \mathfrak {M}<\min \mathfrak {K}<\min \mathfrak {S}<\min \mathfrak {S}^{(1)})$
.
2.1 The proof of Theorem 1.2
Let us start recalling some basic notions that are necessary for the proof of Theorem 1.2.
Definition 2.3. (
$\square $
-sequences)
Let
$\mu \leq \kappa $
be two cardinals. A
$\square _{\kappa ,\mu }$
-sequence is a sequence of sets
$\vec {\mathcal {C}}=\langle \mathcal {C}_{\alpha }:\,\alpha \in \mathrm {Lim}\cap \kappa ^+\rangle $
Footnote
2
such that the following properties hold:
-
(a) For each
$\alpha \in \mathrm {Lim}\cap \kappa ^+$
the set
$\mathcal {C}_{\alpha }$
is a family of club sets on
$\alpha $
with
$1\leq |\mathcal {C}_{\alpha }|\leq \mu $
. -
(b) For each
$\alpha \in \mathrm {Lim}\cap \kappa ^+$
with
$\mathrm {cf}(\alpha )<\kappa $
the family
$\mathcal {C}_{\alpha }$
only contains sets C with
$\mathrm {otp}(C)<\kappa $
. -
(c) For each
$\alpha \in \mathrm {Lim}\cap \kappa ^+$
, the family
$\langle \mathcal {C}_{\beta }:\,\beta \in \mathrm {Lim}\cap \alpha \rangle $
is coherently disposed; namely,
$$ \begin{align*}\forall C\in\mathcal{C}_{\alpha}\,\forall\beta\in \mathrm{Lim}(C)\, C\cap \beta\in\mathcal{C}_{\beta}.\end{align*} $$
We shall say that
$\square _{\kappa ,\mu }$
holds if there is a
$\square _{\kappa ,\mu }$
-sequence. Similarly, we will say that
$\square _{\kappa , <\mu }$
holds if
$\square _{\kappa ,\theta }$
holds, for each
$\theta <\mu $
. We shall denote by
$\square _{\kappa }$
and by
$\square _{\kappa }^*$
the principles
$\square _{\kappa , 1}$
and
$\square _{\kappa ,\kappa }$
, respectively.
There is a canonical forcing for adding a
$\square _{\lambda ,\mu }$
-sequence by approximations but for the purposes of the current paper it will be enough to present the definition of the forcing for adding a
$\square _{\lambda }$
-sequence.
Definition 2.4. Let
$\lambda $
be an uncountable cardinal. The canonical poset for forcing a
$\square _{\lambda }$
-sequence
$\mathbb {P}_{\square _{\lambda }}$
is the set of conditions p such that
-
(a) p is a function with
$dom(p)=(\alpha +1)\cap Lim$
with
$\alpha \in \lambda ^+\cap Lim$
. -
(b) For every
$\beta \in dom(p)$
,
$p(\beta )\subseteq \beta $
is a club subset with
$otp(p(\beta ))\leq \lambda $
. -
(c) If
$\beta \in dom(p) \forall \gamma \in p(\beta )\cap Lim (p(\gamma )=p(\beta )\cap \gamma )$
.
endowed with the reverse end-extension order.
Standard arguments show that
$\mathbb {P}_{\square _{\lambda }}$
is a
$(\lambda +1)$
-strategically closed forcing (see [Reference Cummings10]) and under
$\mathrm {GCH}$
, since
$|\mathbb {P}_{\square _{\lambda }}|=\lambda ^+$
, it preserves cofinalities and respects the
$\mathrm {GCH}$
pattern.
Many times it is helpful for carrying out lifting arguments that our iteration is defined in a sparse enough set of cardinals. The standard setting for such kind of arguments is described by a forcing iteration
$\mathbb {P}$
, an elementary embedding
$j: V\rightarrow M$
and a factorization of the form
$j(\mathbb {P})\cong \mathbb {P}\ast \dot {\mathbb {Q}}$
. Under these conditions one expects that
$\dot {\mathbb {Q}}$
enjoys of some closure property that helps to find a
$\dot {\mathbb {Q}}$
-generic filter over
$M^{\mathbb {P}}$
. For instance, if
$\mathbb {Q}$
is closed enough in
$M^{\mathbb {P}}$
it is usual to build such a generic filter by means a diagonalization argument.
One of the standard procedures to build such iterations consists in guiding the iteration with a function
$\ell $
presenting some fast behavior. Despite that we will need to consider slightly more general fast functions (see the preliminary discussion of §3), in this part we will only be interested in the case where
$\ell $
is a Laver function. Recall that if
$\kappa $
is a supercompact cardinal a function
$\ell : \kappa \rightarrow V_{\kappa }$
is called a Laver function if for every
$\lambda>\kappa $
there is a
$\lambda $
-supercompact elementary embedding
$j:V\rightarrow M$
with
$j(\ell )(\kappa )>\lambda $
[Reference Laver14].
Without loss of generality we may and do assume that the domain of
$\ell $
is the club set of closure points
$\alpha $
of
$\ell $
(i.e.
$\ell ''\alpha \subseteq V_{\alpha }$
) that are also strong limit cardinals.
Definition 2.5. Let
$\mathbb {P}^{\ell }_{\kappa }$
be the
$\kappa $
-Easton support iterationFootnote
3
where
$\mathbb {P}^{\ell }_0$
is the trivial forcing and for each ordinal
$\alpha <\kappa $
, if
$\alpha \in dom(\ell )\cap E^{\kappa }_{\omega }$
and
$\Vdash _{\mathbb {P}^{\ell }_{\alpha }}\text {``}\check {\alpha }^+\text { is a cardinal''}$
then
$\Vdash _{\mathbb {P}^{\ell }_{\alpha }}\text {``}\mathbb {\dot {Q}}_{\alpha }=\mathbb {P}_{\square _{\alpha }}\text {''}$
and
$\Vdash _{\mathbb {P}^{\ell }_{\alpha }}\text {``}\mathbb {\dot {Q}}_{\alpha }\text { is trivial''}$
, otherwise.
The next proposition shows that
$\mathbb {P}^{\ell }_{\kappa }$
forces a
$\square _{\lambda }$
-sequence for each
$\lambda \in \text {dom}\,(\ell )\cap E^{\kappa }_{\omega }$
and thus
$\square _{\lambda }$
holds in a stationary subset of
$\kappa $
.
Proposition 2.6. Assume
$GCH$
. The iteration
$\mathbb {P}^{\ell }_{\kappa }$
preserves cardinals, the
$\mathrm {GCH}$
pattern and yields a generic extension
$V^{\mathbb {P}^{\ell }_{\kappa }}$
where
$\square _{\lambda }$
holds, for all cardinal
$\lambda \in E^{\kappa }_{\omega }\cap dom(\ell )$
.
Proof. The first claim easily follows from the comments after Definition 2.4 so it is enough to prove the claim about the
$\square _{\lambda }$
-sequences. Let
$\lambda \in dom(\ell )\cap E^{\kappa }_{\omega }$
be a cardinal and notice that
$\mathbb {P}^{\ell }_{\kappa }$
factorizes as
$ \mathbb {P}^{\ell }_{\lambda +1}\ast \dot {\mathbb {P}}^{\ell }_{tail}$
, where
$\dot {\mathbb {P}}^{\ell }_{tail}$
is some
$\mathbb {P}^{\ell }_{\lambda +1}$
-name for a
$\lambda ^+$
-strategically closed iteration. Now notice that
$\mathbb {P}^{\ell }_{\lambda }$
is
$\lambda ^+$
-cc, hence
$\mathbb {P}^{\ell }_{\lambda +1}$
forces
$\square _{\lambda }$
, and
$\mathbb {P}^{\ell }_{tail}$
preserves
$(\lambda ^+)^{V^{\mathbb {P}^{\ell }_{\lambda +1}}}$
so
$\vdash _{\mathbb {P}^{\ell }_{\kappa }}\text {``}\square _{\lambda } \text {holds''}$
. ⊣
Proposition 2.7. Forcing with
$\mathbb {P}^{\ell }_{\kappa }$
preserves the supercompactness of
$\kappa $
. Moreover in
$V^{\mathbb {P}^{\ell }_{\kappa }}$
,
$\kappa $
is the first supercompact.
Proof. The last claim follows immediately from the result of Solovay, [Reference Solovay16]. Working in V, let
$\lambda>\kappa $
,
$\theta =(2^{\lambda ^{<\kappa }})^+$
and
$j:V\rightarrow M$
be some
$\theta $
-supercompact embedding such that
$j(\ell )(\kappa )>\theta $
and
$G\subseteq \mathbb {P}^{\ell }_{\kappa }$
a generic filter over V. First of all, since
$j(\ell )\upharpoonright \kappa =\ell $
, the forcing
$j(\mathbb {P}^{\ell }_{\kappa })$
factorizes as
$$\begin{align*}j(\mathbb{P}^{\ell}_{\kappa})\cong \mathbb{P}^{\ell}_{\kappa}\ast \mathbb{Q}\ast \mathbb{P}_{tail}.\end{align*}$$
where
$\mathbb {Q}$
is forced to be the trivial poset because
$\mathrm {cf}^M(\kappa )>\omega $
. On the other hand,
$\Vdash _{\mathbb {P}^{\ell }_{\kappa }}\text {``} \mathbb {Q}\ast \mathbb {P}_{tail} \text { is } \theta \text {-strategically closed''}$
since
$j(\ell )(\kappa )>\theta $
. For the ease of notation we shall denote by
$\mathbb {P}^*_{tail}$
the iteration
$\mathbb {Q}\ast \mathbb {P}_{tail}$
. The conditions in
$\mathbb {P}^{\ell }_{\kappa }$
have bounded supports in
$\kappa $
, hence
$j\upharpoonright \mathbb {P}^{\ell }_{\kappa }=id$
, so
$j''G\subseteq G\ast H$
, for any
$H\subseteq ({\mathbb {P}^*_{tail}})_G$
generic filter over
$M[G]$
. Set
$j^*:V[G]\rightarrow M[G\ast H]\subseteq V[G\ast H]$
be the corresponding lifting. Since
$\kappa $
is a Mahlo cardinal and
$\mathbb {P}^{\ell }_{\kappa }$
is a
$\kappa $
-Easton support iteration of forcings in
$V_{\kappa }$
the iteration
$\mathbb {P}^{\ell }_{\kappa }$
is
$\kappa $
-cc and thus
$M[G]$
remains closed by
$\theta $
-sequences. Similarly, since
$({\mathbb {P}^*_{tail}})_G$
is
$\theta ^+$
-strategically closed in
$M[G]$
and
$M[G]^{\theta }\subseteq M[G]$
, one may argue that
$M[G\ast H]$
is closed under
$\theta $
-sequences and that
$({\mathbb {P}^*_{tail}})_G$
is also
$\theta $
-strategically closed in the model
$V[G]$
.
Working in the generic extension
$V[G\ast H]$
, it is straightforward to show that
$$ \begin{align*}X\in\mathcal{U}\,\longleftrightarrow\, X\subseteq (\mathcal{P}_{\kappa}(\lambda))^{V[G]}\,\wedge\, j''\lambda\in j(X)\end{align*} $$
defines a
$\lambda $
-supercompact measure over
$\mathcal {P}_{\kappa }(\lambda )^{V[G]}$
. By standard arguments of counting nice names it can be checked that
$\mathcal {U}$
has cardinality less than
$\theta $
. On the other hand,
$({\mathbb {P}^*_{tail}})_G$
is
$\theta ^+$
-strategically closed in
$V[G]$
and thus the measure
$\mathcal {U}$
was not introduced by the forcing
$({\mathbb {P}^*_{tail}})_G$
. Altogether this argument shows that
$\mathcal {U}\in V[G]$
; hence
$\kappa $
is
$\lambda $
-supercompact in
$V[G]$
. Provided that
$\lambda $
was chosen arbitrarily we have already proved that
$\kappa $
remains fully supercompact after forcing with
$\mathbb {P}^{\ell } _{\kappa }$
.⊣
We have all we need to prove Theorem 1.2:
Proof of Theorem 1.2
For the rest of the proof fix
$G\subseteq \mathbb {P}^{\ell }_{\kappa }$
a generic filter over V. Aiming for a contradiction let us assume that there is a supercompact embedding
$j:V[G]\rightarrow M$
with
$\mathrm {crit}(j)=\kappa $
,
$M^{\omega }\subseteq M$
and
$j(\kappa )$
being a limit cardinal. Appealing to the closure properties of M and to the elementarity of j it is not hard to realize that the cardinal
$j(\kappa )$
has uncountable cofinality in
$V[G]$
and that there is a
$\square _{\lambda }$
-sequence in M, for each
$\lambda \in j(\text {dom}\,(\ell )\cap E^{\kappa }_{\omega })$
.
On the other hand, since
$\mathrm {cf}(j(\kappa ))>\omega $
,
$E^{j(\kappa )}_{\omega }$
is a stationary set in
$V[G]$
and thus also the set
$j(E^{\kappa }_{\omega } \cap \text {dom}\,(\ell ))$
. Let
$\lambda \in j(E^{\kappa }_{\omega } \cap \text {dom}\,(\ell ))$
be some ordinal greater than
$\kappa $
and notice that, of course,
$\square _{\lambda }$
holds in M. Nevertheless we shall prove that this is also the case in
$V[G]$
, thus yielding the desired contradiction. Aiming for this, it will be enough with proving that M and
$V[G]$
agree on the computations of the successor of
$\lambda $
: namely,
$\left (\lambda ^+\right )^{V[G]}=\left (\lambda ^+\right )^M$
. Since GCH holds in
$V[G]$
, hence also in M, and M is closed by
$\omega $
-sequences,
$({{\hspace {-0.0001pt}}}^{\omega }\lambda )^M= {{\hspace {-0.0001pt}}}^{\omega } \lambda $
,
$\lambda ^{+}=\lambda ^{\omega }$
and
$(\lambda ^{+})^M=(\lambda ^{\omega })^M$
. Combining these expressions the equality
$\lambda ^+=(\lambda ^+)^M$
follows. Finally this have proved that
$\square _{\lambda }$
holds in
$V[G]$
contradicting the supercompactness of
$\kappa $
. ⊣
The same argument as before actually proves something stronger: for each cardinal
$\lambda>\kappa $
the notion of
$\lambda $
-
$C^{(1)}$
-supercompactness is incompatible with
$\square _{\theta }$
holding at each
$\theta \in E^{\kappa }_{\leq \lambda }$
.
Proposition 2.8. Assume
$\mathrm {GCH}$
holds. Let
$\kappa $
be a supercompact cardinal,
$\lambda>\kappa $
and assume that for each
$\theta \in E^{\kappa }_{\leq \lambda }$
,
$\square _{\theta }$
-holds. Then there is no elementary embedding
$j:V\rightarrow M$
such that
$\mathrm {crit}(j)=\kappa $
,
$M^{\lambda }\subseteq M$
and
$j(\kappa )$
being a limit cardinal.
Remark 2.9. Another similar proof of Theorem 1.4 using Radin forcing appears in the third author’s Ph.D. dissertation [Reference Poveda15, §3.1.1].
We will finish this section with the proof of Corollary 2.1:
Proof of Corollary 2.1
Let V be a model of
$\mathrm {GCH}\,$
with two
$C^{(1)}$
-supercompact cardinals
$\kappa <\lambda $
. The previous theorem shows that
$V^{\mathbb {P}}$
is a model where
$\kappa $
is no longer
$C^{(1)}$
-supercompact and in fact it is the first supercompact. Since
$\mathbb {P}$
is a small forcing,
$\lambda $
is still
$C^{(1)}$
-supercompact in
$V^{\mathbb {P}}$
and greater than
$\kappa $
. Combining both things we get a model for the theory
$$ \begin{align*}\text{``}\mathrm{ZFC}\,+\mathrm{GCH}\,+\min\mathfrak{S}<\min\mathfrak{S}^{(1)}\text{''}.\end{align*} $$
□
2.2 Proof of Theorem 1.4
The way we have proceed to make the first supercompact cardinal smaller than the first
$C^{(1)}$
-supercompact is very aggressive: namely, we have forced that scenario paying the prize of making the first supercompact to be the first (
$\omega _1$
-)strongly compact. Therefore it is natural to ask whether these three notions may be forced to be different. Recall that
$\mathfrak {M}$
,
$\mathfrak {K}$
,
$\mathfrak {S}$
and
$\mathfrak {S}^{(1)}$
stand for the class of measurable, strongly compact, supercompact and
$C^{(1)}$
-supercompact cardinals, respectively. In the next pages we shall present some modifications to the arguments of §2.1 that will yield the proof for the consistency of “
$\min \mathfrak {M}<\min \mathfrak {R}<\min \mathfrak {S}<\min \mathfrak {S}^{(1)}$
”.
Assume
$\mathrm {GCH}$
and let
$\lambda <\kappa $
be two supercompact cardinals with a
$C^{(1)}$
-supercompact cardinal
$\mu $
above
$\kappa $
. By virtue of a result of Apter [Reference Apter2], after a preparatory iteration
$\mathbb {Q}\subseteq V_{\lambda }$
of length
$\lambda $
, one can assume that
$\lambda $
is the first strongly compact and the first strong cardinal and besides it is indestructible by
$<\lambda $
-directed closed forcings (i.e.
$\theta $
-directed closed, all
$\theta <\lambda $
) which are also
$\lambda $
-strategically closed. Thereby in
$V^{\mathbb {Q}}$
the
$\mathrm {GCH}$
pattern above
$\lambda $
is preserved,
$\lambda $
is the first strongly compact but not the first measurable cardinal and
$\kappa , \mu $
remain supercompact and
$C^{(1)}$
-supercompact, respectively. For the ease of notation henceforth we will assume that
$V=V^{\mathbb {Q}}$
. Analogously to the former section here we will add many
$\square _{\theta ,\eta }$
-square sequences below
$\kappa $
taking care that both the strong compactness of
$\lambda $
and the supercompactness of
$\kappa $
are preserved. The next forcing notion is discussed with full details in [Reference Cummings, Foreman and Magidor11, section 9] and it is the main ingredient of our argument:
Definition 2.10. Let
$\theta $
be a singular cardinal and let
$\langle \theta _i:\,i\in \mathrm {cf}\theta \rangle $
be an increasing and cofinal sequence in
$\theta $
with
$\theta _0> \mathrm {cf}\theta $
. We will denote by
$\mathbb {S}_{\theta }$
the forcing whose conditions are of the form
$$\begin{align*}p=\langle C^p_{\alpha, i}:\,\lim(\alpha),\, \alpha\leq \gamma^p,\, i^p(\alpha)\leq i < \mathrm{cf}\theta\rangle\end{align*}$$
witnessing
-
1.
$\gamma ^p$
is a limit ordinal less than
$\theta ^+$
. -
2.
$i^p$
is a function such that
$i^p(\alpha )<\mathrm {cf} \theta $
for each limit
$\alpha <\gamma $
. -
3. If
$i^p(\alpha )\leq i<\mu $
then
$C^p_{\alpha , i}$
is a club in
$\alpha $
of
$\mathrm {otp}(C^p_{\alpha ,i})<\theta _i$
. -
4. If
$i^p(\alpha )\leq i<j<\mu $
then
$C^p_{\alpha ,i}\subseteq C^p_{\alpha , j}$
. -
5. If
$i^p(\beta )\leq i<\mu $
and
$\alpha \in \lim (C^p_{\beta , i})$
then
$i(\alpha )\leq i$
and
$C^p_{\alpha ,i}=C^p_{\beta , i}\cap \alpha $
. -
6. If
$\alpha $
and
$\beta $
are limit ordinals with
$\alpha <\beta \leq \gamma $
then there is some
$i(\alpha )\leq i_0$
such that for every
$i_0\leq i<\mathrm {cf}\theta $
then
$\alpha \in \lim (C^p_{\beta , i})$
.
We will say that
$p\leq q$
iff
-
(a)
$\gamma ^q\leq \gamma ^p$
. -
(b) If
$\alpha \leq \gamma ^q$
then
$i^q(\alpha )=i^p(\alpha )$
and
$C^q_{\alpha ,i}=C^p_{\alpha ,i}$
for each
$i^q(\alpha )\leq i< \mathrm {cf} \theta $
.
It is illustrative to think on the conditions of
$\mathbb {S}_{\theta }$
as matrices of clubs which are promises for a potential
$\square _{\theta , \mathrm {cf}(\theta )}$
-sequence. This forcing, besides of adding a
$\square _{\theta ,\mathrm {cf}\theta }$
-sequence, is
$\mathrm {cf} \theta $
-directed and
$<\theta $
-strategically closed. The interested reader may find a detailed proof of both properties in [Reference Cummings, Foreman and Magidor11, section 9]. Since
$\theta $
is singular, hence
$\mathbb {S}_{\theta }$
does not add
$\theta $
-sequences, cardinals and cofinalities up to
$\theta ^+$
are preserved. Furthermore, as
$\mathrm {GCH}\,$
holds above
$\lambda $
, for any singular cardinal
$\theta>\lambda $
the forcing
$\mathbb {S}_{\theta }$
has cardinality
$\theta ^{+}$
and thus preserves all possibles cofinalities as well as the
$\mathrm {GCH}$
pattern above
$\lambda $
. Without loss of generality we will make the assumption that all the cardinals in
$\text {dom}\,(\ell )$
are strong limit above
$\lambda $
that are closed under
$\ell $
.
Definition 2.11. Let
$\mathbb {P}^{\ell }_{\kappa }$
be the
$\kappa $
-Easton support iteration where
$\mathbb {P}^{\ell }_0$
is the trivial forcing and for each ordinal
$\theta <\kappa $
, if
$\theta \in dom(\ell )\cap E^{\kappa }_{\lambda }$
and
$\Vdash _{\mathbb {P}^{\ell }_{\theta }}\text {``}\check {\theta }^+ \text { is a cardinal''}$
then
$\Vdash _{\mathbb {P}^{\ell }_{\theta }}\text {``}\mathbb {\dot {Q}}_{\theta }=\mathbb {S}_{\theta } \text {''} \text {and} \Vdash _{\mathbb {P}^{\ell }_{\theta }}\text {``} \mathbb {\dot {Q}}_{\theta } \text {is trivial''}$
, otherwise.
The iteration
$\mathbb {P}^{\ell }_{\kappa }$
is clearly
$<\lambda $
-directed closed and
$\lambda $
-strategically closed and thus
$\lambda $
remains strongly compact and strong in the generic extension. The next proposition is the corresponding version of Proposition 2.7 in the current setting:
Proposition 2.12. The following statements are true in
$V^{\mathbb {P}^{\ell }_{\kappa }}$
:
-
1.
$\lambda $
is strongly compact and strong and
$\mu $
is
$C^{(1)}$
-supercompact. -
2. There is a stationary set
$S^*\subseteq E^{\kappa }_{\lambda }$
such that for every
$\theta \in S^*$
,
$\square _{\theta ,\lambda }$
holds. In particular, there is no strongly compact between
$\lambda $
and
$\kappa $
. -
3.
$\kappa $
is supercompact but not
$C^{(1)}$
-supercompact. In fact, there is no elementary emebedding
$j: V^{\mathbb {P}^{\ell }_{\kappa }}\rightarrow M$
with
$j(\kappa )$
being a limit cardinal and
$M^{\lambda }\subseteq M$
. In particular,
$\kappa $
is the first supercompact cardinal.
Proof.
-
1. It follows from Apter’s result.
-
2. Let any
$\theta \in \mathrm {dom}(\ell )\cap E^{\kappa }_{\lambda }$
and notice that
$\vdash _{\mathbb {P}^{\ell }_{\theta +1}} \text {``} \square _{\theta ,\lambda } \text {holds''}$
. Set
$\theta ^*$
be the least cardinal in
$\mathrm {dom}(\ell )\,\cap \, E^{\kappa }_{\lambda }$
above
$\theta $
. The iteration restricted to the interval
$[\theta ^*, \kappa )$
is
$\theta ^*$
-startegically closed, hence
$(\theta ^+)^{V^{\mathbb {P}^{\ell }_{\theta +1}}}$
is preserved, and thus
$\Vdash_{\mathbb{P}^\ell_\kappa} \text {``} \square _{\theta ,\lambda } \text {holds''}$
. Finally, the iteration
$\mathbb {P}^{\ell }_{\kappa }$
is
$\kappa $
-cc because
$\kappa $
is Mahlo and thus the set
$S^*:=\mathrm {dom}(\ell )\cap E^{\kappa }_{\lambda }$
remains stationary in the generic extension.The further claim is a consequence of a well-known argument due to Solovay that we exhibit only for completeness. Aiming for a contradiction suppose that there is some
$\lambda < \eta < \kappa $
being
$\theta ^+$
-strongly compact cardinal, some
$\theta \geq \eta $
in
$S^*$
. Let
$j: V\rightarrow M$
be an elementary embedding with
$cp(j)=\eta $
and
$D\in M$
such that
$j''\theta ^+\subseteq D$
and
$M\models |D|<j(\eta )$
. Let
$\vec {C}=\langle \mathcal {C}_{\alpha }:\,\lim (\alpha ), \alpha \in \theta ^+\rangle $
be the
$\square _{\theta , \lambda }$
-sequence forced by
$\mathbb {P}^{\ell }_{\kappa }$
and
$\vec {D}=j(\vec {C})$
. Set
$\theta ^*=\sup (j''\theta ^+)$
and notice that
$\theta ^*<j(\theta )^+$
and
$\mathrm {cf}^M(\theta ^*)<j(\eta )$
. Let
$D_{\theta ^*}\in \mathcal {D}_{\theta ^*}$
and define
$C=\{\alpha \in \theta ^+:\, j(\alpha )\in D_{\theta ^*}\}$
the associated
$<\eta $
-club. Let
$\gamma>\theta $
be a limit point of C with
$cof(\gamma )=\omega $
and
$|C\cap \gamma |=\theta $
. By continuity of j in
$\gamma $
it is the case that
$j(\gamma )\in \lim (D_{\theta ^*})$
. Notice that for every
$\alpha \in C\cap \gamma $
, the formula
$\varphi (\alpha ,\gamma )$
is true in M as witnessed by
$$ \begin{align*} ``\exists\theta'\in j(\theta)^+\, \exists D_{\theta'}\in \vec{D}(\theta')\, (cof(\theta')<j(\eta)\,\\ \wedge\ j(\gamma)\in\lim(D_{\theta'}) \wedge\,j(\alpha)\in D_{\theta'}\cap j(\gamma)) '' \end{align*} $$
$\theta ^*$
. Thus for each
$\alpha \in C\cap \gamma $
there is some
$C_{\theta _{\alpha }}$
such that
$\mathrm {cf}(\theta _{\alpha })<\eta $
,
$\gamma \in lim(C_{\theta _{\alpha }})$
and
$\alpha \in C_{\theta _{\alpha }}\cap \gamma $
. Notice that all of these
$C_{\theta _{\alpha }}\cap \gamma $
lie in
$\mathcal {C}_{\gamma }$
and have cardinality less than
$\theta $
(since
$\mathrm {cf}(\theta _{\alpha })<\eta <\theta $
). Thus
$C\cap \gamma $
can be covered by the union of all clubs in
$\mathcal {C}_{\gamma }$
with cardinality less than
$\theta $
. Since
$|\mathcal {C}_{\gamma }|\leq \mathrm {cf}(\theta )<\theta $
, this union has cardinality less than
$\theta $
. Contradiction.
-
3. The argument is the same as in Proposition 2.7 and Theorem 1.2 noting that
$\mathbb {P}^{\ell }_{\kappa }$
preserve the
$\mathrm {GCH}\,$
pattern above
$\lambda $
.⊣
We can also say something else about the status of
$\lambda $
in the generic extension
$V^{\mathbb {P}^{\ell }_{\kappa }}$
:
Proposition 2.13. The cardinal
$\lambda $
is the first strong cardinal and the first strongly compact in
$V^{\mathbb {P}^{\ell }_{\kappa }}$
. In particular,
$\lambda $
is greater than the first measurable of
$V^{\mathbb {P}^{\ell }_{\kappa }}$
.
Proof. Let us simply show that
$\lambda $
is still the least strong in the generic extension since the claim about strong compactness can be proved similarly. Let
$\lambda ^{\star }<\lambda $
be a strong cardinal in
$V^{\mathbb {P}^{\ell }_{\kappa }}$
. The property of being a strong cardinal is
$\Pi _2$
and any strong cardinal is a
$C^{(2)}$
-cardinal. It then follows from this and from (1) of Proposition 2.12 that
$\lambda ^{\star }$
is strong within
$V[G]_{\lambda }$
. On the other hand notice that
$V[G]_{\lambda }=V_{\lambda }$
because the iteration is
$\lambda $
-distributive, hence
$\lambda ^{\star }$
is strong in
$V_{\lambda }$
. Finally since
$\lambda $
was a strong cardinal in V, hence
$C^{(2)}$
, it is the case that
$\lambda ^{\star }$
is also a strong cardinal in V below
$\lambda $
. This yields a contradiction with the minimality of
$\lambda $
in V. ⊣
Combining Propositions 2.12 and 2.13 the claim of Theorem 1.4 and Corollary 2.2 easily follows.
3 Identity crises: the first
$C^{(n)}$
-supercompact can be the first strongly compact
Let
$\mathscr {L}$
be a large cardinal property and
$\kappa $
be a cardinal such that
$\mathscr {L}(\kappa )$
. We say that
$\ell :\kappa \rightarrow \kappa $
is a
$\mathscr {L}$
-fast function on
$\kappa $
if for every
$\lambda>\kappa $
there is an
$\mathscr {L}$
-elementary embedding
$j:V\rightarrow M$
with
$\mathrm {crit}(j)=\kappa $
and
$j(\ell )(\kappa )>\lambda $
. There are many typical example of such sort of functions among which one must to highlight the Laver functions (see [Reference Laver14]). Under our convention a Laver function on a supercompact cardinals is the same as a
$\mathfrak {S}$
-fast function. Another natural example of this sort of objects is given by Cohen reals where the homogeneity of
$\mathrm {Add}(\kappa ,1)$
yields to the desired fast behaviour (see e.g. Lemma 3.1).
By results of Tsaprounis [Reference Tsaprounis21] it is known that any
$C^{(n)}$
-extendible cardinal carries a
$\mathfrak {E}^{(n)}$
-Laver function and moreover that the standard Jensen iteration to force global
$\mathrm {GCH}$
preserves
$C^{(n)}$
-extendibility. For a general version of Tsaprounis’ theorem see [Reference Bagaria and Poveda8].
Since the discovering of Laver functions fast functions have played a central role in iteration arguments. Essentially this sort of functions allows us to find arbitrary segments of
$j(\mathbb {P})$
where the iteration is trivial which is a crucial property for lifting elementary embeddings.
Regrettably, due to the general lack of understanding of
$C^{(n)}$
-supercompact cardinals, nothing is known about the existence
$\mathfrak {S}^{(n)}$
-fast functions. The naive strategy for proving they exist will lead us to mimic Laver’s construction of a Laver function even though we will eventually realize that this does not work. More precisely, there are obstacles to reflect the formula asserting that there is a counterexample for the existence of a
$\mathfrak {S}^{(n)}$
-fast function since it is
$\Pi _{n+2}$
while
$C^{(n)}$
-supercompact cardinals are not necessarily
$C^{(n+2)}$
-correct.Footnote
4
An alternative strategy is to discuss whether some forcing notion adding a
$\mathfrak {S}^{(n)}$
-fast function preserves
$C^{(n)}$
-supercompact cardinals. Nevertheless this strategy turns to be very problematic as we shall argue in §5. Anyway if we are given a
$C^{(n)}$
-supercompact cardinal
$\kappa $
in a generic extension
$V[\ell ]$
with
$\ell \subseteq \kappa $
being a Cohen real (e.g. as in Tsaprounis’s theorem), we may assume that
$\ell $
is a
$\mathfrak {S}^{(n)}$
-fast function in
$V[\ell ]$
by virtue of the next result:
Lemma 3.1. Let
$\ell :\kappa \rightarrow \kappa $
be a Cohen function over V. Let
$j\colon V\to M$
be an elementary embedding with critical point
$\kappa $
and let
$\lambda < j(\kappa )$
. If there is an extension of j to an elementary embedding
$\tilde {j} \colon V[\ell ] \to M[\tilde \ell ]$
with
$\tilde {j}(\ell ) = \tilde {\ell }$
that extends j then there is another extension of j,
$\tilde {j}'\colon V[\ell ] \to M[\tilde {\ell }']$
, such that
$\tilde {j}'(\ell ) = \tilde {\ell }'$
and
$\tilde {\ell }'(\kappa ) = \lambda $
. Moreover, if
$\tilde {j}$
witness that
$\kappa $
be a
$\lambda $
-
$C^{(n)}$
-supercompact cardinal in
$V[\ell ]$
then so does
$\tilde {j}'$
.
Proof. Let
$p=\{\langle \kappa ,\lambda \rangle \}\in \mathrm {Add}(j(\kappa ),1)^M$
. Since the Cohen forcing is homogeneous, one can find a M-generic filter H for the forcing
$\mathrm {Add}(j(\kappa ),1)^M$
such that
$p\in H$
,
$\bigcup H \restriction \kappa = \tilde {\ell }\restriction \kappa $
and
$M[\tilde {\ell }]=M[H]$
. By the elementarity of
$\tilde {j}$
,
$\tilde {\ell }\restriction \kappa = \tilde {j}(\ell )\restriction \kappa = \ell $
. Let
$\tilde {\ell }' = \bigcup H$
. By Silver’s argument, j extends to an elementary embedding
$\tilde {j}' \colon V[\ell ] \to M[\tilde {\ell }'] = M[\tilde {\ell }]$
. If
$\tilde {j}$
was a
$\lambda $
-
$C^{(n)}$
-supercompact embedding then so is
$\tilde {j}'$
since
$M[\tilde {\ell }] = M[\tilde {\ell }']$
and
$\tilde {j}(\kappa ) = \tilde {j}'(\kappa ) = j(\kappa )$
. ⊣
All the issues described so far can be framed within the setting of preservation of
$C^{(n)}$
-supercompactness by forcing. Broadly speaking, the main obstacle for developing a general theory of preservation for
$C^{(n)}$
-supercompact cardinals is the disagreement between the strong correctness of
$j(\kappa )$
and the little resemblance between M and the universe. More precisely
$C^{(n)}$
-supercompact embeddings may not be superstrong and thus this opens the door to have target models M that are not more correct than
$\Sigma _2$
-correct (i.e.
$M\prec _2 V$
) regardless
$j(\kappa )\in C^{(n)}$
. At §5 we will cover this problematic with all details.
3.1 Magidor product
Hereafter assume that
$n\geq 1$
and that
$\kappa $
is a
$C^{(n)}$
-supercompact cardinal. We moreover assume that
$\kappa $
carries a
$\mathfrak {S}^{(n)}$
-fast function
$\ell :\kappa \rightarrow \kappa $
with
$\text {range}\, (\ell )=\langle \kappa _{\alpha }:\, \alpha <\kappa \rangle $
, a set of measurable cardinals which does not contain their limit points: i.e., for every
$\alpha <\kappa $
,
$\sup _{\beta <\alpha } \kappa _{\beta }<\kappa _{\alpha }$
. It is not clear to these authors whether any
$C^{(n)}$
-supercompact cardinal carries a
$\mathfrak {S}^{(n)}$
-fast function. Nonetheless, these may obtained by starting with
$\kappa $
a
$C^{(n)}$
-extendible cardinal [Reference Tsaprounis21] or even from the more modest assumption of an
$\mathfrak {a}$
-
$C^{(n)}$
-extendible cardinal [Reference Poveda15, §4.1].
Definition 3.2. (Magidor product of Prikry forcings)
Let
$\kappa $
be a regular cardinal and
$A=\langle \kappa _{\alpha }:\,\alpha <\kappa \rangle $
be a subset of measurable cardinals below
$\kappa $
which does not contain their limit points. Let
$U_{\alpha }$
be a normal measure on
$\kappa _{\alpha }$
, each
$\alpha <\kappa $
. The
$\kappa $
-Magidor product with respect to A,
$\mathbb {M}_{A,\kappa }$
, is the set of all sequences
$p=\langle \langle s(\alpha ), A_{\alpha }\rangle :\, \alpha <\kappa \rangle $
such that
-
(a) For every
$\alpha <\kappa $
,
$(s(\alpha ), A_{\alpha })\in \mathbb {P}_{U_{\alpha }}$
, where
$\mathbb {P}_{U_{\alpha }}$
stands for the Prikry forcing with respect to the normal measure
$U_{\alpha }$
. -
(b)
$\{\alpha <\kappa : \, s(\alpha )\neq \emptyset \}\in [\kappa ]^{<\aleph _0}$
.
Given two conditions
$p,q\in \mathbb {M}_{A,\kappa }$
,
$p\leq q$
(p is stronger than q) if for every
$\alpha <\kappa $
,
$p(\alpha )\leq _{\mathbb {P}_{U_{\alpha }}}q(\alpha )$
. We will also say that p is a direct extension of q,
$p\leq ^{\star } q$
if for every
$\alpha <\kappa $
,
$p(\alpha )\leq ^{\star }_{\mathbb {P}_{U_{\alpha }}}q(\alpha )$
.
It is illustrative to think on
$\mathbb {M}_{A,\kappa }$
as a particular case of a Magidor iteration of Prikry forcings as presented in definition 6.1 of [Reference Gitik12]. Specifically, provided that A does not contain their limit points, one can easily check that
$\mathbb {M}_{A,\kappa }$
is isomorphic to the Magidor iteration of Prikry forcings at each
$\kappa _{\alpha }\in A$
below the condition
$\langle \langle \emptyset , \kappa _{\alpha }\rangle :\,\alpha \in \kappa \rangle $
.
On the sequel we shall adopt the notation
$\mathbb {M}$
instead of the cumbersome
$\mathbb {M}_{\text {range}\, (\ell ), \kappa }$
as long as the set A and the cardinal
$\kappa $
are clear from the context. Our main aim along this section is to prove that
$\mathbb {M}$
preserves
$C^{(n)}$
-supercompactness of
$\kappa $
lifting the corresponding ground model embeddings to
$C^{(n)}$
-supercompact embeddings in the generic extension. As we shall argue in such generic extension the first
$C^{(n)}$
-supercompact cardinal coincides with the first (
$\omega _1$
-)strongly compact cardinal.
The key point to carry out the lifting arguments is that the generics of
$\mathbb {M}$
are not arbitrary objects but are essentially given by sequences of generics for the corresponding Prikry forcings. It is widely known that Mathias criterion of genericity (see e.g. [Reference Gitik12]) implies that the critical sequence
$\langle \theta _n:\,n\in \omega \rangle $
of a
$\omega $
-length iteration of ultrapowers with respect to some measure over
$\kappa $
defines a Prikry generic
$C\in V$
for
$\mathbb {P}_{U_{\omega }}$
over
$M_{\omega }$
Footnote
5
Therefore, combining both things, iterated ultrapowers seem to provide a standard tool to define generic filters for
$\mathbb {M}$
and thus it turns to be necessary to prove a similar version to the Mathias criterion for
$\mathbb {M}$
. In the next section we shall prove that
$\mathbb {M}$
enjoys certain property also satisfied by the Prikry forcing that constitutes the main ingredient for the proof of Mathias criterion of genericity. We have called this property Mathias–Prikry property:
Lemma 3.3. Let
$\mathbb {P}$
be the Prikry forcing with respect to some normal measure U. Then
$\mathbb {P}$
enjoys the Mathias–Prikry property; namely, for every condition
$\langle s,A\rangle \in \mathbb {P}$
and every dense open set
$D\subseteq \mathbb {P}$
there are
$n_s\in \omega $
and
$A\in U$
such that for every
$m\geq n_p$
and every
$t\in [A]^m$
,
$\langle s\frown t, A\setminus \max (t)+1\rangle \in D$
.
Proof. See Lemma 1.13 of [Reference Gitik12]. ⊣
Once we prove that
$\mathbb {M}$
enjoys the Mathias–Prikry property the sketch for the construction of the generics will be the following. Let
$j: V\rightarrow M$
be a
$\lambda $
-
$C^{(n)}$
-supercompact embedding,
$A^{\star }=\langle {\kappa }_{\alpha }: \lambda <\alpha <j(\kappa )\rangle $
be a family of M-measurable cardinals not containing their limit points and
$U^{\star } = \langle \tilde {U}_{\alpha } : \lambda < \alpha < j(\kappa )\rangle $
be a sequence of measures over
${\kappa }_{\alpha }$
. Define over M a
$\omega \cdot j(\kappa )$
-iteration of ultrapowers
$\langle M_{\alpha }, j_{\alpha , \beta } \mid \alpha \leq \beta \leq \omega \cdot \mu \rangle $
where each
${\kappa }_{\alpha }$
is iterated
$\omega $
-many times. By previous comments this iteration yields a family of (M-definable) generic filters
$\langle H_{\alpha }:\,\lambda <\alpha <j(\kappa )\rangle $
for each Prikry forcing
$\mathbb {P}_{U_{\omega \cdot \alpha }}$
which defines—here is where the Mathias–Prikry property comes into play—a
$\mathbb {M}^{M_{\omega \cdot \mu }}$
-generic filter over
$M_{\omega \cdot \mu }$
. We will finally show that the embedding
$j_{0,\omega \cdot } \circ j$
lifts to a
$\lambda $
-
$C^{(n)}$
-supercompact embedding in
$V^{\mathbb {M}}$
thus proving that
$\kappa $
remains
$C^{(n)}$
-supercompact in the generic extension.
3.2
$\mathbb {M}$
and the Mathias–Prikry property
Definition 3.4. A function
$s\in \prod _{\alpha \in \kappa } \kappa _{\alpha }^{<\omega }$
is a stem if
$s(\alpha )$
is a strictly increasing sequence of cardinals and
$\{\alpha <\kappa :\, s(\alpha ) \neq \emptyset \}\in [\kappa ]^{<\aleph _0}$
. Let
$St$
be the set of all stems. For
$s\in St$
, we let the support of s,
$\text {supp}\, s$
, be an increasing enumeration
$\langle \alpha _i:i\leq n\rangle $
of the nontrivial coordinates of s. The length sequence of a stem s is
$\text {len}\, s=\langle \text {len}\, s(\alpha ):\,\alpha <\kappa \rangle $
.
Notice that a length sequence
$\text {len}\, s$
completely determines
$\text {supp}\, s$
. Thus, all the relevant information (i.e. the support and the lengths of the corresponding sequences) about a stem s is encoded within
$\text {len}\, s$
. Let
$ \bigoplus _{\alpha < \kappa } \omega $
denote the set of all
$\kappa $
-sequences of natural numbers which are nonzero only in a finite set. Let
$\vec {\gamma }\in \bigoplus _{\alpha < \kappa } \omega $
, we will set
$\vec {\gamma }_{\neq 0}=\{\alpha \in \kappa :\,\vec {\gamma }(\alpha )\neq 0\}$
. If
$\vec {\gamma },\vec {\gamma }'\in \bigoplus _{\alpha < \kappa } \omega $
we will write
$\vec {\gamma }\leq _p \vec {\gamma }'$
if for every
$\alpha <\kappa $
,
$\vec {\gamma }(\alpha )\leq \vec {\gamma }'(\alpha )$
.
Lemma 3.5. (Finite Diagonal Intersection)
Let
$\vec {\gamma }$
be a length sequence and
$\langle B^s_{\alpha } \mid \alpha < \kappa , s\in St, \textrm{len}\, s = \vec {\gamma }\rangle $
,
$B^s_{\alpha }\in U_{\alpha }$
with
$\min B^s_{\alpha } \geq \max s(\alpha )$
. There is a sequence of large sets
$\langle C_{\alpha } \mid \alpha < \kappa \rangle $
such that for every stem
$s \in \prod _{\alpha \in \kappa } C_{\alpha }^{<\omega }$
,
$\mathrm{len}\, s=\vec {\gamma }$
,
$B_{\alpha }^s \supseteq C_{\alpha } \setminus \max s(\alpha )$
for all
$\alpha $
.
Proof. Let us show that the theorem holds by induction over the amount of nonzero coordinates of
$\vec {\gamma }$
,
$|\vec {\gamma }_{\neq 0}|$
. Suppose that
$|\vec {\gamma }_{\neq 0}| =0$
, then there is only one stem with this support (namely the 0 function). Thus defining
$C_{\alpha }=B^s_{\alpha }$
, we are done. Now suppose by induction that for every length sequence
${\vec {\gamma }{'}}$
with
$|{\vec {\gamma }{'}}_{\neq 0}|\leq n$
, for every ordinal
$\delta $
and every family of large sets
$\langle B^s_{\alpha }:\alpha <\delta ,\, s\in St,\, \text {supp}\, s={\vec {\gamma }{'}}\rangle $
there is
$\langle C_{\alpha }:\,\alpha <\delta \rangle $
witnessing the theorem.
Let
$\vec {\gamma }$
be a length sequence with
$|\vec {\gamma }_{\neq 0}|=n+1$
and
$\langle B^s_{\alpha }:\alpha <\kappa ,\, s\in St,\, \text {len}\, s=\vec {\gamma }\rangle $
be a family of large sets. Say that
$\max (\vec {\gamma }_{\neq 0})=\delta $
. Notice that there are at most
$\kappa _{\delta }$
-many stems with such support and thus for every
$\delta <\alpha $
the set
$C_{\alpha }=\bigcap _{s\in St,\text {len}\, s=\vec {\gamma }} B^s_{\alpha }$
is an element of
$U_{\alpha }$
. Let us work now with the truncated family
$\langle B^s_{\alpha }:\alpha < \delta ,\, s\in St,\, \text{len}\, s=\vec {\gamma }\rangle $
. All the stems with length sequence
$\text{len}\, s=\vec {\gamma }$
are built by some
$s'\in St$
with
$\text{len}\, s'=\vec {\gamma }\upharpoonright n$
and some
$\vec {\eta }\in \kappa _{\delta }^{\vec {\gamma }(\delta )}$
. Namely,
$s=s'\frown \vec {\eta }$
.Footnote
6
For each possible extension
$\vec {\eta }$
, one has a family
$\mathcal {B}_{\vec {\eta }}= \langle B^{s'}_{\alpha }(\vec {\eta }):\alpha < \delta ,\, s'\in St,\, \text{len}\, s'=\vec {\gamma }\upharpoonright n\rangle $
of large sets. By the discreteness of the measurables, there is a large set
$A_{\delta }\in U_{\delta }$
such that the families
$\mathcal {B}_{\vec {\eta }}$
are the same for every
$\vec {\eta }\in A_{\delta }^{\vec {\gamma }(\delta )}$
. Let
$\langle B^{s'}_{\alpha }:\alpha < \delta ,\, s'\in St,\, \text{len}\, s'=\vec {\gamma }\upharpoonright n\rangle $
be this common value and apply the induction hypothesis to obtain a family
$\langle C_{\alpha }:\,\alpha <\delta \rangle $
witnessing the theorem. For the coordinate
$\delta $
define
$C_{\delta }=A_{\delta }\cap \bigtriangleup \{B^s_{\delta }: s\in St,\,\text{len}\, s=\vec {\gamma }\}$
where
$\bigtriangleup \{B^s_{\delta }: s\in St,\,\text{len}\, s=\vec {\gamma }\}$
is defined as:
$$ \begin{align*}\{\beta\in \kappa_{\delta}:\,(s\in St\,\wedge\,\text{len}\, s=\vec{\gamma}\,\wedge\, \max(s(\delta))<\beta)\rightarrow\beta\in B^s_{\delta}\}.\end{align*} $$
It is routine to check that the family
$\langle C_{\alpha }:\,\alpha <\kappa \rangle $
witnesses the theorem for the support
$\vec {\gamma }$
.⊣
Lemma 3.6. (Röwbottom Lemma)
Let
$f\colon St \to 2$
be a function. There is a sequence of large sets
$\langle C_{\alpha } \mid \alpha < \kappa \rangle $
and a function
$g\colon \bigoplus _{\alpha < \kappa }\omega \rightarrow 2 $
such that for every stem
$s\in \prod _{\alpha \in \kappa } C_{\alpha }^{<\omega }$
,
$f(s) = g(\text {supp}\, s)$
.
Proof. Fix
$\alpha \in \kappa $
an let
$St_{\alpha }=\{s\in St:\, \max (\text {supp}\, s)=\alpha \}$
. We are going to define by induction over
$n\in \omega $
a sequence of functions
$f_n\upharpoonright \alpha : St_{\alpha } \rightarrow 2$
and a sequence of
$U_{\alpha }$
-large sets
$\langle A_{\alpha ,n}:\,n\in \omega \rangle $
. Let
$f_0=f$
and
$A_{\alpha ,0}=\kappa _{\alpha }\setminus \{0\}$
and let us show how to proceed on larger n’s. Denote by
$St_{\alpha ,n}$
the set of all stems such that
$\alpha =\max (\text {supp}\, s)$
and
$s(\alpha )\in A_{\alpha , n}^{<\omega }$
. For each
$s\in St_{\alpha ,n}$
, consider
$F^n_{\alpha ,s\upharpoonright \alpha }: \kappa _{\alpha }^{<\omega }\rightarrow 2$
defined by
$\vec {\eta }\mapsto f_n(s^{\alpha }_{\vec {\eta }})$
. Here
$s^{\alpha }_{\vec {\eta }}$
stands for the stem
$s^*$
which coincides with s in all the coordinates except in
$\alpha $
where it is
$\vec {\eta }$
. By Röwbottom theorem one can find a homogeneous set
$H_{s\upharpoonright \alpha ,\alpha }\subseteq A_{\alpha , n}$
for this function. Define
$A_{\alpha , n+1}=\bigcap \{H_{s\upharpoonright \alpha ,\alpha }:\, s\in St_{\alpha ,n}\}$
and notice that this is a
$U_{\alpha }$
-large set because this intersection runs for less than
$\kappa _{\alpha }$
-many sets. For each
$s\in St_{\alpha ,n}$
, with
$s(\alpha )\in A_{\alpha , n+1}^{<\omega }$
, define
$f_{n+1}(s^{\alpha }_{\langle 0\rangle ^{s(\alpha )}})=f_n(s)$
. Here
$\langle 0\rangle ^{s(\alpha )}$
stands for the sequence of length
$\text {len}\, s(\alpha )$
of
$0$
’s.Footnote
7
This finishes the induction over n.
Repeating the above argument for each
$\alpha <\kappa $
, one gets a sequence of large sets
$\langle A_{\alpha , n}:\,\alpha <\kappa , n\in \omega \rangle $
and a sequence of functions
$\langle f_n:\,n\in \omega \rangle $
. Let
$C_{\alpha }=\bigcap _{n\in \omega } A_{\alpha , n}$
and
$St^{\star }_{\alpha }=\bigcap _{n\in \omega } St_{\alpha ,n}$
and notice that
$$ \begin{align} \forall\alpha\in \kappa\,\forall s\in St^{\star}_{\alpha}\,\forall n\in\omega\,(f_{n+1}(s^{\alpha}_{\langle 0\rangle^{s(\alpha)}})=f_n(s)). \end{align} $$
For every
$m\in \omega $
, we will prove by induction that for every stem
$s\in \prod _{\alpha \in \kappa } (C_{\alpha }\cup \{0\})^{<\omega }$
,
$f_m(s){{\kern-2pt}={\kern-2pt}}f_{m+n}(r)$
, where
$n{{\kern-2pt}={\kern-2pt}}|\{\alpha :\, s(\alpha ){{\kern-2pt}\neq{\kern-2pt}} \langle 0\rangle ^{s(\alpha )}\}|$
and r is such that
$r(\alpha ){{\kern-2pt}={\kern-2pt}}\langle 0\rangle ^{s(\alpha )}$
if
$\alpha {{\kern-2pt}\in{\kern-2pt}} \text {supp}\, s$
and
$r(\alpha ){{\kern-2pt}={\kern-2pt}}\emptyset $
, otherwise. The induction runs over these n’s.
Let
$m\in \omega $
be fixed. Let us prove for the sake of clarity the first two inductive steps. If s is a stem such that
$|\{\alpha :\, s(\alpha )\neq \langle 0\rangle ^{s(\alpha )}\}|=0$
then the claim is true since
$r=s$
. On the other hand, if
$\{\alpha :\, s(\alpha )\neq \langle 0\rangle ^{s(\alpha )}\}=\{\beta \}$
, then
$s\in St^{\star }_{\beta }$
and thus
$f_m(s)=f_{m+1}(s^{\beta }_{\langle 0\rangle ^{s(\beta )}})$
by the Equation (1). Notice that
$s^{\beta }_{\langle 0\rangle ^{s(\beta )}}=r$
, and we are done.
Suppose that the claim is true for stems s such that
$|\{\alpha :\, s(\alpha )\neq \langle 0\rangle ^{s(\alpha )}\}|=n$
. Let
$s\in \prod _{\alpha \in \kappa } (C_{\alpha }\cup \{0\})^{<\omega }$
with
$|\{\alpha :\, s(\alpha )\neq \langle 0\rangle ^{s(\alpha )}\}|=n+1$
such that
$s\in St^{\star }_{\alpha }$
, for some ordinal
$\alpha $
. By Equation 1,
$f_m(s)=f_{m+1}(s^{\alpha }_{\langle 0\rangle ^{s(\alpha )}})$
. Now
$s^*=s^{\alpha }_{\langle 0\rangle ^{s(\alpha )}}$
is such that
$|\{\beta :\, s(\beta )\neq \langle 0\rangle ^{s^*(\beta )}\}|=n$
so by induction we know that
$f_{m+1}(s^{\alpha }_{\langle 0\rangle ^{s(\alpha )}})=f_{m+n+1} (r)$
, where
$r(\beta )=\langle 0\rangle ^{s(\beta )}$
for every
$\beta \in \text {supp}\, s$
. This shows that
$f_m(s)=f_{m+n+1}(r)$
. In particular, for each
$s\in \prod _{\alpha \in \kappa } C_{\alpha }^{<\omega }$
,
$f(s)=f_n(r)$
, where
$n=| \text {supp}\, s|$
. Thus defining
$g(\text {supp}\, s)=f_{|\text {supp}\, s|}(r)$
, we are done. ⊣
Both lemmas yields the proof of the Mathias–Prikry Property for
$\mathbb {M}$
.
Lemma 3.7. (Mathias–Prikry Property)
Let D be a dense open subset of
$\mathbb {M}$
and
$p\in \mathbb {M}$
. There is a direct extension
$p^{\star } \leq ^{\star } p$
and some
$\vec {\gamma }$
which is a length sequence of a stem, such that for all
$q \leq p^{\star }$
with stem
$s_q$
and
$\vec {\gamma }\leq _p \mathrm{len}\, s_q$
then
$q\in D$
.
Proof. Let
$s\in St$
be the stem of p. Let
$f_s \colon St \to 2$
be the function that sends a stem t to
$1$
if the concatenation of both stems
$s\frown t$
is an stem and there is a sequence of large sets
$\langle B^{s\frown t}:\, \alpha <\kappa \rangle $
such that the resulting condition is in D. Otherwise, define this value as
$0$
. Applying Lemma 3.6, there is a sequence of large sets
$\langle C_{\alpha }:\,\alpha < \kappa \rangle $
and a function
$g\colon \bigoplus _{\alpha <\kappa }\omega \rightarrow 2$
such that for every
$t\in \prod _{\alpha \in \kappa } C^{<\omega }_{\alpha }$
,
$f_s(t)=g(\text {supp}\, t)$
. Since D is dense open it is clear that there is
$t^*\in \prod _{\alpha \in \kappa } C^{<\omega }_{\alpha }$
such that
$f_s(t^*)=1$
. Thus if
$\text {len}\, t^*=\vec {\gamma }$
we have that
$f_s(t)=1$
, for every
$t\in \prod C^{<\omega }_{\alpha }$
with
$\text {len}\, t=\vec {\gamma }$
. By definition, for every stem t with length sequence
$\vec {\gamma }$
, there is a sequence of large sets
$\langle B_{\alpha }^{s\frown t} \mid \alpha < \kappa \rangle $
such that the corresponding forcing condition lies in D. Apply Lemma 3.5 to
$\langle B_{\alpha }^{s\frown t} \mid \alpha < \kappa ,\,\text {len}\, t=\vec {\gamma }\rangle $
and let
$\langle C^{'}_{\alpha }:\alpha <\kappa \rangle $
be the family of large sets witnessing it. For each
$\alpha <\kappa $
, define
$C^*_{\alpha }=C^{'}_{\alpha }\cap C_{\alpha }$
. Let
$p^{\star }$
be the condition in
$\mathbb {M}$
with stem s and large sets
$\langle C^{*}_{\alpha }:\,\alpha <\kappa \rangle $
. If
$q\leq p^{\star }$
and
$\vec {\gamma }\leq _{p} \text{len}\, s_q$
, then q is stronger than some condition with stem
$s\frown t$
with
$t\in \prod _{\alpha \in \kappa }{ (C^{*}_{\alpha })}^{<\omega }$
and large sets
$\langle B^{s\frown t}_{\alpha }:\,\alpha <\kappa \rangle $
. By the above argument, this condition is in D and thus q also. ⊣
3.3 Preserving
$C^{(n)}$
-supercompactness
Let
$\lambda>\kappa $
and
$j: V\rightarrow M$
be a
$\lambda $
-
$C^{(n)}$
-supercompact embedding such that
$j(\ell )(\kappa )>\lambda $
. Recall that the existence of such embeddings are guaranteed by Lemma 3.1.
Lemma 3.8. Let
$G\subseteq \mathbb {M}$
a V-generic filter. Then there is an elementary embedding
$j^{\star }:V[G]\rightarrow M^{\star }[G\times H]$
witnessing the
$\lambda $
-
$C^{(n)}$
-supercompactness of
$\kappa $
in
$V[G]$
.
Proof. Recall that
$\mathbb {M}=\mathbb {M}_{\text {range}\, (\ell ), \kappa }$
so by elementarity
$j(\mathbb {M})=\mathbb {M}^M_{\text {range}\, (j(\ell )), j(\kappa )}$
. It is obvious that the forcing
$j(\mathbb {M})$
factorizes as
$\mathbb {M}\times j(\mathbb {M})/\mathbb {M}$
where
$j(\mathbb {M})/\mathbb {M}$
is the M-version for the Magidor product
$\mathbb {M}_{(\text {range}\, (j(\ell ))\setminus \text {range}\, \ell ), j(\kappa )}$
. Since we have taken j in such a way that
$j(\ell )(\kappa )>\lambda $
, then
$\text {range}\, (j(\ell ))\setminus \text {range}\, \ell )$
can be written as an increasing sequence of measurable cardinals
$\langle \kappa _{\alpha }:\,\alpha <j(\kappa )\rangle $
such that
$\kappa _0>\lambda $
and that for every
$\alpha <j(\kappa )$
,
$\sup _{\beta <\alpha } \kappa _{\beta }<\kappa _{\alpha }$
. For ease of notation set
$\mu =j(\kappa )$
and
$\mathbb {M}^*= j(\mathbb {M})/\mathbb {M}$
. Working in M we shall build an iteration of ultrapowers
$\langle M_{\alpha }, j_{\alpha , \beta } \mid \alpha \leq \beta \leq \omega \cdot \mu \rangle $
and we will show that
$\langle C_{\alpha } \mid \alpha < \mu \rangle $
generates a
$M_{\omega \cdot \mu }$
-generic for the Magidor product
$j_{\omega \mu }(\mathbb {M}^*)$
, where
$C_{\alpha } = \langle \rho _{\alpha }^n \mid n < \omega \rangle $
is the
$\alpha $
th-critical sequence of the iteration. Let
$M_0 = M$
,
$j_{00}=\mathrm {id}$
and
$\vec {U}=\langle U_{\alpha }:\,\alpha \in \mu \rangle $
. For limit
$\alpha $
, let
$M_{\alpha }$
be the direct limit of the system
$\langle M_{\beta }, j_{\beta ,\gamma } \mid \beta \leq \gamma < \alpha \rangle $
while for successor cases we set
$$\begin{align*}M_{\omega \cdot \alpha + n + 1} = \mathrm{Ult}(M_{\omega \cdot \alpha + n}, j_{\omega \cdot \alpha + n}(\vec{U})_{\alpha}),\end{align*}$$
each
$n\in \omega $
. Let
$j_{\omega \cdot \alpha + n, \omega \cdot \alpha + n + 1}$
be the corresponding ultrapower map and define
$j_{\beta , \omega \cdot \alpha + n + 1}$
, for
$\beta <\omega \cdot \alpha +n+1$
, in the only possible way: namely,
$$\begin{align*}\rho_{\alpha}^n = \mathrm{crit} j_{\omega \cdot \alpha + n, \omega \cdot \alpha + n + 1} = j_{\omega \cdot \alpha + n}(\kappa_{\alpha}).\end{align*}$$
Notice that
$\rho ^0_0>\lambda $
and moreover
$\kappa _{\alpha }=\rho ^0_{\alpha }>\alpha $
for every
$\alpha <\mu $
, by discreteness of the measurables. By standard computations of iterated ultrapowers one can show that
$\bar {j}(\mu )=\mu $
. For the ease of notation, on the sequel we will write
$\bar {j} = j_{\omega \cdot \mu },\, M^{\star } = M_{\omega \cdot \mu }$
. Consider,
$$ \begin{align*}H=\{p\in \bar{j}(\mathbb{M}^*):\, \forall \alpha\in\mu\,\forall q\in H_{\alpha}\; (p(\alpha)\parallel q)\},\end{align*} $$
where
$H_{\alpha }=\{\langle s, A\rangle \in \mathbb {P}_{U_{\alpha }}:\,s\lhd C_{\alpha },\; C_{\alpha }\setminus \max (s)\subseteq A\ \}$
; i.e. the Prikry generic defined by the critical sequence
$C_{\alpha }$
. We claim that H is a generic filter for the Magidor product
$\bar {j}(\mathbb {M}^{\star })$
over
$M^{\star }$
.⊣
Claim 3.9. The filter H is
$M^{\star }$
generic for
$\bar {j}(\mathbb {M}^*)$
.
Proof of claim
Let
$D \in M$
be a dense open subset of
$\bar {j}(\mathbb {M}^*)$
. Then there is some function
$f: \prod _{n < n^{\ast }} \kappa ^{<\omega }_{\alpha _n} \rightarrow \mathcal {P}(\mathbb {M}^*)$
such that for all
$\vec {\eta } \in dom f$
,
$f(\vec {\eta })$
is a dense open subset of
$\mathbb {M}^*$
and there are sequences
$\vec {\rho }_n \in C_{{\alpha _n}}^{<\omega }$
for
$n<n^{\star }$
such that
$D = \bar {j}(f)(\vec {\rho }_0,\dots , \vec {\rho }_{n_{\star } - 1})$
. We do assume that for every
$n<n^{\star }$
the sequences
$\vec {\rho }_n$
are an initial segments of the corresponding
$C_{\alpha _n}$
.
Let
$M' = \{\bar {j}(g)(\vec {\rho }_0,\dots , \vec {\rho }_{n_{\star } - 1}) \mid g \in M\}$
, where we only take the g’s that have the right domain, namely that
$\langle \vec {\rho }_n \mid n < n_{\star -1}\rangle \in \bar {j}(\text {dom}\, g)$
. Working in
$M'$
, let us apply Lemma 3.7 for D and a condition with stem
$\vec {\rho }=\langle \vec {\rho }_n \mid n < n_{\star -1}\rangle \frown \langle \emptyset \rangle $
Footnote
8
and let
$p^{\star }$
and
$\vec {\gamma }$
be the obtained direct extension and support. It is sufficient to show that
$p^{\star }$
belongs to the filter H. Indeed, in such case H will meet
$D^{\star }=\{q\leq p^{\star }:\,\text {len}\,(q)\leq _p \vec {\gamma }\}$
which is a subset of D. Let
$g\colon \prod \kappa ^{<\omega }_{\alpha } \to M$
be a function representing the sequence of large sets in
$p^{\star }$
where
$g(s)$
is of the form
$\langle B^s_{\alpha } \mid \alpha < \mu \rangle $
and s goes over stems with length sequence
$\text {len}\, p^{\star }$
. Say
$\vec {B}=\langle B^s_{\alpha } \mid \alpha < \mu , \, \text {len}\, s=\text {len}\, p^{\star }\rangle $
. Using Lemma 3.5, we have a sequence of large sets
$\vec {A}=\langle A_{\alpha } \mid \alpha < \mu \rangle $
such that for every
$s\in \prod A^{<\omega }_{\alpha }$
,
$A_{\alpha }\setminus \max (s(\alpha ))\subseteq B^s_{\alpha }$
, for every
$\alpha <\mu $
. Clearly, the condition
$p^{**}$
with stem
$\vec {\rho }\frown \langle \emptyset \rangle $
and large sets
$\bar {j}(\vec {A})$
is stronger than
$p^*$
. Let us verify that
$p^{**}$
enters the generic and thus
$p^*$
also.
Let
$\alpha <\mu $
. If
$\alpha $
is no one of the
$\alpha _n$
’s then
$p^{**}(\alpha )=\langle \emptyset , \bar {j}(\vec {A})_{\alpha }\rangle $
. Let us show that
$C_{\alpha }\subseteq \bar {j}(\vec {A})_{\alpha }$
and from this we will conclude that it compatible with all the conditions of
$H_{\alpha }$
. By definition
$j(\vec {A})_{\alpha }\in j(\vec {U})_{\alpha }$
. Since
$\alpha $
is a fixed point of
$j_{\omega \alpha ,\omega \mu }$
then
$j(\vec {A})_{j_{\omega \alpha ,\omega \mu }(\alpha )}\in j(\vec {U})_{j_{\omega \alpha ,\omega \mu }(\alpha )}$
and hence
$j_{\omega \alpha }(\vec {A})_{\alpha }\in j_{\omega \alpha }(\vec {U})_{\alpha }$
. Thus by the definition of the iteration and since
$\mathrm {crit} j_{\omega \alpha ,\omega \alpha +1}>\alpha $
,
$\rho ^0_{\alpha }\in j_{\omega \alpha +1}(\vec {A})_{\alpha }$
. The critical point of
$j_{\omega \alpha +1,\omega \mu }$
is
$\rho ^1_{\alpha }$
an hence
$\rho ^0_{\alpha }$
and
$\alpha $
are fixed by this embedding. This shows that
$\rho ^0_{\alpha }\in j(\vec {A})_{\alpha }$
. Using the same argument one can show that
$\rho ^n_{\alpha }\in j(\vec {A})_{\alpha }$
, for all
$n\in \omega $
.
Now let us suppose that
$\alpha =\alpha _n$
for some
$n<n^{\star }$
. We claim that
$C_{\alpha _n}\setminus \vec {\rho }_n\subseteq \bar {j}(\vec {A})_{\alpha _n}$
. Indeed, notice that
$\bar {j}(\vec {A})_{\alpha _n}\setminus \max \vec {\rho }_n\subseteq j(\vec {B})^{\vec {\rho }}_{\alpha _n}\in j(\vec {U})_{\alpha _n}$
. Thus
$\bar {j}(\vec {A})_{\alpha _n}\setminus \max \vec {\rho }_n\in j(\vec {U})_{\alpha _n}$
. On the other hand
$\max \vec {\rho }_n=\max ({\bar {j}{''}}_{\omega \alpha _n+k+1, \omega \mu } \vec {\rho }_n)$
where
$k=|\vec {\rho }_n|$
. Hence
$\bar {j}_{\omega \alpha _n+k+1}(\vec {A})_{\alpha _n}\setminus \max \vec {\rho }_n\in j_{\omega \alpha _n+k+1}(\vec {U})_{\alpha _n}$
. By definition of the iteration,
$\rho ^{k+1}_{\alpha _n}\in j_{\omega \alpha _n+k+2}(\vec {A})_{\alpha _n}$
and hence
$\rho ^{k+1}_{\alpha _n}\in \bar {j}(\vec {A})_{\alpha _n}$
since
$\mathrm {crit} j_{\omega \alpha _n+k+2,\omega \mu }>\rho ^{k+1}_{\alpha _n}>\alpha _n$
. Repeating this argument, we conclude that
$C_{\alpha _n}\setminus \vec {\rho }_n\subseteq \bar {j}(\vec {A})_{\alpha _n}$
. From this it is obvious that
$p^{**}(\alpha _n)=\langle \vec {\rho }_n, \bar {j}(\vec {A})_{\alpha _n}\rangle \parallel q$
, for each
$q\in H_{\alpha _n}$
. This completes the proof of genericity of H. ⊣
Set
$j^{\star }=\bar {j}\circ j$
. The proof of next claim leads us to the end of the lemma.
Claim 3.10. The embedding
$j^{\star }: V\rightarrow M^{\star }$
lifts to an elementary embedding
$j^{\star }: V[G]\rightarrow M^{\star }[G\times H]$
which is a witness for
$\lambda $
-
$C^{(n)}$
-supercompactness of
$\kappa $
in
$V[G]$
.
Proof of claim. Provide that
$j^{\star }$
lifts, it is clear that this embedding will lie in
$V[G]$
since H is definable within M. Let us first show that
$j^{\star }$
lifts. Let
$p\in G$
and notice that
$j(p)=p\frown q$
Footnote
9
where
$q\in \mathbb {M}^*$
has trivial stem. To be more precise,
$q=\langle \langle (s(\alpha ),B_{\alpha }\rangle :\,\alpha \in \mu \rangle $
such that
$s(\alpha )=\emptyset $
and
$B_{\alpha }\in {U}_{\alpha }$
. Applying the second elementary embedding, we have that p is not moved (since
$\mathrm {crit}(\bar {j})>\kappa $
) whereas
$\bar {j}(q)=\langle \langle \emptyset ,\bar {j}(\vec {B})_{\alpha }\rangle :\,\alpha \in \mu \rangle $
.Footnote
10
For each
$\alpha < \mu $
, one can argue as in the proof of genericity for H that
$C_{\alpha }\subseteq \bar {j}(\vec {B})_{\alpha }$
and thus
$\langle \emptyset , \bar {j}(\vec {B})_{\alpha }\rangle \parallel q$
, for all
$q\in H_{\alpha }$
. In particular,
$\bar {j}(q)\in H$
and hence
$j^{\star }(p)\in G\times H$
.
To finish the claim it remains to show that
$N=M^{\star }[G\times H]$
is closed under
$\lambda $
-sequences since
$j^{\star }(\kappa )=j(\kappa )\in C^{(n)}$
because
$\mathbb {M}$
is mild. Since N is a model of choice, it is sufficient to show that every
$\lambda $
-sequence of ordinals from
$V[G]$
belongs to N. Note that the forcing
$\mathbb {M}$
introduces new
$\omega $
-sequences. First, since j is a
$\lambda $
-supercompact embedding, M is closed under
$\lambda $
-sequences from V. Let
$\sigma \in V$
be an
$\mathbb {M}$
-name for a
$\lambda $
-sequence of ordinals. By the
$\kappa $
-chain condition of
$\mathbb {M}$
, we may assume that
$|\sigma | = \lambda $
and that
$\sigma \subseteq \mathbb {M} \times \mathrm {ON}$
. Therefore
$\sigma \in M$
, and in
$M[G]$
we can interpret it. Let us finally show that
$M[G]$
and
$M^{\star }[G\times H]$
contain the same
$\lambda $
-sequences of ordinals.
Let
$\langle \xi _{\alpha } :\, \alpha < \lambda \rangle $
be a sequence of ordinals. In
$M^{\star }$
, for every
$\alpha $
there is a function
$f_{\alpha }$
such that
$\bar {j}(f_{\alpha })(\vec {\rho }^{\alpha }_0,\dots , \vec {\rho }^{\alpha }_{n^{\alpha }-1}) = \xi _{\alpha }$
, where
$\vec {\rho }^{\alpha }_i$
is a finite sequence of elements of
$C_{\zeta _i}$
, some
$\zeta _i < \mu $
. Since the critical point of
$\bar {j}$
is above
$\lambda $
and the sequence of functions
$\langle f_{\alpha } \mid \alpha < \lambda \rangle \in M[G]$
we conclude that
$\bar {j}(\langle f_{\alpha } \mid \alpha < \lambda \rangle ) = \langle \bar {j}(f_{\alpha }) \mid \alpha < \lambda \rangle \in M^{\star }[G]$
. Thus, it is sufficient to show that the sequence
$\vec {R} = \langle \langle \vec {\rho }^{\alpha }_i \mid i < n^{\alpha }\rangle \mid \alpha < \mu \rangle \in M^{\star }[G][H]$
.
Let us define by induction on
$\gamma < \mu $
a sequence of functions
$p_{\gamma }$
such that
$\bar {j}(p_{\gamma })(H) = \gamma $
. Intuitively,
$p_{\gamma }$
is a procedure for extracting
$\gamma $
, given the information of H. Let us assume that
$p_{\beta }$
is defined for all
$\beta < \gamma $
. Since the critical point of
$j_{\gamma , \mu }$
is above
$\gamma $
, we know that
$\gamma $
is represented in
$M_{\gamma }$
by
$$\begin{align*}\gamma = j_{0,\gamma}(g)(\rho_0, \dots, \rho_{n-1}),\end{align*}$$
for some elements of the sequences in H,
$\rho _0, \dots , \rho _{n-1}$
. Those elements are all below the
$\gamma $
-th member of H in the increasing enumeration and in particular, do not move under
$j_{\gamma , \mu }$
. Let
$h\colon \mu \to \mu $
be the increasing enumeration of H. Let
$\beta _0, \dots , \beta _{n-1}$
be their indices, so
$h(\beta _i) = \rho _i$
. We conclude that:
$$\begin{align*}\gamma = \bar{j}(g)(h(p_{\beta_0}(H)), \dots, h(p_{\beta_{n-1}}(H)) ),\end{align*}$$
so we can define
$p_{\gamma }$
.
Finally, let us show that the sequence
$\vec {R}$
is in
$M^{\star }[G][H]$
. Indeed, one can obtain
$\vec {R}$
from H by just knowing the indices of each
$\vec {\rho }^{\alpha }_i$
. This sequence of indices is equivalent to a sequence of ordinals below
$\mu $
of length
$\lambda $
,
$\vec {\epsilon } = \langle \epsilon _{\alpha } \mid \alpha < \lambda \rangle $
. Letting the condition,
$\vec {p} = \langle p_{\epsilon _{\alpha }} \mid \alpha < \lambda \rangle \in M$
and applying the components of
$\bar {j}(\vec {p})$
to H we obtain
$\vec {\epsilon }$
. Finally, applying h on the components of
$\vec {\epsilon }$
, we obtain
$\vec {R}$
, as wanted. ⊣
This immediately yields the proof Theorem 1.3.
Proof of Theorem 1.3
By results of [Reference Kunen13], it is known that if one changes the cofinality of some inaccessible cardinal
$\delta $
to
$\omega $
but preserves its successor then
$\square _{\delta ,\omega }$
holds in the generic extension. Consequently,
$\mathbb {M}$
adds unboundely many
$\square _{\delta ,\omega }$
-sequences below
$\kappa $
and thus there is no (
$\omega _1$
-)strongly compact cardinal below it. Combining this with Lemma 3.8 we are done. ⊣
To conclude this section we would like to point out that the ideas used in the proof of claim 3.9 can be straightforwardly adapted to proof the following version of Mathias criterion for the Magidor product of Prikry forcings:
Theorem 3.11. (Mathias criterion)
Suppose that M is an inner model of ZFC and
$\langle U_{\alpha }:\alpha <\kappa \rangle $
is a sequence of normal measures over the cardinals
$\langle {\kappa }_{\alpha }:\alpha <\kappa \rangle $
, respectively. A sequence
$\vec {C}\in {\prod }_{\alpha \in \kappa } {{{\hspace {-0.0001pt}}}^{{\kappa }_{\alpha }}{\kappa }_{\alpha }}$
defines a generic filter for
$\mathbb {M}$
if it satisfies the following condition:
$$ \begin{align*}\forall\alpha\in\kappa\,\forall A\in U_{\alpha}\,|\vec{C}(\alpha)\setminus A|<\aleph_0.\end{align*} $$
Moreover, the generic is given by
$$ \begin{align*}G(\vec{C})&=\{p\in\mathbb{M}:\,\forall \alpha\in \kappa\, (p(\alpha)=\langle s(\alpha), A_{\alpha}\rangle\wedge s(\alpha)\\&\qquad\vartriangleleft \vec{C}(\alpha)\,\wedge\, \vec{C}(\alpha)\setminus\max s(\alpha)+1\subseteq A_{\alpha})\}\end{align*} $$
3.4 Some consequences of Theorem 1.3
In this section we shall analyse some of the consequences of Theorem 1.3. For each
$n\geq 1$
let us respectively denote by
$\Gamma _n$
and by
$\Gamma ^*_n$
the first order formulas
$$ \begin{align*} &\text{``}\min\mathfrak{M}<\min\mathfrak{K}_{\omega_1}=\min \mathfrak{K}=\min \mathfrak{S}=\min \mathfrak{S}^{(n)} \text{''}\\ &\text{``}\min\mathfrak{M}<\min\mathfrak{K}_{\omega_1}=\min \mathfrak{K}=\min \mathfrak{S}=\min \mathfrak{S}^{(n)}<\min\mathfrak{E} \text{''.} \end{align*} $$
Corollary 3.12. For every
$n\geq 1$
,
$$ \begin{align*}\mathrm{Con}(\mathrm{ZFC}+\exists \kappa\,(\kappa C^{(n)}\text{-extendible}))\rightarrow \mathrm{Con}(\mathrm{ZFC}+\Gamma_n).\end{align*} $$
In particular, for every
$n\geq 3$
$$ \begin{align*}\mathrm{Con}(\mathrm{ZFC}+\exists \kappa\,(\kappa C^{(n)}\text{-extendible}))\rightarrow \mathrm{Con}(\mathrm{ZFC}+\Gamma^{\star}_n).\end{align*} $$
Proof. The first claim follows automatically from Theorem 1.3. For the second claim it will suffice to show that the existence of a
$C^{(n)}$
-extendible cardinal entails the existence of an extendible cardinal above. Indeed, let
$\kappa $
be a
$C^{(n)}$
-extendible and notice that for every
$\alpha <\kappa $
the formula
$\varphi (\alpha )$
$$ \begin{align*}\text{``}\exists\beta\,(\beta>\alpha\,\wedge\,\beta\,\text{extendible}\,)\text{''}\end{align*} $$
is true and
$\Sigma _4$
, hence,
$V_{\kappa }\models \text {``} \forall \alpha \,\varphi (\alpha )\text {''}$
. Since
$C^{(n)}$
-extendible cardinals are
$C^{(5)}$
-correct (see e.g. [Reference Bagaria3]), the formula
$\text {``}\forall \alpha \,\varphi (\alpha )\text {''}$
is already true and thus there is a proper class of extendible cardinals in the universe. ⊣
Remark 3.13. New results due to the third author have pointed out that any
$C^{(n)}$
-extendible cardinal is a limit of
$C^{(n)}$
-supercompact. In particular, the second claim of the corollary is already true for any
$n\geq 1$
.
At the light of Theorem 1.3 the identity crises for
$C^{(n)}$
-supercompact cardinals turns to be a plausible scenario. One may even ask if this result may be strengthened or, more particularly, if the ultimate identity crises for
$C^{(n)}$
-supercompact cardinals is consistent; namely, provided it exists, if the first
$C^{(n)}$
-supercompact cardinal, for each
$n\geq 1$
, can be the first (
$\omega _1$
)-strongly compact cardinal. On this respect, the natural large cardinal hypothesis to start with is the existence of a
$C^{(<\omega )}$
-extendible cardinal: namely, a cardinal
$\kappa $
which is
$C^{(n)}$
-extendible, for each
$n\geq 1$
. Notice however that, by Tarski’s theorem of undefinability of truth, the existence of such cardinals cannot be expressed by a first order formula but via a countable schema of first order formulae. Let
$\textbf {k}$
be a constant symbol and consider the language of set theory augmented with it,
$\mathcal {L}=\{\in ,\textbf {k}\}$
.
Definition 3.14. We will denote by
$C^{(<\omega )}-\mathrm {EXT}$
the countable schema of first order formulae asserting that for each (meta-theoretic)
$n\in \omega $
the
$\mathcal {L}$
-formula “
$\textbf {k}$
is
$C^{(n)}$
-extendible” holds. If
$\mathfrak {M}=\langle M,\in ,x\rangle $
is a
$\mathcal {L}$
-structure, we agree that the interpretation of the constant symbol
$\textbf {k}$
is x. We will write
$\mathfrak {M}\models C^{(<\omega )}-\mathrm {EXT}$
if for every (meta-theoretic)
$n\in \omega $
the formula “
$\mathfrak {M}\models \textbf {k}$
is
$C^{(n)}$
-extendible” is true. We will also denote by
$\mathrm {ZFC}^{\star }$
the version of all
$\mathrm {ZFC}\,$
axioms where we allow a constant symbol
$\textbf {k}$
to be used in any instance of axioms of replacement and separation.
Definition 3.15.
$C^{(<\omega )}$
-extendible cardinal
Let
$\kappa $
be a cardinal and
$\mathfrak {M}=\langle {M,\in , \kappa} \rangle $
be a
$\mathcal {L}$
-structure. We will say that
$\kappa $
is
$\mathfrak {M}$
-
$C^{(<\omega )}$
-extendible if
$\mathfrak {M}\models C^{(<\omega )}-\mathrm {EXT}$
. If
$\mathfrak {M}=\langle V, \in , \kappa \rangle $
we will simply say that
$\kappa $
is
$C^{(<\omega )}$
-extendible.
In a analogous way, we can define the schema
$C^{(<\omega )}-\mathrm {SUP}$
for the intended notion of
$C^{(<\omega )}$
-supercompactness. Let
$\mathfrak {C}^{(<\omega )}$
and
$\mathfrak {S}^{(<\omega )}$
denote the class of
$C^{(<\omega )}$
-extendible and
$C^{(<\omega )}$
-supercompact cardinals, respectively.
By results of Bagaria [Reference Bagaria3], the schema
$C^{(<\omega )}-\mathrm {EXT}$
implies that Vopěnka Principle holds. Recall that given
$\kappa <\lambda $
the cardinal
$\kappa $
is called
$\lambda $
-superhuge if there is an elementary embedding
$j:V\rightarrow M$
such that
$\mathrm {crit}(j)=\kappa $
,
$j(\kappa )>\lambda $
and
$M^{j(\kappa )}\subseteq M$
. If
$\kappa $
is
$\lambda $
-superhuge for each
$\lambda>\kappa $
, the cardinal
$\kappa $
is called superhuge. If we are given a cardinal
$\theta $
, we will say that
$\theta $
is a target of
$\kappa $
(
$\kappa \rightarrow (\theta )$
) when there is some ordinal
$\lambda>\kappa $
and some
$\lambda $
-superhuge embedding
$j: V\rightarrow M$
such that
$j(\kappa )=\theta $
. It is known that if
$\kappa $
is superhuge then the collection of all of its targets is a proper class.
In [Reference Barbanel, Diprisco and Tan9] the authors introduced an strengthening of the classical notion of superhugness. A cardinal
$\kappa $
is stationarily superhuge if its collection of targets forms a stationary proper class.Footnote
11
Since for every
$n\in \omega $
the class
$C^{(n)}$
is a club class it is obvious that any model with an stationarily superhuge cardinal
$\kappa $
satisfies the schema
$C^{(<\omega )}-\mathrm {EXT}$
as witnessed by
$\kappa $
. As pointed out in theorem 6b of the aforementioned paper, the consistency strenght of a stationarily superhuge cardinal is below the consistency of a
$2$
-huge cardinal. Therefore the consistency strength of the schema
$C^{(<\omega )}-\mathrm {EXT}$
is bounded below by
$\mathrm {VP}\,$
and above by the existence of a
$2$
-huge cardinal.
Let
$\kappa $
be a
$C^{(<\omega )}$
-extendible cardinal. By Tsaprounis’ result [Reference Tsaprounis21], for each
$n\geq 1$
there is a
$\mathfrak {E}^{(n)}$
-fast function
$\ell _n:\kappa \rightarrow \kappa $
in V. Notice that
$V_{\kappa } \prec V$
and thus one can define those functions uniformly in
$V_{\kappa + 1}$
, so the function
$\ell = \sup \ell _n$
is a member of V. Arguing as in Theorem 1.3 the ultimate identity crises theorem follows:
Theorem 3.16. Let
$\langle V,\in ,\kappa \rangle $
be a model of (a large enough fragment of)
$\mathrm {ZFC}^{\star }$
plus
$C^{(<\omega )}-\mathrm {EXT}$
. Then in the generic extension
$V^{\mathbb {M}}$
the chain of relations
$$ \begin{align*}\min\mathfrak{M}<\min\mathfrak{K}_{\omega_1}=\min\mathfrak{K}=\min\mathfrak{S}=\min \mathfrak{S}^{(<\omega)}<\min\mathfrak{E}\end{align*} $$
holds.
This immediately yields the following corollary:
Corollary 3.17.
$$\begin{align*}\mathrm{Con}(\mathrm{ZFC}+\exists\,\kappa\,(\kappa\text{ is }2\text{-huge}))\rightarrow \mathrm{Con}(\mathrm{ZFC}+\Xi)\end{align*}$$
where
$\Xi $
is the scheme
$$\begin{align*}\min \mathfrak {M}<\min \mathfrak {K}_{\omega _1}=\min \mathfrak {K}=\min \mathfrak {S}=\min \mathfrak {S}^{(<\omega )}<\min \mathfrak {E}.\end{align*}$$
4 A summary of what is known
In the present section we shall briefly summarize all the known consistency relations between the classes of supercompact,
$C^{(n)}$
-supercompact and
$C^{(n)}$
-extendible cardinals. Similarly to the classical Magidor’s-like analysis of supercompact cardinals in this setting there are also two critical scenarios: the first one corresponding to the identity crises phenomenon discussed in previous sections and the second one where the expected hierarchic relations between large cardinals hold.
As pointed out earlier, the case of
$C^{(n)}$
-extendible cardinals is paradigmatic in the sense that they are not affected by the identity crises pathology. In other words, the class of
$C^{(n)}$
-extendibles is ordered hierarchically and thus its configuration fits within the second paradigm of the universe described so far. Nonetheless the situation with respect to
$C^{(n)}$
-supercompact cardinals may be completely different by virtue of Theorems 1.3 and 1.5. Specifically, we have shown that an extreme identity crises for these classes of cardinals is possible by making the first
$C^{(<\omega )}$
-supercompact cardinal the first (
$\omega _1$
-)strongly compact cardinal.
Recent investigations of the third author have brought to light that the antagonistic scenario is also possible under the assumption of a new axiom suggested by H. Woodin [Reference Poveda15].
Axiom 1. (Woodin's Extender Embedding Axiom (WEEA))
Let
$j:V \to M$
be an elementary embedding with critical point
$\kappa $
such that
$j(\kappa )$
is a limit cardinal and such that M is closed under
$\omega $
-sequences. Then
$\kappa $
is
$j(\kappa )$
-superstrong. Thus, the rest of the line should be erase
$V_{j(\kappa )}\subseteq M$
.
The point for EEA is that under this axiom the configuration of the different classes
$\mathfrak {S}^{(n)}$
coincide with the standard ordering pattern of the large cardinal hierarchy:
Theorem 4.1. (see [Reference Poveda15])
Assume WEEA. Then the following clauses hold:
-
1. For each
$n\geq 1$
, the class of
$C^{(n)}$
-supercompact cardinal is included in
$C^{(n+2)}$
.Footnote
12
-
2. For each
$n\geq 1$
, “
$\min \mathfrak {S}<\min \mathfrak {S}^{(n)}<\min \mathfrak {E}^{(n)}<\min \mathfrak {S}^{(n+1)}$
” holds.
It is worth to emphasize that the inequality “
$\min \mathfrak {S}^{(n)}<\min \mathfrak {E}^{(n)}$
” is proved without need of WEEA, though. Altogether, it seems that WEEA is the right axiom one has to consider to force the universe to have the expected configuration in the section of the large cardinal hierarchy ranging between the first supercompact cardinal and
$\mathrm {VP}\,$
. Therefore it turns out that a central issue for the study of such cardinals is to clarify the status of WEEA modulo large cardinals: namely if it is already consistent. On this respect the present paper has implicitly made some steps towards solving this issue. More precisely, at the light of theorem 4.1, WEEA can not coexists with the identity crises phenomenon and thus it must fails in the model discussed in the previous section.
5 Open Questions and concluding remarks
We would like to conclude the present paper exposing certain questions of combinatorial flavour that remain open. Broadly speaking we are interested to answer, with the most possible generality, the following question:
Question 4. What can be said about the combinatorics of V under the existence of
$C^{(n)}$
-supercompact cardinals?
Unlike supercompact cardinals it does not seem evident how to develop a theory that studies the consequences of
$C^{(n)}$
-supercompact cardinals on the combinatorics of V. In the context of supercompact cardinal this project has been carried out successfully, mainly by means of the method of forcing, yielding to a rich and vast theory. There are many paradigmatic examples on this respect but one of the most important is Laver’s theorem of indestructibility of supercompact cardinals by
$\kappa $
-directed closed forcing [Reference Laver14]. Speaking in general, Laver’s result shows that supercompactness is a robust notion with respect to a wide family of (set) forcings where one can find
$\mathrm {Add}(\kappa ,\lambda )$
among many others. In particular, Laver’s theorem shows that supercompactness is consistent with any prescribed behaviour of the power set function on
$\kappa $
.Footnote
13
The moral here is that one can get relevant information about the combinatorics of V from the robustness of supercompactness.
Nevertheless, this does not seem to be the case for the class of
$C^{(n)}$
-supercompact cardinals. For instance, as commented in former sections, it is not evident whether these cardinals carry
$\mathfrak {S}^{(n)}$
-fast functions and thus one can not naively adapt Laver’s indestructibility arguments to this new setting. In fact Theorem 4.1 indicates that under EEA any
$C^{(n)}$
-supercompact cardinal is a
$C^{(n+2)}$
-cardinal hence no indestructibility result is available for such cardinals [Reference Bagaria, Hamkins, Tsaprounis and Usuba5]. This suggest the following question:
Question 5. Let
$\kappa $
be a
$C^{(n)}$
-supercompact cardinal. What kind of forcings preserve the
$C^{(n)}$
-supercompactnes of
$\kappa $
? For instance, is it possible to add many Cohen susbsets to
$\kappa $
while preserving its
$C^{(n)}$
-supercompactness?
In the next lines we will give an outline of the main difficulties one faces up with discussing the interplay of forcing with
$C^{(n)}$
-supercompact cardinals. Speaking in general, for any given forcing there are two standard ways to proceed on this respect: either analysing under which hypothesis the corresponding embeddings may be lifted or how can one define extenders witnessing the
$C^{(n)}$
-supercompactness of
$\kappa $
in the generic extension. In the next lines we shall try to argue that any of both strategies seem non trivial to implement.
Let
$\mathbb {P}$
be a forcing notion,
$G\subseteq \mathbb {P}$
a generic filter,
$\lambda>\kappa $
be an arbitrary cardinal and
$j:V\rightarrow M$
be an elementary embedding witnessing the
$\lambda $
-
$C^{(n)}$
-supercompactness of
$\kappa $
. The strategies previously commented may be phrased in the following terms:
-
$\diamondsuit $
Lifting strategy: Lift j to
$j^*$
witnessing the
$\lambda $
-
$C^{(n)}$
-supercompactness of
$\kappa $
in
$V[G]$
.
-
$\diamondsuit $
Extender strategy: Use j to define in
$V[G]$
an extender E such that
$j_E: V[G]\rightarrow M$
witnesses the
$\lambda $
-
$C^{(n)}$
-supercompactness of
$\kappa $
(see section 5 of [Reference Bagaria3] for details).
Notice that regardless of the strategy the cardinal
$j(\kappa )$
remains in the class
$(C^{(n)})^{V[G]}$
since the forcing
$\mathbb {P}$
is mild.
5.1 Lifting strategy
If
$\mathbb {P}$
is a
$\kappa $
-Easton support iteration of forcings within
$V_{\kappa }$
it is not hard to show that j lifts to
$j^*:V[G]\rightarrow M[G\ast H]$
, where
$H\subseteq j(\mathbb {P})/\mathbb {P}$
is generic over
$M[G]$
. Furthermore, with a bit of care, one may make sure that
$M[G\ast H]^{\lambda }\subseteq M[G\ast H]$
.Footnote
14
Thereby the main issue here is how to ensure that
$j^*$
is definable in
$V[G]$
or, in other words, that the
$M[G]$
-generic filter H lies in
$V[G]$
. There are specific situations where one can argue on this direction; for instance, using a diagonalization argument as in Proposition 8.1 of [Reference Cummings10] or appealing to the distributiviness of the tail forcing
$j(\mathbb {P})/\mathbb {P}$
as in Lemma 3.5 in [Reference Tsaprounis17]. Nonetheless both arguments rely in the fact that whilst
$j(\kappa )$
is very large in M it is small in V. It is clear that this is never the case for
$C^{(n)}$
-supercompact cardinals.
Consequently the Lifting strategy amounts to building definable generics for
$j(\mathbb {P})/\mathbb {P}$
which suggests that one has to be able to handmade generics for
$j(\mathbb {P})/\mathbb {P}$
. Notice that this is precisely the procedure we have followed in the proof of Theorem 1.3.
5.2 Extender strategy
This strategy is used for instance in Proposition 2.7 or Lemma 6.4 of [Reference Gitik12]. Assume
$\mathbb {P}$
is a forcing
$\kappa $
-iteration of forcings within
$V_{\kappa }$
with a close enough tail forcing
$j(\mathbb {P})/\mathbb {P}$
. Lift j to
$j^{\star }: V[G]\rightarrow M[G\ast H]$
as before and afterwards define E to be the potential extender derived from
$j^*$
. More precisely, set
$E=\langle E_a:\,a\in [\eta ]^{<\omega } \rangle $
as
$$ \begin{align*}(\star)\;\;\;X\in E_a\;\longleftrightarrow\;\exists p\in G\,\exists q\leq j (p)\setminus\kappa, \; p\frown q\Vdash_{j(\mathbb{P})} \dot{a}\in j(\dot{X})\end{align*} $$
where
$\dot {a},\dot {X}$
are
$\mathbb {P}$
-names and
$\eta $
is some ordinal. Here the closedness of the tail is used to argue that
$E\in V[G]$
.
As it is shown in [Reference Gitik12] if
$\mathbb {P}$
is a suitable Prikry-type iteration and the order relation appearing in
$(\star )$
is
$\leq ^{\star }$
then
$E_a$
is a
$\kappa $
-complete normal measure, each
$a\in [\eta ]^{<\omega }$
. The main issue here thus is not related with the definability of the extender nor with its combinatorial properties but with
$j_E(\kappa )$
. Notice that we have to make sure that
$j_E(\kappa )$
is a
$C^{(n)}$
-cardinal in
$V[G]$
and thus it is natural to ask whether
$j_E(\kappa )=j(\kappa )$
. Nonetheless this technical point seems very hard to fulfil due to the generic definition of E. In summary, the Extender strategy amounts to finding extenders E such that
$j_E(\kappa )=j(\kappa )$
.
Acknowledgments
The present paper has been prepared during a research stay of the third author in the Einstein Institute of Mathematics at the Hebrew University of Jerusalem. The third author wants to express his gratitude to professor S. Shelah for his kindness for inviting him and to professors J. Bagaria, W. H. Woodin and M. Gitik for many illuminating discussions on the matter. In the same way, the third author extends his gratitude to the Einstein Institute of Mathematics for his warmly hospitality during his stay. The authors also thank the anonymous referee for helpful comments on prelimminary versions of this paper.
The third author has been supported by MECD (Spanish Government) Grant no FPU15/00026, MEC project number MTM2017-86777-P and SGR (Catalan Government) project number 2017SGR-270.
