3.1 Surface waves

The spiralling surface waves provide the initial condition of the formation and bursting of the root vortex. The surface waves are organized and start a domino effect of the fluid dynamics, namely, air entrainment, vortex formation, bursting, bubble formation in two sizes and the apportioning of entrainment between the vortex core and the suction side of the foil, which in turn affects the proportions of the coarse and fine bubbles formed. The detailed results are given in A.2 Surface waves (A.2.1 Transient divergence waves; A.2.2 Capillary waves) in SI-TA. An overview is given below.

3.2 Bursting of the ‘disturbed-laminar’ contra-rotating double helix root vortex

Figure 2 shows an aerated DH of contra-rotating vortices of the DL type at $f=1.0~\text{Hz}$. While winding, first it inclines exactly to $45^{\circ }$ to the vertical ($\unicode[STIX]{x1D6FD}$) in panel (1), the pointed apex being buckled by compression load $P_{c}$. In (2), barely higher than $45^{\circ }$, it starts to unwind, spreading immediately laterally in the inner half, but collapsing in the outer half. In (3), it contracts laterally, disintegrating into bubbles. In (2), the pitching motion has removed the foil obstruction in (1). The vortex motion correlates with the axial adverse and favourable pressure gradients imposed by the pitching motion. Measuring from the vertical, the vortex slant increases while the length of the vortex increases between (1) and (2) indicating vortex stretching. There are two stages of bursting: an unwinding and a disintegration into bubbles. Each correlates with the relaxation of the stretching. Comparison of (1) and (2) shows that the sudden vortex relaxation produces amplified vertical oscillations of the free surface. This oscillation occurs prior to the disintegration into bubbles in (3). There is a time delay between the vortex oscillation when released from stretching and the disintegration into bubbles. The vertical oscillation is spread over an axial length of $\unicode[STIX]{x1D706}$, the DH wavelength. The vertical oscillation of the free surface is evidence of vortex oscillation when released of stretching. A monochromatic compression and rarefaction wave train will be produced.

The DH originates from the necklace vortex around the stem (figure 3). Out of the two branches, one dominates (Movie 2). The DH mode does not rotate after unwinding when the effect of pitching is no longer present. It is discussed later that the vortex stretching reaches the maximum value at $\unicode[STIX]{x1D6FD}=45^{\circ }$. The vortex is stable for $\unicode[STIX]{x1D6FD}\leqslant 45^{\circ }$, but unstable for $\unicode[STIX]{x1D6FD}>45^{\circ }$. Here and later, the demarcation becomes clear by observing where the bubbles are rare and where there is a preponderance of bubbles, respectively.

The narrow tip of the vortex buckles under compression load $P_{c}$ (panel 1) because the compression stiffness exceeds the bending stiffness in the aerated elastic vortex. Using the grid on the foil surface, the helix pitch in (2) is ($\unicode[STIX]{x1D6FF}_{1}/2+2c/3$), and the helix spread is $2c/3$, where $c$ is the foil chord length and $\unicode[STIX]{x1D6FF}_{1}$ is the foil stem diameter (see the inset (figure 2(4)) in figure 2(2)). The helix spread is zero in the outer half in (2) where the bursting has commenced. The bursting spreads later to the inner half in (3) where the helix spread is nearly zero. The foil pitches along the stem axis at a distance of $c/3$ from the foil leading edge. Hence, $2c/3$, the maximum pitch radius, is the length scale of the helical mode of the instability in the root vortex that is amplifying. The effective maximum blockage width is $2c/3$, not $c$ (see examples in figures SI-IA-2 and SI-IA-3). The unwound vortex bursts (panel (3) in figure 2) when the foil starts to increase the blockage again at $\unicode[STIX]{x1D719}=105^{\circ }$. The disintegration into bubbles proceeds from the tip of the helix to the foil root (figure SI-IA-4). The bubbles formed have low inertia and show a tendency to remain clustered along the DH. Some spherical bubbles are formed, but they remain coalesced and not fully separated.

The inset in figure 2(3) shows the schematic of the mechanism of bubble formation. The stretched vortex tube is observed as suddenly released. Standing spiralling waves of wavelength $\unicode[STIX]{x1D706}_{d}$ are produced. The red and blue arrows show waves rebounding from the opposite ends of the aerated vortex tube. Ringing bubbles of diameter $d$ are produced. Here, $c_{1}$ is the speed of sound in water. Later, it is shown that the vortex inclination rises from $0^{\circ }$ to $45^{\circ }$ when stretching and turbulence amplification are maximum. The sudden release of the maximally stretched vortex tubes produce three ringings of wavelength $\unicode[STIX]{x1D706}$, $\unicode[STIX]{x1D706}_{d}$ and $d$. Here, $\unicode[STIX]{x1D706}$ is the aerated DH wavelength, $\unicode[STIX]{x1D706}_{d}$ is the wavelength of the standing waves (see the inset in figure 2(3)), and $d$ is the bubble diameter. Since the vortices receive orthogonally oscillating inputs of torque and there are two preferred orthogonal directions of organization in the shear flow (Head & Bandyopadhyay Reference Head and Bandyopadhyay1981), the bubbles can be expected to undergo resonant oscillations. The synchronized vertical oscillation of the free surface is an evidence.

Write that the wavelength $\unicode[STIX]{x1D706}\propto d$ and its values are functions of $f$ (to be modelled later). We estimate that the DH wavelength $\unicode[STIX]{x1D706}=20d$–$30d$. One turn of the bubble gives $\unicode[STIX]{x1D706}_{d}=\unicode[STIX]{x03C0}d$. We get, $\unicode[STIX]{x1D706}=7\unicode[STIX]{x1D706}_{d}$ to $10\unicode[STIX]{x1D706}_{d}$. The inverse of the time scales $(\text{s}^{-1})$ are $c_{1}/\unicode[STIX]{x1D706}$, $c_{1}/\unicode[STIX]{x1D706}_{d}$ and $c_{1}/d$, where $c_{1}$ is the speed of sound in water, $1435~\text{m}~\text{s}^{-1}$. At $f=1~\text{Hz}$, $\unicode[STIX]{x1D706}=0.13~\text{m}$, $\unicode[STIX]{x1D706}_{d}=0.019{-}0.013~\text{m}$ and $d=0.006{-}0.004~\text{m}$. We expect spectral peaks of sound level at 11, 75 and 239–359 kHz. The lower range overlaps the buoy measurements in sea due to breaking surface waves (figure 1 in Nystuen Reference Nystuen2002). The measurements do not extend above 50 kHz. At $f=1.25~\text{Hz}$, the wavelengths and bubble diameter are smaller. The breaking wave sound measurements may be from the ringing of the aerated vortex tubes and the induced oscillations of the free surface and not from the bubbles. Buoy measurements above 50 kHz are needed. The mechanism of bubble formation from the bursting of the aerated root vortex may bear relevance to bubble formation due to breaking waves due to winds of $6{-}10~\text{m}~\text{s}^{-1}$. The upper limit of noise due to the collective oscillation of bubbles of the vortex tube is at least 11 kHz and not 1 kHz (Prosperetti Reference Prosperetti1988).

Figure 2(2) marks the location of vortex breakup where the opposing vorticities cross. Panel 3 shows that the fine bubble DH pattern from the foil is fusing with the main DH at the location of the vortex breakup. The fusing point is a vortex crossing point of the arms of the $\pm \unicode[STIX]{x1D6E4}$ DH ($\unicode[STIX]{x1D6E4}$ is circulation).

3.3 Synthesis of the motion of the ‘disturbed-laminar’ contra-rotating double helix root vortex

The physical processes in figure 2 are shown in figure 3. The streamlines, representing convection of vorticity, and the critical points (saddle points $S_{1,}$, $S_{2}$) for figure 2 are sketched in figure 3(a) (Baker Reference Baker1979; Chong, Perry & Cantwell Reference Chong, Perry and Cantwell1990). The upstream lateral vorticity bends to form two horseshoe vortices of size $c$ (figures 2, 4a, $f=1~\text{Hz}$) and $\unicode[STIX]{x1D6FF}_{1}$ (figure 4d1, $f=1.25~\text{Hz}$). Saddles like $S_{1,}$ are created. The right side of the figure shows the critical point of the cross-section of the dominant wound asymmetric horseshoe vortex in the near wake. The cross-section has saddle points ($S_{2}$) where stretching takes place amplifying turbulence. The vortex stretching is due to an axial velocity $U_{a}$ which is the $\unicode[STIX]{x1D6FD}$-component of $U_{ext}$ that creates the vertical shear in the wake (figure 3a, inset 2, and figure 3b; Bandyopadhyay Reference Bandyopadhyay1980).

Figure 4. Vortex slant $\unicode[STIX]{x1D6FD}$ increases to the angle of principal strain ($45^{\circ }$) when vortex stretching and turbulence amplification become maximum and the vortex bursts. (a) Examples of the maximum vortex stretching just prior to bursting; also see figure SI-IA-3 in SI. (b) Vortex slant at the time of (in 1), and after bursting (in 2). (c) The increasing slant $\unicode[STIX]{x1D6FD}$ of the root vortex before (in 1 to 3) and at the time of bursting (in 4) can be seen. (d) A multi pitch thin double helix grows and slants to $45^{\circ }$ in the time step of mere 0.03 s (1 and 2) and bursts (in 3). The acute angle subtended by the thin dotted lines represents a slant $\unicode[STIX]{x1D6FD}$ of $45^{\circ }$ to the vertical direction. The nominal external flow is left to right.

In a cylindrical gas–liquid separator (length $L$, diameter $D$) which has a tangential entrance and exit, an aerated core vortex is formed that stands. A rectilinear vortex spirals when the ratio $L/D=\unicode[STIX]{x03C0}$, $2\unicode[STIX]{x03C0}$ or $3\unicode[STIX]{x03C0}$ (see figure 3 in Bandyopadhyay & Gad-El-Hak Reference Bandyopadhyay and Gad-El-Hak1996). This positioning allows, between the ends, an axial spacing of $L/D=N\unicode[STIX]{x03C0}$, where $N$ is an integer $1,2,3,\ldots$ . The root vortex is anchored at the root and the other end experiences a compression, making the geometry essentially confined. Hence, the aerated root vortex is also standing. Assume $D$ is spiral diameter and vortex diameter $d_{v}$ is proportional to $D$. With increasing $Re$, if $L$ is constant, then, $N$ will increase with drop in spiral diameter $D$. Compare figures 9(b) and SI-IA-2 at $f=1~\text{Hz}$ with 4(d1) at $f=1.25~\text{Hz}$. For the similar cylindrical lengths of 8 cm, $D$ is 2 cm versus 1 cm, $N$ is 1 versus 2, respectively. The vortex diameter also drops with increasing $N$.

The aerated vortex has structural properties such as compression $(K_{c})$ and bending $(K_{b})$ stiffness. If $K_{c}>K_{b}$, the vortex will buckle. In both figures 2(1) and 6(b) the buckling moves toward the stable zone of $\unicode[STIX]{x1D6FD}\leqslant 45^{\circ }$. In figure 2(1), $f=1~\text{Hz}$ and the centrifugal force is lower and the buckling creates a zig-zag shape. However, in figure 6(b), $f=1.25~\text{Hz}$, the centrifugal force is higher and the buckling makes a toroid. The differences in buckling are due to differences in $K_{c}$ and $K_{b}$. The difference in fact proves that the vortex is an elastic structure. The example of the toroidal buckling for high centrifugal forces will be considered again later in figure 6(b2). The compression stiffness increases because surface tension acts to reduce the surface area of the vortex to counter the centrifugal force. At $f=1~\text{Hz}$, the root double spiral has one full turn (of the $\unicode[STIX]{x03C0}$-type) in figures 2, SI-IA-2 to SI-IA-4 and 9(b). At $f=1.25~\text{Hz}$, the number of full turns may be 2 (of the $2\unicode[STIX]{x03C0}$-type) in figure 4(c,d). Therefore, the apex of the vortex is a stagnation point for the wave to be standing. The vortex breakup at the apex is a stagnation point (Saffman Reference Saffman1990). We are seeing evidence of elasticity of an aerated vortex. Therefore, the root vortex is a standing vortex. Extending this result for increasing $N$, the standing DH appears as contra-rotating Taylor cells (see figure 9e,g).

The funnelling and entrainment of air along the stretched vortex axis are shown in figure 3. When the DH in (a) unwinds (b), the free surface oscillates vertically over an axial length of $\unicode[STIX]{x1D706}$, the wavelength of the unwound DH (figure 2(2)), radiating noise. The lateral oscillations of the vortex tube, that start when the vortex is suddenly released of the axial stretching, also oscillate the local air–water interface radially within the vortex tube to form the bubbles. In figure 2 between panels 2 and 3, the bubbles take 0.125 s to form after the onset of the oscillations of the interface. This time scale is a 40 Hz bubble oscillation if five damped oscillations are present as is common in spring, mass and damper analogues (Bandyopadhyay Reference Bandyopadhyay2019).

In figure 2(2), there is a narrowing where the two arms of the DH meet with vorticities ($\pm \unicode[STIX]{x1D714}$) that viscosity acts to cancel. The vortex breaks at this location (Saffman Reference Saffman1990). After the pitching blockage begins to relax at $\unicode[STIX]{x1D6FD}=45^{\circ }$, $\unicode[STIX]{x1D6FD}\rightarrow 90^{\circ }$, $(V_{\unicode[STIX]{x1D703}1},V_{\unicode[STIX]{x1D703}2},V_{\unicode[STIX]{x1D703}})\rightarrow 0$, $U_{a}\rightarrow U_{ext}$, and the vortex bursting, indicated by the turbulence of the bubbles, proceeds towards the root. How Kelvin waves produced at the tip initiate the bursting is shown later. The bubbles form in the air tubes when stretching is suddenly released.

Downstream of the intermittent turbulence patches, conical relaminarescent regions have also been reported in the so called ‘puffs’ of transitional pipe flows (Bandyopadhyay Reference Bandyopadhyay1986) and in the turbulent trailing vortex cores (Bandyopadhyay et al. Reference Bandyopadhyay, Riester and Ash1992) just as in the conical relaminarescent vortex tip in figure 2(2). It was shown in Bandyopadhyay et al. (Reference Bandyopadhyay, Riester and Ash1992) that the puff flow and the trailing vortex contain helical motions which certainly is the case in figure 2.

3.4 The $45^{\circ }$ vortex slant at the time of bursting

In figure 2(1) at $f=1~\text{Hz}$, the vortex slope $\unicode[STIX]{x1D6FD}$ was $45^{\circ }$. In figure 4, $f=1~\text{Hz}$ in (a,b) and 1.25 Hz in (c,d). Angle $\unicode[STIX]{x1D6FD}$ increases to $45^{\circ }$ until the root vortex bursts. In the examples from different cycles in figure 4(a1–a3), $\unicode[STIX]{x1D6FD}=45^{\circ }$. Such well-formed root vortices are not seen for $\unicode[STIX]{x1D6FD}>45^{\circ }$. In figure 4(b), the vortex is about to burst in (1), when still at $\unicode[STIX]{x1D6FD}=45^{\circ }$; but in (2), the vortex has burst and the slope $\unicode[STIX]{x1D6FD}>45^{\circ }$.

Figure 4(c) shows an example from the same vortex of the time sequence of increasing $\unicode[STIX]{x1D6FD}$ until bursting at $\unicode[STIX]{x1D6FD}=45^{\circ }$. Figure 4(c1) shows a small diameter DH wound to a nearly vertical cone at $f=1.25~\text{Hz}$. This vortex radially enlarges initially but without increasing $\unicode[STIX]{x1D6FD}$. Its slant increases in (3) while also enlarging. In (4), while still at $\unicode[STIX]{x1D6FD}=45^{\circ }$, the vortex has just burst. Figure 4(d) shows a long cylindrical DH of uniform diameter at $f=1.25~\text{Hz}$ at a shallow angle of $\unicode[STIX]{x1D6FD}$ in (1), rising to $45^{\circ }$ in (2) and bursting in (3). In (c), the starting DH is conical and shorter in length. There are more modes of DH at the root at $f=1.25~\text{Hz}$.

The root vortex slant $\unicode[STIX]{x1D6FD}$ increases to $45^{\circ }$ when bursting occurs (figures 4, 6 and 7). The slanting of the Taylor tubes (figure 9) are close to $45^{\circ }$ without much variation. In figure 4(c,d), the Taylor tube slanting approach $45^{\circ }$ before the root vortex axis does. The vortex tubes of the foil-tip flow reach a straight slant of $45^{\circ }$ to the external stream (figure 11). The knotting of the tip of the DH in the final stages of bursting is also into a cone of $45^{\circ }$, slanted at $45^{\circ }$ (figure 7(a6), (a7), (b3)). There is a wide prevalence of the $45^{\circ }$ slant of the vortex tubes just prior to bursting.

The vortex inclinations of $45^{\circ }$ have been visualized in a wide range of $Re$ in turbulent boundary layers by Head & Bandyopadhyay (Reference Head and Bandyopadhyay1981), confirmed by particle image velocimetry by Adrian, Meinhart & Tomkins (Reference Adrian, Meinhart and Tomkins2000) and also by direct numerical simulation at low Reynolds numbers by Wu & Moin (Reference Wu and Moin2009).

Consider a parallel shear flow invariant with distance. Concentrations of vorticity can appear only when a periodic disturbance is superimposed. As per Theodorsen’s thesis (Reference Theodorsen1952), these concentrations of vorticity will die down unless there is some existing three-dimensionality. If the flow is three-dimensional, and some vorticity is present, turbulence can be produced from the vorticity only if it is stretched. In a turbulent boundary layer, which happens to be three-dimensional, Theodorsen (Reference Theodorsen1952) predicted the appearance of horseshoe vortices at $45^{\circ }$. These arguments apply in the present case.

The three-dimensionality introduces a term $\unicode[STIX]{x1D714}_{i}\unicode[STIX]{x1D714}_{j}\unicode[STIX]{x2202}u_{i}/\unicode[STIX]{x2202}x_{j}$ in the vorticity equation which implicitly expresses the effects of stretching which must precede and accompany the production of turbulence (Head & Bandyopadhyay Reference Head and Bandyopadhyay1981). Multiplying the vorticity equation by $\unicode[STIX]{x1D714}$, a vector in ($x,y,z$), in tensor notation, we get $\text{D}/\text{D}t[1/2\unicode[STIX]{x1D714}_{i}\unicode[STIX]{x1D714}_{i}]=\unicode[STIX]{x1D714}_{i}\unicode[STIX]{x1D714}_{j}\unicode[STIX]{x2202}u_{i}/\unicode[STIX]{x2202}x_{j}+\unicode[STIX]{x1D714}_{i}\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D714}_{i}$, where $\unicode[STIX]{x1D708}$ is kinematic viscosity. If the vorticity vectors in a concentration of vorticity are ($\unicode[STIX]{x1D714}_{x},\unicode[STIX]{x1D714}_{y},\unicode[STIX]{x1D714}_{z}$), since $\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}y$ is greater than any other component, the stretching term is approximated to $\unicode[STIX]{x1D714}_{x}\unicode[STIX]{x1D714}_{y}\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}y$. This term will be a maximum when the component of the vorticity vector in the ($x,y$) plane is at $45^{\circ }$ to the main flow direction. In a horizontal shear flow, the downstream angle of $45^{\circ }$ represents the direction of principal axis along which the strain is of pure extension and the rate of stretching is at maximum. The abrupt drop in the external velocity when the foil blockage is removed eliminates the term $\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}y$ making the stretching term vanish in the vortex tubes. This event produces axial and radial waves in the tubes precipitating the bursting and bubble formation.

Significantly, in four sets of examples of the present work, the varieties of vortices have this inclination of $45^{\circ }$ to the external flow just prior to bursting. The root vortex slope $\unicode[STIX]{x1D6FD}$ is given by the opposing effects of axial stretching on the induced velocity and the external shear. See Bandyopadhyay (Reference Bandyopadhyay1980), where this balance accurately gives the slope of the arrays of vortices formed sequentially in a turbulent boundary layer large structure. The velocity balance is shown in figure 3(a, inset 2). The wall-normal shear tries to rotate the horseshoe vortex in the boundary layer back, parallel to the wall (see figure 33 in Head & Bandyopadhyay Reference Head and Bandyopadhyay1981). Similarly, in the present flow, the direct effect of the shear tries to rotate the root vortex horizontally along the flow direction near the free surface. As $\unicode[STIX]{x1D6FD}$ increases from $0^{\circ }$ to $45^{\circ }$, the stretching increases to the maximum value. The increased induced velocity then resists the direct effect of the shear exactly. At $\unicode[STIX]{x1D6FD}=45^{\circ }$, the vortex is in neutral equilibrium. It is sensitive to disturbances and is prone to breakdown. The root vortex therefore is stable in the range $0\leqslant \unicode[STIX]{x1D6FD}\leqslant 45^{\circ }$. However, for $45^{\circ }<\unicode[STIX]{x1D6FD}<90^{\circ }$, the stretching drops and there is nothing to resist the shear whereby $\unicode[STIX]{x1D6FD}$ rapidly approaches $90^{\circ }$ (figure SI-IA-4). In support of this argument, we do see a preponderance of pre-burst root vortices for $0\leqslant \unicode[STIX]{x1D6FD}\leqslant 45^{\circ }$, but no pre-burst vortex is seen at $45^{\circ }<\unicode[STIX]{x1D6FD}<90^{\circ }$. Since bubbles can form only where the vortex is unstable, they are confined to $45^{\circ }<\unicode[STIX]{x1D6FD}<90^{\circ }$ and virtually none will appear where 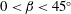$0<\unicode[STIX]{x1D6FD}<45^{\circ }$. The regions where $\unicode[STIX]{x1D6FD}$ is stable and unstable are shown schematically in figure 3(a). The statement on the relationship of bubble formation and vortex instability is confirmed in figures 6(b) and 8(b–d).

Figure 6(d) and Movie 3 at a time stamp of 01:58 (m:s) show that a single coiled vortex, marked V, migrates on the pressure side after formation, shown in panel (1). It shows up over the leading edge from the pressure side in panel (4), stretching at $45^{\circ }$ in (5). The pressure side vortex V bursts at the same time as the suction side root vortex. Here also, the $45^{\circ }$ slope demarcation of stability exists and the unstable zone is complementary. The movie shows that, over time, the $45^{\circ }$ unstable front of the coarse bubble filled region over the foil coming from the pressure side, advances diagonally upward and right toward the standing lower edge of the unstable region of the root vortex closing the bubble-free alleyway shown in figure 6(b2). In this manner, the advancing unstable region of the pressure side joins up with that of the suction side obliterating the intervening stable region. Finally, one could also argue conversely that since the bubbles are formed only in certain triangular sectors, the vortex must be unstable only there.

3.5 Modelling of the nonlinear vortex lift of the root vortex

Figure 5 draws an analogy between the delta-wing high lift leading edge vortex and the root vortex. Both are produced by salient edge separation. The lift producing the root vortex is estimated in the following manner. The hydrostatic pressure $p$ increases with depth $y$. Therefore, the vortex grows axially in an adverse pressure gradient $\unicode[STIX]{x2202}p/\unicode[STIX]{x2202}y>0$, the depth acting like a diffuser. The vortex bursting experiments by Sarpkaya (Reference Sarpkaya1995) and the Kelvin wave vortex experiments by Tsoy et al. (Reference Tsoy, Skripkin, Kuibin, Shtork and Alekseenko2018) have been carried out in small angle diffusers. While pitching up or down in continuously pitching delta wings, the bursting occurs farther back or forward compared to the steady case, respectively. There is hysteresis in the measurements of lift compared to the steady state case (Heron & Myose Reference Heron and Myose2009). The unsteady measurements of lift force in a flapping foil in the absence of any air entrainment show a similar hysteresis with quasi-steady models (figure 7 in Bandyopadhyay et al. Reference Bandyopadhyay, Beal and Menozzi2008a). For these similarities, as shown in figure 5, an analogy is drawn between the root vortex and the leading edge vortex of an asymmetric delta wing with salient leading edges. The vortex in the inset in figure 5 is from figure 2(1).

Figure 5. Modelling of the root vortex lift based on the analogy of delta wing vortex lift. Inset 1: pre-bursting root vortex in figure 2(1) superimposed on the schematic of the delta wing leading edge vortex. Inset 2: quasi-steady model and measurements showing nonlinear vortex lift $C_{LV}$ (Bandyopadhyay et al. Reference Bandyopadhyay, Beal and Menozzi2008a).

The vortex lift model makes no distinction between the DL and the turbulent root vortices. The root vortex is generally conical with the apex pointing diagonally downward. Since the foil input torque does not change cycle to cycle, the lift values are assumed to be similar to those modelled here. Measurements on flapping foils show that lift force coefficient $C_{L}\propto \,f^{2}$ (Menozzi et al. Reference Menozzi, Leinhos, Beal and Bandyopadhyay2008). Equation (2.6) is used to model the linear and nonlinear components of the force, the variation with $\unicode[STIX]{x1D6FD}$, and the nonlinear vortex lift just prior to bursting when $\unicode[STIX]{x1D6FD}=45^{\circ }$.

Unsteady lift measurements in flapping foils can be modelled by assuming the flow to be quasi-steady (Bandyopadhyay et al. Reference Bandyopadhyay, Beal and Menozzi2008a). Define the aspect ratio $(A)$ of a delta wing as $b^{2}/a_{w}$, where $b$ is the wing span and $a_{w}$ is the wing area. Theory and measurements of lift forces in steady delta wings in figure 12 in Polhamus (Reference Polhamus1966) show that the vortex lift in a delta wing is a function of $A$ and the AOA $\unicode[STIX]{x1D6FD}$. Consider using equation (2.6), where the total lift $C_{L}=C_{LP}+C_{LV}$ where $C_{LP}$ is the linear part of wing lift obtained by potential flow method and $C_{LV}$ is the vortex lift component, which is nonlinear. See inset 2 in figure 5. For $A\rightarrow 0$, $C_{LV}\rightarrow 0$ and $C_{L}\rightarrow C_{LP}$. To make the vortex predominantly one sided, the delta wing in figure 5 is shown asymmetric, since smaller values of $A$ produce lower values of lift. We assume that the asymmetry is large and the entire lift force can be attributed to just one edge. It is assumed that the vortex slant is the same as the angle of attack of the delta wing. The maximum value of $C_{L}$ and $C_{LP}$ at an angle of attack, say $\unicode[STIX]{x1D6FD}$ of $25^{\circ }$, increases with $A$. But $C_{LV}$ does not change much between the $A$ values at the same AOA. The difference is understandable because the nonlinear vortex lift is not produced by the foil area. It is produced by the salient edge and $\unicode[STIX]{x1D6FD}$. The potential flow lift is produced by the source–sink distributions over $A$ and $\unicode[STIX]{x1D6FD}$. For example, at $A=0.5$ and $\unicode[STIX]{x1D6FD}=25^{\circ }$, $C_{L}=0.7$ and $C_{LP}=0.24$, giving $C_{LV}=0.46$. At $A=1.5$ and $\unicode[STIX]{x1D6FD}=25^{\circ }$, $C_{L}=1.1$ and $C_{LP}=0.62$ giving $C_{LV}=0.48$. Hence $C_{LV}$ trend with $A$ and $\unicode[STIX]{x1D6FD}$ is universal: $C_{LV}$ increases with $\unicode[STIX]{x1D6FD}$, but is independent of $A$.

The value of $A$ determines $C_{L}$, $C_{LP}$ and $C_{LV}$. In figure 6(a1), $b=c$ and $a_{w}=c^{2}$, giving $A=1.0$. For $\unicode[STIX]{x1D6FD}=15^{\circ }$, $C_{L}=0.5$, $C_{LP}=0.35$, giving $C_{LV}=0.15$. For $\unicode[STIX]{x1D6FD}=25^{\circ }$, $C_{L}=0.90$ and $C_{LP}=0.45$, giving $C_{LV}=0.45$. The vortex lift due to the root vortex in figure 6(a1) is then 0.45 – the linear and nonlinear components of lift are the same. When entrainment is prevented, these values are close to our unsteady flapping foil lift measurements (figure 9 in Bandyopadhyay et al. Reference Bandyopadhyay, Beal and Menozzi2008a). Hence, to estimate $C_{LV}$ alone, figure 9 in Bandyopadhyay et al. (Reference Bandyopadhyay, Beal and Menozzi2008a) may be used since the present apparatus uses the same flapping foil and the delta wing analogy need not be invoked. The suction lift analogy gives the origin of the root vortex a theoretical foundation and helps to isolate the origins of the linear and nonlinear lift forces.

Figure 6. Sets of three images each of two examples of turbulent vortex bursting (a,b) and the schematic (c) of variations in velocity profiles across the vortex axis from jet to wake with changes in blockage. Panels b1 and b2: rotational effect (marking a to b); panels a2, a3 and b3: $45^{\circ }$ slope shows maximum axial stretching. The tiny aerated Taylor cells in the root vortex are normal to the $25^{\circ }$ slope in a1, and normal to the $45^{\circ }$ slope in b1 and in figure 9(e). (d) Sequence of successive frames explaining how the compact vortex in (b) is formed from the stretching and relieving of the trailing edge vertically coiled vortex in panel (5); also shows the migration of the vortex V in the pressure side. In (a), relative phase of $\unicode[STIX]{x1D719}=(1)~0^{\circ }$, (2) $30^{\circ }$, (3) $60^{\circ }$. In (b), relative phase of $\unicode[STIX]{x1D719}=(1)~0^{\circ }$, (2) $76.5^{\circ }$, (3) $135^{\circ }$. Foil parameters are $\unicode[STIX]{x1D719}_{o}=40^{\circ }$, $\unicode[STIX]{x1D703}_{o}=45^{\circ }$, $\unicode[STIX]{x1D703}_{to}=75^{\circ }$, $f=1.25~\text{Hz}$, $\unicode[STIX]{x1D713}=90^{\circ }$.

As per the measurements in figure 9 of Bandyopadhyay et al. (Reference Bandyopadhyay, Beal and Menozzi2008a), the nonlinear vortex lift in the root vortex of 1.0 would be achievable at $\unicode[STIX]{x1D6FD}=45^{\circ }$ when the vortex is about to burst. In figure 6(a), $\unicode[STIX]{x1D6FD}=25^{\circ }$ at vortex formation and $\unicode[STIX]{x1D6FD}=45^{\circ }$ at bursting, being horizontal after bursting.

Figure 9 in Bandyopadhyay et al. (Reference Bandyopadhyay, Beal and Menozzi2008a) shows that the scatter in the lift measurements is higher at AOA of $45^{\circ }$ and $-45^{\circ }$ and negligible at other AOA. The $\unicode[STIX]{x1D6FD}=45^{\circ }$ slope of the root vortex, which is the boundary of the stable and the unstable postures, is a neutral equilibrium posture, and cannot be held there for long. Angle $\unicode[STIX]{x1D6FD}$ increases rapidly after $45^{\circ }$ because shear rotation is not counteracted.

The ‘reattachment lines’ ($R_{1}$ and $R_{2}$) of the wound vortices shown in figure 5 would be saddles assuming mirror images of induced flows in the water. Vorticity stretching is taking place along the downward line of the saddle points whereby entrainment and rotational velocity are being accentuated.

The generally tapering shape of the DH root vortex (figures 2(1), 4, 9g,i,n) in the stable region where $0^{\circ }\leqslant \unicode[STIX]{x1D6FD}\leqslant 45^{\circ }$ is set by the balance between the centrifugal force $\unicode[STIX]{x1D6E4}_{c}$ of the vortex and the force of radial pressure (difference) gradient $P_{r}$. In this region, at a given $\unicode[STIX]{x1D6FD}$, stretching is constant, hence $\unicode[STIX]{x1D6E4}_{c}$ is constant with length, but $P_{r}$ increases with depth. With increasing depth, a cone is produced. At the point where the DH crosses, $\unicode[STIX]{x1D6E4}_{c}$ drops to zero because the opposing vorticities ($\pm \unicode[STIX]{x1D714}$) cancel each other (Saffman Reference Saffman1990) causing vortex breaking and reconnection. In the unstable region $45^{\circ }>\unicode[STIX]{x1D6FD}\geqslant 90^{\circ }$, as $\unicode[STIX]{x1D6E4}_{c}$ drops with loss of stretching, $P_{r}>\unicode[STIX]{x1D6E4}_{c}$ crushing the vortex radially inwards continuing toward the root. In panels (2, 3) of figure 2, $\unicode[STIX]{x1D6FD}$ in panel 3 is greater than in panel 2 which lowers the stretching (by 11 %) and $\unicode[STIX]{x1D6E4}_{c}$. The two arms of the unwound vortex do collapse closer to the axis, first in the outer half in panel 2, and then in the inner half in panel 3. In the vortex, breakdown proceeds toward the root and radially inward.

At $\unicode[STIX]{x1D6FD}=45^{\circ }$, $U_{i}=U_{a}$. The velocity of the external flow is set by $\unicode[STIX]{x1D719}$ and a disc model shows that $U_{ext}=0.08{-}0.09~\text{m}~\text{s}^{-1}$ (Bandyopadhyay Reference Bandyopadhyay2015). Taking the component of $U_{ext}$, the value of $U_{a}$ and $U_{i}$ rise to $0.06~\text{m}~\text{s}^{-1}$ at $\unicode[STIX]{x1D6FD}=45^{\circ }$.

Rossby number $Ro$ is estimated as follows. Ascribe the axial velocity in the vortex to $\dot{\unicode[STIX]{x1D719}}$, which produces the foil load and $U_{ext}$, and the rotational velocity to $\dot{\unicode[STIX]{x1D703}}$. Define $Ro$ as the ratio of the inertial to the Coriolis force components as $Ro=U_{ext}/V_{\unicode[STIX]{x1D703}max}$. The maximum azimuthal velocity of the vortex $V_{\unicode[STIX]{x1D703}max}$ is $2\unicode[STIX]{x03C0}fr$, where the pitch radius $r$ is $2c/3$. For $c=0.10~\text{m}$ and $f=1~\text{Hz}$, $V_{\unicode[STIX]{x1D703}max}=0.419~\text{m}~\text{s}^{-1}$. If the inertia force is given by $0.085~\text{m}~\text{s}^{-1}$, then $Ro=0.203$. This estimate matches the value of 0.20, the critical value when the ‘dramatic’ formation and bursting of small vortices occur in a large rotating flow ascribable to the interaction between spiralling waves (Hopfinger et al. Reference Hopfinger, Browand and Gagne1982).

3.6 Modelling of the bubble diameter

Consider the scaling law of the bubbles. Movie 3 shows a large drop in the bubble diameter with increasing torque input into the vortices from $f=1~\text{Hz}$ (figure 2) to 1.25 Hz (figure 6). The effects can be seen in the reductions in the diameters of the individual arms of the DH vortices in figures 2 and 4(c1,c2). The DH is formed as the foil undergoes $\unicode[STIX]{x2202}\unicode[STIX]{x1D703}/\unicode[STIX]{x2202}t$ motion at the origin of the coordinate system in the inset of figure 6(a) where the foil pierces the surface. Increasing centrifugal force (N) lowers the vortex core pressure $p$ ($\text{N}~\text{m}^{-2}$). The pressure of the surrounding water at the same depth lowers the diameter of the tube and of the bubbles $d$ (m). Surface tension $\unicode[STIX]{x1D6FE}$ ($\text{N}~\text{m}^{-1}$) balances the pressure. The length scale of the vortex and bubble diameters is $\unicode[STIX]{x1D6FE}/p$ (m). The scaling parameter ($N_{b}$) of the bubbles is

(3.1a)$$\begin{eqnarray}N_{b}=pd/\unicode[STIX]{x1D6FE}.\end{eqnarray}$$

The velocity scale $(\text{m}~\text{s}^{-1})$ is $\unicode[STIX]{x1D6E4}/d$ ($\text{m}~\text{s}^{-1}$), where $\unicode[STIX]{x1D6E4}$ ($\text{m}^{2}~\text{s}^{-1}$) is circulation. The bubble scaling parameter ($N_{B}$), in terms of $V_{\unicode[STIX]{x1D703}max}$, is

(3.1b)$$\begin{eqnarray}N_{B}=\unicode[STIX]{x1D70C}V_{\unicode[STIX]{x1D703}max}^{2}d/\unicode[STIX]{x1D6FE}.\end{eqnarray}$$

Here, $V_{\unicode[STIX]{x1D703}max}$ ($\text{m}~\text{s}^{-1}$) is the maximum rotational velocity in the vortex and $\unicode[STIX]{x1D70C}\,(\text{kg}~\text{m}^{-3})$ is density. At $f=1~\text{Hz}$, $V_{\unicode[STIX]{x1D703}_{max}}=0.42~\text{m}~\text{s}^{-1}$, $d=0.005~\text{m}$, $\unicode[STIX]{x1D6FE}=0.072~(\text{N}~\text{m}^{-1})$, $\unicode[STIX]{x1D70C}=1000~\text{kg}~\text{m}^{-3}$ and $N_{B}=12$. At $f=1.25~\text{Hz}$, $V_{\unicode[STIX]{x1D703}max}=0.523~\text{m}~\text{s}^{-1}$, $d=0.003~\text{m}$ and $N_{B}=11.3$. With the limited data and the uncertainties in the estimation of $d$, $N_{B}=\unicode[STIX]{x1D70C}V_{\unicode[STIX]{x1D703}max}^{2}d/\unicode[STIX]{x1D6FE}=11$ to 12.

Figure 6(b) is a limiting case of the model. The vortex of Kelvin mode $m=0$ has too small a diameter to be visible. (Figure 9(i) shows an example of the abrupt reduction in diameter.) The hydrostatic pressure is larger down span. The vortex core is compressed. The pre-bursting high circumferential velocity is obvious post-bursting. From the core, the bubbles are thrown out in an arc of $70^{\circ }$ at the foil roll velocity of the local span. The bubbles formed are most numerous per unit surface area and also the smallest observed out of all cases. In (3.1b), the bubble diameter is inversely proportional to the square of the circumferential velocity. Qualitatively, the model extrapolates to figure 6(b).

3.7 Bursting of contra-rotating turbulent vortex

Two examples of turbulent vortex bursting at $f=1.25~\text{Hz}$ are shown in figure 6 and may be contrasted with the DL case in figure 2 at $f=1.0~\text{Hz}$. A root vortex of shorter length but larger diameter is formed. Along its axis, the tightly wound vortex has an array of small diameter, parallel Taylor–Couette roll cells. (The curved surface of the air tubes acts as a lens producing the white lines.) As shown in figure 6(a1,b1), these are tubes of air: the conventional cylinders have been substituted by the surrounding rotating water and the inner air core. See the schematic in figure 6(c) for the velocity profiles inside and outside the root vortex structure corresponding to figures 6(a1–a3) and 6(b1–b3) following Batchelor (Reference Batchelor1967). The Reynolds number is higher than in figure 2. The DH unwinding is not obvious. The free surface shows a dip as in a funnel, and there is an abrupt breakdown into bubbles aligned in a circumferential trajectory marked ‘a–b’ in figure 6(b2). As the blockage is reduced further, the surface dip closes (figure 6b3) and the bubbles become aligned radially at $45^{\circ }$ to the flow direction (marked ‘c–d’; see figure 6b).

Figure 6(b) shows that the bubbles formed after bursting lie where $45^{\circ }<\unicode[STIX]{x1D6FD}\leqslant 90^{\circ }$ and hardly any where $0^{\circ }\leqslant \unicode[STIX]{x1D6FD}\leqslant 45^{\circ }$. These coincide with the regions where $\unicode[STIX]{x1D6FD}$ is unstable and stable, respectively. Over $45^{\circ }<\unicode[STIX]{x1D6FD}\leqslant 90^{\circ }$, there is a declining force of the induced velocity of the vortex available that counters the shear – a negative feedback loop. The mean shear time scale is $(\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}y)^{-1}$, and the vortex time scale of induction is $(\unicode[STIX]{x2202}V_{\unicode[STIX]{x1D703}}/\unicode[STIX]{x2202}r)^{-1}$, where $V_{\unicode[STIX]{x1D703}}$ is the rotational velocity of the vortex and $r$ is the radius. Here, $(\unicode[STIX]{x2202}V_{\unicode[STIX]{x1D703}}/\unicode[STIX]{x2202}r)^{-1}\ll (\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}y)^{-1}$, changing to $(\unicode[STIX]{x2202}V_{\unicode[STIX]{x1D703}}/\unicode[STIX]{x2202}r)^{-1}<(\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}y)^{-1}$. This change exists because the exiting bubbles are carrying away the compressed elastic energy, which serves as the main source of energy. This mechanism would explain the short time scale of the bursting. The time interval between panels 1 and 2 is 0.17 s, whereas the quarter of the foil oscillation time scale is 0.2 s ($=$ the stretching duration) and the mean $(\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}y)^{-1}$ is approximately 1.5 s. There is a cumulative depletion of the reserve vortex kinetic energy remaining over the duration of bursting. Recall equation (1.3) where $\unicode[STIX]{x1D708}$ is absent; and dissipation, being a slow process, can be neglected. The bubbles are being released gradually as the $\unicode[STIX]{x1D6FD}$ of the weakening vortex approaches $90^{\circ }$. The arc ‘a b’ in figure 6(b panel 2) is created through this process.

The horizontally lying bright groups of individually identifiable tubes near the root are segments of the root vortex which release bubbles later. Over $45^{\circ }<\unicode[STIX]{x1D6FD}\leqslant 90^{\circ }$, the oscillating vortex breaks into axial segments. Bubbles are released, not from the entire length simultaneously, but in about six to ten axial groups over an arc of $70^{\circ }$. (Unlike in the turbulent boundary layer analogy in Bandyopadhyay (Reference Bandyopadhyay1980) where there is a solid wall, here, the vertical oscillation of the free surface allows $\unicode[STIX]{x1D6FD}$ to go beyond $90^{\circ }$ to $115^{\circ }$.) The time scale of the bubble release is assumed to be given by the time it takes for the vortex to change its slanting by $7^{\circ }{-}12^{\circ }$. The bubble release time duration from the compressed aerated vortex is estimated to be $(0.17~\text{s})/6=0.03~\text{s}$ to 0.02 s, approximately $1/10$th or less of the stretching duration. This release signifies that as the balance between the centrifugal force and the surface tension is disturbed, the bubbles would experience resonant oscillation and radiate sound.

The schematic in figure 6(c) shows four velocity $(U)$ profiles to relate the vortex state to the changes across the vortex axis from jet to wake with changes in blockage. Also see Movie 3 in the SI. The early understanding of vortex bursting was based on the distribution of velocity profiles as in figure 6(c) (Batchelor Reference Batchelor1967). Later, it shifted to the mechanisms of vortex breakup and reconnection (Saffman Reference Saffman1990). In both, jetting has roles making them easier to see in visualization. Local vorticity cancellation, reduction of centrifugal forces and pressure build up result in jetting. The present work takes the understanding toward maximum stretching in the direction of principal strain just prior to terminal bursting.

Due to stretching, the root vortex elongates with time and the diameter decreases with axial distance from the root. The aspect ratio (length/diameter) is $2\unicode[STIX]{x03C0}$ in the DL vortex case (figure 2) and $\unicode[STIX]{x03C0}$ in the turbulent case (figure 6). Figure 6(c) shows an axial velocity inside the vortex. In figure 6(c), $U_{1L}$ is the DL jet velocity when the spread is narrow, $U_{1T}$ is the turbulent jet velocity when the spread is wider, $U_{2}$ is the external axial velocity outside the jet, and $U_{1w}$ is the axial velocity along the vortex axis when the jet weakens to a wake. In the short axial length of a cylindrical vortex, consider the ratio $U_{1}/U_{2}$, where $U_{1}=U_{1L}$ or $U_{1T}$. At the roll extremity farthest away from the reader of the images, when the foil starts pitching, generating the vortex at the trailing edge near the free surface, $U_{1}>U_{2}$. When the foil pitches back reducing the obstruction, the funnel dip closes (figure 6(b3)), stopping further entrainment of air.

When the fluid outside the vortex decelerates, the vortex diameter increases. The increase causes an additional pressure gradient effect within the vortex which causes further deceleration and thickening of the vortex. Small changes in the velocity outside the vortex cause a large change in $U_{1}$ and $a$ (Batchelor Reference Batchelor1967, p. 553). A time is reached when the ratio $U_{1}/U_{2}$ crosses a critical threshold value at which the velocity profile becomes unstable and causes the vortex to break. The thickening of the vortex and bursting are rapid in the turbulent cases in figure 6 and cannot be delineated. However, in the DL case in figure 2, they can be delineated as the stages of formation of the DH and the subsequent bursting.

Figure 6(d) explains how the compact vortex in (b) is formed and why the bubbles are spread in arcs extending over a span equalling the foil span while bursting. The vertical trailing edge vortex in panel (5), not seen in (4), is joined to the slanted root vortex at the kink; the vortex follows the trailing edge geometry in figure 1(b) which has a diagonal cut near the root. The entire coiled vortex is experiencing stretching in panel (5). However, in (6), the stretched vortex is suddenly released and the vertical part coils up to the slanted root vortex to form the compact vortex.

Consider a spring, mass and damper system where the mass models the axial compression of the distal end due to the stagnation point against the root. Ignore the damper because the time scales are small in elastic effects as the rapidity of the change between panels (5) and (6) shows. When the mass pulled down is released, it will jump up axially to the uppermost position using the energy of the stretching. The mass will oscillate backdown after that continuing the oscillation. The full vortex is undergoing such axial oscillation and releases the bubbles radially from the root in the process in the unstable range $45^{\circ }<\unicode[STIX]{x1D6FD}\leqslant 90^{\circ }$ only during one half of the oscillation. (In a low-friction mechanical apparatus of small forces $({<}1~\text{N})$, up to five damped oscillations have been seen when the mass is released (Bandyopadhyay Reference Bandyopadhyay2019).) The time period of axial oscillation is 0.067 s, which is two to three times the estimated bubble release time. As per this model, the aerated coil is stretched radially outward in the unstable range, then returns to the root to coil back and the cycle goes on. The bubbles, and the compressed energy are released during the journey of the distal end back to the root. The radial arrays of bubbles in (b3) do show some lateral spacing. This explains the synchronous lateral discharge of bubbles in figure 8(f) in the boxed area.

In figures 2(2), 6(a1) and SI-IA-2 to SI-IA-4, the ratio of the wavelength ($\unicode[STIX]{x1D706}$) to the lateral spread ($\unicode[STIX]{x1D6E5}$) of the double helix is $\unicode[STIX]{x03C0}/2$ to $\unicode[STIX]{x03C0}$. If the circulation number $\unicode[STIX]{x1D6E4}/(v\unicode[STIX]{x1D6FF}_{2})$ remains constant, then the kinetic energy of the vortex is proportional to $v^{2}\propto \unicode[STIX]{x1D6E4}^{2}/{\unicode[STIX]{x1D6FF}_{2}}^{2}\propto \,f^{4}/{\unicode[STIX]{x1D6FF}_{2}}^{2}$. Hence, from $f=1.0~\text{Hz}$ to 1.25 Hz, the kinetic energy rises by a factor of at least 2.44 since the vortex diameter $\unicode[STIX]{x1D6FF}_{2}$ drops. If the vortex diameter drops abruptly by a factor of 2 as in Tsoy et al. (Reference Tsoy, Skripkin, Kuibin, Shtork and Alekseenko2018) due to Kelvin mode $m=0$, the kinetic energy stored increases by a total factor 10. Instead of any $m=0$ mode, figure 6(d) shows that a vertical coiled vortex does exist connected to the slanted root vortex undergoing stretching (see left panel in figure SI-IA-6 for greater clarity). In figure 6(d5), the vortex diameter does drop by half for at least part of the length. (Compressibility is another mechanism of storing elastic energy, discussed later.) When the stretching is relieved, like a spring–mass system, the vortex jumps up to the root vortex and forms a compacted coil together. This is compacting of vorticity and elastic energy. An oscillation along the vortex axis would ensue. The compacted vortex expands and shrinks axially, bursting and filling up the sector over the span with bubbles where the vortex inclination is unstable. The bubble arrays are radial in figure 6(b3) aligning with the axis of the root vortex. But in earlier time, the arrays are orthogonal circular arcs as seen in figure 6(b2), aligning along the direction of the Taylor axis. The bubble separation from the tubes is incomplete in the inner half of the sector in figure 6(b2), but is complete later in figure 6(b3). Figure 2 also did show that bursting proceeds radially inward. Hence, on relaxation, the vortex coil experiences orthogonal oscillations, along the Taylor and the DH axes, and more complete bubble separation proceeding inward from the distal end. When the turbulent vortex bursts, the energy is immediately spread over sometimes $70^{\circ }$ of the quadrant extending over the entire span (figure 6b2).

The foil circulation is sensitive to any air entrainment (figure SI-DA-4), hence variations in the spread of the vortex bursting, particularly in the case when $f=1.25~\text{Hz}$, can be expected. Because of a lack of perfect lock-in between the foil oscillation and the wake, the wake frequency would have a jittering effect, but the foil would have none. The variation in the wake frequency would result in an amplified variation in the kinetic energy of the root vortex which is what is seen cycle to cycle.

Because of fluid rotation, wave motion is possible in the root, the foil leading edge vortices and vortices in the rolled-up flow in the foil tip (to be shown below). The entrainment of air in the core, which is compressible, increases the elasticity (Batchelor Reference Batchelor1967, p. 555). The Kelvin mode $m=0$, energy amplification factors of up to 10 and the post-bursting vortex spread angle of $70^{\circ }$ are net measures of the elastic energy in the vortex.

3.8 Vortex breaking and jetting near the apex of the root vortex just prior to bursting

The vortex narrowing in figure 7 shows a breaking point where the DH ($\pm \unicode[STIX]{x1D6E4}$) crosses and the vorticities cancel. See figure 3(b) sketch. The breakup point has fragmented or there is no aeration. The growth of a vortex blob after that point and its bursting are shown in figure 7. In figure 7(a), in (1) and (2), the main part of the root is slanted at $\unicode[STIX]{x1D6FD}=45^{\circ }$ meaning that it is undergoing maximum turbulence amplification. The bottom tip of the vortex shows a breaking, a growth of the vortex beyond and reconnection. In Saffman’s (Reference Saffman1990) model, viscosity cancels the vorticity at the breakup point, centrifugal forces drop and pressure builds up which produces a jet. The jet convects vorticity away and an ‘apparent reconnection’ is produced. The breakup point is stretched in the visualization. The visualization shows that the breakup and reconnection do not immediately lead to bursting. There is one more event involved, considered below.

Figure 7. Vortex breaking, jetting, reconnection and stretching along $45^{\circ }$ to flow direction just prior to terminal bursting (a,b), and mechanism of formation of roll vortex at vortex tip (c). (a,b) These sequences take place after the slant $\unicode[STIX]{x1D6FD}$ of the main root vortex reaches $45^{\circ }$; repeated jetting and spiralling at vortex tip are shown, and formation of spiralling cones and stretching along $45^{\circ }$ are shown. (c) Insets 1 and 2 in (A) show examples of ‘vortex rods’ which are swirling jets as in (a2); (B) schematic of the mechanism of the formation of the roll vortex cones at the tip of the swirling jets shown in (a,b).

Beyond the breakup, the vortex is radially growing. The tip of the jet in figure 7(a) shows unexpected examples of vortices spiralling on a conical surface: one in panel 2 and one in panels 6 and 7. The concentration of bubbles is inclined. The time interval between panels 1 and 2, and between 5 and 6 is 0.033 s and a higher framing rate than in Movie 3 is needed. The cone becomes upright in panel 7. The surface of the cone is at $45^{\circ }$ to the flow direction. The cone is also radially stretching at $45^{\circ }$ to the flow direction, but this time in the orthogonal direction. What occurs is a maximum vorticity and turbulence intensification in all possible directions. Due to the finiteness of the lateral rolling excursion, the shear is not confined to the longitudinal plane only. There is shear in the lateral direction also (see the triangular region in figure SI-IA-5). Between panels 6 and 7 in figure 7(a), the cone becomes upright because it is moving to the stable posture of maximum stretching. The DH is spiralling from the base to the apex in one example and from the apex to the base in another. The formation of the cones is modelled below.

Panels 2 and 5 in figure 7(a) show that the tip of the root vortex is jetting twice. The vortex grows radially in between. Figure 7(b) shows breaking in panels 1 and 2, and reconnection in panel 3; the terminal bursting is shown in panel 4.

The root vortex, formed by the pitching motion of the foil, is a pitch vortex. But the vortex formed in figure 7 after the breakup and reconnection has a horizontal axis and is modelled to be produced by the rolling motion. It is a roll vortex. The breakup has eliminated the memory of the initial condition.

Mechanism of the formation of the roll vortex and Kelvin mode $m=1$. After the breakup point, the vortex in figure 7 develops a swirling jet of velocity $U_{j}$. The swirling jet is straight, horizontal and of uniform diameter. It is called a ‘vortex rod’. The examples appear in figures 7(a2) and 7(cA); also see figure 9(n). The vortex rod and the conical vortex flows are modelled. See Movie 3 at time stamps 01:10 and 01:12 (m:s) for two examples of the formation of the $m=1$ vortex.

The rolling ($\unicode[STIX]{x1D719}$) ‘vortex rod’ (see figure 7c) is not expanding. Hence, the local circumferential velocity $V_{\unicode[STIX]{x1D719}}$ is ${\geqslant}U_{j}$, the local jet velocity, which is subcritical. Assume $V_{\unicode[STIX]{x1D703}max}=V_{\unicode[STIX]{x1D719}}=0.43~\text{m}~\text{s}^{-1}$. The transverse boundary layer thickness $\unicode[STIX]{x1D6FF}_{tr}=0.5\unicode[STIX]{x1D716}$, half of the local vortex rod diameter, where the estimated $\unicode[STIX]{x1D716}=0.0043~\text{m}$. Transverse boundary layer Reynolds number $Re_{\unicode[STIX]{x1D719}}=(V_{\unicode[STIX]{x1D719}}\unicode[STIX]{x1D6FF}_{tr})\unicode[STIX]{x1D708}=921$, a low value. Axially, the jet $Re$ of the vortex rod is $Re_{j}=U_{j}\unicode[STIX]{x1D716}/\unicode[STIX]{x1D708}=1843$, taking $\unicode[STIX]{x1D708}$ of water $(1.003\times 10^{-6}~\text{m}^{2}~\text{s}^{-1})$, also a low value. The $j$ and $\unicode[STIX]{x1D719}$ motions, although treated separately, produce a spiral. The air flow can be neglected whereby, on the water side of the interface, the flow is of a stabilizing convex curvature and not of a destabilizing concave curvature air flow. The rod is straight, so longitudinal curvature effects are not present, and the transverse curvature effects are present throughout the transverse water boundary layer. At low $Re$, such transverse curvature boundary layers are relaminarizing (Piquet & Patel Reference Piquet and Patel1999). For these reasons the Taylor number $Ta$ (defined later in the context of figure 9) is subcritical, and the aerated transverse pairs of contra-rotating vortex tubes are not formed, although some striations on the interface are present. This vortex rod is stable and is not a source of bubbles.

The mechanism of the Kelvin mode $m=1$ is shown schematically in figure 7(cB, cC). Define a cylindrical coordinate system ($x,r,\unicode[STIX]{x1D719}$). At the terminal stage, the horizontal jet impinges on the cross-stream vortex-free body of water, creating a stagnation point. The swirling jet does not translate horizontally to any significant extent (about 0.02 m) confirming the formation of a stagnation point. Under certain conditions of the Reynolds number $Re_{j}=U_{j}\unicode[STIX]{x1D716}/\unicode[STIX]{x1D708}$, based on $U_{j}$, the vortex diameter $\unicode[STIX]{x1D716}$ and kinematic viscosity $\unicode[STIX]{x1D708}$, the flow very near the stagnation point becomes unstable to azimuthal foil roll oscillation ($\unicode[STIX]{x1D719}$). The DH tip experiences a motion that combines the axial displacement of the jet and the instability of the stagnation point flow which causes a motion in the cross-stream plane. As a result, the tip traverses a conical surface, as seen in figure 7. There is a vertical shear ($\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}y$) normal to $x$. In order to maximize stretching, the vortex is oriented along $45^{\circ }$ to $x$ (the $-45^{\circ }$ orientation is also present). Depending on the initial conditions, this $45^{\circ }$ cone can have a source or a sink type, radially outward or inward flow (figures 7(a6,a7) and 7(b3,b4)). In the cross-stream plane, the equation of a source spiral (growing spiral) can be fitted as $r=K\unicode[STIX]{x1D719}$, and of a sink spiral (damping spiral) as $r=-K\unicode[STIX]{x1D719}$, where $K$ is a constant. The position vector on the cone is $s=(x,r)$. The cone in figure 7(a) shows that $K$ is a constant. Accounting for the axial jet and maximum stretching, $\unicode[STIX]{x2202}r/\unicode[STIX]{x2202}x=\tan (\unicode[STIX]{x03C0}/4)$. The mechanism of the elastic vortex (which is more viscous and less elastic) is both similar and dissimilar to the viscoelastic fluid buckling (which is more elastic and less viscous) (Mahadevan, Ryu & Samuel Reference Mahadevan, Ryu and Samuel1998).

The annotation on the right of figure 7(c) mentions that the vorticity in the cross-stream plane develops a negative component ($-\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D719}}$) with respect to that found in the upstream ‘vortex rod’. This negative component causes a spiral to form (Batchelor Reference Batchelor1967). The spiral is stretched to the maximum extent, triggering the bursting of the entire articulated vortex. The mechanism is discussed in § 3.10.1 in the context of the formation of similar Kelvin $m=1$ spirals in the rolled up foil-tip flow.

From figure 7, it is estimated that $U_{j}$ is $0.13~\text{m}~\text{s}^{-1}$, which is less than the maximum foil velocity. Radial velocity $\text{d}r/\text{d}t=1.5V_{\unicode[STIX]{x1D703}max}$, and $V_{\unicode[STIX]{x1D703}max}=4.6U_{j}$. The radial velocity $(0.9~\text{m}~\text{s}^{-1})$ is close to the foil velocity and is 6.9 times $U_{j}$. The maximum swirl velocity of the jet may be just below $V_{\unicode[STIX]{x1D703}max}$ of the root vortex, assuming some dissipation, because the diameter $\unicode[STIX]{x1D716}$ is similar to the root vortex or pitch vortex diameter, as in figure 7(d1).

What happens if two co-rotating vortex tubes ($\unicode[STIX]{x1D6E4},\unicode[STIX]{x1D6E4}$) come close to one another? Comparison of figures 7 ($\pm \unicode[STIX]{x1D6E4}$) and 11 ($\unicode[STIX]{x1D6E4},\unicode[STIX]{x1D6E4}$; appears later) show that the vortex breakup is not present in the ($\unicode[STIX]{x1D6E4},\unicode[STIX]{x1D6E4}$) case. Both flows encounter regions of $\unicode[STIX]{x2202}p/\unicode[STIX]{x2202}x>0$ and develop a stagnation point. The instability of the stagnation point flow leading to the development of a Kelvin $m=1$ mode single spiral occurs in the ($\unicode[STIX]{x1D6E4},\unicode[STIX]{x1D6E4}$) case. This case is similar to the spiralling cone in the ($\pm \unicode[STIX]{x1D6E4}$) example. Both undergo stretching along the principal plane direction ($45^{\circ }$ to $x$). Finally, the form after bursting is similar: bursting into an arrowhead in the ($\unicode[STIX]{x1D6E4},\unicode[STIX]{x1D6E4}$) case, and into a cone in the ($\pm \unicode[STIX]{x1D6E4}$) case. In the region of $\unicode[STIX]{x2202}p/\unicode[STIX]{x2202}x>0$, ahead of the stagnation point, the displacement of a vortex line radially outward creates an imbalance between the Coriolis and the viscous components, setting up a resonant oscillation. This event creates the $m=1$ Kelvin spiral in both.

3.9 Two mechanisms of bubble formation in turbulent vortex bursting

Figures 1(c), 8(a) and 10 show that two sizes of bubbles are formed (more examples appear in the SI). The coarse bubbles are formed near the free surface mostly in the foil wake-free surface quadrant. Here, the spiralling tubes (figures SI-TA-1(a), 1(e), 6(a1)) of the capillary surface waves are first stretched into the funnel of the root vortex by the pitch oscillation. Arrays of bubbles of fairly uniform diameter are formed (figure 8b–d) when the foil blockage is removed. Fine bubbles form on the foil surface farther from the foil root where the bubble size would be influenced by the wetting properties and viscous drag forces (Lepercq-Bost et al. Reference Lepercq-Bost, Giorgi, Isambert and Arnaud2008).

Figure 8. Bubbles are formed in clusters: fine bubbles in the foil boundary layer (a) and coarse bubbles near the free surface or away from the foil (b–d); see figure SI-TA-4 for ranges of $Re$ and $We$ where coarse and fine bubbles are formed in relation to $Re$ versus $C_{d}$ and $We$ versus $C_{d}$ due to Haberman & Morton (Reference Haberman and Morton1953) for bubbles rising at terminal velocities in filtered water. Arrays of coarse bubbles are formed when a stretched aerated vortex tube is suddenly released (b). All coarse bubbles are formed at the same time.

3.9.1 Mechanism of the formation of coarse bubbles: Taylor air tubes of the root vortex

From the images, the diameters in the DH, where $Re$ is lowest, are from $7.0\times 10^{-3}$ to $20.0\times 10^{-3}~\text{m}$. These bubbles are arched and distorted ellipsoids, and the diameter refers to the minor axis. The diameters of the bubbles at higher $Re$ are from $1.5\times 10^{-3}$ to $20.0\times 10^{-3}~\text{m}$ (Talaia Reference Talaia2007). As shown in figure SI-TA-4(g,h), the present work lies in these ranges. The coarse bubbles are in these ranges: $d=0.0015{-}0.02~\text{m}$, $v_{\infty }=0.20{-}0.40~\text{m}~\text{s}^{-1}$, $Bo=0.303{-}53.82$, $Ca=0.0028{-}0.0055$, $Fr=2.72{-}0.8155$, $Mo=2.5638\times 10^{-11}{-}2.5638\times 10^{-11}$, $Re=300{-}8000$ and $We=0.8239{-}44$. Because $Bo$ is close to 1.0 at $d=0.0015~\text{m}$, both surface tension and gravity forces act as stabilizing forces in the Taylor air tube case. But $Bo$ is $\gg 1.0$ when $d$ is 0.02 m; hence, only gravity, not surface tension, will dominate as a stabilizing force in the DH case. Repeating the helix experiment at 6 and $49\,^{\circ }\text{C}$ would vary the $Mo$ by a factor of 10. The coarse to fine diameter ratio is $10^{4}{-}10^{5}$ (see § 3.9.2).

The marked example in figure 8(b) shows the presence of an array of coarse bubbles of nearly the same size slanted at precisely $45^{\circ }$ to the flow direction. Near the foil, the slant of the bubble array is shallow. But downstream and away from the foil, the slope of the bubble array is largely $45^{\circ }$. The diagonally arrayed bubbles are formed simultaneously in the entire field of view. This idea supports the hypothesis of bubble diameter number ($N_{B}$) modelling given earlier, namely that maximum stretching of the vortex at $45^{\circ }$ followed by sudden relaxation causes the discrete bubbles to form out of the continuous aerated tube. In the modelling of $N_{B}$ in § 3.6, the vortex core pressure due to centrifugal effects is balanced by surface tension. Equations (3.2) and (3.3), on the other hand, do not include any property of the vortex.

The elliptic region in figure 8(c) is in reference to figure 3(a), where there are two scales of foci. Short bubble arrays meet where the foil stem pierces the free surface. These capillary tubes are forming small horseshoe vortices and may be the origin of the small diameter DH root spirals in figure 4(c1, d1). Future research on the stability of the contra rotating foci in figure 3(a) would be useful.

What happens if aerated capillary tubes in proximity are suddenly released en masse? Figure 8(c,d) shows the near-surface bubble arrays upstream and midstream of the foil in (c) and in the immediate downstream root region in (d). There are few bubbles in the stable region of the root vortex $0^{\circ }\leqslant \unicode[STIX]{x1D6FD}<45^{\circ }$, but there is a dense cluster of bubbles in the unstable region of the vortex $45^{\circ }<\unicode[STIX]{x1D6FD}\leqslant 90^{\circ }$. The linear bubble arrays upstream are at an inclination of $\ll 45^{\circ }$ (figure SI-IA-4). A few plausible short segments of dashed lines are shown of bubble arrays originating from the same aerated vortex tube. As marked by the box, the neighbouring tubes discharge the bubbles simultaneously. The neighbouring tubes are oscillating synchronously when suddenly released after stretching.

Figure 9 shows the formation of stacks of aerated tubes whose diameter is similar to the coarse bubbles. Figure 9 has two parts: 9(a) and 9(b–n), with part 9(b–n) being subdivided into 9(b–h) and 9(i–n). Figure 9(a) shows an unwound DH where the bubbles, one of them marked by the arrow, are forming at axial intervals ($\unicode[STIX]{x1D706}_{d}/2$) approximately equal to half the diameter $d$ of the tube locally. However, $\unicode[STIX]{x1D706}_{d}$ varies axially, and the bubbles do not separate at axial distances of $d$ (figure 2). The interface necks locally because of the sudden loss of the tube stretching and the onset of radial oscillation. Theoretically, in progressive capillary waves, the maximum value of the ratio $d/\unicode[STIX]{x1D706}$ is 0.73 (where $d$ is the height of the crest relative to the trough) if $g$ is ignored and $\unicode[STIX]{x1D6FE}$ is the only restoring force on a nominally flat free surface (Crapper Reference Crapper1957).

Figure 9. Aerated Taylor tubes of the root vortex: $f=1~\text{Hz}$ (a–h) and $f=1.25~\text{Hz}$ (i–n). The images are arranged in order of increasing but stable complexity such as the emergence of fine pitch spiralling and patches of disorganization. The increasing complexities are reminiscent of increasing $Re$ in Taylor–Couette experiments but with solid cylinders (Coles Reference Coles1965; Andereck, Liu & Swinney Reference Andereck, Liu and Swinney1986). In the air tubes of the double helix (a), the pitching motion has suddenly removed the flow obstruction, and discrete bubbles are forming in the tube but are not separated yet; the necking about one bubble is marked by the arrow. The helical root vortex (b), modelled in (c,d) has one full turn (the previous panel showing clear one turn appears in the inset, image reduced by half; see figure SI-IA-2) and is experiencing maximum stretching (given by the $45^{\circ }$ slope). Organized Taylor roll cells of air tubes (e) are shown in contra-rotation in a schematic (f). Taylor tubes on a top-like root vortex (g,i–k) are modelled in (h,m). The flow in (i,j,k) is modelled in (l,m). A root vortex with multiple azimuthal lobes of instability is shown in (n). The curved arrow in (e) marks the curl over at the tip of the Taylor tube. The abrupt reductions in diameter at the apex, marked in (g,i), indicate the presence of Kelvin mode $m=0$ (Tsoy et al. Reference Tsoy, Skripkin, Kuibin, Shtork and Alekseenko2018). The root vortex cone (i–k) has just been relaxed after maximum stretching and the cone diameter shrinks; surface tension is reducing the surface area; see notes in (l).

In figure 9(b–h), $f=1.0~\text{Hz}$; in figure 9(i–n), $f=1.25~\text{Hz}$. Figure 9(b–n) shows the foil root vortex and a stack of air tubes wrapped around. They are arranged in order of increasing complexity. Further examples of air tubes appear in figure SI-IA-6.

Taking centrifugal force as the destabilizing force and viscosity as a stabilizing force, define $Ta=(V_{\unicode[STIX]{x1D703}max}^{2}/R_{1}^{2})R_{1}(R_{2}-R_{1})^{3}/\unicode[STIX]{x1D708}^{2}$ for concentric rotation cylinders (White Reference White1994). Here, $R_{1}$ is the external radius of the internal cylinder, and $R_{2}$ is the internal radius of the external cylinder. Applying to the present case and taking the gap ($R_{2}-R_{1}$) to be $d$ ($=\,0.006~\text{m}$), the high value of $R_{2}/R_{1}$ is 0.85. The ratio can vary cycle to cycle from 0.22 to 0.61. In solid cylinders, $R_{2}/R_{1}$ is 0.883 in Andereck et al. (Reference Andereck, Liu and Swinney1986). It is easier to measure the diameter of the root vortex, than the diameters of the vortices or bubbles. The critical value of $Ta$ is 1700 is taken to calculate the ‘cylinder’ gap which in the present case is the diameter of a Taylor roll cell or bubble diameter (d). Taking all cases, the root vortex diameter near the origin is 0.0154 m to 0.08 m. At $f=1~\text{Hz}$, take $2R_{2}$ as 0.08 m in one example of a large value and $V_{\unicode[STIX]{x1D703}max}=0.419~\text{m}~\text{s}^{-1}$. For critical $Ta$, these give $d=0.0008~\text{m}$, a reasonable value. Due to high background turbulence, the critical $Ta$ may be ${<}1700$; $U_{\infty }c/\unicode[STIX]{x1D708}$ is 750, a transitional value for reverse Kármán jets (Bandyopadhyay et al. Reference Bandyopadhyay, Beal, Hrubes and Mangalam2012).

The conical form of the root vortex sets up an internal helical flow toward the apex. Hence, the flow is open axially (Wereley & Lueptow Reference Wereley and Lueptow1999). The spiralling core vortex is represented by the eigenvector shown schematically in figures 9(c), 9(d), 9(h) and 9(m). The flow is closed radially because it is rotating. The rotary motion of the air–water interface forms ripples (millimetre scale) creating the air tubes in figure 9(d–n). The tubes may also be originating in the free surface when the ripples are drawn into the funnel. In the lowest $Re$ case in figure 9(b) at $f=1~\text{Hz}$, the Taylor tubes are incipient and formed in pairs. Hence, the Taylor number $(Ta)$ is barely critical $(Ta_{c})$. Owing to a lack of accurate lock-in, $Re$ is slightly higher in figure 9(g), although figure 9(f) is still at 1 Hz. A model of the top-shaped vortex in figure 9(g) is shown in figure 9(h), which shows the spiralling eigenvector and an interesting narrowing of the tip where the rotational velocity is high. Stacks of Taylor tubes appear at the interface with some waviness. The nipple in figure 9(b) is rounded, but it is conical in figure 9(g). In both figures 9(b) and 9(g), the vortex has a narrowing half-way along the axis, meaning that the mode of the eigenvector has developed a ‘coning’ in figure 9(g). This conical mode of the root vortex is stable because, overall, it is identical at $f=1.25~\text{Hz}$, as shown in figure 9(i–k). It has been shown earlier that the stability is due to the fact that the vortex is stable for $\unicode[STIX]{x1D6FD}\leqslant 45^{\circ }$. In figure 9(n), $Re$ is higher, and the vortex cross-section has circumferential (but non-axisymmetric) Widnall-type instabilities (Pierrehumbert & Widnall Reference Pierrehumbert and Widnall1982).

In figures 9(i–k) and 9(n), $Ta>Ta_{c}$ because the number of air tubes is large. In the case of figures 9(i–k) and 9(n), the number of bubbles formed per unit length of the tube would be numerous since the air tube diameter is smaller than in figure 9(a).

Compared to figure 9(e), as shown schematically in figure 9(f), the Taylor tubes in figure 9(i–k) show breaks that are the twisting of the air tubes. The breaks indicate that spiralling waves are present in the Taylor tube stacks, in figure 9(i) an example is marked by a pair of arrows, and the wavelength of the spiral is similar to the tube diameter. The elasticity magnifies the effect. From the standing wave model in an air tube, the local $L/D=N\unicode[STIX]{x03C0}$, where $N$ is an increasingly large integer. The bubbles formed would spin in relation to $N$.

Figure 9(g) is modelled in figure 9(h), and figure 9(i–k) is modelled in figure 9(m). While the vortex eigenvectors are identical, the $Re$ of the Taylor tubes has increased, and the tubes are distorting and showing intermittency in the distortion. The dispersed packets of unstable vorticity in the sequence (i–k) co-exist below the stable stacks of air tubes still being stretched at $45^{\circ }$. The unstable packets appear down below in the increasing adverse pressure gradient region where the root vortex is narrowing. They are already bursting in (k). The air tube in the straight part of the root vortex, however, is able to sustain the standing waves by selecting a higher value of $N$. This feature is not seen in the narrowing part. It is suggested that, for instability and bursting to be triggered, the waves must stop standing first due to some larger-scale $(\ll D)$ non-uniformity in the boundary condition.

The side-to-side rolling motion of the foil produces an overall horizontal jet flow from left to right in the images in figure 9. In figure 9(e,g,i–k), the Taylor tubes are inclined to the horizontal external flow direction at a mean angle of $45^{\circ }$ which is the direction of principal strain. A few examples are marked by the pairs of thin arrows in (e,g,i), and the direction of each arrow indicating the direction each stretches. In (e), the curved arrow marks an upstream curling over of the tip. The air tubes are expected to be elliptical in the transverse plane. Near the tip, if the induced flow between the legs of a Taylor tube lying in the transverse plane (not visible) is upward, then, in the absence of any external mean flow shear, an upstream curling over would be produced. In turbulent boundary layers, which are jungles of hairpin vortices, in the outer part of the layer and away from the wall, the hairpins also lie at a mean angle of $45^{\circ }$ to the flow direction, and at low $Re$, similar upstream curling over do occur (Bandyopadhyay Reference Bandyopadhyay1980; Head & Bandyopadhyay Reference Head and Bandyopadhyay1981; Perry & Chong Reference Perry and Chong1982; Adrian et al. Reference Adrian, Meinhart and Tomkins2000; Wu & Moin Reference Wu and Moin2009).

The slanting of the Taylor tubes is close to $45^{\circ }$ without much variation. We attribute this organization to the external forcing of the flapping foil. In low $Re$ turbulent boundary layers, such a forcing mechanism accurately models the spatio-temporal drag reduction (Bandyopadhyay & Hellum Reference Bandyopadhyay and Hellum2014).

Although the no-slip boundary condition of conventional Taylor–Couette cylinders (Taylor Reference Taylor1923) is modified to a slip condition of a rippled free surface, the growth of waviness, spiralling and intermittency of the air tubes with $Re$ are similar (Coles Reference Coles1965; Andereck et al. Reference Andereck, Liu and Swinney1986; Tritton Reference Tritton1989). The states of the Taylor air tubes are stable, organized and not turbulent (Gollub & Sweeny Reference Gollub and Sweeny1975). The bubbles from neighbouring tubes would rotate in the opposite directions (figures 9d, 9f and 9l). The rotation helps provide the stable trajectory in figure 9(b2). The above is an uncommon example of Taylor–Couette flow.

3.9.2 Mechanism of the formation of fine bubbles: wall effects

In the foil boundary layer, with increasing wall shear stress (decreasing viscous sublayer thickness $\unicode[STIX]{x1D6FF}_{s}$) with increasing $f$, the fine bubble diameter would decrease. The capillary number $Ca$ is defined as the ratio of the viscous force to the interfacial tension force and is given by

(3.2)$$\begin{eqnarray}Ca=\unicode[STIX]{x1D707}U/\unicode[STIX]{x1D6FE},\end{eqnarray}$$

where $\unicode[STIX]{x1D707}$ (Pa s) is the absolute viscosity of water, $U(\text{m}~\text{s}^{-1})$ is the velocity at the edge of the viscous sublayer and $\unicode[STIX]{x1D6FE}$ is the surface tension $(\text{N}~\text{m}^{-1})$. The bubble diameter would be smaller than $\unicode[STIX]{x1D6FF}_{s}$.

The bubbles would form when the difference in pressure, $\unicode[STIX]{x0394}P$, between the surrounding water and the air jacket overcomes the capillary pressure difference. From Young’s thermodynamic equation, the minimum pressure difference, $P_{min}$, is a function of the contact angle (the wetting property), as

(3.3)$$\begin{eqnarray}P_{min}=4\unicode[STIX]{x1D6FE}\cos \unicode[STIX]{x1D703}/d,\end{eqnarray}$$

where $\unicode[STIX]{x1D703}$ is the contact angle between the water and air on the foil surface, and $d$ is the bubble diameter. Here, $\unicode[STIX]{x1D6FE}$ remains constant, but the head increases with the span of the foil. So, near the foil tip, the water will advance into the air jacket, but, at a shallower span, the air jacket will advance into the surrounding water. Depending on whether the interface on the foil surface is advancing or receding, $\unicode[STIX]{x1D703}$ can be acute or obtuse. This mechanism can be called a wall-based mechanism.

Figure 1(b,e) and SI-TA-3(c) show two paths of air entrainment (see Eggers Reference Eggers2001). Figure 10 shows the wall-based mechanism of the formation of fine bubbles. The funnel centre, marked by a point source of pressure $-p$, is moving closer to the fin while air is sucked in jacketing the suction side of the foil. Clouds of bubbles form near the trailing edge of the jacket toward the foil tip. The edge of the fine bubble cloud toward the foil tip is moving upstream. But the trailing edge of the air jacket closer to the root is moving slightly toward the foil trailing edge. Near the foil root, there is an advancing wave front forming bellows in the jacket – the arcs around the centre $-p$, as shown in the schematic in figure 10(c). As shown in the elliptical insets in figure 10(c), near the root, the air front advances toward the trailing edge, following the arc of the bellows, while the water front advances upstream toward the foil leading edge. Hence, the contact angle on the water side recedes near the root ($\unicode[STIX]{x1D6FE}_{R}<90^{\circ }$), while it advances near the foil tip ($\unicode[STIX]{x1D6FE}_{R}>90^{\circ }$). The contact angle is at equilibrium near the foil root where the spanwise edge of the cloud is.

Figure 10. Formation of fine bubbles on the foil surface: time sequence of air jacket and regions of clouds of fine bubbles over the suction side of the fin (a,b); schematic of surface tension mechanism of the formation of fine bubbles (c). Two elliptical insets in (c) show cross-sections of areas where the foil surface and the air and water interfaces meet. In (a), the markings ‘a’ and ‘b’ draw attention to an extremely thin aerated vortex with small amplitude waves, aligned with the centre of the funnel; when stretched to the maximum extent due to the $45^{\circ }$ slope, this vortex buckles to a sinusoid marked (c,d) in (b).

The fine bubbles are produced by the bursting of the air-jacketed boundary layer over the suction side of the foil near the outer end of the span where the foil surface velocity is higher (figure 10). The fine bubbles are not formed at $f=0.75~\text{Hz}$. Assuming a Blasius boundary layer to be developing over the foil, the foil velocity is $V=2\unicode[STIX]{x03C0}fr$, where $r$, the average foil $\text{span}=0.15~\text{m}$. Assuming a Blasius profile, the boundary layer thickness at the half-chord distance of $l=0.05~\text{m}$ from the leading edge is $\unicode[STIX]{x1D6FF}=\sqrt{\unicode[STIX]{x1D708}l/V}=1.9952\times 10^{-4}~\text{m}$ at $f=1.0~\text{Hz}$ and $=1.7846\times 10^{-4}~\text{m}$ at $f=1.25~\text{Hz}$. These values are the upper limit of the fine bubble diameters. Use $v_{\infty }=gd^{2}(\unicode[STIX]{x1D70C}_{w}-\unicode[STIX]{x1D70C}_{a})/(18\unicode[STIX]{x1D707}_{w})$ (Stokes Reference Stokes1880) to get the terminal $v_{\infty }=0.0216~\text{m}~\text{s}^{-1}$ at $f=1.0~\text{Hz}$ and $0.0173~\text{m}~\text{s}^{-1}$ at $f=1.25~\text{Hz}$. We estimate these values: at $f=1.0~\text{Hz}$, $Bo=0.0054$, $Ca=2.98\times 10^{-4}$, $Fr=0.2394$, $Mo=2.5638\times 10^{-11}$, $Re=4.30$ and $We=0.0013$; at $f=1.25~\text{Hz}$, $Bo=0.0043$, $Ca=2.38\times 10^{-4}$, $Fr=0.1713$, $Mo=2.5638\times 10^{-11}$, $Re=3.08$ and $We=7.3487\times 10^{-4}$. Because $Bo<1.0$, $\unicode[STIX]{x1D6FE}$, not $g$, dominates as a stabilizing force, unlike in the coarse bubbles (see figure SI-TA-4(g,h) to compare).

3.10 Co-rotating vortex tubes of rolled-up foil tip flow

The boundary layer flow from the pressure side near the foil tip rolls up to the suction side in a $270^{\circ }$ arc, as shown in figures 11, 12, SI-IA-7 and SI-IA-8. The rolled-up foil-tip vortex is marked by fine bubbles. Due to the absence of any breakup, the vortex tubes are inferred to be co-rotating, represented as ($\unicode[STIX]{x1D6E4},\unicode[STIX]{x1D6E4}$).

Figure 11. Time sequence showing that the foil-tip vortex and the root vortex burst simultaneously at $f=1.25~\text{Hz}$. A row of two spiralling vortices $(m=1)$ from the foil tip is being stretched at $45^{\circ }$ to the vertical, moving diagonally upwards. Subsequently, they burst simultaneously with the root vortex. Arrows of the tiny spiral schematics on the right side of the panels in (1) and (2) show the eigenvector of the vortex line. The inset in panel 1 shows how a pair of co-rotating vortex lines spiral to produce the chevron; they then fuse and produce the single spiral bursting eventually as shown in panel 2. Regions of favourable and adverse pressure gradients are marked in (1); $x$ is along foil chord.

In figure 11, the rolled up foil-tip flow has a row of two single spirals (they are not DH) that are being stretched at $45^{\circ }$ to the horizontal external flow direction as the DH root vortex does. The spirals, $2~\text{cm}\times 2~\text{cm}$ in size, are larger than the local boundary layer thickness. In figure SI-IA-7, the formation, bursting and the continued motions of the two spirals downstream of the foil are tracked frame by frame (see Movie 3, time stamp 01:38 (m:s)). Due to the passage over the accelerating part of the foil boundary layer, the spirals 1 and 2 in figure 11 form beyond the chord location of maximum foil thickness after the vortex tube has thinned. The spiral 1 bursts into an arrowhead form (see figure 3b), first seen in panel (2), where the external flow velocity has dropped in conformity with Batchelor (Reference Batchelor1967).

Panels 3 to 6 in figure SI-IA-7 show two sequences of the formation of a single spiral, bursting into an arrowhead and the formation of chevron in the rear. The rear end of the burst arrowhead does not move over the time step of one frame indicating, the presence of a stagnation point.

The inset in panel 1 of figure 11 clarifies that the chevron in the rear of the spiral is actually the helical interaction of two co-rotating vortex tubes. On entering the adverse pressure gradient boundary layer, the chevron widens laterally, the two vortex tubes subsequently fuse and a single spiral (or coil) is produced which eventually bursts. Spirals form when vorticity becomes negative (figure 7(cB)). The spirals in figure 11(1) exist outside the Blasius layer which is only 2 mm thick. The spirals and the chevrons are not associated with any externally imposed perturbation, such as boundary layer injection, and do not trigger any boundary layer transition and thickening over the foil (Perry, Lim & Teh Reference Perry, Lim and Teh1981).

Apart from providing direct experimental evidence in support of Batchelor’s (Reference Batchelor1967) theoretical statements on vortex elasticity, we show that vortex bursting requires a necessary condition to be satisfied, namely, that the vorticity amplification needs to be maximized prior to bursting by bringing the alignment of the vortex to the direction of principal strain. Cross-stream views of principal strain may be explored in vortex bursting where the maximum vortex stretching has not yet been reported. In future research, turbulent boundary layer over the underside of a horizontal plate in water would subject the hairpin vortices to both principal strain stretching and adverse pressure gradient.

The foil-tip rolled up flow has signs ($\unicode[STIX]{x1D6E4},\unicode[STIX]{x1D6E4}$) because it originates from the boundary layer vorticity on the pressure side where there is no separation. The stretching along the $45^{\circ }$ inclination intensifies the vorticity bringing the two vortex cores closer. The vortex tubes fuse into one $(2\unicode[STIX]{x1D6E4})$, and do not cancel their vorticities as in the contra-rotating DH $(\pm \unicode[STIX]{x1D6E4})$. The fused tube $(2\unicode[STIX]{x1D6E4})$ develops Kelvin instability of mode $m=1$ (Tsoy et al. Reference Tsoy, Skripkin, Kuibin, Shtork and Alekseenko2018) in the adverse pressure gradient region of the foil boundary layer. The foil-tip single spiral $(2\unicode[STIX]{x1D6E4})$ bursts simultaneously with the root vortex DH $(\pm \unicode[STIX]{x1D6E4})$.

3.10.2 Modelling of chevrons of co-rotating vortex tubes

Waves form past the stagnation points of vortex crossings in both types ($\pm \unicode[STIX]{x1D6E4}$) and ($\unicode[STIX]{x1D6E4},\unicode[STIX]{x1D6E4}$). In ($\unicode[STIX]{x1D6E4},\unicode[STIX]{x1D6E4}$), we look for waves in the chevrons in figure 12 ahead of the vortex fusion. The chevron is spread apart further when the co-rotating tubes in figure 11 enter the adverse pressure gradient region of the foil. The spread out chevron, resisting fusing, is modelled below as experiencing trains of Kelvin divergent waves. This example is similar to what is briefly seen on the surface in figure SI-TA-1 also at $f=1.25~\text{Hz}$. The chevron has symmetrical branches lying in a plane. This occurrence is consistent with that for $Ro\ll 1$, where the waves are planar and at an angle to the axis of rotation of the upstream vortex (Batchelor Reference Batchelor1967). Assume that the stagnation point at the apex of the chevron and upstream of the burst vortex is translating along the $45^{\circ }$ slope, producing a divergent wave train. Figure 12 shows a plausible empirical explanation that the plane waves divide symmetrically at angles of $\pm 19^{\circ }$ to the upstream vortex axis. The agreement is good. The transverse waves being weak are not seen. The pressure point in the parlance of divergent waves (say, a sailboat is being dragged in a channel), or the stagnation point, also match.

Figure 12. Kelvin divergent wave model of a foil-tip chevron; $f=1.25~\text{Hz}$. The model is empirical. A pair of co-rotating spiralling vortex tubes are coming from the pressure side of the foil tip. While being stretched at $45^{\circ }$, the combined vortex tube bursts into an arrowhead shape. This panel appears in between the panels in figure 11(1 and 2). Curved big arrow represents the bundle of streamlines of the rolled up flow of the foil tip. Regions of favourable and adverse pressure gradients are marked; $x$ is along the foil chord, $U_{ext}$ is the external flow velocity.

We use the dispersion relationship $\unicode[STIX]{x1D706}_{g}=2\unicode[STIX]{x03C0}U^{2}(\cos \unicode[STIX]{x1D703})^{2}/g$ to estimate the wavelength $\unicode[STIX]{x1D706}_{g}$. The stagnation point moves at an estimated velocity of $0.14~\text{m}~\text{s}^{-1}$. For $\unicode[STIX]{x1D703}=45^{\circ }$, $\unicode[STIX]{x1D706}_{g}=0.006~\text{m}$. This value is in agreement with figure 12. The pitch of the spirals is similar to $\unicode[STIX]{x1D706}_{g}$. Independent verification of the hypothesis is required. The stretched aerated vortex line at $45^{\circ }$ slope sustains waves and is elastic.

3.11 Initial condition dependence: cycle-to-cycle concatenation

Like equation (2.7), the sum of roll ($\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D719}}$), pitch ($\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D703}}$) and twist ($\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D703}t}$) torques introduced is conserved cycle to cycle. If the sharp leading edge of the foil at its root penetrates the funnel, entrainment by the foil leading edge takes place. The funnel oscillates. The root vortex may spawn small funnels in the large funnel above it (figure 13c,d, SI, Movies 1 and 4). A concatenation model of this variation is given below.

Figure 13. Time frames of lee-side air-entrained secondary surface vortices: ‘laminar’ (a,b) and turbulent (c,d). In (a,b), the upper arrow marks a surface indentation that is the funnel mouth of diameter $q$. This funnel translates down with the air-entrained vortex, as marked by the lower arrow, at a depth of $p$; $p\gg q$. The Kelvin mode $m=0$ is formed, shown by the dotted line part (the upper wave of buckling). The vortex in (a) is a spiral of two turns (see figure 3 in Bandyopadhyay & Gad-El-Hak Reference Bandyopadhyay and Gad-El-Hak1996). Ignoring the spiralling, this is simplified to a buckling aerated ‘bar’ of third mode. That is, a wave of two wavelengths lying between the stagnation point and the free surface (the dashed and dotted lines) can be fitted to the elastic vortex in (a). $K_{\unicode[STIX]{x1D6F9}}$ is torsional spring constant. In (c,d), the dashed perimeters enclose the turbulent secondary surface vortex; $p\leqslant q$ in (d). Coordinate $y$ is downwards from the free surface; $P_{3}$ is axial load for the third mode of buckling.

The entrainment at the root ($\unicode[STIX]{x1D6FA}_{root}$) and the foil ($\unicode[STIX]{x1D6FA}_{foil}$) shown in figure SI-DA-4 are given by

(3.4)$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FA}_{root}=\text{erf}(x)=\frac{2}{\sqrt{\unicode[STIX]{x03C0}}}\int _{0}^{x}\text{e}^{-t^{2}}\,\text{d}t,\quad \text{and} & \displaystyle\end{eqnarray}$$

(3.5)$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FA}_{foil}=\text{erf}\,c(x)=1-\text{erf}(x). & \displaystyle\end{eqnarray}$$

Here, $t$ is time, and $x$ is the surplus or deficiency in entrainment (mass or volume of air) from a long time average. In figure SI-DA-4, the total normalized entrainment of 1.0 is given by the applied torque.

Figure 13 shows vertical secondary DL and turbulent surface vortices on the lee side, translating horizontally. Figures 13(a) and 13(b) show that the funnel mouth, of diameter $q$, indicated by the dark spot on the free surface – an indentation on the surface – is small and translates with the air-entrained vortex below it, at a depth of $p$. Due to a pressure difference with the vortex core, the cusp of the tiny funnel sends air to the vortex through a very thin (invisible) tube. The elastic vortex is pinned between the unstable stagnation point below and the free surface as it pushes against the pressure gradient downwards. A leeward shear of the stagnation point buckles the vortex producing a standing Kelvin wave. A third mode of buckling – a two wavelength long dashed and dotted line – is fitted. Since $p\gg q$, the unstable elastic vortex has an abrupt drop in the diameter as in Kelvin mode $m=0$. For $p\leqslant q$, there is nothing to buckle as in $(d)$. The $m=0$ mode does not undergo maximum stretching because it is not aligned to the direction of principal strain and is not active in the production of visible bubbles. In the turbulent case in figures 13(c) and 13(d), the funnel is wider. The funnel oscillations and the secondary surface vortices in the near wake control the apportioning of the air entrainment between the foil and the root vortex.

3.12 Modelling of the modulus of elasticity of an aerated vortex

Figure 10(a) shows a thin vortex with small amplitude waves, aligned with the centre of the funnel, later buckling to a sinusoid in (b) when stretching reaches the maximum level due to the mean vortex slope of $45^{\circ }$. Below, a buckling model of the modulus of elasticity $E$ of the vertical elastic vortex tube, near the free surface in figure 13(a,b), is given. Added mass effects are ignored. The vortex length in (a) allows a spiral of two turns; see figure 3 in Bandyopadhyay & Gad-El-Hak (Reference Bandyopadhyay and Gad-El-Hak1996). Ignoring the spiralling, this is simplified to a planar buckling and aerated ‘bar’ of third mode. Two wavelengths lying between the stagnation point and the free surface (the dashed and dotted lines) can be fitted to the elastic vortex in (a).

The deflection of an elastic solid bar undergoing the third mode of buckling is given by $P_{3}=9\unicode[STIX]{x03C0}^{2}EI/p^{2}$, where $P_{3}$ is axial load (N), and $p$ is the length $(\text{m})=1.2c$, where $c$ is the foil chord, and $I$ is the second moment of $\text{area}=\unicode[STIX]{x03C0}(q/2)^{4}/4$. For critical buckling, $I$ should be from the minimum value of the diameter $q~(\text{m})$. The value of the visible $q$ varies from 0.01 m at the axial location where the deflection is zero to just under 0.02 m where the deflection is the maximum. Take $P_{3}=\unicode[STIX]{x1D70C}gp(\unicode[STIX]{x03C0}q^{2}/4)$ (N). Ignoring the reduction in the vortex diameter, $P_{3}=0.37$ (N) for $q=0.02~\text{m}$, and $P_{3}=0.0924$ (N), for 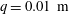$q=0.01~\text{m}$. For $P_{3}=0.37~\text{N}$, $E=7.6\times 10^{3}~\text{N}~\text{m}^{-2}$. For $P_{3}=0.0924~\text{N}$, $E=3.05\times 10^{4}~\text{N}~\text{m}^{-2}$. For comparison, $E$ for gelatin gels is $1\times 10^{3}~\text{N}~\text{m}^{-2}$ (Lucas et al. Reference Lucas, María, Patricia, Laura and Fasce2015), and for water, $E$ is $2.2\times 10^{9}~\text{N}~\text{m}^{-2}$.

The above simplification holds for the lower wavelength since the axis remains vertical where the foil trailing edge effect is uniformly felt. For the upper wavelength, the foil trailing edge effect is less due to a foil truncation (figure 1a). There is a resistance of torsional spring constant $K_{\unicode[STIX]{x1D6F9}}$ due to the effects of the lower trailing edge vortex, and this applies at the lower boundary condition. See figure 13(a). A net lateral buckling displacement of $p\text{Sin}\,\unicode[STIX]{x1D6F9}$ is produced. Since $\unicode[STIX]{x1D6F9}$ is small, the critical value of the compression load is $P_{cr}=K_{\unicode[STIX]{x1D6F9}}/p$. Assuming $P_{cr}=P_{3}=0.0924~\text{N}$, the estimated spring constant $K_{\unicode[STIX]{x1D6F9}}$ is $0.011~\text{Nm}~\text{rad}^{-1}$.

A force of 0.0924 N is $1/10$th of the lowest load in air in a small flapping fin produced in our gearless hemispherical motor drive, which is the lowest-friction drive built by us (Bandyopadhyay Reference Bandyopadhyay2019). Say, the root vortex in figure 6(b) oscillates axially 10 to 20 times while discharging bubbles in the unstable zone. Assume that such loss of energy due to release of compressed air in the form of bubbles is similar to the frictional losses in the flapping mechanism of flying insects, and that the number of natural damped oscillations in the spring–mass–damper system is equal to the quality factor $Q$. Then the $Q$ of the damped oscillation of the bursting root vortex is similar to that of fruit fly, hawkmoth and bumblebee (Ellington Reference Ellington1999).