Published online by Cambridge University Press: 23 March 2005
The concept of generalized order statistics was introduced as a unified approach to a variety of models of ordered random variables. The purpose of this article is to investigate the conditions on the parameters that enable one to establish several stochastic comparisons of general p-spacings for a subclass of generalized order statistics in the likelihood ratio and the hazard rate orders. Preservation properties of the logconvexity and logconcavity of p-spacings are also given.
The concept of generalized order statistics was introduced by Kamps [17,18] as a unified approach to a varity of models of ordered random variables (rv's). Choosing the parameters appropriately, several other models of ordered rv's are seen to be particular cases. One may refer to Kamps [18] for ordinary order statistics, record values, order statistics with nonintegral sample size, k-record values, sequential order statistics, and Pfeifers records, refer to Balakrishnan, Cramer, and Kamps [2] for progressive type II censored order statistics, and refer to Belzunce, Mercader, and Ruiz [6] and references therein for order statistics under multivariate imperfect repair. Generalized order statistics have been of interest during the last few years because they are more flexible in statistical modeling and inference (see, e.g., AL-Hussaini and Ahmd [1], Cramer and Kamps [9], Cramer, Kamps, and Rychlik [10], Gajek and Okolewski [13], Keseling [19], and Nasri-Roudsari [24]).
Stochastic comparisons of spacings of order statistics have been studied by several authors. Kochar [21], Khaledi and Kochar [20], and others compared (normalized) simple spacings, and Hu and Wei [15], Misra and van der Meulen [22], and Hu and Zhuang [16] considered general p-spacings. It is natural and interesting to obtain stochastic properties of spacings of generalized order statistics by analogy with ordinary order statistics. Franco, Ruiz, and Ruiz [12] and Belzunce et al. [6] have made some contributions to this direction. Belzunce et al. [6] touched upon one comparison of general p-spacings of generalized order statistics in the usual stochastic order.
The purpose of this article is to investigate the conditions on the parameters that enable one to establish several stochastic comparisons of general p-spacings for a subclass of generalized order statistics in the likelihood ratio and the hazard rate orders. In Section 2, we recall the definitions of generalized order statistics, some stochastic orders, and some aging notions, and we give some useful lemmas that will be used in Sections 3 and 4. Preservation properties of the logconvexity and logconcavity of p-spacings are given in Section 3. Finally, in Section 4, general p-spacings of generalized order statistics are compared in the likelihood ratio and the hazard rate orders.
Throughout, the terms “increasing” and “decreasing” mean “nondecreasing” and “nonincreasing,” respectively. a/0 is understood to be ∞ whenever a > 0. All integrals and expectations are implicitly assumed to exist whenever they are written. For any rv X with distribution function F, F = 1 − F denotes its survival function. All distribution functions under consideration are restricted to be continuous with its support in the positive real line
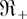
.
Uniform generalized order statistics are defined via some joint density function on a cone of the
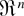
. Generalized order statistics based on an arbitrary distribution function F are defined by means of the inverse function of F.
Definition 2.1 (see Kamps [17]): Let
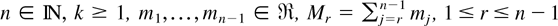
, be parameters such that γr,n = k + n − r + Mr ≥ 1 for all r = 1,…,n − 1, and let

. If the rv's

, possess a joint density of the form
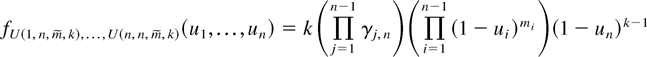
on the cone 0 ≤ u1 ≤ u2 ≤ ··· ≤ un < 1 of
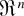
, then they are called uniform generalized order statistics. Now, let F be an arbitrary distribution function. The rv's,
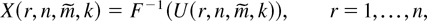
are called the generalized order statistics (GOSs, for short) based on F, where F−1 is the inverse of F defined by F−1(u) = sup{x : F(x) ≤ u} for u ∈ [0,1]. In the particular case m1 = ··· = mn−1 = m, the above rv's are denoted by U(r,n,m,k) and X(r,n,m,k), r = 1,…,n, respectively.
Ordinary order statistics of a random sample from a distribution F are a particular case of GOSs when k = 1 and mr = 0 for all r = 1,…,n − 1. When k = 1 and mr = −1 for all r = 1,…,n − 1, then we get the first n record values from a sequence of rv's with distribution F. Choosing the parameters appropriately, several other models of ordered rv's are seen to be particular cases.
It is well known that GOSs from a continuous distribution form a Markov chain with transition probabilities
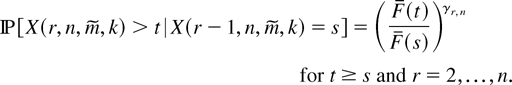
Throughout this article, we consider the special case of GOSs (m1 = ··· = mn−1 = m) in which the marginal distribution and density functions of the rth GOS have closed forms. Stochastic properties of p-spacings of general GOSs are still under our investigation. If F is absolutely continuous with density function f, Lemma 3.3 of Kamps [18] states that, for each r = 1,…,n, the marginal density function of the rth GOS X(r,n,m,k) based on F is given by
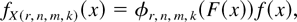
where
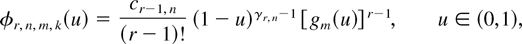
is the marginal density function of
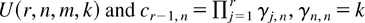
, and Mn = 0. Here, the function
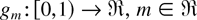
, is defined by

It is easy to see that
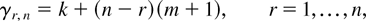
and that gm(x) is nonnegative and increasing in x ∈ [0,1) for each
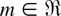
.
Let F be a distribution function of some nonnegative rv. For a given positive integer p, p ≤ n, let
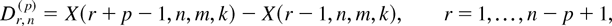
denote the p-spacings of the GOSs X(1,n,m,k) ≤ X(2,n,m,k) ≤ ··· ≤ X(n,n,m,k). Here, X(0,n,m,k) ≡ 0. For p = 1, 1-spacings are simple spacings in the literature. Let fr,n(p)(x), Fr,n(p)(x), and Fr,n(p)(x) denote the respective density, distribution, and survival functions of Dr,n(p), r = 1,…,n − p + 1. Clearly, f1,n(p)(x) = fX(p,n,m,k)(x) given by (2.2). From Lemma 3.5 of Kamps [18], it follows that

and, hence,

for r = 2,…,n − p + 1 and x ≥ 0.
The next proposition states that under suitable restrictions on the parameters of GOSs, the conditional distribution of one GOS given another lower-indexed one based on a continuous distribution has the same distribution as some GOS based on the truncated parent distribution. We denote by [Y |A] any rv whose distribution is the conditional distribution of Y given event A.
Proposition 2.1: Let X(r,n,m,k), r = 1,…,n, be GOSs based on a continuous distribution function F. For each u ∈ Supp(F), the support of F, denote Fu(x) = F(u + x)/F(u) for x ≥ 0. Then
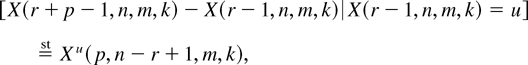
where p ≥ 1 and r = 2,…,n − p + 1, and Xu(p,n − r + 1,m,k) is a GOS based on Fu.
Proof: The proof of the case m ≠ −1 is the immediate consequence of Theorem 3.2 in Keseling [19]. A limiting argument can establish the case of m = −1. █
For the sake of brevity, the constant n in γr,n and cr,n is suppressed when there is no confusion in the following context.
Some stochastic orders and aging notions that will be used in this article are recalled in the following two definitions respectively.
Definition 2.2: Let X and Y be two rv's with respective survival functions F and G. We say that X is smaller than Y if the following hold:
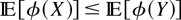
The relationships among these orders are shown in the following diagram (see Shaked and Shanthikumar [27], and Müller and Stoyan [23]):

Definition 2.3: Let X be a nonnegative rv with distribution function F. X or F is said to be
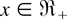
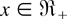

If f is logconcave, then F and F are also logconcave (see, e.g., Chandra and Roy [8], Barlow and Proschan [4, p.77]). If f is logconvex, then F is also logconvex while F is logconcave (see Sengupta and Nanda [26]). Furthermore, Block, Savits, and Singh [7] proved that if F is logconvex then F is logconcave. Therefore,
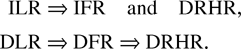
The following lemmas are useful in deriving the main results of this article. Lemma 2.1 is due to Misra and van der Meulen [22], hereafter referred to as MM. Lemma 2.2 is the extension of Lemma 2.1 in MM.
Lemma 2.1: Let Θ be a subset of the real line
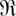
and let X be a nonnegative rv having a distribution function belonging to the family
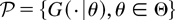
, which satisfies that
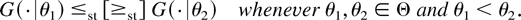
Let Ψ(x,θ) be a real-valued function defined on

. Then the following hold:

Lemma 2.2: Let X be a nonnegative rv with distribution function F. If X is DLR [ILR] and if m ≥ 0, then the following hold:

Proof: Denote Lm(x) = gm(F(x)). Observe that
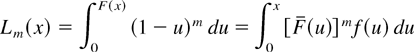
holds for each
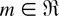
, where f is the density of F. Since the logconvexity [logconcavity] of f (x) implies that F(x) is logconvex [logconcave] in x, it follows that
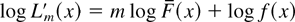
is also logconvex [logconcave] in x for m ≥ 0. The rest of the proof is the same as that of Lemma 2.1 in MM. █
Remark 2.1: For m = 0, Lemma 2.2 reduces to Lemma 2.1 in MM. It is worthwhile pointing out that Lemma 2.2 is, in general, not true when m < 0, as illustrated by the following counterexample: Let X be uniformly distributed on the interval (0,1). Then X is ILR. For each fixed u ∈ (0,1) and x ∈ (0,1 − u), we have
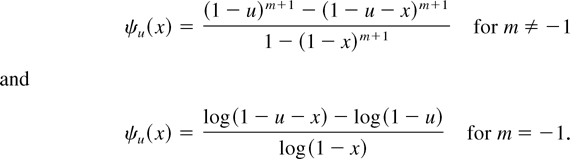
Observe that

for m ≠ −1 and m < 0, where
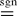
means equality in sign, and
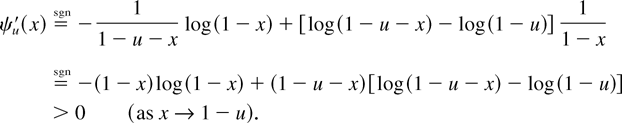
Therefore, ψu(x) is not decreasing in x; that is, Lemma 2.2(i) is not true in this example. Similarly, it can be checked that Lemma 2.2(ii) does not hold in this example.
Remark 2.2: Observe that (2.7) holds for each m, and that (2.7) can be written as
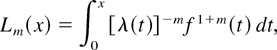
where λ(t) = f (t)/F(t) is the failure rate function of F. Since the logconcavity of λ(t) implies that f (t) and −log F(t) are both logconcave (see Pellerey, Shaked, and Zinn [25, Appendix]), it follows that the integrand in (2.8) is logconcave when m ∈ [−1,0). Therefore, if λ(t) is logconcave and m ∈ [−1,0), then ψu(x) is decreasing in
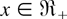
for each fixed
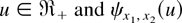
is decreasing in
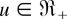
for fixed x2 > x1 > 0.
To state Lemma 2.4, we first recall the following Prekopa's theorem.
Lemma 2.3 (see Eaton [11, Thm. 5.1]): Suppose that
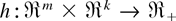
is a logconcave function and
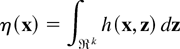
is finite for each
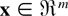
. Then η(x) is logconcave in
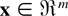
.
Lemma 2.4: Let X be a nonnegative rv with distribution function F. If X is ILR and m ≥ 0, or if the failure rate function of F is logconcave and m ∈ [−1,0), then the following hold:
(i) gm(F(x)) is logconcave in
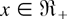
+.
(ii) gm(F(x + u)) − gm(F(u)) is logconcave in
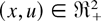
.
Proof: The logconcavity of gm(F(x)) follows from the proof of Lemma 2.2 and Remark 2.2. The same argument as that of the proof of Lemma 3.1 in MM yields part (ii) by applying Lemma 2.3. █
The next lemma gives conditions on the parameters to compare GOSs based on two different distributions in the hazard rate order, which follows from Theorem 3.6 in Franco et al. [12].
Lemma 2.5: Let X(r,n,m,k) and Y(r′,n′,m,k) be two GOSs based on distribution functions F and G, respectively. If F ≤hr G and m ≥ −1, then
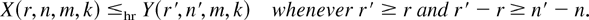
For ordinary order statistics, Barlow and Proschan [3] established that if the parent distribution F is DFR, then the corresponding simple spacings Dk,n(1), k = 1,…,n, are also DFR, and MM [12] proved that if F is DLR, then the Dk,n(1) are also DLR. For record values, Gupta and Kirmani [14] noticed that if F is DFR, then the Dk,n(1) are also DFR. In the following theorem, we extend these results to the simple spacings of GOSs.
Theorem 3.1: Let X(r,n,m,k), r = 1,…,n, be GOSs based on distribution function F.
(1) If F is DFR, then Dr,n(1), r = 1,…,n, are also DFR.
(2) If F is DLR, then Dr,n(1), r = 1,…,n, are also DLR.
Proof:
(1) It follows from (2.1) that the survival function of Dr,n(1) is given by
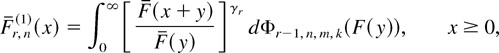
where Φr−1,n,m,k(F(·)) is the distribution function of X(r − 1,n,m,k). The DFR property of F implies that [F(x + y)/F(y)]γr is logconvex in x for each
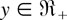
. Since the logconvexity is closed under mixture (see Barlow and Proschan [4, p.103]), it follows from (3.1) that Fr,n(1)(x) is logconvex in
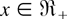
. Hence, Dr,n(1) is DFR.
(2) From (2.2) and (2.3), we have
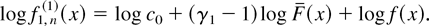
Since the logconvexity of f implies that F is logconvex, it follows that f1,n(1) is also logconvex. To consider the logconvexity of fr,n(1) for r = 2,…,n, fix δ > 0 and consider the ratio
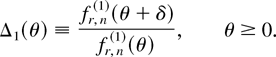
From (2.5), we get that
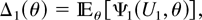
where
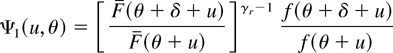
is increasing in
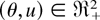
by using the DLR property of F, and the nonnegative rv U1 has a distribution function belonging to the family
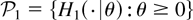
with corresponding densities given by
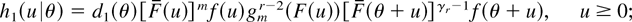
here d1(θ) is the normalizing constant. It is seen that H1(·|θ1) ≤lr H1(·|θ2) and, hence, H1(·|θ1) ≤st H1(·|θ2) whenever θ2 ≥ θ1 ≥ 0 since γr ≥ 1 and
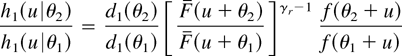
is increasing in
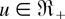
. Therefore, Δ1(θ) is increasing in
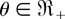
by using Lemma 2.1. This completes the proof. █
From the proof of Theorem 3.1(1), we know that the conclusion is also true for the simple spacings of the GOSs without restriction m1 = ··· = mn−1 = m. For p ≥ 2, the p-spacings do not preserve the DFR or DLR property of the parent distribution (see MM [22, Remark 3.1]).
MM also established that the general p-spacings (1 ≤ p ≤ n) of ordinary order statistics preserve the ILR property of the parent distribution. This result is generalized from ordinary order statistics to GOSs under some restriction on the parameters in the following theorem.
Theorem 3.2: Let X(r,n,m,k), r = 1,…,n, be GOSs based on a distribution function F. If F is ILR and m ≥ 0, then Dr,n(p), r = 1,…,n − p + 1, are also ILR for p = 1,…,n.
Proof: For r = 1, the result follows from (2.2) and (2.3) by using Lemma 2.4(i). For r ≥ 2, a similar argument to that in the proof of Theorem 3.3 in MM yields the desired result by applying Lemmas 2.3 and 2.4 in (2.5). █
Notice that the epoch times of a nonhomogeneous Poisson process with intensity function λ(t) are the record values of a sequence of independent and identically distributed (i.i.d.) nonnegative rv's with the failure rate being λ(t), where
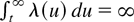
for all
. From Theorem 3.1 in Pellerey et al. [25], we know that if the hazard rate function λ(t) of the underlying distribution is logconcave, then the simple spacings of record values are ILR. This result can be extended to the general spacings of GOSs with m ∈ [−1,0) under the same condition.
Theorem 3.3: Let X(r,n,m,k), r = 1,…,n, be GOSs based on a distribution function F. If the hazard rate function λ(t) of F is logconcave and m ∈ [−1,0), then Dr,n(p), r = 1,…,n − p + 1, are ILR for p = 1,…,n.
Proof: For r ≥ 2, rewrite (2.5) as

The desired result now follows from Remark 2.2 and Lemmas 2.3 and 2.4.
The proof of the case r = 1 is trivial. █
Remark 3.1: Choosing r = 1 in Theorem 3.3, we obtain that if the hazard rate function λ(t) of F is logconcave, then X(r,n,m,k), r = 1,…,n, are ILR for m ∈ [−1,0). Pellerey et al. [25] considered the special case m = −1 in their Corollary 2.2.
For ordinary order statistics, the following are comparison results for general p-spacings:

In this section, we investigate conditions on the parameters to extend the above comparison results (P1)–(P7) from ordinary order statistics to GOSs. Theorems 4.1 and 4.4 deal with the likelihood ratio ordering, whereas Theorems 4.2 and 4.3 deal with the hazard rate ordering.
Theorem 4.1: Let X(r,n,m,k), r = 1,…,n, be GOSs based on a distribution function F, where m ≥ 0. Then the following hold:

Proof:
(a) Suppose that F is DLR. It suffices to verify that for each fixed r = 1,…, n − p,

is increasing in
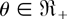
. We consider two cases.
Case 1: For r = 2,…,n − p, it follows from (2.5) that
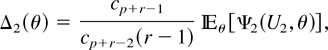
where

and the nonnegative rv U2 has a distribution function belonging to the family
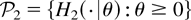
with corresponding densities given by

here, d2(θ) is the normalizing constant. It is seen that, for m ≥ 0, the following hold:

is increasing in
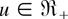
by using Lemma 2.2 and the fact that the logconvexity of f implies the logconvexity of F.
Then, by Lemma 2.1, we conclude that Δ2(θ) is increasing in
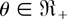
.
Case 2: For r = 1, it follows from (2.2) and (2.5) that

is increasing in
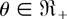
by using Lemma 2.2. This completes the proof of part (a).
(b) Suppose that F is DLR. It suffices to verify that for each fixed r = 1,…,n − p + 1,
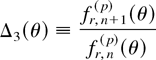
is decreasing in
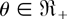
. For r = 1, from (2.2), we get that
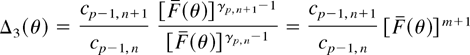
is decreasing in
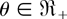
. For r ≥ 2, from (2.5), we get that
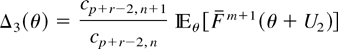
is also decreasing in

by Lemma 2.1, where the nonnegative rv U2 has a distribution function belonging to the family
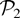
. This completes the proof of part (b).
(c) Suppose that F is DLR [ILR]. It suffices to verify that for each fixed r = 1,…,n − p + 1,
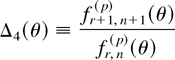
is increasing [decreasing] in
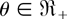
. For r = 1, from (2.2) and (2.5), we get that

is increasing [decreasing] in
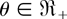
by Lemma 2.2. For r ≥ 2, from (2.5), we get that
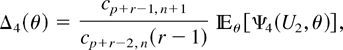
where
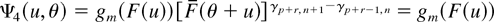
does not depend on θ and is increasing in
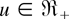
since γp+r,n+1 = k + (n + 1 − p − r)(m + 1) = γp+r−1,n, and U2 has the distribution belonging to the family
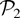
. It can be checked that H2(·|θ1) ≤lr [≥lr] H2(·|θ2) for θ2 ≥ θ1 ≥ 0 if F is DLR [ILR]. Therefore, applying Lemma 2.1 yields that Δ4(θ) is increasing [decreasing] in

. This completes the proof. █
Remark 4.1: In views of Remark 2.2, the proof of Theorem 4.1(c) is still valid for m ∈ [−1,0) under the stronger condition that the failure rate of F is logconcave. Therefore, for GOSs, if m ∈ [−1,0) and the failure rate of F is logconcave, then Dr,n(p) ≥lr Dr+1,n+1(p) for r = 1,…,n − p + 1.
An immediate consequence of Theorem 4.1 is the following corollary.
Corollary 4.1: Let X(r,n,m,k), r = 1,…,n, be GOSs based on a distribution function F. If F is DLR and m ≥ 0, then
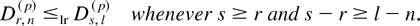
Choosing m = −1 in Remark 4.1, we have the following corollary.
Corollary 4.2: Let XL(1),XL(2),… be record values based on a sequence of i.i.d. rv's with distribution function F. If the failure rate λ(t) of F is logconcave, then
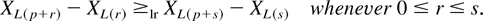
In Theorem 4.1, if, instead, F is assumed to be DFR [IFR], then the results can be weakened from the likelihood ratio order to the hazard rate order (see Theorems 4.2 and 4.3).
Theorem 4.2: Let X(r,n,m,k), r = 1,…,n, be GOSs based on a distribution function F. If F is DFR and m ≥ −1, then the following hold:
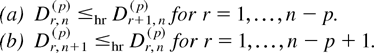
Proof: We give the proof of the case that m > −1; the proof of the case m = −1 follows from the closure property of the hazard rate order under weak convergence. Let λr,n(p)(t) denote the hazard rate function of Dr,n(p), and set Fu(x) = F(u + x)/F(u) for x ≥ 0 and u ∈ Supp(F).
(a) First consider r ∈ Θ1 ≡ {2,3,…,n − p + 1}. From (2.5) and (2.6), we get that
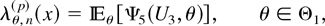
where
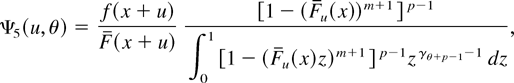
and the nonnegative rv U3 has a distribution function belonging to the family
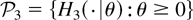
with corresponding densities given by
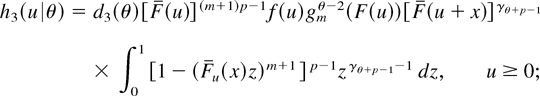
here, d3(θ) is the normalizing constant. Observe the following:

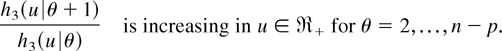
Note that
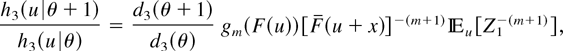
where the nonnegative rv Z1 has a distribution function belonging to the family

with corresponding densities given by
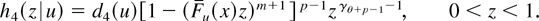
From the DFR property of F, it follows that h4(z|u′)/h4(z|u) is decreasing in z ∈ (0,1) whenever u′ ≥ u ≥ 0 and, hence, H4(·|u) ≥lr H4(·|u′) whenever u′ ≥ u ≥ 0. Applying Lemma 2.1 yields (4.2).
Again, applying Lemma 2.1 in (4.1) yields that λθ,n(p)(x) is decreasing in θ ∈ Θ1 for each fixed

. This means that Dr,n(p) ≤hr Dr+1,n(p) for r ∈ Θ1.
It remains to show that D1,n(p) ≤hr D2,n(p). For this, consider

where the last equality follows from Proposition 2.1, and Xu(p,n − 1,m,k) is a GOS based on Fu. Since the DFR property of F, F ≤hr Fu. By Lemma 2.5, we get that X(p,n,m,k) ≤hr Xu(p,n − 1,m,k) for
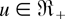
, which, in turn, implies that the ratio in the integrand in (4.3) is increasing in

. Therefore, D1,n(p) ≤hr D2,n(p). This completes the proof of part (a).
(b) For r = 1, the desired result D1,n+1(p) = X(p,n + 1,m,k) ≤hr X(p,n,m,k) = D1,n(p) follows from Lemma 2.5. Now, consider r ≥ 2, and let p and r be fixed. From (2.5) and (2.6), the failure rate function of Dr,θ(p) is given by
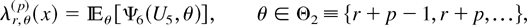
where
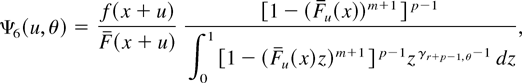
and the nonnegative rv U5 has a distribution function belonging to the family
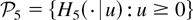
with corresponding densities given by
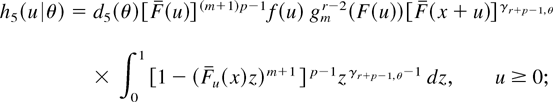
here, d5(θ) is the normalizing constant. Observe that the following hold:

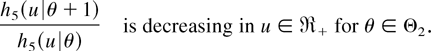
Note that

where Ψ7(z,u) = zm+1 is increasing in z ∈ (0,1), not depending on u, and the nonnegative rv Z2 has a distribution function belonging to the family
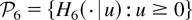
with corresponding densities given by

here, d6(u) is the normalizing constant. Since
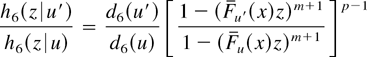
is decreasing in z ∈ (0,1) for u′ ≥ u ≥ 0 by using DFR property of F, it follows from Lemma 2.1 that (4.5) holds.
Again, applying Lemma 2.1 in (4.4) yields that λr,θ(p)(x) is increasing in θ ∈ Θ2 for each fixed

. Therefore, Dr,n+1(p) ≤hr Dr,n(p) for r ≥ 2. This completes the proof of the theorem. █
Remark 4.2: The reversed inequalities in Theorem 4.2 do not, in general, hold when F is IFR, as shown by a counterexample in Hu and Zhuang [16]. Hence, the inequalities in parts (a) and (b) of Theorem 4.1 cannot be reversed when F is ILR.
Remark 4.3: Theorem 4.2 is not true for m < −1, as illustrated by the following counterexample. Let X(r,n,m,k), r = 1,2,…,n, be GOSs based on the exponential distribution F(x) = 1 − e−x, x ≥ 0, where m < −1. Then γr,n < γr+1,n for r = 1,…,n − p, and γr,n+1 < γr,n for r = 1,…,n − p + 1. Denote Yr,n = γr,n Dr,n(1) for r = 1,…,n. From Theorem 3.10 in Kamps [18], we know that F is also the distribution function of Yr,n. Hence,
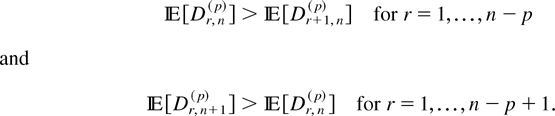
Therefore, Theorem 4.2 cannot be true in this example (even in the usual stochastic order).
In the next theorem, there is no further restriction (like m ≥ −1) on the parameter m.
Theorem 4.3: Let X(r,n,m,k), r = 1,…,n, be GOSs based on a distribution function F. If F is DFR [IFR], then Dr,n(p) ≤hr [≥hr] Dr+1,n+1(p) for r = 1,…,n − p + 1.
Proof: We give the proof of the case m > −1; the proof of the case m < −1 is similar and the proof of the case m = −1 follows by a limiting argument. From (2.5) and (2.6), the failure rate function of Dr+θ,n+θ(p), θ ∈ Θ3 ≡ {0,1}, r = 1,…,n − p + 1, is given by

where

and the nonnegative rv U6 has a distribution function belonging to the family
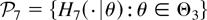
with corresponding densities given by
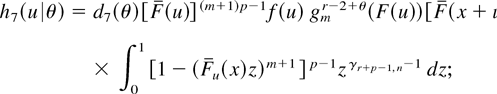
here, d7(θ) is the normalizing constant, and we use the identity that γr+p−1+θ,n+θ = γr+p−1,n for θ ∈ Θ3. Observe the following:

By Lemma 2.1, we obtain that λr+θ,n+θ(p)(x) is decreasing [increasing] in θ ∈ Θ3. So we prove the desired result for r ≥ 2.
It remains to verify that D1,n(p) ≤hr D2,n+1(p). For this, consider

where the last equality follows from Proposition 2.1, and Xu(p,n,m,k) is a GOS based on Fu. Note that the DFR [IFR] property of F implies that F ≤hr [≥hr] Fu. By Lemma 2.5, we get that X(p,n,m,k) ≤hr [≥hr] Xu(p,n,m,k) for

, which, in turn, implies that the ratio in the integrand in (4.6) is increasing [decreasing] in
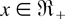
. Therefore, D1,n(p) ≤hr [≥hr]D2,n+1(p). This completes the proof of the theorem. █
In views of Theorems 4.2 and 4.3, we have the following two corollaries.
Corollary 4.3: Let X(r,n,m,k), r = 1,…,n, be GOSs based on a distribution function F. If F is DFR and m ≥ −1, then
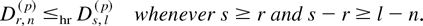
Corollary 4.4: Let XL(1),XL(2),… be the same as in Corollary 4.2. If the failure rate λ(t) of F is decreasing [increasing], then

Finally, the following theorem extends (P7) from ordinary order statistics to GOSs.
Theorem 4.4: Let X(r,n,m,k), r = 1,…,n, be GOSs based on a distribution function F with failure rate function λ(t). If m ≥ 0 and F is ILR, or if m ∈ [−1,0) and λ(t) is logconcave, then
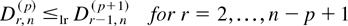
or, equivalently,
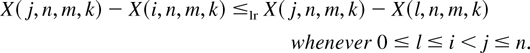
Proof: The equivalence of (4.7) and (4.8) is trivial. We give the proof of (4.7) only. It suffices to prove that for r = 2,…,n − p + 1,
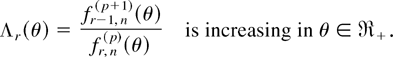
(i) For r = 3,…,n − m + 1, Λr(θ) can be written as
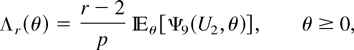
where
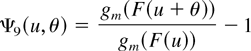
is increasing in
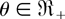
and decreasing in
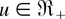
for m ≥ −1 by Lemma 2.4, and the rv U2 is defined as in Theorem 4.2. Since H2(·|θ1) ≥lr H2(·|θ1) for θ2 > θ1 ≥ 0, applying Lemma 2.1 in (4.9) yields that Λr(θ) is increasing in
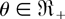
.
(ii) For r = 2, it follows from (2.2) and (2.5) that

which is decreasing in
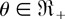
by using Lemma 2.2 and Remark 2.2. This thus completes the proof. █
Theorem 4.4 cannot be, in general, true when F is DLR, as shown by Example 3.1 in Hu and Zhuang [16].
Choosing m = −1 in Theorem 4.4, we have the following corollary.
Corollary 4.5: Let XL(1),XL(2),… be the same as in Corollary 4.2. If the failure rate λ(t) of F is logconcave, then
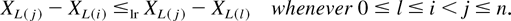
In Corollaries 4.2, 4.4, and 4.5, {XL(1),XL(2),…} can be interpreted as the epoch times {T1,T2,…} of a nonhomogeneous Poisson process with intensity function λ(t) (see the paragraph before Theorem 3.3). For various comparison results of nonhomogeneous Poisson processes, one can refer to Belzunce, Lillo, Ruiz, and Shaked [5] and references therein.
It is still an open problem whether (P8) holds for GOSs.
This work was supported by the National Natural Science Foundation of China (Grant No. 10171093), a Ph.D. Program Foundation of Ministry of Education of China, and one grant from USTC.