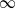1. Introduction and main results
Hawkes processes were introduced by Hawkes [Reference Hawkes18] and are now widely used in many applications, including modeling of earthquake occurrences [Reference Hawkes and Adamopoulos19], [Reference Ogata27], finance [Reference Bacry, Delattre, Hoffmann and Muzy2], [Reference Bacry, Delattre, Hoffmann and Muzy1], [Reference Bacry and Muzy3], genetics [Reference Reynaud-Bouret and Schbath31], and neuroscience [Reference Chevallier, Caceres, Doumic and Reynaud-Bouret9], [Reference Ditlevsen and Löcherbach14], [Reference Reynaud-Bouret, Rivoirard and Tuleau-Malot29]. Hawkes processes are random point processes on the real line (see [Reference Daley and Vere-Jones10], [Reference Daley and Vere-Jones11], [Reference Jacod and Shiryaev21] for an introduction) where each atom is associated with a (possibly signed) reproduction measure generating further atoms or adding repulsion.
When the reproduction measure is nonnegative, Hawkes and Oakes [Reference Hawkes and Oakes20] have provided a cluster representation of Hawkes processes based on immigration of ancestors, each of which is at the head of the branching point process of its offspring. Exponential concentration inequalities for ergodic theorems and tools for statistical applications have been developed, e.g., by Reynaud-Bouret and Roy [Reference Reynaud-Bouret and Roy30] using a coupling à la Berbee [Reference Berbee4].
For many applications, however, it is important to allow the reproduction measure to be a signed measure. The positive part of the measure can be interpreted as self-excitation, and its negative part as self-inhibition. For instance, in neuroscience this can be used to model the existence of a latency period before the successive activations of a neuron; see e.g. [Reference Reynaud-Bouret, Rivoirard and Tuleau-Malot29]. Brémaud and Massoulié [Reference Brémaud and Massoulié5] have devised efficient techniques based on Poisson point process thinning (or embedding) for this framework. The recent works [Reference Chen, Shojaie, Shea-Brown and Witten7] and [Reference Raad28] provide interesting contributions from this perspective, which will be further discussed at the end of Section 1.
A large part of the literature on Hawkes processes for neuroscience uses large systems approximations by mean-field limits (e.g. [Reference Chevallier8], [Reference Delattre, Fournier and Hoffmann13], [Reference Delattre and Fournier12], [Reference Ditlevsen and Löcherbach14]) or stabilization properties (e.g. [Reference Duarte, Löcherbach and Ost15] using Erlang kernels). Here, we consider a single Hawkes process for which the reproduction measure is a signed measure and concentrate on extending the ergodic theorem and concentration inequalities obtained in [Reference Reynaud-Bouret and Roy30] for a nonnegative reproduction measure. Similarly to [Reference Reynaud-Bouret and Roy30], the reproduction measure is assumed to have bounded support.
A main issue here is that when inhibition is present, the cluster representation of [Reference Hawkes and Oakes20] is no longer valid. An important tool in our study is the construction of a coupling of the Hawkes process with signed reproduction measure and a Hawkes process with a positive measure. The former is shown to be a thinning of the latter, for which the cluster representation is valid.
We then define renewal times for these general Hawkes processes. For this purpose, we introduce an auxiliary strong Markov process with states given by point processes. This allows us to split the sample paths into the delay and the cycles, the latter being independent and identically distributed (i.i.d.) excursions for which we use limit theorems for i.i.d. sequences.
In deriving concentration inequalities, a main difficulty is to obtain exponential bounds for the tail distribution of the renewal times. In the case in which the reproduction function is nonnegative, we associate to the Hawkes process an M/G/![]() $\infty$ queue. To our knowledge, this is the first time that the connection with M/G/
$\infty$ queue. To our knowledge, this is the first time that the connection with M/G/![]() $\infty$ queues has been made. This allows us to control the length of the excursions of the Hawkes process by using powerful Laplace transform techniques from queuing theory. These results have independent interest in themselves. We then extend our techniques to Hawkes processes with signed reproduction functions using the coupling.
$\infty$ queues has been made. This allows us to control the length of the excursions of the Hawkes process by using powerful Laplace transform techniques from queuing theory. These results have independent interest in themselves. We then extend our techniques to Hawkes processes with signed reproduction functions using the coupling.
We shall explain in Remark 1.2 how the coupling method presented in this paper in a simple framework can be extended to a much broader framework.
1.1. Definitions and notation
Measure-theoretic and topological framework. Throughout this paper, an appropriate filtered probability space ![]() $(\Omega,\mathcal{F},(\mathcal{F}_t)_{t \ge 0},{\mathbb{P}})$ satisfying the usual assumptions is given. All processes will be assumed to be adapted.
$(\Omega,\mathcal{F},(\mathcal{F}_t)_{t \ge 0},{\mathbb{P}})$ satisfying the usual assumptions is given. All processes will be assumed to be adapted.
Let ![]() $\mathcal{N}(\mathbb{R})$ denote the space of counting measures on the real line
$\mathcal{N}(\mathbb{R})$ denote the space of counting measures on the real line ![]() $\mathbb{R}=(\!-\infty, +\infty)$ which are boundedly finite; these are the Borel measures with values in
$\mathbb{R}=(\!-\infty, +\infty)$ which are boundedly finite; these are the Borel measures with values in ![]() $\mathbb{N}_0\cup \{+\infty\}$ (where
$\mathbb{N}_0\cup \{+\infty\}$ (where ![]() $\mathbb{N}_0=\{0,1,\ldots\}$) which are finite on any bounded set. The space
$\mathbb{N}_0=\{0,1,\ldots\}$) which are finite on any bounded set. The space ![]() $\mathcal{N}(\mathbb{R})$ is endowed with the weak topology
$\mathcal{N}(\mathbb{R})$ is endowed with the weak topology ![]() $\sigma(\mathcal{N}(\mathbb{R}),\mathcal{C}_{bs}(\mathbb{R}))$ and the corresponding Borel
$\sigma(\mathcal{N}(\mathbb{R}),\mathcal{C}_{bs}(\mathbb{R}))$ and the corresponding Borel ![]() $\sigma$-field, where
$\sigma$-field, where ![]() $\mathcal{C}_{bs}$ denotes the space of continuous functions with bounded support.
$\mathcal{C}_{bs}$ denotes the space of continuous functions with bounded support.
If N is in ![]() $\mathcal{N}(\mathbb{R})$ and
$\mathcal{N}(\mathbb{R})$ and ![]() $I\subset \mathbb{R}$ is an interval, then
$I\subset \mathbb{R}$ is an interval, then ![]() $N|_I$ denotes the restriction of N to I, and
$N|_I$ denotes the restriction of N to I, and ![]() $N|_I$ belongs to the space
$N|_I$ belongs to the space ![]() $\mathcal{N}(I)$ of boundedly finite counting measures on I. By abuse of notation, a point process on I is often identified with its extension which is null outside of I, and in particular
$\mathcal{N}(I)$ of boundedly finite counting measures on I. By abuse of notation, a point process on I is often identified with its extension which is null outside of I, and in particular ![]() $N|_I \in \mathcal{N}(I)$ is identified with
$N|_I \in \mathcal{N}(I)$ is identified with ![]() $\mathds{1}_I N \in \mathcal{N}(\mathbb{R})$. Accordingly,
$\mathds{1}_I N \in \mathcal{N}(\mathbb{R})$. Accordingly, ![]() $\mathcal{N}(I)$ is endowed with the trace topology and
$\mathcal{N}(I)$ is endowed with the trace topology and ![]() $\sigma$-field.
$\sigma$-field.
A random point process on ![]() $I\subset \mathbb{R}$ will be considered as a random variable taking values in the Polish space
$I\subset \mathbb{R}$ will be considered as a random variable taking values in the Polish space ![]() $\mathcal{N}(I)$. We shall also consider random processes with sample paths in the Skorokhod space
$\mathcal{N}(I)$. We shall also consider random processes with sample paths in the Skorokhod space ![]() $\mathbb{D}(\mathbb{R}_+,\mathcal{N}(I))$.
$\mathbb{D}(\mathbb{R}_+,\mathcal{N}(I))$.
All these spaces are Polish; see [Reference Daley and Vere-Jones10, Prop. A2.5.III, Prop. A2.6.III].
Hawkes processes. In this paper we study a random point process on the real line ![]() $\mathbb{R}=\break (\!-\infty,+\infty)$ specified by a stochastic evolution on the half-line
$\mathbb{R}=\break (\!-\infty,+\infty)$ specified by a stochastic evolution on the half-line ![]() $(0,+\infty)$ and an initial condition given by a point process on the complementary half-line
$(0,+\infty)$ and an initial condition given by a point process on the complementary half-line ![]() $(\!-\infty,0]$. This is more general than considering a stationary version of the point process (as was done in early papers [Reference Hawkes18], [Reference Hawkes and Oakes20]), does not require its existence, and can be used to prove the latter, as in [Reference Brémaud and Massoulié5]. The time origin 0 can be interpreted as the start of some sort of action with regard to the process (e.g. observation, or computation of statistical estimators).
$(\!-\infty,0]$. This is more general than considering a stationary version of the point process (as was done in early papers [Reference Hawkes18], [Reference Hawkes and Oakes20]), does not require its existence, and can be used to prove the latter, as in [Reference Brémaud and Massoulié5]. The time origin 0 can be interpreted as the start of some sort of action with regard to the process (e.g. observation, or computation of statistical estimators).
In the following definition of a Hawkes process with a signed reproduction measure, the initial condition ![]() $N^0$ is always assumed to be
$N^0$ is always assumed to be ![]() $\mathcal{F}_0$-measurable, and
$\mathcal{F}_0$-measurable, and ![]() $N^h|_{(0,+\infty)}$ is assumed to be adapted to
$N^h|_{(0,+\infty)}$ is assumed to be adapted to ![]() $(\mathcal{F}_t)_{t\ge0}$. We refer to [Reference Daley and Vere-Jones10, Sec. 7.2] for the definition of the conditional intensity measure, and for
$(\mathcal{F}_t)_{t\ge0}$. We refer to [Reference Daley and Vere-Jones10, Sec. 7.2] for the definition of the conditional intensity measure, and for ![]() $x \in \mathbb{R}$ we define
$x \in \mathbb{R}$ we define ![]() $x^+ = \max(x,0)$,
$x^+ = \max(x,0)$, ![]() $x^- = \max({-}x,0)$.
$x^- = \max({-}x,0)$.
Definition 1.1. Let ![]() $\lambda>0$, a signed measurable function
$\lambda>0$, a signed measurable function ![]() $h\,{:}\,(0,+\infty) \to \mathbb{R}$, and a boundedly finite point process
$h\,{:}\,(0,+\infty) \to \mathbb{R}$, and a boundedly finite point process ![]() $N^0$ on
$N^0$ on ![]() $(\!-\infty,0]$ with law
$(\!-\infty,0]$ with law ![]() $\mathfrak{m}$ be given. The point process
$\mathfrak{m}$ be given. The point process ![]() $N^h$ on
$N^h$ on ![]() $\mathbb{R}$ is a Hawkes process on
$\mathbb{R}$ is a Hawkes process on ![]() $(0,+\infty)$ with initial condition
$(0,+\infty)$ with initial condition ![]() $N^0$ and reproduction measure
$N^0$ and reproduction measure ![]() $\mu(dt) \triangleq h(t)\,dt$ if
$\mu(dt) \triangleq h(t)\,dt$ if ![]() $N^h|_{(\!-\infty,0]}=N^0$ and the conditional intensity measure of
$N^h|_{(\!-\infty,0]}=N^0$ and the conditional intensity measure of ![]() $N^h|_{(0,+\infty)}$ with respect to
$N^h|_{(0,+\infty)}$ with respect to ![]() $(\mathcal{F}_t)_{t\ge0}$ is absolutely continuous with respect to the Lebesgue measure and has density
$(\mathcal{F}_t)_{t\ge0}$ is absolutely continuous with respect to the Lebesgue measure and has density
This is a special case of the nonlinear Hawkes process defined in [Reference Brémaud and Massoulié5], corresponding to choosing ![]() $x\mapsto (\lambda + x)^+$ as the function
$x\mapsto (\lambda + x)^+$ as the function ![]() $\phi\,{:}\,\mathbb{R}\to\mathbb{R}_+$ in a conditional intensity of the more general form
$\phi\,{:}\,\mathbb{R}\to\mathbb{R}_+$ in a conditional intensity of the more general form ![]() $\Lambda^{h,\phi}(t)= \phi\bigl(\int_{(\!-\infty,t)} h(t-u)\,N^h(du)\bigr)$. We made this choice in order to streamline the mathematical reasoning and keep formulas reasonably readable. We shall later detail in Remark 1.2 how to extend the results to the more general setting.
$\Lambda^{h,\phi}(t)= \phi\bigl(\int_{(\!-\infty,t)} h(t-u)\,N^h(du)\bigr)$. We made this choice in order to streamline the mathematical reasoning and keep formulas reasonably readable. We shall later detail in Remark 1.2 how to extend the results to the more general setting.
Hawkes processes can be defined for reproduction measures ![]() $\mu$ which are not absolutely continuous with respect to the Lebesgue measure, but we shall consider here this case only. This avoids in particular the issue of multiplicities of points in
$\mu$ which are not absolutely continuous with respect to the Lebesgue measure, but we shall consider here this case only. This avoids in particular the issue of multiplicities of points in ![]() $N^h$. Since h is the density of
$N^h$. Since h is the density of ![]() $\mu$, the support of h is naturally defined as the support of the measure
$\mu$, the support of h is naturally defined as the support of the measure ![]() $\mu$:
$\mu$:
where ![]() $|\mu|(dt)=|h(t)|\,dt$ is the total variation measure of
$|\mu|(dt)=|h(t)|\,dt$ is the total variation measure of ![]() $\mu$. We assume without loss of generality that
$\mu$. We assume without loss of generality that ![]() $h = h{\mathds{1}}_{\textnormal{supp}(h)}$ and define
$h = h{\mathds{1}}_{\textnormal{supp}(h)}$ and define
The constant ![]() $\lambda$ can be viewed as the intensity of a Poisson immigration phenomenon on
$\lambda$ can be viewed as the intensity of a Poisson immigration phenomenon on ![]() $(0,+\infty)$. The function h corresponds to self-excitation and self-repulsion phenomena: each point of
$(0,+\infty)$. The function h corresponds to self-excitation and self-repulsion phenomena: each point of ![]() $N^h$ increases, or respectively decreases, the conditional intensity measure wherever the appropriately translated function h is positive (self-excitation), or respectively negative (self-inhibition).
$N^h$ increases, or respectively decreases, the conditional intensity measure wherever the appropriately translated function h is positive (self-excitation), or respectively negative (self-inhibition).
In the sequel, the notation ![]() $\mathbb{P}_\mathfrak{m}$ and
$\mathbb{P}_\mathfrak{m}$ and ![]() $\mathbb{E}_\mathfrak{m}$ is used to specify that
$\mathbb{E}_\mathfrak{m}$ is used to specify that ![]() $N^0$ has distribution
$N^0$ has distribution ![]() $\mathfrak{m}$. In the case where
$\mathfrak{m}$. In the case where ![]() $\mathfrak{m}=\delta_{\nu}$ for some
$\mathfrak{m}=\delta_{\nu}$ for some ![]() $\nu\in \mathcal{N}((\!-\infty,0])$, we use the notation
$\nu\in \mathcal{N}((\!-\infty,0])$, we use the notation ![]() $\mathbb{E}_\nu$ and
$\mathbb{E}_\nu$ and ![]() $\mathbb{P}_\nu$. We often consider the case when
$\mathbb{P}_\nu$. We often consider the case when ![]() $\nu=\emptyset$, the null measure for which there is no point on
$\nu=\emptyset$, the null measure for which there is no point on ![]() $(\!-\infty,0]$.
$(\!-\infty,0]$.
In Definition 1.1, the density ![]() $\Lambda^h$ of the conditional intensity measure of
$\Lambda^h$ of the conditional intensity measure of ![]() $N^h$ depends on
$N^h$ depends on ![]() $N^h$ itself; hence existence and uniqueness results are needed. In Proposition 2.1, under the further assumptions that
$N^h$ itself; hence existence and uniqueness results are needed. In Proposition 2.1, under the further assumptions that ![]() $\|h^+\|_1 <1$ and that
$\|h^+\|_1 <1$ and that
we prove that Hawkes processes can be constructed as the solution of the equation
 \begin{equation}\left\{\begin{aligned} &N^{h} = N^0+\int_{(0,+\infty)\times(0,+\infty)} \delta_u {\mathds{1}}_{\{\theta\leq \Lambda^{h}(u)\}}\,Q(du,d\theta)\,,\\&\Lambda^h(u) =\biggl(\lambda+\int_{(\!-\infty,u)} h(u-s)\,N^h(ds)\biggr)^+ \,, &&u >0,\end{aligned}\right.\end{equation}
\begin{equation}\left\{\begin{aligned} &N^{h} = N^0+\int_{(0,+\infty)\times(0,+\infty)} \delta_u {\mathds{1}}_{\{\theta\leq \Lambda^{h}(u)\}}\,Q(du,d\theta)\,,\\&\Lambda^h(u) =\biggl(\lambda+\int_{(\!-\infty,u)} h(u-s)\,N^h(ds)\biggr)^+ \,, &&u >0,\end{aligned}\right.\end{equation}where Q is an ![]() $(\mathcal{F}_t)_{t\ge0}$-Poisson point process on
$(\mathcal{F}_t)_{t\ge0}$-Poisson point process on ![]() $(0,+\infty)\times (0,+\infty)$ with unit intensity, characterized by the fact that for every
$(0,+\infty)\times (0,+\infty)$ with unit intensity, characterized by the fact that for every ![]() $t,h,a>0$, the random variable
$t,h,a>0$, the random variable ![]() $Q((t,t+h]\times (0,a])$ is
$Q((t,t+h]\times (0,a])$ is ![]() $\mathcal{F}_{t+h}$-measurable, independent of
$\mathcal{F}_{t+h}$-measurable, independent of ![]() $\mathcal{F}_t$, and Poisson of parameter h a. Such equations have been introduced and studied in this context by Brémaud and Massoulié [Reference Brémaud and Massoulié5]; see also [Reference Brémaud, Nappo and Torrisi6], [Reference Massoulié26].
$\mathcal{F}_t$, and Poisson of parameter h a. Such equations have been introduced and studied in this context by Brémaud and Massoulié [Reference Brémaud and Massoulié5]; see also [Reference Brémaud, Nappo and Torrisi6], [Reference Massoulié26].
Let us remark that the counting process ![]() $(N^h_t)_{t\ge0}$ with sample paths in
$(N^h_t)_{t\ge0}$ with sample paths in ![]() $\mathbb{D}(\mathbb{R}_+,\mathbb{N})$ defined by
$\mathbb{D}(\mathbb{R}_+,\mathbb{N})$ defined by ![]() $N^h_t=N^h((0,t])$ satisfies a pure jump time-inhomogeneous stochastic differential equation which is equivalent to the formulation (1.2).
$N^h_t=N^h((0,t])$ satisfies a pure jump time-inhomogeneous stochastic differential equation which is equivalent to the formulation (1.2).
If h is a nonnegative function satisfying ![]() $\|h\|_1<1$, then there exists an alternate existence and uniqueness proof based on a cluster representation involving subcritical continuous-time Galton–Watson trees (see [Reference Hawkes and Oakes20]), which we shall describe and use later.
$\|h\|_1<1$, then there exists an alternate existence and uniqueness proof based on a cluster representation involving subcritical continuous-time Galton–Watson trees (see [Reference Hawkes and Oakes20]), which we shall describe and use later.
1.2. Main results
Our goal in this paper is to establish limit theorems for a Hawkes process ![]() $N^h$ with general reproduction function h. We aim at studying the limiting behavior of the process on a sliding finite time window of length A. We therefore introduce a time-shifted version of the Hawkes process. Using classical notation for point processes, for
$N^h$ with general reproduction function h. We aim at studying the limiting behavior of the process on a sliding finite time window of length A. We therefore introduce a time-shifted version of the Hawkes process. Using classical notation for point processes, for ![]() $t\in\mathbb{R}$ we define
$t\in\mathbb{R}$ we define
Then ![]() $S_t N$ is the image measure of N by the shift by t units of time, and if
$S_t N$ is the image measure of N by the shift by t units of time, and if ![]() $a<b$ then
$a<b$ then
(with abuse of notation between ![]() $N|_{(t+a,t+b]}$ and
$N|_{(t+a,t+b]}$ and ![]() ${\mathds{1}}_{(t+a,t+b]}N$, etc.).
${\mathds{1}}_{(t+a,t+b]}N$, etc.).
The quantities of interest will be of the form
in which ![]() $T>0$ is a finite time horizon,
$T>0$ is a finite time horizon, ![]() $A>0$ is a finite window length, and f belongs to the set
$A>0$ is a finite window length, and f belongs to the set ![]() $\mathcal{B}_{lb}(\mathcal{N}((\!-A,0]))$ of real Borel functions on
$\mathcal{B}_{lb}(\mathcal{N}((\!-A,0]))$ of real Borel functions on ![]() $\mathcal{N}((\!-A,0])$ which are locally bounded, i.e., uniformly bounded on
$\mathcal{N}((\!-A,0])$ which are locally bounded, i.e., uniformly bounded on ![]() $\{\nu \in \mathcal{N}((\!-A,0]) \,{:}\, \nu((\!-A,0])\le n\}$ for each
$\{\nu \in \mathcal{N}((\!-A,0]) \,{:}\, \nu((\!-A,0])\le n\}$ for each ![]() $n\ge1$. Such quantities appear commonly in the field of statistical inference of random processes; by convention, time is labeled so that observation has started by time
$n\ge1$. Such quantities appear commonly in the field of statistical inference of random processes; by convention, time is labeled so that observation has started by time ![]() $-A$.
$-A$.
Using renewal theory, we are able to obtain results without any nonnegativity assumption on the reproduction function h. We first establish an ergodic theorem and a central limit theorem for such quantities. We then generalize the concentration inequalities which were obtained by Reynaud-Bouret and Roy [Reference Reynaud-Bouret and Roy30] under the assumption that h is a nonnegative subcritical reproduction law. This leads us to make the following hypotheses. Recall that ![]() $h = h{\mathds{1}}_{\textnormal{supp}(h)}$ and
$h = h{\mathds{1}}_{\textnormal{supp}(h)}$ and ![]() $L(h) \triangleq \sup(\textnormal{supp}(h)) \triangleq \sup\{t >0 , |h(t)|>0\}$.
$L(h) \triangleq \sup(\textnormal{supp}(h)) \triangleq \sup\{t >0 , |h(t)|>0\}$.
Assumption 1.1. The signed measurable function ![]() $h\,{:}\,(0,+\infty) \to \mathbb{R}$ is such that
$h\,{:}\,(0,+\infty) \to \mathbb{R}$ is such that
The distribution ![]() $\mathfrak{m}$ of the initial condition
$\mathfrak{m}$ of the initial condition ![]() $N^0$ is such that
$N^0$ is such that
We consider only the case of bounded support, i.e. of ![]() $L(h)<\infty$, and focus on treating the difficulties due to h being signed. The techniques we use exploit this bounded support assumption, which is not very restrictive for the statistical estimation techniques that we have in mind (e.g. [Reference Hansen, Reynaud-Bouret and Rivoirard17], [Reference Lambert24], [Reference Reynaud-Bouret, Rivoirard and Tuleau-Malot29]). The assumption
$L(h)<\infty$, and focus on treating the difficulties due to h being signed. The techniques we use exploit this bounded support assumption, which is not very restrictive for the statistical estimation techniques that we have in mind (e.g. [Reference Hansen, Reynaud-Bouret and Rivoirard17], [Reference Lambert24], [Reference Reynaud-Bouret, Rivoirard and Tuleau-Malot29]). The assumption ![]() $\int_{(0,+\infty)} h^+(t)\,dt <1$ will be used to exploit the coupling we will construct between the process with reproduction function h and a dominating process with reproduction function
$\int_{(0,+\infty)} h^+(t)\,dt <1$ will be used to exploit the coupling we will construct between the process with reproduction function h and a dominating process with reproduction function ![]() $h^+$. Similar assumptions involving
$h^+$. Similar assumptions involving ![]() $h^+$ or
$h^+$ or ![]() $|h|$ are often made in the literature; see [Reference Chen, Shojaie, Shea-Brown and Witten7, Assumption 1] and [Reference Raad28, p. 6], for example.
$|h|$ are often made in the literature; see [Reference Chen, Shojaie, Shea-Brown and Witten7, Assumption 1] and [Reference Raad28, p. 6], for example.
Under these assumptions, we may and will assume that the window ![]() $A<\infty$ is such that
$A<\infty$ is such that ![]() $A\ge L(h)$. Then the quantities (1.5) actually depend only on the restriction
$A\ge L(h)$. Then the quantities (1.5) actually depend only on the restriction ![]() $N^0 |_{(\!-A,0]}$ of the initial condition
$N^0 |_{(\!-A,0]}$ of the initial condition ![]() $N^0$ to
$N^0$ to ![]() $(\!-A,0]$. Thus, in the sequel, by abuse of notation, we identify
$(\!-A,0]$. Thus, in the sequel, by abuse of notation, we identify ![]() $\mathfrak{m}$ with its marginal on
$\mathfrak{m}$ with its marginal on ![]() $\mathcal{N}((\!-A,0])$. Note that even though (1.6) does not imply that
$\mathcal{N}((\!-A,0])$. Note that even though (1.6) does not imply that ![]() $\mathbb{E}_\mathfrak{m}\big(N^0((\!-A,0])\big)\break <\infty$, our results hold under (1.6); see Remark 1.1 below.
$\mathbb{E}_\mathfrak{m}\big(N^0((\!-A,0])\big)\break <\infty$, our results hold under (1.6); see Remark 1.1 below.
The following important results for the Hawkes process ![]() $N^h$ are obtained using its regeneration structure, which will be investigated using a Markov process we now introduce.
$N^h$ are obtained using its regeneration structure, which will be investigated using a Markov process we now introduce.
In Proposition 3.1 we prove that if ![]() $A\ge L(h)$ then the process
$A\ge L(h)$ then the process ![]() $(X_t)_{t\ge 0}$ defined by
$(X_t)_{t\ge 0}$ defined by
is a strong Markov process which admits a unique invariant law denoted by ![]() $\pi_A$; see Theorem 3.1 below.
$\pi_A$; see Theorem 3.1 below.
We define ![]() $\tau$, the first return time to
$\tau$, the first return time to ![]() $\emptyset$ (the null point process) for this Markov process, by
$\emptyset$ (the null point process) for this Markov process, by
The probability measure ![]() $\pi_A$ on
$\pi_A$ on ![]() $\mathcal{N}((\!-A,0])$ can be classically represented as the intensity of an occupation measure over an excursion: for any nonnegative Borel function f,
$\mathcal{N}((\!-A,0])$ can be classically represented as the intensity of an occupation measure over an excursion: for any nonnegative Borel function f,
Note that we may then construct a Markov process ![]() $X_t$ in equilibrium on
$X_t$ in equilibrium on ![]() $\mathbb{R}_+$ and a time-reversed Markov process in equilibrium on
$\mathbb{R}_+$ and a time-reversed Markov process in equilibrium on ![]() $\mathbb{R}_+$, with identical initial conditions (drawn according to
$\mathbb{R}_+$, with identical initial conditions (drawn according to ![]() $\pi_A$) and independent transitions, and build from these a Markov process in equilibrium on
$\pi_A$) and independent transitions, and build from these a Markov process in equilibrium on ![]() $\mathbb{R}$. This construction yields a stationary version of
$\mathbb{R}$. This construction yields a stationary version of ![]() $N^h$ on
$N^h$ on ![]() $\mathbb{R}$.
$\mathbb{R}$.
We now state our main results, whose proofs are postponed to Section 4.
Theorem 1.2. (Ergodic theorems.) Let ![]() $N^h$ be a Hawkes process with immigration rate
$N^h$ be a Hawkes process with immigration rate ![]() $\lambda >0$, reproduction function
$\lambda >0$, reproduction function ![]() $h\,{:}\,(0,+\infty) \to \mathbb{R}$, and initial condition
$h\,{:}\,(0,+\infty) \to \mathbb{R}$, and initial condition ![]() $N^0$ with law
$N^0$ with law ![]() $\mathfrak{m}$, satisfying Assumption 1.1. Let
$\mathfrak{m}$, satisfying Assumption 1.1. Let ![]() $A<\infty$ be such that
$A<\infty$ be such that ![]() $A\ge L(h)$, and let
$A\ge L(h)$, and let ![]() $\pi_A$ be the probability measure on
$\pi_A$ be the probability measure on ![]() $\mathcal{N}((\!-A,0])$ defined by (1.8).
$\mathcal{N}((\!-A,0])$ defined by (1.8).
1. If
 $f \in \mathcal{B}_{lb}(\mathcal{N}((\!-A,0]))$ is nonnegative or
$f \in \mathcal{B}_{lb}(\mathcal{N}((\!-A,0]))$ is nonnegative or  $\pi_A$-integrable, then
$\pi_A$-integrable, then
 \begin{equation*} \frac1T \int_0^T f((S_tN^h)|_{(\!-A,0]})\,dt \xrightarrow[T\to\infty]{\mathbb{P}_{\mathfrak{m}}-\textnormal{a.s.}} \pi_A\,f\,.\end{equation*}
\begin{equation*} \frac1T \int_0^T f((S_tN^h)|_{(\!-A,0]})\,dt \xrightarrow[T\to\infty]{\mathbb{P}_{\mathfrak{m}}-\textnormal{a.s.}} \pi_A\,f\,.\end{equation*}2. Convergence to equilibrium for large times holds in the following sense:
 \begin{equation*} \mathbb{P}_\mathfrak{m}\bigl((S_tN^h)|_{[0,+\infty)} \in \cdot \bigr)\xrightarrow[t\to\infty]{\textnormal{total variation}}\mathbb{P}_{\pi_A}(N^h|_{[0,+\infty)}\in \cdot) \,.\end{equation*}
\begin{equation*} \mathbb{P}_\mathfrak{m}\bigl((S_tN^h)|_{[0,+\infty)} \in \cdot \bigr)\xrightarrow[t\to\infty]{\textnormal{total variation}}\mathbb{P}_{\pi_A}(N^h|_{[0,+\infty)}\in \cdot) \,.\end{equation*}
The following result provides the asymptotics of the fluctuations around the convergence result (1), and yields asymptotically exact confidence intervals for it. We define the variance
Theorem 1.3. (Central limit theorem.) Let ![]() $N^h$ be a Hawkes process with immigration rate
$N^h$ be a Hawkes process with immigration rate ![]() $\lambda >0$, reproduction function
$\lambda >0$, reproduction function ![]() $h\,{:}\, (0,+\infty) \to \mathbb{R}$, and initial law
$h\,{:}\, (0,+\infty) \to \mathbb{R}$, and initial law ![]() $\mathfrak{m}$, satisfying Assumption 1.1. Let
$\mathfrak{m}$, satisfying Assumption 1.1. Let ![]() $A<\infty$ be such that
$A<\infty$ be such that ![]() $A\ge L(h)$, let the hitting time
$A\ge L(h)$, let the hitting time ![]() $\tau$ be given by (1.7), and let the probability measure
$\tau$ be given by (1.7), and let the probability measure ![]() $\pi_A$ on
$\pi_A$ on ![]() $\mathcal{N}((\!-A,0])$ be given by (1.8). If
$\mathcal{N}((\!-A,0])$ be given by (1.8). If ![]() $f \in \mathcal{B}_{lb}(\mathcal{N}((\!-A,0]))$ is
$f \in \mathcal{B}_{lb}(\mathcal{N}((\!-A,0]))$ is ![]() $\pi_A$-integrable and satisfies
$\pi_A$-integrable and satisfies ![]() $\sigma^2(\,f)<\infty$, then
$\sigma^2(\,f)<\infty$, then
Laws of large numbers and central limit theorems for Hawkes processes, as ![]() $T\rightarrow +\infty$, have been much investigated in the case of nonnegative reproduction functions h (e.g. [Reference Bacry, Delattre, Hoffmann and Muzy2], [Reference Jaisson and Rosenbaum22], [Reference Jaisson and Rosenbaum23, Reference Zhu38]). The convergences in these papers concern the instantaneous values of the counting process of the point measure
$T\rightarrow +\infty$, have been much investigated in the case of nonnegative reproduction functions h (e.g. [Reference Bacry, Delattre, Hoffmann and Muzy2], [Reference Jaisson and Rosenbaum22], [Reference Jaisson and Rosenbaum23, Reference Zhu38]). The convergences in these papers concern the instantaneous values of the counting process of the point measure ![]() $N^h$, and the proofs usually rely on martingale techniques. Here the results concern sliding windows of arbitrary finite length of the point measure
$N^h$, and the proofs usually rely on martingale techniques. Here the results concern sliding windows of arbitrary finite length of the point measure ![]() $N^h$, and are obtained with the renewal approach that is also developed for establishing non-asymptotic exponential concentration bounds, as explained below.
$N^h$, and are obtained with the renewal approach that is also developed for establishing non-asymptotic exponential concentration bounds, as explained below.
The first entrance time at ![]() $\emptyset$ is defined by
$\emptyset$ is defined by
Recall that ![]() $x^+=\max(x,0)$ and
$x^+=\max(x,0)$ and ![]() $x^-=\max(\!-x,0)$ for
$x^-=\max(\!-x,0)$ for ![]() $x\in\mathbb{R}$, and let
$x\in\mathbb{R}$, and let ![]() $(x)_{\pm}^k = (x^{\pm})^k$.
$(x)_{\pm}^k = (x^{\pm})^k$.
Theorem 1.4. (Concentration inequalities.) Let ![]() $N^h$ be a Hawkes process with immigration rate
$N^h$ be a Hawkes process with immigration rate ![]() $\lambda >0$, reproduction function
$\lambda >0$, reproduction function ![]() $h\,{:}\,(0,+\infty) \to \mathbb{R}$, and initial law
$h\,{:}\,(0,+\infty) \to \mathbb{R}$, and initial law ![]() $\mathfrak{m}$, satisfying Assumption 1.1. Let
$\mathfrak{m}$, satisfying Assumption 1.1. Let ![]() $A<\infty$ be such that
$A<\infty$ be such that ![]() $A\ge L(h)$. Consider the hitting time
$A\ge L(h)$. Consider the hitting time ![]() $\tau$ given by (1.7), the entrance time
$\tau$ given by (1.7), the entrance time ![]() $\tau_0$ given by (1.10), and the probability measure on
$\tau_0$ given by (1.10), and the probability measure on ![]() $\mathcal{N}((\!-A,0])$ defined in (1.8). Consider
$\mathcal{N}((\!-A,0])$ defined in (1.8). Consider ![]() $f \in \mathcal{B}_{lb}(\mathcal{N}((\!-A,0]))$ taking its values in a bounded interval [a,b], and define
$f \in \mathcal{B}_{lb}(\mathcal{N}((\!-A,0]))$ taking its values in a bounded interval [a,b], and define ![]() $\sigma^2(\,f)$ as in (1.9) and
$\sigma^2(\,f)$ as in (1.9) and
 \begin{align*}& c^\pm(\,f) \triangleq\sup_{k\ge3}\Biggl(\frac2{k!}\frac{\mathbb{E}_\emptyset\bigl(\bigl(\int_0^{\tau} (\,f((S_tN^h)|_{(\!-A,0]}) -\pi_A\,f)\,dt\bigr)^k_\pm \bigr)}{\mathbb{E}_\emptyset(\tau) \sigma^2(\,f)}\Biggr)^{\frac1{k-2}}\,,\\[3pt]
& c^\pm(\tau)\triangleq\sup_{k\ge3}\biggl(\frac2{k!}\frac{\mathbb{E}_\emptyset\bigl( (\tau-\mathbb{E}_\emptyset(\tau))_\pm^k \bigr)}{\mbox{Var}_\emptyset (\tau)}\biggr)^{\frac1{k-2}}\,,\\[3pt]
&c^+(\tau_0)\triangleq\sup_{k\ge3}\biggl(\frac2{k!}\frac{\mathbb{E}_{\mathfrak{m}}\bigl((\tau_0-\mathbb{E}_\mathfrak{m}(\tau_0))_+^k\bigr)}{\mbox{Var}_\mathfrak{m}(\tau_0)}\biggr)^{\frac1{k-2}}\,.\end{align*}
\begin{align*}& c^\pm(\,f) \triangleq\sup_{k\ge3}\Biggl(\frac2{k!}\frac{\mathbb{E}_\emptyset\bigl(\bigl(\int_0^{\tau} (\,f((S_tN^h)|_{(\!-A,0]}) -\pi_A\,f)\,dt\bigr)^k_\pm \bigr)}{\mathbb{E}_\emptyset(\tau) \sigma^2(\,f)}\Biggr)^{\frac1{k-2}}\,,\\[3pt]
& c^\pm(\tau)\triangleq\sup_{k\ge3}\biggl(\frac2{k!}\frac{\mathbb{E}_\emptyset\bigl( (\tau-\mathbb{E}_\emptyset(\tau))_\pm^k \bigr)}{\mbox{Var}_\emptyset (\tau)}\biggr)^{\frac1{k-2}}\,,\\[3pt]
&c^+(\tau_0)\triangleq\sup_{k\ge3}\biggl(\frac2{k!}\frac{\mathbb{E}_{\mathfrak{m}}\bigl((\tau_0-\mathbb{E}_\mathfrak{m}(\tau_0))_+^k\bigr)}{\mbox{Var}_\mathfrak{m}(\tau_0)}\biggr)^{\frac1{k-2}}\,.\end{align*}Then, for all ![]() $\varepsilon>0$,
$\varepsilon>0$, ![]() $T>0$, and
$T>0$, and ![]() $u\in [0,1)$, we have
$u\in [0,1)$, we have
 \begin{align}&\mathbb{P}_\mathfrak{m}\biggl( \biggl|\frac1T \int_0^T f((S_tN^h)|_{(\!-A,0]})\,dt - \pi_A\,f \biggr| \ge \varepsilon \biggr)\notag\\[3pt]
&\quad \le\exp\left(\!-\frac{((1-u)T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau))^2}{8 T \sigma^2(\,f) + 4 c^+(\,f)((1-u)T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau)) }\right)\notag\\[3pt]
&\qquad +\exp\left(\!-\frac{((1-u)T)\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau))^2}{8 T \sigma^2(\,f) + 4 c^-(\,f)((1-u)T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau)) }\right)\notag\\[3pt]
&\qquad +\exp\left(\!-\frac{((1-u)T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau))^2}{8T |b-a|^2\frac{\mbox{Var}_\emptyset (\tau)}{\mathbb{E}_\emptyset(\tau)}+ 4 |b-a| c^+(\tau)((1-u)T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau)) }\right)\notag\\[3pt]
&\qquad +\exp\left(\!-\frac{((1-u)T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau))^2}{8T |b-a|^2\frac{\mbox{Var}_\emptyset (\tau)}{\mathbb{E}_\emptyset(\tau)}+ 4 |b-a| c^-(\tau)((1-u)T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau)) }\right)\notag\\[3pt]
&\qquad +\exp\left(\!-\frac{(uT\varepsilon - 2|b-a| \mathbb{E}_\mathfrak{m}(\tau_0))^2}{8|b-a|^2\mbox{Var}_\mathfrak{m} (\tau_0) + 4 |b-a| c^+(\tau_0)(uT\varepsilon - 2|b-a| \mathbb{E}_\mathfrak{m}(\tau_0)) }\right)\!.\end{align}
\begin{align}&\mathbb{P}_\mathfrak{m}\biggl( \biggl|\frac1T \int_0^T f((S_tN^h)|_{(\!-A,0]})\,dt - \pi_A\,f \biggr| \ge \varepsilon \biggr)\notag\\[3pt]
&\quad \le\exp\left(\!-\frac{((1-u)T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau))^2}{8 T \sigma^2(\,f) + 4 c^+(\,f)((1-u)T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau)) }\right)\notag\\[3pt]
&\qquad +\exp\left(\!-\frac{((1-u)T)\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau))^2}{8 T \sigma^2(\,f) + 4 c^-(\,f)((1-u)T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau)) }\right)\notag\\[3pt]
&\qquad +\exp\left(\!-\frac{((1-u)T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau))^2}{8T |b-a|^2\frac{\mbox{Var}_\emptyset (\tau)}{\mathbb{E}_\emptyset(\tau)}+ 4 |b-a| c^+(\tau)((1-u)T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau)) }\right)\notag\\[3pt]
&\qquad +\exp\left(\!-\frac{((1-u)T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau))^2}{8T |b-a|^2\frac{\mbox{Var}_\emptyset (\tau)}{\mathbb{E}_\emptyset(\tau)}+ 4 |b-a| c^-(\tau)((1-u)T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau)) }\right)\notag\\[3pt]
&\qquad +\exp\left(\!-\frac{(uT\varepsilon - 2|b-a| \mathbb{E}_\mathfrak{m}(\tau_0))^2}{8|b-a|^2\mbox{Var}_\mathfrak{m} (\tau_0) + 4 |b-a| c^+(\tau_0)(uT\varepsilon - 2|b-a| \mathbb{E}_\mathfrak{m}(\tau_0)) }\right)\!.\end{align}If ![]() $N|_{(\!-A,0]} =\emptyset$ then the last term of the right-hand side is null and the upper bound holds with
$N|_{(\!-A,0]} =\emptyset$ then the last term of the right-hand side is null and the upper bound holds with ![]() $u=0$ in the other terms.
$u=0$ in the other terms.
In the proof of this theorem, we split the integral from 0 to T into three parts: an initial integral from 0 to ![]() $\tau_0$, a sum of a deterministic number converging to infinity of i.i.d. integrals over cycles, and a last integral ending at T; see (4.5) below. The control of the first integral requires us to control
$\tau_0$, a sum of a deterministic number converging to infinity of i.i.d. integrals over cycles, and a last integral ending at T; see (4.5) below. The control of the first integral requires us to control ![]() $\tau_0$, and the control of the last integral requires us to control
$\tau_0$, and the control of the last integral requires us to control ![]() $\tau_0$ and a similar sum of i.i.d. random variables. We control the two sums of i.i.d. random variables by separating the deviations above and below the mean for precision and using Bernstein’s inequality, which explains the presence of four terms involving
$\tau_0$ and a similar sum of i.i.d. random variables. We control the two sums of i.i.d. random variables by separating the deviations above and below the mean for precision and using Bernstein’s inequality, which explains the presence of four terms involving ![]() $\tau$ in the right-hand side of (1.11). The fifth term is obtained from the control of
$\tau$ in the right-hand side of (1.11). The fifth term is obtained from the control of ![]() $\tau_0$ and depends heavily on the initial condition
$\tau_0$ and depends heavily on the initial condition ![]() $\mathfrak{m}$. This explains the introduction of the constant u which can be chosen null when
$\mathfrak{m}$. This explains the introduction of the constant u which can be chosen null when ![]() $\tau_0=0$.
$\tau_0=0$.
We now provide a tractable upper bound, using the fact that the hitting time ![]() $\tau$ admits an exponential moment (see Proposition 3.3). For simplicity the process starts at
$\tau$ admits an exponential moment (see Proposition 3.3). For simplicity the process starts at ![]() $\emptyset$.
$\emptyset$.
Corollary 1.1. Under the assumptions and notation of Theorem 1.4, there exists ![]() $\alpha>0$ such that
$\alpha>0$ such that ![]() $\mathbb{E}_\emptyset(e^{\alpha\tau})<\infty$. Let
$\mathbb{E}_\emptyset(e^{\alpha\tau})<\infty$. Let
Then for all ![]() $T>0$, we have that for all
$T>0$, we have that for all ![]() $\varepsilon>0$,
$\varepsilon>0$,
 \begin{align*}\mathbb{P}_\emptyset\biggl( &\biggl|\frac1T \int_0^T f((S_tN^h)|_{(\!-A,0]}) \,dt - \pi_A\,f \biggr| \ge \varepsilon \biggr)\le 4 \exp\left(\!-\frac{\Bigl( T\varepsilon-|b-a|\mathbb{E}_\emptyset(\tau) \Bigr)^2}{4 \left(2v+ c(T\varepsilon-|b-a|\mathbb{E}_\emptyset(\tau)) \right)} \right)\!,\end{align*}
\begin{align*}\mathbb{P}_\emptyset\biggl( &\biggl|\frac1T \int_0^T f((S_tN^h)|_{(\!-A,0]}) \,dt - \pi_A\,f \biggr| \ge \varepsilon \biggr)\le 4 \exp\left(\!-\frac{\Bigl( T\varepsilon-|b-a|\mathbb{E}_\emptyset(\tau) \Bigr)^2}{4 \left(2v+ c(T\varepsilon-|b-a|\mathbb{E}_\emptyset(\tau)) \right)} \right)\!,\end{align*}or equivalently, for all ![]() $1 \ge \eta>0$,
$1 \ge \eta>0$,
where
Remark 1.1. All these results hold under (1.6) even if ![]() $\mathbb{E}_\mathfrak{m}(N^0((\!-A,0]))=+\infty$. Indeed,
$\mathbb{E}_\mathfrak{m}(N^0((\!-A,0]))=+\infty$. Indeed,
 \begin{align*} \frac{1}{T}\int_0^T f\big(N^h(\cdot+t)|_{(\!-A,0]}\big) \,dt&=\frac{1}{T}\int_0^{A-L(h)} f\big(N^h(\cdot+t)|_{(\!-A,0]}\big) \,dt\\[4pt]
&\qquad +\frac{1}{T}\int_{A-L(h)}^T f\big(N^h(.+t)|_{(\!-A,0]}\big) \,dt\,.\end{align*}
\begin{align*} \frac{1}{T}\int_0^T f\big(N^h(\cdot+t)|_{(\!-A,0]}\big) \,dt&=\frac{1}{T}\int_0^{A-L(h)} f\big(N^h(\cdot+t)|_{(\!-A,0]}\big) \,dt\\[4pt]
&\qquad +\frac{1}{T}\int_{A-L(h)}^T f\big(N^h(.+t)|_{(\!-A,0]}\big) \,dt\,.\end{align*}The first right-hand side term converges ![]() $\mathbb{P}_\mathfrak{m}$-almost surely (
$\mathbb{P}_\mathfrak{m}$-almost surely (![]() $\mathbb{P}_\mathfrak{m}$-a.s.) to zero, even when multiplied by
$\mathbb{P}_\mathfrak{m}$-a.s.) to zero, even when multiplied by ![]() $\sqrt{T}$. For the second right-hand side term, we can apply the Markov property at time
$\sqrt{T}$. For the second right-hand side term, we can apply the Markov property at time ![]() $A-L(h)$ (which will be justified during the proof that
$A-L(h)$ (which will be justified during the proof that ![]() $(S_.N^h)|_{(\!-A,0]}$ is a Markov process) and show that
$(S_.N^h)|_{(\!-A,0]}$ is a Markov process) and show that
Remark 1.2. As noted after Definition 1.1, the Hawkes process ![]() $N^h$ is the special case for
$N^h$ is the special case for ![]() $\phi(x)=(\lambda+x)^+$ of the more general setting in which a function
$\phi(x)=(\lambda+x)^+$ of the more general setting in which a function ![]() $\phi\,{:}\,\mathbb{R}\to\mathbb{R}^+$ is given and the Hawkes process
$\phi\,{:}\,\mathbb{R}\to\mathbb{R}^+$ is given and the Hawkes process ![]() $N^{h,\phi}$ is required to have conditional intensity
$N^{h,\phi}$ is required to have conditional intensity
The results of this article can be extended to this more general setting under the growth assumption that there exist ![]() $\lambda$ and a in
$\lambda$ and a in ![]() $[0,\infty)$ such that
$[0,\infty)$ such that
and the stability assumption that the compactly supported function h satisfies
without any additional regularity or monotonicity assumption on ![]() $\phi$. The main point for this is to construct a thinning coupling
$\phi$. The main point for this is to construct a thinning coupling ![]() $N^{h,\phi}\le N^{h^+}$ similar to the coupling
$N^{h,\phi}\le N^{h^+}$ similar to the coupling ![]() $N^h\le N^{h^+}$ in Proposition 2.1(2) below, for which technical details can be found in Appendix A.2. We chose to present this special case first since it contains all the difficulties and constitutes the case where the loss of information by coupling is the lowest.
$N^h\le N^{h^+}$ in Proposition 2.1(2) below, for which technical details can be found in Appendix A.2. We chose to present this special case first since it contains all the difficulties and constitutes the case where the loss of information by coupling is the lowest.
Two other recent works also consider the case of signed reproduction functions. In [Reference Chen, Shojaie, Shea-Brown and Witten7], an alternative approach for analyzing multidimensional Hawkes processes with self-inhibition is proposed. The intensity functions are of the form
 \begin{equation*}\lambda_j(t)=\phi_j\left( \mu_j +\sum_{k=1}^p \int_{0}^\infty \omega_{k,j}(u)dN_j(t-u)\right)\!,\quad j=1,\dots,p\,,\end{equation*}
\begin{equation*}\lambda_j(t)=\phi_j\left( \mu_j +\sum_{k=1}^p \int_{0}^\infty \omega_{k,j}(u)dN_j(t-u)\right)\!,\quad j=1,\dots,p\,,\end{equation*}under a number of assumptions, in particular that the ![]() $\phi_j$ are
$\phi_j$ are ![]() $\alpha_j$-Lipschitz, that the Perron–Frobenius eigenvalue of the matrix
$\alpha_j$-Lipschitz, that the Perron–Frobenius eigenvalue of the matrix ![]() $(\alpha_j\sum_{k} \int_{0}^\infty |\omega_{k,j}(\Delta)| d\Delta)_{j,k}$ is strictly less than 1, and that either the functions
$(\alpha_j\sum_{k} \int_{0}^\infty |\omega_{k,j}(\Delta)| d\Delta)_{j,k}$ is strictly less than 1, and that either the functions ![]() $\phi_j$ have a common uniform bound or the signed functions
$\phi_j$ have a common uniform bound or the signed functions ![]() $\omega_{k,j}$ vanish outside a common bounded interval [Reference Chen, Shojaie, Shea-Brown and Witten7, Assumption 1, Assumption 4]. In order to derive concentration inequalities for the Hawkes processes, the authors of [Reference Chen, Shojaie, Shea-Brown and Witten7] apply the theory of weakly dependent sequences and therefore develop specific coupling techniques in order to control time dependencies. The very recent work [Reference Raad28] provides renewal time points for rather general one-dimensional Hawkes processes with self-inhibition, using technical splitting methods requiring specific couplings.
$\omega_{k,j}$ vanish outside a common bounded interval [Reference Chen, Shojaie, Shea-Brown and Witten7, Assumption 1, Assumption 4]. In order to derive concentration inequalities for the Hawkes processes, the authors of [Reference Chen, Shojaie, Shea-Brown and Witten7] apply the theory of weakly dependent sequences and therefore develop specific coupling techniques in order to control time dependencies. The very recent work [Reference Raad28] provides renewal time points for rather general one-dimensional Hawkes processes with self-inhibition, using technical splitting methods requiring specific couplings.
Both papers [Reference Chen, Shojaie, Shea-Brown and Witten7] and [Reference Raad28] involve sets of assumptions on the reproduction functions that differ from the ones here. Note that (1.14) is the natural stability assumption involving the growth bound at infinity for the dominating process, and that in the present paper we do not need regularity or monotonicity assumptions on ![]() $\phi$. In contrast, [Reference Chen, Shojaie, Shea-Brown and Witten7] and [Reference Raad28], in the spirit of [Reference Brémaud and Massoulié5, Th. 1], make Lipschitz assumptions on
$\phi$. In contrast, [Reference Chen, Shojaie, Shea-Brown and Witten7] and [Reference Raad28], in the spirit of [Reference Brémaud and Massoulié5, Th. 1], make Lipschitz assumptions on ![]() $\phi$ and a stability assumption involving the global Lispschitz constant of
$\phi$ and a stability assumption involving the global Lispschitz constant of ![]() $\phi$ which hence involves its worst local modulus of continuity. Additionally, [Reference Chen, Shojaie, Shea-Brown and Witten7] uses the equivalent of
$\phi$ which hence involves its worst local modulus of continuity. Additionally, [Reference Chen, Shojaie, Shea-Brown and Witten7] uses the equivalent of ![]() $|h|$ instead of
$|h|$ instead of ![]() $h^+$, while [Reference Raad28] requires that
$h^+$, while [Reference Raad28] requires that ![]() $\phi$ be nondecreasing. Moreover, the methods in [Reference Chen, Shojaie, Shea-Brown and Witten7] and [Reference Raad28] are drastically different from ours, and require other technical assumptions which we do not need to make.
$\phi$ be nondecreasing. Moreover, the methods in [Reference Chen, Shojaie, Shea-Brown and Witten7] and [Reference Raad28] are drastically different from ours, and require other technical assumptions which we do not need to make.
2. Hawkes processes
In this section, we first provide a constructive solution of Equation (1.2), which yields a coupling between ![]() $N^h$ and
$N^h$ and ![]() $N^{h^+}$ satisfying
$N^{h^+}$ satisfying ![]() $N^h\leq N^{h^+}$. The renewal times on which the proofs of our main results are based are the instants at which the intensity
$N^h\leq N^{h^+}$. The renewal times on which the proofs of our main results are based are the instants at which the intensity ![]() $\Lambda^h$ has returned and then stayed at
$\Lambda^h$ has returned and then stayed at ![]() $\lambda$ for a duration long enough to guarantee that the dependence on the past has vanished, which allows us to write the process in terms of i.i.d. excursions. The coupling will allow us to control the renewal times for
$\lambda$ for a duration long enough to guarantee that the dependence on the past has vanished, which allows us to write the process in terms of i.i.d. excursions. The coupling will allow us to control the renewal times for ![]() $N^h$ using the renewal times for
$N^h$ using the renewal times for ![]() $N^{h^+}$.
$N^{h^+}$.
When dealing with ![]() $h^+$, we use the well-known cluster representation for a Hawkes process with nonnegative reproduction function. This representation allows us to interpret the renewal times as times at which an M/G/
$h^+$, we use the well-known cluster representation for a Hawkes process with nonnegative reproduction function. This representation allows us to interpret the renewal times as times at which an M/G/![]() $\infty$ queue is empty, and we use this interpretation to obtain tail estimates for the interval between these times.
$\infty$ queue is empty, and we use this interpretation to obtain tail estimates for the interval between these times.
2.1. Solving the equation for the Hawkes process
The result below follows from an algorithmic proof which will be given in Appendix A.1. The algorithmic construction can be used for simulations, which are shown in Figure 1.

Figure 1: (a) Hawkes process with a positive reproduction function h. (b) Hawkes process with a general reproduction function h. The dots in the plane represent the atoms of the Poisson point process Q used for the construction. The atoms of the Hawkes processes are the green dots on the abscissa axis. The bold red curve corresponds to the intensity ![]() $\Lambda^h$ and the colored curves represent the partial cumulative contributions of the successive atoms of the Hawkes process. In (b), the bold blue curve corresponds to the intensity of the dominating Hawkes process with reproduction function
$\Lambda^h$ and the colored curves represent the partial cumulative contributions of the successive atoms of the Hawkes process. In (b), the bold blue curve corresponds to the intensity of the dominating Hawkes process with reproduction function ![]() $h^+$.
$h^+$.
Proposition 2.1. Let Q be an ![]() $(\mathcal{F}_t)_{t\ge0}$-Poisson point process on
$(\mathcal{F}_t)_{t\ge0}$-Poisson point process on ![]() $(0,+\infty)\times (0,+\infty)$ with unit intensity. Consider Equation (1.2), i.e.
$(0,+\infty)\times (0,+\infty)$ with unit intensity. Consider Equation (1.2), i.e.
 \begin{equation*}\left\{\begin{aligned} &N^{h} = N^0+\int_{(0,+\infty)\times(0,+\infty)} \delta_u {\mathds{1}}_{\{\theta\leq \Lambda^{h}(u)\}}\,Q(du,d\theta)\,,\\&\Lambda^h(u) =\biggl(\lambda+\int_{(\!-\infty,u)} h(u-s)\,N^h(ds)\biggr)^+ \,, &&u >0\,,\end{aligned}\right.\end{equation*}
\begin{equation*}\left\{\begin{aligned} &N^{h} = N^0+\int_{(0,+\infty)\times(0,+\infty)} \delta_u {\mathds{1}}_{\{\theta\leq \Lambda^{h}(u)\}}\,Q(du,d\theta)\,,\\&\Lambda^h(u) =\biggl(\lambda+\int_{(\!-\infty,u)} h(u-s)\,N^h(ds)\biggr)^+ \,, &&u >0\,,\end{aligned}\right.\end{equation*}in which ![]() $h\,{:}\, (0,+\infty)\to \mathbb{R}$ is a signed measurable reproduction function,
$h\,{:}\, (0,+\infty)\to \mathbb{R}$ is a signed measurable reproduction function, ![]() $\lambda>0$ an immigration rate, and
$\lambda>0$ an immigration rate, and ![]() $N^0$ an initial condition in
$N^0$ an initial condition in ![]() $\mathcal{N}((\!-\infty,0])$ with law
$\mathcal{N}((\!-\infty,0])$ with law ![]() $\mathfrak{m}$. Consider the similar equation for
$\mathfrak{m}$. Consider the similar equation for ![]() $N^{h^+}$ in which h is replaced by
$N^{h^+}$ in which h is replaced by ![]() $h^+$. Assume that
$h^+$. Assume that
and that the distribution ![]() $\mathfrak{m}$ of the initial condition
$\mathfrak{m}$ of the initial condition ![]() $N^0$ satisfies
$N^0$ satisfies
The main novelty of this proposition is the coupling obtained in (2). Let us first note that the coupling is very strong since the comparison between ![]() $N^h$ and
$N^h$ and ![]() $N^{h^+ }$ holds in the sense of measures: each atom of
$N^{h^+ }$ holds in the sense of measures: each atom of ![]() $N^h$ is an atom of
$N^h$ is an atom of ![]() $N^{h^+ }$. Moreover, even though couplings are easily derived for Hawkes processes associated with nonnegative reproduction functions, it is not so when the reproductive functions are signed: if h and g are two signed functions such that
$N^{h^+ }$. Moreover, even though couplings are easily derived for Hawkes processes associated with nonnegative reproduction functions, it is not so when the reproductive functions are signed: if h and g are two signed functions such that ![]() $h\le g$, then it is not always possible to couple
$h\le g$, then it is not always possible to couple ![]() $N^h$ and
$N^h$ and ![]() $N^g$ in such a way that atoms of
$N^g$ in such a way that atoms of ![]() $N^h$ are atoms of
$N^h$ are atoms of ![]() $N^g$ as well. However, if h is signed and g is nonnegative, then our construction applies and
$N^g$ as well. However, if h is signed and g is nonnegative, then our construction applies and ![]() $N^h\le N^g$; see Appendix A.1 for details. We present the result above using h and
$N^h\le N^g$; see Appendix A.1 for details. We present the result above using h and ![]() $h^+$ since
$h^+$ since ![]() $h^+$ is the least positive upper bound of h.
$h^+$ is the least positive upper bound of h.
Remark 2.1. In order to prove the strong existence and pathwise uniqueness of the solution of Equation (1.2), we propose a proof based on an algorithmic construction similar to the Poisson embedding of [Reference Brémaud and Massoulié5], also referred to in [Reference Daley and Vere-Jones11] as thinning. Since this construction is rather classical, we postpone the proof to Appendix A.1. A similar result is also proved in these references using Picard iteration techniques, with the assumption (2.2) replaced by the stronger hypothesis that there exists ![]() $D_{\mathfrak{m}}>0$ such that
$D_{\mathfrak{m}}>0$ such that
When h is nonnegative, the result can be deduced from the cluster representation of the self-exciting Hawkes process, since ![]() $N^h([0,t])$ is bounded above by the sum of the sizes of a Poisson number of subcritical Galton–Watson trees; see [Reference Hawkes and Oakes20], [Reference Reynaud-Bouret and Roy30].
$N^h([0,t])$ is bounded above by the sum of the sizes of a Poisson number of subcritical Galton–Watson trees; see [Reference Hawkes and Oakes20], [Reference Reynaud-Bouret and Roy30].
Remark 2.2. Proposition 2.1 does not require that L(h) be finite. When ![]() $L(h)<\infty$, the assumption (2.2) can be rewritten as
$L(h)<\infty$, the assumption (2.2) can be rewritten as
A sufficient condition for (2.4) to hold is that ![]() $\mathbb{E}_\mathfrak{m}(N^0(\!-L(h),0])<+\infty$. Indeed, using the Fubini–Tonelli theorem, the left-hand side of (2.4) can be bounded by
$\mathbb{E}_\mathfrak{m}(N^0(\!-L(h),0])<+\infty$. Indeed, using the Fubini–Tonelli theorem, the left-hand side of (2.4) can be bounded by ![]() $\|h^+\|_1 \,\mathbb{E}_\mathfrak{m}(N^0(\!-L(h),0])$. Therefore, the results of Proposition 2.1 hold under Assumption 1.1.
$\|h^+\|_1 \,\mathbb{E}_\mathfrak{m}(N^0(\!-L(h),0])$. Therefore, the results of Proposition 2.1 hold under Assumption 1.1.
2.2. The cluster representation for nonnegative reproduction functions
In this subsection, we consider the case in which the reproduction function h is nonnegative. The intensity process of a corresponding Hawkes process can be written, for ![]() $t>0$, as
$t>0$, as
The first term can be interpreted as an immigration rate of ancestors. Let ![]() $(V_k)_{k\ge1}$ be the corresponding sequence of arrival times, forming a Poisson process of intensity
$(V_k)_{k\ge1}$ be the corresponding sequence of arrival times, forming a Poisson process of intensity ![]() $\lambda$.
$\lambda$.
The second term is the sum of all the contributions of the atoms of ![]() $N^h$ before time t and can be seen as self-excitation. If U is an atom of
$N^h$ before time t and can be seen as self-excitation. If U is an atom of ![]() $N^h$, it contributes to the intensity by the addition of the function
$N^h$, it contributes to the intensity by the addition of the function ![]() $t \mapsto h(t-U)$, hence generating new points regarded as its descendants or offspring. Each individual has a lifelength
$t \mapsto h(t-U)$, hence generating new points regarded as its descendants or offspring. Each individual has a lifelength ![]() $L(h)=\sup(\textnormal{supp}(h))$, the number of its descendants follows a Poisson distribution with mean
$L(h)=\sup(\textnormal{supp}(h))$, the number of its descendants follows a Poisson distribution with mean ![]() $\|h\|_1$, and the ages at which it gives birth to them have density
$\|h\|_1$, and the ages at which it gives birth to them have density ![]() $h/\|h\|_1$, all this independently. This induces a Galton–Watson process in continuous time; see [Reference Hawkes and Oakes20], [Reference Reynaud-Bouret and Roy30], and Figure 2.
$h/\|h\|_1$, all this independently. This induces a Galton–Watson process in continuous time; see [Reference Hawkes and Oakes20], [Reference Reynaud-Bouret and Roy30], and Figure 2.

Figure 2: Cluster representation of a Hawkes process with positive reproduction function. The abscissas of the dots give its atoms. Offspring are colored according to their ancestor, and their ordinates correspond to their generation in this age-structured Galton–Watson tree.
To each ancestor arrival time ![]() $V_k$ we can associate a cluster of times composed of the times of birth of its descendants. The condition
$V_k$ we can associate a cluster of times composed of the times of birth of its descendants. The condition ![]() $\|h\|_1<1$ is a necessary and sufficient condition for the corresponding Galton–Watson process to be subcritical, which implies that the cluster sizes are finite a.s. More precisely, if we define
$\|h\|_1<1$ is a necessary and sufficient condition for the corresponding Galton–Watson process to be subcritical, which implies that the cluster sizes are finite a.s. More precisely, if we define ![]() $H_k$ by saying that
$H_k$ by saying that ![]() $V_k+H_k$ is the largest time in the cluster associated with
$V_k+H_k$ is the largest time in the cluster associated with ![]() $V_k$, then the
$V_k$, then the ![]() $(H_k)_{k\ge1}$ are i.i.d. random variables independent from the sequence
$(H_k)_{k\ge1}$ are i.i.d. random variables independent from the sequence ![]() $(V_k)_{k\ge1}$.
$(V_k)_{k\ge1}$.
Reynaud-Bouret and Roy [Reference Reynaud-Bouret and Roy30] proved the following tail estimate for ![]() $H_1$.
$H_1$.
Proposition 2.2. ([Reference Reynaud-Bouret and Roy30, Prop. 1.2]) Let us define
Under Assumption 1.1, we have that
which provides a lower bound for the rate of decay of the cluster length.
When h is nonnegative, it is possible to associate to the Hawkes process an M/G/![]() $\infty$ queue. For
$\infty$ queue. For ![]() $A \ge L(h)$, we consider that the arrival times of ancestors
$A \ge L(h)$, we consider that the arrival times of ancestors ![]() $(V_k)_{k\ge1}$ correspond to the arrivals of customers in the queue and associate to the kth customer a service time
$(V_k)_{k\ge1}$ correspond to the arrivals of customers in the queue and associate to the kth customer a service time ![]() $\widetilde{H}_k(A) \triangleq H_k+A$. We assume that the queue is empty at time 0, and then the number
$\widetilde{H}_k(A) \triangleq H_k+A$. We assume that the queue is empty at time 0, and then the number ![]() $Y_t$ of customers in the queue at time
$Y_t$ of customers in the queue at time ![]() $t\ge0$ is given by
$t\ge0$ is given by
Let ![]() $\mathcal{T}_0=0$, and let the successive hitting times of 0 by the process
$\mathcal{T}_0=0$, and let the successive hitting times of 0 by the process ![]() $(Y_t)_{t\geq 0}$ be given by
$(Y_t)_{t\geq 0}$ be given by
The time interval ![]() $[V_1,\mathcal{T}_1)$ is called the first busy period, and is the first time interval during which the queue is never empty. Note that the
$[V_1,\mathcal{T}_1)$ is called the first busy period, and is the first time interval during which the queue is never empty. Note that the ![]() $\mathcal{T}_{k}$ are times at which the conditional intensity of the underlying Hawkes process has returned to
$\mathcal{T}_{k}$ are times at which the conditional intensity of the underlying Hawkes process has returned to ![]() $\lambda$ and there is no remaining influence of its previous atoms, since
$\lambda$ and there is no remaining influence of its previous atoms, since ![]() $\widetilde{H}_k(A) \triangleq H_k+A \ge H_k+L(h)$.
$\widetilde{H}_k(A) \triangleq H_k+A \ge H_k+L(h)$.
Thus the Hawkes process after ![]() $\mathcal{T}_{k}$ has the same law as the Hawkes process with initial condition the null point process
$\mathcal{T}_{k}$ has the same law as the Hawkes process with initial condition the null point process ![]() $\emptyset \in \mathcal{N}((\!-A,0])$, translated by
$\emptyset \in \mathcal{N}((\!-A,0])$, translated by ![]() $\mathcal{T}_{k}$. This allows us to split the random measure
$\mathcal{T}_{k}$. This allows us to split the random measure ![]() $N^h$ into i.i.d. parts. We will prove all this in the next section.
$N^h$ into i.i.d. parts. We will prove all this in the next section.
We end this part by giving tail estimates for the ![]() $\mathcal{T}_{k}$, which depend on
$\mathcal{T}_{k}$, which depend on ![]() $\lambda$ and on
$\lambda$ and on ![]() $\gamma$ given in (2.5), which respectively control the exponential decays of
$\gamma$ given in (2.5), which respectively control the exponential decays of ![]() $\mathbb{P}(V_1>x)$ and
$\mathbb{P}(V_1>x)$ and ![]() $\mathbb{P}(H_1>x)$.
$\mathbb{P}(H_1>x)$.
Proposition 2.3. Let Assumption 1.1 hold, and let ![]() $\gamma$ be given by (2.5). Then for all
$\gamma$ be given by (2.5). Then for all ![]() $x\ge 0$, if
$x\ge 0$, if ![]() $\lambda<\gamma$ then
$\lambda<\gamma$ then ![]() $\mathbb{P}(\mathcal{T}_1>x) = O(\text{e}^{-\lambda x})$, and if
$\mathbb{P}(\mathcal{T}_1>x) = O(\text{e}^{-\lambda x})$, and if ![]() $0<\alpha <\gamma\le\lambda$ then
$0<\alpha <\gamma\le\lambda$ then ![]() $\mathbb{P}(\mathcal{T}_1>x)= O(\text{e}^{-\alpha x})$. In particular, if
$\mathbb{P}(\mathcal{T}_1>x)= O(\text{e}^{-\alpha x})$. In particular, if ![]() $0<\alpha < \min(\lambda, \gamma)$ then
$0<\alpha < \min(\lambda, \gamma)$ then ![]() $\mathbb{E}(\text{e}^{\alpha\mathcal{T}_1})$ is finite.
$\mathbb{E}(\text{e}^{\alpha\mathcal{T}_1})$ is finite.
Proof of Proposition 2.3. The proof follows from Proposition 2.2, from which we deduce that the service time ![]() $\widetilde{H}_1=H_1+A$ satisfies
$\widetilde{H}_1=H_1+A$ satisfies
We then conclude by applying Theorem A.1 to the queue ![]() $(Y_t)_{t\geq 0}$ defined by (2.6).
$(Y_t)_{t\geq 0}$ defined by (2.6).
Theorem A.1 in the appendix establishes the decay rates for the tail distributions of ![]() $\mathcal{T}_1$ and of the length of the busy period
$\mathcal{T}_1$ and of the length of the busy period ![]() $[V_1,\mathcal{T}_1)$. This result is of interest in itself, independently of the results for Hawkes processes considered here.
$[V_1,\mathcal{T}_1)$. This result is of interest in itself, independently of the results for Hawkes processes considered here.
3. An auxiliary Markov process
When the reproduction function h has bounded support, ![]() $N^h|_{(t,+\infty)}$ depends on
$N^h|_{(t,+\infty)}$ depends on ![]() $N^h|_{(\!-\infty,t]}$ only through
$N^h|_{(\!-\infty,t]}$ only through ![]() $N^h|_{(t-L(h),t]}$. The process
$N^h|_{(t-L(h),t]}$. The process ![]() $t \mapsto N^h|_{(t-L(h),t]}$ will be seen to be strong Markov, which yields regenerative properties for
$t \mapsto N^h|_{(t-L(h),t]}$ will be seen to be strong Markov, which yields regenerative properties for ![]() $N^h$. It is the purpose of this section to formalize this idea by introducing an auxiliary Markov process.
$N^h$. It is the purpose of this section to formalize this idea by introducing an auxiliary Markov process.
3.1. Definition of a strong Markov process
We suppose that Assumption 1.1 holds and consider the Hawkes process ![]() $N^h$ that is the solution of the corresponding Equation (1.2) constructed in Proposition 2.1. We recall that
$N^h$ that is the solution of the corresponding Equation (1.2) constructed in Proposition 2.1. We recall that ![]() $L(h)<\infty$. Then, for any
$L(h)<\infty$. Then, for any ![]() $t>0$ and
$t>0$ and ![]() $u\in (\!-\infty,-L(h)]$, we have
$u\in (\!-\infty,-L(h)]$, we have ![]() $h(t-u)=0$, and thus
$h(t-u)=0$, and thus
In particular, ![]() $N^h|_{(0,+\infty)}$ depends only on the restriction
$N^h|_{(0,+\infty)}$ depends only on the restriction ![]() $N^0|_{(\!-L(h),0]}$ of the initial condition.
$N^0|_{(\!-L(h),0]}$ of the initial condition.
Recall the shift operator ![]() $S_t$ defined in (1.3) and (1.4). Note that if
$S_t$ defined in (1.3) and (1.4). Note that if ![]() $t,s\geq 0$ then
$t,s\geq 0$ then ![]() $S_{s+t}N^h=S_t S_s N^h=S_s S_tN^h$. Let
$S_{s+t}N^h=S_t S_s N^h=S_s S_tN^h$. Let ![]() $A<\infty$ be such that
$A<\infty$ be such that ![]() $A \ge L(h)$. Consider the
$A \ge L(h)$. Consider the ![]() $(\mathcal{F}_t)$-adapted process
$(\mathcal{F}_t)$-adapted process ![]() $X=(X_t)_{t\ge 0}$ defined by
$X=(X_t)_{t\ge 0}$ defined by
i.e.,
The measure ![]() $X_t$ is the point process
$X_t$ is the point process ![]() $N^h$ in the time window
$N^h$ in the time window ![]() $(t-A,t]$, shifted back to
$(t-A,t]$, shifted back to ![]() $(\!-A,0]$. This is a function of
$(\!-A,0]$. This is a function of ![]() $N^h|_{(\!-A,+\infty)}$. Using Equation (3.1) and the remark below it, we see that the law of
$N^h|_{(\!-A,+\infty)}$. Using Equation (3.1) and the remark below it, we see that the law of ![]() $N^h|_{(\!-A,+\infty)}$ depends on the initial condition
$N^h|_{(\!-A,+\infty)}$ depends on the initial condition ![]() $N^0$ only through
$N^0$ only through ![]() $N^0|_{(\!-A,0]}$. Therefore, with abuse of notation, when dealing with the process
$N^0|_{(\!-A,0]}$. Therefore, with abuse of notation, when dealing with the process ![]() $(X_t)_{t \ge 0}$ we shall use the notation
$(X_t)_{t \ge 0}$ we shall use the notation ![]() $\mathbb{P}_\mathfrak{m}$ and
$\mathbb{P}_\mathfrak{m}$ and ![]() $\mathbb{E}_\mathfrak{m}$ even when
$\mathbb{E}_\mathfrak{m}$ even when ![]() $\mathfrak{m}$ is a law on
$\mathfrak{m}$ is a law on ![]() $\mathcal{N}((\!-A,0])$, and
$\mathcal{N}((\!-A,0])$, and ![]() $\mathbb{P}_{\nu}$ and
$\mathbb{P}_{\nu}$ and ![]() $\mathbb{E}_{\nu}$ even when
$\mathbb{E}_{\nu}$ even when ![]() $\nu$ is an element of
$\nu$ is an element of ![]() $\mathcal{N}((\!-A,0])$.
$\mathcal{N}((\!-A,0])$.
Note that X depends on A, and that we omit this in the notation.
Proposition 3.1. Let Assumption 1.1 hold. Let ![]() $A<\infty$ be such that
$A<\infty$ be such that ![]() $A \ge L(h)$. Then
$A \ge L(h)$. Then ![]() $(X_t)_{t\geq 0}$ defined in (3.2) is a strong
$(X_t)_{t\geq 0}$ defined in (3.2) is a strong ![]() $(\mathcal{F}_t)_{t\ge0}$-Markov process with initial condition
$(\mathcal{F}_t)_{t\ge0}$-Markov process with initial condition ![]() $X_0=N^0|_{(\!-A,0]}$ and sample paths in the Skorokhod space
$X_0=N^0|_{(\!-A,0]}$ and sample paths in the Skorokhod space ![]() $\mathbb{D}(\mathbb{R}_+,\mathcal{N}((\!-A,0]))$.
$\mathbb{D}(\mathbb{R}_+,\mathcal{N}((\!-A,0]))$.
Proof. This follows from the fact that ![]() $N^h$ is the unique solution of Equation (1.2). Indeed, let T be a stopping time. On
$N^h$ is the unique solution of Equation (1.2). Indeed, let T be a stopping time. On ![]() $\{T<\infty\}$, by definition
$\{T<\infty\}$, by definition
Using that ![]() $N^h$ satisfies Equation (1.2) driven by the process Q, we have
$N^h$ satisfies Equation (1.2) driven by the process Q, we have
 \begin{align*}S_T N^h & = S_T (N^h|_{(\!-\infty,T]}) +S_T (N^h|_{(T,+\infty)})\\[3pt]
& = (S_T N^h)|_{(\!-\infty,0]} +\int_{(T,+\infty)\times (0,+\infty)} \delta_{u-T} {\mathds{1}}_{\{\theta\leq \Lambda^h(u)\}}Q(du,d\theta)\\[3pt]
& = (S_T N^h)|_{(\!-\infty,0]} +\int_{(0,+\infty)\times (0,+\infty)} \delta_{v}{\mathds{1}}_{\{\theta\leq \widetilde{\Lambda}^h(v)\}} \ S_T Q(dv,d\theta),\end{align*}
\begin{align*}S_T N^h & = S_T (N^h|_{(\!-\infty,T]}) +S_T (N^h|_{(T,+\infty)})\\[3pt]
& = (S_T N^h)|_{(\!-\infty,0]} +\int_{(T,+\infty)\times (0,+\infty)} \delta_{u-T} {\mathds{1}}_{\{\theta\leq \Lambda^h(u)\}}Q(du,d\theta)\\[3pt]
& = (S_T N^h)|_{(\!-\infty,0]} +\int_{(0,+\infty)\times (0,+\infty)} \delta_{v}{\mathds{1}}_{\{\theta\leq \widetilde{\Lambda}^h(v)\}} \ S_T Q(dv,d\theta),\end{align*}where ![]() $S_T Q$ is the (randomly) shifted process with bivariate cumulative distribution function given by
$S_T Q$ is the (randomly) shifted process with bivariate cumulative distribution function given by
and where for ![]() $v>0$,
$v>0$,
This shows that ![]() $S_T N^h$ satisfies Equation (1.2) driven by
$S_T N^h$ satisfies Equation (1.2) driven by ![]() $S_TQ$ with initial condition
$S_TQ$ with initial condition ![]() $(S_T N^h)|_{(\!-\infty,0]}$. Since
$(S_T N^h)|_{(\!-\infty,0]}$. Since ![]() $A\ge L(h)$, moreover
$A\ge L(h)$, moreover ![]() $S_TN^h|_{(0,+\infty)}$ actually depends only on
$S_TN^h|_{(0,+\infty)}$ actually depends only on ![]() $(S_T N^h) |_{(\!-A,0]} \triangleq X_T$.
$(S_T N^h) |_{(\!-A,0]} \triangleq X_T$.
Let us now condition on ![]() $\{T<\infty\}$ and on
$\{T<\infty\}$ and on ![]() $\mathcal{F}_T$. Since Q is an
$\mathcal{F}_T$. Since Q is an ![]() $(\mathcal{F}_t)_{t\ge0}$-Poisson point process with unit intensity,
$(\mathcal{F}_t)_{t\ge0}$-Poisson point process with unit intensity, ![]() $S_TQ$ is an
$S_TQ$ is an ![]() $(\mathcal{F}_{T+t})_{t\ge0}$-Poisson point process with unit intensity; see Lemma A.2 for this classic fact. In particular it is independent of the
$(\mathcal{F}_{T+t})_{t\ge0}$-Poisson point process with unit intensity; see Lemma A.2 for this classic fact. In particular it is independent of the ![]() $\mathcal{F}_T$-measurable random variable
$\mathcal{F}_T$-measurable random variable ![]() $X_T$. Additionally,
$X_T$. Additionally, ![]() $X_T$ satisfies the assumption (2.2), which becomes in this case the following: for all
$X_T$ satisfies the assumption (2.2), which becomes in this case the following: for all ![]() $r>0$,
$r>0$,
We have indeed that
 \begin{align*}\int_0^r \int_{(\!-A,0]} & h^+(u-s) (S_TN^h)(ds) du \nonumber \\[3pt]
& = \int_0^r \int_{(\!-A+T,T]}h^+(T+u-s) N^h(ds) \ du \nonumber \\[3pt]
&= \int_T^{T+r} \int_{(\!-A+T,T]}h^+(v-s) N^h(ds) \ dv \nonumber \\[3pt]
& \le \int_T^{T+r} \int_{(\!-\infty,0]}h^+(v-s) N^0(ds) \ dv + \int_T^{T+r} \int_{(0,T]}h^+(v-s) N^h(ds) \ dv \nonumber \\[3pt]
& \le \int_T^{T+r} \int_{(\!-\infty,0]}h^+(v-s) N^0(ds) \ dv + \|h^+\|_1 N^h(0,T] \nonumber\\[3pt]
& < +\infty\qquad \mathbb{P}_{\mathfrak{m}}\textnormal{-a.s.},\end{align*}
\begin{align*}\int_0^r \int_{(\!-A,0]} & h^+(u-s) (S_TN^h)(ds) du \nonumber \\[3pt]
& = \int_0^r \int_{(\!-A+T,T]}h^+(T+u-s) N^h(ds) \ du \nonumber \\[3pt]
&= \int_T^{T+r} \int_{(\!-A+T,T]}h^+(v-s) N^h(ds) \ dv \nonumber \\[3pt]
& \le \int_T^{T+r} \int_{(\!-\infty,0]}h^+(v-s) N^0(ds) \ dv + \int_T^{T+r} \int_{(0,T]}h^+(v-s) N^h(ds) \ dv \nonumber \\[3pt]
& \le \int_T^{T+r} \int_{(\!-\infty,0]}h^+(v-s) N^0(ds) \ dv + \|h^+\|_1 N^h(0,T] \nonumber\\[3pt]
& < +\infty\qquad \mathbb{P}_{\mathfrak{m}}\textnormal{-a.s.},\end{align*}since the distribution ![]() $\mathfrak{m}$ of
$\mathfrak{m}$ of ![]() $N^0$ satisfies (2.2), and since we have shown at the end of the proof of Proposition 2.1 that
$N^0$ satisfies (2.2), and since we have shown at the end of the proof of Proposition 2.1 that ![]() $\mathbb{E}_{\mathfrak{m}}(N^h(0,t]) < +\infty$ for all
$\mathbb{E}_{\mathfrak{m}}(N^h(0,t]) < +\infty$ for all ![]() $t >0$.
$t >0$.
Thus the assumptions of Proposition 2.1 are satisfied, which yields that ![]() $(X_{T+t} )_{t\ge0}$ is the pathwise unique, and hence weakly unique, strong solution of Equation (1.2) started at
$(X_{T+t} )_{t\ge0}$ is the pathwise unique, and hence weakly unique, strong solution of Equation (1.2) started at ![]() $X_T$ and driven by the
$X_T$ and driven by the ![]() $(\mathcal{F}_{T+t})_{t\ge0}$-Poisson point process
$(\mathcal{F}_{T+t})_{t\ge0}$-Poisson point process ![]() $S_TQ$. Hence, it is a process started at
$S_TQ$. Hence, it is a process started at ![]() $X_T$ which is an
$X_T$ which is an ![]() $(\mathcal{F}_{T+t})_{t\ge0}$-Markov process with same transition semi-group as
$(\mathcal{F}_{T+t})_{t\ge0}$-Markov process with same transition semi-group as ![]() $(X_t)_{t\geq 0}$. If we wish to be more specific, for every bounded Borel function F on
$(X_t)_{t\geq 0}$. If we wish to be more specific, for every bounded Borel function F on ![]() $\mathbb{D}(\mathbb{R}_+,\mathcal{N}((\!-A,0]))$ we set
$\mathbb{D}(\mathbb{R}_+,\mathcal{N}((\!-A,0]))$ we set
and note that existence and uniqueness in law for (1.2) yield that
This is the strong Markov property we set out to prove.
3.2. Renewal of X at  $\emptyset$
$\emptyset$
Using ![]() $(X_t)_{t\geq 0}$ and Proposition 3.1, we obtain that if T is a stopping time such that
$(X_t)_{t\geq 0}$ and Proposition 3.1, we obtain that if T is a stopping time such that ![]() $N^h|_{(T-A,T]}=\emptyset$, then
$N^h|_{(T-A,T]}=\emptyset$, then ![]() $N^h|_{(T,+\infty)}$ is independent of
$N^h|_{(T,+\infty)}$ is independent of ![]() $N^h|_{(\!-\infty,T]}$ and behaves the same as
$N^h|_{(\!-\infty,T]}$ and behaves the same as ![]() $N^h$ started from
$N^h$ started from ![]() $\emptyset$ and translated by T. Such renewal times lead to an interesting decomposition of
$\emptyset$ and translated by T. Such renewal times lead to an interesting decomposition of ![]() $N^h$ which illuminates its dependence structure.
$N^h$ which illuminates its dependence structure.
The successive hitting times of ![]() $\emptyset \in \mathcal{N}((\!-A,0])$ for the Markov process X are such renewal times. This subsection is devoted to the study of their properties. Recall that we have introduced in (1.7) the first hitting time of
$\emptyset \in \mathcal{N}((\!-A,0])$ for the Markov process X are such renewal times. This subsection is devoted to the study of their properties. Recall that we have introduced in (1.7) the first hitting time of ![]() $\emptyset \in \mathcal{N}((\!-A,0])$ for X, given by
$\emptyset \in \mathcal{N}((\!-A,0])$ for X, given by
It depends on A, but this is omitted in the notation. It is natural to study whether ![]() $\tau$ is finite or not. When the reproduction function h is nonnegative, we introduce the queue
$\tau$ is finite or not. When the reproduction function h is nonnegative, we introduce the queue ![]() $(Y_t)_{t \ge 0}$ defined by (2.6), and its return time to zero,
$(Y_t)_{t \ge 0}$ defined by (2.6), and its return time to zero, ![]() $\mathcal{T}_1$, defined in (2.7). The following result will yield the finiteness of
$\mathcal{T}_1$, defined in (2.7). The following result will yield the finiteness of ![]() $\tau$.
$\tau$.
Lemma 3.1. Let Assumption 1.1 hold. Let ![]() $A<\infty$ be such that
$A<\infty$ be such that ![]() $A \ge L(h)$. Let
$A \ge L(h)$. Let ![]() $\tau$ and
$\tau$ and ![]() $\mathcal{T}_1$ be as defined in (1.7) and (2.7). If h is nonnegative then
$\mathcal{T}_1$ be as defined in (1.7) and (2.7). If h is nonnegative then ![]() $\mathbb{P}_{\emptyset}(\tau = \mathcal{T}_1)=1$.
$\mathbb{P}_{\emptyset}(\tau = \mathcal{T}_1)=1$.
Proof. We use the notation defined in Section 2.2. To begin with, we remark that ![]() $\tau >V_1$. First, let us consider t such that
$\tau >V_1$. First, let us consider t such that ![]() $V_1<t< \mathcal{T}_1$. By definition, there exists
$V_1<t< \mathcal{T}_1$. By definition, there exists ![]() $i\ge1$ such that
$i\ge1$ such that
Since the interval ![]() $[V_i, V_i+H_i]$ corresponds to the cluster of descendants of
$[V_i, V_i+H_i]$ corresponds to the cluster of descendants of ![]() $V_i$, there exists a sequence of points of
$V_i$, there exists a sequence of points of ![]() $N^h$ in
$N^h$ in ![]() $[V_i, V_i+H_i]$ which are distant by less than L(h) and thus by less than A. Therefore, if
$[V_i, V_i+H_i]$ which are distant by less than L(h) and thus by less than A. Therefore, if ![]() $t\in[V_i, V_i+H_i]$, then
$t\in[V_i, V_i+H_i]$, then ![]() $N^h(t-A,t]>0$.
$N^h(t-A,t]>0$.
If ![]() $t\in[ V_i+H_i, V_i+H_i+A]$, then
$t\in[ V_i+H_i, V_i+H_i+A]$, then ![]() $N^h(t-A,t]>0$ as well, since
$N^h(t-A,t]>0$ as well, since ![]() $V_i+H_i \in N^h$ (it is the last birth time in the Galton–Watson tree stemming from
$V_i+H_i \in N^h$ (it is the last birth time in the Galton–Watson tree stemming from ![]() $V_i$, by definition of
$V_i$, by definition of ![]() $H_i$). Since this reasoning holds for any
$H_i$). Since this reasoning holds for any ![]() $t\le \mathcal{T}_1$, it follows that
$t\le \mathcal{T}_1$, it follows that ![]() $\tau \ge\mathcal{T}_1$.
$\tau \ge\mathcal{T}_1$.
Conversely, for any ![]() $t \in [V_1,\tau)$, by definition of
$t \in [V_1,\tau)$, by definition of ![]() $\tau$, necessarily
$\tau$, necessarily ![]() $N^h(t-A,t]>0$. Thus there exists an atom of
$N^h(t-A,t]>0$. Thus there exists an atom of ![]() $N^h$ in
$N^h$ in ![]() $(t-A,t]$, and from the cluster representation, there exists
$(t-A,t]$, and from the cluster representation, there exists ![]() $i \ge 1$ such that this atom belongs to the cluster of
$i \ge 1$ such that this atom belongs to the cluster of ![]() $V_i$, hence to
$V_i$, hence to ![]() $[V_i,V_i+H_i]$. We easily deduce that
$[V_i,V_i+H_i]$. We easily deduce that
and thus ![]() $Y_t\ge1$, for all
$Y_t\ge1$, for all ![]() $t \in [V_1,\tau)$. This proves that
$t \in [V_1,\tau)$. This proves that ![]() $\tau\le \mathcal{T}_1$ and concludes the proof.□
$\tau\le \mathcal{T}_1$ and concludes the proof.□
To extend the result concerning the finiteness of ![]() $\tau$ to the case where no assumption is made on the sign of h, we use the coupling between
$\tau$ to the case where no assumption is made on the sign of h, we use the coupling between ![]() $N^h$ and
$N^h$ and ![]() $N^{h^+}$ stated in Proposition 2.1(2).
$N^{h^+}$ stated in Proposition 2.1(2).
Proposition 3.2. Let Assumption 1.1 hold. Let ![]() $A<\infty$ be such that
$A<\infty$ be such that ![]() $A \ge L(h)$. Let
$A \ge L(h)$. Let ![]() $\tau$ be as defined in (1.7), and let
$\tau$ be as defined in (1.7), and let ![]() $\tau^+$ be defined similarly with
$\tau^+$ be defined similarly with ![]() $h^+$ instead of h. Then
$h^+$ instead of h. Then ![]() $\mathbb{P}_{\mathfrak{m}}(\tau \le \tau^+)=1$.
$\mathbb{P}_{\mathfrak{m}}(\tau \le \tau^+)=1$.
Proof. We use the coupling ![]() $(N^h,N^{h^+})$ of Proposition 2.1(2), which satisfies
$(N^h,N^{h^+})$ of Proposition 2.1(2), which satisfies ![]() $N^h \le N^{h^+}$. If
$N^h \le N^{h^+}$. If ![]() $\tau=+\infty$, since the immigration rate
$\tau=+\infty$, since the immigration rate ![]() $\lambda$ is positive, for any
$\lambda$ is positive, for any ![]() $t\ge0$ we necessarily have
$t\ge0$ we necessarily have ![]() $N^h(t-A,t]>0$ and thus
$N^h(t-A,t]>0$ and thus ![]() $N^{h^+}(t-A,t]>0$, which implies that
$N^{h^+}(t-A,t]>0$, which implies that ![]() $\tau^+=+\infty$ also, a.s.
$\tau^+=+\infty$ also, a.s.
Now, it is enough to prove that ![]() $\tau\leq \tau^+$ when both times are finite. In this case, since
$\tau\leq \tau^+$ when both times are finite. In this case, since ![]() $N^{h^+}$ is locally finite a.s.,
$N^{h^+}$ is locally finite a.s., ![]() $\tau^+-A$ is an atom of
$\tau^+-A$ is an atom of ![]() $N^{h^+}$ such that
$N^{h^+}$ such that ![]() $N^{h^+}(\tau^+-A,\tau^+]=0$. This implies that
$N^{h^+}(\tau^+-A,\tau^+]=0$. This implies that ![]() $N^{h}(\tau^+-A,\tau^+]=0$. If
$N^{h}(\tau^+-A,\tau^+]=0$. If ![]() $\tau^+-A $ is also an atom of
$\tau^+-A $ is also an atom of ![]() $N^h$, then
$N^h$, then ![]() $\tau\leq \tau^+$.
$\tau\leq \tau^+$.
Otherwise, we first prove that ![]() $N^h(\!-A,\tau^+-A)>0$. The result is obviously true if
$N^h(\!-A,\tau^+-A)>0$. The result is obviously true if ![]() $N^0\not= \emptyset$. When
$N^0\not= \emptyset$. When ![]() $N^0=\emptyset$, the first atoms of
$N^0=\emptyset$, the first atoms of ![]() $N^h$ and
$N^h$ and ![]() $N^{h^+}$ coincide because
$N^{h^+}$ coincide because ![]() $\Lambda^h_0=\Lambda_0^{h^+}$, where these functions are as defined in (A.1). This first atom is necessarily before
$\Lambda^h_0=\Lambda_0^{h^+}$, where these functions are as defined in (A.1). This first atom is necessarily before ![]() $\tau^+-A$, and hence
$\tau^+-A$, and hence ![]() $N^h(\!-A,\tau^+-A)>0$. The last atom U of
$N^h(\!-A,\tau^+-A)>0$. The last atom U of ![]() $N^h$ before
$N^h$ before ![]() $\tau^+-A$ is thus well defined, and necessarily satisfies
$\tau^+-A$ is thus well defined, and necessarily satisfies ![]() $N^h(U,U+A]=0$ and
$N^h(U,U+A]=0$ and ![]() $N^h [U, U+A)\neq 0$, so that
$N^h [U, U+A)\neq 0$, so that ![]() $\tau\leq U+A\leq \tau^+$. We have thus proved that
$\tau\leq U+A\leq \tau^+$. We have thus proved that ![]() $\tau\leq \tau^+$,
$\tau\leq \tau^+$, ![]() $\mathbb{P}_{\mathfrak{m}}$-a.s., as needed.□
$\mathbb{P}_{\mathfrak{m}}$-a.s., as needed.□
We now prove that the regeneration time ![]() $\tau$ admits an exponential moment which ensures that it is finite a.s. The results will rely on the coupling between
$\tau$ admits an exponential moment which ensures that it is finite a.s. The results will rely on the coupling between ![]() $N^h$ and
$N^h$ and ![]() $N^{h^+}$ and on the results obtained in Section 2.1. Let us define
$N^{h^+}$ and on the results obtained in Section 2.1. Let us define
Proposition 3.3. Let Assumption 1.1 hold. Let ![]() $A<\infty$ be such that
$A<\infty$ be such that ![]() $A \ge L(h)$, and assume that
$A \ge L(h)$, and assume that ![]() $\mathbb{E}_\mathfrak{m}(N^0(\!-A,0])<+\infty$. Then
$\mathbb{E}_\mathfrak{m}(N^0(\!-A,0])<+\infty$. Then ![]() $\tau$ given by (1.7) satisfies
$\tau$ given by (1.7) satisfies
In particular ![]() $\tau$ is finite,
$\tau$ is finite, ![]() $\mathbb{P}_{\mathfrak{m}}$-a.s., and
$\mathbb{P}_{\mathfrak{m}}$-a.s., and ![]() $\mathbb{E}_{\mathfrak{m}}(\tau) < +\infty$.
$\mathbb{E}_{\mathfrak{m}}(\tau) < +\infty$.
Proof. By Proposition 3.2, it is sufficient to prove this for ![]() $\tau^+$. When
$\tau^+$. When ![]() $\mathfrak{m}$ is the Dirac measure at
$\mathfrak{m}$ is the Dirac measure at ![]() $\emptyset$, the result is a direct consequence of Lemma 3.1 and Proposition 2.3. We now turn to the case when
$\emptyset$, the result is a direct consequence of Lemma 3.1 and Proposition 2.3. We now turn to the case when ![]() $\mathfrak{m}$ is different from
$\mathfrak{m}$ is different from ![]() $\delta_{\emptyset}$. The proof is separated into three steps.□
$\delta_{\emptyset}$. The proof is separated into three steps.□
Step 1: Analysis of the problem. To control ![]() $\tau^+$, we distinguish the points of
$\tau^+$, we distinguish the points of ![]() $N^h$ coming from the initial condition from the points coming from ancestors that arrived after zero. We thus let
$N^h$ coming from the initial condition from the points coming from ancestors that arrived after zero. We thus let ![]() $K= N^0((\!-A,0])$ denote the number of atoms of
$K= N^0((\!-A,0])$ denote the number of atoms of ![]() $N^0$,
$N^0$, ![]() $(V_i^0)_{1\le i \le K}$ the atoms themselves, and
$(V_i^0)_{1\le i \le K}$ the atoms themselves, and ![]() $(\widetilde{H}_i^0(A))_{1\le i \le K}$ the durations such that
$(\widetilde{H}_i^0(A))_{1\le i \le K}$ the durations such that ![]() $V_i^0 + \widetilde{H}_i^0(A)-A$ is the time of birth of the last descendant of
$V_i^0 + \widetilde{H}_i^0(A)-A$ is the time of birth of the last descendant of ![]() $V_i^0$. Note that
$V_i^0$. Note that ![]() $V_i^0$ has no offspring before time 0, so that the reproduction function of
$V_i^0$ has no offspring before time 0, so that the reproduction function of ![]() $V_i^0$ is a truncation of h. We finally define the time when the influence of the past before 0 has vanished, given by
$V_i^0$ is a truncation of h. We finally define the time when the influence of the past before 0 has vanished, given by
with the convention that ![]() $E=0$ if
$E=0$ if ![]() $K=0$. If
$K=0$. If ![]() $K>0$, since
$K>0$, since ![]() $V_i^0\in (\!-A,0]$ and
$V_i^0\in (\!-A,0]$ and ![]() $\widetilde{H}_i^0(A)\geq A$, we have
$\widetilde{H}_i^0(A)\geq A$, we have ![]() $E>0$. Note that
$E>0$. Note that ![]() $\tau^+ \ge E$.
$\tau^+ \ge E$.
We now consider the sequence ![]() $(V_i)_{i \ge 1}$ of ancestors arriving after time 0 at rate
$(V_i)_{i \ge 1}$ of ancestors arriving after time 0 at rate ![]() $\lambda$. We recall that these can be viewed as customers arriving in an M/G/
$\lambda$. We recall that these can be viewed as customers arriving in an M/G/![]() $\infty$ queue with service times given by
$\infty$ queue with service times given by ![]() $\widetilde{H}_1(A)$. In our case, the queue may not be empty at time 0, when
$\widetilde{H}_1(A)$. In our case, the queue may not be empty at time 0, when ![]() $E>0$. In that case, the queue returns to 0 when all the customers that arrived before time 0 have left the system (which is the case at time E) and when all the busy periods containing the customers that arrived at times between 0 and E are over. The first hitting time of 0 for the queue is thus equal to
$E>0$. In that case, the queue returns to 0 when all the customers that arrived before time 0 have left the system (which is the case at time E) and when all the busy periods containing the customers that arrived at times between 0 and E are over. The first hitting time of 0 for the queue is thus equal to
 \begin{equation} \tau^+ = \left\{ \begin{array}{ccl} E & \quad \mbox{ if } & \quad Y_E=0\,, \\[5pt]
\inf\{t \ge E\,{:}\, Y_t=0 \} & \quad\mbox{ if } & \quad Y_E>0\,, \end{array}\right. \end{equation}
\begin{equation} \tau^+ = \left\{ \begin{array}{ccl} E & \quad \mbox{ if } & \quad Y_E=0\,, \\[5pt]
\inf\{t \ge E\,{:}\, Y_t=0 \} & \quad\mbox{ if } & \quad Y_E>0\,, \end{array}\right. \end{equation}where ![]() $Y_t$ is as given in (2.6):
$Y_t$ is as given in (2.6):
Step 2: Exponential moments ofE. In (3.4), E depends only on ![]() $N^0$, and
$N^0$, and ![]() $(Y_t)_{t\geq 0}$ depends only on the arrivals and service times of customers entering the queue after time 0. A natural idea is then to condition with respect to E, and for this it is important to gather estimates on the moments of E. Since
$(Y_t)_{t\geq 0}$ depends only on the arrivals and service times of customers entering the queue after time 0. A natural idea is then to condition with respect to E, and for this it is important to gather estimates on the moments of E. Since ![]() $V_i^0\leq 0$, we have that
$V_i^0\leq 0$, we have that
The truncation mentioned in Step 1 implies that the ![]() $\widetilde{H}^0_i(A)$ are stochastically dominated by independent random variables distributed as
$\widetilde{H}^0_i(A)$ are stochastically dominated by independent random variables distributed as ![]() $\widetilde{H}_1$, which we denote by
$\widetilde{H}_1$, which we denote by ![]() $\bar{H}^0_i(A)$. Thus, for
$\bar{H}^0_i(A)$. Thus, for ![]() $t>0$, using (2.8), we have
$t>0$, using (2.8), we have
 \begin{align*}\mathbb{P}_{\mathfrak{m}}(E>t)&\leq \mathbb{P}_{\mathfrak{m}}\Big(\max_{1\leq i\leq K} \bar{H}^0_i(A)>t\Big)\\&= 1-\mathbb{E}_{\mathfrak{m}}\Big(\big(1-\mathbb{P}(\widetilde{H}_1(A)> t)\big)^K\Big)\\&\leq 1 -\mathbb{E}_{\mathfrak{m}}\big((1-C \text{e}^{-{\gamma^+} t})^K\big)\,.\end{align*}
\begin{align*}\mathbb{P}_{\mathfrak{m}}(E>t)&\leq \mathbb{P}_{\mathfrak{m}}\Big(\max_{1\leq i\leq K} \bar{H}^0_i(A)>t\Big)\\&= 1-\mathbb{E}_{\mathfrak{m}}\Big(\big(1-\mathbb{P}(\widetilde{H}_1(A)> t)\big)^K\Big)\\&\leq 1 -\mathbb{E}_{\mathfrak{m}}\big((1-C \text{e}^{-{\gamma^+} t})^K\big)\,.\end{align*}Thus there exists ![]() $t_0>0$ such that for any
$t_0>0$ such that for any ![]() $t>t_0$,
$t>t_0$,
As a corollary, we have for any ![]() $\beta \in (0,{\gamma^+})$ that
$\beta \in (0,{\gamma^+})$ that
Step 3: Estimate of the tail distribution of![]() $\tau^+$. For
$\tau^+$. For ![]() $t>0$, we have
$t>0$, we have
 \begin{align*}\mathbb{P}_{\mathfrak{m}}(\tau^+>t)& = \mathbb{P}_{\mathfrak{m}}\big(\tau^+>t,\,E> t\big)+\mathbb{P}_{\mathfrak{m}}\big(\tau^+>t,\,E\leq t\big)\\& \leq\mathbb{P}_{\mathfrak{m}}(E> t)+\mathbb{E}_{\mathfrak{m}}\Big({\mathds{1}}_{\{E\leq t\}}\, \mathbb{P}_{\mathfrak{m}}\big(\tau^+>t \,|\, E\big)\Big).\end{align*}
\begin{align*}\mathbb{P}_{\mathfrak{m}}(\tau^+>t)& = \mathbb{P}_{\mathfrak{m}}\big(\tau^+>t,\,E> t\big)+\mathbb{P}_{\mathfrak{m}}\big(\tau^+>t,\,E\leq t\big)\\& \leq\mathbb{P}_{\mathfrak{m}}(E> t)+\mathbb{E}_{\mathfrak{m}}\Big({\mathds{1}}_{\{E\leq t\}}\, \mathbb{P}_{\mathfrak{m}}\big(\tau^+>t \,|\, E\big)\Big).\end{align*}The first term is controlled by (3.5). For the second term, we use Proposition A.2, which is a consequence of Theorem A.1. For this, let us introduce a constant ![]() $\kappa$ such that
$\kappa$ such that ![]() $\kappa <{\gamma^+}$ if
$\kappa <{\gamma^+}$ if ![]() ${\gamma^+} \leq \lambda$ and
${\gamma^+} \leq \lambda$ and ![]() $\kappa=\lambda$ if
$\kappa=\lambda$ if ![]() $\lambda<{\gamma^+}$. We have
$\lambda<{\gamma^+}$. We have
Since ![]() $\kappa<{\gamma^+}$, it is always possible to choose
$\kappa<{\gamma^+}$, it is always possible to choose ![]() $\beta\in (\kappa,{\gamma^+})$ such that (3.6) holds, which implies that
$\beta\in (\kappa,{\gamma^+})$ such that (3.6) holds, which implies that ![]() $\mathbb{E}_\mathfrak{m}\big({\mathds{1}}_{\{E\leq t\}} \,E\,\text{e}^{\kappa E}\big)$ can be bounded by a finite constant independent of t.
$\mathbb{E}_\mathfrak{m}\big({\mathds{1}}_{\{E\leq t\}} \,E\,\text{e}^{\kappa E}\big)$ can be bounded by a finite constant independent of t.
Gathering all the results, we have
This yields that ![]() $\mathbb{E}_\mathfrak{m}(\text{e}^{\alpha \tau^+})<+\infty$ for any
$\mathbb{E}_\mathfrak{m}(\text{e}^{\alpha \tau^+})<+\infty$ for any ![]() $\alpha<\kappa$, i.e.
$\alpha<\kappa$, i.e. ![]() $\alpha<\min (\lambda,{\gamma^+})$.
$\alpha<\min (\lambda,{\gamma^+})$.
Note that if Assumption 1.1 holds, then ![]() $\tau$ given by (1.7) satisfies
$\tau$ given by (1.7) satisfies ![]() $\mathbb{E}_\emptyset(\tau)<\infty$, and hence the null measure
$\mathbb{E}_\emptyset(\tau)<\infty$, and hence the null measure ![]() $\emptyset$ is a positive recurrent state for the strong Markov process
$\emptyset$ is a positive recurrent state for the strong Markov process ![]() $X=(X_t)_{t\ge 0}$.
$X=(X_t)_{t\ge 0}$.
Theorem 3.1. Let Assumption 1.1 hold. The strong Markov process ![]() $X=(X_t)_{t\ge 0}$ with values in
$X=(X_t)_{t\ge 0}$ with values in ![]() $\mathcal{N}((\!-A,0])$ defined by (3.2) admits a unique invariant law
$\mathcal{N}((\!-A,0])$ defined by (3.2) admits a unique invariant law ![]() $\pi_A$ defined as in (1.8); i.e., for every Borel nonnegative function f on
$\pi_A$ defined as in (1.8); i.e., for every Borel nonnegative function f on ![]() $\mathcal{N}((\!-A,0])$,
$\mathcal{N}((\!-A,0])$,
Moreover, ![]() $\pi_A\{\emptyset\} = 1/(\lambda \mathbb{E}_\emptyset(\tau))$.
$\pi_A\{\emptyset\} = 1/(\lambda \mathbb{E}_\emptyset(\tau))$.
Proof. These facts are classic in the presence of the positive recurrent state ![]() $\emptyset$, which is reachable from all states.□
$\emptyset$, which is reachable from all states.□
The strong Markov property of X yields a sequence of regeneration times ![]() $(\tau_k)_{k\geq 0}$, which are the successive visits of X to the positive recurrent state
$(\tau_k)_{k\geq 0}$, which are the successive visits of X to the positive recurrent state ![]() $\emptyset$, defined as follows (the time
$\emptyset$, defined as follows (the time ![]() $\tau_0$ has already been introduced in (1.10)):
$\tau_0$ has already been introduced in (1.10)):
These provide a useful decomposition of the path of X into i.i.d. excursions.
Theorem 3.2. Let ![]() $N^h$ be a Hawkes process satisfying Assumption 1.1, and
$N^h$ be a Hawkes process satisfying Assumption 1.1, and ![]() $A \ge L(h)$. Consider the Markov process X defined in (3.2). Under
$A \ge L(h)$. Consider the Markov process X defined in (3.2). Under ![]() $\mathbb{P}_\mathfrak{m}$ the following hold:
$\mathbb{P}_\mathfrak{m}$ the following hold:
1. The
 $\tau_k$ for
$\tau_k$ for  $k\ge0$ are finite stopping times, a.s.
$k\ge0$ are finite stopping times, a.s.2. The delay
 $(X_{t})_{ t \in [0,\tau_0) }$ is independent of the cycles
$(X_{t})_{ t \in [0,\tau_0) }$ is independent of the cycles  $(X_{\tau_{k-1} + t})_{ t \in [0, \tau_k- \tau_{k-1}) }$ for
$(X_{\tau_{k-1} + t})_{ t \in [0, \tau_k- \tau_{k-1}) }$ for  $k\ge1$.
$k\ge1$.3. These cycles are i.i.d. and distributed as
 $(X_t)_{t \in[0, \tau)}$ under
$(X_t)_{t \in[0, \tau)}$ under  $\mathbb{P}_\emptyset$. In particular their durations
$\mathbb{P}_\emptyset$. In particular their durations  $(\tau_k-\tau_{k-1})_{k\geq 1}$ are distributed as
$(\tau_k-\tau_{k-1})_{k\geq 1}$ are distributed as  $\tau$ under
$\tau$ under  $\mathbb{P}_\emptyset$, and
$\mathbb{P}_\emptyset$, and  $\lim_{k\rightarrow +\infty}\tau_k=+\infty$,
$\lim_{k\rightarrow +\infty}\tau_k=+\infty$,  $\mathbb{P}_\mathfrak{m}$-a.s.
$\mathbb{P}_\mathfrak{m}$-a.s.
Proof. The above items follow classically from the strong Markov property of X. Let us first prove the finiteness of the return times ![]() $\tau_k$. For any
$\tau_k$. For any ![]() $\mathfrak{m}$, from the definition of
$\mathfrak{m}$, from the definition of ![]() $\tau_0$ and
$\tau_0$ and ![]() $\tau$, we have that
$\tau$, we have that ![]() $\tau_0\leq \tau$,
$\tau_0\leq \tau$, ![]() $\mathbb{P}_\mathfrak{m}$-a.s. Then
$\mathbb{P}_\mathfrak{m}$-a.s. Then ![]() $\mathbb{P}_\mathfrak{m}(\tau_0<+\infty)=1$ follows from Proposition 3.3. For
$\mathbb{P}_\mathfrak{m}(\tau_0<+\infty)=1$ follows from Proposition 3.3. For ![]() $k\geq 1$, using the strong Markov property of X, we have for any
$k\geq 1$, using the strong Markov property of X, we have for any ![]() $\mathfrak{m}$ that
$\mathfrak{m}$ that
 \begin{align*}\mathbb{P}_\mathfrak{m}(\tau_k<+\infty)&= \mathbb{E}_\mathfrak{m} \big( {\mathds{1}}_{\{\tau_{k-1}<+\infty\}} \, \mathbb{P}_{X_{\tau_{k-1}}}(\tau<+\infty)\big)\\ &= \mathbb{E}_\mathfrak{m}\big({\mathds{1}}_{\{\tau_{k-1}<+\infty\}} \,\mathbb{P}_\emptyset(\tau<+\infty)\big)\\& = \mathbb{P}_\mathfrak{m}(\tau_{k-1}<+\infty)=\cdots = \mathbb{P}_{\mathfrak{m}}(\tau_0<+\infty)=1.\end{align*}
\begin{align*}\mathbb{P}_\mathfrak{m}(\tau_k<+\infty)&= \mathbb{E}_\mathfrak{m} \big( {\mathds{1}}_{\{\tau_{k-1}<+\infty\}} \, \mathbb{P}_{X_{\tau_{k-1}}}(\tau<+\infty)\big)\\ &= \mathbb{E}_\mathfrak{m}\big({\mathds{1}}_{\{\tau_{k-1}<+\infty\}} \,\mathbb{P}_\emptyset(\tau<+\infty)\big)\\& = \mathbb{P}_\mathfrak{m}(\tau_{k-1}<+\infty)=\cdots = \mathbb{P}_{\mathfrak{m}}(\tau_0<+\infty)=1.\end{align*} Let us now prove (2) and (3). It is sufficient to consider ![]() $(X_t)_{t\in [0,\tau_0)}$,
$(X_t)_{t\in [0,\tau_0)}$, ![]() $(X_{\tau_0+t})_{t\in [0,\tau_1-\tau_0)}$, and
$(X_{\tau_0+t})_{t\in [0,\tau_1-\tau_0)}$, and ![]() $(X_{\tau_1+t})_{t\in [0,\tau_2-\tau_1)}$. Let
$(X_{\tau_1+t})_{t\in [0,\tau_2-\tau_1)}$. Let ![]() $F_0$,
$F_0$, ![]() $F_1$, and
$F_1$, and ![]() $F_2$ be three measurable bounded real functions on
$F_2$ be three measurable bounded real functions on ![]() $\mathbb{D}(\mathbb{R}_+,\mathcal{N}(\!-A,0])$. Then, using the strong Markov property successively at
$\mathbb{D}(\mathbb{R}_+,\mathcal{N}(\!-A,0])$. Then, using the strong Markov property successively at ![]() $\tau_1$ and
$\tau_1$ and ![]() $\tau_0$, we obtain
$\tau_0$, we obtain
 \begin{align*}&\mathbb{E}_{\mathfrak{m}} \Big(F_0\big((X_t)_{t\in [0,\tau_0)}\big)\, F_1\big((X_{\tau_0+t})_{t\in [0,\tau_1-\tau_0)}\big) \,F_2\big((X_{\tau_1+t})_{t\in [0,\tau_2-\tau_1)}\big)\Big)\\&\quad = \mathbb{E}_{\mathfrak{m}} \Big(F_0\big((X_t)_{t\in [0,\tau_0)}\big)\Big) \,\mathbb{E}_{\emptyset}\Big(F_1\big((X_{t})_{t\in [0,\tau)}\big)\Big) \,\mathbb{E}_\emptyset\Big( F_2\big((X_{t})_{t\in [0,\tau)}\big)\Big).\end{align*}
\begin{align*}&\mathbb{E}_{\mathfrak{m}} \Big(F_0\big((X_t)_{t\in [0,\tau_0)}\big)\, F_1\big((X_{\tau_0+t})_{t\in [0,\tau_1-\tau_0)}\big) \,F_2\big((X_{\tau_1+t})_{t\in [0,\tau_2-\tau_1)}\big)\Big)\\&\quad = \mathbb{E}_{\mathfrak{m}} \Big(F_0\big((X_t)_{t\in [0,\tau_0)}\big)\Big) \,\mathbb{E}_{\emptyset}\Big(F_1\big((X_{t})_{t\in [0,\tau)}\big)\Big) \,\mathbb{E}_\emptyset\Big( F_2\big((X_{t})_{t\in [0,\tau)}\big)\Big).\end{align*}This concludes the proof.□
4. Proofs of the main results
We reinterpret the statements of the main results in terms of the Markov process X. Let ![]() $T>0$ be fixed; since the sequence
$T>0$ be fixed; since the sequence ![]() $(\tau_k)_{k\geq 0}$ increases to infinity,
$(\tau_k)_{k\geq 0}$ increases to infinity,
For a locally bounded Borel function f on ![]() $\mathcal{N}((\!-A,0])$ we define the random variables
$\mathcal{N}((\!-A,0])$ we define the random variables
which are finite a.s., i.i.d., and of the same law as ![]() $\int_{0}^{\tau} f (X_t)\,dt$ under
$\int_{0}^{\tau} f (X_t)\,dt$ under ![]() $\mathbb{P}_\emptyset$; see Theorem 3.2.
$\mathbb{P}_\emptyset$; see Theorem 3.2.
Proof of Theorem 1.2(1)
This classic proof assumes first that ![]() $f\ge0$. Then using (4.1) and (4.2),
$f\ge0$. Then using (4.1) and (4.2),
 \begin{equation*}\frac1{K_T}\sum_{k=1}^{K_T} I_k f\le \frac1{K_T}\int_0^T f(X_t)\,dt\le\frac1{K_T}\int_0^{\tau_0} f(X_t)\,dt + \frac1{K_T}\sum_{k=1}^{K_T+1} I_kf,\end{equation*}
\begin{equation*}\frac1{K_T}\sum_{k=1}^{K_T} I_k f\le \frac1{K_T}\int_0^T f(X_t)\,dt\le\frac1{K_T}\int_0^{\tau_0} f(X_t)\,dt + \frac1{K_T}\sum_{k=1}^{K_T+1} I_kf,\end{equation*}and the strong law of large numbers applied to the i.i.d. ![]() $I_k f$ yields that
$I_k f$ yields that
Choosing ![]() $f=1$ yields that
$f=1$ yields that
and dividing the first limit by the second concludes the proof for ![]() $f\ge0$. The case of
$f\ge0$. The case of ![]() $\pi_A$-integrable signed f follows using the decomposition
$\pi_A$-integrable signed f follows using the decomposition ![]() $f=f^+ - f^-$.
$f=f^+ - f^-$.
Proof of Theorem 1.2(2)
This follows from a general result in Thorisson [Reference Thorisson36, Th. 10.3.3, p. 351], which says that if the distribution of ![]() $\tau$ under
$\tau$ under ![]() $\mathbb{P}_\emptyset$ has a density with respect to the Lebesgue measure and if
$\mathbb{P}_\emptyset$ has a density with respect to the Lebesgue measure and if ![]() $\mathbb{E}_\emptyset(\tau)<+\infty$, then there exists a probability measure
$\mathbb{E}_\emptyset(\tau)<+\infty$, then there exists a probability measure ![]() $\mathbb{Q}$ on
$\mathbb{Q}$ on ![]() $\mathbb{D}(\mathbb{R}_+,\mathcal{N}(\!-A,0])$ such that, for any initial law
$\mathbb{D}(\mathbb{R}_+,\mathcal{N}(\!-A,0])$ such that, for any initial law ![]() $\mathfrak{m}$,
$\mathfrak{m}$,
Since ![]() $\pi_A$ is an invariant law,
$\pi_A$ is an invariant law, ![]() $ \mathbb{P}_{\pi_A}\bigl((X_{t+u})_{u\ge0}\in \cdot \bigr) = \mathbb{P}_{\pi_A}(X\in \cdot) $ for every
$ \mathbb{P}_{\pi_A}\bigl((X_{t+u})_{u\ge0}\in \cdot \bigr) = \mathbb{P}_{\pi_A}(X\in \cdot) $ for every ![]() $t\geq 0$. Hence, taking
$t\geq 0$. Hence, taking ![]() $\mathfrak{m}=\pi_A$ in the above convergence yields that
$\mathfrak{m}=\pi_A$ in the above convergence yields that ![]() $\mathbb{Q}=\mathbb{P}_{\pi_A}(X\in \cdot)$.
$\mathbb{Q}=\mathbb{P}_{\pi_A}(X\in \cdot)$.
It remains to check the assumptions of the theorem above. Proposition 3.3 yields that ![]() $\mathbb{E}_\emptyset(\tau)<+\infty$. Moreover, under
$\mathbb{E}_\emptyset(\tau)<+\infty$. Moreover, under ![]() $\mathbb{P}_{\emptyset}$ we can rewrite
$\mathbb{P}_{\emptyset}$ we can rewrite ![]() $\tau$ as
$\tau$ as
Using the strong Markov property, we easily prove independence of the two terms in the right-hand side. Since ![]() $U_1^h$ has an exponential distribution under
$U_1^h$ has an exponential distribution under ![]() $\mathbb{P}_{\emptyset}$,
$\mathbb{P}_{\emptyset}$, ![]() $\tau$ has a density under
$\tau$ has a density under ![]() $\mathbb{P}_\emptyset$.
$\mathbb{P}_\emptyset$.
Proof of Theorem 1.3
Let ![]() $\tilde{f} \triangleq f -\pi_A\,f$, so that
$\tilde{f} \triangleq f -\pi_A\,f$, so that ![]() $\frac1T \int_0^T \tilde{f} (X_t)\,dt = \frac1T \int_0^T f(X_t)\,dt - \pi_A\,f $. With the notation (4.1) and (4.2), we have the decomposition
$\frac1T \int_0^T \tilde{f} (X_t)\,dt = \frac1T \int_0^T f(X_t)\,dt - \pi_A\,f $. With the notation (4.1) and (4.2), we have the decomposition
 \begin{equation}\int_0^T \tilde{f}(X_t)\,dt= \int_0^{\tau_0} \tilde{f}(X_t)\,dt+ \sum_{k=1}^{K_T} I_k \tilde{f} + \int_{\tau_{K_T}}^T \tilde{f}(X_t)\,dt\,.\end{equation}
\begin{equation}\int_0^T \tilde{f}(X_t)\,dt= \int_0^{\tau_0} \tilde{f}(X_t)\,dt+ \sum_{k=1}^{K_T} I_k \tilde{f} + \int_{\tau_{K_T}}^T \tilde{f}(X_t)\,dt\,.\end{equation}The ![]() $I_k \tilde{f}$ are i.i.d. and are distributed as
$I_k \tilde{f}$ are i.i.d. and are distributed as ![]() $\int_{0}^{\tau} \tilde{f} (X_t)\,dt$ under
$\int_{0}^{\tau} \tilde{f} (X_t)\,dt$ under ![]() $\mathbb{P}_\emptyset$, with expectation 0 and variance
$\mathbb{P}_\emptyset$, with expectation 0 and variance ![]() $\mathbb{E}_\emptyset(\tau) \sigma^2(\,f)$; see Theorem 3.2. Since f is locally bounded, so is
$\mathbb{E}_\emptyset(\tau) \sigma^2(\,f)$; see Theorem 3.2. Since f is locally bounded, so is ![]() $\tilde{f}$, and
$\tilde{f}$, and
Now, let ![]() $\varepsilon >0$. For arbitrary
$\varepsilon >0$. For arbitrary ![]() $a>0$ and
$a>0$ and ![]() $0<u\le T$,
$0<u\le T$,
But
and Theorem 1.2(2) yields that
so that there exists ![]() $u_0$ large enough such that
$u_0$ large enough such that
Moreover, Theorem 1.2(2) yields that
thus there exists ![]() $a_0$ large enough that
$a_0$ large enough that
and hence
This implies in particular that
It now remains to treat the second term in the right-hand side of (4.4). The classic central limit theorem yields that
 \begin{equation*}\frac1{\sqrt{T}} \sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} I_k\tilde{f}\xrightarrow[T\to\infty]{\textnormal{in law}}\frac1{\sqrt{\mathbb{E}_\emptyset(\tau)}} \mathcal{N}(0, \mathbb{E}_\emptyset(\tau)\sigma^2(\,f)) = \mathcal{N}(0, \sigma^2(\,f)),\end{equation*}
\begin{equation*}\frac1{\sqrt{T}} \sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} I_k\tilde{f}\xrightarrow[T\to\infty]{\textnormal{in law}}\frac1{\sqrt{\mathbb{E}_\emptyset(\tau)}} \mathcal{N}(0, \mathbb{E}_\emptyset(\tau)\sigma^2(\,f)) = \mathcal{N}(0, \sigma^2(\,f)),\end{equation*}and we are left to control
 \begin{equation*}\Delta_T \triangleq\frac1{\sqrt{T}}\sum_{k=1}^{K_T} I_k\tilde{f}- \frac1{\sqrt{T}}\sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} I_k\tilde{f}\,.\end{equation*}
\begin{equation*}\Delta_T \triangleq\frac1{\sqrt{T}}\sum_{k=1}^{K_T} I_k\tilde{f}- \frac1{\sqrt{T}}\sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} I_k\tilde{f}\,.\end{equation*}Let ![]() $\varepsilon>0$ and
$\varepsilon>0$ and
Note that ![]() $(1-\varepsilon^3)T/\mathbb{E}_\emptyset(\tau)<T/\mathbb{E}_\emptyset(\tau)<(1+\varepsilon^3)T/\mathbb{E}_\emptyset(\tau)$ and hence that
$(1-\varepsilon^3)T/\mathbb{E}_\emptyset(\tau)<T/\mathbb{E}_\emptyset(\tau)<(1+\varepsilon^3)T/\mathbb{E}_\emptyset(\tau)$ and hence that ![]() $\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor$ belongs to
$\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor$ belongs to ![]() $v(T,\varepsilon) $. In view of (4.3), there exists
$v(T,\varepsilon) $. In view of (4.3), there exists ![]() $t_\varepsilon$ such that if
$t_\varepsilon$ such that if ![]() $T\ge t_\varepsilon$, then
$T\ge t_\varepsilon$, then
For ![]() $T\ge t_\varepsilon$ we thus have on
$T\ge t_\varepsilon$ we thus have on ![]() $\{K_T \in v(T,\varepsilon)\}$ that
$\{K_T \in v(T,\varepsilon)\}$ that
 \begin{align*}|\Delta_T |& \leq \Biggl| \frac{1}{\sqrt{T}} \sum_{k=\lfloor (1 -\varepsilon^3)T/\mathbb{E}_\emptyset(\tau)\rfloor}^{K_T} I_k\tilde{f} \Biggr|+ \Biggl| \frac{1}{\sqrt{T}}\sum_{k=\lfloor (1 -\varepsilon^3)T/\mathbb{E}_\emptyset(\tau)\rfloor}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} I_k\tilde{f} \Biggr|\\[5pt]
& \leq \frac{2}{\sqrt{T}}\max_{n\in v(T,\varepsilon)}\Biggl|\sum_{k=\lfloor (1 -\varepsilon^3)T/\mathbb{E}_\emptyset(\tau)\rfloor}^n I_k\tilde{f}\Biggr|\, .\end{align*}
\begin{align*}|\Delta_T |& \leq \Biggl| \frac{1}{\sqrt{T}} \sum_{k=\lfloor (1 -\varepsilon^3)T/\mathbb{E}_\emptyset(\tau)\rfloor}^{K_T} I_k\tilde{f} \Biggr|+ \Biggl| \frac{1}{\sqrt{T}}\sum_{k=\lfloor (1 -\varepsilon^3)T/\mathbb{E}_\emptyset(\tau)\rfloor}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} I_k\tilde{f} \Biggr|\\[5pt]
& \leq \frac{2}{\sqrt{T}}\max_{n\in v(T,\varepsilon)}\Biggl|\sum_{k=\lfloor (1 -\varepsilon^3)T/\mathbb{E}_\emptyset(\tau)\rfloor}^n I_k\tilde{f}\Biggr|\, .\end{align*}Using now Kolmogorov’s maximal inequality [Reference Feller16, Sec. IX.7, p. 234], we obtain that
Since ![]() $\varepsilon >0$ is arbitrary, we conclude that
$\varepsilon >0$ is arbitrary, we conclude that
 \begin{equation*}\Biggl| \frac1{\sqrt{T}}\sum_{k=1}^{K_T} I_k\tilde{f}- \frac1{\sqrt{T}}\sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} I_k\tilde{f}\Biggr| \xrightarrow[T\to\infty]{\text{probab.}} 0\,.\end{equation*}
\begin{equation*}\Biggl| \frac1{\sqrt{T}}\sum_{k=1}^{K_T} I_k\tilde{f}- \frac1{\sqrt{T}}\sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} I_k\tilde{f}\Biggr| \xrightarrow[T\to\infty]{\text{probab.}} 0\,.\end{equation*}These three convergence results and Slutsky’s theorem yield the desired convergence result.
Proof of Theorem 1.4
With the notation ![]() $\tilde{f} \triangleq f -\pi_A\,f$, so that
$\tilde{f} \triangleq f -\pi_A\,f$, so that ![]() $\frac1T \int_0^T \tilde{f} (X_t)\,dt = \frac1T \int_0^T f(X_t)\,dt - \pi_A\,f $, and (4.2), let us consider the decomposition
$\frac1T \int_0^T \tilde{f} (X_t)\,dt = \frac1T \int_0^T f(X_t)\,dt - \pi_A\,f $, and (4.2), let us consider the decomposition
 \begin{align}\int_0^T \tilde{f} (X_t)\,dt=\int_0^{\tau_0} \tilde{f}(X_t)\,dt+ \sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} I_k \tilde{f}+ \int_{\tau_{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor}}^T \tilde{f}(X_t)\,dt \,.\end{align}
\begin{align}\int_0^T \tilde{f} (X_t)\,dt=\int_0^{\tau_0} \tilde{f}(X_t)\,dt+ \sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} I_k \tilde{f}+ \int_{\tau_{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor}}^T \tilde{f}(X_t)\,dt \,.\end{align}The ![]() $I_k \tilde{f}$ are i.i.d. and distributed as
$I_k \tilde{f}$ are i.i.d. and distributed as ![]() $\int_{0}^{\tau} \tilde{f} (X_t)\,dt$ under
$\int_{0}^{\tau} \tilde{f} (X_t)\,dt$ under ![]() $\mathbb{P}_\emptyset$, with expectation 0 and variance
$\mathbb{P}_\emptyset$, with expectation 0 and variance ![]() $\mathbb{E}_\emptyset(\tau) \sigma^2(\,f)$; see Theorem 3.2. Since f takes its values in [a, b], we have
$\mathbb{E}_\emptyset(\tau) \sigma^2(\,f)$; see Theorem 3.2. Since f takes its values in [a, b], we have
and
Now,
 \begin{align*}T-\tau_{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor}&= - \tau_0 - \sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} (\tau_k-\tau_{k-1}) +T\\[5pt]
&= - \tau_0 -\sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} (\tau_k-\tau_{k-1}-\mathbb{E}_\emptyset(\tau)) + T -\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor \mathbb{E}_\emptyset(\tau);\end{align*}
\begin{align*}T-\tau_{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor}&= - \tau_0 - \sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} (\tau_k-\tau_{k-1}) +T\\[5pt]
&= - \tau_0 -\sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} (\tau_k-\tau_{k-1}-\mathbb{E}_\emptyset(\tau)) + T -\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor \mathbb{E}_\emptyset(\tau);\end{align*}here
and the ![]() $\tau_k-\tau_{k-1}-\mathbb{E}_\emptyset(\tau)$ are i.i.d., have the same law as
$\tau_k-\tau_{k-1}-\mathbb{E}_\emptyset(\tau)$ are i.i.d., have the same law as ![]() $\tau-\mathbb{E}_\emptyset(\tau) $ under
$\tau-\mathbb{E}_\emptyset(\tau) $ under ![]() $\mathbb{P}_\emptyset$, and have expectation 0 and variance
$\mathbb{P}_\emptyset$, and have expectation 0 and variance ![]() $\mbox{Var}_\emptyset (\tau)$. Thus,
$\mbox{Var}_\emptyset (\tau)$. Thus,
 \begin{align*}&\mathbb{P}_\mathfrak{m}\biggl( \biggl|\frac1T \int_0^T f(X_t)\,dt - \pi_A\,f \biggr| \ge \varepsilon \biggr)\\[5pt]
&\le \mathbb{P}_\mathfrak{m}\!\left( \left| \sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} I_k \tilde{f} \right| + |b-a| \left( 2\tau_0 +\left|\sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} (\tau_k-\tau_{k-1}-\mathbb{E}_\emptyset(\tau))\right|+ \mathbb{E}_\emptyset(\tau)\right)\ge T\varepsilon\right)\!.\end{align*}
\begin{align*}&\mathbb{P}_\mathfrak{m}\biggl( \biggl|\frac1T \int_0^T f(X_t)\,dt - \pi_A\,f \biggr| \ge \varepsilon \biggr)\\[5pt]
&\le \mathbb{P}_\mathfrak{m}\!\left( \left| \sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} I_k \tilde{f} \right| + |b-a| \left( 2\tau_0 +\left|\sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} (\tau_k-\tau_{k-1}-\mathbb{E}_\emptyset(\tau))\right|+ \mathbb{E}_\emptyset(\tau)\right)\ge T\varepsilon\right)\!.\end{align*}Now, using that for any ![]() $u \in [0,1)$
$u \in [0,1)$
we obtain that
 \begin{align}&\mathbb{P}_\mathfrak{m}\biggl( \biggl|\frac1T \int_0^T f(X_t)\,dt - \pi_A\,f \biggr| \ge \varepsilon \biggr)\notag\\[4pt]
&\quad \le\mathbb{P}_\mathfrak{m}\!\left(\left| \sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} I_k \tilde{f} \right|\ge \frac{(1-u)T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau)}2\right)\notag\\[4pt]
&\qquad +\mathbb{P}_\mathfrak{m}\!\left(\left|\sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} (\tau_k-\tau_{k-1}-\mathbb{E}_\emptyset(\tau))\right|\ge \frac{(1-u)T\varepsilon- |b-a| \mathbb{E}_\emptyset(\tau)}{2|b-a|}\right)\notag\\[4pt]
&\qquad +\mathbb{P}_\mathfrak{m}\!\left(\tau_0-\mathbb{E}_\mathfrak{m}(\tau_0)\ge \frac{uT\varepsilon - 2|b-a| \mathbb{E}_{\mathfrak{m}}(\tau_0)}{2|b-a|}\right)\!.\end{align}
\begin{align}&\mathbb{P}_\mathfrak{m}\biggl( \biggl|\frac1T \int_0^T f(X_t)\,dt - \pi_A\,f \biggr| \ge \varepsilon \biggr)\notag\\[4pt]
&\quad \le\mathbb{P}_\mathfrak{m}\!\left(\left| \sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} I_k \tilde{f} \right|\ge \frac{(1-u)T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau)}2\right)\notag\\[4pt]
&\qquad +\mathbb{P}_\mathfrak{m}\!\left(\left|\sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} (\tau_k-\tau_{k-1}-\mathbb{E}_\emptyset(\tau))\right|\ge \frac{(1-u)T\varepsilon- |b-a| \mathbb{E}_\emptyset(\tau)}{2|b-a|}\right)\notag\\[4pt]
&\qquad +\mathbb{P}_\mathfrak{m}\!\left(\tau_0-\mathbb{E}_\mathfrak{m}(\tau_0)\ge \frac{uT\varepsilon - 2|b-a| \mathbb{E}_{\mathfrak{m}}(\tau_0)}{2|b-a|}\right)\!.\end{align}We aim to apply Bernstein’s inequality [Reference Massart25, Cor. 2.10, p. 25; (2.17), (2.18), p. 24] to bound the three terms of the right-hand side. We recall that for the application of Bernstein’s inequality to random variables ![]() $X_1,\dots X_N$, there should exist constants c and v such that
$X_1,\dots X_N$, there should exist constants c and v such that
 \begin{equation*} \sum_{k=1}^N\mathbb{E}_\mathfrak{m}\!\left[X_k^2\right]\le v \quad \text{ and } \quad \sum_{k=1}^N\mathbb{E}_\mathfrak{m}\!\left[(X_k)_+^n\right]\le \frac{n!}{2}vc^{n-2} \quad \forall n\ge3.\end{equation*}
\begin{equation*} \sum_{k=1}^N\mathbb{E}_\mathfrak{m}\!\left[X_k^2\right]\le v \quad \text{ and } \quad \sum_{k=1}^N\mathbb{E}_\mathfrak{m}\!\left[(X_k)_+^n\right]\le \frac{n!}{2}vc^{n-2} \quad \forall n\ge3.\end{equation*}First,
 \begin{equation*}\sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} \mathbb{E}_\mathfrak{m}\bigl( ( I_k \tilde{f})^2 \bigr)= \Big\lfloor\frac{T}{\mathbb{E}_\emptyset(\tau)}\Big\rfloor \mathbb{E}_\emptyset(\tau) \sigma^2(\,f)\le T \sigma^2(\,f)\end{equation*}
\begin{equation*}\sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} \mathbb{E}_\mathfrak{m}\bigl( ( I_k \tilde{f})^2 \bigr)= \Big\lfloor\frac{T}{\mathbb{E}_\emptyset(\tau)}\Big\rfloor \mathbb{E}_\emptyset(\tau) \sigma^2(\,f)\le T \sigma^2(\,f)\end{equation*}and, for ![]() $n\ge3$,
$n\ge3$,
 \begin{multline*}\sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} \mathbb{E}_\mathfrak{m}\bigl( (I_k \tilde{f})_\pm^n \bigr)= \Big\lfloor \frac{T}{\mathbb{E}_\emptyset(\tau)}\Big\rfloor \mathbb{E}_\mathfrak{m}\bigl( (I \tilde{f})_\pm^n\bigr)\\ \le\frac{n!}2 T \sigma^2(\,f)\biggl(\sup_{k\ge3}\biggl(\frac2{k!}\frac{\mathbb{E}_\mathfrak{m}\bigl( (I\tilde{f})_\pm^k \bigr)}{\mathbb{E}_\emptyset(\tau)\sigma^2(\,f)}\biggr)^{\frac1{k-2}}\biggr)^{n-2}\triangleq\frac{n!}2 T \sigma^2(\,f)(c^\pm(\,f))^{n-2}\,.\end{multline*}
\begin{multline*}\sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} \mathbb{E}_\mathfrak{m}\bigl( (I_k \tilde{f})_\pm^n \bigr)= \Big\lfloor \frac{T}{\mathbb{E}_\emptyset(\tau)}\Big\rfloor \mathbb{E}_\mathfrak{m}\bigl( (I \tilde{f})_\pm^n\bigr)\\ \le\frac{n!}2 T \sigma^2(\,f)\biggl(\sup_{k\ge3}\biggl(\frac2{k!}\frac{\mathbb{E}_\mathfrak{m}\bigl( (I\tilde{f})_\pm^k \bigr)}{\mathbb{E}_\emptyset(\tau)\sigma^2(\,f)}\biggr)^{\frac1{k-2}}\biggr)^{n-2}\triangleq\frac{n!}2 T \sigma^2(\,f)(c^\pm(\,f))^{n-2}\,.\end{multline*}Then,
 \begin{equation*}\sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} \mathbb{E}_\mathfrak{m}\bigl( (\tau_k-\tau_{k-1}-\mathbb{E}_\emptyset(\tau))^2 \bigr)= \Big\lfloor\frac{T}{\mathbb{E}_\emptyset(\tau)}\Big\rfloor \mbox{Var}_\emptyset (\tau)\le T \frac{\mbox{Var}_\emptyset (\tau)}{\mathbb{E}_\emptyset(\tau)}\end{equation*}
\begin{equation*}\sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} \mathbb{E}_\mathfrak{m}\bigl( (\tau_k-\tau_{k-1}-\mathbb{E}_\emptyset(\tau))^2 \bigr)= \Big\lfloor\frac{T}{\mathbb{E}_\emptyset(\tau)}\Big\rfloor \mbox{Var}_\emptyset (\tau)\le T \frac{\mbox{Var}_\emptyset (\tau)}{\mathbb{E}_\emptyset(\tau)}\end{equation*}and, for ![]() $n\ge3$,
$n\ge3$,
 \begin{multline*}\sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} \mathbb{E}_\mathfrak{m}\bigl( (\tau_k-\tau_{k-1}-\mathbb{E}_\emptyset(\tau))_\pm^n \bigr) =\Big\lfloor T/\mathbb{E}_\emptyset(\tau)\Big\rfloor \mathbb{E}_\emptyset\bigl( (\tau-\mathbb{E}_\emptyset(\tau))_\pm^n \bigr)\\\le\frac{n!}2 T \frac{\mbox{Var}_\emptyset (\tau)}{\mathbb{E}_\emptyset(\tau)}\biggl(\sup_{k\ge3}\biggl(\frac2{k!}\frac{\mathbb{E}_\emptyset\bigl( (\tau-\mathbb{E}_\emptyset(\tau))_\pm^k \bigr)}{\mbox{Var}_\emptyset (\tau)}\biggr)^{\frac1{k-2}}\biggr)^{n-2}\triangleq\frac{n!}2 T \frac{\mbox{Var}_\emptyset (\tau)}{\mathbb{E}_\emptyset(\tau)}(c^\pm(\tau))^{n-2}\,.\end{multline*}
\begin{multline*}\sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} \mathbb{E}_\mathfrak{m}\bigl( (\tau_k-\tau_{k-1}-\mathbb{E}_\emptyset(\tau))_\pm^n \bigr) =\Big\lfloor T/\mathbb{E}_\emptyset(\tau)\Big\rfloor \mathbb{E}_\emptyset\bigl( (\tau-\mathbb{E}_\emptyset(\tau))_\pm^n \bigr)\\\le\frac{n!}2 T \frac{\mbox{Var}_\emptyset (\tau)}{\mathbb{E}_\emptyset(\tau)}\biggl(\sup_{k\ge3}\biggl(\frac2{k!}\frac{\mathbb{E}_\emptyset\bigl( (\tau-\mathbb{E}_\emptyset(\tau))_\pm^k \bigr)}{\mbox{Var}_\emptyset (\tau)}\biggr)^{\frac1{k-2}}\biggr)^{n-2}\triangleq\frac{n!}2 T \frac{\mbox{Var}_\emptyset (\tau)}{\mathbb{E}_\emptyset(\tau)}(c^\pm(\tau))^{n-2}\,.\end{multline*}Lastly, ![]() $\mathbb{E}_\mathfrak{m}\bigl((\tau_0-\mathbb{E}_\mathfrak{m}(\tau_0))^2\bigr) = \mbox{Var}_\mathfrak{m}(\tau_0)$ and, for
$\mathbb{E}_\mathfrak{m}\bigl((\tau_0-\mathbb{E}_\mathfrak{m}(\tau_0))^2\bigr) = \mbox{Var}_\mathfrak{m}(\tau_0)$ and, for ![]() $n\ge3$,
$n\ge3$,
 \begin{align*}&\mathbb{E}_\mathfrak{m}\bigl((\tau_0-\mathbb{E}_\mathfrak{m}(\tau_0))_+^n\bigr)\\[4pt]
&\quad \le \frac{n!}2 \mbox{Var}_\mathfrak{m}(\tau_0)\biggl(\sup_{k\ge3}\biggl(\frac2{k!}\frac{\mathbb{E}_\mathfrak{m}\bigl((\tau_0-\mathbb{E}_\mathfrak{m}(\tau_0))_+^k\bigr)}{\mbox{Var}_\mathfrak{m}(\tau_0)}\biggr)^{\frac1{k-2}}\biggr)^{n-2}\triangleq\frac{n!}2 \mbox{Var}_\mathfrak{m}(\tau_0)(c^+(\tau_0))^{n-2}\,.\end{align*}
\begin{align*}&\mathbb{E}_\mathfrak{m}\bigl((\tau_0-\mathbb{E}_\mathfrak{m}(\tau_0))_+^n\bigr)\\[4pt]
&\quad \le \frac{n!}2 \mbox{Var}_\mathfrak{m}(\tau_0)\biggl(\sup_{k\ge3}\biggl(\frac2{k!}\frac{\mathbb{E}_\mathfrak{m}\bigl((\tau_0-\mathbb{E}_\mathfrak{m}(\tau_0))_+^k\bigr)}{\mbox{Var}_\mathfrak{m}(\tau_0)}\biggr)^{\frac1{k-2}}\biggr)^{n-2}\triangleq\frac{n!}2 \mbox{Var}_\mathfrak{m}(\tau_0)(c^+(\tau_0))^{n-2}\,.\end{align*}Applying [Reference Massart25, Cor. 2.10, p. 25; (2.17), (2.18), p. 24] to the right-hand side of (4.6) yields that
 \begin{align*}&\mathbb{P}_\mathfrak{m}\biggl( \biggl|\frac1T \int_0^T f(X_t)\,dt - \pi_A\,f \biggr| \ge \varepsilon \biggr)\notag\\[4pt]
&\quad \le\exp\left(\!-\frac{((1-u)T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau))^2}{8 T \sigma^2(\,f) + 4 c^+(\,f)((1-u)T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau)) }\right)\notag\\[4pt]
&\qquad +\exp\left(\!-\frac{((1-u)T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau))^2}{8 T \sigma^2(\,f) + 4 c^-(\,f)((1-u)T\varepsilon - |b-a|\mathbb{E}_\emptyset(\tau)) }\right)\notag\\[4pt]
&\qquad +\exp\left(\!-\frac{((1-u)T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau))^2}{8T |b-a|^2\frac{\mbox{Var}_\emptyset (\tau)}{\mathbb{E}_\emptyset(\tau)}+ 4 |b-a| c^+(\tau)((1-u)T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau)) }\right)\notag\\[4pt]
&\qquad +\exp\left(\!-\frac{((1-u)T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau))^2}{8T |b-a|^2\frac{\mbox{Var}_\emptyset (\tau)}{\mathbb{E}_\emptyset(\tau)}+ 4 |b-a| c^-(\tau)((1-u)T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau)) }\right)\notag\\[4pt]
&\qquad +\exp\left(\!-\frac{(uT\varepsilon - 2|b-a| \mathbb{E}_\mathfrak{m}(\tau_0))^2}{8|b-a|^2\mbox{Var}_\mathfrak{m} (\tau_0) + 4 |b-a| c^+(\tau_0)(uT\varepsilon - 2|b-a| \mathbb{E}_\mathfrak{m}(\tau_0)) }\right)\!,\end{align*}
\begin{align*}&\mathbb{P}_\mathfrak{m}\biggl( \biggl|\frac1T \int_0^T f(X_t)\,dt - \pi_A\,f \biggr| \ge \varepsilon \biggr)\notag\\[4pt]
&\quad \le\exp\left(\!-\frac{((1-u)T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau))^2}{8 T \sigma^2(\,f) + 4 c^+(\,f)((1-u)T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau)) }\right)\notag\\[4pt]
&\qquad +\exp\left(\!-\frac{((1-u)T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau))^2}{8 T \sigma^2(\,f) + 4 c^-(\,f)((1-u)T\varepsilon - |b-a|\mathbb{E}_\emptyset(\tau)) }\right)\notag\\[4pt]
&\qquad +\exp\left(\!-\frac{((1-u)T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau))^2}{8T |b-a|^2\frac{\mbox{Var}_\emptyset (\tau)}{\mathbb{E}_\emptyset(\tau)}+ 4 |b-a| c^+(\tau)((1-u)T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau)) }\right)\notag\\[4pt]
&\qquad +\exp\left(\!-\frac{((1-u)T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau))^2}{8T |b-a|^2\frac{\mbox{Var}_\emptyset (\tau)}{\mathbb{E}_\emptyset(\tau)}+ 4 |b-a| c^-(\tau)((1-u)T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau)) }\right)\notag\\[4pt]
&\qquad +\exp\left(\!-\frac{(uT\varepsilon - 2|b-a| \mathbb{E}_\mathfrak{m}(\tau_0))^2}{8|b-a|^2\mbox{Var}_\mathfrak{m} (\tau_0) + 4 |b-a| c^+(\tau_0)(uT\varepsilon - 2|b-a| \mathbb{E}_\mathfrak{m}(\tau_0)) }\right)\!,\end{align*}which is (1.11).
Proof of Corollary 1.1
Under ![]() $\mathbb{P}_\emptyset$, we have
$\mathbb{P}_\emptyset$, we have ![]() $\tau_0=0$, and thus (4.6) reads as follows:
$\tau_0=0$, and thus (4.6) reads as follows:
 \begin{align}\mathbb{P}_\emptyset\biggl( \biggl|\frac1T \int_0^T f(X_t)\,dt - \pi_A\,f \biggr| \ge \varepsilon \biggr)&\le\mathbb{P}_\emptyset\!\left(\left| \sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} I_k \tilde{f} \right|\ge \frac{T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau)}2\right)\\[5pt]
&+\mathbb{P}_\emptyset\!\left(\left|\sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor}\! (\tau_k{-}\tau_{k-1}{-}\mathbb{E}_\emptyset(\tau))\right|{\ge} \frac{T\varepsilon- |b-a| \mathbb{E}_\emptyset(\tau)}{2|b-a|}\!\right)\!.\nonumber\end{align}
\begin{align}\mathbb{P}_\emptyset\biggl( \biggl|\frac1T \int_0^T f(X_t)\,dt - \pi_A\,f \biggr| \ge \varepsilon \biggr)&\le\mathbb{P}_\emptyset\!\left(\left| \sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} I_k \tilde{f} \right|\ge \frac{T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau)}2\right)\\[5pt]
&+\mathbb{P}_\emptyset\!\left(\left|\sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor}\! (\tau_k{-}\tau_{k-1}{-}\mathbb{E}_\emptyset(\tau))\right|{\ge} \frac{T\varepsilon- |b-a| \mathbb{E}_\emptyset(\tau)}{2|b-a|}\!\right)\!.\nonumber\end{align}As in the proof of Theorem 1.4, we apply Bernstein’s inequality for each of the terms in the right-hand side. However, in order to simplify the obtained bound, we change the upper bounds of the moments of ![]() $I_k\tilde{f}$ and
$I_k\tilde{f}$ and ![]() $\tau_k-\tau_{k-1}-\mathbb{E}_\emptyset(\tau)$. Namely, we use the fact that for all
$\tau_k-\tau_{k-1}-\mathbb{E}_\emptyset(\tau)$. Namely, we use the fact that for all ![]() $n\ge1$,
$n\ge1$,
Since ![]() $\tau$ is a nonnegative random variable, we have
$\tau$ is a nonnegative random variable, we have ![]() $e^{\alpha \mathbb{E}_\emptyset(\tau)} \ge 1$, and in the sequel it will be more convenient to use the following upper bound: for all
$e^{\alpha \mathbb{E}_\emptyset(\tau)} \ge 1$, and in the sequel it will be more convenient to use the following upper bound: for all ![]() $n\ge1$,
$n\ge1$,
Then
 \begin{equation*}\sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} \mathbb{E}_\emptyset\bigl( ( I_k \tilde{f})^2 \bigr)\le \Big\lfloor\frac{T}{\mathbb{E}_\emptyset(\tau)}\Big\rfloor \mathbb{E}_\emptyset(\tau^2) (b-a)^2\le \frac{2(b-a)^2}{\alpha^2}\Big\lfloor\frac{T}{\mathbb{E}_\emptyset(\tau)}\Big\rfloor \mathbb{E}_\emptyset(e^{\alpha\tau}) e^{\alpha \mathbb{E}_\emptyset(\tau)}\,,\end{equation*}
\begin{equation*}\sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} \mathbb{E}_\emptyset\bigl( ( I_k \tilde{f})^2 \bigr)\le \Big\lfloor\frac{T}{\mathbb{E}_\emptyset(\tau)}\Big\rfloor \mathbb{E}_\emptyset(\tau^2) (b-a)^2\le \frac{2(b-a)^2}{\alpha^2}\Big\lfloor\frac{T}{\mathbb{E}_\emptyset(\tau)}\Big\rfloor \mathbb{E}_\emptyset(e^{\alpha\tau}) e^{\alpha \mathbb{E}_\emptyset(\tau)}\,,\end{equation*}and, for ![]() $n\ge3$,
$n\ge3$,
 \begin{equation*}\sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} \mathbb{E}_\emptyset\bigl( |I_k \tilde{f})|^n \bigr) \le \frac{n!}{2} \left(\Big\lfloor\frac{T}{\mathbb{E}_\emptyset(\tau)}\Big\rfloor |b-a|^2 \frac{2}{\alpha^2}\mathbb{E}_\emptyset(e^{\alpha\tau})e^{\alpha \mathbb{E}_\emptyset(\tau)}\right) \ \Big(\frac{|b-a|}{\alpha}\Big)^{n-2}\,.\end{equation*}
\begin{equation*}\sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} \mathbb{E}_\emptyset\bigl( |I_k \tilde{f})|^n \bigr) \le \frac{n!}{2} \left(\Big\lfloor\frac{T}{\mathbb{E}_\emptyset(\tau)}\Big\rfloor |b-a|^2 \frac{2}{\alpha^2}\mathbb{E}_\emptyset(e^{\alpha\tau})e^{\alpha \mathbb{E}_\emptyset(\tau)}\right) \ \Big(\frac{|b-a|}{\alpha}\Big)^{n-2}\,.\end{equation*}Setting
and applying Bernstein’s inequality, we obtain that
 \begin{equation*} \mathbb{P}_\emptyset\!\left(\left| \sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} I_k \tilde{f} \right|\ge \frac{T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau)}2\right) \le 2 \exp\left(\!-\frac{\Bigl( T\varepsilon-|b-a|\mathbb{E}_\emptyset(\tau) \Bigr)^2}{4 \left(2v + (T\varepsilon-|b-a|\mathbb{E}_\emptyset(\tau))c \right)} \right)\!.\end{equation*}
\begin{equation*} \mathbb{P}_\emptyset\!\left(\left| \sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} I_k \tilde{f} \right|\ge \frac{T\varepsilon - |b-a| \mathbb{E}_\emptyset(\tau)}2\right) \le 2 \exp\left(\!-\frac{\Bigl( T\varepsilon-|b-a|\mathbb{E}_\emptyset(\tau) \Bigr)^2}{4 \left(2v + (T\varepsilon-|b-a|\mathbb{E}_\emptyset(\tau))c \right)} \right)\!.\end{equation*}Also,
 \begin{equation*}\sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} \mathbb{E}_\emptyset\bigl( (\tau_k-\tau_{k-1}-\mathbb{E}_\emptyset(\tau))^2 \bigr)\le \frac{2}{\alpha^2} \Big\lfloor \frac{T}{\mathbb{E}_\emptyset(\tau)}\Big\rfloor \mathbb{E}_\emptyset(e^{\alpha\tau})e^{\alpha \mathbb{E}_\emptyset(\tau)} \,,\end{equation*}
\begin{equation*}\sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} \mathbb{E}_\emptyset\bigl( (\tau_k-\tau_{k-1}-\mathbb{E}_\emptyset(\tau))^2 \bigr)\le \frac{2}{\alpha^2} \Big\lfloor \frac{T}{\mathbb{E}_\emptyset(\tau)}\Big\rfloor \mathbb{E}_\emptyset(e^{\alpha\tau})e^{\alpha \mathbb{E}_\emptyset(\tau)} \,,\end{equation*}and, for ![]() $n\ge3$,
$n\ge3$,
 \begin{equation*}\sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} \mathbb{E}_\emptyset\bigl( |\tau_k-\tau_{k-1}-\mathbb{E}_\emptyset(\tau)|^n \bigr)\le \frac{n!}{2}\left(\Big\lfloor\frac{T}{\mathbb{E}_\emptyset(\tau)}\Big\rfloor \frac{2}{\alpha^2}\mathbb{E}_\emptyset(e^{\alpha\tau})e^{\alpha \mathbb{E}_\emptyset(\tau)} \right) \frac{1}{\alpha^{n-2}}\,.\end{equation*}
\begin{equation*}\sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} \mathbb{E}_\emptyset\bigl( |\tau_k-\tau_{k-1}-\mathbb{E}_\emptyset(\tau)|^n \bigr)\le \frac{n!}{2}\left(\Big\lfloor\frac{T}{\mathbb{E}_\emptyset(\tau)}\Big\rfloor \frac{2}{\alpha^2}\mathbb{E}_\emptyset(e^{\alpha\tau})e^{\alpha \mathbb{E}_\emptyset(\tau)} \right) \frac{1}{\alpha^{n-2}}\,.\end{equation*}Applying Bernstein’s inequality again, we obtain that
 \begin{align*} &\mathbb{P}_\emptyset\!\left(\left|\sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} (\tau_k-\tau_{k-1}-\mathbb{E}_\emptyset(\tau))\right|\ge \frac{T\varepsilon- |b-a| \mathbb{E}_\emptyset(\tau)}{2|b-a|}\right)\\&\qquad \le2 \exp\left(\!-\frac{\Bigl( T\varepsilon-|b-a|\mathbb{E}_\emptyset(\tau) \Bigr)^2}{4 \left(2v + (T\varepsilon-|b-a|\mathbb{E}_\emptyset(\tau))c \right)} \right)\!.\end{align*}
\begin{align*} &\mathbb{P}_\emptyset\!\left(\left|\sum_{k=1}^{\lfloor T/\mathbb{E}_\emptyset(\tau)\rfloor} (\tau_k-\tau_{k-1}-\mathbb{E}_\emptyset(\tau))\right|\ge \frac{T\varepsilon- |b-a| \mathbb{E}_\emptyset(\tau)}{2|b-a|}\right)\\&\qquad \le2 \exp\left(\!-\frac{\Bigl( T\varepsilon-|b-a|\mathbb{E}_\emptyset(\tau) \Bigr)^2}{4 \left(2v + (T\varepsilon-|b-a|\mathbb{E}_\emptyset(\tau))c \right)} \right)\!.\end{align*}The inequality (4.7) gives that
 \begin{align*}\mathbb{P}_\emptyset\biggl( \biggl|\frac1T \int_0^T f(X_t)\,dt - \pi_A\,f \biggr| \ge \varepsilon \biggr)&\le 4 \exp\left(\!-\frac{\Bigl( T\varepsilon-|b-a|\mathbb{E}_\emptyset(\tau) \Bigr)^2}{4 \left(2v + (T\varepsilon-|b-a|\mathbb{E}_\emptyset(\tau))c \right)} \right)\!.\end{align*}
\begin{align*}\mathbb{P}_\emptyset\biggl( \biggl|\frac1T \int_0^T f(X_t)\,dt - \pi_A\,f \biggr| \ge \varepsilon \biggr)&\le 4 \exp\left(\!-\frac{\Bigl( T\varepsilon-|b-a|\mathbb{E}_\emptyset(\tau) \Bigr)^2}{4 \left(2v + (T\varepsilon-|b-a|\mathbb{E}_\emptyset(\tau))c \right)} \right)\!.\end{align*}To prove the second part of Corollary 1.1 we have to solve
 \begin{equation}\eta=4 \exp\left(\!-\frac{\Bigl( T\varepsilon-|b-a|\mathbb{E}_\emptyset(\tau) \Bigr)^2}{4 \left(2v + (T\varepsilon-|b-a|\mathbb{E}_\emptyset(\tau))c \right)} \right)\end{equation}
\begin{equation}\eta=4 \exp\left(\!-\frac{\Bigl( T\varepsilon-|b-a|\mathbb{E}_\emptyset(\tau) \Bigr)^2}{4 \left(2v + (T\varepsilon-|b-a|\mathbb{E}_\emptyset(\tau))c \right)} \right)\end{equation}by expressing ![]() $\varepsilon$ as function of
$\varepsilon$ as function of ![]() $\eta$, for any
$\eta$, for any ![]() $\eta\in (0,1)$.
$\eta\in (0,1)$.
Let us define the following decreasing bijection from ![]() $\mathbb{R}_+$ into
$\mathbb{R}_+$ into ![]() $\mathbb{R}_-$:
$\mathbb{R}_-$:
The solution of (4.8) is then ![]() $\varepsilon_\eta=(|b-a|\mathbb{E}_\emptyset(\tau)+x_0)/T$, where
$\varepsilon_\eta=(|b-a|\mathbb{E}_\emptyset(\tau)+x_0)/T$, where ![]() $x_0$ is the unique positive solution of
$x_0$ is the unique positive solution of
Computing the roots of this second-order polynomial, we can show that there always exist one negative and one positive root as soon as ![]() $\eta<4$. More precisely,
$\eta<4$. More precisely,
which concludes the proof.
Appendix A.
A.1. Proof of Proposition 2.1
Before proving Proposition 2.1, we start with a lemma showing that the assumption (2.2) implies a milder condition which will be used repeatedly in the proof of the proposition.
Lemma A.1. Suppose that the assumption (2.2) is satisfied. Then for any nonnegative random variable U and ![]() $r>0$,
$r>0$,
Proof. First note that, for every integer n,
using the condition (2.2) and the Fubini–Tonelli theorem. This leads easily to
and, for a positive real number r, to
which gives the stated result.
Proof of Proposition 2.1. Proofs of both (1) and (2) will be obtained by induction on the successive atoms of ![]() $N^h$.
$N^h$.
Proof of (1): initialization. Let
with the usual convention that ![]() $\inf \emptyset = +\infty$. First note that conditionally on
$\inf \emptyset = +\infty$. First note that conditionally on ![]() $N^0$,
$N^0$,
follows a Poisson law with parameter ![]() $\int_0^{\varepsilon} \Lambda^h_0(t) dt$. Using the assumption (2.2) and Lemma A.1, we can find
$\int_0^{\varepsilon} \Lambda^h_0(t) dt$. Using the assumption (2.2) and Lemma A.1, we can find ![]() $\varepsilon_0 >0$ such that
$\varepsilon_0 >0$ such that ![]() $\int_0^{\varepsilon_0} \int_{(\!-\infty,0]}h^+(t-s) \,N^0(ds) dt < +\infty$. We thus have,
$\int_0^{\varepsilon_0} \int_{(\!-\infty,0]}h^+(t-s) \,N^0(ds) dt < +\infty$. We thus have, ![]() $\mathbb{P}_{\mathfrak{m}}$-a.s.,
$\mathbb{P}_{\mathfrak{m}}$-a.s.,
 \begin{align*} \int_0^{\varepsilon_0} \Lambda^h_0(t) dt &= \int_0^{\varepsilon_0} \biggl(\lambda+\int_{(\!-\infty,0]}h(t-s) \,N^0(ds)\biggr)^+\, dt \\[4pt]
&\le \lambda \varepsilon_0 +\int_0^{\varepsilon_0} \int_{(\!-\infty,0]}h^+(t-s) \,N^0(ds) dt
< + \infty\,.\end{align*}
\begin{align*} \int_0^{\varepsilon_0} \Lambda^h_0(t) dt &= \int_0^{\varepsilon_0} \biggl(\lambda+\int_{(\!-\infty,0]}h(t-s) \,N^0(ds)\biggr)^+\, dt \\[4pt]
&\le \lambda \varepsilon_0 +\int_0^{\varepsilon_0} \int_{(\!-\infty,0]}h^+(t-s) \,N^0(ds) dt
< + \infty\,.\end{align*}Consequently,
is finite ![]() $\mathbb{P}_{\mathfrak{m}}$-a.s. Hence
$\mathbb{P}_{\mathfrak{m}}$-a.s. Hence ![]() $U_1^h>0$
$U_1^h>0$![]() $\mathbb{P}_{\mathfrak{m}}$-a.s. If
$\mathbb{P}_{\mathfrak{m}}$-a.s. If ![]() $U_1^h=+\infty$ then
$U_1^h=+\infty$ then ![]() $N^h=N^0$, and we define
$N^h=N^0$, and we define ![]() $U_k^h =+\infty$ for all
$U_k^h =+\infty$ for all ![]() $k \ge 2$. Otherwise,
$k \ge 2$. Otherwise, ![]() $U_1^h$ is the first atom on
$U_1^h$ is the first atom on ![]() $(0,+\infty)$ of the point process of conditional intensity
$(0,+\infty)$ of the point process of conditional intensity ![]() $\Lambda_0^h$. Since
$\Lambda_0^h$. Since ![]() $\Lambda^h_0(t)= \Lambda^h(t)$ for
$\Lambda^h_0(t)= \Lambda^h(t)$ for ![]() $t\in (0,U_1^h]$, this implies that
$t\in (0,U_1^h]$, this implies that ![]() $U^h_1$ is also the first atom of
$U^h_1$ is also the first atom of ![]() $N^h$ on
$N^h$ on ![]() $(0,+\infty)$.
$(0,+\infty)$.
Proof of (1): recursion. Assume that we have built ![]() $U_1^h, \dots ,U_k^h$ such that on the event
$U_1^h, \dots ,U_k^h$ such that on the event ![]() $\{U_k^h < +\infty\}$ these are the first k atoms of
$\{U_k^h < +\infty\}$ these are the first k atoms of ![]() $N^h$ in increasing order. We are going to construct
$N^h$ in increasing order. We are going to construct ![]() $U_{k+1}^h$, which will be an atom of
$U_{k+1}^h$, which will be an atom of ![]() $N^h$ greater than
$N^h$ greater than ![]() $U_k^h$.
$U_k^h$.
On ![]() $\{U_k^h = +\infty\}$ we set
$\{U_k^h = +\infty\}$ we set ![]() $U_{k+1}^h = +\infty$. Henceforth, we work on
$U_{k+1}^h = +\infty$. Henceforth, we work on ![]() $\{U_k^h < +\infty\}$. Let
$\{U_k^h < +\infty\}$. Let
 \begin{align} \Lambda^h_k(t) & = \biggl(\lambda+\int_{(\!-\infty,0]}h(t-s) \,N^0(ds) + \int_{(0,U_k^h]} h(t-s) \,N^h (ds)\biggr)^+\,,\qquad t>0\,,\\[5pt]
U_{k+1}^h & = \inf\biggl\{u > U_k^h\,{:}\, \int_{(U_k^h,u]}\int_{(0,\Lambda_k^h(v)]} \,Q(dv,d\theta)>0 \biggr\}\,.\nonumber\end{align}
\begin{align} \Lambda^h_k(t) & = \biggl(\lambda+\int_{(\!-\infty,0]}h(t-s) \,N^0(ds) + \int_{(0,U_k^h]} h(t-s) \,N^h (ds)\biggr)^+\,,\qquad t>0\,,\\[5pt]
U_{k+1}^h & = \inf\biggl\{u > U_k^h\,{:}\, \int_{(U_k^h,u]}\int_{(0,\Lambda_k^h(v)]} \,Q(dv,d\theta)>0 \biggr\}\,.\nonumber\end{align}As in Step 1, we first prove that there exists ![]() $\varepsilon >0$ such that
$\varepsilon >0$ such that ![]() $Q(\mathcal{R}_{\varepsilon})$ is a.s. finite, where
$Q(\mathcal{R}_{\varepsilon})$ is a.s. finite, where
Since the random function ![]() $\Lambda_k^h$ is measurable with respect to
$\Lambda_k^h$ is measurable with respect to ![]() $\mathcal{F}_{U_k^h}$, conditionally on
$\mathcal{F}_{U_k^h}$, conditionally on ![]() $\mathcal{F}_{U_k^h}$,
$\mathcal{F}_{U_k^h}$, ![]() $Q(\mathcal{R}_{\varepsilon})$ follows a Poisson law with parameter
$Q(\mathcal{R}_{\varepsilon})$ follows a Poisson law with parameter
 \begin{equation*}\int_{U_k^h}^{U_k^h +\varepsilon} \Lambda^h_k(t) dt\end{equation*}
\begin{equation*}\int_{U_k^h}^{U_k^h +\varepsilon} \Lambda^h_k(t) dt\end{equation*}(see Lemma A.2), so that
 \begin{equation*}\mathbb{P}(Q(\mathcal{R}_{\varepsilon}) < +\infty) = \mathbb{E}\Big(\mathbb{P}(Q(\mathcal{R}_{\varepsilon}) < +\infty \,|\,\mathcal{F}_{U_k^h} )\Big) = \mathbb{E}\!\left(\mathbb{P}\!\left(\int_{U_k^h}^{U_k^h +\varepsilon} \Lambda^h_k(t) dt
< +\infty \,\bigg|\,\mathcal{F}_{U_k^h} \right)\right)\!.\end{equation*}
\begin{equation*}\mathbb{P}(Q(\mathcal{R}_{\varepsilon}) < +\infty) = \mathbb{E}\Big(\mathbb{P}(Q(\mathcal{R}_{\varepsilon}) < +\infty \,|\,\mathcal{F}_{U_k^h} )\Big) = \mathbb{E}\!\left(\mathbb{P}\!\left(\int_{U_k^h}^{U_k^h +\varepsilon} \Lambda^h_k(t) dt
< +\infty \,\bigg|\,\mathcal{F}_{U_k^h} \right)\right)\!.\end{equation*}Using the fact that ![]() $x \le x^+$ and the monotonicity of
$x \le x^+$ and the monotonicity of ![]() $x \mapsto x^+$, we obtain from (A.3) that
$x \mapsto x^+$, we obtain from (A.3) that
 \begin{align*}\int_{U_k^h}^{U_k^h +\varepsilon} \Lambda^h_k(t) dt\le \lambda \varepsilon&+ \int_{U_k^h}^{U_k^h +\varepsilon} \int_{(\!-\infty,0]}h^+(t-s) \,N^0(ds) dt\\[4pt]
&+ \int_{U_k^h}^{U_k^h +\varepsilon} \int_{(0,U_k^h]} h^+(t-s) \,N^h (ds) dt\,.\end{align*}
\begin{align*}\int_{U_k^h}^{U_k^h +\varepsilon} \Lambda^h_k(t) dt\le \lambda \varepsilon&+ \int_{U_k^h}^{U_k^h +\varepsilon} \int_{(\!-\infty,0]}h^+(t-s) \,N^0(ds) dt\\[4pt]
&+ \int_{U_k^h}^{U_k^h +\varepsilon} \int_{(0,U_k^h]} h^+(t-s) \,N^h (ds) dt\,.\end{align*}On ![]() $\{U_k^h <+\infty\}$ the second term in the right-hand side is finite thanks to the assumption (2.2) and Lemma A.1. It is thus also finite, a.s., on
$\{U_k^h <+\infty\}$ the second term in the right-hand side is finite thanks to the assumption (2.2) and Lemma A.1. It is thus also finite, a.s., on ![]() $\{U_k^h <+\infty\}$, conditionally on
$\{U_k^h <+\infty\}$, conditionally on ![]() $\mathcal{F}_{U_k^h}$. Now, using the Fubini–Tonelli theorem and the assumption (2.1), we obtain that
$\mathcal{F}_{U_k^h}$. Now, using the Fubini–Tonelli theorem and the assumption (2.1), we obtain that
 \begin{align*} \int_{U_k^h}^{U_k^h +\varepsilon} \int_{(0,U_k^h]} h^+(t-s) \,N^h (ds) dt &= \int_{(0,U_k^h]} \biggl(\int_{U_k^h}^{U_k^h +\varepsilon} h^+(t-s)dt \biggr) \,N^h (ds) \\[5pt]
& \le \|h^+\|_1 \,N^h((0,U_k^h]) = k \|h^+\|_1
< +\infty.\end{align*}
\begin{align*} \int_{U_k^h}^{U_k^h +\varepsilon} \int_{(0,U_k^h]} h^+(t-s) \,N^h (ds) dt &= \int_{(0,U_k^h]} \biggl(\int_{U_k^h}^{U_k^h +\varepsilon} h^+(t-s)dt \biggr) \,N^h (ds) \\[5pt]
& \le \|h^+\|_1 \,N^h((0,U_k^h]) = k \|h^+\|_1
< +\infty.\end{align*}This concludes the proof of the finiteness of
 \begin{equation*}\int_{U_k^h}^{U_k^h +\varepsilon} \Lambda^h_k(t) dt ,\end{equation*}
\begin{equation*}\int_{U_k^h}^{U_k^h +\varepsilon} \Lambda^h_k(t) dt ,\end{equation*}so that ![]() $Q(\mathcal{R}_{\varepsilon}) <+\infty$,
$Q(\mathcal{R}_{\varepsilon}) <+\infty$, ![]() $\mathbb{P}_{\mathfrak{m}}$-a.s.
$\mathbb{P}_{\mathfrak{m}}$-a.s.
If ![]() $Q(\mathcal{R}_{\varepsilon}) $ is null then
$Q(\mathcal{R}_{\varepsilon}) $ is null then ![]() $U_{k+1}^h = +\infty$ and thus
$U_{k+1}^h = +\infty$ and thus ![]() $N^h = N^0 +\sum_{i=1}^k \delta_{U_i^h}$. Otherwise,
$N^h = N^0 +\sum_{i=1}^k \delta_{U_i^h}$. Otherwise, ![]() $U_{k+1}^h$ is actually a minimum, implying that
$U_{k+1}^h$ is actually a minimum, implying that ![]() $U_k^h < U_{k+1}^h$ and, since
$U_k^h < U_{k+1}^h$ and, since ![]() $\Lambda^h$ and
$\Lambda^h$ and ![]() $\Lambda^h_k$ coincide on
$\Lambda^h_k$ coincide on ![]() $(0,U_{k+1}^h)$, that
$(0,U_{k+1}^h)$, that ![]() $U_{k+1}^h$ is the
$U_{k+1}^h$ is the ![]() $(k+1)$th atom of
$(k+1)$th atom of ![]() $N^h$.
$N^h$.
We have now proved by induction the existence of a random sequence ![]() $(U_k^h)_{k \ge 1}$ which is strictly increasing until the first rank where it (possibly) hits
$(U_k^h)_{k \ge 1}$ which is strictly increasing until the first rank where it (possibly) hits ![]() $+\infty$, after which point it stays there. On the event that this first rank is finite, the finite
$+\infty$, after which point it stays there. On the event that this first rank is finite, the finite ![]() $U_k^h$ are exactly the atoms of the random point process
$U_k^h$ are exactly the atoms of the random point process ![]() $N^h$ on
$N^h$ on ![]() $(0, +\infty)$.
$(0, +\infty)$.
To complete the proof, it is thus enough to prove that ![]() $\lim_{k \rightarrow +\infty} U_k^h = +\infty$,
$\lim_{k \rightarrow +\infty} U_k^h = +\infty$, ![]() $\mathbb{P}_{\mathfrak{m}}$-a.s. For this, we compute
$\mathbb{P}_{\mathfrak{m}}$-a.s. For this, we compute ![]() $\mathbb{E}_{\mathfrak{m}}(N^h(0,t))$ for
$\mathbb{E}_{\mathfrak{m}}(N^h(0,t))$ for ![]() $t >0$. For all
$t >0$. For all ![]() $k \ge 1$,
$k \ge 1$,
 \begin{align*}\mathbb{E}_{\mathfrak{m}}\big(N^h (0,t \wedge U_k^h)\big)&=\mathbb{E}_{\mathfrak{m}}\bigg(\int_0^{t\wedge U_k^h} \Lambda^h(u)du\bigg)\\[3pt]
&=\mathbb{E}_{\mathfrak{m}}\bigg(\int_0^{t\wedge U_k^h} \bigg(\lambda+ \int_{(\!-\infty ,u)} h(u-s)\,N^h(ds)\bigg)^+\ du\bigg)\\[3pt]
& \le \lambda t+\mathbb{E}_{\mathfrak{m}}\bigg(\int_0^t\int_{(\!-\infty,0]} h^+(u-s)\,N^0(ds)du \bigg)\\[3pt]
&\quad + \mathbb{E}_{\mathfrak{m}}\bigg(\int_0^{t\wedge U_k^h}\int_{(0,u)}h^+(u-s)\,N^h(ds) du \bigg).\end{align*}
\begin{align*}\mathbb{E}_{\mathfrak{m}}\big(N^h (0,t \wedge U_k^h)\big)&=\mathbb{E}_{\mathfrak{m}}\bigg(\int_0^{t\wedge U_k^h} \Lambda^h(u)du\bigg)\\[3pt]
&=\mathbb{E}_{\mathfrak{m}}\bigg(\int_0^{t\wedge U_k^h} \bigg(\lambda+ \int_{(\!-\infty ,u)} h(u-s)\,N^h(ds)\bigg)^+\ du\bigg)\\[3pt]
& \le \lambda t+\mathbb{E}_{\mathfrak{m}}\bigg(\int_0^t\int_{(\!-\infty,0]} h^+(u-s)\,N^0(ds)du \bigg)\\[3pt]
&\quad + \mathbb{E}_{\mathfrak{m}}\bigg(\int_0^{t\wedge U_k^h}\int_{(0,u)}h^+(u-s)\,N^h(ds) du \bigg).\end{align*}Using the nonnegativity of ![]() $h^+$ and the assumption (2.2),
$h^+$ and the assumption (2.2),
For the last term, we use again the Fubini–Tonelli theorem and obtain
 \begin{align*}\mathbb{E}_{\mathfrak{m}}\bigg(\int_0^{t\wedge U_k^h} \int_{(0,u)} h^+(u-s) \,N^h(ds)\ du\bigg)& = \mathbb{E}_{\mathfrak{m}}\bigg(\int_{(0,t\wedge U_k^h)} \int_s^{t\wedge U_k^h} h^+(u-s)du \,N^h(ds)\bigg)\\& \leq \|h^+\|_1 \,\mathbb{E}_{\mathfrak{m}}\bigg( N^h(0,t\wedge U_k^h)\bigg).\end{align*}
\begin{align*}\mathbb{E}_{\mathfrak{m}}\bigg(\int_0^{t\wedge U_k^h} \int_{(0,u)} h^+(u-s) \,N^h(ds)\ du\bigg)& = \mathbb{E}_{\mathfrak{m}}\bigg(\int_{(0,t\wedge U_k^h)} \int_s^{t\wedge U_k^h} h^+(u-s)du \,N^h(ds)\bigg)\\& \leq \|h^+\|_1 \,\mathbb{E}_{\mathfrak{m}}\bigg( N^h(0,t\wedge U_k^h)\bigg).\end{align*}These three inequalities and the fact that ![]() $\|h^+\|_1<1$ (see Assumption (2.1)) yield that
$\|h^+\|_1<1$ (see Assumption (2.1)) yield that
where the upper bound is finite and independent of k.
As a consequence, we necessarily have that ![]() $\lim_{k\rightarrow +\infty} U_k^h=+\infty$ a.s., which we now prove by contradiction. If
$\lim_{k\rightarrow +\infty} U_k^h=+\infty$ a.s., which we now prove by contradiction. If ![]() $\mathbb{P}(\lim_{k\rightarrow +\infty} U_k^h<+\infty)>0$ then there would exist
$\mathbb{P}(\lim_{k\rightarrow +\infty} U_k^h<+\infty)>0$ then there would exist ![]() $T>0$ and
$T>0$ and ![]() $\Omega_0$ such that
$\Omega_0$ such that ![]() $\mathbb{P}(\Omega_0)>0$ and
$\mathbb{P}(\Omega_0)>0$ and ![]() $\lim_{k\rightarrow +\infty} U_k^h\leq T$ on
$\lim_{k\rightarrow +\infty} U_k^h\leq T$ on ![]() $\Omega_0$. But this would entail that
$\Omega_0$. But this would entail that ![]() $\mathbb{E}_{\mathfrak{m}}(N^h(0,T\wedge U_k^h))\geq (k-1) \mathbb{P}_{\mathfrak{m}}(\Omega_0)$, which converges to
$\mathbb{E}_{\mathfrak{m}}(N^h(0,T\wedge U_k^h))\geq (k-1) \mathbb{P}_{\mathfrak{m}}(\Omega_0)$, which converges to ![]() $+\infty$ with k and cannot be bounded above by (A.4).
$+\infty$ with k and cannot be bounded above by (A.4).
Note additionally that once we know that ![]() $\lim_{k\rightarrow +\infty} U_k^h=+\infty$, a.s., we can use the Beppo Levi theorem, which leads to
$\lim_{k\rightarrow +\infty} U_k^h=+\infty$, a.s., we can use the Beppo Levi theorem, which leads to ![]() $\mathbb{E}_{\mathfrak{m}}\big(N^h(0,t)\big) < +\infty$ for all
$\mathbb{E}_{\mathfrak{m}}\big(N^h(0,t)\big) < +\infty$ for all ![]() $t>0$.
$t>0$.
Note that uniqueness comes from the algorithmic construction of the sequence ![]() $(U^h_k)_{k\geq 1}$.
$(U^h_k)_{k\geq 1}$.
Proof of (2). The assumptions of the theorem are valid both for h and for ![]() $h^+$, and the result (1) which we have just proved allows us to construct strong solutions
$h^+$, and the result (1) which we have just proved allows us to construct strong solutions ![]() $N^h$ and
$N^h$ and ![]() $N^{h^+}$ of Equation (1.2) driven by the same Poisson point process Q. Proving (2) is equivalent to showing that the atoms of
$N^{h^+}$ of Equation (1.2) driven by the same Poisson point process Q. Proving (2) is equivalent to showing that the atoms of ![]() $N^h$ are also atoms of
$N^h$ are also atoms of ![]() $N^{h^+}$, which we do using the following recursion.
$N^{h^+}$, which we do using the following recursion.
If ![]() $U_1^h = +\infty$ then
$U_1^h = +\infty$ then ![]() $N^h$ has no atom on
$N^h$ has no atom on ![]() $(0,+\infty)$ and there is nothing to prove.
$(0,+\infty)$ and there is nothing to prove.
Otherwise, we first show that the first atom ![]() $U^h_1$ of
$U^h_1$ of ![]() $N^h$ is also an atom of
$N^h$ is also an atom of ![]() $N^{h^+}$. The key point is to establish that
$N^{h^+}$. The key point is to establish that
Indeed, from the definition of ![]() $U_1^h$, there exists an atom of the Poisson measure Q at some
$U_1^h$, there exists an atom of the Poisson measure Q at some ![]() $(U_1^h,\theta)$ with
$(U_1^h,\theta)$ with ![]() $\theta \le \Lambda^h\big((U_1^h)_-\big)$. If (A.5) is true we may deduce that
$\theta \le \Lambda^h\big((U_1^h)_-\big)$. If (A.5) is true we may deduce that ![]() $(U_1^h,\theta)$ is also an atom of Q satisfying
$(U_1^h,\theta)$ is also an atom of Q satisfying ![]() $\theta \le \Lambda^{h^+}\big((U_1^h)_-\big)$, and thus that
$\theta \le \Lambda^{h^+}\big((U_1^h)_-\big)$, and thus that ![]() $U_1^h$ is also an atom of
$U_1^h$ is also an atom of ![]() $N^{h^+}$.
$N^{h^+}$.
We now turn to the proof of (A.5). For every ![]() $t\in (0,U_1^h)$, we clearly have
$t\in (0,U_1^h)$, we clearly have
we use the fact that ![]() $x \mapsto x^+$ is nondecreasing on
$x \mapsto x^+$ is nondecreasing on ![]() $\mathbb{R}$ to obtain that
$\mathbb{R}$ to obtain that
We now prove that if ![]() $U_1^h, \dots , U_k^h$ are atoms of
$U_1^h, \dots , U_k^h$ are atoms of ![]() $N^{h^+}$ and
$N^{h^+}$ and ![]() $U_{k+1}^h<+\infty$, then
$U_{k+1}^h<+\infty$, then ![]() $U_{k+1}^h$ is also an atom of
$U_{k+1}^h$ is also an atom of ![]() $N^{h^+}$. By construction,
$N^{h^+}$. By construction, ![]() $\Lambda^h(t)=\Lambda^h_k(t)$ for all
$\Lambda^h(t)=\Lambda^h_k(t)$ for all ![]() $t \in (0, U_{k+1}^h)$, and there exists
$t \in (0, U_{k+1}^h)$, and there exists ![]() $\theta >0$ such that
$\theta >0$ such that ![]() $(U_{k+1}^h, \theta)$ is an atom of Q satisfying
$(U_{k+1}^h, \theta)$ is an atom of Q satisfying ![]() $\theta \le \Lambda^h((U_{k+1}^h)_-)$. To obtain that
$\theta \le \Lambda^h((U_{k+1}^h)_-)$. To obtain that ![]() $U_{k+1}^h$ is also an atom of
$U_{k+1}^h$ is also an atom of ![]() $N^{h^+}$, it is thus enough to prove that
$N^{h^+}$, it is thus enough to prove that
Using that ![]() $h \le h^+$ and the induction hypothesis that the first k atoms
$h \le h^+$ and the induction hypothesis that the first k atoms ![]() $U_1^h, \dots , U_k^h$ of
$U_1^h, \dots , U_k^h$ of ![]() $N^h$ are also atoms of
$N^h$ are also atoms of ![]() $N^{h^+}$, we obtain for all
$N^{h^+}$, we obtain for all ![]() $t \in (U_k^h,U_{k+1}^h)$ that
$t \in (U_k^h,U_{k+1}^h)$ that
This upper bound and the definition (A.3) of ![]() $\Lambda_k^h$ yield that, for all
$\Lambda_k^h$ yield that, for all ![]() $t \in (U_k^h,U_{k+1}^h)$,
$t \in (U_k^h,U_{k+1}^h)$,
and since ![]() $\Lambda_k^h$ and
$\Lambda_k^h$ and ![]() $\Lambda^h$ coincide on
$\Lambda^h$ coincide on ![]() $(0, U_{k+1}^h)$, we have finally proved that
$(0, U_{k+1}^h)$, we have finally proved that ![]() $U_{k+1}^h$ is an atom of
$U_{k+1}^h$ is an atom of ![]() $N^{h^+}$. This concludes the proof of the proposition.
$N^{h^+}$. This concludes the proof of the proposition.
A.2 Extension to the more general setting of Remark 1.2
As noted in Remark 1.2, the results of this article can be extended to a more general setting. A critical point for this extension is to construct a coupling of the Hawkes process ![]() $N^{h,\phi}$ with a Hawkes process
$N^{h,\phi}$ with a Hawkes process ![]() $N^g$ satisfying Definition 1.1 for a nonnegative function g, in such a way that
$N^g$ satisfying Definition 1.1 for a nonnegative function g, in such a way that ![]() $N^{h,\phi} \le N^g$ (thinning). Then
$N^{h,\phi} \le N^g$ (thinning). Then ![]() $N^g=\emptyset$ implies that
$N^g=\emptyset$ implies that ![]() $N^{h,\phi} =\emptyset$, and in particular this allows us to derive exponential bounds on the renewal time
$N^{h,\phi} =\emptyset$, and in particular this allows us to derive exponential bounds on the renewal time ![]() $\tau$ of
$\tau$ of ![]() $N^{h,\phi}$.
$N^{h,\phi}$.
Proposition A.1. Assume that ![]() $N^{h,\phi}$ is a Hawkes process with conditional intensity
$N^{h,\phi}$ is a Hawkes process with conditional intensity ![]() $\Lambda^{h,\phi}$ defined in (1.13), and that the functions
$\Lambda^{h,\phi}$ defined in (1.13), and that the functions ![]() $\phi$ and h have the property that there exist
$\phi$ and h have the property that there exist ![]() $\lambda$ and a in
$\lambda$ and a in ![]() $[0,\infty)$ such that for all
$[0,\infty)$ such that for all ![]() $x\in\mathbb{R}$,
$x\in\mathbb{R}$,
Let us define ![]() $g=a h^+$. Then there exists a coupling of
$g=a h^+$. Then there exists a coupling of ![]() $N^{h,\phi}$ with a Hawkes process
$N^{h,\phi}$ with a Hawkes process ![]() $N^g$ in the sense of Definition 1.1 such that a.s.
$N^g$ in the sense of Definition 1.1 such that a.s. ![]() $N^{h,\phi}\le N^{g}$.
$N^{h,\phi}\le N^{g}$.
Scheme of the proof. As in the previous case, a key point is to establish an upper bound for the intensity ![]() $\Lambda^{h,\phi}$ on given time intervals. We have
$\Lambda^{h,\phi}$ on given time intervals. We have
 \begin{align*}\phi\left(\int_{(\!-\infty,t)} h(t-u) N^{h,\phi} (du)\right)&\le \lambda + a \left(\int_{(\!-\infty,t)} h(t-u) N^{h,\phi} (du)\right)^+&&\text{(by assumption)}\\&\le \lambda + \int_{(\!-\infty,t)} g(t-u) N^{h,\phi} (du)&&\text{(since $g = a h^+$)}\\&\le \lambda + \int_{(\!-\infty,t)} g(t-u) N^g (du)&&\text{(thinning),}\end{align*}
\begin{align*}\phi\left(\int_{(\!-\infty,t)} h(t-u) N^{h,\phi} (du)\right)&\le \lambda + a \left(\int_{(\!-\infty,t)} h(t-u) N^{h,\phi} (du)\right)^+&&\text{(by assumption)}\\&\le \lambda + \int_{(\!-\infty,t)} g(t-u) N^{h,\phi} (du)&&\text{(since $g = a h^+$)}\\&\le \lambda + \int_{(\!-\infty,t)} g(t-u) N^g (du)&&\text{(thinning),}\end{align*}and thus it is possible at each point U of ![]() $N^{g}$ to either include it into
$N^{g}$ to either include it into ![]() $N^{h,\phi}$ with probability
$N^{h,\phi}$ with probability
 \begin{equation*}\frac{\phi\left(\int_{(\!-\infty,U)} h(U-u) N^{h,\phi} (du)\right)}{\lambda + \int_{(\!-\infty,U)} g(U-u) N^{g} (du)} \le1\end{equation*}
\begin{equation*}\frac{\phi\left(\int_{(\!-\infty,U)} h(U-u) N^{h,\phi} (du)\right)}{\lambda + \int_{(\!-\infty,U)} g(U-u) N^{g} (du)} \le1\end{equation*}or else to reject it, independently of the rest. Then the conditional intensity of ![]() $N^{h,\phi}$ is given by
$N^{h,\phi}$ is given by
 \begin{equation*}\frac{\phi\left(\int_{(\!-\infty,U)} h(t-u) N^{h,\phi} (du)\right)}{\lambda + \int_{(\!-\infty,t)} g(t-u) N^{g} (du)}\left(\lambda + \int_{(\!-\infty,t)} g(t-u) N^{g} (du)\right)= \phi\left(\int_{(\!-\infty,t)} h(t-u) N^{h,\phi} (du)\right)\!.\end{equation*}
\begin{equation*}\frac{\phi\left(\int_{(\!-\infty,U)} h(t-u) N^{h,\phi} (du)\right)}{\lambda + \int_{(\!-\infty,t)} g(t-u) N^{g} (du)}\left(\lambda + \int_{(\!-\infty,t)} g(t-u) N^{g} (du)\right)= \phi\left(\int_{(\!-\infty,t)} h(t-u) N^{h,\phi} (du)\right)\!.\end{equation*}A.3. Return time for M/G/ $\infty$ queues
$\infty$ queues
We now state a general result for the tail behavior of the time of return to zero ![]() $\mathcal{T}_1$ of an M/G/
$\mathcal{T}_1$ of an M/G/![]() $\infty$ queue with a service time admitting exponential moments. All queues in this section start empty.
$\infty$ queue with a service time admitting exponential moments. All queues in this section start empty.
We recall that an M/G/![]() $\infty$ queue has a Poisson process of customer arrivals with i.i.d. service times with a general distribution, and each customer starts its service immediately at arrival and leaves the system at its completion. For the Hawkes process with nonnegative reproduction function, we consider the ancestors to be customers (arriving as a Poisson process of intensity
$\infty$ queue has a Poisson process of customer arrivals with i.i.d. service times with a general distribution, and each customer starts its service immediately at arrival and leaves the system at its completion. For the Hawkes process with nonnegative reproduction function, we consider the ancestors to be customers (arriving as a Poisson process of intensity ![]() $\lambda$) with service times distributed as
$\lambda$) with service times distributed as ![]() $\widetilde{H}_1(A) \triangleq H_1+A$, where
$\widetilde{H}_1(A) \triangleq H_1+A$, where ![]() $H_1$ is a cluster length (see Section 2.2), and then the queue empties exactly at the hitting times of
$H_1$ is a cluster length (see Section 2.2), and then the queue empties exactly at the hitting times of ![]() $\emptyset$ by the auxiliary Markov process.
$\emptyset$ by the auxiliary Markov process.
This result is of interest in itself, independently of the Hawkes process interpretation. Its proof is based on the computation of the Laplace transform ![]() $\mathbb{E}(\text{e}^{-s\mathcal{T}_1})$ on the half-plane
$\mathbb{E}(\text{e}^{-s\mathcal{T}_1})$ on the half-plane ![]() $\{s\in\mathbb{C}\,{:}\, \Re(s) > 0\}$ by Takács [Reference Takács34, Reference Takács35]. We analytically extend this Laplace transform to
$\{s\in\mathbb{C}\,{:}\, \Re(s) > 0\}$ by Takács [Reference Takács34, Reference Takács35]. We analytically extend this Laplace transform to ![]() $\{s\in\mathbb{C}\,{:}\, \Re(s) > s_c\}$ for an appropriate
$\{s\in\mathbb{C}\,{:}\, \Re(s) > s_c\}$ for an appropriate ![]() $s_c<0$, which yields exponential moments.
$s_c<0$, which yields exponential moments.
Theorem A.1. Consider an M/G/![]() $\infty$ queue with arrival rate
$\infty$ queue with arrival rate ![]() $\lambda >0$ and generic service duration H satisfying for some
$\lambda >0$ and generic service duration H satisfying for some ![]() $\gamma >0$ that, for
$\gamma >0$ that, for ![]() $t\ge0$,
$t\ge0$,
Let ![]() $V_1$ denote the arrival time of the first customer,
$V_1$ denote the arrival time of the first customer, ![]() $\mathcal{T}_1$ the subsequent time of return of the queue to zero, and
$\mathcal{T}_1$ the subsequent time of return of the queue to zero, and ![]() $B=\mathcal{T}_1-V_1$ the corresponding busy period.
$B=\mathcal{T}_1-V_1$ the corresponding busy period.
1. If
 $\beta <\gamma$ then
$\beta <\gamma$ then  $\mathbb{E}(\text{e}^{\beta B}) < \infty$. In particular
$\mathbb{E}(\text{e}^{\beta B}) < \infty$. In particular  $\mathbb{P}(B \ge t) = O(\text{e}^{-\beta t})$.
$\mathbb{P}(B \ge t) = O(\text{e}^{-\beta t})$.2. If
 $\lambda <\gamma$, then
$\lambda <\gamma$, then  $\mathbb{P}(\mathcal{T}_1 \ge t) = O(\text{e}^{-\lambda t})$. If
$\mathbb{P}(\mathcal{T}_1 \ge t) = O(\text{e}^{-\lambda t})$. If  $\gamma \le \lambda$, then
$\gamma \le \lambda$, then  $\mathbb{P}(\mathcal{T}_1 \ge t) = O(\text{e}^{-\alpha t})$ for
$\mathbb{P}(\mathcal{T}_1 \ge t) = O(\text{e}^{-\alpha t})$ for  $\alpha<\gamma$.
$\alpha<\gamma$.
Proof. We have ![]() $\mathcal{T}_1=V_1+B$, and the strong Markov property of the Poisson process yields that
$\mathcal{T}_1=V_1+B$, and the strong Markov property of the Poisson process yields that ![]() $V_1$ and B are independent. Since
$V_1$ and B are independent. Since ![]() $V_1$ is exponential of parameter
$V_1$ is exponential of parameter ![]() $\lambda$, we need mainly to study B. Takács has proved in [Reference Takács34, Eq. (37)] (see also [Reference Takács35, Th. 1, p. 210]) that the Laplace transform of
$\lambda$, we need mainly to study B. Takács has proved in [Reference Takács34, Eq. (37)] (see also [Reference Takács35, Th. 1, p. 210]) that the Laplace transform of ![]() $\mathcal{T}_1$ satisfies
$\mathcal{T}_1$ satisfies
Since the Laplace transform of ![]() $V_1$ is
$V_1$ is ![]() $\frac{\lambda}{\lambda + s}$, the Laplace transform of B satisfies
$\frac{\lambda}{\lambda + s}$, the Laplace transform of B satisfies
There is an apparent singularity in the right-hand sides of (A.6) and of (A.7), since the integral term increases to infinity as s decreases to 0. This is normal, since these formulas remain valid for heavy-tailed service. Moreover, (A.6) is proved in [Reference Takács34] and [Reference Takács35] using the Laplace transform of a measure with infinite mass. We shall remove this apparent singularity and compute the abscissa of convergence of the Laplace transform in the left-hand side of (A.7).
The main point to prove is that the abscissa of convergence ![]() $\sigma_c$ of the Laplace transform in the left-hand side of (A.7) satisfies
$\sigma_c$ of the Laplace transform in the left-hand side of (A.7) satisfies ![]() $\sigma_c \le -\gamma$. In order to remove the apparent singularity in the right-hand side of (A.7), we use integration by parts: on the half-line
$\sigma_c \le -\gamma$. In order to remove the apparent singularity in the right-hand side of (A.7), we use integration by parts: on the half-line ![]() $\{s\in\mathbb{R}\,{:}\, s> 0\}$,
$\{s\in\mathbb{R}\,{:}\, s> 0\}$,
 \begin{align}\int_0^\infty \text{e}^{-st - \lambda \int_0^t[1-G(u)]\,\text{d} u}\,\text{d}t&= \left[\frac{\text{e}^{-st}}{-s} \text{e}^{- \lambda \int_0^t[1-G(u)]\,\text{d} u} \right]_{t=0}^\infty\notag\\[4pt]
&\qquad - \int_0^\infty \frac{\text{e}^{-st}}{-s} (\!-\lambda[1-G(t)])\, \text{e}^{- \lambda \int_0^t[1-G(u)]\,\text{d} u}\,\text{d}t\notag\\[4pt]
&= \frac1s - \frac{\lambda}s \int_0^\infty [1-G(t)]\, \text{e}^{-st- \lambda \int_0^t[1-G(u)]\,\text{d} u}\,\text{d}t\,.\end{align}
\begin{align}\int_0^\infty \text{e}^{-st - \lambda \int_0^t[1-G(u)]\,\text{d} u}\,\text{d}t&= \left[\frac{\text{e}^{-st}}{-s} \text{e}^{- \lambda \int_0^t[1-G(u)]\,\text{d} u} \right]_{t=0}^\infty\notag\\[4pt]
&\qquad - \int_0^\infty \frac{\text{e}^{-st}}{-s} (\!-\lambda[1-G(t)])\, \text{e}^{- \lambda \int_0^t[1-G(u)]\,\text{d} u}\,\text{d}t\notag\\[4pt]
&= \frac1s - \frac{\lambda}s \int_0^\infty [1-G(t)]\, \text{e}^{-st- \lambda \int_0^t[1-G(u)]\,\text{d} u}\,\text{d}t\,.\end{align}After inspection of the integral on the right-hand side, since ![]() $1-G(t) = O(\text{e}^{-\gamma t})$ and
$1-G(t) = O(\text{e}^{-\gamma t})$ and
we are able to define a constant ![]() $\theta <0$ and an analytic function f by setting
$\theta <0$ and an analytic function f by setting
 \begin{align}\theta &= \inf \left\{s \le 0\,{:}\, \lambda \int_0^\infty [1-G(t)] \,\text{e}^{-st- \lambda \int_0^t[1-G(u)]\,\text{d} u}\,\text{d}t <1\right\} \vee(\!- \gamma) \,,\notag\\[4pt]
f(s) &=\frac{\lambda + s}{\lambda} - \frac{s}{\lambda}\frac1{1 - \lambda \int_0^\infty [1-G(t)]\, \text{e}^{-st- \lambda \int_0^t[1-G(u)]\,\text{d} u}\,\text{d}t}\,,\qquad s\in\mathbb{C}\,,\; \Re(s) > \theta \,.\nonumber\\\end{align}
\begin{align}\theta &= \inf \left\{s \le 0\,{:}\, \lambda \int_0^\infty [1-G(t)] \,\text{e}^{-st- \lambda \int_0^t[1-G(u)]\,\text{d} u}\,\text{d}t <1\right\} \vee(\!- \gamma) \,,\notag\\[4pt]
f(s) &=\frac{\lambda + s}{\lambda} - \frac{s}{\lambda}\frac1{1 - \lambda \int_0^\infty [1-G(t)]\, \text{e}^{-st- \lambda \int_0^t[1-G(u)]\,\text{d} u}\,\text{d}t}\,,\qquad s\in\mathbb{C}\,,\; \Re(s) > \theta \,.\nonumber\\\end{align} The Laplace transform in the left-hand side of (A.7) has an abscissa of convergence ![]() $\sigma_c\le 0$ and is analytic in the half-plane
$\sigma_c\le 0$ and is analytic in the half-plane ![]() $\{s\in\mathbb{C}\,{:}\, \Re(s) > \sigma_c\}$; see Widder [Reference Widder37, Th. 5a, p. 57]. Both this Laplace transform and f are analytic in the domain
$\{s\in\mathbb{C}\,{:}\, \Re(s) > \sigma_c\}$; see Widder [Reference Widder37, Th. 5a, p. 57]. Both this Laplace transform and f are analytic in the domain ![]() $\{s\in\mathbb{C}\,{:}\, \Re(s) > \max(\theta, \sigma_c)\}$, and since these two analytic functions coincide there on the half-line
$\{s\in\mathbb{C}\,{:}\, \Re(s) > \max(\theta, \sigma_c)\}$, and since these two analytic functions coincide there on the half-line ![]() $\{s\in\mathbb{R}\,{:}\, s> 0\}$, they must coincide in the whole domain (see Rudin [Reference Rudin33, Th. 10.18, p. 208]), so that
$\{s\in\mathbb{R}\,{:}\, s> 0\}$, they must coincide in the whole domain (see Rudin [Reference Rudin33, Th. 10.18, p. 208]), so that
This Laplace transform must have an analytic singularity at ![]() $s=\sigma_c$ (see Widder [Reference Widder37, Th. 5b, p. 58]), and since f is analytic in
$s=\sigma_c$ (see Widder [Reference Widder37, Th. 5b, p. 58]), and since f is analytic in ![]() $\{s\in\mathbb{C}\,{:}\, \Re(s) > \theta\}$, necessarily
$\{s\in\mathbb{C}\,{:}\, \Re(s) > \theta\}$, necessarily ![]() $\sigma_c \le \theta$.
$\sigma_c \le \theta$.
Since ![]() $\theta<0$, by monotone convergence we have
$\theta<0$, by monotone convergence we have
which implies that
and thus that ![]() $\theta = -\gamma$.
$\theta = -\gamma$.
We conclude that ![]() $\sigma_c \le -\gamma$. Thus, if
$\sigma_c \le -\gamma$. Thus, if ![]() $\beta <\gamma$, then
$\beta <\gamma$, then ![]() $\mathbb{E}(\text{e}^{\beta B}) < \infty$, and
$\mathbb{E}(\text{e}^{\beta B}) < \infty$, and ![]() $\mathbb{P}(B \ge t) = O(\text{e}^{-\beta t})$ using the Markov inequality. Moreover, if
$\mathbb{P}(B \ge t) = O(\text{e}^{-\beta t})$ using the Markov inequality. Moreover, if ![]() $\mathbb{P}(B \ge t) = O(\text{e}^{-\alpha t})$ then
$\mathbb{P}(B \ge t) = O(\text{e}^{-\alpha t})$ then
 \begin{align*}\mathbb{P}(\mathcal{T}_1 \ge t) = \mathbb{P}(B+V_1 \ge t) &= \text{e}^{-\lambda t}+ \lambda \int_0^t \text{e}^{-\lambda u}\mathbb{P}(B \ge t-u)\,\text{d}u\\[4pt]
&\le \text{e}^{-\lambda t} + C \int_0^t \text{e}^{-\lambda u -\alpha (t-u)} \,\text{d}u\,;\end{align*}
\begin{align*}\mathbb{P}(\mathcal{T}_1 \ge t) = \mathbb{P}(B+V_1 \ge t) &= \text{e}^{-\lambda t}+ \lambda \int_0^t \text{e}^{-\lambda u}\mathbb{P}(B \ge t-u)\,\text{d}u\\[4pt]
&\le \text{e}^{-\lambda t} + C \int_0^t \text{e}^{-\lambda u -\alpha (t-u)} \,\text{d}u\,;\end{align*}hence, if ![]() $\lambda <\gamma$, then choosing
$\lambda <\gamma$, then choosing ![]() $\lambda < \alpha < \gamma$ yields that
$\lambda < \alpha < \gamma$ yields that
and if ![]() $\alpha <\gamma \le \lambda $, then
$\alpha <\gamma \le \lambda $, then
We now provide a corollary to the previous result.
Proposition A.2. Consider an M/G/![]() $\infty$ queue with arrival rate
$\infty$ queue with arrival rate ![]() $\lambda >0$ and generic service duration H satisfying for some
$\lambda >0$ and generic service duration H satisfying for some ![]() $\gamma >0$ that
$\gamma >0$ that
Let ![]() $Y_t$ denote the number of customers at time
$Y_t$ denote the number of customers at time ![]() $t\ge0$, and for each
$t\ge0$, and for each ![]() $E\ge 0$ let
$E\ge 0$ let
be the first hitting time of zero after E. If ![]() $\lambda<\gamma$ then let
$\lambda<\gamma$ then let ![]() $\alpha=\lambda$, and if
$\alpha=\lambda$, and if ![]() $\gamma\leq \lambda$ then let
$\gamma\leq \lambda$ then let ![]() $0<\alpha<\gamma$. Then there exists a constant
$0<\alpha<\gamma$. Then there exists a constant ![]() $C<\infty$ such that
$C<\infty$ such that
Proof. The successive return times to zero ![]() $(\mathcal{T}_k)_{k\geq 0}$ of the process
$(\mathcal{T}_k)_{k\geq 0}$ of the process ![]() $(Y_t)_{t\geq 0}$ have been defined in (2.7). The events
$(Y_t)_{t\geq 0}$ have been defined in (2.7). The events ![]() $\{\mathcal{T}_{k-1}\leq E,\ \mathcal{T}_k>E\}$ for
$\{\mathcal{T}_{k-1}\leq E,\ \mathcal{T}_k>E\}$ for ![]() $k\geq 1$ define a partition of
$k\geq 1$ define a partition of ![]() $\Omega$, and for
$\Omega$, and for ![]() $t>E$,
$t>E$,
 \begin{align*}\mathbb{P}(\tau_E \ge t)& = \sum_{k=1}^{+\infty} \mathbb{P}\big(\tau_E \ge t,\,\mathcal{T}_{k-1}\leq E,\,\mathcal{T}_k>E\big)\\& = \sum_{k=1}^{+\infty}\mathbb{P}\big( \mathcal{T}_{k-1}\leq E,\,\mathcal{T}_k\ge t\big)\\& = \sum_{k=1}^{+\infty}\mathbb{E}\Big( {\mathds{1}}_{\{\mathcal{T}_{k-1}\leq E\}} \mathbb{P}\big(\mathcal{T}_k\ge t \,|\,\mathcal{F}_{\mathcal{T}_{k-1}}\big)\Big)\\&\leq \sum_{k=1}^{+\infty}\mathbb{E}\Big( {\mathds{1}}_{\{\mathcal{T}_{k-1}\leq E\}} \mathbb{P}\big(\mathcal{T}_k-\mathcal{T}_{k-1} \ge t-E \,|\,\mathcal{F}_{\mathcal{T}_{k-1}}\big)\Big),\end{align*}
\begin{align*}\mathbb{P}(\tau_E \ge t)& = \sum_{k=1}^{+\infty} \mathbb{P}\big(\tau_E \ge t,\,\mathcal{T}_{k-1}\leq E,\,\mathcal{T}_k>E\big)\\& = \sum_{k=1}^{+\infty}\mathbb{P}\big( \mathcal{T}_{k-1}\leq E,\,\mathcal{T}_k\ge t\big)\\& = \sum_{k=1}^{+\infty}\mathbb{E}\Big( {\mathds{1}}_{\{\mathcal{T}_{k-1}\leq E\}} \mathbb{P}\big(\mathcal{T}_k\ge t \,|\,\mathcal{F}_{\mathcal{T}_{k-1}}\big)\Big)\\&\leq \sum_{k=1}^{+\infty}\mathbb{E}\Big( {\mathds{1}}_{\{\mathcal{T}_{k-1}\leq E\}} \mathbb{P}\big(\mathcal{T}_k-\mathcal{T}_{k-1} \ge t-E \,|\,\mathcal{F}_{\mathcal{T}_{k-1}}\big)\Big),\end{align*}so that, since ![]() $\mathcal{T}_k-\mathcal{T}_{k-1} $ is independent of
$\mathcal{T}_k-\mathcal{T}_{k-1} $ is independent of ![]() $\mathcal{F}_{\mathcal{T}_{k-1}}$ and distributed as
$\mathcal{F}_{\mathcal{T}_{k-1}}$ and distributed as ![]() $\mathcal{T}_1$,
$\mathcal{T}_1$,
 \begin{equation*}\mathbb{P}(\tau_E \ge t)\le \sum_{k=1}^{+\infty}\mathbb{E}\Big( {\mathds{1}}_{\{\mathcal{T}_{k-1}\leq E\}} \Big) \mathbb{P}\big(\mathcal{T}_1 \ge t-E\big)= \mathbb{P}\big(\mathcal{T}_1 \ge t-E\big) \mathbb{E}\Bigg(\sum_{k=1}^{+\infty} {\mathds{1}}_{\{\mathcal{T}_{k-1}\leq E\}} \Bigg)\,.\end{equation*}
\begin{equation*}\mathbb{P}(\tau_E \ge t)\le \sum_{k=1}^{+\infty}\mathbb{E}\Big( {\mathds{1}}_{\{\mathcal{T}_{k-1}\leq E\}} \Big) \mathbb{P}\big(\mathcal{T}_1 \ge t-E\big)= \mathbb{P}\big(\mathcal{T}_1 \ge t-E\big) \mathbb{E}\Bigg(\sum_{k=1}^{+\infty} {\mathds{1}}_{\{\mathcal{T}_{k-1}\leq E\}} \Bigg)\,.\end{equation*}By Theorem A.1, under the assumptions there exists a constant C such that
Moreover, ![]() $\sum_{k=1}^{+\infty} {\mathds{1}}_{\{\mathcal{T}_{k-1}\leq E\}}$ is the number of returns to zero before time E. It is bounded by the number of arrivals between times 0 and E, which follows a Poisson law of parameter and expectation
$\sum_{k=1}^{+\infty} {\mathds{1}}_{\{\mathcal{T}_{k-1}\leq E\}}$ is the number of returns to zero before time E. It is bounded by the number of arrivals between times 0 and E, which follows a Poisson law of parameter and expectation ![]() $\lambda E$. This leads to the stated inequality.□
$\lambda E$. This leads to the stated inequality.□
A.4. Strong Markov property for homogeneous Poisson point processes
In this appendix, we prove a strong Markov property for homogeneous Poisson point processes on the line. This classic result is stated in [Reference Robert32, Prop. 1.18, p. 18] in the case when the filtration is the canonical filtration generated by the Poisson point process. Here, the filtration ![]() $(\mathcal{F}_t)_{t\ge 0}$ may contain additional information, for example coming from configurations on
$(\mathcal{F}_t)_{t\ge 0}$ may contain additional information, for example coming from configurations on ![]() $\mathbb{R}_-$.
$\mathbb{R}_-$.
Lemma A.2. Let Q be an ![]() $(\mathcal{F}_t)_{t\ge0}$-Poisson point process on
$(\mathcal{F}_t)_{t\ge0}$-Poisson point process on ![]() $(0,+\infty)\times (0,+\infty)$ with unit intensity. Then Q is a strong
$(0,+\infty)\times (0,+\infty)$ with unit intensity. Then Q is a strong ![]() $(\mathcal{F}_t)_{t\ge0}$-Markov process in the following sense: for any stopping time T for
$(\mathcal{F}_t)_{t\ge0}$-Markov process in the following sense: for any stopping time T for ![]() $(\mathcal{F}_t)_{t\ge0}$, conditionally on
$(\mathcal{F}_t)_{t\ge0}$, conditionally on ![]() $T<\infty$ the shifted process
$T<\infty$ the shifted process ![]() $S_TQ$ defined by (3.3) is an
$S_TQ$ defined by (3.3) is an ![]() $(\mathcal{F}_{T+t})_{t\ge0}$-Poisson point process with unit intensity.
$(\mathcal{F}_{T+t})_{t\ge0}$-Poisson point process with unit intensity.
Proof. It is enough to prove that, for any stopping time T and any ![]() $h,a>0$, conditionally on
$h,a>0$, conditionally on ![]() $T<\infty$ the random variable
$T<\infty$ the random variable ![]() $Q((T,T+h]\times (0,a])$ is
$Q((T,T+h]\times (0,a])$ is ![]() $\mathcal{F}_{T+h}$-measurable, independent of
$\mathcal{F}_{T+h}$-measurable, independent of ![]() $\mathcal{F}_T$, and Poisson of parameter ha. Indeed, in order to prove the strong Markov property at a given stopping time T, it is enough to apply the above to the stopping times
$\mathcal{F}_T$, and Poisson of parameter ha. Indeed, in order to prove the strong Markov property at a given stopping time T, it is enough to apply the above to the stopping times ![]() $T+t$ for
$T+t$ for ![]() $t>0$ in order to see that
$t>0$ in order to see that ![]() $S_TQ$ satisfies that for every
$S_TQ$ satisfies that for every ![]() $t,h,a>0$, the random variable
$t,h,a>0$, the random variable ![]() $Q((t,t+h]\times (0,a])$ is
$Q((t,t+h]\times (0,a])$ is ![]() $\mathcal{F}_{t+h}$-measurable, independent of
$\mathcal{F}_{t+h}$-measurable, independent of ![]() $\mathcal{F}_t$, and Poisson of parameter ha.
$\mathcal{F}_t$, and Poisson of parameter ha.
We first prove this for an arbitrary stopping time T with finite values belonging to an increasing deterministic sequence ![]() $(t_n)_{n\ge1}$. For each B in
$(t_n)_{n\ge1}$. For each B in ![]() $\mathcal{F}_T$ and
$\mathcal{F}_T$ and ![]() $k\ge0$, we have
$k\ge0$, we have
 \begin{align*}&\mathbb{P}(B\cap\{T<\infty\}\cap \{Q((T,T+h]\times (0,a])=k\})\\&\quad =\sum_{n\ge1} \mathbb{P}(B\cap\{T=t_n\}\cap\{Q((t_n,t_n+h]\times (0,a])=k\}),\end{align*}
\begin{align*}&\mathbb{P}(B\cap\{T<\infty\}\cap \{Q((T,T+h]\times (0,a])=k\})\\&\quad =\sum_{n\ge1} \mathbb{P}(B\cap\{T=t_n\}\cap\{Q((t_n,t_n+h]\times (0,a])=k\}),\end{align*}in which, by definition of ![]() $\mathcal{F}_T$ and since
$\mathcal{F}_T$ and since ![]() $\mathcal{F}_{t_{n-1}}\subset \mathcal{F}_{t_n}$,
$\mathcal{F}_{t_{n-1}}\subset \mathcal{F}_{t_n}$,
The ![]() $(\mathcal{F}_t)_{t\ge0}$-Poisson point process property then yields that
$(\mathcal{F}_t)_{t\ge0}$-Poisson point process property then yields that
and summation of the series yields that
Hence ![]() $Q((T,T+h]\times (0,a])$ is independent of
$Q((T,T+h]\times (0,a])$ is independent of ![]() $\mathcal{F}_T$ and Poisson of parameter ha. Moreover, for
$\mathcal{F}_T$ and Poisson of parameter ha. Moreover, for ![]() $k\ge0$, similarly
$k\ge0$, similarly
 \begin{align*} &\{T<\infty,\, Q((T,T+h]\times (0,a])=k\} \cap \{T+h\le t\} \\ &\quad = \bigcup_{n\ge1} \{T=t_n,\, Q((t_n,t_n+h]\times (0,a])=k\} \cap \{t_n+h\le t\} \subset\mathcal{F}_t,\end{align*}
\begin{align*} &\{T<\infty,\, Q((T,T+h]\times (0,a])=k\} \cap \{T+h\le t\} \\ &\quad = \bigcup_{n\ge1} \{T=t_n,\, Q((t_n,t_n+h]\times (0,a])=k\} \cap \{t_n+h\le t\} \subset\mathcal{F}_t,\end{align*}and hence ![]() $Q((T,T+h]\times (0,a])$ is
$Q((T,T+h]\times (0,a])$ is ![]() $\mathcal{F}_{T+h}$-measurable.
$\mathcal{F}_{T+h}$-measurable.
In order to extend this to a general stopping time T, we approximate T by the discrete stopping times
 \begin{equation*}T_n = \sum_{k=1}^{+\infty} \frac{k}{2^n} {\mathds{1}}_{\{\frac{k-1}{2^n}
< T \le \frac{k}{2^n}\}}\,,\qquad n\ge1\,.\end{equation*}
\begin{equation*}T_n = \sum_{k=1}^{+\infty} \frac{k}{2^n} {\mathds{1}}_{\{\frac{k-1}{2^n}
< T \le \frac{k}{2^n}\}}\,,\qquad n\ge1\,.\end{equation*}The nondecreasing sequence ![]() $(T_n)$ satisfies
$(T_n)$ satisfies ![]() $T_n \ge T$ a.s. As n goes to infinity, the right continuity of
$T_n \ge T$ a.s. As n goes to infinity, the right continuity of ![]() $t\mapsto Q((0,t]\times(0,a])$ and of
$t\mapsto Q((0,t]\times(0,a])$ and of ![]() $(\mathcal{F}_t)_{t\ge0}$ allows us to conclude.
$(\mathcal{F}_t)_{t\ge0}$ allows us to conclude.
Acknowledgements
The authors thank Patricia Reynaud-Bouret for introducing them to Hawkes processes and for proposing the problem of inhibition in Hawkes processes. All the authors have been supported by the Chair ‘Modélisation Mathématique et Biodiversité’ of Veolia Environnement, the École Polytechnique, the Muséum National d’Histoire Naturelle, and the Fondation X. Finally, L. Marsalle and V. C. Tran acknowledge support from Labex CEMPI (ANR-11-LABX-0007-01).