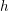1 Introduction
Let 
$M$ be a smooth 
$n$-dimensional manifold. By definition, an 
$m$-dimensional smooth distribution 
$E\subset TM$ is a smooth section of the Grassmannian bundle 
$\text{Gr}_{m}(TM)\longrightarrow M$. Distributions are a core geometric structure in the modern perspective of differential geometry and control theory [Reference Bryant and HsuBH93, Reference Gershkovich and VershikGV87, Reference MontgomeryMon02, Reference Montgomery and ZhitomirskiiMZ09], which in particular subsumes the smooth dynamics of non-vanishing vector fields, the theory of foliations, and contact geometry. The integrability of geometric structures, including the existence of complex structures, and the symmetries (and solvability) of differential equations are part of the theory of distributions [Reference CartanCar01, Reference CartanCar24, Reference Gershkovich and VershikGV87].
Cartan addressed in [Reference CartanCar01] the existence of a local normal form for a generic distribution, that is,the lack of local invariants when the distribution is given by an open condition. The main result [Reference CartanCar01, Reference MontgomeryMon93, Reference MontgomeryMon99] is that a generic distribution 
$E\subset TM$ has a unique local normal form if and only if it belongs to one of the following families: smooth line fields, contact structures (even or odd), or Engel structures. The study of the first two geometries, smooth dynamics and contact topology, has been of major interest and activity in the last four decades.
Engel structures, maximally non-integrable 2-distributions in 4-manifolds, have proven themselves more elusive: in [Reference Eliashberg and MishachevEM02, Intrigue F], Eliashberg and Mishachev identified the classification of Engel structures as an outstanding problem in the theory of 
$h$-principles. The first modern breakthrough in Engel geometry was the existence theorem proven by Vogel [Reference VogelVog09, Theorem 6.1]. In the last two years, the study of Engel structures has seen further significant developments [Reference Casals and del PinoCdP18, Reference Casals, Pérez, del Pino and PresasCPdPP17, Reference Colin, Presas and VogelCPV18, Reference del PinodP18, Reference del Pino and VogeldPV18, Reference Kotschick and VogelKV18, Reference MitsumatsuMit18, Reference PiaPia19, Reference YamazakiYam18, Reference ZhaoZha18a, Reference ZhaoZha18b], exhibiting unique properties of Engel structures and connections with smooth dynamics and contact and symplectic geometry. In particular, the authors proved the parametric existence 
$h$-principle for Engel structures in [Reference Casals, Pérez, del Pino and PresasCPdPP17], and the first two authors developed the complete 
$h$-principle for non-singular Engel knots in [Reference Casals and del PinoCdP18].
The present paper continues this work by providing a classification 
$h$-principle for a class of Engel structures called loose (see § 3.1 for a definition). Our result should be compared (see the Appendix) to the work in [Reference del Pino and VogeldPV18], which defines and classifies another class of Engel structures, called overtwisted. The latter is closer in behaviour to the class of overtwisted contact structures, which were shown to satisfy a complete 
$h$-principle in [Reference Borman, Eliashberg and MurphyBEM15].
Let us now state the main theorems of this paper in precise terms.
1.1 Main results
Let 
$M$ be a closed smooth 
$4$-manifold, 
$\mathscr{E}(M)$ the space of Engel structures on 
$M$, and 
$\mathscr{E}^{\text{f}}(M)$ its formal counterpart [Reference Casals, Pérez, del Pino and PresasCPdPP17, Reference GromovGro86, Reference del Pino and VogeldPV18] (see § 2.1 for a definition). It was proven in [Reference Casals, Pérez, del Pino and PresasCPdPP17] that the scanning map given by the inclusion
$$\begin{eqnarray}\displaystyle \mathscr{E}(M)\longrightarrow \mathscr{E}^{\text{f}}(M) & & \displaystyle \nonumber\end{eqnarray}$$induces a surjection in homotopy groups.
The aim of the present work is to show that every homotopy class in 
$\unicode[STIX]{x1D70B}_{k}(\mathscr{E}^{\text{f}}(M))$ can be represented by a 
$k$-dimensional sphere in 
$\mathscr{E}(M)$ which is unique up to Engel homotopy, that is, there is a subgroup 
$\mathscr{L}_{k}(M)\subset \unicode[STIX]{x1D70B}_{k}(\mathscr{E}(M))$ isomorphic to 
$\unicode[STIX]{x1D70B}_{k}(\mathscr{E}^{\text{f}}(M))$ that can be characterized in a geometric fashion. This is the content of our two main results.
Theorem 1. Let 
$M$ be a smooth 
$4$-manifold, 
$K$ a compact CW-complex, and 
$N$ a positive integer. Then any family 
${\mathcal{D}}:K\longrightarrow \mathscr{E}^{\text{f}}(M)$ is formally homotopic to an 
$N$-loose family.
We strengthen the existence 
$h$-principle in Theorem 1 to the following uniqueness 
$h$-principle.
Theorem 2. Let 
$M$ be a smooth 
$4$-manifold and 
$K$ a compact CW-complex. There exists a positive integer 
$N_{0}$, depending only on 
$\dim (K)$, such that any two 
$N$-loose families 
${\mathcal{D}}_{0},{\mathcal{D}}_{1}:K\longrightarrow \mathscr{E}(M)$, 
$N\geqslant N_{0}$, are Engel homotopic if they are formally homotopic. In addition, the resulting Engel homotopy 
$({\mathcal{D}}_{t})_{t\in [0,1]}$ can be realized as an 
$(N-N_{0})$-loose 
$K\times [0,1]$-family of Engel structures.
Theorem 1 provides existence and Theorem 2 shows uniqueness. The notion of looseness for a family of Engel structures will be introduced in Definition 19, § 3. Roughly, it is a quantitative property which measures the rotation of the Engel plane field 
${\mathcal{D}}$ with respect to a line field 
$\mathscr{Y}\subset {\mathcal{D}}$, captured by a positive integer 
$N$. In particular, if a family of Engel structures 
${\mathcal{D}}:K\longrightarrow \mathscr{E}^{\text{f}}(M)$ is 
$N_{2}$-loose, then it is 
$N_{1}$-loose for any 
$N_{1}\leqslant N_{2}$. By definition, the line field 
$\mathscr{Y}$ is called the certificate and a family that is 
$N$-loose with 
$N\geqslant N_{0}$, with 
$N_{0}$ as in the statement of Theorem 2, is said to be simply loose.
Let 
$\mathscr{E}^{\text{f}}(M,\mathscr{Y})$ be the space of formal Engel structures containing some fixed 
$\mathscr{Y}\subset {\mathcal{D}}$ transverse to the formal kernel 
${\mathcal{W}}$. If 
$\mathscr{Y}$ has no periodic orbits, Theorem 1 can be strengthened to yield families that are 
$N$-loose for all 
$N$. Such a family is said to be 
$\infty$-loose. We denote by 
$\mathscr{L}(M,\mathscr{Y})$ the subspace of Engel structures having 
$\mathscr{Y}$ as their certificate of 
$\infty$-looseness. Using Theorems 1 and 2, we can deduce the following complete 
$h$-principle.
Theorem 3. Let 
$M$ be a closed smooth 
$4$-manifold and 
$\mathscr{Y}$ a line field without periodic orbits. Then the forgetful inclusion 
$\mathscr{L}(M,\mathscr{Y})\longrightarrow \mathscr{E}^{\text{f}}(M,\mathscr{Y})$ is a weak homotopy equivalence.
In § 4 we compare these statements with other recent developments regarding flexibility in Engel topology. In § 4.1 we define the notion of Cartan/Lorentz prolongation and we prove the following result which subsumes one of the main results in [Reference del PinodP18].
Corollary 4. Any family of Lorentz or orientable Cartan prolongations is loose, up to Engel homotopy. In particular, such families are classified, up to Engel homotopy, by their formal data.
In § 4.2 we prove that the Engel structures produced in [Reference Casals, Pérez, del Pino and PresasCPdPP17] are homotopic to loose ones, and that those constructed using Engel open books in [Reference Colin, Presas and VogelCPV18] are loose.
The paper is organized as follows. Section 2 is dedicated to convexity in Engel topology, including all the basic theory needed for our results. Section 3 defines and explores Engel looseness. The proof of Theorems 1, 2, and 3 is structured in two parts: existence of loose families (§ 3.3) and uniqueness (§ 3.4). Section 4 contains applications, including the proof of Corollary 4. Appendix A provides a detailed discussion comparing flexibility phenomena for Engel structures and contact structures. In particular, we discuss the relation between the present paper and the work in [Reference del Pino and VogeldPV18].
2 Engel structures and convexity
In this section we state the basic facts and techniques used in the study of Engel structures. We focus on the interaction between Engel structures and families of convex curves in the 
$2$-sphere. This relationship will allow us to prove Theorems 1, 2, and 3.
We use the notation 
${\mathcal{O}}p(A)$ to denote an arbitrarily small neighbourhood of the subset 
$A$.
2.1 Engel structures
The central objects of study are the following geometric structures.
Definition 5. An Engel structure is a maximally non-integrable 
$2$-plane field 
${\mathcal{D}}\subset TM$. That is, 
${\mathcal{E}}=[{\mathcal{D}},{\mathcal{D}}]$ is an everywhere non-integrable 
$3$-distribution (i.e. 
$TM=[{\mathcal{E}},{\mathcal{E}}]$).
The distribution 
${\mathcal{E}}$ is said to be an even-contact structure. It contains a line field 
${\mathcal{W}}$ uniquely defined by the equation 
$[{\mathcal{W}},{\mathcal{E}}]\subset {\mathcal{E}}$. The line field 
${\mathcal{W}}$ is said to be the kernel of 
${\mathcal{E}}$.
It follows from its definition that the line field 
${\mathcal{W}}$ is contained in the Engel structure 
${\mathcal{D}}$. In consequence, an Engel structure 
${\mathcal{D}}$ induces a complete flag 
${\mathcal{W}}\subset {\mathcal{D}}\subset {\mathcal{E}}$ on the 4-manifold 
$M$ [Reference Casals, Pérez, del Pino and PresasCPdPP17]. In addition, the Lie bracket induces two canonical bundle isomorphisms:
$$\begin{eqnarray}\displaystyle & \displaystyle \det ({\mathcal{D}})\cong {\mathcal{E}}/{\mathcal{D}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \det ({\mathcal{E}}/{\mathcal{W}})\cong TM/{\mathcal{E}}. & \displaystyle\end{eqnarray}$$ Decoupling the differential relation that determines Engel structures leads us to define their formal counterpart as follows: a formal Engel structure is a complete flag 
${\mathcal{W}}\subset {\mathcal{D}}\subset {\mathcal{E}}\subset TM$ endowed with bundle isomorphisms as in equations (1) and (2). In this case there is no differential relationship between the different distributions that constitute the flag. We will often refer to 
${\mathcal{W}}$ as the formal kernel of the formal even-contact structure 
${\mathcal{E}}$.
Let 
$\mathscr{E}(M)$ be the space of Engel structures endowed with the 
$C^{0}$-topology, and 
$\mathscr{E}^{\text{f}}(M)$ the space of formal Engel structure endowed with the 
$C^{2}$-topology. The present work focuses on the homotopy theoretic nature of the inclusion
$$\begin{eqnarray}\displaystyle s:\mathscr{E}(M)\longrightarrow \mathscr{E}^{\text{f}}(M). & & \displaystyle \nonumber\end{eqnarray}$$ This forgetful inclusion is continuous with the chosen topologies. This map is classically called the scanning map [Reference Casals, Pérez, del Pino and PresasCPdPP17, Reference GromovGro86] and it is the main focus in the study of 
$h$-principles [Reference Eliashberg and MishachevEM02].
2.2 Engel flowboxes and convexity
Let us explain a useful method to construct Engel structures locally. For reference, a 
$2$-plane in a smooth 
$3$-manifold is maximally non-integrable (i.e. a contact structure) if and only if the contact planes strictly rotate with respect to a foliation by Legendrian lines [Reference GeigesGei08]. In the same vein, the Engel condition can be geometrically described in terms of a flowbox for a line field contained in the Engel structure, as follows.
Fix coordinates 
$(p,t)$ in the product 
$\mathbb{D}^{3}\times [0,1]$ and consider the bundle isomorphism
$$\begin{eqnarray}\displaystyle d_{(p,t)}\unicode[STIX]{x1D70B}:T_{(p,t)}(\mathbb{D}^{3}\times \{t\})\longrightarrow T_{p}\mathbb{D}^{3}, & & \displaystyle \nonumber\end{eqnarray}$$ where 
$\unicode[STIX]{x1D70B}:\mathbb{D}^{3}\times [0,1]\longrightarrow \mathbb{D}^{3}$ is the projection onto the first factor. Any given fibrewise identification of the projectivized bundle 
$\mathbb{P}(T\mathbb{D}^{3})$ with 
$\mathbb{R}\mathbb{P}^{2}$ obtained by fixing a framing of 
$T\mathbb{D}^{3}$ can be lifted to an identification
$$\begin{eqnarray}\displaystyle d_{(p,t)}\unicode[STIX]{x1D70B}:\mathbb{P}T_{(p,t)}(\mathbb{D}^{3}\times \{t\})\longrightarrow \mathbb{R}\mathbb{P}^{2}. & & \displaystyle \nonumber\end{eqnarray}$$ We focus on the 
$2$-distributions 
${\mathcal{D}}$ of the form 
$\langle \unicode[STIX]{x2202}_{t},X(t)\rangle$, with 
$X(t)$ a vector field tangent to the slice 
$\mathbb{D}^{3}\times \{t\}$. The vector field 
$X$ can be regarded as a 
$\mathbb{D}^{3}$-family of curves
$$\begin{eqnarray}\displaystyle & X_{p}:[0,1]\longrightarrow \mathbb{R}\mathbb{P}^{2}, & \displaystyle \nonumber\\ \displaystyle & X_{p}(t)=d_{(p,t)}\unicode[STIX]{x1D70B}([X(p,t)]), & \displaystyle \nonumber\end{eqnarray}$$ where 
$[-]$ denotes the associated line. The characterization of the Engel condition for 
${\mathcal{D}}$ then reads as follows.
Proposition 6 [Reference Casals, Pérez, del Pino and PresasCPdPP17].
The module 
${\mathcal{E}}=[{\mathcal{D}},{\mathcal{D}}]$ is a 
$3$-distribution on 
${\mathcal{O}}p(p,t)$ if and only if the curve 
$X_{p}$ is immersed at time 
$t$.
The 
$2$-plane field 
${\mathcal{D}}$ is an Engel structure on a neighbourhood of the point 
$(p,t)$ if and only if, additionally, at least one of the following two conditions holds:
(A) the curve
$X_{p}(t)$ has no inflection point at time $t$;(B) the
$2$-distribution $\langle X(q,t),X^{\prime }(q,t)\rangle$ is a contact structure in ${\mathcal{O}}p(p)\times \{t\}$.
If 
${\mathcal{D}}$ is Engel, its kernel 
${\mathcal{W}}$ is spanned by 
$\unicode[STIX]{x2202}_{t}$ at the point 
$(p,t)$ if and only if the curve 
$X_{p}$ has an inflection point at time 
$t$.
By definition, 
$t$ is an inflection point for the curve 
$X_{p}(t)$ if 
$X_{p}$ has a tangency at 
$t$ of order at least 
$2$ with the great circle 
$\langle X_{p}(t),X_{p}^{\prime }(t)\rangle$. We will focus on assumption (A), that is, the curves 
$X_{p}$ will be everywhere convex (or concave); in particular, 
$\unicode[STIX]{x2202}_{t}$ will be transverse to the kernel.
Remark 7. The techniques developed in [Reference Casals, Pérez, del Pino and PresasCPdPP17] are based on the interaction between conditions (A) and (B). For completeness, we prove in § 4.2 that the families constructed in [Reference Casals, Pérez, del Pino and PresasCPdPP17] are loose.
2.3 Convex curves and little wiggles
Proposition 6 connects the study of Engel structures with the theory of convex curves in 
$\mathbb{R}\mathbb{P}^{2}$. The classical results in this direction [Reference LittleLit70, Reference SaldanhaSal15] are stated for convex curves into the 2-sphere 
$\mathbb{S}^{2}$, but they easily translate to the 
$\mathbb{R}\mathbb{P}^{2}$ setting. Let us explain this in detail.
Fix a 
$1$-manifold 
$I$. Let 
${\mathcal{I}}(I)$ be the space of immersions of 
$I$ into 
$\mathbb{R}\mathbb{P}^{2}$, endowed with the 
$C^{1}$-topology. Consider the space 
${\mathcal{I}}^{\text{f}}(I)$ of formal immersions of 
$I$ into 
$\mathbb{R}\mathbb{P}^{2}$, endowed with the 
$C^{0}$-topology, and the subspace 
${\mathcal{L}}(I)\subset {\mathcal{I}}(I)$ of locally convex curves, endowed with the 
$C^{2}$-topology. The inclusion of 
${\mathcal{L}}(I)$ into 
${\mathcal{I}}(I)$ is continuous and the formal counterpart of 
${\mathcal{L}}(I)$ is homotopy equivalent to 
${\mathcal{I}}^{\text{f}}(I)$ [Reference Eliashberg and MishachevEM02, Reference GromovGro86].
The following notion will be important to us.
Definition 8. A curve 
$g\in {\mathcal{I}}(I)$ has a wiggle in the interval 
$[a,b]\subsetneq I$ if 
$g(a)=g(b)$, and, after identifying endpoints, 
$g|_{[a,b]}$ is a smooth closed convex embedded curve.
The curve 
$g$ has 
$n$ wiggles if there are 
$n$ intervals 
$\{I_{i}\subsetneq I\}_{i=1}^{n}$, each of them a wiggle of 
$g$. We require the interiors of these intervals to be pairwise disjoint, but we allow their endpoints to agree. When this happens, we say that the wiggles are concatenated.
Remark 9. Suppose 
$n$ wiggles 
$\{I_{i}\}_{i=1}^{n}$ are concatenated. Then one may be able to choose some other interval 
$I^{\prime }\subset I$ different from them, contained in their union, which is also a wiggle. Due to the embeddedness of a wiggle, we deduce that 
$I^{\prime }$ either is one of the 
$I_{i}$ or intersects exactly two of the original intervals.
We depict wiggles in several figures. For clarity, we often do so up to a small homotopy through convex curves.
2.3.1 Adding wiggles to curves
Let 
$K$ be a compact manifold, 
$n\in \mathbb{N}$ a positive integer, and fix maps 
$f:K\longrightarrow {\mathcal{I}}(I)$ and 
$t:K\longrightarrow I$. From this data, we construct a new map
$$\begin{eqnarray}\displaystyle f^{[n\#t]}:K\longrightarrow {\mathcal{I}}(I) & & \displaystyle \nonumber\end{eqnarray}$$ as follows: for each 
$k\in K$, we cut the curve 
$f(k)$ at the point 
$f(k)(t(k))$ and we add 
$n$ small convex loops, smoothing the result. This defines the map 
$f^{[n\#t]}$, which has (as least) 
$n$ concatenated wiggles. We can and do assume that the two maps 
$f$ and 
$f^{[n\#t]}$ agree as parametrized curves outside of an arbitrarily small neighbourhood of the inserted loops. The insertion of wiggles can be done over different points as long as we have functions 
$t_{0},\ldots ,t_{m}:K\longrightarrow I$ with disjoint images; we then write 
$f^{[n_{0}\#t_{0},\ldots ,n_{m}\#t_{m}]}$ for the resulting family.
Work by Little [Reference LittleLit70] implies that the space of wiggles passing through a point with a given direction is contractible. Therefore, our cutting process is unique up to a convex homotopy of the added wiggle.
Remark 10. Wiggles which are concatenated may have different images (unlike in the construction just provided). However, again invoking the contractibility result due to Little, we deduce that we can make the images be the same by a homotopy through convex curves.
2.3.2 Achieving convexity
The purpose of adding wiggles is that they provide convexity. The first ingredient we need is that any immersed curve 
$f\in {\mathcal{I}}(I)$ is homotopic to a curve with sufficiently many wiggles.
Lemma 11 [Reference LittleLit70, Reference SaldanhaSal15].
Let 
$f:K\longrightarrow {\mathcal{I}}(I)$ be a 
$K$-family of immersed curves and 
$t_{0}\in I$. Then the families 
$f^{[n_{0}\#t_{0}]}$ and 
$f^{[n_{0}+2\#t_{0}]}$ are homotopic through immersions. The homotopy can be assumed to have support in a small neighbourhood 
$(t_{0}-\unicode[STIX]{x1D700},t_{0}+\unicode[STIX]{x1D700})$ of the cutting point 
$t_{0}$.
The homotopy of immersed curves described in Lemma 11 is shown in Figure 1.
Figure 1. Homotopy of immersed curves where two wiggles are introduced. In the last step, we take the concave wiggle and we push it around 
$\mathbb{R}\mathbb{P}^{2}$ so that it appears as a convex wiggle.
The key result in [Reference LittleLit70], explained in detail in [Reference SaldanhaSal15, § 6], states that if 
$f$ is already convex and one extra loop is introduced, additional wiggles may be added using a homotopy through convex curves.
Lemma 12 [Reference LittleLit70, Reference SaldanhaSal15].
Let 
$f:K\longrightarrow {\mathcal{L}}(I)$ be a 
$K$-family of convex curves and 
$t_{0}\in I$. Then the families 
$f^{[n_{0}\#t_{0}]}$ and 
$f^{[n_{0}+2\#t_{0}]}$ are homotopic through convex curves as soon as 
$n_{0}>0$. The homotopy can be assumed to have support in a small neighbourhood 
$(t_{0}-\unicode[STIX]{x1D700},t_{0}+\unicode[STIX]{x1D700})$ of 
$t_{0}$ containing the existing wiggle.
This homotopy of convex curves from Lemma 12 is shown in Figure 2; we refer to it as Little’s homotopy.
Figure 2. (Colour online) Little’s homotopy for convex curves in 
$\mathbb{S}^{2}$. The closed curves correspond to great circles. The first figure shows a convex curve with a little wiggle. By pushing the wiggle down, it can be taken to the second figure. It is convex because it is comprised of three segments that are slight push-offs of equators whose corners have been rounded to preserve convexity. The same is true for the third and fourth figures. In the last two images we push towards the opposite hemisphere, yielding a curve with three wiggles. As shown, this process is relative, in the domain, to the complement of a small neighbourhood of the wiggle.
The last remark we need is that, given any curve 
$f\in {\mathcal{I}}(I)$ and any sufficiently dense collection of points 
$t_{0},\ldots ,t_{m}:K\longrightarrow I$, the curve 
$f^{[1\#t_{0},\ldots ,1\#t_{m}]}$ will be homotopic to a convex curve. Furthermore, the 
$C^{1}$-size of the homotopy needed to achieve convexity will be inversely proportional to the number of wiggles introduced. This is the content of the following proposition, which is the crucial geometric ingredient behind Theorem 3.
Proposition 13. Let 
$K$ be a compact manifold, 
$A\subset K$ a closed submanifold, and 
$0<a<1/2$ a positive real constant. Suppose that 
$f:K\longrightarrow {\mathcal{I}}([0,1])$ is a family of immersions such that 
$f(A)\subset {\mathcal{L}}([0,1])$ and there exists 
$F:K\longrightarrow {\mathcal{L}}([0,a]\cup [1-a,1])$ such that 
$f(k)(t)=F^{[1\#a]}(k)(t)$. Then there exists a family 
$f:K\times [0,\infty )\longrightarrow {\mathcal{I}}([0,1])$ such that the following statements hold.
– For
$s$ large enough $f(k,s)$ is everywhere convex.–
$f(k,s)(t)=f(k)(t)$ if $s=0$, $k\in A$, or $t\in [0,a/2]\cup [1-a,1]$.– The number of wiggles of
$f(k,s)$ in $[a,1-a]$ goes to infinity as $s\longrightarrow \infty$ if $k\notin {\mathcal{O}}p(A)$. The maximum distance between two consecutive wiggles in this segment is $O(1/s)$ and the radius of each wiggle is $O(1/s)$.
Figure 3. (Colour online) We use Little’s homotopy to create several wiggles from a given one. These wiggles are then distributed along the curve to achieve convexity everywhere.
Figure 3 depicts the content of Proposition 13. The density of wiggles goes to infinity as 
$s$ does, as we will see in the proof, while their size has order 
$O(1/s)$.
Proof of Proposition 13.
We construct 
$f(k,s)$ in each interval 
$s=(n,n+1)$ by induction on 
$n\in \mathbb{N}$. For 
$s\in [n,n+1]$ and 
$k$ in the complement of an arbitrarily small neighbourhood 
${\mathcal{O}}p(A)$ of 
$A$, we obtain the following properties.
–
$f(k,n)=f(k)^{[1\#a,1\#(a+(1/2n)(1-2a)),\ldots ,1\#(a+((2n-1)/2n)(1-2a)),1\#(1-a)]}$.–
$f(k,n+1)=f(k)^{[1\#a,1\#(a+(1/(2n+2))(1-2a)),\ldots ,1\#(a+((2n+1)/(2n+2))(1-2a)),1\#(1-a)]}$.– There are
$2n$ paths sliding the last $2n$ wiggles of $f(k,n)$ to the last $2n$ wiggles of $f(k,n+1)$. We change the insertion points from $t=a+(j/2n)(1-2a)$ to $t=a+((j+2)/(2n+2))(1-2a)$, $j=1,\ldots ,2n$, by linear interpolation.– The radius of those
$2n$ wiggles is exactly $1/s$.– In
$Op(A)$, $f(k,s)$ remains convex. Moreover, $f(k,s)=f(k,0)$ for $k\in A$.
Indeed, this is simple to build: the only geometrically non-trivial part corresponds to the family in the interval 
$t\in (a,a+(2/2n)(1-2a))$. In the parameter interval 
$s\in (n,n+1/2)$ we use Little’s homotopy to produce three wiggles out of the existing wiggle at time 
$t=a$, always ensuring that they have radius 
$1/n$. For 
$s\in (n+1/2,n+1)$, we linearly move the insertion points to place them at times 
$a$, 
$a+(1/(2n+2))(1-2a)$, 
$a+(2/(2n+2))(1-2a)$ for 
$s=n+1$. Since convexity is preserved during Little’s homotopy, we can assume that the insertion of the additional wiggles is done relative to 
$A$ by cutting off Little’s homotopy for 
$k\in {\mathcal{O}}p(A)\setminus A$.
To conclude the argument we need to distribute the convexity of the wiggles to make 
$f(k,s)$ everywhere convex for 
$s$ large enough. For that, use only half of the wiggles to create convexity, that is, the ones placed in even positions with respect to the order provided by the insertion time. As explained before, this makes the new family convex for 
$s$ large. Moreover, the odd wiggles are unaffected by this process. Therefore, the number of wiggles is 
$O(s)$ and they are uniformly distributed.◻
2.4 The development map
Let us now introduce the notion of development map, which is used in order to define loose Engel structures. Geometrically, the development map allows us to intrinsically describe the turning of an Engel structure 
${\mathcal{D}}$ with respect to a line field 
$\mathscr{Y}$ contained inside it. Note that this time we are not resorting to the use of charts/flowboxes, as in § 2.2. The development map is well known in the particular case where the line field is the kernel, and under this assumption it was first studied by Montgomery [Reference MontgomeryMon99].
Since the development map encodes how the 2-plane 
${\mathcal{D}}$ moves along 
$\mathscr{Y}$ in terms of the linear holonomy of 
$\mathscr{Y}$, it is natural to define it using the language of groupoids. The monodromy groupoid [Reference Moerdijk and MrčunMM03] is defined as follows.
Definition 14. Let 
$(M,\mathscr{Y})$ be a foliated manifold. The monodromy groupoid 
$\operatorname{Mon}(M,\mathscr{Y})$ is the set of triples 
$(p,q,\unicode[STIX]{x1D6FC})$ where 
$p$ and 
$q$ belong to the same leaf of 
$\mathscr{Y}$ and 
$\unicode[STIX]{x1D6FC}$ is a homotopy class of leafwise paths connecting 
$p$ with 
$q$.
The monodromy groupoid is endowed with the following operations:
– source and target maps
$s,t:\operatorname{Mon}(M,\mathscr{Y})\longrightarrow M$ defined by $s(p,q,\unicode[STIX]{x1D6FC})=p$, $t(p,q,\unicode[STIX]{x1D6FC})=q$;– a partially defined multiplication map
$\operatorname{Mon}(M,\mathscr{Y})\times _{M}\operatorname{Mon}(M,\mathscr{Y})\longrightarrow M$where$$\begin{eqnarray}\displaystyle (p,q,\unicode[STIX]{x1D6FC})\times (q,q^{\prime },\unicode[STIX]{x1D6FC}^{\prime })\longmapsto (p,q^{\prime },\unicode[STIX]{x1D6FC}\,.\,\unicode[STIX]{x1D6FC}^{\prime }), & & \displaystyle \nonumber\end{eqnarray}$$$.$ denotes concatenation of homotopy classes of paths;– unit map
$M\longrightarrow \operatorname{Mon}(M,\mathscr{Y})$ that takes $p$ to $(p,p,[p])$, the class of the constant path at $p$;– inverse map
$\operatorname{Mon}(M,\mathscr{Y})\longrightarrow \operatorname{Mon}(M,\mathscr{Y})$ that takes $(p,q,\unicode[STIX]{x1D6FC})$ to $(q,p,\unicode[STIX]{x1D6FC}^{-1})$;– a partially defined action
$\bullet :\operatorname{Mon}(M,\mathscr{Y})\times _{M}M\longrightarrow M$ on $M$ defined as $(p,q,\unicode[STIX]{x1D6FC})\bullet p=q$.
By construction, the orbit of a point 
$p\in M$ under the action is exactly the leaf 
$L$ of 
$\mathscr{Y}$ in which it is contained. The following result [Reference Moerdijk and MrčunMM03] states that 
$\operatorname{Mon}(M,\mathscr{Y})$ can be endowed with a smooth structure,
Lemma 15. 
$\operatorname{Mon}(M,\mathscr{Y})$ is a Lie groupoid, that is, it is a smooth manifold, possibly non-Hausdorff and non-second-countable, with smooth structure maps. Its dimension is 
$\dim (\mathscr{Y})+\dim (M)$.
The linear holonomy of 
$(p,q,\unicode[STIX]{x1D6FC})$ in 
$\operatorname{Mon}(M,\mathscr{Y})$ is the identification of the normal fibre 
$(TM/\mathscr{Y})_{p}$ with 
$(TM/\mathscr{Y})_{q}$ provided by parallel transport along 
$\unicode[STIX]{x1D6FC}$ using 
$\mathscr{Y}$. Globally, this translates into the action 
$M\unicode[STIX]{x27F2}_{M}\operatorname{Mon}(M,\mathscr{Y})$ lifting to an action 
$\mathbb{P}(TM/\mathscr{Y})\unicode[STIX]{x27F2}_{M}\operatorname{Mon}(M,\mathscr{Y})$ on the projective normal bundle, which is projective linear between fibres.
Let us focus on the Engel structure 
${\mathcal{D}}$. In this case 
$M$ is four-dimensional and 
$\mathscr{Y}\subset {\mathcal{D}}$ is a line field. Over each point 
$p\in M$ the Engel structure determines a point 
$\mathbb{P}({\mathcal{D}}/\mathscr{Y})_{p}\subset \mathbb{P}(TM/\mathscr{Y})_{p}$. This line can be transported using the action 
$\mathbb{P}(TM/\mathscr{Y})\unicode[STIX]{x27F2}_{M}\operatorname{Mon}(M,\mathscr{Y})$ described previously:
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}_{\mathscr{Y}}({\mathcal{D}})_{p}:s^{-1}(p)\longrightarrow \mathbb{P}(TM/\mathscr{Y})_{p},\quad \unicode[STIX]{x1D6FE}_{\mathscr{Y}}({\mathcal{D}})_{p}(p,q,\unicode[STIX]{x1D6FC})=(q,p,\unicode[STIX]{x1D6FC}^{-1})\bullet \mathbb{P}({\mathcal{D}}/\mathscr{Y})_{q}. & & \displaystyle \nonumber\end{eqnarray}$$ Note that the domain 
$s^{-1}(p)$ of the curve 
$\unicode[STIX]{x1D6FE}_{\mathscr{Y}}({\mathcal{D}})_{p}$ is diffeomorphic to 
$\mathbb{R}$.
Definition 16. The smooth map 
$\unicode[STIX]{x1D6FE}_{\mathscr{Y}}({\mathcal{D}}):\operatorname{Mon}(M,\mathscr{Y})\longrightarrow \mathbb{P}(TM/\mathscr{Y})$ obtained by gluing the collection of all maps 
$\unicode[STIX]{x1D6FE}_{\mathscr{Y}}({\mathcal{D}})_{p}$ is called the development map of 
${\mathcal{D}}$ along 
$\mathscr{Y}$.
In § 2.2 we explained how the 2-plane field 
${\mathcal{D}}$ can be described as a family of curves in 
$\mathbb{R}\mathbb{P}^{2}$. The development map provides an intrinsic description of the same phenomenon. By construction, the map 
$\unicode[STIX]{x1D6FE}_{\mathscr{Y}}({\mathcal{D}})$ is equivariant for the action 
$\mathbb{P}(TM/\mathscr{Y})\unicode[STIX]{x27F2}_{M}\operatorname{Mon}(M,\mathscr{Y})$:
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}_{\mathscr{Y}}({\mathcal{D}})(p,q,\unicode[STIX]{x1D6FC})=(p^{\prime },p,\unicode[STIX]{x1D6FC}^{\prime })\bullet \unicode[STIX]{x1D6FE}_{\mathscr{Y}}({\mathcal{D}})((p^{\prime },p,\unicode[STIX]{x1D6FC}^{\prime })\,.\,(p,q,\unicode[STIX]{x1D6FC})). & & \displaystyle \nonumber\end{eqnarray}$$ That is, the curve 
$\unicode[STIX]{x1D6FE}_{\mathscr{Y}}({\mathcal{D}})_{p}\subset \mathbb{P}(TM/\mathscr{Y})_{p}$ is obtained from the curve 
$\unicode[STIX]{x1D6FE}_{\mathscr{Y}}({\mathcal{D}})_{p^{\prime }}\subset \mathbb{P}(TM/\mathscr{Y})_{p^{\prime }}$ using the linear holonomy identification between the two spaces. Condition (A) in Proposition 6 implies the following lemma.
Lemma 17. The module 
$[{\mathcal{D}},{\mathcal{D}}]$ is a 
$3$-distribution if and only if each curve 
$\unicode[STIX]{x1D6FE}_{\mathscr{Y}}({\mathcal{D}})_{p}$ is an immersion. Furthermore, if the curves 
$\unicode[STIX]{x1D6FE}_{\mathscr{Y}}({\mathcal{D}})_{p}$ have no inflection points, 
${\mathcal{D}}$ is an Engel structure.
In Definition 8 we defined a wiggle as an immersion of the interval into 
$\mathbb{R}\mathbb{P}^{2}$ which closes up to a smooth, convex, embedded curve. As such, wiggles are defined in terms of self-intersections and tangencies, implying that being a wiggle is well defined up to projective transformations of 
$\mathbb{R}\mathbb{P}^{2}$. This allows us to speak of intervals of 
$\unicode[STIX]{x1D6FE}_{\mathscr{Y}}({\mathcal{D}})_{p}$ being wiggles in an intrinsic manner, without referring to any particular identification of 
$\mathbb{P}(TM/\mathscr{Y})_{p}$ with 
$\mathbb{R}\mathbb{P}^{2}$. This fact will be important for our arguments.
Remark 18. Definition 16 recovers the notion introduced by Montgomery in [Reference MontgomeryMon99]. Indeed, if 
${\mathcal{D}}$ is Engel and 
$\mathscr{Y}$ is the kernel 
${\mathcal{W}}$, its linearized holonomy preserves the planes 
$({\mathcal{E}}/{\mathcal{W}})_{p}$. In consequence, the monodromy groupoid 
$\operatorname{Mon}(M,\mathscr{Y})$ acts on the projectivized bundle 
$\mathbb{P}({\mathcal{E}}/{\mathcal{W}})$. Since 
${\mathcal{D}}\subset {\mathcal{E}}$, the development map takes values in 
$\mathbb{P}({\mathcal{E}}/{\mathcal{W}})$ and therefore the Engel condition (B) in Proposition 6 implies that each curve 
$\unicode[STIX]{x1D6FE}_{{\mathcal{W}}}({\mathcal{D}})_{p}$ is an immersion.
3 $h$-principle for loose Engel families
In the theory of 
$h$-principles [Reference Eliashberg and MishachevEM02, Reference GromovGro86] there is particular value in finding the correct subclass of structures adhering to an 
$h$-principle [Reference Borman, Eliashberg and MurphyBEM15, Reference Casals and del PinoCdP18, Reference EliashbergEli89]. In the present paper, the 
$h$-principle is a consequence of the flexibility provided by a global dynamical property called looseness. This notion is given in Definition 19 (§ 3.1).
Then we prove our existence and uniqueness theorems: Theorem 1 (§ 3.3) and the uniqueness Theorem 2 (§ 3.4), respectively. Bringing the two of them together allows us to deduce Theorem 3 (§ 3.5).
3.1 Loose Engel structures
Lemma 12 implies that adding enough loops to an immersed curve in 
$\mathbb{R}\mathbb{P}^{2}$ makes it convex (after a suitable modification in-between the cutting points). In line with other 
$h$-principles [Reference Borman, Eliashberg and MurphyBEM15, Reference GromovGro86], once the curve is convex and a loop is added, arbitrarily many new loops can be introduced while preserving convexity. These two phenomena have direct implications in the world of Engel structures.
First, given a 
$2$-plane distribution in a smooth 
$4$-manifold 
$M$, we can make it Engel by adding sufficiently many wiggles to its development map, proceeding carefully over a covering of 
$M$. Secondly, if convexity has been achieved and there are enough wiggles available, we can add arbitrarily many more while keeping the development map convex. These are the two main ingredients to prove a relative 
$h$-principle for this particular class of Engel structures.
The precise definition of this subclass can be detailed as follows. Let 
$M$ be a smooth 
$4$-manifold, 
$K$ a compact CW-complex, and 
$N$ a positive integer. Consider a continuous family of Engel structures 
${\mathcal{D}}:K\longrightarrow \mathscr{E}(M)$ and line fields 
$(\mathscr{Y}(k))_{k\in K}$ with 
$\mathscr{Y}(k)\subset {\mathcal{D}}(k)$. Let 
$\unicode[STIX]{x1D6FE}_{\mathscr{Y}(k)}({\mathcal{D}}(k))$ denote the corresponding development maps.
Definition 19. A family of Engel structures 
${\mathcal{D}}$ is 
$N$-loose with certificate 
$\mathscr{Y}$ if:
– the development curves
$\unicode[STIX]{x1D6FE}_{\mathscr{Y}(k)}({\mathcal{D}}(k))_{p}$ are convex and– for each
$k\in K$ and $p\in M$, there is a segment $\unicode[STIX]{x1D6FE}\subset \unicode[STIX]{x1D6FE}_{\mathscr{Y}(k)}({\mathcal{D}}(k))_{p}$ containing $N$ wiggles that projects to an embedded curve $t(\unicode[STIX]{x1D6FE})$ under the target map.
The family 
${\mathcal{D}}$ is said to be 
$\infty$-loose if this holds for every positive 
$N$.
The convexity condition for the development map implies that the line field 
$\mathscr{Y}(k)$ is always transverse to the kernel of the Engel structure 
${\mathcal{D}}(k)$. The embedding condition for the segment 
$\unicode[STIX]{x1D6FE}$ implies that 
$\infty$-looseness can only hold for line fields 
$\mathscr{Y}(k)$ with no closed orbits; see Proposition 28.
Remark 20. In [Reference SaldanhaSal15], Saldanha describes the homotopy type of the space of convex curves in 
$\mathbb{S}^{2}$. He shows that convex curves behave flexibly as soon as a loop is introduced. He called such families of curves loose. We have decided to name our flexible families of Engel structures accordingly. The geometric intuition we have is that the flexibility of loose Engel structures is a manifestation of the flexibility displayed by convex curves.
Remark 21. In [Reference SaldanhaSal15, Lemma 4.1] it is proven that certain bounds on the total curvature imply that a convex curve has a wiggle (up to homotopy through convex curves). In Definition 19 we introduce looseness using wiggles, but one could define it instead by requiring that the development map has sufficiently large total curvature. This would in fact yield a larger class of Engel structures that would, nonetheless, be weakly homotopy equivalent to the one presented here.
3.2 Convex shells
In our proof of Theorem 1 we first upgrade M. Gromov’s Engel 
$h$-principle for open manifolds [Reference GromovGro86] to a quantitative statement. This is the content of Proposition 24. This effectively reduces the proof to a extension problem for Engel germs in 
$\unicode[STIX]{x2202}\mathbb{D}^{4}$ to the interior of 
$\mathbb{D}^{4}$. Following the geometric set-up explained in § 2.2, we introduce the following definition.
Definition 22. A convex shell is a 
$2$-distribution 
${\mathcal{D}}=\langle \unicode[STIX]{x2202}_{t},X\rangle$ in 
$\mathbb{D}^{3}\times [0,1]$ such that the curves 
$X_{p}$ are immersed for all 
$p$ and convex at time 
$t$ whenever 
$(p,t)\in {\mathcal{O}}p(\unicode[STIX]{x2202}(\mathbb{D}^{3}\times [0,1]))$.
In particular, 
${\mathcal{D}}$ is everywhere non-integrable and defines a germ of Engel structure along the boundary. A convex shell is said to be solid if 
${\mathcal{D}}$ is everywhere Engel.
The quantitative version reads as follows. Let 
$N$ be a positive integer. A convex shell is 
$N$-convex if there exist:
– a constant
$\unicode[STIX]{x1D700}\in (0,1)$,– functions
$(t_{i}:\mathbb{D}^{3}\longrightarrow (0,\unicode[STIX]{x1D700}))_{i=1,\ldots ,n}$ with $0<t_{1}(p)<\cdots <t_{n}(p)<\unicode[STIX]{x1D700}$, and– a
$\mathbb{D}^{3}$-family of convex curves $(f_{p}:[0,\unicode[STIX]{x1D700}]\longrightarrow \mathbb{R}\mathbb{P}^{2})_{p\in \mathbb{D}^{3}}$ such that $X_{p}=f_{p}^{[1\#t_{1}(p),\ldots ,1\#t_{N}(p)]}.$
The definition of parametric families of 
$N$-convex shells is given by the natural extension to higher-dimensional families of curves.
3.3 Existence of loose Engel families
In this subsection we solve the parametric extension problem for convex shells. We will prove the following version of Theorem 1.
Proposition 23. Let 
$M$ be a smooth 
$4$-manifold, 
$K$ a compact CW-complex, and 
$N$ a positive integer. Then any family 
${\mathcal{D}}_{0}:K\longrightarrow \mathscr{E}^{\text{f}}(M)$ is formally homotopic to an 
$N$-loose family 
${\mathcal{D}}_{1}$.
Fix a family of line fields 
$\mathscr{Y}=(\mathscr{Y}(k))_{k\in K}$ with 
$\mathscr{Y}(k)\subset {\mathcal{D}}_{0}(k)$ transverse to the kernel 
${\mathcal{W}}_{0}(k)$. Then 
${\mathcal{D}}_{1}$ can be assumed to have 
$\mathscr{Y}$ as its certificate of 
$N$-looseness. Additionally, the constant 
$N$ can be taken to be 
$\infty$ if the 
$\mathscr{Y}(k)$ have no closed orbits.
Proposition 23 is proven in two stages, following the structure in 
$h$-principles of reducing to a standard model and then extending the boundary germ to the interior. The first step is achieved in the following proposition.
Proposition 24. Let 
$M$ be a smooth 
$4$-manifold, 
$K$ a compact CW-complex, and 
$N$ a positive integer. Consider a family of formal Engel structures 
${\mathcal{D}}_{0}:K\longrightarrow \mathscr{E}^{\text{f}}(M)$ and line fields 
$\mathscr{Y}(k)\subset {\mathcal{D}}_{0}(k)$ transverse to the formal kernel 
${\mathcal{W}}_{0}(k)$. Then there exist a collection of disjoint balls 
$\{{B_{i}\}}_{i\in I}\subset M\times K$ and a homotopy
$$\begin{eqnarray}\displaystyle {\mathcal{D}}_{s}:K\longrightarrow \mathscr{E}^{\text{f}}(M),\quad s\in [0,1], & & \displaystyle \nonumber\end{eqnarray}$$ such that 
$\mathscr{Y}(k)\subset {\mathcal{D}}_{s}(k)$ is transverse to the formal kernel 
${\mathcal{W}}_{s}(k)$, and
– for each
$i\in I$, ${\mathcal{D}}_{1}|_{B_{i}}$ is a $\mathbb{D}^{\dim (K)}$-family of $N$-convex shells with respect to $\mathscr{Y}$,–
${\mathcal{D}}_{1}(k)$ is Engel in $p\in M$ if $(p,k)\in (M\times K)\setminus \bigcup _{i\in I}B_{i}$.
We will prove Proposition 24 by using the following auxiliary lemma.
Lemma 25. Let 
$M$ be a smooth 
$4$-manifold, 
$K$ a compact CW-complex. Consider a family of formal Engel structures 
${\mathcal{D}}_{0}:K\longrightarrow \mathscr{E}^{\text{f}}(M)$ and line fields 
$\mathscr{Y}(k)\subset {\mathcal{D}}_{0}(k)$ transverse to the formal kernel 
${\mathcal{W}}_{0}(k)$. Then there is a homotopy
$$\begin{eqnarray}\displaystyle {\mathcal{D}}_{s}:K\longrightarrow \mathscr{E}^{\text{f}}(M),\quad s\in [0,1], & & \displaystyle \nonumber\end{eqnarray}$$ such that 
$\mathscr{Y}(k)\subset {\mathcal{D}}_{s}(k)$ is transverse to the formal kernel 
${\mathcal{W}}_{s}(k)$ and the formal even-contact structure 
${\mathcal{E}}_{1}(k)$ is given by 
$[{\mathcal{D}}_{1}(k),{\mathcal{D}}_{1}(k)]$.
Proof. Let us assume first that 
$K$ is a compact manifold. Consider a triangulation 
${\mathcal{T}}$ of 
$M\times K$. Regard the family of line fields 
$\mathscr{Y}$ as a line field in 
$M\times K$. Then assume that the triangulation 
${\mathcal{T}}$ is in general position [Reference ThurstonThu74, Reference ThurstonThu76] with respect to 
$\mathscr{Y}$ and the foliation by fibres of 
$M\times K\longrightarrow K$. In particular, all lower-dimensional simplices are transverse to the line field 
$\mathscr{Y}$.
Now, to each simplex 
$\unicode[STIX]{x1D70E}$ of 
${\mathcal{T}}$ we associate a 
$\mathscr{Y}$-flowbox 
${\mathcal{U}}(\unicode[STIX]{x1D70E})$ such that:
– the set of all such flowboxes is a covering of
$M\times K$;– two flowboxes only intersect each other if one of the simplices is contained in the other;
– if
$\unicode[STIX]{x1D70E}$ is top-dimensional, ${\mathcal{U}}(\unicode[STIX]{x1D70E})$ is obtained from $\unicode[STIX]{x1D70E}$ by a $C^{0}$-small shrinking;– if
$\unicode[STIX]{x1D70E}$ is not top-dimensional, any $\mathscr{Y}$-interval in ${\mathcal{U}}(\unicode[STIX]{x1D70E})$ is either fully contained or completely disjoint from the flowboxes corresponding to subsimplices.
These 
$\mathscr{Y}$-flowboxes are constructed in [Reference Casals, Pérez, del Pino and PresasCPdPP17, Proposition 29]. In short, 
${\mathcal{U}}(\unicode[STIX]{x1D70E})$ is obtained by shrinking 
$\unicode[STIX]{x1D70E}$ and then thickening in the directions complementary to 
$\unicode[STIX]{x1D70E}$.
The 2-distribution 
${\mathcal{D}}_{0}$ can be modified over each 
${\mathcal{U}}(\unicode[STIX]{x1D70E})$ inductively in the dimension of 
$\unicode[STIX]{x1D70E}$, relatively to previous steps. Let us denote by 
${\mathcal{E}}_{0}$ the 
$K$-family of 
$3$-distributions which is part of the formal data. Note that, over each flowbox, the Engel family 
${\mathcal{D}}_{0}$ can be regarded as a 
$\mathbb{D}^{3}\times \mathbb{D}^{\dim (K)}$-family of formal immersions of the interval into the projective plane. Indeed, the 
$2$-distribution 
${\mathcal{D}}_{0}$ provides a family of curves into 
$\mathbb{R}\mathbb{P}^{2}$ and the 
$3$-distribution 
${\mathcal{E}}_{0}$ provides a great circle at each point of the curves. The isomorphism 
$\det ({\mathcal{D}}_{0})\equiv {\mathcal{E}}_{0}/{\mathcal{D}}_{0}$ encoded in the formal data (equation (1)) provides an orientationFootnote 1 of each great circle. Then the relative nature of the Smale–Hirsch theorem [Reference Eliashberg and MishachevEM02, Reference GromovGro86] implies that we can modify the curves so that they become immersions, relative to previous flowboxes. In terms of the formal Engel structure this means that 
${\mathcal{D}}_{0}$ is formally homotopic to a family of non-integrable plane fields that bracket-generate a 
$3$-distribution homotopic to 
${\mathcal{E}}_{0}$.
This proves the claim. For 
$K$ an arbitrary CW-complex, we proceed cell by cell as just explained, using again the fact that the Smale–Hirsch theorem is relative both in parameter and domain.◻
Proof of Proposition 24.
We use the set-up explained in the proof of Lemma 25: we may assume that 
$K$ is a compact manifold. We fix a triangulation 
${\mathcal{T}}$ of 
$M\times K$ in general position with respect to 
$\mathscr{Y}$ and the fibres of 
$M\times K\longrightarrow K$. This allows us to cover 
$M\times K$ by 
$\mathscr{Y}$-flowboxes. By the lemma, we can assume that 
$[{\mathcal{D}}_{0},{\mathcal{D}}_{0}]$ is the 
$3$-distribution 
${\mathcal{E}}_{0}$ given by the formal data.
Now we modify the 2-distribution 
${\mathcal{D}}_{0}$ over each flowbox 
${\mathcal{U}}(\unicode[STIX]{x1D70E})$, inductively in the dimension of 
$\unicode[STIX]{x1D70E}$ for 
$\dim (\unicode[STIX]{x1D70E})<\dim (M\times K)$. We regard the restriction 
${\mathcal{D}}_{0}|_{{\mathcal{U}}(\unicode[STIX]{x1D70E})}$ to each flowbox as a 
$\mathbb{D}^{3}\times \mathbb{D}^{\dim (K)}$-family of immersions 
$X_{p,k}$ of the interval 
$I$ into 
$\mathbb{R}\mathbb{P}^{2}$. The isomorphism 
$\det ({\mathcal{E}}_{0}/{\mathcal{W}}_{0})\equiv TM/{\mathcal{E}}_{0}$ provided by the formal data (equation (2)) provides a local orientationFootnote 2 of 
$\mathbb{R}\mathbb{P}^{2}$; we want the curves 
$X_{p,k}$ to be convex with respect to this orientation.
In line with Proposition 13, we first use Lemma 12 to add arbitrarily many wiggles to each 
$X_{p,k}$ close to the endpoints 
$\unicode[STIX]{x2202}I$ and then we distribute them evenly in the interior 
$I\setminus {\mathcal{O}}p(\unicode[STIX]{x2202}I)$. This is done parametrically in the band 
$\{1-\unicode[STIX]{x1D700}\leqslant |p|,|k|\leqslant 1\}$, with 
$\unicode[STIX]{x1D700}>0$ arbitrarily small. Hence, we can assume that 
$X_{p,k}$ is convex and has arbitrarily many wiggles away from its endpoints if 
$\{|p|,|k|\leqslant 1-\unicode[STIX]{x1D700}\}$. Note that the behaviour of 
$X_{p,k}$ will be quite complicated close to 
$\unicode[STIX]{x2202}I$.
This process is relative to the boundary of the flowbox and it can also be made relative to previous flowboxes: by assumption, the development map of the 2-distribution 
${\mathcal{D}}_{0}$ along a 
$\mathscr{Y}$-curve 
$X_{p,k}$ contained in a previous flowbox is already convex. Since the development map is intrinsically defined, we have precise control over how many wiggles such a 
$X_{p,k}$ has. In particular, it can be assumed to be arbitrarily large by evenly introducing sufficiently many wiggles in the previous steps. Proposition 13 can be applied relative to the set of these curves.
The argument can now be repeated until we reach the top-dimensional cells. The collection of balls 
$\{{B_{i}\}}_{i\in I}$ in the statement of Proposition 24 is taken to be the collection of flowboxes 
${\mathcal{U}}(\unicode[STIX]{x1D70E})\subset \unicode[STIX]{x1D70E}$ with 
$\unicode[STIX]{x1D70E}$ top-dimensional. Since we have added arbitrarily many wiggles along the codimension-1 skeleton, the formal Engel structure is a genuine Engel structure in the boundary of each ball 
$B_{i}$, for all 
$i\in I$. In addition, each ball 
$B_{i}$ is a 
$\mathbb{D}^{\dim (K)}$-family of 
$N$-convex shells as required for the statement. Finally, observe that 
$\mathscr{Y}$ has remained fixed during this formal homotopy, which concludes the proof.◻
Proposition 24 solves the reduction process for Proposition 23. Let us now address the extension problem.
Consider the 
$\mathbb{D}^{\dim (K)}$-families of shells 
$\{{B_{i}\}}_{i\in I}$ produced by Proposition 24. Observe that the restriction of the 2-distribution 
${\mathcal{D}}_{1}|_{B_{i}}$ can be regarded as a 
$\mathbb{D}^{3}\times \mathbb{D}^{\dim (k)}$-family of curves 
$X_{p,k}$ satisfying the hypothesis of Proposition 13. Here 
$\mathbb{D}^{3}\times \mathbb{D}^{\dim (k)}$ plays the role of 
$K$ and 
$A$ is its boundary. From this we deduce that there is a deformation, relative to the boundary of the model, that makes all curves convex. This implies that there is an Engel family 
${\mathcal{D}}_{2}$ that is formally homotopic to 
${\mathcal{D}}_{1}$. Additionally, 
${\mathcal{D}}_{2}|_{B_{i}}$ is an 
$(N-1)$-convex shell, since we only needed to use one of the wiggles during the homotopy. This argument proves the following proposition.
Proposition 26. Let 
$K$ be a compact CW-complex. Any family 
$(\mathbb{D}^{3}\times [0,1],{\mathcal{D}}_{k})_{k\in K}$ of 
$N$-convex shells is homotopic to a family of solid 
$(N-1)$-convex shells. This is relative to the boundary of the shells, and relative to the parameter region in which they are already solid.
Proof of Proposition 23 and Theorem 1.
Consider the shells 
$B_{i}$ constructed in Proposition 24. Since these are obtained by shrinking a top-dimensional simplex of the triangulation 
${\mathcal{T}}$ of 
$M\times K$, every orbit of 
$\mathscr{Y}$ must intersect some ball 
$B_{i}$ in the collection. An application of Proposition 26 turns each 
$B_{i}$ into a solid 
$(N-1)$-convex shell, and therefore 
${\mathcal{D}}_{2}$ is 
$(N-1)$-loose. This proves Theorem 1.
Assume now that 
$\mathscr{Y}$ has no closed orbits. Then every orbit accumulates somewhere and therefore intersects one of the 
$B_{i}$ infinitely many times. Since wiggles are intrinsically defined using the development map, we deduce that each orbit of 
$\mathscr{Y}$ has infinitely many of them and therefore 
${\mathcal{D}}_{1}$ is 
$\infty$-loose.◻
This concludes the existence 
$h$-principle for the class of 
$\infty$-loose Engel structures, as stated in Theorem 3. In particular, we have an existence 
$h$-principle refining our previous result [Reference Casals, Pérez, del Pino and PresasCPdPP17], which we will now further improve to a uniqueness 
$h$-principle.
3.4 Uniqueness of loose Engel families
In this subsection we show that the 
$N$-loose Engel families constructed in Theorem 1 are unique up to homotopy if 
$N$ is large enough. This is precisely the content of Theorem 2; its quantitative nature is in line with other quantitative phenomena appearing in higher-dimensional contact flexibility [Reference Borman, Eliashberg and MurphyBEM15, Reference Casals, Murphy and PresasCMP19]. We have included a discussion on this in § 4.
Theorem 2 will be proven by first showing that any loose family can be homotoped to resemble a family produced by Theorem 1. This is the content of the following proposition.
Proposition 27. Let 
$M$ be a smooth 
$4$-manifold and 
$K$ a compact CW-complex. There exists a positive integer 
$N_{0}$, depending only on the dimension of 
$K$, such that for any
–
$N$-loose family ${\mathcal{D}}_{0}:K\longrightarrow \mathscr{E}(M)$, $N\geqslant N_{0}$, with certificate $\mathscr{Y}$,– triangulation
${\mathcal{T}}$ of $M\times K$ in general position with respect to $\mathscr{Y}$ and $M\times K\rightarrow K$,– covering
$\{{\mathcal{U}}(\unicode[STIX]{x1D70E})\}_{\unicode[STIX]{x1D70E}\in {\mathcal{T}}}$ as in Proposition 24,– non-negative integer
$N_{1}$,
there is a homotopy 
${\mathcal{D}}_{s}:K\longrightarrow \mathscr{E}(M)$ satisfying
–
$\mathscr{Y}(k)\subset {\mathcal{D}}_{s}(k)$ is transverse to the kernel ${\mathcal{W}}_{s}(k)$,–
${\mathcal{D}}_{s}$ is $(N-N_{0})$-loose for all $s$, with $\mathscr{Y}$ as its certificate of looseness,– for any top-dimensional simplex
$\unicode[STIX]{x1D70E}\in {\mathcal{T}}$, ${\mathcal{D}}_{1}|_{{\mathcal{U}}(\unicode[STIX]{x1D70E})}$ is a family of solid $N_{1}$-convex shells.
We will say that a family of Engel structures is simply loose if it is 
$N_{0}$-loose. During the proof we will provide a bound for the constant 
$N_{0}$.
Proof. Since the Engel structure 
${\mathcal{D}}_{0}$ is 
$N$-loose, at any point 
$(p,k)\in M\times K$ we can find an embedded interval 
$\unicode[STIX]{x1D6FE}\subset M\times \{k\}$ tangent to 
$\mathscr{Y}$, containing 
$(p,k)$, and whose development map has 
$N$ wiggles. By thickening such intervals, we find a covering 
$\{{\mathcal{U}}_{i}\}$ of 
$M\times K$ by solid 
$N$-convex shells. It is sufficient for us to show that there is an Engel homotopy 
$({\mathcal{D}}_{s})_{s\in [0,1]}$ through 
$(N-N_{0})$-loose Engel structures such that the development map of 
${\mathcal{D}}_{1}$ has arbitrarily many uniformly distributed wiggles. This can be achieved by modifying the development map inductively over each element 
${\mathcal{U}}_{i}$ of the covering, as follows.
Start with the first shell 
${\mathcal{U}}_{0}$, where 
${\mathcal{D}}_{0}$ is considered as a family of convex intervals 
$(X_{p,k})_{(p,k)\in \mathbb{D}^{3}\times \mathbb{D}^{\dim (k)}}$, and fix 
$\unicode[STIX]{x1D700}>0$ arbitrarily small. Since we have 
$N$ wiggles, we can apply Proposition 13 to one of them to produce arbitrarily many more wiggles in the region 
$\{|p|,|k|\leqslant 1-\unicode[STIX]{x1D700}\}$. These wiggles can be assumed to be uniformly distributed in the domain. Note that in doing this, the wiggle we chose in the region 
$\{1-\unicode[STIX]{x1D700}\leqslant |p|\}\cup \{1-\unicode[STIX]{x1D700}\leqslant |k|\}$ disappears as Little’s homotopy is performed. In particular, 
${\mathcal{U}}_{0}$ is only an 
$(N-1)$-convex shell for the new Engel structure.
Now consider 
${\mathcal{U}}_{1}$ and suppose that it intersects 
${\mathcal{U}}_{0}$. From the perspective of 
${\mathcal{U}}_{1}$, the homotopy in 
${\mathcal{U}}_{0}$ could have destroyed two wiggles. Indeed, the wiggle we used for the homotopy in 
${\mathcal{U}}_{0}$ may intersect at most two wiggles in 
${\mathcal{U}}_{1}$ (see Remark 9). However, if we assume that 
$N>2$, there is at least one wiggle remaining and we can repeat the argument above. This allows us to arbitrarily increase the number of wiggles in the interior of 
${\mathcal{U}}_{1}$. It is natural to proceed by repeating this process inductively over the covering index 
$i$. In order to do that, denote the projection to the orbit space by 
$\unicode[STIX]{x1D70B}:{\mathcal{U}}_{i}\longrightarrow U_{i}={\mathcal{U}}_{i}/\mathscr{Y}$, where each 
$U_{i}$ is diffeomorphic to 
$\mathbb{D}^{3}\times \mathbb{D}^{\dim (K)}$.
The main geometric ingredient in the proof is showing that the covering 
$\{{\mathcal{U}}_{i}\}$ can be chosen such that:
(I) only
$N_{0}-1$ of the wiggles of a given shell ${\mathcal{U}}_{i}$ get destroyed by previous homotopies;(II) there exists a continuous section
$U_{i}\longrightarrow {\mathcal{U}}_{i}$ that provides a marked wiggle in each flowline.
For that, fix a cover 
$\{{\mathcal{V}}_{i}\}$ using the process described in the first paragraph, and write
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{i}:{\mathcal{V}}_{i}\longrightarrow V_{i}={\mathcal{V}}_{i}/\mathscr{Y} & & \displaystyle \nonumber\end{eqnarray}$$ for the canonical projection. The intersection 
$\unicode[STIX]{x1D70B}_{i}(\unicode[STIX]{x2202}{\mathcal{V}}_{i^{\prime }}\bigcap {\mathcal{V}}_{i})$ defines a codimension-
$1$ submanifold 
$S_{i^{\prime }}\subset V_{i}$, and by a small perturbation of the flowboxes 
$\{{\mathcal{V}}_{i^{\prime }}\}$, we can assume that the submanifolds 
$\{{S_{i^{\prime }}\}}_{i^{\prime }\neq i}$ of 
$V_{i}$ intersect transversely. In particular, a point in 
$V_{i}$ may only lie in 
$C=\dim (K)+4$ different manifolds 
$S_{i^{\prime }}$. In the previous steps (
$i^{\prime }<i$) of the induction, Little’s homotopy destroyed two wiggles in each region 
${\mathcal{O}}p(\unicode[STIX]{x2202}{\mathcal{V}}_{i^{\prime }})$. Hence, by setting 
$N_{0}\geqslant 2C+1$, it follows that each 
$\mathscr{Y}|_{{\mathcal{V}}_{i}}$ flowline contains still one wiggle, so condition (I) holds.
In order to show that the wiggles can be chosen in a continuous way (condition (II)), we construct a finer covering 
$\{{\mathcal{U}}_{i}^{j}\}$ of 
$M\times K$. This is done inductively on 
$i$ as follows. Set 
${\mathcal{U}}_{0}^{0}={\mathcal{V}}_{0}$ and fix some continuous choice of wiggle 
$V_{0}\longrightarrow {\mathcal{V}}_{0}$. Suppose that we have already subdivided all 
${\mathcal{V}}_{i^{\prime }}$ with 
$i^{\prime }<i$, yielding some partial covering 
${\{{\mathcal{U}}_{i^{\prime }}^{j}\}}_{i^{\prime }<i}$ with corresponding choices of wiggles 
$\{\unicode[STIX]{x1D70B}_{i^{\prime }}({\mathcal{U}}_{i^{\prime }}^{j})\longrightarrow {\mathcal{U}}_{i^{\prime }}^{j}\}$. Now choose a very fine triangulation 
${\mathcal{T}}_{i}$ of 
$V_{i}$ and fix small contractible open neighbourhoods 
$\{U_{i}^{j}\}$ of each simplex in 
${\mathcal{T}}_{i}$. Then 
$\{{\mathcal{U}}_{i}^{j}=\unicode[STIX]{x1D70B}_{i}^{-1}(U_{i}^{j})\}$ is a covering of 
${\mathcal{V}}_{i}$ by flowboxes and we claim that this is enough to conclude.
Indeed, using transversality as above, we can assume that each point in 
$\unicode[STIX]{x1D70B}_{i}({\mathcal{U}}_{i}^{j})\subset V_{i}$ meets at most 
$C$ of the manifolds 
${\{\unicode[STIX]{x1D70B}_{i}(\unicode[STIX]{x2202}{\mathcal{U}}_{i^{\prime }}^{j^{\prime }}\cap {\mathcal{U}}_{i}^{j})\}}_{i^{\prime }<i}$. Additionally, there is a constant 
$D$, depending only on 
$\dim (K)$, bounding from above the number of simplices of 
${\mathcal{T}}_{i}$ intersecting a given simplex. Therefore, 
${\mathcal{U}}_{i}^{j}$ intersects at most 
$D$ of the flowboxes 
${\{{\mathcal{U}}_{i}^{j^{\prime }}\}}_{j^{\prime }\neq j}$. Condition (I) then holds by setting 
$N_{0}\geqslant 2C+2D+1$. Additionally, if 
${\mathcal{T}}_{i}$ is fine enough, each element 
$U_{i}^{j}$ is a neighbourhood of a point so it is possible to make a continuous choice of wiggle.◻
We will need one more ingredient before we prove Theorem 2.
Proposition 28 [Reference Peralta-Salas, del Pino and PresasPdPP16].
Denote by 
$\mathfrak{X}(M)$ the space of line fields on a manifold 
$M$. Denote by 
$\mathfrak{X}_{\operatorname{n.o.}}(M)\subset \mathfrak{X}(M)$ the subset of line fields without periodic orbits. The inclusion 
$\mathfrak{X}_{\operatorname{n.o.}}(M)\subset \mathfrak{X}(M)$ induces a weak homotopy equivalence provided that 
$\dim (M)\geqslant 3$.
This result relies on the existence of parametric versions of the plugs of Wilson and Kuperberg. In particular, it states that the choice of a line field without periodic orbits in the statement of Theorem 3 is not a restriction from a homotopical point of view.
Proof of Theorem 2.
Let 
$\mathscr{Y}_{i}\subset {\mathcal{D}}_{i}$ be the certificate of 
$N$-looseness of 
${\mathcal{D}}_{i}$, and fix
$$\begin{eqnarray}\displaystyle \tilde{{\mathcal{D}}}:K\times [0,1]\longrightarrow \mathscr{E}^{\text{f}}(M) & & \displaystyle \nonumber\end{eqnarray}$$ a family of formal Engel structures connecting 
${\mathcal{D}}_{0}$ and 
${\mathcal{D}}_{1}$. Write 
$\tilde{{\mathcal{W}}}$ for the formal kernel of 
$\tilde{{\mathcal{D}}}$. Fix a family of line fields 
$\mathscr{Y}\subset \tilde{{\mathcal{D}}}$ connecting 
$\mathscr{Y}_{0}$ and 
$\mathscr{Y}_{1}$ and transverse to 
$\tilde{{\mathcal{W}}}$. Construct a triangulation 
${\mathcal{T}}$ of 
$M\times K\times [0,1]$ in general position with 
$\mathscr{Y}$, in general position with 
$M\times K\times [0,1]\longrightarrow K\times [0,1]$, and restricting to triangulations 
${\mathcal{T}}_{i}$ on 
$M\times K\times \{i\}$ also in general position [Reference Casals, Pérez, del Pino and PresasCPdPP17, Reference ThurstonThu76].
Then apply Proposition 27 to achieve that for any top-dimensional simplex 
$\unicode[STIX]{x1D70E}\in {\mathcal{T}}_{i}$, the restriction 
${\mathcal{D}}_{i}|_{{\mathcal{U}}(\unicode[STIX]{x1D70E})}$ is a family of solid 
$N_{1}$-convex shells. This allows us to apply the reduction in Proposition 24 relative to the ends 
$M\times K\times \{0,1\}$. Then Proposition 26 can be used to achieve the Engel condition in the interior of the top cells. Following the proof of Theorem 1, we have deformed the 2-distribution 
$\tilde{{\mathcal{D}}}$ to a family of Engel structures 
${\mathcal{D}}:K\times I\longrightarrow \mathscr{E}(M)$. By construction, the 2-distribution 
${\mathcal{D}}$ restricts to 
${\mathcal{D}}_{i}$ in 
$M\times K\times \{i\}$ as desired. Finally, if 
$\mathscr{Y}_{0}$ and 
$\mathscr{Y}_{1}$ have no periodic orbits, the same can be assumed about 
$\mathscr{Y}$ after an application of Proposition 28. Therefore, if the Engel structure 
${\mathcal{D}}_{i}$ is 
$\infty$-loose, the same holds for the homotopy 
${\mathcal{D}}$.◻
3.5 Proof of Theorem 3
Consider a family 
${\mathcal{D}}:(\mathbb{D}^{k},\unicode[STIX]{x2202}\mathbb{D}^{k})\longrightarrow (\mathscr{E}^{\text{f}}(M,\mathscr{Y}),\mathscr{L}(M,\mathscr{Y}))$. Theorem 1 implies that 
${\mathcal{D}}(0)$ can be homotoped to be 
$\infty$-loose. Then we can regard 
${\mathcal{D}}$ as a formal homotopy between the family 
${\mathcal{D}}|_{\unicode[STIX]{x2202}\mathbb{D}^{k}}$ and the constant family 
${\mathcal{D}}(0)$. Applying Theorem 2 shows that 
${\mathcal{D}}$ can be homotoped to have image in 
$\mathscr{L}(M,\mathscr{Y})$, as desired.◻
This concludes the 
$h$-principle for loose Engel structures.
4 Applications
In this section we prove Corollary 4 on Engel prolongations, and discuss two additional families of examples of loose Engel structures. It follows from Theorem 2 that these families satisfy the 
$h$-principle, and thus exhibit completely flexible behaviour.
4.1 Prolongations
Cartan introduced in [Reference CartanCar24] the notion of prolongation for contact structures and Lorentzian metrics, which we exploited in recent work [Reference Casals, Pérez, del Pino and PresasCPdPP17] to manipulate Engel structures locally. Let us review these two constructions and prove Corollary 4.
Let 
$V$ be a smooth oriented 
$3$-manifold and 
$\unicode[STIX]{x1D709}$ an oriented 
$2$-plane distribution. By definition, the associated oriented formal Cartan prolongation 
$(M(\unicode[STIX]{x1D709}),{\mathcal{D}}(\unicode[STIX]{x1D709}))$ is the sphere bundle 
$M(\unicode[STIX]{x1D709}):=\mathbb{S}(\unicode[STIX]{x1D709})\stackrel{\unicode[STIX]{x1D70B}}{\longrightarrow }V$ endowed with the tautological distribution
$$\begin{eqnarray}\displaystyle {\mathcal{D}}(\unicode[STIX]{x1D709})(p,l)=\unicode[STIX]{x1D70B}^{\ast }[l]. & & \displaystyle\end{eqnarray}$$ The distribution is Engel if and only if 
$\unicode[STIX]{x1D709}$ is a contact distribution. Indeed, this is condition (B) in Proposition 6. In this case, the Engel structure 
$(M(\unicode[STIX]{x1D709}),{\mathcal{D}}(\unicode[STIX]{x1D709}))$ is called the Cartan prolongation of the contact structure 
$\unicode[STIX]{x1D709}$.
Suppose instead that the 
$3$-manifold manifold 
$V$ is endowed with a Lorentzian metric 
$g$. The kernel 
$C_{g}$ of the Lorentzian metric, known as the light cone, defines a sphere bundle 
$M(g):=\mathbb{P}(C_{g})\stackrel{\unicode[STIX]{x1D70B}}{\longrightarrow }V$ endowed with a tautological distribution 
${\mathcal{D}}(g)$ defined again by equation (3). This distribution is always an Engel structure, since it satisfies condition (A) in Proposition 6. By definition, the Engel structure 
$(M(g),{\mathcal{D}}(g))$ is the Lorentz prolongation of 
$g$.
A particular case which is of interest to us is as follows. Consider an orientable and coorientable plane field 
$\unicode[STIX]{x1D709}$. Endow it with a metric 
$g_{\unicode[STIX]{x1D709}}$ and pick a complementary vector field 
$\unicode[STIX]{x1D708}$. Then the pair 
$(g_{\unicode[STIX]{x1D709}},\unicode[STIX]{x1D708})$ defines a family of Lorentz metrics 
$(g_{r})_{r\in \mathbb{R}^{+}}$ by declaring the vector field 
$\unicode[STIX]{x1D708}$ to be orthogonal to 
$\unicode[STIX]{x1D709}$ and of norm 
$-r$. As 
$r$ goes to infinity, the light cone 
$C_{g_{r}}$ converges to the plane field 
$\unicode[STIX]{x1D709}$. We can apply the prolongation construction parametrically in 
$r$. This allows us to think of the structures 
$(M(g_{r}),{\mathcal{D}}(g_{r}))$ as convex push-offs [Reference del PinodP18] of the formal Cartan prolongation 
$(M(\unicode[STIX]{x1D709}),{\mathcal{D}}(\unicode[STIX]{x1D709}))$.
Conversely, given any Lorentz structure 
$g$ and any space-like plane field 
$\unicode[STIX]{x1D709}$, there exists a unique line complement such that 
$g$ is a push-off of a metric in 
$\unicode[STIX]{x1D709}$ by the recipe above.
Corollary 4 states that these Engel structures are all loose. The key ingredient is the observation that the light-cone intersects the unit sphere in a convex curve which is embedded (i.e. a wiggle).
Proof of Corollary 4.
Let 
$K$ be a compact parameter space, 
${\mathcal{D}}$ a 
$K$-family of Lorentz prolongations, and 
$\unicode[STIX]{x1D709}$ a 
$K$-family of plane fields in 
$V$ such that 
${\mathcal{D}}(k)$ is a convex push-off of 
${\mathcal{D}}(\unicode[STIX]{x1D709}(k))$ given by a family of functions 
$r(k)$ (and a corresponding family of metrics in the plane fields 
$\unicode[STIX]{x1D709}(k)$). By performing an Engel homotopy, given by increasing the real numbers 
$r(k)$, we can assume that 
$d\unicode[STIX]{x1D70B}({\mathcal{D}}(k))$ is arbitrarily close to 
$\unicode[STIX]{x1D708}(k)$, where 
$\unicode[STIX]{x1D708}(k):V\longrightarrow TV$, 
$k\in K$, is a vector field transverse to 
$\unicode[STIX]{x1D709}(k)$.
Now consider a family of line fields 
$\mathscr{Y}_{s}(k)\subset {\mathcal{D}}(k)$, 
$s\in [0,1]$, spanned by vector fields 
$Y_{s}(k)$, with 
$\mathscr{Y}_{0}(k)$ contained in the fibre direction and all others transverse to it. Over any 
$3$-disc in 
$V$ (lifted to the fibre bundle by taking a section), the vector fields 
$Y_{s}(k)$ provide a family of return maps 
$\unicode[STIX]{x1D719}_{k,s}$, with 
$\unicode[STIX]{x1D719}_{k,0}$ the identity.
We claim that, for any fixed 
$N\in \mathbb{N}$, the iterates of the return maps
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{k,s}^{(j)},\quad j=1,\ldots ,N, & & \displaystyle \nonumber\end{eqnarray}$$ have no fixed points if 
$s\neq 0$ is close enough to 
$0$. Indeed, since we have pushed the prolongations to be very convex, 
$\unicode[STIX]{x1D719}_{k,s}^{(j)}$ becomes a map that approximates an arbitrarily short time flow of 
$\unicode[STIX]{x1D708}(k)$. By compactness of 
$V$, the map cannot have fixed points. Now the claim follows by taking 
$N$ larger than the universal constant 
$N_{0}$ corresponding to a family of dimension 
$\dim (K)$: the resulting family of Engel structures is 
$N$-loose. This proves the claim in the Lorentz case. Suppose now that 
${\mathcal{D}}$ is family of orientable Cartan prolongations. Then 
${\mathcal{D}}$ is homotopic to a family of Lorentz prolongations by a convex push-off, which proves the statement as desired.◻
A striking consequence of Corollary 4 is that, given two non-isotopic contact structures homotopic as plane fields, their Cartan prolongations are Engel homotopic. In particular, any non-formal contact invariant becomes formal by taking Cartan prolongations.
Remark 29. In the literature (see, for instance, [Reference del PinodP18]) a more general notion of Cartan prolongation is considered. Assume, imposing the obvious condition on the Euler class, that there is a sphere bundle 
$E$ that 
$m:\!1$ covers 
$\mathbb{S}(\unicode[STIX]{x1D709})$. We can then define Engel structures on 
$E$ by pulling back 
${\mathcal{D}}(\unicode[STIX]{x1D709})$; similarly, we can construct 
$m:\!1$ coverings of Lorentzian prolongations. The general statement is then that, given 
${\mathcal{D}}:K\rightarrow \mathscr{E}(M)$ and 
$\unicode[STIX]{x1D70B}:\hat{M}\rightarrow M$ a 
$m:\!1$ cover, we can construct a family 
$\unicode[STIX]{x1D70B}^{\ast }{\mathcal{D}}:K\rightarrow \mathscr{E}(M)$ by pull-back. If 
${\mathcal{D}}$ is 
$N$-loose, then 
$\unicode[STIX]{x1D70B}^{\ast }{\mathcal{D}}$ is 
$mN$-loose.
4.2 Other loose families in the literature
In this subsection we show that the families of Engel structures constructed in [Reference Casals, Pérez, del Pino and PresasCPdPP17] and [Reference Colin, Presas and VogelCPV18] are loose. This is shown for the former class in the following proposition.
Proposition 30. Let 
$M$ be a closed 
$4$-manifold and let 
$K$ be a compact manifold. Any family of Engel structures 
${\mathcal{D}}:K\longrightarrow \mathscr{E}(M)$ constructed using the 
$h$-principle in [Reference Casals, Pérez, del Pino and PresasCPdPP17] is loose up to Engel homotopy.
Proof. The construction in [Reference Casals, Pérez, del Pino and PresasCPdPP17] produces a family 
${\mathcal{D}}:K\longrightarrow \mathscr{E}(M)$ of Engel structures with corresponding line fields 
$\mathscr{Y}:K\longrightarrow \mathfrak{X}(M)$, 
$\mathscr{Y}(k)\subset {\mathcal{D}}(k)$, such that the associated development maps 
$\unicode[STIX]{x1D6FE}_{\mathscr{Y}(k)}({\mathcal{D}}(k))$ satisfy the following requirements.
– The curves
$\unicode[STIX]{x1D6FE}_{\mathscr{Y}(k)}({\mathcal{D}}(k))_{p}$ are immersed and weakly convex.– There is a finite number of disjoint
$3$-weakly convex shells ${\mathcal{U}}_{i}$ that together cover the orbit space $(M\times K)/\mathscr{Y}$.
A curve in 
$\mathbb{R}\mathbb{P}^{2}$ is said to be weakly convex if its curvature is greater than or equal to zero. Weakly convex wiggles and 
$N$-weakly convex shells are defined in the natural manner. The balls 
${\mathcal{U}}_{i}$ are of the form introduced in Proposition 24: they are flowboxes obtained by shrinking the top cells of a triangulation of 
$M\times K$ in general position with respect to 
$\mathscr{Y}$.
It follows from Proposition 6 that 
$\mathscr{Y}(k)_{p}={\mathcal{W}}(k)_{p}$ if and only if the development map has an inflection point at 
$p$. This implies that the tangencies, defined by 
$\mathscr{Y}(k)={\mathcal{W}}(k)$, are all degenerate and there is a 
$C^{\infty }$-perturbation 
$\mathscr{Y}^{\prime }\subset {\mathcal{D}}$ of 
$\mathscr{Y}$ that is everywhere transverse to 
${\mathcal{W}}$. The development map of 
${\mathcal{D}}$ along 
$\mathscr{Y}^{\prime }$ is everywhere convex. We can then perturb the collection 
$\{{\mathcal{U}}_{i}\}$ to a collection of 
$\mathscr{Y}^{\prime }$-flowboxes 
$\{{\mathcal{U}}_{i}^{\prime }\}$ covering the orbit space 
$(M\times K)/\mathscr{Y}^{\prime }$ such that 
${\mathcal{U}}_{i}^{\prime }$ is a 
$3$-convex shell. By applying Proposition 13 we can deform the Engel structure on each 
${\mathcal{U}}_{i}^{\prime }$ so that it becomes a solid 
$N$-convex shell, with 
$N$ arbitrarily large. This produces a new family 
${\mathcal{D}}^{\prime }:K\longrightarrow \mathscr{E}(M)$. Since each orbit of 
$\mathscr{Y}^{\prime }$ intersects at least one 
$U_{i}$, we obtain that the family is loose with 
$\mathscr{Y}^{\prime }$ its certificate of looseness.◻
Remark 31. The following is a technical observation. The Engel structures constructed in [Reference Casals, Pérez, del Pino and PresasCPdPP17] depend on a real parameter 
$E>0$ that needs to be chosen large enough. There is also an increasing function 
$N:\mathbb{R}^{+}\longrightarrow \mathbb{Z}^{+}$, such that 
$\lim _{E\longrightarrow \infty }N(E)=\infty$. Now, the families of Engel structures 
${\mathcal{D}}:K\longrightarrow \mathscr{E}(M)$ constructed using the 
$h$-principle in [Reference Casals, Pérez, del Pino and PresasCPdPP17] satisfy that the open balls 
${\mathcal{U}}_{i}^{\prime }$ are 
$N(E)$-convex shells. Hence, for 
$E$ large enough, the original family is already loose, without having to deform it.
The recent article [Reference Colin, Presas and VogelCPV18] constructs Engel structures adapted to open books, in line with the contact Giroux correspondence. Away from the binding, which is a disjoint union of tori, the structures can be understood as Cartan prolongations of a contact manifold with trivial Euler class. The following statement is proven in [Reference Colin, Presas and VogelCPV18].
Proposition 32. The Engel structures constructed in [Reference Colin, Presas and VogelCPV18] are loose.
Proof. The construction in [Reference Colin, Presas and VogelCPV18] depends on a constant 
$k\in \mathbb{Z}^{+}$ which measures the number of turns performed by the Engel structure in terms of a Legendrian framing on the page. We denote by 
${\mathcal{D}}_{k}$ the Engel structure that turns 
$k$ times. In order to extend it to the binding we need a canonical model on it that requires 
$k$ to be odd. Little’s homotopy implies that 
${\mathcal{D}}_{k}$ and 
${\mathcal{D}}_{k+2}$ are homotopic. For 
$k$ large enough the structure is loose, since the number 
$k$ precisely accounts for the turning of 
${\mathcal{D}}_{k}$ in terms of the development map.◻
Acknowledgements
The authors are grateful to the American Institute of Mathematics and to the organizers and participants of the ‘Engel structures’ workshop for their interest in this work. They are particularly thankful to T. Vogel for reading a preliminary version of these results. The authors are also grateful to the referees of this paper, whose suggestions and comments have greatly improved the present work. The authors are supported by Spanish National Research Projects MTM2016–79400–P, MTM2015-72876-EXP and SEV2015-0554. R. Casals is supported by the NSF grant DMS-1841913 and a BBVA Research Fellowship. Á. del Pino is supported by the NWO Vici Grant no. 639.033.312 of Marius Crainic.
Appendix A Flexibility in Engel and contact topology
In this appendix we discuss the interaction between Engel structures [Reference Casals and del PinoCdP18, Reference Casals, Pérez, del Pino and PresasCPdPP17], contact structures [Reference EliashbergEli89, Reference GeigesGei08], and the 
$h$-principle [Reference Eliashberg and MishachevEM02, Reference GromovGro86]. Our aim is to study the manifestations and subtleties of the 
$h$-principle as seen from the recent new perspectives [Reference Borman, Eliashberg and MurphyBEM15, Reference Casals, Pérez, del Pino and PresasCPdPP17, Reference del Pino and VogeldPV18, Reference VogelVog18]. Let us start with contact structures as the prism through which we are used to looking at the 
$h$-principle.
A.1 Contact flexibility
Even though contact structures do not abide by the 
$h$-principle [Reference GeigesGei08], there is a subset of overtwisted contact structures whose behaviour is flexible, that is, their classification up to homotopy is governed by the underlying formal data. This display of flexibility is precise at the 
$\unicode[STIX]{x1D70B}_{0}$-level, but for higher homotopy groups the picture is more subtle, as we explain.
Let 
$N$ be a closed orientable 
$(2n+1)$-manifold, 
$\mathscr{C}^{\text{f}}(N,\unicode[STIX]{x1D6E5})$ the space of almost contact structures with overtwisted disc 
$\unicode[STIX]{x1D6E5}$ [Reference GromovGro86], and 
$\mathscr{C}_{\operatorname{OT}}(N,\unicode[STIX]{x1D6E5})$ the subspace of contact structures also overtwisted with disc 
$\unicode[STIX]{x1D6E5}$. The main result in [Reference Borman, Eliashberg and MurphyBEM15, Reference EliashbergEli89] is that the forgetful inclusion
$$\begin{eqnarray}\displaystyle \mathscr{C}_{\operatorname{OT}}(N,\unicode[STIX]{x1D6E5})\longrightarrow \mathscr{C}^{\text{f}}(N,\unicode[STIX]{x1D6E5}) & & \displaystyle \nonumber\end{eqnarray}$$ is a weak homotopy equivalence. This is where the first subtlety arises: the overtwisted disk 
$\unicode[STIX]{x1D6E5}$ has been fixed. Recently, it has been shown that the space of overtwisted contact structures does not necessarily have the homotopy type of the space of formal contact structures [Reference VogelVog18]. This failure of flexibility is precisely related to the homotopy type of the space of overtwisted discs in a fixed contact structure.
The articles [Reference Borman, Eliashberg and MurphyBEM15, Reference EliashbergEli89] actually prove a stronger result, in which the overtwisted disc is allowed to vary. Let 
$\unicode[STIX]{x1D709}_{0},\unicode[STIX]{x1D709}_{1}:K\longrightarrow \mathscr{C}(N)$ be two 
$K$-families of contact structures, with 
$K$ a compact CW-complex. Let 
$\unicode[STIX]{x1D6E5}_{0},\unicode[STIX]{x1D6E5}_{1}$ be corresponding 
$K$-families of overtwisted discs and assume that there is a homotopy of pairs 
$(\unicode[STIX]{x1D709}_{t},\unicode[STIX]{x1D6E5}_{t})$ with 
$\unicode[STIX]{x1D709}_{t}:K\longrightarrow \mathscr{C}^{\text{f}}(N)$ having 
$\unicode[STIX]{x1D6E5}_{t}$ as overtwisted discs. Then the families 
$\unicode[STIX]{x1D709}_{0}$ and 
$\unicode[STIX]{x1D709}_{1}$ are homotopic through contact structures relative to 
$\unicode[STIX]{x1D6E5}_{t}$. Conversely, if 
$\unicode[STIX]{x1D709}_{t}:K\longrightarrow \mathscr{C}(N)$ is a homotopy between 
$\unicode[STIX]{x1D709}_{0}$ and 
$\unicode[STIX]{x1D709}_{1}$, and 
$\unicode[STIX]{x1D709}_{0}$ admits a family of overtwisted discs 
$\unicode[STIX]{x1D6E5}_{0}$, we deduce from Gray stability that 
$\unicode[STIX]{x1D709}_{t}$ lifts to a homotopy of pairs 
$(\unicode[STIX]{x1D709}_{t},\unicode[STIX]{x1D6E5}_{t})$.
That is, the 
$K$-family 
$\unicode[STIX]{x1D709}_{0}$ exhibits flexible behaviour if a choice of 
$\unicode[STIX]{x1D6E5}_{0}$ exists. This leads us to introduce the following definition, formalizing a ubiquitous idea in the theory of 
$h$-principles [Reference Eliashberg and MishachevEM02].
Definition A.1. Let 
$\unicode[STIX]{x1D709}_{0}$ be a 
$K$-family of contact structures. A continuous choice of 
$\unicode[STIX]{x1D6E5}_{0}$ is said to be a certificate of overtwistedness for the overtwisted family 
$\unicode[STIX]{x1D709}_{0}$.
A.1.1 Overtwisted classes
The 
$h$-principle in contact geometry does not hold without the mediation of a certificate, and the central obstruction is its homotopy type. At the most basic level, the family 
$\unicode[STIX]{x1D709}_{0}$ might not even admit a continuous choice of certificate 
$\unicode[STIX]{x1D6E5}_{0}$, even if all the structures are individually overtwisted. This is known to happen [Reference VogelVog18]: there exists a formally contractible loop of overtwisted contact structures in 
$\mathbb{S}^{3}$ that admits no certificate and therefore is not contractible geometrically.
Two overtwisted families of contact structures may be formally homotopic but have certificates in different homotopy classes. However, there is a stable range in which this obstruction vanishes and an algebraic form of the 
$h$-principle holds: recall the forgetful inclusion 
$i:\mathscr{C}(N)\longrightarrow \mathscr{C}^{\text{f}}(N)$, and fix an overtwisted basepoint 
$\unicode[STIX]{x1D709}\in \mathscr{C}(N)\subset \mathscr{C}^{\text{f}}(N)$. We consider the homotopy groups 
$\unicode[STIX]{x1D70B}_{k}(\mathscr{C}(N))$ and 
$\unicode[STIX]{x1D70B}_{k}(\mathscr{C}^{\text{f}}(N))$ based at 
$\unicode[STIX]{x1D709}$. A class 
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D70B}_{k}(\mathscr{C}(N))$ is said to be overtwisted if it can be represented by an overtwisted family.
Proposition A.2. Let 
$N$ be a closed 
$(2n+1)$-manifold. Consider the subgroup 
$\operatorname{OT}_{k}(N)\subset \unicode[STIX]{x1D70B}_{k}(\mathscr{C}(N))$ consisting of overtwisted classes, for 
$0\leqslant k\leqslant 2n$. Then the inclusion 
$\unicode[STIX]{x1D70B}_{k}(i):\operatorname{OT}_{k}(N)\longrightarrow \unicode[STIX]{x1D70B}_{k}(\mathscr{C}^{\text{f}}(N))$ is a group isomorphism.
Proof. Let 
$\unicode[STIX]{x1D709}:\mathbb{S}^{k}\longrightarrow \mathscr{C}(N)$ be an overtwisted family of contact structures with certificate 
$\unicode[STIX]{x1D6E5}$. Since 
$k<2n+1$, after an isotopy we may assume that there is a point 
$p\in N$ which is not contained in any of the overtwisted discs 
$\unicode[STIX]{x1D6E5}(a)$, 
$a\in \mathbb{S}^{k}$. This allows us to use the 
$h$-principle to introduce an overtwisted disc at 
$p$, for all 
$\unicode[STIX]{x1D709}(a)$. Even if they are all based at the same point, the family of overtwisted discs might be non-trivial, but this non-triviality is carried by the formal type of the family 
$\unicode[STIX]{x1D709}$ encoded by the value of the distribution 
$\unicode[STIX]{x1D709}(a)$ at the point 
$p$. Any formal homotopy between overtwisted families having overtwisted discs centred at a fixed point lifts to a homotopy of pairs, concluding the proof.◻
We say that a class not belonging to the overtwisted subgroup 
$\operatorname{OT}_{k}(N)$ is a tight class. T. Vogel’s loop of overtwisted contact structures [Reference VogelVog18] is the first instance of a one-dimensional tight family of individually overtwisted contact structures.
A.1.2 Tight classes
One can also observe that the tight classes have a natural group structure. First, we claim that 
$\operatorname{Tight}_{k}(N)=\unicode[STIX]{x1D70B}_{k}(\mathscr{C}(N))/\operatorname{OT}_{k}(N)$ is a group, 
$k>0$. For this to hold, we must show that 
$\operatorname{OT}_{k}(N)$ is a normal subgroup. If 
$2\leqslant k\leqslant 2n$, this is true since the groups are abelian. For 
$k=1$, we have the following sequence of inclusions:
$$\begin{eqnarray}\displaystyle \operatorname{OT}_{1}(N)\rightarrow \unicode[STIX]{x1D70B}_{1}(\mathscr{C}(N))\stackrel{\unicode[STIX]{x1D70B}_{1}(i)}{\rightarrow }\unicode[STIX]{x1D70B}_{1}(\mathscr{C}^{\text{f}}(N))\simeq \operatorname{OT}_{1}(N). & & \displaystyle \nonumber\end{eqnarray}$$ And therefore 
$\operatorname{Tight}_{1}(N)$ is the kernel of the map 
$\unicode[STIX]{x1D70B}_{1}(i)$. Then we may interpret the quotient 
$\operatorname{Tight}_{k}(N)$ as a subgroup of 
$\unicode[STIX]{x1D70B}_{k}(\mathscr{C}(N))$: it corresponds precisely to the homotopy classes of contact spheres that are homotopically trivial as almost contact spheres. Left multiplication with the overtwisted representative identifies the fibres over any other formal class, and therefore all the fibres of the map 
$\unicode[STIX]{x1D70B}_{k}(i)$ are conjugated subgroups.
This stands in sharp contrast to the case 
$k=0$: the projection map 
$\unicode[STIX]{x1D70B}_{0}(\mathscr{C}(\mathbb{S}^{3}))\rightarrow \operatorname{OT}_{0}(\mathbb{S}^{3})$ has one element in each fibre except for the fibre containing the standard contact structure, which contains two [Reference EliashbergEli89, Reference EliashbergEli92].
A.2 Engel flexibility
We can now look at the same concepts through the lens of Engel topology.
A.2.1 Local and global
Engel looseness differs from contact overtwistedness in that the definition of certificate we have given is not local. The contact overtwisted disc is a particular model in a ball (or a particular contact germ over a 
$2n$-disc). In contrast, Engel looseness must be checked globally on the manifold 
$M$ using the line field 
$\mathscr{Y}$.
In [Reference del Pino and VogeldPV18] a local Engel overtwisted disc is defined. It allows flexibility to be proven in a manner that is analogous to the contact case. The main result there reads as follows. Let 
$\mathscr{E}_{\operatorname{OT}}(M,\unicode[STIX]{x1D6E5})$ be the space of Engel structures on 
$M$ having 
$\unicode[STIX]{x1D6E5}$ as a (local) overtwisted disc. Let 
$\mathscr{E}^{\text{f}}(M,\unicode[STIX]{x1D6E5})$ be the corresponding formal space. Then the inclusion 
$\mathscr{E}_{\operatorname{OT}}(M,\unicode[STIX]{x1D6E5})\rightarrow \mathscr{E}^{\text{f}}(M,\unicode[STIX]{x1D6E5})$ is a weak homotopy equivalence. Statements where the overtwisted disc is allowed to move parametrically also hold and overtwisted homotopy subgroups can be defined as well.
This leads to a surprising situation. On the one hand, Engel flexibility holds once a particular local model is found in the manifold; this is a consequence of the fact that the overtwisted disc appears to be the necessary ingredient to solve the Engel extension problem for any germ on 
$\unicode[STIX]{x2202}\mathbb{D}^{4}$. On the other hand, families that seemingly do not possess this local model might still behave flexibly if they ‘turn sufficiently with respect to some line field’, that is, they are loose.
We then observe that looseness cannot yield an 
$h$-principle relative in the domain, as overtwistedness does. The reason behind this is that the reduction process (achieving enough convexity in the codimension-
$1$ skeleton, Proposition 24) cannot be completed when the Engel structure is already fixed in some part of the domain (possibly having very little convexity). In particular, the problem of extension of a germ in 
$\unicode[STIX]{x2202}\mathbb{D}^{4}$ to the interior cannot be solved in full generality using looseness.
Using the relative nature of the 
$h$-principle, one can show that an overtwisted Engel structure contains all possible local models up to Engel homotopy. From this one can deduce that any two definitions of local overtwistedness are equivalent. However, since looseness is a global property, it cannot be compared to overtwistedness. In particular, looseness has no known analogue in contact topology.
A.2.2 Loose classes
Recall the forgetful inclusion 
$\mathscr{E}(M)\longrightarrow \mathscr{E}^{\text{f}}(M)$ and fix a loose basepoint 
${\mathcal{D}}\in \mathscr{E}(M)$. We may look at the groups 
$\unicode[STIX]{x1D70B}_{k}(\mathscr{E}(M))$ and 
$\unicode[STIX]{x1D70B}_{k}(\mathscr{E}^{\text{f}}(M))$ based at 
${\mathcal{D}}$. A class 
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D70B}_{k}(\mathscr{E}(M))$ is loose if it can be represented by a loose family. Note that conjugating by a loose loop takes loose classes to loose classes.
In the 
$h$-principle for loose Engel structures, the homotopy type of the certificate is encoded in the formal type (since the certificate is always transverse to the kernel of the Engel structure). From this, we deduce the 
$h$-principle in its algebraic form for all homotopy groups (and not just in some stable range). This is yet another significant difference between loose Engel structures and overtwisted contact structures; see Proposition A.2.
Corollary A.3. Given a closed 
$4$-manifold 
$M$, let 
$\mathscr{L}_{k}(M)\subset \unicode[STIX]{x1D70B}_{k}(\mathscr{E}(M))$ be the subgroup of loose classes. Then 
$\mathscr{L}_{k}(M)\longrightarrow \unicode[STIX]{x1D70B}_{k}(\mathscr{E}^{\text{f}}(M))$ is a group isomorphism.
Similarly, in [Reference del Pino and VogeldPV18] it is shown that overtwisted Engel families yield subgroups 
$\operatorname{OT}_{k}(M)\subset \unicode[STIX]{x1D70B}_{k}(\mathscr{E}(M))$ in the range 
$0\leqslant k\leqslant 3$ (where the basepoint is instead taken to be overtwisted). We may then speak of tight classes: those that may not be represented by either loose or overtwisted families. We do not know whether tight classes actually exist or whether loose and overtwisted classes might actually coincide in some cases (after conjugating).
