1. Introduction
Accessibility percolation models were inspired by some recent work in evolutionary biology and were developed in order to answer questions of mathematical interest. Consider a rooted graph G with a unique root o. To each vertex v ∊ G, a continuous random variable, denoted by Xv, is assigned. We always assume that these random variables {Xv, v ∊ G} are independently and identically distributed (i.i.d.). Let P = ov 1v 2 ⋯ vkv be a path from the root to vertex v in G, where k ≥ 0 is an integer. If the assigned random variables form an increasing sequence, i.e.
$${X_o} < {X_{{v_1}}} \lt \ldots \lt {X_{{v_k}}} \lt {X_v},$$
we say that vertex v is accessible and the path P is increasing.
Interest in increasing paths and accessible vertices was motivated by the classical model for the evolution of an organism involving genetic mutation and selection (see Weinreich et al. (Reference Weinreich, Delaney, Depristo and Hartl2006); Weinreich, Watson, and Chao (Reference Weinreich, Watson and Chao2005)). In evolutionary biology literature, the assigned random variables are known as fitness values, and increasing paths as selectively accessible paths (see, for example, Franke et al. (Reference Franke, Klözer, De Visser and Krug2011)). The existence of increasing paths is also called accessibility percolation by Nowak and Krug (Reference Nowak and Krug2013). For more details on biological motivation, we refer to Roberts and Zhao (Reference Roberts and Zhao2013) and Berestycki, Brunet and Shi (Reference Berestycki, Brunet and Shi2016).
The phase transition of existence or the numbers of increasing paths in different determin- istic graphs have been studied by several authors. For such problems in regular n-ary rooted trees, where each vertex has exactly n children, see Roberts and Zhao (Reference Roberts and Zhao2013) and Chen (Reference Chen2014). Recently, Coletti, Gava, and Rodrίguez (Reference Coletti, Gava and Rodríguez2018) considered the existence problem of increasing paths in infinite spherically symmetric trees, where the degrees of vertices grow exponentially as their depth increases. And for the increasing paths from (0, 0, …, 0) to (1, 1, …, 1) in an n-dimensional binary hypercube {0, 1}n under various assumptions, we refer to Hegarty and Martinsson (Reference Hegarty and Martinsson2014), Berestycki, Brunet and Shi (Reference Berestycki, Brunet and Shi2016), and Li (Reference Li2017).
The purpose of this work is to establish several limiting theorems of the accessibility percolation model on a class of rooted trees, not only for the number of increasing paths but also the cluster size in this percolation. Furthermore, the underlying graphs we consider here are random trees: random rooted labeled trees (or uniform rooted Cayley trees), which are a classic combinatorial model. According to Cayley’s formula, the number of unrooted labeled trees on n vertices is nn−2. Thus, the set of rooted labeled trees on n vertices has cardinality nn−1. It is natural to assume a uniform model on the set of such trees of the same size. That is, we always assume that all nn−1 rooted labeled trees on n vertices occur with equal probability. Let Tn be a random rooted labeled tree on n vertices.
In a rooted tree, there is a unique path from the root to any non-root vertex. However, we only consider the paths from the root to leaves when the increasing paths are counted. As a result, the number of increasing paths is equal to that of accessible leaves in any rooted tree. Moreover, it is easy to see that the cluster size in accessibility percolation is exactly the number of accessible vertices in any rooted graph. We denote by Zn the number of accessible leaves and Cn the number of accessible vertices in a random rooted labeled tree Tn. The asymptotic distributions of these two random variables are our main concern.
Since we are only concerned with the order of the fitness values, under the assumption of continuity of their distribution, changing the precise distribution will not influence the results. Without loss of generality, we can assume throughout this work that all the fitness values of vertices in a tree are mutually independent and uniformly distributed on the interval [0, 1].It is not hard to see that the probability that a path of length n is increasing (or a vertex with depth n is accessible) is equal to 1/(n + 1)!.
Our main result in this work is stated in the following.
Theorem 1. Let Zn and Cn be the numbers of accessible leaves and accessible vertices in a random rooted labeled tree Tn, respectively. Then the probability generating function of the random vector (Zn, Cn) satisfies that, for any 0 ≤ s, t ≤ 1,
$$\mathop {\lim }\limits_{n \to \infty } {\rm{E}}[{s^{{Z_n}}}{t^{{C_n}}}] = {1 \over {{s_1}}} + {{t - 1} \over {t{{\rm{e}}^{ - {s_1}}} + {s_1} - t}},$$
where s 1 = e−1(1 − s)t + 1. Consequently, the asymptotic distributions of Zn + 1 and Cn are geometric distributions with parameters e/(1 + e) and 1/e, respectively. That is,
$$\mathop {\lim }\limits_{n \to \infty } {\rm{P}}({Z_n} = k) = {{\rm{e}} \over {{{(1 + {\rm{e}})}^{k + 1}}}},\quad \quad k = 0,1,2, \ldots $$
and
$$\mathop {\lim }\limits_{n \to \infty } {\rm{P}}({C_n} = k) = {{{{({\rm{e}} - 1)}^{k - 1}}} \over {{{\rm{e}}^{{\kern 1pt} k}}}},\quad \quad k = 1,2, \ldots $$
Throughout, we shall use the following notation. We denote by |T| the size of a tree T, i.e. the number of vertices in T.Let 1(E) denote the indicator of the event E. For probabilistic convergence we use 
$\mathop \to \limits^{\rm{D}} $ and 
$\mathop \to \limits^{\rm{P}} $ to denote convergence in distribution and in probability, respectively.
The rest of the paper is organized as follows. In Section 2 we introduce several definitions and state some basic results. In addition, the numbers of accessible leaves and accessible vertices in two related random trees are also discussed. Section 3 is devoted to the proof of our main theorem stated above.
2. Preliminaries
In order to obtain the asymptotic distributions of the number of accessible leaves Zn and the number of accessible vertices Cn in a random rooted labeled tree Tn, our analysis is performed in the context of the local weak convergence of such random trees as the size n → ∞. We shall first introduce the basic concept of local weak convergence, and then precisely describe the limiting distribution of random rooted labeled trees.
We also consider in this section the probability measure under the condition that the fitness value of the root Xo = x ∊ [0, 1] is given, i.e.,
$${{\rm{P}}_x}( \cdot ) = {\rm{P}}( \cdot |{X_o} = x),$$
and denote by Ex the expectation with respect to Px.
2.1. Local weak convergence
We now formally introduce the definition of local weak convergence of random rooted trees. Let T denote the set of locally finite rooted trees, considered up to rooted isomor- phism. Here, the terminology rooted isomorphism means that there exists an isomorphism ϕ :(T 1, o 1) → (T 2, o 2) for the two rooted trees T 1 and T 2. Then, each vertex in any tree T ∊ T has finite degree, and for any two trees T 1, T 2 ∊ T, we regard them as an identical element in T if T 1 ≅ T 2 wherer ‘≅’ denotes rooted isomorphism. For any tree T ∊ T and integer m ≥ 0, let T (m) denoted the subgraph induced by all vertices whose depths are at most m. That is, T (m) contains all the vertices which are at a distance of at most m from the root, and all edges of T that join these vertices. Then we can make T into a metric space by endowing it with the distance d loc defined by
$${d_{{\rm{l}}oc}}({T_1},{T_2}{) = 2^{ - \sup \{ m \ge 0:T_1^{(m)} \cong T_2^{(m)}\} }},{\rm{ }}{T_1},{T_2} \in {\cal T}.$$
Now let T and Tn(n = 1, 2, … ) be random rooted locally finite trees. Then, following Benjamini and Schramm (Reference Benjamini and Schramm2001) and Aldous and Steele (Reference Aldous, Steele and Kesten2004), if 
${T_n}\mathop \to \limits^{\rm{D}} T$ as n → ∞ with respect to this topology, we say T is the local weak limit of Tn,or Tn converges weakly in T to T.
The concept of local weak convergence can be easily extended to random rooted locally finite graphs. For more information on this field, we refer to Aldous and Steele (Reference Aldous, Steele and Kesten2004). We shall precisely describe the local weak limit of random rooted labeled trees in the following subsections.
2.2. The branching Poisson tree
The family of branching Poisson trees is a subset of Galton–Watson trees (see, for example, Drmota (Reference Drmota2009)), where the common offspring distribution is a Poisson distribution. Let λ> 0 be a given real number. A branching Poisson tree with parameter λ can be generated in a plane as follows. Start with a single vertex (the root); each vertex independently has a number of children distributed as a Poisson distribution with parameter λ. Let PGW(λ) denote the distribution law of the family of branching Poisson trees with parameter λ.
In a rooted tree T,let Wi(T) denote the number of vertices of depth i for any i ≥ 0. Several properties of PGW(λ) trees are listed in the following.
Lemma 1. In a random rooted labeled tree Tn, the sequence {Wi(Tn), 1 ≤ i ≤ n − 1} has the same joint distribution as {Wi(PGW(λ)):1 ≤ i ≤ n − 1} conditioned on |PGW, (λ)|= n. That is, for any sequence of nonnegative integers a 1, a 2, …, an −1 such that 
$\sum\nolimits_{i = 1}^{n - 1} {a_i} = n - 1$, we have
$${\rm{P}}({W_i}({T_n}) = {a_i},1 \le i \le n - 1) = {\rm{P}}({W_i}(PGW(\lambda )) = {a_i},1 \le i \le n - 1|{\kern 1pt} |PGW(\lambda )| = n).$$
Proof. See Kolchin (Reference Kolchin1977), or Theorem 1 in Grimmett (Reference Grimmett1980).
Lemma 2. For all n and i ≥ 1, we have
$${\rm{E}}[W_i^r(PGW(\lambda ))|{\kern 1pt} |PGW(\lambda )| = n] \le c{\kern 1pt} {i^r},\quad \quad r = 1,2, \ldots ,$$
where c is a constant depending on r only.
Proof. This is an immediate consequence of Theorem 1.13 in Janson (Reference Janson2006).
We point out that the known results in the above two lemmas are independent of λ, and they are applied in the next section only in the critical case λ = 1.
For the numbers of accessible leaves and accessible vertices in a PGW(λ) tree, we have the following results, which are of interest in their own right.
Lemma 3. Let Zλ and Cλ be the numbers of accessible leaves and accessible vertices in a PGW(λ) tree, respectively. If the fitness value of the root x ∊ [0, 1] is given, then the conditional probability generating function of (Zλ, Cλ) is
$${f_\lambda }(x,s,t) = {{\rm{E}}_x}[{s^{{Z_\lambda }}}{t^{{C_\lambda }}}] = {{{s_\lambda }t{{\rm{e}}^{ - \lambda (1 - x){s_\lambda }}}} \over {t{{\rm{e}}^{ - \lambda (1 - x){s_\lambda }}} + {s_\lambda } - t}},\quad \quad 0 \le s,t \le 1,$$
where sλ ≔ e−λ(1 − s)t + 1.
Proof. Without loss of generality, we may assume that the children of the root o are labeled by v 1, …, vN, where N is a random variable, Poisson distributed with parameter λ. If a graph only contains a single vertex, there does not exist a path. Therefore, we always define Zλ = 0 (and Cλ = 1) if N = 0. However, it is more convenient to work with a modified version of Zλ that does not get affected if N ≥ 1, but rather only requires to replace its value by 1 if N = 0. Denote the modified version of Zλ by 
${\tilde Z_\lambda }$. We also define 
${\tilde Z_{{v_i}}}$ as the modified number of accessible leaves in the subtree rooted at vi. Recall that the fitness values Xo, Xv 1, Xv 2, … are i.i.d. random variables uniformly distributed on [0, 1]. Then, it is not hard to see that
$${Z_\lambda } = \sum\limits_{i = 1}^N {\tilde Z_{{v_i}}}{\bf{1}}({X_{{v_i}}} > {X_o})$$
and
$${\tilde Z_\lambda } = \sum\limits_{i = 1}^N {\tilde Z_{{v_i}}}{\bf{1}}({X_{{v_i}}} > {X_o}) + {\bf{1}}(N = 0).$$
Similarly, we can see that
$${C_\lambda } = \sum\limits_{i = 1}^N {C_{{v_i}}}{\bf{1}}({X_{{v_i}}} > {X_o}) + 1,$$
where Cvi is the number of accessible vertices in the subtree rooted at vi. Conditioning on the fitness value of the root Xo = x, it then follows that the relation between fλ(x, s, t) and 
${\tilde f_\lambda }(x,s,t): = {{\rm{E}}_x}[{s^{{{\tilde Z}_\lambda }}}{t^{{C_\lambda }}}]$, the probability generating function of 
$({\tilde Z_\lambda },{C_\lambda })$, is given by
$${f_\lambda }(x,s,t) = {\tilde f_\lambda }(x,s,t) + {\rm{P}}(N = 0)(1 - s)t = {\tilde f_\lambda }(x,s,t) + {s_\lambda } - 1,$$
where s λ = e−λ(1 − s)t + 1. If N = n > 1 is given, it is easy to see that 
$\{ ({\tilde Z_{{v_i}}},{C_{{v_i}}},{X_{{v_i}}}),i{\kern 1pt} = {\kern 1pt} 1, \ldots ,n\} $ are i.i.d. random vectors, and have the same distribution as 
$({\tilde Z_\lambda },{C_\lambda },{X_o})$. Hence, by (3) and (4),
$$\matrix{
{{{\tilde f}_\lambda }(x,s,t) = {{\rm{e}}^{ - \lambda }}st + t\sum\limits_{n = 1}^\infty {{({\rm{E}}[{s^{{{\tilde Z}_\lambda }{\bf{1}}({X_o} > x)}}{t^{{C_\lambda }{\bf{1}}({X_o} > x)}}])}^n}{{{\lambda ^n}} \over {n!}}{{\rm{e}}^{ - \lambda }}} \cr
{ = {{\rm{e}}^{ - \lambda }}t\sum\limits_{n = 0}^\infty {{(\int_x^1 {{\tilde f}_\lambda }({\kern 1pt} y,s,t){\kern 1pt} {\rm{d}}y + x)}^n}{{{\lambda ^n}} \over {n!}} - {{\rm{e}}^{ - \lambda }}(1 - s)t} \cr
{ = t\exp \{ \lambda \int_x^1 {{\tilde f}_\lambda }({\kern 1pt} y,s,t){\kern 1pt} {\rm{d}}y + \lambda (x - 1)\} - ({s_\lambda } - 1).} \cr
} $$
We now fix s and t, and regard 
${\tilde f_\lambda }(x,s,t)$ as a univariate function of x and (6) as a functional equation for it. Taking the common logarithm of both sides of (6) yields that
$$\ln ({\kern 1pt} {\tilde f_\lambda }(x,s,t) + {s_\lambda } - 1) - \ln t = \lambda \int_x^1 {\tilde f_\lambda }({\kern 1pt} y,s,t){\kern 1pt} {\rm{d}}y + \lambda (x - 1).$$
Further, differentiating both sides of the above equation on x, we obtain
$${{\tilde f_\lambda ^{{\kern 1pt} '}(x,s,t)} \over {{{\tilde f}_\lambda }(x,s,t) + {s_\lambda } - 1}} = \lambda [1 - {\tilde f_\lambda }(x,s,t)].$$
Note that for any 0 < y < 1,
$$\eqalign{
& \int_y^1 {{{\tilde f_\lambda ^{^\prime }(x,s,t)} \over {({{\tilde f}_\lambda }(x,s,t) + {s_\lambda } - 1)(1 - {{\tilde f}_\lambda }(x,s,t))}}} {\rm{d}}x{\mkern 1mu} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {1 \over {{s_\lambda }}}\int_y^1 {({{\tilde f_\lambda ^{^\prime }(x,s,t)} \over {{{\tilde f}_\lambda }(x,s,t) + {s_\lambda } - 1}} + {{\tilde f_\lambda ^{^\prime }(x,s,t)} \over {1 - {{\tilde f}_\lambda }(x,s,t)}})} {\rm{d}}x \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\mkern 1mu} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {1 \over {{s_\lambda }}}(\ln {{{{\tilde f}_\lambda }(1,s,t) + {s_\lambda } - 1} \over {1 - {{\tilde f}_\lambda }(1,s,t)}} - \ln {{{{\tilde f}_\lambda }(y,s,t) + {s_\lambda } - 1} \over {1 - {{\tilde f}_\lambda }(y,s,t)}}), \cr} $$
and (6) also indicates the boundary condition 
${\tilde f_\lambda }(1,s,t) = 1 + t - {s_\lambda }$. Thus, by (7), we have
$$\ln t - \ln ({s_\lambda } - t) - \ln {{{{\tilde f}_\lambda }({\kern 1pt} y,s,t) + {s_\lambda } - 1} \over {1 - {{\tilde f}_\lambda }({\kern 1pt} y,s,t)}} = \lambda (1 - y){s_\lambda },$$
from which it follows that, for any x, s, t ∊ [0, 1],
$${{{{\tilde f}_\lambda }(x,s,t) + {s_\lambda } - 1} \over {1 - {{\tilde f}_\lambda }(x,s,t)}} = {t \over {{s_\lambda } - t}}{{\rm{e}}^{ - \lambda (1 - x){s_\lambda }}}.$$
After simple calculations, one can get
$${\tilde f_\lambda }(x,s,t) = {{t{{\rm{e}}^{ - \lambda (1 - x){s_\lambda }}} - ({s_\lambda } - 1)({s_\lambda } - t)} \over {t{{\rm{e}}^{ - \lambda (1 - x){s_\lambda }}} + {s_\lambda } - t}},$$
from which (2) follows by (5).
Applying Lemma 3, we can get the probability generating functions of random variables Zλ and Cλ by setting t = 1 or s = 1 in the function fλ(x, s, t), and also their distributional properties.
Proposition 1. Let Zλ be the number of accessible leaves in a PGW(λ) tree. Then the probability generating function of Zλ is given by
$${\rm{E}}[{s^{{Z_\lambda }}}] = {1 \over \lambda }\ln {{s_\lambda ^*} \over {{{\rm{e}}^{ - \lambda s_\lambda ^*}} + s_\lambda ^* - 1}},\quad \quad 0 \le s \le 1,$$
where 
$s_\lambda ^* = {{\rm{e}}^{ - \lambda }}(1 - s) + 1$.
Proof. Letting t = 1 in(2) gives that the conditional probability generating function of Zλ is
$${{\rm{E}}_x}[{s^{{Z_\lambda }}}] = {{s_\lambda ^*{{\rm{e}}^{ - \lambda (1 - x)s_\lambda ^*}}} \over {{{\rm{e}}^{ - \lambda (1 - x)s_\lambda ^*}} + s_\lambda ^* - 1}},\quad \quad 0 \le s \le 1.$$
Since the fitness value of the root is uniformly distributed on [0, 1], the integral of this conditional probability generating function over x from 0 to 1 gives the desired result, (8).
Theoretically, one can get the exact distribution law of Zλ from Proposition 1. However, we only give the probability of a special event in what follows, since the probability mass function of Zλ cannot be expressed in a simple form.
Corollary 1. In a PGW(λ) tree, we have
P(there exists an accessible leaf in a 
$PGW{\rm{ (}}\lambda {\rm{) }}tree) = 1 - {1 \over \lambda }\ln {{{{\rm{e}}^\lambda } + 1} \over {{{\rm{e}}^{ - \lambda {{\rm{e}}^{ - \lambda }}}} + 1}}.$.
Proof. It follows by Proposition 1 and the fact that the desired probability is 1 − E[sZλ ]|s =0.
The probability that there exists an accessible leaf in a PGW(λ) tree is, of course, a function of λ. Figure 1 illustrates that this probability trends to 0 when λ → 0 or λ → ∞. Using Mathematica®, we find that it achieves the maximum value 0.22558725 … when λ = 1.53366758 …
For the number of accessible vertices in a PGW(λ) tree, we can derive the exact distribution law of Cλ from its probability generating function.
Figure 1: The probability that there exists an accessible leaf in a PGW(λ) tree.
Proposition 2. Let Cλ be the number of accessible vertices in a PGW(λ) tree. Then the random variable Cλ follows the logarithmic series distribution with parameter 1 − e−λ. That is, the probability mass function of Cλ is given by
$${\rm{P}}({C_\lambda } = k) = {{{{(1 - {{\rm{e}}^{ - \lambda }})}^k}} \over {\lambda k}},\quad \quad k = 1,2, \ldots $$
Proof. Similar to the proof of Proposition 1, we can get the probability generating function of Cλ via its conditional probability generating function, and then we can further derive its exact distribution law in a simple form. In fact, letting s = 1 in the probability generating function (2) gives that
$${{\rm{E}}_x}[{t^{{C_\lambda }}}] = {{t{{\rm{e}}^{ - \lambda (1 - x)}}} \over {1 - t + t{{\rm{e}}^{ - \lambda (1 - x)}}}},\quad \quad 0 \le t \le 1.$$
Therefore, the probability generating function of Cλ is given by
$$\eqalign{
& {\rm{E}}[{t^{{C_\lambda }}}] = \int_0^1 {{{\rm{E}}_x}} [{t^{{C_\lambda }}}]{\rm{d}}x \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \int_0^1 {{{t{{\rm{e}}^{ - \lambda (1 - x)}}} \over {1 - t + t{{\rm{e}}^{ - \lambda (1 - x)}}}}} {\rm{d}}x \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,{\mkern 1mu} {\mkern 1mu} = - {1 \over \lambda }\ln (1 - t + t{{\rm{e}}^{ - \lambda }}),\quad \quad 0 \le t \le 1 \cr} $$
It follows from the Maclaurin series expansion
$$\ln (1 + z) = \sum\limits_{k = 1}^\infty {{{{( - 1)}^{k - 1}}} \over k}{z^k}$$
Figure 2: An illustration for the infinite random tree with distribution law PGW∞(1).
for any |z| < 1 that
$$ - {1 \over \lambda }\ln (1 - t + t{{\rm{e}}^{ - \lambda }}) = \sum\limits_{k = 1}^\infty {{{{(1 - {{\rm{e}}^{ - \lambda }})}^k}} \over {\lambda k}}{t^k},$$
since |t(e−λ − 1)| < 1 for 0 ≤ t ≤ 1 and λ> 0. Then (9) follows from the definition of the probability generating function and (10).
2.3. The limiting tree
We now describe an infinite random tree model as follows. Let P = ov 1v 2 ⋯ be an infinite path with root o. To every vertex in P, an independent PGW(λ) tree is attached as a subtree rooted at it. And we still keep vertex o as the unique root of the whole tree (see Figure 2). Let PGW∞(λ) be the distribution law of the family of these infinite random trees; we call such a random tree a PGW∞(λ) tree.
The relation between PGW∞(λ) trees with the special case λ = 1 and random rooted labeled trees is given in the following lemma, which plays an essential role in the proof of our main result. Recall that T is the set of locally finite rooted trees, considered up to rooted isomorphism.
Lemma 4. The random rooted labeled tree Tn on n vertices converges weakly in T to the PGW ∞(1) tree as n → ∞.
Proof. This result was first formalized and proved in Grimmett (Reference Grimmett1980). See also Lemma 2.3 in Aldous and Steele (Reference Aldous, Steele and Kesten2004).
We now state the result analogous to Lemma 3 for the numbers of accessible leaves and accessible vertices in a PGW∞(λ) tree.
Lemma 5. Let Z ∞ and C ∞ be the numbers of accessible leaves and accessible vertices in a PGW ∞(λ) tree, respectively. If the fitness value of root Xo = x ∊ [0, 1] is given, then gλ(x, s, t), the conditional probability generating function of (Z ∞, C ∞), satisfies the equation
$${g_\lambda }(x,s,t) = {{\rm{E}}_x}[{s^{{Z_\infty }}}{t^{{C_\infty }}}] = {\kern 1pt} {f_\lambda }(x,s,t)(\int_x^1 {g_\lambda }(y,s,t){\kern 1pt} {\rm{d}}y + x),\quad \quad 0 \le s,t \le 1,$$
where fλ(x, s, t) is defined in (2).
Proof. First, we introduce some notation in a PGW∞(λ) tree. Let Xv be the fitness value of vertex v. We also denote by Zv 1 and Cv 1 the numbers of accessible leaves and accessible vertices in the (sub)tree rooted at v 1, respectively. Then it is easy to see that
$${Z_\infty } = {Z_o} + {Z_{{v_1}}}{\bf{1}}({X_{{v_1}}} > {X_o}),\quad {C_\infty } = {C_o} + {C_{{v_1}}}{\bf{1}}({X_{{v_1}}} > {X_o}),$$
where Zo (Co) denotes the number of accessible leaves (accessible vertices) only in the PGW(λ) tree rooted at o. It is obvious that the random vector (Zo, Co) defined in a PGW∞(λ) tree has the same distribution as (Zλ, Cλ) defined in Lemma 3, and that the random vector (Zv 1, Cv 1, Xv 1) also has the same distribution as (Z ∞, C ∞, Xo).
We next consider the situation under the condition that Xo = x ∊ [0, 1]. Note that the random vectors (Zo, Co) and (Zv 1, Cv 1) are now (conditionally) independent. Then it follows by (11) that
$$\eqalign{
& {g_\lambda }(x,s,t) = {{\rm{E}}_x}[{s^{{Z_\lambda }}}{t^{{C_\lambda }}}]{\rm{E}}[{s^{{Z_\infty }{\bf{1}}({X_o} > x)}}{t^{{C_\infty }{\bf{1}}({X_o} > x)}}] \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {f_\lambda }(x,s,t)(\int_x^1 {{g_\lambda }} (y,s,t){\rm{d}}y + x), \cr} $$
which completes the proof.
In principle, one can further derive the corresponding results on the numbers of accessible leaves and accessible vertices for PGW∞(λ) trees from Lemma 5, as we have done in Propositions 1 and 2. But now it becomes much more complicated, since neither of the probability generating functions of Z ∞ and C ∞ has a closed form expression for general λ > 0. Fortunately, as Lemma 4 has indicated, for our main purpose it is sufficient to treat the special case λ = 1 only. We shall give the explicit results on PGW∞(1) trees in the next section.
3. Proof of main result
For the proof of our main result, we need the following auxiliary lemma.
Lemma 6. Let Xm, Xn,m, Y, Yn be random vectors in the k-dimensional real space ℝk and 
$n,m \ge 1$. If 
${X_{n,m}}\mathop \to \limits^{\rm{D}} {X_m}$ as n → ∞ for any fixed 
$m,\,\,{X_m}\mathop \to \limits^{\rm{D}} Y$ as m → ∞, and, for any ε > 0,
$$\mathop {\lim }\limits_{m \to \infty } \mathop {\limsup }\limits_{n \to \infty } {\rm{P}}(\parallel {X_{n,m}} - {Y_n}\parallel \ge \varepsilon ) = 0,$$
where ||·|| denotes the Euclidean norm on ℝk, then 
${Y_n}\mathop \to \limits^{\rm{D}} Y$.
Proof. See, for example, Theorem 4.28 in Kallenberg (Reference Kallenberg2002).
To apply Lemma 6, we introduce another piece of notation as follows. For any m ≥ 1, let 
$T_n^{(m)}$ be the subgraph of the random rooted labeled tree Tn induced by all vertices whose depths are at most m.
Proof of Theorem 1. For any rooted tree T,let Z(T) and C(T) denote the numbers of accessible leaves and accessible vertices in it, respectively. Recall that Zn (Cn) denotes the number of accessible leaves (accessible vertices) in a random rooted labeled tree Tn.
For the difference between Zn and 
$Z(T_n^{(m)})$, we have
$$|Z(T_n^{(m)}) - {Z_n}| \le \sum\limits_{i = m}^{n - 1} {\kern 1pt} \sum\limits_{o{v_1} \cdots {v_i} \in {\cal A}} {\bf{1}}({X_o} \lt {X_{{v_1}}} \lt \ldots \lt {X_{{v_i}}}),$$
where A denotes the set of all paths from the root in Tn. Thus,
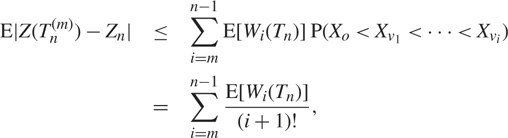$$\eqalign{
& {\rm{E}}|Z(T_n^{(m)}) - {Z_n}| \le \sum\limits_{i = m}^{n - 1} {\rm{E}} [{W_i}({T_n})]{\rm{P}}({X_o} < {X_{{v_1}}}\, < \ldots \, < {X_{{v_i}}}) \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \sum\limits_{i = m}^{n - 1} {{{{\rm{E}}[{W_i}({T_n})]} \over {(i + 1)!}}} , \cr} $$
where Wi(Tn) denotes the number of vertices of depth i in Tn. By Lemmas 1 and 2, we have
$${\rm{E}}[{W_i}({T_n})] = {\rm{E}}[{W_i}({\rm{PGW}}(1))||{\rm{PGW}}(1))| = n] \le ci,$$
for some absolute constant c and 1 ≤ i ≤ n − 1. By (12) and (13), it follows from Markov’s inequality that, for any ε > 0,
$$\eqalign{
& \mathop {\lim }\limits_{m \to \infty } \mathop {\lim \sup }\limits_{n \to \infty } {\rm{P}}(|Z(T_n^{(m)}) - {Z_n}| \ge \varepsilon ) \le \mathop {\lim }\limits_{m \to \infty } \mathop {\lim \sup }\limits_{n \to \infty } {{{\rm{E}}|Z(T_n^{(m)}) - {Z_n}|} \over \varepsilon } \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \le \mathop {\lim }\limits_{m \to \infty } \sum\limits_{i = m}^\infty {{{{\rm{E}}[{W_i}({T_n})]} \over {(i + 1)!\varepsilon }}} {\mkern 1mu} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\mkern 1mu} \le \mathop {\lim }\limits_{m \to \infty } \sum\limits_{i = m}^\infty {{{ci} \over {(i + 1)!\varepsilon }}} {\mkern 1mu} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 0. \cr} $$
Similarly, it is also follows that
$$\mathop {\lim }\limits_{m \to \infty } \mathop {\limsup }\limits_{n \to \infty } {\kern 1pt} {\rm{P}}(|C(T_n^{(m)}) - {C_n}| \ge \varepsilon ) = 0$$
holds for any ε > 0, so that
$$\mathop {\lim }\limits_{m \to \infty } \mathop {\limsup }\limits_{n \to \infty } {\kern 1pt} {\rm{P}}(\parallel (Z(T_n^{(m)}),C(T_n^{(m)})) - ({Z_n},{C_n})\parallel \ge \varepsilon ) = 0.$$
By Lemma 4, we can obtain that for any fixed integer m ≥ 1,
$$(Z(T_n^{(m)}),C(T_n^{(m)}))\mathop \to \limits^{\rm{D}} (Z({\rm{PGW}}_\infty ^{(m)}(1)),C({\rm{PGW}}_\infty ^{(m)}(1)))$$
as n → ∞, where PGW 
$_\infty ^{(m)}(1)$(1) also denotes the subgraph of the PGW∞(1) tree induced by all vertices whose depths are at most m. An analogous technique to (12)–(14) gives that, as m → ∞,
$$\parallel (Z({\rm{PGW}}_\infty ^{(m)}(1)),C({\rm{PGW}}_\infty ^{(m)}(1))) - (Z({\rm{PG}}{{\rm{W}}_\infty }(1)),C({\rm{PG}}{{\rm{W}}_\infty }(1)))\parallel \mathop \to \limits^{\rm{P}} 0,$$
which implies that
$$(Z({\rm{PGW}}_\infty ^{(m)}(1)),C({\rm{PGW}}_\infty ^{(m)}(1)))\mathop \to \limits^{\rm{D}} (Z({\rm{PG}}{{\rm{W}}_\infty }(1)),C({\rm{PG}}{{\rm{W}}_\infty }(1)))$$
as m → ∞. Collecting the above results and applying Lemma 6, we have
$$({Z_n},{C_n})\mathop \to \limits^{\rm{D}} (Z({\rm{PG}}{{\rm{W}}_\infty }(1)),C({\rm{PG}}{{\rm{W}}_\infty }(1)))$$
as n → ∞. From Levy’s continuity theorem, the probability generating function of (Zn, Cn) thus converges to that of (Z(PGW∞(1)), C(PGW∞(1))). That is, it follows that as n → ∞, for any 0 ≤ s, t ≤ 1,
$$\mathop {\lim }\limits_{n \to \infty } {\rm{E}}[{s^{{Z_n}}}{t^{{C_n}}}] = {\rm{E}}[{s^{Z({\rm{PG}}{{\rm{W}}_\infty }(1))}}{t^{C({\rm{PG}}{{\rm{W}}_\infty }(1))}}].$$
Letting λ = 1 and x = 0 in Lemma 5 yields that
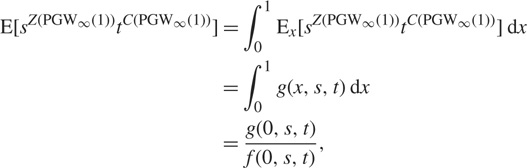$$\eqalign{
& {\rm{E}}[{s^{Z({\rm{PG}}{{\rm{W}}_\infty }(1))}}{t^{C({\rm{PG}}{{\rm{W}}_\infty }(1))}}] = \int_0^1 {{{\rm{E}}_x}} [{s^{Z({\rm{PG}}{{\rm{W}}_\infty }(1))}}{t^{C({\rm{PG}}{{\rm{W}}_\infty }(1))}}]{\rm{d}}x \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \int_0^1 g (x,s,t){\rm{d}}x \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {{g(0,s,t)} \over {f(0,s,t)}}, \cr} $$
where g(x, s, t) ≔ g 1(x, s, t) and
$$f(x,s,t): = {f_1}(x,s,t) = {{{s_1}t{{\rm{e}}^{{s_1}(x - 1)}}} \over {t{{\rm{e}}^{{s_1}(x - 1)}} + {s_1} - t}},$$
with s 1 = e−1(1 − s)t + 1.
We next find the exact expression for the probability generating function of the random vector (Z(PGW∞(1), C(PGW∞(1))). By Lemma 5, the relation between g(x, s, t) and f (x, s, t) reduces to
$$g(x,s,t) = {\kern 1pt} f(x,s,t)(\int_x^1 g(y,s,t){\kern 1pt} {\rm{d}}y + x),\quad \quad 0 \le x,s,t \le 1.$$
We can also fix s and t, and regard g(x, s, t) and f (x, s, t) as univariate functions of x. Taking the derivative of both sides of (18) with respect to x yields
$$g'(x,s,t) + p(x,s,t)g(x,s,t) = {\kern 1pt} f(x,s,t),$$
which is a standard first-order differential equation for g(x, s, t) with
$$p(x,s,t): = f(x,s,t) - {{f'(x,s,t)} \over {f(x,s,t)}} = 2f(x,s,t) - {s_1},$$
by (17). With the boundary condition g(1, s, t) = f (1, s, t) = t, it is well known that the solution of (19) can be given as
$$g(x,s,t) = \exp \{ - \int_1^x p({\kern 1pt} y,s,t){\kern 1pt} {\rm{d}}y\} (\int_1^x f({\kern 1pt} y,s,t)\exp \{ \int_1^y p(z,s,t){\rm{d}}z\} {\kern 1pt} {\rm{d}}y + t).$$
After straightforward calculations, we get that
$$g(x,s,t) = {{t{{\rm{e}}^{{s_1}(x - 1)}}(t{{\rm{e}}^{{s_1}(x - 1)}} + s_1^2x - t - {s_1}t(x - 1))} \over {{{(t{{\rm{e}}^{{s_1}(x - 1)}} + {s_1} - t)}^2}}}.$$
Inserting x = 0 into (17) and (20), it thus follows by (16) that, for 0 ≤ s, t ≤ 1,
$${\rm{E}}[{s^{Z({\rm{PG}}{{\rm{W}}_\infty }(1))}}{t^{C({\rm{PG}}{{\rm{W}}_\infty }(1))}}] = {1 \over {{s_1}}} + {{t - 1} \over {t{{\rm{e}}^{ - {s_1}}} + {s_1} - t}},$$
which, together with (15), implies that (1) holds.
One can immediately obtain the asymptotic distributions of Zn and Cn through (1). In fact, letting t = 1 in (1) yields that the limiting probability generating function of Zn is given by
$$\mathop {\lim }\limits_{n \to \infty } {\rm{E}}[{s^{{Z_n}}}] = {{\rm{e}} \over {1 + {\rm{e}} - s}} = \sum\limits_{k = 0}^\infty {{{\rm{e}}{s^k}} \over {{{(1 + {\rm{e}})}^{k + 1}}}},$$
which implies that
$$\mathop {\lim }\limits_{n \to \infty } {\rm{P}}({Z_n} = k) = {{\rm{e}} \over {{{(1 + {\rm{e}})}^{k + 1}}}},\quad \quad k = 0,1,2, \ldots $$
For Cn, it also follows directly by (1) that
$$\mathop {\lim }\limits_{n \to \infty } {\rm{E}}[{t^{{C_n}}}] = {{t/{\rm{e}}} \over {1 - t(1 - 1/{\rm{e}})}},$$
which is the probability generating function of the geometric distribution with parameter 1/e. That is,
$$\mathop {\lim }\limits_{n \to \infty } {\rm{P}}({C_n} = k) = {{{{({\rm{e}} - 1)}^{k - 1}}} \over {{{\rm{e}}^{{\kern 1pt} k}}}},\quad \quad k = 1,2, \ldots $$
The proof of Theorem 1 is complete.
Acknowledgements
We thank the anonymous referee for useful suggestions that greatly improved the presentation of this work. This work is supported by NSFC grant numbers 11671373 and 11771418.
