Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-06T08:57:11.008Z Has data issue: false hasContentIssue false
  • English
  • Français

Analytical and numerical investigation of the pulse-shape effect on the longitudinal electric field of a tightly focused ultrafast few-cycle TM01 laser beam

Published online by Cambridge University Press:  05 January 2012

Harish Malav ,
K.P. Maheshwari  and
Y. Choyal
Harish Malav
Affiliation:
DST-Project, Vardhaman Mahaveer Open University, Kota, India
K.P. Maheshwari*
Affiliation:
DST-Project, Vardhaman Mahaveer Open University, Kota, India
Y. Choyal
Affiliation:
School of Physics, Devi Ahilya Vishwavidyalaya, Indore, India
*
Address correspondence and reprint requests to: K.P. Maheshwari, DST-Project, Vardhaman Mahaveer Open University, Rawatbhata road, Kota-324010, India. E-mail: malavh@yahoo.co.in
Rights & Permissions [Opens in a new window]

Abstract

The effect of temporal pulse-shape on the characterization of the longitudinal electric field resulting from the tight-focusing of an ultrashort few-cycle TM01 laser beam in free space is investigated analytically and numerically. The longitudinal field is found to be sensitive to the pulse-shape of the driving field. The temporal pulse-shapes considered are Gaussian, Lorentzian, and hyperbolic secant having identical full width at half maximum of intensity. Analytical calculations are made beyond the paraxial and slowly varying envelope approximations. From the numerical results we find that due to finite duration of the signal, the evolution of the pulse envelope before the waist is faster (negative time-delay) but slowed down (positive time-delay) after the waist. This time-delay, for single-cycle pulses of wavelength λ0, and for spot-size w0f in the range 0.6λ0 > w0f > 0.25λ0, is pulse-shape dependent. The time delay is maximum for the Gaussian pulse and minimum for the Lorentzian pulse. The carrier frequency shift depends on the temporal profile of the pulse, beam spot size, axial propagating distance and also on the number of cycles in a pulse. In addition, a comparative study of the variation of the corrected axial Gouy- phase of the longitudinal electric field of single-cycle pulse (spot size w0f = 0.5λ0) with normalized retarded time shows that the phase variation is maximum for Gaussian and minimum for the Lorentzian pulse shape.

Keywords

Axial Gouy phaseCarrier frequency shiftLaser pulse-shapeTightly focused TM01 laser beam
Type
Research Article
Information
Laser and Particle Beams , Volume 30 , Issue 1 , March 2012 , pp. 75 - 86
Copyright
Copyright © Cambridge University Press 2011

1. INTRODUCTION

The recent progress in the technologies leading to the generation (Schenkel et al., Reference Schenkel, Biegert, Keller, Vozzi, Nisoli, Sansone, Stagira, De Silvestri and Svelto2003), phase-measurement (Paulus et al., Reference Paulus, Lindner, Walther, Baltuška, Gouliemakis, Lezius and Krausz2003; Kröll et al., Reference Kröll, Darmo, Dhillon, Marcadet, Calligaro, Sirtori and Unterrainer2007; Wittmann et al., Reference Wittmann, Horvath, Helml, Schätzel, Gu, Cavalieri, Paulus and Kienberger2009), and control of the sub-cycle evolution (Apolonski et al., Reference Apolonski, Poppe, Tempea, Spielmann, Udem, Holzwarth, Hänsch and Krausz2000) of few-cycle light wave has opened the door to the observations of atomic-scale electron dynamics (Krausz & Ivanov, Reference Krausz and Ivanov2009), electron acceleration (Sprangle et al., Reference Sprangle, Hafizi, Penano, Hubbard, Ting, Zigler and Antonsen2000; Varin & Piché, Reference Varin and Piché2002; Varin et al., Reference Varin, Piché and Porras2005; Esarey et al., Reference Esarey, Scchroeder and Leemans2009; Malav et al., Reference Malav, Maheshwari and Choyal2011a) and high-order harmonic generation (Lichters et al.,Reference Lichters, Meyer-Ter-Vehn and Pukhov1996; Villoresi et al., Reference Villoresi, Barbiero, Poletto, Nisoli, Cerullo, Priori, Stagira, De Lisco, Bruzzese and Altucci2001; Baeva et al., Reference Baeva, Gordienko and Pukhov2006; Dromey et al., Reference Dromey, Kar, Bellei, Carroll, Clarke, Green, Kneip, Markey, Nagel, Simpson, Willingale, Mckenna, Neely, Najmudin, Krushelnick, Norreys and Zepf2007, Reference Dromey, Rykovanov, Adams, Hörlein, Nomura, Carroll, Foster, Kar, Markey, Mckenna, Neely, Geissler, Tsakiris and Zepf2009; Gupta et al., Reference Gupta, Sharma and Mahmoud2007; Corkum & Krausz Reference Corkum and Krausz2007; Varro, Reference Varro2007; Malav et al., Reference Malav, Maheshwari and Senecha2011b). These physical processes are dependent on the electric field, rather than just the intensity envelope of a pulse (Varin & Piché, Reference Varin and Piché2002). Recent experimental results show that a radially polarized field can be focused to a spot size significantly smaller (0.16λ02) than for linear polarization (0.26λ02) (Dorn et al., Reference Dorn, Quabis and Leuchs2003). The effect of the vector properties of light is shown by a comparison of the focal intensity distribution for radially and azimuthally polarized input laser-fields. For strong focusing, a radially polarized field leads to a longitudinal electric field component at the focus which is sharp and centered at the optical axis. Since such laser fields consist of merely a few field oscillations, therefore, the actual time variation of the electric field affects all physical processes driven by the laser. Consequently, the physical processes such as high-harmonic generation, intense laser-matter interaction, diffraction effects etc., depend on the phase of the carrier wave with respect to the envelope, the so called carrier envelope phase (Porras, Reference Porras2002, Reference Porras2009; Nisoli et al., Reference Nisoli, Sansone, Stagira, Silvestri, Vozzi, Pascolini, Poletto, Villoresi and Tondello2003). Attention is therefore being paid to the characterization of the axial longitudinal electric field of tightly focused few-cycle pulses in free space.

Our main concern in this work is to investigate the pulse-shape effect on the characterization of the axial longitudinal electric field resulting from the tight focusing of an ultrashort few-cycle TM01 laser beam in free space. The temporal pulse-shape effects due to ultrashort pulse duration may have important implications for several applications such as acceleration of charge particles (Malav et al., Reference Malav, Maheshwari and Choyal2011a), high order harmonic generation (Malav et al., Reference Malav, Maheshwari and Senecha2011b). The present numerical study extends the work by Varin et al. (Reference Varin, Piché and Porras2006) that includes the effect of temporal profile of the incident laser pulse on the characterization of the longitudinal electric field.

Following Brabec and Krausz (Reference Brabec and Krausz1997), we express the temporal form of the pulsed beam as enveloped carrier oscillations of the averaged carrier frequency ω0. The temporal pulse-shapes considered are Gaussian, Lorentzian, and hyperbolic secant having identical full-width at half maximum of intensity. Using a complete vectorial description of an ultrafast tightly focused TM01 laser beam in free space having different temporal pulse-shapes, analytical expressions beyond the paraxial and slowly varying envelope approximations are obtained for longitudinal electric field. The results show that due to the finite duration of the signal, the evolution of the pulse envelope before the waist is faster (negative time-delay) but slowed down (positive time-delay) after the waist, and this time-delay is pulse-shape dependent for single-cycle pulses having spot-size in the range 0.6λ0 > w 0f > 0.25λ0. The magnitude of the time delay is maximum for the Gaussian pulse- shape and minimum for the Lorentzian pulse-shape. With smaller spot size, the laser beam divergence is faster than predicted by the paraxial theory. There is also a carrier-frequency- shift that depends on the pulse-shape, beam spot-size, axial propagating distance, and also on the number of cycles in a pulse. It is also found that there is a faster evolution of the axial Gouy phase shift in the vicinity of the focus that depends on the pulse-shape. However, the Gouy phase at the Rayleigh range for single-cycle tightly focused laser beam does not depend on the pulse shape.

The work is organized as follows: In Section 2, we present the field equations of tightly focused ultrafast TM01 beam in free space. In Section 3, we present expressions that exhibit the pulse-shape dependence of the axial longitudinal electric field of the tightly focused TM01 laser beam in free space. In Section 4, we analyze the results and give discussion. Section 5 presents our conclusions.

2. FIELD EQUATIONS OF TIGHTLY FOCUSED ULTRAFAST TM01 BEAM IN FREE SPACE

The electric field vector E of electromagnetic wave in free-space can be expressed as

(1)
E = \hbox{Re} \left[\widetilde{E} \exp \left\{\,j \, \left({\rm \omega}_0 t - k_0 z \right)\right\}\right]\comma \;

with Ẽ being the complex envelope of electric field vector, ω0 is of center carrier frequency and k 0 is free space wave vector. In terms of the reduced variables $t^{\prime} = t - {z / c}\comma \; z^{\prime} = z$, the vector Ẽ satisfies the perturbed paraxial wave equation (Porras, Reference Porras2001; Varin et al., Reference Varin, Piché and Porras2006):

(2)
\nabla_{\bot}^2 \widetilde{E} - \, 2j\, k_0 \, \partial_{z^{\prime}} \, \left[1 - \Theta \right]\, \widetilde{E} = 0\comma \;

with

(3)
\Theta = j \left\{{\rm \omega}_0^{ - 1} \partial_{t^{\prime}} - \left(2 k_0 \right)^{ - 1} \partial_{z^{\prime}} \right\}.

A solution to perturbed paraxial wave equation can be found by expanding the envelope of the electric field vector as a power series. The complex envelope of the longitudinal electric field E z can be expressed as:

(4)
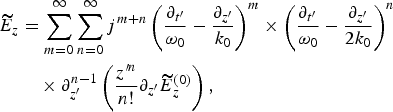
\eqalign{\widetilde{E}_z &= \sum_{m = 0}^{\infty} \sum_{n = 0}^{\infty} j^{m+n} \left({\partial_{t^{\prime}} \over {\rm \omega}_0} - {\partial_{z^{\prime}} \over k_0} \right)^m \times \left({\partial_{t^{\prime}} \over {\rm \omega}_0} - {\partial_{z^{\prime}} \over 2k_0} \right)^n \cr &\quad \times \partial_{z^{\prime}}^{n - 1} \left({z^{\prime n} \over n!} \partial_{z^{\prime}} \widetilde{E}_z^{\lpar 0\rpar } \right)\comma \; }

where Ẽ z(0) is the paraxial and slowly varying envelope of the longitudinal electric field.

Higher order terms follow from elemental operations on the zeroth order solution. These are the corrections up to the order of $\left({1 / {\rm \omega}_0 {\rm \tau}} \right)^n \left({1 / k_0 z_{Rf}} \right)^m $ for n, m ≥ 1, are expected to decrease with growing n and m for ${1 / {\rm \omega}_0 {\rm \tau}} \lt 1\comma \; {1 / k_0 z_{Rf}} \lt 1.$

Here, we consider the case of an ultrafast TM01 beam (B z = B r = E θ = 0) that is tightly focused by an ideal lens free of all aberrations.

The waist of the entrance beam E i is at z′ = 0. A lens of focal length f is placed at z′ = z l. The waist of the output beam E f is located at z′ = z f (Fig. 1 of Varin et al., Reference Varin, Piché and Porras2006).

Fig. 1. Shows the temporal distribution of on-axis longitudinal electric field of a ultrafast, single cycle tightly focused laser beam (beam spot-size w 0f = λ0) having Gaussian pulse-shape at (a) for Δz′ = −z Rf, (b) Δz′ = 0, and (c) Δz′ = z Rf. Bold and dashed lines represent the results of paraxial and non-paraxial approximation, respectively. The absolute value of the fields has been normalized so that their envelopes are equal to 1 at the centre of the pulse (t′ = 0) and at the waist (Δz′ = 0).

The paraxial and slowly varying envelope of the longitudinal electric field after the lens can be expressed as

(5)
\eqalign{\widetilde{E}_z^{\,f\lpar 0\rpar } &= - {2\sqrt{2} jE_{0f} \over k_0 w_{0f}} \exp \lpar 1/2\rpar \left({\,jz_{Rf} \over \widetilde{q}_f} \right)^2 \left(1 - {\,jk_0 r^2 \over 2\widetilde{q}_f} \right)\cr &\quad \times \exp \left(- {\,jk_0 r^2 \over 2\widetilde{q}_f} \right)A_f \lpar t^{\prime}\rpar \comma \; }

where E 0f is the amplitude of the transverse field after the lens, Ẽ f = Δz′ + jz Rf = z′ − z f + jz Rf is the complex parameter of the Gaussian beam, $z_{Rf} = {k_0 w_{0f}^{\ \ \ 2} \over 2}$ is the Rayleigh distance, w 0f is the beam-spot-size at the waist and A f(t′) is the temporal profile of the pulse envelope after the lens.

The temporal profiles of the envelopes for a Gaussian, Lorentzian, and hyperbolic secant pulses are taken to be (Brabec & Krausz, Reference Brabec and Krausz2000)

(6.1)
A_{\,fg} \left(t^{\prime} \right)= \exp \left[- \left({1.17t^{\prime} \over {\rm \tau}} \right)^2 \right]\comma \;
(6.2)
A_{\,fl} \left(t^{\prime} \right)= \left[1 + \left({1.29t^{\prime} \over {\rm \tau}} \right)^2 \right]^{ - 1}\comma \;

and

(6.3)
A_{\,fh} \left(t^{\prime} \right)= \hbox{sech}\, \left({1.76t^{\prime} \over {\rm \tau}} \right)\comma \;

respectively, where τ is full width at half maximum of pulse intensity.

Ẽ z has been expressed as an infinite series in terms of successive derivatives of zeroth order solution Ẽ z(0). The series expansions are converging for on axis longitudinal electric field of few-cycle ultra-short tightly focused TM01 beams in free space for ${1 / {\rm \omega}_0 {\rm \tau}}\lt 1\comma \; {1 / k_0 z_{Rf}}\lt 1$ (Porras, Reference Porras2002). The series expansion truncated to second order in temporal and spatial parts contains terms proportional to ${1 / \left(k_0 z_{Rf} \right)^2}\comma \; {1 / \left({\rm \omega}_0 {\rm \tau} \right)^2}$ and ${1 / {\rm \omega}_0 {\rm \tau} k_0 z_{Rf}}$.

For the single-cycle pulse, the zeroth, first order, second order, third order terms compare as 1 : 0.159: 0.025: 0.004 and for two-cycle pulse, the zeroth, first order, second order, third order terms compare as 1 : 0.079: 0.0061: 0.0005. It is seen that the higher-order terms give insignificant contribution to the field.

3. PULSE-SHAPE DEPENDENCE OF THE AXIAL LONGITUDINAL ELECTRIC FIELD OF THE TIGHTLY FOCUSED TM01 LASER BEAM IN FREE SPACE

Following Varin et al. (Reference Varin, Piché and Porras2006), one finds that at the center of the TM01 tightly focused pulsed laser beam, the longitudinal electric field reaches its maximum amplitude. When the spot size approaches the wave-length, second order intensity corrections to the paraxial approximation become important.

The second order electric field E zf of a few cycle TM01 beam at r = 0 can be expressed as the real part of the complex envelope times the carrier wave. Thus,

(7)
E_z^f = \hbox{Re} \left[\widetilde{E}_z^f \exp \!\lpar j{\rm \omega}_0 t^{\prime}\rpar \right]= \left\vert \widetilde{E}_z^{\,f0} \right\vert \Big\vert \widetilde{C} \Big\vert \cos \left[\Phi \lpar \Delta z^{\prime}\comma \; t^{\prime}\rpar \right]\comma \;

where Ẽ zf = Ẽ zf0C̃ and Ẽ zf0 is axial zeroth order field.

(8)
\Phi \lpar \Delta z^{\prime}\comma \; t^{\prime}\rpar = {\rm \omega}_0 t^{\prime} + 2\tan ^{ - 1} \left(\Delta z^{\prime}/z_{Rf} \right)+ {\rm \phi}_c - {\rm \pi} /2\comma \;

is total phase of the longitudinal electric fields, where ϕc = argument 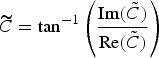${\widetilde C}=\tan^{-1}\left({{\rm Im}(\tilde{C})\over {\rm Re}(\tilde {C})}\right)$. In the following we derive expressions for the second-order on-axis longitudinal electric field of a few-cycle ultrashort tightly focused TM01 beam in free space for the different pulse shapes.

Substituting for Gaussian, Lorentzian, and hyperbolic secant temporal profile pulse-shape i.e Eq. (6) in Eq. (5) and using Eq. (4), the field at the focus of the ideal lens is given by the following expressions:

(1) Gaussian pulse-shape

(9)
\eqalignno{\widetilde{E}_z^{\; f} &= \widetilde{E}_z^{\,f0} \left[1 + {3j \over k_0 \widetilde{q}_f} \left(1 - {\Delta z^{\prime} \over \widetilde{q}_f} \right)- {2j\left(1.17 \right)^2 t^{\prime} \over {\rm \omega}_0 {\rm \tau}^2} \right. \cr &\quad \times \left. \left(1 - {2\Delta z^{\prime} \over \widetilde{q}_f} \right)+ {2\left(1.17 \right)^2 \over {\rm \omega}_0^2 {\rm \tau}^2} \left(1 - {2\left(1.17 \right)^2 t^{\prime 2} \over {\rm \tau}^2} \right)\right. \cr &\quad \times \left. \left(1 - 4{\Delta z^{\prime} \over \widetilde{q}_f} + 3{\Delta z^{\prime 2} \over \widetilde{q}_f^{\ 2}} \right)+ {2\left(1.17 \right)^2 t^{\prime} \over k_0 \widetilde{q}_f {\rm \omega}_0 {\rm \tau}^2} \right. \cr &\quad \times \left. \left(9 - 21 {\Delta z^{\prime} \over \widetilde{q}_f} + 12 {\Delta z^{\prime 2} \over \widetilde{q}_f^{\ 2}} \right)+ {3 \over 2\left(k_0 \widetilde{q}_f \right)^2} \right. \cr &\quad \times \left. \left(- 11 + 20 {\Delta z^{\prime} \over \widetilde{q}_f} - 10 {\Delta z^{\prime 2} \over \widetilde{q}_f^{\ 2}} \right)\right]\comma \;}

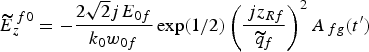where $\widetilde{E}_z^{\,f0} = - \displaystyle{2\sqrt{2} jE_{0f} \over k_0 w_{0f}} \exp \lpar 1/2\rpar \left(\displaystyle{\,jz_{Rf} \over \widetilde{q}_f} \right)^2 A_{\,fg} \lpar t^{\prime}\rpar $.

(10)
\eqalignno{\hbox{Re} \lpar \widetilde{C}\rpar &= 1 + {4\lpar 1.17\rpar ^2 t^{\prime} z_0 \over {\rm \omega}_0 {\rm \tau}^2 \left(1 + z_0^2 \right)} + {3\left(1 - z_0^2 \right)\over k_0 z_{Rf} \left(1 + z_0^2 \right)^2} \cr &\quad + {2\lpar 1.17\rpar ^2 \left(1 - 5z_0^2 \right)\over {\rm \omega}_0^2 {\rm \tau}^2 \left(1 + z_0^2 \right)^2} \left\{1 - {2\lpar 1.17\rpar ^2 \lpar t^{\prime}\rpar ^2 \over {\rm \tau}^2} \right\}\cr &\quad +{2\lpar 1.17\rpar ^2 t^{\prime} \left(30z_0 - 18z_0^3 \right)\over k_0 z_{Rf} {\rm \omega}_0 {\rm \tau}^2 \left(1 + z_0^2 \right)^3} \cr &\quad + {3\left(11 - 59z_0^2 + 9z_0^4 - z_0^6 \right)\over 2k_0^2 z_{Rf}^2 \left(1 + z_0^2 \right)^4}\comma \;}

where $z_0 = \displaystyle{\Delta z^{\prime} \over z_{Rf}}$.

(11)
\eqalignno{\hbox{Im} \lpar \widetilde{C}\rpar &= {6z_0 \over k_0 z_{Rf} \left(1 + z_0^2 \right)^2} - {2\lpar 1.17\rpar ^2 t^{\prime} \left(1 - z_0^2 \right)\over {\rm \omega}_0 {\rm \tau} ^2 \left(1 + z_0^2 \right)} \cr &\quad + {2\lpar 1.17\rpar ^2 \left(4z_0 - 2z_0^3 \right)\over {\rm \omega}_0^2 {\rm \tau}^2 \left(1 + z_0^2 \right)^2} \left\{1 - {2\lpar 1.17\rpar ^2 \lpar t^{\prime}\rpar ^2 \over {\rm \tau}^2} \right\}\cr &\quad + {2\lpar 1.17\rpar ^2 t^{\prime} \left(- 9 + 36z_0^2 - 3z_0^4 \right)\over k_0 z_{Rf} {\rm \omega}_0 {\rm \tau}^2 \left(1 + z_0^2 \right)^3} \cr &\quad + {3\left(42z_0 - 36z_0^3+2z_0^5 \right)\over 2k_0^2 z_{Rf}^2 \left(1 + z_0^2 \right)^4}}

(2) Lorentzian pulse-shape

(12)
\eqalignno{\widetilde{E}_z^{\ f} &= \widetilde{E}_z^{\,f0} \left[1 + {3j \over k_0 \widetilde{q}_f} \left(1 - {\Delta z^{\prime} \over \widetilde{q}_f} \right)- {2j\left(1.29 \right)^2 t^{\prime} A_{\,fl} \over {\rm \omega}_0 {\rm \tau}^2} \right. \cr &\quad \times \left.\left(1 - {2\Delta z^{\prime} \over \widetilde{q}_f} \right)+ {2\lpar 1.29\rpar ^2 A_{\,fl} \over {\rm \omega}_0^2 {\rm \tau}^2} \right. \cr &\quad \times \left. \left\{1 - {4\lpar 1.29\rpar ^2 t^{\prime 2} A_{\,fl} \over {\rm \tau}^2} \right\}\left(1 - 4 {\Delta z^{\prime} \over \widetilde{q}_f} + 3{\Delta z^{\prime 2} \over \widetilde{q}_f^{\ 2}} \right)\right. \cr &\quad \left. + {2\left(1.29 \right)^2 t^{\prime}A_{\,fl} \over k_0 \widetilde{q}_f {\rm \omega}_0 {\rm \tau}^2} \left(9 - 21 {\Delta z^{\prime} \over \widetilde{q}_f} + 12 {\Delta z^{\prime 2} \over \widetilde{q}_f^{\ 2}} \right)\right. \cr &\quad \left. + {3 \over 2\left(k_0 \widetilde{q}_f \right)^2} \left(- 11 + 20 {\Delta z^{\prime} \over \widetilde{q}_f} - 10 {\Delta z^{\prime 2} \over \widetilde{q}_f^{\ 2}} \right)\right]\comma \; }

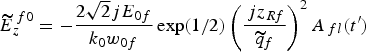where $\widetilde{E}_z^{\,f0} = - \displaystyle{{2\sqrt{2} jE_{0f} \over k_0 w_{0f}}} \exp \lpar 1/2\rpar \left(\displaystyle{{\,jz_{Rf} \over \widetilde{q}_f}} \right)^2 A_{\,fl} \lpar t^{\prime}\rpar $.

(13)
\eqalignno{\hbox{Re} \lpar \widetilde{C}\rpar &= 1 + {4\lpar 1.29\rpar ^2 t \, A_{\,fl} z_0 \over {\rm \omega}_0 {\rm \tau}^2 \left(1 + z_0^2 \right)} + {3 \lpar 1 - z_0^2\rpar \over k_0 z_{Rf} \lpar 1 + z_0^2\rpar ^2} \cr &\quad + {2\lpar 1.29\rpar ^2 A_{\,fl} \lpar 1 - 5z_0^2\rpar \over {\rm \omega}_0^2 {\rm \tau}^2 \lpar 1 + z_0^2\rpar ^2} \left\{1 - {4\lpar 1.29\rpar ^2 t^2 A_{\,fl} \over {\rm \tau}^2} \right\}\cr &\quad + {2\lpar 1.29\rpar ^2 A_{\,fl} t \lpar 30z_0 - 18z_0^3\rpar \over k_0 z_{Rf} {\rm \omega}_0 {\rm \tau} ^2 \lpar 1 + z_0^2\rpar ^3} \cr &\quad + {3\lpar 11 - 59z_0^2+9z_0^4 - z_0^6\rpar \over 2k_0^2 Z_R^2 \lpar 1 + z_0^2\rpar ^4}\comma \;}

where $z_0 = \displaystyle{{\Delta z^{\prime} \over z_{Rf}}}$.

(14)
\eqalignno{\hbox{Im} \lpar \widetilde{C}\rpar &= {{\rm 6z}_{\rm 0} \over k_0 z_{Rf} \lpar 1 + z_0^2\rpar ^2} - {2\lpar 1.29\rpar ^2 t \, A_{\,fl} \lpar 1 - z_0^2\rpar \over {\rm \omega}_0 {\rm \tau}^2 \lpar 1 + z_0^2\rpar } \cr &\quad + {2\lpar 1.29\rpar ^2 A_{\,fl} \lpar 4z_0 - 2z_0^3\rpar \over {\rm \omega}_0^2 {\rm \tau}^2 \lpar 1 + z_0^2\rpar ^2} \left\{1 - {4\lpar 1.29\rpar ^2 t^2 A_{\,fl} \over {\rm \tau}^2} \right\}\cr &\quad + {2\lpar 1.29\rpar ^2 A_{\,fl} t \lpar - 9 + 36z_0^2 - 3z_0^4\rpar \over k_0 z_{Rf} {\rm \omega}_0 {\rm \tau}^2 \lpar 1 + z_0^2\rpar ^3} \cr &\quad + {3 \lpar 42z_0 - 36z_0^3 + 2z_0^5\rpar \over 2k_0^2 z_{Rf}^2 \lpar 1 + z_0^2\rpar ^4}}

(3) Hyperbolic secant pulse-shape

(15)
\eqalignno{\widetilde{E}_z^{\; f} &= \widetilde{E}_z^{\,f0} \left[1 + {3j \over k_0 \widetilde{q}_f} \left(1 - {\Delta z^{\prime} \over \widetilde{q}_f} \right)- {\,j\lpar 1.76\rpar \tanh \left({1.76t^{\prime} \over {\rm \tau}} \right)\over {\rm \omega}_0 {\rm \tau}} \right. \cr &\quad \times \left. \left(1 - {2\Delta z^{\prime} \over \widetilde{q}_f} \right)- {\lpar 1.76\rpar ^2 \lpar 1 - 2A_{\,fh}^2\rpar \over {\rm \omega}_0^2 {\rm \tau}^2} \right. \cr &\quad \times \left. \left(1 - 4 {\Delta z^{\prime} \over \widetilde{q}_f} + 3 {\Delta z^{\prime 2} \over \widetilde{q}_f^2} \right)+ {\lpar 1.76\rpar \tanh \left({1.76t^{\prime} \over {\rm \tau}} \right)\over k_0 \widetilde{q}_f {\rm \omega}_0 {\rm \tau}} \right. \cr &\quad \times \left. \left(9 - 21 {\Delta z^{\prime} \over \widetilde{q}_f} + 12 {\Delta z^{\prime 2} \over \widetilde{q}_f^2} \right)+ {3 \over 2 \lpar k_0 \widetilde{q}_f\rpar ^2} \right. \cr &\quad \times \left. \left(- 11 + 20 {\Delta z^{\prime} \over \widetilde{q}_f} - 10 {\Delta z^{\prime 2} \over \widetilde{q}_f^2} \right)\right]\comma \;}

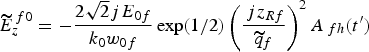where $\widetilde{E}_z^{\,f0} = - \displaystyle{2\sqrt{2} jE_{0f} \over k_0 w_{0f}} \exp \lpar 1/2\rpar \left(\displaystyle{\,jz_{Rf} \over \widetilde{q}_f} \right)^2 A_{\,fh}\lpar t^{\prime}\rpar $.

(16)
\eqalignno{\hbox{Re} \lpar \widetilde{C}\rpar &= 1 + {2\lpar 1.76\rpar z_0 \tanh \left({1.76t^{\prime} \over {\rm \tau}} \right)\over {\rm \omega}_0 {\rm \tau} \lpar 1 + z_0^2\rpar } + {3 \lpar 1 - z_0^2\rpar \over k_0 z_{Rf} \lpar 1 + z_0^2\rpar ^2} \cr &\quad - {\lpar 1.76\rpar ^2 \lpar 1 - 2A_{\,fh}^2\rpar \lpar 1 - 5z_0^2\rpar \over {\rm \omega}_0^2 {\rm \tau}^2 \lpar 1 + z_0^2\rpar ^2} \cr &\quad + {\lpar 1.76\rpar \tanh \left({1.76t^{\prime} \over {\rm \tau}} \right)\lpar 30z_0 - 18z_0^3\rpar \over k_0 z_{Rf} {\rm \omega}_0 {\rm \tau} \lpar 1 + z_0^2\rpar ^3} \cr &\quad + {3\lpar 11 - 59z_0^2 + 9z_0^4 - z_0^6\rpar \over 2k_0^2 Z_R^2 \lpar 1 + z_0^2\rpar ^4}\comma \;}

where $z_0 = \displaystyle{\Delta z^{\prime} \over z_{Rf}}$.

(17)
\eqalignno{\hbox{Im} \lpar \widetilde{C}\rpar &= {{\rm 6z}_0 \over k_0 z_{Rf} \lpar 1 + z_0^2\rpar ^2} - {\lpar 1.76\rpar z_0 \tanh \left({1.76t^{\prime} \over {\rm \tau}} \right)\lpar 1 - z_0^2\rpar \over {\rm \omega}_0 {\rm \tau} \lpar 1 + z_0^2\rpar } \cr &\quad - {\lpar 1.76\rpar ^2 \lpar 1 - 2A_{\,fh}^2\rpar \lpar 4z_0 - 2z_0^3\rpar \over {\rm \omega}_0^2 {\rm \tau}^2 \lpar 1 + z_0^2\rpar ^2} \cr &\quad + {\lpar 1.76\rpar \tanh \left({1.76t^{\prime} \over {\rm \tau}} \right)\lpar - 9 + 36z_0^2 - 3z_0^4\rpar \over k_0 z_{Rf} {\rm \omega}_0 {\rm \tau} \lpar 1 + z_0^2\rpar ^3} \cr &\quad + {3\lpar 42z_0 - 36z_0^3 + 2z_0^5\rpar \over 2k_0^2 z_{Rf}^2 \lpar 1 + z_0^2\rpar ^4}}

For a given axial distance we have a phase correction due to the corrected field i.e. C̃, which gives a shift in carrier frequency. The total phase of the field can be expressed as

(18)
\eqalignno{\Phi \lpar \Delta z^{\prime}\comma \; t^{\prime}\rpar &= {\rm \omega}_0 t^{\prime} + 2\tan ^{ - 1} \left({\Delta z^{\prime} \over z_{Rf}} \right)+ {\rm \phi}_c - {{\rm \pi}/2}\cr & = {\rm \omega}_0^{\prime} \lpar \Delta z^{\prime}\comma \; t^{\prime}\rpar t^{\prime} - {{\rm \pi} \over 2}\comma \;}

where ${\rm \omega}_0^{\prime} = {\rm \omega}_0 + \displaystyle{{\rm \phi}_c \lpar 0\comma \; t^{\prime}\rpar \over t^{\prime}} + 2\lpar t^{\prime}\rpar ^{ - 1} \tan^{ - 1} \left(\displaystyle{\Delta z^{\prime} / z_{Rf}} \right)$.

The carrier frequency shift can be defined as

(19)
\Delta {\rm \omega} = {\rm \omega}_0^{\prime} \lpar \Delta z^{\prime}\comma \; t^{\prime}\rpar - {\rm \omega}_0 = {2\tan^{ - 1} \left({\Delta z^{\prime} \over z_{Rf}} \right)+ {\rm \phi}_c \over t^{\prime}}.

Normalized frequency shift at the beam waist can be expressed as:

For Gaussian pulse shape

(20)
\left({{\rm \omega}_0^{\prime} - {\rm \omega}_0 \over {\rm \omega}_0} \right)_{\Delta z^{\prime} = 0} = - {1 \over {\rm \omega}_0 t^{\prime}} \tan^{ - 1} \left\{{2\lpar 1.17\rpar ^2\, k_g t^{\prime} \over {\rm \omega}_0 {\rm \tau}^2} \right\}\comma \;

where

(20.1)
k_g= \displaystyle{1 + \displaystyle{9 \over k_o z_{Rf}} \over \matrix{1 + \displaystyle{3 \over k_o z_{Rf}} + \displaystyle{2\lpar 1.17\rpar ^2 \over {\rm \omega}_0^2 {\rm \tau}^2} \left\{1 - \displaystyle{2\lpar 1.17\rpar ^2 \lpar t^{\prime}\rpar ^2 \over {\rm \tau}^2} \right\} + \displaystyle{33 \over 2k_0^2 z_{Rf}^2}.}}

For Lorentzian pulse shape

(21)
\left({{\rm \omega}_0^{\prime} - {\rm \omega}_0 \over {\rm \omega}_0} \right)_{\Delta z^{\prime} = 0} = - {1 \over {\rm \omega}_0 t^{\prime}} \tan^{ - 1} \left\{{2\lpar 1.29\rpar ^2\, k_l t^{\prime}A_{\,fl} \over {\rm \omega}_0 {\rm \tau}^2} \right\}\comma \;

where

(21.1)
k_l = \displaystyle{1 + \displaystyle{9 \over k_o z_{Rf}} \over \matrix{1 + \displaystyle{3 \over k_o z_{Rf}} + \displaystyle{2\lpar 1.29\rpar ^2 A_{\,fl} \over {\rm \omega}_0^2 {\rm \tau} ^2} \left\{1 - \displaystyle{4\lpar 1.17\rpar ^2 \lpar t^{\prime}\rpar ^2 A_{\,fl} \over {\rm \tau}^2} \right\} + \displaystyle{33 \over 2k_0^2 z_{Rf}^2}}}

For hyperbolic secant pulse shape

(22)
\eqalignno{\left({{\rm \omega}_0^{\prime} - {\rm \omega}_0 \over {\rm \omega}_0} \right)_{\Delta z^{\prime} = 0} &= - {1 \over {\rm \omega}_0 t^{\prime}} \tan^{ - 1} \cr &\quad \times \left\{{\lpar 1.76\rpar k_s \tanh \left(1.76t^{\prime}/{\rm \tau} \right)\over {\rm \omega}_0 {\rm \tau}} \right\}\comma \;}

where

(22.1)
k_s = \displaystyle{1 + \displaystyle{9 \over k_o z_{Rf}} \over 1 + \displaystyle{3 \over k_o z_{Rf}} - \displaystyle{\lpar 1.76\rpar ^2 \over {\rm \omega}_0^2 {\rm \tau}^2} \left\{1 - 2A_{\,fh}^2 \right\}+ \displaystyle{33 \over 2k_0^2 z_{Rf}^2}}.

and the phase shift is given by

(23)
\Delta \Phi \lpar \Delta z^{\prime}\comma \; t^{\prime}\rpar = {\rm \omega}_0 t^{\prime} + 2\tan^{ - 1} \left({\Delta z^{\prime} \over z_{Rf}} \right)+ {\rm \phi}_c.

The corrected axial Gouy phase at the centre of the pulse is

(24)
{\rm \phi}_{GC} = 2\tan^{ - 1} \left({\Delta z^{\prime} \over z_{Rf}} \right)+ {\rm \phi}_c.

4. RESULTS AND DISCUSSION

In Figures 1 and 2, we demonstrate the temporal distribution of the axial longitudinal electric field of a Gaussian laser pulse at various positions along the z′ axis for beam spot-size w 0f = λ0 and w 0f = 0.5λ0, respectively. The absolute value of the fields has been normalized so that their envelopes are equal to 1 at the center of the pulse (t′ = 0) and at the waist (Δz′ = 0). The dotted curve is obtained in the paraxial approximation (zeroth –order), while the solid line curve has been obtained incorporating second order fields. We note that the distribution of the field differs from what is expected from the paraxial wave theory. Although pulses emitted from many lasers can be approximated by a Gaussian shape, it is also important to consider the effect of other pulse-shapes viz. Lorentzian and the hyperbolic-secant on the axial longitudinal electric field. Figures 3 and 4, depict the temporal distribution of the longitudinal electric field for a TM01 Lorentzian pulse along the z′ axis at the beam center for spot size w 0f = λ0 and w 0f = 0.5λ0, respectively. Figures 5 and 6, represent the temporal distribution of the longitudinal electric field of a hyperbolic secant laser pulse along the z′ axis at the beam centre for spot size w 0f = λ0 and w 0f = 0.5λ0, respectively. From these results it is seen that in the non-paraxial approximation the pulse envelope attains its maximum faster as compared to paraxial approximation for Δz′ < 0 and slower for Δz′ > 0. Figure 7 shows the temporal distribution of the longitudinal electric field for different single-cycle pulse shapes at Δz′ = z Rf corresponding to different values of the beam spot size. It depicts that for 0.6λ0 > w 0λ > 0.25λ0 the time delay is sensitive to the pulse-shape of the single cycle laser beam. As a comparison, the magnitude of the time delay for Gaussian pulse-shape is maximum and minimum for Lorentzian pulse-shape. For bigger beam-spot-size e.g., w 0λ > 0.6λ0, we note that these time delays are almost the same for all the temporal profiles of the pulse. We also observe that for spot size at the waist comparable to the wavelength, the beam of single-cycle pulse diverges more rapidly than expected from the paraxial theory.

Fig. 2. Shows the temporal distribution of on-axis longitudinal electric field of a ultrafast, single cycle tightly-focused laser beam (beam spot-size w 0f = 0.5λ0) having Gaussian pulse at (a) Δz′ = −z Rf, (b) Δz′ = 0, and (c) Δz′ = z Rf. Bold and dashed lines represent the results of paraxial and non-paraxial approximation respectively. For normalization see caption of Figure 1.

Fig. 3. Shows the temporal distribution of on-axis longitudinal electric field of a ultrafast, single cycle tightly focused beam (beam spot-size w 0f = λ0) having Lorentzian pulse-shape at (a) Δz′ = −z Rf, (b) Δz′ = 0, and (c) Δz′ = z Rf. Bold and dashed lines represent the results of paraxial and non-paraxial approximation respectively. For normalization see caption of Figure 1.

Fig. 4. Shows the temporal distribution of on-axis longitudinal electric field of a ultrafast, single cycle tightly-focused laser beam (beam spot-size w 0f = 0.5λ0) having Lorentzian pulse at (a) Δz′ = −z Rf, (b) Δz′ = 0, and (c) Δz′ = z Rf. Bold and dashed lines represent the results of paraxial and non-paraxial approximation respectively. For normalization see caption of Figure 1.

Fig. 5. Shows the temporal distribution of on-axis longitudinal electric field of a ultrafast, single cycle tightly-focused beam (beam spot-size w 0f = λ0) having hyperbolic secant pulse-shape at (a) Δz′ = −z Rf, (b) Δz′ = 0, and (c) Δz′ = z Rf. Bold and dashed lines represent the results of paraxial and non-paraxial approximation respectively. For normalization see caption of Figure 1.

Fig. 6. Shows the temporal distribution of on-axis longitudinal electric field of a ultrafast, single cycle tightly focused beam (beam spot-size w 0f = 0.5λ0) having hyperbolic secant pulse at (a) Δz′ = −z Rf, (b) Δz′ = 0, and (c) Δz′ = z Rf. Bold and dashed lines represent the results of paraxial and non-paraxial approximation respectively. For normalization see caption of Figure 1.

Fig. 7. Shows the temporal distribution of the on-axis longitudinal electric field for different single-cycle pulse envelopes corresponding to different values of the beam spot size atΔz′ = z Rf. The absolute value of the fields have been normalized so that Gaussian envelopes are equal to 1 at t′ = 0 and Δz′ = 0.

In addition, it is also found that the frequency-shift depends on the temporal profile of the pulse, beam spot size, axial propagating distance, and also on the number of cycles in a pulse. Figure 8a, shows the variation of the axial frequency shift of an ultrafast tightly focused TM01 beam at the waist (τ = 2π/ω0 and w 0f = λ0) as a function of time. Figure 8b, represents the frequency-shift at far from the waist (Δz′ = ∞). The frequency-shift at Δz′ = ∞ is independent of beam-spot-size; however, it depends on the pulse-shape. It is observed from Figure 8a, that the frequency is red shifted for Gaussian, Lorentzian, and hyperbolic secant pulses. The amount of the red shift increases with time for Gaussian pulse, while it decreases for Lorentzian and hyperbolic secant pulse. The rate of decrease of the magnitude of red shift is more in case of the Lorentzian pulse as compared to hyperbolic secant and Gaussian pulses. It may be remarked that the variation of the red shift in case of the Gaussian pulse is found to be different from the Figure 7a of Varin et al. (Reference Varin, Piché and Porras2006). This is because an additional term ${2\lpar 1.17\rpar ^2 / {\rm \omega}_0^2 {\rm \tau}^2} \left\{1 - {2\lpar 1.17\rpar ^2 \lpar t^{\prime}\rpar ^2 / {\rm \tau}^2} \right\}$ appears in the Eq. (20.1) because of the inclusion of the pulse-shape effect. In the absence of this term, the results agree with Varin et al. (Reference Varin, Piché and Porras2006). The effect of variation of the spot size on the frequency shift with retarded time is shown in Figure 9. We note that for the spot-size in the range w 0λ ≥ 0.6λ0, the amount of red frequency shift increases with retarded time for the Gaussian shape, whereas for the range 0.6λ0 > w 0λ > 0.25λ0, it decreases. The effect of the number of cycles in a pulse, on the frequency shift is shown in Figure 10. It is found that in the case of single-cycle pulse, the shift in frequency is enhanced as compared to the double-cycle pulse. Figure 11, depicts the variation of the frequency shift as a function of the axial coordinate for all the three single-cycle pulses for spot size w 0f = 0.5λ0 and at retarded time t′ = τ. It is observed from the figure that at $\displaystyle{\Delta z^{\prime} / z_{Rf}} \approx 1.1\comma \; $ the frequency shift is approximately same. For lower values of the axial coordinates, we get red shift whereas blue shift at higher values.

Fig. 8. (a) Shows the variation of the axial frequency shift of a single-cycle ultrafast tightly focused TM01 beam (w 0f = λ0) at the beam waist as a function of retarded time. (b) Shows the variation of the axial frequency shift of an single-cycle ultrafast tightly focused TM01 beam at far from the waist (Δz′ = ∞) as a function of retarded time.

Fig. 9. Shows the variation of the axial frequency shift of a single-cycle ultrafast tightly focused TM01 beam as a function of retarded time, corresponding to different values of the beam spot size at the beam waist. (a) Gaussian, (b) Lorentzian, and (c) Hyperbolic secant pulse-shape.

Fig. 10. Shows the temporal variation of the axial frequency-shift of an ultrafast tightly focused (w 0f = λ0) TM01 beam, corresponding to single and double cycle in a pulse at the beam waist. (a) Gaussian, (b) Lorentzian, and (c) Hyperbolic secant pulse-shape.

Fig. 11. Shows the pulse-shape dependence of the frequency-shift of the on-axis longitudinal electric field of a ultrafast, single-cycle tightly focused beam as a function of axial coordinate for spot size w 0f = 0.5λ0, and at retarded time t′ = τ.

Figure 12, shows a comparative study of the variation of the corrected axial Gouy-phase ϕGC of the longitudinal electric field of Gaussian, Lorentzian, and hyperbolic secant single-cycle pulses with normalized axial distance $\left({\Delta z^{\prime} / z_{Rf}}\right)$. From our results we observe that the Gouy phase at the Rayleigh range is independent of the pulse-shape. At a specific axial distance Δz′ ≈ −z Rf we get an inflexion point, and in the range −2z Rf  ≤ Δz′ ≤ 0 there is a rapid change in phase which is maximum for the Gaussian pulse-shape and minimum for the Lorentzian pulse-shape.

Fig. 12. Shows a comparative study of the variation of the corrected axial Gouy-phase ϕGC of the longitudinal electric field of an ultrafast, single-cycle, tightly focused (w 0f = 0.5λ0) TM01 beam with normalized axial distance $\left(\displaystyle{\Delta z^{\prime} / z_{Rf}} \right)$ at retarded time t′ = τ.

Figure 13, represent a comparative study of the variation of the corrected axial Gouy- phase of the longitudinal electric field of Gaussian, Lorentzian, and hyperbolic secant single-cycle pulse (spot size w 0f = 0.5λ0) with normalized retarded time. We see that the phase variation is maximum for Gaussian and minimum for the Lorentzian pulse shape.

Fig. 13. Shows a comparative study of the variation of the corrected axial Gouy- phase of the longitudinal electric field of an ultrafast, single-cycle tightly focused (w 0f = 0.5λ0) TM01 beam with normalized retarded time. (a) Δz′ = 0 and (b) Δz′ = z Rf.

5. CONCLUSION

While estimating the strength of the longitudinal electric field of tightly focused TM01 laser beam in non-paraxial approximation, it is important to include the effect of the pulse-shape in addition to the number of cycles, size of the beam-spot. The evolution of the pulse envelope before the waist is faster (negative time-delay) but slowed down (positive time-delay) after the waist. This time-delay, for single-cycle pulses and for beam-spot size w 0f in the range 0.6λ0 > w 0f > 0.25λ0, is pulse-shape dependent for single-cycle pulses. The carrier frequency shift and the corrected axial Gouy- phase depend on the temporal profile of the pulse, beam spot size, axial propagating distance and also on the number of cycles in a pulse.

ACKNOWLEDGMENTS

Financial support from the Department of Science & Technology, New- Delhi, (Government of India) is thankfully acknowledged. The authors are thankful to the reviewers of the paper for their valuable suggestions. The authors express thanks to Professor Naresh Dadhich, Vice-Chancellor, V. M. O. U. Kota for support and encouragement. Authors are thankful to Dr. H. B. Nandwana, Director, Science & Technology, VMOU, Kota for his kind support.

References

REFERENCES

Apolonski, A., Poppe, A., Tempea, G., Spielmann, Ch., Udem, Th., Holzwarth, R., Hänsch, T.W. & Krausz, F. (2000). Controlling the phase evolution of few-cycle light pulses. Phys. Rev. Lett. 85, 740–743.CrossRefGoogle ScholarPubMed
Baeva, T., Gordienko, S. & Pukhov, A. (2006). Theory of high-order harmonic generation in relativistic laser interaction with over dense plasma. Phys. Rev. E 74, 046404/1–11.CrossRefGoogle Scholar
Brabec, T. & Krausz, F. (1997). Nonlinear optical pulse propagation in the single-cycle regime. Phys. Rev. Lett. 78, 3282–3285.CrossRefGoogle Scholar
Brabec, T. & Krausz, F. (2000). Intense few-cycle laser fields: Frontier of nonlinear optics. Rev. Mod. Phys. 72, 545–591.CrossRefGoogle Scholar
Corkum, P.B. & Krausz, F. (2007). Attosecond science. Nat. Phys. 3, 281–287.CrossRefGoogle Scholar
Dorn, R., Quabis, S. & Leuchs, G. (2003). Sharper focus for a radially polarized light beam. Phys. Rev. Lett. 91, 23390/1–4.CrossRefGoogle ScholarPubMed
Dromey, B., Kar, S., Bellei, C., Carroll, D.C., Clarke, R.J., Green, J.S., Kneip, S., Markey, K., Nagel, S.R., Simpson, P.T., Willingale, L., Mckenna, P., Neely, D., Najmudin, Z., Krushelnick, K., Norreys, P. A. & Zepf, M. (2007). Bright multi-KeV harmonic generation from relativistically oscillating plasma surfaces. Phys. Rev. Lett. 99, 0850011/1–14.CrossRefGoogle ScholarPubMed
Dromey, B., Rykovanov, S.G., Adams, D., Hörlein, R., Nomura, Y., Carroll, D.C., Foster, P.S., Kar, S., Markey, K., Mckenna, P., Neely, D., Geissler, M., Tsakiris, G.D. & Zepf, M. (2009). Tunable enhancement of high harmonic emission from laser solid interactions. Phys. Rev. Lett. 102, 225002/1–4.CrossRefGoogle ScholarPubMed
Esarey, E., Scchroeder, C.B. & Leemans, W.P. (2009). Physics of laser-driven plasma–based electron accelerators. Rev. Mod. Phys. 81, 1229–1285.CrossRefGoogle Scholar
Gupta, M.K., Sharma, R.P. & Mahmoud, S.T. (2007). Generation of plasma wave and third harmonic generation at ultra relativistic laser power. Laser Part. Beams 25, 211–218.CrossRefGoogle Scholar
Krausz, F. & Ivanov, M. (2009). Attosecond physics. Rev. Mod. Phys. 81, 163–234.CrossRefGoogle Scholar
Kröll, J., Darmo, J., Dhillon, S.S., Marcadet, X., Calligaro, M., Sirtori, C. & Unterrainer, K. (2007). Phase- resolved measurements of stimulated emission in a laser. Nat. Lett. 449, 698–701.CrossRefGoogle ScholarPubMed
Lichters, R., Meyer-Ter-Vehn, J. & Pukhov, A. (1996). Short-pulse laser harmonics from oscillating plasma surfaces driven at relativistic intensity. Phys. Plasmas 3, 3425–3437.Google Scholar
Malav, H., Maheshwari, K.P. & Choyal, Y. (2011 b). Analytical and numerical investigation of pulse-shape effect on the interaction of an ultrashort, intense, few-cycle laser pulse with a thin plasma layer. Laser Part. Beams 29, 45–54.CrossRefGoogle Scholar
Malav, H., Maheshwari, K.P. & Senecha, V. (2011 a). Analytical and numerical investigation of the effect of pulse shape of intense, few-cycle TM01 laser on the acceleration of charged particles. Indian J. Pure Appl.Phys. 49, 251–256.Google Scholar
Malav, H., Maheshwari, K.P., Meghwal, R.S., Choyal, Y. & Sharma, R. (2010). Analytical and numerical investigation of diffraction effects on the nonlinear propagation of ultra-intense few-cycle optical pulses in plasmas. J. Plasma Phys. 76, 209–227.Google Scholar
Nisoli, M., Sansone, G., Stagira, S., Silvestri, S.D., Vozzi, C., Pascolini, M., Poletto, L., Villoresi, P. & Tondello, G. (2003). Effects of carrier-envelope phase differences of few-optical-cycle light pulses in single-shot high- order-harmonic spectra. Phys. Rev. Letters 91, 2139051/1–54.CrossRefGoogle ScholarPubMed
Paulus, G.G., Lindner, F., Walther, H., Baltuška, A., Gouliemakis, E., Lezius, M. & Krausz, F. (2003). Measurement of the phase of few-cycle laser pulses. Phys. Rev. Lett. 91, 253004 (1–4).Google Scholar
Porras, M.A. (2001). Pulse correction to monochromatic light-beam propagation. Opt. Lett. 26, 44–46.CrossRefGoogle ScholarPubMed
Porras, M.A. (2002). Diffraction effects in few-cycle optical pulses., Phys. Rev. E 65, 026606/1–11.CrossRefGoogle ScholarPubMed
Porras, M.A. (2009). Characterization of the electric field of focused pulsed Gaussian beams for phase –sensitive interactions with matter. Opt. Lett. 34, 1546–1548.CrossRefGoogle ScholarPubMed
Schenkel, B., Biegert, J., Keller, U., Vozzi, C., Nisoli, M., Sansone, G., Stagira, S., De Silvestri, S., & Svelto, O. (2003). Generation of 3.8-fs pulses from adaptive compression of a cascaded hollow fiber supercontinuum. Opt. Lett. 28, 1987–1989.CrossRefGoogle ScholarPubMed
Sprangle, P., Hafizi, B., Penano, J.R., Hubbard, R.F., Ting, A., Zigler, A. & Antonsen, T.M. (2000). Stable laser-pulse propagation in plasma channels for GeV electron acceleration. Phys. Rev. Lett. 85, 5110–5113.CrossRefGoogle ScholarPubMed
Varin, C. & Piché, M. (2002). Acceleration of ultra-relativistic electrons using high-intensity TM01 laser beams. Appl. Phys. B 74, S83–S88.CrossRefGoogle Scholar
Varin, C., Piché, M. & Porras, M.A. (2005). Acceleration of electron from rest to GeV energies by ultrashort transverse magnetic laser pulses in free space. Phys. Rev. E 71, 026603/1–10.Google Scholar
Varin, C., Piché, M. & Porras, M.A. (2006). Analytical calculation of the longitudinal electric field resulting from the tight focusing of an ultrafast transverse-magnetic laser beam. J. Opt. Soc. Am. A 23, 2027–2038.CrossRefGoogle ScholarPubMed
Varro, S. (2007). Linear and nonlinear absolute phase effects in interactions of ultrashort laser pulses with a metal nano-layer or with a thin plasma layer. Laser part. Beams 25, 379–390.CrossRefGoogle Scholar
Villoresi, P., Barbiero, P., Poletto, L., Nisoli, M., Cerullo, G., Priori, E., Stagira, S., De Lisco, C., Bruzzese, R. & Altucci, C. (2001). Study of few-optical-cycles generation of high-order harmonics. Laser Part. Beams 19, 41–45.CrossRefGoogle Scholar
Wittmann, T., Horvath, B., Helml, W., Schätzel, M.G., Gu, X., Cavalieri, A.L., Paulus, G.G. & Kienberger, R. (2009). Single-shot carrier-envelope phase measurement of few-cycle laser pulses. Nat. Phys. 5, 357–362.Google Scholar
Figure 0

Fig. 1. Shows the temporal distribution of on-axis longitudinal electric field of a ultrafast, single cycle tightly focused laser beam (beam spot-size w0f = λ0) having Gaussian pulse-shape at (a) for Δz′ = −zRf, (b) Δz′ = 0, and (c) Δz′ = zRf. Bold and dashed lines represent the results of paraxial and non-paraxial approximation, respectively. The absolute value of the fields has been normalized so that their envelopes are equal to 1 at the centre of the pulse (t′ = 0) and at the waist (Δz′ = 0).

Figure 1

Fig. 2. Shows the temporal distribution of on-axis longitudinal electric field of a ultrafast, single cycle tightly-focused laser beam (beam spot-size w0f = 0.5λ0) having Gaussian pulse at (a) Δz′ = −zRf, (b) Δz′ = 0, and (c) Δz′ = zRf. Bold and dashed lines represent the results of paraxial and non-paraxial approximation respectively. For normalization see caption of Figure 1.

Figure 2

Fig. 3. Shows the temporal distribution of on-axis longitudinal electric field of a ultrafast, single cycle tightly focused beam (beam spot-size w0f = λ0) having Lorentzian pulse-shape at (a) Δz′ = −zRf, (b) Δz′ = 0, and (c) Δz′ = zRf. Bold and dashed lines represent the results of paraxial and non-paraxial approximation respectively. For normalization see caption of Figure 1.

Figure 3

Fig. 4. Shows the temporal distribution of on-axis longitudinal electric field of a ultrafast, single cycle tightly-focused laser beam (beam spot-size w0f = 0.5λ0) having Lorentzian pulse at (a) Δz′ = −zRf, (b) Δz′ = 0, and (c) Δz′ = zRf. Bold and dashed lines represent the results of paraxial and non-paraxial approximation respectively. For normalization see caption of Figure 1.

Figure 4

Fig. 5. Shows the temporal distribution of on-axis longitudinal electric field of a ultrafast, single cycle tightly-focused beam (beam spot-size w0f = λ0) having hyperbolic secant pulse-shape at (a) Δz′ = −zRf, (b) Δz′ = 0, and (c) Δz′ = zRf. Bold and dashed lines represent the results of paraxial and non-paraxial approximation respectively. For normalization see caption of Figure 1.

Figure 5

Fig. 6. Shows the temporal distribution of on-axis longitudinal electric field of a ultrafast, single cycle tightly focused beam (beam spot-size w0f = 0.5λ0) having hyperbolic secant pulse at (a) Δz′ = −zRf, (b) Δz′ = 0, and (c) Δz′ = zRf. Bold and dashed lines represent the results of paraxial and non-paraxial approximation respectively. For normalization see caption of Figure 1.

Figure 6

Fig. 7. Shows the temporal distribution of the on-axis longitudinal electric field for different single-cycle pulse envelopes corresponding to different values of the beam spot size atΔz′ = zRf. The absolute value of the fields have been normalized so that Gaussian envelopes are equal to 1 at t′ = 0 and Δz′ = 0.

Figure 7

Fig. 8. (a) Shows the variation of the axial frequency shift of a single-cycle ultrafast tightly focused TM01 beam (w0f = λ0) at the beam waist as a function of retarded time. (b) Shows the variation of the axial frequency shift of an single-cycle ultrafast tightly focused TM01 beam at far from the waist (Δz′ = ∞) as a function of retarded time.

Figure 8

Fig. 9. Shows the variation of the axial frequency shift of a single-cycle ultrafast tightly focused TM01 beam as a function of retarded time, corresponding to different values of the beam spot size at the beam waist. (a) Gaussian, (b) Lorentzian, and (c) Hyperbolic secant pulse-shape.

Figure 9

Fig. 10. Shows the temporal variation of the axial frequency-shift of an ultrafast tightly focused (w0f = λ0) TM01 beam, corresponding to single and double cycle in a pulse at the beam waist. (a) Gaussian, (b) Lorentzian, and (c) Hyperbolic secant pulse-shape.

Figure 10

Fig. 11. Shows the pulse-shape dependence of the frequency-shift of the on-axis longitudinal electric field of a ultrafast, single-cycle tightly focused beam as a function of axial coordinate for spot size w0f = 0.5λ0, and at retarded time t′ = τ.

Figure 11

Fig. 12. Shows a comparative study of the variation of the corrected axial Gouy-phase ϕGC of the longitudinal electric field of an ultrafast, single-cycle, tightly focused (w0f = 0.5λ0) TM01 beam with normalized axial distance $\left(\displaystyle{\Delta z^{\prime} / z_{Rf}} \right)$ at retarded time t′ = τ.

Figure 12

Fig. 13. Shows a comparative study of the variation of the corrected axial Gouy- phase of the longitudinal electric field of an ultrafast, single-cycle tightly focused (w0f = 0.5λ0) TM01 beam with normalized retarded time. (a) Δz′ = 0 and (b) Δz′ = zRf.