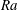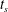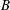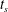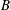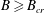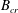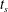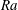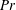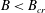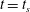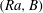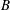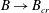1. Introduction
Viscoplastic fluids are those with a yield stress. Such fluids are commonplace in everyday life and present in a variety of both industrial and natural settings; see Balmforth, Frigaard & Ovarlez (Reference Balmforth, Frigaard and Ovarlez2014) and Coussot (Reference Coussot2014). Yield stress fluids only deform if the applied shear stress surpasses a critical value called the yield stress. Below this critical limit such fluids undergo rigid-body motion. A typical flow field may consist of yielded and unyielded regions, according to whether the local stress is above or below the yield stress respectively. Unyielded regions may be further categorized as being stationary or in motion, with the former typically abutting a wall of the flow domain.
This paper is motivated by the recent experimental study of Davaille et al. (Reference Davaille, Gueslin, Massmeyer and Giuseppe2013) in which thermal plumes are induced in a stationary viscoplastic fluid reservoir (rectangular tank), by means of localized heating applied at the lower wall of the tank. In natural convection, buoyancy forces resulting from thermal expansion induce fluid motion. In the case of a viscoplastic fluid, these buoyancy forces may be balanced by stress gradients that do not exceed the yield stress, allowing such fluids to remain motionless in situations where purely viscous fluids would convect. This yield-stress–buoyancy balance allows for interesting new phenomena to arise.
Natural convection of viscoplastic fluid is of particular interest to (at least) the food industry and to geoscientists. Pancakes are one of the oldest foods known to mankind, common across global civilizations and dating back to prehistory. Many similar foods are made from batters that vary in rheological properties according to composition, but frequently have a yield stress (Xue Reference Xue2007). Rheology, boundary conditions, onset of natural convection and the occurrence of dynamical structures such as thermal plumes result in quite different culinary products, e.g. blini, waffles, crêpes and crumpets. Geophysical interest in viscoplastic natural convection ranges from mantle dynamics to basaltic lava flows, mud pots, mud volcanoes and mud baths.
There has only been relatively limited study of natural convection of yield stress fluids despite the relatively common occurrence of such flows. The additional complexity of strong coupling between energy and momentum balances in natural convection flows has meant that the limited number of existing studies tend to be computational. The largest body of work concerns the effect of the yield stress on steady-state naturally convecting flows. In the first place there are a number of one-dimensional naturally convecting flows that admit analytical solution (Yang & Yeh Reference Yang and Yeh1965; Gershuni & Zhukhovitski Reference Gershuni and Zhukhovitski1973; Cherkasov Reference Cherkasov1979; Patel & Ingham Reference Patel and Ingham1994; Bayazitoglu, Paslay & Cernocky Reference Bayazitoglu, Paslay and Cernocky2007). Although one-dimensional, these solutions can exhibit a rich structure, e.g. Karimfazli & Frigaard (Reference Karimfazli and Frigaard2013) show the potential for an infinite number of plug regions in a finite domain!
A number of authors have studied steady-state heat transfer characteristics (Lyubimova Reference Lyubimova1977; Vikhansky Reference Vikhansky2009; Turan, Chakraborty & Poole Reference Turan, Chakraborty and Poole2010, Reference Turan, Chakraborty and Poole2012; Turan, Poole & Chakraborty Reference Turan, Poole and Chakraborty2011), most commonly in a rectangular enclosure with differentially heated sidewalls. The more recent studies of Turan and coauthors have focused largely on using computational fluid dynamics tools to extend Newtonian fluid Nusselt number closure expressions into non-Newtonian parameter regimes. Within the context of steady-state flow, a sufficiently large yield stress suppresses buoyancy-induced stresses, resulting in a static regime (zero velocity everywhere). The temperature field then evolves to its steady conductive limit. A few studies have explicitly considered flows in which this limiting value of the yield stress is evaluated (e.g. Lyubimova Reference Lyubimova1977; Vikhansky Reference Vikhansky2010a ,Reference Vikhansky b ; Karimfazli & Frigaard Reference Karimfazli and Frigaard2013; Huilgol & Kefayati Reference Huilgol and Kefayati2014; Karimfazli, Frigaard & Wachs Reference Karimfazli, Frigaard and Wachs2015).
The most classical setting for instability in natural convection is the Rayleigh–Bénard problem, in which a horizontal layer of stationary fluid is heated from below. It is well established now that flow onset due to linear instability is fundamentally altered due to the yield stress. Zhang, Vola & Frigaard (Reference Zhang, Vola and Frigaard2006) demonstrated that the static conductive state of a Bingham fluid is linearly stable at all values of the Rayleigh number,
$Ra$
,
$$\begin{eqnarray}Ra=\frac{{\hat{g}}\hat{{\it\beta}}{\rm\Delta}\hat{T}\hat{L}^{3}}{\hat{{\it\nu}}\hat{{\it\kappa}}}.\end{eqnarray}$$
The Rayleigh number represents the ratio of time scales for advective and conductive heat transfer in buoyancy-driven flows. Here,
$\hat{{\it\beta}}$
,
$\hat{{\it\nu}}$
and
$\hat{{\it\kappa}}$
represent respectively the coefficients of thermal expansion, kinematic viscosity and thermal diffusivity;
$\hat{L}$
is the height of the fluid layer,
${\rm\Delta}\hat{T}$
is the temperature difference imposed across the fluid layer and
${\hat{g}}$
is the acceleration due to gravity.
Balmforth & Rust (Reference Balmforth and Rust2009) studied the limit of small yield stress, using weakly nonlinear stability analysis to show that an unstable subcritical branch of nonlinear convective states bifurcates from infinite Rayleigh number. Vikhansky (Reference Vikhansky2009) also briefly visited flow transition in the Rayleigh–Bénard problem, exploring the yield stress needed to suppress steady Newtonian natural convection and speculating on the effect of the yield stress on flow transients. The energy stability results of Zhang et al. (Reference Zhang, Vola and Frigaard2006) have been extended by the present authors (Karimfazli et al.
Reference Karimfazli, Frigaard and Wachs2015) to include stationary states in differentially heated vertical cavities. The static state is shown to be energy stable to arbitrary amplitude disturbances for
$Ra$
below the Newtonian limit and conditionally stable for larger
$Ra$
. Karimfazli et al. (Reference Karimfazli, Frigaard and Wachs2015) also study various controlled transitions between steady states, including establishing the interesting possibility of temporary flow arrest between convecting steady states. While the majority of these results are established for Bingham fluids, for reasons of analytical and parametric simplicity, the main qualitative conclusions are expected to be true for other simple yield stress models, e.g. Herschel–Bulkley and Casson fluids.
Although the theoretical background is well established, experimental studies do not fully agree. Both Darbouli et al. (Reference Darbouli, Metivier, Piau, Magnin and Abdelali2013) and Kebiche, Castelain & Burghelea (Reference Kebiche, Castelain and Burghelea2014) have studied flow onset in the Rayleigh–Bénard set-up experimentally and, although their results do not agree quantitatively, both groups find that above a certain heating rate, natural convection starts without any manual agitation of the fluid. Darbouli et al. (Reference Darbouli, Metivier, Piau, Magnin and Abdelali2013) use Carbopol gels at relatively weak concentrations and yield stresses (
${\lesssim}0.1$
Pa). They offer a variety of explanations for the disagreement with theory. First, they outline the difficulty of specifying a relevant viscosity for
$Ra$
at low (zero) shear rates. Second, they speculate that at low concentrations a more appropriate microstructural model might be that of a porous media flow of water through a swollen microgel matrix. Kebiche et al. (Reference Kebiche, Castelain and Burghelea2014) consider a wider range of yield stresses, again with Carbopol. They show the onset of convective rolls above a critical power threshold that increases exponentially with yield stress.
In discussing transient natural convection, a wide range of phenomena may occur. In particular, regarding the effect of the yield stress on the onset of flow from a stationary state we must first distinguish two different mechanisms. Due to the yield stress the static state may be a solution to the flow problem for all values of the dimensionless groups and all time. Typically this depends on the domain geometry and boundary conditions. In this case, flow onset is a consequence of a hydrodynamic instability. Alternatively, if the static state is not always a solution, flow onset from a static initial state might be merely the result of temporal evolution of the driving (buoyancy) and/or resisting (yield) stresses.
Moving now specifically to the subject of this paper, thermal plumes have long received interest both as convective flows that develop due to localized heat sources and as instabilities that rise from a thermal boundary layer (see, e.g., Batchelor Reference Batchelor1954; Sparrow, Husar & Goldstein Reference Sparrow, Husar and Goldstein1970; Moses, Zocchi & Libchaber Reference Moses, Zocchi and Libchaber1993; Kaminski & Jaupart Reference Kaminski and Jaupart2003). A review of the vast body of research on Newtonian plumes can be found in Ribe, Davaille & Christensen (Reference Ribe, Davaille and Christensen2007). To the best of authors’ knowledge, the first experimental studies of viscoplastic plumes were conducted very recently by Davaille et al. (Reference Davaille, Gueslin, Massmeyer and Giuseppe2013).
Davaille et al. examined natural convection of yield stress fluids in a rectangular tank driven by a localized heater placed centrally on the bottom wall. They mainly focused on illustrating various flow morphologies observed at different heating rates. The effect of the heating rate is captured by the yield number,
$Y$
, which represents the relative strength of thermal stresses and the yield stress,
$$\begin{eqnarray}Y=\frac{\hat{{\it\beta}}\hat{{\it\rho}}\,\hat{\dot{q}}}{\hat{{\it\tau}}_{y}\hat{k}}.\end{eqnarray}$$
Here,
$\hat{{\it\rho}}$
,
$\hat{k}$
and
$\hat{{\it\tau}}_{y}$
represent the density, thermal conductivity and yield stress;
$\hat{\dot{q}}$
is the constant power supply applied to the heater. The effect of the yield number on the transition between three different regimes is investigated, classified solely on the value of the yield number,
$Y$
. The fluid is deemed motionless when
$Y\lesssim 120$
. When
$120\lesssim Y\lesssim 260$
, cellular convection is expected, i.e. a localized motion around the heater. With
$Y>260$
, finger-like plumes form above the heater and ascend upwards into the tank. Within this range of
$Y$
, the developing plumes show pulsing trends, in some cases resulting in complete stoppage of the flow between consecutive pulses. In all of the convecting cases, it was observed that yielding and advection started a long time after heating was initiated. In this work there was no study of the effects of
$Ra$
on transition between the three regimes.
In a subsequent paper, Massmeyer et al. (Reference Massmeyer, Giuseppe, Davaille, Rolf and Tackley2013) studied a similar flow numerically. They considered a taller 3D cavity with insulated walls and imposed a constant temperature at the heater, which gradually increased with time. This temperature history was not produced using any particular mathematical function. Instead it was derived from the temperature history of the heater in the experiments of Davaille et al. (Reference Davaille, Gueslin, Massmeyer and Giuseppe2013) and was only provided for a very limited number of simulations. This significantly limits the possibility of quantitative benchmarking against their work. The main focus of Massmeyer et al. (Reference Massmeyer, Giuseppe, Davaille, Rolf and Tackley2013) appears to be on capturing the plume onset time and maximum plume rise. They also briefly considered the effect of small changes in fluid rheology on plume development. The simulations succeeded in reproducing a few of the experimental features qualitatively well, e.g. the formation of plume heads at high values of
$Y$
. However, the hydrodynamics of transition from no motion to cellular motion and the processes affecting the features of cellular motion as
$Ra$
and
$B$
change were not investigated or explained. Furthermore, the intermittent pulsing of plumes observed by Davaille et al. (Reference Davaille, Gueslin, Massmeyer and Giuseppe2013) was not reported in the numerical study. Hassan, Pathak & Khan (Reference Hassan, Pathak and Khan2013) have numerically studied steady-state convection of viscoplastic fluids in a similar set-up, with their focus firmly on heat transfer.
A common technical issue with numerical studies such as those of Hassan et al. (Reference Hassan, Pathak and Khan2013) and Massmeyer et al. (Reference Massmeyer, Giuseppe, Davaille, Rolf and Tackley2013) is their reliance on regularized effective viscosity models in simulating yield stress behaviour. Although exact yield stress models are purportedly studied, the numerical code sees only a very viscous fluid at low shear rates. This range is precisely that which is important for the study of flow onset or stoppage. Although such methods may be used effectively, it is necessary to understand the degree to which the constitutive law is regularized, i.e. in terms of typical shear rates of the flow studied. The second issue with such methods for yielding problems is that the shape and position of the (apparent) yield surfaces are known to be sensitive to the form of regularization used.
The main focus of our paper is to understand the effect of localized heating in viscoplastic fluids from the mechanical perspective of a simple yield stress fluid. We feel that localized heating is the key feature of the work of Davaille et al. (Reference Davaille, Gueslin, Massmeyer and Giuseppe2013) that merits further investigation. Where possible, we have tried to make analogies between the phenomena observed by Davaille et al. (Reference Davaille, Gueslin, Massmeyer and Giuseppe2013) and the simplified problem studied here. However, the intention is not to reproduce experiments, but to clarify what may be expected in terms of dynamical behaviour. For example, it is intuitive that a critical ratio of buoyancy to yield stress should play a governing role, and we seek to expose that in as simple a way as possible. Equally, the role of the Rayleigh number in the flow onset and plume formation and development should be clarified. For those flows that do convect we explore the variation of flow features with the controlling dimensionless parameters, and look for processes that could promote pulsing features.
We employ both analytical and numerical techniques, always assuming an ideal yield stress fluid. We consider a two-dimensional (2D) rectangular cavity with all walls maintained at a temperature
$\hat{T}_{C}$
, except in the middle of the lower wall where a centrally positioned heater is maintained at a higher temperature
$\hat{T}_{H}$
. Although in 2D, key geometric ratios are chosen similar to those of the experiments in (Davaille et al.
Reference Davaille, Gueslin, Massmeyer and Giuseppe2013). The heater thus covers 10 % of the bottom wall of a square cavity and the geometry is fixed throughout the paper. As the focus is on yielding and yield stress, we adopt the simplest (Bingham fluid) rheological model, for which the effective viscosity is
$$\begin{eqnarray}\hat{{\it\mu}}_{e}=\frac{\hat{{\it\tau}}_{y}}{\hat{\dot{{\it\gamma}}}}+\hat{{\it\mu}},\end{eqnarray}$$
where
$\hat{{\it\mu}}$
is the plastic viscosity of the fluid and the rate of strain is denoted by
$\hat{\dot{{\it\gamma}}}$
. Although different yield stress models can be used to describe the shear-thinning behaviour, e.g. the Herschel–Bulkley model, this mainly affects the role of the plastic viscosity. The commonality between all such models is the singularity of the effective viscosity as yield surfaces are approached. Indeed, in studying flow onset the plastic viscosity matters only if
$\hat{\dot{{\it\gamma}}}>0$
, i.e. after onset.
As commented above in discussing the Rayleigh–Bénard studies, note the distinction between analytical and computational studies involving simplified rheological constitutive models and related experimental studies with yield stress fluids. The latter necessarily involve additional complexities associated with the nature of yield stress fluids, on which there has been a long-standing scientific discourse; see, e.g., Barnes (Reference Barnes1999), Divoux, Barentin & Manneville (Reference Divoux, Barentin and Manneville2011), Ovarlez et al. (Reference Ovarlez, Cohen-Addad, Krishan, Goyon and Coussot2013), Balmforth et al. (Reference Balmforth, Frigaard and Ovarlez2014), Coussot (Reference Coussot2014) and Bonn et al. (Reference Bonn, Paredes, Denn, Berthier, Divoux and Manneville2015). As much of the interest and concern is focused on regimes of low strain rates and/or subyield stresses, where different materials exhibit different characteristic behaviours, care must be taken in widely interpreting the results of systematic studies for other materials. In this context, one of the key values of using simplified rheological constitutive models (as here) is in removing the ambiguity of results, i.e. in determining which phenomena have their origin in pure yield stress behaviour.
A brief outline of the paper is as follows. In § 2 we formulate the problem, identify the governing dimensionless groups and briefly explain our computational method. In § 3 we investigate the conditions that precede yielding (flow onset) and the role of the yield stress in the transition from a motionless state to an advective one. In § 4 we carefully consider the effect of the yield stress on the dynamics of flow development after the start of yielding. This allows us to identify the mechanisms that play the key role in transition between different regimes. We close in § 5 with a qualitative comparison of our results with those of Davaille et al. (Reference Davaille, Gueslin, Massmeyer and Giuseppe2013), and an overview of the main characteristics of viscoplastic plumes.
2. Formulation
We consider a square (two-dimensional) cavity of side
$\hat{L}$
filled with a Bingham fluid with the following properties: yield stress
$\hat{{\it\tau}}_{y}$
, plastic viscosity
$\hat{{\it\mu}}$
, thermal diffusivity
$\hat{{\it\kappa}}$
, thermal expansion
$\hat{{\it\beta}}$
and density
$\hat{{\it\rho}}$
. The cavity walls are maintained at temperature
$\hat{T}_{c}$
, except the bottom wall where a heater of width
${\hat{h}}_{w}$
is positioned in the middle (
$-{\hat{h}}_{w}/2\leqslant \hat{x}\leqslant {\hat{h}}_{w}/2$
) and is maintained at temperature
$\hat{T}_{H}$
for
$\hat{t}>0$
. Figure 1 illustrates the flow geometry and boundary conditions. In this paper we will denote dimensional quantities with the
$\hat{\cdot }$
symbol and dimensionless quantities without.
Figure 1. Schematic of the domain geometry and temperature boundary conditions. No-slip conditions are assumed on all walls and on the heater.
At
$\hat{t}=0$
the fluid is at temperature
$\hat{T}_{C}$
everywhere and the fluid is stationary. Heat transfer and the onset of flow are driven by the temperature difference
${\rm\Delta}\hat{T}=\hat{T}_{H}-\hat{T}_{C}$
. The hydrodynamics is governed by the momentum, energy and continuity equations. Assuming the Boussinesq approximation and using dimensionless variables, these equations are
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{Pr}\frac{\partial u_{i}}{\partial t}+Gr\;u_{j}\frac{\partial u_{i}}{\partial x_{j}}=-\frac{\partial p}{\partial x_{i}}+\frac{\partial {\it\tau}_{ij}}{\partial x_{j}}+T{\it\delta}_{i2}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial T}{\partial t}+Ra\,u_{j}\frac{\partial T}{\partial x_{j}}=\frac{\partial ^{2}T}{\partial x_{i}\partial x_{i}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial u_{i}}{\partial x_{i}}=0, & \displaystyle\end{eqnarray}$$
$i,j=1,2$
, with
$(x_{1},x_{2})=(x,y)$
. Here, the convention of implicit summation over repeated indices is adopted. In (2.1)–(2.3),
$u_{i}$
,
$p$
,
${\it\tau}_{ij}$
and
$T$
are the velocity, pressure, deviatoric stress and temperature, respectively. The Bingham model is described by the constitutive equations 
$$\begin{eqnarray}\left.\begin{array}{@{}cl@{}}{\it\tau}_{ij}=\displaystyle \left(1+\frac{B}{\dot{{\it\gamma}}}\right)\dot{{\it\gamma}}_{ij}, & \text{iff}~{\it\tau}>B,\\ \dot{{\it\gamma}}=0, & \text{iff}~{\it\tau}\leqslant B.\end{array}\right\}\end{eqnarray}$$
The cavity is denoted by
${\it\Omega}=[-1/2,1/2]\times [0,1]$
and the boundary conditions are
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \hspace{-28.79993pt}u_{i}=0,\quad T=0,\quad \text{at }x_{1}=\pm 1/2,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \hspace{-46.79993pt}u_{i}=0,\quad T=0,\quad \text{at }x_{2}=1,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle u_{i}=0,\quad T=\left\{\begin{array}{@{}l@{}}1,\quad \text{at}~x_{2}=0,|x_{1}|\leqslant r,\\ 0,\quad \text{at}~x_{2}=0,|x_{1}|>r.\end{array}\right.\end{eqnarray}$$
It should be noted that the solution is symmetric with respect to
$x=0$
. Thus, one only needs to analyse half of the domain,
$0\leqslant x<1/2$
, subject to the boundary conditions
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \hspace{-48.0pt}u_{i}=0,\quad T=0,\quad \text{at }x_{1}=1/2,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \hspace{-49.20007pt}u_{1}=0,\quad \frac{\partial T}{\partial x}=0,\quad \text{at }x_{1}=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \hspace{-58.79993pt}u_{i}=0,\quad T=0,\quad \text{at }x_{2}=1,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle u_{i}=0,\quad T=\left\{\begin{array}{@{}l@{}}1,\quad \text{at }x_{2}=0,0\leqslant x_{1}\leqslant r,\\ 0,\quad \text{at }x_{2}=0,r<x_{1}.\end{array}\right.\end{eqnarray}$$
In (2.1)–(2.3) dimensionless variables have been defined as follows:
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle x_{i}=\frac{\hat{x_{i}}}{\hat{L}},\quad \displaystyle T=\frac{\hat{T}-\hat{T}_{C}}{\hat{T}_{H}-\hat{T}_{C}},\quad \displaystyle u_{i}=\frac{\hat{{\it\nu}}\,\hat{u_{i}}}{{\hat{g}}\hat{{\it\beta}}{\rm\Delta}\hat{T}\hat{L}^{2}},\\ \displaystyle p=\frac{\hat{p}-\hat{{\it\rho}}_{0}{\hat{g}}{\hat{y}}}{\hat{{\it\rho}}_{0}{\hat{g}}\hat{{\it\beta}}{\rm\Delta}\hat{T}\hat{L}},\quad \displaystyle t=\frac{\hat{{\it\kappa}}\hat{t}}{\hat{L}^{2}},\quad \displaystyle {\it\tau}_{ij}=\frac{\hat{{\it\tau}}_{ij}}{\hat{{\it\rho}}_{0}{\hat{g}}\hat{{\it\beta}}{\rm\Delta}\hat{T}\hat{L}}.\end{array}\right\}\end{eqnarray}$$
The four independent dimensionless groups that describe this flow are the Rayleigh number,
$Ra$
, Prandtl number,
$Pr$
, Bingham number,
$B$
, and width ratio
$r$
:
$$\begin{eqnarray}\displaystyle Ra=\frac{{\hat{g}}\hat{{\it\beta}}{\rm\Delta}\hat{T}\hat{L}^{3}}{\hat{{\it\nu}}\hat{{\it\kappa}}},\quad Pr=\frac{\hat{{\it\nu}}}{\hat{{\it\kappa}}},\quad B=\frac{\hat{{\it\tau}}_{y}}{\hat{{\it\rho}}_{0}{\hat{g}}\hat{{\it\beta}}{\rm\Delta}\hat{T}\hat{L}},\quad r=\frac{{\hat{h}}_{w}}{2\hat{L}}. & & \displaystyle\end{eqnarray}$$
It should be noted that the Grashof number
$Gr=Ra/Pr$
. The Bingham number
$B$
reflects the ratio of the yield stress to a representative buoyancy stress. As the velocity scale above comes from balancing buoyant stresses with viscous stresses, an alternative interpretation for
$B$
is as the balance of yield stress and viscous stress. The type of stress balance captured in
$B$
is sometimes referred to as the Oldroyd number or yield number.
2.1. Computational method
We give now an outline of the computational method that has been used throughout this paper. Adopting the constitutive equation of a Bingham fluid (or similar) gives rise to two specific properties: (i) the stress field is undetermined when the strain-rate field is zero and (ii) the equation is non-differentiable at the yield point. Two families of numerical methods have been used to circumvent these issues. The first is the well-known regularization method, which approximates the exact yield stress law with a smoothed and bounded effective viscosity. This transforms the problem into a generalized Newtonian flow, in which the material is treated as highly viscous in regions where it is supposed not to yield. At the computational level, classical solution methods for shear-thinning/shear-thickening fluid flows are used. This type of method is apparently used in Massmeyer et al. (Reference Massmeyer, Giuseppe, Davaille, Rolf and Tackley2013). Although practical, this technique raises issues in terms of the determination of the yield surface positions and in determining limits of flow/no flow, e.g. onset and stopping. These defects are simply because generalized Newtonian (i.e. purely viscous) materials move under any applied deviatoric stress, even if their viscosity is very high.
The second method relies on Lagrange multiplier and decomposition–coordination methods and is referred to in the literature as an augmented Lagrangian algorithm. It has been shown that, when combined with a fully implicit backward Euler time discretization, this algorithm computes return to rest in finite time in an accurate way (in the sense that at rest the strain-rate field is computationally zero everywhere in the flow domain). This is because the original form of the Bingham constitutive equation is considered directly, with the Lagrange multiplier representing an admissible stress. For an extended discussion on regularization techniques and the augmented Lagrangian algorithm, the interested reader is referred to Frigaard & Nouar (Reference Frigaard and Nouar2005) and Glowinski & Wachs (Reference Glowinski and Wachs2011) respectively.
In this study (2.1)–(2.3) with corresponding boundary conditions are solved using an augmented Lagrangian algorithm combined with a finite volume/staggered grid space discretization. The numerical strategy employed here is identical to that in Karimfazli et al. (Reference Karimfazli, Frigaard and Wachs2015), wherein more details about the numerical scheme can be found. All simulations are performed with PeliGRIFF, a code that has been developed for numerical computation of two-phase flows (e.g. particles, drops or bubbles suspended in Newtonian or yield stress fluids); see, e.g., Wachs et al. (Reference Wachs, Hammouti, Vinay and Rahmani2015) for more details. A number of benchmark flows have been computed to verify that this code does faithfully reproduce published results on steady-state natural convection with Newtonian fluids (de Vahl Davis Reference de Vahl Davis1983) and with Bingham fluids (Turan et al. Reference Turan, Chakraborty and Poole2010), and compares well with available analytical results for the termination of flow. These benchmark comparisons are detailed in Karimfazli et al. (Reference Karimfazli, Frigaard and Wachs2015) and are not repeated here for brevity.
3. Onset of yielding and flow
At
$t=0$
, the velocity is zero everywhere and the fluid is at the reference temperature (
$T=0$
) everywhere in the domain. On neglecting all nonlinear advective terms that are quadratic in the solution variables, the initial behaviour is governed by
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{1}{Pr}\frac{\partial u_{i}}{\partial t}=-\frac{\partial p}{\partial x_{i}}+\frac{\partial {\it\tau}_{ij}}{\partial x_{j}}+T{\it\delta}_{i2}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial T}{\partial t}=\frac{\partial ^{2}T}{\partial x_{i}\partial x_{i}}. & \displaystyle\end{eqnarray}$$
$T(0,x,y)=0$
, we might expect that the convection cell will not immediately start, i.e. a time is required for the fluid to heat sufficiently to generate a large enough buoyancy force. If the yield stress is sufficiently large, yielding of the fluid will not occur and the flow remains static.
The minimum yield stress that is sufficient to suppress the flow indefinitely is called the critical yield stress, denoted in dimensionless variables by
$B_{cr}$
. Suppose instead that yielding starts at
$t=t_{s}$
. Before yielding starts, for
$t<t_{s}$
, we have
$\boldsymbol{u}(t,x,y)=0$
and
$T$
satisfies (3.2), with initial condition
$T(0,x,y)=0$
. The temperature distribution in the cavity is thus governed purely by conduction and the analytical solution is easily found in series form:
$$\begin{eqnarray}\displaystyle & \displaystyle T_{c}(t,x_{1},x_{2})=T_{s}(x_{1},x_{2})+T_{t}(t,x_{1},x_{2}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle T_{s}(x_{1},x_{2})=\mathop{\sum }_{m=0}^{\infty }C_{m}\sin [a_{2m+1}(x_{1}+0.5)]\sinh [a_{2m+1}(1-x_{2})], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle T_{t}(t,x_{1},x_{2})=\mathop{\sum }_{m=1}^{\infty }\mathop{\sum }_{p=0}^{\infty }A_{2p+1,m}\exp (-(a_{2p+1}^{2}+b_{m}^{2})t)\sin (a_{2p+1}(x_{1}+0.5))\sin (b_{m}(1-x_{2})), & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle C_{m}=\frac{4(-1)^{m}}{a_{2m+1}}\frac{\sin (a_{2m+1}r)}{\sinh (a_{2m+1})}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle A_{2p+1,q}=\frac{8(-1)^{p+q}\,b_{q}}{a_{2p+1}(b_{q}^{2}+a_{2p+1}^{2})}\sin (a_{2p+1}r), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle a_{2p+1}=(2p+1){\rm\pi}\quad \text{and}\quad b_{m}=m{\rm\pi}. & \displaystyle\end{eqnarray}$$
$T_{s}$
and
$T_{t}$
are respectively the steady-state and transient components of the conductive temperature field
$T_{c}(t,x_{1},x_{2})$
, and the exact solution to (2.1)–(2.3) is 
$$\begin{eqnarray}\displaystyle \boldsymbol{u}(t,x_{1},x_{2})=0,\quad T(t,x_{1},x_{2})=T_{c}(t,x_{1},x_{2});\quad t\in [0,t_{s}). & & \displaystyle\end{eqnarray}$$
It should be noted that although the velocity is determined during the phase
$t\in [0,t_{s})$
, the stress field is not. The static momentum balance is
$$\begin{eqnarray}0=-\frac{\partial p}{\partial x_{i}}+\frac{\partial {\it\tau}_{ij}}{\partial x_{j}}+T_{c}{\it\delta}_{i2}.\end{eqnarray}$$
During this time period heat diffuses into the cavity from the heated plate, eventually approaching the steady state. As initially
$T=0$
, we expect that everywhere in the cavity the size of the buoyancy force will increase monotonically with time. However,
$t$
appears essentially as a parameter in (3.10) contained in
$T_{c}(t,x,y)$
. The stress components are not fully determined by (3.10), which is properly considered as an admissibility condition for the stress. We denote by
$\mathscr{S}$
the set of admissible stress tensors
$\tilde{{\it\sigma}}_{ij}=-\tilde{p}{\it\delta}_{ij}+\tilde{{\it\tau}}_{ij}$
that satisfy (3.10). In other words, at any time
$t\in [0,t_{s})$
,
$\mathscr{S}$
depends on the buoyancy force
$T_{c}{\it\delta}_{i2}$
. It is known that the stress tensor in a viscoplastic fluid (Stokes) flow satisfies a stress maximization principle, which in this case takes the following form; see, e.g., Prager (Reference Prager1954). The true stress tensor
${\it\sigma}_{ij}\in \mathscr{S}$
maximizes
$$\begin{eqnarray}{\it\Psi}(\tilde{{\it\tau}})=-\frac{1}{2}\int _{{\it\Omega}}[\max \{\tilde{{\it\tau}}-B,0\}]^{2}\,\text{d}V\end{eqnarray}$$
over
$\mathscr{S}$
. From this we may deduce that if any (admissible) stress tensor has
$\tilde{{\it\tau}}\leqslant B$
, then
${\it\tau}\leqslant B$
for the actual stress field. In other words, suppose that at each
$t\in [0,t_{s})$
we may find the admissible stress tensor
$\tilde{{\it\sigma}}_{ij}$
with smallest
$\tilde{{\it\tau}}$
, this defines the limiting yield stress, say
$B=B_{c}(T_{c}(t,x_{1},x_{2}))$
, required to keep the fluid static; i.e. a yield stress fluid will not yield unless it has to.
We observe that
$T_{c}(t,x,y)$
depends only on the dimensionless parameter
$r$
. The admissibility condition (3.10) is independent of
$Ra$
and
$Pr$
. Thus, any admissible stress field depends only on
$r$
. It follows that the limiting yield stress
$B_{c}$
must be independent of
$Ra$
and
$Pr$
at each
$t\in [0,t_{s})$
. It should be noted that this argument is valid for more general cavity shapes
${\it\Omega}$
and heater configurations, i.e. the conductive temperature field would first be solved (depending on domain geometry and heater configuration only), and (3.10) then depends only on
${\it\Omega}$
and
$T_{c}$
.
A discontinuity in the initial temperature conditions may allow large admissible stresses, causing localized yielding. However, for the present problem, the only discontinuity is due to the wall temperature. For
$t>0$
, the heat equation (3.2) smooths the temperature field and, therefore, no singular stress values are expected within the domain. We expect that the main physical effect will be a monotone increase in
$T_{c}(t,x_{1},x_{2})$
and hence the buoyancy-induced stresses. In other words, we would expect that
$B_{c}(t)$
increases with
$T_{c}(t,x,y)$
. To suppress the flow indefinitely, taking
$t_{s}\rightarrow \infty$
we see that
$T_{c}(t_{s},x_{1},x_{2})\rightarrow T_{s}(x_{1},x_{2})$
. Therefore, provided that
$B_{c}(t)$
increases monotonically with
$t$
, we can associate
$B_{cr}$
with the stress field induced by the steady-state conductive temperature
$T_{s}(x_{1},x_{2})$
.
3.1. Computational determination of the critical Bingham number
As we have demonstrated, the actual conditions for motion onset are independent of
$Ra$
and
$Pr$
. However, once started these parameters affect the evolution of the solution. At higher
$Ra$
, the yielded area propagates more rapidly. Therefore, at identical time instances, the yield surfaces deviate more noticeably from the initial shape at onset. The geometry of the yield surfaces shortly after yielding is illustrated for different values of
$Ra$
at
$B=0.002$
in figure 2.
Figure 2. Speed,
$|\boldsymbol{u}|(t)$
, and yield surfaces (white lines) at
$t=0.006$
,
$B=0.002$
and
$Pr=10^{4}$
, at different values of
$Ra$
: (a)
$Ra=10^{4}$
, (b)
$Ra=10^{5}$
, (c)
$Ra=10^{6}$
.
As
$B$
is increased it takes progressively longer for the flow to be initiated (
$t_{s}$
increases). However, the computed steady-state velocity decreases with
$B$
. Figure 3 illustrates the steady-state flow structure at a Bingham number close to the critical value, where the convection is relatively weak for
$Ra=10^{4}$
.
Figure 3. Flow field at
$Ra=10^{4},Pr=10^{4}$
and
$B=0.0028$
. (a) Colourmap of the speed
$|\boldsymbol{u}|$
; white lines represent the yield surfaces. (b) Colourmap of the temperature
$T$
; white lines represent the streamlines.
The critical Bingham number may be approximated from the results of numerical solution of the flow. We have already determined that the initial yielding (flow onset) is independent of both
$Ra$
and
$Pr$
. Thus, we fix
$Ra=10^{4}$
and
$Pr=10^{4}$
for our main computations. Starting from an initially static and cold fluid we integrate forward in time at a fixed
$B$
. If the flow starts we integrate until steady velocity and temperature are achieved. We then use the following criterion to approximate
$t_{s}$
from the norm of the shear rate:
$$\begin{eqnarray}\frac{\Vert \dot{{\it\gamma}}\Vert (t_{s})}{\Vert \dot{{\it\gamma}}\Vert (\infty )}=10^{-3}.\end{eqnarray}$$
We use linear interpolation to evaluate
$\Vert \dot{{\it\gamma}}\Vert (t)$
between the discrete numerical data points. The results of the above explained computational approach are illustrated later in figure 6(a).
To numerically estimate
$B_{cr}$
we extrapolate using the steady-state
$\Vert \dot{{\it\gamma}}\Vert (\infty )$
at three values of the Bingham number close to the critical value, to find
$B_{cr}$
where
$\Vert \dot{{\it\gamma}}\Vert (\infty )=0$
. Using this approach we find
$$\begin{eqnarray}B_{cr}=0.0030.\end{eqnarray}$$
This limit is verified by additional computations at different values of
$Ra$
and
$Pr$
. It should be noted that
$B_{cr}$
does change with
$r$
and the cavity aspect ratio. Variation of
$B_{cr}$
with
$r$
is illustrated in figure 4. Increasing
$r$
increases the heat transferred to the domain. On the other hand, as
$r\rightarrow 0.5$
it is expected that the effect of the sidewalls will become more important as the shape and position of yield surfaces are limited by the walls. Moreover, more thermal energy is dissipated through the sidewalls as they get closer to the heater. On increasing
$r$
from zero to
$0.5$
, therefore,
$B_{cr}$
initially increases to a maximum before decreasing to its limiting value
$B_{cr}=0.0087$
at
$r=0.5$
. It should be noted that had we assumed a zero heat flux at the vertical sidewalls, we would have expected
$B_{cr}\rightarrow 0$
as
$r\rightarrow 0.5$
.
Figure 4. Variation of
$B_{cr}$
with
$r$
. Estimates of
$B_{cr}$
are calculated using the computational technique described in § 3.1.
3.2. Analytical determination of the critical Bingham number
There are a number of ways in which
$B_{cr}$
might be estimated analytically. First, we might try a direct constructive method. The series form of
$T_{c}(t,x,y)$
inserted into (3.10) suggests that
$p$
and
${\it\tau}_{ij}$
can be expressed similarly in series structure, e.g.
$$\begin{eqnarray}{\it\tau}_{ij}=\mathop{\sum }_{m}F_{ij,m}(x_{1},x_{2})+\mathop{\sum }_{m}\mathop{\sum }_{p}A_{ij,(2p+1,m)}\exp (-{\it\alpha}_{p,m}t)G_{ij,(p,m)}(x_{1},x_{2}).\end{eqnarray}$$
Here, the first summation represents the stress tensor needed to balance the buoyancy force from
$T_{s}(x_{1},x_{2})$
and the second summation balances the transient component. We note that even in attempting to evaluate a single modal term of the above expression the (modal) stresses are indeterminate, i.e.
$p$
,
${\it\tau}_{11}=-{\it\tau}_{22}$
and
${\it\tau}_{12}={\it\tau}_{21}$
must be found from two momentum equations. Nevertheless, we can speculate regarding
$B_{c}(t)$
using (3.14). As
$t\rightarrow \infty$
,
$$\begin{eqnarray}{\it\tau}_{ij}\sim \mathop{\sum }_{m}F_{ij,m}(x_{1},x_{2})+A_{ij,(1,1)}\exp (-{\it\alpha}_{0,1}t)G_{ij,(0,1)}(x_{1},x_{2}).\end{eqnarray}$$
As discussed earlier in § 3,
$B_{c}(t)\propto {\it\tau}$
and
$B_{c}(t)$
is expected to increase monotonically with time and
$\lim _{t\rightarrow \infty }B_{c}(t)=B_{cr}$
. We therefore hypothesize that
$$\begin{eqnarray}B_{c}(t)\sim B_{cr}(1-\exp (-{\it\alpha}t)),\end{eqnarray}$$
i.e. as
$B\rightarrow B_{cr}$
, the flow start time increases to infinity logarithmically, as
$\ln (1-B/B_{cr})$
.
Alternatively, we may approach the limiting yield stress considering the energy equation at the onset of motion. Suppose that the flow starts at
$t=t_{s}$
, with
$\Vert \boldsymbol{u}\Vert >0$
for
$t>t_{s}$
. We multiply (2.1) by
$u_{i}$
and integrate over the cavity
${\it\Omega}$
to derive the energy equation:
$$\begin{eqnarray}\frac{1}{Pr}\frac{\text{d}H}{\text{d}t}=-\langle \dot{{\it\gamma}}^{2}(\boldsymbol{u})\rangle -B\langle \dot{{\it\gamma}}(\boldsymbol{u})\rangle +\langle u_{2}T\rangle ,\end{eqnarray}$$
where
$H$
represents the kinetic energy of the fluid,
$$\begin{eqnarray}H=\frac{1}{2}\langle \boldsymbol{u}^{2}\rangle \quad \text{and}\quad \langle {\it\phi}\rangle =\int _{{\it\Omega}}{\it\phi}\,\text{d}x.\end{eqnarray}$$
Assuming that when
$B=B_{c}$
yielding starts at
$t_{s}$
, for sufficiently small
$0<{\it\epsilon}\ll 1$
, the flow field at
$t^{\ast }=t_{s}+{\it\epsilon}\tilde{t}$
can be described as
$$\begin{eqnarray}\displaystyle & u(t^{\ast })=u(t_{s})+{\it\delta}_{u}\tilde{u} , & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & T(t^{\ast })=T(t_{s})+{\it\delta}_{T}\tilde{T}, & \displaystyle\end{eqnarray}$$
${\it\delta}_{u}\ll 1$
,
${\it\delta}_{T}\ll 1$
and the
$\tilde{\cdot }$
denoting rescaled quantities local to starting. The rescaled energy equation thus becomes 
$$\begin{eqnarray}\frac{{\it\delta}_{T}}{{\it\epsilon}}\frac{\partial \tilde{T}}{\tilde{t}}+Ra{\it\delta}_{u}{\it\delta}_{T}\tilde{u} _{j}\frac{\partial \tilde{T}}{\partial x_{j}}=\frac{\partial ^{2}T_{c}(t_{s})}{\partial x_{j}\partial x_{j}}+{\it\delta}_{T}\frac{\partial ^{2}\tilde{T}}{\partial x_{j}\partial x_{j}},\end{eqnarray}$$
which yields
${\it\delta}_{T}={\it\epsilon}$
, i.e. the heat transfer is still dominated by conduction at
$t^{\ast }$
, and
$T(t^{\ast })=T_{c}(t_{s})+{\it\epsilon}\tilde{T}^{\ast }$
. The rescaled kinetic energy equation is therefore
$$\begin{eqnarray}\frac{{\it\delta}_{u}^{2}}{{\it\epsilon}Pr}\frac{\text{d}\tilde{H}}{\text{d}\tilde{t}}=-{\it\delta}_{u}^{2}\langle \dot{{\it\gamma}}^{2}(\tilde{\boldsymbol{u}})\rangle -B_{c}{\it\delta}_{u}\langle \dot{{\it\gamma}}(\tilde{\boldsymbol{u}})\rangle +{\it\delta}_{u}\langle \tilde{u} _{2}(T_{c}(t_{s})+{\it\epsilon}\tilde{T})\rangle .\end{eqnarray}$$
Alternatively we may write
$$\begin{eqnarray}0<\frac{{\it\delta}_{u}}{{\it\epsilon}Pr}\frac{\text{d}\tilde{H}}{\text{d}\tilde{t}}+{\it\delta}_{u}\langle \dot{{\it\gamma}}^{2}(\tilde{\boldsymbol{u}})\rangle \leqslant -\langle \dot{{\it\gamma}}(\tilde{\boldsymbol{u}})\rangle \left[B_{c}-\sup _{\boldsymbol{v}\in \mathscr{V},\boldsymbol{v}\not =0}\left\{\frac{\langle \tilde{v}_{2}(T_{c}(t_{s})+{\it\epsilon}\tilde{T})\rangle }{\langle \dot{{\it\gamma}}(\tilde{\boldsymbol{v}})\rangle }\right\}\right],\end{eqnarray}$$
where
$\mathscr{V}=\{\boldsymbol{v}\in [H_{0}^{1}({\it\Omega})]^{2};\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{v}=0\}$
. Defining
$$\begin{eqnarray}B_{c}(t_{s})=\sup _{\boldsymbol{v}\in \mathscr{V},\boldsymbol{v}\not =0}\left\{\frac{\langle \tilde{v}_{2}T_{c}(t_{s})\rangle }{\langle \dot{{\it\gamma}}(\tilde{\boldsymbol{v}})\rangle }\right\},\end{eqnarray}$$
we observe that a necessary condition for
$H$
(or
$\tilde{H}$
) to grow in time at
$t=t_{s}$
is that
$B\leqslant B_{c}(t_{s})$
, i.e. taking
$B>B_{c}(t_{s})$
contradicts the assumption that
$\Vert \boldsymbol{u}\Vert >0$
for
$t>t_{s}$
. Moreover, a comparison of (3.22) and (3.24) reveals that
${\it\delta}_{u}={\it\epsilon}^{2}$
, i.e. the viscous dissipation does not affect the kinetic energy balance (at the leading order) and the excess buoyancy at
$t^{\ast }$
accelerates the otherwise static fluid. Whether the condition
$B>B_{c}(t_{s})$
is sharp or not depends on whether the actual solution attains the supremum in (3.24). Nevertheless, as
$t\rightarrow \infty$
we have
$T_{c}\rightarrow T_{s}$
and
$B_{c}(t)$
exponentially approaches a constant limiting value (see (3.16)).
Quantities such as
$B_{c}(t)$
are well defined, according to the theoretical development in Temam & Strang (Reference Temam and Strang1980). Exact evaluation is difficult, but crude estimates may be made analytically. For example, using integration by parts we have
$$\begin{eqnarray}\frac{\partial }{\partial x_{2}}\left(u_{2}\int _{0}^{x_{2}}T_{c}(t,x_{1},s)\,\text{d}s\right)=u_{2}T_{c}+\frac{\partial u_{2}}{\partial x_{2}}\int _{0}^{x_{2}}T_{c}(t,x_{1},s)\,\text{d}s.\end{eqnarray}$$
Using the above directly in (3.22) and simplifying the resulting integral we get
$$\begin{eqnarray}\frac{{\it\epsilon}}{Pr}\frac{\text{d}\tilde{H}}{\text{d}\tilde{t}}\leqslant -\langle \dot{{\it\gamma}}^{2}(\tilde{\boldsymbol{u}})\rangle \int _{{\it\Omega}}\dot{{\it\gamma}}(\tilde{\boldsymbol{u}})\left[\frac{1}{2}\int _{0}^{x_{2}}T_{c}(t,x_{1},s)\,\text{d}s-B+O({\it\epsilon})\right]\text{d}x_{2}\,\text{d}x_{1}.\end{eqnarray}$$
Choosing
$B$
such that
$$\begin{eqnarray}B\geqslant \frac{1}{2}\int _{0}^{1}T_{c}(t,x_{1},s)\,\text{d}s\end{eqnarray}$$
is sufficient to ensure that the flow does not start at
$t$
. As
$t\rightarrow \infty$
we may use the steady-state temperature in the above estimate and evaluate numerically, giving
$B\gtrsim 0.054$
as sufficient to suppress flow, i.e.
$B_{cr}\leqslant 0.054$
. In comparison to the numerical estimate given in (3.13), this estimate is very conservative.
We may also derive a semianalytical estimate based on the flow field just after onset. The flow structure at a Bingham number close to the critical value was illustrated in figure 3. We see that the flow is confined to the vicinity of the heater, rises vertically above the heater and then recirculates within a yielded envelope. In figure 5, we see that for
$B<B_{cr}$
, the yield surfaces shortly after
$t_{s}$
are qualitatively similar to the test function shape. This explains the relatively good approximation of
$t_{s}$
illustrated in figure 6.
It should be noted that evaluating the supremum in (3.24) does not depend on the magnitude of the test velocity, but on the distribution of the velocity field. A flow field with similar distribution of velocity to that observed in figure 3 just after flow onset is illustrated in figure 5. Here, the
$P_{i}$
are plugs where the fluid is in rigid-body motion. In
$P_{1}$
, the velocity is in pure rotation about
$O_{1}$
. In
$P_{2}$
and
$P_{3}$
, the fluid is undergoing pure translation:
$$\begin{eqnarray}\boldsymbol{u}(\boldsymbol{x})=\left\{\begin{array}{@{}ll@{}}r{\it\omega}\,\boldsymbol{e}_{{\it\alpha}},\quad & \text{if}~\boldsymbol{x}\in P_{1},\\ u_{p2}\,\boldsymbol{e}_{1},\quad & \text{if}~\boldsymbol{x}\in P_{2},\\ u_{p3}\,\boldsymbol{e}_{2},\quad & \text{if}~\boldsymbol{x}\in P_{3}.\end{array}\right.\end{eqnarray}$$
Here,
${\it\omega}$
is the angular velocity of
$P_{1}$
. Fluid is assumed to be yielded in asymptotically thin layers of width
${\it\varepsilon}_{i}$
that separate the plugs, allowing adjustment of the flow direction. Given the parameters
${\it\theta}_{i}$
and
$u_{p1}/(R{\it\omega})$
, the geometry of the thin yielded layers between the three moving plugs can be calculated using conservation of mass. Similarly, using conservation of mass over control volumes where the static and moving plugs meet suggests
$u_{pi}/(R{\it\omega})=\cos ({\it\theta}_{i})$
. The idea of such test solutions is that they might represent functions that approximate the supremum in (3.24).
Figure 5. Schematic of the suggested flow geometry as
$t\rightarrow t_{s}^{+}$
. The dashed red lines represent moving yield surfaces. The black solid lines represent static yield surfaces and the bottom wall.
Figure 6. (a) Comparison of numerical and analytical estimates of variation of
$t_{s}$
with
$B$
. (b) Variation of the analytical estimate of
$R$
with
$B$
.
On substituting such a test function into (3.24), the problem of (approximately) finding
$B_{c}$
is reduced to solving the optimization problem (3.24) with respect to
${\it\theta}_{2}$
,
${\it\theta}_{3}$
and
$R$
. Using this method we find
$$\begin{eqnarray}B_{cr}=0.00307,\end{eqnarray}$$
which is very close to our numerical estimate.
Strictly speaking, we should only expect such an approach to give a good estimate when
$T_{c}$
becomes sufficiently steady, i.e. use of the steady-state
$T_{s}(x,y)$
with the above test functions should give an approximate value for
$B_{cr}$
. However, this same test function approach may be used for
$B<B_{cr}$
in the following way. Fixing
$t=t_{s}$
, for any conductive temperature
$T_{c}(t_{s},x,y)$
we insert the test function into (3.24), optimize with respect to
${\it\theta}_{2}$
,
${\it\theta}_{3}$
and
$R$
, and hence derive an estimate for
$B_{c}(t_{s})$
. We now compare
$B=B_{c}(t_{s})$
with the numerical value of
$B$
for which onset occurs at
$t=t_{s}$
. Figure 6(a) illustrates analytical and numerical estimates of variation of start time with Bingham number. It should be noted that
$t_{s}$
is independent of
$Ra$
and
$Pr$
and varies only with
$B$
(domain geometry and boundary conditions).
Not surprisingly, the numerical estimates are consistently larger than the analytical ones. First, the computationally evaluated velocity norm increases to a numerically meaningful magnitude only after the exact velocity field has increased to a level that falls above the resolution of the computational scheme. Second, the definition of the numerical estimate in (3.12) may facilitate numerical consistency and precision but it also introduces an intrinsic positive error. Third, it should be noted that the semianalytical approach is also expected to overestimate
$t_{s}(B)$
as it is not a perfect evaluation of the supremum in (3.24) that defines
$B_{c}(t)$
. It should be noted that
$B_{cr}$
and the flow geometry as
$t\rightarrow t_{s}^{+}$
change with
$r$
and the cavity aspect ratio. We only expect the flow geometry illustrated in figure 5 to provide reasonable estimates of
$B_{cr}$
at those values of
$r$
and the cavity aspect ratio for which the yielded structure does not touch the top or sidewalls of the cavity as
$t\rightarrow t_{s}^{+}$
.
4. Convective flow regimes
In the preceding section we have focused on stationary states and the onset of motion. Now we explore the range of convective flows that are found for
$B<B_{cr}$
. We start with a qualitative analysis. Throughout we focus on high
$Pr$
, which is realistic for most yield stress fluids. At large
$Pr$
the nonlinear advective terms in the momentum equation are small relative to the viscous dissipation. Thus, except on progressively smaller transient time scales, the left-hand side of the momentum equation vanishes as
$Pr\rightarrow \infty$
. Unless otherwise specified, the results presented here are obtained at
$Pr=10^{4}$
. The computed results were very similar for any
$Pr\geqslant 10^{2}$
.
At critical flow conditions a yield stress (say
$\hat{{\it\tau}}_{y,c}$
) balances with the buoyancy stresses, as captured in
$B_{cr}$
:
$$\begin{eqnarray}B_{cr}\hat{{\it\rho}}_{0}{\rm\Delta}\hat{T}{\hat{g}}\hat{L}\approx \hat{{\it\tau}}_{y,c}.\end{eqnarray}$$
As we have discussed,
$B_{cr}$
depends upon the domain geometry and boundary conditions. Suppose now that
$B<B_{cr}$
so that motion starts at
$t_{s}$
. Part of the buoyancy stresses are balanced by the yield stress
$\hat{{\it\tau}}_{y}<\hat{{\it\tau}}_{y,c}$
, while the remainder may contribute towards fluid motion, being balanced by developing viscous stresses. Assuming that
$\hat{d}$
is the length scale of the subdomain containing the moving fluid, the characteristic velocity of the convective flow that develops close to the heater is
$$\begin{eqnarray}\hat{U} \approx \frac{\hat{d}(B_{cr}\hat{{\it\rho}}_{0}\hat{{\it\beta}}{\rm\Delta}\hat{T}{\hat{g}}\hat{L}-\hat{{\it\tau}}_{y})}{\hat{{\it\mu}}}.\end{eqnarray}$$
Thus,
$\hat{U}$
defines a time scale
$\hat{t}_{a}$
for advection in the cell:
$$\begin{eqnarray}\hat{t}_{a}\approx \frac{\hat{d}}{\hat{U} }=\frac{\hat{{\it\mu}}}{B_{cr}\hat{{\it\rho}}_{0}\hat{{\it\beta}}{\rm\Delta}\hat{T}{\hat{g}}\hat{L}-\hat{{\it\tau}}_{y}}=\frac{\hat{{\it\mu}}}{\hat{{\it\tau}}_{y}}\frac{B}{B_{cr}-B}.\end{eqnarray}$$
We may compare
$\hat{t}_{a}$
with the conductive time scale
$\hat{t}_{c}=\hat{d}^{2}/\hat{{\it\kappa}}$
. The ratio of the conductive to the advective time scale is
$$\begin{eqnarray}\frac{\hat{t}_{c}}{\hat{t}_{a}}\approx \frac{(B_{cr}\hat{{\it\rho}}_{0}\hat{{\it\beta}}{\rm\Delta}\hat{T}{\hat{g}}\hat{L}-\hat{{\it\tau}}_{y})\hat{d}^{2}}{\hat{{\it\mu}}\hat{{\it\kappa}}}=\frac{\hat{d}^{2}}{\hat{L}^{2}}Ra(B_{cr}-B).\end{eqnarray}$$
Alternatively, we may interpret
$\hat{t}_{a}^{-1}=\hat{U} /\hat{d}$
as a representative strain rate, and use this to define an effective viscosity:
$$\begin{eqnarray}\hat{{\it\mu}}_{e}=\hat{{\it\mu}}+\frac{\hat{{\it\tau}}_{y}}{\hat{\dot{{\it\gamma}}}}\approx \hat{{\it\mu}}+\hat{{\it\tau}}_{y}\hat{t}_{a}=\hat{{\it\mu}}\frac{B_{cr}}{B_{cr}-B}.\end{eqnarray}$$
On replacing
$\hat{{\it\mu}}$
with
$\hat{{\it\mu}}_{e}$
in (4.4) we obtain
$$\begin{eqnarray}\frac{\hat{t}_{c}}{\hat{t}_{a}}\approx \frac{\hat{d}^{2}}{\hat{L}^{2}}Ra(B_{cr}-B)=\frac{\hat{d}^{2}}{\hat{L}^{2}}B_{cr}Ra_{e}.\end{eqnarray}$$
Essentially, as
$B$
is varied from zero to the critical limit at fixed
$Ra$
, the flow characteristics transition from those of the Newtonian limit, where the effective Rayleigh number,
$Ra_{e}$
, equals the nominal Rayleigh number,
$Ra$
, to the purely conductive regime with zero velocity everywhere and
$Ra_{e}=0$
.
We separate our analysis into two regimes. First, when
$\hat{t}_{c}\lesssim \hat{t}_{a}$
, advective effects are not dominant and we expect that flow development is qualitatively more similar to the diffusive regime where
$t_{c}\ll t_{a}$
. We see clearly that this behaviour is characteristic of flows at low
$Ra_{e}$
, generally meaning either low
$Ra$
or moderate/high
$Ra$
with
$B/B_{cr}\sim 1$
. Weak advection is studied in § 4.1. The second regime we study is for
$\hat{t}_{c}\gg \hat{t}_{a}$
, when we expect that advection effects will become significant. From (4.6) we see that this is only possible if
$Ra$
is sufficiently large, for fixed
$B/B_{cr}<1$
. Strong advection is studied in § 4.2.
Some insight into the transition between weak and strong convection is gained from the simpler Newtonian flow (
$B=0$
). The signature of the flow is given by monitoring the heat flux through the heater,
$\dot{q}$
,
$$\begin{eqnarray}\dot{q}(t)=\int _{-r}^{r}\frac{\partial T}{\partial x_{2}}(t,x_{1},0)\,\text{d}x_{1}.\end{eqnarray}$$
In figure 7 we plot the computed
$\dot{q}(t)$
for
$B=0$
at four different
$Ra$
. Over the time scale illustrated, for smaller
$Ra$
the heat flux decays monotonically in an analogous way to the heat flux of the purely conductive temperature (see
$Ra=10^{4}$
and
$Ra=10^{5}$
). However, for higher
$Ra$
(see
$Ra=10^{6}$
and
$Ra=10^{7}$
in the same figure), stronger advection enhances the heat transfer around the heater, resulting in the formation of a thermal plume head which then advects upwards. This sudden removal of hot fluid away from the heater leads to increased thermal gradients close to the heater, which then conduct heat away more effectively. Thus, at higher
$Ra$
we often observe a local minimum in
$\dot{q}(t)$
, related to initial plume formation, followed by a local maximum related to the enhanced conduction due to the removal of the plume head.
Figure 7. Heat flux rate,
$\dot{q}(t)$
, through the heater for
$B=0$
(Newtonian fluid),
$Pr=10^{4}$
. The heat flux in the purely conductive regime is represented by
$\times$
.
Figure 8. Evolution of the speed
$|\boldsymbol{u}|$
(a–d) and the temperature
$T$
(e–h), for
$Ra=10^{4}$
,
$B=0.001$
,
$Pr=10^{4}$
, at
$t=0.006$
(a,e),
$t=0.033$
(b,f),
$t=0.129$
(c,g) and
$t=0.399$
(d,h). The white contours in (a–h) denote the yield surface positions. (i,j) The evolution of
$U_{a}$
and
$\Vert T\Vert$
respectively. The red markers in (i,j) represent the times when the snapshots are taken.
4.1. Weak advection,
$\hat{t}_{c}\lesssim \hat{t}_{a}$
For
$\hat{t}_{c}<\hat{t}_{a}$
, i.e. sufficiently small effective Rayleigh number
$Ra_{e}$
, we observe a slow and smooth development of the yielded region around the heater. The velocity gradually increases from zero and the static plugs that separate the walls and the yielded region next to the heater shrink. Eventually the convective cellular motion expands and attains a steady state. An illustration of this sequence is given in figure 8 at different stages of flow development, for
$Ra=10^{4},B=0.001$
. We observe that the velocity and temperature increase monotonically towards their steady values. Qualitatively similar results are found for larger
$B$
, except that the velocity and steady temperature are reduced.
While the analysis leading to (4.6) is based on bulk scaling arguments, we may also analyse the computational solution directly to give more accurate estimates and interpretation of the system behaviour. First, we recall that the scaling of our equations in (2.12) is based on a length scale
$\hat{L}$
, a velocity scale
$\hat{U} _{v}={\hat{g}}\hat{{\it\beta}}{\rm\Delta}\hat{T}\hat{L}^{2}/\hat{{\it\nu}}$
(balancing buoyant and viscous stresses) and the conductive time scale
$\hat{t}_{c}=\hat{L}^{2}/\hat{{\it\kappa}}$
. From the numerical solution, at any time
$t$
we find that only a limited subdomain of the cavity has
$|u|>0$
, and we call this the advecting domain. We can compute the average speed over the advecting domain,
$U_{a}$
, and also the height
$d$
of the advecting domain. In dimensional terms, the improved advective and conductive time scales are given by
$\hat{t}_{a}=d\hat{L}/(U_{a}\hat{U} _{v})$
,
$\hat{t}_{c}=d^{2}\hat{L}^{2}/\hat{{\it\kappa}}$
and thus the (dimensionless) ratio of the two time scales is
$$\begin{eqnarray}\frac{\hat{t}_{c}}{\hat{t}_{a}}=\frac{t_{c}}{t_{a}}\approx Ra\,U_{a}\,d.\end{eqnarray}$$
Now
$d$
has to be larger than the size of the yielded structure at
$t_{s}$
, i.e.
$R\leqslant d\leqslant 1$
(see figure 5). Therefore, for the range of
$B$
considered here and at a constant
$Ra$
, the changes in
$U_{a}$
are the main factors indicating changes in
$t_{c}/t_{a}$
.
Figure 9. Effect of
$B$
on the development of
$t_{c}/t_{a}$
,
${\it\phi}$
and
$\Vert T\Vert$
at
$Ra=10^{4}$
(a–c) and
$10^{5}$
(d–f);
$Pr=10^{4}$
. The broken red lines represent the development of the conductive temperature field.
Figure 10. Evolution of the speed
$|\boldsymbol{u}|$
(a–d) and the temperature
$T$
(e–h), for
$Ra=10^{5}$
,
$B=0.001$
,
$Pr=10^{4}$
, at
$t=0.006$
(a,e),
$t=0.029$
(b,f),
$t=0.031$
(c,g) and
$t=0.078$
(d,h). The white contours in (a–h) denote the yield surface positions. (i,j) The evolution of
$U_{a}$
and
$\Vert T\Vert$
respectively. The red markers in (i,j) represent the times when the snapshots are taken.
Conductive heat transfer in the cell is driven by the temperature difference between the heater and the periphery of the cell,
${\it\delta}T_{c}\approx 1$
. Advective heat transfer, however, is driven by the difference between the mean temperature of the fluid in the advecting domain and that of the periphery of the cell, say
${\it\delta}T_{a}$
. The ratio of advective and conductive heat fluxes, which we denote by
${\it\phi}$
, can therefore be estimated by
$$\begin{eqnarray}{\it\phi}\approx Ra\,U_{a}\,d\,{\it\delta}T_{a},\end{eqnarray}$$
which is similar to the time scale ratio, except for the inclusion of
${\it\delta}T_{a}$
again postprocessed from the numerical solution. While not directly predictive (as they need the computed numerical solution), quantities such as
$t_{c}/t_{a},{\it\phi},U_{a},\ldots$
do give a more accurate picture of the system at time
$t$
.
Figure 9(a–c) illustrates the variation of
$t_{c}/t_{a}$
,
${\it\phi}$
and
$\Vert T\Vert$
with
$B$
when advection is weak. At
$Ra=10^{4}$
the advective time scale slowly decreases with time to a minimum that is at most comparable with the conductive time scale. During flow development, therefore, conductive heat transfer is dominant and
${\it\phi}\ll 1$
. On increasing
$Ra$
(and hence
$Ra_{e}$
), we observe that the advective time scale decreases faster and advection plays a more significant role during flow development,
${\it\phi}\approx 1$
(figure 9
d–f). An example of this flow type is given in figure 10(h–j), for
$Ra=10^{5},B=0.001$
. Two effects now compete. First, since advective time scales are shorter, the velocity field develops faster, improving the heating of the fluid close to the heater more rapidly. The heated fluid around the heater perhaps temporarily rises, contributing to a local maximum in
$t_{c}/t_{a}$
. However, since the advective time scale is not sufficiently small, this weak dominance of advection is quite short lived. As thermal energy diffuses away from the heated core,
$t_{c}/t_{a}$
decreases and the steady state is gradually achieved. The dominant effect of increasing Bingham number, within this range of
$Ra$
, is the increase in effective viscosity, which results in a decrease in the steady values of
$U_{a}$
,
$t_{c}/t_{a}$
,
${\it\phi}$
and
$\Vert T\Vert$
. At moderate
$Ra_{e}$
, advective and conductive heat transfer become comparable,
${\it\phi}\approx 1$
, signalling the end of the weak-advection regime.
The vertical component of velocity and the temperature profiles along the centreline of the cavity at different stages of the flow development are plotted in figure 11. One should notice the persistence of a plug close to the heater around the centreline. The size of this plug generally increases with time and with
$B$
. In the weak-advection regime considered here, the temperature of the fluid immediately surrounding the heater does not become significantly higher than that of the surrounding fluid at any stage.
Phenomenologically, the cellular motion observed by Davaille et al. (Reference Davaille, Gueslin, Massmeyer and Giuseppe2013) is analogous to a subset of the weak-advection regime presented here: when
$t_{a}\gg t_{c}$
temperature development deviates negligibly from the conductive regime, motion develops in an expanding cellular pattern around the heater and steady state is achieved rather slowly. See, for example, the slow development of
${\it\phi}$
in figure 9(b,e) at large values of
$B$
.
Figure 11. Effect of the Bingham number on the development of
$u_{2}$
and
$T$
along the centreline of the cavity at
$Ra=10^{4},10^{5}$
: (a,d)
$Ra=10^{4}$
,
$B=0$
; (b,e)
$Ra=10^{4}$
,
$B=0.001$
; (c,f)
$Ra=10^{4}$
,
$B=0.0025$
; (g,j)
$Ra=10^{5}$
,
$B=0$
; (h,k)
$Ra=10^{5}$
,
$B=0.001$
; (i,l)
$Ra=10^{5}$
,
$B=0.0025$
.
4.2. Strong advection,
$\hat{t}_{c}\gg \hat{t}_{a}$
At sufficiently high
$Ra$
, when the fluid has no yield stress, cellular convection next to the heater increases the average local temperature. The pocket of hot fluid then advects upwards, eventually decelerating due to dissipation of thermal and kinetic energy at the upper wall. This event results in the first pulse observed in
$t_{c}/t_{a}$
and improves the advective heat transfer within the cavity. For Newtonian fluids, transition to the steady state is typically relatively smooth after the first pulse, although non-monotone at larger
$Ra$
.
For
$0<B<B_{cr}$
, a variety of flow features can emerge. The time development of
$t_{c}/t_{a}$
and
${\it\phi}$
is illustrated in figure 12. We see that
$t_{a}$
decreases quickly once yielding starts and advective heat transfer dominates conduction. Thus, we find
$t_{c}/t_{a}\gg 1$
and
${\it\phi}>1$
. A few characteristic trends are evident in figure 12. First, considering
${\it\phi}$
as an illustrative measure of the domination of convection over conduction, it is clear that at a fixed
$Ra$
the dominant effect of yield stress at lower values of
$B$
is to increase the effective viscosity, resulting in a decrease in maximal
$t_{c}/t_{a}$
and
${\it\phi}$
. However, as
$B$
is increased further we observe a range of
$B$
over which there is an increase in maximum
${\it\phi}$
, i.e. advection is temporarily enhanced. Finally, as
$B$
approaches the critical limit, we expect the maximum
${\it\phi}$
to decrease with
$B$
and to recover the ‘weak-advection’ regime sufficiently close to
$B_{cr}$
. Further, in comparison to the Newtonian flow, progressively stronger oscillatory trends are observed in the development of
${\it\phi}$
as
$Ra$
is increased.
Figure 12. Effect of
$B$
on the development of
$t_{c}/t_{a}$
,
${\it\phi}$
and
$\Vert T\Vert$
at
$Ra=10^{6}$
(a–c) and
$10^{7}$
(d–f);
$Pr=10^{4}$
. The broken red lines represent the development of the conductive temperature field. The red circular markers represent
$t_{p1}$
on each curve.
It must be recognized that a number of competing effects govern this complex transient behaviour. The onset time is governed by
$B$
. However, once yielding starts, both
$Ra$
and
$B$
affect the flow. Different features observed in the flow development are due to the relative importance of such effects. In what follows we rely on a simplistic analogy to explain the physics of the process more intuitively.
Figure 13 illustrates in more detail the evolution of a thermal plume, for
$Ra=10^{6}$
,
$B=0.0025$
. The initial development (figure 13
a,e) is reminiscent of the flows observed close to yielding (as illustrated in, e.g., figure 5). The formation and upward advection of a ‘packet’ of hot fluid is evident in figure 13(c,g) and onward. As the packet of hot fluid approaches the top wall,
$U_{a}$
decays. There is a short delay in which a local minimum in
$U_{a}$
is attained, but no secondary ‘pulse’ of hot fluid detaches from the plume, which becomes progressively steady. No secondary pulses were observed at
$Ra=10^{6}$
over the range of Bingham numbers considered. Although details of the flow regimes are different at different values of
$B$
, no significant qualitative differences were observed at this
$Ra$
. Once the first ‘pulse’ in
$t_{c}/t_{a}$
passes, convergence to the steady state is relatively smooth.
Figure 13. Evolution of the speed
$|\boldsymbol{u}|$
(a–d,i–j) and the temperature
$T$
(e–h,k–l), for
$Ra=10^{6},B=0.0025,Pr=10^{4}$
, at (a,e)
$t=0.033$
, (b,f)
$t=0.036$
, (c,g)
$t=0.038$
, (d,h)
$t=0.04$
, (i,k)
$t=0.045$
and (j,l)
$t=0.05$
. The white contours in (a–d,i–j) denote the yield surface positions. (m,n) The evolution of
$U_{a}$
and
$\Vert T\Vert$
respectively. The red markers in (m,n) represent the times when the snapshots are taken.
Consideration of the advection of fluid along the centreline in more detail can facilitate an understanding of the effects of the yield stress. The development of the velocity and temperature profiles along the symmetry line at
$Ra=10^{6}$
is illustrated in figure 14 for both Newtonian and viscoplastic fluids. When the flow starts, there is a plug on the centreline close to the heater. At the Bingham numbers illustrated here, this plug initially moves upwards before approaching its steady shape and position closer to the heater.
Figure 14. Effect of the Bingham number on the development of
$u_{2}$
and
$T$
along the centreline of the cavity at
$Ra=10^{6}$
: (a,d)
$Ra=10^{6}$
,
$B=0$
; (b,e)
$Ra=10^{6}$
,
$B=0.001$
; (c,f)
$Ra=10^{6}$
,
$B=0.0025$
.
Shortly after the start of the flow a local maximum is noticeable in the temperature profile along the centreline. Existence of this maximum is the hallmark of strong advection. Figure 15 illustrates the local maximum temperature (
$T^{\ast }$
) and the location (
$y^{\ast }$
) of the temperature maxima, from the instant that they are (numerically) distinguishable until they disappear, close to the top wall. Although
$y^{\ast }$
and
$T^{\ast }$
are indeed not identical to the location and average temperature of the plume head, they are representative of parametric changes that occur. It should be noted that even for Newtonian fluid, there is a finite delay between the start of the flow (at
$t_{s}=0$
) and the formation of the first distinct plume head (at
$t_{p1}$
).
Figure 15. (a,b) The variation of the location,
$x_{2}^{\ast }$
, and temperature,
$T^{\ast }$
, of the local maxima of temperature along the centreline, at
$Ra=10^{6}$
. The legend in (b) is applicable to (a) as well. (a) Illustration of the effect of
$B$
on the development of
$x_{2}^{\ast }$
with time. Time is measured with reference to
$t_{s}$
, when yielding starts. The increase in
$t_{p1}-t_{s}$
with
$B$
is evident in this figure. Variation of
$T^{\ast }$
with distance from the heater is illustrated in (b). It should be noted that the absolute maximum at
$y=0$
is excluded.
Figure 16. (a) The times
$t_{s}$
and
$t_{p1}$
when yielding starts and when the first extremum is observed along the centreline respectively. (b,c) Contours of
$T=0.5T^{\ast }$
at
$t\approx t_{p1}$
illustrating the variation of plume head shape with
$B$
and
$Ra$
: (b)
$Ra=10^{6}$
, (c)
$Ra=10^{7}$
.
Precise identification of the instant that a plume head forms, say
$t_{p1}$
, and the precise shape of its boundaries at
$t=t_{p1}$
is not practical. This is mainly because at
$t_{p1}$
the plume head is not distinguishable from the heated fluid layer that it is emerging from. As the plume head advects away from the heater and a plume stem forms, identification of the plume head becomes more feasible. A reproducible measure of
$t_{p1}$
can therefore be defined as the instant when a local maximum is observed on the centreline at
$y>0$
. This reproducibility is gained at the cost of an inherent positive error in the plume onset time. Using this definition,
$t_{p1}$
effectively represents the instant when a plume-head-like feature is identifiable. Figure 16(a) illustrates how
$t_{p1}-t_{s}$
changes with
$B$
and
$Ra$
;
$t_{p1}-t_{s}$
represents the time interval over which the cellular motion develops around the heater before the plume emerges. Figure 16(b,c) illustrates contours of
$T=0.5T^{\ast }$
at
$t\approx t_{p1}$
. These contours are representative of the plume shape and size at
$t_{p1}$
. It can be inferred from this figure that the plume onset time and plume head size increase with
$B$
and decrease with
$Ra$
.
Simplistically, the rise of the plume head is analogous to the rise of a buoyant ‘packet’ of fluid. The packet is restricted by the yield stress of the surrounding fluid and is pushed upwards by buoyancy. The packet is thus expected to rise only if
$B_{p}<B_{p,cr}$
, where
$$\begin{eqnarray}B_{p}=\frac{\hat{{\it\tau}}_{y}}{(\hat{{\it\rho}}_{0}-\hat{{\it\rho}}_{p}){\hat{g}}\hat{R}_{p}}=B\frac{{\rm\Delta}\hat{T}}{{\rm\Delta}\hat{T}_{p}}\frac{\hat{L}}{\hat{R}_{p}}=\frac{B}{T_{p}r_{p}}.\end{eqnarray}$$
Here,
${\rm\Delta}\hat{T}_{p}=\hat{T}_{p}-\hat{T}_{0}$
, and
$\hat{T}_{p}$
and
$\hat{R}_{p}$
are the average dimensional temperature and characteristic radius of the packet respectively;
$\hat{T}_{0}$
represents the average temperature of the surrounding body of fluid.
The Bingham number affects
$T_{p}$
through two different mechanisms. First,
$t_{s}$
and thus
$T(t_{s})$
increases with
$B$
. This does not necessarily indicate an increase in the average plume head temperature,
$T_{p}$
, with
$B$
, but we hypothesize that it is the main reason for the observed increase in
$T^{\ast }$
with
$B$
(see figure 15
b). Second, the effective viscosity and hence the advective time scale in the convecting cell increases with
$B$
. Given that at a higher
$B$
, higher buoyancy stresses are needed for a packet to float upwards, it is expected that the formation of a critically buoyant fluid packet is delayed, i.e.
$t_{p1}-t_{s}$
increases with
$B$
(see figure 16
a).
When yielding starts at
$t_{s}$
,
$B$
is the only dimensionless parameter that defines
$d(t)$
, the width of the convecting cell. It is illustrated in figure 6(b) that
$d(t_{s})$
increases with
$B$
. This is suggestive of an increase in
$r_{p}$
with
$B$
. Moreover, since
$t_{p1}-t_{s}$
increases with
$B$
, diffusive length scales also increase with
$B$
and contribute to a larger
$r_{p}$
. Arguably this variation of
$r_{p}$
with
$B$
constitutes a favourable effect on the formation of a buoyant packet of fluid.
Once
$B_{p}<B_{p,cr}$
, the hot fluid packet starts to accelerate upwards, shaping the first pulse observed in
$t_{c}/t_{a}$
. This positive acceleration is enhanced by the favourable temperature gradient of the surrounding stagnant fluid. However, in addition to the dependence of the average temperature and size of the plume head on the Bingham number, the effective viscosity that it experiences while advecting upwards increases with
$B$
.
When the dominant consequence of increasing
$B$
is the increase in
$T_{p}$
and
$r_{p}$
, the local maximum in
$t_{c}/t_{a}$
also increases with
$B$
. This balance of the abovementioned mechanisms endures over a limited interval of
$B$
. As
$B$
approaches the critical limit, the effective viscosity increases more rapidly while
$T_{p}$
and
$r_{p}$
asymptote to finite values of
$O(1)$
. On increasing
$B$
beyond this interval, the local maximum of
$t_{c}/t_{a}$
decreases with
$B$
, and, eventually, we expect to recover the weakly advective regime,
${\it\phi}\lesssim 1$
.
For a very tall cavity, the acceleration diminishes as the temperature gradient vanishes away from the heat source. The advecting plume head then slowly decelerates due to dissipation of internal and kinetic energy. For cavities that are not sufficiently tall, viscous dissipation dominates as the hot fluid approaches the top wall. As the buoyant plume head ‘impinges’ on the wall, it deforms and is dispersed horizontally. Considering the kinetic energy equation (3.17), this is equivalent to a major loss of the driving buoyancy force, i.e.
$\langle u_{2}T\rangle$
. Dissipation thus dominates the (transient) balance of kinetic energy in the cavity, at least temporarily, and the advective velocity decreases significantly, i.e. stronger pulses are affected more severely by the presence of the wall. This explains the sharp decay of the strong pulses in
$t_{c}/t_{a}$
in figure 12.
Understanding the effect of
$Ra$
on the evolution of the plume head is perhaps more straightforward. The decrease in
$t_{p1}-t_{s}$
with increasing
$Ra$
can be attributed to the improved heat transfer in the convecting cell: when yielding starts at
$t_{s}$
, a higher
$Ra$
means enhanced advection around the heater as
$t_{c}/t_{a}$
increases with
$Ra$
(see figure 16
a).
Going back to the simplistic rising fluid packet analogy, it is clear in (4.10) that the critical buoyancy stress (
$\propto T_{p}\,r_{p}$
) needed to enable the rise of a bubble does not explicitly depend on
$Ra$
and varies only with
$B$
. Given that
$t_{p1}-t_{s}$
decreases with
$Ra$
, we expect the average plume head temperature, analogous to
$T_{p}$
, to increase with
$Ra$
, while its size, analogous to
$r_{p}$
, decreases. This leads to enhanced acceleration of the plume head, and thus the increase in
$T^{\ast }(t_{p1})$
with
$Ra$
.
Overall, shorter transition times indicate limited diffusion. This implies that a more significant share of the buoyant forces is carried within the plume head. We hypothesize that this is the prime reason behind sharper decay of the kinetic energy of the pulse at higher
$Ra$
.
The flow development for
$Ra=10^{7}$
and relatively low
$B=0.001$
is illustrated in figure 17. At this value of
$B$
only a single plume forms, with the flow thereafter approaching steady state. To compare, the flow development for
$Ra=10^{7}$
and
$B=0.0025$
is illustrated in figure 18. The formation of a second plume head is evident in figure 18(j,l). At sufficiently high
$Ra$
and over a certain range of
$B$
, the kinetic energy dissipation after the decay of the first plume becomes sufficiently strong to significantly decelerate the flow, bringing it close to complete stoppage. Consequently,
$t_{c}/t_{a}$
decreases and the heat transfer is mostly localized around the heater. This brings about favourable conditions for the formation of a second pulse, at
$t_{p2}$
. In figure 19 the location and temperature at the local temperature maxima are traced with time. It is evident that the number of identified pulses increases with
$Ra$
.
Figure 17. (a–l) The evolution of the speed
$|\boldsymbol{u}|$
(a–d,i–j) and the temperature
$T$
(e–h,k–l), for
$Ra=10^{7},B=0.001,Pr=10^{4}$
, at (a,e)
$t=0.0010$
, (b,f)
$t=0.0012$
, (c,g)
$t=0.0014$
, (d,h)
$t=0.0020$
, (i,k)
$t=0.0023$
and (j,l)
$t=0.0040$
. The white contours denote the yield surface positions. (m,n) The evolution of
$U_{a}$
and
$\Vert T\Vert$
respectively. The red markers in (m,n) represent the times when the snapshots are taken.
Figure 18. (a–n) The evolution of the speed
$|\boldsymbol{u}|$
(a–d,i–l) and the temperature
$T$
(e–h,m–p), for
$Ra=10^{7},B=0.0025,Pr=10^{4}$
, during the flow onset and the formation of the first two pulses, at (a,e)
$t=0.0257$
, (b,f)
$t=0.0259$
, (c,g)
$t=0.0260$
, (d,h)
$t=0.0262$
, (i,m)
$t=0.0280$
, (j,n)
$t=0.0287$
, (k,o)
$t=0.0290$
, (l,p)
$t=0.0297$
. The white contours denote the yield surface positions. (q,r) The evolution of
$U_{a}$
and
$\Vert T\Vert$
respectively. The red markers in (q,r) represent the times when the snapshots are taken.
Figure 19. Variation of the location,
$x_{2}^{\ast }$
, and temperature,
$T^{\ast }$
, of the local maxima of temperature along the centreline, at
$Ra=10^{7}$
. The curves representing the first and second maxima are tagged using ○, ▫ respectively, and the legend in (b) is applicable to (a) and (c) as well. (a) The effect of
$B$
on the development of
$x_{2}^{\ast }$
with time. Time is measured with reference to
$t_{s}$
, when yielding starts. The increase in
$t_{p1}-t_{s}$
with
$B$
is evident in this figure. The variation of
$T^{\ast }$
with distance from the heater is illustrated in (b,c). It should be noted that the absolute maximum at
$y=0$
is excluded.
Comparing the state of the flow at
$t=0$
and
$t=t_{p1}$
, it is not surprising that the formation of the second pulse occurs faster than the first one, i.e.
$t_{p2}-t_{p1}<t_{p1}$
. First, at
$t_{p1}$
the fluid temperature around the heater is above the reference temperature, so less time is needed for its temperature to increase to a desired value. Second, the yield stress of the fluid in the cavity is partly balanced by the buoyancy stresses (effected by the temperature increases in the domain). This decrease in the effective yield stress of the fluid implies lower critical
$T_{b2}r_{b2}$
for the second pulse in comparison to the first. Since momentum and heat diffusive length scales increase with time, it is expected that
$r_{b2}\gtrsim r_{b1}$
. This suggests that the average plume temperature decreases for consecutive pulses (and this is what is observed). Further, the fluid temperature in the domain has generally increased in comparison to
$t_{p1}$
. This results in weaker acceleration of the successive plume heads and, hence, a decrease in the plume head velocity. As each pulse approaches the top wall and decelerates, the distribution of buoyancy forces and the magnitude of the effective viscous dissipation determine whether the kinetic energy decays sufficiently to allow the formation of yet another pulsing plume.
The strongly advective flows described here are analogous to a subset of plume flows observed by Davaille et al. (Reference Davaille, Gueslin, Massmeyer and Giuseppe2013). Although quantitative comparison is not feasible, certain similarities can be identified. When the plume forms, we have observed a sudden uplift of isotherms away from the heater, and
$t_{p1}$
varies noticeably with both
$Ra$
and
$B$
. Moreover, for sufficiently large values of
$Ra$
, which are analogous to high heating rates, we have observed episodic features during flow development.
5. Summary and discussion
Taking as inspiration the experimental work of Davaille et al. (Reference Davaille, Gueslin, Massmeyer and Giuseppe2013), we have investigated the flow of a yield stress fluid in a cavity, driven by a localized heat source at the bottom wall. We have taken a simple viscoplastic fluid (Bingham) and a 2D square cavity as a representative model problem with which to explore the general features of buoyancy-driven flow of viscoplastic fluids due to localized heating. The main contributions of our study are threefold. (i) We have clarified the temporal aspect of flow onset, starting from an initially stationary state, and explained how this is influenced by the yield stress. (ii) We have given an explanation for the transition between weakly and strongly convecting steady flows as the Rayleigh number is increased, including new observations on the interesting phenomenon of pulsing of thermal plumes. (iii) We have systematically explored the effect of varying
$Ra$
and
$B$
on features of weak and strong advective flows. We give below a qualitative description of the occurrence of different flow regimes within the dimensionless parameter space.
Regarding flow onset (§ 3), a number of insights have been gained. First, a simple dimensional analysis reveals that both the Prandtl and Rayleigh numbers are irrelevant insofar as determining when and if a given static initial condition will yield and flow. This conclusion is quite generic, applying to arbitrary cavity shapes and different boundary conditions. Equally, as the viscous stresses are unimportant in flow onset, this insight is independent of the precise yield stress fluid model, i.e. it is equally valid for, e.g., Herschel–Bulkley or Casson fluids.
Realizing the above allowed us in § 3 to focus on the role of the conductive temperature field
$T_{c}(t,\boldsymbol{x})$
in determining onset. The conductive temperature field
$T_{c}(t,\boldsymbol{x})$
may be calculated analytically or otherwise for general problems of the type considered. At each time
$t$
, the conductive temperature
$T_{c}(t,\boldsymbol{x})$
produces a buoyancy force, and it is the balance of this buoyancy force with a statically admissible stress field that determines whether or not the flow commences at that time. This leads to the (precise) notion of a time-evolving
$B_{c}(t)$
such that yielding occurs at
$t=t_{s}$
if
$B=B_{c}(t_{s})$
. This captures, at each time, the fundamental balance between buoyancy and yield stresses in determining yielding. Furthermore, since
$T_{c}(t,\boldsymbol{x})$
approaches a steady conductive temperature distribution, exponentially in time, the onset time
$t_{s}\rightarrow \infty$
logarithmically as
$B\rightarrow B_{cr}$
.
With regard to the experimental study of Davaille et al. (Reference Davaille, Gueslin, Massmeyer and Giuseppe2013), differences in the boundary conditions at the heater, the spatial dimension of the problem and the precise fluid rheology prevent quantitative comparison. Nevertheless, the physical mechanisms responsible for the observed phenomena are analogous. The balance of buoyancy and yield stresses, represented here by
$B$
, is the decisive dimensionless group characterizing the transition from the purely conductive regime to convecting flows. This is in full agreement with the observation of Davaille et al. (Reference Davaille, Gueslin, Massmeyer and Giuseppe2013) that identifies transition from conductive to convective regimes as occurring at a constant yield number,
$Y_{c1}$
. In fact, because of the relatively small width of the heater, the binary nature of (non)existence of motion and the indifference of this limit to viscosity, comparison of
$Y_{c1}$
and
$B_{cr}$
is the most feasible quantitative comparison between our study and the experimental work of Davaille et al. (Reference Davaille, Gueslin, Massmeyer and Giuseppe2013). Assuming that the steady-state temperature difference of the heater,
${\rm\Delta}\hat{T}$
, and the heat transfer rate through the heater,
$\hat{\dot{q}}$
, scale as
${\rm\Delta}\hat{T}=\hat{\dot{q}}/(4\hat{k}\hat{R}_{eff})$
, where
$\hat{R}_{eff}$
is the effective radius of the heater (Davaille et al.
Reference Davaille, Gueslin, Massmeyer and Giuseppe2013), we have
$$\begin{eqnarray}Y=\frac{4}{B}\frac{\hat{R}_{eff}}{\hat{L}}.\end{eqnarray}$$
Thus, based on our simplified 2D geometry and uniform heater temperature, we have
$Y_{c1}=119$
, which is in close agreement with the value found by Davaille et al. (Reference Davaille, Gueslin, Massmeyer and Giuseppe2013),
$Y_{c1}=120$
.
Flow onset as described in § 3 is the result of the evolution of the temperature field in time. When
$B<B_{cr}$
at a certain time,
$t_{s}$
, the yield stress is not sufficient to balance the buoyancy stresses, thus yielding and the start of flow are inevitable. The onset time is thus decided by the value of
$B$
and is independent of viscous forces, i.e.
$Ra$
. This should be distinguished from flow onset in set-ups such as the Rayleigh–Bénard paradigm where, due to the domain geometry and boundary conditions, the yield stress is always capable of suppressing the buoyancy stresses in a motionless fluid domain. Therefore, in such cases yielding starts only if sufficiently strong initial disturbances are present in the domain. Viscous stresses then play a key role in determining the start of yielding: at a given
$B$
yielding may start due to hydrodynamic instability if
$Ra$
is sufficiently large to promote growth of the initial disturbances. Flow onset is no longer determined by the Bingham number alone, and determination of an onset time is not practical as it depends on the properties of the disturbances present in the domain. Given the fundamentally different processes that can lead to the onset of yielding and flow, great care must be taken in extending the results of Zhang et al. (Reference Zhang, Vola and Frigaard2006) and Balmforth & Rust (Reference Balmforth and Rust2009) to other problems. The applicability of their analysis relies on the existence of a steady motionless background state.
Finally, regarding onset, some caution must be exercised in interpreting the generality of our results for all domains, and boundary and initial conditions. Here, we considered a simple geometry and boundary conditions, such that the calculated
$T_{c}(t,\boldsymbol{x})$
increased monotonically in time to approach the steady conductive state. The consequence was that
$B_{c}(t)$
apparently increased monotonically, approaching
$B_{cr}$
as
$t\rightarrow \infty$
. Although the conductive problem is generally diffusive, smoothing the initial temperature distribution and any boundary discontinuities, we may conceive of different domain geometries, and initial and boundary conditions that allow temperature discontinuity within the domain (at
$t=0$
) or lead to
$T_{c}(t,\boldsymbol{x})$
that develops non-monotonically. Ongoing work is aimed at clarifying transient characteristics in such situations.
Once yielding starts viscous stresses become important. Because yield stress fluids tend to be relatively viscous, practically speaking we can restrict our attention to large Prandtl number, meaning that velocity transients evolve rapidly to a pseudosteady equilibrium. The relative size of advective and conductive time scales plays the key role in determining flow dynamics and the strength of convection. Therefore, when
$B<B_{cr}$
, both
$Ra$
and
$B$
govern the flow characteristics. After the onset of convection, the yield stress acts to increase the effective viscosity of the fluid, so that an effective Rayleigh number
$Ra_{e}$
should be considered in determining the strength of advection. If
$Ra_{e}$
is sufficiently high to prompt the formation of a plume head and pulsing, further to viscosification of the flow, the yield stress affects flow development through other mechanisms described in § 4.2, i.e. mere incorporation of the yield stress in defining
$Ra_{e}$
no longer reveals the complicated role of the yield stress in flow development. We feel that for an evolving transient such as here,
$Ra_{e}$
is conceptually useful in general flow classification, but should be used along with
$B$
to identify flow characteristics more specifically.
Assuming
$B<B_{cr}$
, high values of
$Ra$
, which signify strong buoyancy stresses in comparison to viscous stresses, are imperative to the formation of plume heads and subsequent pulsing. For progressively larger
$Ra$
we have observed an increased tendency for plumes to form and to do so in a pulsing manner. Over a certain range of
$(Ra,B)$
flow becomes temporarily frozen between two consecutive pulses. Such characteristics are distinctly reminiscent of the experimental work of Davaille et al. (Reference Davaille, Gueslin, Massmeyer and Giuseppe2013). Unlike Massmeyer et al. (Reference Massmeyer, Giuseppe, Davaille, Rolf and Tackley2013), we had no difficulty in finding repeated pulsation in our numerical results. The yield stress plays a dual role here, at high
$Ra$
. On the one hand, starting at
$B=0$
, we have seen that increasing
$B$
tends to increase the intensity of the pulses: the presence of the yield stress accelerates the return to rest of parts of the fluid away from the plume head, thus restricting advective heat transfer and focusing the heat closer to the heater. On the other hand, for larger
$B\rightarrow B_{cr}$
, the plume never starts.
It was observed in our simulations that successive pulses become weaker and eventually all of our flows approach a steady-state configuration at long times. This is in qualitative agreement with the experimental work of Davaille et al. (Reference Davaille, Gueslin, Massmeyer and Giuseppe2013). They report observing a maximum of three pulses before steady state is achieved.
In terms of classifying the flows, we have established that convecting (yielded) flows are governed by two dimensionless groups
$(Ra,B)$
that balance the ratios of three competing stresses: buoyancy, viscous and yield stress. Presence of a yield stress is fundamental in creating intense pulsing behaviour at high
$Ra$
and moderate
$B<B_{cr}$
, which is quite unlike the Newtonian regime at any
$Ra$
that we have observed. We have established necessary conditions for the onset of yielding in a cavity subject to localized heating at the bottom wall and qualitatively described the transition from smooth flow development (
$t_{c}\lesssim t_{a}$
) to pulsing (
$t_{a}\ll t_{c}$
). We can thus illustrate, schematically, the main three observed flow regimes in the
$(Ra,B)$
-plane: see figure 20.
Figure 20. Schematic of the flow regimes in
$(Ra,B)$
-plane. The dashed line,
$B^{\ast }(Ra)$
, represents the transition from weak to strong advection. The strength and number of the observed pulses increases with
$Ra$
, away from
$B=0$
and
$B^{\ast }(Ra)$
.
The broken line marked
$B=B^{\ast }(Ra)$
signifies a transition from weak to strong advection. Simplistically, using the hot-packet analogy,
$B^{\ast }(Ra)$
corresponds to the Bingham number at which
$\max \big(B_{p}(t)\big)=B_{p,cr}$
; i.e. during the flow development the most buoyant packet of fluid is critically buoyant. It should be noted that precise positioning of
$B^{\ast }(Ra)$
has not been the focus of this work. This requires populating the
$(Ra,B)$
-plane with more data points from individual simulations. Nevertheless, figure 20 may seem to be in contradiction with Davaille et al. (Reference Davaille, Gueslin, Massmeyer and Giuseppe2013), where transition from cellular motion to plumes is attributed to a critical ratio of buoyancy and yield stresses,
$Y=Y_{c2}$
. Interpreting a criterion such as
$Y=Y_{c2}$
as the transition from weak to strong convection, as in the description of Davaille et al. (Reference Davaille, Gueslin, Massmeyer and Giuseppe2013), we believe to be incomplete. As we have seen, a more systematic study of the regimes reveals the
$Ra$
dependence of many transition features and not only dependence on
$B$
(equivalently
$Y$
). Although
$Y=Y_{c2}$
may seem to adequately describe the experimental data, use of
$Y$
negates the effects of the viscous stresses in influencing the transition. We postulate that limited sampling of the dimensionless parameter space in the experimental study of Davaille et al. (Reference Davaille, Gueslin, Massmeyer and Giuseppe2013) has obscured the variation of
$Y_{c2}$
with
$Ra$
.
Acknowledgements
We gratefully acknowledge financial support from the Natural Sciences and Engineering Research Council of Canada. I.K. acknowledges the support of the University of British Columbia via a 4YF graduate fellowship. This research was enabled in part by support provided by WestGrid (www.westgrid.ca) and Compute Canada/Calcul Canada (www.computecanada.ca).
