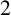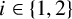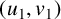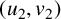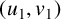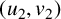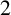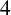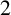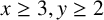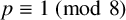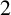1 Introduction
An arc of a graph is an ordered pair of adjacent vertices. A graph
![]() $\Gamma $
is said to be arc-transitive if its automorphism group is transitive on the set of arcs. Let u and v be two distinct vertices of
$\Gamma $
is said to be arc-transitive if its automorphism group is transitive on the set of arcs. Let u and v be two distinct vertices of
![]() $\Gamma $
. Then the smallest positive integer n such that there is a path of length n from u to v is called the distance from u to v and is denoted by
$\Gamma $
. Then the smallest positive integer n such that there is a path of length n from u to v is called the distance from u to v and is denoted by
![]() $d_{\Gamma }(u, v)$
. A noncomplete arc-transitive graph
$d_{\Gamma }(u, v)$
. A noncomplete arc-transitive graph
![]() $\Gamma $
is said to be
$\Gamma $
is said to be
![]() $2$
-distance-transitive if, for any two distinct vertex pairs
$2$
-distance-transitive if, for any two distinct vertex pairs
![]() $(u_1,v_1)$
and
$(u_1,v_1)$
and
![]() $(u_2,v_2)$
with
$(u_2,v_2)$
with
![]() $d_{\Gamma }(u_1,v_1)=d_{\Gamma }(u_2,v_2)=2$
, there exists an element of
$d_{\Gamma }(u_1,v_1)=d_{\Gamma }(u_2,v_2)=2$
, there exists an element of
![]() ${\mathrm {Aut}}(\Gamma )$
that maps
${\mathrm {Aut}}(\Gamma )$
that maps
![]() $(u_1,v_1)$
to
$(u_1,v_1)$
to
![]() $(u_2,v_2)$
.
$(u_2,v_2)$
.
The systematic investigation of (locally)
![]() $2$
-distance-transitive graphs was initiated recently. Devillers et al. [Reference Devillers, Giudici, Li and Praeger7] studied the class of locally s-distance-transitive graphs using the normal quotient strategy developed for s-arc-transitive graphs in [Reference Paley29]. Corr et al. [Reference Corr, Jin and Schneider6] investigated the family of
$2$
-distance-transitive graphs was initiated recently. Devillers et al. [Reference Devillers, Giudici, Li and Praeger7] studied the class of locally s-distance-transitive graphs using the normal quotient strategy developed for s-arc-transitive graphs in [Reference Paley29]. Corr et al. [Reference Corr, Jin and Schneider6] investigated the family of
![]() $2$
-distance-transitive graphs, and they determined the family of
$2$
-distance-transitive graphs, and they determined the family of
![]() $2$
-distance-transitive but not
$2$
-distance-transitive but not
![]() $2$
-arc-transitive graphs of valency at most five. Then the authors [Reference Jin and Tan21] gave a classification of the class of
$2$
-arc-transitive graphs of valency at most five. Then the authors [Reference Jin and Tan21] gave a classification of the class of
![]() $2$
-distance-transitive but not
$2$
-distance-transitive but not
![]() $2$
-arc-transitive graphs of valency six.
$2$
-arc-transitive graphs of valency six.
The family of
![]() $2$
-distance-transitive Cayley graphs over cyclic groups (circulants) was recently classified in [Reference Chen, Jin and Li4]. In this paper, we continue the study of the family of
$2$
-distance-transitive Cayley graphs over cyclic groups (circulants) was recently classified in [Reference Chen, Jin and Li4]. In this paper, we continue the study of the family of
![]() $2$
-distance-transitive Cayley graphs; precisely, we are interested in
$2$
-distance-transitive Cayley graphs; precisely, we are interested in
![]() $2$
-distance-transitive Cayley graphs over dihedral groups. The graph in Figure 1 is the octahedron that is a
$2$
-distance-transitive Cayley graphs over dihedral groups. The graph in Figure 1 is the octahedron that is a
![]() $2$
-distance-transitive Cayley graph over the dihedral group
$2$
-distance-transitive Cayley graph over the dihedral group
![]() $D_6$
.
$D_6$
.

Figure 1 Octahedron.
It is easy to see that every noncomplete
![]() $2$
-arc-transitive graph is
$2$
-arc-transitive graph is
![]() $2$
-distance- transitive. The converse is not necessarily true. If a
$2$
-distance- transitive. The converse is not necessarily true. If a
![]() $2$
-distance-transitive graph has girth
$2$
-distance-transitive graph has girth
![]() $3$
(length of the shortest cycle is 3), then this graph is not
$3$
(length of the shortest cycle is 3), then this graph is not
![]() $2$
-arc-transitive. Hence, the family of noncomplete
$2$
-arc-transitive. Hence, the family of noncomplete
![]() $2$
-arc-transitive graphs is properly contained in the family of
$2$
-arc-transitive graphs is properly contained in the family of
![]() $2$
-distance-transitive graphs.
$2$
-distance-transitive graphs.
The family of
![]() $2$
-arc-transitive dihedrants has been classified in [Reference Du, Malnič and Marušič13, Reference Marušič28, Reference Praeger34]. Thus, we are particularly interested in
$2$
-arc-transitive dihedrants has been classified in [Reference Du, Malnič and Marušič13, Reference Marušič28, Reference Praeger34]. Thus, we are particularly interested in
![]() $2$
-distance-transitive dihedrants that are not
$2$
-distance-transitive dihedrants that are not
![]() $2$
-arc-transitive, and the following is a family of examples.
$2$
-arc-transitive, and the following is a family of examples.
Example 1.1. Let
![]() $T= \langle a,b|a^n=1,b^2=1,a^b=a^{-1}\rangle \cong D_{2n}$
with
$T= \langle a,b|a^n=1,b^2=1,a^b=a^{-1}\rangle \cong D_{2n}$
with
![]() $n\geq 3$
,
$n\geq 3$
,
![]() $S=T\setminus \langle b\rangle $
and
$S=T\setminus \langle b\rangle $
and
![]() $\Gamma ={\mathrm {Cay}}(T,S)$
. Let
$\Gamma ={\mathrm {Cay}}(T,S)$
. Let
![]() $u=1$
. Then
$u=1$
. Then
![]() $\Gamma _2(u)=\{b\}$
, and
$\Gamma _2(u)=\{b\}$
, and
![]() $\{u\}\cup S\cup \Gamma _2(u)=T$
. Since
$\{u\}\cup S\cup \Gamma _2(u)=T$
. Since
![]() $\Gamma $
is vertex-transitive, it follows that
$\Gamma $
is vertex-transitive, it follows that
![]() $\Gamma $
has diameter 2 and is antipodal with each fold having two vertices, and so
$\Gamma $
has diameter 2 and is antipodal with each fold having two vertices, and so
![]() $\Gamma \cong {\mathrm {K}}_{n[2]}$
.
$\Gamma \cong {\mathrm {K}}_{n[2]}$
.
Moreover,
![]() ${\mathrm {Aut}} (\Gamma )=S_2\wr S_n$
is transitive on both the set of vertices and the set of arcs. For each arc
${\mathrm {Aut}} (\Gamma )=S_2\wr S_n$
is transitive on both the set of vertices and the set of arcs. For each arc
![]() $(u,v)$
of
$(u,v)$
of
![]() $\Gamma $
, we have
$\Gamma $
, we have
![]() $|\Gamma _2(u)\cap \Gamma (v)|=1$
, and so
$|\Gamma _2(u)\cap \Gamma (v)|=1$
, and so
![]() $\Gamma $
is
$\Gamma $
is
![]() $2$
-distance-transitive. Since
$2$
-distance-transitive. Since
![]() $\Gamma $
has girth 3 and is noncomplete, it follows that
$\Gamma $
has girth 3 and is noncomplete, it follows that
![]() $\Gamma $
is not 2-arc-transitive.
$\Gamma $
is not 2-arc-transitive.
The graph in Figure 1 is the dihedrant
![]() ${\mathrm {K}}_{3[2]}$
.
${\mathrm {K}}_{3[2]}$
.
Our first theorem gives a complete classification of the family of
![]() $2$
-distance-transitive Cayley graphs with triangles over dihedral groups.
$2$
-distance-transitive Cayley graphs with triangles over dihedral groups.
Theorem 1.2. Let
![]() $\Gamma $
be a connected
$\Gamma $
be a connected
![]() $2$
-distance-transitive Cayley graph over a dihedral group. Then
$2$
-distance-transitive Cayley graph over a dihedral group. Then
![]() $\Gamma $
has girth
$\Gamma $
has girth
![]() $3$
if and only if
$3$
if and only if
![]() $\Gamma $
is isomorphic to either
$\Gamma $
is isomorphic to either
![]() $ {\mathrm {K}}_{x[y]}$
for some
$ {\mathrm {K}}_{x[y]}$
for some
![]() $x\geq 3,y\geq 2$
or
$x\geq 3,y\geq 2$
or
![]() $G(2,p,({p-1})/{4})$
, where p is a prime and
$G(2,p,({p-1})/{4})$
, where p is a prime and
![]() $p \equiv 1 \ (\operatorname {mod}\, 8)$
.
$p \equiv 1 \ (\operatorname {mod}\, 8)$
.
The definitions of the graphs arising in Theorem 1.2 are given in the next section.
We give a remark on Theorem 1.2.
Remark 1.3. Let
![]() $\Gamma $
be a connected
$\Gamma $
be a connected
![]() $(G,2)$
-distance-transitive graph. If
$(G,2)$
-distance-transitive graph. If
![]() $\Gamma $
has girth at least
$\Gamma $
has girth at least
![]() $5$
, then, for any two vertices with distance 2 in
$5$
, then, for any two vertices with distance 2 in
![]() $\Gamma $
, there is a unique 2-arc between these two vertices. Hence,
$\Gamma $
, there is a unique 2-arc between these two vertices. Hence,
![]() $\Gamma $
being
$\Gamma $
being
![]() $(G,2)$
-distance-transitive implies that it is
$(G,2)$
-distance-transitive implies that it is
![]() $(G,2)$
-arc-transitive. Thus,
$(G,2)$
-arc-transitive. Thus,
![]() $\Gamma $
has girth
$\Gamma $
has girth
![]() $3$
or
$3$
or
![]() $4$
whenever it is not
$4$
whenever it is not
![]() $(G,2)$
-arc-transitive.
$(G,2)$
-arc-transitive.
At the moment, all the
![]() $(G,2)$
-distance-transitive but not
$(G,2)$
-distance-transitive but not
![]() $(G,2)$
-arc-transitive graphs of girth greater than 3 that we know about are
$(G,2)$
-arc-transitive graphs of girth greater than 3 that we know about are
![]() $2$
-arc-transitive. Moreover, the family of
$2$
-arc-transitive. Moreover, the family of
![]() $2$
-arc-transitive dihedrants has been classified in [Reference Du, Malnič and Marušič13, Reference Marušič28, Reference Praeger34]. By Theorem 1.2, we give the following conjecture.
$2$
-arc-transitive dihedrants has been classified in [Reference Du, Malnič and Marušič13, Reference Marušič28, Reference Praeger34]. By Theorem 1.2, we give the following conjecture.
Conjecture 1.4. A connected
![]() $2$
-distance-transitive dihedrant either is a known
$2$
-distance-transitive dihedrant either is a known
![]() $2$
-arc-transitive dihedrant or is isomorphic to one of the following two graphs:
$2$
-arc-transitive dihedrant or is isomorphic to one of the following two graphs:
![]() $ {\mathrm {K}}_{x[y]}$
for some
$ {\mathrm {K}}_{x[y]}$
for some
![]() $x\geq 3,y\geq 2$
and
$x\geq 3,y\geq 2$
and
![]() $G(2,p,({p-1})/{4})$
, where p is a prime and
$G(2,p,({p-1})/{4})$
, where p is a prime and
![]() $p \equiv 1 \ (\operatorname {mod}\, 8)$
.
$p \equiv 1 \ (\operatorname {mod}\, 8)$
.
A vertex triple
![]() $(u,v,w)$
of a graph
$(u,v,w)$
of a graph
![]() $\Gamma $
with v adjacent to both u and w is called a
$\Gamma $
with v adjacent to both u and w is called a
![]() $2$
-geodesic if
$2$
-geodesic if
![]() $u\neq w$
and
$u\neq w$
and
![]() $u,w$
are not adjacent. An arc-transitive and noncomplete graph is said to be
$u,w$
are not adjacent. An arc-transitive and noncomplete graph is said to be
![]() $2$
-geodesic-transitive if its graph automorphism group is transitive on the set of 2-geodesics. During the past ten years, several papers regarding 2-geodesic-transitive graphs have appeared. The possible local structures of 2-geodesic-transitive graphs were determined in [Reference Devillers, Jin, Li and Praeger8]. Then Devillers et al. [Reference Devillers, Jin, Li and Praeger9, Reference Devillers, Jin, Li and Praeger11] gave classifications of all finite graphs that are
$2$
-geodesic-transitive if its graph automorphism group is transitive on the set of 2-geodesics. During the past ten years, several papers regarding 2-geodesic-transitive graphs have appeared. The possible local structures of 2-geodesic-transitive graphs were determined in [Reference Devillers, Jin, Li and Praeger8]. Then Devillers et al. [Reference Devillers, Jin, Li and Praeger9, Reference Devillers, Jin, Li and Praeger11] gave classifications of all finite graphs that are
![]() $2$
-geodesic-transitive but not 2-arc-transitive, and which have valency four or prime valency. Later, in [Reference Devillers, Jin, Li and Praeger10], a reduction theorem for the family of normal
$2$
-geodesic-transitive but not 2-arc-transitive, and which have valency four or prime valency. Later, in [Reference Devillers, Jin, Li and Praeger10], a reduction theorem for the family of normal
![]() $2$
-geodesic-transitive Cayley graphs was produced and those which are complete multipartite graphs were also classified.
$2$
-geodesic-transitive Cayley graphs was produced and those which are complete multipartite graphs were also classified.
By definition, every 2-geodesic-transitive graph must be a 2-distance-transitive graph, but some 2-distance-transitive graphs may not be 2-geodesic-transitive. For instance, Paley graphs with at least 13 vertices are 2-distance-transitive but not 2-geodesic-transitive (see [Reference Jin, Devillers, Li and Praeger18]).
There is an investigation of the family of connected
![]() $2$
-geodesic-transitive Cayley graphs of dihedral groups in [Reference Jin and Ma20, Theorem 1.2], where a reduction result was given and also basic normal quotient graphs were determined. In this paper, as an application of Theorem 1.2, we determine precisely the family of connected
$2$
-geodesic-transitive Cayley graphs of dihedral groups in [Reference Jin and Ma20, Theorem 1.2], where a reduction result was given and also basic normal quotient graphs were determined. In this paper, as an application of Theorem 1.2, we determine precisely the family of connected
![]() $2$
-geodesic-transitive Cayley graphs of dihedral groups.
$2$
-geodesic-transitive Cayley graphs of dihedral groups.
Theorem 1.5. Let
![]() $\Gamma $
be a connected
$\Gamma $
be a connected
![]() $2$
-geodesic-transitive Cayley graph over a dihedral group. Then
$2$
-geodesic-transitive Cayley graph over a dihedral group. Then
![]() $\Gamma $
is isomorphic to a noncomplete
$\Gamma $
is isomorphic to a noncomplete
![]() $2$
-arc-transitive dihedrant or to
$2$
-arc-transitive dihedrant or to
![]() $ {\mathrm{K}}_{x[y]}$
for some
$ {\mathrm{K}}_{x[y]}$
for some
![]() $x\geq 3,y\geq 2$
.
$x\geq 3,y\geq 2$
.
Note that, in Theorem 1.5, all connected
![]() $2$
-arc-transitive dihedrants are known, and there is a classification result in [Reference Du, Malnič and Marušič13, Reference Marušič28, Reference Praeger34]. Thus, all connected
$2$
-arc-transitive dihedrants are known, and there is a classification result in [Reference Du, Malnič and Marušič13, Reference Marušič28, Reference Praeger34]. Thus, all connected
![]() $2$
-geodesic-transitive dihedrants are known.
$2$
-geodesic-transitive dihedrants are known.
2 Preliminaries
In this section, we give some definitions about groups and graphs that are used in the paper.
All graphs in this paper are finite, simple, connected and undirected. For a graph
![]() $\Gamma $
, we use
$\Gamma $
, we use
![]() $V(\Gamma )$
and
$V(\Gamma )$
and
![]() ${\mathrm {Aut}}(\Gamma )$
to denote its vertex set and automorphism group, respectively. For the group theoretic terminology not defined here we refer the reader to [Reference Cameron3, Reference Dixon and Mortimer12, Reference Weiss39].
${\mathrm {Aut}}(\Gamma )$
to denote its vertex set and automorphism group, respectively. For the group theoretic terminology not defined here we refer the reader to [Reference Cameron3, Reference Dixon and Mortimer12, Reference Weiss39].
2.1 Groups and graphs
Let T be a finite group and let S be a subset of T such that
![]() $1\notin S$
and
$1\notin S$
and
![]() $S=S^{-1}$
. Then the Cayley graph
$S=S^{-1}$
. Then the Cayley graph
![]() $\Gamma ={\mathrm {Cay}}(T,S)$
of T with respect to S is the graph with vertex set T and edge set
$\Gamma ={\mathrm {Cay}}(T,S)$
of T with respect to S is the graph with vertex set T and edge set
![]() $\{\{g,sg\} \,|\,g\in T,s\in S\}$
. In particular, the Cayley graph
$\{\{g,sg\} \,|\,g\in T,s\in S\}$
. In particular, the Cayley graph
![]() ${\mathrm {Cay}}(T,S)$
is connected if and only if
${\mathrm {Cay}}(T,S)$
is connected if and only if
![]() $T=\langle S\rangle $
. The group
$T=\langle S\rangle $
. The group
![]() $R(T) = \{ \sigma _t|t\in T\}$
consists of right translations
$R(T) = \{ \sigma _t|t\in T\}$
consists of right translations
![]() $\sigma _t : x \mapsto xt$
and is a subgroup of the automorphism group
$\sigma _t : x \mapsto xt$
and is a subgroup of the automorphism group
![]() ${\mathrm {Aut}}(\Gamma )$
acting regularly on the vertex set. We may identify T with
${\mathrm {Aut}}(\Gamma )$
acting regularly on the vertex set. We may identify T with
![]() $R(T)$
. Godsil [Reference Godsil15, Lemma 2.1] observed that
$R(T)$
. Godsil [Reference Godsil15, Lemma 2.1] observed that
![]() $N_{{\mathrm {Aut}}(\Gamma )}(T)=T:{\mathrm {Aut}}(T,S)$
, where
$N_{{\mathrm {Aut}}(\Gamma )}(T)=T:{\mathrm {Aut}}(T,S)$
, where
![]() ${\mathrm {Aut}}(T,S)=\{\sigma \in {\mathrm {Aut}}(T)|S^\sigma =S\}$
. If
${\mathrm {Aut}}(T,S)=\{\sigma \in {\mathrm {Aut}}(T)|S^\sigma =S\}$
. If
![]() ${\mathrm {Aut}}(\Gamma )=N_{{\mathrm {Aut}}(\Gamma )}(T)$
, then the graph
${\mathrm {Aut}}(\Gamma )=N_{{\mathrm {Aut}}(\Gamma )}(T)$
, then the graph
![]() $\Gamma $
was called a normal Cayley graph by Xu [Reference Wielandt40] and such graphs have been studied under various additional conditions (see [Reference Du, Wang and Xu14, Reference Kwak and Oh23, Reference Lu and Xu27, Reference Pan30, Reference Pan, Yu, Zhang and Huang31, Reference Praeger33]).
$\Gamma $
was called a normal Cayley graph by Xu [Reference Wielandt40] and such graphs have been studied under various additional conditions (see [Reference Du, Wang and Xu14, Reference Kwak and Oh23, Reference Lu and Xu27, Reference Pan30, Reference Pan, Yu, Zhang and Huang31, Reference Praeger33]).
We call a graph with n vertices a circulant if it has an automorphism that is an n-cycle. Thus, a circulant is a Cayley graph over a cyclic group.
A dihedral group of order
![]() $2n$
is denoted by
$2n$
is denoted by
![]() $D_{2n}$
and is defined by the presentation
$D_{2n}$
and is defined by the presentation
![]() $D_{2n}=\langle a,b{\kern2pt}|{\kern2pt}a^n=1, b^2=1,a^b=a^{-1}\rangle $
. A Cayley graph
$D_{2n}=\langle a,b{\kern2pt}|{\kern2pt}a^n=1, b^2=1,a^b=a^{-1}\rangle $
. A Cayley graph
![]() ${\mathrm {Cay}}(T,S)$
is called a dihedrant if the group T is a dihedral group.
${\mathrm {Cay}}(T,S)$
is called a dihedrant if the group T is a dihedral group.
The following lemma about normal subgroups of dihedral groups is well known.
Lemma 2.1. Let
![]() $D_{2n}=\langle a,b|a^n=1,b^2=1,bab=a^{-1}\rangle $
, where
$D_{2n}=\langle a,b|a^n=1,b^2=1,bab=a^{-1}\rangle $
, where
![]() $n\geq 2$
. Then all the normal subgroups N of
$n\geq 2$
. Then all the normal subgroups N of
![]() $D_{2n}$
are the following.
$D_{2n}$
are the following.
-
(1) If n is odd, then
 $N=\langle a^i\rangle $
, where
$N=\langle a^i\rangle $
, where
 $i|n$
.
$i|n$
. -
(2) If n is even, then N is one of the following groups:
 $\langle a^i\rangle $
, where
$\langle a^i\rangle $
, where
 $i|n$
,
$i|n$
,
 $\langle a^2,b\rangle $
or
$\langle a^2,b\rangle $
or
 $\langle a^2,ab\rangle $
.
$\langle a^2,ab\rangle $
.
Let
![]() $\Omega =\{\omega _1,\omega _2,\ldots ,\omega _n\}$
and let
$\Omega =\{\omega _1,\omega _2,\ldots ,\omega _n\}$
and let
![]() $\Omega ^{(k)}$
be the set of k-tuples of points of
$\Omega ^{(k)}$
be the set of k-tuples of points of
![]() $\Omega $
. Then
$\Omega $
. Then
![]() $G\leq {\mathrm {Sym}}(\Omega )$
is said to be k-transitive on
$G\leq {\mathrm {Sym}}(\Omega )$
is said to be k-transitive on
![]() $\Omega $
if G is transitive on
$\Omega $
if G is transitive on
![]() $\Omega ^{(k)}$
.
$\Omega ^{(k)}$
.
For a vertex-transitive graph
![]() $\Gamma $
and a set of
$\Gamma $
and a set of
![]() ${\mathrm {Aut}}(\Gamma )$
-invariant partitions
${\mathrm {Aut}}(\Gamma )$
-invariant partitions
![]() $\mathcal {B}$
of
$\mathcal {B}$
of
![]() $V(\Gamma )$
, the quotient graph
$V(\Gamma )$
, the quotient graph
![]() $\Gamma _{\mathcal {B}}$
of
$\Gamma _{\mathcal {B}}$
of
![]() $\Gamma $
is the graph whose vertex set is the set
$\Gamma $
is the graph whose vertex set is the set
![]() $\mathcal {B}$
such that two elements
$\mathcal {B}$
such that two elements
![]() $B_i,B_j \in \mathcal {B}$
are adjacent in
$B_i,B_j \in \mathcal {B}$
are adjacent in
![]() $\Gamma _{\mathcal {B}}$
if and only if there exist
$\Gamma _{\mathcal {B}}$
if and only if there exist
![]() $x\in B_i$
and
$x\in B_i$
and
![]() $ y\in B_j$
such that
$ y\in B_j$
such that
![]() $x,y$
are adjacent in
$x,y$
are adjacent in
![]() $\Gamma $
. The graph
$\Gamma $
. The graph
![]() $\Gamma $
is called a cover of
$\Gamma $
is called a cover of
![]() $\Gamma _{\mathcal {B}}$
if, for each edge
$\Gamma _{\mathcal {B}}$
if, for each edge
![]() $\{B_i,B_j\}$
of
$\{B_i,B_j\}$
of
![]() $\Gamma _{\mathcal {B}}$
and
$\Gamma _{\mathcal {B}}$
and
![]() $v\in B_i$
, the vertex v is adjacent to exactly one vertex in
$v\in B_i$
, the vertex v is adjacent to exactly one vertex in
![]() $B_j$
; and, further, if
$B_j$
; and, further, if
![]() $|B_i|=n$
and we want to emphasize this value, we call
$|B_i|=n$
and we want to emphasize this value, we call
![]() $\Gamma $
a n-cover of
$\Gamma $
a n-cover of
![]() $\Gamma _{\mathcal {B}}$
. Whenever the blocks in
$\Gamma _{\mathcal {B}}$
. Whenever the blocks in
![]() $\mathcal {B}$
are the N-orbits, for some nontrivial normal subgroup N of
$\mathcal {B}$
are the N-orbits, for some nontrivial normal subgroup N of
![]() ${\mathrm {Aut}}(\Gamma )$
, we write
${\mathrm {Aut}}(\Gamma )$
, we write
![]() $\Gamma _{\mathcal {B}}=\Gamma _{N}$
. Suppose that
$\Gamma _{\mathcal {B}}=\Gamma _{N}$
. Suppose that
![]() $\Gamma $
is a cover of
$\Gamma $
is a cover of
![]() $\Gamma _{\mathcal {B}}$
. Then
$\Gamma _{\mathcal {B}}$
. Then
![]() $\Gamma $
is further called an antipodal cover of
$\Gamma $
is further called an antipodal cover of
![]() $\Gamma _{\mathcal {B}}$
if, for any
$\Gamma _{\mathcal {B}}$
if, for any
![]() $B\in \mathcal {B}$
and
$B\in \mathcal {B}$
and
![]() $u,v\in B$
, the distance between
$u,v\in B$
, the distance between
![]() $u,v$
in
$u,v$
in
![]() $\Gamma $
is equal to the diameter of
$\Gamma $
is equal to the diameter of
![]() $\Gamma $
.
$\Gamma $
.
For a graph
![]() $\Gamma $
, its diameter is the maximum of the distances between its pairs of vertices. For
$\Gamma $
, its diameter is the maximum of the distances between its pairs of vertices. For
![]() $u\in V(\Gamma )$
and each integer i less than or equal to the diameter of
$u\in V(\Gamma )$
and each integer i less than or equal to the diameter of
![]() $\Gamma $
, we use
$\Gamma $
, we use
![]() $\Gamma _i(u)$
to denote the set of vertices at distance i from vertex u in
$\Gamma _i(u)$
to denote the set of vertices at distance i from vertex u in
![]() $\Gamma $
. Further,
$\Gamma $
. Further,
![]() $\Gamma _1(u)$
is usually denoted by
$\Gamma _1(u)$
is usually denoted by
![]() $\Gamma (u)$
.
$\Gamma (u)$
.
A vertex triple
![]() $(u,v,w)$
of
$(u,v,w)$
of
![]() $\Gamma $
with v adjacent to both u and w is called a
$\Gamma $
with v adjacent to both u and w is called a
![]() $2$
-arc if
$2$
-arc if
![]() $u\neq w$
. A G-arc-transitive graph
$u\neq w$
. A G-arc-transitive graph
![]() $\Gamma $
is said to be
$\Gamma $
is said to be
![]() $(G,2)$
-arc-transitive if G is transitive on the set of 2-arcs. Moreover, if
$(G,2)$
-arc-transitive if G is transitive on the set of 2-arcs. Moreover, if
![]() $G={\mathrm {Aut}}(\Gamma )$
, then G is usually omitted in the previous notation. The first remarkable result about the class of finite
$G={\mathrm {Aut}}(\Gamma )$
, then G is usually omitted in the previous notation. The first remarkable result about the class of finite
![]() $2$
-arc-transitive graphs comes from Tutte [Reference Song, Li and Zhang36, Reference Tutte37]. Due to the influence of Tutte’s work, this class of graphs has been studied extensively in the literature (see [Reference Alspach, Conder, Marušič and Xu1, Reference Ivanov and Praeger17, Reference Li and Pan26, Reference Praeger32]).
$2$
-arc-transitive graphs comes from Tutte [Reference Song, Li and Zhang36, Reference Tutte37]. Due to the influence of Tutte’s work, this class of graphs has been studied extensively in the literature (see [Reference Alspach, Conder, Marušič and Xu1, Reference Ivanov and Praeger17, Reference Li and Pan26, Reference Praeger32]).
We denote by
![]() ${\mathrm {K}}_{m[b]}$
the complete multipartite graph with m parts, with each part having b vertices, where
${\mathrm {K}}_{m[b]}$
the complete multipartite graph with m parts, with each part having b vertices, where
![]() $m\geq 3, b\geq 2$
.
$m\geq 3, b\geq 2$
.
Let
![]() $q=p^e$
be a prime power such that
$q=p^e$
be a prime power such that
![]() $q\equiv 1 \ (\operatorname {mod}\, 4)$
. Let
$q\equiv 1 \ (\operatorname {mod}\, 4)$
. Let
![]() $GF(q)$
be the finite field of order q. Then the Paley graph
$GF(q)$
be the finite field of order q. Then the Paley graph
![]() $P(q)$
is defined as the graph with vertex set
$P(q)$
is defined as the graph with vertex set
![]() $GF(q)$
, and two distinct vertices
$GF(q)$
, and two distinct vertices
![]() $u,v$
are adjacent if and only if
$u,v$
are adjacent if and only if
![]() $u-v$
is a nonzero square in
$u-v$
is a nonzero square in
![]() $GF(q)$
. Note that the congruence condition on the prime power q implies that
$GF(q)$
. Note that the congruence condition on the prime power q implies that
![]() $-1$
is a square in
$-1$
is a square in
![]() $GF(q)$
, and hence
$GF(q)$
, and hence
![]() $P(q)$
is an undirected graph. Paley first defined this family of graphs in 1933 (see [Reference Paley29]). Note that the field
$P(q)$
is an undirected graph. Paley first defined this family of graphs in 1933 (see [Reference Paley29]). Note that the field
![]() $GF(q)$
has
$GF(q)$
has
![]() $(q-1)/2$
elements that are nonzero squares, and so
$(q-1)/2$
elements that are nonzero squares, and so
![]() $P(q)$
has valency
$P(q)$
has valency
![]() $(q-1)/2$
. Moreover,
$(q-1)/2$
. Moreover,
![]() $P(q)$
is a Cayley graph for the additive group
$P(q)$
is a Cayley graph for the additive group
![]() $GF(q)^+\cong \mathbb {Z}_{p}^e$
; and
$GF(q)^+\cong \mathbb {Z}_{p}^e$
; and
![]() $P(q)$
is
$P(q)$
is
![]() $2$
-distance-transitive, by [Reference Brouwer, Cohen and Neumaier2, Reference Jin, Devillers, Li and Praeger18].
$2$
-distance-transitive, by [Reference Brouwer, Cohen and Neumaier2, Reference Jin, Devillers, Li and Praeger18].
Let p be an odd prime and let r be a positive even integer dividing
![]() $p-1$
. Let A and
$p-1$
. Let A and
![]() $A'$
denote two disjoint copies of
$A'$
denote two disjoint copies of
![]() $\mathbb {Z}_p$
and denote the corresponding elements of A and
$\mathbb {Z}_p$
and denote the corresponding elements of A and
![]() $A'$
by i and
$A'$
by i and
![]() $i'$
, respectively. Denote the unique subgroup of order r of the multiplicative group of
$i'$
, respectively. Denote the unique subgroup of order r of the multiplicative group of
![]() $\mathbb {Z}_p$
by
$\mathbb {Z}_p$
by
![]() $L(p,r)$
. We define the graph
$L(p,r)$
. We define the graph
![]() $G(2,p,r)$
to be the graph with vertex set
$G(2,p,r)$
to be the graph with vertex set
![]() $A\cup A'$
and edge set
$A\cup A'$
and edge set
![]() $\{\{x,y\},\{x',y\},\{x,y'\},\{x',y'\}|x,y\in \mathbb {Z}_p,y-x\in L(p,r)\}.$
Note that
$\{\{x,y\},\{x',y\},\{x,y'\},\{x',y'\}|x,y\in \mathbb {Z}_p,y-x\in L(p,r)\}.$
Note that
![]() $G(2,p,r)$
is a nonbipartite bicirculant of valency
$G(2,p,r)$
is a nonbipartite bicirculant of valency
![]() $2r$
as it contains a p-cycle. Moreover, if
$2r$
as it contains a p-cycle. Moreover, if
![]() $r=p-1$
, then
$r=p-1$
, then
![]() $G(2,p,r)$
is the graph
$G(2,p,r)$
is the graph
![]() ${\mathrm {K}}_{p[2]}$
and is also the complement graph of a complete matching.
${\mathrm {K}}_{p[2]}$
and is also the complement graph of a complete matching.
2.2 Some lemmas
Lemma 2.2. Let
![]() $\Gamma =G(2,p,r)$
, where p is an odd prime,
$\Gamma =G(2,p,r)$
, where p is an odd prime,
![]() $r>1$
is even and r divides
$r>1$
is even and r divides
![]() $p-1$
. Then
$p-1$
. Then
![]() $\Gamma $
is a Cayley graph of the dihedral group
$\Gamma $
is a Cayley graph of the dihedral group
![]() $D_{2p}$
.
$D_{2p}$
.
Proof. Recall that
![]() $V(\Gamma )$
consists of the elements i and
$V(\Gamma )$
consists of the elements i and
![]() $i'$
for
$i'$
for
![]() $i\in \mathbb {Z}_p$
. Let
$i\in \mathbb {Z}_p$
. Let
 $$ \begin{align*} \tau: & \ V(\Gamma)\mapsto V(\Gamma),i\mapsto i+1,i'\mapsto (i+1)',\\ \sigma: & \ V(\Gamma)\mapsto V(\Gamma),i\mapsto (-i)', i'\mapsto -i. \end{align*} $$
$$ \begin{align*} \tau: & \ V(\Gamma)\mapsto V(\Gamma),i\mapsto i+1,i'\mapsto (i+1)',\\ \sigma: & \ V(\Gamma)\mapsto V(\Gamma),i\mapsto (-i)', i'\mapsto -i. \end{align*} $$
Then
![]() $\tau $
is an automorphism of
$\tau $
is an automorphism of
![]() $\Gamma $
of order p with two orbits being p-cycles, and
$\Gamma $
of order p with two orbits being p-cycles, and
![]() $\sigma $
is an automorphism of
$\sigma $
is an automorphism of
![]() $\Gamma $
of order two swapping the two orbits of
$\Gamma $
of order two swapping the two orbits of
![]() $\tau $
. Moreover,
$\tau $
. Moreover,
![]() $\sigma \tau \sigma =\tau ^{-1}$
, and
$\sigma \tau \sigma =\tau ^{-1}$
, and
![]() $\langle \sigma ,\rho \rangle \cong D_{2p}$
is a dihedral group of order
$\langle \sigma ,\rho \rangle \cong D_{2p}$
is a dihedral group of order
![]() $2p$
which acts regularly on the vertex set. Thus,
$2p$
which acts regularly on the vertex set. Thus,
![]() $\Gamma $
is a Cayley graph of the dihedral group
$\Gamma $
is a Cayley graph of the dihedral group
![]() $D_{2p}$
.
$D_{2p}$
.
The following useful result about Cayley graphs is observed by Godsil and Xu.
Lemma 2.3 [Reference Godsil15] and [Reference Wielandt40, Propositions 1.3 and 1.5].
The graph
![]() $\Gamma ={\mathrm {Cay}}(T,S)$
is a normal Cayley graph if and only if
$\Gamma ={\mathrm {Cay}}(T,S)$
is a normal Cayley graph if and only if
![]() ${\mathrm {Aut}}(\Gamma )=T:{\mathrm {Aut}}(T,S)$
.
${\mathrm {Aut}}(\Gamma )=T:{\mathrm {Aut}}(T,S)$
.
We cite two important results about quasiprimitive permutation groups.
Theorem 2.4 [Reference Jones22, Reference Li24, Reference Qiao, Du and Koolen35].
Let G be a quasiprimitive permutation group on
![]() $\Omega $
that contains a regular cyclic subgroup T of degree n. Then G is primitive on
$\Omega $
that contains a regular cyclic subgroup T of degree n. Then G is primitive on
![]() $\Omega $
, and either
$\Omega $
, and either
![]() $n=p$
is prime and
$n=p$
is prime and
![]() $G\leq AGL(1,p)$
or G is
$G\leq AGL(1,p)$
or G is
![]() $2$
-transitive, as listed in Table 1.
$2$
-transitive, as listed in Table 1.
Table 1 Quasiprimitive groups containing regular cyclic subgroups.

Theorem 2.5 [Reference Li25, Theorem 1.5].
Let G be a quasiprimitive permutation group on
![]() $\Omega $
that contains a regular dihedral subgroup T. Then G is
$\Omega $
that contains a regular dihedral subgroup T. Then G is
![]() $2$
-transitive on
$2$
-transitive on
![]() $\Omega $
and
$\Omega $
and
![]() $(G,T,G_u)$
is one of the triples in Table 2.
$(G,T,G_u)$
is one of the triples in Table 2.
Table 2 Quasiprimitive groups containing regular dihedral subgroups.

The following lemma is obvious and is a generalization of [Reference Du, Malnič and Marušič13, Lemma 2.6].
Lemma 2.6. Let
![]() $X\mapsto Y$
be a regular cyclic covering of a connected graph such that some
$X\mapsto Y$
be a regular cyclic covering of a connected graph such that some
![]() $2$
-geodesic-transitive group
$2$
-geodesic-transitive group
![]() $G\leq {\mathrm {Aut}}(X)$
projects along
$G\leq {\mathrm {Aut}}(X)$
projects along
![]() $X\mapsto Y$
. Then there exists a regular prime cyclic covering
$X\mapsto Y$
. Then there exists a regular prime cyclic covering
![]() $X'\mapsto Y$
such that some
$X'\mapsto Y$
such that some
![]() $2$
-geodesic-transitive group
$2$
-geodesic-transitive group
![]() $G'\leq {\mathrm {Aut}}(X')$
projects along
$G'\leq {\mathrm {Aut}}(X')$
projects along
![]() $X'\mapsto Y$
.
$X'\mapsto Y$
.
Lemma 2.7 [Reference Devillers, Giudici, Li and Praeger7, Lemma 5.3].
Let
![]() $\Gamma $
be a connected locally
$\Gamma $
be a connected locally
![]() $(G, s)$
-distance-transitive graph with
$(G, s)$
-distance-transitive graph with
![]() $s\geq 2$
. Let
$s\geq 2$
. Let
![]() $1\neq N \lhd G$
be intransitive on
$1\neq N \lhd G$
be intransitive on
![]() $V(\Gamma )$
and let
$V(\Gamma )$
and let
![]() $\mathcal {B}$
be the set of N-orbits on
$\mathcal {B}$
be the set of N-orbits on
![]() $V(\Gamma )$
. Then one of the following holds.
$V(\Gamma )$
. Then one of the following holds.
-
(i)
 $|\mathcal {B}| = 2$
.
$|\mathcal {B}| = 2$
. -
(ii)
 $\Gamma $
is bipartite,
$\Gamma $
is bipartite,
 $\Gamma _N\cong {\mathrm {K}}_{1,r}$
where
$\Gamma _N\cong {\mathrm {K}}_{1,r}$
where
 $r\geq 2$
and G is intransitive on
$r\geq 2$
and G is intransitive on
 $V(\Gamma )$
.
$V(\Gamma )$
. -
(iii)
 $s=2$
,
$s=2$
,
 $\Gamma \cong {\mathrm {K}}_{m[b]}$
and
$\Gamma \cong {\mathrm {K}}_{m[b]}$
and
 $\Gamma _N \cong {\mathrm {K}}_{m}$
where
$\Gamma _N \cong {\mathrm {K}}_{m}$
where
 $m\geq 3$
and
$m\geq 3$
and
 $b\geq 2$
.
$b\geq 2$
. -
(iv) N is semiregular on
 $V(\Gamma )$
,
$V(\Gamma )$
,
 $\Gamma $
is a cover of
$\Gamma $
is a cover of
 $\Gamma _N$
,
$\Gamma _N$
,
 $|V(\Gamma _N)|<|V(\Gamma )|$
and
$|V(\Gamma _N)|<|V(\Gamma )|$
and
 $\Gamma _N$
is
$\Gamma _N$
is
 $(G/N,s')$
-distance-transitive, where
$(G/N,s')$
-distance-transitive, where
 $s'=\min \{s,{\mathrm {diam}}(\Gamma _N)\}$
.
$s'=\min \{s,{\mathrm {diam}}(\Gamma _N)\}$
.
We use the following lemma frequently.
Lemma 2.8. Let
![]() $\Gamma $
be a connected
$\Gamma $
be a connected
![]() $2$
-distance-transitive graph of girth
$2$
-distance-transitive graph of girth
![]() $3$
. Let N be a nontrivial intransitive normal subgroup of
$3$
. Let N be a nontrivial intransitive normal subgroup of
![]() $A:={\mathrm {Aut}}(\Gamma )$
. Suppose that
$A:={\mathrm {Aut}}(\Gamma )$
. Suppose that
![]() $\Gamma \ncong {\mathrm {K}}_{x[y]}$
for any
$\Gamma \ncong {\mathrm {K}}_{x[y]}$
for any
![]() $x\geq 3,y\geq 2$
. Then N is regular on each orbit,
$x\geq 3,y\geq 2$
. Then N is regular on each orbit,
![]() $\Gamma $
is a cover of
$\Gamma $
is a cover of
![]() $\Gamma _N$
and either
$\Gamma _N$
and either
![]() $\Gamma _N$
is a complete
$\Gamma _N$
is a complete
![]() $A/N$
-arc-transitive graph or
$A/N$
-arc-transitive graph or
![]() $\Gamma _N$
is a noncomplete
$\Gamma _N$
is a noncomplete
![]() $(A/N,2)$
-distance-transitive graph of girth
$(A/N,2)$
-distance-transitive graph of girth
![]() $3$
.
$3$
.
Proof. Since
![]() $\Gamma $
is a
$\Gamma $
is a
![]() $2$
-distance-transitive graph, it follows that it is locally
$2$
-distance-transitive graph, it follows that it is locally
![]() $2$
-distance-transitive, and so Lemma 2.7 applies. Since N is intransitive on
$2$
-distance-transitive, and so Lemma 2.7 applies. Since N is intransitive on
![]() $V(\Gamma )$
and using the A-arc-transitivity of
$V(\Gamma )$
and using the A-arc-transitivity of
![]() $\Gamma $
, we know that each nontrivial N-orbit does not contain any edge of
$\Gamma $
, we know that each nontrivial N-orbit does not contain any edge of
![]() $\Gamma $
. Thus,
$\Gamma $
. Thus,
![]() $\Gamma $
is a nonbipartite graph and N has at least three orbits in
$\Gamma $
is a nonbipartite graph and N has at least three orbits in
![]() $V(\Gamma )$
, as the girth of
$V(\Gamma )$
, as the girth of
![]() $\Gamma $
is
$\Gamma $
is
![]() $3$
. Moreover,
$3$
. Moreover,
![]() $\Gamma \ncong {\mathrm {K}}_{x[y]}$
for any
$\Gamma \ncong {\mathrm {K}}_{x[y]}$
for any
![]() $x\geq 3$
and
$x\geq 3$
and
![]() $y\geq 2$
implies that only Lemma 2.7(iv) occurs. Hence, N is semiregular on the vertex set and
$y\geq 2$
implies that only Lemma 2.7(iv) occurs. Hence, N is semiregular on the vertex set and
![]() $\Gamma $
is a cover of
$\Gamma $
is a cover of
![]() $\Gamma _N$
. In particular,
$\Gamma _N$
. In particular,
![]() $\Gamma _N$
has girth 3.
$\Gamma _N$
has girth 3.
Since
![]() $\Gamma $
is A-arc-transitive, we can easily show that
$\Gamma $
is A-arc-transitive, we can easily show that
![]() $\Gamma _N$
is
$\Gamma _N$
is
![]() $A/N$
-arc-transitive. Assume that
$A/N$
-arc-transitive. Assume that
![]() $\Gamma _N$
is a noncomplete graph. Let
$\Gamma _N$
is a noncomplete graph. Let
![]() $(C_1,C_3)$
and
$(C_1,C_3)$
and
![]() $(C_1',C_3')$
be two pairs of vertices of
$(C_1',C_3')$
be two pairs of vertices of
![]() $\Gamma _N$
such that
$\Gamma _N$
such that
![]() $d_{\Gamma _N}(C_1,C_3)=d_{\Gamma _N}(C_1',C_3')=2$
. Then there exist
$d_{\Gamma _N}(C_1,C_3)=d_{\Gamma _N}(C_1',C_3')=2$
. Then there exist
![]() $c_i\in C_i$
and
$c_i\in C_i$
and
![]() $c_i'\in C_i'$
such that
$c_i'\in C_i'$
such that
![]() $(c_1,c_3)$
and
$(c_1,c_3)$
and
![]() $(c_1',c_3')$
are two pairs of vertices of
$(c_1',c_3')$
are two pairs of vertices of
![]() $\Gamma $
with
$\Gamma $
with
![]() $d_{\Gamma }(c_1,c_3)=d_{\Gamma }(c_1',c_3')=2$
. Since
$d_{\Gamma }(c_1,c_3)=d_{\Gamma }(c_1',c_3')=2$
. Since
![]() $\Gamma $
is
$\Gamma $
is
![]() $2$
-distance-transitive, there exists
$2$
-distance-transitive, there exists
![]() $\alpha \in A$
such that
$\alpha \in A$
such that
![]() $(c_1,c_3)^\alpha =(c_1',c_3')$
. Hence,
$(c_1,c_3)^\alpha =(c_1',c_3')$
. Hence,
![]() $(C_1,C_3)^\alpha =(C_1',C_3')$
. In particular,
$(C_1,C_3)^\alpha =(C_1',C_3')$
. In particular,
![]() $\alpha $
induces an element of
$\alpha $
induces an element of
![]() $ A/N$
that maps
$ A/N$
that maps
![]() $(C_1,C_3)$
to
$(C_1,C_3)$
to
![]() $(C_1',C_3')$
. Therefore,
$(C_1',C_3')$
. Therefore,
![]() $\Gamma _N$
is
$\Gamma _N$
is
![]() $(A/N,2)$
-distance-transitive.
$(A/N,2)$
-distance-transitive.
3 Proof of main theorem
In this section, we prove our main theorem by a series of lemmas.
Lemma 3.1. Let
![]() $\Gamma $
be a connected
$\Gamma $
be a connected
![]() $2$
-distance-transitive graph of girth
$2$
-distance-transitive graph of girth
![]() $3$
. Let N be an intransitive normal subgroup of
$3$
. Let N be an intransitive normal subgroup of
![]() ${\mathrm {Aut}}(\Gamma )$
such that
${\mathrm {Aut}}(\Gamma )$
such that
![]() $\Gamma _N\cong {\mathrm {K}}_{|V(\Gamma )|/2}$
. Then either
$\Gamma _N\cong {\mathrm {K}}_{|V(\Gamma )|/2}$
. Then either
![]() $\Gamma \cong {\mathrm {K}}_{x[y]}$
for some
$\Gamma \cong {\mathrm {K}}_{x[y]}$
for some
![]() $x\geq 3,y\geq 2$
or
$x\geq 3,y\geq 2$
or
![]() $\Gamma $
is a diameter
$\Gamma $
is a diameter
![]() $3$
, distance-transitive antipodal
$3$
, distance-transitive antipodal
![]() $2$
-cover of
$2$
-cover of
![]() ${\mathrm {K}}_{|V(\Gamma )|/2}$
and, in particular,
${\mathrm {K}}_{|V(\Gamma )|/2}$
and, in particular,
![]() $\Gamma $
is isomorphic to one of the graphs in [Reference Godsil, Liebler and Praeger16, Main Theorem].
$\Gamma $
is isomorphic to one of the graphs in [Reference Godsil, Liebler and Praeger16, Main Theorem].
Proof. Suppose that
![]() $\Gamma \ncong {\mathrm {K}}_{x[y]}$
for any
$\Gamma \ncong {\mathrm {K}}_{x[y]}$
for any
![]() $x\geq 3,y\geq 2$
. Since
$x\geq 3,y\geq 2$
. Since
![]() $\Gamma $
is a
$\Gamma $
is a
![]() $2$
-distance-transitive graph of girth
$2$
-distance-transitive graph of girth
![]() $3$
, it follows from Lemma 2.8 that N is regular on each orbit and
$3$
, it follows from Lemma 2.8 that N is regular on each orbit and
![]() $\Gamma $
is a cover of the normal quotient graph
$\Gamma $
is a cover of the normal quotient graph
![]() $\Gamma _N$
. Furthermore, the assumption that the quotient graph
$\Gamma _N$
. Furthermore, the assumption that the quotient graph
![]() $\Gamma _N$
is isomorphic to
$\Gamma _N$
is isomorphic to
![]() $ {\mathrm {K}}_n$
, where
$ {\mathrm {K}}_n$
, where
![]() $n=|V(\Gamma )|/2$
, implies that
$n=|V(\Gamma )|/2$
, implies that
![]() $N\cong \mathbb {Z}_2$
and
$N\cong \mathbb {Z}_2$
and
![]() $\Gamma _N$
has valency
$\Gamma _N$
has valency
![]() $n-1$
, and so
$n-1$
, and so
![]() $\Gamma $
has valency
$\Gamma $
has valency
![]() $n-1$
and each N-orbit has two vertices. Let
$n-1$
and each N-orbit has two vertices. Let
![]() $B=\{u,u'\}$
be an N-orbit. By the arc-transitivity of
$B=\{u,u'\}$
be an N-orbit. By the arc-transitivity of
![]() $\Gamma $
, we know that each N-orbit does not contain any edge of
$\Gamma $
, we know that each N-orbit does not contain any edge of
![]() $\Gamma $
, and hence the distance between u and
$\Gamma $
, and hence the distance between u and
![]() $u'$
in
$u'$
in
![]() $\Gamma $
is at least
$\Gamma $
is at least
![]() $2$
.
$2$
.
If the distance between u and
![]() $u'$
is
$u'$
is
![]() $2$
, then there exists a vertex w that is adjacent to both u and
$2$
, then there exists a vertex w that is adjacent to both u and
![]() $u'$
, and so
$u'$
, and so
![]() $|\Gamma (w)\cap B|=2$
, which is impossible since
$|\Gamma (w)\cap B|=2$
, which is impossible since
![]() $\Gamma $
is a cover of
$\Gamma $
is a cover of
![]() $\Gamma _N$
by Lemma 2.8.
$\Gamma _N$
by Lemma 2.8.
Thus, the distance between u and
![]() $u'$
in
$u'$
in
![]() $\Gamma $
is at least 3. Hence,
$\Gamma $
is at least 3. Hence,
![]() $\Gamma (u)\cap \Gamma (u')=\emptyset $
. Since
$\Gamma (u)\cap \Gamma (u')=\emptyset $
. Since
![]() $\Gamma $
has valency
$\Gamma $
has valency
![]() $n-1$
, it follows that
$n-1$
, it follows that
![]() $|\Gamma (u)|=|\Gamma (u')|=n-1$
. As
$|\Gamma (u)|=|\Gamma (u')|=n-1$
. As
![]() $\Gamma $
is a connected graph with
$\Gamma $
is a connected graph with
![]() $2n$
vertices, we must have
$2n$
vertices, we must have
![]() $\Gamma _2(u)=\Gamma (u')$
. Therefore, the distance between u and
$\Gamma _2(u)=\Gamma (u')$
. Therefore, the distance between u and
![]() $u'$
in
$u'$
in
![]() $\Gamma $
is exactly 3. Moreover,
$\Gamma $
is exactly 3. Moreover,
![]() $\Gamma _3(u)=\{u'\}$
,
$\Gamma _3(u)=\{u'\}$
,
![]() $\Gamma _3(u')=\{u\}$
and
$\Gamma _3(u')=\{u\}$
and
![]() $V(\Gamma )=\{u\}\cup \Gamma (u)\cup \Gamma _2(u)\cup \{u'\}$
. By the
$V(\Gamma )=\{u\}\cup \Gamma (u)\cup \Gamma _2(u)\cup \{u'\}$
. By the
![]() $2$
-distance-transitivity of
$2$
-distance-transitivity of
![]() $\Gamma $
, for any 2-geodesic
$\Gamma $
, for any 2-geodesic
![]() $(u,v,w)$
, we have
$(u,v,w)$
, we have
![]() $|\Gamma _3(u)\cap \Gamma (w)|=1$
. This forces
$|\Gamma _3(u)\cap \Gamma (w)|=1$
. This forces
![]() $\Gamma $
to be distance-transitive. Thus,
$\Gamma $
to be distance-transitive. Thus,
![]() $\Gamma $
is a distance-transitive antipodal 2-cover of
$\Gamma $
is a distance-transitive antipodal 2-cover of
![]() ${\mathrm {K}}_n$
with diameter 3 and, in particular, this graph is isomorphic to one of the graphs in [Reference Godsil, Liebler and Praeger16, Main Theorem].
${\mathrm {K}}_n$
with diameter 3 and, in particular, this graph is isomorphic to one of the graphs in [Reference Godsil, Liebler and Praeger16, Main Theorem].
Lemma 3.2. Let
![]() $\Gamma $
be a connected
$\Gamma $
be a connected
![]() $2$
-distance-transitive graph of girth
$2$
-distance-transitive graph of girth
![]() $3$
that is not isomorphic to
$3$
that is not isomorphic to
![]() $ {\mathrm {K}}_{x[y]}$
for any
$ {\mathrm {K}}_{x[y]}$
for any
![]() $x\geq 3,y\geq 2$
. Let N be an intransitive normal subgroup of
$x\geq 3,y\geq 2$
. Let N be an intransitive normal subgroup of
![]() $A:={\mathrm {Aut}}(\Gamma )$
such that
$A:={\mathrm {Aut}}(\Gamma )$
such that
![]() $\Gamma _N$
is a complete graph. Then
$\Gamma _N$
is a complete graph. Then
![]() $A/N$
is
$A/N$
is
![]() $3$
-transitive on
$3$
-transitive on
![]() $V(\Gamma _N)$
if and only if
$V(\Gamma _N)$
if and only if
![]() $\Gamma _N$
is
$\Gamma _N$
is
![]() $(A/N,2)$
-arc-transitive, or, equivalently, if and only if
$(A/N,2)$
-arc-transitive, or, equivalently, if and only if
![]() $\Gamma $
is
$\Gamma $
is
![]() $2$
-arc-transitive.
$2$
-arc-transitive.
Proof. Since
![]() $\Gamma $
is a
$\Gamma $
is a
![]() $2$
-distance-transitive graph of girth 3 that is not isomorphic to
$2$
-distance-transitive graph of girth 3 that is not isomorphic to
![]() $ {\mathrm {K}}_{x[y]}$
for any
$ {\mathrm {K}}_{x[y]}$
for any
![]() $x\geq 3,y\geq 2$
, it follows from Lemma 2.8 that N is regular on each orbit,
$x\geq 3,y\geq 2$
, it follows from Lemma 2.8 that N is regular on each orbit,
![]() $\Gamma $
is a cover of
$\Gamma $
is a cover of
![]() $\Gamma _{N}$
and
$\Gamma _{N}$
and
![]() $|V(\Gamma _{N})|\geq 3$
.
$|V(\Gamma _{N})|\geq 3$
.
Assume that
![]() $A/N$
is
$A/N$
is
![]() $3$
-transitive on
$3$
-transitive on
![]() $V(\Gamma _N)$
. Then, for each N-orbit
$V(\Gamma _N)$
. Then, for each N-orbit
![]() $B\in V(\Gamma _{N})$
, the stabilizer
$B\in V(\Gamma _{N})$
, the stabilizer
![]() $(A/N)_B$
is 2-transitive on
$(A/N)_B$
is 2-transitive on
![]() $\Gamma _N(B)$
, and so
$\Gamma _N(B)$
, and so
![]() $\Gamma _N$
is
$\Gamma _N$
is
![]() $(A/N,2)$
-arc-transitive.
$(A/N,2)$
-arc-transitive.
Let
![]() $(b_0,b_1,b_2)$
and
$(b_0,b_1,b_2)$
and
![]() $(c_0,c_1,c_2)$
be two 2-arcs of
$(c_0,c_1,c_2)$
be two 2-arcs of
![]() $\Gamma $
, where
$\Gamma $
, where
![]() $b_i\in B_i\in V(\Gamma _{N})$
and
$b_i\in B_i\in V(\Gamma _{N})$
and
![]() $c_i\in C_i \in V(\Gamma _{N})$
. Then
$c_i\in C_i \in V(\Gamma _{N})$
. Then
![]() $(B_0,B_1,B_2)$
and
$(B_0,B_1,B_2)$
and
![]() $(C_0,C_1,C_2)$
are two 2-arcs of
$(C_0,C_1,C_2)$
are two 2-arcs of
![]() $\Gamma _N$
. Since
$\Gamma _N$
. Since
![]() $\Gamma _N$
is
$\Gamma _N$
is
![]() $(A/N,2)$
-arc-transitive, it follows that
$(A/N,2)$
-arc-transitive, it follows that
![]() $(B_0,B_1,B_2)^{gN}=(C_0,C_1,C_2)$
for some
$(B_0,B_1,B_2)^{gN}=(C_0,C_1,C_2)$
for some
![]() $gN\in A/N$
, and so there exists
$gN\in A/N$
, and so there exists
![]() $n\in N$
such that
$n\in N$
such that
![]() $(b_0,b_1,b_2)^{gn}=(c_0',c_1',c_2')$
, where
$(b_0,b_1,b_2)^{gn}=(c_0',c_1',c_2')$
, where
![]() $c_i'\in C_i$
.
$c_i'\in C_i$
.
Since N is regular on each orbit, there exists
![]() $n'\in N$
such that
$n'\in N$
such that
![]() $(c_0')^{n'}=c_0$
. Hence,
$(c_0')^{n'}=c_0$
. Hence,
![]() $(c_1')^{n'}\in C_1\cap \Gamma (c_0)$
. As
$(c_1')^{n'}\in C_1\cap \Gamma (c_0)$
. As
![]() $\Gamma $
is a cover of
$\Gamma $
is a cover of
![]() $\Gamma _N$
, it follows that
$\Gamma _N$
, it follows that
![]() $[C_i\cup C_j]\cong |N|{\mathrm {K}}_2$
, and so
$[C_i\cup C_j]\cong |N|{\mathrm {K}}_2$
, and so
![]() $|C_1\cap \Gamma (c_0)|=1$
. Hence,
$|C_1\cap \Gamma (c_0)|=1$
. Hence,
![]() $\{(c_1')^{n'}\}= C_1\cap \Gamma (c_0)=\{c_1\}$
, that is,
$\{(c_1')^{n'}\}= C_1\cap \Gamma (c_0)=\{c_1\}$
, that is,
![]() $(c_1')^{n'}=c_1$
. Similarly, we can get that
$(c_1')^{n'}=c_1$
. Similarly, we can get that
![]() $(c_2')^{n'}=c_2$
. Thus,
$(c_2')^{n'}=c_2$
. Thus,
![]() $(c_0',c_1',c_2')^{n'}=(c_0,c_1,c_2)$
, and so
$(c_0',c_1',c_2')^{n'}=(c_0,c_1,c_2)$
, and so
![]() $(b_0,b_1,b_2)^{gnn'}=(c_0,c_1,c_2)$
. Therefore,
$(b_0,b_1,b_2)^{gnn'}=(c_0,c_1,c_2)$
. Therefore,
![]() $\Gamma $
is
$\Gamma $
is
![]() $2$
-arc-transitive.
$2$
-arc-transitive.
Conversely, if
![]() $\Gamma $
is
$\Gamma $
is
![]() $2$
-arc-transitive, then, for each vertex u of
$2$
-arc-transitive, then, for each vertex u of
![]() $\Gamma $
, the stabilizer
$\Gamma $
, the stabilizer
![]() $A_u$
is 2-transitive on
$A_u$
is 2-transitive on
![]() $\Gamma (u)$
. Since
$\Gamma (u)$
. Since
![]() $\Gamma $
is a cover of the graph
$\Gamma $
is a cover of the graph
![]() $\Gamma _N$
, it follows that, for each N-orbit B,
$\Gamma _N$
, it follows that, for each N-orbit B,
![]() $(A/N)_B$
is 2-transitive on
$(A/N)_B$
is 2-transitive on
![]() $\Gamma _N(B)$
. Moreover,
$\Gamma _N(B)$
. Moreover,
![]() $\Gamma _N$
being a complete graph implies that
$\Gamma _N$
being a complete graph implies that
![]() $A/N$
is
$A/N$
is
![]() $3$
-transitive on
$3$
-transitive on
![]() $V(\Gamma _N)$
.
$V(\Gamma _N)$
.
Lemma 3.3. Let
![]() $\Gamma $
be a connected
$\Gamma $
be a connected
![]() $2$
-distance-transitive Cayley graph of girth
$2$
-distance-transitive Cayley graph of girth
![]() $3$
over the dihedral group T. Let N be a maximal intransitive normal subgroup of
$3$
over the dihedral group T. Let N be a maximal intransitive normal subgroup of
![]() $A:={\mathrm {Aut}}(\Gamma )$
. If
$A:={\mathrm {Aut}}(\Gamma )$
. If
![]() $ T\cap N= 1$
, then either
$ T\cap N= 1$
, then either
![]() $\Gamma \cong {\mathrm {K}}_{x[y]}$
for some
$\Gamma \cong {\mathrm {K}}_{x[y]}$
for some
![]() $x\geq 3,y\geq 2$
or
$x\geq 3,y\geq 2$
or
![]() $\Gamma \cong G(2,p,({p-1})/{4})$
, where p is a prime and
$\Gamma \cong G(2,p,({p-1})/{4})$
, where p is a prime and
![]() $p \equiv 1 \ (\operatorname {mod}\, 8)$
.
$p \equiv 1 \ (\operatorname {mod}\, 8)$
.
Proof. Assume that
![]() $ T\cap N= 1$
. Let
$ T\cap N= 1$
. Let
Since
![]() $\Gamma $
is a Cayley graph over the group T, we have
$\Gamma $
is a Cayley graph over the group T, we have
![]() $|V(\Gamma )|=|T|$
. Suppose that
$|V(\Gamma )|=|T|$
. Suppose that
![]() $\Gamma \ncong {\mathrm {K}}_{x[y]}$
for any
$\Gamma \ncong {\mathrm {K}}_{x[y]}$
for any
![]() $x\geq 3,y\geq 2$
. As
$x\geq 3,y\geq 2$
. As
![]() $\Gamma $
is
$\Gamma $
is
![]() $2$
-distance-transitive of girth 3, it follows from Lemma 2.8 that the normal subgroup N of A is regular on each of its orbits and
$2$
-distance-transitive of girth 3, it follows from Lemma 2.8 that the normal subgroup N of A is regular on each of its orbits and
![]() $\Gamma $
is a cover of
$\Gamma $
is a cover of
![]() $\Gamma _N$
, and either
$\Gamma _N$
, and either
![]() $\Gamma _N$
is isomorphic to the complete graph
$\Gamma _N$
is isomorphic to the complete graph
![]() ${\mathrm {K}}_n$
or
${\mathrm {K}}_n$
or
![]() $\Gamma _N$
is a
$\Gamma _N$
is a
![]() $(A/N,2)$
-distance-transitive circulant of girth
$(A/N,2)$
-distance-transitive circulant of girth
![]() $3$
. Moreover,
$3$
. Moreover,
![]() $\Gamma $
has girth 3 which also indicates that N has at least three orbits on
$\Gamma $
has girth 3 which also indicates that N has at least three orbits on
![]() $V(\Gamma )$
, and so
$V(\Gamma )$
, and so
![]() $|T|/|N|=|V(\Gamma _N)|\geq 3$
.
$|T|/|N|=|V(\Gamma _N)|\geq 3$
.
Since
![]() $T\cap N=1$
, it follows that
$T\cap N=1$
, it follows that
![]() $\overline {T}=TN/N\cong T/T\cap N\cong T$
. Let t be an element of T that fixes every N-orbit setwisely. Then t is in the kernel of the T-action on
$\overline {T}=TN/N\cong T/T\cap N\cong T$
. Let t be an element of T that fixes every N-orbit setwisely. Then t is in the kernel of the T-action on
![]() $V(\Gamma _N)$
, and so t is in the kernel of the A-action on
$V(\Gamma _N)$
, and so t is in the kernel of the A-action on
![]() $V(\Gamma _N)$
. Let K be the kernel of the A-action on
$V(\Gamma _N)$
. Let K be the kernel of the A-action on
![]() $V(\Gamma _N)$
. Then
$V(\Gamma _N)$
. Then
![]() $N\leq K$
. Let B be an N-orbit and let
$N\leq K$
. Let B be an N-orbit and let
![]() $u_1\in B$
. Suppose that
$u_1\in B$
. Suppose that
![]() $K_{u_1}\neq 1$
. Then, as
$K_{u_1}\neq 1$
. Then, as
![]() $\Gamma $
is connected, there exists a path
$\Gamma $
is connected, there exists a path
![]() $(u_1,u_2,\ldots ,u_i,u_{i+1})$
of
$(u_1,u_2,\ldots ,u_i,u_{i+1})$
of
![]() $\Gamma $
such that
$\Gamma $
such that
![]() $K_{u_1}$
fixes each of
$K_{u_1}$
fixes each of
![]() $u_1,u_2,\ldots ,u_i$
, but not
$u_1,u_2,\ldots ,u_i$
, but not
![]() $u_{i+1}$
. Let
$u_{i+1}$
. Let
![]() $\alpha $
be an element of
$\alpha $
be an element of
![]() $K_{u_1}$
fixing
$K_{u_1}$
fixing
![]() $u_{i}$
but not
$u_{i}$
but not
![]() $u_{i+1}$
. Then
$u_{i+1}$
. Then
![]() $u_{i+1}^\alpha $
is a distinct vertex to
$u_{i+1}^\alpha $
is a distinct vertex to
![]() $u_{i+1}$
and
$u_{i+1}$
and
![]() $u_{i+1}^\alpha \in \Gamma (u_{i})$
. Furthermore, since K fixes every N-orbit, it follows that
$u_{i+1}^\alpha \in \Gamma (u_{i})$
. Furthermore, since K fixes every N-orbit, it follows that
![]() $u_{i+1}^\alpha $
is in the same N-orbit
$u_{i+1}^\alpha $
is in the same N-orbit
![]() $B'$
as
$B'$
as
![]() $u_{i+1}$
. Thus,
$u_{i+1}$
. Thus,
![]() $\{u_{i+1},u_{i+1}^\alpha \}\subseteq \Gamma (u_{i})\cap B'$
. However, since
$\{u_{i+1},u_{i+1}^\alpha \}\subseteq \Gamma (u_{i})\cap B'$
. However, since
![]() $\Gamma $
is a cover of
$\Gamma $
is a cover of
![]() $\Gamma _N$
, it follows that any two distinct vertices of the same N-orbit have distance at least 3, which is a contradiction. Therefore,
$\Gamma _N$
, it follows that any two distinct vertices of the same N-orbit have distance at least 3, which is a contradiction. Therefore,
![]() $K_{u_1}= 1$
and K is semiregular on
$K_{u_1}= 1$
and K is semiregular on
![]() $V(\Gamma )$
. Hence,
$V(\Gamma )$
. Hence,
![]() $|K|=|N|$
. It follows that
$|K|=|N|$
. It follows that
![]() $N= K$
, as
$N= K$
, as
![]() $N\leq K$
. Thus,
$N\leq K$
. Thus,
![]() $t\in T\cap N=1$
, and so T acts faithfully on
$t\in T\cap N=1$
, and so T acts faithfully on
![]() $V(\Gamma _N)$
. Since T is transitive on
$V(\Gamma _N)$
. Since T is transitive on
![]() $V(\Gamma _N)$
, the vertex stabilizer
$V(\Gamma _N)$
, the vertex stabilizer
![]() $\overline {T}_{B}=T_B$
is a core-free subgroup of T. As the only nontrivial core-free subgroup of T is
$\overline {T}_{B}=T_B$
is a core-free subgroup of T. As the only nontrivial core-free subgroup of T is
![]() $\langle b\rangle \cong \mathbb {Z}_2$
, we conclude that
$\langle b\rangle \cong \mathbb {Z}_2$
, we conclude that
![]() $\overline {T}_{B}=\langle b\rangle \cong \mathbb {Z}_2$
. Thus,
$\overline {T}_{B}=\langle b\rangle \cong \mathbb {Z}_2$
. Thus,
![]() $H:=\langle a\rangle $
is transitive and so regular on
$H:=\langle a\rangle $
is transitive and so regular on
![]() $V(\Gamma _N)$
. Since N is regular on each orbit, it follows that
$V(\Gamma _N)$
. Since N is regular on each orbit, it follows that
![]() $|N|\times |H|=|V(\Gamma )|=|T|$
, and so
$|N|\times |H|=|V(\Gamma )|=|T|$
, and so
![]() $|N|=2$
. Thus, each N-orbit in the vertex set has cardinality two and H is regular on
$|N|=2$
. Thus, each N-orbit in the vertex set has cardinality two and H is regular on
![]() $V(\Gamma _N)$
.
$V(\Gamma _N)$
.
Therefore,
![]() $\Gamma _{N}$
is a Cayley graph of H with
$\Gamma _{N}$
is a Cayley graph of H with
![]() $|V(\Gamma _N)|=n$
. Since H is a cyclic group, it follows that
$|V(\Gamma _N)|=n$
. Since H is a cyclic group, it follows that
![]() $\Gamma _{N}$
is a circulant, and so
$\Gamma _{N}$
is a circulant, and so
![]() $\Gamma _{N}$
is a graph in [Reference Jin, Liu and Wang19, Theorem 1.3]. Recall that
$\Gamma _{N}$
is a graph in [Reference Jin, Liu and Wang19, Theorem 1.3]. Recall that
![]() $\Gamma $
is a cover of
$\Gamma $
is a cover of
![]() $\Gamma _N$
, and either
$\Gamma _N$
, and either
![]() $\Gamma _N$
is isomorphic to the complete graph
$\Gamma _N$
is isomorphic to the complete graph
![]() ${\mathrm {K}}_n$
, where
${\mathrm {K}}_n$
, where
![]() $n\geq 3$
, or
$n\geq 3$
, or
![]() $\Gamma _N$
is an
$\Gamma _N$
is an
![]() $(A/N,2)$
-distance-transitive circulant of girth
$(A/N,2)$
-distance-transitive circulant of girth
![]() $3$
. If the latter case holds, then, by [Reference Chen, Jin and Li4, Theorem 1.1], we get that
$3$
. If the latter case holds, then, by [Reference Chen, Jin and Li4, Theorem 1.1], we get that
![]() $\Gamma _N\cong {\mathrm {K}}_{(n/2)[2]}$
or a Paley graph.
$\Gamma _N\cong {\mathrm {K}}_{(n/2)[2]}$
or a Paley graph.
On the other hand, as N is a maximal intransitive normal subgroup of A, the quotient group
![]() $A/N$
is quasiprimitive on
$A/N$
is quasiprimitive on
![]() $V(\Gamma _N)$
, and so
$V(\Gamma _N)$
, and so
![]() $\Gamma _N\ncong {\mathrm {K}}_{(n/2)[2]}$
. Thus, either
$\Gamma _N\ncong {\mathrm {K}}_{(n/2)[2]}$
. Thus, either
![]() $\Gamma _N$
is isomorphic to the complete graph
$\Gamma _N$
is isomorphic to the complete graph
![]() ${\mathrm {K}}_n$
, where
${\mathrm {K}}_n$
, where
![]() $n\geq 3$
, or it is isomorphic to a Paley graph.
$n\geq 3$
, or it is isomorphic to a Paley graph.
Since
![]() $T\cap N=1$
, we have
$T\cap N=1$
, we have
![]() $H\cap N=1$
, and so
$H\cap N=1$
, and so
![]() $H\cong H/(H\cap N) \cong HN/N\leq A/N$
. Hence,
$H\cong H/(H\cap N) \cong HN/N\leq A/N$
. Hence,
![]() $A/N$
contains a regular cyclic subgroup. As
$A/N$
contains a regular cyclic subgroup. As
![]() $A/N$
is quasiprimitive on
$A/N$
is quasiprimitive on
![]() $V(\Gamma _N)$
, it follows from Theorem 2.4 that either:
$V(\Gamma _N)$
, it follows from Theorem 2.4 that either:
-
(1)
 $A/N$
is a
$A/N$
is a
 $2$
-transitive group in Table 1 on
$2$
-transitive group in Table 1 on
 $V(\Gamma _N)$
; or
$V(\Gamma _N)$
; or -
(2)
 $n=p$
and
$n=p$
and
 $A/N\leq AGL(1,p)$
, where p is a prime.
$A/N\leq AGL(1,p)$
, where p is a prime.
Assume that
![]() $\Gamma _N$
is isomorphic to the complete graph
$\Gamma _N$
is isomorphic to the complete graph
![]() ${\mathrm {K}}_n$
, where
${\mathrm {K}}_n$
, where
![]() $n\geq 3$
. If
$n\geq 3$
. If
![]() $n=3$
, then
$n=3$
, then
![]() $\Gamma _N$
has valency two. Since
$\Gamma _N$
has valency two. Since
![]() $\Gamma $
is a cover of
$\Gamma $
is a cover of
![]() $\Gamma _N$
, it follows that
$\Gamma _N$
, it follows that
![]() $\Gamma $
also has valency two, and this forces
$\Gamma $
also has valency two, and this forces
![]() $\Gamma $
to be the complete graph
$\Gamma $
to be the complete graph
![]() ${\mathrm {K}}_3$
, as it has girth 3, which is a contradiction. Hence,
${\mathrm {K}}_3$
, as it has girth 3, which is a contradiction. Hence,
![]() $n\geq 4$
. Moreover, Lemma 3.1 indicates that
$n\geq 4$
. Moreover, Lemma 3.1 indicates that
![]() $\Gamma $
is isomorphic to one of the graphs in [Reference Godsil, Liebler and Praeger16, Main Theorem]. Then on inspection of the graphs in [Reference Godsil, Liebler and Praeger16, Main Theorem], the case
$\Gamma $
is isomorphic to one of the graphs in [Reference Godsil, Liebler and Praeger16, Main Theorem]. Then on inspection of the graphs in [Reference Godsil, Liebler and Praeger16, Main Theorem], the case
![]() $n=p$
and
$n=p$
and
![]() $A/N\leq AGL(1,p)$
does not occur. Suppose that case (1) holds, that is,
$A/N\leq AGL(1,p)$
does not occur. Suppose that case (1) holds, that is,
![]() $A/N$
acts 2-transitively on
$A/N$
acts 2-transitively on
![]() $V(\Gamma _N)$
and
$V(\Gamma _N)$
and
![]() $A/N$
is in Table 1. By inspecting the candidates in Table 1, either
$A/N$
is in Table 1. By inspecting the candidates in Table 1, either
![]() $A/N$
is 3-transitive on
$A/N$
is 3-transitive on
![]() $V(\Gamma _N)$
or
$V(\Gamma _N)$
or
![]() $n=|V(\Gamma _N)|=11,({q^d-1})/({q-1})$
, where
$n=|V(\Gamma _N)|=11,({q^d-1})/({q-1})$
, where
![]() $d\geq 3$
and q is a prime power. By Lemma 3.2,
$d\geq 3$
and q is a prime power. By Lemma 3.2,
![]() $A/N$
is not 3-transitive on
$A/N$
is not 3-transitive on
![]() $V(\Gamma _N)$
. Thus,
$V(\Gamma _N)$
. Thus,
![]() $n=11$
or
$n=11$
or
![]() $({q^d-1})/({q-1})$
, where
$({q^d-1})/({q-1})$
, where
![]() $d\geq 3$
and q is a prime power. However, a check of the graphs listed in [Reference Godsil, Liebler and Praeger16, Main Theorem] reveals that such a graph does not exist.
$d\geq 3$
and q is a prime power. However, a check of the graphs listed in [Reference Godsil, Liebler and Praeger16, Main Theorem] reveals that such a graph does not exist.
Therefore,
![]() $\Gamma _N$
is isomorphic to a Paley graph
$\Gamma _N$
is isomorphic to a Paley graph
![]() $P(q^f)$
, where q is a prime and
$P(q^f)$
, where q is a prime and
![]() $q^f \equiv 1 \ (\operatorname {mod}\, 4)$
. Moreover, in this case,
$q^f \equiv 1 \ (\operatorname {mod}\, 4)$
. Moreover, in this case,
![]() $A/N$
is not
$A/N$
is not
![]() $2$
-transitive on
$2$
-transitive on
![]() $V(\Gamma _N)$
, and so
$V(\Gamma _N)$
, and so
![]() $q^f=p$
and
$q^f=p$
and
![]() $A/N\leq AGL(1,p)$
, where p is a prime and
$A/N\leq AGL(1,p)$
, where p is a prime and
![]() $p \equiv 1 \ (\operatorname {mod}\, 4)$
. Recall that
$p \equiv 1 \ (\operatorname {mod}\, 4)$
. Recall that
![]() $|V(\Gamma )|=2n$
and
$|V(\Gamma )|=2n$
and
![]() $n=|V(\Gamma _N)|$
. Hence, the graph
$n=|V(\Gamma _N)|$
. Hence, the graph
![]() $\Gamma $
is a 2-cover of the Paley graph
$\Gamma $
is a 2-cover of the Paley graph
![]() $P(p)$
. Thus,
$P(p)$
. Thus,
![]() $|V(\Gamma )|=2p$
, and it follows that such a graph is isomorphic to one of the ones listed in [Reference Cheng and Oxley5, Theorem 2.4].
$|V(\Gamma )|=2p$
, and it follows that such a graph is isomorphic to one of the ones listed in [Reference Cheng and Oxley5, Theorem 2.4].
By inspecting the candidates in [Reference Cheng and Oxley5, Theorem 2.4], the only connected nonbipartite graph is
![]() $G(2,p,r)$
of valency
$G(2,p,r)$
of valency
![]() $2r$
, where r is even and
$2r$
, where r is even and
![]() $r | p-1$
. The fact that
$r | p-1$
. The fact that
![]() $\Gamma $
is a cover of
$\Gamma $
is a cover of
![]() $\Gamma _N$
which is a Paley graph of valency
$\Gamma _N$
which is a Paley graph of valency
![]() $({p-1})/{2}$
implies that
$({p-1})/{2}$
implies that
![]() $2r=({p-1})/{2}$
, and hence
$2r=({p-1})/{2}$
, and hence
![]() $r=({p-1})/{4}$
. Since r is an even integer, we have
$r=({p-1})/{4}$
. Since r is an even integer, we have
![]() $p \equiv 1 \ (\operatorname {mod}\, 8)$
. Thus,
$p \equiv 1 \ (\operatorname {mod}\, 8)$
. Thus,
![]() $\Gamma =G(2,p,({p-1})/{4})$
, where p is a prime and
$\Gamma =G(2,p,({p-1})/{4})$
, where p is a prime and
![]() $p \equiv 1 \ (\operatorname {mod}\, 8)$
. Moreover, by Lemma 2.2,
$p \equiv 1 \ (\operatorname {mod}\, 8)$
. Moreover, by Lemma 2.2,
![]() $G(2,p,({p-1})/{4})$
is a Cayley graph of a dihedral group. This completes the proof.
$G(2,p,({p-1})/{4})$
is a Cayley graph of a dihedral group. This completes the proof.
Lemma 3.4. Let
![]() $\Gamma $
be a connected
$\Gamma $
be a connected
![]() $2$
-distance-transitive Cayley graph of girth
$2$
-distance-transitive Cayley graph of girth
![]() $3$
over the dihedral group
$3$
over the dihedral group
![]() $T=\langle a,b|a^n=b^2=1,a^b=a^{-1}\rangle $
, where
$T=\langle a,b|a^n=b^2=1,a^b=a^{-1}\rangle $
, where
![]() $n\geq 3$
. Suppose that
$n\geq 3$
. Suppose that
![]() $\Gamma \ncong {\mathrm {K}}_{x[y]}$
for any
$\Gamma \ncong {\mathrm {K}}_{x[y]}$
for any
![]() $x\geq 3,y\geq 2$
. Then either:
$x\geq 3,y\geq 2$
. Then either:
-
(i)
 $\Gamma =G(2,p,({p-1})/{4})$
where p is a prime and
$\Gamma =G(2,p,({p-1})/{4})$
where p is a prime and
 $p \equiv 1 \ (\operatorname {mod}\, 8)$
; or
$p \equiv 1 \ (\operatorname {mod}\, 8)$
; or -
(ii) every maximal intransitive normal subgroup of
 ${\mathrm {Aut}}(\Gamma )$
is a proper subgroup of
${\mathrm {Aut}}(\Gamma )$
is a proper subgroup of
 $ \langle a \rangle $
.
$ \langle a \rangle $
.
Proof. Let N be a maximal intransitive normal subgroup of
![]() $A:={\mathrm {Aut}}(\Gamma )$
. Then each N-orbit is a block of the A-action on
$A:={\mathrm {Aut}}(\Gamma )$
. Then each N-orbit is a block of the A-action on
![]() $V(\Gamma )$
and
$V(\Gamma )$
and
![]() $A/N$
acts quasiprimitively on the set of N-orbits. Since
$A/N$
acts quasiprimitively on the set of N-orbits. Since
![]() $\Gamma $
is arc-transitive, each N-orbit does not contain any edge of
$\Gamma $
is arc-transitive, each N-orbit does not contain any edge of
![]() $\Gamma $
. Since
$\Gamma $
. Since
![]() $\Gamma $
has girth
$\Gamma $
has girth
![]() $3$
, it follows that N has at least three orbits. Let
$3$
, it follows that N has at least three orbits. Let
![]() $\mathcal {B}=\{B_1,\ldots ,B_t\}$
be the set of N-orbits. Then
$\mathcal {B}=\{B_1,\ldots ,B_t\}$
be the set of N-orbits. Then
![]() $t \geq 3$
.
$t \geq 3$
.
Let
![]() $H_0$
and
$H_0$
and
![]() $H_1$
be the two orbits of
$H_1$
be the two orbits of
![]() $H:=\langle a \rangle $
on
$H:=\langle a \rangle $
on
![]() $V(\Gamma )$
. Suppose that there exists some N-orbit
$V(\Gamma )$
. Suppose that there exists some N-orbit
![]() $B\in \mathcal {B}$
such that
$B\in \mathcal {B}$
such that
![]() $B\subseteq H_i$
for some
$B\subseteq H_i$
for some
![]() $i\in \{0,1\}$
, and assume that there is another block
$i\in \{0,1\}$
, and assume that there is another block
![]() $B'\in \mathcal {B}$
such that
$B'\in \mathcal {B}$
such that
![]() $B'\cap H_0\neq \varnothing $
and
$B'\cap H_0\neq \varnothing $
and
![]() $B'\cap H_{1}\neq \varnothing $
. Then, for each vertex
$B'\cap H_{1}\neq \varnothing $
. Then, for each vertex
![]() $u\in B$
, there exists
$u\in B$
, there exists
![]() $h\in H$
such that
$h\in H$
such that
![]() $u^{h}\in B'\cap H_i$
, as H acts transitively on
$u^{h}\in B'\cap H_i$
, as H acts transitively on
![]() $H_i$
. Thus,
$H_i$
. Thus,
![]() $u^{h}\in B'\cap B^{h}$
. Since
$u^{h}\in B'\cap B^{h}$
. Since
![]() $B^{h}\in \mathcal {B}$
and
$B^{h}\in \mathcal {B}$
and
![]() $\mathcal {B}$
is a block system, we get
$\mathcal {B}$
is a block system, we get
![]() $B'=B^{h}\subseteq H_i$
, which is a contradiction. Therefore, either:
$B'=B^{h}\subseteq H_i$
, which is a contradiction. Therefore, either:
-
(1) all elements of
 $\mathcal {B}$
are subsets of
$\mathcal {B}$
are subsets of
 $H_0$
or
$H_0$
or
 $H_1$
; or
$H_1$
; or -
(2) the intersections of each
 $B\in \mathcal {B}$
with both
$B\in \mathcal {B}$
with both
 $H_0$
and
$H_0$
and
 $H_1$
are nonempty.
$H_1$
are nonempty.
Let
![]() $B\in \mathcal {B}$
. First, suppose that (1) occurs, that is,
$B\in \mathcal {B}$
. First, suppose that (1) occurs, that is,
![]() $B\subset H_i$
for some
$B\subset H_i$
for some
![]() $H_i$
. Then, since H acts regularly on
$H_i$
. Then, since H acts regularly on
![]() $ H_i$
, it follows that
$ H_i$
, it follows that
![]() $HN/N\cong H/(H\cap N)$
is regular on
$HN/N\cong H/(H\cap N)$
is regular on
![]() $\mathcal {B}\cap H_i$
. Hence,
$\mathcal {B}\cap H_i$
. Hence,
![]() $H\cap N$
is regular on B, and so
$H\cap N$
is regular on B, and so
![]() $|H\cap N|=|B|=|N|$
and we have
$|H\cap N|=|B|=|N|$
and we have
![]() $H\cap N=N$
. Thus,
$H\cap N=N$
. Thus,
![]() $N\leq H$
is a cyclic group, so (ii) holds.
$N\leq H$
is a cyclic group, so (ii) holds.
Now assume that (2) holds, that is,
![]() $B\cap H_i\neq \varnothing $
. As B is a block of H, for each
$B\cap H_i\neq \varnothing $
. As B is a block of H, for each
![]() $h\in H$
, we have
$h\in H$
, we have
![]() $B^{h}= B$
or
$B^{h}= B$
or
![]() $B^{h}\cap B=\varnothing $
. Since
$B^{h}\cap B=\varnothing $
. Since
![]() $(B\cap H_i)^{h}\subseteq H_i$
, it follows that
$(B\cap H_i)^{h}\subseteq H_i$
, it follows that
![]() $(B\cap H_i)^{h}=B\cap H_i$
or
$(B\cap H_i)^{h}=B\cap H_i$
or
![]() $(B\cap H_i)^{h}\cap (B\cap H_i)=\varnothing $
and so
$(B\cap H_i)^{h}\cap (B\cap H_i)=\varnothing $
and so
![]() $B\cap H_i$
is a block for H on
$B\cap H_i$
is a block for H on
![]() $H_i$
. Further,
$H_i$
. Further,
![]() $HN/N\cong H/(H\cap N)$
is regular on
$HN/N\cong H/(H\cap N)$
is regular on
![]() $\mathcal {B}$
, and so
$\mathcal {B}$
, and so
![]() $H\cap N$
is semiregular on B with two orbits. Thus,
$H\cap N$
is semiregular on B with two orbits. Thus,
![]() $H\cap N$
is a cyclic index two subgroup of N, and
$H\cap N$
is a cyclic index two subgroup of N, and
![]() $|B\cap H_0|= |B\cap H_1|$
.
$|B\cap H_0|= |B\cap H_1|$
.
Since
![]() $\Gamma $
is a
$\Gamma $
is a
![]() $2$
-distance-transitive graph of girth
$2$
-distance-transitive graph of girth
![]() $3$
and
$3$
and
![]() $\Gamma \ncong {\mathrm {K}}_{x[y]}$
for any
$\Gamma \ncong {\mathrm {K}}_{x[y]}$
for any
![]() $x\geq 3$
and
$x\geq 3$
and
![]() $y\geq 2$
, it follows from Lemma 2.8 that N is regular on each orbit,
$y\geq 2$
, it follows from Lemma 2.8 that N is regular on each orbit,
![]() $\Gamma $
is a cover of
$\Gamma $
is a cover of
![]() $\Gamma _{N}$
, and either
$\Gamma _{N}$
, and either
![]() $\Gamma _N$
is isomorphic to a complete graph or
$\Gamma _N$
is isomorphic to a complete graph or
![]() $\Gamma _{N}$
is a
$\Gamma _{N}$
is a
![]() $(A/N,2)$
-distance-transitive noncomplete graph.
$(A/N,2)$
-distance-transitive noncomplete graph.
Since
![]() $B\cap H_i$
is a block for H on
$B\cap H_i$
is a block for H on
![]() $H_i$
and
$H_i$
and
![]() $HN/N\cong H/(H\cap N)$
is regular on
$HN/N\cong H/(H\cap N)$
is regular on
![]() $\mathcal {B}$
, it follows that
$\mathcal {B}$
, it follows that
![]() $\Gamma _{N}$
is a circulant of the cyclic group
$\Gamma _{N}$
is a circulant of the cyclic group
![]() $H/(H\cap N)$
.
$H/(H\cap N)$
.
Suppose that
![]() $\Gamma _{N}$
is a
$\Gamma _{N}$
is a
![]() $(A/N,2)$
-distance-transitive noncomplete graph.
$(A/N,2)$
-distance-transitive noncomplete graph.
![]() $\Gamma _{N}$
is one of the graphs listed in [Reference Jin, Liu and Wang19, Theorem 1.3]. Since
$\Gamma _{N}$
is one of the graphs listed in [Reference Jin, Liu and Wang19, Theorem 1.3]. Since
![]() $\Gamma _{N}$
has girth 3 and valency at least three, and since
$\Gamma _{N}$
has girth 3 and valency at least three, and since
![]() $A/N$
acts quasiprimitively on
$A/N$
acts quasiprimitively on
![]() $\mathcal {B}$
, by inspecting the graphs in [Reference Jin, Liu and Wang19, Theorem 1.3],
$\mathcal {B}$
, by inspecting the graphs in [Reference Jin, Liu and Wang19, Theorem 1.3],
![]() $\Gamma _{N}$
is a complete graph, which yields a contradiction.
$\Gamma _{N}$
is a complete graph, which yields a contradiction.
Thus,
![]() $\Gamma _{N}$
is a complete graph. For
$\Gamma _{N}$
is a complete graph. For
![]() $i\in \{0,1\}$
, let
$i\in \{0,1\}$
, let
![]() $\mathcal {B}_i=\{B_1\cap H_i,\ldots ,B_t\cap H_i\}$
. Since each
$\mathcal {B}_i=\{B_1\cap H_i,\ldots ,B_t\cap H_i\}$
. Since each
![]() $B_j$
meets each
$B_j$
meets each
![]() $H_i$
nontrivially, we have that
$H_i$
nontrivially, we have that
![]() $|\mathcal {B}_0|=|\mathcal {B}_1|=t$
. Moreover, as H is transitive on each
$|\mathcal {B}_0|=|\mathcal {B}_1|=t$
. Moreover, as H is transitive on each
![]() $H_i$
, it is transitive on each
$H_i$
, it is transitive on each
![]() $\mathcal {B}_i$
. Since H is cyclic, it has a unique subgroup of each order and so the kernel of H on
$\mathcal {B}_i$
. Since H is cyclic, it has a unique subgroup of each order and so the kernel of H on
![]() $\mathcal {B}_0$
is equal to the kernel of H on
$\mathcal {B}_0$
is equal to the kernel of H on
![]() $\mathcal {B}_1$
, and so is in the kernel of H on
$\mathcal {B}_1$
, and so is in the kernel of H on
![]() $\mathcal {B}$
. It follows that H acts faithfully and hence regularly on each
$\mathcal {B}$
. It follows that H acts faithfully and hence regularly on each
![]() $\mathcal {B}_i$
. Thus,
$\mathcal {B}_i$
. Thus,
![]() $|H|=t=|\mathcal {B}_i|$
, and so each
$|H|=t=|\mathcal {B}_i|$
, and so each
![]() $B\in \mathcal {B}$
has size two. This indicates that
$B\in \mathcal {B}$
has size two. This indicates that
![]() $|B\cap H_0|=|B\cap H_1|=1$
. Hence,
$|B\cap H_0|=|B\cap H_1|=1$
. Hence,
![]() $|N|=|B|=2$
. Since N has a cyclic index two normal subgroup
$|N|=|B|=2$
. Since N has a cyclic index two normal subgroup
![]() $H\cap N$
, we have
$H\cap N$
, we have
![]() $H\cap N=1$
.
$H\cap N=1$
.
Since
![]() $N\lhd A$
, we have
$N\lhd A$
, we have
![]() $T\cap N\lhd T$
. Further,
$T\cap N\lhd T$
. Further,
![]() $|T:T\cap N|\geq |T|/|N|\geq 3$
, and it follows from Lemma 2.1 that
$|T:T\cap N|\geq |T|/|N|\geq 3$
, and it follows from Lemma 2.1 that
![]() $T\cap N\leq H $
.
$T\cap N\leq H $
.
If
![]() $T\cap N= H $
, then
$T\cap N= H $
, then
![]() $\overline {T}\cong T/T\cap N\cong \mathbb {Z}_2$
and
$\overline {T}\cong T/T\cap N\cong \mathbb {Z}_2$
and
![]() $|\overline {T}|=2$
, which contradicts that
$|\overline {T}|=2$
, which contradicts that
![]() $|\overline {T}|=|TN/N|= |T/T\cap N|\geq |T/N|=|\mathcal {B}|\geq 3$
. Thus,
$|\overline {T}|=|TN/N|= |T/T\cap N|\geq |T/N|=|\mathcal {B}|\geq 3$
. Thus,
If
![]() $1\neq T\cap N< H$
, then
$1\neq T\cap N< H$
, then
![]() $H\cap N=T\cap N\neq 1$
, which is a contradiction. Thus,
$H\cap N=T\cap N\neq 1$
, which is a contradiction. Thus,
![]() $T\cap N=1$
, and, by Lemma 3.3,
$T\cap N=1$
, and, by Lemma 3.3,
![]() $\Gamma =G(2,p,({p-1})/{4})$
, where p is a prime and
$\Gamma =G(2,p,({p-1})/{4})$
, where p is a prime and
![]() $p \equiv 1 (\operatorname {mod}\, 8)$
, so (i) holds.
$p \equiv 1 (\operatorname {mod}\, 8)$
, so (i) holds.
Lemma 3.5. Let
![]() $\Gamma $
be a connected
$\Gamma $
be a connected
![]() $2$
-distance-transitive Cayley graph over a dihedral group T. Suppose that
$2$
-distance-transitive Cayley graph over a dihedral group T. Suppose that
![]() $\Gamma $
has girth
$\Gamma $
has girth
![]() $3$
and is isomorphic to neither
$3$
and is isomorphic to neither
![]() $ {\mathrm {K}}_{x[y]}$
, where
$ {\mathrm {K}}_{x[y]}$
, where
![]() $x\geq 3,y\geq 2$
, nor
$x\geq 3,y\geq 2$
, nor
![]() $G(2,p,({p-1})/{4})$
, where p is a prime and
$G(2,p,({p-1})/{4})$
, where p is a prime and
![]() $p \equiv 1 \ (\operatorname {mod}\, 8)$
. Then, for each maximal intransitive normal subgroup N of
$p \equiv 1 \ (\operatorname {mod}\, 8)$
. Then, for each maximal intransitive normal subgroup N of
![]() ${\mathrm {Aut}}(\Gamma )$
,
${\mathrm {Aut}}(\Gamma )$
,
![]() $T^{V(\Gamma _N)}$
is regular on
$T^{V(\Gamma _N)}$
is regular on
![]() $V(\Gamma _N)$
and
$V(\Gamma _N)$
and
![]() $|T^{V(\Gamma _N)}|=|T/N|=|V(\Gamma _N)|$
.
$|T^{V(\Gamma _N)}|=|T/N|=|V(\Gamma _N)|$
.
Proof. Let N be a maximal intransitive normal subgroup of
![]() $A:={\mathrm {Aut}}(\Gamma )$
. Then, since
$A:={\mathrm {Aut}}(\Gamma )$
. Then, since
![]() $\Gamma $
is a
$\Gamma $
is a
![]() $2$
-distance-transitive graph of girth
$2$
-distance-transitive graph of girth
![]() $3$
and
$3$
and
![]() $\Gamma \ncong {\mathrm {K}}_{x[y]}$
for any
$\Gamma \ncong {\mathrm {K}}_{x[y]}$
for any
![]() $x\geq 3$
and
$x\geq 3$
and
![]() $y\geq 2$
, it follows from Lemma 2.8 that N is regular on each orbit and N is the kernel of A acting on
$y\geq 2$
, it follows from Lemma 2.8 that N is regular on each orbit and N is the kernel of A acting on
![]() $V(\Gamma _N)$
. Hence,
$V(\Gamma _N)$
. Hence,
![]() $N\cap T$
is the kernel of T acting on
$N\cap T$
is the kernel of T acting on
![]() $V(\Gamma _N)$
, and so
$V(\Gamma _N)$
, and so
![]() $T^{V(\Gamma _N)}\cong T/T\cap N$
.
$T^{V(\Gamma _N)}\cong T/T\cap N$
.
Let
![]() $T=\langle a,b|a^n=b^2=1,a^b=a^{-1}\rangle \cong D_{2n}$
, where
$T=\langle a,b|a^n=b^2=1,a^b=a^{-1}\rangle \cong D_{2n}$
, where
![]() $n\geq 3$
. Then, as
$n\geq 3$
. Then, as
![]() $\Gamma $
is isomorphic to neither
$\Gamma $
is isomorphic to neither
![]() $ {\mathrm {K}}_{x[y]}$
, where
$ {\mathrm {K}}_{x[y]}$
, where
![]() $x\geq 3,y\geq 2$
, nor
$x\geq 3,y\geq 2$
, nor
![]() $G(2,p,({p-1})/{4})$
, where p is a prime and
$G(2,p,({p-1})/{4})$
, where p is a prime and
![]() $p \equiv 1 \, (\operatorname {mod}\, 8)$
, it follows from Lemma 3.4 that
$p \equiv 1 \, (\operatorname {mod}\, 8)$
, it follows from Lemma 3.4 that
![]() $ N< \langle a\rangle <T$
, and so
$ N< \langle a\rangle <T$
, and so
![]() $ T\cap N=N$
. Thus,
$ T\cap N=N$
. Thus,
![]() $|T^{V(\Gamma _N)}|=| T/T\cap N|=|T/N|$
. Since T is regular on
$|T^{V(\Gamma _N)}|=| T/T\cap N|=|T/N|$
. Since T is regular on
![]() $V(\Gamma )$
, it follows that
$V(\Gamma )$
, it follows that
![]() $|T/N|=|V(\Gamma _N)|$
. Hence,
$|T/N|=|V(\Gamma _N)|$
. Hence,
![]() $|T^{V(\Gamma _N)}|=|T/N|=|V(\Gamma _N)|$
, and
$|T^{V(\Gamma _N)}|=|T/N|=|V(\Gamma _N)|$
, and
![]() $T^{V(\Gamma _N)}$
is regular on
$T^{V(\Gamma _N)}$
is regular on
![]() $V(\Gamma _N)$
.
$V(\Gamma _N)$
.
Lemma 3.6. Let
![]() $\Gamma $
be a connected
$\Gamma $
be a connected
![]() $2$
-distance-transitive Cayley graph over a dihedral group T. Then
$2$
-distance-transitive Cayley graph over a dihedral group T. Then
![]() $\Gamma $
has girth
$\Gamma $
has girth
![]() $3$
if and only if
$3$
if and only if
![]() $\Gamma $
is isomorphic to either
$\Gamma $
is isomorphic to either
![]() $ {\mathrm {K}}_{x[y]}$
for some
$ {\mathrm {K}}_{x[y]}$
for some
![]() $x\geq 3,y\geq 2$
or
$x\geq 3,y\geq 2$
or
![]() $G(2,p,({p-1})/{4})$
, where p is a prime and
$G(2,p,({p-1})/{4})$
, where p is a prime and
![]() $p \equiv 1 \ (\operatorname {mod}\, 8)$
.
$p \equiv 1 \ (\operatorname {mod}\, 8)$
.
Proof. If
![]() $\Gamma \cong {\mathrm {K}}_{x[y]}$
for some
$\Gamma \cong {\mathrm {K}}_{x[y]}$
for some
![]() $x\geq 3,y\geq 2$
or
$x\geq 3,y\geq 2$
or
![]() $G(2,p,({p-1})/{4})$
, where p is a prime and
$G(2,p,({p-1})/{4})$
, where p is a prime and
![]() $p \equiv 1 \, (\operatorname {mod}\, 8)$
, then, clearly,
$p \equiv 1 \, (\operatorname {mod}\, 8)$
, then, clearly,
![]() $\Gamma $
has girth
$\Gamma $
has girth
![]() $3$
. Conversely, suppose that
$3$
. Conversely, suppose that
![]() $\Gamma $
has girth
$\Gamma $
has girth
![]() $3$
. Assume further that
$3$
. Assume further that
![]() $\Gamma $
is isomorphic to neither
$\Gamma $
is isomorphic to neither
![]() $ {\mathrm {K}}_{x[y]}$
, where
$ {\mathrm {K}}_{x[y]}$
, where
![]() $x\geq 3,y\geq 2$
, nor
$x\geq 3,y\geq 2$
, nor
![]() $G(2,p,({p-1})/{4})$
, where p is a prime and
$G(2,p,({p-1})/{4})$
, where p is a prime and
![]() $p \equiv 1 \ (\operatorname {mod}\, 8)$
.
$p \equiv 1 \ (\operatorname {mod}\, 8)$
.
Let
![]() $A:={\mathrm {Aut}}(\Gamma )$
. If A is quasiprimitive on the vertex set
$A:={\mathrm {Aut}}(\Gamma )$
. If A is quasiprimitive on the vertex set
![]() $V(\Gamma )$
, then, as T is a dihedral regular subgroup of A, it follows from Theorem 2.5 that A is 2-transitive on
$V(\Gamma )$
, then, as T is a dihedral regular subgroup of A, it follows from Theorem 2.5 that A is 2-transitive on
![]() $V(\Gamma )$
, and so
$V(\Gamma )$
, and so
![]() $\Gamma $
is a complete graph, which is a contradiction. Thus, A is not quasiprimitive on
$\Gamma $
is a complete graph, which is a contradiction. Thus, A is not quasiprimitive on
![]() $V(\Gamma )$
. Hence, A has at least one nontrivial intransitive normal subgroup. Let N be a maximal intransitive normal subgroup of A. Then N is the kernel of A acting on
$V(\Gamma )$
. Hence, A has at least one nontrivial intransitive normal subgroup. Let N be a maximal intransitive normal subgroup of A. Then N is the kernel of A acting on
![]() $V(\Gamma _N)$
. Thus,
$V(\Gamma _N)$
. Thus,
![]() $N\cap T$
is the kernel of T acting on
$N\cap T$
is the kernel of T acting on
![]() $V(\Gamma _N)$
, and so
$V(\Gamma _N)$
, and so
![]() $T^{V(\Gamma _N)}\cong T/T\cap N$
. By Lemma 3.5, the group
$T^{V(\Gamma _N)}\cong T/T\cap N$
. By Lemma 3.5, the group
![]() $T^{V(\Gamma _N)}$
is regular on
$T^{V(\Gamma _N)}$
is regular on
![]() $V(\Gamma _N)$
, and hence
$V(\Gamma _N)$
, and hence
![]() $V(\Gamma _N)$
is the set of
$V(\Gamma _N)$
is the set of
![]() $T\cap N$
-orbits. It follows that the set of
$T\cap N$
-orbits. It follows that the set of
![]() $T\cap N$
-orbits is exactly the set of N-orbits, and
$T\cap N$
-orbits is exactly the set of N-orbits, and
![]() $T\cap N$
is transitive on each N-orbit.
$T\cap N$
is transitive on each N-orbit.
Let
![]() $T=\langle a,b|a^n=b^2=1,a^b=a^{-1}\rangle \cong D_{2n}$
, where
$T=\langle a,b|a^n=b^2=1,a^b=a^{-1}\rangle \cong D_{2n}$
, where
![]() $n\geq 3$
. Then, since
$n\geq 3$
. Then, since
![]() $\Gamma $
is not isomorphic to
$\Gamma $
is not isomorphic to
![]() $G(2,p,({p-1})/{4})$
, it follows from Lemma 3.4 that
$G(2,p,({p-1})/{4})$
, it follows from Lemma 3.4 that
![]() $ N< \langle a\rangle <T$
, and so
$ N< \langle a\rangle <T$
, and so
![]() $ T\cap N=N$
. Hence,
$ T\cap N=N$
. Hence,
![]() $T^{V(\Gamma _N)}\cong T/T\cap N=T/N$
is a dihedral subgroup of
$T^{V(\Gamma _N)}\cong T/T\cap N=T/N$
is a dihedral subgroup of
![]() $A/N$
. Since N is a maximal intransitive normal subgroup of A, it follows that
$A/N$
. Since N is a maximal intransitive normal subgroup of A, it follows that
![]() $A/N$
is quasiprimitive on
$A/N$
is quasiprimitive on
![]() $V(\Gamma _N)$
. Recall that
$V(\Gamma _N)$
. Recall that
![]() $T^{V(\Gamma _N)}$
acts regularly on
$T^{V(\Gamma _N)}$
acts regularly on
![]() $V(\Gamma _N)$
. Thus,
$V(\Gamma _N)$
. Thus,
![]() $A/N,T/N$
and
$A/N,T/N$
and
![]() $|V(\Gamma _N)|$
lie in Table 2 of Theorem 2.5. In particular,
$|V(\Gamma _N)|$
lie in Table 2 of Theorem 2.5. In particular,
![]() $A/N$
is
$A/N$
is
![]() $2$
-transitive on
$2$
-transitive on
![]() $V(\Gamma _N)$
, and so
$V(\Gamma _N)$
, and so
![]() $\Gamma _N$
is a complete graph.
$\Gamma _N$
is a complete graph.
Since
![]() $\Gamma $
is a
$\Gamma $
is a
![]() $2$
-distance-transitive graph of girth
$2$
-distance-transitive graph of girth
![]() $3$
, it follows that
$3$
, it follows that
![]() $\Gamma $
is not
$\Gamma $
is not
![]() $2$
-arc-transitive. Thus, by Lemma 3.2,
$2$
-arc-transitive. Thus, by Lemma 3.2,
![]() $A/N$
is 2-transitive but not 3-transitive on
$A/N$
is 2-transitive but not 3-transitive on
![]() $V(\Gamma _N)$
. By inspecting the groups in Table 2, one of the following holds.
$V(\Gamma _N)$
. By inspecting the groups in Table 2, one of the following holds.
-
(1)
 $T/N\cong D_{4}$
and
$T/N\cong D_{4}$
and
 $|V(\Gamma _N)|=4$
.
$|V(\Gamma _N)|=4$
. -
(2)
 $T/N\cong D_{16}$
and
$T/N\cong D_{16}$
and
 $|V(\Gamma _N)|=16$
.
$|V(\Gamma _N)|=16$
. -
(3)
 $A/N=PSL(2,r^f)$
,
$A/N=PSL(2,r^f)$
,
 $T/N=D_{r^f+1}$
, and
$T/N=D_{r^f+1}$
, and
 $|V(\Gamma _N)|=r^f+1$
,
$|V(\Gamma _N)|=r^f+1$
,
 $r^f \equiv 3 \ (\operatorname {mod}\, 4)$
.
$r^f \equiv 3 \ (\operatorname {mod}\, 4)$
.
Since N is a cyclic group, it follows that subgroups of N are characteristic subgroups, and so subgroups of N are normal subgroups of A. Thus, by Lemma 2.6, it is sufficient to prove the lemma when
![]() $|N|$
is a prime. In the remainder of the proof, we suppose that
$|N|$
is a prime. In the remainder of the proof, we suppose that
![]() $N\cong \mathbb {Z}_p$
, where p is a prime number.
$N\cong \mathbb {Z}_p$
, where p is a prime number.
First, assume that case (1) holds. Then
![]() $T/N\cong D_{4}$
and
$T/N\cong D_{4}$
and
![]() $|V(\Gamma _N)|=4$
. By Lemma 2.8,
$|V(\Gamma _N)|=4$
. By Lemma 2.8,
![]() $\Gamma $
is a cover of
$\Gamma $
is a cover of
![]() $\Gamma _N$
. Thus,
$\Gamma _N$
. Thus,
![]() $\Gamma $
has valency three. Since
$\Gamma $
has valency three. Since
![]() $\Gamma $
is symmetric and has girth 3,
$\Gamma $
is symmetric and has girth 3,
![]() $\Gamma $
is a complete graph, which is a contradiction.
$\Gamma $
is a complete graph, which is a contradiction.
Next, assume that case (3) occurs. Then
![]() $A/N=PSL(2,r^f)$
, where
$A/N=PSL(2,r^f)$
, where
![]() $r^f \equiv 3 \ (\operatorname {mod}\, 4)$
is a nonabelian simple group. Note that
$r^f \equiv 3 \ (\operatorname {mod}\, 4)$
is a nonabelian simple group. Note that
![]() $C_A(N)/N\unlhd A/N$
. We have
$C_A(N)/N\unlhd A/N$
. We have
![]() $C_A(N)/N=1$
or
$C_A(N)/N=1$
or
![]() $A/N$
. Assume that
$A/N$
. Assume that
![]() $C_A(N)/N=1$
. Then
$C_A(N)/N=1$
. Then
![]() $C_A(N)=N$
, and so
$C_A(N)=N$
, and so
![]() $A/C_A(N)=A/N\leq {\mathrm {Aut}}(N)$
is a cyclic group, which is a contradiction. Thus,
$A/C_A(N)=A/N\leq {\mathrm {Aut}}(N)$
is a cyclic group, which is a contradiction. Thus,
![]() $C_A(N)/N=A/N$
, and so
$C_A(N)/N=A/N$
, and so
![]() $C_A(N)=A$
. Hence,
$C_A(N)=A$
. Hence,
![]() $N\leq Z(A)$
, and
$N\leq Z(A)$
, and
![]() $A=N\times PSL(2,r^f)$
,
$A=N\times PSL(2,r^f)$
,
![]() $r^f \equiv 3 \ (\operatorname {mod}\, 4)$
. Moreover,
$r^f \equiv 3 \ (\operatorname {mod}\, 4)$
. Moreover,
![]() $PSL(2,r^f)$
is a maximal intransitive normal subgroup of A as
$PSL(2,r^f)$
is a maximal intransitive normal subgroup of A as
![]() $|N|$
is a prime. However, by Lemma 3.4,
$|N|$
is a prime. However, by Lemma 3.4,
![]() $ PSL(2,r^f)< \langle a\rangle $
is cyclic, which is a contradiction.
$ PSL(2,r^f)< \langle a\rangle $
is cyclic, which is a contradiction.
From now on, we suppose that case (2) holds, that is,
![]() $T/N\cong D_{16}$
,
$T/N\cong D_{16}$
,
![]() $\mathrm{soc}( A/N) = \mathbb {Z}_2^4$
and
$\mathrm{soc}( A/N) = \mathbb {Z}_2^4$
and
![]() $|V(\Gamma _N)|=16$
. Thus,
$|V(\Gamma _N)|=16$
. Thus,
![]() $\Gamma _N\cong {\mathrm {K}}_{16}$
. Moreover, Theorem 2.5 says that the quotient group
$\Gamma _N\cong {\mathrm {K}}_{16}$
. Moreover, Theorem 2.5 says that the quotient group
![]() $A/N \in \{ \mathbb {Z}_2^4: A_6$
,
$A/N \in \{ \mathbb {Z}_2^4: A_6$
,
![]() $\mathbb {Z}_2^4: S_6$
,
$\mathbb {Z}_2^4: S_6$
,
![]() $\mathbb {Z}_2^4: S_5, \mathbb {Z}_2^4: \Gamma L(2,4)\}$
. Let
$\mathbb {Z}_2^4: S_5, \mathbb {Z}_2^4: \Gamma L(2,4)\}$
. Let
![]() $\overline {A}:=A/N$
.
$\overline {A}:=A/N$
.
Let
![]() $Y = N. \mathrm{soc}( \overline {A})= N .\mathbb {Z}_2^4$
. Then
$Y = N. \mathrm{soc}( \overline {A})= N .\mathbb {Z}_2^4$
. Then
![]() $ A=N.\overline {A}=Y.(\overline {A}/\mathrm{soc}(\overline {A}))$
. Thus, for each
$ A=N.\overline {A}=Y.(\overline {A}/\mathrm{soc}(\overline {A}))$
. Thus, for each
![]() $g\in A$
, we have
$g\in A$
, we have
![]() $g=xy$
, where
$g=xy$
, where
![]() $x\in Y$
and
$x\in Y$
and
![]() $y\in \overline {A}\setminus \mathbb {Z}_2^4$
. Since
$y\in \overline {A}\setminus \mathbb {Z}_2^4$
. Since
![]() $N \lhd A$
and
$N \lhd A$
and
![]() $\mathrm{soc}( \overline {A})= \mathbb {Z}_2^4$
, it follows that
$\mathrm{soc}( \overline {A})= \mathbb {Z}_2^4$
, it follows that
![]() $Y^g=Y^{y}=Y$
. Hence,
$Y^g=Y^{y}=Y$
. Hence,
![]() $Y \lhd A$
.
$Y \lhd A$
.
Since
![]() $\mathbb {Z}_2^4$
is regular on
$\mathbb {Z}_2^4$
is regular on
![]() $V(\Gamma _N)$
, it follows that
$V(\Gamma _N)$
, it follows that
![]() $\Gamma _N$
is a Cayley graph of
$\Gamma _N$
is a Cayley graph of
![]() $\mathbb {Z}_2^4$
. Moreover,
$\mathbb {Z}_2^4$
. Moreover,
![]() $\mathrm{soc}( \overline {A})=\mathbb {Z}_2^4 \lhd \overline {A}$
implies that
$\mathrm{soc}( \overline {A})=\mathbb {Z}_2^4 \lhd \overline {A}$
implies that
![]() $\Gamma _N$
is a
$\Gamma _N$
is a
![]() $\overline {A}$
-normal Cayley graph of
$\overline {A}$
-normal Cayley graph of
![]() $\mathbb {Z}_2^4$
. Since N is regular on each orbit, it follows that
$\mathbb {Z}_2^4$
. Since N is regular on each orbit, it follows that
![]() $Y=N.\mathbb {Z}_2^4$
is regular on
$Y=N.\mathbb {Z}_2^4$
is regular on
![]() $V(\Gamma )$
, and so
$V(\Gamma )$
, and so
![]() $\Gamma $
is a Cayley graph of Y, say,
$\Gamma $
is a Cayley graph of Y, say,
![]() $\Gamma ={\mathrm {Cay}}(Y,S')$
. As
$\Gamma ={\mathrm {Cay}}(Y,S')$
. As
![]() $Y \lhd A$
, we know that
$Y \lhd A$
, we know that
![]() $\Gamma $
is an A-normal Cayley graph of Y. Thus, by Lemma 2.3, for the vertex
$\Gamma $
is an A-normal Cayley graph of Y. Thus, by Lemma 2.3, for the vertex
![]() $u=1_A \in V(\Gamma )$
, we must have
$u=1_A \in V(\Gamma )$
, we must have
![]() $A_u\leq {\mathrm {Aut}}(Y,S')$
. Since
$A_u\leq {\mathrm {Aut}}(Y,S')$
. Since
![]() $\Gamma $
is a connected
$\Gamma $
is a connected
![]() $2$
-distance-transitive graph,
$2$
-distance-transitive graph,
![]() $A_u$
is transitive on
$A_u$
is transitive on
![]() $S'$
. Thus, all elements of
$S'$
. Thus, all elements of
![]() $S'$
have the same order. Since
$S'$
have the same order. Since
![]() $Y=\langle S'\rangle $
and
$Y=\langle S'\rangle $
and
![]() $Y = N. \mathrm{soc}( \overline {A})= N .\mathbb {Z}_2^4$
, it follows that Y is nonabelian.
$Y = N. \mathrm{soc}( \overline {A})= N .\mathbb {Z}_2^4$
, it follows that Y is nonabelian.
First, assume that p is an odd prime. Note that
![]() $N\leq C_Y (N)$
. If
$N\leq C_Y (N)$
. If
![]() $C_Y (N)=N$
, then
$C_Y (N)=N$
, then
![]() $Y=N .\mathbb {Z}_2^4\leq N.\mathbb {Z}_{p-1}$
, which is not possible. Thus,
$Y=N .\mathbb {Z}_2^4\leq N.\mathbb {Z}_{p-1}$
, which is not possible. Thus,
![]() $N<C_Y(N)<Y$
. Since
$N<C_Y(N)<Y$
. Since
![]() $Y/C_Y (N)\leq {\mathrm {Aut}}(N)\cong \mathbb {Z}_{p-1}$
, we have
$Y/C_Y (N)\leq {\mathrm {Aut}}(N)\cong \mathbb {Z}_{p-1}$
, we have
![]() $Y=N .\mathbb {Z}_2^4\leq C_Y (N).\mathbb {Z}_{p-1}$
, and so
$Y=N .\mathbb {Z}_2^4\leq C_Y (N).\mathbb {Z}_{p-1}$
, and so
![]() ${C_Y (N) = N. \mathbb {Z}_2^3\cong \mathbb {Z}_p\times \mathbb {Z}_2^3}$
and
${C_Y (N) = N. \mathbb {Z}_2^3\cong \mathbb {Z}_p\times \mathbb {Z}_2^3}$
and
![]() $\mathbb {Z}_{p-1}=\mathbb {Z}_{2}$
. Thus,
$\mathbb {Z}_{p-1}=\mathbb {Z}_{2}$
. Thus,
![]() $\mathrm{soc}(Y) \cong \mathbb {Z}_p\times \mathbb {Z}_2^3$
has characteristic subgroup
$\mathrm{soc}(Y) \cong \mathbb {Z}_p\times \mathbb {Z}_2^3$
has characteristic subgroup
![]() $P\cong \mathbb {Z}_2^3$
, and hence the group P is a normal subgroup of A. It follows that
$P\cong \mathbb {Z}_2^3$
, and hence the group P is a normal subgroup of A. It follows that
![]() $N\times P$
is normal in A and
$N\times P$
is normal in A and
![]() $|Y:N\times P|=2$
. Therefore,
$|Y:N\times P|=2$
. Therefore,
![]() $N\times P$
has two orbits on
$N\times P$
has two orbits on
![]() $V(\Gamma )$
, and it induces a normal quotient graph
$V(\Gamma )$
, and it induces a normal quotient graph
![]() $\Gamma _{N\times P}\cong {\mathrm {K}}_2$
. However, by Lemma 2.8,
$\Gamma _{N\times P}\cong {\mathrm {K}}_2$
. However, by Lemma 2.8,
![]() $\Gamma $
is a cover of
$\Gamma $
is a cover of
![]() $\Gamma _{N\times P}$
, since
$\Gamma _{N\times P}$
, since
![]() $\Gamma $
has girth 3, and it follows that
$\Gamma $
has girth 3, and it follows that
![]() $\Gamma _{N\times P}$
has girth 3, which is a contradiction.
$\Gamma _{N\times P}$
has girth 3, which is a contradiction.
Next, assume that
![]() $p = 2$
. Then
$p = 2$
. Then
![]() $Y = \mathbb {Z}_2. \mathbb {Z}_2^4$
. Let
$Y = \mathbb {Z}_2. \mathbb {Z}_2^4$
. Let
![]() $Z(Y)$
denote the center of Y. Then, as Y is a 2-group, we know that
$Z(Y)$
denote the center of Y. Then, as Y is a 2-group, we know that
![]() $Z(Y) \neq 1$
. Further,
$Z(Y) \neq 1$
. Further,
![]() $|Z(Y)|$
divides 8, as Y is nonabelian. If
$|Z(Y)|$
divides 8, as Y is nonabelian. If
![]() $|Z(Y)| = 4$
or 8, then
$|Z(Y)| = 4$
or 8, then
![]() $Z(Y) \lhd A$
has at least four orbits on
$Z(Y) \lhd A$
has at least four orbits on
![]() $V(\Gamma )$
. Hence,
$V(\Gamma )$
. Hence,
![]() $\Gamma $
is a cover of
$\Gamma $
is a cover of
![]() $\Gamma _{Z(Y)}$
. Since
$\Gamma _{Z(Y)}$
. Since
![]() $\Gamma _N\cong {\mathrm {K}}_{16}$
and
$\Gamma _N\cong {\mathrm {K}}_{16}$
and
![]() $\Gamma $
covers the graph
$\Gamma $
covers the graph
![]() $\Gamma _N$
,
$\Gamma _N$
,
![]() $\Gamma $
has valency 15. Thus, as the valency of
$\Gamma $
has valency 15. Thus, as the valency of
![]() $\Gamma _{Z(Y)}$
is equal to the valency of
$\Gamma _{Z(Y)}$
is equal to the valency of
![]() $\Gamma $
, it is
$\Gamma $
, it is
![]() $ 15$
, which is impossible as
$ 15$
, which is impossible as
![]() $|V(\Gamma _{Z(Y)})| \leq 8$
. So
$|V(\Gamma _{Z(Y)})| \leq 8$
. So
![]() $|Z(Y)| = 2$
.
$|Z(Y)| = 2$
.
Now, either
![]() $Y\cong D_8 \cdot D_8$
or Y is the central product of
$Y\cong D_8 \cdot D_8$
or Y is the central product of
![]() $D_8$
and
$D_8$
and
![]() $Q_8$
, and
$Q_8$
, and
![]() ${\mathrm {Aut}}(Y)\cong \mathbb {Z}_2^4. O_4^+ (2)$
or
${\mathrm {Aut}}(Y)\cong \mathbb {Z}_2^4. O_4^+ (2)$
or
![]() $ \mathbb {Z}_2^4. O_4^-(2)$
, respectively, where
$ \mathbb {Z}_2^4. O_4^-(2)$
, respectively, where
![]() $O_4^+ (2)$
and
$O_4^+ (2)$
and
![]() $O_4^- (2)$
are the orthogonal groups. Recall that
$O_4^- (2)$
are the orthogonal groups. Recall that
![]() $A/N \in \{ \mathbb {Z}_2^4: A_6$
,
$A/N \in \{ \mathbb {Z}_2^4: A_6$
,
![]() $\mathbb {Z}_2^4: S_6$
,
$\mathbb {Z}_2^4: S_6$
,
![]() $\mathbb {Z}_2^4: S_5, \mathbb {Z}_2^4: \Gamma L(2,4)\}$
. Since
$\mathbb {Z}_2^4: S_5, \mathbb {Z}_2^4: \Gamma L(2,4)\}$
. Since
![]() $Y = N. \mathrm{soc}( \overline {A})= N .\mathbb {Z}_2^4$
and
$Y = N. \mathrm{soc}( \overline {A})= N .\mathbb {Z}_2^4$
and
![]() $ A=N.\overline {A}=Y.(\overline {A}/\mathrm{soc}(\overline {A}))$
, it follows that
$ A=N.\overline {A}=Y.(\overline {A}/\mathrm{soc}(\overline {A}))$
, it follows that
![]() $\overline {A}/\mathrm{soc}(\overline {A}) \in \{ A_6, S_6, S_5, \Gamma L(2,4)\}$
. However, as
$\overline {A}/\mathrm{soc}(\overline {A}) \in \{ A_6, S_6, S_5, \Gamma L(2,4)\}$
. However, as
![]() $\Gamma $
is an A-normal Cayley graph of Y and
$\Gamma $
is an A-normal Cayley graph of Y and
![]() $A = Y. (\overline {A}/\mathrm{soc}(\overline {A}))$
, we have
$A = Y. (\overline {A}/\mathrm{soc}(\overline {A}))$
, we have
![]() $\overline {A}/\mathrm{soc}(\overline {A}) \leq {\mathrm {Aut}}(Y)$
, which is a contradiction. This completes the proof.
$\overline {A}/\mathrm{soc}(\overline {A}) \leq {\mathrm {Aut}}(Y)$
, which is a contradiction. This completes the proof.
From Lemma 3.6, we can get Theorem 1.2 directly.
Now, as an application of Theorem 1.2, we prove our second theorem, that is, we determine the family of
![]() $2$
-geodesic-transitive Cayley graphs over dihedral groups.
$2$
-geodesic-transitive Cayley graphs over dihedral groups.
Proof of Theorem 1.5. Let
![]() $\Gamma $
be a connected
$\Gamma $
be a connected
![]() $2$
-geodesic-transitive Cayley graph over a dihedral group
$2$
-geodesic-transitive Cayley graph over a dihedral group
![]() $T\cong D_{2n}$
, where
$T\cong D_{2n}$
, where
![]() $n\geq 3$
. First, suppose that
$n\geq 3$
. First, suppose that
![]() $\Gamma $
has girth at least 4. Then every 2-arc of
$\Gamma $
has girth at least 4. Then every 2-arc of
![]() $\Gamma $
is a 2-geodesic, and every 2-geodesic is a 2-arc. Thus,
$\Gamma $
is a 2-geodesic, and every 2-geodesic is a 2-arc. Thus,
![]() $\Gamma $
is a noncomplete
$\Gamma $
is a noncomplete
![]() $2$
-arc-transitive dihedrant.
$2$
-arc-transitive dihedrant.
Now suppose that
![]() $\Gamma $
has girth 3. Then
$\Gamma $
has girth 3. Then
![]() $\Gamma $
contains cycles of length
$\Gamma $
contains cycles of length
![]() $3$
, and so
$3$
, and so
![]() $\Gamma $
contains some
$\Gamma $
contains some
![]() $2$
-arcs that are not
$2$
-arcs that are not
![]() $2$
-geodesics. Thus,
$2$
-geodesics. Thus,
![]() $\Gamma $
is not
$\Gamma $
is not
![]() $2$
-arc-transitive. Since
$2$
-arc-transitive. Since
![]() $\Gamma $
is
$\Gamma $
is
![]() $2$
-geodesic-transitive, it follows that
$2$
-geodesic-transitive, it follows that
![]() $\Gamma $
is a
$\Gamma $
is a
![]() $2$
-distance-transitive graph. Then by Theorem 1.2,
$2$
-distance-transitive graph. Then by Theorem 1.2,
![]() $\Gamma $
is isomorphic to either
$\Gamma $
is isomorphic to either
![]() $ {\mathrm {K}}_{x[y]}$
for some
$ {\mathrm {K}}_{x[y]}$
for some
![]() $x\geq 3,y\geq 2$
or
$x\geq 3,y\geq 2$
or
![]() $G(2,p,({p-1})/{4})$
, where p is a prime and
$G(2,p,({p-1})/{4})$
, where p is a prime and
![]() $p \equiv 1 \ (\operatorname {mod}\, 8)$
.
$p \equiv 1 \ (\operatorname {mod}\, 8)$
.
Suppose that
![]() $\Gamma $
is isomorphic to
$\Gamma $
is isomorphic to
![]() $G(2,p,({p-1})/{4})$
, where p is a prime and
$G(2,p,({p-1})/{4})$
, where p is a prime and
![]() $p \equiv 1 \ (\operatorname {mod}\, 8)$
. Then, by the proof of the Lemma 3.3, we know that
$p \equiv 1 \ (\operatorname {mod}\, 8)$
. Then, by the proof of the Lemma 3.3, we know that
![]() $\Gamma $
is a cover of the Paley graph
$\Gamma $
is a cover of the Paley graph
![]() $P(p)$
with p vertices. Since
$P(p)$
with p vertices. Since
![]() $\Gamma $
is
$\Gamma $
is
![]() $2$
-geodesic-transitive, it follows that the quotient graph
$2$
-geodesic-transitive, it follows that the quotient graph
![]() $P(p)$
is also 2-geodesic-transitive. Moreover, since p is a prime and
$P(p)$
is also 2-geodesic-transitive. Moreover, since p is a prime and
![]() $p \equiv 1 \ (\operatorname {mod}\, 8)$
, we have
$p \equiv 1 \ (\operatorname {mod}\, 8)$
, we have
![]() $p\geq 17$
. However, by [Reference Jin, Devillers, Li and Praeger18, Theorem 1.2], Paley graphs with at least 13 vertices are 2-distance-transitive but not 2-geodesic-transitive, which is a contradiction. Thus,
$p\geq 17$
. However, by [Reference Jin, Devillers, Li and Praeger18, Theorem 1.2], Paley graphs with at least 13 vertices are 2-distance-transitive but not 2-geodesic-transitive, which is a contradiction. Thus,
![]() $\Gamma $
is not isomorphic to
$\Gamma $
is not isomorphic to
![]() $G(2,p,({p-1})/{4})$
, and hence
$G(2,p,({p-1})/{4})$
, and hence
![]() $\Gamma $
is isomorphic to
$\Gamma $
is isomorphic to
![]() $ {\mathrm {K}}_{x[y]}$
for some
$ {\mathrm {K}}_{x[y]}$
for some
![]() $x\geq 3,y\geq 2$
. This completes the proof.
$x\geq 3,y\geq 2$
. This completes the proof.